Bộ đề ôn tập kiểm tra 1 tiết Giải tích 12 chương 2 chủ đề mũ – logarit có đáp án

Tài liệu gồm 70 trang được biên soạn bởi thầy Trần Quốc Nghĩa tuyển tập một số đề trắc nghiệm kiểm tra 1 tiết Giải tích 12 chương 2 chủ đề mũ – logarit có đáp án.

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

70 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 1/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 001
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Giả sử
a
,
b
là các số thực dương. Biểu thức
5
3
b a
a b
được viết dưới dạng
a
b
. Tìm
giá trị
.
A.
4
15
. B.
. C.
2
15
. D.
2
15
.
Câu 2. [2D2-1] Cho
a
,
b
là các số thực dương khác
1
. Trong các khẳng định sau, chọn khẳng định
đúng.
A.
, .
m m
a b a b m
B.
1 1
, 0
m m
a b m
a b
.
C.
1 1
, 0
m m
a b m
a b
. D.
1 1
, 0
m m
a b m
a b
.
Câu 3. [2D2-1] Tìm tập xác định của hàm số
2
3
2
y x .
A.
\ 2
. B.
2;

. C.
0;

. D.
.
Câu 4. [2D2-2] Cho
3
2 2
.
f x x x
. Tính giá trị của
1
f
.
A.
2
. B.
8
3
. C.
4
. D.
3
8
.
Câu 5. [2D2-2]Cho đồ thị ba hàm số
x
y a
,
x
y b
,
x
y c
như hình vẽ. Kết luận nào sau đây đúng.
A.
0 1
a b c
.
B.
0 1
c a b
.
C.
0 1
c b a
.
D.
0 1
a c b
Câu 6. [2D2-1] Tính
3 7
1
log 0, 1
a
a a a
.
A.
7
3
. B.
. C.
3
7
. D.
.
Câu 7. [2D2-2] Cho
a
là hai số thực dương khác. Đặt
3
log
a m
. Tính theo
m
giá trị của biểu thức
1
3
3
log log log 9
a
D a a .
A.
2
2 3
m
D
m
. B.
2
3 2
m
D
m
. C.
2
4 3
2
m
D
m
. D.
3
D m
.
Câu 8. [2D2-2]Cho
2
log 5
a
,
3
log 5
b
. Hãy biểu diễn
6
log 5
theo
a
và
b
.
A.
6
1
log 5
a b
. B.
6
log 5
ab
a b
.
C.
6
log 5
a b
. D.
2 2
6
log 5
a b
.
O
x
1
x
y a
x
y b
x
y c
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 2/69 - Mã đề 2D2
Câu 9. [2D2-3] Biết
2 2
a b ab
,
0
a
,
0
b
. Chọn đẳng thức đúng.
A.
2ln ln2 ln ln
a b a b
. B.
2 2
ln ln ln
a b a b
.
C.
2 2
lg lg lg
a b a b
. D.
2lg lg3 lg lg
a b a b
.
Câu 10. [2D2-3] Cho hàm số
2
5
2
x
x
f x . Khẳng định nào sau đây là khẳng định sai?
A.
2
5
1 0
log 2
x
f x
x
. B.
2
2
1 log 5 0
f x x x
.
C.
2
5
5
1 log 0
2
x
x
f x
. D.
2
5
1 log 2 0
f x x x
.
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
2 1
log 3
x
f x
x x
.
A.
0;3
D . B.
3 5
0;3 \
2
D
C.
\ 0;3
D
. D.
D
.
Câu 12. [2D2-2] Tìm đạo hàm của hàm số
2
2 3 e 3
x
y x x
trong điều kiện xác định.
A.
2
4 4 e 3
x
y x
. B.
2
4 4 e 3
x
y x x
.
C.
2
4.e 3
x
y
. D.
2
2 1 e 3
x
y x
.
Câu 13. [2D2-2] Mệnh đề nào sau đây là sai?
A. Cho hàm số
2
x
y
thì
1 ln 4
y
.
B. Cho hàm số
log 2 1
y x
thì
2
1
3ln10
y
.
C. Cho hàm số
e
x
y
thì
1 e
x
y
.
D. Cho hàm số
ln
y x
thì
1 1
y
.
Câu 14. [2D2-3] Gọi
M
và
m
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
x
y xe
trên
1;2
.
Tính
.
M n
.
A.
3
2e
. B.
2
2e
. C.
e
. D.
0
.
Câu 15. [2D2-4] Ông A vay ngân hàng T (triệu đồng) với lãi suất
12
% năm. Ông A thỏa thuận với ngân
hàng cách thức trả nợ như sau: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai
lần hoàn nợ liên tiếp cách nhau đúng một tháng. Nhưng cuối tháng thứ ba kể từ lúc vay ông A
mới hoàn nợ lần thứ nhất, cuối tháng thứ tư ông A hoàn nợ lần thứ hai, cuối tháng thứ năm ông
A hoàn nợ lần thứ ba (hoàn hết nợ). Biết rằng số tiền hoàn nợ lần thứ hai gấp đôi số tiền hoàn
nợ lần thứ nhất và số tiền hoàn nợ lần thứ ba bằng tổng số tiền hoàn nợ của hai lần trước. Tính
số tiền ông A đã hoàn nợ ngân hàng lần thứ nhất.
A.
5
2
1 0,01
2,01 2
T
. B.
5
2
1 0,01
1,01 5
T
. C.
5
1 0,01
6
T
. D.
5
1
100
6
T
.
Câu 16. [2D2-1] Tìm nghiệm của phương trình
1
3 27
x
.
A.
9
x
. B.
3
x
.C.
4
x
. D.
10
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 3/69 - Mã đề 2D2
Câu 17. [2D2-2] Gọi
S
là tập nghiệm của phương trình
2
2 3
1
1
7 .
7
x x
x
Tính tổng tất cả các phần tử
của
S
.
A.
5.
B.
0.
C.
1.
D.
2.
Câu 18. [2D2-2] Gọi
S
là tập nghiệm của phương trình
4 8 2 5
2
3 4.3 28 2log 2
x x
. Tính tích tất cả
các phần tử của
S
.
A.
4.
B.
3
.
2
C.
3
.
2
D.
1.
Câu 19. [2D2-1] Cho phương trình
2 2 2 2
2 2 2 2
log 1 .log 2 4 6 log 1 1 4log 2 4 0 1
x x x x x x
Gọi
1
x
,
2
x
là hai nghiệm thực dương của phương trình đã cho
1 2
x x
. Tính
2
1 2
2
T x x
.
A.
3 2 5
T . B.
1 3 5
T . C.
7
T
. D.
6
T
.
Câu 20. [2D2-4] Tìm nghiệm của phương trình
2
0,5
log sin 5sin .cos 2
1
4
9
x x x
.
A.
2
1
arctan
5
x k
k
x k
. B.
2
1
arctan
3
x k
k
x k
C.
1
arctan
3
x k
k
x k
. D.
1
arctan
5
x k
k
x k
.
Câu 21. [2D2-1] Tìm tập nghiệm của bất phương trình
2
2 4
2 3 1
1
4
2
x
x x
.
A.
5
0;
4
. B.
1
.
C.
;0 1;
 
. D.
5
;1 ;
4
 
.
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình
1
2
log 1 2
x
.
A.
1;S

. B.
3
0;
4
S
. C.
3
1;
4
S
. D.
3
;
4
S

.
Câu 23. [2D2-3] Tìm tập nghiệm của bất phương trình
2
1
5 2 5 2
x
x
x
.
A.
; 1 0;1
 . B.
1;0
. C.
; 1 0;
 
.
D.
1;0 1;

.
Câu 24. [2D2-2] Phương trình
2 4
log 1 2log 3 2 2 0
x x
có mấy nghiệm?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên bé hơn
10
của tham số
m
sao cho bất phương trình
2 2
2 2
log 1 2 log 1 0
x x m
thỏa mãn với mọi
3
1;2
?
A.
3
. B.
4
. C.
5
. D.
6
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 4/69 - Mã đề 2D2
TOÁN HỌC BẮC – TRUNG - NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 002
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Rút gọn biểu thức
1
3
0
M a a a
.
A.
5
6
M a
. B.
1
6
M a
. C.
6
5
M a
. D.
3
2
M a
.
Câu 2. [2D2-2] Cho
a
là số thực dương. Đơn giản biểu thức
4 1 2
3 3 3
1 3 1
4 4 4
a a a
P
a a a
.
A.
P a
. B.
1
P a a
. C.
1
P a
. D.
1
P a
.
Câu 3. [2D2-3] Với
, 0
a b
bất kì. Cho biểu thức
2 1
3 3
6 6
a b b a
P
a b
. Tìm mệnh đề đúng.
A.
3
P ab
. B.
P ab
. C.
6
P ab
. D.
P ab
.
Câu 4. [2D2-1] Cho
a
là số thực dương
1
a
và
3
3
log
a
P a
. Mệnh đề nào dưới đây đúng?
A.
3
P
. B.
1
P
. C.
9
P
. D.
1
3
P
.
Câu 5. [2D2-1] Giá trị của
2 3 4 63
log 3.log 4.log 5...log 64
A bằng
A.
5
. B.
4
. C.
6
. D.
3
.
Câu 6. [2D2-2] Với các số thực dương
a
,
b
bất kì. Khẳng định nào sau đây là khẳng định đúng?
A.
log log
ab a b
. B.
log log
b
a
a
b
.
C.
log log log
ab a b
. D.
log log
a
a b
b
.
Câu 7. [2D2-2] Cho log
b
a x
và log
b
c y
. Hãy biểu diễn
2
3
5 4
log
a
b c
theo
x
và
:
A.
5 4
6
y
x
. B.
20
3
y
x
. C.
4
2
5 3
3
y
x
. D.
20
20
3
y
x .
Câu 8. [2D2-3] Cho
14 14
log 7 ,log 5
a b
. Tính
35
log 28
theo
,
a b
A.
35
2
log 28
a
a b
. B.
35
2
log 28
a b
. C.
35
2
log 28
a
a b
. D.
35
log 28
a
a b
.
Câu 9. [2D2-1] Tìm tập xác định
D
của hàm số
1
x
y
.
A.
D
. B.
1;D
. C.
1;D
. D.
;1
D

.
Câu 10. [2D2-1] Tìm tập xác định
D
của hàm số
3
log 2 1
y x
.
A.
1
;
2
D

. B.
1
;
2
D
. C.
0;D
. D.
1
;
2
D
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 5/69 - Mã đề 2D2
Câu 11. [2D2-2] Tìm đạo hàm của hàm số
2
log2
.
x
y
x
A.
3
1 4ln 2
.
2 ln10
x
y
x
B.
2
1
.
2 ln10
y
x
C.
3
1 2ln 2
.
ln10
x
y
x
D.
3
1 2log 2
.
x
y
x
Câu 12. [2D2-1] Đạo hàm của hàm số
3
e
x
y
là
A.
e
x
y
. B.
3 1
3 e
x
y x
. C.
3
3 e
x
y x
. D.
3
3e
x
y
.
Câu 13. [2D2-1] Tìm giá trị nhỏ nhất của hàm số
ln
y x
trên
1;e
A. Không xác định được giá trị nhỏ nhất. B.
min 1
y
khi
1
x
.
C.
min e
y
, khi
e
x
. D.
min 0
y
, khi
1
x
.
Câu 14. [2D2-1] Tìm giá trị nhỏ nhất của hàm số
1
2
x
y
trên
1;0
A.
min 1
y
, khi
0
x
. B.
1
min
2
y
khi
1
x
.
C.
min 2
y
, khi
1
x
. D.
1
min
2
y
, khi
1
x
.
Câu 15. [2D2-1] Hình vẽ sau đây là đồ thị của hàm số nào?
A.
ln
y x x
.
B.
ln
y x
.
C.
e
x
y
.
D.
e
x
y x
.
Câu 16. [2D2-2] Cho hàm số
2
ln
y x x
, khẳng định nào sau đây là đúng
A.
3 0
y x y
. B.
2 0
y x y

. C.
2 0
y x y
. D.
3 0
y x y

.
Câu 17. [2D2-2] Nghiệm của phương trình
2 1
1
3
27
x
là
A.
2
x
. B.
2
x
. C.
1
x
. D.
1
x
.
Câu 18. [2D2-2] Nghiệm của phương trình
2
2 2
log 1 log 3 2
x x x
A.
1; 3
x x
. B.
3
x
. C.
1; 3
x x
. D.
3
x
.
Câu 19. [2D2-2] Tập nghiệm của bất phương trình
2
3 1
1
2
2
x x
.
A.
;1 2;T

. B.
;1 2;T
 
.
C.
1;2
T . D.
1;2
T .
Câu 20. [2D2-2] Tập nghiệm của bất phương trình
2
3
log 2 4 5 2
x x
.
A.
T
. B.
\ 1
T
. C.
\ 1
T
. D.
T
.
Câu 21. [2D2-3] Bác Hiếu đầu tư
99
triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8,25%
một năm. Hỏi sau
5
năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi).
A.
48,155
triệu. B.
147,155
triệu. C.
58,004
triệu. D.
8,7
triệu.
O
x
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 6/69 - Mã đề 2D2
Câu 22. [2D2-3] Giá trị
m
để phương trình
2
2
5 .5 3 0
x
x
m m
có
2
nghiệm phân biệt sao cho
1 2
2
x x
là
A.
2
. B.
2
. C.
3
. D.
4
.
Câu 23. [2D2-3] Có bao nhiêu số nguyên thỏa mãnbất phương trình
1
2
2.3 9 9 ?
x
x x x
A.
3.
B.
4.
C.
5.
D.
6.
Câu 24. [2D2-2] Số nghiệm nguyên của bất phương trình
3 1
1 3
10 3 10 3
x x
x x
trong khoảng
2018;2018
là
A.
4033
. B.
4032
. C.
4031
. D.
4030
.
Câu 25. [2D2-4] Biết
15
2
x
là một nghiệm của bất phương trình
2
2log 23 23 log 2 15 *
a
a
x x x . Tập nghiệm
T
của bất phương trình
*
là
A.
19
;
2
T
. B.
17
1;
2
T
. C.
2;8
T . D.
2;9
T .
-----------HẾT---------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 7/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 003
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho góc
, giá trị của biểu thức
2 2
sin cos
5 .5
bằng
A.
1
. B.
5
. C.
25
. D.
2 2
sin .cos
5
.
Câu 2. [2D2-2] Cho
a
,
b
là các số thực dương khác
1
. Hình
vẽ bên là đồ thị của
2
hàm số
1
:
x
C y a
,
2
:
x
C y b
. Mệnh đề nào sau đây là đúng?
A.
1
b a
. B.
1
a b
.
C.
1
a b
. D.
1
b a
.
Câu 3. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
2
y x x
.
A.
D
. B.
\ 1;2
D
.
C.
; 1 2;D

. D.
0;D
.
Câu 4. [2D2-2] Tính đạo hàm của hàm số
13
x
y
x
.
A.
1
13
x
y
. B.
2
13 ln13 1
x
x
y
x
.
C.
13 1
x
y
x
. D.
13 ln13 1
.ln13
x
y
x
.
Câu 5. [2D2-2] Cho hàm số
2
ln 1
2
x
y x
. Khẳng định nào sau đây là đúng.
A. Hàm số đồng biến trên khoảng
0;
. B. Hàm số đạt cực tiểu tại
1
x
.
C. Hàm số nghịch biến trên khoảng
0;1
. D. Hàm số đạt cực đại tại
1
x
.
Câu 6. [2D2-1] Cho
0
a
,
1
a
và
x
,
là hai số dương. Mệnh đề nào sau đây là đúng?
A.
log log log
a a a
x y x y
. B.
log log .log
a a a
x y x y
.
C.
log . log log
a a a
x y x y
. D.
log . log .log
a a a
x y x y
.
Câu 7. [2D2-2] Đặt
ln3
a
,
ln5
b
. Tính
3 4 5 123 124
ln ln ln ... ln ln
4 5 6 124 125
S theo
a
và
b
.
A.
2
I a b
. B.
3
I a b
. C.
2
I a b
. D.
3
I a b
.
Câu 8. [2D2-2] Biết
sin 0
x
,
cos 0
x
và
3 3
log sin log cos 1
x x
. Giá trị của
3
log sin cos
x x
bằng
A.
1
. B.
1
3
. C.
3
1
log 5 1
2
. D.
3
log 5 1
.
Câu 9. [2D2-3] Cho
0
a
,
0
b
,
0
c
là các số thực khác
0
thỏa
5 15 45
a b c
. Tính
b b
T
a c
.
A.
15
log 5
T . B.
3
T
. C.
2
T
. D.
5
log 45
T .
O
x
1
1
C
2
C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 8/69 - Mã đề 2D2
Câu 10. [2D2-3] Cho hàm số
2
1 2
log
2 1
x
f x
x
.
Tính tổng:
1 2 3 2015 2016
...
2017 2017 2017 2017 2017
S f f f f f
.
A.
2017
. B.
2016
. C.
4032
. D.
1008
.
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
3
0,5
log 3 2
y x x
.
A.
2;
. B.
0;1
. C.
1;
. D.
2; \ 1
.
Câu 12. [2D2-2] Cho bốn hàm số
1
1
2
x
y
,
3 2
x
y ,
1
3
2
x
y
,
4 4
x
y và bốn đường cong
1
C
,
2
C
,
3
C
,
4
C
như hình vẽ bên. Đồ thị hàm số
1
,
2
,
3
,
4
lần lượt là
A.
1 2 3 4
, , ,
C C C C
. B.
3 2 4 1
, , ,
C C C C
.
C.
2 4 1 3
, , ,
C C C C
. D.
4 1 3 2
, , ,
C C C C
.
Câu 13. [2D2-2] Tìm tất cả giá trị thực của tham số
m
để hàm số
2
ln 2
y x mx m
có tập xác định
là
.
A.
0
m
hoặc
1
m
. B.
0 1
m
.
C.
0
m
hoặc
1
m
. D.
0 1
m
.
Câu 14. [2D2-3] Trong mặt phẳng tọa độ
Oxy
cho hình vuông
ABCD
có diện tích bằng
36
, đường
thẳng
AB
song song với trục
Ox
, các đỉnh
A
,
B
và
C
lần lượt nằm trên đồ thị của các hàm
số
log
a
y x
, log
a
y x
,
3
log
a
y x
và
a
là một số thực lớn hơn
1
. Tìm
a
.
A.
3
a . B.
3
6
a .
C.
6
a . D.
6
3
a .
Câu 15. [2D2-4] Cho
a
,
b
là hai số thực dương thỏa mãn
2 4 8
2 2 4 8
a
a b
b
a b
. Tính giá trị của biểu
thức
2017
2017
a
b
P .
A.
1
. B.
2
2017
. C.
2017
a
. D.
2017
b
.
Câu 16. [2D2-1] Tập nghiệm
S
của phương trình
1 2
2 3
3 2
x x
là
A.
1
S . B.
1
3
S
.
C.
1
S
. D.
2
S .
Câu 17. [2D2-2] Tìm tọa độ giao điểm của đồ thị hàm số
3 2
x
y
và đường thẳng
5
y
.
A.
1;5
. B.
1;5
. C.
2;5
. D.
2;5
.
O
x
1
2
C
1
C
4
C
3
C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 9/69 - Mã đề 2D2
Câu 18. [2D2-2] Biết rằng phương trình
8
log 9
2018
3 2 0
x
có nghiệm duy nhất
0
x x
. Khẳng định nào
sau đây là đúng?
A.
0
x
là số nguyên tố. B.
0
x
là số chính phương.
C.
0
x
chia hết cho
3
. D.
0
x
là một số chẵn.
Câu 19. [2D2-3] Tính tổng
T
tất cả các nghiệm của phương trình
2 2
3.25 3 10 .5 3 0
x x
x x
.
A.
5
2
4 log
7
T
. B.
5
3 log 2
T . C.
5
4 log 3
T . D.
5
2 log 6
T .
Câu 20. [2D2-4] Tính tổng
T
tất cả các giá trị của tham số
m
để phương trình
2
1
2
2 2
2 log 2 3 4 log 2 2
x mx
x x x m
có đúng ba nghiệm phân biệt.
A.
1
T
. B.
2
T
. C.
3
T
. D.
4
T
.
Câu 21. [2D2-1] Tập nghiệm của bất phương trình
1
1
3
9
x
là
A.
3;
. B.
1;
. C.
; 1

. D.
1;3
.
Câu 22. [2D2-2] Tập nghiệm của bất phương trình
0,5
log 1 2
x
là
A.
5
;
4

. B.
5
;
4
. C.
5
1;
4
. D.
1;3
.
Câu 23. [2D2-2] Gọi
S
là tập nghiệm của bất phương trình
2
2 3
1
0,25
4
x
x
. Khi đó
S
có dạng
;
a b
với
a b
. Tính
P a b
.
A.
2
. B.
2
. C.
1
. D.
0
.
Câu 24. [2D2-2] Có bao nhiêu số nguyên
x
thỏa mãn bất phương trình
log 40 log 60 2
x x
.
A.
20
. B.
18
. C.
21
. D.
19
.
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
2018;2018
để bất
phương trình
2 2
1 4 1 4
9 20 .3 2 5 0
x x
m m
có tập nghiệm
2;2
.
A.
2057
. B.
2060
. C.
2058
. D.
2056
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 10/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 004
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho
. Kết luận nào sau đây là đúng?
A.
0
. B.
. 1
. C.
. D.
.
Câu 2. [2D2-2] Cho biểu thức
3
5
2 3
P x x x
. Mệnh đề nào dưới đây đúng.
A.
14
15
P x
. B.
17
P x
. C.
13
15
P x
. D.
16
15
P x
.
Câu 3. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
3 1
y x
A.
1
\
3
D
. B.
1
3
D
.
C.
1 1
; ;
3 3
 
. D.
1 1
;
3 3
D
.
Câu 4. [2D2-2] Đường cong ở hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào?
A.
2
2 1
y x x
. B.
0,5
log
y x
.
C.
1
2
x
y . D.
2
x
y
.
Câu 5. [2D2-1] Hàm số
1
3
1
y x
có đạo hàm là
A.
2
3
1
3 1
y
x
. B.
3
1
3 1
y
x
. C.
2
3
1
3
x
y
. D.
3
1
3
x
y
.
Câu 6. [2D2-2] Cho
30
log 3
a và
30
log 5
b . Tính
30
log 1350
theo
a
và
b
.
A.
1 2
a b
B.
1 2 .
a b
C.
1 2
a b
D.
1 2
a b
Câu 7. [2D2-2] Nếu
2 2 2
log 5log 4log ,( , 0)
x a b a b
thì
x
bằng
A.
5 4
a b
. B.
4 5
a b
. C.
5 4 .
a b
D.
4 5 .
a b
Câu 8. [2D2-2] Cho
3 5
2 2 4
3
. . .
log
a
a a a a
A
a
với
0; 1
a a
. Giá trị
A
bằng
A.
16
5
B.
67
5
C.
22
5
D.
62
15
Câu 9. [2D2-3] Cho
x
,
là các số thực dương thỏa mãn
9 6 4
log log log
6
x y
x y
. Tính tỉ số
x
y
.
A.
3
x
y
. B.
5
x
y
. C.
2
x
y
. D.
4
x
y
.
O
x
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 11/69 - Mã đề 2D2
Câu 10. [2D2-3] Cho các số thực dương khác
1
là
a
,
b
,
c
. Rút gọn
2
2
2
log .log .log
a
b
c
b c a
ta được
, ,
2
m
m n N
n
, với
m
n
là phân số tối giản. Chọn khẳng định đúng.
A.
2
m n
B.
2 0
m n
C.
2 0
m n
D.
2
4 0
n m
Câu 11. [2D2-1] Đồ thị sau là của hàm số nào sau đây?
A.
3
log
y x
. B.
2
log 2
y x
.
C.
3
2log
y x
. D.
5
log
y x
.
Câu 12. [2D2-2] Hàm số
2
ln 2 4
y x mx
có tập xác định
D
khi:
A.
2
m
. B.
2
2
m
m
. C.
2
m
. D.
2 2
m
.
Câu 13. [2D2-3] Biết rằng giá trị lớn nhất của hàm số
2
ln
x
y
x
trên đoạn
3
1;e
là
e
n
m
M
trong đó
M
,
n
là các số tự nhiên. Tính
2 3
2 .
S m n
A.
22.
S
B.
24.
S
C.
32.
S
D.
135.
S
Câu 14. [2D2-1] Cho
ln
f x x x
. Đạo hàm cấp hai
e
f
bằng:
A.
2.
B.
1
.
e
C.
3.
D.
e
.
Câu 15. [2D2-2] Đồ thị hàm số
ln
x
y
x
có tọa độ điểm cực đại là
;
a b
. Khi đó
ab
bằng
A.
e
. B.
2e
. C.
1
D.
1
Câu 16. [2D2-1] Tìm các nghiệm của phương trình
1
3 27.
x
A.
9.
x
B.
3.
x
C.
4.
x
D.
10.
x
Câu 17. [2D2-1] Phương trình
2
3
log 4 12 2
x x
. Chọn phương án đúng?
A. Có hai nghiệm cùng dương. B. Có hai nghiệm trái dấu.
C. Có hai nghiệm cùng âm. D. Vô nghiệm.
Câu 18. [2D2-2] Cho phương trình
25
log 4.5 2 1
x
x
có hai nghiệm là
1
x
,
2
x
. Tổng
1 2
x x
bằng
A.
50.
B.
5
log 100
C.
30.
D.
5
log 50.
Câu 19. [2D2-2] Bất phương trình
2
2 3 2 3
x x
có tập nghiệm là
A.
1; .

B.
; 1 .

C.
(2; ).

D.
( ; 2).

Câu 20. [2D2-2] Tập nghiệm của bất phương trình
1
3
log 3 1 0
x
có dạng
;
a b
. Khi đó giá trị
3
a b
bằng
A.
15
. B.
13
.
C.
37
3
. D.
30
.
Câu 21. [2D2-2] Tìm số nghiệm nguyên của bất phương trình:
3
log 1 3
x
.
A.
7
.
B.
26
.
C.
15
.
D.
27
.
O
x
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 12/69 - Mã đề 2D2
Câu 22. [2D2-2] Anh Nam vay tiền ngân hàng
1
tỷ đồng theo phương thức trả góp (chịu lãi số tiền chưa
trả) với lãi suất
0,5%
/tháng. Nếu cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả
30
triệu đồng. Hỏi sau bao nhiêu tháng anh Nam trả hết nợ?
A.
35
tháng. B.
36
tháng. C.
37
tháng. D.
38
tháng.
Câu 23. [2D2-3] Tìm tất cả các giá trị của tham số
m
để phương trình
2
3 3
log 2 log 3 1 0
x m x m
có 2 nghiệm
1
x
,
2
x
sao cho
1 2
27
x x
.
A.
4
3
m
. B.
25
m
. C.
28
3
m . D.
1
m
.
Câu 24. [2D2-4] Tìm tập hợp các giá trị của tham số thực
m
để phương trình
6 3 2 0
x x
m m
có
nghiệm thuộc khoảng
0;1
.
A.
3;4
. B.
2;4
. C.
2;4
. D.
3;4
.
Câu 25. [2D2-4] Tìm giá trị nhỏ nhất của biểu thức
2
2
2
log 6 log
a
b
a
b
P b
a
với
a
,
b
là các số
thực thay đổi thỏa mãn
1.
b a
A.
30.
B.
40.
C.
50.
D.
60.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 13/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 005
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Tính:
3 2 1 2 4 2
4 .2 : 2K
, ta được
A.
5
. B.
6
. C.
7
. D.
8
.
Câu 2. [2D1-2] Với biểu thức
3 5
4 6
2 1 2 1
a a
. Khi đó cơ số
a
phải thỏa điều kiện
A.
1
a
. B.
0 1
a
. C.
1
1
2
a
. D.
1
a
.
Câu 3. [2D2-1] Hàm số y =
4
2
4 1
x
có tập xác định là
A.
. B.
0;

. C.
1 1
\ ;
2 2
. D.
1 1
;
2 2
.
Câu 4. [2D2-2] Tìm đạo hàm của hàm số
e
2
2
1
y x trên
.
A.
e
1
2
2
2 1
y x x
. B.
e 2
2
e 1y x x
.
C.
e
1
2
2
e
1
2
y x
. D.
e
2 2
2
1 ln 1
y x x
.
Câu 5. [2D2-2] Tìm điểm cực trị của hàm số
e
2
2
1
y x trên
.
A.
1
x
. B.
0
x
. C.
1
x
. D.
2
x
.
Câu 6. [2D2-1] Giá trị của biểu thức
2
log 3
4
A
bằng
A.
6
. B.
2
. C.
12
. D.
9
.
Câu 7. [2D2-2] Biết
5
log 3
a
, khi đó giá trị của
3
27
log
25
được tính theo
a
là
A.
3 2
a
a
. B.
3
2
a
. C.
3
2
a
. D.
3 2
a
a
.
Câu 8. [2D2-2] Nếu
30
log 3
a và
30
log 5
b thì
A.
30
log 1350 2 2.
a b
B.
30
log 1350 2 1.
a b
C.
30
log 1350 2 1.
a b
D.
30
log 1350 2 2.
a b
Câu 9. [2D2-3] Giả sử ta có hệ thức
2 2
7 , 0 .
a b ab a b Hệ thức nào sau đây là đúng?
A.
2 2 2
4log log log
6
a b
a b
. B.
2 2 2
log 2 log log
3
a b
a b
.
C.
2 2 2
2log log log
a b a b
. D.
2 2 2
2log log log
3
a b
a b
.
Câu 10. [2D2-3] Tìm tất cả các giá trị thực của tham số
m
để bất phương trình sau có nghiệm
3 4
log 3 12
x
m x x x
.
A.
2 3
m . B.
0
m
. C.
3
2 3 12log 5
m . D.
3
12log 5
m .
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
log 6 5
y x x
.
A.
;1 5;D
 
. B.
1;5
D .
C.
;1 5;D

. D.
1;5
D .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 14/69 - Mã đề 2D2
Câu 12. [2D2-2] Hàm số y =
2
2 2 e
x
x x có đạo hàm là
A.
2
e
x
y x
. B.
2
4 4 e
x
y x x
. C.
2
e
x
y x
. D.
2
e
2
x
y x
.
Câu 13. [2D2-3.2-2] Tính đạo hàm của hàm số
2
9
x
x
y
tại điểm
2
x
.
A.
1
2
3
y
. B.
1
2
5
y
. C.
1
2
9
y
. D.
2
1
2
9
y
.
Câu 14. [2D2-3] Hàm số
2
3
1
e
x x
x
y
có giá trị lớn nhất trên đoạn
0;3
là:
A.
2
e
. B.
1
. C.
e
. D.
3
e
.
Câu 15. [2D2-4] Bạn Hùng trúng tuyển vào trường đại học A nhưng vì do không đủ nộp học phí nên
Hùng quyết định vay ngân hàng trong 4 năm mỗi năm vay
3.000.000
đồng để nộp học phí với
lãi suất
3%
/năm. Sau khi tốt nghiệp đại học bạn Hùng phải trả góp hàng tháng số tiền
T
(không đổi) cùng với lãi suất
0,25%
/tháng trong vòng 5 năm. Số tiền
T
hàng tháng mà bạn
Hùng phải trả cho ngân hàng (làm tròn đến kết quả hàng đơn vị) là:
A.
309604
đồng. B.
232518
đồng. C.
232289
đồng. D.
215456
đồng.
Câu 16. [2D2-1] Nghiệm của phương trình
2 1
1
2 0
8
x
là.
A.
2
x
. B.
2
x
. C.
1
x
. D.
1
x
.
Câu 17. [2D2-2] Tìm tập nghiệm
S
của phương trình
2
0,5 2
log 10 23 log 5 0
x x x
.
A.
7
S . B.
2;9
S . C.
9
S . D.
4;7
S .
Câu 18. [2D2-2] Tìm tích các nghiệm của phương trình
2 1 2 1 2 2 0
x x
.
A.
0
. B.
2
. C.
1
. D.
1
.
Câu 19. [2D2-3] Phương trình
3 3
3 log log 3 1 0
x x
có tổng các nghiệm bằng
A.
81
. B.
3
. C.
78
. D.
84
.
Câu 20. [2D2-4] Tổng các nghiệm của phương trình
2
2 1 2
1 .2 2 1 4 2
x x
x x x x
bằng
A.
3
. B.
5
. C.
4
. D.
2
.
Câu 21. [2D2-1] Tập nghiệm của bất phương trình
2 1 2
4 4
5 5
x x
là
A.
. B.
;1

. C.
3;

. D.
1;

.
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình
2
1
2
log 3 2 1.
x x
A.
0;2
. B.
;1

. C.
0;1 2;3
. D.
0;2 3;7
.
Câu 23. [2D2-2] Tìm số nghiệm nguyên của bất phương trình
2
3 10 2
1 1
3 3
x x x
.
A.
0
. B.
1
. C.
9
. D.
11
.
Câu 24. [2D2-2] Bất phương trình
2 3
log log 1
x x
có nghiệm là
A.
log 6
3x . B.
3
log 6
2x . C.
6
x
. D.
6
log 2
3x .
Câu 25. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số
m
để bất phương trình
2 2 2
sin cos cos
4 5 .7
x x x
m
có nghiệm.
A.
6
7
m
. B.
6
7
m
. C.
6
7
m
. D.
6
7
m
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 15/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 006
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Viết biểu thức
a a
0
a
về dạng lũy thừa của
a
là
A.
5
4
a
. B.
1
4
a
. C.
3
4
a
. D.
1
2
a
.
Câu 2. [2D2-2] Trong các khẳng định sau đây, khẳng định nào sai?
A.
2 2
0,01 10
. B.
2 2
0,01 10
.
C.
2 2
0,1 10
. D.
0
1, 0
a a
.
Câu 3. [2D2-1] Tập xác định của hàm số
2017
(2 1)
y x là
A.
D
.
B.
1
;
2
D

. C.
1
;
2
D

. D.
1
\
2
D
Câu 4. [2D2-2] Hàm số
1
3
1
y x
có đạo hàm là
A.
2
3
1
3 1
y
x
. B.
3
1
3 1
y
x
. C.
2
3
1
3
x
y
. D.
3
1
3
x
y
Câu 5. [2D2-2] Đồ thị hàm số
ln
x
y
x
có tọa độ điểm cực đại là
;
a b
. Khi đó
ab
bằng
A.
e
. B.
2e
. C.
1
. D.
1
.
Câu 6. [2D2-1] Cho
0
a
,
1
a
, giá trị của biểu thức
log 4
a
a
bằng bao nhiêu?
A.
16
. B.
4
. C.
8
. D.
2
.
Câu 7. [2D2-2] Cho
2
log 6
a
. Khi đó giá trị của
3
log 18
được tính theo
a
là
A.
a
. B.
1
a
a
. C.
2 3
a
. D.
2 1
1
a
a
.
Câu 8. [2D2-2] Cho
2
log 5
a
,
3
log 5
b
. Khi đó
6
log 5
tính theo
a
và
b
là
A.
1
a b
. B.
ab
a b
. C.
a b
. D.
2 2
a b
.
Câu 9. [2D2-3] Cho
, 0
a b
và
2 2
7
a b ab
. Khẳng định nào sau đây là khẳng định đúng?
A.
2log log log
a b a b
. B.
4log log log
6
a b
a b
.
C.
1
log log log
3 2
a b
a b
. D.
log 3 log log
3
a b
a b
.
Câu 10. [2D2-3] Cho hàm số
2
2 sin
2 .3
x x
f x . Khẳng định nào sau đây là khẳng định đúng?
A.
2
1 ln4 sin x ln3 0
f x x
. B.
2
1 2 2sin log 3 0
f x x x
.
C.
2
3
1 log 2 sin 0
f x x x
. D.
2
2
1 2 log 3 0
f x x
.
Câu 11. [2D2-1] Với giá trị nào của
x
thì biểu thức:
2
6
log 2
f x x x
xác định?
A.
0 2
x
. B.
2
x
. C.
1 1
x
. D.
3
x
.
Câu 12. [2D2-2] Đạo hàm của hàm số
2
4
x
y là
A.
2
2.4 ln 4
x
y
. B.
2
4 .ln 2
x
y
. C.
2
4 ln 4
x
y
. D.
2
2.4 ln 2
x
y
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 16/69 - Mã đề 2D2
Câu 13. [2D2-2] Cho hàm số
2
3
log 2 .
f x x x
Tập nghiệm
S
của phương trình
0
f x
là
A.
1
S . B.
1 2
S
. C.
0;2
S . D.
1
S
.
Câu 14. [2D2-3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2 2
x
y xe x x
trên đoạn
1
;2
2
là
A.
1
;2
2
1
;2
2
max 4e 8
min 0
y
y
. B.
1
;2
2
1
;2
2
max 0
1 5
min
4
e
y
y
.C.
2
1
;2
2
1
;2
2
max 4e 8
min 0
y
y
. D.
2
1
;2
2
1
;2
2
max 4e 8
min 0
y
y
.
Câu 15. [2D2-4] Bạn Duy Anh trúng tuyển vào đại học nhung vì không đủ nộp tiền học phí Duy Anh
quyết định vay ngân hàng trong
4
năm mỗi năm
3.000.000
đồng để nộp học với lãi suất
3%
/năm. Sau khi tốt nghiệp đại học Duy Anh phải trả góp hàng tháng số tiền
T
(không đổi)
cùng với lãi suất
0,25%
/tháng trong vòng
5
năm. Số tiền
T
mà Duy Anh phải trả cho ngân
hàng (làm tròn đến hàng đơn vị) là
A.
232518
đồng. B.
309604
đồng. C.
215456
đồng. D.
232289
đồng.
Câu 16. [2D2-1] Số nghiệm của phương trình
2
2 7 5
2 1
x x
là
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 17. [2D2-2] Phương trình
2
2 4
log 2 3 2log 1
x x x
có nghiệm là
A.
4
x
. B.
1
x
. C.
4; 1
x x
. D.
2
x
.
Câu 18. [2D2-2] Phương trình
9 3.3 2 0
x x
có hai nghiệm
1
x
,
2
x
với
1 2
x x
. Giá trị
1 2
2 3
A x x
là
A.
2
2log 3
. B.
1
. C.
3
3log 2
. D.
3
4log 2
.
Câu 19. [2D2-3] Phương trình
2 2
4 4
log 7log 4 10 0
x x
có hai nghiệm
1
x
,
2
x
với
1 2
x x
. Giá trị
4
1
2
x
A
x
là
A.
. B.
16
. C.
64
. D.
1
16
.
Câu 20. [2D2-1] Biết rằng phương trình
2
log 4 2 3
2 4. 2
x
x x
có hai nghiệm
1
x
,
2 1 2
x x x
.
Tính
1 2
2
x x
.
A.
1
. B.
3
. C.
5
. D.
1
.
Câu 21. [2D2-1] Tìm tập nghiệm
S
của bất phương trình
1
1
5 0
5
x
.
A.
1;S
. B.
1;S
. C.
2;S
. D.
; 2
S

.
Câu 22. [2D2-1] Tập nghiệm của bất phương trình:
1
3
log 3 1
x
có dạng
;
a b
. Khi đó giá trị
3
a b
bằng
A.
15
. B.
13
. C.
37
3
. D.
30
.
Câu 23. [2D2-2] Bất phương trình
2
2 10
3 4
1
2
2
x
x x
có bao nhiêu nghiệm nguyên dương?
A.
2
. B.
4
. C.
6
. D.
3
.
Câu 24. [2D2-2] Tập nghiệm của bất phương trình
3 1
3
2log 4 3 log 2 3 2
x x
là
A.
3
;3
8
S
. B.
3
;3
8
S
. C.
; 3
S  . D.
3
;3
4
S
.
Câu 25. [2D2-3] Tìm
m
để bất phương trình
2 2
5 5
1 log 1 log 4
x mx x m
thỏa mãn với mọi
x
.
A.
1 0
m
. B.
1 0
m
. C.
2 3
m
. D.
2 3
m
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 17/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 007
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho
a
là số thực dương. Rút gọn biểu thức
2 1
2 2
2 1
1
.
P a
a
A.
3
P a
. B.
2
P a
. C.
2 2
P a
. D.
2
P a
.
Câu 2. [2D2-2] Mệnh đề nào sau đây là đúng?
A.
1
1
1 1
. B.
0,5 0,5
e
. C.
1 1
e
. D.
3
0
2 0
.
Câu 3. [2D2-1] Tập xác định của hàm số
1
3
1 2
y x
là
A.
. B.
1
;
2

. C.
0;
. D.
1
;
2

.
Câu 4. [2D2-2] Hàm số
4
2
3
3y x
có đạo hàm trên khoảng
3; 3
là
A.
7
2
3
4
3
3
y x
. B.
7
2
3
8
3
3
y x x
.
C.
7
2
3
8
3
3
y x x
. D.
7
2 2
3
4
3
3
y x x
Câu 5. [2D2-2] Hàm số nào sau đây có cực trị?
A.
3
y x
. B.
4
y x
. C.
1
y x
. D.
1
3
y x
.
Câu 6. [2D2-1] Với các số thực dương
a
,
b
bất kì, đặt
0,3
10
3 5
a
M
b
. Mệnh đề nào dưới đây đúng?
A.
1
log 3log log
2
M a b
. B.
1
log 3log log
2
M a b
.
C.
log 3log 2log
M a b
. D.
log 3log 2log
M a b
.
Câu 7. [2D2-2] Cho
3
log 5
a
,
3
log 6
b
,
3
log 22
c
. Mệnh đề nào dưới đây đúng?
A.
3
270
log
121
3 2
a b c
. B.
3
270
log
121
3 2
a b c
.
C.
3
270
log
121
3 2
a b c
. D.
3
270
log
121
3 2
a b c
.
Câu 8. [2D2-2] Với các số thực dương
a
,
b
bất kì. Mệnh đề nào dưới đây đúng?
A.
7 3
3
2
ln
3ln
log log
3
a
b
b
a
. B.
3
27 3
ln
3ln3
log log
a
a
b b
.
C.
7 3
3
2
ln
3ln
log log
3
a
b
b
a
. D.
3
27 3
ln
3ln3
log log
a
a
b b
.
Câu 9. [2D2-3] Cho
a
,
b
,
x
là các số thực dương và khác 1 và các mệnh đề:
Mệnh đề (I) :
log log
b
b
a
a
x x
. Mệnh đề (II) :
log 1 log
log
log
b b
a
b
a x
ab
x a
.
Khẳng định nào dưới đây là đúng ?
A. (II) đúng, (I) sai. B. (I) đúng, (II) sai. C. (I), (II) đều sai. D. (I), (II) đều đúng.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 18/69 - Mã đề 2D2
Câu 10. [2D2-3] Cho hàm số
2
3 .4
x x
f x . Khẳng định nào sau đây sai?
A.
2
3
9 2 log 2 2
f x x x
. B.
2
9 ln3 ln 4 2ln3
f x x x .
C.
2
2 2
9 log 3 2 2log 3
f x x x . D.
9 2 log3 log4 log9
f x x x .
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
2
log 2
y x x
.
A.
0;D

. B.
;0 2;D
 
.
C.
;0 2;D
 
. D.
;0 2;D
 
.
Câu 12. [2D2-2] Đạo hàm của hàm số
2
log e 1
x
y
là
A.
e
e 1 ln2
x
x
y
. B.
2 ln 2
2 1
x
x
y
. C.
2
2 1 ln 2
x
x
y
. D.
e ln2
e 1
x
x
y
.
Câu 13. [2D2-2] Cho hàm số
2 .5
x x
f x . Tính giá trị của
0
f
.
A.
0 10
f
. B.
0 1
f
. C.
1
0
ln10
f
. D.
0 ln10
f
.
Câu 14. [2D2-3] Cho ba số thực
a
,
b
,
1
;1
4
c
.
Tìm giá trị nhỏ nhất
min
P
của biểu thức
1 1 1
log log log
4 4 4
a b c
P b c a
.
A.
min
3
P
. B.
min
6
P
. C.
min
3 3
P . D.
min
1
P
.
Câu 15. [2D2-4] Bác Hiếu đầu tư
99
triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8,25%
một năm. Hỏi sau
5
năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi).
A.
48,155
triệu. B.
147,155
triệu. C.
58,004
triệu. D.
8,7
triệu.
Câu 16. [2D2-1] Tìm nghiệm của phương trình
1 ln81
9 e
x
.
A.
5
x
. B.
4
x
. C.
6
x
. D.
17
x
.
Câu 17. [2D2-2] Phương trình
2
3 3
log log 9 0
x x
có 2 nghiệm là
1
x
,
2
x
,
1 2
x x
. Khi đó
1 2
3
x x
bằng
A.
28
9
. B.
3
. C.
8
9
. D.
10
.
Câu 18. [2D2-2] Phương trình
3 3
3 log log 3 1 0
x x
có tổng các nghiệm bằng
A.
3
. B.
84
. C.
81
. D.
78
.
Câu 19. [2D2-3] Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1
x
,
2
x
thì tổng
1 2
x
x
là
A.
4
. B.
2
. C.
2
log 6 4 2
. D.
6 4 2
.
Câu 20. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số thực
m
đề phương trình
2 2
log 5 1 .log 2.5 2
z z
m
có nghiệm thuộc khoảng
0; .

A.
1
;
4

. B.
1
;
4

. C.
;0 2;

. D.
0;2
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 19/69 - Mã đề 2D2
Câu 21. [2D2-1] Tìm tập nghiệm
S
của bất phương trình
1
3 1 4 2 3
x
A.
1;S

. B.
1;S

. C.
;1
S

. D.
;1
S

.
Câu 22. [2D2-1] Tìm tập hợp nghiệm
S
của bất phương trình
2
4 4
log 1 log 2 4
x x
.
A.
2; 1
S
. B.
2;S

.
C.
3; 2; 1
S

. D.
3;S

.
Câu 23. [2D2-2] Nghiệm của bất phương trình
1
1
1
5 2 5 2
x
x
x
là
A.
2 1
x
hoặc
1
x
. B.
1
x
.
C.
2 1
x
. D.
3 1
x
.
Câu 24. [2D2-2] Nghiệm của bất phương trình
2
2 1 2
2
log log 2 log 2 3
x x x
là
A.
3
2
x
. B.
3
2
x
.
C.
1 0
x
hoặc
0
x
. D.
3
1
2
x
.
Câu 25. [2D2-4] Tìm tập hợp
X
gồm tất cả các giá trị của tham số thực
m
để bất phương trình
2 2
5 5
1 log 1 log 4
x mx x m
có tập nghiệm là
.
A.
2;3
X . B.
3;5
X . C.
2;3
X . D.
3;5
X .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 20/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 008
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Rút gọn biểu thức
5
3
3
:
Q a a
với
0.
a
A.
4
3
.
Q a
B.
.
Q a
C.
5
9
.
Q a
D.
2
.
Q a
Câu 2. [2D2-1] Nếu
2 3 2 3
x y
thì kết luận nào sau đây đúng?
A.
x y
. B.
x y
. C.
x y
. D.
x y
.
Câu 3. [2D2-1] Tìm tập xác định
D
của hàm số
e
.
y x
A.
;0 .
D  B.
.
D
C.
0; .
D

D.
\ 0 .
D
Câu 4. [2D2-2] Tính đạo hàm của hàm số
1
2
x
y
.
A.
1 2 ln2
x
y x
. B.
1
2 log2
x
y
. C.
1
2
ln2
x
y
. D.
1
2 ln2
x
y
.
Câu 5. [2D2-2] Hình bên là đồ thị của ba hàm số
x
y a
,
x
y b
,
x
y c
0 , , 1
a b c
được vẽ trên cùng một hệ trục tọa độ.
Khẳng định nào sau đây là khẳng định đúng?
A.
b a c
. B.
a b c
.
C.
a c b
. D.
c b a
Câu 6. [2D2-2] Cho
a
là số thực dương khác
2
. Tính
2
2
log
4
a
a
I
.
A.
1
2
I
. B.
2
I
. C.
2
I
. D.
2
I
.
Câu 7. [2D2-2] Cho
6
log 9 .
a
Tính
3
log 2
theo
a
.
A.
.
2
a
a
B.
2
.
a
a
C.
2
.
a
a
D.
2
.
a
a
Câu 8. [2D2-2] Cho
3
log 2
a
và
2
1
log
2
b
. Tính
2
3 3 1
4
2log log 3 log
I a b
.
A.
5
4
I
. B.
4
I
. C.
0
I
. D.
3
2
I
.
Câu 9. [2D2-3] Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
A.
2
log
y x
. B.
1
2
log
y x
.
C.
2
log
y x
. D.
2
log 2
y x
Câu 10. [2D2-3] Cho
a
và
b
là hai số thực dương và
1
a
. Mệnh đề nào sau đây là đúng?
A.
log
x
b
a b x a
. B.
log
x
a
a b x b
.
C.
log
x
a
a b x b
. D.
0 log
x
a
a b x b
O
x
x
y c
x
y b
x
y a
1
O
x
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 21/69 - Mã đề 2D2
Câu 11. [2D2-1] Tìm tập xác định
D
của hàm số
2
3
log 4 3
y x x
.
A.
2 2;1 3;2 2
D
. B.
1;3
D .
C.
;1 3;D
 
. D.
;2 2 2 2;D
 
.
Câu 12. [2D2-2] Tính đạo hàm của hàm số
1
2
4
1 xy
.
A.
5
2
4
1
1
4
xy
. B.
5
2
4
5
1
2
x xy
.
C.
5
2
4
5
1
2
xy x
. D.
5
2
4
1
1
2
xy x
.
Câu 13. [2D2-2] Cho hàm số
2
ln 2
f x x x
. Chọn khẳng định đúng trong các khẳng định sau:
A.
3
f
. B.
1
3
12
f
. C.
1
3
3
f
. D.
3 ln3
f
Câu 14. [2D2-2] Cho hàm số
x
y ex e
. Nghiệm của phương trình
0
y
?
A.
1
x
. B.
1
x
. C.
0
x
. D.
ln 2
x
Câu 15. [2D2-4] Xét các số thực dương
a
,
b
thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ
nhất
min
P
của
2
P a b
.
A.
min
2 10 3
2
P
. B.
min
2 10 5
2
P
. C.
min
3 10 7
2
P
. D.
min
2 10 1
2
P
.
Câu 16. [2D2-2] Gọi
1
x
,
2
x
là hai nghiệm của phương trình:
2
6 10
1
5
5
x x
x
; khi đó
1 2
x x
bằng:
A.
. B.
7
2
. C.
7
. D.
7
.
Câu 17. [2D2-2] Tìm nghiệm của phương trình
2
log 5 4
x
.
A.
21
x
. B.
3
x
. C.
11
x
. D.
13
x
.
Câu 18. [2D2-3] Số nghiệm của phương trình
1
3 4 0
9
x x
:
A.
1
n
. B.
2
n
. C.
3
n
. D.
4
n
.
Câu 19. [2D2-2] Nghiệm nguyên nhỏ nhất của bất phương trình
3
log 3 log 3 0
x x
là:
A.
3
x
. B.
1
x
. C.
2
x
. D.
4
x
.
Câu 20. [2D2-3] Giá trị của
m
để phương trình
1
4 .2 2 0
x x
m m
có hai nghiệm
1
x
,
2
x
thỏa mãn
1 2
3
x x
là
A.
3
m
. B.
4
. C.
9
2
m
. D.
3
2
m
.
Câu 21. [2D2-1] Nghiệm của bất phương trình
2
3
x
là
A.
4
x
. B.
0
x
. C.
0
x
. D.
4
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 22/69 - Mã đề 2D2
Câu 22. [2D2-1] Tập nghiệm của bất phương trình
2
1
2
log 1
x
là
A.
2;

. B.
2;0 0; 2
.
C.
2; 2
. D.
0; 2
.
Câu 23. [2D2-2] Tập nghiệm của bất phương trình
1 1
2 2 3 3
x x x x
A.
2;x

. B.
2;x

. C.
;2
x  . D.
2;

.
Câu 24. [2D2-2] Bất phương trình
4 2
log 7 log 1
x x
có tập nghiệm là
A.
1;4
. B.
5;

. C.
1;2
. D.
;1

.
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số
m
để hàm số
3
1
log
2 1
y x m
m x
xác định trên
2;3
.
A.
1 2
m
. B.
1 2
m
. C.
1 2
m
. D.
1 2
m
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 23/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 008
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho các số thực dương
a
,
b
. Khi đó biểu thức
1 4 4 1
3 3 3 3
3 3
a b a b
a b
bằng
A.
.
a b
B.
1 1
3 3
.
a b
C.
.
ab
D.
2 2
3 3
.
a b
Câu 2. [2D2-2] Cho
m
,
n
thoả mãn
5 2 5 2
m n
. Khi đó ta có
A.
.
m n
B.
.
m n
C.
.
m n
D.
.
m n
Câu 3. [2D2-1] Tập xác định của hàm số
1
2
3
4
y x
là
A.
0; .

B.
.
C.
2;2 .
D.
;2 .

Câu 4. [2D2-2] Đạo hàm của hàm số
4
2
3
2 3
y x x là
A.
1
2
3
2 3 .
x x B.
1
2
3
4
2 3 .
3
x x
C.
1
2
3
4
2 3 .
3
x x
D.
1
2
3
8
1 2 3 .
3
x x x
Câu 5. [2D2-2] Số cực trị của hàm số
1
3
y x x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 6. [2D2-1] Cho
0 1
a
,
b
. Rút gọn biểu thức
2
2 4
log log
a
a
b b
ta được
A.
4log .
a
b
B.
6log .
a
b
C.
4log .
a
b
D.
6log .
a
b
Câu 7. [2D2-2] Biết
5
log 3,
a khi đó
15
log 27
bằng
A.
3
.
1
a
a
B.
2
.
1
a
a
C.
4 1
.
1
a
a
D.
4 1
.
2 1
a
a
Câu 8. [2D2-2] Đặt
2 2
log 3,b log 5.
a Khi đó
2
log 675
bằng
A.
3 2 .
a b
B.
2 3 .
a b
C.
3 .
a b
D.
3 .
a b
Câu 9. [2D2-3] Cho các số thực dương
a
,
b
thỏa mãn
a b
và
2 2
3 0.
a ab b
Trong các đẳng
thức sau, đẳng thức nào đúng
A.
ln ln
ln .
2
a b
a b
B.
ln ln
ln .
3
a b
a b
C.
ln ln
ln 2 2 .
2
a b
a b
D.
ln ln
ln .
2
a b
a b
Câu 10. [2D2-3] Cho hai số thực
,
m n
thỏa mãn
2 2
m n
. Khẳng định nào sau đấy đúng
A.
3 3
1 1
2 2
log 3 log 3 .
m m n n
B.
3 3
1 1
2 2
log 3 log 3 .
m m n n
C.
3 3
1 1
2 2
log 3 log 3 .
m m n n
D.
3 3
1 1
2 2
log 3 log 3 .
m m n n
Câu 11. [2D2-1] Tập xác định của hàm số
2
5
log 2
y x x
là
A.
0; .

B.
.
C.
0;2 .
D.
0;2 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 24/69 - Mã đề 2D2
Câu 12. [2D2-2] Đạo hàm của hàm số
2 .e
x x
y x
A.
1 1
2 e .e .
x x x
x
B.
2 ln2 1 e .
x x
x C.
2 1 e .
x x
x D.
2
1 e .
ln2
x
x
x
Câu 13. [2D2-2] Tìm tất cả các khoảng đồng biến của hàm số
2
2
log 2 3
y x x
A.
1; .

B.
;1 .
 C.
0; .

D.
;2 .

Câu 14. [2D2-3] Gọi
M
,
m
lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số
3
e 3e 4
x x
y
trên
1;1 .
Khi đó
M m
bằng
A.
3
e 3e 4.
B.
3
e 3e 6.
C.
3
e 3e 2.
D.
3
1 3
6.
e e
Câu 15. [2D2-4] Một người gửi ngân hàng
100
triệu đồng theo thể thức lãi kép định kì liên tục, với lãi
suất không đổi mỗi năm. Sau
5
năm thì thu được cả vốn lẫn lãi là
200
triệu đồng. Hỏi người
đó muốn thu được
300
triệu đồng khi gửi
100
triều đồng thì cần bao nhiêu năm
A.
7.
B.
8.
C.
9.
D.
10
Câu 16. [2D2-1] Số nghiệm của phương trình
2
2
1
9
3
x x
x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 17. [2D2-2] Số nghiệm của phương trình
3
2
2 8
log 1 log 1
x x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 18. [2D2-2] Tổng các nghiệm của phương trình
16 10.4 16 0
x x
là
A.
10.
B.
16.
C.
2.
D.
6.
Câu 19. [2D2-3] Tích các nghiệm của phương trình
2 3 3 2
log .log 4 log 4log
x x x x
là
A.
83.
B.
54.
C.
4.
D.
60.
Câu 20. [2D2-4] Số nghiệm của phương trình
3 1 .2 3 1
x
x x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 21. [2D2-1] Tập nghiệm của bất phương trình
2
3 1
2
2
x x
là
A.
1;2 .
B.
1;3 .
C.
;1 2; .
 
D.
2; .

Câu 22. [2D2-1] Tập nghiệm của bất phương trình
1
2
log 2 2 1
x
là
A.
1;0 .
B.
0;1 .
C.
;0 .
 D.
1; .

Câu 23. [2D2-2] Tập nghiệm của bất phương trình
2
2 2
3 9
x x x
là
A.
2;3 .
B.
2;3 .
C.
3;2 .
D.
1;3 .
Câu 24. [2D2-2] Khoảng
;
a b
là tập nghiệm của bất phương trình
5
5
log 1 log 3
x x
. Khi đó
2 2
a b
bằng
A.
29.
B.
27.
C.
34.
D.
30.
Câu 25. [2D2-3] Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
log 6 < log 2 m
x x x x
có tập nghiệm chứa
3;4
A.
3
m
B.
4
m
C.
5
m
D.
6
m
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 25/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 010
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Cho
m
là số nguyên dương, biểu thức nào sau đây sai?
A.
2
16 4
m m
. B.
3
16 2 . 2
m m m
. C.
16 4 . 2
m m m
. D.
4
16 2
m m
.
Câu 2. [2D2-2] Với
0, 0
a b
. Giá trị của biểu thức
3 1 3 5
2 3
2
. .
. : .
a a b b
A
a b a b b
là:
A.
b a
A
a
. B.
1
A a
. C.
1
a
A
b
. D.
a b
A
b
.
Câu 3. [2D2-1] Tập xác định của hàm số
3
3 1
y x
là tập:
A.
3;

. B.
1
;
3

. C.
1
;
3

. D.
1
\
3
.
Câu 4. [2D2-2] Đạo hàm của hàm số
y x x
A.
4
3
4
y
x
. B.
4
4
3
y
x
. C.
3
4
y
x
. D.
4
3
4
y
x
.
Câu 5. [2D2-2] Hàm số
2
1
x
y x e
có bao nhiêu cực trị?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 6. [2D2-1] Cho
0
a
và
1.
a
Tìm mệnh đề đúng trong các mệnh đề sau:
A.
log
a
x
có nghĩa với
x
. B. log 1
a
a
và log
0.
a
a
C.
log
.
log
log
a
a
a
x
x y
y
D.
log . log log
a a a
x y x y
0
)
0, .
(x y
Câu 7. [2D2-2] Với
0
m
, cho
3
log
a m
với. Tính
log 27
m
P m
theo
a
A.
6 2
.
a
P
a
B.
6 . .
P a a
C.
6
.
a
P
a
D.
6 2 . .
A a a
Câu 8. [2D2-2] Đặt
2
log 3,
a
5
log 3.
b Hãy biểu diễn
6
log 45
theo
a
và
.
b
A.
6
2
log 45 .
a ab
ab
B.
2
6
2 2
log 45 .
a ab
ab
C.
6
2
log 45 .
a ab
ab b
D.
2
6
2 2
log 45 .
a ab
ab b
Câu 9. [2D2-3] Khẳng định nào sau đây đúng:
A.
2
3 3
log 2log
a a
. B.
3
2 2 2
3
log 4log
a a
. C.
3
2 2 2
3
log 4log
a a
. D.
2
3 3
1
log log
2
a a
.
Câu 10. [2D2-3] Nếu
2
2
3
2
a a
và
3 4
log log
4 5
b b
thì khẳng định nào sau đây đúng?
A.
0 1
a
và
0 1.
b
B.
0 1
a
và
1.
b
C.
1
a
và
0 1.
b
D.
1
a
và
1.
b
Câu 11. [2D2-2] Tìm tập xác định
D
của hàm số
2
3
log 2 1
y x x
.
A.
;1
D

. B.
1;D
.
C.
;D

. D.
;1 1;D

.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 26/69 - Mã đề 2D2
Câu 12. [2D2-1] Đạo hàm
f x
của hàm số
2
e
x
f x
là
A.
2e
x
f x
. B.
2e
x
f x
. C.
2e
f x
x
. D.
2
2e
x
f x
.
Câu 13. [2D2-2] Cho hàm số
ln
y x x
, khi đó đạo hàm cấp hai tại
e
x
là
e
y
có giá trị bằng bao
nhiêu?
A.
e
. B.
2
. C.
1
e
. D.
1
.
Câu 14. [2D2-3] Bác Anh đem gửi tiết kiệm ở ngân hàng với lãi suất là
12%
một năm. Biết rằng cứ sau
mỗi một quý (
3
tháng) thì lãi được cộng dồn vào gốc. Hỏi sau tối thiểu bao nhiêu năm thì Bác
Anh nhận lại được số tiền (cả vốn lẫn lãi) gấp ba số tiền ban đầu.
A.
8
năm. B.
9
năm. C.
10
năm. D.
11
năm.
Câu 15. [2D2-4] Tìm giá trị lớn nhất của
2 2
sin cos
2 2
x x
y
A.
3
. B.
2
. C.
4
. D.
5
.
Câu 16. [2D2-1] Cho phương trình
2
4 5
3 9
x x
tổng lập phương các nghiệm thực của phương trình là
A.
28.
B.
27.
C.
26.
D.
25.
Câu 17. [2D2-2] Gọi
1 2
,
x x
là nghiệm của phương trình
16
log 2 log 0
x
x
. Khi đó giá trị
1 2
.
2
x x
bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 18. [2D2-2] Tổng các nghiệm của phương trình:
3 1
1 1
2 5 2
x x
x x
là
A.
0
. B.
2
. C.
2
. D. 4.
Câu 19. [2D2-3] Số nghiệm của phương trình
4 2 2 4
log log log log 2
x x
là
A.
0
. B.
2
. C.
3
. D.
1.
Câu 20. [2D2-4] Biết phương trình
1
5 .8 500
x
x
x
hai nghiệm
1
x
,
2
x
. Tính
1 2
.
5
x x
P .
A.
8
P
. B.
1
8
P
. C.
3
P
. D.
1
3
P
.
Câu 21. [2D2-1] Bất phương trình
2
1 3 1
3 3
2 2
x x
có tập nghiệm là
A.
(2;5)
. B.
1;2
. C.
1;3
. D.
; 1

.
Câu 22. [2D2-1] Tìm tập nghiệm
S
của bất phương trình
1
2
log 4 3 4
x
.
A.
; 4 .
S

B.
4
;2 .
3
S
C.
4
; .
3
S

D.
.
S
Câu 23. [2D2-2] Nghiệm của bất phương trình
2 4 2 2
3 45.6 9.2 0
x x x
A.
2
x
. B.
2
x
. C.
2
x
. D.
2
x
.
Câu 24. [2D2-2] Có bao nhiêu giá trị nguyên dương của
x
thỏa mãn bất phương trình
log 40 log 60 2
x x
.
A.
10
. B.
19
. C.
18
. D.
20
.
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
2 2
log 5 1 .log 2.5 2
x x
m
nghiệm đúng với mọi
1
x
.
A.
6
m
. B.
6
m
. C.
6
m
. D.
6
m
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 27/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
Nhóm: THBTN – ĐỀ KIỂM TRA
(25 câu trắc nghiệm)
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
MÃ ĐỀ 011
Thời gian làm bài: 45 phút, không kể thời gian phát đề.
Câu 1. [2D2-1] Biểu thức
4
3
1
27
3
a
( với
0
a
) viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
1 1
4 12
3 .
a
. B.
1 1
4 2
3 .
a
. C.
1
9.
a
. D.
1
1
3
4
3 .
a
Câu 2. [2D2-1] Cho
a
,
b
là các số thực dương thỏa mãn
4
3
5
4
a a
và
1 2
log log
2 3
b b
. Mệnh đề nào
sau đây đúng?
A.
1, 1
a b
. B. 1,0
a b a
. C.
0 1,0 1
a b
. D.
0 1, 1
a b
.
Câu 3. [2D2-1] Tìm
x
để biểu thức
1
2
3
1
x
có nghĩa:
A.
;1 1;x
 
. B.
; 1 1;x

.
C.
1;1
x . D.
\ 1
x
.
Câu 4. [2D2-2] Đạo hàm của hàm số
1
2
3
5 2
y x x là
A.
3 2
10 1
3 5 2
x
y
x x
. B.
3 2
10 1
5 2
x
y
x x
.
C.
2
2
3
10 1
3 5 2
x
y
x x
. D.
3 2
1
3 5 2
y
x x
.
Câu 5. [2D2-2] Hàm số
2
3 10 2
x
y a a đồng biến trên
;
 
khi:
A.
1
;
3
a

. B.
3;a

. C.
1
;
3
a

. D.
1
;3
3
a
.
Câu 6. [2D2-1] Nếu
1
1
6
2
a a
và
2 3
b b
thì
A.
1;0 1
a b
.
B.
1; 1
a b
.
C.
0 1; 1
a b
.
D.
1;0 1
a b
.
Câu 7. [2D2-2] Cho
0
a
,
0
b
. Nếu viết
0,2
10
5 5 5
6 5
log log log
a
x a y b
b
thì
xy
bằng bao nhiêu?
A.
3
. B.
1
3
. C.
1
3
. D.
3
.
Câu 8. [2D2-2] Cho
, 0
x y
và
2 2
4 12
x y xy
. Khẳng định nào sau đây là khẳng định đúng?
A.
2 2 2
2
log log log
4
x y
x y
. B.
2 2 2
1
log 2 2 log log
2
x y x y
.
C.
2 2 2
log 2 log log 1
x y x y
. D.
2 2 2
4log 2 log log
x y x y
.
Câu 9. [2D2-2] Cho
2
log 3
a
,
2
log 7
b
. Tính
2
log 2016
theo
a
và
b
.
A.
5 2
a b
. B.
5 3 2
a b
.
C.
2 2 3
a b
. D.
2 3 2
a b
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 28/69 - Mã đề 2D2
Câu 10. [2D2-3] Hình bên là đồ thị của ba hàm số
x
y a
,
x
y b
,
x
y c
0 , , 1
a b c
được vẽ trên cùng một hệ
trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
A.
b a c
.
B.
a b c
.
C.
a c b
.
D.
c b a
.
Câu 11. [2D2-2] ] Cho
a
là số thực dương khác
1
. Xét hai số thực
1
x
,
2
x
. Phát biểu nào sau đây là
đúng?
A. Nếu
1 2
x x
a a
thì
1 2
x x
. B. Nếu
1 2
x x
a a
thì
1 2
1 0
a x x
.
C. Nếu
1 2
x x
a a
thì
1 2
1 0
a x x
. D. Nếu
1 2
x x
a a
thì
1 2
x x
.
Câu 12. [2D2-1] Hàm số
1
log
x
y x
xác định khi và chỉ khi:
A.
1
2
x
x
. B.
1
x
. C.
0
x
. D.
2
x
Câu 13. [2D2-1] Cho hàm số
e
x
f x x
. Gọi
f x
là đạo hàm cấp hai của
f x
. Ta có
1
f
bằng
A.
3e
. B.
2
3e
. C.
3
e
. D.
2
5e
Câu 14. [2D2-1] Cho hàm số
e e
x
y x
.
Nghiệm của phương trình
0
y
?
A.
1
x
. B.
1
x
. C.
0
x
. D.
ln 2
x
Câu 15. [2D2-2] Tính giá trị của biểu thức
ln tan1° ln tan 2 ln tan3 ... ln tan89
P
.
A.
1.
P
B.
1
.
2
P
C.
0.
P
D.
2.
P
Câu 16. [2D2-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền
T
theo hình thức lãi
kép với lãi suất
0,6
% mỗi tháng. Biết sau
15
tháng người đó có số tiền là
10
triệu đồng.Hỏi số
tiền
T
gần với số tiền nào nhất trong các số sau?
A.
535000
. B.
635000
. C.
613000
. D.
643000
.
Câu 17. [2D2-1] Nghiệm của phương trình
1 1
2 2 3 3
x x x x
là
A.
3
2
3
log
4
x . B.
1
x
. C.
0
x
. D.
4
3
2
log
3
x .
Câu 18. [2D2-1] Số nghiệm của phương trình
2
2 2
log 3 log 6 10 1 0
x x
là
A. Vô nghiệm. B.
1
. C.
2
. D.
3
.
Câu 19. [2D2-1] Phương trình
9 5.3 6 0
x x
có tổng các nghiệm là
A.
3
log 6
. B.
3
2
log
3
. C.
3
3
log
2
. D.
3
log 6
.
Câu 20. [2D2-2] Tìm số nghiệm thực của phương trình
3 2
1
log 2 2 3 1
x
x x x
.
A.
0
. B.
1
.
C.
2
.
D.
3
.
Câu 21. [2D2-3] Hỏi phương trình
3.2 4.3 5.4 6.5
x x x x
có tất cả bao nhiêu nghiệm thực?
A.
2
. B.
4
. C.
1
. D.
3
.
O
x
x
y c
x
y b
x
y a
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 29/69 - Mã đề 2D2
Câu 22. [2D2-3] Phương trình
3 2
23 3 2
2 .2 1024 23 10
x x x
x x x
có tổng các nghiệm gần nhất với số
nào dưới đây
A.
0,35.
B.
0,40.
C.
0,50.
D.
0,45.
Câu 23. [2D2-3] Tìm
m
để phương trình
2
2 2
log log 0
x x m
có nghiệm
0;1
x ?
A.
1
m
. B.
1
4
m
. C.
1
4
m
. D.
1
m
.
Câu 24. [2D2-2] Cho hàm số
2
2 sin
2 .3
x x
f x . Khẳng định nào sau đây là khẳng định đúng?
A.
2
1 ln4 sin x ln3 0
f x x
. B.
2
1 2 2sin log 3 0
f x x x
.
C.
2
3
1 log 2 sin 0
f x x x
. D.
2
2
1 2 log 3 0
f x x
.
Câu 25. [2D2-4] Cho hàm số
3
e 1 e 1
4
2017
x x
m
y
. Tìm
m
để hàm số đồng biến trên khoảng
1;2
.
A.
3 4
3e 1 3e 1
m
. B.
4
3e 1
m
.
C.
2 3
3e 1 3e 1
m
. D.
2
3e 1
m
.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 30/69 - Mã đề 2D2
BẢNG ĐÁP ÁN CÁC ĐỀ ÔN TẬP
ĐÁP ÁN ĐỀ 001
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
C
B B C
A
A
B D
A
B
A
C
A
A
C
C
C
D
A
A
C
D
A
B
ĐÁP ÁN ĐỀ 002
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
A
B C
C
C
A
A
D
D
C
D
D
A
A
C
B D
D
D
A
B A
D
D
ĐÁP ÁN ĐỀ 003
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
C
B
B D
C
D
C
C
D
D
B D
D
B B A
C
C
C
A
C
A
B
D
ĐÁP ÁN ĐỀ 004
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
A
A
C
A
B
A
D
C
A
A
D
C
B
D
C
C
D
B B B
C
D
C
D
ĐÁP ÁN ĐỀ 005
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
C C B B
D
A
C D
B C A
D
B
C
D
A
D
D
B D C C D A
ĐÁP ÁN ĐỀ 006
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C B A
A
C
A
D
B C A
A
A
A
D
D
A
A
C C D
C B
D
D
C
ĐÁP ÁN ĐỀ 007
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B B B B
A
A
A
D
D
B A
D
B
A
A
D
B B D
D
C
B
C
C
ĐÁP ÁN ĐỀ 008
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B A
C D
A
B
D
D
A
B C D
A
A
A
D
A
A
D
B A
B
A
C
A
ĐÁP ÁN ĐỀ 009
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B C D
B
C
A
A
A
B D
B A
B
B
C B C B C C A
A
C
B
ĐÁP ÁN ĐỀ 010
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C C B D
5 D
A
C B B D
D
C
C
A
A
C C D
B B A
D
C
C
ĐÁP ÁN ĐỀ 11
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
D
B C D
A
C B A
A
B A
A
A
C
B A
B A
B C D
C
A
B
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 31/69 - Mã đề 2D2
TRƯỜNG THPT TRẦN QUỐC TUẤN
TỔ TOÁN
ĐỀ KIỂM TRA 1 TIẾT LẦN 3 - HKI
MÔN: GIẢI TÍCH - LỚP 12
(Thời gian làm bài:45 phút)
Họ, tên thí sinh:................................... SBD:...............
Mã đề: 132
Câu 1. Cho hàm số
2
1
3
log 2 4
y x x
. Tập nghiệm của bất phương trình
0
y
là
A.
;0
 . B.
1;

. C.
;1

. D.
2;

.
Câu 2. Cho 3 số dương
a
,
b
,
c
và khác
1
. Chọn khẳng định sai trong các khẳng định sau:
A.
log log log
a a a
bc b c
. B.
log log .log
a a b
c b c
.
C.
log
a
b
a a
. D.
1
log
log
a
b
b
.
Câu 3. Gọi
1
x
,
2
x
là hai nghiệm của phương trình
4 8.2 4 0
x x
. Giá trị biểu thức
1 2
P x x
bằng
A.
4
. B.
4
. C.
0
. D.
2
.
Câu 4. Phương trình
3
2 4
x
có nghiệm thuộc tập nào?
A.
;4
 . B.
;8
 . C.
;5
 . D.
;3
 .
Câu 5. Gọi
1
x
,
2
x
là hai nghiệm của phương trình
2
2 2
log 3log 2 0
x x
. Giá trị biểu thức
2 2
1 2
P x x
bằng bao nhiêu?
A.
20
. B.
5
. C.
36
. D.
25
.
Câu 6. Tìm tập hợp các giá trị của tham số thực
m
để phương trình
6 3 .2 0
x x
x m
có nghiệm
thuộc khoảng
0;1
A.
4;10
. B.
3;4
. C.
2;4
. D.
3;4
.
Câu 7. Anh Thành vay
20
triệu đồng của ngân hàng để mua laptop và phải trả góp trong vòng
3
năm
với lãi suất
1,1%
mỗi tháng. Hàng tháng anh Thành phải trả
1
số tiền cố định là bao nhiêu để
sau
3
năm hết nợ (làm tròn đến đơn vị đồng)
A.
675.807
đồng. B.
673.807
đồng. C.
672807
đồng. D.
677807
đồng.
Câu 8. Cho
3
số dương
a
,
b
,
c
khác
1
và thỏa mãn: bbb
caca
log.2017logloglog . Chọn khẳng
định đúng trong các khẳng định sau:
A.
2017
ac
. B.
2017
ab
. C.
2017
bc
. D.
2017
abc
.
Câu 9. Cho
log 16
m
P m
và
2
log
a m
, với
m
là số dương khác
1
. Mệnh đề nào dưới đây đúng?
A. 1
4
a
P
. B.
2
3
P a
. C.
4
a
P
a
. D.
3
a
P
a
.
Câu 10. Tập xác định của hàm số
10
2
2
y x x
là
A.
\ 0;2
D
. B.
D
. C.
\ 0;2
D
. D.
\ 2
D
.
Câu 11. Tập nghiệm của bất phương trình:
2
1 0,2
25
4log 5log 6 0
x x
là
A.
S R
. B.
S
. C.
1 1
;
125 25
S
. D.
1
;
25
S
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 32/69 - Mã đề 2D2
Câu 12. Cho hai số dương
a
,
b
khác
1
. Đồ thị hàm số
log
a
y x
,
log
b
y x
(như hình vẽ bên). Mệnh
đề nào sau đây là mệnh đề đúng?
A.
1
a b
. B.
1
b a
.
C.
1
b a
. D.
1
a b
.
Câu 13. Tập nghiệm của bất phương trình
1 1
2 2
log 2 1 log 1
x x
là
A.
2;

. B.
1
;2
2
. C.
;2
 . D.
1
;2
2
.
Câu 14. Hàm số nào trong các hàm số dưới đây có đồ
thị phù hợp với hình vẽ bên
A.
1
2
log
y x
. B.
2
log
y x
.
C.
1
2
x
y
. D.
2
x
y
.
Câu 15. Giải phương trình
3
5
log log 3
2
x
x
ta được hai nghiệm
1 2
x x
. Khẳng định nào sau đây
đúng?
A.
2
1
3 0
3
x
x
. B.
2
1
3 0
3
x
x
. C.
1
2
10
3
x
x
. D.
1
2
9
3
x
x
.
Câu 16. Tập xác định của hàm số
ln 2
y x
là
A.
\ 2
. B.
2;

. C.
;2
 . D.
2;

.
Câu 17. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hàm số
log
a
y x
với
1
a
nghịch biến trên khoảng
0;

.
B. Hàm số
x
y a
với
0 1
a
đồng biến trên khoảng
0;

.
C. Hàm số
log
y x
với nghịch biến trên khoảng
0;

.
D. Hàm số
x
y a
với
0 1
a
nghịch biến trên khoảng
;
 
.
Câu 18. Tập nghiệm của bất phương trình
2 3
3 27
x
là
A.
3;

. B.
0;

. C.
3;

. D.
0;

.
Câu 19. Phương trình
2
2
log ( 2 3) 1
x x
có mấy nghiệm?
A. 2. B. 3. C. 0. D. 1.
Câu 20. Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A.
1
2
y log
x
. B.
2
y
3
x
. C.
e
y
3
x
. D.
ln
y x
.
Câu 21. Tính đạo hàm của hàm số
8 5
x x x
y
x
(
0
x
)
A.
3
4
1
4
y
x
. B.
3
4
1
4
y
x
. C.
3
4
1
4
y x
. D.
3
4
4
y x
.
O
x
1
x
O
1
2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 33/69 - Mã đề 2D2
Câu 22. Hàm số
2
n
l
xf
x
x đạt cực trị tại điểm:
A.
e
x . B.
1
e
x
. C.
e
x
. D.
1
e
x
.
Câu 23. Theo tài liệu thống kê cho biết năm
2001
dân số Việt nam có khoảng
78.695.000
người và tỉ
lệ tăng dân số trung bình hằng năm là
1,3%
trên
1
năm. Nếu tỉ lệ tăng dân số không đổi thì
năm
2016
dân số nước ta khoảng bao nhiêu người
A.
95.638.898
. B.
96.890.320
. C.
98.158.117
. D.
94.403.638
.
Câu 24. Phương trình
2 2
4 6.2 8 0
x x
có mấy nghiệm?
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 25. Giá trị nhỏ nhất của hàm số
2
e
x
y
là
A.
1
. B.
1
. C.
e
. D.
0
.
----------- HẾT ----------
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
C
D
B
A
A
A
A
C
A
C
C
B
D
B
B
D
C
D
D
B
B
A
D
A
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 34/69 - Mã đề 2D2
SỞ GD & ĐT HÀ NỘI
TRƯỜNG THPT LÝ THÁNH TÔNG
..........*..........
ĐỀ KIỂM TRA KHẢO SÁT LẦN 2
MÔN:TOÁN 12
NĂM HỌC: 2017-2018
(Thời gian làm bài:45 phút)
Câu 1. Hàm số nào có bảng biến thiên như hình sau:.
A.
2 5
2
x
x
y
. B.
2 3
2
x
x
y
. C.
3
2
x
x
y
. D.
2 1
2
x
x
y
.
Câu 2. Hàm số
e
x
y
có giá trị lớn nhất trên đoạn
1;ln3
là
A.
e
. B.
2
e
. C.
3
. D.
1
.
Câu 3. Đồ thị của hàm số nào dưới đây nhận đường thẳng
1
x
là tiệm cận đứng?
A.
2
2
3 2
1
x x
x
y
. B.
2
1
x
x
y
. C.
2 1
1
x
x
y
. D.
1
1
x
x
y
.
Câu 4.
Tập xác định của hàm số
5
3
3
2 9 3
y x x là
A.
3;

. B.
3
\
. C.
9
;
2

. D.
9
3;
2
\
.
Câu 5. Cho
27
log 5
a
,
8
log 7
b
và
2
log 3
c
. Biểu diễn
12
log 35
theo
a
,
b
,
c
?
A.
3 3
3
b ac
y
c
. B.
3 2
2
b ac
y
c
. C.
3 3
2
b ac
y
c
. D.
3 3
1
b ac
y
c
.
Câu 6.
Đạo hàm của hàm số
2
log e
x
y x là
A.
1 e
ln2
x
. B.
1 e
e
x
x
x
. C.
1
e ln2
x
x
. D.
1 e
e ln2
x
x
x
.
Câu 7. Tập nghiệm của phương trình
3
log 1 2
x
là
A.
3;2
. B.
10;2
. C.
3
. D.
4;2
.
Câu 8. Tập nghiệm của bất phương trình
1 3
3
log log 2 0
x
là
A.
5;

. B.
3;5
. C.
4;1
. D.
;5
 .
Câu 9. Cho một khối chóp có thể tích bằng
V
. Khi giảm diện tích đa giác đáy xuống
1
3
lần thì thể tích
khối chóp lúc đó bằng
A.
9
V
. B.
6
V
. C.
3
V
. D.
27
V
.
Câu 10. Thể tích của khối nón có chiều cao bằng
a
và độ dài đường sinh bằng
5
a
là
A.
3
4
3
V a
. B.
3
4
V a
. C.
3
2
3
V a
. D.
3
5
3
V a
.
x

2

y
–
–
2


2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 35/69 - Mã đề 2D2
Câu 11. Đồ thị hàm số
3
2 1
x
x
y
có bao nhiêu tiếp tuyến song song với đường thẳng :
d y x
?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 12. Đồ thị hàm số
ln
x
y
x
có điểm cực đại là
A.
1;
e
. B.
1;0
. C.
;1
e
. D.
1
;
e
e
.
Câu 13. Rút gọn biểu thức
3 3
2 2
1 1
2 2
.
a b a b a b
a b
ab
a b
M
(với điều kiện
M
có nghĩa) ta được:
A.
1
. B.
2
. C.
1
. D.
3
.
Câu 14. Cho
0,2 0,2
log log
x y
. Chọn khẳng định đúng?
A.
0
y x
. B.
0
x y
. C.
0
x y
. D.
0
y x
.
Câu 15. Số nghiệm của phương trình
2
2 2
2
x x
là
A.
0
. B.
2
. C.
1
. D.
4
.
Câu 16. Cho hàm số
3 2
y x bx x d
.
Các đồ thị nào có thể là đồ thị biểu diễn hàm số đã cho?
A.
I
. B.
I
và
II
. C.
III
. D.
I
và
III
.
Câu 17. Tìm
m
để hàm số
3 2
6 9
y x x x m
có giá trị nhỏ nhất trên đoạn
0;2
bằng
4
?
A.
8
m
. B.
4
m
. C.
0
m
. D.
4
m
.
Câu 18. Với giá trị nào của
m
thì đồ thị hàm số
1
1
mx
x
y
có hai đường tiệm cận?
A.
1
m
. B.
m
. C.
0
m
. D.
2
m
.
Câu 19. Có thể kết luận gì về cơ số
a
nếu
3 1
2 1 > 2 1
a a
?
A.
1
;
2

. B.
1
;0
2
. C.
0;

. D.
;0
 .
Câu 20. Kết quả thống kê cho biết ở thời điểm năm
2013
dân số Việt Nam là
90
triệu người, tốc độ
tăng dân số là
1,1%
/năm. Nếu mức tăng dân số ở mức ổn định như vậy thì dân số Việt Nam sẽ
gấp đôi ( đạt ngưỡng
180
triệu người) vào năm nào?
A.
2050
. B.
2077
. C.
2093
. D.
2070
.
Câu 21. Cho ba số thực dương
a
,
b
,
c
khác
1
thỏa mãn
log log log 2016.log .
a c a c
b b b
. Khẳng định
nào sau đây là đúng?
A.
2016
ab
. B.
2016
bc
. C.
2016
abc
. D.
2016
ac
.
O
x
O
x
O
x
I
II
III
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 36/69 - Mã đề 2D2
Câu 22. Phát biểu nào sau đây không đúng?
A. Hai hàm số
x
y a
và
log
a
y x
có cùng tập giá trị.
B. Hai đồ thị hàm số
x
y a
và
log
a
y x
đối xứng nhau qua đường thẳng
y x
.
C. Hai hàm số
x
y a
và
log
a
y x
có cùng tính đơn điệu.
D. Hai đồ thị hàm số
x
y a
và
log
a
y x
đều có đường tiệm cận.
Câu 23. Tìm
m
để phương trình
2 2
2
4 2 6
x x
m
có đúng 3 nghiệm?.
A.
3
m
. B.
2
m
. C.
3
m
. D.
2 3
m
.
Câu 24. Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật biết rằng
SA
vuông góc với mặt
phẳng đáy,
SC
hợp với đáy một góc
45
và
3
AB a
,
4
BC a
. Tính thể tích khối chóp
.
S ABCD
theo
a
?
A.
3
40
a
. B.
3
6
0
a
. C.
3
10 3
3
a
. D.
3
20
a
.
Câu 25. Một hình thang vuông
ABCD
có đường cao
AD
, đáy nhỏ
AB
, đáy lớn
2
CD
.
Cho hình thang đó quay quanh
CD
ta được khối tròn xoay có thể tích bằng
A.
4
2
V
. B.
4
4
3
V
. C.
3
4
3
V
. D.
2
4
3
V
.
--------- Hết ----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 37/69 - Mã đề 2D2
TRƯỜNG THPT THANH HÀ KIỂM TRA 45' GIẢI TÍCH CHƯƠNG II LỚP 12
Họ tên:............................................................................. Lớp:…………………..... Mã đề 064
Câu 1. Trong các số sau số nào lớn nhất:
A.
2
log 5
. B.
1
2
1
log
6
. C.
4
log 15
. D.
3
log 8
.
Câu 2. Tập xác định của hàm số
1
3
1
y x
là
A.
;1

. B.
\ 1
. C.
;1

. D.
.
Câu 3. Phương trình
3
log (3 2) 3
x
có nghiệm là
A.
25
3
x . B.
13
x
. C.
29
3
x . D.
11
3
x
.
Câu 4. Tập xác định của hàm số
ln 1
y x
là
A.
;e

. B.
0;

. C.
1;

. D.
1;

.
Câu 5. Giả sử tỷ lệ lạm phát của Việt Nam mỗi năm trong
10
năm tới là
5%
. Hỏi nếu năm
2017
giá
xăng A92 là
18000
VNĐ /lít thì năm 2025 giá xăng A92 là bao nhiêu tiền một lít?
A.
29320,10
VNĐ/lit. B.
25327,81
VNĐ/lít.
C.
27923,91
VNĐ/lít. D.
26594,20
VNĐ/lít.
Câu 6. Đạo hàm của hàm số
e
2 1
y x
là
A.
e 1
e 2 1
y x
. B.
e 1
2 2 1
y x
. C.
e
2 2 1
y x
. D.
e 1
2e 2 1
y x
.
Câu 7. Phương trình
2
2 2
log 4log 3 0
x x
có tập nghiệm là
A.
6;8
. B.
1;3
. C.
6;2
. D.
8;2
.
Câu 8. Với mọi số thực dương a và b thỏa mãn
2 2
6
a b ab
, mệnh đề nào dưới đây đúng?
A.
8 8 8
log log log
a b a b
. B.
8 8 8
1
log 1 log log
2
a b a b
.
C.
8 8 8
log 1 log log
a b a b
. D.
8 8 8
1
log log log
2
a b a b
.
Câu 9. Phương trình:
3.4 3 10 .2 3 0
x x
x x
có 1 nghiệm dạng
log
a
b
. Tìm
4
a b
.
A.
12
. B.
14
. C.
8
. D.
16
.
Câu 10. Biết
9
log 5
a
. Khi đó giá trị của
3
log 5
được tính theo
a
là
A.
4
a
. B.
1
4
a
. C.
1
2
a
. D.
2
a
.
Câu 11. Phương trình
1
3.2 4 8 0
x x
có
2
nghiệm
1
x
,
2
x
và tổng
1 2
x x
là
A.
4
. B.
2
. C.
5
. D.
3
.
Câu 12. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2 2
3 3
log log 1 4 1 0
x x m
có ít
nhất một nghiệm thuộc đoạn
3
1;3
.
A.
0;2
m . B.
[ 1;0]
m
. C.
0;1
m . D.
0;4
m .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 38/69 - Mã đề 2D2
Câu 13. Chọn đáp án đúng: Phương trình
1 1
3 3 10
x x
A. Vô nghiệm. B. Có hai nghiệm cùng dương.
C. Có 2 nghiệm trái dâu. D. Có hai nghiệm âm.
Câu 14. Tập nghiệm của phương trình
2
2
1
log 2 1 0
2
x
là
A.
0; 4
. B.
4
. C.
1;0
. D.
0
.
Câu 15. Hàm số nào sau đây đồng biến trên tập xác định của nó:
A.
y
e
x
. B.
0,5
x
y .
C.
2
2
x
y
. D.
2
3
x
y
.
Câu 16. Cho hàm số
1
ln
1
y
x
. Trong các khẳng định sau đây khẳng định nào đúng?
A.
e 1
y
xy
. B.
e 1
y
xy
.
C.
e 1
y
xy
. D.
e 1
y
xy
.
Câu 17. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Hàm số
2
log 2
y x
đồng biến trên
2;

.
B. Hàm số
1
3
log 1
y x
nghịch biến trên
1;

.
C. Đồ thị hàm số
log 0 1
a
y x a
nằm phía trên trục
Ox
.
D. Đồ thị các hàm số
x
y a
và
log
a
y x
(với
0 1
a
) đối xứng với nhau qua đường
thẳng
y x
.
Câu 18. Phương trình
2 1
3 1
x
có nghiệm là
A.
1.
x
B.
1
.
3
x
C.
1
.
2
x
D.
0.
x
Câu 19. Tổng các nghiệm của phương trình
2
5 .3 1
x x
là:
A.
5
log 3
. B.
5
log 3
. C.
3
log 5
. D.
3
log 5
.
Câu 20. Nghiệm của bất phương trình
1
2
1
3
9
x
x
là
A.
6
.
7
x
B.
0
x
. C.
4
.
3
x
D.
4
.
3
x
Câu 21. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Đồ thị hàm số
3
x
y
nhận trục
Oy
là tiệm cận đứng.
B. Hàm số
2 1
e
x
y
có đạo hàm là
2 1
2e
x
y
.
C. Hàm số
1
2
x
y
nghịch biến trên
.
D. Hàm số
2
x
y
đồng biến trên
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 39/69 - Mã đề 2D2
Câu 22. Tính
4
0,75
3
1 1
16 8
K
, ta được
A.
18
K
. B.
16
K
. C.
12
K
. D.
24
K
.
Câu 23. Tập nghiệm của bất phương trình
2
1 1
2 2
log log 2
x x
là
A.
2;T

. B.
2;2
T .
C.
1;2
T . D.
2; 1 2;T

.
Câu 24. Tìm m để phương trình
2 2
1 1
4 4.2 3 4 0
x x x x
m
có nghiệm
A.
3
0
4
m
. B.
9
0
4
m
. C.
3
0
4
m
. D.
0
m
.
Câu 25. Biết
2
log 5
a
,
5
log 3
b
. Khi đó giá trị của
15
log 24
A.
3
1
ab
a b
. B.
1
1
a
ab
. C.
1
1
a
b
. D.
1
b
ab
.
----------HẾT----------
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
A
C
D
D
D
D
B B
D
C
B C
A
A
A
C
C
D
D
A
D
D
A
A
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 40/69 - Mã đề 2D2
SỞ GD&ĐT DAKLAK
TRƯỜNG THCS _THPT ĐÔNG DU
(Đề thi có 04 trang)
KIỂM TRA 1 TIẾT TOÁN 12 CHƯƠNG 2
NĂM HỌC 2017 - 2018
MÔN GT 12 – Khối lớp 12
Thời gian làm bài : 45 phút (không kể thời gian phát đề)
Họ và tên thí sinh:...................................................SBD:.....................
Mã đề thi 981
Câu 1. Cho hàm số
1
2
4 1
y x
có tập xác định là
A.
0;

. B.
1 1
\ ;
2 2
. C.
1 1
;
2 2
. D.
.
Câu 2. Cho hai biểu thức
9 9 9
log 15 log 18 log 10
A và
36 1
6
1
log 2 log 3.
2
B Giá trị của
A
B
là
A.
4
. B.
8
. C.
9
. D.
3
.
Câu 3. Biến đổi
5
3
4
0
x x x
thành dạng lũy thừa với số mũ hữu tỉ, ta được
A.
20
3
x
. B.
23
12
x
. C.
21
12
x
. D.
12
5
x
.
Câu 4. Cho hàm số
3 2
1
f x x x
. giá trị
0
f
là
A.
3
. B.
1
. C.
. D.
1
3
.
Câu 5. Cho
a
,
0
b
và
a
,
1
b
,
x
và
là hai số dương. Tìm khẳng định sai trong các khẳng định
sau:
A.
log log log
a a a
xy x y
. B.
2016
log 2016log
a a
x x
.
C.
2 2 2
1
log 4log
a
a
x x
. D.
log
log
log
b
a
b
x
x
a
.
Câu 6. Giải phương trình
2 3
1 2
2
log 2log 75 0
x x
(1) một học sinh thực hiện theo các bước sau:.
(I) Điều kiện xác định
0
x
.
(II)
2
2 2
(1) 9log 2log 75 0
x x
.
(III)
2
2
log 3
25
log
9
x
x
.
(IV)
2
log 3 8
x x
. Vậy (1) có nghiệm duy nhất là
9
x
.
Các bước đúng là
A. (I), (II), (III). B. (I), (II), (III), (IV).
C. (I), (II). D. Không bước nào đúng.
Câu 7. Phương trình
9 3.3 2 0
x x
có hai nghiệm
1
x
,
2 1 2
x x x
. Giá trị của
1 2
2 3
A x x
là
A.
1
. B.
3
4log 2
. C.
3
3log 2
. D.
3
2log 4
.
Câu 8. Tích các nghiệm của phương trình
2 2
log log 1 1
x x
là
A.
2.
B.
1.
C.
3.
D.
2.
Câu 9. Cho
x
,
là hai số thực dương và
m
,
n
là hai số thực tùy ý. Đẳng thức nào sau đây là sai ?
A.
.
n
n n
xy x y
. B.
.
m n
m n
x y xy
. C.
.
m
n n m
x x
. D. .
m n m n
x x x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 41/69 - Mã đề 2D2
Câu 10. Số nghiệm của phương trình
2 1 1
8 2
x
x
là
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 11. Hàm số
2
e
x
y x
nghịch biến trên khoảng:
A.
2;0
. B.
; 2

. C.
1;

. D.
;1

.
Câu 12. Nghiệm của bất phương trình
5.4 2.25 7.10 0
x x x
là
A.
0 1
x
. B.
1 1
x
. C.
0 1
x
. D.
0 2
x
.
Câu 13. Cho log3
m
,
ln3
n
thì
ln30
là
A.
ln30 1
n
m
. B. Đáp số khác. C. ln30
n
n
m
. D. ln30
n m
n
.
Câu 14. Tìm tập nghiệm
S
của bất phương trình
2
2 2
log 5log 4 0
x x
A.
0;2 16;S
. B.
;1 4;S
 
.
C.
2;16
S . D.
;2 16;S
 
.
Câu 15. Giải bất phương trình
2
log 3 1 3.
x
A.
10
3
x
. B.
3
x
. C.
3
x
. D.
1
3
3
x
.
Câu 16. Hàm số
1 2
ln
1 e
x
x
y
x
có đạo hàm là
A.
1 2
1 e
x
x
y
x
. B.
1 2
ln2 1
1 e
x
x
y
x
.
C.
1 2
ln2
1 e
x
x
y
x
. D.
1 2
ln2 1
1 e
x
x
y
x
.
Câu 17. Cho ba số thực dương
, ,
a b c
khác
1
. Đồ thị
các hàm số
x
y a
,
x
y b
,
x
y c
được cho
trong hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
c a b
. B.
b c a
.
C.
a c b
. D.
a b c
.
Câu 18. Phương trình
4 2 .2 2 0
x x
m m
có 2 nghiệm phân biệt khi và chỉ khi:
A.
2 2
m
. B.
2
m
.
C.
2
m
. D. Không có giá trị nào của
m
.
Câu 19. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 1
.e
x
y x
trên đoạn
1
;3
2
lần lượt là
A.
4 e
;
e 4
. B.
2
9 e
;
e 4
. C.
4
;0
e
. D.
e
;0
4
.
Câu 20. Tập xác định của hàm số
2
3 2
log 1 log
y x x
là
A.
0;

. B.
1;

. C.
1;0 0;
. D.
1;0
.
Câu 21. Các khẳng định sau khẳng định nào sai?
A. Hàm số
2
x
y
đồng biến trên
.
B. Hàm số
2
log
y x
đồng biến trên khoảng
0;

.
C. Đồ thị hàm số
3
x
y
có tiệm cận đứng là đường thẳng
0
x
.
D. Đồ thị hàm số
ln
y x
có tiệm cận đứng là đường thẳng
0
x
.
O
x
x
y a
x
y b
x
y c
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 42/69 - Mã đề 2D2
Câu 22. Tập nghiệm của bất phương trình
2 2
2log 1 log 5 1
x x
là
A.
3;3
. B.
3;5
. C.
1;5
. D.
1;3
.
Câu 23. Cho hàm số
ln 1
y x x
. Khẳng định nào sau đây là đúng?
A. Hàm có tập xác định là
\ 1
. B. Hàm số nghịch biến trên
1;0
.
C. Hàm số đồng biến trên
;0
 . D. Hàm số đồng biến trên
1;

.
Câu 24. Số nghiệm nguyên nhỏ hơn 5 của bất phương trình:
2
2 1 2 3 0
x
x x
là
A.
6
nghiệm. B.
5
nghiệm. C.
7
nghiệm. D. vô số.
Câu 25. Đạo hàm của hàm số
2
ln 1
y x x
là
A.
2
1
ln 1
x x
. B.
2
1
1
x x
. C.
2
2 1
ln 1
x
x x
. D.
2
2 1
1
x
x x
.
Câu 26. Khi tới nhà bạn gái chơi, mẹ bạn gái của anh Lang hỏi cháu có xe hơi chưa? Anh Lang vì muốn
cưa đổ cô nàng nên về quyết định mua trả góp chiếc KIA MORING với giá
300
triệu đồng
theo hình thức trả góp. Anh Lang muốn trả trong vòng 2 năm, với lãi suất
0,6%
. Hỏi hàng
tháng anh Lang phải trả khoản tiền cố định là bao nhiêu?
A.
13.46
triệu đồng. B.
14,45
triệu đồng. C.
14,09
triệu đồng. D.
12,88
triệu đồng.
Câu 27. Phương trình
2
log 1 log 2
x x x m
có nghiệm duy nhất khi và chỉ khi
A.
5
4
1
m
m
. B.
5
4
m
. C.
5
4
1
m
m
. D.
5
4
1
m
m
.
Câu 28. Khẳng định nào dưới đây là sai?
A.
2 1 3
2 2
. B.
2016 2017
2 1 2 1 .
C.
2017 2016
3 1 3 1 . D.
2018 2017
2 2
1 1
2 2
.
Câu 29. Sự tăng trưởng của một loại vi khuẩn theo công thức
.e
rt
S A
trong đó
A
là số lượng vi khuẩn
ban đầu,
r
là tỉ lệ tăng trưởng
0
r
,
t
là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn
ban đầu là
100
con và sau
5
giờ có
300
con. Khi đó sau thời gian bao lâu thì số lượng vi
khuẩn tăng gấp
10
lần so với số lượng ban đầu:
A.
5
log3
t
(giờ ). B.
3
log5
t
(giờ ). C.
3ln5
ln10
t (giờ ). D.
5ln3
ln10
t (giờ ).
Câu 30. Nghiệm của phương trình
5 5 5
log log 6 log 2
x x x
là
A.
0 ; 1
x x
. B.
–3 ; 2
x x
. C.
2
x
. D.
1
x
.
Câu 31. Một người gửi tiết kiệm
50
triệu đồng vào ngân hàng với lãi suất
7%
một năm. Biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu.
Nếu sau
5
năm mới rút lãi thì người đó thu được số tiền lãi là
A.
70,128
triệu đồng. B.
50,7
triệu đồng. C.
20,128
triệu đồng. D.
3,5
triệu đồng.
Câu 32. Phương trình
2 2
2 4 4 2
x x
x x
có tập nghiệm là
A.
1; 2
. B.
1;1;4
. C.
1;4
. D.
1;2
.
------ HẾT ------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
1
2
C
D
C
A
C
A
B
B
A
A
C
A
C
B
C
B
A
C
C
D
B
B
D
A
A
C
A
C
C
C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 43/69 - Mã đề 2D2
UBNN HUYỆN CHÂU THÀNH
TRUNG TÂM GDNN - GDTX
ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG II GIẢI TÍCH 12
(25 câu trắc nghiệm)
Họ, tên thí sinh:.................................... Lớp:……….
Mã đề thi 132
Câu 1. Hàm số
3
2
2 1
y x x
có đạo hàm
0
f
là
A. 2.
B.
1
3
.
C.
1
3
. D.
4
.
Câu 2. Giá trị của
log 5
a
a
là
A.
25
. B.
5
. C.
5
. D.
1
5
.
Câu 3. Trong các hàm số sau, hàm số nào đồng biến trên khoảng
0;

:
A.
6
log
y x
. B.
log , 3 2
a
y x a .
C.
1
4
log
y x
. D.
3
log
y x
.
Câu 4. Cho
27 8 2
log 5 ;log 7 ;log 3
a b c
.Tính
12
log 35
bằng:
A.
3 2
3
b ac
c
. B.
3 3
2
b ac
c
. C.
3 3
1
b ac
c
. D.
3 2
2
b ac
c
.
Câu 5. Biểu thức
4
3
2
3
:
a a
viết dưới dạng lũy thừa:
A.
5
3
a
. B.
2
3
a
. C.
5
8
a
. D.
7
3
a
.
Câu 6. Cho
2
log 6
a
. Khi đó
3
log 18
tính theo
a
là
A.
2 1
1
a
a
.
B.
1
a
a
. C.
2 3
a
. D.
2 3
a
.
Câu 7.
4
1
8
log 32
bằng
A.
. B.
. C.
5
12
. D.
3
.
Câu 8. Đạo hàm của hàm số
3
y x
là:
A.
4
3
1
3
x
. B.
3
2
1
3
x
. C.
3
1
2
x
. D.
3
2
1
x
.
Câu 9. Hàm số
2
2
log 5
y x x
có đạo hàm là :
A.
2
2 1
5 ln 2
x
y
x x
. B.
2
2 1 ln2
5
x
y
x x
. C.
2 1 ln 2
y x
. D.
2
2 1
5
x
y
x x
.
Câu 10. Hàm số nào dưới đây là hàm số lũy thừa:
A.
1
3
( 0)
y x x
. B. Cả 3 câu còn lại đều đúng.
C.
1
( 0)
y x x
. D.
3
y x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 44/69 - Mã đề 2D2
Câu 11. Cho
2
ln
f x x
. Đạo hàm
e
f
bằng
A.
3
e
. B.
e
. C.
1
e
. D.
e
.
Câu 12. Biến đổi
53
4
,( 0)
x x x
thành dạng lũy thừa với số mũ hữu tỉ ta được:
A.
20
3
x
. B.
23
12
x
. C.
21
12
x
. D.
12
5
x
.
Câu 13. Giá trị của
2
8log 19
a
a
là:
A.
2
19
. B.
8
19
. C.
16
19
. D.
4
19
.
Câu 14. Hàm số
2
2 2 e
x
y x x có đạo hàm là
A.
2 e
x
y x
. B.
2 2 e
x
y x
. C.
2
e
x
y x
. D. Kết quả khác.
Câu 15. Nếu log4
a
thì
log4000
bằng:
A.
3
a
. B.
4
a
. C.
3 2
a
. D.
4 2
a
.
Câu 16. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Đồ thị hàm số
x
y a
và
1
x
y
a
(
0 1
a
) thì đối xứng với nhau qua trục tung.
B. Hàm số
x
y a
với
0 1
a
là một hàm số đồng biến trên
:
 
.
C. Đồ thị hàm số
x
y a
(
0 1
a
) luôn đi qua điểm
;1
a
.
D. Hàm số
x
y a
với
1
a
là một hàm số nghịch biến trên
:
 
.
Câu 17. Giá trị của
5
3
log
a
a a a a
là:
A.
. B.
4
. C.
. D.
13
10
.
Câu 18. Hàm số
2
5
log 4
y x x
có tập xác định là
A.
. B.
2;6
. C.
0;4
. D. (
0;
)
¥
.
Câu 19. Cho
1
ln
1
y
x
. Hệ thức liên hệ giữa
và
y
không phụ thuộc vào x là
A.
2 1
y y
. B.
e 0
y
y
. C.
4e 0
y
y
. D.
2 0
yy
.
Câu 20. Cho
a
,
b
là các số dương. Khi đó,
4 1 2
3 3 3
1 3 1
4 4 4
a a a
A
a a a
có giá trị là
A.
4
a
. B.
2
a
. C.
3
a
. D.
a
.
Câu 21. Tính:
4
0,75
3
1 1
16 8
K
, ta được:
A.
16
. B.
12
. C.
18
. D.
24
.
Câu 22. Tính:
2
1,5
3
0,04 0,125
K
, ta được:
A.
125
. B.
90
. C.
121
. D.
120
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 45/69 - Mã đề 2D2
Câu 23. Hàm số
2
ln 5 6
y x x
có tập xác định là
A.
0;

. B.
;0
 . C.
2;3
. D.
;2 3;
 
.
Câu 24. Cho
a
,
b
là các số dương. Khi đó,
2
1 1
2 2
1 2 :
b b
B a b
a a
có giá trị là
A.
. B.
2
a
. C.
3
2
a
. D.
a
.
Câu 25. Hàm số
1 ln
x
y
x x
có đạo hàm là
A.
2
ln
x
x
. B.
4
ln
x
x
. C. Kết quả khác. D.
ln
x
x
.
----------- HẾT ----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 46/69 - Mã đề 2D2
SỞ GD-ĐT TỈNH BÌNH ĐỊNH
ĐỀ KIỂM TRA CHƯƠNG II
TRƯỜNG THPT NGUYỄN TRUNG TRỰC Môn: Toán
Thời gian: 45 phút.
Họ tên học sinh:........................................ Lớp: 12A ……...
I - Phần trắc nghiệm (6 điểm)
Câu 1.
3
7
1
log
a
a
(
0
a
,
1
a
) bằng
A.
7
3
.
B.
.
C.
4
.
D.
5
3
.
Câu 2.
Cho
0
a
và
1
a
. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
log
a
x
có nghĩa với mọi
x
.
B.
log log .log
a a a
xy x y
.
C.
log 1
a
a
và
log 0
a
a
.
D.
log log
n
a a
x n x
(
0
x
,
0
n
).
Câu 3.
Hàm số
3
2
9 1
y x
có tập xác định là
A.
.
B.
1 1
;
3 3
.
C.
0;

.
D.
1 1
\ ;
3 3
.
Câu 4.
Cho
sin2
e
x
xf
. Đạo hàm
0
f
bằng
A.
3
.
B.
1
.
C.
2
.
D.
4
.
Câu 5.
Hàm số
3 2
2 1
f x x x
có đạo hàm
0
f
là
A.
2
.
B.
1
3
.
C.
1
3
.
D.
4
.
Câu 6.
Tính
2
1,5
3
0,04 0,125
K
, ta được
A.
120
.
B.
90
.
C.
121
.
D.
125
.
Câu 7.
Cho
1
a
. Tìm mệnh đề
sai
trong các mệnh đề sau:
A.
log 0
a
x
khi
1
x
.
B.
log 0
a
x
khi
0 1
x
.
C.
Đồ thị hàm số
log
a
y x
có tiệm cận ngang là trục hoành.
D.
Nếu
1 2
0
x x
thì
1 2
log log
a a
x x
.
Câu 8.
Cho
a
là một số dương, biểu thức
2
3
a a
viết dưới dạng luỹ thừa với số mũ hữu tỷ là
A.
6
5
a
.
B.
11
6
a
.
C.
5
6
a
.
D.
7
6
a
.
Câu 9.
Bất phương trình:
2 2
log 3 2 log 6 5
x x
có tập nghiệm là
A.
3;1
.
B.
1
;3
2
.
C.
6
1;
5
.
D.
0;

.
Câu 10.
Phương trình
3 2
4 16
x
có nghiệm là
A.
3
.
B.
5
.
C.
3
4
x
.
D.
4
3
x
.
Câu 11.
Cho
. Kết luận nào sau đây là đúng?
A.
.
B.
. 1
.
C.
0
.
D.
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 47/69 - Mã đề 2D2
Câu 12.
Cho
0
a
và
1
a
. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
Tập giá trị của hàm số
log
a
y x
là khoảng
0;

.
B.
Tập giá trị của hàm số
x
y a
là tập
.
C.
Tập xác định của hàm số
log
a
y x
là khoảng
0;

.
D.
Tập xác định của hàm số
x
y a
là khoảng
0;

.
II - Phần tự luận (4 điểm)
Giải các phương trình và bất phương trình sau:
a)
2
3 1
4 2
x x
.
b)
x
9 3 6 0
x
.
c)
log log 6 log 4
x x x
.
Bài làm:
ĐÁP ÁN THAM KHẢO
I - Phần trắc nghiệm (6 điểm)
1 2 3 4 5 6 7 8 9 10 11 12
A D D C B C C D C D A C
II - Phần tự luận (4 điểm)
a)
x
hoặc
1
x
. b)
1
x
c)
6
x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 48/69 - Mã đề 2D2
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT CÂY DƯƠNG
KIỂM TRA TOÁN 12 - MŨ LOGARIT
Thời gian: 45 phút
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 213
Câu 1. Cho các số thực dương
a
và
b
,
1
a
. Tìm mệnh đề sai trong các mệnh đề dưới đây
A.
log 1 0
a
. B.
log .log
a a
b b
.
C.
log .log 0
a
a
b b
. D.
log 1
a
a
.
Câu 2. Biết
log 3
a
b
và
log 4
a
c
. Tính giá trị của biểu thức
5 2
log .
a
T b c
.
A.
12
T
. B.
259
T
. C.
23
T
. D.
3888
T
.
Câu 3. Cho hàm số
1
e
x
x
y
. Tìm khẳng định đúng
A.
2 0
y y y
. B.
2 0
y y y
. C.
2 0
y y y
. D.
2 0
y y y

.
Câu 4. Tìm tập xác định của hàm số
2
y x
.
A.
2;

. B.
2;

. C.
; 2

. D.
;2
 .
Câu 5. Tìm tập nghiệm của phương trình
1
2.9 3 1 0
x x
.
A.
1
. B.
1
2
. C.
1
1;
2
. D.
.
Câu 6. Tìm tập xác định của hàm số
4
lg
2
x
y
x
.
A.
4;2
. B.
2;4
. C.
; 2 4;
 
. D.
2;4
.
Câu 7. Một người mỗi tháng đều đặn gởi vào ngân hàng cùng một số tiền là
10
triệu đồng vào một
ngày cố định của mỗi tháng với lãi suất kép
7%
/năm. Hỏi sau ít nhất bao lâu thì người đó thu
được cả vốn và lãi là
1
tỷ đồng? Giả sử trong quá trình gởi người đó không rút tiền ra và lãi
suất không thay đổi
A.
2
năm
6
tháng. B.
7
năm
5
tháng. C.
6
năm
7
tháng. D.
8
năm
2
tháng.
Câu 8. Gọi
S
là tập hợp các số nguyên
m
nhỏ hơn
2018
sao cho hàm số
2 1
x
y m
xác định
trên nửa khoảng
2;

. Tìm số phần tử của S.
A.
2016
. B.
2021
. C.
2018
. D.
2022
.
Câu 9. Biết
18
log 3
a
và
18
log 5
b
. Tính theo
a
và
b
giá trị của
18
log 2430
.
A.
3 1
a b
. B.
3 1
a b
. C.
3 1
a b
. D.
3 1
a b
.
Câu 10. Giải bất phương trình
1
2
log 0
x
.
A.
1
x
. B.
1
x
. C.
0 1
x
. D.
0
x
.
Câu 11. Đồ thị của hàm số
y x
luôn đi qua điểm có tọa độ nào dưới đây?
A.
1;1
. B.
1; 1
. C.
0;1
. D.
1;0
.
Câu 12. Tìm nghiệm của phương trình
3
log 1 2
x
.
A.
9
x
. B.
4
x
. C.
8
x
. D.
10
x
.
Câu 13. Tính giá trị biểu thức
0,75
5
2
1
0,04
81
P
.
A.
1523
P
. B.
3152
P
. C.
2315
P
. D.
5231
P
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 49/69 - Mã đề 2D2
Câu 14. Tìm tham số thực
m
để phương trình
2 2
5 5
log 2 1 .log 4 0
x m x m
có hai nghiệm thực
phân biệt
1
x
,
2
x
thỏa mãn
1 2
. 25
x x
.
A.
6
m . B.
1
2
m
. C.
29
m . D.
3
2
m
.
Câu 15. Tìm mệnh đề đúng trong các mệnh đề sau
A. Đồ thị hàm số
log 0, 1
a
y x a a
có tiệm cận đứng là trục
Oy
.
B. Hàm số
0, 1
x
y a a a
có tập xác định là
0;

.
C. Hàm số
log 0, 1
a
y x a a
có tập xác định là
.
D. Đồ thị hàm số
0, 1
x
y a a a
có tiệm cận đứng là trục
Oy
.
Câu 16. Giải bất phương trình
7 2
x
.
A.
7
log 2
x . B.
2
log 7
x . C.
7
log 2
x . D.
2
log 7
x .
Câu 17. Tìm đạo hàm của hàm số
2
2
5
1
y x x
A.
3
2
5
2
. 1
5
y x x
. B.
3
2
5
2
. 1 2 . 1
5
y x x x
.
C.
3
2
5
5
. 1 2 . 1
2
y x x x
. D.
3
2
5
2
. 1 2 . 1
5
y x x x
.
Câu 18. Phương trình
2
lg lg 1 0
x x
có tất cả bao nhiêu nghiệm?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 19. Cho số thực
x
dương. Viết biểu thức
1
3
4
2
.
Q x x
dưới dạng lũy thừa với số mũ hữu tỉ
A.
6
Q x
. B.
4
5
Q x
. C.
5
4
Q x
. D.
Q x
.
Câu 20. Tìm tất cả các tham số thực
m
để bất phương trình
1
4 2 3 0
x x
m
có nghiệm.
A.
4
m
. B.
3
m
. C.
3
m
. D.
4
m
.
Câu 21. Cho các số thực dương
a
và
b
thỏa mãn
2 2
23
a b ab
. Tìm mệnh đề đúng trong các mệnh
đề sau
A.
5 5 5
1 1
log 1 log log
2 2
a b a b
. B.
2 2 2
1 1
log 1 log log
2 2
a b a b
.
C.
5 5 5
1 1
log 1 log log
2 2
a b a b
. D.
2 2 2
log log log
a b a b
.
Câu 22. Cho số thực dương
a
,
1
a
. Tính giá trị của
3
log
a
a
.
A.
6
. B.
1
6
. C.
. D.
.
Câu 23. Tìm tập nghiệm của bất phương trình
lg 2 3 lg
x x
.
A.
;3

. B.
3;

. C.
3
3;
2
. D.
3
;3
2
.
Câu 24. Đồ thị nào dưới đây là đồ thị của hàm số mũ
x
y a
với
0 1
a
.
A. . B. . C. . D. .
Câu 25. Bất phương trình
1
4 129.2 32 0
x x
có tất cả bao nhiêu nghiệm nguyên?
A.
8
. B.
31
. C.
32
. D.
6
.
……….HẾT……….
O
x
1
O
x
O
x
1
O
x
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 50/69 - Mã đề 2D2
SỞ GD & ĐT LONG AN
TRƯỜNG THPT CHUYÊN LONG AN
ĐỀ KIỂM TRA TẬP TRUNG HỌC KỲ 1 – LẦN 3
MÔN: GIẢI TÍCH 12
(Thời gian làm bài 45 phút)
I. PHẦN TRẮC NGHIỆM:
Câu 1. Tìm mệnh đề đúng trong các mệnh đề sau?
A. Đồ thị hàm số
log
a
y x
và
1
log
a
y x
với
0 1
a
đối xứng nhau qua trục hoành.
B. Hàm số
log
a
y x
với
0 1
a
là hàm số đồng biến trên khoảng
0;

.
C. Hàm số
log
a
y x
với
0 1
a
có tập xác định là
.
D. Hàm số
log
a
y x
với
1
a
là hàm số đồng biến trên khoảng
0;

.
Câu 2. Giả sử
a
là số thực dương khác 1. Biểu thức
3
a a
được viết dưới dạng
a
. Khi đó giá trị
của
là
A.
5
3
. B.
2
3
. C.
11
6
. D.
1
6
.
Câu 3. Tập xác định của hàm số
4
2
1
y x
là
A.
D \ 1
. B.
D ; 1 1;
 
.
C.
D ; 4 1;
 
. D.
D
.
Câu 4. Viết biểu thức
4
3
. 0, 1
P x x x x
dưới dạng lũy thừa với số mũ hữu tỉ là
A.
5
12
P x
. B.
5
4
P x
. C.
1
7
P x
. D.
1
12
P x
.
Câu 5. Cho
1
n
là một số nguyên. Tính giá trị của
2 3
1 1 1
...
log ! log ! log !
n
P
n n n
?
A.
P n
. B.
1
P
. C.
0
P
. D.
!
P n
.
Câu 6. Cho các số thực
, , ,
a b m n
với
, 0
a b
. Mệnh đề nào sau đây là sai?
A.
.
m
m m
a
a b
b
. B.
n
m m n
a a
. C.
2
a a
. D.
. .
m
m m
a b a b
.
Câu 7. Hàm số nào sau đây đồng biến trên
?
A.
2
1
4
log 1
y x
. B.
2
x
y
. C.
2
4
log 2 1
y x x
. D.
1
3
x
y
.
Câu 8. Cho các số thực
, 0
a b
. Khi rút gọn biểu thức
2
2 1
2
2log log
P a b
được biểu thức nào sau đây?
A.
2
2
log
a
P
b
. B.
2
2
log
P ab
. C.
2
2
2
log
a
P
b
. D.
2
2
log 2
P ab
.
Câu 9. Tìm tất cả các giá trị của tham số
m
để phương trình
2
3
3 1
3
9 log log 0
x x m
có nghiệm
thuộc khoảng
0;1
?
A.
;0
m  . B.
1
;
4
m

. C.
1
0;
4
m
. D.
1
;
4
m

.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 51/69 - Mã đề 2D2
Câu 10. Cho các số thực dương
,
a b
. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
2
2 2
1
log log
2
a a
. B.
2 2
1 1
log log
a a
a b
.
C.
2 2
2 2
log 2log
a b a b
. D.
3 3
4 4
log log
a b a b
.
Câu 11. Cho
2 1
3 3
1 1
a a
. Khi đó ta có thể kết luận gì về
a
?
A.
0 1
a
. B.
2
a
. C.
1 2
a
. D.
2
a
.
Câu 12. Tìm nghiệm của phương trình
2
log 1 3
x
?
A.
7
x
. B.
10
x
. C.
9
x
. D.
8
x
.
Câu 13. Hình bên là đồ thị của hàm số nào sau đây?
A.
2
log
y x
. B.
2
x
y
.
C.
1
2
x
y
. D.
3
log
y x
.
Câu 14. Cho
3
log 5
x
. Tính giá trị của biểu thức
3
log
P x
?
A.
5
P . B.
25
P
. C.
5
2
P
. D.
5
3
P
.
Câu 15. Với các số thực dương
a
,
b
bất kỳ. Khẳng định nào sau đây là khẳng định đúng?
A.
log log
ab a b
. B.
log log
b
a
a
b
.
C.
log log log
ab a b
. D.
log
log
log
a
a b
b
.
Câu 16. Tính đạo hàm của hàm số
log ln 2
y x
. Khi đó, ta thu được kết quả nào sau đây?
A.
1
ln2
y
x
. B.
1
.ln 2 .ln10
y
x x
. C.
1
2 .ln 2 .ln10
y
x x
. D.
2
.ln 2 .ln10
y
x x
.
Câu 17. Tìm tất cả giá trị của tham số
m
để phương trình
3 2
3
3 1 log 0
x x m
có đúng một
nghiệm?
A.
3
1
27
m
m
. B.
1
27
m . C.
3
1
0
27
m
m
. D.
3
m
.
Câu 18. Tìm tập nghiệm của phương trình
2
2
2
2log 1 log 1
x x x
.
A.
0
S . B.
2
S . C.
0;2
S . D. S
.
Câu 19. Cho số thực dương
x
thỏa
3 27 27 3
log log log log
x x
. Tính giá trị của
3
log
T x
.
A.
27
T
. B.
3 3
T . C.
1
3
T
. D.
3
3
T .
Câu 20. Số nghiệm của phương trình
2
log 1 2
x
là bao nhiêu?
A.
1
. B.
0
. C.
2
. D.
3
.
O
x
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 52/69 - Mã đề 2D2
Câu 21. Một người lần đầu gửi ngân hàng 100 triệu đồng với kì hạn 3 tháng với lãi suất 3% của một
quý (một quý có 3 tháng) và tiền lãi từng quý sẽ nhập vào vốn (hình thức lãi kép). Sau đúng 6
tháng, người đó gửi thêm vào 100 triệu đồng với kì hạn và lãi suất như trước đó. Tổng số tiền
người đó nhận được 1 năm kể từ khi gửi thêm tiền lần hai sẽ gần nhất với số tiền nào sau đây?
A.
219
triệu đồng. B.
262
triệu đồng. C.
232
triệu đồng. D.
313
triệu đồng.
Câu 22. Cho
a
,
b
là các số dương
1
a
,
1
b
thỏa mãn
53
7
4
3 5
, log log
4 7
b b
a a . Phát biểu đúng là
A.
log 0
b
a
. B.
0 log 1
a
b
. C.
0 log 1
b
a
. D.
log 1
a
b
.
II. PHẦN TỰ LUẬN:
Giải các phương trình sau: a)
2 2
2 1 2 2
2 9.2 2 0
x x x x
. b)
1 3
2
log log 1
x x
.
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
A
B B A
B B B B C
D
D
C
B C
C
B C
B B B C
A
Đáp số tự luận: a)
1, 2
x x
b)
2
3
log 2
3x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 53/69 - Mã đề 2D2
SỞ GD & ĐT TUYÊN QUANG
TRƯỜNG THPT ĐÔNG THỌ
ĐỀ KHẢO SÁT ÔN THI THPT QUỐC GIA LẦN 1
MÔN: TOÁN 11
(Thời gian làm bài 90 phút)
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 101
Câu 1. Cho
.
x
f x x
. Đạo hàm
1
f
bằng
A.
ln
. B.
2
ln
. C.
ln
. D.
1
ln
.
Câu 2. Giá trị của
2 8
1
log 3 3log 5
2
4
bằng
A.
25
. B.
50
. C.
75
. D.
45
.
Câu 3. Cho
a
là một số dương, biểu thức
2
3
a a
viết dưới dạng luỹ thừa với số mũ hữu tỷ là
A.
6
5
a
. B.
11
6
a
. C.
5
6
a
. D.
7
6
a
.
Câu 4.
3 52 2 4
15 7
log
a
a a a
a
bằng
A. 3. B.
12
5
. C.
9
5
. D.
2
.
Câu 5. Giỏ trị của
0,5
log 0,125
bằng
A.
5
. B.
3
. C.
4
. D.
2
.
Câu 6. 6. Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng nó xác định?
A.
3
y x
. B.
4
y x
. C.
4
y x
. D. y =
3
4
x
.
Câu 7. Cho
2
e
x
f x
x
. Đạo hàm
1
f
bằng
A.
6e
. B.
4e
. C.
2
e
. D.
e
.
Câu 8. Cho
0
a
và
1
a
,
x
và
y
là hai số dương. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
log log log
a a a
x y x y
. B.
1 1
log
log
a
a
x x
.
C.
log
log
log
a
a
a
x
y y
. D.
log log .log
b b a
x a x
.
Câu 9. Nếu
1
log log 9 log 5 log 2
2
a a a a
x (
0
a
,
1
a
) thì x bằng
A.
. B.
3
5
. C.
6
5
. D.
3
.
Câu 10. Tính:
4
0,75
3
1 1
16 8
K , ta được:
A.
24
. B.
12
. C.
16
. D.
18
.
Câu 11. Đạo hàm của hàm số
2 3
2
x
y là
A.
2 3
2 .ln 2
x
. B.
2 2
2 3 2 ln 2
x
x . C.
2 3
2.2
x
. D.
2 3
2.2 .ln2
x
.
Câu 12. Hàm số nào dới đây thì nghịch biến trên tập xác định của nó?
A.
3
log
y x
. B.
e
log
y x
. C.
2
log
y x
. D.
log
y x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 54/69 - Mã đề 2D2
Câu 13. Biểu thức
6
5
3
. .
x x x
(
0
x
) viết dưới dạng luỹ thừa với số mũ hữu tỷ là
A.
7
3
x
. B.
5
2
x
. C.
2
3
x
. D.
5
3
x
.
Câu 14. Cho
. Kết luận nào sau đây là đúng?
A.
. B.
1
.
. C.
D.
0
.
Câu 15. Rút gọn biểu thức
2
3 1
2 3
:b b
(
0
b
), ta đợc:
A.
4
b
. B.
3
b
. C.
2
b
. D.
b
.
Câu 16. Hàm số
2
5
log 4
y x x
có tập xác định là
A.
0;

. B.
0 4
;
. C.
. D.
2 6
;
.
Câu 17. Cho
sin2
e
x
f x . Đạo hàm
0
f
bằng
A.
1
. B.
4
. C.
3
. D. 2.
Câu 18. Một khu rừng có trữ lượng gỗ
5
4.10
mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng
đó là
4
%
mỗi năm. Tìm khối lượng gỗ của khu rừng đó sau
5
năm
A.
5 3
4,8666.10 (m ).
B.
5 3
4,0806.10 (m ).
C.
5 3
4,6666.10 (m ).
D.
5 3
4,6888.10 (m ).
Câu 19. Giá trị của
3
7
1
log
a
a
(
0
a
,
1
a
)bằng
A.
5
3
. B.
. C. 4. D.
7
3
.
Câu 20. Giá trị của
2
1
log 10
2
64
bằng
A.
400
. B.
1000
. C.
200
. D.
1200
.
Câu 21. Hàm số
2
ln
2
x x
y
có đạo hàm
y
là
A.
2
ln
1
2 2 .
x x
x
x
B.
2
ln
1
2 2 ln2.
x x
x
x
C.
2
ln
2
.
ln2
x x
D.
2
ln
1 2
2 .
ln2
x x
x
x
Câu 22. Cho
0
a
và
1
a
. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
log log .log
a a a
xy x y
. B.
log
a
x
có nghĩa với
x
.
C.
log log
n
a a
x n x
(
0
x
,
0
n
). D. 1log
a
a
và
0
log
a
a
.
Câu 23.
4
1
8
log 32
bằng
A.
. B. 3. C. -
5
12
. D.
.
Câu 24. Cho
4
ln 1
f x x . Đạo hàm
1
f
bằng
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 25. Cho
9 9 23
x x
. Khi đó biểu thức
1 3 3
5 3 3
x x
x x
K có giá trị bằng
A.
5
2
. B.
2
5
. C.
. D.
2
.
----------- HẾT ----------
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
C
D
A
B A
D
D
C
A
D
B D
C
A
B D
A
D
B B C
C
A
B
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 55/69 - Mã đề 2D2
SỞ GD & ĐT ĐÀ NẴNG
TRƯỜNG THPT TÔN THẤT TÙNG
ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG II
MÔN: TOÁN 12
(Thời gian làm bài 90 phút)
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 817
I. Phần trắc nghiệm: (6 điểm).
Câu 1. Tập xác định của hàm số
2
log
1
x
y
x
là:
A.
;1 2;

. B.
1;2
. C.
\ 1
. D.
\ 1;2
.
Câu 2. Khẳng định nào sai trong các khẳng định sau:
A.
ln 0 1
x x
. B.
2
log 0 0 1
x x
.
C.
1 1
3 3
log log 0
a b a b . D.
1 1
2 2
log log 0
a b a b .
Câu 3. Cho hàm số
ln 1
y x
. Chọn khẳng định đúng trong các khẳng định sau:
A.
1
2
2
y . B.
1
2
3
y . C.
6
5
5
y . D.
1
y .
Câu 4. Trong các hàm số:
1
ln
sin
f x
x
;
1 sin
ln
cos
x
g x
x
;
1
ln
cos
h x
x
. Hàm số nào có đạo
hàm là
1
cos
x
A.
f x
. B.
g x
. C.
h x
. D.
g x
và
h x
.
Câu 5. Tập xác định
1
4 4
x
y là:
A.
;1 2;

. B.
1;

. C.
\ 1
. D.
\ 1;3
.
Câu 6. Tập xác định của hàm số
9 3
x x
y là:
A.
0;

. B.
5;

. C.
\ 5
. D.
\ 0;5
.
Câu 7. Điều kiện xác định của phươg trình
2 3
log 16 2
x
là:
A.
3
\ ;2
2
x . B.
2
x
. C.
3
2
2
x . D.
3
2
x .
Câu 8. Phương trình
3
log 3 2 3
x có nghiệm là:
A.
29
3
x . B.
11
3
x . C.
25
3
x . D.
87
x
.
Câu 9. Phương trình
2
3 3
log 6 log 2 1
x x có tập nghiệm là:
A.
0;3
T . B.
T
. C.
3
T . D.
1;3
T .
Câu 10. Số nghiệm của phương trình
2 3 2
log .log 2 1 2log
x x x
là:
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 11. Tập nghiệm của bất phương trình
2
1
2
log 5 7 0
x x là:
A.
2 3
x
. B.
3
x
. C.
2
x
. D.
2
x
hoặc
3
x
.
Câu 12. Biết phương trình
16 17.4 16 0
x x
có
2
nghiệm là
1
x
và
2
x
. Tính tổng
1 2
x x
?
A.
0
. B.
1
. C.
2
. D.
3
.
II. Phần tự luận: (4 điểm)
Câu 1. (2,0 điểm) Giải các phương trình sau: a)
2
2 7 5
2 1
x x
. b)
2
2 2
log 9.log 10
x x .
Câu 2. (2,0 điểm) Giải các bất phương trình sau: a)
1 2
4 2 3
x x
. b)
2
2 3
log 2
1
x
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 56/69 - Mã đề 2D2
SỞ GD & ĐT BÌNH DƯƠNG
TRƯỜNG THPT BÌNH AN
ĐỀ KIỂM TRA 1 TIẾT
MÔN: TOÁN 12
(Thời gian làm bài 45 phút)
Họ và tên thí sinh:..............................................................SBD:.....................
Mã đề thi 485
Câu 1. [2D2-3] Cho bất phương trình:
9 1 .3 0 1
x x
m m . Tìm tất cả các giá trị của tham số
m
để bất phương trình
1
có nghiệm đúng
1
x
?
A.
3
2
m
. B.
3 2 2
m
. C.
3 2 2
m
. D.
3
2
m
.
Câu 2. [2D2-2] Cho phương trình:
2
4 5
3 9
x x
. Tổng lập phương các nghiệm của phương trình là
A.
28.
B.
26.
C.
25.
D.
27.
Câu 3. [2D2-2] Cho
,
a b
là hai số thực dương.và
1
a
. Khẳng định nào đúng?
A.
2
log . 2 2log .
a
a
a b b
B.
2
1
log . log .
2
a
a
a b b
C.
2
1
log . log .
4
a
a
a b b
D.
2
1 1
log . log .
2 2
a
a
a b b
Câu 4. [2D2-2] Số nghiệm của phương trình:
6.9 13.6 6.4 0
x x x
là
A.
3.
B.
0.
C.
2.
D.
1.
Câu 5. [2D2-2] Đạo hàm của hàm số:
2 1
5
x
x
y
là
A.
2 2
.ln 5 .ln5.
5 5
x
x
y
B.
1 1
2 1
.
5 5
x x
y x x
C.
2 2 1
ln ln5.
5 5 5
x x
y
D.
1 1
2 1
.
5 5
x x
y x x
Câu 6. [2D2-2] Số thực
a
thỏa mãn điều kiện
3 2
log log 0
a
là
A.
. B.
3
. C.
2
. D.
1
3
.
Câu 7. [2D2-3] Bất phương trình
2
0.2 0.2
log 5log 6
x x
có tập nghiệm là
A.
0;3
. B.
1 1
;
125 25
. C.
1
0;
25
. D.
2;3
.
Câu 8. [2D2-2] Cho hàm số
1
ln
1
y
x
, hệ thức liên hệ giữa
và
y
không phụ thuộc vào
x
là
A.
2 0
yy
. B.
e 0
y
y
. C.
2 1
y y
. D.
4 0
y
y e
.
Câu 9. [2D2-3] Tìm tất cả các giá trị thực của tham số
m
để hàm số
3
1
log
2 1
y x m
m x
xác định trên
2;3
.
A.
1 2
m
. B.
1 2
m
. C.
1 2
m
. D.
1 2
m
.
Câu 10. [2D2-2] Với
0 1
x
, ta có
4
2
1
1
1
x
x
.
A.
3
4
1
1
x
x
. B.
3
4
1
1
x
x
. C.
4
1
1
. D.
4
1
1
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 57/69 - Mã đề 2D2
Câu 11. [2D2-2] Cho
30
log 3 ;
a
30
log 5
b
thì
30
log 8
tính theo
,
a b
là
A.
3 1
a b
. B.
3
a b
. C.
3 1
a b
. D.
a b
.
Câu 12. [2D2-2] Phương trình
2
3
log 4 12 2
x x
A. Có hai nghiệm trái dấu. B. Có hai nghiệm dương.
C. Vô nghiệm. D. Có hai nghiệm âm.
Câu 13. [2D2-2] Giá trị lớn nhất của hàm số
2
e
x
f x x
trên
1; 1
là
A.
0
. B.
1
e
. C.
e
. D.
2e
.
Câu 14. [2D2-1] Cho
a
là một số dương,
2
3
a a
viết dưới dạng lũy thừa với số mũ hữu tỷ là
A.
2
6
a
. B.
11
6
a
. C.
7
6
a
. D.
6
5
a
.
Câu 15. [2D2-1] Cho
a
và
*
2 1 n k k
,
n
a
có căn bậc
n
là
A.
a
. B.
a
. C.
a
. D.
2 1
n
n
a
.
Câu 16. [2D2-2] Bất phương trình
1
1
1
5 2 5 2
x
x
x
tương đương với bất phương trình nào sau đây?
A.
5 2
1
1 log 5 2
1
x
x
x
. B.
1
1
1
x
x
x
.
C.
1
1
1
x
x
x
. D.
5 2
1
1 log 5 2
1
x
x
x
.
Câu 17. [2D2-2] Phương trình
3 2 3 2 10
x x x
có tất cả bao nhiêu nghiệm thực?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 18. [2D2-1] Tập giá trị của hàm số
x
y a
0, 1
a a
là
A.
\ 0
. B.
0;
. C.
. D.
0;
.
Câu 19. [2D2-2] Đồ thị
L
của hàm số
ln
f x x
cắt trục hoành tại điểm
A
, tiếp tuyến của
L
tại
A
có phương trình là
A.
3
y x
. B.
2 1
y x
. C.
4 3
y x
. D.
1
y x
.
Câu 20. [2D2-2] Hình bên là đồ thị của ba hàm số
x
y a
,
x
y b
,
x
y c
(
0 , , 1
a b c
) được vẽ trên cùng một hệ
trục toạ độ. Khẳng định nào sau đây là khẳng định đúng?
A.
a b c
. B.
b a c
.
C.
a c b
. D.
c b a
.
Câu 21. [2D2-2] Số nghiệm của phương trình:
2 2
log 1 2log 3 2 2 0
x x
là
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 22. [2D2-2] Hàm số
3
2
y x
có tập xác định:
A.
. B.
\ 2
. C.
2;
. D.
2;
.
x
O
1
x
y a
x
y c
x
y b
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 58/69 - Mã đề 2D2
Câu 23. [2D2-4] Khách hàng
A
vay ưu đãi vốn ngân hàng
150
triệu đồng với lãi suất
0,68%
/tháng.
Ông hoàn nợ cho ngân hàng theo cách như sau: sau đúng một tháng kể từ ngày vay ông ta bắt
đầu hoàn nợ, hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ trong mỗi
tháng là như nhau và hoàn nợ trong 5 năm thì hết nợ. Hỏi theo cách đó mỗi lần hoàn nợ ông
A
phải trả cho ngân hàng bao nhiêu? Biết rằng lãi suất ngân hàng không đổi trong thời gian ông
hoàn nợ.
A.
5
5
1020000. 1,0068
1,0068 1
(đồng). B.
60
60
1020000. 1,0068
1,0068 1
(đồng).
C.
60
60
1020000. 1,0068
1,0068
(đồng). D.
5
5
1020000. 1,0068
1,0068
(đồng).
Câu 24. [2D2-1] Trong các hàm số sau đây, hàm số nào đồng biến trên
:
A.
1
3
x
y
. B.
3
x
y
. C.
1
2
x
y
. D.
2
e
x
y
.
Câu 25. [2D2-2] Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án
A
,
B
,
C
,
D
dưới đây. Hỏi hàm số đó là hàm số nào?
A.
2
log
y x
. B.
2
log
y x
. C.
2
log 2
y x
. D.
1
2
log
y x
.
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
A
D
C C C B B A
A
C D
C C C C B D
D
B A
B B A
A
x
O
1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 59/69 - Mã đề 2D2
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT QUỐC OAI
(Đề thi có 06 trang)
KIỂM TRA ĐỊNH KÌ
NĂM HỌC 2017 - 2018
MÔN TOÁN – Lớp 12A2
Thời gian làm bài : 90 phút (không kể thời gian phát đề)
Họ và tên học sinh :................................................... Số báo danh :.............................
Mã đề A
Câu 1. Gọi
S
là tập nghiệm của bất phương trình
2
2 3
1
0,25
4
x
x
. Khi đó
S
có dạng
;
a b
với
a b
. Tính
P a b
.
A.
2
. B.
1
. C.
0
. D.
2
.
Câu 2. Có bao nhiêu số nguyên
x
thỏa mãn bất phương trình
log 40 log 60 2
x x
.
A.
19
. B.
20
. C.
21
. D.
18
.
Câu 3. Tính tổng
T
tất cả các nghiệm của phương trình
2 2
3.25 3 10 .5 3 0
x x
x x
.
A.
5
2 log 6
T . B.
5
2
4 log
7
T
. C.
5
4 log 3
T . D.
5
3 log 2
T .
Câu 4. Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
2018;2018
để bất phương trình
2 2
1 4 1 4
9 20 .3 2 5 0
x x
m m
có tập nghiệm
2;2
.
A.
2056
. B.
2057
. C.
2058
. D.
2060
.
Câu 5. Cho bốn hàm số
1
1
2
x
y
,
3 2
x
y ,
1
3
2
x
y
,
4 4
x
y và bốn đường cong
1
C
,
2
C
,
3
C
,
4
C
như hình vẽ bên.
Đồ thị hàm số
1
,
2
,
3
,
4
lần lượt là
A.
4 1 3 2
, , ,
C C C C
.
B.
1 2 3 4
, , ,
C C C C
.
C.
2 4 1 3
, , ,
C C C C
.
D.
3 2 4 1
, , ,
C C C C
.
Câu 6. Cho hàm số
2
5
2
x
x
f x . Khẳng định nào sau đây là khẳng định sai?
A.
2
5
1 log 2 0
f x x x
. B.
2
5
1 0
log 2
x
f x
x
.
C.
2
5
5
1 log 0
2
x
x
f x
. D.
2
2
1 log 5 0
f x x x
.
Câu 7. Cho phương trình
2 2 2 2
2 2 2 2
log 1 .log 2 4 6 log 1 1 4log 2 4 0 1
x x x x x x
Gọi
1
x
,
2
x
là hai nghiệm thực dương của phương trình đã cho
1 2
x x
. Tính
2
1 2
2
T x x
.
A.
6
T
. B.
3 2 5
T . C.
7
T
. D.
1 3 5
T .
O
x
1
2
C
1
C
4
C
3
C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 60/69 - Mã đề 2D2
Câu 8. Cho
a
,
b
là các số thực dương khác
1
. Hình vẽ bên
là đồ thị của
2
hàm số
1
:
x
C y a
,
2
:
x
C y b
.
Mệnh đề nào sau đây là đúng?
A.
1
b a
. B.
1
b a
.
C.
1
a b
. D.
1
a b
.
Câu 9. Tìm tập xác định
D
của hàm số
3
0,5
log 3 2
y x x
.
A.
2; \ 1
. B.
2;
. C.
1;
. D.
0;1
.
Câu 10. Tập nghiệm của bất phương trình
1
1
3
9
x
là
A.
; 1

. B.
1;3
. C.
3;
. D.
1;
.
Câu 11. Tìm tập xác định của hàm số
2
3
2
y x .
A.
0;

. B.
. C.
\ 2
. D.
2;

.
Câu 12. Tìm nghiệm của phương trình
2
0,5
log sin 5sin .cos 2
1
4
9
x x x
.
A.
1
arctan
3
x k
k
x k
. B.
1
arctan
5
x k
k
x k
.
C.
2
1
arctan
5
x k
k
x k
. D.
2
1
arctan
3
x k
k
x k
Câu 13. Đặt
ln3
a
,
ln5
b
. Tính
3 4 5 123 124
ln ln ln ... ln ln
4 5 6 124 125
S theo
a
và
b
.
A.
2
I a b
. B.
3
I a b
. C.
2
I a b
. D.
3
I a b
.
Câu 14. Cho hàm số
2
1 2
log
2 1
x
f x
x
.
Tính tổng:
1 2 3 2015 2016
...
2017 2017 2017 2017 2017
S f f f f f
.
A.
4032
. B.
1008
. C.
2017
. D.
2016
.
Câu 15. Tìm tất cả giá trị thực của tham số
m
để hàm số
2
ln 2
y x mx m
có tập xác định là
.
A.
0
m
hoặc
1
m
. B.
0 1
m
.
C.
0
m
hoặc
1
m
. D.
0 1
m
.
Câu 16. Tìm tập xác định
D
của hàm số
2
2
2 1
log 3
x
f x
x x
.
A.
0;3
D
. B.
3 5
0;3 \
2
D
C.
D
. D.
\ 0;3
D
.
O
x
1
1
C
2
C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 61/69 - Mã đề 2D2
Câu 17. Gọi
S
là tập nghiệm của phương trình
4 8 2 5
2
3 4.3 28 2log 2
x x
. Tính tích tất cả các phần
tử của
S
.
A.
4.
B.
3
.
2
C.
1.
D.
3
.
2
Câu 18. Phương trình
2 4
log 1 2log 3 2 2 0
x x
có mấy nghiệm?
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 19. Mệnh đề nào sau đây là sai?
A. Cho hàm số
2
x
y
thì
1 ln4
y
.
B. Cho hàm số
log 2 1
y x
thì
2
1
3ln10
y
.
C. Cho hàm số
ln
y x
thì
1 1
y
.
D. Cho hàm số
e
x
y
thì
1 e
x
y
.
Câu 20. Tìm tập nghiệm của bất phương trình
1
2
log 1 2
x
.
A.
1;S

. B.
3
0;
4
S
. C.
3
;
4
S

. D.
3
1;
4
S
.
Câu 21. Trong mặt phẳng tọa độ
Oxy
cho hình vuông
ABCD
có diện tích bằng
36
, đường thẳng
AB
song song với trục
Ox
, các đỉnh
,
A B
và
C
lần lượt nằm trên đồ thị của các hàm số
log
a
y x
,
log
a
y x
,
3
log
a
y x
và
a
là một số thực lớn hơn
1
. Tìm
a
.
A.
3
a . B.
3
6
a . C.
6
3
a . D.
6
a .
Câu 22. Cho đồ thị ba hàm số
x
y a
,
x
y b
,
x
y c
như
hình vẽ. Kết luận nào sau đây đúng.
A. 0 1
a b c
.
B. 0 1
c a b
.
C. 0 1
a c b
.
D. 0 1
c b a
.
Câu 23. Gọi
S
là tập nghiệm của phương trình
2
2 3
1
1
7 .
7
x x
x
Tính tổng tất cả các phần tử của
S
.
A.
5.
B.
0.
C.
2.
D.
1.
Câu 24. Tính tổng
T
tất cả các giá trị của tham số
m
để phương trình
2
1
2
2 2
2 log 2 3 4 log 2 2
x mx
x x x m
có đúng ba nghiệm phân biệt.
A.
1
T
. B.
2
T
. C.
4
T
. D.
3
T
.
Câu 25. Tập nghiệm
S
của phương trình
1 2
2 3
3 2
x x
là
A.
1
S
. B.
1
3
S
. C.
2
S
. D.
1
S
.
Câu 26. Tập nghiệm của bất phương trình
0,5
log 1 2
x
là
A.
5
;
4

. B.
5
;
4
. C.
1;3
. D.
5
1;
4
.
O
x
1
x
y a
x
y b
x
y c
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 62/69 - Mã đề 2D2
Câu 27. Cho
a
,
b
là các số thực dương khác
1
. Trong các khẳng định sau, chọn khẳng định đúng.
A.
1 1
, 0
m m
a b m
a b
. B.
1 1
, 0
m m
a b m
a b
.
C.
, .
m m
a b a b m
D.
1 1
, 0
m m
a b m
a b
.
Câu 28. Giả sử
a
,
b
là các số thực dương. Biểu thức
5
3
b a
a b
được viết dưới dạng
a
b
. Tìm giá trị
.
A.
2
5
. B.
2
15
. C.
4
15
. D.
2
15
.
Câu 29. Gọi
M
và
m
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
e
x
y x
trên
1;2
. Tính
.
M n
.
A.
2
2e
. B.
0
. C.
3
2e
. D.
e
.
Câu 30. Tính
3 7
1
log 0, 1
a
a a a
.
A.
3
. B.
3
. C.
3
. D.
3
.
Câu 31. Biết
sin 0
x
,
cos 0
x
và
3 3
log sin log cos 1
x x
. Giá trị của
3
log sin cos
x x
bằng
A.
1
3
. B.
3
log 5 1
. C.
1
. D.
3
1
log 5 1
2
.
Câu 32. Tìm tập nghiệm của bất phương trình
2
2 4
2 3 1
1
4
2
x
x x
.
A.
1
. B.
5
;1 ;
4
 
. C.
5
0;
4
. D.
;0 1;
 
.
Câu 33. Tìm tọa độ giao điểm của đồ thị hàm số
3 2
x
y
và đường thẳng
5
y
.
A.
1;5
. B.
2;5
. C.
1;5
. D.
2;5
.
Câu 34. Biết
2 2
a b ab
,
0
a
,
0
b
. Chọn đẳng thức đúng.
A.
2 2
ln ln ln
a b a b
. B.
2lg lg3 lg lg
a b a b
.
C.
2ln ln2 ln ln
a b a b
. D.
2 2
lg lg lg
a b a b
.
Câu 35. Biết rằng phương trình
8
log 9
2018
3 2 0
x
có nghiệm duy nhất
0
x x
. Khẳng định nào sau đây là đúng?
A.
0
x
là số chính phương. B.
0
x
là một số chẵn.
C.
0
x
là số nguyên tố. D.
0
x
chia hết cho
3
.
Câu 36. Ông A vay ngân hàng T (triệu đồng) với lãi suất
12
% năm. Ông A thỏa thuận với ngân hàng
cách thức trả nợ như sau: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần
hoàn nợ liên tiếp cách nhau đúng một tháng. Nhưng cuối tháng thứ ba kể từ lúc vay ông A mới
hoàn nợ lần thứ nhất, cuối tháng thứ tư ông A hoàn nợ lần thứ hai, cuối tháng thứ năm ông A
hoàn nợ lần thứ ba (hoàn hết nợ). Biết rằng số tiền hoàn nợ lần thứ hai gấp đôi số tiền hoàn nợ
lần thứ nhất và số tiền hoàn nợ lần thứ ba bằng tổng số tiền hoàn nợ của hai lần trước Tính số
tiền ông A đã hoàn nợ ngân hàng lần thứ nhất.
A.
5
2
1 0,01
1,01 5
T
. B.
5
1
100
6
T
. C.
5
2
1 0,01
2,01 2
T
. D.
5
1 0,01
6
T
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 63/69 - Mã đề 2D2
Câu 37. Tìm tập nghiệm của bất phương trình
2
1
5 2 5 2
x
x
x
.
A.
; 1 0;1

. B.
1;0
. C.
; 1 0;
 
. D.
1;0 1;

.
Câu 38. Cho
2
log 5
a
,
3
log 5
b
. Hãy biểu diễn
6
log 5
theo
a
và
b
.
A.
6
1
log 5
a b
. B.
6
log 5
ab
a b
. C.
6
log 5
a b
. D.
2 2
6
log 5
a b
.
Câu 39. Cho
0
a
,
0
b
,
0
c
là các số thực khác
0
thỏa
5 15 45
a b c
. Tính
b b
T
a c
.
A.
15
log 5
T . B.
3
T
. C.
2
T
. D.
5
log 45
T .
Câu 40. Cho
3
2 2
.
f x x x
. Tính giá trị của
1
f
.
A.
2
. B.
8
3
. C.
4
. D.
3
8
.
Câu 41. Có bao nhiêu giá trị nguyên bé hơn
10
của tham số
m
sao cho bất phương trình
2 2
2 2
log 1 2 log 1 0
x x m
thỏa mãn với mọi
3
1;2
?
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 42. Cho góc
, giá trị của biểu thức
2 2
sin cos
5 .5
bằng
A.
1
. B.
5
. C.
25
. D.
2 2
sin .cos
5
.
Câu 43. Cho
a
là hai số thực dương khác Đặt
3
log
a m
. Tính theo
m
giá trị của biểu thức
1
3
3
log log log 9
a
D a a
.
A.
2
2 3
m
D
m
. B.
2
3 2
m
D
m
. C.
2
4 3
2
m
D
m
. D.
3
D m
.
Câu 44. Tìm đạo hàm của hàm số
2
2 3 e 3
x
y x x
trong điều kiện xác định.
A.
2
4 4 e 3
x
y x
. B.
2
4 4 e 3
x
y x x
.
C.
2
4.e 3
x
y
. D.
2
2 1 e 3
x
y x
.
Câu 45. Cho
a
,
b
là hai số thực dương thỏa mãn
2 4 8
2 2 4 8
a
a b
b
a b
. Tính giá trị của biểu thức
2017
2017
a
b
P .
A.
2017
b
. B.
2017
a
. C.
2
2017
. D.
1
.
Câu 46. Tìm tập xác định
D
của hàm số
2
2
2
y x x
.
A.
0;D
. B.
; 1 2;D

.
C.
\ 1;2
D
. D.
D
.
Câu 47. Tìm nghiệm của phương trình
1
3 27
x
.
A.
10
x
. B.
4
x
. C.
3
x
. D.
9
x
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 64/69 - Mã đề 2D2
Câu 48. Cho hàm số
2
ln 1
2
x
y x
. Khẳng định nào sau đây là đúng.
A. Hàm số đạt cực đại tại
1
x
. B. Hàm số nghịch biến trên khoảng
0;1
.
C. Hàm số đạt cực tiểu tại
1
x
. D. Hàm số đồng biến trên khoảng
0;
.
Câu 49. Tính đạo hàm của hàm số
13
x
y
x
.
A.
13 ln13 1
.ln13
x
y
x
. B.
13 1
x
y
x
. C.
2
13 ln13 1
x
x
y
x
.D.
1
13
x
y
.
Câu 50. Cho
0
a
,
1
a
và
x
,
là hai số dương. Mệnh đề nào sau đây là đúng?
A.
log . log .log
a a a
x y x y
. B.
log . log log
a a a
x y x y
.
C.
log log .log
a a a
x y x y
. D.
log log log
a a a
x y x y
.
------ HẾT ------
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
D
C
A
D
B
A
C
A
C
D
C
B
B
B
B
D
A
D
D
C
D
D
D
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
D
D
C
C
D
C
C
B
D
C
D
B
C
B
B
B
A
A
C
C
B
A
C
B
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 65/69 - Mã đề 2D2
SỞ GD VÀ ĐT HẢI DƯƠNG
TRƯỜNG THPT ĐOÀN THƯỢNG
ĐỀ KIỂM TRA 45 PHÚT NĂM HỌC 2017 – 2018
Môn: Giải tích 12 – Chương 2
Thời gian làm bài: 45 phút;
Họ, tên thí sinh:................................... Số báo danh:...............
Mã đề thi 132
Câu 1. Tập nghiệm của bất phương trình
2x-5
3 9
là
A.
7
;
2

. B.
7
;
2

. C.
5
;
2

. D.
5
;
2

.
Câu 2. Cho số dương
a
, biểu thức
6
5
3
. .
a a a
viết dưới dạng lũy thừa hữu tỉ là
A.
5
7
a
. B.
1
6
a
. C.
7
3
a
. D.
5
3
a
.
Câu 3. Cho hàm số
2
2
2 log 2 2 2 1
f x x m mx m x m
(
m
là tham số). Tìm tất cả các
giá trị
m
để hàm số
f x
xác định với mọi
x
.
A.
0
m
. B.
1
m
. C.
1 4
m m
. D.
4
m
.
Câu 4. Tính đạo hàm của hàm số
2
3 2
e
x x
y
.
A.
2 3 e
x
y x
. B.
2
-3x 2
e
x
y
.
C.
2
2 3 2
3 2 e
x x
y x x
. D.
2
-3 2
2 3 e
x x
y x
.
Câu 5. Giá trị của tham số
m
để phương trình
4 .2 2 5 0
x x
m m
có hai nghiệm trái dấu là
A.
5
2
m
. B.
5
2
m
. C.
5
4
2
m
. D.
4
m
.
Câu 6. Tập nghiệm của bất phương trình
2
2 2
log 4log 3 0
x x
là
A.
0;2 8;

. B.
;2 8;
 
.
C.
2;8
. D.
8;

.
Câu 7. Số
756839
2 1
p
là một số nguyên tố. Hỏi nếu viết trong hệ thập phân, số đó có bao nhiêu chữ số?
A.
227831
chữ số. B.
227834
chữ số.
C.
227832
chữ số. D.
227835
chữ số.
Câu 8. Ông Minh gửi ngân hàng số tiền
100
triệu đồng với lãi suất
7%
một năm theo hình thức lãi
kép. Biết rằng trong suốt quá trình gửi ông không rút tiền lãi. Hỏi sau ít nhất bao nhiêu năm thì
ông có nhiều hơn
500
triệu.
A.
24
năm. B.
23
năm.
C.
22
năm. D.
25
năm.
Câu 9. Hàm số
2
ln
y x x
đạt cực trị tại điểm
A.
1
0;
e
x x
. B.
1
e
x
. C.
0
x
. D.
e
x .
Câu 10. Hàm số
4
2
4 1
y x
có tập xác định là
A.
. B.
1 1
;
2 2
. C.
1 1
\ ;
2 2
. D.
0;

.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 66/69 - Mã đề 2D2
Câu 11. Tìm tập xác định của hàm số sau
2
2
3 2
log
1
x x
f x
x
.
A.
3 17 3 17
; 1;
2 2
D

. B.
; 3 1;

.
C.
3 17 3 17
; 1 ;1
2 2
D
. D.
; 3 1;1
 .
Câu 12. Bạn An gửi tiết kiệm số tiền
58.000.000
đồng trong
8
tháng tại một ngân hàng thì nhận được
61.329.000
đồng. Khi đó, lãi suất hàng tháng gần với giá trị nào nhất trong các giá trị sau:
A.
9%
. B.
6%
. C.
5%
. D.
7%
.
Câu 13. Nếu
2
log 3
a ,
2
log 5
b thì:
A.
6
2
1
log 360
6 2 3
a b
. B.
6
2
1
log 360
3 4 6
a b
.
C.
6
2
1
log 360
2 6 3
a b
. D.
6
2
1
log 360
2 3 6
a b
.
Câu 14. Một người gửi ngân hàng số tiền
100
triệu đồng với lãi suất
7%
một năm theo hình thức lãi
kép. Biết rằng trong suốt quá trình gửi không rút tiền lãi. Hỏi sau 5 năm số tiền của người ấy
gần với giá trị nào dưới đây nhất
A.
142
triệu. B.
140
triệu. C.
130
triệu. D.
150
triệu.
Câu 15. Phương trình
2 2
1
4 2 3
x x x x
có nghiệm là chọn 1 đáp án đúng
A.
1
2
x
x
. B.
1
1
x
x
. C.
0
2
x
x
. D.
0
1
x
x
.
Câu 16. Biểu thức
0
x x x x x
được viết dưới dạng lũy thừa số mũ hữu tỉ là
A.
15
16
x
. B.
15
18
x
. C.
3
16
x
. D.
7
18
x
.
Câu 17. Phương trình tiếp tuyến của đồ thị hàm số
2
y x
tại điểm thuộc đồ thị có hoành độ bằng
1
là
A.
1
2
y x
. B.
1
2 2
y x
. C.
1
2 2
y x
. D.
1
2
y x
.
Câu 18. Tìm tập xác định
D
của hàm số
2
log 3 2
y x x
A.
2;1
D . B.
1;D

.
C.
2;D

. D.
;1 2;D
 
.
Câu 19. Cho hàm số
2 2
x
y x
. Khẳng định nào sau đây sai?
A. Đồ thị hàm số luôn cắt trục tung.
B. Hàm số có giá trị nhỏ nhất lớn hơn
1
.
C. Đồ thị hàm số cắt trục hoành tại duy nhất một điểm.
D. Đồ thị hàm số luôn cắt đường thẳng
2
y
.
Câu 20. Cho
0 1
a
và
x
,
là hai số dương. Phát biểu nào sau là đúng
A.
log log . og
a a a
xy x l y
. B.
log log . og
a a a
x y x l y
.
C.
log log og
a a a
xy x l y
. D.
log log og
a a a
x y x l y
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 67/69 - Mã đề 2D2
Câu 21. Cho phương trình
ln ln 1 0
x x
. Chọn khẳng định đúng.
A. Phương trình vô nghiệm. B. Phương trình có hai nghiệm.
C. Phương trình có nghiệm
1;2
. D. Phương trình có nghiệm thuộc
0;1
.
Câu 22. Số nghiệm của phương trình
3
3
log 3x
2
x
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 23. Giải bất phương trình
2 1
2
15
log log 2 2
16
x
A.
0
x
. B.
2 2
15 31
log log
16 16
x .
C.
2
31
0 log
16
x . D.
2
15
log 0
16
x
.
Câu 24. Một người gửi ngân hàng số tiền
T
với lãi suất
7%
một năm theo hình thức lãi kép. Biết rằng
trong suốt quá trình gửi không rút tiền lãi. Hỏi sau bao nhiêu năm số tiền của người gấp đôi số
tiền ban đầu
A.
11
năm. B.
12
năm. C.
14
năm. D.
10
năm.
Câu 25. Để giải phương trình
2
2
log 1 6
x
. Một học sinh giải như sau:
Bước 1: Điều kiện
2
1 0 1
x x
.
Bước 2: Phương trình tương đương:
2 2
2log 1 6 log 1 3 1 8 7
x x x x
.
Bước 3: Vậy phương trình đã cho có nghiệm là
7
x
.
Dựa vào bài giải trên chọn khẳng định đúng trong các khẳng định sau:
A. Bài giải trên hoàn toàn chính xác. B. Bài giải trên sai từ Bước 1.
C. Bài giải trên sai từ Bước 2. D. Bài giải trên sai từ Bước 3.
----------- HẾT -----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 68/69 - Mã đề 2D2
TRƯỜNG THPT NGUYỄN TRÃI
TỔ TOÁN
ĐỀ KIỂM TRA 1 TIẾT
MÔN: GIẢI TÍCH - LỚP 12
Họ, tên thí sinh:................................... SBD:...............
Mã đề: 132
Câu 1. Cho
a
là số thực dương
,
là các số thực. Mệnh đề nào sau đây sai?
A.
.
a a a
. B.
a a

. C.
a
a
a
. D.
( )
a b ab
.
Câu 2. Cho
a
,
b
,
c
là
3
số dương khác
1
. Chọn khẳng định sai trong các khẳng định sau:
A.
log log log
a a a
bc b c
. B.
log log b.log
a a b
c c
.
C. log log
a
a
b b
. D.
1
log log ( 0)
a
a
b b
.
Câu 3. Tìm tất cả các giá trị thực của
m
để phương trình
2
3
x
m
có nghiệm:
A.
1;m

. B.
3;m
. C.
1;m

. D.
0;m
.
Câu 4. Gọi
1
x
,
2
x
là hai nghiệm của phương trình
9 8.3 9 0
x x
. Giá trị biểu thức
1 2
P x x
bằng
A.
2
. B.
4
. C.
9
. D.
8
.
Câu 5. Gọi
1
x
,
2
x
là hai nghiệm của phương trình
2
3 3
log 3log 2 0
x x
. Giá trị biểu thức
2 2
1 2
P x x
bằng bao nhiêu?
A.
20
. B.
92
. C.
90
. D.
9
.
Câu 6. Với
a
,
b
,
c
là các số thực dương tùy ý
a
khác
1
. Đặt
2
8 4
log log
a
a
Q b b
. Mệnh đề nào
dưới đây đúng?
A.
5log
a
b
. B.
7log
a
b
. C.
8log
a
b
. D.
12log
a
b
.
Câu 7. Anh Hùng vay
40
triệu đồng của ngân hàng để mua xe máy và phải trả góp trong vòng
3
năm
với lãi suất
1,2%
mỗi tháng. Hàng tháng anh Hùng phải trả
1
số tiền cố định là bao nhiêu để
sau
3
năm hết nợ (làm tròn đến đơn vị đồng)
A.
1.374.807
đồng. B.
1.374.889
đồng. C.
1.374.907
đồng. D.
1.378.222
đồng.
Câu 8. Tập xác định
D
của hàm số:
3
3
log
2
x
y
x
là
A.
\ 3;2
D
. B.
3;2
D .
C.
; 3 2;D
 
. D.
3;2
D .
Câu 9. Cho
log 3
m
a và
log 3
n
b , với
m
,
n
là các số thực dương khác
1
.Tính
2
3
log ( )
P nm
A.
ab
P
a b
. B.
2
a b
P
ab
. C.
2
ab
P
a b
. D.
2
a b
P
ab
.
Câu 10. Tập xác định của hàm số
3
2
2
2
y x x
là
A.
\ 0;2
D
. B.
D
. C.
\ 0;2
D
. D.
\ 2
D
.
Câu 11. Rút gọn biểu thức
5
3
:
Q a a
với
0
a
.
A.
2
3
Q a
. B.
2
3
Q a
. C.
4
3
Q a
. D.
7
6
a
.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện Trang 69/69 - Mã đề 2D2
Câu 12. Tìm tất cả các giá trị thực của
m
để phương trình:
2
2 2
log 1 log 3 0
x x x m
có
2
nghiệm phân biệt.
A.
2 3
m
. B.
2 3
m
. C.
2 3
m
. D.
2
m
.
Câu 13. Đạo hàm của hàm số y =
4
x
x
là
A.
2
1 ln4
4
x
x
. B.
1
4 ln4
x
. C.
1
4 ln4
x
x
. D.
1 ln4
4
x
x
.
Câu 14. Chọn khẳng định Sai trong các khẳng định sau:
A.
ln 0 1
x x
. B.
log 0 10
x x
.
C.
1 1
2 2
log log 0.
a b a b
. D.
2 2
log log 0
a b a b
.
Câu 15. Cho
3 0
a b
và
2 2
9 10
a b ab
, mệnh đề nào dưới đây đúng?
A.
ln ln
ln 3 ln 2
2
a b
a b
. B.
ln .ln
ln 3 ln2
2
a b
a b .
C.
ln ln
ln 3 ln2
2
a b
a b
. D.
ln .ln
ln 3 ln 2
2
a b
a b .
Câu 16. Tổng các nghiệm của phương trình
2
2
log 1 1
x
là
A.
2
. B.
2 2
. C.
2 2
. D.
2 1
.
Câu 17. Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A.
1
2
y log
x
. B.
2
y
3
x
. C.
e
y
3
x
. D.
ln
y x
.
Câu 18. Tìm giá trị thực của tham số
m
để giá trị nhỏ nhất của hàm số:
2
2 log
x
f x x m
trên
đoạn
1;2
bằng
.
A.
3
m
. B.
3
m
. C.
1
m
. D.
2
m
.
Câu 19. Cho
3 3 15
x x
. Giá trị biểu thức:
9 9
x x
P
là
A.
221
. B.
225
. C.
223
. D.
227
.
Câu 20. Tìm tất cả các giá trị thực của
m
để phương trình
2 2
2 1 2 2
4 .2 6 5 0
x x x x
m m
có
4
nghiệm phân biệt.
A.
5
m
. B.
5 6
m
. C.
5
m
. D.
5 6
m
.
----------- HẾT -----------
ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
C C A A C C B D B A D C D B C A D A C A
| 1/70
| | Tải xuống

Có thể bạn quan tâm:

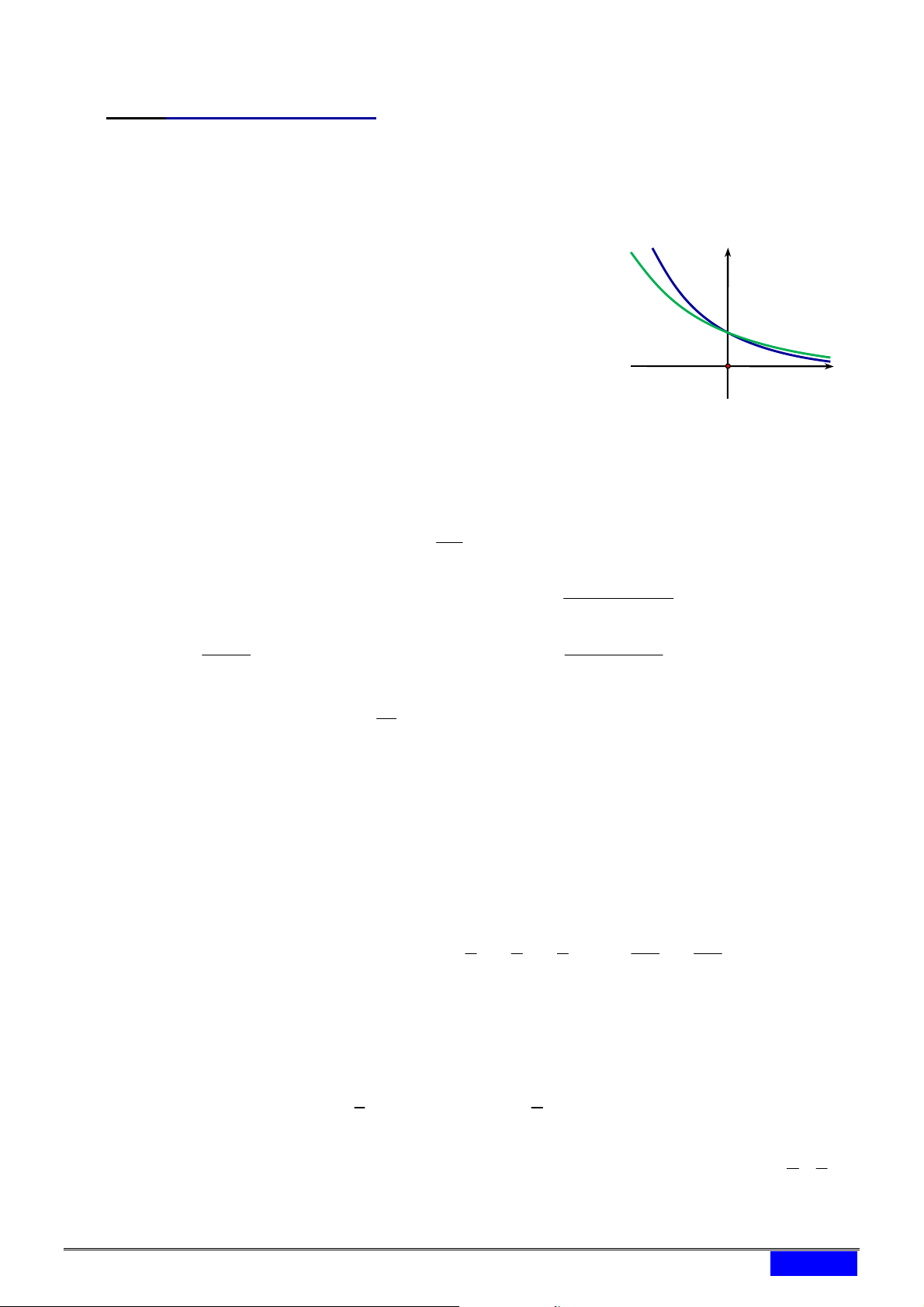
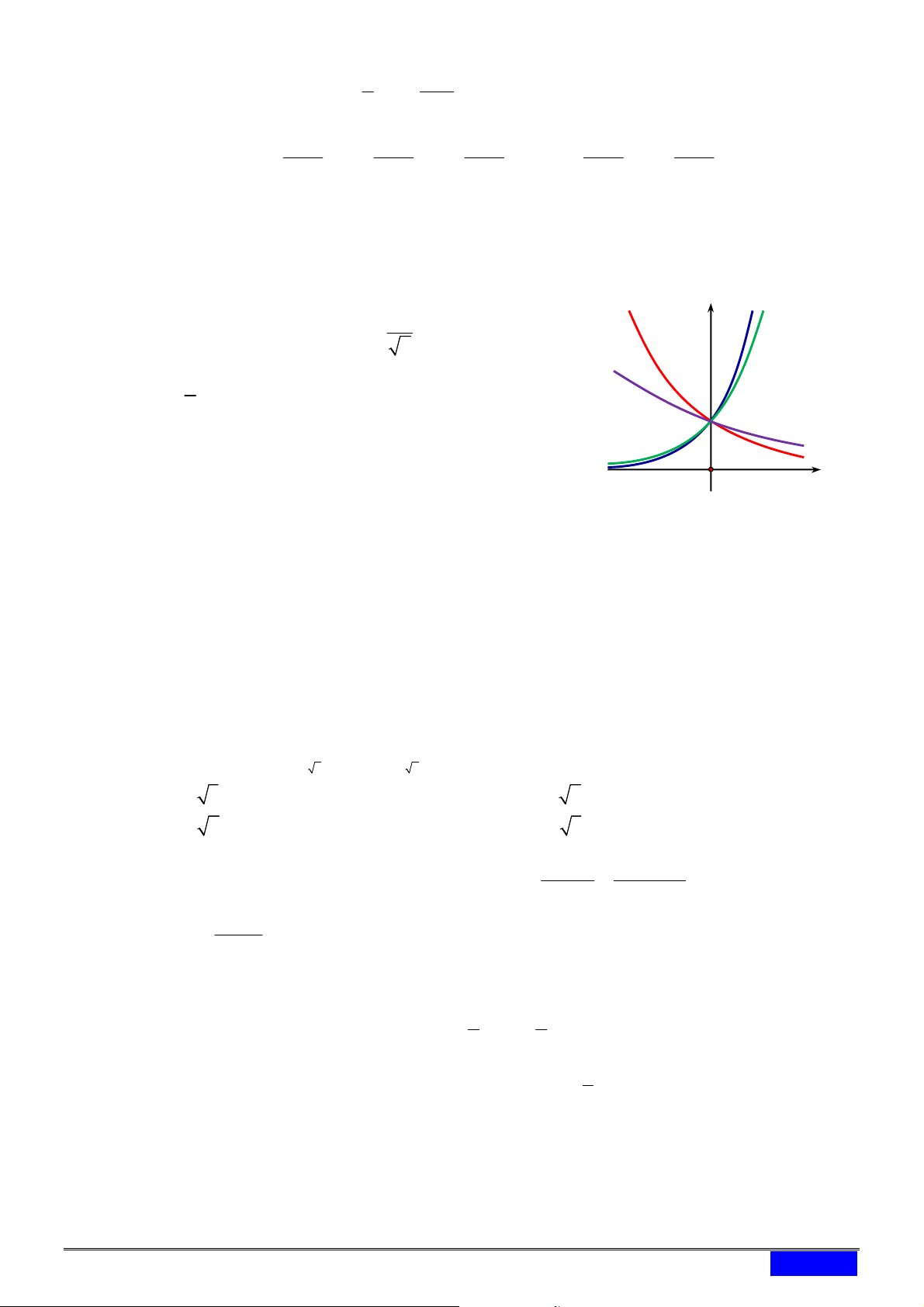
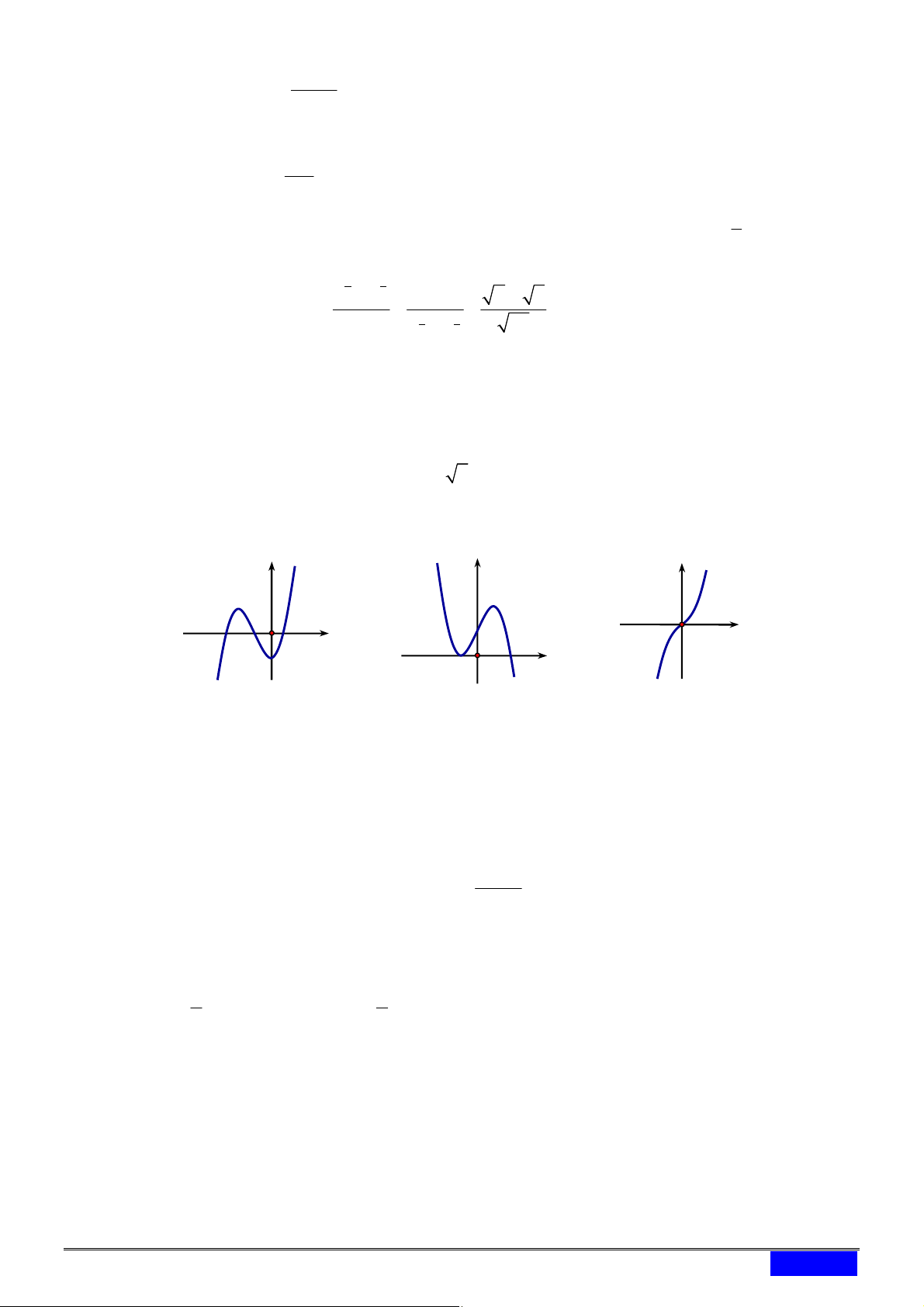
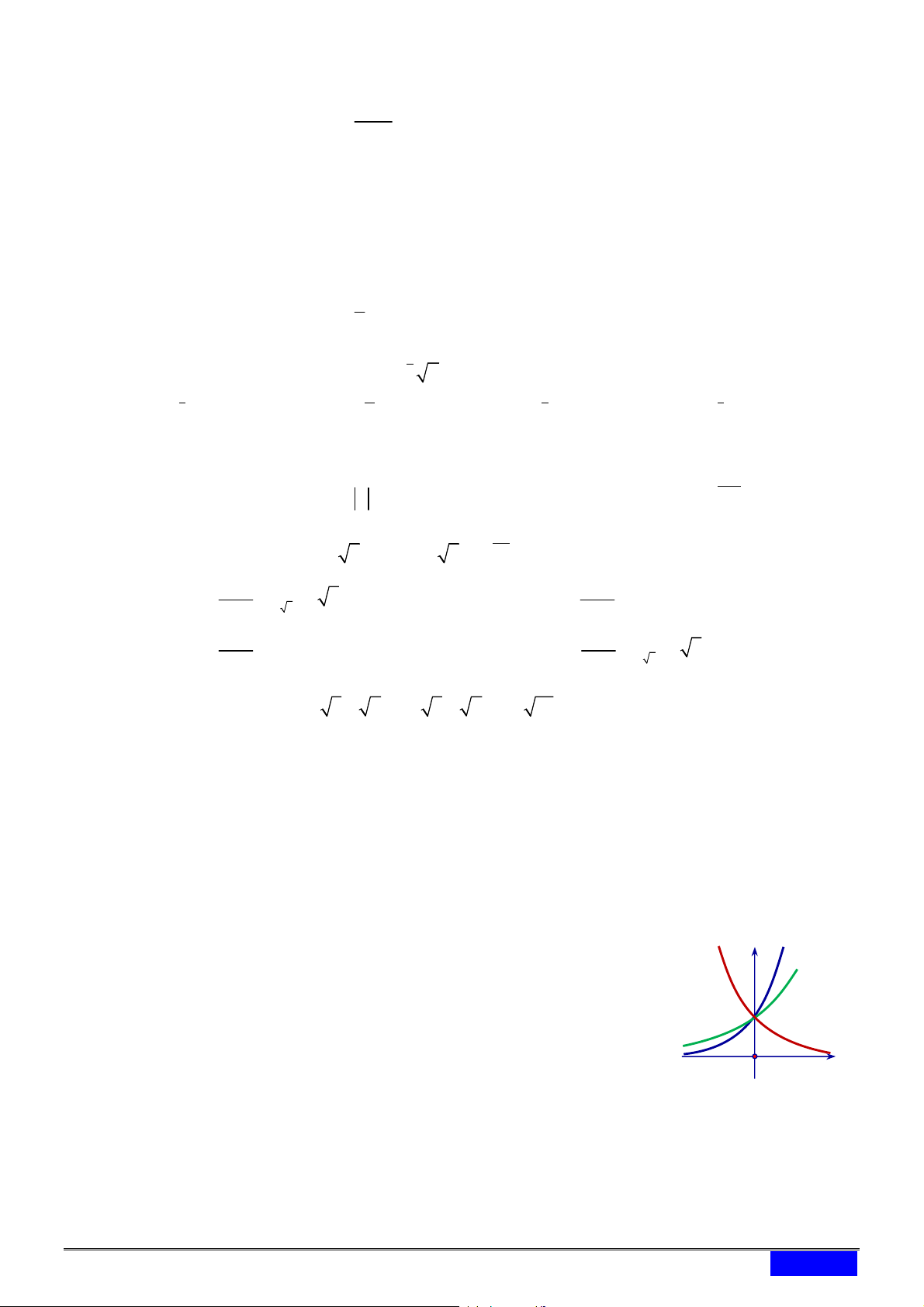
Preview text:

TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 001
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. b aa Câu 1.
[2D2-1] Giả sử a , b là các số thực dương. Biểu thức 5 3
được viết dưới dạng   . Tìm a bb  giá trị . 4 2 2 2 A. . B. . C.  . D. . 15 5 15 15 Câu 2.
[2D2-1] Cho a , b là các số thực dương khác 1. Trong các khẳng định sau, chọn khẳng định đúng. m m  1   1  A. m m
a b a b , . m
B. a b   , m   0     .  a   b m m m m  1   1   1   1 
C. a b   ,m  0     .
D. a b   , m   0     .  a   b   a   b  2 Câu 3.
[2D2-1] Tìm tập xác định của hàm số y   x   3 2 . A.  \   2 . B.  2  ;  . C. 0;  . D.  . Câu 4.
[2D2-2] Cho f x 2 3 2
x . x . Tính giá trị của f   1 . 8 3 A. 2 . B. . C. 4 . D. . 3 8 Câu 5.
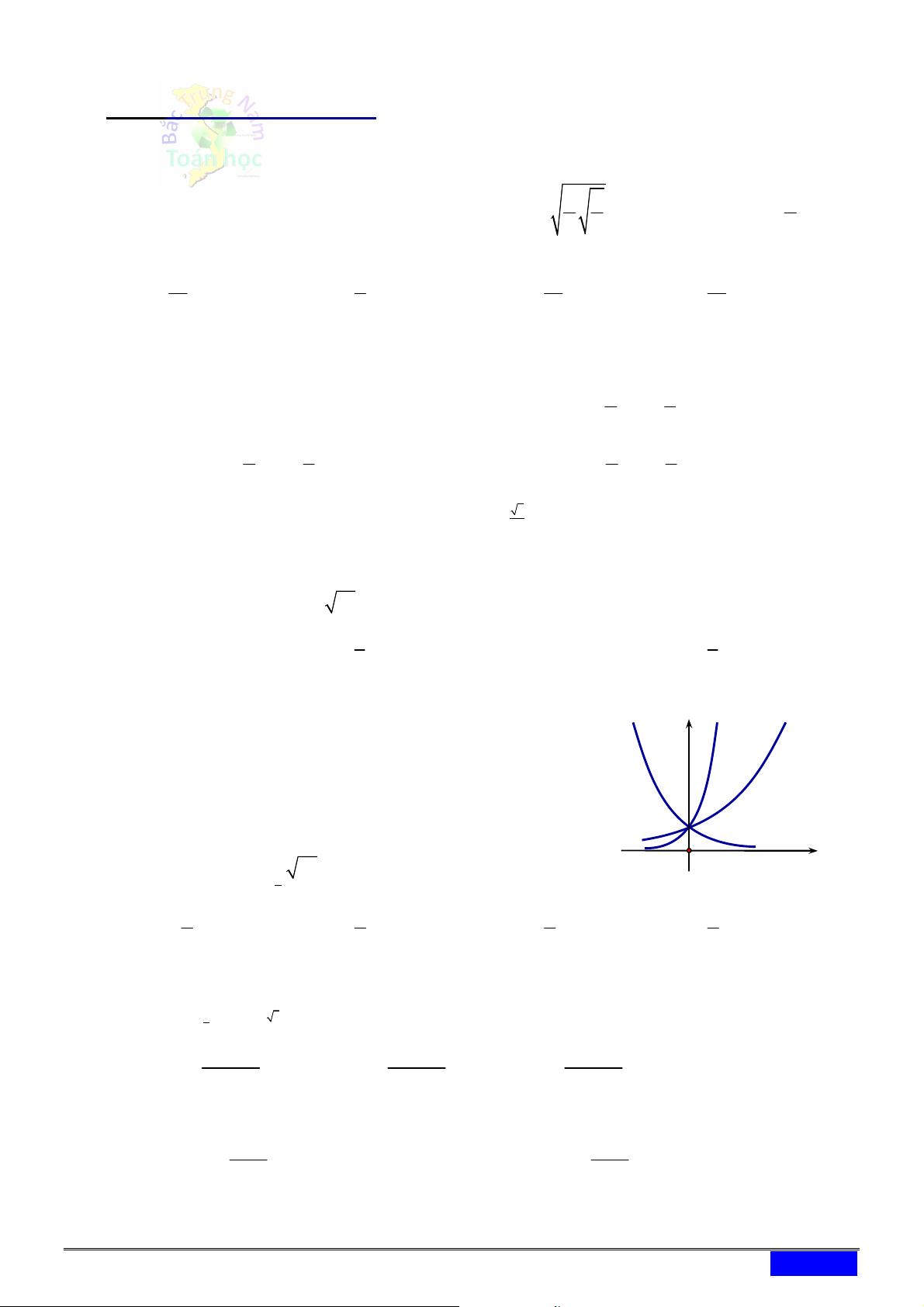
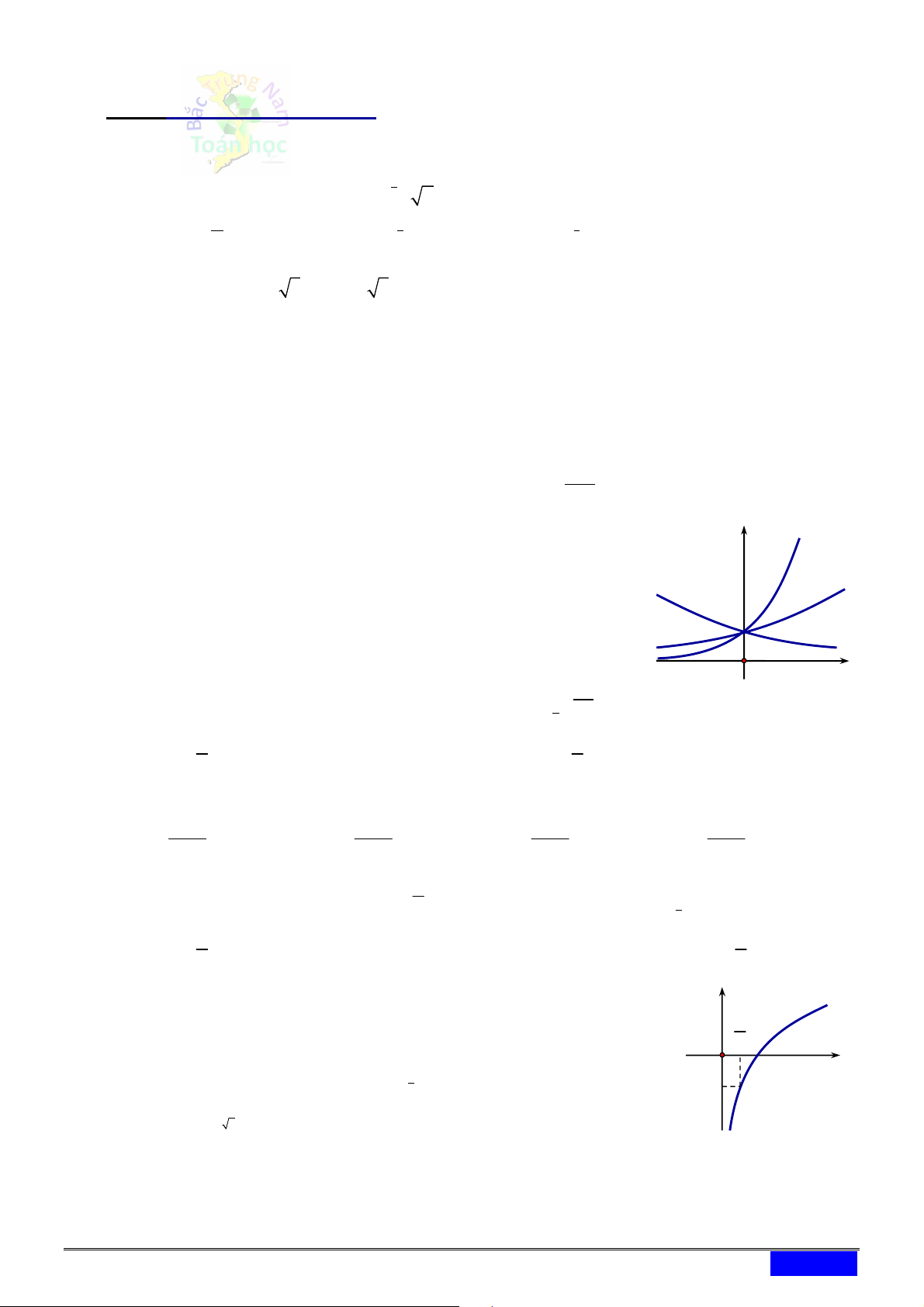
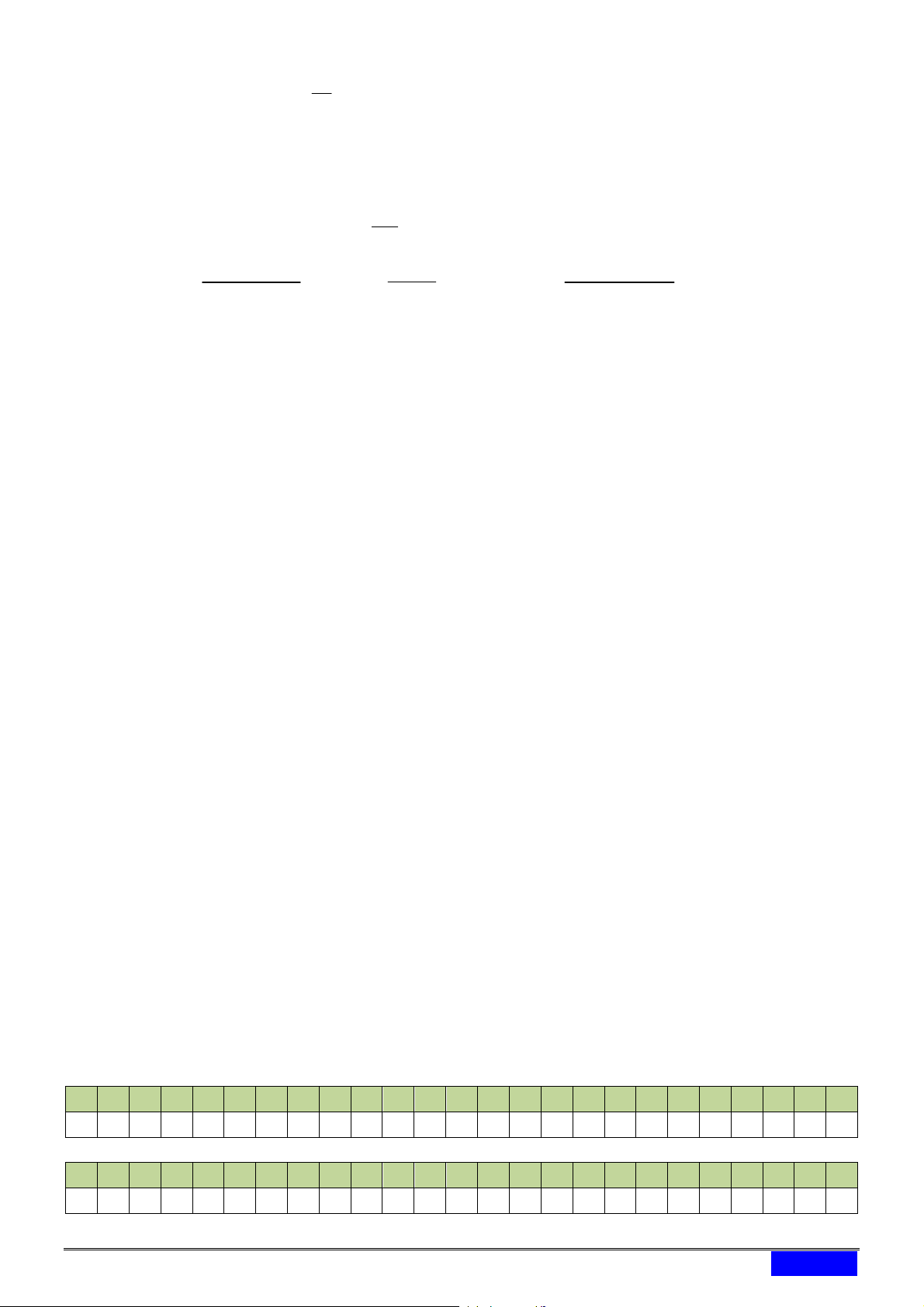
[2D2-2]Cho đồ thị ba hàm số x y a , x y b , x y c x x x
như hình vẽ. Kết luận nào sau đây đúng. y c y y a y b
A. 0  a  1  b c .
B. 0  c  1  a b .
C. 0  c  1  b a .
D. 0  a  1  c b 1 O x Câu 6. [2D2-1] Tính 3 7 log a
a  0, a  1 . 1   a 7 7 3 3 A.  . B. . C.  . D. . 3 3 7 7 Câu 7.
[2D2-2] Cho a là hai số thực dương khác. Đặt log a m . Tính theo m giá trị của biểu thức 3
D  log a  log a  log 9 . 1 3 a 3 2 2  3m 2 3m  2 2 4  3m A. D  . B. D  . C. D  . D. D  3  m . m m 2m Câu 8.
[2D2-2]Cho log 5  a , log 5  b . Hãy biểu diễn log 5 theo a và b . 2 3 6 1 ab A. log 5  . B. log 5  . 6 a b 6 a b
C. log 5  a b . D. 2 2
log 5  a b . 6 6
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 1/69 - Mã đề 2D2 Câu 9. [2D2-3] Biết 2 2
a b ab , a  0 , b  0 . Chọn đẳng thức đúng.
A. 2 ln a b  ln 2  ln a  ln b . B.  2 2
ln a b   ln a  ln b . C.  2 2
lg a b   lg a  lg b .
D. 2 lg a b  lg 3  lg a  lg b . 2 5x
Câu 10. [2D2-3] Cho hàm số f x 
. Khẳng định nào sau đây là khẳng định sai? 2x 2 x
A. f x  1   0 .
B. f x 2
 1  x log 5  x  0 . x log 2 2 5 2  5x
C. f x  1  log    0 .
D. f x 2
 1  x x log 2  0 . 5  2x  5   2x 1
Câu 11. [2D2-1] Tìm tập xác định D của hàm số f x  . log  2  x  3x 2    3   5  
A. D  0;3 .
B. D  0;3 \    2   
C. D   \ 0;  3 .
D. D   .
Câu 12. [2D2-2] Tìm đạo hàm của hàm số     2 2 3 e x y x
 3x trong điều kiện xác định. A.      2 4 4 e x y x  3 . B.      2 4 4 e x y x  3x . C. 2 4.e x y   3 . D.      2 2 1 e x y x  3 .
Câu 13. [2D2-2] Mệnh đề nào sau đây là sai? A. Cho hàm số 2x y  thì y  1  ln 4 . 2
B. Cho hàm số y  log 2x   1 thì y  1  . 3ln10 C. Cho hàm số ex y  thì   1 ex y  .
D. Cho hàm số y  ln x thì y  1  1.
Câu 14. [2D2-3] Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số x
y xe trên 1;2. Tính M .n . A. 3 2e . B. 2 2e . C. e . D. 0 .
Câu 15. [2D2-4] Ông A vay ngân hàng T (triệu đồng) với lãi suất 12 % năm. Ông A thỏa thuận với ngân
hàng cách thức trả nợ như sau: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai
lần hoàn nợ liên tiếp cách nhau đúng một tháng. Nhưng cuối tháng thứ ba kể từ lúc vay ông A
mới hoàn nợ lần thứ nhất, cuối tháng thứ tư ông A hoàn nợ lần thứ hai, cuối tháng thứ năm ông
A hoàn nợ lần thứ ba (hoàn hết nợ). Biết rằng số tiền hoàn nợ lần thứ hai gấp đôi số tiền hoàn
nợ lần thứ nhất và số tiền hoàn nợ lần thứ ba bằng tổng số tiền hoàn nợ của hai lần trước. Tính
số tiền ông A đã hoàn nợ ngân hàng lần thứ nhất.  5  5 T 1 T 1 0, 5 01 T 1 0,  01 T   5 1 0, 01    100  A. . B. . C. . D. .  2 2, 2 01  2 1,  01  5 6 6
Câu 16. [2D2-1] Tìm nghiệm của phương trình x 1 3   27 . A. x  9 .
B. x  3 .C. x  4 . D. x  10 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 2/69 - Mã đề 2D2 2 x 2x3  1 
Câu 17. [2D2-2] Gọi S là tập nghiệm của phương trình x 1  7  .  
Tính tổng tất cả các phần tử  7  của S . A. 5. B. 0. C. 1. D. 2.
Câu 18. [2D2-2] Gọi S là tập nghiệm của phương trình 4x8 2 x5 3  4.3  28  2 log 2 . Tính tích tất cả 2
các phần tử của S . 3 3 A. 4. B.  . C. . D. 1  . 2 2
Câu 19. [2D2-1] Cho phương trình log  2 x  1 .log  2 x 2x 4 2 2 6 log x 1 1        4 log
x  2x  4  0 1 2 2 2 2    
Gọi x , x là hai nghiệm thực dương của phương trình đã cho  x x . Tính 2
T x  2x . 1 2  1 2 1 2
A. T  3  2 5 . B. T  1   3 5 . C. T  7 .
D. T  6 . log  2 xx x 1 0,5 sin 5sin .cos 2
Câu 20. [2D2-4] Tìm nghiệm của phương trình 4  . 9  x   kx   k 2  2 A.
k  . B.  k  1  1 x  arctan  k
x  arctan  k  5  3  x kx k C.   1
k  . D. 1
k  .
x  arctan  k
x  arctan  k  3  5 2 x4 2 x x  1 
Câu 21. [2D2-1] Tìm tập nghiệm của bất phương trình 2 3 1 4    .  2   5  A. 0;  . B.   1 . 4     5  C.  ;
 0 1;  . D.  ;   1  ;    .  4 
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình log x 1  2 . 1   2  3   3   3 
A. S  1;  . B. S  0;    .
C. S  1;    .
D. S   ;    .  4   4   4  2 x x
Câu 23. [2D2-3] Tìm tập nghiệm của bất phương trình  x 1 5 2     5  2 . A.  ;    1  0;  1 . B.  1  ; 0 . C.  ;   
1  0;  . D.  1
 ; 0  1;  .
Câu 24. [2D2-2] Phương trình log x 1  2 log
3x  2  2  0 có mấy nghiệm? 2   4   A. 1. B. 2 . C. 3 . D. 4 .
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên bé hơn 10 của tham số m sao cho bất phương trình 2 2
log x 1 2 log x 1  m  0 thỏa mãn với mọi 3 1  ;2  ? 2 2   A. 3 . B. 4 . C. 5 . D. 6 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 3/69 - Mã đề 2D2
TOÁN HỌC BẮC – TRUNG - NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 002
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 1 Câu 1.
[2D2-1] Rút gọn biểu thức 3 M a
a a  0 . 5 1 6 3 A. 6 M a . B. 6 M a . C. 5 M a . D. 2 M a . 4 1 2   3 3 3 a aa   Câu 2.
[2D2-2] Cho a là số thực dương. Đơn giản biểu thức   P  . 1 3 1    4 4 4 a a a    
A. P a .
B. P a a   1 .
C. P a 1 .
D. P a 1. 2 1 3 3 a b b a Câu 3. [2D2-3] Với ,
a b  0 bất kì. Cho biểu thức P  . Tìm mệnh đề đúng. 6 6 a b A. 3 P ab . B. P ab . C. 6 P ab .
D. P ab . Câu 4.
[2D2-1] Cho a là số thực dương a  1 và 3 P  log
a . Mệnh đề nào dưới đây đúng? 3 a 1 A. P  3 . B. P  1 . C. P  9 . D. P  . 3 Câu 5.
[2D2-1] Giá trị của A  log 3.log 4.log 5...log 64 bằng 2 3 4 63 A. 5 . B. 4 . C. 6 . D. 3 . Câu 6.
[2D2-2] Với các số thực dương a , b bất kì. Khẳng định nào sau đây là khẳng định đúng?  a
A. log ab  log a b . B. log  log a   . b    b   a
C. log ab  log a  log b . D. log  log   a b .  b Câu 7.
[2D2-2] Cho log a x và log c y . Hãy biểu diễn 3 5 4 log b c
theo x và y : 2 a   b b 5  4 y 20 y 4 5  3y 20 y A. . B. . C. . D. 20x  . 6x 3x 2 3x 3 Câu 8.
[2D2-3] Cho log 7  a, log 5  b . Tính log 28 theo , a b 14 14 35 2  a 2 2  a a A. log 28  . B. log 28  . C. log 28  . D. log 28  . 35 a b 35 a b 35 a b 35 a b Câu 9.
[2D2-1] Tìm tập xác định D của hàm số 1 x y   . A. D   .
B. D  1;  .
C. D  1;  .
D. D  ;  1 .
Câu 10. [2D2-1] Tìm tập xác định D của hàm số y  log 2x  1 . 3    1   1   1 
A. D  ;    . B. D  ;     .
C. D  0;   .
D. D   ;     .  2   2   2 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 4/69 - Mã đề 2D2 log 2x
Câu 11. [2D2-2] Tìm đạo hàm của hàm số y  . 2 x 1 4 ln 2x 1 1 2 ln 2x 1 2 log 2x A. y  . B. y  . C. y  . D. y  . 3 2x ln10 2 2x ln10 3 x ln10 3 x
Câu 12. [2D2-1] Đạo hàm của hàm số 3 e x y  là A. 3 e x y  . B. 3 1 3 e x y x    . C. 3   3 e x y x . D. 3 3e x y  .
Câu 13. [2D2-1] Tìm giá trị nhỏ nhất của hàm số y  ln x trên 1;e
A. Không xác định được giá trị nhỏ nhất.
B. min y  1 khi x  1 .
C. min y  e , khi x  e .
D. min y  0 , khi x  1 . x  1 
Câu 14. [2D2-1] Tìm giá trị nhỏ nhất của hàm số y    trên  1  ; 0  2  1
A. min y  1, khi x  0 . B. min y  khi x  1  . 2 1 
C. min y  2 , khi x  1  . D. min y  , khi x  1  . 2
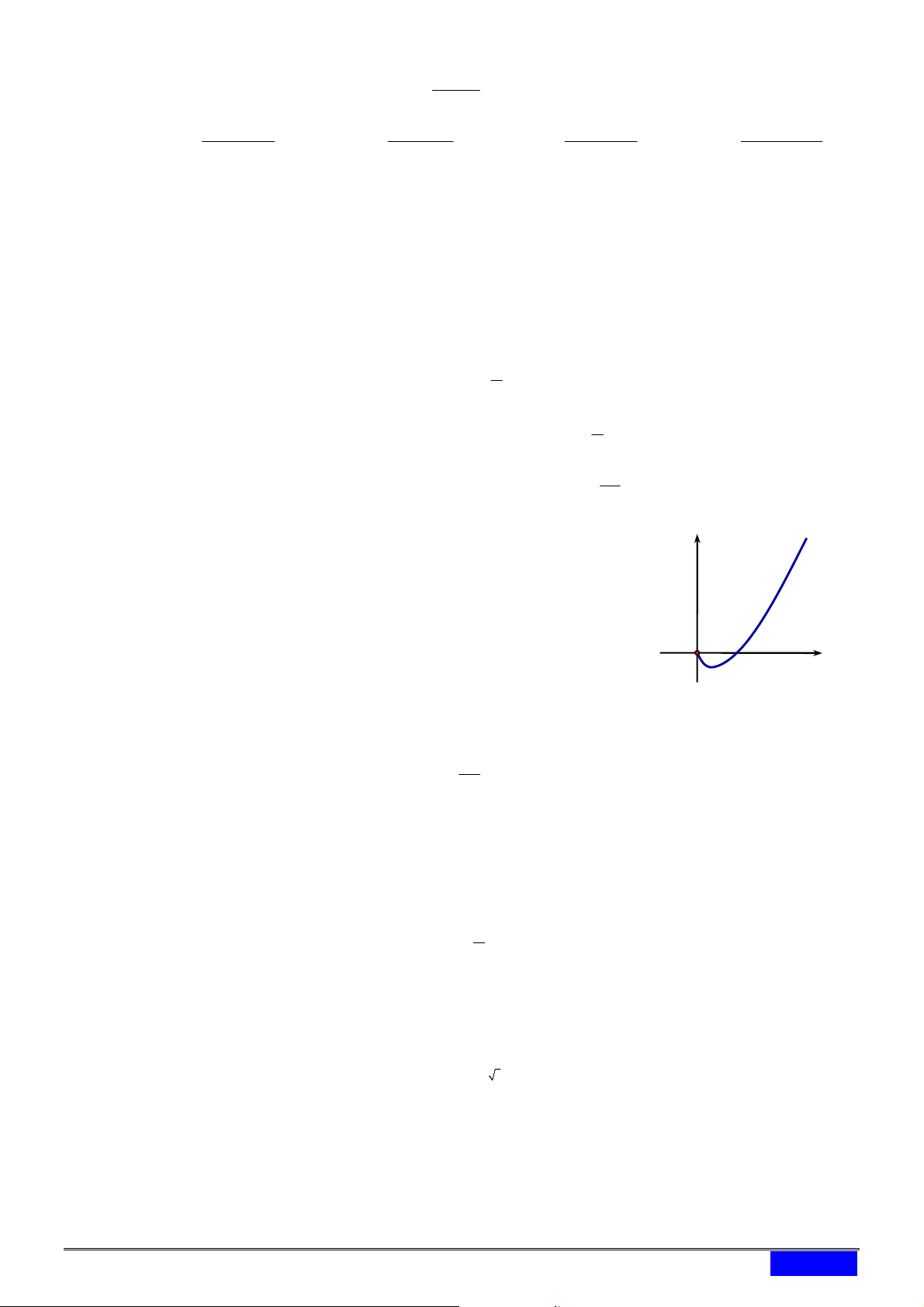
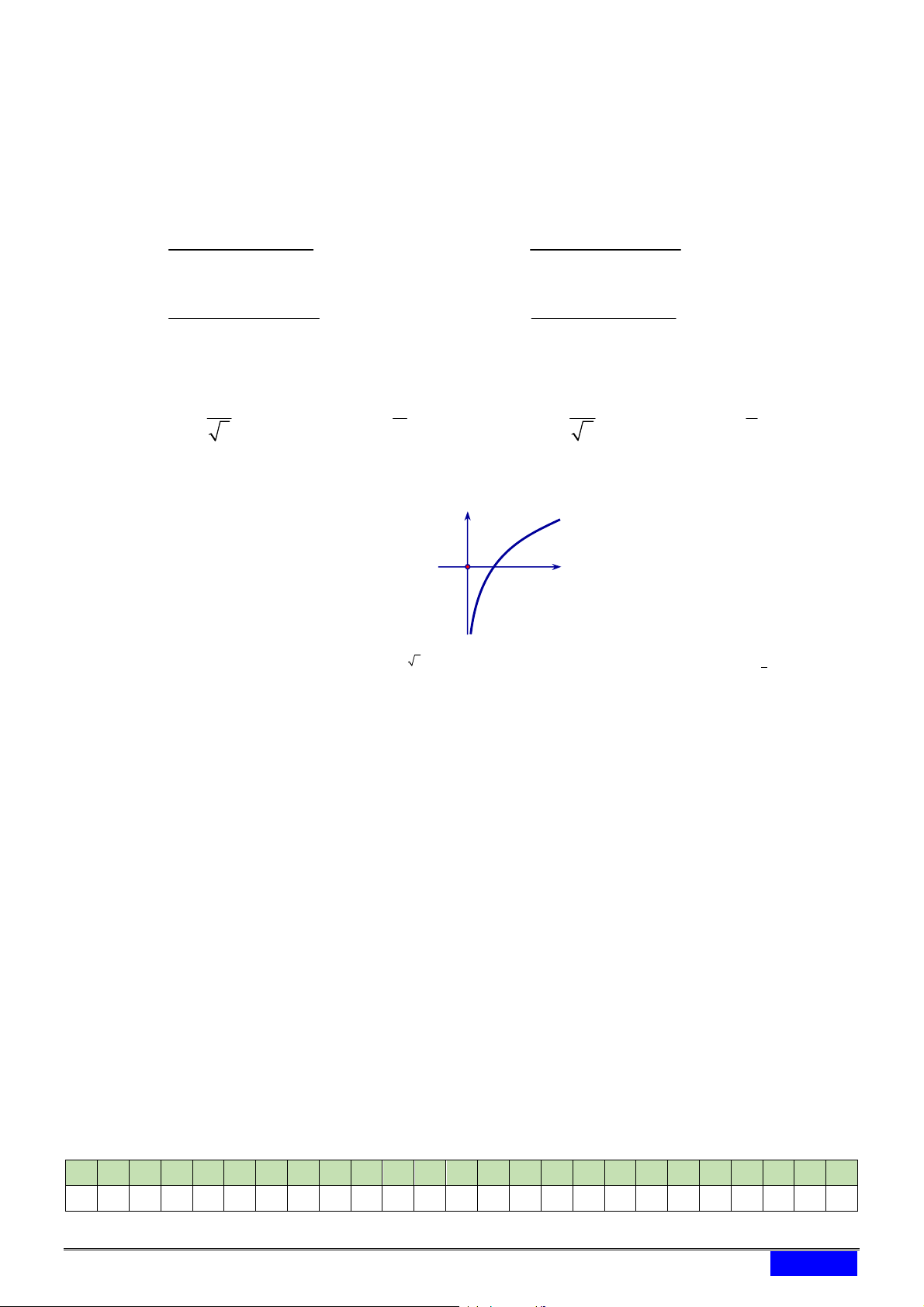
Câu 15. [2D2-1] Hình vẽ sau đây là đồ thị của hàm số nào? y
A. y x ln x .
B. y  ln x . C. ex y  . D.  ex y x . O x 1
Câu 16. [2D2-2] Cho hàm số 2
y x ln x , khẳng định nào sau đây là đúng
A. y  x 3  y  0 .
B. y  x 2  y  0 . C. y  x 2  y  0 . D. y  x 3  y  0 . x 1
Câu 17. [2D2-2] Nghiệm của phương trình 2 1 3  là 27 A. x  2 . B. x  2  . C. x  1 . D. x  1  .
Câu 18. [2D2-2] Nghiệm của phương trình log  x   1  log  2 x  3x  2 2 2 
A. x  1; x  3 . B. x  3  .
C. x  1; x  3 . D. x  3 . 2 x 3x 1   1 
Câu 19. [2D2-2] Tập nghiệm của bất phương trình  2   .  2 
A. T   ;   1  2;  .
B. T   ;   1  2;  .
C. T  1; 2 .
D. T  1; 2 .
Câu 20. [2D2-2] Tập nghiệm của bất phương trình log  2
2x  4x  5  2 . 3  A. T   .
B. T   \   1 .
C. T   \   1 . D. T   .
Câu 21. [2D2-3] Bác Hiếu đầu tư 99 triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8, 25% một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi). A. 48,155 triệu. B. 147,155 triệu. C. 58, 004 triệu. D. 8, 7 triệu.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 5/69 - Mã đề 2D2 x2
Câu 22. [2D2-3] Giá trị m để phương trình x 2 5  . m 5
 3  m  0 có 2 nghiệm phân biệt sao cho
x x  2 là 1 2 A. 2  . B. 2 . C. 3 . D. 4 . 1 x
Câu 23. [2D2-3] Có bao nhiêu số nguyên thỏa mãnbất phương trình xx 2 2.3  9  9x ? A. 3. B. 4. C. 5. D. 6. 3 x x 1 
Câu 24. [2D2-2] Số nghiệm nguyên của bất phương trình    x 1    x3 10 3 10 3 trong khoảng  2  018; 2018 là A. 4033 . B. 4032 . C. 4031 . D. 4030 . 15 Câu 25. [2D2-4] Biết x  là một nghiệm của bất phương trình 2  x    x x
. Tập nghiệm T của bất phương trình * là a  2 2 log 23 23 log 2 15 * a   19   17  A. T   ;    . B. T  1;   .
C. T  2;8 .
D. T  2;9 .  2   2 
-----------HẾT---------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 6/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 003
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 2 2 Câu 1.
[2D2-1] Cho góc , giá trị của biểu thức sin cos 5 .5 bằng 2 2 A. 1. B. 5 . C. 25 . D. sin .cos 5 . Câu 2.
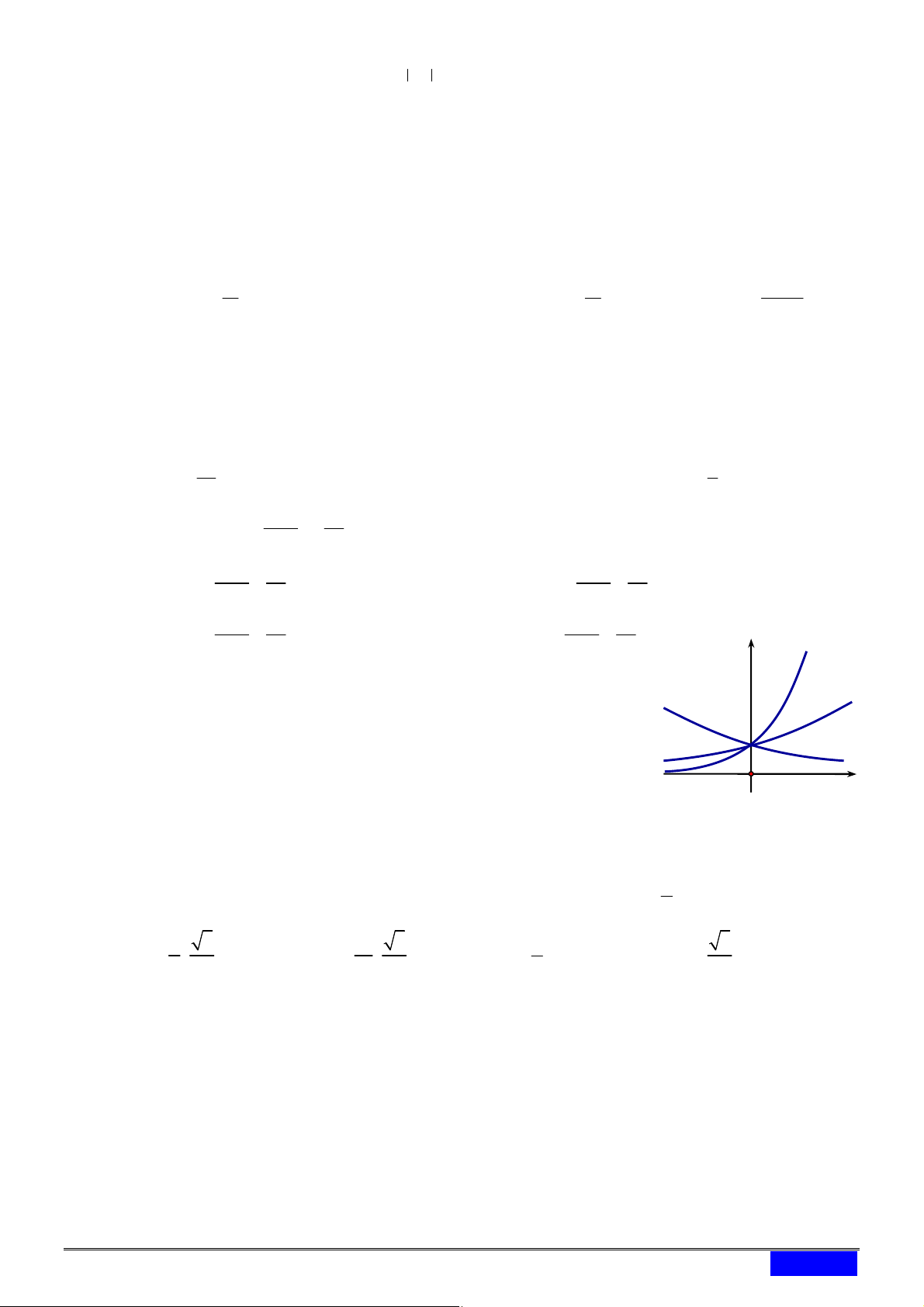
[2D2-2] Cho a , b là các số thực dương khác 1. Hình yC1
vẽ bên là đồ thị của 2 hàm số  : x C y a , 1  C2   : x C
y b . Mệnh đề nào sau đây là đúng? 2  1
A. b a  1 .
B. a b  1 .
C. a b  1.
D. b a  1. O xCâu 3.
[2D2-1] Tìm tập xác định D của hàm số y   x x   2 2 2 . A. D   .
B. D   \  1  ;  2 .
C. D   ;    1  2;  .
D. D  0;   . 13x Câu 4.
[2D2-2] Tính đạo hàm của hàm số y  . x
13x x ln13   1 A. 1 13x y    . B. y  . 2 x 13x 1 13x ln13   1 C. y  . D. y  . x . x ln13 2 x Câu 5.
[2D2-2] Cho hàm số y  ln x
1. Khẳng định nào sau đây là đúng. 2
A. Hàm số đồng biến trên khoảng 0;   .
B. Hàm số đạt cực tiểu tại x  1 .
C. Hàm số nghịch biến trên khoảng 0;  1 .
D. Hàm số đạt cực đại tại x  1 . Câu 6.
[2D2-1] Cho a  0 , a  1 và x , y là hai số dương. Mệnh đề nào sau đây là đúng?
A. log  x y  log x  log y . B. log x y x y . a   log .log a a a a a C. log  .
x y   log x  log y . D. log x y x y . a  .  log .log a a a a a 3 4 5 123 124 Câu 7.
[2D2-2] Đặt a  ln 3 , b  ln 5 . Tính S  ln  ln  ln  ...  ln  ln
theo a và b . 4 5 6 124 125
A. I a  2b .
B. I a  3b .
C. I a  2b .
D. I a  3b . Câu 8.
[2D2-2] Biết sin x  0 , cos x  0 và log sin x  log cos x  1  . Giá trị của 3   3   log
sin x  cos x bằng 3   1 1 A. 1  . B. . C. log 5 1 . D. log 5 1. 3  3 2 3 b b Câu 9.
[2D2-3] Cho a  0 , b  0 , c  0 là các số thực khác 0 thỏa 5a 15b 45c   . Tính T   . a c
A. T  log 5 . B. T  3. C. T  2 .
D. T  log 45 . 15 5
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 7/69 - Mã đề 2D2 1  2x
Câu 10. [2D2-3] Cho hàm số f x  log . 2   2  1 x   1   2   3   2015   2016 
Tính tổng: S fff  ...  ff           .  2017   2017   2017   2017   2017  A. 2017 . B. 2016 . C. 4032 . D. 1008 .
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y  log  3
x  3x  2 . 0,5  A.  2  ;   . B. 0;  1 . C. 1;  . D.  2  ;   \   1 . x y  1  C4 
C1 C2 
Câu 12. [2D2-2] Cho bốn hàm số y x     1 , y  3 2 ,  2  x  1  y x
  3 , y  4  4 và bốn đường cong C , 1  C3   2  1
C , C , C như hình vẽ bên. Đồ thị hàm số 4  3  2   
1 , 2 , 3 , 4 lần lượt là O x
A. C , C , C , C .
B. C , C , C , C . 3   2   4   1  1   2   3   4 
C. C , C , C , C .
D. C , C , C , C . 4   1   3   2  2   4   1   3 
Câu 13. [2D2-2] Tìm tất cả giá trị thực của tham số m để hàm số y   2
ln x  2mx m có tập xác định là  .
A. m  0 hoặc m  1.
B. 0  m  1 .
C. m  0 hoặc m  1.
D. 0  m  1 .
Câu 14. [2D2-3] Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có diện tích bằng 36 , đường
thẳng AB song song với trục Ox , các đỉnh A , B và C lần lượt nằm trên đồ thị của các hàm
số y  log x , y  log x , y  log
x và a là một số thực lớn hơn 1. Tìm a . a a 3 a A. a  3 . B. 3 a  6 . C. a  6 . D. 6 a  3 . 2a 4b  8
Câu 15. [2D2-4] Cho a , b là hai số thực dương thỏa mãn 
. Tính giá trị của biểu 2a  2b a  4b  8 2017a thức P  . 2017b A. 1. B. 2 2017 . C. 2017a . D. 2017b . x 1  2x  2   3 
Câu 16. [2D2-1] Tập nghiệm S của phương trình      là  3   2   1  A. S    1 .
B. S    .  3
C. S    1 . D. S    2 .
Câu 17. [2D2-2] Tìm tọa độ giao điểm của đồ thị hàm số 3 x y  
 2 và đường thẳng y  5 . A.  1  ;5 . B. 1;5 . C. 2;5 . D.  2  ;5 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 8/69 - Mã đề 2D2
Câu 18. [2D2-2] Biết rằng phương trình 2018 x log 9 8 3  2
 0 có nghiệm duy nhất x x . Khẳng định nào 0 sau đây là đúng?
A. x là số nguyên tố.
B. x là số chính phương. 0 0
C. x chia hết cho 3 .
D. x là một số chẵn. 0 0
Câu 19. [2D2-3] Tính tổng T tất cả các nghiệm của phương trình
x2   x   x2 3.25 3 10 .5  3  x  0 .  2 
A. T  4  log .
B. T  3  log 2 .
C. T  4  log 3 .
D. T  2  log 6 . 5   5 5 5  7 
Câu 20. [2D2-4] Tính tổng T tất cả các giá trị của tham số m để phương trình  x 2 1 2 log  2
x  2x  3  4 xm log
2 x m  2 có đúng ba nghiệm phân biệt. 2  2   A. T  1. B. T  2 . C. T  3. D. T  4 . x 1
Câu 21. [2D2-1] Tập nghiệm của bất phương trình 1 3  là 9 A.  3  ;    . B. 1;  . C.  ;    1 . D.  1  ;3 .
Câu 22. [2D2-2] Tập nghiệm của bất phương trình log x 1  2 là 0,5    5   5   5  A.  ;    . B. ;     . C. 1;   . D. 1;3 .  4   4   4  2 x3 2 x  1 
Câu 23. [2D2-2] Gọi S là tập nghiệm của bất phương trình 0, 25   
. Khi đó S có dạng  4 
a;b với a b . Tính P a b . A. 2 . B. 2  . C. 1. D. 0 .
Câu 24. [2D2-2] Có bao nhiêu số nguyên x thỏa mãn bất phương trình log  x  40  log 60  x  2 . A. 20 . B. 18 . C. 21 . D. 19 .
Câu 25. [2D2-4] Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  2  018; 2018 để bất 2 2
phương trình 1 4x     1 4 9 20 .3  x m
 2m  5  0 có tập nghiệm  2  ; 2 . A. 2057 . B. 2060 . C. 2058 . D. 2056 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 9/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 004
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. Câu 1. [2D2-1] Cho
. Kết luận nào sau đây là đúng?
A.  0 .
B. . 1.
C. .
D. . Câu 2.
[2D2-2] Cho biểu thức 3 2 5 3 P x
x x . Mệnh đề nào dưới đây đúng. 14 17 13 16 A. 15 P x . B. 36 P x . C. 15 P x . D. 15 P x .  Câu 3.
[2D2-1] Tìm tập xác định D của hàm số y   x   2 2 3 1  1   1 
A. D   \   . B. D    .  3   3   1   1   1 1  C. ;   ;      . D. D   ;   .  3   3   3 3  Câu 4.
[2D2-2] Đường cong ở hình bên là đồ thị của một hàm số trong y
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào? 1 A. 2
y   x  2x  1. B. y  log x . 0,5 1 O x C. y  . D. 2x y  . 2x 1 Câu 5.
[2D2-1] Hàm số y   x  3 1 có đạo hàm là 1 1  x  2 3 1  x  3 1 A. y  . B. y  . C. y  . D. y  . 3  x  2 3 1 3  x  3 1 3 3 Câu 6.
[2D2-2] Cho a  log 3 và b  log 5 . Tính log 1350 theo a và b . 30 30 30
A. 1 2a b B. 1 2a  . b
C. 1 2a b D. 1
  2a b Câu 7.
[2D2-2] Nếu log x  5 log a  4 log b, (a,b  0) thì x bằng 2 2 2 A. 5 4 a b . B. 4 5 a b . C. 5a  4 . b D. 4a  5 . b 2 3 2 5 4 a . a . . a a Câu 8.
[2D2-2] Cho A  log
với a  0; a  1 . Giá trị A bằng a 3 a 16 67 22 62 A. B. C. D. 5 5 5 15 x y x Câu 9.
[2D2-3] Cho x , y là các số thực dương thỏa mãn log x  log y  log . Tính tỉ số . 9 6 4 6 y x x x x A.  3 . B.  5 . C.  2 . D.  4 . y y y y
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 10/69 - Mã đề 2D2
Câu 10. [2D2-3] Cho các số thực dương khác 1 là a , b , c . Rút gọn 2 log b.log c .log a ta được 2 a 2 b c m m ,  ,
m n N  , với
là phân số tối giản. Chọn khẳng định đúng. n 2 n
A. m  2n
B. m  2n  0
C. m  2n  0 D. 2 n  4m  0
Câu 11. [2D2-1] Đồ thị sau là của hàm số nào sau đây? y
A. y  log x . B. y  log 2x . 2   3
C. y  2 log x .
D. y  log x . O 1 x 3 5
Câu 12. [2D2-2] Hàm số y   2
ln x  2mx  4 có tập xác định D   khi:  m  2 A. m  2 . B.  . C. m  2 . D. 2   m  2 . m  2   2 ln x m
Câu 13. [2D2-3] Biết rằng giá trị lớn nhất của hàm số y  trên đoạn 3 1  ; e  M  trong đó x   là en
M , n là các số tự nhiên. Tính 2 3
S m  2n . A. S  22. B. S  24. C. S  32. D. S  135.
Câu 14. [2D2-1] Cho f x  x ln x . Đạo hàm cấp hai f e bằng: 1 A. 2. B. . C. 3. D. e . e ln x
Câu 15. [2D2-2] Đồ thị hàm số y
có tọa độ điểm cực đại là a;b . Khi đó ab bằng x A. e . B. 2e . C. 1  D. 1
Câu 16. [2D2-1] Tìm các nghiệm của phương trình x 1 3   27. A. x  9. B. x  3. C. x  4. D. x  10.
Câu 17. [2D2-1] Phương trình log  2
x  4x 12  2 . Chọn phương án đúng? 3 
A. Có hai nghiệm cùng dương.
B. Có hai nghiệm trái dấu.
C. Có hai nghiệm cùng âm. D. Vô nghiệm.
Câu 18. [2D2-2] Cho phương trình log
4.5x  2  x 1 có hai nghiệm là x , x . Tổng x x bằng 25   1 2 1 2 A. 50. B. log 100 C. 30. D. log 50. 5 5 x x
Câu 19. [2D2-2] Bất phương trình        2 2 3 2 3 có tập nghiệm là A.  1  ; . B.  ;    1 . C. (2; ). D. ( ;  2  ).
Câu 20. [2D2-2] Tập nghiệm của bất phương trình log
x  3 1  0 có dạng a;b . Khi đó giá trị 1   3
a  3b bằng 37 A. 15 . B. 13 . C. . D. 30 . 3
Câu 21. [2D2-2] Tìm số nghiệm nguyên của bất phương trình: log x 1  3 . 3   A. 7 . B. 26 . C. 15 . D. 27 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 11/69 - Mã đề 2D2
Câu 22. [2D2-2] Anh Nam vay tiền ngân hàng 1 tỷ đồng theo phương thức trả góp (chịu lãi số tiền chưa
trả) với lãi suất 0,5% /tháng. Nếu cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả 30
triệu đồng. Hỏi sau bao nhiêu tháng anh Nam trả hết nợ? A. 35 tháng. B. 36 tháng. C. 37 tháng. D. 38 tháng. Câu 23. [2D2-3] Tìm tất cả các giá trị của tham số m để phương trình 2
log x m  2 log x  3m 1  0 có 2 nghiệm x , x sao cho x x  27 . 3   3 1 2 1 2 4 28 A. m  . B. m  25 . C. m  . D. m  1. 3 3
Câu 24. [2D2-4] Tìm tập hợp các giá trị của tham số thực m để phương trình 6x  3   2x mm  0 có
nghiệm thuộc khoảng 0;  1 . A. 3; 4 . B. 2; 4 . C. 2; 4 . D. 3; 4 . 2 2  b
Câu 25. [2D2-4] Tìm giá trị nhỏ nhất của biểu thức P   2 log b   6 log
 với a , b là các số a ba   a
thực thay đổi thỏa mãn b a  1. A. 30. B. 40. C. 50. D. 60.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 12/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 005
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. Câu 1. [2D2-1] Tính: 3 2 1 2 4 2 K  4 .2 : 2 , ta được A. 5 . B. 6 . C. 7 . D. 8 . 3 5 Câu 2.
[2D1-2] Với biểu thức  a  4   a  6 2 1 2 1
. Khi đó cơ số a phải thỏa điều kiện 1 A. a  1 .
B. 0  a  1. C. a  1. D. a  1 . 2  Câu 3.
[2D2-1] Hàm số y =  x   4 2 4 1 có tập xác định là  1 1   1 1  A.  . B. 0;  .
C.  \  ;  . D.  ;   .  2 2   2 2  e Câu 4.
[2D2-2] Tìm đạo hàm của hàm số y   2 x  2 1 trên  . e 1  
A. y  x  2 x  2 2 1 .
B. y  x x  e 2 2 e 1 . e e 1 e  C. y   2 x  2 1 .
D. y   2 x    2 2 1 ln x   1 . 2 e Câu 5.
[2D2-2] Tìm điểm cực trị của hàm số y   2 x  2 1 trên  . A. x  1  . B. x  0 . C. x  1 . D. x  2 . Câu 6.
[2D2-1] Giá trị của biểu thức log2 3 A  4 bằng A. 6 . B. 2 . C. 12 . D. 9 . 27 Câu 7.
[2D2-2] Biết log 3  a , khi đó giá trị của log
được tính theo a là 5 3 25 3a  2 3a 3 a A. . B. . C. . D. . a 2 2a 3a  2 Câu 8.
[2D2-2] Nếu a  log 3 và b  log 5 thì 30 30
A. log 1350  2a b  2.
B. log 1350  a  2b  1. 30 30
C. log 1350  2a b  1.
D. log 1350  a  2b  2. 30 30 Câu 9.
[2D2-3] Giả sử ta có hệ thức 2 2
a b  7ab a,b  0. Hệ thức nào sau đây là đúng? a b a b A. 4 log
 log a  log b . B. log
 2 log a  log b . 2  2 2  2 2 2 6 3 a b C. 2 log
a b  log a  log b . D. 2 log
 log a  log b . 2   2 2 2 2 2 3
Câu 10. [2D2-3] Tìm tất cả các giá trị thực của tham số m để bất phương trình sau có nghiệm m log 3  x x x 12 . 3 4 x   A. m  2 3 . B. m  0 .
C. 2 3  m  12 log 5 .
D. m  12 log 5 . 3 3
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y   2
log x  6x  5 .
A. D   ;   1  5;  .
B. D  1;5 .
C. D   ;   1  5;  .
D. D  1;5 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 13/69 - Mã đề 2D2
Câu 12. [2D2-2] Hàm số y =  2  2  2ex x x có đạo hàm là A. 2   ex y x . B.    2   4  4ex y x x .
C.   2 ex y x .
D.   2  2 ex y x . x  2
Câu 13. [2D2-3.2-2] Tính đạo hàm của hàm số y
tại điểm x  2 . 9x 1 1 1 1
A. y2  .
B. y2  .
C. y2  .
D. y2  . 3 5 9 2 9 2 x 3x
Câu 14. [2D2-3] Hàm số x 1 y e  
có giá trị lớn nhất trên đoạn 0;3 là: A. 2 e . B. 1. C. e . D. 3 e .
Câu 15. [2D2-4] Bạn Hùng trúng tuyển vào trường đại học A nhưng vì do không đủ nộp học phí nên
Hùng quyết định vay ngân hàng trong 4 năm mỗi năm vay 3.000.000 đồng để nộp học phí với
lãi suất 3% /năm. Sau khi tốt nghiệp đại học bạn Hùng phải trả góp hàng tháng số tiền T
(không đổi) cùng với lãi suất 0, 25% /tháng trong vòng 5 năm. Số tiền T hàng tháng mà bạn
Hùng phải trả cho ngân hàng (làm tròn đến kết quả hàng đơn vị) là: A. 309604 đồng. B. 232518 đồng. C. 232289 đồng. D. 215456 đồng. x 1
Câu 16. [2D2-1] Nghiệm của phương trình 2 1 2   0 là. 8 A. x  2 . B. x  2  . C. x  1 . D. x  1  .
Câu 17. [2D2-2] Tìm tập nghiệm S của phương trình log  2
x 10x  23  log x  5  0 . 0,5  2   A. S    7 .
B. S  2;  9 . C. S    9 .
D. S  4;  7 . x x
Câu 18. [2D2-2] Tìm tích các nghiệm của phương trình  2   1   2   1  2 2  0 . A. 0 . B. 2 . C. 1. D. 1  .
Câu 19. [2D2-3] Phương trình 3 log x  log 3x 1  0 có tổng các nghiệm bằng 3 3 A. 81. B. 3 . C. 78 . D. 84 . 2
Câu 20. [2D2-4] Tổng các nghiệm của phương trình  x   x x  2
x     x 1  2 1 .2 2 1 4 2  x  bằng A. 3 . B. 5 . C. 4 . D. 2 . 2x 1  2 x  4   4 
Câu 21. [2D2-1] Tập nghiệm của bất phương trình      là  5   5  A.  . B.  ;   1 . C. 3; . D. 1; .
Câu 22. [2D2-1] Tìm tập nghiệm của bất phương trình log  2
x  3x  2  1.  1  2 A. 0; 2 . B.  ;   1 . C. 0;  1  2;  3 .
D. 0; 2  3;7 . 2 x 3x 1  0 x2  1   1 
Câu 23. [2D2-2] Tìm số nghiệm nguyên của bất phương trình      .  3   3  A. 0 . B. 1. C. 9 . D. 11.
Câu 24. [2D2-2] Bất phương trình log x  log x  1 có nghiệm là 2 3 A. log log 6 log 2 2 6 x  3 . B. 3 x  2 . C. x  6 . D. 6 x  3 . 2 2 2
Câu 25. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số m để bất phương trình sin x cos x cos 4  5  .7 x m có nghiệm. 6 6 6 6 A. m  . B. m  . C. m   . D. m   . 7 7 7 7
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 14/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 006
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. Câu 1.
[2D2-1] Viết biểu thức a a a  0 về dạng lũy thừa của a là 5 1 3 1 A. 4 a . B. 4 a . C. 4 a . D. 2 a . Câu 2.
[2D2-2] Trong các khẳng định sau đây, khẳng định nào sai?  2  2  2  2 A. 0, 0  1  10 . B. 0, 0  1  10 . 2  2 C. 0,  1  10 . D. 0 a  1, a   0 . Câu 3.
[2D2-1] Tập xác định của hàm số 2017 y  (2x 1) là  1   1  1  A. D   . B. D  ;    . C. D  ;     . D. D  \    2   2   2  1 Câu 4.
[2D2-2] Hàm số y   x  3 1 có đạo hàm là 1 1  x  2 3 1  x  3 1 A. y  . B. y  . C. y  . D. y  3  x  2 3 1 3  x  3 1 3 3 ln x Câu 5.
[2D2-2] Đồ thị hàm số y
có tọa độ điểm cực đại là a;b . Khi đó ab bằng x A. e . B. 2e . C. 1. D. 1  . log 4 Câu 6.
[2D2-1] Cho a  0 , a  1, giá trị của biểu thức a a bằng bao nhiêu? A. 16 . B. 4 . C. 8 . D. 2 . Câu 7.
[2D2-2] Cho log 6  a . Khi đó giá trị của log 18 được tính theo a là 2 3 a 2a 1 A. a . B. . C. 2a  3 . D. . a 1 a 1 Câu 8.
[2D2-2] Cho log 5  a , log 5  b . Khi đó log 5 tính theo a và b là 2 3 6 1 ab A. . B. .
C. a b . D. 2 2 a b . a b a b Câu 9. [2D2-3] Cho , a b  0 và 2 2
a b  7ab . Khẳng định nào sau đây là khẳng định đúng?  a b
A. 2 log a b  log a  log b . B. 4 log
 log a  log b   .  6   a b  1  a b C. log   
log a  logb . D. log  3  
log a  log b .  3  2  3 
Câu 10. [2D2-3] Cho hàm số   2 2 x sin 2 .3 x f x
. Khẳng định nào sau đây là khẳng định đúng?
A. f x 2
 1  x ln 4  sin x ln 3  0 .
B. f x  1  2x  2sin x log 3  0 . 2
C. f x 2
 1  x log 2  sin x  0 .
D. f x 2
 1  2  x log 3  0 . 3 2
Câu 11. [2D2-1] Với giá trị nào của x thì biểu thức: f x  log  2 2x x xác định? 6 
A. 0  x  2 . B. x  2 . C. 1   x  1. D. x  3 .
Câu 12. [2D2-2] Đạo hàm của hàm số 2 4 x y  là A. 2 2.4 x y  ln 4 . B. 2 4 x y  .ln 2 . C. 2 4 x y  ln 4 . D. 2 2.4 x y  ln 2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 15/69 - Mã đề 2D2
Câu 13. [2D2-2] Cho hàm số f x  log  2
x  2x . Tập nghiệm S của phương trình f  x  0 là 3  A. S    1 .
B. S  1 2 .
C. S  0;  2 .
D. S    1 .  1 
Câu 14. [2D2-3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số x 2
y  2xe  2x x trên đoạn  ; 2  là 2    max y  4e  8 max y  0 2 max y  4e  8 2 max y  4e  8  1   1   ;2   1  1    ;2         2   ;2  ;2  2         A.   2   2   . B.  .C.  . D.  . min y  0 1 5  min y    min y  0  min y  0   1   1  1    ;2    1    e 4  ;2  ;2 2    ;2         2   2 2     
Câu 15. [2D2-4] Bạn Duy Anh trúng tuyển vào đại học nhung vì không đủ nộp tiền học phí Duy Anh
quyết định vay ngân hàng trong 4 năm mỗi năm 3.000.000 đồng để nộp học với lãi suất
3% /năm. Sau khi tốt nghiệp đại học Duy Anh phải trả góp hàng tháng số tiền T (không đổi)
cùng với lãi suất 0, 25% /tháng trong vòng 5 năm. Số tiền T mà Duy Anh phải trả cho ngân
hàng (làm tròn đến hàng đơn vị) là A. 232518 đồng. B. 309604 đồng. C. 215456 đồng. D. 232289 đồng. 2
Câu 16. [2D2-1] Số nghiệm của phương trình 2x 7x5 2  1 là A. 2 . B. 0 . C. 3 . D. 1.
Câu 17. [2D2-2] Phương trình log  2
x  2x  3  2 log
x 1 có nghiệm là 2  4   A. x  4 . B. x  1 .
C. x  4; x  1 . D. x  2 .
Câu 18. [2D2-2] Phương trình 9x 3.3x
 2  0 có hai nghiệm x , x với x x . Giá trị A  2x  3x là 1 2 1 2 1 2 A. 2 log 3. B. 1. C. 3log 2 . D. 4 log 2 . 2 3 3 4 x
Câu 19. [2D2-3] Phương trình 2 2
log x  7 log 4x  10  0 có hai nghiệm x , x với x x . Giá trị 1 A  là 4 4 1 2 1 2 x2 1 1 A. . B. 16 . C. 64 . D. . 4 16 log 4 x2  3
Câu 20. [2D2-1] Biết rằng phương trình  x 2 2     
 4. x  2 có hai nghiệm x , x x x . 2  1 2  1
Tính 2x x . 1 2 A. 1. B. 3 . C. 5  . D. 1  . x 1
Câu 21. [2D2-1] Tìm tập nghiệm S của bất phương trình 1 5   0 . 5
A. S  1;   .
B. S  1;   . C. S   2  ;    .
D. S  ; 2 .
Câu 22. [2D2-1] Tập nghiệm của bất phương trình: log
x  3  1 có dạng a;b . Khi đó giá trị a  3b bằng 1   3 37 A. 15 . B. 13 . C. . D. 30 . 3 2 x 1  0 2 x x  1 
Câu 23. [2D2-2] Bất phương trình 3 4 2   
có bao nhiêu nghiệm nguyên dương?  2  A. 2 . B. 4 . C. 6 . D. 3 .
Câu 24. [2D2-2] Tập nghiệm của bất phương trình 2 log 4x  3  log 2x  3  2 là 3   1   3  3   3   3  A. S   ;3  .
B. S   ;3 .
C. S   ;  3 . D. S  ;3  . 8      8   4 
Câu 25. [2D2-3] Tìm m để bất phương trình 1 log  2 x   1  log  2
mx  4x m thỏa mãn với mọi x   . 5 5  A. 1   m  0 . B. 1   m  0 .
C. 2  m  3 .
D. 2  m  3 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 16/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 007
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 2 1    1  Câu 1.
[2D2-1] Cho a là số thực dương. Rút gọn biểu thức 2 2 P a .    2 1  a   A. 3 P a . B. 2 P a . C. 2 2 P a . D. 2 P a . Câu 2.
[2D2-2] Mệnh đề nào sau đây là đúng?  A.   1 1 1  1 . B. 0,5 0,5  e . C. 1 1   e . D.  3 0 2  0 . 1 Câu 3.
[2D2-1] Tập xác định của hàm số y    x3 1 2 là  1   1  A.  . B.  ;    . C. 0;   . D.  ;    .  2   2  4  Câu 4.
[2D2-2] Hàm số y   2  x  3 3
có đạo hàm trên khoảng  3; 3 là 7 4 7 8 A. y    2 3  x  3 . B. y x  2 3  x  3 . 3 3 7 8  7 4 C. y   x  2 3  x  3 . D. 2 y   x  2 3  x  3 3 3 Câu 5.
[2D2-2] Hàm số nào sau đây có cực trị? 1 A. 3 y x . B. 4 y x . C. 1 y x  . D. 3 y x . 0,3 10  aCâu 6.
[2D2-1] Với các số thực dương a , b bất kì, đặt M   
. Mệnh đề nào dưới đây đúng? 3 5  b  1 1 A. log M  3  log a  log b . B. log M  3  log a  log b . 2 2 C. log M  3
 log a  2 log b .
D. log M  3log a  2 log b . Câu 7.
[2D2-2] Cho log 5  a , log 6  b , log 22  c . Mệnh đề nào dưới đây đúng? 3 3 3  270   270  A. log
a 3b 2c . B. log  a 3b 2c . 3     3      121   121   270   270  C. log
a 3b 2c . D. log
a 3b 2c . 3     3      121   121  Câu 8.
[2D2-2] Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng? 3  a  ln b 3  a  3ln 3 A. log  log a  . B. log  log a  . 7 2   3   b 3ln 3 27 3   b ln b   3  a  ln b 3  a  3ln 3 C. log  log a  . D. log  log a  . 7 2   3   b 3ln 3 27 3   b ln b   Câu 9.
[2D2-3] Cho a , b , x là các số thực dương và khác 1 và các mệnh đề:  ab
log a  1 log x Mệnh đề (I) : log b x x . Mệnh đề (II) : log b b  . b loga a a    x  log a b
Khẳng định nào dưới đây là đúng ?
A. (II) đúng, (I) sai.
B. (I) đúng, (II) sai.
C. (I), (II) đều sai.
D. (I), (II) đều đúng.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 17/69 - Mã đề 2D2
Câu 10. [2D2-3] Cho hàm số   2 3x .4x f x
. Khẳng định nào sau đây sai?
A. f x 2
 9  x  2x log 2  2 .
B. f x 2
 9  x ln 3  x ln 4  2 ln 3 . 3
C. f x 2
 9  x log 3  2x  2 log 3 .
D. f x  9  2x log 3  x log 4  log 9 . 2 2
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y  log  2 x  2x . 2 
A. D  0;  .
B. D   ;
 0  2;  .
C. D   ;  0 2; .
D. D   ;  0 2; .
Câu 12. [2D2-2] Đạo hàm của hàm số log ex y  1 là 2   ex 2x ln 2 2x ex ln 2 A. y  . B. y  . C. y  . D. y  . ex   1 ln 2 2x 1 2x   1 ln 2 ex 1
Câu 13. [2D2-2] Cho hàm số   2x.5x f x
. Tính giá trị của f 0 . 1
A. f 0  10 .
B. f 0  1.
C. f 0  .
D. f 0  ln10 . ln10  1 
Câu 14. [2D2-3] Cho ba số thực a , b , c  ;1   .  4   1   1   1 
Tìm giá trị nhỏ nhất P
của biểu thức P  log b   log c   log a  . min a        4 b   4 c   4  A. P  3 . B. P  6 . C. P  3 3 . D. P  1 . min min min min
Câu 15. [2D2-4] Bác Hiếu đầu tư 99 triệu đồng vào một công ty theo thể thức lãi kép với lãi suất
8, 25% một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (Giả
sử rằng lãi suất hàng năm không đổi). A. 48,155 triệu. B. 147,155 triệu. C. 58, 004 triệu. D. 8, 7 triệu.
Câu 16. [2D2-1] Tìm nghiệm của phương trình x 1  ln81 9  e . A. x  5 . B. x  4 . C. x  6 . D. x  17 .
Câu 17. [2D2-2] Phương trình 2 log x  log
9x  0 có 2 nghiệm là x , x ,  x x . Khi đó 3x x 1 2  3 3   1 2 1 2 bằng 28 8 A. . B. 3 . C. . D. 10 . 9 9
Câu 18. [2D2-2] Phương trình 3 log x  log 3x 1  0 có tổng các nghiệm bằng 3 3 A. 3 . B. 84 . C. 81. D. 78 .
Câu 19. [2D2-3] Phương trình log
3.2x 1  x 1 có hai nghiệm x , x thì tổng x x là 4   1 2 1 2 A. 4 . B. 2 . C. log 6  4 2 . D. 6  4 2 . 2  
Câu 20. [2D2-4] Tìm tập hợp tất cả các giá trị của tham số thực m đề phương trình log 5z 1 .log
2.5z  2  m có nghiệm thuộc khoảng 0; . 2   2    1   1  A.  ;    . B.  ;     . C.  ;
 0  2; . D. 0; 2 .  4   4 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 18/69 - Mã đề 2D2 x
Câu 21. [2D2-1] Tìm tập nghiệm S của bất phương trình    1 3 1  4  2 3
A. S  1;  .
B. S  1;  .
C. S  ;  1 .
D. S   ;   1 .
Câu 22. [2D2-1] Tìm tập hợp nghiệm S của bất phương trình log    .  2 x  1
log2x 4 4 4 A. S   2  ;   1 .
B. S  2;  .
C. S  3;  2;   1 .
D. S  3; . x 1  x 1 
Câu 23. [2D2-2] Nghiệm của bất phương trình    x 1 5 2 5 2     là A. 2
  x  1 hoặc x  1. B. x  1. C. 2   x  1 . D. 3   x  1  .
Câu 24. [2D2-2] Nghiệm của bất phương trình 2 log x  log x  2  log 2x  3 là 2 1   2   2 3 3 A. x   . B. x   . 2 2 3 C. 1
  x  0 hoặc x  0 . D.   x  1  . 2
Câu 25. [2D2-4] Tìm tập hợp X gồm tất cả các giá trị của tham số thực m để bất phương trình 1 log  2 x   1  log  2
mx  4x m có tập nghiệm là .  5 5 
A. X  2;  3 .
B. X  3;5 .
C. X  2;  3 .
D. X  3;5.
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 19/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 008
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 5 Câu 1.
[2D2-1] Rút gọn biểu thức 3 3
Q a : a với a  0. 4 4 5 A. 3 Q a . B. 3 Q a . C. 9 Q a . D. 2 Q a . x y Câu 2.
[2D2-1] Nếu 2  3  2  3 thì kết luận nào sau đây đúng?
A. x y .
B. x y .
C. x y .
D. x y . Câu 3.
[2D2-1] Tìm tập xác định D của hàm số e y x .
A. D  ;0. B. D  . 
C. D  0;.
D. D   \   0 . Câu 4.
[2D2-2] Tính đạo hàm của hàm số 1 2x y   . x 1 2  A.      1 2x y x ln 2 . B. x 1 y 2    log 2 . C. y  . D. x 1 y 2    ln 2 . ln 2 Câu 5.
[2D2-2] Hình bên là đồ thị của ba hàm số x y a , x y b , y x y b x
y c 0  a,b, c  
1 được vẽ trên cùng một hệ trục tọa độ. x y c
Khẳng định nào sau đây là khẳng định đúng? x
A. b a c .
B. a b c . y a
C. a c b .
D. c b a 1 O x 2  a Câu 6.
[2D2-2] Cho a là số thực dương khác 2 . Tính I  log . a   4 2   1 1 A. I  . B. I  2 . C. I   . D. I  2  . 2 2 Câu 7. [2D2-2] Cho log 9  .
a Tính log 2 theo a . 6 3 a a  2 a  2 2  a A. . B. . C. . D. . 2  a a a a 1 Câu 8.
[2D2-2] Cho log a  2 và log b
. Tính I  2 log log 3a   log b 3 3   2 3 2 2 1   . 4 5 3 A. I  . B. I  4 . C. I  0 . D. I  . 4 2 Câu 9.
[2D2-3] Đường cong trong hình bên là đồ thị của một hàm số y
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới 1
đây. Hỏi hàm số đó là hàm số nào? 2
A. y  log x .
B. y  log x . O x 2 1 2 1  C. y  log x . D. y  log 2x 2   2
Câu 10. [2D2-3] Cho a và b là hai số thực dương và a  1 . Mệnh đề nào sau đây là đúng? A. x
a b x  log a . B. x
a b x  log b . b a C. x
a b x  log b . D. x
a b  0  x  log b a a
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 20/69 - Mã đề 2D2
Câu 11. [2D2-1] Tìm tập xác định D của hàm số y  log  2
x  4x  3 . 3 
A. D  2  2;  1  3;2  2  .
B. D  1;3 .
C. D   ;   1  3; .
D. D   ;
 2  2  2  2; . 1
Câu 12. [2D2-2] Tính đạo hàm của hàm số y   2   4 1 x . 5 1  5 5  A. y   2 1 x  4 . B. y  x  2 1 x  4 . 4 2 5 5 5 1 C. y  x  2 1 x  4 . D. y  x  2 1 x  4 . 2 2
Câu 13. [2D2-2] Cho hàm số f x   2
ln x  2x . Chọn khẳng định đúng trong các khẳng định sau: 4 1 1
A. f  3  .
B. f 3  .
C. f 3  .
D. f 3  ln 3 3 12 3
Câu 14. [2D2-2] Cho hàm số x y ex e  
. Nghiệm của phương trình y  0 ? A. x  1  . B. x  1 . C. x  0 . D. x  ln 2 1 ab
Câu 15. [2D2-4] Xét các số thực dương a , b thỏa mãn log
 2ab a b  3 . Tìm giá trị nhỏ 2 a b nhất P
của P a  2b . min 2 10  3 2 10  5 3 10  7 2 10 1 A. P  . B. P  . C. P  . D. P  . min 2 min 2 min 2 min 2 2 xx  1 
Câu 16. [2D2-2] Gọi x , x là hai nghiệm của phương trình: 6 x 1  0  5
; khi đó x x bằng: 1 2  5  1 2   7 7 A. . B.  . C. 7  . D. 7 . 2 2
Câu 17. [2D2-2] Tìm nghiệm của phương trình log x  5  4 . 2   A. x  21. B. x  3 . C. x  11 . D. x  13 .
Câu 18. [2D2-3] Số nghiệm của phương trình x 1 9x 3    4  0 : A. n  1 . B. n  2 . C. n  3 . D. n  4 .
Câu 19. [2D2-2] Nghiệm nguyên nhỏ nhất của bất phương trình log 3  log 3  0 là: x x 3 A. x  3 . B. x  1 . C. x  2 . D. x  4 .
Câu 20. [2D2-3] Giá trị của m để phương trình x x 1 4 . m 2  
 2m  0 có hai nghiệm x , x thỏa mãn 1 2
x x  3 là 1 2 9 3 A. m  3 . B. 4 . C. m  . D. m  . 2 2 x 1
Câu 21. [2D2-1] Nghiệm của bất phương trình 2 3  là 9 A. x  4  . B. x  0 . C. x  0 . D. x  4 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 21/69 - Mã đề 2D2
Câu 22. [2D2-1] Tập nghiệm của bất phương trình 2 log x  1  là 1 2 A.  2;  . B.  2; 0  .  0; 2    C.  2; 2  . D. 0; 2 .   
Câu 23. [2D2-2] Tập nghiệm của bất phương trình x x 1  x x 1 2 2 3 3    
A. x 2;  .
B. x 2;  . C. x  ;  2 . D. 2;  .
Câu 24. [2D2-2] Bất phương trình log x  7  log
x 1 có tập nghiệm là 4   2   A. 1; 4 . B. 5; . C.  1  ; 2 . D.  ;   1 . 1
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số m để hàm số y   log x m 3 2m 1 x
xác định trên 2;3 .
A. 1  m  2 .
B. 1  m  2 . C. 1   m  2 . D. 1   m  2
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 22/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 008
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 1 4 4 1   3 3 3 3 a b a b     Câu 1.
[2D2-1] Cho các số thực dương a , b . Khi đó biểu thức bằng 3 3 a b 1 1 2 2
A. a b. B. 3 3 a b . C. a . b D. 3 3 a b . m n Câu 2.
[2D2-2] Cho m , n thoả mãn  5  2    5  2 . Khi đó ta có A. m  . n B. m  . n C. m  . n D. m  . n 1 Câu 3.
[2D2-1] Tập xác định của hàm số y   2  x 3 4 là A. 0; . B. . C.  2  ; 2. D.  ;  2. 4 Câu 4.
[2D2-2] Đạo hàm của hàm số y   2 x x  3 2 3 là 1 1 4 A.  2 x x  3 2 3 . B.  2
x  2x  33 . 3 1 4 1  8 C.  2
x  2x  3 3 .
D. x   1  2
x  2x  33 . 3 3 1 Câu 5.
[2D2-2] Số cực trị của hàm số 3
y x x là A. 0. B. 1. C. 2. D. 3. Câu 6.
[2D2-1] Cho 0  a  1, b   . Rút gọn biểu thức 2 4
log b  log b ta được 2 a a A. 4 log . b B. 6 log . b C. 4 log b . D. 6 log b . a a a a Câu 7.
[2D2-2] Biết a  log 3, khi đó log 27 bằng 5 15 3a 2a 4a 1 4a 1 A. . B. . C. . D. . 1 a 1 a 1 a 2a 1 Câu 8.
[2D2-2] Đặt a  log 3, b  log 5. Khi đó log 675 bằng 2 2 2 A. 3a  2 . b B. 2a  3 . b C. a  3 . b D. 3a  . b Câu 9.
[2D2-3] Cho các số thực dương a , b thỏa mãn a b và 2 2
a  3ab b  0. Trong các đẳng
thức sau, đẳng thức nào đúng ln a  ln b ln a  ln b
A. ln a b  .
B. ln a b  . 2 3 ln a  ln b ln a  ln b
C. ln 2a  2b  .
D. ln a b  . 2 2
Câu 10. [2D2-3] Cho hai số thực ,
m n thỏa mãn 2m 2n
. Khẳng định nào sau đấy đúng A. log  3
m  3m   log  3 n  3n . B. log  3
m  3m   log  3 n  3n . 1 1  1 1  2 2 2 2 C. log  3
m  3m   log  3 n  3n . D. log  3
m  3m   log  3 n  3n . 1 1  1 1  2 2 2 2
Câu 11. [2D2-1] Tập xác định của hàm số y  log  2 2x x là 5  A. 0; . B. . C. 0;2. D. 0; 2.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 23/69 - Mã đề 2D2
Câu 12. [2D2-2] Đạo hàm của hàm số  2x  .ex y x 2x A. x 1  x x 1 2 e . x e    .
B. 2x ln 2     1 ex x
. C. 2x     1 ex x . D.     1 ex x . ln 2
Câu 13. [2D2-2] Tìm tất cả các khoảng đồng biến của hàm số y  log  2 x  2x  3 2  A. 1; . B.  ;   1 . C. 0; . D.  ;  2.
Câu 14. [2D2-3] Gọi M , m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số 3 e x 3ex y    4 trên 1 
;1 . Khi đó M m bằng 1 3 A. 3 e  3e  4. B. 3 e  3e  6. C. 3 e  3e  2. D.   6. 3 e e
Câu 15. [2D2-4] Một người gửi ngân hàng 100 triệu đồng theo thể thức lãi kép định kì liên tục, với lãi
suất không đổi mỗi năm. Sau 5 năm thì thu được cả vốn lẫn lãi là 200 triệu đồng. Hỏi người
đó muốn thu được 300 triệu đồng khi gửi 100 triều đồng thì cần bao nhiêu năm A. 7. B. 8. C. 9. D. 10 2 1
Câu 16. [2D2-1] Số nghiệm của phương trình x 2  9 x là 3x A. 0. B. 1. C. 2. D. 3.
Câu 17. [2D2-2] Số nghiệm của phương trình log  x  
1  log  x  3 2 1 là 2 8 A. 0. B. 1. C. 2. D. 3.
Câu 18. [2D2-2] Tổng các nghiệm của phương trình 16x 10.4x  16  0 là A. 10. B. 16. C. 2. D. 6.
Câu 19. [2D2-3] Tích các nghiệm của phương trình log .
x log x  4  log x  4 log x là 2 3 3 2 A. 83. B. 54. C. 4. D. 60.
Câu 20. [2D2-4] Số nghiệm của phương trình 3   1 .2x x  3x 1 là A. 0. B. 1. C. 2. D. 3. 2 x x 1
Câu 21. [2D2-1] Tập nghiệm của bất phương trình 3 1 2  là 2 A. 1;2. B. 1;3. C.  
;1  2;. D. 2; .
Câu 22. [2D2-1] Tập nghiệm của bất phương trình log 2x  2  1  là 1   2 A.  1  ; 0. B. 0  ;1 . C.  ;  0. D.  1  ; . 2
Câu 23. [2D2-2] Tập nghiệm của bất phương trình x x2 x2 3  9 là A. 2;3. B.  2  ;3. C.  3  ; 2. D. 1;3.
Câu 24. [2D2-2] Khoảng  ;
a b là tập nghiệm của bất phương trình log x 1  log x  3 . Khi đó 5     5 2 2 a b bằng A. 29. B. 27. C. 34. D. 30.
Câu 25. [2D2-3] Tìm tất cả các giá trị của tham số m để bất phương trình  2
log x x  6  x < log  x  2  m có tập nghiệm chứa 3; 4 A. m  3 B. m  4 C. m  5 D. m  6
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 24/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 010
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. Câu 1.
[2D2-1] Cho m là số nguyên dương, biểu thức nào sau đây sai? A. m 2 16 4 m  . B. m m  3 16 2 . 2 m   . C. 16m 4m.2m   . D. m 4 16 2 m  . 3 1  3 5
a .a b .b Câu 2.
[2D2-2] Với a  0, b  0 . Giá trị của biểu thức A  là:    . a b 2 :  . a b 3 2  b b a a a b A. A  .
B. A a 1. C. A  1. D. A  . a b b Câu 3.
[2D2-1] Tập xác định của hàm số y   x   3 3 1 là tập:  1   1  1  A.  3  ;  . B.  ;    . C.  ;    . D. \   .  3   3  3 Câu 4.
[2D2-2] Đạo hàm của hàm số y x x 3 4 3 3 A. y   . B. y  . C. y  . D. y  . 4 4 x 4 3 x 4 x 4 4 x Câu 5. [2D2-2] Hàm số   2   1 x y x
e có bao nhiêu cực trị? A. 0 . B. 1. C. 2 . D. 3 . Câu 6.
[2D2-1] Cho a  0 và a  1. Tìm mệnh đề đúng trong các mệnh đề sau:
A. log x có nghĩa với x  .
B. log 1  a và log a  0. a a a log x C. log x y D. log x y x
y (x  0, y  0). a  .  log log a   a . log y a a a Câu 7.
[2D2-2] Với m  0 , cho a  log m với. Tính P  log
27m theo a 3 m 6  2a 6  a A. P  .
B. P  6  a. . a C. P  .
D. A  6  2a. . a a a Câu 8.
[2D2-2] Đặt a  log 3, b  log 3. Hãy biểu diễn log 45 theo a và . b 2 5 6 a  2ab 2 2a  2ab A. log 45  . B. log 45  . 6 ab 6 ab a  2ab 2 2a  2ab C. log 45  . D. log 45  . 6 ab b 6 ab b Câu 9.
[2D2-3] Khẳng định nào sau đây đúng: 1 A. 2
log a  2 log a . B. 2 2 2
log a  4 log a . C. 2 2 2
log a  4 log a . D. 2 log a  log a . 3 3 3 3 3 3 3 3 2 2 2 3 4 Câu 10. [2D2-3] Nếu 3 2 aa và log  log
thì khẳng định nào sau đây đúng? b 4 b 5
A. 0  a  1 và 0  b  1.
B. 0  a  1 và b  1.
C. a  1 và 0  b  1.
D. a  1 và b  1.
Câu 11. [2D2-2] Tìm tập xác định D của hàm số y  log  2
x  2x  1 . 3 
A. D  ;  1 .
B. D  1;  .
C. D   ;    .
D. D   ;   1  1; .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 25/69 - Mã đề 2D2
Câu 12. [2D2-1] Đạo hàm f  x của hàm số   2 e x f x   là 2e A.   2e x f x    . B.    2  ex f x .
C. f  x   . D.   2 2e x f x     . x
Câu 13. [2D2-2] Cho hàm số y x ln x , khi đó đạo hàm cấp hai tại x  e là ye có giá trị bằng bao nhiêu? 1 A. e . B. 2 . C. . D. 1. e
Câu 14. [2D2-3] Bác Anh đem gửi tiết kiệm ở ngân hàng với lãi suất là 12% một năm. Biết rằng cứ sau
mỗi một quý ( 3 tháng) thì lãi được cộng dồn vào gốc. Hỏi sau tối thiểu bao nhiêu năm thì Bác
Anh nhận lại được số tiền (cả vốn lẫn lãi) gấp ba số tiền ban đầu. A. 8 năm. B. 9 năm. C. 10 năm. D. 11 năm. 2 2
Câu 15. [2D2-4] Tìm giá trị lớn nhất của sin x cos 2 2 x y   A. 3 . B. 2 . C. 4 . D. 5 . 2
Câu 16. [2D2-1] Cho phương trình x 4x5 3
 9 tổng lập phương các nghiệm thực của phương trình là A. 28. B. 27. C. 26. D. 25.
Câu 17. [2D2-2] Gọi x , x là nghiệm của phương trình log 2  log x  0 . Khi đó giá trị 1 . 2 2x x bằng 1 2 x 16 A. 1  . B. 1. C. 2 . D. 2  . x3 x 1 
Câu 18. [2D2-2] Tổng các nghiệm của phương trình: x 1  x 1 2 5 2    là A. 0 . B. 2 . C. 2  . D. 4.
Câu 19. [2D2-3] Số nghiệm của phương trình log log x  log log x  2 là 4  2  2  4  A. 0 . B. 2 . C. 3 . D. 1. x 1 
Câu 20. [2D2-4] Biết phương trình 5x.8 x  500 hai nghiệm x , x . Tính 1 . 2 5x x P  . 1 2 1 1 A. P  8 . B. P  . C. P  3 . D. P  . 8 3 2 x 1  3x 1   3   3 
Câu 21. [2D2-1] Bất phương trình      có tập nghiệm là  2   2      A. (2;5) . B. 1;2. C.  1  ;  3 . D.  ;    1 .
Câu 22. [2D2-1] Tìm tập nghiệm S của bất phương trình log 4  3x  4  . 1   2  4   4 
A. S   ;  4  . B. S  ; 2 .   C. S   ;  .   D. S  .   3   3 
Câu 23. [2D2-2] Nghiệm của bất phương trình 2x4 x 2 x2 3  45.6  9.2  0 A. x  2 . B. x  2 . C. x  2  . D. x  2  .
Câu 24. [2D2-2] Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình
log  x  40  log 60  x  2 . A. 10 . B. 19 . C. 18 . D. 20 .
Câu 25. [2D2-4] Tìm tất cả các giá trị thực của tham số
m để bất phương trình log 5x 1 .log
2.5x  2  m nghiệm đúng với mọi x  1. 2   2   A. m  6 . B. m  6 . C. m  6 . D. m  6 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 26/69 - Mã đề 2D2
TOÁN HỌC BẮC–TRUNG–NAM
KIỂM TRA CHƯƠNG 2 GIẢI TÍCH 12
Nhóm: THBTN – ĐỀ KIỂM TRA MÃ ĐỀ 011
(25 câu trắc nghiệm)
Thời gian làm bài: 45 phút, không kể thời gian phát đề. 1 Câu 1. [2D2-1] Biểu thức 4 3
27 a ( với a  0 ) viết dưới dạng lũy thừa với số mũ hữu tỉ là 3 1 1 1 1 1 1 1 A. 4 12 3 .a . B. 4 2 3 .a . C. 12 9.a . D. 4 3 3 .a 3 4 1 2 Câu 2.
[2D2-1] Cho a , b là các số thực dương thỏa mãn 4 5 a a và log  log . Mệnh đề nào b 2 b 3 sau đây đúng?
A. a  1,b  1 .
B. a  1, 0  b a .
C. 0  a  1, 0  b  1 . D. 0  a  1,b  1. 1 Câu 3.
[2D2-1] Tìm x để biểu thức  2 x  3 1 có nghĩa: A. x    ;   1  1; . B. x    ;    1  1;  . C. x    1  ;  1 . D. x    \   1 . 1 Câu 4.
[2D2-2] Đạo hàm của hàm số y   2 x x  3 5 2 là 10x 1 10x 1 A. y  . B. y  . 3 2 3 5x x  2 3 2 5x x  2 10x 1 1 C. y  . D. y  . 3 2
3 5x x  22 2 3 3 5x x  2 x Câu 5.
[2D2-2] Hàm số y   2
3a 10a  2 đồng biến trên  ;   khi:  1   1   1  A. a   ;    .
B. a 3;  . C. a   ;    . D. a  ;3   .  3   3  3  1 1 Câu 6. [2D2-1] Nếu 2 6 a a và 2 3 bb thì
A. a  1; 0  b  1.
B. a  1;b  1 .
C. 0  a  1;b  1.
D. a  1;0  b  1. 0  ,2 10  aCâu 7.
[2D2-2] Cho a  0 , b  0 . Nếu viết log
x log a y log b thì xy bằng bao nhiêu? 5   5 5 6 5  b  1 1 A. 3 . B. . C.  . D. 3  . 3 3 Câu 8.
[2D2-2] Cho x, y  0 và 2 2
x  4 y  12xy . Khẳng định nào sau đây là khẳng định đúng?
x  2 y  1 A. log
 log x  log y . B. log
x  2 y  2 
log x  log y . 2    2 2  2   2 2  4  2 C. log
x  2 y  log x  log y 1. D. 4 log
x  2 y  log x  log y . 2   2   2 2 2 2 Câu 9.
[2D2-2] Cho log 3  a , log 7  b . Tính log 2016 theo a và b . 2 2 2
A. 5  2a b .
B. 5  3a  2b .
C. 2  2a  3b .
D. 2  3a  2b .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 27/69 - Mã đề 2D2
Câu 10. [2D2-3] Hình bên là đồ thị của ba hàm số x y a , y x y b , x
y c 0  a,b, c  
1 được vẽ trên cùng một hệ x y b
trục tọa độ. Khẳng định nào sau đây là khẳng định đúng? x y c
A. b a c . x y a
B. a b c .
C. a c b . 1
D. c b a . O x
Câu 11. [2D2-2] ] Cho a là số thực dương khác 1. Xét hai số thực x , x . Phát biểu nào sau đây là 1 2 đúng? A. Nếu 1 x 2 x
a a thì x x . B. Nếu 1 x 2 x
a a thì a  
1  x x  0 . 1 2  1 2 C. Nếu 1 x 2 x
a a thì a  
1  x x  0 . D. Nếu 1 x 2 x
a a thì x x . 1 2  1 2
Câu 12. [2D2-1] Hàm số y  log
x xác định khi và chỉ khi: x 1  x  1 A.  . B. x  1 . C. x  0 . D. x  2 x  2 
Câu 13. [2D2-1] Cho hàm số    ex f x x
. Gọi f  x là đạo hàm cấp hai của f x . Ta có f   1 bằng A. 3e . B. 2 3  e . C. 3 e . D. 2 5  e
Câu 14. [2D2-1] Cho hàm số e e x y x   
.Nghiệm của phương trình y  0 ? A. x  1  . B. x  1 . C. x  0 . D. x  ln 2
Câu 15. [2D2-2] Tính giá trị của biểu thức P  ln tan1°  ln  tan 2  ln tan 3  ...  ln tan 89 . 1 A. P  1. B. P  . C. P  0. D. P  2. 2
Câu 16. [2D2-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức lãi
kép với lãi suất 0, 6 % mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng.Hỏi số
tiền T gần với số tiền nào nhất trong các số sau? A. 535000 . B. 635000 . C. 613000 . D. 643000 .
Câu 17. [2D2-1] Nghiệm của phương trình x x 1  x x 1 2 2 3 3     là 3 2 A. x  log . B. x  1 . C. x  0 . D. x  log . 3 4 4 3 2 3
Câu 18. [2D2-1] Số nghiệm của phương trình log  2 x  3  log
6x 10 1  0 là 2  2   A. Vô nghiệm. B. 1. C. 2 . D. 3 .
Câu 19. [2D2-1] Phương trình 9x 5.3x
 6  0 có tổng các nghiệm là 2 3 A. log 6 . B. log . C. log . D.  log 6 . 3 3 3 3 2 3
Câu 20. [2D2-2] Tìm số nghiệm thực của phương trình log    .   3 2 2x 2x 3x 1 x 1  A. 0 . B. 1. C. 2 . D. 3 .
Câu 21. [2D2-3] Hỏi phương trình 3.2x 4.3x 5.4x 6.5x   
có tất cả bao nhiêu nghiệm thực? A. 2 . B. 4 . C. 1. D. 3 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 28/69 - Mã đề 2D2 3 2
Câu 22. [2D2-3] Phương trình 23x x x 3 2 2
.2 1024  23x  10x x có tổng các nghiệm gần nhất với số nào dưới đây A. 0,35. B. 0, 40. C. 0,50. D. 0, 45.
Câu 23. [2D2-3] Tìm m để phương trình 2 log
x  log x m  0 có nghiệm x  0;  1 ? 2 2 1 1 A. m  1. B. m  . C. m  . D. m  1. 4 4
Câu 24. [2D2-2] Cho hàm số   2 2 x sin 2 .3 x f x
. Khẳng định nào sau đây là khẳng định đúng?
A. f x 2
 1  x ln 4  sin x ln 3  0 .
B. f x  1  2x  2sin x log 3  0 . 2
C. f x 2
 1  x log 2  sin x  0 .
D. f x 2
 1  2  x log 3  0 . 3 2 3 e x    1 ex m 1   4 
Câu 25. [2D2-4] Cho hàm số y   
. Tìm m để hàm số đồng biến trên khoảng 1; 2 .  2017  A. 3 4
3e 1  m  3e  1. B. 4 m  3e 1 . C. 2 3
3e 1  m  3e  1. D. 2 m  3e 1 .
----------HẾT----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 29/69 - Mã đề 2D2
BẢNG ĐÁP ÁN CÁC ĐỀ ÔN TẬP ĐÁP ÁN ĐỀ 001 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C C B B C A A B D A B A C A A C C C D A A C D A B ĐÁP ÁN ĐỀ 002 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A A B C C C A A D D C D D A A C B D D D A B A D D ĐÁP ÁN ĐỀ 003 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B C B B D C D C C D D B D D B B A C C C A C A B D ĐÁP ÁN ĐỀ 004 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D A A C A B A D C A A D C B D C C D B B B C D C D ĐÁP ÁN ĐỀ 005 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D C C B B D A C D B C A D B C D A D D B D C C D A ĐÁP ÁN ĐỀ 006 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C B A A C A D B C A A A A D D A A C C D C B D D C ĐÁP ÁN ĐỀ 007 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B B B B A A A D D B A D B A A D B B D D C B C C ĐÁP ÁN ĐỀ 008 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A C D A B D D A B C D A A A D A A D B A B A C A ĐÁP ÁN ĐỀ 009 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B C D B C A A A B D B A B B C B C B C C A A C B ĐÁP ÁN ĐỀ 010 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C C B D 5 D A C B B D D C C A A C C D B B A D C C ĐÁP ÁN ĐỀ 11 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A D B C D A C B A A B A A A C B A B A B C D C A B
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 30/69 - Mã đề 2D2
TRƯỜNG THPT TRẦN QUỐC TUẤN
ĐỀ KIỂM TRA 1 TIẾT LẦN 3 - HKI TỔ TOÁN
MÔN: GIẢI TÍCH - LỚP 12
(Thời gian làm bài:45 phút)
Họ, tên thí sinh:................................... SBD:............... Mã đề: 132 Câu 1. Cho hàm số y  log  2
x  2x  4 . Tập nghiệm của bất phương trình y  0 là 1  3 A.  ;  0 . B. 1; . C.  ;   1 . D. 2; . Câu 2.
Cho 3 số dương a , b , c và khác 1. Chọn khẳng định sai trong các khẳng định sau:
A. log bc  log b  log c . B. log c  log . b log c . a a a a a b 1 C. log b a aa . D. log b  . a log a b Câu 3.
Gọi x , x là hai nghiệm của phương trình 4x 8.2x
 4  0 . Giá trị biểu thức P x x bằng 1 2 1 2 A. 4  . B. 4 . C. 0 . D. 2 . Câu 4. Phương trình x3 2
 4 có nghiệm thuộc tập nào? A.  ;  4 . B.  ;  8 . C.  ;  5 . D.  ;  3 . Câu 5.
Gọi x , x là hai nghiệm của phương trình 2
log x  3log x  2  0 . Giá trị biểu thức 1 2 2 2 2 2
P x x bằng bao nhiêu? 1 2 A. 20 . B. 5 . C. 36 . D. 25 . Câu 6.
Tìm tập hợp các giá trị của tham số thực m để phương trình 6x  3  .2x x
m  0 có nghiệm thuộc khoảng 0;  1 A. 4;10 . B. 3; 4 . C. 2; 4 . D. 3; 4 . Câu 7.
Anh Thành vay 20 triệu đồng của ngân hàng để mua laptop và phải trả góp trong vòng 3 năm
với lãi suất 1,1% mỗi tháng. Hàng tháng anh Thành phải trả 1 số tiền cố định là bao nhiêu để
sau 3 năm hết nợ (làm tròn đến đơn vị đồng) A. 675.807 đồng. B. 673.807 đồng. C. 672807 đồng. D. 677807 đồng. Câu 8.
Cho 3 số dương a , b , c khác 1 và thỏa mãn: log b  log b  log 2017.log b . Chọn khẳng a c a c
định đúng trong các khẳng định sau:
A. ac  2017 .
B. ab  2017 .
C. bc  2017 .
D. abc  2017 . Câu 9.
Cho P  log 16m và a  log m , với m là số dương khác 1. Mệnh đề nào dưới đây đúng? m 2 a a  4 a  3 A. P  1 . B. 2 P  3  a . C. P  . D. P  . 4 a a
Câu 10. Tập xác định của hàm số y   x x 10 2 2 là
A. D   \ 0;  2 . B. D   .
C. D   \ 0;2 .
D. D   \   2 .
Câu 11. Tập nghiệm của bất phương trình: 2 4 log x  5log x  6  0 là 1 0,2 25  1 1   1 
A. S R . B. S   . C. S  ;   . D. S   ;    .  125 25   25 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 31/69 - Mã đề 2D2
Câu 12. Cho hai số dương a , b khác1. Đồ thị hàm số y
y  log x , y  log x (như hình vẽ bên). Mệnh a b
đề nào sau đây là mệnh đề đúng? O x 1
A. a  1  b .
B. b a  1.
C. b  1  a .
D. a b  1.
Câu 13. Tập nghiệm của bất phương trình log 2x 1  log x  1 là 1   1   2 2  1   1  A. 2; . B. ; 2   . C.  ;  2 . D.  ; 2   .  2   2 
Câu 14. Hàm số nào trong các hàm số dưới đây có đồ y
thị phù hợp với hình vẽ bên
A. y  log x .
B. y  log x . 1 2 2 2 x  1 
C. y    . D. 2x y  .  2  O 1 x 5
Câu 15. Giải phương trình log x  log 3 
ta được hai nghiệm x x . Khẳng định nào sau đây 3 x 2 1 2 đúng? x x x x A. 2 3x   0 . B. 2 3x   0 .
C. 1  x  10 .
D. 1  x  9 . 1 3 1 3 2 2 3 3
Câu 16. Tập xác định của hàm số y  ln  x  2 là A.  \   2 . B. 2; . C.  ;  2 . D. 2; .
Câu 17. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hàm số y  log x với a  1 nghịch biến trên khoảng 0;  . a B. Hàm số x
y a với 0  a  1 đồng biến trên khoảng 0;  .
C. Hàm số y  log x với nghịch biến trên khoảng 0;  . D. Hàm số x
y a với 0  a  1 nghịch biến trên khoảng  ;   .
Câu 18. Tập nghiệm của bất phương trình 2x3 3  27 là A. 3; . B. 0;  . C. 3; . D. 0;  .
Câu 19. Phương trình 2
log (x  2x  3)  1 có mấy nghiệm? 2 A. 2. B. 3. C. 0. D. 1.
Câu 20. Hàm số nào dưới đây đồng biến trên tập xác định của nó? x x  2   e 
A. y  log x . B. y  . C. y  .
D. y  ln x . 1      3   3  2 x x x
Câu 21. Tính đạo hàm của hàm số y  ( x  0 ) 8 5 x 1 1 1 A. y  . B. y  . C. 3 4 y  x . D. 3 4 y  4 x . 3 4 4 x 4 3 4 x 4
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 32/69 - Mã đề 2D2
Câu 22. Hàm số f x 2  x n
l x đạt cực trị tại điểm: 1 1 A. x  e . B. x  . C. x  e . D. x  . e e
Câu 23. Theo tài liệu thống kê cho biết năm 2001 dân số Việt nam có khoảng 78.695.000 người và tỉ
lệ tăng dân số trung bình hằng năm là 1, 3% trên 1 năm. Nếu tỉ lệ tăng dân số không đổi thì
năm 2016 dân số nước ta khoảng bao nhiêu người A. 95.638.898 . B. 96.890.320 . C. 98.158.117 . D. 94.403.638 . 2 2
Câu 24. Phương trình 4x 6.2x
 8  0 có mấy nghiệm? A. 3 . B. 1. C. 2 . D. 4 . 2
Câu 25. Giá trị nhỏ nhất của hàm số ex y  là A. 1. B. 1  . C. e . D. 0 . ----------- HẾT ---------- ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C C D B A A A A C A C C B D B B D C D D B B A D A
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 33/69 - Mã đề 2D2 SỞ GD & ĐT HÀ NỘI
ĐỀ KIỂM TRA KHẢO SÁT LẦN 2
TRƯỜNG THPT LÝ THÁNH TÔNG MÔN:TOÁN 12 ..........*.......... NĂM HỌC: 2017-2018
(Thời gian làm bài:45 phút) Câu 1.
Hàm số nào có bảng biến thiên như hình sau:. x  2  y – – 2  y  2 2x  5 2x  3 x  3 2x 1 A. y  . B. y  . C. y  . D. y  . x  2 x  2 x  2 x  2 Câu 2. Hàm số ex y
có giá trị lớn nhất trên đoạn 1;ln  3 là A. e . B. 2 e . C. 3 . D. 1. Câu 3.
Đồ thị của hàm số nào dưới đây nhận đường thẳng x  1 là tiệm cận đứng? 2 x 3x 2 x 2x 1 x 1 A. y    . B. y  . C. y   . D. y   . 2 x 1 2 x 1 x 1 x 1 5 Câu 4. 3
Tập xác định của hàm số y
x    x  3 2 9 3 là  9  9 A. 3; . B.  \   3 . C. ;     . D. \   3;  .  2   2  Câu 5.
Cho log 5  a , log 7  b và log 3  c . Biểu diễn log 35 theo a , b , c ? 27 8 2 12 3b  3ac 3b  2ac 3b  3ac 3b  3ac A. y  . B. y  . C. y  . D. y  . c  3 c  2 c  2 c 1 Câu 6.
Đạo hàm của hàm số  log  ex y x là 2   1 ex  1 ex 1 1 ex A. . B. . C. . D. . ln 2  ex x  ex x  ln 2   ex x ln 2 Câu 7.
Tập nghiệm của phương trình log x 1  2 là 3 A.  3  ;  2 . B.  1  0;  2 . C.   3 . D.  4  ;  2 . Câu 8.
Tập nghiệm của bất phương trình log log x  2   0 1 3     là 3 A. 5; . B. 3;5 . C.  4  ;  1 . D.  ;  5 . 1 Câu 9.
Cho một khối chóp có thể tích bằng V . Khi giảm diện tích đa giác đáy xuống lần thì thể tích 3 khối chóp lúc đó bằng V V V V A. . B. . C. . D. . 9 6 3 27
Câu 10. Thể tích của khối nón có chiều cao bằng a và độ dài đường sinh bằng a 5 là 4 2 5 A. 3 V  a . B. 3 V  4 a . C. 3 V  a . D. 3 V  a . 3 3 3
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 34/69 - Mã đề 2D2 x 3
Câu 11. Đồ thị hàm số y  
có bao nhiêu tiếp tuyến song song với đường thẳng d : y x ? 2x 1 A. 0 . B. 1. C. 2 . D. 3 . ln x
Câu 12. Đồ thị hàm số y  có điểm cực đại là x  1  A. 1;e . B. 1;0 . C.  ; e  1 . D. ; e   .  e  3 3   2 2 a b a b a b
Câu 13. Rút gọn biểu thức M     .
(với điều kiện M có nghĩa) ta được: 1 1  a b   ab  2 2 a b     A. 1  . B. 2 . C. 1. D. 3  . Câu 14. Cho log x  log
y . Chọn khẳng định đúng? 0,2 0,2
A. y x  0 .
B. x y  0 .
C. x y  0 .
D. y x  0 .
Câu 15. Số nghiệm của phương trình 2
2x  2 x  2 là A. 0 . B. 2 . C. 1. D. 4 . Câu 16. Cho hàm số 3 2
y x bx x d . y y y O x O x O xI  II  III
Các đồ thị nào có thể là đồ thị biểu diễn hàm số đã cho? A. I  .
B. I  và  II  .
C. III  .
D. I  và  III  .
Câu 17. Tìm m để hàm số 3 2
y x  6x  9x m có giá trị nhỏ nhất trên đoạn 0; 2 bằng 4  ? A. m  8 . B. m  4 . C. m  0 . D. m  4 . mx 1
Câu 18. Với giá trị nào của m thì đồ thị hàm số y
có hai đường tiệm cận? x 1 A. m  1. B. m   . C. m  0 . D. m  2 . 3  1 
Câu 19. Có thể kết luận gì về cơ số a nếu 2a   1 > 2a   1 ?  1   1  A.  ;    . B.  ; 0   . C. 0;  . D.  ;  0 .  2   2 
Câu 20. Kết quả thống kê cho biết ở thời điểm năm 2013 dân số Việt Nam là 90 triệu người, tốc độ
tăng dân số là 1,1% /năm. Nếu mức tăng dân số ở mức ổn định như vậy thì dân số Việt Nam sẽ
gấp đôi ( đạt ngưỡng 180 triệu người) vào năm nào? A. 2050 . B. 2077 . C. 2093 . D. 2070 .
Câu 21. Cho ba số thực dương a , b , c khác 1 thỏa mãn log b  log b  log 2016.log .b . Khẳng định a c a c nào sau đây là đúng?
A. ab  2016 .
B. bc  2016 .
C. abc  2016 .
D. ac  2016 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 35/69 - Mã đề 2D2
Câu 22. Phát biểu nào sau đây không đúng? A. Hai hàm số x
y a và y  log x có cùng tập giá trị. a
B. Hai đồ thị hàm số x
y a và y  log x đối xứng nhau qua đường thẳng y x . a C. Hai hàm số x
y a và y  log x có cùng tính đơn điệu. a
D. Hai đồ thị hàm số x
y a và y  log x đều có đường tiệm cận. a 2 2
Câu 23. Tìm m để phương trình x x 2 4  2
 6  m có đúng 3 nghiệm?. A. m  3 . B. m  2 . C. m  3 .
D. 2  m  3 .
Câu 24. Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật biết rằng SA vuông góc với mặt
phẳng đáy, SC hợp với đáy một góc 45 và AB  3a , BC  4a . Tính thể tích khối chóp
S.ABCD theo a ? 3 10a 3 A. 3 40a . B. 3 60a . C. . D. 3 20a . 3
Câu 25. Một hình thang vuông ABCD có đường cao AD , đáy nhỏ AB , đáy lớn CD  2.
Cho hình thang đó quay quanh CD ta được khối tròn xoay có thể tích bằng 4 4 4 A. 4 V  2. B. 4 V . C. 3 V . D. 2 V . 3 3 3 --------- Hết ----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 36/69 - Mã đề 2D2
TRƯỜNG THPT THANH HÀ
KIỂM TRA 45' GIẢI TÍCH CHƯƠNG II LỚP 12
Họ tên:............................................................................. Lớp:…………………..... Mã đề 064 Câu 1.
Trong các số sau số nào lớn nhất: 1 A. log 5 . B. log . C. log 15 . D. log 8 . 2 1 6 4 3 2 1 Câu 2.
Tập xác định của hàm số y    x3 1 là A.  ;   1 . B.  \   1 . C.  ;   1 . D.  . Câu 3.
Phương trình log (3x  2)  3 có nghiệm là 3 25 29 11 A. x  . B. x  13 . C. x  . D. x  . 3 3 3 Câu 4.
Tập xác định của hàm số y  ln  x   1 là A.  ; e  . B. 0;  . C. 1; . D. 1; . Câu 5.
Giả sử tỷ lệ lạm phát của Việt Nam mỗi năm trong 10 năm tới là 5% . Hỏi nếu năm 2017 giá
xăng A92 là 18000 VNĐ /lít thì năm 2025 giá xăng A92 là bao nhiêu tiền một lít? A. 29320,10 VNĐ/lit. B. 25327,81 VNĐ/lít. C. 27923,91 VNĐ/lít.
D. 26594, 20 VNĐ/lít. Câu 6.
Đạo hàm của hàm số y   x  e 2 1 là   
A. y   x  e 1 e 2 1 .
B. y   x  e 1 2 2 1 .
C. y   x  e 2 2 1 . D. y   x  e 1 2e 2 1 . Câu 7. Phương trình 2
log x  4 log x  3  0 có tập nghiệm là 2 2 A. 6;  8 . B. 1;  3 . C. 6;  2 . D. 8;  2 . Câu 8.
Với mọi số thực dương a và b thỏa mãn 2 2
a b  6ab , mệnh đề nào dưới đây đúng? 1 A. log
a b  log a  log b . B. log a b
1 log a  log b . 8    8 8  8   8 8 2 1 C. log
a b  1 log a  log b . D. log a b
 log a  log b . 8   8   8 8 8 8 2 Câu 9.
Phương trình: 3.4x  3 10.2x x
 3  x  0 có 1 nghiệm dạng  log b . Tìm a  4b . a A. 12 . B. 14 . C. 8 . D. 16 .
Câu 10. Biết log 5  a . Khi đó giá trị của log 5 được tính theo a là 9 3 1 1 A. 4a . B. a . C. a . D. 2a . 4 2
Câu 11. Phương trình x x 1 3.2 4  
 8  0 có 2 nghiệm x , x và tổng x x là 1 2 1 2 A. 4 . B. 2 . C. 5 . D. 3 .
Câu 12. Tìm tất cả các giá trị thực của tham số m để phương trình 2 2
log x  log x 1  4m 1  0 có ít 3 3
nhất một nghiệm thuộc đoạn 3 1  ;3  .  
A. m 0;2 . B. m [ 1  ; 0] .
C. m 0;  1 .
D. m 0;4 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 37/69 - Mã đề 2D2
Câu 13. Chọn đáp án đúng: Phương trình 1x 1 3  3 x  10 A. Vô nghiệm.
B. Có hai nghiệm cùng dương.
C. Có 2 nghiệm trái dâu.
D. Có hai nghiệm âm. 1
Câu 14. Tập nghiệm của phương trình
log  x  22 1  0 là 2 2 A. 0;  4  . B.   4 . C.  1  ;  0 . D.   0 .
Câu 15. Hàm số nào sau đây đồng biến trên tập xác định của nó: xx
A. y    .
B. y  0, 5 .  e  xx 2   2  C. y    . D. y  .    2     3  1
Câu 16. Cho hàm số y  ln
. Trong các khẳng định sau đây khẳng định nào đúng? x 1 A. e y xy  1. B. e y xy  1. C. ey xy   1. D. e y xy  1.
Câu 17. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Hàm số y  log
x  2 đồng biến trên 2;  . 2  
B. Hàm số y  log
x 1 nghịch biến trên  1  ;  . 1   3
C. Đồ thị hàm số y  log x 0  a  
1 nằm phía trên trục Ox . a
D. Đồ thị các hàm số x
y a và y  log x (với 0  a  1 ) đối xứng với nhau qua đường a
thẳng y x .
Câu 18. Phương trình 2x 1 3   1 có nghiệm là 1 1 A. x  1. B. x  . C. x   . D. x  0. 3 2 2
Câu 19. Tổng các nghiệm của phương trình 5x.3x  1 là: A. log 3 . B.  log 3 . C. log 5 . D.  log 5 . 5 5 3 3 x 1  x  1 
Câu 20. Nghiệm của bất phương trình 2 3    là  9  6 4 4 A. x  . B. x  0 . C. x  . D. x  . 7 3 3
Câu 21. Trong các mệnh đề sau đây mệnh đề nào sai?
A. Đồ thị hàm số 3x y
nhận trục Oy là tiệm cận đứng. B. Hàm số 2 1 e x y   có đạo hàm là 2 1 2e x y    . x  1 
C. Hàm số y    nghịch biến trên  .  2  D. Hàm số 2x y  đồng biến trên  .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 38/69 - Mã đề 2D2 4 0,75  3  1   1 
Câu 22. Tính K       , ta được  16   8  A. K  18 . B. K  16 . C. K  12 . D. K  24 .
Câu 23. Tập nghiệm của bất phương trình 2 log x  log x  2 là 1 1   2 2 A. T   2  ;  . B. T   2  ; 2 . C. T   1  ; 2 . D. T   2  ;   1  2;  . 2 2
Câu 24. Tìm m để phương trình x 1x x 1 4  4.2  x
 3m  4  0 có nghiệm 3 9 3 A. 0  m  . B. 0  m  . C. 0  m  . D. m  0 . 4 4 4
Câu 25. Biết log 5  a , log 3  b . Khi đó giá trị của log 24 2 5 15 3  ab a 1 a 1 b A. . B. . C. . D. . a b   1 ab 1 b 1 ab 1
----------HẾT---------- ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A C D D D D B B D C B C A A A C C D D A D D A A
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 39/69 - Mã đề 2D2 SỞ GD&ĐT DAKLAK
KIỂM TRA 1 TIẾT TOÁN 12 CHƯƠNG 2
TRƯỜNG THCS _THPT ĐÔNG DU NĂM HỌC 2017 - 2018
(Đề thi có 04 trang)
MÔN GT 12 – Khối lớp 12
Thời gian làm bài : 45 phút (không kể thời gian phát đề)
Họ và tên thí sinh:...................................................SBD:..................... Mã đề thi 981 Câu 1.
Cho hàm số y   x   1 2 4 1 có tập xác định là  1  1   1  1  A. 0;  . B.  \  ;  . C. ;   . D.  .  2 2   2 2  1 A Câu 2.
Cho hai biểu thức A  log 15  log 18  log 10 và B  log 2  log 3. Giá trị của là 9 9 9 36 1 2 B 6 A. 4 . B. 8 . C. 9 . D. 3 . Câu 3. Biến đổi 3 5 4 x
x x  0 thành dạng lũy thừa với số mũ hữu tỉ, ta được 20 23 21 12 A. 3 x . B. 12 x . C. 12 x . D. 5 x . Câu 4.
Cho hàm số f x 3 2 
x x  1 . giá trị f 0 là 2 1 A. 3 . B. 1. C. . D. . 3 3 Câu 5.
Cho a , b  0 và a , b  1, x và y là hai số dương. Tìm khẳng định sai trong các khẳng định sau:
A. log  xy  log x  log y . B. 2016 log x  2016 log x . a a a a a log x C. 2 2 2 log x  4  log x . D. log b x  . 1 a a log a a b Câu 6. Giải phương trình 2 3
log x  2 log x  75  0 (1) một học sinh thực hiện theo các bước sau:. 1 2 2
(I) Điều kiện xác định x  0 . (II) 2
(1)  9 log x  2 log x  75  0 . 2 2 log x  3 2 (III)   25 . log x   2  9
(IV)  log x  3  x  8 . Vậy (1) có nghiệm duy nhất là x  9 . 2 Các bước đúng là A. (I), (II), (III).
B. (I), (II), (III), (IV). C. (I), (II).
D. Không bước nào đúng. Câu 7. Phương trình 9x 3.3x
 2  0 có hai nghiệm x , x x x
. Giá trị của A  2x  3x là 2  1 2  1 1 2 A. 1. B. 4 log 2 . C. 3log 2 . D. 2 log 4 . 3 3 3 Câu 8.
Tích các nghiệm của phương trình log x  log x 1  1là 2 2   A. 2. B. 1. C. 3. D. 2  . Câu 9.
Cho x , y là hai số thực dương và m , n là hai số thực tùy ý. Đẳng thức nào sau đây là sai ? n mn m A.   n  . n xy x y . B. m. n
x y   xy . C. n n.m xx . D. m. n m n x x x   .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 40/69 - Mã đề 2D2
Câu 10. Số nghiệm của phương trình x 2 1  1 8 2 x   là A. 2 . B. 1. C. 0 . D. 3 . Câu 11. Hàm số 2  ex y x
nghịch biến trên khoảng: A.  2  ;0 . B.  ;  2   . C. 1; . D.  ;   1 .
Câu 12. Nghiệm của bất phương trình 5.4x 2.25x 7.10x    0 là
A. 0  x  1. B. 1   x  1.
C. 0  x  1.
D. 0  x  2 .
Câu 13. Cho log 3  m , ln 3  n thì ln 30 là n n n m A. ln 30  1 . B. Đáp số khác. C. ln 30   n . D. ln 30  . m m n
Câu 14. Tìm tập nghiệm S của bất phương trình 2
log x  5 log x  4  0 2 2
A. S  0; 2 16; .
B. S   ;   1  4;  .
C. S  2;16 .
D. S  ;2 16;  .
Câu 15. Giải bất phương trình log 3x 1  3. 2   10 1 A. x  . B. x  3 . C. x  3 . D. x  3 . 3 3  1  2x
Câu 16. Hàm số y  ln    có đạo hàm là  x 1  ex 1 2x 1 2x A. y    . B. y     . x  ln 2  1 x 1 ex x 1 e 1 2x 1 2x C. y    ln 2 . D. y    . x  ln 2  1 x 1 ex x 1 e y x y b
Câu 17. Cho ba số thực dương , a ,
b c khác 1. Đồ thị x y a các hàm số x y a , x y b , x
y c được cho x
trong hình vẽ bên. Mệnh đề nào dưới đây đúng? y c
A. c a b .
B. b c a . 1
C. a c b .
D. a b c . O x
Câu 18. Phương trình 4x  2 .2x m
m  2  0 có 2 nghiệm phân biệt khi và chỉ khi:
A.  2  m  2 . B. m  2 . C. m  2 .
D. Không có giá trị nào của m .  1 
Câu 19. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 1 .e x y x   trên đoạn ;3  lần lượt là 2    4 e 9 e 4 e A. ; . B. ; . C. ; 0 . D. ; 0 . e 4 2 e 4 e 4
Câu 20. Tập xác định của hàm số y  log  x   2 1  log x là 3 2 A. 0;  . B.  1  ;  . C.  1
 ;0  0; . D.  1  ;0 .
Câu 21. Các khẳng định sau khẳng định nào sai? A. Hàm số 2x y  đồng biến trên  .
B. Hàm số y  log x đồng biến trên khoảng 0;  . 2
C. Đồ thị hàm số 3x y
có tiệm cận đứng là đường thẳng x  0 .
D. Đồ thị hàm số y  ln x có tiệm cận đứng là đường thẳng x  0 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 41/69 - Mã đề 2D2
Câu 22. Tập nghiệm của bất phương trình 2 log x 1  log 5  x 1 là 2   2   A.  3  ;3 . B. 3;5. C. 1;5 . D. 1;  3 .
Câu 23. Cho hàm số y x  ln  x  
1 . Khẳng định nào sau đây là đúng?
A. Hàm có tập xác định là  \   1  .
B. Hàm số nghịch biến trên  1  ;0 .
C. Hàm số đồng biến trên  ;  0 .
D. Hàm số đồng biến trên  1  ;  .
Câu 24. Số nghiệm nguyên nhỏ hơn 5 của bất phương trình:  x   2 2
1 x  2x  3  0 là A. 6 nghiệm. B. 5 nghiệm. C. 7 nghiệm. D. vô số.
Câu 25. Đạo hàm của hàm số y   2
ln x x   1 là 1 1 2x 1 2x 1 A. . B. . C. . D. . ln  2 x x   1 2 x x 1 ln  2 x x   1 2 x x 1
Câu 26. Khi tới nhà bạn gái chơi, mẹ bạn gái của anh Lang hỏi cháu có xe hơi chưa? Anh Lang vì muốn
cưa đổ cô nàng nên về quyết định mua trả góp chiếc KIA MORING với giá 300 triệu đồng
theo hình thức trả góp. Anh Lang muốn trả trong vòng 2 năm, với lãi suất 0, 6% . Hỏi hàng
tháng anh Lang phải trả khoản tiền cố định là bao nhiêu?
A. 13.46 triệu đồng.
B. 14, 45 triệu đồng. C. 14, 09 triệu đồng. D. 12,88 triệu đồng.
Câu 27. Phương trình  x     2 log 1
log x  2x m có nghiệm duy nhất khi và chỉ khi  5  5  5 m  5 m m A.  4 . B. m  . C.  4 . D.  4 .  4   m  1  m  1  m  1 
Câu 28. Khẳng định nào dưới đây là sai? 2016 2017 A. 2 1  3 2  2 . B.  2   1   2   1 . 2018 2017 2017 2016  2   2  C.  3   1   3   1 . D. 1   1  .  2   2     
Câu 29. Sự tăng trưởng của một loại vi khuẩn theo công thức  .ert S A
trong đó A là số lượng vi khuẩn
ban đầu, r là tỉ lệ tăng trưởng r  0 , t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn
ban đầu là 100 con và sau 5 giờ có 300 con. Khi đó sau thời gian bao lâu thì số lượng vi
khuẩn tăng gấp 10 lần so với số lượng ban đầu: 5 3 3ln 5 5ln 3 A. t  (giờ ). B. t  (giờ ). C. t  (giờ ). D. t  (giờ ). log 3 log 5 ln10 ln10
Câu 30. Nghiệm của phương trình log x  log x  6  log x  2 là 5 5   5  
A. x  0 ; x  1 .
B. x  –3 ; x  2 . C. x  2 . D. x  1 .
Câu 31. Một người gửi tiết kiệm 50 triệu đồng vào ngân hàng với lãi suất 7% một năm. Biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu.
Nếu sau 5 năm mới rút lãi thì người đó thu được số tiền lãi là
A. 70,128 triệu đồng.
B. 50, 7 triệu đồng.
C. 20,128 triệu đồng. D. 3,5 triệu đồng.
Câu 32. Phương trình 2 x 2 2  4  4  2 x x x có tập nghiệm là A. 1; 2. B. 1;1;  4 . C. 1;  4 . D. 1;  2 . ------ HẾT ------
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
1 2 C D C A C A B B A A C A C B C B A C C D B B D A A C A C C C
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 42/69 - Mã đề 2D2 UBNN HUYỆN CHÂU THÀNH
ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG II GIẢI TÍCH 12 TRUNG TÂM GDNN - GDTX
(25 câu trắc nghiệm)
Họ, tên thí sinh:.................................... Lớp:………. Mã đề thi 132 Câu 1. Hàm số 3 2 y
2x x 1 có đạo hàm f 0 là 1 1 A. 2. B.  . C. . D. 4 . 3 3 log 5 Câu 2. Giá trị của a a là 1 A. 25 . B. 5 . C. 5 . D. . 5 Câu 3.
Trong các hàm số sau, hàm số nào đồng biến trên khoảng 0;  :
A. y  log x .
B. y  log x, a  3  2 . a 6
C. y  log x . D. y  log x . 1 3 4 Câu 4.
Cho log 5  a;log 7  b;log 3  c .Tính log 35 bằng: 27 8 2 12 3b  2ac 3b  3ac 3b  3ac 3b  2ac A. . B. . C. . D. . c  3 c  2 c 1 c  2 4 Câu 5. Biểu thức 3 2 3
a : a viết dưới dạng lũy thừa: 5 2 5 7 A. 3 a . B. 3 a . C. 8 a . D. 3 a . Câu 6.
Cho log 6  a . Khi đó log 18 tính theo a là 2 3 2a 1 a A. . B. . C. 2a  3 . D. 2  3a . a 1 a 1 Câu 7. 4 log 32 bằng 1 8 5 4 5 A. . B. . C.  . D. 3 . 4 5 12 Câu 8. Đạo hàm của hàm số 3 y x là: 4 1 1 1 1 A. 3 x . B. . C. . D. . 3 3 2 3 3 x 2 x 3 2 x Câu 9.
Hàm số y  log  2
x x  5 có đạo hàm là : 2  2x 1 2x   1 ln 2 2x 1 A. y  . B. y  .
C. y  2x   1 ln 2 . D. y  .  2
x x  5ln 2 2 x x  5 2 x x  5
Câu 10. Hàm số nào dưới đây là hàm số lũy thừa: 1 A. 3
y x (x  0) .
B. Cả 3 câu còn lại đều đúng. C. 1 y x (x  0) . D. 3 y x .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 43/69 - Mã đề 2D2
Câu 11. Cho f x 2
 ln x . Đạo hàm f e bằng 3 4 1 2 A. . B. . C. . D. . e e e e
Câu 12. Biến đổi 3 5 4 x
x , (x  0) thành dạng lũy thừa với số mũ hữu tỉ ta được: 20 23 21 12 A. 3 x . B. 12 x . C. 12 x . D. 5 x . 8log 19
Câu 13. Giá trị của 2 a a là: A. 2 19 . B. 8 19 . C. 16 19 . D. 4 19 . Câu 14. Hàm số
  2  2  2ex y x x có đạo hàm là
A.   2 ex y x .
B.   2  2 ex y x . C. 2   ex y x . D. Kết quả khác.
Câu 15. Nếu log 4  a thì log 4000 bằng: A. 3  a . B. 4  a . C. 3  2a . D. 4  2a .
Câu 16. Tìm mệnh đề đúng trong các mệnh đề sau: x  1 
A. Đồ thị hàm số x
y a và y    ( 0  a  1) thì đối xứng với nhau qua trục tung.  a B. Hàm số x
y a với 0  a  1 là một hàm số đồng biến trên  :  .
C. Đồ thị hàm số x
y a ( 0  a  1 ) luôn đi qua điểm a;  1 . D. Hàm số x
y a với a  1 là một hàm số nghịch biến trên  :  .
Câu 17. Giá trị của 5 3 log a a a a là: a 1 1 13 A. . B. 4 . C. . D. . 2 4 10
Câu 18. Hàm số y  log  2 4x x có tập xác định là 5  A.  . B. 2;6 . C. 0; 4 . D. (0; ) ¥  . 1
Câu 19. Cho y  ln
. Hệ thức liên hệ giữa y và y không phụ thuộc vào x là 1 x
A. y  2 y  1 . B. e y y   0 . C. 4e y y   0 .
D. yy  2  0 . 4 1 2    3 3 3 a aa  
Câu 20. Cho a ,  
b là các số dương. Khi đó, A  có giá trị là 1 3 1    4 4 4 a a a     A. 4a . B. 2a . C. 3a . D. a . 4 0,75  3  1   1 
Câu 21. Tính: K       , ta được:  16   8  A. 16 . B. 12 . C. 18 . D. 24 . 2 1,5 
Câu 22. Tính: K       3 0, 04 0,125 , ta được: A. 125 . B. 90 . C. 121. D. 120 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 44/69 - Mã đề 2D2
Câu 23. Hàm số y   2
ln x  5x  6 có tập xác định là A. 0;  . B.  ;  0 . C. 2;3 . D.  ;
 2  3;  . 2 1 1  b b   
Câu 24. Cho a , b là các số dương. Khi đó, 2 2 B  1 2   : a b   có giá trị là  a a      1 3a A. . B. 2a . C. . D. a . a 2 1 ln x
Câu 25. Hàm số y   có đạo hàm là x x ln x ln x ln x A.  . B. . C. Kết quả khác. D. . 2 x 4 x x
----------- HẾT ----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 45/69 - Mã đề 2D2
SỞ GD-ĐT TỈNH BÌNH ĐỊNH
ĐỀ KIỂM TRA CHƯƠNG II
TRƯỜNG THPT NGUYỄN TRUNG TRỰC Môn: Toán Thời gian: 45 phút.
Họ tên học sinh:........................................ Lớp: 12A ……...
I - Phần trắc nghiệm (6 điểm) 3 7 Câu 1. log a 1
( a  0 , a  1) bằng a 7 2 5 A.  . B. . C. 4 . D. . 3 3 3 Câu 2.
Cho a  0 và a  1. Tìm mệnh đề đúng trong các mệnh đề sau: A. log x xy x y a
có nghĩa với mọi x . B. log log .log a a a . C. log 1  a a n x n x a và log 0 a . D. log log
( x  0 , n  0 ). a aCâu 3.
Hàm số y   x   3 2 9 1 có tập xác định là  1 1   1 1  A.  . B.  ;   . C. 0;  .
D.  \  ;  .  3 3   3 3 Câu 4. Cho f   sin 2  e x x
. Đạo hàm f 0 bằng A. 3 . B. 1. C. 2 . D. 4 . Câu 5.
Hàm số f x 3 2
 2x x 1 có đạo hàm f 0 là 1 1 A. 2 . B.  . C. . D. 4 . 3 3 2 Câu 6. Tính   K    1,5    3 0, 04 0,125 , ta được A. 120 . B. 90 . C. 121. D. 125 . Câu 7.
Cho a  1 . Tìm mệnh đề sai trong các mệnh đề sau: A. log x  0 a khi x  1 . B. log x  0   a khi 0 x 1.
C. Đồ thị hàm số y  log x a
có tiệm cận ngang là trục hoành.
D. Nếu 0  x x log x  log x 1 2 thì a 1 a 2 . 2 Câu 8.
Cho a là một số dương, biểu thức 3 a
a viết dưới dạng luỹ thừa với số mũ hữu tỷ là 6 11 5 7 A. 5 a . B. 6 a . C. 6 a . D. 6 a . Câu 9. Bất phương trình: log 3x  2  log 6  5x 2   2   có tập nghiệm là  1   6  A.  3  ;  1 . B. ;3   . C. 1;   . D. 0;  .  2   5 
Câu 10. Phương trình 3x2 4  16 có nghiệm là 3 4 A. 3 . B. 5 . C. x  . D. x  . 4 3 Câu 11. Cho
. Kết luận nào sau đây là đúng?
A. .
B. . 1.
C.  0 .
D. .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 46/69 - Mã đề 2D2
Câu 12. Cho a  0 và a  1. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Tập giá trị của hàm số y  log x 0;  a là khoảng   .
B. Tập giá trị của hàm số x
y a là tập  .
C. Tập xác định của hàm số y  log x 0;  a là khoảng   .
D. Tập xác định của hàm số x
y a là khoảng 0;  .
II - Phần tự luận (4 điểm)
Giải các phương trình và bất phương trình sau: 2 a) x 3x 1 4 2   . b) x 9 3x   6  0 .
c) log x  log  x  6  log  x  4 . Bài làm: ĐÁP ÁN THAM KHẢO
I - Phần trắc nghiệm (6 điểm) 1 2 3 4 5 6 7 8 9 10 11 12 A D D C B C C D C D A C
II - Phần tự luận (4 điểm) 1 a) x  hoặc x  1 . b) x  1 c) x  6 2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 47/69 - Mã đề 2D2
SỞ GD&ĐT KIÊN GIANG
KIỂM TRA TOÁN 12 - MŨ LOGARIT
TRƯỜNG THPT CÂY DƯƠNG Thời gian: 45 phút
Họ và tên thí sinh:..............................................................SBD:..................... Mã đề thi 213 Câu 1.
Cho các số thực dương a và b , a  
1 . Tìm mệnh đề sai trong các mệnh đề dưới đây A. log 1  0 .
B. log b .log b . a a a C. log   . D. log a  1.  b .log b  0 aa a Câu 2.
Biết log b  3 và log c  4 . Tính giá trị của biểu thức T   5 2 log b .c . aa a A. T  12 . B. T  259 . C. T  23 . D. T  3888 . x  1 Câu 3. Cho hàm số y  . Tìm khẳng định đúng ex
A. y  2 y  y  0 .
B. y  2 y  y  0 .
C. y  2 y  y  0 .
D. y  2 y  y  0 . Câu 4.
Tìm tập xác định của hàm số y   x  2 . A. 2;  . B.  2  ;  . C.  ;  2   . D.  ;  2 . Câu 5.
Tìm tập nghiệm của phương trình x 1
2.9  3 x 1  0 .  1   1  A.   1 . B.   . C.  1  ;   . D.  .  2   2  4  x Câu 6.
Tìm tập xác định của hàm số y  lg . x  2 A.  4  ; 2 . B. 2; 4 . C.  ;  2
   4;  . D.  2  ; 4 . Câu 7.
Một người mỗi tháng đều đặn gởi vào ngân hàng cùng một số tiền là 10 triệu đồng vào một
ngày cố định của mỗi tháng với lãi suất kép 7% /năm. Hỏi sau ít nhất bao lâu thì người đó thu
được cả vốn và lãi là 1 tỷ đồng? Giả sử trong quá trình gởi người đó không rút tiền ra và lãi suất không thay đổi A. 2 năm 6 tháng. B. 7 năm 5 tháng. C. 6 năm 7 tháng. D. 8 năm 2 tháng. Câu 8.
Gọi S là tập hợp các số nguyên m nhỏ hơn 2018 sao cho hàm số  2x y
m 1 xác định
trên nửa khoảng 2; . Tìm số phần tử của S. A. 2016 . B. 2021 . C. 2018 . D. 2022 . Câu 9.
Biết log 3  a và log 5  b . Tính theo a và b giá trị của log 2430 . 18 18 18
A. 3a b 1.
B. 3a b 1.
C. a  3b 1.
D. a  3b 1.
Câu 10. Giải bất phương trình log x  0 . 1 2 A. x  1 . B. x  1.
C. 0  x  1. D. x  0 .
Câu 11. Đồ thị của hàm số y x   luôn đi qua điểm có tọa độ nào dưới đây? A. 1;  1 . B. 1;  1  . C. 0;  1 . D. 1;0 .
Câu 12. Tìm nghiệm của phương trình log x 1  2 . 3   A. x  9 . B. x  4 . C. x  8 . D. x  10 . 0  ,75 5 1   
Câu 13. Tính giá trị biểu thức 2 P   0, 04  . 81    A. P  1523 . B. P  3152 . C. P  2315 . D. P  5231.
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 48/69 - Mã đề 2D2
Câu 14. Tìm tham số thực m để phương trình 2
log x  2m   2
1 .log x m  4  0 có hai nghiệm thực 5 5
phân biệt x , x thỏa mãn x .x  25 . 1 2 1 2 1 3 A. m  6 . B. m  . C. m  29 . D. m   . 2 2
Câu 15. Tìm mệnh đề đúng trong các mệnh đề sau
A. Đồ thị hàm số y  log xa  0, a  
1 có tiệm cận đứng là trục Oy . a B. Hàm số x
y a a  0, a  
1 có tập xác định là 0;  .
C. Hàm số y  log xa  0, a  
1 có tập xác định là  . a
D. Đồ thị hàm số x
y a a  0, a  
1 có tiệm cận đứng là trục Oy .
Câu 16. Giải bất phương trình 7x  2 .
A. x  log 2 .
B. x  log 7 .
C. x  log 2 .
D. x  log 7 . 7 2 7 2 2
Câu 17. Tìm đạo hàm của hàm số y   2  x x 5 1 3 2 3  2 A. y  . 2
1 x x  5 . B. y  .1 2x. 2
1 x x 5 . 5 5 3 5 3  2  C. y  .1 2x. 2
1 x x  5 . D. y  .1 2x. 2
1 x x  5 . 2 5
Câu 18. Phương trình 2
lg x  lg x 1  0 có tất cả bao nhiêu nghiệm? A. 1. B. 2 . C. 3 . D. 0 . 1
Câu 19. Cho số thực x dương. Viết biểu thức 4 3 2
Q x . x dưới dạng lũy thừa với số mũ hữu tỉ 11 4 5 A. 6 Q x . B. 5 Q x . C. 4 Q x .
D. Q x .
Câu 20. Tìm tất cả các tham số thực m để bất phương trình x 1
4  2 x m  3  0 có nghiệm. A. m  4 . B. m  3 . C. m  3 . D. m  4 .
Câu 21. Cho các số thực dương a và b thỏa mãn 2 2
a b  23ab . Tìm mệnh đề đúng trong các mệnh đề sau 1 1 1 1 A. log a b  1 log a  log b . B. log a b  1 log a  log b . 2   5   5 5 2 2 2 2 2 2 1 1 C. log a b  1 log a  log b . D. log
a b  log a  log b . 2   5   5 5 2 2 2 2
Câu 22. Cho số thực dương a , a   1 . Tính giá trị của 3 log a . a 1 2 3 A. 6 . B. . C. . D. . 6 3 2
Câu 23. Tìm tập nghiệm của bất phương trình lg 2x  3  lg x .  3   3  A.  ;  3 . B. 3; . C. 3  ;   . D. ;3   .  2   2 
Câu 24. Đồ thị nào dưới đây là đồ thị của hàm số mũ x
y a với 0  a  1. y y y y 1 1 O 1 x O x O x A. . B. . C. O x . D. .
Câu 25. Bất phương trình 1
4 x 129.2x  32  0 có tất cả bao nhiêu nghiệm nguyên? A. 8 . B. 31. C. 32 . D. 6 .
……….HẾT……….
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 49/69 - Mã đề 2D2 SỞ GD & ĐT LONG AN
ĐỀ KIỂM TRA TẬP TRUNG HỌC KỲ 1 – LẦN 3
TRƯỜNG THPT CHUYÊN LONG AN MÔN: GIẢI TÍCH 12
(Thời gian làm bài 45 phút)
I. PHẦN TRẮC NGHIỆM: Câu 1.
Tìm mệnh đề đúng trong các mệnh đề sau?
A. Đồ thị hàm số y  log x và y  log x với 0  a  1 đối xứng nhau qua trục hoành. a 1 a
B. Hàm số y  log x với 0  a  1 là hàm số đồng biến trên khoảng 0;  . a
C. Hàm số y  log x với 0  a  1 có tập xác định là  . a
D. Hàm số y  log x với a  1 là hàm số đồng biến trên khoảng 0;  . a Câu 2.
Giả sử a là số thực dương khác 1. Biểu thức 3
a a được viết dưới dạng a . Khi đó giá trị của là 5 2 11 1 A.  . B.  . C.  . D.  . 3 3 6 6  Câu 3.
Tập xác định của hàm số y   x   4 2 1 là
A. D   \   1 .
B. D  ;   1  1;  . C. D  ; 4    1;  . D. D   . Câu 4. Viết biểu thức 3 4 P
x . x x  0, x  
1 dưới dạng lũy thừa với số mũ hữu tỉ là 5 5 1 1 A. 12
P x . B. 4 P x . C. 7 P x . D. 12 P x . 1 1 1 Câu 5.
Cho n  1 là một số nguyên. Tính giá trị của P    ...  ? log n! log n! log n! 2 3 n
A. P n . B. P  1 . C. P  0 .
D. P n!. Câu 6.
Cho các số thực a, b, m, n với a, b  0 . Mệnh đề nào sau đây là sai? ma m A. ma . m b m m   . B.  n m m n a a   . C. 2 a a . D.  .
a b  a .b .  b Câu 7.
Hàm số nào sau đây đồng biến trên  ? x x  1 
A. y  log  2 x 1 .
B. y   2 .
C. y  log  2 x  2x 1 . D. y  . 4  1     3  4 Câu 8.
Cho các số thực a, b  0 . Khi rút gọn biểu thức 2
P  2 log a  log b được biểu thức nào sau đây? 2 1 2 2  a   2a A. P  log . B. P  log ab . C. P  log . D. P  log  2 2ab . 2  2  2 2   2    b  2  b Câu 9.
Tìm tất cả các giá trị của tham số m để phương trình 9 log x 2 3
 log x m  0 có nghiệm 3 1 3 thuộc khoảng 0;  1 ?  1   1   1 
A. m   ;0 .
B. m  ;   . C. m  0;  . D. m  ;    . 4      4   4 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 50/69 - Mã đề 2D2
Câu 10. Cho các số thực dương a, b . Trong các mệnh đề sau, mệnh đề nào đúng? 1 A. 2 log a  log a . B. log a  log b . 2 2 2 2 2 a 1  a 1  C. log  2 2 a b  2 log a b .
D. log a  log b a b . 2  2   3 3 4 4 2 1  
Câu 11. Cho a   3  a   3 1 1
. Khi đó ta có thể kết luận gì về a ?
A. 0  a  1. B. a  2 .
C. 1  a  2 . D. a  2 .
Câu 12. Tìm nghiệm của phương trình log x 1  3 ? 2  
A. x  7 . B. x  10 . C. x  9 . D. x  8 .
Câu 13. Hình bên là đồ thị của hàm số nào sau đây? y
A. y  log x . B. 2x y  . 2 x  1  1
C. y    .
D. y  log x . 3  2  O x
Câu 14. Cho log x  5 . Tính giá trị của biểu thức P  log x ? 3 3 5 5
A. P  5 . B. P  25 . C. P  . D. P  . 2 3
Câu 15. Với các số thực dương a , b bất kỳ. Khẳng định nào sau đây là khẳng định đúng?a
A. log ab  log a b . B. log  log a   . bb  log a
C. log ab  log a  log b . D.
 log a b . log b
Câu 16. Tính đạo hàm của hàm số y  log ln 2x . Khi đó, ta thu được kết quả nào sau đây? 1 1 1 2 A. y  . B. y  . C. y  . D. y  . x ln 2 . x ln 2 . x ln10 2 . x ln 2 . x ln10 . x ln 2 . x ln10
Câu 17. Tìm tất cả giá trị của tham số m để phương trình 3 2
x  3x 1 log m  0 có đúng một 3 nghiệm? m  3 m  3 1 A.   1 . B. m  . C. 1 . D. m  3 . m  27 0  m   27  27
Câu 18. Tìm tập nghiệm của phương trình 2 log  2
x x 1  log x 1 . 2    2 A. S    0 . B. S    2 .
C. S  0;  2 . D. S   .
Câu 19. Cho số thực dương x thỏa log log x  log
log x . Tính giá trị của T  log x . 3  27  27  3  3 1 3
A. T  27 . B. T  3 3 . C. T  . D. T  . 3 3
Câu 20. Số nghiệm của phương trình  x  2 log 1  2 là bao nhiêu? A. 1. B. 0 . C. 2 . D. 3 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 51/69 - Mã đề 2D2
Câu 21. Một người lần đầu gửi ngân hàng 100 triệu đồng với kì hạn 3 tháng với lãi suất 3% của một
quý (một quý có 3 tháng) và tiền lãi từng quý sẽ nhập vào vốn (hình thức lãi kép). Sau đúng 6
tháng, người đó gửi thêm vào 100 triệu đồng với kì hạn và lãi suất như trước đó. Tổng số tiền
người đó nhận được 1 năm kể từ khi gửi thêm tiền lần hai sẽ gần nhất với số tiền nào sau đây?
A. 219 triệu đồng.
B. 262 triệu đồng.
C. 232 triệu đồng.
D. 313 triệu đồng. 3 5 3 5
Câu 22. Cho a , b là các số dương a  1, b  1 thỏa mãn 4 7 a a , log  log
. Phát biểu đúng là b 4 b 7
A. log a  0 .
B. 0  log b  1.
C. 0  log a  1. D. log b  1. b a b a
II. PHẦN TỰ LUẬN: 2 2
Giải các phương trình sau: a) 2x 1  x x 2x2 2  9.2  2
 0 . b) log x  log x  1. 1 3 2 ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22
A B B A B B B B C D D C B C C B C B B B C A log 2 2
Đáp số tự luận: a) x  1, x  2 b) 3 x  3
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 52/69 - Mã đề 2D2
SỞ GD & ĐT TUYÊN QUANG
ĐỀ KHẢO SÁT ÔN THI THPT QUỐC GIA LẦN 1
TRƯỜNG THPT ĐÔNG THỌ MÔN: TOÁN 11
(Thời gian làm bài 90 phút)
Họ và tên thí sinh:..............................................................SBD:..................... Mã đề thi 101 Câu 1. Cho    . x f x
x  . Đạo hàm f   1 bằng
A.  ln . B. 2 ln.
C. ln.
D. 1 ln . 1 log2 33lo 8g 5 Câu 2. Giá trị của 2 4 bằng A. 25 . B. 50 . C. 75 . D. 45 . 2 Câu 3.
Cho a là một số dương, biểu thức 3 a
a viết dưới dạng luỹ thừa với số mũ hữu tỷ là 6 11 5 7 A. 5 a . B. 6 a . C. 6 a . D. 6 a . 2 3 2 5 4  a a a Câu 4. log   bằng a  15 7 a    12 9 A. 3. B. . C. . D. 2 . 5 5 Câu 5. Giỏ trị của log 0,125 bằng 0,5 A. 5 . B. 3 . C. 4 . D. 2 . Câu 6.
6. Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng nó xác định? 3  A. 3 y x . B. 4 y x . C. 4 y x  . D. y = 4 x . ex Câu 7.
Cho f x 
. Đạo hàm f   1 bằng 2 x A. 6e . B. 4e . C. 2 e . D. e . Câu 8.
Cho a  0 và a  1 , x và y là hai số dương. Tìm mệnh đề đúng trong các mệnh đề sau: 1 1
A. log  x y  log x  log y . B. log  . a a a a x log x a x log x C. log a  .
D. log x  log a.log x . a y log y b b a a 1 Câu 9. Nếu log x
log 9  log 5  log 2 ( a  0 , a  1 ) thì x bằng a 2 a a a 2 3 6 A. . B. . C. . D. 3 . 5 5 5 4 0,75  3  1   1 
Câu 10. Tính: K       , ta được:  16   8  A. 24 . B. 12 . C. 16 . D. 18 .
Câu 11. Đạo hàm của hàm số 2 3 2   x y là A. 2x3 2 .ln 2 .
B. x   2x2 2 3 2 ln 2 . C. 2 3 2.2 x . D. 2 x3 2.2 .ln 2 .
Câu 12. Hàm số nào dới đây thì nghịch biến trên tập xác định của nó? A. y  log x .
B. y  log x .
C. y  log x .
D. y  log x . 3 e 2
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 53/69 - Mã đề 2D2 Câu 13. Biểu thức 3 6 5
x. x. x ( x  0 ) viết dưới dạng luỹ thừa với số mũ hữu tỷ là 7 5 2 5 A. 3 x . B. 2 x . C. 3 x . D. 3 x . Câu 14. Cho
. Kết luận nào sau đây là đúng?
A. .
B. . 1.
C.
D.  0 .   2 3 1
Câu 15. Rút gọn biểu thức 2  3 b : b
( b  0 ), ta đợc: A. 4 b . B. 3 b . C. 2 b . D. b .
Câu 16. Hàm số y  log  2 4x x có tập xác định là 5  A. 0;  . B. 0;4 . C.  . D. 2;6 . Câu 17. Cho   sin 2 e x f x
. Đạo hàm f 0 bằng A. 1. B. 4 . C. 3 . D. 2.
Câu 18. Một khu rừng có trữ lượng gỗ 5
4.10 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng
đó là 4% mỗi năm. Tìm khối lượng gỗ của khu rừng đó sau 5 năm A. 5 3 4,8666.10 (m ). B. 5 3 4, 0806.10 (m ). C. 5 3 4, 6666.10 (m ). D. 5 3 4, 6888.10 (m ).
Câu 19. Giá trị của 3 7 log
a ( a  0 , a  1 )bằng 1 a 5 2 7 A. . B. . C. 4. D.  . 3 3 3 1 log210
Câu 20. Giá trị của 2 64 bằng A. 400 . B. 1000 . C. 200 . D. 1200 . 2 Câu 21. Hàm số ln 2 x x y  
có đạo hàm y là 2  1  2  1  A. ln  2 2 xx x . ln xx   B.  2x 2 ln 2.    x   x  2 ln 2 2 xx ln  1  2 xx C. . D.  2x .   ln 2  x  ln 2
Câu 22. Cho a  0 và a  1 . Tìm mệnh đề đúng trong các mệnh đề sau:
A. log xy  log x.log y .
B. log x có nghĩa với x  . a a a a C. log n
x n log x ( x  0 , n  0 ).
D. log 1  a và log a  0 . a a a a Câu 23. 4 log 32 bằng 1 8 5 5 4 A. . B. 3. C. - . D. . 4 12 5
Câu 24. Cho f x   4 ln x  
1 . Đạo hàm f   1 bằng A. 2 . B. 1. C. 4 . D. 3 .
1 3x  3x
Câu 25. Cho 9x  9x  23 . Khi đó biểu thức K  có giá trị bằng
5  3x  3x 5 2 3 A.  . B.  . C. . D. 2 . 2 5 2
----------- HẾT ---------- 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A C D A B A D D C A D B D C A B D A D B B C C A B
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 54/69 - Mã đề 2D2 SỞ GD & ĐT ĐÀ NẴNG
ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG II
TRƯỜNG THPT TÔN THẤT TÙNG MÔN: TOÁN 12
(Thời gian làm bài 90 phút)
Họ và tên thí sinh:..............................................................SBD:..................... Mã đề thi 817
I. Phần trắc nghiệm: (6 điểm). x  2 Câu 1.
Tập xác định của hàm số y  log là: 1 x A.  ;   1  2;  . B. 1; 2 . C.  \   1 . D.  \ 1;  2 . Câu 2.
Khẳng định nào sai trong các khẳng định sau:
A. ln x  0  x  1.
B. log x  0  0  x  1. 2
C. log a  log b a b  0 .
D. log a  log b a b  0 . 1 1 1 1 3 3 2 2 Câu 3.
Cho hàm số y  ln 1 x . Chọn khẳng định đúng trong các khẳng định sau: 1 1 6 6
A. y2  .
B. y2  .
C. y5  .
D. y  1   . 2 3 5 5 1 1 sin x 1 Câu 4.
Trong các hàm số: f x  ln
; g x  ln
; h x  ln . Hàm số nào có đạo sin x cos x cos x 1 hàm là cos x
A. f x .
B. g x .
C. h x .
D. g x và hx . 1 Câu 5.
Tập xác định y  là: 4x  4 A.  ;   1  2;  . B. 1; . C.  \   1 . D.  \ 1;  3 . Câu 6.
Tập xác định của hàm số  9x  3x y là: A. 0;  . B. 5; . C.  \   5 . D.  \ 0;  5 . Câu 7.
Điều kiện xác định của phươg trình log 16  2 là: 2 x3  3  3 3 A. x   \ ; 2  . B. x  2 . C. x  2 . D. x  . 2    2 2 Câu 8.
Phương trình log 3x  2  3 có nghiệm là: 3   29 11 25 A. x  . B. x  . C. x  . D. x  87 . 3 3 3 Câu 9. Phương trình log  2 x  6  log
x  2  1 có tập nghiệm là: 3  3  
A. T  0;  3 . B. T   . C. T    3 .
D. T  1;  3 .
Câu 10. Số nghiệm của phương trình log . x log
2x 1  2 log x là: 2 3   2 A. 2 . B. 1. C. 3 . D. 0 .
Câu 11. Tập nghiệm của bất phương trình log  2
x  5x  7  0 là: 1  2
A. 2  x  3 . B. x  3 . C. x  2 .
D. x  2 hoặc x  3 .
Câu 12. Biết phương trình 16x 17.4x 16  0 có 2 nghiệm là x và x . Tính tổng x x ? 1 2 1 2 A. 0 . B. 1. C. 2 . D. 3 .
II. Phần tự luận: (4 điểm) 2 Câu 1.
(2,0 điểm) Giải các phương trình sau: a) 2x 7x5 2  1. b) 2
log x  9.log x  10 . 2 2 2x  3 Câu 2.
(2,0 điểm) Giải các bất phương trình sau: a) x 1  x2 4  2  3 . b) log  2 . 2 x 1
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 55/69 - Mã đề 2D2
SỞ GD & ĐT BÌNH DƯƠNG
ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT BÌNH AN MÔN: TOÁN 12
(Thời gian làm bài 45 phút)
Họ và tên thí sinh:..............................................................SBD:..................... Mã đề thi 485 Câu 1.
[2D2-3] Cho bất phương trình: 9x     1 .3x mm  0  
1 . Tìm tất cả các giá trị của tham số m
để bất phương trình   1 có nghiệm đúng x   1? 3 3 A. m   .
B. m  3  2 2 .
C. m  3  2 2 . D. m   . 2 2 2 Câu 2.
[2D2-2] Cho phương trình: x 4x5 3
 9 . Tổng lập phương các nghiệm của phương trình là A. 28. B. 26. C. 25. D. 27. Câu 3. [2D2-2] Cho ,
a b là hai số thực dương.và a  1. Khẳng định nào đúng? 1 A. log . a b  2  2 log . b B. log . a b  log . b 2   2   a a 2 a a 1 1 1 C. log . a b  log . b D. log . a b   log . b 2   2   4 a a 2 2 a a Câu 4.
[2D2-2] Số nghiệm của phương trình: 6.9x 13.6x 6.4x    0 là A. 3. B. 0. C. 2. D. 1. 2x 1 Câu 5.
[2D2-2] Đạo hàm của hàm số: y  là 5x x x 1  x 1   2  2  2   1  A.   .ln  5 x y  .ln 5.  
B. y  xx .      5  5  5   5  x x x 1  x 1   2  2  1   2   1  C. y  ln  ln 5.    
D. y  xx .      5  5  5   5   5  Câu 6.
[2D2-2] Số thực a thỏa mãn điều kiện log log a  0 là 3  2  1 1 A. . B. 3 . C. 2 . D. . 2 3 Câu 7.
[2D2-3] Bất phương trình 2 log x  5 log x  6  có tập nghiệm là 0.2 0.2  1 1   1  A. 0;3 . B. ;   . C. 0;   . D. 2;3 .  125 25   25  1 Câu 8.
[2D2-2] Cho hàm số y  ln
, hệ thức liên hệ giữa y và y không phụ thuộc vào x là x 1
A. yy  2  0 . B. e y y   0 .
C. y  2 y  1 . D.   4 y y e  0 . 1 Câu 9.
[2D2-3] Tìm tất cả các giá trị thực của tham số m để hàm số y   log x m 3 2m 1 x
xác định trên 2;3 .
A. 1  m  2 . B. 1   m  2 .
C. 1  m  2 . D. 1   m  2 . 1
Câu 10. [2D2-2] Với 0  x  1, ta có 1 x 4 . 2 1 x 1 x3 1 x3 1 x 1 x A. 4 . B. 4  . C. 4 . D. 4  . 1 x 1 x 1 x 1 x
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 56/69 - Mã đề 2D2
Câu 11. [2D2-2] Cho log 3  a; log 5  b thì log 8 tính theo a, b là 30 30 30 3
A. 31 a b . B. .
C. 31 a b .
D. a b . a b
Câu 12. [2D2-2] Phương trình log  2
x  4x 12  2 3 
A. Có hai nghiệm trái dấu.
B. Có hai nghiệm dương. C. Vô nghiệm.
D. Có hai nghiệm âm.
Câu 13. [2D2-2] Giá trị lớn nhất của hàm số   2  ex f x x trên  1  ;  1 là 1 A. 0 . B. . C. e . D. 2e . e 2
Câu 14. [2D2-1] Cho a là một số dương, 3 a
a viết dưới dạng lũy thừa với số mũ hữu tỷ là 2 11 7 6 A. 6 a . B. 6 a . C. 6 a . D. 5 a .
Câu 15. [2D2-1] Cho a   và n k   * 2
1 k    , n
a có căn bậc n là n A. a . B. a . C. a . D. 2n 1 a  . x 1  x 1 
Câu 16. [2D2-2] Bất phương trình    x 1 5 2 5 2    
tương đương với bất phương trình nào sau đây? 1 x 1 x A. x 1  log 5  2 . B. x 1  . 5 2   x 1 x 1 1 x 1 x C. x 1  . D. x 1  log 5  2 . 5 2   x 1 x 1 x x x
Câu 17. [2D2-2] Phương trình  3  2   3  2   10 có tất cả bao nhiêu nghiệm thực? A. 4 . B. 1. C. 2 . D. 3 .
Câu 18. [2D2-1] Tập giá trị của hàm số x
y a a  0, a   1 là A.  \   0 . B. 0;   . C.  . D. 0;   .
Câu 19. [2D2-2] Đồ thị  L của hàm số f x  ln x cắt trục hoành tại điểm A , tiếp tuyến của  L tại
A có phương trình là
A. y  3x .
B. y  2x 1.
C. y  4x  3 .
D. y x 1. x
Câu 20. [2D2-2] Hình bên là đồ thị của ba hàm số x y a , y y b x y a x y b , x
y c ( 0  a, ,
b c  1 ) được vẽ trên cùng một hệ
trục toạ độ. Khẳng định nào sau đây là khẳng định đúng? 1 x
A. a b c .
B. b a c . y c
C. a c b .
D. c b a . x O
Câu 21. [2D2-2] Số nghiệm của phương trình: log x 1  2 log
3x  2  2  0 là 2   2   A. 0 . B. 3 . C. 1. D. 2 . 
Câu 22. [2D2-2] Hàm số y   x   3 2 có tập xác định: A.  . B.  \   2 . C. 2;  . D. 2;  .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 57/69 - Mã đề 2D2
Câu 23. [2D2-4] Khách hàng A vay ưu đãi vốn ngân hàng 150 triệu đồng với lãi suất 0, 68% /tháng.
Ông hoàn nợ cho ngân hàng theo cách như sau: sau đúng một tháng kể từ ngày vay ông ta bắt
đầu hoàn nợ, hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ trong mỗi
tháng là như nhau và hoàn nợ trong 5 năm thì hết nợ. Hỏi theo cách đó mỗi lần hoàn nợ ông A
phải trả cho ngân hàng bao nhiêu? Biết rằng lãi suất ngân hàng không đổi trong thời gian ông hoàn nợ. 60 1020 000.1, 00685 1020 000.1, 0068 A. (đồng). B. (đồng).  60 1, 00685 1 1,0068 1 5 1020 000.1, 006860 1020 000.1, 0068 C. (đồng). D. (đồng).  5 1, 006860 1,0068
Câu 24. [2D2-1] Trong các hàm số sau đây, hàm số nào đồng biến trên  : x x x x  1     1   2  A. y    .
B. y    . C. y    .
D. y    .  3   3   2   e 
Câu 25. [2D2-2] Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A , B , C , D dưới đây. Hỏi hàm số đó là hàm số nào? y x O 1
A. y  log x . B. y  log x .
C. y  log 2x .
D. y  log x . 2 2 2 1 2 BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A A D C C C B B A A C D C C C C B D D B A B B A A
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 58/69 - Mã đề 2D2
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI KIỂM TRA ĐỊNH KÌ
TRƯỜNG THPT QUỐC OAI NĂM HỌC 2017 - 2018
MÔN TOÁN – Lớp 12A2
(Đề thi có 06 trang)
Thời gian làm bài : 90 phút (không kể thời gian phát đề)
Họ và tên học sinh :................................................... Số báo danh :............................. Mã đề A 2 x3 2 x  1  Câu 1.
Gọi S là tập nghiệm của bất phương trình 0, 25   
. Khi đó S có dạng  ; a b với  4 
a b . Tính P a b . A. 2  . B. 1. C. 0 . D. 2 . Câu 2.
Có bao nhiêu số nguyên x thỏa mãn bất phương trình log  x  40  log 60  x  2 . A. 19 . B. 20 . C. 21 . D. 18 . Câu 3.
Tính tổng T tất cả các nghiệm của phương trình
x2   x   x2 3.25 3 10 .5  3  x  0 .  2 
A. T  2  log 6 .
B. T  4  log .
C. T  4  log 3 .
D. T  3  log 2 . 5 5   5 5  7  Câu 4.
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng  2
 018; 2018 để bất phương trình 2   x     2 1 4 1 4 9 20 .3  x m
 2m  5  0 có tập nghiệm 2;2 . A. 2056 . B. 2057 . C. 2058 . D. 2060 . x x  1   1  Câu 5.
Cho bốn hàm số y x x    
1 , y  3 2 , y    3 , y  4 4 và bốn đường cong C , 1   2   2 
C , C , C như hình vẽ bên. 4  3  2  yC4 
C1 C2  Đồ thị hàm số  
1 , 2 , 3 , 4 lần lượt là
A. C , C , C , C . 4   1   3   2 
B. C , C , C , C . C3  1   2   3   4  1
C. C , C , C , C . 2   4   1   3 
D. C , C , C , C . 3   2   4   1  O x 2 5x Câu 6.
Cho hàm số f x 
. Khẳng định nào sau đây là khẳng định sai? 2x 2 x
A. f x 2
 1  x x log 2  0 .
B. f x  1   0 . 5 x log 2 5 2  5x
C. f x  1  log    0 .
D. f x 2
 1  x log 5  x  0 . 5  2x  2   Câu 7. Cho phương trình log  2 x  1 .log  2 x 2x 4 2 2 6 log x 1 1        4 log
x  2x  4  0 1 2 2 2 2    
Gọi x , x là hai nghiệm thực dương của phương trình đã cho  x x . Tính 2
T x  2x . 1 2  1 2 1 2
A. T  6 .
B. T  3  2 5 .
C. T  7 . D. T  1   3 5 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 59/69 - Mã đề 2D2 Câu 8.
Cho a , b là các số thực dương khác 1. Hình vẽ bên yC1
là đồ thị của 2 hàm số  : x C y a ,  : x C y b . 2  1  C2 
Mệnh đề nào sau đây là đúng? 1
A. b a  1.
B. b a  1 .
C. a b  1.
D. a b  1 . O x Câu 9.
Tìm tập xác định D của hàm số y  log  3
x  3x  2 . 0,5  A.  2  ;   \  1 . B.  2  ;   .
C. 1;   . D. 0;  1 . x 1
Câu 10. Tập nghiệm của bất phương trình 1 3  là 9 A.  ;    1 . B.  1  ;3 . C.  3  ;   . D. 1;   . 2
Câu 11. Tìm tập xác định của hàm số y   x   3 2 .
A. 0; . B.  . C.  \   2 . D.  2  ;  . log  2
sin x5sin x.cos x2 1 0,5 
Câu 12. Tìm nghiệm của phương trình 4  . 9  x kx k A.   1
k  . B. 1
k  .
x  arctan  k
x  arctan  k  3  5  x   kx   k 2  2 C.
k  . D.  k  1  1 x  arctan  k
x  arctan  k  5  3 3 4 5 123 124
Câu 13. Đặt a  ln 3 , b  ln 5 . Tính S  ln  ln  ln  ...  ln  ln
theo a và b . 4 5 6 124 125
A. I a  2b .
B. I a  3b .
C. I a  2b .
D. I a  3b . 1  2x
Câu 14. Cho hàm số f x  log . 2   2  1 x   1   2   3   2015   2016 
Tính tổng: S fff  ...  ff           .  2017   2017   2017   2017   2017  A. 4032 . B. 1008 . C. 2017 . D. 2016 .
Câu 15. Tìm tất cả giá trị thực của tham số m để hàm số y   2
ln x  2mx m có tập xác định là  .
A. m  0 hoặc m  1.
B. 0  m  1.
C. m  0 hoặc m  1.
D. 0  m  1. 2x 1
Câu 16. Tìm tập xác định D của hàm số f x  . log  2  x  3x 2    3   5  
A. D  0;3 .
B. D  0;3 \   2    
C. D   .
D. D   \ 0;  3 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 60/69 - Mã đề 2D2
Câu 17. Gọi S là tập nghiệm của phương trình 4x8 2x5 3  4.3  28  2log
2 . Tính tích tất cả các phần 2 tử của S . 3 3 A. 4. B.  . C. 1  . D. . 2 2
Câu 18. Phương trình log x 1  2 log
3x  2  2  0 có mấy nghiệm? 2   4   A. 1. B. 2 . C. 4 . D. 3 .
Câu 19. Mệnh đề nào sau đây là sai? A. Cho hàm số 2x y  thì y  1  ln 4 . 2
B. Cho hàm số y  log 2x   1 thì y  1  . 3ln10
C. Cho hàm số y  ln x thì y  1  1. D. Cho hàm số ex y  thì   1 ex y  .
Câu 20. Tìm tập nghiệm của bất phương trình log x 1  2 . 1   2  3   3   3  A. S   1  ;  . B. S  0;    .
C. S   ;    . D. S  1  ;    .  4   4   4 
Câu 21. Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có diện tích bằng 36 , đường thẳng AB
song song với trục Ox , các đỉnh ,
A B và C lần lượt nằm trên đồ thị của các hàm số
y  log x , y  log x , y  log
x và a là một số thực lớn hơn 1. Tìm a . a a 3 a
A. a  3 . B. 3 a  6 . C. 6 a  3 . D. a  6 .
Câu 22. Cho đồ thị ba hàm số x y a , x y b , x y c như x y c y x y a x y b
hình vẽ. Kết luận nào sau đây đúng.
A. 0  a  1  b c .
B. 0  c  1  a b .
C. 0  a  1  c b . 1
D. 0  c  1  b a . O x 2 x 2 x3  1 
Câu 23. Gọi S là tập nghiệm của phương trình x 1  7  .  
Tính tổng tất cả các phần tử của S .  7  A. 5. B. 0. C. 2. D. 1. Câu 24. Tính tổng T tất cả các giá trị của tham số m để phương trình  x 2 1 2 log  2
x  2x  3  4 xm log
2 x m  2 có đúng ba nghiệm phân biệt. 2  2  
A. T  1.
B. T  2 .
C. T  4 . D. T  3. x 1  2 x  2   3 
Câu 25. Tập nghiệm S của phương trình      là  3   2   1  A. S    1 .
B. S    . C. S    2 .
D. S    1 .  3
Câu 26. Tập nghiệm của bất phương trình log x 1  2 là 0,5    5   5   5  A.  ;    . B. ;     . C. 1;3 . D. 1;   .  4   4   4 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 61/69 - Mã đề 2D2
Câu 27. Cho a , b là các số thực dương khác 1. Trong các khẳng định sau, chọn khẳng định đúng. m m m m  1   1   1   1 
A. a b   , m   0     .
B. a b   , m   0     .  a   b   a   b m m  1   1  C. m m
a b a b , . m
D. a b   , m  0     .  a   b b aa
Câu 28. Giả sử a , b là các số thực dương. Biểu thức 5 3
được viết dưới dạng   . Tìm giá trị . a bb  2 2 4 2 A. . B. . C. . D.  . 5 15 15 15
Câu 29. Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số  ex y x trên 1; 
2 . Tính M .n . A. 2 2e . B. 0 . C. 3 2e . D. e . Câu 30. Tính 3 7 log a
a  0, a  1 . 1   a 7 3 7 3 A. . B. . C.  . D.  . 3 7 3 7
Câu 31. Biết sin x  0 , cos x  0 và log sin x  log cos x  1
 . Giá trị của log sin x  cos x bằng 3   3   3   1 1 A. . B. log 5 1. C. 1  . D. log 5 1 . 3  3 3 2 2 x4 2  x x  1
Câu 32. Tìm tập nghiệm của bất phương trình 2 3 1 4    .  2     5  A.   1 . B.   5 ;1  ;    . C. 0;   . D.  ;  0 1; .  4   4 
Câu 33. Tìm tọa độ giao điểm của đồ thị hàm số 3 x y  
 2 và đường thẳng y  5 . A. 1;5 .
B. 2;5 . C.  1  ;5 . D. 2;5 . Câu 34. Biết 2 2
a b ab , a  0 , b  0 . Chọn đẳng thức đúng. A.  2 2
ln a b   ln a  ln b .
B. 2lg a b  lg 3  lg a  lg b .
C. 2ln a b  ln 2  ln a  ln b . D.  2 2
lg a b   lg a  lg b .
Câu 35. Biết rằng phương trình 2018 x log 9 8 3  2
 0 có nghiệm duy nhất x x . Khẳng định nào sau đây là đúng? 0
A. x là số chính phương.
B. x là một số chẵn. 0 0
C. x là số nguyên tố.
D. x chia hết cho 3 . 0 0
Câu 36. Ông A vay ngân hàng T (triệu đồng) với lãi suất 12 % năm. Ông A thỏa thuận với ngân hàng
cách thức trả nợ như sau: sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần
hoàn nợ liên tiếp cách nhau đúng một tháng. Nhưng cuối tháng thứ ba kể từ lúc vay ông A mới
hoàn nợ lần thứ nhất, cuối tháng thứ tư ông A hoàn nợ lần thứ hai, cuối tháng thứ năm ông A
hoàn nợ lần thứ ba (hoàn hết nợ). Biết rằng số tiền hoàn nợ lần thứ hai gấp đôi số tiền hoàn nợ
lần thứ nhất và số tiền hoàn nợ lần thứ ba bằng tổng số tiền hoàn nợ của hai lần trước Tính số
tiền ông A đã hoàn nợ ngân hàng lần thứ nhất.  5  T 1 5 T 1 0, 5 01    100 T 1 0,  01 T   5 1 0, 01 A. . B.  . C. . D. .  2 1, 2 01  5 6 2,  01  2 6
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 62/69 - Mã đề 2D2 2 x x
Câu 37. Tìm tập nghiệm của bất phương trình  x 1 5 2     5  2 . A.  ;    1 0;  1 . B.  1  ; 0 . C.  ;   
1 0;  . D. 1;01; .
Câu 38. Cho log 5  a , log 5  b . Hãy biểu diễn log 5 theo a và b . 2 3 6 1 ab A. log 5  . B. log 5  .
C. log 5  a b . D. 2 2
log 5  a b . 6 a b 6 a b 6 6 a b c b b
Câu 39. Cho a  0 , b  0 , c  0 là các số thực khác 0 thỏa 5  15  45 . Tính T   . a c
A. T  log 5 .
B. T  3.
C. T  2 .
D. T  log 45 . 15 5
Câu 40. Cho f x 2 3 2
x . x . Tính giá trị của f   1 . 8 3 A. 2 . B. . C. 4 . D. . 3 8
Câu 41. Có bao nhiêu giá trị nguyên bé hơn 10 của tham số m sao cho bất phương trình 2 2
log x 1 2 log x 1  m  0 thỏa mãn với mọi 3 1  ; 2  ? 2 2   A. 3 . B. 4 . C. 5 . D. 6 . 2 2
Câu 42. Cho góc , giá trị của biểu thức sin cos 5 .5 bằng 2 2 A. 1. B. 5 . C. 25 . D. sin .cos 5 .
Câu 43. Cho a là hai số thực dương khác Đặt log a m . Tính theo m giá trị của biểu thức 3
D  log a  log a  log 9 . 1 3 a 3 2 2  3m 2 3m  2 2 4  3m A. D  . B. D  . C. D  . D. D  3  m . m m 2m
Câu 44. Tìm đạo hàm của hàm số     2 2 3 e x y x
 3x trong điều kiện xác định. A.      2 4 4 e x y x  3 . B.      2 4 4 e x y x  3x . C. 2 4.e x y   3 . D.      2 2 1 e x y x  3 . 2a 4b  8
Câu 45. Cho a , b là hai số thực dương thỏa mãn 
. Tính giá trị của biểu thức 2a  2b a  4b  8 2017a P  . 2017b
A. 2017b .
B. 2017a . C. 2 2017 . D. 1. 
Câu 46. Tìm tập xác định D của hàm số y   x x   2 2 2 .
A. D  0;   .
B. D   ;    1  2;  .
C. D   \  1  ;  2 . D. D   .
Câu 47. Tìm nghiệm của phương trình x 1 3   27 .
A. x  10 .
B. x  4 .
C. x  3 . D. x  9 .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 63/69 - Mã đề 2D2 2 x
Câu 48. Cho hàm số y  ln x
1. Khẳng định nào sau đây là đúng. 2
A. Hàm số đạt cực đại tại x  1 .
B. Hàm số nghịch biến trên khoảng 0;  1 .
C. Hàm số đạt cực tiểu tại x  1 .
D. Hàm số đồng biến trên khoảng 0;   . 13x
Câu 49. Tính đạo hàm của hàm số y  . x 13x ln13   1 13x 1
13x x ln13   1 A. y  . B. y  . C. y  .D. 1 13x y    . . x ln13 x 2 x
Câu 50. Cho a  0 , a  1 và x , y là hai số dương. Mệnh đề nào sau đây là đúng? A. log  . x y  log .
x log y . B. log x y x y . a  .  log log a a a a a
C. log  x y  log .
x log y . D. log x y x y . a   log log a a a a a ------ HẾT ------ ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D D C A D B A C A C D C B B B B D A D D C D D D B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D D D C C D C C B D C D B C B B B A A C C B A C B
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 64/69 - Mã đề 2D2 SỞ GD VÀ ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA 45 PHÚT NĂM HỌC 2017 – 2018
TRƯỜNG THPT ĐOÀN THƯỢNG
Môn: Giải tích 12 – Chương 2
Thời gian làm bài: 45 phút;
Họ, tên thí sinh:................................... Số báo danh:............... Mã đề thi 132 Câu 1.
Tập nghiệm của bất phương trình 2x-5 3  9 là  7   7   5   5  A.  ;    . B. ;    . C.  ;    . D. ;    .  2   2   2   2  Câu 2.
Cho số dương a , biểu thức 3 6 5
a. a. a viết dưới dạng lũy thừa hữu tỉ là 5 1 7 5 A. 7 a . B. 6 a . C. 3 a . D. 3 a . Câu 3.
Cho hàm số f x 2
 2x m  log mx  2 m  2 x  2m 1 2   
 ( m là tham số). Tìm tất cả các
giá trị m để hàm số f x xác định với mọi x   . A. m  0 . B. m  1.
C. m  1 m  4  . D. m  4 . 2 Câu 4.
Tính đạo hàm của hàm số 3 2 ex x y    . 2
A.   2  3 ex y x . B. -3x 2 ex y    . C.   2 2 3 2 3 2 ex x y x x       . D.   2-3 2 2 3 ex x y x     . Câu 5.
Giá trị của tham số m để phương trình 4x  .2x m
 2m  5  0 có hai nghiệm trái dấu là 5 5 5 A. m  . B. m  . C. m  4 . D. m  4 . 2 2 2 Câu 6.
Tập nghiệm của bất phương trình log x2  4 log x  3  0 là 2 2
A. 0; 2  8; . B.  ;
 2  8;  . C. 2;8 . D. 8; . Câu 7. Số 756839 p  2
1 là một số nguyên tố. Hỏi nếu viết trong hệ thập phân, số đó có bao nhiêu chữ số? A. 227831 chữ số. B. 227834 chữ số. C. 227832 chữ số. D. 227835 chữ số. Câu 8.
Ông Minh gửi ngân hàng số tiền 100 triệu đồng với lãi suất 7% một năm theo hình thức lãi
kép. Biết rằng trong suốt quá trình gửi ông không rút tiền lãi. Hỏi sau ít nhất bao nhiêu năm thì
ông có nhiều hơn 500 triệu. A. 24 năm. B. 23 năm. C. 22 năm. D. 25 năm. Câu 9. Hàm số 2
y x ln x đạt cực trị tại điểm 1 1
A. x  0; x  . B. x  . C. x  0 . D. x  e . e e 
Câu 10. Hàm số y   x   4 2 4 1 có tập xác định là  1 1   1 1  A.  . B.  ;   .
C.  \  ;  . D. 0;  .  2 2   2 2 
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 65/69 - Mã đề 2D2 2 3  2x x
Câu 11. Tìm tập xác định của hàm số sau f x  log . 2 x 1  3   17   3   17 
A. D   ;    1;  . B.  ;  3   1; .  2  2      3   17   3   17  C. D   ; 1   ;1 . D.  ;  3     1  ;  1 . 2  2     
Câu 12. Bạn An gửi tiết kiệm số tiền 58.000.000 đồng trong 8 tháng tại một ngân hàng thì nhận được
61.329.000 đồng. Khi đó, lãi suất hàng tháng gần với giá trị nào nhất trong các giá trị sau: A. 9% . B. 6% . C. 5% . D. 7% .
Câu 13. Nếu a  log 3 , b  log 5 thì: 2 2 1 a b 1 a b A. 6 log 360    . B. 6 log 360    . 2 6 2 3 2 3 4 6 1 a b 1 a b C. 6 log 360    . D. 6 log 360    . 2 2 6 3 2 2 3 6
Câu 14. Một người gửi ngân hàng số tiền 100 triệu đồng với lãi suất 7% một năm theo hình thức lãi
kép. Biết rằng trong suốt quá trình gửi không rút tiền lãi. Hỏi sau 5 năm số tiền của người ấy
gần với giá trị nào dưới đây nhất A. 142 triệu. B. 140 triệu. C. 130 triệu. D. 150 triệu. 2 2
Câu 15. Phương trình x x x x 1 4 2  
 3 có nghiệm là chọn 1 đáp án đúng  x  1  x  1   x  0  x  0 A.  . B.  . C.  . D.  . x  2  x  1  x  2  x  1  Câu 16. Biểu thức
x x x x x  0 được viết dưới dạng lũy thừa số mũ hữu tỉ là 15 15 3 7 A. 16 x . B. 18 x . C. 16 x . D. 18 x .
Câu 17. Phương trình tiếp tuyến của đồ thị hàm số 2
y x tại điểm thuộc đồ thị có hoành độ bằng 1 là A. y x 1. B. y x  1. C. y x  1. D. y x 1. 2 2 2 2 2 2
Câu 18. Tìm tập xác định D của hàm số y   2
log x  3x  2 A. D   2  ;  1 .
B. D  1;  . C. D   2  ;   .
D. D   ;   1  2; . Câu 19. Cho hàm số  2x y
 2x . Khẳng định nào sau đây sai?
A. Đồ thị hàm số luôn cắt trục tung.
B. Hàm số có giá trị nhỏ nhất lớn hơn 1  .
C. Đồ thị hàm số cắt trục hoành tại duy nhất một điểm.
D. Đồ thị hàm số luôn cắt đường thẳng y  2 .
Câu 20. Cho 0  a  1 và x , y là hai số dương. Phát biểu nào sau là đúng
A. log  xy  log . x l og y . B. log x y x l y . a   log . og a a a a a
C. log  xy  log x l og y . D. log x y x l y . a   log og a a a a a
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 66/69 - Mã đề 2D2
Câu 21. Cho phương trình ln x  ln  x  
1  0 . Chọn khẳng định đúng.
A. Phương trình vô nghiệm.
B. Phương trình có hai nghiệm.
C. Phương trình có nghiệm  1;2 .
D. Phương trình có nghiệm thuộc 0;  1 . 1
Câu 22. Số nghiệm của phương trình log  3 x  3x  3  2 A. 2 . B. 3 . C. 0 . D. 1 .     x 15
Câu 23. Giải bất phương trình log  log 2      2 2 1   16  2  15 31 A. x  0 . B. log  x  log . 2 2 16 16 31 15
C. 0  x  log . D. log  x  0 . 2 16 2 16
Câu 24. Một người gửi ngân hàng số tiền T với lãi suất 7% một năm theo hình thức lãi kép. Biết rằng
trong suốt quá trình gửi không rút tiền lãi. Hỏi sau bao nhiêu năm số tiền của người gấp đôi số tiền ban đầu A. 11 năm. B. 12 năm. C. 14 năm. D. 10 năm.
Câu 25. Để giải phương trình log  x  2 1
 6 . Một học sinh giải như sau: 2
Bước 1: Điều kiện  x  2 1  0  x  1  .
Bước 2: Phương trình tương đương: 2 log x 1  6  log
x 1  3  x  1  8  x  7 . 2   2  
Bước 3: Vậy phương trình đã cho có nghiệm là x  7 .
Dựa vào bài giải trên chọn khẳng định đúng trong các khẳng định sau:
A. Bài giải trên hoàn toàn chính xác.
B. Bài giải trên sai từ Bước 1.
C. Bài giải trên sai từ Bước 2.
D. Bài giải trên sai từ Bước 3.
----------- HẾT -----------
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 67/69 - Mã đề 2D2
ĐỀ KIỂM TRA 1 TIẾT
TRƯỜNG THPT NGUYỄN TRÃI
MÔN: GIẢI TÍCH - LỚP 12 TỔ TOÁN
Họ, tên thí sinh:................................... SBD:............... Mã đề: 132 Câu 1.
Cho a là số thực dương , là các số thực. Mệnh đề nào sau đây sai? a
A. a a .a . B. aa   . C. a  . D. a b (ab)  . a Câu 2.
Cho a , b , c là 3 số dương khác 1. Chọn khẳng định sai trong các khẳng định sau:
A. log bc  log b  log c .
B. log c  log b.log c . a a a a a b 1 C. log  . D. log   .  b log b ( 0)  b log b a a a a 2 Câu 3.
Tìm tất cả các giá trị thực của m để phương trình 3x m có nghiệm:
A. m 1; .
B. m 3; .
C. m  1;  .
D. m 0; . Câu 4.
Gọi x , x là hai nghiệm của phương trình 9x 8.3x
 9  0 . Giá trị biểu thức P x x bằng 1 2 1 2 A. 2 . B. 4 . C. 9 . D. 8 . Câu 5.
Gọi x , x là hai nghiệm của phương trình 2
log x  3log x  2  0 . Giá trị biểu thức 1 2 3 3 2 2
P x x bằng bao nhiêu? 1 2 A. 20 . B. 92 . C. 90 . D. 9 . Câu 6.
Với a , b , c là các số thực dương tùy ý a khác 1. Đặt 8 4
Q  log b  log b . Mệnh đề nào 2 a a dưới đây đúng? A. 5 log b . B. 7 log b . C. 8 log b . D. 12 log b . a a a a Câu 7.
Anh Hùng vay 40 triệu đồng của ngân hàng để mua xe máy và phải trả góp trong vòng 3 năm
với lãi suất 1, 2% mỗi tháng. Hàng tháng anh Hùng phải trả 1 số tiền cố định là bao nhiêu để
sau 3 năm hết nợ (làm tròn đến đơn vị đồng) A. 1.374.807 đồng. B. 1.374.889 đồng. C. 1.374.907 đồng. D. 1.378.222 đồng. x  3 Câu 8.
Tập xác định D của hàm số: y  log là 3 2  x
A. D   \  3  ;  2 . B. D   3  ; 2 .
C. D   ;  3    2;  . D. D   3  ; 2 . Câu 9.
Cho a  log 3 và b  log 3 , với m , n là các số thực dương khác 1.Tính 2 P  log (nm ) m n 3 ab a  2b 2ab 2a b A. P  . B. P  . C. P  . D. P  . a b ab a b ab 3
Câu 10. Tập xác định của hàm số y   2 x x2 2 là
A. D   \ 0;2 . B. D   .
C. D   \ 0;2 .
D. D   \   2 . 5
Câu 11. Rút gọn biểu thức 3
Q a : a với a  0 . 2 2 4 7  A. 3 Q a . B. 3 Q a . C. 3 Q a . D. 6 a .
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 68/69 - Mã đề 2D2
Câu 12. Tìm tất cả các giá trị thực của m để phương trình: log  x   1  log  2
x  3x m  0 có 2 2 2  nghiệm phân biệt.
A. 2  m  3 .
B. 2  m  3 .
C. 2  m  3 . D. m  2 . x
Câu 13. Đạo hàm của hàm số y = là 4x 1 x ln 4 1 1 x 1 x ln 4 A. . B. . C. . D. . 2 4 x 4x ln 4 4x ln 4 4x
Câu 14. Chọn khẳng định Sai trong các khẳng định sau:
A. ln x  0  x  1.
B. log x  0  x  10 .
C. log a  log b a b  0..
D. log a  log b a b  0 . 1 1 2 2 2 2
Câu 15. Cho a  3b  0 và 2 2
a  9b  10ab , mệnh đề nào dưới đây đúng? ln a  ln b ln . a ln b
A. ln a  3b  ln 2  .
B. ln a  3b  ln 2  . 2 2 ln a  ln b ln . a ln b
C. ln a  3b  ln 2  .
D. ln a  3b  ln 2  . 2 2
Câu 16. Tổng các nghiệm của phương trình log  x  2 1  1 là 2 A. 2 . B. 2 2 . C. 2  2 . D. 2 1.
Câu 17. Hàm số nào dưới đây đồng biến trên tập xác định của nó? x x  2   e 
A. y  log x . B. y  . C. y  .
D. y  ln x . 1      3   3  2
Câu 18. Tìm giá trị thực của tham số m để giá trị nhỏ nhất của hàm số:    2x f x
 log x m trên 2 9 đoạn 1;2 bằng . 4 A. m  3 . B. m  3 . C. m  1. D. m  2 .
Câu 19. Cho 3x  3x  15 . Giá trị biểu thức: 9x 9 x P    là A. 221 . B. 225 . C. 223 . D. 227 . 2 2
Câu 20. Tìm tất cả các giá trị thực của m để phương trình x 2 x 1  x 2 x2 4  . m 2
 6m  5  0 có 4 nghiệm phân biệt. A. m  5 .
B. 5  m  6 . C. m  5 .
D. 5  m  6 .
----------- HẾT ----------- ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 C C A A C C B D B A D C D B C A D A C A
Nhóm biên tập TOÁN HỌC BẮC–TRUNG–NAM thực hiện
Trang 69/69 - Mã đề 2D2