Bộ Đề Ôn Tập Toán Tuyển Sinh Lớp 10 Quận Phú Nhuận TP HCM 2025-2026 Giải Chi Tiết
Với sự phát triển của khoa học kĩ thuật hiện nay, người ta tạo ra nhiều mẫu xe lăn đẹp và tiện dụng cho người khuyết tật. Công ty Ađã sản xuất ra những chiếc xe lăn cho người khuyết tật với số vốn ban đầu là 500000000 đồng và thêm chi phí để sản xuất ra một chiếc xe lăn là 2500000 đồng. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 216 tài liệu
Môn: Toán 9 3 K tài liệu
Tác giả:
Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN PHUÙ NHUAÄN MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận. ĐỀ TH AM KHẢO
Thời gian: 120 phút (không kể thời gian phát đề)
MÃ ĐỀ: Quận Phú Nhuận - 1
Câu 1. (1,5 điểm). Cho hàm số 2
y = −x có đồ thị (P) và hàm số y = 2
− x + 1 có đồ thị (D) .
a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.
Câu 2. (1 điểm). Cho phương trình: 2
x − 6x + 8 = 0 có 2 nghiệm x ,x .Không giải phương trình, 1 2 2 2 x x
hãy tình giá trị của biểu thức biểu thức 1 2 A = − x + − x . 1 2 x x 2 1
Câu 3. (0,75 điểm). Với sự phát triển của khoa học kĩ thuật hiện nay, người ta tạo ra nhiều mẫu xe
lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn
cho người khuyết tật với số vốn ban đầu là 500 000 000 đồng và thêm chi phí để sản xuất
ra một chiếc xe lăn là 2 500 000 đồng. Biết rằng giá bán ra mỗi chiếc là 3 500 000 đồng.
a) Viết hàm số biểu diễn số tiền lời hoặc lỗ y (đồng) khi bán ra x (chiếc xe lăn).
b) Hỏi cần phải bán ít nhất bao nhiêu chiếc xe lăn thì công ty A không bị lỗ?
Câu 4. (1 điểm). Hai lớp 9A và 9B có tổng cộng 86 học sinh. Trong đợt thu nhặt giấy báo cũ thực
hiện kế hoạch nhỏ, có 1 học sinh lớp 9A góp được 5kg , các bạn còn lại trong lớp, mỗi bạn
góp được 4kg . Lớp 9B có 1 học sinh góp được 7kg , các bạn còn lại trong lớp, mỗi bạn góp
được 8kg . Tính số học sinh của mỗi lớp, biết cả hai lớp góp được 520kg giấy báo cũ?
Câu 5. (1 điểm). Một nhóm học sinh tham gia thực hành môn Sinh học với nhiệm vụ được giao là
chăm sóc và ghi nhận sự phát triển về chiều cao của cây. Nhóm được giáo viên giao chăm
sóc một cây non có chiều cao ban đầu là 2,56cm . Sau hai tuần chăm sóc, nhóm ghi nhận
chiều cao của cây đã tăng thêm 1,28cm . Gọi (
h cm) là chiều cao của cây sau . t . (tuần) chăm
sóc, h và t liên hệ với nhau bằng hàm số h = at + b (giả sử, mức tăng chiều cao trung bình
của cây ở mỗi tuần chênh lệch không đáng kể)
a) Xác định hệ số a,b của hàm số h = at + b
b) Hỏi sau bao nhiêu ngày thì cây sẽ đạt chiều cao 5,76cm , tính từ khi cây được giao cho nhóm chăm sóc.
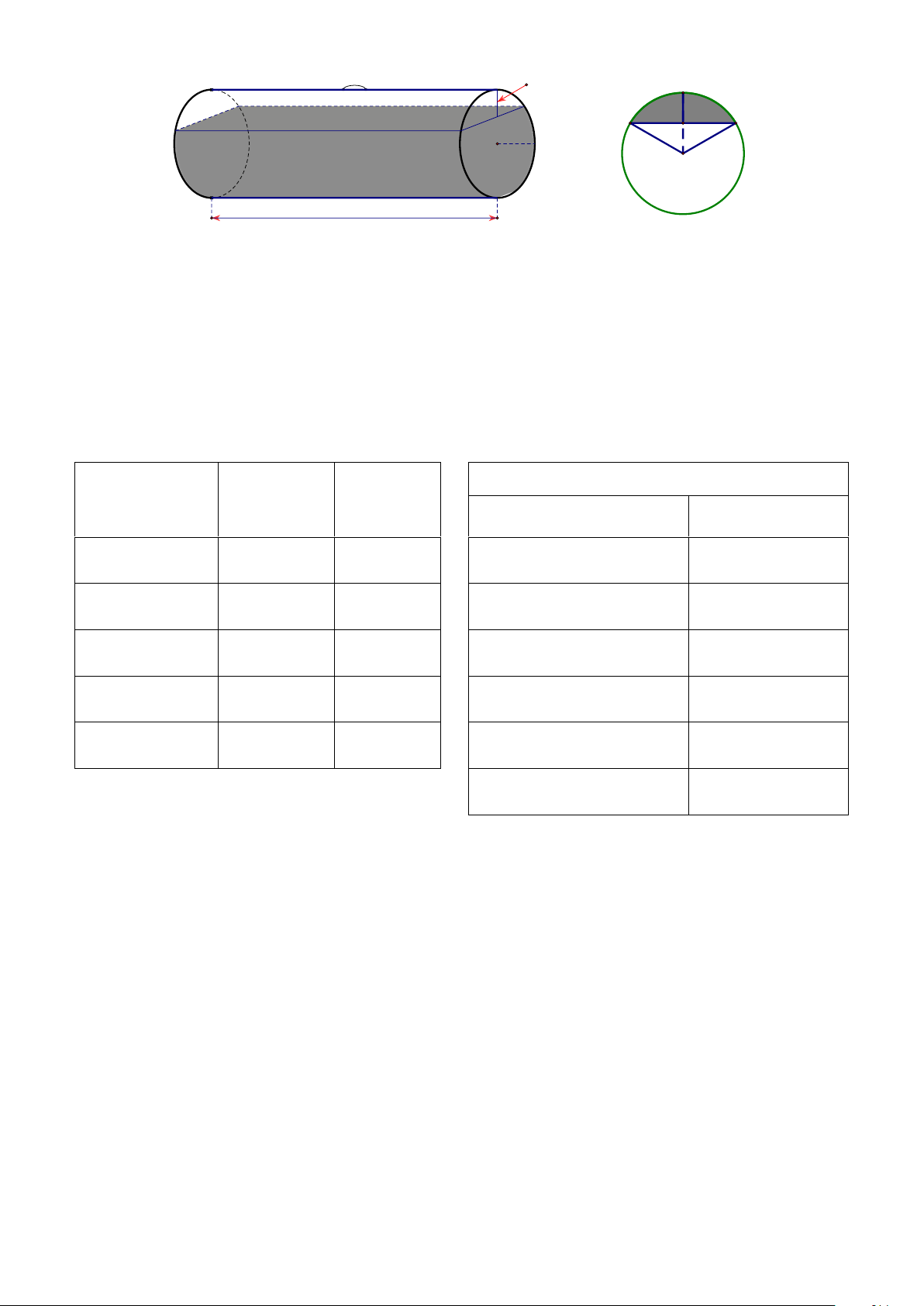
Câu 6. (1 điểm). Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là 5m ,
bán kính đáy 1m , với nắp bồn đặt trên mặt nằm ngang của hình trụ. Người ta đã rút dầu
trong bồn tương ứng với 0,5m của đường kính đáy (như hình vẽ). Tính lượng dầu còn lại
trong bồn (giả sử độ dày của bồn là không đáng kể và kết quả làm tròn đến chữ số thập phân thứ 2 ). Biết: 2 V
= R .h , R : bán kính đáy, h : chiều cao hình trụ. hinh truï Trang 1 0.5m B A C H 1m O 5m
Câu 7. (0,75 điểm) Để tính tiền điện của một thiết bị điện ta lấy lượng điện thiết bị tiêu thụ nhân
với giá điện tại thời điểm đó. Công thức tính lượng điện tiêu tiêu thụ của thiết bị điện như
sau: T = P.t (trong đó: T là lượng điện tiêu thụ trong khoảng thời gian t (giờ); P công suất của thiết bị).
a) Một máy lạnh có công suất 800W , một ngày sử dụng trung bình 4 giờ. Tính lượng điện
tiêu thụ của máy lạnh đó trong tháng 5 / 2022 ?
b) Nhà anh An có các thiết bị như sau:
BẢNG GIÁ ĐIỆN SINH HOẠT Công suất Thời gian Số lượng 1 thiết bị dùng 1 ngày Số kWh sử dụng Giá (đồng/kWh) 4 đèn Led 18W /giờ 4 giờ
Cho 50 kWh đầu tiên 1 678 1 máy lạnh 100W /giờ 8 giờ Cho kWh 51 đến 100 1734
1 nồi cơm điện 900W /giờ 3 giờ Cho kWh 101 đến 200 2 014 1 tủ lạnh 1040W /ngày 24 giờ Cho kWh 201 đến 300 2 536 2 quạt máy 48W /giờ 10 giờ Cho kWh 301 đến 400 2 834
Cho kWh từ 401 trở lên 2 927
Tính tiền điện gia đình anh An phải trả trong tháng 5 / 2022 ? Biết thuế giá trị gia tăng là
10% . (làm tròn kết quả đến hàng nghìn)
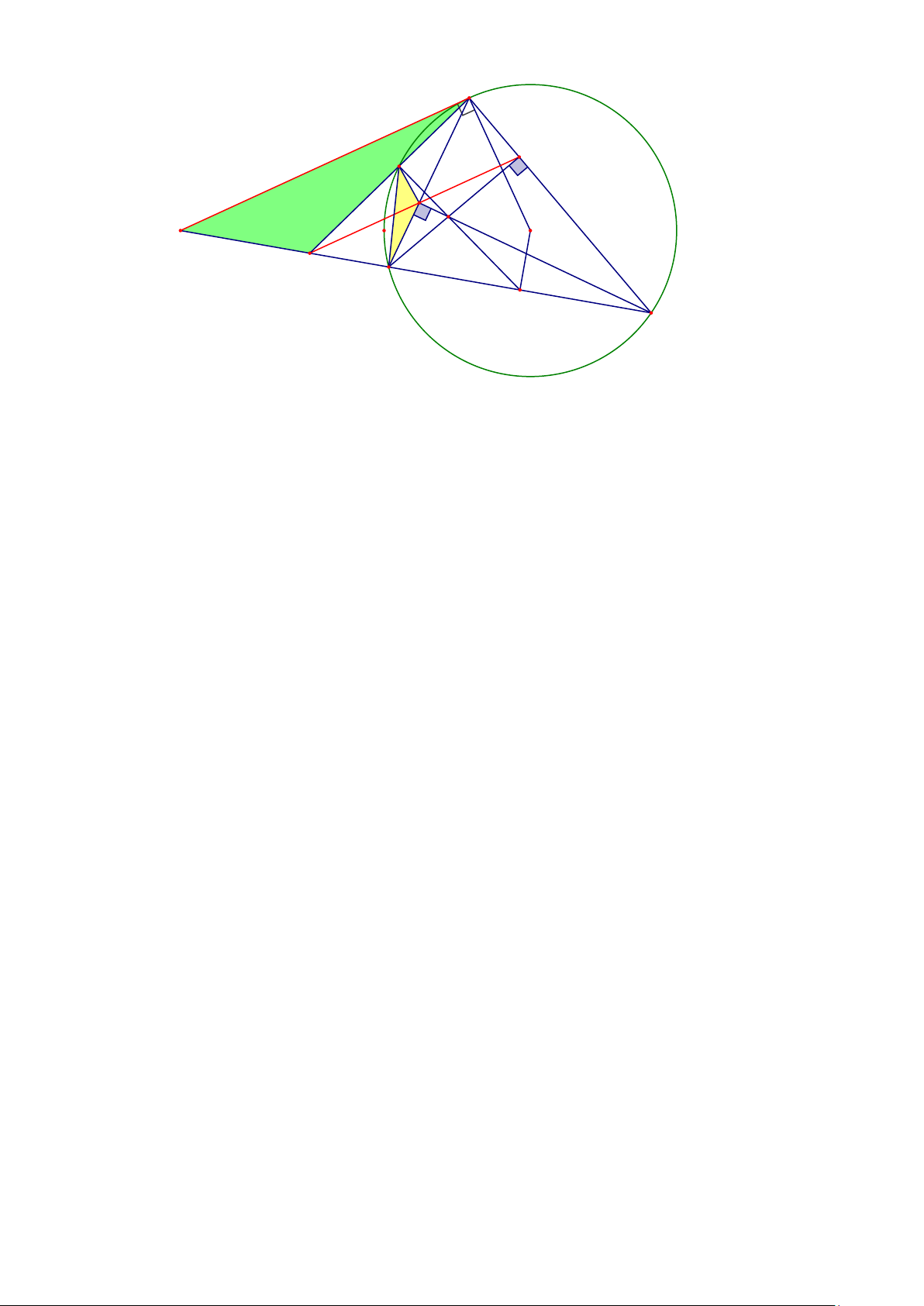
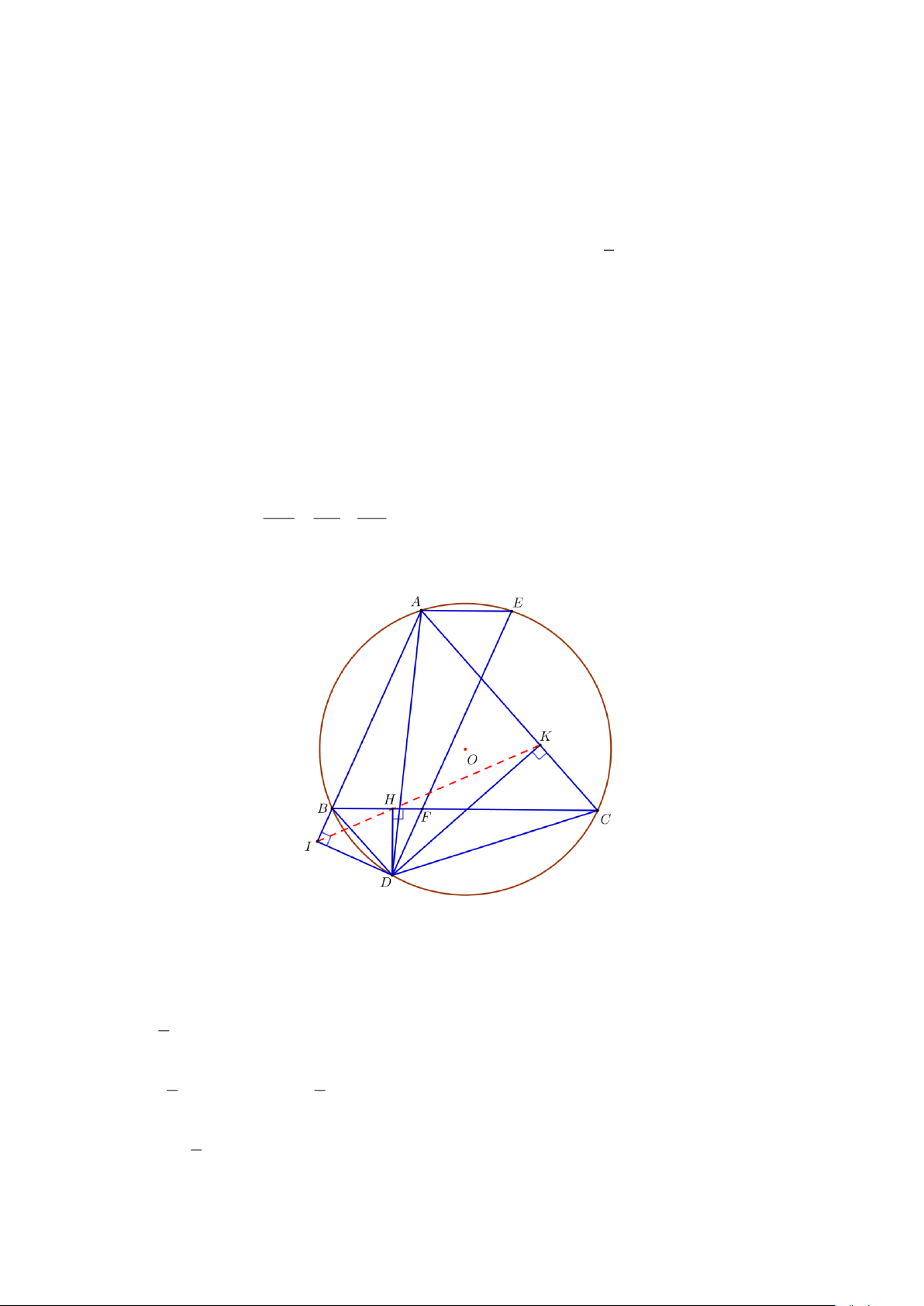
Câu 8. (3 điểm) Từ điểm A nằm ngoài đường tròn (O,R) với OA 2R . Vẽ tiếp tuyến AB và cát
tuyến ACD với đường tròn (O) , ( B là tiếp điểm; AC AD , tia AD không cắt đoạn thẳng
OB ). Gọi CE,DF là các đường cao của tam giác BCD .
a) Chứng minh: tứ giác DEFC nội tiếp và EF // AB .
b) Tia EF cắt AD tại G , BG cắt (O) tại H . Chứng minh: FHC đồng dạng GAB .
c) Gọi I là giao điểm của CE và DF . Tia HI cắt DC tại M . Chứng minh: OM ⊥ CD ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm). Cho hàm số 2
y = −x có đồ thị (P) và hàm số y = 2
− x + 1 có đồ thị (D) .
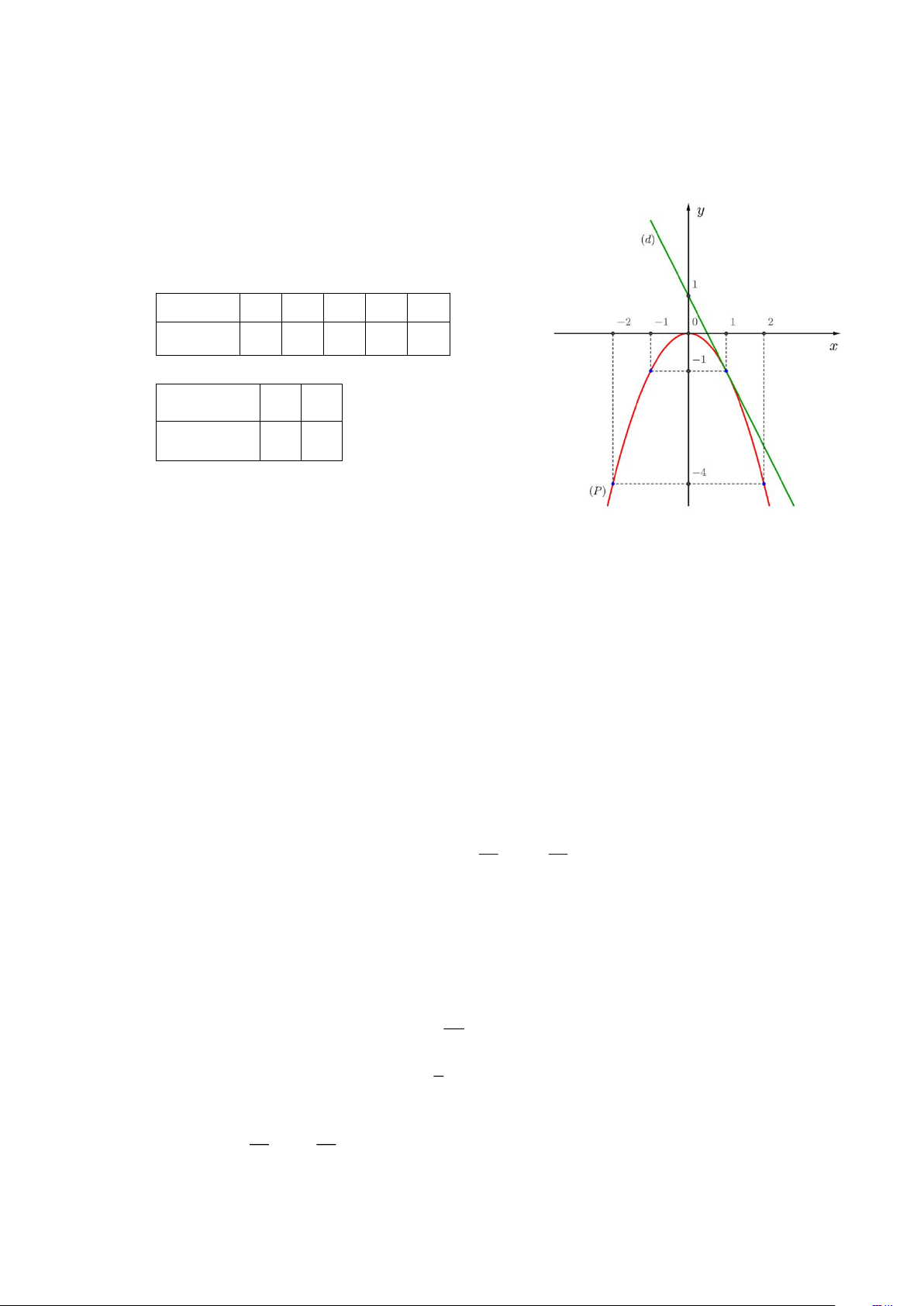
a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán. Lời giải
a) Vẽ đồ thị (P) và(D) trên cùng hệ trục tọa độ. BGT: x −2 1 − 0 1 2 2 y = −x −4 1 − 0 1 − −4 x 0 1 y = 2 − x + 1 1 1 −
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (D) : 2
−x = −2x + 1 2
x − 2x + 1 = 0 x = 1 Thay x = 1 vào 2
y = −x , ta được: 2 y = 1 − = −1 .
Vậy (1; − 1) là hai giao điểm cần tìm.
Câu 2. (1 điểm). Cho phương trình: 2
x − 6x + 8 = 0 có 2 nghiệm x ,x .Không giải phương trình, 1 2 2 2 x x
hãy tình giá trị của biểu thức biểu thức 1 2 A = − x + − x . 1 2 x x 2 1 Lời giải Vì 2 2
= b − 4ac = 6 − 4.1.8 = 4 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 −b
S = x + x = = 6 1 2
Theo định lí Vi-et, ta có: a c
P = x .x = = 8 1 2 a 2 2 x x Ta có: 1 2 A = − x + − x 1 2 x x 2 1 Trang 3 2 2 x x 1 2 A = − x + − x 1 2 x x 2 1 2 2 x x 1 2 A = + − ( x + x 1 2 ) x x 2 1 3 3 x + x 1 2 A = − (x + x 1 2 ) x x 1 2
(x + x )3 −3x x x + x 1 2 1 2 ( 1 2 ) A = − (x + x 1 2 ) x x 1 2 3 S − 3PS A = − S P 3 6 − 3.8.6 A = − 6 = 3 8
Câu 3. (0,75 điểm). Với sự phát triển của khoa học kĩ thuật hiện nay, người ta tạo ra nhiều mẫu xe
lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn
cho người khuyết tật với số vốn ban đầu là 500 000 000 đồng và thêm chi phí để sản xuất
ra một chiếc xe lăn là 2 500 000 đồng. Biết rằng giá bán ra mỗi chiếc là 3 500 000 đồng.
a) Viết hàm số biểu diễn số tiền lời hoặc lỗ y (đồng) khi bán ra x (chiếc xe lăn).
b) Hỏi cần phải bán ít nhất bao nhiêu chiếc xe lăn thì công ty A không bị lỗ? Lời giải
a) Viết hàm số biểu diễn số tiền lời hoặc lỗ y (đồng) khi bán ra x (chiếc xe lăn).
Gọi y (đồng) số tiền lời hoặc lỗ khi bán ra được x chiếc xe lăn:
y = (3 500 000 − 2 500 000)x − 500 000 000 = 1 000 000x − 500 000 000 (đồng)
b) Hỏi cần phải bán ít nhất bao nhiêu chiếc xe lăn thì công ty A không bị lỗ?
Số chiếc xe ít nhất công ty A cần bán để không bị lỗ là:
3,5x = 2,5x + 500 x = 500
Vậy công ty A cần bán được ít nhất 500 chiếc xe lăn sẽ không bị lỗ.
Câu 4. (1 điểm). Hai lớp 9A và 9B có tổng cộng 86 học sinh. Trong đợt thu nhặt giấy báo cũ thực
hiện kế hoạch nhỏ, có 1 học sinh lớp 9A góp được 5kg , các bạn còn lại trong lớp, mỗi bạn
góp được 4kg . Lớp 9B có 1 học sinh góp được 7kg , các bạn còn lại trong lớp, mỗi bạn góp
được 8kg . Tính số học sinh của mỗi lớp, biết cả hai lớp góp được 520kg giấy báo cũ? Lời giải
Gọi x (học sinh), y (học sinh), lần lượt là số học sinh của lớp 9A, 9B
(x * ,y * ,x 86,y 86) )
Vì hai lớp 9A và 9B có tổng cộng 86 học sinh nên ta có phương trình: x + y = 86 ( ) 1
Lớp 9A góp được: 5+ (x − )
1 .4 = 4x +1(kg)
Lớp 9B góp được: 7 + (y − )
1 .8 = 8y −1(kg) Trang 4
Vì cả hai lớp góp được 520kg giấy báo cũ nên ta có phương trình
4x +1+ 8y −1 = 520 x + 2y = 130 (2) x + y = 86 x = 42 Từ ( ) 1 và (2) ta có hpt: (nhận) x + 2y = 130 y = 44
Vậy lớp 9A có 42 học sinh, lớp 9B có 44 học sinh.
Câu 5. (1 điểm). Một nhóm học sinh tham gia thực hành môn Sinh học với nhiệm vụ được giao là
chăm sóc và ghi nhận sự phát triển về chiều cao của cây. Nhóm được giáo viên giao chăm
sóc một cây non có chiều cao ban đầu là 2,56cm . Sau hai tuần chăm sóc, nhóm ghi nhận
chiều cao của cây đã tăng thêm 1,28cm . Gọi (
h cm) là chiều cao của cây sau . t . (tuần) chăm
sóc, h và t liên hệ với nhau bằng hàm số h = at + b (giả sử, mức tăng chiều cao trung bình
của cây ở mỗi tuần chênh lệch không đáng kể)
a) Xác định hệ số a,b của hàm số h = at + b
b) Hỏi sau bao nhiêu ngày thì cây sẽ đạt chiều cao 5,76cm , tính từ khi cây được giao cho nhóm chăm sóc. Lời giải a) Xác định hệ số ,
a b của hàm số h = at + b
Vì cây non có chiều cao ban đầu là 2,56cm nên =
t 0 và h = 2,56 2,56 = .
a 0 + b b = 2,56 ( ) 1
Vì sau hai tuần chăm sóc, nhóm ghi nhận chiều cao của cây đã tăng thêm 1,28cm =
t 2 và h = 2,56 +1,28 = 3,84 3,84 = . a 2 + b (2) Từ ( )
1 và (2) ta có hệ phương trình b = 2,56 b = 2,56 2a + b = 3,84 a = 0,64
b) Hỏi sau bao nhiêu ngày thì cây sẽ đạt chiều cao 5,76cm, tính từ khi cây được giao cho nhóm chăm sóc.
Ta có: h = 0,64t + 2,56
Thay h = 5,67vào h = 0,64t + 2,56 ta có: 5,67 = 0,64t + 2,56 0,64t = 3,2 t = 5
Vậy sau 5.7 = 35 ngày thì cây đạt chiều cao 5,76cm.
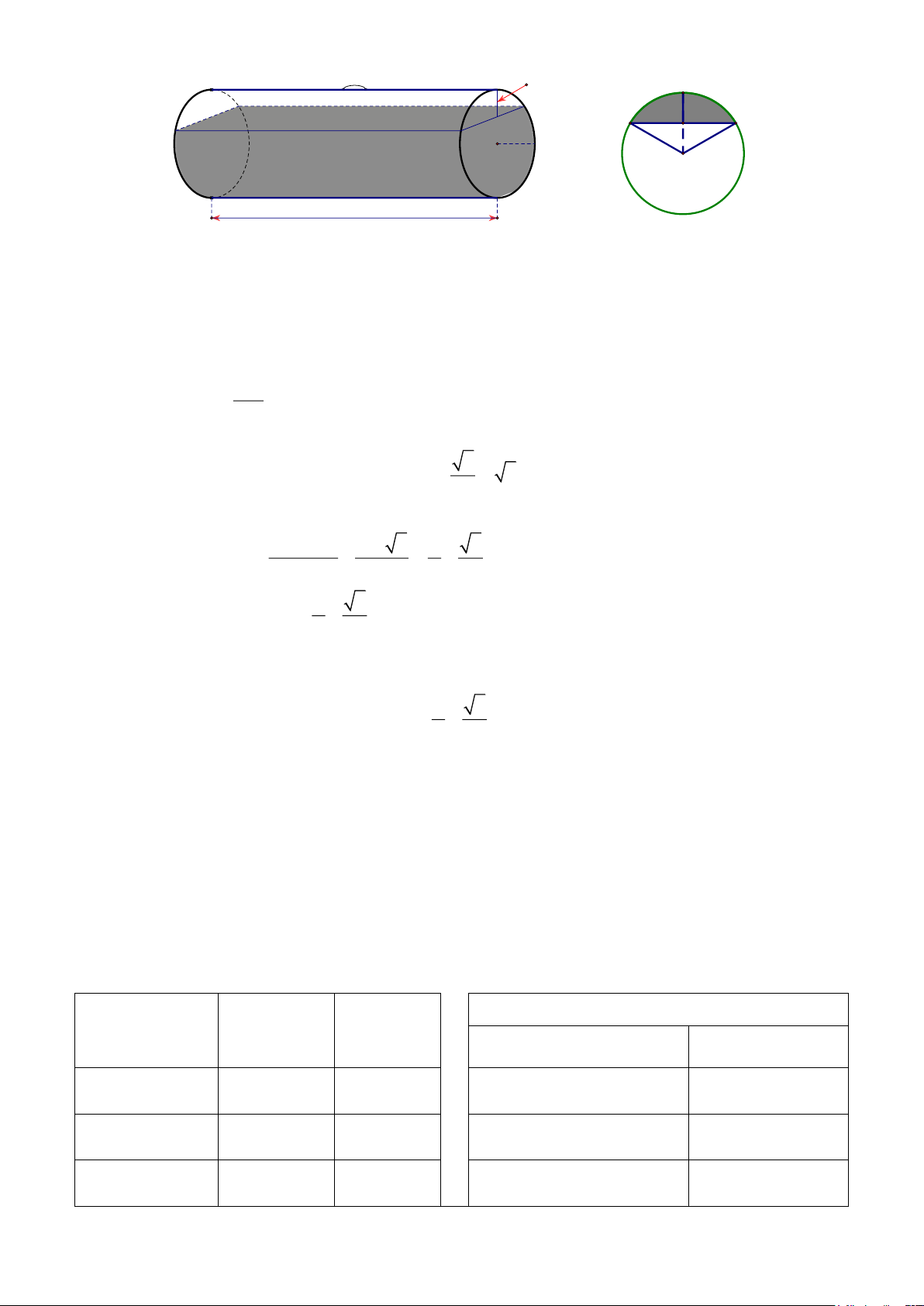
Câu 6. (1 điểm). Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là 5m ,
bán kính đáy 1m , với nắp bồn đặt trên mặt nằm ngang của hình trụ. Người ta đã rút dầu
trong bồn tương ứng với 0,5m của đường kính đáy (như hình vẽ). Tính lượng dầu còn lại
trong bồn (giả sử độ dày của bồn là không đáng kể và kết quả làm tròn đến chữ số thập phân thứ 2 ). Biết: 2 V
= R .h , R : bán kính đáy, h : chiều cao hình trụ. hinh truï Trang 5 0.5m B A C H 1m O 5m Lời giải
Ta có: OH = OB − BH = 1 − 0,5 = 0,5m
Xét OHC vuông tại H ta có: OH cos HOC =
HOC = 60 AOC = 2HOC = 120 OC 3
Ta có: AC = 2HC = 2OC.sin HOC = 2.1. = 3 2
Diện tích mặt đáy phần dầu rút ra : 2 .1 .120 0,5. 3 3 S −S = − = − m q AOC A OC ( 2) ( ) 360 2 3 4 3 Thể tích dầu rút ra: − .5 ( 3 m ) 3 4 2 2 V
= R .h = .1 .5 = 5 m hinh ( 3 truï ) 3
Lượng dầu còn lại trong bồn: 5 − − .5 12,64 ( 3 m ) 3 4
Câu 7. (0,75 điểm) Để tính tiền điện của một thiết bị điện ta lấy lượng điện thiết bị tiêu thụ nhân
với giá điện tại thời điểm đó. Công thức tính lượng điện tiêu tiêu thụ của thiết bị điện như
sau: T = P.t (trong đó: T là lượng điện tiêu thụ trong khoảng thời gian t (giờ); P công suất của thiết bị).
c) Một máy lạnh có công suất 800W , một ngày sử dụng trung bình 4 giờ. Tính lượng điện
tiêu thụ của máy lạnh đó trong tháng 5 / 2022 ?
d) Nhà anh An có các thiết bị như sau:
BẢNG GIÁ ĐIỆN SINH HOẠT Công suất Thời gian Số lượng 1 thiết bị dùng 1 ngày Số kWh sử dụng Giá (đồng/kWh) 4 đèn Led 18W /giờ 4 giờ
Cho 50 kWh đầu tiên 1 678 1 máy lạnh 100W /giờ 8 giờ Cho kWh 51 đến 100 1734
1 nồi cơm điện 900W /giờ 3 giờ Cho kWh 101 đến 200 2 014 Trang 6 1 tủ lạnh 1040W /ngày 24 giờ Cho kWh 201 đến 300 2 536 2 quạt máy 48W /giờ 10 giờ Cho kWh 301 đến 400 2834
Cho kWh từ 401 trở lên 2927
Tính tiền điện gia đình anh An phải trả trong tháng 5 / 2022 ? Biết thuế giá trị gia tăng là
10% . (làm tròn kết quả đến hàng nghìn). Lời giải
a) Một máy lạnh có công suất 800W , một ngày sử dụng trung bình 4 giờ. Tính lượng điện
tiêu thụ của máy lạnh đó trong tháng 5 / 2022 ?
Lượng điện tiêu thụ trung bình của máy lạnh đó trong 1 ngày là: T = P.t = 8.400 = 3200W
Vì tháng 5 / 2022 có 31 ngày nên lượng điện tiêu thụ của máy lạnh trong tháng 5 / 2022 là: 3200.31 = 99200W
b) Tính tiền điện gia đình anh An phải trả trong tháng 5 / 2022 ? Biết thuế giá trị gia tăng là
10% . (làm tròn kết quả đến hàng nghìn)
Lượng điện tiêu thụ của nhà anh An trong tháng 5 / 2022 là:
(4.18.4 + 100.8 + 900.3 + 1040.24 + 2.48.10).31 = 920 948W = 920, 948kWh
Tiền điện gia đình anh An phải trả trong tháng 5 / 2022 là:
(1678.50 + 1734.50 + 2014.100 + 2536.100 + 2834.100 + 2927.520,948).(100% + 10%) = 2 677 000 (đồng)
Câu 8. (3 điểm) Từ điểm A nằm ngoài đường tròn (O,R) với OA 2R . Vẽ tiếp tuyến AB và cát
tuyến ACD với đường tròn (O) , ( B là tiếp điểm; AC AD , tia AD không cắt đoạn thẳng
OB ). Gọi CE,DF là các đường cao của tam giác BCD .
d) Chứng minh: tứ giác DEFC nội tiếp và EF // AB .
e) Tia EF cắt AD tại G , BG cắt (O) tại H . Chứng minh: FHC đồng dạng GAB .
f) Gọi I là giao điểm của CE và DF . Tia HI cắt DC tại M . Chứng minh: OM ⊥ CD Lời giải Trang 7 B E H F I A O G C M D
a) Chứng minh: tứ giác DEFC nội tiếp và EF // AB .
Xét tứ giác DEFC ta có :
DEC = DFC = 90 ( CE, DF là đường cao của BCD)
Tứ giác DEFC nội tiếp ( 2 đỉnh E,F liên tiếp cùng nhìn cạnh DC dưới góc không đổi) Ta có:
+ ABC = EDC (Góc nt và góc tạo bởi tia tiếp tuyến và dây cùng chắn BC )
+ BFE = EDC (Tứ giác DEFC nội tiếp) ABC = BFE
Mà ABC,BFE nằm ở vị trí so le trong EF // AB
b) Tia EF cắt AD tại G , BG cắt (O) tại H . Chứng minh: FHC đồng dạng GAB
Ta có EF // AB ABH = FGH (so le trong)
Mà ABH = FCH (Góc nt và góc tạo bởi tia tiếp tuyến và dây cùng chắn BH ) FGH = FCH
Tứ giác FHGC nội tiếp ( 2 đỉnh C,G liên tiếp cùng nhìn cạnh FH dưới 1 góc không đổi)
BGA = CFH (góc ngoài bằng góc đối trong)
Xét FHC và GAB , có: + BGA = CFH
+ ABH = FCH (cmt)
FHC đồng dạng GAB
c) Gọi I là giao điểm của CE và DF . Tia HI cắt DC tại M . Chứng minh: OM ⊥ CD
Kéo dài HM cắt (O) tại K
Ta có: FHG = FCD (tg FHGC nội tiếp)
Mà FCD = BEF ( tg DEFC nội tiếp) Trang 8
FHG = BEF tg BEFH nội tiếp vì có góc ngoài bằng góc đối trong ( ) 1
Xét tứ giác BEIF ta có :
BEI = BFI = 90 ( CE, DF là đường cao của BCD)
BEI + BFI = 180
Tứ giác BEIF nội tiếp đường tròn đường kính BI vì có tổng số đo 2 góc đối bằng 180 (2) Từ ( ) 1 và (2) B
,E,F,H,I cùng thuộc một đường tròn đường kính BI
BHK = 90 (Góc nội tiếp chắn nửa đường tròn đường kính BI )
BK là đường kính của đường tròn (O) Ta có:
+ DF ⊥ BC ( DF là đường cao của BCD)
+ KC ⊥ BC ( BCK là gnt chắn nửa đường tròn đường kính BK )
DF // KC (3) Ta có:
+ CI ⊥ DB ( CE là đường cao của BCD)
+ DK ⊥ DB ( BDK là gnt chắn nửa đường tròn đường kính BK )
CI // DK (4)
Từ (3) và (4) Tứ giác DICK là hình bình hành
Mà M là giao điểm của 2 đường chéo KI và DC
M là trung điểm của DC
OM ⊥ CD (Quan hệ giữa đường kính và dây) ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN PHUÙ NHUAÄN
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: Quận Phú Nhuận -
Thời gian: 120 phút (không kể thời gian phát đề) 2 1
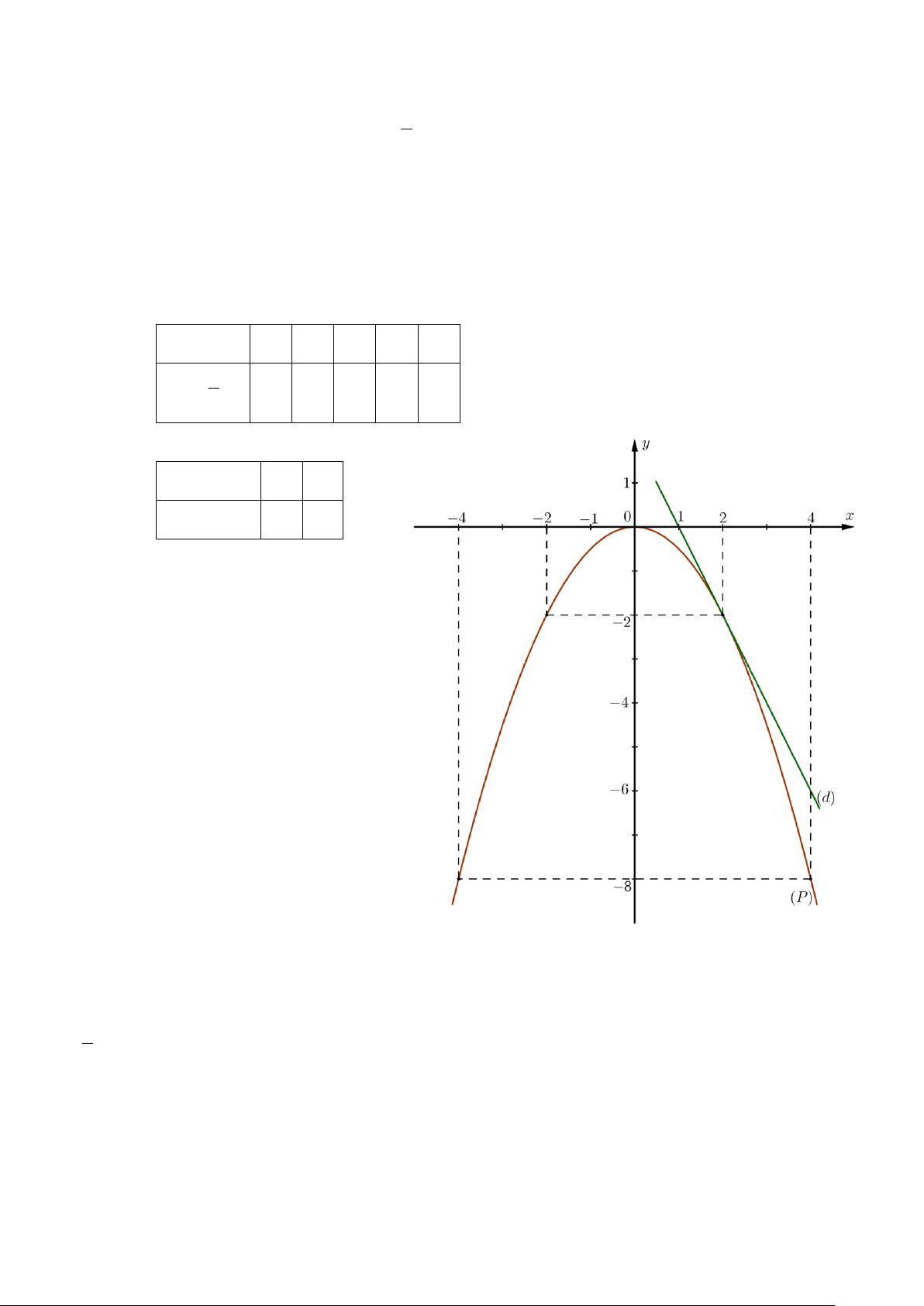
Câu 1. (1,5 điểm). Cho Parabol (P) : y = − 2
x và đường thẳng (d) : y = −2x + 2 . 2
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
2x − 3x − 3 = 0 có hai nghiệm là x và x . Tính giá trị biểu 1 2 thức sau: B = 2 x x + 2 x x . 1 2 2 1 Trang 9
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 3. (1 điểm). Tháng thứ nhất hai tổ sản xuất được 800 chi tiết máy. Tháng thứ hai tổ I vượt
mức 10% và tổ II vượt mức 20% so với tháng thứ nhất, vì vậy hai tổ đã sản xuất được
910 chi tiết máy. Hỏi tháng thứ nhất mỗi tổ sản xuất được bao nhiêu chi tiết máy.
Câu 4. (0,75 điểm). Một người gửi tiết kiệm 300 triệu đồng vào tài khoản ngân hàng Nam Á. Có 2 sự lựa chọn:
Lựa chọn 1 : Người gửi có thể nhận được lãi suất 7% một năm.
Lựa chọn 2 : Người gửi nhận tiền thưởng ngay là 4 triệu với lãi suất 6% một năm.
Người gửi nên chọn lựa chọn nào để nhận được tiền lãi cao hơn sau thời hạn 1 năm? Sau thời hạn 2 năm?
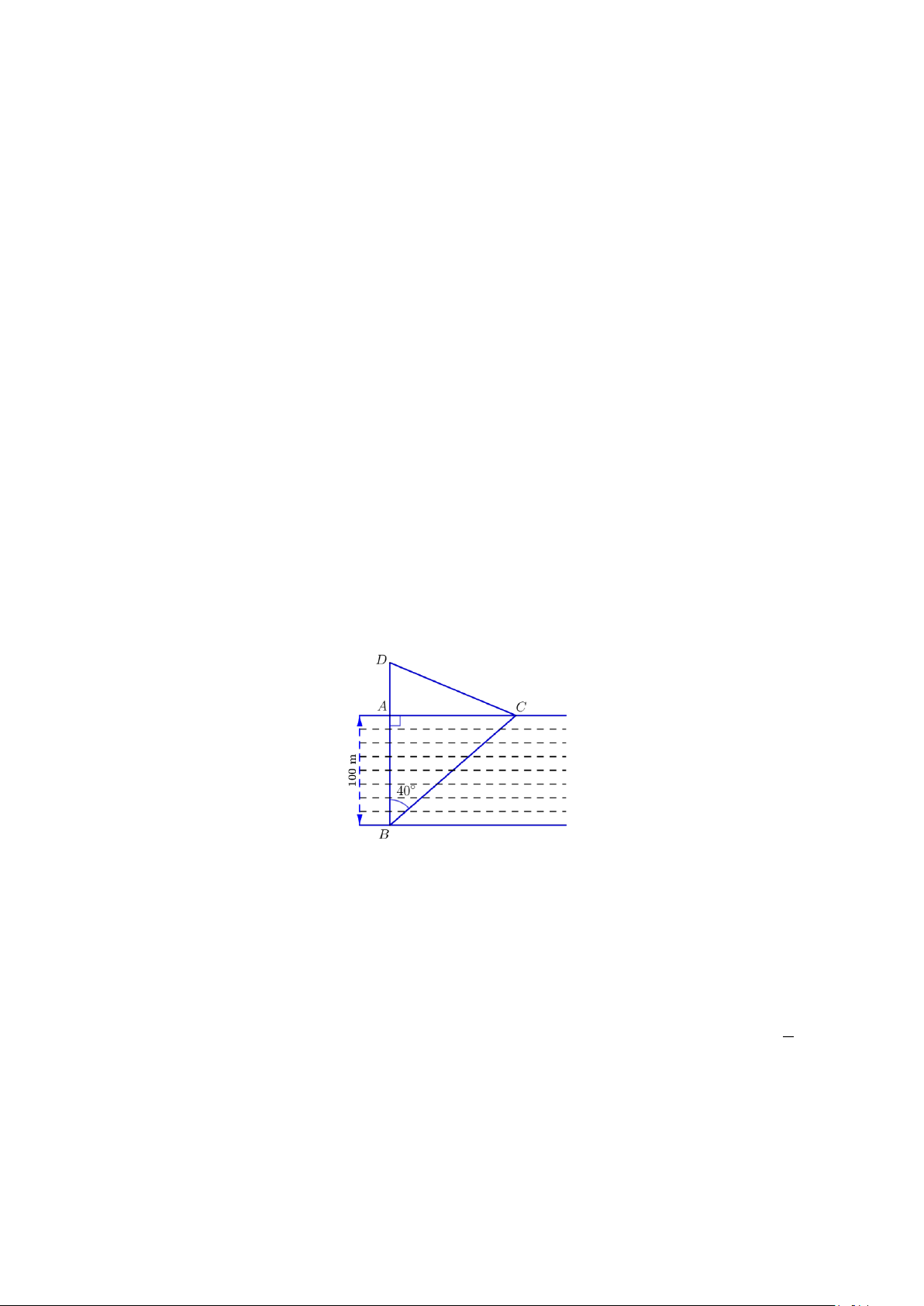
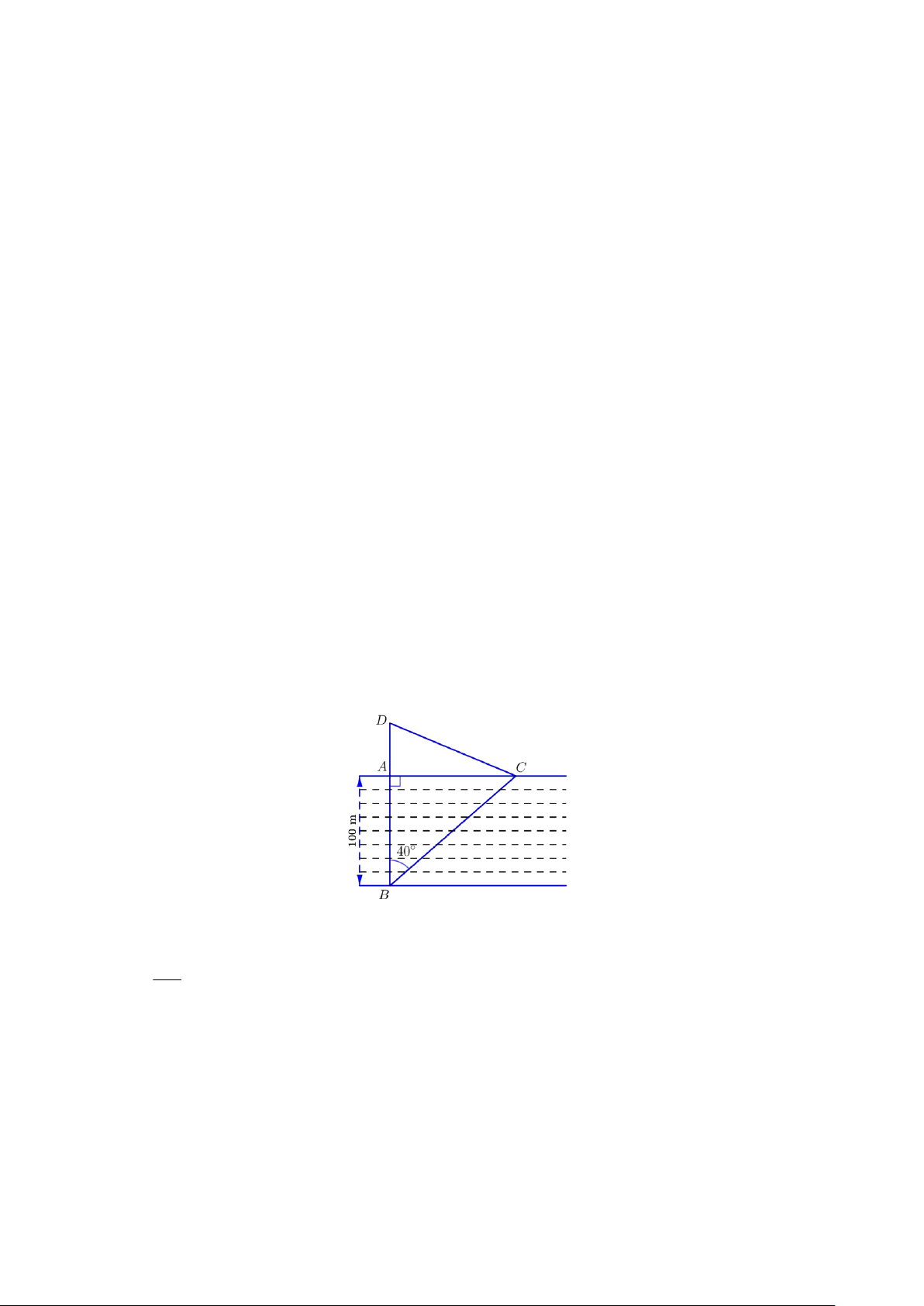
Câu 5. (1 điểm). Từ nhà bạn Nam đến trường phải qua một khúc sông rộng 100 m (Từ B đến A ).
Nhưng thực tế khi bạn Nam đi đò qua sông thì dòng nước đẩy xiên chiếc đò một góc 40
(đến điểm C ở bờ bên kia). Từ C bạn Nam phải đi bộ đến trường (điểm D ) mất thời gian
gấp đôi khi đi từ A . Hỏi quãng đường mà Nam đi bộ đến trường là bao nhiêu mét? Biết
rằng vận tốc Nam đi bộ là không thay đổi.
Câu 6. (1 điểm). Người ta trộn 8g chất lỏng này với 6g chất lỏng khác có khối lượng riêng lớn hơn nó là 3
0,2 g / cm để được hỗn hợp có khối lượng riêng 3
0,7 g / cm . Tìm khối lượng riêng của mỗi chất lỏng.
Câu 7. (1 điểm). Bạn Hưng làm việc tại nhà hàng nọ, bạn ấy được trả 2 triệu đồng cho 40 giờ làm 1
việc tại quán trong một tuần. Mỗi giờ làm thêm trong tuần bạn được trả bằng 1 số tiền 2
mà mỗi giờ bạn ấy kiếm được trong 40 giờ đầu. Nếu trong tuần đó bạn Hung được trả 2,3
triệu đồng thì bạn ấy đã phải làm thêm bao nhiêu giờ ?
Câu 8. (3 điểm) Cho ABC nhọn nội tiếp trong (O) . Lấy D BC nhỏ, kẻ dây AE// BC , DE cắt
BC tại F . Vẽ DH , DK , DI lần lượt vuông góc với các cạnh BC , AC , AB . Trang 10
a) Chứng minh BDF ” ADC , DCF ” DAB .
b) Chúng minh ba điểm H , I ¸ K thẳng hàng . BC AB AC c) Chứng minh = + . DH DI DK ----HẾT--- Trang 11 HƯỚNG DẪN GIẢI 1
Câu 1. (1,5 điểm). Cho Parabol (P) : y = − 2
x và đường thẳng (d) : y = −2x + 2 . 2
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải a) BGT: x −4 −2 0 2 4 y = − 1 2
x −8 −2 0 −2 −8 2 x 1 2 y = −2x + 2 0 −2
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : − 1 2 x = −2x + 2 2 2
x − 4x + 4 = 0 x = 2
Thay x = 2 vào y = −2x + 2 , ta được: y = −2.2 + 2 = −2 .
Vậy (2; − 2) là hai giao điểm cần tìm. Trang 12
Câu 2. (1 điểm). Cho phương trình 2
2x − 3x − 3 = 0 có hai nghiệm là x và x . Tính giá trị biểu 1 2 thức sau: B = 2 x x + 2 x x . 1 2 2 1 Lời giải 2 Vì = 2
b − 4ac = (−3) − 4.2.(−3) = 33 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 − = + = b S x x = 3 1 2
Theo định lí Vi-et, ta có: a 2 = c P x .x = = − 3 1 2 a 2 3 3 9 Ta có: A = 2 x x + 2 x x = x x x x . . 1 2 2 1 1 2 ( + 1 2 ) = − = − 2 2 4
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 3. (1 điểm). Tháng thứ nhất hai tổ sản xuất được 800 chi tiết máy. Tháng thứ hai tổ I vượt
mức 10% và tổ II vượt mức 20% so với tháng thứ nhất, vì vậy hai tổ đã sản xuất được
910 chi tiết máy. Hỏi tháng thứ nhất mỗi tổ sản xuất được bao nhiêu chi tiết máy. Lời giải
Gọi x , y lần lượt là số chi tiết máy tổ I và tổ II sản xuất được trong tháng thứ nhất (x,y *)
Vì trong tháng thứ nhất, cả hai tổ sản xuất được 800 chi tiết máy nên ta có phương trình: x + y = 800 ( ) 1
Tháng thứ hai, cả hai tổ đã vượt mức và sản xuất được 910 chi tiết máy, nên ta có phương trình:
x(1+ 10%) + y(1+ 20%) = 910 1,1x + 1,2y = 910 (2) x + y = 800 x = 500(n) Từ ( )
1 và (2) ta có hệ phương trình: . 1,1x + 1,2y = 910 y = 300(n)
Vậy tháng thứ nhất, tổ I sản xuất được 500 chi tiết máy, tổ II sản xuất được 300 chi tiết máy.
Câu 4. (0,75 điểm). Một người gửi tiết kiệm 300 triệu đồng vào tài khoản ngân hàng Nam Á. Có 2 sự lựa chọn:
Lựa chọn 1 : Người gửi có thể nhận được lãi suất 7% một năm.
Lựa chọn 2 : Người gửi nhận tiền thưởng ngay là 4 triệu với lãi suất 6% một năm.
Người gửi nên chọn lựa chọn nào để nhận được tiền lãi cao hơn sau thời hạn 1 năm? Sau thời hạn 2 năm? Trang 13 Lời giải
Trường hợp khách hàng gửi kỳ hạn 1 năm:
Tổng số tiền nhận được sau 1 năm với lựa chọn 1 : 300.(1+ 7%) = 321 triệu đồng.
Tổng số tiền nhận được sau 1 năm với lựa chọn 2 : 300.(1 + 6%) + 4 = 322 triệu đồng.
Vậy khách hàng nên chọn lựa chọn 2 sẽ nhận được tổng số tiền nhiều hơn.
Trường hợp khách hàng gửi kỳ hạn 2 năm:
Tổng số tiền nhận được sau 2 năm với lựa chọn 1 : 321.(1 + 7%) = 343,47 triệu đồng.
Tổng số tiền nhận được sau 2 năm với lựa chọn 2 : 300.(1+ 6%)(1+ 6%) + 4 = 341,08 triệu đồng.
Vậy khách hàng nên chọn lựa chọn 1 sẽ nhận được tổng số tiền nhiều hơn.
Câu 5. (1 điểm). Từ nhà bạn Nam đến trường phải qua một khúc sông rộng 100 m (Từ B đến A ).
Nhưng thực tế khi bạn Nam đi đò qua sông thì dòng nước đẩy xiên chiếc đò một góc 40
(đến điểm C ở bờ bên kia). Từ C bạn Nam phải đi bộ đến trường (điểm D ) mất thời gian
gấp đôi khi đi từ A . Hỏi quãng đường mà Nam đi bộ đến trường là bao nhiêu mét? Biết
rằng vận tốc Nam đi bộ là không thay đổi. Lời giải
Xét ABC vuông tại A , ta có: AC tan ABC = AC = A . B tan 4 0 = 100.tan 4 0 83,9 m . AB
Với vận tốc đi bộ trên các tuyến đường khác nhau không đổi và thời gian đi từ C → D gấp đôi thời gian
đi từ A → D nên DC = 2AD .
Xét ACD vuông tại A , ta có: 2 = 2 + 2 DC AD AC (ĐL Pytago) Trang 14 DC 2 2 DC = + 2 83,9 2 3 2 DC = 2 83,9 4 DC = 2 3 83,9 : 96,9 . m 4
Vậy Nam đã đi bộ quãng đường DC 96,9m .
Câu 6. (1 điểm). Người ta trộn 8g chất lỏng này với 6g chất lỏng khác có khối lượng riêng lớn hơn nó là 3
0,2 g / cm để được hỗn hợp có khối lượng riêng 3
0,7 g / cm . Tìm khối lượng riêng của mỗi chất lỏng. Lời giải Gọi V , V ( 3
cm ) lần lượt là thể tích của mỗi chất lỏng (V ,V 0 1 2 ) 1 2 m 8 m 6
Khối lượng riêng của mỗi chất lỏng: D = 1 = và D = 2 = . 1 V V 2 V V 1 1 2 2 8 6
Vì khối lượng riêng D lớn hơn D nên ta có phương trình: D - D = 0, 2 Þ - = 0, 2 ( ) 1 1 2 1 2 V V 1 2
Vì hỗn hợp sau khi trộn có khối lượng riêng là 3
0, 7g / cm nên ta có phương trình: m + m m + m 1 2 1 2 D =
= 0, 7 Þ V + V =
= 20 Þ V = 20 - V 2 1 2 2 1 ( ) V + V 0, 7 1 2 8 6 Thay (2) vào ( ) 1 , ta được: - = 0, 2 V 20 - V 1 1
Û 8(20 - V - 6V = 0,2V . 20 - V 1 ) 1 1 ( 1 ) 2
Û 160 - 8V - 6V = 4V - 0, 2V 1 1 1 1 2
Û 0, 2V - 14V + 160 = 0 1 1 V é = 80 V é = 20 - 80 = - 60 l ê 1 ê 2 ( ) Û Þ V ê = 10 V ê = 20 - 10 = 10 n ê 1 ê 2 ( ) ë ë 8 6
Vậy khối lượng riêng của mỗi chất lỏng: 3 D = = 0, 8g / cm , 3 D = = 0, 6g / cm . 1 10 2 10
Câu 7. (1 điểm). Bạn Hưng làm việc tại nhà hàng nọ, bạn ấy được trả 2 triệu đồng cho 40 giờ làm 1
việc tại quán trong một tuần. Mỗi giờ làm thêm trong tuần bạn được trả bằng 1 số tiền 2 Trang 15
mà mỗi giờ bạn ấy kiếm được trong 40 giờ đầu. Nếu trong tuần đó bạn Hưng được trả 2,3
triệu đồng thì bạn ấy đã phải làm thêm bao nhiêu giờ ? Lời giải
Số tiền bạn Hưng được trả trong 1 giờ làm việc trong tuần: 2 : 40 = 0, 05 triệu đồng 50 000 đồng. 1
Số tiền một giờ làm thêm bạn Hưng nhận được trong tuần: 50 000.1 = 75 000 đồng. 2
Số giờ làm thêm trong tuần của bạn Hưng: (2 300 000 - 2 000 00 ) 0 : 75 000 = 4 giờ.
Câu 8. (3 điểm) Cho ABC nhọn nội tiếp trong (O) . Lấy D BC nhỏ, kẻ dây AE// BC , DE cắt
BC tại F . Vẽ DH , DK , DI lần lượt vuông góc với các cạnh BC , AC , AB .
a) Chứng minh BDF ” ADC , DCF ” DAB .
b) Chúng minh ba điểm H , I ¸ K thẳng hàng . BC AB AC c) Chứng minh = + . DH DI DK Lời giải
a) Chứng minh BDF ” ADC , DCF ” DAB .
Trong (O) , ta có: AE// BC (gt) sñAB = sñCE . 1
Mà: BFD = (sñBD = sñCE) (góc có đỉnh ở trong đường tròn chắn BD và CE ) 2 1 1
Nên: BFD = (sñBD = sñAB) = sñAD 2 2
Lại có: ACD == 1 sñAD (gnt (O) chắn AD ) 2
Suy ra: BFD = ACD Trang 16 Xét B
DF và ADC , ta có:
DBF = DAC ( 2 gnt (O) cùng chắn DC ) BFD = ACD (cmt) B DF” A DC (g.g).
Xét DCF và D AB, ta có:
DCF = DAB ( 2 gnt (O) cùng chắn BD )
CDF = ADB ( 2 gnt (O) cùng chắn 2 cung AB = CE ) DCF ” DA B (g.g).
b) Chúng minh ba điểm H , I ¸ K thẳng hàng .
Xét tứ giác BHDI , có:
BHD = 90(DH ⊥ BC ) BID = 90 (DI ⊥ AB)
BHD + BID = 180
Tứ giác BHDI nội tiếp vì có hai góc đối bù nhau.
Xét tứ giác DHKC , có:
DHC = 90(DH ⊥ BC ) DKC = 90 (DK ⊥ AC)
DHC = DKC(= 90)
Tứ giác DHKC nội tiếp vì có hai đỉnh kề cùng nhìn một cạnh dưới hai góc bằng nhau.
DHK + DCL = 180
Mà: DBI = DCK (tg ABDC nội tiếp)
Và DBI = DHI (tg BIDH nội tiếp)
Nên: DHK + DHI = 180 KHI = 180 . BC AB AC c) Chứng minh = + . DH DI DK Trang 17
Xét AID và CHD , ta có:
IAD = HCD ( 2 gnt (O) cùng chắn BD )
AID = CHD(= 90) A ID” CHD (g.g). AI ID = (tsđd) AI CH = ( ) 1 CH DH ID DH Xét A KD và B HD , ta có:
DAK = DBH ( 2 gnt (O) cùng chắn DC )
AKD = BHD(= 90) AK D” BHD (g.g). AK DK = (tsđd) AK BH = (2) BH DH DK DH Xét B
ID và CKD , ta có:
DBI = DCK (Tứ giác ABDC nội tiếp)
DIB = DKC (= 90) B ID” CK D (g.g). BI ID = (tsđd) BI CK = (2) CK BK ID BK Cộng ( )
1 và (2) theo vế, ta được: AI AK CH BH + = + ID DK DH DH AB + BI AC − KC BC + = ID DK DH AB BI AC KC BC + + − = ID ID DK DK DH AB AC BC BI KC + = = ID DK DH ID DK ----HẾT--- Trang 18