Bộ Đề Ôn Thi Toán Tuyển Sinh 10 Quận 10 TP HCM 2025-2026 Giải Chi Tiết
Bác Năm dùng hai xô nước để lấy nước từ một hồ để sử dụng trong sinh hoạt và trồng trọt. Gia đình bác sử dụng trung bình mỗi ngày 150lít nước. Hỏi bác Năm cần phải lấy ít nhất bao nhiêu lần mỗi ngày (mỗi lần xách 2 xô) để phục vụ cho sinh hoạt và trồng trọt, biết rằng mỗi lần xách nước về thì lượng nước bị hao hụt khoảng 5%. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 216 tài liệu
Môn: Toán 9 3 K tài liệu
Tác giả:
Preview text:
SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN 10 MÔN: TOÁN 9
MÃ ĐỀ: Quận 10 - 1
Đê thi gồm 8 câu hỏi tự luận
Thời gian: 120 phút (không kể thời gian phát đề) ĐỀ THAM KHẢO 1 1 −
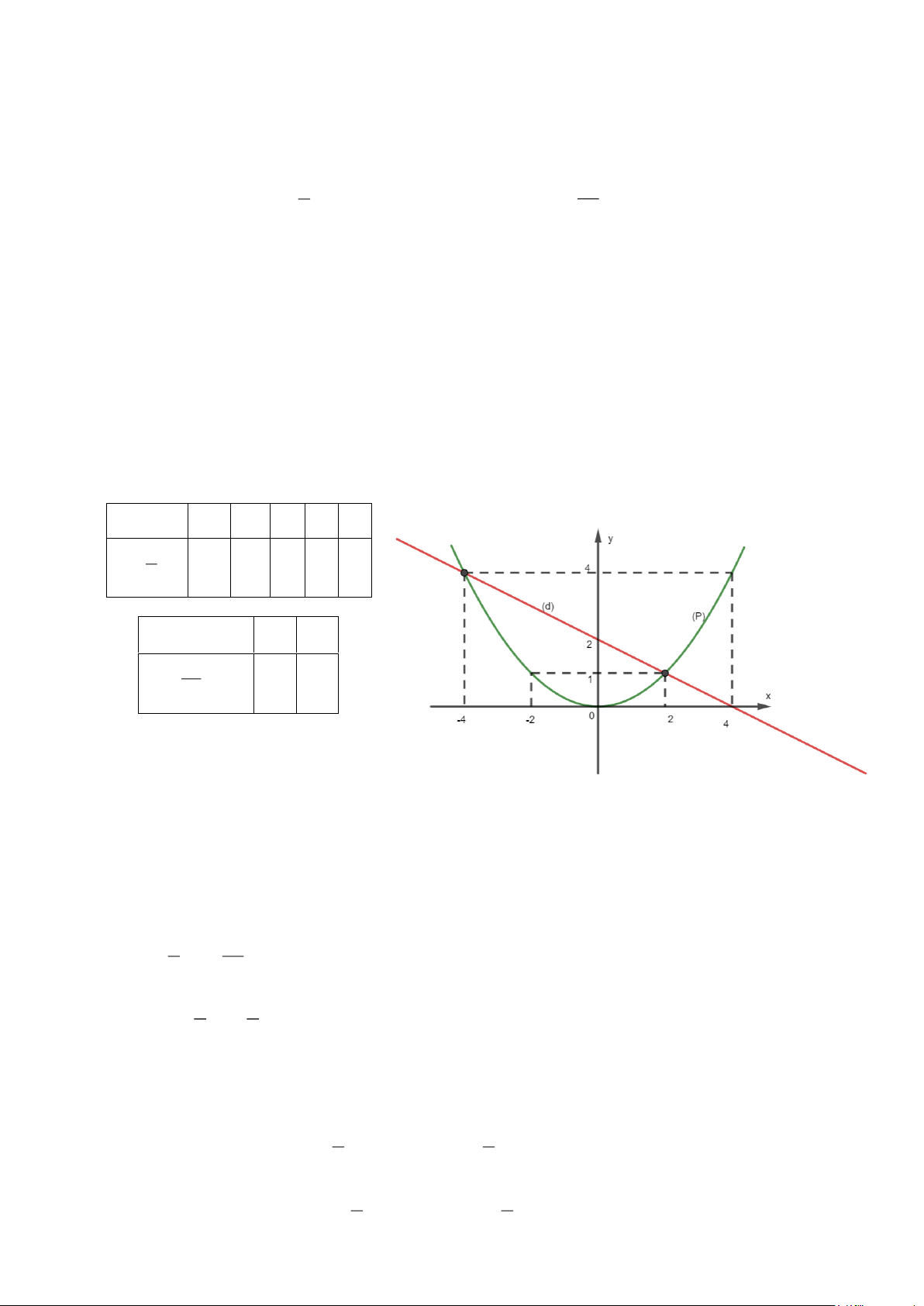
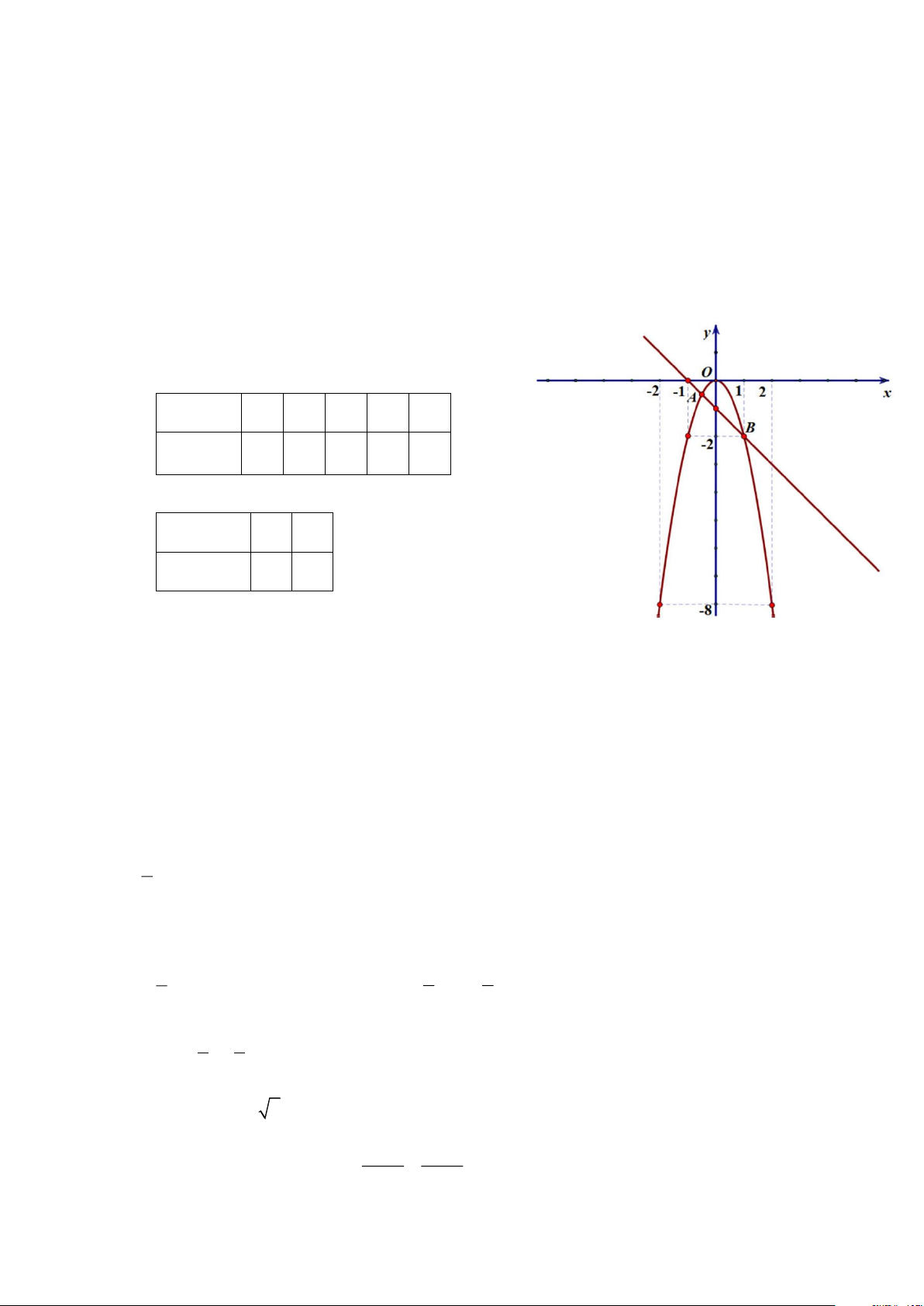
Bài 1. (1,5 điểm). Cho 2 y =
x có đồ thị (P) và hàm số y =
x + 2 có đồ thị là đường thẳng (d) 4 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Bài 2. (1,0 điểm). Cho phương trình 2
3x + 5x − 1 = 0 có 2 nghiệm là x , x . 1 2
Không giải phương trình, hãy tính giá trị của biểu thức 2 2
A = x + x − x x 1 2 1 2
Bài 3. (1,0 điểm). Nhân dịp Tết Nguyên đán, một cửa hàng bán đồ dùng thể thao có chương trình
giảm giá toàn bộ sản phẩm trong cửa hàng như sau: Một áo thể thao giảm 10% , một quần
thể thao giảm 20% , một đôi giày thể thao giảm 30% . Đặc biệt nếu mua đủ 3 sản phẩm
bao gồm 1 quần, 1 áo, 1 đôi giày thì sẽ được giảm tiếp 5% trên giá đã giảm. Bạn An vào
cửa hàng này và mua 3 áo với giá 300 000 đồng/cái, 2 quần với giá 250 000 đồng/cái và 1
đôi giày với giá 1 000 000 đồng/đôi (giá trên là giá chưa giảm). Vậy số tiền bạn An phải trả là bao nhiêu?
Bài 4. (0,75 điểm). Một vật rơi tự do từ độ cao 150m so với mặt đất. Bỏ qua sức cản của không
khí, quãng đường chuyển động s (mét) của vật rơi sau thời gian t (giây) được biểu diễn
gần đúng bởi công thức: 2 s = 5t .
a) Sau 3 giây (tính từ lúc bắt đầu rơi) vật này cách mặt đất bao nhiêu mét?
b) Tính quãng đường đi được của vật đó trong giây thứ 4 .
Bài 5. (1,0 điểm). Còn một tuần nữa sẽ đến ngày 20 / 11 , các bạn học sinh lớp 9A đăng kí thi đua
hoa điểm 10 với mong muốn đạt thật nhiều điểm 10 để tặng thầy cô giáo. Đến ngày
19 / 11 , lớp trưởng tổng kết số điểm 10 của các bạn trong lớp và được như sau:
• Không có bạn nào trong lớp không có điểm 10 trong tuần vừa qua.
• Có 20 bạn có ít nhất 2 điểm 10 .
• Có 10 bạn có ít nhất 3 điểm 10 .
• Có 5 bạn có ít nhất 4 điểm 10 .
• Không có ai có nhiều hơn 4 điểm 10 .
Hỏi lớp 9A có bao nhiêu điểm 10 tuần vừa qua? Biết rằng lớp 9A có 35 học sinh. Trang 1
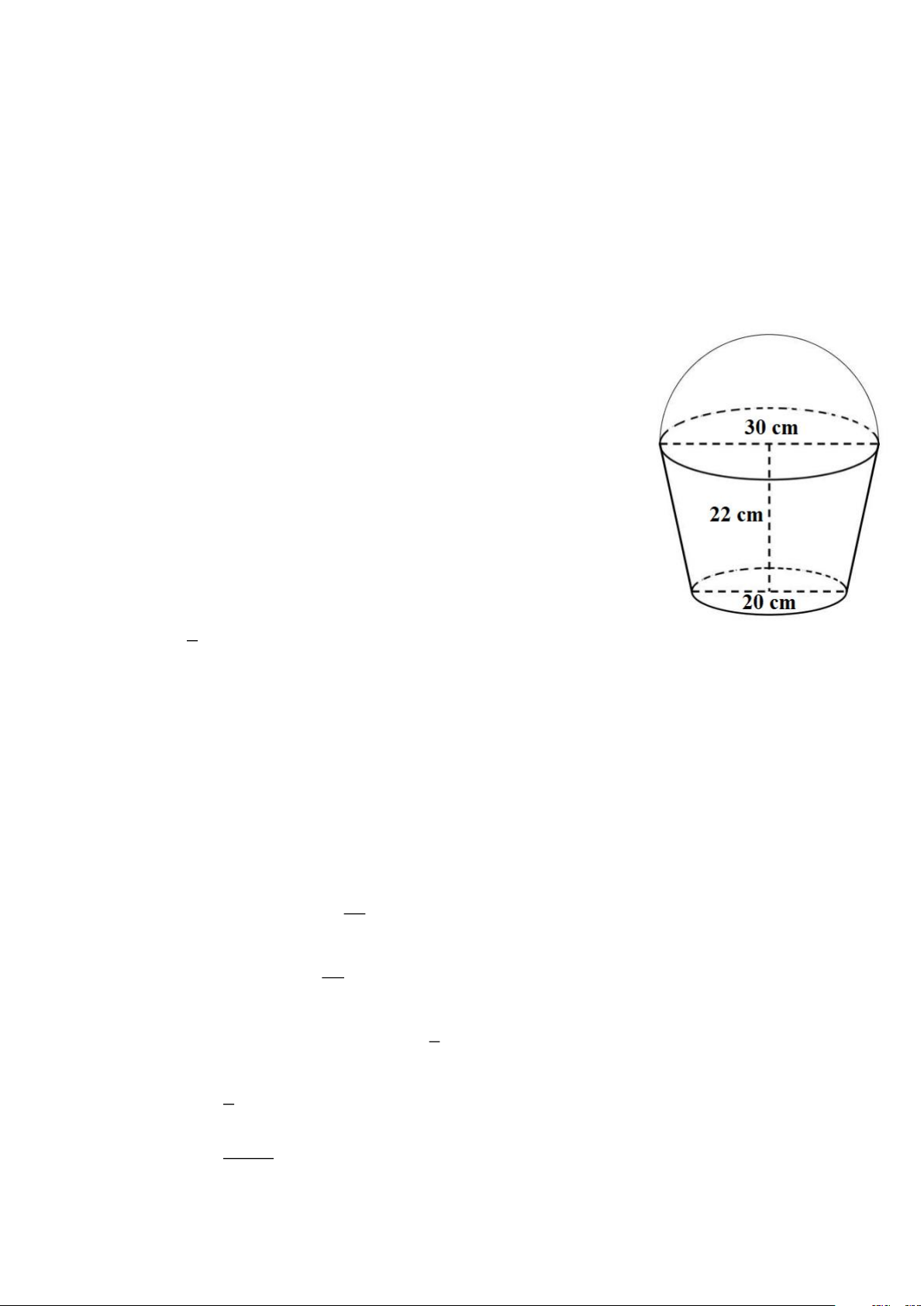
Bài 6. (1,0 điểm). Một xô đựng nước có dạng hình nón cụt (có các kích thước như hình). Đáy xô có
đường kính là 20cm , miệng xô là đáy lớn của hình nón cụt có đường kính 30cm và chiều
cao của xô là 22cm .
a) Xô có thể chứa tối đa bao nhiêu lít nước? Biết rằng thể tích của hình nón cụt có R , r , h 1
lần lượt là bán kính đáy lớn, bán kính đáy nhỏ và chiều cao là: V = h( 2 2
R + Rr + r ) ( 3
kết quả làm tròn đến hàng đơn vị)
b) Bác Năm dùng hai xô nước để lấy nước từ một hồ để sử dụng trong sinh hoạt và trồng
trọt. Gia đình bác sử dụng trung bình mỗi ngày 150 lít nước. Hỏi bác Năm cần phải lấy
ít nhất bao nhiêu lần mỗi ngày (mỗi lần xách 2 xô) để phục vụ cho sinh hoạt và trồng
trọt, biết rằng mỗi lần xách nước về thì lượng nước bị hao hụt khoảng 5% .
Bài 7. (1,0 điểm)Tổng số học sinh của lớp 9A và 9B vào đầu năm học là 90 học sinh. Đến đầu
học kì II , lớp 9A có 2 học sinh đi du học và 4 học sinh chuyển qua lớp 9B nên lúc này số 5
học sinh lớp 9A chỉ bằng
số học sinh lớp 9B . Tính số học sinh đầu năm của lớp 9A và 6 9B .
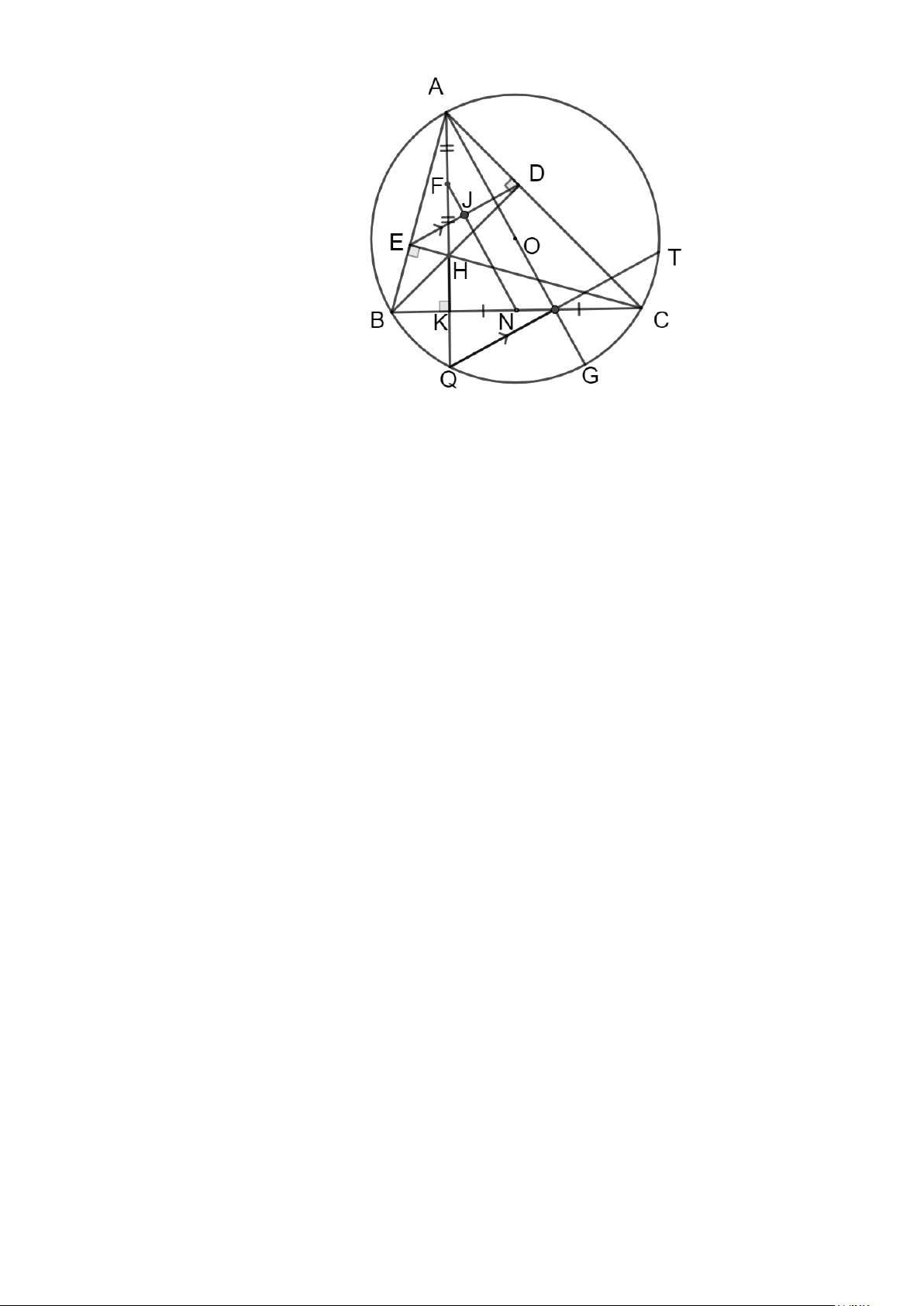
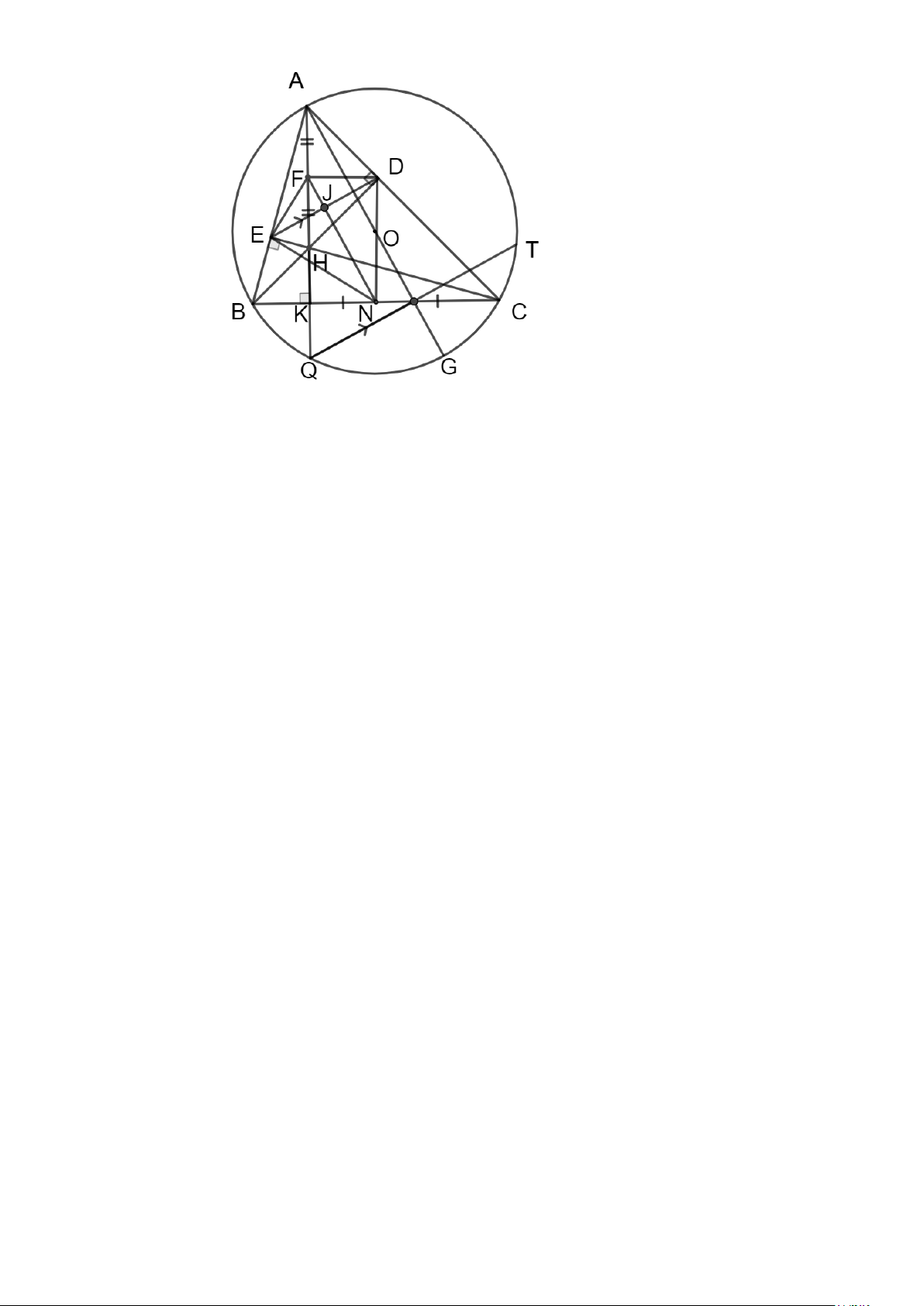
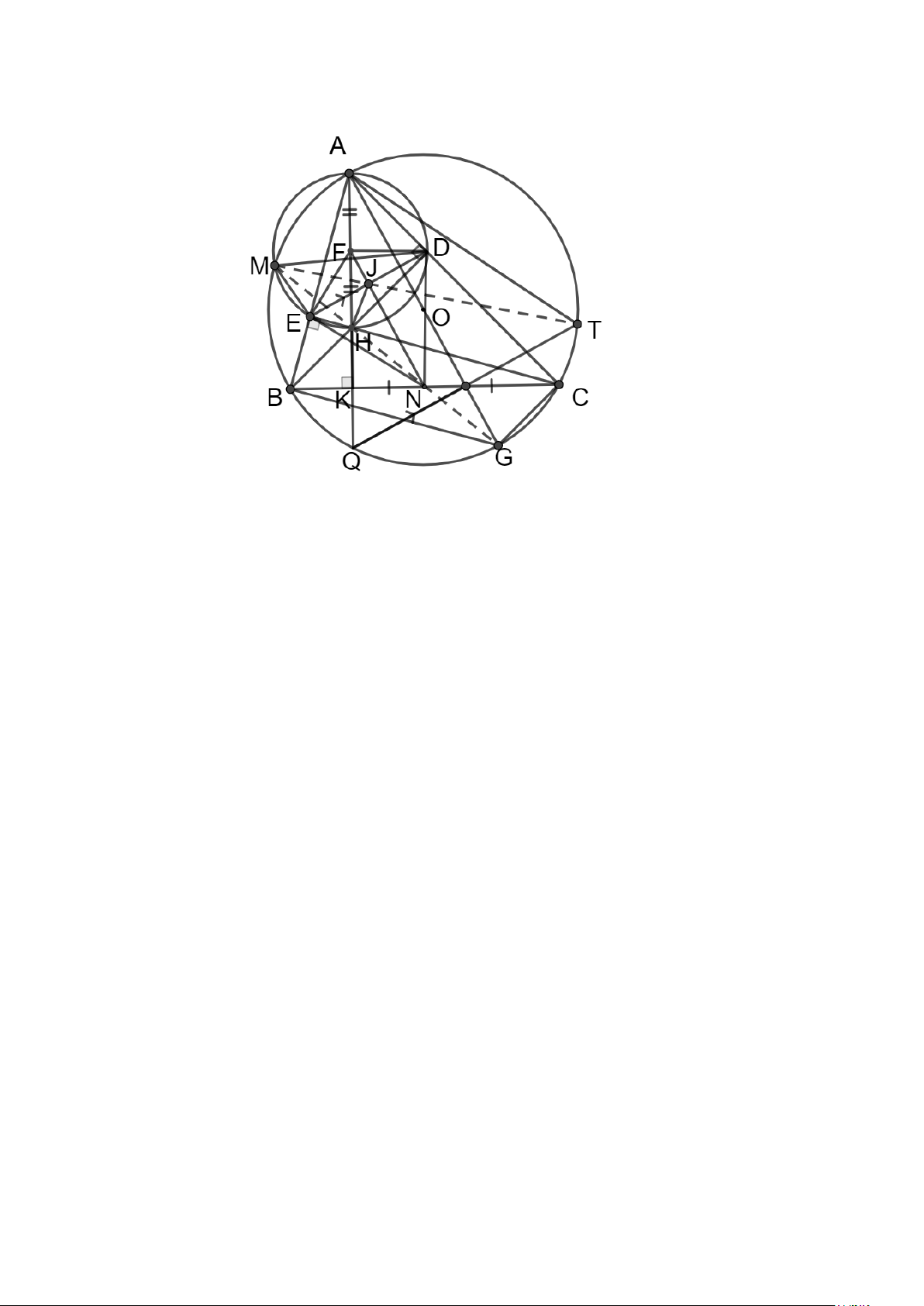
Bài 8. (3,0 điểm) Cho ABC nhọn nội tiếp đường tròn (O) có các đường cao AK, BD, CE cắt nhau
tại H , tia AK cắt (O) tại Q . Gọi N là trung điểm của BC , F là trung điểm AH . Kẻ đường
kính AG của (O) , đường thẳng qua Q song song với ED cắt (O) tại giao điểm thứ 2 là T (
T khác Q ). Gọi J là giao điểm của NF và ED .
a) Chứng minh BEDC và AEHD là các tứ giác nội tiếp.
b) Chứng minh: FD ⊥ ND . Từ đó suy ra 2
ND = NJ.NF
c) Đường tròn đường kính AH cắt (O) tại giao điểm thứ hai là M ( M khác A ). Chứng minh: 2
ND = NH.NM và M , J, T thẳng hàng. ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI 1 1 −
Bài 1. (1,5 điểm) Cho 2
y = x có đồ thị (P) và hàm số y =
x + 2 có đồ thị là đường thẳng 4 2 (d)
a) Vẽ đồ thị (P) và (d ) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d ) bằng phép tính. Lời giải
a) Vẽ đồ thị (P) và (d ) trên cùng hệ trục tọa độ. BGT: x −4 −2 0 2 4 y = 1 2 x 4 1 0 1 4 4 x 0 2 − y = 1 x + 2 2 1 2
b) Tìm tọa độ giao điểm của (P) và (d ) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d ) : 1 − 2 1 x = x + 2 4 2 1 2 1
x + x − 2 = 0 4 2 x = 2 x = −4 1 1 Thay x = 2 vào 2
y = x , ta được: 2 y = .2 = 1 4 4 1 1 Thay x = − 4 vào 2
y = x , ta được: y = .( 4 − )2 = 4 4 4 Trang 3 Vậy (2; )
1 , (− 4; 4) là hai giao điểm cần tìm.
Bài 2. (1,0 điểm). Cho phương trình 2
3x + 5x −1 = 0 có 2 nghiệm là x , x . 1 2
Không giải phương trình, hãy tính giá trị của biểu thức 2 2
A = x + x − x x 1 2 1 2 Lời giải Vì 2 2
= b − 4ac = 5 − 4.3.(− ) 1 = 37 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 −b 5
S = x + x = = − 1 2
Theo định lí Vi-et, ta có: a 3 c 1
P = x .x = = − 1 2 a 3 Ta có: 2 2
A = x + x − x x 1 2 1 2 2 2
A = x + x − x x 1 2 1 2
A = ( x + x )2 − 2x x − x x 1 2 1 2 1 2
A = ( x + x )2 − 3x x 1 2 1 2 2 5 1 A = − − 3 − 3 3 34 A = 9
Bài 3. (1,0 điểm). Nhân dịp Tết Nguyên đán, một cửa hàng bán đồ dùng thể thao có chương trình
giảm giá toàn bộ sản phẩm trong cửa hàng như sau: Một áo thể thao giảm 10% , một quần
thể thao giảm 20% , một đôi giày thể thao giảm 30% . Đặc biệt nếu mua đủ 3 sản phẩm
bao gồm 1 quần, 1 áo, 1 đôi giày thì sẽ được giảm tiếp 5% trên giá đã giảm. Bạn An vào
cửa hàng này và mua 3 áo với giá 300 000 đồng/cái, 2 quần với giá 250 000 đồng/cái và
1 đôi giày với giá 1 000 000 đồng/đôi (giá trên là giá chưa giảm). Vậy số tiền bạn An phải trả là bao nhiêu? Lời giải
Giá của 1 áo thể thao sau khi giảm 10% là :
300 000.(100% −10%) = 270 000 (đồng)
Giá của 1 quần thể thao sau khi giảm 20% là :
250 000.(100% − 20%) = 200 000 (đồng)
Giá của 1 đôi giày thể thao sau khi giảm 30% là : Trang 4
1 000 000.(100% − 30%) = 700 000 (đồng)
Giá của 1 quần, 1 áo, 1 đôi giày sau khi giảm tiếp 5% là:
(270 000 + 200 000 + 700 000).(100% − 5%) = 1 111 500 (đồng)
Vậy số tiền bạn An phải trả là:
1 111 500 + 2 . 270 000 + 200 000 = 1 851 500 (đồng)
Bài 4. (0,75 điểm). Một vật rơi tự do từ độ cao 150m so với mặt đất. Bỏ qua sức cản của không
khí, quãng đường chuyển động s (mét) của vật rơi sau thời gian t (giây) được biểu diễn
gần đúng bởi công thức: 2 s = 5t .
a) Sau 3 giây (tính từ lúc bắt đầu rơi) vật này cách mặt đất bao nhiêu mét?
b) Tính quãng đường đi được của vật đó trong giây thứ 4 . Lời giải a) Thay t = 3 vào 2
s = 5t ta có: 2 s = 5.3 s = 45
Vậy sau 3 giây (tính từ lúc bắt đầu rơi) vật này cách mặt đất: 150 − 45 = 105(m) b) Thay t = 4 vào 2
s = 5t ta có: 2 s = 5.4 s = 80
Vậy quãng đường đi được của vật đó trong giây thứ 4 là 80m
Bài 5. (1,0 điểm). Còn một tuần nữa sẽ đến ngày 20 / 11, các bạn học sinh lớp 9A đăng kí thi
đua hoa điểm 10 với mong muốn đạt thật nhiều điểm 10 để tặng thầy cô giáo. Đến ngày
19 / 11, lớp trưởng tổng kết số điểm 10 của các bạn trong lớp và được như sau:
• Không có bạn nào trong lớp không có điểm 10 trong tuần vừa qua.
• Có 20 bạn có ít nhất 2 điểm 10 .
• Có 10 bạn có ít nhất 3 điểm 10 .
• Có 5 bạn có ít nhất 4 điểm 10 .
• Không có ai có nhiều hơn 4 điểm 10 .
Hỏi lớp 9A có bao nhiêu điểm 10 tuần vừa qua? Biết rằng lớp 9A có 35 học sinh. Lời giải
Vì không có bạn nào trong lớp không có điểm 10 nên số bạn được 1 điểm 10 là: 35− 20 = 15 (baïn) Trang 5
Số bạn được 2 điểm 10 là: 20 −10 = 10 (baïn)
Số bạn được 3 điểm 10 là: 10 − 5 = 5 (baïn)
Do không có bạn nào được nhiều hơn 4 điểm 10 nên số bạn được 4 điểm 10 là: 5 bạn
Vậy số điểm 10 trong tuần vừa qua của lớp là:
15+10.2 + 5.3+ 5.4 = 70(ñieå ) m
Bài 6. (1,0 điểm). Một xô đựng nước có dạng hình nón cụt (có các
kích thước như hình). Đáy xô có đường kính là 20cm , miệng
xô là đáy lớn của hình nón cụt có đường kính 30cm và chiều
cao của xô là 22cm .
a) Xô có thể chứa tối đa bao nhiêu lít nước? Biết rằng thể
tích của hình nón cụt có R , r , h lần lượt là bán kính đáy
lớn, bán kính đáy nhỏ và chiều cao là: 1 V = h( 2 2
R + Rr + r ) ( kết quả làm tròn đến hàng đơn 3 vị)
b) Bác Năm dùng hai xô nước để lấy nước từ một hồ để sử dụng trong sinh hoạt và trồng
trọt. Gia đình bác sử dụng trung bình mỗi ngày 150 lít nước. Hỏi bác Năm cần phải lấy
ít nhất bao nhiêu lần mỗi ngày (mỗi lần xách 2 xô) để phục vụ cho sinh hoạt và trồng
trọt, biết rằng mỗi lần xách nước về thì lượng nước bị hao hụt khoảng 5% . Lời giải 30
a) Bán kính miệng xô là: R = =15 (cm) 2 20
Bán kính đáy xô là: r = =10 (cm) 2 1
Thay h = 22, R = 15, r = 10 vào V = h( 2 2
R + Rr + r ) ta có: 3 1 V = .22.( 2 2 15 +15.10 +10 ) 3 10450 V = ( 3 cm ) 3 Trang 6 209 V = (lít) 60 V 11 (lít)
Vậy xô có thể chứa tối đa 11 lít nước
b) Lượng nước mỗi lần xách là: 209 ( − ) = 3971 2. . 100% 5% (lít) 60 600
Bác Năm cần phải lấy ít nhất số lần là: 3971 150 : 8 (laà) n 600
Vậy bác Năm cần phải lấy ít nhất 8 lần
Bài 7. (1,0 điểm)Tổng số học sinh của lớp 9A và 9B vào đầu năm học là 90 học sinh. Đến đầu
học kì II , lớp 9A có 2 học sinh đi du học và 4 học sinh chuyển qua lớp 9B nên lúc này số 5
học sinh lớp 9A chỉ bằng số học sinh lớp 9B . Tính số học sinh đầu năm của lớp 9A và 6 9B . Lời giải
Gọi số học sinh của lớp 9A là x(hoïc sinh) (x Î ¥ *, x < 90)
Gọi số học sinh của lớp 9B là y(hoïc sinh) (y Î ¥ *, y < ) 90
Vì tổng số học sinh của lớp 9A và 9B vào đầu năm học là 90 học sinh nên ta có phương trình: x + y = 90
Số học sinh 9A đầu học kì II là:
x - 2 - 4 = x - 6 (hoïcsinh)
Số học sinh 9B đầu học kì II là:
x + 4(hoïcsinh) 5
Vì đến đầu học kì II số học sinh lớp 9A chỉ bằng số học sinh lớp 9B nên ta có phương 6 trình: Trang 7 5
x - 6 = .( y + 4) 6 5 10 x - 6 = y + 6 3 5 10 x - y = + 6 6 3 5 28 x - y = 6 3 Ta có hệ phương trình: x + y = 90 5 28 x - y = 6 3
Giải hệ phương trình ta được:
x = 46 (nhaän) y = 44 (nhaän)
Vậy số học sinh đầu năm của lớp 9A là 46 học sinh
Số học sinh đầu năm của lớp 9B là 44 học sinh
Bài 8. (3,0 điểm) Cho ABC nhọn nội tiếp đường tròn (O) có các đường cao AK, BD, CE cắt
nhau tại H , tia AK cắt (O) tại Q . Gọi N là trung điểm của BC , F là trung điểm AH .
Kẻ đường kính AG của (O) , đường thẳng qua Q song song với ED cắt (O) tại giao điểm
thứ 2 là T ( T khác Q ). Gọi J là giao điểm của NF và ED .
a) Chứng minh BEDC và AEHD là các tứ giác nội tiếp.
b) Chứng minh: FD ⊥ ND . Từ đó suy ra 2
ND = NJ.NF
c) Đường tròn đường kính AH cắt (O) tại giao điểm thứ hai là M ( M khác A ). Chứng minh: 2
ND = NH.NM và M , J , T thẳng hàng. Lời giải Trang 8
a) Chứng minh BEDC và AEHD là các tứ giác nội tiếp.
Xét tứ giác BEDC có: BEC = 90 (CE ⊥ AB) BDC = 90 (BD ⊥ AC) BEC = BDC
Tứ giác BEDC nội tiếp ( 2 đỉnh liền kề cùng nhìn 1 cạnh)
Xét tứ giác AEHD có: AEH = 90 (CE ⊥ AB) ADH = 90 (BD ⊥ AC)
AEH + ADH = 180
Tứ giác AEHD nội tiếp (tổng 2 góc đối = 180 )
b) Chứng minh: FD ⊥ ND . Từ đó suy ra 2
ND = NJ.NF Trang 9
Vì tứ giác AEHD nội tiếp (cmt) có ADH là góc nội tiếp mà ADH = 90
AH là đường kính
F là tâm (vì F là trung điểm của AH )
AF = FD (bán kính)
AFD cân tại F FAD = FDA
Vì tứ giác BEDC nội tiếp (cmt) có BDC là góc nội tiếp mà BDC = 90
BC là đường kính
N là tâm(vì N là trung điểm của BC )
ND = NC (bán kính)
NDC cân tại N NDC = NCD
Xét AKC vuông tại K (vì AK ⊥ BC ) có:
KAC + KCA = 90
FAD + NCD = 90
FDA + NDC = 90
Mà FDA + NDC + FDN = 180 FDN = 90 FD ⊥ ND
FDN vuông tại D
Vì FE = FD (bán kính, tứ giác AEHD nội tiếp (F))
NE = ND (bán kính, tứ giác BEDC nội tiếp (N) )
NF là trung trực của ED
NF ⊥ ED tại J
Xét FDN vuông tại D có DJ là đường cao 2
ND = NJ.NF (hệ thức lượng trong tam giác vuông)
c) Đường tròn đường kính AH cắt (O) tại giao điểm thứ hai là M ( M khác A ). Trang 10 Chứng minh: 2
ND = NH.NM và M , J , T thẳng hàng.
Ta có HMA = 90 (góc nội tiếp chắn nửa (F)) HM ⊥ AM
GMA = 90 (góc nội tiếp chắn nửa (O) ) GM ⊥ AM
G, H , M thẳng hàng
GCA = 90 (góc nội tiếp chắn nửa (O) ) GC ⊥ AC
Mà BD ⊥ AC (gt) GC / /BD
GC / /BH
GBA = 90 (góc nội tiếp chắn nửa (O) ) GB ⊥ AB
Mà CE ⊥ AB (gt) GB / /CE
GB / /CH
Xét tứ giác BHCG có:
GC / /BH (cmt)
GB/ /CH (cmt) Trang 11
BHCG là hình bình hành
Mà N là trung điểm BC
N là trung điểm HG
H , N, G thẳng hàng
Mà G, H , M thẳng hàng (cmt)
M , H , N, G thẳng hàng
Xét NEH và NME có: MNE chung 1 NEH =
NME = sñME 2 NE H ” NM
E ( g − g ) NE NH = NM NE 2
NE = NH.NM
Mà NE = ND (cmt) 2
ND = NH.NM Mà 2
ND = NJ.NF (chứng minh câu b)
NH.NM = NJ.NF NH NJ = NF NM
Xét NJH và NMF có: MNF chung NH NJ = (cmt) NF NM N JH ” N
MF (c − g − c) NJH = NMF
tứ giác MHJF nội tiếp (góc trong = góc đối ngoài)
HMJ = HFJ ( 2 góc nội tiếp cùng chắn JH )
Ta có GMT = GAT ( 2 góc nội tiếp cùng chắn GT của (O) )
Vì tứ giác BEDC nội tiếp
ADE = ABC (góc trong = góc đối ngoài) Trang 12
ABC = 1 sñAC = 1 AOC = 1(18 0 − 2.OAC) = 9 0 − OAC 2 2 2
ABC + OAC = 90
ADE + OAC = 90 AG ⊥ ED
Mà NF ⊥ ED (cmt) AG / /NF
QAG = HFJ(ñoàn g v ) ò
Mặt khác AG ⊥ ED (cmt); ED / /QT ( gt) AG ⊥ QT
Mà AG là đường kính
AG đi qua trung điểm của QT (quan hệ đường kính và dây)
AG vừa là đường cao, vừa là trung tuyến của AQT AQT cân tại A
AG là phân giác QAT QAG = GAT
GAT = HFJ (cùng = QAG )
GMT = HFJ (cùng = GAT )
GMT = HMJ (cùng = HFJ )
Mà G, H , M thẳng hàng
M , J, T thẳng hàng (điều phải chứng minh) ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 10
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 10 - 2
Thời gian: 120 phút (không kể thời gian phát đề) a)
Cho (P) y = − 2 :
2x và đường thẳng (d) : y = −x − 1 .
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Trang 13 b) Cho phương trình − 2
2x + 2x + 3 = 0 có 2 nghiệm phân biệt là x ,x . Không giải phương 1 2 x + 1 x + 1
trình, hãy tính giá trị của biểu thức A = 2 + 1 1 − x 1 − x 1 2 c)
Ở Bạc Liêu ngành nông nghiệp khuyến khích bà con nông dân phương thức nuôi trồng :
“con tôm, cây lúa”, cải tạo đồng lúa năng suất thấp thành các hồ nuôi tôm nước mặn. Dung
dịch nước muối nuôi tôm có nồng độ 5% . Nhưng nơi đây chỉ có nước biển nồng độ 10%
và nước lợ nồng độ muối 1% . Để đổ đầy hồ nuôi tôm có dung tích 1000 lít phải cần bơm
vào hồ mỗi loại nước bao nhiêu kg ? Biết khối lượng riêng của dung dịch nước muối 5% là 1, 8kg / l d)
Đối với người Á Đông, Âm lịch luôn giữ vai trò quan trọng giúp chúng ta xác định các dịp
lễ Tết trong năm. Và cũng như Dương lịch, Âm lịch cũng sẽ có năm nhuận. Để biết được
năm Âm lịch có nhuận hay không, ta lấy năm Dương lịch tương ứng chia cho 19 . Nếu số
dư của phép chia này là 0; 3; 6; 9; 11; 14; 17 thì năm đó sẽ là năm Âm lịch nhuận.
a) Hãy tính xem năm 2020 có phải năm Âm lịch nhuận hay không? Vì sao?
b) Biết rằng một năm dương lịch được gọi là nhuận nếu năm Dương lịch đó chia hết cho 4 .
Bác Năm sinh ra vào cuối thế kỉ 20 , bác Năm chưa quá 50 tuổi . Hãy tính xem bác Năm
sinh ra năm bao nhiêu biết rằng năm sinh của bác là một năm vừa nhuận Âm lịch, vừa nhuận Dương lịch. e)
Giá cước gọi quốc tế của một công ty X trong dịp khuyến mãi mừng ngày thành lập công
ty được cho bởi bảng sau: Thời gian Giá cước (VNĐ) 5 phút đầu 6000 Từ phút thứ 6 - 10 5800 Từ phút thứ 11 - 20 5200 Từ phút thứ 21 - 30 5000 Trên 30 phút 4500
a) Bác Lan gọi cho người thân ở nước ngoài trong thời gian 24 phút thì số tiền bác Lan trả là bao nhiêu?
b) Một người đã trả 197 000 đồng để gọi điện cho người thân ở nước ngoài . Tính thời gian
người đó đã gọi điện cho người thân. f)
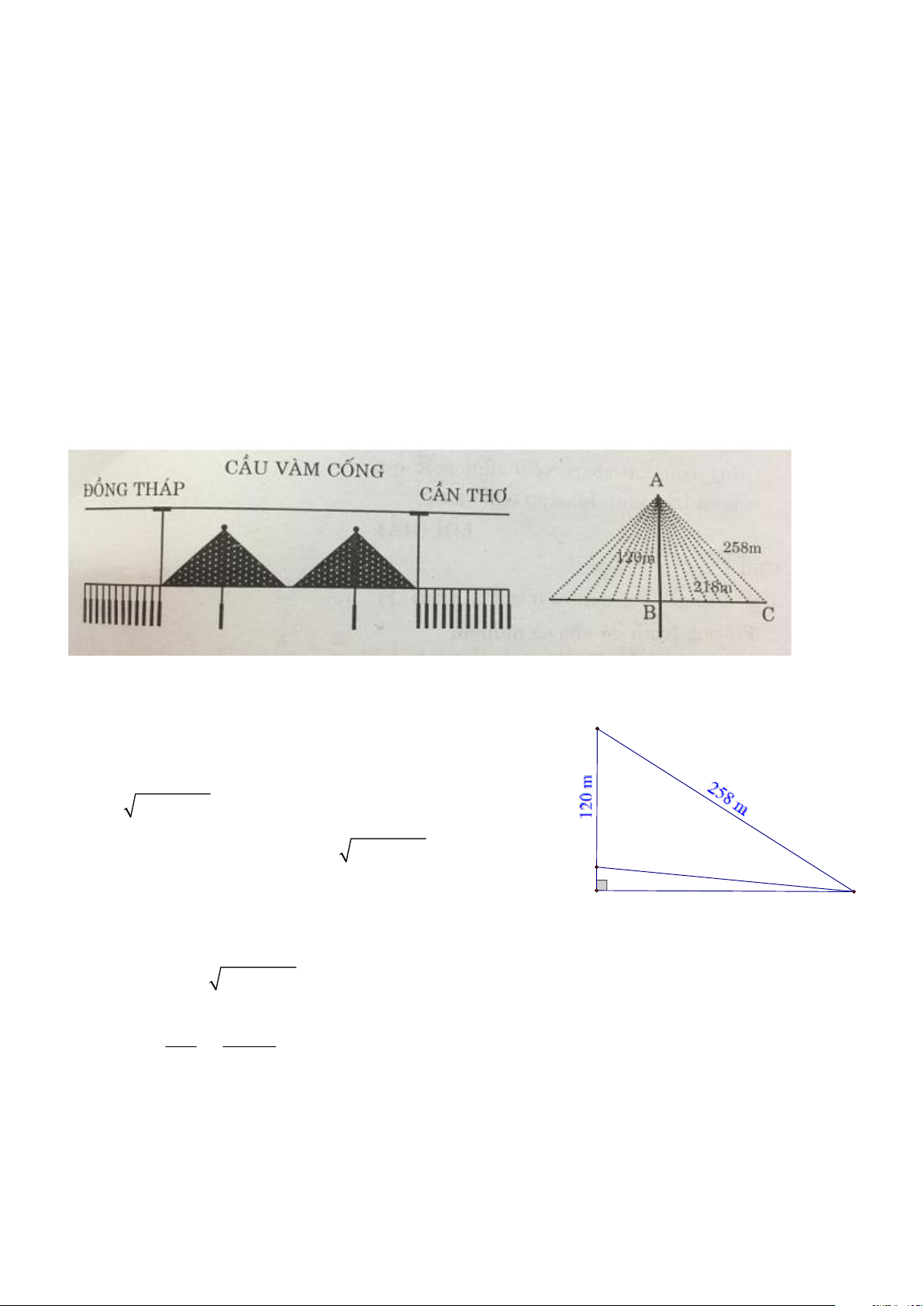
Cầu Vàm Cống bắc ngang sông Hậu nối hai tỉnh Cần Thơ và Đồng Tháp thiết kế theo kiểu
dây văng như hình vẽ. Chiều cao từ sàn đến đỉnhA B = 120m , dây văngA C = 258 m , Trang 14
chiều dài sàn cầu từ B đến C là 218m Hỏi góc nghiêng của sàn cầu BC so với mặt sàn
nằm ngang (giả thiết xem như trụ đỡ A B thẳng đứng (Làm tròn đến phút) g)
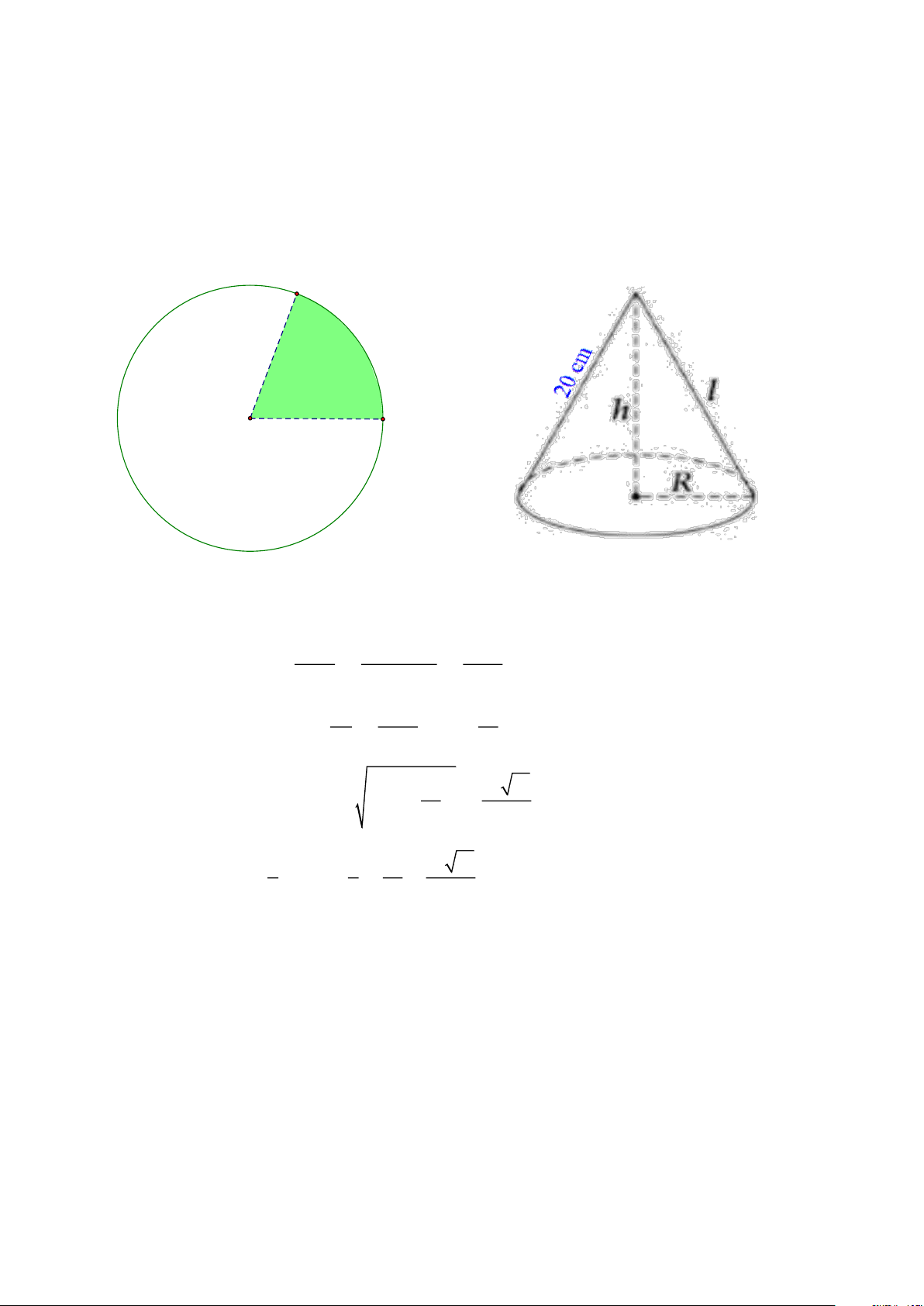
Để làm mũ sinh nhật hình nón từ miếng giấy hình tròn bán kính 20cm . Bạn An cắt bỏ phần ·
quạt tròn A OB với A OB = 60° . Sau đó dán phần hình quạt lớn còn lại sao cho A º B để làm cái mũ.
a) Tính độ dài cung lớn A B
b) Hỏi thể tích cái nón là bao nhiêu? h)
Từ điểm M nằm ngoài đường tròn (O ), vẽ hai tiếp tuyến MP, MQ (P,Q là hai tiếp điểm).
Từ điểm N trên cung nhỏ PQ ta vẽ tiếp tuyến với đường tròn (O ) , tiếp tuyến này cắt
MP, MQ lần lượt tạiE , F a) Chứng minh: P = 2MP . DMEF · ·
b) Chứng minh: EOF + OMP = 90° . ·
c) Hạ EH ^ OF, FK ^ OE . Chứng minh: NO là phân giác của HNK .
d) Chứng minh: 4 điểm P,Q, H , K thẳng hàng. ----HẾT--- Trang 15 HƯỚNG DẪN GIẢI
Bài 1. (1,5 điểm) Cho (P) y = − 2 :
2x và đường thẳng (d) : y = −x − 1 .
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. BGT: x −2 1 − 0 1 2 y = − 2
2x −8 −2 0 −2 −8 x 0 1
y = −x − 1 −1 −2
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : − 2 2x = −x − 1 2
2x − x − 1 = 0 x = 1 x = −1 2
Thay x = 1 vào y = − 2
2x , ta được: y = − 2 2.1 = −2 . 2 1 1
Thay x = − 1 vào y = − 2
2x , ta được: y = − − = − . 2 2 4 1 1 Vậy (1; − 2) , − ; −
là hai giao điểm cần tìm. 2 4
Bài 2. Cho phương trình − 2
2x + 2x + 3 = 0 có 2 nghiệm phân biệt là x ,x . Không giải phương trình, 1 2 x + 1 x + 1
hãy tính giá trị của biểu thức A = 2 + 1 1 − x 1 − x 1 2 Lời giải Trang 16 Vì = 2 b − ac = 2 4
2 − 4.(− 2 ).3 = 4 + 12 2 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 − = + = b S x x = − 2 = 1 1 2 a − 2 2
Theo định lí Vi-et, ta có: = c P x .x = = 3 = − 3 1 2 a − 2 2 x + 1 x + 1 Ta có: A = 2 + 1 1 − x 1 − x 1 2 (x +1 1 x x 1 1 x 2 )( − 2) ( + 1 )( − 1)
A = (1 x 1 x 1 x 1 x 1 ) ( 2 ) + − − ( − 2)( − 1) x − 2
x + 1 − x + x − 2 x + 1 − A = x 2 2 2 1 1 1
1 − x − x + x x 2 1 1 2 2 − ( 2 x + 2 x 2 S 2P 1 2 ) − ( 2 − ) A = 1 − (x + x x x 1 S P 1 2 ) = + − + 1 2 2 1 3 2 − − 2. − 2 2 A = = 3 1 3 1 − + 2 − 2 2
Bài 3. Ở Bạc Liêu ngành nông nghiệp khuyến khích bà con nông dân phương thức nuôi trồng : “con
tôm, cây lúa”, cải tạo đồng lúa năng suất thấp thành các hồ nuôi tôm nước mặn. Dung dịch
nước muối nuôi tôm có nồng độ 5% . Nhưng nơi đây chỉ có nước biển nồng độ 10% và nước lợ
nồng độ muối 1% . Để đổ đầy hồ nuôi tôm có dung tích 1000 lít phải cần bơm vào hồ mỗi loại
nước bao nhiêu kg ? Biết khối lượng riêng của dung dịch nước muối 5% là 1, 8kg / l Lời giải
Số kg nước muối cần bơm vào hồ nuôi tôm là: 1, 8 . 1000 = 1800 kg
Gọi x (kg)là số kg nước biển ( x > 0),y (kg) là số kg nước lợ (y > 0 ).
Vì số kg nước cần bơm vào hồ là 1800 kg nên: x + y = 1800 ( ) 1
Vì dung dịch nước nước cần bơm vào có nồng độ 5% nên:
10%x + 1%y = 5%.1800 Û 0 x ,1 + 0, 1 0 y = 0 9 (2) x + y = 1800 x = 800 Từ ( )
1 và (2) ta có hệ phương trình: .
0,1a + 0,01y = 90 y = 1000
Vậy: phải bơm vào hồ 800 kg nước biển và 1000 kg nước lợ. Trang 17 Bài 4.
Đối với người Á Đông, Âm lịch luôn giữ vai trò quan trọng giúp chúng ta xác định các
dịp lễ Tết trong năm. Và cũng như Dương lịch, Âm lịch cũng sẽ có năm nhuận. Để biết
được năm Âm lịch có nhuận hay không, ta lấy năm Dương lịch tương ứng chia cho19 .
Nếu số dư của phép chia này là 0; 3; 6; 9; 11; 14; 17 thì năm đó sẽ là năm Âm lịch nhuận.
a) Hãy tính xem năm 2020 có phải năm Âm lịch nhuận hay không? Vì sao?
b) Biết rằng một năm dương lịch được gọi là nhuận nếu năm Dương lịch đó chia hết cho 4
Bác Năm sinh ra vào cuối thế kỉ 20 , bác Năm chưa quá 50 tuổi . Hãy tính xem bác Năm
sinh ra năm bao nhiêu biết rằng năm sinh của bác là một năm vừa nhuận Âm lịch, vừa nhuận Dương lịch. Lời giải
a) Vì 2020 : 19 dư 6 nên năm 2020 là năm nhuận Âm lịch.
b) Vì bác Năm chưa quá 50 tuổi và sinh vào cuối thế kỉ 20 nên ta tính từ năm 1973 đến
năm 1999 có các năm nhuận Dương lịch (chia hết cho 4 ) là:
1976; 1980; 1984; 1988; 1992; 1996 . Trong các năm trên chỉ có năm 1976 chia 3 dư
0 là năm nhuận Âm lịch.
Vậy bác Năm sinh năm 1976. Bài 5.
Giá cước gọi quốc tế của một công ty X trong dịp khuyến mãi mừng ngày thành lập
công ty được cho bởi bảng sau: Thời gian Giá cước (VNĐ) 5 phút đầu 6000 Từ phút thứ 6 - 10 5800 Từ phút thứ 11 - 20 5200 Từ phút thứ 21 - 30 5000 Trên 30 phút 4500
a) Bác Lan gọi cho người thân ở nước ngoài trong thời gian 24 phút thì số tiền bác Lan trả là bao nhiêu?
b) Một người đã trả 197 000 đồng để gọi điện cho người thân ở nước ngoài . Tính thời gian
người đó đã gọi điện cho người thân. Lời giải Trang 18
a) Số tiền Bác Lan phải trả khi gọi 24 phút là:
5.6000 + 5.5800 + 10.5200 + 4.5000 = 131000 (đồng)
b) Số tiền phải trả cho cuộc gọi từ lúc bắt đầu đến phút thứ 30 là:
5.6000 + 5.5800 + 10.5200 + 10.5000 = 161000 (đồng)
Thời gian gọi vượt quá 30 phút là: (197000 - 161000): 4500 = 8 (phút)
Vậy thời gian gọi điện cho người thân là: 30 + 8 = 38 (phút)
Bài 6. Cầu Vàm Cống bắc ngang sông Hậu nối hai tỉnh Cần Thơ và Đồng Tháp thiết kế theo kiểu dây
văng như hình vẽ. Chiều cao từ sàn đến đỉnh A B = 120m , dây văngA C = 258 m , chiều dài
sàn cầu từ B đến C là 218m Hỏi góc nghiêng của sàn cầu BC so với mặt sàn nằm ngang (giả
thiết xem như trụ đỡ A B thẳng đứng (Làm tròn đến phút) Lời giải A
GọiCH = x (0 < x < 258 ) Ta có: 2 2 BH = 218 - x (Pitago) Suy ra: 2 2
A H = 120 + BH = 120 + 218 - x B 218 m Trong D A HC có: H ? C x 2 2 2
A C = A H + HC (Pitago) Þ = ( + - x )2 2 2 2 2 258 120 218
+ x Û x » 217,14m · HC 217,14 · cos BCH = = Þ BCH » 5 5 ° ' BC 218
Vậy góc tạo bởi sàn cầu và sàn nằm ngang là 5°5 ' Bài 7.
Để làm mũ sinh nhật hình nón từ miếng giấy hình tròn bán kính 20cm . Bạn An cắt bỏ ·
phần quạt tròn A OB với A OB = 60° . Sau đó dán phần hình quạt lớn còn lại sao cho A º B để làm cái mũ. Trang 19
a) Tính độ dài cung lớn A B
b) Hỏi thể tích cái nón là bao nhiêu? Lời giải A O 60° B O 20cm H A≡B
a) Số đo cung lớn A B là: 0 0 360 - 60 = 300° . pR.n p.20.300° 100p
Độ dài cung lớn A B là: l = = = » 104, 72cm . 180° 180° 3 C 100p 50
b) Bán kính đáy là: R = = : 2p = cm . 2p 3 3 2 50 æ ö ç ÷ 10 11
Đường cao của hình nón là: 2 OH = 20 - ç ÷ = cm ç . çè 3 ÷÷ø 3 2 1 1 5 æ 0ö ç ÷ 10 11 Thể tích cái nón là: 2 3 V = pR h = p ç ÷ . » 3215, 89cm . 3 3 çè 3 ÷÷ø 3
Bài 8. Từ điểm M nằm ngoài đường tròn (O ), vẽ hai tiếp tuyến MP, MQ (P,Q là hai tiếp điểm). Từ
điểm N trên cung nhỏ PQ ta vẽ tiếp tuyến với đường tròn (O ) , tiếp tuyến này cắt MP, MQ lần
lượt tại E , F a) Chứng minh: P = 2MP DMEF b) · ·
Chứng minh: EOF + OMP = 90° c) ·
Hạ EH ^ OF, FK ^ OE . Chứng minh: NO là phân giác của HNK
d) Chứng minh: bốn điểm P, Q, H, K thẳng hàng Trang 20