Bộ Đề Ôn Thi Toán Tuyển Sinh 10 Quận 12 TP HCM 2025-2026 Giải Chi Tiết
Một người mang cam đi đổi lấy táo và lê. Cứ 9 quả cam thì đổi được 2 quả táo và 1 quả lê, 5 quả táo thì đổi được 2 quả lê. Nếu người đó đổi hết số cam mang đi thì được 17 quả táo và 13 quả lê. Hỏi người đó mang đi bao nhiêu quả cam? Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 216 tài liệu
Môn: Toán 9 3 K tài liệu
Tác giả:
Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 12 MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận. ĐỀ TH AM KHẢO
Thời gian: 120 phút (không kể thời gian phát đề) MÃ ĐỀ: Quận 12 - 1 2 x x
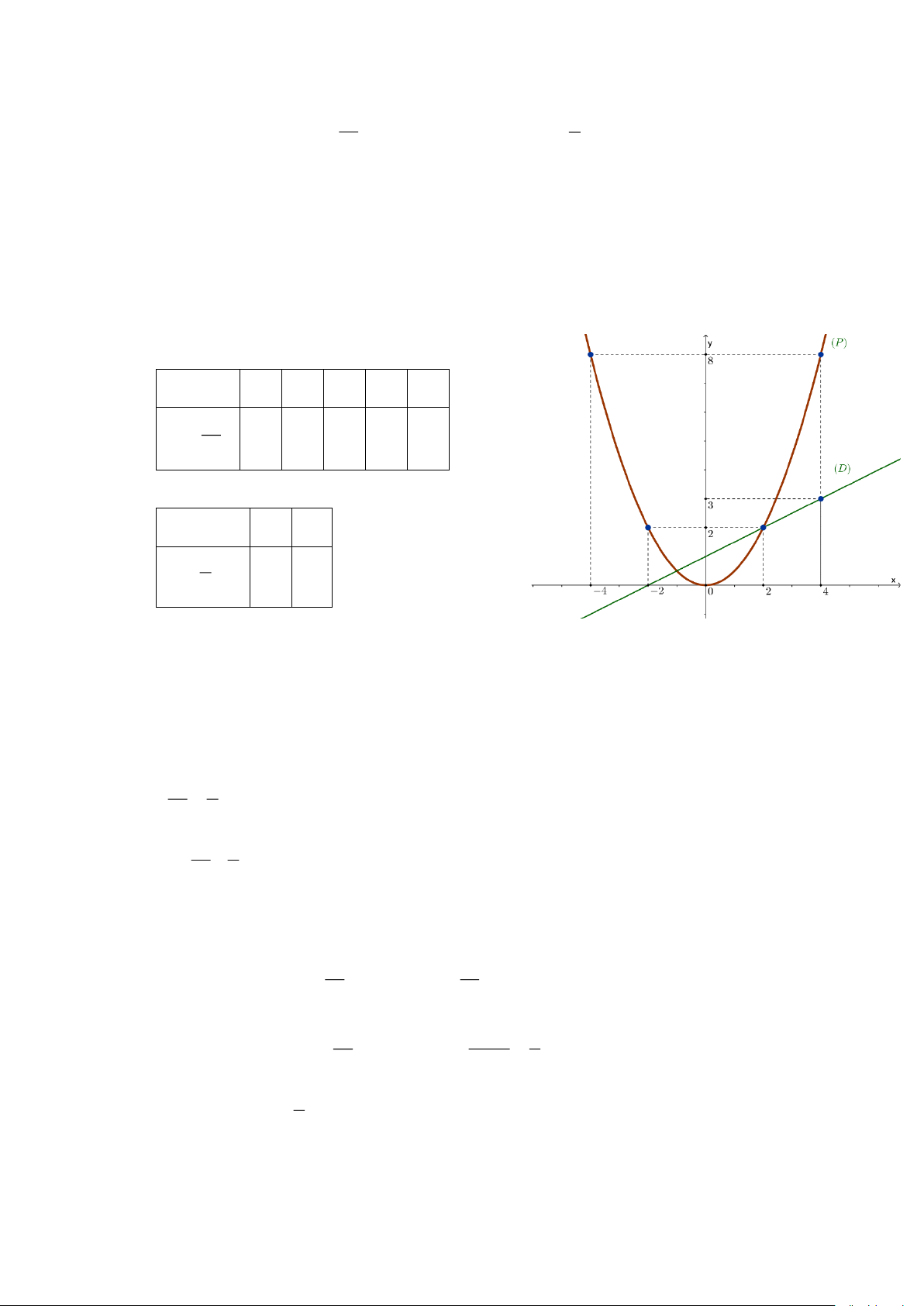
Câu 1. (1,5 điểm). Cho (P) : y =
và đường thẳng (D) : y = + 1 . 2 2
a) Vẽ đồ thị (P) và (D) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Câu 2. (1,0 điểm). Cho phương trình 2
3x + 2x − 4 = 0 có 2 nghiệm là x , x . Không giải phương 1 2 2 3x + 5x x + 2 3x
trình, hãy tính giá trị của biểu thức A = 1 1 2 2 3 4x x + 3 4x x 1 2 1 2
Câu 3. (1,0 điểm). Giá bán một cái bánh ở hai cửa hàng A và B đều là 15000 đồng, nhưng mỗi
cửa hàng có hình thức khuyến mãi khác nhau.
- Cửa hàng A : nếu khách hàng mua bốn cái bánh trở lên thì ba cái bánh đầu tiên giá mỗi
cái bánh vẫn là 15000 đồng nhưng từ cái bánh thứ tư trở đi khách hàng chỉ phải trả 80 % giá đang bán.
- Cửa hàng B : nếu khách hàng mua 3 cái bánh thì được tặng một cái bánh miễn phí.
Một nhóm bạn học sinh mua 15 cái bánh thì chọn cửa hàng nào có lợi hơn và lợi hơn bao nhiêu?
Câu 4. (0,75 điểm). Ba làng A, B, C nằm trên cùng một quốc lộ, làng B nằm giữa làng A và làng
C , làng A cách làng B 5 km. Một người đi bộ theo hướng từ làng B đến làng C mỗi giờ
cách làng A thêm 4 km. Biết rằng mối liên hệ giữa khoảng cách từ làng A đến người đi bộ
y (km) và thời gian đi bộ của người đó là x (giờ) là một hàm số bậc nhất có dạng y = ax + . b
a) Xác định các hệ số a và b.
b) Nếu người đi bộ cách làng A 7 km thì người ấy phải đi bộ trong bao nhiêu phút?
Câu 5. (0,75 điểm). Một người mang cam đi đổi lấy táo và lê. Cứ 9 quả cam thì đổi được 2 quả táo
và 1 quả lê, 5 quả táo thì đổi được 2 quả lê. Nếu người đó đổi hết số cam mang đi thì
được 17 quả táo và 13 quả lê. Hỏi người đó mang đi bao nhiêu quả cam?
Câu 6. (1,0 điểm). Một xe chở xăng dầu, bên trên có một bồn chứa hình trụ dài 2, 6 m và đường
kính đáy là 1, 4 m. Theo tiêu chuẩn an toàn thì bồn chỉ chứa được tối đa 80 % thể tích khi
xe di chuyển trên đường. Trang 1
a) Mỗi chuyến xe có thể chở nhiều nhất bao nhiêu lít nhiên liệu? (cho p = 3,14 ).
b) Trên đường vận chuyển, xe chở xăng dầu trên phải đi qua 1 cây cầu có tải trọng 5 tấn.
Biết xe khi chưa chở hàng nặng 3 tấn. Hỏi nếu muốn đi qua cây cầu đó thì xe chở tối đa
bao nhiêu lít xăng? Biết khối lượng riêng của xăng là 0, 713 kg/lít (Các kết quả làm tròn đến hàng đơn vị).
Câu 7. (1 điểm). Điểm trung bình của 100 học sinh trong hai lớp 9A và 9B là 7, 608. Tính điểm
trung bình của các học sinh mỗi lớp, biết rằng số học sinh của lớp 9A hơn lớp 9B 2 học 9
sinh và điểm trung bình của học sinh lớp 9B bằng
điểm trung bình của học sinh lớp 10 9A.
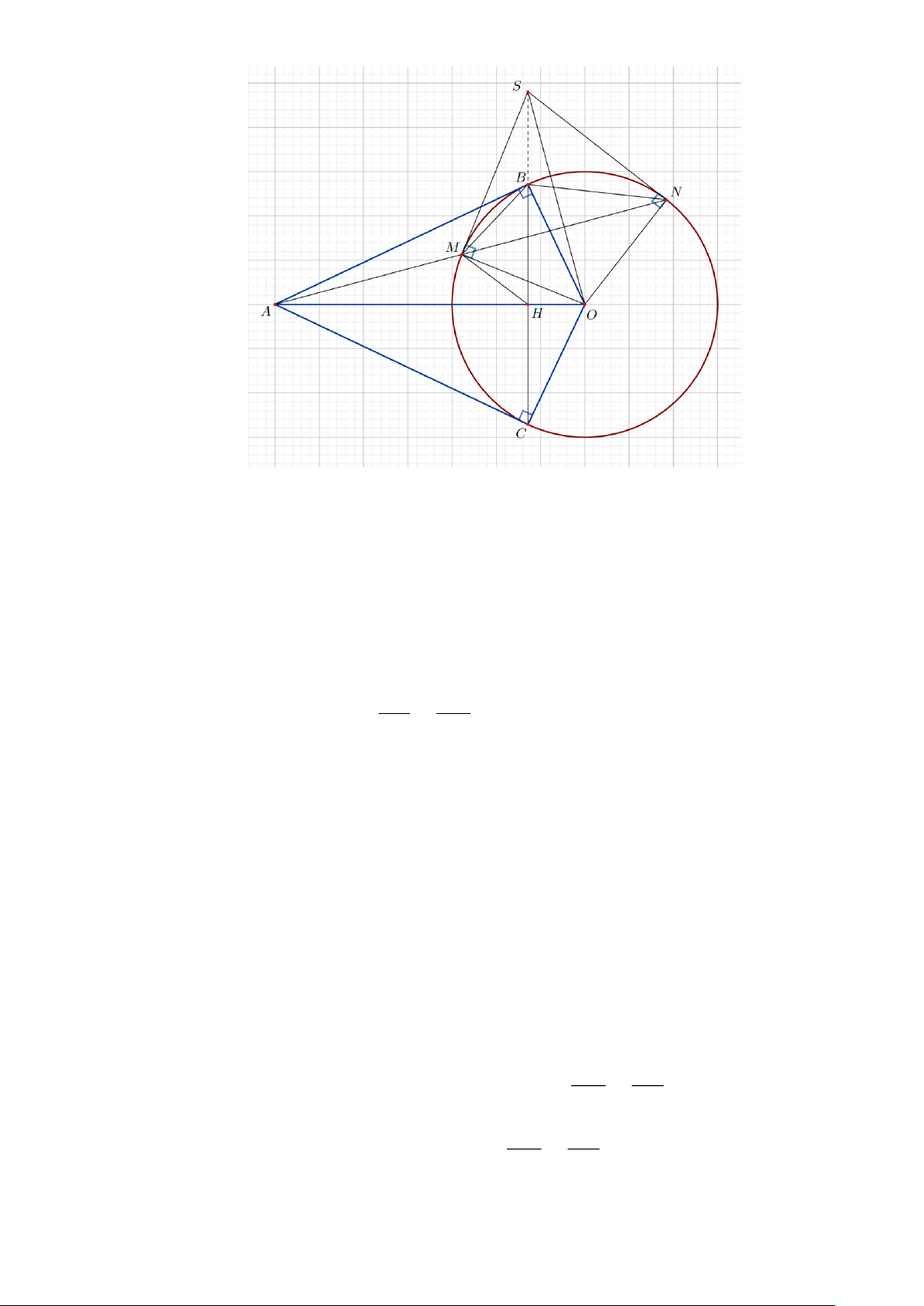
Câu 8. (3 điểm) Từ điểm A nằm ngoài đường tròn (O; R) kẻ hai tiếp tuyến A B và A C . Vẽ cát ·
tuyến A MN với (O ) ( M nằm giữa A và N ; điểm O nằm ngoài BA N ). Gọi H là giao
điểm của OA và CB .
a) Chứng minh tứ giác OB A C nội tiếp. b) Chứng minh 2 2 2
A B = A M .A N = OA - R .
c) Tiếp tuyến tại M và N của (O ) cắt nhau tại S . Chứng minh tứ giác OHMN nội tiếp và
ba điểm S , B, C thẳng hàng. ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI 2 x x
Câu 1. (1,5 điểm) Cho (P) : y =
và đường thẳng (D) : y = + 1 . 2 2
a) Vẽ đồ thị (P) và (D) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính. Lời giải
a) Vẽ đồ thị (P) và (D) trên cùng hệ trục tọa độ. BGT: x −4 −2 0 2 4 2 = x y 8 2 0 2 8 2 x 2 4 = x y + 1 2 3 2
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (D) : 2 x = x +1 2 2 2
x − x − 1 = 0 2 2 x = 2 x = − 1 2 x 2 2
Thay x = 2 vào y = , ta được: y = = 2. 2 2 2 2 x (− )1 1
Thay x = −1 vào y = , ta được: y = = . 2 2 2 1 Vậy (2;2) , −
1; là hai giao điểm cần tìm. 2 Trang 3 Câu 2.
(1 điểm) Cho phương trình 2
3x + 2x − 4 = 0 có 2 nghiệm là x , x . Không giải phương 1 2 2 3x + 5x x + 2 3x
trình, hãy tính giá trị của biểu thức A = 1 1 2 2 . 3 4x x + 3 4x x 1 2 1 2 Lời giải Vì .
a c = 3.(−4) = −12 0
Nên phương trình có hai nghiệm phân biệt trái dấu x ,x . 1 2 − = + = b S x x = − 2 1 2
Theo định lí Vi-et, ta có: a 3 = c P x .x = = − 4 1 2 a 3 2 3x + 5x x + 2 3x Ta có: A = 1 1 2 2 3 4x x + 3 4x x 1 2 1 2 3( 2 x + 2 x 5x x 1 2 ) + A = 1 2 4x x ( 2 x + 2 x 1 2 1 2 ) 3( 2
S − 2P) + 5P A = 4P ( 2 S − 2P) 2 3S − = P A 2 4S P − 2 8P −2 2 4 3. − − 3 3 − A = = 9 . − 2 4 4 2 56 2 4 − − 8 − 3 3 3
Câu 3. (1,0 điểm). Giá bán một cái bánh ở hai cửa hàng A và B đều là 15000 đồng, nhưng mỗi
cửa hàng có hình thức khuyến mãi khác nhau.
- Cửa hàng A : nếu khách hàng mua bốn cái bánh trở lên thì ba cái bánh đầu tiên giá mỗi
cái bánh vẫn là 15000 đồng nhưng từ cái bánh thứ tư trở đi khách hàng chỉ phải trả 80 % giá đang bán.
- Cửa hàng B : nếu khách hàng mua 3 cái bánh thì được tặng một cái bánh miễn phí.
Một nhóm bạn học sinh mua 15 cái bánh thì chọn cửa hàng nào có lợi hơn và lợi hơn bao nhiêu? Lời giải
Số tiền phải trả khi mua ở cửa hàng A
15000.3 + 15000.80%.12 = 189000 (đồng)
Ta có 15 : 4 = 3 dư 3 Þ được tặng 3 cái bánh Trang 4
Số tiền phải trả khi mua ở cửa hàng B 15000.12 = 180000 (đồng)
Vậy mua ở cửa hàng B lợi hơn và lợi hơn 9000 đồng.
Câu 4. (0,75 điểm). Ba làng A, B, C nằm trên cùng một quốc lộ, làng B nằm giữa làng A và
làng C , làng A cách làng B 5 km. Một người đi bộ theo hướng từ làng B đến làng C
mỗi giờ cách làng A thêm 4 km. Biết rằng mối liên hệ giữa khoảng cách từ làng A đến
người đi bộ y (km) và thời gian đi bộ của người đó là x (giờ) là một hàm số bậc nhất có
dạng y = ax + . b
a. Xác định các hệ số a và b.
b. Nếu người đi bộ cách làng A 7 km thì người ấy phải đi bộ trong bao nhiêu phút? Lời giải
a. Xác định các hệ số a và b.
Khoảng cách từ làng A đến người đi bộ = Vận tốc x thời gian + khoảng cách từ làng
A cách làng B y = 4x + 5
Vậy a = 4, b = 5.
b. Nếu người đi bộ cách làng A 7 km thì người ấy phải đi bộ trong bao nhiêu phút?
Thế y = 7 vào y = 4x + 5 Û 7 = 4x + 5 Û x = 0, 5
Vậy người đó phải đi bộ trong 30 phút. Câu 5.
(0,75 điểm). Một người mang cam đi đổi lấy táo và lê. Cứ 9 quả cam thì đổi được 2 quả
táo và 1 quả lê, 5 quả táo thì đổi được 2 quả lê. Nếu người đó đổi hết số cam mang đi
thì được 17 quả táo và 13 quả lê. Hỏi người đó mang đi bao nhiêu quả cam? Lời giải
Cách 1: Cứ 9 quả cam thì đổi được 2 quả táo và 1 quả lê
Þ 18 quả cam thì đổi được 4 quả táo và 2 quả lê
Mà 2 quả lê thì đổi được 5 quả táo
Nên 18 quả cam thì đổi được 9 quả táo
Þ 2 quả cam thì đổi được 1 quả táo
Mà 5 quả táo thì đổi được 2 quả lê Trang 5
Þ 10 quả cam thì đổi được 2 quả lê Þ 5 quả cam thì đổi được 1 quả lê
Vậy số quả cam người đó mang đi 17.2 + 13.5 = 99 (quả)
Cách 2: Gọi số quả cam đổi được 1 quả táo là x (quả)
Gọi số quả cam đổi được 1 quả lê là y (quả) (ĐK: * x, y Î ¥ )
Cứ 9 quả cam thì đổi được 2 quả táo và 1 quả lê, nên ta có phương trình: 2x + 1y = 9 ( ) 1
5 quả táo thì đổi được 2 quả lê, nên ta có phương trình:
5x = 2y Û 5x - 2y = 0 ( ) 1 ìï 2x + y = 9 ìï x = 2 ï ï Từ ( )
1 và (2) ta có hệ phương trình:í Û í ï (nhận). 5x - 2y = 0 ï y = 5 ïî ïî
Vậy số quả cam người đó mang đi 17.2 + 13.5 = 99 (quả).
Câu 6. (1 điểm) Một xe chở xăng dầu, bên trên có một bồn chứa hình trụ dài 2, 6 m và đường kính
đáy là 1, 4 m. Theo tiêu chuẩn an toàn thì bồn chỉ chứa được tối đa 80 % thể tích khi xe di chuyển trên đường.
a. Mỗi chuyến xe có thể chở nhiều nhất bao nhiêu lít nhiên liệu? (cho p = 3,14 ).
b. Trên đường vận chuyển, xe chở xăng dầu trên phải đi qua 1 cây cầu có tải trọng 5 tấn.
Biết xe khi chưa chở hàng nặng 3 tấn. Hỏi nếu muốn đi qua cây cầu đó thì xe chở tối đa
bao nhiêu lít xăng? Biết khối lượng riêng của xăng là 0, 713 kg/lít (Các kết quả làm tròn đến hàng đơn vị). Lời giải
a) Mỗi chuyến xe có thể chở nhiều nhất bao nhiêu lít nhiên liệu? (cho p = 3,14 ).
Bán kính đáy: 1, 4 : 2 = 0, 7 (m)
Số lít nhiên liệu xe có thể chở nhiều nhất: 2 » ( 3 3,14.2, 6.0, 7 .80% 3, 2 m ) = 3200 (lít)
b) Trên đường vận chuyển, xe chở xăng dầu trên phải đi qua 1 cây cầu có tải trọng 5 tấn.
Biết xe khi chưa chở hàng nặng 3 tấn. Hỏi nếu muốn đi qua cây cầu đó thì xe chở tối đa
bao nhiêu lít xăng? Biết khối lượng riêng của xăng là 0, 713 kg/lít (Các kết quả làm tròn đến hàng đơn vị).
Khối lượng xăng xe có thể chở tối đa để qua cầu 5 - 3 = 2 (tấn) = 2000 (kg)
Số lít xăng xe chở tối đa để qua cầu Trang 6 2000 : 0, 713 » 2805 (lít).
Câu 7. (1 điểm). Điểm trung bình của 100 học sinh trong hai lớp 9A và 9B là 7, 608. Tính điểm
trung bình của các học sinh mỗi lớp, biết rằng số học sinh của lớp 9A hơn lớp 9B 2 học 9
sinh và điểm trung bình của học sinh lớp 9B bằng
điểm trung bình của học sinh lớp 9A. 10 Lời giải
Số học sinh lớp 9A : (100 + 2): 2 = 51 (học sinh)
Số học sinh lớp 9B : (100 - 2): 2 = 49 (học sinh)
Gọi điểm trung bình của lớp 9A và 9B lần lượt là x, y (ĐK x, y > 0 ) 9
Điểm trung bình của học sinh lớp 9B bằng
điểm trung bình của học sinh lớp 9A. , nên ta 10 9 9
có phương trình: y = x Û x - y = 0 ( ) 1 10 10
Điểm trung bình của 100 học sinh trong hai lớp 9A và 9B là 7, 608. , nên ta có phương trình:
51x + 49y = 100.7, 608 = 760, 8 (2) ìï 9 ïï x - y = 0 ìï x = 8 Từ ( )
1 và (2) ta có hệ phương trình: ï ï í 10 Û í (nhận). ï ï y = 7, 2
ï 51x + 49y = 760, 8 ïî ïî
Vậy điểm trung bình của lớp 9A và 9B lần lượt là 8 và 7, 2.
Câu 8. (3 điểm) Từ điểm A nằm ngoài đường tròn (O; R) kẻ hai tiếp tuyến A B và A C . Vẽ cát ·
tuyến A MN với (O ) ( M nằm giữa A và N ; điểm O nằm ngoài BA N ). Gọi H là giao
điểm của OA và CB .
a) Chứng minh tứ giác OB A C nội tiếp. b) Chứng minh 2 2 2
A B = A M .A N = OA - R .
c) Tiếp tuyến tại M và N của (O ) cắt nhau tại S . Chứng minh tứ giác OHMN nội tiếp và
ba điểm S , B, C thẳng hàng. Lời giải Trang 7
a) Chứng minh tứ giác OB A C nội tiếp. · ·
Xét tứ giác OB A C ta có OBA = OCA = ° ( ) · ·
90 g.t Þ OBA + OCA = 180°
Þ Tứ giác OBA C nội tiếp (tổng hai góc đối bằng 180° ) b) Chứng minh 2 2 2
A B = A M .A N = OA - R . · · · ¼
Xét D A B M và D A N B ta có BA N chung và A BM = A NB (cùng chắn BM )
Þ DA BM ∽ DA NB ( ) A B A M 2 g.g Þ =
Þ A B = A M .A N . A N A B
Xét D A B O vuông tại B , ta có: 2 2 2 2 2 2
OA = OB + A B Þ A B = OA - R .
c) Tiếp tuyến tại M và N của (O ) cắt nhau tại S . Chứng minh tứ giác OHMN nội tiếp và
ba điểm S , B, C thẳng hàng.
Ta có OB = OC = R .
Và A B = A C (tính chất hai tiếp tuyến cắt nhau)
Þ OA là đường trung trực của BC .
Þ OA ^ BC tại H .
Xét D A B O vuông tại B có đường cao BH , ta có: 2
A B = A H .A O A M A O Mà 2
A B = A M .A N (c.m.t) Þ AM .AN = AH.AO Þ = . A H A N · A M A O
Xét D A HM và D A N O ta có OA N chung và = (c.m.t) A H A N
Þ DA HM ∽ DA NO ( ) · ·
c.g.c Þ A HM = A NO . Trang 8
Þ Tứ giác OHMN nội tiếp (góc ngoài bằng góc đối trong) ( ) 1
Chứng minh tương tự câu a
Þ Tứ giác OMSN nội tiếp đường tròn đường kính OS (2) Từ ( )
1 và (2) Þ 5 điểm O,H,M ,S,N cùng thuộc đường tròn đường kính OS Þ · 0
SHO = 90 (góc nội tiếp chắn nửa đường tròn)
Þ SH ^ OA tại H
Mà BC ^ OA tại H (c.m.t)
Þ ba điểm S , B, C thẳng hàng. ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 12
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 12 - 2
Thời gian: 120 phút (không kể thời gian phát đề) 2 x
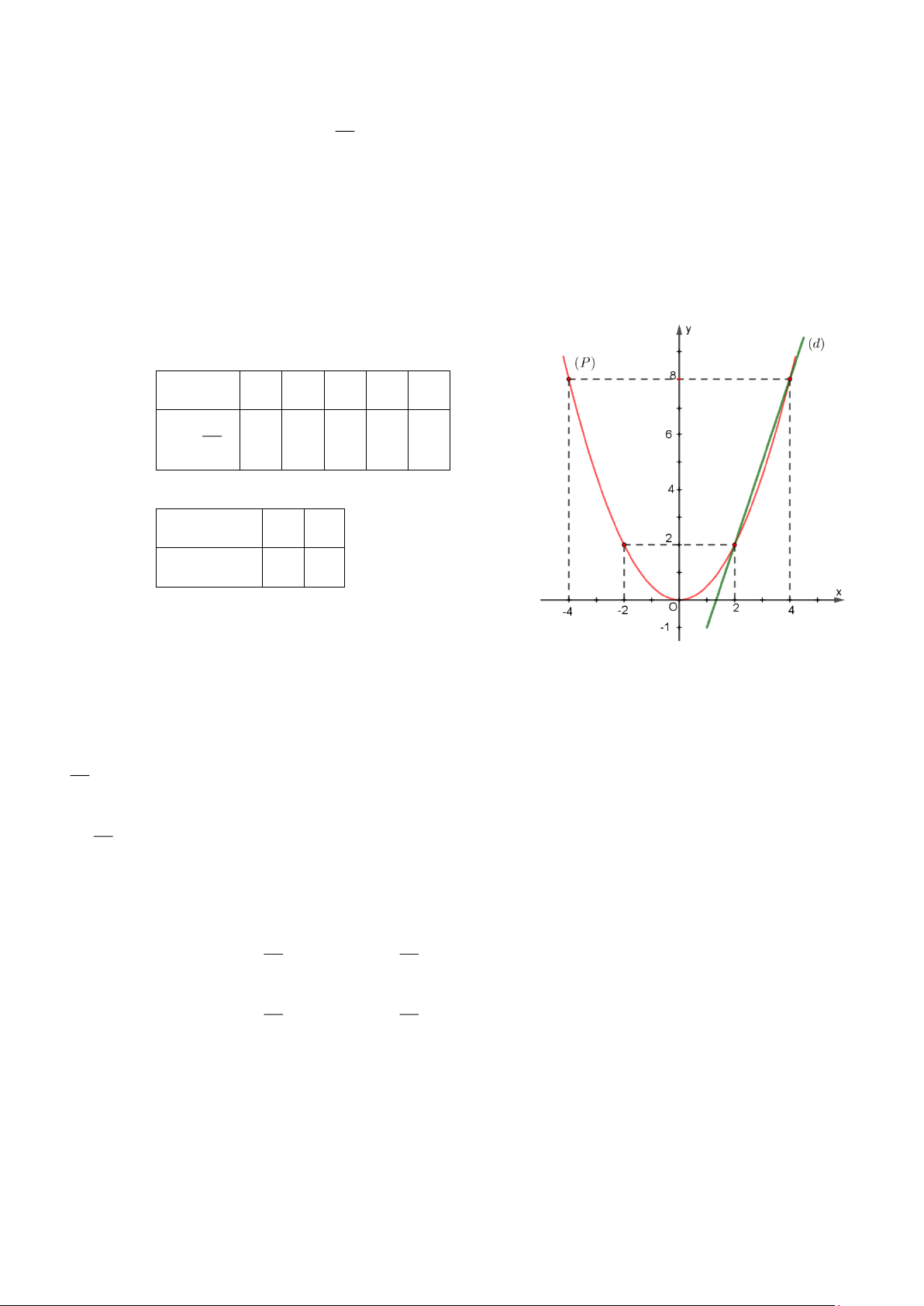
Câu 1. (1,5 điểm). Cho (P) : y =
và đường thẳng (d) : y = −4 + 3x . 2
a) Vẽ đồ thị (P) và (d) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình x2 3
+ 5x − 6 = 0 có 2 nghiệm là x ,x . 1 2 2 2 x x
Không giải phương trình, hãy tính giá trị của biểu thức A = 1 + 2 . x − 1 x − 1 2 1
Câu 3. (1 điểm). Hiện nay, các em học sinh trung học ngày càng quan tâm hơn về, cân nặng và
chiều cao của bản thân. Các bạn nam thường chú trọng đến chiều cao còn các bạn nữ lại rất
hay để ý đến cân nặng. Cân nặng lý tưởng ứng với chiều cao của một người được tính theo công thức sau : h − w = h − − 150 100 ( )1 c
Trong đó : w là cân nặng (tính theo kg ), h là chiều cao (tính theo cm ) và c = 4 nếu người đó là nam
và c = 2 nếu người đó là nữ. Công thức này cho phép tính được cân nặng lý tưởng của một người để
có một cơ thể cân đối, ưa nhìn khi biết chiều cao của người đó.
a) Một bạn nữ có chiều cao là 1,52m thì cân nặng lý tưởng của bạn ấy là bao nhiêu kg ?
b) Nếu một bạn nam có cân nặng là 56 kg thì chiều cao của bạn nam này cần phải là bao
nhiêu để 56 kg là cân nặng lý tưởng cho bạn ấy ?
Câu 4. (0,75 điểm). Lớp 9A có 30 học sinh, mỗi bạn dự định đóng mỗi tháng 70 000 đồng để mua
quà tặng các trẻ em ở mái ấm tình thương và sau 3 tháng sẽ đủ tiền để tặng mỗi em ở mái Trang 9
ấm 3 gói quà (giá trị mỗi gói quà là như nhau). Khi các học sinh đã đóng đủ tiền thì mái
ấm nhận chăm sóc thêm 9 em và giá tiền mỗi gói quà tăng thêm 5% nên chỉ tặng được
mỗi em 2 gói quà. Hỏi lúc đầu có bao nhiêu em ở mái ấm được tặng quà?
Câu 5. (1 điểm). Để lập đội tuyển năng khiếu về bóng rổ của trường thầy thể dục đưa ra quy định
tuyển chọn như sau: mỗi bạn dự tuyển sẽ được ném 10 quả bóng vào rổ, quả bóng vào rổ
được cộng 4 điểm; quả bóng ném ra ngoài thì bị trừ 2 điểm. Nếu bạn nào có số điểm từ 22
điểm trở lên thì sẽ được chọn vào đội tuyển. Hỏi một học sinh muốn được chọn vào đội
tuyển thì phải ném ít nhất bao nhiêu quả vào rổ?
Câu 6. (1 điểm). Bảng cước phí dịch vụ Mobiphone áp dụng cho thuê bao trả trước, cước gọi liên
mạng trong nước (đã bao gồm VAT) quy định rằng : nếu gọi trong 5 giây đầu thì tính cước
200 đồng/ 5 giây đầu, còn kể từ sau giây thứ 5 trở đi, họ tính thêm 28 đồng cho mỗi giây.
a) Gọi m là số tiền phải trả (tính bằng đồng) và n là thời gian gọi nhiều hơn 5 giây ( t 5 ).
Hãy lập công thức biểu thị m theo n ?
b) Hỏi bạn Anh gọi trong bao lâu mà bạn trả 3420 đồng ?
Câu 7. (0,75 điểm): Nước giải khát thường đựng trong lon nhôm và cỡ lon phổ biến trên thế giới
thường chứa được khoảng 335 ml chất lỏng, được thiết kế hình trụ với chiều cao gần gấp
đôi đường kính đáy (cao 12 cm , đường kính đáy 6,5cm ). Nhưng hiện nay các nhà sản xuất
có xu hướng tạo ra những lon nhôm với kiểu dáng thon cao dài. Tuy chi phí sản xuất của
những chiếc lon này tốn kém hơn, do nó có diện tích mặt ngoài (diện tích toàn phần của
hình trụ) lớn hơn, nhưng nó lại dễ đánh lừa thị giác và được người tiêu dùng ưa chuộng hơn.
a) Một lon nước ngọt cao 14,2 cm , đường kính đáy 5,9 cm . Hỏi lon nước ngọt cao này có
thể chứa được hết lượng nước ngọt của một lon cỡ phổ biến không ? Vì sao ? Biết thể
tích hình trụ V = R2h với 3,14 (kết quả làm tròn đến chữ số thập phân thứ hai).
b) Hỏi chi phí sản xuất lon nước ngọt cao ở câu a, tăng bao nhiêu phần trăm so với sản xuất
lon nước ngọt cỡ phổ biến ? Biết S = 2 .
Rhvà S = S + 2.S . xq tp xq ñ
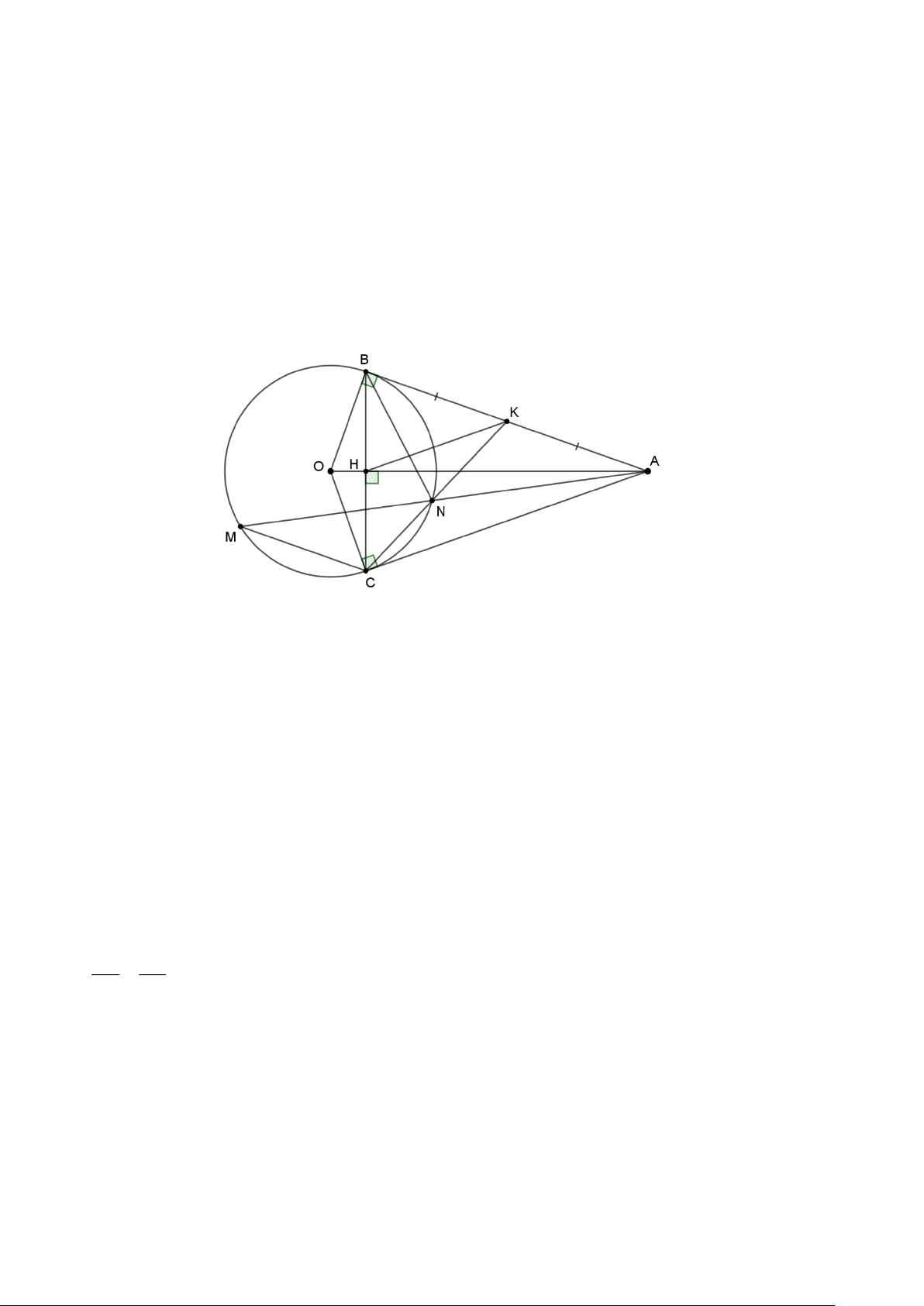
Câu 8. (3 điểm): Từ điểm A nằm ngoài đường tròn (O; R) sao cho OA 2R ; vẽ hai tiếp tuyến AB ,
AC ( C , B là hai tiếp điểm). Gọi K là trung điểm của AB ; CK cắt (O) tại N ; tia AN cắt
(O) tại M .
a) Chứng minh: OA ⊥ BC tại H và 2
BK = KN.KC . Trang 10
b) Chứng minh: MC / / AB .
c) Chứng minh: Tứ giác BHNK nội tiếp và tia NB là tia phân giác của MNK . ----HẾT--- Trang 11 HƯỚNG DẪN GIẢI 2 x
Câu 1. (1,5 điểm). Cho (P) : y =
và đường thẳng (d) : y = −4 + 3x . 2
a) Vẽ đồ thị (P) và (d) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. a) BGT: x −4 −2 0 2 4 2 = x y 8 2 0 2 8 2 x 2 4 y = − 4 + 3x 2 8
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : x2 = 3x − 4 2 x2 − 3x + 4 = 0 2 x = 4 x = 2 2 x 2 4
Thay x = 4 vào (P) : y = , ta được: y = = 8 . 2 2 2 x 2 2
Thay x = 2 vào (P) : y = , ta được: y = = 2 . 2 2
Vậy (4; 8) , (2; 2) là hai giao điểm cần tìm. Trang 12
Câu 2. (1 điểm) Cho phương trình x2 3
+ 5x − 6 = 0 có 2 nghiệm là x ,x . Không giải phương 1 2 2 2 x x
trình, hãy tính giá trị của biểu thức A = 1 + 2 x − 1 x − 1 2 1 Lời giải 2
Vì = b2 − 4ac = (5) − 4.3.(−6) = 97 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 −b 5
S = x + x = = − 1 2
Theo định lí Vi-et, ta có: a 3 c
P = x x. = = − 2 1 2 a 2 2 x x Ta có: A = 1 + 2 x − 1 x − 1 2 1 x2 x2 A = 1 + 2 x − 1 x − 1 2 1 x2. 1 . 1 1 ( x − 1 )+ x22 (x − 2 ) A = (x −1 1 2 )(x − 1 )
x3 − x2 + x3 − x2 A = 1 1 2 2 x x . − x − x + 1 1 2 1 2
x3 + x3 − x2 − x2 A = 1 2 1 2 x x . − 1 1 2 (x + x 1 2 ) +
(x + x )(x2 − x x. + x2)−(x2 + x2 1 2 1 1 2 2 1 2 ) A = x x . − 1 1 2 (x + x 1 2 ) +
(x + x )(x2 + x2 − x x. )−(x2 + x2 1 2 1 2 1 2 1 2 ) A = x x . − 1 1 2 (x + x 1 2 ) + ( 2 2 x + x ( 2x x . − x x . 2 . 1 2 1 2 ) − (( x + x 1 2 ) − x x 1 2 ) 1 2 ) ( x + x 1 2 ) − A = x x . − 1 1 2 (x + x 1 2 ) + −5 − 2 2 5 − (− ) − − 5 3. 2 − 2.(− 2) 3 3 3 −289 A = = (−2) −5 − + 9 1 3 Trang 13
Câu 3. (1 điểm). Hiện nay, các em học sinh trung học ngày càng quan tâm hơn về, cân nặng và
chiều cao của bản thân. Các bạn nam thường chú trọng đến chiều cao còn các bạn nữ lại rất
hay để ý đến cân nặng. Cân nặng lý tưởng ứng với chiều cao của một người được tính theo công thức sau : h − w = h − − 150 100 ( )1 c
Trong đó : w là cân nặng (tính theo kg ), h là chiều cao (tính theo cm ) và c = 4 nếu người đó là nam
và c = 2 nếu người đó là nữ. Công thức này cho phép tính được cân nặng lý tưởng của một người để
có một cơ thể cân đối, ưa nhìn khi biết chiều cao của người đó.
a) Một bạn nữ có chiều cao là 1,52m thì cân nặng lý tưởng của bạn ấy là bao nhiêu kg ?
b) Nếu một bạn nam có cân nặng là 56 kg thì chiều cao của bạn nam này cần phải là bao
nhiêu để 56 kg là cân nặng lý tưởng cho bạn ấy ? Lời giải h −
a) Ta có công thức w = h − − 150 100 ( )1 c
Một bạn nữ có chiều cao là 1,52m thì c = 2 và h = 152 . 152 − 150
Thay c = 2 và h = 152 vào công thức ( )
1 , ta được w = 152 − 100 − = 51 . 2
Bạn nữ có chiều cao là 1,52m thì cân nặng lý tưởng của bạn ấy là 51kg .
b) Bạn nam có cân nặng là 56 kg thì c = 4 và w = 56
Thay c = 4 và w = 56 vào công thức ( ) 1 h −
Ta được 56 = h − − 150 100 4 h − 150 h − 100 − = 56 4
4h − 400 − (h − 150) = 224 4 4
4h − 400 − (h −150) = 224
4h − 400 − h + 150 = 224
4h − h = 224 + 400 − 150 3h = 474 h = 158
Vậy bạn nam có cân nặng là 56 kg thì chiều cao của bạn nam này là 1,58m để 56 kg là cân nặng lý tưởng cho bạn ấy Trang 14
Câu 4. (0,75 điểm). Lớp 9A có 30 học sinh, mỗi bạn dự định đóng mỗi tháng 70 000 đồng để mua
quà tặng các trẻ em ở mái ấm tình thương và sau 3 tháng sẽ đủ tiền để tặng mỗi em ở mái
ấm 3 gói quà (giá trị mỗi gói quà là như nhau). Khi các học sinh đã đóng đủ tiền thì mái
ấm nhận chăm sóc thêm 9 em và giá tiền mỗi gói quà tăng thêm 5% nên chỉ tặng được
mỗi em 2 gói quà. Hỏi lúc đầu có bao nhiêu em ở mái ấm được tặng quà? Lời giải
Gọi x (người) là số em ở mái ấm được tặng quà lúc đầu ( * x ).
Tổng tiền 30 bạn dự định đóng trong 3 tháng là : 70 000 . 30 . 3 = 6 300 000 (đồng).
Số phần quà các em được nhận ban đầu là 3x (phần quà). 6 300000
Giá trị 1 phần quà ban đầu là (đồng). 3x
Số em ở mái ấm được tặng quà lúc sau là x + 9 (em).
Số phần quà các em được nhận 2.(x + 9) (phần quà). 6 300000
Giá trị 1 phần quà lúc sau là (đồng). 2(x + 9)
Vì giá tiền mỗi gói quà tăng thêm 5% giá trị của các phần quà là như nhau , Nên ta có phương trình: 6 300000 ( + ) = 6300000 . 1 5% 3x 2(x + 9) 1 ( + ) = 1 . 1 5% 3x 2(x + 9) 0,35 = 1 x 2(x + 9)
x = 0,35.2(x + 9)
x = 0,7x + 6,3 0,3x = 6,3 x = 21(nhận)
Vậy có 21 em ở mái ấm được tặng quà lúc đầu. Trang 15
Câu 5. (1 điểm). Để lập đội tuyển năng khiếu về bóng rổ của trường thầy thể dục đưa ra quy định
tuyển chọn như sau: mỗi bạn dự tuyển sẽ được ném 10 quả bóng vào rổ, quả bóng vào rổ
được cộng 4 điểm; quả bóng ném ra ngoài thì bị trừ 2 điểm. Nếu bạn nào có số điểm từ 22
điểm trở lên thì sẽ được chọn vào đội tuyển. Hỏi một học sinh muốn được chọn vào đội
tuyển thì phải ném ít nhất bao nhiêu quả vào rổ? Lời giải Cách 1:
Gọi x (quả bóng) là số quả bóng một học sinh ném vào rổ (x * ,x 10) .
Gọi y (quả bóng) là số quả bóng một học sinh ném ra ngoài (y * ,y 10) .
Vì mỗi bạn dự tuyển sẽ được ném 10 quả bóng vào rổ Nên x + y = 10 (1) .
Vì quả bóng vào rổ được cộng 4 điểm, quả bóng ném ra ngoài bị trừ 2 điểm và tổng điểm là 22
điểm, nên 4x − 2y = 22 (2) . Từ ( )
1 và (2) ta có hệ phương trình : x + y = 10 x = 7 (n)
4x − 2y = 22 y = 3 (n)
Vậy mỗi học sinh cần ném vào rỗ ít nhất là 7 quả. Cách 2:
Gọi x (quả bóng) là số quả bóng một học sinh ném vào rổ (x * ,x 10)
Suy ra: 10 − x là số quả bóng một học sinh ném ra ngoài.
Vì quả bóng vào rổ được cộng 4 điểm; quả bóng ném ra ngoài thì bị trừ 2 điểm và số điểm từ 22 điểm trở lên.
Nên ta có bất phương trình : 4x − 2(10 − x) 22
4x − 20 + 2x 22 6x 42 x 7
Vậy mỗi học sinh cần ném vào rỗ ít nhất là 7 quả. Trang 16
Câu 6. (1 điểm). Bảng cước phí dịch vụ Mobiphone áp dụng cho thuê bao trả trước, cước gọi liên
mạng trong nước (đã bao gồm VAT) quy định rằng : nếu gọi trong 5 giây đầu thì tính cước
200 đồng/ 5 giây đầu, còn kể từ sau giây thứ 5 trở đi, họ tính thêm 28 đồng cho mỗi giây.
a) Gọi m là số tiền phải trả (tính bằng đồng) và n là thời gian gọi nhiều hơn 5 giây
(t 5).Hãy lập công thức biểu thị mtheo n?
b) Hỏi bạn Anh gọi trong bao lâu mà bạn trả 3420 đồng ? Lời giải
a) Công thức biểu thị m theo n có dạng m = a n . + b . Theo đề bài, ta có: n = 6 Với = . ( ) 1 200 + (6 − 5) 228 = 6 a . + b m .28 = 228 n = 7 Với = . (2) 200 + (7 − 5) 256 = 7 a . + b m .28 = 256 6a + b = 228 a = 28 Từ ( )
1 và (2) ta có hệ phương trình: . 7a + b = 256 b = 60
Vậy: a = 28 , b = 60 và m = 28n + 60 .
b) Hỏi bạn Anh gọi trong bao lâu mà bạn trả 3420 đồng ?
Thay m = 3420 vào biểu thức m = 28n + 60
Ta được : 3420 = 28n + 60 n = 120 .
Vậy bạn Anh gọi 120 giây, bạn trả 3420 đồng. Trang 17
Câu 7. (0,75 điểm): Nước giải khát thường đựng trong lon nhôm và cỡ lon
phổ biến trên thế giới thường chứa được khoảng 335 ml chất lỏng,
được thiết kế hình trụ với chiều cao gần gấp đôi đường kính đáy
(cao 12 cm , đường kính đáy 6,5cm ). Nhưng hiện nay các nhà sản
xuất có xu hướng tạo ra những lon nhôm với kiểu dáng thon cao
dài. Tuy chi phí sản xuất của những chiếc lon này tốn kém hơn, do
nó có diện tích mặt ngoài (diện tích toàn phần của hình trụ) lớn hơn, nhưng nó lại dễ đánh
lừa thị giác và được người tiêu dùng ưa chuộng hơn.
c) Một lon nước ngọt cao 14,2 cm , đường kính đáy 5,9 cm . Hỏi lon nước ngọt cao này có
thể chứa được hết lượng nước ngọt của một lon cỡ phổ biến không ? Vì sao ? Biết thể
tích hình trụ V = R2h với 3,14 (kết quả làm tròn đến chữ số thập phân thứ hai)
d) Hỏi chi phí sản xuất lon nước ngọt cao ở câu a, tăng bao nhiêu phần trăm so với sản xuất
lon nước ngọt cỡ phổ biến ? Biết S = 2 .
Rhvà S = S + 2.S xq tp xq ñ Lời giải
a) Bán kính đáy lon cao : 5,9 : 2 = 2,95(cm) . 2
Thể tích lon cao : V = R2h = ( ) = (cm3 3,14. 2,95 .14,2 388,03 ) = 388,03ml.
Vì 388,03ml 335ml Nên Lon nước ngọt cao này có thể chứa được hết lượng nước ngọt của một lon cỡ phổ biến.
b) Diện tích toàn phần lon phổ biến
S = S + S = Rh + R = ( ) + ( )2 2 = ( 3 2. 2 . 2. 2.3,14. 3,25 .12 2.3,14. 3,25 311,25 cm . tp xq ñ )
Diện tích toàn phần lon cao
S = S + S = Rh + R = ( ) + ( )2 2 = ( 3 2. 2 . 2.
2.3,14. 2,95 .14,2 2.3,14. 2.95 317,72 cm . tp xq ñ )
% Nguyên liệu để sản xuất lon nước ngọt cao tăng so với sản xuất lon nước ngọt cỡ phổ biến là:
317,72 − 311,25 0,0208= 2,08%. 311,25
Vậy chi phí sản xuất lon nước ngọt cao ở câu a, tăng 2,08%so với sản xuất lon nước ngọt cỡ phổ biến. Trang 18
Câu 8. (3 điểm): Từ điểm A nằm ngoài đường tròn (O; R) sao cho OA 2R ; vẽ hai tiếp tuyến
AB , AC ( C , B là hai tiếp điểm). Gọi K là trung điểm của AB ; CK cắt (O) tại N ; tia
AN cắt (O) tại M .
c) Chứng minh: OA ⊥ BC tại H và 2
BK = KN.KC .
d) Chứng minh: MC // AB .
e) Chứng minh: Tứ giác BHNK nội tiếp và tia NB là tia phân giác của MNK . Lời giải
a) Chứng minh: OA ⊥ BC tại H và 2
BK = KN.KC . Taco :ù AB =
AC( AC,ABlaøtieáptuyeáncuûa( ) O ) OB = OC (O ,
A OBlaøbaùnkínhcuûa( ) O )
OAlaøñöôøng trung tröïc cuûa BC
OA ⊥ BC taïi H Xe ùt BKN va ø CK , B tacoù K laøgoùc chung
KBN = KCB cuøng chaén cung BN ( ) Va
äy BKN∽CKB(g − ) g
BK = CK (tæsoáñoàngdaïng) KN BK 2
BK = KN.KC Trang 19
b) Chứng minh: MC / / AB Ta co :ù 2 BK =
KN.KC(cmcaâua) KB =
KA (K laøtrungñieåmAB) KA KC 2
AK = KN.KC = KN KA Xe ùt AKN va ø CK , A tacoù K laøgoùc chung KA KC = (cmt) KN KA Va
äy AKN∽CKA(g − ) g
KAN = ACK (hai goùc töông öùng)
Laïico :ùCMN = ACK (cuø ng chaén cung CN) KAN = CMN
MC / / AB
c) Chứng minh: Tứ giác BHNK nội tiếp và tia NB là tia phân giác của MNK Trang 20