Bộ Đề Ôn Thi Toán Tuyển Sinh Lớp 10 Quận Tân Bình TP HCM 2025-2026 Giải Chi Tiết
Vào dịp khai trương, nhà sách khuyến mãi mỗi cây viết bi được giảm 20% so với giá niêm yết, còn mỗi quyển tập giảm 20% so với giá niêm yết. Bạn An vào nhà sách mua 20 quyển tập và 10 cây viết bi. Khi tính tiền, bạn An đưa 175 000 đồng và được thối lại 3 000 đồng. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 216 tài liệu
Môn: Toán 9 3 K tài liệu
Tác giả:
Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN BÌNH TAÂN MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận. ĐỀ TH AM KHẢO
Thời gian: 120 phút (không kể thời gian phát đề)
MÃ ĐỀ: Quận Bình Tân - 2
Câu 1. (1,5 điểm). Cho (P) y = 2 :
x và đường thẳng (d) : y = 3x − 2 .
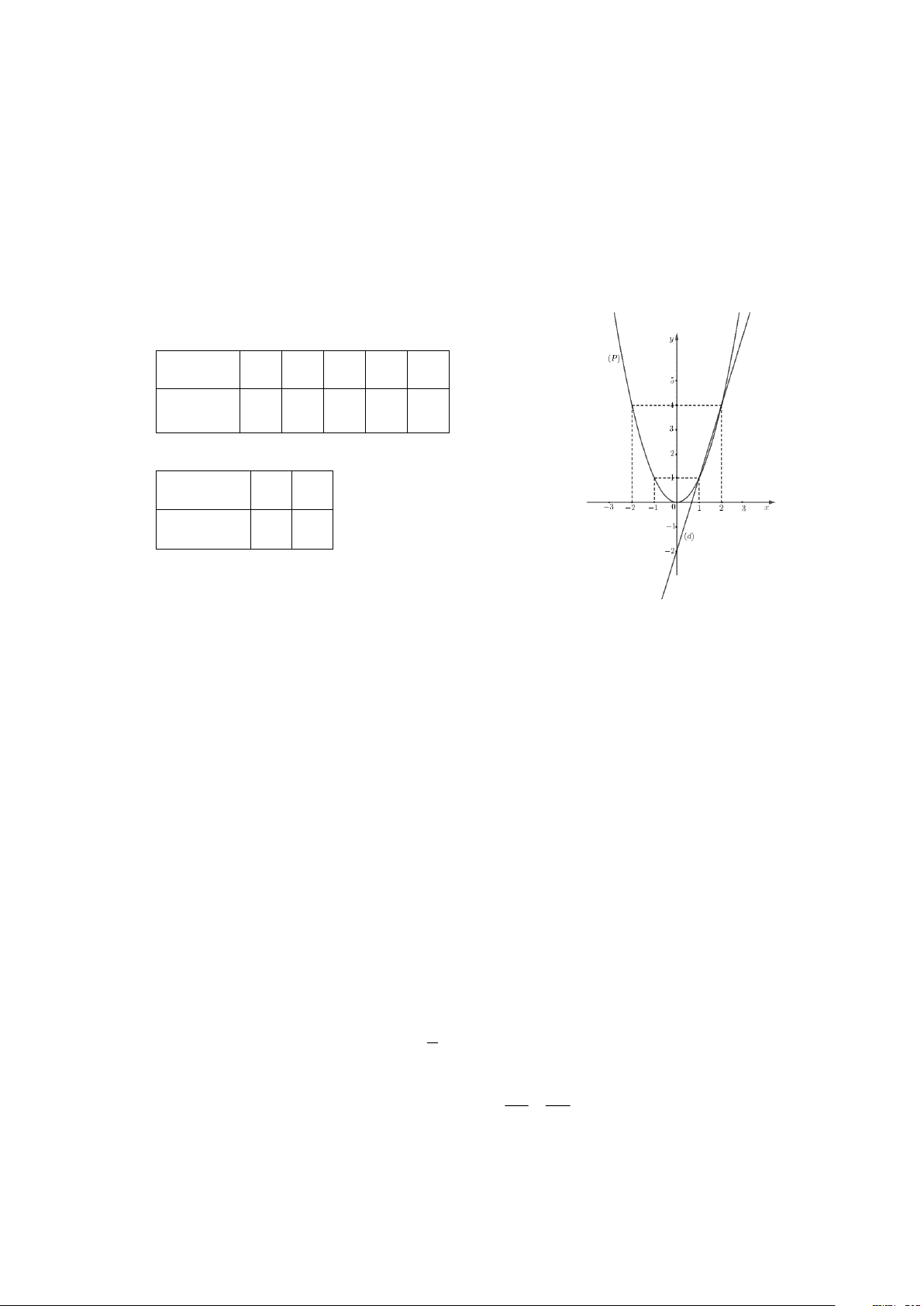
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. 5
Câu 2. (1 điểm). Cho phương trình 2 x − 5x +
= 0 . Gọi x ,x là hai nghiệm (nếu có) . Không giải 3 1 2 2 2 x x
phương trình, hãy tính giá trị của biểu thức A = 1 + 2 x x 2 1 Câu 3.
(0,75 điểm). Bên cạnh việc xem đua chó, nhiều người thích tham gia chương trình dự
thưởng để cuộc đua thêm phấn khích. Trước khi chọn chó để đạt thưởng, bạn sẽ được
phát một cuốn tài liệu có giới thiệu khá chi tiết về từng chú chó, từ những thành tích tốt,
xấu đến tình trạng sức khỏe, cuộc đua gần nhất có tham gia…sẽ giúp bạn dễ dàng chọn
lựa. Và có 5 kiểu thắng giải áp dụng cho các đợt đua là:
- Thắng nhất là Win nếu con chó mà bạn chọn về nhất.
- Thắng nhất – nhì (Exacta) là 2 con chó bạn chọn về nhất – nhì theo đúng thứ tự.
- Thắng nhất – nhì – ba (Trifecta) là cả 3 con chó bạn chọn đều về 3 thứ hạng đầu theo đúng thứ tự.
Các giải tiếp theo là Quartet (4) , Superfecta (6) . Càng lên cao càng trúng đậm.
Hỏi trong một đợt đua có 8 chú khuyển, ta có bao nhiêu cách chọn vé dự thưởng theo
giải nhất – nhì – ba?
Câu 4. (1 điểm). Cuối năm 2009 , một bản báo cáo được trình lên chính phủ Anh. Theo đó, nếu
nhiệt độ trái đất tăng lên 2 C
thì tổng giá trị kinh tế thế giới sẽ bị giảm đi 3% , nếu nhiệt
độ tăng lên 5C kinh tế sẽ giảm đi 10% Từ đó, thông qua nghiên cứu một nhóm nhà kinh
tế học đã đưa ra dự đoán về mối liên hệ giữa nhiệt độ thế giới và tổng giá trị kinh tế của thế
giới. Kết quả nghiên cứu đưa ra rằng tổng giá trị kinh tế bị giảm y % là hàm số bậc nhất
theo x là nhiệt độ tăng lên của Trái đất (tính theo C ).
a) Xác định mối liên hệ giữa y và x
b) Theo nghiên cứu đó, tổng giá trị kinh tế sẽ giảm bao nhiêu nếu thế giới tăng thêm 10C
(làm tròn đến hàng đơn vị). Trang 1
Câu 5. (0,75 điểm). Lớp 9A dự định tổ chức liên hoan lớp cuối năm, trong phần nước cần chuẩn bị
42 ly trà sữa. Để tiết kiệm chi phí lớp đã tìm hiểu giá của hai cửa hàng A và B như sau:
- Cửa hàng A : mua 5 ly bất kì sẽ được tặng 1 ly (cùng loại) và hóa đơn trên 400 000đồng
thì sẽ giảm thêm 10% trên hóa đơn.
- Cửa hàng B : chỉ khuyến mãi khi đặt qua App Grab Food mua từ 10 ly trở lên thì giảm
30% mỗi ly so với giá niêm yết và phí giao hàng thì khách tự trả theo khoảng cách từ cửa
hàng đến nơi nhận hàng.
Hỏi lớp 9A nên mua ở cửa hàng nào sẽ tiết kiệm hơn và tiết kiệm hơn bao nhiêu tiền? Biết
giá niêm yết 1 ly trà sữa ở hai cửa hàng đều là 30 000đồng, khoảng cách từ địa điểm liên
hoan đến cửa hàng B là 12km. Phí giao hàng được tính theo bảng sau: Khoảng cách Giá tiền (đồng) Dưới 10km 25 000 Từ 10kmđến 20km 26 000 Từ 20kmđến 40km 30 000 Trên 40km 5% giá trị đơn hàng
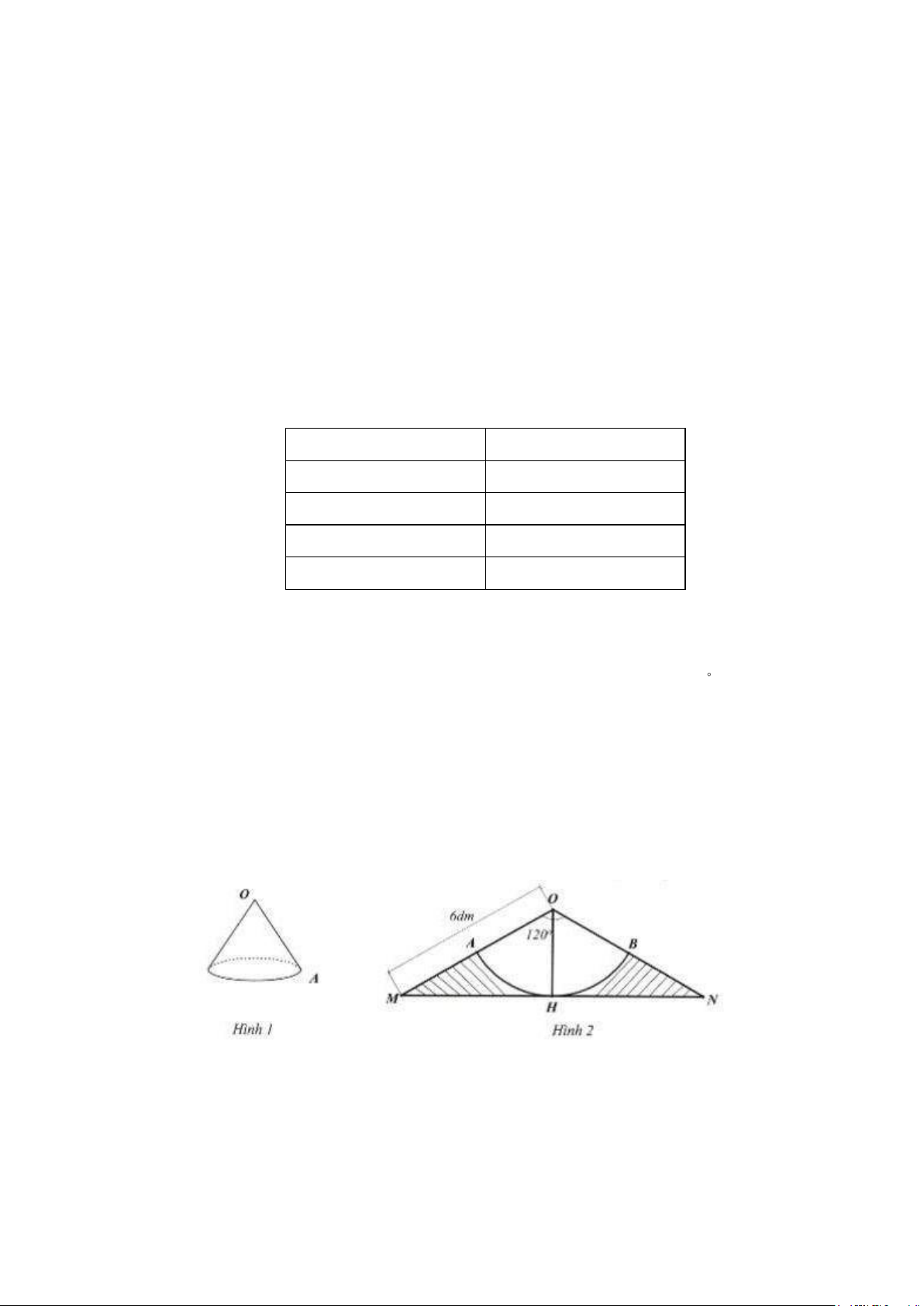
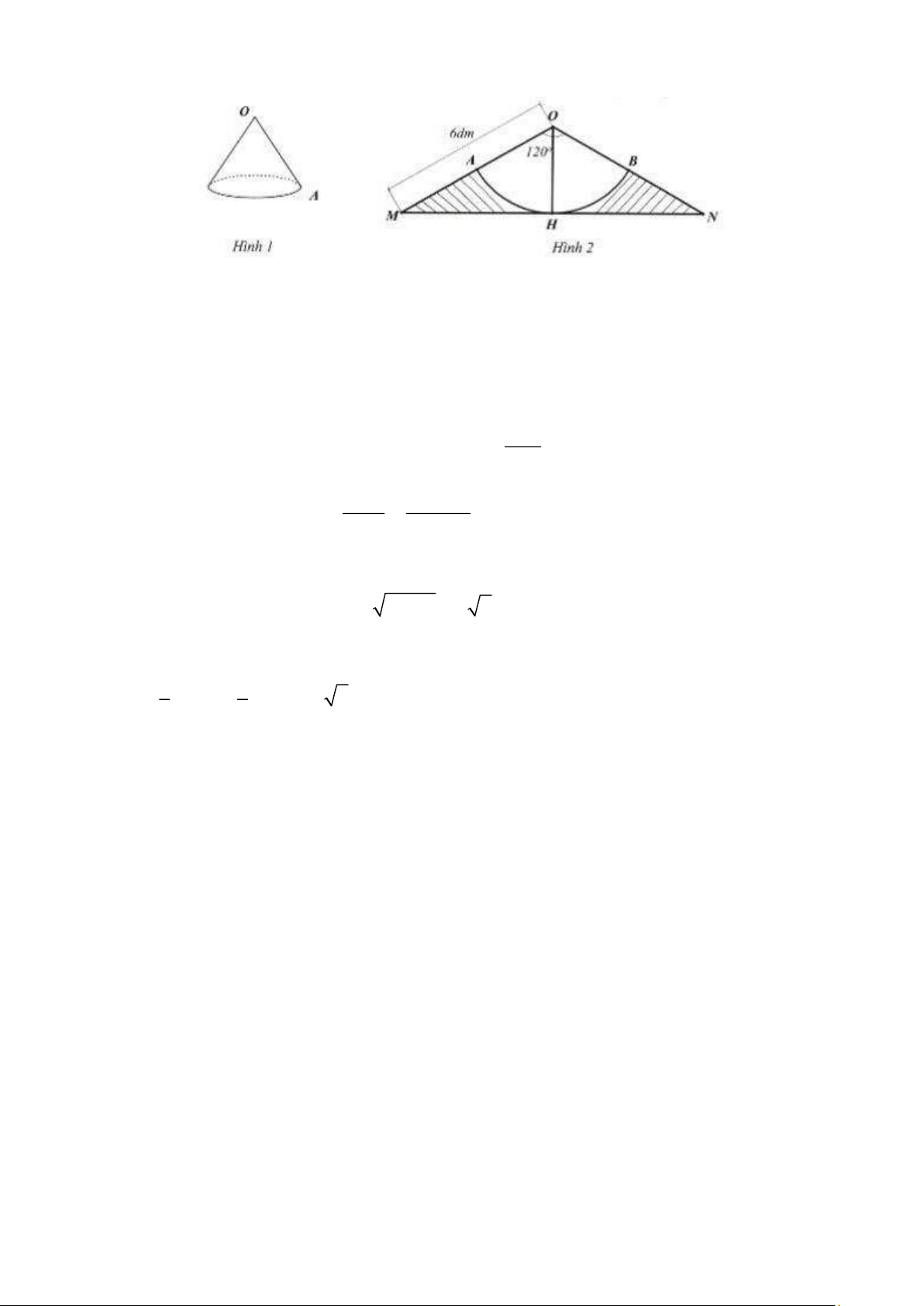
Câu 6. (1 điểm). Để làm một cái gàu tát nước có dạng hình nón (hình 1), bác An dùng một tấm tôn
hình tam giác OMN cân tại O có cạnh bên OM = 6 m
d , góc MON = 120 (hình 2 ). Bác xác
định trung điểm H của MN , vẽ cung tròn tâm O bán kính OH cắt các cạnh OM, ON lần
lượt tại A, B . Sau đó bác cắt bỏ phần gạch sọc, cuộn phần còn lại của tấm tôn sao cho mép
OA trùng khít với mép OBtạo thành chiếc gàu (giả sử phần diện tích của mép nối không
đáng kể). Hỏi khi múc đầy thì chiếc gàu chứa được bao nhiêu lít nước? (kết quả làm tròn
đến một chữ số thập phân, lấy 3,14 )
Câu 7. (1 điểm). Vào dịp khai trương, nhà sách khuyến mãi mỗi cây viết bi được giảm 20% so với
giá niêm yết, còn mỗi quyển tập giảm 20% so với giá niêm yết. Bạn An vào nhà sách mua
20 quyển tập và 10 cây viết bi. Khi tính tiền, bạn An đưa 175 000 đồng và được thối lại Trang 2
3 000 đồng. Tính giá niêm yết của mỗi quyển tập và mỗi cây viết bi mà bạn An đã mua.
Biết rằng khi An nhìn vào hóa đơn, tổng số tiền phải trả khi chưa giảm giá là 195 000 đồng.
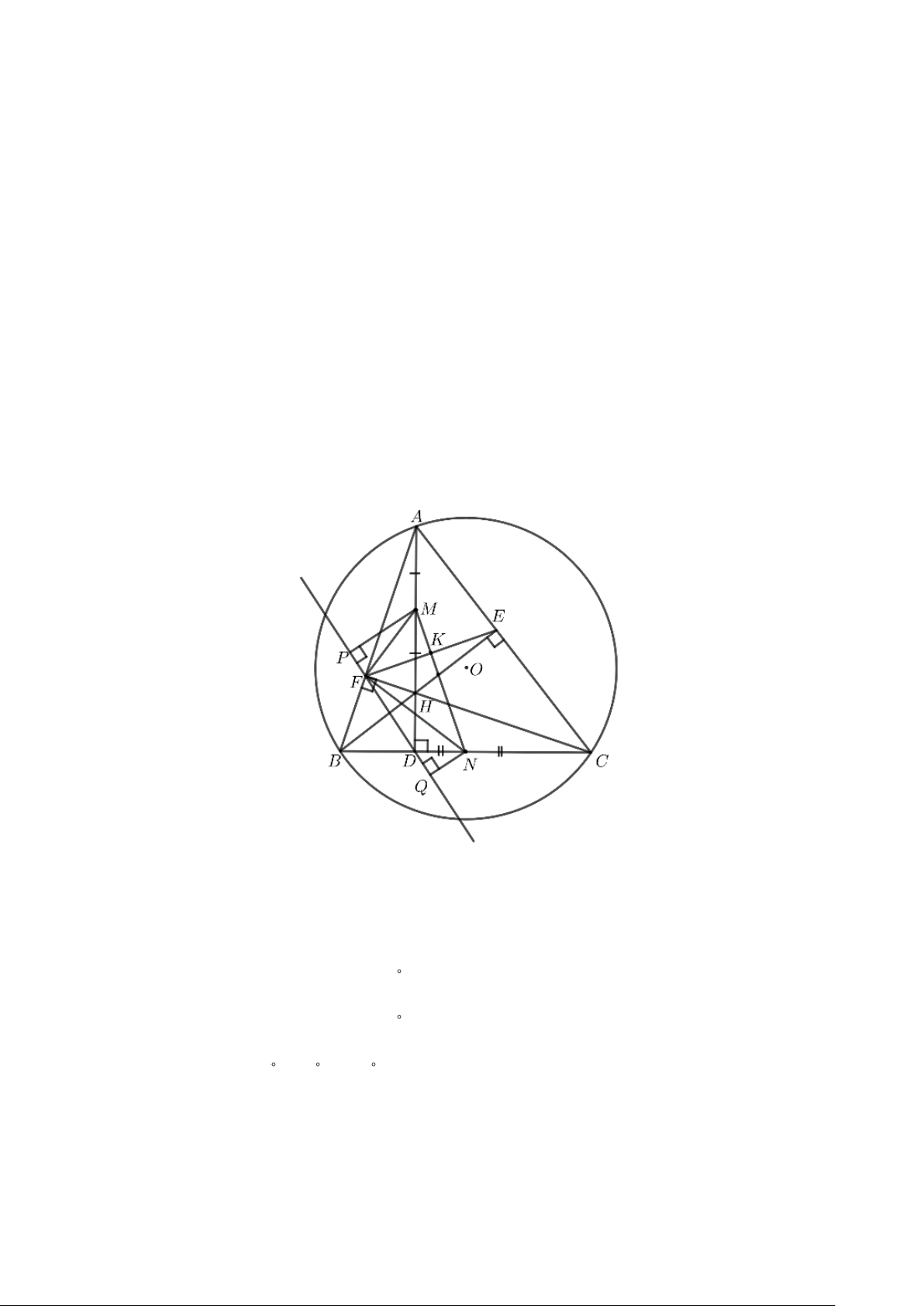
Câu 8. (3 điểm) Cho tam giác ABC có 3 góc nhọn AB AC . Vẽ đường cao AD, BE, CF của tam
giác đó. Gọi H là giao điểm của các đường cao vừa vẽ.
a) Chứng minh: các tứ giác E
A HF và BFEC nội tiếp.
b) Gọi M, N lần lượt là trung điểm của các đoạn AH, BC . Chứng minh: FM.FC = FN.FA .
c) Gọi P,Q lần lượt là chân các đường vuông góc kẻ từ M, N đến đường thẳng DF . Chứng
minh rằng đường tròn đường kính PQ đi qua giao điểm của FE và MN . ----HẾT--- Trang 3 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm) Cho (P) y = 2 :
x và đường thẳng (d) : y = 3x − 2 .
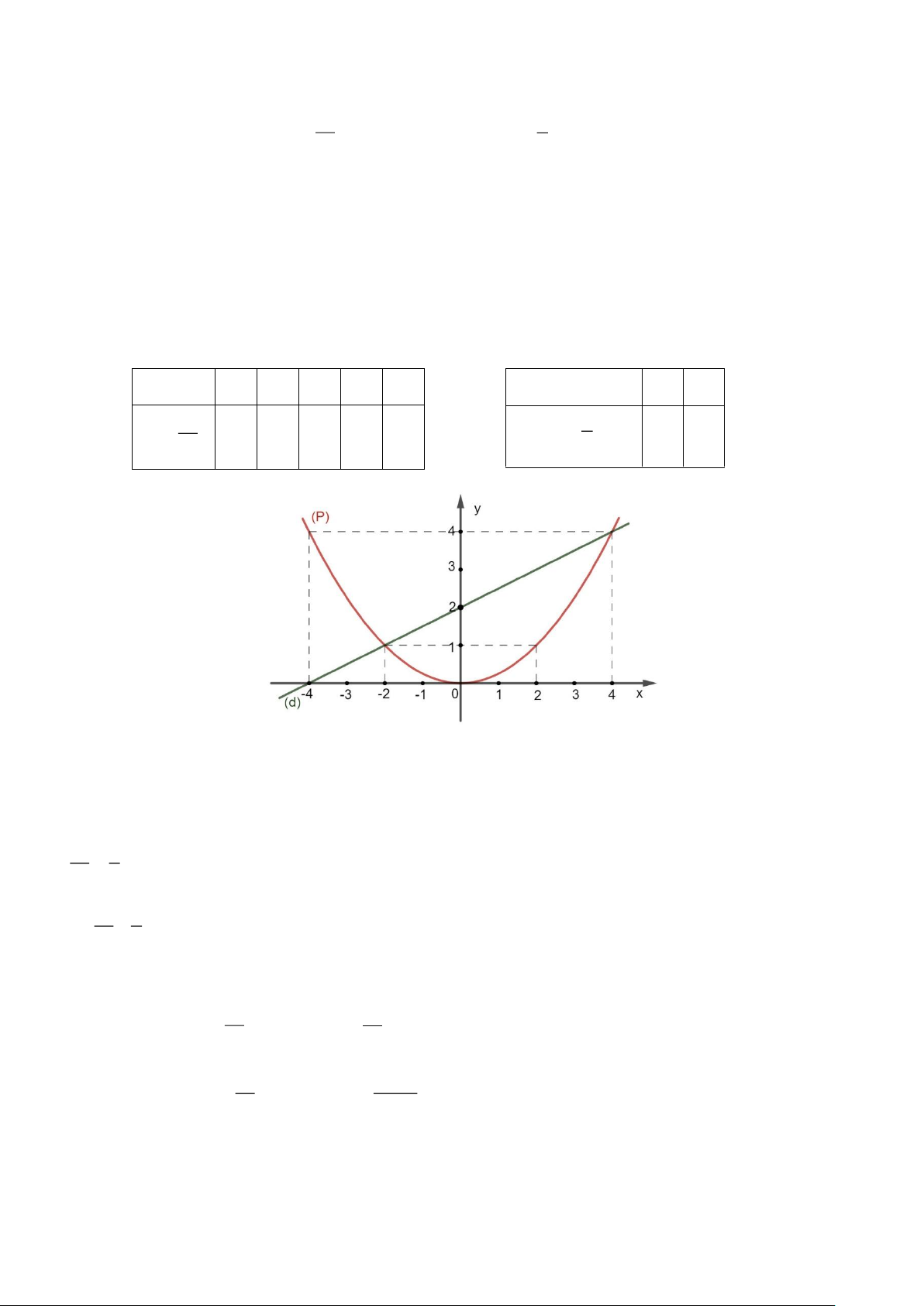
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. a) BGT: x −2 1 − 0 1 2 = 2 y x 4 1 0 1 4 x 0 1
y = 3x − 2 −2 1
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : 2 x = 3x − 2 2
x − 3x + 2 = 0 x = 1 x = 2 Thay x = 1 vào = 2 y
x , ta được: y = 2 1 = 1 . Thay x = 2 vào = 2 y
x , ta được: y = 2 2 = 4 .
Vậy (1; 1) , (2; 4) là hai giao điểm cần tìm. 5
Câu 2. (1 điểm) Cho phương trình 2 x − 5x +
= 0 . Gọi x ,x là hai nghiệm (nếu có) . Không giải 3 1 2 2 2 x x
phương trình, hãy tính giá trị của biểu thức A = 1 + 2 . x x 2 1 Lời giải Trang 4 5 5 Phương trình: 2
x − 5x + = 0 (a = 1, b = - 5, c = ) 3 3 5 55
Vì = b − 4ac = ( 5 − )2 2 − 4.1. = 0 3 3
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 −b −( 5 − )
S = x + x = = = 5 1 2 a 1
Theo định lí Vi-et, ta có: 5 c 5 3
P = x .x = = = 1 2 a 1 3 Ta có: 3 3 x + x 1 2 A = x .x 1 2
(x + x )3 −3x .x x + x 1 2 1 2 ( 1 2 ) A = x .x 1 2 5 3 5 − 3. .5 3 A = = 60 5 3 Vậy A = 60
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ
số thập phân, số đo góc làm tròn đến phút.
Câu 3. (1 điểm) Bên cạnh việc xem đua chó, nhiều người thích tham gia chương trình dự thưởng
để cuộc đua thêm phấn khích. Trước khi chọn chó để đạt thưởng, bạn sẽ được phát một
cuốn tài liệu có giới thiệu khá chi tiết về từng chú chó, từ những thành tích tốt, xấu đến tình
trạng sức khỏe, cuộc đua gần nhất có tham gia…sẽ giúp bạn dễ dàng chọn lựa. Và có 5 kiểu
thắng giải áp dụng cho các đợt đua là:
- Thắng nhất là Win nếu con chó mà bạn chọn về nhất.
- Thắng nhất – nhì (Exacta) là 2 con chó bạn chọn về nhất – nhì theo đúng thứ tự.
- Thắng nhất – nhì – ba (Trifecta) là cả 3 con chó bạn chọn đều về 3 thứ hạng đầu theo đúng thứ tự.
Các giải tiếp theo là Quartet (4) , Superfecta (6) . Càng lên cao càng trúng đậm.
Hỏi trong một đợt đua có 8 chú khuyển, ta có bao nhiêu cách chọn vé dự thưởng theo
giải nhất – nhì – ba? Lời giải Trang 5
Con về nhất có: 8 cách chọn
Con về nhì có: 7 cách chọn
Con về ba có: 6 cách chọn
Vậy có: 8.7.6 = 336 cách chọn vé dự thưởng theo giải nhất – nhì – ba.
Câu 4. (0,75 điểm). Cuối năm 2009 , một bản báo cáo được trình lên chính phủ Anh. Theo đó, nếu
nhiệt độ trái đất tăng lên 2 C
thì tổng giá trị kinh tế thế giới sẽ bị giảm đi 3% , nếu nhiệt độ
tăng lên 5C kinh tế sẽ giảm đi 10% Từ đó, thông qua nghiên cứu một nhóm nhà kinh tế
học đã đưa ra dự đoán về mối liên hệ giữa nhiệt độ thế giới và tổng giá trị kinh tế của thế
giới. Kết quả nghiên cứu đưa ra rằng tổng giá trị kinh tế bị giảm y % là hàm số bậc nhất
theo x là nhiệt độ tăng lên của Trái đất (tính theo C ).
a) Xác định mối liên hệ giữa y và x
b) Theo nghiên cứu đó, tổng giá trị kinh tế sẽ giảm bao nhiêu nếu thế giới tăng thêm 10C
(làm tròn đến hàng đơn vị ) Lời giải
a) Xác định mối liên hệ giữa y và x.
y = ax + b(a 0)
Gọi hàm số biểu thị mối liên hệ giữa y và x là:
Khi x = 2 thì y = 3 nên ta có: 3 = .2
a + b 2.a + b = 3 (1)
Khi x =5 thì y = 10 nên ta có: 10 = .5
a + b 5.a + b = 10 (2) 2a + b = 3 5 a + b =10
Từ (1) và (1) ta có hệ phương trình: 7 5 − a = ;b =
Giải hệ phương trình ta được: 3 3 7 5 y = x −
Vậy hàm số biểu thị mối liên hệ giữa y và x là: 3 3 7 5 y = .10 − 22
b) Thay x = 10 vào ta được: 3 3 0
Vậy tổng giá trị kinh tế sẽ giảm khoảng 22% nếu thế giới tăng thêm 10 C
Câu 5. (1 điểm) Lớp 9A dự định tổ chức liên hoan lớp cuối năm, trong phần nước cần chuẩn bị
42 ly trà sữa. Để tiết kiệm chi phí lớp đã tìm hiểu giá của hai cửa hàng A và B như sau: Trang 6
- Cửa hàng A : mua 5 ly bất kì sẽ được tặng 1 ly (cùng loại) và hóa đơn trên 400 000đồng
thì sẽ giảm thêm 10% trên hóa đơn.
- Cửa hàng B : chỉ khuyến mãi khi đặt qua App Grab Food mua từ 10 ly trở lên thì giảm
30% mỗi ly so với giá niêm yết và phí giao hàng thì khách tự trả theo khoảng cách từ cửa
hàng đến nơi nhận hàng.
Hỏi lớp 9A nên mua ở cửa hàng nào sẽ tiết kiệm hơn và tiết kiệm hơn bao nhiêu tiền? Biết
giá niêm yết 1 ly trà sữa ở hai cửa hàng đều là 30 000đồng, khoảng cách từ địa điểm liên
hoan đến cửa hàng B là 12km. Phí giao hàng được tính theo bảng sau: Khoảng cách Giá tiền (đồng) Dưới 10km 25 000 Từ 10kmđến 20km 26 000 Từ 20kmđến 40km 30 000 Trên 40km 5% giá trị đơn hàng Lời giải
Số tiền phải trả nếu mua 42 ly trà sữa ở cửa hàng A là: (42 − 7).30 0 0.(
0 1−10%) = 945 000 (đồng)
Số tiền phải trả nếu mua 42 ly trà sữa ở cửa hàng B là: 42.30 0 0.(
0 1− 30%) + 26 000 = 908 000 (đồng)
Lớp 9A nên mua ở cửa hàng B sẽ tiết kiệm hơn vì 908 000 < 945 000
Và tiết kiệm hơn: 908 000 − 945 000 = 37 000 (đồng)
Câu 6. (1 điểm) Để làm một cái gàu tát nước có dạng hình nón (hình 1), bác An dùng một tấm tôn
hình tam giác OMN cân tại O có cạnh bên OM = 6 m
d , góc MON = 120 (hình 2 ). Bác xác
định trung điểm H của MN , vẽ cung tròn tâm O bán kính OH cắt các cạnh OM, ON lần
lượt tại A, B . Sau đó bác cắt bỏ phần gạch sọc, cuộn phần còn lại của tấm tôn sao cho mép
OA trùng khít với mép OBtạo thành chiếc gàu (giả sử phần diện tích của mép nối không
đáng kể). Hỏi khi múc đầy thì chiếc gàu chứa được bao nhiêu lít nước? (kết quả làm tròn
đến một chữ số thập phân, lấy 3,14 ) Trang 7 Lời giải
Tam giác OMN cân, H là trung điểm
OH là đường cao, là phân giác OH
Xét tam giác OHM vuông tại H , ta có: 0 0 cos60 =
OH = 6.cos60 = 3(d ) m OM . R n .3.120
Độ dài cung tròn ABlà: l = = = 2 (dm) 180 180
Bán kính đường tròn miệng của chiếc gàu là: R = C : 2 = 2 : 2 = 1 (dm)
Chiều cao của chiếc gàu là: 2 2 h = 3 −1 = 2 2 (dm)
Khi múc đầy thì chiếc gàu chứa được số lít nước là: 1 1 2 2 3
V = R h = .3,14.1 .2 2 = 3,0(dm ) = 3(l) 3 3
Câu 7. (1 điểm) Vào dịp khai trương, nhà sách khuyến mãi mỗi cây viết bi được giảm 20% so với
giá niêm yết, còn mỗi quyển tập giảm 20% so với giá niêm yết. Bạn An vào nhà sách mua
20 quyển tập và 10 cây viết bi. Khi tính tiền, bạn An đưa 175 000 đồng và được thối lại
3 000 đồng. Tính giá niêm yết của mỗi quyển tập và mỗi cây viết bi mà bạn An đã mua. Biết
rằng khi An nhìn vào hóa đơn, tổng số tiền phải trả khi chưa giảm giá là 195 000 đồng. Lời giải
Gọi giá niêm yết của mỗi quyển tập là x ( x 0 ; đồng)
Giá niêm yết của mỗi cây viết bi là y ( y 0 ; đồng)
Vì tổng số tiền mua 20 quyển tập và 10 cây viết bi khi chưa giảm giá là 195 000 đồng nên ta
có phương trình: 20x +10 y = 195000 (1)
Vì tổng số tiền mua 20 quyển tập và 10 cây viết bi khi đã giảm giá là 175000 − 3000 =172000 đồng nên ta có phương trình:
20(1−10%)x +10(1− 20%)y =172000
18x + 8y = 172000 (2) Trang 8
20x +10y = 195000
Từ (1) và (2) ta có hệ phương trình: 1
8x + 8y = 172000 x = 8000(n)
Giải hệ phương trình, ta được: y = 3500(n)
Vậy giá niêm yết của mỗi quyển tập là 8000 đồng và mỗi cây viết bi 3500 đồng.
Câu 8. (3 điểm) Cho tam giác ABC có 3 góc nhọn AB AC . Vẽ đường cao AD, BE, CF của tam giác
đó. Gọi H là giao điểm của các đường cao vừa vẽ.
a) Chứng minh: các tứ giác E
A HF và BFEC nội tiếp.
b) Gọi M, N lần lượt là trung điểm của các đoạn AH, BC . Chứng minh: FM.FC = FN.FA .
c) Gọi P,Q lần lượt là chân các đường vuông góc kẻ từ M, N đến đường thẳng DF . Chứng
minh rằng đường tròn đường kính PQ đi qua giao điểm của FE và MN . Lời giải
a) Chứng minh: các tứ giác E
A HF và BFEC nội tiếp. Chứng minh: Tứ giác E A HF nội tiếp AEH = 90 Xét tứ giác E A HF có:
(Vì CF, BE là đường cao) AFH = 90
AEH + AFH = 90 + 90 = 180 Tứ giác E A HF nội tiếp
Chứng minh: Tứ giác BFEC nội tiếp Trang 9 BEC = 90
Xét tứ giác BFEC có:
(Vì CF, BE là đường cao) BFC = 90 BEC = BFC
Tứ giác BFEC nội tiếp
Gọi M, N lần lượt là trung điểm của các đoạn AH,BC . Chứng minh: FM.FC = FN.FA Tam giác H
AF vuông tại F,FM là trung tuyến
MF = MA (tính chất đường trung tuyến trong tam giác vuông)
AMF cân tại M MAF = MFA
Tam giác BFC vuông tại F,FN là trung tuyến
NF = NC (tính chất đường trung tuyến trong tam giác vuông)
CNF cân tại N NCF = NFC AFC = 90 • Xét tứ giác A C F D có: (Vì CF,BE là đường cao) ADC = 90 AFC = ADC Tứ giác A C F D nội tiếp
FAD = FCD (cùng chắn cung FD )
MAF = MFA = NCF = NFC FAM = FCN
• Xét AFM và CFN có: AFM = CFN
AFM ∽ CFN (g – g) FM FA =
= FM.FC = FN.FA FN FC
d) Gọi P, Q lần lượt là chân các đường vuông góc kẻ từ M, N đến đường thẳng DF. Chứng
minh rằng đường tròn đường kính PQ đi qua giao điểm của FE và MN.
Gọi K là giao điểm của EF và MN
Ta có MAF ∽ NCF
Suy ra: MFA = NFC Trang 10 Mà 0
AFC = 90 MFN = 90 MFP + NFQ = 90
Ta lại có MFP + FMQ = 90
Suy ra NFQ = FMP (1)
Vì M là tâm đường tròn ngoại tiếp tứ giác HF AE
, N là tâm đường tròn ngoại tiếp tứ giác BCEF do đó MN ⊥ EF tại K
Suy ra tứ giác MKFP nội tiếp FMP = PKF (2)
Từ (1),(2) suy ra NFQ = PKF
Và tứ giác NKFQ nội tiếp QNF = QKF
Mà QNF + NFQ = 90 suy ra QKF + PKF = 90 Suy ra QKP = 90
Do đó K thuộc đường tròn đường kính PQ . ----HẾT---
SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN TÂN BÌNH
NĂM HỌC: 2023 - 2024 MÔN: TOÁN
Đê thi gồm 8 câu hỏi tự luận. ĐỀ THAM KHẢO
MÃ ĐỀ: Quận Tân Bình -
Thời gian: 120 phút (không kể thời gian phát đề) 3 2 x 1
Câu 1. (1,5 điểm). Cho (P) : y =
và đường thẳng (d ) : y = x + 2 . 4 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
4x − 5x − 3 = 0 có hai nghiệm x ; x 1 2 .
5x − 3 5x − 3
Không giải phương trình tìm x ; x M = + 1
2 , tính giá trị của biểu thức 1 2 x x 2 1 Trang 11
Câu 3. (0,75 điểm). Các nhà khoa học về thống kê đã thiết lập được hàm số để tính về độ tuổi
trung bình các phụ nữ kết hôn lần đầu của thế giới như sau: A(t ) = 0, 08t +19, 7 . Trong đó:
A(t) là tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới, t là năm kết hôn với gốc
thời gian tính từ năm 1950 nghĩa là năm 1950 thì t = 0 , năm 1951 t = 1,…
a) Hãy tính độ tuổi trung bình các phụ nữ kết hôn lần đầu trên thế giới lần lượt vào các năm 1980 , 2005 .
b) Vào năm bao nhiêu thì độ tuổi trung bình các phụ nữ kết hôn lần đầu là 25, 7 tuổi?
Câu 4. (0,75 điểm). Cước điện thoại y (nghìn đồng) là số tiền mà người sử dụng điện thoại cần trả
hàng tháng, nó phụ thuộc vào lượng thời gian gọi x (phút) của người đó trong tháng. Mối
liên hệ giữa hai đại lượng này là một hàm số bậc nhất y = ax + b . Hãy tìm a,b biết rằng
nhà bạn An trong tháng 5 đã gọi 100 phút với số tiền là 40 nghìn đồng và trong tháng 6
gọi 40 phút với số tiền là 28 nghìn đồng.
Câu 5. (1 điểm). Hôm qua mẹ của Lan đi chợ mua 2 kg táo và 2 kg xoài thì phải trả số tiền là
220000 đồng. Hôm nay mẹ Lan mua 4 kg táo và 5 kg xoài thì phải trả số tiền là 505000
đồng. Hỏi giá của táo và xoài là bao nhiêu đồng/kg? (biết giá táo và xoài không thay đổi)
Câu 6. (1 điểm). Một xô nước hình trụ có đường kính là 28cm và chiều cao 30cm , được dùng để
lấy nước từ một hồ trữ nước hình lập phương có cạnh là 1,8m . Hồ đang chứa đầy nước.
a) Tính thể tích của xô nước. Biết rằng thể tích hình trụ được tính theo công thức 2
V = 3,14R h . Trong đó là R bán kính mặt đáy; h là chiều cao của hình trụ.
b) Giả sử mội ngày gia đình bạn A sử dụng 30 xô nước lấy từ hồ. Hỏi trong ngày hồ hết
nước, nước trong hồ sử dụng được đến xô thứ bao nhiêu thì hết nước (bỏ qua thể tích
thành hồ, mỗi lần múc đầy xô nước).
Câu 7. (1 điểm). Một cửa hàng nhập về 20 cái tivi và bán với giá tăng 40% so với giá nhập.
Nhưng sau khi bán được 12 cái thì cửa hàng muốn tăng lợi nhuận nên đã tăng 20% giá Trang 12
bán so với giá đang bán. Sau khi bán hết 20 cái tivi cửa hàng thu được 272160000 đồng.
Hỏi cửa hàng đã nhập mỗi các tivi với giá là bao nhiêu đồng?
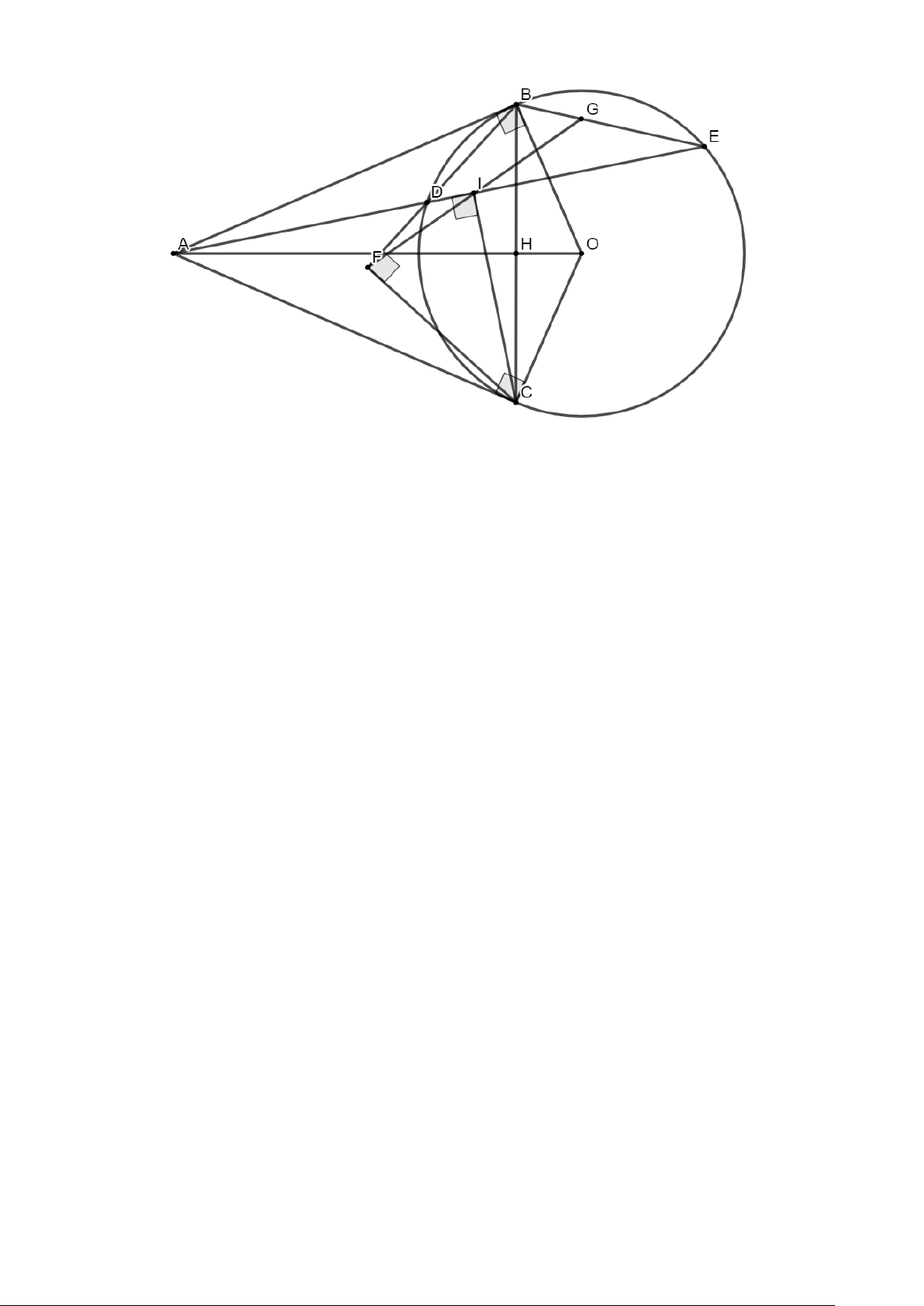
Câu 8. (3 điểm). Cho AB, AC là tiếp tuyến của (O) với B,C là tiếp điểm. Gọi H là giao điểm của
OA và BC . Lấy điểm E thuộc cung lớn BC của (O) sao cho EB EC cắt (O) tại D .
( D khác E ) . Vẽ CI ⊥ AE tại I .
a) Chứng minh OA ⊥ BD tại H và tứ giác AIHC nội tiếp.
b) Vẽ CF ⊥ BD tại F và FI cắt BE tại G . Chứng minh tứ giác IDFC nội tiếp và CG ⊥ BE .
c) Chứng minh I là trung điểm của GF . ----HẾT--- Trang 13 HƯỚNG DẪN GIẢI 2 x 1
Câu 1. (1,5 điểm) Cho (P) : y =
và đường thẳng (d ) : y = x + 2 . 4 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. BGT: x −4 −2 0 2 4 x 0 2 2 x 1 y = 4 1 0 1 4
(d) : y = x + 2 2 1 4 2
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : 2 x 1 = x + 2 4 2 2 x 1 − x − 2 = 0 4 2
x = 4 hay x = −2 2 x 2 4
Thay x = 4 vào y = , ta được:. y = = 4 4 4 2 x (− )2 2
Thay x = −2 vào y = , ta được:. y = =1 4 4 Vậy (4, 4) và (−2, )
1 là giao điểm cần tìm. Trang 14
Câu 2. (1 điểm) Cho phương trình 2
4x − 5x − 3 = 0 có hai nghiệm x ; x 1 2 .
5x − 3 5x − 3
Không giải phương trình tìm x ; x M = + 1
2 , tính giá trị của biểu thức 1 2 x x 2 1 Lời giải Vì . a c = 4.( 3 − ) = 12 − 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b − 5
S = x + x = = 1 2 a 4
Theo định lí Vi-et, ta có: c 3 −
P = x .x = = 1 2 a 4
5x − 3 5x − 3 Ta có: 1 2 M = + x x 2 1 x 5x − 3 x 5x − 3 1 ( 1 ) 2 ( 2 ) M = + x x x x 2 1 1 2 2 2
5x − 3x + 5x − 3x 1 1 2 2 M = x x 1 2 5( 2 2 x + x − 3 x + x 1 2 ) ( 1 2 ) M = x x 1 2 5( 2
S − 2P) − 3S M = P 2 5 −3 5 5 − 2. − 3. 4 4 4 185 − M = = 3 − 12 4
Câu 3. (0,75 điểm) Các nhà khoa học về thống kê đã thiết lập được hàm số để tính về độ tuổi
trung bình các phụ nữ kết hôn lần đầu của thế giới như sau: A(t ) = 0, 08t +19, 7 . Trong đó:
A(t) là tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới, t là năm kết hôn với gốc thời
gian tính từ năm 1950 nghĩa là năm 1950 thì t = 0 , năm 1951 t = 1,…
a) Hãy tính độ tuổi trung bình các phụ nữ kết hôn lần đầu trên thế giới lần lượt vào các năm 1980 , 2005 .
Vào năm bao nhiêu thì độ tuổi trung bình các phụ nữ kết hôn lần đầu là 25, 7 tuổi. Lời giải Trang 15
a) Vào năm 1980 thì t = 1980 −1950 = 30 thế vào công thức ta được:
A(t) = 0,08.30 +19,7 = 22,1
Vào năm 2005 thì t = 2005 −1950 = 55 thế vào công thức ta được:
A(t) = 0,08.55 +19,7 = 24,1
Vậy độ tuổi trung bình các phụ nữ kết hôn lần đầu trên thế giới lần lượt vào các năm 1980 là 22,1 tuổi; 2005 là 24,1 tuổi.
b) Ta có A(t ) = 25, 7 thế vào công thức ta được: 25,7 = 0,08t +19,7 t = 75
Vậy vào năm 2025 thì độ tuổi trung bình các phụ nữ kết hôn lần đầu là 25, 7 tuổi.
Câu 4. (0,75 điểm) Cước điện thoại y (nghìn đồng) là số tiền mà người sử dụng điện thoại cần trả
hàng tháng, nó phụ thuộc vào lượng thời gian gọi x (phút) của người đó trong tháng. Mối
liên hệ giữa hai đại lượng này là một hàm số bậc nhất y = ax + b . Hãy tìm a,b biết rằng nhà
bạn An trong tháng 5 đã gọi 100 phút với số tiền là 40 nghìn đồng và trong tháng 6 gọi 40
phút với số tiền là 28 nghìn đồng. Lời giải
Thế x = 100 và y = 40 vào hàm số ta được: 40 = .1 a 00 + b ( ) 1
Thế x = 40 và y = 28 vào hàm số ta được: 28 = .4 a 0 + b (2) 40 = .1 a 00 + b Từ ( )
1 và (2) ta có hệ phương trình: 28 = .4 a 0 + b 1 a = 5 b = 20 1
Vậy a = và b = 20 5 Trang 16
Câu 5. (1 điểm) Hôm qua mẹ của Lan đi chợ mua 2 kg táo và 2 kg xoài thì phải trả số tiền là
220000 đồng. Hôm nay mẹ Lan mua 4 kg táo và 5 kg xoài thì phải trả số tiền là 505000
đồng. Hỏi giá của táo và xoài là bao nhiêu đồng/kg? (biết giá táo và xoài không thay đổi) Lời giải
Gọi x là số tiền 1kg táo ( x, y 0)
y là số tiền 1kg xoài
Theo bài ra: mua 2 kg táo và 2 kg xoài thì phải trả số tiền là 220000 đồng.
2x + 2y = 220000 ( ) 1
Mua 4 kg táo và 5 kg xoài thì phải trả số tiền là 505000 đồng.
4x + 5y = 505000 (2)
2x + 2y = 220000 Từ ( )
1 và (2) ta có hệ phương trình:
4x + 5y = 505000 x = 45000 (nhận) y = 65000
Vậy giá 1kg táo lả 45000 đồng, giá 1kg xoài là 65000 đồng.
Câu 6. (1 điểm) Một xô nước hình trụ có đường kính là 28cm và chiều cao 30cm , được dùng để lấy
nước từ một hồ trữ nước hình lập phương có cạnh là 1,8m . Hồ đang chứa đầy nước.
a) Tính thể tích của xô nước. Biết rằng thể tích hình trụ được tính theo công thức 2
V = 3,14R h . Trong đó là R bán kính mặt đáy; h là chiều cao của hình trụ.
b) Giả sử mội ngày gia đình bạn A sử dụng 30 xô nước lấy từ hồ. Hỏi trong ngày hồ hết
nước, nước trong hồ sử dụng được đến xô thứ bao nhiêu thì hết nước (bỏ qua thể tích
thành hồ, mỗi lần múc đầy xô nước). Lời giải d 28
a) Bán kính xô nước: R = = =14cm . 2 2 Trang 17 Thể tích xô nước: 2 2
V = 3,14R h = 3,14.14 .30 = 18463, 2 ( 3 cm ) b) Thể tích hồ nước: 3 3
V = a = 1,8 = 5,832 ( 3 m ) Đổi: 3 3
5,832m = 5832000cm .
Số ngày sử dụng hết nước trong hồ:
5832000 :18463, 2 : 30 = 10 (ngày) dư 293040 ( 3 cm ).
Số xô nước dư trong ngày: 293040 :18463, 2 15,87 (xô)
Vậy trong ngày hồ hết nước, nước trong hồ sử dụng được đến xô thứ 16 .
Câu 7. (1 điểm) Một cửa hàng nhập về 20 cái tivi và bán với giá tăng 40% so với giá nhập. Nhưng
sau khi bán được 12 cái thì cửa hàng muốn tăng lợi nhuận nên đã tăng 20% giá bán so với
giá đang bán. Sau khi bán hết 20 cái tivi cửa hàng thu được 272160000 đồng. Hỏi cửa hàng
đã nhập mỗi các tivi với giá là bao nhiêu đồng? Lời giải
Gọi x là giá nhập của một cái tivi. (x 0)
x(1+ 40%) =1,4x là giá bán lúc đầu của một cái tivi.
1,4x(1+ 20%) =1,68x là giá bán lúc sau của một cái tivi.
Theo bài ra: tổng số tiền bán hết 20 cái tivi là 272160000 đồng. 1, 4 .12 x + 8.1,68x = 272160000
30, 24x = 272160000
x = 9000000 (nhận)
Vậy giá nhập một cái tivi là 9000000 đồng.
Câu 8. (3 điểm) Cho AB, AC là tiếp tuyến của (O) với B,C là tiếp điểm. Gọi H là giao điểm của
OA và BC . Lấy điểm E thuộc cung lớn BC của (O) sao cho EB EC cắt (O) tại D
( D khác E ) . Vẽ CI ⊥ AE tại I .
a) Chứng minh OA ⊥ BD tại H và tứ giác AIHC nội tiếp.
b) Vẽ CF ⊥ BD tại F và FI cắt BE tại G . Chứng minh tứ giác IDFC nội tiếp và CG ⊥ BE
c) Chứng minh I là trung điểm của GF . Trang 18 Lời giải
a) Ta có OB = OC (bán kính)
AB = AC (tính chất 2 tiếp tuyến cắt nhau)
OA là đường trung trực của BC . OA ⊥ BC Xét tg AIHC có:
AIC = AHC = 90 và cùng nhìn cạnh AC .
Vậy tg AIHC nội tiếp đường tròn. b) Xét tg IDFC có: DFC = 90 DIC = 90
DFC + DFC = 180
Vậy tg IDFC nội tiếp đường tròn.
Ta có: CDI = CFI (cùng chắn CI )
Mà CDI = CBE (cùng chắn CE ) CFI = CBE
Tg CFBG nội tiếp đường tròn.
CFB + CGB = 180 Trang 19 Mà CFB = 90
CGB = 90 CG ⊥ BE
c) Ta có: FIC = FDC (tg IDFC nội tiếp)
Xét ADC và ACE có: CAE chung
ACD = AEC (cùng chắn CD )
Þ D A DC ” D A CE (g.g) ADC = ACE
ADF + FDC = ACB + BCF
DFC + BCE = ACB + BCE
Mà BCE = BCE (cùng chắn BE ) DFC = ACB ( ) 1
Ta có: CIH = HAC (tg AIHC nội tiếp) (2)
Mà HAC + ACH = 90 (3)
CIH + FIC = 90 Từ ( ) 1 ,(2),(3) IH ⊥ FG
Ta có: BGC vuông tại G , H là trung điểm BC . 1 GH = BC 2 1
Chứng minh tương tự, ta được: FH = BC 2 GH = FH HGF cân tại H . Mà IH ⊥ FG
IH cũng là đường trung tuyến.
I là trung điểm FG . ----HẾT--- Trang 20