












Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT HUYỆN NHÀ BÈ MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận. ĐỀ TH AM KHẢO
Thời gian: 120 phút (không kể thời gian phát đề)
MÃ ĐỀ: Huyện Nhà Bè - 1
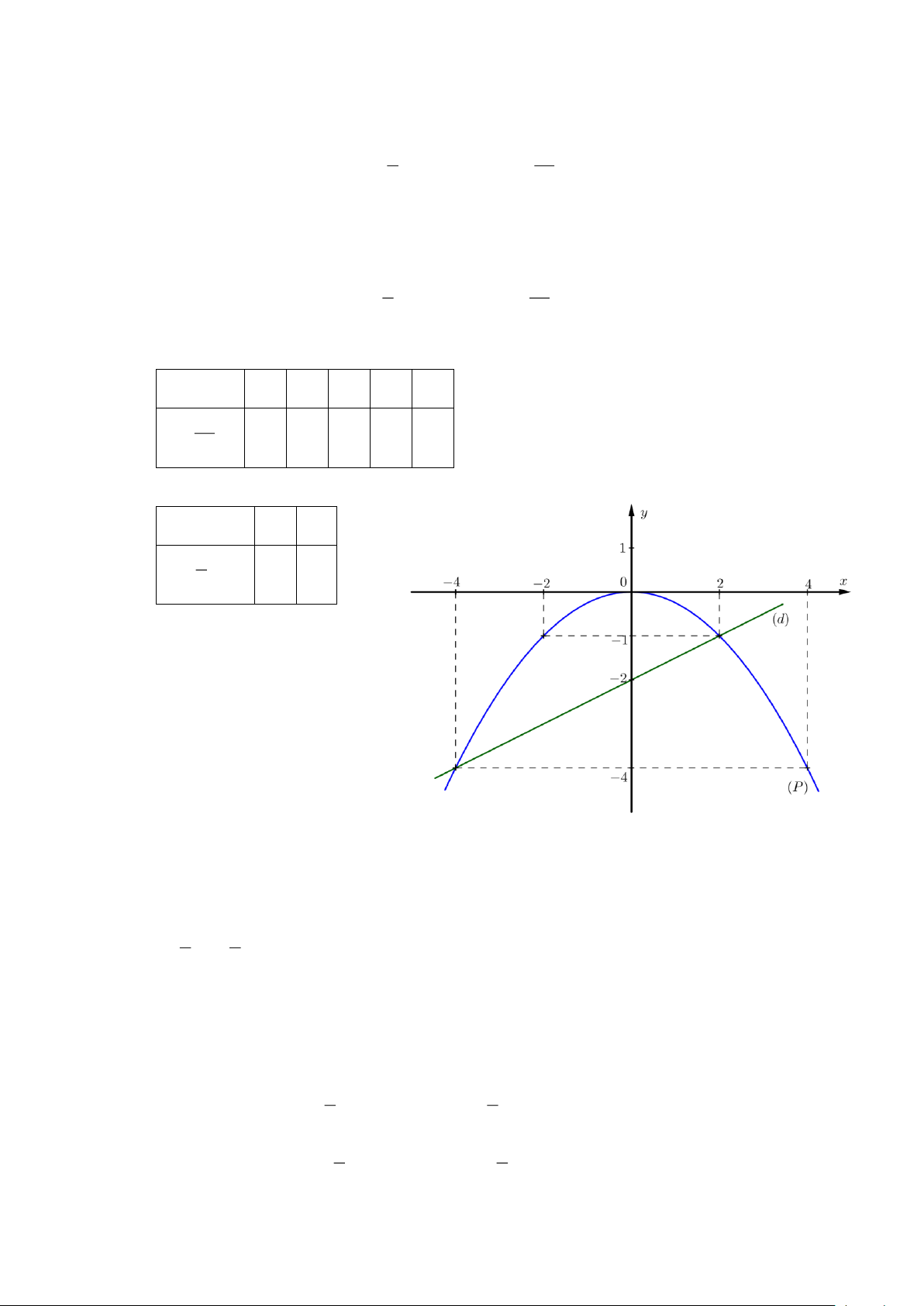
Câu 1. (1,5 điểm). 1 −
a) Vẽ hai đồ thị hàm số (d) 1 : y = x − 2 và (P) 2 : y =
x trên cùng một mặt phẳng tọa độ. 2 4
b) Tìm tọa độ giao điểm của hai đồ thị bằng phép toán.
Câu 2. (1 điểm). Cho phương trình 2
2x − 9x + 4 = 0 . Không giải phương trình, hãy tính giá trị của 49 biểu thức C = .
x x − x + x x − x 1 ( 1 2 ) 2 ( 2 1 )
Câu 3. (1 điểm). Một cửa hàng tạp hoá nhập về 1 thùng coca với giá gốc phân phối từ đại lý là
192 000 đồng/ 1 thùng. Sau đó bán lẻ cho khách với giá 10 000 đồng/ 1 lon.
a) Hỏi với việc mua và bán như thế thì cửa hàng đã thu lời bao nhiêu phần trăm so với giá
gốc? (Biết một thùng coca có 24 lon)
b) Để thu lời là 50% thì cửa hàng cần bán lẻ cho khách với giá là bao nhiêu trên 1 lon.
Câu 4. (0,75 điểm). Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Gọi y là
đại lượng biểu thị cho áp suất của khí quyển (tính bằng mmHg ) và x là đại lượng biểu thị
cho độ cao so với mặt nước biển (tính bằng mét). Người ta thấy với những độ cao không
lớn lắm thì mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất y = ax + b có đồ thị như hình vẽ sau:
a) Hãy xác định các hệ số a và b
b) Tại cực bắc của Việt Nam có một địa danh khá nổi tiếng là Cột cờ Lũng Cú ở xã Đồng
Văn, tỉnh Hà Giang nằm ở độ cao khoảng 1470m so với mực nước biển. Hỏi áp suất khí
quyển tại đây là bao nhiêu?
Câu 5. (0,75 điểm). Một doanh nghiệp vận tải dự định sẽ chở 40 tấn gạo trong một ngày để phân
phối đến các đại lý từ một kho hàng lương thực. Nhưng trên thực tế, doanh nghiệp vận tải
đã chở được vượt mức 25% , vì vậy mà đã thực hiện được sớm hơn 4 ngày so với dự định.
Hỏi ban đầu trong kho có bao nhiêu tấn gạo?
Câu 6. (1 điểm). Hai cửa hàng A và B đều nhập về (giá gốc) một nhãn hàng ti vi với giá là
10 000000 đồng. Cửa hàng A niêm yết sản phẩm đó với giá tăng 40% so với giá nhập về,
nhưng lại bán với giá giảm 20% so với giá niêm yết. Cửa hàng B niêm yết sản phẩm đó
với giá tăng 20% so với giá nhập về, nhưng lại bán với giá giảm 5% so với giá niêm yết.
Biết giá niêm yết là giá mà cửa hàng đề xuất với người tiêu dùng. Theo em, người tiêu
dùng chọn mua ti vi từ cửa hàng nào sẽ có lợi hơn? Em hãy giải thích?
Câu 7. (1 điểm). Nón lá là biểu tượng cho sự dịu dàng, bình dị, thân thiện của người phụ nữ Việt
Nam từ ngàn đời nay; nón lá bài thơ là một đặc trưng của xứ Huế. Một chiếc nón lá hoàn
thiện cần qua nhiều công đoạn từ lên rừng hái lá, rồi sấy lá, mở, ủi, chọn lá, xây độn vành, Trang 1
chằm, cắt lá, nức vành, cắt chỉ, … Nhằm làm đẹp và tôn vinh thêm cho chiếc nón lá xứ
Huế, các nghệ nhân còn ép tranh và vài dòng thơ vào giữa hai lớp lá:
Khung của nón lá có dạng hình nón được làm bởi các thanh gỗ nối từ đỉnh tới đáy như các
đường sinh ( ) , 16 vành nón được làm từ những thanh tre mảnh nhỏ, dẻo dai uốn thành
những vòng tròn có đường kính to, nhỏ khác nhau, cái nhỏ nhất to bằng đồng xu.
• Đường kính (d = 2r) của vành nón lớn nhất khoảng 40(cm) .
• Chiều cao (h) của chiếc nón lá khoảng 18(cm) .
a) Tính độ dài của thanh tre uốn thành vòng tròn lớn nhất của vành chiếc nón lá. (Không
kể phần chắp nối, biết 3,14 ).
b) Tính diện tích phần lá phủ xung quanh của chiếc nón lá. (Không kể phần chắp nối tính
gần đúng đến hàng đơn vị). Biết diện tích xung quanh của hình nón là S = .r. .
Câu 8. (3 điểm) Cho ABC nhọn ( AB AC) nội tiếp đường tròn (O) có 2 đường cao BE và CF
cắt nhau tại H . EF kéo dài cắt BC tại M , và MD là tiếp tuyến của đường tròn (O) ( D
thuộc cung nhỏ BC )
a) Chứng minh: AEHF nội tiếp, và BFEC nội tiếp.
b) Chứng minh: OA vuông góc với EF và 2 MD = M . E MF
c) Chứng minh: DA là phân giác của góc EDF . ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm). 1 1
a) Vẽ hai đồ thị hàm số (d) : y = x − 2 và (P) − : y = 2
x trên cùng một mặt phẳng tọa độ. 2 4
b) Tìm tọa độ giao điểm của hai đồ thị bằng phép toán. Lời giải 1
a) Vẽ hai đồ thị hàm số (d) 1 : y = x − 2 và (P) − : y = 2
x trên cùng một mặt phẳng tọa độ. 2 4 BGT: x −4 −2 0 2 4 − y = 1 2 x −4 1 − 0 1 − −4 4 x 0 2
y = 1 x − 2 −2 1 − 2
b) Tìm tọa độ giao điểm của của hai đồ thị bằng phép toán.
Phương trình hoành độ giao điểm của (P) và (d) : − 1 2 x = 1 x − 2 4 2 2 x + 2x − 8 = 0 x = 2 x = − 4 1 1
Thay x = 2 vào y = x − 2 , ta được: y = .2 − 2 = −1 . 2 2 1 1
Thay x = −4 vào y = x − 2 , ta được: y = .(−4) − 2 = −4 . 2 2
Vậy (2; − 1) , (−4; − 4) là hai giao điểm cần tìm. Trang 3
Câu 2. (1 điểm) Cho phương trình 2
2x − 9x + 4 = 0 . Không giải phương trình, hãy tính giá trị của 49 biểu thức C =
x (x − x ) + x (x − x 1 1 2 2 2 1 ) Lời giải 2 Vì = 2
b − 4ac = (−9) − 4.2.4 = 49 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 − = + = b S x x = 9 1 2
Theo định lí Vi-et, ta có: a 2 = c P x .x = = 2 1 2 a 49 Ta có: C =
x (x − x ) + x (x − x 1 1 2 2 2 1 ) C = 49 2 x − x x + 2 x − x x 1 1 2 2 1 2 C = 49 2
S − 2P − 2P 49 C = 2 S − 4P C = 49 9 2 − 4.2 2 C = 4
Câu 3. (1 điểm) Một cửa hàng tạp hoá nhập về 1 thùng coca với giá gốc phân phối từ đại lý là
192 000đồng/ 1 thùng. Sau đó bán lẻ cho khách với giá 10 000 đồng/ 1 lon.
a) Hỏi với việc mua và bán như thế thì cửa hàng đã thu lời bao nhiêu phần trăm so với giá
gốc? (Biết một thùng coca có 24 lon)
b) Để thu lời là 50% thì cửa hàng cần bán lẻ cho khách với giá là bao nhiêu trên 1 lon. Lời giải
a) Hỏi với việc mua và bán như thế thì cửa hàng đã thu lời bao nhiêu phần trăm so với
giá gốc? (Biết một thùng coca có 24 lon)
Phần trăm lãi so với giá gốc :
24.10 000 - 192 000 .100% = 25% 192 000
b) Để thu lời là 50% thì cửa hàng cần bán lẻ cho khách với giá là bao nhiêu trên 1 lon.
Gọi x (đồng) là giá tiền 1 lon nước (x > 0) Trang 4
24.x - 192 000 .100% = 50% 192 000
Û 24.x - 192 000 = 0, 5.192 000
Û x = 12 000(n )
Vậy giá tiền 1 lon nước là 12 000 đồng để thu lời là 50%
Câu 4. (0,75 điểm) Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Gọi y
là đại lượng biểu thị cho áp suất của khí quyển (tính bằng m m Hg ) và x là đại lượng biểu thị
cho độ cao so với mặt nước biển (tính bằng mét). Người ta thấy với những độ cao không lớn
lắm thì mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất y = ax + b có đồ thị như hình vẽ sau:
a) Hãy xác định các hệ số a và b
b) Tại cực bắc của Việt Nam có một địa danh khá nổi tiếng là Cột cờ Lũng Cú ở xã Đồng
Văn, tỉnh Hà Giang nằm ở độ cao khoảng 1470m so với mực nước biển. Hỏi áp suất khí
quyển tại đây là bao nhiêu? Lời giải
a) Hãy xác định các hệ số a và b Theo đề bài, ta có: x = 1600 Với
632 = 1600.a + . ( ) 1 y = b 632 x = 0 Với 760 = 0.a + . (2) y = b 760 a + b = a = − 2 0 760 Từ ( )
1 và (2) ta có hệ phương trình: . 1600a + b = 25 632 b = 760 2
Vậy: a = − 2 , b = 760 và y = − x + 760 . 25 25
b) Tại cực bắc của Việt Nam có một địa danh khá nổi tiếng là Cột cờ Lũng Cú ở xã Đồng
Văn, tỉnh Hà Giang nằm ở độ cao khoảng 1470m so với mực nước biển. Hỏi áp suất
khí quyển tại đây là bao nhiêu? 2
Thay x = 1470 vào y = − x + 760 ta được: 25 y = − 2 .1470 + 760 25 y = 642,4 Trang 5
Vậy áp suất khí quyển tại đây là 642, 4mmHg
Câu 5. (0,75 điểm). Một doanh nghiệp vận tải dự định sẽ chở 40 tấn gạo trong một ngày để phân
phối đến các đại lý từ một kho hàng lương thực. Nhưng trên thực tế, doanh nghiệp vận tải đã
chở được vượt mức 25% , vì vậy mà đã thực hiện được sớm hơn 4 ngày so với dự định. Hỏi
ban đầu trong kho có bao nhiêu tấn gạo? Lời giải
Gọi x (tấn) là số tấn gạo ban đầu (x > 0)
x (ngày) là số ngày giao hàng dự định để giao hết số tấn gạo. 40
x (ngày) là số ngày giao hàng thực tế để giao hết số tấn gạo. 50 x x Ta có phương trình: - = 4 40 50 50x - 40x Û = 4 2000 Û 10x = 8000 Û x = 800(n )
Vậy ban đầu có 800 tấn gạo.
Câu 6. (1 điểm). Hai cửa hàng A và B đều nhập về (giá gốc) một nhãn hàng ti vi với giá là
10 000 000 đồng. Cửa hàng A niêm yết sản phẩm đó với giá tăng 40% so với giá nhập về,
nhưng lại bán với giá giảm 20% so với giá niêm yết. Cửa hàng B niêm yết sản phẩm đó với
giá tăng 20% so với giá nhập về, nhưng lại bán với giá giảm 5% so với giá niêm yết. Biết giá
niêm yết là giá mà cửa hàng đề xuất với người tiêu dùng. Theo em, người tiêu dùng chọn
mua ti vi từ cửa hàng nào sẽ có lợi hơn? Em hãy giải thích? Lời giải
Giá niêm yết ti vi ở cửa hàng A : 10 000 000.(1 + 40 ) % .(1 - 20 ) % = 11200 000 (đồng)
Giá niêm yết ti vi ở cửa hàng B : 10 000 000.(1 + 20 ) % .(1 - 5 ) % = 11400 000 (đồng)
Vì 11200 000 < 11400 000 nên mua ở cửa hàng A sẽ lợi hơn.
Câu 7. (1 điểm). Nón lá là biểu tượng cho sự dịu dàng, bình dị, thân thiện của người phụ nữ Việt
Nam từ ngàn đời nay; nón lá bài thơ là một đặc trưng của xứ Huế. Một chiếc nón lá hoàn Trang 6
thiện cần qua nhiều công đoạn từ lên rừng hái lá, rồi sấy lá, mở, ủi, chọn lá, xây độn vành,
chằm, cắt lá, nức vành, cắt chỉ, … Nhằm làm đẹp và tôn vinh thêm cho chiếc nón lá xứ Huế,
các nghệ nhân còn ép tranh và vài dòng thơ vào giữa hai lớp lá:
Khung của nón lá có dạng hình nón được làm bởi các thanh gỗ nối từ đỉnh tới đáy như các
đường sinh (l ), 16 vành nón được làm từ những thanh tre mảnh nhỏ, dẻo dai uốn thành
những vòng tròn có đường kính to, nhỏ khác nhau, cái nhỏ nhất to bằng đồng xu.
• Đường kính (d = 2r ) của vành nón lớn nhất khoảng 40(cm )
• Chiều cao (h) của chiếc nón lá khoảng 18(cm )
a) Tính độ dài của thanh tre uốn thành vòng tròn lớn nhất của vành chiếc nón lá. (Không kể
phần chắp nối, biết p » 3,14 )
b) Tính diện tích phần lá phủ xung quanh của chiếc nón lá. (Không kể phần chắp nối tính gần
đúng đến hàng đơn vị). Biết diện tích xung quanh của hình nón là S = p.r.l Lời giải
a) Tính độ dài của thanh tre uốn thành vòng tròn lớn nhất của vành chiếc nón lá. (Không kể
phần chắp nối, biết p » 3,14 )
Độ dài của thanh tre uốn thành vòng tròn lớn là:
20p » 20.3,14 » 62, 83(cm )
b. Tính diện tích phần lá phủ xung quanh của chiếc nón lá. (Không kể phần chắp nối tính gần
đúng đến hàng đơn vị). Biết diện tích xung quanh của hình nón là S = p.r.l
Xét D A B C vuông tại B 2 2 2
A B + BC = A C 2 2 2 Û 18 + 20 = A C 2 Û 724 = A C
Û A C = 2 181(cm )
Diện tích phần lá phủ xung quanh: S = p r l » » ( 2 . . 3,14.20.2 181 1690, 63 cm ) Trang 7
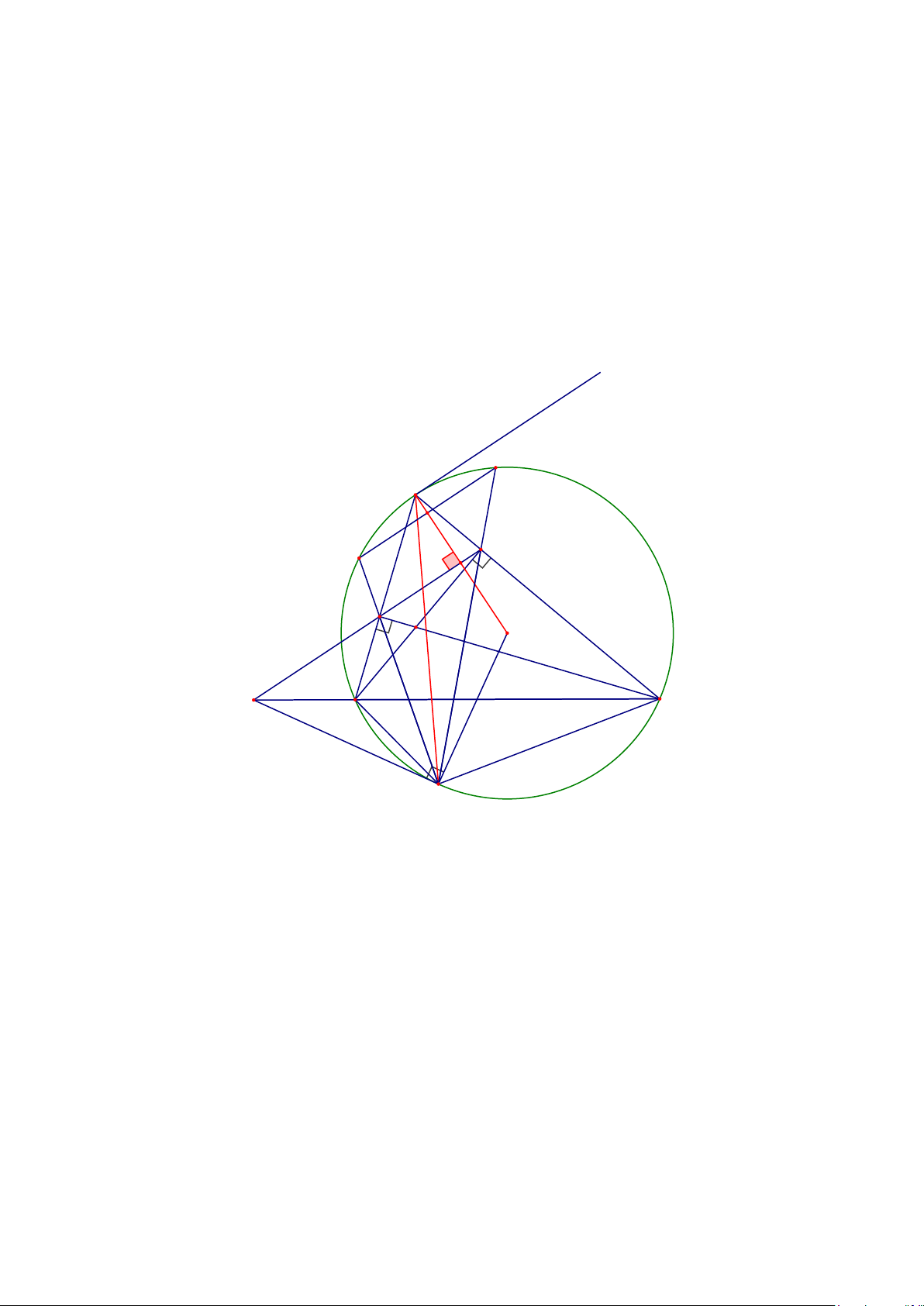
Câu 8. (3 điểm) Cho ABC nhọn ( AB AC) nội tiếp đường tròn (O) có 2 đường cao BE và CF
cắt nhau tại H . EF kéo dài cắt BC tại M , và MD là tiếp tuyến của đường tròn (O ) (D thuộc cung nhỏ BC )
a) Chứng minh: AEHF nội tiếp, và BFEC nội tiếp.
b) Chứng minh: OA vuông góc với EF và 2
MD = ME .MF
c) Chứng minh: DA là phân giác của góc EDF. Lời giải x Q A S I E F O H C M B D
a) Chứng minh: AEHF nội tiếp, và BFEC nội tiếp.
Xét tứ giác AEHF , có:
AEH = 90(BE ⊥ AC ) AFH = 90 (CF ⊥ AB) AEH + AFH = 180
Tứ giác AEHF nội tiếp vì có hai góc đối bù nhau.
Xét tứ giác BFEC , có: BFC = 90 (CF ⊥ AB) BEC = 90 (BE ⊥ AC) Trang 8
BFC = BEC = 90
Tứ giác BFEC nội tiếp vì có hai đỉnh kề cùng nhìn một cạnh dưới hai góc bằng nhau.
b) Chứng minh: OA vuông góc với EF và 2
MD = ME .MF
Vẽ Ax là tiếp tuyến của (O ) · · xA E = A BC ¼ (cùng chắn A C ) · ·
A EF = A BC ( BFEC nội tiếp, góc ngoài bằng góc đối trong) · · Þ xA E = A EF
Mà hai góc này ở vị trí so le trong Ax// EF Mà OA ^ A x Þ OA ^ EF
Chứng minh D MB D đồng dạng D MDC (g-g) Suy ra 2
MD = MB .MC
Chứng minh D MFB đồng dạng D MEC (g-g)
Suy ra MF .ME = MB .MC Do đó 2
MD = ME .MF
c) Chứng minh: DA là phân giác của góc EDF.
Kéo dài DF , DE cắt (O ) tại I và Q
Chứng minh được D MFD đồng dạng D MDE (c-g-c) · · Þ MDF = MED · · · »
Mà MDF = MDI = IQD (cùng chắn DI ) · ·
Þ EFD = IQD mà hai góc này ở vị trí đồng vị IQ // EF
Þ IQ ^ OA tại S
D A IQ có A S là đường trung trực
Þ DA IQ cân tại A Þ IA = IQ Þ º ¼
sđ IA = sđ A Q · · Þ IDA = A DQ · ·
hay FDA = A DE Trang 9
Þ DA là phân giác của góc DEF . ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT HUYỆN NHÀ BÈ
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: Huyện Nhà Bè -
Thời gian: 120 phút (không kể thời gian phát đề) 2
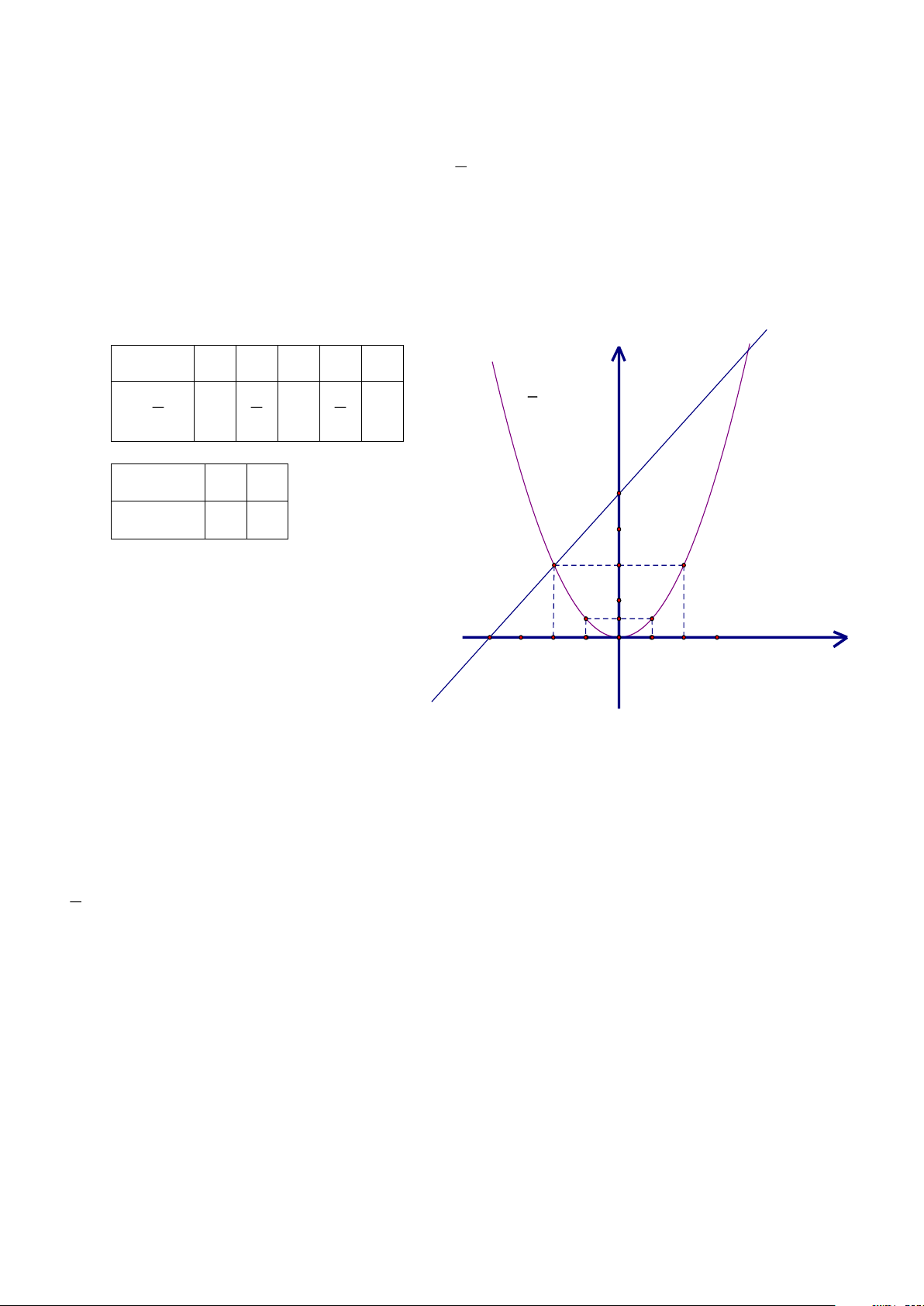
Bài 1. (1,5 điểm) 1
a) Vẽ hai đồ thị hàm số (d ) : y = x + 4 và ( P) 2
: y = x trên cùng một mặt phẳng tọa độ 2
b) Tìm tọa độ giao điểm của hai đồ thị bằng phép toán.
Bài 2. (1 điểm) Cho phương trình: 2
2x − 7x + 6 = 0 . 2x 2x
Không giải phương trình hãy tính giá trị biểu thức: 1 2 A = + 3x − x 3x − x 1 2 2 1
Bài 3. (0,75 điểm) Theo quy định của công ty, một công nhân được trả lương như sau: 400 000
đồng cho một ngày làm việc bình thường (từ thứ hai đến thứ sáu hàng tuần, một ngày làm 8 giờ).
Nếu làm tăng ca vào các ngày thứ 7 - chủ nhật hoặc lễ thì được hưởng lương bằng 150% tiền
lương của một ngày làm việc bình thường Anh Thắng là nhân viên của công ty trên và trong tháng
5 / 2022 vừa qua anh đã được trả lương là 10 400 000 .
Hỏi anh đã làm việc bao nhiêu ngày tăng ca? (biết số ngày làm việc bình thường trong tháng 5 của anh là 20 ngày).
Bài 4. (1 điểm)Một hộ gia đình có ý định mua một cái máy bơm để phục vụ cho việc tưới tiêu. Khi
đến cửa hàng thì được nhân viên giới thiệu 2 loại máy bơm có lưu lượng nước trong một
giờ và chất lượng máy là như nhau. Giá bán và hao phí điện năng của mỗi máy như sau :
Máy thứ nhất : giá 3 triệu và trong một giờ tiêu thụ hết 1,5 kWh.
Máy thứ hai : giá 2 triệu và trong một giờ tiêu thụ hết 2 kWh. Biết giá 1 kWh là 2 000 đồng và một
a) Gọi y là tổng chi phí (bao gồm tiền mua máy bơm và tiền điện phải trả) khi mua mỗi
loại máy bơm và sử dụng trong x giờ. Hãy lập công thức biểu diễn y theo x của từng loại máy bơm.
b) Nếu người nông dân chỉ sử dụng trong hai năm và mỗi ngày chỉ sử dụng 3 giờ thì nên
chọn mua loại máy nào có lợi hơn.
Bài 5. (1 điểm)Một năm bình thường sẽ có 12 tháng và 365 ngày. Khi một năm có số ngày hoặc
số tháng tăng lên (theo Dương lịch hoặc Âm lịch) thì sẽ được gọi là năm nhuận, trong đó có
những ngày nhuận và tháng nhuận. Năm nhuận là năm có ngày 29 tháng 2 Dương lịch Trang 10
(không nhuận là 28 ngày). Cách tính năm nhuận theo dương lịch là những năm dương lịch
nào chia cho 4 thì đó sẽ là năm nhuận.
Ví dụ: 2016 chia hết cho 4 nên năm 2016 là năm nhuận.
Ngoài ra, đối với những tròn thế kỷ (những năm có hai số cuối là số 0 ) thì chúng ta sẽ lấy số năm
đem chia cho 400 , nếu như chia hết thì đó sẽ là năm nhuận.
Ví dụ: 1600 và 2000 là các năm nhuận nhưng 1700 ,1800 và 1900 không phải năm nhuận.
a) Em hãy dùng quy tắc trên để xác định năm 2022 , năm 2024 có phải là năm nhuận dương lịch không?
b) Biết rằng ngày 30 / 04 / 2022 là rơi vào thứ bảy. Hỏi ngày 30 / 04 / 1975 là rơi vào thứ mấy? Em hãy giải thích.
Bài 6. (1 điểm)Trong kì thi HK2 môn Toán lớp 9 , một phòng thi có 24 thí sinh dự thi. Các thí sinh
đều phải làm bài trên giấy thi của trường phát cho. Cuối buổi thi, sau khi thu bài, giám thị
coi thi đếm được tổng số tờ giấy thi là 49 tờ. Hỏi trong phòng thi đó có bao nhiêu thí sinh
làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 5 thí sinh chỉ
làm 1 tờ giấy thi, và không có thí sinh nào làm trên 3 tờ giấy thi.
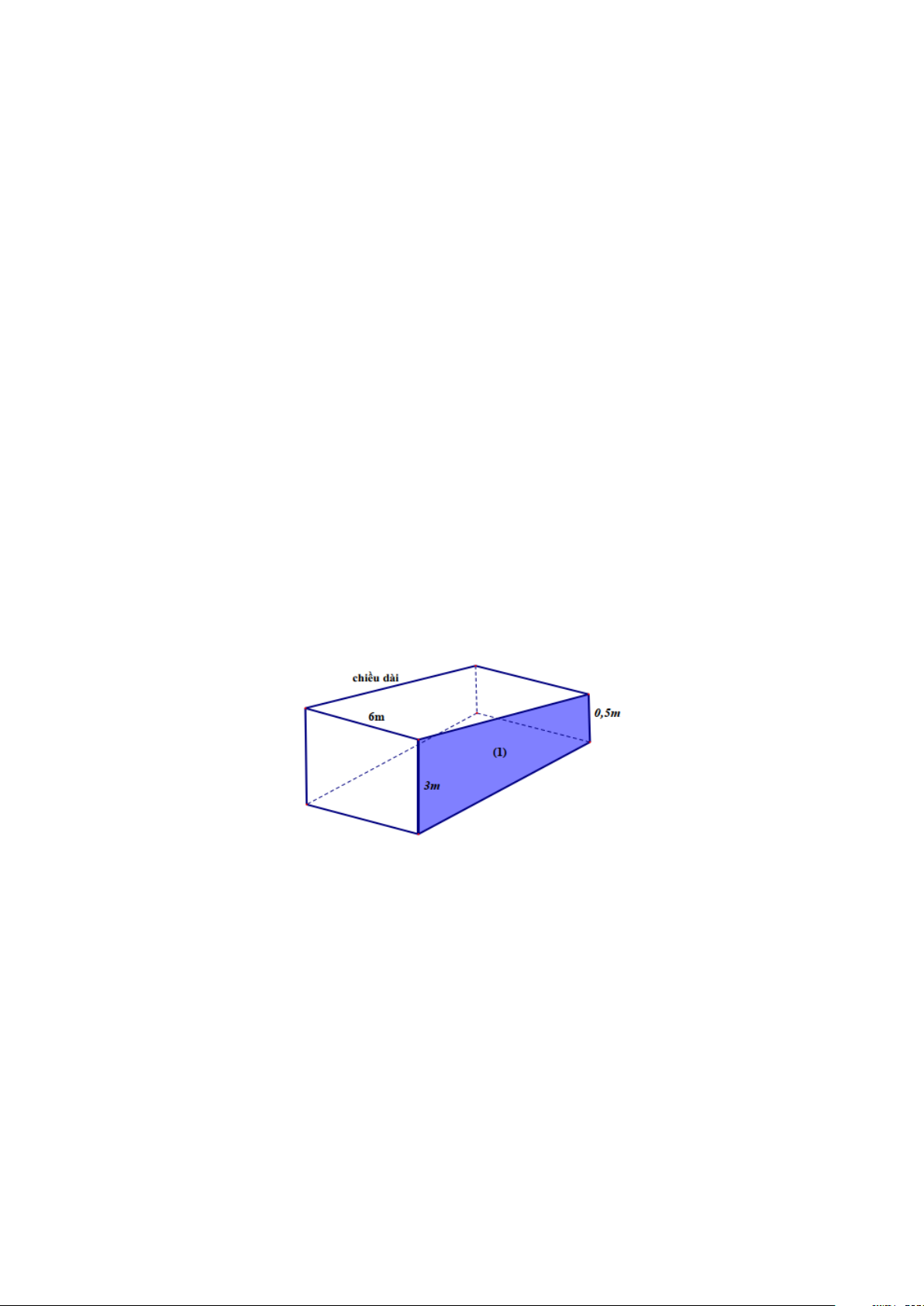
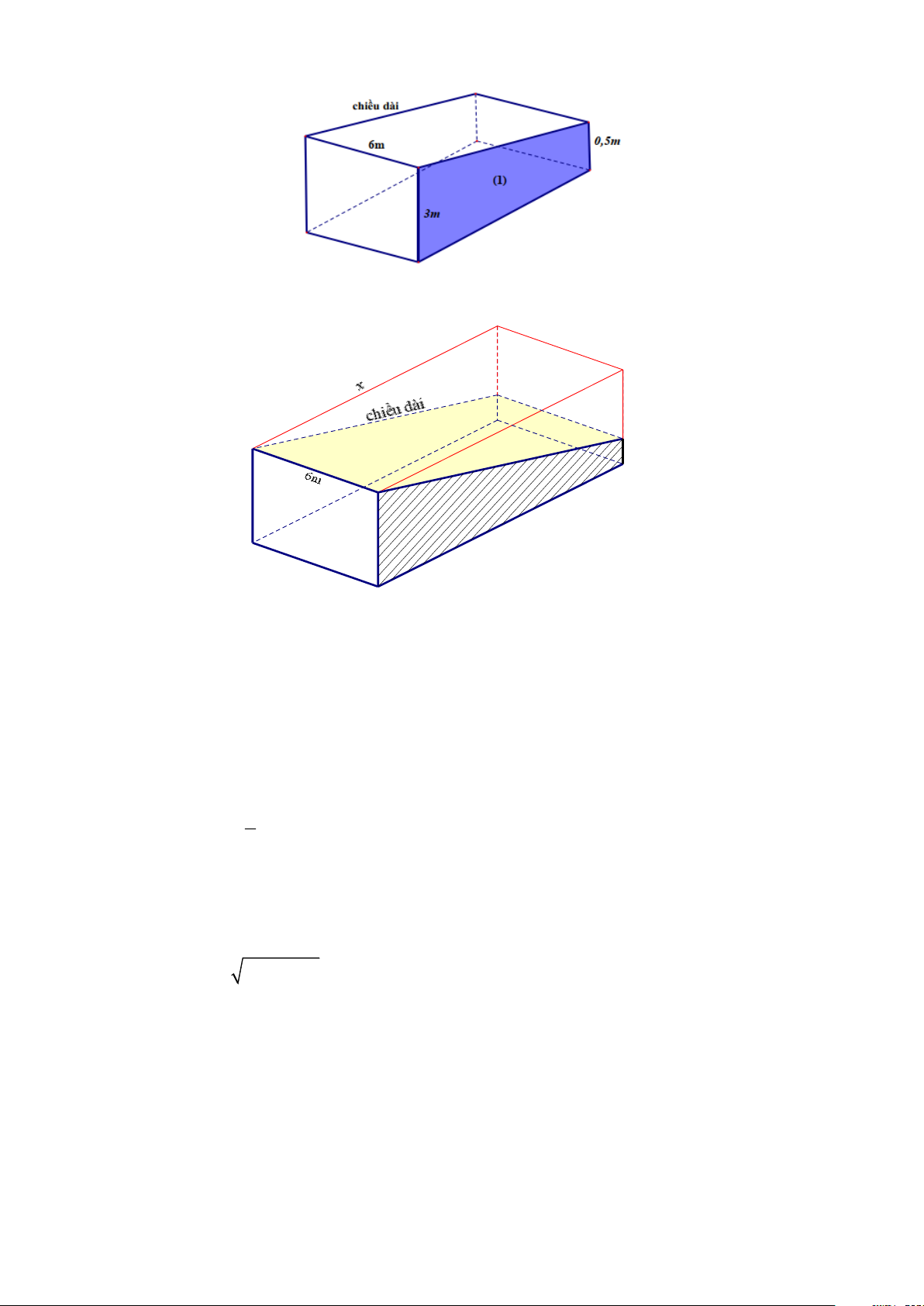
Bài 7. (0,75 điểm) Người ta thiết kế một hồ bơi có dạng là một lăng trụ đứng tứ giác với đáy là
hình thang vuông (mặt số 1 ) của hồ bơi, cùng các kích thước như đã cho (xem hình vẽ). Biết
rằng người ta dùng một máy bơm với lưu lượng là 3
6m / phút và sẽ bơm đầy hồ mất 35
phút. Em hãy tính chiều dài của hồ.
Bài 8. (3 điểm) Từ điểm A ở ngoài đường tròn tâm O , vẽ hai tiếp tuyến AB, AC với (O) (B , C
là hai tiếp điểm). Vẽ cát tuyến AMN với (O) sao cho AM AN và tia AM nằm giữa tia
OA và tia OC . Gọi E là trung điểm của MN .
a) Chứng minh tứ giác ABOE nội tiếp, và 2
AB = AM .AN
b) Đoạn thẳng BC cắt OA và MN lần lượt tại H và K .
Chứng minh: OA vuông góc với BC tại H và AE.AK = AM .AN .
c) Cho biết OA = 2R . Trên đoạn thẳng BC lấy một điểm F bất kì, qua F vẽ đường thẳng
vuông góc với OF tại F cắt AB và AC tại P và Q . Chứng minh góc POQ luôn
không đổi khi F di chuyển trên đoạn BC . ----HẾT--- Trang 11 HƯỚNG DẪN GIẢI
Bài 1. (1,5 điểm) 1
a) Vẽ hai đồ thị hàm số (d ) : y = x + 4 và 2
(P) : y = x trên cùng một mặt phẳng tọa độ. 2
b) Tìm tọa độ giao điểm của hai đồ thị bằng phép toán. Lời giải
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. BGT: x −2 1 − 0 1 2 y 1 1 1 y = ∙x2 y = 1 2 x 2 0 2 2 2 2 2 y = x + 4 x 0 −2 4 y = x + 4 4 2 3 2 1 1/2 -4 O -3 -2 -1 1 2 3 x
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : 1 2 x = x + 4 2 2
x − 2x − 8 = 0 x = 4 x = − 2
Thay x = 4 vào y = x + 4 , ta được: y = 4 + 4 = 8 .
Thay x = −2 vào y = x + 4 , ta được: y = −2 + 4 = 2 .
Vậy (4; 8) , (−2; 2) là hai giao điểm cần tìm.
Bài 2. (1 điểm) Cho phương trình: 2
2x − 7x + 6 = 0 Trang 12 2x 2x
Không giải phương trình hãy tính giá trị biểu thức: 1 2 A = + 3x − x 3x − x 1 2 2 1 Lời giải 2 Vì = 2
b − 4ac = (−7) − 4.2.6 = 1 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 −b −
S = x + x = = − 7 = 7 1 2
Theo định lí Vi-et, ta có: a 2 2 = = c P x x = 6 . = 3 1 2 a 2 2x 2x Ta có: 1 2 A = + 3x − x 3x − x 1 2 2 1
2x 3x − x + 2x 3x − x 1 ( 2 1 ) 2 ( 1 2 ) A = (3x − x 3x − x 1 2 ) ( 2 1 ) 2 7 16.3 − 2. 16x x 2 x + x − 1 2 ( 2 1 2 ) 2 94 A = = =
16x x − 3 x + x 7 45 2 ( 2 )2 2 1 1 16.3 − 3. 2
Bài 3. (0,75 điểm)
Theo quy định của công ty, một công nhân được trả lương như sau: 400 000 đồng cho một ngày
làm việc bình thường (từ thứ hai đến thứ sáu hàng tuần, một ngày làm 8 giờ).
Nếu làm tăng ca vào các ngày thứ 7 - chủ nhật hoặc lễ thì được hưởng lương bằng 150% tiền
lương của một ngày làm việc bình thường Anh Thắng là nhân viên của công ty trên và trong tháng
5 / 2022 vừa qua anh đã được trả lương là 10 400 000 .
Hỏi anh đã làm việc bao nhiêu ngày tăng ca? (biết số ngày làm việc bình thường trong tháng 5 của anh là 20 ngày). Lời giải
Một ngày tăng ca anh Thắng được trả lương là: 400000.150% = 600000 ( đồng)
Tiền lương 1 tháng anh Thắng được trả( không tăng ca) là: 400000.20 = 8000000 ( đồng)
Số tiền anh Thắng được nhận khi tăng ca là: 10400000 − 8000000 = 2400000 ( đồng)
Số ngày anh Thắng đã làm tăng ca trong tháng 5 là: 2400000 : 600000 = 4 ( ngày)
Bài 4. (1 điểm)
Một hộ gia đình có ý định mua một cái máy bơm để phục vụ cho việc tưới tiêu. Khi đến cửa hàng
thì được nhân viên giới thiệu 2 loại máy bơm có lưu lượng nước trong một giờ và chất lượng máy
là như nhau. Giá bán và hao phí điện năng của mỗi máy như sau : Trang 13
Máy thứ nhất : giá 3 triệu và trong một giờ tiêu thụ hết 1,5 kWh.
a) Máy thứ hai : giá 2 triệu và trong một giờ tiêu thụ hết 2 kWh. Biết giá 1 kWh là 2 000 đồng và một
Gọi y là tổng chi phí (bao gồm tiền mua máy bơm và tiền điện phải trả) khi mua mỗi loại máy bơm
và sử dụng trong x giờ. Hãy lập công thức biểu diễn y theo x của từng loại máy bơm.
b) Nếu người nông dân chỉ sử dụng trong hai năm và mỗi ngày chỉ sử dụng 3 giờ thì nên
chọn mua loại máy nào có lợi hơn. Lời giải
a) Công thức biểu diễn y theo x của từng loại máy bơm
- Máy bơm I : y = 3000000 +1,5x 1500 = 3000000 + 2250x (đồng)
- Máy bơm II : y = 2000000 + 2x 1500 = 2000000 + 3000x (đồng) b) Số giờ sử dụng: 23653 = 2190 (giờ)
Thay x = 2190 , ta có: - Số tiền
phải trả nếu sử dụng máy bơm I là:
y = 3000000 + 2250 2190 = 7927500 (đồng) - Số tiền
phải trả nếu sử dụng máy bơm II là:
y = 2000000 + 3000 2190 = 8570000 (đồng)
Vậy nên sử dụng máy I có lợi hơn.
Bài 5. (1 điểm)
Một năm bình thường sẽ có 12 tháng và 365 ngày. Khi một năm có số ngày hoặc số tháng tăng lên
(theo Dương lịch hoặc Âm lịch) thì sẽ được gọi là năm nhuận, trong đó có những ngày nhuận và
tháng nhuận. Năm nhuận là năm có ngày 29 tháng 2 Dương lịch (không nhuận là 28 ngày). Cách
tính năm nhuận theo dương lịch là những năm dương lịch nào chia cho 4 thì đó sẽ là năm nhuận.
Ví dụ: 2016 chia hết cho 4 nên năm 2016 là năm nhuận.
Ngoài ra, đối với những tròn thế kỷ (những năm có hai số cuối là số 0 ) thì chúng ta sẽ lấy số năm
đem chia cho 400 , nếu như chia hết thì đó sẽ là năm nhuận.
Ví dụ: 1600 và 2000 là các năm nhuận nhưng 1700 ,1800 và 1900 không phải năm nhuận.
a) Em hãy dùng quy tắc trên để xác định năm 2022 , năm 2024 có phải là năm nhuận dương lịch không? Trang 14
b) Biết rằng ngày 30 / 04 / 2022 là rơi vào thứ bảy. Hỏi ngày 30 / 04 / 1975 là rơi vào thứ mấy? Em hãy giải thích. Lời giải
a) 2022 4 nên năm 2022 không là năm nhuận
2022 4 nên năm 2022 là năm nhuận
b) Số năm nhuận là: (2020 −1976) : 4 +1 = 12 (năm)
Từ 30 / 04 / 1975 đến 30 / 04 / 2022 có số năm là (2022 −1975) +1 = 48 (năm)
Số ngày từ 30 / 04 / 1975 đến 30 / 04 / 2022 là: (48.365 + 12. ) 1 + 1 = 17533 (ngày) 17533 chia 7 dư 3
Vì 30 / 04 / 2022 là rơi vào thứ bảy nên ngày 30 / 04 / 1975 trước ba ngày kể từ ngày thứ Bảy và là ngày Thứ Tư.
Bài 6. (1 điểm)
Trong kì thi HK2 môn Toán lớp 9, một phòng thi có 24 thí sinh dự thi. Các thí sinh đều phải làm
bài trên giấy thi của trường phát cho. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng
số tờ giấy thi là 49 tờ. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu
thí sinh làm bài 3 tờ giấy thi? Biết rằng có 5 thí sinh chỉ làm 1 tờ giấy thi, và không có thí sinh nào làm trên 3 tờ giấy thi Lời giải
Vì phòng thi 24 thí sinh có 5 thí sinh chỉ làm 1 tờ giấy thi và không có thí sinh nào làm trên 3 tờ
giấy thi nên tổng số thí sinh làm 2 tờ hoặc 3 tờ giấy thi là 24 − 5 = 19 thí sinh và tổng số tờ là 49 − 5 = 44
Gọi x , y (thí sinh) lần lượt là số thí sinh làm 2 tờ hoặc 3 tờ giấy thi.
(Điều kiện: 0 x, y 19 ) x + y = 19 x = 13
Theo đề bài ta có hệ phương trình: Giải hệ ta được: (Thảo mãn điều kiện) 2x + 3y = 44 y = 6
Vậy có 13 thí sinh làm 2 tờ và 6 thí sinh làm 3 tờ.
Bài 7. (0,75 điểm)
Người ta thiết kế một hồ bơi có dạng là một lăng trụ đứng tứ giác với đáy là hình thang vuông (mặt
số (1)) của hồ bơi, cùng các kích thước như đã cho (xem hình vẽ). Biết rằng người ta dùng một máy bơm với lưu lượng là 3
6m / phút và sẽ bơm đầy hồ mất 35 phút. Em hãy tính chiều dài của hồ. Trang 15 Lời giải 2,5m 0,5m 3m
Ghép thêm vào lăng trụ tứ giác một lăng trụ đứng có đáy là tam giác vuông (như hình vẽ) sao cho
tạo thành một hình hộp chữ nhật.
Gọi x là độ dài cạnh còn lại của hình hộp chữ nhật đó. Ta có: V = x = x ( 3 6.3. 18 m hhcn ) V = = ( 3 6.35 210 m hoboi ) 1 V = 2,5. . x 6. = 3.2,5.x m langtrudungtamgiac ( 3) 2 Khi đó V = V −V
18x − 3.2,5x = 210 hoboi hhcn langtrudungtamgiac x = 20(m) 2 2
Chiều dài của hồ là: 2,5 + 20 20,16(m)
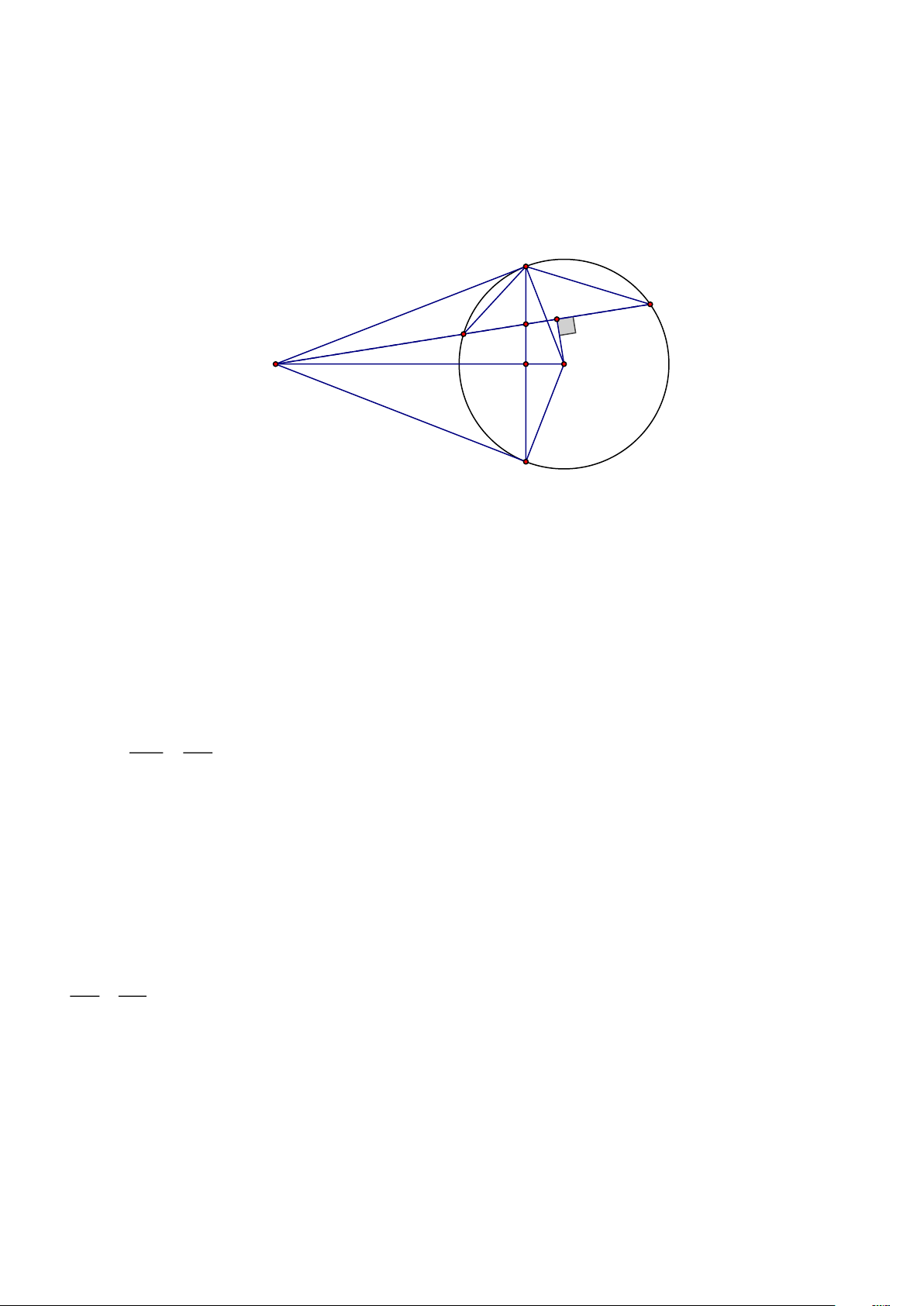
Bài 8. (3 điểm) Từ điểm A ở ngoài đường tròn tâm O , vẽ hai tiếp tuyến AB, AC với (O) (B , C là
hai tiếp điểm). Vẽ cát tuyến AMN với (O) sao cho AM AN và tia AM nằm giữa tia OA và tia
OC . Gọi E là trung điểm của MN . 2
a) Chứng minh tứ giác ABOE nội tiếp, và AB = AM .AN
b) Đoạn thẳng BC cắt OA và MN lần lượt tại H và K .
Chứng minh: OA vuông góc với BC tại H và AE.AK = AM .AN . Trang 16
c) Cho biết OA = 2R . Trên đoạn thẳng BC lấy một điểm F bất kì, qua F vẽ đường thẳng vuông
góc với OF tại F cắt AB và AC tại P và Q . Chứng minh góc POQ luôn không đổi khi F di
chuyển trên đoạn BC . Lời giải C N E K M A H O B
a) Xét (O) có AB là tiếp tuyến tại B .Suy ra ABO = 90 . Lại có EM = EN nên OE ⊥ MN hay AEO = 90
Xét tứ giác ABOE có ABO + AEO = 90 + 90 = 180 . Suy ra tứ giác ABOE nội tiếp đường tròn đường kính AO .
Xét AMC và ACN có : AMC góc chung ;
ANC = ACM ( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung MC ÁÃÃÃÂ)
AMC ∽ AC N (g-g) AM AC Suy ra: 2 =
AC = AM.AN ( ) 1 AC AN AB, AC 2
là hai tiếp tuyến cắt nhau tại A . Suy ra AB = AC hay AB = AM .AN
b) Vì AB = AC ; OB = OC = R nên OA là trung trực của BC OA ⊥ BC tại H
Xét ACO vuông tại C có CH ⊥ 2
OA AC = AH.AO (2)( hệ thức lượng trong tam giác vuông).
Xét AHK và AEO có
AHK = AEO = 90 EOA góc chung
AMC ∽ AC N (g-g) AH AK =
AK.AE = AH.AO (3) AE AO Từ ( )
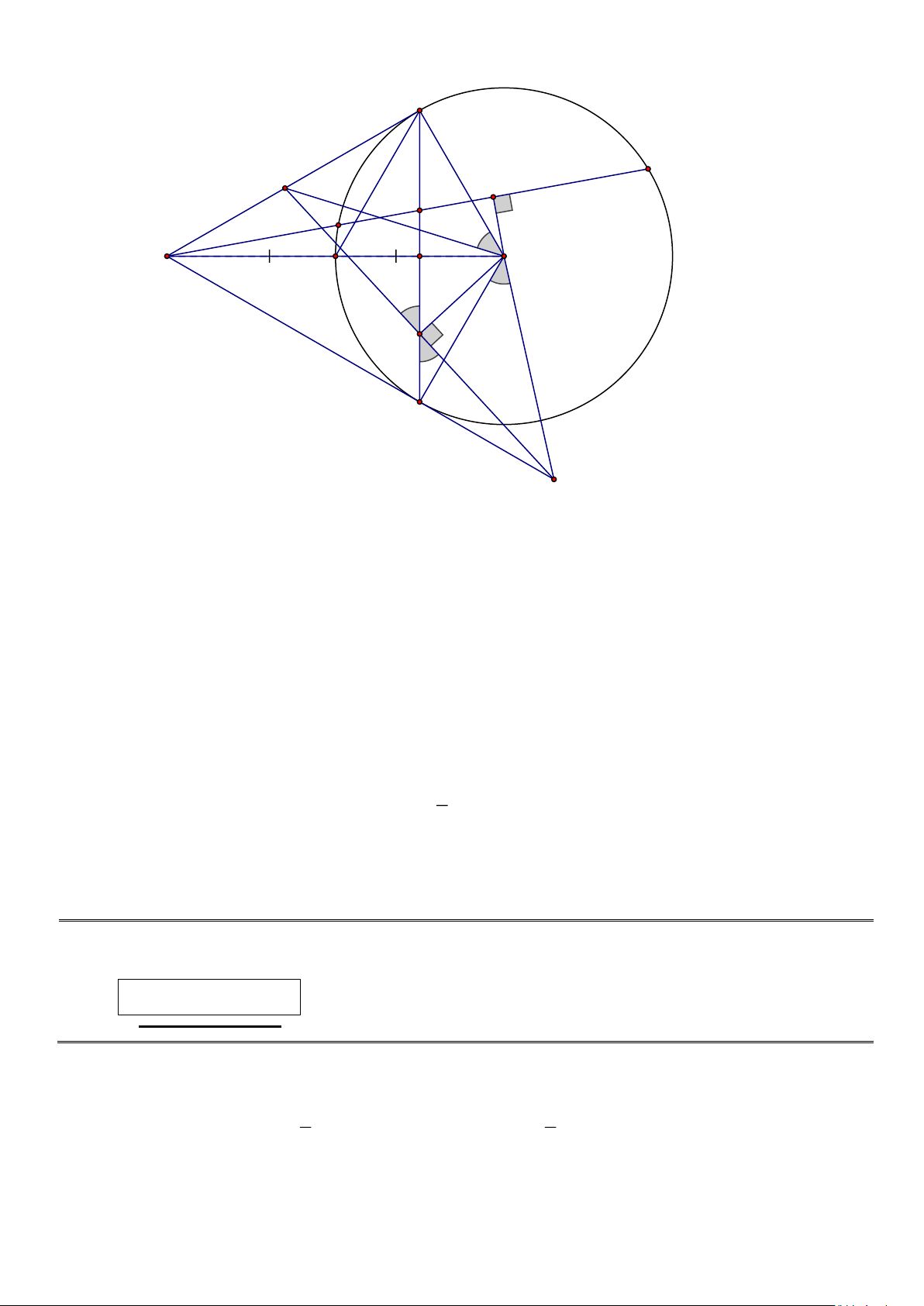
1 ,(2),(3) ta có AK.AE = AM .AN . Trang 17 C N Q E K M A I O H F B P c)
Xét tứ giác OFQC có OFC + OQC = 90 + 90 = 180 . Suy ra tứ giác OFQC nội tiếp đường tròn.
COQ = CFQ (*) hai góc nội tiếp cùng chắn cung CQ .
Xét tứ giác OFBP có OFP = OBP = 90 . Hai điểm B, F cùng nhìn đoạn OP dưới 1 góc bằng nhau
90 . Suy ra tứ giác OFBP nội tiếp đường tròn đường kính OP .
Suy ra BFP = BOQ (**) hai góc nội tiếp cùng chắn cung BP .
Mà CFQ = BFP (***) (đối đỉnh).
Từ (*), (**), (***) ta có: CFQ = BOP
COQ + QOB = QOB + BOP COB = QOP
Xét (O) có AB , AC là hai tiếp tuyến tại B và C COA = AOB . 1
Vì OA = 2R . Xét ACO vuông tại C , có CI =
AO = R ( trung tuyến thuộc cạnh huyền) C OI 2
đều ( OI = CI = OC = R ) . Suy ra COI = 0
6 hay COA = AOB = 90 COB = 120 COB = POQ = 120 .
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT HUYỆN NHÀ BÈ
NAÊM HOÏC: 2023 - 2024 PHUÙ MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: Huyện Nhà Bè - 3
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm). 1 3
a) Vẽ đồ thị (P) : y = 2
x và đường thẳng (d) : y = − x + 2 trên cùng hệ trục tọa độ. 2 2
b) Tìm tọa độ giao điểm của (P) và (d) ở câu trên bằng phép tính. Trang 18
Câu 2. (1 điểm). Cho phương trình 2
2x − x − 6 = 0 có 2 nghiệm là x , x . Không giải phương 1 2 2
trình, hãy tính giá trị của biểu thức (x − x 1 2 )
Câu 3. (1 điểm). Nhân dịp khai trương, cửa hàng chị Hương đã quyết định giảm giá 20% cho một
quyển tập và nếu khách hàng mua 10 quyển tập trở lên thì từ quyển thứ 11 trở đi, khách
hàng chỉ phải trả 90% giá đã giảm. Biết rằng ban đầu giá một quyển tập là 8 000 đồng.
a) Mẹ bạn An đặt mua cho hai chị em bạn An 60 quyển tập. Tính số tiền mẹ bạn An phải trả.
b) Một khách hàng đã mua tập ở cửa hàng chị Hương và tổng số tiền mà vị khách này phải
trả là 928 000 đồng. Hỏi khách hàng này đã mua bao nhiêu quyển tập?
Câu 4. (1 điểm). Hai bạn Thanh và Liên đi cùng trên một con đường. Lúc đầu hai bạn ở cùng một
phía đối với trạm xe bus và cách trạm xe bus lần lượt là 200m và 500m ; hai bạn cùng đi
ngược hướng với trạm xe bus . Trung bình mỗi giờ Thanh đi được 3km và Liên đi được
1km . Gọi d là khoảng cách của Thanh, Liên với trạm xe bus sau khi đi được t giờ.
a) Lập hàm số của d theo t đối với mỗi bạn
b) Sau bao lâu thì hai bạn gặp nhau?
Câu 5. (0,75 điểm). Vào dịp liên hoan cuối năm gia đình bạn Phương dự định mua một số bánh
pizza để dùng. Biết bánh pizza cỡ 7 inch có giá 99 000 đồng và cỡ 9 inch có giá 189 000
đồng (chất lượng và bề dày của hai cỡ bánh là như nhau). Em hãy tính xem mua bánh cỡ
nào sẽ có lợi hơn?
Câu 6. (1 điểm). “Vàng 24K còn được gọi là vàng ròng (là loại vàng tinh khiết nhất, gần như
không có pha lẫn tạp chất, có giá trị cao nhất trong các loại vàng) là một kim loại có ánh
kim đậm nhất nhưng khá mềm. Trong ngành công nghệ chế tạo trang sức, người ta ít dùng
vàng 24K mà thay thế bằng vàng 14K là hợp kim của vàng và đồng để dễ đánh bóng và
tạo ra nhiều kiểu dáng đa dạng”. Một món trang sức được làm từ vàng 14K có thể tích 3
10cm và nặng 151,8g . Hãy tính thể tích vàng nguyên chất và đồng được dùng để làm ra
món trang sức; biết khối lượng riêng của vàng nguyên chất là 3
19, 3g / cm , khối lượng riêng của đồng là 3
9g / cm và công thức liên hệ giữa khối lượng riêng và thể tích là m = . D V . Trang 19
Câu 7. (1 điểm). Vào khoảng năm 200 trước Công Nguyên, Ơratôxten, một nhà toán học và thiên
văn học Hi Lạp, đã ước lượng được "chu vi" của Trái Đất (chu vi đường Xích Đạo) nhờ hai quan sát sau:
1) Một ngày trong năm, ông ta để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố
Xy-en (nay gọi là At-xu-an), tức là tia sáng chiếu thẳng đứng
2) Cùng lúc đó ở thành phố A-lếch-xăng-đria cách Xy-en 800km , một tháp cao 25m có
bóng trên mặt đất dài 3,1m . Từ hai quan sát trên, em hãy tính xấp xỉ "chu vi" của Trái
Đất. (Trên hình điểm S tượng trưng cho thành phố Xy-en, điểm A tượng trưng cho
thành phố A-lếch-xăng-đri-a, bóng của tháp trên mặt đất được coi là đoạn thẳng AB )
Câu 8. (3 điểm) Từ điểm A nằm ngoài đường tròn (O; R) , vẽ hai tiếp tuyến AM, AN ( M, N là
hai tiếp điểm) và cát tuyến ABC ( B nằm giữa A và C , tia AC nằm giữa hai tia AO, AN ).
Gọi I là trung điểm BC .
a) Chứng minh năm điểm A, M, N , O, I cùng thuộc một đường tròn. BC KC
b) MN cắt BC tại K . Chứng minh K .
B KC = KM.KN và = 2 . BA KA
c) MN cắt OA tại H . Gọi S là trung điểm của AH ; MS cắt đường tròn (O) tại E . Vẽ
đường kính MF của đường tròn (O) . Chứng minh F, H, E thẳng hàng. Trang 20




