










Preview text:
SỞ GD & ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH LỚP 10
PHÒNG GD & ĐT QUẬN GÒ VẤP MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận. ĐỀ THAM KHẢO
Thời gian: 120 phút (không kể thời gian phát đề)
MÃ ĐỀ: Quận Gò Vấp - 1 1
Câu 1. (1,5 điểm). Cho (P) − : y = 2
x và đường thẳng (d) − y = 3 : x . 4 4
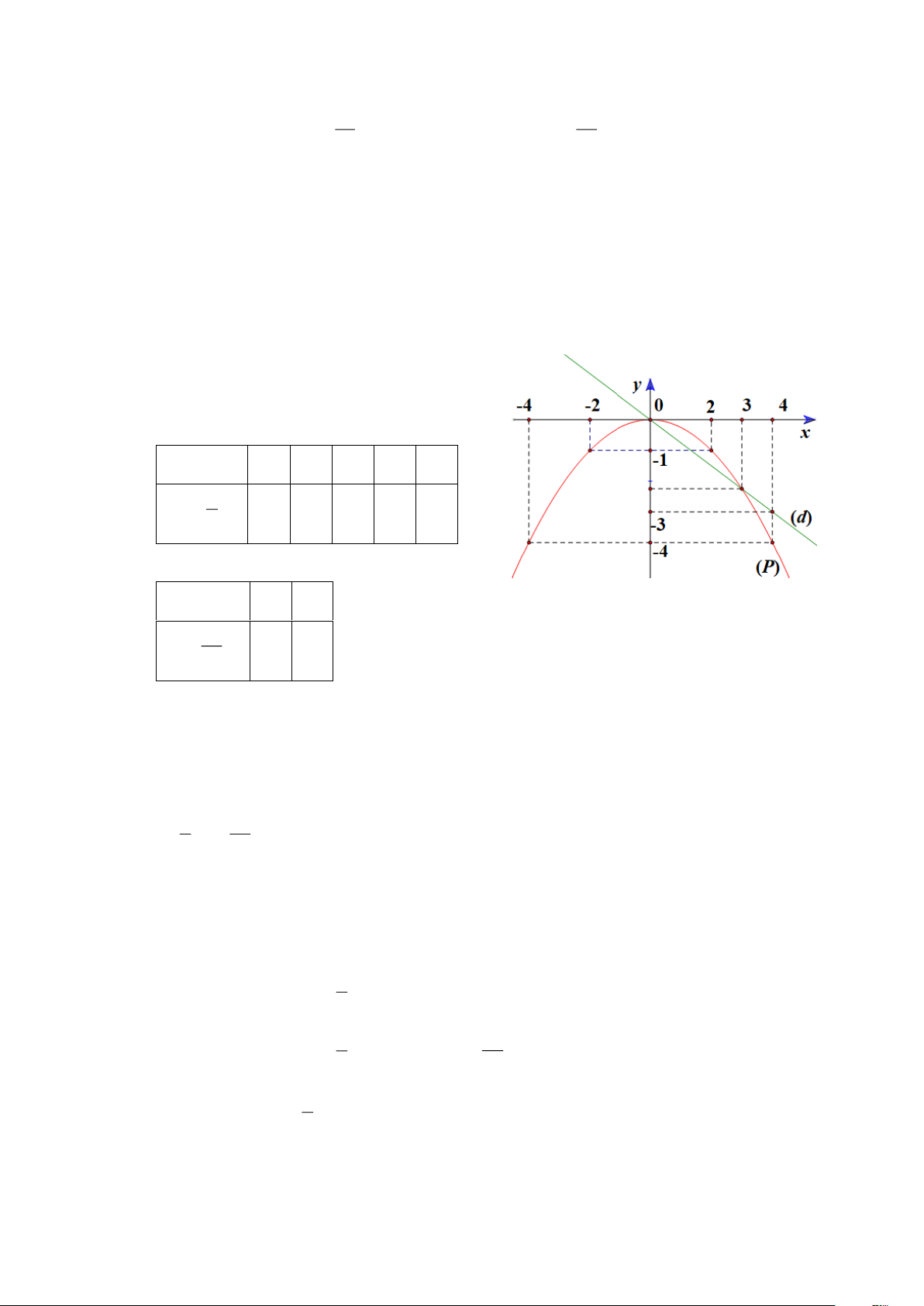
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
3x − 5x − 4 = 0 . Không giải phương trình. 2 2
Tính giá trị của biểu thức A =
x (3x − 2023) + x (3x − 2023 1 2 2 1 ) 3 3
Câu 3. (1 điểm). Bến xe Miền Đông mới được thiết kế theo mô hình Transit Oriented Development
(viết tắt là TOD) – là mô hình định hướng phát triển giao thông công cộng làm cơ sở quy
hoạch phát triển của đô thị, lấy giao thông làm điểm tập trung dân cư để từ đó hình thành
hệ thống giao thông phân tán, mô hình này rất phát triển
trên thế giới. Một xe ô tô chở khách đi từ bến xe Miền
Đông mới hướng về Miền Trung; quãng đường đi được
của xe cách Trung tâm Thành phố Hồ Chí Minh là (s) và
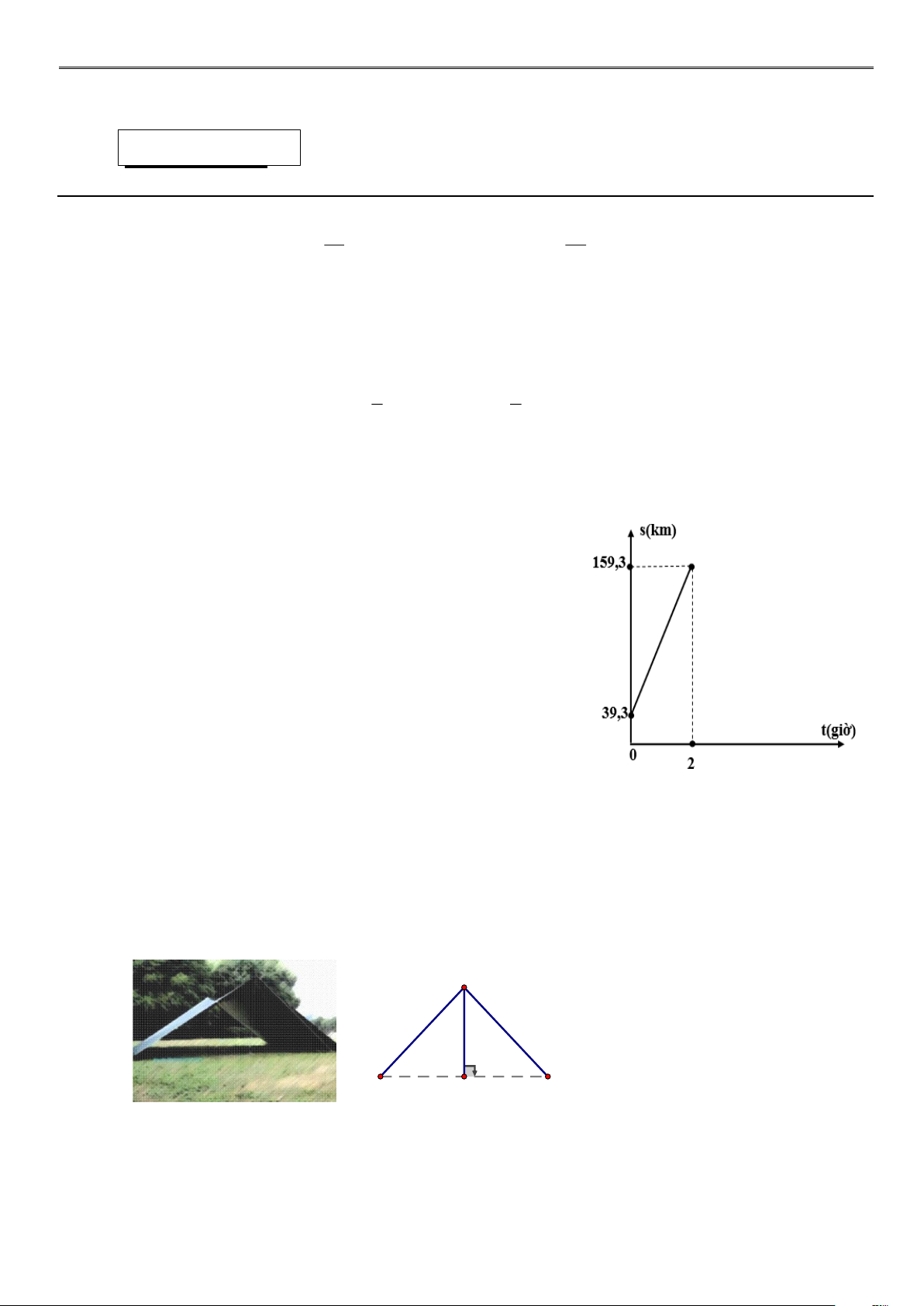
thời gian xe chạy (t ) được cho bởi hàm số bậc nhất
s = at + b và có đồ thị như sau:
(Lưu ý: Học sinh không cần vẽ hình)
a) Xác định các hệ số a và b của hàm số trên.
b) Sau 4 giờ, xe đã cách trung tâm Thành phố Hồ Chí Minh bao nhiêu km; biết xe có ghé
nghỉ ngơi tại trạm dừng chân 45 phút
Câu 4. (0,75 điểm). Cuối tuần, một nhóm bạn muốn đi thư giãn bằng cách cắm trại ngoài trời. Để
che nắng che mưa trong lúc cắm trại, các bạn quyết định dựng lều chữ A . Theo tính toán
của nhóm, các bạn có sẵn hai cây cọc có chiều cao 2m . Nhóm có tấm bạt dài 6m thì có thể
dựng lều chữ A với góc tạo bởi tấm bạt và mặt đất là bao nhiêu độ? A 2m B H C
Câu 5. (1 điểm). Một người đi siêu thị mua hai món hàng. Món thứ nhất có giá niêm yết là 4 triệu.
Nhưng đúng vào đợt khuyến mãi nên món hàng thứ nhất được giảm 10% , còn món hàng
thứ hai được giảm 8% nên người đó phải trả 6,36 triệu đồng. Hỏi giá niêm yết của món
hàng thứ hai là bao nhiêu? Trang 1
Câu 6. (1 điểm). Một quán trà sữa có chương trình khuyến mãi mua 4 tặng 1 với mặt hang trà sữa giá 30000 đồng /ly
Trong một ngày, số lượng người mua trà sữa được thống kê lại qua bảng sau: Số ly Số người 1 ly 15 2 ly 20 3 ly 10 4 ly 20 5 ly 10 6 ly 5
a) Tính số ly trà sữa mà quán đã làm cho khách hàng?
b) Nếu giá vốn để làm một ly trà sữa là 25000 đồng, thuế phải nộp là 10% trên tổng số tiền
bán thì ngày hôm đó quán có lời hay không? Và lời bao nhiêu tiền?
Câu 7. (1 điểm). Trò Chơi XÂY THÁP WOODY TOWER WD012 bao
gồm 48 thanh 6 màu được làm từ chất liệu gỗ, có thể chơi một hoặc
nhiều người, mỗi lượt người chơi rút ra một thanh gỗ từ tòa tháp và
đặt thanh gỗ rút ra đó lên trên đỉnh mà không làm đổ tháp. Trò chơi
tiếp tục như vậy, với mỗi lượt của từng người chơi cho đến khi tháp
đổ. Mỗi thanh là một hình hộp chữ nhật có kích thước 1,5cm x 2cm x
7,5cm ; được đựng vào một hộp có kích thước 8cm x 8cm x 27cm .
a) Tính thể tích của hộp đựng 48 thanh gỗ?
b) Hỏi thể tích các thanh gỗ màu đỏ và tím trong hộp chiếm bao nhiêu phần trăm thể tích
hộp (Các kết quả làm tròn đến chữ số thập phân thứ hai sau dấu phẩy)
Câu 8. (3 điểm) Cho đường tròn (O) và điểm A nằm ngoài (O) . Từ A vẽ hai tiếp tuyến AB, AC
của (O) ( B,C là hai tiếp điểm). Gọi H là giao điểm của AO và BC . Qua A vẽ cát tuyến
ADE của đường tròn (O) (D, E thuộc (O)) sao cho đường thẳng AE cắt đoạn thẳng HB tại
I . Gọi M là trung điểm dây cung DE . a) Chứng minh: 5 điểm ,
A B,O, M ,C cùng thuộc một đường tròn; suy ra MA là tia phân giác góc BMC .
b) Chứng minh: tứ giác OHDE nội tiếp.
c) Trên tia đối của tia HD lấy điểm F sao cho H là trung điểm DF . Tia AO cắt đường
thẳng EF tại K . Chứng minh: IK / / DF . ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI 1
Câu 1. (1,5 điểm). Cho (P) − : y = 2
x và đường thẳng (d) − y = 3 : x . 4 4
a. Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b. Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. BGT: x −4 −2 0 2 4 y = − 1 2 x −4 1 − 0 1 − −4 4 x 0 4 − y = 3 x 0 −3 4
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : 1 − − 2 x = 3 x 4 4 2 x − 3x = 0 x = 0 x = 3 1
Thay x = 0 vào y = − 2
x , ta được: y = 0 . 4 1 −
Thay x = 3 vào y = − 2
x , ta được: y = 9 . 4 4 9 Vậy (0;0 ) , 3; −
là hai giao điểm cần tìm. 4
Câu 2. (1 điểm). Cho phương trình 2
3x − 5x − 4 = 0 . Không giải phương trình. Trang 3 2 2
Tính giá trị của biểu thức A =
x (3x − 2023) + x (3x − 2023 1 2 2 1 ) 3 3 Lời giải Vì .
a c = 3.(−4) = −12 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 − = + = b S x x = 5 1 2
Theo định lí Vi-et, ta có: a 3 = c P x .x = = − 4 1 2 a 3 2 2
Ta có: A = x (3x − 2023) + x (3x − 2023 1 2 2 1 ) 3 3
A = x x − 4046 x + x x − 4046 2 2 x 1 2 1 1 2 2 3 3 A = x x − 4046 4 x x 1 2 ( + 1 2 ) 3 −4 4046 5 − A = − = 20278 4. 3 3 3 9
Câu 3. (1 điểm). Bến xe Miền Đông mới được thiết kế theo mô hình Transit Oriented
Development (viết tắt là TOD) – là mô hình định hướng
phát triển giao thông công cộng làm cơ sở quy hoạch
phát triển của đô thị, lấy giao thông làm điểm tập trung
dân cư để từ đó hình thành hệ thống giao thông phân
tán, mô hình này rất phát triển trên thế giới. Một xe ô tô
chở khách đi từ bến xe Miền Đông mới hướng về Miền
Trung; quãng đường đi được của xe cách Trung tâm
Thành phố Hồ Chí Minh là (s) và thời gian xe chạy
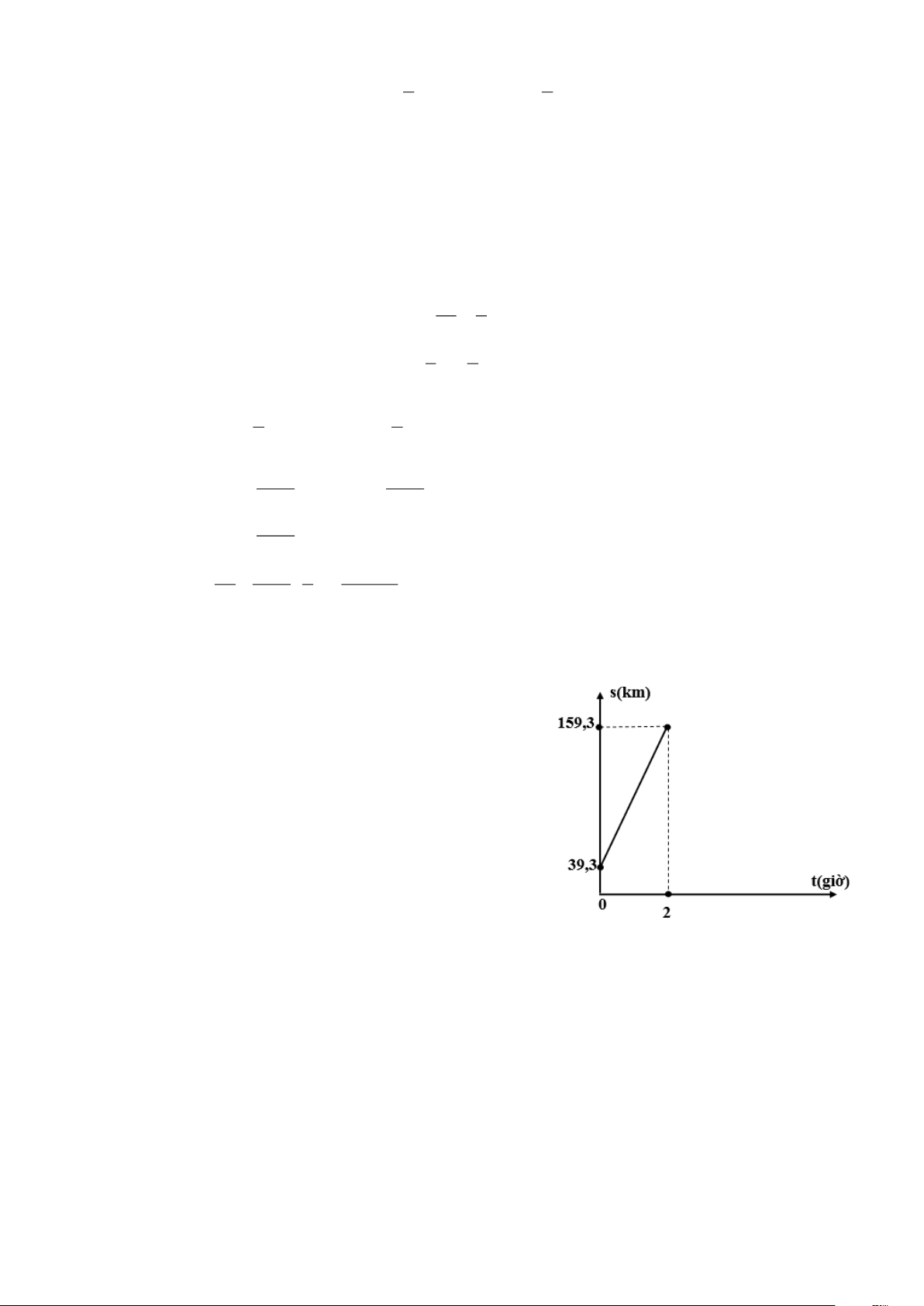
(t) được cho bởi hàm số bậc nhất s = at +b và có đồ thị như sau:
(Lưu ý: Học sinh không cần vẽ hình)
a) Xác định các hệ số a và b của hàm số trên
b) Sau 4 giờ, xe đã cách trung tâm Thành phố Hồ Chí Minh bao nhiêu km; biết xe có ghé
nghỉ ngơi tại trạm dừng chân 45 phút Lời giải
a) Xác định các hệ số a và b của hàm số trên. Trang 4 Theo đề bài, ta có: t = 0 Với 39,3 = 0.a + . ( ) 1 s = b 39,3 t = 2 Với
159,3 = 2.a + . (2) s = b 159,3 0a + b = 39,3 a = 60 Từ ( )
1 và (2) ta có hệ phương trình: . 2a + b = 159,3 b = 39,3
Vậy: a = 60 , b = 39,3 và s = 60t + 39,3 .
b) Sau 4 giờ, xe đã cách trung tâm Thành phố Hồ Chí Minh bao nhiêu km; biết xe có ghé
nghỉ ngơi tại trạm dừng chân 45 phút 45 3 13
Thời gian xe chạy là: 4 − = 4 − = (h) 60 4 4 13 Thế t =
(h) vào hàm số s = 60t + 39,3 , ta được: 4 13 s = 60. + 39,3 = 234,3(km) 4
Vậy xe đã cách trung tâm Thành phố Hồ Chí Minh 234,3(km)
Câu 4. (0,75 điểm). Cuối tuần một nhóm bạn muốn đi thư giãn bằng cách cắm trại ngoài trời.
Để che nắng che mưa trong lúc cắm trại, các bạn quyết định dựng lều chữ A . Theo tính
toán của nhóm, các bạn có sẵn hai cây cọc có chiều cao 2m . Nhóm có tấm bạt dài 6m thì
có thể dựng lều chữ A với góc tạo bởi tấm bạt và mặt đất là bao nhiêu độ? A 2m B H C Lời giải
AB = AC = 6: 2 = 3(m)
Ta có: ABC cân tai A HB = HC
Xét ABH vuông ở H , ta có: AH 2 sin ABH = = ABH 42 AB 3 Trang 5
Vậy góc tạo bởi tấm bạt và mặt đất là 42
Câu 5. (1 điểm) Một người đi siêu thị mua hai món hàng. Món thứ nhất có giá niêm yết là 4
triệu. Nhưng đúng vào đợt khuyến mãi nên món hàng thứ nhất được giảm 10% , còn
món hàng thứ hai được giảm 8% nên người đó phải trả 6,36 triệu đồng. Hỏi giá niêm yết
của món hàng thứ hai là bao nhiêu? Lời giải
Giá tiền của món hàng thứ nhất sau khi được giảm giá là: 4.90% = 3, 6 (triệu đồng)
Giá tiền của món hang thứ hai sau khi được giảm giá là: 6,36 − 3, 6 = 2, 76 (triệu đồng)
Giá niêm yết của món hàng thứ hai là: 2, 76 : 92% = 3 (triệu đồng)
Câu 6. (1 điểm) Một quán trà sữa có chương trình khuyến mãi mua 4 tặng 1 với mặt hàng trà sữa giá 30000 đồng /ly
Trong một ngày, số lượng người mua trà sữa được thống kê lại qua bảng sau: Số ly Số người 1 ly 15 2 ly 20 3 ly 10 4 ly 20 5 ly 10 6 ly 5
a) Tính số ly trà sữa mà quán đã làm cho khách hàng?
b) Nếu giá vốn để làm một ly trà sữa là 25000 đồng, thuế phải nộp là 10% trên tổng số tiền
bán thì ngày hôm đó quán có lời hay không? Và lời bao nhiêu tiền? Lời giải
a) Tính số ly trà sữa mà quán đã làm cho khách hàng?
Tổng số ly trà sữa quán đã làm cho khách là: 1.15 + 2.20 + 3.10 + 4.20 + 5.10 + 6.5 = 245(ly)
b) Nếu giá vốn để làm một ly trà sữa là 25000 đồng, thuế phải nộp là 10% trên tổng số tiền
bán thì ngày hôm đó quán có lời hay không? Và lời bao nhiêu tiền?
Khách hàng được khuyến mãi mua 4 tặng 1 thì số tiền phải trả cho 5 ly trà sữa là: 30000.4 = 120000 (đồng) Trang 6 245
Số tiền cửa hàng thu về ngày hôm đó là: 120000. = 5880000 (đồng) 5
Số tiền cửa hàng đóng thuế và tiền vốn của ngày hôm đó là:
5880000.10% + 25000.245 = 6713000 (đồng)
Vậy ngày hôm đó quán bị lỗ
Câu 7. (1 điểm) Trò Chơi XÂY THÁP WOODY TOWER WD012 bao
gồm 48 thanh 6 màu được làm từ chất liệu gỗ, có thể chơi một
hoặc nhiều người, mỗi lượt người chơi rút ra một thanh gỗ từ tòa
tháp và đặt thanh gỗ rút ra đó lên trên đỉnh mà không làm đổ
tháp. Trò chơi tiếp tục như vậy, với mỗi lượt của từng người chơi
cho đến khi tháp đổ. Mỗi thanh là một hình hộp chữ nhật có kích
thước 1,5cm x 2cm x 7,5cm ; được đựng vào một hộp có kích
thước 8cm x 8cm x 27cm .
c) Tính thể tích của hộp đựng 48 thanh gỗ?
d) Hỏi thể tích các thanh gỗ màu đỏ và tím trong hộp chiếm bao nhiêu phần trăm thể
tích hộp (Các kết quả làm tròn đến chữ số thập phân thứ hai sau dấu phẩy) Lời giải
a) Tính thể tích của hộp đựng 48 thanh gỗ?
Thể tích của hộp đựng 48 thanh gỗ là: = ( 3 8.8.27 1728 cm )
b) Hỏi thể tích các thanh gỗ màu đỏ và tím trong hộp chiếm bao nhiêu phần trăm thể
tích hộp (Các kết quả làm tròn đến chữ số thập phân thứ hai sau dấu phẩy)
Thể tích một thanh gỗ là: = ( 3 1,5.2.7,5 22,5 cm )
Tổng thể tích các khối gỗ màu đỏ và tím có trong hộp là: = ( 3
(48 : 6).2.22,5 360 cm ) 360
Vậy thể tích các thanh gỗ màu đỏ và tím trong hộp chiếm .100 20,83% thể tích 1728 hộp
Câu 8. (3 điểm) Cho đường tròn (O) và điểm A nằm ngoài (O) . Từ A vẽ hai tiếp tuyến AB, AC
của (O) ( B,C là hai tiếp điểm). Gọi H là giao điểm của AO và BC . Qua A vẽ cát tuyến Trang 7
ADE của đường tròn (O) (D, E thuộc (O)) sao cho đường thẳng AE cắt đoạn thẳng HB
tại I . Gọi M là trung điểm dây cung DE a) Chứng minh: 5 điểm ,
A B,O, M ,C cùng thuộc một đường tròn; suy ra MA là tia phân giác góc BMC (1đ)
b) Chứng minh: tứ giác OHDE nội tiếp (1đ)
c) Trên tia đối của tia HD lấy điểm F sao cho H là trung điểm DF . Tia AO cắt đường
thẳng EF tại K . Chứng minh: IK / /DF (1đ) Lời giải B E M I D K A O H F C a) Chứng minh: 5 điểm ,
A B,O, M ,C cùng thuộc một đường tròn; suy ra MA là tia phân giác góc BMC (1đ)
Ta có: M là trung điểm dây cung DE(gt)
OM ⊥ DE (quan hệ đường kính dây cung)
OMA = OBA = OCA = 90 ,
A B,O, M ,C cùng thuộc một đường tròn đường kính OA
Xét đường tròn đường kính OA , ta có:
Dây cung AB = dây cung AC (tính chất 2 tiếp tuyến cắt nhau tại ) A AB = AC
BMA = CMA ( 2 góc nội tiếp chắn AB = AC)
MA là tia phân giác góc BMC
b) Chứng minh: tứ giác OHDE nội tiếp (1đ) Ta có: Trang 8
AB = AC(cmt) O
A = OC = R
OA là trung trực BC
OA ⊥ BC ở H
Xét OBA vuông tại B có AH là đường cao: 2
AB = AH.AO(htl)( ) 1
Xét ABD & AEB có:
BAD = EAB (góc chung)
ABD = AEB (góc tạo bởi tiếp tuyến và dây cung với góc nội tiếp cùng chắn BD ) A
BD ∽ A EB( gg) AB AD 2 =
AB = AE.AD(2) AE AB AH AD Từ ( )
1 & (2) AH.AO = AE.AD = AE AO Xét AHD & AEO có:
HAD = EAO(chung) AH AD = (cmt) AE AO
AHD ∽ AEO (cgc)
AHD = AEO (3)
Xét tứ giác OHDE ta có: AHD = AEO (cmt )
tứ giác OHDE nội tiếp (góc ngoài = góc trong đối diện)
c) Chứng minh: IK / /DF (1đ)
Xét ODE ta có: OD = OE = R ODE
cân tại O ODE = OED (4)
Do tứ giác OHDE nội tiếp nên ODE = OHE (5)
Từ (3),(4),(5) AHD = OHE
Mà AHD = FHK (đối đỉnh) Nên OHE = FHK KF HF
HK là phân giác của EHF =
(tính chất đường phân giác trong EHF ) KE HE
Mà HF = HD (do H là trung điểm DF ) Trang 9 KF HD Nên = (6) KE HE Ta có:
AHD = OHE (cmt)
AHD+IHD = BHD =90
OHE + IHE = BHO = 90 IHD = IHE ID HD
HI là phân giác của EHD =
(7) (tính chất đường phân giác trong EHD ) IE HE KF ID Từ (6),(7) = KE IE KF ID Xét EFD ta có: =
(cmt) IK / /DF (định lý Talet đảo) KE IE ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN Gò vấp
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ THAM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận Gò Vấp
Thời gian: 120 phút (không kể thời gian phát đề) - 2
Câu 1. (1,5 điểm): Cho parabol (P) y = 2 :
x và đường thẳng (d) : y = −x + 2
a) Vẽ (P) và (d) trên cùng hệ trục toạ độ.
b) Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm) Cho phương trình 2
3x + 5x − 1 = 0 có hai nghiệm x ; x . Không giải phương trình 1 2
hãy tính giá trị của biểu thức A = (3x − 2x )(3x − 2x ) − 2023 . 1 2 2 1
Câu 3. (0,75 điểm) Để ước tính chiều cao tối đa của trẻ em khi đạt đến độ trưởng thành, hoàn toàn
có thể dựa vào chiều cao của bố mẹ. Cách tính chiều cao của con theo bố mẹ được các
chuyên gia đánh giá cao bởi thực tế, sự di truyền các thế hệ có ảnh hưởng nhất định đến
chiều cao của trẻ. Ta có công thức tính như sau: C = (B + M + 13A) : 2 .
Trong đó: C là chiều cao của người con (cm)
B là chiều cao của người bố (cm)
M là chiều cao của người mẹ (cm)
A = 1 khi người con có giới tính là Nam
A = −1 khi người con có giới tính là Nữ Trang 10
a) Em hãy dùng công thức trên để tìm chiều cao tối đa của bạn Nam (giới tính là nam) biết
Ba của bạn Nam có chiều cao là 175 cm và Mẹ của bạn Nam có chiều cao là 168 cm .
b) Bạn Hương (giới tính là nữ) có chiều cao là 164 cm . Em hãy tính xem chiều cao tối đa của
Mẹ bạn Hương khi biết chiều cao của Ba bạn Hương là 180 cm .
Câu 4. (1,0 điểm) Một hãng hàng không quy định xử phạt hành lý kí gửi vượt quá quy định miễn
phí (hành lý quá cước). Cứ vượt quá x(kg) hành lý thì khách hàng phải trả tiền phạt
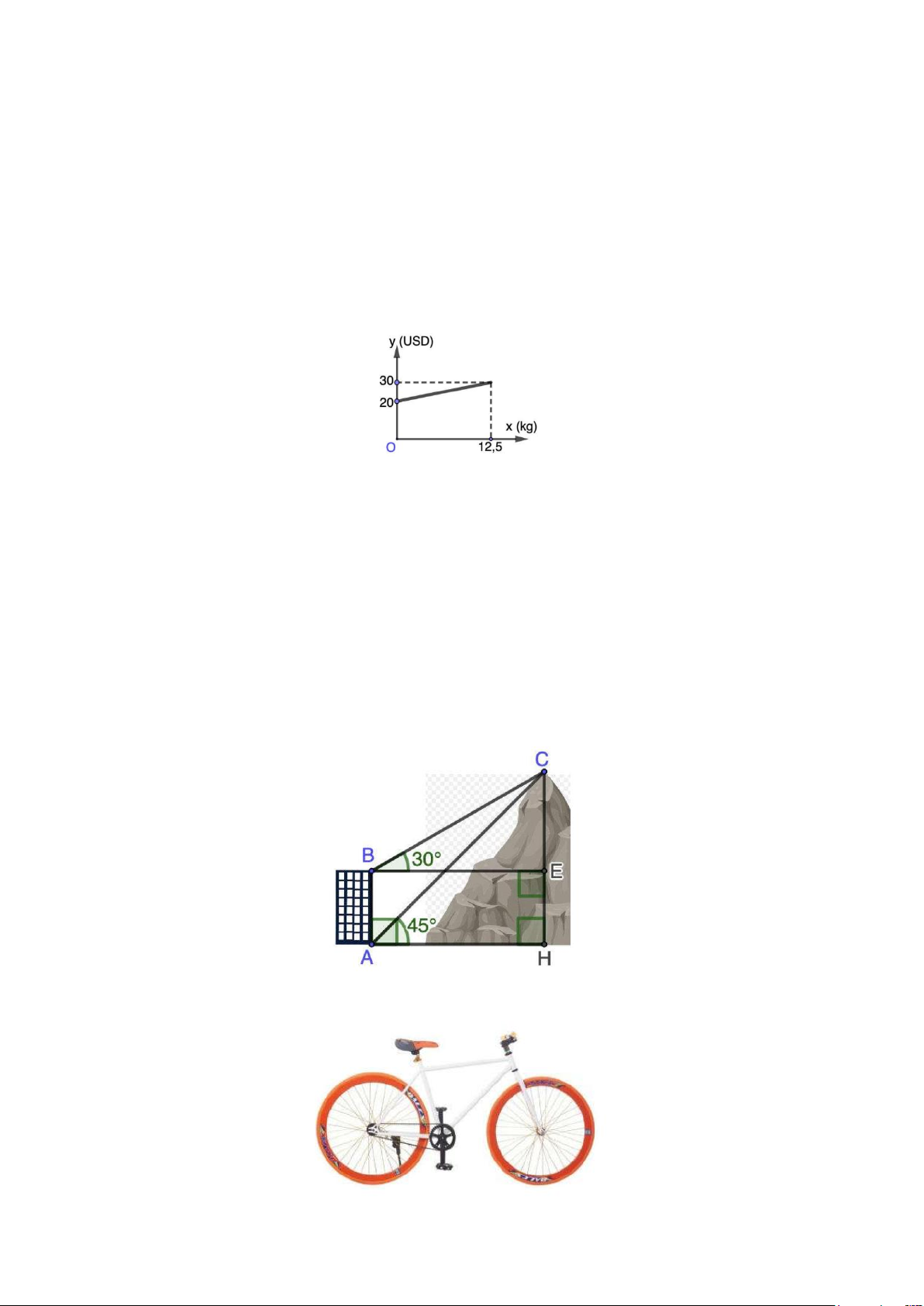
y (USD) . Người ta thấy mối quan hệ giữa hai đại lượng này là một hàm số bậc nhất
y = ax + b có đồ thị như hình bên:
a) Xác định các hệ số a và b
b) Hãy tính số tiền phạt của một hành khách có 20 kg hành lý quá cước.
Câu 5. (0,75 điểm) Đầu mỗi tháng ông Mạnh gửi vào ngân hàng 2000000 đồng với lãi suất 0,65%
/tháng và không rút gốc, lãi tháng trước. Sau 3 tháng thì số tiền ông Mạnh nhận được cả
gốc lẫn lãi (sau khi ngân hàng đã tính lãi tháng cuối cùng) là bao nhiêu?
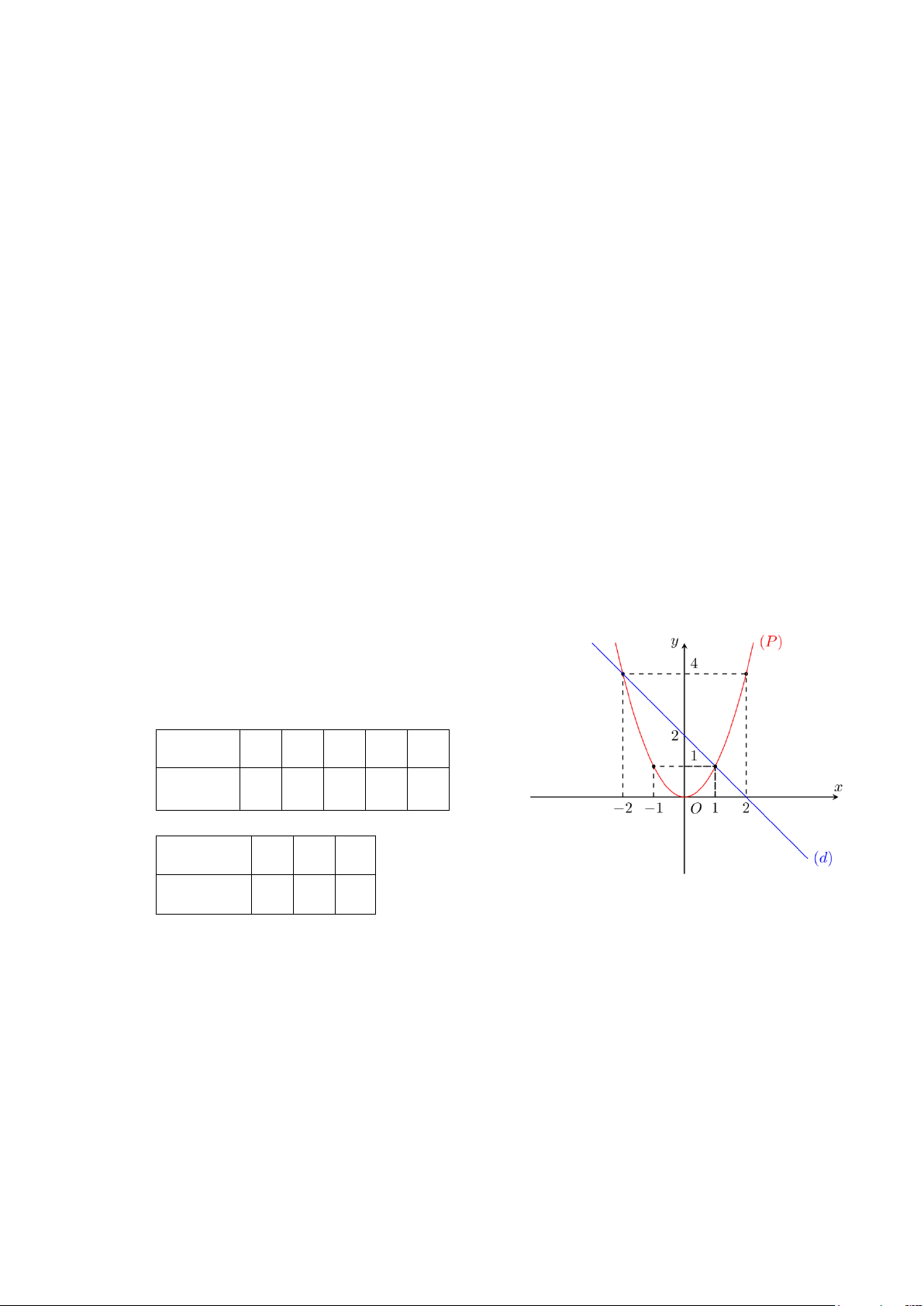
Câu 6. (1 điểm) Để đo chiều cao một ngọn đồi, người ta đặt giác kế tại hai vị trí là A (chân toà
nhà) và B (sân thượng toà nhà). Thông qua giác kế người ta đo được CAH = 45 và CBE =
30 . Tính độ cao của ngọn đồi? Biết toà nhà cao 50 m . (Kết quả làm tròn đến hàng đơn vị).
Câu 7. (0,75 điểm) Bánh xe đạp bơm căng có đường kính là 73 cm . Trang 11
a) Hỏi xe đạp đi được bao nhiêu {km} nếu bánh xe quay được 1000 vòng? Kết quả làm tròn
đến chữ số thập phân thứ ba.
b) Hỏi bánh xe quay được bao nhiêu vòng khi xe đi được 4,64km ? Kết quả làm tròn đến hàng đơn vị.
Câu 8. Cho ABC nhọn ( AB AC) , nội tiếp đường tròn (O; R) có hai đường cao BE , CF cắt
nhau tại H và cắt đường tròn (O) lần lượt tại Y và X . Kẻ đường kính AK của (O) , HK
cắt (O) tại P .
a) Chứng minh: tứ giác APFE nội tiếp đường tròn. b) Chứng minh: .
PB PE = PC.PF
c) Gọi M là điểm chính giữa của cung nhỏ BC , MX và MY cắt AB , AC lần lượt tại I và
J . Chứng minh: H ,I , J thẳng hàng. ----HẾT--- HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm): Cho parabol (P) y = 2 :
x và đường thẳng (d) : y = −x + 2
a) Vẽ (P) và (d) trên cùng hệ trục toạ độ.
b) Tìm toạ độ giao điểm của (P) và (d) bằng phép tính. Lời giải
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. BGT: x −2 −1 0 1 2 = 2 y x 4 1 0 1 4 x −2 1 2 y = −x + 2 4 1 0
a) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm (nếu có) của (P) và (d) : 2 x = −x + 2 2 x + x − 2 = 0 x = − 2 x = 1 Trang 12 2 Thay x = −2 vào = 2 y
x , ta được: y = (−2) y = 4 Thay x = 1 vào = 2 y
x , ta được: y = 2 1 y = 1
Vậy tọa độ giao điểm của (P) và (d) là A(−2;4) và B(1;1) .
Câu 2. (1 điểm) Cho phương trình 2
3x + 5x − 1 = 0 có hai nghiệm x ; x . Không giải phương 1 2
trình hãy tính giá trị của biểu thức A = (3x − 2x )(3x − 2x ) − 2023 . 1 2 2 1 Lời giải Ta có: 2
3x + 5x − 1 = 0 ( )1 (
a = 3,b = 5,c = − ) 1
Vì phương trình (1) có hai nghiệm x ,x ` 2 1
Áp dụng định lý Vi – ét, ta có: −b −
S = x + x = = 5 1 2 a 3 c − P = x x = = 1 . 1 2 a 3 Ta có:
A = (3x − 2x 3x 2x 2023 1 2 ) ( − 2 1 ) − = 9x .x − 2 6x − 2
6x + 4x .x − 2023 1 2 1 2 1 2
= 13x .x − 6( 2 x + 2 x 2023 1 2 1 2 ) − −1 13. 6 (x x 2x .x 1 2 )2 = − + − 3 1 2 2 −13 −5 − = − − 1 6 2. − 2023 = − 2048 3 3 3 Vậy A = −2048 .
Câu 3. (0,75 điểm) Để ước tính chiều cao tối đa của trẻ em khi đạt đến độ trưởng thành, hoàn
toàn có thể dựa vào chiều cao của bố mẹ. Cách tính chiều cao của con theo bố mẹ được
các chuyên gia đánh giá cao bởi thực tế, sự di truyền các thế hệ có ảnh hưởng nhất định
đến chiều cao của trẻ. Ta có công thức tính như sau: C = (B + M + 13A) : 2 .
Trong đó: C là chiều cao của người con (cm)
B là chiều cao của người bố (cm)
M là chiều cao của người mẹ (cm)
A = 1 khi người con có giới tính là Nam
A = −1 khi người con có giới tính là Nữ
a) Em hãy dùng công thức trên để tìm chiều cao tối đa của bạn Nam (giới tính là nam)
biết Ba của bạn Nam có chiều cao là 175 cm và Mẹ của bạn Nam có chiều cao là 168 cm .
b) Bạn Hương (giới tính là nữ) có chiều cao là 164 cm . Em hãy tính xem chiều cao tối đa
của Mẹ bạn Hương khi biết chiều cao của Ba bạn Hương là 180 cm . Lời giải Trang 13
a) Em hãy dùng công thức trên để tìm chiều cao tối đa của bạn Nam (giới tính là nam)
biết Ba của bạn Nam có chiều cao là 175 cm và Mẹ của bạn Nam có chiều cao là 168 cm . 175 + 168 + 13.1
Chiều cao tối đa của Nam là: = 178(cm) 2
Vậy chiều cao tối đa của Nam là: 178cm
b) Bạn Hương (giới tính là nữ) có chiều cao là 164 cm . Em hãy tính xem chiều cao tối đa
của Mẹ bạn Hương khi biết chiều cao của Ba bạn Hương là 180 cm .
Chiều cao tối đa của mẹ bạn Hương là: 1809 + M + 13.(− ) 1 164 = 2
180 + M − 13 = 328 M + 167 = 328 M = 161(cm)
Vậy chiều cao tối đa của mẹ bạn Hương là: 161cm .
Câu 4. (1,0 điểm) Một hãng hàng không quy định xử phạt hành lý kí gửi vượt quá quy định
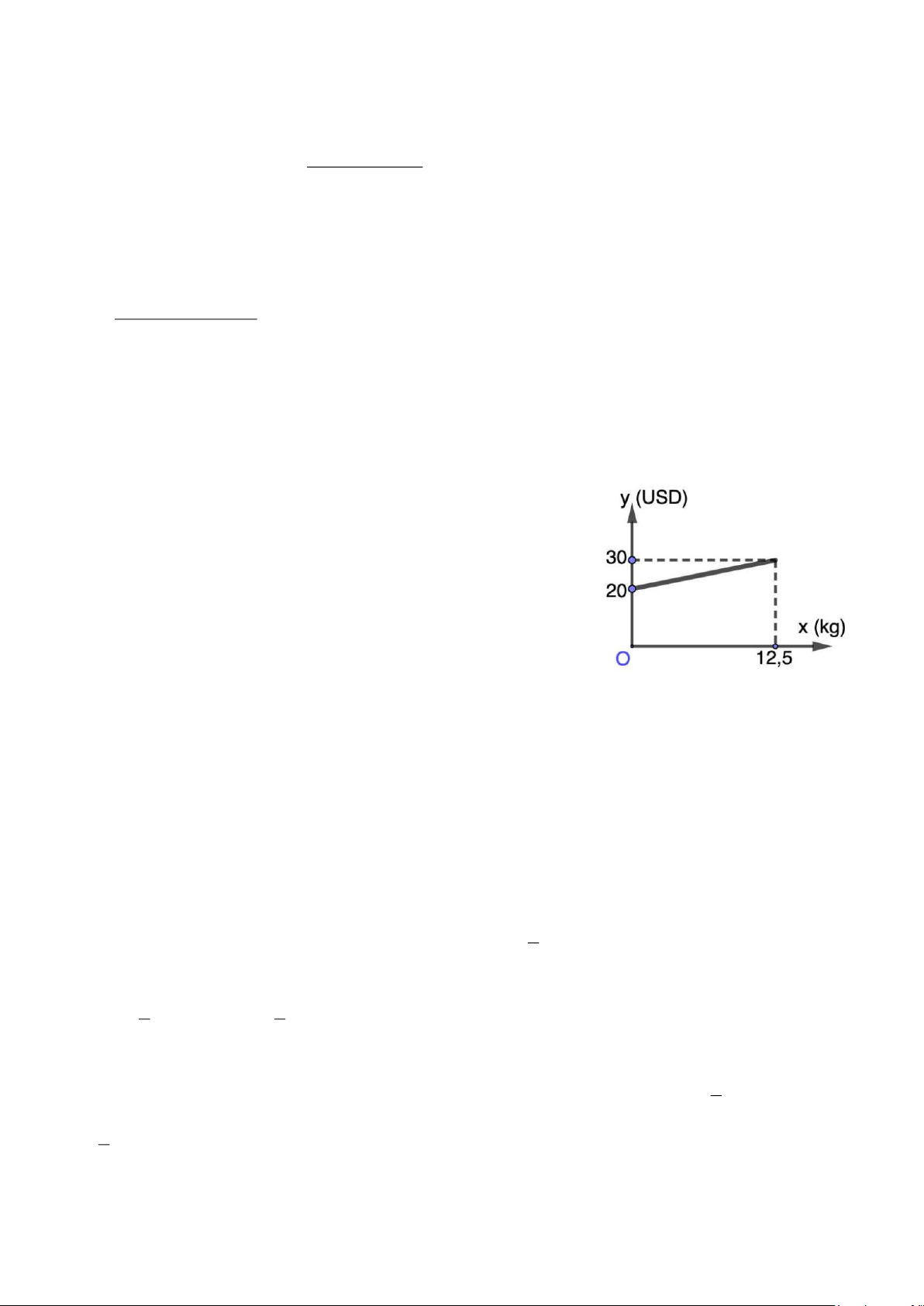
miễn phí (hành lý quá cước). Cứ vượt quá x(kg) hành lý
thì khách hàng phải trả tiền phạt y (USD) . Người ta thấy
mối quan hệ giữa hai đại lượng này là một hàm số bậc
nhất y = ax + b có đồ thị như hình bên:
a) Xác định các hệ số a và b
b) Hãy tính số tiền phạt của một hành khách có 20 kg
hành lý quá cước. Lời giải
a) Xác định các hệ số a và b . Theo đề bài, ta có: x = 0 Với 20 = 0.a + .( ) 1 y = b 20 x = 12,5 Với
30 = 12,5.a + . (2) y = b 30 a + b = a = 4 0 20 Từ ( )
1 và (2) ta có hệ phương trình: . 12,5a + b = 5 30 b = 20 4
Vậy: a = 4 , b = 20 và y = x + 20 . 5 5
b) Hãy tính số tiền phạt của một hành khách có 20kg hành lý quá cước. 4
Vì một hành khách có 20kg hành lý quá cước nên ta thay x = 20 vào y = x + 20 , ta được: 5
y = 4 .20 + 20 y = 36 5
Vậy số tiền phạt của một hành khách có 20kg hành lý quá cước là 36USD . Trang 14
Câu 5. (0,75 điểm) Đầu mỗi tháng ông Mạnh gửi vào ngân hàng 2000000 đồng với lãi suất
0,65% /tháng và không rút gốc, lãi tháng trước. Sau 3 tháng thì số tiền ông Mạnh nhận
được cả gốc lẫn lãi (sau khi ngân hàng đã tính lãi tháng cuối cùng) là bao nhiêu? Lời giải
Số tiền lãi ông Mạnh nhận được sau ba tháng là: ( + )3
2000000. 1 0,65% = 2 039 254 049 (đồng)
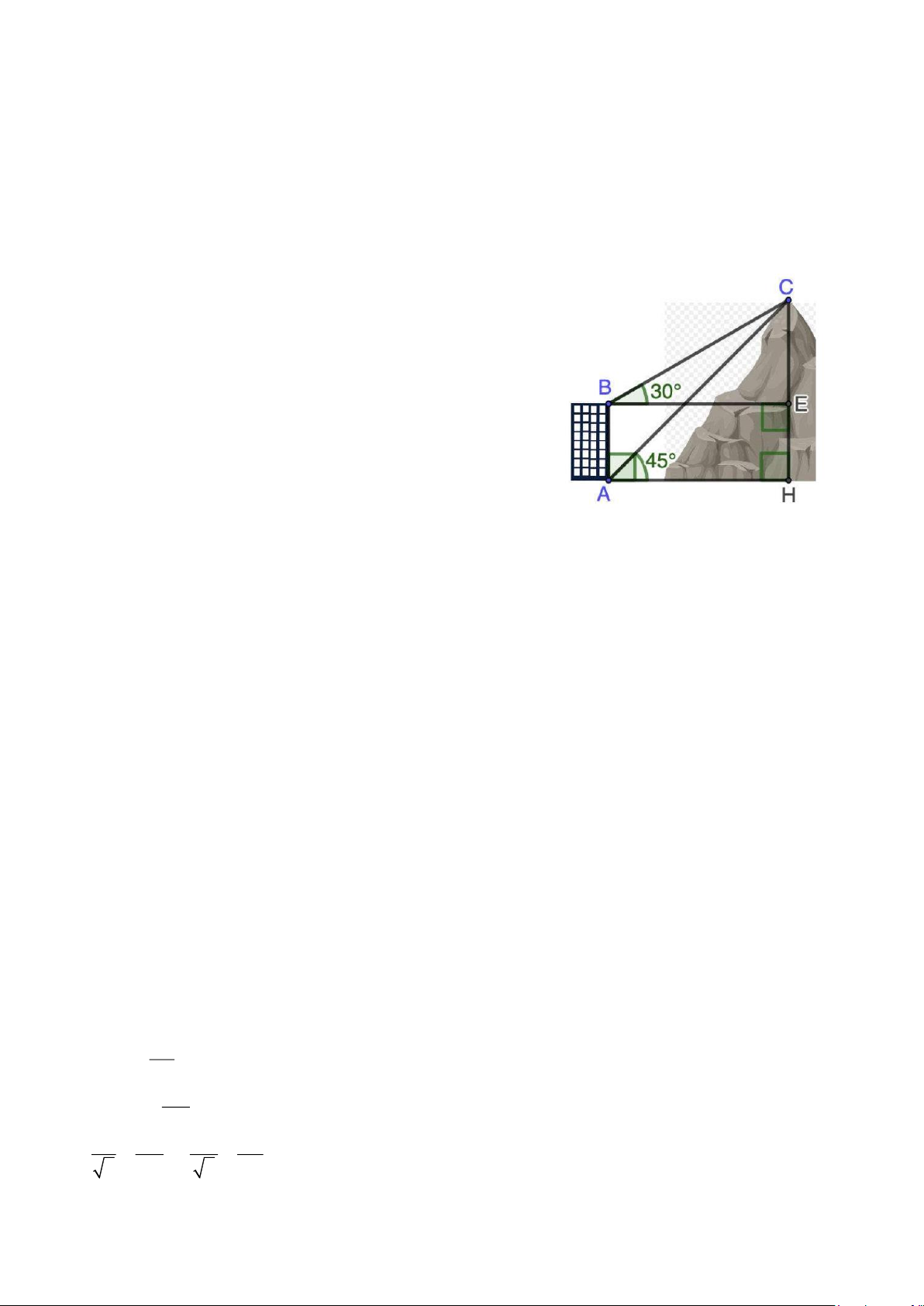
Câu 6. (1 điểm) Để đo chiều cao một ngọn đồi, người ta
đặt giác kế tại hai vị trí là A (chân toà nhà) và B
(sân thượng toà nhà). Thông qua giác kế người ta
đo được CAH = 45 và CBE = 30 . Tính độ cao của
ngọn đồi? Biết toà nhà cao 50 m . (Kết quả làm tròn đến hàng đơn vị) . Lời giải
Xét tứ giác ABEH , ta có:
BAH = 90(gt)
BEH = 90(gt)
AHE = 90(gt)
Tứ giác ABEH là hình chữ nhật (tứ giác có 3 góc vuông) BE = AH AB = EH
Mà AB = 50m ( AB là chiều cao tòa nhà bằng 50m ) Nên EH = 50m
Xét ACH vuông tại H , ta có: CAH = 45(gt)
ACH vuông cân tại H AH = CH
Mà AH = BE(cmt) Nên CH = BE
Xét BEC vuông tại E , ta có: FC tanCBE = (tỉ số lượng giác) BE FC tan 3 0 =
(CBE=3 0,BE=CH) CH
1 = EC CH = EC 3 CH 3 1
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: Trang 15 CH EC CH − = =
EC = EH = 50 (CH = CE+ EH,ECH,EH = 50m) 3 1 5 − 1 3 − 1 3 − 1 CH =
50 CH = 50 3 CH 118(m) 3 3 − 1 3 − 1
Vậy chiều cao của ngọn đồi khoảng 118m
Câu 7. (0,75 điểm) Bánh xe đạp bơm căng có đường kính là 73 cm .
a) Hỏi xe đạp đi được bao nhiêu {km} nếu bánh xe quay
được 1000 vòng? Kết quả làm tròn đến chữ số thập phân thứ ba.
b) Hỏi bánh xe quay được bao nhiêu vòng khi xe đi
được 4,64km ? Kết quả làm tròn đến hàng đơn vị. Lời giải
a) Xe đạp đi được bao nhiêu km nếu bánh xe quay 1000 vòng?
Chu vi của bánh xe đạp là: C = 73 . (cm) = 0,0007 3 (km) .
Quãng đường xe máy đi được nếu bánh xe quay 1000 vòng:
L = N.C = 1000.0,0007 3 2,293(km) .
Vậy xe đạp đi được khoảng 2,293km nếu bánh xe quay 1000 vòng
b) Bánh xe quay được bao nhiêu vòng khi xe đi 4,64km ?
Số vòng bánh xe quay được khi xe đi 4,64m là: = L N = 4,64 (vòng). C 2023 0,00073
Vậy bánh xe quay được khoảng 2023 vòng khi xe đi được 4,64km .
Câu 8. Cho ABC nhọn ( AB AC) , nội tiếp đường tròn (O; R) có hai đường cao BE , CF cắt
nhau tại H và cắt đường tròn (O) lần lượt tại Y và X . Kẻ đường kính AK của (O) , HK
cắt (O) tại P .
a) Chứng minh: tứ giác APFE nội tiếp đường tròn. b) Chứng minh: .
PB PE = PC.PF
c) Gọi M là điểm chính giữa của cung nhỏ BC , MX và MY cắt AB , AC lần lượt tại I
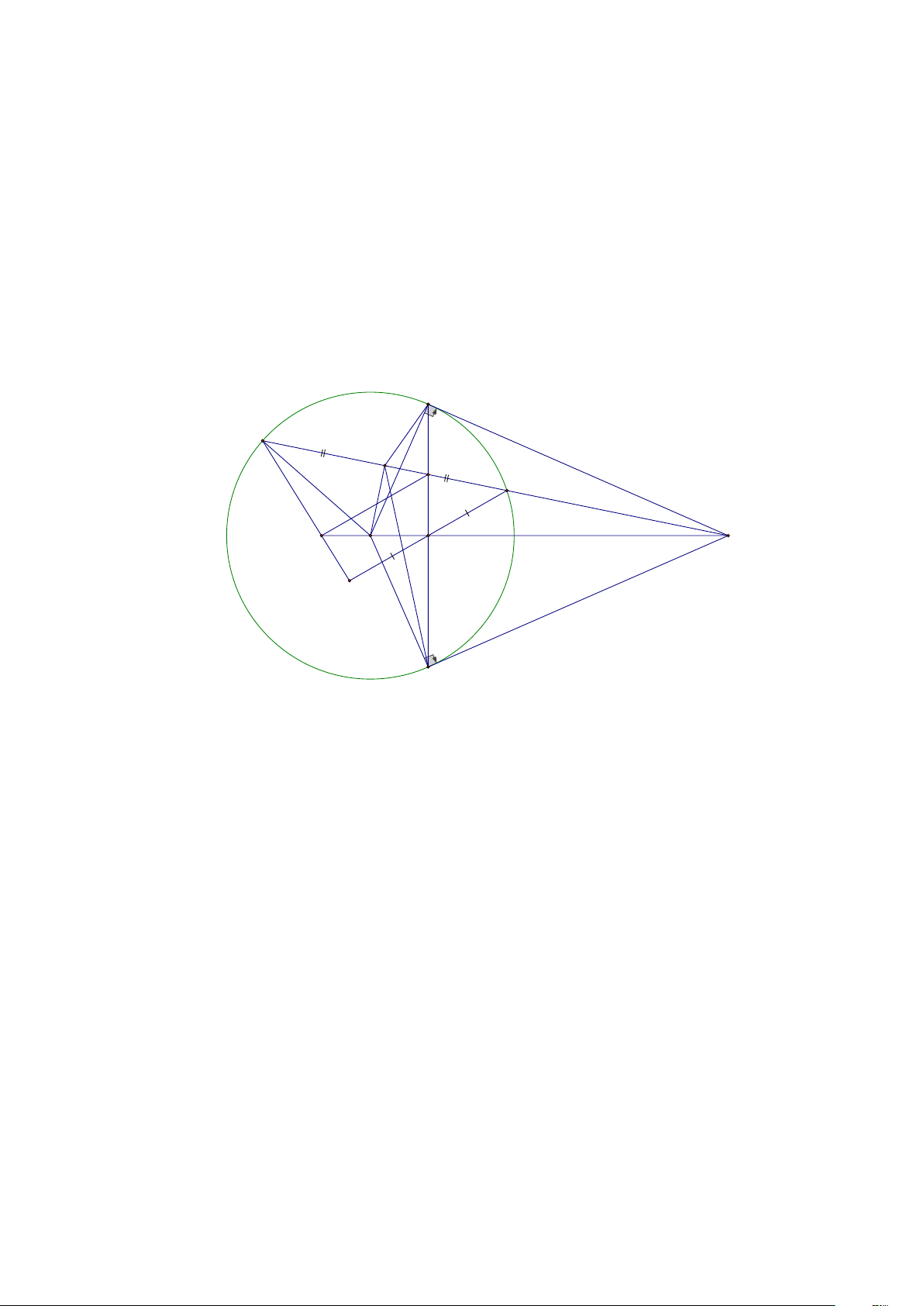
và J . Chứng minh: H ,I , J thẳng hàng. Lời giải Trang 16 A P Y E X F J O I H C B M K
a) Chứng minh: tứ giác APFE nội tiếp đường tròn. Xét (O) , ta có:
HPA là góc nội tiếp chắn nửa đường tròn đường kính AK (gt) HPA = 90
Xét tứ giác APHE , ta có: APH = 90 (cmt) AEH = 90
(BE ⊥ AC taïi E;H BE) APH + AEH = 180
Tứ giác APHE nội tiếp đường tròn đường kính AH (tứ giác có 2 góc đối bù nhau)
A , P , H , E nội tiếp đường tròn đường kính AH (1)
Xét tứ giác AFHE , ta có:
AFH = 90(CF ⊥ AB taïi F;H CF ) AEH = 90
(BE ⊥ ACtaïi E;H BE)
AFH + AEH = 90 + 90 = 180
Tứ giác AFHE nội tiếp đường tròn đường kính AH (tứ giác có hai góc đối bù nhau)
A , F , H , E thuộc đường tròn đường kính AH (2) Từ (1) và (2) suy ra: ,
A P, F, E thuộc đường tròn đường kính AH
Tứ giác APFE nội tiếp đường tròn đường kính AH b) Chứng minh: .
PB PE = PC.PF . Ta có:
BPC = BAC (2 góc nội tiếp cùng chắn BC của (O) )
Mà BAC = FPE (2 góc nội tiếp cùng chắn EF của đường tròn đường kính AH)
Nên BPC = FPE(= BAC) Ta có:
BCP = BAP (2 góc nội tiếp cùng chắn BP của (O) ) Trang 17
Mà BAP = FEP (2 góc nội tiếp cùng chắn PF của đường tròn đường kính AH)
Nên BCP = FEP(= BAP)
Xét BPC và FPE, ta có: BPC = FPE(cmt) BCP = FPE(cmt)
BPC ∽ FPE( . g g)
PB = PC (tsđd) PF PE .
PB PE = PC.PF
c) Chứng minh: H , I , J thẳng hàng.
Xét tứ giác BFEC , ta có: BFC = 90
(CF ⊥ ABtaïi F ) BEC = 90
(BE ⊥ AC taïi E)
BFC = BEC(= 90)
Tứ giác BFEC nội tiếp (tứ giác có hai đỉnh liên tiếp cùng nhìn cạnh dưới hai góc bằng nhau) FBE = FCE
Mà XBF = FCE (hai góc nội tiếp cùng chắn PX của (O ))
Nên FBE = XPF (= FCE)
BF là tia phân giác của XBH Xét (O) , ta có: 1 BXI = sñ BM
(goùc noäi tieáp chaénBM) 2 1
FXI = sñCM (goùc noäi tieáp chaé n CM) 2 sñBM = sñCM
la øñieåm chính giöõa (M BC ) X B I = FXI
XI là tia phân giác của BXF Xét D B X H , ta có
XI la ø tia phaân giaùc cuûa BXF (cmt)
BF la ø tia phaân giaùc cuûa XBH (cmt) XI caétBF taïi I (gt)
HI là tia phân giác của BHX 1 BHI = BHX 2
Chứng minh tương tự: ta được EHJ = 1 EHC 2 Trang 18 Ta có: 1 BHI = BHX (cmt) 2 1
EHJ = EHC (cmt) 2
BHX = EHC(hai goùc ñoái ñænh) BHI = EHJ
Mà EHJ + BHJ = 180(hai goùc keà b ) uø
Nên BHI + BHJ = 180 IHJ = 180
I,H, J thẳng hàng ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN GÒ VẤP
NAÊM HOÏC: 2023 – 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: Quận Gò Vấp - 3
Thời gian: 120 phút (không kể thời gian phát đề) 1
Câu 9. (1,5 điểm). Cho (P) 2 : y =
x và đường thẳng (d) : y = x + 4 . 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 10. (1 điểm). Cho phương trình 2
2x − 7x − 3 = 0 có 2 nghiệm là x ,x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức 2 2
A = x x − x − x . 1 2 1 2
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 11. (0,75 điểm).
a) Nước đóng vai trò cấp thiết cho một sức khỏe ổn định. Nó giúp cho máu được lưu thông tuần
hoàn, tăng cường đào thải độc tố trong cơ thể. Số lít nước cần nạp mỗi ngày sẽ theo cân nặng là lấy
số cân nặng (theo kg ) nhân với 0,033 . Bạn Nga nặng 50 kg thì phải nạp bao nhiêu lít nước mỗi ngày?
b) Chỉ số khối cơ thể hay còn gọi là BMI được sử dụng để xác định xem bạn có đang ở phạm vi
cân nặng khỏe mạnh so với chiều cao của bạn hay không. Chỉ số khối cơ thể (Body Mass Index – Trang 19
BMI ), được tính bằng cân nặng (kg) chia cho bình phương của chiều cao (mét), để đánh giá tình
trạng dinh dưỡng của người trưởng thành. Phân loại IDI & WPRO, BMI ( 2 2000
kg / m ) Nhẹ cân (CED) 18,5
Tình trạng dinh dưỡng bình thường 18,5 − 22,9 Thừa cân 23,0 Tiền béo phì 23,0 − 24,9 Béo phì độ I 25,0 − 29,9 Béo phì độ II 30,0
Bạn Hằng nặng 50 kg ; cao 160 cm thì thuộc loại thể trạng nào?
c) BFP (Body Fat Percentage) – Phần trăm Mỡ cơ thể là tỷ lệ mỡ so với khối lượng cơ thể.
Công thức phần trăm mỡ cơ thể (BFP) đối với nam giới trưởng thành:
BFP(%) = 1,20 BMI + 0,23Tuoi – 16,2
Công thức tỷ lệ phần trăm mỡ cơ thể (BFP) đối với phụ nữ trưởng thành:
BFP(%) = 1,20 BMI + 0,23Tuoi – 5,4
Một bạn nam 20 tuổi; cao 162 cm ; có tỉ lệ mỡ là 25% . Hỏi bạn này cần nạp vào cơ thể bao nhiêu lít
nước mỗi ngày (kết quả làm tròn 1 số thập phân).
Câu 12. (0,75 điểm). Vào đầu năm 2021 , anh Hoàng chia khoản tiền 1 tỉ 500 triệu đồng mà anh
đang có thành hai thành phần: một phần anh gửi tiết kiệm kì hạn 1 năm vào ngân hàng với
mức lãi suất 7 % /năm (theo hình thức lãi kép); một phần anh đầu tư vào một công ty
thương mại. Biết rằng sau đúng 1 năm, dưới sự ảnh hưởng của dịch COVID-19 thì tình
hình kinh doanh khó khăn, khoản đầu tư vào công ty đã bị lỗ 10,5% . Anh Hoàng rút
khoản tiền lãi từ ngân hàng ra thì vừa đủ để bù lỗ. Tính số tiền anh Hoàng đã đầu tư vào công ty thương mại.
Câu 13. (1 điểm). Trong tiết thực hành vật lý; nhóm bạn An được cô giao ghi lại thời gian đun sôi
của nước đá làm từ nước cất (bỏ qua sự phụ thuộc độ cao). Nhóm bạn ghi lại như sau: Tại
phút thứ 10 nước đá đã chuyển hoàn toàn từ thể rắn sang thể lỏng và nhiệt độ đo được từ nhiệt kế là 0 C
. Cứ mỗi một phút đun tiếp theo với cùng nhiệt độ lửa thì nhóm bạn ghi
nhận nhiệt độ của nước tăng thêm 10 C . Gọi h( C
) là nhiệt độ nước đo được tại t (phút)
từ lúc nước ở 0 C
đến khi nước sôi có liên hệ bởi hàm số h = at + b(t 10) . Trang 20




