Bộ đề tham khảo kiểm tra cuối chương 1 Hình học 12 có đáp án và lời giải chi tiết

Tài liệu gồm 73 trang được tổng hợp và biên soạn bởi thầy Nguyễn Hoàng Việt tuyển tập 5 đề tham khảo kiểm tra cuối chương 1 Hình học 12 có đáp án và lời giải chi tiết, nội dung kiểm tra

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

73 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 1/73
luyenthitracnghi
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 2/73
luyenthitracnghi
MỤC LỤC
............................................................................................................................................................................................ 1
ĐỀ THAM KHẢO SỐ 1 ......................................................................................................................................................... 3
ĐỀ THAM KHẢO SỐ 2 ......................................................................................................................................................... 6
ĐỀ THAM KHẢO SỐ 3 ....................................................................................................................................................... 10
ĐỀ THAM KHẢO SỐ 4 ....................................................................................................................................................... 13
ĐỀ THAM KHẢO SỐ 5 ....................................................................................................................................................... 16
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 1 .............................................................................................................................. 19
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 2 .............................................................................................................................. 19
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 3 .............................................................................................................................. 19
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 4 .............................................................................................................................. 19
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 5 .............................................................................................................................. 19
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 1 ................................................................................................................................................. 20
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 2 ................................................................................................................................................. 30
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 3 ................................................................................................................................................. 42
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 4 ................................................................................................................................................. 52
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 5 ................................................................................................................................................. 63
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 3/73
luyenthitracnghi
ĐỀ THAM KHẢO SỐ 1
Câu 1. [2H1-1] Hình nào dưới đây không phải là một khối đa diện?
A. B. C. D.
Câu 2. [2H1-1] Khối đa diện nào được cho dưới đây là khối đa diện đều?
A. Khối chóp tam giác đều. B. Khối lăng trụ đều.
C. Khối chóp tứ giác đều D. Khối lập phương.
Câu 3. [2H1-2] Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống, mệnh
đề sau trở thành mệnh đề đúng:
“Khối đa diện (H) được gọi là khối đa diện lồi nếu. nối hai điểm bất kì của (H) luôn thuộc (H)”.
A. Đường thẳng. B. Đoạn thẳng.
C. Đường gấp khúc. D. Đường cong.
Câu 4. [2H1-1] Khối tứ diện đều là khối đa diện đều loại nào?
A.
4;3 .
B.
3;4 .
C.
3;3 .
D.
5;3 .
Câu 5. [2H1-1] Cho khối hộp có diện tích đáy là
,S
chiều cao tương ứng là
.h
Khi đó thể tích khối
hộp là
A.
2
.Sh
. B.
2
1
.
3
Sh
. C.
. D.
1
.
3
Sh
.
Câu 6. [2H1-2] Mặt phẳng
AB C

chia khối lăng trụ
.ABC A B C
thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp tứ giác.
B. Hai khối chóp tam giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
D. Hai khối chóp tứ giác.
Câu 7. [2H1-2] Tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A.
1
. B.
4
. C.
5
. D.
6
.
Câu 8. [2H1-2] Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần
lượt là
15cm
và
5cm
. Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ
nhật sao cho cây nến nằm khít trong hộp. Thể tích của chiếc hộp đó bằng:
A.
1500 ml
. B.
600 6 ml
. C.
1800 ml
. D.
750 3 ml
.
Câu 9. [2H1-3] Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng
.a
Thể tích khối tứ diện
A B AC

là
A.
3
3
.
6
a
B.
3
.
6
a
C.
3
3
.
12
a
D.
3
3
.
4
a
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 4/73
luyenthitracnghi
Câu 10. [2H1-3] Cho hình lập phương có tổng diện tích các mặt bằng
3
12a
. Tính theo
a
thể tích
khối lập phương đó.
A.
3
8a
. B.
3
2a
. C.
3
a
. D.
3
3
a
.
Câu 11. [2H1-2] Cho hình lập phương
.ABCD A B C D
có diện tích mặt chéo
ACC A

bằng
2
22a
. Thể tích của khối lập phương
.ABCD A B C D
là
A.
3
a
. B.
3
2a
. C.
3
22a
. D.
3
8a
.
Câu 12. [2H1-2] Một hình chóp tứ giác đều có cạnh đáy bằng
a
, các mặt bên tạo với đáy một góc
. Thể tích của khối chóp đó là
A.
3
sin .
2
a
B.
3
tan .
2
a
C.
3
cot .
6
a
D.
3
tan .
6
a
Câu 13. [2H1-3] Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
A
,
AC a
,
60ACB 
. Đường chéo
BC
của mặt bên
BCC B

tạo với mặt phẳng
ACC A

một góc
30
. Tính thể tích của khối lăng trụ theo
a
.
A.
3
46
3
a
V
. B.
3
6Va
. C.
3
26
3
a
V
. D.
3
6
3
a
V
.
Câu 14. [2H1-3] Cho khối chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2a
.
Tính thể tích
V
của khối chóp
.S ABC
A.
3
13
12
a
V
. B.
3
11
12
a
V
. C.
3
11
6
a
V
. D.
3
11
4
a
V
.
Câu 15. [2H1-2] Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật, mặt bên
SAD
là tam giác
đều cạnh
2a
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích khối
chóp
.S ABCD
biết rằng mặt phẳng
()SBC
tạo với mặt phẳng đáy một góc
30 .
A.
3
3
.
2
a
B.
3
2 3 .a
C.
3
23
.
3
a
D.
3
43
.
3
a
Câu 16. [2H1-3] Cho hình chóp tứ giác đều có cạnh đáy bằng
x
. Diện tích xung quanh gấp đôi
diện tích đáy. Khi đó thể tích của khối chóp bằng:
A.
3
.3
6
x
. B.
3
.3
2
x
. C.
3
.3
12
x
. D.
3
.3
3
x
.
Câu 17. [2H1-3] Một hình chóp tam giác đều có cạnh bên bằng
b
và cạnh bên tạo với mặt phẳng
đáy một góc
. Thể tích của hình chóp đó là
A.
32
3
cos sin
4
b

. B.
32
3
sin cos
4
b

. C.
32
3
cos sin
4
b

. D.
3
3
cos sin
4
b

.
Câu 18. [2H1-1] Cho tứ diện
ABCD
. Gọi
'B
và
'C
lần lượt là trung điểm của
AB
và
AC
. Tính tỉ
số thể tích của khối tứ diện
''AB C D
và khối tứ diện
ABCD
.
A.
1
4
. B.
1
2
. C.
1
6
. D.
1
8
.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 5/73
luyenthitracnghi
Câu 19. [2H1-2] Cho khối chóp
.S ABC
có thể tích bằng
16
. Gọi
,,M N P
lần lượt là trung điểm của
các cạnh
,,SA SB SC
. Tính thể tích V của khối tứ diện
AMNP
.
A.
2V
. B.
6V
. C.
4V
. D.
8V
.
Câu 20. [2H1-2] Cho tứ diện
ABCD
có hai mặt
ABC
,
BCD
là các tam giác đều cạnh
a
và nằm
trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện
ABCD
là:
A.
3
3
4
a
. B.
3
8
a
. C.
3
4
a
. D.
3
3
8
a
.
Câu 21. [2H1-3] Một hình hộp chữ nhật
.ABCD A B C D
có ba kích thước là
2cm
,
3cm
và
6cm
.
Thể tích của khối tứ diện
.A CB D

bằng
A.
3
8 cm
. B.
3
12 cm
. C.
3
6 cm
. D.
3
4 cm
.
Câu 22. [2H1-3] Cho khối chóp
.S ABC
có
6, 2, 4, 2 10SA SB SC AB
và góc
90SBC
,
120ASC
. Mặt phẳng
P
đi qua
B
và trung điểm
N
của cạnh
đồng thời vuông góc
với mặt phẳng
SAC
cắt
SA
tại
M
. Tính tỉ số thể tích
.
.
.
S BMN
S ABC
V
k
V
A.
1
6
k
. B.
2
5
k
. C.
2
9
k
. D.
1
4
k
.
Câu 23. [2H1-3] Cho khối lăng trụ
.ABC A B C
có thể tích
V
, điểm
P
thuộc cạnh
,AA Q
thuộc
BB
sao cho
1
;
3
PA QB
R
PA QB

là trung điểm
CC
. Tính thể tích khối chóp tứ giác
.R ABQP
theo
V
.
A.
2
3
V
. B.
1
3
V
. C.
3
4
V
. D.
1
2
V
.
Câu 24. [2H1-4] Người ta muốn xây một bể chứa nước dạng khối hộp chữ nhật trong một phòng
tắm. Biết chiều dài, chiều rộng, chiều cao của khối hộp đó lần lượt là
3m
;
1,2m
;
1,8m
(người ta chỉ xây hai mặt thành bể như hình vẽ bên). Biết mỗi viên gạch có chiều dài
20cm
, chiều rộng
10cm
, chiều cao
5cm
. Hỏi
người ta sử dụng ít nhất bao nhiêu viên
gạch để xây bể đó và thể tích thực của
bể chứa bao nhiêu lít nước? (Giả sử
lượng xi măng và cát không đáng kể).
A.
738
viên,
5742
lít. B.
730
viên,
5742
lít.
C.
738
viên,
5740
lít. D.
730
viên,
5740
lít.
Câu 25. [2H1-3] Cho hình chóp
.S ABCD
có đáy
là hình vuông cạnh
a
, mặt bên
SAB
là
tam giác đều, mặt bên
SCD
là tam giác
vuông cân đỉnh
S
. Thể tích khối chóp
.S ABCD
là
A.
3
3
.
6
a
B.
3
3
.
12
a
C.
3
.
6
a
D.
3
3
.
4
a
1,8dm
1dm
1dm
3m
1,2m
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 6/73
luyenthitracnghi
ĐỀ THAM KHẢO SỐ 2
Câu 1. [2H1-1]
hình (a) hình (b) hình (c) hình (d)
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là
A. hình (a). B. hình (b). C. hình (c). D. hình (d).
Câu 2. [2H1-1]
hình (a). hình (b). hình (c). hình (d).
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 3. [2H1-1]Phát biểu nào sau đây là đúng?
A. Hình bát diện đều có 8 đỉnh, 12 cạnh, 6 mặt.
B. Hình bát diện đều có 6 đỉnh, 12 cạnh, 8 mặt.
C. Hình bát diện đều có 12 đỉnh, 8 cạnh, 6 mặt.
D. Hình bát diện đều có 8 đỉnh, 6 cạnh, 12 mặt.
Câu 4. [2H1-2]Một hình hộp đứng có hai đáy là hình thoi (không phải là hình vuông) có bao
nhiêu mặt phẳng đối xứng?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 5. [2H1-1]Thể tích khối chóp có diện tích đáy B và chiều cao h là:
A.
V Bh
.
B.
1
2
V Bh
. C.
2V Bh
. D.
1
3
V Bh
.
Câu 6. [2H1-2]Trong các mệnh đề sau mệnh đề nào sai ?
A.Lắp ghép hai khối hộp sẽ được một khối đa diện lồi
B.Khối hộp là khối đa diện lồi
C.Khối tứ diện là khối đa diện lồi
D.Khối lăng trụ tam giác là khối đa diện lồi
Câu 7. [2H1-2]Nếu không sử dụngthêm điểm nào khác ngoài các đỉnh của hình lập phương thì
có thể chia hình lập phương thành
A.Một tứ diện đều và bốn hình chóp tam giác giác đều
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 7/73
luyenthitracnghi
B.Năm tứ diện đều
C.Bốn tứ diện đều và một hình chóp tam giác đều
D.Năm hình chóp tam giác giác đều,không có tứ diện đều
Câu 8. [2H1-1]Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là
A.
.V B h
B.
1
.
3
V B h
C.
1
.
2
V B h
D.
4
.
3
V B h
.
Câu 9. [2H1-3] Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
2,AD a AB a
.Gọi
H
là
trung điểm của
AD
,biết
SH ABCD
.Tính thể tích khối chóp biết
5SA a
.
A.
3
23
3
a
B.
3
43
3
a
C.
3
4
3
a
D.
3
2
3
a
.
Câu 10. [2H1-3]
Cho hình lập phương ABCDA’B’C’D’.I là trung điểm
BB’.Mặt phẳng (DIC’)chia khối lập phương thành 2 phần có
tỉ số thể tích phần bé chia phần lớn bằng:
A.
1
3
. B.
7
17
. C.
4
14
. D.
1
2
.
Câu 11. [2H1-2] Cho hình lập phương
. ' ' ' 'ABCD A B C D
có
' 4 3AC
. Thể tích khối lập phương
. ' ' ' 'ABCD A B C D
là
A.
32.
B.
43
C.
64.
D.
16.
Câu 12. [2H1-2] Cho khối chóp đều
.S ABCD
có cạnh đáy bằng
3a
. Tính thể tích khối chóp
.S ABCD
biết góc giữa cạnh bên và mặt đáy bằng 60°.
A.
3
2
2
a
B.
3
32
2
a
C.
3
36
2
a
D.
3
6
2
a
Câu 13: [2H1-3] Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông tại
A
với
; 60AC a ACB
. Biết
'BC
hợp với
'ACC A
một góc
0
30
. Thể tích của khối lăng trụ
. ' ' 'ABC A B C
là:
A.
3
6a
B.
3
2a
C.
3
3a
D.
3
23a
Câu 14: [2H1-3] Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, góc giữa đường thẳng
SA
và mặt phẳng
ABC
bằng
0
45
. Hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là điểm
H
thuộc
BC
sao cho
3BC BH
. Thể tích khối chóp
.S ABC
là:
A.
3
21
18
a
B.
3
21
36
a
C.
3
21
12
a
D.
3
21
27
a
Câu 15: [2H1-2] Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh a. Hai mặt phẳng
SAB
và
SAD
cùng vuông góc với mặt phẳng
ABCD
. Đường thẳng
SC
tạo với đáy
một góc bằng
0
45
. Gọi
,MN
lần lượt là trung điểm của cạnh
,AB AC
. Thể tích của khối
chóp
.S MCDN
là bao nhiêu?
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 8/73
luyenthitracnghi
A.
3
52
12
a
B.
3
52
6
a
C.
3
52
8
a
D.
3
52
24
a
Câu 16: [2-H1-3] Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Gọi
SH
là chiều cao
của hình chóp, khoảng cách từ trung điểm
I
của
SH
đến mặt bên
SBC
bằng
b
. Tính
thể tích
V
của khối chóp
.S ABCD
.
A.
22
3 16
ab
V
ab
. B.
3
22
2
3 16
ab
V
ab
. C.
22
16
ab
V
ab
. D.
22
2
16
ab
V
ab
.
Câu 17: [2-H1-3] Hình chóp tam giác đều
.S ABC
có
AB a
, góc giữa
SA
và đáy bằng
0
30
. Thể
tích khối chóp là.
A.
3
2
12
a
. B.
3
3
72
a
. C.
3
3
12
a
. D.
3
3
.
36
a
Câu 18: [2-H1-1] Cho tứ diện
ABCD
. Gọi
'B
và
'C
lần lượt là trung điểm của
AB
và
AC
. Tính tỉ
số thể tích của khối tứ diện
''AB C D
và khối tứ diện
ABCD
.
A.
1
6
. B.
1
8
. C.
1
2
. D.
1
4
.
Câu 19: [2-H1-2] Cho khối chóp
.S ABC
có
9, 4, 8SA SB SC
và đôi một vuông góc. Các điểm
,,A B C
thỏa mãn
2. ,SA SA
3. ,SB SB
4. .SC SC
Thể tích khối chóp
.S A B C
là.
A.
16
. B.
12
. C.
2
. D.
24
.
Câu 20: [2-H1-2] Cho tứ diện
ABCD
có thể tích bằng 12 và
G
là trọng tâm tam giác
BCD
. Tính
thể tích
V
của khối chóp
.AGBC
.
A.
4V
. B.
5V
. C.
6V
. D.
3V
.
Câu 21: [2-H1-3] Cho khối hộp
. ' ' ' 'ABCD A B C D
có thể tích bằng
12
( đơn vị thể tích). Gọi
,,M N P
lần lượt là trung điểm của các cạnh
, , 'AD DC AA
. Tính thể tích khối chóp
.P BMN
.
A.
3
4
V
. B.
2V
. C.
3
2
V
. D.
3V
.
Câu 22: [2-H1-3] Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy
một góc
60
. Gọi
M
là điểm đối xứng với
C
qua
D
;
N
là trung điểm của
SC
, mặt
phẳng (
BMN
) chia khối chóp
.S ABCD
thành hai phần. Tính tỉ số thể tích giữa hai phần
đó.
A.
1
7
. B.
7
5
. C.
7
3
. D.
1
5
.
Câu 23: [2-H1-3] Cho khối lập phương
. ’ ’ ’ ’ABCD A B C D
cạnh
a
. Gọi
O
và
’O
lần lượt là tâm của
ABCD
và
’ ’ ’ ’A B C D
. Thể tích phần chung nhau của hai khối chóp
. ’ ’ ’ ’O A B C D
và
’.O ABCD
là:
A.
3
.
12
a
V
B.
3
.
6
a
V
C.
3
.
4
a
V
D.
3
.
3
a
V
Câu 24: [2-H1-4] Người ta muốn mạ vàng cho bề mặt phía ngoài của một cái hộp dạng hình hộp
đứng không nắp (nắp trên), có đáy là một hình vuông. Tìm chiều cao của hộp để lượng
vàng phải dùng để mạ là ít nhất, biết lớp mạ ở mọi nơi như nhau, giao giữa các mặt là
không đáng kể và thể tích của hộp là
3
4 dm
.
A.
1,5 dm
. B.
1 dm
. C.
0,5 dm
. D.
2 dm
.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 9/73
luyenthitracnghi
Câu 25: [2-H1-3] Cho hình chóp
.S ABC
có
SA a
, tam giác
ABC
đều, tam giác
SAB
vuông cân
tại
S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp
.S ABC
bằng?
A.
3
6
12
a
. B.
3
6
4
a
. C.
3
6
8
a
. D.
3
6
24
a
.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 10/73
luyenthitracnghi
ĐỀ THAM KHẢO SỐ 3
Câu 1. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mỗi hình đa diện có ít nhất bốn đỉnh.
B. Mỗi hình đa diện có ít nhất ba đỉnh.
C. Số đỉnh của một hình đa diện lớn hơn hoặc bằng số cạnh của nó.
D. Số mặt của một hình đa diện lớn hơn hoặc bằng số cạnh của nó.
Câu 2. Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất:
A. Năm cạnh. B. Bốn cạnh. C. Ba cạnh. D. Hai cạnh.
Câu 3. Trong các mệnh đề sau, mệnh đề nào sai?
A. Khối tứ diện là khối đa diện lồi.
B. Lắp ghép hai khối hộp luôn được một khối đa diện.
C. Khối hộp là khối đa diện lồi.
D. Khối lăng trụ tam giác đều là khối đa diện lồi.
Câu 4. Trong không gian có tất cả bao nhiêu loại khối đa diện đều?
A.
2.
B.
3.
C.
4.
D.
5.
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA vuông góc với đáy,
2SA a
.
Tính thể tích khối chóp S.ABCD?
A.
3
2
.
6
a
V
B.
3
2
.
2
a
V
C.
3
2.Va
D.
3
2
.
3
a
V
Câu 6. Phân chia khối lập phương
.ABCD A B C D
bởi ba mặt phẳng
A BD
,
DDBB

,
B CD

ta
được những khối đa diện nào?
A. Hai khối tứ diện và một khối lăng trụ tứ giác.
B. Ba khối tứ diện và một khối lăng trụ tam giác.
C. Hai khối tứ diện và một khối lăng trụ tam giác.
D. Hai khối tứ diện và hai khối chóp tứ giác.
Câu 7. Phân chia khối lăng trụ
.ABC A B C
bởi hai mặt phẳng
AB D

và
AB D
ta được các khối nào
sau đây?
A. Khối chóp tứ giác
.DAB D B

và khối tứ diện
ABDB
.
B. Khối chóp tứ giác
.DA B D B

và khối tứ diện
ADD B

.
C. Khối chóp tứ giác
.DA B D B

và khối tứ diện
AA B D
.
D. Ba khối tứ diện
ABDB
,
ADD B

và
AA B D
Câu 8. Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
I
là trung điểm
của
BC
,
6BC a
. Mặt phẳng
A BC
tạo với mặt phẳng
ABC
một góc
60
. Thể tích khối lăng
trụ
.ABC A B C
là
A.
3
92
4
a
. B.
3
92
2
a
. C.
3
92
12
a
. D.
3
92
6
a
.
Câu 9. Cho khối hộp
.ABCD A B C D
có thể tích bằng
72
(ĐVTT). Gọi
1
V
là thể tích khối chóp
.A ABC
. Khi đó, chọn kết quả đúng trong các kết quả cho dưới đây?
A.
1
12V
. B.
1
24V
. C.
1
36V
. D.
1
18V
.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 11/73
luyenthitracnghi
Câu 10. Cho khối lập phương
.ABCD A B C D
, có đường chéo
3BD
. Thể tích của khối lập phương
.ABCD A B C D
bằng bao nhiêu?
A.
3
. B.
63
. C.
3
. D.
33
.
Câu 11. Tổng diện tích các mặt bên của khối lập phương bằng 54 .Thể tích khối lập phương bằng?
A.
27.
B.
9.
C.
3 3.
D.
3.
Câu 12.
Cho hình chóp tứ giác đều S.ABCD cạnh đáy AB =a , góc SAC bằng 45
0
.Thể tích khối chóp
bằng:
A.
3
.
3
a
B.
3
2
2
a
C.
3
3
6
a
D.
3
2
6
a
Câu 13. Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác đều cạnh
a
. Mặt phẳng
''AB C
tạo với mặt
đáy góc
0
60
. Tính theo
a
thể tích lăng trụ
. ' ' 'ABC A B C
.
A.
3
3
2
a
V
. B.
3
33
4
a
V
. C.
3
3
8
a
V
. D.
3
33
8
a
V
.
Câu 14. Cho khối chóp
.S ABC
có
SA
vuông góc với đáy,
46,,SA AB
10BC
và
8CA
. Tính thể
tích
V
của khối chóp
..S ABC
A.
40.V
B.
192.V
C.
32.V
D.
24.V
Câu 15. Cho khối chóp
.S ABCD
có đáy là hình chữ nhật,
3,,AB a AD a
SA
vuông góc với đáy và
mặt phẳng
SBC
tạo với đáy một góc
0
60
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
3
.
a
V
B.
3
3
3
.
a
V
C.
3
.Va
D.
3
3 .Va
Câu 16. Cho hình chóp đều
.S ABCD
có
AB a
. Gọi
M
là trung điểm
AD
và góc tạo bởi mặt phẳng
SCM
và mặt đáy bằng
0
60
. Tính theo
a
thể tích
V
của khối chóp
..S ABCD
A.
3
15
30
.
a
V
B.
3
15
10
.
a
V
C.
3
5
15
.
a
V
D.
3
5
5
.
a
V
Câu 17. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên tạo với đáy một góc
. Tính
thể tích khối chóp đó
A.
3
cot
.
12
a
B.
3
tan
.
12
a
C.
2
tan
.
12
a
D.
3
tan
.
4
a
Câu 18. Cho tứ diện ABCD, gọi B’, C’ lần lượt là trung điểm của AB, AC. Khi đó tỉ số thể tích của khối tứ
diện AB’C’D và khối tứ diện ABCD bằng:
A.
1
.
2
B.
1
.
4
C.
1
.
6
D.
1
.
8
Câu 19.
Cho hình chóp S.ABC có SA vuông góc mặt đáy , SA=a, tam giác ABC đều cạnh 2a. Gọi M,N lần
lượt thuộc cạnh SB,SC sao cho SM=MB,
2SN CN
.
Tính thể tích khối AMNCB.
A.
3
23
.
9
a
B.
3
3
.
9
a
C.
3
3
.
18
a
D.
3
23
.
3
a
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 12/73
luyenthitracnghi
Câu 20. Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D , (ABC)
(BCD)
và AD hợp với (BCD) một góc 60
o
.Tính thể tích tứ diện ABCD.
A.
3
a3
9
B.
3
a3
3
C.
3
a3
27
D.
3
2a 3
9
Câu 21. Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh bằng
a
. Gọi
O
là giao điểm của
AC
và
BD
. Tính
thể tích của tứ diện
'OA BC
.
A.
3
.
6
a
B.
3
6
.
24
a
C.
3
.
12
a
D.
3
.
4
a
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a , AD = 2a. Cạnh SA vuông
góc với mặt phẳng đáy, cạnh bên SB tạo với mặt phắng đáy một góc
0
60
. Trên cạnh SA lấy điểm M sao cho
AM =
3
3
a
, mặt phẳng (BCM) cắt cạnh SD tại N. Tính thể tích khối chóp S.BCNM
A.
10 3
.
27
B.
3
10 3
.
9
a
C.
3
10 3
.
27
a
D.
3
10
.
27
a
Câu 23. Cho hình lăng trụ ABC. A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên hợp với đáy một góc
là 45
0
. Gọi P là trung điểm BC, chân đường vuông góc hạ từ A’ xuống (ABC) là H sao cho
1
2
AP AH
. gọi
K là trung điểm AA’,
là mặt phẳng chứa HK và song song với BC cắt BB’ và CC’ tại M, N. Tính tỉ số thể
tích
' ' '
ABCKMN
A B C KMN
V
V
A.
1
2
B.
2
3
C.
1
3
D.
3
4
Câu 24. Cho một tấm bìa hình chữ nhật chiều dài
90AB cm
, chiều rộng
60BC cm
. Người ta cắt 6
hình vuông bằng nhau như hình vẽ, mỗi hình vuông cạnh bằng
x cm
, rồi gập tấm bìa lại như hình vẽ dưới
đây để được một hộp quà có nắp. Tìm
x
để hộp nhận được thể tích lớn nhất?
A.
10 .cm
B.
9.cm
C.
15 .cm
D.
10
.
3
cm
Câu 25. Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy và khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2
2
.
a
Tính thể tích
V
của khối chóp đã cho.
A.
3
2
.
a
V
B.
3
.Va
C.
3
3
.
a
V
D.
3
3
.
a
V
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 13/73
luyenthitracnghi
ĐỀ THAM KHẢO SỐ 4
Câu 1. [2H1-1] Cho khối chóp có là n – giác
3;n n N
. Mệnh đề nào đúng sau đây:
A. Số cạnh của khối chóp bằng n + 1. B. Số mặt của khối chóp bằng 2n.
C. Số đỉnh của khối chóp bằng n + 1. D. Số mặt của khối chóp bằng số đỉnh của nó.
Câu 2. [2H1-1] Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh. B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt. D. Mỗi mặt có ít nhất ba cạnh.
Câu 3. [2H1-2] Trong các mệnh đề sau mệnh đề nào sai ?
A. Lắp ghép hai khối hộp sẽ được một khối đa diện lồi.
B. Khối hộp là khối đa diện lồi.
C. Khối tứ diện là khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi.
Câu 4. [2H1-1] Có bao nhiêu loại khối đa diện đều?
A.
2
. B.
4
. C.
5
. D. Vô số.
Câu 5. [2H1-1] Khối đa điện nào sau đây có công thức tính thể tích là
1
3
V Bh
(
B
là diện tích đáy;
h
là chiều
cao)
A. Khối lăng trụ. B. Khối chóp.
C. Khối lập phương. D. Khối hộp chữ nhật.
Câu 6. [2H1-2] Trong Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và D .
Bằng hai mặt phẳng và ta chia khối tứ diện đã cho thành bốn khối tứ diện:
A. AMCN, AMND, AMCD, BMCN. B. AMNC, AMND, BMNC, BMND.
C. AMCD, AMND, BMCN, BMND. D. BMCD, BMND, AMCN, AMDN.
Câu 7. [2H1-2] Có thể chia hình lập phương thành bao nhiêu hình tứ diện bằng nhau?
A.
2
. B. Vô số. C.
4
. D.
6
.
Câu 8. [2H1-2] Trong cách mệnh đề sau, mệnh đề nào sai?
A. Hai khối hộp chữ nhật có diện tích xung quanh bằng nhau thì có thể tích bằng nhau.
B. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
C. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
D. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
Câu 9. [2H1-3] Cho hình hộp
D.ABC A B C D
. Tỉ số thể tích của khối tứ diện
''ACB D
và khối hộp
D.ABC A B C D
là:
A.
1
5
. B.
1
4
. C.
1
3
. D.
1
6
.
Câu 10. [1H1-3] Cho hình lập phương
. ’ ’ ’ ’ABCD A B C D
có khoảng cách giữa
’AC
và
’’CD
là
1
cm. Thể
tích khối lập phương
. ’ ’ ’ ’ABCD A B C D
là:
A.
3
8.cm
B.
3
2 2 .cm
C.
3
3 3 .cm
D.
3
27 .cm
Câu 11. [1H1-2] Tính thể tích
V
của khối lập phương
.ABCD A B C D
, biết
3AC a
.
A.
3
Va
. B.
3
36
4
a
V
. C.
3
33Va
. D.
3
1
3
Va
.
Câu 12: [1H1-2] Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
a
là
A.
3
2
6
a
. B.
3
3
4
a
. C.
3
3
2
a
. D.
3
3
a
.
Câu 13: [1H1-3] Cho lăng trụ đứng tam giác
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
với
BA BC a
, biết
AB
hợp với đáy
ABC
một góc
60
. Tính thể tích khối lăng trụ.
A. . B. . C. . D. .
MCD
NAB
3
3
2
a
3
a
3
2a
3
2
a
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 14/73
luyenthitracnghi
Câu 14: [1H1-3] Cho hình chóp
.S ABC
có tam giác
ABC
là tam giác đều cạnh
a
. Hình chiếu vuông góc
của
S
trên mặt phẳng
ABC
là trung điểm của cạnh
AB
, góc tạo bởi cạnh
SC
và mặt phẳng
ABC
bằng
o
30
. Tính thể tích của khối chóp
.S ABC
.
A.
3
3
8
a
. B.
3
8
a
. C.
3
3
4
a
. D.
3
3
24
a
.
Câu 15: [1H1-2] Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
, a SA
vuông góc với mặt đáy
, SD
tạo
với mặt phẳng
SAB
một góc bằng
30
. Tính thể tích
V
của khối chóp.
A.
3
6
18
a
. B.
3
3a
. C.
3
6
3
a
. D.
3
3
3
a
.
Câu 16: [1H1-3] Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên gấp hai lần cạnh đáy. Tính tích V
của khối chóp tứ giác đã cho.
A.
3
2
2
a
V
. B.
3
2
6
a
V
. C.
3
14
2
a
V
. D.
3
14
6
a
V
.
Câu 17: [1H1-3] Cho hình chóp tam giác đều
.S ABC
. Tính theo
a
thể tích khối chóp
.S ABC
biết rằng
AB a
,
( ),( ) 60SBC ABC 
.
A.
3
3
24
a
.
B.
3
4
a
.
C.
3
3
4
a
.
D.
3
3
12
a
.
Câu 18: [1H1-1] Cho hình chóp tam giác
.S ABC
. Gọi
M
lần lượt là trung điểm của
SB
và
N
nằm trên
cạnh
SC
sao cho
2SN NC
. Khi đó tỉ số thể tích của khối tứ diện
.S AMN
và khối tứ diện
.S ABC
bằng:
A.
1
6
. B.
1
3
. C.
1
6
. D.
1
2
.
Câu 19: [1H1-2] Cho khối chóp
.S ABC
có thể tích bằng
16
. Gọi
,,M N P
lần lượt là trung điểm của các
cạnh
,,SA SB SC
. Tính thể tích V của khối tứ diện
AMNP
.
A.
2V
. B.
6V
. C.
4V
. D.
8V
.
Câu 20: [1H1-2] Cho hình chóp tam giác
.S ABC
có
ABC
là tam giác đều cạnh
a
, hai mặt phẳng
SAB
và
SAC
cùng vuông góc với mặt đáy
ABC
và
2SC a
. Tính theo
a
thể tích
V
của khối chóp
.S ABC
.
A.
3
1
4
Va
. B.
3
3
2
Va
. C.
3
3
6
Va
. D.
3
3
4
Va
.
Câu 21: [1H1-3] Cho hình lập phương
. ' ' ' 'ABCD A B C D
có cạnh bằng
6
. Gọi
G
là trọng tâm tam giác
'A BD
. Tính thể tích
V
của khối tứ diện
GABC
.
A.
12V
. B.
18V
. C.
24V
. D.
36V
.
Câu 22. [2H1-3] Cho khối chóp
.O ABC
. Trên ba cạnh
,,OA OB OC
lần lượt lấy ba điểm
’, ,A B C

sao cho
2 , 4 , 3OA OA OB OB OC OC
. Tính tỉ số
. ' ' '
.
O A B C
O ABC
V
V
A.
1
12
. B.
1
24
. C.
1
16
. D.
1
32
.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 15/73
luyenthitracnghi
Câu 23. [2H1-3] Cho khối lăng trụ tam giác đều
. ’ ’ ’ABC A B C
có tất cả các cạnh đều bằng
a
. Thể tích khối tứ
diện
’ ’ ’A BB C
là
A.
3
3
12
a
B.
3
3
4
a
C.
3
3
6
a
D.
3
12
a
Câu 24. [2H1-4] Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các
đỉnh là các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng
a
. Hãy tính thể tích
của khối tám mặt đều đó:
A.
3
4
a
. B.
3
6
a
. C.
3
12
a
. D.
3
8
a
.
Câu 25. [2H1-3] Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
, cạnh
SB
vuông góc với
đáy và mặt phẳng
SAD
tạo với đáy một góc
60
. Tính thể tích khối chóp
.S ABCD
.
A.
3
33
4
a
V
. B.
3
33
8
a
V
. C.
3
83
3
a
V
. D.
3
43
3
a
V
.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 16/73
luyenthitracnghi
ĐỀ THAM KHẢO SỐ 5
Câu 1. [2D4-2] Hình đa diện đều có tất cả các mặt là ngũ giác có bao nhiêu cạnh?
A.
20
. B.
60
. C.
30
. D.
12
.
Câu 2. [2H1-1] Hình nào sau đây không phải là hình đa diện .
A. Hình trụ. B. Hình tứ diện. C. Hình lập phương. D. Hình chóp.
Câu 3. [2H1-2] Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ sau
Khối tứ diện đều Khối lập phương Bát diện đều Hình
12
mặt đều Hình
20
mặt đều
Mệnh đề nào sau đây đúng?
A. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.
B. Khối lập phương và khối bát diện đều có cùng số cạnh.
C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.
Câu 4. [2D4-1] Số đỉnh của khối bát diện đều là:
A. 6. B. 8. C. 12. D. 4.
Câu 5. [2H1-1]Công thức nào sau đây là công thức tính thể tích khối chóp?
A.
1
.
6
V S h
. B.
.V S h
. C.
1
.
3
V S h
. D.
1
.
2
V S h
.
Câu 6. [2H1-2]Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi
M
là trung điểm
.SC
Mặt phẳng
qua
M
song song với
DC
chia khối chóp thành bao nhiêu khối chóp tứ giác.
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 7. [2D4-2] Cắt khối lăng trụ
.MNP M N P
bởi các mặt phẳng
MN P

và
MNP
ta được những khối
đa diện nào?
A. Hai khối tứ diện và hai khối chóp tứ giác. B. Một khối tứ diện và một khối chóp tứ giác.
C. Ba khối tứ diện.
D. Hai khối tứ diện và một khối chóp tứ giác.
Câu 8. [2H1-1] Thể tích khối lăng trụ đứng tam giác
.ABC A B C
có tất cả các cạnh bằng
a
là .
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
4
a
. D.
3
4
a
.
Câu 9. [2H1-1] Tính theo a thể tích V của khối lập phương
.ABCD A B C D
biết
.AC a
A.
3
3 3 .Va
B.
3
.Va
C.
3
.
27
a
V
D.
3
3
.
9
a
V
Câu 10. [2D4-2] Tính thể tích của khối hộp chữ nhật có diện tích của các mặt bên và mặt đáy lần lượt là
2
10cm
,
2
16 cm
và
2
40cm
.
A.
3
160 cm
. B.
3
400 cm
. C.
3
80 cm
. D.
3
640 cm
.
Câu 11. [2H1-2] Cho hình lập phương
.ABCD A B C D
có cạnh bằng a. Tính thể tích khối tứ diện
ACB D

theo
a
.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 17/73
luyenthitracnghi
A.
3
6
a
. B.
3
2
a
. C.
3
3
a
. D.
3
4
a
.
Câu 12. [2H1-3] Cho hình chóp tứ giác đều
.S ABCD
có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên
và mặt phẳng đáy là
. Mặt phẳng
P
qua AC và vuông góc với mặt phẳng
SAD
chia khối chóp
.S ABCD
thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là
MACD
SABCM
V
V
?
A.
2
cos
B.
2
sin
C.
2
tan
D.
0,9
Câu 13. [2D4-2] Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác vuông tại
0
, , 60A AC a ACB
.
Đường chéo
'BC
của mặt bên
''BCC B
tạo với mặt phẳng
''AA C C
một góc
0
30
. Tính thể tích
của khối lăng trụ theo
a
.
A.
3
6
2
a
. B.
3
6
3
a
. C.
3
6a
. D.
3
26
3
a
.
Câu 14. [2H1-3] Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
A
và
2AB AC a
. Tam giác
SBC
có diện tích bằng
2
2a
và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích
V
của
khối chóp
.S ABC
.
A.
3
4
3
a
V
. B.
3
3
a
V
. C.
3
2Va
. D.
3
2
3
a
V
.
Câu 15. [1H2-3] Tính thể tích khối chóp
.S ABCD
có
ABCD
là hình thang vuông tại
,AB
có
2,AD a AB BC a
,
SA ABCD
, Góc giữa
SCD
và
ABC
là
0
60
. Tính thể tích khối
chóp
.S ABCD
A.
3
6
4
a
. B.
3
33
4
a
. C.
3
63
4
a
. D.
3
6
2
a
.
Câu 16. [2D4-3] Cho hình chóp tứ giác đều S.ABCD. Gọi O là tâm mặt đáy, biết
20SO cm
và khoảng
cách từ điểm O tới mặt bên của khối chóp bằng
12cm
. Tính thể tích khối chóp S.ABCD.
A.
3
3840V cm
. B.
3
6000V cm
. C.
3
1920V cm
. D.
3
3000V cm
.
Câu 17. [2H1-3] Cho một hình chóp tứ giác đều có cạnh đáy bằng
a
và diện tích xung quanh gấp đôi diện
tích đáy. Khi đó thể tích của khối chóp là.
A.
3
3
12
a
. B.
3
2
3
a
. C.
3
3
3
a
. D.
3
3
6
a
.
Câu 18. [2H1-1] Cho tứ diện
ABCD
. Gọi
,MN
lần lượt là trung điểm của
AB
và
AC
. Khi đó tỉ số thể tích
của khối tứ diện
AMND
và khối tứ diện
ABCD
bằng:
A.
1
2
B.
1
4
C.
1
6
D.
1
8
Câu 19. [2D4-2] Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích bằng 1. Trên cạnh
SC
lấy điểm
E
sao cho
2SE EC
. Tính thể tích
V
của khối tứ diện
SEBD
.
A.
2
3
V
. B.
1
12
V
. C.
1
3
V
. D.
1
6
V
.
Câu 20. [2H1-3] Cho hình chóp đều
.S ABC
có cạnh đáy bằng
a
, khoảng cách giữa cạnh bên
SA
và cạnh
đáy
BC
bằng
3
4
a
. Thể tích khối chóp
.S ABC
tính theo
a
là .
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 18/73
luyenthitracnghi
A.
3
33
16
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
33
8
a
.
Câu 21. [1H2-2] Cho khối hộp
. ' ' ' 'ABCD A B C D
có thể tích bằng
3
24dm
.Gọi
M
là trung điểm của
'AD
Tính thể tích khối chóp
M.ABC
?
A.
3
6dm
. B.
3
2dm
. C.
3
3dm
. D.
3
9dm
.
Câu 22. [2D4-3] Cho hình chóp S.ABCD có thể tích bằng 1. Biết mặt đáy là hình vuông tâm O và SO vuông
góc với mặt phẳng
ABCD
. Gọi I là trung điểm cạnh SD, tính thể tích khối tứ diện IOBC.
A.
1
2
IOBC
V
. B.
1
12
IOBC
V
. C.
1
8
IOBC
V
. D.
1
24
IOBC
V
.
Câu 23. [2H1-4] Cho hình hộp
.ABCD A B C D
. Tỉ số thể tích của khối tứ diện
ACB D

và khối hộp
.ABCD A B C D
bằng
A.
1
2
. B.
1
3
. C.
1
4
. D.
1
6
.
Câu 24. [2H1-3] Một túp lều có dạng hình lăng trụ đứng có kích thước như hình bên. Tính thể tích của túp
lều.
A.
3
280m
B.
3
280
m
3
C.
3
560m
D.
3
560
m
3
Câu 25. [2H1-4] Cho tứ diện
ABCD
có các cạnh
AB AC,
và
AD
đôi một vuông góc nhau;
6 ,AB a
AC a AD a 7 , 4 .
Gọi
M N P, ,
tương ứng là trung điểm các cạnh
BC CD BD, , .
Thể tích
V
của tứ diện
.AMNP
A.
3
7a
2
. B.
3
14a
. C.
3
28
a
3
. D.
3
7a
.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 19/73
luyenthitracnghi
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 1
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
A
D
B
C
A
A
D
D
C
A
11
12
13
14
15
16
17
18
19
20
C
D
B
B
B
A
A
A
A
B
21
22
23
24
25
B
A
B
A
B
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 2
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
A
C
B
C
D
A
A
A
C
A
11
12
13
14
15
16
17
18
19
20
B
B
A
B
D
B
D
D
C
A
21
22
23
24
25
A
B
A
B
A
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 3
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
A
C
B
D
D
D
D
A
A
D
11
12
13
14
15
16
17
18
19
20
A
D
D
C
C
A
B
B
A
A
21
22
23
24
25
C
C
A
A
D
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 4
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
C
C
A
C
B
C
B
A
C
B
11
12
13
14
15
16
17
18
19
20
A
A
A
D
D
D
A
B
A
A
21
22
23
24
25
A
B
A
B
C
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 5
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
C
A
B
A
C
C
C
C
D
C
11
12
13
14
15
16
17
18
19
20
C
A
C
D
A
B
D
A
C
B
21
22
23
24
25
B
C
B
A
D
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 20/73
luyenthitracnghi
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 1
Câu 1. [2H1-1] Hình nào dưới đây không phải là một khối đa diện?
A. B. C. D.
Hướng dẫn giải
Chọn A.
Câu 2. [2H1-1] Khối đa diện nào được cho dưới đây là khối đa diện đều?
A. Khối chóp tam giác đều. B. Khối lăng trụ đều.
C. Khối chóp tứ giác đều D. Khối lập phương.
Hướng dẫn giải:
Chọn D.
Câu 3. [2H1-2] Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống, mệnh
đề sau trở thành mệnh đề đúng:
“Khối đa diện (H) được gọi là khối đa diện lồi nếu. nối hai điểm bất kì của (H) luôn thuộc (H)”.
A. Đường thẳng. B. Đoạn thẳng.
C. Đường gấp khúc. D. Đường cong.
Hướng dẫn giải.
Chọn B.
Câu 4. [2H1-1] Khối tứ diện đều là khối đa diện đều loại nào?
A.
4;3 .
B.
3;4 .
C.
3;3 .
D.
5;3 .
Hướng dẫn giải
Chọn C.
Câu 5. [2H1-1] Cho khối hộp có diện tích đáy là
,S
chiều cao tương ứng là
.h
Khi đó thể tích khối
hộp là
A.
2
.Sh
. B.
2
1
.
3
Sh
. C.
. D.
1
.
3
Sh
.
Hướng dẫn giải
Chọn C.
Công thức tính thể tích hình hộp là
.V S h
.
Câu 6. [2H1-2] Mặt phẳng
AB C

chia khối lăng trụ
.ABC A B C
thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp tứ giác.
B. Hai khối chóp tam giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 21/73
luyenthitracnghi
D. Hai khối chóp tứ giác.
Lời giải
Chọn A.
Mặt phẳng
AB C

chia khối lăng trụ
.ABC A B C
thành hai khối chóp
Chóp tam giác:
.A A B C
và chóp tứ giác:
.A BB C C

.
Câu 7. [2H1-2] Tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A.
1
. B.
4
.
C.
5
. D.
6
.
Hướng dẫn giải
Chọn D.
Giả sử hình tứ diện đều
ABCD
sẽ có
6
mặt phẳng đối xứng, đó là mặt phẳng đi qua
1
cạnh và trung
điểm cạnh đối diện.
Câu 8. [2H1-2] Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần
lượt là
15cm
và
5cm
. Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ
nhật sao cho cây nến nằm khít trong hộp. Thể tích của chiếc hộp đó bằng:
A.
1500 ml
. B.
600 6 ml
. C.
1800 ml
. D.
750 3 ml
.
Chọn D.
Ta có
10AB cm
,
53AD cm
50 3
ABCD
S
. 750 3
ABCD
V S h
Câu 9. [2H1-3] Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng
.a
Thể tích khối tứ diện
A B AC

là
A.
3
3
.
6
a
B.
3
.
6
a
C.
3
3
.
12
a
D.
3
3
.
4
a
Hướng dẫn giải
Chọn C
Gọi
H
là hình chiếu của
C
lên
AB
.
Ta có
( ' ')CH AA B
B'
C'
A
C
B
A'
B'
C'
A
A'
B'
C'
A
C
B
S
R
Q
P
N
M
D
C
B
A
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 22/73
luyenthitracnghi
3
2
a
CH
2
''
11
'. ' .
2 2 2
AA B
a
S AA A B a a
23
AA'
1 1 3 3
..
3 3 2 2 12
A B AC B
a a a
V CH S

.
Câu 10. [2H1-3] Cho hình lập phương có tổng diện tích các
mặt bằng
3
12a
. Tính theo
a
thể tích khối lập phương đó.
A.
3
8a
. B.
3
2a
. C.
3
a
. D.
3
3
a
.
Hướng dẫn giải
Chọn A.
Khối lập phương có
6
mặt là hình vuông bằng nhau
Từ giả thiết suy ra diện tích một mặt là
2
2
12
2
6
a
a
.
Cạnh của khối lập phương là
2
22aa
.
Thể tích của khối lập phương là:
3
3
28V a a
.
Câu 11. [2H1-2] Cho hình lập phương
.ABCD A B C D
có diện tích mặt chéo
ACC A

bằng
2
22a
. Thể tích của khối lập phương
.ABCD A B C D
là
A.
3
a
. B.
3
2a
. C.
3
22a
. D.
3
8a
.
Hướng dẫn giải.
Chọn C.
Giả sử hình lập phương có cạnh bằng
x
,
0x
.
Ta có:
2
A
.AC . 2 2 2 2
ACC
S AA x x a x a

.
Vậy
3
3
.
2 2 2
ABCD A B C D
V a a

.
Câu 12. [2H1-2] Một hình chóp tứ giác đều có cạnh đáy bằng
a
,
các mặt
bên tạo với đáy một góc
. Thể tích của khối chóp đó là
A.
3
sin .
2
a
B.
3
tan .
2
a
C.
3
cot .
6
a
D.
3
tan .
6
a
Hướng dẫn giải
Chọn D.
S
A
B
C
D
O
N
H
D'
C'
B'
A'
D
B
C
A
A'
B'
C'
C
B
A
H
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 23/73
luyenthitracnghi
Trong mặt phẳng
ABCD
, gọi
O AC BD
()SO ABCD
M
là trung điểm
CD
.Khi đó
SMO
.
Có
.tan
.tan
2
a
SO OM

nên thể tích khối chóp đã cho là
3
1 tan
..
36
ABCD
a
V SO S

.
Câu 13. [2H1-3] Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
A
,
AC a
,
60ACB 
. Đường chéo
BC
của mặt bên
BCC B

tạo với mặt phẳng
ACC A

một góc
30
. Tính thể tích của khối lăng trụ theo
a
.
A.
3
46
3
a
V
. B.
3
6Va
. C.
3
26
3
a
V
. D.
3
6
3
a
V
.
Hướng dẫn giải
Chọn B.
Xét
ABC
có
0
tan 60 3 3 3.
AB
AB AC a
AC
Ta có
' ' '; ' ' ' .
'
AB AC
AB ACC A BC ACC A BC A
AB AA
Bài ra
0 0 0
1
'; ' ' 30 ' 30 tan 30
'
3
AB
BC ACC A BC A
AC
2 2 2 2 2
' 3 3 ' ' 9 ' 2 2AC AB a CC AC AC a a CC a
3
. ' ' '
11
'. '. . 2 2. 3. 6.
22
ABC A B C ABC
V CC S CC AB AC a a a a
Câu 14. [2H1-3] Cho khối chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2a
.
Tính thể tích
V
của khối chóp
.S ABC
A.
3
13
12
a
V
. B.
3
11
12
a
V
. C.
3
11
6
a
V
. D.
3
11
4
a
V
.
Lời giải
Chọn B.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 24/73
luyenthitracnghi
Do đáy là tam giác đều nên gọi
I
là trung điểm cạnh
, khi đó
AI
là đường cao của tam giác
đáy. Theo định lý Pitago ta có
2
2
3
42
aa
AI a
, và
2 2 3 3
3 3.2 3
aa
AO AI
.
Trong tam giác
SOA
vuông tại
O
ta có
2
2
11
4
3
3
aa
SO a
Vậy thể tích khối chóp
.S ABC
là
3
1 1 3 11 11
..
3 2 2 12
3
a a a
Va
.
Câu 15. [2H1-2] Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật, mặt bên
SAD
là tam giác
đều cạnh
2a
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích khối
chóp
.S ABCD
biết rằng mặt phẳng
()SBC
tạo với mặt phẳng đáy một góc
30 .
A.
3
3
.
2
a
B.
3
2 3 .a
C.
3
23
.
3
a
D.
3
43
.
3
a
Hướng dẫn giải
.
Chọn B.
Gọi
lần lượt là trung điểm của
,AD BC
23
3
2
a
SI a
(
SI
là đường cao của tam giác đều
SAD
).
Ta có
,
SAD ABCD AD
SI AD SI SAD SI ABCD
SAD ABCD

JI
là hình chiếu vuông góc của
JS
lên
ABCD
.
O
I
A
C
B
S
S
A
D
B
C
I
J
30
a2
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 25/73
luyenthitracnghi
Khi đó,
, , 30SBC ABCD JS JI SJI
SIJ
vuông tại
I
3
tan 3
t an30
tan
SI SI a
SJI IJ a
IJ
SJI
3
1 1 1
. . . .2 .3 . 3 2 3
3 3 3
SABCD ABCD
V S SI AD IJSI a a a a
(đơn vị thể tích).
Câu 16. [2H1-3] Cho hình chóp tứ giác đều có cạnh đáy bằng
x
. Diện tích xung quanh gấp đôi
diện tích đáy. Khi đó thể tích của khối chóp bằng:
A.
3
.3
6
x
. B.
3
.3
2
x
. C.
3
.3
12
x
. D.
3
.3
3
x
.
Hướng dẫn giải
Chọn A.
2
; S 4. 2 .
ABCD xq SCD
S x S SI x
Theo yêu cầu bài toán
2
2.SI x x SI x
2
2 2 2
3
42
x
SO SI OI x x
3
2
1 1 3 . 3
. . .
3 3 2 6
SABCD ABCD
x
V SO S x x
Câu 17. [2H1-3] Một hình chóp tam giác đều có cạnh bên bằng
b
và cạnh bên tạo với mặt phẳng
đáy một góc
. Thể tích của hình chóp đó là
A.
32
3
cos sin
4
b

. B.
32
3
sin cos
4
b

. C.
32
3
cos sin
4
b

. D.
3
3
cos sin
4
b

.
Hướng dẫn giải
O
A
D
B
C
S
I
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 26/73
luyenthitracnghi
Chọn A.
Gọi
M
là trung điểm
,
H
là tâm tam giác
ABC
.
Ta có:
SH ABC
.
Xét tam giác
SHA
vuông tại
H
, ta có:
sin sin
cos cos
SH SA b
AH SA b




33
cos
22
AM AH b
.
Mà:
32
3 cos
2
3
AB AM
AM AB b
.
2
32
3 3 cos
11
. . . sin .
3 3 4
3
cos sin
4
SABC ABC
b
V SH S b
b


Câu 18. [2H1-1] Cho tứ diện
ABCD
. Gọi
'B
và
'C
lần lượt là trung điểm của
AB
và
AC
. Tính tỉ
số thể tích của khối tứ diện
''AB C D
và khối tứ diện
ABCD
.
A.
1
4
. B.
1
2
. C.
1
6
. D.
1
8
.
Hướng dẫn giải:
Chọn A.
Ta có:
1 1 1
2 2 4
AB C D
ABCD
V
AB AC
V AB AC


.
Câu 19. [2H1-2] Cho khối chóp
.S ABC
có thể tích bằng
16
.
Gọi
,,M N P
lần lượt là trung điểm của các cạnh
,,SA SB SC
. Tính thể tích V của khối tứ diện
AMNP
.
A.
2V
. B.
6V
.
C.
4V
. D.
8V
.
Hướng dẫn giải
Chọn A.
Ta có
3
.
.
11
..
28
S MNP
S ABC
V
SM SN SP
V SA SB SC



Do đó
.
16
2
8
S MNP
V 
.
Do
M
là trung điểm
, ta có
( ,( )) ( ,( ))d A MNP d S MNP
Suy ra
.
2
AMNP S MNP
VV
.
Câu 20. [2H1-2] Cho tứ diện
ABCD
có hai mặt
ABC
,
BCD
là các tam giác đều cạnh
a
và nằm
trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện
ABCD
là:
A.
3
3
4
a
. B.
3
8
a
. C.
3
4
a
. D.
3
3
8
a
.
B
C
S
M
A
N
P
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 27/73
luyenthitracnghi
Hướng dẫn giải
Chọn B
Gọi
H
là trung điểm
. Tam giác
DBC
đều nên
DH
vừa là trung tuyến vừa là đường cao, do
đó
DH BC
và
3
2
a
DH
Mặt khác
DBC ABC
và
DBC ABC BC
nên
DH ABC
.
Thể tích:
23
1 1 3 3
. . .
3 3 2 4 8
ABC
a a a
V DH S
Câu 21. [2H1-3] Một hình hộp chữ nhật
.ABCD A B C D
có ba kích thước là
2cm
,
3cm
và
6cm
.
Thể tích của khối tứ diện
.A CB D

bằng
A.
3
8 cm
. B.
3
12 cm
. C.
3
6 cm
. D.
3
4 cm
.
Hướng dẫn giải
Chọn B.
Ta có :
Cách 1:
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 28/73
luyenthitracnghi
. . . . . .
. . .
. . .
. . .
..
4
4
1
4.
6
11
.2.
33
ABCD A B C D B AB C D ACD A B AD C B C D A CB D
ABCD A B C D B AB C A CB D
A CB D ABCD A B C D B AB C
A CB D ABCD A B C D ABCD A B C D
A CB D ABCD A B C D
V V V V V V
V V V
V V V
V V V
VV
3
3.6 12cm
Cách 2 :
3
. ' ' .A BC D
11
.2.3.6 12
33
A CB D ABCD
V V cm
Câu 22. [2H1-3] Cho khối chóp
.S ABC
có
6, 2, 4, 2 10SA SB SC AB
và góc
90SBC
,
120ASC
. Mặt phẳng
P
đi qua
B
và trung điểm
N
của cạnh
đồng thời vuông góc
với mặt phẳng
SAC
cắt
SA
tại
M
. Tính tỉ số thể tích
.
.
.
S BMN
S ABC
V
k
V
A.
1
6
k
. B.
2
5
k
. C.
2
9
k
. D.
1
4
k
.
Hướng dẫn giải
Chọn A.
Trên cạnh
lấy điểm
1
A
sao cho
1
2SA
. Khi đó ta có
2 2 2 2 2 2
11
1
cos
2 . 2 .
AS AB SB AB AA A B
SAB
AS AB AB AA

1
22AB
Mặt khác
1
2
2
BN SC
,
1
23AN
. Suy ra tam giác
1
A BN
vuông tại
B
.
Gọi
D
là hình chiếu của
S
xuống mặt phẳng
1
A BN
. Do
1
2SA SB SN
nên
D
là tâm đường tròn ngoại tiếp tam giác
1
A BN
. Do đó
D
trung điểm
1
AN
.
Vậy ta có
1
SD A BN
nên
11
SAC A BN A M
.
Từ đó ta có
.
1
.
1 1 1
..
3 2 6
S BMN
S ABC
V
SA SN
k
V SA SC
.
Câu 23. [2H1-3] Cho khối lăng trụ
.ABC A B C
có thể tích
V
, điểm
P
thuộc cạnh
,AA Q
thuộc
BB
sao cho
1
;
3
PA QB
R
PA QB

là trung điểm
CC
. Tính thể tích khối chóp tứ giác
.R ABQP
theo
V
.
A.
2
3
V
. B.
1
3
V
. C.
3
4
V
. D.
1
2
V
.
Hướng dẫn giải
Chọn B
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 29/73
luyenthitracnghi
Cách 1: Nếu bài toán đúng với mọi hình lăng trụ thì bài toán cũng phải đúng với hình lăng trụ đặc
biệt.
Giả sử
.ABC A B C
là khối lăng trụ đứng có đáy là tam giác
ABC
vuông cân tại
A
và
4; 4AB AC AA
.
Chọn hệ trục tọa độ với
; ; .AB Ax AC Ay AA Az
Thể tích khối lăng trụ
.
1
4 4 4 32
2
ABC A B C ABC
V S AA
.
Diện tích
1
4.1 .4.2 8
2
ABQP APTB PTQ
S S S
Chiều cao hình chóp
.R ABQP
:
, , 4
R
d R ABQP d R Oxz y
( Vì
0;4;2 ; : 0R Oxz y
).
Suy ra thể tích khối chóp:
.
1 1 32
. , .8.4
3 3 3
R ABQP ABQP
V S d R ABQP
Vậy
.
.
1
3
R ABPQ
ABC A B C
V
V
.
Cách 2:
. . . .
1 1 2 1
2 2 3 3
R ABQP R ABB A ABC A B C ABC A B C
V V V V
.
Câu 24.
[2H1-4] Người ta muốn xây một bể chứa nước dạng khối hộp chữ nhật trong một phòng
tắm. Biết chiều dài, chiều rộng, chiều cao của khối hộp đó lần lượt là
3m
;
1,2m
;
1,8m
(người ta chỉ xây hai mặt thành bể như hình vẽ bên). Biết mỗi viên gạch có chiều dài
20cm
, chiều rộng
10cm
, chiều cao
5cm
. Hỏi người ta sử dụng ít nhất bao nhiêu viên gạch để xây
bể đó và thể tích thực của bể chứa bao nhiêu lít nước? (Giả sử lượng xi măng và cát không
đáng kể).
A
C
B
A'
C'
B'
P
Q
R
A'
A
B'
B
P
Q
T
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 30/73
luyenthitracnghi
A.
738
viên,
5742
lít. B.
730
viên,
5742
lít.
C.
738
viên,
5740
lít. D.
730
viên,
5740
lít.
Hướng dẫn giải
Chọn A.
Thể tích của bể là
18.11.29 5742Vl
.
Thể tích của
1
viên gạch là
3
1dm
, thể tích cần xây
dựng là
3
(30 11).18 738dm
, suy ra số viên ít
nhất cần dùng là
738
viên.
Câu 25. [2H1-3] Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
, mặt bên
SAB
là tam giác
đều, mặt bên
SCD
là tam giác vuông cân đỉnh
S
. Thể tích khối chóp
.S ABCD
là
A.
3
3
.
6
a
B.
3
3
.
12
a
C.
3
.
6
a
D.
3
3
.
4
a
Hướng dẫn giải
Chọn B
Gọi
M
,
N
lần lượt là trung điểm của
,AB CD
.
Ta có
()SMN ABCD
nên hình chiếu
H
của
S
lên mp
ABCD
thuộc
MN
.
3
,,
22
aa
SM SN MN a
2
2
2 2 2 2
3
22
aa
SM SN a MN






nên tam giác
SMN
vuông tại
S
.
3
.
.3
22
..
4
aa
SM SN a
SH MN SM SN SH
MN a
3
2
1 1 3 3
..
3 3 4 12
ABCD
aa
V SH S a
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 2
Câu 1. [2H1-1]
hình (a) hình (b) hình (c) hình (d)
1,8dm
1dm
1dm
3m
1,2m
H
A
B
C
D
S
M
N
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 31/73
luyenthitracnghi
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là
A. hình (a). B. hình (b). C. hình (c). D. hình (d).
Lời giải
Chọn A.
Hình đa diện là hình tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
1. Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung hoặc chỉ có một đỉnh chung hoặc chỉ
có một cạnh chung.
2. Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Các hình (b), (c), (d) đều không thỏa mãn tính chất số 2.
Câu 2. [2H1-1]
hình (a). hình (b). hình (c). hình (d).
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C.
Hình (b) không thỏa mãn tính chất số 2.
Câu 3. [2H1-1]Phát biểu nào sau đây là đúng?
A. Hình bát diện đều có 8 đỉnh, 12 cạnh, 6 mặt.
B.Hình bát diện đều có 6 đỉnh, 12 cạnh, 8 mặt.
C. Hình bát diện đều có 12 đỉnh, 8 cạnh, 6 mặt.
D. Hình bát diện đều có 8 đỉnh, 6 cạnh, 12 mặt.
Lời giải
Chọn B
Hình bát diện đều có 6 đỉnh, 12 cạnh, 8 mặt.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 32/73
luyenthitracnghi
Câu 4. [2H1-2]Một hình hộp đứng có hai đáy là hình thoi (không phải là hình vuông) có bao
nhiêu mặt phẳng đối xứng?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C.
Gọi
.ABCD A B C D
là hình hộp đứng đã cho và gọi
1 1 1 1
, , ,A B C D
lần lượt là trung điểm của
, , ,AA BB CC DD
khi đó các phép đối xứng qua mặt phẳng
1 1 1 1
;;ACC A BDD B ABC D
đều biến
hình hộp thành chính nó. Vậy hình hộp nói trên có 3 mặt phẳng đối xứng.
Câu 5. [2H1-1]Thể tích khối chóp có diện tích đáy B và chiều cao h là:
A.
V Bh
.
B.
1
2
V Bh
. C.
2V Bh
. D.
1
3
V Bh
.
Lời giải
Chọn D.
Câu 6. [2H1-2]Trong các mệnh đề sau mệnh đề nào sai ?
A.Lắp ghép hai khối hộp sẽ được một khối đa diện lồi
B.Khối hộp là khối đa diện lồi
C.Khối tứ diện là khối đa diện lồi
D.Khối lăng trụ tam giác là khối đa diện lồi
Lời giải
Chọn A.
Lắp ghép hai khối hộp bất kỳ có thể thu được một khối đa diện không phải là đa diện lồi. Ví dụ:
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 33/73
luyenthitracnghi
Câu 7. [2H1-2]Nếu không sử dụngthêm điểm nào khác ngoài các đỉnh của hình lập phương thì
có thể chia hình lập phương thành
A.Một tứ diện đều và bốn hình chóp tam giác giác đều
B.Năm tứ diện đều
C.Bốn tứ diện đều và một hình chóp tam giác đều
D.Năm hình chóp tam giác giác đều,không có tứ diện đều
Lời giải
Chọn A.
Câu 8. [2H1-1]Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
.V B h
B.
1
.
3
V B h
C.
1
.
2
V B h
D.
4
.
3
V B h
.
Lời giải
Chọn A.
Câu 9. [2H1-3] Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
2,AD a AB a
.Gọi
H
là
trung điểm của
AD
,biết
SH ABCD
.Tính thể tích khối chóp biết
5SA a
.
A.
3
23
3
a
B.
3
43
3
a
C.
3
4
3
a
D.
3
2
3
a
.
Lời giải
Chọn C.
H là trung điểm của AD => AH=AD:2=a.
SH ABCD
=> SH là đường cao của khối chóp.
2 2 2 2
52SH SA AH a a a
.
3
.
1 1 4
. 2 .2 .
3 3 3
S ABCD ABCD
a
V SH S a a a
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 34/73
luyenthitracnghi
Câu 10. [2H1-3] Cho hình lập phương
’ ’ ’ ’.ABCDA B C D I
là trung điểm
’BB
.Mặt phẳng
’DIC
chia
khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng:
A.
1
3
. B.
3
4
. C.
4
14
. D.
1
2
.
Lời giải
Chọn A.
Kéo dài C’I cắt BC tại E.
3
1 1 1
. . 2 .
3 3 2 3
C CDE DCE
a
V CC S a a a
3 3 3 3
11
2 sin135
3 3 2 2 3 12 4
DIBCC CC DE DIBE
a a a a a
V V V a a

33
3
3
44
A ABIC D B ABCDA B C D DIBCC
aa
V V V a
3
3
1
4
3
3
4
DIBCC
A ABIC D B
a
V
a
V
.
Câu 11: [1D1-2] Cho hình lập phương
. ' ' ' 'ABCD A B C D
có
' 4 3AC
. Thể tích khối lập phương
. ' ' ' 'ABCD A B C D
là
A.
32.
B.
43
C.
64.
D.
16.
Lời giải
Chọn B.
Đặt
' , . ' ' ' 'AA a ABCD A B C D
là hình lập phương
2AB a AC a
.
Tam giác
'A AC
vuông tại
A
, có
2 2 2 2
' ' 3 48 4A C A A AC a a
.
Thể tích khối lập phương là
33
. ' ' ' '
4 64
ABCD A B C D
Va
Câu 12: [2H1-2] Cho khối chóp đều S.ABCD có cạnh đáy bằng
3a
. Tính thể tích khối chóp
S.ABCD biết góc giữa cạnh bên và mặt đáy bằng 60°.
A.
3
2
2
a
B.
3
32
2
a
C.
3
36
2
a
D.
3
6
2
a
Lời giải
Chọn B.
Gọi O là tâm của hình vuông ABCD khi đó
SO ABCD
Gọi
O
là tâm của hình vuông
ABCD
khi đó
0
60SDO
chính là góc giữa cạnh bên
SD
và mặt
phẳng
ABCD
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 35/73
luyenthitracnghi
Lại có
6
6
22
BD a
BD a OD
Suy ra
0
0
6 tan60 3 2
tan60
22
aa
SO OD
Vậy
3
.
1 3 2
.
32
S ABCD ABCD
a
V SO S
Câu 13: [2H1-3] Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông tại
A
với
; 60AC a ACB
. Biết
'BC
hợp với
'ACC A
một
góc
0
30
. Thể tích của khối lăng trụ
. ' ' 'ABC A B C
là:
A.
3
6a
B.
3
2a
C.
3
3a
D.
3
23a
Lời giải
Chọn A.
Lăng trụ đứng
. ' ' ' 'ABC A B C AA ABC
.
Ta có
0
tan60 3 3
AB
AB a
AC
.
Lại có
' ' ' '
' ' ' '
' ' '
B A A C
B A ACC A
B A A A

góc giữa
'BC
và mặt phẳng
''ACC A
là
00
' ' 1
' ' 30 tan30
'
3
AB
B CA
AC
' ' ' 3 3. 3 3A C A B a a
2 2 2 2
' ' 9 2 2AA A C AC a a a
Vậy
3
. ' ' '
1
' . 2 2. . 3 6
2
ABC A B C ABC
V A A S a a a a
Câu 14: [2H1-3] Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, góc giữa đường
thẳng
SA
và mặt phẳng
ABC
bằng
0
45
. Hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là điểm
H
thuộc
BC
sao cho
3BC BH
. Thể tích khối chóp
.S ABC
là:
A.
3
21
18
a
B.
3
21
36
a
C.
3
21
12
a
D.
3
21
27
a
Lời giải
Chọn B.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 36/73
luyenthitracnghi
Gọi
M
là trung điểm của
BC
Ta có:
3
;
2 2 3 6
a a a a
AM MH BM BH
22
7
3
a
AH AM HM
Lại có
7
45
3
a
SH ABC SAH SH HA
Suy ra
23
1 1 7 3 21
. . .
3 3 3 4 36
ABC
a a a
V SH S
.
Câu 15: [2H1-2] Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh a. Hai mặt phẳng
SAB
và
SAD
cùng vuông góc với mặt phẳng
ABCD
. Đường thẳng
SC
tạo với đáy
một góc bằng
0
45
. Gọi
,MN
lần lượt là trung điểm của cạnh
,AB AC
. Thể tích của khối
chóp
.S MCDN
là bao nhiêu?
A.
3
52
12
a
B.
3
52
6
a
C.
3
52
8
a
D.
3
52
24
a
Lời giải
Chọn D.
Ta có:
SAB ABCD
SA ABCD
SAD ABCD

Lại có
2 .tan45 2AC a SA AC a
Mặt khác
MNDC ABCD AMN MBC
S S S S
2 2 2
2
5
8 4 8
a a a
a
Do đó
3
.
1 5 2
.
3 24
S MNDC MNDC
a
V SA S
.
Câu 16: [2-H1-3] Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Gọi
SH
là chiều cao
của hình chóp, khoảng cách từ trung điểm
I
của
SH
đến mặt bên
SBC
bằng
b
. Tính
thể tích
V
của khối chóp
.S ABCD
.
A.
22
3 16
ab
V
ab
. B.
3
22
2
3 16
ab
V
ab
. C.
22
16
ab
V
ab
. D.
22
2
16
ab
V
ab
.
Lời giải
Chọn B.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 37/73
luyenthitracnghi
.
Vì
.S ABCD
là hình chóp tứ giác đều suy ra
H
là tâm của hình vuông
ABCD
.
Gọi
M
là trung điểm
BC
,
K
là hình chiếu vuông góc của
H
lên
SM
.
Ta có:
BC SH
BC SHM
BC HM

.
SBC SHM
, mà
HK SM HK SBC
.
Suy ra
22HK IJ b
, ta có.
22
22
22
.2
16
HK HM ab
SH
HM HK
ab

. Vậy
3
22
2
3 16
ab
V
ab
.
Câu 17: [2-H1-3] Hình chóp tam giác đều
.S ABC
có
AB a
, góc giữa
SA
và đáy bằng
0
30
. Thể
tích khối chóp là.
A.
3
2
12
a
. B.
3
3
72
a
. C.
3
3
12
a
. D.
3
3
.
36
a
Lời giải
Chọn D.
Gọi
O
là tâm của đường tròn ngoại tiếp tam giác
ABC
.
Vì
.S ABC
là hình chóp tam giác đều nên
SO ABC
.
.
Ta có
OA
là hình chiếu vuông góc của
SA
lên
ABC
nên
0
, 30SA ABC SAO
.
Tam giác
ABC
đều, cạnh
a
nên
2
3
4
ABC
a
S
và
3
2
a
AM
.
Xét tam giác vuông
SAO
, ta có
3
tan
2
2
3
SO SO SO
SAO
AO AM
AM
.
H
A
D
C
S
B
M
K
I
J
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 38/73
luyenthitracnghi
2 tan
33
AM SAO a
SO
.
Thể tích
.S ABC
là.
23
1 3 3
..
3 3 4 36
a a a
V
.
Câu 18: [2-H1-1] Cho tứ diện
ABCD
. Gọi
'B
và
'C
lần lượt là trung điểm của
AB
và
AC
. Tính tỉ
số thể tích của khối tứ diện
''AB C D
và khối tứ diện
ABCD
.
A.
1
6
. B.
1
8
. C.
1
2
. D.
1
4
.
Lời giải
Chọn D.
Ta có:
1 1 1
2 2 4
AB C D
ABCD
V
AB AC
V AB AC


.
Câu 19: [2-H1-2] Cho khối chóp
.S ABC
có
9, 4, 8SA SB SC
và đôi một vuông góc. Các điểm
,,A B C
thỏa mãn
2. ,SA SA
3. ,SB SB
4. .SC SC
Thể tích khối chóp
.S A B C
là.
A.
16
. B.
12
. C.
2
. D.
24
.
Lời giải
Chọn C.
.
11
. . . . .
36
S ABC SBC
V SAS SASB SC
.
Ta có:
1
..
24
SA B C
SABC
V
SA SB SC
V SA SB SC
.
2
SA B C
V
.
.
Câu 20: [2-H1-2] Cho tứ diện
ABCD
có thể tích bằng 12 và
G
là trọng tâm tam giác
BCD
. Tính
thể tích
V
của khối chóp
.AGBC
.
A.
4V
. B.
5V
. C.
6V
. D.
3V
.
C'
B'
A'
C
B
A
S
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 39/73
luyenthitracnghi
Lời giải
Chọn A.
.
Cách 1:
Phân tích: tứ diện
ABCD
và khối chóp
.AGBC
có cùng đường cao là khoảng cách từ
A
đến mặt
phẳng
BCD
. Do
G
là trọng tâm tam giác
BCD
nên ta có

BGC BGD CGD
S S S
3


BCD BGC
SS
(xem phần chứng minh).
Áp dụng công thức thể tích hình chóp ta có:
.
.
1
1
.
.
3
3
3
1
1
.
.
3
3
ABCD BCD
BCD
ABCD BCD
A GBC GBC
GBC
A GBC GBC
V h S
hS
VS
VS
hS
V h S
.
11
.12 4
33
A GBC ABCD
VV
.
Cách 2:
,
11
,,
33
,
d G ABC
GI
d G ABC d D ABC
DI
d D ABC
.
Nên
.
11
, . . 4.
33
G ABC ABC DABC
V d G ABC S V
.
.
Câu 21: [2-H1-3] Cho khối hộp
. ' ' ' 'ABCD A B C D
có thể tích bằng
12
( đơn vị thể tích). Gọi
,,M N P
lần lượt là trung điểm của các cạnh
, , 'AD DC AA
. Tính thể tích khối chóp
.P BMN
.
A.
3
4
V
. B.
2V
. C.
3
2
V
. D.
3V
.
Lời giải
G
I
D
B
C
A
H
1
H
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 40/73
luyenthitracnghi
Chọn A.
.
Vì
P
là trung điểm
'AA
nên chiều cao khối chóp
.P BMN
bằng một nữa chiều cao khối
. ' ' ' 'ABCD A B C D
.
3
8
BMN ABCD
SS
. Tính bằng cách cho cạnh độ dài rồi tính bằng cách trừ phần dư.
Vậy
. ' ' ' '
1 1 3 3
. . .
3 2 8 4
P BMN ABCDA B C D
VV
.
Câu 22: [2-H1-3] Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy
một góc
60
. Gọi
M
là điểm đối xứng với
C
qua
D
;
N
là trung điểm của
SC
, mặt
phẳng (
BMN
) chia khối chóp
.S ABCD
thành hai phần. Tính tỉ số thể tích giữa hai phần
đó.
A.
1
7
. B.
7
5
. C.
7
3
. D.
1
5
.
Lời giải
Chọn B.
.
Đặt
1
1
2
2
?
SABIKN
NBCDIK
VV
V
VV
V

.
*
23
.
1 6 6
.
3 2 6
S ABCD
a
V a a
.
*
3
.
1 1 1 6 1 6
. . . . . . .2
3 3 2 3 4 2 12
N BMC BMC BMC
SO a
V NH S S a a a

.
* Nhận thấy
K
là trọng tâm của tam giác
SMC
2
3
MK
MN

.
*
.
.
1 1 2 1
. . . .
2 2 3 6
M DIK
M CBN
V
MD MI MK
V MC MB MN
.
P
N
M
B'
C'
D'
D
A
B
C
A'
H
N
M
D
A
B
C
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 41/73
luyenthitracnghi
33
2 . . .CBN
5 5 6 5 6
.
6 6 12 72
M CBN M DIK M
V V V V a a
.
3
3 3 3
1
1 . 2
3
2
76
6 5 6 7 6 7
72
6 72 72 5
56
72
S ABCD
a
V
V V V a a a
V
a
.
Câu 23: [2-H1-3] Cho khối lập phương
. ’ ’ ’ ’ABCD A B C D
cạnh
a
. Gọi
O
và
’O
lần lượt là tâm của
ABCD
và
’ ’ ’ ’A B C D
. Thể tích phần chung nhau của hai khối chóp
. ’ ’ ’ ’O A B C D
và
’.O ABCD
là:
A.
3
.
12
a
V
B.
3
.
6
a
V
C.
3
.
4
a
V
D.
3
.
3
a
V
Lời giải
Chọn A. – NVP
Trắc nghiệm:
Tự luận:
- Dễ xác định được phần giao nhau của hai khối
chóp O.A’B’C’D’ và O’.ABCD là khối bát diện:
OMNPQO’.
- Và
'
1
.OO'.
3
OMNPQO MNPQ
VS
.
- Với
OO' , .
2
a
a MN
-
2
3
'
1
. . .
3 2 12
OMNPQO
aa
Va




Câu 24: [2-H1-4] Người ta muốn mạ vàng cho bề mặt phía ngoài của một cái hộp dạng hình hộp
đứng không nắp (nắp trên), có đáy là một hình vuông. Tìm chiều cao của hộp để lượng
vàng phải dùng để mạ là ít nhất, biết lớp mạ ở mọi nơi như nhau, giao giữa các mặt là
không đáng kể và thể tích của hộp là
3
4 dm
.
A.
1,5 dm
. B.
1 dm
. C.
0,5 dm
. D.
2 dm
.
Lời giải
Chọn B.
Gọi
, , 0x y x y
lần lượt là độ dài cạnh đáy, chiều cao của hình hộp.
Thể tích khối hộp là
22
2
4
4V x y x y y
x
.
Diện tích cần mạ vàng
2 2 2
3
16 8 8
4 3 64S x xy x x
x x x
đạt giá trị nhỏ nhất khi chỉ khi.
8
21x x y
x
.
Câu 25: [2-H1-3] Cho hình chóp
.S ABC
có
SA a
, tam giác
ABC
đều, tam giác
SAB
vuông cân
tại
S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp
.S ABC
bằng?
A.
3
6
12
a
. B.
3
6
4
a
. C.
3
6
8
a
. D.
3
6
24
a
.
Lời giải
M
N
P
Q
O'
O
B'
A'
C'
D'
D
A
B
C
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 42/73
luyenthitracnghi
Chọn A.
.
Tam giác
SAB
vuông cân tại
S
và
SA a
nên
2AB a
.
Gọi
M
là trung điểm
AB
, ta có
SM AB
và
2
22
AB a
SM 
(
SM
là đường trung tuyến của tam
giác
SAB
vuông cân tại
S
).
Mặt khác
SAB ABC
,
SM AB
và
SAB ABC AB
nên
SM ABC
.
Suy ra
SM
là đường cao của hình chóp
.S ABC
ứng với đáy là tam giác
ABC
.
Thể tích khối chóp
.S ABC
là.
2
3
.
23
1 1 2 6
. . .
3 3 2 4 12
S ABC ABC
a
aa
V SM S
.
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 3
Câu 1. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mỗi hình đa diện có ít nhất bốn đỉnh.
B. Mỗi hình đa diện có ít nhất ba đỉnh.
C. Số đỉnh của một hình đa diện lớn hơn hoặc bằng số cạnh của nó.
D. Số mặt của một hình đa diện lớn hơn hoặc bằng số cạnh của nó.
Hướng dẫn giải
Chọn A.
Vì hình chóp tam giác (tứ diện) có số đỉnh, số cạnh, số mặt là ít nhất trong tất cả các hình đa diện. Do đó
"Mỗi hình đa diện có ít nhất bốn đỉnh" là đúng.
Chú ý: Do A đúng nên B sai. Ví dụ chóp tam giác có 4 đỉnh, 4 mặt và 6 cạnh nên C, D sai.
Câu 2. Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất:
A. Năm cạnh. B. Bốn cạnh. C. Ba cạnh. D. Hai cạnh.
Hướng dẫn giải
Chọn C.
Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.
Câu 3. Trong các mệnh đề sau, mệnh đề nào sai?
A. Khối tứ diện là khối đa diện lồi.
B. Lắp ghép hai khối hộp luôn được một khối đa diện.
C. Khối hộp là khối đa diện lồi.
D. Khối lăng trụ tam giác đều là khối đa diện lồi.
Hướng dẫn giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 43/73
luyenthitracnghi
Chọn B.
Khối tứ diện, khối hộp và khối lăng trụ tam giác đều đều là các khối đa diện lồi. Suy ra B sai.
Chú ý: B sai vì ta có thể ghép 2 khối hộp sao cho hai mặt (đa giác) phân biệt có hai cạnh chung, suy ra
không thỏa mãn tính chất 1 nên B sai.
Câu 4. Trong không gian có tất cả bao nhiêu loại khối đa diện đều?
A.
2.
B.
3.
C.
4.
D.
5.
Hướng dẫn giải
Chọn D.
Trong không gian có tất cả 5 loại khối đa diện đều.
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA vuông góc với đáy,
2SA a
.
Tính thể tích khối chóp S.ABCD?
A.
3
2
.
6
a
V
B.
3
2
.
2
a
V
C.
3
2.Va
D.
3
2
.
3
a
V
Hướng dẫn giải
Chọn D
B = S
đáy
= a
2
; h =
3
12
2 . )
33
a
SA a V B h
Câu 6. Phân chia khối lập phương
.ABCD A B C D
bởi ba mặt phẳng
A BD
,
DDBB

,
B CD

ta
được những khối đa diện nào?
A. Hai khối tứ diện và một khối lăng trụ tứ giác.
B. Ba khối tứ diện và một khối lăng trụ tam giác.
C. Hai khối tứ diện và một khối lăng trụ tam giác.
D. Hai khối tứ diện và hai khối chóp tứ giác.
Hướng dẫn giải
Chọn D.
Câu 7. Phân chia khối lăng trụ
.ABC A B C
bởi hai mặt phẳng
AB D

và
AB D
ta được các khối nào
sau đây?
A. Khối chóp tứ giác
.DA B D B

và khối tứ diện
ABDB
.
B. Khối chóp tứ giác
.DAB D B

và khối tứ diện
ADD B

.
C'
C
B
A
D
B'
D'
A'
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 44/73
luyenthitracnghi
C. Khối chóp tứ giác
.DAB D B

và khối tứ diện
AA B D
.
D. Ba khối tứ diện
ABDB
,
ADD B

và
AA B D
Hướng dẫn giải
Chọn D.
Câu 8. Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
I
là trung điểm
của
BC
,
6BC a
. Mặt phẳng
A BC
tạo với mặt phẳng
ABC
một góc
60
. Thể tích khối lăng
trụ
.ABC A B C
là
A.
3
92
4
a
. B.
3
92
2
a
. C.
3
92
12
a
. D.
3
92
6
a
.
Hướng dẫn giải
Chọn A.
D
D'
D
D'
D
D'
B
A
A'
B'
B'
A'
A
B'
B
A
A
B'
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 45/73
luyenthitracnghi
2 2 2 2 2 2 2 2
2 6 3 3AB AC BC AB BC a AB a AB a
2
1 1 3
. 3. 3
2 2 2
ABC
a
S AB AC a a
2
2
36
2
6
ABC
S
aa
AI
BC
a
32
tan 60
2
a
AA AI
Vậy
23
.
3 2 3 9 2
.
2 2 4
ABC A B C
a a a
V

.
Câu 9. Cho khối hộp
.ABCD A B C D
có thể tích bằng
72
(ĐVTT). Gọi
1
V
là thể tích khối chóp
.A ABC
. Khi đó, chọn kết quả đúng trong các kết quả cho dưới đây?
A.
1
12V
. B.
1
24V
. C.
1
36V
. D.
1
18V
.
Hướng dẫn giải
Chọn A.
Ta có,
1 . 2 2
1 1 1 1
. 12.
3 3 2 6
A B C ABC
V V V V



Câu 10. Cho khối lập phương
.ABCD A B C D
, có đường chéo
3BD
. Thể tích của khối lập phương
.ABCD A B C D
bằng bao nhiêu?
A.
3
. B.
63
. C.
3
. D.
33
.
Hướng dẫn giải
Chọn D.
60
°
a
6
C
B
A'
B'
C'
A
I
D
D'
A'
B'
C'
A
B
C
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 46/73
luyenthitracnghi
B
C
B'
C'
M
A
A'
Gọi
a
là độ dài cạnh hình lập phương.
Ta có,
22
3BD a
2
33aa
.
Vậy thể tích khối lập phương bằng:
3
33Va
.
Câu 11. Tổng diện tích các mặt bên của khối lập phương bằng 54 .Thể tích khối lập phương bằng?
A.
27.
B.
9.
C.
3 3.
D.
3.
Hướng dẫn giải
Chọn A.
Một mặt của hình lập phương có diện tích bằng : 54:6 = 9
Cạnh của hình lập phương bằng 3
Thể tích khối lập phương bằng : 27
Câu 12.
Cho hình chóp tứ giác đều S.ABCD cạnh đáy AB =a , góc SAC bằng 45
0
.Thể tích khối chóp
bằng:
A.
3
.
3
a
B.
3
2
2
a
C.
3
3
6
a
D.
3
2
6
a
Hướng dẫn giải
Chọn D.
O là tâm hình vuông , h=SO là đường cao hình chóp.
2
22
AC a
SO 
Diện tích đáy : B = a
2
Thể tích :
3
2
6
a
V
Câu 13. Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác đều cạnh
a
. Mặt phẳng
''AB C
tạo với mặt
đáy góc
0
60
. Tính theo
a
thể tích lăng trụ
. ' ' 'ABC A B C
.
A.
3
3
2
a
V
. B.
3
33
4
a
V
. C.
3
3
8
a
V
. D.
3
33
8
a
V
.
Hướng dẫn giải
Chọn D.
Vì
. ' ' 'ABC A B C
là lăng trụ đứng nên
'AA ABC
.
Gọi
M
là trung điểm
''BC
, do tam giác
'''A B C
đều
nên suy ra
' ' 'A M B C
.
Khi đó
0
60 ' ' , ' ' ' , ' 'AB C A B C AM A M AMA
.
Tam giác
'AA M
, có
3
'
2
a
AM
;
3
' ' .tan '
2
a
AA A M AMA
.
Diện tích tam giác đều
2
' ' '
3
4
A B C
a
S
.
D
D'
B'
C'
A'
A
C
B
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 47/73
luyenthitracnghi
Vậy
3
33
.'
8
ABC
a
V S AA
(đvtt).
Câu 14. Cho khối chóp
.S ABC
có
SA
vuông góc với đáy,
46,,SA AB
10BC
và
8CA
. Tính thể
tích
V
của khối chóp
..S ABC
A.
40.V
B.
192.V
C.
32.V
D.
24.V
Lời giải
Chọn C.
Ta có:
2 2 2
100BC AB CA
ABC
vuông tại
A
11
6 8 24
22
. . . .
ABC
S AB AC
Suy ra:
11
4 24 32
33
. . . . .
ABC
V SA S
Câu 15. Cho khối chóp
.S ABCD
có đáy là hình chữ nhật,
3,,AB a AD a
SA
vuông góc với đáy và
mặt phẳng
SBC
tạo với đáy một góc
0
60
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
3
.
a
V
B.
3
3
3
.
a
V
C.
3
.Va
D.
3
3 .Va
Lời giải
Chọn C.
Do
0
60,.BC SAB SBC ABCD SBA
Ta có:
0
2
60 3
3
.tan .tan
.
ABCD
SA AB SBA a a
S AB AD a

Suy ra:
23
11
33
33
. . . .
ABCD
V SA S a a a
Câu 16. Cho hình chóp đều
.S ABCD
có
AB a
. Gọi
M
là trung điểm
AD
và góc tạo bởi mặt phẳng
SCM
và mặt đáy bằng
0
60
. Tính theo
a
thể tích
V
của khối chóp
..S ABCD
A.
3
15
30
.
a
V
B.
3
15
10
.
a
V
C.
3
5
15
.
a
V
D.
3
5
5
.
a
V
Lời giải
Chọn A.
Gọi
AC BD O
. Do
.S ABCD
là hình chóp đều nên
SO ABCD
.
Kẻ
0
60,.OI DM I DM SCM ABCD SIO
8
10
6
4
A
C
B
S
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 48/73
luyenthitracnghi
Do
ABCD
là hình vuông cạnh
a
nên
2
.
ABCD
Sa
Ta có:
22
.
AD a
DM 
Xét tam giác
CDM
ta có:
2
2 2 2
5
22
.
aa
CM CD DM a



Mặt khác:
2
1 1 1
2 2 4 8 8
..
ABCD
COM CAM ABCD
S
a
S S S
Suy ra:
2
2
2 5 5
8 2 10
:
COM
S
a a a
OI
CM
5
10
.tan .
a
SO OI SIO
Vậy
3
2
1 1 15 15
3 3 10 30
. . . . .
ABCD
aa
V SO S a
Câu 17. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên tạo với đáy một góc
. Tính
thể tích khối chóp đó
A.
3
cot
.
12
a
B.
3
tan
.
12
a
C.
2
tan
.
12
a
D.
3
tan
.
4
a
Hướng dẫn giải
Chọn B.
Gọi G là trọng tâm tam giác ABC khi đó SG là chiều cao
SAG
=>
3
tan tan
3
a
SG AG


V=
3
1 tan
.
3 12
ABC
a
S SG
Câu 18. Cho tứ diện ABCD, gọi B’, C’ lần lượt là trung điểm của AB, AC. Khi đó tỉ số thể tích của khối tứ
diện AB’C’D và khối tứ diện ABCD bằng:
A.
1
.
2
B.
1
.
4
C.
1
.
6
D.
1
.
8
Hướng dẫn giải
Chọn B.
Ta có:
''
'. '. 1
. . 4
AB C D
ABCD
AB AC AD
V
V AB AC AD

Câu 19.
Cho hình chóp S.ABC có SA vuông góc mặt đáy , SA=a, tam giác ABC đều cạnh 2a. Gọi M,N lần
lượt thuộc cạnh SB,SC sao cho SM=MB,
2SN CN
.
Tính thể tích khối AMNCB.
A.
3
23
.
9
a
B.
3
3
.
9
a
C.
3
3
.
18
a
D.
3
23
.
3
a
Hướng dẫn giải
Chọn A.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 49/73
luyenthitracnghi
O
B'
A'
D
C
D'
C'
B
A
3
. 1 2 2 3
. 3 3 9
SAMN
AMNCB SABC
SABC
V
SM SN a
VV
S SB SC
, suy ra đáp án A
Câu 20. Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D , (ABC)
(BCD)
và AD hợp với (BCD) một góc 60
o
.Tính thể tích tứ diện ABCD.
A.
3
a3
9
B.
3
a3
3
C.
3
a3
27
D.
3
2a 3
9
Hướng dẫn giải
Chọn A.
Gọi H là trung điểm của BC.
Ta có tam giác ABC đều nên AH
(BCD) , mà (ABC)
(BCD)
AH
(BCD)
.
Ta có AH
HD
AH = AD. tan60
o
=
a3
và HD = AD. cot60
o
=
a3
3
BCD
BC = 2HD =
2a 3
3
suy ra
V =
3
BCD
1 1 1 a 3
S .AH . BC.HD.AH
3 3 2 9

Câu 21. Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh bằng
a
. Gọi
O
là giao điểm của
AC
và
BD
. Tính
thể tích của tứ diện
'OA BC
.
A.
3
.
6
a
B.
3
6
.
24
a
C.
3
.
12
a
D.
3
.
4
a
Hướng dẫn giải
Ta có
3
2
'
1 1 1
'.
4 4 3 12
BOC ABCD OA BC BOC
a
S S a V AA S
.
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a , AD = 2a. Cạnh SA vuông
góc với mặt phẳng đáy, cạnh bên SB tạo với mặt phắng đáy một góc
0
60
. Trên cạnh SA lấy điểm M sao cho
AM =
3
3
a
, mặt phẳng (BCM) cắt cạnh SD tại N. Tính thể tích khối chóp S.BCNM
o
60
a
H
D
C
B
A
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 50/73
luyenthitracnghi
A.
10 3
.
27
B.
3
10 3
.
9
a
C.
3
10 3
.
27
a
D.
3
10
.
27
a
Hướng dẫn giải
Chọn C.
Ta có SA =
0
tan tan60 3AB SBA AB a
V
S.ABCD
=
3
1 2 3
..
33
a
AB AD SA
V
S.ABC
= V
S.ACD
=
1
2
V
S.ABCD
=
3
3
3
a
3
.
..
.
2 2 2 3
3 3 9
S MBC
S MBC S ABC
S ABC
V
SM a
VV
V SA
3
.
..
.
4 4 4 3
.
9 9 27
S MCN
S MCN S ACD
S ACD
V
SM SN a
VV
V SA SD
Vậy
.MBCN . .S S MBC S MCN
V V V
3
10 3
27
a
Câu 23. Cho hình lăng trụ ABC. A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên hợp với đáy một góc
là 45
0
. Gọi P là trung điểm BC, chân đường vuông góc hạ từ A’ xuống (ABC) là H sao cho
1
2
AP AH
. gọi
K là trung điểm AA’,
là mặt phẳng chứa HK và song song với BC cắt BB’ và CC’ tại M, N. Tính tỉ số thể
tích
' ' '
ABCKMN
A B C KMN
V
V
A.
1
2
B.
2
3
C.
1
3
D.
3
4
Hướng dẫn giải
Chọn A
Gọi Q, I, J lần lượt là
trung điểm B’C’, BB’, CC’
ta có:
2
3a
AP
3aAH
Vì
''AHA
vuông cân tại H.
Vậy
3' aHA
HASV
ABCCBABCA
'.
'''
Ta có
4
3
2
3
.
2
1
2
aa
aS
ABC
(đvdt)
4
3
4
3
.3
32
'''
aa
aV
CBABCA
(đvtt) (1)
Vì
''AHA
vuông cân
CCBBHKAAHK '''
G ọi E = MN
KH BM = PE = CN (2)
mà AA’ =
22
' AHHA
=
633
22
aaa
4
6
2
6 a
CNPEBM
a
AK
C
A
D
B
S
M
N
45
E
K
J
I
A
B
C
C'
B'
A'
P
H
Q
N
M
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 51/73
luyenthitracnghi
Ta có thể tích K.MNJI là:
1
.
3
MNJI
V S KE
mà
1 1 6
'
2 4 4
a
KE KH AA
2
66
. . ( )
44
MNJI
aa
S MN MI a dvdt
23
1 6 6
()
3 4 4 8
KMNJI
a a a
V dvtt
33
23
' ' '
3
1
88
3
2
88
ABCKMN
A B C KMN
aa
V
aa
V
Câu 24. Cho một tấm bìa hình chữ nhật chiều dài
90AB cm
, chiều rộng
60BC cm
. Người ta cắt 6
hình vuông bằng nhau như hình vẽ, mỗi hình vuông cạnh bằng
x cm
, rồi gập tấm bìa lại như hình vẽ dưới
đây để được một hộp quà có nắp. Tìm
x
để hộp nhận được thể tích lớn nhất?
A.
10 .cm
B.
9.cm
C.
15 .cm
D.
10
.
3
cm
Hướng dẫn giải
Chọn A.
Hộp quà là hình hộp chữ nhật có chiều cao là h = x cm.
Đáy là hình chữ nhật với hai kích thước lần lượt là
1
90 3
2
x
l
và
2
60 2lx
.
Vậy thể tích của hộp quà là
12
90 3
. . . 60 2 . 30 90 3
2
x
V hl l x x x x x
.
Ta có
3
3
6 90 3 90 3
11
30 90 3 .6 . 90 3 . 90 3 . 12000
18 18 27
xxx
x x x x x x cm
.
Dấu "=" xảy ra khi và chỉ khi
6 90 3 9 90 10x x x x cm
.
Câu 25. Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy và khoảng cách từ
A
đến mặt phẳng
SBC
bằng
2
2
.
a
Tính thể tích
V
của khối chóp đã cho.
A.
3
2
.
a
V
B.
3
.Va
C.
3
3
.
a
V
D.
3
3
.
a
V
Lời giải
Chọn D.
Kẻ
AH SB H SB
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 52/73
luyenthitracnghi
2
2
,.
a
d A SBC AH
Ta có:
2 2 2
1 1 1
AH SA AB

2 2 2 2 2 2
1 1 1 2 1 1
SA AH AB a a a
.SA a
Suy ra:
3
2
11
3 3 3
. . . . .
ABCD
a
V SA S a a
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 4
Câu 1. [2H1-1] Cho khối chóp có là n – giác
3;n n N
. Mệnh đề nào đúng sau đây:
A. Số cạnh của khối chóp bằng n + 1. B. Số mặt của khối chóp bằng 2n.
C. Số đỉnh của khối chóp bằng n + 1. D. Số mặt của khối chóp bằng số đỉnh của nó.
Lời giải
Chọn C.
Vì mặt đáy có n đỉnh và thêm 1 đỉnh của hình chóp không nằm trong mặt đáy.
Ví dụ: Hình chóp tứ giác có 5 điỉnh
Câu 2. [2H1-1] Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh. B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt. D. Mỗi mặt có ít nhất ba cạnh.
Lời giải
Chọn C.
Đáp án C sai vì hình đa diện là hình thõa mãn tính chất: mỗi cạnh của đa giác nào cũng là cạnh chung của đúng
hai đa giác.
Câu 3. [2H1-2] Trong các mệnh đề sau mệnh đề nào sai ?
A. Lắp ghép hai khối hộp sẽ được một khối đa diện lồi.
B. Khối hộp là khối đa diện lồi.
C. Khối tứ diện là khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi.
Lời giải
Chọn A.
Ví dụ: Ghép hai khối trên không được một khối đa diện lồi
Câu 4. [2H1-1] Có bao nhiêu loại khối đa diện đều?
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 53/73
luyenthitracnghi
A.
2
. B.
4
. C.
5
. D. Vô số.
Lời giải
Chọn C.
Vì chỉ có 5 loại khối đa diện đều là:tứ diện đều, lập phương, bát diện đều, mười hai mặt đều, hai mươi mặt đều.
Câu 5. [2H1-1] Khối đa điện nào sau đây có công thức tính thể tích là
1
3
V Bh
(
B
là diện tích đáy;
h
là chiều
cao)
A. Khối lăng trụ. B. Khối chóp.
C. Khối lập phương. D. Khối hộp chữ nhật.
Lời giải
Chọn B.
Câu 6. [2H1-2] Trong Cho khối tứ diện
DABC
. Lấy một điểm
M
nằm giữa
A
và
B
, một điểm
N
nằm giữa
C
và
D
. Bằng hai mặt phẳng
DMC
và
NAB
ta chia khối tứ diện đã cho thành bốn khối tứ diện:
A. AMCN, AMND, AMCD, BMCN. B. AMNC, AMND, BMNC, BMND.
C. AMCD, AMND, BMCN, BMND. D. BMCD, BMND, AMCN, AMDN.
Lời giải
Chọn C.
Dựa vào hình vẽ suy ra đáp án C đúng.
Câu 7. [2H1-2] Có thể chia hình lập phương thành bao nhiêu hình tứ diện bằng nhau?
A.
2
. B. Vô số. C.
4
. D.
6
.
Lời giải
Chọn B.
Vì 1 khối lập phương có thẻ chia được 6 khối tứ diện bằng nhau mà từ một khối lập phương có thể chia nhỏ
ra thành vô số khối lập phương nên chọn đáp án B.
Câu 8. [2H1-2] Trong cách mệnh đề sau, mệnh đề nào sai?
A. Hai khối hộp chữ nhật có diện tích xung quanh bằng nhau thì có thể tích bằng nhau.
B. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
C. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
D. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
Lời giải
Chọn A.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 54/73
luyenthitracnghi
Ví dụ như hai khối trên (Khối hộp chữ nhật có các kích thước là
1,7,1
và khối lập phương có cạnh là
2
) đều
só diện tích xung quanh là 16 nhưng thể tích khác nhau.
Câu 9. [2H1-3] Cho hình hộp
D.ABC A B C D
. Tỉ số thể tích của khối tứ diện
''ACB D
và khối hộp
D.ABC A B C D
là:
A.
1
5
. B.
1
4
. C.
1
3
. D.
1
6
.
Lời giải
Chọn C.
Gọi
h
là chiều cao của khối hộp.
Ta có
D. D
.
ABC A B C D ABC
V S h
D. . D D D
1 1 1 1
4 . 4. . . 4. . . .
3 3 2 3
ACB D ABC A B C D A ABC ABC ABC ABC ABCD ABC
V V V S h S h S h S h S h
Vậy
D.
1
3
ACB D
ABC A B C D
V
V

.
Câu 10: [1H1-3] Cho hình lập phương
. ’ ’ ’ ’ABCD A B C D
có khoảng cách giữa
’AC
và
’’CD
là
1
cm. Thể
tích khối lập phương
. ’ ’ ’ ’ABCD A B C D
là:
A.
3
8.cm
B.
3
2 2 .cm
C.
3
3 3 .cm
D.
3
27 .cm
Lời giải
Chọn B.
Để tìm khoảng cách giữa
’AC
và
’’CD
, ta dựng một mặt phẳng chứa
’AC
và song song với
’ ’.CD
Dễ thấy
đó là mặt phẳng
’ ’ .CA B
Gọi
a
là độ dài cạnh của khối lập phương, lúc này ta có:
(C'D',A'C) d[ ' ',(CA'B')] [ ',(CA'B')]d C D d D
Để tính khoảng cách từ điểm
’D
đến mặt phẳng
’ ’ ,CA B
ta xét khối tứ diện
’ ’ ’.D CA B
23
3
' ' ' ' ' '
11
'. . (cm )
3 3 2 6
D CA B B A D
aa
V CC S a
2
2
''
1 1 2
'. ' ' .a 2 (cm )
2 2 2
CA B
a
V CB B A a
D’
A’
C’
B’
D
A
B
C
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 55/73
luyenthitracnghi
Suy ra
3
' ' '
2
''
3
2
2
[ D',(CA'B')] (cm)
2
2
2
D CA B
CA B
a
V
a
d
S
a
2.a
Do đó

33
2 2(cm )Va
Câu 11: [1H1-2] Tính thể tích
V
của khối lập phương
.ABCD A B C D
, biết
3AC a
.
A.
3
Va
. B.
3
36
4
a
V
. C.
3
33Va
. D.
3
1
3
Va
.
Lời giải
Chọn A.
Gọi
x
là cạnh của khối lập phương thì đường chéo
33AC x a x a
. Vậy
33
V x a
.
Câu 12: [1H1-2] Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng
a
là
A.
3
2
6
a
.
B.
3
3
4
a
.
C.
3
3
2
a
.
D.
3
3
a
.
Lời giải
Chọn A.
Vì khối chóp tứ giác đều.
Nên giả sử
SO ABCD
.
Hay tam giác
SAO
vuông tại
O
.
12
2
22
a
AC a AO AC
.
2
2
22
22
22
aa
SO SA AO a




.
Vì hình chóp đều
.S ABCD
nên
ABCD
là hình vuông
22
ABCD
S AB a
.
3
2
.
1 1 2 2
. . . .
3 3 2 6
S ABC ABCD
aa
V SO S a
Câu 13: [1H1-3] Cho lăng trụ đứng tam giác
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
với
BA BC a
, biết
AB
hợp với đáy
ABC
một góc
60
. Tính thể tích khối lăng trụ.
A. . B. . C. . D. .
Lời giải
3
3
2
a
3
a
3
2a
3
2
a
A
B
C
D
S
O
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 56/73
luyenthitracnghi
Chọn A.
Hình chiếu vuông góc của
AB
lên mặt đáy là
AB
.
Nên góc tạo bởi
AB
với mặt đáy là góc
60A BA
.
Ta có:
tan60 . 3
AA
AA a
AB
Thể tích khối lăng trụ tam giác:
3
2
1 1 3
. . . . . 3
2 2 2
a
V B h AB BC A A a a
Câu 14: [1H1-3] Cho hình chóp
.S ABC
có tam giác
ABC
là tam giác đều cạnh
a
. Hình chiếu vuông góc
của
S
trên mặt phẳng
ABC
là trung điểm của cạnh
AB
, góc tạo bởi cạnh
SC
và mặt phẳng
ABC
bằng
o
30
. Tính thể tích của khối chóp
.S ABC
.
A.
3
3
8
a
. B.
3
8
a
. C.
3
3
4
a
. D.
3
3
24
a
.
Lời giải
Chọn D.
Ta có
2
3
4
ABC
a
S
.
60
a
a
A
C
B
B'
C'
A'
S
A
B
C
H
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 57/73
luyenthitracnghi
Gọi
H
là trung điểm
AB
thì
SH ABC
nên
, 3, 0SC ABC SC HC SCH
.
Ta có
3
2
a
HC
nên
.tan30
2
a
SH HC
.
Vậy
3
.
13
.
3 24
S ABC ABC
a
V SH S
.
Câu 15: [1H1-2] Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
, a SA
vuông góc với mặt đáy
, SD
tạo
với mặt phẳng
SAB
một góc bằng
30
. Tính thể tích
V
của khối chóp.
A.
3
6
18
a
. B.
3
3a
. C.
3
6
3
a
. D.
3
3
3
a
.
Lời giải
Chọn D.
0
, 30SD SAB DSA
Xét trong tam giác vuông
SAD
:
0
3
tan30
33
3
DA a a
SA
2
ABCD
Sa
Thể tích
V
của khối chóp là
3
2
.
1 1 3 3
. . .
3 3 3
3
S ABCD ABCD
aa
V SA S a
Câu 16: [1H1-3] Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên gấp hai lần cạnh đáy. Tính tích V
của khối chóp tứ giác đã cho.
A.
3
2
2
a
V
. B.
3
2
6
a
V
. C.
3
14
2
a
V
. D.
3
14
6
a
V
.
Lời giải
Chọn D.
30
0
C
D
B
A
S
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 58/73
luyenthitracnghi
Xét hình chóp đều
.S ABCD
với đáy
ABCD
là hình vuông cạnh bằng
a
. Gọi
O
là tâm của hình
vuông
ABCD
,
SO ABCD
.
Ta có:
22
2 14
;.
2 2 2
AC a a
OA SO SA OA
Vậy thể tích khối chóp
.S ABCD
là
3
2
1 1 14 14
..
3 3 2 6
ABCD
aa
V S SO a
.
Câu 17: [1H1-3] Cho hình chóp tam giác đều
.S ABC
. Tính theo
a
thể tích khối chóp
.S ABC
biết rằng
AB a
,
( ),( ) 60SBC ABC 
.
A.
3
3
24
a
.
B.
3
4
a
.
C.
3
3
4
a
.
D.
3
3
12
a
.
Lời giải
Chọn A.
Gọi
O
là tâm của tam giác
ABC
.
M
là trung điểm
BC
.
Vì hình chóp tam giác đều
.S ABC
nên
SO ABC
.
Ta có
AM BC
(
AM
là đường cao tam giác
ABC
đều ).
Lại có tam giác
SBC
cân tại
S
nên
SM BC
.
Do đó
,( ) , 60SBC ABC SM AM SMO
.
Vì
O
là trọng tâm tam giác
ABC
nên.
1 1 3 3
.
3 3 2 6
aa
MO AM
.
2
3
4
ABC
a
S
.
A
B
C
O
M
60
S
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 59/73
luyenthitracnghi
Xét tam giác
SMO
vuông tại
O
, ta có
3
.tan60 . 3
62
aa
SO MO
.
Vậy
23
.
1 1 3 3
. . .
3 3 2 4 24
S ABC ABC
a a a
V SO S
.
Câu 18: [1H1-1] Cho hình chóp tam giác
.S ABC
. Gọi
M
lần lượt là trung điểm của
SB
và
N
nằm
trên cạnh
SC
sao cho
2SN NC
. Khi đó tỉ số thể tích của khối tứ diện
.S AMN
và khối tứ
diện
.S ABC
bằng:
A.
1
6
. B.
1
3
. C.
1
4
. D.
1
2
.
Lời giải
Chọn B.
Theo giả thiết ta có
1
2
SM
SA
và
2
2
3
SN
SN NC
SC
.
Khi đó
.
.
1 2 1
..
2 3 3
S AMN
S ABC
V
SM SN
V SB SC
.
Phân tích phương án nhiễu.
A, C sai Do tính sai tỉ số
SN
SC
.
D sai do tính sai.
Câu 19: [1H1-2] Cho khối chóp
.S ABC
có thể tích bằng
16
. Gọi
,,M N P
lần lượt là trung điểm của
các cạnh
,,SA SB SC
. Tính thể tích V của khối tứ diện
AMNP
.
A.
2V
. B.
8
3
V
. C.
4V
. D.
8V
.
Lời giải
Chọn A.
B
C
S
M
A
N
P
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 60/73
luyenthitracnghi
Ta có
3
.
.
11
..
28
S MNP
S ABC
V
SM SN SP
V SA SB SC



Do đó
.
16
2
8
S MNP
V 
.
Do
M
là trung điểm
SA
, ta có
( ,( )) ( ,( ))d A MNP d S MNP
Suy ra
.
2
AMNP S MNP
VV
.
Phân tích phương án nhiễu.
B sai do tính
3
26
.
C sai do áp dụng công thức tỉ số khoảng cách sai
2 ( ,( )) ( ,( ))d A MNP d S MNP
.
D sai do thấy trung điểm là phân nữa nên lấy thể tích chia 2.
Câu 20: [1H1-2] Cho hình chóp tam giác
.S ABC
có
ABC
là tam giác đều cạnh
a
, hai mặt phẳng
SAB
và
SAC
cùng vuông góc với mặt đáy
ABC
và
2SC a
. Tính theo
a
thể tích
V
của khối chóp
.S ABC
.
A.
3
1
4
Va
. B.
3
3
3
Va
. C.
3
3
6
Va
. D.
3
3
4
Va
.
Lời giải
Chọn A.
Ta có:
SAB ABC
SAC ABC
SA ABC
;
SAC
vuông tại
A
:
22
3SA SC AC a
.
Vậy
23
.
1 1 3
. 3.
3 3 4 4
S ABC ABC
aa
V SAS a
.
Phân tích phương án nhiễu.
B sai do tính diện tích tam giác
ABC
là
2
3
2
a
.
a
a
a
2a
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 61/73
luyenthitracnghi
C sai do xác định đường cao là
SC
.
D sai do tính công thức thể tích thiếu chia 3.
Câu 21: [1H1-3] Cho hình lập phương
. ' ' ' 'ABCD A B C D
có cạnh bằng
6
. Gọi
G
là trọng tâm tam
giác
'A BD
. Tính thể tích
V
của khối tứ diện
GABC
.
A.
12V
. B.
18V
. C.
24V
. D.
36V
.
Hướng dẫn giải
Chọn A.
Ta có
11
, D , D 2
33
d G ABC d A ABC SA
Và
D
1
18
2
ABC ABC
SS
.
1
,.
3
GABC ABC
V d G ABCD S
1
.18.2 12
3

Phân tích phương án nhiễu.
B sai do tính tỉ số khoảng cách sai
22
, D , D 4
33
d G ABC d A ABC SA
.
C sai do tính diện tích tam giác
ABC
bằng
36
.
D sai do tính thể tích thiếu chia 3.
Câu 22. [2H1-3] Cho khối chóp
.O ABC
. Trên ba cạnh
,,OA OB OC
lần lượt lấy ba điểm
’, ,A B C

sao cho
2 , 4 , 3OA OA OB OB OC OC
. Tính tỉ số
. ' ' '
.
O A B C
O ABC
V
V
A.
1
12
. B.
1
24
. C.
1
16
. D.
1
32
.
Lời giải:
Chọn B.
G
D'
D
A
B
C
B'
C'
A'
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 62/73
luyenthitracnghi
Ta có:
. ’ ’
.
1 1 1
; ;
2 4 3
1 1 1 1
2 4 3 24
O
A
ABC
O B C
OA OB OC
OA OB OC
V
OA OB OC
V OA OB OC
Câu 23. [2H1-3] Cho khối lăng trụ tam giác đều
. ’ ’ ’ABC A B C
có tất cả các cạnh đều bằng
a
. Thể tích khối tứ
diện
’ ’ ’A BB C
là
A.
3
3
12
a
B.
3
3
4
a
C.
3
3
6
a
D.
3
12
a
Lời giải:
Chọn A.
2
3
3
4
13
.
3 12
ABC
A BB C A B C
h BB a
a
S
a
V BB S

Câu 24. [2H1-4] Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có
các đỉnh là các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng
a
. Hãy tính thể
tích của khối tám mặt đều đó:
A.
3
4
a
. B.
3
6
a
. C.
3
12
a
. D.
3
8
a
.
Lời giải:
Đáp án B.
Dựng được hình như hình bên.
+ Thấy được thể tích khối cần tính bằng 2 lần thể tích của hình chóp
S.ABCD.
+ Nhiệm vụ bây giờ đi tìm thể tích của S.ABCD.
+ ABCD là hình vuông có tâm O đồng thời chính là hình chiếu của
S lên mặt đáy.
A
B
C
A'
B'
C'
O
A
B
C
C
B
A
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 63/73
luyenthitracnghi
2
a
SO
;
BD
cạnh của hình lập phương
a
. Suy ra các cạnh của hình vuông
2
2
ABCD a
.
3
3
.
1 1 1 2 2
..
3 3 2 2 2 12
S ABCD
a
V Sh a
.
3
đa diên .
2.
6
khôi S ABCD
a
VV
.
Câu 25. [2H1-3] Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
, cạnh
SB
vuông góc với
đáy và mặt phẳng
SAD
tạo với đáy một góc
60
. Tính thể tích khối chóp
.S ABCD
.
A.
3
33
4
a
V
. B.
3
33
8
a
V
. C.
3
83
3
a
V
. D.
3
43
3
a
V
.
Lời giải:
Chọn C.
Ta có:
AD AB
AD SB
AD
(SAB)
AD
SA.
0
60SAB
.
S
ABCD
= 4a
2
.
Xét tam giác SAB tại vuông tại B, ta có:
0
tan60 2 3SB AB a
.
Vậy V =
1
3
.4a
2
. 2a
3
=
3
83
3
a
.
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 5
Câu 1. [2D4-2] Hình đa diện đều có tất cả các mặt là ngũ giác có bao nhiêu cạnh?
A.
20
. B.
60
. C.
30
. D.
12
.
Lời giải
Chọn C .
Hình đa diện đều có tất cả các mặt là ngũ giác đều là hình mười hai mặt đều (loại
5;3
) có 20
đỉnh, 30 cạnh, 12 mặt.
Phân tích phương án nhiễu.
A – sai do nhớ nhầm số đỉnh.
B – sai do quên kiến thức.
D – sai do nhớ nhầm số mặt.
Câu 2. [2H1-1] Hình nào sau đây không phải là hình đa diện .
A. Hình trụ. B. Hình tứ diện. C. Hình lập phương. D. Hình chóp.
Lời giải
B
S
A
D
C
2a
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 64/73
luyenthitracnghi
Chọn A.
Câu 3. [2H1-2] Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ sau
Khối tứ diện đều Khối lập phương Bát diện đều Hình
12
mặt đều Hình
20
mặt đều
Mệnh đề nào sau đây đúng?
A. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.
B. Khối lập phương và khối bát diện đều có cùng số cạnh.
C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.
Lời giải
Chọn B.
+ B đúng, vì khối lập phương có 12 cạnh; khối bát diện đều có 12 cạnh.
Phân tích phương án nhiễu
+ A- sai, vì khối lập phương có
6
mặt và
64
.
+ C- sai, vì khối tứ diện đều không có tâm đối xứng.
+ D -sai, vì khối
12
mặt đều có
20
đỉnh, còn khối
20
mặt đều có
12
đỉnh.
Câu 4. [2D4-1] Số đỉnh của khối bát diện đều là:
A. 6. B. 8. C. 12. D. 4.
Lời giải
Chọn A.
Phân tích phương án nhiễu.
B – Sai do 8 là số đỉnh của khối lập phương.
C – Sai do 12 là số đỉnh của khối 20 mặt đều.
D – Sai do 4 là số đỉnh của khối tứ diện đều.
Câu 5. [2H1-1]Công thức nào sau đây là công thức tính thể tích khối chóp?
A.
1
.
6
V S h
. B.
.V S h
. C.
1
.
3
V S h
. D.
1
.
2
V S h
.
Câu 6. [2H1-2]Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi
M
là trung điểm
.SC
Mặt phẳng
qua
M
song song với
DC
chia khối chóp thành bao nhiêu khối chóp tứ giác.
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn C.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 65/73
luyenthitracnghi
Một khối chóp tứ giác
Phân tích phương án nhiễu.
A – sai do không xác định đúng mặt phẳng
.
C – sai do không xác định đúng mặt phẳng
.
D – sai do không xác định đúng mặt phẳng
.
Câu 7. [2D4-2] Cắt khối lăng trụ
.MNP M N P
bởi các mặt phẳng
MN P

và
MNP
ta được những khối
đa diện nào?
A. Hai khối tứ diện và hai khối chóp tứ giác. B. Một khối tứ diện và một khối chóp tứ giác.
C. Ba khối tứ diện.
D. Hai khối tứ diện và một khối chóp tứ giác.
Lời giải
Chọn C .
Cắt khối lăng trụ
.MNP M N P
bởi các mặt phẳng
MN P

và
MNP
ta được ba khối tứ diện là
.;P MNP
.;P MNN
M .MN P .
Phân tích phương án nhiễu.
A – sai do học sinh không vẽ được hình hoặc nhầm lẫn tên các khối.
B – sai do học sinh không vẽ được hình hoặc nhầm lẫn tên các khối.
D – sai do học sinh không vẽ được hình hoặc nhầm lẫn tên các khối.
Câu 8. [2H1-1] Thể tích khối lăng trụ đứng tam giác
.ABC A B C
có tất cả các cạnh bằng
a
là .
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
3
4
a
. D.
3
4
a
.
Lời giải
Chọn C.
M
N
P
M'
P'
N'
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 66/73
luyenthitracnghi
Vì
.ABC A B C
là khối lăng trụ đứng có tất cả các cạnh bằng
a
nên có hai đáy là các tam giác đều
cạnh
a
, các mặt bên là hình vuông cạnh
a
. Suy ra thể tích khối lăng trụ là
23
33
..
44
ABC
aa
V S AA a
(đvtt) .
Câu 9. [2H1-1] Tính theo a thể tích V của khối lập phương
.ABCD A B C D
biết
.AC a
A.
3
3 3 .Va
B.
3
.Va
C.
3
.
27
a
V
D.
3
3
.
9
a
V
Lời giải
Chọn D.
Ta có
3.
3
a
AC AB AB
Thể tích khối lập phương là:
3
33
3
3
9
3 3 3
a a a
V AB



.
Phân tích phương án nhiễu
+ A- sai, do nhớ nhầm công thức thành
3 3.AB AC a

+ B- sai, do học sinh đọc đề ko kĩ và nhớ công thức là lấy cạnh lập phương mà ko để ý cạnh nào.
+ C -sai, do tính sai cạnh của hình lập phương thành
3
a
hoặc do tính sai lập phương cảu
AB
.
Câu 10. [2D4-2] Tính thể tích của khối hộp chữ nhật có diện tích của các mặt bên và mặt đáy lần lượt là
2
10cm
,
2
16 cm
và
2
40cm
.
A.
3
160 cm
. B.
3
400 cm
. C.
3
80 cm
. D.
3
640 cm
.
Lời giải
Chọn C.
Gọi kích thước của khối hộp chữ nhật là x, y và z.
Ta có
10, 16xy xz
và
40yz
. Khi đó
2 2 2
6400 80x y z xyz
.
Vậy thể tích khối hộp chữ nhật là
3
80 cm
.
Câu 11. [2H1-2] Cho hình lập phương
.ABCD A B C D
có cạnh bằng a. Tính thể tích khối tứ diện
ACB D

theo
a
.
A.
3
6
a
. B.
3
2
a
. C.
3
3
a
. D.
3
4
a
.
Câu 12. [2H1-3] Cho hình chóp tứ giác đều
.S ABCD
có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên
và mặt phẳng đáy là
. Mặt phẳng
P
qua AC và vuông góc với mặt phẳng
SAD
chia khối chóp
.S ABCD
thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là
MACD
SABCM
V
V
?
A
B
C
D
A
B
C
D
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 67/73
luyenthitracnghi
A.
2
cos
B.
2
sin
C.
2
tan
D.
0,9
Lời giải
Chọn A.
Ta có:
2 2 2 2 2
2
2
11
. 1 cos 1
2 cos 2.cos
cos
aa
SD SN ND ON ND
SNO

Ta có :
11
..
22
SCD
S CM SD SN CD

2
2
1
.
.
2 cos
1 cos
cos 1
2.cos
a
a
SN CD a
CM
a
SD
2
2 2 2
2
2
.cos
1 cos
1 cos
aa
DM CD CM a
2
2
2
2
.cos
1 1 1 cos
1 cos
. . . .
2. 2 2 2 1 cos
1 cos
2.cos
MACD MACD
SABCD SACD
a
VV
DM DA DC DM
a
V V DS DA DA DS
22
2 2 2
cos cos 1
1
1 cos 1 cos 1 cos
MACD SABCD SABCM SABCD SABCD
V V V V V




Do vậy :
2
cos
MACD
SABCM
V
V
Câu 13. [2D4-2] Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác vuông tại
0
, , 60A AC a ACB
. Đường
chéo
'BC
của mặt bên
''BCC B
tạo với mặt phẳng
''AA C C
một góc
0
30
. Tính thể tích của
khối lăng trụ theo
a
.
A.
3
6
2
a
. B.
3
6
3
a
. C.
3
6a
. D.
3
26
3
a
.
Lời giải
Chọn C .
Ta có
''BA AA C C
nên
0
', ' ' ', ' ' 30BC AA C C BC AC AC B
.
Trong
ABC
vuông tại
A
,
0
.tan60 3AB AC a
.
Trong
'ABC
vuông tại
A
,
0
' .cot30 3AC AB a
.
Trong
'CC A
vuông tại
C
,
22
' ' 2 2CC AC AC a
.
2
1 1 3
. 3.
2 2 2
ABC
a
S AB AC a a
.
2
3
3
'. 2 2. 6
2
ABC
a
V CC S a a
.
Phân tích phương án nhiễu.
A – sai do nhớ nhầm công thức thể tích hoặc gặp lỗi trong tính toán.
B – sai do nhớ nhầm công thức thể tích hoặc gặp lỗi trong tính toán.
D – sai do nhớ nhầm công thức thể tích hoặc gặp lỗi trong tính toán.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 68/73
luyenthitracnghi
Câu 14. [2H1-3] Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
A
và
2AB AC a
. Tam giác
SBC
có diện tích bằng
2
2a
và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích
V
của
khối chóp
.S ABC
.
A.
3
4
3
a
V
. B.
3
3
a
V
. C.
3
2Va
. D.
3
2
3
a
V
.
Lời giải
Chọn D.
( ):
SBC ABC
SBC ABC BC AH SBC
Trong ABC AH BC
ABC
vuông cân tại
A
nên
1
22
2
BC AB a AH BC a
.
23
1 1 2
. .2 .
3 3 3
SABC SBC
V S AH a a a
.
Câu 15. [1H2-3] Tính thể tích khối chóp
.S ABCD
có
ABCD
là hình thang vuông tại
,AB
có
2,AD a AB BC a
,
SA ABCD
, Góc giữa
SCD
và
ABC
là
0
60
. Tính thể tích khối chóp
.S ABCD
A.
3
6
4
a
. B.
3
33
4
a
. C.
3
63
4
a
. D.
3
6
2
a
.
Lời giải
Chọn A.
Gọi
M
là trung điểm của
AD
suy ra
0
90ACD
suy ra
ACD CD
Góc giữa mặt phẳng
SCD
và
ABC
là
0
60ACD
Chiều cao :
0
.tan60 2. 3 6SA AC a a
2a
a
a
60
M
A
D
B
S
C
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 69/73
luyenthitracnghi
Diện tích đáy:
2
1 1 3
. 2 .
2 2 4
a
S BC AD AB a a a
Thể tích là :
23
1 3 6
6
3 4 4
aa
Va
, chọn đáp án A.
Phân tích phương án nhiễu
B-sai, do học sinh xác định nhầm góc giữa hai mặt phẳng là góc
SBD
đẫn đến đường cao
SA
tính
sai là
2a
C –sai, do học sinh xác định nhầm góc giữa hai mặt phẳng là góc
SDA
đẫn đến đường cao
SA
tính sai là
23a
D-sai, do học sinh tính nhầm công thức diện tích hính thang.
.S AD BC AB
Câu 16. [2D4-3] Cho hình chóp tứ giác đều S.ABCD. Gọi O là tâm mặt đáy, biết
20SO cm
và khoảng cách
từ điểm O tới mặt bên của khối chóp bằng
12cm
. Tính thể tích khối chóp S.ABCD.
A.
3
3840V cm
. B.
3
6000V cm
. C.
3
1920V cm
. D.
3
3000V cm
.
Lời giải
Chọn B.
Gọi E là trung điểm CD.
Dựng
0; 12OF SE d SCD OF


.
Ta có
2 2 2
1 1 1
15OE cm
OF OS OE
.
Vậy
2 30AD OE cm
.
Khi đó
23
1
.30 .20 6000
3
V cm
.
Phân tích phương án nhiễu.
A – Sai do nghĩ rằng khoảng cách từ O tới mặt (SCD) là OE.
C – Sai do nghĩ rằng khoảng cách từ O tới mặt (SCD) là OD.
D – Sai do nghĩ rằng khoảng cách từ O tới mặt (SCD) là đoạn kẻ vuông góc từ O lên SD.
Câu 17. [2H1-3] Cho một hình chóp tứ giác đều có cạnh đáy bằng
a
và diện tích xung quanh gấp đôi diện
tích đáy. Khi đó thể tích của khối chóp là.
A.
3
3
12
a
. B.
3
2
3
a
. C.
3
3
3
a
. D.
3
3
6
a
.
Câu 18. [2H1-1] Cho tứ diện
ABCD
. Gọi
,MN
lần lượt là trung điểm của
AB
và
AC
. Khi đó tỉ số thể tích
của khối tứ diện
AMND
và khối tứ diện
ABCD
bằng:
A.
1
2
B.
1
4
C.
1
6
D.
1
8
Lời giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 70/73
luyenthitracnghi
Chọn A.
Ta có
1
..
4
AMND
ABCD
V
AM AN AD
V AB AC AD

.
Phân tích phương án nhiễu.
B – sai do tính toán.
C – sai do tính toán.
D – sai do tính toán.
Câu 19. [2D4-2] Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích bằng 1. Trên cạnh
SC
lấy điểm
E
sao cho
2SE EC
. Tính thể tích
V
của khối tứ diện
SEBD
.
A.
2
3
V
. B.
1
12
V
. C.
1
3
V
. D.
1
6
V
.
Lời giải
Chọn C .
.
Ta có
11
22
SBCD SABCD
VV
.
Mà
. . 2
. . 3
SEBD
SCBD
V
SE SB SD
V SC SB SD

. Do đó
1
3
SEBD
V
.
Phân tích phương án nhiễu.
A – sai do nhớ nhầm thể tích
1
SBCD
V
.
B – sai do lập tỉ số
SEBD
SBCD
V
V
sai.
D – sai do lập tỉ số
SEBD
SBCD
V
V
sai.
Câu 20. [2H1-3] Cho hình chóp đều
.S ABC
có cạnh đáy bằng
a
, khoảng cách giữa cạnh bên
SA
và cạnh
đáy
BC
bằng
3
4
a
. Thể tích khối chóp
.S ABC
tính theo
a
là .
A.
3
33
16
a
. B.
3
3
12
a
. C.
3
3
8
a
. D.
3
33
8
a
.
Lời giải
Chọn B.
E
A
D
B
C
S
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 71/73
luyenthitracnghi
Gọi
M
là trung điểm của
BC
,
O
là trọng tâm tam giác
ABC
Khi đó ta có :
AM BC
,
SM BC
suy ra
BC SAM
Kẻ
MH SA
, do
3
4
a
BC SAM BC MH MH
Tam giác
ABC
đều cạnh
a
suy ra
3
2
a
AM
Tam giác
HAM
vuông tại
H
suy ra
22
3
4
a
HA AM HA
Do
SO ABC SO AM
nên tam giác
SOA
vuông tại
O
,
23
33
a
OA AM
Tính được
.
tan
HM SO HM AO
SAO SO a
AH AO AH
Thể tích khối chóp
.S ABC
là :
23
1 1 3 3
. . .
3 3 4 12
ABC
aa
V S SO a
.
Câu 21. [1H2-2] Cho khối hộp
. ' ' ' 'ABCD A B C D
có thể tích bằng
3
24dm
.Gọi
M
là trung điểm của
'AD
Tính thể tích khối chóp
M.ABC
?
A.
3
6dm
. B.
3
2dm
. C.
3
3dm
. D.
3
9dm
.
Lời giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 72/73
luyenthitracnghi
Chọn B.
Thể tích khối hộp
.
day
V S h
Do đó chiều cao khối hộp
. ' ' ' 'ABCD A B C D
bằng chiều cao
khối chóp
M.ABC
Diện tích
ABC
bằng
1
2
day
S
do đó:
'. . ' ' ' '
1
12
A ABC ABCD A B C D
VS
Phân tích phương án nhiễu
A-sai, Học sinh quên công thức thể tích khối chóp
1
.
3
day
S S h
.
C –sai, do Học sinh nhầm tưởng công thức tỷ số thể tích.
D-sai, do học sinh khoanh bừa.
Câu 22. [2D4-3] Cho hình chóp S.ABCD có thể tích bằng 1. Biết mặt đáy là hình vuông tâm O và SO vuông
góc với mặt phẳng
ABCD
. Gọi I là trung điểm cạnh SD, tính thể tích khối tứ diện IOBC.
A.
1
2
IOBC
V
. B.
1
12
IOBC
V
. C.
1
8
IOBC
V
. D.
1
24
IOBC
V
.
Lời giải
Chọn C.
Ta có
1 1 1 1
. . .
3 3 2 4
IOBC I OBC ABCD
V h S SO S

1 1 1
.
8 3 8
ABCD
SO S




.
Câu 23. [2H1-4] Cho hình hộp
.ABCD A B C D
. Tỉ số thể tích của khối tứ diện
ACB D

và khối hộp
.ABCD A B C D
bằng
A.
1
2
. B.
1
3
. C.
1
4
. D.
1
6
.
Câu 24. [2H1-3] Một túp lều có dạng hình lăng trụ đứng có kích thước như hình bên. Tính thể tích của túp
lều.
A.
3
280m
B.
3
280
m
3
C.
3
560m
D.
3
560
m
3
A'
D'
C'
B'
A
D
C
B
M
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12 Năm học 2018 – 2019
THẦY VIỆT
0905.193.688
Trang 73/73
luyenthitracnghi
Lời giải
Chọn A.
Thể tích của túp lều là
3
1
. 10. .7.8 280m
2
V h S
.
Phân tích phương án nhiễu.
B – sai do tính toán.
C – sai do tính toán.
D – sai do tính toán
Câu 25. [2H1-4] Cho tứ diện
ABCD
có các cạnh
AB AC,
và
AD
đôi một vuông góc nhau;
6 ,AB a
AC a AD a 7 , 4 .
Gọi
M N P, ,
tương ứng là trung điểm các cạnh
BC CD BD, , .
Thể tích
V
của tứ diện
.AMNP
A.
3
7a
2
. B.
3
14a
. C.
3
28
a
3
. D.
3
7a
.
Lời giải
Chọn D.
3
11
. 28 .
32
ABCD
V AB AC AD a




3
. .AMP .
1
7.
4
D AND B C MNA ABCD
V V V V a
3
. .AMP .
7.
AMNP ABCD D AND B C MNA
V V V V V a
Phân tích phương án nhiễu.
B – sai do tính toán.
C – sai do tính toán.
D – sai do tính toán
| 1/73
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

THẦY VIỆT 0905.193.688
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 1/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 MỤC LỤC
............................................................................................................................................................................................ 1
ĐỀ THAM KHẢO SỐ 1 ......................................................................................................................................................... 3
ĐỀ THAM KHẢO SỐ 2 ......................................................................................................................................................... 6
ĐỀ THAM KHẢO SỐ 3 ....................................................................................................................................................... 10
ĐỀ THAM KHẢO SỐ 4 ....................................................................................................................................................... 13
ĐỀ THAM KHẢO SỐ 5 ....................................................................................................................................................... 16
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 1 .............................................................................................................................. 19
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 2 .............................................................................................................................. 19
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 3 .............................................................................................................................. 19
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 4 .............................................................................................................................. 19
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 5 .............................................................................................................................. 19
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 1 ................................................................................................................................................. 20
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 2 ................................................................................................................................................. 30
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 3 ................................................................................................................................................. 42
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 4 ................................................................................................................................................. 52
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 5 ................................................................................................................................................. 63
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 2/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 ĐỀ THAM KHẢO SỐ 1 Câu 1.
[2H1-1] Hình nào dưới đây không phải là một khối đa diện? A. B. C. D. Câu 2.
[2H1-1] Khối đa diện nào được cho dưới đây là khối đa diện đều?
A. Khối chóp tam giác đều.
B. Khối lăng trụ đều.
C. Khối chóp tứ giác đều
D. Khối lập phương. Câu 3.
[2H1-2] Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống, mệnh
đề sau trở thành mệnh đề đúng:
“Khối đa diện (H) được gọi là khối đa diện lồi nếu. nối hai điểm bất kì của (H) luôn thuộc (H)”. A. Đường thẳng. B. Đoạn thẳng.
C. Đường gấp khúc. D. Đường cong. Câu 4.
[2H1-1] Khối tứ diện đều là khối đa diện đều loại nào? A. 4;  3 . B. 3;  4 . C. 3;  3 . D. 5;  3 . Câu 5.
[2H1-1] Cho khối hộp có diện tích đáy là S, chiều cao tương ứng là .
h Khi đó thể tích khối hộp là 1 1 A. 2 S .h . B. 2 S .h . C. S.h . D. S.h . 3 3 Câu 6.
[2H1-2] Mặt phẳng AB C
  chia khối lăng trụ AB . C A BC
  thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp tứ giác.
B. Hai khối chóp tam giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
D. Hai khối chóp tứ giác. Câu 7.
[2H1-2] Tứ diện đều có bao nhiêu mặt phẳng đối xứng? A. 1 . B. 4 . C. 5 . D. 6 . Câu 8.
[2H1-2] Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần
lượt là 15 cm và 5 cm . Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ
nhật sao cho cây nến nằm khít trong hộp. Thể tích của chiếc hộp đó bằng: A. 1500 ml . B. 600 6 ml . C. 1800 ml . D. 750 3 ml . Câu 9.
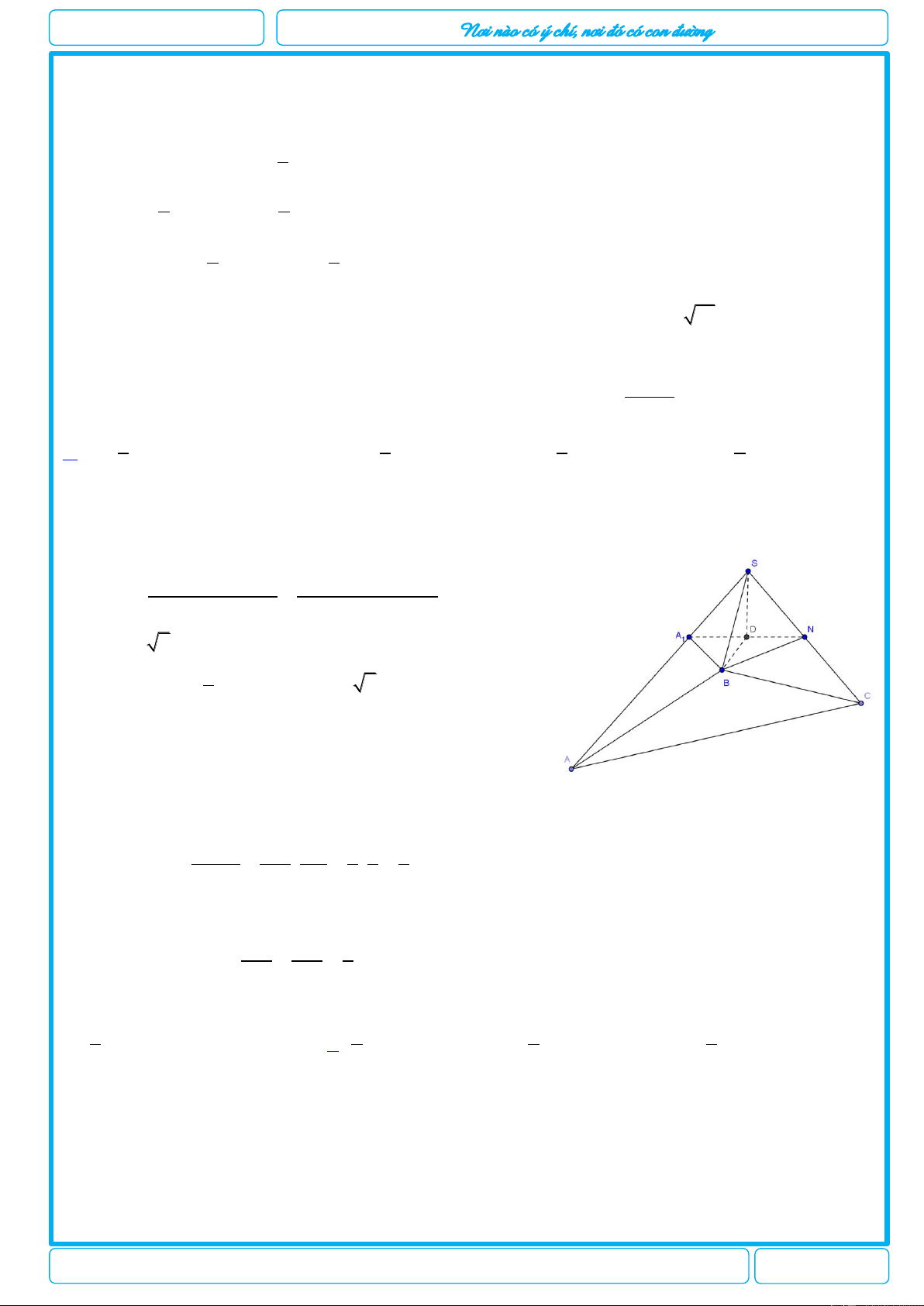
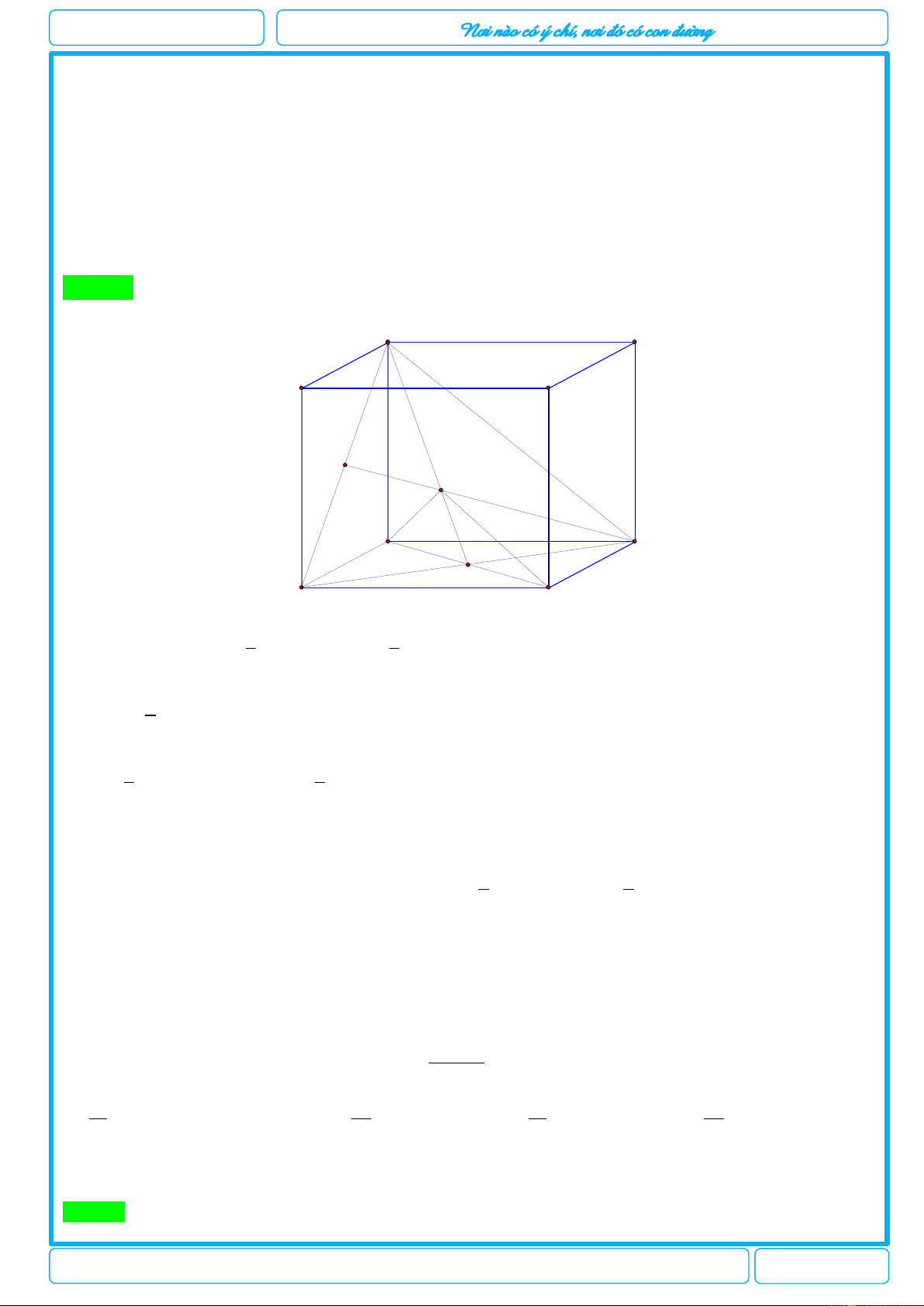
[2H1-3] Cho hình lăng trụ đứng AB . C A BC
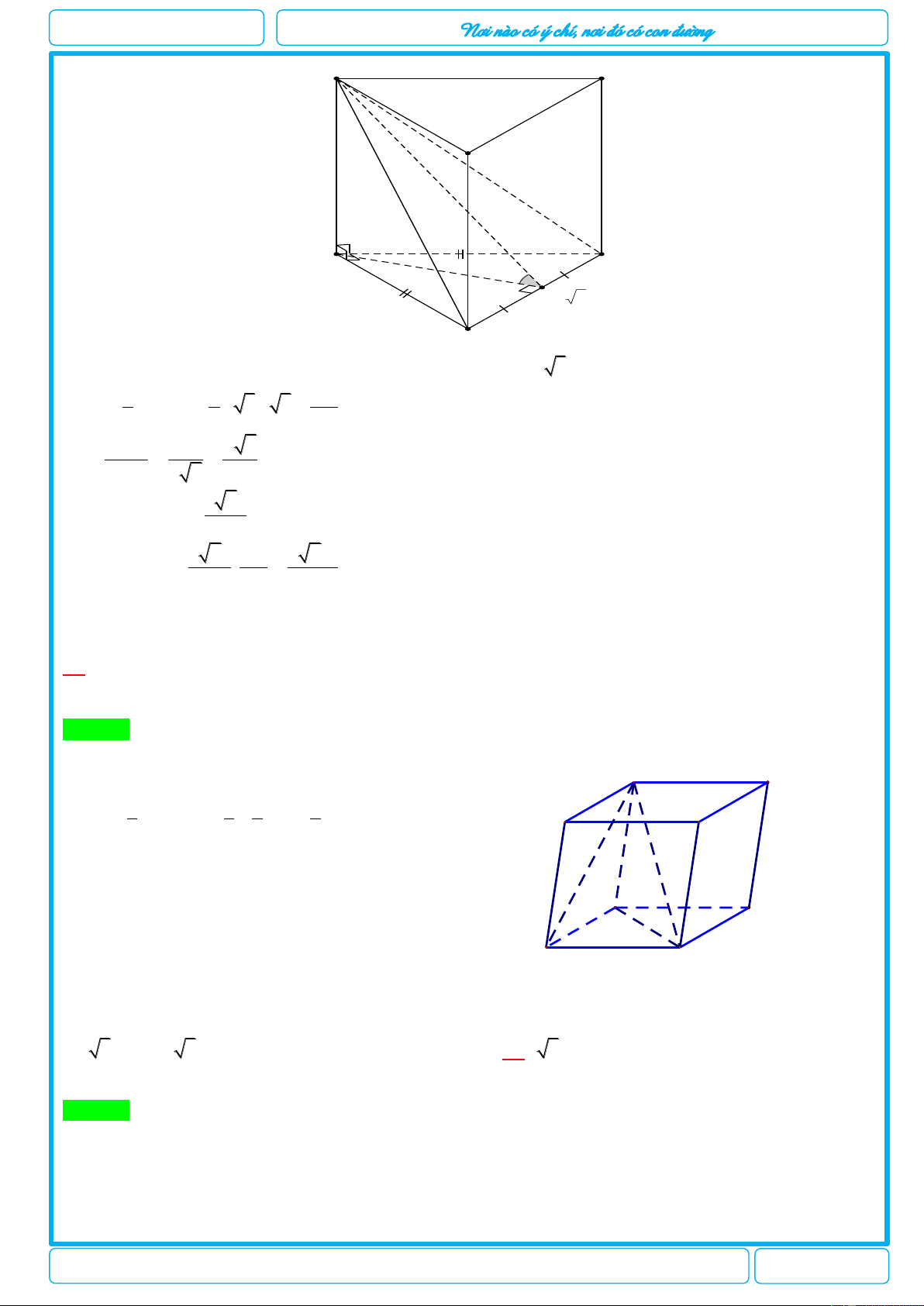
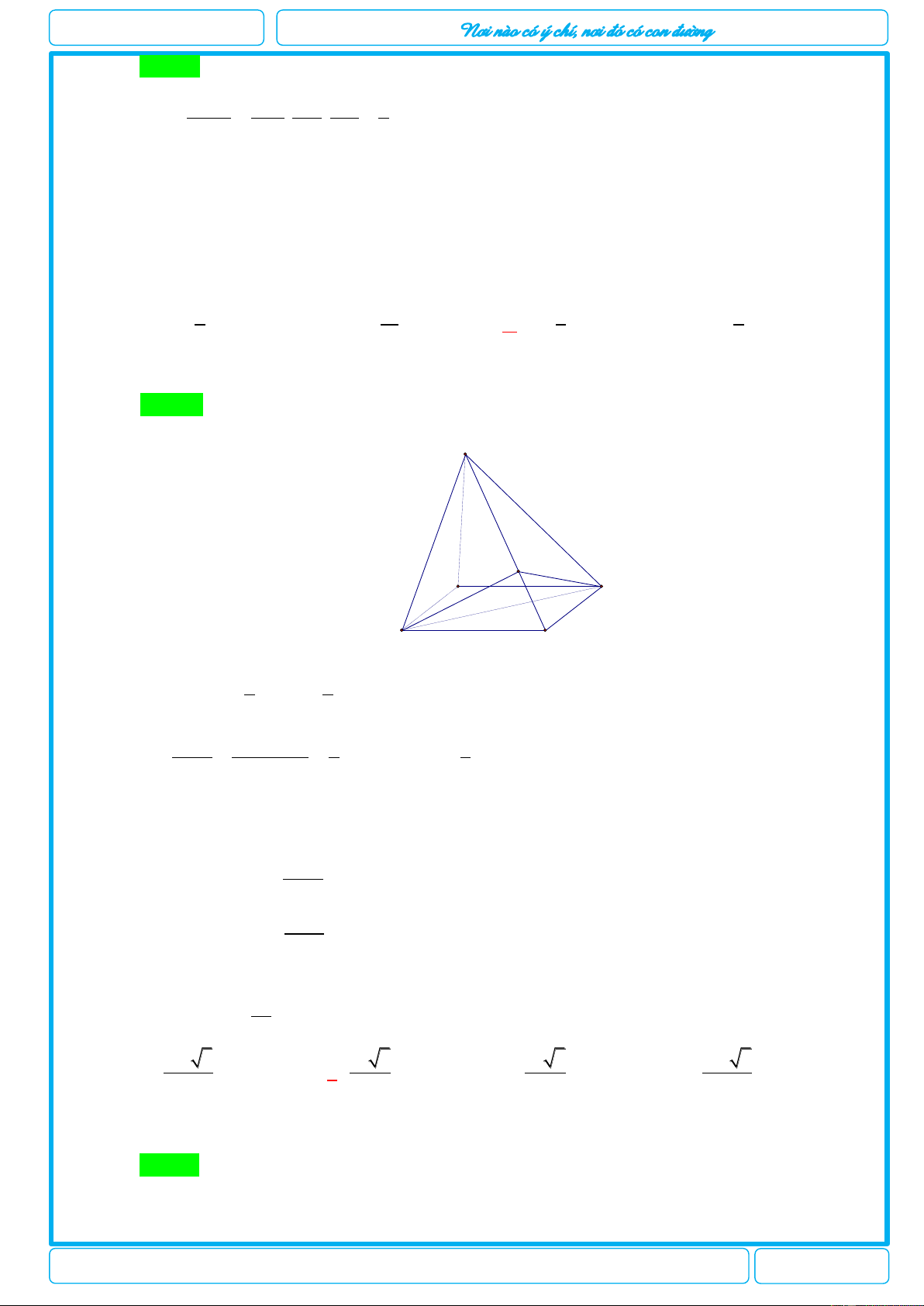
  có tất cả các cạnh bằng .a Thể tích khối tứ diện A BAC là 3 3a 3 a 3 3a 3 3a A. . B. . C. . D. . 6 6 12 4
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 3/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Câu 10. [2H1-3] Cho hình lập phương có tổng diện tích các mặt bằng 3
12a . Tính theo a thể tích khối lập phương đó. 3 a A. 3 8a . B. 3 2a . C. 3 a . D. . 3
Câu 11. [2H1-2] Cho hình lập phương ABCD.A BCD
  có diện tích mặt chéo ACC A   bằng 2 2 2a
. Thể tích của khối lập phương ABCD.A BCD   là A. 3 a . B. 3 2a . C. 3 2 2a . D. 3 8a .
Câu 12. [2H1-2] Một hình chóp tứ giác đều có cạnh đáy bằng a, các mặt bên tạo với đáy một góc
 . Thể tích của khối chóp đó là 3 a 3 a 3 a 3 a A. sin . B. tan . C. cot . D. tan . 2 2 6 6
Câu 13. [2H1-3] Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại A , AC a
, ACB  60 . Đường chéo BC của mặt bên BCC B
  tạo với mặt phẳng ACC A   một góc
30 . Tính thể tích của khối lăng trụ theo a. 3 4a 6 3 2a 6 3 a 6 A. V  . B. 3 V a 6 . C. V  . D. V  . 3 3 3
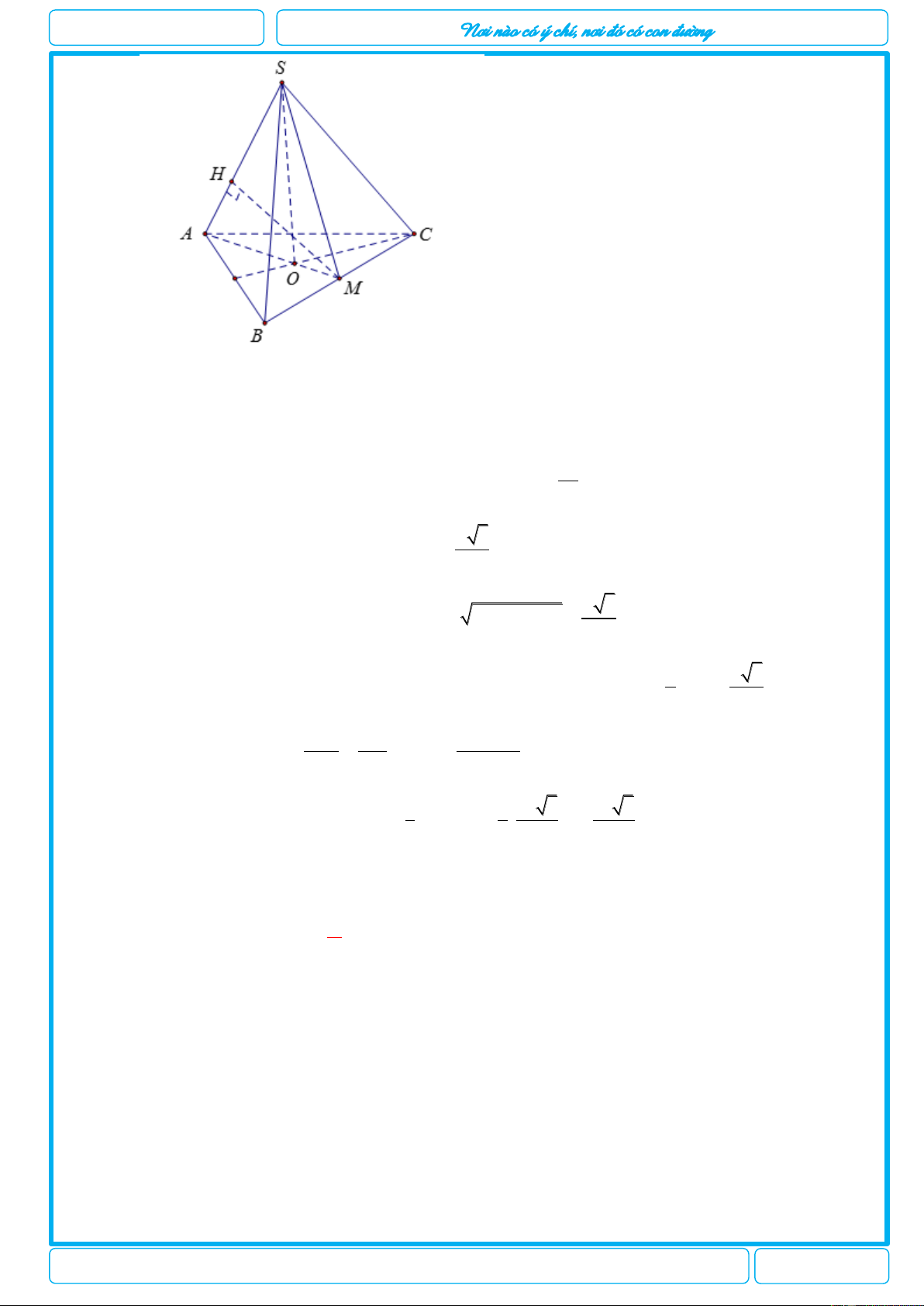
Câu 14. [2H1-3] Cho khối chóp tam giác đều .
S ABC có cạnh đáy bằng a và cạnh bên bằng 2a .
Tính thể tích V của khối chóp . S ABC 3 13a 3 11a 3 11a 3 11a A. V  . B. V  . C. V  . D. V  . 12 12 6 4
Câu 15. [2H1-2] Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác
đều cạnh 2a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích khối chóp .
S ABCD biết rằng mặt phẳng (SBC) tạo với mặt phẳng đáy một góc 30 .  3 3a 3 2 3a 3 4 3a A. . B. 3 2 3a . C. . D. . 2 3 3
Câu 16. [2H1-3] Cho hình chóp tứ giác đều có cạnh đáy bằng x . Diện tích xung quanh gấp đôi
diện tích đáy. Khi đó thể tích của khối chóp bằng: 3 x . 3 3 x . 3 3 x . 3 3 x . 3 A. . B. . C. . D. . 6 2 12 3
Câu 17. [2H1-3] Một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng
đáy một góc  . Thể tích của hình chóp đó là 3 3 3 3 A. 3 2 b cos  sin  . B. 3 2
b sin  cos  . C. 3 2
b cos  sin  . D. 3 b cos  sin  . 4 4 4 4
Câu 18. [2H1-1] Cho tứ diện ABCD . Gọi B' và C ' lần lượt là trung điểm của AB và AC . Tính tỉ
số thể tích của khối tứ diện AB' C' D và khối tứ diện ABCD . 1 1 1 1 A. . B. . C. . D. . 4 2 6 8
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 4/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Câu 19. [2H1-2] Cho khối chóp .
S ABC có thể tích bằng 16 . Gọi M , N , P lần lượt là trung điểm của
các cạnh SA,S ,
B SC . Tính thể tích V của khối tứ diện AMNP . A. V  2 . B. V  6 . C. V  4 . D. V  8 .
Câu 20. [2H1-2] Cho tứ diện ABCD có hai mặt ABC , BCD là các tam giác đều cạnh a và nằm
trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là: 3 a 3 3 a 3 a 3 3a A. . B. . C. . D. . 4 8 4 8
Câu 21. [2H1-3] Một hình hộp chữ nhật ABCD.A BCD
  có ba kích thước là 2cm , 3cm và 6cm .
Thể tích của khối tứ diện A.CB D   bằng A. 3 8 cm . B. 3 12 cm . C. 3 6 cm . D. 3 4 cm .
Câu 22. [2H1-3] Cho khối chóp .
S ABC có SA  6, SB  2, SC  4, AB  2 10 và góc SBC 90  , ASC 120 
. Mặt phẳng P đi qua B và trung điểm N của cạnh SC đồng thời vuông góc V
với mặt phẳng SAC cắt SA tại M . Tính tỉ số thể tích S.BM N k  . VS.ABC 1 2 2 1 A. k  . B. k  . C. k  . D. k  . 6 5 9 4
Câu 23. [2H1-3] Cho khối lăng trụ AB . C A BC
  có thể tích V , điểm P thuộc cạnh AA ,Q thuộc PA QB 1 BB sao cho   ; R R ABQP PA
là trung điểm CC. Tính thể tích khối chóp tứ giác . QB 3 theo V . 2 1 3 1 A. V . B. V . C. V . D. V . 3 3 4 2
Câu 24. [2H1-4] Người ta muốn xây một bể chứa nước dạng khối hộp chữ nhật trong một phòng
tắm. Biết chiều dài, chiều rộng, chiều cao của khối hộp đó lần lượt là 3m ; 1, 2m ; 1, 8m
(người ta chỉ xây hai mặt thành bể như hình vẽ bên). Biết mỗi viên gạch có chiều dài 20cm
, chiều rộng 10cm , chiều cao 5cm . Hỏi
người ta sử dụng ít nhất bao nhiêu viên 1dm
gạch để xây bể đó và thể tích thực của
bể chứa bao nhiêu lít nước? (Giả sử 1dm
lượng xi măng và cát không đáng kể).
A. 738 viên, 5742 lít. B. 730 viên, 5742 lít. 1,8 dm
C. 738 viên, 5740 lít. D. 730 viên, 5740 lít.
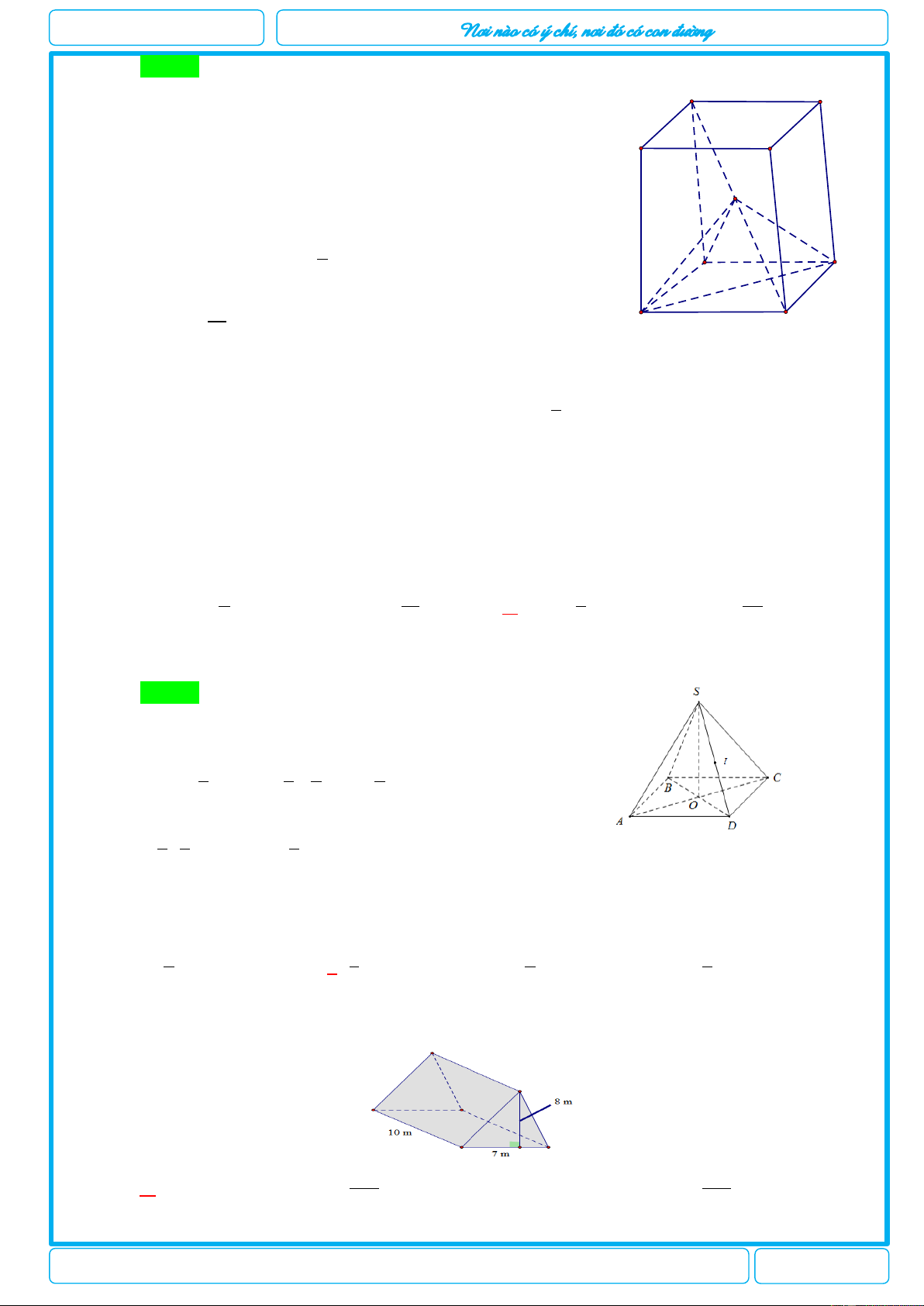
Câu 25. [2H1-3] Cho hình chóp . S ABCD có đáy 1, 2 m
là hình vuông cạnh a, mặt bên SAB là 3m
tam giác đều, mặt bên SCD là tam giác
vuông cân đỉnh S . Thể tích khối chóp . S ABCD là 3 3a 3 3a 3 a 3 3a A. . B. . C. . D. . 6 12 6 4
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 5/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 ĐỀ THAM KHẢO SỐ 2 Câu 1. [2H1-1] hình (a) hình (b) hình (c) hình (d)
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là A. hình (a). B. hình (b). C. hình (c). D. hình (d). Câu 2. [2H1-1] hình (a). hình (b). hình (c). hình (d).
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là A.1. B. 2 . C. 3 . D. 4 . Câu 3.
[2H1-1]Phát biểu nào sau đây là đúng?
A. Hình bát diện đều có 8 đỉnh, 12 cạnh, 6 mặt.
B. Hình bát diện đều có 6 đỉnh, 12 cạnh, 8 mặt.
C. Hình bát diện đều có 12 đỉnh, 8 cạnh, 6 mặt.
D. Hình bát diện đều có 8 đỉnh, 6 cạnh, 12 mặt. Câu 4.
[2H1-2]Một hình hộp đứng có hai đáy là hình thoi (không phải là hình vuông) có bao
nhiêu mặt phẳng đối xứng? A.1 . B. 2 . C. 3 . D. 4 . Câu 5.
[2H1-1]Thể tích khối chóp có diện tích đáy B và chiều cao h là: 1 1
A.V Bh . B.V Bh .
C.V  2Bh .
D.V Bh . 2 3 Câu 6.
[2H1-2]Trong các mệnh đề sau mệnh đề nào sai ?
A.Lắp ghép hai khối hộp sẽ được một khối đa diện lồi
B.Khối hộp là khối đa diện lồi
C.Khối tứ diện là khối đa diện lồi
D.Khối lăng trụ tam giác là khối đa diện lồi Câu 7.
[2H1-2]Nếu không sử dụngthêm điểm nào khác ngoài các đỉnh của hình lập phương thì
có thể chia hình lập phương thành
A.Một tứ diện đều và bốn hình chóp tam giác giác đều
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 6/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
B.Năm tứ diện đều
C.Bốn tứ diện đều và một hình chóp tam giác đều
D.Năm hình chóp tam giác giác đều,không có tứ diện đều Câu 8.
[2H1-1]Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là 1 1 4 A.V  . B h B.V  . B h C.V  . B h D.V  . B h . 3 2 3 Câu 9.
[2H1-3] Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật AD  2 ,
a AB a .Gọi H là
trung điểm của AD ,biết SH   ABCD .Tính thể tích khối chóp biết SA a 5 . 3 2a 3 3 4a 3 3 4a 3 2a A. B. C. D. . 3 3 3 3
Câu 10. [2H1-3]
Cho hình lập phương ABCDA’B’C’D’.I là trung điểm
BB’.Mặt phẳng (DIC’)chia khối lập phương thành 2 phần có
tỉ số thể tích phần bé chia phần lớn bằng: 1 7 4 1 A. . B. . C. . D. . 3 17 14 2
Câu 11. [2H1-2] Cho hình lập phương ABC .
D A' B'C' D' có A'C  4 3 . Thể tích khối lập phương ABC .
D A' B'C' D' là A. 32. B. 4 3 C. 64. D. 16.
Câu 12. [2H1-2] Cho khối chóp đều .
S ABCD có cạnh đáy bằng a 3 . Tính thể tích khối chóp .
S ABCD biết góc giữa cạnh bên và mặt đáy bằng 60°. 3 a 2 3 3a 2 3 3a 6 3 a 6 A. B. C. D. 2 2 2 2
Câu 13: [2H1-3] Cho lăng trụ đứng AB .
C A' B'C ' có đáy ABC là tam giác vuông tại A với AC  ;
a ACB  60 . Biết B 'C hợp với  ACC ' A một góc 0
30 . Thể tích của khối lăng trụ AB .
C A' B'C ' là: A. 3 6a B. 3 2a C. 3 3a D. 3 2 3a
Câu 14: [2H1-3] Cho hình chóp .
S ABC có đáy ABC là tam giác đều cạnh a , góc giữa đường thẳng
SA và mặt phẳng  ABC bằng 0
45 . Hình chiếu vuông góc của S trên mặt phẳng  ABC
là điểm H thuộc BC sao cho BC  3BH . Thể tích khối chóp . S ABC là: 3 a 21 3 a 21 3 a 21 3 a 21 A. B. C. D. 18 36 12 27
Câu 15: [2H1-2] Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng
SAB và SAD cùng vuông góc với mặt phẳng ABCD. Đường thẳng SC tạo với đáy một góc bằng 0
45 . Gọi M, N lần lượt là trung điểm của cạnh AB, AC . Thể tích của khối chóp . S MCDN là bao nhiêu?
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 7/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 3 5a 2 3 5a 2 3 5a 2 3 5a 2 A. B. C. D. 12 6 8 24
Câu 16: [2-H1-3] Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi SH là chiều cao
của hình chóp, khoảng cách từ trung điểm I của SH đến mặt bên SBC bằng b . Tính
thể tích V của khối chóp S.ABCD . ab 3 2a b ab 2ab A. V  . B. V  . C. V  . D. V  . 2 2 3 a 16b 2 2 3 a 16b 2 2 a 16b 2 2 a 16b
Câu 17: [2-H1-3] Hình chóp tam giác đều S.ABC có AB
a , góc giữa SA và đáy bằng 0 30 . Thể tích khối chóp là. 3 a 2 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 72 12 36
Câu 18: [2-H1-1] Cho tứ diện ABCD . Gọi B ' và C ' lần lượt là trung điểm của AB và AC . Tính tỉ
số thể tích của khối tứ diện AB 'C ' D và khối tứ diện ABCD . 1 1 1 1 A. . B. . C. . D. . 6 8 2 4
Câu 19: [2-H1-2] Cho khối chóp S.ABC có SA  9, SB  4, SC  8 và đôi một vuông góc. Các điểm A ,
B ,C thỏa mãn SA  2.SA , SB  3.SB , SC  4.SC . Thể tích khối chóp S.A BC   là. A. 16 . B. 12 . C. 2 . D. 24 .
Câu 20: [2-H1-2] Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm tam giác BCD . Tính
thể tích V của khối chóp . A GBC . A. V  4 . B. V  5 . C. V  6 . D. V  3 .
Câu 21: [2-H1-3] Cho khối hộp ABC .
D A' B' C ' D' có thể tích bằng 12 ( đơn vị thể tích). Gọi
M , N, P lần lượt là trung điểm của các cạnh A ,
D DC, AA' . Tính thể tích khối chóp . P BMN . 3 3 A. V . B. V 2 . C. V . D. V 3 . 4 2
Câu 22: [2-H1-3] Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy
một góc 60 . Gọi M là điểm đối xứng với C qua D ; N là trung điểm của SC , mặt
phẳng ( BMN ) chia khối chóp S.ABCD thành hai phần. Tính tỉ số thể tích giữa hai phần đó. 1 7 7 1 A. . B. . C. . D. . 7 5 3 5
Câu 23: [2-H1-3] Cho khối lập phương ABC . D ’ A ’ B C’ ’
D cạnh a . Gọi O và O’ lần lượt là tâm của ABCD và ’ A ’ B C’ ’
D . Thể tích phần chung nhau của hai khối chóp . O ’ A ’ B C’ ’ D và ’. O ABCD là: 3 a 3 a 3 a 3 a A. V  . B. V  . C. V  . D. V  . 12 6 4 3
Câu 24: [2-H1-4] Người ta muốn mạ vàng cho bề mặt phía ngoài của một cái hộp dạng hình hộp
đứng không nắp (nắp trên), có đáy là một hình vuông. Tìm chiều cao của hộp để lượng
vàng phải dùng để mạ là ít nhất, biết lớp mạ ở mọi nơi như nhau, giao giữa các mặt là
không đáng kể và thể tích của hộp là 3 4 dm . A. 1,5 dm . B. 1 dm . C. 0,5 dm . D. 2 dm .
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 8/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
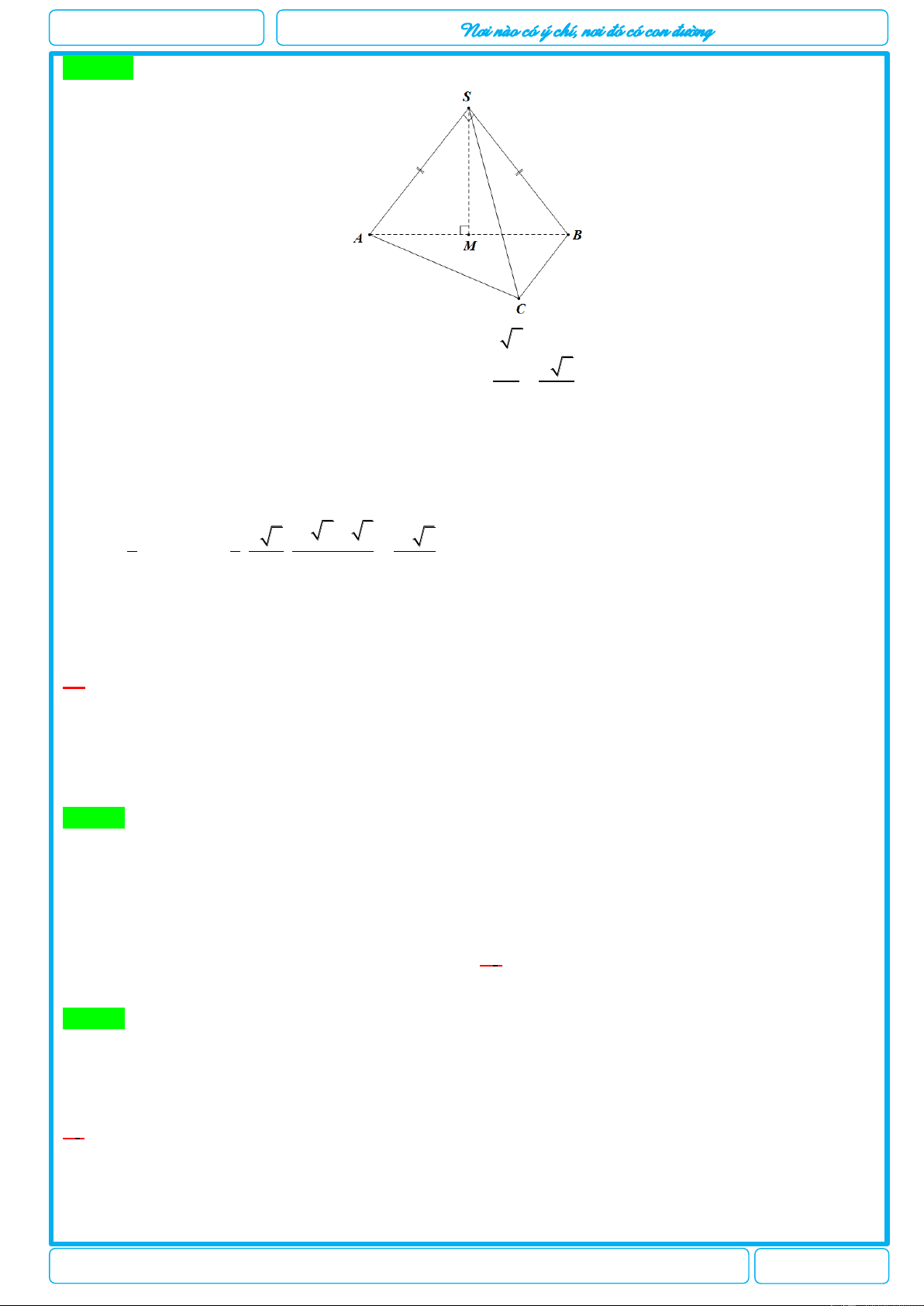
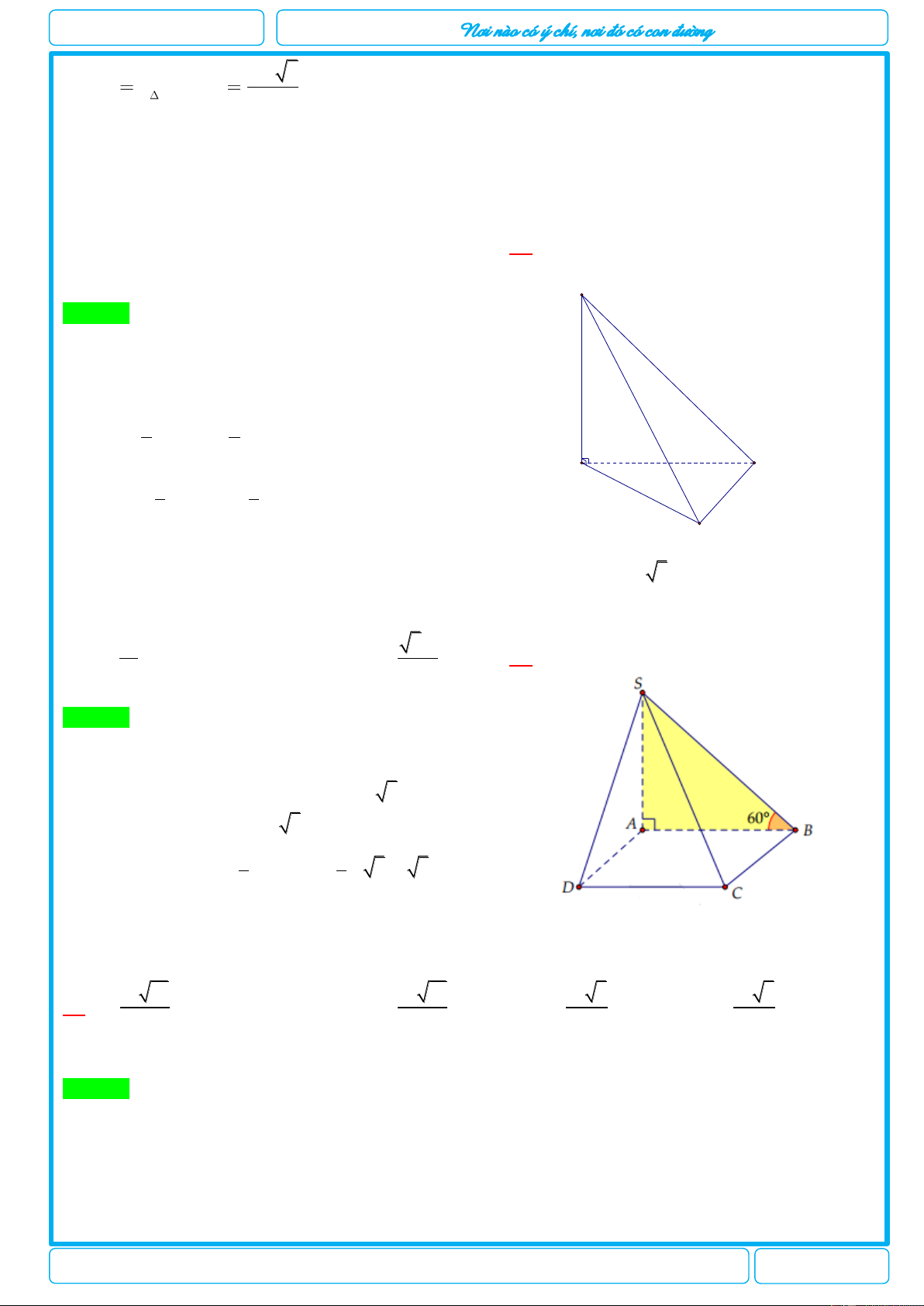
Câu 25: [2-H1-3] Cho hình chóp S.ABC có SA a , tam giác ABC đều, tam giác SAB vuông cân
tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng? 3 6a 3 6a 3 6a 3 6a A. . B. . C. . D. . 12 4 8 24
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 9/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 ĐỀ THAM KHẢO SỐ 3 Câu 1.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mỗi hình đa diện có ít nhất bốn đỉnh.
B. Mỗi hình đa diện có ít nhất ba đỉnh.
C. Số đỉnh của một hình đa diện lớn hơn hoặc bằng số cạnh của nó.
D. Số mặt của một hình đa diện lớn hơn hoặc bằng số cạnh của nó. Câu 2.
Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất: A. Năm cạnh.
B. Bốn cạnh. C. Ba cạnh. D. Hai cạnh. Câu 3.
Trong các mệnh đề sau, mệnh đề nào sai?
A. Khối tứ diện là khối đa diện lồi.
B. Lắp ghép hai khối hộp luôn được một khối đa diện.
C. Khối hộp là khối đa diện lồi.
D. Khối lăng trụ tam giác đều là khối đa diện lồi. Câu 4.
Trong không gian có tất cả bao nhiêu loại khối đa diện đều? A. 2. B. 3. C. 4. D. 5. Câu 5.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA vuông góc với đáy, SA a 2 .
Tính thể tích khối chóp S.ABCD? 3 a 2 3 a 2 3 a 2 A. V  . B. V  . C. 3 V a 2. D. V  . 6 2 3 Câu 6.
Phân chia khối lập phương ABC . D A BCD
  bởi ba mặt phẳng  A BD ,  DD B B   , B CD ta
được những khối đa diện nào?
A. Hai khối tứ diện và một khối lăng trụ tứ giác.
B. Ba khối tứ diện và một khối lăng trụ tam giác.
C. Hai khối tứ diện và một khối lăng trụ tam giác.
D. Hai khối tứ diện và hai khối chóp tứ giác. Câu 7.
Phân chia khối lăng trụ AB . C A BC
  bởi hai mặt phẳng  AB D   và  AB D
  ta được các khối nào sau đây?
A. Khối chóp tứ giác . A D B D B
  và khối tứ diện ABDB.
B. Khối chóp tứ giác . A D B D B
  và khối tứ diện ADD B  .
C. Khối chóp tứ giác . A D B D B
  và khối tứ diện AA BD  .
D. Ba khối tứ diện ABDB , ADD B  và AA BD   Câu 8.
Cho lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại A , I là trung điểm
của BC , BC a 6 . Mặt phẳng  A B
C tạo với mặt phẳng  ABC một góc 60. Thể tích khối lăng trụ AB . C A BC  là 3 9 2a 3 9 2a 3 9 2a 3 9 2a A. . B. . C. . D. . 4 2 12 6 Câu 9. Cho khối hộp ABC . D A BCD
  có thể tích bằng 72 (ĐVTT). Gọi V là thể tích khối chóp A.ABC 1
. Khi đó, chọn kết quả đúng trong các kết quả cho dưới đây?
A. V  12 .
B. V  24 .
C. V  36 . D. V  18 . 1 1 1 1
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 10/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Câu 10. Cho khối lập phương ABC . D A BCD
  , có đường chéo BD  3. Thể tích của khối lập phương ABC . D A BCD   bằng bao nhiêu? A. 3 . B. 6 3 . C. 3 . D. 3 3 .
Câu 11. Tổng diện tích các mặt bên của khối lập phương bằng 54 .Thể tích khối lập phương bằng?
A. 27. B. 9. C. 3 3. D. 3.
Câu 12. Cho hình chóp tứ giác đều S.ABCD cạnh đáy AB =a , góc SAC bằng 450 .Thể tích khối chóp bằng: 3 a 3 a 2 3 a 3 3 a 2 A. . B. C. D. 3 2 6 6
Câu 13. Cho lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác đều cạnh a . Mặt phẳng AB 'C ' tạo với mặt đáy góc 0
60 . Tính theo a thể tích lăng trụ ABC.A'B 'C ' . 3 a 3 3 3a 3 3 a 3 3 3a 3 A. V . B. V . C. V . D. V . 2 4 8 8
Câu 14. Cho khối chóp S.ABC có SA vuông góc với đáy, SA  4, AB  6, BC  10 và CA  8 . Tính thể
tích V của khối chóp S.ABC.
A. V  40.
B. V  192.
C. V  32.
D. V  24.
Câu 15. Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB a, AD a 3, SA vuông góc với đáy và
mặt phẳng SBC tạo với đáy một góc 0
60 . Tính thể tích V của khối chóp S.ABCD . 3 a 3 3a A. V  . B. V  . C. 3
V a . D. 3
V  3a . 3 3
Câu 16. Cho hình chóp đều S.ABCD có AB a . Gọi M là trung điểm AD và góc tạo bởi mặt phẳng
SCM  và mặt đáy bằng 0
60 . Tính theo a thể tích V của khối chóp S.ABC . D 3 a 15 3 a 15 3 a 5 3 a 5 A. V  . B. V  . C. V  . D. V  . 30 10 15 5
Câu 17. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên tạo với đáy một góc  . Tính thể tích khối chóp đó 3 a cot 3 a tan 2 a tan 3 a tan A. . B. . C. . D. . 12 12 12 4
Câu 18. Cho tứ diện ABCD, gọi B’, C’ lần lượt là trung điểm của AB, AC. Khi đó tỉ số thể tích của khối tứ
diện AB’C’D và khối tứ diện ABCD bằng: 1 1 1 1 A. . B. . C. . D. . 2 4 6 8
Câu 19. Cho hình chóp S.ABC có SA vuông góc mặt đáy , SA=a, tam giác ABC đều cạnh 2a. Gọi M,N lần
lượt thuộc cạnh SB,SC sao cho SM=MB,   SN
2CN . Tính thể tích khối AMNCB. 3 2 3a 3 3a 3 3a 3 2 3a A. . B. . C. . D. . 9 9 18 3
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 11/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Câu 20. Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D , (ABC)  (BCD)
và AD hợp với (BCD) một góc 60o .Tính thể tích tứ diện ABCD. 3 a 3 3 a 3 3 a 3 3 2a 3 A. 9 B. 3 C. 27 D. 9
Câu 21. Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh bằng a . Gọi O là giao điểm của AC và BD . Tính
thể tích của tứ diện OA' BC . 3 a 3 a 6 3 a 3 a A. . B. . C. . D. . 6 24 12 4
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a , AD = 2a. Cạnh SA vuông
góc với mặt phẳng đáy, cạnh bên SB tạo với mặt phắng đáy một góc 0
60 . Trên cạnh SA lấy điểm M sao cho a 3 AM =
, mặt phẳng (BCM) cắt cạnh SD tại N. Tính thể tích khối chóp S.BCNM 3 10 3 3 10 3a 3 10 3a 3 10a A. . B. . C. . D. . 27 9 27 27
Câu 23. Cho hình lăng trụ ABC. A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên hợp với đáy một góc
là 450. Gọi P là trung điểm BC, chân đường vuông góc hạ từ A’ xuống (ABC) là H sao cho 1 AP AH . gọi 2
K là trung điểm AA’,   là mặt phẳng chứa HK và song song với BC cắt BB’ và CC’ tại M, N. Tính tỉ số thể V tích ABCKMN
VA'B'C'KMN 1 2 1 3 A. B. C. D. 2 3 3 4
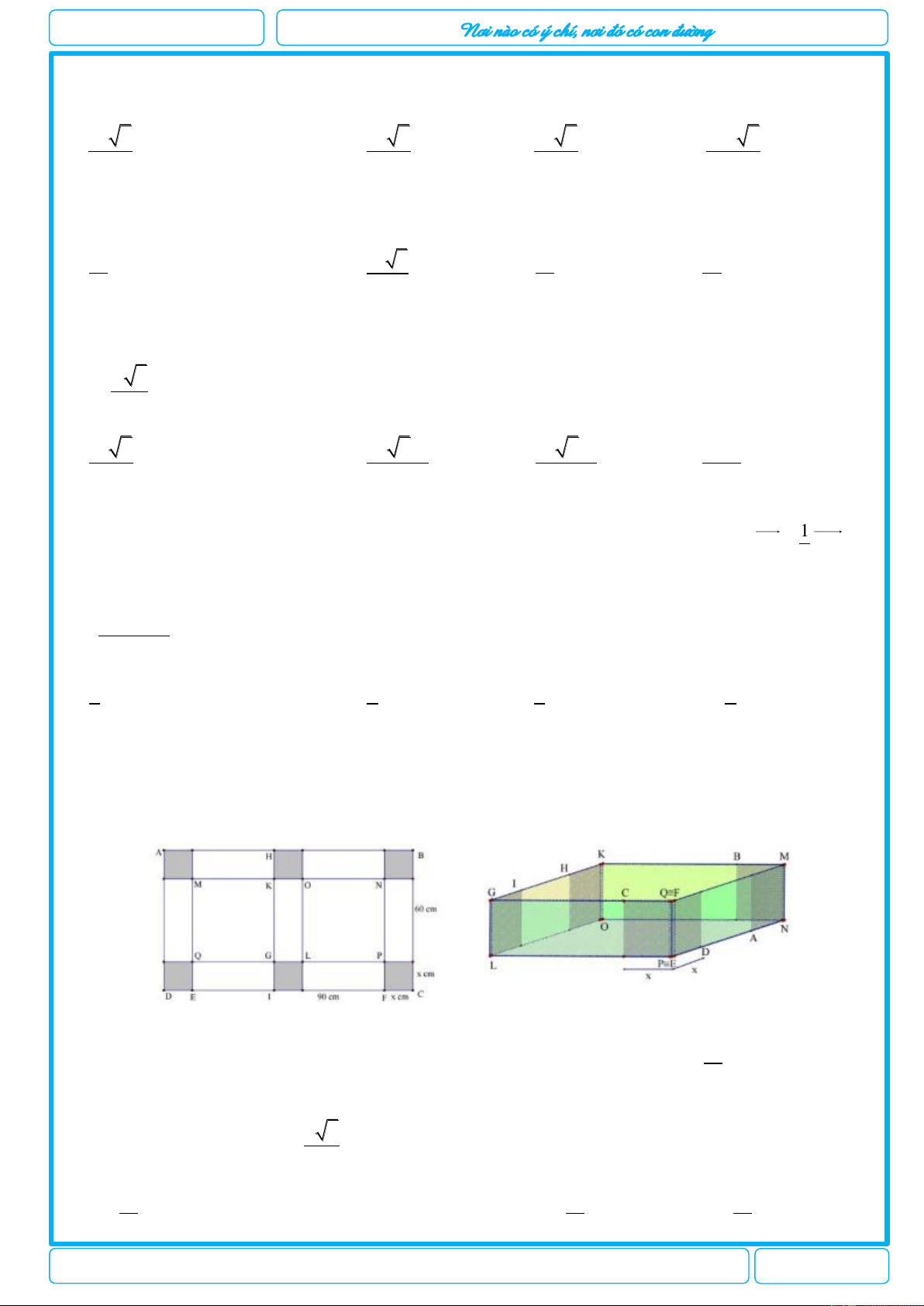
Câu 24. Cho một tấm bìa hình chữ nhật chiều dài AB  90cm , chiều rộng BC  60cm . Người ta cắt 6
hình vuông bằng nhau như hình vẽ, mỗi hình vuông cạnh bằng x cm , rồi gập tấm bìa lại như hình vẽ dưới
đây để được một hộp quà có nắp. Tìm x để hộp nhận được thể tích lớn nhất? 10 A. 10cm. B. 9cm. C. 15cm. D. cm. 3
Câu 25. Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy và khoảng cách từ a
A đến mặt phẳng SBC bằng
2 . Tính thể tích V của khối chóp đã cho. 2 3 a 3 a 3 a A. V  . B. 3
V a . C. V  . D. V  . 2 3 3
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 12/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 ĐỀ THAM KHẢO SỐ 4
Câu 1. [2H1-1] Cho khối chóp có là n – giác n  3;nN  . Mệnh đề nào đúng sau đây:
A. Số cạnh của khối chóp bằng n + 1.
B. Số mặt của khối chóp bằng 2n.
C. Số đỉnh của khối chóp bằng n + 1.
D. Số mặt của khối chóp bằng số đỉnh của nó.
Câu 2. [2H1-1] Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
D. Mỗi mặt có ít nhất ba cạnh.
Câu 3. [2H1-2] Trong các mệnh đề sau mệnh đề nào sai ?
A. Lắp ghép hai khối hộp sẽ được một khối đa diện lồi.
B. Khối hộp là khối đa diện lồi.
C. Khối tứ diện là khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi.
Câu 4. [2H1-1] Có bao nhiêu loại khối đa diện đều? A. 2 . B. 4 . C. 5 . D. Vô số. Câu 5. 1
[2H1-1] Khối đa điện nào sau đây có công thức tính thể tích là V
Bh ( B là diện tích đáy; h là chiều 3 cao) A. Khối lăng trụ. B. Khối chóp.
C. Khối lập phương.
D. Khối hộp chữ nhật.
Câu 6. [2H1-2] Trong Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và D .
Bằng hai mặt phẳng MCD và  NAB ta chia khối tứ diện đã cho thành bốn khối tứ diện:
A. AMCN, AMND, AMCD, BMCN.
B. AMNC, AMND, BMNC, BMND.
C. AMCD, AMND, BMCN, BMND.
D. BMCD, BMND, AMCN, AMDN.
Câu 7. [2H1-2] Có thể chia hình lập phương thành bao nhiêu hình tứ diện bằng nhau? A. 2 . B. Vô số. C. 4 . D. 6 .
Câu 8. [2H1-2] Trong cách mệnh đề sau, mệnh đề nào sai?
A. Hai khối hộp chữ nhật có diện tích xung quanh bằng nhau thì có thể tích bằng nhau.
B. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
C. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
D. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
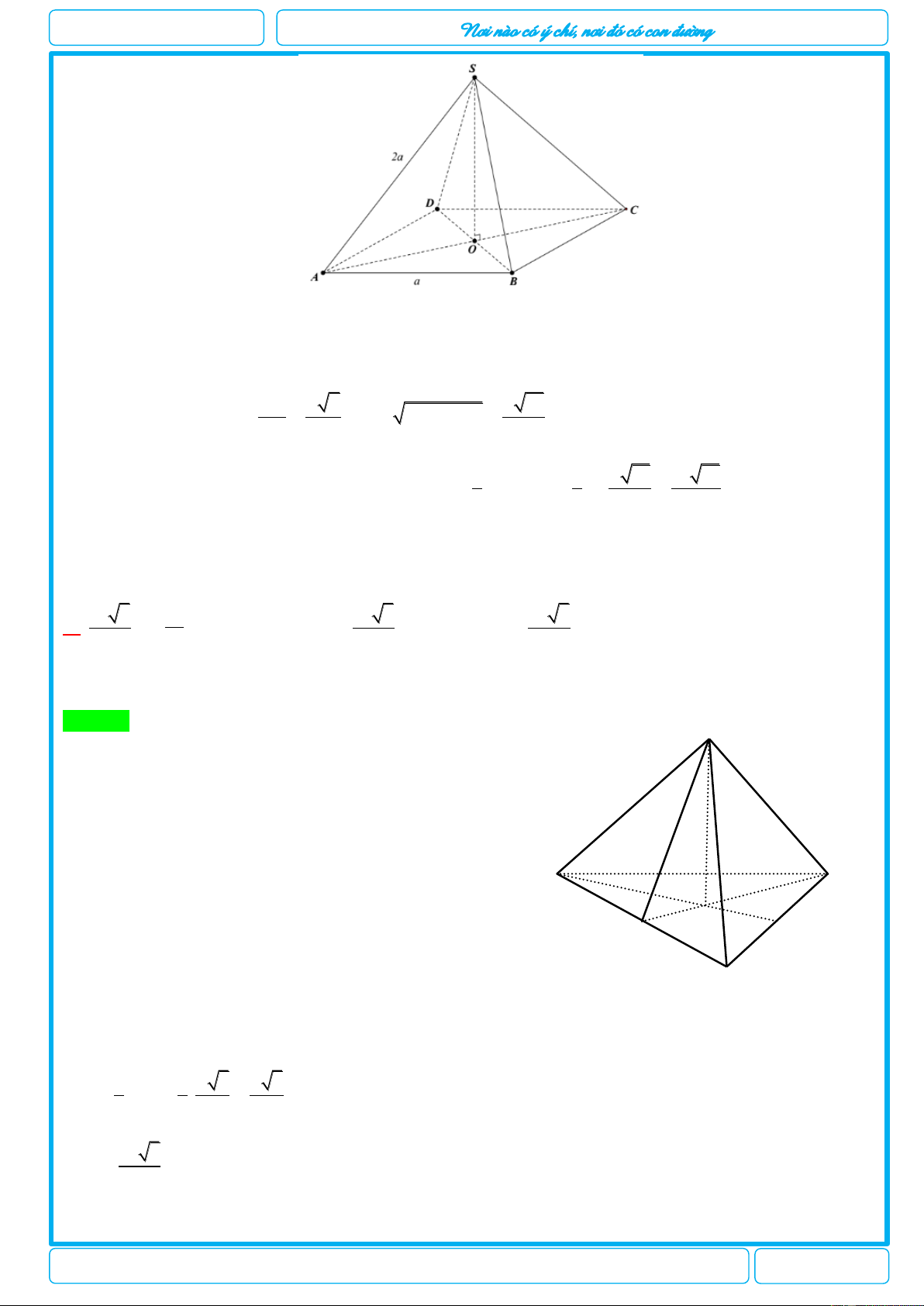
Câu 9. [2H1-3] Cho hình hộp AB D. C A BCD
 . Tỉ số thể tích của khối tứ diện ACB'D' và khối hộp AB D. C A BCD   là: 1 1 1 1 A. . B. . C. . D. . 5 4 3 6
Câu 10. [1H1-3] Cho hình lập phương ABC . D ’ A ’ B ’ C ’
D có khoảng cách giữa ’ A C và ’ C ’ D là 1 cm. Thể
tích khối lập phương ABC . D ’ A ’ B ’ C ’ D là: A. 3 8cm . B. 3 2 2 cm . C. 3 3 3 cm . D. 3 27cm .
Câu 11. [1H1-2] Tính thể tích V của khối lập phương ABC . D A BCD
  , biết AC  a 3 . 3 3 6a 1 A. 3 V a . B. V  . C. 3 V  3 3a . D. 3 V a . 4 3
Câu 12: [1H1-2] Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a là 3 2a 3 3a 3 3a 3 a A. . B. . C. . D. . 6 4 2 3
Câu 13: [1H1-3] Cho lăng trụ đứng tam giác AB . C A BC
  có đáy ABC là tam giác vuông cân tại B với
BA BC a , biết A B
 hợp với đáy ABC một góc 60 . Tính thể tích khối lăng trụ. 3 a 3 3 a A. . B. 3 a . C. 3 2a . D. . 2 2
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 13/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Câu 14: [1H1-3] Cho hình chóp S.ABC có tam giác ABC là tam giác đều cạnh a . Hình chiếu vuông góc
của S trên mặt phẳng  ABC là trung điểm của cạnh AB , góc tạo bởi cạnh SC và mặt phẳng  ABC bằng o
30 . Tính thể tích của khối chóp S.ABC . 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 8 8 4 24
Câu 15: [1H1-2] Cho hình chóp S.ABCD có đáy là hình vuông cạnh ,
a SA vuông góc với mặt đáy , SD tạo
với mặt phẳng SAB một góc bằng 
30 . Tính thể tích V của khối chóp. 3 6a 3 6a 3 3a A. . B. 3 3a . C. . D. . 18 3 3
Câu 16: [1H1-3] Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên gấp hai lần cạnh đáy. Tính tích V
của khối chóp tứ giác đã cho. 3 2a 3 2a 3 14a 3 14a A. V  . B. V  . C. V  . D. V  . 2 6 2 6
Câu 17: [1H1-3] Cho hình chóp tam giác đều S.ABC . Tính theo a thể tích khối chóp S.ABC biết rằng
AB a , (SBC),(ABC)  60 . 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 24 4 4 12
Câu 18: [1H1-1] Cho hình chóp tam giác S.ABC . Gọi M lần lượt là trung điểm của SB và N nằm trên
cạnh SC sao cho SN  2NC . Khi đó tỉ số thể tích của khối tứ diện S.AMN và khối tứ diện S.ABC bằng: 1 1 1 1 A. . B. . C. . D. . 6 3 6 2
Câu 19: [1H1-2] Cho khối chóp S.ABC có thể tích bằng 16 . Gọi M , N, P lần lượt là trung điểm của các cạnh S , A S ,
B SC . Tính thể tích V của khối tứ diện AMNP . A. V  2 . B. V  6 . C. V  4 . D. V  8 .
Câu 20: [1H1-2] Cho hình chóp tam giác S.ABC có ABC là tam giác đều cạnh a , hai mặt phẳng SAB và
SAC cùng vuông góc với mặt đáy ABC và SC  2a. Tính theo a thể tích V của khối chóp S.ABC . 1 3 3 3 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 4 2 6 4
Câu 21: [1H1-3] Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng 6 . Gọi G là trọng tâm tam giác
A' BD . Tính thể tích V của khối tứ diện GABC . A. V  12 . B. V  18 . C. V  24 . D. V  36 .
Câu 22. [2H1-3] Cho khối chóp .
O ABC . Trên ba cạnh O , A O ,
B OC lần lượt lấy ba điểm ’, A B ,  C sao cho V 2OA  O ,
A 4OB  O ,
B 3OC  OC . Tính tỉ số O.A'B'C' VO.ABC 1 1 1 1 A. . B. . C. . D. . 12 24 16 32
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 14/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Câu 23. [2H1-3] Cho khối lăng trụ tam giác đều AB . C ’ A ’ B ’
C có tất cả các cạnh đều bằng a . Thể tích khối tứ diện ’ A B ’ B ’ C là 3 a 3 3 a 3 3 a 3 3 a A.B.C.D.  12 4 6 12
Câu 24. [2H1-4] Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các
đỉnh là các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng a . Hãy tính thể tích
của khối tám mặt đều đó: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 6 12 8
Câu 25. [2H1-3] Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , cạnh SB vuông góc với
đáy và mặt phẳng SAD tạo với đáy một góc 60. Tính thể tích khối chóp S.ABCD . 3 3a 3 3 3a 3 3 8a 3 3 4a 3 A. V  . B. V  . C. V  . D. V  . 4 8 3 3
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 15/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 ĐỀ THAM KHẢO SỐ 5 Câu 1.
[2D4-2] Hình đa diện đều có tất cả các mặt là ngũ giác có bao nhiêu cạnh? A. 20 . B. 60 . C. 30 . D. 12 . Câu 2.
[2H1-1] Hình nào sau đây không phải là hình đa diện . A. Hình trụ. B. Hình tứ diện.
C. Hình lập phương. D. Hình chóp. Câu 3.
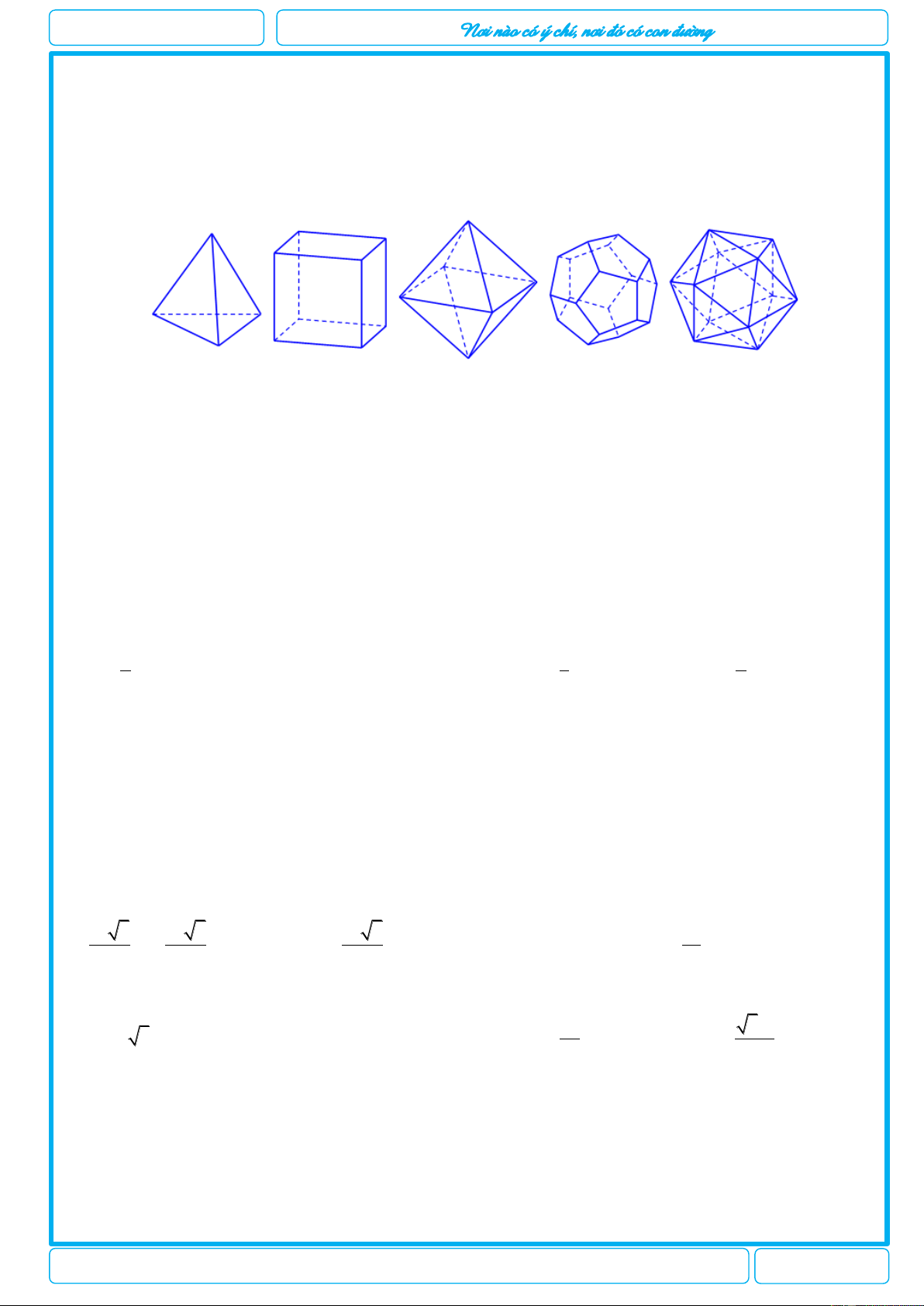
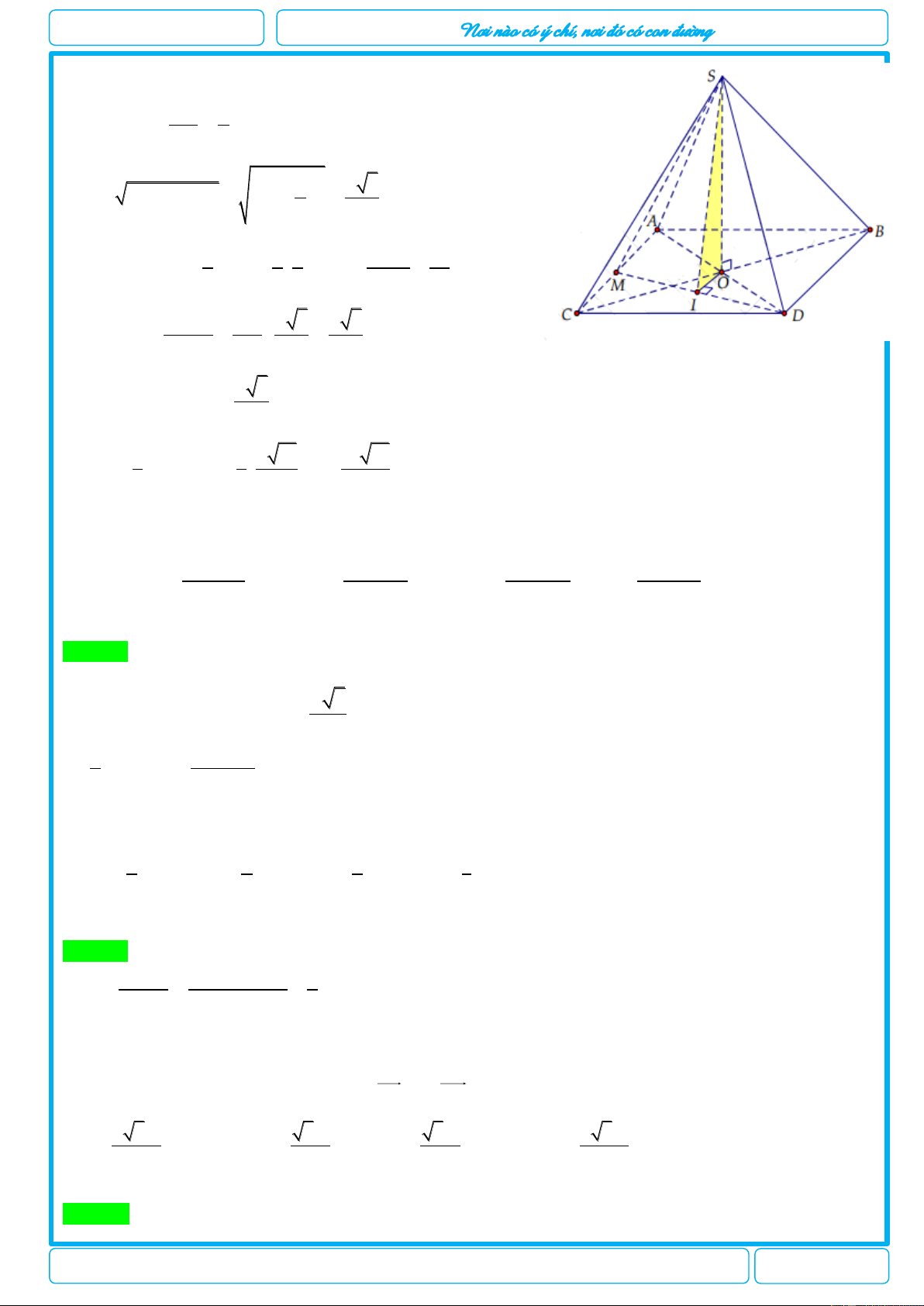
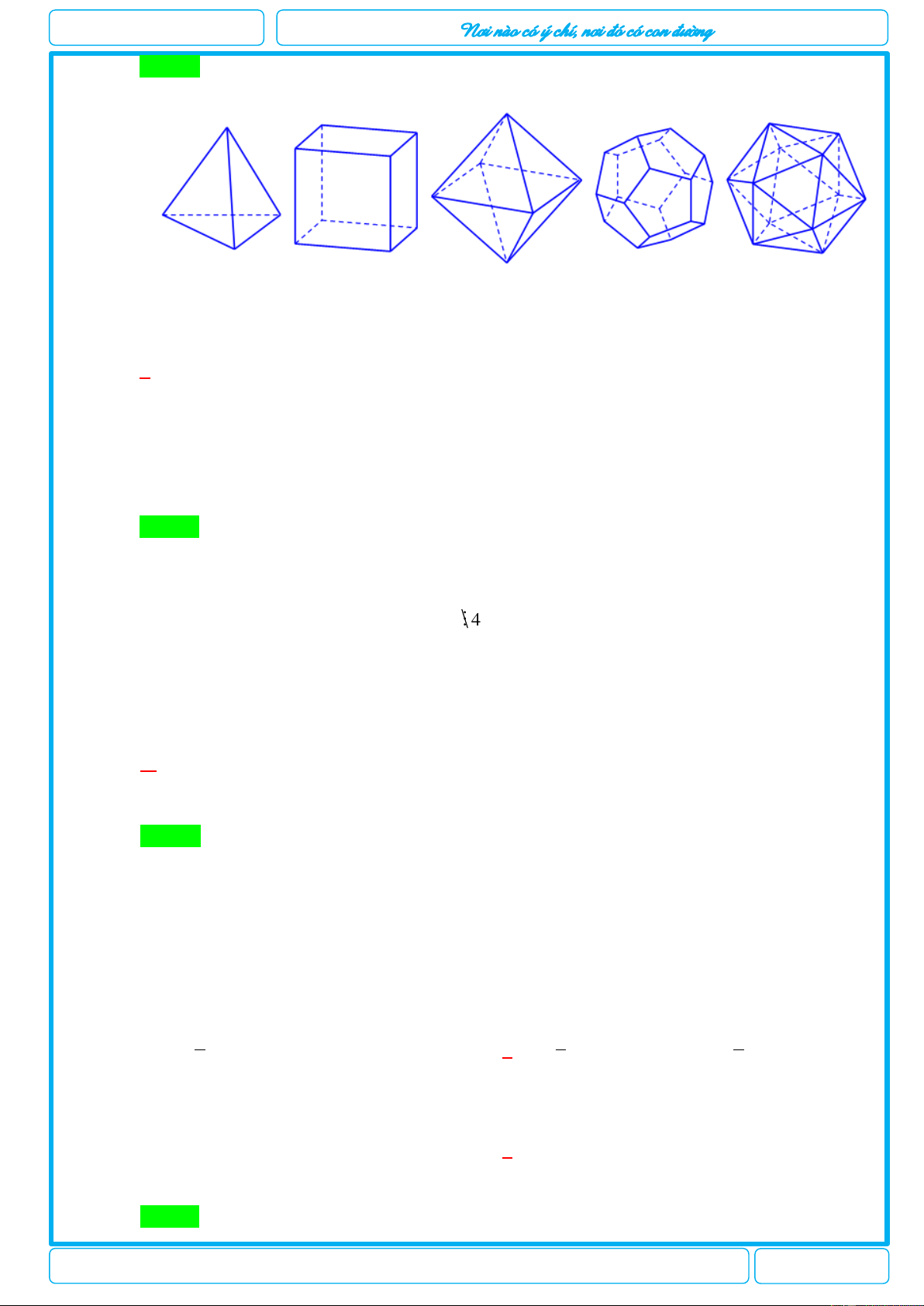
[2H1-2] Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ sau
Khối tứ diện đều Khối lập phương Bát diện đều Hình 12 mặt đều Hình 20 mặt đều
Mệnh đề nào sau đây đúng?
A. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.
B. Khối lập phương và khối bát diện đều có cùng số cạnh.
C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh. Câu 4.
[2D4-1] Số đỉnh của khối bát diện đều là: A. 6. B. 8. C. 12. D. 4. Câu 5.
[2H1-1]Công thức nào sau đây là công thức tính thể tích khối chóp? 1 1 1 A. V S.h .
B. V S.h . C. V S.h . D. V S.h . 6 3 2 Câu 6.
[2H1-2]Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm SC. Mặt phẳng
  qua M song song với DC chia khối chóp thành bao nhiêu khối chóp tứ giác. A. 4 . B. 3 . C.1 . D. 2 . Câu 7.
[2D4-2] Cắt khối lăng trụ MN . P M NP
  bởi các mặt phẳng MN P
  và MNPta được những khối đa diện nào?
A. Hai khối tứ diện và hai khối chóp tứ giác.
B. Một khối tứ diện và một khối chóp tứ giác.
C. Ba khối tứ diện.
D. Hai khối tứ diện và một khối chóp tứ giác. Câu 8.
[2H1-1] Thể tích khối lăng trụ đứng tam giác AB . C A BC
  có tất cả các cạnh bằng a là . 3 a 3 3 a 3 3 a 3 3 a A. . B. . C. . D. . 6 3 4 4 Câu 9.
[2H1-1] Tính theo a thể tích V của khối lập phương ABC . D A BCD
  biết AC  . a 3 a 3 3a A. 3 V  3 3a . B. 3 V a . C. V  . D. V  . 27 9
Câu 10. [2D4-2] Tính thể tích của khối hộp chữ nhật có diện tích của các mặt bên và mặt đáy lần lượt là 2 10 cm , 2 16 cm và 2 40 cm . A. 3 160 cm . B. 3 400 cm . C. 3 80 cm . D. 3 640 cm .
Câu 11. [2H1-2] Cho hình lập phương ABC . D A BCD
  có cạnh bằng a. Tính thể tích khối tứ diện ACB D   theo a .
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 16/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 3 a 3 a 3 a 3 a A. . B. . C. . D. . 6 2 3 4
Câu 12. [2H1-3] Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên
và mặt phẳng đáy là  . Mặt phẳng  P qua AC và vuông góc với mặt phẳng SAD chia khối chóp V
S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là MACD ? VSABCM A. 2 cos  B. 2 sin  C. 2 tan  D. 0, 9
Câu 13. [2D4-2] Cho lăng trụ đứng AB .
C A' B 'C ' có đáy là tam giác vuông tại 0 , A AC  , a ACB  60 .
Đường chéo BC ' của mặt bên BCC ' B' tạo với mặt phẳng  AA'C 'C một góc 0 30 . Tính thể tích
của khối lăng trụ theo a . 3 a 6 3 a 6 3 2 6a A. . B. . C. 3 a 6 . D. . 2 3 3
Câu 14. [2H1-3] Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A và AB AC a 2 . Tam giác
SBC có diện tích bằng 2
2a và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của
khối chóp S.ABC . 3 4a 3 a 3 2a A. V  . B. V  . C. 3 V  2a . D. V  . 3 3 3
Câu 15. [1H2-3] Tính thể tích khối chóp S.ABCD có ABCD là hình thang vuông tại , A B có AD  2 ,
a AB BC a , SA   ABCD , Góc giữa SCD và  ABC là 0 60 . Tính thể tích khối chóp S.ABCD 3 a 6 3 3 3a 3 6 3a 3 a 6 A. . B. . C. . D. . 4 4 4 2
Câu 16. [2D4-3] Cho hình chóp tứ giác đều S.ABCD. Gọi O là tâm mặt đáy, biết SO  20cm và khoảng
cách từ điểm O tới mặt bên của khối chóp bằng 12 cm . Tính thể tích khối chóp S.ABCD. A. 3 V  3840cm . B. 3 V  6000cm . C. 3 V  1920cm . D. 3 V  3000cm .
Câu 17. [2H1-3] Cho một hình chóp tứ giác đều có cạnh đáy bằng a và diện tích xung quanh gấp đôi diện
tích đáy. Khi đó thể tích của khối chóp là. 3 a 3 3 a 2 3 a 3 3 a 3 A. . B. . C. . D. . 12 3 3 6
Câu 18. [2H1-1] Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB và AC . Khi đó tỉ số thể tích
của khối tứ diện AMND và khối tứ diện ABCD bằng: 1 1 1 1 A. B. C. D. 2 4 6 8
Câu 19. [2D4-2] Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh
SC lấy điểm E sao cho SE  2EC . Tính thể tích V của khối tứ diện SEBD . 2 1 1 1 A. V  . B. V  . C. V  . D. V  . 3 12 3 6
Câu 20. [2H1-3] Cho hình chóp đều S.ABC có cạnh đáy bằng a , khoảng cách giữa cạnh bên SA và cạnh đáy 3a BC bằng
. Thể tích khối chóp S.ABC tính theo a là . 4
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 17/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 3 3a 3 3 a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 16 12 8 8
Câu 21. [1H2-2] Cho khối hộp ABC .
D A' B 'C ' D ' có thể tích bằng 3
24dm .Gọi M là trung điểm của A' D
Tính thể tích khối chóp M.ABC ? A. 3 6dm . B. 3 2dm . C. 3 3dm . D. 3 9dm .
Câu 22. [2D4-3] Cho hình chóp S.ABCD có thể tích bằng 1. Biết mặt đáy là hình vuông tâm O và SO vuông
góc với mặt phẳng  ABCD . Gọi I là trung điểm cạnh SD, tính thể tích khối tứ diện IOBC. 1 1 1 1 A. V  . B.V  . C.V  . D.V  . IOBC 2 IOBC 12 IOBC 8 IOBC 24
Câu 23. [2H1-4] Cho hình hộp ABC . D A BCD
  . Tỉ số thể tích của khối tứ diện ACB D   và khối hộp ABC . D AB CD   bằng 1 1 1 1 A. . B. . C. . D. . 2 3 4 6
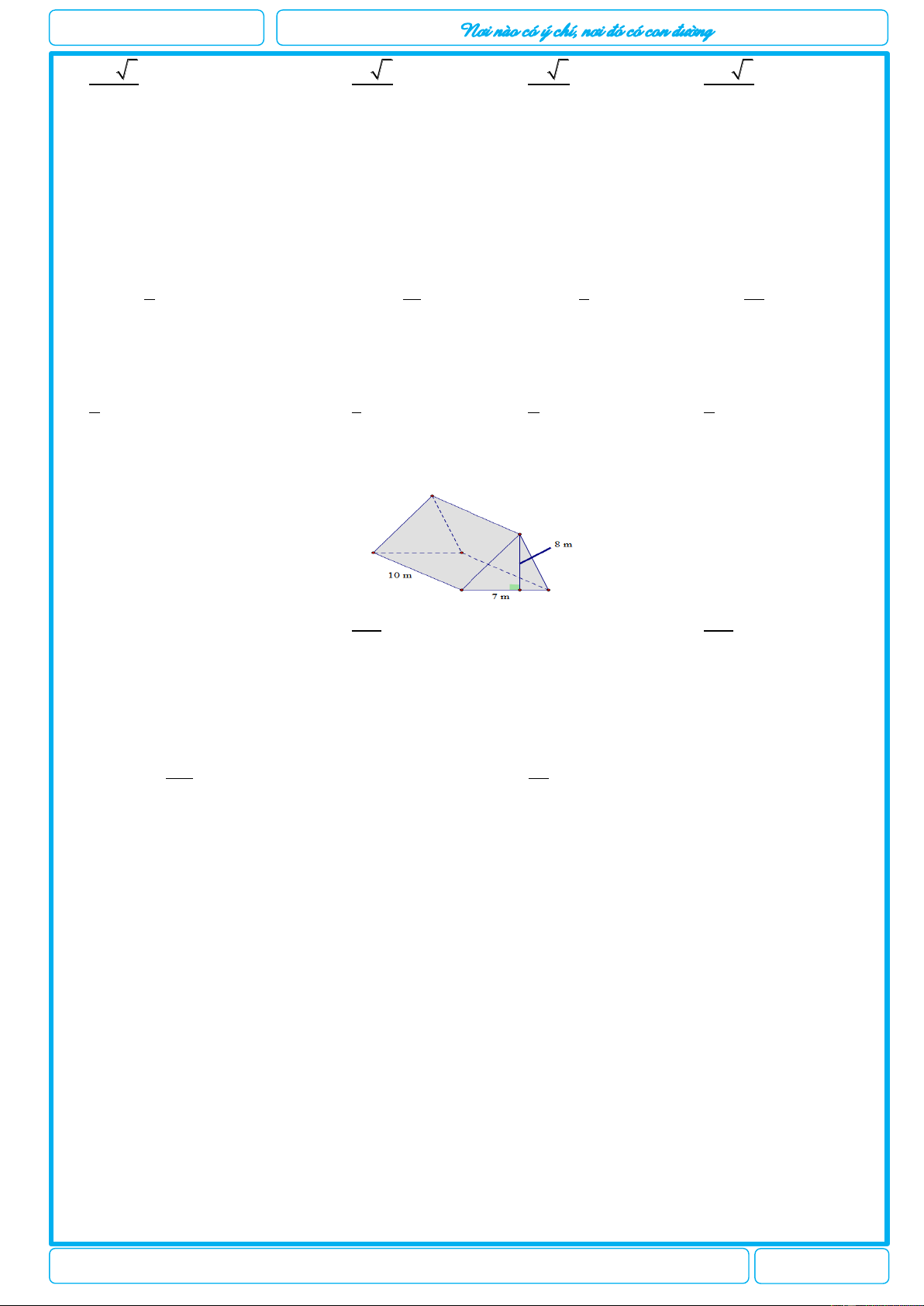
Câu 24. [2H1-3] Một túp lều có dạng hình lăng trụ đứng có kích thước như hình bên. Tính thể tích của túp lều. 280 560 A. 3 280 m B. 3 m C. 3 560 m D. 3 m 3 3
Câu 25. [2H1-4] Cho tứ diện ABCD có các cạnh AB A
, C và AD đôi một vuông góc nhau; AB  6 , a
AC 7a, A
D 4a. Gọi M, N , P
tương ứng là trung điểm các cạnh BC, C D, B
D. Thể tích V của tứ diện AMN . P 3 7a 28 A. . B. 3 14a . C. 3 a . D. 3 7a . 2 3
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 18/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 1 ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 A D B C A A D D C A 11 12 13 14 15 16 17 18 19 20 C D B B B A A A A B 21 22 23 24 25 B A B A B
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 2 ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 A C B C D A A A C A 11 12 13 14 15 16 17 18 19 20 B B A B D B D D C A 21 22 23 24 25 A B A B A
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 3 ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 A C B D D D D A A D 11 12 13 14 15 16 17 18 19 20 A D D C C A B B A A 21 22 23 24 25 C C A A D
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 4 ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 C C A C B C B A C B 11 12 13 14 15 16 17 18 19 20 A A A D D D A B A A 21 22 23 24 25 A B A B C
BẢNG ĐÁP ÁN ĐỀ THAM KHẢO SỐ 5 ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 C A B A C C C C D C 11 12 13 14 15 16 17 18 19 20 C A C D A B D A C B 21 22 23 24 25 B C B A D
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 19/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 1 Câu 1.
[2H1-1] Hình nào dưới đây không phải là một khối đa diện? A. B. C. D. Hướng dẫn giải Chọn A. Câu 2.
[2H1-1] Khối đa diện nào được cho dưới đây là khối đa diện đều?
A. Khối chóp tam giác đều.
B. Khối lăng trụ đều.
C. Khối chóp tứ giác đều
D. Khối lập phương. Hướng dẫn giải: Chọn D. Câu 3.
[2H1-2] Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống, mệnh
đề sau trở thành mệnh đề đúng:
“Khối đa diện (H) được gọi là khối đa diện lồi nếu. nối hai điểm bất kì của (H) luôn thuộc (H)”. A. Đường thẳng. B. Đoạn thẳng.
C. Đường gấp khúc. D. Đường cong. Hướng dẫn giải. Chọn B. Câu 4.
[2H1-1] Khối tứ diện đều là khối đa diện đều loại nào? A. 4;  3 . B. 3;  4 . C. 3;  3 . D. 5;  3 . Hướng dẫn giải Chọn C. Câu 5.
[2H1-1] Cho khối hộp có diện tích đáy là S, chiều cao tương ứng là .
h Khi đó thể tích khối hộp là 1 1 A. 2 S .h . B. 2 S .h . C. S.h . D. S.h . 3 3 Hướng dẫn giải Chọn C.
Công thức tính thể tích hình hộp là V  . S h . Câu 6.
[2H1-2] Mặt phẳng AB C
  chia khối lăng trụ AB . C A BC
  thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp tứ giác.
B. Hai khối chóp tam giác.
C. Một khối chóp tam giác và một khối chóp ngũ giác.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 20/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
D. Hai khối chóp tứ giác. Lời giải Chọn A. C A A C A B B C' A' C' A' C' B' B' B' Mặt phẳng AB C
  chia khối lăng trụ AB . C A BC
  thành hai khối chóp
Chóp tam giác: A.A BC
  và chóp tứ giác: A.BB CC  . Câu 7.
[2H1-2] Tứ diện đều có bao nhiêu mặt phẳng đối xứng? A. 1 . B. 4 . C. 5 . D. 6 . Hướng dẫn giải Chọn D.
Giả sử hình tứ diện đều ABCD sẽ có 6 mặt phẳng đối xứng, đó là mặt phẳng đi qua 1 cạnh và trung điểm cạnh đối diện. Câu 8.
[2H1-2] Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần
lượt là 15 cm và 5 cm . Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ
nhật sao cho cây nến nằm khít trong hộp. Thể tích của chiếc hộp đó bằng: A. 1500 ml . B. 600 6 ml . C. 1800 ml . D. 750 3 ml . Chọn D. A M N B
Ta có AB  10 cm , AD  5 3 cm S  50 3 ABCD S P V S .h  750 3 ABCD Câu 9.
[2H1-3] Cho hình lăng trụ đứng AB . C A BC
  có tất cả các cạnh Rbằng .a Th D Q ể tích C khối tứ diện A BAC là 3 3a 3 a 3 3a 3 3a A. . B. . C. . D. . 6 6 12 4 Hướng dẫn giải Chọn C
Gọi H là hình chiếu của C lên AB .
Ta có CH  (AA ' B')
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 21/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 a 3 A CH C 2 H 2 1 1 a S
AA '.A ' B  . a a AA ' B' B 2 2 2 2 3 1 1 a 3 a a 3 V      CH.S . . A B AC AA ' 3 B 3 2 2 12 A' C'
Câu 10. [2H1-3] Cho hình lập phương có tổng diện tích các mặt bằng 3
12a . Tính theo a thể tích khối lập phương đó. B' 3 a A. 3 8a . B. 3 2a . C. 3 a . D. . 3 Hướng dẫn giải Chọn A.
Khối lập phương có 6 mặt là hình vuông bằng nhau 2 12a
Từ giả thiết suy ra diện tích một mặt là 2  2a . 6
Cạnh của khối lập phương là 2 2a a 2 .
Thể tích của khối lập phương là: V  a 3 3 2  8a .
Câu 11. [2H1-2] Cho hình lập phương ABCD.A BCD
  có diện tích mặt chéo ACC A   bằng 2 2 2a
. Thể tích của khối lập phương ABCD.A BCD   là A. 3 a . B. 3 2a . C. 3 2 2a . D. 3 8a . Hướng dẫn giải. Chọn C. D C
Giả sử hình lập phương có cạnh bằng x , x  0 . A Ta có: 2 S         AA .AC x.x 2 2 2a x a 2 . ACC A B D' C' Vậy V       a a . A B C D  23 3 2 2 ABCD. H A' B'
Câu 12. [2H1-2] Một hình chóp tứ giác đều có cạnh đáy bằng a, các mặt
bên tạo với đáy một góc  . Thể tích của khối chóp đó là 3 a 3 a 3 a 3 a A. sin . B. tan . C. cot . D. tan . 2 2 6 6 Hướng dẫn giải Chọn D. S A DO N B C
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 22/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Trong mặt phẳng ABCD , gọi O AC BD SO  (ABCD)
M là trung điểm CD .Khi đó   SMO . . a tan  3 1 a tan 
Có SO OM .tan  
nên thể tích khối chóp đã cho là V  .SO.S  . 2 3 ABCD 6
Câu 13. [2H1-3] Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại A , AC a
, ACB  60 . Đường chéo BC của mặt bên BCC B
  tạo với mặt phẳng ACC A   một góc
30 . Tính thể tích của khối lăng trụ theo a. 3 4a 6 3 2a 6 3 a 6 A. V  . B. 3 V a 6 . C. V  . D. V  . 3 3 3 Hướng dẫn giải Chọn B. AB Xét ABC có 0 tan 60 
 3  AB AC 3  a 3. ACAB AC Ta có 
AB  ACC' A '  BC';ACC' A '  BC' A. A B A A '  A B 1
Bài ra BC';ACC' A ' 0 0 0
 30  BC' A  30  tan 30   A C ' 3 2 2 2 2 2
AC'  AB 3  3aCC'  AC'  AC  9a a CC'  2a 2 1 1 3  VCC'.SCC'. A . B AC  2a 2.
a 3.a a 6.
ABC.A ' B'C' ABC 2 2
Câu 14. [2H1-3] Cho khối chóp tam giác đều .
S ABC có cạnh đáy bằng a và cạnh bên bằng 2a .
Tính thể tích V của khối chóp . S ABC 3 13a 3 11a 3 11a 3 11a A. V  . B. V  . C. V  . D. V  . 12 12 6 4 Lời giải Chọn B.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 23/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 S A C O I B
Do đáy là tam giác đều nên gọi I là trung điểm cạnh BC , khi đó AI là đường cao của tam giác 2 a a 3 2 2a 3 a 3
đáy. Theo định lý Pitago ta có 2 A I a   , và AO A I   . 4 2 3 3.2 3 2 a 11a
Trong tam giác SOA vuông tại O ta có 2 SO  4a   3 3 3 1 1 a 3 11a 11a
Vậy thể tích khối chóp .
S ABC là V  . a .  . 3 2 2 3 12
Câu 15. [2H1-2] Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác
đều cạnh 2a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích khối chóp .
S ABCD biết rằng mặt phẳng (SBC) tạo với mặt phẳng đáy một góc 30 .  3 3a 3 2 3a 3 4 3a A. . B. 3 2 3a . C. . D. . 2 3 3 Hướng dẫn giải S a 2 A B  30 I J C . D Chọn B. 2a 3
Gọi I, J lần lượt là trung điểm của AD, BC SI
a 3 (SI là đường cao của tam giác đều 2 SAD ). 
SAD ABCD  AD  Ta có S
I AD, SI  SAD   SI  ABCD   JI là hình chiếu vuông góc của JS lên ABCD .   SAD   ABCD
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 24/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Khi đó, SBC,ABCD  JS, JI   SJI  30 SI SI a 3 S
IJ vuông tại I  tan SJI   IJ    3a IJ tan SJI t an30 1 1 1 3 VS .SI AD.I . J SI  .2 . a 3 . a a 3  2a 3 (đơn vị thể tích). SABCD 3 ABCD 3 3
Câu 16. [2H1-3] Cho hình chóp tứ giác đều có cạnh đáy bằng x . Diện tích xung quanh gấp đôi
diện tích đáy. Khi đó thể tích của khối chóp bằng: 3 x . 3 3 x . 3 3 x . 3 3 x . 3 A. . B. . C. . D. . 6 2 12 3 Hướng dẫn giải Chọn A. S A D O I B C 2 S
x ; S  4.S  2SI.x ABCD xq SCD Theo yêu cầu bài toán 2
2SI.x x SI x 2 x 3 2 2 2
SO SI OI x   x 4 2 3 1 1 3 x . 3 2 VSO.S  .x .x SABCD 3 ABCD 3 2 6
Câu 17. [2H1-3] Một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng
đáy một góc  . Thể tích của hình chóp đó là 3 3 3 3 A. 3 2 b cos  sin  . B. 3 2
b sin  cos  . C. 3 2
b cos  sin  . D. 3 b cos  sin  . 4 4 4 4 Hướng dẫn giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 25/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Chọn A.
Gọi M là trung điểm BC , H là tâm tam giác ABC .
Ta có: SH  ABC. Xét tam giác SHA vuông tại H , ta có: S
H SA sin   bsin  
A H SA cos  bcos  3 3
AM AH bcos . 2 2 A B 3 2A M Mà: AM   AB   3bcos . 2 3 3  3bcos 1 1 2 V  .SH.S  .bsin . SA BC 3 A BC 3 4 3 3 2  b cos  sin  4
Câu 18. [2H1-1] Cho tứ diện ABCD . Gọi B' và C ' lần lượt là trung điểm của AB và AC . Tính tỉ
số thể tích của khối tứ diện AB' C' D và khối tứ diện ABCD . 1 1 1 1 A. . B. . C. . D. . 4 2 6 8 Hướng dẫn giải: Chọn A. V     A B A C 1 1 1 Ta có: AB C D      . V A B A C 2 2 4 ABCD
Câu 19. [2H1-2] Cho khối chóp .
S ABC có thể tích bằng 16 .
Gọi M , N , P lần lượt là trung điểm của các cạnh SA , S ,
B SC . Tính thể tích V của khối tứ diện AMNP . A. V  2 . B. V  6 . C. V  4 . D. V  8 . Hướng dẫn giải S Chọn A. 3 V SM SN SP  1  1 Ta có S.MNP  . .     M P V SA SB SC  2  8 S.A BC 16 N Do đó V   2 . S.MN P A C 8
Do M là trung điểm SA , ta có (
d A ,(MNP))  ( d S,(MNP)) Suy ra VV  2. AMNP S.MNP B
Câu 20. [2H1-2] Cho tứ diện ABCD có hai mặt ABC , BCD là các tam giác đều cạnh a và nằm
trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là: 3 a 3 3 a 3 a 3 3a A. . B. . C. . D. . 4 8 4 8
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 26/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Hướng dẫn giải Chọn B
Gọi H là trung điểm BC . Tam giác DBC đều nên DH vừa là trung tuyến vừa là đường cao, do a 3
đó DH BC và DH  2
Mặt khác DBC  ABC và DBC ABC  BC nên DH  ABC . 2 3 1 1 a 3 a 3 a
Thể tích: V DH.S  . .   3 ABC 3 2 4 8
Câu 21. [2H1-3] Một hình hộp chữ nhật ABCD.A BCD
  có ba kích thước là 2cm , 3cm và 6cm .
Thể tích của khối tứ diện A.CB D   bằng A. 3 8 cm . B. 3 12 cm . C. 3 6 cm . D. 3 4 cm . Hướng dẫn giải Chọn B. Ta có : Cách 1:
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 27/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 V          VV
V    V    V A BCD .A B C D B.A B C D .A CD A .B A D C.B C D A .CB D    V       4VV A BCD .A B C D B.A B C A .CB D    V     V     4V A .CB D A BCD .A B C D B.A B C  1  V     V     4. V A .CB D A BCD .A B C D A BCD .     6 A B C D 1 1  V   3    V     .2.3.6 12cm A .CB D A BCD . 3 A B C D 3 1 1 Cách 2 : 3 VV       .2.3.6 12 cm
A .CB' D ' ABCD.A B C D 3 3
Câu 22. [2H1-3] Cho khối chóp .
S ABC có SA  6, SB  2, SC  4, AB  2 10 và góc SBC 90  , ASC 120 
. Mặt phẳng P đi qua B và trung điểm N của cạnh SC đồng thời vuông góc V
với mặt phẳng SAC cắt SA tại M . Tính tỉ số thể tích S.BM N k  . VS.ABC 1 2 2 1 A. k  . B. k  . C. k  . D. k  . 6 5 9 4 Hướng dẫn giải Chọn A.
Trên cạnh SA lấy điểm A sao cho SA  2 . Khi đó ta có 1 1 2 2 2 2 2 2
A S A B SB
A B A A A B 1 1 cos SA B   2A S.A B 2A . B A A1  A B  2 2 1 1
Mặt khác BN SC  2 , A N  2 3 . Suy ra tam giác 2 1
A BN vuông tại B . 1
Gọi D là hình chiếu của S xuống mặt phẳng A BN . Do 1 
SA SB SN  2 nên D là tâm đường tròn ngoại tiếp tam giác A BN . Do đó D trung điểm A N . 1 1 1
Vậy ta có SD  A BN nên SAC  A BN A M . 1  1  1 V SA SN 1 1 1 Từ đó ta có S.BMN 1 k   .  .  . V SA SC 3 2 6 S.ABC
Câu 23. [2H1-3] Cho khối lăng trụ AB . C A BC
  có thể tích V , điểm P thuộc cạnh AA ,Q thuộc PA QB 1 BB sao cho   ; R R ABQP PA
là trung điểm CC. Tính thể tích khối chóp tứ giác . QB 3 theo V . 2 1 3 1 A. V . B. V . C. V . D. V . 3 3 4 2 Hướng dẫn giải Chọn B
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 28/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 A' C' B' R A' B' P Q Q A C P T B A B
Cách 1: Nếu bài toán đúng với mọi hình lăng trụ thì bài toán cũng phải đúng với hình lăng trụ đặc biệt. Giả sử AB . C A BC
  là khối lăng trụ đứng có đáy là tam giác ABC vuông cân tại A và
AB AC  4; AA  4 .
Chọn hệ trục tọa độ với AB Ax ;AC Ay ;AA   Az . 1
Thể tích khối lăng trụ V            S A A 4 4 4 32 . ABC.A B C ABC 2 1 Diện tích SSS  4.1 .4.2  8 ABQP APTB PTQ 2
Chiều cao hình chóp R.ABQP : dR,ABQP  dR,Oxz  y  4 R
( Vì R 0; 4;2;Oxz : y  0 ). 1 1 32
Suy ra thể tích khối chóp: VS .d R, ABQP  .8.4  R.ABQP ABQP    3 3 3 VR ABPQ 1 Vậy .  . V    3 A BC.A B C 1 1 2 1 Cách 2: VV      V    V . R.ABQP R .ABB A ABC.A B C ABC.    2 2 3 3 A B C
[2H1-4] Người ta muốn xây một bể chứa nước dạng khối hộp chữ nhật trong một phòng
Câu 24. tắm. Biết chiều dài, chiều rộng, chiều cao của khối hộp đó lần lượt là 3m; 1,2m; 1,8m
(người ta chỉ xây hai mặt thành bể như hình vẽ bên). Biết mỗi viên gạch có chiều dài 20cm
, chiều rộng 10cm , chiều cao 5cm . Hỏi người ta sử dụng ít nhất bao nhiêu viên gạch để xây
bể đó và thể tích thực của bể chứa bao nhiêu lít nước? (Giả sử lượng xi măng và cát không đáng kể).
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 29/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 A. 738 viên, 1dm 5742 lít. B. 730 viên, 5742 lít. 1dm
C. 738 viên, 5740 lít. D. 730 viên, 5740 lít. Hướng dẫn giải 1,8 dm Chọn A.
Thể tích của bể là V  18.11.29  5742l . 1, 2 m
Thể tích của 1 viên gạch là 3
1dm , thể tích cần xây 3m dựng là 3
(30  11).18  738dm , suy ra số viên ít
nhất cần dùng là 738 viên.
Câu 25. [2H1-3] Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác
đều, mặt bên SCD là tam giác vuông cân đỉnh S . Thể tích khối chóp . S ABCD là 3 3a 3 3a 3 a 3 3a A. . B. . C. . D. . 6 12 6 4 Hướng dẫn giải Chọn B S
Gọi M , N lần lượt là trung điểm của A , B CD .
Ta có SMN   (ABCD) nên hình chiếu H của S lên mp
ABCD thuộc MN . A D a 3 a SM  , SN  , MN a 2 2 M N 2 2  H a 3   a  2 2 2 2
SM SN      a MN   nên tam giác SMN 2    2  B C vuông tại S . a 3 a . SM .SN a 3 2 2
SH.MN SM .SN SH    MN a 4 3 1 1 a 3 a 3 2 V SH.S  .a  3 ABCD 3 4 12
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 2 Câu 1. [2H1-1] hình (a) hình (b) hình (c) hình (d)
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 30/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là A. hình (a). B. hình (b). C. hình (c). D. hình (d). Lời giải Chọn A.
Hình đa diện là hình tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
1. Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung hoặc chỉ có một đỉnh chung hoặc chỉ có một cạnh chung.
2. Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Các hình (b), (c), (d) đều không thỏa mãn tính chất số 2. Câu 2. [2H1-1] hình (a). hình (b). hình (c). hình (d).
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là A.1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C.
Hình (b) không thỏa mãn tính chất số 2. Câu 3.
[2H1-1]Phát biểu nào sau đây là đúng?
A. Hình bát diện đều có 8 đỉnh, 12 cạnh, 6 mặt.
B.Hình bát diện đều có 6 đỉnh, 12 cạnh, 8 mặt.
C. Hình bát diện đều có 12 đỉnh, 8 cạnh, 6 mặt.
D. Hình bát diện đều có 8 đỉnh, 6 cạnh, 12 mặt. Lời giải Chọn B
Hình bát diện đều có 6 đỉnh, 12 cạnh, 8 mặt.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 31/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Câu 4.
[2H1-2]Một hình hộp đứng có hai đáy là hình thoi (không phải là hình vuông) có bao
nhiêu mặt phẳng đối xứng? A.1 . B. 2 . C. 3 . D. 4 . Lời giải Chọn C. Gọi ABC . D A BCD
  là hình hộp đứng đã cho và gọi A , B ,C , D lần lượt là trung điểm của 1 1 1 1 AA ,
BB ,CC , DD khi đó các phép đối xứng qua mặt phẳng  ACC A  ;BDD B
 ; ABC D đều biến 1 1 1 1 
hình hộp thành chính nó. Vậy hình hộp nói trên có 3 mặt phẳng đối xứng. Câu 5.
[2H1-1]Thể tích khối chóp có diện tích đáy B và chiều cao h là: 1 1
A.V Bh . B.V Bh .
C.V  2Bh .
D.V Bh . 2 3 Lời giải Chọn D. Câu 6.
[2H1-2]Trong các mệnh đề sau mệnh đề nào sai ?
A.Lắp ghép hai khối hộp sẽ được một khối đa diện lồi
B.Khối hộp là khối đa diện lồi
C.Khối tứ diện là khối đa diện lồi
D.Khối lăng trụ tam giác là khối đa diện lồi Lời giải Chọn A.
Lắp ghép hai khối hộp bất kỳ có thể thu được một khối đa diện không phải là đa diện lồi. Ví dụ:
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 32/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Câu 7.
[2H1-2]Nếu không sử dụngthêm điểm nào khác ngoài các đỉnh của hình lập phương thì
có thể chia hình lập phương thành
A.Một tứ diện đều và bốn hình chóp tam giác giác đều
B.Năm tứ diện đều
C.Bốn tứ diện đều và một hình chóp tam giác đều
D.Năm hình chóp tam giác giác đều,không có tứ diện đều Lời giải Chọn A. Câu 8.
[2H1-1]Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là 1 1 4 A.V  . B h B.V  . B h C.V  . B h D.V  . B h . 3 2 3 Lời giải Chọn A. Câu 9.
[2H1-3] Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật AD  2 ,
a AB a .Gọi H là
trung điểm của AD ,biết SH   ABCD .Tính thể tích khối chóp biết SA a 5 . 3 2a 3 3 4a 3 3 4a 3 2a A. B. C. D. . 3 3 3 3 Lời giải Chọn C.
H là trung điểm của AD => AH=AD:2=a. SH   ABCD => SH là đường cao của khối chóp. 3 2 2 2 2 1 1 4a
SH SA AH  5a a  2a .VSH.S  2 . a 2 . a a S .ABCD 3 ABCD 3 3
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 33/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Câu 10. [2H1-3] Cho hình lập phương ABCD ’ A ’ B ’ C ’
D .I là trung điểm ’
BB .Mặt phẳng  DI ’ C  chia
khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng: 1 3 4 1 A. . B. . C. . D. . 3 4 14 2 Lời giải Chọn A. 3 1 1 1 a
Kéo dài C’I cắt BC tại E. V      CC .S . a 2 . a a C CDE 3 DCE 3 2 3 3 3 3 3 a 1 a 1 a a aV         V V a 2a sin135 DIBCC CC DE DIBE 3 3 2 2 3 12 4 3 a 3 3 a 3a V  1 3 V      DIBCC 4        V     Va . A ABIC D B ABCDA B C D DIBCC 4 4 3 V 3a     3 A ABIC D B 4
Câu 11: [1D1-2] Cho hình lập phương ABC .
D A' B'C' D' có A'C  4 3 . Thể tích khối lập phương ABC .
D A' B'C' D' là A. 32. B. 4 3 C. 64. D. 16. Lời giải Chọn B.
Đặt AA'  a, ABC .
D A' B'C' D' là hình lập phương  AB a AC a 2 .
Tam giác A' AC vuông tại A , có 2 2 2 2
A'C A' A AC  3a  48  a  4 .
Thể tích khối lập phương là 3 3 Va  4  64
ABCD.A'B'C'D'
Câu 12: [2H1-2] Cho khối chóp đều S.ABCD có cạnh đáy bằng a 3 . Tính thể tích khối chóp
S.ABCD biết góc giữa cạnh bên và mặt đáy bằng 60°. 3 a 2 3 3a 2 3 3a 6 3 a 6 A. B. C. D. 2 2 2 2 Lời giải Chọn B.
Gọi O là tâm của hình vuông ABCD khi đó SO   ABCD
Gọi O là tâm của hình vuông ABCD khi đó 0
SDO  60 chính là góc giữa cạnh bên SD và mặt phẳng  ABCD
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 34/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Lại có BD a 6
BD a 6  OD   2 2 Suy ra 0 0 a 6 tan 60 3a 2
SO OD tan 60   2 2 3 1 3a 2 VS . O S  Vậy S.ABCD 3 ABCD 2
Câu 13: [2H1-3] Cho lăng trụ đứng AB .
C A' B'C ' có đáy
ABC là tam giác vuông tại A với AC  ;
a ACB  60 . Biết B 'C hợp với  ACC ' A một góc 0
30 . Thể tích của khối lăng trụ AB .
C A' B'C ' là: A. 3 6a B. 3 2a C. 3 3a D. 3 2 3a Lời giải Chọn A.
Lăng trụ đứng AB .
C A' B'C '  AA'  ABC . AB Ta có 0 tan 60 
 3  AB a 3 . AC
B' A'  A'C' Lại có 
B' A'  ACC' A' B' A'   A' A
 góc giữa B'C và mặt phẳng ACC' A' là 0 0 A' B' 1
B'CA'  30  tan 30   A'C 3
A'C A'B' 3  a 3. 3  3a 2 2 2 2
AA'  A'C AC  9a a  2a 2 1 Vậy 3 VA' . A S  2a 2. . a a 3  a 6
ABC.A' B'C' ABC 2
Câu 14: [2H1-3] Cho hình chóp .
S ABC có đáy ABC là tam giác đều cạnh a , góc giữa đường
thẳng SA và mặt phẳng  ABC bằng 0
45 . Hình chiếu vuông góc của S trên mặt phẳng
ABC là điểm H thuộc BC sao cho BC  3BH . Thể tích khối chóp .SABClà: 3 a 21 3 a 21 3 a 21 3 a 21 A. B. C. D. 18 36 12 27 Lời giải Chọn B.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 35/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Gọi M là trung điểm của BC a 3 a a a Ta có: AM
; MH BM BH    2 2 3 6 2 2 a 7
AH AM HM  3 a
Lại có SH   ABC 7
SAH  45  SH HA  3 2 3 1 1 a 7 a 3 a 21
Suy ra V SH.S  . .  . 3 ABC 3 3 4 36
Câu 15: [2H1-2] Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng
SAB và SAD cùng vuông góc với mặt phẳng ABCD. Đường thẳng SC tạo với đáy một góc bằng 0
45 . Gọi M, N lần lượt là trung điểm của cạnh AB, AC . Thể tích của khối chóp . S MCDN là bao nhiêu? 3 5a 2 3 5a 2 3 5a 2 3 5a 2 A. B. C. D. 12 6 8 24 Lời giải Chọn D. SAB   ABCD Ta có:    SAD  
ABCDSA ABCD
Lại có AC a 2  SA A .
C tan 45  a 2 Mặt khác SSSS MNDC ABCD AMN MBC 2 2 2 2 a a 5aa    8 4 8 3 1 5a 2 Do đó VS . A S  . S.MNDC 3 MNDC 24
Câu 16: [2-H1-3] Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi SH là chiều cao
của hình chóp, khoảng cách từ trung điểm I của SH đến mặt bên SBC bằng b . Tính
thể tích V của khối chóp S.ABCD . ab 3 2a b ab 2ab A. V  . B. V  . C. V  . D. V  . 2 2 3 a 16b 2 2 3 a 16b 2 2 a 16b 2 2 a 16b Lời giải Chọn B.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 36/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 S J I D K C H A M B .
Vì S.ABCD là hình chóp tứ giác đều suy ra H là tâm của hình vuông ABCD .
Gọi M là trung điểm BC , K là hình chiếu vuông góc của H lên SM . BC SH  Ta có:
  BC  SHM . BC HM
 SBC  SHM  , mà HK SM HK  SBC .
Suy ra HK  2IJ  2b , ta có. 2 2 HK .HM 2ab 3 2a b SH   . Vậy V  . 2 2 2 2 HM HK a 16b 2 2 3 a 16b
Câu 17: [2-H1-3] Hình chóp tam giác đều S.ABC có AB
a , góc giữa SA và đáy bằng 0 30 . Thể tích khối chóp là. 3 a 2 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 72 12 36 Lời giải Chọn D.
Gọi O là tâm của đường tròn ngoại tiếp tam giác ABC .
Vì S.ABC là hình chóp tam giác đều nên SO ABC . .
Ta có OA là hình chiếu vuông góc của SA lên ABC nên 0 S , A ABC SAO 30 . 2 a 3 a 3
Tam giác ABC đều, cạnh a nên S và AM . ABC 4 2 SO SO 3SO
Xét tam giác vuông SAO , ta có tan SAO . AO 2 2AM AM 3
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 37/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 2AM tan SAO a SO . 3 3
Thể tích S.ABC là. 2 3 1 a a 3 a 3 V . . . 3 3 4 36
Câu 18: [2-H1-1] Cho tứ diện ABCD . Gọi B ' và C ' lần lượt là trung điểm của AB và AC . Tính tỉ
số thể tích của khối tứ diện AB 'C ' D và khối tứ diện ABCD . 1 1 1 1 A. . B. . C. . D. . 6 8 2 4 Lời giải Chọn D. V     AB AC 1 1 1 Ta có: AB C D      . V AB AC 2 2 4 ABCD
Câu 19: [2-H1-2] Cho khối chóp S.ABC có SA  9, SB  4, SC  8 và đôi một vuông góc. Các điểm A ,
B ,C thỏa mãn SA  2.SA , SB  3.SB , SC  4.SC . Thể tích khối chóp S.A BC   là. A. 16 . B. 12 . C. 2 . D. 24 . Lời giải Chọn C. 1 1 S V . .S . A S .S . A S . ABC SBC B SC . 3 6 V SA SB SC 1 Ta có: SA B C . . . V SA SB SC 24 SABC V 2 . SA B C S C' A' B' A C B .
Câu 20: [2-H1-2] Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm tam giác BCD . Tính
thể tích V của khối chóp . A GBC . A. V  4 . B. V  5 . C. V  6 . D. V  3 .
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 38/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Lời giải Chọn A. . Cách 1:
Phân tích: tứ diện ABCD và khối chóp .
A GBC có cùng đường cao là khoảng cách từ A đến mặt
phẳng BCD . Do G là trọng tâm tam giác BCD nên ta có SS   S   S 3S BGCBGDCGDBCDBGC (xem phần chứng minh).
Áp dụng công thức thể tích hình chóp ta có: 1  1 V  . h S ABCDBCD .  h S 3   V 3 BCD S 1 1 ABCD    
BCD  3 VV  .12  4 . 1 V 1  S . A GBC 3 ABCD 3 . V  . A GBC h S . GBC h S .   GBC A GBC 3 GBC  3 Cách 2:
d G, ABC  GI 1 1     . d
d G, ABC
d D, ABC  , D ABC      DI 3 3 1 1 Nên V
d G, ABC .S  .V  4. . G. ABC     3 ABC 3 DABC D G A C H1 H I B .
Câu 21: [2-H1-3] Cho khối hộp ABC .
D A' B' C ' D' có thể tích bằng 12 ( đơn vị thể tích). Gọi
M , N, P lần lượt là trung điểm của các cạnh A ,
D DC, AA' . Tính thể tích khối chóp . P BMN . 3 3 A. V . B. V 2 . C. V . D. V 3 . 4 2 Lời giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 39/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Chọn A. A' B' D' C' P A B M A B M D D N C H N C .
Vì P là trung điểm AA' nên chiều cao khối chóp .
P BMN bằng một nữa chiều cao khối ABC .
D A' B 'C ' D ' . 3 S S
. Tính bằng cách cho cạnh độ dài rồi tính bằng cách trừ phần dư. BMN 8 ABCD 1 1 3 3 Vậy V . . .V . P.BMN
ABCDA' B 'C ' D ' 3 2 8 4
Câu 22: [2-H1-3] Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy
một góc 60 . Gọi M là điểm đối xứng với C qua D ; N là trung điểm của SC , mặt
phẳng ( BMN ) chia khối chóp S.ABCD thành hai phần. Tính tỉ số thể tích giữa hai phần đó. 1 7 7 1 A. . B. . C. . D. . 7 5 3 5 Lời giải Chọn B. . V   V V Đặt 1 SABIKN 1    ?. V V V  2 NBCDIK 2 1 a 6 6 * 2 3 V  . a a . S . ABCD 3 2 6 1 1 SO 1 a 6 1 6 * 3 V  .NH.S  . .S  . . . a 2a a . N .BMC   3 BMC 3 2 BMC 3 4 2 12 MK 2
* Nhận thấy K là trọng tâm của tam giác SMC   . MN 3 V MD MI MK 1 1 2 1 * M.DIK  . .  . .  . V MC MB MN 2 2 3 6 M .CBN
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 40/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 5 5 6 5 6 3 3 V VVV  . a a . 2 M .CBN M .DIK M .CBN 6 6 12 72 7 6 3 a 6 5 6 7 6 V 7 3 3 3 1 72 V VV a a a    . 1 S . ABCD 2 6 72 72 V 5 6 5 2 3 a 72
Câu 23: [2-H1-3] Cho khối lập phương ABC . D ’ A ’ B C’ ’
D cạnh a . Gọi O và O’ lần lượt là tâm của ABCD và ’ A ’ B C’ ’
D . Thể tích phần chung nhau của hai khối chóp . O ’ A ’ B C’ ’ D và ’. O ABCD là: 3 a 3 a 3 a 3 a A. V  . B. V  . C. V  . D. V  . 12 6 4 3 Lời giải Chọn A. – NVP  Trắc nghiệm: B C Tự luận: O
- Dễ xác định được phần giao nhau của hai khối A D
chóp O.A’B’C’D’ và O’.ABCD là khối bát diện: Q P OMNPQO’. M N 1 - Và V  .OO'.S . B' A' OMNPQO' 3 MNPQ a O'
- Với OO'  a, MN  . D' C' 2 2 3 1  a a - V  . . a    . OMNPQO' 3  2  12
Câu 24: [2-H1-4] Người ta muốn mạ vàng cho bề mặt phía ngoài của một cái hộp dạng hình hộp
đứng không nắp (nắp trên), có đáy là một hình vuông. Tìm chiều cao của hộp để lượng
vàng phải dùng để mạ là ít nhất, biết lớp mạ ở mọi nơi như nhau, giao giữa các mặt là
không đáng kể và thể tích của hộp là 3 4 dm . A. 1,5 dm . B. 1 dm . C. 0,5 dm . D. 2 dm . Lời giải Chọn B. Gọi , x y  ,
x y  0 lần lượt là độ dài cạnh đáy, chiều cao của hình hộp. 4 Thể tích khối hộp là 2 2
V x y  4  x y y  . 2 x 16 8 8 Diện tích cần mạ vàng 2 2 2 3
S x  4xy x
x    3 64 đạt giá trị nhỏ nhất khi chỉ khi. x x x 8 x
x  2  y 1. x
Câu 25: [2-H1-3] Cho hình chóp S.ABC có SA a , tam giác ABC đều, tam giác SAB vuông cân
tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng? 3 6a 3 6a 3 6a 3 6a A. . B. . C. . D. . 12 4 8 24 Lời giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 41/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Chọn A. .
Tam giác SAB vuông cân tại S và SA a nên AB a 2 . AB a 2
Gọi M là trung điểm AB , ta có SM AB và SM  
( SM là đường trung tuyến của tam 2 2
giác SAB vuông cân tại S ).
Mặt khác SAB   ABC , SM AB và SAB  ABC  AB nên SM   ABC .
Suy ra SM là đường cao của hình chóp S.ABC ứng với đáy là tam giác ABC .
Thể tích khối chóp S.ABC là. aa 22 3 3 1 1 2 a 6 VSM.S  . .  . S . ABC  3 ABC 3 2 4 12
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 3 Câu 1.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mỗi hình đa diện có ít nhất bốn đỉnh.
B. Mỗi hình đa diện có ít nhất ba đỉnh.
C. Số đỉnh của một hình đa diện lớn hơn hoặc bằng số cạnh của nó.
D. Số mặt của một hình đa diện lớn hơn hoặc bằng số cạnh của nó. Hướng dẫn giải Chọn A.
Vì hình chóp tam giác (tứ diện) có số đỉnh, số cạnh, số mặt là ít nhất trong tất cả các hình đa diện. Do đó
"Mỗi hình đa diện có ít nhất bốn đỉnh" là đúng.
Chú ý: Do A đúng nên B sai. Ví dụ chóp tam giác có 4 đỉnh, 4 mặt và 6 cạnh nên C, D sai. Câu 2.
Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất: A. Năm cạnh.
B. Bốn cạnh. C. Ba cạnh. D. Hai cạnh. Hướng dẫn giải Chọn C.
Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh. Câu 3.
Trong các mệnh đề sau, mệnh đề nào sai?
A. Khối tứ diện là khối đa diện lồi.
B. Lắp ghép hai khối hộp luôn được một khối đa diện.
C. Khối hộp là khối đa diện lồi.
D. Khối lăng trụ tam giác đều là khối đa diện lồi. Hướng dẫn giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 42/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Chọn B.
Khối tứ diện, khối hộp và khối lăng trụ tam giác đều đều là các khối đa diện lồi. Suy ra B sai.
Chú ý: B sai vì ta có thể ghép 2 khối hộp sao cho hai mặt (đa giác) phân biệt có hai cạnh chung, suy ra
không thỏa mãn tính chất 1 nên B sai. Câu 4.
Trong không gian có tất cả bao nhiêu loại khối đa diện đều? A. 2. B. 3. C. 4. D. 5. Hướng dẫn giải Chọn D.
Trong không gian có tất cả 5 loại khối đa diện đều. Câu 5.
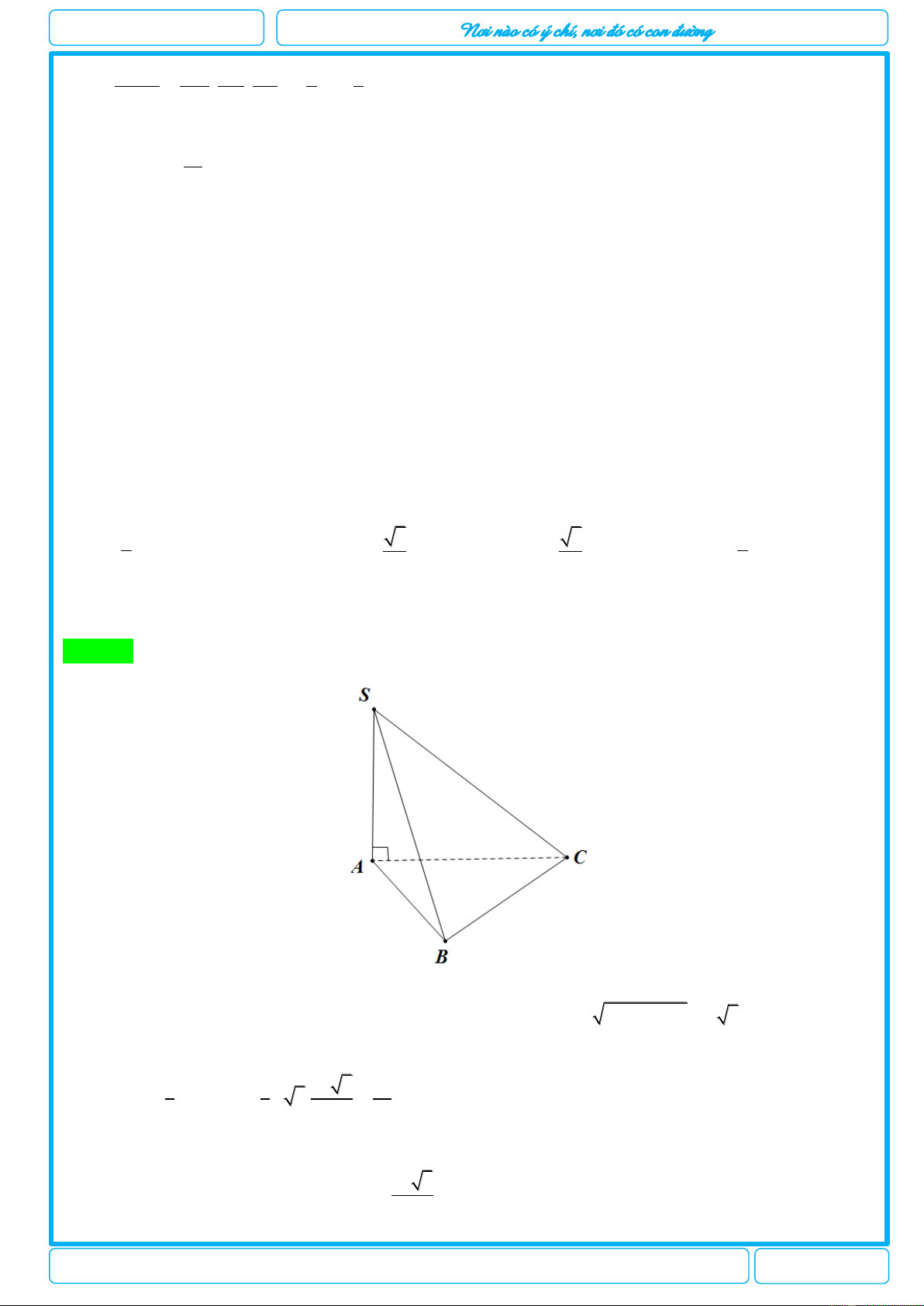
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA vuông góc với đáy, SA a 2 .
Tính thể tích khối chóp S.ABCD? 3 a 2 3 a 2 3 a 2 A. V  . B. V  . C. 3 V a 2. D. V  . 6 2 3 Hướng dẫn giải Chọn D 3 1 a 2
B = Sđáy = a2; h = SA a 2  V  . B h  ) 3 3 Câu 6.
Phân chia khối lập phương ABC . D A BCD
  bởi ba mặt phẳng  A BD ,  DD B B   , B CD ta
được những khối đa diện nào?
A. Hai khối tứ diện và một khối lăng trụ tứ giác.
B. Ba khối tứ diện và một khối lăng trụ tam giác.
C. Hai khối tứ diện và một khối lăng trụ tam giác.
D. Hai khối tứ diện và hai khối chóp tứ giác. Hướng dẫn giải Chọn D. B C A D C' B' A' D' Câu 7.
Phân chia khối lăng trụ AB . C A BC
  bởi hai mặt phẳng  AB D   và  AB D
  ta được các khối nào sau đây?
A. Khối chóp tứ giác . A D B D B
  và khối tứ diện ABDB.
B. Khối chóp tứ giác . A D B D B
  và khối tứ diện ADD B  .
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 43/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 C. Khối chóp tứ giác . A D B D B
  và khối tứ diện AA BD  .
D. Ba khối tứ diện ABDB , ADD B  và AA BD   Hướng dẫn giải Chọn D. B A D B' B D A A D B' B' A D' A' D' B' D' A' Câu 8.
Cho lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại A , I là trung điểm
của BC , BC a 6 . Mặt phẳng  A B
C tạo với mặt phẳng  ABC một góc 60. Thể tích khối lăng trụ AB . C A BC  là 3 9 2a 3 9 2a 3 9 2a 3 9 2a A. . B. . C. . D. . 4 2 12 6 Hướng dẫn giải Chọn A.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 44/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 A' C' B' A C 60° I a 6 B 2 2 2 2 2 2 2 2
AB AC BC  2AB BC  6a AB  3a AB a 3 2 1 1 3a SA . B AC a 3.a 3  ABC 2 2 2 2 2S 3a a 6 ABC AI    BC a 6 2 3 2a
AA  AI tan 60  2 2 3 Vậy 3 2a 3a 9 2a V  .  . ABC. A BC   2 2 4 Câu 9. Cho khối hộp ABC . D A BCD
  có thể tích bằng 72 (ĐVTT). Gọi V là thể tích khối chóp A.ABC 1
. Khi đó, chọn kết quả đúng trong các kết quả cho dưới đây?
A. V  12 .
B. V  24 .
C. V  36 . D. V  18 . 1 1 1 1 Hướng dẫn giải Chọn A. Ta có, A' D' 1 1  1  1 V V       . V V 12. B' C' 1 A B C . ABC  2  2 3 3  2  6 D A B C
Câu 10. Cho khối lập phương ABC . D A BCD
  , có đường chéo BD  3. Thể tích của khối lập phương ABC . D A BCD   bằng bao nhiêu? A. 3 . B. 6 3 . C. 3 . D. 3 3 . Hướng dẫn giải Chọn D.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 45/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Gọi a là độ dài cạnh hình lập phương. B C Ta có, 2 2 BD  3a 2
a  3  a  3 . A
Vậy thể tích khối lập phương bằng: 3 D
V a  3 3 . B' C' A' D'
Câu 11. Tổng diện tích các mặt bên của khối lập phương bằng 54 .Thể tích khối lập phương bằng?
A. 27. B. 9. C. 3 3. D. 3. Hướng dẫn giải Chọn A.
Một mặt của hình lập phương có diện tích bằng : 54:6 = 9
Cạnh của hình lập phương bằng 3
Thể tích khối lập phương bằng : 27
Câu 12. Cho hình chóp tứ giác đều S.ABCD cạnh đáy AB =a , góc SAC bằng 450 .Thể tích khối chóp bằng: 3 a 3 a 2 3 a 3 3 a 2 A. . B. C. D. 3 2 6 6 Hướng dẫn giải Chọn D.
O là tâm hình vuông , h=SO là đường cao hình chóp. AC a 2 SO   2 2
Diện tích đáy : B = a2 3 a 2 Thể tích :V  6
Câu 13. Cho lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác đều cạnh a . Mặt phẳng AB 'C ' tạo với mặt đáy góc 0
60 . Tính theo a thể tích lăng trụ ABC.A'B 'C ' . 3 a 3 3 3a 3 3 a 3 3 3a 3 A. V . B. V . C. V . D. V . 2 4 8 8 A C Hướng dẫn giải B Chọn D.
Vì ABC.A' B 'C ' là lăng trụ đứng nên AA' ABC .
Gọi M là trung điểm B 'C ' , do tam giác A'B 'C ' đều A' C' nên suy ra A' M B 'C ' . M Khi đó 0 60
AB 'C ' , A'B 'C ' AM,A'M AMA' . B' a 3 3a
Tam giác AA' M , có A ' M ; AA'
A' M.tan AMA' . 2 2 2 a 3
Diện tích tam giác đều S . A' B 'C ' 4
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 46/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 3 3a 3 Vậy V S .AA' (đvtt). ABC 8
Câu 14. Cho khối chóp S.ABC có SA vuông góc với đáy, SA  4, AB  6, BC  10 và CA  8 . Tính thể
tích V của khối chóp S.ABC.
A. V  40.
B. V  192.
C. V  32.
D. V  24. Lời giải S Chọn C. Ta có: 2 2 2
BC  100  AB CA 4 ABC  vuông tại A 1 1  SA . B AC  6 . 8 .  24. ABC 2 2 8 A C 1 1
Suy ra: V  .S . A S  4 . 2 . 4  32. 10 6 3 ABC 3 B
Câu 15. Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB a, AD a 3, SA vuông góc với đáy và
mặt phẳng SBC tạo với đáy một góc 0
60 . Tính thể tích V của khối chóp S.ABCD . 3 a 3 3a A. V  . B. V  . C. 3
V a . D. 3
V  3a . 3 3 Lời giải Chọn C.
Do BC  SAB  SBC, ABCD 0  SBA  60 . 0 SA A . B tan SBA  . a tan 60  a 3 Ta có:  2 SA . B AD a 3  ABCD 1 1 Suy ra: 2 3 V S . A S
 .a 3.a 3  a . 3 ABCD 3
Câu 16. Cho hình chóp đều S.ABCD có AB a . Gọi M là trung điểm AD và góc tạo bởi mặt phẳng
SCM  và mặt đáy bằng 0
60 . Tính theo a thể tích V của khối chóp S.ABC . D 3 a 15 3 a 15 3 a 5 3 a 5 A. V  . B. V  . C. V  . D. V  . 30 10 15 5 Lời giải Chọn A.
Gọi AC BD   
O . Do S.ABCD là hình chóp đều nên SO   ABCD .
Kẻ OI DM I DM    SCM , ABCD 0  SIO  60 .
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 47/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Do ABCD là hình vuông cạnh a nên 2 Sa . ABCD AD a Ta có: DM
 . Xét tam giác CDM ta có: 2 2 2  a a 5 2 2 2
CM CD DM a     .  2  2 2 S Mặt khác: 1 1 1 a SS  . ABCD S   . COM 2 CAM 2 4 ABCD 8 8 2 2S 2a a 5 a 5 Suy ra: COM OI   :  CM 8 2 10 a 5
SO OI.tan SIO  . 10 3 Vậy 1 1 a 15 a 15 2 V  .S . O S  . .a  . 3 ABCD 3 10 30
Câu 17. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên tạo với đáy một góc  . Tính thể tích khối chóp đó 3 a cot 3 a tan 2 a tan 3 a tan A. . B. . C. . D. . 12 12 12 4 Hướng dẫn giải Chọn B.
Gọi G là trọng tâm tam giác ABC khi đó SG là chiều cao a 3
SAG   => SG AG tan  tan 3 3 1 a tan V= S .SG  3 ABC 12
Câu 18. Cho tứ diện ABCD, gọi B’, C’ lần lượt là trung điểm của AB, AC. Khi đó tỉ số thể tích của khối tứ
diện AB’C’D và khối tứ diện ABCD bằng: 1 1 1 1 A. . B. . C. . D. . 2 4 6 8 Hướng dẫn giải Chọn B. V
AB '.AC '.AD 1
Ta có: AB'C'D   V A . B AC.AD 4 ABCD
Câu 19. Cho hình chóp S.ABC có SA vuông góc mặt đáy , SA=a, tam giác ABC đều cạnh 2a. Gọi M,N lần
lượt thuộc cạnh SB,SC sao cho SM=MB,   SN
2CN . Tính thể tích khối AMNCB. 3 2 3a 3 3a 3 3a 3 2 3a A. . B. . C. . D. . 9 9 18 3 Hướng dẫn giải Chọn A.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 48/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 3 V SM .SN 1 2 2 3a SAMN   VV  , suy ra đáp án A S S . B SC 3 AMNCB 3 SABC 9 SABC
Câu 20. Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D , (ABC)  (BCD)
và AD hợp với (BCD) một góc 60o .Tính thể tích tứ diện ABCD. 3 a 3 3 a 3 3 a 3 3 2a 3 A. 9 B. 3 C. 27 D. 9 Hướng dẫn giải Chọn A. A a B o H 60 D C
Gọi H là trung điểm của BC.
Ta có tam giác ABC đều nên AH  (BCD) , mà (ABC)  (BCD)  AH  (BCD). a 3
Ta có AH  HD  AH = AD. tan60o = a 3 và HD = AD. cot60o = 3 BCD 2a 3 BC = 2HD = 3 suy ra 3 1 1 1 a 3 V = S .AH  . BC.HD.AH BCD  3 3 2 9
Câu 21. Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh bằng a . Gọi O là giao điểm của AC và BD . Tính
thể tích của tứ diện OA' BC . 3 a 3 a 6 3 a 3 a A. . B. . C. . D. . 6 24 12 A 4 B Hướng dẫn giải O D C 3 1 1 1 a 2 A' B' Ta có SSa VAA'.S  . BOC ABCD OA' 4 4 BC 3 BOC 12 D' C'
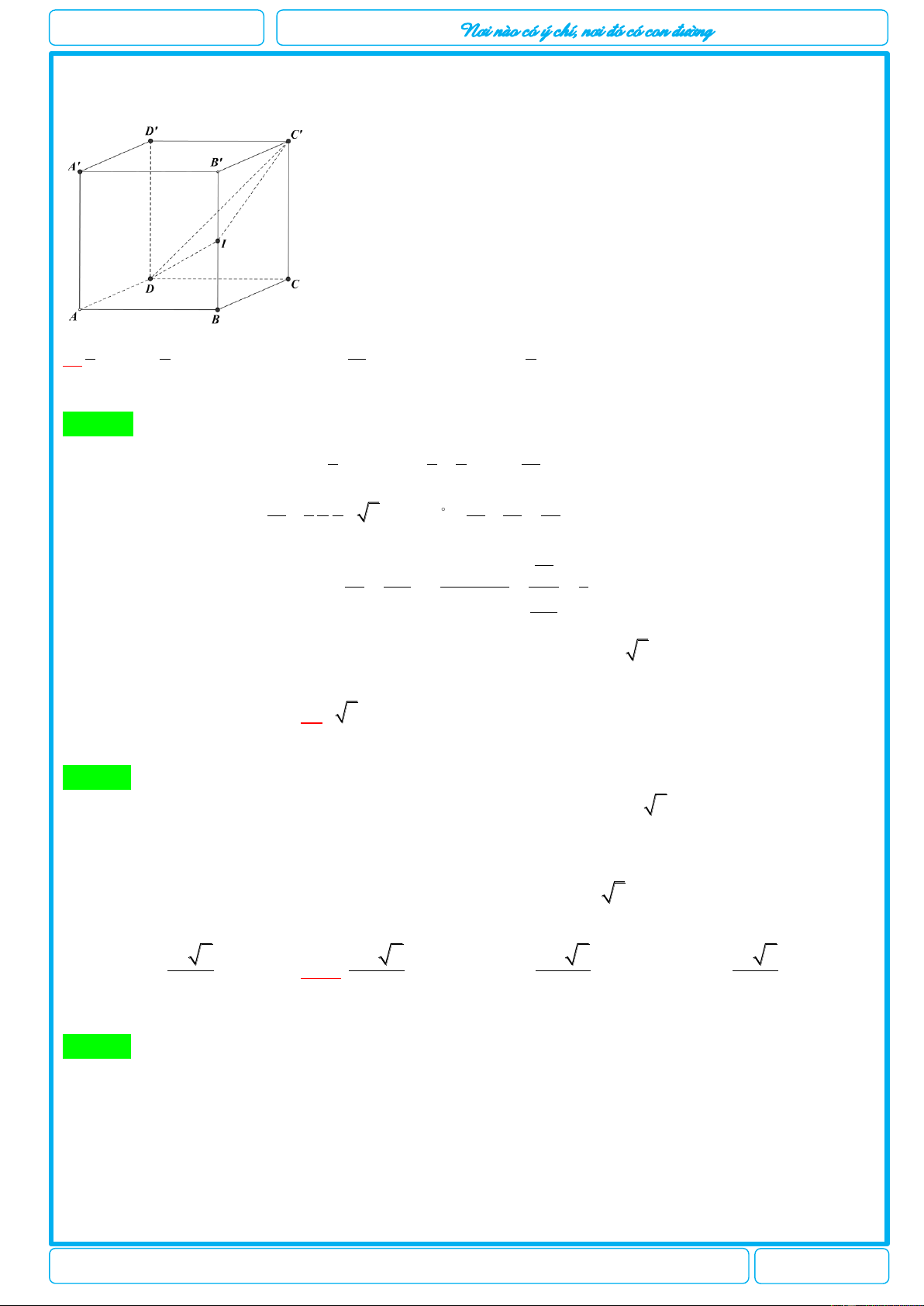
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a , AD = 2a. Cạnh SA vuông
góc với mặt phẳng đáy, cạnh bên SB tạo với mặt phắng đáy một góc 0
60 . Trên cạnh SA lấy điểm M sao cho a 3 AM =
, mặt phẳng (BCM) cắt cạnh SD tại N. Tính thể tích khối chóp S.BCNM 3
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 49/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 10 3 3 10 3a 3 10 3a 3 10a A. . B. . C. . D. . 27 9 27 27 Hướng dẫn giải Chọn C. Ta có SA = 0
AB tan SBA AB tan 60  a 3 S 3 1 2a 3 VS.ABCD = A . B A . D SA  3 3 3 M 1 a 3 N V = S.ABC= VS.ACD = VS.ABCD 2 3 3 V SM 2 2 2a 3 S .MBC    VVS .MBC S . V SA 3 3 ABC 9 S . ABC A D 3 V SM SN 4 4 4a 3 S .MCN  .  VVS .MCN S . V SA SD 9 9 ACD 27 S . ACD B 3 C 10 3a Vậy VVVS.MBCN S.MBC S.MCN 27
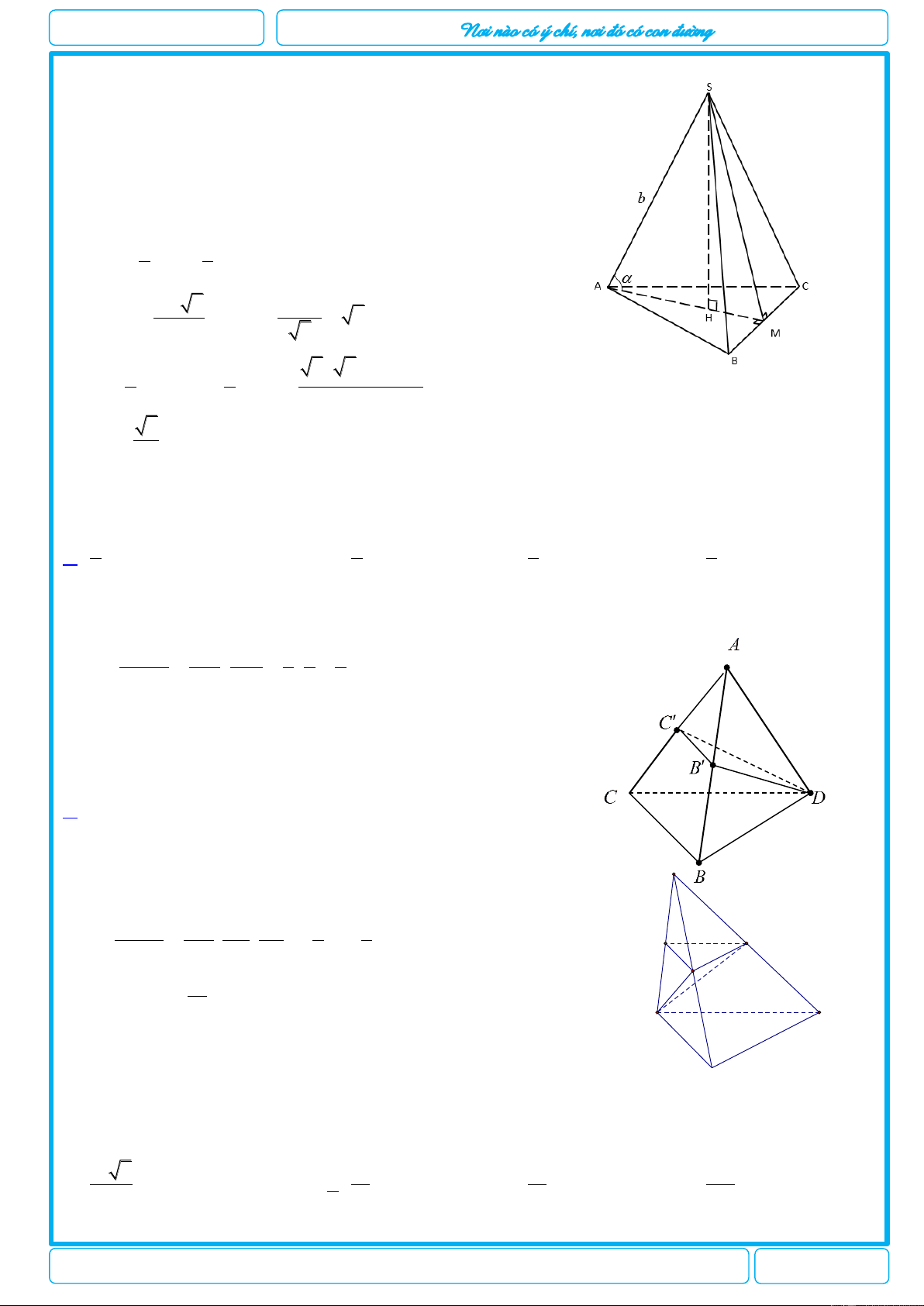
Câu 23. Cho hình lăng trụ ABC. A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên hợp với đáy một góc
là 450. Gọi P là trung điểm BC, chân đường vuông góc hạ từ A’ xuống (ABC) là H sao cho 1 AP AH . gọi 2
K là trung điểm AA’,   là mặt phẳng chứa HK và song song với BC cắt BB’ và CC’ tại M, N. Tính tỉ số thể V tích ABCKMN
VA'B'C'KMN 1 2 1 3 A. B. C. D. 2 3 3 4 Hướng dẫn giải Chọn A A' C'
Gọi Q, I, J lần lượt là
trung điểm B’C’, BB’, CC’ Q B' ta có: K a 3 J AP  2  N AH a 3 E I A 45 Vì '  AH '
A vuông cân tại H. C M Vậy ' A H a 3 P VS .A' H ABCA'B C ' ' ABC B H 1 a 3 2 a 3 Ta có S  . a  (đvdt) ABC 2 2 4 2 a 3 3 3 aVa . 3  (đvtt) (1)
ABCA'B'C ' 4 4 Vì '  AH '
A vuông cân  HK AA' HK  BB'C'C
G ọi E = MN  KH  BM = PE = CN (2) mà AA’ = a 6 a 6 2 2 ' A H AH = 3 2 a  3 2
a a 6  AK
BM PE CN  2 4
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 50/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Ta có thể tích K.MNJI là: 1 1 1 a 6 V S .KE mà KE KH AA'  3 MNJI 2 4 4 2 a 6 a 6 2 3 1 a 6 a 6 a SMN.MI  . a  (dvdt)  V   (dvtt) MNJI 4 4 KMNJI 3 4 4 8 3 3 3a aV 1 ABCKMN 8 8    2 3 V 3a a 2
A' B 'C ' KMN  8 8
Câu 24. Cho một tấm bìa hình chữ nhật chiều dài AB  90cm , chiều rộng BC  60cm . Người ta cắt 6
hình vuông bằng nhau như hình vẽ, mỗi hình vuông cạnh bằng x cm , rồi gập tấm bìa lại như hình vẽ dưới
đây để được một hộp quà có nắp. Tìm x để hộp nhận được thể tích lớn nhất? 10 A. 10cm. B. 9cm. C. 15cm. D. cm. 3 Hướng dẫn giải Chọn A.
Hộp quà là hình hộp chữ nhật có chiều cao là h = x cm.  Đáy là hình chữ 90 3x
nhật với hai kích thước lần lượt là l
và l  60  2x . 1 2 2 90  3x
Vậy thể tích của hộp quà là V  . h l .l  . x 60  2x .
x 30  x 90 3x . 1 2      2 Ta có  x   x   x
x 30  x90  3x 1  .6 .
x 90  3x.90  3x 1 6 90 3 90 3 3 3  . 12000cm . 18 18 27
Dấu "=" xảy ra khi và chỉ khi 6x  90  3x  9x  90  x 10cm .
Câu 25. Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy và khoảng cách từ a
A đến mặt phẳng SBC bằng
2 . Tính thể tích V của khối chóp đã cho. 2 3 a 3 a 3 a A. V  . B. 3
V a . C. V  . D. V  . 2 3 3 Lời giải Chọn D.
Kẻ AH SBH SB
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 51/73 luyenthitracnghi
THẦY VIỆT 0905.193.688   a d A,SBC 2  AH  . 2 1 1 1 Ta có:   2 2 2 AH SA AB 1 1 1 2 1 1       2 2 2 2 2 2 SA AH AB a a aSA  . a 3 1 1 a Suy ra: 2 V  .S . A S  . . a a  . 3 ABCD 3 3
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 4
Câu 1. [2H1-1] Cho khối chóp có là n – giác n  3;nN  . Mệnh đề nào đúng sau đây:
A. Số cạnh của khối chóp bằng n + 1.
B. Số mặt của khối chóp bằng 2n.
C. Số đỉnh của khối chóp bằng n + 1.
D. Số mặt của khối chóp bằng số đỉnh của nó. Lời giải Chọn C.
Vì mặt đáy có n đỉnh và thêm 1 đỉnh của hình chóp không nằm trong mặt đáy.
Ví dụ: Hình chóp tứ giác có 5 điỉnh
Câu 2. [2H1-1] Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
D. Mỗi mặt có ít nhất ba cạnh. Lời giải Chọn C.
Đáp án C sai vì hình đa diện là hình thõa mãn tính chất: mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Câu 3. [2H1-2] Trong các mệnh đề sau mệnh đề nào sai ?
A. Lắp ghép hai khối hộp sẽ được một khối đa diện lồi.
B. Khối hộp là khối đa diện lồi.
C. Khối tứ diện là khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi. Lời giải Chọn A.
Ví dụ: Ghép hai khối trên không được một khối đa diện lồi
Câu 4. [2H1-1] Có bao nhiêu loại khối đa diện đều?
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 52/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 A. 2 . B. 4 . C. 5 . D. Vô số. Lời giải Chọn C.
Vì chỉ có 5 loại khối đa diện đều là:tứ diện đều, lập phương, bát diện đều, mười hai mặt đều, hai mươi mặt đều. Câu 5. 1
[2H1-1] Khối đa điện nào sau đây có công thức tính thể tích là V
Bh ( B là diện tích đáy; h là chiều 3 cao) A. Khối lăng trụ. B. Khối chóp.
C. Khối lập phương.
D. Khối hộp chữ nhật. Lời giải Chọn B.
Câu 6. [2H1-2] Trong Cho khối tứ diện D
ABC . Lấy một điểm M nằm giữa A và B , một điểm N nằm giữa C
và D . Bằng hai mặt phẳng  D
MC  và  NAB ta chia khối tứ diện đã cho thành bốn khối tứ diện:
A. AMCN, AMND, AMCD, BMCN.
B. AMNC, AMND, BMNC, BMND.
C. AMCD, AMND, BMCN, BMND.
D. BMCD, BMND, AMCN, AMDN. Lời giải Chọn C.
Dựa vào hình vẽ suy ra đáp án C đúng.
Câu 7. [2H1-2] Có thể chia hình lập phương thành bao nhiêu hình tứ diện bằng nhau? A. 2 . B. Vô số. C. 4 . D. 6 . Lời giải Chọn B.
Vì 1 khối lập phương có thẻ chia được 6 khối tứ diện bằng nhau mà từ một khối lập phương có thể chia nhỏ
ra thành vô số khối lập phương nên chọn đáp án B.
Câu 8. [2H1-2] Trong cách mệnh đề sau, mệnh đề nào sai?
A. Hai khối hộp chữ nhật có diện tích xung quanh bằng nhau thì có thể tích bằng nhau.
B. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
C. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
D. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau. Lời giải Chọn A.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 53/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Ví dụ như hai khối trên (Khối hộp chữ nhật có các kích thước là 1, 7,1 và khối lập phương có cạnh là 2 ) đều
só diện tích xung quanh là 16 nhưng thể tích khác nhau.
Câu 9. [2H1-3] Cho hình hộp AB D. C A BCD
 . Tỉ số thể tích của khối tứ diện ACB'D' và khối hộp AB D. C A BCD   là: 1 1 1 1 A. . B. . C. . D. . 5 4 3 6 Lời giải Chọn C.
Gọi h là chiều cao của khối hộp. Ta có V      S .h AB D C .A B C D AB D C 1 1 1 1 V          V     4V S .h 4. S .h S .h 4. . S .h S .h ACB D AB D. C A B C D A .ABC AB D C ABC AB D C ABCD AB D 3 3 2 3 C V   1 Vậy ACB D  . V     3 AB D. C A B C D
Câu 10: [1H1-3] Cho hình lập phương ABC . D ’ A ’ B ’ C ’
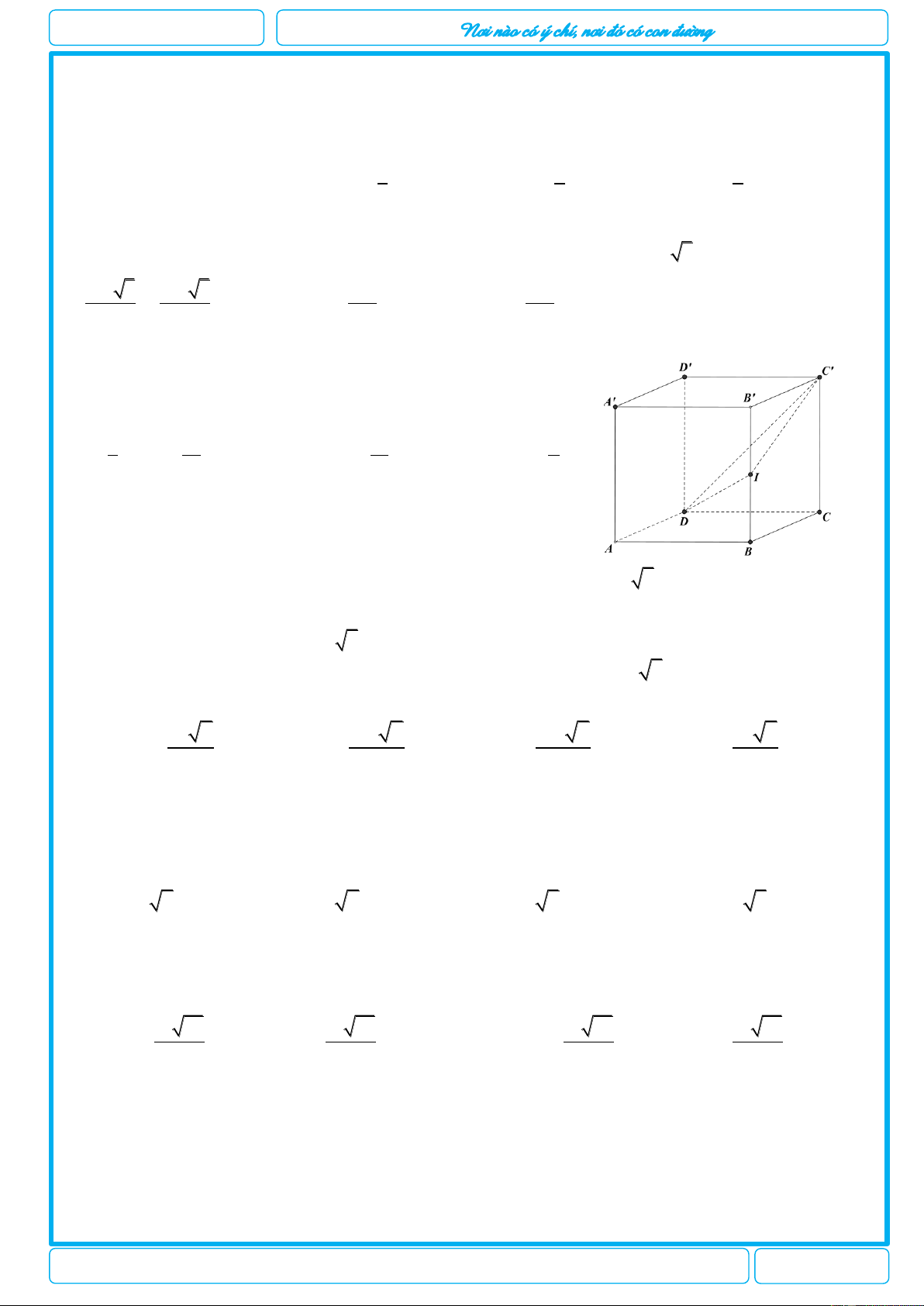
D có khoảng cách giữa ’ A C và ’ C ’ D là 1 cm. Thể
tích khối lập phương ABC . D ’ A ’ B ’ C ’ D là: A. 3 8cm . B. 3 2 2 cm . C. 3 3 3 cm . D. 3 27cm . Lời giải Chọn B. D’ C’ A’ B’ D C A B
Để tìm khoảng cách giữa ’ A C và ’ C ’
D , ta dựng một mặt phẳng chứa ’
A C và song song với ’ C ’. D Dễ thấy
đó là mặt phẳng C ’ A ’
B . Gọi a là độ dài cạnh của khối lập phương, lúc này ta có:
d(C'D', A'C)  d[C ' D ',(CA'B')]  [ d D ',(CA'B')]
Để tính khoảng cách từ điểm ’
D đến mặt phẳng C ’ A ’
B , ta xét khối tứ diện ’ D C ’ A ’ B . 2 3  1 S  1 a a V CC '. a.  3 (cm )
D 'CA' B '
B ' A' D ' 3 3 2 6 2  1 a V
CB '.B ' A'  1 a.a 2  2 2 (cm ) CA' B ' 2 2 2
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 54/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 3 a 3V a 2 Suy ra d
D 'CA' B '  2 [ D',(CA'B')]  (cm) 2 S 2 CA' B ' a 2 2
a  2.Do đó V  3 a  3 2 2(cm )
Câu 11: [1H1-2] Tính thể tích V của khối lập phương ABC . D A BCD
  , biết AC  a 3 . 3 3 6a 1 A. 3 V a . B. V  . C. 3 V  3 3a . D. 3 V a . 4 3 Lời giải Chọn A.
Gọi x là cạnh của khối lập phương thì đường chéo AC  x 3  a 3  x a . Vậy 3 3
V x a .
Câu 12: [1H1-2] Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a là 3 2a 3 3a 3 3a 3 a A. . B. . C. . D. . 6 4 2 3 Lời giải Chọn A.
Vì khối chóp tứ giác đều. S
Nên giả sử SO   ABCD .
Hay tam giác SAO vuông tại O . 1 a 2
AC a 2  AO AC  . D C 2 2 2  a 2  a 2 O
SO SA AO  a2 2 2       . 2 2   A B
Vì hình chóp đều S.ABCD nên ABCD là hình vuông 2 2  SAB a . ABCD 3 1 1 a 2 a 2 2 VS . O S  . .a  . S . ABC 3 ABCD 3 2 6
Câu 13: [1H1-3] Cho lăng trụ đứng tam giác AB . C A BC
  có đáy ABC là tam giác vuông cân tại B với
BA BC a , biết A B
 hợp với đáy ABC một góc 60 . Tính thể tích khối lăng trụ. 3 a 3 3 a A. . B. 3 a . C. 3 2a . D. . 2 2 Lời giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 55/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Chọn A. A' C' B' A C 60 a a B
Hình chiếu vuông góc của A B
 lên mặt đáy là AB .
Nên góc tạo bởi A B
 với mặt đáy là góc A BA  60 . AA Ta có: tan 60   AA  . a 3 AB 3 1 1 a 3
Thể tích khối lăng trụ tam giác: 2 V  . B h  .A . B BC.A A
  a .a 3  2 2 2
Câu 14: [1H1-3] Cho hình chóp S.ABC có tam giác ABC là tam giác đều cạnh a . Hình chiếu vuông góc
của S trên mặt phẳng  ABC là trung điểm của cạnh AB , góc tạo bởi cạnh SC và mặt phẳng  ABC bằng o
30 . Tính thể tích của khối chóp S.ABC . 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 8 8 4 24 Lời giải Chọn D. S A H B C 2 a 3 Ta có S  . ABC 4
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 56/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Gọi H là trung điểm AB thì SH   ABC nên SC, ABC  SC, HC  SCH  30 . a 3 a Ta có HC
nên SH HC.tan 30  . 2 2 3 1 a 3 Vậy VSH.S  . S .ABC 3 ABC 24
Câu 15: [1H1-2] Cho hình chóp S.ABCD có đáy là hình vuông cạnh ,
a SA vuông góc với mặt đáy , SD tạo
với mặt phẳng SAB một góc bằng 
30 . Tính thể tích V của khối chóp. 3 6a 3 6a 3 3a A. . B. 3 3a . C. . D. . 18 3 3 Lời giải Chọn D. S 300 A B C D 0 S , D SAB DSA 30 DA a 3a
Xét trong tam giác vuông SAD : SA 0 tan 30 3 3 3 2 S a ABCD 3 1 1 3a a 3
Thể tích V của khối chóp là 2 V S . A S . .a S . ABCD 3 ABCD 3 3 3
Câu 16: [1H1-3] Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên gấp hai lần cạnh đáy. Tính tích V
của khối chóp tứ giác đã cho. 3 2a 3 2a 3 14a 3 14a A. V  . B. V  . C. V  . D. V  . 2 6 2 6 Lời giải Chọn D.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 57/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Xét hình chóp đều S.ABCD với đáy ABCD là hình vuông cạnh bằng a . Gọi O là tâm của hình
vuông ABCD , SO   ABCD . AC a 2 a 14 Ta có: 2 2 OA   ; SO SA OA  . 2 2 2 3 1 1 a 14 a 14
Vậy thể tích khối chóp S.ABCD là 2 V S .SO a .  . 3 ABCD 3 2 6
Câu 17: [1H1-3] Cho hình chóp tam giác đều S.ABC . Tính theo a thể tích khối chóp S.ABC biết rằng
AB a , (SBC),(ABC)  60 . 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 24 4 4 12 Lời giải Chọn A. S
Gọi O là tâm của tam giác ABC .
M là trung điểm BC .
Vì hình chóp tam giác đều S.ABC nên SO   ABC . B A
Ta có AM BC ( AM là đường cao tam giác ABC đều ). 60 O
Lại có tam giác SBC cân tại S nên SM BC . M
Do đó SBC,(ABC)  SM, AM   SMO  60. C
Vì O là trọng tâm tam giác ABC nên. 1 1 a 3 a 3 MO AM  .  . 3 3 2 6 2 a 3 S  . ABC 4
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 58/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 a 3 a
Xét tam giác SMO vuông tại O , ta có SO M . O tan 60  . 3  . 6 2 2 3 1 1 a a 3 a 3 VậyVS . O S  . .  . S. ABC 3 ABC 3 2 4 24
Câu 18: [1H1-1] Cho hình chóp tam giác S.ABC . Gọi M lần lượt là trung điểm của SB và N nằm
trên cạnh SC sao cho SN  2NC . Khi đó tỉ số thể tích của khối tứ diện S.AMN và khối tứ
diện S.ABC bằng: 1 1 1 1 A. . B. . C. . D. . 6 3 4 2 Lời giải Chọn B. SM 1 SN 2 Theo giả thiết ta có
 và SN  2NC   . SA 2 SC 3 V SM SN 1 2 1
Khi đó S.AMN  .  .  . V SB SC 2 3 3 S .ABC
Phân tích phương án nhiễu. SN
A, C sai Do tính sai tỉ số . SC D sai do tính sai.
Câu 19: [1H1-2] Cho khối chóp S.ABC có thể tích bằng 16 . Gọi M , N, P lần lượt là trung điểm của các cạnh S , A S ,
B SC . Tính thể tích V của khối tứ diện AMNP . 8 A. V  2 . B. V  . C. V  4 . D. V  8 . 3 Lời giải Chọn A. S M P N A C B
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 59/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 3 V SM SN SP  1  1 Ta có S.MNP  . .     V SA SB SC  2  8 S . ABC 16 Do đó V   2 . S .MNP 8
Do M là trung điểm SA , ta có d( , A (MN )
P )  d(S, (MN ) P ) Suy ra VV  2 . AMNP S.MNP
Phân tích phương án nhiễu. B sai do tính 3 2  6 .
C sai do áp dụng công thức tỉ số khoảng cách sai 2d( , A (MN )
P )  d(S, (MN ) P ) .
D sai do thấy trung điểm là phân nữa nên lấy thể tích chia 2.
Câu 20: [1H1-2] Cho hình chóp tam giác S.ABC có ABC là tam giác đều cạnh a , hai mặt phẳng
SAB và SAC cùng vuông góc với mặt đáy ABC và SC  2a. Tính theo a thể tích V
của khối chóp S.ABC . 1 3 3 3 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 4 3 6 4 Lời giải Chọn A. 2a a a a   SAB     ABC Ta có:
SA   ABC      
; SAC vuông tại A : 2 2 SA SC AC a 3 .  SAC     ABC 2 3 1 1 a 3 a Vậy VS . A Sa 3.  . S .ABC  3 ABC 3 4 4
Phân tích phương án nhiễu. 2 a 3
B sai do tính diện tích tam giác ABC là . 2
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 60/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
C sai do xác định đường cao là SC .
D sai do tính công thức thể tích thiếu chia 3.
Câu 21: [1H1-3] Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng 6 . Gọi G là trọng tâm tam
giác A' BD . Tính thể tích V của khối tứ diện GABC . A. V 12. B. V 18. C. V  24 . D. V  36 . Hướng dẫn giải Chọn A. A' B' D' C' G A B D C 1 1
Ta có d G, AB D
C   d  , A AB D
C   SA  2 3 3 1 Và SS 18. ABC AB D 2 C 1 V  1 d G ABCD S  .18.2 12 GABC  , .  3 ABC 3
Phân tích phương án nhiễu. 2 2
B sai do tính tỉ số khoảng cách sai d G, AB D
C   d  , A AB D
C   SA  4 . 3 3
C sai do tính diện tích tam giác ABC bằng 36 .
D sai do tính thể tích thiếu chia 3.
Câu 22. [2H1-3] Cho khối chóp .
O ABC . Trên ba cạnh O , A O ,
B OC lần lượt lấy ba điểm ’, A B ,  C sao cho V 2OA  O ,
A 4OB  O ,
B 3OC  OC . Tính tỉ số O.A'B'C' VO.ABC 1 1 1 1 A. . B. . C. . D. . 12 24 16 32 Lời giải: Chọn B.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 61/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 O Ta có: BCAOA 1 OB 1 OC 1  ;  ;  OA 2 OB 4 OC 3 V    A COA OB OC
O. A B’C’ 1 1 1 1         V OA OB OC 2 4 3 24 O. ABC B
Câu 23. [2H1-3] Cho khối lăng trụ tam giác đều AB . C ’ A ’ B ’
C có tất cả các cạnh đều bằng a . Thể tích khối tứ diện ’ A B ’ B ’ C là 3 a 3 3 a 3 3 a 3 3 a A.B.C.D.  12 4 6 12 Lời giải: Chọn A. A ' C '
h BB  a  B ' 2  a 3 SAB C    4 3 1 a 3  A C V       BB .S A BB C    3 A B C 12 B
Câu 24. [2H1-4] Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có
các đỉnh là các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng a . Hãy tính thể
tích của khối tám mặt đều đó: 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 6 12 8 Lời giải: Đáp án B.
Dựng được hình như hình bên.
+ Thấy được thể tích khối cần tính bằng 2 lần thể tích của hình chóp S.ABCD.
+ Nhiệm vụ bây giờ đi tìm thể tích của S.ABCD.
+ ABCD là hình vuông có tâm O đồng thời chính là hình chiếu của S lên mặt đáy.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 62/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 a SO
; BD  cạnh của hình lập phương  a . Suy ra các cạnh của hình vuông 2 ABCD a . 2 2 3 1 1 1  2   2  a 3 VSh  . .   a  . S . ABCD    3 3 2 2 2 12    3 a V  2.V  . khôi đa diên S. ABCD 6
Câu 25. [2H1-3] Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , cạnh SB vuông góc với
đáy và mặt phẳng SAD tạo với đáy một góc 60. Tính thể tích khối chóp S.ABCD . 3 3a 3 3 3a 3 3 8a 3 3 4a 3 A. V  . B. V  . C. V  . D. V  . 4 8 3 3 Lời giải: Chọn C. AD AB Ta có: 
AD (SAB) AD SAD SBSA. 0  SAB  60 . SABCD = 4a2. A D
Xét tam giác SAB tại vuông tại B, ta có:  0
SB AB tan 60  2a 3 . 2a 1 3 8a 3 B C Vậy V = .4a2. 2a 3 = . 3 3
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 5 Câu 1.
[2D4-2] Hình đa diện đều có tất cả các mặt là ngũ giác có bao nhiêu cạnh? A. 20 . B. 60 . C. 30 . D. 12 . Lời giải Chọn C .
Hình đa diện đều có tất cả các mặt là ngũ giác đều là hình mười hai mặt đều (loại 5;  3 ) có 20
đỉnh, 30 cạnh, 12 mặt.
Phân tích phương án nhiễu.
A – sai do nhớ nhầm số đỉnh.
B – sai do quên kiến thức.
D – sai do nhớ nhầm số mặt. Câu 2.
[2H1-1] Hình nào sau đây không phải là hình đa diện . A. Hình trụ. B. Hình tứ diện.
C. Hình lập phương. D. Hình chóp. Lời giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 63/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Chọn A. Câu 3.
[2H1-2] Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ sau
Khối tứ diện đều Khối lập phương Bát diện đều Hình 12 mặt đều Hình 20 mặt đều
Mệnh đề nào sau đây đúng?
A. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.
B. Khối lập phương và khối bát diện đều có cùng số cạnh.
C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
D. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh. Lời giải Chọn B.
+ B đúng, vì khối lập phương có 12 cạnh; khối bát diện đều có 12 cạnh.
Phân tích phương án nhiễu
+ A- sai, vì khối lập phương có 6 mặt và 6 4 .
+ C- sai, vì khối tứ diện đều không có tâm đối xứng.
+ D -sai, vì khối 12 mặt đều có 20 đỉnh, còn khối 20 mặt đều có 12 đỉnh. Câu 4.
[2D4-1] Số đỉnh của khối bát diện đều là: A. 6. B. 8. C. 12. D. 4. Lời giải Chọn A.
Phân tích phương án nhiễu.
B – Sai do 8 là số đỉnh của khối lập phương.
C – Sai do 12 là số đỉnh của khối 20 mặt đều.
D – Sai do 4 là số đỉnh của khối tứ diện đều. Câu 5.
[2H1-1]Công thức nào sau đây là công thức tính thể tích khối chóp? 1 1 1 A. V S.h .
B. V S.h .
C. V S.h . D. V S.h . 6 3 2 Câu 6.
[2H1-2]Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm SC. Mặt phẳng
  qua M song song với DC chia khối chóp thành bao nhiêu khối chóp tứ giác. A. 4 . B. 3 . C.1 . D. 2 . Lời giải Chọn C.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 64/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Một khối chóp tứ giác
Phân tích phương án nhiễu.
A – sai do không xác định đúng mặt phẳng   .
C – sai do không xác định đúng mặt phẳng   .
D – sai do không xác định đúng mặt phẳng   . Câu 7.
[2D4-2] Cắt khối lăng trụ MN . P M NP
  bởi các mặt phẳng MN P
  và MNPta được những khối đa diện nào?
A. Hai khối tứ diện và hai khối chóp tứ giác.
B. Một khối tứ diện và một khối chóp tứ giác.
C. Ba khối tứ diện.
D. Hai khối tứ diện và một khối chóp tứ giác. Lời giải Chọn C . M N P M' N' P'
Cắt khối lăng trụ MN . P M NP
  bởi các mặt phẳng MN P
  và MNP ta được ba khối tứ diện là . P MNP ;  . P MNN ;  M.MN P  .
Phân tích phương án nhiễu.
A – sai do học sinh không vẽ được hình hoặc nhầm lẫn tên các khối.
B – sai do học sinh không vẽ được hình hoặc nhầm lẫn tên các khối.
D – sai do học sinh không vẽ được hình hoặc nhầm lẫn tên các khối. Câu 8.
[2H1-1] Thể tích khối lăng trụ đứng tam giác AB . C A BC
  có tất cả các cạnh bằng a là . 3 a 3 3 a 3 3 a 3 3 a A. . B. . C. . D. . 6 3 4 4 Lời giải Chọn C.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 65/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Vì AB . C A BC
  là khối lăng trụ đứng có tất cả các cạnh bằng a nên có hai đáy là các tam giác đều
cạnh a , các mặt bên là hình vuông cạnh a . Suy ra thể tích khối lăng trụ là 2 3 a 3 a 3 V S .AA  .a  (đvtt) . ABC  4 4 Câu 9.
[2H1-1] Tính theo a thể tích V của khối lập phương ABC . D A BCD
  biết AC  . a 3 a 3 3a A. 3 V  3 3a . B. 3 V a . C. V  . D. V  . 27 9 Lời giải Chọn D. A a D
Ta có AC  AB 3  AB  . 3 B C
Thể tích khối lập phương là: 3 3 3  a a a 3 A 3 V AB      . D  3  3 3 9 B C
Phân tích phương án nhiễu
+ A- sai, do nhớ nhầm công thức thành AB AC 3  a 3.
+ B- sai, do học sinh đọc đề ko kĩ và nhớ công thức là lấy cạnh lập phương mà ko để ý cạnh nào. a
+ C -sai, do tính sai cạnh của hình lập phương thành
hoặc do tính sai lập phương cảu AB . 3
Câu 10. [2D4-2] Tính thể tích của khối hộp chữ nhật có diện tích của các mặt bên và mặt đáy lần lượt là 2 10 cm , 2 16 cm và 2 40 cm . A. 3 160 cm . B. 3 400 cm . C. 3 80 cm . D. 3 640 cm . Lời giải Chọn C.
Gọi kích thước của khối hộp chữ nhật là x, y và z.
Ta có xy 10, xz 16 và yz  40 . Khi đó 2 2 2
x y z  6400  xyz  80 .
Vậy thể tích khối hộp chữ nhật là 3 80 cm .
Câu 11. [2H1-2] Cho hình lập phương ABC . D A BCD
  có cạnh bằng a. Tính thể tích khối tứ diện ACB D   theo a . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 6 2 3 4
Câu 12. [2H1-3] Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên
và mặt phẳng đáy là  . Mặt phẳng  P qua AC và vuông góc với mặt phẳng SAD chia khối chóp V
S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là MACD ? VSABCM
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 66/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 A. 2 cos  B. 2 sin  C. 2 tan  D. 0,9 Lời giải Chọn A. Ta có: 1 a 1 a 2 2 2 2 2 SD
SN ND ON .  ND  1  cos  1 2 2   cos SNO 2 cos 2.cos a 1 .a 1 1 SN.CDa Ta có : S
CM.SD SN.CD 2 cos  CM    SCD  2 2 2 SD a 2 1 cos  cos  1 2.cos 2 a . a cos 2 2 2
DM CD CM a   2 2 1 cos   1 cos . a cos 2 2 V V 1 DM DA DC 1 DM 1    MACD MACD 1 cos cos   . . .  .   2 V 2.V 2 DS DA DA 2 DS 2 a   2 1 cos SABCD SACD 1 cos  2.cos 2 2 cos   cos   1 VVV  1 VV MACD 2 SABCD SABCM 2 SABCD 2 1 cos   1 cos   1 cos SABCDV Do vậy : MACD 2  cos  VSABCM
Câu 13. [2D4-2] Cho lăng trụ đứng AB .
C A' B 'C ' có đáy là tam giác vuông tại 0 ,
A AC a, ACB  60 . Đường
chéo BC ' của mặt bên BCC ' B ' tạo với mặt phẳng  AA'C 'C một góc 0 30 . Tính thể tích của
khối lăng trụ theo a . 3 a 6 3 a 6 3 2 6a A. . B. . C. 3 a 6 . D. . 2 3 3 Lời giải Chọn C .
Ta có BA   AA'C 'C nên BC AA C C  BC AC  0 ', ' ' ',
'  AC ' B  30 . Trong ABC  vuông tại A , 0 AB A .
C tan 60  a 3 . Trong ABC  ' vuông tại A , 0 AC '  A .
B cot 30  3a . Trong C
C ' A vuông tại C , 2 2 CC ' 
AC '  AC  2a 2 . 2 1 1 a 3 SA . B AC a 3.a  . ABC 2 2 2 2 a 3 3
V CC '.S  2a 2.  a 6 . ABC 2
Phân tích phương án nhiễu.
A – sai do nhớ nhầm công thức thể tích hoặc gặp lỗi trong tính toán.
B – sai do nhớ nhầm công thức thể tích hoặc gặp lỗi trong tính toán.
D – sai do nhớ nhầm công thức thể tích hoặc gặp lỗi trong tính toán.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 67/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Câu 14. [2H1-3] Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A và AB AC a 2 . Tam giác
SBC có diện tích bằng 2
2a và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của
khối chóp S.ABC . 3 4a 3 a 3 2a A. V  . B. V  . C. 3 V  2a . D. V  . 3 3 3 Lời giải Chọn D.
SBC  ABC   
SBC    ABC   BC
  AH  SBC 
Trong ( ABC) : AH BC ABC  vuông cân tại A nên 1
BC AB 2  2a AH BC a . 2 1 1 2 2 3 VS
.AH  .2a .a a . SABC  3 SBC 3 3
Câu 15. [1H2-3] Tính thể tích khối chóp S.ABCD có ABCD là hình thang vuông tại , A B có AD  2 ,
a AB BC a , SA   ABCD , Góc giữa SCD và  ABC là 0
60 . Tính thể tích khối chóp S.ABCD 3 a 6 3 3 3a 3 6 3a 3 a 6 A. . B. . C. . D. . 4 4 4 2 Lời giải Chọn A. S 2a M A D a 60 B a C
Gọi M là trung điểm của AD suy ra 0
ACD  90 suy ra  ACD  CD
Góc giữa mặt phẳng SCD và  ABC là 0 ACD  60 Chiều cao : 0 SA A .
C tan 60  a 2. 3  a 6
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 68/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 a
Diện tích đáy: S  BC ADAB   a a 2 1 1 3 . 2 .a  2 2 4 2 3 1 3a a 6 Thể tích là : V a 6  , chọn đáp án A. 3 4 4
Phân tích phương án nhiễu
B-sai, do học sinh xác định nhầm góc giữa hai mặt phẳng là góc SBD đẫn đến đường cao SA tính sai là a 2
C –sai, do học sinh xác định nhầm góc giữa hai mặt phẳng là góc SDA đẫn đến đường cao SA tính sai là 2a 3
D-sai, do học sinh tính nhầm công thức diện tích hính thang. S   AD BC.AB
Câu 16. [2D4-3] Cho hình chóp tứ giác đều S.ABCD. Gọi O là tâm mặt đáy, biết SO  20cm và khoảng cách
từ điểm O tới mặt bên của khối chóp bằng 12cm . Tính thể tích khối chóp S.ABCD. A. 3 V  3840cm . B. 3 V  6000cm . C. 3 V  1920cm . D. 3 V  3000cm . Lời giải Chọn B. Gọi E là trung điểm CD.
Dựng OF SE d 0;
 SCD  OF 12  . 1 1 1 Ta có  
OE 15cm . 2 2 2 OF OS OE
Vậy AD  2OE  30cm . 1 Khi đó 2 3
V  .30 .20  6000 cm . 3
Phân tích phương án nhiễu.
A – Sai do nghĩ rằng khoảng cách từ O tới mặt (SCD) là OE.
C – Sai do nghĩ rằng khoảng cách từ O tới mặt (SCD) là OD.
D – Sai do nghĩ rằng khoảng cách từ O tới mặt (SCD) là đoạn kẻ vuông góc từ O lên SD.
Câu 17. [2H1-3] Cho một hình chóp tứ giác đều có cạnh đáy bằng a và diện tích xung quanh gấp đôi diện
tích đáy. Khi đó thể tích của khối chóp là. 3 a 3 3 a 2 3 a 3 3 a 3 A. . B. . C. . D. . 12 3 3 6
Câu 18. [2H1-1] Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB và AC . Khi đó tỉ số thể tích
của khối tứ diện AMND và khối tứ diện ABCD bằng: 1 1 1 1 A. B. C. D. 2 4 6 8 Lời giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 69/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Chọn A. V AM AN AD 1 Ta có AMND  . .  . V AB AC AD 4 ABCD
Phân tích phương án nhiễu. B – sai do tính toán.
C – sai do tính toán.
D – sai do tính toán.
Câu 19. [2D4-2] Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh
SC lấy điểm E sao cho SE  2EC . Tính thể tích V của khối tứ diện SEBD . 2 1 1 1 A. V  . B. V  . C. V  . D. V  . 3 12 3 6 Lời giải Chọn C . S E A D B C . 1 1 Ta có VV  . SBCD 2 SABCD 2 V SE.S . B SD 2 1 Mà SEBD   . Do đó V  . V SC.S . B SD 3 SEBD 3 SCBD
Phân tích phương án nhiễu.
A – sai do nhớ nhầm thể tích V 1. SBCD V
B – sai do lập tỉ số SEBD sai. VSBCD V
D – sai do lập tỉ số SEBD sai. VSBCD
Câu 20. [2H1-3] Cho hình chóp đều S.ABC có cạnh đáy bằng a , khoảng cách giữa cạnh bên SA và cạnh 3a đáy BC bằng
. Thể tích khối chóp S.ABC tính theo a là . 4 3 3a 3 3 a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 16 12 8 8 Lời giải Chọn B.
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 70/73 luyenthitracnghi
THẦY VIỆT 0905.193.688
Gọi M là trung điểm của BC , O là trọng tâm tam giác ABC
Khi đó ta có : AM BC , SM BC suy ra BC  SAM a
Kẻ MH SA , do BC  SAM  3
BC MH MH  4 a 3
Tam giác ABC đều cạnh a suy ra AM  2 a 3
Tam giác HAM vuông tại H suy ra 2 2 HA AM HA  4 2 a 3
Do SO   ABC  SO AM nên tam giác SOA vuông tại O , OA AM  3 3 HM SO HM .AO
Tính được tan SAO    SO   a AH AO AH 2 3 1 1 a 3 a 3
Thể tích khối chóp S.ABC là : V S .SO  . .a  . 3 ABC 3 4 12
Câu 21. [1H2-2] Cho khối hộp ABC .
D A' B'C ' D' có thể tích bằng 3
24dm .Gọi M là trung điểm của A' D
Tính thể tích khối chóp M.ABC ? A. 3 6dm . B. 3 2dm . C. 3 3dm . D. 3 9dm . Lời giải
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 71/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Chọn B. A' D'
Thể tích khối hộp V S .h C' day B'
Do đó chiều cao khối hộp ABC .
D A' B'C ' D' bằng chiều cao M khối chóp M.ABC 1 Diện tích ABC  bằng S do đó: D 2 day A 1 VS B C A'. ABC
ABCD.A' B 'C ' D ' 12
Phân tích phương án nhiễu 1
A-sai, Học sinh quên công thức thể tích khối chóp S S .h . 3 day
C –sai, do Học sinh nhầm tưởng công thức tỷ số thể tích.
D-sai, do học sinh khoanh bừa.
Câu 22. [2D4-3] Cho hình chóp S.ABCD có thể tích bằng 1. Biết mặt đáy là hình vuông tâm O và SO vuông
góc với mặt phẳng  ABCD . Gọi I là trung điểm cạnh SD, tính thể tích khối tứ diện IOBC. 1 1 1 1 A. V  . B.V  . C.V  . D.V  . IOBC 2 IOBC 12 IOBC 8 IOBC 24 Lời giải Chọn C. Ta có 1 1  1   1  Vh .S  . SO . S IOBC     3 I OBC 3  2   4 ABCD  1  1  1  S . O S    . 8  3 ABCD  8
Câu 23. [2H1-4] Cho hình hộp ABC . D A BCD
  . Tỉ số thể tích của khối tứ diện ACB D   và khối hộp ABC . D AB CD   bằng 1 1 1 1 A. . B. . C. . D. . 2 3 4 6
Câu 24. [2H1-3] Một túp lều có dạng hình lăng trụ đứng có kích thước như hình bên. Tính thể tích của túp lều. 280 560 A. 3 280 m B. 3 m C. 3 560 m D. 3 m 3 3
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 72/73 luyenthitracnghi
THẦY VIỆT 0905.193.688 Lời giải Chọn A. 1
Thể tích của túp lều là 3 V  .
h S  10. .7.8  280 m . 2
Phân tích phương án nhiễu. B – sai do tính toán.
C – sai do tính toán.
D – sai do tính toán
Câu 25. [2H1-4] Cho tứ diện ABCD có các cạnh AB A
, C và AD đôi một vuông góc nhau; AB  6 , a
AC 7a, A
D 4a. Gọi M, N , P
tương ứng là trung điểm các cạnh BC, C D, B
D. Thể tích V của tứ diện AMN . P 3 7a 28 A. . B. 3 14a . C. 3 a . D. 3 7a . 2 3 Lời giải Chọn D. 1  1  3 VA .
B AC AD  28a . ABCD   3  2  1 3 VVVV  7a . D.AND B.AMP C.MNA 4 ABCD VV VVVa AND B C MNA  3 7 . AMNP ABCD D. .AMP .
Phân tích phương án nhiễu. B – sai do tính toán.
C – sai do tính toán.
D – sai do tính toán
Chuyên đề: Kiểm tra thể tích khối đa diện chương I lớp 12
Năm học 2018 – 2019 Trang 73/73 luyenthitracnghi