Bộ Đề Tham Khảo Môn Toán Tuyển Sinh 10 Quận 3 TP HCM 2025-2026 Giải Chi Tiết
Trong tháng giêng cả hai tổ I và II sản xuất được 720 chi tiết máy. Trong tháng hai, tổ I sản xuất vượt15%, tổ II sản xuất vượt 12% so với tháng giêng nên cả hai tổ sản xuất được tất cả là 819 chi tiết máy. Tính xem trong tháng giêng mỗi tổ sản xuất được bao nhiêu chi tiết máy. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 216 tài liệu
Môn: Toán 9 3 K tài liệu
Tác giả:
Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 3 MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận. ĐỀ TH AM KHẢO
Thời gian: 120 phút (không kể thời gian phát đề) MÃ ĐỀ: Quận 3 - 1
Câu 1. (1,5 điểm). Cho (P) 2
: y = −x và đường thẳng (d) : y = 2x − 3 .
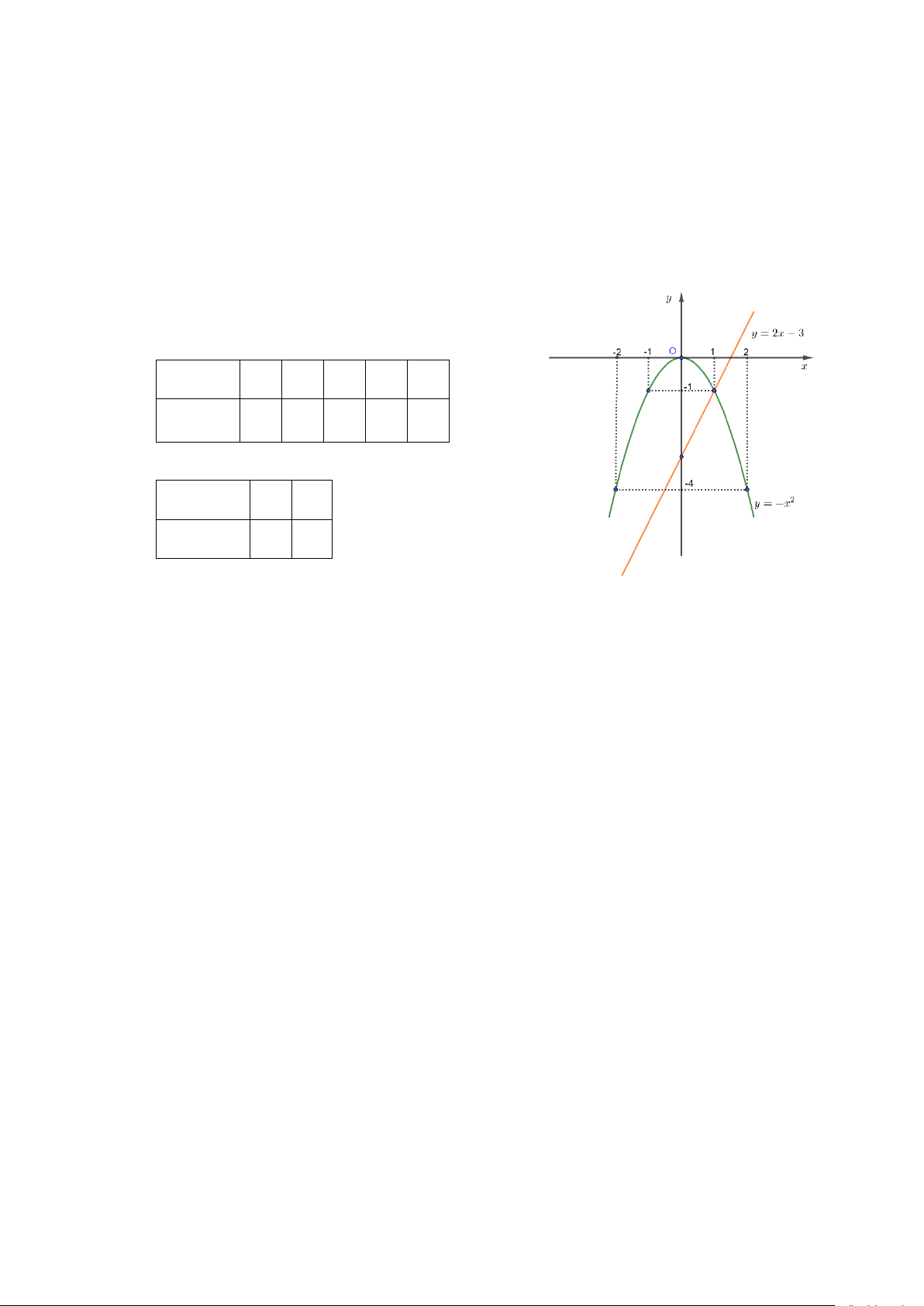
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1,0 điểm). Cho phương trình 2
2x − x − 3 = 0 có 2 nghiệm là x , x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức A = 2 x + 2 x − 2 2 x x . 1 2 1 2
Câu 3. (1,0 điểm). Nồng độ cồn trong máu (BAC – Blood
Alcohol Conentration) là tỉ lệ lượng rượu (gam) trong 100 mililit máu.
Ví dụ: BAC 0, 03 nghĩa là 0, 03g rượu trong 100ml.
máu. Uống càng nhiều rượu bia thì nồng độ cồn
trong máu càng cao và càng dễ gây ra tai nạn khi
điều khiển phương tiện giao thông.
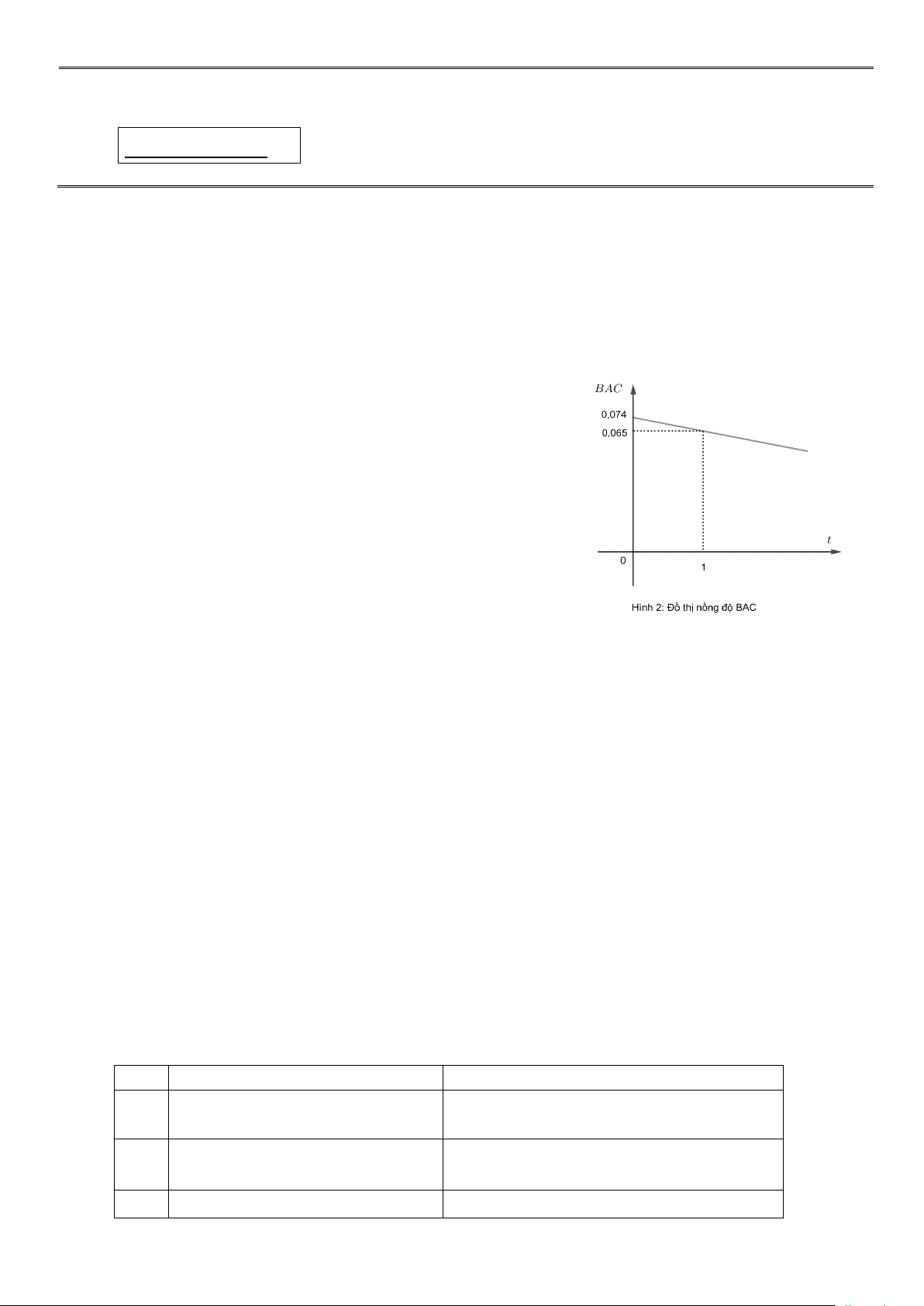
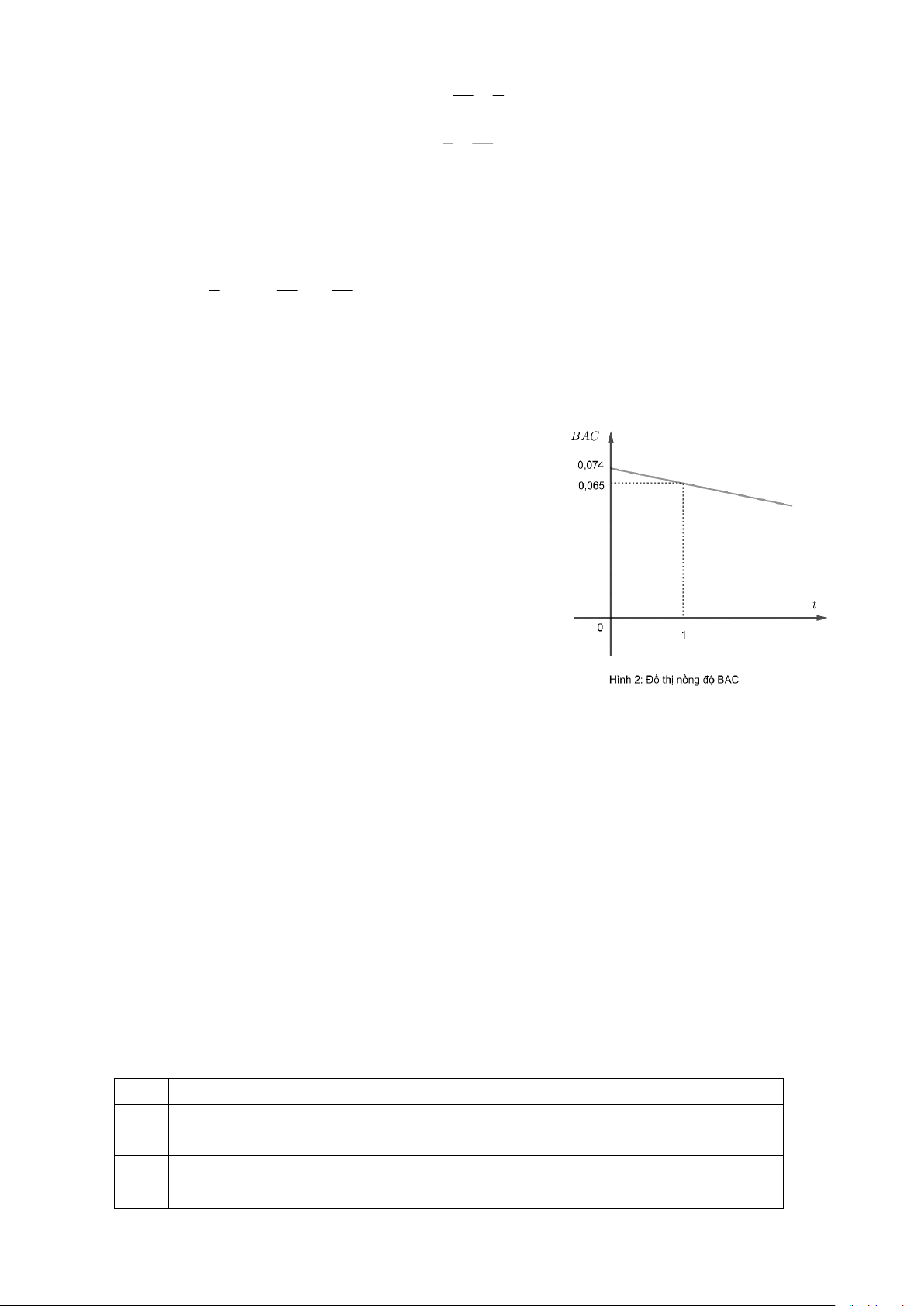
Với một người đã uống khoảng 100g rượu (rượu ethyl hoặc ethanol) thì nồng độ BAC sau t
giờ được thể hiện qua đồ thị như hình 2 .
a) Gọi y là nồng độ BAC của một người sau khi uống khoảng 100g rượu trong t giờ. Viết công
thức biểu thị y theo t , biết y là một hàm số bậc nhất của t .
b) Theo nghị định 100 / 2019 / NĐ-CP ngày 30 /12 / 2019 của chính phủ nước Cộng hòa xã hội
chủ nghĩa Việt Nam về quy định xử phạt vi phạm hành chính trong lĩnh vực giao thông
đường bộ và đường sắt; mức xử phạt các lỗi vi phạm giao thông đối với người điều khiển xe
máy được tính theo bảng 1 . Hỏi sau khi uống 100g rượu khoảng 2 giờ, nếu người này điều
khiển xe máy tham gia giao thông đường bộ thì sẽ bị xử phạt ở mức nào?
Bảng 1 : Tra cứu mức phạt các lỗi vi phạm giao thông. STT Lỗi vi phạm
Mức phạt tiền và hình phạt 1
Nồng độ chưa vượt quá BAC
• 02 − 03 triệu đồng. 0, 05
• Thu bằng lái xe từ 10 −12 tháng. 2
Nồng độ từ BAC 0, 05 đến BAC
• 04 − 05 triệu đồng. 0, 08
• Thu bằng lái xe từ 16 −18 tháng. 3
Nồng độ lớn hơn BAC 0, 08
• 06 − 08 triệu đồng. Trang 1
• Thu bằng lái xe từ 22 − 24 tháng.
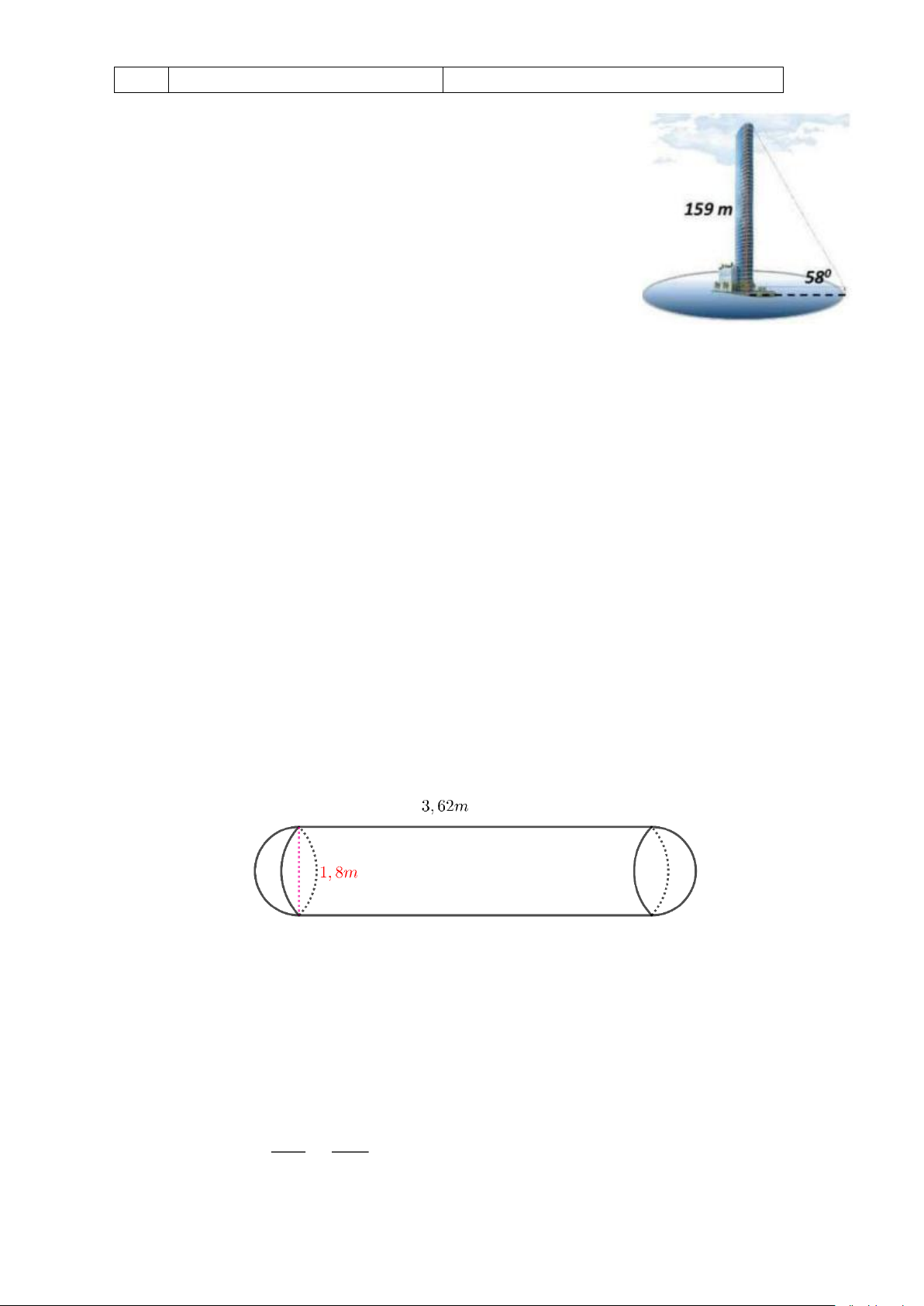
Câu 4. (1,0 điểm). Một người cao 175cm đứng trên bờ hồ và nhìn lên
đỉnh một tòa cao ốc 159m xây giữa hồ (mặt hồ có dạng hình
tròn, cao ốc xem như vuông góc với mặt hình tròn tại tâm hình
tròn) dưới một góc 58° . Em hãy tính diện tích và chu vi của hồ
này biết chu vi C và diện tích S của hình tròn được tính theo
công thức C = 3,14.d và 2
S = 3,14.R trong đó d là đường kính
và R là bán kính của hình tròn (kết quả làm tròn đến chữ số thập phân thứ hai).
Câu 5. (1,0 điểm). Trong tháng giêng cả hai tổ I và II sản xuất được 720 chi tiết máy. Trong tháng
hai, tổ I sản xuất vượt15% , tổ II sản xuất vượt 12% so với tháng giêng nên cả hai tổ sản
xuất được tất cả là 819 chi tiết máy. Tính xem trong tháng giêng mỗi tổ sản xuất được bao nhiêu chi tiết máy.
Câu 6. (0,75 điểm). Một vé xem phim đang có giá là 120 000 đồng. Trong đợt giảm giá cuối năm
2022 , số lượng người xem phim tăng thêm 50% nên tổng doanh thu cũng tăng lên 20% (so
với lúc chưa giảm giá). Hỏi giá mỗi vé khi đã giảm là bao nhiêu đồng?
Câu 7. (0,75 điểm). Một xe bồn chở nước sạch cho một khu dân cư có 200 hộ dân. Bồn xe có hình
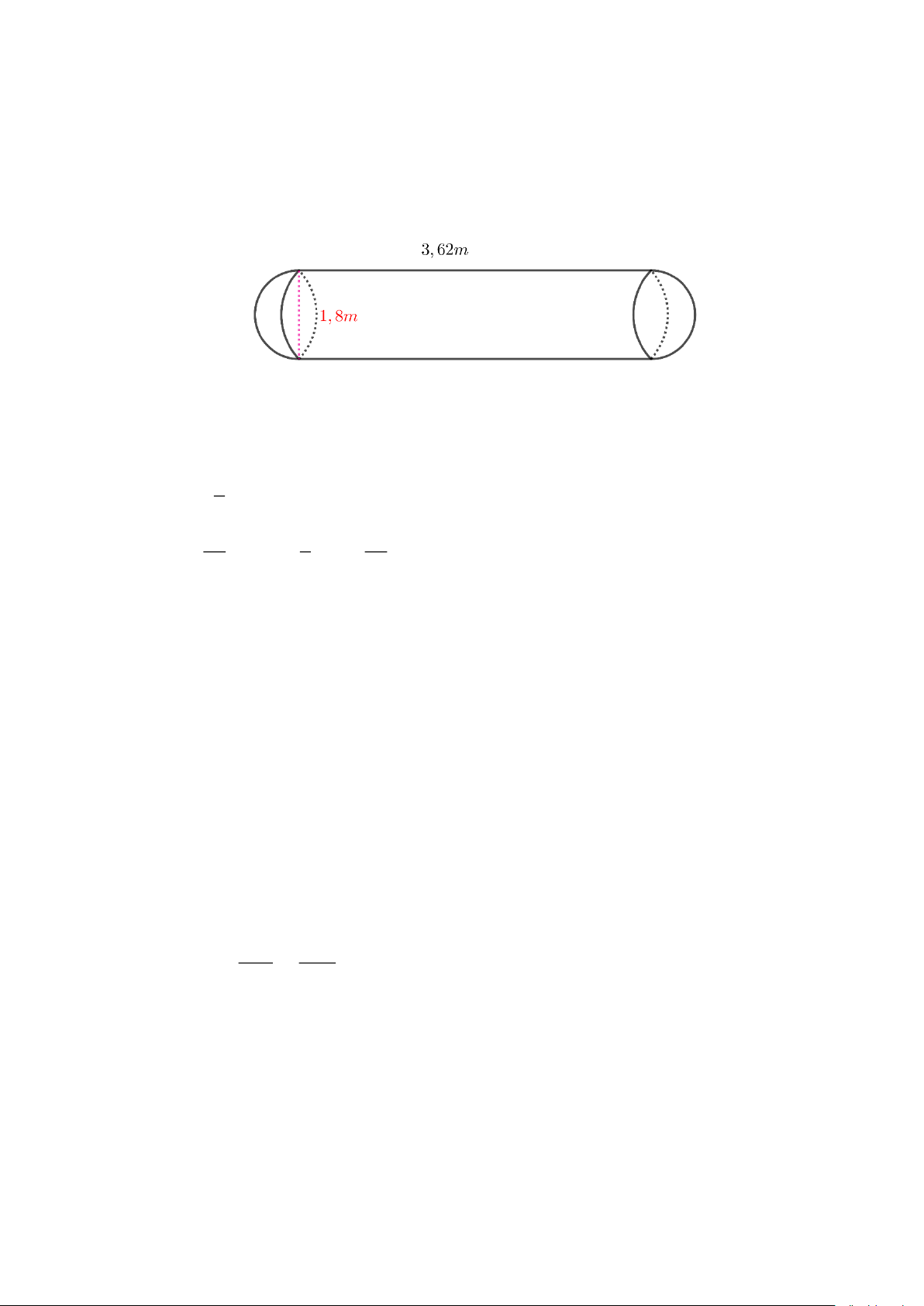
dạng và kích thước như hình vẽ bên dưới, mỗi đầu của bồn xe là nửa hình cầu. Xe chở đầy
nước và lượng nước chia đều cho từng hộ dân. Tính xem mỗi hộ dân được nhận bao nhiêu lít nước sạch.
Câu 8. (3,0 điểm) Từ điểmM nằm ở ngoài đường tròn (O;R )vẽ hao tiếp tuyến MA, MC vơi đường
tròn ( A,C là hai tiếp điểm). Vẽ đường kính A B của đường tròn (O ).
a) Chứng minh tứ giác A MCO nội tiếp và OM / / BC .
b) Kẻ CD ^ A B (D Î A B ). BM cắt (O)tại N (N ¹ B ). Chứng minh DMA O và DCDB 2 MN CN đồng dạng và = . 2 MB CB Trang 2
c) Gọi I là giao điểm của OM và A C ; K là giao điểm của BM và CD . Khi OM = A B ,
tính theo R diện tích D MIK . ----HẾT--- Trang 3 HƯỚNG DẪN GIẢI Câu 1.
(1,5 điểm) Cho (P) 2
: y = −x và đường thẳng (d) : y = 2x − 3 .
a. Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b. Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
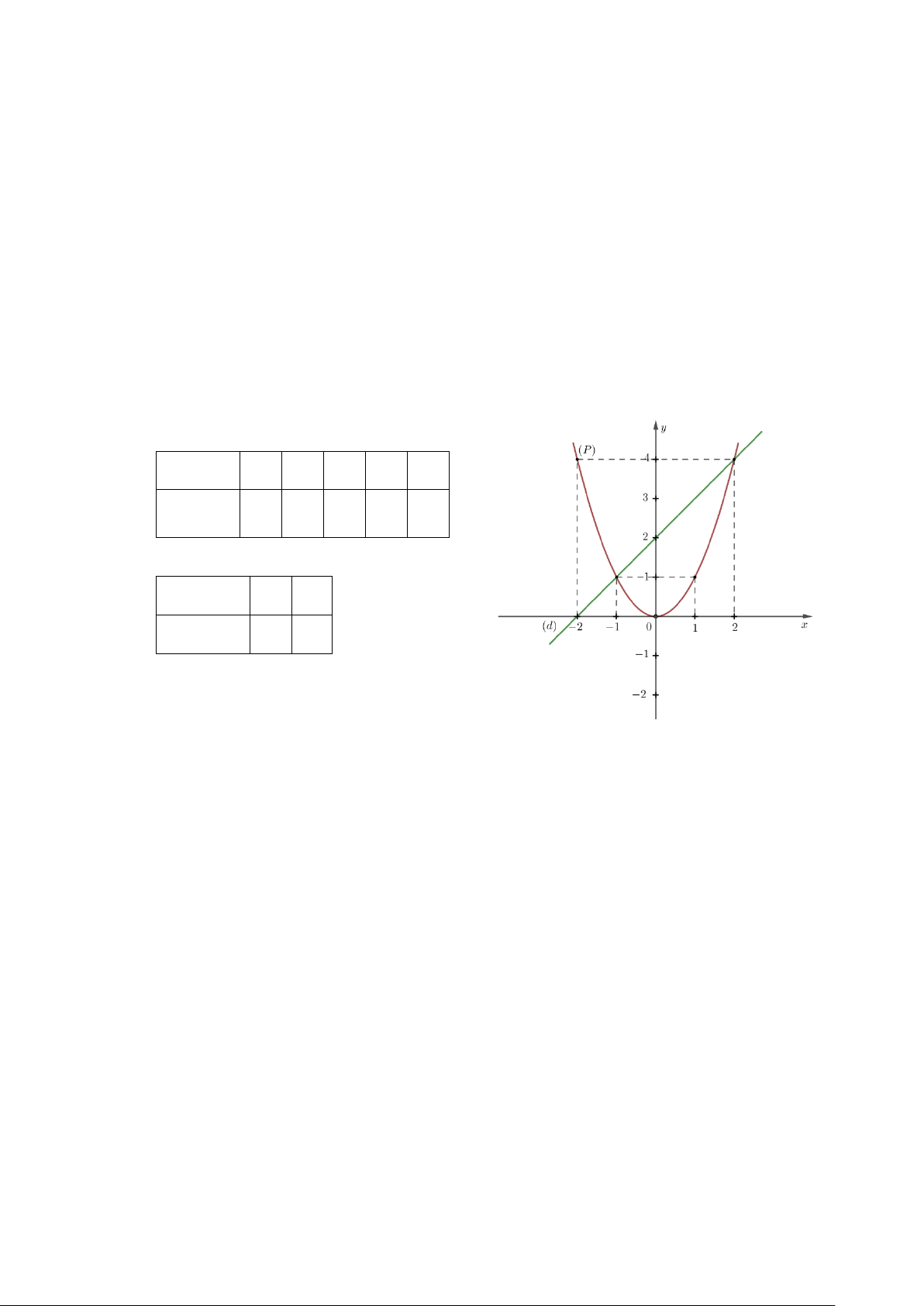
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. BGT: x −2 1 − 0 1 2 2 y = −x −4 1 − 0 1 − −4 x 0 1
y = 3x − 4 −3 1 −
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : − 2 x = 2x − 3 − 2 x − 2x + 3 = 0 x = 1 x = − 3 Thay x = 1 vào 2
y = −x , ta được: 2 y = 1 − = −1 . 2 Thay x = −3 vào 2
y = −x , ta được: y = −(−3) = −9 .
Câu 2. (1 điểm) Cho phương trình 2
2x − x − 3 = 0 có 2 nghiệm là x , x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức A = 2 x + 2 x − 2 2 x x . 1 2 1 2 Lời giải 2 Vì = 2
b − 4ac = (− ) 1 − 4.2.(−3) = 25 0 .
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 Trang 4 − = + = b S x x = 1 1 2
Theo định lí Vi-et, ta có: a 2 c −
P = x .x = = 3 1 2 a 2 Ta có: A = 2 x + 2 x − 2 2 x x 1 2 1 2
A = (x + x )2 − 2x x − (x x )2 1 2 1 2 1 2 1 2 −3 −3 2 A = − 2. − 2 2 2 A = 1
Câu 3. (1 điểm) Nồng độ cồn trong máu (BAC – Blood Alcohol Conentration) là tỉ lệ lượng rượu
(gam) trong 100 mililit máu.
Ví dụ: BAC 0, 03 nghĩa là 0, 03g rượu trong
100ml. máu. Uống càng nhiều rượu bia thì
nồng độ cồn trong máu càng cao và càng dễ
gây ra tai nạn khi điều khiển phương tiện giao thông.
Với một người đã uống khoảng 100g rượu
(rượu ethyl hoặc ethanol) thì nồng độ BAC
sau t giờ được thể hiện qua đồ thị như hình 2 .
a) Gọi y là nồng độ BAC của một người sau khi uống khoảng 100g rượu trong t giờ. Viết
công thức biểu thị y theo t , biết y là một hàm số bậc nhất của t .
b) Theo nghị định 100 / 2019 / NĐ-CP ngày 30 /12 / 2019 của chính phủ nước Cộng hòa xã
hội chủ nghĩa Việt Nam về quy định xử phạt vi phạm hành chính trong lĩnh vực giao
thông đường bộ và đường sắt; mức xử phạt các lỗi vi phạm giao thông đối với người
điều khiển xe máy được tính theo bảng 1. Hỏi sau khi uống 100g rượu khoảng 2 giờ, nếu
người này điều khiển xe máy tham gia giao thông đường bộ thì sẽ bị xử phạt ở mức nào?
Bảng 1: Tra cứu mức phạt các lỗi vi phạm giao thông. STT Lỗi vi phạm
Mức phạt tiền và hình phạt 1
Nồng độ chưa vượt quá BAC
• 02 − 03 triệu đồng. 0, 05
• Thu bằng lái xe từ 10 −12 tháng. 2
Nồng độ từ BAC 0, 05 đến BAC
• 04 − 05 triệu đồng. 0, 08
• Thu bằng lái xe từ 16 −18 tháng. Trang 5 3
Nồng độ lớn hơn BAC 0, 08
• 06 − 08 triệu đồng.
• Thu bằng lái xe từ 22 − 24 tháng. Lời giải
a) Vì y là hàm số bậc nhất của t . Nên hàm số của y có dạng: y = at + b Theo đề bài, ta có: t = 0 Với 0,074 = 0.a + . ( ) 1 y = b 0,074 t = 1 Với 0,065 = a + . (2) y = b 0,065
0a + b = 0,074 a = −0,009 Từ ( )
1 và (2) ta có hệ phương trình: . 12a + b = 0,065 b = 0,074
Vậy: a = −0,009 , b = 0,074 và y = −0,009t + 0,074 .
b) Thay t = 2 vào y = −0, 009t + 0, 074 y = 0, 056 .
So với bảng mức phạt thì người này bị phạt ở mức thứ 2.
Câu 4. (0,75 điểm). Một người cao 175cm đứng trên bờ hồ và nhìn
lên đỉnh một tòa cao ốc 159m xây giữa hồ (mặt hồ có dạng
hình tròn, cao ốc xem như vuông góc với mặt hình tròn tại
tâm hình tròn) dưới một góc 58o . Em hãy tính diện tích và
chu vi của hồ này biết chu vi C và diện tích S của hình tròn
được tính theo công thức C = 3,14.d và 2
S = 3,14.R trong đó
d là đường kính và R là bán kính của hình tròn (kết quả làm
tròn đến chữ số thập phân thứ hai). Lời giải
Đổi 175cm = 1, 75m
Chiều cao của tòa nhà tính từ đầu của người đó đến đỉnh của tòa nhà:
159 - 1, 75 = 157, 25(m ) 157, 25
Bán kính của hồ: R = (m) tan 58o Trang 6 2 157 æ , 25 ö ç ÷ Diện tích của hồ: 2
S = 3,14.R = 3,14.ç ÷ » 30317, 22 ç ÷ ( 2 m ) ç èt an 58o ÷ø 157, 25
Chu vi của hồ: C = 3,14.d = 3,14.2.R = 3,14.2. » 617, 08(m ) tan 58o
Câu 5. (1 điểm) Trong tháng giêng cả hai tổ I và II sản xuất được 720 chi tiết máy. Trong
tháng hai, tổ I sản xuất vượt15% , tổ II sản xuất vượt 12% so với tháng giêng nên cả
hai tổ sản xuất được tất cả là 819 chi tiết máy. Tính xem trong tháng giêng mỗi tổ sản
xuất được bao nhiêu chi tiết máy. Lời giải
Gọi số chi tiết máy trong tháng giêng của tổ I và II lần lượt là x;y (0 < x,y < 720)
Vì trong tháng giêng cả hai tổ I và II sản xuất được 720 chi tiết máy, nên ta có phương
trình: x + y = 720 ( ) 1
Trong tháng hai cả hai tổ I và II sản xuất được 819 chi tiết máy, nên ta có phương
trình: 115%x + 112%y = 819 ( ) 2 ìï x + y = 720 ìï x = 420 ï ï Từ ( )
1 và (2) ta có hệ phương trình: í Û í ï (thỏa mãn)
115%x + 112%y = 819 ï y = 300 ïî ïî
Vậy số chi tiết máy trong tháng giêng của tổ I và II lần lượt là 420; 300 chi tiết máy.
Câu 6. (1 điểm) Một vé xem phim đang có giá là 120 000 đồng. Trong đợt giảm giá cuối năm
2022 , số lượng người xem phim tăng thêm 50% nên tổng doanh thu cũng tăng lên 20%
(so với lúc chưa giảm giá). Hỏi giá mỗi vé khi đã giảm là bao nhiêu đồng? Lời giải
Gọi số lượng người xem trước khi giảm giá vé là x (x Î ¥ ) *
Doanh thu lúc trước:120 000x (đồng)
Số lượng người xem sau khi giảm giá vé: 150%.x = 1, 5x (người)
Doanh thu lúc sau:120 000x.120% = 144 000x (đồng)
Giá mỗi vé sau khi đã giảm:144 000x : 1, 5x = 96000 (đồng)
Vậy giá mỗi vé sau khi đã giảm là 96000 (đồng) Trang 7
Câu 7. (1 điểm) Một xe bồn chở nước sạch cho một khu dân cư có 200 hộ dân. Bồn xe có hình
dạng và kích thước như hình vẽ bên dưới, mỗi đầu của bồn xe là nửa hình cầu. Xe chở
đầy nước và lượng nước chia đều cho từng hộ dân. Tính xem mỗi hộ dân được nhận bao nhiêu lít nước sạch. Lời giải
Thể tích của bồn chở nước là : 4 2 3
V = R h + R 3 2 3 1,8 4 1,8 V = 3,14. .3,62 + .3,14. 2 3 2 V 12, 259 ( 3 m ) Đổi 3
12, 259 m = 12259 l
Số lít nước mỗi hộ dân nhận được là :
12259 : 200 = 61, 295 (l)
Câu 8. (3 điểm) Từ điểm M nằm ở ngoài đường tròn (O;R )vẽ hao tiếp tuyến MA, MC vơi đường
tròn ( A,C là hai tiếp điểm). Vẽ đường kính A B của đường tròn (O ).
a) Chứng minh tứ giác A MCO nội tiếp và OM / / BC .
b) Kẻ CD ^ A B (D Î A B ) . BM cắt (O ) tại N (N ¹ B ) . Chứng minh D MA O và D CDB 2 MN CN đồng dạng và = . 2 MB CB
c) Gọi I là giao điểm của OM và A C ; K là giao điểm của BM và CD . Khi OM = A B , tính
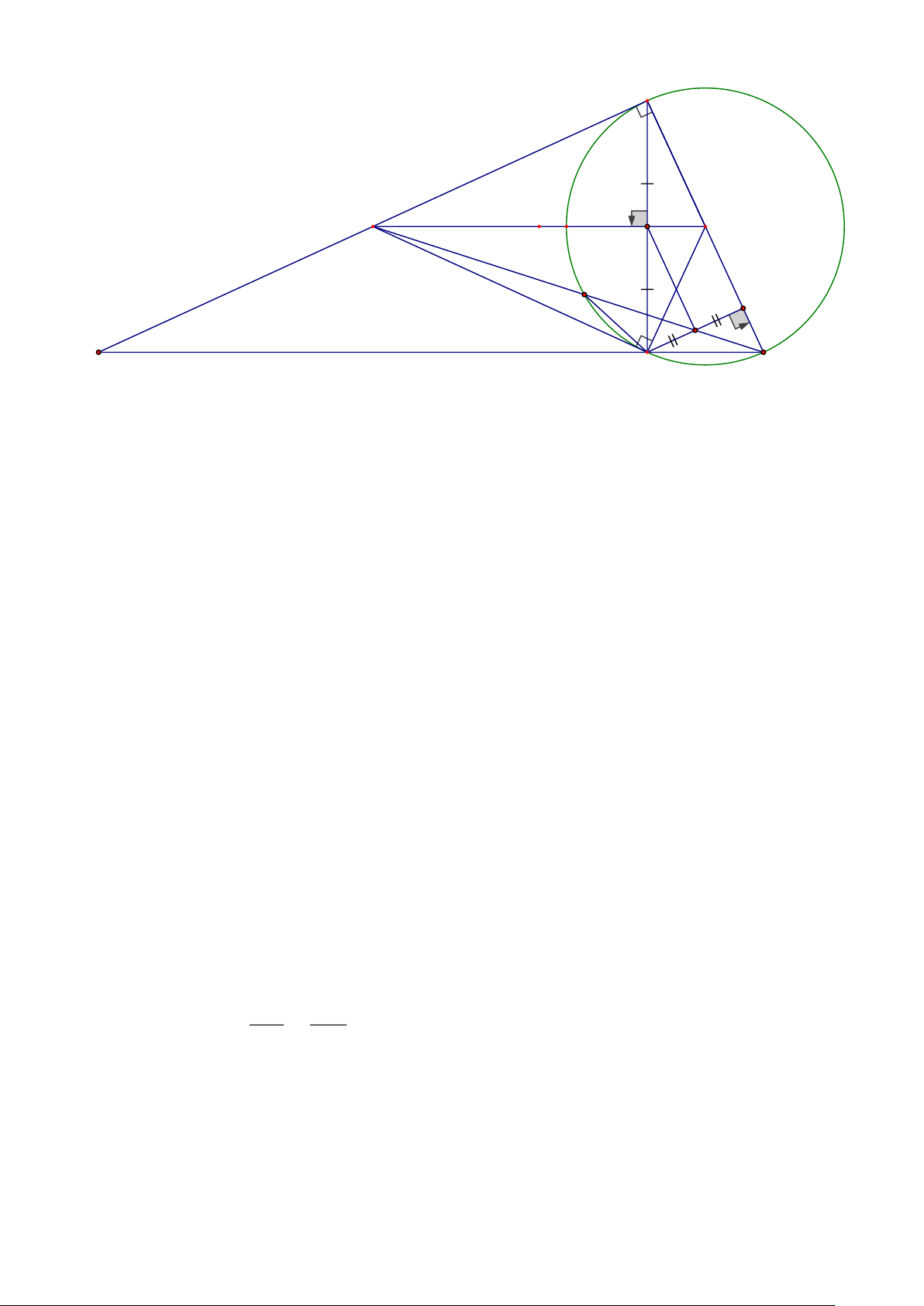
theo R diện tích D MIK . Lời giải Trang 8 A M I O N D K H C B
a) Chứng minh tứ giác A MCO nội tiếp và OM / / BC .
Xét tứ giác A MCO , có:
MAO = 90(MA ⊥ OA) MCO = 90 (MC ⊥ OC)
MAO + MCO = 180
Tứ giác BDEM nội tiếp vì có hai góc đối bù nhau. Ta có :
+ MA = MC ( tính chất hai tiếp tuyến cắt nhau)
+ OA = OC = R
Þ MO là đường trung trực của đoạn A C Þ MO ^ A C ·
Ta lại có : A CB = 90° (góc nội tiếp chắn nửa đường tròn ) Þ CB ^ A C
Vì vậy : MO / / BC
b) Kẻ CD ^ A B (D Î A B ). BM cắt (O )tại N (N ¹ B ). Chứng minh D MA O và D CDB 2 MN CN đồng dạng và = . 2 MB CB
Xét D MA O và D CDB có : · ·
+ MA O = CDB = 90° · ·
+ MOA = CBD ( hai góc đồng vị)
Þ DMA O ∽ DCDB ( . g g) Trang 9
Xét D MCN và D MB C có : · + NMN là góc chung · · »
+ MCN = MBC ( cùng chắn CN )
Þ D MCN ∽ DMBC ( . g g) MC MN CN Þ = = ( tỉ lệ đồng dạng) MB MC CB MC MN Vì 2 =
Þ MC = MN .MB MB MC 2 2 2 2 MC CN MC CN MN .MB CN MN CN Và vì = Þ = Þ = Þ = 2 2 2 2 2 MB CB MB CB MB CB MB CB
c) Gọi I là giao điểm của OM và A C ; K là giao điểm của BM và CD . Khi OM = A B , tính
theo R diện tích D MIK .
Vì MO là đường trung trực của A C và cắt A C tại I
Nên A I ^ MO và I là trung điểm AC
Xét D MA O vuông tại A có đường cao A I + 2 2 2
MO = MA + A O ( định lí Py-ta-go) 2 2 2
Û 4R = MA + R Þ MA = R 3 + 2
MA = MI .MO ( Hệ thức lượng trong tam giác vuông) 3R 2
Û 3R = MI .2R Þ MI = 2 2 1 1 R 3 Ta có : S = BO.MA = .R.R 3 = DMOB 2 2 2
Gọi H là giao điểm của A M và BC .
Vì MO / / BC Þ MO / / BH Xét D B A H có :
+ O là trung điểm A B + MO / / BC
Þ M là trung điểm của đoạn AH. Trang 10 Þ MA = MH
Xét D B A M có DK / / A M BD DK Þ =
( Hệ quả định lí Ta lét) BM A M
Xét D B MH có CK / / MH BK CK Þ =
( Hệ quả định lí Ta lét) BM MH DK CK Từ đó suy ra : = A M MH
Mà A M = MH (cmt )
Nên K D = CK Þ K là trung điểm CD Xét D CDA có
+ K là trung điểm CD
+ I là trung điểm A C
Þ IK là đường trung bình của D CDA
Þ IK / / A D Þ IK / /OB
Xét D MIK và D MOB có : · + B MO là góc chung. · ·
+ MK I = MBO ( hai góc đồng vị)
Þ DMIK ∽ DMOB ( . g g) 9 2 2 R S MI 9 DMIK 4 Þ = = = 2 2 S MO 4R 16 DMOB 2 2 9 9 R 3 9R 3 Þ S = S = . = (đvdt). DMIK 16 DMOB 16 2 32 ----HẾT--- Trang 11
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 3
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 3 - 2
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm). Cho hàm số = 2
y x có đồ thị (P) và hàm số y = x + 2 có đồ thị là (d) .
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ Oxy .
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
5x − 7x + 1 = 0 ( ) 1 (x là ẩn số).
a) Chứng minh phương trình (1) có hai nghiệm phân biệt x , x . 1 2 æ 7ö ç ÷ 1
b) Tính giá trị biểu thức 2 A = x ç - x ÷ + + x . 1 ç ÷ 1 2 2 çè 5÷ ø 25x2
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 3. (1 điểm). Trên một khúc sông, vận tốc dòng chảy (của nước) ở bề mặt lớn hơn vận tốc dòng
chảy ở đáy sông. Gọi v (km / h) là vận tốc dòng chảy ở bề mặt sông, f (km / h) là vận tốc
dòng chảy ở đáy sông, các nhà khoa học đã tìm được công thức thể hiện mối liên hệ giữa
vận tốc này là: f = v - 1, 31 .
a) Nếu vận tốc dòng chảy ở bề mặt sông là 9, 31km / h thì vận tốc dòng chảy ở đáy sông là
bao nhiêu? (làm tròn kết quả đến phần trăm km / h )
b) Nếu vận tốc dòng chảy ở đáy sông là 20, 32km / h thì vận tốc dòng chảy ở bề mặt sông
là bao nhiêu? (làm tròn kết quả đến phần trăm km / h )
Câu 4. (1 điểm). Thớt là dụng cụ sử dụng trong bếp của mỗi gia
đình. Xét một cái thớt bằng gỗ có hình trụ với đường
kính đáy 22cm , chiều cao 4cm .
a) Tính tổng diện tích hai mặt thớt (làm tròn đến đơn vị 2 cm ). 3
b) Cho biết loại gỗ làm thớt có khối lượng riêng là 500kg / m . Tính khối lượng (theo đơn
vị gam) của cái thớt trên. Biết công thức tính thể tích V của hình trụ là V = S .h ( S là
diện tích đáy và h là chiều cao hình trụ). Trang 12
Câu 5. (1 điểm). Trong môn bóng đá, ban đầu các quả bóng thường được làm bằng bàng quang
hoặc dạ dày của động vật. Những quả bóng này dễ bị vỡ. Đến thể kỷ 19, với những khám
phá về lưu hóa của Charles Goodyear, bóng được làm bằng cao su. Cuối thể kỷ 20, quả
bóng thường được làm từ 32 mảnh ghép nhỏ do Eigil Nielsen phát triển vào năm 1962. Cho
đến hôm nay, người ta đã ứng dụng thêm nhiều công nghệ khác nữa để làm quả bóng.
Xét một quả bóng được ghép từ 32 mảnh da gồm các mảnh hình
lục giác màu trắng và hình ngũ giác màu đen. Mỗi mảnh màu
đen ráp với 5 mảnh màu trắng. Mỗi mảnh màu trắng ráp với 3
mảnh màu đen và 3 mảnh màu trắng (Hình 1). Hỏi quả bóng
này có bao nhiêu mảnh màu trắng?
Câu 6. (0,75 điểm). Một cửa hàng thực hiện chương trình khuyến mãi một sản phẩm bánh kem:
Mua 4 tặng 1. Giá bán 1 bánh là 50 000 đồng. Bình mua 12 bánh, Mai mua 13 bánh. Bình nói
với Mai ghóp tiền mua chung sẽ tốn ít tiền hơn khi từng người mua riêng. Hãy tính xem
khi Mai và Bình mua chung thì sẽ đỡ tốn hơn bao nhiêu tiền và mỗi người sẽ chi trả bao nhiêu.
Câu 7. (0,75 điểm). Các bạn học sinh của lớp 9A dự định đóng ghóp một số tiền để mua tặng cho
mỗi em ở Mái ấm tính thương ba món quà (giá tiền các món quà đều như nhau). Khi các
bạn đóng đủ số tiền như dự định thì Mái ấm đã nhận chăm sóc thêm 9 em và giá tiền mỗi
món quà lại tăng thêm 5% nên số tiền có được chỉ vừa đủ để tặng mỗi em hai món quà.
Hỏi hiện tại Mái ấm có bao nhiêu em?
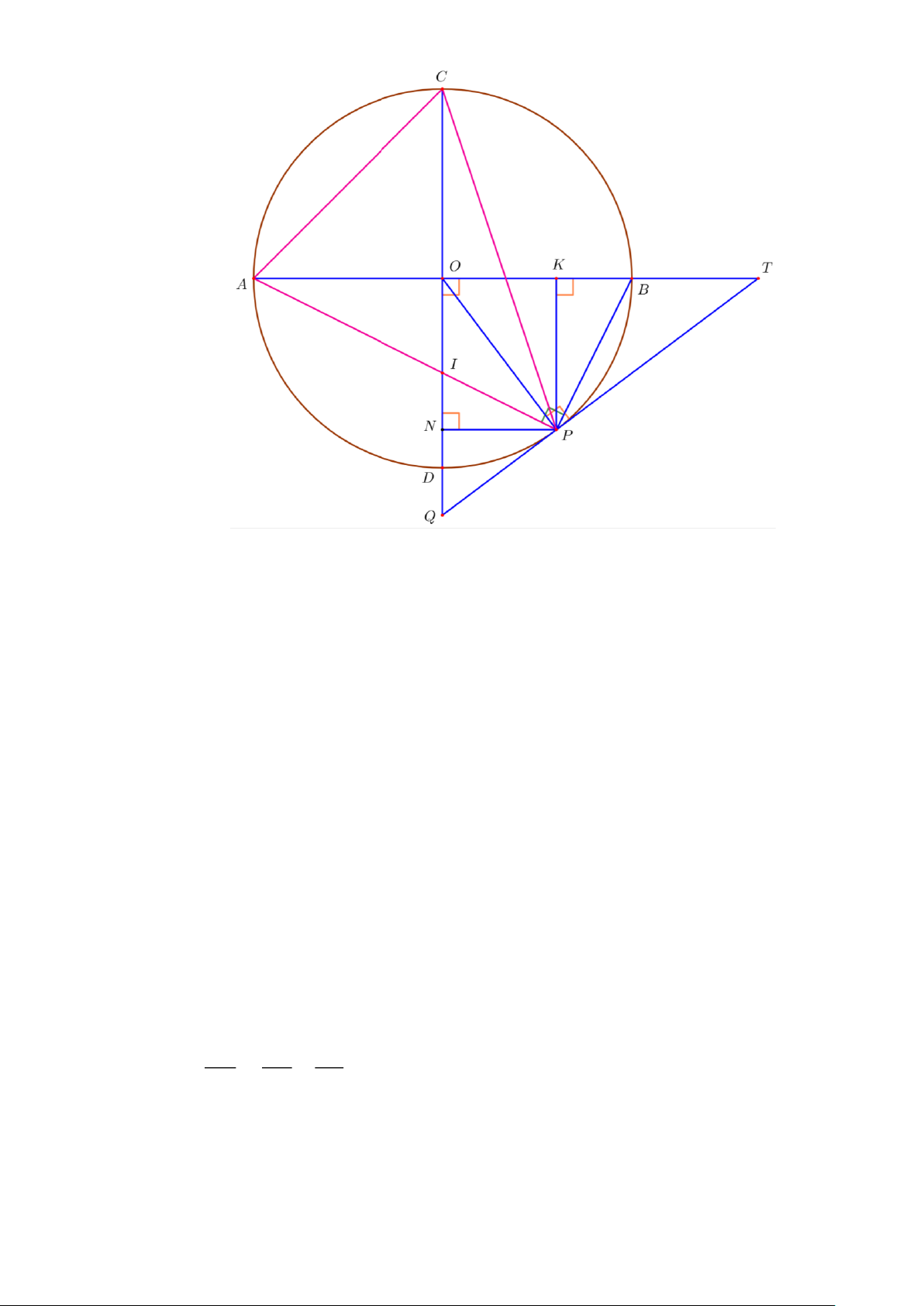
Câu 8. (3 điểm) Cho A B và CD là hai đường kính vuông góc của đường tròn (O;R ). Gọi I là
trung điểm của bán kính OD . Tia A I cắt (O ) tại P (P ¹ A). Tiếp tuyến tại P của
đường tròn (O ) cắt tia A B tại T .
a) Chứng minh tứ giác PIOB nội tiếp và BTP + 2TPB = 90 .
b) Kẻ PK ^ A B (K Î A B ). Gọi Q là giao điểm của T P và CD . Chứng minh P V QI 2 1 1 cân và = - . KT KB KA
c) Tính theo R diện tích A V CP . Trang 13 ----HẾT--- HƯỚNG DẪN GIẢI
Câu 4. (1,5 điểm Cho hàm số = 2
y x có đồ thị (P) và hàm số y = x + 2 có đồ thị là (d) .
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ Oxy .
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
c) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ Oxy . BGT: x −2 1 − 0 1 2 = 2 y x 4 1 0 1 4 x 0 1 y = x + 2 2 3
d) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : 2 x = x + 2 2
x − x − 2 = 0 x = −1 x = 2 Thay x = - 1 vào 2
y = x , ta được: y = (- )2 1 = 1. Thay x = 2 vào 2
y = x , ta được: 2 y = 2 = 4 . Vậy (- 1; )
1 , (2;4) là hai giao điểm cần tìm.
Câu 5. (1 điểm) Cho phương trình 2
5x − 7x + 1 = 0 ( ) 1 (x là ẩn số).
a) Chứng minh phương trình (1) có hai nghiệm phân biệt x , x . 1 2 Trang 14 æ 7ö ç ÷ 1
b) Tính giá trị biểu thức 2 A = x ç - x ÷ + + x . 1 ç ÷ 1 2 2 çè 5÷ ø 25x2 Lời giải
a) Chứng minh phương trình ( )
1 có hai nghiệm phân biệt x , x . 1 2 Phương trình 2
5x − 7x + 1 = 0 ( )
1 ( x là ẩn số).
Vì = b − ac = (− )2 2 4 7 − 4.5.1 = 29 0
Nên phương trình (1) có hai nghiệm phân biệt x ,x . 1 2 æ 7ö ç ÷ 1
b) Tính giá trị biểu thức 2 A = x ç - x ÷ + + x . 1 ç ÷ 1 2 2 çè 5÷ ø 25x2 − = + = b S x x = 7 1 2
Theo định lí Vi-et, ta có: a 5 = c P x .x = = 1 1 2 a 5 æ 7ö ç ÷ 1 Ta có: 2 A = x ç - x ÷ + + x 1 ç ÷ 1 2 2 çè 5÷ ø 25x2 2 A = x − 1 1 2 x x x . x 1 ( + 1 2 ) + + 1 5 2 2 x2
A = −x x + (x x )2 1 . . . + 2 x 2 1 1 2 2 2 x2
A = −x .x + 2 x + 2 x 1 2 1 2
A = (x + x 3x .x 1 2 )2 − 1 2 7 2 A = − 1 3. 5 5 A = 49 − 3 25 5 A = 34 25
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một
chữ số thập phân, số đo góc làm tròn đến phút.
Câu 6. (1 điểm) Trên một khúc sông, vận tốc dòng chảy (của nước) ở bề mặt lớn hơn vận tốc
dòng chảy ở đáy sông. Gọi v (km / h) là vận tốc dòng chảy ở bề mặt sông, f (km / h) là
vận tốc dòng chảy ở đáy sông, các nhà khoa học đã tìm được công thức thể hiện mối
liên hệ giữa vận tốc này là: f = v - 1, 31 . Trang 15
a) Nếu vận tốc dòng chảy ở bề mặt sông là 9, 31km / h thì vận tốc dòng chảy ở đáy sông
là bao nhiêu? (làm tròn kết quả đến phần trăm km / h )
b) Nếu vận tốc dòng chảy ở đáy sông là 20, 32km / h thì vận tốc dòng chảy ở bề mặt
sông là bao nhiêu? (làm tròn kết quả đến phần trăm km / h ) Lời giải
a) Nếu vận tốc dòng chảy ở bề mặt sông là 9, 31km / h thì vận tốc dòng chảy ở đáy sông
là bao nhiêu? (làm tròn kết quả đến phần trăm km / h )
Ta có: v = 9, 31km / h thay vào công thức f = v - 1, 31 Þ f = 9, 31 - 1, 31 Þ f = ( 9, 31 - 1, )2
31 = 3, 03(km / h)
Vậy nếu vận tốc dòng chảy ở bề mặt sông là 9, 31km / h thì vận tốc dòng chảy ở đáy
sông là 3, 03(km / h).
b) Nếu vận tốc dòng chảy ở đáy sông là 20, 32km / h thì vận tốc dòng chảy ở bề mặt
sông là bao nhiêu? (làm tròn kết quả đến phần trăm km / h )
Ta có: f = 20, 32km / h thay vào công thức f = v - 1, 31 Þ 20, 32 = v - 1, 31 Þ v = 20, 32 + 1, 31 Þ v = ( 20,32 + 1, )2 31
Þ v = 33, 85(km / h)
Vậy nếu vận tốc dòng chảy ở đáy sông là 20, 32km / h thì vận tốc dòng chảy ở bề mặt
sông là 33, 85(km / h).
Câu 7. (1 điểm) Thớt là dụng cụ sử dụng trong bếp của mỗi
gia đình. Xét một cái thớt bằng gỗ có hình trụ với
đường kính đáy 22cm , chiều cao 4cm .
a) Tính tổng diện tích hai mặt thớt (làm tròn đến đơn vị 2 cm ). Trang 16 3
b) Cho biết loại gỗ làm thớt có khối lượng riêng là 500kg / m . Tính khối lượng (theo
đơn vị gam) của cái thớt trên. Biết công thức tính thể tích V của hình trụ là V = S .h (
S là diện tích đáy và h là chiều cao hình trụ). Lời giải
a) Tính tổng diện tích hai mặt thớt (làm tròn đến đơn vị 2 cm ).
Bán kính đáy thớt là: r = 22 : 2 = 11(cm )
Tổng diện tích hai mặt thớt là: 2 2 pr = p = ( 2 2 2 .11 760 cm ) 3
b) Cho biết loại gỗ làm thớt có khối lượng riêng là 500kg / m . Tính khối lượng (theo
đơn vị gam) của cái thớt trên. Biết công thức tính thể tích V của hình trụ là V = S .h (
S là diện tích đáy và h là chiều cao hình trụ). 2 2 3 3
Thể tích của thớt là: V = S .h = p.r .h = p.11 .4 = 1520, 53(cm ) = 0, 00152053(m )
Khối lượng của thớt là: 0, 00152053.500 = 0, 76(kg) = 760(g)
Câu 8. (1 điểm) Trong môn bóng đá, ban đầu các quả bóng thường được làm bằng bàng quang
hoặc dạ dày của động vật. Những quả bóng này dễ bị vỡ. Đến thể kỷ 19, với những
khám phá về lưu hóa của Charles Goodyear, bóng được làm bằng cao su. Cuối thể kỷ
20, quả bóng thường được làm từ 32 mảnh ghép nhỏ do Eigil Nielsen phát triển vào
năm 1962. Cho đến hôm nay, người ta đã ứng dụng thêm
nhiều công nghệ khác nữa để làm quả bóng.
Xét một quả bóng được ghép từ 32 mảnh da gồm các
mảnh hình lục giác màu trắng và hình ngũ giác màu đen.
Mỗi mảnh màu đen ráp với 5 mảnh màu trắng. Mỗi mảnh
màu trắng ráp với 3 mảnh màu đen và 3 mảnh màu trắng
(Hình 1). Hỏi quả bóng này có bao nhiêu mảnh màu trắng? Lời giải
Gọi số mảnh màu trắng là x (mảnh)
số mảnh màu đen là y (mảnh) Đk: * x, y Î ¥
Tổng số mảnh ghép là 32 Þ x + y = 32( ) 1 Trang 17
Vì mỗi mảnh màu đen ráp với 5 mảnh màu trắng và mỗi mảnh màu trắng ráp với 3
mảnh màu đen Þ 3x = 5y (2) Từ ( )
1 ,(2) ta có hệ phương trình: ìï x + y = 32 ìï x + y = 32 ìï x = 20 ï ï ï í Û í Û í ï (nhận) 3x = 5y ï 3x - 5y = 0 ï y = 12 ïî ïî ïî
Vậy quả bóng này có 20 mảnh màu trắng.
Câu 6. (0,75 điểm) Một cửa hàng thực hiện chương trình khuyến mãi một sản phẩm bánh
kem: Mua 4 tặng 1. Giá bán 1 bánh là 50 000 đồng. Bình mua 12 bánh, Mai mua 13
bánh. Bình nói với Mai ghóp tiền mua chung sẽ tốn ít tiền hơn khi từng người mua
riêng. Hãy tính xem khi Mai và Bình mua chung thì sẽ đỡ tốn hơn bao nhiêu tiền và
mỗi người sẽ chi trả bao nhiêu. Lời giải
TH1. Hai bạn mua bánh riêng
Bình mua 12 bánh nên Bình chỉ cần mua 10 bánh (vì mua 8 tặng 2 )
Số tiền Bình phải trả là: 10.50 000 = 500 000 (đồng)
Mai mua 13 bánh nên Mai chỉ cần mua 11 bánh (vì mua 8 tặng 2 )
Số tiền Mai phải trả là: 11.50 000 = 550 000 (đồng)
Tổng số tiền mua riêng phải trả của 2 bạn là: 500 000 + 550 000 = 1050 000 (đồng)
TH2. Hai bạn ghóp tiền mua bánh chung
Tổng số bánh 2 bạn mua chung là 25 bánh nên 2 bạn chỉ cần mua 20 bánh (vì mua 20 tặng 5 )
Tổng số tiền phải trả khi 2 bạn mua chung là: 20.50 000 = 1000 000 (đồng)
Số tiền tiết kiệm khi 2 bạn mua chung là: 1050 000 - 1000 000 = 50 000 (đồng) 1000 000.12
Số tiền Bình phải trả khi mua chung là: = 480 000 (đồng) 25 1000 000.13
Số tiền Mai phải trả khi mua chung là: = 520 000 (đồng) 25
Câu 7. (0,75 điểm) Các bạn học sinh của lớp 9A dự định đóng ghóp một số tiền để mua tặng
cho mỗi em ở Mái ấm tình thương ba món quà (giá tiền các món quà đều như nhau). Trang 18
Khi các bạn đóng đủ số tiền như dự định thì Mái ấm đã nhận chăm sóc thêm 9 em và
giá tiền mỗi món quà lại tăng thêm 5% nên số tiền có được chỉ vừa đủ để tặng mỗi
em hai món quà. Hỏi hiện tại Mái ấm có bao nhiêu em? Lời giải
Gọi số em lúc ban đầu ở Mái ấm là x (em)
Số em lúc tặng quà ở Mái ấm là x + 9 (em) Đk: * x Î ¥
Theo đề bài, ta có phương trình:
x.3 = (x + 9).2.105%
Û 3x = (x + 9).2,1
Û 3x = 2,1x + 18, 9 Û 0, 9x = 18, 9
Û x = 21(nh ?n )
Vậy hiện tại Mái ấm có: 21 + 9 = 30 (em)
Câu 8. (3 điểm) Cho A B và CD là hai đường kính vuông góc của đường tròn (O;R ). Gọi I
là trung điểm của bán kính OD . Tia A I cắt (O ) tại P (P ¹ A). Tiếp tuyến tại P của
đường tròn (O ) cắt tia A B tại T .
a) Chứng minh tứ giác PIOB nội tiếp và BTP + 2TPB = 9 0 .
b) Kẻ PK ^ A B (K Î A B ). Gọi Q là giao điểm của T P và CD . Chứng minh P V QI 2 1 1 cân và = - . KT KB KA
c) Tính theo R diện tích A V CP . Lời giải Trang 19
a) Chứng minh tứ giác PIOB nội tiếp và BTP + 2TPB = 9 0 .
Xét tứ giác PIOB , có: ìï · ï IOB = 90° ï (AB ^ CD) íï ·
ï IPB = 90°(A P ^ PB ) ïî
IOB + IPB = 180
Þ Tứ giác PIOB nội tiếp vì có hai góc đối bù nhau. Xét O V PT có:
OP ^ PT (tính chất tiếp tuyến ) Þ O
V PT vuông tại P · ·
Þ POT + PT O = 90° · · »
Mà POT = 2T PB (Góc ở tâm, góc tạo bởi tiếp tuyến và dây cung cùng chắn BP ) · ·
Þ BT P + 2.T PB = 90°
b) Kẻ PK ^ A B (K Î A B ). Gọi Q là giao điểm của T P và CD . Chứng minh P V QI 2 1 1 cân và = - . KT KB KA
Ta có: tứ giác PIOB nội tiếp · ·
Þ PIQ = OBP (góc ngoài = góc đối trong) · · »
Mà A BP = A PQ (Góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung cùng chắn A P ) Trang 20