









Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THAM KHẢO TUYỂN SINH 10
THÀNH PHỐ HỒ CHÍ MINH MÔN: TOÁN 9
PHÒNG GDĐT BÌNH CHÁNH
Đê thi gồm 8 câu hỏi tự luận.
Thời gian: 120 phút (không kể thời gian phát đề) ĐỀ TH AM KHẢO
MÃ ĐỀ: Quận Bình Chánh - 1
Câu 1. (1,5 điểm). Cho ( P) 2
: y = x và (d ) : y = −x + 2
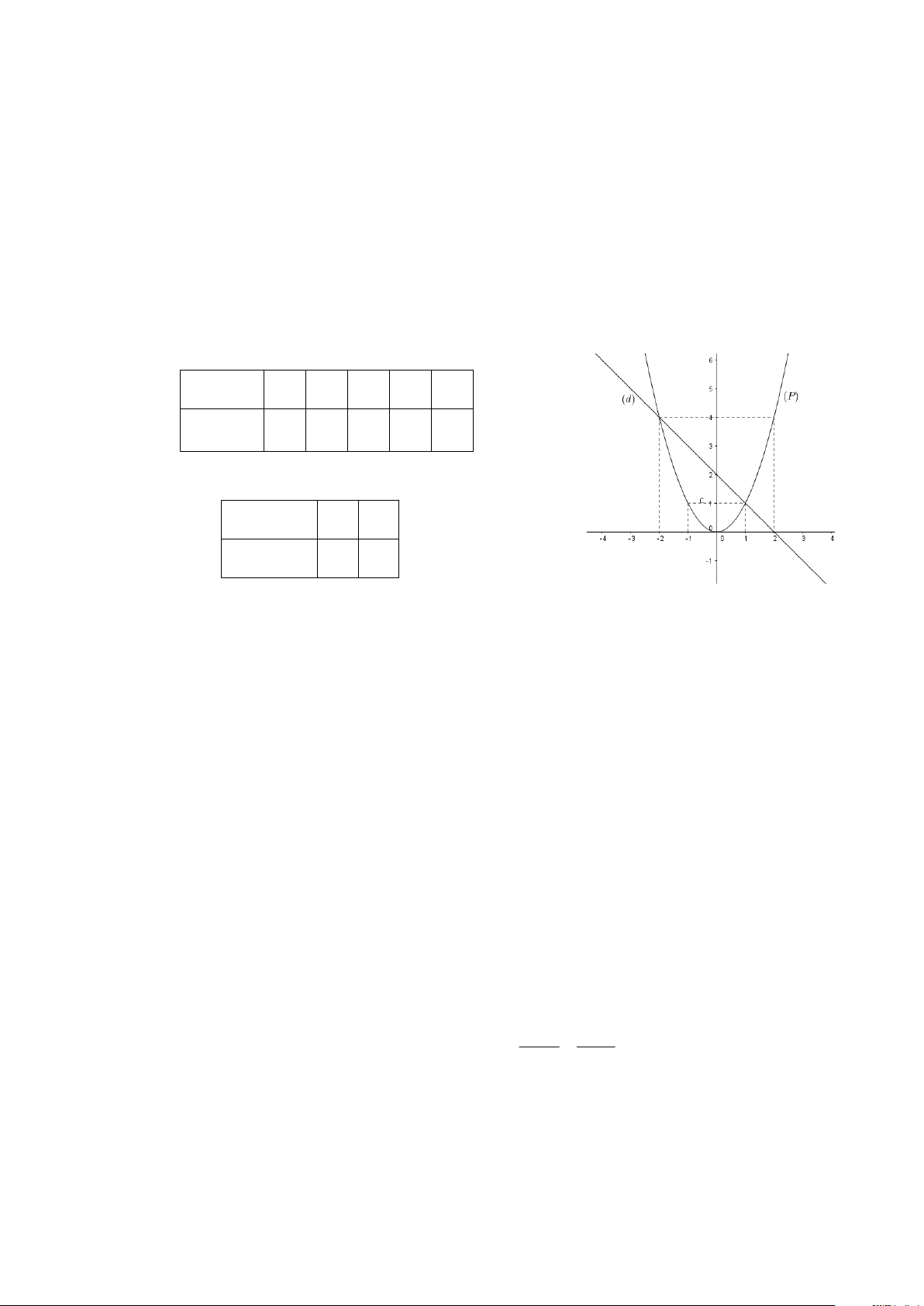
a) Vẽ đồ thị ( P) và (d ) trên cùng một mặt phẳng tọa độ Oxy .
b) Tìm tọa độ giao điểm của ( P) và (d ) bằng phép toán.
Câu 2. (1 điểm). Cho phương trình 2
−x − 2x + 5 = 0 có hai nghiệm phân biệt x , x 1 2 . Không giải x x
phương trình, hãy tính giá trị của biểu thức 1 2 A = − + 2022 x −1 1− . x 2 1
Câu 3. (0,75 điểm). Một cửa hàng đồng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu
mua từ gói kẹo thứ hai trở đi thì sẽ được giảm 10% so với giá ban đầu là 50000 đồng.
a) Nếu gọi số kẹo đã mua là x và số tiền phải trả là y . Hãy biểu diễn y theo x .
b) Bạn Thư muốn mua 10 gói kẹo thì hết bao nhiêu tiền.
Câu 4. (1 điểm). Trong kì thi HKII môn Toán lớp 9 , một phòng thi của trường có 24 thí sinh dự
thi. Các thí sinh đều phải làm bài trên giấy trường phát. Cuối buổi thi, giám thị coi thi đếm
được tổng số tờ giấy thi là 53 tờ. Hỏi trong phòng thi đó có bao nhiêu học sinh làm 2 tờ
giấy thi, bao nhiêu học sinh làm 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.
Câu 5. (0,75 điểm). Nhân ngày "Phụ nữ Việt Nam 20/10", cửa hàng giỏ xách giảm giá 30% cho tất
cả các sản phẩm và ai có thẻ “khách hàng thân thiết” sẽ được giảm tiếp 10% trên giá đã giảm.
Hỏi mẹ bạn An có thẻ khách hàng thân thiết khi mua 1 cái túi xách trị giá 500000 đồng thì phải trả bao nhiêu?
Mẹ bạn An mua thêm 1 cái bóp nên trả tất cả 693000 đ. Hỏi giá ban đầu của cái bóp là bao nhiêu?
Câu 6. (1 điểm). Người ta hỏi Pytago về số học trò của ông. Ông nói: "Một nửa số học trò của tôi
đang học toán, một phần tư đang học nhạc, một phần bảy đang suy nghĩ và còn lại 3
người". Hỏi ông có bao nhiêu học trò?
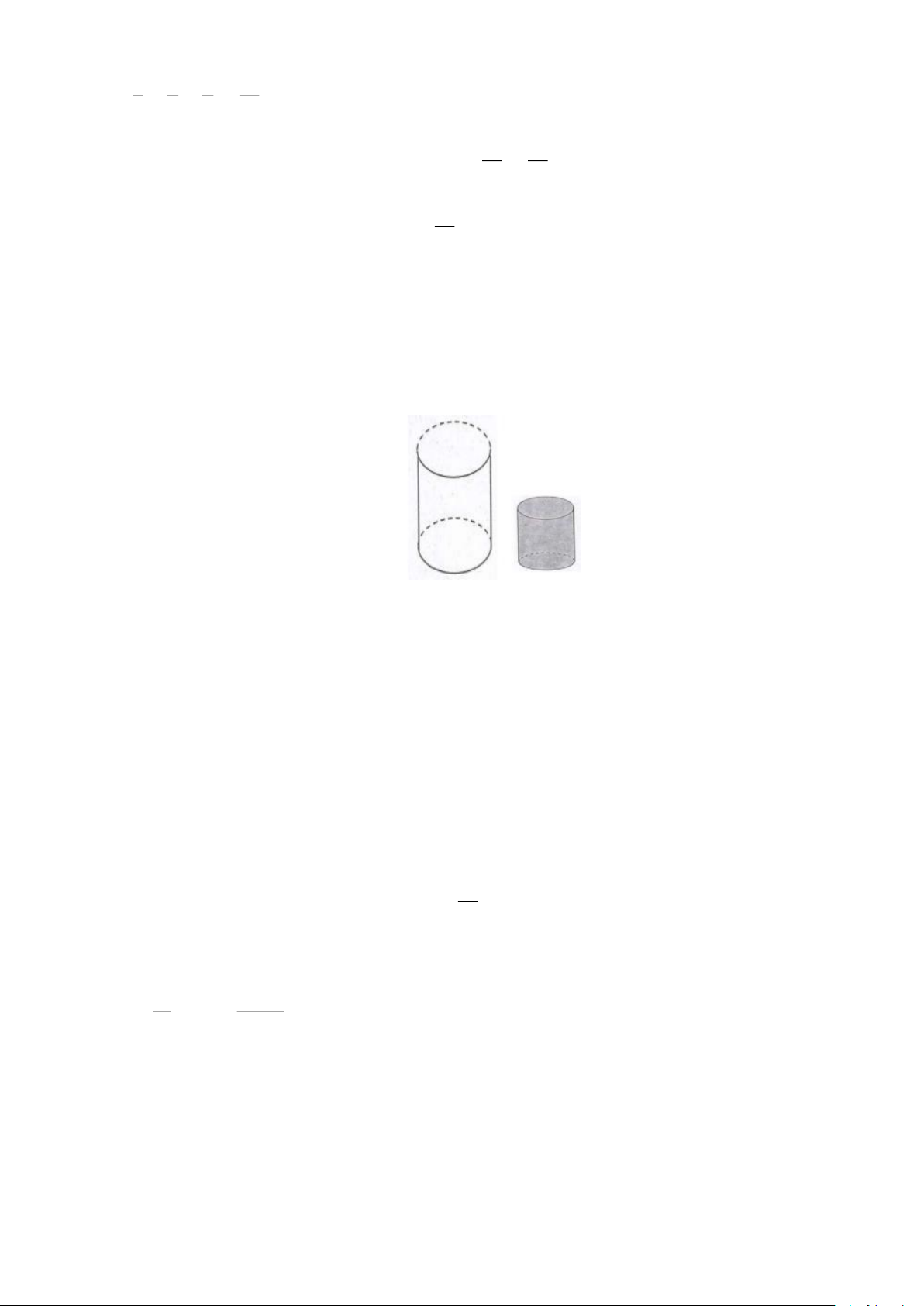
Câu 7. (1 điểm). Có một bình thủy tinh hình trụ phía bên trong có đường
kính đáy là 30cm , chiều cao 20cm , đựng một nửa bình nước và
một khối thủy tinh hình trụ có bán kính đáy là 14cm , chiều cao là
11cm . (Cho thể tích hình trụ tính theo công thức: 2
V = R h với R
là bán kính đáy, h là chiều cao của hình trụ)
a) Tính thể tích khối thủy tinh (làm tròn đến chữ số thập phân thứ nhất)
b) Hỏi nếu bỏ lọt khối thủy tinh vào bình thủy tinh thì lượng nước trong bình có bị tràn ra ngoài hay không? Tại sao? Trang 1
Câu 8. (3 điểm) Cho tam giác ABC nhọn ( AB AC ) , nội tiếp đường tròn (O; R) . Các tiếp tuyến
tại B và C cắt nhau tại M . Gọi H là giao điểm của OM và BC . Từ M kẻ đường thẳng
song song với AC , đường thẳng này cắt (O) tại E và F ( E thuộc cung nhỏ BC ), cắt BC
tại I , cắt AB tại K .
a) Chứng minh: MO ⊥ BC và ME.MF = MH.MO .
b) Chứng minh rằng: tứ giác MBKC nội tiếp đường tròn. Từ đó suy ra 5 điểm M , B, K ,
O,C cùng thuộc một đường tròn.
c) Đường thẳng OK cắt (O) tại N và P ( N thuộc cung nhỏ AC ). Đường thẳng PI cắt
(O) tại Q ( Q khác P ). Chứng minh ba điểm M , N,Q thẳng hàng. ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm) Cho (P) y = 2 :
x và đường thẳng (d) : y = −x + 2 .
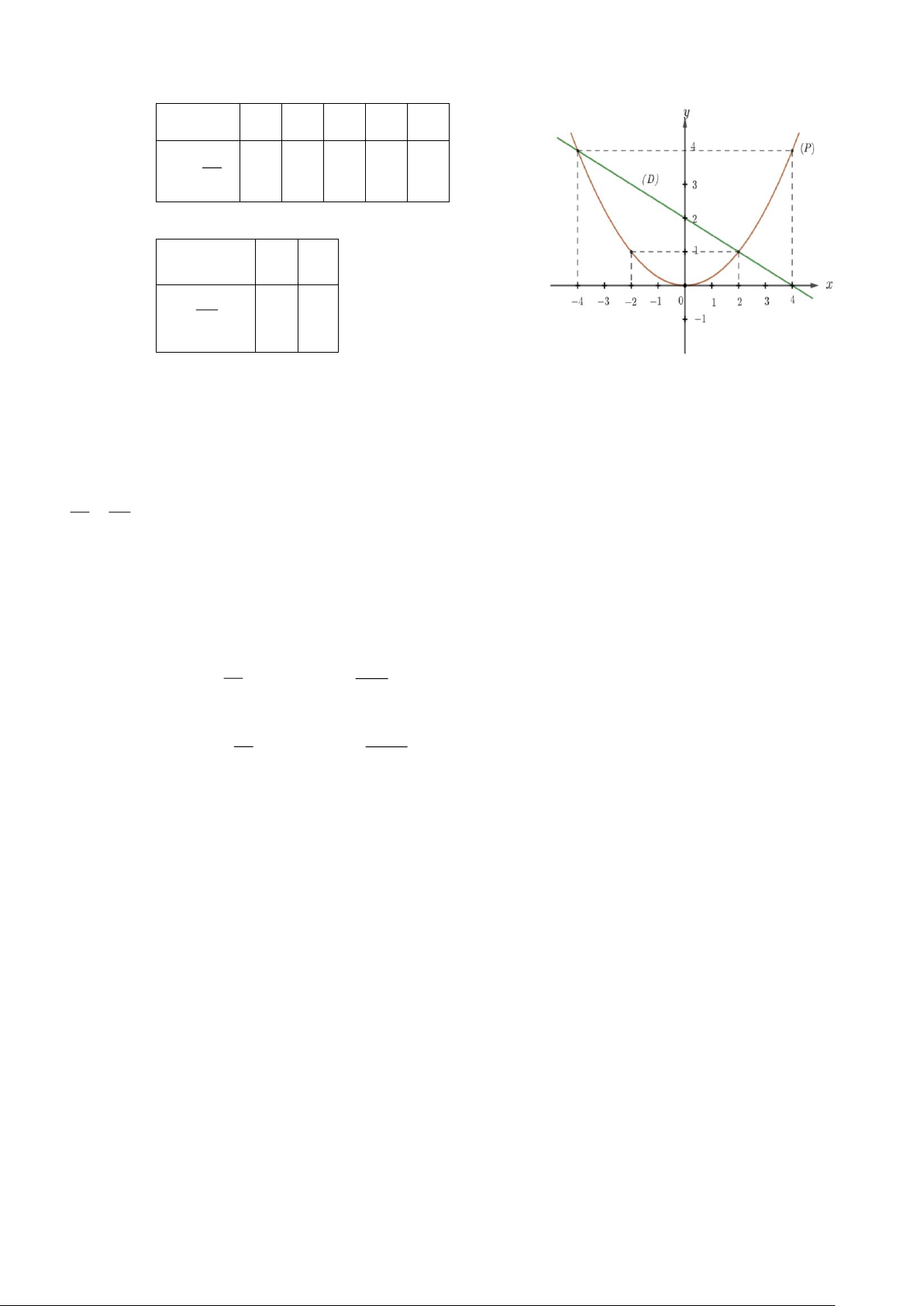
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
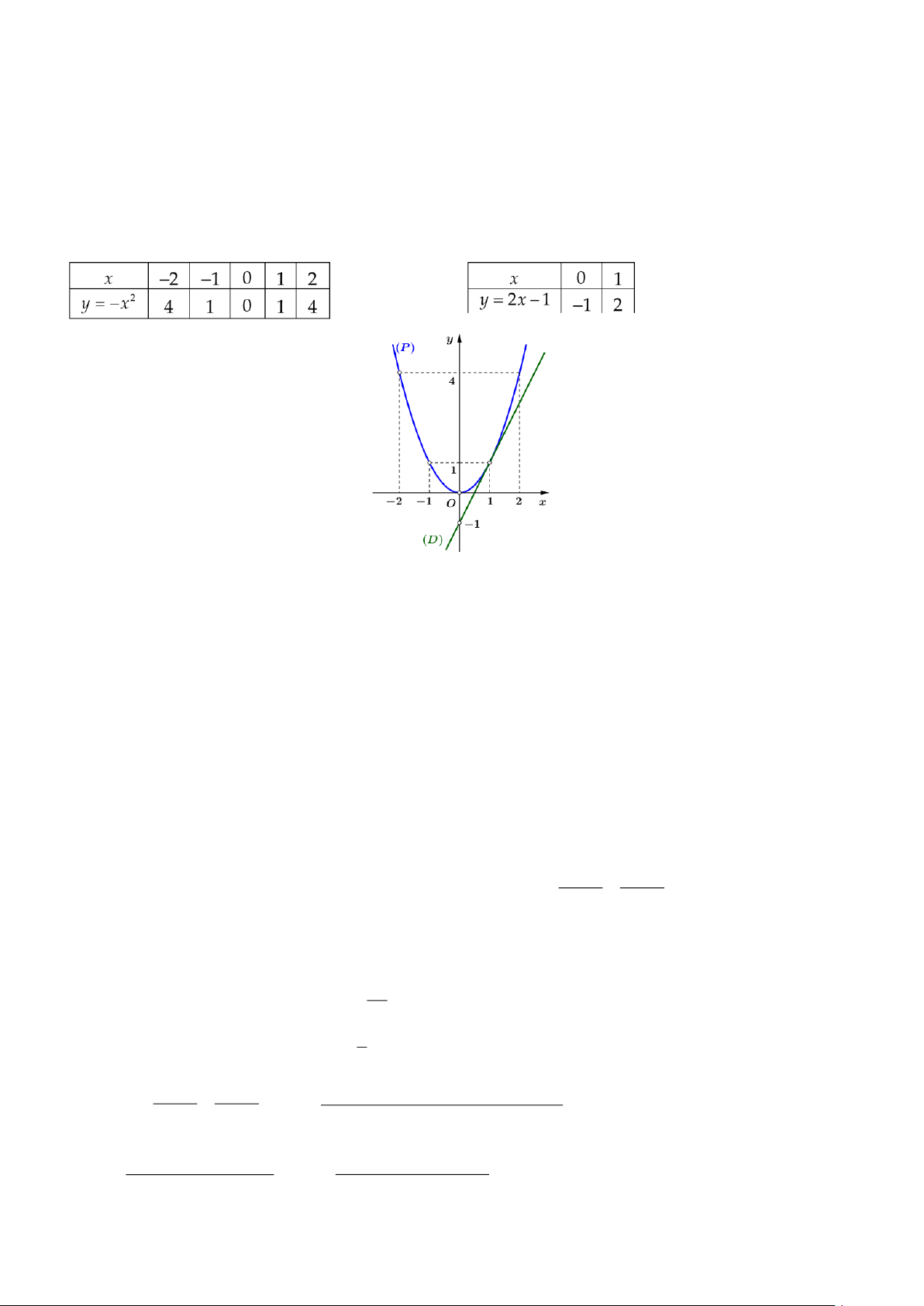
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. BGT: x −2 1 − 0 1 2 = 2 y x 4 1 0 1 4 x 0 1 y = −x + 2 2 1
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : 2 x = −x + 2 2 x + x − 2 = 0 x = 1 x = − 2 Thay x = 1 vào = 2 y
x , ta được: y = 2 1 = 1 . 2 Thay x = −2 vào 2
y = −x , ta được: y = (−2) = 4 .
Vậy (1; 1) , (−2; 4) là hai giao điểm cần tìm.
Câu 2. (1 điểm) Cho phương trình 2
−x − 2x + 5 = 0 có hai nghiệm phân biệt x , x 1 2 . Không giải x x
phương trình, hãy tính giá trị của biểu thức 1 2 A = − + 2022 x −1 1− . x 2 1 Lời giải
Ta có: ac < 0 nên phương trình đã cho luôn có hai nghiệm phân biệt x , x 1 2 . Trang 3 − = + = b S x x = − 2 1 2
Theo định lí Vi-et, ta có: a = c P x .x = = − 5 1 2 a x x Ta có: 1 2 A = − + 2022 x −1 1− x 2 1 x x 1 2 = + + 2022 x −1 x −1 2 1
x x −1 + x x −1 1 ( 1 ) 2 ( 2 ) = ( x −1 x −1 1 )( 2 ) 2 2
x + x − x + x 1 2 ( 1 2) =
x x − x + x +1 1 2 ( 1 2)
(x + x )2 −2x x − x + x 1 2 1 2 ( 1 2) =
x x − x + x +1 1 2 ( 1 2) (− )2 2 − 2.( 5 − ) −( 2 − ) = 5 − − ( 2 − ) +1 = −8.
Câu 3. (0,75 điểm) Một cửa hàng đồng loạt giảm giá các sản phẩm. Trong đó có chương trình
nếu mua từ gói kẹo thứ hai trở đi thì sẽ được giảm 10% so với giá ban đầu là 50000 đồng.
a) Nếu gọi số kẹo đã mua là x và số tiền phải trả là y . Hãy biểu diễn y theo x .
b) Bạn Thư muốn mua 10 gói kẹo thì hết bao nhiêu tiền. Lời giải
a) Số tiền khi mua một gói kẹo (từ gói thứ hai trở đi) là:
50000 - 50000.10% = 45000 (đồng).
Nếu gọi số kẹo đã mua là x và số tiền phải trả là y , khi đó:
y = 50000 + 45000(x - ) 1 = 45000x + 5000 .
b) Bạn Thư mua 10 gói kẹo thì phải trả:
45000.10 + 5000 = 455000 (đồng).
Câu 4. (1 điểm). Trong kì thi HKII môn Toán lớp 9, một phòng thi của trường có 24 thí sinh dự
thi. Các thí sinh đều phải làm bài trên giấy trường phát. Cuối buổi thi, giám thị coi thi
đếm được tổng số tờ giấy thi là 53 tờ. Hỏi trong phòng thi đó có bao nhiêu học sinh làm Trang 4
2 tờ giấy thi, bao nhiêu học sinh làm 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi. Lời giải
Gọi số học sinh làm 2 tờ giấy thi là x (học sinh), số học sinh làm 3 tờ giấy thi là y (học sinh); ( *
x,y Î ¥ ; x,y < 24).
Phòng thi có 24 thí sinh nên: x + y + 3 = 24 Û x + y = 21 .
Tổng số tờ giấy thi là 53 tờ nên: 2x + 3y = 53 - 3 = 50 . ìï x + y = 21 ìï x = 13 ï ï Ta có hệ phương trình í Û í ï (thỏa mãn). 2x + 3y = 50 ï y = 8 ïî ïî
Vậy có 13 học sinh làm 2 tờ giấy thi, 8 học sinh làm 3 tờ giấy thi.
Câu 5. (0,75 điểm) Nhân ngày "Phụ nữ Việt Nam 20/10", cửa hàng giỏ xách giảm giá 30% cho
tất cả các sản phẩm và ai có thẻ “khách hàng thân thiết” sẽ được giảm tiếp 10% trên giá đã giảm.
Hỏi mẹ bạn An có thẻ khách hàng thân thiết khi mua 1 cái túi xách trị giá 500000 đồng thì phải trả bao nhiêu?
Mẹ bạn An mua thêm 1 cái bóp nên trả tất cả 693000 đ. Hỏi giá ban đầu của cái bóp là bao nhiêu? Lời giải
+) Phần trăm giá tiền sản phẩm sau khi giảm là:
(100 - 30)%.(100 - 10)% = 63% .
Nên mẹ bạn An có thẻ khách hàng thân thiết khi mua 1 cái túi xách trị giá 500000 đồng thì phải trả:
500000.63% = 315000 (đồng).
+) Giá tiền ban đầu của cái bóp là: (693000 - 31500 )
0 : 63.100 = 600000 (đồng).
Câu 6. (1 điểm) Người ta hỏi Pytago về số học trò của ông. Ông nói: "Một nửa số học trò của tôi
đang học toán, một phần tư đang học nhạc, một phần bảy đang suy nghĩ và còn lại 3
người". Hỏi ông có bao nhiêu học trò? Lời giải
Phân số chỉ số phần số học trò học toán, học nhạc và suy nghĩ là: Trang 5 1 1 1 25 + + = . 2 4 7 28 25 3
Nên 3 người còn lại chiếm số phần là: 1 - = . 28 28 3
Vậy số học trò của ông Pytago là: 3 : = 28 (học trò). 28
Câu 7. (1 điểm) Có một bình thủy tinh hình trụ phía bên trong có đường kính đáy là 30cm ,
chiều cao 20cm , đựng một nửa bình nước và một khối thủy tinh hình trụ có bán kính
đáy là 14cm , chiều cao là 11cm . (Cho thể tích hình trụ tính theo công thức: 2 V = R h
với R là bán kính đáy, h là chiều cao của hình trụ)
a) Tính thể tích khối thủy tinh (làm tròn đến chữ số thập phân thứ nhất)
b) Hỏi nếu bỏ lọt khối thủy tinh vào bình thủy tinh thì lượng nước trong bình có bị tràn
ra ngoài hay không? Tại sao? Lời giải
a) Thể tích khối thủy tinh là: 2
V = 3,14.14 .11 = 6769, 8( 3 cm . 2 ) 2 30 æ ö ç ÷
b) Thể tích bình thủy tinh là: V = 3,14.ç ÷ .20 = 14130 ç ÷ ( 3 cm . 1 ) çè 2 ÷ø
Thể tích khi bỏ khối thủy tinh vào bình thủy tinh là: V 14130 1 + V = + 6769, 8 = 13834, 8 cm < V . 2 ( 3) 1 2 2
Vậy nước không bị tràn ra ngoài.
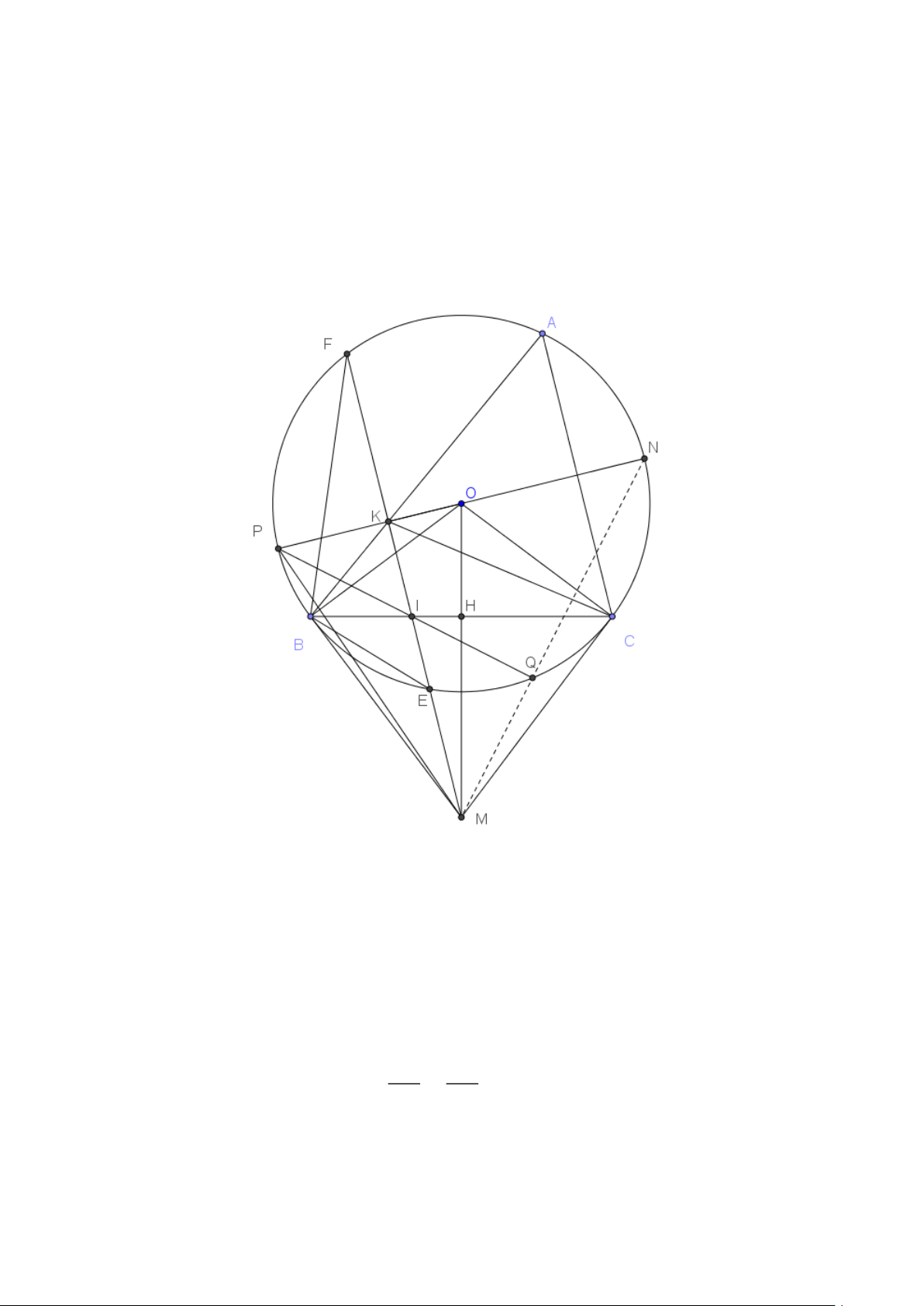
Câu 8. (3 điểm) Cho tam giác ABC nhọn ( AB AC) , nội tiếp đường tròn (O; R) . Các tiếp
tuyến tại B và C cắt nhau tại M . Gọi H là giao điểm của OM và BC . Từ M kẻ
đường thẳng song song với AC , đường thẳng này cắt (O) tại E và F (E thuộc cung
nhỏ BC) , cắt BC tại I , cắt AB tại K . Trang 6
a) Chứng minh: MO ⊥ BC và ME.MF = MH.MO .
b) Chứng minh rằng: tứ giác MBKC nội tiếp đường tròn. Từ đó suy ra 5 điểm
M , B, K , O,C cùng thuộc một đường tròn.
c) Đường thẳng OK cắt (O) tại N và P(N thuộc cung nhỏ AC) . Đường thẳng PI
cắt (O) tại Q(Q khác P) . Chứng minh ba điểm M , N ,Q thẳng hàng. Lời giải
a) +) Ta có: OB = OC (= R ) và MB = MC (tính chất hai tiếp tuyến cắt nhau) nên
MO là đường trung trực của BC Þ MO ^ BC .
+) Xét D MB O vuông tại B , đường cao BH có: 2
MH .MO = MB ( ) 1 · · ·
Xét D MB E và D MFB có BMF chung và MBE = MFB (cùng bằng nửa số đo cung BE ) MB ME Do đó: 2 DMBE # DMFB Þ =
Û MB = ME .MF (2) MF MB Từ ( )
1 và (2) ta suy ra: ME.MF = MH.MO . · ·
b) Vì KM / / A C Þ BKM = BA C (đồng vị). Trang 7 · ·
Mặt khác: BA C = BCM (cùng bằng nửa số đo cung BC ) · ·
Khi đó: BKM = BCM .
Xét tứ giác B K CM có hai đỉnh kề nhau là K và C cùng nhìn cạnh BM dưới hai góc · ·
bằng nhau (BKM = BCM ) nên nó nội tiếp. · ·
Tứ giác B OCM có OBM + OCM = 180° nên nó nội tiếp được đường tròn đường
kính OM . Do đó: 5 điểm M , B, K , O,C cùng thuộc một đường tròn đường kính OM .
c) Theo câu b) 5 điểm M , B, K , O,C cùng thuộc một đường tròn đường kính OM , khi ·
đó: OKM = 90° (góc nội tiếp chắn nửa đường tròn).
Tứ giác MBKC nội tiếp nên IB .IC = IK .IM .
Tứ giác PBQC nội tiếp nên IB .IC = IP .IQ . IK IQ
Suy ra: IK .IM = IP .IQ Û = . IP IM IK IQ · ·
Xét D K IP và D QIM có: =
và KIP = QIM nên DKIP # DQIM . IP IM · ·
Do đó: IQM = IKP = 90° . ·
Mặt khác: PQN = 90° (góc nội tiếp chắn nửa đường tròn) · · ·
Þ MQN = MQI + PQN = 180° .
Vậy ba điểm M , N ,Q thẳng hàng. ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN BÌNH CHAÙNH
NAÊM HOÏC: 2023 - 2024 ĐỀ TH MÔN: TOÁN 9 AM KHẢO-2
(Đề thi gồm 02 trang)
Đê thi gồm 8 câu hỏi tự luận.
Thời gian: 120 phút (không kể thời gian phát đề)
Bài 1. (1,5 điểm ) Cho parabol ( P) 2
: y = x và đường thẳng (D) : y = 2x −1 .
a) Vẽ ( P) và ( D) trên cùng mặt phẳng tọa độ Oxy .
b) Tìm giao điểm của ( P) và ( D) bằng phép toán. Trang 8
Bài 2. (1 điểm ) Cho phương trình: 2
−x + 3x + 5 = 0 có 2 nghiệm x ,x 1 2 x + 2 x + 2
Không giải phương trình , hãy tính giá trị của biểu thức : 1 2 A = + . x − 2 x − 2 2 1
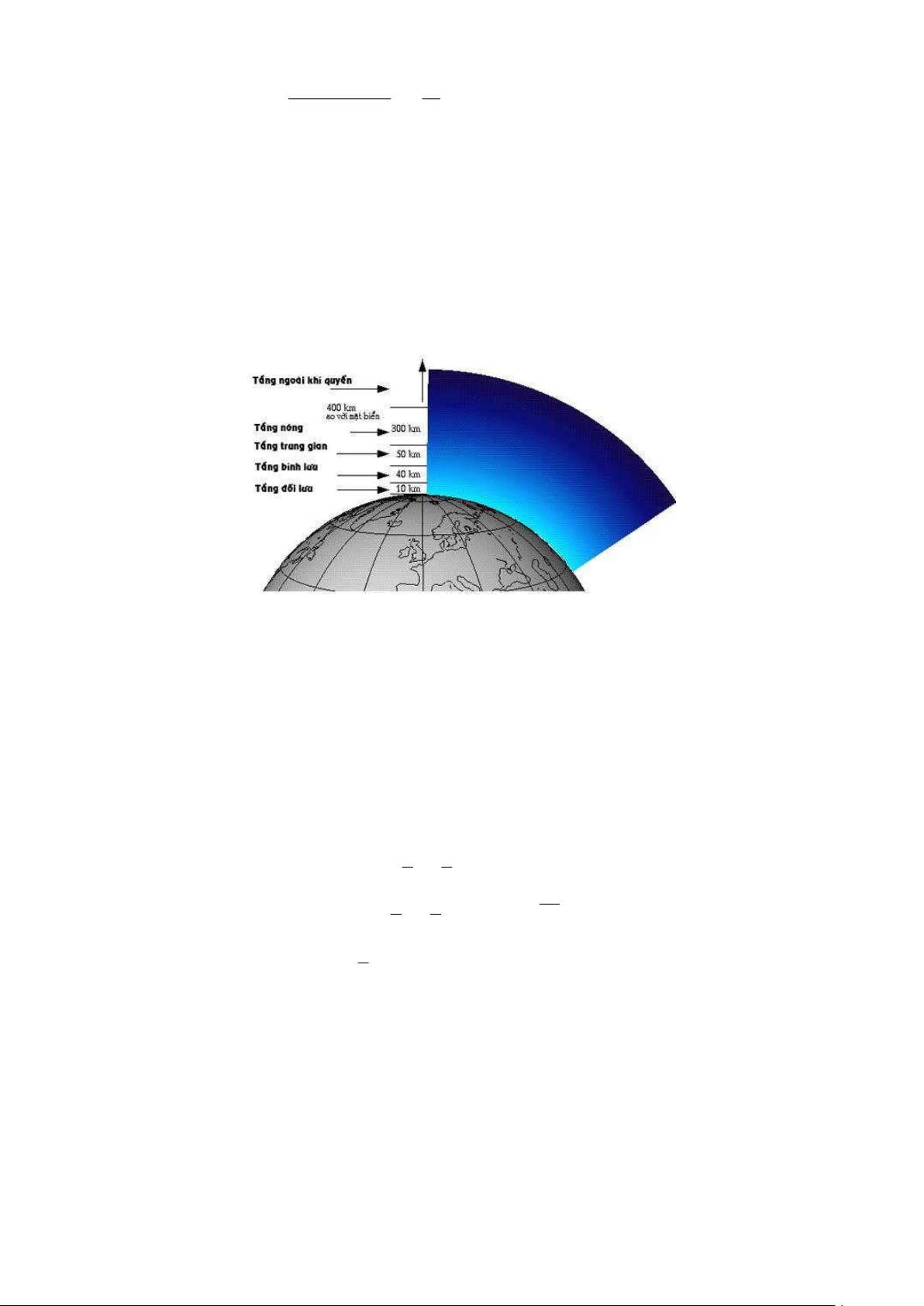
Bài 3. (0,75 điểm) Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm, ví dụ
ở khu vực TP.Hồ Chí Minh có độ cao sát mực nước biển nên có áp suất khí quyển là
p = 760 mmHg còn ở thành phố Addis Ababa ở Ethiopia có độ cao h = 2355 m thì có áp
suất khí quyển là p = 571,6 mmHg Với những độ cao không quá lớn, người ta nhận
thấy mối liên hệ giữa độ cao và áp suất khí quyển có dạng hàm số bậc nhất p = .
a h + b (a 0).
a) Xác định hệ số a, . b
b) Hỏi ở cao nguyên Pleiku có độ cao 1000 m so với mực nước biển thì có áp suất khí quyển là bao nhiêu?
Bài 4. (0,75điểm ) Cô Minh mua 100 cái áo với giá mỗi cái là 200 000 đồng. Cô bán 60 cái áo,
mỗi cái so với giá mua cô lời được 20% và 40 cái áo còn lại cô bán lỗ vốn hết 5%. Việc
mua và bán 100 cái áo cô Minh lời bao nhiêu tiền?
Bài 5. (1 điểm ) Cận thị trong học sinh ngày càng tăng. Lớp 9A có 35 học sinh, trong đó chỉ 1 1 có số học sinh nam và
số học sinh nữ không bị cận thị. Biết tổng số học sinh nam 4 5
và học sinh nữ không bị cận thị là 8 học sinh. Tính số học sinh nữ không bị cận thị?
Bài 6. (1 điểm) Một lọ vitamin C có dạng hình trụ với bán kính đáy là 1,5 cm và chiều cao là
8 cm Những viên sủi vitamin C được đựng trong lọ cũng có dạng hình trụ với diện 9
tích đáy bằng diện tích đáy lọ và thể tích mỗi viên là ( 3 cm ) . 5
a) Hỏi trong lọ có tổng cộng bao nhiêu viên vitamin C?
b) Những lọ vitamin này được xếp thẳng đứng sát nhau vào một khay hình hộp chữ
nhật. Hỏi chiều dài và chiều rộng của khay là bao nhiêu để chứa được 20 lọ xếp
thành 5 hàng, mỗi hàng 4 lọ?
Bài 7. (1 điểm ) Lớp 9A đăng kí tham gia vệ sinh trường học, với số lượng đăng kí cô giáo
chủ nhiệm dự định chia lớp thành 3 tổ có số học sinh như nhau. Nhưng sau đó lớp có
thêm 4 học sinh đăng kí nữa. Do đó, cô giáo chủ nhiệm đã chia đều số học sinh của lớp
thành 4 tổ. Hỏi lớp 9A hiện có bao nhiêu học sinh, biết rằng so với phương án dự định
ban đầu, số học sinh của mỗi tổ hiện nay có ít hơn 2 học sinh ?
Bài 8. (3 điểm ) Cho tam giác ABC vuông tại A (AB AC). Vẽ đường tròn (O) đường kính
AC , đường tròn (O) cắt BC tại .
D Vẽ tiếp tuyến BE của (O) ( E là tiếp điểm). BO cắt
AE tại H .
a) Chứng minh: OB ⊥ AE và BH.BO = . BD BC Trang 9
b) Chứng minh: DHOC là tứ giác nội tiếp và BHD = OHC
c) Vẽ tiếp tuyến tại C của đường tròn (O) cắt AE tại F . AD cắt CE tại K. Chứng
minh: 3 điểm B,K, F thẳng hàng.
........... HẾT ............ Trang 10
Bài 1. (1,5 điểm ) Cho parabol (P) 2
: y = x và đường thẳng (D) : y = 2x − 1 .
a) Vẽ (P) và ( D) trên cùng mặt phẳng tọa độ Oxy .
b) Tìm giao điểm của (P) và ( D) bằng phép toán. Lời giải
a) Vẽ (P) và ( D) trên cùng mặt phẳng tọa độ Oxy . Bảng giá trị:
b) Tìm giao điểm của (P) và ( D) bằng phép toán.
Phương trình hoành độ giao điểm của (P) và ( D) : 2 x = 2x − 1 2
x − 2x + 1 = 0 (x − 2 1) = 0 x = 1 Thay x = 1 vào = 2 y
x , ta được: y = 2 1 = 1 .
Vậy (P) tiếp xúc ( D) tại điểm (1; 1) .
Bài 2. (1 điểm ) Cho phương trình: − 2
x + 3x + 5 = 0 có 2 nghiệm x , x 1 2 x + 2 x + 2
Không giải phương trình , hãy tính giá trị của biểu thức : A = 1 + 2 . x − 2 x − 2 2 1 Lời giải
Vì phương trình đã cho có .
a c = −3 0 nên nó luôn có hai nghiệm trái dấu x ,x . 1 2 − = + = b S x x = 3 1 2
Theo định lí Vi-et, ta có: a ( ) 1 = c P x .x = = − 5 1 2 a x + 2 x + 2
(x + 2 x 2 x 2 x 2 1 )( − 1 )+( + 2 )( − 2 ) Ta có: A = 1 + 2 A = x − 2 x − 2 (x −2 x 2 1 )( − 2 ) 2 1 2 2 x − 4 + 2 x −
(x + x −2x x −8 1 2 ) A = 4 1 2 1 2 A = x x − 2 x x 4
x x − 2 x + x + 4 1 2 ( 1 2) 1 2 ( + 1 2 ) + Trang 11 2 3 − 2(−5) − 8 11 Thế ( )
1 và (2) ta được A = = − . − 5 − 2.3 + 4 7
Bài 3. (0,75 điểm) Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm, ví dụ
ở khu vực TP.Hồ Chí Minh có độ cao sát mực nước biển nên có áp suất khí quyển là
p = 760 mmHg còn ở thành phố Addis Ababa ở Ethiopia có độ cao h = 2355 m thì có áp
suất khí quyển là p = 571,6 mmHg Với những độ cao không quá lớn, người ta nhận
thấy mối liên hệ giữa độ cao và áp suất khí quyển có dạng hàm số bậc nhất p = .
a h + b (a 0).
c) Xác định hệ số a, . b
d) Hỏi ở cao nguyên Pleiku có độ cao 1000 m so với mực nước biển thì có áp suất khí quyển là bao nhiêu? Lời giải
a) Ta xem TP.Hồ Chí Minh và thành phố Addis Ababa ở Ethiopia là hai điểm thuộc đồ thị hàm số p = .
a h + b (a 0).
Với h = 0 m và p = 760 mmHg nên ta có .0 a + b = 760 (1)
Với h = 2355 m và p = 571,6 mmHg nên ta có .2355 a + b = 571,6 (2) .0 a + b = 760 a = −0,08 .235 a 5 + b = 571,6 b = 760
− 1 x− 1 y = −7 x+ y = x = 20 5 5 35 y = 15 1 1 1 x = 1 x + y = 8 20 BH.BO = B . D BC 4 5 9 ( 3 cm ) 5 V = 2 r h = 2 .1,5 .8 = 3 18 (cm ).
Từ (1) và (2) ta có hệ phương trình , 1 5 2 4 = 2 1 (cm) 2 AB = . BD BC (2) 2
AB = BH.BO (2) BCO BHD = OHC . a 0 + b = 760 a = −0,08 . .
a 2355 + b = 571,6 b = 760 Trang 12
Vậy p = −0,08h + 760.
b) Áp suất khí quyển tại cao nguyên Pleiku có độ cao 1000 m so với mực nước biển là
p = −0,08.1000 + 760 = 680mmH . g
Bài 4. (0,75điểm ) Cô Minh mua 100 cái áo với giá mỗi cái là 200 000 đồng. Cô bán 60 cái áo,
mỗi cái so với giá mua cô lời được 20% và 40 cái áo còn lại cô bán lỗ vốn hết 5%. Việc
mua và bán 100 cái áo cô Minh lời bao nhiêu tiền? Lời giải
Tổng số tiền mua 100 cái áo là 100 200 000 = 20 000 000 (đồng).
Số tiền lời khi Cô bán 60 cái áo là 60 200 000 120% = 14 400 000 (đồng).
Số tiền lời khi Cô bán 40 cái áo là 40 200 000 95% = 7 600 000 (đồng).
Tổng số tiền bán hai đợt là 14 400 000 + 7 600 000 = 22 000 000 đồng).
Vì 22 000 000 − 20 000 000 = 2 000 000 0 nên sau khi bán 100 cái áo cô Minh lời 2 000 00 (đồng).
Bài 5. (1 điểm ) Cận thị trong học sinh ngày càng tăng. Lớp 9A có 35 học sinh, trong đó chỉ 1 1 có số học sinh nam và
số học sinh nữ không bị cận thị. Biết tổng số học sinh nam 4 5
và học sinh nữ không bị cận thị là 8 học sinh. Tính số học sinh nữ không bị cận thị? Lời giải
Gọi x, y lần lượt là số học sinh nam và nữ của lớp 9A .
Điều kiện: 0 x, y 35; x, y . 1
Số học sinh nam không bị cận là x . 4 1
Số học sinh nữ không bị cận là y . 5
Lớp 9A có 35 học sinh: x + y = 35 (1) 1 1
Tổng số học sinh nam và học sinh nữ không bị cận thị là 8 học sinh: x + y = 8 (2) 4 5 x + y = 35 x = 20
Theo giả thiết, ta có hệ phương trình 1 x + 1 y = 8 y = 15 4 5 1
Vậy số học sinh nữ không bị cận thị là 15 = 3 (học sinh). 5
Bài 6. (1 điểm) Một lọ vitamin C có dạng hình trụ với bán kính đáy là 1,5 cm và chiều cao là
8 cm Những viên sủi vitamin C được đựng trong lọ cũng có dạng hình trụ với diện 9
tích đáy bằng diện tích đáy lọ và thể tích mỗi viên là ( 3 cm ) . 5
c) Hỏi trong lọ có tổng cộng bao nhiêu viên vitamin C?
d) Những lọ vitamin này được xếp thẳng đứng sát nhau vào một khay hình hộp chữ
nhật. Hỏi chiều dài và chiều rộng của khay là bao nhiêu để chứa được 20 lọ xếp
thành 5 hàng, mỗi hàng 4 lọ? Lời giải
a) Thể tích lọ V = 2 r h = 2 = 3 .1,5 .8 18 (cm ). Trang 13 9
Số viên vitamin C trong lọ 1 8 : = 10 (viên). 5
b) Chiều dài hình hộp chữ nhật là 1,5 2 5 = 15(cm) .
Chiều rộng hình hộp chữ nhật là 1,5 2 4 = 12(cm) .
Bài 7. (1 điểm ) Lớp 9A đăng kí tham gia vệ sinh trường học, với số lượng đăng kí cô giáo
chủ nhiệm dự định chia lớp thành 3 tổ có số học sinh như nhau. Nhưng sau đó lớp có
thêm 4 học sinh đăng kí nữa. Do đó, cô giáo chủ nhiệm đã chia đều số học sinh của lớp
thành 4 tổ. Hỏi lớp 9A hiện có bao nhiêu học sinh, biết rằng so với phương án dự định
ban đầu, số học sinh của mỗi tổ hiện nay có ít hơn 2 học sinh ? Lời giải
Gọi 3x là số học sinh đăng kí tham gia vệ sinh trường học của lớp 9A , với * x
Số học sinh mỗi tổ theo dự định ban đầu là x (học sinh). 3x + 4
Số học sinh lúc sau 3x + 4 và số tổ lúc sau là (học sinh). 4
Vì số học sinh mỗi tổ hiện nay kém số học sinh mỗi tổ lúc đầu 2 học sinh, nên ta có phương 3x + 4 trình: x −
= 2 x = 12 (nhận) 4
Vậy lớp 9A có 40 học sinh
Bài 8. (3 điểm ) Cho tam giác ABC vuông tại A (AB AC). Vẽ đường tròn (O) đường kính
AC , đường tròn (O) cắt BC tại .
D Vẽ tiếp tuyến BE của (O) ( E là tiếp điểm). BO cắt
AE tại H .
d) Chứng minh: OB ⊥ AE và BH.BO = . BD BC
e) Chứng minh: DHOC là tứ giác nội tiếp và BHD = OHC
f) Vẽ tiếp tuyến tại C của đường tròn (O) cắt AE tại F . AD cắt CE tại K. Chứng
minh: 3 điểm B,K, F thẳng hàng. Lời giải
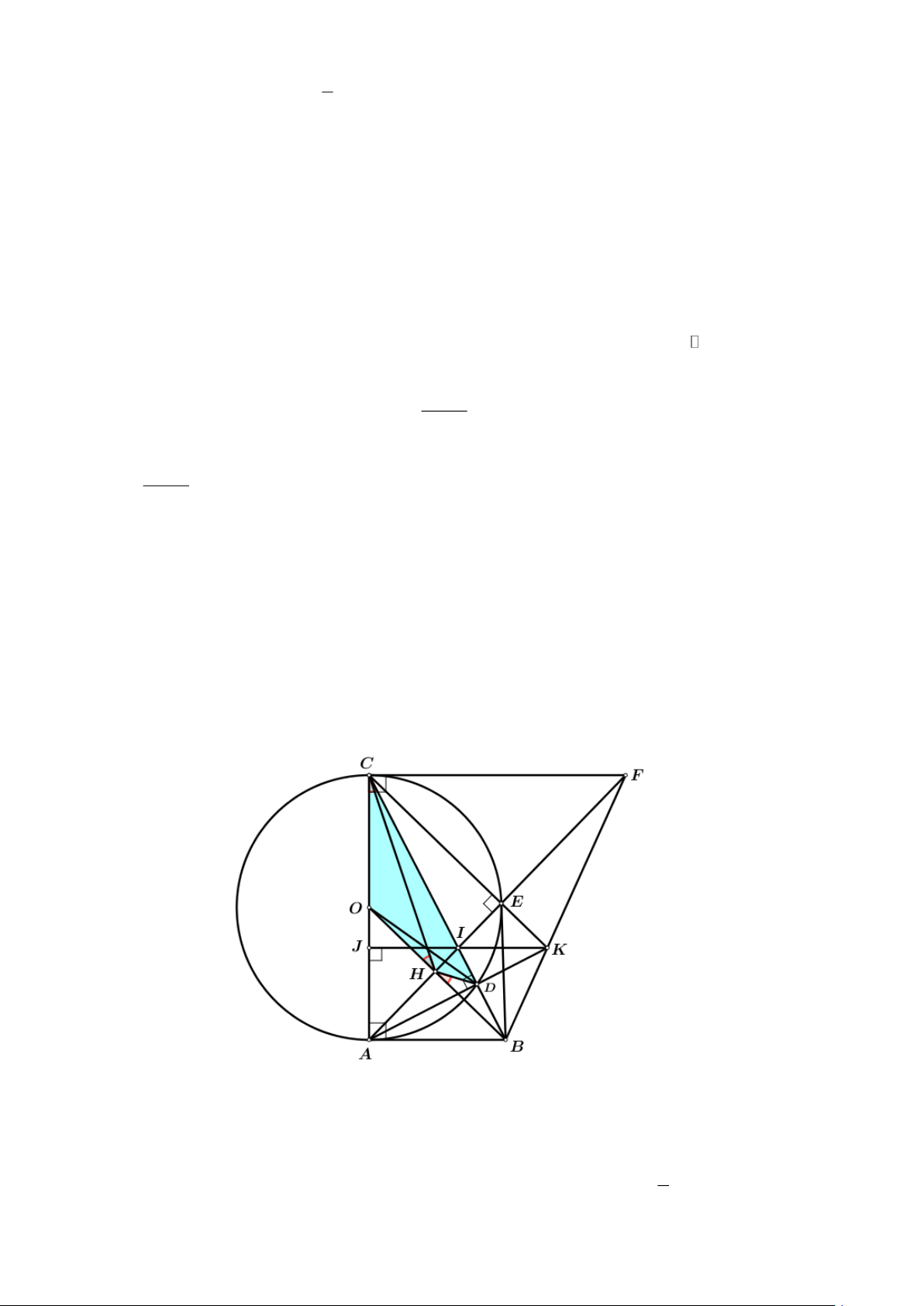
a) Chứng minh: OB ⊥ AE
Xét đường tròn đường kính AC ta có AB ⊥ AC
AB là tiếp tuyến của đường tròn (O) 1
Mà BE cũng là tiếp tuyến của đường tròn (O) nên BA = BE, OE = OA = AC OB là trung 2
trực của AE hay OB ⊥ AE . Trang 14
Chứng minh: BH.BO = . BD BC
Ta có D thuộc đường tròn đường kính AC nên ABC vuông tại A có đường cao AD 2 AB = . BD BC (1)
Mặt khác OAB vuông tại A có đường cao AH (do OB ⊥ AE ) 2
AB = BH.BO (2) Từ ( ) 1 và (2) suy ra .
BD BC = BH.BO
b) Chứng minh: DHOC là tứ giác nội tiếp.
Xét hai tam giác BDH và BCO , ta có B là góc chung BD BH Mà .
BD BC = BH.BO (do câu a) = BO BC Suy ra BDH #
BOC BHD = OCB
Khi đó tứ giác DHOC có ngoài BHD = OCB nên nó nội tiếp
Chứng minh: BHD = OHC 1
OHC = ODC = sđOC (* *)
Ta có tứ giác DHOC nội tiếp (chứng minh trên) nên 2 (3) (6) BHD = OCB = OCD
Mà OCD cân tại O (do OC = OD = 1 AC ) OCD = ODC (4) 2
Từ (3) và (4) suy ra BHD = OHC .
c) Vẽ tiếp tuyến tại C của đường tròn (O) cắt AE tại F . AD cắt CE tại K. Chứng minh: Ba
điểm B,K, F thẳng hàng.
Ta có CF ⊥ AC (do CF là tiếp tuyến tại C của đường tròn (O) ) (5)
AB ⊥ AC (do ABC vuông tại A ) (6)
Từ (5) và (6) suy ra CF//AB tứ giác ABFC là hình thang (*)
Mặt khác ADC = AEC =
90 (góc nội tiếp chắn nửa đường tròn (O) )
Do đó ACK có hai đường cao CD, AE cắt nhau tại I KI là đường cao thứ ba
Gọi J là giao điểm của KI và AC thì KJ ⊥ AC KJ//AB//CF (* *)
Từ (*) và (* *) suy ra ba điểm B,K,F thẳng hàng.
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT H BÌNH CHÁNH
NAÊM HOÏC: 2023 - 2024 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: HUYỆN BÌNH
Thời gian: 120 phút (không kể thời gian phát đề) CHÁNH - 3 1 1
Câu 1. (1,5 điểm). Cho (P) 2 : y =
x và đường thẳng (d) − : y = x + 2 . 4 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. Trang 15
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
x − 2x − 3 = 0 có 2 nghiệm là x ,x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức A = 2x + 2 x 1 2
Câu 3. (0,75 điểm). Hai lớp 9A và 9B cùng tham gia quyên góp tiền giúp các bạn học sinh có
hoàn cảnh khó khăn mua thiết bị học tập. Trung bình một học sinh lớp 9A góp 18 000
đồng, một học sinh lớp 9B góp 20 000 đồng. Hỏi mỗi lớp có bao nhiêu học sinh, biết rằng
cả hai lớp có 85 học sinh và tổng số tiền góp được là 1 610 000 đồng?
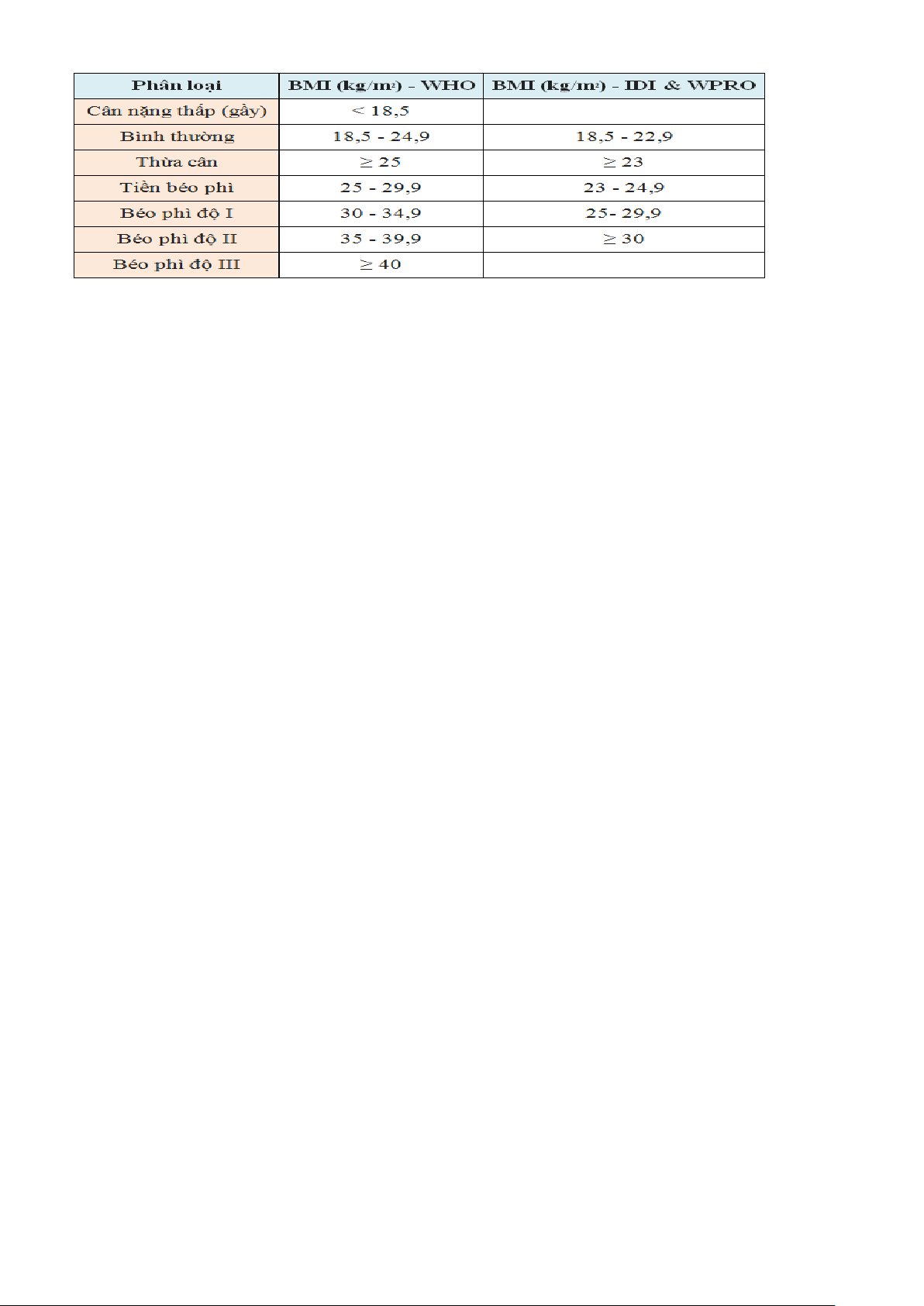
Câu 4. (0,75 điểm). Dưới đây là bảng phân loại mức độ gầy - béo của một người dựa vào chỉ số
BMI. Thang phân loại của Tổ chức y tế thế giới (WHO) dành cho người châu Âu và thang
phân loại của Hiệp hội đái đường các nước châu Á (IDI & WPRO) được áp dụng cho người châu Á.
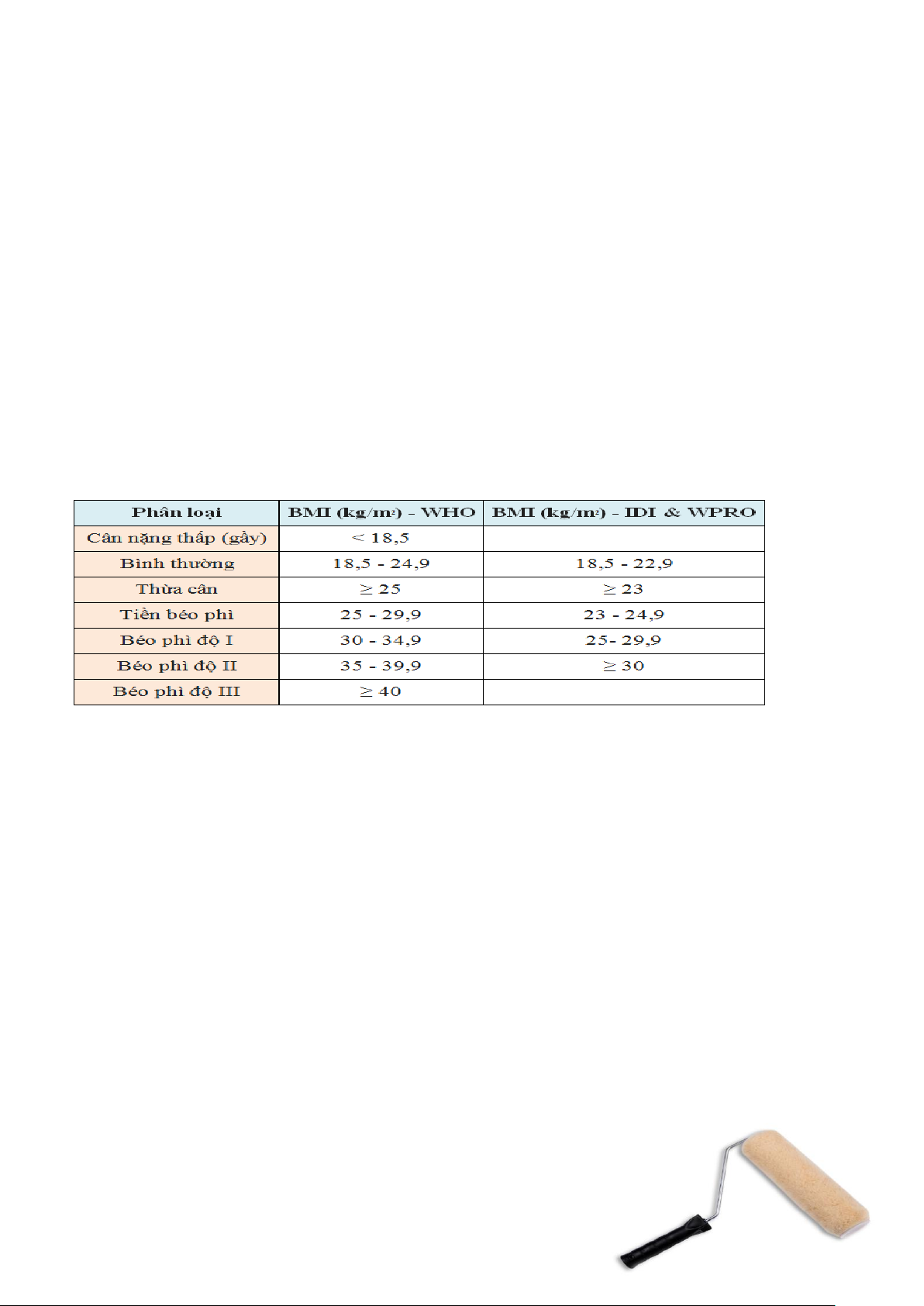
Bảng phân loại mức độ gầy - béo của một người dựa vào chỉ số BMI
Dựa vào thang phân loại của IDI & WPRO dành cho người châu Á thì BMI lý tưởng của người Việt
Nam là từ 18,5 đến 22,9 . Ngoài ra bạn có thể tính nhẩm nhanh cân nặng lý tưởng của mình dựa
vào chiều cao theo cách sau:
Cân nặng lý tưởng = Số lẻ của chiều cao (tính bằng cm ) x 9 rồi chia 10 .
Mức cân tối đa = Bằng số lẻ của chiều cao (tính bằng cm ).
Mức cân tối thiểu = Số lẻ của chiều cao (tính bằng cm ) x 8 rồi chia 10 .
Hỏi, bạn Nam cao 1,7 m thì cân nặng lý tưởng, cân nặng tối đa và cân nặng tối thiểu của bạn đó là bao nhiêu?
Câu 5. (1 điểm). Anh An làm việc cho một công ty sản xuất hàng cao cấp, anh được trả năm triệu
bảy trăm sáu mươi ngàn đồng cho 48 tiếng làm việc
trong một tuần. Sau đó để tăng thêm thu nhập, anh An
đã đăng ký làm thêm một số giờ nửa trong tuần, mỗi giờ Trang 16
làm thêm này anh An được trả bằng 150% số tiền mà mỗi giờ anh An được trả trong 48
giờ đầu. Cuối tuần sau khi xong việc, anh An được lãnh số tiền là bảy triệu hai trăm ngàn
đồng. Hỏi anh An đã làm thêm bao nhiêu giờ trong tuần đó?
Câu 6. (1 điểm). Một cái trục lăng sơn nước có dạng hình trụ. Đường kính của đường tròn đáy là
5cm , chiều dài lăn là 23cm (hình bên). Hỏi, người thợ cần sơn một mặt của bức tường hình
chữ nhật có chiều dài 5m và chiều rộng 4 m thì lăn sơn nước sẽ quay bao nhiêu vòng. Biết
bức tường có một cửa sổ hình chữ nhật kích thước 1m 2m . Biết diện tích xung quanh
hình trụ là 2Rh với R là bán kính đáy; h là chiều cao hình trụ.
Câu 7. (1 điểm) Một công ty xây dựng hướng dẫn tính chi phí xây dựng một ngôi nhà như sau:
Đầu tiên ta sẽ tính tổng diện tích 2
(m ) toàn bộ ngôi nhà rồi nhân với đơn giá 2
1m xây dựng.
Diện tích phần móng nhà được tính bằng 50% diện tích tầng trệt.
Diện tích tầng trệt được tính bằng 100% diện tích nền nhà.
Diện tích một lầu bằng diện tích tầng trệt
Diện tích mái nhà bằng 35% diện tích tầng trệt
Đơn giá xây dựng trọn gói là 6 triệu đồng 2 1m
Ba bạn An muốn xây dựng một căn nhà 3 tầng (ngang 5 m, dài 16m ). Hỏi chi phí xây dựng là bao nhiêu?
Câu 8. (3 điểm) Cho tam giác ABC nhọn ( AB AC) nội tiếp (O) . Gọi H là giao điểm ba đường
cao AD,BE,CF và đường thẳng EF cắt BC tại M . Đường thẳng MA cắt (O) tại K .
a) Chứng minh: Tứ giác BCEF và tứ giác MBFK nội tiếp.
b) Chứng minh: 5 điểm A,K,F,H ,E cùng thuộc một đường tròn. AB AC BC
c) Tia KH cắt (O) tại N . Chứng minh AN = . . . 2. S ABC ----HẾT--- HƯỚNG DẪN GIẢI 1 1
Câu 1. (1,5 điểm) Cho (P) 2 : y =
x và đường thẳng (d) − : y = x + 2 . 4 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ. Trang 17 a) BGT: x −4 −2 0 2 4 2 = x y 4 1 0 1 4 4 x −4 2 − = x y + 2 4 1 2
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.
Phương trình hoành độ giao điểm của (P) và (D) : 2 x − = x + 2 4 2 2 x + 2x − 8 = 0 x = 2 x = − 4 2 2 x (2)
Thay x = 2 vào y = , ta được: y = = 1. 4 4 2 2 x (−4)
Thay x = −4 vào y = , ta được: y = = 4 . 4 4
Vậy (2; 1) , (−4; 4) là hai giao điểm cần tìm.
Câu 2. (1 điểm) Cho phương trình 2
x − 2x − 3 = 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức A = 2x + 2 x 1 2 Lời giải 2 Vì 2
= b − 4ac = ( 2 − ) − 4.1.( 3 − ) = 16 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 Trang 18 − = + = b S x x = 2 = 2 1 2
Theo định lí Vi-et, ta có: a 1 c − P = x x = = 3 . = − 3 1 2 a 1
Ta có: A = 2x + 2 x 1 2
A = x (x + x ) 2 + x 1 1 2 2 2 2
A = x + x x + x 1 1 2 2 2 2
A = x + x + x x 1 2 1 2 2 2
A = S − 2P + P = S − P 2 A = 2 − ( 3 − ) = 7
Câu 3. (0,75 điểm) Hai lớp 9A và 9B cùng tham gia quyên góp tiền giúp các bạn học sinh có hoàn
cảnh khó khăn mua thiết bị học tập. Trung bình một học sinh lớp 9A góp 18 000 đồng, một
học sinh lớp 9B góp 20 000 đồng. Hỏi mỗi lớp có bao nhiêu học sinh, biết rằng cả hai lớp có
85 học sinh và tổng số tiền góp được là 1 610 000 đồng?
Lời giải
Gọi số học sinh lớp 9A là x (học sinh)
Gọi số học sinh lớp 9B là y (học sinh) (x y * , )
Vì cả hai lớp có 85 học sinh nên:
Vì trung bình một học sinh lớp 9A góp 18 000 đồng, một học sinh lớp 9B góp 20 000 đồng và
tổng số tiền góp được là 1 610 000 nghìn đồng nên:
18000x + 20000y = 1 610 000 (2) x + y = 85 (1) Từ ( ) 1 và (2) ta được hpt:
18 000x + 20 000y = 1 610 000 (2) x = 45 Giải ra ta được: (nhận) y = 40
Vậy lớp 9A có 45 học sinh, 9B có 40 học sinh Câu 4.
(0,75 điểm). Dưới đây là bảng phân loại mức độ gầy - béo của một người dựa vào chỉ số
BMI. Thang phân loại của Tổ chức y tế thế giới (WHO) dành cho người châu Âu và thang
phân loại của Hiệp hội đái đường các nước châu Á (IDI & WPRO) được áp dụng cho người châu Á. Trang 19
Bảng phân loại mức độ gầy - béo của một người dựa vào chỉ số BMI
Dựa vào thang phân loại của IDI & WPRO dành cho người châu Á thì BMI lý tưởng của người Việt
Nam là từ 18,5 đến 22,9 . Ngoài ra bạn có thể tính nhẩm nhanh cân nặng lý tưởng của mình dựa
vào chiều cao theo cách sau:
Cân nặng lý tưởng = Số lẻ của chiều cao (tính bằng cm) x 9 rồi chia 10
Mức cân tối đa = Bằng số lẻ của chiều cao (tính bằng cm)
Mức cân tối thiểu = Số lẻ của chiều cao (tính bằng cm) x 8 rồi chia 10
Hỏi, bạn Nam cao 1,7 m thì cân nặng lý tưởng, cân nặng tối đa và cân nặng tối thiểu của bạn đó là bao nhiêu? Lời giải
Như vậy, nếu bạn cao 1,7 m = 170 cm thì :
Cân cân nặng lý tưởng của bạn là: 70.9 : 10 = 63(kg)
Cân nặng tối đa là: 70kg
Cân nặng tối thiểu là: 70.8 : 10 = 56(kg)
Câu 5. (1 điểm) Anh An làm việc cho một công ty sản xuất hàng cao cấp, anh được trả năm triệu bảy
trăm sáu mươi ngàn đồng cho 48 tiếng làm việc trong một tuần. Sau đó để tăng thêm thu
nhập, anh An đã đăng ký làm thêm một số giờ nửa trong tuần, mỗi giờ làm thêm này anh An
được trả bằng 150% số tiền mà mỗi giờ anh An được trả trong 48 giờ đầu. Cuối tuần sau khi
xong việc, anh An được lãnh số tiền là bảy triệu hai trăm ngàn đồng. Hỏi anh An đã làm
thêm bao nhiêu giờ trong tuần đó? Lời giải
Số tiền mỗi giờ anh An làm trong 48 giờ đầu: 5 760 000 : 48 = 120 000 (đồng)
Số tiền anh An làm thêm là: 7 200 000 − 5 760 000 = 1 440 000 (đồng)
Số tiền mỗi giờ làm thêm anh An được trả là: 120 000 150% = 180 000 (đồng) Trang 20




