Bộ Đề Tham Khảo Tuyển Sinh 10 TPHCM Môn Toán Năm 2025-2026 Có Lời Giải Chi Tiết (Bộ 4)
Vào cuối học kì I, trường trung học cơ sở A có tỉ lệ học sinh xếp loại học lực trung bình trở lên ở khối 7 là 90% học sinh toàn khối 7 và ở khối 9 là 84% học sinh toàn khối 9. Nếu tính chung cả hai khối thì số học sinh xếp loại học lực trung bình trở lên là 864 em, chiếm tỉ lệ 86,4% số học sinh cả khối 7 và khối 9. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 216 tài liệu
Môn: Toán 9 2.9 K tài liệu
Tác giả:
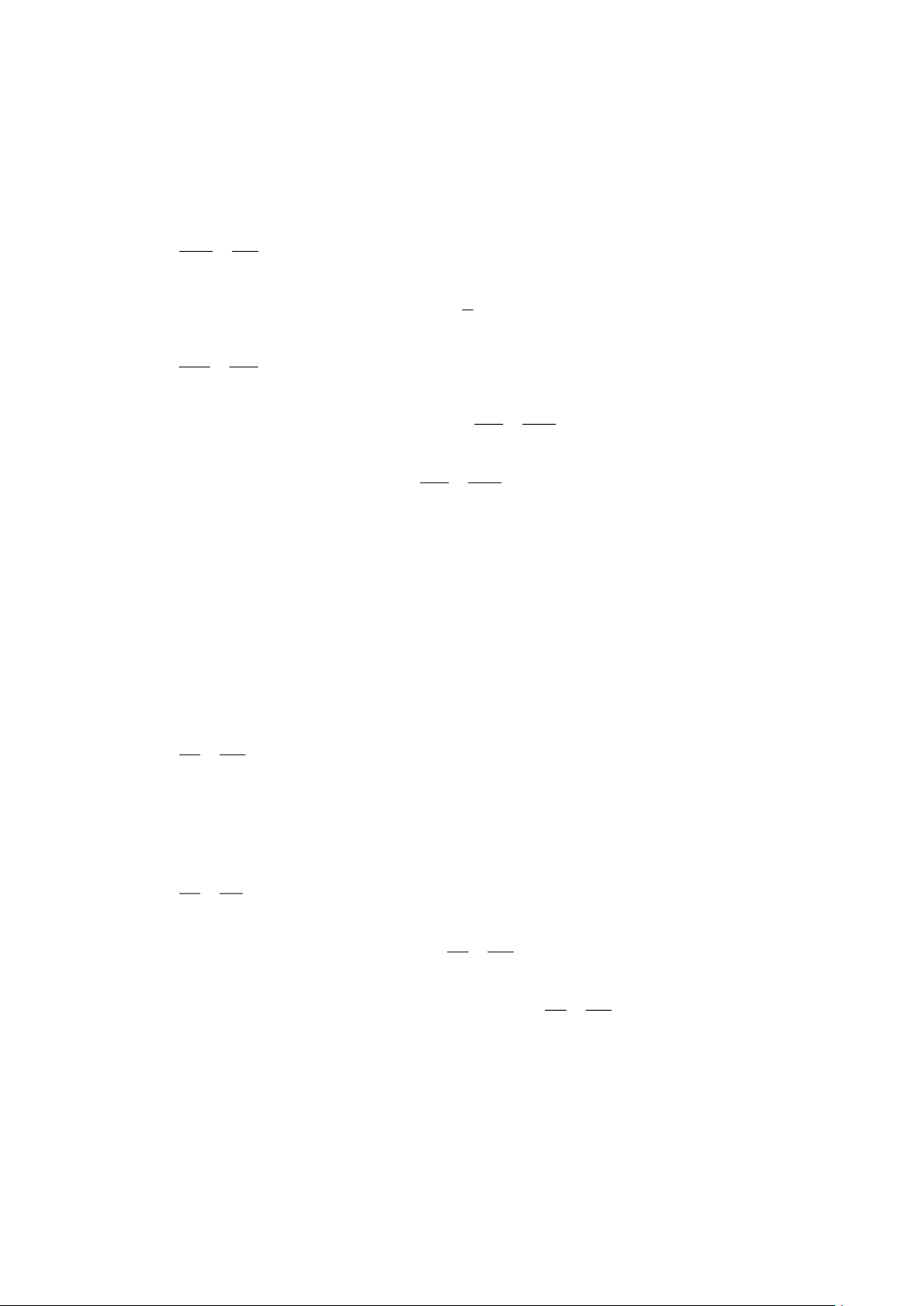
Preview text:
SỞ GD VÀ ĐT TPHCM
ĐỀ THAM KHẢO SINH 10 PHÒNG GD QUẬN 6 MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận. ĐỀ THAM KHẢO
Thời gian: 120 phút (không kể thời gian phát đề) MÃ ĐỀ: Quận 6 - 1
Câu 1. (1,5 điểm). Cho (P) 2
: y = −x và đường thẳng (d) : y = 3x − 4 .
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
4x + 3x − 1 = 0 có 2 nghiệm là x , x . Không giải phương trình, hãy 1 2
tính giá trị của biểu thức A = (x − 2)(x − 2 . 1 2 )
Câu 3. (0,75 điểm) Trong kết quả xét nghiệm lượng đường trong máu có bệnh viện tính theo đơn
vị là mg / dl nhưng cũng có bệnh viện tính theo đơn vị là mmol / l . Công thức chuyển đổi
là 1 mmol / l = 18 mg / dl . Hai bạn Châu và Lâm nhịn ăn sáng sau khi thử đường huyết tại
nhà có chỉ số đường huyết lần lượt là 110 mg / dl và 90 mg / dl . Căn cứ vào bảng sau, em
hãy cho biết tình trạng sức khỏe của hai bạn Châu và Lâm: Tên xét nghiệm Hạ đường Đường huyết Giai đoạn tiền Chuẩn đoán huyết bình thường tiểu đường bệnh tiểu đường
Đường huyết lúc x 4.0 4.0 x 5.6 5.6 x 7.0 x 7.0 đói mmol / l mmol / l mmol / l mmol / l ( x mml / l )
Câu 4. (1 điểm). Minh đến nhà sách mua một quyển tập và một quyển sách thì phải thanh toán số tiền là
25000 đồng. Nếu Minh mua thêm 1 quyển tập cùng loại nữa thì số tiền phải thanh toán là 30 000
đồng. Biết rằng mối liên hệ giữa số tiền phải thanh toán y (đồng) cho nhà sách và số tập x (quyển)
mà Minh mua là một hàm số bậc nhất có dạng y = ax + b (a 0) .
a) Xác định các hệ số a và b .
b) Minh mang theo khi đến nhà sách là 70 000 đồng thì có thể mua được bao nhiêu quyển tập và giá
của quyển tập mà Minh mua là bao nhiêu tiền?
Câu 5. (0,75 điểm). Vào cuối học kì I, trường trung học cơ sở A có tỉ lệ học sinh xếp loại học lực trung
bình trở lên ở khối 7 là 90% học sinh toàn khối 7 và ở khối 9 là 84% học sinh toàn khối 9 . Nếu
tính chung cả hai khối thì số học sinh xếp loại học lực trung bình trở lên là 864 em, chiếm tỉ lệ 86,4%
số học sinh cả khối 7 và khối 9 . Hãy cho biết mỗi khối trên có bao nhiêu học sinh?
Câu 6. (1 điểm) Các viên kẹo mút có dang hình cầu, bán kính 1,6 cm. Người ta dùng môt que nhựa hình
trụ tròn, bán kính 0,2 cm cắm vào đến phân nửa viên kẹo để người dùng dễ sử dụng.
a) Tính thể tích phần ống nhựa hình trụ cắm vào phân nửa viên kẹo. Trang 1
b) Tính thể tích thực của viên kẹo sau khi trừ phần ống nhựa cắm vào.
Câu 7. (1 điểm). Thống kê điểm một bài kiểm tra môn toán của lớp 9A , người ta đã tính được điểm trung
bình kiểm tra của lớp là 6,4 . Nhưng do sai sót khi nhập liệu, số học sinh đạt điểm 6 và điểm 7 đã bị
mất. Dựa vào bảng thống kê dưới đây em hãy tìm lại hai số bị mất đó , biết lớp 9A có 40 học sinh. Điểm 3 4 5 6 7 8 9 10 Số học sinh 1 2 7 6 2 1
Câu 8. (3 điểm) Cho điểm A nằm ngoài đường tròn tâm O . Kẻ hai tiếp tuyến AB và AC ( B , C là tiếp
điểm) và một cát tuyến AHK (AH AK) với đường tròn. Lấy điểm I thuộc đoạn BC (IB IC) , I
không thuôc cát tuyến AHK . Kẻ OM ⊥ AI tại M . a)
Chứng minh: 5 điểm M,O,C,B, A cùng thuộc một đường tròn. b) Chứng minh: AI AM = 2 .
AB và tứ giác MIHK nội tiếp đường tròn. c)
Kẻ KI cắt đường tròn (O) tại N (khác K ) và AN cắt đường tròn (O) ở E . Chứng minh H , I , E thẳng hàng. ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm) Cho (P) 2
: y = −x và đường thẳng (d) : y = 3x − 4 .
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
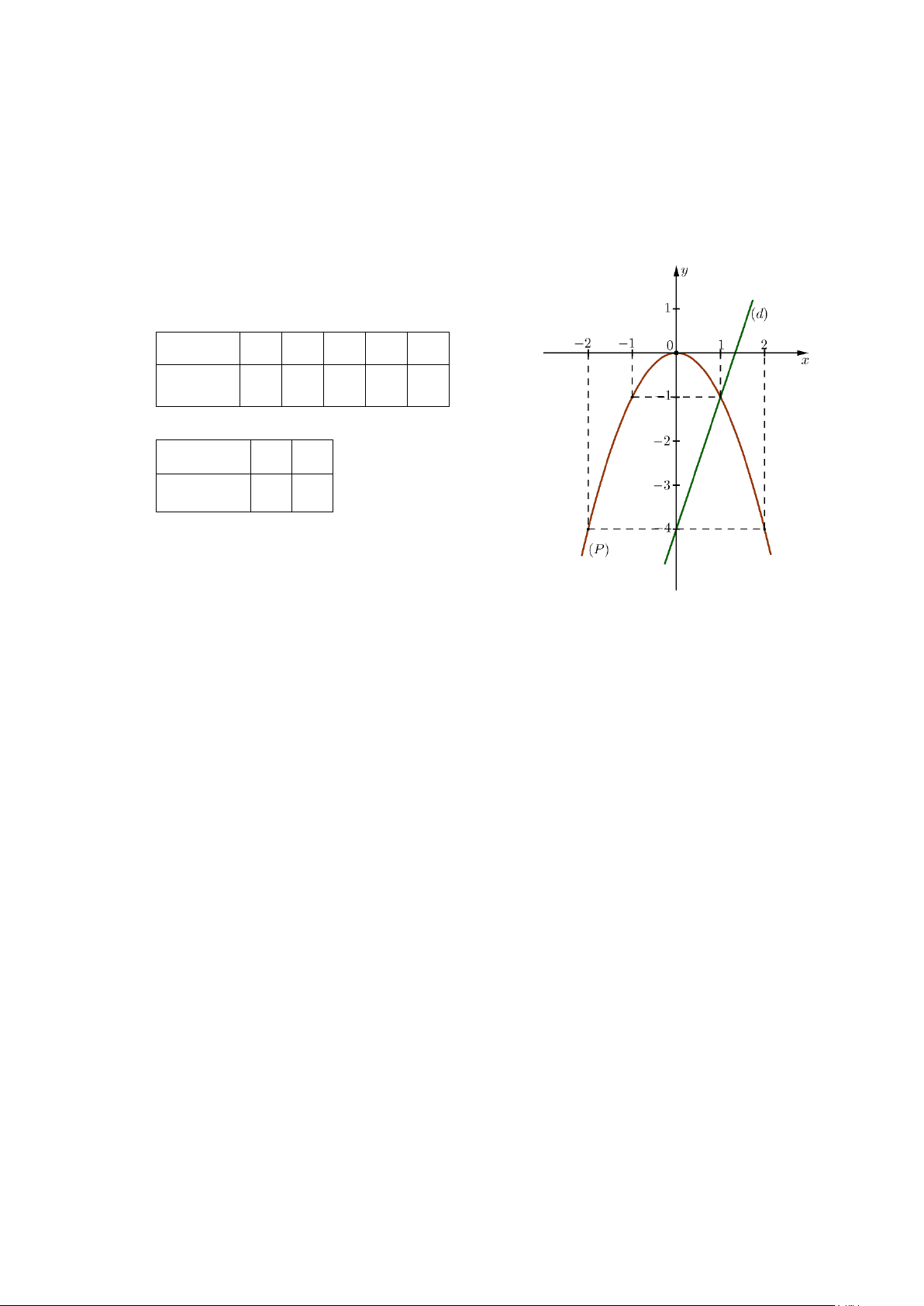
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. a) BGT: x −2 1 − 0 1 2 2 y = −x −4 1 − 0 1 − −4 x 0 1
y = 3x − 4 −4 1 −
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : 2 −x = 3x − 4 2
x + 3x − 4 = 0 x = 1 x = 4 − Thay x = 1 vào 2
y = −x , ta được: 2 y = 1 − = −1 . Thay x = −4 vào 2
y = −x , ta được: y = −(− )2 4 = 1 − 6 . Vậy (1; − 1) , ( 4
− ; −16) là hai giao điểm cần tìm.
Câu 2. (1 điểm) Cho phương trình 2
4x + 3x − 1 = 0 có 2 nghiệm là x , x . Không giải phương trình, hãy 1 2
tính giá trị của biểu thức A = (x − 2)(x − 2 .. 1 2 ) Lời giải Vì = 2 b − ac = 2 4 3 − 4.4.(−1) = 25 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 Trang 3 − = + = b S x x − 3 1 2
Theo định lí Vi-et, ta có: a 4 c −
P = x .x = = 1 1 2 a 4
Ta có: A = (x − 2)(x − 2 1 2 )
A = x x − 2x − 2x + 4 1 2 1 2
A = x x − 2 x x 4 1 2 ( + 1 2 ) +
A = P − 2S + 4 A = − 1 − 3 + = 21 2. 4 4 4 4
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập
phân, số đo góc làm tròn đến phút.
Câu 3. (0,75 điểm) Trong kết quả xét nghiệm lượng đường trong máu có bệnh viện tính theo đơn
vị là mg / dl nhưng cũng có bệnh viện tính theo đơn vị là mmol / l . Công thức chuyển đổi
là 1 mmol / l = 18 mg / dl . Hai bạn Châu và Lâm nhịn ăn sáng sau khi thử đường huyết tại
nhà có chỉ số đường huyết lần lượt là 110 mg / dl và 90 mg / dl . Căn cứ vào bảng sau, em
hãy cho biết tình trạng sức khỏe của hai bạn Châu và Lâm: Tên xét nghiệm Hạ đường Đường huyết Giai đoạn tiền Chuẩn đoán huyết bình thường tiểu đường bệnh tiểu đường
Đường huyết lúc x 4.0 4.0 x 5.6 5.6 x 7.0 x 7.0 đói mmol / l mmol / l mmol / l mmol / l ( x mml / l ) Lời giải
Chỉ số đường huyết của Châu là mg dl = 1 = 55 100 / .110
6,1mmol / l . 18 9
Chỉ số đường huyết của Lâm là mg dl = 1 90 /
.90 = 5mmol / l . 18
Căn cứ vào bảng đề bài cho, ta có thể kết luận: bạn lâm đường huyết bình thường, còn bạn Châu
thuộc giai đoạn tiền tiểu đường.
Câu 4. (1 điểm). Minh đến nhà sách mua một quyển tập và một quyển sách thì phải thanh toán số tiền là
25000 đồng. Nếu Minh mua thêm 1 quyển tập cùng loại nữa thì số tiền phải thanh toán là 30 000
đồng. Biết rằng mối liên hệ giữa số tiền phải thanh toán y (đồng) cho nhà sách và số tập x (quyển)
mà Minh mua là một hàm số bậc nhất có dạng y = ax + b (a 0) .
a) Xác định các hệ số a và b .
b) Minh mang theo khi đến nhà sách là 70 000 đồng thì có thể mua được bao nhiêu quyển tập và giá
của quyển tập mà Minh mua là bao nhiêu tiền? Trang 4 Lời giải
a) Theo đề bài, một quyển tập và một quyển sách thì phải thanh toán số tiền là 25000 đồng tức là 25000 = .1
a + b = a + b .
Nếu Minh mua thêm 1 quyển tập cùng loại nữa thì số tiền phải thanh toán là 30000 đồng tức là 30000 = .2
a + b = 2a + b .
a + b = 25000 a = 5000
Suy ra a và b là nghiệm của hệ phương trình . 2a + b = 30000 b = 20000
Vâỵ: y = 5000x + 20000 .
b) Minh mang theo khi đến nhà sách là 70 000 đồng tức là y = 70000 , khi đó
70 000 = 5000x + 20 000 x = 10 .
Vậy minh mua được 10 quyển tập và giá của mỗi quyển tập là 5000 .
Câu 5. (0,75 điểm). Vào cuối học kì I, trường trung học cơ sở A có tỉ lệ học sinh xếp loại học lực trung bình
trở lên ở khối 7 là 90% học sinh toàn khối 7 và ở khối 9 là 84% học sinh toàn khối 9 . Nếu tính
chung cả hai khối thì số học sinh xếp loại học lực trung bình trở lên là 864 em, chiếm tỉ lệ 86,4% số
học sinh cả khối 7 và khối 9 . Hãy cho biết mỗi khối trên có bao nhiêu học sinh? Lời giải
Tổng số học sinh khối 7 và 9 là 864 : 86,4% = 1000 (học sinh).
Gọi x là số học sinh khối 7 ( x 0 ).
Tỉ lệ xếp loại học lực trung bình trở lên của khối 7 là 90% và khối 9 là 84% nên ta có phương trình
0,9x + 0,84(1000 − x) = 864
0,9x + 840 − 0,84x = 864 0,06x = 24 x = 400
Với x = 400 thỏa điêu kiện, do đó số học sinh khối 7 là 400 em, khối 9 là 1000 − 400 = 600 em.
Câu 6. (1 điểm) Các viên kẹo mút có dang hình cầu, bán kính 1,6 cm. Người ta dùng môt que nhựa hình trụ
tròn, bán kính 0,2 cm cắm vào đến phân nửa viên kẹo để người dùng dễ sử dụng.
a) Tính thể tích phần ống nhựa hình trụ cắm vào phân nửa viên kẹo.
b) Tính thể tích thực của viên kẹo sau khi trừ phần ống nhựa cắm vào. Lời giải
a) Thể tích phần ống nhựa hình trụ cắm vào viên kẹo: V = 2 r h = 2 = 3 .0,2 .1,6 0,064 (cm ) .
b) Thể tích hình cầu có bán kính 4 4
1,6 cm: V = 2 R = 2 .1,6 = 5,4 3 6 (cm ) . 3 3
Thể tích thực của viên kẹo: − = 3 5,46 0,064 5,396(cm ) Trang 5
Câu 7. (1 điểm) Thống kê điểm một bài kiểm tra môn toán của lớp 9A , người ta đã tính được điểm trung
bình kiểm tra của lớp là 6,4 . Nhưng do sai sót khi nhập liệu, số học sinh đạt điểm 6 và điểm 7 đã bị
mất. Dựa vào bảng thống kê dưới đây em hãy tìm lại hai số bị mất đó , biết lớp 9A có 40 học sinh. Điểm 3 4 5 6 7 8 9 10 Số học sinh 1 2 7 6 2 1 Lời giải
Gọi x là số học sinh đạt điểm 6 , y là số học sinh đạt điểm 7 (x,y *,x,y 40) .
Theo đề bài, ta có hệ phương trình: x + y = 21 x + y = 21 x = 13 6x + 7y = 6,4.40 6x + 7y = 134 y = 8
Vậy có 13 học sinh đạt điểm 6 và 8 học sinh đạt điểm 7 .
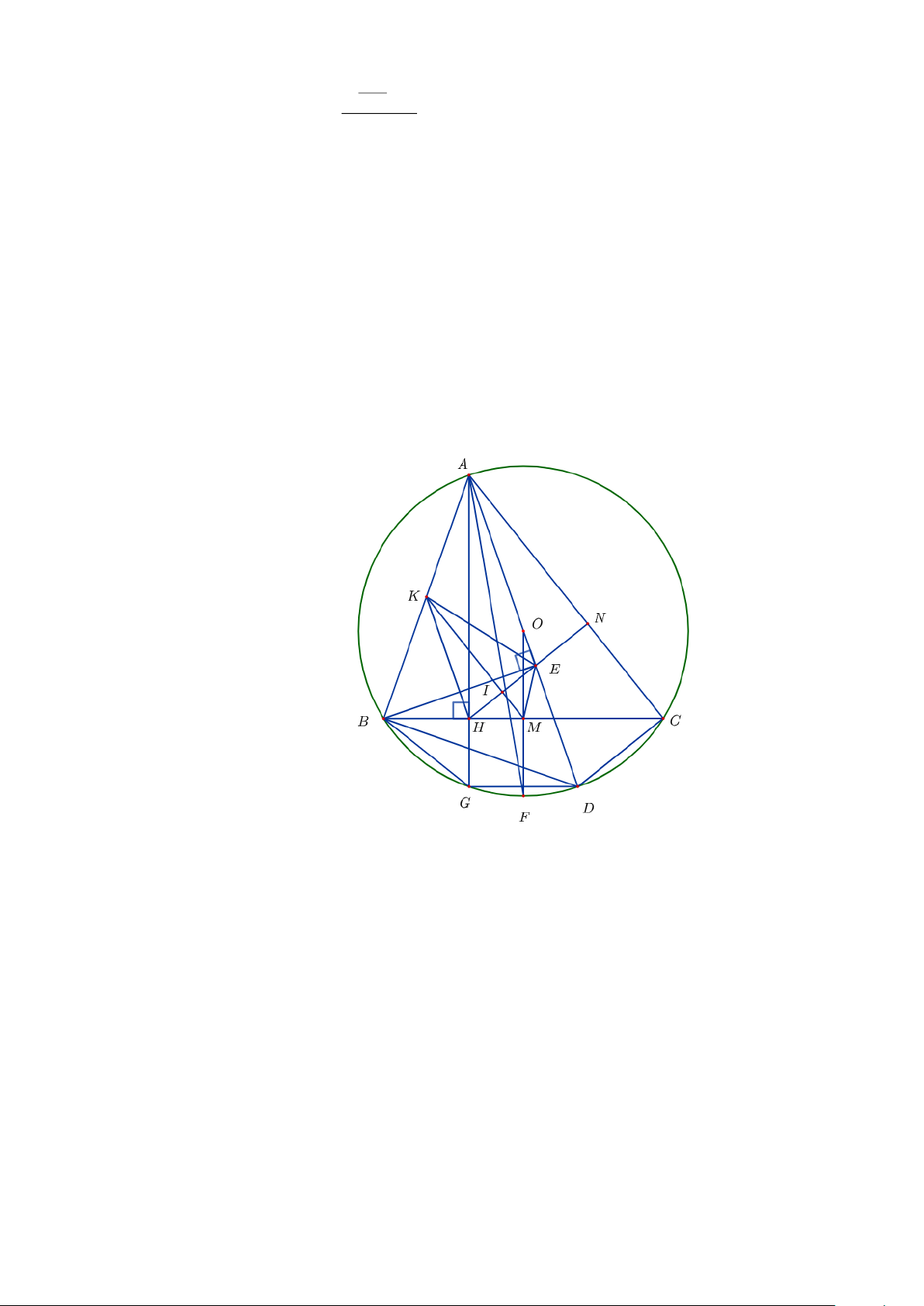
Câu 8. (3 điểm) Cho điểm A nằm ngoài đường tròn tâm O . Kẻ hai tiếp tuyến AB và AC ( B , C là tiếp
điểm) và một cát tuyến AHK (AH AK) với đường tròn. Lấy điểm I thuộc đoạn BC (IB IC) , I
không thuôc cát tuyến AHK . Kẻ OM ⊥ AI tại M .
a) Chứng minh: 5 điểm M,O,C,B, A cùng thuộc một đường tròn.
b) Chứng minh: AI AM = 2 .
AB và tứ giác MIHK nội tiếp đường tròn.
c) Kẻ KI cắt đường tròn (O) tại N (khác K ) và AN cắt đường tròn (O) ở E . Chứng minh H , I , E thẳng hàng. Lời giải a)
Chứng minh: 5 điểm M,O,C,B, A cùng thuộc một đường tròn.
Ta có: ABO = ACO = AMO = 90 (gt)
Nên 5 điểm A,B,C,O,M cùng thuộc một đường tròn đường kính AO .
b) Chứng minh: AI AM = 2 .
AB và tứ giác MIHK nội tiếp đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau, ta có AB = AC nên ABC cân tại A Trang 6 CBA = ACB.
Mà BMA = ACB (góc nội tiếp đường tròn đường kính AO , cùng chắn cung BA)
Suy ra ABC = AMB .
Xét ABI và AMB có BAI chung và ABI = AMB (cmt) suy ra ABI# AMB (g-g).
AB = AI AM AI = 2 . AB (1) . AM AB
Xét ABK và AHB có BKA = ABH = 1 sđ HB và BAH chung ABK# AHB(g-g) 2
AB = AK AH AK = 2 . AB (2) AH AB Từ AI AH
(1) và (2) suy ra AM.AI = AH.AK = AK AM Xét AI AH
AIH và AKM có AHI và =
(cmt) suy ra AIH# AKM (c-g-c) AK AM AIH = AKM
Vậy tứ giác IMKH nội tiếp.
c) Kẻ KI cắt đường tròn (O) tại N (khác K ) và AN cắt đường tròn (O) ở E . Chứng minh H , I , E thẳng hàng.
Xét IBM và IAC có BIM = AIC (đối đỉnh) và MBC = MAC (2 góc nội tiếp đường tròn
đường kính AO , chắn cung MC ) suy ra IBM# IAC (g-g).
IB = IM I . A IM = I . B IC (3) . IA IC
Xét IKC và IBN có KIC = BIN (đối đỉnh) và CKN = NBC (góc nội tiếp (O) , chắn cung
NC ) suy ra IKC# IBN (g-g)
IK = IC IK.IN = I . B IC (4) IB IN Từ IA IN (3) và (4) suy ra .
A IM = IK.IN = . IK IM Xét IA IN
INA và IMK có KIM = AIN (đối đỉnh) và =
(cmt) suy ra INA# IMK IK IM MKN = MAN
Suy ra tứ giác ANMK nội tiếp ( tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới một góc bằng nhau). Do đó IHK = 180 − IMK =
180 − ANK = ENK = EHK . Vậy H , I , E thẳng hàng. Trang 7
SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN 5
NĂM HỌC: 2021 - 2022 MÔN: TOÁN 9 ĐỀ THAM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 5 - 1
Thời gian: 120 phút (không kể thời gian phát đề) 2
Câu 9. (1,5 điểm). Cho parabol ( ) −x P : y =
và đường thẳng (d) : y = −4x + 6 . 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 10. (1 điểm). Cho phương trình 1 2
x − x − 1 = 0 (1) 2
Không giải phương trình, hãy tính giá trị của biểu thức sau A = x x
1 + 2 − x x với x ,x là hai 1 2 x x 1 2 2 1
nghiệm của phương trình (1)
Câu 11. (0,75 điểm). Để tính múi giờ của một địa điểm ta làm như sau:
− Ở Đông bán cầu (kí hiệu là o Đ ): múi giờ = kinh độ Đông : 15o
− Ở Tây bán cầu (kí hiệu là oT ): múi giờ = ( 360o − kinh độ Tây) : 15o
(Kết quả làm tròn đến hàng đơn vị)
Để tính giờ của một địa điểm, ta tính theo công thức sau: T = GMT + H với T là giờ tại nơi đó,
GMT là giờ gốc, H được quy đổi như sau: Múi giờ 0 1 2 3 4 5 6 7 8 9 10 11 H 0 1 2 3 4 5 6 7 8 9 10 11 Múi giờ 12 13 14 15 16 17 18 19 20 21 22 23 H 12 − −11 −10 −9 −8 −7 −6 −5 −4 −3 −2 1 −
a) Lúc 19h00 ở Hà Nội (105o Đ ) ngày 15 / 06 / 2021 thì lúc đó ở Los Angeles (120oT ) là mấy giờ?
b) Một chiếc máy bay cất cánh ở sân bay New York ( 75oT ) với vận tốc 750 km / h trên quãng
đường chim bay dài 14250km để hạ cánh xuống sân bay Tân Sơn Nhất (105o Đ ) của Việt Nam
đúng 2 giờ sáng ngày 01 / 10 / 2021. Hỏi máy bay cất cánh tại New York ngày nào? Lúc mấy giờ?
Câu 12. (0,75 điểm). Áp suất của nước P (đơn vị: atm ) lên một người thợ lặn ở độ sâu d (tính theo feet ) là
một hàm số bậc nhất P(d) = ad + b .
a) Tính các hệ số a và b biết các điểm ( A 0;1) và (
B 33; 2) thuộc đồ thị hàm số.
b) Tính áp suất của nước lên người thợ lặn ở độ sâu 100 feet (kểt quả làm tròn đến hàng đơn vị).
Biết feet là đơn vị đo độ dài, 1 feet = 0,3048m Trang 8
Câu 13. (1 điểm). Hãng viễn thông Văn có ba phương án trả tiền cước điện thoại cho mỗi cuộc gọi như sau:
− Phương án I: Trả tổng cộng 99 cent cho 20 phút đầu, sau đó từ phút thứ 21 thì mỗi phút trả 5 cent .
− Phương án II: Kể từ lúc đầu tiên, mỗi phút trả 10 cent .
− Phương án III: Trả 25 cent tiền thuê bao, sau đó kể từ phút đầu tiên mỗi phút trả 8 cent .
Anh Toàn là nhân viên Sale bất động sản. Trung bình mỗi tháng thì anh Toàn thực hiện 200 cuộc
gọi với 10% cuộc gọi 1 phút, 10% cuộc gọi 5 phút, 30% cuộc gọi 10 phút, 30% cuộc gọi 20
phút, 20% cuộc gọi 30 phút. Hỏi anh Toàn nên chọn phương án nào của hãng viễn thông Văn để có lợi nhất?
Câu 14. (1 điểm). Thầy Bảo, nhân viên y tế, được nhà trường phân công mua một số hộp khẩu trang để phục
vụ cho công tác phòng chống dịch Covid của nhà trường. Thầy dự định mua một số hộp khẩu trang
tại nhà thuốc Pharmacity. Khi tham khảo giá trang web thì tổng số tiền thầy sẽ trả là 600 nghìn
đồng. Tuy nhiên, khi đến mua trực tiếp, Pharmacity có chương trình khuyến mãi mỗi hộp khẩu trang
được giảm 2 nghìn đồng nên thầy quyết định mua thêm 2 hộp. Khi đó tổng số tiền phải trả là 672
nghìn đồng. Hỏi thầy Bảo đã mua tất cả bao nhiêu hộp khẩu trang?
Câu 15. (1 điểm). Một bồn nước hình trụ có bán kính đáy là 3m , chiều cao là 4m . Người ta đổ nước vào
trong bồn sao cho chiều cao của nước bằng đúng một nửa chiều cao của bồn và tiếp tục đặt vào trong
bồn một phao nước có dạng hình cầu bằng kim loại không thấm nước có bán kính là 50cm và chìm hoàn toàn trong nước.
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ ba) ?
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có công suất chảy là 3 0,0024m cho
mỗi giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)?
Câu 16. (3 điểm) Cho tam giác ABC nhọn (AB AC) nội tiếp đường tròn (O) . Kẻ
AD là đường kình của
(O), AH vuông góc với BC tại H, BE vuông góc với AD tại E. Gọi G là giao điểm của AH với (O) .
a) Chứng minh tứ giác ABHE nội tiếp và GD / / BC ;
b) Gọi N là giao điểm giữa HE và AC. Chứng minh tam giác AHN vuông tại N ;
c) Tia phân giác của góc BAC cắt đường tròn (O) tại F. Gọi M là giao điểm của OF và BC,K là
trung điểm của AB,I là giao điểm của KM và . HE Chứng minh rằng . AB EI = . AE EM. ----HẾT--- Trang 9 HƯỚNG DẪN GIẢI 2
Câu 9. (1,5 điểm) Cho ( ) −x P : y =
và đường thẳng (d) : y = −4x + 6 . 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
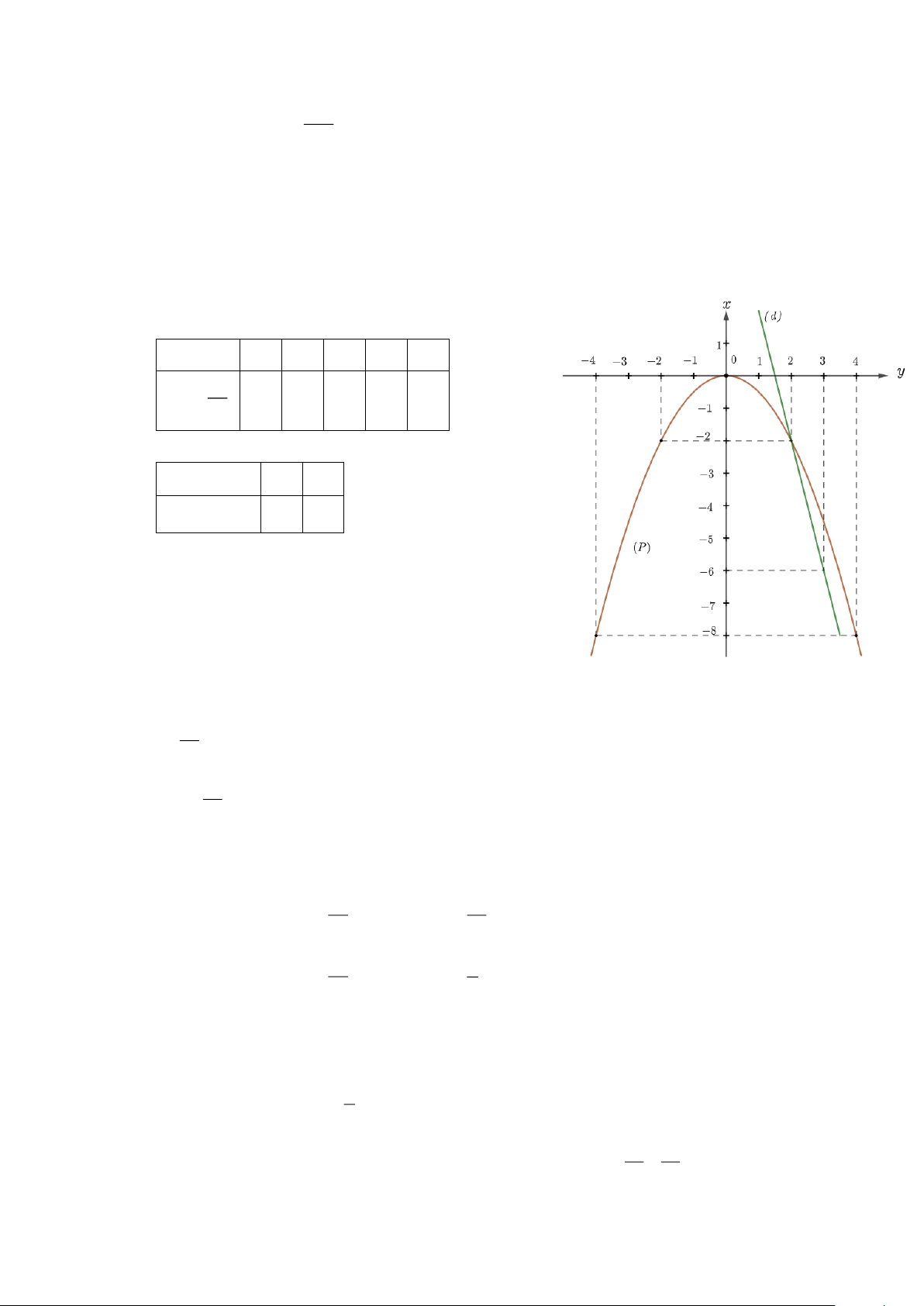
c) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. b) BGT: x −4 −2 0 2 4 2 x y = − −8 −2 0 −2 −8 2 x 2 3 y = 4 − x + 6 −2 −6
d) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : 2 x − = 4 − x + 6 2 2 x − + 4x − 6 = 0 2 x = 2 x = 6 2 2 Thay x 2
x = 2 vào y = − , ta được: y = − = 2 − . 2 2 2 2 Thay x 6
x = 6 vào y = − , ta được: y = − = 18 − . 2 2
Vậy (2; − 2) , (6; − 18) là hai giao điểm cần tìm.
Câu 10. (1 điểm) Cho phương trình 1 2
x − x − 1 = 0 (1) 2
Không giải phương trình, hãy tính giá trị của biểu thức sau A = x x
1 + 2 − x x với x ,x là hai 1 2 x x 1 2 2 1
nghiệm của phương trình (1) Trang 10 Lời giải
Vì = b − ac = (− )2 2 1 4 1 − 4. .( 1 − ) = 3 0 2
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 −b ( 1 − )
S = x + x = = − = 2 1 2 a 1
Theo định lí Vi-et, ta có: 2 c 1 −
P = x .x = = = −2 1 2 a 1 2 Ta có: A = x x 1 + 2 − x x 1 2 x x 2 1 x x 1 2 A = + − x x 1 2 x x 2 1 2 2 x + x 1 2 A = − x x 1 2 x x 1 2 2
(x + x ) − 2x x 1 2 1 2 A = − x x 1 2 x x 1 2 2 2 − 2(−2) A = − (−2) −2 A = −2
Câu 3. (0,75 điểm) Để tính múi giờ của một địa điểm ta làm như sau:
− Ở Đông bán cầu (kí hiệu là o Đ ): múi giờ = kinh độ Đông : 15o
− Ở Tây bán cầu (kí hiệu là oT ): múi giờ = ( 360o − kinh độ Tây) : 15o
(Kết quả làm tròn đến hàng đơn vị)
Để tính giờ của một địa điểm, ta tính theo công thức sau: T = GMT + H với T là giờ tại nơi đó,
GMT là giờ gốc, H được quy đổi như sau: Múi giờ 0 1 2 3 4 5 6 7 8 9 10 11 H 0 1 2 3 4 5 6 7 8 9 10 11 Múi giờ 12 13 14 15 16 17 18 19 20 21 22 23 H 12 − −11 −10 −9 −8 −7 −6 −5 −4 −3 −2 1 −
a) Lúc 19h00 ở Hà Nội (105o Đ ) ngày 15 / 06 / 2021 thì lúc đó ở Los Angeles (120oT ) là mấy giờ?
b) Một chiếc máy bay cất cánh ở sân bay New York ( 75oT ) với vận tốc 750 km / h trên quãng
đường chim bay dài 14250km để hạ cánh xuống sân bay Tân Sơn Nhất ( 105o Đ ) của Việt Nam
đúng 2 giờ sáng ngày 01 / 10 / 2021. Hỏi máy bay cất cánh tại New York ngày nào? Lúc mấy giờ? Trang 11 Lời giải
a) Lúc 19h00 ở Hà Nội (105o Đ ) ngày 15 / 06 / 2021 thì lúc đó ở Los Angeles (120oT ) là mấy giờ? o
Múi giờ tại Hà Nội là: 105 = 7 H = 7 15 o o −
Múi giờ tại Los Angles là: 360 120 = 16 H = 8 − 15
Vậy giờ gốc là: 19 = GMT + 7 GMT = 12 giờ
Vậy lúc 19h00 ở Hà Nội (105o Đ ) ngày 15 / 06 / 2021 thì lúc đó ở Los Angles là 12 − 8 = 4 giờ
b) Một chiếc máy bay cất cánh ở sân bay New York ( 75oT ) với vận tốc 750 km / h trên quãng
đường chim bay dài 14250km để hạ cánh xuống sân bay Tân Sơn Nhất (105o Đ ) của Việt Nam
đúng 2 giờ sáng ngày 01 / 10 / 2021. Hỏi máy bay cất cánh tại New York ngày nào? Lúc mấy giờ?
Thời gian để di chuyển từ New York đến sân bay Tân Sơn Nhất là: s 14250 t = = = 9 1 giờ v 750
Như vậy máy bay cất cánh vào lúc 7 giờ ngày 30 / 09 / 2021 theo giờ tại sân bay Tân Sơn Nhất. o o −
Múi giờ tại New York là: 360 75 = 19 H = 5 − 15
Vậy giờ gốc là: 7 = GMT + 7 GMT = 0
Vậy thời gian máy bay cất cánh ở New York là: 24 − 5 = 19 giờ vào ngày 29 / 09 / 2021
Câu 4. (0,75 điểm). Áp suất của nước P (đơn vị: atm ) lên một người thợ lặn ở độ sâu d (tính theo feet ) là
một hàm số bậc nhất P(d) = ad + b .
a) Tính các hệ số a và b biết các điểm ( A 0;1) và (
B 33; 2) thuộc đồ thị hàm số.
b) Tính áp suất của nước lên người thợ lặn ở độ sâu 100 feet (kểt quả làm tròn đến hàng đơn vị). Biết
feet là đơn vị đo độ dài, 1 feet = 0,3048m Lời giải
a. Tính các hệ số a và b biết các điểm ( A 0;1) và (
B 33; 2) thuộc đồ thị hàm số. Theo đề bài, ta có: d = 0 Với
1 = 0.a + b .( ) 1 ( P d) = 1 d = 33 Với
2 = 33.a + b.(2) ( P d) = 2 1 0a + b = 1 = Từ ( ) a
1 và (2) ta có hệ phương trình: 33 . 33a + b = 2 b = 1 Vậy: 1 a = , b = 1 và 1 ( P d) = d + 1. 33 33 Trang 12
b) Tính áp suất của nước lên người thợ lặn ở độ sâu 100 feet (kểt quả làm tròn đến hàng đơn vị). Biết
feet là đơn vị đo độ dài, 1 feet = 0,3048m
Áp suất của nước lên người thợ lặn ở độ sâu 100 feet: 1 ( P 100) = .100 + 1 4 atm 33
Câu 17. (1 điểm) Hãng viễn thông Văn có ba phương án trả tiền cước điện thoại cho mỗi cuộc gọi như sau:
− Phương án I: Trả tổng cộng 99 cent cho 20 phút đầu, sau đó từ phút thứ 21 thì mỗi phút trả 5 cent .
− Phương án II: Kể từ lúc đầu tiên, mỗi phút trả 10 cent .
− Phương án III: Trả 25 cent tiền thuê bao, sau đó kể từ phút đầu tiên mỗi phút trả 8 cent .
Anh Toàn là nhân viên Sale bất động sản. Trung bình mỗi tháng thì anh Toàn thực hiện 200 cuộc gọi
với 10% cuộc gọi 1 phút, 10% cuộc gọi 5 phút, 30% cuộc gọi 10 phút, 30% cuộc gọi 20 phút,
20% cuộc gọi 30 phút. Hỏi anh Toàn nên chọn phương án nào của hãng viễn thông Văn để có lợi nhất? Lời giải
Số cuộc gọi 1 phút là: 200.10% = 20 cuộc gọi
Số cuộc gọi 5 phút là: 200.10% = 20 cuộc gọi
Số cuộc gọi 10 phút là: 200.30% = 60 cuộc gọi
Số cuộc gọi 20 phút là: 200.30% = 60 cuộc gọi
Số cuộc gọi 30 phút: 200.20% = 40 cuộc gọi
Vậy tổng số phút để thực hiện số cuộc gọi trên là: 20.1 + 20.5 + 60.10 + 60.20 + 30.40 = 3120 phút.
Số tiền phải trả ở phương án I là: 99 + (3120 − 21).5 = 15594 cent
Số tiền phải trả ở phương án II là: 3120.10 = 31200 cent
Số tiền phải trả ở phương án III là: 25 + 3120.8 = 24985cent
Vậy anh Toàn nên chọn phương án I để có lợi nhất
Câu 6. (1 điểm) Thầy Bảo, nhân viên y tế, được nhà trường phân công mua một số hộp khẩu trang để phục
vụ cho công tác phòng chống dịch Covid của nhà trường. Thầy dự định mua một số hộp khẩu trang tại
nhà thuốc Pharmacity. Khi tham khảo giá trang web thì tổng số tiền thầy sẽ trả là 600 nghìn đồng.
Tuy nhiên, khi đến mua trực tiếp, Pharmacity có chương trình khuyến mãi mỗi hộp khẩu trang được
giảm 2 nghìn đồng nên thầy quyết định mua thêm 2 hộp. Khi đó tổng số tiền phải trả là 672 nghìn
đồng. Hỏi thầy Bảo đã mua tất cả bao nhiêu hộp khẩu trang? Lời giải
Gọi số tiền mua một hộp khẩu trang trước khi giảm giá là x (nghìn đồng) (x 2)
Số tiền mua một hộp khẩu trang sau khi giảm giá là x − 2 (nghìn đồng)
Số hộp khẩu trang mua được trước khi giảm giá là 600 (hộp) x Trang 13
Số hộp khẩu trang mua được sau khi giảm giá là 672 (hộp) x − 2 Theo đề bài, ta có: 600 672 = − 2 x x − 2
600(x − 2) = 672x − 2 ( x x − 2) 2
600x − 1200 = 672x − 2x + 4x 2
2x − 76x − 1200 = 0 x = 50 x = 12 −
Do x 2 nên ta nhận x = 50
Vậy số hộp khẩu trang mà thầy Bảo đã mua là: 672 = 14 hộp 50 − 2
Câu 7. (1 điểm) Một bồn nước hình trụ có bán kính đáy là 3 m , chiều cao là 4 m . Người ta đổ nước vào
trong bồn sao cho chiều cao của nước bằng đúng một nửa chiều cao của bồn và tiếp tục đặt vào trong
bồn một phao nước có dạng hình cầu bằng kim loại không thấm nước có bán kính là 50 cm và chìm hoàn toàn trong nước.
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ ba) ?
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có công suất chảy là 3 0,0024m cho mỗi
giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)? Lời giải
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ ba) ?
Thể tích của nước đã đổ vào trong bồn là: 2 2 3
V = r h = .3 .2 = 18 (m ) 1 1
Thể tích của quả cầu kim loại là: 4 3 4 3 3
V = R = . .0,5 = (m ) 2 3 3 6
Thể tích của cả nước đã đổ vào trong bồn và quả cầu kim loại là: 109 3
V = V + V = 18 + = (m ) 3 1 2 6 6 109 V
Vậy mực nước trong bồn cao: 3 6 h = = 2,019 m 3 2 2 r .3
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có công suất chảy là 0,0024 m3 cho mỗi
giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)?
Thể tích của toàn bộ cái bồn hình trụ là: 2 3
V = .3 .4 = 36 (m )
Thể tích nước cần bơm thêm vào để đầy bồn là: 109 107 3 36 − = (m ) 6 6 Trang 14 107
Vậy bồn nước sẽ đầy sau: 6 389 phút 0,0024.60
Câu 8. (3 điểm) Cho tam giác ABC nhọn (AB AC) nội tiếp đường tròn (O) . Kẻ
AD là đường kình của
(O), AH vuông góc với BC tại H, BE vuông góc với AD tại E. Gọi G là giao điểm của AH với (O).
a) Chứng minh tứ giác ABHE nội tiếp và GD / / BC ;
b) Gọi N là giao điểm giữa HE và AC. Chứng minh tam giác AHN vuông tại N ;
c) Tia phân giác của góc BAC cắt đường tròn (O) tại F. Gọi M là giao điểm của OF và BC,K là
trung điểm của AB,I là giao điểm của KM và . HE Chứng minh rằng . AB EI = . AE EM. Lời giải
d) Chứng minh tứ giác ABHE nội tiếp và GD / / BC ;
Xét tứ giác ABHE , có:
AHB = 90(AH ⊥ BC) AEB = 90 (BE ⊥ AD)
Tứ giác ABHE nội tiếp vì có hai đỉnh kề cùng nhìn một cạnh dưới hai góc bằng nhau.
Ta có: AGD nội tiếp đường tròn đường kính AD = 90o AGD
AG ⊥ GD mà H AG
AH ⊥ GD mà AH ⊥ BC Trang 15 GD / /BC
e) Gọi N là giao điểm giữa HE và AC. Chứng minh tam giác AHN vuông tại N ;
Vì ABHE là tứ giác nội tiếp nên NHC = BAD (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó)
Xét đường tròn (O) , ta có: BAD = BCD (2 góc nội tiếp cùng chắn BD ) Ta có: NHC = BAD
BAD = BCD NHC = BCD
Mà hai góc NHC và BCD nằm ở vị trí so le trong HN / /CD
Ta có: ACD nội tiếp đường tròn đường kính AD = 90o ACD AC ⊥ CD mà HN / /CD
HN ⊥ AC (từ vuông góc tới song song)
AHN vuông tại N
f) Tia phân giác của góc BAC cắt đường tròn (O) tại F. Gọi M là giao điểm của OF và BC,K là
trung điểm của AB,I là giao điểm của KM và . HE Chứng minh rằng . AB EI = . AE EM.
Ta có AF là tia phân giác BAC nên BAF = CAF BF = CF BF = CF
F thuộc trung trực của BC
Ta có: OB = OC = R O thuộc trung trực của BC
OF là đường trung trực của BC
Mà M là giao điểm của OF và BC
Nên M là trung điểm của BC
ABC có M là trung điểm của BC và K là trung điểm của AB
KM là đường trung bình ABC
KM / /AC HE ⊥ KM HE ⊥ AC
Ta có ABHE là tứ giác nội tiếp đường tròn đường kính AB nên K là tâm của đường tròn này Trang 16
Do đó KH = KE K
EH cân tại K
KM vừa là đường cao vừa là đường trung trực của HE MH = ME
Vậy MEH cân tại M
Ta có ABHE là tứ giác nội tiếp nên EHM = EAB (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp)
Mà MEH cân tại M MEH = EHM MEH = MEI = EAB Xét E
AB và IEM , ta có: MEI = EAB
MIE = AEB = 90o E AB∽ I EM AB AE = EM EI A .
B EI = EM.AE ----HẾT---
SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN 5
NĂM HỌC: 2021 - 2022 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 5 - 2
Thời gian: 120 phút (không kể thời gian phát đề)
Giáo viên sửa phần màu đỏ theo mã đề của mình 2
Câu 18. (1,5 điểm). Cho parabol ( ) x 1 P : y =
và đường thẳng (d) : y = − x + 2 . 4 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 19. (1 điểm). Gọi x ,x là hai nghiệm của phương trình 2
5x − 3x + 2 = 0 . Không giải phương trình, hãy 1 2
tính giá trị của biểu thức sau: = 1 + 1 A x x 1 2
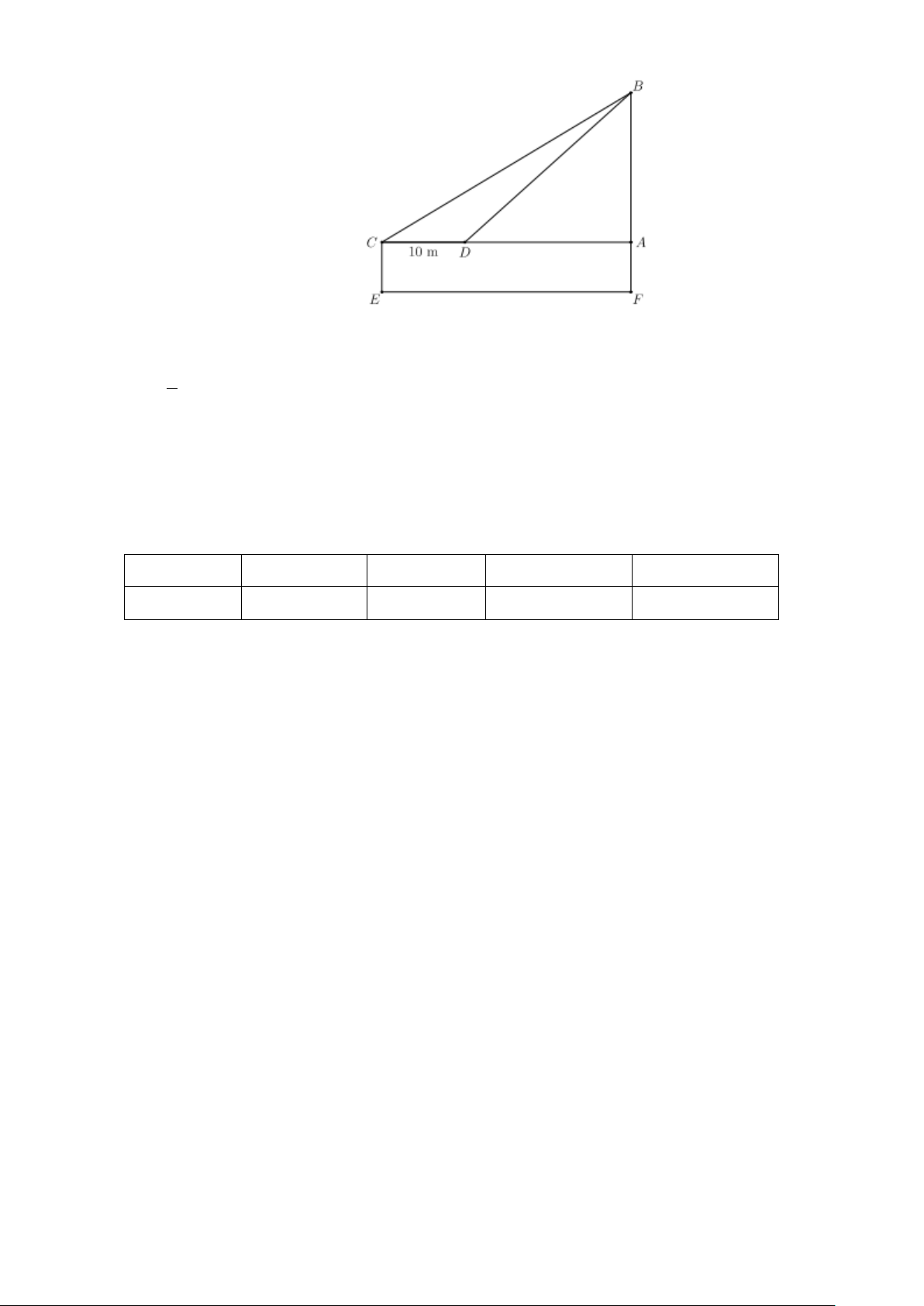
Câu 20. (1 điểm). Một người đứng tại hai điểm cách 10m nhìn thấy đỉnh tháp với góc nâng lần lượt là 40o
và 50o . Tính chiều cao của tháp (làm tròn đến mét), biết khoảng cách từ mắt người đó đến mặt đất là 1,6m . Trang 17
Câu 21. (1 điểm). Để đổi từ nhiệt độ F (Fahrentheit) sang độ C (Celsius), ta dùng công thức sau:
C = 5 (F − 32) 9
a) Hãy tính nhiệt độ C khi biết nhiệt độ F là 30o F .
b) Hãy viết biểu thức biểu diễn hàm số bậc nhất F theo biến số C . Tính nhiệt độ F khi biết nhiệt độ
C là 25oC .
Câu 22. (1 điểm). Cho bảng thống kê điểm trung bình như sau: Lớp 9A Lớp 9B Lớp 9C Lớp 9A và 9B Lớp 9B và 9C 9,2 7,55 8,5 8,3 8
Biết số học sinh lớp 9A là 25 em. Tìm số học sinh của hai lớp 9B và 9C.
Câu 23. (1 điểm). Tính diện tích tôn cần thiết để làm một cái thùng hình trụ có chiều cao là 80cm và đáy có diện tích là 2
5024cm (không tính diện tích các chỗ mối ghép và nắp thùng). Lấy = 3,14.
Câu 24. (1 điểm). Một cửa hàng điện máy thực hiện chương trình khuyến mãi giảm giá tất cả
các mặt hàng 10% theo giá niêm yết, và nếu hóa đơn khách hàng trên 10 triệu sẽ được giảm thêm
2% số tiền trên hóa đơn, hóa đơn trên 15 triệu sẽ được giảm thêm 3% số tiền trên hóa đơn, hóa
đơn trên 40 triệu sẽ được giảm thêm 6% số tiền trên hóa đơn. Ông An muốn mua một tỉ vi với giá
niêm yết là 9 200 000 đồng và một tủ lạnh với giá niêm yết là 8 000 000 đồng. Hỏi với chương
trình khuyến mãi của cửa hàng, ông An phải trã bao nhiêu tiền?
Câu 25. (2,5 điểm) Từ một điểm A nằm ngoài đường tròn (O; R) với OA 2R . Vẽ hai tiếp tuyến AD, AE
với (O) ( D,E là các tiếp điểm). Gọi H là giao điểm của DE và AO . Lấy điểm M thuộc cung
nhỏ DE ( M khác D, khác E, MD ME ). Tia AM cắt đường tròn (O; R) tại N . Đoạn thẳng
AO cắt cung nhỏ DE tại K.
a) Chứng minh AO ⊥ DE và 2
AD = AM.AN .
b) Chứng minh rằng NK là tia phân giác của góc DNE và tứ giác MHON nội tiếp.
c) Kẻ đường kính KQ của đường tròn (O; R) . Tia QN cắt tia ED tại C . Chứng minh . MD CE = . ME CD . Trang 18 ----HẾT--- Trang 19 HƯỚNG DẪN GIẢI 2
Câu 11. (1,5 điểm) Cho parabol ( ) x 1 P : y =
và đường thẳng (d) : y = − x + 2 . 4 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
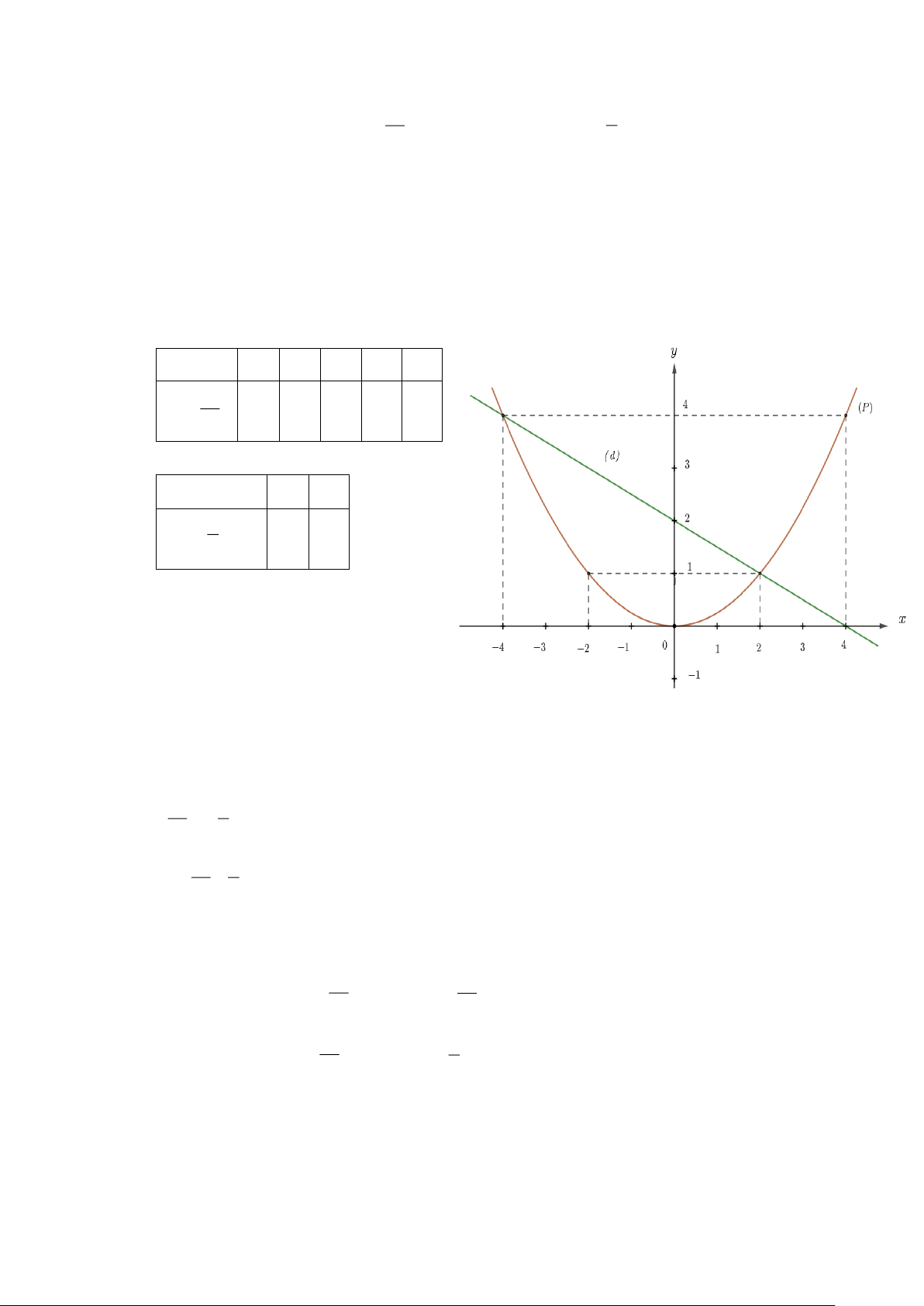
e) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. c) BGT: x −4 −2 0 2 4 2 x y = 4 1 0 1 4 4 x −4 0 1 y = − x + 2 4 2 2
f) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : 2 x 1 = − x + 2 4 2 2 x 1 + x − 2 = 0 4 2 x = 2 x = 4 − 2 2 Thay x 4
x = −4 vào y = , ta được: y = = 4 . 4 4 2 2 Thay x 2 x = 2 vào y = , ta được: y = = 1. 4 4
Vậy (−4; 4) , (2; 1) là hai giao điểm cần tìm. Trang 20