

















Preview text:
Bộ đề thi khảo sát chất lượng đầu năm môn Toán lớp 10
năm học 2020 – 2021
Đề thi khảo sát chất lượng đầu năm lớp 10 năm 2020 – 2021
Môn: Toán – Đề số 1
Câu 1: Cho biểu thức
x x +1 x −1 x − 4 A = − : x + x − 1 x − 1 x − 1
a. Tìm điều kiện xác định của biểu thức b. Rút gọn biểu thức
c. Tìm giá trị x nguyên để A nguyên
Câu 2: Cho phương trình 2 2
x − 2mx + m + m − 1 = 0
a. Giải phương trình khi m = 1
b. Xác định m để phương trình có hai nghiệm phân biệt x ,x thỏa mãn điều kiện 1 2 sau: 2 2
x + x + 2x − 3x x + 2x = 4 1 2 1 1 2 2 x
Câu 3: Cho parabol (P) 2 =
và đường thẳng (d) : y = 2x + 3 2
a. Vẽ (P) và d trên cùng hệ trục tọa độ
b. Tìm tọa độ giao điểm của (P) và d
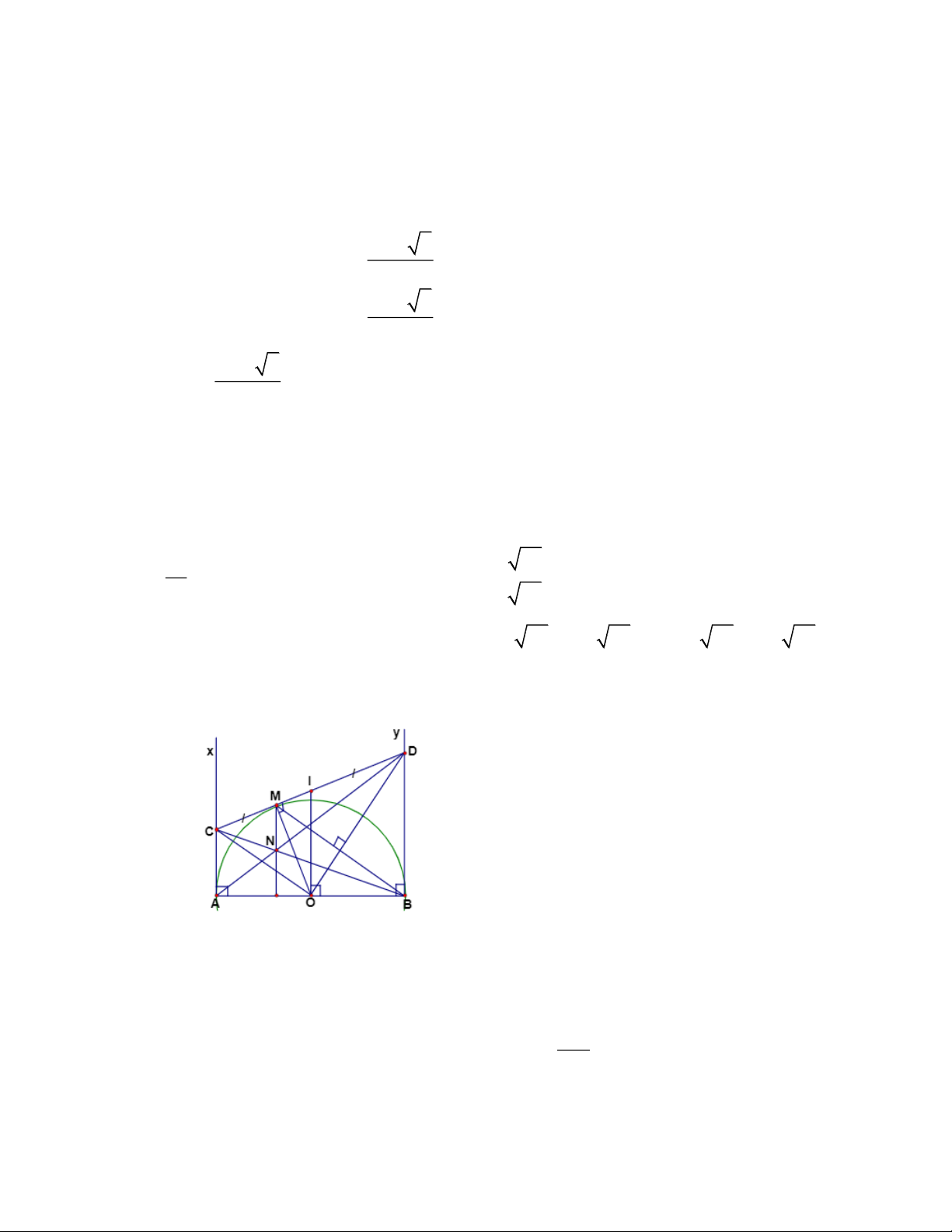
Câu 4: Cho nửa đường tròn đường kính AB = 2R . Từ A và B kẻ hai tiếp tuyến
Ax và By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ 3 cắt các tiếp
tuyến Ax, By lần lượt ở C, D. Các đường thẳng AD, BC cắt nhau tại N.
a. Chứng minh 4 điểm O, M, B, D cùng nằm trên một đường tròn, xác định tâm đường tròn đó b. Chứng minh: 0 COD = 90
c. Chứng minh AB là tiếp tuyến của đường tròn đường kính CD
d. Xác định vị trí của P để ACDB đạt giá trị nhỏ nhất
Câu 5: Cho 3 số thực dương thỏa mãn điều kiện xyz = 1. Chứng minh rằng: 1 1 1 + + 1 2 2 2 2 2 2 x + y + 1 y + z + 1 z + x + 1
Đề thi khảo sát chất lượng đầu năm lớp 10 năm 2020 – 2021
Môn: Toán – Đề số 2
Câu 1: Cho biểu thức x x 2 2 − x A = + : −
,x 0,x 1 − −
x 1 x 1 x x x + x a. Rút gọn biểu thức
b. Biết P (x) = 4 . Tìm x
c. Tìm giá trị của x để P (x) 1
Câu 2: Cho phương trình 2
mx − x − 5m + 2 = 0
a. Giải phương trình khi m = 2
b. Tìm điều kiện của m để phương trình có 2 nghiệm phân biệt x ,x thỏa mãn 1 2 2 2
x + x − 2 x + x = 1 1 2 ( 1 2)
Câu 3: Cho parabol (P) 2
= x + 5x + 2 và đường thẳng (d) : y = mx
a. Vẽ (P) và d trên cùng hệ trục tọa độ
b. Tìm điều kiện của m để d cắt (P) tại 2 điểm phân biệt sao cho một điểm có hoành độ bằng 1
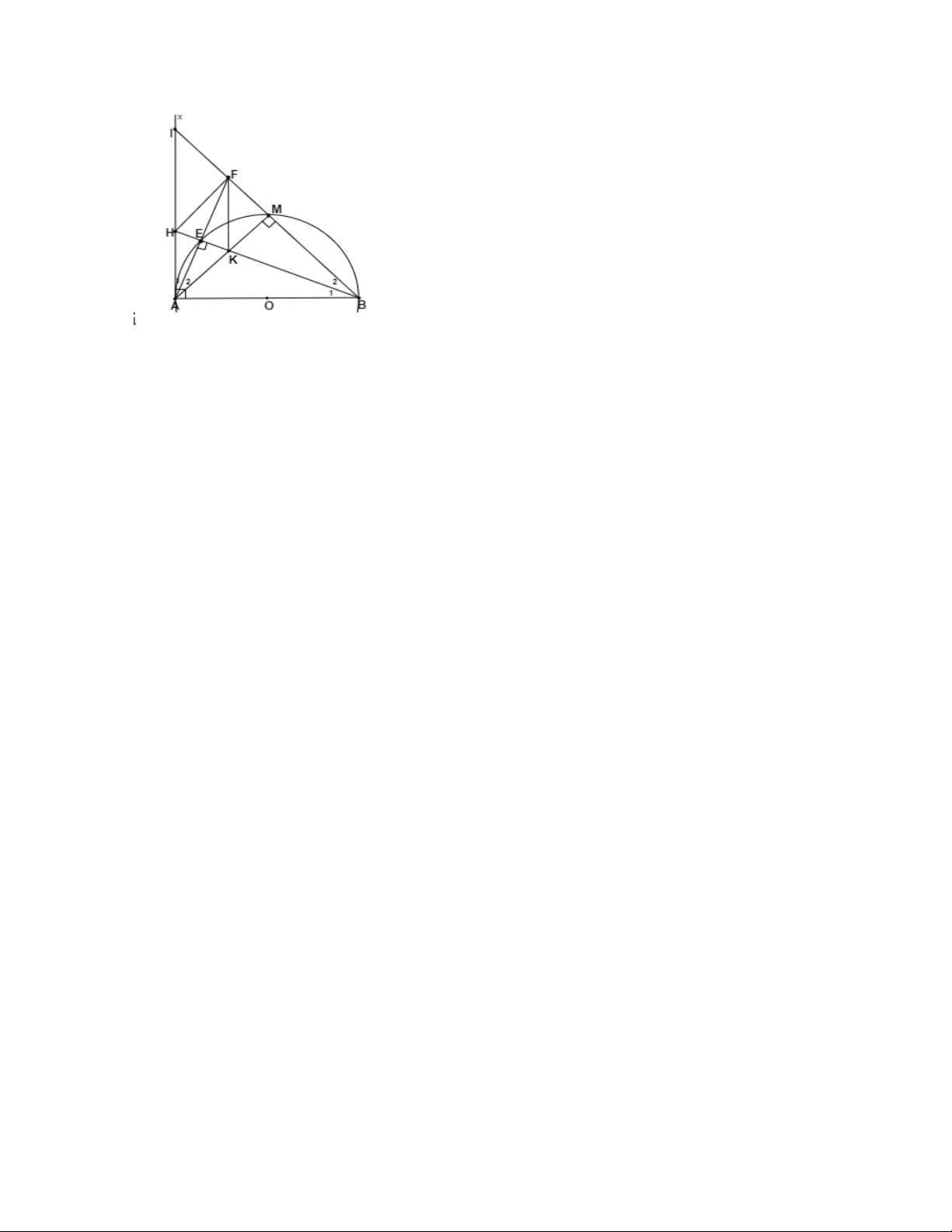
Câu 4: Cho nửa đường tròn tâm O đường kính AB điểm M bất kì nằm trên nửa
đường tròn. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn kẻ tiếp tuyến Ax.
Tia BM cắt Ax tại I, tia phân giác của MAI cắt nửa đường tròn tại E, cắt tia MN
tại F tia BE cắt Ax tại H, cắt AM tại K.
a. Chứng minh rằng: Tứ giác EFMK là tứ giác nội tiếp
b. Chứng minh tam giác BAF là tam giác cân c. AKFH là hình thoi
d. Xác định M để AKFI nội tiếp nửa đường tròn
Câu 5: Cho 2 số thực x, y không âm thay đổi. Tính giá trị lớn nhất, giá trị nhỏ
(1 − xy)(x − y)
nhất của biểu thức: A = ( 1 + x)2 (1+ y)2
Đề thi khảo sát chất lượng đầu năm lớp 10 năm 2020 – 2021
Môn: Toán – Đề số 3
Câu 1: Cho biểu thức
x x −1 x x +1 x − 2 P = − . x − x
x + x x + 2 a. Rút gọn biểu thức.
b. Tìm giá trị của x nguyên để P đạt giá trị nguyên. Câu 2: 2 2
x + xy + y −1 = 0
a. Giải hệ phương trình:
x − y = 3 + xy b. Giải phương trình: 2 2
25 − x − 10 − x = 3
Câu 3: Cho phương trình: 2 x − (m − ) 2 2
1 x + m − 3m = 0
Tìm giá trị tham số m để phương trình có 2 nghiệm phân biệt cùng âm
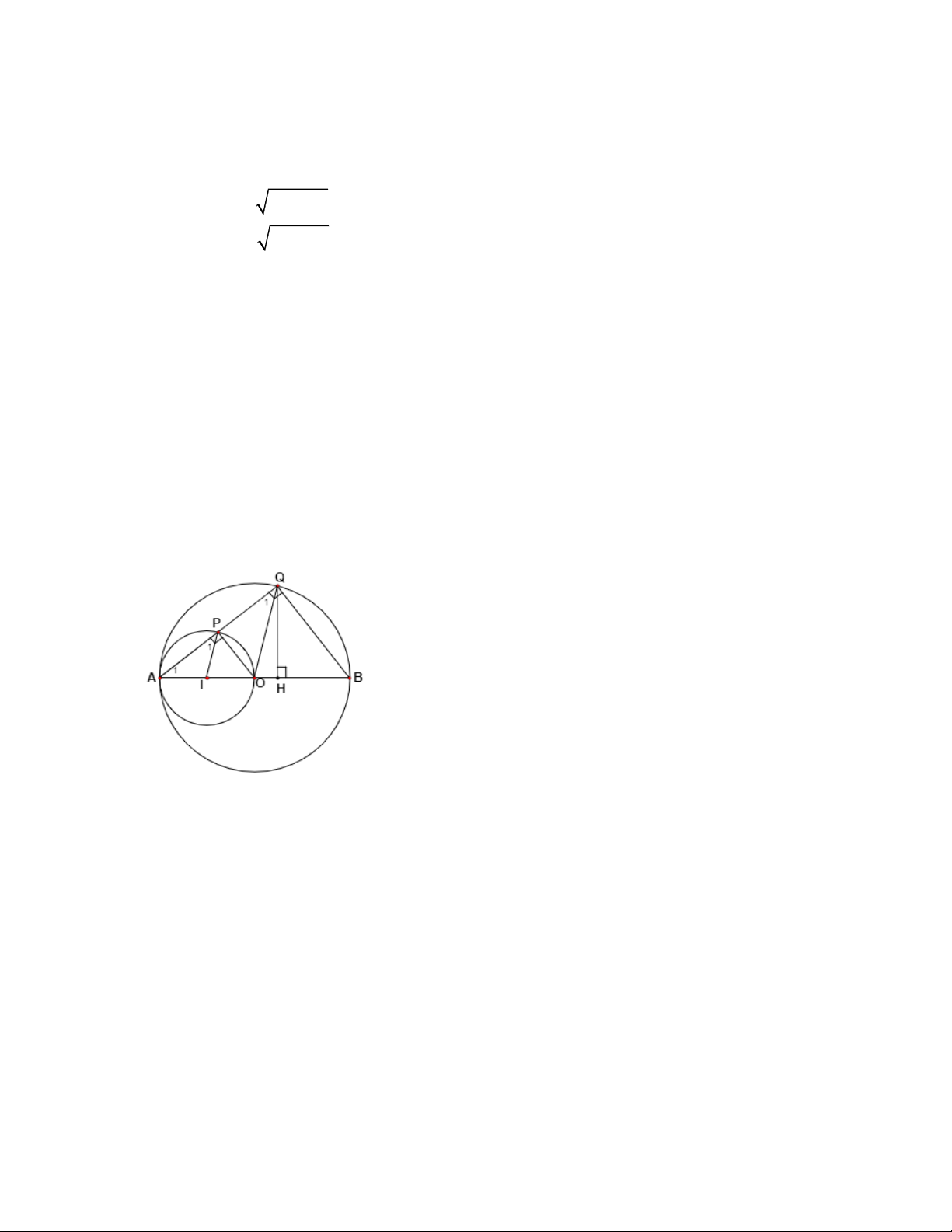
Câu 4: Cho đường tròn tâm O đường kính AB. I là trung điểm của OA. Đường
tròn tâm I đi qua A, P là điểm bất kì nằm trên đường tròn tâm I, AP cắ (O) tại Q
a. Chứng minh rằng (I), (O) tiếp xúc với nhau tại A
b. Chứng minh: IP / /OQ c. Chứng minh: PQ = PA
d. Xác định vị trí của P để tam giác ABQ có diện tích lớn nhất 1 1
Câu 5: Chứng minh rằng: x − 1 + y − 1 = x + y biết x 0, y 0, + = 1 x y
Đề thi khảo sát chất lượng đầu năm lớp 10 năm 2020 – 2021
Môn: Toán – Đề số 4
Câu 1: Chứng minh biểu thức sau không phụ thuộc vào x + − 3 2 x 2 x
x + x − x − 1 A = + . + + − x 2 x 1 x 1 x Câu 2:
1. Không sử dụng máy tính cầm tay giải phương trình và hệ phương trình sau: 2x + y = 7 b. 4 2
x − 6x + 8 = 0 a. x − 3y = 7
2. Tìm tham số m để hàm số y = (m − 2) x + 3m − 1 nghịch biến trên
Câu 3: Cho phương trình: 2 x − 2(m − )
1 x + m − 2 = 0
a. Giải phương trình với m = 1
b. Tìm m để phương trình có 2 nghiệm phân biệt x ,x thỏa mãn biểu thức: 1 2 2 2
x + x − x x = 4 1 2 1 2
Câu 4: Một người đi xe máy từ A đến B với vận tốc 40km/h. Khi đến B người đó
nghỉ 30 phút rồi quay về A với vận tốc 50km/h. Tính quãng đường AB biết tổng
thời gian người đó đi từ A đến B , từ B về A và thời gian nghỉ là 7 giờ 15 phút.
Câu 5: Cho đường tròn (O, R). BC là một dây cung (BC 2R ). Một điểm A di
động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC. Các đường cao
AD, CF, BE cắt nhau tại điểm H.
a. Chứng minh rằng: A EF A BC
b. Gọi A’ là trung điểm của BC. Chứng minh AH = 2OA'
c. Gọi A Là trung điểm của EF. Chứng minh rằng: RAA = OA'.AA' 1 1
d. Tìm vị trí của A để EF + FD + DE đạt giá trị lớn nhất 1 1 1
Câu 6: Cho x, y, z là những số thực dương và + + = 2 x + 1 y + 1 z + . Chứng 1 1 minh rằng: xyz 8
Đề thi khảo sát chất lượng đầu năm lớp 10 năm 2020 – 2021
Môn: Toán – Đề số 5
Câu 1: Cho biểu thức: 2x + 1 1 x + 4 P = − : 1− 2 x − 1 x − 1 x + x + 1 a. Rút gọn P
b. Tìm giá trị x dương để P nhận giá trị nguyên.
Câu 2: Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Một mảnh vườn hình chữ nhật có diện tích 2
420m . Nếu tăng chiều dài lên 10m
và giảm chiều rộng đi 6m thì diện tích mảnh vườn không đổi. Tính chiều dài và
chiều rộng của mảnh vườn. Câu 3: 1 3 + = 5
x − 2 y −1
1. Giải hệ phương trình: 2 7 + = 11
x − 2 y − 1
2. Trong mặt phẳng tọa độ Oxy cho đường thẳng 2
d : 3x − y = 1− m và parabol (P): 2 y = 2x
a. Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt với mọi m .
b. Gọi x ,x lần lượt là hoành độ giao điểm của 2 giao điểm.Tìm m để 1 2
(x −1 x −1 = 4 1 )( 2 )
Câu 4: Cho đường tròn tâm O đường kính AB = 2R, dây MN vuông góc với đáy
AB tại I sao cho IA < IB. Trên đoạn MI lấy điểm E (E không trùng M và I). Tia EA
cắt đường tròn tại điểm thứ 2 là K.
a. Chứng minh: IEKB nội tiếp đường tròn b. Chứng minh: 2 AM = A . E AK c. Chứng minh: 2 A .
E AK + BI.BA = 4R
d. Xác định vị trí điểm I sao cho tam giác MIO đạt giá trị lớn nhất
Câu 5: Cho x, y, z là những số thực dương. Chứng minh: x y z + + 1 y + 2z z + 2x 2y + x
Đáp án Đề thi khảo sát chất lượng đầu năm năm 2020 – 2021 Đề số 1 Câu 1: x − 1 0 x 1
a. Điều kiện xác định: x − 1 0 x 0 x 0
x x +1 x −1 x − 4 b. A = − : x + x − 1 x − 1 x − 1
( x 1)(x x 1) ( x 1)( x 1) x( x 1) x 4 + − + + − − + − A = − : x − 1 x − 1 x − 1 x − x +1 x − 4 A = −( x + 1) : x − 1 x −1
x − x +1− x +1 x −1 A = . x − 1 x − 4
− x + 2 x − 1 1 − A = . = x − 1 x − 4 x + 2 +
c. Để A đạt giá trị nguyên thì x + 2 U (1) = 1 x + 2 2 1
không có giá trị x nguyên nào để A đạt giá trị nguyên Câu 2:
a. Thay m = 1vào phương trình ta có:
x − x + = (x − )2 2 2 1 0 1 = 0 x = 1
Kết luận với m = 1 thì phương trình có nghiệm x = 1
b. Để phương trình có 2 nghiệm phân biệt x ,x thì: 1 2 ' 0 2 2
' = m − m − m + 1 = 1− m 0 m 1 b
x + x = − = 2m 1 2
Áp dụng hệ thức Vi – et ta có: a c 2 x .x = = m + m − 1 1 2 a 2 2
x + x + 2x − 3x x + 2x = 4 1 2 1 1 2 2
(x + x )2 − 5x x + 2 x + x = 4 1 2 1 2 ( 1 2) (2m)2 − 5( 2
m + m − 1) + 4m = 4 1 − + 5 m = 2 − − + = 2 m m 1 0 (Tm) 1 − − 5 m = 2 1 − 5 Vậy m =
thì phương trình có 2 nghiệm phân biệt thỏa 2 mãn: 2 2
x + x + 2x − 3x x + 2x = 4 1 2 1 1 2 2 Câu 3: a. Học sinh tự vẽ
b. Phương trình hoành độ giao điểm là: 2 x x = 2 + 10 2
= 2x + 3 x − 4x − 6 = 0 2 x = 2 − 10
Vậy tọa độ gia điểm của (P) và d là: A(2 + 10,7 + 2 10),B(2 − 10,7 − 2 10 ) Câu 4: Chứng minh a. Xét tứ giác OMBD có: 0
OMD + OBD = 180 Tứ giác OMBD nội tiếp đường OD
tròn tâm là trung điểm của OD và bán kính 2
b. Ta có : OC là phân giác góc AOM , OD là phân giác góc MOB Mặt khác 0
AOM + MOB = 180 0 COD = 90
c. Gọi I là trung điểm của CD
I là tâm đường tròn ngoại tiếp tam giác COD, IO là bán kính
Theo tính chất tiếp tuyến ta có: AC ⊥ AB, BD ⊥ AB BD / / AC . Vậy ACDB là hình thang
Ta lại có I là trung điểm của CD, O là trung điểm AB. Vậy OI là đường trung bình của hình thang ACDB
IO//AC, mà AC ⊥ AB IO ⊥ AB tại O. Vậy AB là tiếp tuyến tại O của
đường tròn đường kính CD
d. Ta có chu vi tứ giác ACDB = AB + AC + CD + BD mà AC + BD = CD nên chu
vi ACBD = AB + 2CD mà AB không đổi nên chu vi tứ giác ACDB nhỏ nhất
khi CD CD là khoảng cách giữa Ax và By tức là CD vuông góc với Ax và
By. Khi đó CD//AB. Vậy M là trung điểm của AB Câu 5: 2 2
x + y xy (x + y)( 2 2 2
x + y ) 2xy(x + y) 2 2 1 1
1 + x + y (x + y + z)xy 2 2 1 + x + y
(x + y + z)xy 1 z 1 x 1 y , , 2 2 2 2 2 2 1 + x + y
x + y + z 1 + y + z
x + y + z 1 + z + x x + y + z 1 1 1 z x y x + y + z + + + + = 1 = Vp 2 2 2 2 2 2 1 + x + y 1 + y + z 1 + z + x x + y + z x + y + z x + y + z x + y + z
Đáp án Đề thi khảo sát chất lượng đầu năm năm 2020 – 2021 Đề số 2 Câu 1: x x 2 2 − x A = + : − − −
x 1 x 1 x x x + x x ( x 1) + x 2 2 − x A = + : − x − 1 x − 1 x ( x x + 1) + 2 ( x 1) 2 + − + 2 x x x A = : x −1 x ( x +1)
x ( x + 2) x( x + 1) x A = . = x − 1 x ( x + 2) x − 1 x b. P (x) = 4 = x −
x + = ( x − )2 4 4 4 0 2 = 0 x = 2 x − 1
Vậy x = 2 thì P (x) = 4 2 1 3 x − + x x − x + 1 2 4
c. P (x) 1 1 0 0 x − 1 x − 1 x − 1 2 1 3 3 Do x − + x
x − 1 0 x 1 0 x 1 2 4 4 Vậy…… Câu 2:
a. Thay m = 2 vào phương trình ta có: 2 1 65
2x − x − 8 = 0 x = 4 1 65
Vậy với m = 2 phương trình có 2 nghiệm phân biệt x = 4
b. Để phương trình có 2 nghiệm phân biệt x ,x ta có: 0 1 2 2 = − ( − m) 2 1 4 2 5
m = 20m − 8m + 1 0 m 0 b 1 x + x = − = 1 2
Áp dụng hệ thức Viet ta có: a m c 2 − 5m x .x = = 1 2 a m Ta có biểu thức 2 −
x + x − (x + x ) = (x + x )2 2 2 1 2 5m 2 2
− 2x x − 2 x + x = − 2 − − 1 = 0 1 2 1 2 1 2 1 2
( 1 2) m m m 2 + 13 m = 2 − − = 9 9m 4m 1 0 (tm) 2 − 13 m = 9 Kết luận: …… Câu 3: a. Học sinh tự vẽ hình
b. Phương trình hoành độ giao điểm là: 2 2
x + 5x + 2 − mx = 0 x + (5 − m)x + 2 = 0
Để d cắt (P) tại 2 điểm phân biệt thì 0 = ( − m)2 2 5
− 4.2 = m − 10m + 17 0(*)
Áp dụng hệ thức Viet ta có: b
x + x = − = 5 − m 1 2 a c x .x = = 2 1 2 a
Do một giao điểm có hoành độ bằng 1 ta giả sử x = 1 x = 2 1 2
1+ 2 = 5 − m m = 2 thỏa mãn (*)
Vậy m = 1 thì d cắt (P) tại 2 điểm phân biệt sao cho có một điểm có hoành độ bằng 1 Câu 4: Chứng minh
a. Do M nằm trên nửa đường tròn nên 0 0
AMB = 90 AMF = 90
Do M nằm trên nửa đường tròn nên 0 0
AEB = 90 BEF = 90 0
AMF + BEF = 180 EFMK là tứ giác nội tiếp
b. Ta có AE là phân giác góc MAI IEM = MAE EA = ME EAB = MBE
Vậy BE là tia phân giác góc ABF (1)
Mặt khác BE ⊥ AF (2)
Từ (1) và (2) ta có tam giác BAF cân tại B
c. Theo chứng minh trên ta có tam giác BAF là tam giác cân tại B, BE là đường
cao nên BE cũng là trung tuyến EA = EF (3)
AF ⊥ HK (4), AE là phân giác của HAK Tam giác AHK là tam giác cân tại
A có AE là đường cao nên cũng là đường trung tuyến. Vậy EK = EH (5)
Từ (3), (4), (5) ta có AKHF là hình thoi
d. Ta có AKHF là hình thoi HA / /FK hay IA / /FK AKFI là hình thang
Để AKFI nột tiếp đường tròn thì AKFI là hình thang cân
AKFI là hình thang cân khi M là trung điểm của AB M là trung điểm của AB 0
ABM = IAM = 45
Tam giác ABI vuông tại A có 0 0
ABI = 45 AIB = 45 0
KAI = AIF = 45 AKFI là hình thang cân
Vậy khi M là trung điểm của cung AB thì tứ giác AKFI nội tiếp nửa đường tròn Câu 5: 2
x + y + xy + 1
(1 − xy)(x − y)
(1 − xy)(x − y) 2 1 A = = (
+ x)2 ( + y)2 ( + x)2 ( + y)2 (x + y + xy + )2 4 1 1 1 1 1 −1 1 P 4 4 1 − P = khi x = 0, y = 1 thì 4 1 P = khi x = 1, y = 0 4
Đáp án Đề thi khảo sát chất lượng đầu năm năm 2020 – 2021 Đề số 3
Câu 1: Điện kiện: x 0, x 1, x 2, x 0
x x −1 x x +1 x − 2 P = − . x − x
x + x x + 2 − ( x + x )3 3 1 ( ) 1 x − 2 P = − x ( x − ) x ( x + ) .x+2 1 1
( x 1)(x x 1) ( x 1)(x x 1) − + + + − + x − 2 P = − x ( x − ) x ( x + ) .x+2 1 1
(x x 1) (x x 1) + + − + x − 2 P = − . x x x + 2 2 x x − 2 2.(x − 2) P = . = x x + 2 x + 2 2 x − 2 8 b. P (x) ( ) = = 2 − x + 2 x + 2
Để P(x) nguyên thì x + 2U (8) = 1 , 2 , 4 , 8 ta có bảng sau x +2 -8 -4 -2 -1 1 2 4 8 x -10 -6 -4 -3 -1 0 2 6
Kết hợp với điều kiện xác định ta có: x = 6 thỏa mãn
Vậy x = 6 thì P(x) đạt giá trị nguyên Câu 2: a.
x + xy + y −1 = 0 (x − y)2 2 2 = 1− 3xy
x − y = 3 + xy
x − y = 3 + xy (3+ xy)2 2 2 = 1− 3xy
9 + 6xy + x y = 1− 3xy
x − y = 3 + xy
x − y = 3 + xy 2 2
x y + 9xy + 8 = 0 (1)
x−y = 3+xy (2)
Từ phương trình (1) ta đặt xy = t. Phương trình trở thành t = 1 − xy = 1 − 2
t + 9t + 8 = 0 t = 8 − xy = 8 − Với xy = 1
− kết hợp với phương trình (2) ta có : xy = 1 − (y + 2).y = 1 − y = 1 −
(x, y) = (1,− ) 1 x − y = 2 x = y + 2 x =1
Với xy = 8 kết hợp với phương trình (2) ta có :
Vậy hệ phương trình có nghiệm (x y) 11+ 3 17 1 − 1+ 3 17 11− 3 17 1 − 1− 3 17 , = , = , ( 2 2 2 2
x, y ) = (1, − ) 1 11+ 3 17 1 − 1+ 3 17 11− 3 17 1 − 1− 3 17 = , = , 2 2 2 2 b. 2 2
25 − x − 10 − x = 3 2 25− x 0 5 − x 5
Điều kiện xác định:
− 10 x 10 2 10 − x 0
− 10 x 10 2
a = 25− x Đặt ,(a,b 0) 2
b = 10 − x Phương trình trở thành:
a − b = 3 a − b = 3 a − b = 3 2 2 a − b = 15 ( a − b
)(a+b) = 15 a+b = 5 2 a = 4 25 − x = 4 x = 3 2 x = 9 (tm) = 2 b 1 − = x = 3 10 x 1 −
Vậy phương trình có nghiệm x = 3 hoặc x = -3 Câu 3: 2 x − (m − ) 2 2
1 x + m − 3m = 0
Để phương trình có hai nghiệm âm phân biệt ta có: ' 0 ( m − )2 2
1 − m + 3m 0 m 1 1 m 3 2 x .x 0 m − 3m 0 0 m 3 1 2 Vây 1 Câu 4: Chứng minh
a. Ta có: OI = OA − IA (O) và (I) tiếp xúc với nhau tại A
b. Tam giác OAQ cân tại O Q = A 1 1
Tam giác IAP cân tại O P = A 1 1
Q = P IP / /OQ 1 1 c. 0
APO = 90 (góc nội tiếp chắn nửa đường tròn) OP ⊥ AQ OP là đường
cao của tam giác OAQ mà OAQ cân tại O nên OP là đường trung tuyến AP = PQ
d. Kẻ HQ vuông góc với AB. 1 Ta có: S = . AB QH ABQ 2
Mà AB là đường kính không đổi nên S
lớn nhất khi QH lớn nhất hay Q ABQ
trùng với trung điểm của AB
Muốn Q trùng với trung điểm của AB thì P là trung điểm của cung AO
Thật vậy P là trung điểm của cung AO thì PI ⊥ AO mà IP / /OQ QO ⊥ AB tại O
Vậy Q là trung điểm của AB kéo theo H trùng với O, OQ lớn nhất neenn QH lớn nhất 1 1 Câu 5: + = 1 (1) x y 1 1 Ta có: +
= 1 x 1,y 1, x − 1, y − 1 x y
Từ (1) ta có: x + y = xy xy − x − y + 1 = 1 (x − 1)(y − 1) = 0 (x − )
1 (y − 1) = 1 2 (x − 1)(y − 1) = 2
x + y = x + y + 2 (x −1)(y −1) − 2 = ( x −1 + y −1)2
x + y = x − 1 + y − 1
Đáp án Đề thi khảo sát chất lượng đầu năm năm 2020 – 2021 Đề số 4
Câu 1: Điều kiện xác định: x 0, x 1 + − 3 2 x 2 x
x + x − x − 1 A = + . + + − x 2 x 1 x 1 x x + − + + x − x
( x 1) ( x 1 2 2 ) A = ( + x ) . 2 ( x −1)( x + + 1 1 ) x + − 2 + x 2 − x
( x 1)(x 1) A = ( + x ) . 2 ( x −1)( x + + 1 1 ) x ( 2 x )( x 1) (2
x )( x 1) ( x 1)( x 1)( x 1) + − + − + + − + A = ( + 1) . 2 ( −1)( +1) x x x x
(2+ x)( x − )1+(2− x)( x + )1 2 x A = = = 2 = const x x Câu 2: 1. 2x + y = 7 2x + y = 7 2x + y = 7 x = 4 a. x − 3y = 7
2x − 6y = 14 7y = 7 − y = 1 −
Vậy hệ phương trình có nghiệm (x, y) = (4, 1 − ) b. 4 2
x − 6x + 8 = 0 Đặt 2
x = t,(t 0) phương trình trở thành: 2
t − 6t + 8 = 0 2
' = 3 − 8 = 1 ' = 1 0 x = 2 2
x = 4 x = 2 t 3 1 4 − = + = 1 t = 3 − 1 = 2 x = 2 2 2 x = 2 x = − 2
Vậy phương trình có 4 nghiệm x = 2 ,x = 2
b. Để hàm số nghịch biến trên R thì m − 2 0 m 2
vậy m < 2 thì hàm số nghịch biến trên R Câu 3:
a. Thay m = 1 vào phương trình ta có: x = 1 2 2
x − 1 = 0 x = 1 x = 1 −
b. Để phương trình có 2 nghiệm phân biệt ta có: ' 0 ' = (m − )2 2
1 − m + 2 = m − 3m + 3 0 −b x + x = = 2 m − 1 1 2 ( )
Áp dụng hệ thức Viet ta có: a c x .x = = m − 2 1 2 a Theo bài ra: 2 2
x + x − x x = 3 1 2 1 2
(x + x )2 − 3x x = 3 1 2 1 2 2
4(m − 1) − 3(m − 2) = 3 7 m = 2 4m 11m 7 0 − + = 4 (tm) m = 1 7 Vậy m =
hoặc m = 1thì phương trình có 2 nghiệm phân biệt x ,x thỏa mãn biểu 4 1 2 thức: 2 2
x + x − x x = 4 1 2 1 2 Câu 4:
Gọi quãng đường AB là x (km) x > 0 x
Thời gian lúc đi từ A đến B của xe máy là: (km/h) 40 x
Thời gian lúc đi về từ B đến A của xe máy là: (km/h) 50
Do tổng thời gian người đó đi từ A đến B, từ B về A và thời gian nghỉ là 7,25 giờ
Khi đó ta có phương trình: x x 1 + + = 7,25 40 50 2
Dễ dàng tìm được x = 150 km
Vậy quãng đường AB là 150 km Câu 5: Chứng minh
a. Tứ giác BFEC nội tiếp
AEF = ACB ( cùng bù BEF )
AEF = ABC ( cùng bù FEC ). Vậy A EF A BC
b. Kẻ đường kính AK nên ta có KB // CH, KC // BH
BHKC là hình bình hànhA’ là trung điểm của KH KO là đường trung
bình của tam giác AHK AH = 2AO AA' R c. Ta có: A EF A BC =
(1) R là bán kính đường tròn ngoại tiếp AA R' 1
tam giác ABC, R’ là bán kính đường tròn ngoại tiếp tam giác AEF, AA’ là
trung tuyến tam giác ABC, AA là trung tuyến tam giác AEF 1
Ta lại có AEHF nội tiếp đường tròn đường kính AH nên đây cũng là đường
tròn ngoại tiếp tam giác AEF AH 2OA' Từ (1) .
R AA = AA'.R' = AA'. = AA'. .
R AA = AA'.OA' 1 1 2 2
d. Gọi M, N lần lượt là trung điểm của AC, AB
Ta có: OM ⊥ AC,ON ⊥ AB OA’, OM, ON lần lượt là các đường cao của tam giác OBC, OCA, OAB 1 S = S + S + S =
OA BC + OM AC + ON AB (2) ABC OCA OCB OAB ( '. . . ) 2 2S
= OA'.BC + OM.AC + ON.AB ABC . R AA AA Ta có: 1 OA' =
(theo chứng minh câu c). Mà
1 là tỉ số 2 trung tuyến AA' AA' AA EF
của 2 tam giác đồng dạng AEF và ABC nên 1 = . Tương tự ta có: AA' BC . R FD . R DE OM = , ON = AC AB . R AA . R FD . R DE 1 2S = R .BC + .AC + .AB Thay vào (2) ta được: ABC AA' AC AB 2S
= R EF + FD + DE ABC ( )
Do R không đổi nên EF + FD + DE đạt giá trị lớn nhất khi diện tích tam giác ABC đạt max 1 Ta có S
= BC.AD do BC không đổi nên diện tích tam giác ABC lớn nhất ABC 2 khi AD lớn nhất
Mà AD lớn nhất khi A nằm chính giữa cung BC . Câu 6: Ta có: 1 1 1 1 1 = 2 − − = 1− + 1− x + 1 y + 1 z + 1 y + 1 z + 1 y z yz = + 2 y + 1 z + 1 (y +1)(z +1) 1 xz 1 xy Tương tự ta có: 2 y + (x+ )1(z+ ) , 2 1 1 z + 1 (x+ )1(y + )1
Nhân các vế của bất dẳng thức ta được điều phải chứng minh
Đáp án Đề thi khảo sát chất lượng đầu năm năm 2020 – 2021 Đề số 5
Câu 1: Điều kiện xác đinh: x 0, x 1 2x + 1 1 x + 4 a. P = − : 1− 3 x − 1 x − 1 x + x + 1 2x + 1 1
x + x + 1− x − 4 P = ( −
x − 1)(x + x + 1) : x − 1 x + x + 1
2x + 1 − x − x − 1 x − 3 P = ( x − ) 1 (x + x + ) : 1 x + x + 1
x − 3 U (3) = 1 , 3 x ( x −1) x + x + 1 P = (
x − 1)(x + x + 1) . x − 3 x 3 P = = 1+ x − 3 x − 3
b. Để P nhận giá trị nguyên thì x − 3 U (3) = 1 , 3 x − 3 -1 1 -3 3 4 (TM) 16 (TM) 0 ( L) 81 (TM)
Kết luận : Vậy để P nhận giá trị nguyên thì x {1,16,81} Câu 2:
Gọi chiều dài mảnh vườn là x (m), x > 0. Diện tích mảnh vườn là 420 2 m 420
Chiều rộng của mảnh vườn là (m) x
Khi tăng chiều dài thêm 10 m thì chiều dài thay đổi là: x + 10 (m) 420
Khi giảm chiều rộng đi 6 m thì chiều rộng thay đổi là: – 6 (m) x
Do diện tích mảnh vườn không đổi nên ta có phương trình: ( x + ) 420 10 − 6 = 420 x x = 5 − + 5 29(TM) Dễ dàng tìm được x = 5 − − 5 29(L)
Kết luận: Vậy chiều dài mảnh vườn là 5
− + 5 29 m, chiều rộng của mảnh vườn là 3 + 3 29 m Câu 3:
1. Điều kiện: x 2, y 1 1 1 Đặt a = ,b = x − 2 y − 1
Hệ phương trình trở thành: a + 3b = 5 2a + 6b = 10 b = 1 2a + 7b = 11 2a + 7b = 11 a = 2 1 = 2 5 x − 2 x = 2 1 = 1 y = 1 y −1
Vậy hệ phương trình có nghiệm (x y) 5 , = ,1 2 2.
a. Phương trình hoành độ giao điểm: 2 2 2 2
2x = 3x − 1 + m 2x − 3x + 1 − m = 0 2 = − ( 2 − m ) 2 3 4.2. 1 = 1+ 8m 0 m
Vậy (d) luôn cắt (P) tại 2 điểm phân biệt −b 3 x + x = = 1 2
b. Áp dụng hệ thức Viet ta có: a 2 c 2 x .x = = 1− m 1 2 a Từ hệ thức: ( − −
x − 1)(x − 1) = 4 x .x − (x + x ) 7 + 1 = ( 2 1 − m ) 1 7 2 − =
m = 4 m = 2 1 2 1 2 1 2 2 2 2 Vậy m = 2 …… Câu 4: Chứng minh
a. Ta có AB là đường kính, K thuộc đường tròn nên 0 AKB = 90 Ta có: 0
KEB = EIB = 90 nên tứ giác IEKB nội tiếp
b. Ta có: EAM = MAK ( cùng chắn cung nhỏ MK) 1 1 EMA = sdAN =
sdAM = MKA AM E AK M 2 2 AE MA 2 = . AE AK = MA MA KA
Tam giác MAB vuông tại M và MI là đường cao nên 2 I .
B BA = MB . Do đó: 2 2 2 A .
E AK + BI.BA = AM + MB = 4R
d. Chu vi tam giác OIM bằng MI + OI + MO
Mà MO = R không đổi nên chu vi tam giác IMO lớn nhất khi MI + MO lớn nhất 2
Ta có: (MI+MO) 2( 2 2 MI + IO ) 2 2
− 2OM = 2R MI + MO R 2 R 2
Dấu bằng xảy ra khi MI = MO = 2
Vậy chu vi tam giác OIM lớn nhất khi I nằm trên AB và cách O một khoảng R 2 bằng 2 Câu 5: Ta có: 2 2 x y z x y z
(x+ y + z)2 2 + + = + + y + 2z z + 2x 2y + x xy + 2xz yz + 2xy xz + 2yz
3(xy + yz + zx)
(x+ y + z)2
Có nghĩa là ta sẽ chứng minh ( hay
xy + yz + zx) 1 3
(x + y + z)2 3(xy + yz + zx)
Đây là bất đẳng thức quen thuộc. Bạn đọc tự chứng minh




