Bộ đề thi Quốc Gia 2020 môn Toán phát triển từ đề minh họa-Tập 2

Bộ đề thi Quốc Gia 2020 môn Toán phát triển từ đề minh họa-Tập 2. Tài liệu được biên soạn dưới dạng file PDF bao gồm 92 trang tổng hợp các kiến thức tổng hợp giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!

43 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2020

Môn: Toán

Thông tin:

92 trang 8 tháng trước

Tác giả:

Profile Mỹ Duyên
Trang 1
ĐỀ 1
PHÁT TRIỂN TỪ ĐỀ MINH HỌA
LẦN 2 NĂM 2020
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Trong một hộp bút gồm có 8 cây bút bi, 6 cây bút chì và 10 cây bút màu. Hỏi có bao nhiêu cách
chọn ra một cây bút từ hộp bút đó?
A.
48.
B.
60.
C.
480.
D.
24.
Câu 2: Cho cấp số cộng
( )
n
u
với
và
13 6
u 2u 5.=+
Khi đó số hạng đầu
1
u
và công sai
d
bằng
A.
1
v5u4àd= =
. B.
1
v4u3àd= =
.
C.
1
v3u4àd= =
. D.
1
v5u3àd= =
.
Câu 3: Nghiệm của phương trình
3
3
log ( 3) 3x -=
là
A.
33x =+
. B.
3x =
. C.
33x =
. D.
33x =-
.
Câu 4: Cho khối lập phương
.ABCD A B C D
có
( )
20AC a a=
. Thể tích của khối lập phương đã
cho bằng
A.
2
.a
B.
3
.
3
a
C.
3
.a
D.
3.a
. Câu 5: Tập xc đnh của hm số
( )
2
32y x x
= − +
l:
A.
( ) ( )
;1 2;− +
. B. . C.
( )
0;+
. D.
( )
1;2
.
Câu 6: Tìm nguyên hàm của hàm số
( )
sin2f x x=
.
A.
2cos2xC−+
. B.
1
cos2
2
xC+
. C.
2cos2xC+
. D.
1
cos2
2
xC−+
.
Câu 7: Cho khối lăng trụ
.ABC A B C
có thể tích là
V
, thể tích của khối chóp
.C ABC
là:
A.
1
6
V
. B.
1
2
V
. C.
1
3
V
. D.
2V
.
Câu 8: Hình nón có bn kính đy bằng
2
(cm), góc ở đỉnh bằng
60
. Thể tích khối nón là
A.
( )
3
83
cm
9
V
=
. B.
( )
3
83
cm
2
V
=
.
C.
( )
3
8 3 cmV
=
. D.
( )
3
83
cm
3
V
=
.
Trang 2
Câu 9: Tính bán kính
r
của khối cầu có thể tích là
( )
3
36 cmV
=
.
A.
( )
3 cmr =
. B.
( )
6 cmr =
. C.
( )
4 cmr =
. D.
( )
9 cmr =
.
Câu 10: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng no dưới đây?
A.
( )
0;1
B.
( )
1;0−
. C.
( )
1;1−
. D.
( )
1; +
.
Câu 11: Với
a
là số thực dương tùy ý,
( )
5
3
log a
bằng
A.
3
5
log
3
a



. B.
3
1
log
5
a
. C.
3
5 log a+
. D.
3
5log a
.
Câu 12: Diện tích xung quanh của hình nón có độ di đường sinh
l
v bn kính đy
r
bằng
A.
4 rl
. B.
rl
. C.
1
3
rl
. D.
2 rl
.
Câu 13: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại điểm
A.
2x =−
. B.
2x =
. C.
1x =
. D.
1x =−
.
Câu 14: Đồ th của hàm số no dưới đây có dạng như đường cong trong hình dưới?
A.
32
y x 3x 4= - + -
B.
32
y x 3x 4= - +
Trang 3
C.
42
y x 2x 3= - -
D.
x1
y
x1
-
=
+
Câu 15: Tiệm cận ngang của đồ th hàm số
32
1
x
y
x
+
=
−
là
A.
2y =−
. B.
3y =
. C.
2x =−
. D.
3x =
.
Câu 16: Tập nghiệm của bất phương trình
ln 1x
là
A.
( )
;e +
. B.
( )
0;+
. C.
)
;e +
. D.
( )
;e−
.
Câu 17: Cho hàm số . Đồ th của hàm số như hình vẽ bên.
Số nghiệm của phương trình là
A. . B. . C. . D. .
Câu 18: Nếu
( )
2
0
d6f x x =
thì
( )
2
0
3df x x
bằng
A. 18. B. 6. C.
3
. D.
2
.
Câu 19: Số phức liên hợp của số phức
34zi=+
là
A.
43zi= − +
. B.
34zi=−
. C.
34zi= − −
. D.
43zi=+
.
Câu 20: Cho hai số phức
1
1zi= − +
và
2
32zi=+
. Phần thực của số phức
12
zz+
bằng
A.
1
. B. 2. C. 4. D. -1
.
Câu 21: Trong mặt phẳng toạ độ, hai điểm
( )
1;2A −
,
( )
3; 4B −
lần lượt l điểm biểu diễn cho số phức
1
z
,
2
z
. Điểm biểu diễn cho số phức
12
z z z=
l điểm no sau đây?
A.
( )
10;5N
. B.
( )
5;10M
. C.
( )
11;10P −
. D.
( )
10; 11Q −
.
Câu 22: Trong không gian
Oxyz
, cho điểm
( )
1;2;3A −
. Tìm tọa độ điểm điểm
B
đối xứng với điểm
A
qua mặt phẳng
( )
Oyz
.
( )
42
f x ax bx c++=
( )
,,abcÎ
( )
y f x=
( )
4 3 0fx-=
4
3
2
0
Trang 4
A.
( )
1;2;3B
. B.
( )
1;2; 3B −
. C.
( )
1; 2; 3B − − −
. D.
( )
1; 2;3B −
.
Câu 23: Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 4 2 6 5 0S x y z x y z+ + + − + + =
. Mặt cầu
( )
S
có
bán kính là
A.
3
. B.
5
. C.
2
. D.
7
.
Câu 24:Trong không gian với hệ trục toạ độ
Oxyz
, cho mặt phẳng
( )
P
:
2 3 0zx− + =
. Một vectơ php
tuyến của
( )
P
là:
A.
( )
0;1; 2u =−
. B.
( )
1; 2;3v =−
. C.
( )
2;0; 1n =−
. D.
( )
1; 2;0w =−
.
Câu 25: Trong không gian
Oxyz
, cho đường thẳng
:d
1
2
xt
yt
zt
=
=−
=+
. Đường thẳng
d
đi qua điểm no sau
đây?
A.
( )
1; 1;1K −
. B.
( )
1;2;0H
. C.
( )
1;1;2E
. D.
( )
0;1;2F
.
Câu 26. Cho hình chóp tứ giác  có đy l hình vuông , AC=
2a
, 
󰇛

󰇜
và
3SA a=
.
Góc giữa đường thẳng  và (ABCD) là
A. . B. . C.
0
60
. D. .
Câu 27. Cho hàm số
󰇛
󰇜
, bảng xét dấu của
󰆒
󰇛
󰇜
như sau:
Số điểm cực tr của hàm số đã cho l
A.  B. 3 C. . D. .
Câu 28. Biết giá tr lớn nhất và giá tr nhỏ nhất của hàm số

 trên
󰇟

󰇠
lần lượt
là và . Giá tr của bằng
A.
. B.
28
3
−
. C. . D.
.
Câu 29. Xét tất cả cc số thực dương và thỏa mãn
( )
2
2
ln . ln
b
ab
e

=


. Tích  thuộc khoảng no
trong cc khoảng sau đây?
A.
( )
0;1
. B.
󰇛

󰇜
. C. 󰇡
󰇢. D.
󰇛

󰇜
..
Câu 30. Cho hàm số
󰇛
󰇜
có bảng biến thiên như sau:
Số nghiệm thực của phương trình 
󰇛
󰇜
là
Trang 5
A. . B.
1
. C. . D. .
Câu 31: Tập nghiệm của bất phương trình
2
33
log 2log 3 0xx+ −
là :
A.
1
;3 .
27



B.
( ) ( )
; 3 1; .− − +
C.
( )
3;1 .−
D.
1
;27 .
3



Lời giải
Đặt
3
logtx=
bất phương trình đã cho trở thành
2
2 3 0 3 1t t t+ − −
3
1
3 log 1 3
27
xx −
Câu 32 : Cho khối nón có đường sinh bằng 5 v bn kính đy bằng 3. Thể tích khối nón bằng?
A.
18
. B.
12
. C.
24
. D.
15
.
Câu 33 : Cho tích phân
2
0
cosI x xdx
=
và
2
, cosu x dv xdx==
. Khẳng đnh no sau đây đúng?
A.
2
0
2 sinsin
0
I x x x xdx
=+
. B.
2
0
sin
0
sinI x x x xdx
=−
.
C.
2
0
sin
0
sinI x x x xdx
=+
. D.
2
0
2 sinsin
0
I x x x xdx
=−
.
Câu 34 : Cho hình phẳng (D) được giới hạn bởi cc đường
( )
2 1, , 0, 1f x x Ox x x= + = =
. Tính thể
tích V của khối tròn xoay tạo thnh khi quay (D) xung quanh trục
Ox
được tính theo công thức?
A.
1
0
21V x dxp=+
ò
B.
( )
1
0
21V x dxp=+
ò
C.
( )
1
0
21V x dx=+
ò
D.
1
0
21V x dx=+
ò
Câu 35 : Cho hai số phức
12
3 2 ; 1 3 .= − = +z i z i
Tổng của hai số phức
12
;zz
là :
A.
4.+ i
B.
9.− i
C.
1 9 .−−i
D.
4 5 .− i
Câu 36: Gọi
12
,zz
là nghiệm của phương trình
2
2 10 0zz+ + =
. Giá tr của biểu thức
22
12
A z z=+
là:
A.
10
B. 2
10
C. 0 D. 20
Câu 37: Trong không gian hệ tọa độ Oxyzx, cho A(-1;0;1), B(-2;1;1). Phương trình mặt trung trực của
đoạn AB có phương trình l:
A.
20xy− − =
B.
10xy− + =
C.
20xy−+=
D.
20xy− + + =
Trang 6
Câu 38: Trong không gian với hệ tọa độ Oxyz, cho
( )
:2 2 3 0x y z
− + − =
. Phương trình đường thẳng
d đi qua A(2;-3;-1) song song
( )
và mặt phẳng (Oyz) là:
A.
2
3
1
xt
y
zt
=−
=−
= − +
B.
2
32
1
x
yt
zt
=
= − +
= − +
C.
2
32
1
x
yt
zt
=
= − −
= − +
D.
2
23
1
xt
yt
zt
=
=−
=−
Câu 39: Câu 39. Lớp 11A có
40
học sinh trong đó có
12
học sinh đạt điểm tổng kết môn Hóa học loại
giỏi và
13
học sinh đạt điểm tổng kết môn Vật lí loại giỏi. Biết rằng khi chọn một học sinh của lớp đạt
điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi có xác suất là
0,5
. Số học sinh đạt điểm tổng kết giỏi
cả hai môn Hóa học và Vật lí là
A.
4
. B.
7
. C.
6
. D.
5
.
Câu 40: Cho hình chóp S.ABCD có đy ABCD l hình chữ nhật, AB = a,
23AD a=
Cạnh bên SA vuông góc với đy, biết tam giác SAD có diện tích
2
3Sa=
. Tính khoảng cách
từ C đến (SBD).
Câu 41: Cho hàm số
32
( 3 6) 5y x mx m x= − − + − + +
với m là tham số. Có bao nhiêu giá tr
nguyên của m để hàm số nghch biến trên khoảng
( )
;− +
?
A. 2. B. 3. C. 4. D. 5.
Câu 42:Tỉ lệ tăng dân số hng năm của Nhật l 0,2%. Năm 1998, dân số của Nhật l
125 932 000. Vo năm no dân số của Nhật sẽ l 140 000 000 ? ( Kết quả làm tròn đến hàng đơn vị)
A. 2061. B. 2055. C. 2051. D. 2045.
Câu 43: Ta xc đnh được các số a, b, c để đồ th hàm số
32
y x ax bx c= + + +
đi qua điểm
( )
1;0
và
có điểm cực tr
( )
2;0−
. Tính giá tr biểu thức
2 2 2
T a b c= + +
.
A. 25. B. -1. C. 7. D. 14.
Câu 44: Cho hình trụ có bn kính đy bằng a. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng
2
a
, thiết diện thu được là một hình vuông.Thể tích của
khối trụ được giới hạn bằng hình trụ đã cho bằng
A.
3
3.a
B.
3
3.a
C.
3
3
.
4
a
D.
3
.a
Trang 7
Câu 45: Cho hàm số
()y f x=
thỏa mãn
(ln3) 3f =
và
2
'( )
11
x
xx
e
f x x
ee
=
+ − +
.
Khi đó
ln3
0
()
x
e f x dx
bằng
A.
10 8 2
3
−−
B.
20 8 2
.
3
−
C.
20 8 2
.
3
+
D.
10 8 2
3
−
Câu 46: Cho hàm số
()y f x=
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
3
;
2

−


của phương trình
2 (2cos ) 9 0fx−=
là:
A.
5.
B.
4
C.
3.
D.
2.
Câu 47: Cho
x
,
y
là các số thực dương thỏa mãn
2
log 4 1
9 24
xy
xy
xy

+
= − + −

+

. Tính giá tr nhỏ nhất
của biểu thức
2
2
Px
y
=+
bằng.
A.
4
B.
10
C.
6
D.
2
Câu 48:Cho hàm số
2
1
x mx m
y
x
++
=
+
gọi
S
là tập hợp tất cả các giá tr thực của tham số
m
sao cho
1;2
2Max y =
.Tổng các phần tử của
S
là.
A.
2
3
. B.
11
6
. C.
11
6
−
. D.
5
2
−
.
Lời giải.
Trang 8
Câu 49: Cho hình chóp đều
.S ABC
có tất cả các cạnh bằng
3
và
,,M N P
lần lượt là trọng tâm của
tam giác
,,SAB SBC SAC
. Thể tích khối đa diện có cc đỉnh là
, , , , ,A B C M N P
là
A.
2
.
12
B.
42
.
3
C.
82
.
3
D.
92
.
4
Câu 50: Cho hàm số
( )
(
)
2
ln 1y f x x x= = + +
. Số giá tr nguyên dương
a
thỏa mãn bất phương
trình
( ) ( )
3 ln 0f a f a− +
là
A.
1.
B.
2.
C.
3.
D.
4.
ĐÁP ÁN CHI TIẾT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
B
A
C
A
D
C
D
A
A
D
B
B
A
B
C
A
A
B
B
B
A
A
C
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
B
B
A
B
A
B
D
B
A
D
C
B
D
D
C
C
A
B
B
A
C
C
B
B
Câu 1: Trong một hộp bút gồm có 8 cây bút bi, 6 cây bút chì và 10 cây bút màu. Hỏi có bao nhiêu cách chọn
ra một cây bút từ hộp bút đó?
A.
48.
B.
60.
C.
480.
D.
24.
Lời giải
Chọn D
Áp dụng quy tắc cộng:
Số cách chọn ra một cây bút từ hộp bút đó l
8 6 10 24.+ + =
Câu 2: Cho cấp số cộng
( )
n
u
với
và
13 6
u 2u 5.=+
Khi đó số hạng đầu
1
u
và công sai
d
bằng
A.
1
v5u4àd= =
. B.
1
v4u3àd= =
.
C.
1
v3u4àd= =
. D.
1
v5u3àd= =
.
Lời giải
Chọn B
Ta có
( )
( )
11
92
1
1
13 6 1
11
85
5
4 3 0
3
2 5 2 5
4
12 2 5 5
u d u d
uu
ud
u
u u u d
d
u d u d
+ = +
=
−=
=
= + − = −
=
+ = + +
.
Trang 9
Câu 3: Nghiệm của phương trình
3
3
log ( 3) 3x -=
là
A.
33x =+
. B.
3x =
. C.
33x =
. D.
33x =-
.
Lời giải
Chọn A
( )
( )
3
3
3
3
30
33
log 3 3 3 3
3 3 3 3
33
x
xx
xx
xx
x
ì
ï
ìì
ïï
->
ï
>>
ïï
ï
ï ï ï
- = Û Û Û Û = +
í í í
ï ï ï
- = = +
-=
ï ï ï
ïï
îî
ï
ï
î
Câu 4: Cho khối lập phương
.ABCD A B C D
có
( )
20AC a a=
. Thể tích của khối lập phương đã
cho bằng
A.
2
.a
B.
3
.
3
a
C.
3
.a
D.
3.a
Lời Giải
Chọn C
Gọi
x
là cạnh hình lập phương.
.ABCD A B C D
là hình lập phương nên
ABCD
l hình vuông do đó
2AC x=
.
Mặt khc, theo đề bài ta có
( )
2, 0AC a a=
. Suy ra cạnh của hình lập phương bằng
xa=
.
Vậy thể tích của khối lập phương bằng
3
.Va=
. Câu 5: Tập xc đnh của hm số
( )
2
32y x x
= − +
l:
A.
( ) ( )
;1 2;− +
. B. . C.
( )
0;+
. D.
( )
1;2
.
Lời giải
Chọn A
Hm số
( )
2
32y x x
= − +
l hm ly thừa có số m
nên hm số xc đnh khi
2
3 2 0xx− +
( ) ( )
;1 2;x − +
. Vậy tập xc đnh của hm số l
( ) ( )
;1 2;− +
.
Câu 6: Tìm nguyên hàm của hàm số
( )
sin2f x x=
.
A.
2cos2xC−+
. B.
1
cos2
2
xC+
. C.
2cos2xC+
. D.
1
cos2
2
xC−+
.
Trang 10
Lời giải
Chọn D
1
sin2 d cos2
2
x x x C= − +
.
Câu 7: Cho khối lăng trụ
.ABC A B C
có thể tích là
V
, thể tích của khối chóp
.C ABC
là:
A.
1
6
V
. B.
1
2
V
. C.
1
3
V
. D.
2V
.
Lời giải
Chọn C
Gọi
h
là khoảng cách từ
C
đến mặt phẳng
( )
ABC
và
B
là diện tích tam giác
ABC
. Khi
đó, thể tích lăng trụ
V Bh=
, thể tích khối chóp
.C ABC
là
.
1
3
C ABC
V Bh
=
. Do đó,
.
1
3
C ABC
VV
=
.
Câu 8: Hình nón có bn kính đy bằng
2
(cm), góc ở đỉnh bằng
60
. Thể tích khối nón là
A.
( )
3
83
cm
9
V
=
. B.
( )
3
83
cm
2
V
=
.
C.
( )
3
8 3 cmV
=
. D.
( )
3
83
cm
3
V
=
.
Lời giải
Ta có bn kính đy
2r =
, đường cao
tan30
r
h =
23h=
.
Vậy thể tích khối nón
2
1
3
V r h
=
1
.4.2 3
3
=
( )
3
83
cm
3
=
.
Câu 9: Tính bán kính
r
của khối cầu có thể tích là
( )
3
36 cmV
=
.
A.
( )
3 cmr =
. B.
( )
6 cmr =
. C.
( )
4 cmr =
. D.
( )
9 cmr =
.
Trang 11
Lời giải
Chọn A
Ta có
3
4
3
Vr
=
3
3
4
V
r
=
3
27r=
3r=
. Vậy
( )
3 cmr =
.
Câu 10: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng no dưới đây?
A.
( )
0;1
B.
( )
1;0−
. C.
( )
1;1−
. D.
( )
1; +
.
Lời giải
Chọn A
Câu 11: Với
a
là số thực dương tùy ý,
( )
5
3
log a
bằng
A.
3
5
log
3
a



. B.
3
1
log
5
a
. C.
3
5 log a+
. D.
3
5log a
.
Lời giải
Công thức
( )
5
3
log a
=5
( )
3
log a
chọn câu D
Câu 12: Diện tích xung quanh của hình nón có độ di đường sinh
l
v bn kính đy
r
bằng
A.
4 rl
. B.
rl
. C.
1
3
rl
. D.
2 rl
.
Lời giải
Công thức B
Câu 13: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Trang 12
Hàm số đã cho đạt cực tiểu tại điểm
A.
2x =−
. B.
2x =
. C.
1x =
. D.
1x =−
.
Lời giải
Dựa vào bảng biến thiên chọn B
Câu 14: Đồ th của hàm số no dưới đây có dạng như đường cong trong hình dưới?
A.
32
y x 3x 4= - + -
B.
32
y x 3x 4= - +
C.
42
y x 2x 3= - -
D.
x1
y
x1
-
=
+
Lời giải
Đồ th hàm bậc 3 với a<0 chọn câu A
Câu 15: Tiệm cận ngang của đồ th hàm số
32
1
x
y
x
+
=
−
là
A.
2y =−
. B.
3y =
. C.
2x =−
. D.
3x =
.
Lời giải
Ta có TCN:
3
a
y
c
==
chọn B
Câu 16: Tập nghiệm của bất phương trình
ln 1x
là
A.
( )
;e +
. B.
( )
0;+
. C.
)
;e +
. D.
( )
;e−
.
Lời giải
ln 1x x e
nên chọn C
Câu 17: Cho hàm số . Đồ th của hàm số như hình vẽ bên.
Số nghiệm của phương trình là
( )
42
f x ax bx c++=
( )
,,abcÎ
( )
y f x=
( )
4 3 0fx-=
Trang 13
A. . B. . C. . D. .
Lời giải
( )
3
4
fx=
dựa vo đồ th chọn A
Câu 18: Nếu
( )
2
0
d6f x x =
thì
( )
2
0
3df x x
bằng
A. 18. B. 6. C.
3
. D.
2
.
Lời giải
( )
2
0
3df x x
=3
( )
2
0
df x x =
3.6=18 chọn A
Câu 19: Số phức liên hợp của số phức
34zi=+
là
A.
43zi= − +
. B.
34zi=−
. C.
34zi= − −
. D.
43zi=+
.
Lời giải
Số phức liên hợp a-bi chọn B 3-4i
Câu 20: Cho hai số phức
1
1zi= − +
và
2
32zi=+
. Phần thực của số phức
12
zz+
bằng
A.
1
. B. 2. C. 4. D. -1
.
Lời giải
12
zz+
= -1+3+3i=2+3i chọn B
Câu 21: Trong mặt phẳng toạ độ, hai điểm
( )
1;2A −
,
( )
3; 4B −
lần lượt l điểm biểu diễn cho số phức
1
z
,
2
z
. Điểm biểu diễn cho số phức
12
z z z=
l điểm no sau đây?
A.
( )
10;5N
. B.
( )
5;10M
. C.
( )
11;10P −
. D.
( )
10; 11Q −
.
Lời giải
Chọn B
Ta có:
1
12zi= − +
,
2
34zi=−
( )( )
1 2 3 4 5 10z i i i= − + − = +
Vậy điểm biểu diễn số phức
z
là
( )
5;10
.
4
3
2
0
( )
4 3 0fx-=
Trang 14
Câu 22: Trong không gian
Oxyz
, cho điểm
( )
1;2;3A −
. Tìm tọa độ điểm điểm
B
đối xứng với điểm
A
qua mặt phẳng
( )
Oyz
.
A.
( )
1;2;3B
. B.
( )
1;2; 3B −
. C.
( )
1; 2; 3B − − −
. D.
( )
1; 2;3B −
.
Lời giải
Chọn A.
Hình chiếu của điểm
A
xuống mặt phẳng
( )
Oyz
là
( )
0;2;3I
. Khi đó
I
l trung điểm của
AB
nên tọa độ điểm
( )
1;2;3B
.
Câu 23: Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 4 2 6 5 0S x y z x y z+ + + − + + =
. Mặt cầu
( )
S
có
bán kính là
A.
3
. B.
5
. C.
2
. D.
7
.
Lời giải
Chọn A.
Mặt cầu
( )
S
có tâm
( )
2;1; 3I −−
và bán kính
( ) ( )
22
2
2 1 3 5 3R = − + + − − =
.
Câu 24:Trong không gian với hệ trục toạ độ
Oxyz
, cho mặt phẳng
( )
P
:
2 3 0zx− + =
. Một vectơ php
tuyến của
( )
P
là:
A.
( )
0;1; 2u =−
. B.
( )
1; 2;3v =−
. C.
( )
2;0; 1n =−
. D.
( )
1; 2;0w =−
.
Lời giải
Chọn C
Ta có:
2 3 0zx− + =
2 3 0xz − − =
. Do đó mặt phẳng
( )
P
có một vectơ php tuyến l
( )
2;0; 1n =−
.
Câu 25: Trong không gian
Oxyz
, cho đường thẳng
:d
1
2
xt
yt
zt
=
=−
=+
. Đường thẳng
d
đi qua điểm no sau
đây?
A.
( )
1; 1;1K −
. B.
( )
1;2;0H
. C.
( )
1;1;2E
. D.
( )
0;1;2F
.
Lời giải
Chọn D
Đường thẳng
d
đi qua điểm
( )
0;1;2F
.
Câu 26. Cho hình chóp tứ giác  có đy l hình vuông , AC=
2a
, 
󰇛

󰇜
và
3SA a=
.
Góc giữa đường thẳng  và (ABCD) là
A. . B. . C. . D. .
Lời giải
Chọn C
Trang 15
Hình chiếu của SB lên (ABCD) là SA
Suy ra góc giữa đường thẳng SB và 󰇛󰇜à góc
SBA
.
ABCD là hình vuông, AC=
2a
nên AB = a
Trong tam giác  vuông tại , ta có: AB = a,
3SA a=



3

.
Câu 27. Cho hàm số
󰇛
󰇜
, bảng xét dấu của
󰆒
󰇛
󰇜
như sau:
Số điểm cực tr của hàm số đã cho l
A.  B.  C. . D. .
Lời giải
Chọn B
Dựa vào bảng xét dấu
󰆒
󰇛
󰇜
ta thấy hàm số đạt cực tiểu tại  v đạt cực đại tại
Vậy hàm số có cực tr.
Câu 28. Biết giá tr lớn nhất và giá tr nhỏ nhất của hàm số

 trên
󰇟

󰇠
lần lượt
là và . Giá tr của bằng
A.
. B.

. C. . D.
.
Lời giải
Chọn B
Hàm số

 xc đnh và liên tục trên
󰇟

󰇠
.
󰆒
 ,
󰆒

󰇛
󰇜

󰇛
󰇜
.
󰇛
󰇜
,
󰇛

󰇜

,
󰇛

󰇜
,
󰇛

󰇜

.
Trang 16
Vậy ,

nên

.
Câu 29. Xét tất cả các số thực dương và thỏa mãn
( )
2
2
ln . ln
b
ab
e

=


. Tích  thuộc khoảng no
trong cc khoảng sau đây?
A.
󰇛

󰇜
. B.
󰇛

󰇜
. C. 󰇡
󰇢. D.
󰇛

󰇜
.
Lời giải
Chọn A
Ta có
( )
22
2
ln . ln ln 2ln ln( ) 2 ln ln 2 ln( . ) 2 .
b
ab a b b a b a b a b e
e
−

= + = − + = − = − =


.
Câu 30. Cho hàm số
󰇛
󰇜
có bảng biến thiên như sau:
Số nghiệm thực của phương trình 
󰇛
󰇜
là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có 
󰇛
󰇜
󰇛
󰇜
.
Số nghiệm của phương trình l số giao điểm của đường thẳng
v đồ th hàm số
󰇛
󰇜
.
Từ bảng biến thiên suy ra phương trình có nghiệm thực.
Câu 31: Tập nghiệm của bất phương trình
2
33
log 2log 3 0xx+ −
là :
A.
1
;3 .
27



B.
( ) ( )
; 3 1; .− − +
C.
( )
3;1 .−
D.
1
;27 .
3



Lời giải
Đặt
3
logtx=
bất phương trình đã cho trở thành
2
2 3 0 3 1t t t+ − −
3
1
3 log 1 3
27
xx −
Câu 32 : Cho khối nón có đường sinh bằng 5 v bn kính đy bằng 3. Thể tích khối nón bằng?
Trang 17
A.
18
. B.
12
. C.
24
. D.
15
.
Lời giải
Chiều cao hình nón
2 2 2 2
5 3 4h l r= − = − =
.
Thể tích khối nón
22
11
.3 .4 12
33
V r h
= = =
.
Câu 33 : Cho tích phân
2
0
cosI x xdx
=
và
2
, cosu x dv xdx==
. Khẳng đnh no sau đây đúng?
A.
2
0
2 sinsin
0
I x x x xdx
=+
. B.
2
0
sin
0
sinI x x x xdx
=−
.
C.
2
0
sin
0
sinI x x x xdx
=+
. D.
2
0
2 sinsin
0
I x x x xdx
=−
.
Lời giải
2
2
s
cos
inx
du xdx
ux
v
dv xdx
=
=
→

=
=
22
00
sicos 2 sin
0
nI x xdx x x x xdx

= = −

Câu 34 : Cho hình phẳng (D) được giới hạn bởi cc đường
( )
2 1, , 0, 1f x x Ox x x= + = =
. Tính thể
tích V của khối tròn xoay tạo thnh khi quay (D) xung quanh trục
Ox
được tính theo công thức?
A.
1
0
21V x dxp=+
ò
B.
( )
1
0
21V x dxp=+
ò
C.
( )
1
0
21V x dx=+
ò
D.
1
0
21V x dx=+
ò
Lời giải
Thể tích cần tìm:
( )
( )
11
2
00
2 1 2 1V x dx x dxpp= + = +
òò
Câu 35 : Cho hai số phức
12
3 2 ; 1 3 .= − = +z i z i
Tổng của hai số phức
12
;zz
là :
A.
4.+ i
B.
9.− i
C.
1 9 .−−i
D.
4 5 .− i
Lời giải
( ) ( ) ( ) ( )
+ = − + + = + + − + = +
12
3 2 1 3 3 1 2 3 4 .z z i i i i
Câu 36: Gọi
12
,zz
là nghiệm của phương trình
2
2 10 0zz+ + =
. Giá tr của biểu thức
22
12
A z z=+
là:
Trang 18
A.
10
B. 2
10
C. 0 D. 2
Giải:
+ + = = − + = − −
+=
2
12
22
12
2 10 0 coù hai nghieäm z 1 3 ; z 1 3
20
z z i i
Neân z z
Câu 37: Trong không gian hệ tọa độ Oxyzx, cho A(-1;0;1), B(-2;1;1). Phương trình mặt trung trực của
đoạn AB có phương trình l:
A.
20xy− − =
B.
10xy− + =
C.
20xy−+=
D.
20xy− + + =
Giải:
. PT mặt phẳng
( )
-3 1
qua I( ; ;1)
p
22
VTPT (-1;1;0)
có phương trình:
20xy−+=
Câu 38: Trong không gian với hệ tọa độ Oxyz, cho
( )
:2 2 3 0x y z
− + − =
. Phương trình đường thẳng
d đi qua A(2;-3;-1) song song
( )
và mặt phẳng (Oyz) là:
A.
2
3
1
xt
y
zt
=−
=−
= − +
B.
2
32
1
x
yt
zt
=
= − +
= − +
C.
2
32
1
x
yt
zt
=
= − −
= − +
D.
2
23
1
xt
yt
zt
=
=−
=−
Giải: Đường thẳng

==

qua A(2;-3;-1)
d
VTCP ; (0;2;1)u n i
có phương trình:
2
32
1
x
yt
zt
=
= − +
= − +
Câu 39. Lớp 11A có
40
học sinh trong đó có
12
học sinh đạt điểm tổng kết môn Hóa học loại giỏi và
13
học sinh đạt điểm tổng kết môn Vật lí loại giỏi. Biết rằng khi chọn một học sinh của lớp đạt điểm
tổng kết môn Hóa học hoặc Vật lí loại giỏi có xác suất là
0,5
. Số học sinh đạt điểm tổng kết giỏi cả hai
môn Hóa học và Vật lí là
A.
4
. B.
7
. C.
6
. D.
5
.
Lời giải
Gọi
A
là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Hóa học”.
B
là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Vật lí”.
AB
là biến cố “Học sinh được chọn đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi”.
AB
là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi cả hai môn Hóa học và Vật lí”.
Ta có:
( )
0,5.40n A B=
20=
.
Trang 19
Mặt khác:
( ) ( ) ( ) ( )
.n A B n A n B n AB = + −
( ) ( ) ( ) ( )
.n AB n A n B n A B = + −
12 13 20= + −
5=
.
Đáp án D.
Câu 40: Cho hình chóp S.ABCD có đy ABCD l hình chữ nhật, AB = a,
23AD a=
Cạnh bên SA vuông góc với đy, biết tam giác SAD có diện tích
2
3Sa=
. Tính khoảng cách
từ C đến (SBD).
A.
39
13
a
d =
. B.
39
5
a
d =
. C.
2 39
13
a
d =
. D.
2 51
17
a
d =
.
Lời giải: Chọn D
Ta có:
2
11
. 3 .2a 3 3
22
SAD
S SA AD a SA SA a= = =
Gọi O l giao điểm của AC v BD. Suy ra O l giao điểm của AC và mặt phẳng (SBD).
( )
( )
( ) ( )
,( )
1 ,( ) A,( )
A,( )
d C SBD
CO
d C SBD d SBD
d SBD AO
= = =
Kẻ
AK BD⊥
tại K
SK BD⊥
(Đnh lý 3 đường vuông góc).
( )
BD SAK⊥
Kẻ
AH SK⊥
tại H (1).
Mà
( )
BD SAK BD AH ⊥ ⊥
(2).
Từ (1) và (2) suy ra
( )
AH SBD⊥
( )
( )
,A SBD
d AH=
Trang 20
Xét tam giác SAK vuông tại A ta có:
2 2 2
1 1 1
AH AS AK
=+
.
Lại có tam giác ABD vuông tại A nên ta có:
2 2 2
1 1 1
AK AB AD
=+
.
2 2 2 2 2 2 3
1 1 1 1 1 1 17
12AH AS AK AS AB AD a
= + = + + =
2 51
17
a
AH =
( ) ( )
2 51
,( ) A,( )
17
a
d C SBD d SBD==
Câu 41: Cho hàm số
32
( 3 6) 5y x mx m x= − − + − + +
với m là tham số. Có bao nhiêu giá tr
nguyên của m để hàm số nghch biến trên khoảng
( )
;− +
?
A. 2. B. 3. C. 4. D. 5.
Lời giải: Chọn C.
'2
3 2 ( 3 6)y x mx m= − − + − +
Để hàm số nghch biến trên R
'
0,y x R
( )
22
3 3 6 0 9 18 0 3 6m m m m m + − + − +
Các giá tr cần tìm là : 3, 4, 5, 6.
Câu 42:Tỉ lệ tăng dân số hng năm của Nhật l 0,2%. Năm 1998, dân số của Nhật l
125 932 000. Vo năm no dân số của Nhật sẽ l 140 000 000 ? ( Kết quả làm tròn đến hàng đơn vị)
A. 2061. B. 2055. C. 2051. D. 2045.
Lời giải: Chọn C.
Áp dụng công thức lãi kép liên tục
Với A
0
= 125 932 000; r= 0,2%; A
n
= 140 000 000. Ta đi tính n.
Ta có:
0,2%.n
125932000 140000000
n
Pe==
140000000
0,2%. ln
125932000
n=
Trang 21
53n
Đến năm 53 + 1998 = 2051 thì dân số của Nhật xấp xỉ l 140 000 000
Câu 43: Ta xc đnh được các số a, b, c để đồ th hàm số
32
y x ax bx c= + + +
đi qua điểm
( )
1;0
và
có điểm cực tr
( )
2;0−
. Tính giá tr biểu thức
2 2 2
T a b c= + +
.
A. 25. B. -1. C. 7. D. 14.
Lời giải: Chọn A
Ta có:
2
32y x ax b= + +
.
Đồ th hàm số
32
y x ax bx c= + + +
đi qua điểm
( )
1;0
nên ta có: a + b + c = -1.
Đồ th hàm số có điểm cực tr
( )
2;0−
nên
( )
'
4 2 8
4 2 8
4 12
20
a b c
a b c
ab
y
− + =
− + =

− + = −
−=
.
Ta có hệ phương trình
13
4 2 8 0
4 12 4
a b c a
a b c b
a b c
+ + = − =


− + = =


− + = − = −

2 2 2
25T a b c= + + =
Câu 44: Cho hình trụ có bn kính đy bằng a. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng
2
a
, thiết diện thu được là một hình vuông.Thể tích của
khối trụ được giới hạn bằng hình trụ đã cho bằng
A.
3
3.a
B.
3
3.a
C.
3
3
.
4
a
D.
3
.a
Giải: Chọn B
Giả sử ABCD là thiết diện hình vuông như hình trên.
Gọi O v O’ lần lượt l tâm 2 đy của hình trụ.
Ta có :
( ) ( )
;
',( ) ,( ) ( '/ /( ))
2
OA r a
a
d OO ABCD d O ABCD do OO ABCD
==
==
Gọi H là hình chiếu của O lên AB ( H l trung điểm AB).
Trang 22
Khi đó :
( )
,( )
2
a
d O ABCD OH==
Xét tam giác OAH vuông tại H có :
2
2 2 2
2 2 3
2
a
AB AH OA OH a a

= = − = − =


.
Vì ABCD là hình vuông nên :
'3h OO AB BC a= = = =
Vậy
2 2 3
. 3 3.V r h a a a
= = =
Câu 45: Cho hàm số
()y f x=
thỏa mãn
(ln3) 3f =
và
2
'( )
11
x
xx
e
f x x
ee
=
+ − +
.
Khi đó
ln3
0
()
x
e f x dx
bằng
A.
10 8 2
3
−−
B.
20 8 2
.
3
−
C.
20 8 2
.
3
+
D.
10 8 2
3
−
Giải: Chọn B
( )
( )
2
2
2
2
( ) '( )
11
( 1 1)
1 ( 1)
( 1 1)
e ( 1)
1
21
11
x
xx
x x x
xx
x x x
xx
x
x
x x x x
xx
e
f x f x dx dx
ee
e e e
dx
ee
e e e
dx
e
de
e
e dx e dx e e C
ee
==
+ − +
+ + +
=
+ − +
+ + +
=
+
+

= + = + = + + +

++


Mà
(ln3) 3 4 ( ) 2 1 4
xx
f C f x e e= = − = + + −
.
Khi đó:
(
)
( )
ln3 ln3
2
00
ln3
3
2
2
( ) 2 1 4
1 4 20 8 2
14
2 3 3
x x x x x
x x x
o
e f x dx e e e e dx
e e e
= + + −

−
= + + − =



Trang 23
Câu 46: Cho hàm số
()y f x=
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
3
;
2

−


của phương trình
2 (2cos ) 9 0fx−=
là:
A.
5.
B.
4
C.
3.
D.
2.
Giải
Chọn A
Đặt
3
2cos , ; 2;2
2
t x x t

= − −


thì
2 (2cos ) 9 0fx−=
trở thành
9
2 (t) 9 0 ( ) (1)
2
f f t− = =
Nhận xét: Số nghiệm pt (1) là số giao điểm của hai đồ th (C) :
v đường thẳng d:
9
2
y =
.
Bảng biến thiên của hàm số
(t)yf=
trên
2;2−
Dựa vào bảng biến thiên , số nghiệm
2;2t −
của (1) là 2 nghiệm phân biệt
( ) ( )
12
2;0 ; 0;2tt −
Ta có đồ th hàm số
cosyx=
trên
3
;
2

−


Trang 24
+ Với
( ) ( ) ( )
1
11
2;0 2cos 2;0 cos 1;0
2
t
t x t x − = − = −
Dựa vo đồ th
cosyx=
trên
3
;
2

−


ta thấy phương trình
( )
1
cos 1;0
2
t
x = −
có 3 nghiệm phân biệt
1 2 3
3
2 2 2
x x x

−
−
+ Với
( ) ( ) ( )
2
22
0;2 2cos 0;2 cos 0;1
2
t
t x t x = =
Dựa vo đồ th
cosyx=
trên
3
;
2

−


ta thấy phương trình
( )
2
cos 0;1
2
t
x =
có 2 nghiệm phân biệt
45
0
22
xx

−
Vậy số nghiệm thuộc đoạn
3
;
2

−


của phương trình
2 (2cos ) 9 0fx−=
là
2 3 5+=
Câu 47: Cho
x
,
y
là các số thực dương thỏa mãn
2
log 4 1
9 24
xy
xy
xy

+
= − + −

+

. Tính giá tr nhỏ nhất
của biểu thức
2
2
Px
y
=+
bằng.
A.
4
B.
10
C.
6
D.
2
Lời giải
Do
,0xy
nên
2
0
9 24
xy
xy
+
+
.
Ta có
2 10 20
log 4 1 log 4
9 24 9 24
x y x y
x y x y
x y x y
++
= − + − = − +
++
( ) ( ) ( ) ( )
log 10 20 log 9 24 9 24 10 20x y x y x y x y + − + = + − +
( ) ( ) ( ) ( )
log 10 20 10 20 log 9 24 9 24x y x y x y x y + + + = + + +
Trang 25
Xét hàm số
( )
logf t t t=+
với
( )
0;t +
( )
1
10
ln10
ft
t
= +
với
( )
0;t +
nên hàm số
( )
ft
đồng biến trên
( )
0;t +
.
Nên
( ) ( )
9 24 10 20 4x y x y x y+ = + =
.
3
2 2 2 2
2 1 1 1
4 2 2 2 2.3 . . 6P y y y y y y
y y y y
= + = + = + + =
Dấu bằng xảy ra khi
3
1
14y y x
y
= = =
Vậy Giá tr nhỏ nhất của P là 6 Chọn C
Câu 48:Cho hàm số
2
1
x mx m
y
x
++
=
+
gọi
S
là tập hợp tất cả các giá tr thực của tham số
m
sao cho
1;2
2Max y =
.Tổng các phần tử của
S
là.
A.
2
3
. B.
11
6
. C.
11
6
−
. D.
5
2
−
.
Lời giải.
Xét hàm số:
2
1
x mx m
y
x
++
=
+
.
( )
2
2
2
1
xx
y
x
+
=
+
;
0y
=
( )
2
2
2
0
1
xx
x
+
=
+
2
20xx + =
0 1;2
2 1;2
x
x
=
= −
.
Khi đó ta có bảng biến thiên sau:
Xét TH1:
2 1 1
0
22
m
m
+
−
Suy ra
1;2
3 4 2
2
33
m
Max y m
+
= = =
(Nhận).
Xét TH2:
3 4 4
0
33
m
m
+
−
Suy ra
1;2
2 1 5
2
22
m
Max y m
+
= − = = −
(Nhận).
Trang 26
TH3:Xét
2 1 3 4 4 1
0
2 3 3 2
mm
m
++
− −
Suyra
1;2
1;2
21
5
2
()
2
2
2
34
()
2
3
3
m
Max y
ml
m
ml
Max y
+
= − =
=−
+
=
==
Tổng các phần tử của S là
2 5 11
3 2 6
− = −
Chọn đp n C.
Câu 49: Cho hình chóp đều
.S ABC
có tất cả các cạnh bằng
3
và
,,M N P
lần lượt là trọng tâm của
tam giác
,,SAB SBC SAC
. Thể tích khối đa diện có cc đỉnh là
, , , , ,A B C M N P
là
A.
2
.
12
B.
42
.
3
C.
82
.
3
D.
92
.
4
Lời giải:
Hình chóp
.S ABC
có
2
3 3 9 3
44
6
.3 6
3
ABC
S
h
==
==
.
1 9 2
34
S ABC
V Sh==
( )
mp MNP
cắt
,,SA SB SC
tại
1 1 1
,,A B C
nên
1 1 1
.
.
2 2 2 8
..
3 3 3 27
S A B C
S ABC
V
V
==
1 1 1
.
8 9 2 2 2
.
27 4 3
S A B C
V = =
N
P
M
A1
B1
C1
C
B
A
S
Trang 27
Khối chóp
1
BB MN
có
1
1
1
3
2
4
12
16
33
B MN
BB MN
S
V
hh
=
=
==
Thể tích cần tìm là V
1 1 1 1 1 1
..S ABC S A B C AA MP BB MN CC NP
V V V V V V= − − − −
1 1 1
. . 1
3
42
3
S ABC S A B C BB MN
V V V= − −
=
Câu 50: Cho hàm số
( )
(
)
2
ln 1y f x x x= = + +
. Số giá tr nguyên dương
a
thỏa mãn bất phương
trình
( ) ( )
3 ln 0f a f a− +
là
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
( )
2
1
' 0, ,
1
f x x
x
=
+
nên
( )
fx
đồng biến trên
( )
(
)
(
)
( )
22
2
1
ln 1 ln ln 1
1
f x x x x x f x
xx
− = + − = = − + + = −
++
,
x
, nên
( )
fx
là hàm số lẻ
Mà
( ) ( )
3 ln 0f a f a− +
( ) ( )
( ) ( )
ln 3
ln 3
f a f a
f a f a
− −
−
ln 3aa −
ln 3 1;2a a a +
do a nguyên dương.
ĐỀ 7
PHÁT TRIỂN TỪ ĐỀ MINH HỌA
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Trang 28
LẦN 2 NĂM 2020
Thời gian: 90 phút
Câu 1: (NB). Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là.
A.
7!
3!
B. 21. C.
3
7
A
D.
3
7
.C
Câu 2: (NB). Cho dãy cấp số nhân
()
n
u
, biết
12
3, 6uu= = −
. Công bội của cấp số nhân
()
n
u
bằng:
A. q = - 9 B. q = 9 C. q = - 2 D. q = 2
Câu 3: (NB).Tìm tập nghiệm
S
của phương trình
++
=
2
23
2 8 .
xx
x
A.
{ }
1;3 .S =
B.
{ }
1;3 .S =-
C.
{ }
3;1 .S =-
D.
{ }
3.S =-
Câu 4: (NB). Thể tích khối lăng trụ có diện tích đy B v chiều cao h là:
A.
=V Bh
B.
=
1
2
V Bh
C.
= 2V Bh
D.
=
1
3
V Bh
Câu 5: (NB). Giá tr của biểu thức
3
log ( . )
a
aa
(với
01a
) là
A.
2
3
. B.
4
3
. C.
3
2
. D. 3.
Câu 6: (NB). Hm số no sau đây l một nguyên hàm của hm số
5
yx=
?
A.
6
.yx=
B.
4
5.yx=
C.
6
.
6
x
y =
D.
5
6.yx=
Câu 7: (NB). Chiều cao của khối lăng trụ có diện tích đy bằng
B
và thể tích bằng
V
là
A.
3V
h
B
=
. B.
6V
h
B
=
. C.
2V
h
B
=
. D.
V
h
B
=
.
Câu 8: (NB). Một hình nón có diện tích xung quanh bằng
2
2 cm
v bn kính đy
1
.
2
r cm=
Khi đó độ
di đường sinh của hình nón là:
A.
3cm
. B.
4cm
. C.
2cm
. D.
1cm
.
Câu 9: (NB). Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu?
A.
2
4
.
3
=
a
S
B.
2
.
3
=
a
S
C.
2
.=
Sa
D.
2
4.=
Sa
Câu 10: (NB). Hàm số
4
21yx=+
đồng biến trên khoảng nào?
Trang 29
A.
1
;
2
æö
÷
ç
- ¥ -
÷
ç
÷
ç
èø
. B.
( )
0;+¥
. C.
1
;
2
æö
÷
ç
- + ¥
÷
ç
÷
ç
èø
. D.
( )
;0-¥
.
Câu 11: (NB). Với a là số thực dương tùy,
2
5
log a
bằng
A.
5
2log .a
B.
5
2 log .a+
C.
5
1
log .
2
a+
D.
5
1
log .
2
a
Câu 12: (NB). Một hình trụ có bán kính bằng 3 v đường cao bằng 4 có diện tích xung quanh bằng bao
nhiêu ?
A.
24p
. B.
12p
. C.
15p
. D.
20p
.
Câu 13: (NB). Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
x
- 0 2 +
y’
- 0 + 0 -
y
+
5
1
-
Giá tr cực tiểu của hàm số đã cho bằng
A. 1. B. 2. C. 0. D. 5.
Câu 14: (TH). Đường cong trong hình vẽ l đồ th của hàm số no dưới đây?
A.
1
.
1
x
y
x
−
=
−−
B.
1
.
1
x
y
x
+
=
−
C.
1
.
1
x
y
x
+
=
−+
D.
1
.
1
x
y
x
−
=
+
Câu 15: (NB). Đồ th hàm số no dưới đây có tiệm cận ngang?
Trang 30
A.
3
1
x
y
x
−
=
+
B.
2
9 x
y
x
−
=
C.
2
3yx=−
D.
2
21x
y
x
+
=
Câu 16: (NB). Nghiệm của bất phương trình
+−
xx2 1 3
33
là
A.
x
3
.
2
B.
x
2
.
3
C.
x
2
.
3
−
D.
x
2
.
3
Câu 17: (TH). Cho hàm số
( )
32
y f x ax bx cx d= = + + +
có bảng biến thiên như sau:
x
- ∞ -1 1 +∞
y’
+ 0 - 0 +
y
2 +∞
-∞ -2
A.
3
3y x x=−
B.
3
32y x x= − +
C.
3
3
2
2
y x x= − +
D.
3
3y x x= − +
Câu 18: (NB). Biết
( )
5
2
d3f x x =
,
( )
5
2
d9g x x =
. Tích phân
( ) ( )
5
2
f x g x dx +

bằng
A.
10
. B.
3
. C.
6
. D.
12
.
Câu 19: (NB). Cho số phức
2 5 .=+zi
Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là:
A. (5;2) B. (2;5) C.
( 2;5)−
D.
(2; 5)−
Câu 20: (NB). Cho
( ) ( )
2 2
11z i i= + − −
, tính phần ảo của số phức z.
A.–4 B. 4 C.–2 D.2
Câu 21: (NB). Cho số phức
5 4 .zi=−
Số phức đối của z có tọa độ điểm biểu diễn là.
A.
( )
5; 4−−
B.
( )
5;4
C.
( )
5;4−
D.
( )
5; 4−
Câu 22: (TH). Trong không gian Oxyz cho hai điểm
( ) ( )
2;3;4 3;0;1 .A và B
Khi đó độ di véctơ
AB
là.
A.
19.
B. 19. C.
13.
D. 13.
Trang 31
Câu 23: (NB). Tọa độ tâm
A
của mặt cầu
( )
2 2 2
: 2 4 2 3 0S x y z x y z+ + − + + − =
là:
A.
( )
1;2; 1A −
B.
( )
1;2;1A −
C.
( )
1;2; 1A −−
D.
( )
1; 2; 1A −−
Câu 24: (NB). Cho mặt phẳng
( )
: 2 3 4 0P x y z− + + =
. Pht biểu no sau đây l đúng?
A.
( )
1
1;2;3n =
l một vectơ php tuyến của mặt phẳng
( )
P
.
B.
( )
2
1; 2;3n =−
l một vectơ php tuyến của mặt phẳng
( )
P
.
C.
( )
3
1;3;4n =
l một vectơ php tuyến của mặt phẳng
( )
P
.
D.
( )
1
2;3;4n =−
l một vectơ php tuyến của mặt phẳng
( )
P
.
Câu 25: (TH). Trong không gian tọa độ Oxyz, viết phương trình tham số của đường thẳng
( )
d
đi qua
điểm
( )
1; 2;4A −
và có một vectơ chỉ phương là
( )
2;3; 5u =−
.
A.
12
23
45
xt
yt
zt
=+
= − +
=−
B.
11 2
23
45
xt
yt
zt
= − +
= − +
= − −
C.
12
23
45
xt
yt
zt
=+
= − −
=−
D.
12
23
45
xt
yt
zt
=−
= − +
=+
Câu 26: (TH). Cho hình chóp S.ABCD có SA vuông góc với mặt đy (ABCD). Góc giữa SC và
(ABCD) là:
A.
SBA
. B.
SAC
. C.
SDA
. D.
SCA
.
Câu 27: (TH). Cho hàm số phù hợp với bảng biến thiên sau:
Phát biểu no sau đây l đúng?
A. Hàm số đạt cực tiểu tại x = 0 v đạt cực đại tại x = 1
B. Giá tr cực tiểu của hàm số là 1
C. Giá tr cực đại của hàm số là 0
D. Hàm số đạt cực đại tại x = 0 v đạt cực tiểu tại x = 1
Trang 32
Câu 28: (TH). Gọi M là giá tr lớn nhất của hàm số
( )
2
ln 3y x x= − −
trên đoạn
2;5
. Trong các khẳng
đnh sau, khẳng đnh nào đúng?
A.
3
6
M
e
+
=
. B.
0M
. C.
5
22 0
M
e
+
−=
. D.
20M +=
Câu 29: (TH). Nếu
log3 a=
thì
log9000
bằng:
A.
32a+
B.
2
a
C.
2
3a +
D.
2
3a
Câu 30: (TH). Tìm tất cả giá tr thực của tham số
m
để phương trình
32
3x x m+=
có ba nghiệm phân
biệt.
A.
2.m=
B.
0 4.m
C.
0.m
D.
4.m
Câu 31: (TH). Số nghiệm nguyên dương của bất phương trình
1 2 3
11
39
xx−+
thuộc
5;5−
là:
A. 10 B. 11 C. 8 D. 6
Câu 32. (TH). Cho tứ diện đều
ABCD
cạnh bằng
3a
. Tính diện tích xung quanh
xq
S
của hình trụ có
đy l đường tròn ngoại tiếp tam giác
BCD
và có chiều cao bằng chiều cao của tứ diện đều
ABCD
.
A.
2
23
xq
Sa
=
. B.
2
2
xq
Sa
=
. C.
2
3
xq
Sa
=
. D.
2
22
xq
Sa
=
.
Câu 33: (TH). Cho nguyên hàm
22
4I x x dx=−
. Nếu đặt
2sinxt=
với
;
22
t


−


thì
A.
cos4
2
2
t
I t C= + +
B.
sin8
2
4
t
I t C= + +
C.
cos4
2
2
t
I t C= − +
D.
sin4
2
2
t
I t C= − +
Câu 34: (TH). Kết quả của diện tích hình phẳng giới hạn bởi đồ th hàm số , trục
hoành, trục tung v đường thẳng
2x =
có dạng
a
b
(với
a
b
là phân số tối giản). Khi đó mối liên hệ giữa
a
và
b
là:
A.
-=2.ab
B.
-=3ab
. C.
- = - 2.ab
D.
- = - 3.ab
Câu 35: (TH). Trong mặt phẳng phức, điểm
( )
2; 3M −
l điểm biểu diễn số phức z. Khẳng đnh nào
sau đây l khẳng đnh đúng?
A.
( )
21i z i+ = −
. B.
( )
13i z i− = +
. C.
32iz i=+
. D.
( )
1 1 2i z i− = +
.
Câu 36: (TH). Gọi
12
,zz
là hai nghiệm phức của phương trình
2
4 13 0zz− + =
. Khi đó
1 2 1
.z z z+
bằng
A.
26
. B.
13 13+
. C.
13
. D.
13 5+
.
Trang 33
Câu 37: (TH). Cho ba điểm
( ) ( ) ( )
0;1;2 ; 2; 2;1 ; 2;0;1A B C−−
. Phương trình mặt phẳng đi qua
A
v
vuông góc với
BC
l
A.
2 1 0xy− + =
. B.
2 3 0yz− + − =
. C.
2 5 0yz+ − =
. D.
2 1 0xy− − =
.
Câu 38: (TH). Trong không gian Oxyz, cho mặt phẳng
( )
: 3 0P x y z+ + − =
v đường thẳng
12
:.
1 2 1
x y z
d
+−
==
−
Đường thẳng d' đối xứng với d qua mặt phẳng (P) có phương trình l:
A.
1 1 1
.
1 2 7
x y z− − −
==
−
B.
1 1 1
.
1 2 7
x y z+ + +
==
−
C.
1 1 1
.
1 2 7
x y z− − −
==
D.
1 1 1
.
1 2 7
x y z+ + +
==
Câu 39: (VD). Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên 4 bóng từ
hộp, xác suất để có đủ 3 màu bóng là
A.
35
.
816
B.
35
.
68
C.
175
.
5832
D.
35
.
1632
Câu 40: (VD). Cho hình chóp S.ABC có đy ABC là tam giác vuông tại B có
3AB =
,
4BC =
.
( )
SA ABC⊥
và
5SA =
. Gọi H là hình chiếu vuông góc của A lên SB và K l trung điểm của SC. Khẳng
đnh no sau đây đúng?
A.
( )
//AHK BC
. B.
( ) ( )
⊥AHK SBC
. C.
( )
⊥AHK SB
. D.
( ) ( )
⊥AHK SAB
.
Câu 41: (VD). Hàm số nào trong các hàm số sau đồng biến trên
R
?
A.
7 2sin3 .y x x=−
B.
32
2 1.y x x= + +
C.
tan .yx=
D.
41
.
2
x
y
x
+
=
+
Câu 42: (VD). Một số tiền 58.000.000đ gửi tiết kiệm theo hình thức lãi kép với lãi suất 0,7%/tháng. Số
tiền có được gồm vốn lẫn lãi sau 8 tháng gửi là:
A. 61.328.699 đ B. 62.328.699 đ C. 60.328.699 đ D. 63.328.699
đ
Câu 43: (VD). Cho hàm số
( ) ( )
= - + + +
42
1
3 1 2 1
4
y x m x m
với
m
là tham số thực. Tìmgiá tr của
m
để đồ th hàm sốcó ba điểm cực tr tạo thành tam giác có trọng tâm là gốc tọa độ.
A.
2
3
m =-
. B.
2
3
m =
. C.
1
3
m =-
. D.
1
3
m =
.
Câu 44: (VD). Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình
vuông có cạnh bằng a . Tính diện tích xung quanh S của khối trụ đó.
Trang 34
A.
2
2.Sa
=
B.
2
.
2
a
S
=
C.
2
.Sa
=
D.
2
4.Sa
=
Câu 45: (VD). Cho tích phân
( )
( )
--
= = + +
+
ò
2
2
1
21
d ln 2 ln 3
1
x x x
I x a b c
x
với . Chọn
khẳng đnh đúng trong các khẳng đnh sau:
A.
> 0b
. B.
< 0c
. C.
< 0a
. D.
++>0a b c
.
Câu 46: (VDC). Một mảnh giấy hình chữ nhật có chiều dài 12cm và
chiều rộng 6cm. Thực hiện thao tác gấp góc dưới bên phải sao cho
đỉnh được gấp nằm trên cạnh chiều dài còn lại. Hỏi chiều dài
L
tối
thiểu của nếp gấp là bao nhiêu?
A.
min 6 2 cmL =
. B.
93
min cm
2
L =
.
C.
73
min cm
2
L =
. D.
min 9 2 cmL =
.
Câu 47: (VDC). Nếu
4
3
5
4
aa
và
12
log log
23
bb
thì
,ab
thoả mãn điều kiện no trong cc điều kiện
sau?
A.
1, 1.ab
B.
1,0 1.ab
C.
0 1,0 1.ab
D.
0 1, 1.ab
Câu 48: (VDC). Hàm số
2
xm
y
x
−
=
+
thỏa mãn
0;3 0;3
7
min max
6
xx
yy

+=
. Hỏi giá tr m thuộc khoảng nào trong
các khoảng dưới đây?
A.
( )
1;0−
. B.
( )
;1− −
. C.
( )
2;+
. D.
( )
0;2
.
Câu 49: (VDC). Cho hai hình vuông
ABCD
và
ABEF
có cạnh bằng
a
, lần lượt nằm trên hai mặt
phẳng vuông góc với nhau. Lấy điểm
H
trên đoạn
DE
sao cho
3HD HE=
. Gọi
S
l điểm đối xứng
với
B
qua
H
. Thể tích của khối đa diện
ABCDSEF
bằng
A.
3
8
3
a
B.
3
5
6
a
C.
3
9
8
a
D.
3
2
3
a
Câu 50: (VDC). Xét các số nguyên dương
,ab
sao cho phương trình
2
ln ln 5 0a x b x+ + =
có hai
nghiệm phân biệt
12
,xx
v phương trình
2
5log log 0x b x a+ + =
có hai nghiệm phân biệt
34
,xx
sao
cho
1 2 3 4
x x x x
. Tìm giá tr nhỏ nhất của
23S a b=+
.
A.
30
. B.
25
. C.
33
. D.
17
Trang 35
BẢNG ĐÁP ÁN
1
D
11
A
21
B
31
C
41
A
2
C
12
A
22
A
32
D
42
A
3
A
13
A
23
D
33
D
43
D
4
A
14
B
24
B
34
B
44
C
5
B
15
A
25
A
35
C
45
D
6
C
16
D
26
D
36
B
46
B
7
D
17
A
27
D
37
A
47
D
8
B
18
D
28
A
38
A
48
A
9
C
19
B
29
A
39
B
49
B
10
B
20
B
30
B
40
B
50
B
ĐỀ 8
PHÁT TRIỂN TỪ ĐỀ MINH HỌA
LẦN 2 NĂM 2020
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Một tổ có 5 học sinh nam và 7 học sinh nữ, số cách chọn ra hai học sinh có cả nam và nữ?
A.
11
57
.CC
B.
11
57
CC+
C.
2
12
C
D.
11
57
CC+
Câu 2: Cho
( )
n
u
là cấp số cộng với công sai
.d
Biết
3
4u =−
và
5
10.u =−
Số hạng đầu tiên
1
u
bằng
A.
1
2u =
B.
1
3u =−
C.
1
6u =−
D.
1
7u =−
Câu 3: Số nghiệm của phương trình
2
33
xx
=
là
A. 2 B. 1 C. 0 D. Vô số
Câu 4: Một khối lập phương có thể tích là
3
8.a
Cạnh của khối lập phương đó bằng
A.
2a
B.
a
C.
2
a
D.
3
a
Câu 5: Tập xc đnh của hàm số
3
log 3 )(yx=−
là
A.
( )
;3−
B. C.
( )
3; +
D.
( )
0 ;+
Câu 6: Họ nguyên hàm của hàm số
( )
3
x
f x e=+
là
Trang 36
A.
( )
3
x
F x e x=+
B.
( )
3
x
F x e x=−
C.
( )
3
x
F x e x= − +
D.
( )
3
x
F x e x= − −
Câu 7: Một khối chóp có đy l hình vuông cạnh
3a =
v đường cao
5.h =
Thể tích khối chóp là
A.
15V =
B.
45V =
C.
25V =
D.
35V =
Câu 8: Cho hình nón có bn kính đy r = 4 v diện tích xung quanh bằng 20π. Thể tích
của khối nón đã cho bằng
A. 4π. B. 16π. C.163π. D.803π.
Câu 9: Thể tích V của một khối cầu có bán kính R là
A.
3
4
3
VR
=
B.
3
1
3
VR
=
C.
2
4
3
VR
=
D.
3
4VR
=
Câu 10: Cho hm số y = f(x) có bảng biến thiên như sau :
x
-∞
0
2
+ ∞
y’
+
0 -
0 +
y
0
1
-3
+ ∞
Hàm số đã cho đồng biến trên khoảng no dưới đây?
A. (2;+∞) B. (-∞;1) C. (0;+∞) D. (0;2)
Câu 11: Với
,ab
l hai số thực dương tùy ý,
4
ln
ae
b
bằng
A.
4ln – ln 1ab+
. B.
4ln ln 1.ba−+
C.
4ln ln –1.ab+
D.
4ln ln 1.ab++
Câu 12: Công thức tính diện tích xung quanh của hình trụ có chiều cao
,h
bn kính đy
R
là
A. S
xq
= 2πRh. B. S
xq
= π
2
Rh. C. S
xq
= πRh. D. S
xq
= 4πRh.
Câu 13: Hm số y = f(x) liên tục trên v có bảng biến thiên như hình vẽ.
x
-∞
1
2
+ ∞
y’
+
0 −
|| +
y
−∞
3
0
+ ∞
Mệnh đề no sau đây l đúng?
A. Hm số đã cho có hai điểm cực tr.
B. Hm số đã cho có đúng một điểm cực tr.
C. Hm số đã cho không có gi tr cực tiểu.
D. Hm số đã cho không có gi tr cực đại.
Câu 14: Đường cong trong hình vẽ bên l đồ th của hm số no dưới đây?
O
x
y
1−
2
3−
1
Trang 37
A.
32
3 1y x x= − +
B.
32
31y x x= − − +
C.
32
3 1y x x= + +
D.
32
3 1y x x= − + +
Câu 15: Đường thẳng no dưới đây l tiệm cận ngang của đồ th hm số
14
?
21
x
y
x
−
=
−
A.
2.y =
B.
1
2
y =
. C.
4.y =
D.
2.y =−
Câu 16: Tập nghiệm của bất phương trình log
3
(x - 2) ≥ 2 l
A.
)
11; .+
B.
( )
2; .+
C.
( )
;11 .−
D.
(11; )+
Câu 17: Cho hàm số bậc bốn
()y f x=
có đồ th như hình vẽ
Số nghiệm của phương trình
() 1fx=−
là:
A.
4.
B.
3.
C.
2.
D.
1.
Câu 18: Cho hàm số
( )
fx
liên tục trên [0;3]. Nếu
3
0
( ) 2f x dx =
thì
3
0
[ 3 ( )]x f x dx−
có giá tr bằng
A.
3
2
−
B.
3−
C.
3
D.
3
.
2
Câu 19: Số phức liên hợp của số phức
4 – 3zi=
là
A.
43zi=+
B.
43zi= − −
C.
43zi= − +
D.
34zi=−
Câu 20: Cho hai số phức:
1
1– 2 zi=
và
2
3 – 2 .zi=
Tìm số phức
2
1
z
z
z
=
A.
74
55
zi=+
B.
74
55
zi= − +
C.
74
55
zi=−
D.
74
55
zi= − −
Câu 21: Cho số phức z = 4 – 3i có điểm biểu diễn trên mặt phẳng tọa độ Oxy là M. Độ di
OM
bằng
A.
5
B.
25
C.
7
D.
4
Câu 22: Trong không gian Oxyz , cho điểm A(1; 2; 3). Hình chiếu vuông góc của điểm A trên trục Oz là
điểm
A.
0;0;3 .()Q
B.
1;0;3 .()M
C.
( )
0;2;3 .P
D.
1;0;0 .()N −
Trang 38
Câu 23: Trong không gian với hệ tọa độ
,Oxyz
cho mặt cầu có phương trình
2 2 2
2 4 6 9 0.x y z x y z+ + − + − + =
Tọa độ tâm I và bán kính R của mặt cầu l
A.
()1; 2;3I −
và R = 5. B.
()1; 2;3I −
và R =
5
.
C.
)1;2 3( ;I −−
và R = 5. D.
)1;2 3( ;I −−
và R =
5
.
Câu 24: Trong không gian Oxyz, cho mặt phẳng (α) : x - 2y + 2z - 3 = 0. Điểm no sau đây nằm trên
mặt phẳng (α)?
A. N(1;0;1). B.
( )
2;1;1 .Q
C.
2; 1;1 .()P −
D.
( )
2;0;1 .M
Câu 25: Trong không gian
,Oxyz
cho đường thẳng
d
có phương trình:
12
2 3 1
x y z−+
==
−
. Một vectơ
chỉ phương của đường thẳng d có tọa độ
A.
( )
2;3; 1 .−
B.
( )
1; 2;0 .−
C.
( )
1;3;2 .−
D.
( )
4;6;2 .
Câu 26: Cho hình chóp
.,S ABCD
đy
ABCD
là hình vuông cạnh
bằng
a
,
( )
SA ABCD^
và
6
3
SA
a
=
(minh họa như hình bên).
Góc giữa đường thẳng
SC
và mặt phẳng
( )
ABCD
bằng
A.
0
30 .
B.
0
60 .
C.
0
75 .
D.
0
45 .
Câu 27: Cho hàm số
()y f x=
xc đnh, liên tục trên
\2
và có
bảng biến thiên như hình dưới đây:
Khẳng đnh no sau đây l đúng?
A. Hàm số đã cho nghch biến trên khoảng
B. Hàm số đã cho có gi tr cực đại bằng
C. Hàm số đã cho đồng biến trên khoảng và
D. Hàm số đã cho có điểm cực tiểu là
Câu 28: Biết rằng hàm số
( )
32
3 9 28f x x x x= - - +
đạt giá tr nhỏ nhất trên đoạn
[ ]
0;4
tại
0
x
. Tính
0
2018.Px=+
A.
3.P =
B.
2019.P =
C.
2021.P =
D.
2018.P =
Câu 29: Tính
P
là tích tất cả các nghiệm của phương trình
3.9 10.3 3 0.
xx
- + =
( ) ( )
3; 2 2; 1 .- - È - -
3.-
( )
;3- ¥ -
( )
1; .- + ¥
2.
Trang 39
A.
1P =
. B.
1P =-
. C.
0P =
. D.
9.P =
Câu 30: Cho hàm số
( )
( )
2
21y x x= − +
có đồ th
( )
.C
Mệnh đề no sau đây l đúng?
A.
( )
C
không cắt trục hoành. B.
( )
C
cắt trục hoành tại một điểm.
C.
( )
C
cắt trục hoành tại hai điểm. D.
( )
C
cắt trục hoành tại ba điểm.
Câu 31: Có bao nhiêu số nguyên dương
x
thỏa mãn bất phương trình
( ) ( )
log 40 log 60 2xx− + −
A. 20. B. 18. C. 21. D. 19.
Câu 32: Cho khối nón có độ di đường sinh bằng
2a
v bn kính đy bằng
a
. Thể tích của khối nón
đã cho bằng
A.
3
3
3
a
B.
3
3
2
a
C.
3
2
3
a
D.
3
3
a
Câu 33: Cho hai hàm số
( ), ( )y f x y g x==
liên tục trên thỏa mãn
2
1
( ) 3f x dx =
và
2
1
( ) 2.g x dx =
.
Tính
2
[2 ( ) 3 ( ) 1]J f x g x dx= − +
.
A.
1J =
B.
2J =
C.
3J =
D.
6J =
Câu 34: Cho hình phẳng
( )
H
giới hạn bởi cc đường
( ), 0,y f x x x b= = =
và trục hoành (phần tô
màu trong hình vẽ bên). Khi đó diện tích hình phẳng được tính bằng biểu thức nào trong các
biểu thức dưới đây ?
A.
0
()
b
f x dx
B.
0
()
a
f x dx
C.
0
( ) ( )
ab
a
f x dx f x dx−

D.
2
0
()
b
f x dx
Câu 35: Tìm các số thực
,ab
thỏa mãn
2 3 2 6a b bi i+ − = +
A.
2, 6ab= = −
B.
6, 2ab= − =
C.
6, 2ab= − =
D.
6, 2ab= = −
Câu 36: Kí hiệu
0
z
là nghiệm phức có phần ảo dương của phương
trình
2
4 16 17 0.zz− + =
Trên mặt phẳng tọa độ, điểm no dưới đây
l điểm biểu diễn của số phức
0
?w iz=
A.
1
1
;2
2
M



B.
2
1
;2
2
M

−


C.
1
1
;1
4
M

−


D.
1
1
;1
4
M



Câu 37: Trong không gian với hệ tọa độ
,Oxyz
cho ba điểm
( ) ( )
2;1; 1 , 1;0;4 ,AB--
( )
0; 2; 1C --
.
Phương trình no sau đây l phương trình của mặt phẳng đi qua
A
và vuông góc với
BC
?
A.
2 5 5 0x y z− − + =
B.
2 5 0x y z+ - - =
C.
2 5 5 0x y z− − − =
D.
2 5 21 0x y z- - + =
( )
H
Trang 40
Câu 38: Trong không gian với hệ tọa độ
,Oxyz
lập phương trình tham số của đường thẳng
d
đi qua
( )
2;1; 3M −
và vuông góc với hai đường thẳng:
1
11
:
3 1 2
x y z
d
+−
==
−
,
2
0
:
3
x
d y t
zt
=
=−
=
.
A.
2 1 3
:
1 9 3
x y z
d
− − +
==
−−
B.
2
: 1 9
33
xt
d y t
zt
=+
=−
= − −
C.
2
: 1 9
33
xt
d y t
zt
= − +
= − −
=−
D.
2
: 1 9
33
xt
d y t
zt
=+
=+
= − −
Câu 39: Cho 20 tấm thẻ được đnh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất 5 tấm được
chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn; trong đó có ít nhất một tấm thẻ mang số chia
hết cho 4 là:
A.
75
94
B.
225
646
C.
170
646
D.
175
646
Câu 40: Cho hình chóp
.S ABCD
có đy
ABCD
là hình vuông cạnh
.a
Hình chiếu vuông góc của
S
lên
mặt phẳng
( )
ABCD
trùng với trung điểm
H
của cạnh
.AB
Góc tạo bởi
SC
và
( )
ABCD
bằng
0
45 .
Tính theo
a
tính khoảng cách giữa hai đường thẳng
SD
và
.AB
A.
25
3
a
d =
B.
5
13
a
d =
C.
5
3
a
d =
D.
15
3
a
d =
Câu 41: Cho hàm số
()y f x=
có đạo hàm trên và có bảng xét dấu của hàm số
'( )y f x=
như sau:
2−
2
5
'( )fx
−
0
+
0
−
0
+
Hàm số
( ) ( )
32g x f x=−
nghch biến trên khoảng nào trong các khoảng sau ?
A.
( )
0;2 .
B.
( )
; 1 .− −
C.
( )
1;3 .
D.
( )
1; .− +
Câu 42: Dân số thế giới được tính theo công thức 

trong đó A l dân số của năm lấy làm
mốc tính, S là dân số sau n năm, I l tỉ lệ tăng dân số hng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1,47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam gần với số nào nhất sau đây?
A. 99.389.200 B. 99.386.600 C. 100.861.100 D. 99.251.200
x
−
+
Trang 41
Câu 43: Hàm số
bx c
y
xa
−
=
−
(
0;a
)
, , a b c
có đồ th như hình vẽ
bên. Mệnh đề no sau đây l đúng?
A.
0, 0, 0.a b c ab −
B.
0, 0, 0.a b c ab −
C.
0, 0, 0.a b c ab − =
D.
0, 0, 0.a b c ab −
x
y
y
O
Câu 44: Cho hình trụ có bn kinh` đy bằng
2.a
Cắt hình trụ bởi một mặt phẳng song song với trục
của hình trụ và cách trục của hình trụ một khoảng bằng
2
a
ta được thiết diện là một hình vuông.
Tính thể tích V của khối trụ đã cho.
A.
3
3Va
=
B.
3
27
3
a
V
=
C.
3
27Va
=
D.
3
Va
=
Câu 45: Cho hm số
()fx
có đạo hm liên tục trên
.
Biết
(5) 1f =
và
1
0
(5 ) 1xf x dx =
, khi đó
5
2
0
'( )x f x dx
bằng:
A.
15.
B.
23.
C.
123
5
D.
25.−
Câu 46: Cho hàm số
( )
y f x=
liên tục trên
¡
v có đồ th như hình vẽ. Gọi
S
là tập hợp tất cả các
giá tr nguyên của tham số
m
để phương trình
( )
sin 3sinf x x m=+
có nghiệm thuộc khoảng
( )
0;
. Tổng các phần tử của
S
bằng
A.
8.−
B.
10.−
C.
6.−
D.
5.−
Câu 47: Cho hai số thực
1, 1ab
. Biết phương trình
2
1
1
xx
ab
−
=
có hai nghiệm phân biệt
12
,xx
. Tìm
giá tr nhỏ nhất của biểu thức
( )
2
12
12
12
4
xx
S x x
xx

= − +

+

.
Trang 42
A.
3
34
. B.
4
C.
3
32
. D.
3
4
.
Câu 48: Cho hàm số
( )
2
4
1
mx
fx
x
+
=
+
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá tr của
m
sao cho
( )
( )
1;3
1;3
2max min 12f x f x−=
. Số phần tử của
S
là?
A.
0
. B.
2
. C.
4
. D.
6
.
Câu 49: Cho hình hộp
.ABCD A B C D
có chiều cao bằng
10
và diện tích đy bằng
202
. Gọi
M
là
trung điểm của cạnh
.AB
Mặt phẳng
( )
'MB D
chia khối hộp
.ABCD A B C D
thành hai khối đa
diện. Thể tích của khối đa diện lồi chứa đỉnh
A
bằng
A.
3535
3
. B.
1010
3
. C.
505
2
. D.
3535
6
.
Câu 50: Cho
,xy
là các số thực dương thỏa mãn
12
ln 3 1.
x
xy
xy

−
= + −

+

Tìm giá tr nhỏ nhất
min
P
của
11
1.P
x xy
= + +
A.
min
8P =
. B.
min
16P =
. C.
min
9P =
. D.
min
2P =
.
HẾT
HƯỚNG DẪN GIẢI
Câu 1: Một tổ có 5 học sinh nam và 7 học sinh nữ, số cách chọn ra hai học sinh có cả nam và nữ?
A.
11
57
.CC
B.
11
57
CC+
C.
2
12
C
D.
11
57
CC+
Gợi ý giải: Số cách chọn một học sinh nam là : 5 cách(
1
5
C
)
Số cách chọn một học sinh nữ là : 7 cách(
1
7
C
)
Vậy số cách chọn hai học sinh có cả nam và nữ là : 5 x 7 = 35 hay
11
57
.CC
(cách chọn)
Câu 2: Cho
( )
n
u
là cấp số cộng với công sai
.d
Biết
3
4u =−
và
5
10.u =−
Số hạng đầu tiên
1
u
bằng
A.
1
2u =
B.
1
3u =−
C.
1
6u =−
D.
1
7u =−
Gợi ý giải: Ta có :
3
1
1
51
4
24
2
10 4 10
3
u
ud
u
u u d
d
=−
+ = −
=
= − + = −
=−
. Vậy
1
2u =
Câu 3: Số nghiệm của phương trình
2
33
xx
=
là
A. 2 B. 1 C. 0 D. Vô số
Gợi ý giải:
2
22
0
3 3 0
1
xx
x
x x x x
x
=
= = − =
=
Vậy
0, 1xx==
Câu 4: Một khối lập phương có thể tích là
3
8.a
Cạnh của khối lập phương đó bằng
A.
2a
B.
a
C.
2
a
D.
3
a
Trang 43
Gợi ý giải: Ta có :
3
8Va=
suy ra cạnh của hình lập phương bằng
2a
Câu 5: Tập xc đnh của hàm số
3
log 3 )(yx=−
là
A.
( )
;3−
B. C.
( )
3; +
D.
( )
0 ;+
Gợi ý giải: Hàm số xc đnh khi
3– 0 3.xx
Vậy tập xc đnh của hàm số là
( )
;3−
Câu 6: Họ nguyên hàm của hàm số
( )
3
x
f x e=+
là
A.
( )
3
x
F x e x=+
B.
( )
3
x
F x e x=−
C.
( )
3
x
F x e x= − +
D.
( )
3
x
F x e x= − −
Gợi ý giải:
( )
3
x
F x e x=+
Câu 7: Một khối chóp có đy l hình vuông cạnh
3a =
v đường cao
5.h =
Thể tích khối chóp là
A.
15V =
B.
45V =
C.
25V =
D.
35V =
Gợi ý giải: Diện tích đy
2
.Ba=
Thể tích khối chóp
2
11
.3 .5 15
33
V Bh V= = =
Câu 8: Cho hình nón có bn kính đy r = 4 v diện tích xung quanh bằng 20π. Thể tích
của khối nón đã cho bằng
A. 4π. B. 16π. C.163π. D.803π.
Lời giải.
Áp dụng công thức tính diện tích xung quanh của hình nón ta có: Sxq = πrl
20π = π4l
l = 5.
Vì
2 2 2 2
5 4 3h l r h= − = − =
. Khối nón có thể tích l
22
11
.4 .3 16
33
V r h
= = =
Câu 9: Thể tích V của một khối cầu có bán kính R là
A.
3
4
3
VR
=
B.
3
1
3
VR
=
C.
2
4
3
VR
=
D.
3
4VR
=
Lời giải.
Thể tích V của khối cầu có bn kính R là:
3
4
3
VR
=
Câu 10: Cho hm số y = f(x) có bảng biến thiên như sau :
x
-∞
0
2
+ ∞
y’
+
0 -
0 +
y
0
1
-3
+ ∞
Hàm số đã cho đồng biến trên khoảng no dưới đây?
A. (2;+∞) B. (-∞;1) C. (0;+∞) D. (0;2)
Lời giải.
Trang 44
Dựa vo bảng biến thiên, hm số đã cho đồng biến trên cc khoảng
( )
;0−
và
( )
2; .+
Chọn đp n A
Câu 11: Với
,ab
l hai số thực dương tùy ý,
4
ln
ae
b
bằng
A.
4ln – ln 1ab+
. B.
4ln ln 1.ba−+
C.
4ln ln –1.ab+
D.
4ln ln 1.ab++
Lời giải.
Ta có:
4
ln
ae
b
= ln (a
4
e) – ln b = 4 ln a + 1 – ln b. Chọn đp n: A
Câu 12: Công thức tính diện tích xung quanh của hình trụ có chiều cao
,h
bn kính đy
R
là
A. S
xq
= 2πRh. B. S
xq
= π
2
Rh. C. S
xq
= πRh. D. S
xq
= 4πRh.
Lời giải.
Áp dụng công thức tính diện tích xung quanh của hình trụ S
xq
= 2πRh. Chọn đp n: A
Câu 13: Hm số y = f(x) liên tục trên v có bảng biến thiên như hình vẽ.
x
-∞
1
2
+ ∞
y’
+
0 −
|| +
y
−∞
3
0
+ ∞
Mệnh đề no sau đây l đúng?
A. Hm số đã cho có hai điểm cực tr.
B. Hm số đã cho có đúng một điểm cực tr.
C. Hm số đã cho không có gi tr cực tiểu.
D. Hm số đã cho không có gi tr cực đại.
Lời giải.
Dựa vo bảng biến thiên, ta thấy hm số đạt cực đại tại x = 1 v đạt cực tiểu tại x = 2.
Vậy hàm số có hai điểm cực tr. Chọn đp n A
Câu 14: Đường cong trong hình vẽ bên l đồ th của hm số no dưới đây?
A.
32
3 1y x x= − +
B.
32
31y x x= − − +
C.
32
3 1y x x= + +
D.
32
3 1y x x= − + +
Lời giải.
Hình vẽ l đồ th hm số y = ax
3
+ bx
2
+ cx + d với a > 0 v hm số có hai điểm cực tr l x = 0
và x = 2. Ta thấy chỉ có hm số
32
31y x x= − +
thỏa
O
x
y
1−
2
3−
1
Trang 45
Câu 15: Đường thẳng no dưới đây l tiệm cận ngang của đồ th hm số
14
?
21
x
y
x
−
=
−
A.
2.y =
B.
1
2
y =
. C.
4.y =
D.
2.y =−
Lời giải.
Ta có:
lim 2; lim 2
xx
yy
→+ →−
= − = −
, nên đường thẳng
2y =−
l đường tiệm cận ngang của đồ th hm số đã
cho. Chọn đp n D
Câu 16: Tập nghiệm của bất phương trình log
3
(x - 2) ≥ 2 l
A.
)
11; .+
B.
( )
2; .+
C.
( )
;11 .−
D.
(11; )+
Lời giải.
Gợi ý giải:
Điều kiện:
2 0 2.xx−
Vì
31
nên
( )
2
3
log 2 2 2 3 11.x x x − −
Vậy tập nghiệm của bất phương trình l
)
11; .+
Câu 17: Cho hàm số bậc bốn
()y f x=
có đồ th như hình vẽ
Số nghiệm của phương trình
() 1fx=−
là:
A.
4.
B.
3.
C.
2.
D.
1.
Lời giải.
Số nghiệm của phương trình l số giao điểm của
đồ th hai hàm số: y = f(x) và y = -1. Suy ra số nghiệm là 4
Câu 18: Cho hàm số
( )
fx
liên tục trên [0;3]. Nếu
3
0
( ) 2f x dx =
thì
3
0
[ 3 ( )]x f x dx−
có giá tr bằng
A.
3
2
−
B.
3−
C.
3
D.
3
.
2
Lời giải.
Ta có:
3
3 3 3
2
0 0 0
0
3
[ 3 ( )] 3 ( ) 3.2
22
x
x f x dx xdx f x dx− = − = − = −
Câu 19: Số phức liên hợp của số phức
4 – 3zi=
là
Trang 46
A.
43zi=+
B.
43zi= − −
C.
43zi= − +
D.
34zi=−
Lời giải.
Số phức liên hợp của
z
là
43zi=+
Câu 20: Cho hai số phức:
1
1– 2 zi=
và
2
3 – 2 .zi=
Tìm số phức
2
1
z
z
z
=
A.
74
55
zi=+
B.
74
55
zi= − +
C.
74
55
zi=−
D.
74
55
zi= − −
Lời giải.
2
1
(3 2 )(1 2 ) 7 4
(1 2 )(1 2 ) 5
z
i i i
z i i
− + +
==
−+
Câu 21: Cho số phức z = 4 – 3i có điểm biểu diễn trên mặt phẳng tọa độ Oxy là M. Độ di
OM
bằng
A.
5
B.
25
C.
7
D.
4
Lời giải.
Ta có: Tọa độ M(4 ; -3) nên OM =
22
4 ( 3) 5+ − =
Câu 22: Trong không gian Oxyz , cho điểm A(1; 2; 3). Hình chiếu vuông góc của điểm A trên trục Oz là
điểm
A.
0;0;3 .()Q
B.
1;0;3 .()M
C.
( )
0;2;3 .P
D.
1;0;0 .()N −
Lời giải.
Hình chiếu vuông góc của điểm
( )
1;2;3A
lên trục
Oz
l điểm
( )
0;0;3M
Câu 23: Trong không gian với hệ tọa độ
,Oxyz
cho mặt cầu có phương trình
2 2 2
2 4 6 9 0.x y z x y z+ + − + − + =
Tọa độ tâm I và bán kính R của mặt cầu l
A.
()1; 2;3I −
và R = 5. B.
()1; 2;3I −
và R =
5
.
C.
)1;2 3( ;I −−
và R = 5. D.
)1;2 3( ;I −−
và R =
5
.
Lời giải.
Mặt cầu x
2
+ y
2
+ z
2
- 2x + 4y - 6z + 9 = 0 có tâm I (1; - 2; 3) và bán kính
R =
2 2 2
1 ( 2) 3 9 5+ − + − =
Câu 24: Trong không gian Oxyz, cho mặt phẳng (α) : x - 2y + 2z - 3 = 0. Điểm no sau đây nằm trên
mặt phẳng (α)?
A. N(1;0;1). B.
( )
2;1;1 .Q
C.
2; 1;1 .()P −
D.
( )
2;0;1 .M
Lời giải.
Ta thấy tọa độ điểm N(1; 0; 1) thỏa mãn phương trình mặt phẳng (α) nên điểm N nằm trên (α)
Câu 25: Trong không gian
,Oxyz
cho đường thẳng
d
có phương trình:
12
2 3 1
x y z−+
==
−
. Một vectơ
chỉ phương của đường thẳng d có tọa độ
Trang 47
A.
( )
2;3; 1 .−
B.
( )
1; 2;0 .−
C.
( )
1;3;2 .−
D.
( )
4;6;2 .
Lời giải.
d có VTVP
(2;3; 1)u =−
Câu 26: Cho hình chóp
.,S ABCD
đy
ABCD
là hình vuông cạnh
bằng
a
,
( )
SA ABCD^
và
6
3
SA
a
=
(minh họa như hình bên).
Góc giữa đường thẳng
SC
và mặt phẳng
( )
ABCD
bằng
A.
0
30 .
B.
0
60 .
C.
0
75 .
D.
0
45 .
Hướng dẫn giải:
ABCD
là hình vuông cạnh
a
nên
2.AC a=
( )
SA ABCD AC^Þ
là hình chiếu vuông góc của
SC
lên
( )
·
ABCD SCAÞ
là góc giữa
SC
và
( )
.ABCD
Tam giác
SAC
vuông tại
A
nên
· ·
0
6 1 1
tan . 30 .
3
23
SA a
SCA SCA
AC
a
= = = Þ =
Câu 27: Cho hàm số
()y f x=
xc đnh, liên tục trên
\2
và có bảng biến thiên như hình dưới đây:
Khẳng đnh no sau đây l đúng?
A. Hàm số đã cho nghch biến trên khoảng
B. Hàm số đã cho có gi tr cực đại bằng
C. Hàm số đã cho đồng biến trên khoảng và
D. Hàm số đã cho có điểm cực tiểu là
Hướng dẫn giải:
Dựa vào bảng biến thiên, ta có nhận xét sau
Hàm số nghch biến trên khoảng và A sai (sai chỗ dấu ).
Hàm số có giá tr cực đại B sai.
Hàm số đồng biến khoảng và C đúng.
( ) ( )
3; 2 2; 1 .- - È - -
3.-
( )
;3- ¥ -
( )
1; .- + ¥
2.
( )
3; 2--
( )
2; 1- - ¾ ¾®
È
2
C
y = - ¾ ¾®
Đ
( )
;3- ¥ -
( )
1;- + ¥ ¾ ¾®
Trang 48
Hàm số có điểm cực tiểu là D sai. )
Câu 28: Biết rằng hàm số
( )
32
3 9 28f x x x x= - - +
đạt giá tr nhỏ nhất trên đoạn
[ ]
0;4
tại
0
x
. Tính
0
2018.Px=+
A.
3.P =
B.
2019.P =
C.
2021.P =
D.
2018.P =
Hướng dẫn giải:
Đạo hàm
( ) ( )
[ ]
[ ]
2
1 0;4
' 3 6 9 ' 0 .
3 0;4
x
f x x x f x
x
é
= - Ï
ê
= - - ¾ ¾® = Û
ê
=Î
ê
ë
Ta có
( )
( )
( )
[ ]
( )
0;4
0 28
3 1 min 1
48
f
f f x
f
ì
ï
=
ï
ï
ï
= ¾ ¾® =
í
ï
ï
ï
=
ï
î
khi
0
3 2021.x x P= = ¾ ¾® =
Câu 29: Tính
P
là tích tất cả các nghiệm của phương trình
3.9 10.3 3 0.
xx
- + =
A.
1P =
. B.
1P =-
. C.
0P =
. D.
9.P =
Hướng dẫn giải:
Phương trình
2
3.3 10.3 3 0
xx
Û - + =
.
Đặt
3 0.
x
t =>
Phương trình trở thành
2
1
3 10 3 0
3
t t t- + = Û =
hoặc
3t =
.
Với
1
11
3 1 .
33
x
t x x= ¾ ¾® = Û = - =
Với
2
3 3 3 1 .
x
t x x= ¾ ¾® = Û = =
Vậy
12
1.P x x= = -
Câu 30: Cho hàm số
( )
( )
2
21y x x= − +
có đồ th
( )
.C
Mệnh đề no sau đây l đúng?
A.
( )
C
không cắt trục hoành. B.
( )
C
cắt trục hoành tại một điểm.
C.
( )
C
cắt trục hoành tại hai điểm. D.
( )
C
cắt trục hoành tại ba điểm.
Hướng dẫn giải:
Phương trình honh độ giao điểm của
( )
C
với trục hoành:
( )
( )
2
2 1 0 2 0 2.x x x x− + = − = =
Vậy đồ th hàm số cắt trục hoành tại một điểm.
Câu 31: Có bao nhiêu số nguyên dương
x
thỏa mãn bất phương trình
( ) ( )
log 40 log 60 2xx− + −
A. 20. B. 18. C. 21. D. 19.
Hướng dẫn giải:
Điều kiện:
40 60x
.
Bất phương trình
( )( )
log 40 60 2xx − −


( )( ) ( )
2
22
40 60 10 100 2500 0 50 0 50.x x x x x x − − − + −
1- ¾ ¾®
Trang 49
Kết hợp với điều kiện, ta được
40 60
41;...;59 \ 50
50
x
x
x
x
+

⎯⎯⎯→
.
Câu 32: Cho khối nón có độ di đường sinh bằng
2a
v bn kính đy bằng
a
. Thể tích của khối nón
đã cho bằng
A.
3
3
3
a
B.
3
3
2
a
C.
3
2
3
a
D.
3
3
a
Hướng dẫn giải:
22
=−h l r
với
2=
=
la
ra
. Suyra
3=ha
.
3
22
1 1 3
3
3 3 3
= = =
a
V r h a a

.
Câu 33: Cho hai hàm số
( ), ( )y f x y g x==
liên tục trên thỏa mãn
2
1
( ) 3f x dx =
và
2
1
( ) 2.g x dx =
.
Tính
2
[2 ( ) 3 ( ) 1]J f x g x dx= − +
.
A.
1J =
B.
2J =
C.
3J =
D.
6J =
Hướng dẫn giải
Ta có
2 2 2 2
2
1
1 1 1
[2 ( ) 3 ( ) 1] 2 ( ) 3 ( ) 2.3 3.2 1J f x g x dx f x dx g x dx dx x= − + = − + = − + =
Câu 34: Cho hình phẳng
( )
H
giới hạn bởi cc đường
( ), 0,y f x x x b= = =
và trục hoành (phần tô
màu trong hình vẽ bên). Khi đó diện tích hình phẳng được tính bằng biểu thức nào trong các
biểu thức dưới đây ?
A.
0
()
b
f x dx
B.
0
()
a
f x dx
C.
0
( ) ( )
ab
a
f x dx f x dx−

D.
2
0
()
b
f x dx
Hướng dẫn giải
• Ta có diện tích hình phẳng được tính bởi công thức
00
( ) ( ) ( )
b a b
a
S f x dx f x dx f x dx= = +
• Mặt khác, dựa vo đồ th hàm số ta có:
▪ Trên đoạn
[0; ], ( ) 0a f x
▪ Trên đoạn
[ ; ], ( ) 0a b f x
• Từ đó suy ra
0
( ) ( )
ab
a
S f x dx f x dx=−

Câu 35: Tìm các số thực
,ab
thỏa mãn
2 3 2 6a b bi i+ − = +
A.
2, 6ab= = −
B.
6, 2ab= − =
C.
6, 2ab= − =
D.
6, 2ab= = −
Hướng dẫn giải
( )
H
( )
H
( )
y f x=
Trang 50
• Ta có
2 2 6
2 3 2 6
3 6 2
a b a
a b bi i
bb
+ = =
+ − = +

− = = −
Câu 36: Kí hiệu
0
z
là nghiệm phức có phần ảo dương của phương trình
2
4 16 17 0.zz− + =
Trên mặt
phẳng tọa độ, điểm no dưới đây l điểm biểu diễn của số phức
0
?w iz=
A.
1
1
;2
2
M



B.
2
1
;2
2
M

−


C.
1
1
;1
4
M

−


D.
1
1
;1
4
M



Hướng dẫn giải
• Ta có
22
1
2
24
2
4 16 17 0 (2 4) 1
2 4 1
2
2
zi
zi
z z z
zi
zi
=+
−=
− + = − = −
− = −
=−
.
• Vì có phần ảo dương nên
0
1
2.
2
zi=+
. Khi đó
0
11
22
22
w iz i i i

= = + = − +


.
• Suy ra điểm biểu diễn của số phức
1
2
2
wi= − +
l điểm có tọa độ
1
;2
2

−


Câu 37: Trong không gian với hệ tọa độ
,Oxyz
cho ba điểm
( ) ( )
2;1; 1 , 1;0;4 ,AB--
( )
0; 2; 1C --
.
Phương trình no sau đây l phương trình của mặt phẳng đi qua
A
và vuông góc với
BC
?
A.
2 5 5 0x y z− − + =
B.
2 5 0x y z+ - - =
C.
2 5 5 0x y z− − − =
D.
2 5 21 0x y z- - + =
Hướng dẫn giải : Mặt phẳng cần tìm đi qua
( )
2;1; 1A -
và nhận
( )
1; 2; 5BC = - -
uuur
làm một VTPT nên
có phương trình
2 5 5 0x y z- - - =
.
Câu 38: Trong không gian với hệ tọa độ
,Oxyz
lập phương trình tham số của đường thẳng
d
đi qua
( )
2;1; 3M −
và vuông góc với hai đường thẳng:
1
11
:
3 1 2
x y z
d
+−
==
−
,
2
0
:
3
x
d y t
zt
=
=−
=
.
A.
2 1 3
:
1 9 3
x y z
d
− − +
==
−−
B.
2
: 1 9
33
xt
d y t
zt
=+
=−
= − −
C.
2
: 1 9
33
xt
d y t
zt
= − +
= − −
=−
D.
2
: 1 9
33
xt
d y t
zt
=+
=+
= − −
Đường thẳng d qua
( )
2;1; 3M −
, VTCP
( )
12
; 1; 9; 3u u u

= = − −

Câu 39: Cho 20 tấm thẻ được đnh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất 5 tấm được
chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn; trong đó có ít nhất một tấm thẻ mang số chia
hết cho 4 là:
0
z
Trang 51
A.
75
94
B.
225
646
C.
170
646
D.
175
646
Lời giải
Số phần tử không gian mẫu là:
5
20
()nC=
Trong số các số tư 1 đến 20 có 10 số lẻ, 10 số chẵn trong đó 5 số chia hết cho 4 là: 4, 8, 12, 16, 20.
Số cách chọn 3 tấm thẻ mang số lẻ là:
3
10
C
Số cách chọn 2 tấm thẻ mang số chẵn là:
2
10
C
Số cách chọn 2 tấm thẻ mang số chẵn mà không chia hết cho 4 là:
2
5
C
Vậy xác suất để chọn được 5 tấm thẻ thỏa yêu cầu bài toán là:
( )
3 2 2
10 10 5
5
20
175
646
C C C
C
−
=
Câu 40: Cho hình chóp
.S ABCD
có đy
ABCD
là hình vuông cạnh
.a
Hình chiếu vuông góc của
S
lên
mặt phẳng
( )
ABCD
trùng với trung điểm
H
của cạnh
.AB
Góc tạo bởi
SC
và
( )
ABCD
bằng
0
45 .
Tính theo
a
tính khoảng cách giữa hai đường thẳng
SD
và
.AB
A.
25
3
a
d =
B.
5
13
a
d =
C.
5
3
a
d =
D.
15
3
a
d =
Lời giải
Góc giữa SC và (ABCD) là
0
SCH 45=
Tính được
a 5 a 5
HC SH
22
= =
Vì
( )
AB/ / SCD ,H AB
nên
( ) ( )
( )
( )
( )
d AB;SD d AB, SCD d H, SCD==
Gọi I l trung điểm của CD. Trong (SHI), dựng
HK SI⊥
tại K
Chứng minh được
( ) ( )
( )
HK SCD d H; SCD HK⊥ =
Xét tam giác SHI vuông tại H, HK đường cao:
2 2 2 2 2 2
1 1 1 4 1 9 a 5
HK
HK SH HI 5a a 5a 3
= + = + = =
Trang 52
Vậy
( )
a5
d AB;SD HK
3
==
Câu 41: Cho hàm số
()y f x=
có đạo hàm trên và có bảng xét dấu của hàm số
'( )y f x=
như sau:
2−
2
5
'( )fx
−
0
+
0
−
0
+
Hàm số
( ) ( )
32g x f x=−
nghch biến trên khoảng nào trong các khoảng sau ?
A.
( )
0;2 .
B.
( )
; 1 .− −
C.
( )
1;3 .
D.
( )
1; .− +
Lời giải
Dựa vào bảng xét dấu:
22
'( ) 0
5
x
fx
x
−

Ta có
( ) ( )
' 2 ' 3 2g x f x= − −
Xét
( ) ( )
15
2 3 2 2
' 0 ' 3 2 0
22
3 2 5
1
x
x
g x f x
x
x
− −

−
−
−
Vậy g(x) nghch biến trên
15
;
22



và
( )
;1− −
Câu 42: Dân số thế giới được tính theo công thức 

trong đó A l dân số của năm lấy làm
mốc tính, S là dân số sau n năm, I l tỉ lệ tăng dân số hng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1,47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam gần với số nào nhất sau đây?
A. 99.389.200 B. 99.386.600 C. 100.861.100 D. 99.251.200
Hướng dẫn giải:
Áp dụng công thức
.
ni
S Ae=
với A = 80.902.400, n = 2019 - 2005 = 14, i = 1,47% = 0,0147
Dân số Việt Nam đến năm 2019 l
14.0,0147
80.902.400. 99389203,38e==
Như vậy, số dân Việt Nam đến năm 2019 gần với số 99.389.200 nhất.
Chọn đp n A.
x
−
+
Trang 53
Câu 43: Hàm số
bx c
y
xa
−
=
−
(
0;a
)
, , a b c
có đồ th như hình vẽ
bên. Mệnh đề no sau đây l đúng?
A.
0, 0, 0.a b c ab −
B.
0, 0, 0.a b c ab −
C.
0, 0, 0.a b c ab − =
D.
0, 0, 0.a b c ab −
x
y
y
O
Hướng dẫn giải:
Đồ th hàm số có tiệm cận đứng
0xa=
; tiệm cận ngang
0.yb=
Mặt khác, ta thấy dạng đồ th l đường cong đi xuống từ trái sang phải trên các khoảng xc đnh của nó
nên
( )
2
0, 0.
c ab
y x a c ab
xa
−
= ⎯⎯→ −
−
Vậy
0, 0, 0.a b c ab −
Chọn A.
Câu 44: Cho hình trụ có bn kinh` đy bằng
2.a
Cắt hình trụ bởi một mặt phẳng song song với trục
của hình trụ và cách trục của hình trụ một khoảng bằng
2
a
ta được thiết diện là một hình vuông.
Tính thể tích V của khối trụ đã cho.
A.
3
3Va
=
B.
3
27
3
a
V
=
C.
3
27Va
=
D.
3
Va
=
Hướng dẫn giải:
Gọi O, O’ lần lượt là tâm của đy v thiết diện l hình vuông ABB’A’.
Gọi H l trung điểm AB, ta có OH
^
AB , OH
^
AA’ suy ra OH
^
(ABB’A’)
Do đó
’,( ’ ’)
2
()
a
d OO ABB A OH==
Tam giác OAH vuông tại H nên
7
2
a
AH =
Suy ra
’ ’ 2 7AB AA OO AH a= = = =
Vậy thể tích
2 2 3
( 2) 7 2 7V r h a a a
= = =
a
1
a
2
O'
B'
A'
H
B
A
O
Trang 54
Vậy chọn C
Câu 45: Cho hm số
()fx
có đạo hm liên tục trên
.
Biết
(5) 1f =
và
1
0
(5 ) 1xf x dx =
, khi đó
5
2
0
'( )x f x dx
bằng:
A.
15.
B.
23.
C.
123
5
D.
25.−
Cách 1:
5 5 1
5
22
0
0 0 0
'( )d ( ) 2 . ( )d 25.1 2 5 . (5 )d(5 ) 25 50.1 25x f x x x f x x f x x t f t t= − = − = − = −
Cách 2:
Ta có:
1
0
1 (5 )dxf x x=
Đặt
1
5 d 5d d d
5
t x t x t x= = =
5 5 5 5
0 0 0 0
1 1 1
1 ( ) d 1 ( )d ( )d 25 ( )d 25
5 5 25
t f t t t f t t t f t t x f x x = = = =
Đặt
5
2
0
( )dI x f x x
=
Đặt:
2
d 2 d
()
d '( )d
u x x
ux
v f x
v f x x
=
=

=
=
5
5
2
0
0
( ) 2 ( )d 25 (5) 2.25 25I x f x xf x x f = − = − = −
Câu 46: Cho hàm số
( )
y f x=
liên tục trên
¡
v có đồ th như hình vẽ. Gọi
S
là tập hợp tất cả các
giá tr nguyên của tham số
m
để phương trình
( )
sin 3sinf x x m=+
có nghiệm thuộc khoảng
( )
0;
. Tổng các phần tử của
S
bằng
A.
8.−
B.
10.−
C.
6.−
D.
5.−
Đặt
sintx=
, do
( ) (
(
0; sin 0;1 0;1x x t
.
Trang 55
Gọi
1
l đường thẳng qua điểm
( )
1; 1−
và song song với đường thẳng
3yx=
có phương
trình
34yx=−
.
Gọi
2
lđường thẳng qua điểm
( )
0;1
và song song với đường thẳng
3yx=
có phương
trình
31yx=+
.
Do đó phương trình
( )
sin 3sinf x x m=+
có nghiệm thuộc khoảng
( )
0;
khi và chỉ khi
phương trình
( )
3f t t m=+
có nghiệm thuộc nửa khoảng
(
0;1
41m −
.
Câu 47: Cho hai số thực
1, 1ab
. Biết phương trình
2
1
1
xx
ab
−
=
có hai nghiệm phân biệt
12
,xx
. Tìm
giá tr nhỏ nhất của biểu thức
( )
2
12
12
12
4
xx
S x x
xx

= − +

+

.
A.
3
34
. B.
4
C.
3
32
. D.
3
4
.
Ta có
( )
2
1 2 2
1 log 1 0 log 1 0
xx
bb
a b x a x x x a
−
= + − = + − =
Do phương trình có hai nghiệm
12
,xx
nên theo đnh lý Viet ta có:
12
12
log
1
b
x x a
xx
+ = −
=−
Khi đó
2
1
4log
log
b
b
Sa
a
=+
Đặt
log
b
ta=
, do
1, 1 0a b t
. Khi đó
3
22
11
4 2 2 3 4S t t t
tt
= + = + +
Đẳng thức xảy ra khi
2
3
11
2
2
tt
t
= =
. Vậy
3
min 3 4S =
Câu 48: Cho hàm số
( )
2
4
1
mx
fx
x
+
=
+
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá tr của
m
sao cho
( )
( )
1;3
1;3
2max min 12f x f x−=
. Số phần tử của
S
là?
A.
0
. B.
2
. C.
4
. D.
6
.
Lời giải tham khảo
Điều kiện
1x −
Ta có
( )
( )
2
2
4
'
1
m
fx
x
−
=
+
TH1: Nếu
2
4 0 2mm− = =
thì
( )
4fx=
( )
( )
1;3
1;3
2max min 4f x f x−=
( không thỏa ycbt)
Nên ta loại
2m =
TH2: Nếu
2
2
40
2
m
m
m
−
−
thì hàm số đồng biến trên [1;3]
Khi đó:
( )
( )
22
1;3
1;3
3 4 4
2max min 12 12 2 3
22
mm
f x f x m
++
− = − = =
(nhận)
Trang 56
TH3: Nếu
2
4 0 2 2mm− −
thì hàm số nghch biến trên [1;3]
Khi đó:
( )
( )
2
2
1;3
1;3
34
2max min 12 4 12 6
4
m
f x f x m m
+
− = + − = =
(loại)
Vậy có 2 giá tr của
m
thỏa ycbt
Chọn B
Câu 49: Cho hình hộp
.ABCD A B C D
có chiều cao bằng
10
và diện tích đy bằng
202
. Gọi
M
là
trung điểm của cạnh
.AB
Mặt phẳng
( )
'MB D
chia khối hộp
.ABCD A B C D
thành hai khối đa
diện. Thể tích của khối đa diện lồi chứa đỉnh
A
bằng
A.
3535
3
. B.
1010
3
. C.
505
2
. D.
3535
6
.
Lời giải tham khảo
Chọn D
Ta có
.
10.202 2020
ABCD A B C D
V
==
Gọi
' '; 'S B M AA N AD SD==
Suy ra
N
l trung điểm của
'SD
.
. ' ' ' . ' ' '
. ' ' '
17
88
S AMN
AMN A B D S A B D
S A B D
V
VV
V
= =
Mà
. ' ' ' . ' ' '
2
S A B D A A B D
VV=
. ' ' ' . ' ' ' . ' ' ' . ' ' ' '
7 7 7
.2.
8 4 24
AMN A B D A A B D A A B D ABCD A B C D
V V V V = = =
. ' ' '
7 3535
.2020
24 6
AMN A B D
V = =
Câu 50: Cho
,xy
là các số thực dương thỏa mãn
12
ln 3 1.
x
xy
xy

−
= + −

+

Tìm giá tr nhỏ nhất
min
P
của
11
1.P
x xy
= + +
A.
min
8P =
. B.
min
16P =
. C.
min
9P =
. D.
min
2P =
.
Lời giải tham khảo
Chọn A
Điều kiện:
1 2 1
0 1 2 0
2
x
xx
xy
−
−
+
Kết hợp với
0x
ta suy ra
1
0
2
x
Trang 57
Ta có:
( ) ( ) ( ) ( )
12
ln 3 1 ln 1 2 ln 1 2
x
x y x x y x y x
xy

−
= + − − − + = + − −

+

( ) ( ) ( ) ( )
ln 1 2 1 2 lnx x x y x y − + − = + + +
Xét hàm
( ) ( )
lnf t t t=+
. Hàm số xc đnh và liên tục trên
( )
0;+
( )
1
' 1 0, 0f t t
t
= +
. Suy ra hàm số đồng biến trên
( )
0;+
( ) ( )
1 2 1 2 1 3 0f x f x y x x y y x − = + − = + = −
Khi đó
( )
1 1 1 2
11
12
13
P
x x x
xx
= + + + +
−
−
Dấu “=” xảy ra
1
13
4
x x x = − =
Xét hàm
( )
12
1
12
gx
xx
= + +
−
trên
1
0;
3



Hàm số
( )
gx
liên tục trên
1
0;
3



( )
( )
2
2
14
'
12
gx
x
x
= − +
−
( )
1
'0
4
g x x= =
Bảng biến thiên
x
0
1
4
1
3
( )
'gx
−
0
+
( )
gx
+
9
8
Vậy
min
8P =
tại
1
4
x =
Trang 58
ĐỀ 9
PHÁT TRIỂN TỪ ĐỀ MINH HỌA
LẦN 2 NĂM 2020
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1. Một lớp học có 18 bạn nam và 22 bạn nữ. Hỏi có bao nhiêu cách chon ra một cặp nam nữ?
A. 40 B. 576 C. 1 D. 357
Câu 2. Cho cấp số cộng
( )
n
u
với số hạng tổng quát
21
n
un=+
. Số hạng
5
u
bằng
A. 10 B. 8 C. 11 D. 5
Câu 3. Nghiệm của phương trình
25
x
=
là
A.
2
log 5x =
B.
5
log 2x =
C.
32x =
D.
25x =
Câu 4. Một khối chóp có diện tích đy bằng 8 và chiều cao bằng 6. Thể tích khối chóp đó bằng
A. 14 B. 48 C. 16 D. 32
Câu 5. Tập xc đnh của hàm số
( )
ln 1yx=−
là
A.
)
1; +
B.
( )
1; +
C.
( )
1;− +
D.
)
1;− +
Câu 6. Họ tất cả các nguyên hàm của hàm số
cos
x
y e x=+
là
A.
sin
x
e x C++
B.
sin
x
e x C− + +
C.
sin
x
e x C−+
D.
sin
x
y e x C= − − +
Câu 7. Thể tích khối lăng trụ có diện tích đy bằng B và chiều cao bằng h là
A.
1
3
V Bh=
B.
V Bh=
C.
3V Bh=
D.
B
V
h
=
Câu 8. Một mặt nón có độ di đường sinh bằng 6, bn kính đy bằng 3. Diện tích xung quanh của mặt
nón đó bằng
A.
6
B. 6 C.
18
D.
18
Câu 9. Thể tích khối cầu có bán kính bằng a là:
A.
2
4
3
a
B.
2
4 a
C.
3
4
3
a
D.
3
4 a
Câu 10. Cho hm số
()y f x=
có bảng biến thiên như hình vẽ
Trang 59
Mệnh đề no đúng trong cc mệnh đề
sau?
A. Hm số đồng biến trên khoảng
( )
2;+
B. Hm số đồng biến trên khoảng
( )
0;+
C. Hm số nghch biến trên khoảng
( )
;2−
D. Hm số nghch biến trên khoảng
( )
2;+
Câu 11. Đạo hm của hm số
x
ye=
là
A.
/ ln2x
ye=
B.
/ x
ye=
C.
/ x
y xe=
D.
/
ln2
x
ye=
Câu 12. Hình trụ có bn kính đy bằng 5cm, đường cao bằng 7cm Tính thể tích khối trụ tròn xoay giới
hạn bởi hình trụ trên.
A. 175 cm
3
. B. 70 cm
3
. C.
175
3
cm
3
. D. 35 cm
3
.
Câu 13. Cho hàm số
()y f x=
có bảng biến thiên như hình vẽ
Hàm số đạt cực đại tại
A.
2=x
B.
4=x
C.
1=−x
D.
8=x
Câu 14. Cho hàm số
2
1
x
y
x
+
=
−
. Khẳng đnh no đúng trong cc khẳng đnh sau?
A. Hàm số đồng biến trên khoảng
( )
1;−
và
( )
1;+
B. Hàm số nghch biến trên R
C. Hàm số nghch biến trên khoảng
( )
1;−
và
( )
1;+
D. Hàm số đồng biến trên R
Câu 15. Đường tiệm cận đứng của đồ th hàm số
23
1
x
y
x
−
=
+
có phương trình l
Trang 60
A.
1x =−
B.
1x =
C.
3=−x
D.
2x =
Câu 16. Nghiệm của bất phương trình
2
log 3x
là
A.
6x
B.
6x
C.
8x
D.
8x
Câu 17. Hàm số
()y f x=
có bảng biến thiên như hình vẽ. Số nghiệm của phương trình
( ) 3 0fx−=
là
A. 1 B. 2 C. 3 D. 4
Câu 18. Biết
1
0
( ) 1f x dx =
và
2
1
( ) 2f x dx =
. Tính
2
0
()f x dx
bằng
A. -1 B. 3 C. 1 D. 2
Câu 19. Mođun của số phức
12zi=+
bằng
A.
5
B. 3 C. 5 D.
3
Câu 20. Cho số phức
1
23zi=−
và
2
32zi=+
. Điểm biểu diễn số phức
12
zz+
có tọa độ l
A.
( )
1; 5−−
B.
( )
5;1
C.
( )
5; 1−
D.
( )
5;1−
Câu 21. Số phức liên hợp của số phức
z a bi=−
là
A.
z a bi=+
B.
z a bi= − +
C.
z b ai=−
D.
z b ai=+
Câu 22. Trong không gian với hệ tọa độ Oxyz. Khoảng cách giữa điểm A(1;2;-3) và B(2;1;-4) bằng
A. 2 B.
2
C. 1 D.
3
Câu 23. Trong không gian với hệ tọa độ Oxyz cho mặt cầu
( )
S
:
( ) ( )
22
2
5 4 3− + + + =x y z
. Tọa độ tâm
I và bán kính R của mặt cầu
( )
S
là
A.
( )
5; 4;0I −
,
3=R
B.
( )
5;4;0I −
,
6=R
C.
( )
5;4;0I
,
3R =
D.
( )
5; 4;0I −
,
9R =
Trang 61
Câu 24. Cho mặt phẳng
( )
α 2 3 0: xy− + + =
. Một véc tơ php tuyến của mặt phẳng
( )
α
là
A.
( )
1 2 0−;;n
B.
( )
1 2 3;;n −
C.
( )
0 1 2;;n −
D.
( )
1 2 0−−;;n
Câu 25. Phương trình tham số của đường thẳng d đi qua điểm A(1;3;5) và vuông góc với mặt phẳng
3 4 2 0( ):P x y z− + − =
là
A.
3
: 4 3
15
xt
d y t
zt
=+
= − +
=+
B.
13
: 3 4
5
xt
d y t
zt
=+
=−
=+
C.
13
: 3 4
5
xt
d y t
zt
= − +
= − +
= − +
D.
13
: 3 4
5
xt
d y t
zt
= − +
=−
=−
Câu 26. Cho hình chóp S.ABC có đy ABC l tam gic đều, SA vuông góc với đy, gọi M l trung
điểm cạnh BC. Khẳng đnh no sau đây đúng?
A.
( )
⊥SM ABC
B.
( )
⊥AM SBC
C.
( )
⊥SA SBC
D.
( )
⊥BC SAM
Câu 27. Cho hàm số
32
1
21
3
()y x mx m x= + + + +
, hàm số có hai điểm cực tr khi giá tr của tham số m
là:
A.
1
2
m
m
−
B.
1
2
m
m
−
C.
12m−
D.
12m−
Câu 28. Giá tr lớn nhất của hàm số
3
12 2y x x= − + +
trên đoạn
13;
, bằng
A. 28 B.13 C.11 D. 18
Câu 29. Đạo hàm của hàm số
ln
x
y e x=
là
A.
x
e
x
B.
1
ln
x
ex
x

+


C.
( )
1 ln
x
ex+
D.
ln
x
ex
x
Câu 30. Số giao điểm của đồ th hàm số
1
21
x
y
x
+
=
−
v đường thẳng
32yx=−
là
A. 3 B. 2 C. 1 D. 0
Trang 62
Câu 31. Nghiệm của bất phương trình:
2 8 1lg( )x−
là
A.
49x
B.
9x
C.
4x
D.
49x
Câu 32. Thiết diện qua đỉnh của một hình nón là một tam giác vuông có cạnh huyền bằng
2a
. Thể tích
khối nón đó bằng
A.
2
2ap
B.
3
ap
C.
3
1
3
ap
D.
2
22ap
Câu 33. Biết F(x) là một nguyên hàm của hàm số
2
()
x
f x e=
và
24(ln )F =
. Khi đó F(0) bằng:
A. 2 B.
5
2
C.
1
D.
3
2
Câu 34. Diện tích hình phẳng giới hạn bởi đồ th hm số
()y f x=
v trục Ox (phần gạch chéo trong hình
vẽ bên) l
A.
13
01
( ) ( )S f x dx f x dx=−

B.
13
01
( ) ( )S f x dx f x dx=+

C.
3
0
()S f x dx=
D.
3
0
()S f x dx=
Câu 35. Tập hợp điểm biểu diễn của số phức
z
thỏa mãn
1z =
là
A. Đường tròn tâm
( )
0;0O
bán kính
=1R
.
B. Hình tròn tâm
( )
0;0O
bán kính
=1R
.
C. Parabol
2
yx=
.
D. Đường thẳng
10xy+ − =
.
Trang 63
Câu 36. Để phương trình
2
z0z b c+ + =
nhận
1 i+
làm nghiệm thì giá tr của b và c là
A.
1; 1bc= − = −
B.
2; 2bc= = −
. C.
3; 2bc= = −
. D.
2; 2bc= − =
.
Câu 37. Phương trình mặt phẳng
( )
P
qua
( )
2 1 3;;A −
và song song với mặt phẳng
( )
2 1 0:Q x y z− + − =
là
A.
( )
2 5 0:P x y z− + + =
B.
( )
2 6 0:P x y z− + + =
C.
( )
2 4 0:P x y z− + + =
D.
( )
2 3 0:P x y z− + − =
Câu 38. Trong không gian Oxyz. Đường thẳng d đi qua
( )
1 2 1;;M −
song song với mặt phẳng
( )
α 2 1 0: x y z+ − − =
và vuông góc với đường thẳng
1
2
2
:
xt
d y t
zt
=−
=+
=
có phương trình l:
A.
13
2
1
xt
yt
zt
=+
= − +
=+
B.
15
2
13
xt
yt
zt
=+
= − −
=+
C.
16
23
1
xt
yt
zt
=+
= − −
=+
D.
12
2
13
xt
yt
zt
=+
= − +
=+
Câu 39. Một bài thi trắc nghiệm khách quan gồm 10 câu hỏi, mỗi câu có 4 phương n trả lời. Xác suất
để một học sinh lm bi thi được ít nhất 8 câu hỏi là
A.
559
289125
B.
580
252259
. C.
110
262141
. D.
109
262144
.
Câu 40. Cho hình chóp
.S ABCD
có đy
ABCD
là hình vuông tâm
O
cạnh
a
,
SO
vuông góc với mặt
phẳng
( )
ABCD
và
.SO a=
Khoảng cách giữa
SC
và
AB
bằng
A.
3
15
a
B.
5
5
a
C.
23
15
a
D.
25
5
a
Câu 41. Hàm số
( )
42
2 2 3y x m x m= − + − + −
đạt cực đại tại điểm
1x =
khi giá tr của m là
A.
3m =
B.
5m =
C.
3m
D.
5m
Câu 42. Một người gửi vo ngân hng 10 triệu đồng với lãi kép 5%/năm. Tính số tiền cả gốc lẫn lãi m
người đó nhận được sau khi gửi ngân hng 10 năm (gần với số no nhất)?
A. 16,234 triệu B. 16, 289 triệu C. 16, 327 triệu D. 16, 280
triệu
Trang 64
Câu 43. Tất cả cc gi tr của tham số m để hàm số
( )
2
2 2 1y x m x= + − +
đồng biến trên khoảng
( )
1; +
là
A.
1m
B.
1m
C.
0m
D.
0m
Câu 44. Cắt một khối trụ T bằng một mặt phẳng đi qua trục của nó ta được một hình vuông có diện tích
bằng 9. Khẳng đnh no sau đây l sai?
A. Khối trụ T có độ di đường sinh là
l3=
B. Khối trụ T có diện tích toàn phần
tp
27
S
2
=
C. Khối trụ T có diện tích xung quanh
D. Khối trụ T có thể tích
9
V
4
=
Câu 45. Đổi biến
lntx=
thì tích phân
2
1
1 ln
e
x
I dx
x
−
=
trở thành
A.
( )
1
0
1
−
−
t
t e dt
B.
( )
1
0
1−
t dt
C.
( )
1
0
1−
t
t edt
D.
( )
1
2
0
1−
t
t e dt
Câu 46. Cho hàm số
( )
32
f x x ax bx c.= + + +
Nếu phương trình
( )
f x 0=
có ba nghiệm phân biệt thì
phương trình
( ) ( ) ( )
( )
2
2f x .f '' x f ' x=
có bao nhiêu nghiệm.
A.
3
B.
1
C.
2
D.
4
Câu 47. Cho x, y là hai số thực dương thỏa mãn điều kiện
( )
2 2 2
x 2y x 2y 2y x 2
4 9.3 4 9 .7
− − − +
+ = +
.Tìm giá tr
nhỏ nhất của biểu thức
x 2y 18
P.
x
++
=
A.
P6=
B.
P 12=
C.
P9=
D.
P4=
Câu 48. Cho hàm số
()y f x=
có đạo hàm
( )( )
2
/2
14
x
f x x x= − −
. Giá tr lớn nhất của hàm số
2
()y f x=
trên đoạn [−2;2] bằng
A.
f(0)
B.
f(1)
C.
f(2)
D.
f( 2)−
Câu 49. Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N l hai điểm thay đổi lần lượt thuộc cạnh BC,
BD sao cho mặt phẳng
( )
AMN
luôn vuông góc với mặt phẳng
( )
BCD .
Gọi
12
V ;V
lần lượt là giá tr lớn
nhất và giá tr nhỏ nhất của thể tích khối tứ diện ABMN. Tính
12
V V ?+
Trang 65
A.
2
12
B.
17 2
72
C.
17 2
144
D.
17 2
216
Câu 50. Tập hợp cc gi tr thực của tham số m để phương trình
( )
( )
2
2019 1
2019
log 4 log 2 1 0x x m− + + − =
có
hai nghiệm thực phân biệt
12
;xx
. Tính
12
2S x x=+
A. 8 B. 16 C. 18 D. 20
…Hết…
ĐỀ 10
PHÁT TRIỂN TỪ ĐỀ MINH HỌA
LẦN 2 NĂM 2020
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1.(NB) Có bao nhiêu cách xếp khc nhau cho 5 người ngồi vào một bàn dài?
A. 120 B. 5
C. 20 D. 25
Câu 2:(NB) Cho cấp số nhân
( )
n
u
có
1
3u =
và
2
6u =−
. Công bội của cấp số nhân đã cho bằng
A. -2 B.
1
2
−
C. -9 D. -18
Câu 3. (NB)Phương trình
21
5 125
x+
=
có nghiệm là
A.
5
2
x =
. B.
1x =
. C.
3x =
. D.
3
2
x =
.
Câu 4 (NB): Thể tích của khối lập phương bằng
8
. Khi đó cạnh của khối lập phương bằng
A. 2 B.3 C.4 D.5
Câu 5.(NB) Tìm tập xc đnh
D
của hàm số
( )
1
3
f x x
−
=
.
A.
)
0;D = +
. B.
\0D =
. C.
( )
0;D = +
. D.
D =
.
Câu 6.(NB)Mệnh đề no sau đây đúng
A.
xx
e dx e C=+
ò
. B.
1
lndx x C
x
=+
ò
.
C.
2
1
tan
cos
dx x C
x
= - +
ò
. D.
sin cosxdx x C=+
ò
.
Trang 66
Câu 7 (NB): Cho khối lăng trụ có đy l hình vuông cạnh
a
, chiều cao bằng
3a
. Thể tích của khối
lăng trụ đã cho bằng
A.
3
3a
B.
3
a
C.
2
3a
D.
2
a
Câu 8 (NB): Cho khối nón có bn kính đy
5r =
, đường sinh
7l =
. Diện tích xung quanh của khối
nón bằng
A.
35
B.
70
C.
2
35
D.
2
70
Câu 9 (NB): Diện tích mặt cầu có đường kính 2 bằng
A.
4
B.
16
C.
32
D.
8
Câu 10. (NB) Cho hàm số
( )
y f x=
có đồ th như hình vẽ bên. Hỏi hàm số đã cho đồng biến trên
khoảng no dưới đây ?
A.
( )
;8−
. B.
( )
1;4
. C.
( )
4;+
. D.
( )
0;1
.
Câu 11. (NB)Với
,ab
là hai số thực dương khc
1
, ta có
log
b
a
bằng:
A.
log
a
b−
. B.
1
log
a
b
. C.
log logab−
. D.
log
a
b
.
Câu 12 (NB): Thể tích khối trụ có đường cao
h
, bn kinh đy
r
bằng
A.
2
rh
B.
2
1
3
rh
C.
2
rh
D.
2
1
3
rh
Câu 13.(NB)Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Trang 67
Giá tr cực tiểu của hàm số đã cho bằng
A.
0
. B.
2−
. C.
1−
. D.
1
.
Câu 14.(TH) Đường cong trong hình vẽ dưới đây l đồ th của hàm số no trong cc phương n
A
,
B
,
C
,
D
?
A.
2
1
x
y
x
−
=
+
. B.
2
1
x
y
x
−−
=
+
. C.
1
x
y
x
−
=
+
. D.
2
1
x
y
x
−+
=
+
.
Câu 15 (NB). Đường thẳng là tiệm cận đứng của đồ th hàm số nào trong các hàm số sau đây?
A.
23
.
1
x
y
x
−
=
−
B.
32
.
31
x
y
x
+
=
−
C.
3
.
1
x
y
x
+
=
+
D.
2
1
.
1
x
y
x
−
=
+
Câu 16.(NB) Tập nghiệm của bất phương trình
( )
3
log 2 3 0x −
là:
A.
(
;2−
. B.
3
;2
2


. C.
)
2;+
. D.
53
;
2

−
−

.
Câu 17(TH): Cho hàm số
( )
y f x=
liên tục trên
v có đồ th như hình bên. Số nghiệm của
phương trình
( )
2 7 0fx+=
là
A. 1.
B. 4.
C. 2.
D. 3.
1x =
Trang 68
Câu 18. (NB)Nếu
( )
4
1
2f x dx =−
và
( )
4
1
6g x dx =−
thì
( ) ( )
4
1
f x g x dx

−

bằng:
A.
8−
. B.
4
. C.
4−
. D.
8
.
Câu 19.(NB) Số phức liên hợp của số phức z = 2 − 3i là
A. . B. . C. . D. .
Câu 20.(NB) Cho hai số phức
1
32zi=−
và
2
24zi= − −
. Phần ảo của số phức
12
zz−
bằng
A. -6. B.2i . C. 2. D. 5 .
Câu 21.(NB) Điểm M trong hình vẽ bên là điểm biểu diễn của số phức nào
dưới đây ?
A.
1 3 .=−zi
B.
3= − +zi
C.
1 3 .=+zi
D.
3.= − −zi
Câu 22:(TH) Trong không gian Oxyz, hình chiếu vuông góc của điểm M(2; - 3; 5) trên mặt phẳng
(Oyz) l điểm có tọa độ:
A.
(2;0;0)
B.
( )
2; 3;0−
C.
( )
2;0;5
D.
(0; 3;5)−
Câu 23: (NB)Trong không gian Oxyz, tâm của mặt cầu
( ) ( ) ( )
2 2 2
3 2 3 9x y z+ + − + − =
là
A.
( 3;2;3)I −
B.
(3; 2; 3)I −−
C.
( 3; 2;3)I −−
D.
(3;2; 3)I −
Câu 24:(NB) Trong không gian Oxyz, cho mặt phẳng (P):
3 2 4 0x y z− + − =
. Vectơ no sau đây l
vectơ php tuyến của (P)?
A.
1
(3; 2; 4)n = − −
B.
2
(3; 2;0)n =−
C.
3
(3; 2;1)n =−
D.
4
(3;0;1)n =
Câu 25: (TH)Trong không gian Oxyz, cho đường thẳng d :
22
5 3 1
x y z+−
==
−
. Điểm no dưới đây
thuộc đường thẳng d?
A.
(2; 2;0)N −
B.
( 2;2;0)M −
C.
(5;3; 1)P −
D.
( 5; 3;1)Q −−
23zi= − +
32zi=−
23zi=+
32zi=+
Trang 69
Câu 26 (TH): Cho hình chóp tứ gic đều
.S ABCD
, có đy
ABCD
là hình vuông tâm
O
. Các cạnh
bên và các cạnh đy đều bằng
a
. Gọi
M
l trung điểm
SC
. Góc giữa hai mặt phẳng
( )
MBD
và
( )
ABCD
bằng
A.
0
45
B.
0
60
C.
0
90
D.
0
30
Câu 27.(TH) Cho hàm số
( )
y f x=
liên tục trên và có bảng xét dấu của đạo hm như hình bên.
Hàm số đã cho có bao nhiêu điểm cực tr?
A. 3. B. 2. C. 1. D. 4.
Câu 28.(TH) Giá tr lớn nhất của hàm số
( )
32
3 9 17= − − +f x x x x
trên đoạn
2;4−
.bằng
A. 22. B. 55. C. 15. D. 44.
Câu 29. (TH)Cho
,,abc
là các số thực dương v khc 1 thỏa mãn
log log log 2020.log
a b a b
c c c+=
.Mênh đề no dưới đây đúng?.
A.
2020abc =
. B.
2020ac =
. C.
2020bc =
. D.
2020ab =
.
Câu 30.(TH) Số giao điểm của đồ thị hàm số
42
34y x x= − −
và trục hoành là
A. 2. B. 3. C. 4. D. 0.
Câu 31.(TH) Cho bất phương trình
1
4 5.2 16 0
xx+
− +
có tập nghiệm l đoạn
;ab
. Giá tr của
( )
22
log ab+
bằng
A.
2
. B.
1
. C.
0
. D.
10
.
Câu 32 (TH): Cho mặt cầu
()S
có tâm
I
và bán kinh
R
. Một hình nón
()N
tròn xoay có đỉnh
thuộc mặt cầu
()S
, trục của
()N
là một đường kính của
()S
v đường tròn đy của
()N
có tâm là
I
. Diện tích xung quanh của mặt nón là
A.
2
2
xq
SR
=
B.
2
2
xq
SR
=
C.
2
3
2
xq
SR
=
D.
2
xq
SR
=
Câu 33. (TH) Xét
2
1
ln
e
x
dx
x
, nếu đặt
lnux=
thì
2
1
ln
e
x
dx
x
bằng:
Trang 70
A.
1
2
0
duu
. B.
1
2
0
duu−
. C.
1
0
duu
. D.
2
1
d
e
uu
.
Câu 34.(TH) Diện tích
S
của hình phẳng giới hạn bởi đồ th các hàm số
e
x
y =
,
2y =
,
0x =
,
1x =
được tính bởi công thức no dưới đây?
A.
( )
1
0
e 2 d
x
Sx=−
. B.
( ) ( )
ln2 1
0 ln2
e 2 d e 2 d
xx
S x x= − + −

.
C.
( ) ( )
ln2 1
0 ln2
e 2 d e 2 d
xx
S x x= − − −

. D.
( ) ( )
ln2 1
0 ln2
e 2 d e 2 d
xx
S x x= − − + −

.
Câu 35:(TH) Tìm phần ảo
b
của số phức
)24(3 iiz +=
A.
12=b
B.
6=b
C.
ib 12=
D.
3=b
Câu 36(TH)Gọi
1
z
và
2
z
là hai nghiệm phức của pt :
2
9 6 4 0+ + =zz
. Giá tr của biểu thức
12
11
+
zz
bằng
A.
4
.
3
B. 3. C.
3
.
2
D.
9
.
2
Câu 37:(TH) Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 3; 5) vđường thẳng
d :
1 2 2
1 3 2
x y z+ + −
==
. Phương trình mặt phẳng (P) đi qua M v vuông góc với đường thẳng d là:
A.
( )
: 3 2 21 0P x y z+ + + =
B.
( ):2 3 5 21 0P x y z+ + + =
C.
( ): 3 2 21 0P x y z+ + − =
D.
( ):2 3 5 21 0P x y z+ + − =
Câu 38: (TH)Trong không gian với hệ tọa độ Oxyz, cho điểm
(2;3; 5)M −
v đường thẳng
22
: 3 4
5
xt
yt
zt
= − +
= −
=−
. Phương trình tham số của đường thẳng d đi qua M v song song với
là:
A.
22
33
5
xt
yt
z
=−
=+
=−
B.
22
34
55
xt
yt
zt
= − +
=−
= − −
C.
22
34
55
xt
yt
zt
= − +
=−
=−
D.
22
34
55
xt
yt
zt
=+
=−
= − −
Câu 39: (VD)Một người bắn 3 viên đạn. Xác suất để trúng cả 3 viên vòng 10 là 0,008, xác suất để 1
viên trúng vòng 8 là 0,15 và xác suất để 1 viên trúng vòng dưới 8 là 0,4.(Các vòng bắn dĩ nhiên độc
lập với nhau). Xác suất để xạ thủ đạt ít nhất 28 điểm là
A. 0,0935 B. 0,0835
C.0,32 D. 0,035
Trang 71
Câu 40 (VD): Cho hình chóp
.S ABCD
có đy
ABCD
là hình vuông tâm
O
, cạnh
a
. Hai mặt bên
()SAB
và
()SAD
cùng vuông góc với mặt phẳng đy v
2SA a=
. Khoảng cách giữa
SO
và
AB
bằng
A.
2
3
a
B.
a
C.
6
3
a
D.
3
4
a
Câu 41 (VD): Cho hàm số 

󰇛

󰇜
với m là tham số. Có bao nhiêu giá tr
nguyên của m để hàm số nghch biến trên khoảng
󰇛

󰇜
?
A. 2. B. 3. C. 4. D. 5.
Câu 42.(VD) Dân số thế giới được dự đon theo công thức
.
Nr
S Ae=
(trong đó
A
: là dân số của
năm lấy làm mốc tính,
S
là dân số sau
N
năm,
r
là tỉ lệ tăng dân số hng năm). Theo số liệu thực tế,
dân số thế giới năm
1950
là
2560
triệu người; dân số thế giới năm
1980
là
3040
triệu người. Hãy dự
đon dân số thế giới năm
2020
?
A.
3823
triệu. B.
5360
triệu. C.
3954
triệu. D.
4017
triệu.
Câu 43(VD).Cho hàm số
( )
32
y f x x ax bx c= = + + +
có bảng biến thiên như hình vẽ sau:
Tính giá tr của biểu thức
3.P a b c= + +
A.
3P =−
. B.
9P =−
. C.
3P =
. D.
9P =
.
Câu 44 (VD): Trong số các hình trụ có diện tích toàn phần đều bằng
S
thì bán kính
R
và chiều cao
h
của khối trụ có thể tích lớn nhất là:
A..
;2
66
SS
Rh

==
B.
;
44
SS
Rh

==
.
C.
22
;4
33
SS
Rh

==
. D.
1
;
2 2 2
SS
Rh

==
.
Câu 45. (VD) Cho hàm số
( )
fx
có
8
43
f

=−


và
( )
2
16cos4 .sin ,f x x x x
=
. Khi đó
( )
0
df x x
bằng
A.
16
3
. B.
64
27
. C.
4
3
−
. D.
0
.
Câu 46. (VDC)Cho hàm số
( )
2
y f x ax bx c= = + +
có đồ th
( )
C
(như hình vẽ):
Trang 72
Có bao nhiêu giá tr nguyên của tham số
m
để phương trình
( )
( )
2
2 ( ) 3 0f x m f x m+ − + − =
có
6
nghiệm phân biệt?
A.
1.
B.
4.
C.
3.
D.
2.
Câu 47.(VDC) Cho
, , 1abc
. Biết rằng biểu thức
( ) ( ) ( )
log log 4log
a b c
P bc ac ab= + +
đạt giá tr
nhỏ nhất bằng m khi
log
b
cn=
. Tính giá tr
mn+
.
A.
14mn+=
. B.
25
2
mn+=
. C.
12mn+=
. D.
10mn+=
.
Câu 48. (VDC)Bạn Vân chèo thuyền từ điểm
A
trên một bờ sông thẳng rộng
3km
và muốn đến
điểm
B
cách
8km
xuôi dòng trên bờ đối diện, càng nhanh càng tốt (như hình vẽ). Bạn Vân có thể
chèo thuyền của mình trực tiếp qua sông để đến
C
v sau đó chạy đến
B
, hay có thể chèo trực tiếp
đến
B
, hoặc bạn ấy có thể chèo thuyền đến một điểm
D
giữa
C
và
B
v sau đó chạy đến
B
. Biết
bạn ấy có thể chèo thuyền
6/km h
, chạy
8/km h
. Biết tốc độ của dòng nước l không đng kể so với
tốc độ chèo thuyền. Điểm
D
cách
A
bao xa để bạn Vân đến
B
nhanh nhất?
A.
73
B.
( )
9 1 7
7
+
C.
3
D.
12
7
.
Câu 49 (VDC): Cho tứ diện
.S ABC
,
M
và
N
l cc điểm thuộc các cạnh
SA
và
SB
sao cho
2MA SM=
,
2SN NB=
,
()
là mặt phẳng qua
MN
và song song với
SC
. Kí hiệu
1
()H
và
2
()H
là
các khối đa diện có được khi chia khối tứ diện
.S ABC
bởi mặt phẳng
()
, trong đó,
1
()H
chứa
điểm
S
,
2
()H
chứa điểm
A
;
1
V
và
2
V
lần lượt là thể tích của
1
()H
và
2
()H
. Tính tỉ số
1
2
V
V
A.
4
5
B.
5
4
C.
3
4
D.
4
3
Câu 50.(VDC) Có bao nhiêu số nguyên
( )
0;2018m
để phương trình
10
x
m x me+=
có hai
nghiệm phân biệt?
A. 9. B. 2017. C. 2016. D. 2007.
Trang 73
ĐÁP ÁN VÀ LỜI GIẢI
Câu 1.(NB) Có bao nhiêu cách xếp khc nhau cho 5 người ngồi vào một bàn dài?
A. 120 B. 5
C. 20 D. 25
Lời giải. Số cách sắp xếp khc nhau cho 5 người ngồi vào một bàn dài là một hoán v của 5 phần tử
nên có
5! 120=
cách.
Chọn A.
Câu 2:(NB) Cho cấp số nhân
( )
n
u
có
1
3u =
và
2
6u =−
. Công bội của cấp số nhân đã cho bằng
A. -2 B.
1
2
−
C. -9 D. -18
Lời giải. Ta có công bội của cấp số nhân là
2
1
2.
u
q
u
= = −
Chọn A.
Câu 3. (NB)Phương trình
21
5 125
x+
=
có nghiệm là
A.
5
2
x =
. B.
1x =
. C.
3x =
. D.
3
2
x =
.
Ta có:
21
5 125
x+
=
2 1 3
55
x+
=
2 1 3x + =
1x=
.
Chọn B
Câu 4 (NB): Thể tích của khối lập phương bằng
8
. Khi đó cạnh của khối lập phương bằng
A. 2 B.3 C.4 D.5
Đp n A
Câu 5.(NB) Tìm tập xc đnh
D
của hàm số
( )
1
3
f x x
−
=
.
A.
)
0;D = +
. B.
\0D =
. C.
( )
0;D = +
. D.
D =
.
Điều kiện:
0.x
Vậy
( )
0; .D = +
Chọn C
Câu 6. (NB)Mệnh đề no sau đây đúng
A.
xx
e dx e C=+
ò
. B.
1
lndx x C
x
=+
ò
.
Trang 74
C.
2
1
tan
cos
dx x C
x
= - +
ò
. D.
sin cosxdx x C=+
ò
.
Từ bảng nguyên hm cơ bản ta chọn đp n A.
Chọn A
Câu 7 (NB): Cho khối lăng trụ có đy l hình vuông cạnh
a
, chiều cao bằng
3a
. Thể tích của khối
lăng trụ đã cho bằng
A.
3
3a
B.
3
a
C.
2
3a
D.
2
a
Đp n A
Câu 8 (NB): Cho khối nón có bn kính đy
5r =
, đường sinh
7l =
. Diện tích xung quanh của khối
nón bằng
A.
35
B.
70
C.
2
35
D.
2
70
Đp n A
Câu 9 (NB): Diện tích mặt cầu có đường kính 2 bằng
A.
4
B.
16
C.
32
D.
8
Đp n A
Câu 10. (NB) Cho hàm số
( )
y f x=
có đồ th như hình vẽ bên. Hỏi hàm số đã cho đồng biến trên
khoảng no dưới đây ?
A.
( )
;8−
. B.
( )
1;4
. C.
( )
4;+
. D.
( )
0;1
.
Lời giải
Chọn D
Trang 75
Xét từ trái sang phải, Đp n A,B loại vì trong khoảng
( )
1;4
đồ th hàm số đi xuống nên hàm số
nghch biến, đp n C loại vì trong khoảng
( )
4;9
đồ th hàm số là một đường song song trục
Ox
nên hàm số không đổi.
Đp n D, trên khoảng (0;1) đồ th hàm số đi lên liên tục nên hàm số đồng biến trên khoảng đó.
Chọn D.
Câu 11. (NB)Với
,ab
là hai số thực dương khc
1
, ta có
log
b
a
bằng:
A.
log
a
b−
. B.
1
log
a
b
. C.
log logab−
. D.
log
a
b
.
Với
,ab
là hai số thực dương khc
1
và theo công thức đổi cơ số:
1
log .
log
b
a
a
b
=
Chọn B
Câu 12 (NB): Thể tích khối trụ có đường cao
h
, bn kinh đy
r
bằng
A.
2
rh
B.
2
1
3
rh
C.
2
rh
D.
2
1
3
rh
Đp n A
Câu 13.(NB)Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Giá tr cực tiểu của hàm số đã cho bằng
A.
0
. B.
2−
. C.
1−
. D.
1
.
Lời giải
Chọn C
Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại
1x =
và giá tr cực tiểu là
1
CT
y =−
.
Câu 14.(TH) Đường cong trong hình vẽ dưới đây l đồ th của hàm số no trong cc phương n
A
,
B
,
C
,
D
?
Trang 76
A.
2
1
x
y
x
−
=
+
. B.
2
1
x
y
x
−−
=
+
. C.
1
x
y
x
−
=
+
. D.
2
1
x
y
x
−+
=
+
.
Lời giải
Chọn D
Từ hình vẽ ta nhận thấy hàm số cần tìm có đồ th hàm số cắt trục tung, trục hoành lần lượt tại hai
điểm
( )
0;2
và
( )
2;0
nên cc đp n
A
,
B
,
C
đều loại và thấy
D
l đp n đúng. Chọn D.
Câu 15 (NB). Đường thẳng là tiệm cận đứng của đồ th hàm số nào trong các hàm số sau đây?
A.
23
.
1
x
y
x
−
=
−
B.
32
.
31
x
y
x
+
=
−
C.
3
.
1
x
y
x
+
=
+
D.
2
1
.
1
x
y
x
−
=
+
Lời giải
Chọn A
Câu 16.(NB) Tập nghiệm của bất phương trình
( )
3
log 2 3 0x −
là:
A.
(
;2−
. B.
3
;2
2


. C.
)
2;+
. D.
53
;
2

−
−

.
Điều kiện:
3
2
x
.
Do
3 5 1+
nên
( )
53
log 2 3 0 2 3 1 2
+
− − x x x
.
Đối chiếu điều kiện ta có tập nghiệm của bất phương trình l
)
2;+
.
Chọn C.
1x =
Trang 77
Câu 17(TH): Cho hàm số
( )
y f x=
liên tục trên
v có đồ th như hình bên. Số nghiệm của
phương trình
( )
2 7 0fx+=
là
A. 1.
B. 4.
C. 2.
D. 3.
Lời giải
Chọn B
7
2 ( ) 7 0 ( )
2
f x f x+ = = −
Số nghiệm của phương trình
7
()
2
fx=−
bằng số giao điểm của đồ th hàm số
()y f x=
với đường
thẳng
7
2
y =−
. Dựa vo đồ th hàm số
()y f x=
suy ra số nghiệm phương trình bằng 4.
Câu 18. (NB)Nếu
( )
4
1
2f x dx =−
và
( )
4
1
6g x dx =−
thì
( ) ( )
4
1
f x g x dx

−

bằng:
A.
8−
. B.
4
. C.
4−
. D.
8
.
Ta có
( ) ( ) ( ) ( ) ( ) ( )
4 4 4
1 1 1
dx dx dx 2 6 4f x g x f x g x− = − = − − − =


.
Chọn B
Câu 19.(NB) Số phức liên hợp của số phức z = 2 − 3i là
A. . B. . C. . D. .
Câu 20.(NB) Cho hai số phức
1
32zi=−
và
2
24zi= − −
. Phần ảo của số phức
12
zz−
bằng
A. -6. B.2i . C. 2. D. 5 .
Lời giải
Chọn C
23zi= − +
32zi=−
23zi=+
32zi=+
Trang 78
12
52z z i− = +
Phần ảo của
12
zz−
bằng 2
Câu 21.(NB) Điểm M trong hình vẽ bên là điểm biểu diễn của số phức nào
dưới đây ?
A.
1 3 .=−zi
B.
3= − +zi
C.
1 3 .=+zi
D.
3.= − −zi
Lời giải
Chọn A
(1; 3) 1 3M z i− = −
Câu 22:(TH) Trong không gian Oxyz, hình chiếu vuông góc của điểm M(2; - 3; 5) trên mặt phẳng
(Oyz) l điểm có tọa độ:
A.
(2;0;0)
B.
( )
2; 3;0−
C.
( )
2;0;5
D.
(0; 3;5)−
Lời giải.
Hình chiếu vuông góc của điểm M(2; - 3; 5) trên mặt phẳng (Oyz) l điểm có tọa độ:
(0; 3;5)−
Chọn D
Câu 23: (NB)Trong không gian Oxyz, tâm của mặt cầu
( ) ( ) ( )
2 2 2
3 2 3 9x y z+ + − + − =
là
A.
( 3;2;3)I −
B.
(3; 2; 3)I −−
C.
( 3; 2;3)I −−
D.
(3;2; 3)I −
Lời giải.
Mặt cầu có tâm
( 3;2;3)I −
Trang 79
Chọn A.
Câu 24:(NB) Trong không gian Oxyz, cho mặt phẳng (P):
3 2 4 0x y z− + − =
. Vectơ no sau đây l
vectơ php tuyến của (P)?
A.
1
(3; 2; 4)n = − −
B.
2
(3; 2;0)n =−
C.
3
(3; 2;1)n =−
D.
4
(3;0;1)n =
Lời giải.
Vectơ vectơ php tuyến của (P) là
3
(3; 2;1)n =−
Chọn C.
Câu 25: (TH)Trong không gian Oxyz, cho đường thẳng d :
22
5 3 1
x y z+−
==
−
. Điểm no dưới đây
thuộc đường thẳng d?
A.
(2; 2;0)N −
B.
( 2;2;0)M −
C.
(5;3; 1)P −
D.
( 5; 3;1)Q −−
Lời giải.
Điểm thuộc đường thẳng d là
( 2;2;0)M −
Chọn B.
Câu 26 (TH): Cho hình chóp tứ gic đều
.S ABCD
, có đy
ABCD
là hình vuông tâm
O
. Các cạnh
bên và các cạnh đy đều bằng
a
. Gọi
M
l trung điểm
SC
. Góc giữa hai mặt phẳng
( )
MBD
và
( )
ABCD
bằng
A.
0
45
B.
0
60
C.
0
90
D.
0
30
Đp n A
Hướng dẫn giải:
Gọi
'M
l trung điểm
OC
.
Ta có :
2
1 1 2
. . . 2
2 2 2 4
MBD
aa
S MO BD a
= = =
;
2
1 1 1
. . . 2. 2
2 2 4 4
BM D
a
S M O BD a a
= = =
. Do đó
0
2
cos 45
2
BM D
BMD
S
S

= = =
Câu 27.(TH) Cho hàm số
( )
y f x=
liên tục trên và có bảng xét dấu của đạo hm như hình bên.
Hàm số đã cho có bao nhiêu điểm cực tr?
Trang 80
A. 3. B. 2. C. 1. D. 4.
Lời giải
Chọn D
Ta có f’(x) đổi dấu khi qua x = -1 ; x = 0 ; x = 2; x = 4 nên hàm số đã cho có 4 điểm cực tr.
Câu 28.(TH) Giá tr lớn nhất của hàm số
( )
32
3 9 17= − − +f x x x x
trên đoạn
2;4−
.bằng
A. 22. B. 55. C. 15. D. 44.
Lời giải
Chọn A
( )
32
3 9 17= − − +f x x x x
2
'( ) 3 6 9f x x x= − −
3
'( ) 0
1
x
fx
x
=
=
=−
( 2) 15; ( 1) 22; (3) 10; (4) 3f f f f− = − = = − = −
Giá tr lớn nhất của hàm số trên đoạn [-2;4] là 22.
Câu 29. (TH)Cho
,,abc
là các số thực dương v khc 1 thỏa mãn
log log log 2020.log
a b a b
c c c+=
.Mênh đề no dưới đây đúng?.
A.
2020abc =
. B.
2020ac =
. C.
2020bc =
. D.
2020ab =
.
Ta có:
log log log 2020.log
a b a b
c c c+=
log 2020
1 1 1
.
log log log log
c
c c c c
a b a b
+ =
(công thức đổi cơ số)
log log log 2020
c c c
ab + =
log log 2020 2020
cc
ab ab = =
.
Chọn D.
Câu 30.(TH) Số giao điểm của đồ thị hàm số
42
34y x x= − −
và trục hoành là
A. 2. B. 3. C. 4. D. 0.
Trang 81
Lời giải
Chọn A
Phương trình honh độ giao điểm của đồ thị hàm số
42
34y x x= − −
và trục hoành:
2
42
2
2
1 0( )
3 4 0
4
42
xl
xx
x
xx
= −
− − =
=
= =
Số nghiệm phương trình là số giao điểm của đồ thị hàm số
42
34y x x= − −
và trục hoành.
Phương trình có 2 nghiệm phân biệt nên đồ thị hàm số
42
34y x x= − −
và trục hoành có 2 giao
điểm.
Câu 31.(TH) Cho bất phương trình
1
4 5.2 16 0
xx+
− +
có tập nghiệm l đoạn
;ab
. Giá tr của
( )
22
log ab+
bằng
A.
2
. B.
1
. C.
0
. D.
10
.
Bất phương trình
1
4 5.2 16 0
xx+
− +
4 10.2 16 0 2 2 8
x x x
− +
13x
.
Vậy tập nghiệm của bất phương trình l
1;3
.
Suy ra
1; 3ab==
nên
( ) ( )
2 2 2 2
log log 1 3 1ab+ = + =
.
Chọn B
Câu 32 (TH): Cho mặt cầu
()S
có tâm
I
và bán kinh
R
. Một hình nón
()N
tròn xoay có đỉnh
thuộc mặt cầu
()S
, trục của
()N
là một đường kính của
()S
v đường tròn đy của
()N
có tâm là
I
. Diện tích xung quanh của mặt nón là
A.
2
2
xq
SR
=
B.
2
2
xq
SR
=
C.
2
3
2
xq
SR
=
D.
2
xq
SR
=
Đp n A
Hướng dẫn:
Gọi
,rl
lần lượt l bn kinh v đường sinh của hình nón
()N
.
Từ giả thiết, ta có
,r R h R==
2 2 2
2
xq
S rl R R R R
= = + =
Câu 33. (TH) Xét
2
1
ln
e
x
dx
x
, nếu đặt
lnux=
thì
2
1
ln
e
x
dx
x
bằng:
Trang 82
A.
1
2
0
duu
. B.
1
2
0
duu−
. C.
1
0
duu
. D.
2
1
d
e
uu
.
Đặt
1
ln d du x u x
x
= =
.
Với
10xu= =
Với
1x e u= =
Vậy
1
2
2
10
ln
d
e
x
x u du
x
=

.
Chọn A
Câu 34. (TH) Diện tích
S
của hình phẳng giới hạn bởi đồ th các hàm số
e
x
y =
,
2y =
,
0x =
,
1x =
được tính bởi công thức no dưới đây?
A.
( )
1
0
e 2 d
x
Sx=−
. B.
( ) ( )
ln2 1
0 ln2
e 2 d e 2 d
xx
S x x= − + −

.
C.
( ) ( )
ln2 1
0 ln2
e 2 d e 2 d
xx
S x x= − − −

. D.
( ) ( )
ln2 1
0 ln2
e 2 d e 2 d
xx
S x x= − − + −

.
Diện tích cần tìm là:
1
0
e 2 d
x
Sx=−
.
Xét
e 2 0
x
−=
ln2x=
.
Bảng xét dấu
e2
x
−
:
Ta có
1
0
e 2 d
x
Sx=−
( ) ( )
ln2 1
0 ln2
e 2 d e 2 d
xx
xx= − − + −

Chọn D.
Câu 35:(TH) Tìm phần ảo
b
của số phức
)24(3 iiz +=
A.
12=b
B.
6=b
C.
ib 12=
D.
3=b
Lời giải
Chọn A
x
0
1
ln2
e2
x
−
0
−
+
Trang 83
)24(3 iiz +=
= -6+12i
Câu 36(TH)Gọi
1
z
và
2
z
là hai nghiệm phức của pt :
2
9 6 4 0+ + =zz
. Giá tr của biểu thức
12
11
+
zz
bằng
A.
4
.
3
B. 3. C.
3
.
2
D.
9
.
2
Lời giải
Chọn B
Phương trình
2
9 6 4 0+ + =zz
có 2 nghiệm phức :
12
1 3 1 3
;
33
ii
zz
− + − −
==
12
11
3
zz
+=
Câu 37:(TH) Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 3; 5) vđường thẳng
d :
1 2 2
1 3 2
x y z+ + −
==
. Phương trình mặt phẳng (P) đi qua M v vuông góc với đường thẳng d là:
A.
( )
: 3 2 21 0P x y z+ + + =
B.
( ):2 3 5 21 0P x y z+ + + =
C.
( ): 3 2 21 0P x y z+ + − =
D.
( ):2 3 5 21 0P x y z+ + − =
Lời giải
Vì (P) vuông góc với d nên vectơ chỉ phương của d l vectơ php tuyến của (P)
d có vectơ chỉ phương l
(1;3;2)a =
Phương trình mặt phẳng (P) là:
2 3( 3) 2( 5) 0x y z− + − + − =
2 3 9 2 10 0xyz − + − + − =
3 2 21 0x y z + + − =
Chọn C
Câu 38: (TH)Trong không gian với hệ tọa độ Oxyz, cho điểm
(2;3; 5)M −
v đường thẳng
22
: 3 4
5
xt
yt
zt
= − +
= −
=−
. Phương trình tham số của đường thẳng d đi qua M v song song với
là:
Trang 84
A.
22
33
5
xt
yt
z
=−
=+
=−
B.
22
34
55
xt
yt
zt
= − +
=−
= − −
C.
22
34
55
xt
yt
zt
= − +
=−
=−
D.
22
34
55
xt
yt
zt
=+
=−
= − −
Lời giải
Vì d song song với
nên vectơ chỉ phương của
cng l vec tơ chỉ phương của d
có vectơ chỉ phương l
(2; 4; 5)a = − −
Phương trình tham số của đường thẳng d là
22
34
55
xt
yt
zt
=+
=−
= − −
Chọn D.
Câu 39: (VD)Một người bắn 3 viên đạn. Xác suất để trúng cả 3 viên vòng 10 là 0,008, xác suất để 1
viên trúng vòng 8 là 0,15 và xác suất để 1 viên trúng vòng dưới 8 là 0,4.(Các vòng bắn dĩ nhiên độc
lập với nhau). Xác suất để xạ thủ đạt ít nhất 28 điểm là
A. 0,0935 B. 0,0835
C.0,32 D. 0,035
Lời giải.
Gọi A là biến cố “1 viên trúng vòng 10”.
Khi đó theo giả thiết:
3
( ( )) 0,008 ( ) 0,2P A P A= =
Gọi B là biến cố “1 viên trúng vòng 9”.
Gọi C là biến cố “1 viên trúng vòng 8”.
Gọi D là biến cố “1 viên trúng vòng dưới 8”.
Theo giả thiết ta có : P(C)=0,15; P(D)=0,4.
Vì
A B C D =
. Rõ ràng các biến cố ny đôi một xung khắc nên ta có :
1 ( ) ( ) ( ) ( ) ( )
0,2 ( ) 0,15 0,4
( ) 0,25
P A B C D P A P B P C P D
PB
PB
= = + + +
= + + +
=
Gọi X là biến cố “xạ thủ đạt ít nhất 28 điểm”
Để đạt ít nhất 28 điểm thì
- Hoặc là 2 viên trúng vòng 10, 1 viên trúng vòng 8;
- Hoặc là 2 viên trúng vòng 9, 1 viên trúng vòng 10;
- Hoặc là 2 viên trúng vòng 10, 1 viên trúng vòng 9;
- Hoặc là 2 viên trúng vòng 10, 1 viên trúng vòng 9;
- Hoặc là cả 3 viên trúng vòng 10.
Từ đó dựa vào quy tắc nhân và quy tắc cộng xác suất, ta có:
2 2 2 2 2 2
3 3 3
( ) (0,2) (0,15) (0,25) (0,2) (0,2) (0,25) 0,008 0,0935P X C C C= + + + =
Chọn A.
Trang 85
Câu 40 (VD): Cho hình chóp
.S ABCD
có đy
ABCD
là hình vuông tâm
O
, cạnh
a
. Hai mặt bên
()SAB
và
()SAD
cùng vuông góc với mặt phẳng đy v
2SA a=
. Khoảng cách giữa
SO
và
AB
bằng
A.
2
3
a
B.
a
C.
6
3
a
D.
3
4
a
Đp n A
Hướng dẫn:
Gọi l trung điểm của
.
Khi đó:
, với là
hình chiếu của lên .
Ta có.
2 2 2
2
2.
.2
2
3
2
4
a
a
SA AE a
AH
SA AE a
a
= = =
+
+
Câu 41 (VD): Cho hàm số 

󰇛

󰇜
với m là tham số. Có bao nhiêu giá tr
nguyên của m để hàm số nghch biến trên khoảng
󰇛

󰇜
?
A. 2. B. 3. C. 4. D. 5.
Lời giải
Chọn C.
2
y' 3x 2mx ( 3m 6)= − − + − +
Để hàm số nghch biến trên R
y' 0, x R
22
m 3( 3m 6) 0 m 9m 18 0 + − + − +
3 m 6
Suy ra có 4 giá tr nguyên của m thỏa đề bài.
Câu 42.(VD) Dân số thế giới được dự đon theo công thức
.
Nr
S Ae=
(trong đó
A
: là dân số của
năm lấy làm mốc tính,
S
là dân số sau
N
năm,
r
là tỉ lệ tăng dân số hng năm). Theo số liệu thực tế,
dân số thế giới năm
1950
là
2560
triệu người; dân số thế giới năm
1980
là
3040
triệu người. Hãy dự
đon dân số thế giới năm
2020
?
E
AD
( ) ( )
( )
;;d SO AB d AB SOE AH==
H
A
SE
Trang 86
A.
3823
triệu. B.
5360
triệu. C.
3954
triệu. D.
4017
triệu.
Ta có:
( )
( )
1950.
1. 6
6
980
1950 . 2560.10
1980 . 3040.10
r
r
S A e
S A e
ì
ï
==
ï
ï
í
ï
==
ï
ï
î
Suy ra:
3
30
0
304 19
256 16
rr
ee= Þ =
và
1950
6
2560.10
r
A
e
=
Vậy:
( )
( )
( )
( )
2020
6
70
2020. 6
950
6
1
2560.10 .
2020 . 2560.10 . 3823.10
r
rr
r
e
S A e e
e
= = = ;
.
Chọn A
Câu 43(VD). Cho hàm số
( )
32
y f x x ax bx c= = + + +
có bảng biến thiên như hình vẽ sau:
Tính giá tr của biểu thức
3.P a b c= + +
A.
3P =−
. B.
9P =−
. C.
3P =
. D.
9P =
.
Lời giải
Chọn A.
2
'( ) 3 2f x x ax b= + +
Từ bảng biến thiên ta thấy:
'( 1) 0 2 3 3
'(3) 0 6 27 9
f a b a
f a b b
− = − + = − = −

= + = − = −
(3) 24
(3) 24 27 9 3 24 3
( 1) 1( )
f
f a b c c
f a b c hn
=−
= − + + + = − =
− = − + −
P=a+b+3c=-3
Câu 44 (VD): Trong số các hình trụ có diện tích toàn phần đều bằng
S
thì bán kính
R
và chiều cao
h
của khối trụ có thể tích lớn nhất là:
A..
;2
66
SS
Rh

==
B.
;
44
SS
Rh

==
.
C.
22
;4
33
SS
Rh

==
. D.
1
;
2 2 2
SS
Rh

==
.
Trang 87
Đp n A
Hướng dẫn:
Gọi thể tích khối trụ là
V
, diện tích toàn phần của hình trụ là
S
.
Ta có:
2
2
22
day xq
S S S R Rh

= + = +
. Từ đó suy ra:
2
2 2 2
3
2
3
2 2 2 2 4
Cauchy
S S V V V V
R Rh R R
R R R
= + = + = + +
hay
3
23
2
27
4 2 54
V S S
V



.
Vậy
3
max
54
S
V
=
. Dấu “=” xảy ra
2
2
2 2 2
V R h Rh
R
RR

= = =
hay
2hR=
.
Khi đó
2
6
6
S
S R R
= =
và
22
6
S
hR
==
.
Câu 45. (VD) Cho hàm số
( )
fx
có
8
43
f

=−


và
( )
2
16cos4 .sin ,f x x x x
=
. Khi đó
( )
0
df x x
bằng
A.
16
3
. B.
64
27
. C.
4
3
−
. D.
0
.
Ta có
( )
2
16cos4 .sin ,f x x x x
=
nên
( )
fx
là một nguyên hàm của
( )
fx
.
Có
( )
2
1 cos2
d 16cos4 .sin d 16.cos4 . d 8.cos4 d 8cos4 .cos2 d
2
x
f x x x x x x x x x x x x
−
= = = −
( )
2
8 cos4 d 4 cos6 cos2 d 2sin4 sin6 2sin2
3
= − + = − − +

x x x x x x x x C
.
Suy ra
( )
2
2sin4 sin6 2sin2
3
= − − +f x x x x C
. Mà
84
4 3 3

= − = −


fC
.
Do đó. Khi đó:
( )
00
2 4 4
d 2sin4 sin6 2sin2 d
3 3 3


= − − − = −



f x x x x x x
Chọn C.
Câu 46. (VDC)Cho hàm số
( )
2
y f x ax bx c= = + +
có đồ th
( )
C
(như hình vẽ):
Trang 88
Có bao nhiêu giá tr nguyên của tham số
m
để phương trình
( )
( )
2
2 ( ) 3 0f x m f x m+ − + − =
có
6
nghiệm phân biệt?
A.
1.
B.
4.
C.
3.
D.
2.
Lời giải
Chọn C
Phương trình
( )
( )
2
2 ( ) 3 0f x m f x m+ − + − =
( ) 3(1)
( ) 1(2)
f x m
fx
= − +
=−
Từ đồ th hàm số
( )
2
y f x ax bx c= = + +
ta vẽ được đồ th hàm số
( )
y f x=
Từ đồ th hàm số, suy ra phương trình (2) có 2 nghiệm. Để phương trình
( )
( )
2
2 ( ) 3 0f x m f x m+ − + − =
có
6
nghiệm phân biệt thì phương trình (1) có 4 nghiệm phân biệt
khi đó
04m
. Suy ra có 3 giá tr nguyên của m thỏa đề bài.
.
Câu 47.(VDC) Cho
, , 1abc
. Biết rằng biểu thức
( ) ( ) ( )
log log 4log
a b c
P bc ac ab= + +
đạt giá tr
nhỏ nhất bằng m khi
log
b
cn=
. Tính giá tr
mn+
.
8
6
4
2
2
5
5
Trang 89
A.
14mn+=
. B.
25
2
mn+=
. C.
12mn+=
. D.
10mn+=
.
Do
, , 1abc
nên
log ,log ,log 0
a c b
b a c
.
( ) ( ) ( )
log log 4log log log log log 4log 4log
a b c a a b b c a
P bc ac ab b c a c a b= + + = + + + + +
( ) ( ) ( )
log log log 4log log 4log
a b a c b c
b a c a c b= + + + + +
1 1 4
log 4log log
log log log
a c b
a c b
b a c
b a c
= + + + + +
1 1 4
2 log · 2 ·4log 2 log · 2 4 4 10
log log log
a c b
a c b
b a c
b a c
+ + = + + =
.
Dấu “ = ” xảy ra khi và chỉ khi
1
log
log log 1
11
4log log
log 2
log 2
4
log
log
a
aa
cc
c
b
b
c
b
bb
aa
a
c
c
b
=
=
= =


=

=
Vậy, đạt giá tr nhỏ nhất là 10 khi
log 2 10
b
cm= =
,
2 12n m n= + =
.
Chọn C.
Câu 48. (VDC)Bạn Vân chèo thuyền từ điểm
A
trên một bờ sông thẳng rộng
3km
và muốn đến
điểm
B
cách
8km
xuôi dòng trên bờ đối diện, càng nhanh càng tốt (như hình vẽ). Bạn Vân có thể
chèo thuyền của mình trực tiếp qua sông để đến
C
v sau đó chạy đến
B
, hay có thể chèo trực tiếp
đến
B
, hoặc bạn ấy có thể chèo thuyền đến một điểm
D
giữa
C
và
B
v sau đó chạy đến
B
. Biết
bạn ấy có thể chèo thuyền
6/km h
, chạy
8/km h
. Biết tốc độ của dòng nước l không đng kể so với
tốc độ chèo thuyền. Điểm
D
cách
A
bao xa để bạn Vân đến
B
nhanh nhất?
A.
73
B.
( )
9 1 7
7
+
C.
3
D.
12
7
.
Trang 90
Lời giải
Chọn D
Đặt
CD x=
. Quãng đường chạy bộ
8DB x=−
v quãng đường chèo thuyền
2
9AD x=+
.(
(0 8)x
Khi đó, thời gian chèo thuyền là
2
9
6
x+
và thời gian chạy bộ là
8
8
x−
.
Tổng thời gian mà bạn Vân cần có là:
2
98
( ) , [0;8]
68
xx
T x x
+−
= +
.
Ta có:
2
1
'( )
8
69
x
Tx
x
=−
+
.
2 2 2 2
2
19
'( ) 0 4 3 9 16 9( 9) 7 81
8
7
69
x
T x x x x x x x
x
= = = + = + = =
+
.
Ta có:
3
(0)
2
T =
;
97
1
8
7
T

=+


;
73
(8)
6
T =
.
Do đó:
[0;8]
97
min ( ) 1
8
7
T x T

= = +


.
Vậy để bạn Vân đến
B
nhanh nhất :
81
9
7
AD =+
12
7
=
.
Câu 49 (VDC): Cho tứ diện
.S ABC
,
M
và
N
l cc điểm thuộc các cạnh
SA
và
SB
sao cho
2MA SM=
,
2SN NB=
,
()
là mặt phẳng qua
MN
và song song với
SC
. Kí hiệu
1
()H
và
2
()H
là
Trang 91
các khối đa diện có được khi chia khối tứ diện
.S ABC
bởi mặt phẳng
()
, trong đó,
1
()H
chứa
điểm
S
,
2
()H
chứa điểm
A
;
1
V
và
2
V
lần lượt là thể tích của
1
()H
và
2
()H
. Tính tỉ số
1
2
V
V
A.
4
5
B.
5
4
C.
3
4
D.
4
3
Đp n A
Hướng dẫn:
Kí hiệu
V
là thể tích khối tứ diện
SABC
.
Gọi
P
,
Q
lần lượt l giao điểm của
()
với cc đường thẳng
BC
,
AC
.
Ta có
// //NP MQ SC
. Khi chia khối
1
()H
bởi mặt phẳng
()QNC
, ta được hai khối chóp
.N SMQC
và
.N QPC
.
Ta có:
.
.
( ,( ))
(B,( ))
N SMQC SMQC
B ASC SAC
VS
d N SAC
V d SAC S
=
;
( ,( )) 2
(B,( )) 3
d N SAC NS
d SAC BS
==
;
2
45
99
AMQ SMQC
ASC ASC
SS
AM
S AS S

= = =


Suy ra
.
.
2 5 10
3 9 27
N SMQC
B ASC
V
V
= =
.QP
.
( ,(QP ))
(S,(A ))
1 1 2 2
3 3 3 27
QPC
NC
S ABC ABC
S
V
d N C
V d BC S
NB CQ CP
SB CA CB
=
= == =
.
.QP
11
12
. . 1 2
10 2 4 4
54
27 27 9 9
N SMQC
NC
B ASC S ABC
V
V
VV
VV
V V V V V
= + = + = = =
+
1
2
4
5
V
V
=
Câu 50.(VDC) Có bao nhiêu số nguyên
( )
0;2018m
để phương trình
10
x
m x me+=
có hai
nghiệm phân biệt?
P
N
Q
M
A
B
C
S
Trang 92
A. 9. B. 2017. C. 2016. D. 2007.
Với
0x =
, phương trình trở thành
=mm
(luôn đúng), suy ra với mọi
( )
0;2018m
phương trình
luôn có 1 nghiệm
0x =
.
Với
0x
, ta có
10
10
1
x
x
x
m x me m
e
+ = =
−
.
Xét hàm số
( )
10
1
x
x
y f x
e
==
−
trên
\0
, ta có
( )
( )
( )
2
10 1
0 \ 0
1
xx
x
e xe
f x x
e
−−
=
−
.
Thật vậy, xét hàm số
( )
1
xx
g x e xe= − −
. Ta có
( )
( )
x x x x
g x e e xe xe
= − + = −
.
Ta có bảng biến thiên như sau:
x
−
0
+
( )
gx
+
0
–
( )
gx
−
0
−
Bảng biến thiên hàm số
( )
y f x=
x
−
0
+
( )
fx
+
0
–
( )
fx
+
10
10
0
Suy ra yêu cầu bài toán thỏa mãn khi và chỉ khi
0 2018
10
m
m

Do đó, có 2016 số nguyên m thỏa mãn yêu cầu bài toán.
Chọn C.
| 1/92
| | Tải xuống

Có thể bạn quan tâm:

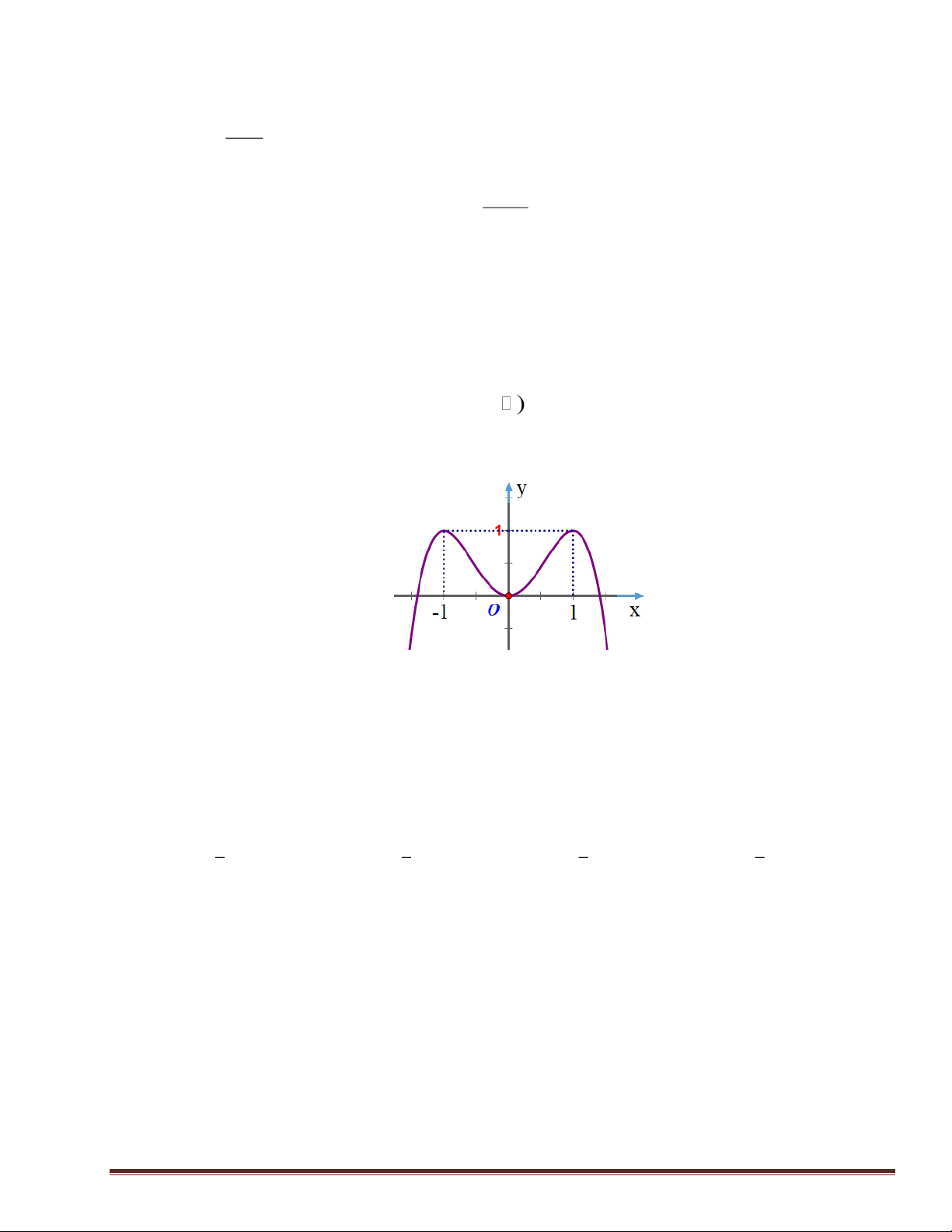
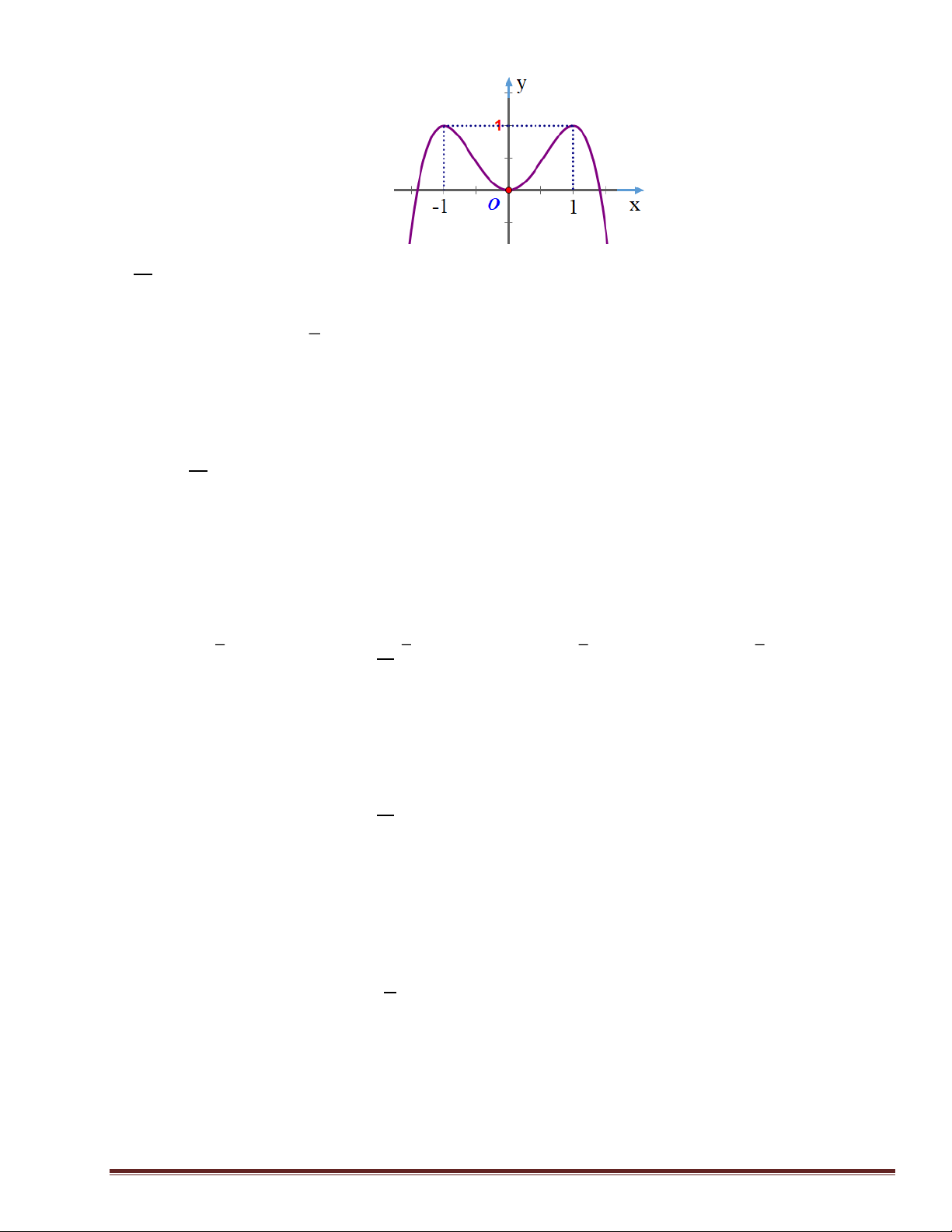
Preview text:

ĐỀ 1
ĐỀ THI THỬ THPT QUỐC GIA 2020
PHÁT TRIỂN TỪ ĐỀ MINH HỌA MÔN TOÁN LẦN 2 NĂM 2020 Thời gian: 90 phút
Câu 1: Trong một hộp bút gồm có 8 cây bút bi, 6 cây bút chì và 10 cây bút màu. Hỏi có bao nhiêu cách
chọn ra một cây bút từ hộp bút đó? A. 48. B. 60. C. 480. D. 24.
Câu 2: Cho cấp số cộng (u với u = 5u và u = 2u + 5. Khi đó số hạng đầu u và công sai d bằng n ) 9 2 13 6 1
A. u = 4 và d = 5 . B. u = 3 và d = 4 . 1 1
C. u = 4 và d = 3 . D. u = 3 và d = 5 . 1 1
Câu 3: Nghiệm của phương trình 3 log (x - 3) = 3 là 3 A. x = 3 + 3 .
B. x = 3 .
C. x = 3 3 . D. x = 3 - 3 .
Câu 4: Cho khối lập phương ABC . D A BCD
  có AC = a 2 (a  0) . Thể tích của khối lập phương đã cho bằng 3 a A. 2 a . B. . C. 3 a . D. 3 . a 3 
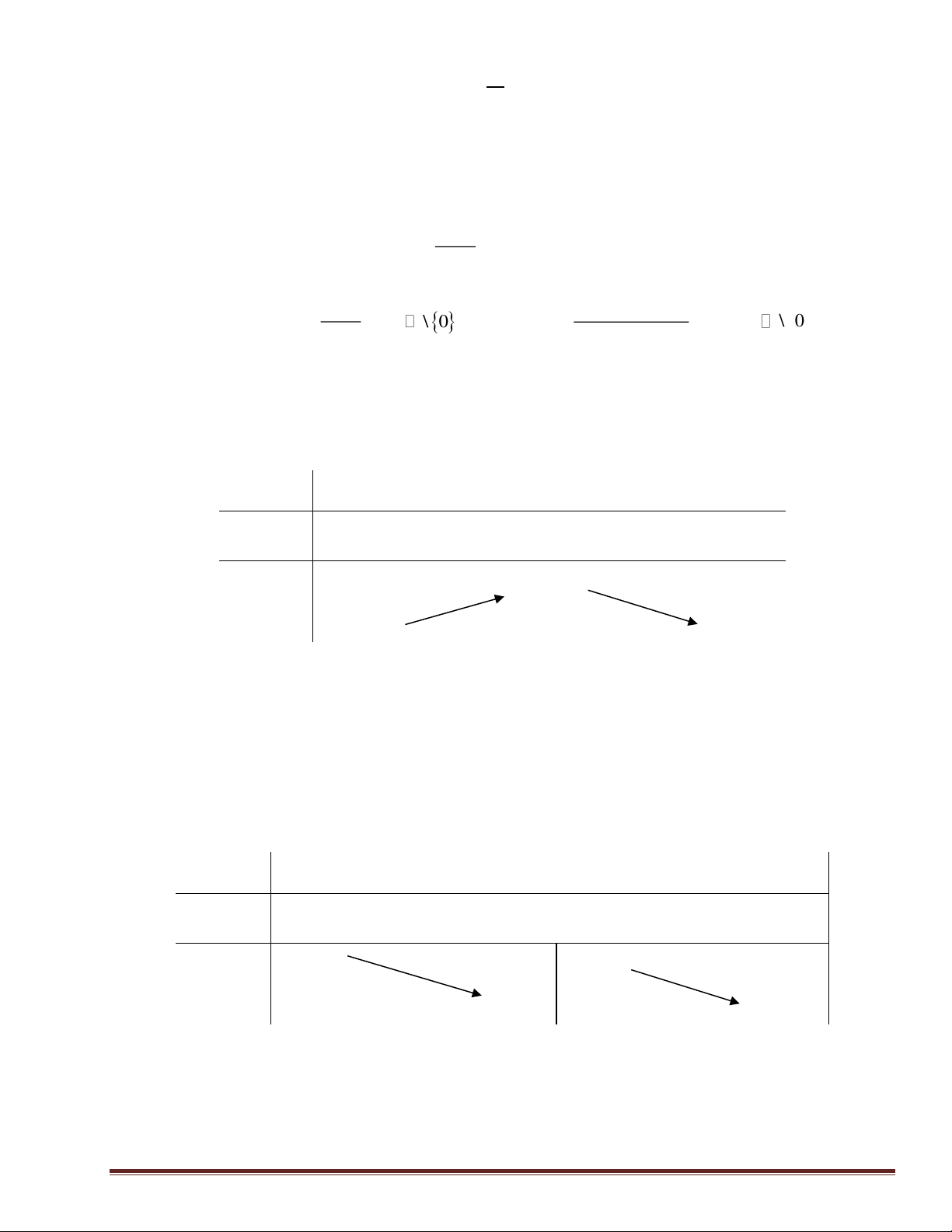
. Câu 5: Tập xác định của hàm số y = ( 2
x − 3x + 2) là: A. (− ;  ) 1 (2;+) . B. . C. (0;+) . D. (1; 2) .
Câu 6: Tìm nguyên hàm của hàm số f ( x) = sin 2x . 1 1 A. 2
− cos2x + C . B.
cos 2x + C .
C. 2cos 2x + C .
D. − cos 2x + C . 2 2
Câu 7: Cho khối lăng trụ AB . C A BC
  có thể tích là V , thể tích của khối chóp C .ABC là: 1 1 1 A. V . B. V . C. V . D. 2V . 6 2 3
Câu 8: Hình nón có bán kính đáy bằng 2 (cm), góc ở đỉnh bằng 60 . Thể tích khối nón là 8 3 8 3 A. V = ( 3 cm ). B. V = ( 3 cm ) . 9 2 8 3 C. V =  ( 3 8 3 cm ) . D. V = ( 3 cm ) . 3 Trang 1
Câu 9: Tính bán kính r của khối cầu có thể tích là V =  ( 3 36 cm ) .
A. r = 3(cm) .
B. r = 6(cm) .
C. r = 4(cm).
D. r = 9(cm) .
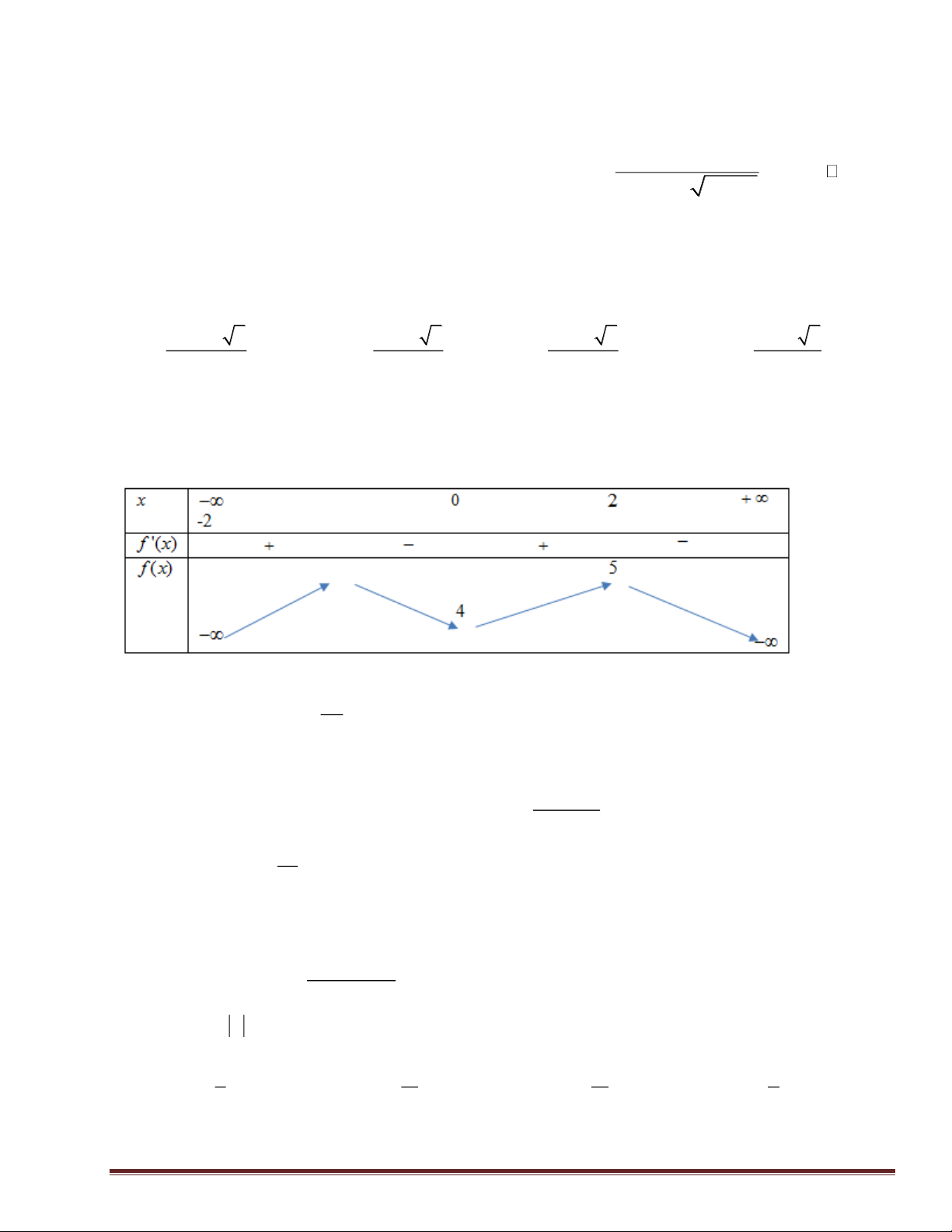
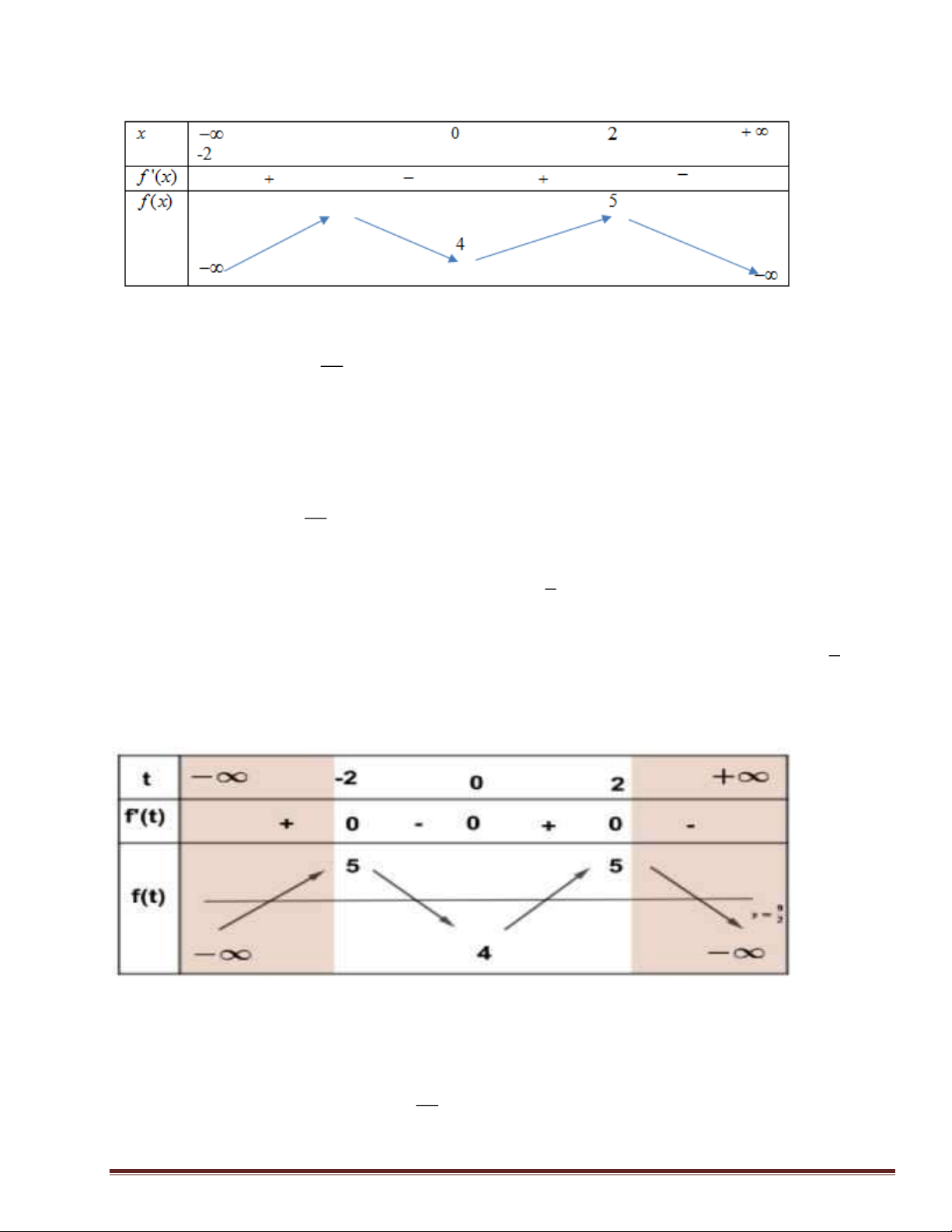
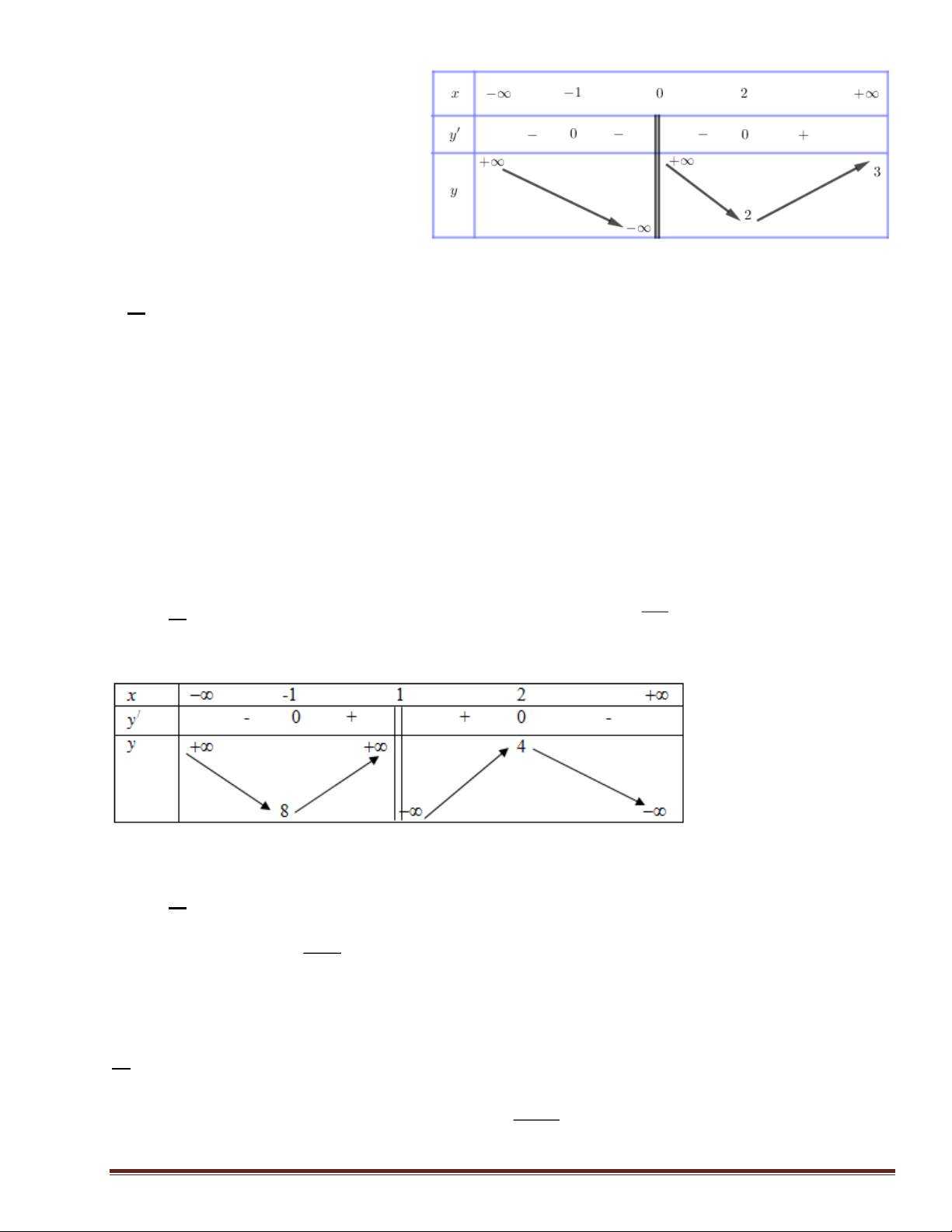
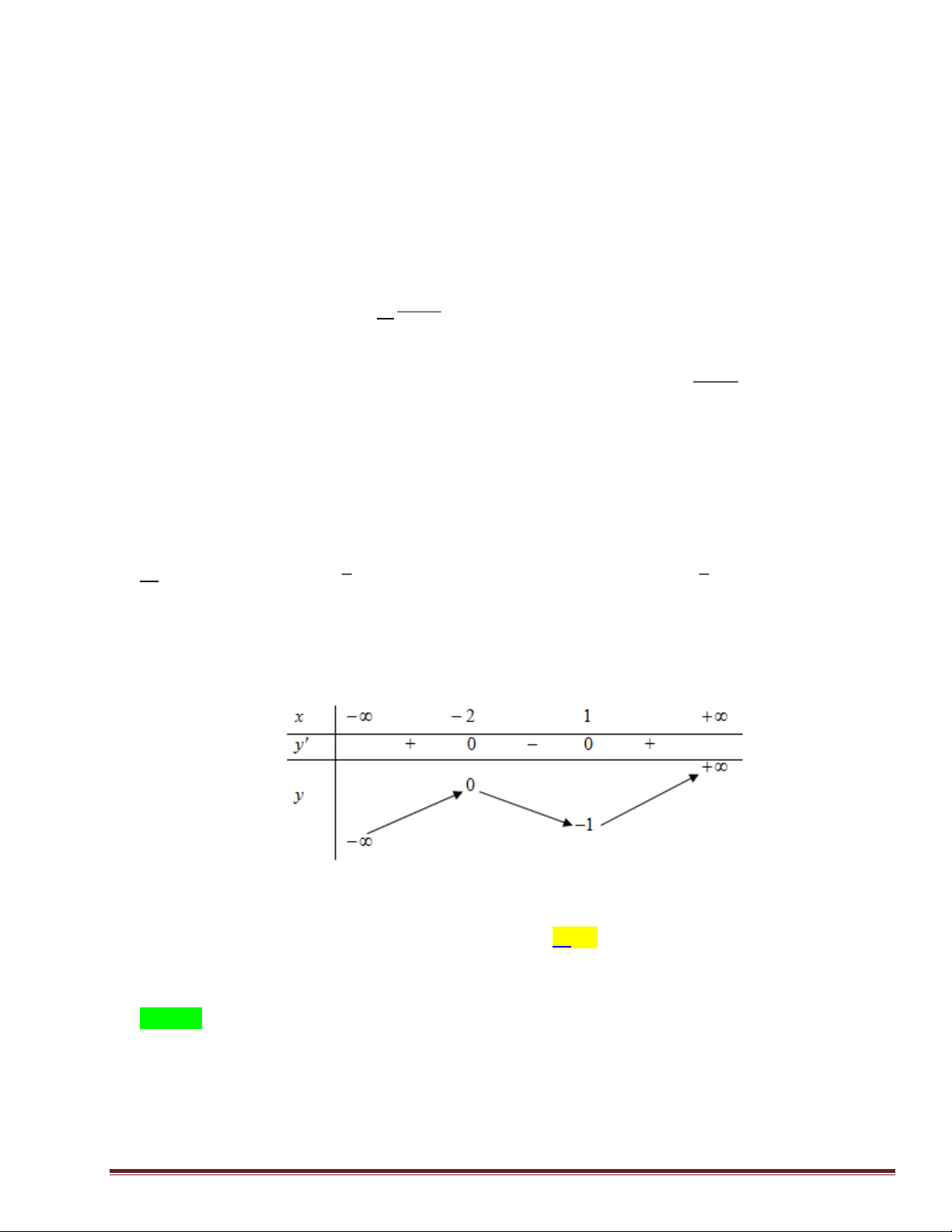
Câu 10: Cho hàm số y = f ( x) có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (0 ) ;1 B. ( 1 − ;0) . C. ( 1 − ; ) 1 . D. (1;+) .
Câu 11: Với a là số thực dương tùy ý, log ( 5 a bằng 3 )  5  1 A. log a  . B. log a . C. 5 + log a . D. 5log a . 3   3  3 5 3 3
Câu 12: Diện tích xung quanh của hình nón có độ dài đường sinh l và bán kính đáy r bằng 1 A. 4 rl . B. rl . C. rl . D. 2 rl . 3
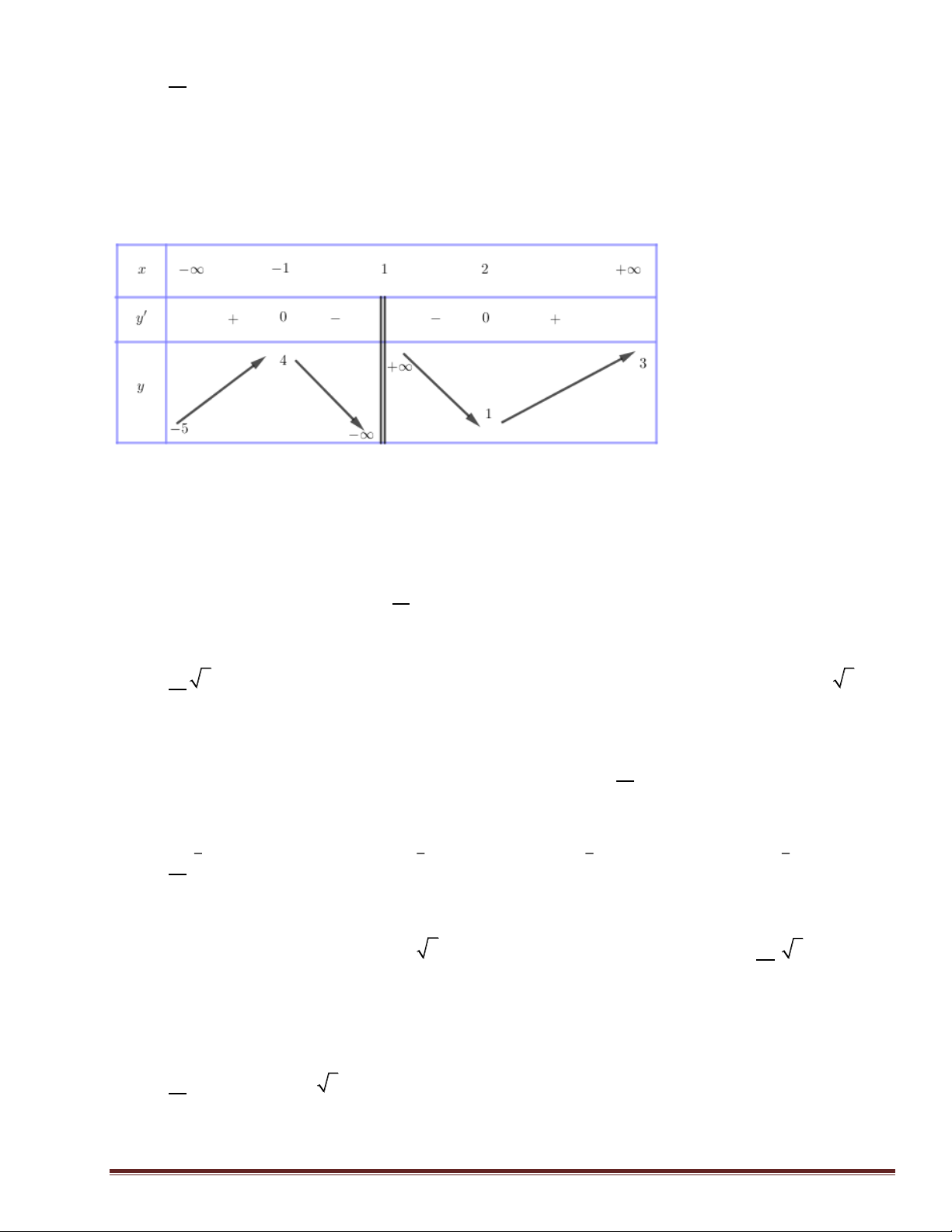
Câu 13: Cho hàm số y = f ( x) có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại điểm A. x = 2 − . B. x = 2 . C. x = 1 . D. x = 1 − .
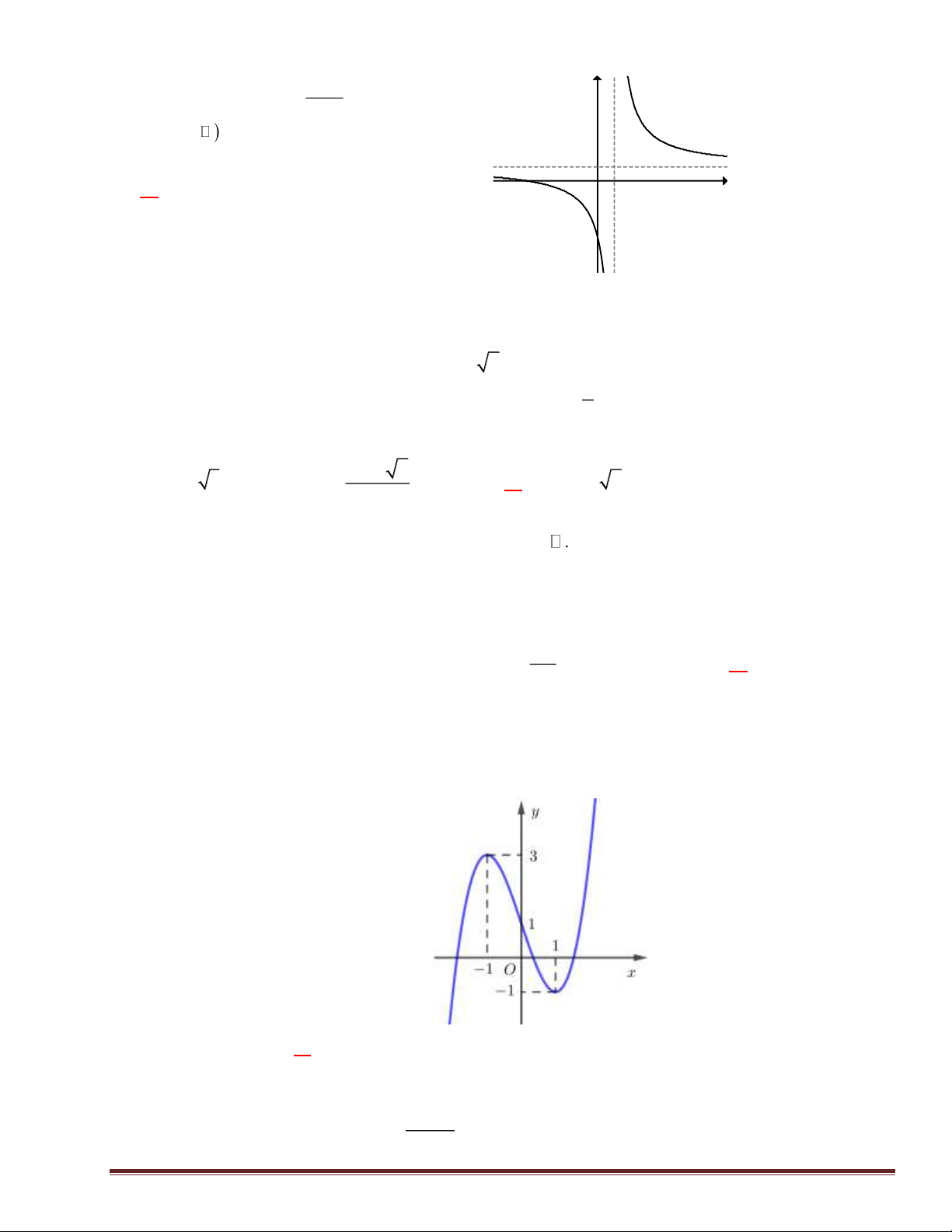
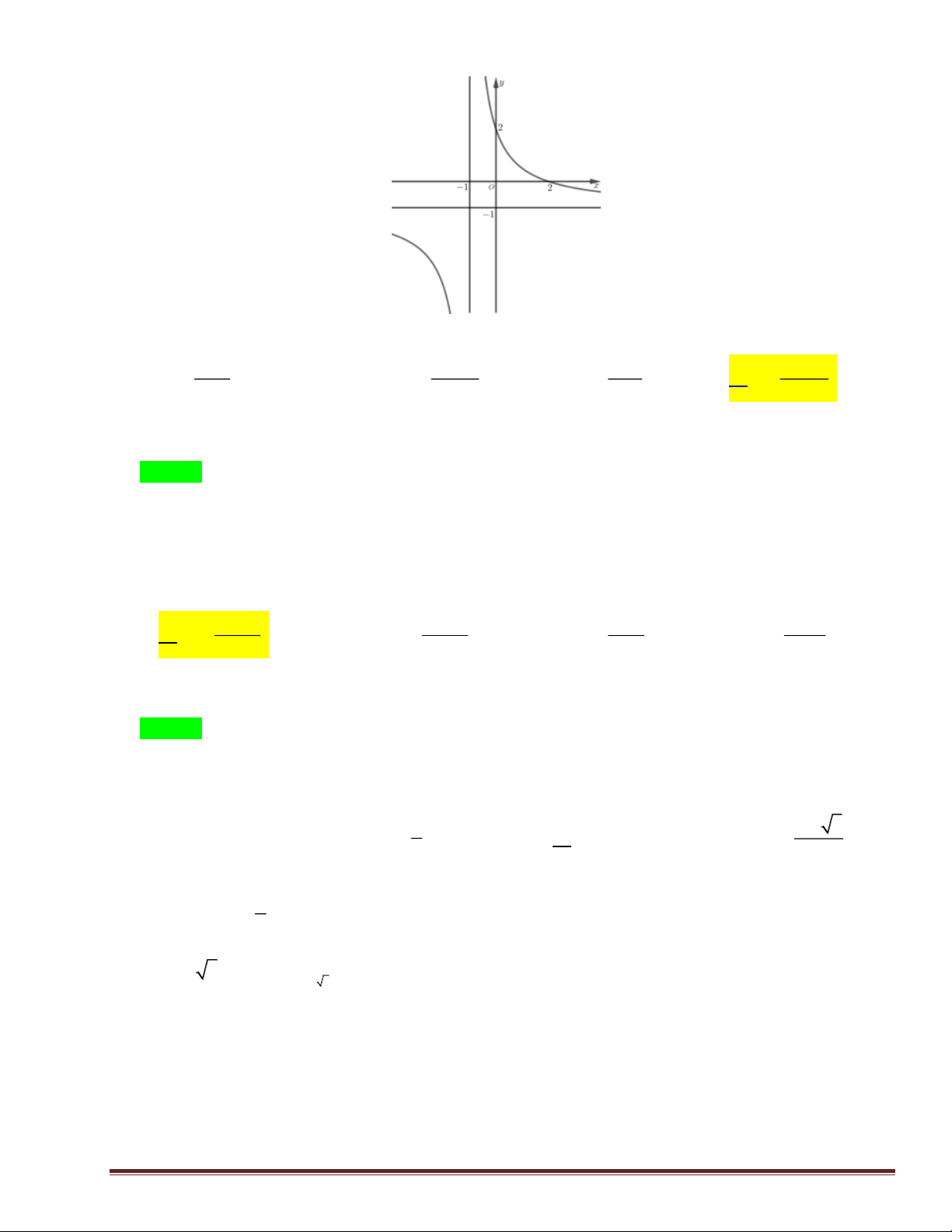
Câu 14: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới? A. 3 2 y = - x + 3x - 4 B. 3 2 y = x - 3x + 4 Trang 2 C. 4 2 y = x - 2x - 3 x - 1 D. y = x + 1 3x + 2
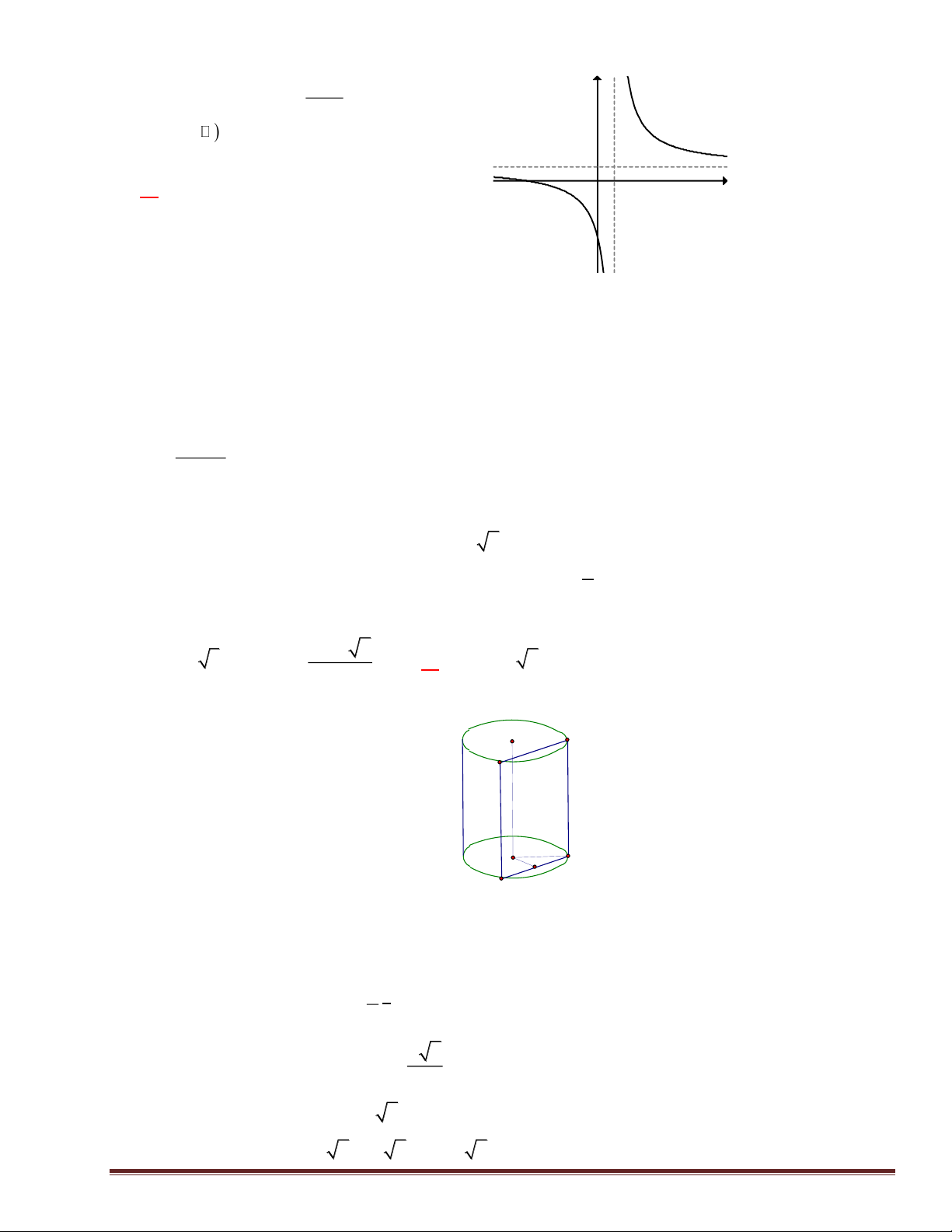
Câu 15: Tiệm cận ngang của đồ thị hàm số y = là x −1 A. y = 2 − . B. y = 3 . C. x = 2 − . D. x = 3 .
Câu 16: Tập nghiệm của bất phương trình ln x  1 là A. ( ; e +) . B. (0;+). C.  ; e +) . D. ( ; − e) . Câu 17: Cho hàm số ( ) 4 2
f x = ax + bx + c ( , a , b c Î
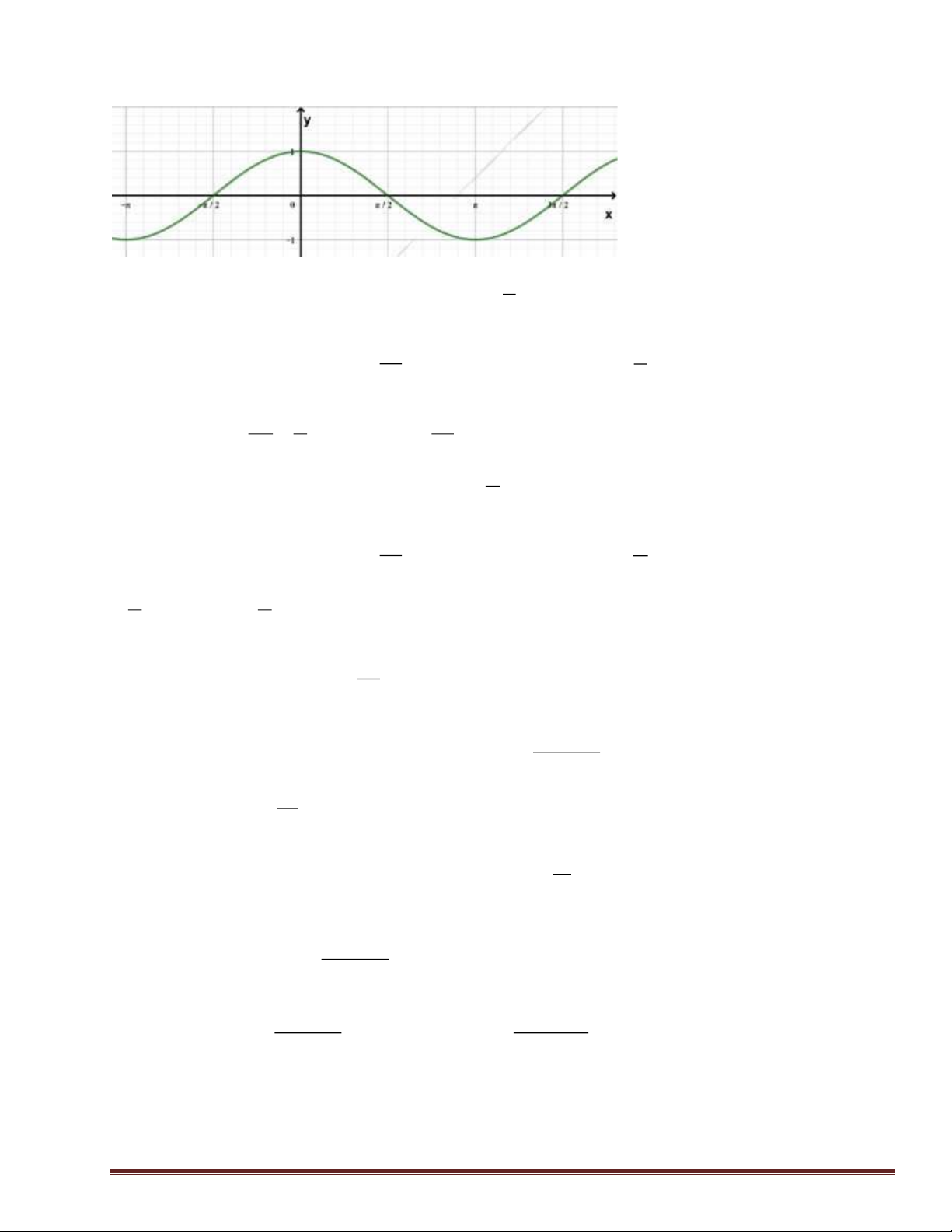
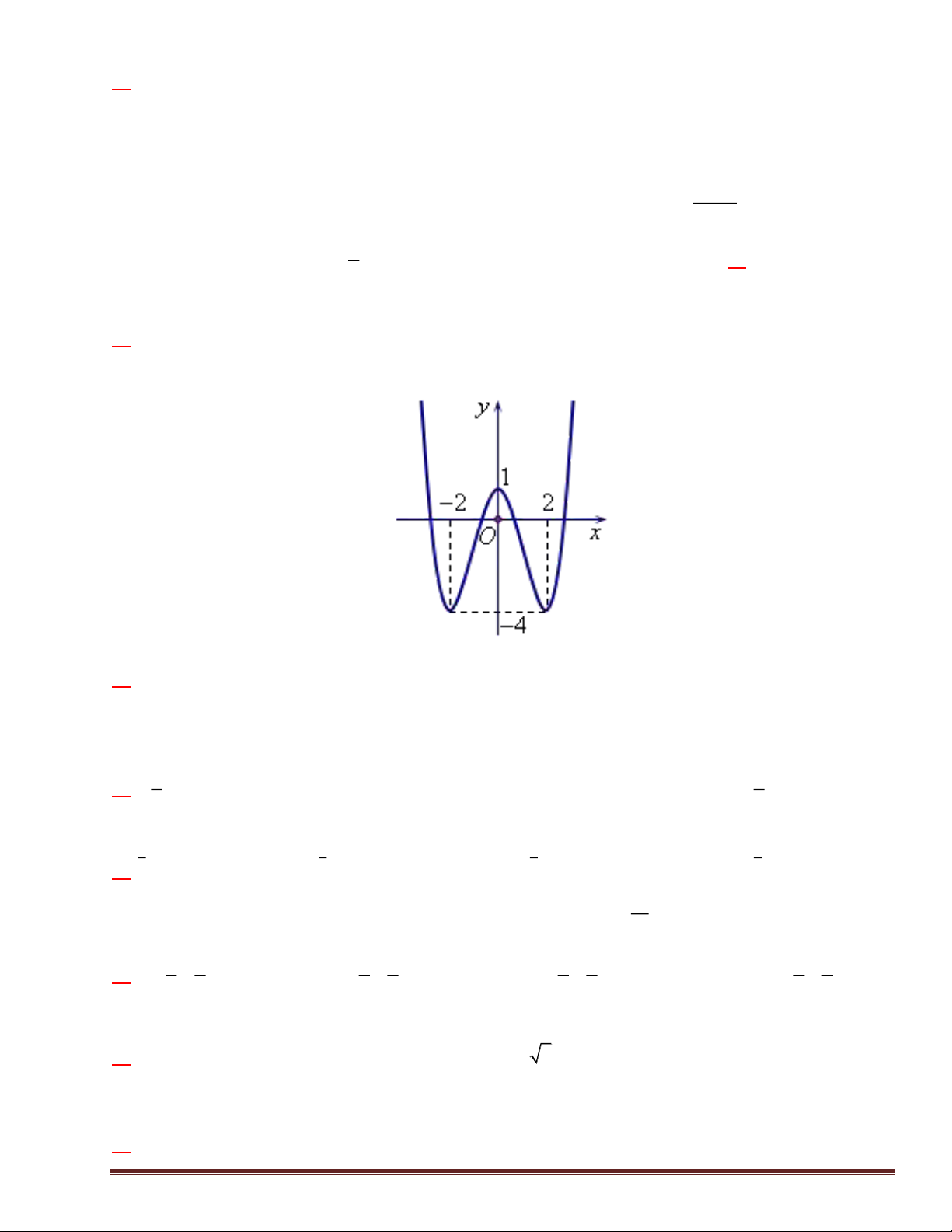
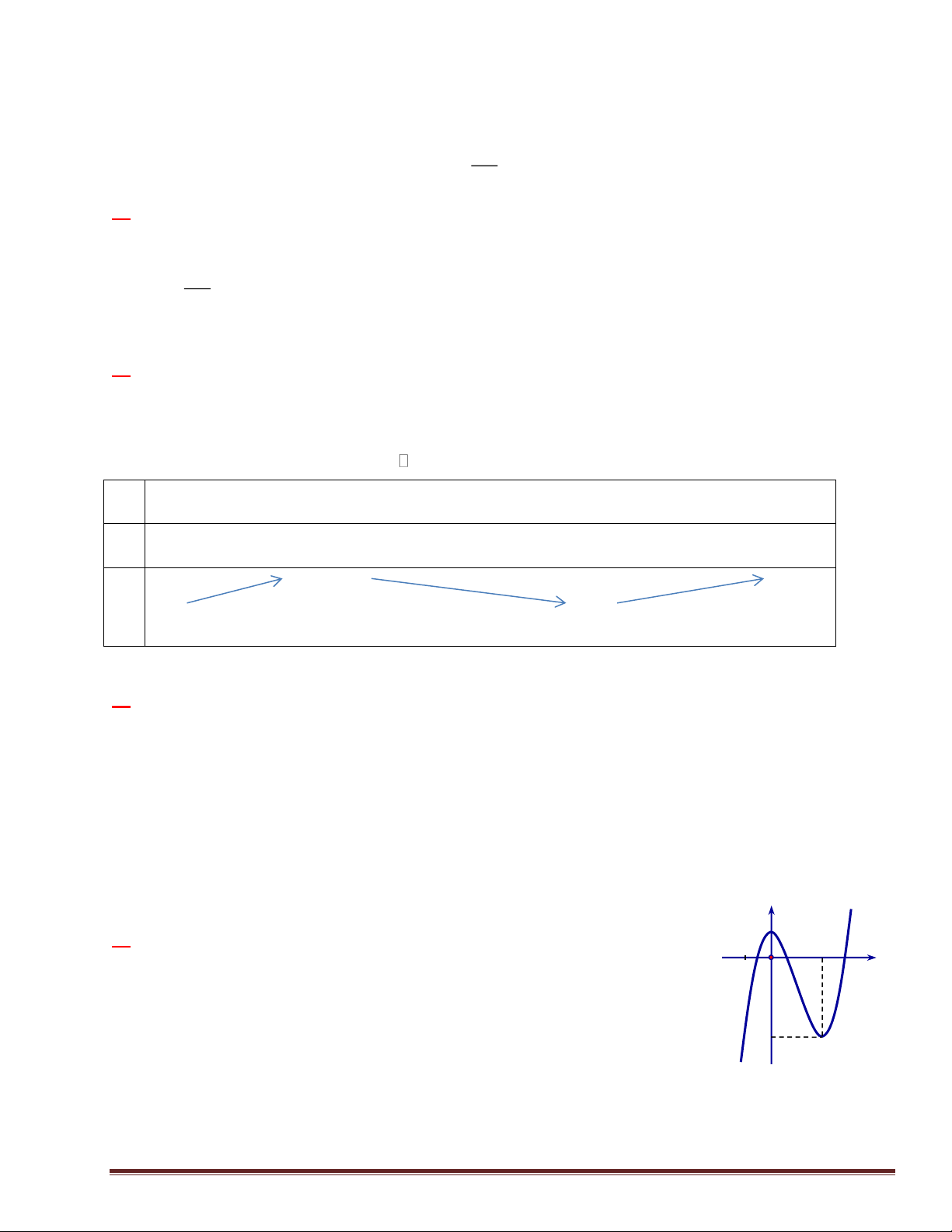
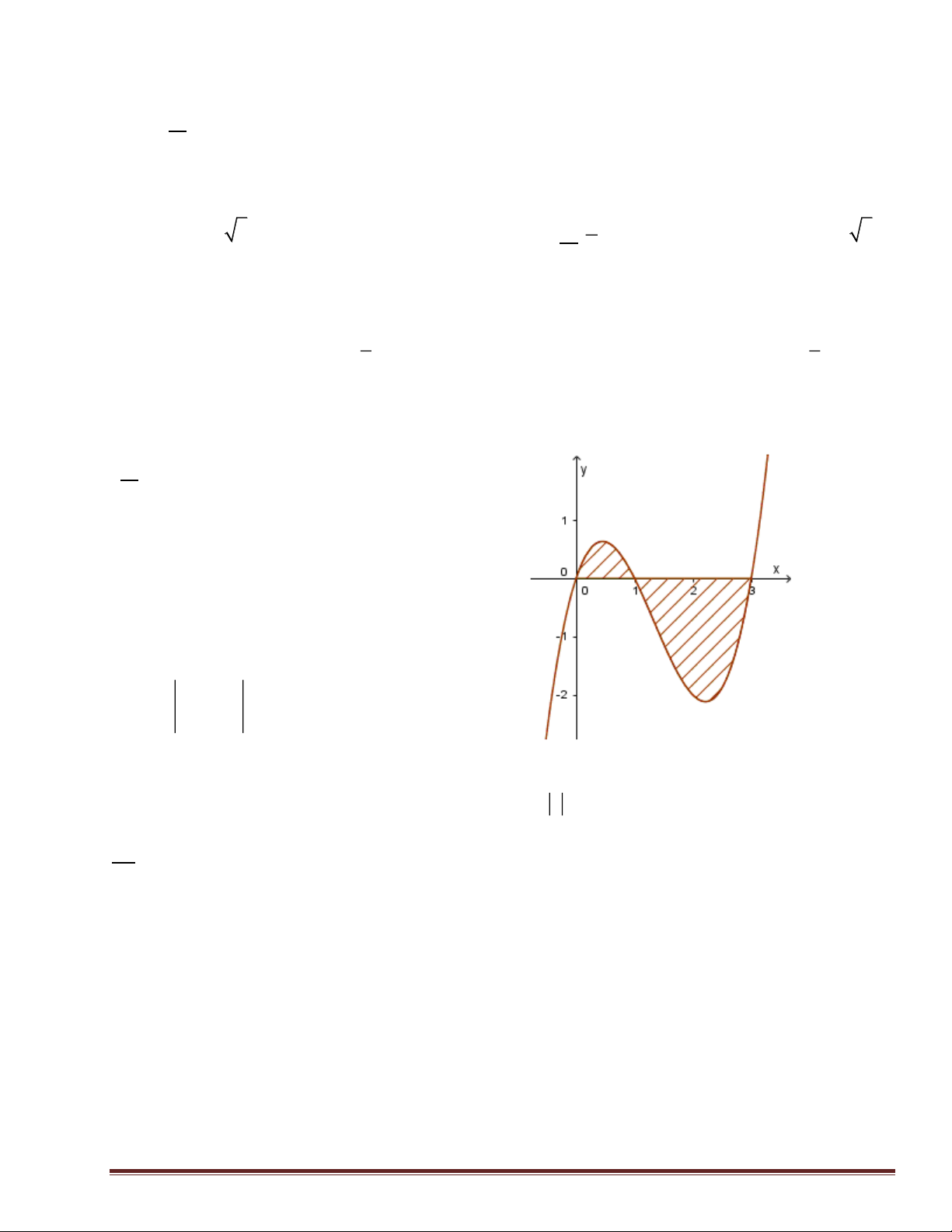
). Đồ thị của hàm số y = f (x) như hình vẽ bên.
Số nghiệm của phương trình 4 f (x)- 3 = 0 là A. 4 . B. 3 . C. 2 . D. 0 . 2 2 Câu 18: Nếu f
 (x)dx =6 thì 3f (x)dx  bằng 0 0 A. 18. B. 6. C. 3. D. 2.
Câu 19: Số phức liên hợp của số phức z = 3 + 4i là A. z = 4 − + 3i .
B. z = 3 − 4i . C. z = 3 − − 4i .
D. z = 4 + 3i .
Câu 20: Cho hai số phức z = 1
− + i và z = 3 + 2i . Phần thực của số phức z + z bằng 1 2 1 2 A. 1. B. 2. C. 4. D. -1 .
Câu 21: Trong mặt phẳng toạ độ, hai điểm A( 1 − ;2), B(3; 4
− ) lần lượt là điểm biểu diễn cho số phức
z , z . Điểm biểu diễn cho số phức z = z z là điểm nào sau đây? 1 2 1 2
A. N (10;5) .
B. M (5;10) . C. P ( 1 − 1;10). D. Q(10; 1 − ) 1 .
Câu 22: Trong không gian Oxyz , cho điểm A( 1 − ;2; )
3 . Tìm tọa độ điểm điểm B đối xứng với điểm A
qua mặt phẳng (Oyz) . Trang 3 A. B(1;2; ) 3 . B. B (1;2;− ) 3 . C. B( 1 − ; 2 − ;− ) 3 . D. B (1; 2 − ; ) 3 .
Câu 23: Trong không gian Oxyz , cho mặt cầu(S ) 2 2 2
: x + y + z + 4x − 2y + 6z + 5 = 0 . Mặt cầu (S ) có bán kính là A. 3 . B. 5 . C. 2 . D. 7 .
Câu 24:Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng ( P) : z − 2x + 3 = 0 . Một vectơ pháp
tuyến của (P) là:
A. u = (0;1; − 2) .
B. v = (1;− 2;3) .
C. n = (2;0; − ) 1 .
D. w = (1;− 2;0) . x = t
Câu 25: Trong không gian Oxyz , cho đường thẳng d :  y = 1− t . Đường thẳng d đi qua điểm nào sau z = 2 + t  đây? A. K (1; 1 − ; ) 1 .
B. H (1;2;0) .
C. E (1;1;2) .
D. F (0;1;2) .
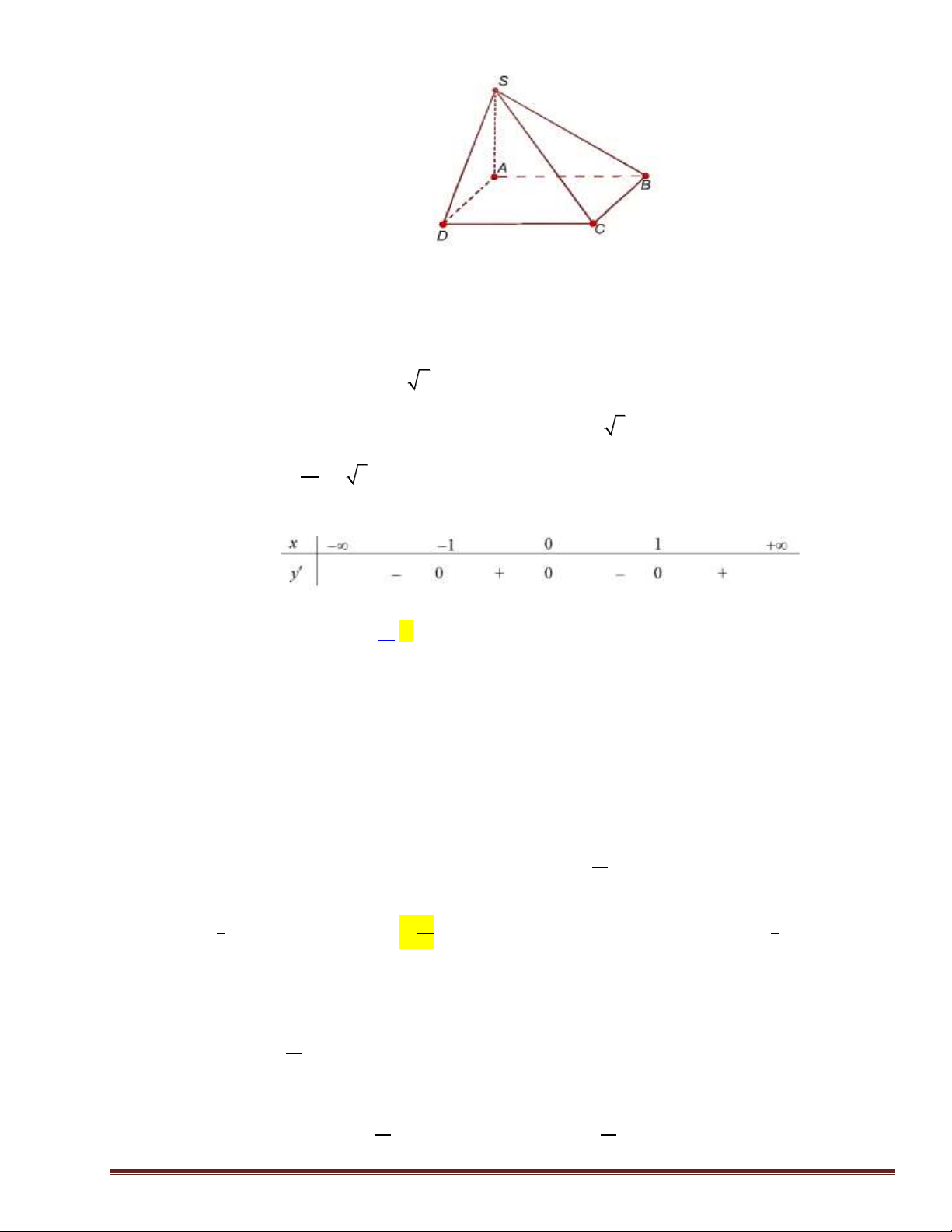
Câu 26. Cho hình chóp tứ giác 𝑆. 𝐴𝐵𝐶𝐷 có đáy là hình vuông , AC= a 2 , 𝑆𝐴 ⊥ (𝐴𝐵𝐶𝐷) và SA = a 3 .
Góc giữa đường thẳng 𝑆𝐵 và (ABCD) là A. 30°. B. 75°. C. 0 60 . D. 45°.
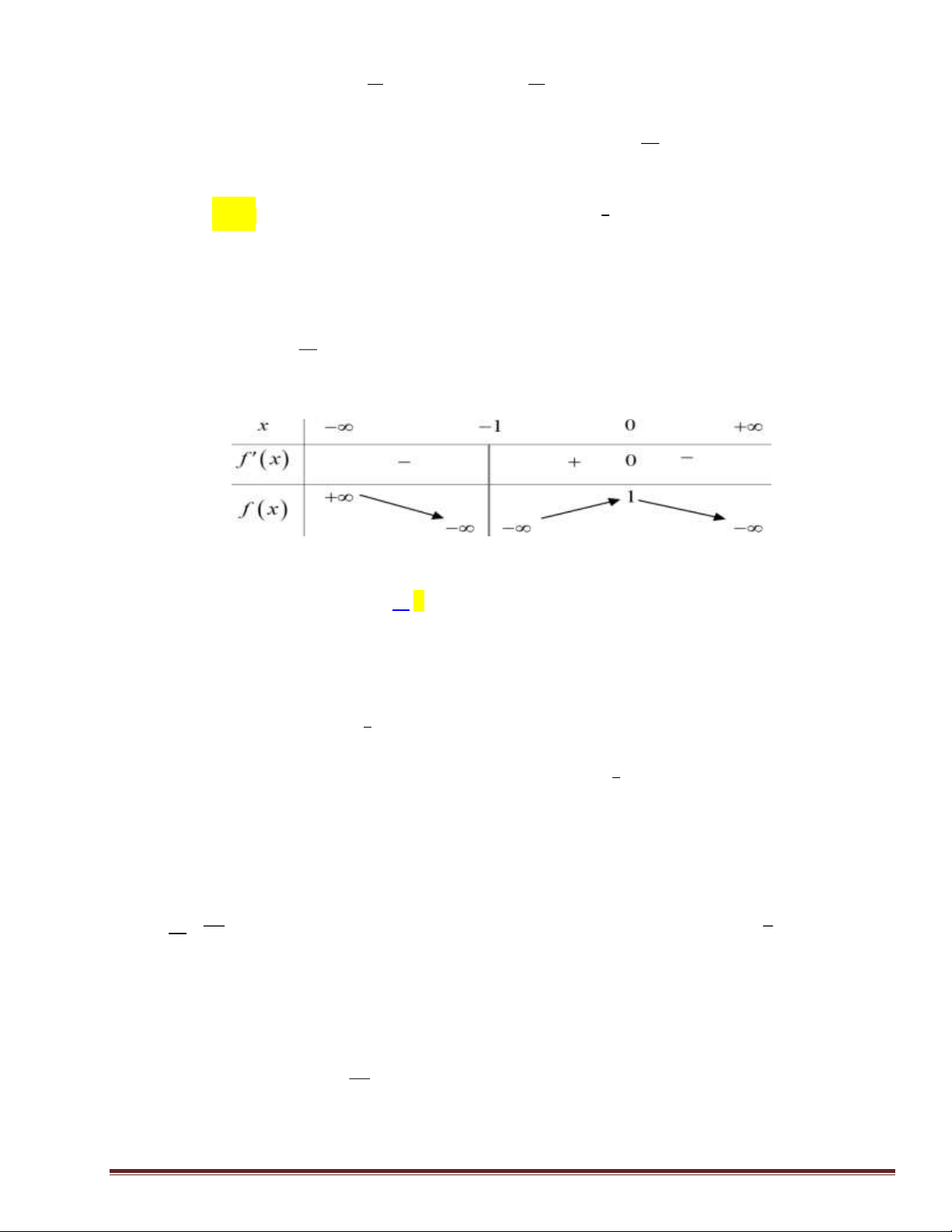
Câu 27. Cho hàm số 𝑓(𝑥), bảng xét dấu của 𝑓′(𝑥) như sau:
Số điểm cực trị của hàm số đã cho là A. 1. B. 3 C. 2. D. 4. 𝑥3
Câu 28. Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số 𝑦 =
+ 2𝑥2 + 3𝑥 − 4 trên [−4; 0] lần lượt 3
là 𝑀 và 𝑚. Giá trị của 𝑀 + 𝑚 bằng 4 28 4 A. . B. − . C. −4. D. − . 3 3 3  b
Câu 29. Xét tất cả các số thực dương 𝑎 và 𝑏 thỏa mãn ln ( 2 . a b ) = ln 
. Tích 𝑎𝑏 thuộc khoảng nào 2  e
trong các khoảng sau đây? 1 A. (0 ) ;1 . B. (−𝑒; 0). C. (− ; 0). D. (1; 2).. 𝑒
Câu 30. Cho hàm số 𝑓(𝑥) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2𝑓(𝑥) − 3 = 0 là Trang 4 A. 3 . B. 1. C. 2. D. 0.
Câu 31: Tập nghiệm của bất phương trình 2
log x + 2 log x − 3  0 là : 3 3  1   1  A. ;3 .   B. (− ;  − ) 3 (1;+). C. ( 3 − ; ) 1 . D. ; 27 .    27   3  Lời giải
Đặt t = log x bất phương trình đã cho trở thành 2
t + 2t −3  0  3 −  t 1 3 1  3 −  log x 1   x  3 3 27
Câu 32 : Cho khối nón có đường sinh bằng 5 và bán kính đáy bằng 3. Thể tích khối nón bằng? A. 18 . B. 12 . C. 24 . D. 15 . 
Câu 33 : Cho tích phân 2
I = x cos xdx  và 2
u = x , dv = cos xdx . Khẳng định nào sau đây đúng? 0     A. 2
I = x sin x + 2 xsin xdx  . B. 2
I = x sin x − xsin xdx  . 0 0 0 0     C. 2
I = x sin x + xsin xdx  . D. 2
I = x sin x − 2 xsin xdx  . 0 0 0 0
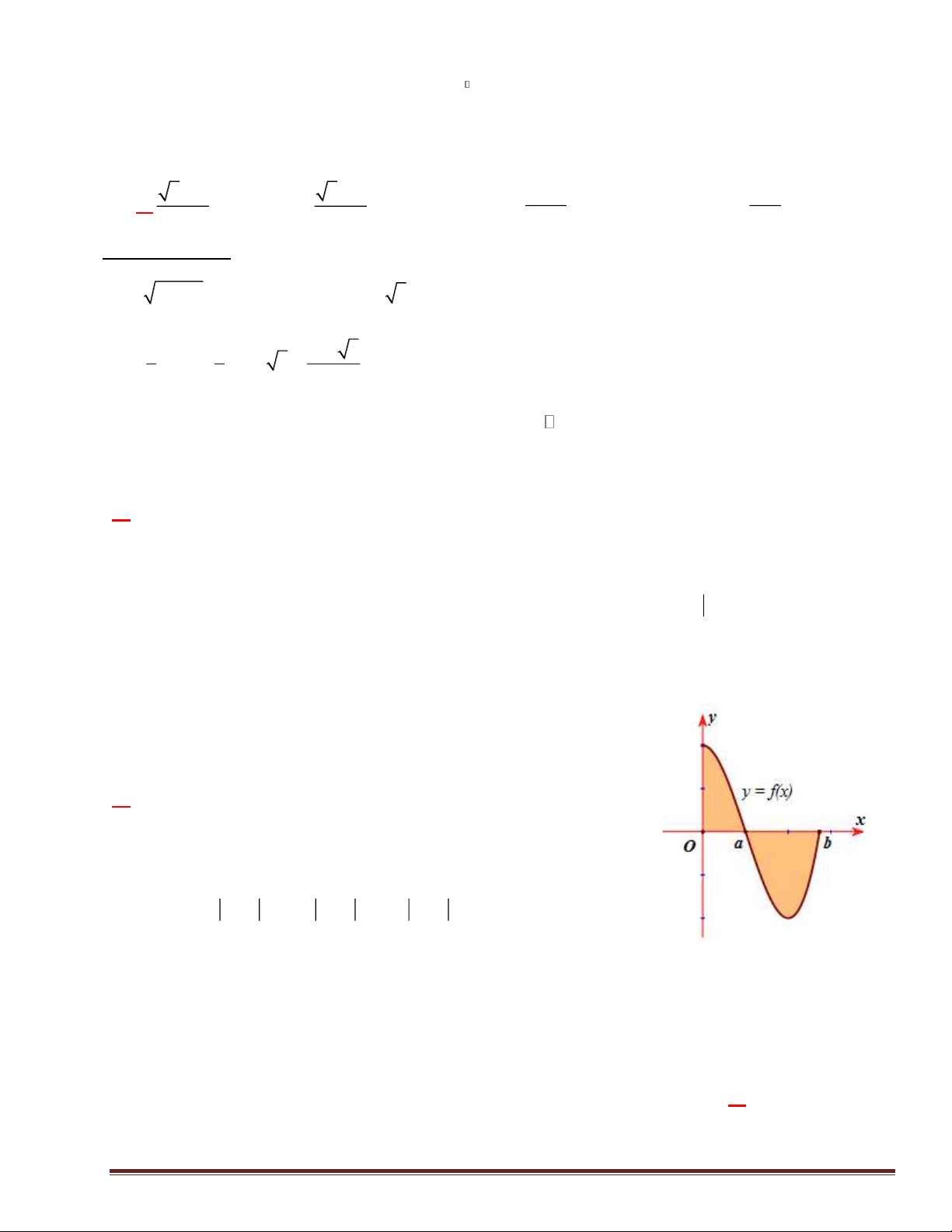
Câu 34 : Cho hình phẳng (D) được giới hạn bởi các đường f ( x) = 2x +1, O ,
x x = 0, x = 1 . Tính thể
tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức? 1 1 A. V = p 2x + 1dx ò B. V = p (2x + ò ) 1 dx 0 0 1 1 C. V = (2x + ò ) 1 dx D. V = 2x + 1dx ò 0 0
Câu 35 : Cho hai số phức z = 3 − 2i; z = 1 + 3 .
i Tổng của hai số phức z ; z là : 1 2 1 2 A. 4 + . i B. 9 − . i C. 1
− − 9 .i D. 4 − 5 .i 2 2
Câu 36: Gọi z , z là nghiệm của phương trình 2
z + 2z +10 = 0 . Giá trị của biểu thức A = z + z là: 1 2 1 2 A. 10 B. 2 10 C. 0 D. 20
Câu 37: Trong không gian hệ tọa độ Oxyzx, cho A(-1;0;1), B(-2;1;1). Phương trình mặt trung trực của
đoạn AB có phương trình là:
A. x − y − 2 = 0
B. x − y +1 = 0
C. x − y + 2 = 0
D. −x + y + 2 = 0 Trang 5
Câu 38: Trong không gian với hệ tọa độ Oxyz, cho ( ) : 2x − y + 2z −3 = 0 . Phương trình đường thẳng
d đi qua A(2;-3;-1) song song ( ) và mặt phẳng (Oyz) là: x = 2 − tx = 2 x = 2 x = 2t     A.  y = 3 −
B.  y = −3 + 2t
C.  y = −3 − 2t
D.  y = 2 − 3t     z = 1 − + tz = −1+ tz = −1+ tz = 1− t
Câu 39: Câu 39. Lớp 11A có 40 học sinh trong đó có 12 học sinh đạt điểm tổng kết môn Hóa học loại
giỏi và 13 học sinh đạt điểm tổng kết môn Vật lí loại giỏi. Biết rằng khi chọn một học sinh của lớp đạt
điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi có xác suất là 0,5. Số học sinh đạt điểm tổng kết giỏi
cả hai môn Hóa học và Vật lí là A. 4 . B. 7 . C. 6 . D. 5 .
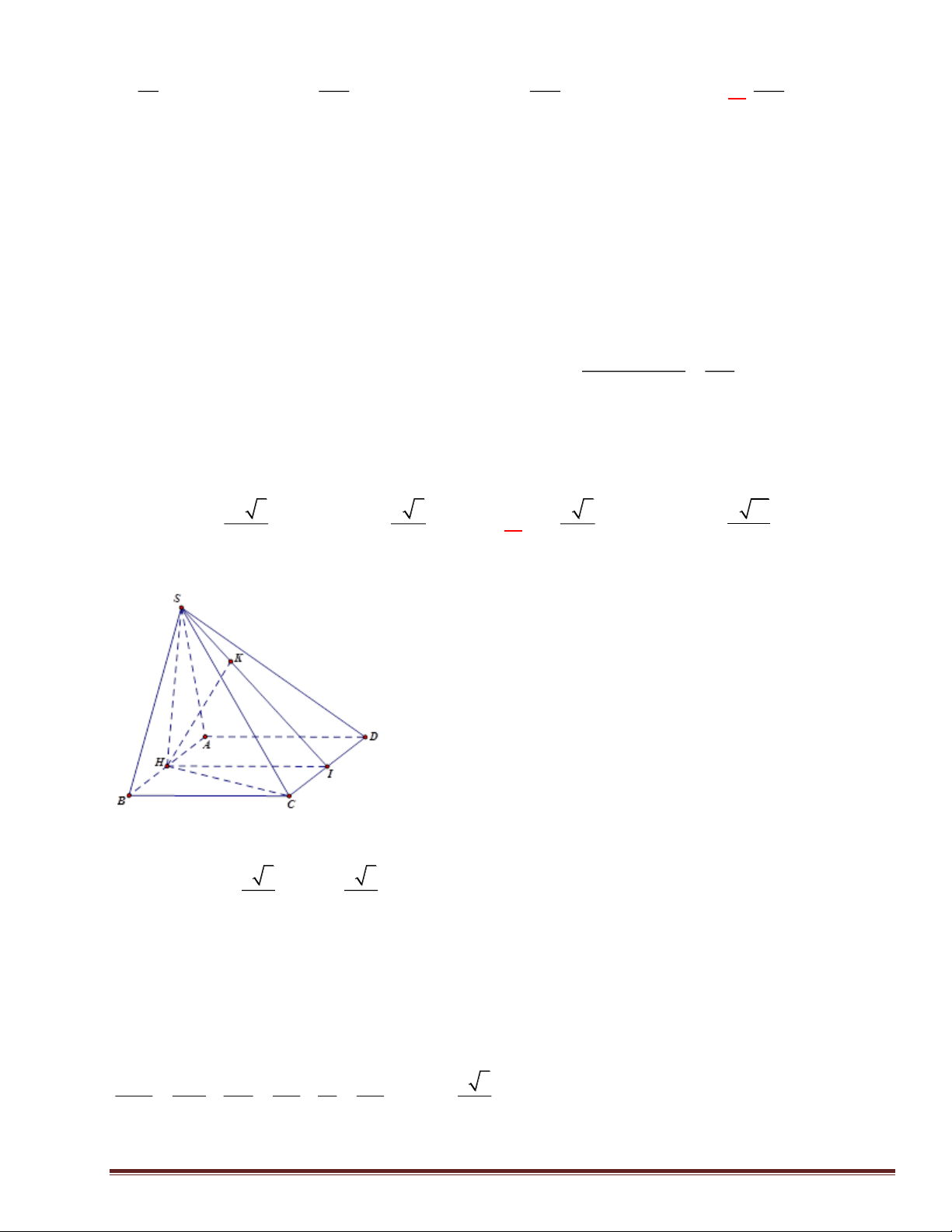
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a 3 2
Cạnh bên SA vuông góc với đáy, biết tam giác SAD có diện tích S = 3a . Tính khoảng cách từ C đến (SBD). Câu 41: Cho hàm số 3 2
y = −x − mx + ( 3
− m + 6)x + 5 với m là tham số. Có bao nhiêu giá trị
nguyên của m để hàm số nghịch biến trên khoảng (− ;  +)? A. 2. B. 3. C. 4. D. 5.
Câu 42:Tỉ lệ tăng dân số hàng năm của Nhật là 0,2%. Năm 1998, dân số của Nhật là
125 932 000. Vào năm nào dân số của Nhật sẽ là 140 000 000 ? ( Kết quả làm tròn đến hàng đơn vị)
A. 2061. B. 2055. C. 2051. D. 2045.
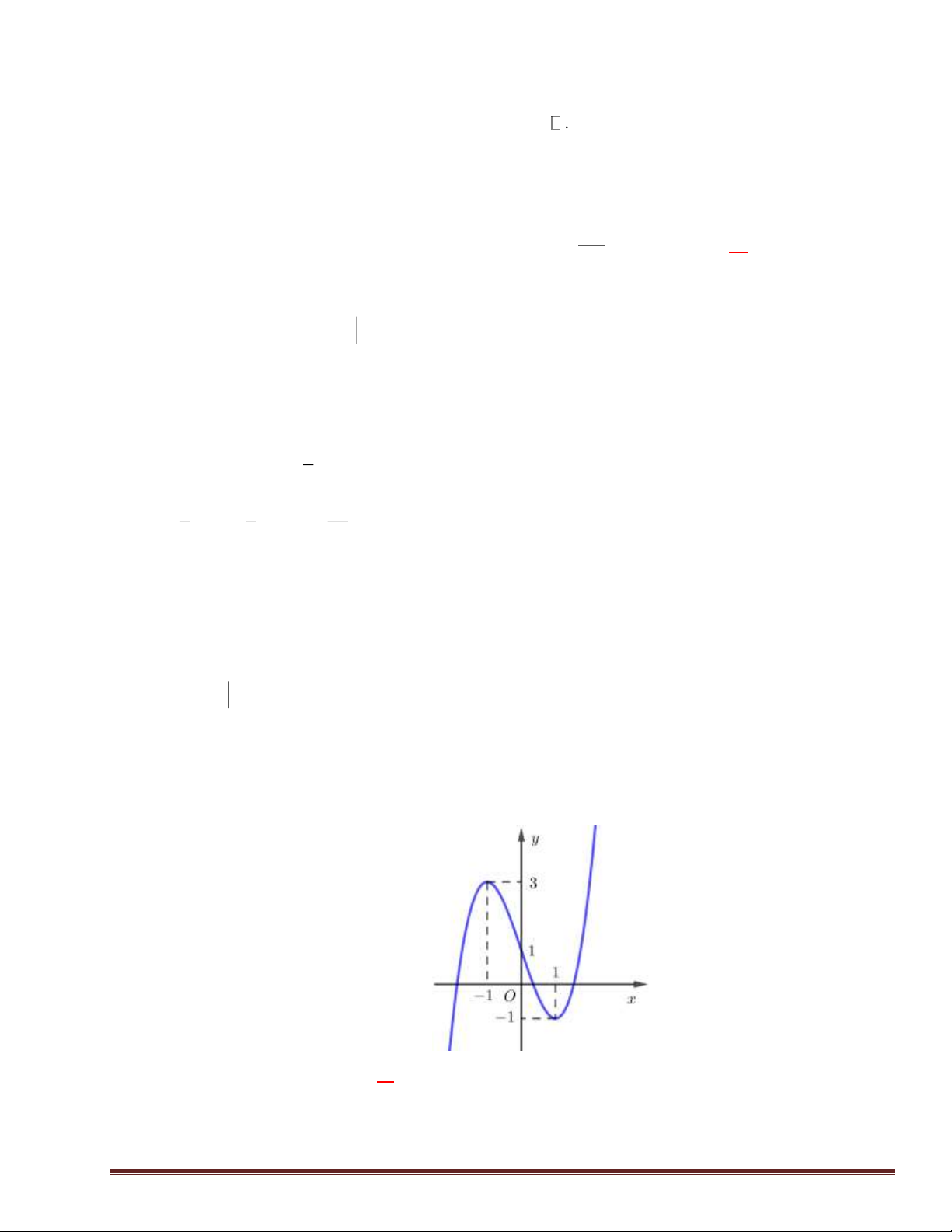
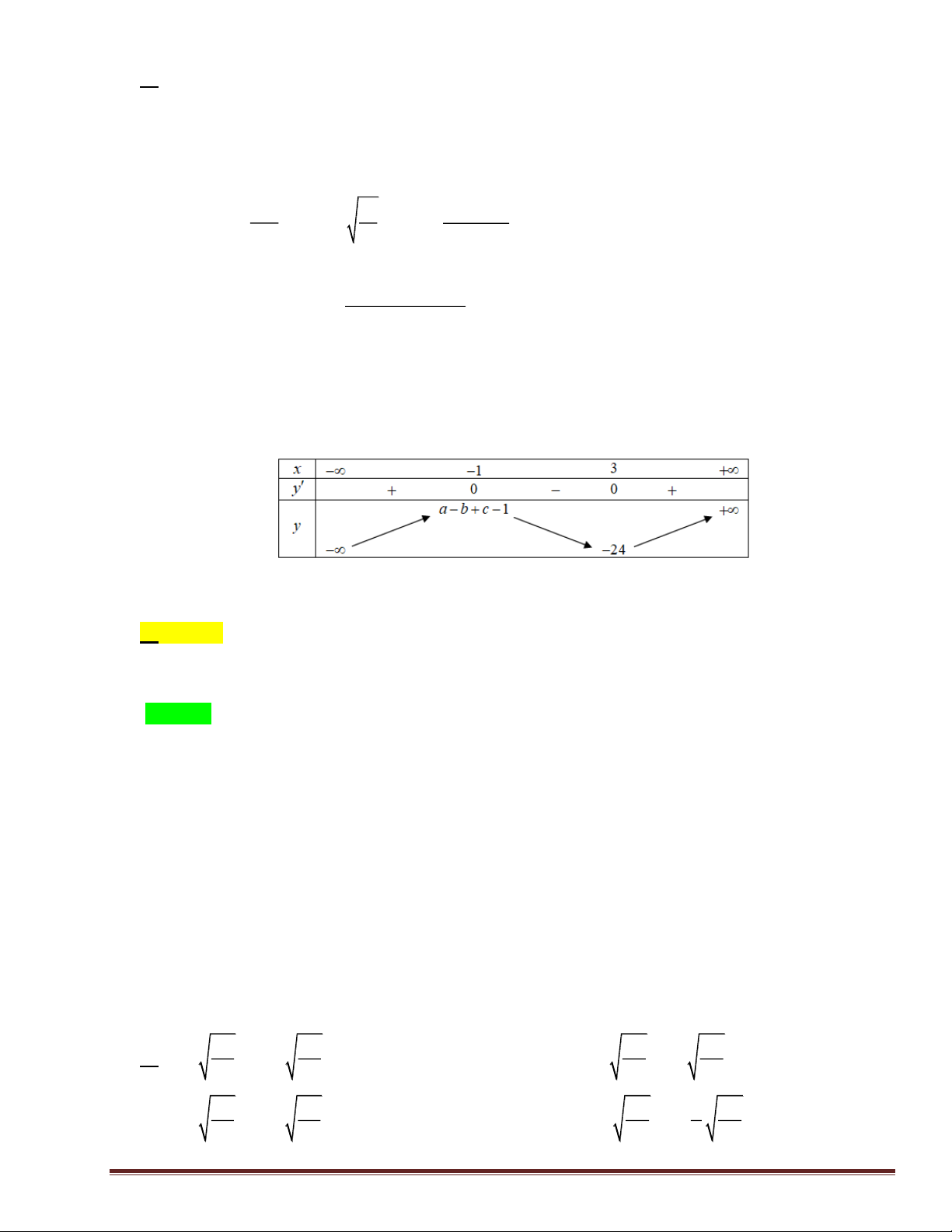
Câu 43: Ta xác định được các số a, b, c để đồ thị hàm số 3 2
y = x + ax + bx + c đi qua điểm (1;0) và có điể 2 2 2 m cực trị ( 2
− ;0). Tính giá trị biểu thức T = a + b + c . A. 25. B. -1. C. 7. D. 14.
Câu 44: Cho hình trụ có bán kính đáy bằng a. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song a
song với trục và cách trục một khoảng bằng
, thiết diện thu được là một hình vuông.Thể tích của 2
khối trụ được giới hạn bằng hình trụ đã cho bằng 3  a 3 A. 3 3 a . B. 3  a 3. C. . D. 3 a . 4 Trang 6 2 x e f '(x) = x  
Câu 45: Cho hàm số y = f ( )
x thỏa mãn f (ln 3) = 3 và x e + 1 x − e + 1 . ln 3 Khi đó x
e f (x) dx  bằng 0 1 − 0 − 8 2 20 − 8 2 20 + 8 2 10 − 8 2 A. B. . C. . D. 3 3 3 3
Câu 46: Cho hàm số y = f ( )
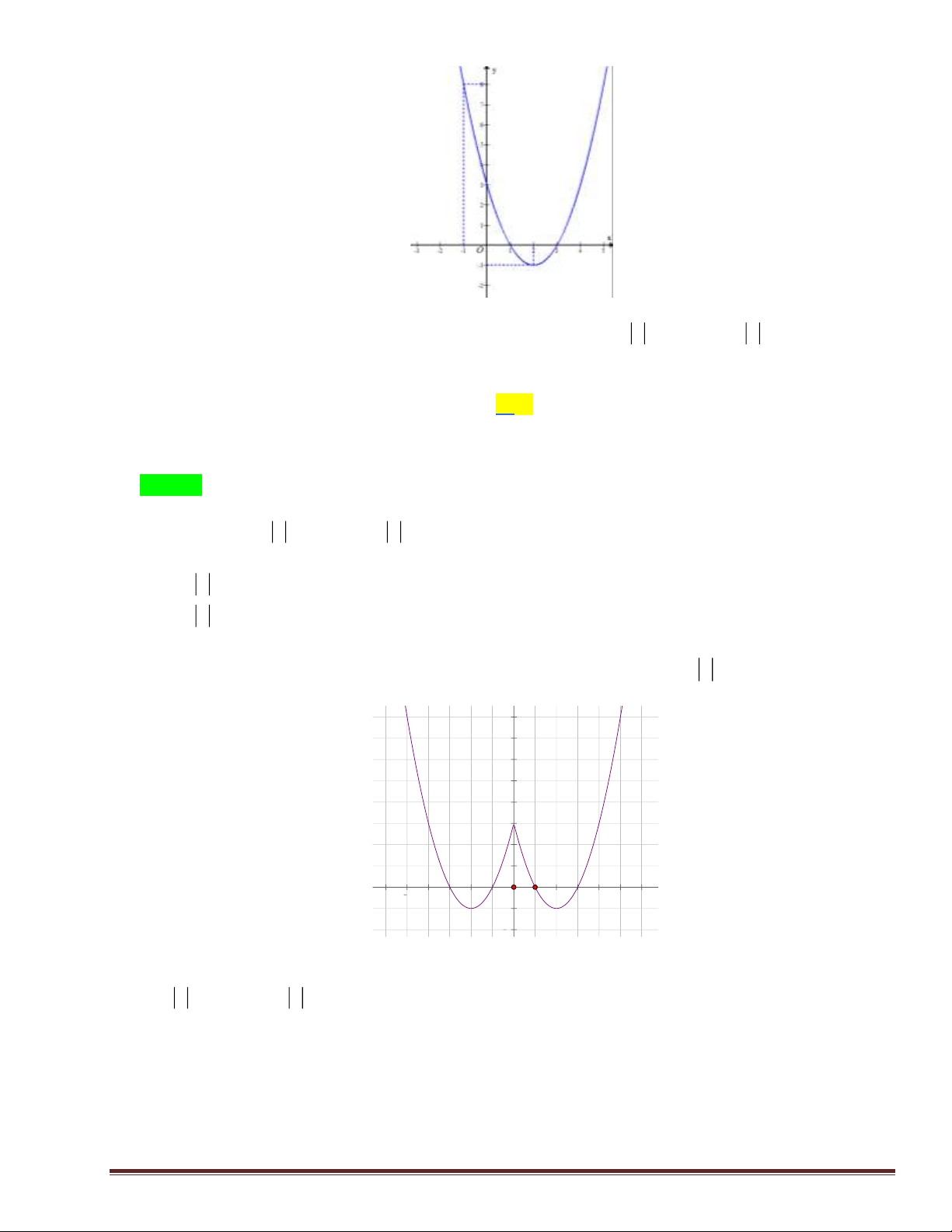
x có bảng biến thiên như sau:  3  Số nghiệm thuộc đoạn  − ; 
 của phương trình 2 f (2cos ) x − 9 = 0 là:  2  A. 5. B. 4 C. 3. D. 2.  x + 2y
Câu 47: Cho x , y là các số thực dương thỏa mãn log = −x + 4y −1  
. Tính giá trị nhỏ nhất  9x + 24y  2
của biểu thức P = x + bằng. 2 y A. 4 B. 10 C. 6 D. 2 2
x + mx + m
Câu 48:Cho hàm số y = x +
gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho 1
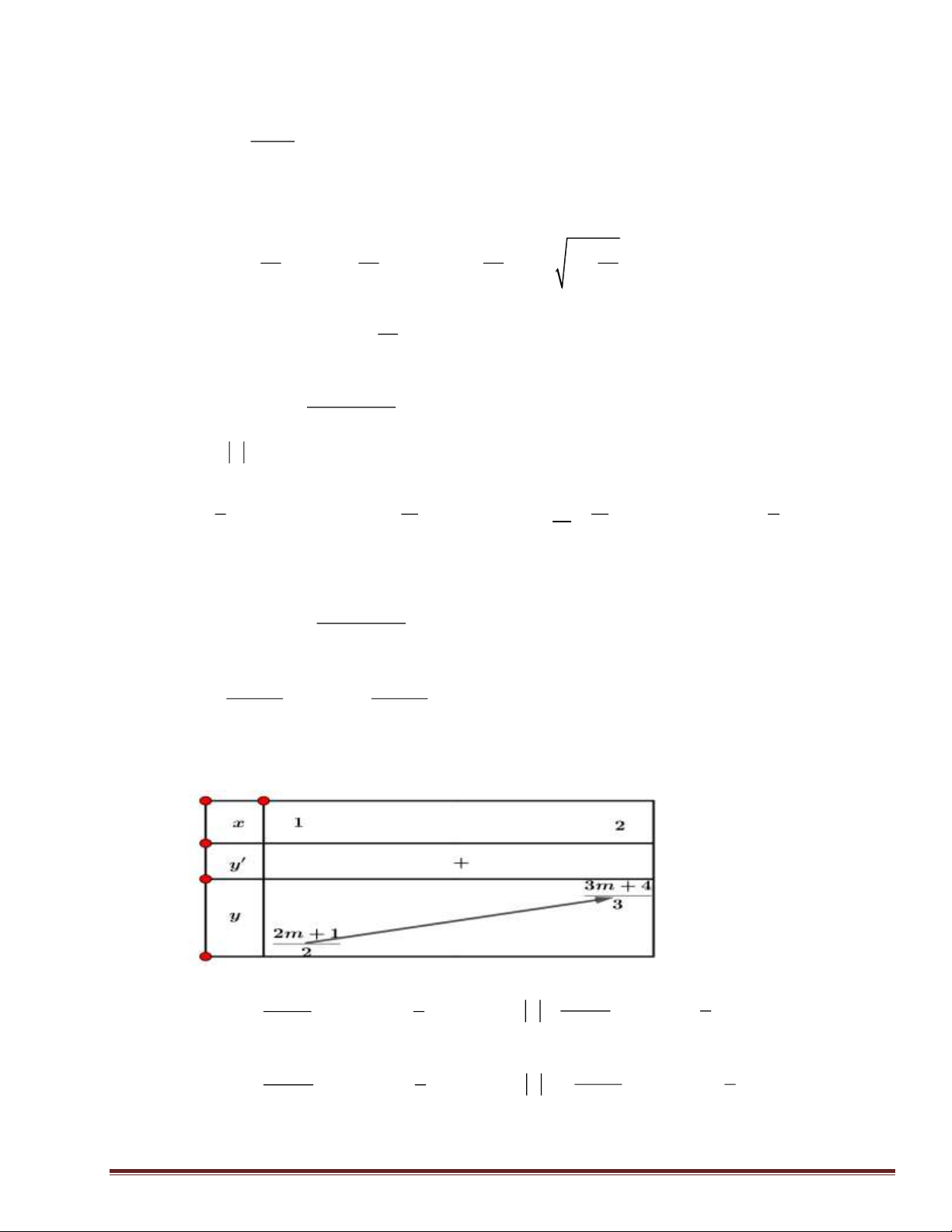
Max y = 2 .Tổng các phần tử của S là. 1;2 2 11 11 5 A. . B. . C. − . D. − . 3 6 6 2 Lời giải. Trang 7
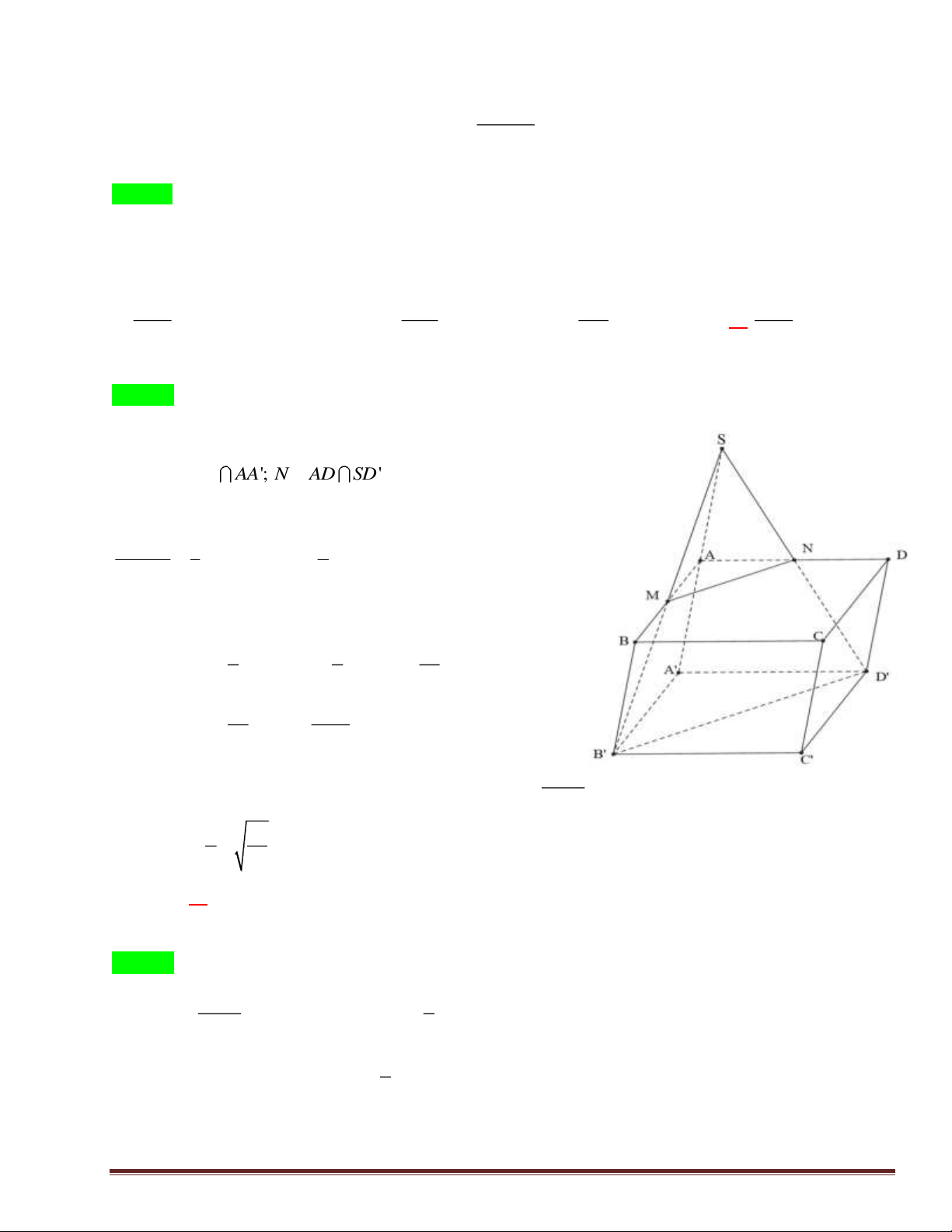
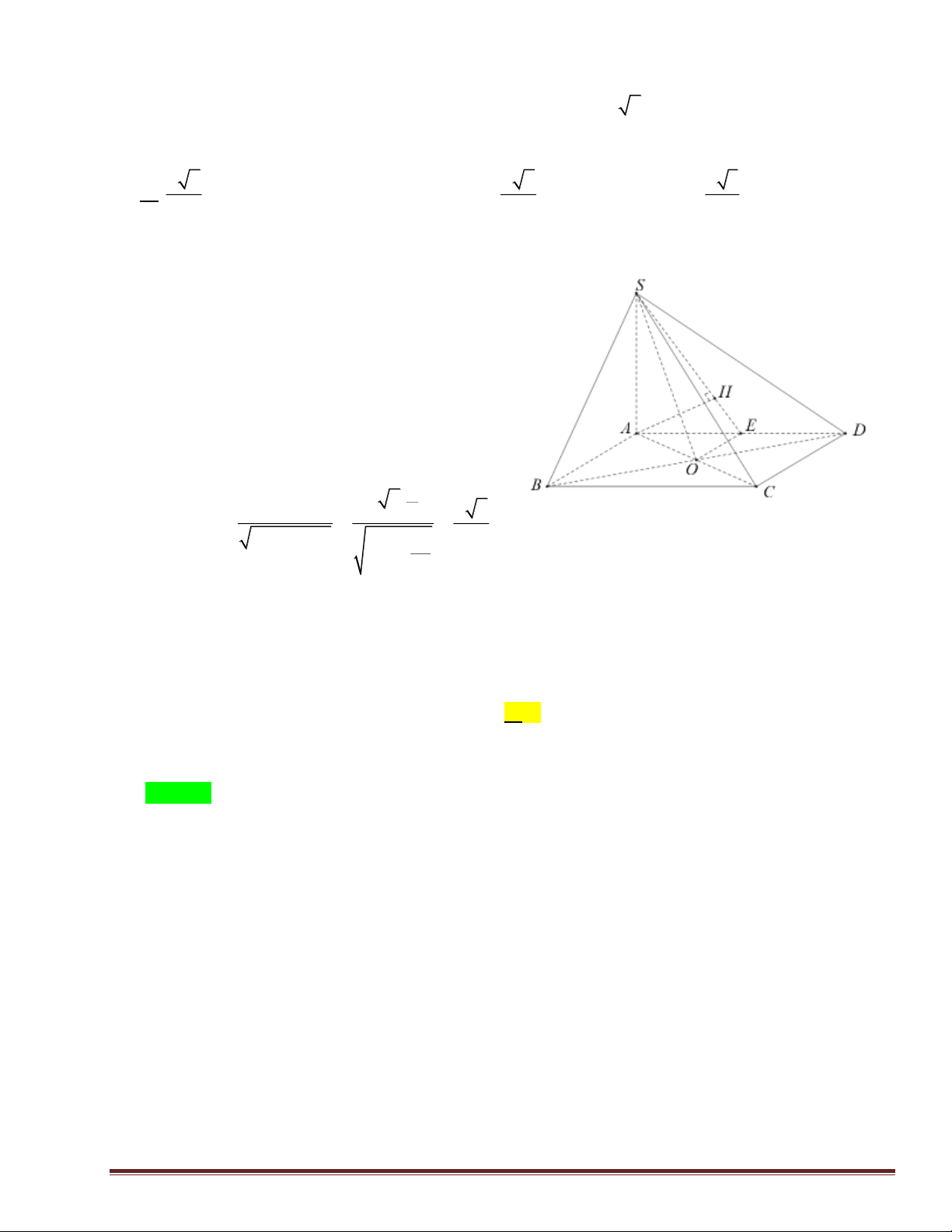
Câu 49: Cho hình chóp đều S.ABC có tất cả các cạnh bằng 3 và M , N, P lần lượt là trọng tâm của tam giác SA ,
B SBC, SAC . Thể tích khối đa diện có các đỉnh là , A , B ,
C M, N, P là 2 4 2 8 2 9 2 A. . B. . C. . D. . 12 3 3 4
Câu 50: Cho hàm số y = f ( x) = ( 2 ln
1+ x + x) . Số giá trị nguyên dương a thỏa mãn bất phương
trình f (a − )
3 + f (ln a)  0 là
A. 1. B. 2. C. 3. D. 4. ĐÁP ÁN CHI TIẾT 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D B A C A D C D A A D B B A B C A A B B B A A C D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C B B A B A B D B A D C B D D C C A B B A C C B B
Câu 1: Trong một hộp bút gồm có 8 cây bút bi, 6 cây bút chì và 10 cây bút màu. Hỏi có bao nhiêu cách chọn
ra một cây bút từ hộp bút đó? A. 48. B. 60. C. 480. D. 24. Lời giải Chọn D Áp dụng quy tắc cộng:
Số cách chọn ra một cây bút từ hộp bút đó là 8 + 6 +10 = 24.
Câu 2: Cho cấp số cộng (u với u = 5u và u = 2u + 5. Khi đó số hạng đầu u và công sai d bằng n ) 9 2 13 6 1
A. u = 4 và d = 5 . B. u = 3 và d = 4 . 1 1
C. u = 4 và d = 3 . D. u = 3 và d = 5 . 1 1 Lời giải Chọn B u  = 5u u
 + 8d = 5 u + d  4u − 3d = 0 u  = 3 9 2 1 ( 1 ) 1 Ta có 1        . u = 2u + 5  u
 +12d = 2 u + 5d + 5 u − 2d = 5 −   d = 4 13 6 1 ( 1 ) 1 Trang 8
Câu 3: Nghiệm của phương trình 3 log (x - 3) = 3 là 3 A. x = 3 + 3 .
B. x = 3 .
C. x = 3 3 . D. x = 3 - 3 . Lời giải Chọn A ìï ì ï - > ï ìï 3 x 3 0 ( ï ï > ï > ï ï ï x - ) x 3 x 3 log 3 = 3 Û í 3 Û í Û í Û x = 3 + 3 3 ïïï(x - 3) 3 = 3 ïï x 3 3 ï - = ï x = 3 + 3 ïî ïî ïî
Câu 4: Cho khối lập phương ABC . D A BCD
  có AC = a 2 (a  0) . Thể tích của khối lập phương đã cho bằng 3 a A. 2 a . B. . C. 3 a . D. 3 . a 3 Lời Giải Chọn C
Gọi x là cạnh hình lập phương. ABC . D A BCD
  là hình lập phương nên ABCD là hình vuông do đó AC = x 2 .
Mặt khác, theo đề bài ta có AC = a 2,(a  0) . Suy ra cạnh của hình lập phương bằng x = a .
Vậy thể tích của khối lập phương bằng 3 V = a . 
. Câu 5: Tập xác định của hàm số y = ( 2
x − 3x + 2) là: A. (− ;  ) 1 (2;+) . B. . C. (0;+) . D. (1; 2) . Lời giải Chọn A  Hàm số y = ( 2
x − 3x + 2) là hàm lũy thừa có số mũ  nên hàm số xác định khi 2
x − 3x + 2  0  x (− ;  )
1 (2;+) . Vậy tập xác định của hàm số là (− ;  ) 1 (2;+) .
Câu 6: Tìm nguyên hàm của hàm số f ( x) = sin 2x . 1 1 A. 2
− cos2x + C . B.
cos 2x + C .
C. 2cos 2x + C .
D. − cos 2x + C . 2 2 Trang 9 Lời giải Chọn D 1 sin 2 d
x x = − cos 2x + C  . 2
Câu 7: Cho khối lăng trụ AB . C A BC
  có thể tích là V , thể tích của khối chóp C .ABC là: 1 1 1 A. V . B. V . C. V . D. 2V . 6 2 3 Lời giải Chọn C
Gọi h là khoảng cách từ C đến mặt phẳng ( ABC ) và B là diện tích tam giác ABC . Khi đó, thể 1
tích lăng trụ V = Bh , thể tích khối chóp C .ABC là V = . Do đó,  Bh C . ABC 3 1 V =  V . C . ABC 3
Câu 8: Hình nón có bán kính đáy bằng 2 (cm), góc ở đỉnh bằng 60 . Thể tích khối nón là 8 3 8 3 A. V = ( 3 cm ). B. V = ( 3 cm ) . 9 2 8 3 C. V =  ( 3 8 3 cm ) . D. V = ( 3 cm ) . 3 Lời giải Ta có bán kính đáy r
r = 2 , đường cao h =  h = 2 3 . tan 30 1 1 8 3 Vậy thể tích khối nón 2
V =  r h =  .4.2 3 = ( 3 cm ) . 3 3 3
Câu 9: Tính bán kính r của khối cầu có thể tích là V =  ( 3 36 cm ) .
A. r = 3(cm) .
B. r = 6(cm) .
C. r = 4(cm) .
D. r = 9(cm) . Trang 10 Lời giải Chọn A 4 3V Ta có 3 V = r 3  r = 3
r = 27  r = 3 . Vậy r = 3(cm) . 3 4
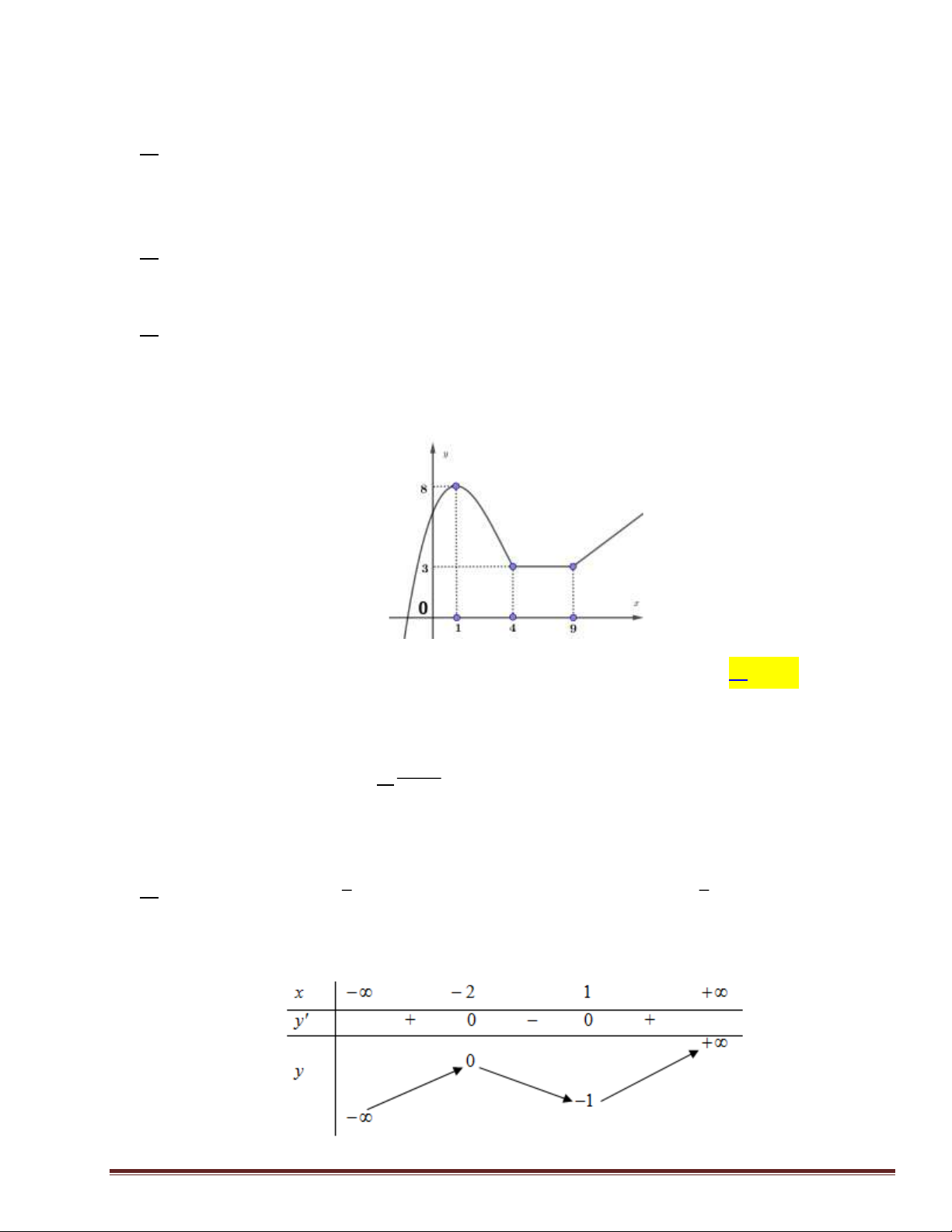
Câu 10: Cho hàm số y = f ( x) có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (0 ) ;1 B. ( 1 − ;0) . C. ( 1 − ; ) 1 . D. (1;+) . Lời giải Chọn A
Câu 11: Với a là số thực dương tùy ý, log ( 5 a bằng 3 )  5  1 A. log a  . B. log a . C. 5 + log a . D. 5log a . 3   3  3 5 3 3 Lời giải Công thức log ( 5 a
=5 log a chọn câu D 3 ( ) 3 )
Câu 12: Diện tích xung quanh của hình nón có độ dài đường sinh l và bán kính đáy r bằng 1 A. 4 rl . B. rl . C. rl . D. 2 rl . 3 Lời giải Công thức B
Câu 13: Cho hàm số y = f ( x) có bảng biến thiên như sau: Trang 11
Hàm số đã cho đạt cực tiểu tại điểm A. x = 2 − . B. x = 2 . C. x = 1 . D. x = 1 − . Lời giải
Dựa vào bảng biến thiên chọn B
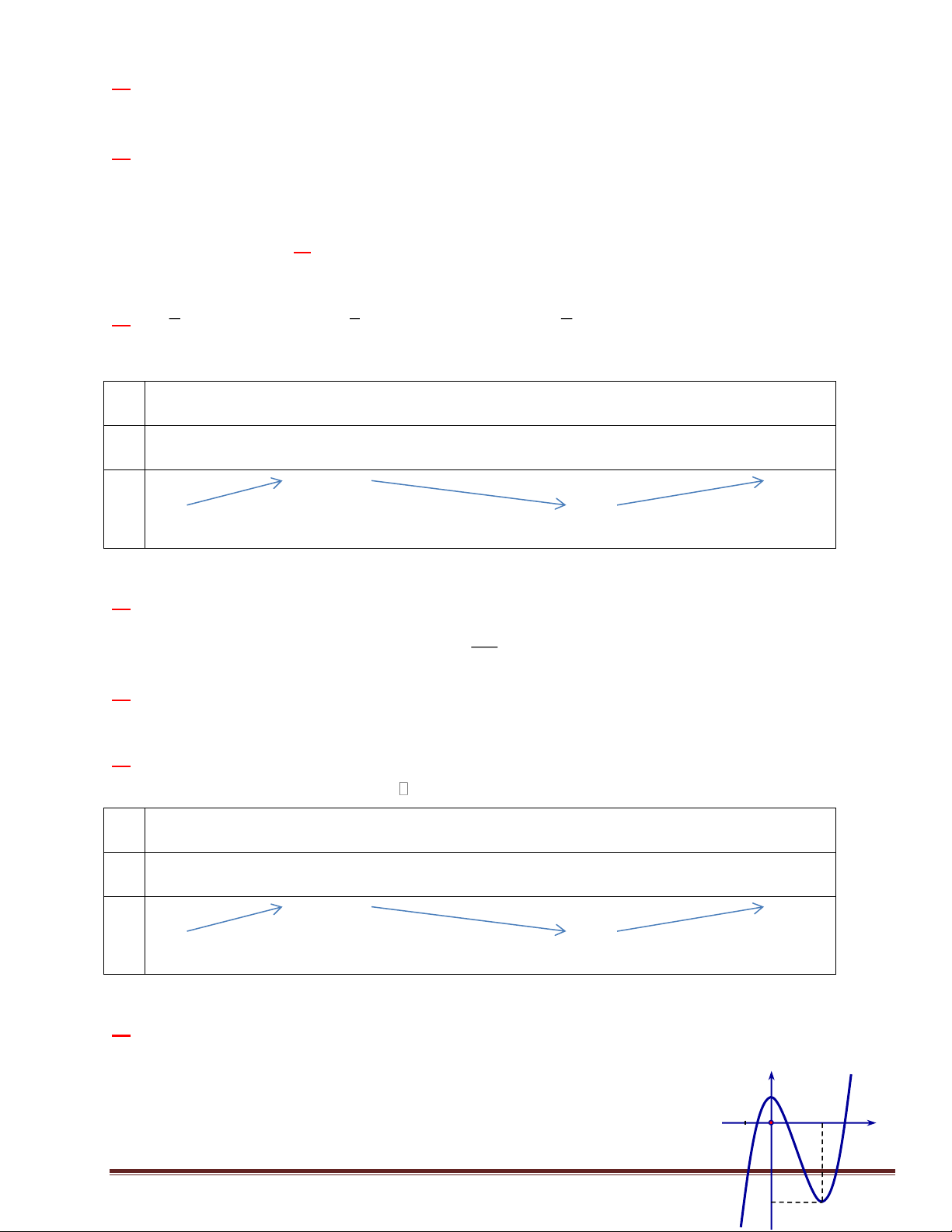
Câu 14: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới? A. 3 2 y = - x + 3x - 4 B. 3 2 y = x - 3x + 4 C. 4 2 y = x - 2x - 3 x - 1 D. y = x + 1 Lời giải
Đồ thị hàm bậc 3 với a<0 chọn câu A 3x + 2
Câu 15: Tiệm cận ngang của đồ thị hàm số y = x − là 1 A. y = 2 − . B. y = 3 . C. x = 2 − . D. x = 3 . Lời giải a Ta có TCN: y = = 3 chọn B c
Câu 16: Tập nghiệm của bất phương trình ln x  1 là A. ( ; e +) . B. (0;+). C.  ; e +) . D. ( ; − e) . Lời giải
ln x  1  x e nên chọn C Câu 17: Cho hàm số ( ) 4 2
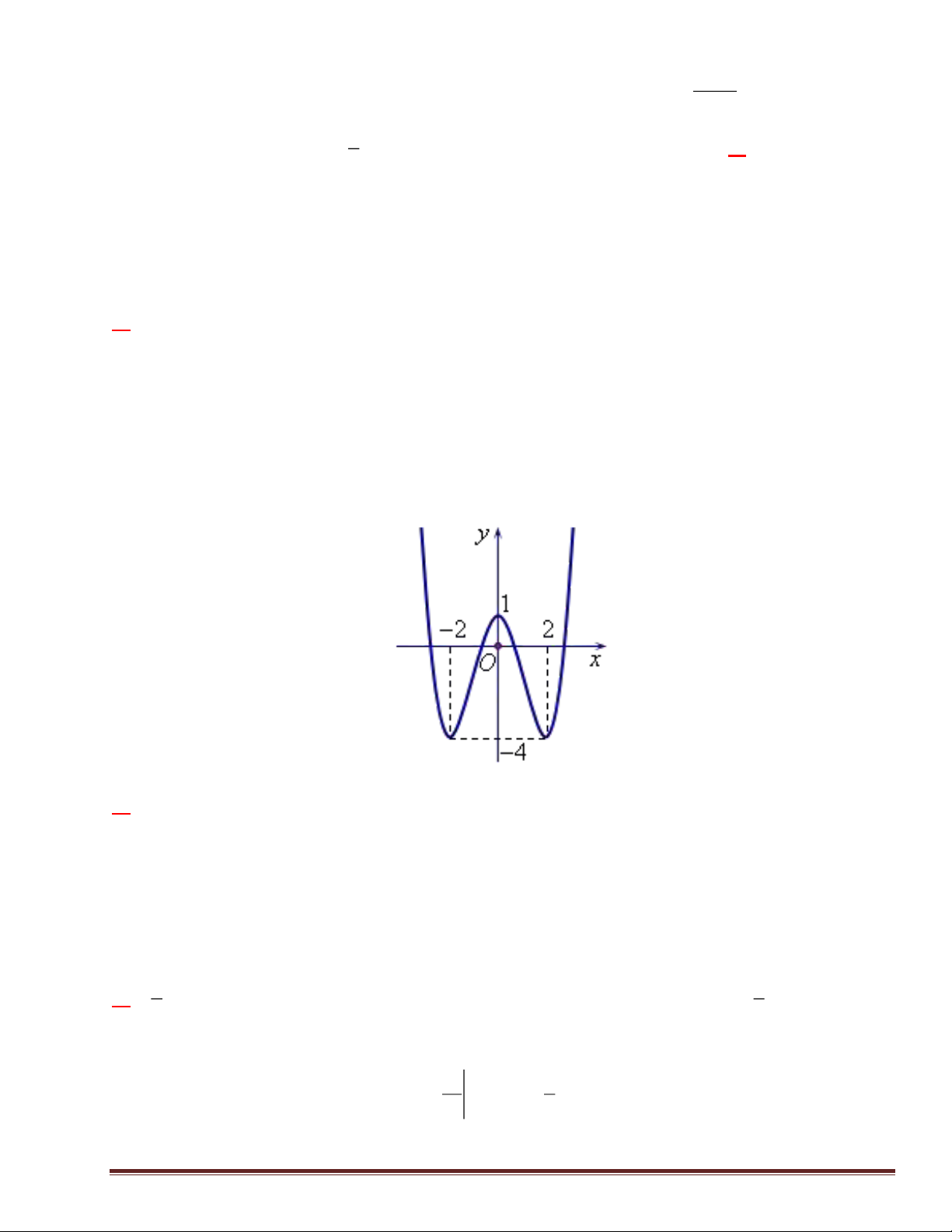
f x = ax + bx + c ( , a , b c Î
). Đồ thị của hàm số y = f (x) như hình vẽ bên.
Số nghiệm của phương trình 4 f (x)- 3 = 0 là Trang 12 A. 4 . B. 3 . C. 2 . D. 0 . Lời giải
4 f (x)- 3 = 0  f ( x) 3
= dựa vào đồ thị chọn A 4 2 2 Câu 18: Nếu f
 (x)dx =6 thì 3f (x)dx  bằng 0 0 A. 18. B. 6. C. 3. D. 2. Lời giải 2 2 3 f (x)dx
=3 f (x)dx =  3.6=18 chọn A 0 0
Câu 19: Số phức liên hợp của số phức z = 3 + 4i là A. z = 4 − + 3i .
B. z = 3 − 4i . C. z = 3 − − 4i .
D. z = 4 + 3i . Lời giải
Số phức liên hợp a-bi chọn B 3-4i
Câu 20: Cho hai số phức z = 1
− + i và z = 3 + 2i . Phần thực của số phức z + z bằng 1 2 1 2 A. 1. B. 2. C. 4. D. -1 . Lời giải
z + z = -1+3+3i=2+3i chọn B 1 2
Câu 21: Trong mặt phẳng toạ độ, hai điểm A( 1 − ;2), B(3; 4
− ) lần lượt là điểm biểu diễn cho số phức
z , z . Điểm biểu diễn cho số phức z = z z là điểm nào sau đây? 1 2 1 2
A. N (10;5) .
B. M (5;10) . C. P ( 1 − 1;10). D. Q(10; 1 − ) 1 . Lời giải Chọn B Ta có: z = 1
− + 2i , z = 3 − 4i z = ( 1
− + 2i)(3−4i) = 5+10i 1 2
Vậy điểm biểu diễn số phức z là (5;10) . Trang 13
Câu 22: Trong không gian Oxyz , cho điểm A( 1 − ;2; )
3 . Tìm tọa độ điểm điểm B đối xứng với điểm A
qua mặt phẳng (Oyz) . A. B(1;2; ) 3 . B. B (1;2;− ) 3 . C. B( 1 − ; 2 − ;− ) 3 . D. B (1; 2 − ; ) 3 . Lời giải Chọn A.
Hình chiếu của điểm A xuống mặt phẳng (Oyz) là I (0;2; )
3 . Khi đó I là trung điểm của
AB nên tọa độ điểm B (1;2; ) 3 .
Câu 23: Trong không gian Oxyz , cho mặt cầu(S ) 2 2 2
: x + y + z + 4x − 2y + 6z + 5 = 0 . Mặt cầu (S ) có bán kính là A. 3 . B. 5 . C. 2 . D. 7 . Lời giải Chọn A. Mặt cầu ( 2 2
S ) có tâm I ( 2 − ;1;− )
3 và bán kính R = (− ) 2 2
+1 + (−3) − 5 = 3 .
Câu 24:Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng ( P) : z − 2x + 3 = 0 . Một vectơ pháp
tuyến của (P) là:
A. u = (0;1; − 2) .
B. v = (1;− 2;3) .
C. n = (2;0; − ) 1 .
D. w = (1;− 2;0) . Lời giải Chọn C
Ta có: z − 2x + 3 = 0  2x − z − 3 = 0 . Do đó mặt phẳng ( P) có một vectơ pháp tuyến là n = (2;0; − ) 1 . x = t
Câu 25: Trong không gian Oxyz , cho đường thẳng d :  y = 1− t . Đường thẳng d đi qua điểm nào sau z = 2 + t  đây? A. K (1; 1 − ; ) 1 .
B. H (1;2;0) .
C. E (1;1;2) .
D. F (0;1;2) . Lời giải Chọn D
Đường thẳng d đi qua điểm F (0;1;2) .
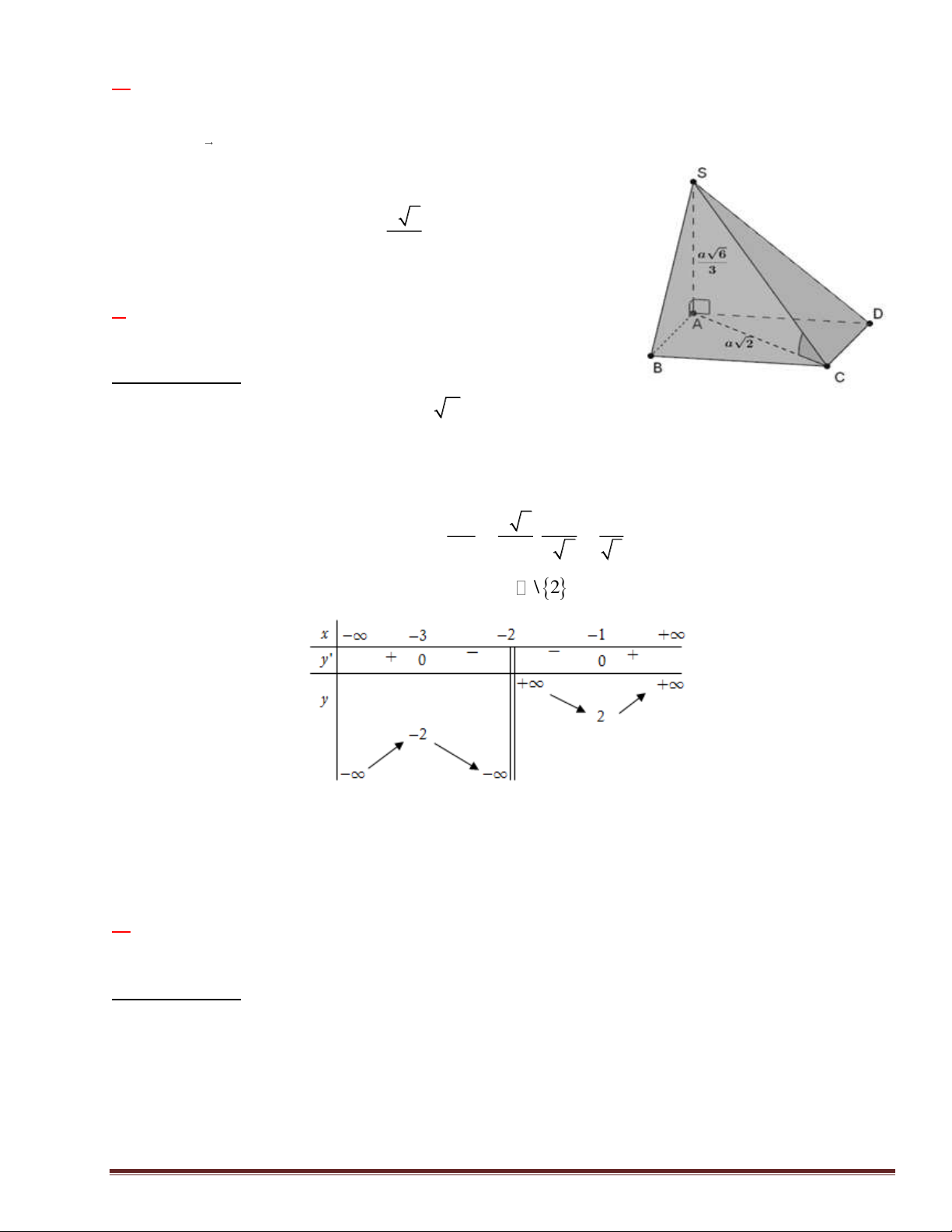
Câu 26. Cho hình chóp tứ giác 𝑆. 𝐴𝐵𝐶𝐷 có đáy là hình vuông , AC= a 2 , 𝑆𝐴 ⊥ (𝐴𝐵𝐶𝐷) và SA = a 3 .
Góc giữa đường thẳng 𝑆𝐵 và (ABCD) là A. 30°. B. 75°. C. 60°. D. 45°. Lời giải Chọn C Trang 14
Hình chiếu của SB lên (ABCD) là SA
Suy ra góc giữa đường thẳng SB và (𝐴𝐵𝐶𝐷) 𝑙à góc SBA .
ABCD là hình vuông, AC= a 2 nên AB = a
Trong tam giác 𝑆𝐵𝐴 vuông tại 𝐴, ta có: AB = a, SA = a 3 𝑆𝐴 ⇒ 𝑡𝑎𝑛 𝑆𝐵𝐴 ̂ = = 3 ⇒ 𝑆𝐵𝐴 ̂ = 60°. 𝐴𝐵
Câu 27. Cho hàm số 𝑓(𝑥), bảng xét dấu của 𝑓′(𝑥) như sau:
Số điểm cực trị của hàm số đã cho là A. 1. B. 3. C. 2. D. 4. Lời giải Chọn B
Dựa vào bảng xét dấu 𝑓′(𝑥) ta thấy hàm số đạt cực tiểu tại 𝑥 = −1; 𝑥 = 1 và đạt cực đại tại 𝑥 = 0
Vậy hàm số có 3 cực trị. 𝑥3
Câu 28. Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số 𝑦 =
+ 2𝑥2 + 3𝑥 − 4 trên [−4; 0] lần lượt 3
là 𝑀 và 𝑚. Giá trị của 𝑀 + 𝑚 bằng 4 28 4 A. . B. − . C. −4. D. − . 3 3 3 Lời giải Chọn B 𝑥3 Hàm số 𝑦 =
+ 2𝑥2 + 3𝑥 − 4 xác định và liên tục trên [−4; 0]. 3 𝑥 = −1(𝑛)
𝑦′ = 𝑥2 + 4𝑥 + 3, 𝑦′ = 0 ⇔ [ . 𝑥 = −3(𝑛) 16 16
𝑓(0) = −4, 𝑓(−1) = − , 𝑓(−3) = −4, 𝑓(−4) = − . 3 3 Trang 15 16 28 Vậy 𝑀 = −4, 𝑚 = − nên 𝑀 + 𝑚 = − . 3 3  b
Câu 29. Xét tất cả các số thực dương 𝑎 và 𝑏 thỏa mãn ln ( 2 . a b ) = ln 
. Tích 𝑎𝑏 thuộc khoảng nào 2  e
trong các khoảng sau đây? 1 A. (0; 1). B. (−𝑒; 0). C. (− ; 0). D. (1; 2). 𝑒 Lời giải Chọn A Ta có  b  ln ( 2 . a b ) 2 = ln
 ln a + 2ln b = ln( )
b − 2  ln a + ln b = 2 −  ln( . a ) b = 2 −  . a b = e−   . 2  e
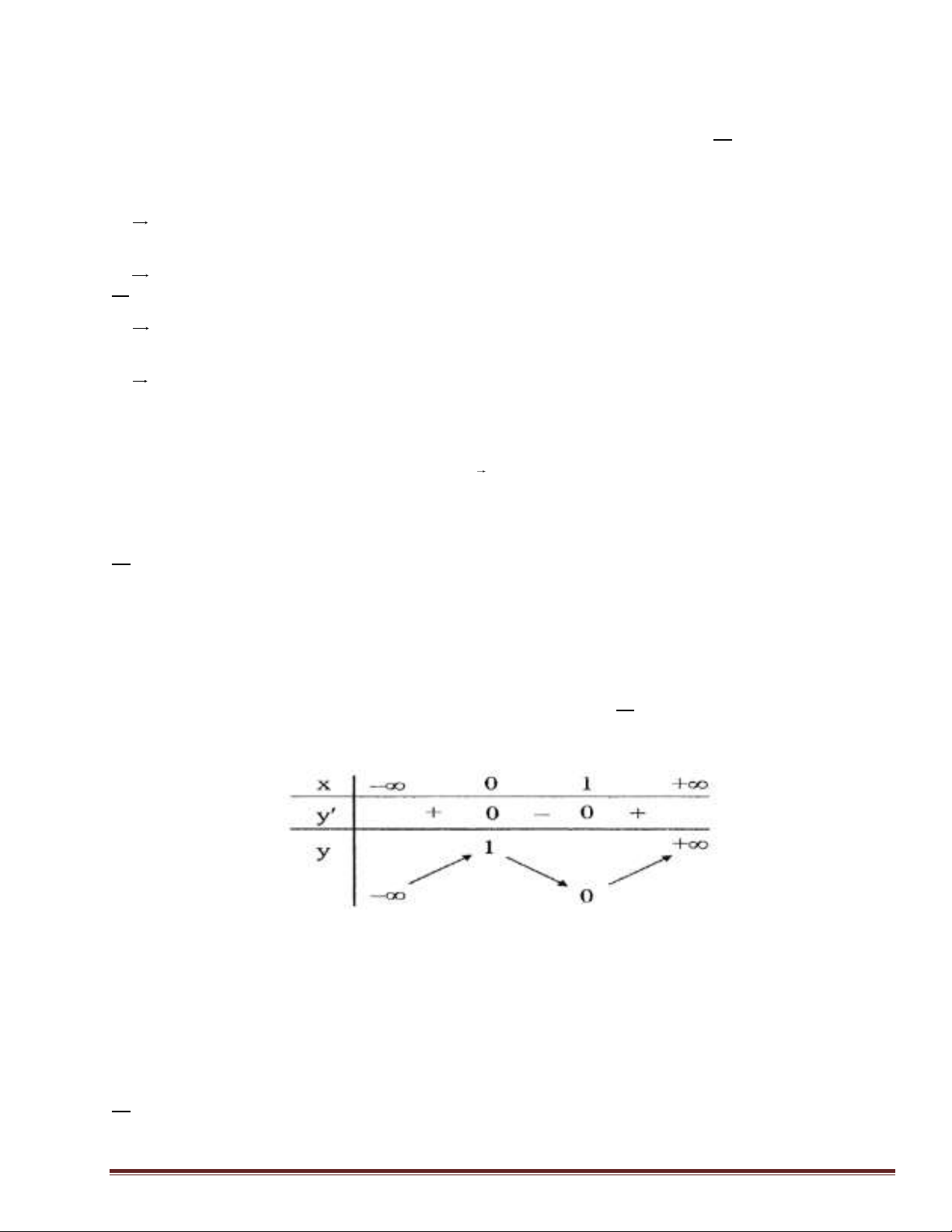
Câu 30. Cho hàm số 𝑓(𝑥) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2𝑓(𝑥) − 3 = 0 là A. 3 . B. 1. C. 2. D. 0. Lời giải Chọn B 3
Ta có 2𝑓(𝑥) − 3 = 0 ⇔ 𝑓(𝑥) = . 2 3
Số nghiệm của phương trình là số giao điểm của đường thẳng 𝑦 = và đồ thị hàm số 𝑦 = 𝑓(𝑥). 2
Từ bảng biến thiên suy ra phương trình có 1 nghiệm thực.
Câu 31: Tập nghiệm của bất phương trình 2
log x + 2 log x − 3  0 là : 3 3  1   1  A. ;3 .   B. (− ;  − ) 3 (1;+). C. ( 3 − ; ) 1 . D. ; 27 .    27   3  Lời giải
Đặt t = log x bất phương trình đã cho trở thành 2
t + 2t −3  0  3 −  t 1 3 1  3 −  log x 1   x  3 3 27
Câu 32 : Cho khối nón có đường sinh bằng 5 và bán kính đáy bằng 3. Thể tích khối nón bằng? Trang 16 A. 18 . B. 12 . C. 24 . D. 15 . Lời giải Chiều cao hình nón 2 2 2 2
h = l − r = 5 − 3 = 4 . 1 1 Thể tích khối nón 2 2
V =  r h =  .3 .4 = 12 . 3 3 
Câu 33 : Cho tích phân 2
I = x cos xdx  và 2
u = x , dv = cos xdx . Khẳng định nào sau đây đúng? 0     A. 2
I = x sin x + 2 xsin xdx  . B. 2
I = x sin x − xsin xdx  . 0 0 0 0     C. 2
I = x sin x + xsin xdx  . D. 2
I = x sin x − 2 xsin xdx  . 0 0 0 0 Lời giải 2 u  = xdu = 2xdx  →  dv = cos xdxv = sinx    2 2
I = x cos xdx = x sin x − 2 xsin xdx   0 0 0
Câu 34 : Cho hình phẳng (D) được giới hạn bởi các đường f ( x) = 2x +1, O ,
x x = 0, x = 1 . Tính thể
tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức? 1 1 A. V = p 2x + 1dx ò B. V = p (2x + ò ) 1 dx 0 0 1 1 C. V = (2x + ò ) 1 dx D. V = 2x + 1dx ò 0 0 Lời giải 1 1 2
Thể tích cần tìm: V = p
( 2x + 1) dx = p (2x + ò ò ) 1 dx 0 0
Câu 35 : Cho hai số phức z = 3 − 2i; z = 1 + 3 .
i Tổng của hai số phức z ; z là : 1 2 1 2 A. 4 + . i B. 9 − . i C. 1
− − 9 .i D. 4 − 5 .i Lời giải
z + z = (3 − 2i) + (1+ 3i) = (3 + 1) + (−2 + 3)i = 4 + .i 1 2 2 2
Câu 36: Gọi z , z là nghiệm của phương trình 2
z + 2z +10 = 0 . Giá trị của biểu thức A = z + z là: 1 2 1 2 Trang 17 A. 10 B. 2 10 C. 0 D. 2 Giải: 2
z + 2z+10 = 0 coù hai nghieä
m z = −1+ 3i; z = −1− 3i 1 2 2 Neâ n z + 2 z = 20 1 2
Câu 37: Trong không gian hệ tọa độ Oxyzx, cho A(-1;0;1), B(-2;1;1). Phương trình mặt trung trực của
đoạn AB có phương trình là:
A. x − y − 2 = 0
B. x − y +1 = 0
C. x − y + 2 = 0
D. −x + y + 2 = 0 Giải:   -3 1 qua I( ; ;1) . PT mặt phẳng (p)  2 2
có phương trình: x − y + 2 = 0 VTPT (-1;1;0)
Câu 38: Trong không gian với hệ tọa độ Oxyz, cho ( ) : 2x − y + 2z −3 = 0 . Phương trình đường thẳng
d đi qua A(2;-3;-1) song song ( ) và mặt phẳng (Oyz) là: x = 2 − tx = 2 x = 2 x = 2t     A.  y = 3 −
B.  y = −3 + 2t
C.  y = −3 − 2t
D.  y = 2 − 3t     z = 1 − + tz = −1+ tz = −1+ tz = 1− t   x = 2 qua A(2;-3;-1) 
Giải: Đường thẳng d 
có phương trình:  y = −3 + 2t VTCP u =   n ;i =      (0;2;1) z = −1+t
Câu 39. Lớp 11A có 40 học sinh trong đó có 12 học sinh đạt điểm tổng kết môn Hóa học loại giỏi và
13 học sinh đạt điểm tổng kết môn Vật lí loại giỏi. Biết rằng khi chọn một học sinh của lớp đạt điểm
tổng kết môn Hóa học hoặc Vật lí loại giỏi có xác suất là 0,5 . Số học sinh đạt điểm tổng kết giỏi cả hai
môn Hóa học và Vật lí là A. 4 . B. 7 . C. 6 . D. 5 . Lời giải
Gọi A là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Hóa học”.
B là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Vật lí”.
AB là biến cố “Học sinh được chọn đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi”.
AB là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi cả hai môn Hóa học và Vật lí”.
Ta có: n( AB) = 0,5.40 = 20 . Trang 18
Mặt khác: n( AB) = n( A) + n(B) − n( . A B)  n( .
A B) = n( A) + n(B) − n( AB) =12 +13− 20 = 5 . Đáp án D.
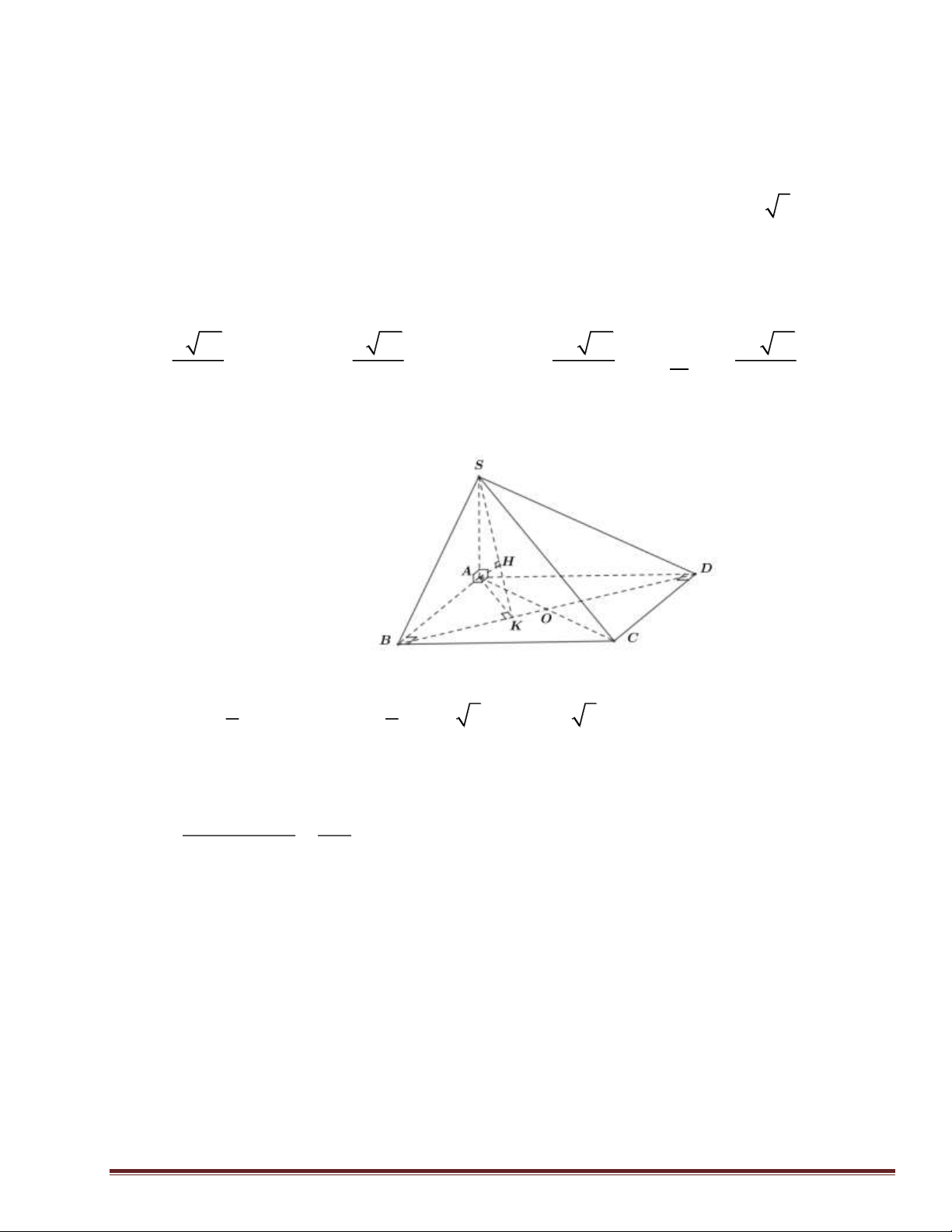
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a 3 2
Cạnh bên SA vuông góc với đáy, biết tam giác SAD có diện tích S = 3a . Tính khoảng cách từ C đến (SBD). a 39 a 39 2a 39 2a 51 A. d = . B. d = . C. d = . D. d = . 13 5 13 17 Lời giải: Chọn D 1 1 Ta có: 2 S = S . A AD  3a = S .
A 2a 3  SA = a 3 SAD 2 2
Gọi O là giao điểm của AC và BD. Suy ra O là giao điểm của AC và mặt phẳng (SBD).
d (C,(SBD)) CO  ( =
=  d C SBD = d SBD d A,(SBD)) 1 ( ,( )) (A,( )) AO
Kẻ AK ⊥ BD tại K  ⊥ SK
BD (Định lý 3 đường vuông góc).
BD ⊥ (SAK )
Kẻ AH ⊥ SK tại H (1).
Mà  BD ⊥ (SAK )  BD ⊥ AH (2).
Từ (1) và (2) suy ra  AH ⊥ (SBD)  d( = ( AH , A SBD)) Trang 19 1 1 1
Xét tam giác SAK vuông tại A ta có: = + . 2 2 2 AH AS AK 1 1 1
Lại có tam giác ABD vuông tại A nên ta có: = + . 2 2 2 AK AB AD 1 1 1 1 1 1 17  = + = + + = 2 2 2 2 2 2 3 AH AS AK AS AB AD 12a 2a 51  a AH =
d (C SBD ) = d ( SBD ) 2 51 ,( ) A,( ) = 17 17 Câu 41: Cho hàm số 3 2
y = −x − mx + ( 3
− m + 6)x + 5 với m là tham số. Có bao nhiêu giá trị
nguyên của m để hàm số nghịch biến trên khoảng (− ;  +)? A. 2. B. 3. C. 4. D. 5.
Lời giải: Chọn C. ' 2 y = 3
− x − 2mx + ( 3 − m + 6)
Để hàm số nghịch biến trên R '  y  0, x   R 2 2  m + 3( 3
− m + 6)  0  m − 9m +18  0  3  m  6
Các giá trị cần tìm là : 3, 4, 5, 6.
Câu 42:Tỉ lệ tăng dân số hàng năm của Nhật là 0,2%. Năm 1998, dân số của Nhật là
125 932 000. Vào năm nào dân số của Nhật sẽ là 140 000 000 ? ( Kết quả làm tròn đến hàng đơn vị)
A. 2061. B. 2055. C. 2051. D. 2045.
Lời giải: Chọn C.
Áp dụng công thức lãi kép liên tục
Với A0= 125 932 000; r= 0,2%; An= 140 000 000. Ta đi tính n. 0,2%.n
Ta có: P = 125932000e =140000000 n 140000000  0, 2%.n = ln 125932000 Trang 20  n  53
Đến năm 53 + 1998 = 2051 thì dân số của Nhật xấp xỉ là 140 000 000
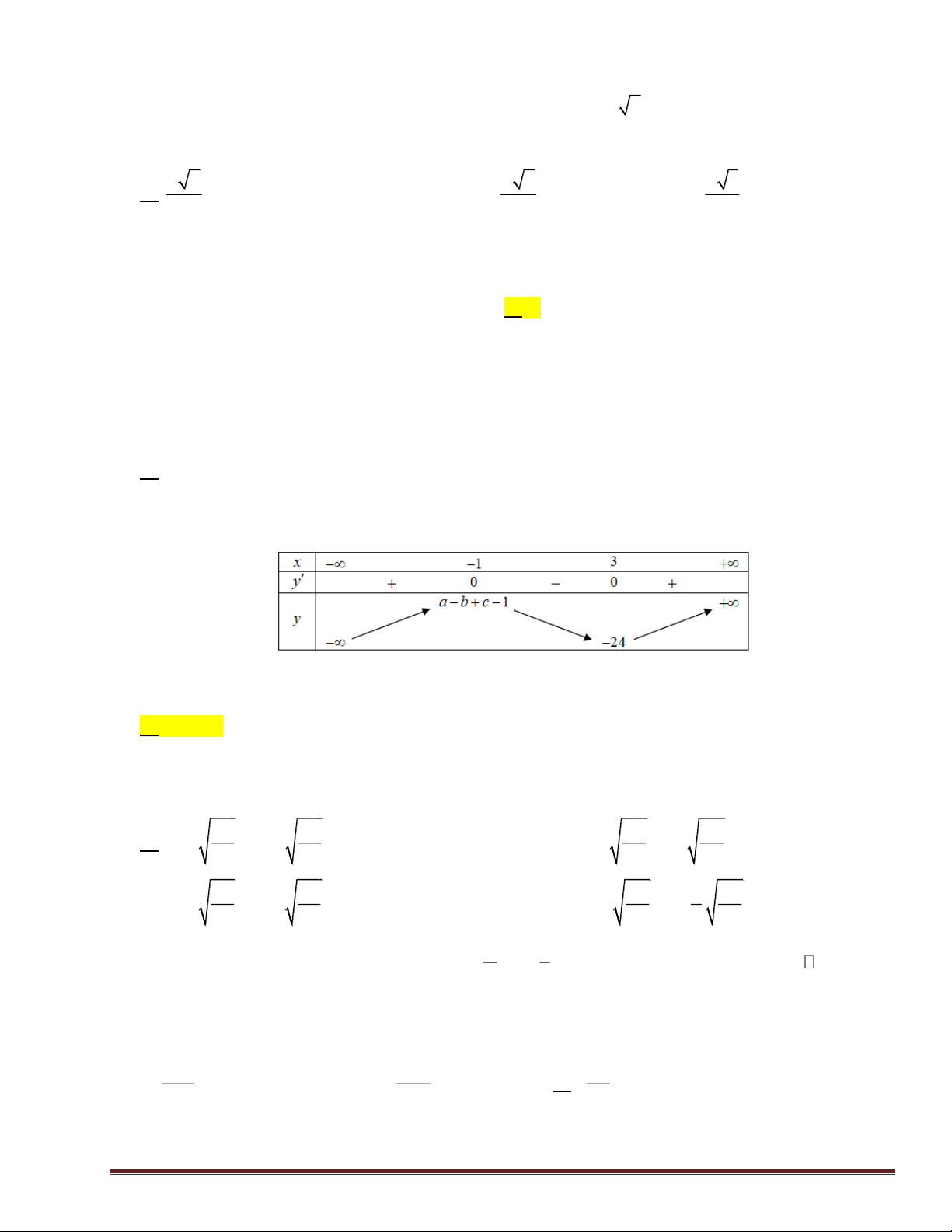
Câu 43: Ta xác định được các số a, b, c để đồ thị hàm số 3 2
y = x + ax + bx + c đi qua điểm (1;0) và có điể 2 2 2 m cực trị ( 2
− ;0). Tính giá trị biểu thức T = a + b + c . A. 25. B. -1. C. 7. D. 14.
Lời giải: Chọn A Ta có: 2
y = 3x + 2ax + b . Đồ thị hàm số 3 2
y = x + ax + bx + c đi qua điểm (1;0) nên ta có: a + b + c = -1.
4a − 2b + c = 8 
4a − 2b + c = 8
Đồ thị hàm số có điểm cực trị ( 2 − ;0) nên    . ' y  ( 2 − ) = 0  4 − a + b = 1 − 2
a + b + c = 1 − a = 3  
Ta có hệ phương trình 4a − 2b + c = 8  b  = 0   4 − a + b = 12 − c = 4 −   2 2 2
T = a + b + c = 25
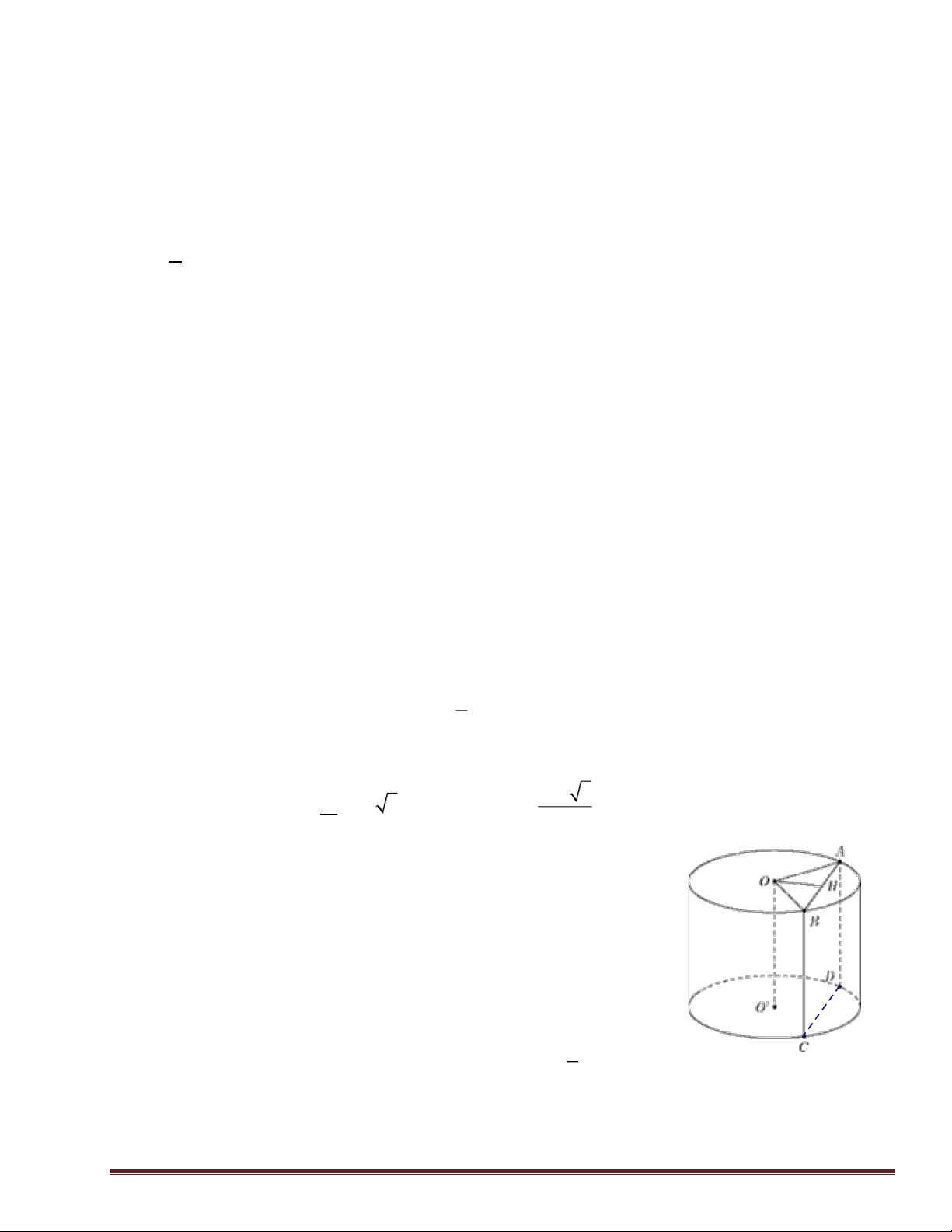
Câu 44: Cho hình trụ có bán kính đáy bằng a. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song a
song với trục và cách trục một khoảng bằng
, thiết diện thu được là một hình vuông.Thể tích của 2
khối trụ được giới hạn bằng hình trụ đã cho bằng 3  a 3 A. 3 3 a . B. 3  a 3. C. . D. 3 a . 4 Giải: Chọn B
Giả sử ABCD là thiết diện hình vuông như hình trên.
Gọi O và O’ lần lượt là tâm 2 đáy của hình trụ. Ta có : OA = r = ; a ( a
d OO ', ( ABCD)) = d ( , O ( ABCD)) =
( do OO '/ /( ABCD)) 2
Gọi H là hình chiếu của O lên AB ( H là trung điểm AB). Trang 21 a Khi đó : d ( ,
O ( ABCD)) = OH = 2
Xét tam giác OAH vuông tại H có : 2  a  2 2 2 AB = 2 AH = OA − OH = 2 a − = a 3   .  2 
Vì ABCD là hình vuông nên : h = OO ' = AB = BC = a 3 Vậy 2 2 3
V =  r h =  a .a 3 =  a 3. 2 x e f '(x) = x  
Câu 45: Cho hàm số y = f ( )
x thỏa mãn f (ln 3) = 3 và x e + 1 x − e + 1 . ln 3 Khi đó x
e f (x) dx  bằng 0 1 − 0 − 8 2 20 − 8 2 20 + 8 2 10 − 8 2 A. B. . C. . D. 3 3 3 3 Giải: Chọn B 2 x e f (x) =
f '(x)dx = dx   xe +1 x − e +1 2 x e ( x e + 1 x + e +1) =  ( dx x e + )2 1 − ( x e + 1) 2 x e ( x e + 1 x + e +1) = dx  ex ( x e + 1)   d ( x x e e + x x )1 x = e + dx  = e dx + = e + 2 x e + 1 + C   xe + 1 xe + 1 Mà (ln 3) = 3  = 4 −  ( ) x = + 2 x f C f x e e +1 − 4 . Khi đó: ln 3 ln 3 x
e f (x)dx =   ( 2x e + 2 x x e e + 1 − 4 x e )dx 0 0 ln 3  1  − x 4 =  e + ( x e + )3 x 20 8 2 2 2 1 − 4e  = 2 3 3   o Trang 22
Câu 46: Cho hàm số y = f ( )
x có bảng biến thiên như sau:  3  Số nghiệm thuộc đoạn  − ; 
 của phương trình 2 f (2cos ) x − 9 = 0 là:  2  A. 5. B. 4 C. 3. D. 2. Giải Chọn A    Đặ 3 t t = 2 cos , x x   − ;  t  2 − ;2    2  9 thì 2 f (2cos )
x − 9 = 0 trở thành 2 f (t) − 9 = 0  f (t) = (1) 2 9
Nhận xét: Số nghiệm pt (1) là số giao điểm của hai đồ thị (C) : y = f (t) và đường thẳng d: y = . 2
Bảng biến thiên của hàm số y = f (t) trên  2 − ;2
Dựa vào bảng biến thiên , số nghiệm t  2 − ; 
2 của (1) là 2 nghiệm phân biệt t  2 − ;0 ; t  0;2 1 ( ) 2 ( )  3 
Ta có đồ thị hàm số y = cos x trên  − ;    2  Trang 23 t + Với t  ( 2
− ;0)  2cos x = t ( 2 − ;0) 1  cos x =  1 − ;0 1 1 ( ) 2  3  t
Dựa vào đồ thị y = cos x trên  − ;   ta thấy phương trình 1 cos x =  ( 1
− ;0) có 3 nghiệm phân biệt  2  2  −  3  −  x  
x    x  1 2 3 2 2 2 t
+ Với t  (0; 2)  2cos x = t  (0; 2) 2  cos x =  0;1 2 2 ( ) 2  3  t
Dựa vào đồ thị y = cos x trên  − ;   ta thấy phương trình 2 cos x = (0 )
;1 có 2 nghiệm phân biệt  2  2  
−  x  0  x  4 5 2 2  3 
Vậy số nghiệm thuộc đoạn  − ; 
 của phương trình 2 f (2cos )
x − 9 = 0 là 2 + 3 = 5  2   x + 2y
Câu 47: Cho x , y là các số thực dương thỏa mãn log = −x + 4y −1  
. Tính giá trị nhỏ nhất  9x + 24y  2
của biểu thức P = x + bằng. 2 y A. 4 B. 10 C. 6 D. 2 Lời giải x + 2 y Do , x y  0 nên  0 9x + . 24 yx + 2y  10x + 20y  Ta có log
= −x + 4y −1  log = −x + 4y      9x + 24y   9x + 24y
 log(10x + 20y) −log(9x + 24y) = (9x + 24y)−(10x + 20y)
 log(10x + 20y) +(10x + 20y) = log(9x + 24y)+(9x + 24y) Trang 24
Xét hàm số f (t) = logt + t với t (0; +) f (t ) 1 =
+1  0 với t (0;+) nên hàm số f (t) đồng biến trên t (0;+) . t ln10
Nên (9x + 24y) = (10x + 20y)  x = 4y . 2  1   1  1 P = 4y + = 2 2y + = 2 y + y +  2.33 . y . y = 6     2 2 2 2 yy   y y 1
Dấu bằng xảy ra khi y =
y = 1 x = 4 Vậy Giá trị nhỏ nhất của P là 6 Chọn C 3 y 2
x + mx + m
Câu 48:Cho hàm số y =
gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho x +1
Max y = 2 .Tổng các phần tử của S là. 1;2 2 11 11 5 A. . B. . C. − . D. − . 3 6 6 2 Lời giải. 2
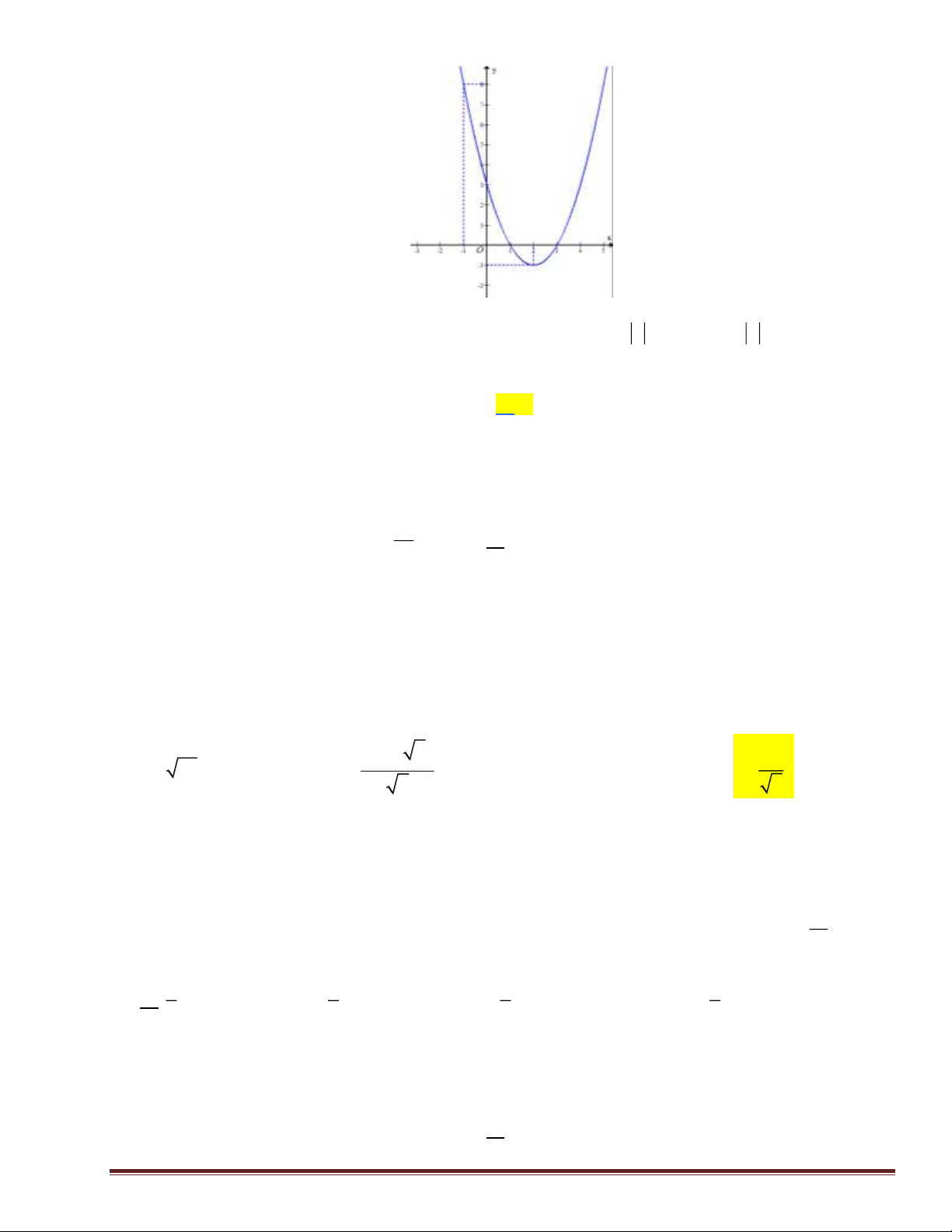
x + mx + m Xét hàm số: y = x + . 1 2 x + 2x 2 x + 2xx = 01;2 y =  = 2  + =  ( ; y = 0 0 x 2x 0  . 2 x + )2 1 (x + ) 1 x = 2 −   1;2
Khi đó ta có bảng biến thiên sau: 2m +1 1 3m + 4 2 Xét TH1:
 0  m  − Suy ra Max y = = 2  m = (Nhận). 2 2 1;2 3 3 3m + 4 4 2m +1 5 Xét TH2:
 0  m  − Suy ra Max y = −
= 2  m = − (Nhận). 3 3 1;2 2 2 Trang 25  2m +1 = − =  5 Max y 2  m = − (l) 2m +1 3m + 4 4 1   1;2 2 2 TH3:Xét  0 
 −  m  − Suyra    2 3 3 2  3m + 4 2  Max y = = 2 m = (l)     1;2 3 3 2 5 11
Tổng các phần tử của S là − = − Chọn đáp án C. 3 2 6
Câu 49: Cho hình chóp đều S.ABC có tất cả các cạnh bằng 3 và M , N, P lần lượt là trọng tâm của tam giác SA ,
B SBC, SAC . Thể tích khối đa diện có các đỉnh là , A , B ,
C M, N, P là 2 4 2 8 2 9 2 A. . B. . C. . D. . 12 3 3 4 Lời giải: S P C1 A1 N M C A B1 B 2  3 3 9 3 S = = ABC   4 4 1 9 2
Hình chóp S.ABC có  V = Sh =  S.ABC 6 3 4 h = .3 = 6  3 VS.A B C 2 2 2 8 8 9 2 2 2
mp (MNP) cắt S , A S ,
B SC tại A , B , C nên 1 1 1 = . . =  V = . = 1 1 1 V 3 3 3 27 S . 1 A 1 B 1 C 27 4 3 S . ABC Trang 26  3 S = 1 B MN  4 2
Khối chóp BB MN có   V = 1 B 1 B MN 12  1 6 h = h = 1  3 3 Thể tích cần tìm là V V = V −V −V −V −V S . ABC S . 1 A 1 B 1 C 1 AA MP 1 BB MN C 1 C NP =V −V −3V S.ABC S. 1 A 1 B C1 B 1 B MN 4 2 = 3
Câu 50: Cho hàm số y = f ( x) = ( 2 ln
1+ x + x) . Số giá trị nguyên dương a thỏa mãn bất phương
trình f (a − )
3 + f (ln a)  0 là
A. 1. B. 2. C. 3. D. 4. Lời giải: f ( x) 1 ' =  0, x
  , nên f (x) đồng biến trên 2 1+ x f (−x) = ln ( 1 2 1+ x − x) = ln = −ln ( 2
1+ x + x = − f x , x
  , nên f (x) là hàm số lẻ 2 ) ( ) 1+ x + x Mà f (a − )
3 + f (ln a)  0
f (ln a)  − f (a − 3)
f (ln a)  f (3− a)
 ln a  3− a
a + ln a  3  a1;  2 do a nguyên dương. ĐỀ 7
ĐỀ THI THỬ THPT QUỐC GIA 2020
PHÁT TRIỂN TỪ ĐỀ MINH HỌA MÔN TOÁN Trang 27 LẦN 2 NĂM 2020 Thời gian: 90 phút
Câu 1: (NB). Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là. 7! A. B. 21. C. 3 A D. 3 C . 7 7 3!
Câu 2: (NB). Cho dãy cấp số nhân (u ) , biết u = 3,u = 6
− . Công bội của cấp số nhân (u ) bằng: n 1 2 n A. q = - 9 B. q = 9 C. q = - 2 D. q = 2 2 x 2x 3
Câu 3: (NB).Tìm tập nghiệm S của phương trình + + 2 = 8x. A. S = {1; } 3 . B. S = {- 1; } 3 . C. S = {- 3; } 1 . D. S = {- } 3 .
Câu 4: (NB). Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: 1 1
A.V = Bh B. V = B h
C. V = 2Bh D.V = B h 2 3
Câu 5: (NB). Giá trị của biểu thức 3 log ( .
a a ) (với 0  a  1 ) là a 2 4 3 A. . B. . C. . D. 3. 3 3 2
Câu 6: (NB). Hàm số nào sau đây là một nguyên hàm của hàm số 5 y = x ? 6 x A. 6 y = x . B. 4 y = 5x . C. y = . D. 5 y = 6x . 6
Câu 7: (NB). Chiều cao của khối lăng trụ có diện tích đáy bằng B và thể tích bằng V là 3V 6V 2V V A. h = . B. h = . C. h = . D. h = . B B B B
Câu 8: (NB). Một hình nón có diện tích xung quanh bằng 2
2 cm và bán kính đáy 1 r = c . m Khi đó độ 2
dài đường sinh của hình nón là: A. 3cm. B. 4cm . C. 2cm . D. 1cm .
Câu 9: (NB). Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu? 2 4 a 2  a A. S = . B. S = . C. 2 S =  a . D. 2 S = 4 a . 3 3
Câu 10: (NB). Hàm số 4
y = 2x + 1 đồng biến trên khoảng nào? Trang 28 æ 1ö æ 1 ö A. ç- ç ¥ ; ÷ - ÷ ç ÷ ç . B.(0;+ ¥ ). C. - ç ;+ ¥ ÷. D.(- ¥ ;0). è 2÷ø çè 2 ÷ø
Câu 11: (NB). Với a là số thực dương tùy, 2 log a bằng 5 1 1 A. 2 log . a B. 2 + log . a C. + log . a D. log . a 5 5 5 2 5 2
Câu 12: (NB). Một hình trụ có bán kính bằng 3 và đường cao bằng 4 có diện tích xung quanh bằng bao nhiêu ? A. 24p . B.12p . C. 15p .
D. 20p .
Câu 13: (NB). Cho hàm số y = f ( x) có bảng biến thiên như sau: x - 0 2 + y’ - 0 + 0 - + 5 y 1 -
Giá trị cực tiểu của hàm số đã cho bằng A. 1. B. 2. C. 0. D. 5.
Câu 14: (TH). Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây? x −1 x +1 A. y = . B. y = . −x −1 x −1 x +1 x −1 C. y = . D. y = . −x +1 x +1
Câu 15: (NB). Đồ thị hàm số nào dưới đây có tiệm cận ngang? Trang 29 x − 3 2 9 − x 2 2x +1 A. y = B. y = C. 2 y = x − 3 D. y = x +1 x x
Câu 16: (NB). Nghiệm của bất phương trình 2x+1 − 3  3 x 3 là 3 2 2 2 A. x  . B. x  . C. x  − . D. x  . 2 3 3 3
Câu 17: (TH). Cho hàm số = ( ) 3 2 y
f x = ax + bx + cx + d có bảng biến thiên như sau: x - ∞ -1 1 +∞ y’ + 0 - 0 + 2 +∞ y -∞ -2 3 A. 3
y = x − 3x B. 3
y = x − 3x + 2 C. 3 y = x − x + 2 D. 3
y = −x + 3x 2 5 5 5 Câu 18: (NB). Biết f
 (x)dx = 3, g
 (x)dx = 9. Tích phân  f
 (x)+ g(x)dx  bằng 2 2 2 A.10 . B. 3 . C. 6 . D.12 .
Câu 19: (NB). Cho số phức z = 2 + 5 .
i Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là: A. (5;2) B. (2;5) C. ( 2 − ;5) D. (2; 5 − ) 2 2
Câu 20: (NB). Cho z = (1+ i) − (1− i) , tính phần ảo của số phức z. A.–4 B. 4 C.–2 D.2
Câu 21: (NB). Cho số phức z = 5 − 4 .
i Số phức đối của z có tọa độ điểm biểu diễn là. A. ( 5 − ; 4 − ) B. (5;4) C. ( 5 − ;4) D. (5; 4 − )
Câu 22: (TH). Trong không gian Oxyz cho hai điểm A(2;3;4) và B(3;0; )
1 . Khi đó độ dài véctơ AB là. A. 19. B. 19. C. 13. D. 13. Trang 30
Câu 23: (NB). Tọa độ tâm A của mặt cầu (S ) 2 2 2
: x + y + z − 2x + 4y + 2z − 3 = 0 là: A. A(1;2;− ) 1 B. A( 1 − ;2; ) 1 C. A( 1 − ;2;− ) 1 D. A(1; 2 − ;− ) 1
Câu 24: (NB). Cho mặt phẳng (P) : x − 2y + 3z + 4 = 0 . Phát biểu nào sau đây là đúng?
A. n = 1; 2;3 là một vectơ pháp tuyến của mặt phẳng (P) . 1 ( ) B. n = 1; 2
− ;3 là một vectơ pháp tuyến của mặt phẳng (P). 2 ( )
C. n = 1;3; 4 là một vectơ pháp tuyến của mặt phẳng (P) . 3 ( ) D. n = 2
− ;3;4 là một vectơ pháp tuyến của mặt phẳng (P). 1 ( )
Câu 25: (TH). Trong không gian tọa độ Oxyz, viết phương trình tham số của đường thẳng (d ) đi qua điểm A(1; 2
− ;4) và có một vectơ chỉ phương là u = (2;3; 5 − ) . x =1+ 2tx = −11+ 2tx =1+ 2tx =1− 2t     A. y = 2 − + 3t
B. y = −2 + 3t C. y = 2 − − 3t D. y = 2 − + 3t     z = 4 − 5tz = 4 − − 5tz = 4 − 5tz = 4 + 5t
Câu 26: (TH). Cho hình chóp S.ABCD có SA vuông góc với mặt đáy (ABCD). Góc giữa SC và (ABCD) là: A. SBA . B. SAC . C. SDA . D. SCA .
Câu 27: (TH). Cho hàm số phù hợp với bảng biến thiên sau:
Phát biểu nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại x = 0 và đạt cực đại tại x = 1
B. Giá trị cực tiểu của hàm số là 1
C. Giá trị cực đại của hàm số là 0
D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1 Trang 31
Câu 28: (TH). Gọi M là giá trị lớn nhất của hàm số y = ( 2
ln x − 3) − x trên đoạn2;  5 . Trong các khẳng
định sau, khẳng định nào đúng? A. 3 M e + = 6. B. M  0 . C. 5 M e + − 22 = 0 . D. M + 2 = 0
Câu 29: (TH). Nếu log 3 = a thì log 9000 bằng: A. 3 + 2a B. 2 a C. 2 a + 3 D. 2 3a
Câu 30: (TH). Tìm tất cả giá trị thực của tham số m để phương trình 3 2
x + 3x = m có ba nghiệm phân biệt. A. m= 2.
B. 0  m  4. C. m 0. D. m  4. x 1 − 2 x+3  1   1 
Câu 31: (TH). Số nghiệm nguyên dương của bất phương trình      thuộc  5 − ;  5 là:  3   9  A. 10 B. 11 C. 8 D. 6
Câu 32. (TH). Cho tứ diện đều ABCD cạnh bằng a 3 . Tính diện tích xung quanh S của hình trụ có xq
đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện đều ABCD . A. 2 S = 2 3 a . B. 2 S = 2 a . C. 2 S = 3 a . D. 2 S = 2 2 a . xq xq xq xq    
Câu 33: (TH). Cho nguyên hàm 2 2 I = x 4 − x dx
. Nếu đặt x = 2sin t với t  − ;   thì  2 2  cos 4t sin 8t cos 4t sin 4t
A. I = 2t + + C
B. I = 2t + + C
C. I = 2t − + C
D. I = 2t − + C 2 4 2 2
Câu 34: (TH). Kết quả của diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục a a
hoành, trục tung và đường thẳng x = 2 có dạng (với là phân số tối giản). Khi đó mối liên hệ giữa b b a và b là:
A. a - b = 2.
B. a - b = 3 .
C. a - b = - 2.
D. a - b = - 3.
Câu 35: (TH). Trong mặt phẳng phức, điểm M (2; 3
− ) là điểm biểu diễn số phức z. Khẳng định nào
sau đây là khẳng định đúng?
A. (2 + i) z =1− i .
B. (1− i) z = 3+ i .
C. iz = 3 + 2i .
D. (1− i) z =1+ 2i .
Câu 36: (TH). Gọi z , z là hai nghiệm phức của phương trình 2
z − 4z +13 = 0 . Khi đó z .z + z 1 2 1 2 1 bằng A. 26 . B.13 + 13 . C. 13 . D. 13 + 5 . Trang 32
Câu 37: (TH). Cho ba điểm A(0;1;2); B(2; 2 − ; ) 1 ;C ( 2 − ;0; )
1 . Phương trình mặt phẳng đi qua A và
vuông góc với BC là
A. 2x − y +1 = 0 .
B. −y + 2z − 3 = 0.
C. y + 2z − 5 = 0 .
D. 2x − y −1 = 0 .
Câu 38: (TH). Trong không gian Oxyz, cho mặt phẳng (P) : x + y + z − 3 = 0 và đường thẳng x y +1 z − 2 d : = =
. Đường thẳng d' đối xứng với d qua mặt phẳng (P) có phương trình là: 1 2 1 − x −1 y −1 z −1 x +1 y +1 z +1 x −1 y −1 z −1 A. = = . B. = = . C. = = . D. 1 2 − 7 1 2 − 7 1 2 7 x +1 y +1 z +1 = = . 1 2 7
Câu 39: (VD). Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên 4 bóng từ
hộp, xác suất để có đủ 3 màu bóng là 35 35 175 35 A. . B. . C. . D. . 816 68 5832 1632
Câu 40: (VD). Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B có AB = 3 , BC = 4 .
SA ⊥ ( ABC) và SA = 5. Gọi H là hình chiếu vuông góc của A lên SB và K là trung điểm của SC. Khẳng
định nào sau đây đúng?
A. ( AHK ) / /BC .
B. ( AHK ) ⊥ (SBC) .
C. ( AHK ) ⊥ SB .
D. ( AHK ) ⊥ (SAB) .
Câu 41: (VD). Hàm số nào trong các hàm số sau đồng biến trên R ? 4x +1
A. y = 7x − 2sin 3 . x B. 3 2
y = x + 2x +1. C. y = tan . x D. y = . x + 2
Câu 42: (VD). Một số tiền 58.000.000đ gửi tiết kiệm theo hình thức lãi kép với lãi suất 0,7%/tháng. Số
tiền có được gồm vốn lẫn lãi sau 8 tháng gửi là: A. 61.328.699 đ B. 62.328.699 đ C. 60.328.699 đ D. 63.328.699 đ 1
Câu 43: (VD). Cho hàm số y = 4 x - (3m + ) 2 1 x + 2(m + )
1 với m là tham số thực. Tìmgiá trị của 4
m để đồ thị hàm sốcó ba điểm cực trị tạo thành tam giác có trọng tâm là gốc tọa độ. 2 2 1 1 A. m = - . B. m = . C. m = - . D. m = . 3 3 3 3
Câu 44: (VD). Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình
vuông có cạnh bằng a . Tính diện tích xung quanh S của khối trụ đó. Trang 33 2  a A. 2 S = 2 a . B. S = . C. 2 S =  a . D. 2 S = 4 a . 2 2 ( 2
x - 2x)(x - ) 1
Câu 45: (VD). Cho tích phân I =
dx = a + b ln 2 + ò c ln 3 với . Chọn x + 1 1
khẳng định đúng trong các khẳng định sau: A. b > 0 . B. c < 0 . C. a < 0 .
D. a + b + c > 0 .
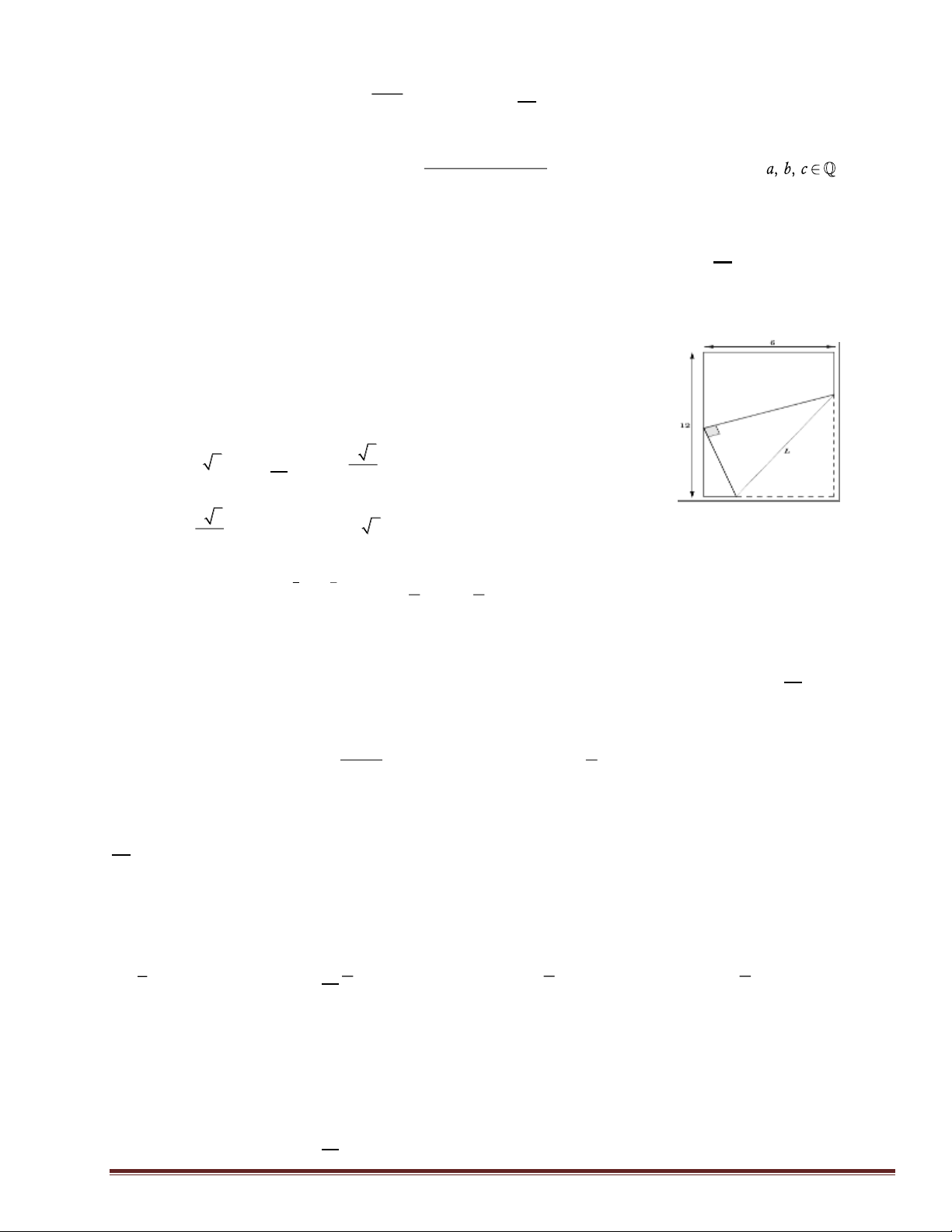
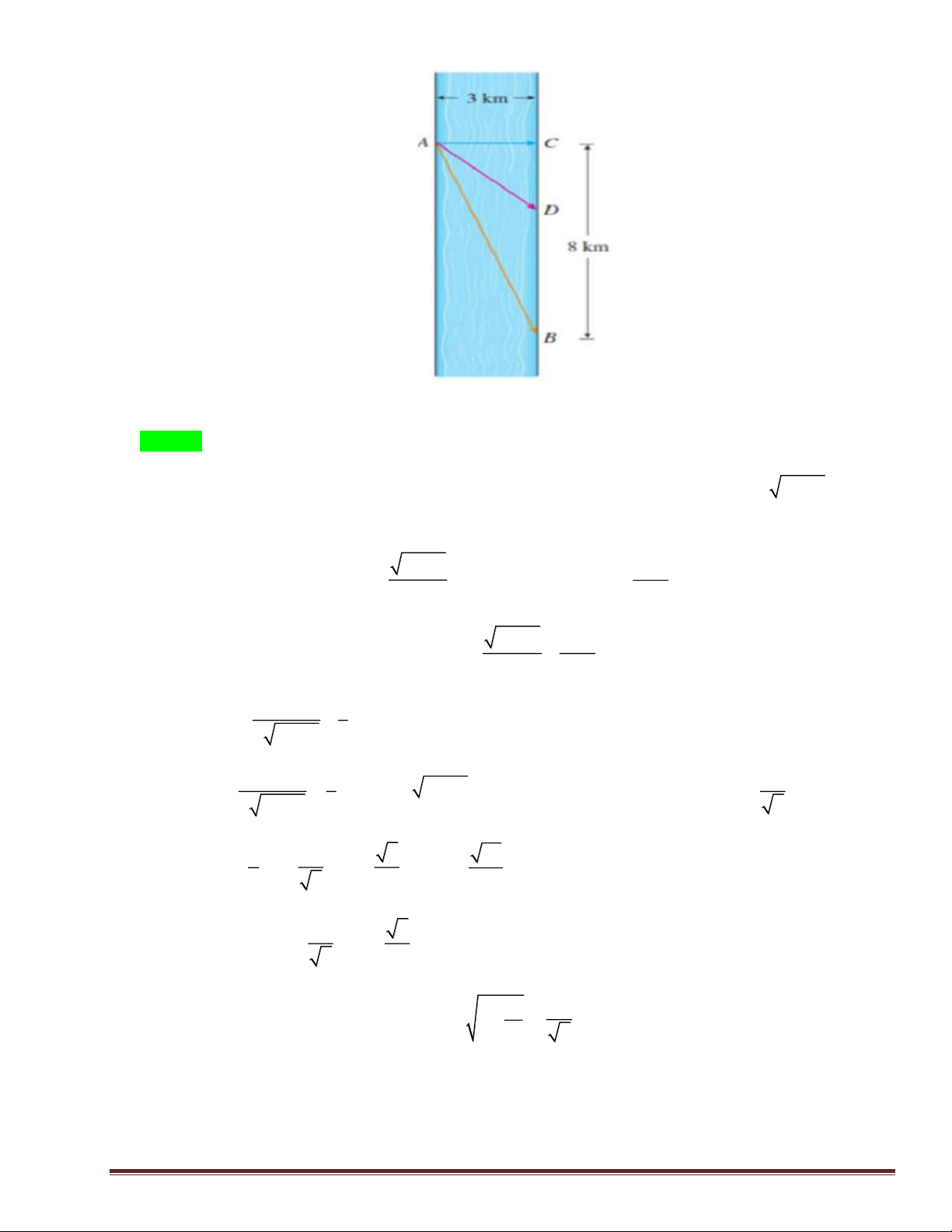
Câu 46: (VDC). Một mảnh giấy hình chữ nhật có chiều dài 12cm và
chiều rộng 6cm. Thực hiện thao tác gấp góc dưới bên phải sao cho
đỉnh được gấp nằm trên cạnh chiều dài còn lại. Hỏi chiều dài L tối
thiểu của nếp gấp là bao nhiêu? 9 3
A. min L = 6 2 cm . B. min L = cm . 2 7 3 C. min L =
cm . D. min L = 9 2 cm . 2 3 4 1 2 Câu 47: (VDC). Nếu 4 5 a a và log  log
thì a,b thoả mãn điều kiện nào trong các điều kiện b 2 b 3 sau?
A. a 1,b 1.
B. a 1,0  b 1.
C. 0  a 1,0  b 1. D.
0  a 1,b 1. x − m 7
Câu 48: (VDC). Hàm số y =
thỏa mãn min y+ max y =
. Hỏi giá trị m thuộc khoảng nào trong x + 2 x   0  ;3 x   0  ;3 6 các khoảng dưới đây? A. ( 1 − ;0) . B. (− ;  − ) 1 . C. (2;+) . D. (0;2) .
Câu 49: (VDC). Cho hai hình vuông ABCD và ABEF có cạnh bằng a , lần lượt nằm trên hai mặt
phẳng vuông góc với nhau. Lấy điểm H trên đoạn DE sao cho HD = 3HE . Gọi S là điểm đối xứng
với B qua H . Thể tích của khối đa diện ABCDSEF bằng 8 5 9 2 A. 3 a B. 3 a C. 3 a D. 3 a 3 6 8 3
Câu 50: (VDC). Xét các số nguyên dương a, b sao cho phương trình 2
a ln x + b ln x + 5 = 0 có hai
nghiệm phân biệt x , x và phương trình 2
5log x + b log x + a = 0 có hai nghiệm phân biệt x , x sao 1 2 3 4
cho x x x x . Tìm giá trị nhỏ nhất của S = 2a + 3b . 1 2 3 4 A. 30 . B. 25 . C. 33 . D. 17 Trang 34 BẢNG ĐÁP ÁN 1 D 11 A 21 B 31 C 41 A 2 C 12 A 22 A 32 D 42 A 3 A 13 A 23 D 33 D 43 D 4 A 14 B 24 B 34 B 44 C 5 B 15 A 25 A 35 C 45 D 6 C 16 D 26 D 36 B 46 B 7 D 17 A 27 D 37 A 47 D 8 B 18 D 28 A 38 A 48 A 9 C 19 B 29 A 39 B 49 B 10 B 20 B 30 B 40 B 50 B ĐỀ 8
ĐỀ THI THỬ THPT QUỐC GIA 2020
PHÁT TRIỂN TỪ ĐỀ MINH HỌA MÔN TOÁN LẦN 2 NĂM 2020 Thời gian: 90 phút
Câu 1: Một tổ có 5 học sinh nam và 7 học sinh nữ, số cách chọn ra hai học sinh có cả nam và nữ? A. 1 1 C .C B. 1 1 C + C C. 2 C D. 1 1 C + C 5 7 5 7 12 5 7
Câu 2: Cho (u là cấp số cộng với công sai d.Biết u = 4 − và u = 10. −
Số hạng đầu tiên u bằng n ) 3 5 1
A. u = 2 B. u = − 3 C. u = 6 − D. u = 7 − 1 1 1 1
Câu 3: Số nghiệm của phương trình 2 3x 3x = là A. 2 B. 1 C. 0 D. Vô số
Câu 4: Một khối lập phương có thể tích là 3
8a . Cạnh của khối lập phương đó bằng a A. 2a B. a C. 2 a D. 3
Câu 5: Tập xác định của hàm số y = log 3 ( − x) là 3 A. (− ;3) B. C. (3;+) D. (0 ;+)
Câu 6: Họ nguyên hàm của hàm số ( ) x f x = e + 3 là Trang 35 A. ( ) x
F x = e + 3x B. ( ) x
F x = e − 3x C. ( ) = − x F x e + 3x D. ( ) = − x F x
e − 3x
Câu 7: Một khối chóp có đáy là hình vuông cạnh a = 3và đường cao h = 5. Thể tích khối chóp là
A. V = 15 B. V = 45 C. V = 25
D. V = 35
Câu 8: Cho hình nón có bán kính đáy r = 4 và diện tích xung quanh bằng 20π. Thể tích
của khối nón đã cho bằng A. 4π. B. 16π. C.163π. D.803π.
Câu 9: Thể tích V của một khối cầu có bán kính R là 4 1 4 A. 3 V =  R B. 3 V =  R C. 2 V =  R D. 3 V = 4 R 3 3 3
Câu 10: Cho hàm số y = f(x) có bảng biến thiên như sau : x -∞ 0 2 + ∞ y’ + 0 - 0 + y 1 + ∞ 0 -3
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (2;+∞) B. (-∞;1) C. (0;+∞) D. (0;2) 4 a e
Câu 11: Với a,b là hai số thực dương tùy ý, ln bằng b
A. 4ln a – ln b +1 .
B. 4ln b − ln a +1.
C. 4ln a + ln b –1.
D. 4ln a + ln b +1.
Câu 12: Công thức tính diện tích xung quanh của hình trụ có chiều cao h, bán kính đáy R là
A. Sxq = 2πRh.
B. Sxq = π2Rh.
C. Sxq = πRh.
D. Sxq = 4πRh.
Câu 13: Hàm số y = f(x) liên tục trên
và có bảng biến thiên như hình vẽ. x -∞ 1 2 + ∞ y’ + 0 − || + y 3 + ∞ −∞ 0
Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho có hai điểm cực trị.
B. Hàm số đã cho có đúng một điểm cực trị. y
C. Hàm số đã cho không có giá trị cực tiểu. 1
D. Hàm số đã cho không có giá trị cực đại. 2 1 − O x
Câu 14: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? Trang 36 −3 A. 3 2
y = x − 3x +1 B. 3 2
y = − x − 3x +1 C. 3 2
y = x + 3x +1 D. 3 2
y = − x + 3x +1 − x
Câu 15: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số 1 4 y = ? 2x −1 1 A. y = 2. B. y = . C. y = 4. D. y = 2. − 2
Câu 16: Tập nghiệm của bất phương trình log3(x - 2) ≥ 2 là A. 11;+). B. (2;+). C. ( ; − 1 ) 1 . D. (11; ) +
Câu 17: Cho hàm số bậc bốn y = f ( )
x có đồ thị như hình vẽ
Số nghiệm của phương trình f ( ) x = 1 − là: A. 4. B. 3. C. 2. D. 1. 3 3
Câu 18: Cho hàm số f ( x) liên tục trên [0;3]. Nếu f (x)dx = 2 
thì [x − 3 f (x)]dx  có giá trị bằng 0 0 3 3 A. − B. −3 C. 3 D. . 2 2
Câu 19: Số phức liên hợp của số phức z = 4 – 3i là
A. z = 4 + 3i B. z = 4 − −3i C. z = 4 − +3i
D. z = 3 − 4i z
Câu 20: Cho hai số phức: z = 1 – 2i và z = 3 – 2 . i Tìm số phức 2 z = 1 2 z1 7 4 7 4 7 4 7 4 A. z = + i B. z = − + i C. z = − i D. z = − − i 5 5 5 5 5 5 5 5
Câu 21: Cho số phức z = 4 – 3i có điểm biểu diễn trên mặt phẳng tọa độ Oxy là M. Độ dài OM bằng A. 5 B. 25 C. 7 D. 4
Câu 22: Trong không gian Oxyz , cho điểm A(1; 2; 3). Hình chiếu vuông góc của điểm A trên trục Oz là điểm A. Q 0 ( ;0;3 . ) B. M 1 ( ;0;3 . ) C. P (0;2;3). D. N( 1 − ;0;0 .) Trang 37
Câu 23: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình 2 2 2
x + y + z − 2x + 4 y − 6z + 9 = 0. Tọa độ tâm I và bán kính R của mặt cầu là A. I (1; 2 − ; ) 3 và R = 5. B. I (1; 2 − ; ) 3 và R = 5 . C. I ( 1 − ;2;− ) 3 và R = 5. D. I ( 1 − ;2;− ) 3 và R = 5 .
Câu 24: Trong không gian Oxyz, cho mặt phẳng (α) : x - 2y + 2z - 3 = 0. Điểm nào sau đây nằm trên mặt phẳng (α)? A. N(1;0;1). B. Q (2;1; ) 1 . C. ( P 2; 1 − ;1 .) D. M (2;0; ) 1 . x − y + z
Câu 25: Trong không gian Oxyz, cho đường thẳng d có phương trình: 1 2 = = . Một vectơ 2 3 1 −
chỉ phương của đường thẳng d có tọa độ A. (2;3;− ) 1 . B. (1; 2 − ;0). C. ( 1 − ;3;2). D. (4;6;2).
Câu 26: Cho hình chóp S.ABC ,
D đáy ABCD là hình vuông cạnh a 6
bằng a , SA ^ (ABCD) và SA =
(minh họa như hình bên). 3
Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng A. 0 30 . B. 0 60 . C. 0 75 . D. 0 45 .
Câu 27: Cho hàm số y = f ( )
x xác định, liên tục trên \   2 và có
bảng biến thiên như hình dưới đây:
Khẳng định nào sau đây là đúng?
A. Hàm số đã cho nghịch biến trên khoảng (- 3;- 2)È(- 2;- ) 1 .
B. Hàm số đã cho có giá trị cực đại bằng - 3.
C. Hàm số đã cho đồng biến trên khoảng (- ¥ ;- ) 3 và (- 1;+ ¥ ).
D. Hàm số đã cho có điểm cực tiểu là 2.
Câu 28: Biết rằng hàm số f (x) 3 2
= x - 3x - 9x + 28 đạt giá trị nhỏ nhất trên đoạn [0;4] tại x0 . Tính P = x + 2018. 0 A. P = 3. B. P = 2019. C. P = 2021. D. P = 2018.
Câu 29: Tính P là tích tất cả các nghiệm của phương trình 3.9x 10.3x - + 3 = 0. Trang 38 A. P = 1 . B. P = - 1 . C. P = 0 . D. P = 9.
Câu 30: Cho hàm số y = ( x − )( 2 2 x + )
1 có đồ thị (C ). Mệnh đề nào sau đây là đúng?
A. (C) không cắt trục hoành.
B. (C) cắt trục hoành tại một điểm.
C. (C) cắt trục hoành tại hai điểm.
D. (C) cắt trục hoành tại ba điểm.
Câu 31: Có bao nhiêu số nguyên dương x thỏa mãn bất phương trình log(x − 40) + log(60 − x)  2 A. 20. B. 18. C. 21. D. 19.
Câu 32: Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng 3 3 a 3 3 a 3 2 a 3  a A. B. C. D. 3 2 3 3 2 2
Câu 33: Cho hai hàm số y = f ( )
x , y = g( ) x liên tục trên thỏa mãn
f (x)dx = 3 
và g(x)dx = 2.  . 1 1 2 Tính J =
[2 f (x) − 3g(x) +1]dx  . A. J = 1 B. J = 2 C. J = 3
D. J = 6
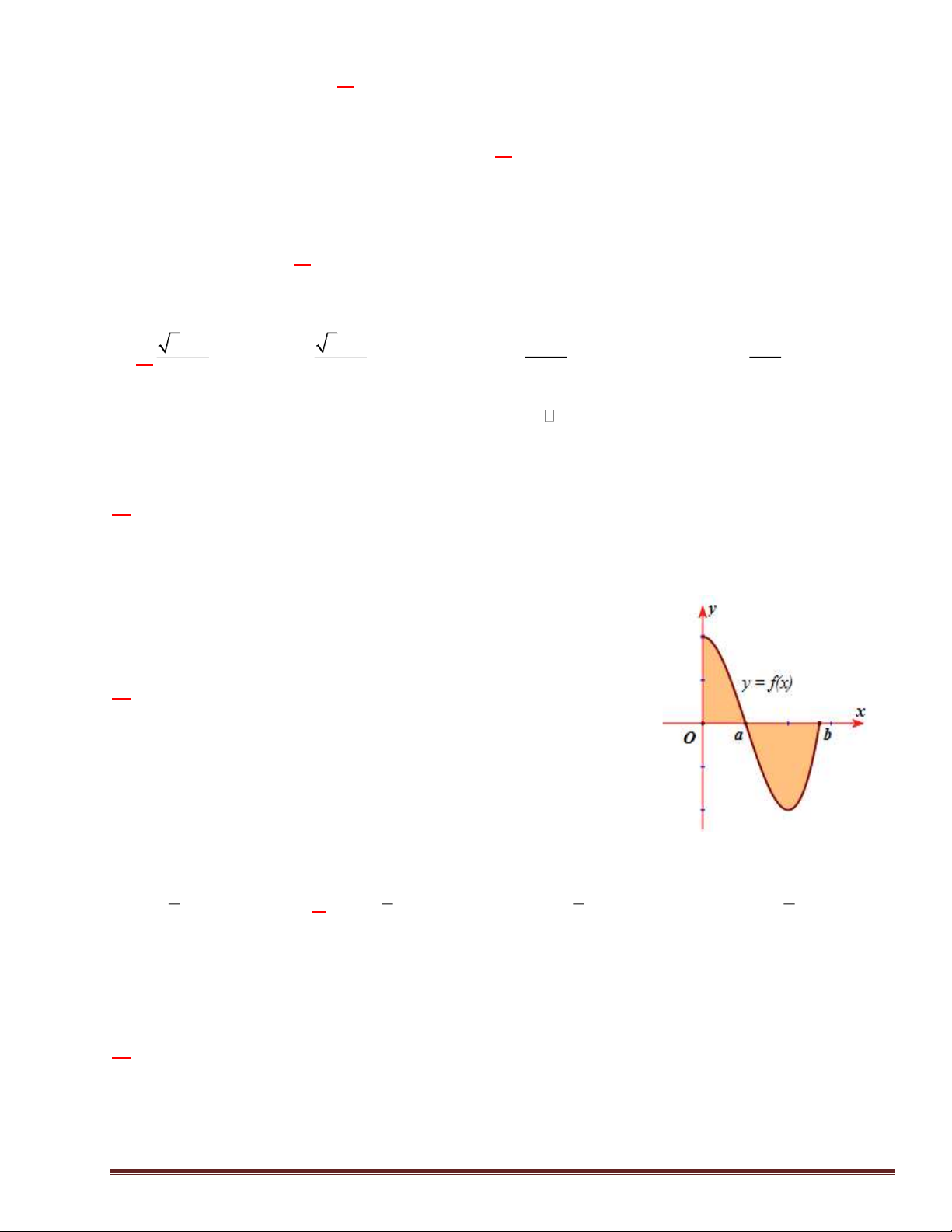
Câu 34: Cho hình phẳng ( H ) giới hạn bởi các đường y = f ( )
x , x = 0, x = b và trục hoành (phần tô
màu trong hình vẽ bên). Khi đó diện tích hình phẳng ( H ) được tính bằng biểu thức nào trong các biểu thức dưới đây ? b a A. f (x)dxB. f (x)dx  0 0 a b b C.
f (x)dx − f (x)dx   D. 2 f (x)dx 0 a 0
Câu 35: Tìm các số thực a,b thỏa mãn a + 2b − 3bi = 2 + 6i
A. a = 2,b = 6 − B. a = 6 − ,b = 2 C. a = 6 − ,b = 2
D. a = 6,b = 2 −
Câu 36: Kí hiệu z là nghiệm phức có phần ảo dương của phương 0 trình 2
4z −16z +17 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây
là điểm biểu diễn của số phức w = iz ? 0  1   1   1   1  A. M ; 2 B. M − ;2 C. M − ;1 D. M ;1 1          2  2  2  1  4  1  4 
Câu 37: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;1;- )
1 , B(- 1;0;4), C (0;- 2;- ) 1 .
Phương trình nào sau đây là phương trình của mặt phẳng đi qua A và vuông góc với BC ?
A. x − 2y −5z + 5 = 0
B. 2x + y - z - 5 = 0
C. x − 2y −5z −5 = 0
D. x- 2y - 5z + 21= 0 Trang 39
Câu 38: Trong không gian với hệ tọa độ Oxyz, lập phương trình tham số của đường thẳng d đi qua x = 0 x +1 y −1 zM (2;1;− )
3 và vuông góc với hai đường thẳng: d : = =
, d :  y = t − . 1 3 1 2 − 2 z = 3t  x = 2 + t x − 2 y −1 z + 3  A. d : = =
B. d :  y = 1− 9t 1 9 − 3 − z = 3 − − 3t  x = 2 − + tx = 2 + t  
C. d :  y = 1 − − 9t
D. d :  y = 1+ 9t   z = 3 − 3tz = 3 − − 3t
Câu 39: Cho 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất 5 tấm được
chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn; trong đó có ít nhất một tấm thẻ mang số chia hết cho 4 là: 75 225 170 175 A. B. C. D. 94 646 646 646
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Hình chiếu vuông góc của S lên
mặt phẳng ( ABCD) trùng với trung điểm H của cạnh .
AB Góc tạo bởi SC và ( ABCD) bằng 0 45 .
Tính theo a tính khoảng cách giữa hai đường thẳng SD và . AB 2a 5 a 5 a 5 a 15 A. d = B. d = C. d = D. d = 3 13 3 3
Câu 41: Cho hàm số y = f ( )
x có đạo hàm trên
và có bảng xét dấu của hàm số y = f '( ) x như sau: x −  2 − 2 5 + 
f '(x) − 0 + 0 − 0 +
Hàm số g ( x) = f (3− 2x) nghịch biến trên khoảng nào trong các khoảng sau ? A. (0;2). B. (− ;  − ) 1 . C. (1; ) 3 . D. ( 1 − ;+).
Câu 42: Dân số thế giới được tính theo công thức 𝑆 = 𝐴. 𝑒𝑛𝑖 trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, I là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1,47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam gần với số nào nhất sau đây? A. 99.389.200 B. 99.386.600 C. 100.861.100 D. 99.251.200 Trang 40 y bx − c y Câu 43: Hàm số y = (a  0; x − a , a ,
b c  ) có đồ thị như hình vẽ
bên. Mệnh đề nào sau đây là đúng?
A. a  0, b  0, c − ab  0. O x
B. a  0, b  0, c − ab  0.
C. a  0, b  0, c − ab = 0.
D. a  0, b  0, c − ab  0.
Câu 44: Cho hình trụ có bán kinh` đáy bằng a 2. Cắt hình trụ bởi một mặt phẳng song song với trục a
của hình trụ và cách trục của hình trụ một khoảng bằng
ta được thiết diện là một hình vuông. 2
Tính thể tích V của khối trụ đã cho. 3 2 a 7 A. 3 V =  a 3 B.V = C. 3 V = 2 a 7 D. 3 V =  a 3 1
Câu 45: Cho hàm số f (x) có đạo hàm liên tục trên
. Biết f (5) =1 và xf (5x)dx = 1  , khi đó 0 5 2
x f '(x)dx  bằng: 0 123 A. 15. B. 23. C. D. 25. − 5
Câu 46: Cho hàm số y = f ( x) liên tục trên ¡ và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các
giá trị nguyên của tham số m để phương trình f (sin x) = 3sin x + m có nghiệm thuộc khoảng
(0; ) . Tổng các phần tử của S bằng A. 8. − B. 10. − C. 6. − D. 5. −
Câu 47: Cho hai số thực a 1,b 1. Biết phương trình 2 x x 1
a b − = 1 có hai nghiệm phân biệt x , x . Tìm 1 2 2  x x
giá trị nhỏ nhất của biểu thức 1 2 S = 
 − 4( x + x . 1 2 ) x + x  1 2  Trang 41 A. 3 3 4 . B. 4 C. 3 3 2 . D. 3 4 . m x +
Câu 48: Cho hàm số f ( x) 2 4 =
( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m x +1
sao cho 2 max f ( x) − min f ( x) = 12 . Số phần tử của S là? 1;  3 1;  3 A. 0 . B. 2 . C. 4 . D. 6 .
Câu 49: Cho hình hộp ABC . D A BCD
  có chiều cao bằng 10 và diện tích đáy bằng 202 . Gọi M là trung điểm của cạnh .
AB Mặt phẳng (MB D
 ') chia khối hộp ABC . D A BCD   thành hai khối đa
diện. Thể tích của khối đa diện lồi chứa đỉnh A bằng 3535 1010 505 3535 A. . B. . C. . D. . 3 3 2 6 1− 2x Câu 50: Cho ,
x y là các số thực dương thỏa mãn ln = 3x + y −1.  
Tìm giá trị nhỏ nhất Px + y  min 1 1 của P = + +1. x xy A. P = 8. B. P =16 . C. P = 9 . D. P = 2 . min min min min HẾT HƯỚNG DẪN GIẢI
Câu 1: Một tổ có 5 học sinh nam và 7 học sinh nữ, số cách chọn ra hai học sinh có cả nam và nữ? A. 1 1 C .C B. 1 1 C + C C. 2 C D. 1 1 C + C 5 7 5 7 12 5 7 Gợi ý giải:
Số cách chọn một học sinh nam là : 5 cách( 1 C ) 5
Số cách chọn một học sinh nữ là : 7 cách( 1 C ) 7
Vậy số cách chọn hai học sinh có cả nam và nữ là : 5 x 7 = 35 hay 1 1
C .C (cách chọn) 5 7
Câu 2: Cho (u là cấp số cộng với công sai d.Biết u = 4 − và u = 10. −
Số hạng đầu tiên u bằng n ) 3 5 1
A. u = 2 B. u = − 3 C. u = 6 − D. u = 7 − 1 1 1 1 u  = 4 − u  + 2d = 4 − u  = 2
Gợi ý giải: Ta có : 3 1 1     . Vậy u = 2 u = 1 − 0 u + 4d = 1 − 0   d = 3 − 1 5 1
Câu 3: Số nghiệm của phương trình 2 3x 3x = là A. 2 B. 1 C. 0 D. Vô số  = 2 x 0
Gợi ý giải: x x 2 2 3
= 3  x = x x − x = 0  
Vậy x = 0, x =1 x =1
Câu 4: Một khối lập phương có thể tích là 3
8a . Cạnh của khối lập phương đó bằng a A. 2a B. a C. 2 a D. 3 Trang 42
Gợi ý giải: Ta có : 3
V = 8a suy ra cạnh của hình lập phương bằng 2a
Câu 5: Tập xác định của hàm số y = log 3 ( − x) là 3 A. (− ;3) B. C. (3;+) D. (0 ;+)
Gợi ý giải: Hàm số xác định khi 3 – x  0  x  3. Vậy tập xác định của hàm số là (− ;3)
Câu 6: Họ nguyên hàm của hàm số ( ) x f x = e + 3 là A. ( ) x
F x = e + 3x B. ( ) x
F x = e − 3x C. ( ) = − x F x e + 3x D. ( ) = − x F x
e − 3x Gợi ý giải: ( ) x
F x = e + 3x
Câu 7: Một khối chóp có đáy là hình vuông cạnh a = 3và đường cao h = 5. Thể tích khối chóp là
A. V = 15 B. V = 45 C. V = 25
D. V = 35 1 1
Gợi ý giải: Diện tích đáy 2
B = a .Thể tích khối chóp 2 V =
Bh V = .3 .5 = 15 3 3
Câu 8: Cho hình nón có bán kính đáy r = 4 và diện tích xung quanh bằng 20π. Thể tích
của khối nón đã cho bằng A. 4π. B. 16π. C.163π. D.803π. Lời giải.
Áp dụng công thức tính diện tích xung quanh của hình nón ta có: Sxq = πrl ⇒ 20π = π4l ⇒ l = 5. 1 1 Vì 2 2 2 2
h = l − r h = 5 − 4 = 3. Khối nón có thể tích là 2 2
V =  r h = .4 .3 = 16 3 3
Câu 9: Thể tích V của một khối cầu có bán kính R là 4 1 4 A. 3 V =  R B. 3 V =  R C. 2 V =  R D. 3 V = 4 R 3 3 3 Lời giải. Thể tích 4
V của khối cầu có bán kính R là: 3 V =  R 3
Câu 10: Cho hàm số y = f(x) có bảng biến thiên như sau : x -∞ 0 2 + ∞ y’ + 0 - 0 + y 1 + ∞ 0 -3
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (2;+∞) B. (-∞;1) C. (0;+∞) D. (0;2) Lời giải. Trang 43
Dựa vào bảng biến thiên, hàm số đã cho đồng biến trên các khoảng ( ;0 − )và (2;+). Chọn đáp án A 4 a e
Câu 11: Với a,b là hai số thực dương tùy ý, ln bằng b
A. 4ln a – ln b +1 .
B. 4ln b − ln a +1.
C. 4ln a + ln b –1.
D. 4ln a + ln b +1. Lời giải. 4 a e Ta có: ln
= ln (a4 e) – ln b = 4 ln a + 1 – ln b. Chọn đáp án: A b
Câu 12: Công thức tính diện tích xung quanh của hình trụ có chiều cao h, bán kính đáy R là
A. Sxq = 2πRh.
B. Sxq = π2Rh.
C. Sxq = πRh.
D. Sxq = 4πRh. Lời giải.
Áp dụng công thức tính diện tích xung quanh của hình trụ Sxq = 2πRh. Chọn đáp án: A
Câu 13: Hàm số y = f(x) liên tục trên
và có bảng biến thiên như hình vẽ. x -∞ 1 2 + ∞ y’ + 0 − || + y 3 + ∞ −∞ 0
Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho có hai điểm cực trị.
B. Hàm số đã cho có đúng một điểm cực trị.
C. Hàm số đã cho không có giá trị cực tiểu.
D. Hàm số đã cho không có giá trị cực đại. Lời giải.
Dựa vào bảng biến thiên, ta thấy hàm số đạt cực đại tại x = 1 và đạt cực tiểu tại x = 2.
Vậy hàm số có hai điểm cực trị. Chọn đáp án A
Câu 14: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y 1 A. 3 2
y = x − 3x +1 2 B. 3 2
y = − x − 3x +1 1 − O x C. 3 2
y = x + 3x +1 D. 3 2
y = − x + 3x +1 −3 Lời giải.
Hình vẽ là đồ thị hàm số y = ax3 + bx2 + cx + d với a > 0 và hàm số có hai điểm cực trị là x = 0
và x = 2. Ta thấy chỉ có hàm số 3 2
y = x − 3x +1 thỏa Trang 44 − x
Câu 15: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số 1 4 y = ? 2x −1 1 A. y = 2. B. y = . C. y = 4. D. y = 2. − 2 Lời giải. Ta có: lim y = 2 − ; lim y = 2
− , nên đường thẳng y = 2
− là đường tiệm cận ngang của đồ thị hàm số đã x→+ x→− cho. Chọn đáp án D
Câu 16: Tập nghiệm của bất phương trình log3(x - 2) ≥ 2 là A. 11;+). B. (2;+). C. ( ; − 1 ) 1 . D. (11; ) + Lời giải. Gợi ý giải:
Điều kiện: x − 2  0  x  2. Vì 3 1nên log (x − 2) 2
 2  x − 2  3  x 11. 3
Vậy tập nghiệm của bất phương trình là 11;+).
Câu 17: Cho hàm số bậc bốn y = f ( )
x có đồ thị như hình vẽ
Số nghiệm của phương trình f ( ) x = 1 − là: A. 4. B. 3. C. 2. D. 1. Lời giải.
Số nghiệm của phương trình là số giao điểm của
đồ thị hai hàm số: y = f(x) và y = -1. Suy ra số nghiệm là 4 3 3
Câu 18: Cho hàm số f ( x) liên tục trên [0;3]. Nếu f (x)dx = 2 
thì [x − 3 f (x)]dx  có giá trị bằng 0 0 3 3 A. − B. −3 C. 3 D. . 2 2 Lời giải. 3 3 3 3 2 x 3
Ta có: [x − 3 f (x)]dx = xdx − 3 f (x)dx = − 3.2 = −    2 2 0 0 0 0
Câu 19: Số phức liên hợp của số phức z = 4 – 3i là Trang 45
A. z = 4 + 3i B. z = 4 − −3i C. z = 4 − +3i
D. z = 3 − 4i Lời giải.
Số phức liên hợp của z là z = 4 + 3i z
Câu 20: Cho hai số phức: z = 1 – 2i và z = 3 – 2 . i Tìm số phức 2 z = 1 2 z1 7 4 7 4 7 4 7 4 A. z = + i
B. z = − + i C. z = − i
D. z = − − i 5 5 5 5 5 5 5 5 Lời giải. z
(3 − 2i)(1+ 2i) 7 + 4i 2 = = z (1− 2i)(1+ 2i) 5 1
Câu 21: Cho số phức z = 4 – 3i có điểm biểu diễn trên mặt phẳng tọa độ Oxy là M. Độ dài OM bằng A. 5 B. 25 C. 7 D. 4 Lời giải.
Ta có: Tọa độ M(4 ; -3) nên OM = 2 2 4 + ( 3 − ) = 5
Câu 22: Trong không gian Oxyz , cho điểm A(1; 2; 3). Hình chiếu vuông góc của điểm A trên trục Oz là điểm A. Q 0 ( ;0;3 . ) B. M 1 ( ;0;3 . ) C. P (0;2;3). D. N( 1 − ;0;0 .) Lời giải.
Hình chiếu vuông góc của điểm A(1;2; )
3 lên trục Oz là điểm M (0;0;3)
Câu 23: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình 2 2 2
x + y + z − 2x + 4 y − 6z + 9 = 0. Tọa độ tâm I và bán kính R của mặt cầu là A. I (1; 2 − ; ) 3 và R = 5. B. I (1; 2 − ; ) 3 và R = 5 . C. I ( 1 − ;2;− ) 3 và R = 5. D. I ( 1 − ;2;− ) 3 và R = 5 . Lời giải.
Mặt cầu x2 + y2 + z2 - 2x + 4y - 6z + 9 = 0 có tâm I (1; - 2; 3) và bán kính R = 2 2 2 1 + ( 2) − + 3 − 9 = 5
Câu 24: Trong không gian Oxyz, cho mặt phẳng (α) : x - 2y + 2z - 3 = 0. Điểm nào sau đây nằm trên mặt phẳng (α)? A. N(1;0;1). B. Q (2;1; ) 1 . C. ( P 2; 1 − ;1 .) D. M (2;0; ) 1 . Lời giải.
Ta thấy tọa độ điểm N(1; 0; 1) thỏa mãn phương trình mặt phẳng (α) nên điểm N nằm trên (α) x − y + z
Câu 25: Trong không gian Oxyz, cho đường thẳng d có phương trình: 1 2 = = . Một vectơ 2 3 1 −
chỉ phương của đường thẳng d có tọa độ Trang 46 A. (2;3;− ) 1 . B. (1; 2 − ;0). C. ( 1 − ;3;2). D. (4;6;2). Lời giải.
d có VTVP u = (2;3; −1)
Câu 26: Cho hình chóp S.ABC ,
D đáy ABCD là hình vuông cạnh a 6
bằng a , SA ^ (ABCD) và SA =
(minh họa như hình bên). 3
Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng A. 0 30 . B. 0 60 . C. 0 75 . D. 0 45 .
Hướng dẫn giải:
ABCD là hình vuông cạnh a nên AC = a 2. SA ^ (ABC )
D Þ AC là hình chiếu vuông góc của SC lên ( ) ·
ABCD Þ SCA là góc giữa SC và (ABCD). · SA a 6 1 1 ·
Tam giác SAC vuông tại A nên 0 tan SCA = = . = Þ SCA = 30 . AC 3 a 2 3
Câu 27: Cho hàm số y = f ( )
x xác định, liên tục trên \  
2 và có bảng biến thiên như hình dưới đây:
Khẳng định nào sau đây là đúng?
A. Hàm số đã cho nghịch biến trên khoảng (- 3;- 2)È(- 2;- ) 1 .
B. Hàm số đã cho có giá trị cực đại bằng - 3.
C. Hàm số đã cho đồng biến trên khoảng (- ¥ ;- ) 3 và (- 1;+ ¥ ).
D. Hàm số đã cho có điểm cực tiểu là 2.
Hướng dẫn giải:
Dựa vào bảng biến thiên, ta có nhận xét sau
Hàm số nghịch biến trên khoảng (- 3;- 2) và (- 2;- )
1 ¾ ¾® A sai (sai chỗ dấu È ).
Hàm số có giá trị cực đại y = - 2 ¾ ¾ ® CĐ B sai.
Hàm số đồng biến khoảng (- ¥ ;- )
3 và (- 1;+ ¥ )¾ ¾® C đúng. Trang 47
Hàm số có điểm cực tiểu là - 1¾ ¾ ® D sai. )
Câu 28: Biết rằng hàm số f (x) 3 2
= x - 3x - 9x + 28 đạt giá trị nhỏ nhất trên đoạn [0;4] tại x0 . Tính P = x + 2018. 0 A. P = 3. B. P = 2019. C. P = 2021. D. P = 2018.
Hướng dẫn giải: x é = - 1Ï [0;4]
Đạo hàm f '(x) 2 3x 6x 9 f '(x) 0 ê = - - ¾ ¾® = Û . x ê = 3Î ê [0;4] ë ìï f (0)= 28 ïï Ta có ïí f ( )
3 = 1 ¾ ¾® min f (x)= 1 khi x = 3 = x ¾ ¾® P = 2021. ï 0 [0;4] ïï f ï (4)= 8 î
Câu 29: Tính P là tích tất cả các nghiệm của phương trình 3.9x 10.3x - + 3 = 0. A. P = 1 . B. P = - 1 . C. P = 0 . D. P = 9.
Hướng dẫn giải: Phương trình 2 3.3 x 10.3x Û - + 3 = 0 . Đặ 1 t 3x t =
> 0. Phương trình trở thành 2
3t - 10t + 3 = 0 Û t = hoặc t = 3 . 3 1 x 1 Với t = ¾ ¾® 3 =
Û x = - 1 = x . 1 3 3 Với = 3 ¾ ¾ ® 3x t
= 3 Û x = 1= x . 2
Vậy P = x x = - 1. 1 2
Câu 30: Cho hàm số y = ( x − )( 2 2 x + )
1 có đồ thị (C ). Mệnh đề nào sau đây là đúng?
A. (C) không cắt trục hoành.
B. (C) cắt trục hoành tại một điểm.
C. (C) cắt trục hoành tại hai điểm.
D. (C) cắt trục hoành tại ba điểm.
Hướng dẫn giải:
Phương trình hoành độ giao điểm của (C) với trục hoành: (x − )( 2 2 x + )
1 = 0  x − 2 = 0  x = 2.
Vậy đồ thị hàm số cắt trục hoành tại một điểm.
Câu 31: Có bao nhiêu số nguyên dương x thỏa mãn bất phương trình log(x − 40) + log(60 − x)  2 A. 20. B. 18. C. 21. D. 19.
Hướng dẫn giải:
Điều kiện: 40  x  60 .
Bất phương trình  log (x − 40)(60 − x)  2 
 (x − )( − x)   x − x +   (x − )2 2 2 40 60 10 100 2500 0 50  0  x  50. Trang 48 40  x  60 +
Kết hợp với điều kiện, ta được x  ⎯⎯⎯
→ x 41;...;5  9 \ 5  0 . x  50
Câu 32: Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng 3 3 a 3 3 a 3 2 a 3  a A. B. C. D. 3 2 3 3
Hướng dẫn giải:l = 2a 2 2
h = l − r với 
. Suyra h = a 3 . r = a 3 1 1  3 2 2 =  =  3 = a V r h a a . 3 3 3 2 2
Câu 33: Cho hai hàm số y = f ( )
x , y = g( ) x liên tục trên thỏa mãn
f (x)dx = 3 
và g(x)dx = 2.  . 1 1 2 Tính J =
[2 f (x) − 3g(x) +1]dx  . A. J = 1 B. J = 2 C. J = 3
D. J = 6
Hướng dẫn giải Ta có 2 2 2 2 2 J =
[2 f (x) − 3g(x) +1]dx = 2
f (x)dx − 3 g(x)dx +
d x = 2.3 − 3.2 + x = 1     1 1 1 1
Câu 34: Cho hình phẳng ( H ) giới hạn bởi các đường y = f ( )
x , x = 0, x = b và trục hoành (phần tô
màu trong hình vẽ bên). Khi đó diện tích hình phẳng ( H ) được tính bằng biểu thức nào trong các biểu thức dưới đây ? b a A. f (x)dxB. f (x)dx  0 0 a b b C.
f (x)dx − f (x)dx   D. 2 f (x)dx 0 a 0
Hướng dẫn giải
• Ta có diện tích hình phẳng (H ) được tính bởi công thức b a b S =
f (x) dx =
f (x) dx + f (x) dx    0 0 a
• Mặt khác, dựa vào đồ thị hàm số y = f (x) ta có: ▪ Trên đoạn [0; ] a , f ( ) x  0 ▪ Trên đoạn [ ; a ] b , f ( ) x  0 • a b Từ đó suy ra S =
f (x)dx − f (x)dx   0 a
Câu 35: Tìm các số thực a,b thỏa mãn a + 2b − 3bi = 2 + 6i
A. a = 2,b = 6 − B. a = 6 − ,b = 2 C. a = 6 − ,b = 2
D. a = 6,b = 2 −
Hướng dẫn giải Trang 49  + =  = • a 2b 2 a 6
Ta có a + 2b − 3bi = 2 + 6i     3 − b = 6 b   = 2 −
Câu 36: Kí hiệu z là nghiệm phức có phần ảo dương của phương trình 2
4z −16z +17 = 0. 0 Trên mặt
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w = iz ? 0  1   1   1   1  A. M ; 2 B. M − ;2 C. M − ;1 D. M ;1 1          2  2  2  1  4  1  4 
Hướng dẫn giải   1 z = 2 + i  − =  • 2z 4 i 2 Ta có 2 2
4z −16z +17 = 0  (2z − 4) = 1 −     . 2z − 4 = i − 1 z = 2− i     2 • 1  1  1
Vì z0 có phần ảo dương nên z = 2 + .
i . Khi đó w = iz = i 2 + i = − + 2i . 0   2 0  2  2 •   Suy ra điể 1 1
m biểu diễn của số phức w = −
+ 2i là điểm có tọa độ − ;2   2  2 
Câu 37: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;1;- )
1 , B(- 1;0;4), C (0;- 2;- ) 1 .
Phương trình nào sau đây là phương trình của mặt phẳng đi qua A và vuông góc với BC ?
A. x − 2y −5z + 5 = 0
B. 2x + y - z - 5 = 0
C. x − 2y −5z −5 = 0
D. x- 2y - 5z + 21= 0 uuur
Hướng dẫn giải : Mặt phẳng cần tìm đi qua A(2;1;- )
1 và nhận BC = (1;- 2;- ) 5 làm một VTPT nên
có phương trình x - 2y - 5z - 5 = 0.
Câu 38: Trong không gian với hệ tọa độ Oxyz, lập phương trình tham số của đường thẳng d đi qua x = 0 x +1 y −1 zM (2;1;− )
3 và vuông góc với hai đường thẳng: d : = =
, d :  y = t − . 1 3 1 2 − 2 z = 3t  x = 2 + t x − 2 y −1 z + 3  A. d : = =
B. d :  y = 1− 9t 1 9 − 3 − z = 3 − − 3t  x = 2 − + tx = 2 + t  
C. d :  y = 1 − − 9t
D. d :  y = 1+ 9t   z = 3 − 3tz = 3 − − 3t
Đường thẳng d qua M (2;1;− ) 3 , VTCP u = u  ;u  = 1; 9 − ; 3 − 1 2 ( )  
Câu 39: Cho 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất 5 tấm được
chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn; trong đó có ít nhất một tấm thẻ mang số chia hết cho 4 là: Trang 50 75 225 170 175 A. B. C. D. 94 646 646 646 Lời giải
Số phần tử không gian mẫu là: 5 n() = C 20
Trong số các số tư 1 đến 20 có 10 số lẻ, 10 số chẵn trong đó 5 số chia hết cho 4 là: 4, 8, 12, 16, 20.
Số cách chọn 3 tấm thẻ mang số lẻ là: 3 C 10
Số cách chọn 2 tấm thẻ mang số chẵn là: 2 C 10
Số cách chọn 2 tấm thẻ mang số chẵn mà không chia hết cho 4 là: 2 C 5 3 C ( 2 2 C − C 10 10 5 ) 175
Vậy xác suất để chọn được 5 tấm thẻ thỏa yêu cầu bài toán là: = 5 C 646 20
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Hình chiếu vuông góc của S lên
mặt phẳng ( ABCD) trùng với trung điểm H của cạnh .
AB Góc tạo bởi SC và ( ABCD) bằng 0 45 .
Tính theo a tính khoảng cách giữa hai đường thẳng SD và . AB 2a 5 a 5 a 5 a 15 A. d = B. d = C. d = D. d = 3 13 3 3 Lời giải Góc giữa SC và (ABCD) là 0 SCH = 45 Tính đượ a 5 a 5 c HC =  SH = 2 2
Vì AB / / (SCD), H AB nên d(AB;SD) = d(AB,(SCD)) = d(H,(SCD))
Gọi I là trung điểm của CD. Trong (SHI), dựng HK ⊥ SI tại K
Chứng minh được HK ⊥ (SCD)  d(H;(SCD)) = HK
Xét tam giác SHI vuông tại H, HK đường cao: 1 1 1 4 1 9 a 5 = + = + =  HK = 2 2 2 2 2 2 HK SH HI 5a a 5a 3 Trang 51 Vậy ( ) a 5 d AB;SD = HK = 3
Câu 41: Cho hàm số y = f ( )
x có đạo hàm trên
và có bảng xét dấu của hàm số y = f '( ) x như sau: x −  2 − 2 5 + 
f '(x) − 0 + 0 − 0 +
Hàm số g ( x) = f (3− 2x) nghịch biến trên khoảng nào trong các khoảng sau ? A. (0;2). B. (− ;  − ) 1 . C. (1; ) 3 . D. ( 1 − ;+). Lời giải  2 −  x  2
Dựa vào bảng xét dấu: f '(x)  0   x  5
Ta có g '( x) = 2 − f '(3−2x) 1 5  2 −  3− 2x  2  x  
Xét g '( x)  0  f '(3 − 2x)  0    2 2 3− 2x  5  x  1 −  1 5 
Vậy g(x) nghịch biến trên ;   và (− ;  − ) 1  2 2 
Câu 42: Dân số thế giới được tính theo công thức 𝑆 = 𝐴. 𝑒𝑛𝑖 trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, I là tỉ lệ tăng dân số hàng năm. Cho biết năm 2005 Việt Nam có
khoảng 80.902.400 người và tỉ lệ tăng dân số là 1,47% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng
năm không đổi thì đến năm 2019 số dân của Việt Nam gần với số nào nhất sau đây?
A. 99.389.200 B. 99.386.600 C. 100.861.100 D. 99.251.200 Hướng dẫn giải: Áp dụng công thức = . ni S
A e với A = 80.902.400, n = 2019 - 2005 = 14, i = 1,47% = 0,0147
Dân số Việt Nam đến năm 2019 là 14.0,0147 = 80.902.400.e = 99389203,38
Như vậy, số dân Việt Nam đến năm 2019 gần với số 99.389.200 nhất. Chọn đáp án A. Trang 52 y bx − c y Câu 43: Hàm số y = (a  0; x − a , a ,
b c  ) có đồ thị như hình vẽ
bên. Mệnh đề nào sau đây là đúng?
A. a  0, b  0, c − ab  0. O x
B. a  0, b  0, c − ab  0.
C. a  0, b  0, c − ab = 0.
D. a  0, b  0, c − ab  0. Hướng dẫn giải:
Đồ thị hàm số có tiệm cận đứng x = a  0 ; tiệm cận ngang y = b  0.
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó c − ab nên y =    ⎯⎯ → −  ( x − a) 0, x a c ab 0. 2
Vậy a  0, b  0, c − ab  0. Chọn A.
Câu 44: Cho hình trụ có bán kinh` đáy bằng a 2. Cắt hình trụ bởi một mặt phẳng song song với trục a
của hình trụ và cách trục của hình trụ một khoảng bằng
ta được thiết diện là một hình vuông. 2
Tính thể tích V của khối trụ đã cho. 3 2 a 7 A. 3 V =  a 3 B.V = C. 3 V = 2 a 7 D. 3 V =  a 3 a2 O' A' B' O A a1 H Hướ B ng dẫn giải:
Gọi O, O’ lần lượt là tâm của đáy và thiết diện là hình vuông ABB’A’.
Gọi H là trung điểm AB, ta có OH ^ AB , OH ^ AA’ suy ra OH ^ (ABB’A’) Do đó a d (O ’, O ( AB ’ B ’) A ) = OH = 𝑎 2 2 a 7
Tam giác OAH vuông tại H nên AH = 2
Suy ra AB = A ’ A = O ’
O = 2AH = a 7 Vậy thể tích 2 2 3
V =  r h =  (a 2)  a 7 = 2 a 7 Trang 53 Vậy chọn C 1
Câu 45: Cho hàm số f (x) có đạo hàm liên tục trên
. Biết f (5) =1 và xf (5x)dx = 1  , khi đó 0 5 2
x f '(x)dx  bằng: 0 123 A. 15. B. 23. C. D. 25. − 5 Cách 1: 5 5 5 1 2 2
x f '(x)dx = x f (x) − 2 .
x f (x)dx = 25.1− 2 5t. f (5t)d(5t) = 25 − 50.1 = 25 −    0 0 0 0 Cách 2: 1 Ta có: 1 =
x f (5x)dx  0 Đặ 1
t t = 5x  dt = 5dx  dt = dx 5 5 5 5 5 1 1 1 1 =
t f (t)  dt  1 =
t f (t)dt
t f (t)dt = 25 
x f (x)dx = 25     0 0 0 0 5 5 25 5 Đặ  t 2 I =
x f (x)dx  0 2 u  = x d  u = 2 d x x Đặt:   
dv = f '(x)dx v   = f (x) 5 5 2
I = x f (x) − 2 x f (x)dx = 25 f (5) − 2.25 = 25 −  0 0
Câu 46: Cho hàm số y = f ( x) liên tục trên ¡ và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các
giá trị nguyên của tham số m để phương trình f (sin x) = 3sin x + m có nghiệm thuộc khoảng
(0; ) . Tổng các phần tử của S bằng A. 8. − B. 10. − C. 6. − D. 5. −
Đặt t = sin x , do x(0; )  sin x(0;  1  t (0;  1 . Trang 54
Gọi  là đường thẳng qua điểm (1;− )
1 và song song với đường thẳng y = 3x có phương 1
trình y = 3x − 4 .
Gọi  là đường thẳng qua điểm (0 )
;1 và song song với đường thẳng y = 3x có phương 2
trình y = 3x +1.
Do đó phương trình f (sin x) = 3sin x + m có nghiệm thuộc khoảng (0; ) khi và chỉ khi
phương trình f (t) = 3t + m có nghiệm thuộc nửa khoảng (0;  1  4 −  m 1.
Câu 47: Cho hai số thực a 1,b 1. Biết phương trình 2 x x 1
a b − = 1 có hai nghiệm phân biệt x , x . Tìm 1 2 2  x x
giá trị nhỏ nhất của biểu thức 1 2 S = 
 − 4( x + x . 1 2 ) x + x  1 2  A. 3 3 4 . B. 4 C. 3 3 2 . D. 3 4 . 2 Ta có x x 1 a b − =  x a + x − =  x + x a − = b ( 2 ) 2 1 log 1 0 log 1 0 b
x + x = −log a
Do phương trình có hai nghiệm x , x nên theo định lý Viet ta có: 1 2 b  1 2 x x = 1 −  1 2 Khi đó 1 S = + 4log a 2 log b a b Đặ 1 1
t t = log a , do a 1,b 1 t  0. Khi đó 3 S = + 4t =
+ 2t + 2t  3 4 b 2 2 t t Đẳ 1 1 ng thức xảy ra khi = 2t t = . Vậy 3 min S = 3 4 2 3 t 2 m x +
Câu 48: Cho hàm số f ( x) 2 4
= x+ (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m 1
sao cho 2 max f ( x) − min f ( x) = 12 . Số phần tử của S là? 1;  3 1;  3 A. 0 . B. 2 . C. 4 . D. 6 .
Lời giải tham khảo Điều kiện x  1 − 2 m − 4
Ta có f '( x) = ( x + )2 1 TH1: Nếu 2
m − 4 = 0  m = 2
 thì f (x) = 4  2max f (x) − min f (x) = 4 ( không thỏa ycbt) 1;  3 1;  3 Nên ta loại m = 2  m  2 − TH2: Nếu 2 m − 4  0  
thì hàm số đồng biến trên [1;3] m  2 + + Khi đó: f ( x) − f ( x) 2 2 3m 4 m 4 2 max min =12  − =12  m = 2  3 (nhận) 1  ;3 1  ;3 2 2 Trang 55 TH3: Nếu 2 m − 4  0  2
−  m  2 thì hàm số nghịch biến trên [1;3] + Khi đó: m
2 max f ( x) − min f ( x) 2 3 4 2 =12  m + 4 − = 12  m = 6  (loại) 1  ;3 1  ;3 4
Vậy có 2 giá trị của m thỏa ycbt Chọn B
Câu 49: Cho hình hộp ABC . D A BCD
  có chiều cao bằng 10 và diện tích đáy bằng 202 . Gọi M là trung điểm của cạnh .
AB Mặt phẳng (MB D
 ') chia khối hộp ABC . D A BCD   thành hai khối đa
diện. Thể tích của khối đa diện lồi chứa đỉnh A bằng 3535 1010 505 3535 A. . B. . C. . D. . 3 3 2 6
Lời giải tham khảo Chọn D Ta có V = =     10.202 2020 ABCD.A B C D
Gọi S = B' M
AA'; N = AD SD'
Suy ra N là trung điểm của SD ' V 1 7 S.AMN = V = V
AMN .A' B ' D'
S.A' B ' D' V 8 8
S.A' B ' D' Mà V = 2V
S . A' B ' D ' .
A A' B ' D ' 7 7 7 V = .2.V = V = V
AMN . A' B ' D ' .
A A' B ' D ' .
A A' B ' D '
ABCD. A' B 'C ' D ' 8 4 24 7 3535 V = .2020 =
AMN .A' B ' D ' 24 6 1− 2x Câu 50: Cho ,
x y là các số thực dương thỏa mãn ln = 3x + y −1.  
Tìm giá trị nhỏ nhất Px + y  min 1 1 của P = + +1. x xy A. P = 8 . B. P =16 . C. P = 9 . D. P = 2 . min min min min
Lời giải tham khảo Chọn A − Điề 1 2x 1 u kiện:
 0  1− 2x  0  x x + y 2 1
Kết hợp với x  0 ta suy ra 0  x  2 Trang 56 1− 2x  Ta có: ln
= 3x + y −1  ln  
(1− 2x)−ln(x + y) = (x + y)−(1− 2x)  x + y
 ln(1−2x)+(1−2x) = ln(x + y)+(x + y)
Xét hàm f (t) = ln (t) + t . Hàm số xác định và liên tục trên (0;+) f (t ) 1 ' = +1  0, t
  0 . Suy ra hàm số đồng biến trên (0;+) t
f (1−2x) = f (x + y) 1−2x = x + y y =1−3x  0 Khi đó 1 1 1 2 P = + +  + + x x (1− 3x) 1 1 x 1− 2x 1
Dấu “=” xảy ra  x = 1− 3x x = 4  1  Xét hàm g ( x) 1 2 = + +1 trên 0;   x 1− 2x  3   1 
Hàm số g ( x) liên tục trên 0;    3  g ( x) 1 4 ' = − + 2 x (1−2x)2 g ( x) 1 ' = 0  x = 4 Bảng biến thiên x 1 1 0 4 3 g '( x) − 0 + g ( x) + 9 8 1 Vậy P = 8 tại x = min 4 Trang 57 ĐỀ 9
ĐỀ THI THỬ THPT QUỐC GIA 2020
PHÁT TRIỂN TỪ ĐỀ MINH HỌA MÔN TOÁN LẦN 2 NĂM 2020 Thời gian: 90 phút
Câu 1. Một lớp học có 18 bạn nam và 22 bạn nữ. Hỏi có bao nhiêu cách chon ra một cặp nam nữ? A. 40 B. 576 C. 1 D. 357
Câu 2. Cho cấp số cộng (u với số hạng tổng quát u = 2n +1. Số hạng u bằng n ) n 5 A. 10 B. 8 C. 11 D. 5
Câu 3. Nghiệm của phương trình 2x = 5 là A. x = log 5 B. x = log 2 C. x = 32 D. x = 25 2 5
Câu 4. Một khối chóp có diện tích đáy bằng 8 và chiều cao bằng 6. Thể tích khối chóp đó bằng A. 14 B. 48 C. 16 D. 32
Câu 5. Tập xác định của hàm số y = ln ( x − ) 1 là A.1;+) B. (1;+) C. ( 1 − ;+) D.  1 − ;+)
Câu 6. Họ tất cả các nguyên hàm của hàm số x
y = e + cos x là A. x
e + sin x + C B. x e − +sin x +C C. x
e − sin x + C D. x y = e
− − sin x + C
Câu 7. Thể tích khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h là 1 B A. V = Bh
B. V = Bh
C. V = 3Bh D. V = 3 h
Câu 8. Một mặt nón có độ dài đường sinh bằng 6, bán kính đáy bằng 3. Diện tích xung quanh của mặt nón đó bằng A. 6 B. 6 C. 18 D. 18
Câu 9. Thể tích khối cầu có bán kính bằng a là: 2 4 a 3 4 a A. B. 2 4 a C. D. 3 4 a 3 3
Câu 10. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ Trang 58
Mệnh đề nào đúng trong các mệnh đề sau?
A. Hàm số đồng biến trên khoảng (2;+ )
B. Hàm số đồng biến trên khoảng (0;+ )
C. Hàm số nghịch biến trên khoảng ( ; − 2)
D. Hàm số nghịch biến trên khoảng (2;+ )
Câu 11. Đạo hàm của hàm số x y = e là A. / x ln 2 y = e B. / x y = e C. / x y = xe D. / x y = e ln 2
Câu 12. Hình trụ có bán kính đáy bằng 5cm, đường cao bằng 7cm Tính thể tích khối trụ tròn xoay giới
hạn bởi hình trụ trên. 175 A. 175 cm3. B. 70 cm3. C.  cm3. D. 35 cm3. 3
Câu 13. Cho hàm số y = f ( )
x có bảng biến thiên như hình vẽ
Hàm số đạt cực đại tại A. x = 2
B. x = 4 C. x = 1 − D. x = 8 x + 2
Câu 14. Cho hàm số y =
. Khẳng định nào đúng trong các khẳng định sau? x −1
A. Hàm số đồng biến trên khoảng ( )1 ; − và(1;+ )
B. Hàm số nghịch biến trên R
C. Hàm số nghịch biến trên khoảng ( )1 ; − và(1;+ )
D. Hàm số đồng biến trên R 2x − 3
Câu 15. Đường tiệm cận đứng của đồ thị hàm số y = có phương trình là x +1 Trang 59 A. x = 1 − B. x = 1 C. x = 3 − D. x = 2
Câu 16. Nghiệm của bất phương trình log x  3 là 2 A. x  6 B. x  6 C. x  8 D. x  8
Câu 17. Hàm số y = f ( )
x có bảng biến thiên như hình vẽ. Số nghiệm của phương trình f ( ) x − 3 = 0 là A. 1 B. 2 C. 3 D. 4 1 2 2 Câu 18. Biết
f (x)dx = 1  và
f (x)dx = 2  . Tính f (x)dx  bằng 0 1 0 A. -1 B. 3 C. 1 D. 2
Câu 19. Mođun của số phức z = 1+ 2i bằng A. 5 B. 3 C. 5 D. 3
Câu 20. Cho số phức z = 2 − 3i và z = 3 + 2i . Điểm biểu diễn số phức z + z có tọa độ là 1 2 1 2 A. ( 1 − ; 5 − ) B. (5; ) 1 C. (5; )1 − D. ( 5 − ; ) 1
Câu 21. Số phức liên hợp của số phức z = a − bi là
A. z = a + bi
B. z = −a + bi
C. z = b − ai
D. z = b + ai
Câu 22. Trong không gian với hệ tọa độ Oxyz. Khoảng cách giữa điểm A(1;2;-3) và B(2;1;-4) bằng A. 2 B. 2 C. 1 D. 3 2 2
Câu 23. Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S ) :( x − ) + ( y + ) 2 5 4
+ z = 3 . Tọa độ tâm
I và bán kính R của mặt cầu (S ) là A. I (5; 4 − ;0) , R = 3 B. I ( 5 − ;4;0) , R = 6
C. I (5;4;0) , R = 3 D. I (5; 4 − ;0) , R = 9 Trang 60
Câu 24. Cho mặt phẳng (α) :− x + 2y + 3 = 0. Một véc tơ pháp tuyến của mặt phẳng (α) là
A. n(1; − 2;0) B. n( 1 − ; 2;3)
C. n(0; 1;− 2) D. n( 1 − ; − 2; 0)
Câu 25. Phương trình tham số của đường thẳng d đi qua điểm A(1;3;5) và vuông góc với mặt phẳng ( )
P : 3x − 4y + z− 2 = 0 là x = 3+ tx =1+ 3tx = 1 − + 3t   
A. d :  y = 4 − + 3t
B. d :  y = 3 − 4t
C. d :  y = 3 − + 4t D.    z = 1+ 5tz = 5 + tz = 5 − + t  x = 1 − + 3t
d :  y = 3 − 4t z = 5−t
Câu 26. Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA vuông góc với đáy, gọi M là trung
điểm cạnh BC. Khẳng định nào sau đây đúng?
A. SM ⊥ ( ABC)
B. AM ⊥ (SBC)
C. SA ⊥ (SB ) C D. BC ⊥ (SAM) 1 Câu 27. Cho hàm số 3 2 y =
x + mx + (m+ 2)x +1 , hàm số có hai điểm cực trị khi giá trị của tham số m 3 là: m  −1 m  −1 A.B.C. 1 −  m 2 D. 1 −  m 2  m  2  m  2
Câu 28. Giá trị lớn nhất của hàm số 3
y = −x +12x + 2 trên đoạn 1;  3 , bằng A. 28 B.13 C.11 D. 18
Câu 29. Đạo hàm của hàm số x
y = e ln x là x e   x e ln x x 1 A. B. e ln x +   C. x e (1+ ln x) D. xx x x +1
Câu 30. Số giao điểm của đồ thị hàm số y =
và đường thẳng y = 3x − 2 là 2x −1 A. 3 B. 2 C. 1 D. 0 Trang 61
Câu 31. Nghiệm của bất phương trình: lg(2x −8) 1 là
A. 4  x  9 B. x  9 C. x  4
D. 4  x  9
Câu 32. Thiết diện qua đỉnh của một hình nón là một tam giác vuông có cạnh huyền bằng 2a . Thể tích khối nón đó bằng 1 A. 2 a p 2 B. 3 pa C. 3 pa D. 2 2 a p 2 3
Câu 33. Biết F(x) là một nguyên hàm của hàm số 2 ( ) x f x = e và (
F ln2) = 4 . Khi đó F(0) bằng: 5 3 A. 2 B. C. 1 D. 2 2
Câu 34. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f ( )
x và trục Ox (phần gạch chéo trong hình vẽ bên) là 1 3 A. S= f ( ) x dx − f ( ) x dx   0 1 1 3 B. S= f ( ) x dx + f ( ) x dx   0 1 3 C. S= f ( ) x dx  0 3 D. S= f (x)dx  0
Câu 35. Tập hợp điểm biểu diễn của số phức z thỏa mãn z = 1 là
A. Đường tròn tâm O(0;0) bán kính R=1.
B. Hình tròn tâm O(0;0) bán kính R=1. C. Parabol 2 y = x .
D. Đường thẳng x + y −1 = 0 . Trang 62
Câu 36. Để phương trình 2 z + z
b + c = 0 nhận 1+ i làm nghiệm thì giá trị của b và c là A. b = 1 − ;c = 1 −
B. b = 2;c = 2 − .
C. b = 3;c = 2 − . D. b = 2 − ;c = 2.
Câu 37. Phương trình mặt phẳng (P) qua A(2 1 ; ;− )
3 và song song với mặt phẳng ( )
Q : x − y + 2z−1 = 0 là A. ( )
P : x − y + 2z+ 5 = 0 B. ( )
P : x − y + 2z+ 6 = 0 C. ( )
P : x − y + 2z+ 4 = 0 D. ( )
P : x − y + 2z− 3 = 0
Câu 38. Trong không gian Oxyz. Đường thẳng d đi qua M (1;− 2; )
1 song song với mặt phẳng  x = 1− t ( 
α) : x + 2y− z−1= 0 và vuông góc với đường thẳng d : y = 2 + t có phương trình là:  z= 2t   x = 1+ 3tx = 1+ 5tx =1+ 6tx = 1+ 2t    
A.y = −2 + t
B.y = −2 − t C.y = 2 − − 3t
D.y = −2 + t     z = 1+ tz = 1+ 3tz = 1+ tz = 1+ 3t
Câu 39. Một bài thi trắc nghiệm khách quan gồm 10 câu hỏi, mỗi câu có 4 phương án trả lời. Xác suất
để một học sinh làm bài thi được ít nhất 8 câu hỏi là 559 580 110 109 A. B. . C. . D. . 289125 252259 262141 262144
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a , SO vuông góc với mặt
phẳng ( ABCD) và SO = .
a Khoảng cách giữa SC và AB bằng a 3 a 5 2a 3 2a 5 A. B. C. D. 15 5 15 5 Câu 41. Hàm số 4
y = −x + (m − ) 2 2
2 x + m − 3 đạt cực đại tại điểm x = 1 khi giá trị của m là A. m = 3 B. m = 5 C. m  3 D. m  5
Câu 42. Một người gửi vào ngân hàng 10 triệu đồng với lãi kép 5%/năm. Tính số tiền cả gốc lẫn lãi mà
người đó nhận được sau khi gửi ngân hàng 10 năm (gần với số nào nhất)? A. 16,234 triệu B. 16, 289 triệu C. 16, 327 triệu D. 16, 280 triệu Trang 63
Câu 43. Tất cả các giá trị của tham số m để hàm số 2
y = x + 2(m − 2) x +1 đồng biến trên khoảng (1;+) là
A. m  1
B. m  1
C. m  0
D. m  0
Câu 44. Cắt một khối trụ T bằng một mặt phẳng đi qua trục của nó ta được một hình vuông có diện tích
bằng 9. Khẳng định nào sau đây là sai? 27
A. Khối trụ T có độ dài đường sinh là l = 3
B. Khối trụ T có diện tích toàn phần S = tp 2 9
C. Khối trụ T có diện tích xung quanh S = 9
D. Khối trụ T có thể tích V = xq 4 e 1− ln x
Câu 45. Đổi biến t = ln x thì tích phân I = dx  trở thành 2 x 1 1 1 1 − A. (1−  ) t t e dt B. (1−  t)dt C. (1−  ) t t e dt D. 0 0 0 1 ( −  ) 2 1 t t e dt 0
Câu 46. Cho hàm số ( ) 3 2
f x = x + ax + bx + c. Nếu phương trình f (x) = 0 có ba nghiệm phân biệt thì phương trình ( ) ( ) = ( ( ))2 2f x .f ' x f ' x có bao nhiêu nghiệm. A. 3 B. 1 C. 2 D. 4 2 2 2 − − − +
Câu 47. Cho x, y là hai số thực dương thỏa mãn điều kiện x 2 y + = ( x 2 y + ) 2y x 2 4 9.3 4 9 .7 .Tìm giá trị x + 2y +18
nhỏ nhất của biểu thức P = . x A. P = 6 B. P =12 C. P = 9 D. P = 4
Câu 48. Cho hàm số y = f ( )
x có đạo hàm f = x ( x − )( x − )2 / 2 1
4 . Giá trị lớn nhất của hàm số 2
y = f (x ) x trên đoạn [−2;2] bằng A. f (0) B. f (1) C. f (2) D. f ( 2 − )
Câu 49. Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC,
BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi V ; V lần lượt là giá trị lớn 1 2
nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V + V ? 1 2 Trang 64 2 17 2 17 2 17 2 A. B. C. D. 12 72 144 216
Câu 50. Tập hợp các giá trị thực của tham số m để phương trình log ( 2 4 − x + log
2x + m −1 = 0 có 2019 ) 1 ( ) 2019
hai nghiệm thực phân biệt x ; x . Tính S = 2x + x 1 2 1 2 A. 8 B. 16 C. 18 D. 20 …Hết… ĐỀ 10
ĐỀ THI THỬ THPT QUỐC GIA 2020
PHÁT TRIỂN TỪ ĐỀ MINH HỌA MÔN TOÁN LẦN 2 NĂM 2020 Thời gian: 90 phút
Câu 1.(NB) Có bao nhiêu cách xếp khác nhau cho 5 người ngồi vào một bàn dài? A. 120 B. 5 C. 20 D. 25
Câu 2:(NB) Cho cấp số nhân (u có u = 3 và u = 6
− . Công bội của cấp số nhân đã cho bằng n ) 1 2 −1 A. -2 B. C. -9 D. -18 2 +
Câu 3. (NB)Phương trình 2x 1 5 =125 có nghiệm là 5 3 A. x =
. B. x = 1 . C. x = 3. D. x = . 2 2
Câu 4 (NB): Thể tích của khối lập phương bằng 8 . Khi đó cạnh của khối lập phương bằng
A. 2 B.3 C.4 D.5 1 −
Câu 5.(NB) Tìm tập xác định D của hàm số ( ) 3 f x = x .
A. D = 0; + ). B. D = \  
0 . C. D = (0; + ) . D. D = .
Câu 6.(NB)Mệnh đề nào sau đây đúng 1 A. x x
e dx = e + C ò . B.
dx = ln x + C ò . x 1 C.
dx = - tan x + C ò . D.
sin x dx = cos x + C ò . 2 cos x Trang 65
Câu 7 (NB): Cho khối lăng trụ có đáy là hình vuông cạnh a , chiều cao bằng 3a . Thể tích của khối lăng trụ đã cho bằng A. 3 3a B. 3 a C. 2 3a D. 2 a
Câu 8 (NB): Cho khối nón có bán kính đáy r = 5 , đường sinh l = 7 . Diện tích xung quanh của khối nón bằng
A. 35 B. 70 C. 2 35 D. 2 70
Câu 9 (NB): Diện tích mặt cầu có đường kính 2 bằng
A. 4 B. 16 C. 32 D. 8
Câu 10. (NB) Cho hàm số y = f ( x) có đồ thị như hình vẽ bên. Hỏi hàm số đã cho đồng biến trên
khoảng nào dưới đây ? A. ( ;8 − ) . B. (1; 4) . C. (4;+) . D. (0 ) ;1 .
Câu 11. (NB)Với a,b là hai số thực dương khác 1, ta có log a bằng: b 1
A. − log b . B. .
C. log a − logb . D. log b . a a log b a
Câu 12 (NB): Thể tích khối trụ có đường cao h , bán kinh đáy r bằng 1 1 A. 2 r h B. 2 r h C. 2 rh D. 2  rh 3 3
Câu 13.(NB)Cho hàm số y = f ( x) có bảng biến thiên như sau Trang 66
Giá trị cực tiểu của hàm số đã cho bằng A. 0 . B. 2 − . C. 1 − . D. 1.
Câu 14.(TH) Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào trong các phương án
A , B , C , D ? x − 2 −x − 2 −x −x + 2 A. y = . B. y = . C. y = . D. y = . x +1 x +1 x +1 x +1
Câu 15 (NB). Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số nào trong các hàm số sau đây? 2x − 3 3x + 2 x + 3 x −1 A. y = . B. y = . C. y = . D. y = . x −1 3x −1 x +1 2 x +1
Câu 16.(NB) Tập nghiệm của bất phương trình log 2x − 3  0 là: 3 ( )  3   5 − 3 
A. (−;2. B. ; 2   .
C. 2;+ ) . D.  ; −  .  2  2  
Câu 17(TH): Cho hàm số y = f ( x) liên tục trên
và có đồ thị như hình bên. Số nghiệm của
phương trình 2 f (x) + 7 = 0 là A. 1. B. 4. C. 2. D. 3. Trang 67 4 4 4
Câu 18. (NB)Nếu f ( x)dx = 2 − 
và g( x)dx = 6 −  thì  f
 (x)−g(x) dx  bằng: 1 1 1
A. −8 . B. 4 . C. 4 − . D. 8 .
Câu 19.(NB) Số phức liên hợp của số phức z = 2 − 3i là A. z = 2
− + 3i . B. z = 3 − 2i .
C. z = 2 + 3i .
D. z = 3 + 2i .
Câu 20.(NB) Cho hai số phức z = 3 − 2i và z = 2
− − 4i . Phần ảo của số phức z − z bằng 1 2 1 2 A. -6. B.2i . C. 2. D. 5 .
Câu 21.(NB) Điểm M trong hình vẽ bên là
điểm biểu diễn của số phức nào dưới đây ? A. z = 1− 3 . i B. z = 3 − + i C. z = 1+ 3 . i D. z = 3 − − .i
Câu 22:(TH) Trong không gian Oxyz, hình chiếu vuông góc của điểm M(2; - 3; 5) trên mặt phẳng
(Oyz) là điểm có tọa độ: A. (2;0;0) B. (2; 3 − ;0) C. (2;0;5) D. (0; 3 − ;5) 2 2 2
Câu 23: (NB)Trong không gian Oxyz, tâm của mặt cầu ( x + 3) + ( y − 2) + ( z − 3) = 9 là A. I( 3 − ;2;3) B. I(3; 2 − ; 3 − ) C. I( 3 − ; 2 − ;3) D. I(3;2; 3 − )
Câu 24:(NB) Trong không gian Oxyz, cho mặt phẳng (P): 3x − 2y + z − 4 = 0 . Vectơ nào sau đây là
vectơ pháp tuyến của (P)? A. n = (3; 2 − ; 4 − ) B. n = (3; 2 − ;0) C. n = (3; 2 − ;1) D. n = (3;0;1) 1 2 3 4 x + 2 y − 2 z
Câu 25: (TH)Trong không gian Oxyz, cho đường thẳng d : = = . Điểm nào dưới đây 5 3 1 − thuộc đường thẳng d? A. N(2; 2 − ;0) B. M ( 2 − ;2;0) C. ( P 5;3; 1 − ) D. ( Q 5 − ; 3 − ;1) Trang 68
Câu 26 (TH): Cho hình chóp tứ giác đều S.ABCD , có đáy ABCD là hình vuông tâm O . Các cạnh
bên và các cạnh đáy đều bằng a . Gọi M là trung điểm SC . Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng A. 0 45 B. 0 60 C. 0 90 D. 0 30
Câu 27.(TH) Cho hàm số y = f ( x) liên tục trên
và có bảng xét dấu của đạo hàm như hình bên.
Hàm số đã cho có bao nhiêu điểm cực trị? A. 3. B. 2. C. 1. D. 4.
Câu 28.(TH) Giá trị lớn nhất của hàm số f ( x) 3 2
= x −3x −9x +17 trên đoạn  2 − ;4.bằng A. 22. B. 55. C. 15. D. 44. Câu 29. (TH)Cho , a ,
b c là các số thực dương và khác 1 thỏa mãn log c + log c = log 2020.log c a b a b
.Mênh đề nào dưới đây đúng?.
A. abc = 2020 . B. ac = 2020. C. bc = 2020 . D. ab = 2020 .
Câu 30.(TH) Số giao điểm của đồ thị hàm số 4 2
y = x − 3x − 4 và trục hoành là A. 2. B. 3. C. 4. D. 0.
Câu 31.(TH) Cho bất phương trình x x 1 4 5.2 + −
+16  0có tập nghiệm là đoạn a;b. Giá trị của ( 2 2
log a + b ) bằng
A. 2 . B. 1. C. 0 . D. 10 .
Câu 32 (TH): Cho mặt cầu (S) có tâm I và bán kinh R . Một hình nón (N) tròn xoay có đỉnh
thuộc mặt cầu (S) , trục của (N) là một đường kính của (S) và đường tròn đáy của (N) có tâm là
I . Diện tích xung quanh của mặt nón là 3 A. 2 S = 2 R B. 2 S = 2 R C. 2 S =  R D. 2 S =  R xq xq xq 2 xq e 2 ln x e 2 ln x Câu 33. (TH) Xét dx
, nếu đặt u = ln x thì dx  bằng: x x 1 1 Trang 69 1 1 1 e A. 2 u du  . B. 2 − u du  . C. d u u  . D. 2 u du  . 0 0 0 1
Câu 34.(TH) Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số ex y =
, y = 2 , x = 0 , x =1
được tính bởi công thức nào dưới đây? 1 ln 2 1 A. = (ex S − 2)dx . B.
=  (ex −2)d +  (ex S x − 2)dx . 0 0 ln 2 ln 2 1 ln 2 1 C.
=  (ex −2)d −  (ex S x − 2)dx. D.
= −  (ex −2)d +  (ex S x − 2)dx . 0 ln 2 0 ln 2
Câu 35:(TH) Tìm phần ảo b của số phức z = 3i(4 + 2i) A. b = 12 B. b = 6
C. b =12i D. b = 3
Câu 36(TH)Gọi z và z là hai nghiệm phức của pt : 2
9z + 6z + 4 = 0. Giá trị của biểu thức 1 2 1 1 + bằng z z 1 2 4 3 9 A. . B. 3. C. . D. . 3 2 2
Câu 37:(TH) Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 3; 5) và đường thẳng x +1 y + 2 z − 2 d : = =
. Phương trình mặt phẳng (P) đi qua M và vuông góc với đường thẳng d là: 1 3 2
A. (P) : x + 3y + 2z + 21 = 0 B. ( )
P : 2x + 3y + 5z + 21 = 0 C. ( )
P : x + 3y + 2z − 21 = 0 D. ( )
P : 2x + 3y + 5z − 21 = 0
Câu 38: (TH)Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;3; 5 − ) và đường thẳng x = −2 + 2t
 : y = 3− 4t . Phương trình tham số của đường thẳng d đi qua M và song song với  là: z = 5 − t  x = 2 − 2tx = 2 − + 2tx = 2 − + 2tx = 2 + 2t    
A. y = 3 + 3t
B. y = 3 − 4t
C. y = 3 − 4t
D. y = 3 − 4t     z = −5  z = 5 − − 5tz = 5 − 5tz = 5 − − 5t
Câu 39: (VD)Một người bắn 3 viên đạn. Xác suất để trúng cả 3 viên vòng 10 là 0,008, xác suất để 1
viên trúng vòng 8 là 0,15 và xác suất để 1 viên trúng vòng dưới 8 là 0,4.(Các vòng bắn dĩ nhiên độc
lập với nhau). Xác suất để xạ thủ đạt ít nhất 28 điểm là A. 0,0935 B. 0,0835 C.0,32 D. 0,035 Trang 70
Câu 40 (VD): Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a . Hai mặt bên (SA ) B và (SA )
D cùng vuông góc với mặt phẳng đáy và SA = a 2 . Khoảng cách giữa SO và AB bằng a 2 a 6 a 3 A.
B. a C. D. 3 3 4
Câu 41 (VD): Cho hàm số y = −x3 − mx2 + (−3m + 6)x + 5 với m là tham số. Có bao nhiêu giá trị
nguyên của m để hàm số nghịch biến trên khoảng (−∞; +∞)? A. 2. B. 3. C. 4. D. 5.
Câu 42.(VD) Dân số thế giới được dự đoán theo công thức = . Nr
S Ae (trong đó A : là dân số của
năm lấy làm mốc tính, Slà dân số sau N năm, r là tỉ lệ tăng dân số hàng năm). Theo số liệu thực tế,
dân số thế giới năm 1950 là 2560 triệu người; dân số thế giới năm 1980 là 3040 triệu người. Hãy dự
đoán dân số thế giới năm 2020? A. 3823triệu.
B. 5360 triệu.
C. 3954 triệu. D. 4017 triệu.
Câu 43(VD).Cho hàm số = ( ) 3 2 y
f x = x + ax + bx + c có bảng biến thiên như hình vẽ sau:
Tính giá trị của biểu thức P = a + b + 3 . c A. P = 3 − . B. P = 9 − . C. P = 3 . D. P = 9 .
Câu 44 (VD): Trong số các hình trụ có diện tích toàn phần đều bằng S thì bán kính R và chiều cao
h của khối trụ có thể tích lớn nhất là: S S S S A.. R = ; h = 2 B. R = ; h = . 6 6 4 4 2S 2S S 1 S C. R = ; h = 4 . D. R = ; h = . 3 3 2 2 2    8
Câu 45. (VD) Cho hàm số f ( x) có f = −   và f ( x) 2 =16cos4 . x sin , x x   . Khi đó  4  3  f  (x)dxbằng 0 16 64 4 A. . B. . C. − . D. 0 . 3 27 3
Câu 46. (VDC)Cho hàm số = ( ) 2 y
f x = ax + bx + c có đồ thị (C) (như hình vẽ): Trang 71
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
f ( x ) + (m − 2) f ( x ) + m − 3 = 0 có 6 nghiệm phân biệt? A. 1. B. 4. C. 3. D. 2. Câu 47.(VDC) Cho , a ,
b c 1. Biết rằng biểu thức P = log (bc) + log (ac) + 4log ab đạt giá trị a b c ( )
nhỏ nhất bằng m khi log c = n . Tính giá trị m + n . b 25
A. m + n = 14 .
B. m + n = .
C. m + n = 12 .
D. m + n = 10 . 2
Câu 48. (VDC)Bạn Vân chèo thuyền từ điểm A trên một bờ sông thẳng rộng 3km và muốn đến
điểm B cách 8km xuôi dòng trên bờ đối diện, càng nhanh càng tốt (như hình vẽ). Bạn Vân có thể
chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B , hay có thể chèo trực tiếp
đến B , hoặc bạn ấy có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B . Biết
bạn ấy có thể chèo thuyền 6km / h , chạy 8km / h . Biết tốc độ của dòng nước là không đáng kể so với
tốc độ chèo thuyền. Điểm D cách A bao xa để bạn Vân đến B nhanh nhất? 9 (1+ 7 ) 12 A. 73 B. C. 3 D. . 7 7
Câu 49 (VDC): Cho tứ diện S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho
MA = 2SM , SN = 2NB , ( ) là mặt phẳng qua MN và song song với SC . Kí hiệu (H ) và (H ) là 1 2
các khối đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng ( ) , trong đó, (H ) chứa 1 điể V
m S , (H ) chứa điểm A ; V và V lần lượt là thể tích của (H ) và (H ) . Tính tỉ số 1 2 1 2 1 2 V2 4 5 3 4 A. B. C. D. 5 4 4 3
Câu 50.(VDC) Có bao nhiêu số nguyên m(0;2018) để phương trình +10 x m x = me có hai nghiệm phân biệt? A. 9. B. 2017. C. 2016. D. 2007. Trang 72
ĐÁP ÁN VÀ LỜI GIẢI
Câu 1.(NB) Có bao nhiêu cách xếp khác nhau cho 5 người ngồi vào một bàn dài? A. 120 B. 5 C. 20 D. 25
Lời giải. Số cách sắp xếp khác nhau cho 5 người ngồi vào một bàn dài là một hoán vị của 5 phần tử nên có 5! = 120 cách. Chọn A.
Câu 2:(NB) Cho cấp số nhân (u có u = 3 và u = 6
− . Công bội của cấp số nhân đã cho bằng n ) 1 2 −1 A. -2 B. C. -9 D. -18 2 u
Lời giải. Ta có công bội của cấp số nhân là 2 q = = 2. − u1 Chọn A. +
Câu 3. (NB)Phương trình 2x 1 5 =125 có nghiệm là 5 3 A. x = .
B. x = 1 .
C. x = 3. D. x = . 2 2 Ta có: 2x 1 5 + =125 2x 1 + 3  5
= 5  2x +1= 3  x =1. Chọn B
Câu 4 (NB): Thể tích của khối lập phương bằng 8 . Khi đó cạnh của khối lập phương bằng
A. 2 B.3 C.4 D.5 Đáp án A 1 −
Câu 5.(NB) Tìm tập xác định D của hàm số ( ) 3 f x = x .
A. D = 0; + ). B. D = \   0 .
C. D = (0; + ) . D. D = .
Điều kiện: x  0. Vậy D = (0;+). Chọn C Câu 6.
(NB)Mệnh đề nào sau đây đúng 1 A. x x
e dx = e + C ò . B.
dx = ln x + C ò . x Trang 73 1 C.
dx = - tan x + C ò . D.
sin x dx = cos x + C ò . 2 cos x
Từ bảng nguyên hàm cơ bản ta chọn đáp án A. Chọn A
Câu 7 (NB): Cho khối lăng trụ có đáy là hình vuông cạnh a , chiều cao bằng 3a . Thể tích của khối lăng trụ đã cho bằng A. 3 3a B. 3 a C. 2 3a D. 2 a Đáp án A
Câu 8 (NB): Cho khối nón có bán kính đáy r = 5 , đường sinh l = 7 . Diện tích xung quanh của khối nón bằng
A. 35 B. 70 C. 2 35 D. 2 70 Đáp án A
Câu 9 (NB): Diện tích mặt cầu có đường kính 2 bằng
A. 4 B. 16 C. 32 D. 8 Đáp án A
Câu 10. (NB) Cho hàm số y = f ( x) có đồ thị như hình vẽ bên. Hỏi hàm số đã cho đồng biến trên
khoảng nào dưới đây ? A. ( ;8 − ) . B. (1; 4) . C. (4;+) . D. (0 ) ;1 . Lời giải Chọn D Trang 74
Xét từ trái sang phải, Đáp án A,B loại vì trong khoảng (1; 4) đồ thị hàm số đi xuống nên hàm số
nghịch biến, đáp án C loại vì trong khoảng (4;9) đồ thị hàm số là một đường song song trục Ox nên hàm số không đổi.
Đáp án D, trên khoảng (0;1) đồ thị hàm số đi lên liên tục nên hàm số đồng biến trên khoảng đó. Chọn D.
Câu 11. (NB)Với a,b là hai số thực dương khác 1, ta có log a bằng: b 1
A. − log b . B. .
C. log a − logb . D. log b . a a log b a 1
Với a,b là hai số thực dương khác 1và theo công thức đổi cơ số: log a = . b log b a Chọn B
Câu 12 (NB): Thể tích khối trụ có đường cao h , bán kinh đáy r bằng 1 1 A. 2 r h B. 2 r h C. 2 rh D. 2  rh 3 3 Đáp án A
Câu 13.(NB)Cho hàm số y = f ( x) có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng A. 0 . B. 2 − . C. 1 − . D. 1. Lời giải Chọn C
Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại x = 1 và giá trị cực tiểu là y = 1 − . CT
Câu 14.(TH) Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào trong các phương án
A , B , C , D ? Trang 75 x − 2 −x − 2 −x −x + 2 A. y = . B. y = . C. y = . D. y = . x +1 x +1 x +1 x +1 Lời giải Chọn D
Từ hình vẽ ta nhận thấy hàm số cần tìm có đồ thị hàm số cắt trục tung, trục hoành lần lượt tại hai
điểm (0;2) và (2;0) nên các đáp án A , B , C đều loại và thấy D là đáp án đúng. Chọn D.
Câu 15 (NB). Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số nào trong các hàm số sau đây? 2x − 3 3x + 2 x + 3 x −1 A. y = . B. y = . C. y = . D. y = . x −1 3x −1 x +1 2 x +1 Lời giải Chọn A
Câu 16.(NB) Tập nghiệm của bất phương trình log 2x − 3  0 là: 3 ( )  3   5 − 3 
A. (−;2. B. ; 2   .
C. 2;+ ) . D.  ; −  .  2  2   3
Điều kiện: x  . 2 Do 3 + 5  1nên log
(2x −3)  0  2x −31 x  2. 3+ 5
Đối chiếu điều kiện ta có tập nghiệm của bất phương trình là 2;+) . Chọn C. Trang 76
Câu 17(TH): Cho hàm số y = f ( x) liên tục trên
và có đồ thị như hình bên. Số nghiệm của
phương trình 2 f (x) + 7 = 0 là A. 1. B. 4. C. 2. D. 3. Lời giải Chọn B 7
2 f (x) + 7 = 0  f (x) = − 2
Số nghiệm của phương trình 7 f (x) = −
bằng số giao điểm của đồ thị hàm số y = f ( ) x với đường 2 7 thẳng y = −
. Dựa vào đồ thị hàm số y = f ( )
x suy ra số nghiệm phương trình bằng 4. 2 4 4 4
Câu 18. (NB)Nếu f ( x)dx = 2 − 
và g( x)dx = 6 −  thì  f
 (x)−g(x) dx  bằng: 1 1 1 A. −8 . B. 4 . C. 4 − . D. 8 . 4 4 4 Ta có  f
 (x)− g(x)dx = f   (x)dx − g  (x)dx = ( 2 − ) − ( 6 − ) = 4 . 1 1 1 Chọn B
Câu 19.(NB) Số phức liên hợp của số phức z = 2 − 3i là A. z = 2
− + 3i . B. z = 3 − 2i . C. z = 2 + 3i .
D. z = 3 + 2i .
Câu 20.(NB) Cho hai số phức z = 3 − 2i và z = 2
− − 4i . Phần ảo của số phức z − z bằng 1 2 1 2 A. -6. B.2i . C. 2. D. 5 . Lời giải Chọn C Trang 77
z − z = 5 + 2i 1 2
Phần ảo của z − z bằng 2 1 2
Câu 21.(NB) Điểm M trong hình vẽ bên là
điểm biểu diễn của số phức nào dưới đây ? A. z = 1− 3 . i B. z = 3 − + i C. z = 1+ 3 . i D. z = 3 − − .i Lời giải Chọn A M (1; 3
− )  z =1−3i
Câu 22:(TH) Trong không gian Oxyz, hình chiếu vuông góc của điểm M(2; - 3; 5) trên mặt phẳng
(Oyz) là điểm có tọa độ: A. (2;0;0) B. (2; 3 − ;0) C. (2;0;5) D. (0; 3 − ;5) Lời giải.
Hình chiếu vuông góc của điểm M(2; - 3; 5) trên mặt phẳng (Oyz) là điểm có tọa độ: (0; 3 − ;5) Chọn D 2 2 2
Câu 23: (NB)Trong không gian Oxyz, tâm của mặt cầu ( x + 3) + ( y − 2) + ( z − 3) = 9 là A. I ( 3 − ;2;3) B. I(3; 2 − ; 3 − ) C. I( 3 − ; 2 − ;3) D. I (3;2; 3 − ) Lời giải.
Mặt cầu có tâm I ( 3 − ;2;3) Trang 78 Chọn A.
Câu 24:(NB) Trong không gian Oxyz, cho mặt phẳng (P): 3x − 2y + z − 4 = 0 . Vectơ nào sau đây là
vectơ pháp tuyến của (P)? A. n = (3; 2 − ; 4 − ) B. n = (3; 2 − ;0) C. n = (3; 2 − ;1) D. n = (3;0;1) 1 2 3 4 Lời giải.
Vectơ vectơ pháp tuyến của (P) là n = (3; 2 − ;1) 3 Chọn C. x + 2 y − 2 z
Câu 25: (TH)Trong không gian Oxyz, cho đường thẳng d : = = . Điểm nào dưới đây 5 3 1 − thuộc đường thẳng d? A. N(2; 2 − ;0) B. M ( 2 − ;2;0) C. ( P 5;3; 1 − ) D. ( Q 5 − ; 3 − ;1) Lời giải.
Điểm thuộc đường thẳng d là M( 2 − ;2;0) Chọn B.
Câu 26 (TH): Cho hình chóp tứ giác đều S.ABCD , có đáy ABCD là hình vuông tâm O . Các cạnh
bên và các cạnh đáy đều bằng a . Gọi M là trung điểm SC . Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng A. 0 45 B. 0 60 C. 0 90 D. 0 30 Đáp án A
Hướng dẫn giải:
Gọi M ' là trung điểm OC . 2 1 1 a a 2 Ta có : S = M . O BD = . .a 2 = ; MBD 2 2 2 4 2 1 1 1 a S =  = =   M . O BD . .a 2.a 2 . Do đó BM D 2 2 4 4 S  2 BM D 0 cos = =  = 45 S 2 BMD
Câu 27.(TH) Cho hàm số y = f ( x) liên tục trên
và có bảng xét dấu của đạo hàm như hình bên.
Hàm số đã cho có bao nhiêu điểm cực trị? Trang 79 A. 3. B. 2. C. 1. D. 4. Lời giải Chọn D
Ta có f’(x) đổi dấu khi qua x = -1 ; x = 0 ; x = 2; x = 4 nên hàm số đã cho có 4 điểm cực trị.
Câu 28.(TH) Giá trị lớn nhất của hàm số f ( x) 3 2
= x −3x −9x +17 trên đoạn  2 − ;4.bằng A. 22. B. 55. C. 15. D. 44. Lời giải Chọn A f ( x) 3 2
= x −3x −9x +17 2
f '(x) = 3x − 6x − 9 x = 3
f '(x) = 0   x = 1 − f ( 2 − ) =15; f ( 1 − ) = 22; f (3) = 1 − 0; f (4) = 3 −
Giá trị lớn nhất của hàm số trên đoạn [-2;4] là 22. Câu 29. (TH)Cho , a ,
b c là các số thực dương và khác 1 thỏa mãn log c + log c = log 2020.log c a b a b
.Mênh đề nào dưới đây đúng?.
A. abc = 2020 .
B. ac = 2020.
C. bc = 2020 . D. ab = 2020 .
Ta có: log c + log c = log 2020.log c a b a b 1 1 log 2020 1 c  + = .
(công thức đổi cơ số) log a log b log a log b c c c c
 log a + log b = log 2020 c c c
 log ab = log 2020  ab = 2020. c c Chọn D.
Câu 30.(TH) Số giao điểm của đồ thị hàm số 4 2
y = x − 3x − 4 và trục hoành là A. 2. B. 3. C. 4. D. 0. Trang 80 Lời giải Chọn A
Phương trình hoành độ giao điểm của đồ thị hàm số 4 2
y = x − 3x − 4 và trục hoành: 2 x = 1 −  0(l) 4 2
x − 3x − 4 = 0   2 x = 4 2 x = 4  x = 2 
Số nghiệm phương trình là số giao điểm của đồ thị hàm số 4 2
y = x − 3x − 4 và trục hoành.
Phương trình có 2 nghiệm phân biệt nên đồ thị hàm số 4 2
y = x − 3x − 4 và trục hoành có 2 giao điểm.
Câu 31.(TH) Cho bất phương trình x x 1 4 5.2 + −
+16  0có tập nghiệm là đoạn a;b. Giá trị của ( 2 2
log a + b ) bằng
A. 2 . B. 1. C. 0 . D. 10 . Bất phương trình x x 1 4 5.2 + − +16  0 4x 10.2x 16 0 2 2x  − +     8 1 x  3.
Vậy tập nghiệm của bất phương trình là 1;  3 .
Suy ra a =1;b = 3 nên ( 2 2 a + b ) = ( 2 2 log log 1 + 3 ) = 1. Chọn B
Câu 32 (TH): Cho mặt cầu (S) có tâm I và bán kinh R . Một hình nón (N) tròn xoay có đỉnh
thuộc mặt cầu (S) , trục của (N) là một đường kính của (S) và đường tròn đáy của (N) có tâm là
I . Diện tích xung quanh của mặt nón là 3 A. 2 S = 2 R B. 2 S = 2 R C. 2 S =  R D. 2 S =  R xq xq xq 2 xq Đáp án A Hướng dẫn:
Gọi r,l lần lượt là bán kinh và đường sinh của hình nón (N) .
Từ giả thiết, ta có r = , R h = R 2 2 2
S =  rl =  R R + R = 2 R xq e 2 ln x e 2 ln x Câu 33. (TH) Xét dx
, nếu đặt u = ln x thì dx  bằng: x x 1 1 Trang 81 1 1 1 e A. 2 u du  . B. 2 − u du  . C. d u u  . D. 2 u du  . 0 0 0 1 Đặ 1
t u = ln x  du = dx . x
Với x = 1 u = 0
Với x = e u = 1 e 2 1 ln x Vậy 2 dx = u du   . x 1 0 Chọn A Câu 34.
(TH) Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số ex y =
, y = 2 , x = 0 ,
x = 1 được tính bởi công thức nào dưới đây? 1 ln 2 1 A. = (ex S − 2)dx . B.
=  (ex −2)d +  (ex S x − 2)dx . 0 0 ln 2 ln 2 1 ln 2 1 C.
=  (ex −2)d −  (ex S x − 2)dx. D.
= −  (ex −2)d +  (ex S x − 2)dx . 0 ln 2 0 ln 2 1 Diện tích cần tìm là: = ex S − 2 dx  . 0
Xét ex − 2 = 0  x = ln 2 .
Bảng xét dấu ex − 2 : x 0 ln 2 1 ex − 2 − 0 + 1 ln 2 1 Ta có = ex S − 2 dx
= −  (ex −2)d +  (ex x − 2)dx 0 0 ln 2 Chọn D.
Câu 35:(TH) Tìm phần ảo b của số phức z = 3i(4 + 2i) A. b = 12 B. b = 6
C. b =12i D. b = 3 Lời giải Chọn A Trang 82
z = 3i(4 + 2i) = -6+12i
Câu 36(TH)Gọi z và z là hai nghiệm phức của pt : 2
9z + 6z + 4 = 0. Giá trị của biểu thức 1 2 1 1 + bằng z z 1 2 4 3 9 A. . B. 3. C. . D. . 3 2 2 Lời giải Chọn B 1 − + 3i 1 − − 3i Phương trình 2
9z + 6z + 4 = 0 có 2 nghiệm phức : z = ; z = 1 2 3 3 1 1 + = 3 z z 1 2
Câu 37:(TH) Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 3; 5) và đường thẳng x +1 y + 2 z − 2 d : = =
. Phương trình mặt phẳng (P) đi qua M và vuông góc với đường thẳng d là: 1 3 2
A. (P) : x + 3y + 2z + 21 = 0 B. ( )
P : 2x + 3y + 5z + 21 = 0 C. ( )
P : x + 3y + 2z − 21 = 0 D. ( )
P : 2x + 3y + 5z − 21 = 0 Lời giải
Vì (P) vuông góc với d nên vectơ chỉ phương của d là vectơ pháp tuyến của (P)
d có vectơ chỉ phương là a = (1;3;2)
Phương trình mặt phẳng (P) là:
x − 2 + 3(y −3) + 2(z −5) = 0
x − 2+3y −9+ 2z −10 = 0
x +3y + 2z − 21= 0 Chọn C
Câu 38: (TH)Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;3; 5 − ) và đường thẳng x = −2 + 2t
 : y = 3− 4t . Phương trình tham số của đường thẳng d đi qua M và song song với  là: z = 5 − t  Trang 83 x = 2 − 2tx = 2 − + 2tx = 2 − + 2tx = 2 + 2t    
A. y = 3 + 3t
B. y = 3 − 4t
C. y = 3 − 4t
D. y = 3 − 4t     z = −5  z = 5 − − 5tz = 5 − 5tz = 5 − − 5t  Lời giải
Vì d song song với  nên vectơ chỉ phương của  cũng là vec tơ chỉ phương của d
 có vectơ chỉ phương là a = (2; 4 − ; 5 − ) x = 2 + 2t
Phương trình tham số của đường thẳng d là y = 3− 4t z = 5 − − 5t  Chọn D.
Câu 39: (VD)Một người bắn 3 viên đạn. Xác suất để trúng cả 3 viên vòng 10 là 0,008, xác suất để 1
viên trúng vòng 8 là 0,15 và xác suất để 1 viên trúng vòng dưới 8 là 0,4.(Các vòng bắn dĩ nhiên độc
lập với nhau). Xác suất để xạ thủ đạt ít nhất 28 điểm là A. 0,0935 B. 0,0835 C.0,32 D. 0,035 Lời giải.
Gọi A là biến cố “1 viên trúng vòng 10”. Khi đó theo giả thiết: 3 (P( )
A ) = 0, 008  P( ) A = 0, 2
Gọi B là biến cố “1 viên trúng vòng 9”.
Gọi C là biến cố “1 viên trúng vòng 8”.
Gọi D là biến cố “1 viên trúng vòng dưới 8”.
Theo giả thiết ta có : P(C)=0,15; P(D)=0,4.
Vì A B C D =  . Rõ ràng các biến cố này đôi một xung khắc nên ta có :
1 = P( A B C D) = P( )
A + P(B) + P(C) + P(D)
= 0,2 + P(B) + 0,15 + 0,4  P(B) = 0,25
Gọi X là biến cố “xạ thủ đạt ít nhất 28 điểm”
Để đạt ít nhất 28 điểm thì
- Hoặc là 2 viên trúng vòng 10, 1 viên trúng vòng 8;
- Hoặc là 2 viên trúng vòng 9, 1 viên trúng vòng 10;
- Hoặc là 2 viên trúng vòng 10, 1 viên trúng vòng 9;
- Hoặc là 2 viên trúng vòng 10, 1 viên trúng vòng 9;
- Hoặc là cả 3 viên trúng vòng 10.
Từ đó dựa vào quy tắc nhân và quy tắc cộng xác suất, ta có: 2 2 2 2 2 2
P( X ) = C (0, 2) (0,15) + C (0, 25) (0, 2) + C (0, 2) (0, 25) + 0, 008 = 0, 0935 3 3 3 Chọn A. Trang 84
Câu 40 (VD): Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a . Hai mặt bên (SA ) B và (SA )
D cùng vuông góc với mặt phẳng đáy và SA = a 2 . Khoảng cách giữa SO và AB bằng a 2 a 6 a 3 A.
B. a C. D. 3 3 4 Đáp án A Hướng dẫn:
Gọi E là trung điểm của AD . Khi đó: d (S ;
O AB) = d ( A ;
B (SOE )) = AH , với H là
hình chiếu của A lên SE . a a 2. S . A AE a 2 Ta có. 2 AH = = = 2 2 2 + 3 SA AE a 2 2a + 4
Câu 41 (VD): Cho hàm số y = −x3 − mx2 + (−3m + 6)x + 5 với m là tham số. Có bao nhiêu giá trị
nguyên của m để hàm số nghịch biến trên khoảng (−∞; +∞)? A. 2. B. 3. C. 4. D. 5. Lời giải Chọn C. 2 y ' = 3x − − 2mx + ( 3 − m + 6)
Để hàm số nghịch biến trên R  y'  0, x  R 2 2  m + 3( 3
− m + 6)  0  m − 9m +18  0  3  m  6
Suy ra có 4 giá trị nguyên của m thỏa đề bài.
Câu 42.(VD) Dân số thế giới được dự đoán theo công thức = . Nr
S Ae (trong đó A : là dân số của
năm lấy làm mốc tính, Slà dân số sau N năm, r là tỉ lệ tăng dân số hàng năm). Theo số liệu thực tế,
dân số thế giới năm 1950 là 2560 triệu người; dân số thế giới năm 1980 là 3040 triệu người. Hãy dự
đoán dân số thế giới năm 2020? Trang 85 A. 3823triệu.
B. 5360 triệu.
C. 3954 triệu. D. 4017 triệu. ìï S ï (195 ) 1950.r 6 0 = A.e = 2560.10 Ta có: í ï S ï (198 ) 1 . 980 r 6 0 = A.e = 3040.10 ïî 6 r 304 r 19 2560.10 Suy ra: 30 30 e = Þ e = và A = 256 16 1950r e 2560.10 .( r e )2020 6 70 Vậy: S (202 ) 2020.r 6 0 = A.e = = 2560.10 . r e ; 3823.10 . 950 1 ( ) 6 ( r e ) Chọn A Câu 43(VD). Cho hàm số = ( ) 3 2 y
f x = x + ax + bx + c có bảng biến thiên như hình vẽ sau:
Tính giá trị của biểu thức P = a + b + 3 . c A. P = 3 − . B. P = 9 − . C. P = 3 . D. P = 9 . Lời giải Chọn A. 2
f '(x) = 3x + 2ax + b f '( 1 − ) = 0  2 − a + b = 3 − a = 3 −
Từ bảng biến thiên ta thấy:       f '(3) = 0 6a + b = 27 − b  = 9 −  f (3) = 2 − 4   f (3) = 2
− 4  27 + 9a + 3b + c = 2 − 4  c = 3  f ( 1
− ) = a − b + c −1(hn) P=a+b+3c=-3
Câu 44 (VD): Trong số các hình trụ có diện tích toàn phần đều bằng S thì bán kính R và chiều cao
h của khối trụ có thể tích lớn nhất là: S S S S A.. R = ; h = 2 B. R = ; h = . 6 6 4 4 2S 2S S 1 S C. R = ; h = 4 . D. R = ; h = . 3 3 2 2 2 Trang 86 Đáp án A Hướng dẫn:
Gọi thể tích khối trụ là V , diện tích toàn phần của hình trụ là S . Ta có: 2 S = S
+ S = 2 R + 2 Rh . Từ đó suy ra: 2day xq Cauchy 2 S S V V V V 2 2 2 3 = R + Rh  = R + = R + + 3  2 2 2  R 2 R 2 R 4 3 2 3 VS S hay 27   V    . 2 4  2  54 3 S 2 VR h Rh Vậy V = . Dấu “=” xảy ra  2 R = = = hay h = 2R . max 54 2 R 2 R 2 Khi đó S S 2
S = 6 R R = và h = 2R = 2 . 6 6    8
Câu 45. (VD) Cho hàm số f ( x) có f = −   và f ( x) 2 =16cos4 . x sin , x x   . Khi đó  4  3  f  (x)dxbằng 0 16 64 4 A. . B. . C. − . D. 0 . 3 27 3 Ta có f ( x) 2 =16cos4 . x sin , x x
  nên f (x) là một nguyên hàm của f (x) . 1− cos 2x Có f   (x) 2 dx = 16 cos 4 . x sin d x x = 16.cos 4 . x dx = 8.cos 4 d x x − 8cos 4 . x cos 2 d x x     2 = x x − ( x + x) 2 8 cos 4 d 4 cos 6 cos 2 dx = 2sin 4x −
sin 6x − 2sin 2x +   C . 3    8 4 Suy ra f ( x) 2
= 2sin 4x − sin 6x − 2sin 2x + C . Mà f = −  C = −   . 3  4  3 3 Do đó. Khi đó:    f (x)  2 4  4 dx =
2sin 4x − sin 6x − 2sin 2x − dx = −    3 3  3 0 0 Chọn C.
Câu 46. (VDC)Cho hàm số = ( ) 2 y
f x = ax + bx + c có đồ thị (C) (như hình vẽ): Trang 87
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
f ( x ) + (m − 2) f ( x ) + m − 3 = 0 có 6 nghiệm phân biệt? A. 1. B. 4. C. 3. D. 2. Lời giải Chọn C Phương trình 2
f ( x ) + (m − 2) f ( x ) + m − 3 = 0
f ( x ) = −m + 3(1)    f ( x ) = 1 − (2)  Từ đồ thị hàm số = ( ) 2 y
f x = ax + bx + c ta vẽ được đồ thị hàm số y = f ( x ) 8 6 4 2 5 5 2
Từ đồ thị hàm số, suy ra phương trình (2) có 2 nghiệm. Để phương trình 2
f ( x ) + (m − 2) f ( x ) + m − 3 = 0 có 6 nghiệm phân biệt thì phương trình (1) có 4 nghiệm phân biệt
khi đó 0  m  4. Suy ra có 3 giá trị nguyên của m thỏa đề bài.. Câu 47.(VDC) Cho , a ,
b c 1. Biết rằng biểu thức P = log (bc) + log (ac) + 4log ab đạt giá trị a b c ( )
nhỏ nhất bằng m khi log c = n . Tính giá trị m + n . b Trang 88 25
A. m + n = 14 .
B. m + n = .
C. m + n = 12 .
D. m + n = 10 . 2 Do , a , b c 1 nên log ,
b log a, log c  0 . a c b
P = log (bc) + log (ac) + 4log (ab) = log b + log c + log a + log c + 4log a + 4log b a b c a a b b c a
= (log b + log a) +(log c + 4log a) +(log c + 4log b a b a c b c )  1   1   4  = log b +  + 
+ 4log a +log c +  a log b log c b a log ca   c   b  1 1 4  2 log · b + 2 ·4 log a + 2 log · c = 2 + 4 + 4 =10 . a log b log c b a log c a c b  1 log b =  a log b log b =1 a a    1  1
Dấu “ = ” xảy ra khi và chỉ khi 
= 4log a  log a = log c c a 2  c   log c = 2 4  b log c = b log bc
Vậy, đạt giá trị nhỏ nhất là 10 khi log c = 2  m = 10 , n = 2  m + n = 12 . b Chọn C.
Câu 48. (VDC)Bạn Vân chèo thuyền từ điểm A trên một bờ sông thẳng rộng 3km và muốn đến
điểm B cách 8km xuôi dòng trên bờ đối diện, càng nhanh càng tốt (như hình vẽ). Bạn Vân có thể
chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B , hay có thể chèo trực tiếp
đến B , hoặc bạn ấy có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B . Biết
bạn ấy có thể chèo thuyền 6km / h , chạy 8km / h . Biết tốc độ của dòng nước là không đáng kể so với
tốc độ chèo thuyền. Điểm D cách A bao xa để bạn Vân đến B nhanh nhất? 9 (1+ 7 ) 12 A. 73 B. C. 3 D. . 7 7 Trang 89 Lời giải Chọn D
Đặt CD = x . Quãng đường chạy bộ DB = 8 − x và quãng đường chèo thuyền 2 AD = 9 + x .( (0  x  8) 2 + − Khi đó, thờ 9 x 8 x i gian chèo thuyền là
và thời gian chạy bộ là . 6 8 2 x + 9 8 − x
Tổng thời gian mà bạn Vân cần có là: T (x) = + , x  [0;8]. 6 8 x 1 Ta có: T '(x) = − . 2 + 8 6 x 9 x 1 9 2 2 2 2 T '(x) = 0 
=  4x = 3 x + 9 16x = 9(x + 9)  7x = 81 x = . 2 + 8 6 x 9 7 3  9  7 73 Ta có: T (0) = ; T =1+   ; T (8) = . 2  7  8 6   Do đó: 9 7
min T (x) = T =1+   . [0;8]  7  8 Vậy để bạn Vân đến 81
B nhanh nhất : AD = 9 + 12 = . 7 7
Câu 49 (VDC): Cho tứ diện S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho
MA = 2SM , SN = 2NB , ( ) là mặt phẳng qua MN và song song với SC . Kí hiệu (H ) và (H ) là 1 2 Trang 90
các khối đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng ( ) , trong đó, (H ) chứa 1 điể V
m S , (H ) chứa điểm A ; V và V lần lượt là thể tích của (H ) và (H ) . Tính tỉ số 1 2 1 2 1 2 V2 4 5 3 4 A. B. C. D. 5 4 4 3 Đáp án A Hướng dẫn:
Kí hiệu V là thể tích khối tứ diện SABC .
Gọi P , Q lần lượt là giao điểm của ( ) với các đường thẳng BC , AC . Ta có NP//M /
Q /SC . Khi chia khối (H ) bởi mặt phẳng (QNC) , ta được hai khối chóp N.SMQC và 1 N.QPC . Ta có: V d N SAC S N SMQC ( , ( )) . SMQC =  ; V d (B, (SAC)) S B. ASC SAC S
d (N , (SAC)) NS 2 = = ; d (B, (SAC)) BS 3 M 2 SAM S AMQ 4 SMQC 5 = =  =   SAS  9 S 9 ASC ASC N VN SMQC 2 5 10 Suy ra . =  = V 3 9 27 C B. ASC A Q P V d N C S B N .QP C ( , (QP )) QPC =  V
d (S, (A BC)) S S . ABC ABC NB CQ CP 1 1 2 2 =   ==   = SB CA CB 3 3 3 27 V V V N .SMQC N .QPC 10 2 4 V 4 V 4 1 1 = + = + =  =  5V = 4V 1  = 1 2 V V V 27 27 9 V +V 9 V 5 B. ASC S . ABC 1 2 2
Câu 50.(VDC) Có bao nhiêu số nguyên m(0;2018) để phương trình +10 x m x = me có hai nghiệm phân biệt? Trang 91 A. 9. B. 2017. C. 2016. D. 2007.
Với x = 0, phương trình trở thành m = m (luôn đúng), suy ra với mọi m(0;2018) phương trình
luôn có 1 nghiệm x = 0. x x 10
Với x  0 , ta có m +10x = me m = . x e −1 10( x x e − xe − ) x 1
Xét hàm số y = f ( x) 10 = trên \  
0 , ta có f ( x) =  0 x   \ 0 . 2   x e −1 ( xe − )1
Thật vậy, xét hàm số ( ) x x
g x = e − xe −1 . Ta có ( ) x = − ( x x + ) x g x e e xe = −xe .
Ta có bảng biến thiên như sau: x − 0 + g( x) + 0 – 0 g ( x) − −
Bảng biến thiên hàm số y = f ( x) x − 0 + f ( x) + 0 – + 10 f ( x) 10 0 0  m  2018
Suy ra yêu cầu bài toán thỏa mãn khi và chỉ khi  m  10
Do đó, có 2016 số nguyên m thỏa mãn yêu cầu bài toán. Chọn C. Trang 92