Bộ đề thi thử thpt quốc gia 2020 toán bám sát đề minh họa - tập 5

SỞ GD & ĐT ĐỒNG THÁP
ĐỀ THI HỌC KỲ II–NĂM HỌC2019 - 2020
TRƯỜNG THPT THANH BÌNH 1
MÔNTOÁN - KHỐI LỚP 12 Ngày thi: 22/06/2020
ĐỀ THI CHÍNH THỨC
Thời gian làm bài : 90Phút; (Đề có 50 câu) (Đề có 6 trang)
Họ tên:............................................................... Số báo danh:................... Mã đề133
Câu 1: Với F (x) là một nguyên hàm của hàm số f (x) khi đó A. kf
 xdx  kF(x)C . B. f
 xdx  F(x). C. kf
 xdx  kF(x). D. kf
 xdx  F(x)C .
Câu 2: Cho số phức z  2
  3i . Số phức liên hợp của z là A. z  13 . B. z  2  3i .
C. z  3 2i .
D. z  2  3i .
Câu 3: Cho hàm số y  f  x liên tục trên [a;b] . Diện tích hình phẳng (H ) giới hạn bởi đồ thị hàm
số y  f  x , trục hoành và hai đường thẳng x  a ; x  b được tính theo công thứclà b b b 1 A. S  f  x dx. B. S  f  xdx.
C. S    f
 x 2 dx  . D. S   f
 x dx . a a a 0
Câu 4: Kí hiệu z , z , z và z là bốn nghiệm phức của phương trình 4 2
z  z 12  0. Tính tổng 1 2 3 4
T  z  z  z  z 1 2 3 4 A. T  4 . B. T  2 3 .
C. T  4  2 3 .
D. T  2  2 3 .
Câu 5: Cho số phức z có số phức liên hợp z  3 2i . Tổng phần thực và phần ảo của số phức z bằng. A. 5 . B. 1  . C. 1. D. 5  .
Câu 6: Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;  3; 4 , đường thẳng x  2 y  5 z  2 d :  
và mặt phẳng  P : 2x  z  2  0 . Viết phương trình đường thẳng  đi qua M 3 5  1 
,vuông góc với d và song song với  P . x 1 y  3 z  4 x 1 y  3 z  4 A.  :   B.  :   1 1 2  . 1 1  2  . x 1 y  3 z  4 x 1 y  3 z  4 C.  :   D.  :   1  1  2  . 1 1  2 .
Câu 7: Họ các nguyên hàm của hàm số f  x 4 2
 5x  6x 1 là x
A. F  x 4 2 
 2x  2x  C .
B. F  x 5 3
 x  2x  x  C . 4
C. F  x 5 3
 20x 12x  x  C .
D. F  x 3
 20x 12x  C .
Câu 8: Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y  x , 2
y  x  2 . 11 20 13 A. S  . B. S  . C. S  . D. S  3. 2 3 3  2
Câu 9: Tính tích phân cos xdx  . 0 A. 0. B. 1. C. 3. D. 2. Trang 1
Câu 10: Trong không gian Oxyz, cho mặt phẳng (P) : x- 2y - 2z = 0 và hai điểm A(1;1;1) . Điểm  A  ; a ; b 
c là điểm đối xứng của A qua mặt phẳng   . Khi đó  2  2  2 T a b c bằng A. T = 5 . B. T = 6 . C. T = 3 . D. T = 2 .    
Câu 11: Trong không gian với hệ trục tọa độ Oxyz , cho a  3; 2 
;1 , b  3; 2;5 . Khi đó:  , a b   có tọa độ bằng A. 8; 1  2;0 . B. 0;8;12 . C. 8; 1  2;5 . D. 0;8; 1  2 . x  y  z
Câu 12: Đâu là phương trình tham số của đường thẳng 1 1   2 3 2  x  1   2t
x  5  2t x  3 2t x  1   2t    
A.  y  1 3t
B.  y  5  3t
C. y  2  3t D.  y  1   3t     z  2  t  z  4  2t z  2   2t z  2t .  .  .  .
Câu 13: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x – 2y – z – 4 = 0 và mặt cầu (S): 2 2 2
x  y  z  2x  4 y  6z 11  0 . Biết rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn
(C). Xác định bán kính của đường tròn (C). A. r  5. B. r  2. C. r  4. D. r  3.
Câu 14: Cho z = x + yi thỏa mãn z + 1- 5i = z + 3- i và z đạt giá trị nhỏ nhất. Tìm x 3 + . y 5 5 12 12 A. - × B. × C. × D. - × 12 12 5 5 Câu 15: Cho hàm số x
y  e có đồ thị như hình vẽ bên. Gọi S là 1
diện tích hình phẳng giới hạn bởi các đường  x y e , x  1  , x  k
và S là diện tích hình phẳng giới hạn bởi các đường 2 x
y  e , x  k, x  1. Xác định k để S  S ? 1 2  1 
A. k  ln e   ln 2  
. B. k  ln 2 .  e   1 
C. k  2ln 2 1.
D. k  2ln e  1   .  e 
Câu 16: Diện tích hình phẳng giới hạn bởi các đường cong y  sin x , y  cos x và các đường thẳng
x  0 , x   bằng A. 3 2 . B. 2 . C. 2 2 . D. 2  2 .
Câu 17: Gọi z , z là hai nghiệm phức của phương trình 2
z  mz  2m 1  0 trong đó m là thamsố 1 2
phức. Giá trị của m để phương trình có hai nghiệm z , z thỏa mãn 2 2 z  z  10  là 1 2 1 2
A. m  2  2 2i .
B. m  2  2 2i .
C. m  2  2 2i . D. m  2   2 2i .
Câu 18: Trong không gian với hệ toạ độ Oxyz , cho điểm I 1;0;  
1 là tâm của mặt cầu S  và   đườ x 1 y 1 z ng thẳng d :  
, đường thẳng d cắt mặt cầu S  tại hai điểm A , B sao cho AB  6 2 2 1 
. Mặt cầu S  có bán kính R bằng A. 2 . B. 10 . C. 2 2 . D. 10 . x - 1 y + 2 z - 3
Câu 19: giá trị nào của m thì đường thẳng d : = =
song song với đường thẳng 2 2 m Trang 2 ìï x = 1 + t ïïï
D : í y = 2 + t, (t Î ¡ )? ï ïï z = 2 + 2t ïî A. m = 1. B. m = 3. C. m = 2. D. m = 4.
Câu 20: Cho số phức z  3 2i . Tìm phần ảo của của số phức liên hợp z . A. 2  i . B. 2i . C. 2  . D. 2 . 1 1
Câu 21: Biết A =
dx = a + b ln 4 + c ln 5 ò
. Tính tổng S = a + b + c . - 2 x + 3 + 3 A. 3 . B. 8 . C. 2 . D. - 2 . 2 2 Câu 22: Cho
f (x )dx = 2 ò . Tính I = 3
[ f (x ) - 2]dx ò . 1 1 A. I = 4 . B. I = 3 . C. I = 2 . D. I = 1.
Câu 23: Cho số phức z có số phức liên hợp z  3 2i . Tổng phần ảo của số phức z và z bằng. A. 3 . B. 6 . C. 0 . D. 4 .
Câu 24: Trong không gian với hệ toạ độ Oxyz , cho ba điểm A4;0;0, B 0;2;0,C 0;0;4 . Tìm tọa
độ điểm D để tứ giác ABCD là hình bình hành A. 4; 2; 2. B.  4  ;2;4 . C. 4; 2  ;4 . D. 2; 2  ;4 .
Câu 25: Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  7z 15  0 . Tính giá trị biểu thức 1 2
P  z  z  z z 1 2 1 2 A. P  7  . B. P  8 . C. P 15 . D. P  22 .
Câu 26: Môđun của số phức z  5  2i bằng A. 7 . B. 29 . C. 29 . D. 3 .
Câu 27: Trong không gian Oxyz , mặt phẳng nào trong các mặt phẳng sau song song với trục Oz ?
A. (b ) : z = 1 .
B. (P) : x + y = 0 .
C. (Q) : x + 11y + 1= 0 . D. (a ) : z = 0 .
Câu 28: Tìm họ nguyên hàm của hàm số f  x  x  cos x . x A. f
 xdx  xsin xcosxC. B. f  x 2 dx 
 sin x  C . 2 x C. f
 xdx 1sin xC. D. f  x 2 dx 
 sin x  C . 2 e 4 (2 ln x + 3)
Câu 29: Tính I = dx ò
bằng cách đặt t = 2 ln x + 3, ta được x 1 e 4 5 5 e t 4 t A. I = dt. ò B. I = dt. ò C. 4 I = 2t dt. ò D. 4 I = 2t dt. ò 2 2 1 3 3 1 1
Câu 30: Hàm số nào sau đây là một nguyên hàm của hàm số y 
với x  0 . x 1 A. y   .
B. y   ln x . C. y  x .
D. y  ln x . 2 x
Câu 31: Tập nghiệm của phương trình z4  z2 2  8  0là Trang 3 A.  ; 2  i 4 . B.  ; 2  i 4 .
C.  2;  i 2  . D.  i; 2   2 . x  2  t 
Câu 32: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d:  y  3  t , vectơ nào dưới đây z  1   5t 
là vectơ chỉ phương của đường thẳng d ?    
A. u  1; 3; 2
B. u  1; 1; 5
C. u  1;1; 5
D. u  2;3;   1 . . . . u   x
Câu 33: Cho tích phân  . x H x e dx  . Nếu đă ̣t  thì ta được x dv  e dx A.  x   x H xe xe dx B.  x   x H xe e dx . . C.  x   x H xe e dx D.  x   x H e xe dx . .
Câu 34: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2; 1
 ;5, B1;2;3 . Mặt phẳng  
đi qua hai điểm A , B và song song với trục Ox có phương trình A. 2
 x  z  7  0 . B. 2
 x  y  7  0 .
C. 2x  z  7  0 . D. 2
 x  z 7  0. 1 1 1 Câu 35: Cho
f (x)dx  1  và
g(x)dx  2  
. Tính  1 f (x)  3g(x)d .x 2  2  2  A. 7.  B. 8. C. 4.  D. 24. Câu 36:Trong không gian với hệ toạ độ Oxyz cho phương trình 2 2 2 2
x  y  z  2mx  4 y  2z  5m  6m  7  0 . Tìm m để phương trình đó là phương trình của một mặt cầu. 1 1 A. m  1
 hoặc m  2 . B.  m  1. C. 1   m  2 . D. m  hoặc m  1. 2 2
Câu 37: Cho hai số phức z  1 2i và z  m  3  2
m  6 i , m    . Tìm tập hợp tất cả các giá trị 2  1
m để z  z là số thực 1 2 A.   2 . B.  2  ;  2 . C.  6; 6. D.   2 . Câu 38: Gọi ,
A B, C là các điểm trong mặt phẳng theo thứ tự biểu diễn số phức 2 + 3i, 3 + i, 1+ 2 . i
Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z. A. z = 2 + 2 . i B. z = 1+ . i C. z = 2 - 2 . i D. z = 1- . i
Câu 39: Trong không gian Oxyz , cho hai điểm M 1; 2;3 và N  1  ;2; 
1 . Mặt cầu đường kính MN có phương trình là 2 2
A. x   y  2   z  2 2 2 1  5. B. 2
x   y  2   z   1  5 . 2 2 C. 2 2 2
x   y  2   z   1  5. D. 2
x   y  2   z   1  5 .
Câu 40: Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng  P : 2x  3z  4  0 . Điểm nào sao
đây thuộc mặt phẳng P ? A. Q(2;-3;4). B. M(-2;0;2). C. K(2;0;-3). D. N(-2;2;0).
Câu 41: Trong không gian với hệ trục tọa độ Oxyz , mặt cầu S  2 2 2
: x  y  z  8x  4 y  2z  4  0 có Trang 4 bán kính R là A. R  5 . B. R  2 . C. R  5 . D. R  25 . x  4t 
Câu 42: Trong không gian Oxyz, cho hai đường thẳng d  :  y  1 6t ;(t   ). Điểm nào dưới z  1   4t 
đây không thuộc đường thẳng d  5  A. M 1; ; 0  
B. M 4;7; 3
C. M 0;1;   1
D. M 0; 1;   1  2  . . . .
Câu 43: Cho đồ thị y  f  x như hình vẽ sau đây. Diện tích S của hình
phẳng (phần gạch chéo) được xác định bởi 1 2 2 A. S  f
 xdx f  xdx. B. S  f  xdx. 2  1 2  1 2 1 2 C. S  f
 xdx f  xdx.
D. S   f
 xdx f  xdx. 2  1 2  1
Câu 44: Gọi z , z là hai nghiệm phức của phương trình 2
z  z 1  0 . Tính giá trị biểu thức 1 2
P  z  z 1 2 A. P  2 . B. P  4 . C. P  1 . D. P  3 . x y  7 z  2
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng  :   và điểm 3 5 2 M 2; 1
 ;3 Gọi M ' là điểm đối xứng với M qua , tính OM '.
A. OM '  5 2. B. OM '  2 5. OM   . C. ' 5 3. . D. OM ' 53..
Câu 46: Trong không gian với hệ trục Oxyz , cho hai mặt phẳng  P : nx  7 y  6z  4  0 ,
Q:3x  my 2z 7  0 . Tìm giá trị của ,
m n để hai mặt phẳng  P, Q song song với nhau. 7 7 7 3
A. m  9, n  . B. m  , n  9 . C. m  , n  1. D. m  , n  9 . 3 3 3 7
Câu 47: Trong không gian với hệ tọa độ Oxyz, cho điểm A 1  ;1  ;1 và đường thẳng x  3 y  2 z 1 d :  
Viết phương trình đường thẳng Δ qua A, Δ cắt và vuông góc với d. 2 1 1 
x  1 t x  1   2t x  1   2t x  2  t    
A.  y  1 2t .
B.  y  1 5t .
C.  y  1 7t .
D.  y  5  t .     z  1 4t  z  1 t  z  1 3t  z  1 t  3
Câu 48: Cho hàm số f (x ) liên tục trên ¡ sao cho
f (x )dx = 4. ò
Mệnh đề nào sau đây đúng? 1 1 7 1 7 A.
f (2x + 1)dx = 8. ò B.
f (2x + 1)dx = 8. ò C.
f (2x + 1)dx = 2. ò D.
f (2x + 1)dx = 2. ò 0 3 0 3
Câu 49: Trong không gian Oxyz , cho hai điểm A1;5; 2
  , B3;1;2 . Viết phương trình mặt phẳng
trung trực của đoạn thẳng AB .
A. x  2 y  2z  8  0 .
B. x  2 y  2z  4  0 . Trang 5
C. x  2 y  2x  0 .
D. 2x  3y  4  0 .
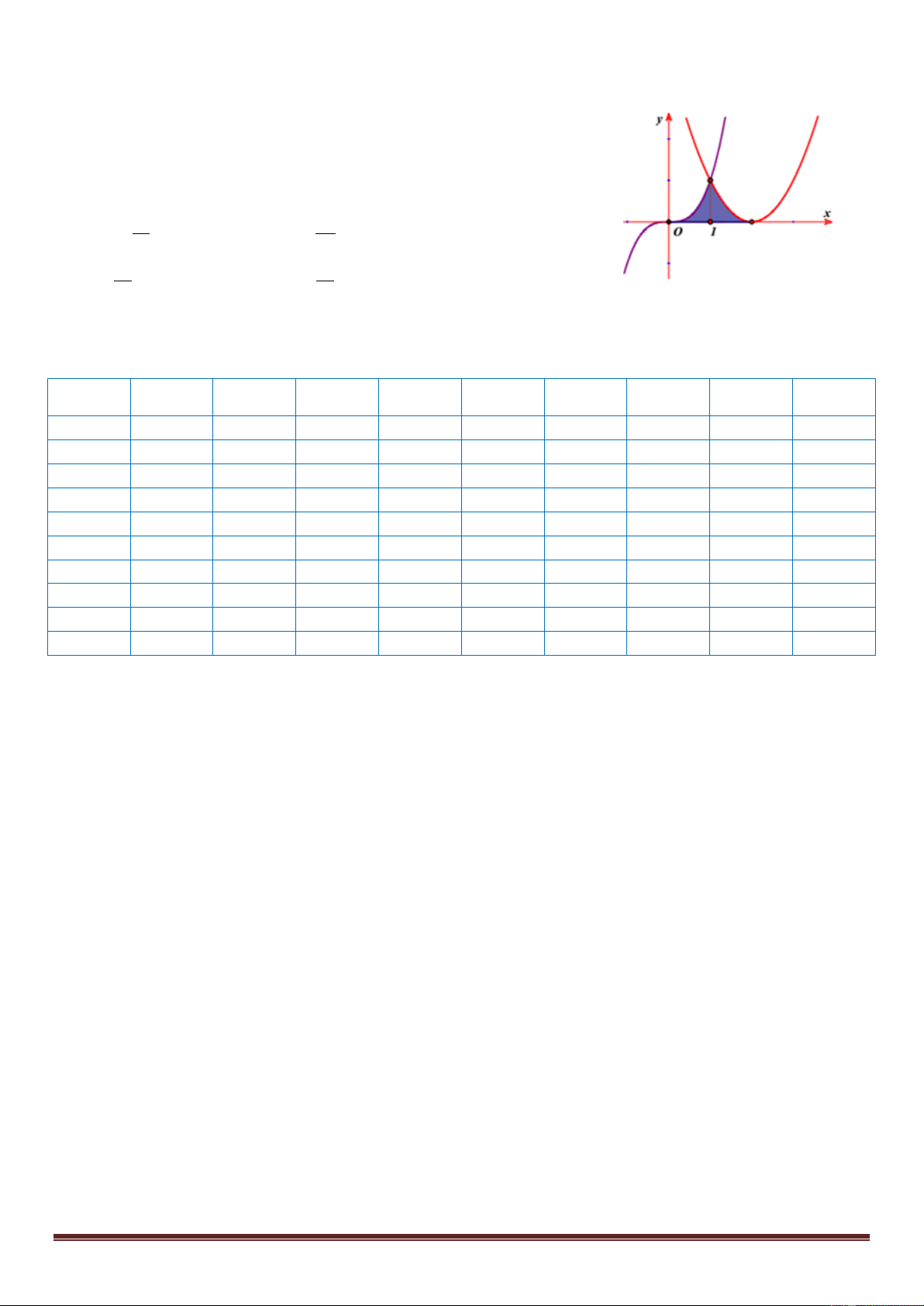
Câu 50: Cho hình  H  là hình phẳng giới hạn bởi parabol 2
y  x  4x  4 , đường cong 3
y  x và trục hoành (phần tô đậm trong
hình vẽ). Tính diện tích S của hình H  . 11 20 A. S  . B. S  . 2 3 7 15 C. S  . D. S  . 12 2
------ HẾT ------
ĐÁP ÁN MÃ ĐỀ 133 Câu ĐA Câu ĐA Câu ĐA Câu ĐA Câu ĐA 1 A 11 A 21 C 31 D 41 A 2 B 12 C 22 A 32 C 42 D 3 A 13 C 23 C 33 C 43 D 4 C 14 C 24 C 34 D 44 A 5 A 15 A 25 B 35 C 45 A 6 A 16 C 26 B 36 B 46 B 7 B 17 C 27 C 37 B 47 C 8 B 18 B 28 B 38 A 48 C 9 B 19 D 29 B 39 A 49 B 10 D 20 D 30 D 40 D 50 C Trang 6