Bộ Đề Thi Thử Toán Vào 10 TPHCM Năm 2025-2026 Có Lời Giải Chi Tiết (Bộ 2)
Với sự phát triển của khoa học kỹ thuật hiện nay, nguời ta tạo ra nhiều mẫu xe lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho nguời khuyết tật với số vốn ban đầu là 500 triệu đồng. Chi phí để sản xuất ra một chiếc xe lăn là 2.500.000 đồng. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 216 tài liệu
Môn: Toán 9 2.9 K tài liệu
Tác giả:
Preview text:
SỞ SD&ĐT TPHCM
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT HUYỆN CẦN GIỜ MÔN: TOÁN 9
Đê thi gồm 8 câu hỏi tự luận. ĐỀ TH AM KHẢO
Thời gian: 120 phút (không kể thời gian phát đề)
MÃ ĐỀ: Quận Cần Giờ - 2
Câu 1. (1,5 điểm).
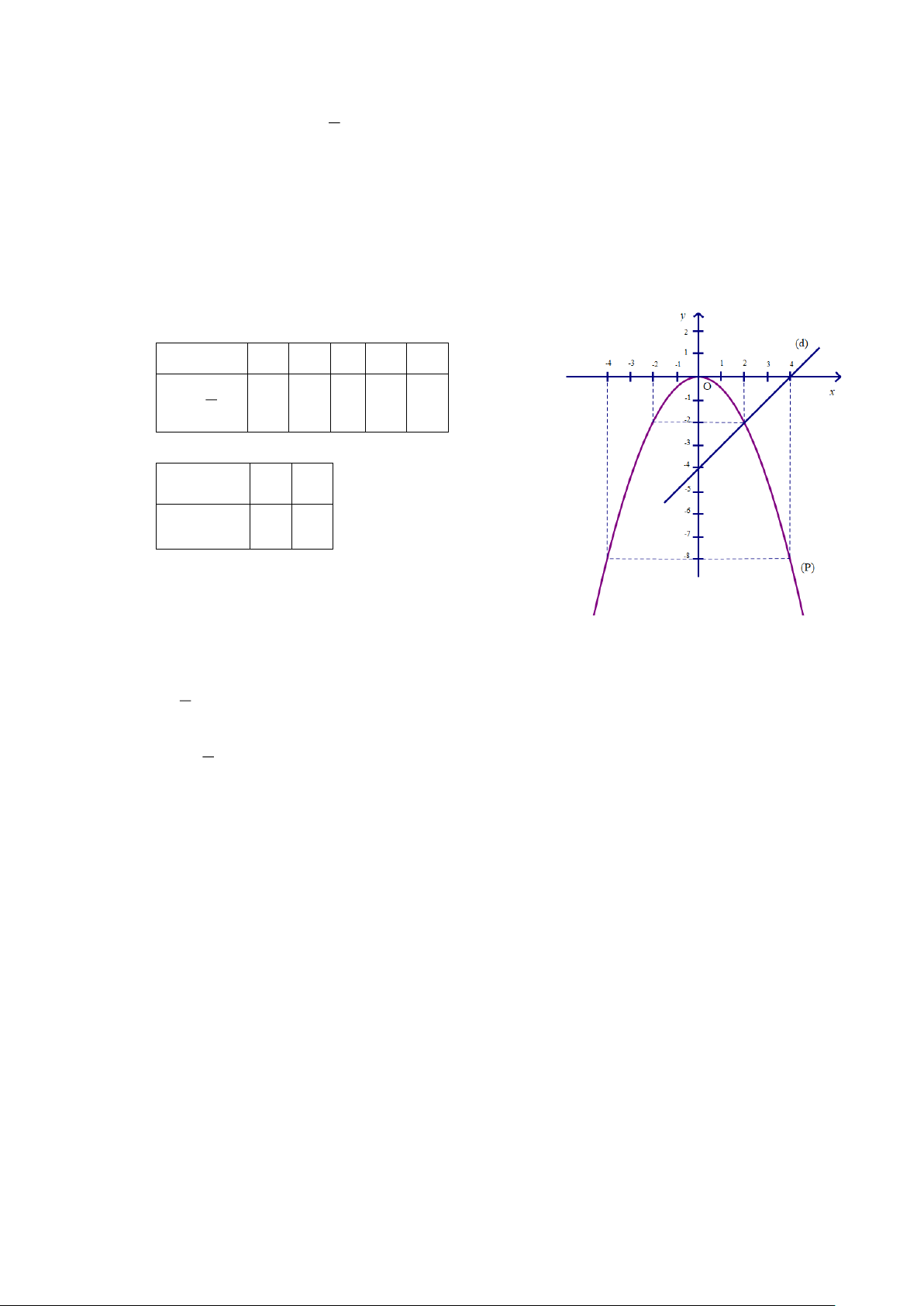
a) Vẽ đồ thị hàm số (P ) 2
: y = - x và đường thẳng (d): y = - 4x + 3 trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P ) và (d) bằng phép toán.
Câu 2. (1 điểm). Cho phương trình: 2
3x + 2x - 9 = 0 có hai nghiệm là x , x . Không giải phương trình 1 2
trên, hãy tính giá trị của biểu thức A = (3x – 2x 3x – 2x 1 2 ) ( 2 1 )
Câu 3. (1 điểm). Ngày 28 / 09 / 2018 , sau trận động đất 7, 5 độ Richter, cơn sóng thần (tiếng Anh là
Tsunami) cao hơn 6 m đã tràn vào đảo Sulawesi của In đô nê xi a, tàn phá thành phố Palu, gây
thiệt hại vô cùng to lớn. Tốc độ của cơn sóng thần và chiều sâu của đại dương, nơi bắt đầu của sóng
thần, liên hệ bởi công thức v = dg . Trong đó, 2
g = 9, 81 m/ s , d là chiều sâu của đại dương tính
bằng m, v là vận tốc của sóng thần tính bằng m/s
a) Biết độ sâu trung bình tại Thái Bình Dương là 4000 m , hãy tính tốc độ trung bình của các con
sóng thần xuất phát từ đáy của Thái Bình Dương.
b) Theo tính toán của các nhà khoa học địa chất, vận tốc của đợt sóng thần ngày 28 / 09 / 2018 có
vận tốc là 800 km/ h , hãy tính chiều sâu của đại dương, nơi tâm chấn động đất gây ra sóng thần là bao nhiêu m?
Câu 4. (1,0 điểm). Với sự phát triển của khoa học kỹ thuật hiện nay, nguời ta tạo ra nhiều mẫu xe lăn đẹp và
tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho nguời khuyết tật với
số vốn ban đầu là 500 triệu đồng. Chi phí để sản xuất ra một chiếc xe lăn là 2.500.000 đồng. Giá
bán ra mỗi chiếc là 3.000.000 đồng.
a) Viết hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn (gồm vốn
ban đầu và chi phí sản xuất) và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn.
b) Công ty A phải bán bao nhiêu chiếc xe mới có thể thu hồi được vốn ban đầu? Trang 1
Câu 5. (1 điểm). Để giúp các bạn trẻ “khởi nghiệp”, ngân hàng cho vay vốn ưu đãi với lãi suất 5% /năm.
Một nhóm bạn trẻ vay 100 triệu đồng làm vốn kinh doanh hàng tiểu thủ công mỹ nghệ.
a) Hỏi sau một năm các bạn trẻ phải trả cho ngân hàng cả vốn lẫn lãi là bao nhiêu?
b) Các bạn trẻ kinh doanh hai đợt trong năm, đợt 1 sau khi trừ các chi phí thấy lãi được 18% so với
vốn bỏ ra nên dồn cả vốn lẫn lãi để kinh doanh tiếp đợt 2 , cuối đợt 2 trừ các chi phí thấy lãi 20% so
với vốn đợt 2 bỏ ra. Hỏi sau 2 đợt kinh doanh, trả hết nợ ngân hàng, các bạn trẻ còn lãi được bao nhiêu tiền?
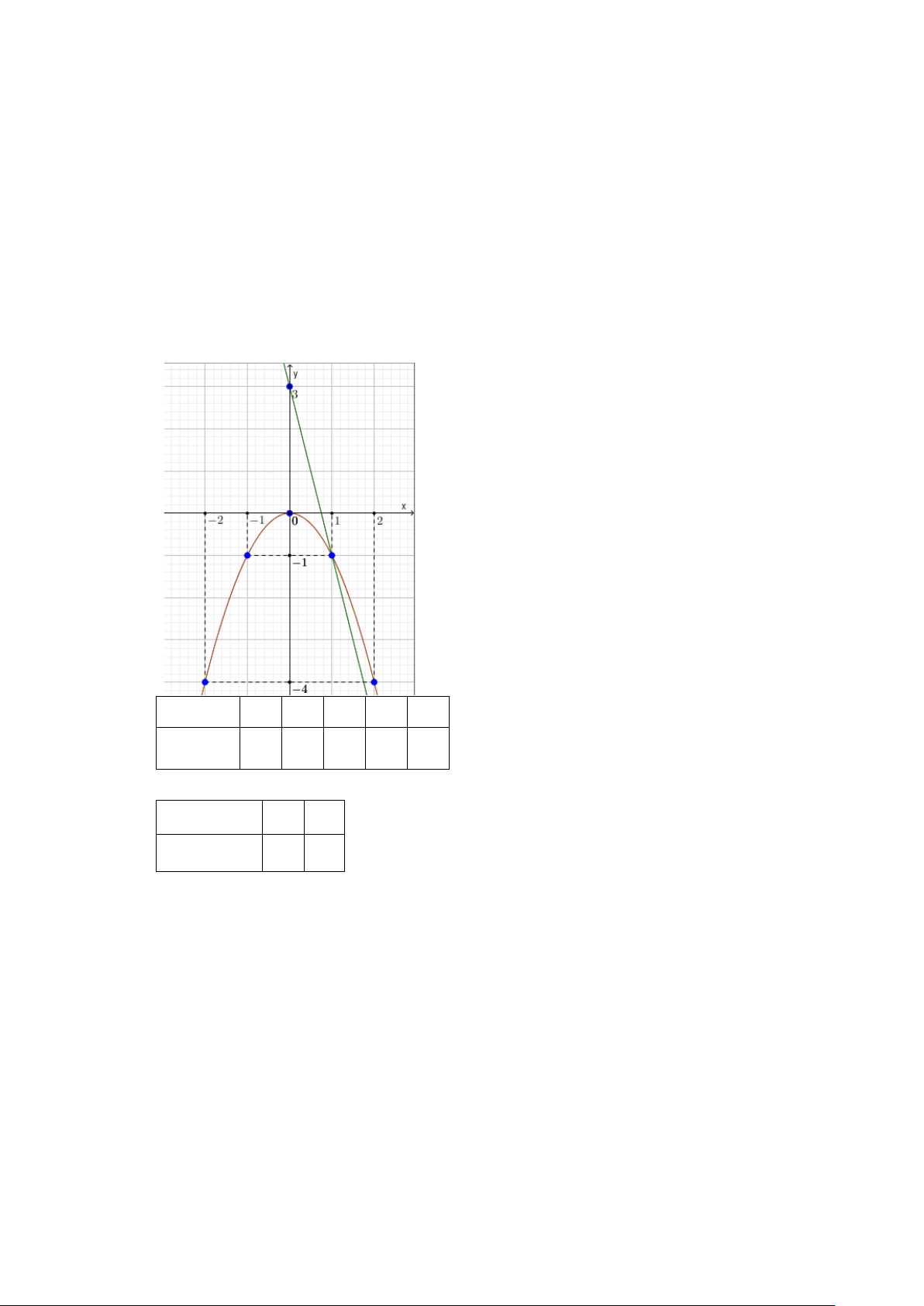
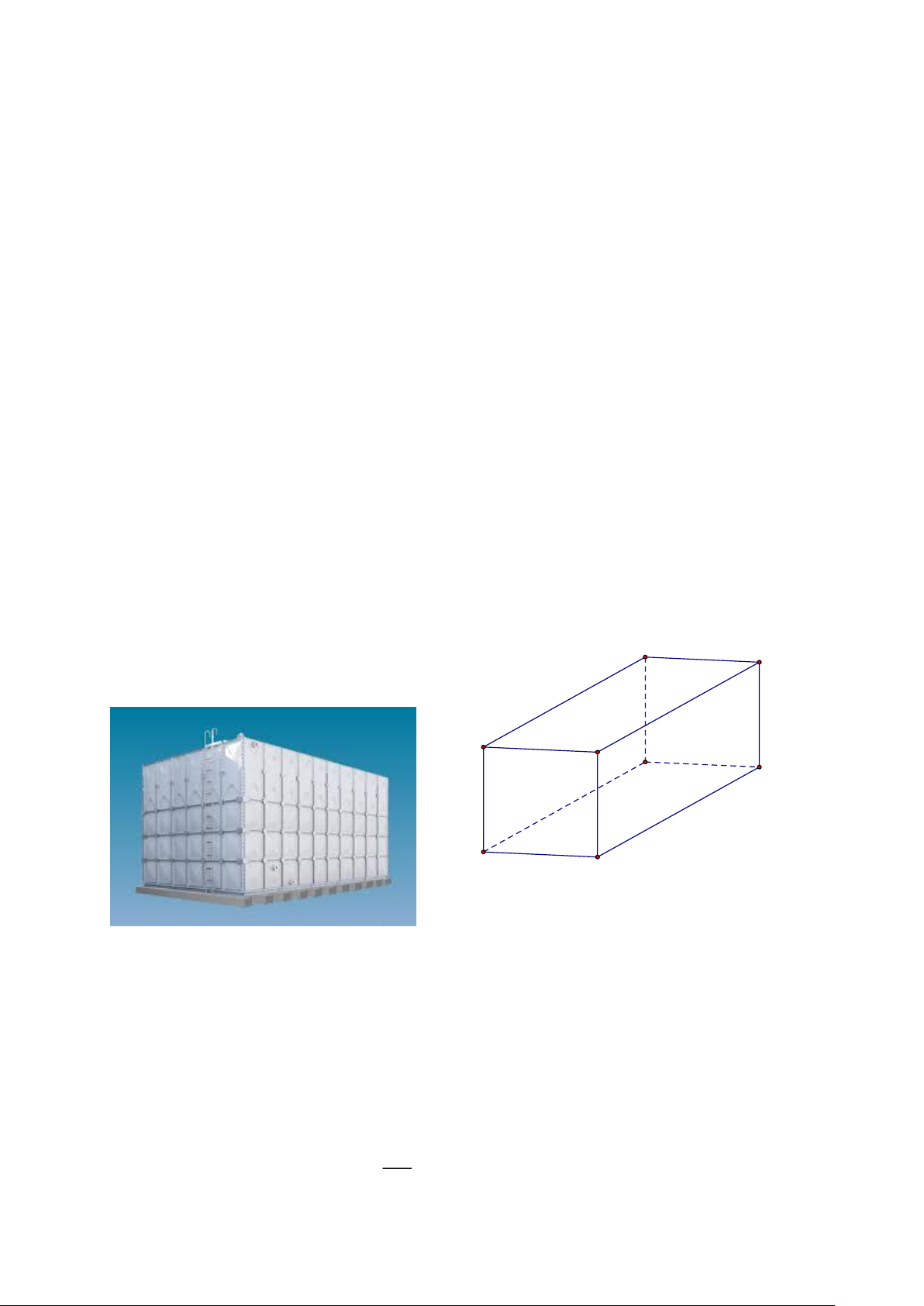
Câu 6. (1 điểm). Một bồn đựng nước có dạng hình hộp chữ nhật có các kích thước cho trên hình vẽ
a) Tính diện tích bề mặt của bồn (không tính nắp)?
b) Một vòi bơm với công suất 120 lít/phút để bơm một lượng nước vào bồn lên độ cao cách nắp bồn
là 1, 5 m thì phải mất bao lâu? (bồn không chứa nước) 2,3 m 11,5m 3,1 m
Câu 7. (1 điểm). Hai trường A và B có 420 học sinh đậu vào lớp 10 đạt tỉ lệ 84% . Riêng trường A tỉ lệ
đậu 80% , riêng trường B tỉ lệ đậu 90% . Tính số học sinh dự thi của mỗi trường?
Câu 8. (3 điểm) Cho đường tròn (O; 4 cm) và điểm A ở ngoài (O) với OA = 8 cm . Tia A O cắt đường
tròn (O) tại hai điểm D và E (D nằm giữa hai điểm A và O ), cát tuyến A CB cắt đường tròn
(O) tại hai điểm C và B (C nằm giữa hai điểm A và B ). a) Chứng minh · ·
A CD = A EB và A C .A B = A D.A E .
b) Gọi H là trung điểm của đoạn thẳng OD . Chứng minh tứ giác OHCB nội tiếp.
c) Tia đối của tia phân giác ·
CHB cắt đường tròn (O) tại M . Chứng minh A M là tiếp tuyến đường
tròn (O) tại M . Trang 2 ----HẾT--- Trang 3 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm)
a) Vẽ đồ thị hàm số (P ) 2 : y = - x
và đường thẳng (d): y = - 4x + 3 trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P ) và (d) bằng phép toán. Lời giải
a) Vẽ đồ thị hàm số (P ) 2 : y = - x
và đường thẳng (d): y = - 4x + 3 trên cùng một mặt phẳng tọa độ. BGT: x −2 1 − 0 1 2 2 y = −x −4 1 − 0 1 − −4 x 0 1 y = 4 − x + 3 3 1 −
(thu nhỏ điểm trên đồ thị chữ x, y chuyển sang in nghiêng cho đồng bộ vs x, y trong bài làm – nên xóa nền ô vuông)
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : − 2 x = −4x + 3 Trang 4 − 2 x + 4x − 3 = 0 x = 1 x = 3 Thay x = 1 vào 2
y = −x , ta được: 2 y = 1 − = −1 . Thay x = 3 vào 2
y = −x , ta được: y = − 2 3 = −9 .
Vậy (1; − 1) , (3; − 9) là hai giao điểm cần tìm.
Câu 2. (1 điểm) Cho phương trình: 2
3x + 2x - 9 = 0 có hai nghiệm là x , x . Không giải phương trình trên, 1 2
hãy tính giá trị của biểu thức A = (3x – 2x 3x – 2x 1 2 ) ( 2 1 ) Lời giải Vì .
a c = 3.(−9) = −27 0
Nên phương trình có hai nghiệm phân biệt trái dấu x ,x . 1 2 −b −
S = x + x = = 2 1 2
Theo định lí Vi-et, ta có: a 3 = c P x .x = = − 3 1 2 a Ta có:
A = (3x – 2x 3x – 2x 1 2 ) ( 2 1 ) 2 2
= 9x x − 6x − 6x + 4x x 1 2 1 2 1 2 2 2
= 13x x − 6(x + x ) 1 2 1 2 2
= 13x x − 6[(x + x ) − 2x x ] (sử dụng sai dấu ( )) 1 2 1 2 1 2 2
= 25x x − 6(x + x ) 1 2 1 2 2 − 2 − = 25.( 3 − ) − 6.( ) = 71 − = 25.(−3) − 6. = −71 3 3
Câu 3. (1 điểm) Ngày 28 / 09 / 2018 , sau trận động đất 7, 5 độ Richter, cơn sóng thần (tiếng Anh là
Tsunami) cao hơn 6 m đã tràn vào đảo Sulawesi của In đô nê xi a, tàn phá thành phố Palu, gây thiệt
hại vô cùng to lớn. Tốc độ của cơn sóng thần và chiều sâu của đại dương, nơi bắt đầu của sóng thần,
liên hệ bởi công thức v = dg . Trong đó, 2
g = 9, 81 m/ s , d là chiều sâu của đại dương tính bằng
m, v là vận tốc của sóng thần tính bằng m/s
a) Biết độ sâu trung bình tại Thái Bình Dương là 4000 m , hãy tính tốc độ trung bình của các con
sóng thần xuất phát từ đáy của Thái Bình Dương.
b) Theo tính toán của các nhà khoa học địa chất, vận tốc của đợt sóng thần ngày 28 / 09 / 2018 có
vận tốc là 800 km/ h , hãy tính chiều sâu của đại dương, nơi tâm chấn động đất gây ra sóng thần là bao nhiêu m? Lời giải
a) Tốc độ trung bình của các con sóng thần xuất phát từ đáy của Thái Bình Dương . Trang 5
v = dg = 4000.9,81 = 198,1 m/s
b) Chiều sâu của đại dương là:
800 km/ h = 800 : 3, 6 = 2000 / 9 (m/ s) Ta có: v = dg 2000 = d.9,81 9 2 2000 = d.9,81 9 2 2000 d = : 9,81 = 5033,9 (m) (m) 9
Câu 4. (1,0 điểm). Với sự phát triển của khoa học kỹ thuật hiện nay, nguời ta tạo ra nhiều mẫu xe lăn đẹp và
tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho nguời khuyết tật với
số vốn ban đầu là 500 triệu đồng. Chi phí để sản xuất ra một chiếc xe lăn là 2.500.000 đồng. Giá bán
ra mỗi chiếc là 3.000.000 đồng.
a) Viết hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn (gồm vốn
ban đầu và chi phí sản xuất) và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn.
b) Công ty A phải bán bao nhiêu chiếc xe mới có thể thu hồi được vốn ban đầu? Lời giải
a) Ðơn vị tính là triệu đồng.
Hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn là:
y = 2,5x + 500 (1)
Hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn y là: y = 3x (2)
b) Giải hệ phương trình (1) và (2) ta được x = 1000;y = 3000 Trang 6
Vậy bán 1000 chiếc thu hồi vốn là 3 tỉ đồng.
Câu 5. (1 điểm) Để giúp các bạn trẻ “khởi nghiệp”, ngân hàng cho vay vốn ưu đãi với lãi suất 5% /năm. Một
nhóm bạn trẻ vay 100 triệu đồng làm vốn kinh doanh hàng tiểu thủ công mỹ nghệ.
a) Hỏi sau một năm các bạn trẻ phải trả cho ngân hàng cả vốn lẫn lãi là bao nhiêu?
b) Các bạn trẻ kinh doanh hai đợt trong năm, đợt 1 sau khi trừ các chi phí thấy lãi được 18% so với
vốn bỏ ra nên dồn cả vốn lẫn lãi để kinh doanh tiếp đợt 2 , cuối đợt 2 trừ các chi phí thấy lãi 20% so
với vốn đợt 2 bỏ ra. Hỏi sau 2 đợt kinh doanh, trả hết nợ ngân hàng, các bạn trẻ còn lãi được bao nhiêu tiền? Lời giải
a) Sau một năm các bạn trẻ phải trả cho ngân hàng cả vốn lẫn lãi
100.105% = 105 (triệu đồng)
b) Số tiền vốn và lãi sau 2 đợt kinh doanh
100.118%.120% = 141, 6 (triệu đồng)
Số tiền lãi có được sau khi trả hết nợ ngân hàng
141, 6 - 105 = 36, 6 (triệu đồng)
Câu 6. (1 điểm) Một bồn đựng nước có dạng hình hộp chữ nhật có các kích thước cho trên hình vẽ
a) Tính diện tích bề mặt của bồn (không tính nắp)?
b) Một vòi bơm với công suất 120 lít/phút để bơm một lượng nước vào bồn lên độ cao cách nắp bồn
là 1, 5 m thì phải mất bao lâu? (bồn không chứa nước) 2,3 m 11,5m 3,1 m Lời giải
a) Diện tích bề mặt của bồn (không tính nắp): S + S = ( + ) + = ( 2
2. 3,1 11,5 .2,3 3,1.11,5 102,81 m xq d ) b) Thể tích cần bơm : − = ( 3
3,1.11,5.(2,3 1,5) 28,52 m ) = 28520(l) 713
Thời gian cần bơm: 28520 :120 =
(phút) 3 giờ 57, 7 phút 3 Trang 7
Câu 7. (1 điểm) Hai trường A và B có 420 học sinh đậu vào lớp 10 đạt tỉ lệ 84% . Riêng trường A tỉ lệ đậu
80% , riêng trường B tỉ lệ đậu 90% . Tính số học sinh dự thi của mỗi trường? Lời giải
Gọi x, y (học sinh) lần lượt là số học sinh dự thi của hai trường A và B. (ĐK: * x, y Î ¥ )
Theo đề bài ta có: (theo khung chấm điểm hiện nay học sinh bắt buộc phải lập được từng phương
trình sau đó kết hợp 2 phương trình thành hệ phương trình thì mới đc điểm tối đa) 8
0%x + 90%y = 420 x = 300
x + y = 420 :84% y = 200
(tách Lời giải ra khỏi border)
Vậy trường A có 300 hs (học sinh) dự thi, trường B có 200 hs (học sinh) dự thi.
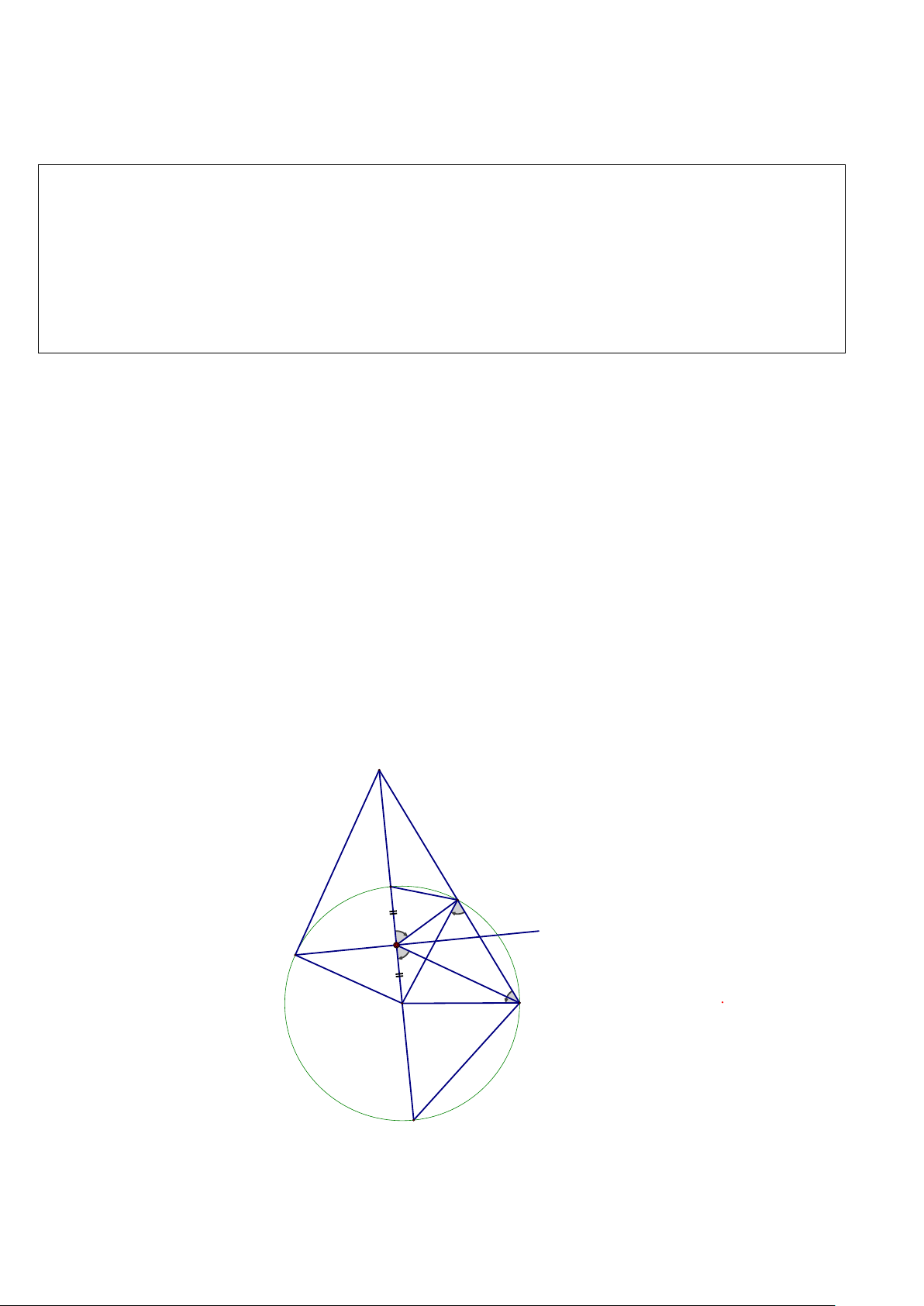
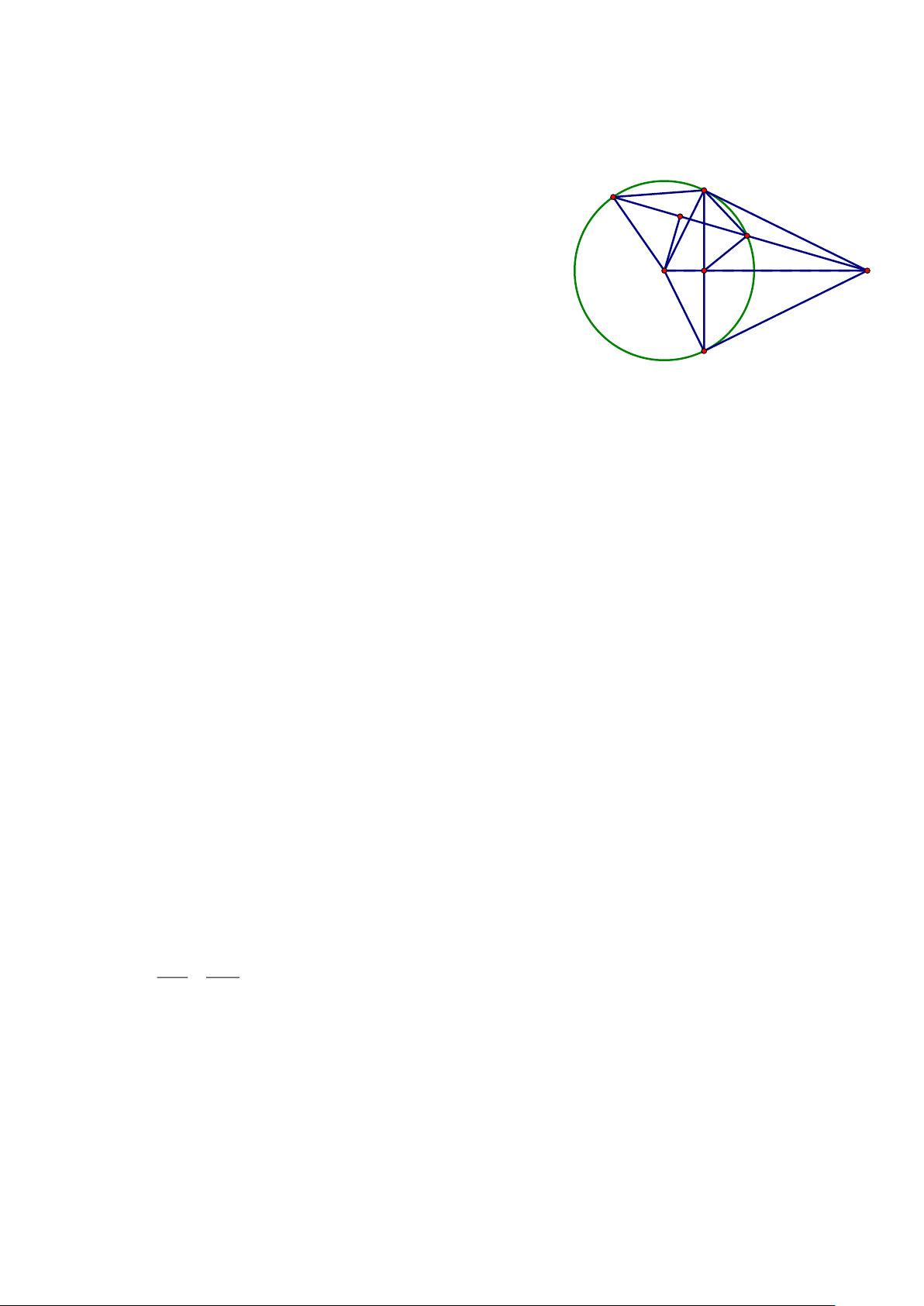
Câu 8. (3 điểm) Cho đường tròn (O; 4 cm) và điểm A ở ngoài (O) với OA = 8 cm . Tia A O cắt đường
tròn (O) tại hai điểm D và E (D nằm giữa hai điểm A và O ), cát tuyến A CB cắt đường tròn
(O) tại hai điểm C và B (C nằm giữa hai điểm A và B ). a) Chứng minh · ·
A CD = A EB và A C .A B = A D.A E .
b) Gọi H là trung điểm của đoạn thẳng OD . Chứng minh tứ giác OHCB nội tiếp.
c) Tia đối của tia phân giác ·
CHB cắt đường tròn (O) tại M . Chứng minh A M là tiếp tuyến
đường tròn (O) tại M . Lời giải A D C x H M O B E
(nên vẽ OA nằm ngang song song với Ox, làm mờ các dấu góc về 0% - xóa bỏ dấu mũi tên) Trang 8 a) Chứng minh · ·
A CD = A EB và A C .A B = A D.A E . Ta có: · ·
A CD = A EB (do tứ giác BCDE nội tiếp)
Xét D A DC và D A BE , ta có: · EA B chung · ·
A CD = A EB (cmt)
Suy ra: D A DC # D A BE (g.g) AC A D = A E A B
AC .AB = AD.AE
b) Gọi H là trung điểm của đoạn thẳng OD . Chứng minh tứ giác OHCB nội tiếp.
Ta có: OH = HD = OD = 2 cm (do H là trung điểm của OD )
A D = A O – OD = 8 – 4 = 4 cm
Suy ra: A E = A D + DE = 4 + 8 = 12 cm và A H = A D + DH = 4 + 2 = 6 cm
Nên: A C .A B = A D.A E = 4.12 = 48
A H .A O = 6.8 = 48
Suy ra: A C .A B = A H .A O A C A H = A O A B Và: µ A chung
DAHC # DABO (c.g.c) · · A HC = A BO
Vậy tứ giác OHCB nội tiếp.
c) Tia đối của tia phân giác ·
CHB cắt đường tròn (O) tại M . Chứng minh A M là tiếp tuyến
đường tròn (O) tại M . Ta có · ·
A HC = A BO (cmt) Mà · ·
A BO = OCB ( D OCB cân tại O do OC = OB = 4 ) 1 Và · ·
OCB = BHO (do = » OB ) 2 Nên · ·
A HC = BHO Mà · ·
CHx = xHB ( Hx là tia phân giác · CHB ) Trang 9 Þ · · · ·
CHx + A HC = xHB + BHO Þ · · A Hx = xHO Mà: · · 0
A Hx + xHO = 180 Þ · · 0 A Hx = xHO = 90
Þ Mx ^ A O tại H
Xét D OHM và D OMA , ta có: µ O chung OH OM 2 4 = (do = ) OM OA 4 8
Do đó: D OHM # D OMA . Þ · · 0 A MO = MHO = 90 Þ A M ^ OM
Þ A M là tiếp tuyến tại M của (O) . ----HẾT---
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT HUYỆN CẦN GIỜ
NAÊM HOÏC: 2022 - 2023 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: Huyện cần giờ - 3
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 9. (1,5 điểm). Cho (P) : y = − 1 2
x và đường thẳng (d) : y = x − 4 . 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 10. (1 điểm). Cho phương trình 2
x – 7x + 12 = 0 có 2 nghiệm là x , x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức A = 2 x + 2
x − x − x 1 2 1 2
Câu 11. (0,75 điểm). Trong một tháng khoảng lợi nhuận y (đồng) của một cửa hàng thu được khi bán x hộp
sữa loại 900g được cho bởi phương trình y = ax + b . Biết rằng trong tháng 10 cửa hàng bán
được 95 hộp sữa thu lợi nhuận 4 870 000 đồng, tháng 11 bán được 180 hộp sữa thu được lợi
nhuận 9 120 000 đồng. Tính hệ số a và b ?
Câu 12. (0,75 điểm). Theo âm lịch thì do một chu kỳ quay của Mặt Trăng quanh Trái Đất là khoảng 29,53
ngày nên một năm âm lịch chỉ có khoảng 354 ngày (làm tròn). Do vậy, cứ sau một vài năm âm lịch Trang 10
thì người ta phải bổ sung một tháng (tháng nhuận) để đảm bảo năm âm lịch tương đối phù hợp với
chu kỳ của thời tiết, là yếu tố phụ thuộc vào chu kỳ quay của Trái Đất xung quanh Mặt Trời. Cách
tính năm nhuận âm lịch như sau:
Lấy số năm chia cho 19 , nếu số dư là một trong các số: 0; 3; 6; 9 ; 11; 14; 17 thì năm âm lịch đó có tháng nhuận. Ví dụ:
2017 là năm nhuận âm lịch vì 2017 chia cho 19 dư 3 .
2015 không phải năm nhuận âm lịch vì 2015 chia cho 19 dư 1 .
a) Em hãy sử dụng quy tắc trên để xác định năm 1995 và 2030 có phải năm nhuận âm lịch hay không?
b) Năm nhuận dương lịch là năm chia hết cho 4 . Ngoài ra, Những năm chia hết cho 100 chỉ được
coi là năm nhuận dương lịch nếu chúng cũng chia hết cho 400 (ví dụ 1600 là năm nhuận dương lịch
nhưng 1700 không phải năm nhuận dương lịch). Trong các năm từ năm 1895 đến năm 1930 , năm
nào vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch.
Câu 13. (1 điểm). Tháng 6 / 2021 gia đình ông Hai thu nhập 15.000.000 đồng và chi tiêu 12.000.000 đồng
. Tháng 7 / 2021 thu nhập giảm 10% mà chi tiêu lại tăng 13% . Hỏi ông Hai còn để dành tiền được không ?
Câu 14. (1 điểm). Một bể kính nuôi cá có dạng hình hộp chữ nhật có chiều dài 100cm , chiều rộng 50cm ,
chiều cao 60cm . Mực nước trong bể cao bằng 3 chiều cao bể. Tính thể tích nước trong bể đó (độ 4
dày kính không đáng kể). Công thức tính thể tích nước trong bể là V = .
S h với S là diện tích mặt
đáy bể và h là chiều cao mực nước trong bể.
Câu 15. (1 điểm). Bà nội dành dụm được một số tiền để thưởng cho các cháu của bà. Nếu bà thưởng cho mỗi
cháu 140000 đồng thì bà còn dư 40000 đồng, nếu bà thưởng cho mỗi cháu 160000 đồng thì bà còn
thiếu 60000 đồng. Hỏi bà nội dành dụm được bao nhiêu tiền và có bao nhiêu cháu ?
Câu 16. (3 điểm) Từ điểm A ở ngoài đường tròn (O; R) , vẽ hai tiếp tuyến AB, AC và cát tuyến AMN
với đường tròn ( B, C là các tiếp điểm, AM AN và tia AM nằm giữa hai tia AB , AO ). Gọi I
là hình chiếu của O trên AN , H là giao điểm của OA và BC . Chứng minh:
a) Tứ giác OABI nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác. Trang 11
b) IA là tia phân giác của BIC
c) Điểm H thuộc đường tròn ngoại tiếp OMN ----HẾT--- Trang 12 HƯỚNG DẪN GIẢI
Câu 9. (1,5 điểm) Cho (P) : y = − 1 2
x và đường thẳng (d) : y = x − 4 . 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Lời giải
c) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. a) BGT: x −4 −2 0 2 4 y = − 1 2
x −8 −2 0 −2 −8 2 x 1 2 y = x − 4 −3 −2
d) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d) : − 1 2 x = x − 4 2 − 1 2 x − x + 4 = 0 2 x = 2 x = − 4
Thay x = 2 vào y = x − 4 , ta được: y = 2 − 4 = −2 .
Thay x = −4 vào y = x − 4 , ta được: y = −4 − 4 = −8 .
Vậy (2; − 2) , (−4; − 8) là hai giao điểm cần tìm.
Câu 2. (1 điểm). Cho phương trình 2
x – 7x + 12 = 0 có 2 nghiệm là x , x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức A = 2 x + 2
x − x − x 1 2 1 2 Lời giải
Vì = b − ac = (− )2 2 4 7 − 4.1.12 = 1 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 Trang 13 − = + = b S x x = 7 1 2
Theo định lí Vi-et, ta có: a = c P x .x = = 12 1 2 c Ta có: A = 2 x + 2
x − x − x 1 2 1 2 A = 2
S − 2P − S A = 2 7 − 2.12 − 7 A = 32
Câu 3. (0,75 điểm). Trong một tháng khoảng lợi nhuận y (đồng) của một cửa hàng thu được khi bán x hộp
sữa loại 900g được cho bởi phương trình y = ax + b . Biết rằng trong tháng 10 cửa hàng bán
được 95 hộp sữa thu lợi nhuận 4 870 000 đồng, tháng 11 bán được 180 hộp sữa thu được lợi
nhuận 9 120 000 đồng. Tính hệ số a và b ? Lời giải
Khi x = 95 thì y = 4 870 000 ta có pt: 95a + b = 4780 000(1)
Khi x = 180 thì y = 9 120 000 ta có pt: 180a + b = 9120 000(2) 95a + b = 4870000 a = 50000
Từ (1) và (2) ta có hpt: 180a + b = 9120000 b = 120000
Vậy a = 50000 và b = 120000
Câu 4. (0,75 điểm). Theo âm lịch thì do một chu kỳ quay của Mặt Trăng quanh Trái Đất là khoảng 29,53
ngày nên một năm âm lịch chỉ có khoảng 354 ngày (làm tròn). Do vậy, cứ sau một vài năm âm lịch
thì người ta phải bổ sung một tháng (tháng nhuận) để đảm bảo năm âm lịch tương đối phù hợp với
chu kỳ của thời tiết, là yếu tố phụ thuộc vào chu kỳ quay của Trái Đất xung quanh Mặt Trời. Cách
tính năm nhuận âm lịch như sau:
Lấy số năm chia cho 19 , nếu số dư là một trong các số: 0; 3; 6; 9 ; 11; 14; 17 thì năm âm lịch đó có tháng nhuận. Ví dụ:
2017 là năm nhuận âm lịch vì 2017 chia cho 19 dư 3 .
2015 không phải năm nhuận âm lịch vì 2015 chia cho 19 dư 1 .
a) Em hãy sử dụng quy tắc trên để xác định năm 1995 và 2030 có phải năm nhuận âm lịch hay không?
b) Năm nhuận dương lịch là năm chia hết cho 4 . Ngoài ra, Những năm chia hết cho 100 chỉ được
coi là năm nhuận dương lịch nếu chúng cũng chia hết cho 400 (ví dụ 1600 là năm nhuận dương
lịch nhưng 1700 không phải năm nhuận dương lịch). Trong các năm từ năm 1895 đến năm
1930 , năm nào vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch. Lời giải
a) 1995 chia 19 dư 0 nên là năm nhuận âm lịch . Trang 14
2030 chia 19 dư 16 nên không là năm nhuận âm lịch.
b) Các năm nhuận dương lịch: 1896, 1904, 1908, 1912, 1916, 1920, 1924, 1928.
Trong đó 1928 chia 19 dư 9 nên cũng là năm nhuận âm lịch.
Vậy năm 1928 vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch.
Câu 5. (1 điểm). Tháng 6 / 2021 gia đình ông Hai thu nhập 15.000.000 đồng và chi tiêu 12.000.000 đồng
. Tháng 7 / 2021 thu nhập giảm 10% mà chi tiêu lại tăng 13% . Hỏi tháng ông Hai còn để dành tiền được không ? Lời giải
Thu nhập của gia đình ông Hai vào tháng 7 / 2021 là: 0 15000000.(100 − 0 10 ) = 13500000 đồng 0 0
Số tiền chi tiêu của gia đình ông Hai vào tháng 7 / 2021 là: 12000000.( 0 100 + 0 13 13560000 đồng 0 0 ) =
Vậy gia đình ông Hai không để dành được tiền trong tháng 7 / 2021 (vì 13500000 13560000 )
Câu 6. (1 điểm). Một bể kính nuôi cá có dạng hình hộp chữ nhật có chiều dài 100cm , chiều rộng 50cm ,
chiều cao 60cm . Mực nước trong bể cao bằng 3 chiều cao bể. Tính thể tích nước trong bể đó (độ 4
dày kính không đáng kể). Công thức tính thể tích nước trong bể là V = .
S h với S là diện tích mặt
đáy bể và h là chiều cao mực nước trong bể. Lời giải
Đổi 100cm = 1m; 50cm = 0,5 ;
m 60cm = 0,6m Thể tích bể cá là: V = S h = = 3 . 1.0,5.0,6 0,3m
Thể tích nước có trong bể cá là: Trang 15 3 0,3 = 3 0,225m 4
Câu 7. (1 điểm). Bà nội dành dụm được một số tiền để thưởng cho các cháu của bà. Nếu bà thưởng cho mỗi
cháu 140000 đồng thì bà còn dư 40000 đồng, nếu bà thưởng cho mỗi cháu 160000 đồng thì bà còn
thiếu 60000 đồng. Hỏi bà nội dành dụm được bao nhiêu tiền và có bao nhiêu cháu ? Lời giải
Gọi x (đồng) là số tiền Bà nội dành dụm ( x 0 )
Gọi y là số cháu của Bà nội ( * y N )
Theo đề bài nếu bà thưởng cho mỗi cháu 140000 đồng thì bà còn dư 40000 đồng nên ta có phương
trình : x – 140000y = 40000 (1)
Ta lại có nếu bà thưởng cho mỗi cháu 160000 đồng thì bà còn thiếu 60000 đồng nên ta có phương
trình: x = 160000y – 60000
x – 160000y = − 60000 (2)
x −140000y = 40000 Từ ( )
1 và (2) ta có hệ phương trình : x−160000y = − 60000 x = 740000( ) n y = 5( ) n
Vậy số tiền Bà nội dành dụm được là 740000 đồng và bà có 5 cháu.
Câu 8. (3 điểm) Từ điểm A ở ngoài đường tròn (O; R) , vẽ hai tiếp tuyến AB, AC và cát tuyến AMN
với đường tròn ( B, C là các tiếp điểm, AM AN và tia AM nằm giữa hai tia AB , AO ). Gọi I
là hình chiếu của O trên AN , H là giao điểm của OA và BC . Chứng minh:
a) Tứ giác OABI nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác.
b) IA là tia phân giác của BIC
c) Điểm H thuộc đường tròn ngoại tiếp OMN Lời giải
a) Chứng minh rằng: Tứ giác OABI nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác.
Xét tứ giác OABI , có: OBA = 0
90 ( AB là tiếp tuyến của (O) ) OIA = 0
90 ( I là hình chiếu của O trên AN )
OBA = OIA = 0 90
Tứ giác OABI nội tiếp. Trang 16 Vì
OBA = 90 nên tâm đường tròn ngoại tiếp tứ giác OABI là trung điểm của OA
b) Chứng minh rằng: IA là tia phân giác của BIC
Xét tứ giác ABOC , có: B N I OBA = 0
90 ( AB là tiếp tuyến của (O) ) M OCA = 0
90 ( AB là tiếp tuyến của (O) ) O H A OBA + OCA = 180 C
Tứ giác ABOC nội tiếp.
Mà tứ giác OABI nội tiếp (cmt)
năm điểm A,B,I,O,C cùng thuộc một đường tròn. AIB = AOB AIC = AOC
Mà AOB = AOC ( AB, AC là tiếp tuyến của (O) ) AIB = AIC
IA là tia phân giác của BIC
c) Chứng minh: Điểm H thuộc đường tròn ngoại tiếp OMN .
Xét ABM và ANB BAN : chung
ABM = ANB (cùng chắn cung BM )
ABM ∽ ANB(g.g) AB = AM 2
AB = AM.AN ( )1 AN AB AB = AC OB = OC
OA là đường trung trực của BC
OA ⊥ BC tại H 2 AB = . AO AH (2) Trang 17
Từ (1), (2) suy ra: AM.AN = . AO AH AM = AH AO AN
Xét AHM và ANO OAN : chung
AM = AH (Chứng minh trên) AO AN
AHM ∽ ANO( . c g.c) AHM = ANO
tứ giác ONMH nội tiếp
H thuộc đường tròn ngoại tiếp OMN . ----HẾT---
SỞ GD&ĐT TP. HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT HUYỆN CỦ CHI
NĂM HỌC: 2022 - 2023 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận.
MÃ ĐỀ: Huyện Củ Chi - 01
Thời gian: 120 phút (không kể thời gian phát đề) −
Câu 17. (1,5 điểm). Cho Parabol ( ) 2 x x P : y =
và đường thẳng (D) : y = + 2 . 4 2
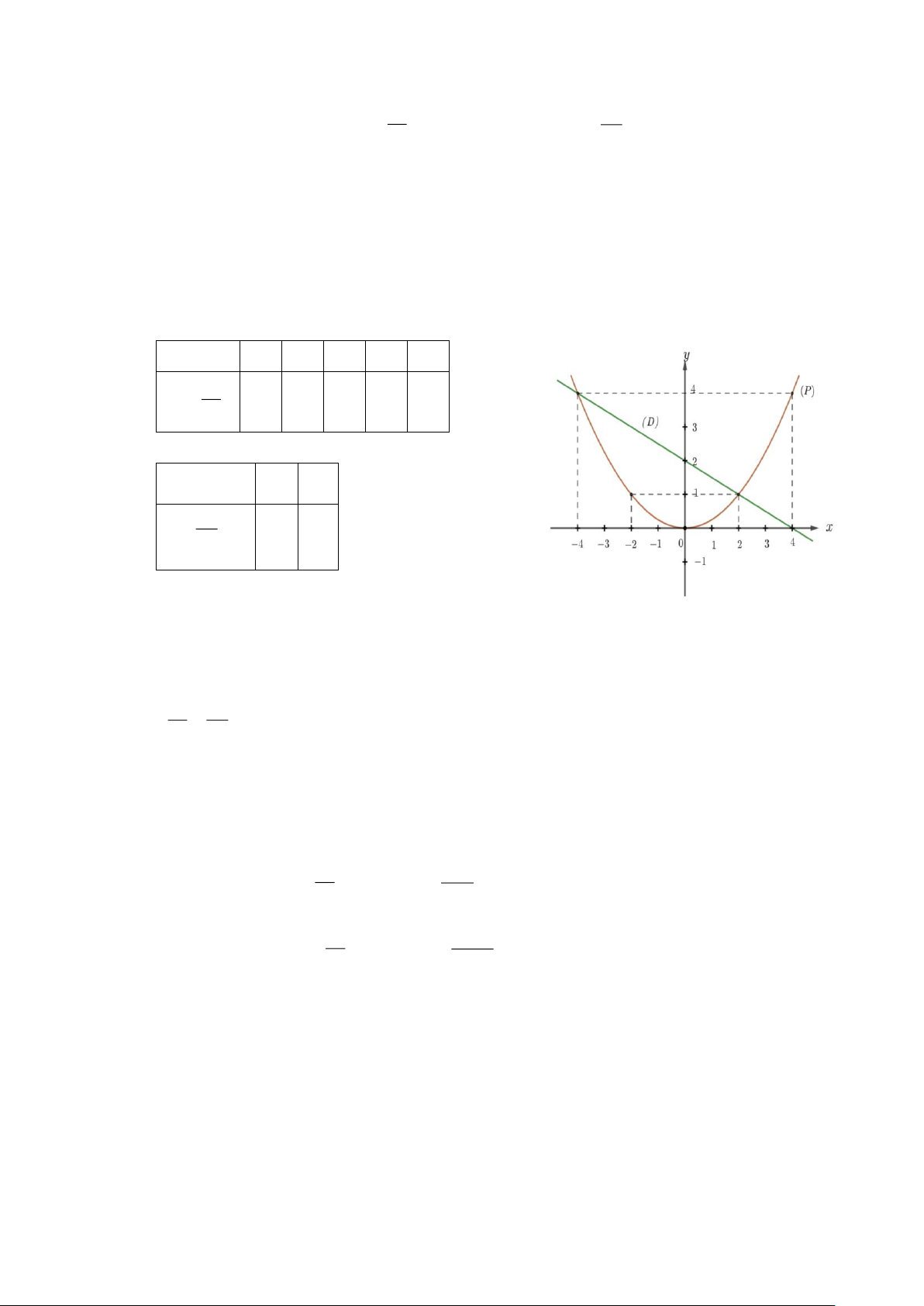
a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.
Câu 18. (1 điểm). Cho phương trình 2
x − 3x + 1 = 0 . Không giải phương trình, hãy tính giá trị của biểu thức 3 3
A = x + x . 1 2
Lưu ý: Từ bài này, các số liệu tính toán về độ dài khi làm tròn (nếu có) lấy đến một chữ số thập phân, số đo góc làm tròn đến phút.
Câu 19. (1 điểm). Ông Ba mua một ký khoai tại vườn là 5 000 đồng một ký, tiền xe vận chuyển từ vườn đến
nơi tiêu thụ là 2 000 000 đồng một chuyến. Gọi x (kg) là số kg khoai ông Ba mua mỗi chuyến, y
(đồng) là tổng chi phí cho một chuyến khoai.
a) Lập công thức tính y theo x .
b) Biết sau một chuyến khoai, ông Ba thu được 30 triệu đồng và lãi được 8 triệu đồng. Hỏi ông Ba
đã mua bao nhiêu kg khoai và đã bán ra với giá bao nhiêu tiến 1 ký? Trang 18
Câu 20. (0,75 điểm). Bạn Nam nhặt được một tấm gỗ bị gãy là một phần của hình tròn (hình 1). Nam muốn
biết bán kính của hình tròn chứa tấm gỗ là bao nhiêu, nên bạn ấy đã kẻ một dây AB bất kỳ trên tấm
gỗ, sau đó dựng đường trung trực của AB và xác định các điểm C và điểm H (hình 2). Nam đo
được AH = 6 cm , CH = 4 cm . Em hãy giúp bạn ấy tính bán kính của hình tròn chứa tấm gỗ.
Câu 21. (1 điểm). Ngày thứ 3 giá một ký thịt Lợn giảm 10% so với ngày thứ 2 , nhưng giá của một ký thịt
Lơn trong ngày thứ 4 lại tăng 5% so với ngày thứ 3 . Biết giá một ký thịt Lợn ở ngày thứ 4 là 94 500 đồng một ký.
a) Tính một ký thịt Lợn ở ngày thứ 2 .
b) Thứ 5 giá một ký thịt Lợn tăng x% so với ngày thứ 4 . Ngày thứ 6 , giá một ký thịt Lợn giảm
x% so với ngày thứ 5 . Giá một ký thịt Lợn ở ngày thứ 6 là 94 000 đồng. Hãy tìm x (làm tròn
đến chữ số thập phân thứ 2 ).
Câu 22. (1 điểm). Hôm qua, bà Tư bán 20 kg gà và 25 kg vịt được tổng cộng 3 050 000 đồng. Hôm nay
giá gà tăng 5% và giá vịt giảm 10% nên bà bán 30 kg gà và 35 kg vịt thu được tổng cộng
4 410 000 đồng. Tính giá một kg gà, một kg vịt của ngày hôm qua.
Câu 23. (1 điểm). Bạn Bình đổ 11 lít nước vào một cái nón lá thì đầy nón. Bình đo được đường kính vòng tròn đáy của nón là 1
40 cm . Biết công thức tính thể tích hình nón là 2
V = r h . Với r là bán kính 3
đáy, h là chiều cao hình nón. Độ dài đường sinh BC của hình nón bằng bao nhiêu dm ? (làm tròn 1 chữ số thập phân).
Câu 24. (3 điểm) Cho (O; R) và dây CD 2R . Gọi B là điểm chính giữa cung nhỏ CD , kẻ đường kính
BA , trên tia đối của tia AB lấy S , SC cắt (O) tại M , MD cắt AB tại K . AC cắt MB tại H
a) Chứng minh tứ giác MAKH nội tiếp.
b) Chứng minh HK∥ CD . c) Chứng minh 2
OK.OS = R . ----HẾT--- Trang 19 HƯỚNG DẪN GIẢI 2
Câu 10. (1,5 điểm) Cho Parabol ( ) x x P : y =
và đường thẳng (D) − : y = + 2 . 4 2
a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán. Lời giải
e) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ. b) BGT: x −4 −2 0 2 4 2 = x y 4 1 0 1 4 4 x −4 2 − = x y + 2 4 1 2
f) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.
Phương trình hoành độ giao điểm của (P) và (D) : 2 x − = x + 2 4 2 2 x + 2x − 8 = 0 x = 2 x = − 4 2 2 (2) Thay x x = 2 vào y = , ta được: y = = 1. 4 4 2 2 (−4) Thay x
x = −4 vào y = , ta được: y = = 4 . 4 4
Vậy (2; 1) , (−4; 4) là hai giao điểm cần tìm.
Câu 11. (1 điểm) Cho phương trình 2
x − 3x + 1 = 0 . Không giải phương trình, hãy tính giá trị của biểu thức A = 3 x + 3 x . 1 2 Lời giải
Vì = b − ac = (− )2 2 4 3 − 4.1.1 = 5 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 Trang 20