














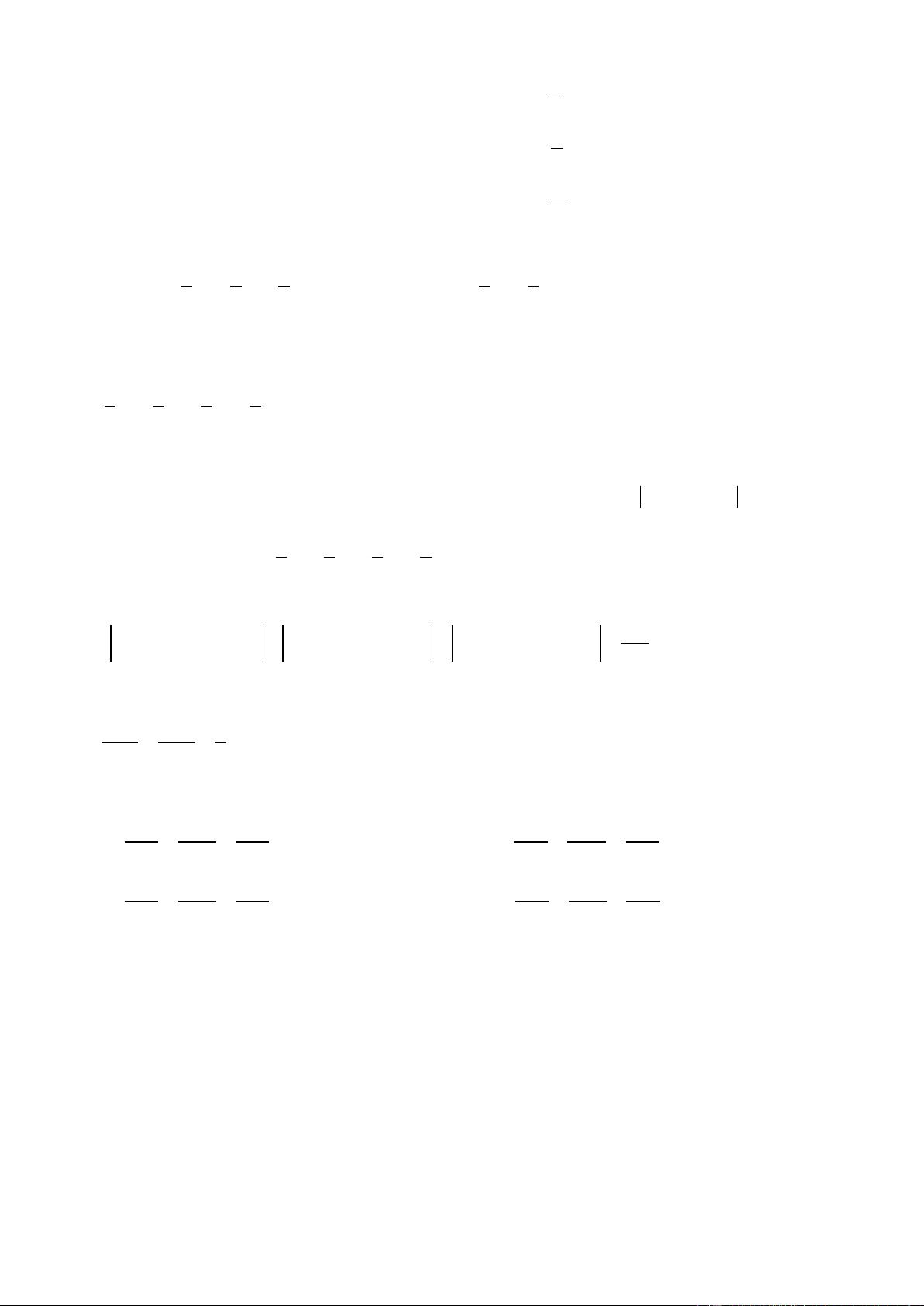















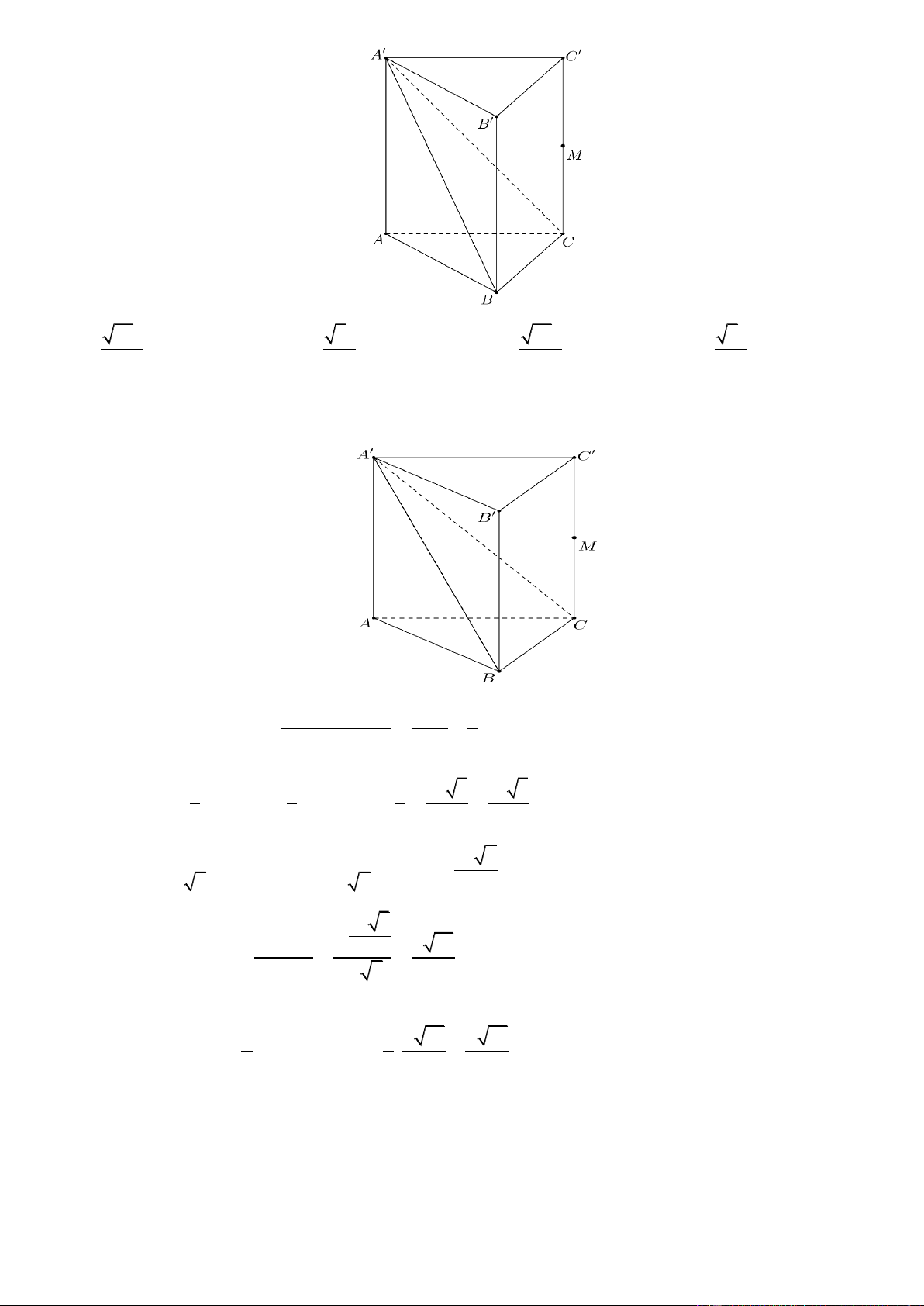


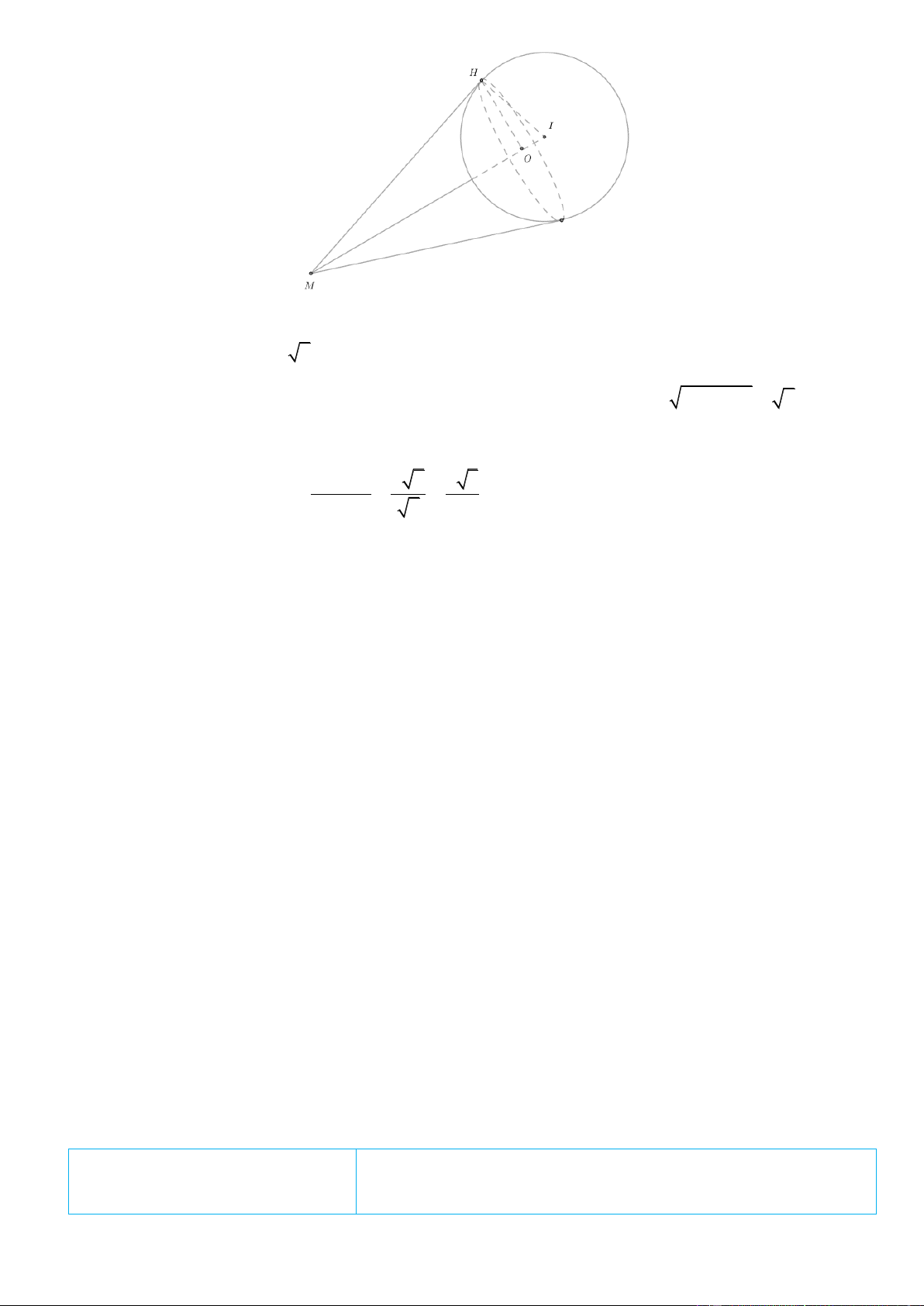







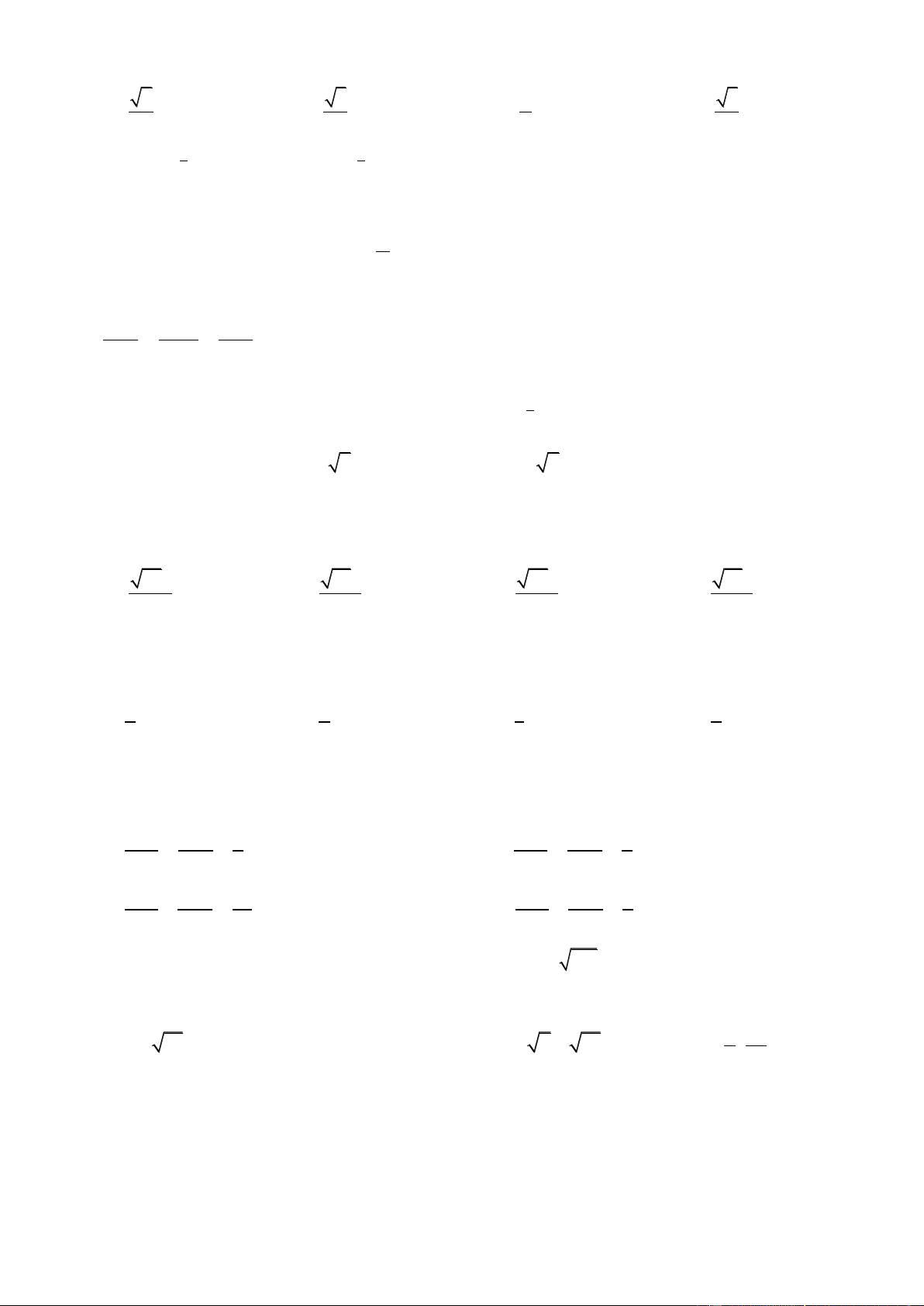








Preview text:
ĐỀ 1
ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2022
BÁM SÁT ĐỀ MINH HỌA MÔN TOÁN Thời gian: 90 phút
Câu 1. Môđun của số phức z 3 i là A. 3 . B. 1. C. 2. D. 2 .
Câu 2. Mặt cầu có phương trình nào sau đây có tâm là I 1 ;1;0 ? A. 2 2 2
x y z 2x 2 y 0. B. 2 2 2
x y z 2x 2 y 1 0.
C. x y x y2 2 2 2 2 2
z 2x 1 2x . y
D. x y2 2
2xy z 1 4 . x
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 4 2
y x 3x 2
A. Điểm M 1; 4 .
B. Điểm N 1 ;0 .
C. Điểm P 0; 2 .
D. Điểm Q 1; 2 .
Câu 4. Tính diện tích S của mặt cầu và thể tích V của khối cầu có bán kính bằng 3cm .
A. S 36 2
cm và V 36 3 cm .
B. S 18 2
cm và V 108 3 cm .
C. S 36 2
cm và V 108 3 cm .
D. S 18 2
cm và V 36 3 cm .
Câu 5. Tìm họ nguyên hàm của hàm số f x 3x sin x . x
A. f x 2
dx 3x cos x C .
B. f x 2 3 dx
cos x C . 2 x
C. f x 2 3 dx
cos x C .
D. f xdx 3 cos x C . 2
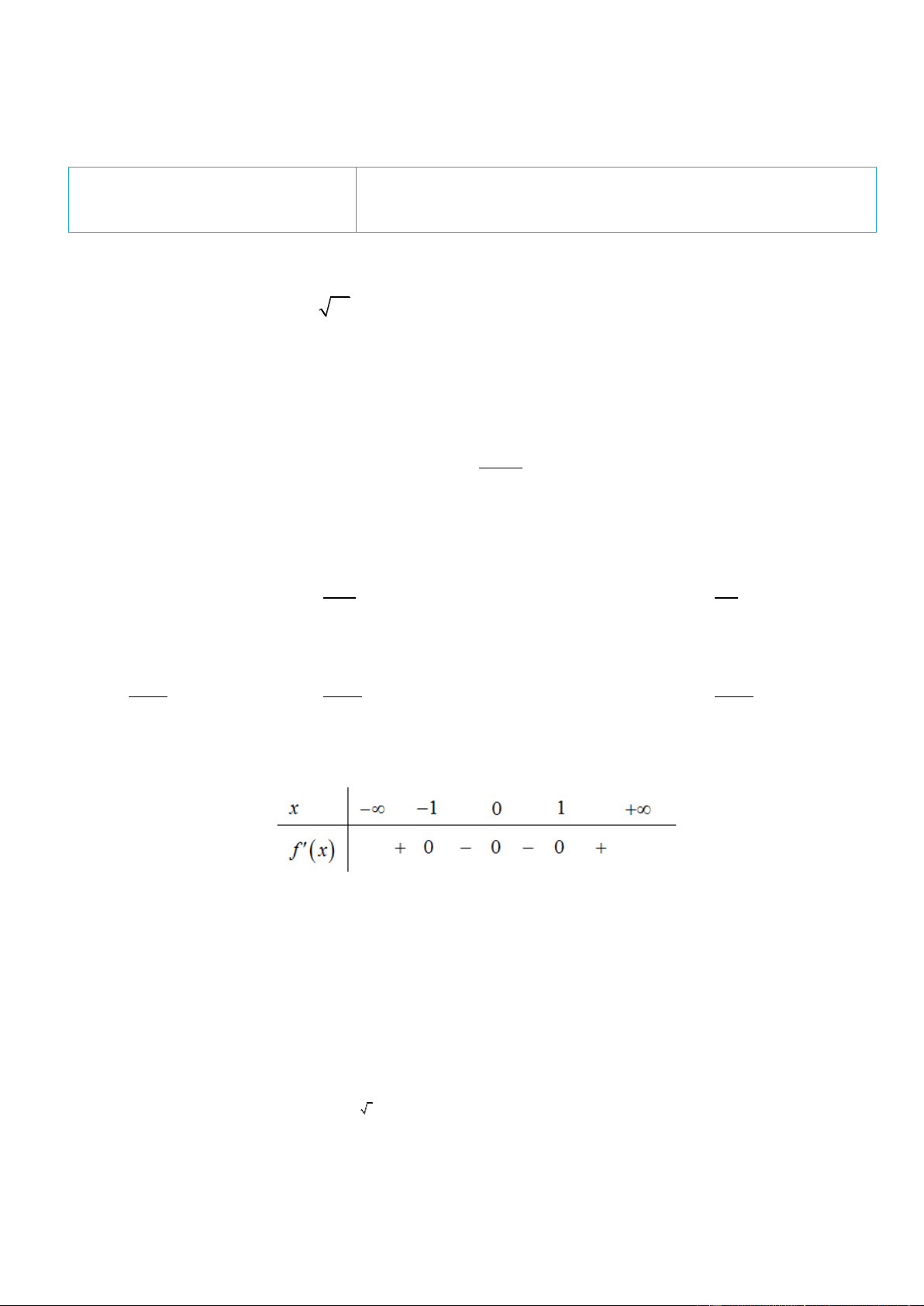
Câu 6. Cho hàm số f x có đạo hàm f x x x x 3 1 4 , x
. Số điểm cực đại của hàm số đã cho là A. 2 . B. 3 . C. 4 . D. 1 . 2 x 23
Câu 7. Tập nghiệm của bất phương trình 3 9 là A. 5 ;5 . B. ;5 . C. 5; . D. 0;5 .
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và thể tích bằng 3
a .Tính chiều cao h của hình chóp đã cho. A. h . a . B. h 2 . a . C. h 3 . a . D. h 3 . a .
Câu 9. Tập xác định của hàm số y 2 x13 là A. .
B. 2; . C. ; 2 . D. \ 2 .
Câu 10. Nghiệm của phương trình log x 7 5 là 2 A. x 18 . B. x 25 . C. x 39 . D. x 3. 1 1 1 Câu 11. Biết
f xdx 2 và g
xdx 3, khi đó f
x gx dx bằng 0 0 0 A. 1. B. 1. C. 5 . D. 5 . Trang1
Câu 12. Cho số phức z thỏa mãn điều kiện: 1 i z 1 3i 0 . Phần ảo của số phức w 1iz z là A. 1. B. 3 . C. 2 . D. 1.
Câu 13. Trong không giam Oxyz, mặt phẳng P : 2x 3y z 1 0 có một vectơ pháp tuyến là A. n 2;3; 1
B. n 1; 3; 2
C. n 2; 3;1
D. n 1; 3; 2 2 4 3 1
Câu 14. Trong không gian Oxyz cho ba vectơ a 1; 1
;2,b 3;0; 1 , c 2 ;5
;1 , vectơ m a b c có tọa độ là A. 6;0; 6 . B. 6 ;6;0 . C. 6; 6 ;0 . D. 0;6; 6 .
Câu 15. Trong mặt phẳng tọa độ, biết điểm M (2;1) là điểm biểu diễn số phức z . Phần thực của z bằng: A. 2 B. 2 C.1 D. 1 x 1
Câu 16. Tiệm cận đứng của đồ thị hàm số y x là 3 A. x 3 . B. x 1 . C. x 1 . D. x 3.
Câu 17. Với a là số thực dương tùy ý, log 5a bằng 5
A. 5 log a .
B. 5 log a . C. 1 log a . D. 1 log a . 5 5 5 5
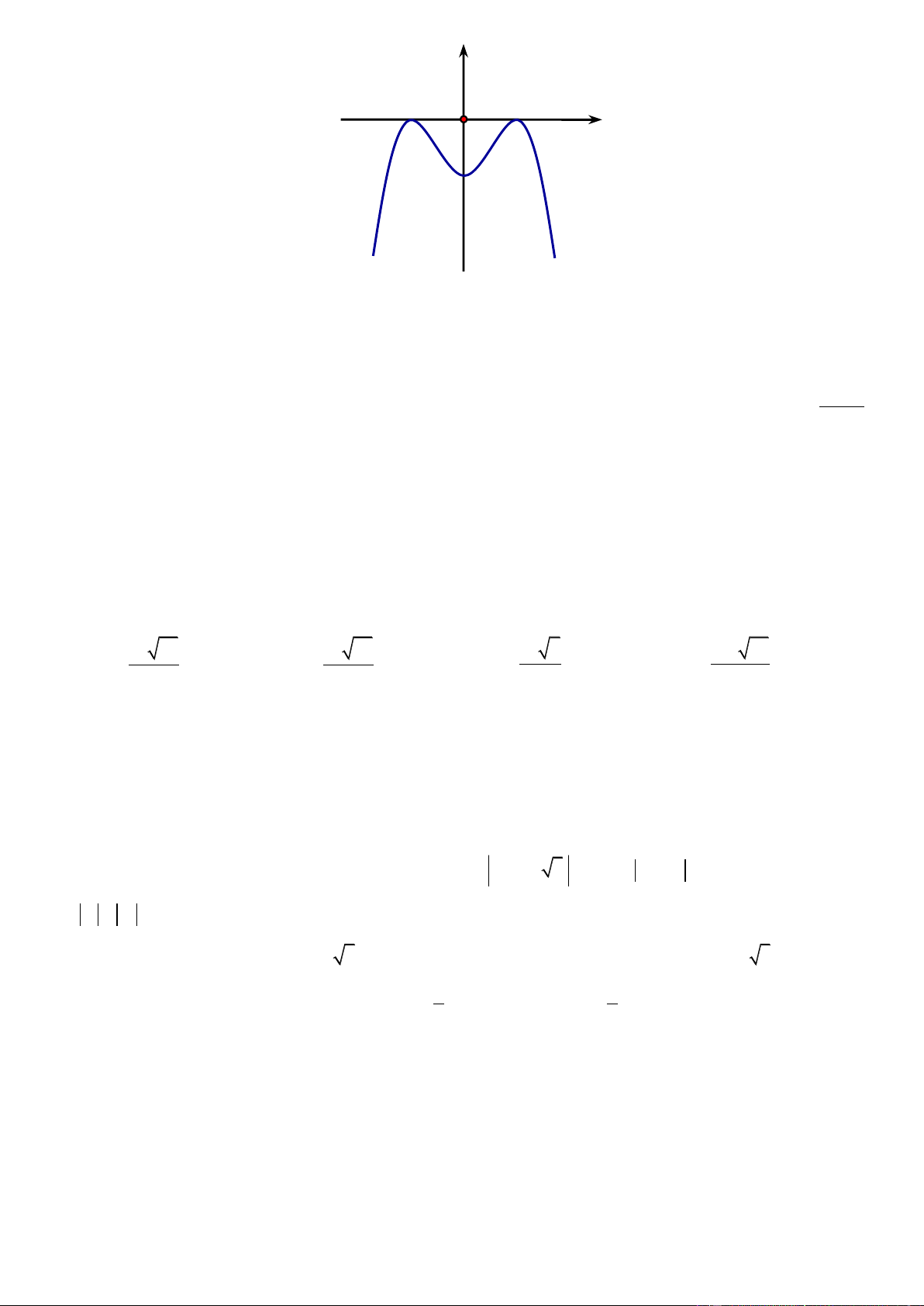
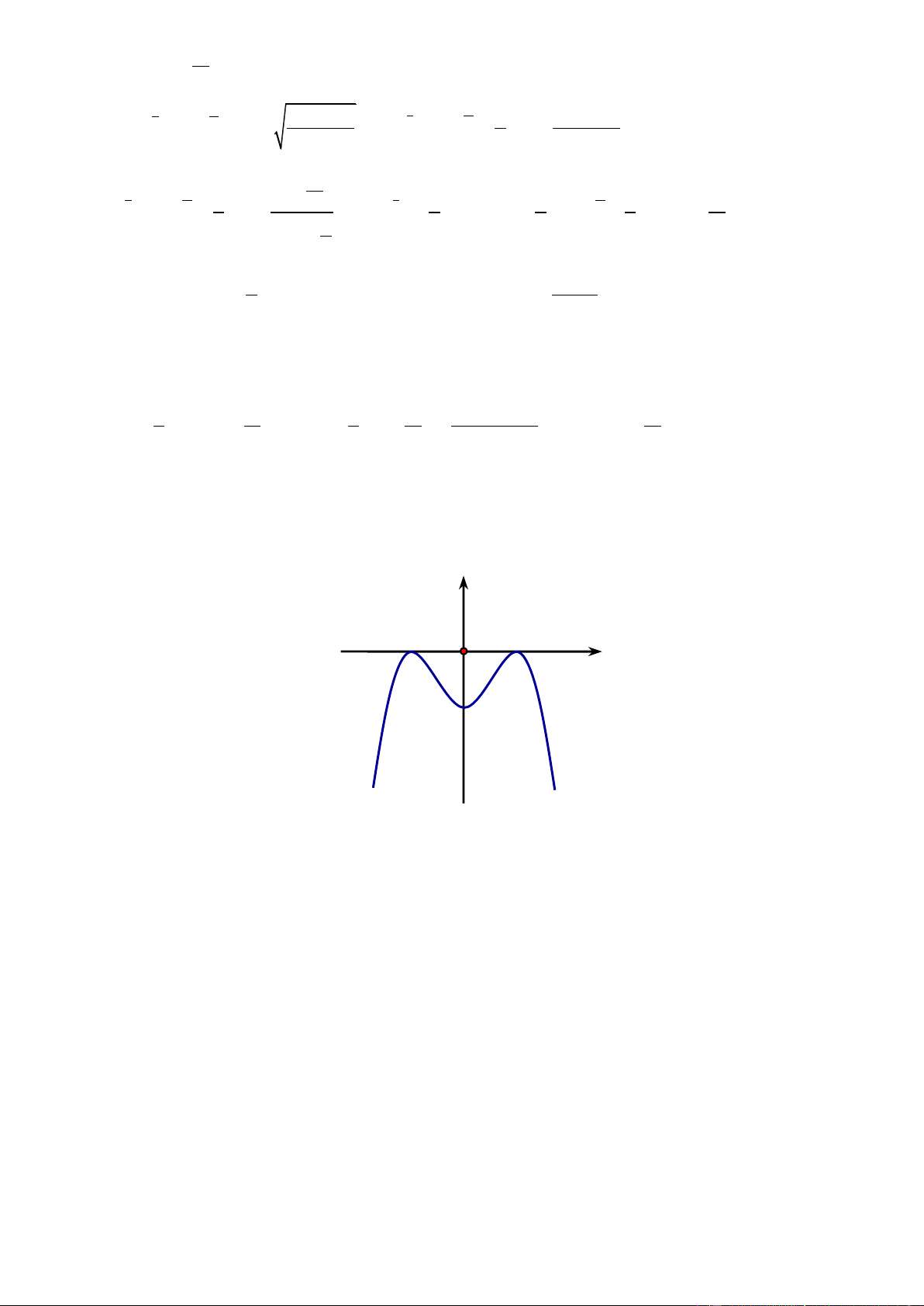
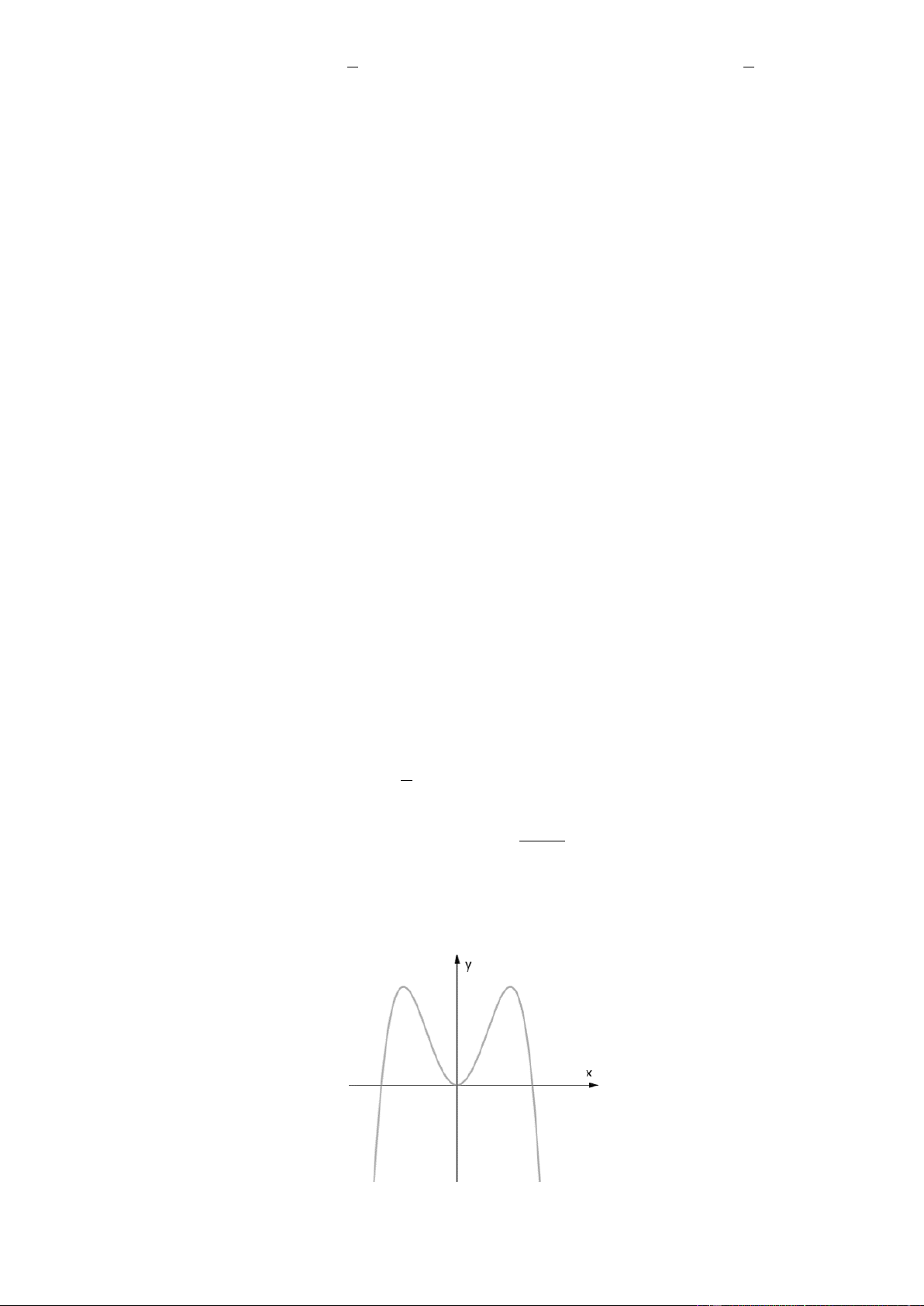
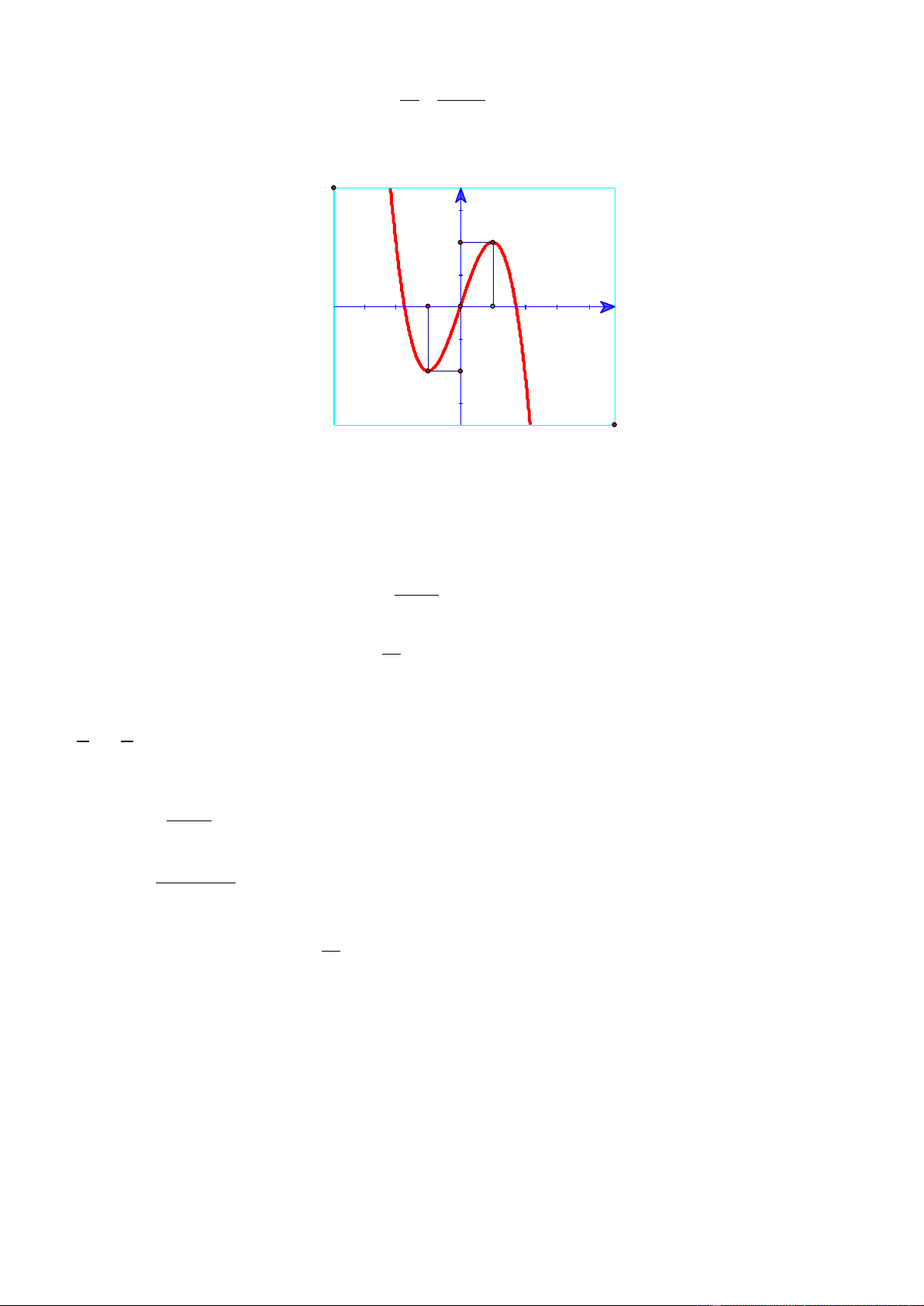
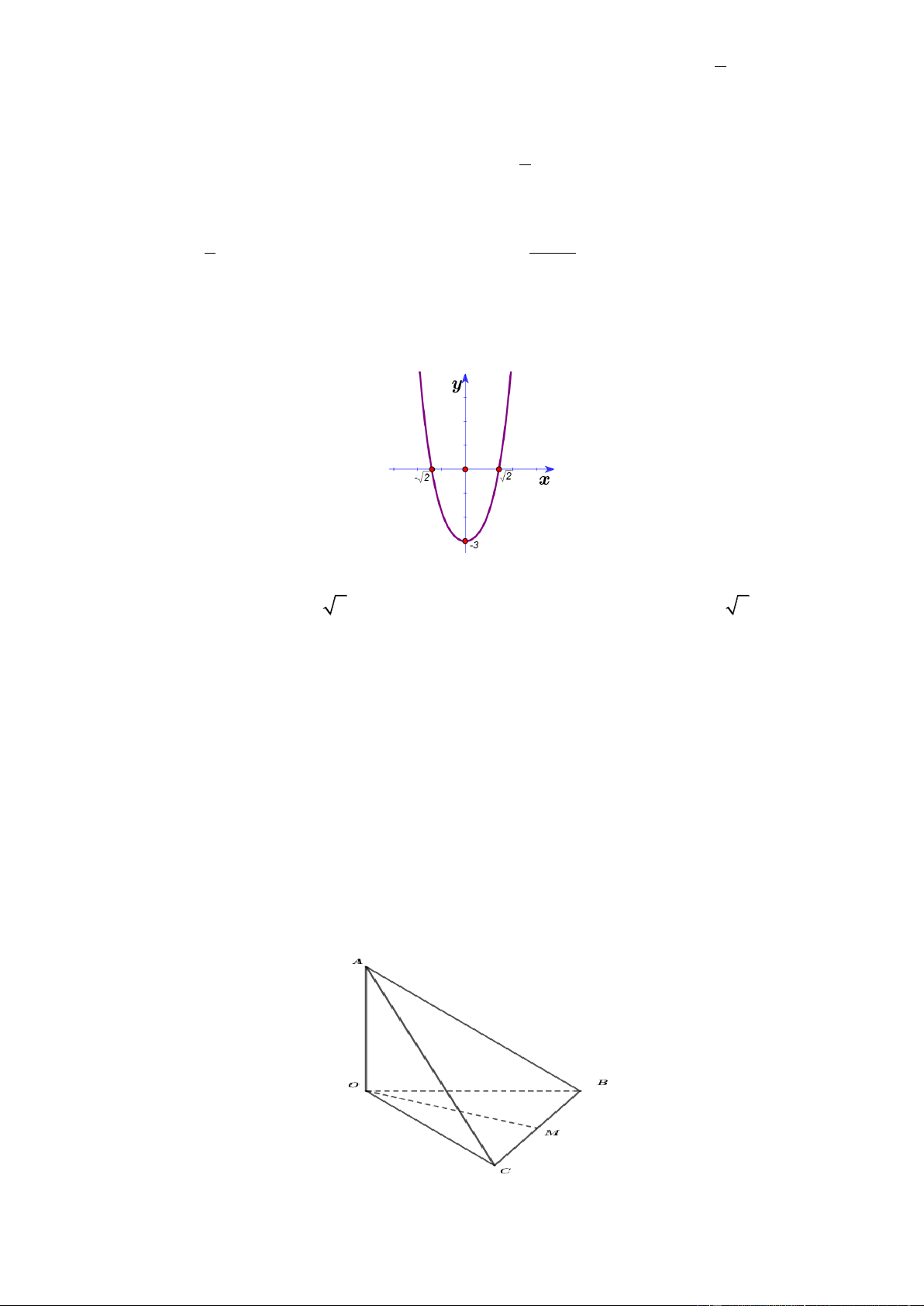
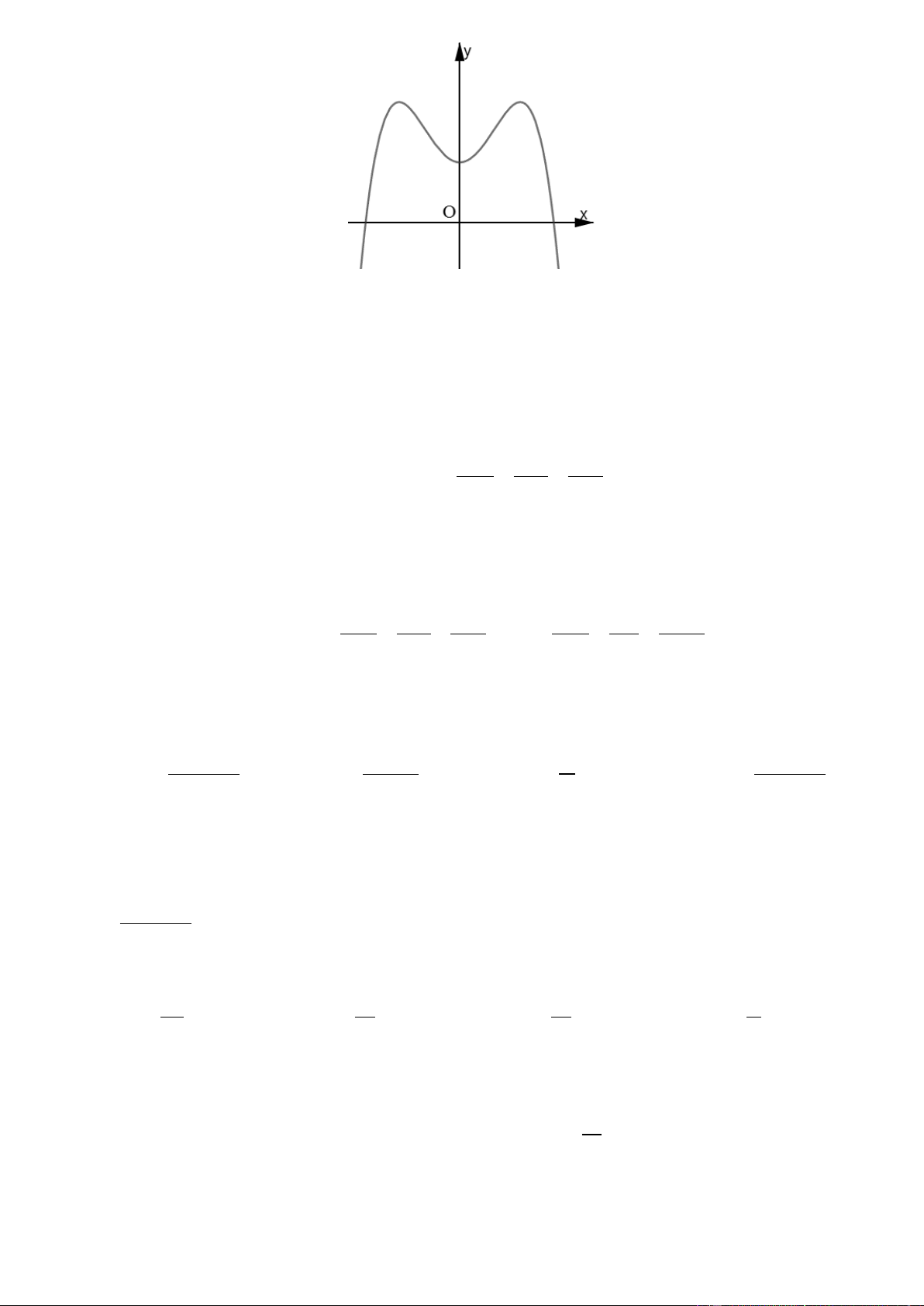
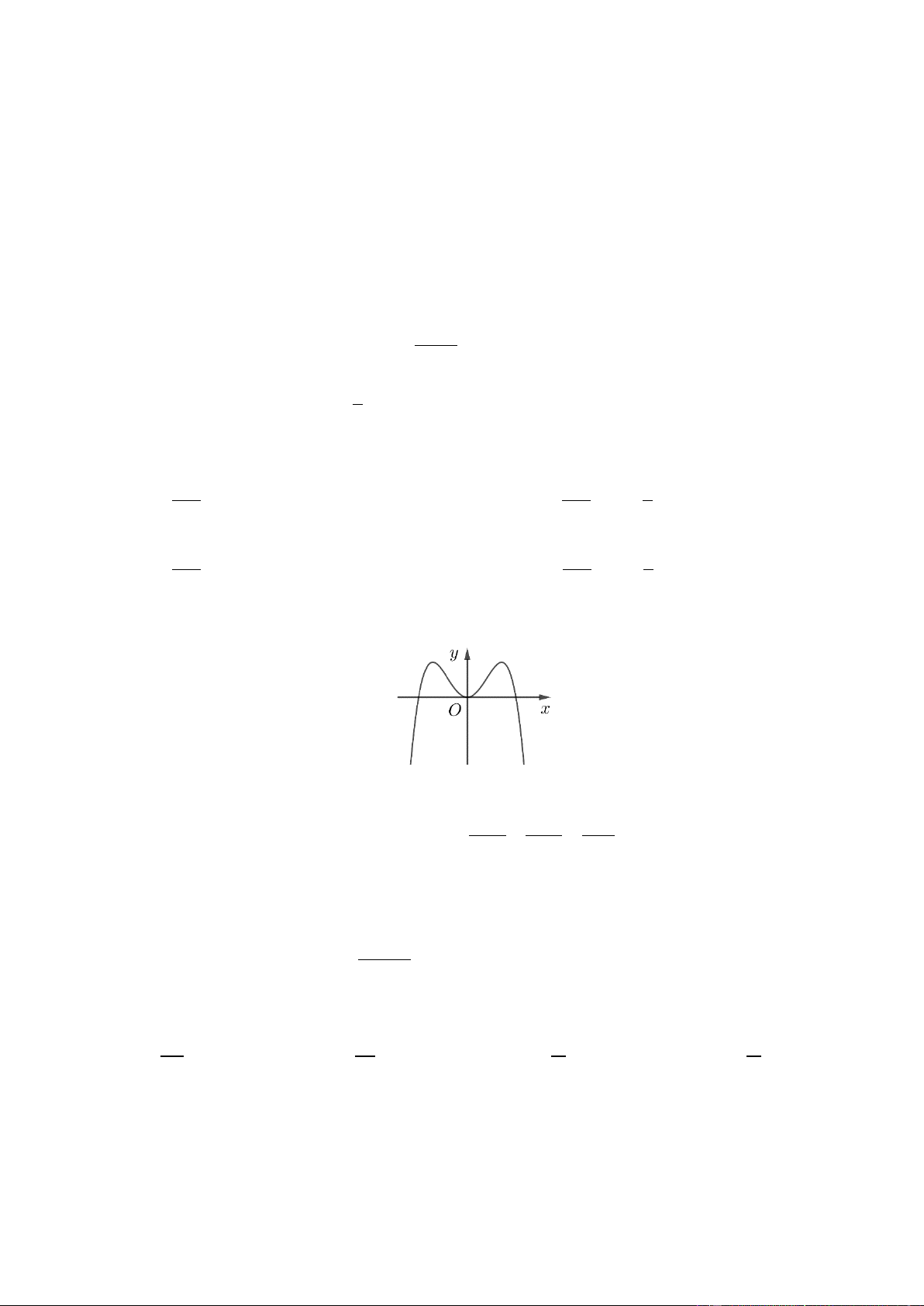
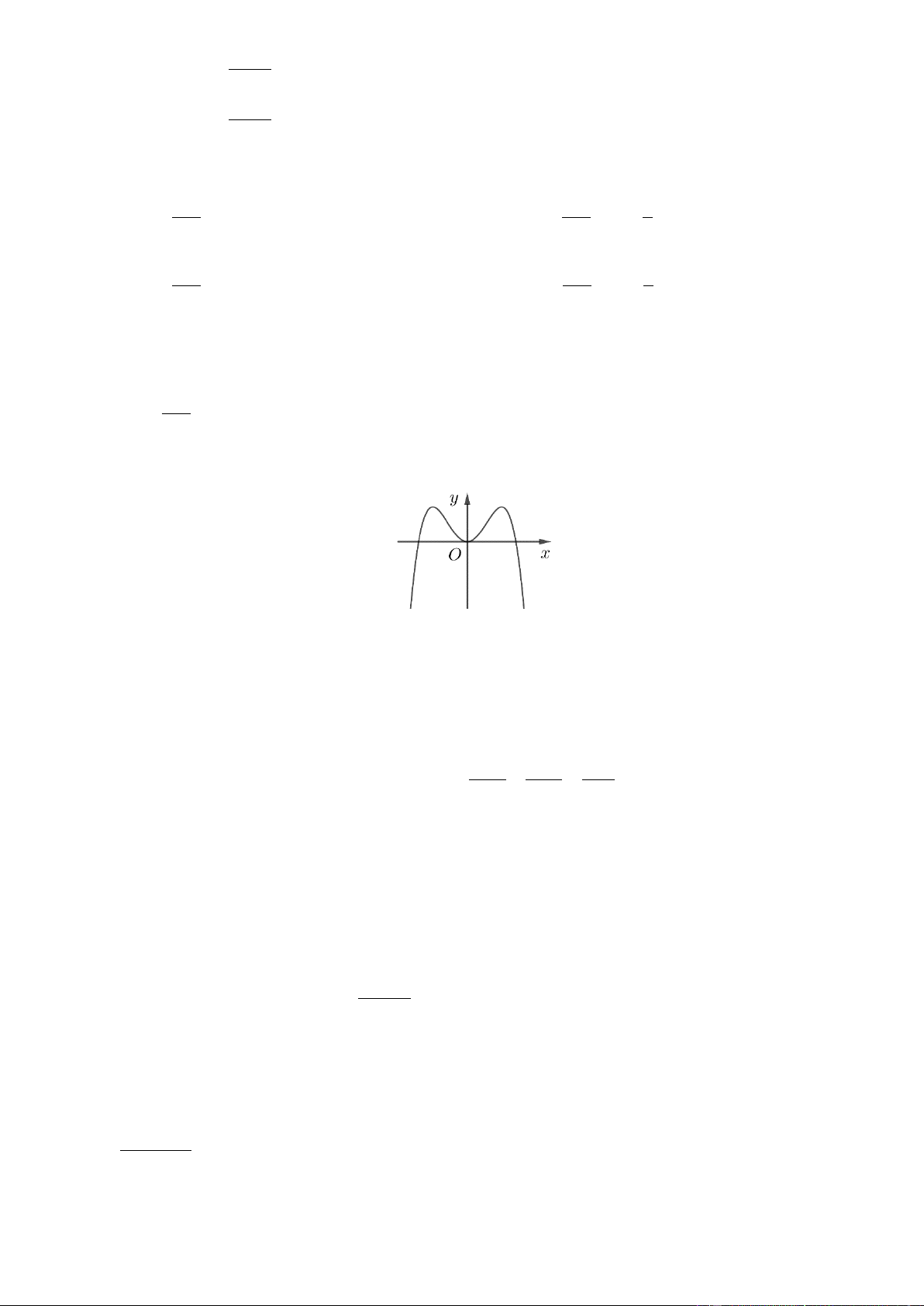
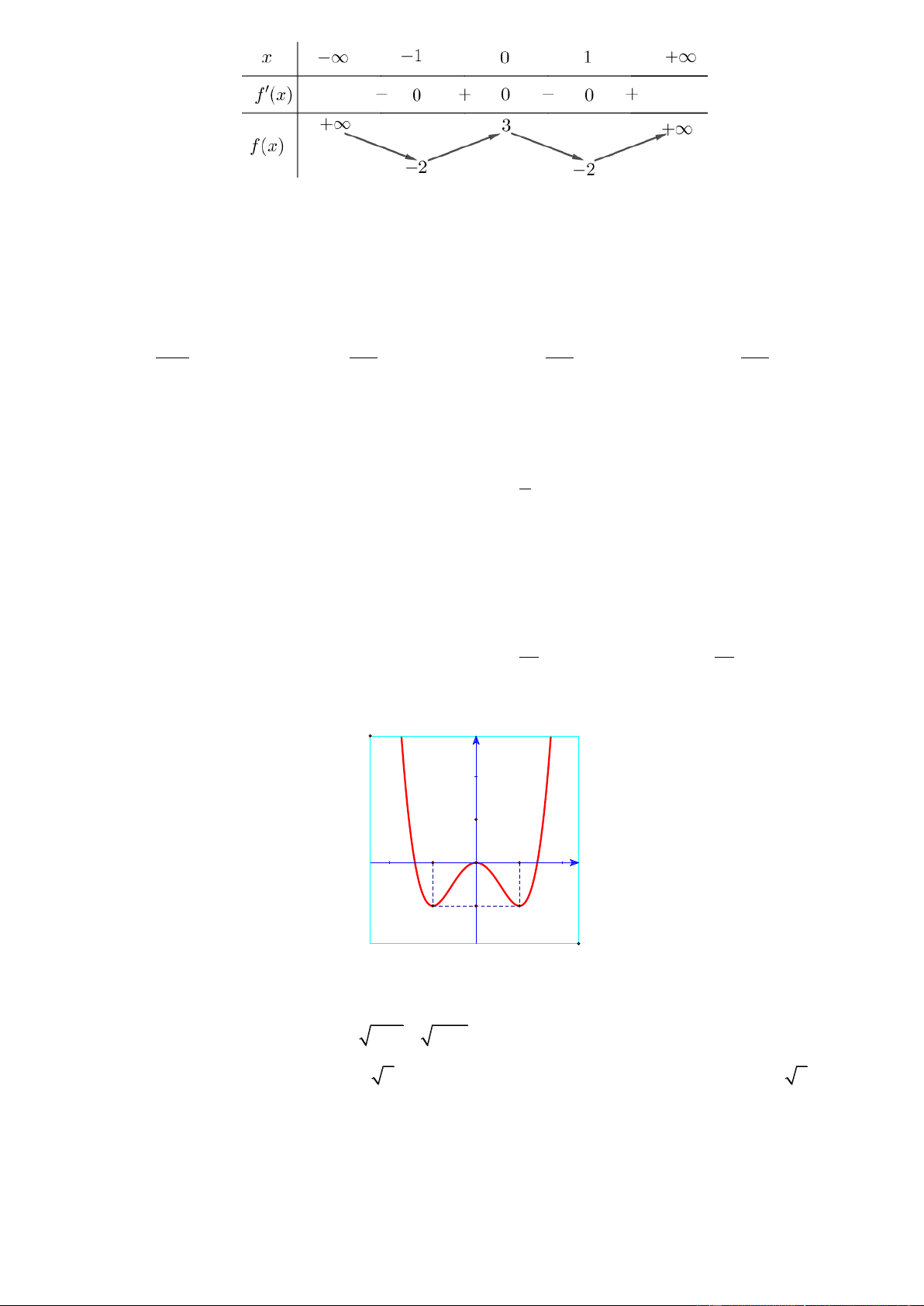
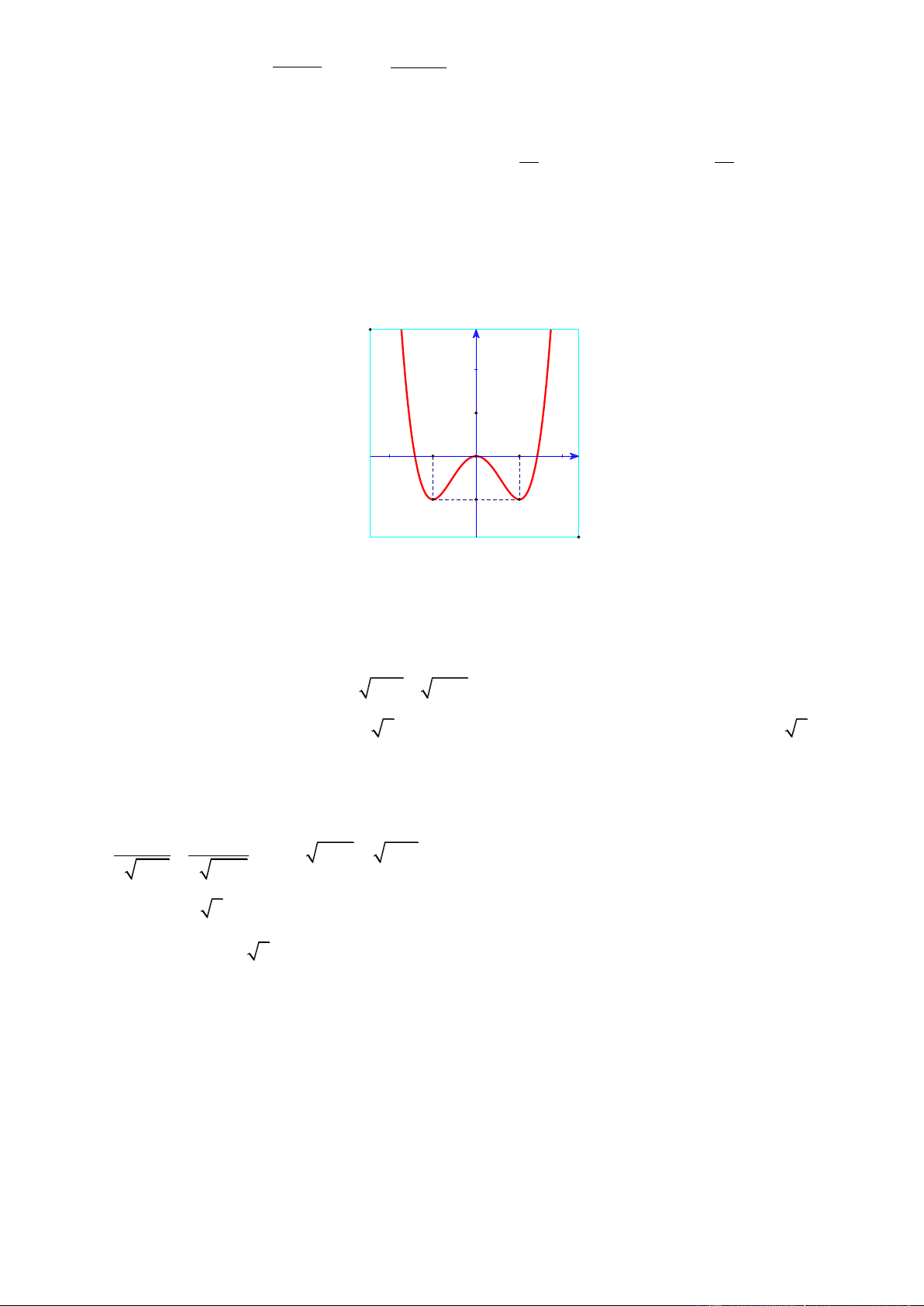
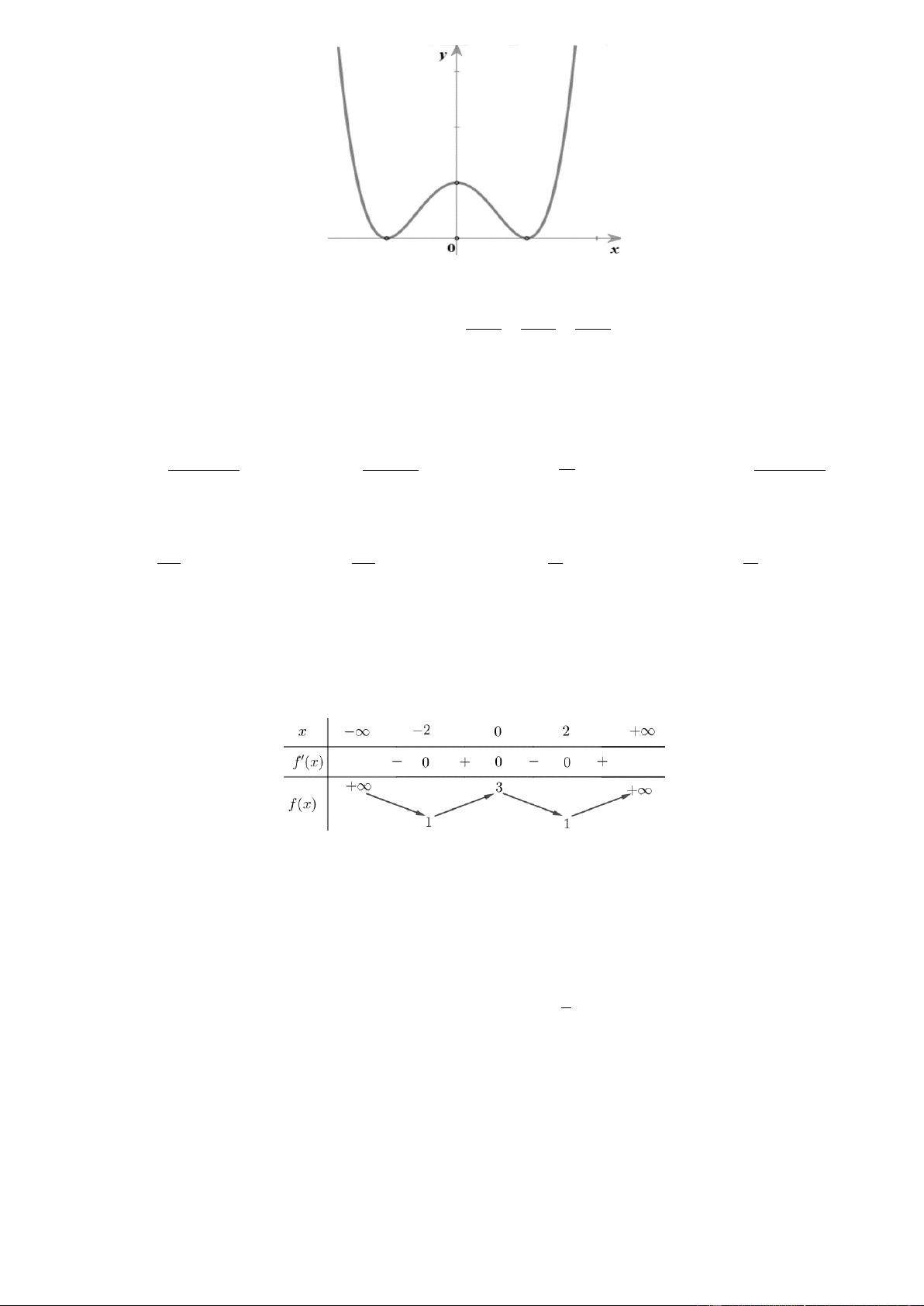
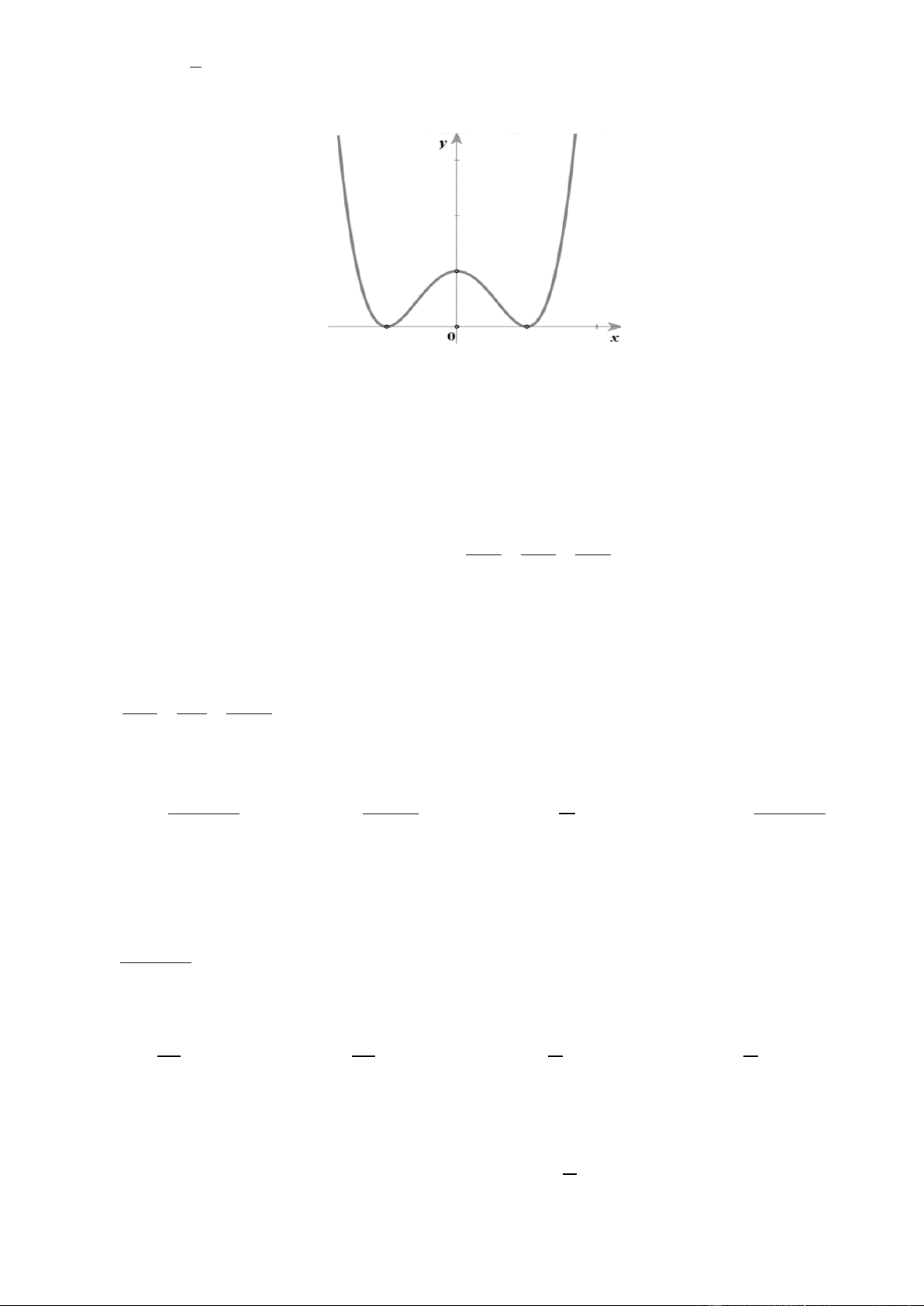
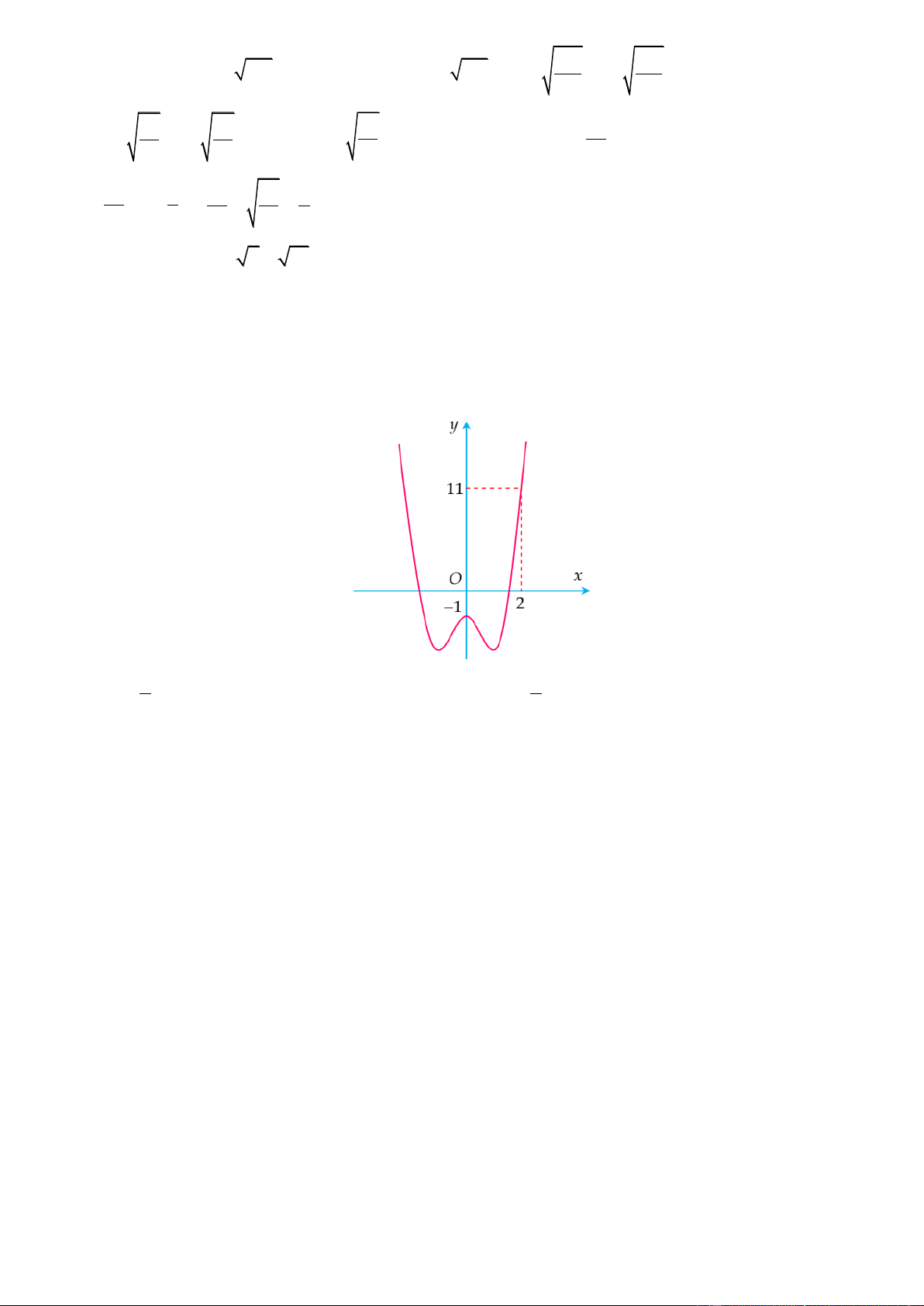
Câu 18. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3
y x 3x 2 B. 4 2
y x x 1 C. 4 2
y x x 1 D. 3
y x 3x 2 x 2 y 1 z 2
Câu 19. Trong không gian Oxyz , điểm nào dưới đây thuộc đường thằng d : . 1 1 2 A. N 2; 1 ;2 B. Q 2 ;1;2 C. M 2 ; 2 ;1
D. P 1;1; 2
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. A A A . D. A n k !(n . B. k)! n (k . C. n)! n k ! n (n . k)!
Câu 21. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là 3V 3h V h A. B . B. B . C. B . D. B . h V h V
Câu 22. Tính đạo hàm của hàm số ex y ln 3x . 1 3 x x 1 x 1
A. y e . B. ex y . C. ex y .
D. y e ln 3x e . 3x x x x
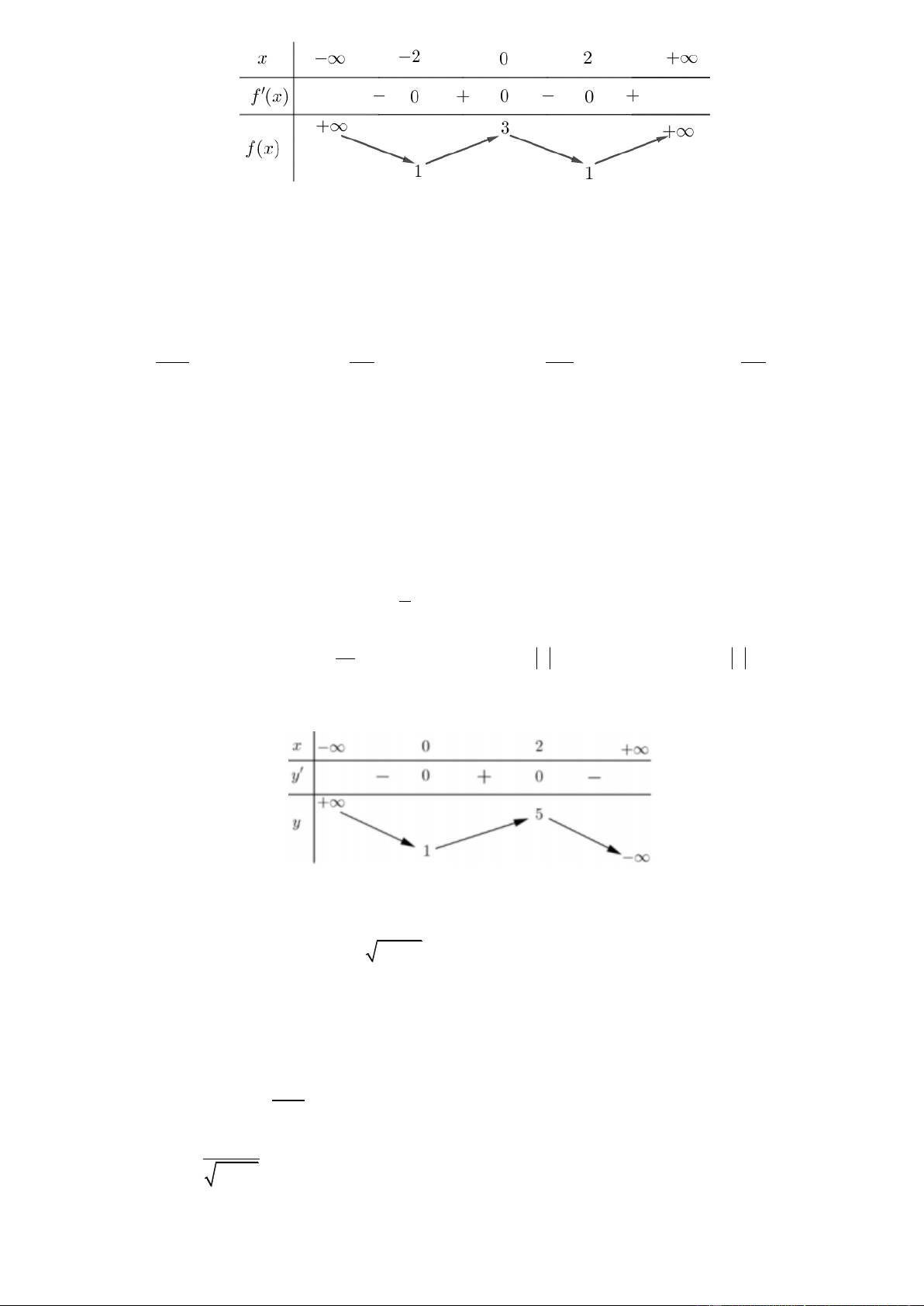
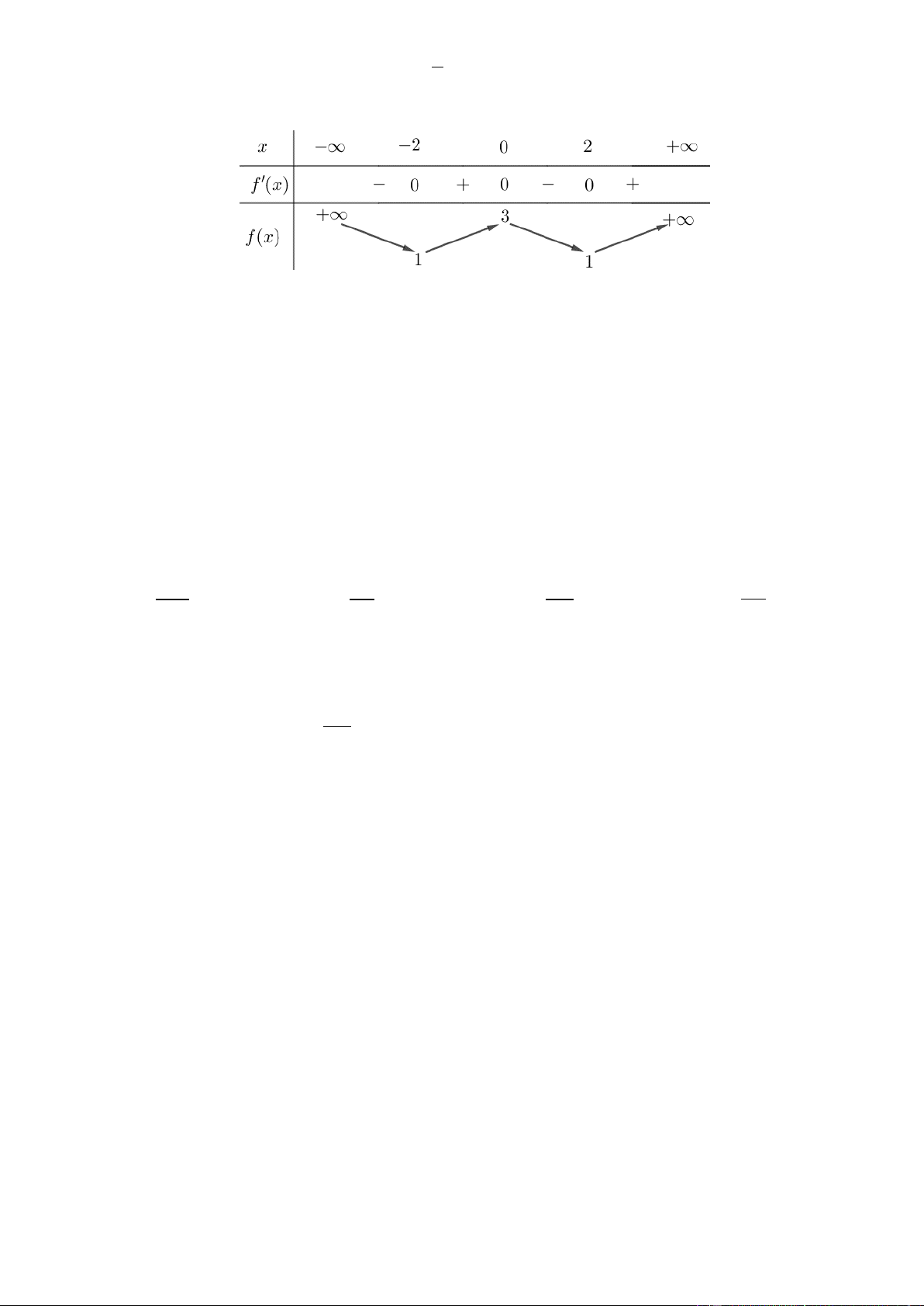
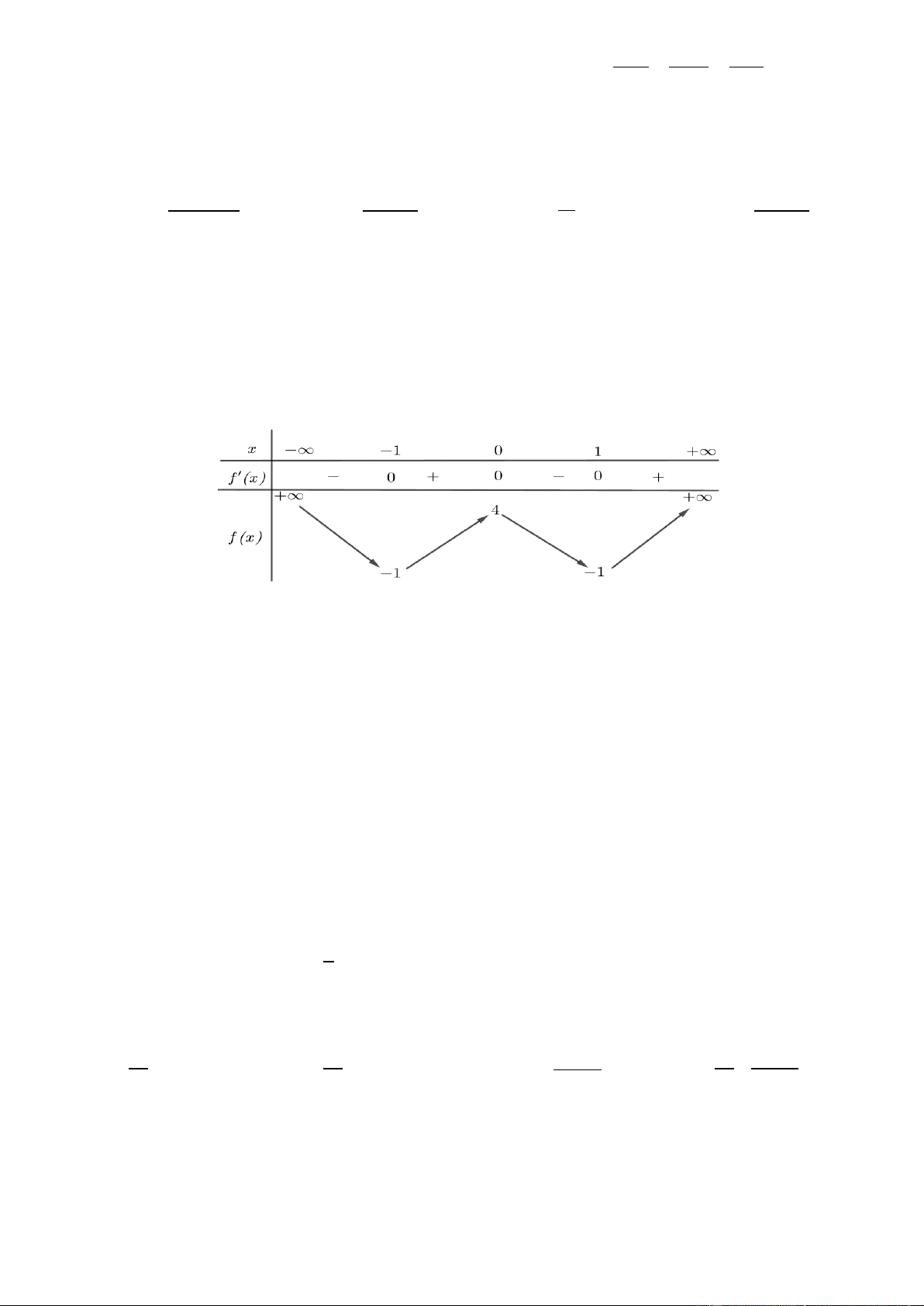
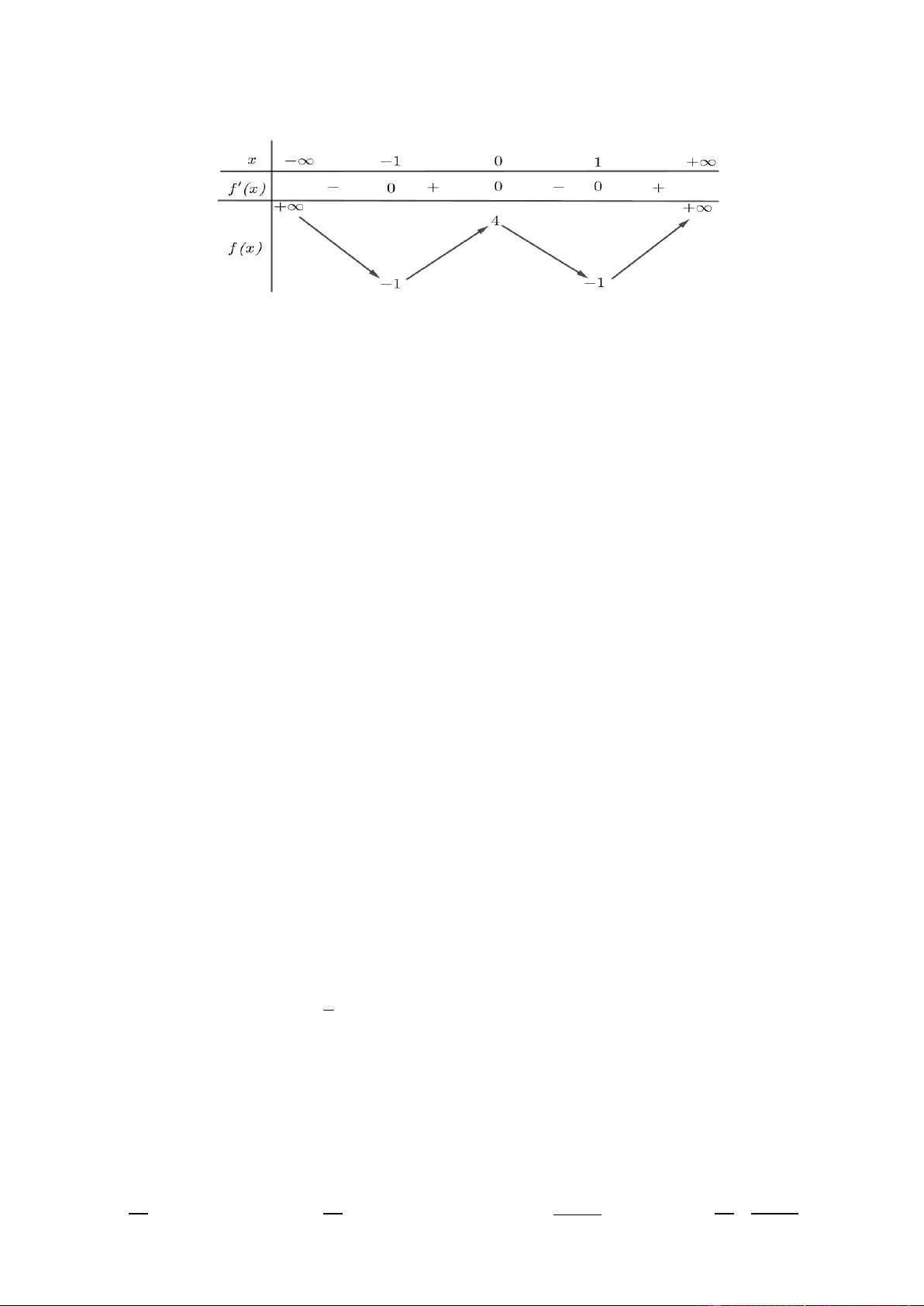
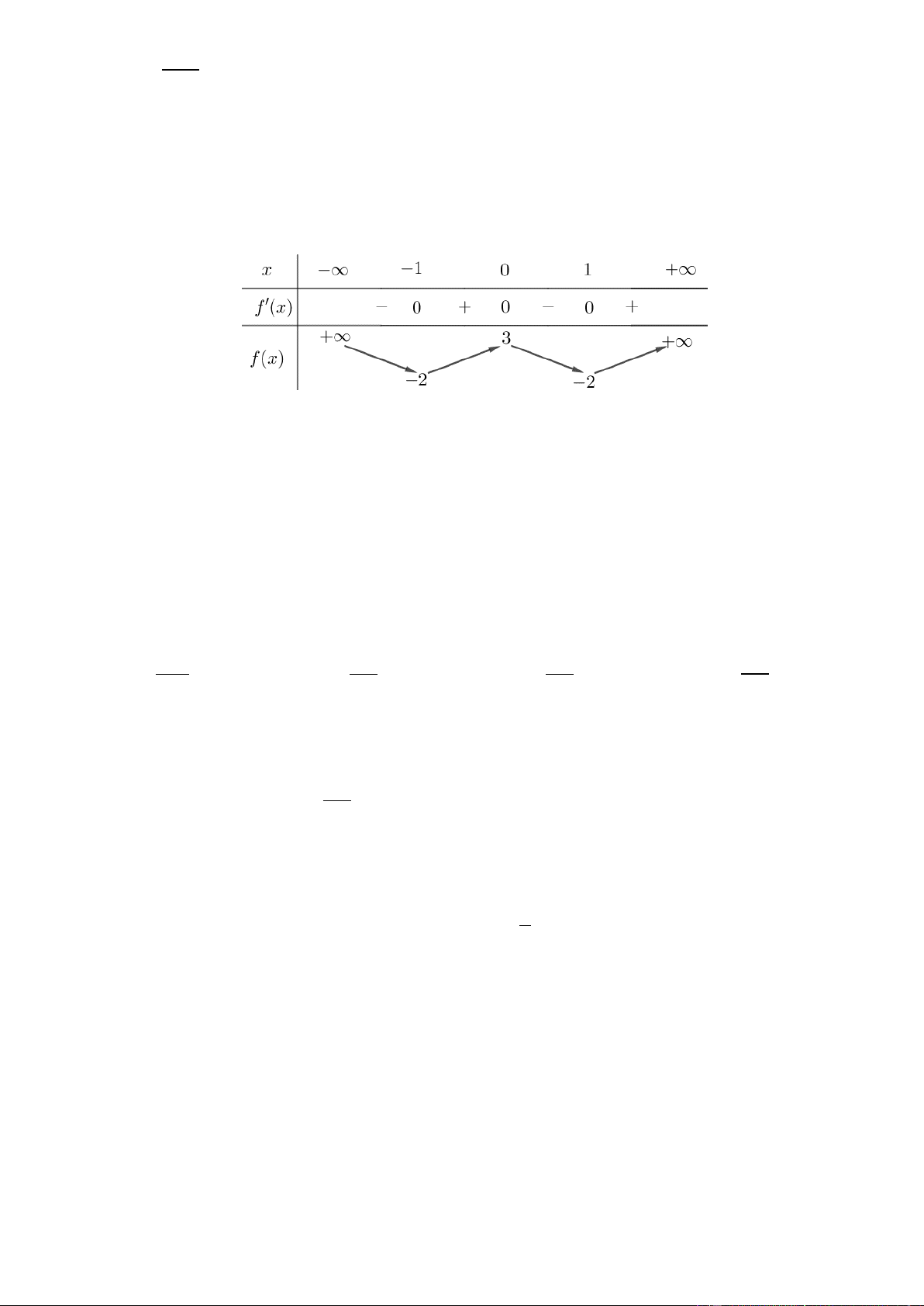
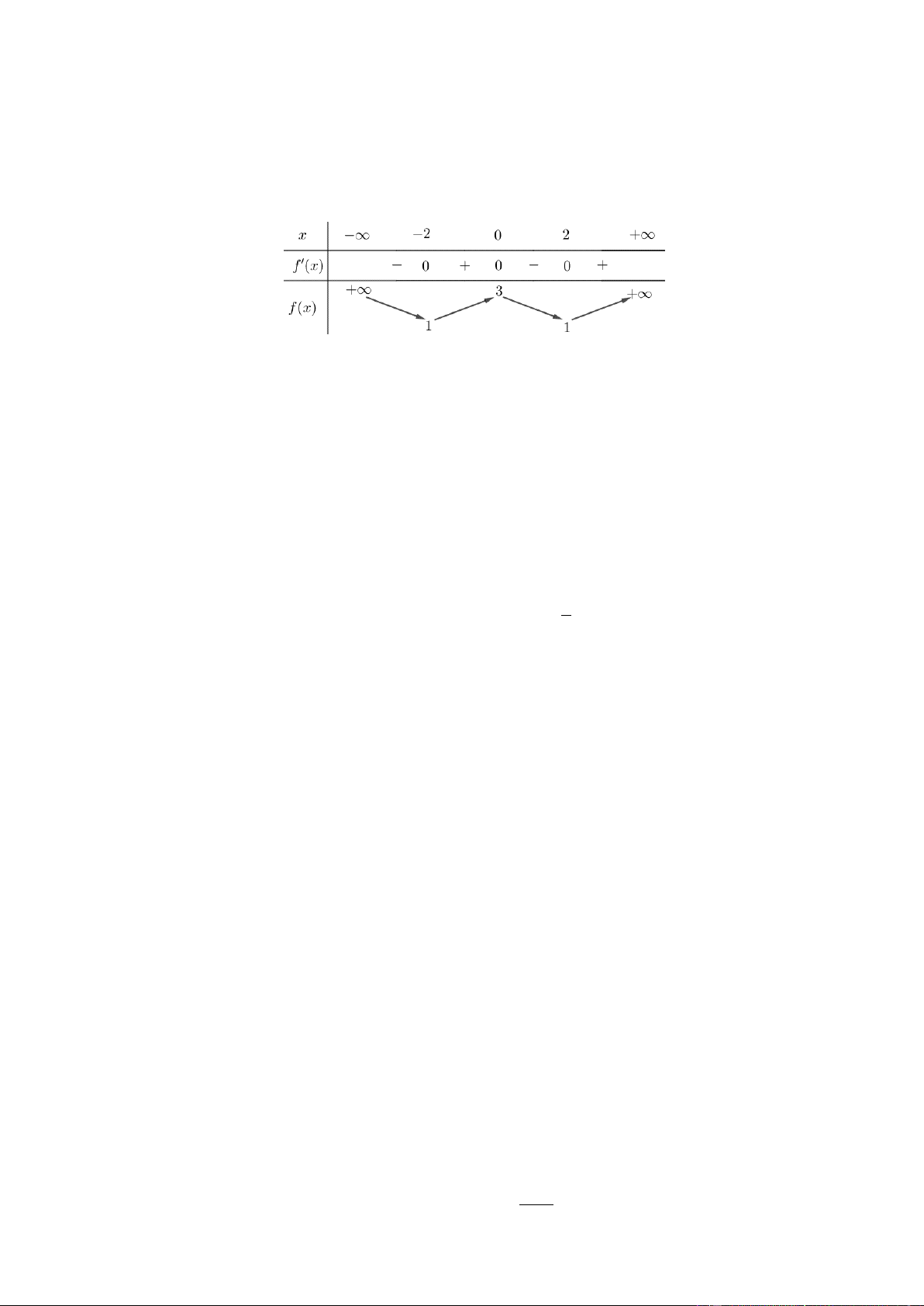
Câu 23. Cho hàm số có bảng biến thiên như sau Trang2
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? 0;2. 0;. 2 ;0. 2;. A. B. C. D.
Câu 24. Cho hình trụ có diện tích xung quanh S và độ dài đường sinh l . Bán kính đáy r của hình trụ đã cho xq
được tính theo công thức nào sau đây? 2S S S xq xq xq l A. r . B. r . C. r . D. r . l l 2 l Sxq 1 1 1 Câu 25. Cho f
xdx 2 và g
xdx 5 , khi f
x2gxdx bằng 0 0 0 A. 8 B. 1 C. 3 D. 12
Câu 26. Cho cấp số cộng u
với u 5;u 10 . Công sai của cấp số cộng đã cho bằng n 1 2 A. 5 . B. 5 . C. 2 . D. 15 .
Câu 27. Họ nguyên hàm của hàm số f x 1
sin x là x 1
A. ln x cos x C . B.
cos x C .
C. ln x cos x C .
D. ln x cos x C . 2 x
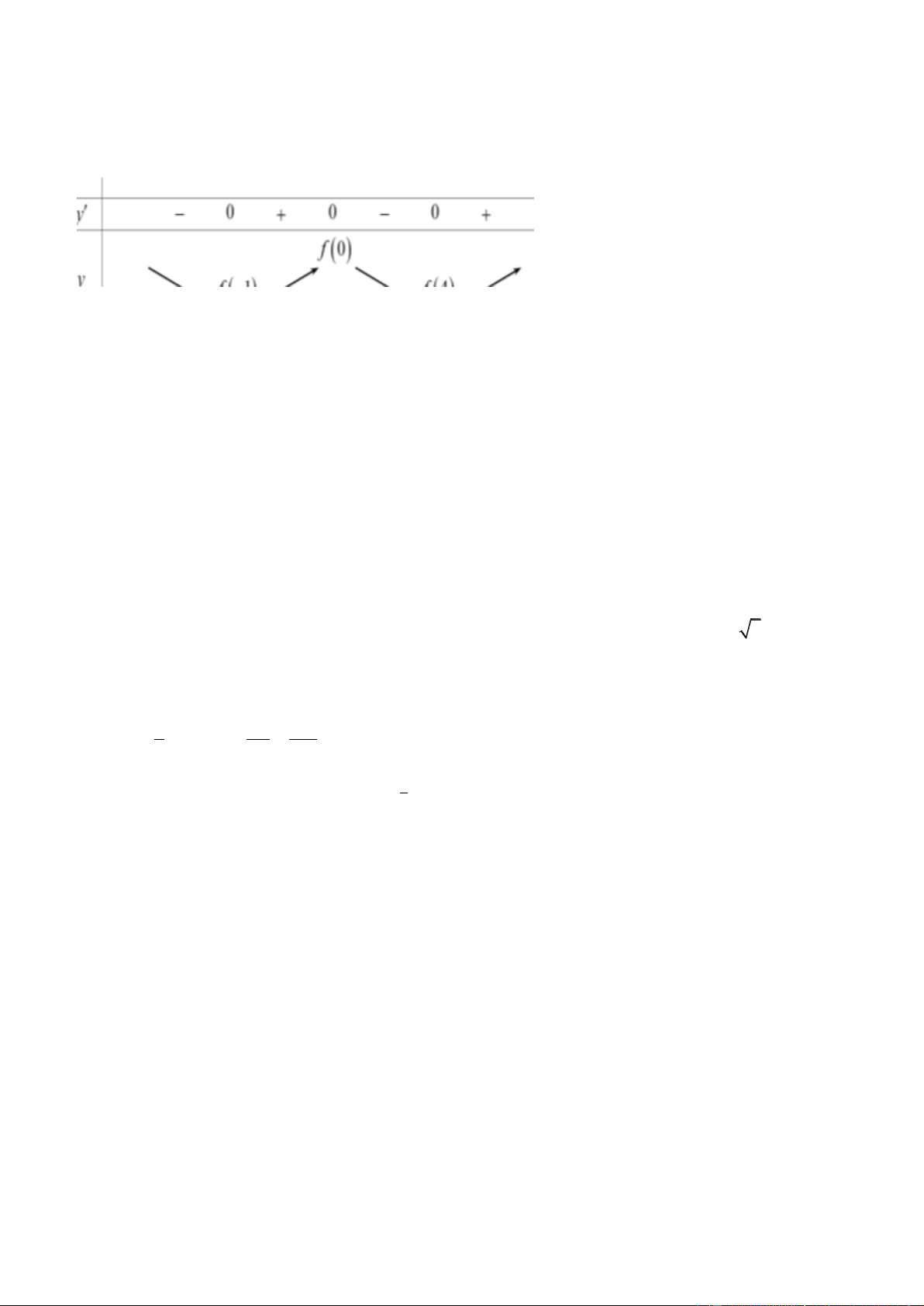
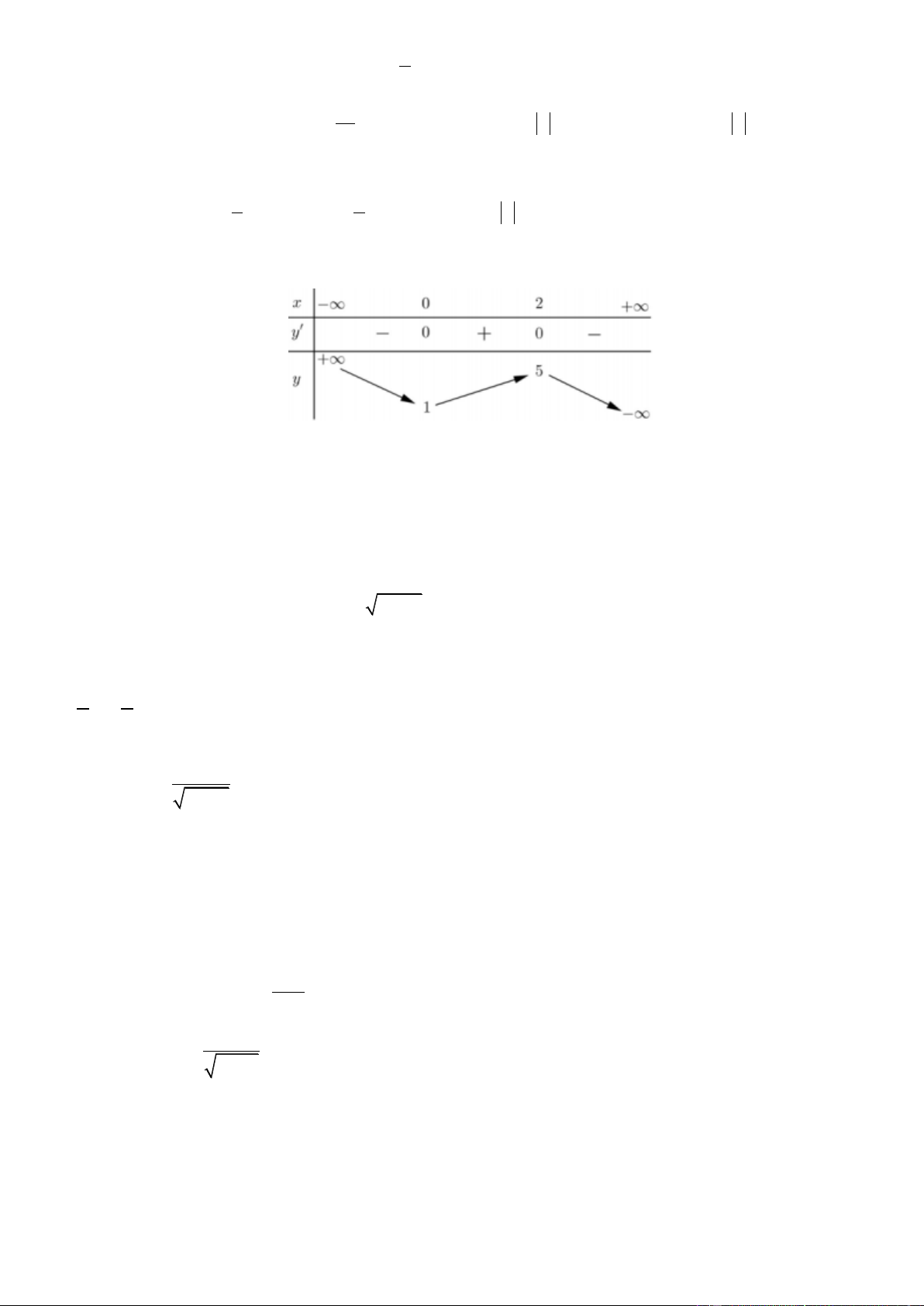
Câu 28. Cho hàm số y f x có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 5 B. 2 C. 0 D. 1
Câu 29. Giá trị lớn nhất của hàm số 2 y 4 x là A. 2. B. 0. C. 4. D. 1.
Câu 30. Xét các mệnh đề sau: (I). Hàm số 3 y (
x 1) nghịch biến trên . x
(II). Hàm số y ln(x 1) x đồng biến trên tập xác định của nó. 1 x (III). Hàm số y đồng biến trên . 2 x 1
Hỏi có bao nhiêu mệnh đề đúng? A. 3. B. 2. C. 1. D. 0. Trang3 log (ab)
Câu 31. Cho a và b là hai số thực dương thỏa mãn 3 9
4a . Giá trị của 2 ab bằng A. 3 . B. 6. C. 2 D. 4
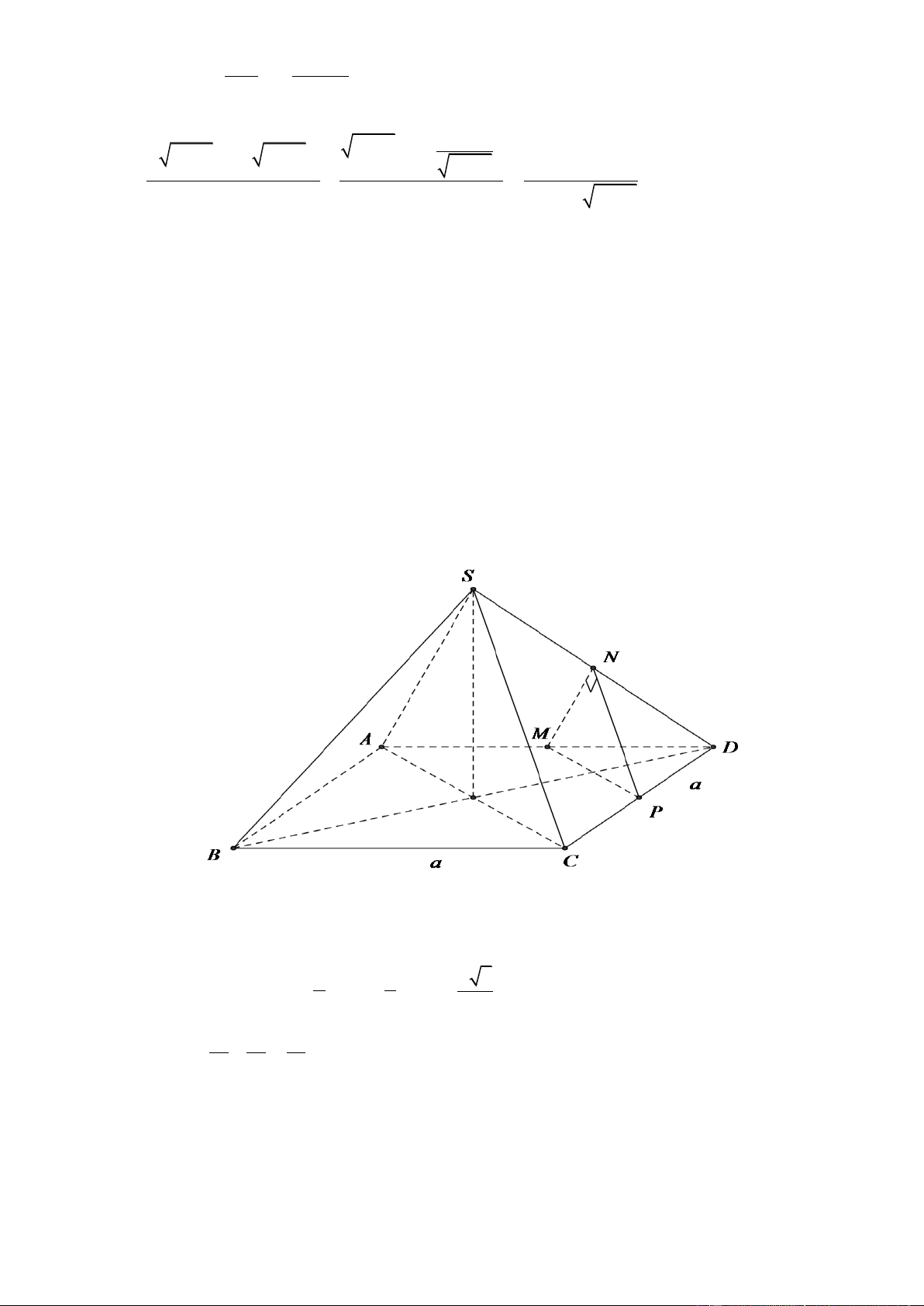
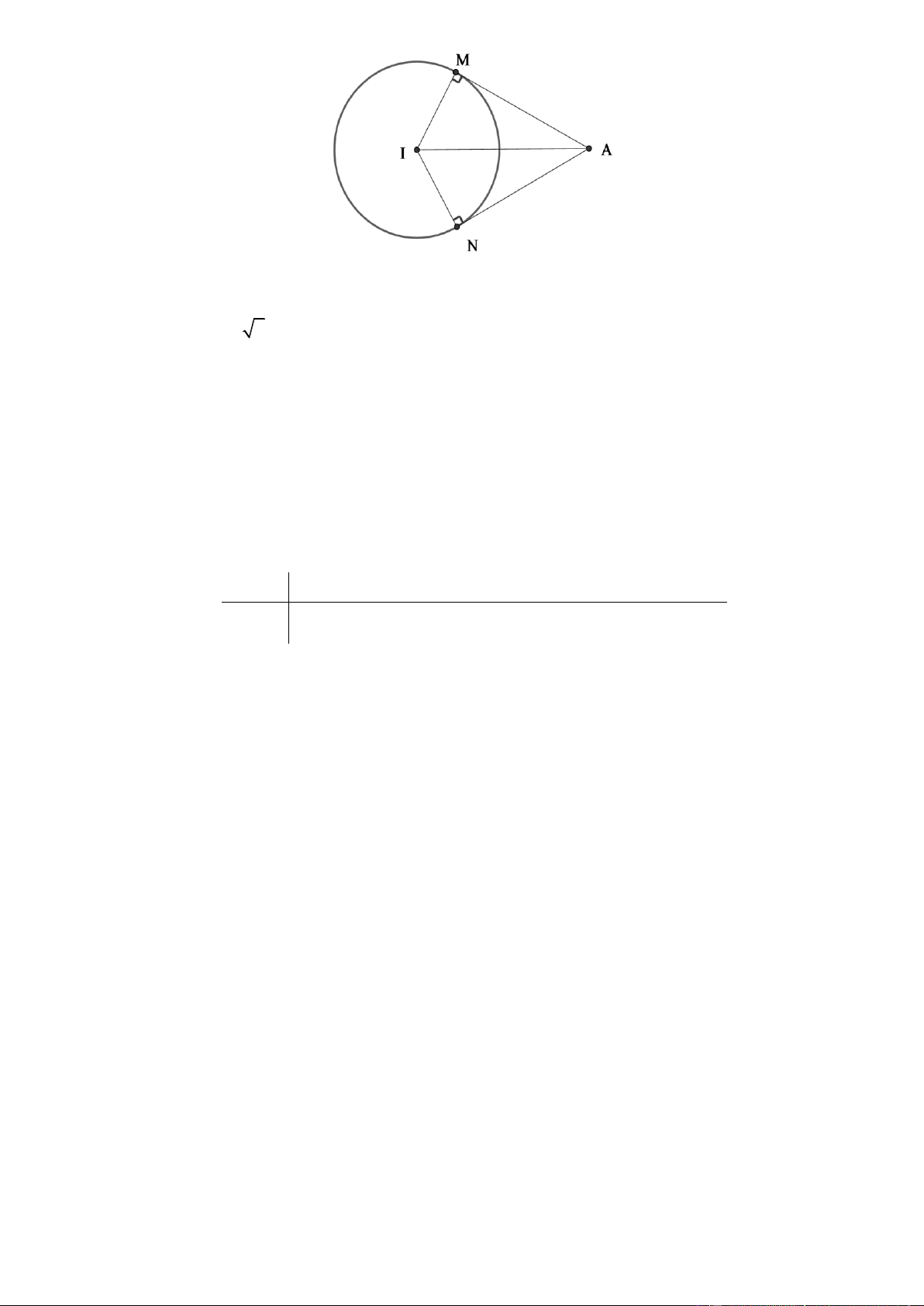
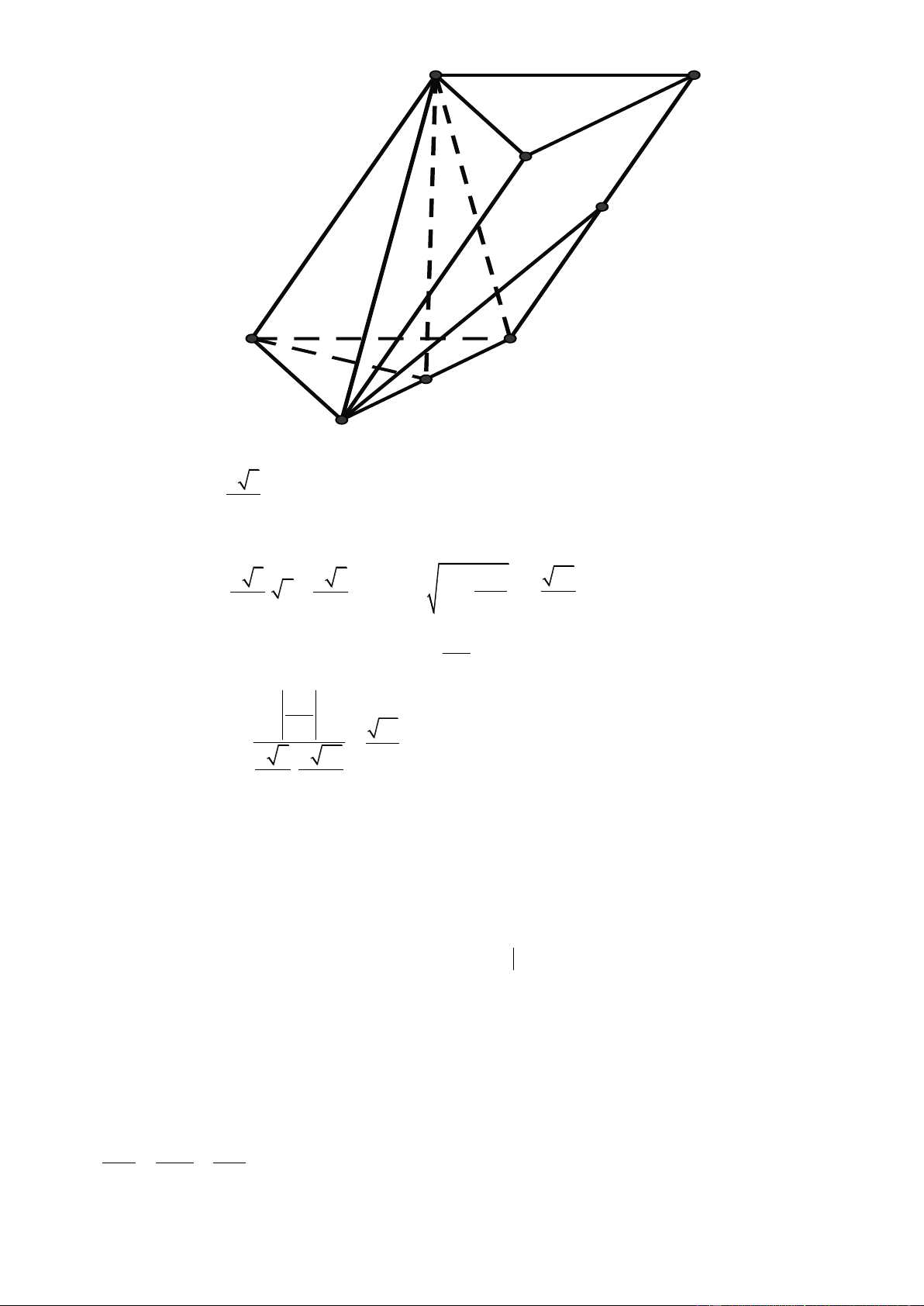
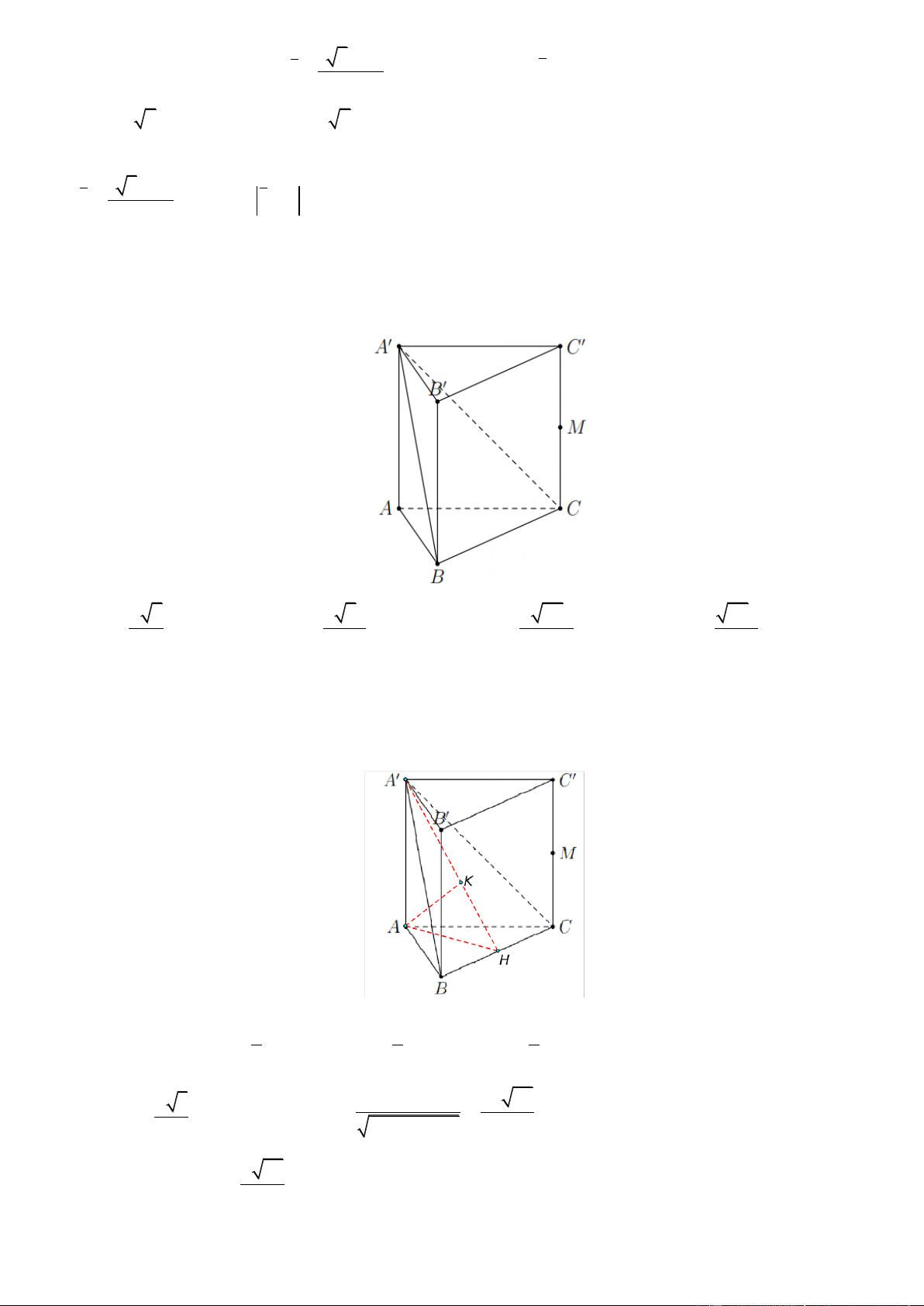
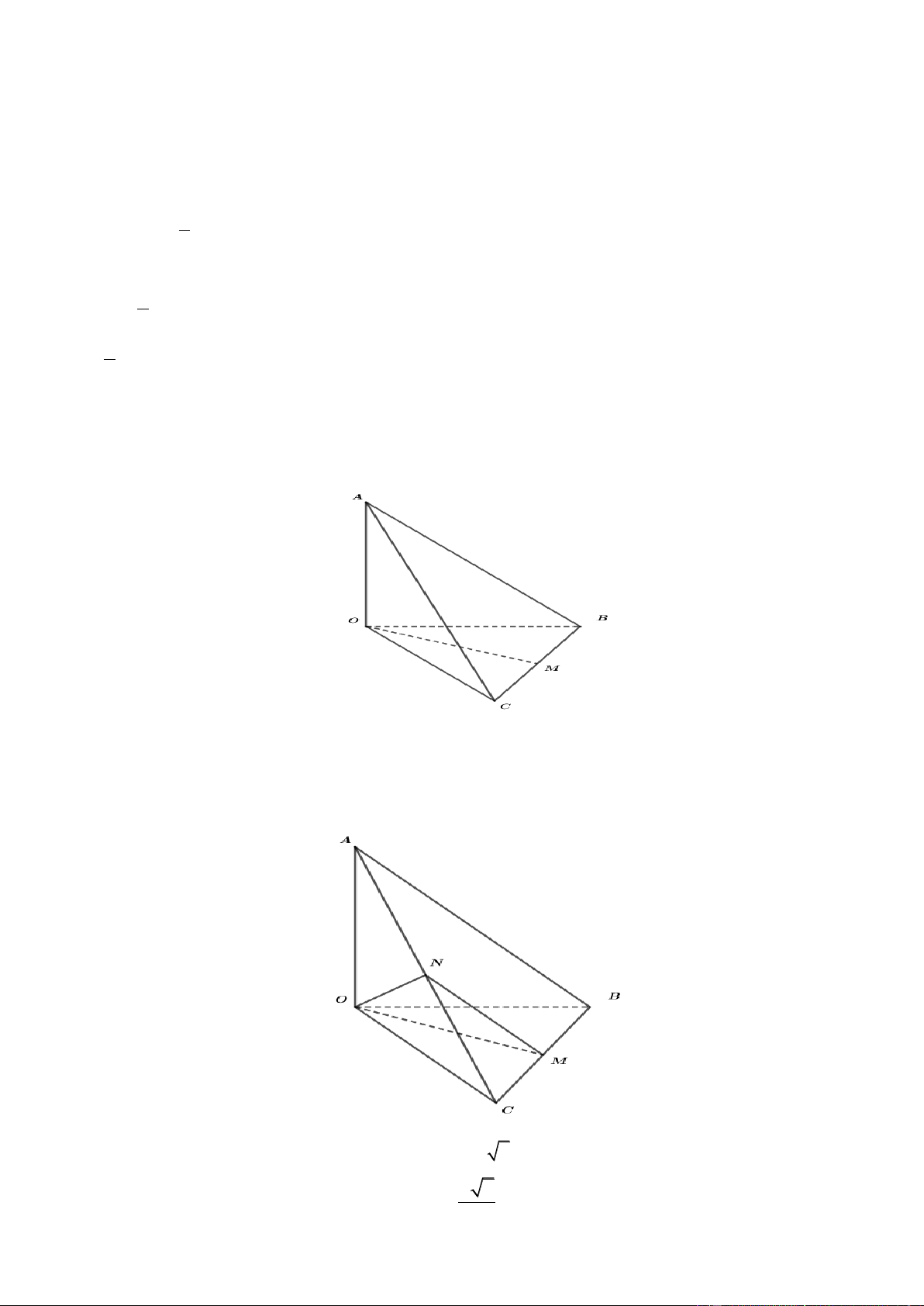
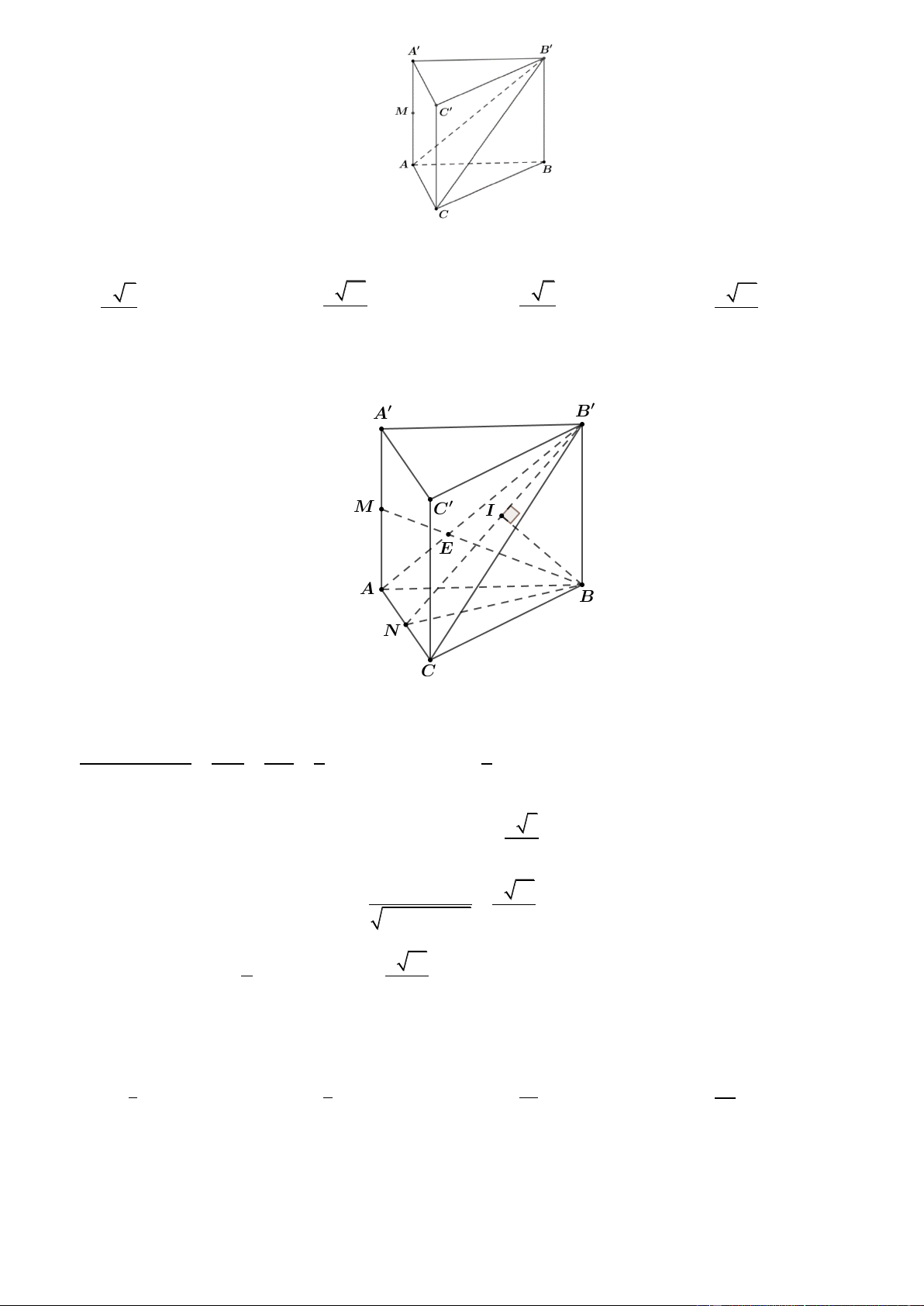
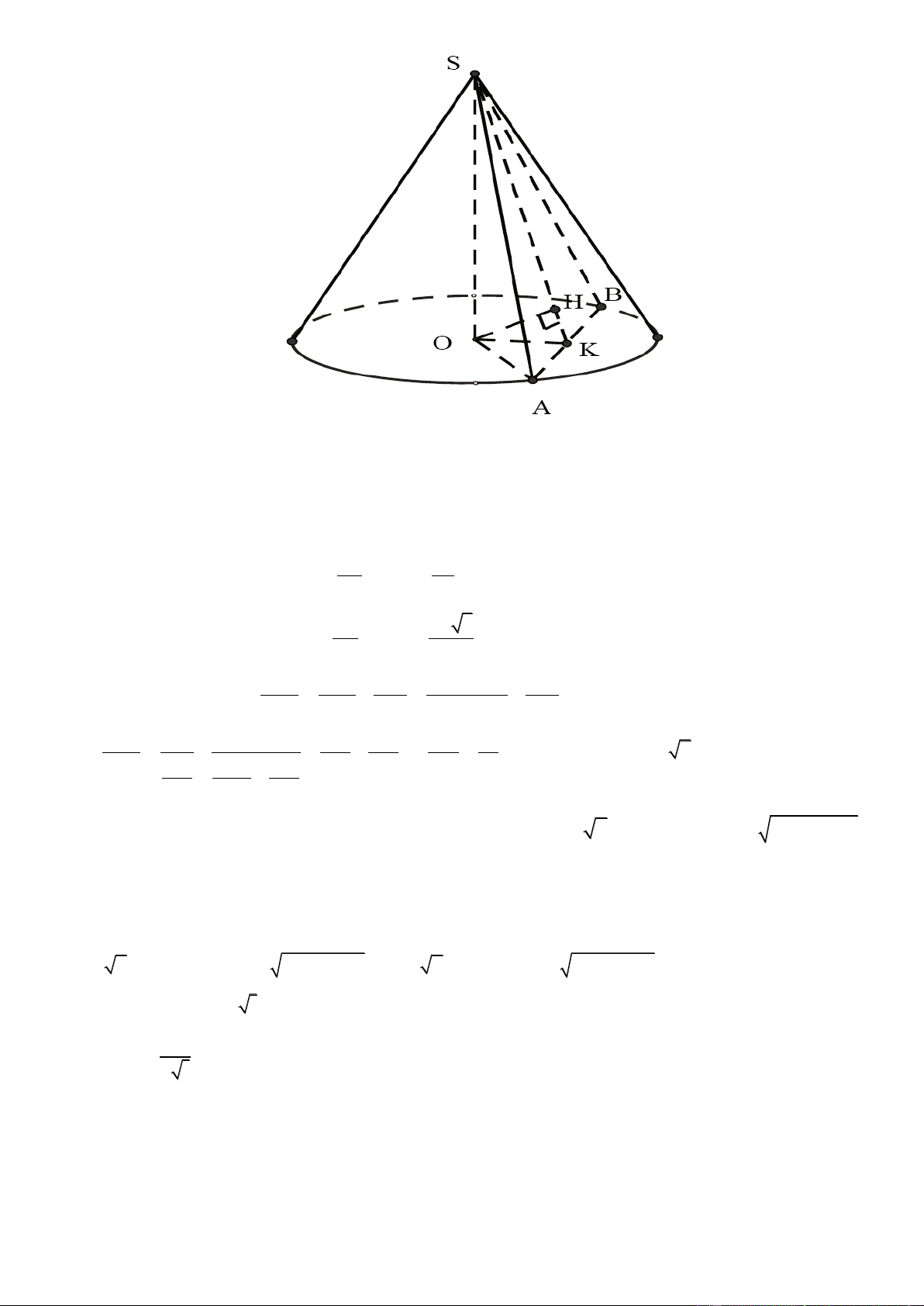
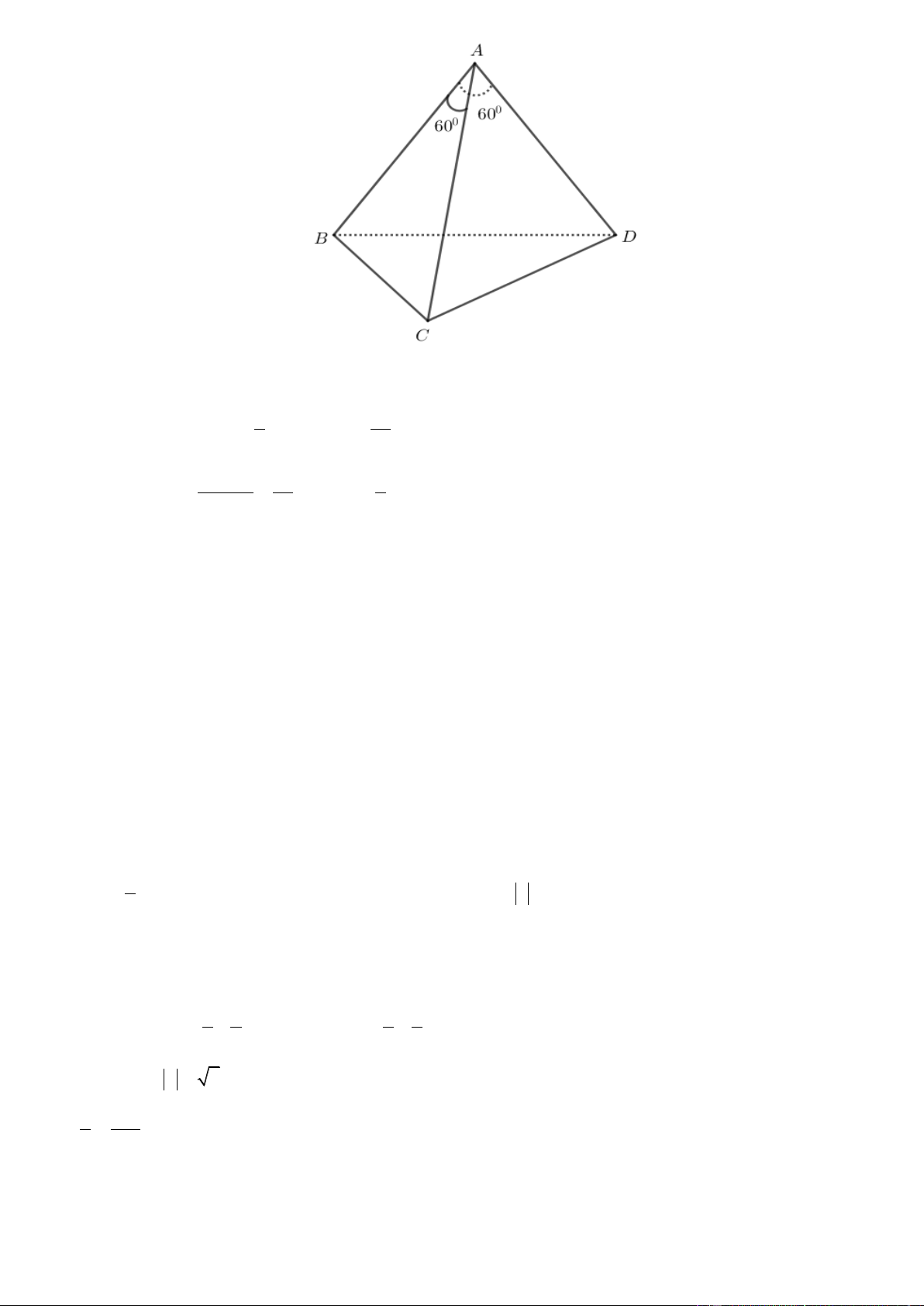
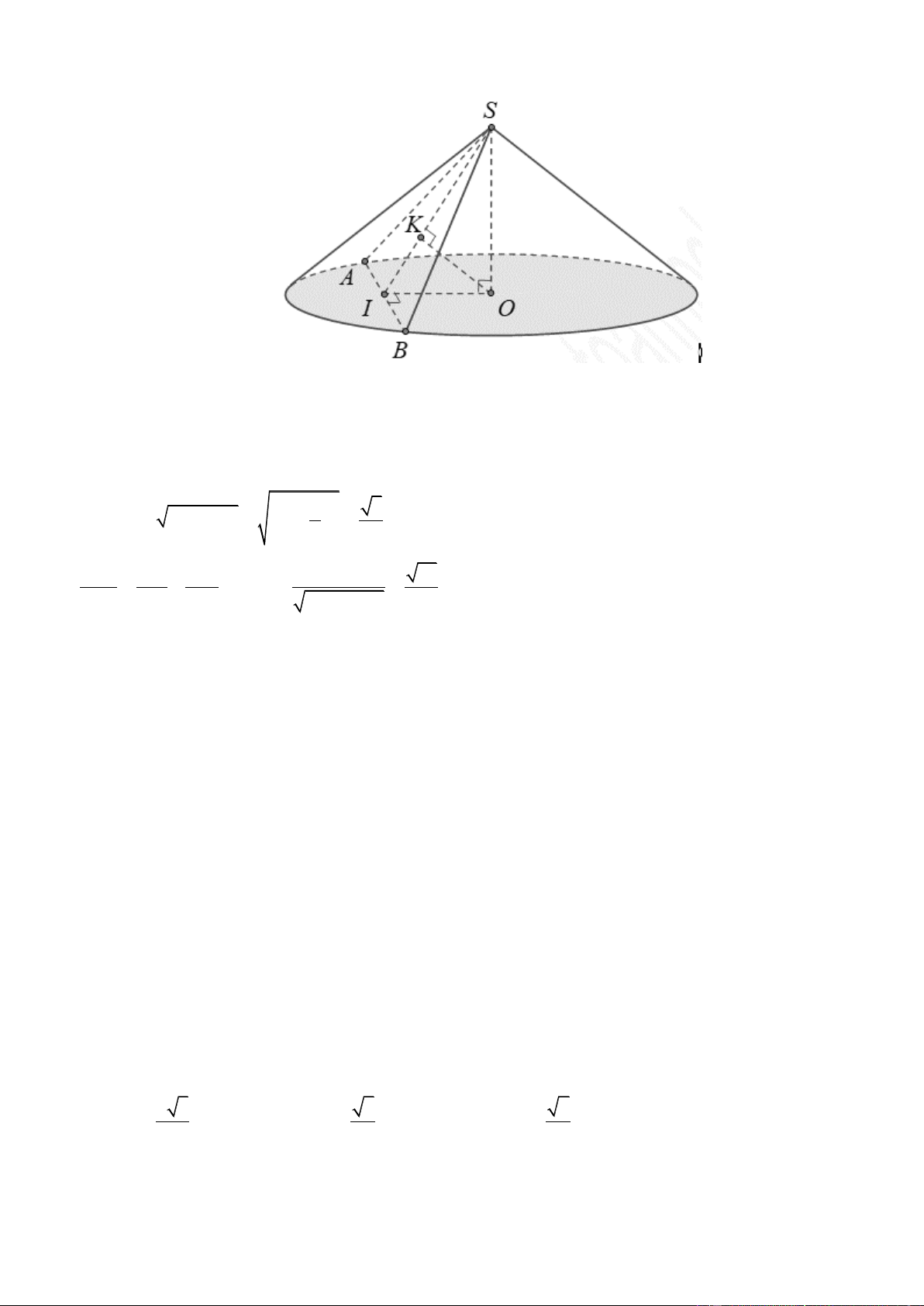
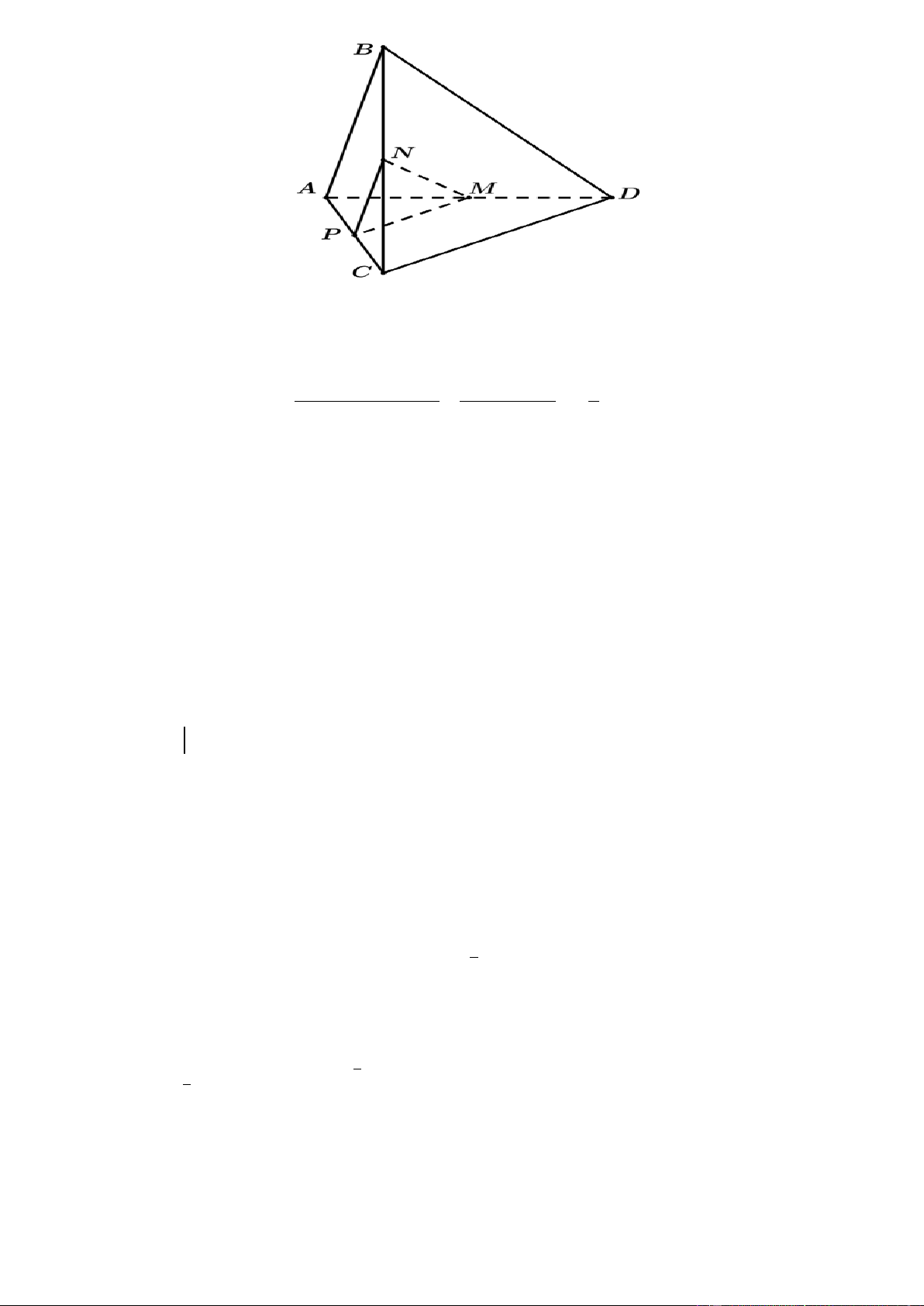
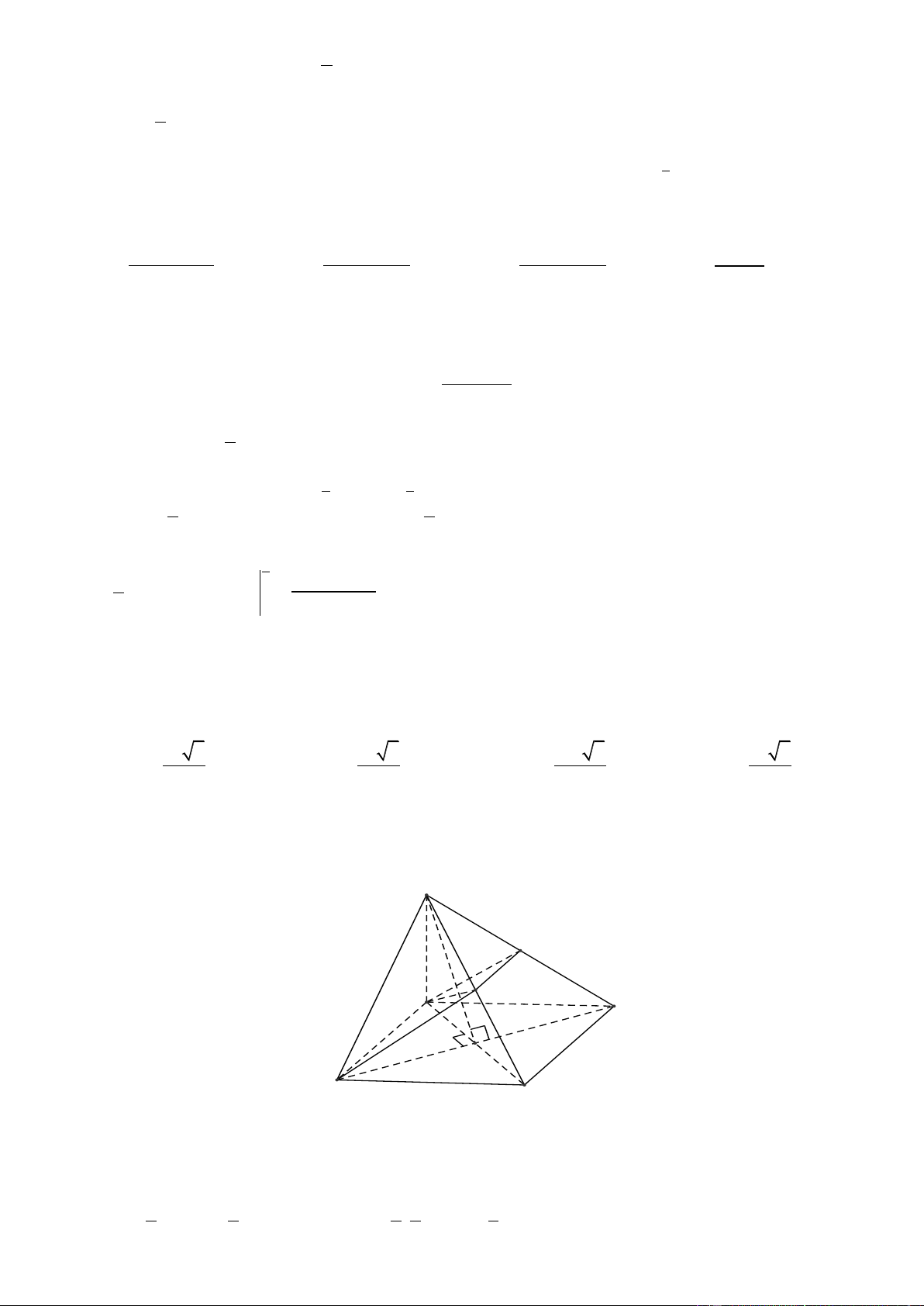
Câu 32. Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a . Gọi M , N lần lượt là trung điểm của AD
và SD . Số đo của góc giữa hai đường thẳng MN và SC là A. 45 . B. 60 . C. 30 . D. 90 . 1 1 Câu 33. Cho f
xdx 1 tích phân 2 f x 2
3x dx bằng 0 0 A. 1. B. 0 . C. 3 . D. 1.
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua A(2 ; 1 ; )
1 và vuông góc với đường thẳng íï x = 1+ 2 ï t ï D : ì y = 2 + t ï
có phương trình là ïï z = 1- 2 ïî t
A. 2x y z - 3 0 .
B. 2x y - 2z - 5 0 .
C. x 2 y z - 5 0 .
D. 2x y - 2z - 3 0 . i
Câu 35. Cho số phức z thỏa mãn điều kiện i 1 2 z
5 i . Môđun của số phức 2
w 1 2z z có giá trị 1 i là A. 10. B. 10 . C. 100. D. 100 .
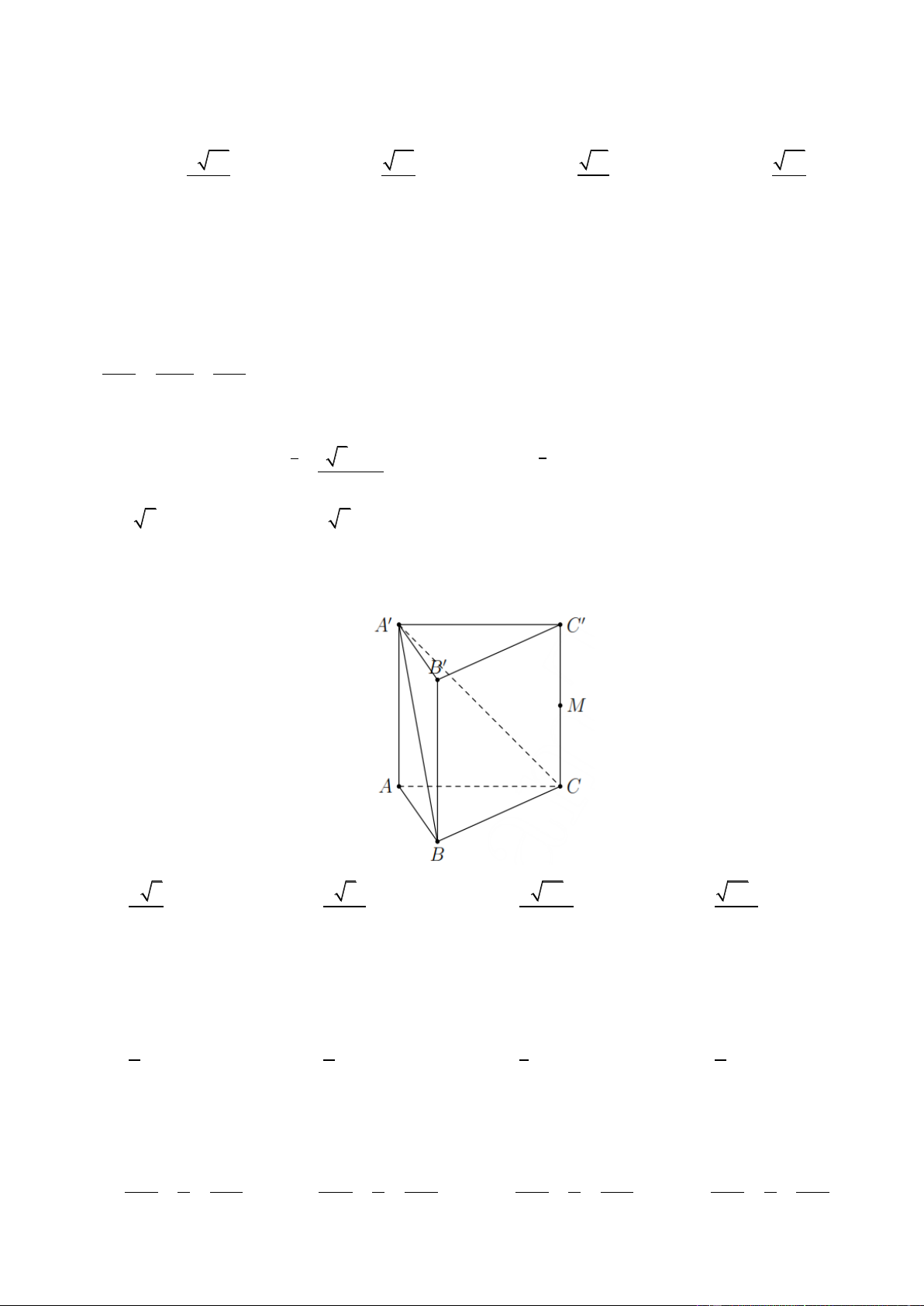
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD a , AB 2a . Cạnh bên SA 2a
và vuông góc với đáy. Gọi M , N lần lượt là trung điểm của SB và SD . Tính khoảng cách d từ S đến mặt
phẳng AMN . a 6 3a A. d .
B. d 2a . C. d . D. d a 5 . 3 2
Câu 37. Cho 14 tấm thẻ được đánh số từ 1 đến 14 . Chọn ngẫu nhiên 3 tấm thẻ. Xác suất để tích 3 số ghi trên 3
tấm thẻ này chia hết cho 3 bằng? 30 61 31 12 A. . B. . C. . D. . 91 91 91 17
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P: 2x y z 3 0 và điểm A1; 2 ;1 .
Phương trình đường thẳng d đi qua A và vuông góc với P là x 1 2t x 1 2t x 2 t x 1 2t
A. d: y 2 t .
B. d: y 2 4t . C. y 1 2t .
D. d: y 2 t . z 1 t z 1 3t z 1 t z 1 3t 1 11 x 1 2 2x 11
Câu 39. Số nghiệm nguyên thuộc khoảng 0;12 của bất phương trình 3 x 3 x log2 2
x x là: 1 A. 7 . B. 8 . C. 5 . D. 11.
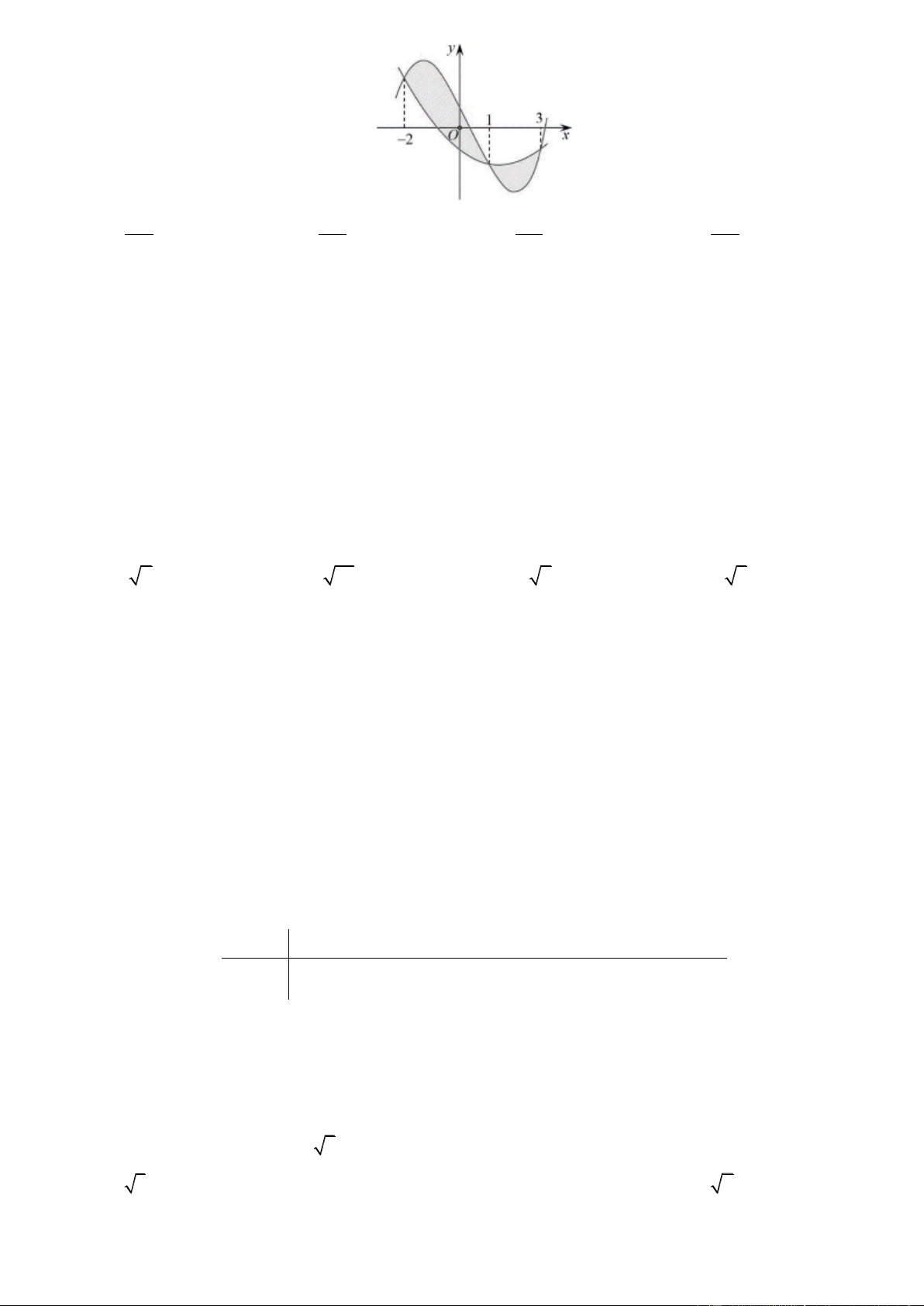
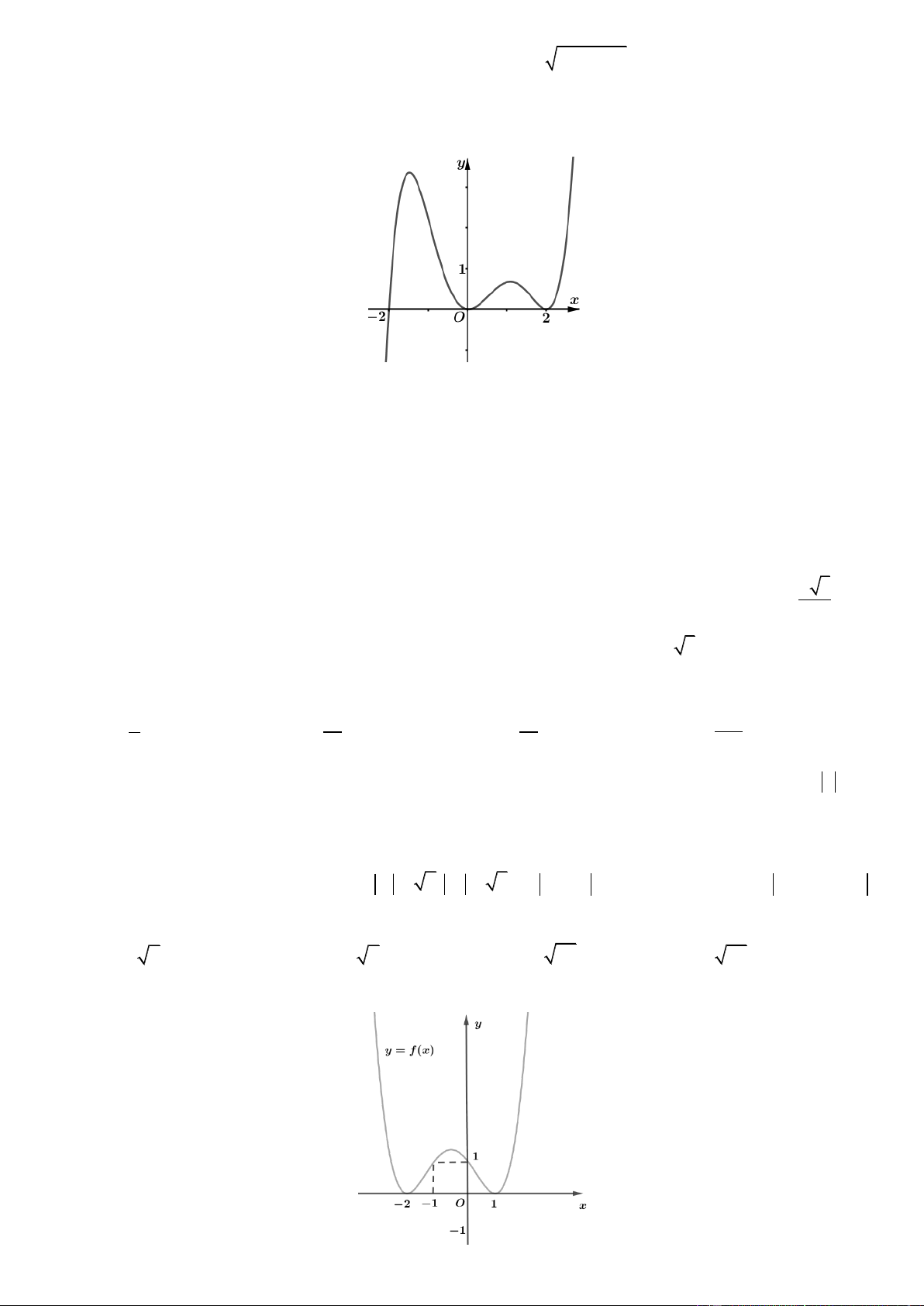
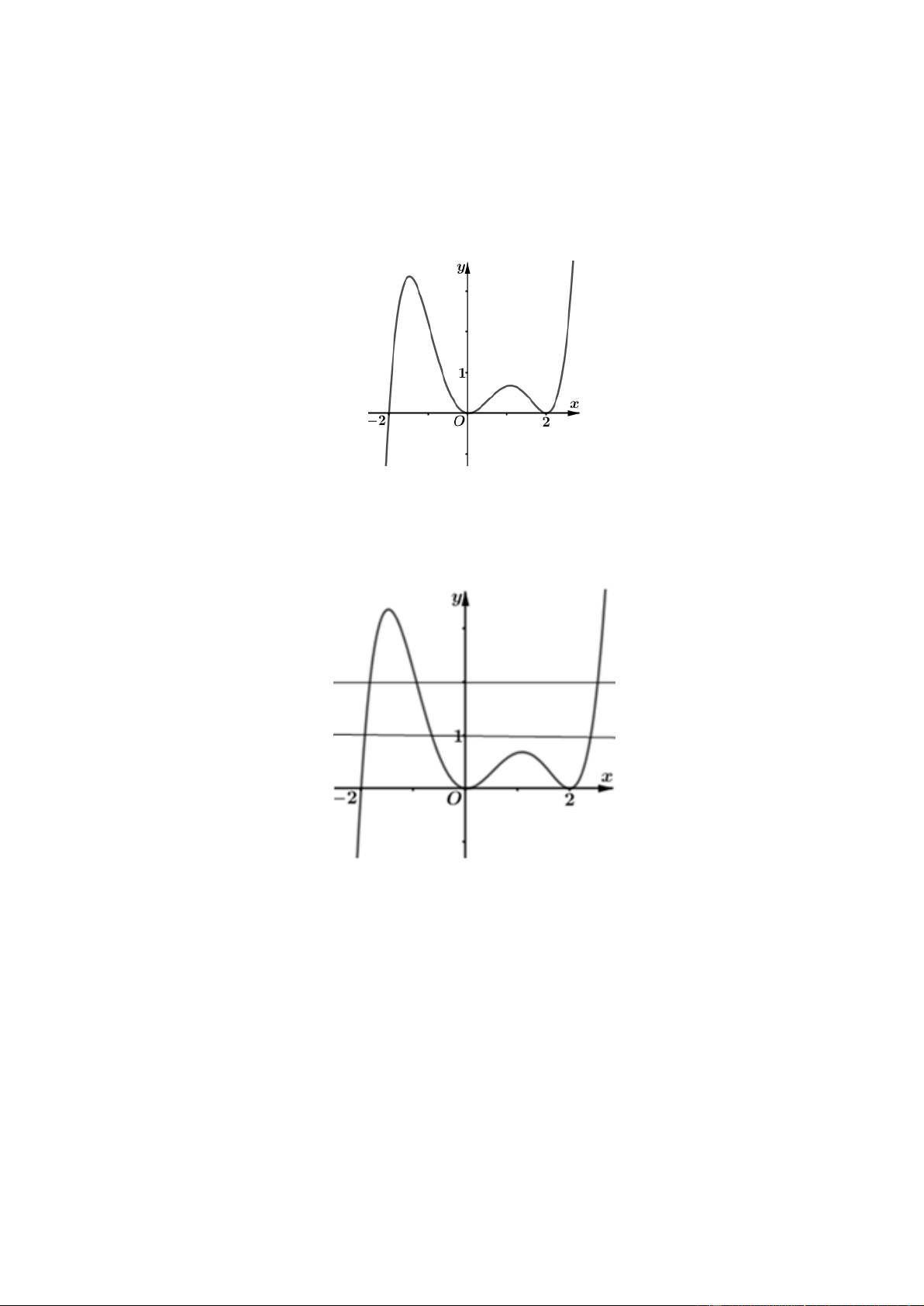
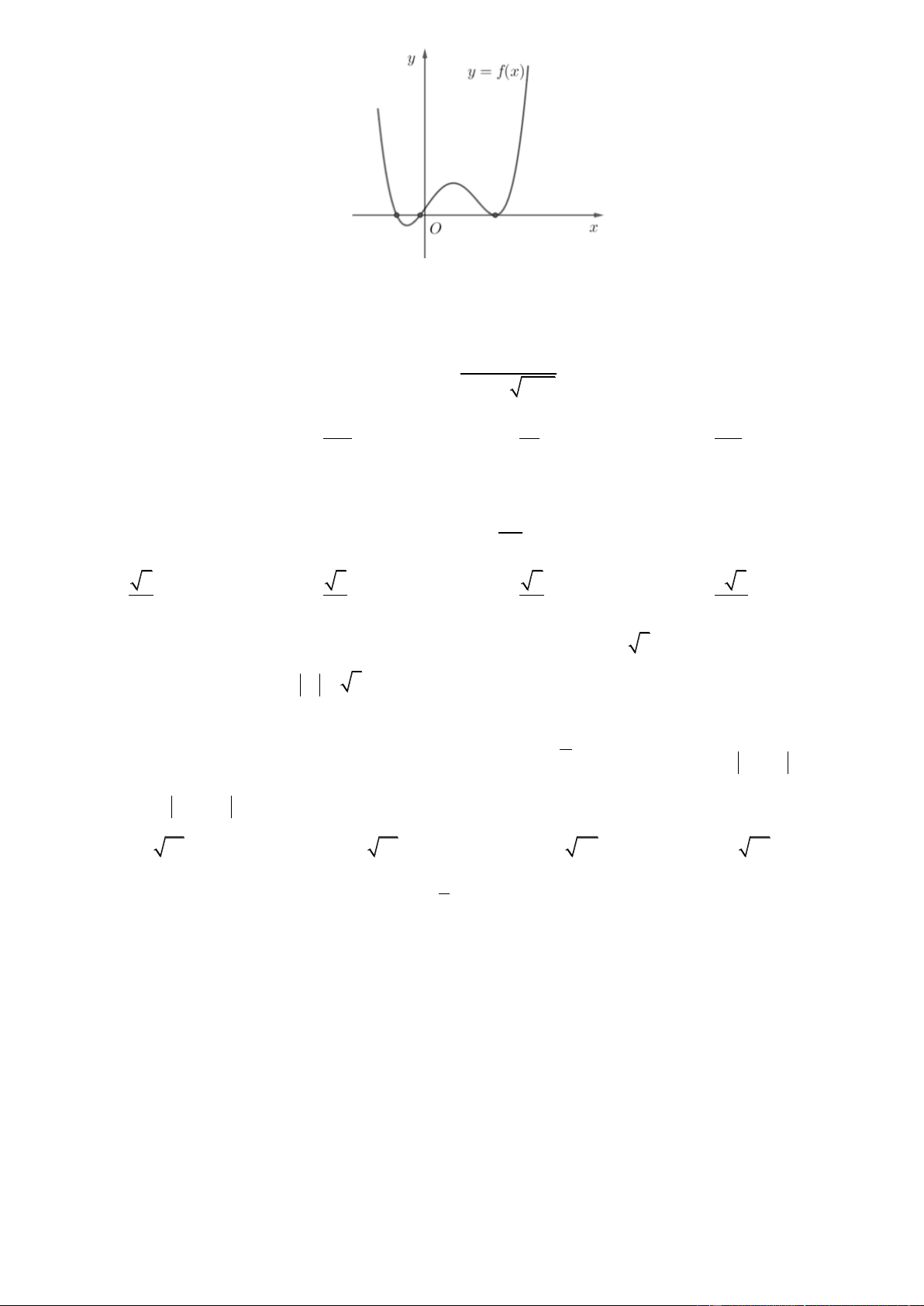
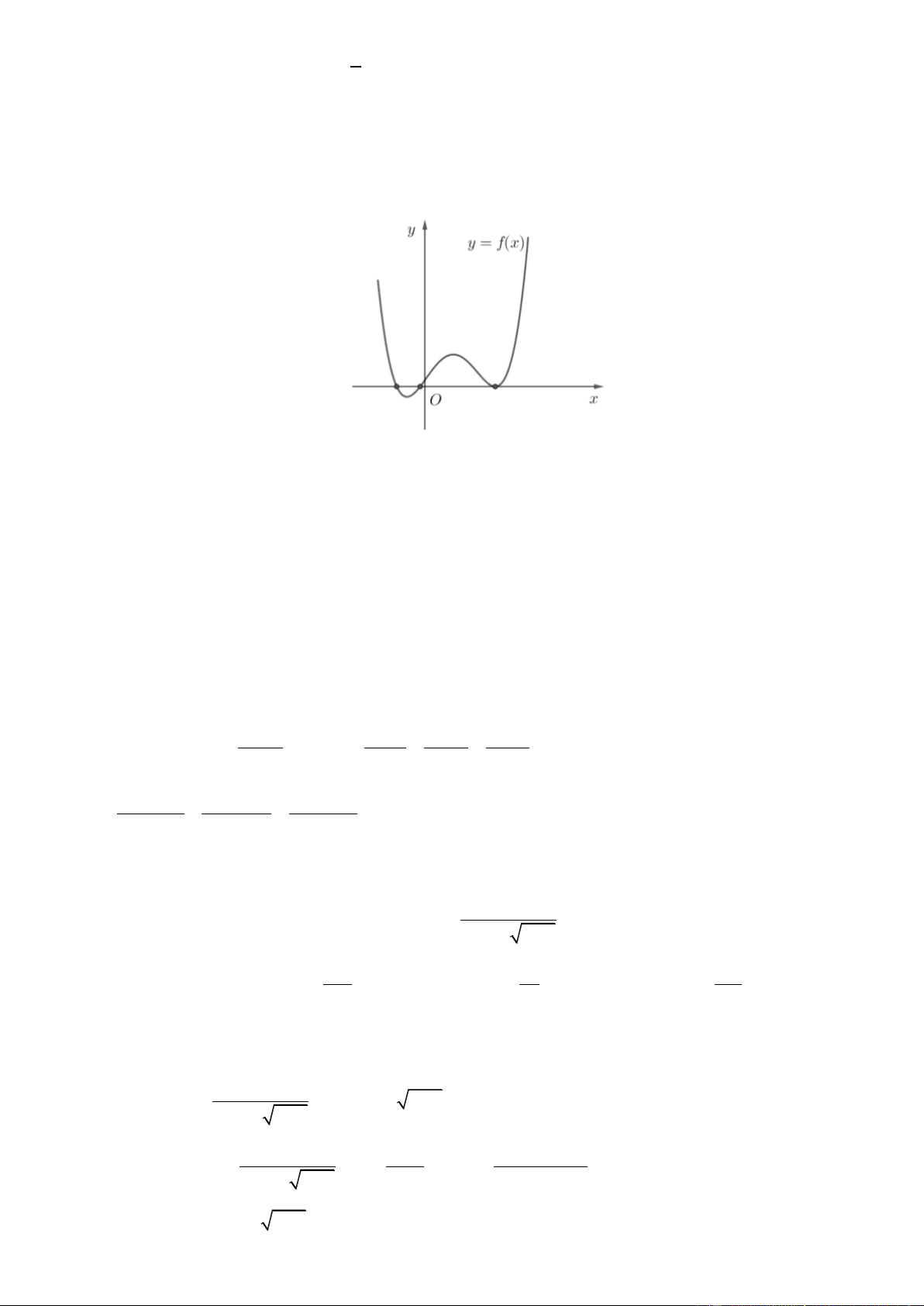
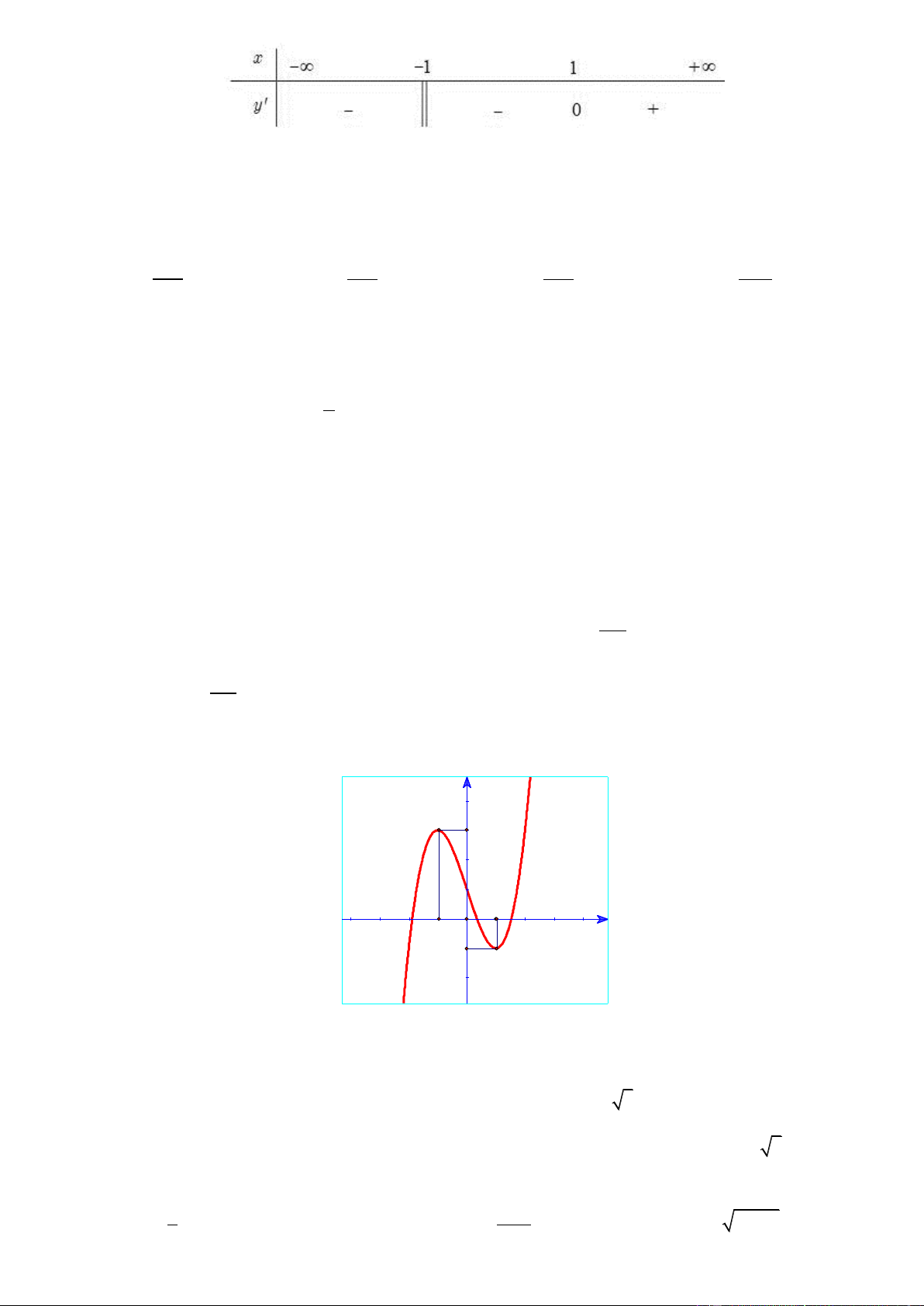
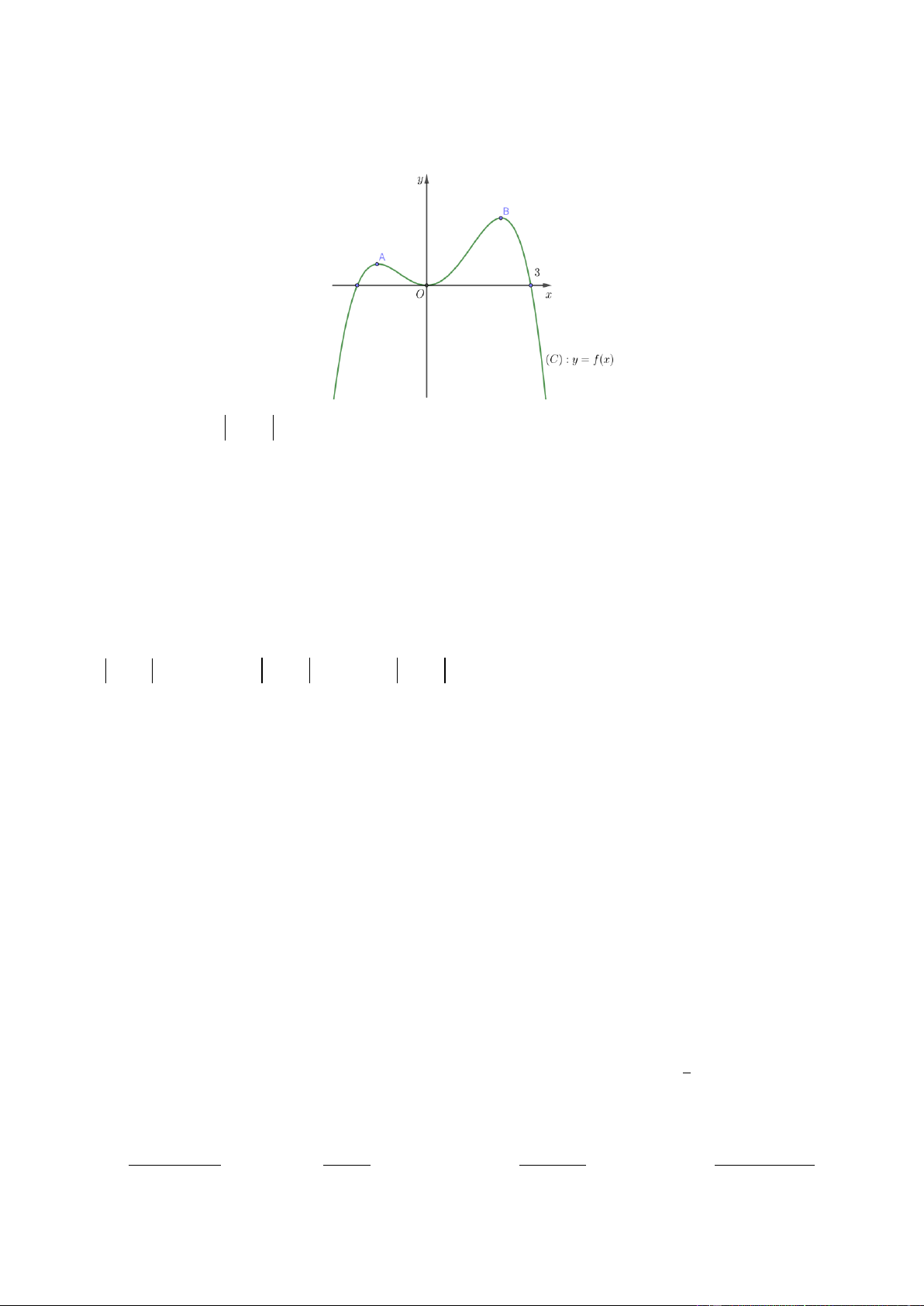
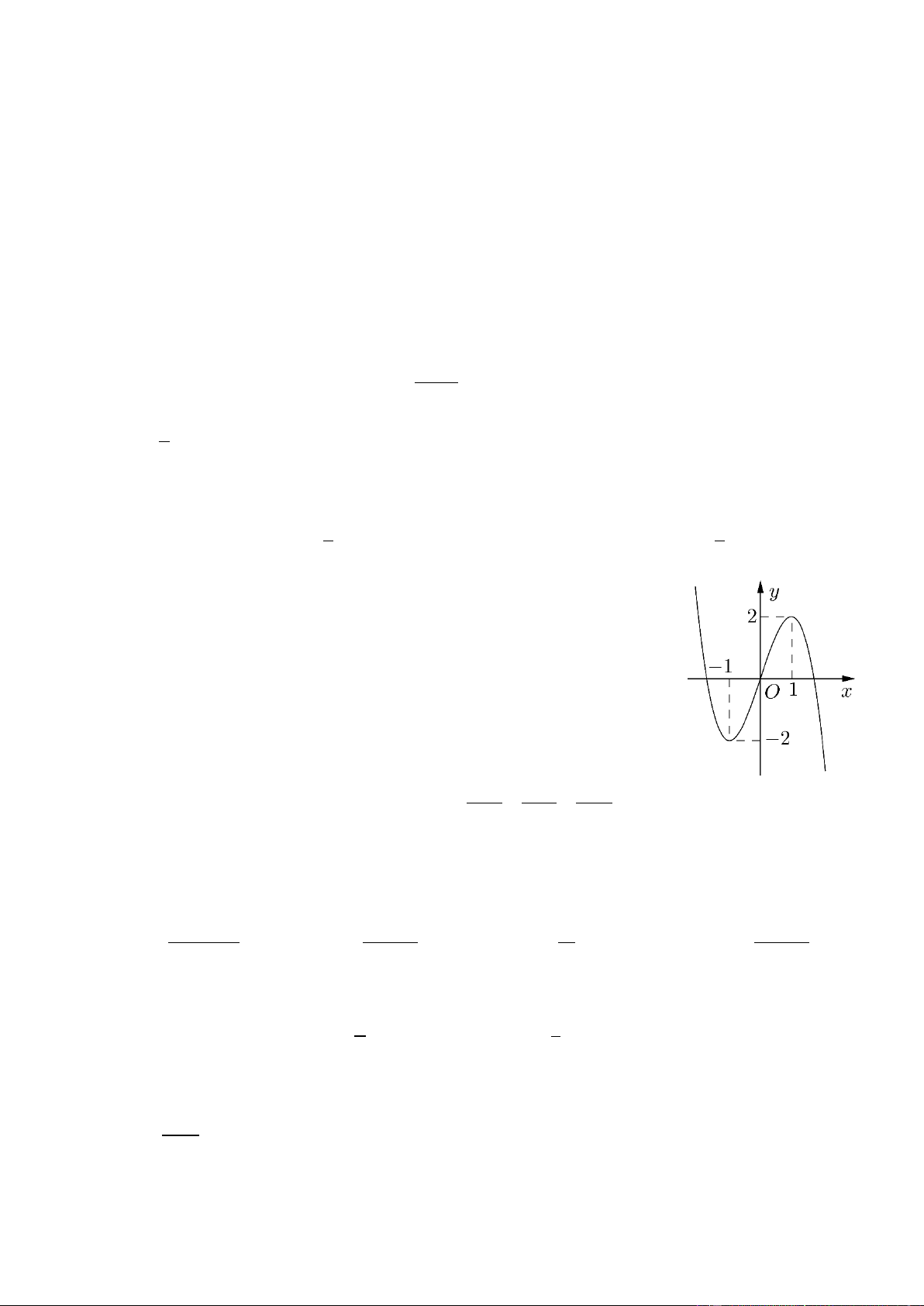
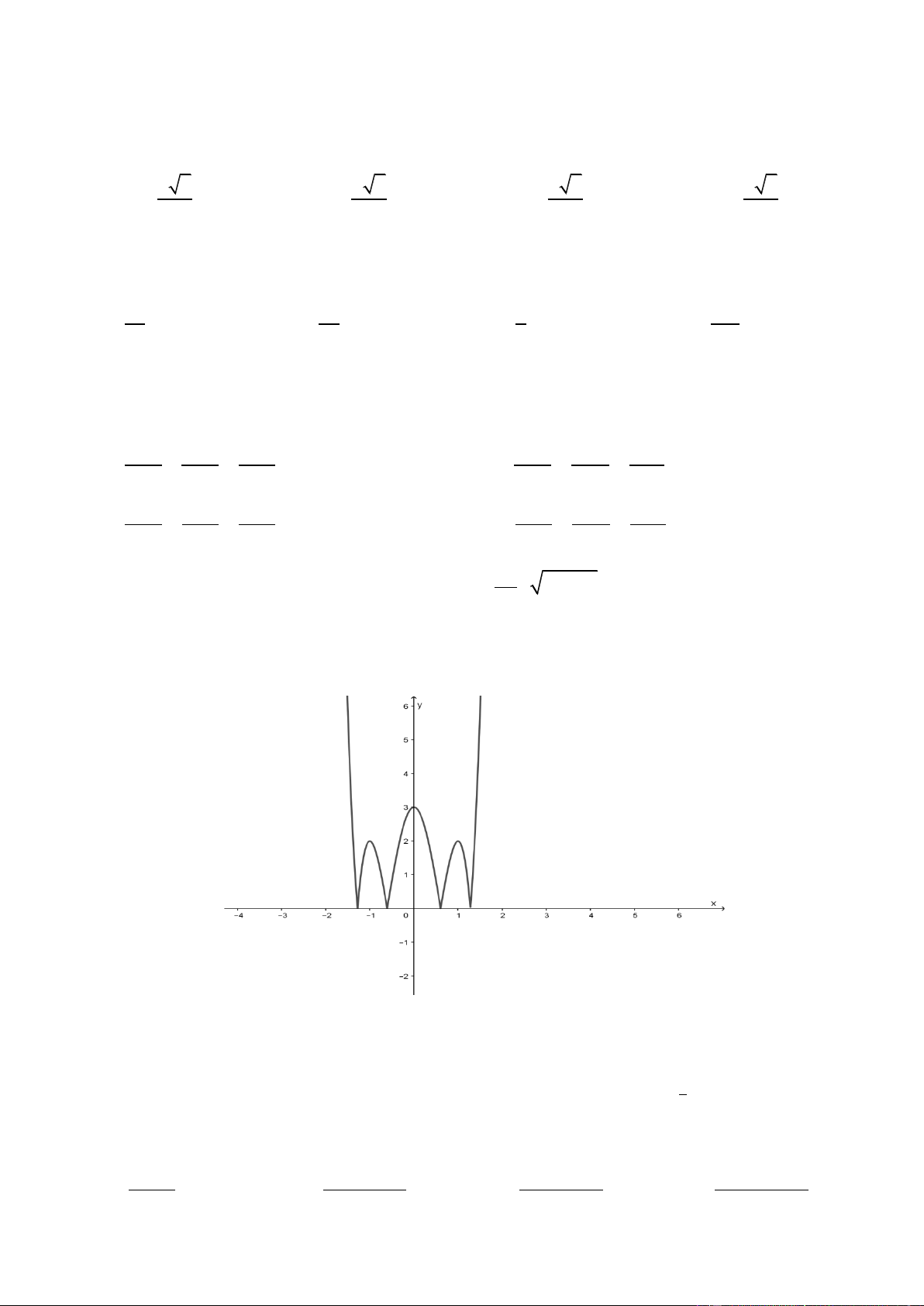
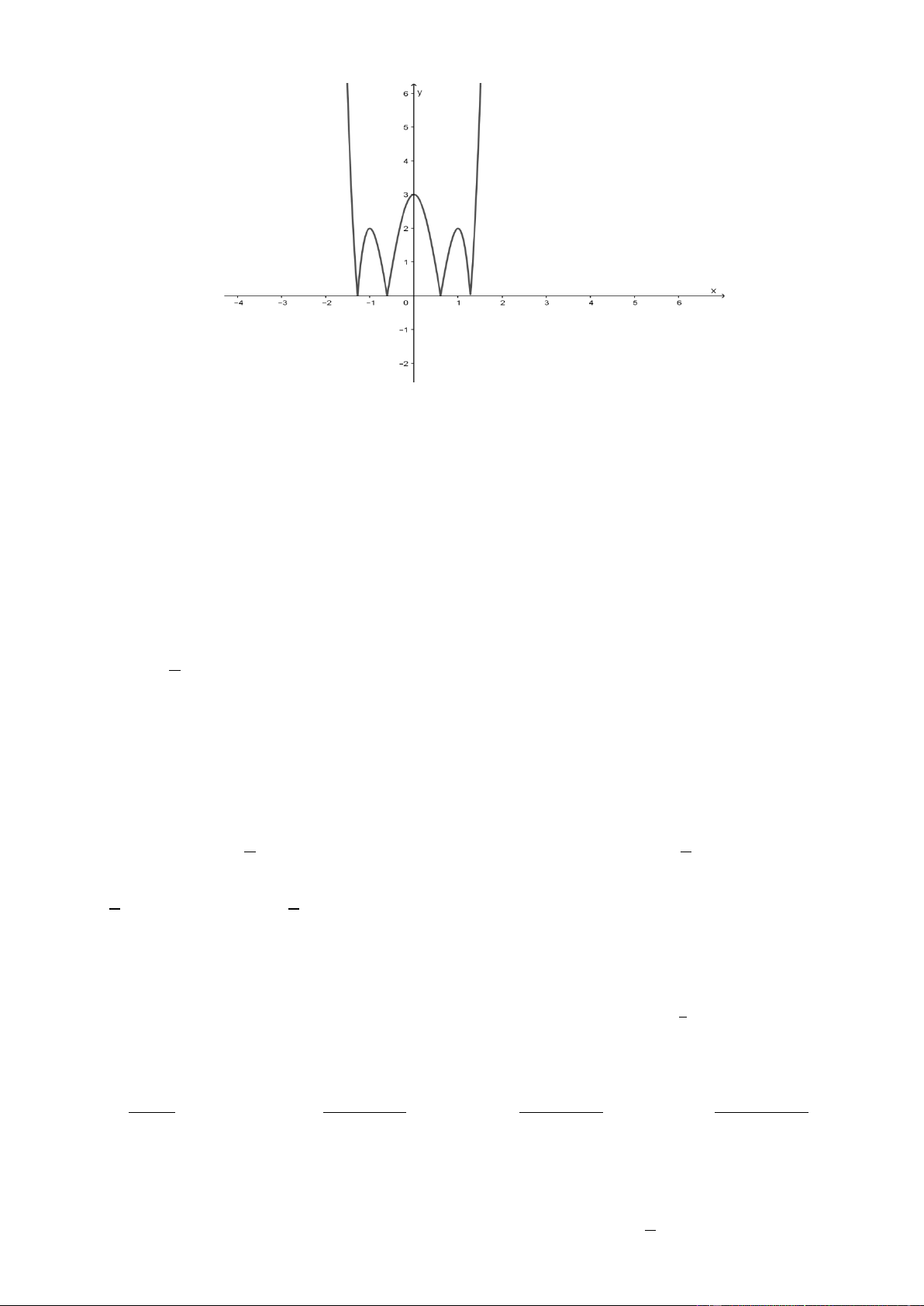
Câu 40. Cho hàm số y f x có đạo hàm f x trên khoảng ;
. Đồ thị của hàm số y f x như hình vẽ Trang4 y 1 1 O x 1 ' 2
Tìm số nghiệm của phương trình f 2x 0 A. 3 . B. 4 . C. 2 . D. 5 . 4 Câu 41. Cho hàm số f x xác định trên R\ 2; 2 thỏa mãn
f x 2 x , 4 f 3
f 3 f 1 f
1 2 . Giá trị biểu thức f 4
f 0 f 4 bằng A. 4 . B. 1. C. 2 . D. 3 .
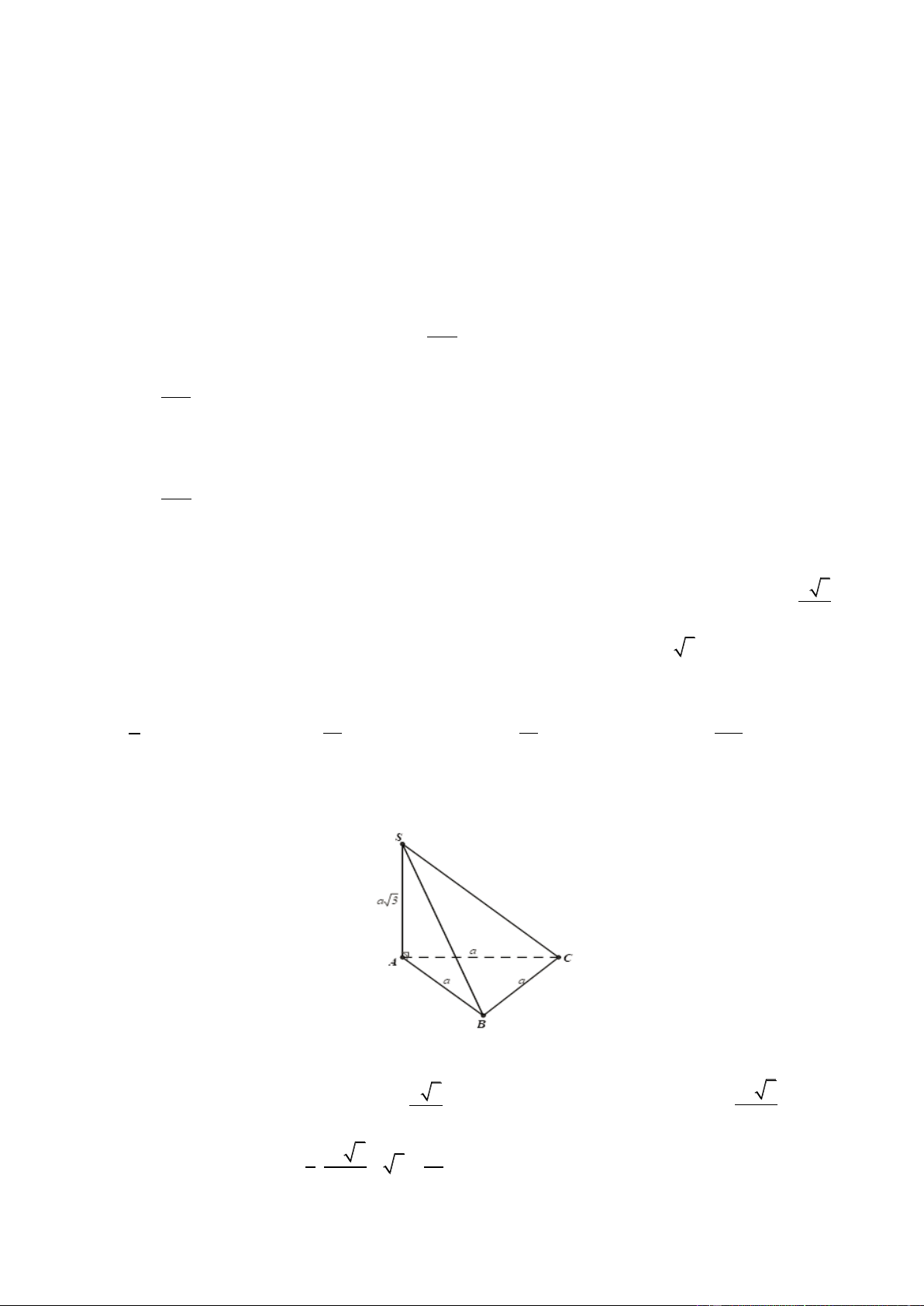
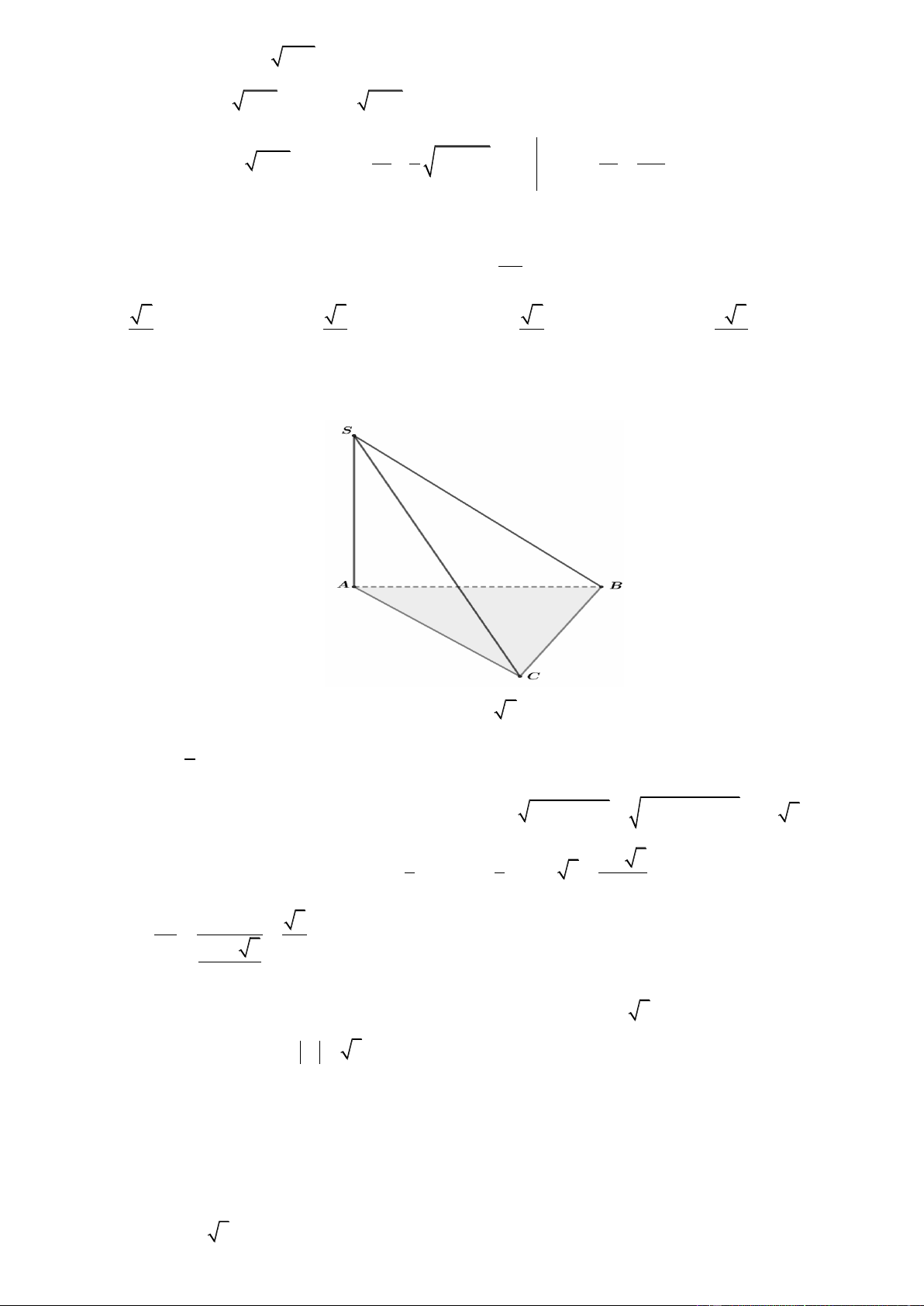
Câu 42. Cho hình chóp S .A B CD có đáy A B CD là hình chữ nhật có A B = a, B C = 2a . Hai mp (SA B )và
mp (SA D)cùng vuông góc với mă ̣t phẳng đáy , cạnh SC hợp với đáy một góc 0
60 . Tính thể tích khối chóp
S .A BCD theo a . 3 a 15 3 a 15 3 a 3 3 2a 15 A. . B. . C. . D. . 5 3 15 3
Câu 43. Tìm các số thực a, b, c sao cho hai phương trình 2 2
az bz c 0, cz bz a 16 16i 0 có nghiệm
chung là z 1 2i A. , a , b c 1; 2 ;5 B. a, , b c 1; 2; 5 C. a, , b c 1 ; 2 ;5 D. a, , b c 1; 2 ; 5
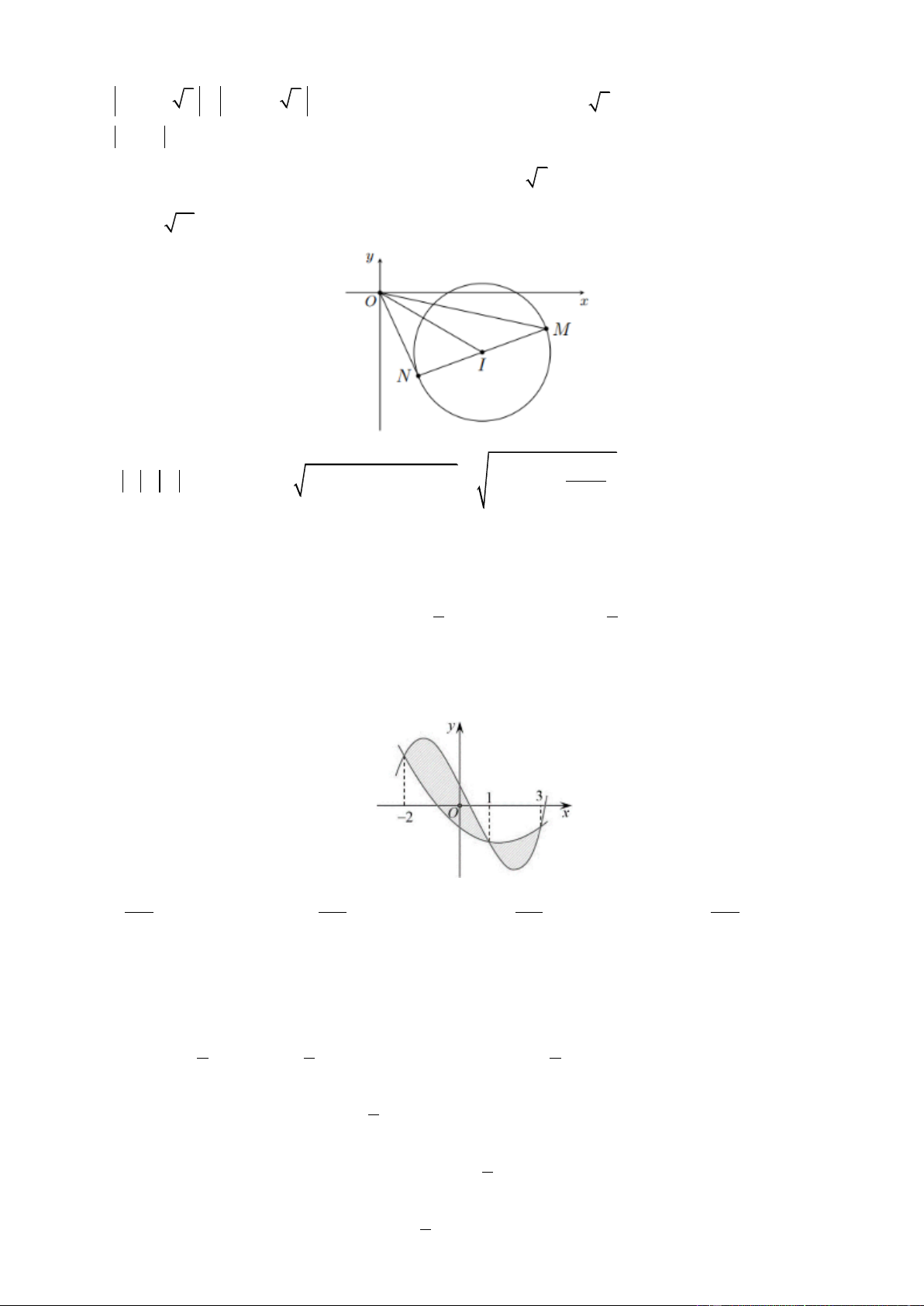
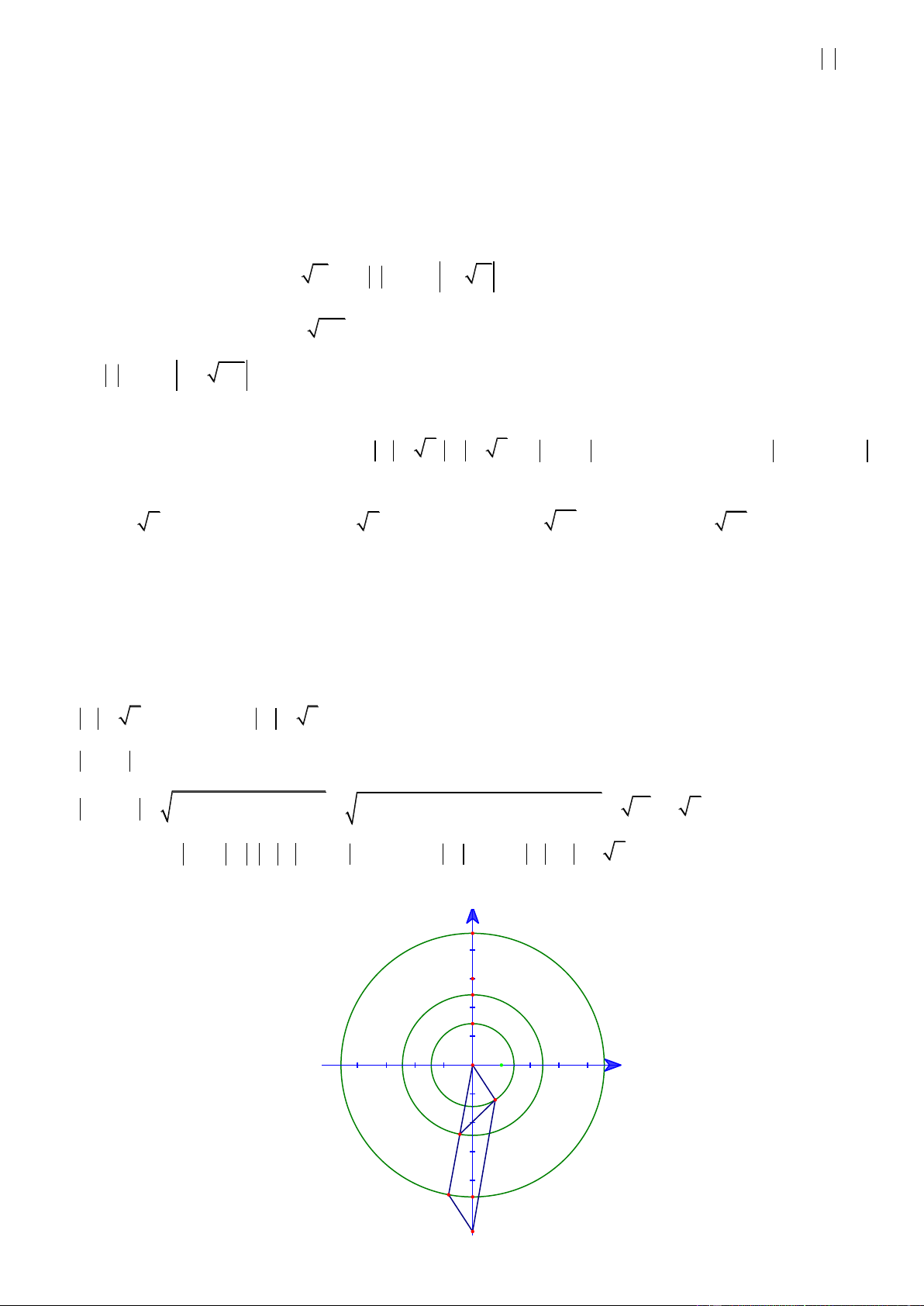
Câu 44. Cho z , z là hai trong các số phức thỏa mãn z 3 3i 2 và z z 4 . Giá trị lớn nhất của 1 2 1 2 z z bằng 1 2 A. 8 . B. 4 3 . C. 4 . D. 2 2 3 . 3 3
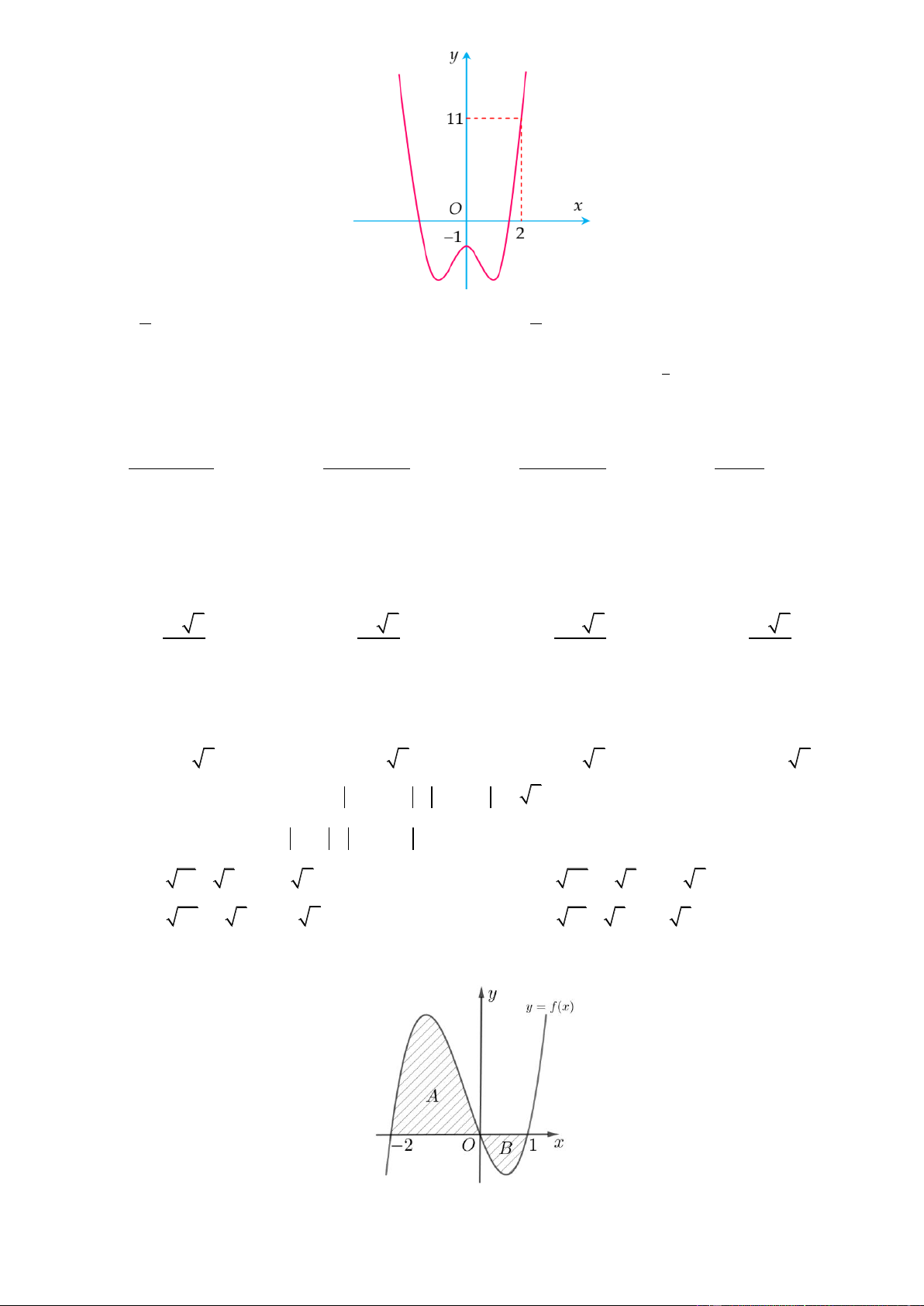
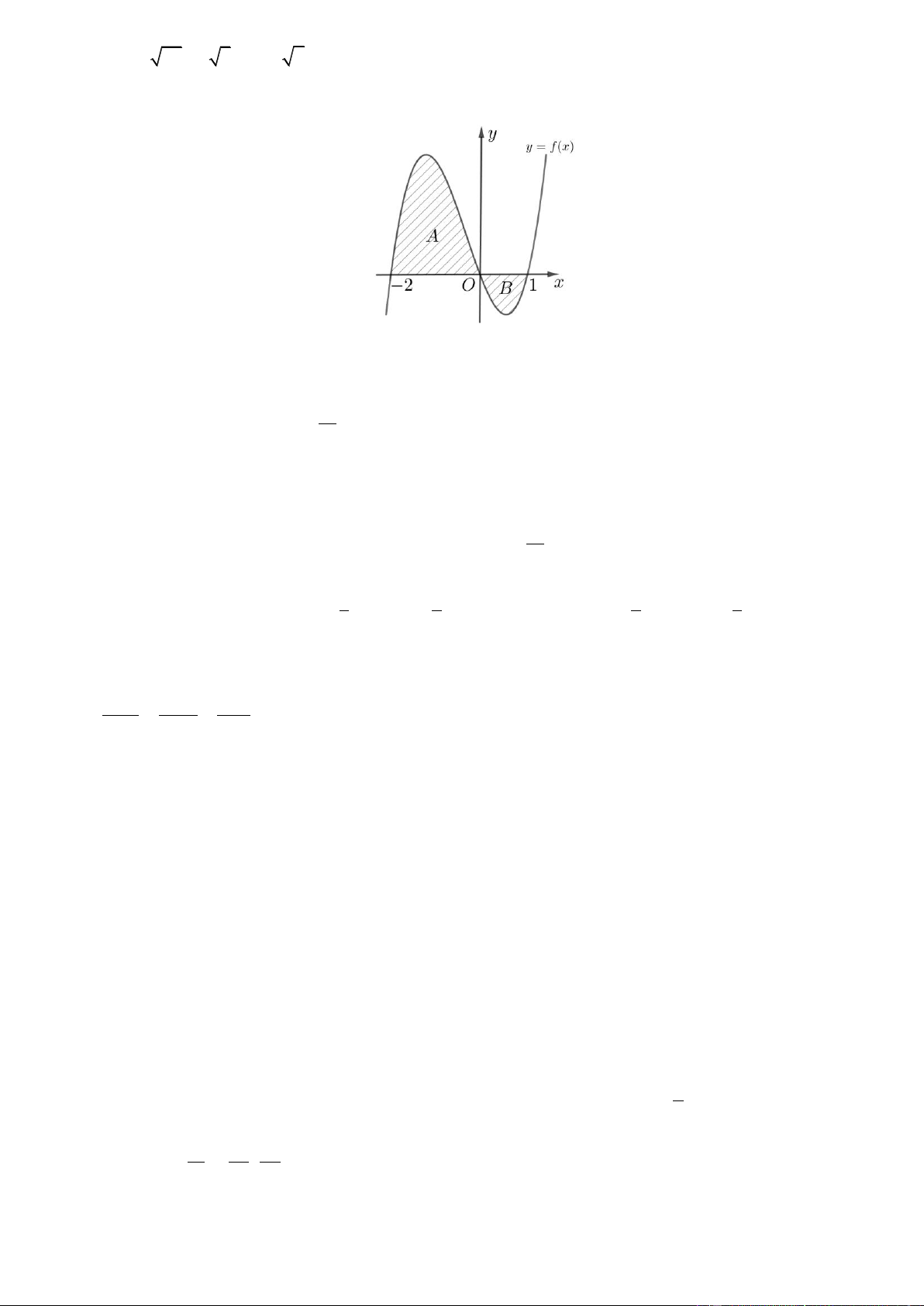
Câu 45. Cho hai hàm số f x 3 2
ax bx cx và g x 2
dx ex , , a , b ,
c d, e . Biết rằng đồ thị 4 4
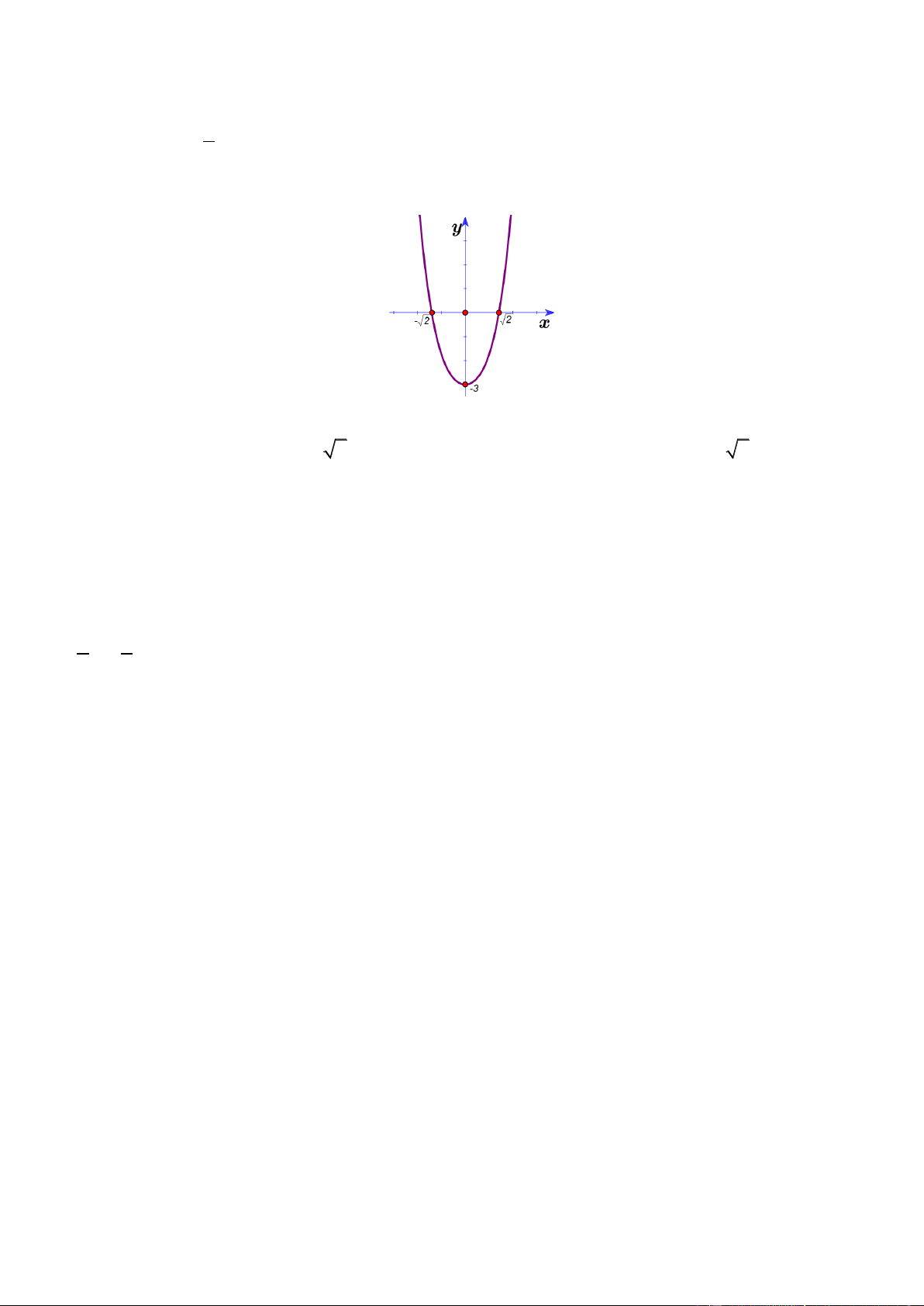
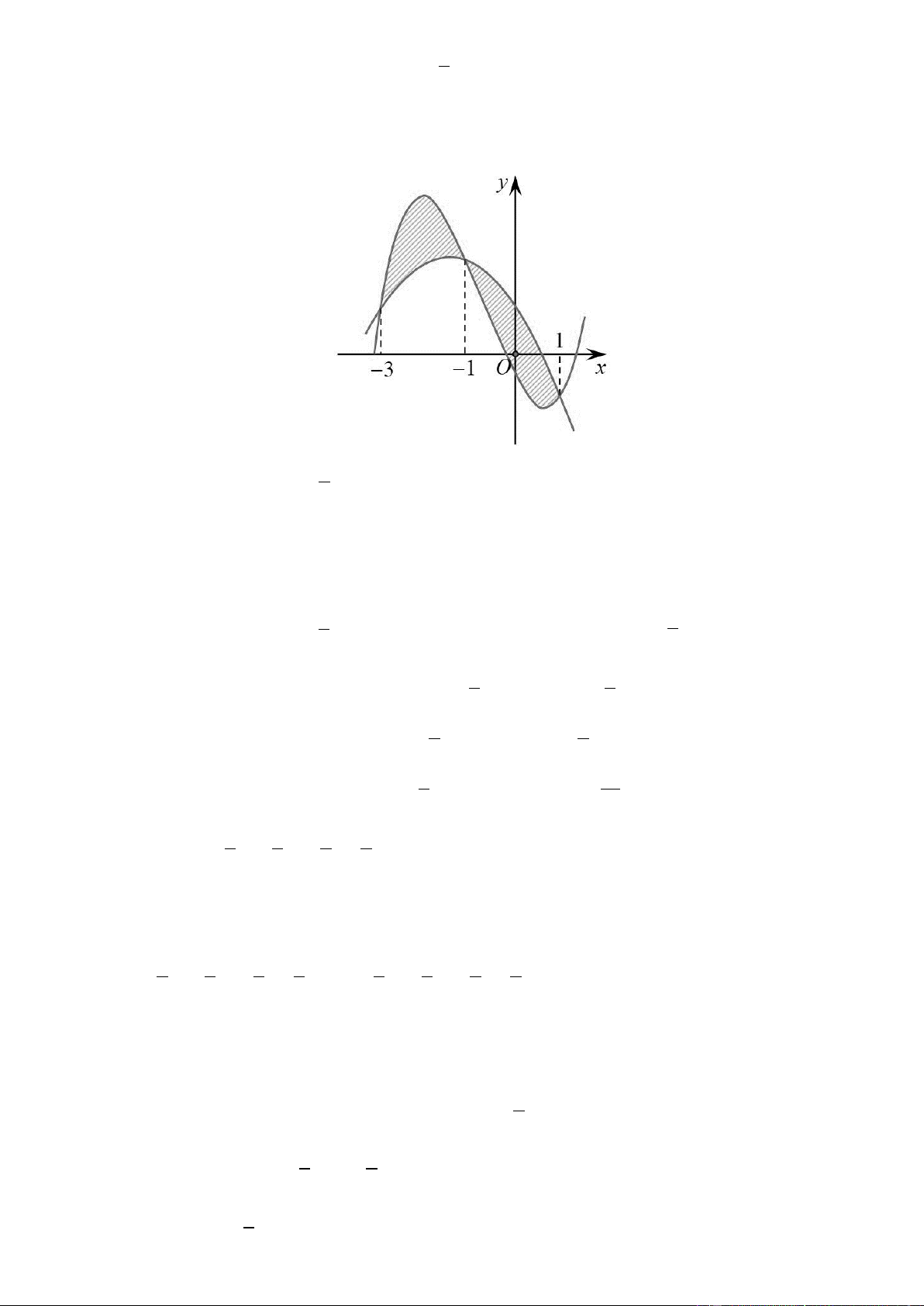
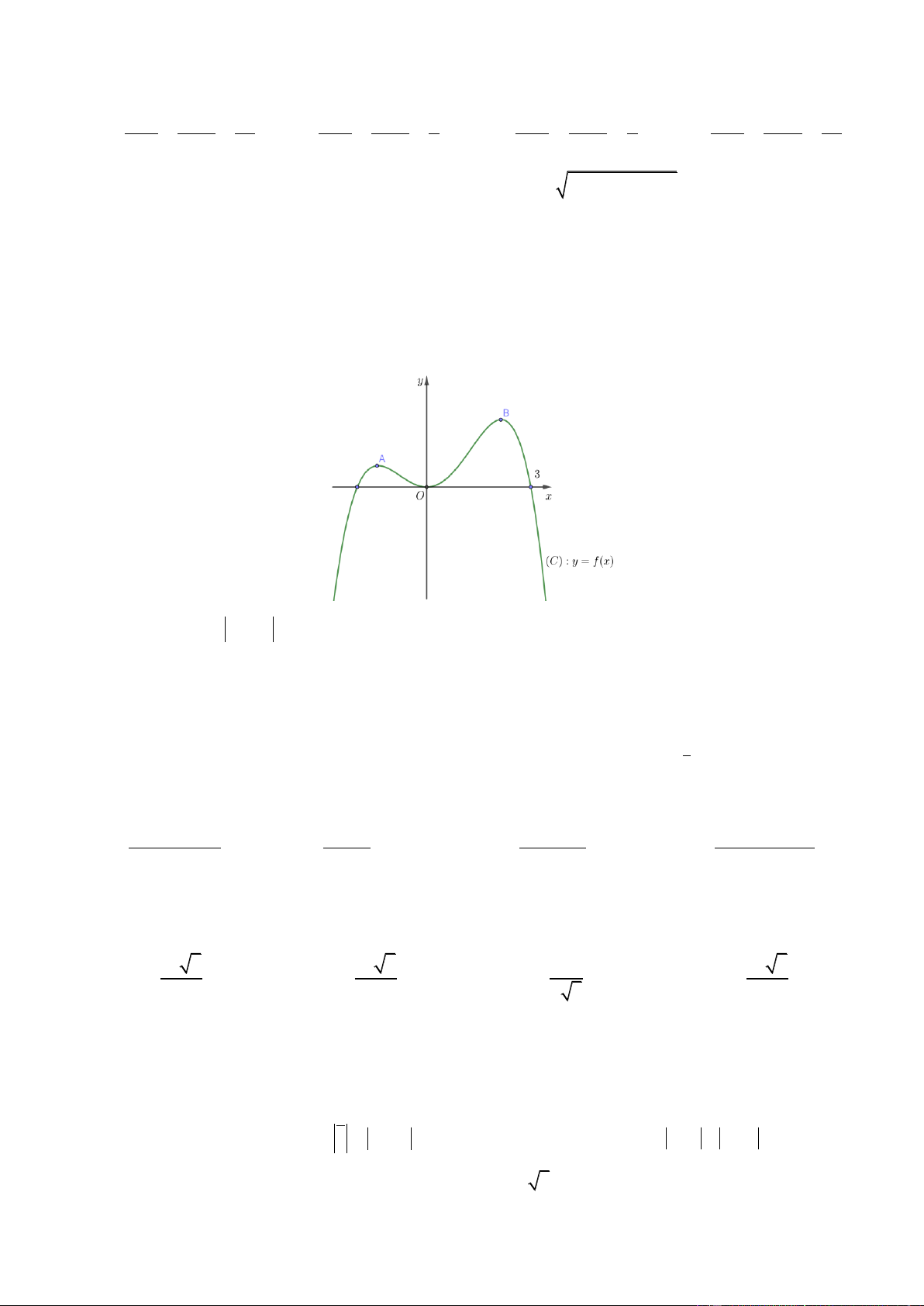
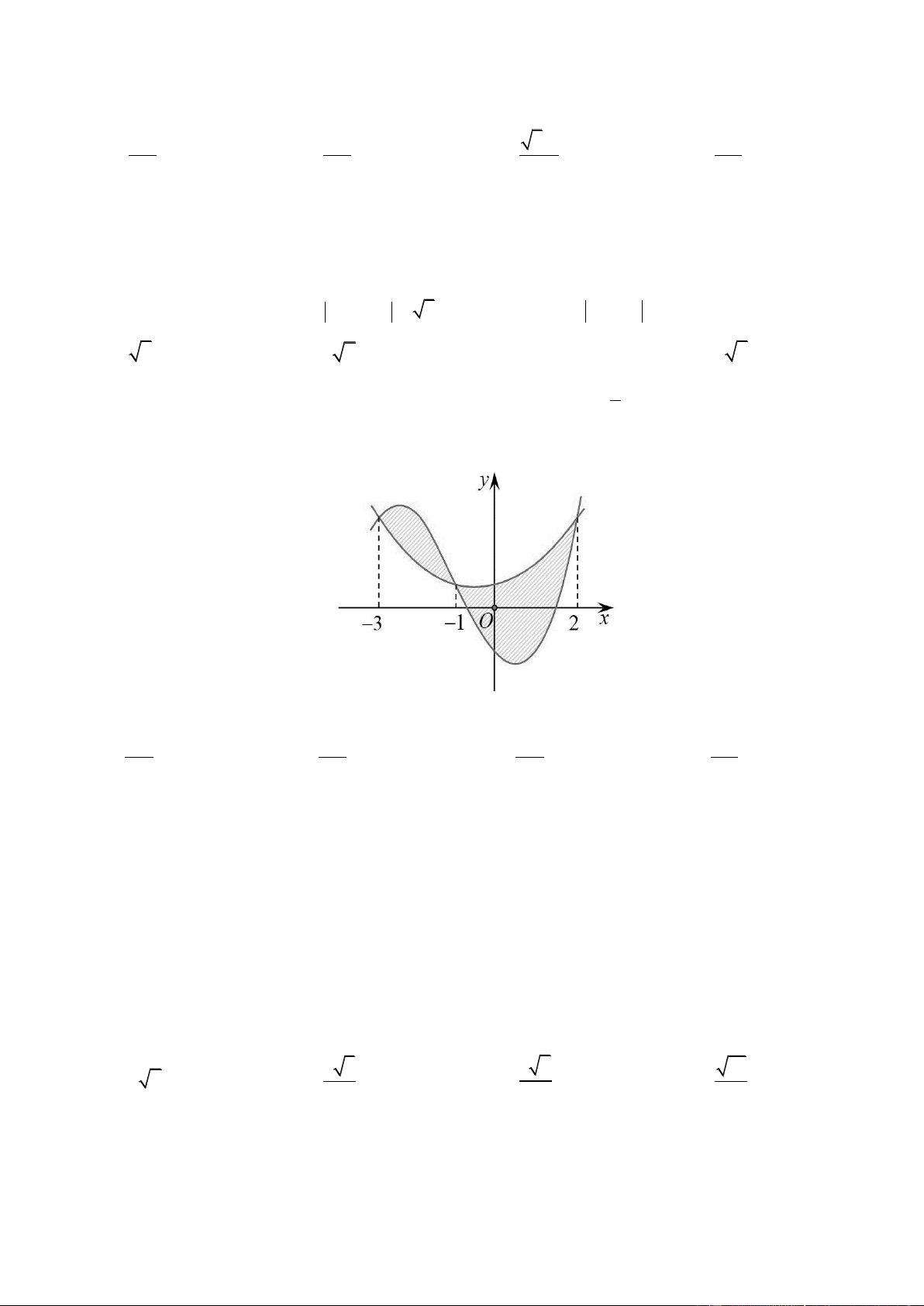
của hàm số y f x và y g x cắt nhau tại ba điểm có hoành độ lần lượt là 2
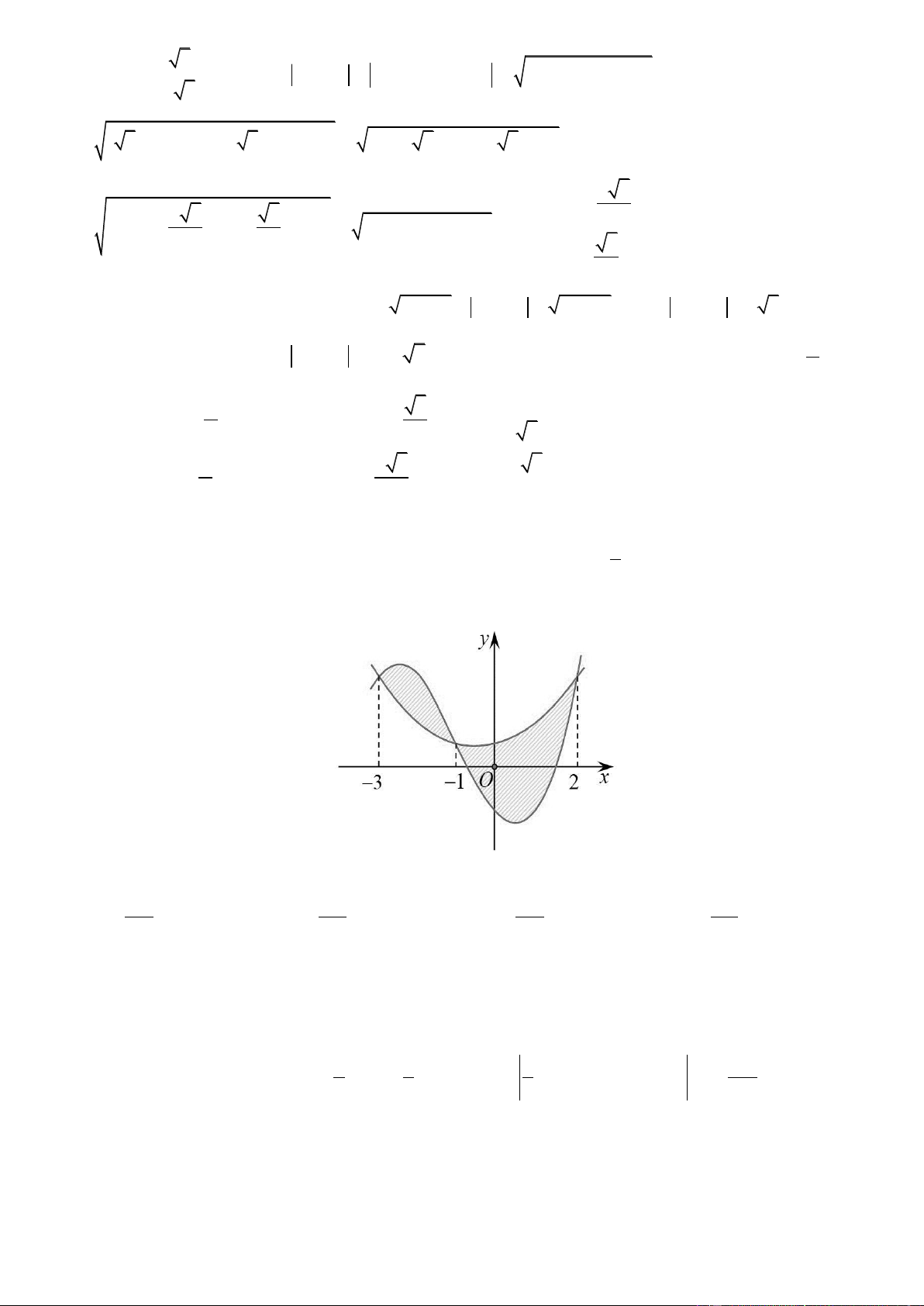
; 1; 3 (tham khảo hình vẽ).
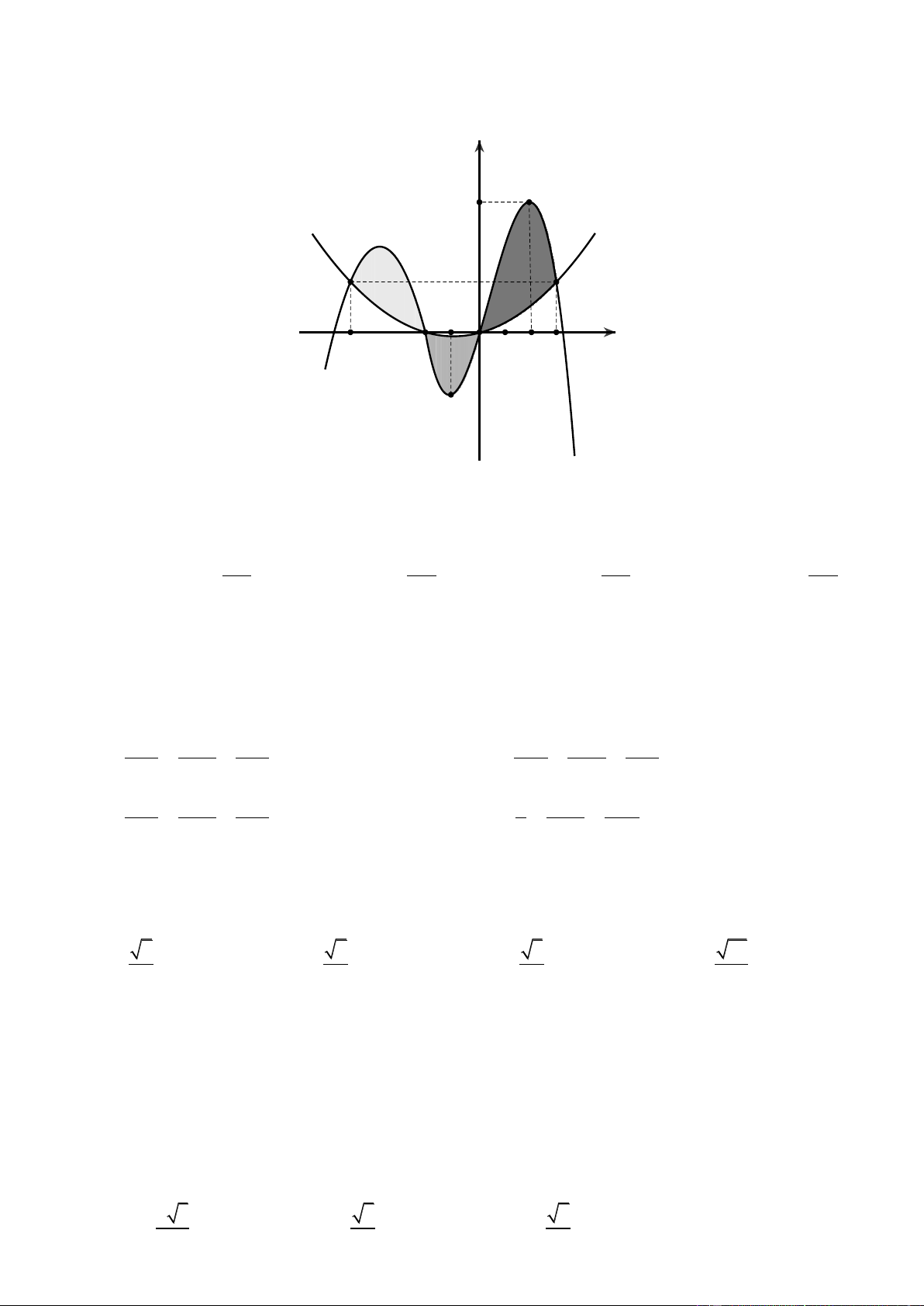
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng Trang5 253 125 125 253 A. B. C. D. 48 24 48 24
Câu 46. Trong không gian với hệ toạ độ Oxyz , cho điểm A1; 2
;3 và hai mặt phẳng P: x y z 1 0 ,
Q: x y z 2 0 . Phương trình nào dưới đây là phương trình đường thẳng đi qua A , song song với P và Q ? x 1 t x 1 t x 1 2t x 1 A. y 2 B. y 2 C. y 2 D. y 2 z 3 t z 3 t z 3 2t z 3 2t
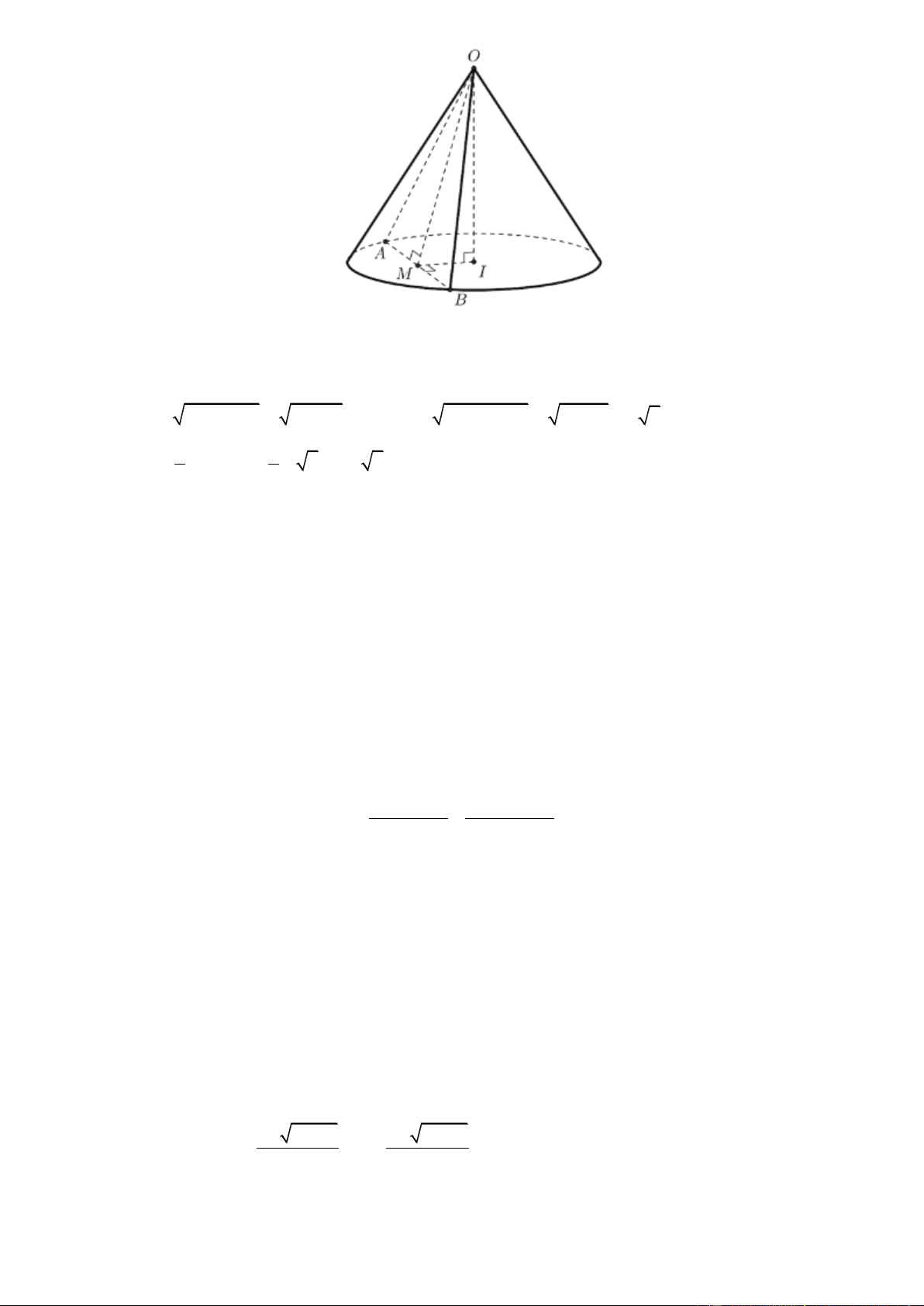
Câu 47. Cho hình nón tròn xoay có chiều cao bằng 4 và bán kính bằng 3. Mặt phẳng P đi qua đỉnh của hình
nón và cắt hình nón theo thiết diện là một tam giác có độ dài cạnh đáy bằng 2 . Diện tích của thiết diện bằng. A. 6 . B. 19 . C. 2 6 . D. 2 3 .
Câu 48. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn log 2
x y log (x y) ? 4 3 A. 59 . B. 58 . C. 116 . D. 115 .
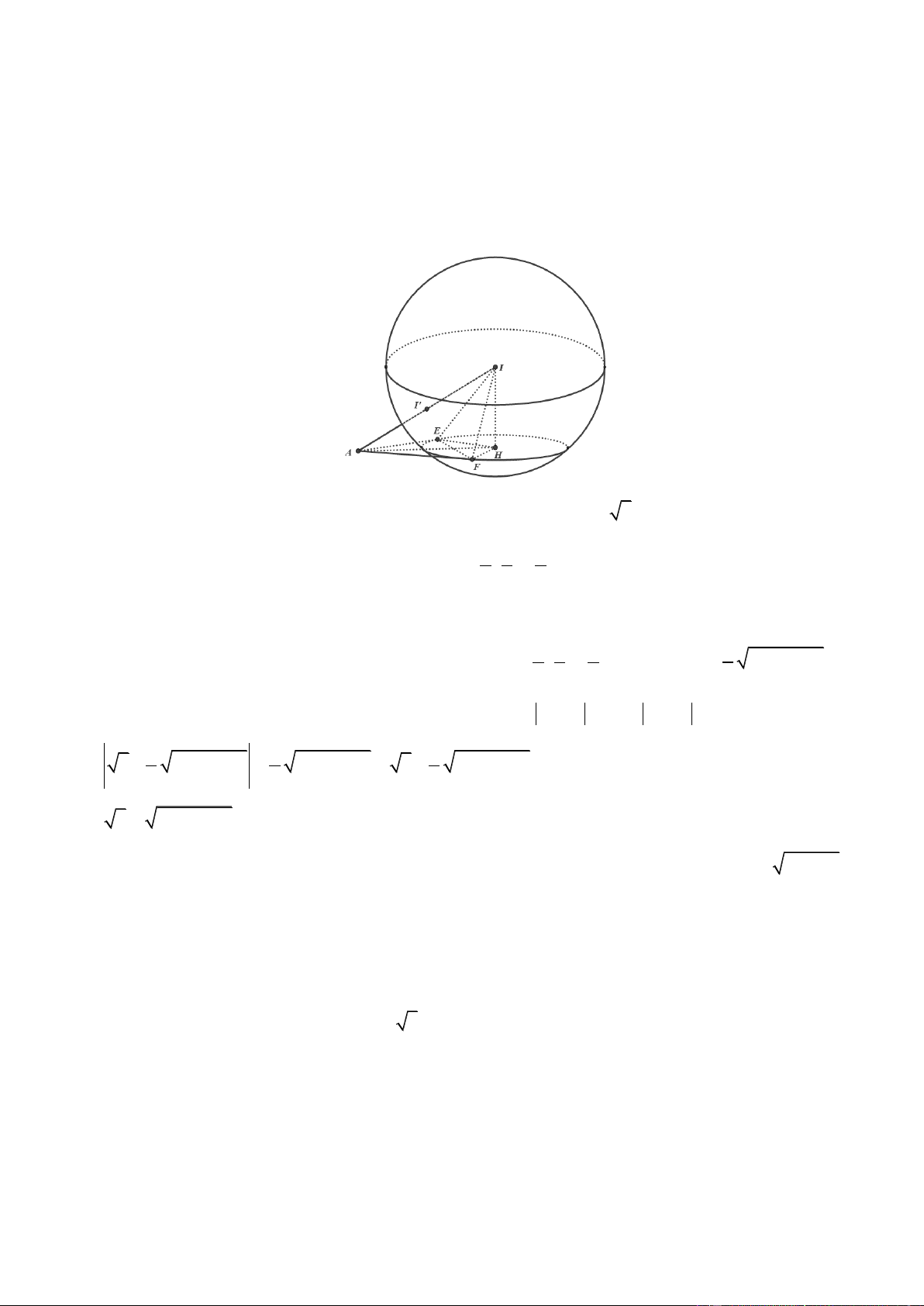
Câu 49. Trong không gian Oxyz , cho mặt cầu: S x y z 2 2 2 : 1
5 . Có tất cả bao nhiêu điểm Aa;b;c (a, ,
b c là các số nguyên) thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp tuyến của S đi qua A và hai tiếp
tuyến đó vuông góc nhau? A. 20 . B. 8 . C. 12 . D. 16 .
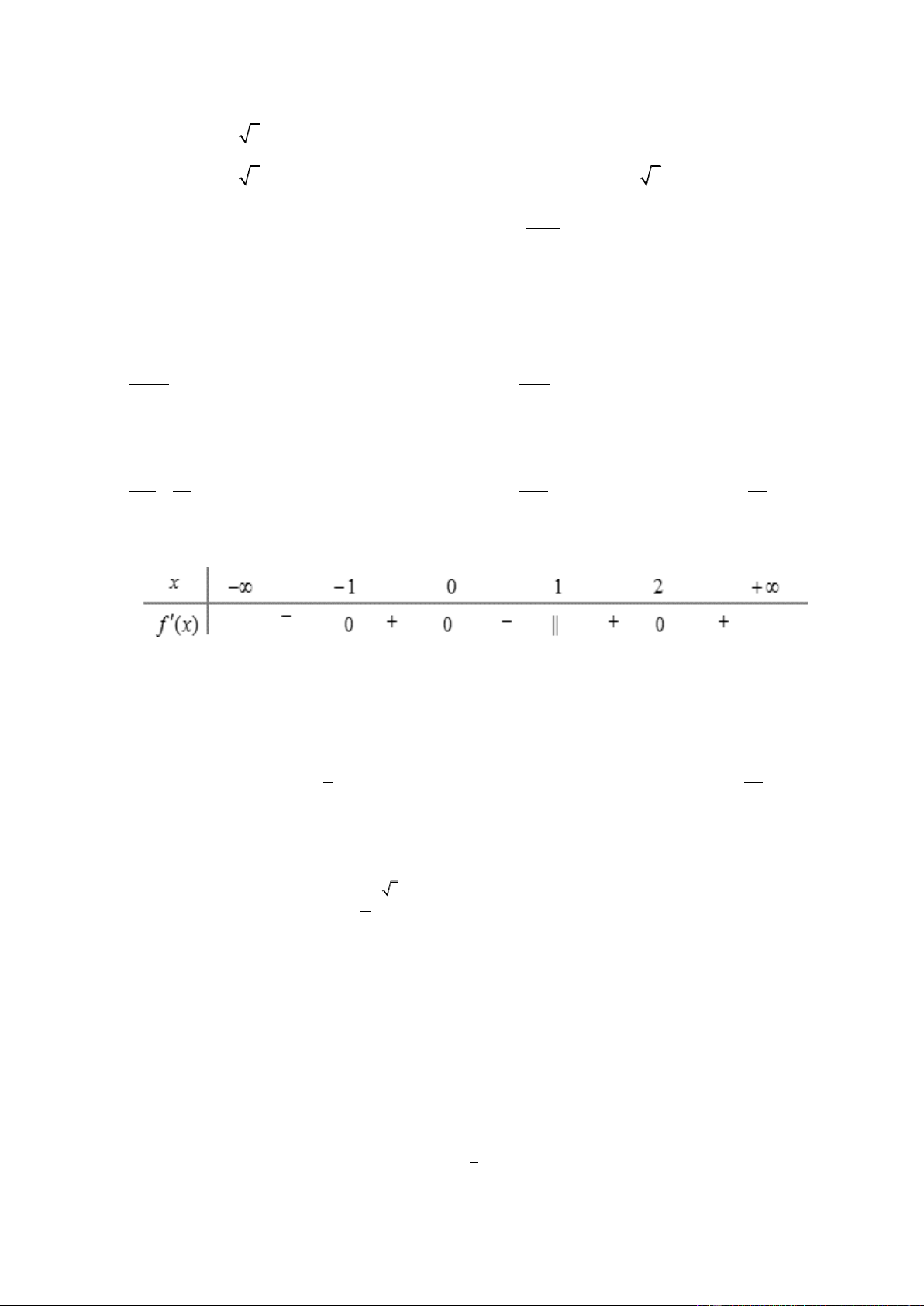
Câu 50. Cho hàm số y f x có bảng xét dấu f ' x như sau x 11 4
f ' x 0 0 0
Có bao nhiêu giá trị nguyên của tham số m thuộc 1
0;10 để g x f 2
x 2x m có 5 điểm cực trị? A. 10. B. 15. C. 20. D. 21.
LỜI GIẢI CHI TIẾT
Câu 1. Môđun của số phức z 3 i là A. 3 . B. 1. C.2. D. 2 . Lờigiải Trang6 z
i z 2 2 3 3 1 2
Vậy chọn đáp án C.
Câu 2. Mặt cầu có phương trình nào sau đây có tâm là I 1 ;1;0 ? A. 2 2 2
x y z 2x 2 y 0. B. 2 2 2
x y z 2x 2 y 1 0.
C. x y x y2 2 2 2 2 2
z 2x 1 2x . y
D. x y2 2
2xy z 1 4 . x Lờigiải
Phương trình mặt cầu S có dạng 2 2 2
x y z 2ax 2by 2cz d 0 với 2 2 2
a b c d 0 , có tâm I ; a ; b c , bán kính 2 2 2
R a b c d .
Lựa chọn đáp án A.
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 4 2
y x 3x 2
A. Điểm M 1; 4 .
B. Điểm N 1 ;0 .
C. Điểm P 0; 2 .
D. Điểm Q 1; 2 . Lờigiải Chọn B
Câu 4. Tính diện tích S của mặt cầu và thể tích V của khối cầu có bán kính bằng 3cm .
A. S 36 2
cm và V 36 3 cm .
B. S 18 2
cm và V 108 3 cm .
C. S 36 2
cm và V 108 3 cm .
D. S 18 2
cm và V 36 3 cm . Lờigiải Chọn A
Mặt cầu bán kính r có diện tích là: 2 2
S 4πr 4π.3 36π 2 cm . 4 4
Khối cầu bán kính r có thể tích là: 3 3 V
πr π.3 36π 3 cm . 3 3
Câu 5. Tìm họ nguyên hàm của hàm số f x 3x sin x . x
A. f x 2
dx 3x cos x C .
B. f x 2 3 dx
cos x C . 2 x
C. f x 2 3 dx
cos x C .
D. f xdx 3 cos x C . 2 Lờigiải ChọnC x
Ta có f x x x x 2 3 d 3 sin dx
cos x C . 2
Câu 6. Cho hàm số f x có đạo hàm f x x x x 3 1 4 , x
. Số điểm cực đại của hàm số đã cho là A. 2 . B. 3 . C. 4 . D. 1 . Lời giải Chọn D Trang7 x 0
f x 0 x x
1 x 43 0 x 1 . x 4
Lập bảng biến thiên của hàm số f x
Vậy hàm số đã cho có một điểm cực đại. 2 x 23
Câu 7. Tập nghiệm của bất phương trình 3 9 là A. 5 ;5 . B. ;5 . C. 5; . D. 0;5 . Lời giải Chọn A 2 x 23 2 2 Ta có 3
9 x 23 2 x 25 5 x 5 . 2
Vậy nghiệm của bất phương trình x 23 3 9 là 5 ;5 .
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và thể tích bằng 3
a .Tính chiều cao h của hình chóp đã cho. A. h . a . B. h 2 . a . C. h 3 . a . D. h 3 . a . Lời giải ChọnC 3 1 3V 3a Ta có:V
S.h h 3 . a . 2 3 S a
Câu 9. Tập xác định của hàm số y 2 x13 là A. .
B. 2; . C. ; 2 . D. \ 2 . Lời giải Chọn C
Câu 10. Nghiệm của phương trình log x 7 5 là 2 A. x 18 . B. x 25 . C. x 39 . D. x 3. Lờigiải ChọnB log x 7 5
5 x 7 2 x 25 . 2 1 1 1 Câu 11. Biết
f xdx 2 và g
xdx 3, khi đó f
x gx dx bằng 0 0 0 A. 1. B. 1. C. 5 . D. 5 . Lờigiải ChọnC Trang8 1 1 1
f x gx dx
f xdx gxdx 2 3 5 . 0 0 0
Câu 12. Cho số phức z thỏa mãn điều kiện: 1 i z 1 3i 0 . Phần ảo của số phức w 1iz z là A. 1. B. 3 . C. 2 . D. 1. Lời giải
1i z 13i 0 1 3i
13i1i 4 2i z i
i i 2 i z 2 i 1 1 1 2
w 1 iz z 1 i 2 i 2 i 2 3i
Phần ảo của w là 3
Vậy chọn đáp án B.
Câu 13. Trong không giam Oxyz, mặt phẳng P : 2x 3y z 1 0 có một vectơ pháp tuyến là A. n 2;3; 1
B. n 1; 3; 2
C. n 2; 3;1
D. n 1; 3; 2 2 4 3 1 Lờigiải ChọnC
Mặt phẳng P : 2x 3y z 1 0 có một vectơ pháp tuyến là n 2;3;1 . 4
Câu 14. Trong không gian Oxyz cho ba vectơ a 1; 1
;2,b 3;0; 1 , c 2 ;5
;1 , vectơ m a b c có tọa độ là A. 6;0; 6 . B. 6 ;6;0 . C. 6; 6 ;0 . D. 0;6; 6 .
Câu 15. Trong mặt phẳng tọa độ, biết điểm M (2;1) là điểm biểu diễn số phức z . Phần thực của z bằng: A. 2 B. 2 C.1 D. 1 Lời giải ChọnA
Điểm M (- 2;1) là điểm biểu diễn số phức z Þ z = - 2+ i
Vậy phần thực của z là - 2 x 1
Câu 16. Tiệm cận đứng của đồ thị hàm số y x là 3 A. x 3 . B. x 1 . C. x 1 . D. x 3. Lời giải. Chọn D x 1 lim x . x3 x
. Suy ta tiệm cận đứng là đường thẳng 3 3
Câu 17. Với a là số thực dương tùy ý, log 5a bằng 5
A. 5 log a .
B. 5 log a . C. 1 log a . D. 1 log a . 5 5 5 5 Lời giải Chọn C Trang9 Ta có: log
5a log 5 log a 1 log a . 5 5 5 5
Câu 18. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3
y x 3x 2 B. 4 2
y x x 1 C. 4 2
y x x 1 D. 3
y x 3x 2 Lờigiải Chọn D
Đồ thị hình vẽ là đồ thị hàm số bậc ba có hệ số a 0 nên chỉ có hàm số 3
y x 3x 2 thỏa mãn điều kiện trên. x 2 y 1 z 2
Câu 19. Trong không gian Oxyz , điểm nào dưới đây thuộc đường thằng d : . 1 1 2 A. N 2; 1 ;2 B. Q 2 ;1;2 C. M 2 ; 2 ;1
D. P 1;1; 2 Lờigiải ChọnB x 2 y 1 z 2 Đường thằng d : đi qua điểm 2 ;1; 2 . 1 1 2
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. A A A . D. A n k !(n . B. k)! n (k . C. n)! n k ! n (n . k)! Lời giải Chọn D n k ! A n (n k)!
Câu 21. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là 3V 3h V h A. B . B. B . C. B . D. B . h V h V Lời giải Chọn C V
Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là: B . h
Câu 22. Tính đạo hàm của hàm số ex y ln 3x . 1 3 x x 1 x 1
A. y e . B. ex y . C. ex y .
D. y e ln 3x e . 3x x x x Lờigiải Chọn B Trang10 Ta có
ex ln 3 ex y x ln 3 1
ln x ex y . x
Câu 23. Cho hàm số có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? 0;2. 0;. 2 ;0. 2;. A. B. C. D. Lời giải Chọn A 0;2 f ' x
Dựa vào bảng biến thiên ta thấy trên khoảng 0 thì . 0;2
Vậy hàm số nghịch biến trên khoảng .
Câu 24. Cho hình trụ có diện tích xung quanh S và độ dài đường sinh l . Bán kính đáy r của hình trụ đã cho xq
được tính theo công thức nào sau đây? 2S S S xq xq xq l A. r . B. r . C. r . D. r . l l 2 l Sxq Lờigiải Chọn C S
Bán kính đáy r của hình trụ là: xq r . 2 l 1 1 1 Câu 25. Cho f
xdx 2 và g
xdx 5 , khi f
x2gxdx bằng 0 0 0 A. 8 B. 1 C. 3 D. 12 Lờigiải ChọnA 1 1 1 Có f
x2gxdx f
xdx2 g
xdx 22.5 8 . 0 0 0
Câu 26. Cho cấp số cộng u
với u 5;u 10 . Công sai của cấp số cộng đã cho bằng n 1 2 A. 5 . B. 5 . C. 2 . D. 15 . Lời giải Chọn B Cấp số cộng u
có số hạng tổng quát là: u u n 1 d ; n 1 n
(Với u là số hạng đầu và d là công sai). 1
Suy ra có: u u d 10 5 d d 5 . 2 1
Vậy công sai của cấp số cộng đã cho bằng 5. Trang11
Câu 27. Họ nguyên hàm của hàm số f x 1
sin x là x 1
A. ln x cos x C . B.
cos x C .
C. ln x cos x C .
D. ln x cos x C . 2 x Lờigiải Ta có f x 1 1 dx sin x dx dx sin d
x x ln x cos x C . x x
Câu 28. Cho hàm số y f x có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 5 B. 2 C. 0 D. 1 Lời giải Chọn A
Dựa bào BBT ta có: Giá trị cực đại của hàm số là y 5 CD
Câu 29. Giá trị lớn nhất của hàm số 2 y 4 x là A. 2. B. 0. C. 4. D. 1. Lời giải Chọn A
• Tập xác định: D 2 ;2 • Ta có: x y '
y 0 x 0 2 ;2 2 4 x y 2
y2 0 • Ta có: . y y 0 max 2 2 ;2 2
Câu 30. Xét các mệnh đề sau: (I). Hàm số 3 y (
x 1) nghịch biến trên . x
(II). Hàm số y ln(x 1) x đồng biến trên tập xác định của nó. 1 x (III). Hàm số y đồng biến trên . 2 x 1
Hỏi có bao nhiêu mệnh đề đúng? A. 3. B. 2. C. 1. D. 0. Lời giải Chọn A. (I) y 3 x 2 ( 1) 3
(x 1) 0,x Trang12 x x
(II) y ln(x 1) x x 1 x 0, 1 2 1 x
x x x 2 2 2 x 1 . x 1. 1 . 1 2 x 1 1 (III) y 0,x 2 2 x 1 x 1 2x 2 1 x 1 log (ab)
Câu 31. Cho a và b là hai số thực dương thỏa mãn 3 9
4a . Giá trị của 2 ab bằng A. 3 . B. 6. C. 2 D. 4 Lời giải Chọn D log3(ab) Ta có : 9
= 4a Û 2 log ab = log 4a Û log ( 2 2 a b = log 4a 2 2 Þ a b = 4a 3 ) 3 ( ) 3 ( ) 3 ( ) 2 Û ab = 4 .
Câu 32. Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a . Gọi M , N lần lượt là trung điểm của AD
và SD . Số đo của góc giữa hai đường thẳng MN và SC là A. 45 . B. 60 . C. 30 . D. 90 . Lờigiải
Gọi P là trung điểm của CD .
Ta có: NP // SC MN, SC MN, NP . a a a 2
Xét tam giác MNP ta có: MN , NP , MP 2 2 2 2 2 a a 2 a 2 2
MN NP 2 MP M
NP vuông tại N 4 4 2
MNP 90 MN,SC MN, NP 90. 1 1 Câu 33. Cho f
xdx 1 tích phân 2 f x 2
3x dx bằng 0 0 A. 1. B. 0 . C. 3 . D. 1. Lờigiải Trang13 Chọn. A. 1 1 1 2 f x 2
3x dx 2 f x 2
dx 3 x dx 2 1 1 . 0 0 0
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua A(2 ; 1 ; )
1 và vuông góc với đường thẳng íï x = 1+ 2 ï t ï D : ì y = 2 + t ï
có phương trình là ïï z = 1- 2 ïî t
A. 2x y z - 3 0 .
B. 2x y - 2z - 5 0 .
C. x 2 y z - 5 0 .
D. 2x y - 2z - 3 0 . i
Câu 35. Cho số phức z thỏa mãn điều kiện i 1 2 z
5 i . Môđun của số phức 2
w 1 2z z có giá trị 1 i là A. 10. B. 10 . C. 100. D. 100 . Lờigiải i 1 i 2 z 5 i 1 i 2 i 2 i 1 z
i i 5 i 1 1 i 2i 2 z 5 i 2 i 5 2
z 5 z 2 i 2 i
w z z z2 i2 i w 2 2 2 1 2 1 3 8 6 8 6 10 .
Vậy chọn đáp án A.
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD a , AB 2a . Cạnh bên SA 2a
và vuông góc với đáy. Gọi M , N lần lượt là trung điểm của SB và SD . Tính khoảng cách d từ S đến mặt
phẳng AMN . a 6 3a A. d .
B. d 2a . C. d . D. d a 5 . 3 2 Lời giải Chọn A 1 2 3 Ta có: V S . A S a S . ABD 3 ABD 3 Trang14 3 V SN SM 1 1 a Vì: S.AMN . V V S. AMN S . V SD SB 4 4 ABD 6 S.ABD 1 a 5 S AD vuông: 2 2
SD SA AD a 5 AN SD 2 2 S AB vuông: 2 2 SD
SA AB 2a 2 AM a 2 1 a 5
MN là đường trung bình của tam giác SBD MN DB 2 2 2 a 6 3V a 6 Khi đó: S d
S;AMN S . AMN
nên chọn đáp án A. AMN 4 S 3 A MN
Câu 37. Cho 14 tấm thẻ được đánh số từ 1 đến 14 . Chọn ngẫu nhiên 3 tấm thẻ. Xác suất để tích 3 số ghi trên 3
tấm thẻ này chia hết cho 3 bằng? 30 61 31 12 A. . B. . C. . D. . 91 91 91 17 Lời giải Chọn B
Không gian mẫu có sốp phần tử là: 3 C 364 . 14
Để tích của ba số ghi trên 3 tấm thẻ chia hết cho 3 thì trong ba số phải có ít nhất 1 số chia hết cho 3 do đó ta có: 1 2 2 1 3
C .C C .C C 244 cách lấy ra ba số để tích ba số ghi trên 3 tấm thẻ chia hết cho 3 . 4 10 4 10 4 244 61
Xác suất cần tính là: P . 364 91
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P: 2x y z 3 0 và điểm A1; 2 ;1 .
Phương trình đường thẳng d đi qua A và vuông góc với P là x 1 2t x 1 2t x 2 t x 1 2t
A. d: y 2 t .
B. d: y 2 4t . C. y 1 2t .
D. d: y 2 t . z 1 t z 1 3t z 1 t z 1 3t Lờigiải ChọnA
Mặt phẳng P có một vectơ pháp tuyến là n 2; 1; 1 .
Đường thẳng d vuông góc với mặt phẳng P nên nhận n 2; 1;
1 làm vectơ chỉ phương. Mà d đi qua x 1 2t A1; 2
;1 nên có phương trình: y 2
t (t ). z 1t 1 11 x 1 2 2x 11
Câu 39. Số nghiệm nguyên thuộc khoảng 0;12 của bất phương trình 3 x 3 x log2 2
x x là: 1 A. 7 . B. 8 . C. 5 . D. 11. Lờigiải ChọnC Trang15 11
Điều kiện x và x 0 . 2 1 11 1 11 x 1 2 2x 11 x 1 2 1 2x 11
Khi đó 3 x 3 x log
3 x 3 x log 2 2 x x 1 2 2 2
x x 1 11 1 11 2 1 11 x 1 2 x 1 2 1 1 1 1 11
3 x 3 x log x
3 x log x 1 3 x log 2 . 2 2 2 2 1 2 x 2 x x 1 x t 1
Xét hàm số f t 3 log t với t 0. Khi đó f t t 1 3 ln 3 0, t
0 nên hàm số đã cho đồng 2 2 2t ln 2 biến trên 0; . Do đó 2 1 11 1 11 x 3x 10 11 f x 1 f 2 x 1 2 0 x ; 2 0;5 . x x x x x 2
Vậy trên khoảng 0;12 có 5 nghiệm nguyên thỏa yêu cầu bài toán.
Câu 40. Cho hàm số y f x có đạo hàm f x trên khoảng ;
. Đồ thị của hàm số y f x như hình vẽ y 1 1 O x 1 ' 2
Tìm số nghiệm của phương trình f 2x 0 A. 3 . B. 4 . C. 2 . D. 5 . Lờigiải Chọn A. Ta có f 2x 2 0 x 1 x 0 2 2
f x ' 2 2 x f 2 x f 2 0 4 . .
x 0 f 2
x x 1
, x 0 x 1 0 . x 0 x 1 x 0
Suy ra phương trình 3 nghiệm. Trang16 4 Câu 41. Cho hàm số f x xác định trên R\ 2; 2 thỏa mãn
f x 2 x , 4 f 3
f 3 f 1 f
1 2 . Giá trị biểu thức f 4
f 0 f 4 bằng A. 4 . B. 1. C. 2 . D. 3 . Lờigiải 4 1 1 dx
dx ln x 2 ln x 2 C Ta có: 2 x 4
x 2 x 2 . x 2 ln C khi x 2 1 x 2 2 x f x ln C khi 2 x 2 Do đó: 2 x 2 x 2 ln C khi x 2 3 x 2 1 1 f 3
ln5 C ; f 3 ln C ; f 0 C ; f
1 ln 3 C ; f 1 ln C ; 1 3 5 2 2 2 3 C C 2 f 3
f 3 f 1 f
1 2 C C 2C 2 1 3 1 3 2 C 1 . 2 1 Vậy f 4
f 0 f 4 ln3 C C ln C C C C 3 . 1 2 3 3 1 2 3
Câu 42. Cho hình chóp S .A B CD có đáy A B CD là hình chữ nhật có A B = a, B C = 2a . Hai mp (SA B )và
mp (SA D)cùng vuông góc với mă ̣t phẳng đáy , cạnh SC hợp với đáy một góc 0
60 . Tính thể tích khối chóp
S .A BCD theo a . 3 a 15 3 a 15 3 a 3 3 2a 15 A. . B. . C. . D. . 5 3 15 3 Lờigiải S A D 600 B C Trang17
íï (SA B) ^ (A BCD) ïïï
+ Ta có: ì (SA D) ^ (A BCD)
Þ SA ^ (A BCD) .
ïïï(SAB) Ç(SAD) = SA ïî
Þ Hình chiếu củaSC lênmp (ABCD)làAC . · é ù Þ S ê C (A BCD) · 0 , = ú SCA = 60 . êë úû 1 + Mà: V = SA.S 1 . S .A BCD A CBD ( ) 3 · SA ·
+ TìmSA ? Trong D SA C vuông ta ̣i A : t an SCA =
Þ SA = A C . t an SCA A C 2 2 0 2 2 =
A B + BC . t an 60 =
a + (2a) . 3 = a 15 (2). + Ta la ̣i có: 2 S
= A B.BC = a.2a = 2a ( ) 3 . A BCD 3 1 2a 15 + Thay( ) 2 , (3)vào( ) 2 1 Þ V = a × 15 2 × a = (đvtt). A BCD 3 3 Chọn Đáp án D
Câu 43. Tìm các số thực a, b, c sao cho hai phương trình 2 2
az bz c 0, cz bz a 16 16i 0 có nghiệm
chung là z 1 2i A. , a , b c 1; 2 ;5 B. a, , b c 1; 2; 5 C. a, , b c 1 ; 2 ;5 D. a, , b c 1; 2 ; 5 Lờigiải
Theo giả thiết phương trình 2
az bz c 0 có nghiệm z 1 2i khi a i
a b c
2 b i c a b c a b 3 0 1 2 1 2 0 3 4 2 i 0 1
4a 2b 0 Tương tự phương trình 2
cz bz a 16 16i 0 có nghiệm z 1 2i khi c i2 1 2
b1 2i a 16 16i 0 c 3
4i b 2bi a 16 16i 0
a b c b c
a b 3c 16 0 3 16 2 2 8 i 0 2
b 2c 8 0 Từ
1 , 2 suy ra a, , b c 1; 2 ;5. Chọn A.
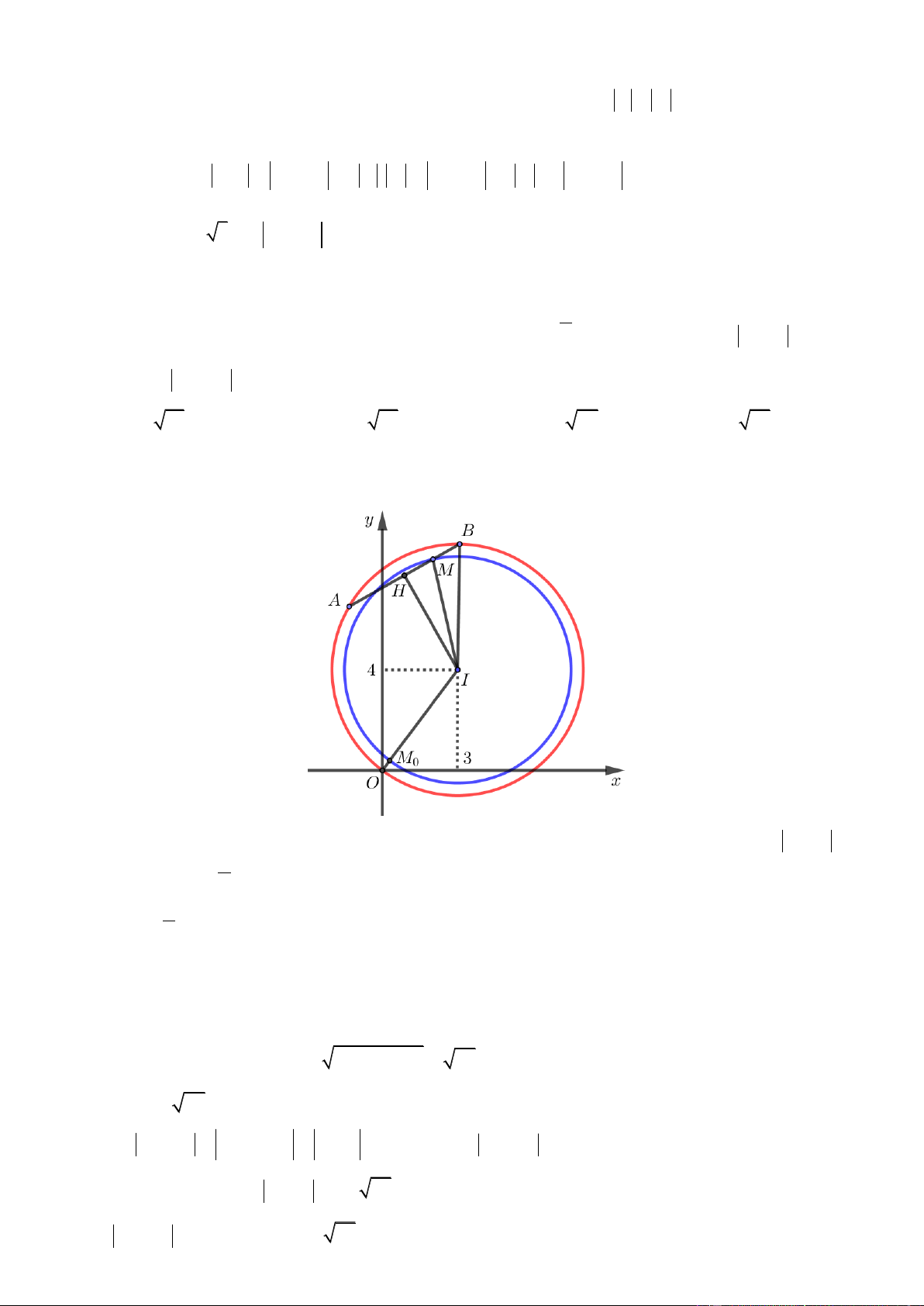
Câu 44. Cho z , z là hai trong các số phức thỏa mãn z 3 3i 2 và z z 4 . Giá trị lớn nhất của 1 2 1 2 z z bằng 1 2 A. 8 . B. 4 3 . C. 4 . D. 2 2 3 . Lờigiải ChọnA Trang18
Gọi M , N lần lượt là điểm biểu diễn của hai số phức z , z . 1 2
z 3 3i z 3 3i 2
M,NC:x3 y 32 2 2 1 2 2 Do nên .
z z 4 1 2 MN 4 2.2
Như vậy MN là đường kính của đường tròn C với tâm I 3; 3 , bán kính R 2 , do đó I là trung điểm
MN , OI 12 . MN
Ta có z z OM ON 1
1 OM ON 2 2 2 2 22OI 8. 1 2 2
Dấu " " xảy ra khi và chỉ khi OM ON MN là đường kính của C vuông góc với OI . 3 3
Câu 45. Cho hai hàm số f x 3 2
ax bx cx và g x 2
dx ex , , a , b ,
c d, e . Biết rằng đồ thị 4 4
của hàm số y f x và y g x cắt nhau tại ba điểm có hoành độ lần lượt là 2
; 1; 3 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 253 125 125 253 A. B. C. D. 48 24 48 24 Lờigiải ChọnA
Ta có phương trình hoành độ giao điểm là: 3 3 3 3 2 2
ax bx cx
dx ex 3
ax b d 2
x c e x 0 . 4 4 2 3
Đặt h x 3
ax b d 2
x c e x 2 3
Dựa vào đồ thị ta có h x 3
ax b d 2
x c e x
có ba nghiệm là x 2
; x 1; x 3. 2 3 Với x 2 ta có 8
a 4b d 2c e , 1 . 2 Trang19 3
Với x 1 ta có a b d c e , 2 . 2 3
Với x 3 ta có 27a 9b d 3c e , 3 . 2 1
a b d c e 3 8 4 2 a 2 4 3 1 Từ
1 , 2 và 3 ta có a b d c e b d . 2 2 5
a b d c e 3 27 9 3 c e 2 4 Hay ta có 3 1 3 1 1 5 3 1 1 5 3 S f
x gx dx 3 2 3 2 x x x dx x x x dx 63 4 253 . 4 2 4 2 4 2 4 2 16 3 48 2 2 1
Câu 46. Trong không gian với hệ toạ độ Oxyz , cho điểm A1; 2
;3 và hai mặt phẳng P: x y z 1 0 ,
Q: x y z 2 0 . Phương trình nào dưới đây là phương trình đường thẳng đi qua A , song song với P và Q ? x 1 t x 1 t x 1 2t x 1 A. y 2 B. y 2 C. y 2 D. y 2 z 3 t z 3 t z 3 2t z 3 2t Lờigiải ChọnA n P 1;1; 1 Ta có và n , n 2;0; 2
. Vì đường thẳng d song song với hai mặt phẳngP và Q , P Q n Q 1; 1; 1
nên d có véctơ chỉ phương u 1;0; 1 . x 1 t
Đường thẳng d đi qua A1; 2
;3 nên có phương trình: y 2 z 3t
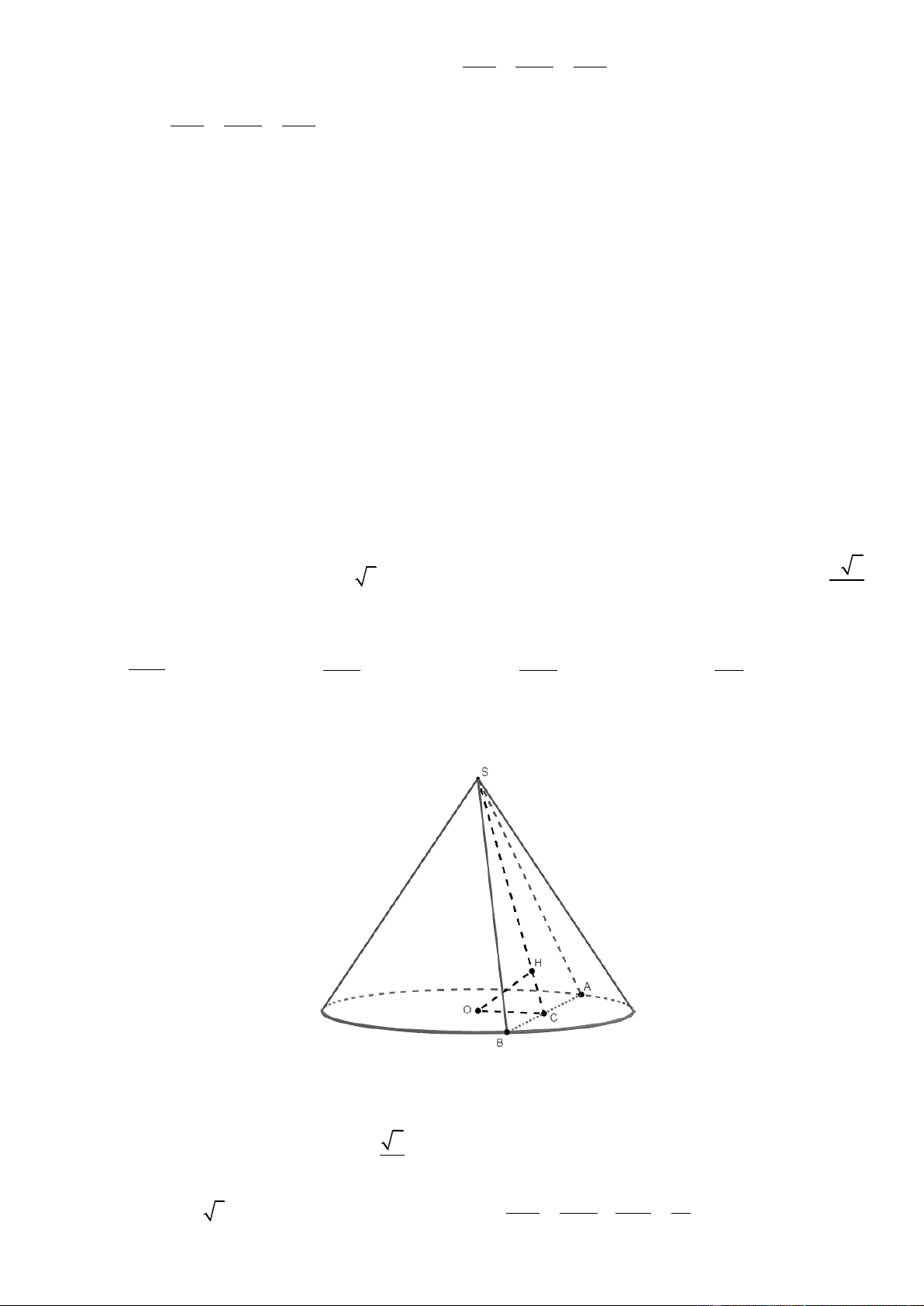
Câu 47. Cho hình nón tròn xoay có chiều cao bằng 4 và bán kính bằng 3. Mặt phẳng P đi qua đỉnh của hình
nón và cắt hình nón theo thiết diện là một tam giác có độ dài cạnh đáy bằng 2 . Diện tích của thiết diện bằng. A. 6 . B. 19 . C. 2 6 . D. 2 3 . Lời giải Trang20
Ta có: h OI 4, R IA IB 3, AB 2 .
Gọi M là trung điểm AB MI AB AB SMI AB SM . Lại có: 2 2 2 2
SB OI IB 4 3 5 ; 2 2 2 2 SM
SB MB 5 1 2 6 . 1 1 Vậy: S
.SM .AB .2 6.2 2 6 . SAB 2 2
Câu 48. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn log 2
x y log (x y) ? 4 3 A. 59 . B. 58 . C. 116 . D. 115 . Lời giải Chọn C
Bất phương trình đã cho tương đương log (x y) log 2
x y 0 (1) 3 4
Xét hàm số f (y) log (x y) log 2 x y . 3 4
Tập xác định D (x ; ) . 1 1 Với mọi x 2
ta có x x nên f ( y) x D (x y) ln 3 0, 2 x yln 4
f ( y) đồng biến trên khoảng (x;) .
Do y là số nguyên thuộc (x ; ) nên y x k, k .
Giả sử y x k là nghiệm của bất phương trình (1) thì f ( y) f (x k) 0 .
Mà x 1 x 2 ... x k và f ( y) đồng biến trên khoảng (x ; ) , suy ra
f (x 1) f (x 2) ... f (x k) 0 , nên các số nguyên x 1, x 2, ..., x k đều là nghiệm của
(1), hay nói cách khác bất phương trình (1) sẽ có k số nguyên y thỏa mãn yêu cầu ứng với mỗi x .
Để có không quá 728 số nguyên y thì f (x 729) 0 log 729 log 2
x x 729 0 3 4 1 13469 1 13469 2
x x 3367 0 x 2 2
Mà x nên x 5 7, 56, ..., 5 8 .
Vậy có 116 số nguyên x thỏa yêu cầu bài toán. Trang21
Câu 49. Trong không gian Oxyz , cho mặt cầu: S x y z 2 2 2 : 1
5 . Có tất cả bao nhiêu điểm Aa;b;c (a, ,
b c là các số nguyên) thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp tuyến của S đi qua A và hai tiếp
tuyến đó vuông góc nhau? A. 20 . B. 8 . C. 12 . D. 16 . Lờigiải ChọnA Mặt cầu S 2 2 2
: x y (z 1) 5 có tâm I 0;0;
1 và có bán kính R 5 a b 1
Aa;b;0 Oxy , Gọi I là trung điểm của AI I ; ; 2 2 2
Gọi E, F lần lượt là hai tiếp điểm của tiếp tuyến đi qua A sao cho AE AF . a b 1 1
Ta có: E, F cùng thuộc mặt cầu S đường kính IA có tâm I ; ; , bán kính 2 2 R a b 1 . 2 2 2 2
Đề tồn tại E, F thì hai mặt cầu S và S phải cắt nhau suy ra R R II R R 1 1 1 2 2 2 2 2 2 5 a b 1
a b 1 5 a b 1 2 2 2 2 2 2 2
5 a b 1 a b 4 1
Gọi H là hình chiếu của I trên AEF khi đó tứ giác AEHF là hình vuông có cạnh 2 AE HF AI 5 . Ta có 2 2 2
IH R HF 2 AI 2 2 2 2 2 5
5 10 AI 0 a b 1 10 a b 92 Từ 1 và 2 ta có 2 2
4 a b 9 mà a, ,
b c nên có 20 điểm thỏa bài toán. Cáchkhác:
Mặt cầu S có tâm I 0,0,
1 bán kính R 5 . Ta có d 1 R
mặt cầu S cắt mặt phẳng Oxy . I Oxy
Để có tiếp tuyến của S đi qua A AI R 1 .
Có Aa b c Oxy Aa b 2 2 , ,
, , 0 , IA a b 1.
Quỹ tích các tiếp tuyến đi qua A của S là một mặt nón nếu AI R và là một mặt phẳng nếu AI R .
Trong trường hợp quỹ tích các tiếp tuyến đi qua A của S là một mặt nón gọi AM , AN là hai tiếp tuyến sao cho ,
A M , I , N đồng phẳng. Trang22
Tồn tại ít nhất hai tiếp tuyến của S đi qua A và hai tiếp tuyến đó vuông góc với nhau khi và chỉ khi 90o MAN
IA R 2 2 . Từ 2 2
1 , 2 4 a b 9 . Vì a, b 2 a 0 2 2 2 2 2 2 a 9 a 4 a 0 a 1 a 4 a 4 hoặc hoặc hoặc hoặc hoặc hoặc . 2 b 9 2 b 0 2 b 0 2 b 4 2 b 4 2 b 1 2 b 4
Bốn hệ phương trình đầu tiên có hai nghiệm, ba hệ sau có 4 nghiệm suy ra số điểm A thỏa mãn là 4.2 3.4 20 .
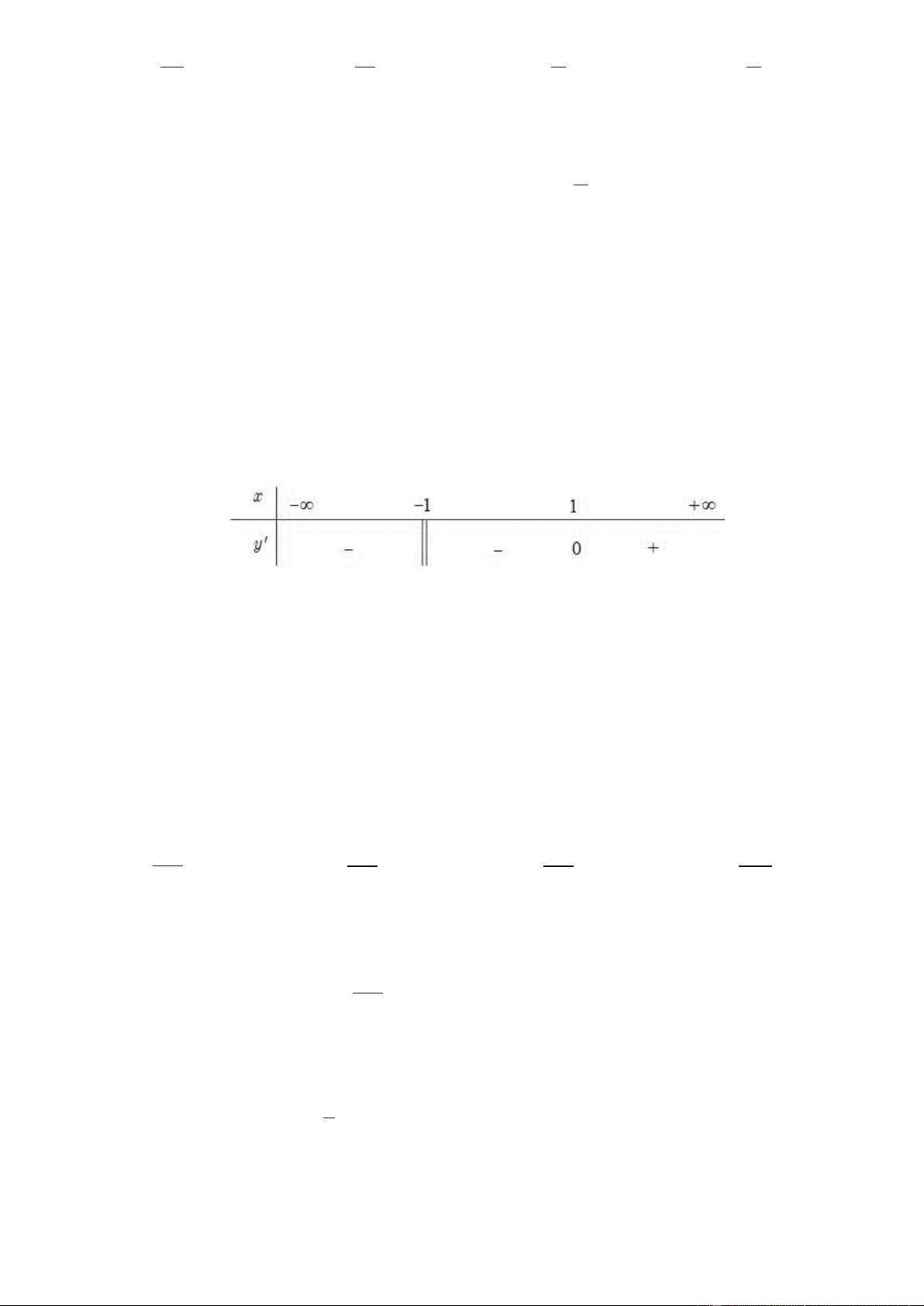
Câu 50. Cho hàm số y f x có bảng xét dấu f ' x như sau x 11 4
f ' x 0 0 0
Có bao nhiêu giá trị nguyên của tham số m thuộc 1
0;10 để g x f 2
x 2x m có 5 điểm cực trị? A. 10. B. 15. C. 20. D. 21. Lời giải Chọn A
Ta có g x x f 2 ' 2 1
' x 2x m x 1 x 1 2 2
x 2x m 1
x 2x m 1 0 g ' x 1 0 2 2
x 2x m 1
x 2x m 1 0 2 2 2
x 2x m 4
x 2x m 4 0 3
Nhận xét: Phương trình (2) nếu có nghiệm là nghiệm bội chẵn; phương trình (1) và (3) nếu có nghiệm thì nghiệm không chung nhau.
Hàm số g x có 5 điểm cực trị phương trình g ' x 0 có 5 nghiệm bội lẻ
Phương trình (1) và (3) có hai nghiệm phân biệt, khác 1. 0 1 m 0 0 3 m 5 0 m 0 V T 0 m 0 1 m 5 0 VT 0 3 Trang23 m Vì m
m 1;2;3;4;5;6;7;8;9;1 0 10;10
Vậy có 10 giá trị của tham số m. ĐỀ 2
ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2022
BÁM SÁT ĐỀ MINH HỌA MÔN TOÁN Thời gian: 90 phút
Câu 1. Cho số phức z 5 4i . Môđun của số phức z là A. 3. B. 41 . C. 1. D. 9. Lờigiải 2 2
Câu 2. Mặt cầu S x y 2 : 1 2
z 9 có tâm là: A. I 1 ; 2 ;0. B. I 1 ;2;0.
C. I 1; 2;0. D. I 1; 2 ;0. 2x 1
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số y x 2
A. Điểm M 1 ; 1 .
B. Điểm N 1; 3 .
C. Điểm P 1;3 .
D. Điểm Q 2;0 .
Câu 4. Cho khối cầu có bán kính r 2 . Thể tích của khối cầu đã cho bằng 32 8 A. 16 . B. . C. 32 . D. . 3 3
Câu 5. Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số 2022 y x ? 2023 x 2023 x 2023 x A. 1. B. . C. 2021 y 2022x . D. 1. 2023 2023 2023
Câu 6. Cho hàm số f x , bảng xét dấu của f x như sau:
Số điểm cực trị của hàm số đã cho là A. 0 . B. 2 . C. 1. D. 3 .
Câu 7. Tập nghiệm của bất phương trình x 1 5 7 là
A. 1 log 7; .
B. 1 log 7; . C. ; 1 log 7 . D. ;1 log 7 . 5 5 5 5
Câu 8. Cho khối chóp có diện tích đáy 2
B 6a và chiều cao h 2a . Thể tích khối chóp đã cho bằng: 3 3 3 3 A. 2a . B. 4a . C. 6a . D. 12a .
Câu 9. Tập xác định của hàm số 3 y x là A. . B. 0; . C. \ 0 . D. 0; .
Câu 10. Nghiệm của phương trình log 2x 1 2 3 là: Trang24 9 7 A. x 3. B. x . C. x 5. D. x . 2 2 3 3 3 Câu 11. Biết f xdx 4 và g
xdx 1. Khi đó: f
xgx dx bằng: 2 2 2 A. 3 . B. 3 . C. 4 . D. 5 .
Câu 12. Cho hai số phức z 1 2i và z 2 3i . Phần ảo của số phức w 3z 2z là 1 2 1 2 A. 12. B. 11. C. 1. D.12i .
Câu 13. Trong không gian Oxyz , cho mặt phẳng : 2x 4 y z 3 0 . Véctơ nào sau đây là véc tơ pháp tuyến của ? A. n 2; 4; 1 .
B. n 2; 4;1 . C. n 2 ;4;1 .
D. n 2; 4;1 . 1 3 2 1
Câu 14. Trong không gian với hệ trục tọa độ Oxyz , cho ba vecto a 1; 2;3;b 2; 2; 1 ; c 4;0; 4 . Tọa độ của
vecto d a b 2c là
A. d 7;0; 4 B. d 7 ;0; 4 C. d 7;0; 4
D. d 7;0; 4
Câu 15. Trên mặt phẳng tọa độ, biết M 3 ;
1 là điểm biểu diễn số phức z . Phần thực của z bằng A.1. B. 3 . C. 1. D. 3 .
Câu 16. Cho hàm số y f (x) có lim f (x) 1và lim f ( ) x 1
. Khẳng định nào sau đây là khẳng định đúng? x x
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x 1 và x 1 .
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y 1và y 1. 3
Câu 17. Với a là số thực dương tùy ý, log bằng: 3 a 1
A. 1 log a
B. 3 log a C. D. 1 log a 3 3 log a 3 3
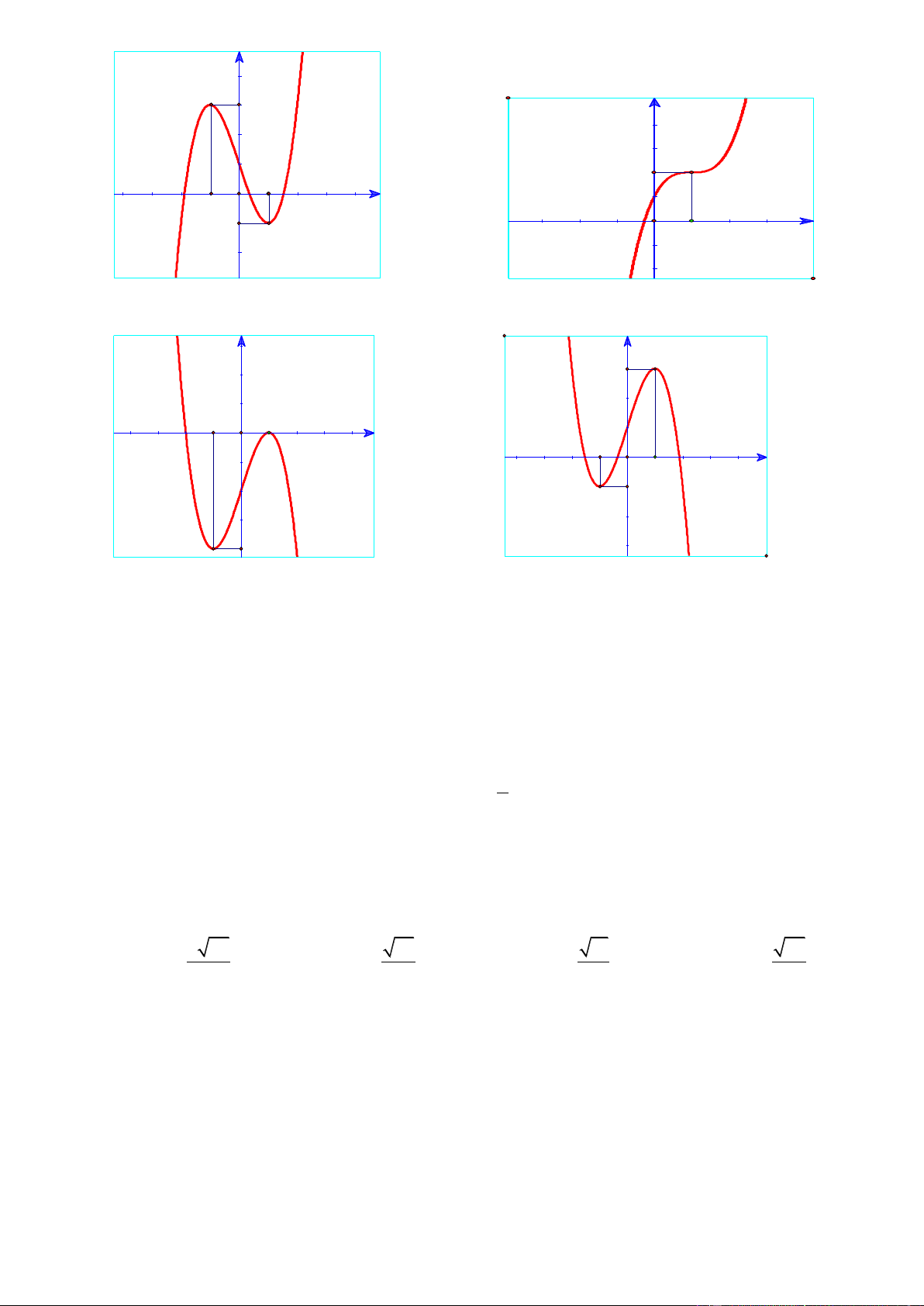
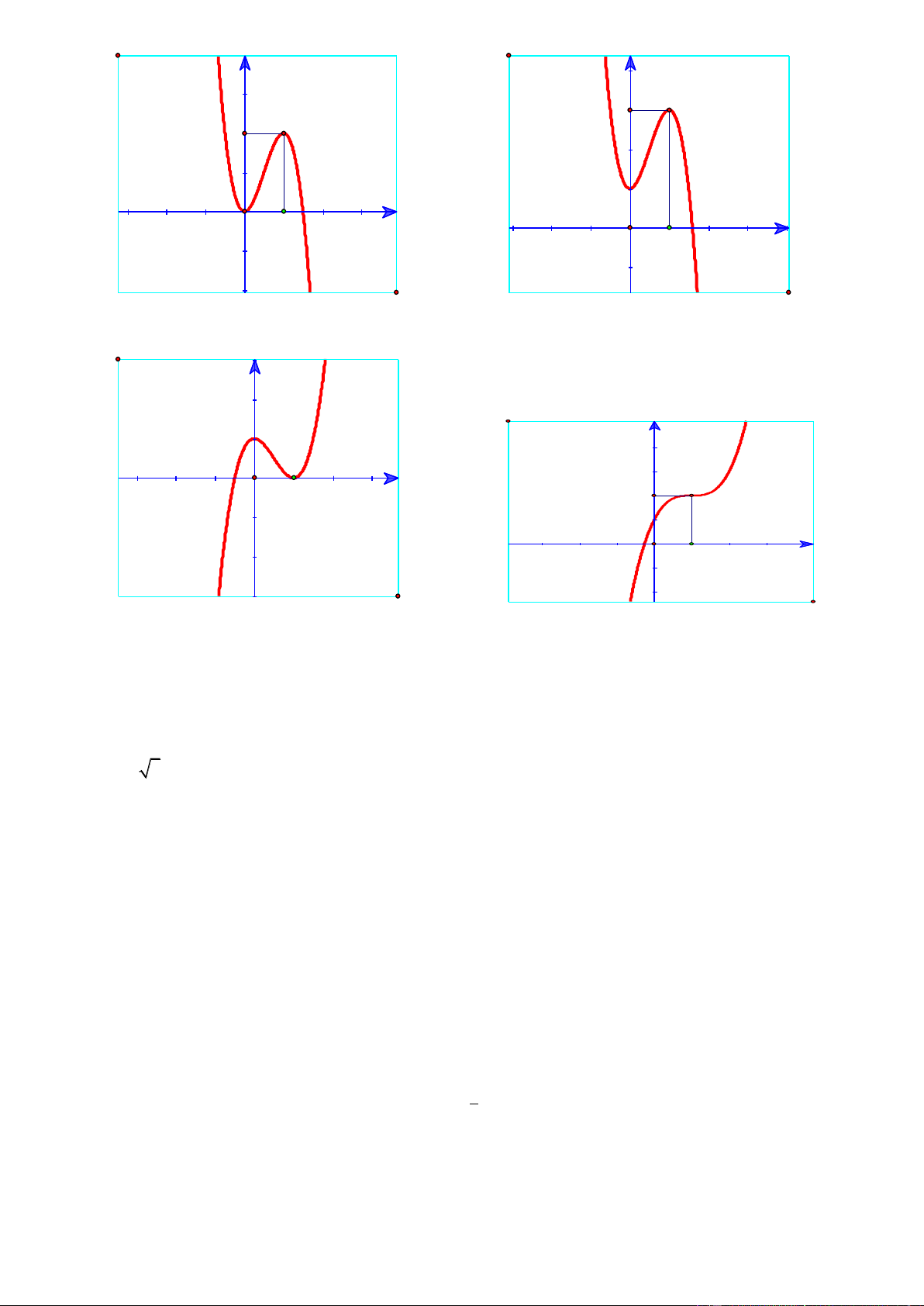
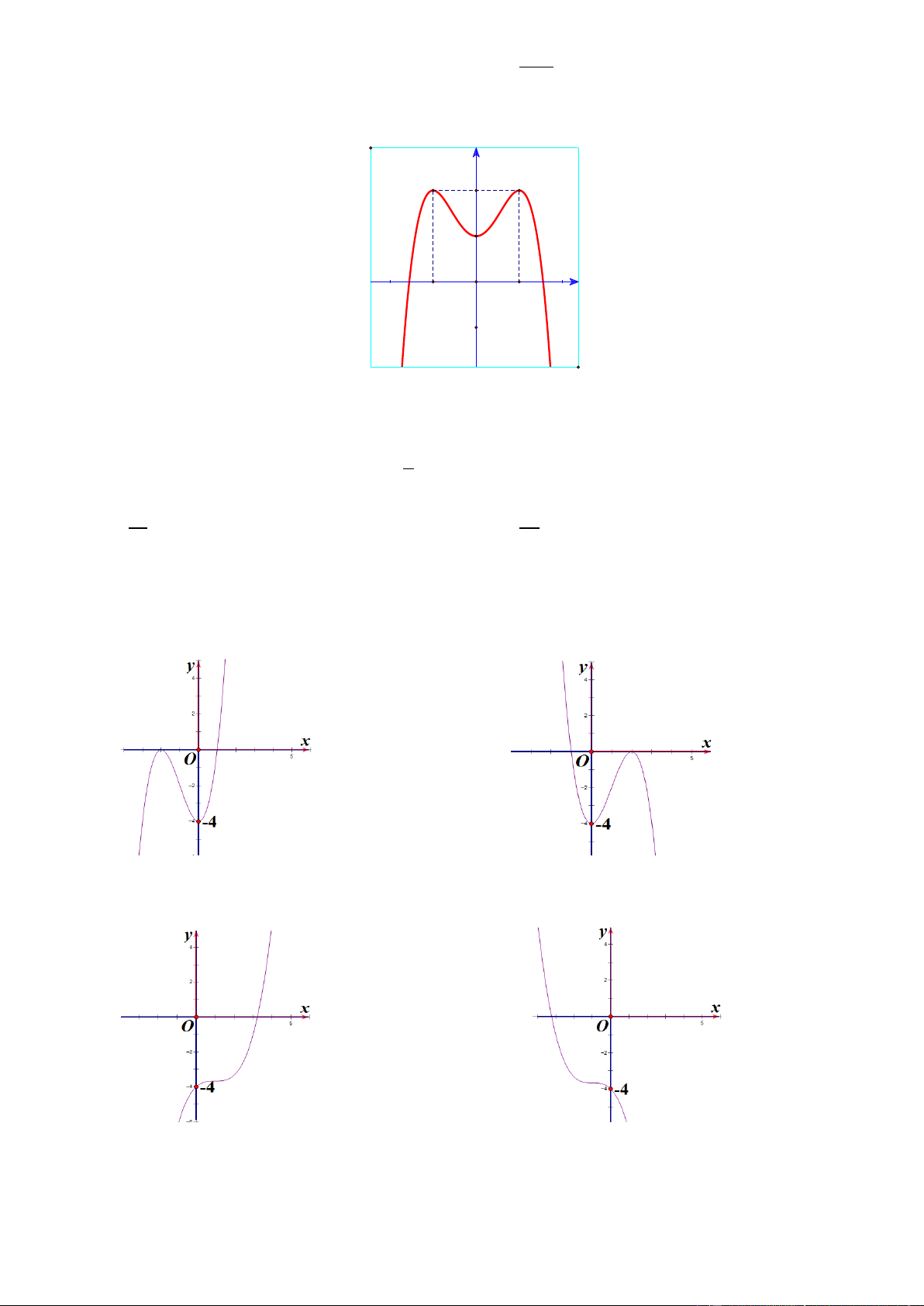
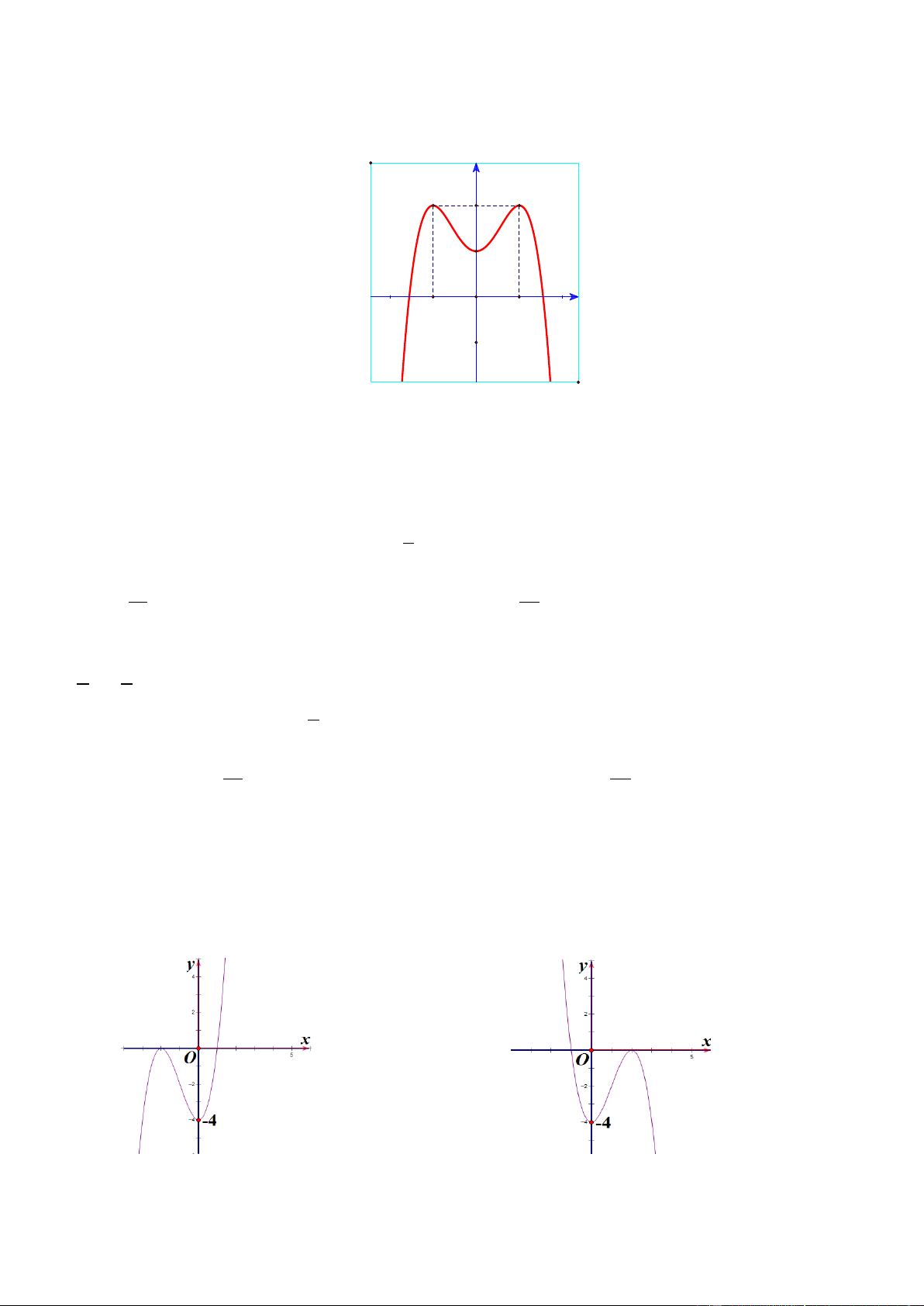
Câu 18. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới đây? 4 2 4 2 3 2
A. y x 2x .
B. y x 2x .
C. y x 3x . D. 3 2
y x 3x . Trang25 x 1 y 2 z 1
Câu 19. Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d : ? 1 3 3 A. P 1; 2 ;1 .
B. Q 1; 2; 1 . C. N 1 ;3;2. D. P 1;2 ;1 .
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. A A A . D. A n k !(n . B. k)! n (k . C. n)! n k ! n (n . k)!
Câu 21. Cho khối lăng trụ có diện tích đáy B 3 và chiều cao h 2 . Thể tích của khối lăng trụ đã cho bằng A. 1. B. 3 . C. 2 . D. 6 .
Câu 22. Tính đạo hàm của hàm số 2 1 2 x y . A. 2 x 1 y 2 ln 4 . B. x 1 y 4 ln 4 . C. 2 2 . x y ln 2 . D. 2 2 x y ln 2 .
Câu 23. Ta có Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ; 1 . B. 0; 1 . C. 1 ;1 . D. 1 ;0
Câu 24. Cho hình trụ có bán kính đáy r 5 và độ dài đường sinh l 3 . Diện tích xung quanh của hình trụ đã cho bằng A. 15 B. 25 . C. 30 . D. 75 .
Áp dụng công thức diện tích xung quanh hình trụ ta được: S 2 rl 30 . xq 6 6 Câu 25. Cho
f (x)dx 12
. Tính I 2022 f (x) . dx 0 0
A. I 5
B. I 12
C. I 24264 D. I 2022
Câu 26. Cho cấp số cộng u
với u 9 và công sai d 2 . Giá trị của u bằng n 1 2 9 A. 11. B. . C. 18 . D. 7 . 2
Câu 27. Tính x sin 2xdx . 2 x 2 x 2 cos 2x x cos 2x A.
sin x C . B.
cos 2x C . C. 2 x C . D. C . 2 2 2 2 2
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ. Trang26 y 2 -1 O x 1 -2
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 2 . C. 1. D. 1 . 2 x 3
Câu 29. Tìm giá trị nhỏ nhất của hàm số y
trên đoạn 2; 4 . x 1 19 A. min y 3 B. min y
C. min y 6 D. min y 2 2;4 2;4 3 2; 4 2;4
Câu 30. Đồ thị hàm số 3 2
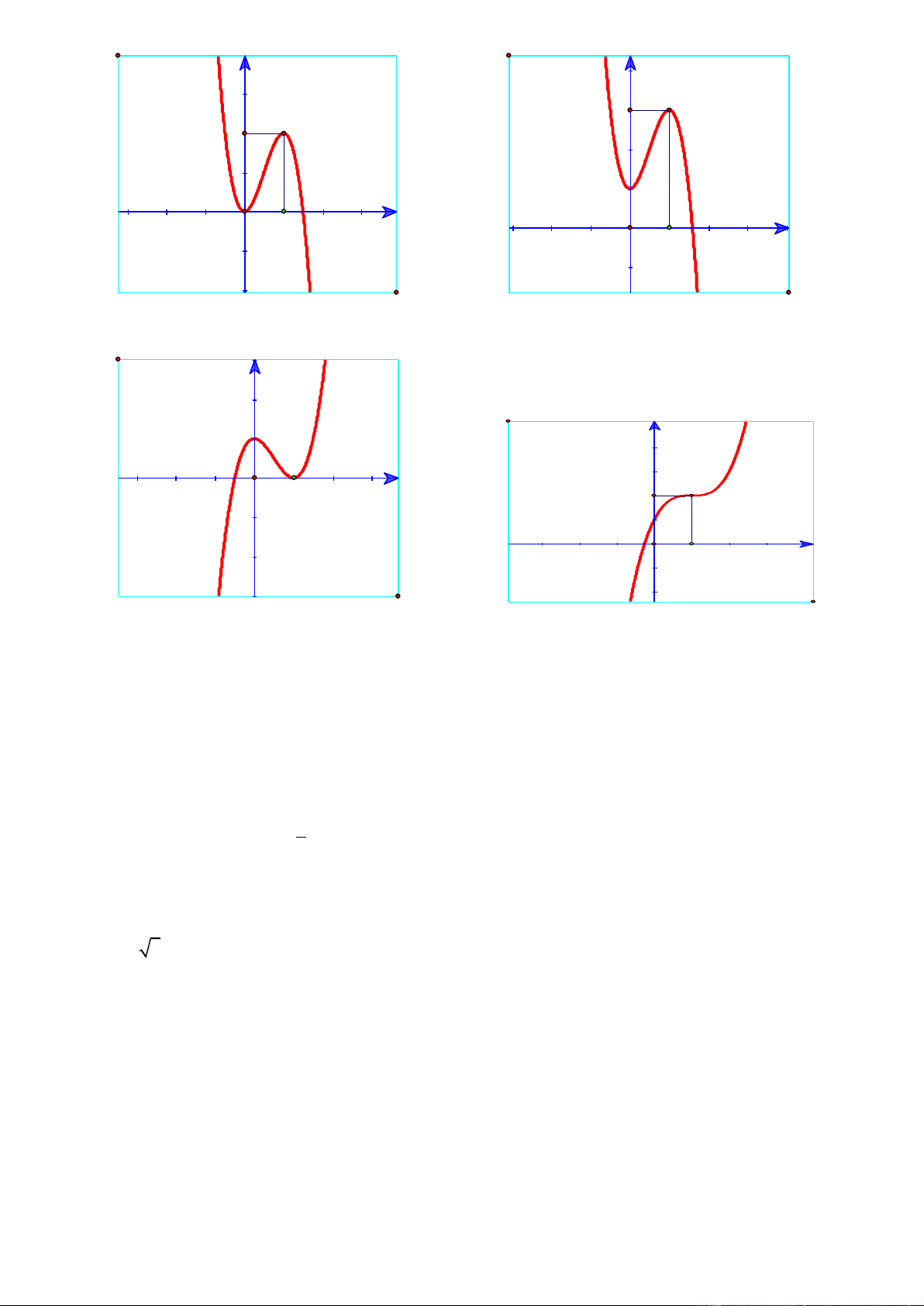
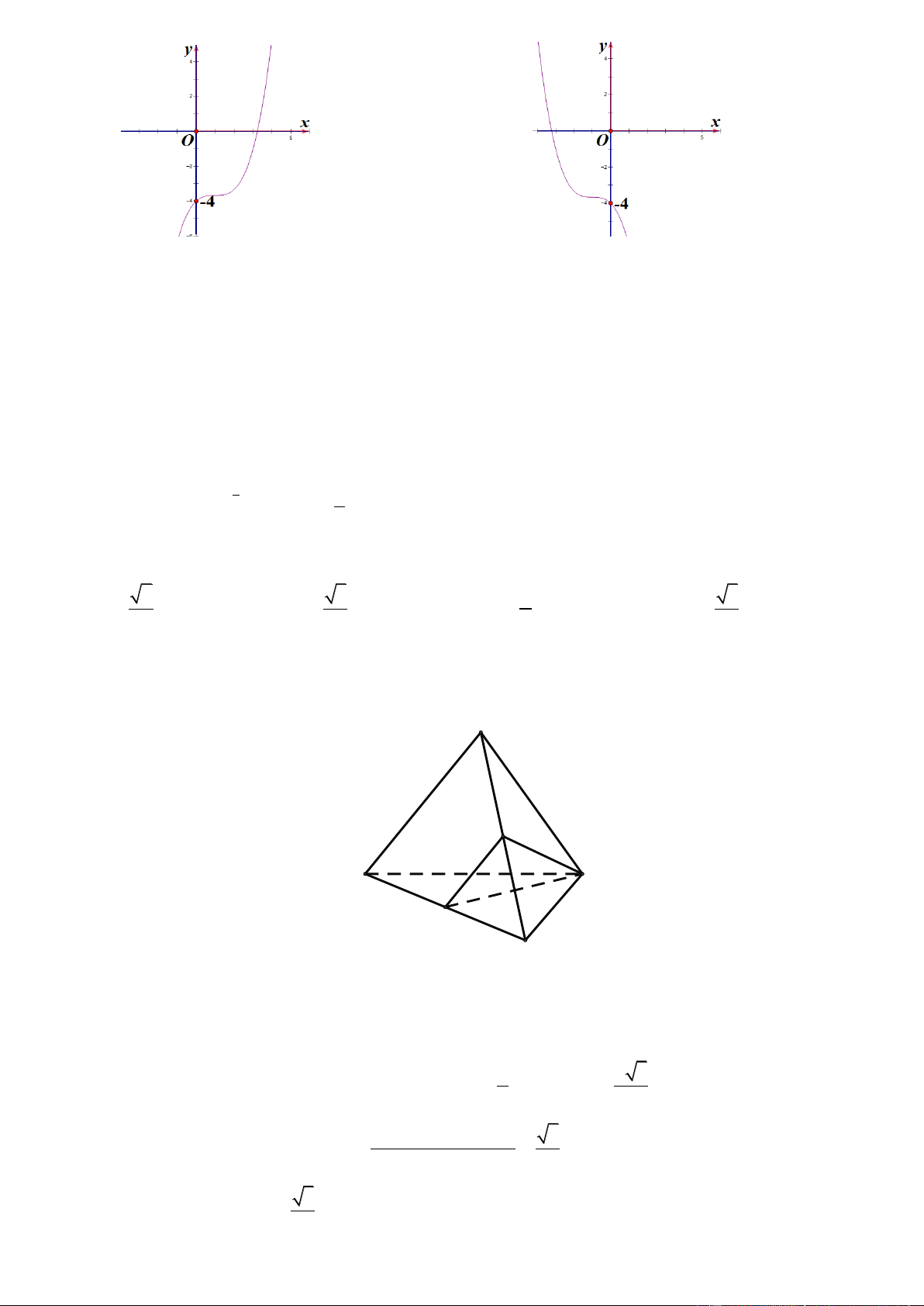
y f (x) ax bx cx d . Hình nào trong 4 hình dưới đây mà hàm số luôn đồng biến trên ? y 4 3 y 1 2 O 1 x 1 -1 O x -1 1 A. Hình 1. B. Hình 2. y y 3 -1 O 1 x 1 -1 O x 1 -2 -1 -4 C. Hình 3. D. Hình 4.
Câu 31. Với a, b là các số thực dương tùy ý thỏa mãn log a 2 log b 2 , mệnh đề nào dưới đây đúng? 3 9 2 2
A. a 9b .
B. a 9b .
C. a 6b .
D. a 9b . Trang27
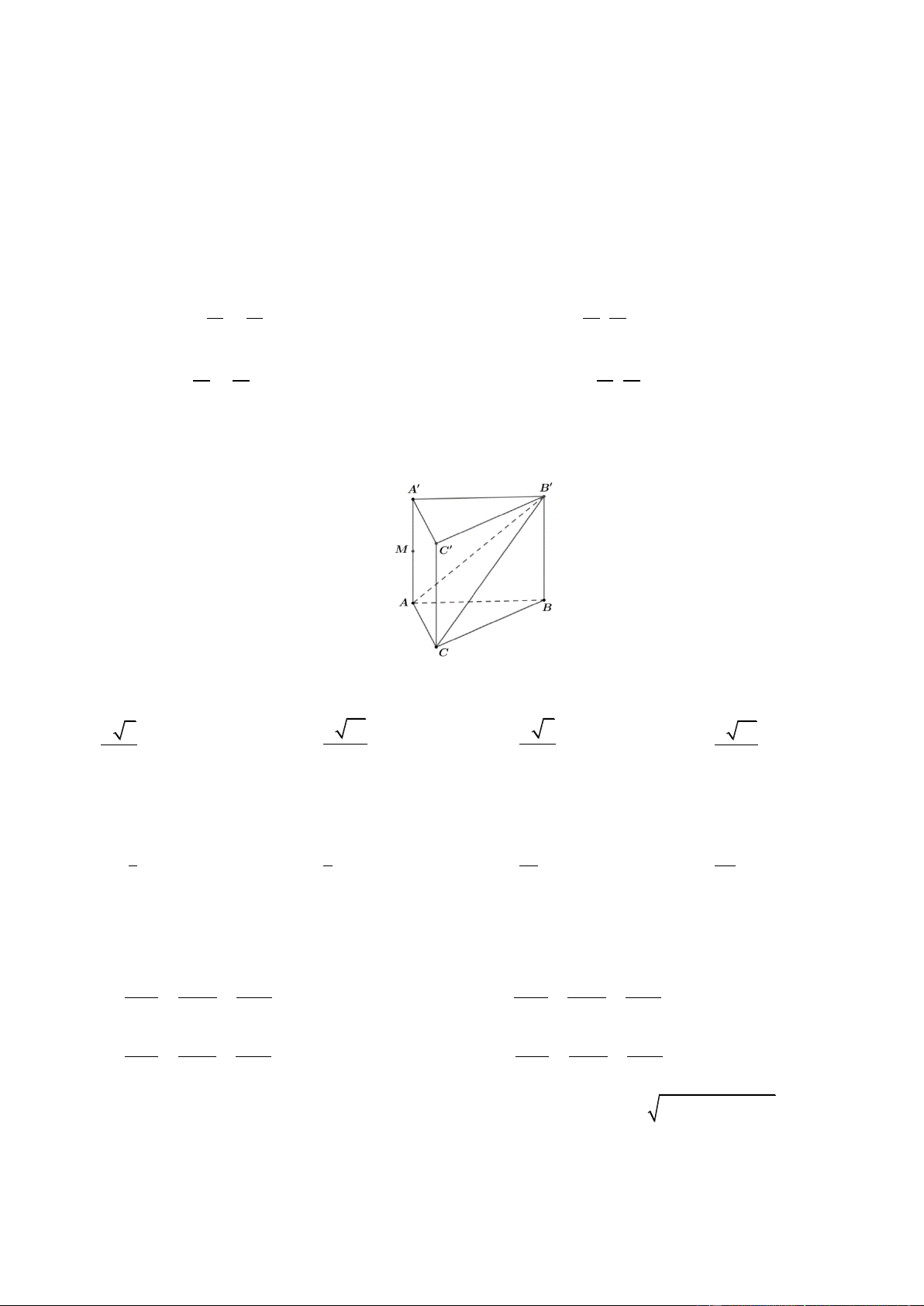
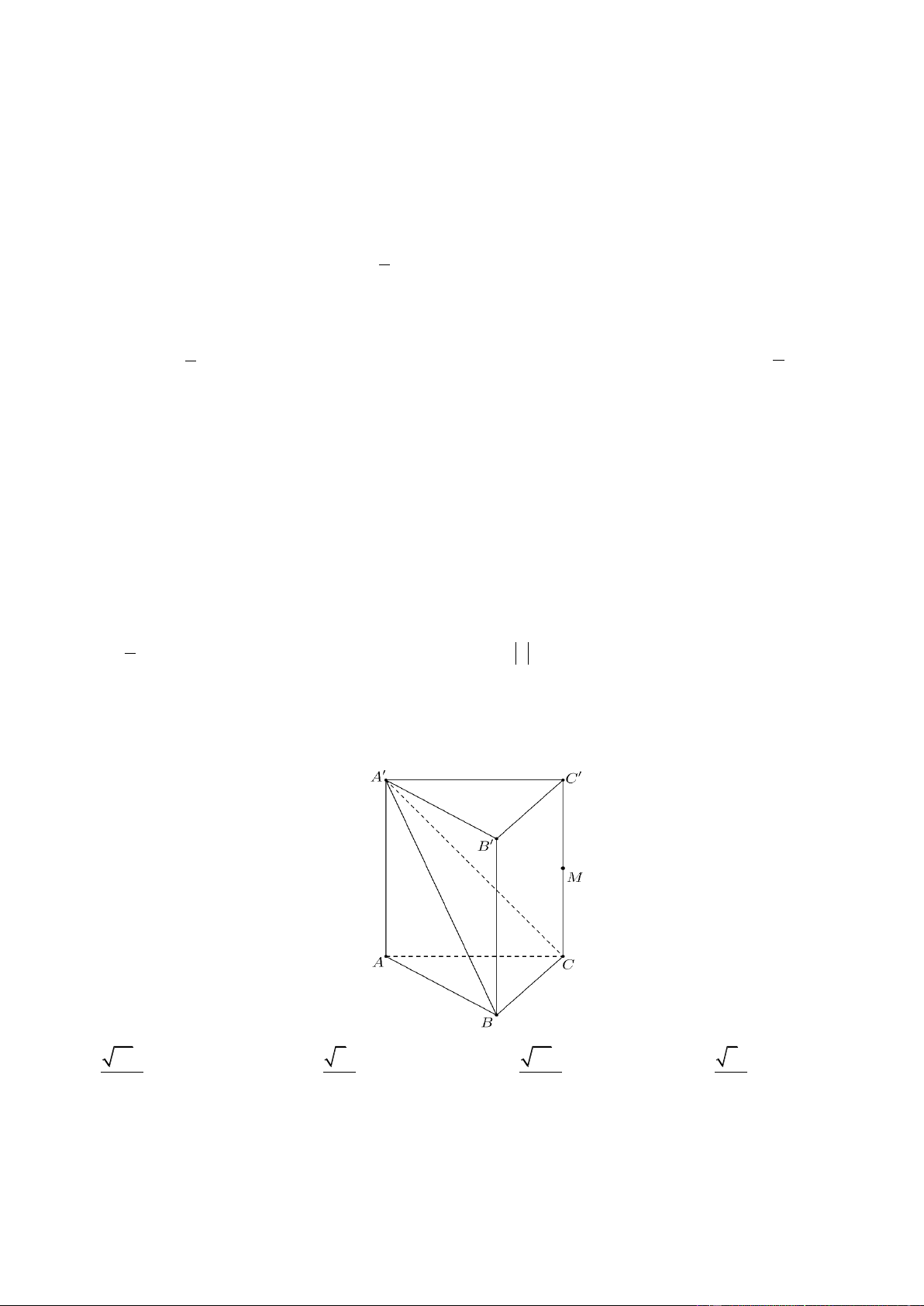
Câu 32. Cho hình lăng trụ AB . C A B C
có đáy ABC là tam giác đều cạnh a , tam giác A B
C đều nằm trong
mặt phẳng vuông góc với ABC . M là trung điểm cạnh CC . Tính cosin góc giữa hai đường thẳng AA và BM . 2 22 33 11 22 A. cos . B. cos . C. cos . D. cos . 11 11 11 11 1 1
Câu 33. Cho hàm số f x liên tục trên đoạn [0; 1] và có 3 2 f
xdx 5 . Tính
f x dx . 0 0 A. 1. B.2. C.1. D. 2 .
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua điểm M 1;1;
1 và vuông góc với đường thẳng x 1 y 2 z 1 :
có phương trình là 2 2 1
A. 2x 2 y z 3 0 .
B. x 2 y z 0 .
C. 2x 2 y z 3 0 .
D. x 2 y z 2 0 . 3 ( 3 i)
Câu 35. Cho số phức z thỏa z
. Môđun của số phức z iz là: i 1 A. 2 2 . B. 4 2 . C. 0. D. 16.
Câu 36. Cho lăng trụ đứng AB . C A B C
có đáy ABC là tam giác đều cạnh a và AA 2a . Gọi M là trung
điểm của CC (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng A B C bằng a 5 2 5a 2 57a 57a A. 5 . B. 5 . C. 19 . D. 19 .
Câu 37. Một hộp chứa 30 quả cầu gồm 10 quả cầu đỏ được đánh số từ 1 đến 10 và 20 quả màu xanh được đánh
số từ 1 đến 20 . Lấy ngẫu nhiên một quả cầu từ hộp đó. Tính xác suất sao cho quả được chọn là quả màu xanh hoặc ghi số lẻ. 2 7 5 3 A. . B. . C. . D. . 3 8 6 4
Câu 38. Trong không gian Oxyz , cho ba điểm A1;0
;1 , B 1;1;0 và C 3; 4;
1 . Đường thẳng đi qua A và
song song với BC có phương trình là x 1 y z 1 x 1 y z 1 x 1 y z 1 x 1 y z 1 A. 4 5 1 . B. 2 3 1 . C. 2 3 1 . D. 4 5 1 . Trang28
Câu 39. Có bao nhiêu số nguyên x thỏa mãn x x 1 25 4.5
125 3log x 0 ? 2 A. 7 . B. 8 . C. 9 . D.10 .
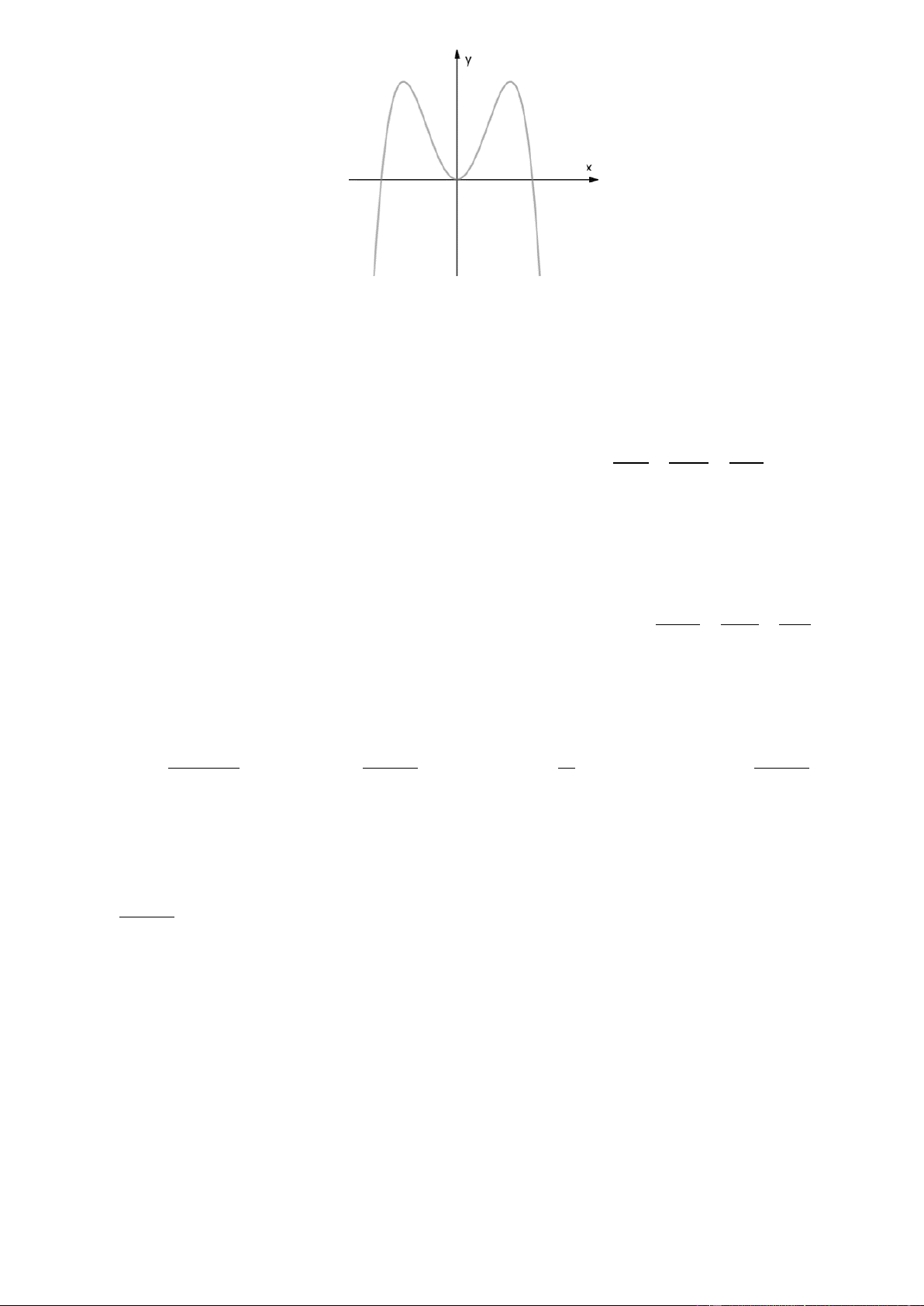
Câu 40. Cho hàm số y f x liên tục trên và có đồ thị là đường cong trơn (không bị gãy khúc), hình vẽ bên.
Gọi hàm g x f f x.
Hỏi phương trình g x 0 có bao nhiêu nghiệm phân biệt? A. 10. B. 12. C. 8. D. 14.
Câu 41. Cho hàm số y f x có đạo hàm là f x 2 ' 3
x 2022, x
và f
1 2021 . Biết F x là
mô ̣t nguyên hàm của f x thỏa mãn F 1 0 . Tính F 2
kết quả là. A. F 2 0 . B. F 2 2022 . C. F 2 4048 . D. F 2 4040 . a
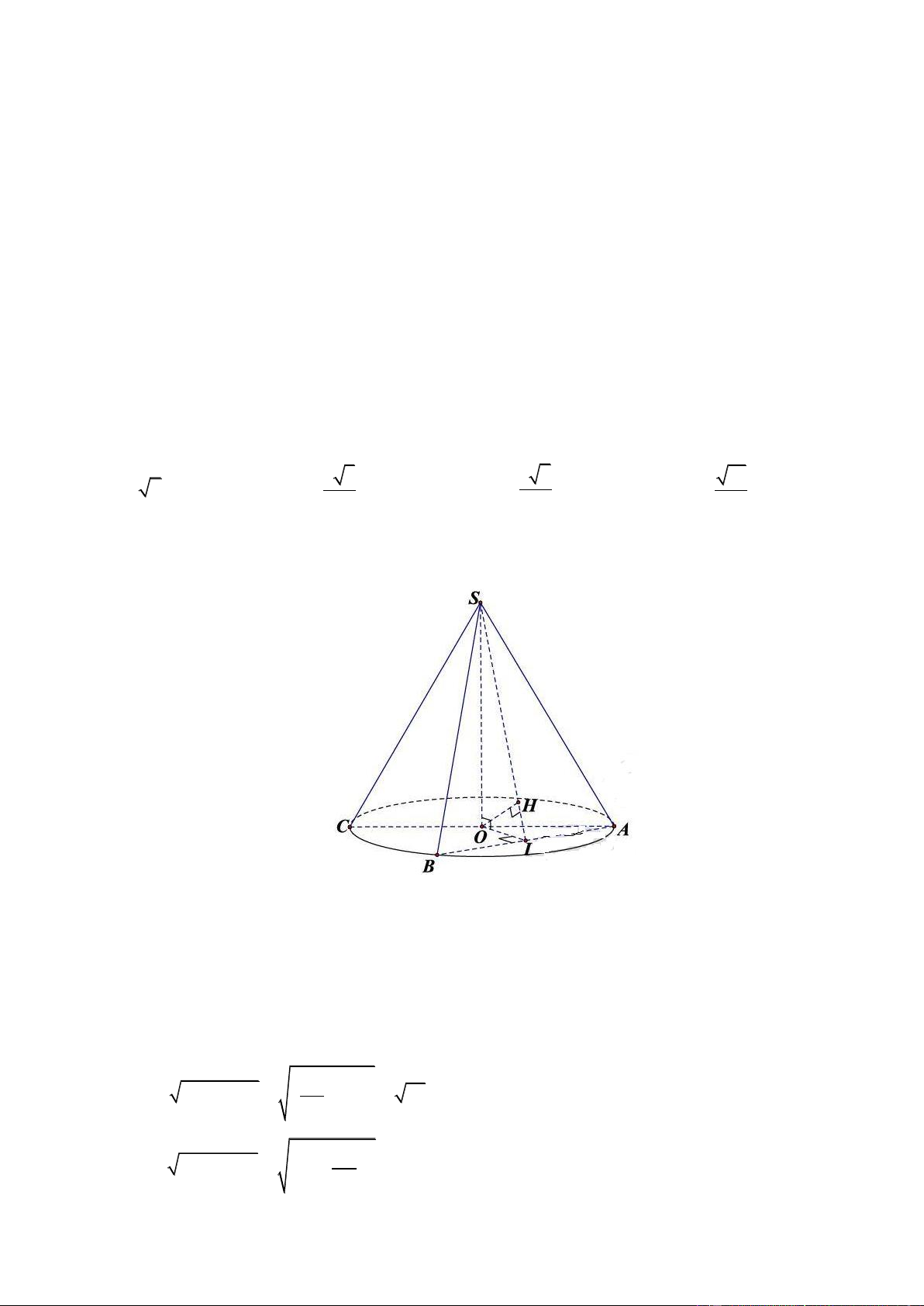
Câu 42. Cho hình chóp S.ABC có đáy ABC là tam giác đều và độ dài đường cao của ABC bằng 3 . Biết 4
mặt phẳng SAB và mặt phẳng SAC cùng vuông góc với mặt đáy. Cho SA a 3 , Tính thể tích khối chóp S.ABC . a 3 a 3 a 3 3a A. B. C. D. 4 2 4 4
Câu 43. Gọi S là tổng các số thực m để phương trình 2
z 2z 1 m 0 có nghiệm phức thỏa mãn z 2. Tính S.
A. S 6. B. S 10. C. S 3. D. S 7.
Câu 44. Xét hai số phức
. Giá trị lớn nhất của 1
z ; z2 thỏa mãn 1 z 2; z2 5 và 1 z z2 3 1 z 2z2 3i bằng A. 3 2 3 . B. 3 3 2 . C. 3 26 . D. 26 3 .
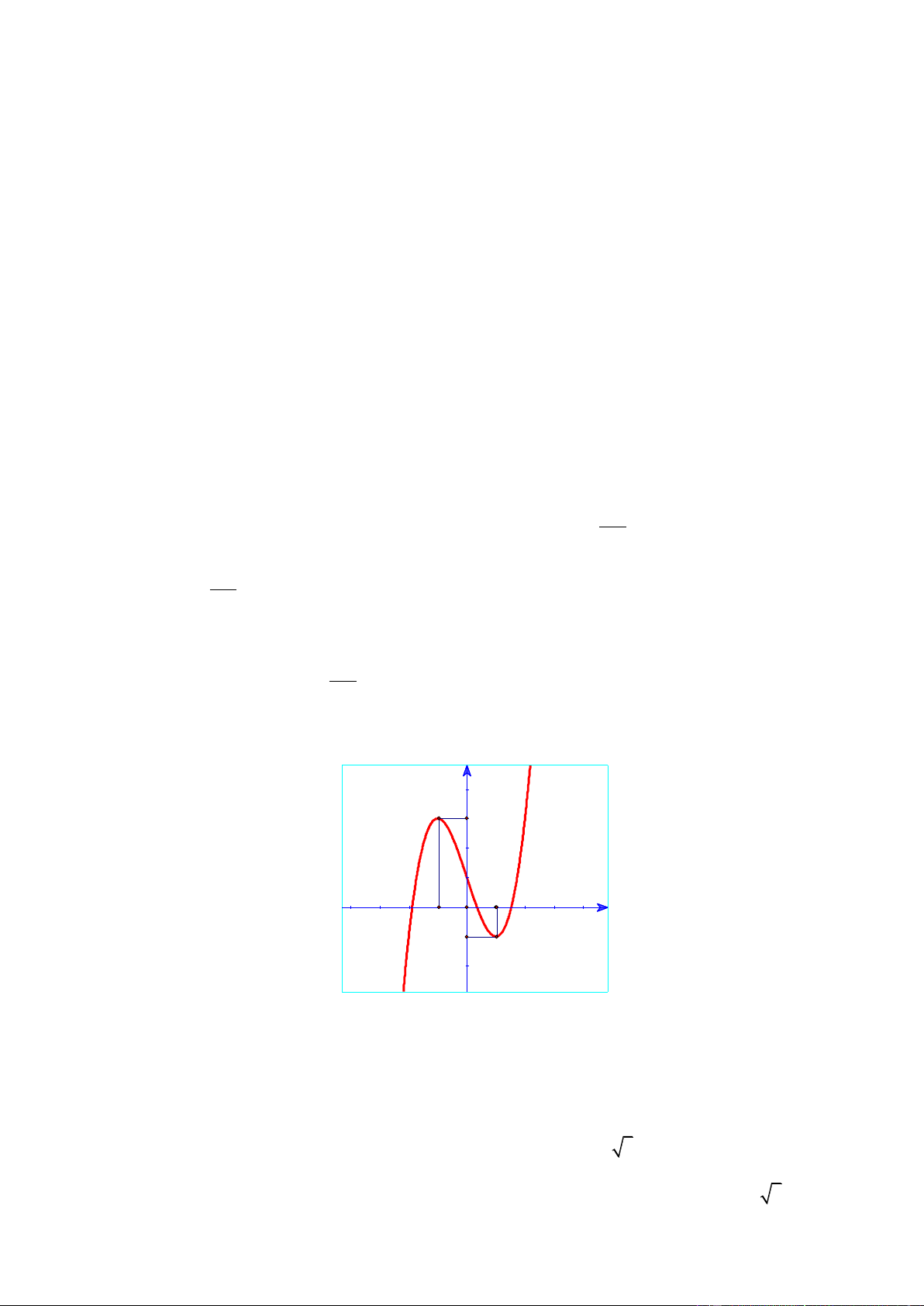
Câu 45. Cho hàm số y f (x) là hàm số đa thức bậc bốn và có đồ thị như hình vẽ. Trang29
Hình phẳng giới hạn bởi đồ thị hai hàm số y f (x); y f '(x) có diện tích bằng 127 127 107 13 A. . B. . C. . D. . 40 10 5 5
Câu 46. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x y z 9 0, đường thẳng x 3 y 3 z d :
và điểm A1;2; 1
. Viết phương trình đường thẳng đi qua điểm A cắt d và song song 1 3 2
với mặt phẳng P . x 1 y 2 z 1 x 1 y 2 z 1 A. . B. 1 2 1 1 2 . 1 x 1 y 2 z 1 x 1 y 2 z 1 C. . D. 1 2 1 1 2 1 .
Câu 47. Cho một hình nón có bán kính đáy bằng 2a . Mặt phẳng P đi qua đỉnh S của hình nón, cắt đường a 2
tròn đáy tại A và B sao cho AB 2a 3 , khoảng cách từ tâm đường tròn đáy đến mặt phẳng P bằng . 2
Thể tích khối nón đã cho bằng 3 8 a 3 4 a 3 2 a 3 a A. . B. . C. . D. . 3 3 3 3
Câu 48. Có bao nhiêu số nguyên x sao cho ứng với mỗi x , tồn tại ít nhất bốn số nguyên y 1 0;10 thỏa mãn 2
5x y 4yx 26 ? A. 4 . B. 5 . C. 6 . D. 7 .
Câu 49. Trong không gian Oxyz , cho mặt cầu S x y z 2 2 2 : 2
3 . Có tất cả bao nhiêu điểm
Aa;b;c ( a,b, c là các số nguyên) thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp tuyến của S đi qua A
và hai tiếp tuyến đó vuông góc với nhau? A. 8 . B. 16 . C. 12 . D. 4 . 2 2
Câu 50. Cho hàm số y f (x) có đạo hàm f x x
1 x 2x với mọi x . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g x f 2
x 8x m có 5 điểm cực trị? A. 15. B. 16. C. 17. D. 18.
LỜI GIẢI CHI TIẾT
Câu 1. Cho số phức z 5 4i . Môđun của số phức z là A. 3. B. 41 . C. 1. D. 9. Lờigiải
z i z 2 2 5 4 5 4 41
Vậy chọn đáp án B. 2 2
Câu 2. Mặt cầu S x y 2 : 1 2
z 9 có tâm là: A. I 1 ; 2 ;0. B. I 1 ;2;0.
C. I 1; 2;0. D. I 1; 2 ;0. Trang30 Lờigiải
Phương trình mặt cầu 2 2 2
S có dạng x a
y b z c 2
R có tâm I ; a ; b c , bán kính . R
Lựa chọn đáp án D. 2x 1
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số y x 2
A. Điểm M 1 ; 1 .
B. Điểm N 1; 3 .
C. Điểm P 1;3 .
D. Điểm Q 2;0 . Lờigiải Chọn B
Câu 4. Cho khối cầu có bán kính r 2 . Thể tích của khối cầu đã cho bằng 32 8 A. 16 . B. . C. 32 . D. . 3 3 Lờigiải Chọn B 4 4 32
Thể tích của khối cầu đã cho 3 3 : V r .2 . 3 3 3
Câu 5. Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số 2022 y x ? 2023 x 2023 x 2023 x A. 1. B. . C. 2021 y 2022x . D. 1. 2023 2023 2023 Lờigiải 2023 x Ta có: 2022 x dx C, C
là hằng số. Nên các phương án A,B,D đều là nguyên hàm của hàm số 2022 y x . 2023
Câu 6. Cho hàm số f x , bảng xét dấu của f x như sau:
Số điểm cực trị của hàm số đã cho là A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn B x 1
Ta có f x 0 x 0 x 1
Từ bảng biến thiên ta thấy f x đổi dấu khi x qua nghiệm 1và nghiệm 1; không đổi dấu khi x qua nghiệm 0
nên hàm số có hai điểm cực trị.
Câu 7. Tập nghiệm của bất phương trình x 1 5 7 là
A. 1 log 7; .
B. 1 log 7; . C. ; 1 log 7 . D. ;1 log 7 . 5 5 5 5 Lời giải Trang31 Chọn A x 1
5 7 x 1 log 7 x 1 log 7 . 5 5
Vậy Tập nghiệm của bất phương trình là 1 log 7; . 5
Câu 8. Cho khối chóp có diện tích đáy 2
B 6a và chiều cao h 2a . Thể tích khối chóp đã cho bằng: A. 3 2a . B. 3 4a . C. 3 6a . D. 3 12a . Lờigiải Chọn B 1 1 2 3 V . B h
6a .2a 4a 3 3
Câu 9. Tập xác định của hàm số 3 y x là A. . B. 0; . C. \ 0 . D. 0; . Lời giải Chọn B
Câu 10. Nghiệm của phương trình log 2x 1 2 là: 3 9 7 A. x 3. B. x . C. x 5. D. x . 2 2 Lờigiải ChọnC 1
Điều kiện: 2x 1 0 x 2 1 1 x x Ta có log 2x 1 2 2 x 5 . 3 2 2 2x 1 3 x 5
Vậy phương trình có nghiệm x 5. 3 3 3 Câu 11. Biết f xdx 4 và g
xdx 1. Khi đó: f
xgx dx bằng: 2 2 2 A. 3 . B. 3 . C. 4 . D. 5 . Lờigiải ChọnB 3 3 3 Ta có f
x gxdx f
xdx g
xdx 41 3 2 2 2
Câu 12. Cho hai số phức z 1 2i và z 2 3i . Phần ảo của số phức w 3z 2z là 1 2 1 2 A. 12. B. 11. C. 1. D.12i . Lờigiải
w 3z 2z 3 1 2i 2 2 3i 1
12i . Vậy phần ảo của số phức w là 12 . 1 2
Vậy chọn đáp án A. Trang32
Câu 13. Trong không gian Oxyz , cho mặt phẳng : 2x 4y z 3 0 . Véctơ nào sau đây là véc tơ pháp tuyến của ? A. n 2; 4; 1 .
B. n 2; 4;1 . C. n 2 ;4;1 .
D. n 2; 4;1 . 1 3 2 1 Lời giải Chọn A
Mặt phẳng : 2x 4y z 3 0 có một véctơ pháp tuyến là n 2;4; 1 .
Câu 14. Trong không gian với hệ trục tọa độ Oxyz , cho ba vecto a 1; 2;3;b 2; 2; 1 ; c 4;0; 4 . Tọa độ của
vecto d a b 2c là
A. d 7;0; 4 B. d 7 ;0; 4 C. d 7;0; 4
D. d 7;0; 4 Lờigiải ChọnC
Ta có: d a b 2c 1 2 2.4; 2 2 2.0;3 1 2.( 4) 7;0; 4 .
Câu 15. Trên mặt phẳng tọa độ, biết M 3 ;
1 là điểm biểu diễn số phức z . Phần thực của z bằng A.1. B. 3 . C. 1. D. 3 . Lờigiải ChọnB Điểm M 3 ;
1 là điểm biểu diễn số phức z , suy ra z 3 i .
Vậy phần thực của z bằng 3 .
Câu 16. Cho hàm số y f (x) có lim f (x) 1và lim f ( ) x 1
. Khẳng định nào sau đây là khẳng định đúng? x x
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x 1 và x 1 .
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y 1và y 1. Lời giải Chọn D
Dựa vào định nghĩa đường tiệm cận ngang của đồ thị hàm số ta chọn đáp án D. 3
Câu 17. Với a là số thực dương tùy ý, log bằng: 3 a 1
A. 1 log a
B. 3 log a C. D. 1 log a 3 3 log a 3 3 Lờigiải ChọnA 3 Ta có log
log 3 log a 1 log a . 3 3 3 a 3
Câu 18. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới đây? 4 2 4 2 3 2
A. y x 2x .
B. y x 2x .
C. y x 3x . D. 3 2
y x 3x . Trang33 Lời giải Chọn A
Từ hình dạng của đồ thị ta loại phương án C và D.
Nhận thấy lim f (x) suy ra hệ số của 4
x âm nên chọn phương án A. x x 1 y 2 z 1
Câu 19. Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d : ? 1 3 3 A. P 1; 2 ;1 .
B. Q 1; 2; 1 . C. N 1 ;3;2. D. P 1;2 ;1 . Lờigiải ChọnA 11 2 2 11
Thay tọa độ các điểm vào phương trình đường thẳng ta thấy điểm P 1; 2 ;1 thỏa 0 . 1 3 3 Vậy điểm P 1; 2
;1 thuộc đường thẳng yêu cầu.
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. A A A . D. A n k !(n . B. k)! n (k . C. n)! n k ! n (n . k)! Lời giải Chọn D n k ! A n (n k)!
Câu 21. Cho khối lăng trụ có diện tích đáy B 3 và chiều cao h 2 . Thể tích của khối lăng trụ đã cho bằng A. 1. B. 3 . C. 2 . D. 6 . Lờigiải Chọn D
Thể tích khối lăng trụ là V . B h 3.2 6 .
Câu 22. Tính đạo hàm của hàm số 2 1 2 x y . A. 2 x 1 y 2 ln 4 . B. x 1 y 4 ln 4 . C. 2 2 . x y ln 2 . D. 2 2 x y ln 2 . Lời giải Chọn C Trang34 u
Áp dụng công thức đạo hàm . u a u a .ln a
Câu 23. Ta có Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ; 1 . B. 0; 1 . C. 1 ;1 . D. 1 ;0 Lời giải Chọn D.
Hàm số đã cho đồng biến trên khoảng 1 ;0 và 1; 2 x 1
2x 1 2 2 2 1 .2 .ln 2 2 . x y x ln 2 .
Câu 24. Cho hình trụ có bán kính đáy r 5 và độ dài đường sinh l 3 . Diện tích xung quanh của hình trụ đã cho bằng A. 15 B. 25 . C. 30 . D. 75 . Lờigiải Chọn C
Áp dụng công thức diện tích xung quanh hình trụ ta được: S 2 rl 30 . xq 6 6 Câu 25. Cho
f (x)dx 12
. Tính I 2022 f (x) . dx 0 0
A. I 5
B. I 12
C. I 24264 D. I 2022 Lờigiải ChọnC 6 6
Ta có: I 2022 f (x)dx 2022 f (x)dx 2022.12 24264 0 0
Câu 26. Cho cấp số cộng u
với u 9 và công sai d 2 . Giá trị của u bằng n 1 2 9 A. 11. B. . C. 18 . D. 7 . 2 Lời giải Chọn A
Ta có: u u d 9 2 11 . 2 1
Câu 27. Tính x sin 2xdx . 2 x 2 x cos 2x 2 x cos 2x A.
sin x C . B.
cos 2x C . C. 2 x C . D. C . 2 2 2 2 2 Trang35 Lờigiải 2 x cos 2x
Ta có x sin 2xdx = d x x sin 2 d x x C . 2 2
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ. y 2 -1 O x 1 -2
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 2 . C. 1. D. 1 . Lời giải Chọn A 2 x 3
Câu 29. Tìm giá trị nhỏ nhất của hàm số y
trên đoạn 2; 4 . x 1 19 A. min y 3 B. min y
C. min y 6 D. min y 2 2;4 2;4 3 2; 4 2;4 Lời giải Chọn C
Tập xác định: D \ 1 2 x 3 Hàm số y
xác định và liên tục trên đoạn 2; 4 x 1 2 x 2x 3 Ta có 2 y
y x x x hoặc x 1 (loại) x ; 0 2 3 0 3 2 1 Suy ra y y y 19 2 7; 3 6; 4
. Vậy min y 6 tại x 3. 3 2;4
Câu 30. Đồ thị hàm số 3 2
y f (x) ax bx cx d . Hình nào trong 4 hình dưới đây mà hàm số luôn đồng biến trên ? Trang36 y 4 3 y 1 2 O 1 x 1 -1 O x -1 1 A. Hình 1. B. Hình 2. y y 3 -1 O 1 x 1 -1 O x 1 -2 -1 -4 C. Hình 3. D. Hình 4.
Câu 31. Với a, b là các số thực dương tùy ý thỏa mãn log a 2 log b 2 , mệnh đề nào dưới đây đúng? 3 9 A. 2 a 9b .
B. a 9b .
C. a 6b . D. 2 a 9b . Lời giải Chọn B a
Ta có: log a 2 log b 2 log a log b 2 log
2 a 9b. 3 9 3 3 3 b
Câu 32. Cho hình lăng trụ AB . C A B C
có đáy ABC là tam giác đều cạnh a , tam giác A B
C đều nằm trong
mặt phẳng vuông góc với ABC . M là trung điểm cạnh CC . Tính cosin góc giữa hai đường thẳng AA và BM . 2 22 33 11 22 A. cos . B. cos . C. cos . D. cos . 11 11 11 11 Lờigiải Trang37 A' C' B' M A C H B a 3
Ta có: AH A H
và AH BC, AH BC BC AA H
BC AA hay 2
BC BB . Do đó: BCC B
là hình chữ nhật. a 3 a 6 2 a .6 22
Khi đó: CC AA . 2 2 BM a a . 2 2 16 4
2 3a Xét: AA .
BM AA.BC CM 0 AA.CM . 4 2 3a 4
Suy ra cos AA , BM 33 . a 6 a 22 11 . 2 4 1 1
Câu 33. Cho hàm số f x liên tục trên đoạn [0; 1] và có 3 2 f
xdx 5 . Tính
f x dx . 0 0 A. 1. B.2. C.1. D. 2 . Lờigiải 1 1 1 1 1 Ta có: 3 2 f
xdx 5 3dx 2 f
xdx 5 3x 2 f
xdx 5 0 0 0 0 0 1 1 2
f x dx 5 3 2 f x dx 1 0 0 Chọn A
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua điểm M 1;1;
1 và vuông góc với đường thẳng x 1 y 2 z 1 :
có phương trình là 2 2 1
A. 2x 2 y z 3 0 .
B. x 2 y z 0 .
C. 2x 2 y z 3 0 .
D. x 2 y z 2 0 . Trang38 3 ( 3 i)
Câu 35. Cho số phức z thỏa z
. Môđun của số phức z iz là: i 1 A. 2 2 . B. 4 2 . C. 0. D. 16. Lờigiải 3 ( 3 i) z
4 4i z iz 0 i 1
Vậy chọn đáp án C.
Câu 36. Cho lăng trụ đứng AB . C A B C
có đáy ABC là tam giác đều cạnh a và AA 2a . Gọi M là trung
điểm của CC (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng A B C bằng a 5 2 5a 2 57a 57a A. 5 . B. 5 . C. 19 . D. 19 . Lờigiải Chọn D Gọi H , K
lần lượt là hình chiếu của A lên BC và A H .
d M ABC 1
d C A BC 1
d A A BC 1 , , , AK Ta có 2 2 2 . a 3 AH.AA 2a 57 AH AK 2 2 Mà
2 ; AA 2a nên 19 AH AA .
d M A B C a 57 ; Vậy 19 . Trang39
Câu 37. Một hộp chứa 30 quả cầu gồm 10 quả cầu đỏ được đánh số từ 1 đến 10 và 20 quả màu xanh được đánh
số từ 1 đến 20 . Lấy ngẫu nhiên một quả cầu từ hộp đó. Tính xác suất sao cho quả được chọn là quả màu xanh hoặc ghi số lẻ. 2 7 5 3 A. . B. . C. . D. . 3 8 6 4 Lời giải Chọn C
Số cách lấy ngẫu nhiên một quả cầu từ hộp: 1 C 30 (cách). 30
Có 5 cách chọn được quả cầu ghi số lẻ và có 20 cách để chọn được quả cầu màu xanh. 5 20 5
Vậy xác suất cần tìm: P . 30 6
Câu 38. Trong không gian Oxyz , cho ba điểm A1;0
;1 , B 1;1;0 và C 3; 4;
1 . Đường thẳng đi qua A và
song song với BC có phương trình là x 1 y z 1 x 1 y z 1 x 1 y z 1 x 1 y z 1 A. 4 5 1 . B. 2 3 1 . C. 2 3 1 . D. 4 5 1 . Lờigiải ChọnC
Đường thẳng d đi qua A và song song với BC nhận BC 2;3;
1 làm một véc tơ chỉ phương. x 1 y z 1
Phương trình của đường thẳng d : 2 3 1 .
Câu 39. Có bao nhiêu số nguyên x thỏa mãn x x 1 25 4.5
125 3log x 0 ? 2 A. 7 . B. 8 . C. 9 . D.10 . Lờigiải ChọnA x 0 Điều kiện
0 x 8 3 log x 0 2 Ta có x x 1 25 4.5
125 3log x 0 2 x x 1 25 4.5 125 0 1 3 log x 0 2 2 Giải 1 : x x 1 25 4.5 125 0 x x 1 25 4.5 125 0 2 5 x 20.5x 125 0 . t 0 t 0
Đặt 5x t 0 ta được t 5 t 25 . 2 t
20t 125 0 t 25 Trang40
Suy ra 5x 25 x 2
Kết hợp điều kiện 2 x 8
Do x là số nguyên x 2;3; 4;5;6;7; 8
Giải 2 : 3 log x 0 x 8 (thỏa điều kiện) 2
Vậy có 7 giá trị x cần tìm
Câu 40. Cho hàm số y f x liên tục trên và có đồ thị là đường cong trơn (không bị gãy khúc), hình vẽ bên.
Gọi hàm g x f f x.
Hỏi phương trình g x 0 có bao nhiêu nghiệm phân biệt? A. 10. B. 12. C. 8. D. 14. Lờigiải
g x f f x
g (x) f (x). f f x . g (
x) 0 f (x). f f x 0 x x 2 ;1 1 x 0
x x 1;2 2
f (x) 0 x 2 . f f
f x x 2
;1 x x 2 1
x 0 3
f (x) 0 x 2 ;0; 2
f (x) x 1;2 x x ;x ;x ,x x x 0 2 x 2 4 5 6 3 4 5 6
f (x) 2 x
x ;x ;x ,x x x x x x 7 8 9 4 7 8 5 6 9
Kết luận phương trình g x 0 có 12 nghiệm phân biệt. Trang41
Câu 41. Cho hàm số y f x có đạo hàm là f x 2 ' 3
x 2022, x
và f
1 2021 . Biết F x là
mô ̣t nguyên hàm của f x thỏa mãn F 1 0 . Tính F 2
kết quả là. A. F 2 0 . B. F 2 2022 . C. F 2 4048 . D. F 2 4040 . Lờigiải Chọn D
Ta có: f x f
xdx 2 x 3 ' 3
2022 dx x 2022x C Với f C
C f x 3 1 2021 1 2022 2021 0
x 2022x x
Do đó: F x f
xdx x x 4 3 2 2022 dx 1011x C 4 F x 4 x 2 1011x C 4 Mà F 1 0 C 0 F x 4 x 2 1011x 4 F 2 4040 a
Câu 42. Cho hình chóp S.ABC có đáy ABC là tam giác đều và độ dài đường cao của ABC bằng 3 . Biết 4
mặt phẳng SAB và mặt phẳng SAC cùng vuông góc với mặt đáy. Cho SA a 3 , Tính thể tích khối chóp S.ABC . a 3 a 3 a 3 3a A. B. C. D. 4 2 4 4 Lờigiải Chọn C
Ta có SA là đường cao hình chóp 2 a a 3
Tam giác ABC đều có độ dài đường cao bằng
3 nên cạnh tam giác bằng a do đó S ABC 4 4 2 3 1 a 3 a
Vậy thể tích cần tìm là: V . .a 3 . S. ABC 3 4 4 Trang42
Câu 43. Gọi S là tổng các số thực m để phương trình 2
z 2z 1 m 0 có nghiệm phức thỏa mãn z 2. Tính S.
A. S 6. B. S 10. C. S 3. D. S 7. Lờigiải ChọnD
Ta có: z z m z 2 2 2 1 0 1 m 1 m 1
+) Với m 0 thì
1 z 1 m . Do z 2 1 m 2 (thỏa mãn). m 9
+) Với m 0 thì
1 z 1 i m.
Do z 2 1 i m 2 1 m 4 m 3 (thỏa mãn).
Vậy S 1 9 3 7 .
Câu 44. Xét hai số phức
. Giá trị lớn nhất của 1
z ; z2 thỏa mãn 1 z 2; z2 5 và 1 z z2 3 1 z 2z2 3i bằng A. 3 2 3 . B. 3 3 2 . C. 3 26 . D. 26 3 . Lời giải Chọn B Cách 1:
Đặt z a bi, z c di (với a,b, c, d ) 1 2 Theo bài ra ta có: 2 2 2 2 z
2 a b 2; z 5 c d 5 1 2
z z 3 a c2 b d 2 2 2 2 2
9 a b c d 2 ac bd 9 ac bd 1 1 2
z 2z a 2c2 b 2d 2 2 2
a b 4 2 2 c d
4 ac bd 18 3 2 1 2
Theo tính chất z z ' z z ' ta có: 1 z 2z2 3i 1 z 2z2 3i 3 2 3 Cách 2: y Q 3 O x M N P R Trang43
Gọi M là điểm biểu diễn cho số phức z , M thuộc đường tròn tâm O bán kính 2 OM 2 1
Gọi N là điểm biểu diễn cho số phức z , N thuộc đường tròn tâm O bán kính 5 ON 5 2
Suy ra NM OM ON là điểm biểu diễn cho z z MN z z 3 1 2 1 2
Gọi P là điểm biểu diễn cho số phức 2z , P thuộc đường tròn tâm O bán kính 2 5 OP 2 5 2
Gọi Q là điểm biểu diễn cho số phức 3i , Q0;3 OQ 3
Dựng hình bình hành OMRP ta có OR OM OP R là điểm biểu diễn cho số phức z 2z 1 2 2 2 2
OM ON MN 2 5 9 1 Ta có: cos MON 2.OM .ON 2. 2. 5 10 2 2 2 2 2
OR OP PR 2.O . P P .
R cos OPR OP OM 2.O . P OM .cos MON 1
OR 20 2 2.2 5. 2. 3 2 10 T 1 z 2 2 z 3i OR OQ QR QR
T đạt giá trị lớn nhất khi QR lớn nhất 0
QOR 180 QR OQ OR 3 3 2
Vậy T đạt giá trị lớn nhất bằng 3 3 2 .
Câu 45. Cho hàm số y f (x) là hàm số đa thức bậc bốn và có đồ thị như hình vẽ.
Hình phẳng giới hạn bởi đồ thị hai hàm số y f (x); y f '(x) có diện tích bằng 127 127 107 13 A. . B. . C. . D. . 40 10 5 5 Lờigiải Hàm số đã cho có dạng 4 3 2 3 2
f (x) ax bx cx dx e f '(x) 4ax 3bx 2cx d .
Từ giả thiết đồ thị hàm số đã cho ta thấy đồ thị hàm số đi qua các điểm (2;0) , (1;1) , (0;1) , (1;0) và có hai
điểm cực tiểu là (1;0) , (2; 0) nên ta có hệ Trang44 e 1 1 f (0) 1 e 1 a 4 f ( 2 ) 0
a b c d 1 1 f (1)
0 16a 8b 4c 2d 1 b . 2 f '( 2 ) 0 3
2a 12b 4c d 0 3 '(1) 0 4 3 2 0 c f a b c d 4 d 1 Do đó 1 1 3 3 3 4 3 2 3 2 f (x) x x
x x 1 f '(x) x x x 1. 4 2 4 2 2
Xét phương trình hoành độ giao điểm f (x) f '(x). x 2 1 1 9 1 x 1 4 3 2
x x x x 2 0 . 4 2 4 2 x 1 x 4 4
Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y f (x); y f '(x) là S
f (x) f ( x) dx 2 1 1 9 1 Vì biểu thức 4 3 2
f (x) f (
x) x x x x 2 không đổi đấu trên các khoảng (2;1) , (1;1) , (1;4) 4 2 4 2 nên ta có 1
S f x f x 1
dx f x f x 4
dx f x f x 107 ( ) '( ) ( ) '( ) ( ) '( ) dx (dvdt). 2 1 1 5
Câu 46. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x y z 9 0, đường thẳng x 3 y 3 z d :
và điểm A1;2; 1
. Viết phương trình đường thẳng đi qua điểm A cắt d và song song 1 3 2
với mặt phẳng P . x 1 y 2 z 1 x 1 y 2 z 1 A. . B. 1 2 1 1 2 . 1 x 1 y 2 z 1 x 1 y 2 z 1 C. . D. 1 2 1 1 2 1 . Lờigiải ChọnA Cách 1:
Ta có: P có vectơ pháp tuyến là: n 1;1; 1 .
d có vectơ chỉ phương là: u 1;3; 2 và B 3;3;0 d .
có vectơ chỉ phương là: u a; ; b c và A1;2; 1 (trong đó 2 2 2 a b c 0 ). AB 2;1 ;1 ; d
P u .n 0 a b c 0 c a b u a; ; b a b .
Do d cắt A ,
B u.u 0 2a b 0 b 2 . a Trang45 x y z
Chọn a b c u 1 2 1 1 2 1 1; 2;1 : . 1 2 1 x 1 y 2 z 1 Kết luận: : . 1 2 1 Cách 2:
Ta có: P có vectơ pháp tuyến là: n 1;1; 1 .
có vectơ chỉ phương là: u a; ; b c và A1;2; 1 (trong đó 2 2 2 a b c 0 ).
Do song song với mặt phẳng P u .n 0 .
Nhận xét đáp án A: u .n 0 .
Nhận xét đáp án B: u .n 4 0 loại đáp án B.
đáp án C: u .n 2 0 loại đáp án C.
đáp án D: u .n 2 0 loại đáp án D.
Kết luận: Chọn đáp án A.
Câu 47. Cho một hình nón có bán kính đáy bằng 2a . Mặt phẳng P đi qua đỉnh S của hình nón, cắt đường a 2
tròn đáy tại A và B sao cho AB 2a 3 , khoảng cách từ tâm đường tròn đáy đến mặt phẳng P bằng . 2
Thể tích khối nón đã cho bằng 3 8 a 3 4 a 3 2 a 3 a A. . B. . C. . D. . 3 3 3 3 Lờigiải Chọn B SO AB
Gọi C là trung điểm của AB , O là tâm của đáy. Khi đó
SOC AB . Gọi H là hình chiếu của O C AB 2
O lên SC thì OH SAB nên OH a . 2 1 1 1 1 OB 2 ,
a BC a 3 OC a . Xét tam giác vuông SOC : SO a . 2 2 2 2 SO OH OC a Trang46 1 4 a
Vậy thể tích khối nón giới hạn bởi hình nón đã cho là .2a 3 2 .a . 3 3
Câu 48. Có bao nhiêu số nguyên x sao cho ứng với mỗi x , tồn tại ít nhất bốn số nguyên y 1 0;10 thỏa mãn 2
5x y 4yx 26 ? A. 4 . B. 5 . C. 6 . D. 7 . Lời giải Chọn B. Ta có: 2
5x y 4yx 26 2
5x y 4yx 26 0 y x 2 x 4 26 5 0 5y 5y y y 2 4 1 1 . 26. 5x 0 5 4x 5 y y
Xét hàm số f y 2 4 1 1 . 26. 5x với y 1 0;10 5 4x 5 y y f y 4 1 4 1 2 ' . .ln 26. .ln 0
. Do đó hàm số f y luôn đồng biến 5 4x 5 5 5
Để f y 0có ít nhất bốn số nguyên y 1 0;10 thì 2 f 6 0 hay x 6 6 5 4 x 26 2 x 6 5 26 (do 6 4 x 0 ) 2 2
x 6 log 26 x 6 log 26 2 ,83 x 2,83 5 5
Do x là số nguyên nên x 2 ; 1 ; 0
Câu 49. Trong không gian Oxyz , cho mặt cầu S x y z 2 2 2 : 2
3 . Có tất cả bao nhiêu điểm
Aa;b;c ( a,b, c là các số nguyên) thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp tuyến của S đi qua A
và hai tiếp tuyến đó vuông góc với nhau? A. 8 . B. 16 . C. 12 . D. 4 . Lờigiải ChọnC
Mặt cầu S có tâm I 0;0; 2 và bán kính R 3 ; AOxy Aa;b;0 .
* Xét trường hợp AS , ta có 2 2
a b 1 . Lúc này các tiếp tuyến của S thuộc tiếp diện của S tại A nên
có vô số các tiếp tuyến vuông góc nhau.
a 0 a 0 a 1 a 1
Trường hợp này ta có 4 cặp giá trị của a;b là ; ; ; . b 1 b 1 b 0 b 0 Trang47
* Xét trường hợp A ở ngoài S . Khi đó, các tiếp tuyến của S đi qua A thuộc mặt nón đỉnh A . Nên các tiếp
tuyến này chỉ có thể vuông góc với nhau tại A .
Điều kiện để có ít nhất 2 tiếp tuyến vuông góc là góc ở đỉnh của mặt nón lớn hơn hoặc bằng 90 .
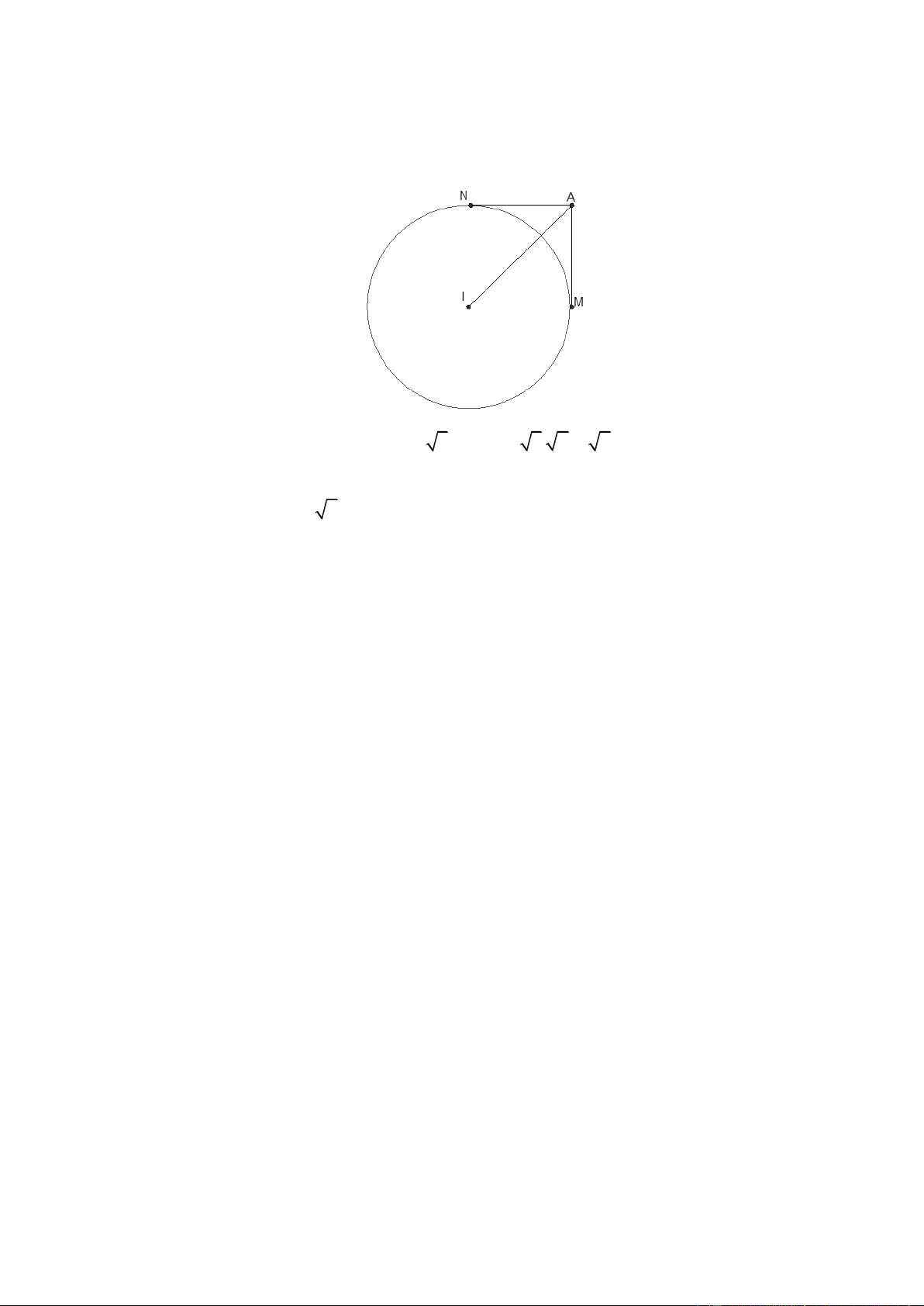
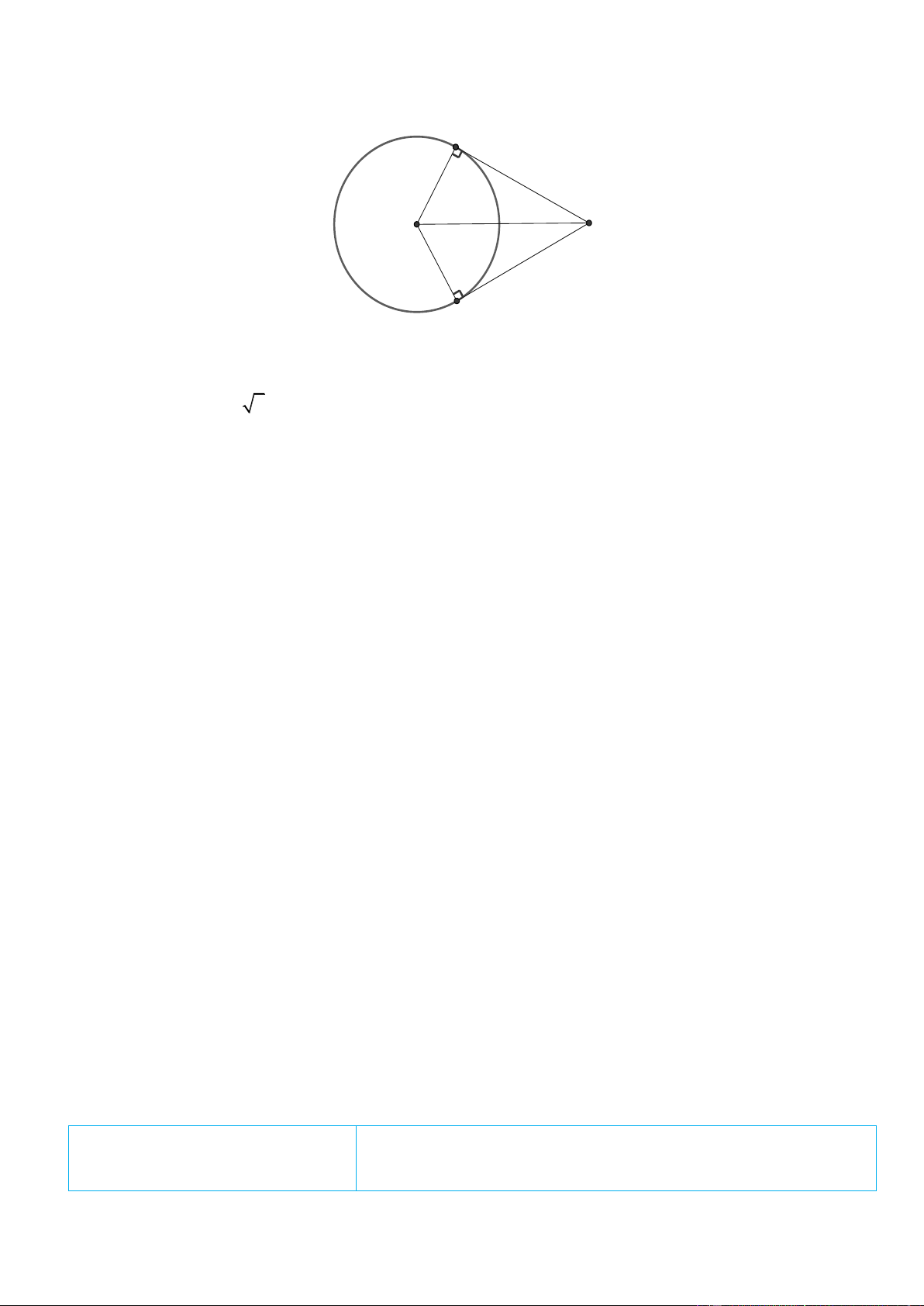
Giả sử AN; AM là các tiếp tuyến của S thỏa mãn AN AM ( N; M là các tiếp điểm) Dễ thấy A N
IM là hình vuông có cạnh IN R 3 và IA 3. 2 6 . IA R 2 2
a b 1
Điều kiện phải tìm là
IA IA 6 2 2
a b 4
Vì a , b là các số nguyên nên ta có các cặp nghiệm a;b là
0;2,0;2,2;0, 2 ;0,1; 1 , 1 ; 1 , 1 ; 1 , 1; 1 .
Vậy có 12 điểm A thỏa mãn yêu cầu. 2 2
Câu 50. Cho hàm số y f (x) có đạo hàm f x x
1 x 2x với mọi x . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g x f 2
x 8x m có 5 điểm cực trị? A. 15. B. 16. C. 17. D. 18. Lờigiải ChọnA x é = 1 (nghiem boi 2) ê 2 ê Xét f (
¢ x)= 0 Û (x- ) 1 ( 2
x - 2x)= 0 Û x = 0 . ê êx = 2 êë Ta có g (
¢ x)= (x- ) f ( 2 2 4 ¢ x - 8x + ) m ; x é = 4
ê 2xê- 8x+ m= 1 (nghiem boi 2) ê g (
¢ x)= 0 Û 2(x- 4) f ( 2
¢ x - 8x + m)= 0 Û ê . 2 x
ê - 8x + m = 0 ( ) 1 ê 2 x
ê - 8x + m = 2 (2) ë
Yêu cầu bài toán Û g (
¢ x)= 0 có 5 nghiệm bội lẻ Û mỗi phương trình ( ) 1 , ( )
2 đều có hai nghiệm phân biệt khác 4. ( ) *
Xét đồ thị (C) của hàm số 2
y = x - 8x và hai đường thẳng d : y = - ,
m d : y = - m + 2 (như hình vẽ). 1 2 Trang48 Khi đó ( )
* Û d , d cắt (C) tại bốn điểm phân biệt Û - m> - 16 Û m < 16. 1 2
Vậy có 15 giá trị m nguyên dương thỏa. 2
Cách 2: Đặt g x f 2
x 8x m . Ta có f x x 2 1 x 2x
g x x x x m 2 2
2x xm 2 ' 2 8 8 1 8
x 8x m 2 x 4 2
x 8x m 1
. Các phương trình 1 , 2, 3 không có nghiệm chung từng đôi một g x 1 0 2
x 8x m 0 2 2
x 8x m 2 0 3
và x x m 2 2 8 2
0 với m nên g x có 5 cực trị khi và chỉ khi
1 và 2 có hai nghiệm phân biệt 1 6 m 0 m 16 m và khác 4 16 2 0 m m 18 16. 16 32 m 0 m 16 1
632m 0 m 18
Vậy m nguyên dương và m 16 nên có 15 giá trị m cần tìm. ĐỀ 3
ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2022
BÁM SÁT ĐỀ MINH HỌA MÔN TOÁN Thời gian: 90 phút
Câu 1. Cho số phức z 2 5i . Môđun của số phức đối của z là A. 3 . B. 29 . C. 7 . D. 14 .
Câu 2. Mặt cầu S 2 2 2
: x y z 8x 2 y 1 0 có tâm là: A. I 8; 2 ;0. B. I 4 ;1;0. C. I 8 ;2;0. D. I 4; 1 ;0.
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 3
y x 2x 1
A. Điểm M 1; 4 .
B. Điểm N 0; 1 .
C. Điểm P 1 ;2.
D. Điểm Q 1 ;0 .
Câu 4. Thể tích của khối cầu bán kính R bằng 3 4 A. 3 R B. 3 R C. 3 4 R D. 3 2 R 4 3 Câu 5. Tính 2
F(x) e dx
, trong đó e là hằng số và e 2, 718 . Trang49 2 2 e x 3 e 2
A. F (x) C .
B. F (x) C .
C. F (x) e x C .
D. F (x) 2ex C . 2 3
Câu 6. Cho hàm số f x liên tục trên ¡ và có bảng xét dấu của f x như sau:
Số điểm cực đại của hàm số đã cho là A. 4 . B. 1. C. 2 . D. 3 .
Câu 7. Tập nghiệm của bất phương trình 3x 1 0 là
A. 0; .
B. 0; .
C. 1; .
D. 1; .
Câu 8. Thể tích V của khối chóp có chiều cao bằng h và diện tích đáy bằng 3B là 1 1
A. V 3Bh . B. V Bh . C. V Bh .
D. V Bh . 3 6
Câu 9. Tập xác định của hàm số y x 2022 3 1 là 1 1 1 A. . B. ; . C. ; . D. \ . 3 3 3
Câu 10. Nghiệm của phương trình log x 1 3 là 2 A. x 10 . B. x 8 . C. x 9 . D. x 7 . 2 2 2 Câu 11. Biết f
xdx 3 và g
xdx 2. Khi đó f
x gxdx bằng? 1 1 1 A. 6 . B. 1 . C. 5 . D. 1.
Câu 12. Cho số phức z 1 6i 2 4i . Phần thực, phần ảo của z lần lượt là
A. 1; 2 . B.1; 2 . C. 2;1. D. – 2;1.
Câu 13. Trong không gian Oxyz , Cho mặt phẳng : 2x y 3z 5 0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của ? A. n 2 ;1;3 .
B. n 2;1; 3 . C. n 2; 1 ;3 .
D. n 2;1;3 . 1 2 4 3
Câu 14. Trong không gian với hệ trục tọa độ Oxyz , cho a 2; 3
;3 , b 0;2; 1 , c 3; 1 ;5 . Tìm tọa độ
của vectơ u 2a 3b 2c . A. 10; 2 ;13 . B. 2 ;2;7 . C. 2 ; 2 ;7 . D. 2 ;2;7 .
Câu 15. Trong mặt phẳng tọa độ, biết điểm M (2;1) là điểm biểu diễn số phức z . Phần thực của z bằng: A. 2 B. 2 C.1 D. 1 4x 1
Câu 16. Tiệm cận ngang của đồ thị hàm số y x là 1 1 A. y . B. y 4 . C. y 1. D. y 1. 4 Trang50 2 a
Câu 17. Với a , b là các số thực dương tùy ý, log bằng 2 4 b
A. 2a 4b .
B. 2 log a 4 log b .
C. log a 2 log b . D. 4 log a b . 2 2 2 2 2
Câu 18. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 2
y x 3x 1. B. 3 2
y x 3x 1. C. 4 2
y x 2x 1. D. 4 2
y x 2x 1. x 2 y 1 z 3
Câu 19. Trong không gian Oxyz, cho đường thẳng d :
. Điểm nào dưới đây thuộc d? 4 2 1 A. Q 4; 2 ;1 . B. N 4; 2 ;1 . C. P 2;1; 3 .
D. M 2;1;3.
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. C C C . D. C n k !(n . B. k)! n (n . C. k)! n k ! n k !(k . n)!
Câu 21. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao 3h là 3V 3h V V A. B . B. B . C. B . D. B . h V 3h h
Câu 22. Đạo hàm của hàm số 1 2 e x y là A. 1 2 2e x y . B. 1 2 e x y . C. 1 2 2e x y . D. 2ex y .
Câu 23. Cho hàm số y f x có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng? ; 2 2 ;0
A. Hàm số nghịch biến trên khoảng
B. Hàm số đồng biến trên khoảng ; 0 0;2
C. Hàm số đồng biến trên khoảng
D. Hàm số nghịch biến trên khoảng
Câu 24. Cho hình trụ có bán kính đáy 3r và độ dài đường sinh l . Diện tích xung quanh S của hình trụ đã cho xq
được tính theo công thức nào sau đây? 1 A. S 2rl . B. S rl . C. S rl . D. S 6rl . xq xq xq 6 xq 3 3 Câu 25. Biết f
xdx 3. Giá trị của 2 f xdx bằng 1 1 Trang51 3 A. 5 . B. 9 . C. 6 . D. . 2
Câu 26. Cho cấp số cộng u
với u 7 công sai d 2 . Giá trị u bằng n 1 2 7 A. 14 . B. 9 . C. . D. 5 2
Câu 27. Công thức nào sau đây là sai? 1 1
A. ln x dx C . B.
dx tan x C . x 2 cos x
C. sin x dx cos x C .
D. ex d ex x C .
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ.
Giá trị cực tiểu của hàm số đã cho bằng A. 0 . B. 2 . C. 3 . D. 2 .
Câu 29. Giá trị nhỏ nhất của hàm số f x 3
x 3x 2 trên đoạn 3 ; 3 bằng A. 0 . B. 16 . C. 20 . D. 4 .
Câu 30. Hàm số nào sau đây nghịch biến trên toàn trục số? A. 3 2
y x 3x . B. 3
y x 3x 1. C. 3 2
y x 3x 3x 2 . D. 3 y x .
Câu 31. Với a,b là các số thực dương tùy ý thỏa mãn log a 2log b 4 , mệnh đề nào dưới đây đúng? 2 4 A. 2 a 16b .
B. a 8b .
C. a 16b . D. 4 a 16b .
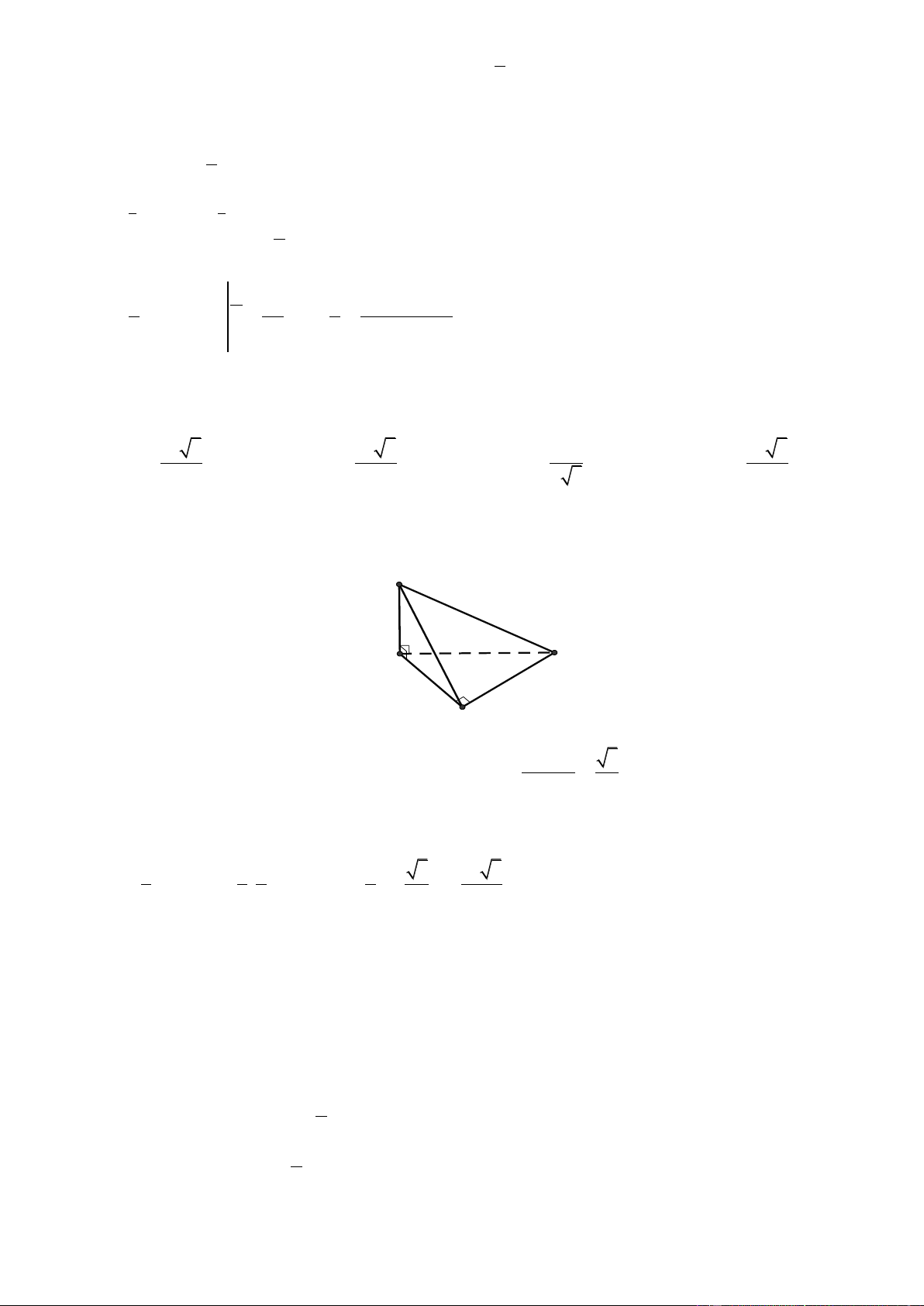
Câu 32. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và OA OB OC . Gọi M là
trung điểm của BC (tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng OM và AB bằng 0 0 0 0 A. 45 B. 90 C. 30 D. 60 Trang52 1 1
Câu 33. Biết f
x2x dx 3
. Khi đó f x dx bằng 0 0 A. 1 . B. 5 . C. 3 . D. 2 .
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua điểm M 2; 1 ; 3
và vuông góc với trục Oy có phương trình là
A. y 1 0 .
B. z 3 0 .
C. x 2 0.
D. y 1 0 .
Câu 35. Các số thực x, y thỏa mãn: 2x 3y
1 x 2yi 3x 2y 2 4x y 3i là A. x y 9 4 ; ; . B. x y 9 4 ; ; . 11 11 11 11 C. x y 9 4 ; ; . D. x y 9 4 ; ; . 11 11 11 11
Câu 36. Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng a . Gọi M là trung điểm của AA (tham khảo hình vẽ). AB C
Khoảng cách từ M đến mặt phẳng bằng a 2 a 21 a 2 a 21 A. 4 . B. 7 . C. 2 . D. 14 .
Câu 37. Có hai cái rương, mỗi rương chứa 5 cái thẻ đánh số tự 1 đến 5 . Rút ngẫu nhiên từ mỗi cái rương một
tấm thẻ. Xác suất để 2 thẻ rút ra đều ghi số lẻ là 1 3 3 9 A. . B. . C. D. . 3 5 10 25
Câu 38. Trong không gian Oxyz , cho ba điểm A1; 2;3, B 1;1;
1 , C 3; 4;0 . Đường thẳng đi qua A và song
song với BC có phương trình là x 1 y 2 z 3 x 1 y 2 z 3 A. . B. . 4 5 1 4 5 1 x 1 y 2 z 3 x 1 y 2 z 3 C. 2 3 1 . D. 2 3 1 .
Câu 39. Có bao nhiêu số nguyên x 2
022;2022 thỏa mãn 2x 1 3
7.3x 2 log 2x 1 2 0 ? 3 A. 2022 . B. 2021. C. 2018 . D. 2017 .
Câu 40. Cho f x là một hàm đa thức bậc bốn có đồ thị như hình dưới đây. Trang53
Tập nghiệm của phương trình f x 2 f
x.f x có số phần tử là A. 1. B. 2. C. 6. D. 0. x 8
Câu 41. Cho hàm số f x có f 3 3 và f x , x
0. Khi đó f xdx bằng x 1 x 1 3 197 29 181 A. 7 . B. . C. . D. . 6 2 6
Câu 42. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, cạnh bên SA vuông góc với mặt đáy, biết 3 a
AB 4a, SB 6a. Thể tích khối chóp S.ABC là V . Tỷ số là 3V 5 5 5 3 5 A. B. C. D. 80 40 20 80
Câu 43. Có bao nhiêu giá trị dương của số thực a sao chophương trình 2 2
z 3z a 2a 0 có nghiệm phức
z với phần ảo khác 0 thỏa mãn z 3. 0 0 A. 3 . B. 2 . C. 1. D. 4 .
Câu 44. Giả sử z , z là hai trong các số phức thỏa mãn z 68 zi là số thực. Biết rằng z z 4 , giá trị 1 2 1 2
nhỏ nhất của z 3z bằng 1 2 A. 5 21 B. 20 4 21 C. 20 4 22 D. 5 22 1
Câu 45. Cho hai hàm số f x 3 2
ax bx cx và g x 2
dx ex 1 , a , b ,
c d, e . Biết rằng đồ thị 2
hàm số y f x và y g x cắt nhau tại 3 điểm có hoành độ lần lượt là 3
; 1; 1 (tham khảo hình vẽ). Hình
phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng Trang54 9 A. 5 B. C. 8 D. 4 2 x y 1 z 2
Câu 46. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : , mặt phẳng 1 2 2
(P) :2x y 2z 5 0 và điểm A1;1; 2
. Phương trình chính tắc của đường thẳng đi qua điểm A song
song với mặt phẳng (P) và vuông góc với d là: x 1 y 1 z 2 x 1 y 1 z 2 A. : : 1 2 2 . B. 2 1 . 2 x 1 y 1 z 2 x 1 y 1 z 2 C. : : . 2 2 3 . D. 1 2 2
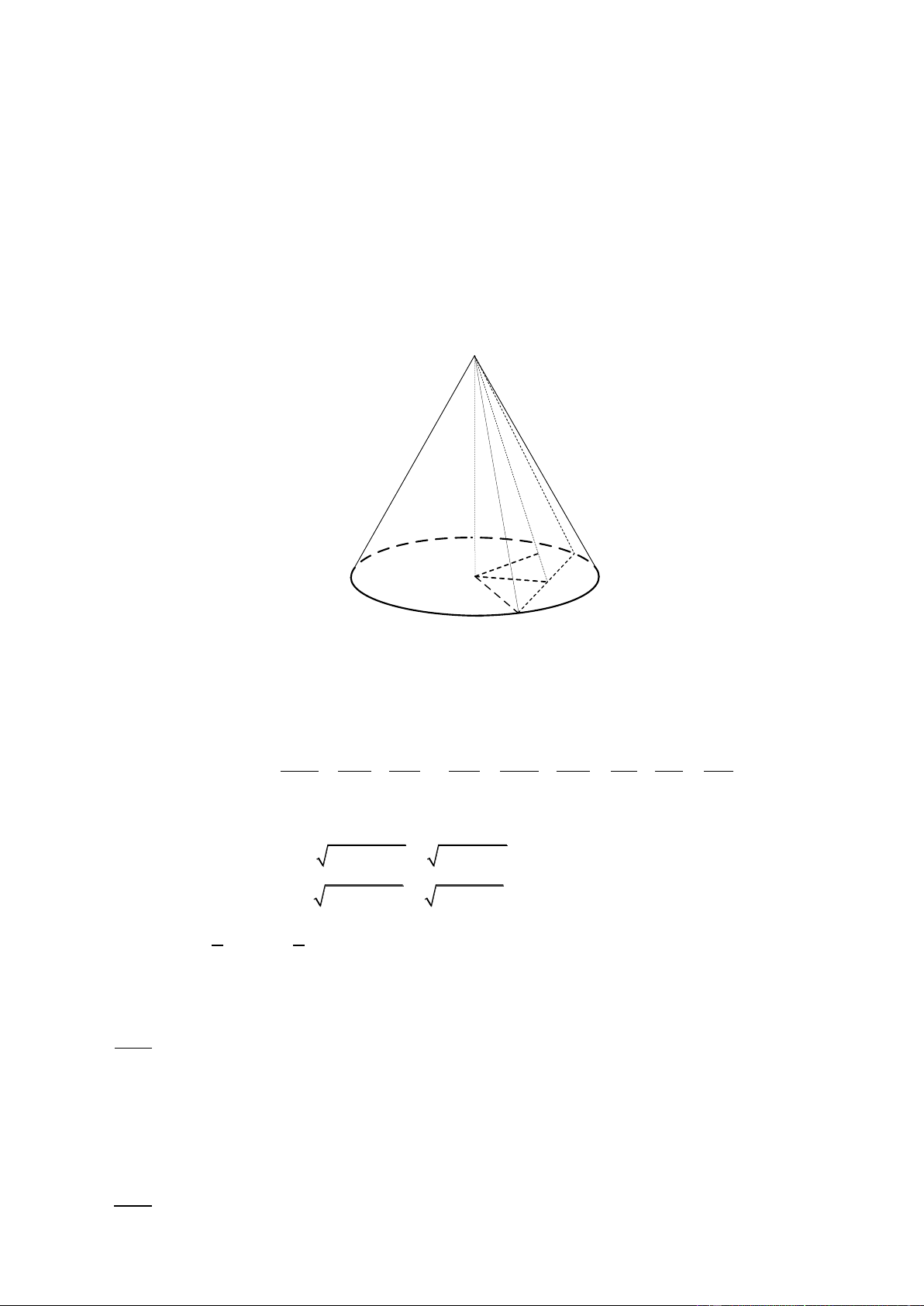
Câu 47. Cho hình nón đỉnh S , đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ a 3 O 0
đến SAB bằng và 0
SAO 30 , SAB 60 . Độ dài đường sinh của hình nón theo a bằng 3 A. a 2 B. a 3 C. 2a 3 D. a 5 2 2
Câu 48. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn x, y 5;50 và x y 2y x 2 y 2y 2 A. 2 . B. 5 . C. 15 . D.11.
Câu 49. Trong không gian Oxyz , cho mặt cầu: S x y z 2 2 2 : 1
5 . Có tất cả bao nhiêu điểm Aa;b;c (a, ,
b c là các số nguyên) thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp tuyến của S đi qua A và hai tiếp
tuyến đó vuông góc nhau? A. 20 . B. 8 . C. 12 . D. 16 .
Câu 50. Cho hàm số y = f (x) có đạo hàm f ( ¢ x) 2 = x ( 2 x - x + )( 2 3
2 x - x), với mọi x Î ¡ . Có bao nhiêu
giá trị nguyên dương của tham số m để hàm số y f 2
x 16x 2m có 5 điểm cực trị? A. 30 . B. 31. C. 32 . D. 33 .
LỜI GIẢI CHI TIẾT
Câu 1. Cho số phức z 2 5i . Môđun của số phức đối của z là A. 3 . B. 29 . C. 7 . D. 14 . Lờigiải Trang55
z i z i z 2 2 3 4 3 4 3 4 5
Vậy chọn đáp án B.
Câu 2. Mặt cầu S 2 2 2
: x y z 8x 2 y 1 0 có tâm là: A. I 8; 2 ;0. B. I 4 ;1;0. C. I 8 ;2;0. D. I 4; 1 ;0. Lờigiải
Phương trình mặt cầu S có dạng 2 2 2
x y z 2ax 2by 2cz d 0 với 2 2 2
a b c d 0 , có tâm I ; a ; b c , bán kính 2 2 2
R a b c d .
Lựa chọn đáp án D.
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 3
y x 2x 1
A. Điểm M 1; 4 .
B. Điểm N 0; 1 .
C. Điểm P 1 ;2.
D. Điểm Q 1 ;0 . Lờigiải Chọn A
Câu 4. Thể tích của khối cầu bán kính R bằng 3 4 A. 3 R B. 3 R C. 3 4 R D. 3 2 R 4 3 Lờigiải ChọnB Câu 5. Tính 2
F(x) e dx
, trong đó e là hằng số và e 2, 718 . 2 2 e x 3 e 2
A. F (x) C .
B. F (x) C .
C. F (x) e x C .
D. F (x) 2ex C . 2 3 Lờigiải Ta có: 2 2
F(x) e dx e x C .
Câu 6. Cho hàm số f x liên tục trên ¡ và có bảng xét dấu của f x như sau:
Số điểm cực đại của hàm số đã cho là A. 4 . B. 1. C. 2 . D. 3 . Lời giải Chọn C
Do hàm số f x liên tục trên ¡ , f 1 0 , f
1 không xác định nhưng do hàm số liên tục trên ¡ nên tồn tại f ( ) 1
và f x đổi dấu từ " " sang " " khi đi qua các điểm x 1
, x 1 nên hàm số đã cho đạt cực đại tại 2 điểm này.
Vậy số điểm cực đại của hàm số đã cho là 2. Trang56
Câu 7. Tập nghiệm của bất phương trình 3x 1 0 là
A. 0; .
B. 0; .
C. 1; .
D. 1; . Lời giải Chọn B 3x 1 0 3x 1 x 0.
Vậy tập nghiệm của bất phương trình đã cho là 0; .
Câu 8. Thể tích V của khối chóp có chiều cao bằng h và diện tích đáy bằng 3B là 1 1
A. V 3Bh . B. V Bh . C. V Bh .
D. V Bh . 3 6 Lời giải Chọn D 1 Ta có V .3 . B h Bh . 3
Câu 9. Tập xác định của hàm số y x 2022 3 1 là 1 1 1 A. . B. ; . C. ; . D. \ . 3 3 3 Lời giải Chọn B
Câu 10. Nghiệm của phương trình log x 1 3 là 2 A. x 10 . B. x 8 . C. x 9 . D. x 7 . Lờigiải ChọnC x 1 0 x Ta có log x 1 3 1 x 9 . 2 3 x 1 2 x 9 2 2 2 Câu 11. Biết f
xdx 3 và g
xdx 2. Khi đó f
x gxdx bằng? 1 1 1 A. 6 . B. 1 . C. 5 . D. 1. Lờigiải ChọnB 2 2 2 Ta có: f
x gxdx f
xdx g
xdx 32 1. 1 1 1
Câu 12. Cho số phức z 1 6i 2 4i . Phần thực, phần ảo của z lần lượt là
A. 1; 2 . B.1; 2 . C. 2;1. D. – 2;1. Lời giải
z 1 6i 2 4i 1 2i
Vậy chọn đáp án A. Trang57
Câu 13. Trong không gian Oxyz , Cho mặt phẳng : 2x y 3z 5 0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của ? A. n 2 ;1;3 .
B. n 2;1; 3 . C. n 2; 1 ;3 .
D. n 2;1;3 . 1 2 4 3 Lời giải Chọn C
Câu 14. Trong không gian với hệ trục tọa độ Oxyz , cho a 2; 3
;3 , b 0;2; 1 , c 3; 1 ;5 . Tìm tọa độ
của vectơ u 2a 3b 2c . A. 10; 2 ;13 . B. 2 ;2;7 . C. 2 ; 2 ;7 . D. 2 ;2;7 . Lờigiải Ta có: 2a 4; 6
;6 , 3b 0;6; 3 , 2 c 6 ;2; 1
0 u 2a 3b 2c 2;2;7.
Câu 15. Trong mặt phẳng tọa độ, biết điểm M (2;1) là điểm biểu diễn số phức z . Phần thực của z bằng: A. 2 B. 2 C.1 D. 1 Lờigiải ChọnA
Điểm M (- 2;1) là điểm biểu diễn số phức z Þ z = - 2+ i
Vậy phần thực của z là - 2 4x 1
Câu 16. Tiệm cận ngang của đồ thị hàm số y x là 1 1 A. y . B. y 4 . C. y 1. D. y 1. 4 Lời giải Chọn B. 4
Tiệm cận ngang lim y lim y 4 x x 1 2 a
Câu 17. Với a , b là các số thực dương tùy ý, log bằng 2 4 b
A. 2a 4b .
B. 2 log a 4 log b .
C. log a 2 log b . D. 4 log a b . 2 2 2 2 2 Lờigiải ChọnB 2 a
Với a 0 , b 0 thì log log 2 a log 4 b
2log a 4log b . 2 2 2 4 b 2 2
Câu 18. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? Trang58 A. 3 2
y x 3x 1. B. 3 2
y x 3x 1. C. 4 2
y x 2x 1. D. 4 2
y x 2x 1. Lời giải Chọn C.
Từ hình có đây là hình dạng của đồ thị hàm bậc 4.
lim f x lim f x a 0 x x x 2 y 1 z 3
Câu 19. Trong không gian Oxyz, cho đường thẳng d :
. Điểm nào dưới đây thuộc d? 4 2 1 A. Q 4; 2 ;1 . B. N 4; 2 ;1 . C. P 2;1; 3 .
D. M 2;1;3. Lờigiải ChọnC x 2 y 1 z 3 2 2 11 3 3
Thay tọa độ điểm P 2;1; 3 vào d : 0 0 0 4 2 ta được 1 4 2 đúng. 1
Vậy điểm P d .
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. C C C . D. C n k !(n . B. k)! n (n . C. k)! n k ! n k !(k . n)! Lời giải Chọn A n k ! C n
k !(n k)!
Câu 21. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao 3h là 3V 3h V V A. B . B. B . C. B . D. B . h V 3h h Lời giải Chọn C V
Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao 3h là: B . 3h
Câu 22. Đạo hàm của hàm số 1 2 e x y là A. 1 2 2e x y . B. 1 2 e x y . C. 1 2 2e x y . D. 2ex y . Trang59 Lờigiải Chọn A Xét hàm số 1 2 e x y . Ta có: 1 2x 1 2 1 2 e 2e x y x .
Câu 23. Cho hàm số y f x có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng? ; 2 2 ;0
A. Hàm số nghịch biến trên khoảng
B. Hàm số đồng biến trên khoảng ; 0 0;2
C. Hàm số đồng biến trên khoảng
D. Hàm số nghịch biến trên khoảng Lời giải Chọn D
Theo bảng xét dấu thì y ' 0 khi x (0; 2) nên hàm số nghịch biến trên khoảng (0; 2) .
Câu 24. Cho hình trụ có bán kính đáy 3r và độ dài đường sinh l . Diện tích xung quanh S của hình trụ đã cho xq
được tính theo công thức nào sau đây? 1 A. S 2rl . B. S rl . C. S rl . D. S 6rl . xq xq xq 6 xq Lờigiải Chọn D
Diện tích xung quanh của hình trụ là: S 2.3rl 6rl . xq 3 3 Câu 25. Biết f
xdx 3. Giá trị của 2 f xdx bằng 1 1 3 A. 5 . B. 9 . C. 6 . D. . 2 Lờigiải ChọnC 3 3 Ta có: 2 f
xdx 2 f
xdx 2.3 6. 1 1
Câu 26. Cho cấp số cộng u
với u 7 công sai d 2 . Giá trị u bằng n 1 2 7 A. 14 . B. 9 . C. . D. 5 2 Lời giải Chọn B Vì u
là một cấp số cộng thì u
u d u u d 7 2 9 n n 1 n 2 1
Câu 27. Công thức nào sau đây là sai? 1 1
A. ln x dx C . B.
dx tan x C . x 2 cos x Trang60
C. sin x dx cos x C .
D. ex d ex x C . Lờigiải 1
Ta có: ln x dx C sai. x
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ.
Giá trị cực tiểu của hàm số đã cho bằng A. 0 . B. 2 . C. 3 . D. 2 . Lời giải Chọn C
Câu 29. Giá trị nhỏ nhất của hàm số f x 3
x 3x 2 trên đoạn 3 ; 3 bằng A. 0 . B. 16 . C. 20 . D. 4 . Lời giải Chọn B
Cách 1:Mode 7 f x 3
x 3x 2 . Start -3 end3step 1 Chọn B
Cách 2: f x 2
3x 3. f x 0 x 1 3 ; 3 . f 3 1 6 ; f 1 4 ; f
1 0 ; f 3 20 .
Giá trị nhỏ nhất là 16 .
Câu 30. Hàm số nào sau đây nghịch biến trên toàn trục số? A. 3 2
y x 3x . B. 3
y x 3x 1. C. 3 2
y x 3x 3x 2 . D. 3 y x . Lời giải Chọn đáp án C 3 2
y x 3x 2
y 3x 6x . Loại A 3
y x 3x 1 2 y 3
x 3 3 . Loại B 3 2
y x 3x 3x 2 y x x x 2 2 3 6 3 3 1 0 .
Câu 31. Với a,b là các số thực dương tùy ý thỏa mãn log a 2log b 4 , mệnh đề nào dưới đây đúng? 2 4 Trang61 A. 2 a 16b .
B. a 8b .
C. a 16b . D. 4 a 16b . Lời giải Chọn C
Ta có log a 2log b 4 2 4
log a 2log b 4 2 2 2 1
log a 2. log b 4 2 2 2
log a log b 4 2 2 a log 4 2 b a 4 2 b a 16b
Câu 32. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và OA OB OC . Gọi M là
trung điểm của BC (tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng OM và AB bằng 0 0 0 0 A. 45 B. 90 C. 30 D. 60 Lờigiải Chọn D
Đặt OA a suy ra OB OC a và AB BC AC a 2 Gọi a 2
N là trung điểm AC ta có MN / / AB và MN 2 Trang62
Suy ra góc OM , AB OM , MN . Xét OMN a 2
Trong tam giác OMN có ON OM MN
nên OMN là tam giác đều 2 0
Suy ra OMN 60 . Vậy OM AB OM MN 0 , , 60 1 1
Câu 33. Biết f
x2x dx 3
. Khi đó f x dx bằng 0 0 A. 1 . B. 5 . C. 3 . D. 2 . Lờigiải ChọnD 1 1 1 1 2 x 1 Ta có f
x2x dx 3 f
xdx2 xdx 3 f
xdx2. 3. 2 0 0 0 0 0 1 1 Suy ra f x 2 dx 3 x 3 1 0 2. 0 0
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua điểm M 2; 1 ; 3
và vuông góc với trục Oy có phương trình là
A. y 1 0 .
B. z 3 0 .
C. x 2 0.
D. y 1 0 .
Câu 35. Các số thực x, y thỏa mãn: 2x 3y
1 x 2yi 3x 2y 2 4x y 3i là A. x y 9 4 ; ; . B. x y 9 4 ; ; . 11 11 11 11 C. x y 9 4 ; ; . D. x y 9 4 ; ; . 11 11 11 11 Lờigiải
2x 3y
1 x 2 yi 3x 2 y 2 4x y 3i 9 x
2x 3y 1 3x 2y 2
x 5y 1 11
x 2y 4x y 3
5x 3y 3 4 y 11 Vậy x y 9 4 ; ; 11 11
Vậy chọn đáp án B.
Câu 36. Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng a . Gọi M là trung điểm của AA (tham khảo hình vẽ). Trang63 AB C
Khoảng cách từ M đến mặt phẳng bằng a 2 a 21 a 2 a 21 A. 4 . B. 7 . C. 2 . D. 14 . Lờigiải Chọn D ABB A Trong
, gọi E là giao điểm của BM và AB . Khi đó hai tam giác EAM và EB B đồng dạng. Do đó
d M , AB C EM MA 1 1 d
d M , AB C
d B, AB C B, AB C EB BB 2 2 . a 3 BN
Từ B kẻ BN AC thì N là trung điểm của AC và
2 , BB a .
d B AB C BB BN a 21 , BI Kẻ 2 2 BI B N thì 7 BB BN .
d M AB C 1
d B AB C a 21 , , Vậy 2 14 .
Câu 37. Có hai cái rương, mỗi rương chứa 5 cái thẻ đánh số tự 1 đến 5 . Rút ngẫu nhiên từ mỗi cái rương một
tấm thẻ. Xác suất để 2 thẻ rút ra đều ghi số lẻ là 1 3 3 9 A. . B. . C. D. . 3 5 10 25 Lời giải Chọn D
Số phần tử không gian mẫu: n 25 . Trang64
Gọi C là biến cố: “ 2 thẻ rút ra đều ghi số lẻ” thì nC 3.3 9 n C 9 Vậy P C . n 25
Câu 38. Trong không gian Oxyz , cho ba điểm A1; 2;3, B 1;1;
1 , C 3; 4;0 . Đường thẳng đi qua A và song
song với BC có phương trình là x 1 y 2 z 3 x 1 y 2 z 3 A. . B. . 4 5 1 4 5 1 x 1 y 2 z 3 x 1 y 2 z 3 C. 2 3 1 . D. 2 3 1 . Lờigiải ChọnC
Ta có BC 2;3;
1 , đường thẳng song song nên có vec tơ chỉ phương cùng phương với BC 2;3; 1 .
Do vậy đường thẳng đi qua A và song song với BC có phương trình là x 1 y 2 z 3 2 3 1
Câu 39. Có bao nhiêu số nguyên x 2
022;2022 thỏa mãn 2x 1 3
7.3x 2 log 2x 1 2 0 ? 3 A. 2022 . B. 2021. C. 2018 . D. 2017 . Lờigiải ChọnD 2x 1 0 9 Điều kiện x
log 2x 1 2 0 2 3 Ta có 2x 1
3 7.3x 2 log 2x 1 2 0 3 2 x 1 3
7.3x 2 0 1 log 2x 1 2 0 2 3 Giải 1 : 2x 1 3 7.3x 2 0 x2 3. 3 7.3x 2 0 . 1 t 0 0 t Đặt
3x t 0 ta được 3 . 2 3
t 7t 2 0 t 2 x 1 0 3 x 1 0 3 3 x 1 Suy ra 3 . x log 2 3 x log 2 3 3 3x 2 3
Vậy bất phương trình có tập nghiệm là ; 1 log 2; . 3 9 9
Kết hợp điều kiện x ; 2 2 Trang65 9
Giải 2 : log 2x 1 2 0 x (thỏa điều kiện) 3 2
Do x là số nguyên , x 2
022;2022 x 5;6;...;202 1
Vậy có 2017 giá trị x cần tìm
Câu 40. Cho f x là một hàm đa thức bậc bốn có đồ thị như hình dưới đây.
Tập nghiệm của phương trình f x 2 f
x.f x có số phần tử là A. 1. B. 2. C. 6. D. 0. Lờigiải Chọn A
Xét phương trình f x 2 f
x.f x 1
Do f x 0 có ba nghiệm x , x , x x x x và f ' x 0 suy ra x là một nghiệm của (1) 3 1 2 2 1 2 3 3 2
Ta có f x a x x x x x x , a 0 1 2 3 f x 1 1 2
Với x x 1 0 0 3 f x x x x x x x 1 2 3 1 1 2 vô nghiệm. x x 0 2
x x 2 x x 2 1 2 3
Vậy, phương trình (1) có đúng một nghiệm x x . 3 x 8
Câu 41. Cho hàm số f x có f 3 3 và f x , x
0. Khi đó f xdx bằng x 1 x 1 3 197 29 181 A. 7 . B. . C. . D. . 6 2 6 Lờigiải ChọnB x Xét f
xdx dx . Đặt 2 2 t
x 1 x 1 t x t 1 dx 2tdt . x 1 x 1 2 x t 1 t 1 . t 1 Khi đó, f x dx dx 2 d t t 2 d t t 2t 2 dt 2 x 1 x 1 t t t.t 1 2
t 2t C x
1 2 x 1 C . Trang66
Mà f 3 3 3
1 2 3 1 C 3 C 5 .
f x x
1 2 x 1 5 x 2 x 1 4 . 8 8 8 f
x x x x 2 x 4 x x 3 19 197 d 2 1 4 d 1 4x 36 . 2 3 6 6 3 3 3
Câu 42. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, cạnh bên SA vuông góc với mặt đáy, biết 3 a
AB 4a, SB 6a. Thể tích khối chóp S.ABC là V . Tỷ số là 3V 5 5 5 3 5 A. B. C. D. 80 40 20 80 Lờigiải Chọn B
+ D ABC vuông cân tại C, AB 4a suy ra AC BC 2a 2. 1 Do đó: 2 S
AC.BC 4a . ABC 2 2 2
+ SA ABC SA AB D ABC vuông tại A 2 2
SA SB AB 6a 4a 2a 5. 3 1 1 8a 5
+ Khối chóp S.ABC có SA ABC 2 V S .SA 4a .2a 5 3 ABC 3 3 3 3 a a 5 Vậy tỷ số: . 3 3V 3.8a 5 40 3
Câu 43. Có bao nhiêu giá trị dương của số thực a sao chophương trình 2 2
z 3z a 2a 0 có nghiệm phức
z với phần ảo khác 0 thỏa mãn z 3. 0 0 A. 3 . B. 2 . C. 1. D. 4 . Lờigiải ChọnC 2 2
Ta có 3 4a 2a 3 4a 8a . Phương trình 2 2
z 3z a 2a 0 có nghiệm phức khi và chỉ khi Trang67 2 2
0 3 4a 8a 0 4a 8a 3 0 * .
Khi đó phương trình có hai nghiệm z , z là hai số phức liên hợp của nhau và z z . 1 2 1 2 Ta có 2 2 2 2 2
z .z a 2a z .z a 2a z . z a 2a z a 2a . 1 2 1 2 1 2 0
a 2a 3 a 1
Theo giả thiết có 3 2 2 2
a 2a ( t/m ĐK(*)). 2
a 2a 3 a 3
Các giá trị của a thỏa mãn điều kiện * . Vậy có 1 giá trị dương a thỏa mãn yêu cầu bài toán.
Câu 44. Giả sử z , z là hai trong các số phức thỏa mãn z 68 zi là số thực. Biết rằng z z 4 , giá trị 1 2 1 2
nhỏ nhất của z 3z bằng 1 2 A. 5 21 B. 20 4 21 C. 20 4 22 D. 5 22 Lờigiải ChọnC
Giả sử z x yi , x, y .Gọi ,
A B lần lượt là điểm biểu diễn cho các số phức z , z . Suy ra AB z z 4 . 1 2 1 2
* Ta có z 68 zi x 6 yi.
8 y xi x y 2 2 8 6 48
x y 6x 8yi . Theo giả thiết
z 68 zi là số thực nên 2 2
ta suy ra x y 6x 8y 0 . Tức là các điểm ,
A B thuộc đường tròn C tâm
I 3;4 , bán kính R 5.
* Xét điểm M thuộc đoạn AB thỏa MA 3MB 0 OA 3OB 4OM .Gọi H là trung điểm AB . Ta tính được 2 2 2 2 2
HI R HB 21; IM HI HM 22 , suy ra điểm M thuộc đường tròn C tâm I 3;4 , bán kính r 22 .
* Ta có z 3z OA 3OB 4OM 4OM , do đó z 3z nhỏ nhất khi OM nhỏ nhất. 1 2 1 2 Ta có OM
OM OI r 5 22 . 0 min Vậy z 3z
4OM 20 4 22 . 1 2 0 min Trang68 1
Câu 45. Cho hai hàm số f x 3 2
ax bx cx và g x 2
dx ex 1 , a , b ,
c d, e . Biết rằng đồ thị 2
hàm số y f x và y g x cắt nhau tại 3 điểm có hoành độ lần lượt là 3
; 1; 1 (tham khảo hình vẽ). Hình
phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng 9 A. 5 B. C. 8 D. 4 2 Lờigiải ChọnD Cách1: 1 3 Xét phương trình 3 2 2
ax bx cx
dx ex 1 3
Û ax + (b- d ) 2
x + (c- e) x-
= 0 có 3 nghiệm lần lượt 2 2 3
a b d c e 3 27 9 3 0 b d 2 2 3 1 là 3
; 1; 1 nên suy ra a b d c e 0 a 2 2 1 a
b dc e 3 0 c e 2 2 1 3 1 3
Vậy f x g x 3 2
x x x . 2 2 2 2 1 1
Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng S f x g xdx g x f xdx 3 1 1 1 1 3 1 3 1 3 1 3 3 2 3 2 S x x x dx x x x dx 2 2 4 . 2 2 2 2 2 2 2 2 3 1 Cách2:
Ta có: f x g x a x 3 x 1 x 1 . 3
Suy ra a x 3 x 1 x 3
1 ax b d 2
x c d x 2 3 1
Xét hệ số tự do suy ra: 3a a . 2 2 1
Do đó: f x g x x 3 x 1 x 1 . 2 Trang69 1 1
Diện tích bằng: S f
x gxdx g
x f xdx 3 1 1 1 1 S
x x x 1 3 1 1 dx
x 3x 1 x 1 dx 4 . 2 2 3 1 x y 1 z 2
Câu 46. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : , mặt phẳng 1 2 2
(P) :2x y 2z 5 0 và điểm A1;1; 2
. Phương trình chính tắc của đường thẳng đi qua điểm A song
song với mặt phẳng (P) và vuông góc với d là: x 1 y 1 z 2 x 1 y 1 z 2 A. : : 1 2 2 . B. 2 1 . 2 x 1 y 1 z 2 x 1 y 1 z 2 C. : : . 2 2 3 . D. 1 2 2 Lờigiải ChọnC x y 1 z 2 d :
d có một vectơ chỉ phương là u 1;2;2 . 1 2 2
(P) :2x y 2z 5 0 (P) có một vectơ pháp tuyến là n 2;1; 2 .
Đường thẳng song song với mặt phẳng (P) và vuông góc với d
có một vectơ chỉ phương là v
u, n 2;2; 3
, và đường thẳng đi qua điểm A1;1; 2 Phương x 1 y 1 z 2
trình chính tắc của đường thẳng là: 2 2 . 3
Câu 47. Cho hình nón đỉnh S , đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ a 3 O 0
đến SAB bằng và 0
SAO 30 , SAB 60 . Độ dài đường sinh của hình nón theo a bằng 3 A. a 2 B. a 3 C. 2a 3 D. a 5 Lời giải ChọnA Trang70
Gọi K là trung điểm của AB ta có OK AB vì tam giác OAB cân tại O
Mà SO AB nên AB SOK SOK SAB mà SOK SAB SK nên từ O dựng
OH SK thì OH SAB OH d , O SAB SO SA
Xét tam giác SAO ta có: sin SAO SO SA 2 SK SA
Xét tam giác SAB ta có: 3 sin SAB SK SA 2 1 1 1 1 1
Xét tam giác SOK ta có: 2 2 2 2 2 2 OH OK OS SK SO SO 1 1 1 4 2 6 3 2
SA 2a SA a 2 2 2 2 2 2 2 OH SA 3SA SA SA SA 2 2 SA a 4 4 4 2 2
Câu 48. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn x, y 5;50 và x y 2y x 2 y 2y 2 A. 2 . B. 5 . C. 15 . D.11. Lờigiải Chọn C Có 2 2 2 2
x y 2 y x 2
y 2 y 2 x
x y 2y 2
y 2y 2 (2)
Xét hàm số f t t t trên khoảng 0; ta có: f t 1 1 0, t
0 f t đồng biến. 2 t
f x f 2 y y 2 2 2
2 x y 2y 2 .
Do x, y 5;50 nên y y y 2 2 5 2 2 50 4 1 49 1 y 6
Do y và y 5;50 nên y 5 hoặc y 6 . Với y 5 có 2
37 y 2 y 2 x 50 x 37;38;...;5 0 có 14 cặp ; x y thỏa mãn. Trang71 Với y 6 có 2
50 y 2 y 2 x 50 x 50 có 1 cặp ; x y thỏa mãn.
Vậy có tất cả 15 cặp ; x y thỏa mãn.
Câu 49. Trong không gian Oxyz , cho mặt cầu: S x y z 2 2 2 : 1
5 . Có tất cả bao nhiêu điểm Aa;b;c (a, ,
b c là các số nguyên) thuộc mặt phẳng Oxy sao cho có ít nhất hai tiếp tuyến của S đi qua A và hai tiếp
tuyến đó vuông góc nhau? A. 20 . B. 8 . C. 12 . D. 16 . Lờigiải ChọnA Mặt cầu S 2 2 2
: x y (z 1) 5 có tâm I 0;0;
1 và có bán kính R 5 a b 1
Aa;b;0 Oxy , Gọi I là trung điểm của AI I ; ; 2 2 2
Gọi E, F lần lượt là hai tiếp điểm của tiếp tuyến đi qua A sao cho AE AF . a b 1 1
Ta có: E, F cùng thuộc mặt cầu S đường kính IA có tâm I ; ; , bán kính 2 2 R a b 1 . 2 2 2 2
Đề tồn tại E, F thì hai mặt cầu S và S phải cắt nhau suy ra R R II R R 1 1 1 2 2 2 2 2 2 5 a b 1
a b 1 5 a b 1 2 2 2 2 2 2 2
5 a b 1 a b 4 1
Gọi H là hình chiếu của I trên AEF khi đó tứ giác AEHF là hình vuông có cạnh 2 AE HF AI 5 . Ta có 2 2 2
IH R HF 2 AI 2 2 2 2 2 5
5 10 AI 0 a b 1 10 a b 92 Từ 1 và 2 ta có 2 2
4 a b 9 mà a, ,
b c nên có 20 điểm thỏa bài toán. Cáchkhác:
Mặt cầu S có tâm I 0,0,
1 bán kính R 5 . Ta có d 1 R
mặt cầu S cắt mặt phẳng Oxy . I Oxy
Để có tiếp tuyến của S đi qua A AI R 1 .
Có Aa b c Oxy Aa b 2 2 , ,
, , 0 , IA a b 1.
Quỹ tích các tiếp tuyến đi qua A của S là một mặt nón nếu AI R và là một mặt phẳng nếu AI R . Trang72
Trong trường hợp quỹ tích các tiếp tuyến đi qua A của S là một mặt nón gọi AM , AN là hai tiếp tuyến sao cho ,
A M , I , N đồng phẳng. M A I N
Tồn tại ít nhất hai tiếp tuyến của S đi qua A và hai tiếp tuyến đó vuông góc với nhau khi và chỉ khi 90o MAN
IA R 2 2 . Từ 2 2
1 , 2 4 a b 9 . Vì a, b 2 a 0 2 2 2 2 2 2 a 9 a 4 a 0 a 1 a 4 a 4 hoặc hoặc hoặc hoặc hoặc hoặc . 2 b 9 2 b 0 2 b 0 2 b 4 2 b 4 2 b 1 2 b 4
Bốn hệ phương trình đầu tiên có hai nghiệm, ba hệ sau có 4 nghiệm suy ra số điểm A thỏa mãn là 4.2 3.4 20
Câu 50. Cho hàm số y = f (x) có đạo hàm f ( ¢ x) 2 = x ( 2 x - x + )( 2 3
2 x - x), với mọi x Î ¡ . Có bao nhiêu
giá trị nguyên dương của tham số m để hàm số y f 2
x 16x 2m có 5 điểm cực trị? A. 30 . B. 31. C. 32 . D. 33 . Lờigiải Chọn B
Ta có: y¢= f ( 2 ¢ x - 16x + 2 ) m (2x - 1 ) 6 . x é = 8 ê 2 x é = 8 x
ê - 16x + 2m = 1 (1) ê ê Cho y¢= 0 Û Û ê ê . f ê ( 2
¢ x - 16x + 2m) 2 = 0 x
ê - 16x + 2m = 0 (2) ë ê 2 x
ê - 16x + 2m = 2 (3) ë
Do các nghiệm của (1) đều là nghiệm bội bậc chẵn còn (2) và (3) không thể có nghiệm trùng nhau nên hàm số đã
cho có 5 điểm cực trị khi (2) và (3) có 2 nghiệm phân biệt khác 8 . ' íï D > 0 ï í 2 ï ï 64- 2m > 0 ï ï ï ' ï D > 0 ï ï 64- 2m + 2 > 0 3 ì ï Û ì
Û m < 32 mà m nguyên dương nên m có 31 giá trị. 2
ïï 8 - 16.8+ m ¹ 0 ï - 64+ m ¹ 0 ï ï ï ïï 2 ï 8 - 16.8+ m ¹ 2 ï ï - + ¹ î 64 m 2 î ĐỀ 4
ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2022
BÁM SÁT ĐỀ MINH HỌA MÔN TOÁN Thời gian: 90 phút
Câu 1. Cho số phức z 6 7i . Số phức liên hợp của z là Trang73
A. z 6 7i . B. z 6 7i . C. z 6 7i .
D. z 6 7i .
Câu 2. Mặt cầu S 2 2 2
: x y z 4x 1 0 có tọa độ tâm và bán kính R là:
A. I 2;0;0, R 3.
B. I 2;0;0, R 3.
C. I 0; 2;0, R 3. D. I 2 ;0;0, R 3. 1 x
Câu 3. Điểm nào dưới đây không thuộc đồ thị của hàm số y x 1 1
A. Điểm M 0 ;1 .
B. Điểm N 1 ;0 .
C. Điểm P 1;0 .
D. Điểm Q 2; . 3
Câu 4. Thể tích khối cầu có đường kính 2a bằng 3 4 a 3 a A. . B. 3 4 a . C. . D. 3 2 a . 3 3
Câu 5. Nguyên hàm của hàm số 2x f x x là x 2 2 x 2x 2 x 2 x A. C . B. 2
2x x C . C. x C . D. 2 C . ln 2 2 ln 2 2
Câu 6. Cho hàm f x liên tục trên và có bảng xét dấu f x như sau:
Số điểm cực tiểu của hàm số là A. 1. B. 2 . C. 3 . D. 4 .
Câu 7. Giải bất phương trình log 3x 1 3 . 2 1 10
A. x 3 B. x 3
C. x 3 D. x 3 3
Câu 8. Khi tăng độ dài các cạnh của một khối chóp lên 2 lần thì thể tích của khối chóp thay đổi như thà nào? A. Tăng 4 lần.. B. Tăng 8 lần.. C. Tăng 2 lần. D. Không thay đổi. 3 1
Câu 9. Tập xác định của hàm số y là x A. . B. 0; . C. \ 0 . D. 0; .
Câu 10. Nghiệm của phương trình log x 2 3 là: 2
A. x 6 .
B. x 8 .
C. x 11.
D. x 10 . 2 2 2 Câu 11. Biết
f (x)dx 2
và g (x)dx 3.
Khi đó [ f (x) g(x)]dx bằng 1 1 1 A. 1 . B. 5 . C. 1. D. 6 .
Câu 12. Cho số phức z 2 5i . Tìm số phức w iz z .
A. w 7 3i . B. w 3 3i .
C. w 3 3i . D. w 7 7i . Trang74
Câu 13. Trong không gian Oxyz , cho mặt phẳng : x 2y 4z 1 0 .Vectơ nào dưới đây là một vectơ pháp
tuyến của mặt phẳng ?
A. n 1; 2; 4 .
B. n 1; 2; 4 .
C. n 1; 2; 4 .
D. n 1; 2; 4 4 2 1 3
Câu 14. Trong không gian với hệ trục tọa độ Oxyz , cho a i
2 j 3k . Tọa độ của vectơ a là A. 1 ;2; 3 . B. 2; 3 ; 1 . C. 2; 1 ; 3 . D. 3 ;2; 1 .
Câu 15. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức z 1 2i ?
A. Q 1; 2 . B. M 2 ;1 . C. P 2 ;1 .
D. N 1; 2 . 5x 1
Câu 16. Tiệm cận ngang của đồ thị hàm số y x là 1 1 A. y 1. B. y . C. y 1. D. y 5 . 5
Câu 17. Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng? 3 2a 3 2a 1 A. log
1 3log a log b . B. log
1 log a log b . 2 2 2 b 2 2 2 b 3 3 2a 3 2a 1 C. log
1 3log a log b . D. log
1 log a log b . 2 2 2 b 2 2 2 b 3
Câu 18. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y x 2x . B. 3
y x 3x . C. 4 2
y x 2x . D. 3
y x 3x . x 4 z 2 z 1
Câu 19. Trong không gian Oxyz , cho đường thẳng d :
. Điểm nào sau đây thuộc d ? 2 5 1 A. N (4; 2; 1 ) . B. Q(2; 5;1) . C. M (4; 2;1) . D. P(2; 5 ;1) .
Câu 20. Với n là số nguyên dương, công thức nào sao đây đúng? n!
A. P n 1 !. B. P .
C. P n .
D. P n! . n n n 1 ! n n
Câu 21. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là 3V 3h V h A. B . B. B . C. B . D. B . h V h V
Câu 22. Tính đạo hàm của hàm số 1 e x f x . A. 1 e x f x .
B. f x x 1 e ln . C. e x f x . D. e x f x ln .
Câu 23. Cho hàm số y f x có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? Trang75 1; ;1 1; ; 1 A. . B. . C. . D. .
Câu 24. Cho hình trụ có diện tích xung quanh S và bán kính đáy 2r . Độ dài đường sinh l của hình trụ đã cho xq
được tính theo công thức nào sau đây? 4 r S S 4S xq xq xq A. l . B. l . C. l . D. l . S 4 r 2 r r xq 5 5 Câu 25. Biết f
xdx 4. Giá trị của 3f xdx bằng 1 1 4 A. 7 . B. . C. 64 . D. 12 . 3
Câu 26. Cho cấp số cộng u
với u 3 ; u 9 . Công sai của cấp số cộng đã cho bằng n 1 2 A. 6. B. 3. C. 12. D. -6.
Câu 27. Tìm họ nguyên hàm của hàm số f x 3x sin x . x
A. f x 2
dx 3x cos x C .
B. f x 2 3 dx
cos x C . 2 x
C. f x 2 3 dx
cos x C .
D. f xdx 3 cos x C . 2
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ. y 4 3 1 O 1 x -1 -1
Hàm số đã cho đạt cực đại tại A. x 1 . B. x 3. C. x 0 . D. x 1 . 4 2
Câu 29. Tìm giá trị lớn nhất M của hàm số y x 2x 3 trên đoạn 0; 3 .
A. M 6
B. M 1
C. M 9
D. M 8 3
Câu 30. Cho các hàm số sau: 1 x 1 3 2 (I) : y
x x 3x 4 ; (II) : y y x ; 2 (III) : 4 3 x 1 Trang76 3
(IV) : y x 4x sin x ; 4 2
(V) : y x x 2 .
Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định? A.2. B. 4. C. 3. D. 5.
Câu 31. Với mọi a , b , x là các số thực dương thoả mãn log x 5 log a 3log b . Mệnh đề nào dưới đây 2 2 2 đúng?
A. x 5a 3b B. 5 3
x a b C. 5 3
x a b
D. x 3a 5b 3
Câu 32. Cho tứ diện ABCD với 0 AC
AD, CAB DAB 60 , CD AD . Gọi là góc giữa hai đường 2
thẳng AB và CD . Chọn khẳng định đúng về góc . 3 1 A. cos B. 0 30 C. 0 60 D. cos 4 4 1 1 Câu 33. Biết f
x 2xdx 4 . Khi đó
f x dx bằng 0 0 A. 3 . B. 2 . C. 6 . D. 4 .
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua điểm M 1;1;
1 và song song với mặt phẳng
:2x2yz 0 có phương trình là
A. 2x 2y z 3 0 .
B. x 2y z 0 .
C. 2x 2y z 3 0 .
D. x 2y z 2 0 .
Câu 35. Cho số phức z 1 i . Khẳng định nào sau đây là khẳng định đúng? z A. 1 i . B. 1 z .z 0 . C. z 2 . D. 2 z 2i . i
Câu 36. Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng a . Gọi M là trung điểm của CC (tham A B C
khảo hình bên). Khoảng cách từ M đến mặt phẳng bằng 21a 2a 21a 2a A. 14 . B. 2 . C. 7 . D. 4 .
Câu 37. Chọn ngẫu nhiên 3 số trong 50 số tự nhiên 1; 2;3; 4...50 . Tính xác suất biến cố A: trong 3 số đó chỉ có 2 số là bội của 5 . A. 0.09 . B. 0, 08 . C. 0,19 . D. 0,18 . Trang77
Câu 38. Trong không gian Oxyz , cho ba điểm (
A 1; 2; 0), B(1;1; 2) và C(2;3;1) . Đường thẳng đi qua A và song
song với BC có phương trình là x 1 y 2 z x 1 y 2 z x 1 y 2 z x 1 y 2 z A. . . C. . D. . 1 2 B. 1 3 4 3 3 4 3 1 2 1
Câu 39. Có bao nhiêu số nguyên x thỏa mãn x x 1 x x 1 2 2
3 3 3log x 2 0 ? 2 A. 7 . B. 8 . C. 9 . D.10 .
Câu 40. Cho hàm số f x có đạo hàm liên tục trên , f x có đồ thị C như hình dưới đây, trong đó , A B
là các điểm cực đại của C , các tiếp tuyến của C tại các tiếp điểm thuộc cung AB đều không song song với
hai đường thẳng đường thẳng y 2x , y 2x , lim f ' x ,
lim f 'x . x x
Xét phương trình f f 'x 1 0
1 , khẳng định nào sau đây đúng? A. 1 cóđúng hai nghiệm. B. 1 cóđúng ba nghiệm. C.
1 có ít nhất hai nghiệm. D. 1 có đúng ba nghiệm. 4
Câu 41. Cho hàm số f x . Biết f 0 4 và f x 2 '
2sin x 1, x , khi đó f
xdx bằng 0 2 16 4 2 4 2 15 2 16 16 A. . B. . C. . D. . 16 16 16 16
Câu 42. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại B , AB a , ACB 60 , cạnh bên
SA vuông góc với mặt đáy và SB hợp với mặt đáy một góc 45 . Tính thể tích V của khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 a 3 A. V B. V C. V D. V 18 12 2 3 9
Câu 43. Cho phương trình 2
z mz 6i 0 . Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có
dạng m a bi ,
a b . Giá trị a 2b là: A. 0 B. 1 C. 2 D. 1
Câu 44. Cho số phức z thỏa mãn : z z 2i . Giá trị nhỏ nhất của biểu thức P z i z 4 là A. 5. B. 4. C. 3 3. D. 6. Trang78
Câu 45. Cho hàm số f x xác định và liên tục trên đoạn 5 ;
3 . Biết rằng diện tích hình phẳng S , S , S giới 1 2 3
hạn bởi đồ thị hàm số f x và đường parabol 2 y
g x ax bx c lần lượt là , m n, p . y 5 y= g(x) S3 2 S1 -1 -5 -2 O 2 3 x S2 y= f(x) 3 Tích phân f
xdx bằng 5 208 208 208 208
A. m n p .
B. m n p
C. m n p .
D. m n p . 45 45 45 45
Câu 46. Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng : x 2y z 1 0 ,
:2x y z 0 và điểm A1;2; 1
. Đường thẳng đi qua điểm A và song song với cả hai mặt phẳng
, có phương trình là x 1 y 2 z 1 x 1 y 2 z 1 A. . 2 4 2 . B. 1 3 5 x 1 y 2 z 1 x y 2 z 3 C. . 1 2 1 . D. 1 2 1
Câu 47. Cho hình nón có chiều cao và bán kính đáy đều bằng 1 . Mặt phẳng P qua đỉnh của hình nón và cắt đáy
theo dây cung có độ dài bằng 1. Khoảng cách từ tâm của đáy tới mặt phẳng P bằng 7 2 3 21 A. . B. . C. . D. 7 2 3 7
Câu 48. Có bao nhiêu cặp số nguyên dương ; x y thỏa mãn 2 x 2 cos 2.2 sin 2 y x y A. 1. B. 0 . C. 2 . D. 3 . 2 2
Câu 49. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x y 2 : 1
1 z 4 và một điểm M 2;3
;1 . Từ M kẻ được vô số các tiếp tuyến tới S , biết tập hợp các tiếp điểm là đường tròn C . Tính bán
kính r của đường tròn C . 2 3 3 2 A. r . B. r . C. r . D. 2 . 3 3 3 Trang79
Câu 50. Cho hàm số y = f (x) có đạo hàm 2
f x = x (x + )( 2 '( ) 1 x + 2mx + )
4 . Có bao nhiêu giá trị nguyên của
m không vượt quá 2021 để hàm số = ( 2 y
f x ) có đúng 1 điểm cực trị? A. 2021. B. 2022 . C. 5 . D. 2024 .
LỜI GIẢI CHI TIẾT
Câu 1. Cho số phức z 6 7i . Số phức liên hợp của z là
A. z 6 7i . B. z 6 7i . C. z 6 7i .
D. z 6 7i . Lời giải
z 6 7i z 6 7i
Vậy chọn đáp án D.
Câu 2. Mặt cầu S 2 2 2
: x y z 4x 1 0 có tọa độ tâm và bán kính R là:
A. I 2;0;0, R 3.
B. I 2;0;0, R 3.
C. I 0; 2;0, R 3. D. I 2 ;0;0, R 3. Lờigiải
Phương trình mặt cầu S có dạng 2 2 2
x y z 2ax 2by 2cz d 0 với 2 2 2
a b c d 0 , có tâm I ; a ; b c , bán kính 2 2 2
R a b c d .
Lựa chọn đáp án A. 1 x
Câu 3. Điểm nào dưới đây không thuộc đồ thị của hàm số y x 1 1
A. Điểm M 0 ;1 .
B. Điểm N 1 ;0 .
C. Điểm P 1;0 .
D. Điểm Q 2; . 3 Lờigiải Chọn B
Câu 4. Thể tích khối cầu có đường kính 2a bằng 3 4 a 3 a A. . B. 3 4 a . C. . D. 3 2 a . 3 3 Lời giải Chọn A 3 4 a
Đường kính của khối cầu là 2a , nên bán kính của nó là a , thể tích khối cầu là . 3
Câu 5. Nguyên hàm của hàm số 2x f x x là x 2 2 x 2x 2 x 2 x A. C . B. 2
2x x C . C. x C . D. 2 C . ln 2 2 ln 2 2 Lờigiải 2x x 1 Ta có 2 x 2 dx x C . ln 2 2
Câu 6. Cho hàm f x liên tục trên và có bảng xét dấu f x như sau: Trang80
Số điểm cực tiểu của hàm số là A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B
Ta thấy f x đổi dấu 2 lần từ sang khi qua các điểm x 1; x 1nênhàm số có 2 điểm cực tiểu.
Câu 7. Giải bất phương trình log 3x 1 3 . 2 1 10
A. x 3 B. x 3
C. x 3 D. x 3 3 Lờigiải ChọnA 1
Đkxđ: 3x 1 0 x 3 Bất phương trình 3
3x 1 2 3x 9 x 3 (t/m đk).
Vậy bpt có nghiệm x > 3.
Câu 8. Khi tăng độ dài các cạnh của một khối chóp lên 2 lần thì thể tích của khối chóp thay đổi như thà nào? A. Tăng 4 lần.. B. Tăng 8 lần.. C. Tăng 2 lần. D. Không thay đổi. Lời giải Chọn B 1
Thể tích khối chóp là: V . B h . 3
Độ dài cạnh đáy tăng lên 2 lần thì diện tích mặt đáy tăng 2 2 4 lần.
Cạnh bên tăng lên 2 lần thì chiều cao của hình chóp tăng lên 2 lần.
Vậy khi tăng độ dài các cạnh của một khối chóp lên 2 lần thì thể tích của khối chóp tăng lên 8 lần. 3 1
Câu 9. Tập xác định của hàm số y là x A. . B. 0; . C. \ 0 . D. 0; . Lời giải Chọn B
Câu 10. Nghiệm của phương trình log x 2 3 là: 2
A. x 6 .
B. x 8 .
C. x 11.
D. x 10 . Lờigiải ChọnD
Điều kiện: x 2 0 x 2 . Trang81 log
x 2 3 x 2 8 x 10 (thỏa). 2
Vậy phương trình có nghiệm x 10 . 2 2 2 Câu 11. Biết
f (x)dx 2
và g (x)dx 3.
Khi đó [ f (x) g(x)]dx bằng 1 1 1 A. 1 . B. 5 . C. 1. D. 6 . Lờigiải ChọnB 2 2 2
Ta có: [ f (x) g(x)]dx
f (x)dx g(x)dx 2 3 5 . 1 1 1
Câu 12. Cho số phức z 2 5i . Tìm số phức w iz z .
A. w 7 3i . B. w 3 3i .
C. w 3 3i . D. w 7 7i . Lời giải iz 5 2i
z 2 5i
w iz z 3 3i .
z 2 5i
Vậy chọn đáp án B.
Câu 13. Trong không gian Oxyz , cho mặt phẳng : x 2y 4z 1 0 .Vectơ nào dưới đây là một vectơ pháp
tuyến của mặt phẳng ?
A. n 1; 2; 4 .
B. n 1; 2; 4 .
C. n 1; 2; 4 .
D. n 1; 2; 4 4 2 1 3 Lời giải Chọn A.
Câu 14. Trong không gian với hệ trục tọa độ Oxyz , cho a i
2 j 3k . Tọa độ của vectơ a là A. 1 ;2; 3 . B. 2; 3 ; 1 . C. 2; 1 ; 3 . D. 3 ;2; 1 . Lời giải a i
2 j 3k a 1 ;2; 3 .
Câu 15. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức z 1 2i ?
A. Q 1; 2 . B. M 2 ;1 . C. P 2 ;1 .
D. N 1; 2 . Lời giải ChọnD
Điểm biểu diễn số phức z 1 2i là điểm N 1; 2 5x 1
Câu 16. Tiệm cận ngang của đồ thị hàm số y x là 1 1 A. y 1. B. y . C. y 1. D. y 5 . 5 Lời giải Chọn D Trang82 5x 1 lim y lim 5 x
x x 1 Ta có
y 5 là tiệm cận ngang của đồ thị hàm số. 5x 1 lim y lim 5 x x x 1
Câu 17. Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng? 3 2a 3 2a 1 A. log
1 3log a log b . B. log
1 log a log b . 2 2 2 b 2 2 2 b 3 3 2a 3 2a 1 C. log
1 3log a log b . D. log
1 log a log b . 2 2 2 b 2 2 2 b 3 Lời giải Chọn A 3 2a Ta có log log 3 2a log b 3
log 2 log a log b 1 3log a log b . 2 2 2 b 2 2 2 2 2
Câu 18. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y x 2x . B. 3
y x 3x . C. 4 2
y x 2x . D. 3
y x 3x . Lời giải Chọn A
Đường cong trong hình là đồ thị hàm trùng phương 4 2
y ax bx c a 0 có hệ số a 0 . x 4 z 2 z 1
Câu 19. Trong không gian Oxyz , cho đường thẳng d :
. Điểm nào sau đây thuộc d ? 2 5 1 A. N (4; 2; 1 ) . B. Q(2; 5;1) . C. M (4; 2;1) . D. P(2; 5 ;1) . Lờigiải ChọnA
Thế điểm N (4; 2; 1
) vào d ta thấy thỏa mãn nên chọn A.
Câu 20. Với n là số nguyên dương, công thức nào sao đây đúng? n!
A. P n 1 !. B. P .
C. P n .
D. P n! . n n n 1 ! n n Lời giải Chọn D n k ! C n
k !(n k)!
Câu 21. Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là Trang83 3V 3h V h A. B . B. B . C. B . D. B . h V h V Lời giải Chọn C V
Diện tích đáy của khối lăng trụ có thể tích V và có chiều cao h là: B . h
Câu 22. Tính đạo hàm của hàm số 1 e x f x . A. 1 e x f x .
B. f x x 1 e ln . C. e x f x . D. e x f x ln . Lời giải Chọn A
Ta có f x x 1 x x 1 x 1 e 1 e e .
Câu 23. Cho hàm số y f x có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? 1; ;1 1; ; 1 A. . B. . C. . D. . Lời giải Chọn D ; 1;
Từ bảng xét dấu ta thấy hàm số đã cho nghịch biến trên khoảng 1 1 và . ;
Vậy hàm số đã cho nghịch biến trên khoảng 1 .
Câu 24. Cho hình trụ có diện tích xung quanh S và bán kính đáy 2r . Độ dài đường sinh l của hình trụ đã cho xq
được tính theo công thức nào sau đây? 4 r S S 4S xq xq xq A. l . B. l . C. l . D. l . S 4 r 2 r r xq Lờigiải Chọn B S
Độ dài đường sinh l của hình trụ là: xq l . 4 r 5 5 Câu 25. Biết f
xdx 4. Giá trị của 3f xdx bằng 1 1 4 A. 7 . B. . C. 64 . D. 12 . 3 Lờigiải ChọnD Trang84 5 5 Ta có 3 f
xdx 3 f
xdx 3.4 12. 1 1
Câu 26. Cho cấp số cộng u
với u 3 ; u 9 . Công sai của cấp số cộng đã cho bằng n 1 2 A. 6. B. 3. C. 12. D. -6. Lời giải Chọn A Cấp số cộng u
có số hạng tổng quát là: u u n 1 d ; n 1 n
(Với u là số hạng đầu và d là công sai). 1
Suy ra có: u u d 9 3 d d 6. 2 1
Vậy công sai của cấp số cộng đã cho bằng 6.
Câu 27. Tìm họ nguyên hàm của hàm số f x 3x sin x . x
A. f x 2
dx 3x cos x C .
B. f x 2 3 dx
cos x C . 2 x
C. f x 2 3 dx
cos x C .
D. f xdx 3 cos x C . 2 Lờigiải x
Ta có f x x x x 2 3 d 3 sin dx
cos x C . 2
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ. y 4 3 1 O 1 x -1 -1
Hàm số đã cho đạt cực đại tại A. x 1 . B. x 3. C. x 0 . D. x 1 . Lời giải Chọn D 4 2
Câu 29. Tìm giá trị lớn nhất M của hàm số y x 2x 3 trên đoạn 0; 3 .
A. M 6
B. M 1
C. M 9
D. M 8 3 Lời giải Trang85 Chọn A Ta có: 3
y x x x 2 4 4 4 x 1 x 0
y 0 x 2 4 x 1 0 x 1 x 1 (l)
Ta có : y 0 3 ; y
1 2 ; y 3 6
Vậy giá trị lớn nhất của hàm số 4 2
y x 2x 3 trên đoạn 0; 3
là M y 3 6
Câu 30. Cho các hàm số sau: 1 x 1 3 2 (I) : y
x x 3x 4 ; (II) : y y x ; 2 (III) : 4 3 x 1 3
(IV) : y x 4x sin x ; 4 2
(V) : y x x 2 .
Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định? A.2. B. 4. C.3. D. 5. Lời giải Chọn C.
(I): y x x x 2 2 2 3
1 2 0, x . x 1 2 (II): y 0, x 1 2 x 1 (x 1) x (III): y 2 x 4 2 x 4 (IV): 2
y 3x 4 cos x 0,x ¡ (V): 3 2
y 4x 2x 2x(2x 1)
Câu 31. Với mọi a , b , x là các số thực dương thoả mãn log x 5 log a 3log b . Mệnh đề nào dưới đây 2 2 2 đúng?
A. x 5a 3b B. 5 3
x a b C. 5 3
x a b
D. x 3a 5b Lờigiải ChọnC Có 5 3 5 3 5 3
log x 5log a 3log b log a log b log a b x a b . 2 2 2 2 2 2 3
Câu 32. Cho tứ diện ABCD với 0 AC
AD, CAB DAB 60 , CD AD . Gọi là góc giữa hai đường 2
thẳng AB và CD . Chọn khẳng định đúng về góc . 3 1 A. cos B. 0 30 C. 0 60 D. cos 4 4 Hướng dẫn giải Chọn D Trang86
Ta có AB CD AB AD AC 0 0 . . A . B AD A . B AC A . B A . D cos 60 A . B A . C cos 60 3 1 0 0 . AB . AD cos 60 . AB . AD cos 60 . AB AD 2 4
cos AB CD A . B CD 1 1 , cos A . B CD 4 4 1 1 Câu 33. Biết f
x 2xdx 4 . Khi đó
f x dx bằng 0 0 A. 3 . B. 2 . C. 6 . D. 4 . Lờigiải ChọnA 1 f x 1
2x dx 4 f x 1 1 dx 2 d x x 4 f
xdx 41 3 0 0 0 0
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua điểm M 1;1;
1 và song song với mặt phẳng
:2x2yz 0 có phương trình là
A. 2x 2y z 3 0 .
B. x 2y z 0 .
C. 2x 2y z 3 0 .
D. x 2y z 2 0 .
Câu 35. Cho số phức z 1 i . Khẳng định nào sau đây là khẳng định đúng? z A. 1 i . B. 1 z .z 0 . C. z 2 . D. 2 z 2i . i Hướng dẫn giải
z i z i2 2 2 2 1 1
1 2.1.i i 2i 1 1 1 1 1 1
z 1 i z
i z .z 1 i i 1 2 2 2 2
z 1 i z 2 z 1 i 1 i i i
Câu 36. Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng a . Gọi M là trung điểm của CC (tham A B C
khảo hình bên). Khoảng cách từ M đến mặt phẳng bằng Trang87 21a 2a 21a 2a A. 14 . B. 2 . C. 7 . D. 4 . Hướng dẫn giải Chọn A.
d M , A B C C M 1 C M A B C C
d C , A B C C C 2 , suy ra . 2 3 1 1 1 a 3 a 3 V V .C C.S . . a C .A BC ABC.A B C A BC Ta có 3 3 3 4 12 . 2 a 7 S Lại có A B a 2 A BC
, CB a , A C a 2 4 . 3 a 3 d 3. C A B
C 3V a 21 C . A BC 12 , 2 S a A BC 7 7 Suy ra 4 .
d M A B C 1
d C A B
C 1 a 21 a 21 , , . Vậy 2 2 7 14
Câu 37. Chọn ngẫu nhiên 3 số trong 50 số tự nhiên 1; 2;3; 4...50 . Tính xác suất biến cố A: trong 3 số đó chỉ có 2 số là bội của 5 . A. 0.09 . B. 0, 08 . C. 0,19 . D. 0,18 . Lời giải Chọn A Trang88 n 3 C . 50
Gọi A :”trong 3 số đó chỉ có 2 số là bội của 5 ”. n A 2 1 C .C . 10 40 n A 9 Vậy P A . n 0, 09 98
Câu 38. Trong không gian Oxyz , cho ba điểm (
A 1; 2; 0), B(1;1; 2) và C(2;3;1) . Đường thẳng đi qua A và song
song với BC có phương trình là x 1 y 2 z x 1 y 2 z x 1 y 2 z x 1 y 2 z A. . . C. . D. . 1 2 B. 1 3 4 3 3 4 3 1 2 1 Lờigiải ChọnA
Gọi d là phương trình đường thẳng qua A1;2;0 và song song với BC . x 1 y 2 z
Ta có BC 1; 2; 1 d : 1 2 1 .
Câu 39. Có bao nhiêu số nguyên x thỏa mãn x x 1 x x 1 2 2
3 3 3log x 2 0 ? 2 A. 7 . B. 8 . C. 9 . D.10 . Lờigiải ChọnB x 2 0 Điều kiện
2 x 10 3
log x 2 0 2 Ta có
x x 1 x x 1 2 2 3 3
log x2 3 0 2 x x 1 x x 1 2 2 3 3 0 1 3 log x 2 0 2 2 Giải 1 : 2x 1 3 7.3x 2 0 x x 1 x x 1 x x 1 x2 x2
2 2 3 3 3.2 4.3 2 3 x2 2
1 x 2 0 x 2 . 3
Kết hợp điều kiện 2 x 10 x 2;10 Giải 2 : 3 log
x 2 0 x 2 8 x 10(thỏa). 2
Do x là số nguyên x 3; 4;5;6;7;8;9;1 0
Vậy có 8 giá trị x cần tìm Trang89
Câu 40. Cho hàm số f x có đạo hàm liên tục trên , f x có đồ thị C như hình dưới đây, trong đó , A B
là các điểm cực đại của C , các tiếp tuyến của C tại các tiếp điểm thuộc cung AB đều không song song với
hai đường thẳng đường thẳng y 2x , y 2x , lim f ' x ,
lim f 'x . x x
Xét phương trình f f 'x 1 0
1 , khẳng định nào sau đây đúng? A. 1 cóđúng hai nghiệm. B. 1 cóđúng ba nghiệm. C.
1 có ít nhất hai nghiệm. D. 1 có đúng ba nghiệm. Hướng dẫn giải Chọn C
Dựa vào đồ thị ta thấy f x 0 có ba nghiệm trong đó có một nghiệm dương là 3.
f 'x 2
Do f ' x 1 1 nên f f ' x
1 0 f ' x 1 3 . Tức . f ' x 2
Gọi x , x lần lượt là hoành độ của ,
A B . Do f ' x liên tục nên ta có: A B f 'x A 0 + x
x sao cho f 'x 2. 1 lim f ' x ; 1 A x f 'x B 0 + x
x sao cho f 'x 2 . 2 lim f ' x ; 2 B x
+ Các tiếp tuyến của C tại các tiếp điểm thuộc cung AB đều không song song với hai đường thẳng đường thẳng f ' x 2
y 2x , y 2x chứng tỏ x
x ; x . A B f ' x 2
Tóm lại, (*) có ít nhất hai nghiệm. 4
Câu 41. Cho hàm số f x . Biết f 0 4 và f x 2 '
2sin x 1, x , khi đó f
xdx bằng 0 2 16 4 2 4 2 15 2 16 16 A. . B. . C. . D. . 16 16 16 16 Lờigiải ChọnA Trang90 1
Ta có f x 2 2 sin x
1 dx 2 cos 2x dx 2x sin 2x C. 2
Vì f 0 4 C 4 Hay f x 1
2x sin 2x 4. 2 4 4 1 Suy ra f
xdx 2x sin2x4 dx 2 0 0 2 2 1 1 16 4 2 x cos 2x 4x 4 . 4 16 4 16 0
Câu 42. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại B , AB a , ACB 60 , cạnh bên
SA vuông góc với mặt đáy và SB hợp với mặt đáy một góc 45 . Tính thể tích V của khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 a 3 A. V B. V C. V D. V 18 12 2 3 9 Hướng dẫn giải Chọn A S A C B AB 3
ABC là tam giác vuông tại B , AB a , ACB 60 BC a 0 tan 60 3 SB ABC SB AB 0 , ,
45 nên tam giác SAB vuông cân tại S SA AB a 3 1 1 1 1 3 a 3 V S .SA . B . A BC.SA . a a a S.ABC 3 ABC 3 2 6 3 18
Câu 43. Cho phương trình 2
z mz 6i 0 . Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có
dạng m a bi ,
a b . Giá trị a 2b là: A. 0 B. 1 C. 2 D. 1 Lờigiải
Gọi z , z là hai nghiệm của phương trình đã cho 1 2 b
S z z m 1 2 a Theo Viet, ta có: c
P z .z 6 i 1 2 a
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có: Trang91
z z S 2P m 12i 5 m 5 12i m 3 2i2 2 2 2 2 2 2 1 2
m 3 2i
a 3;b 2
a 2b 3 4 1 Ta chọn đáp án A.
Câu 44. Cho số phức z thỏa mãn : z z 2i . Giá trị nhỏ nhất của biểu thức P z i z 4 là A. 5. B. 4. C. 3 3. D. 6. Lờigiải ChọnA
Gọi M (x; y) là điểm biểu diễn số phức z. Ta có z z 2i y 1 0, tức biểu diễn hình học của số phức
thỏa mãn giả thiết là đường thẳng y 1 0. Xét điểm A(0;1) và B(4; 0) thì P z i z 4 MA M . B Dễ thấy ,
A B cùng phía với đường thẳng y 1 0 nên MA MB nhỏ nhất bằng BA trong đó A (
0;3) đối xứng với A
qua đường thẳng y 1 0. B A M' M A'
Do đó MA MB nhỏ nhất bằng BA 5.
Câu 45. Cho hàm số f x xác định và liên tục trên đoạn 5 ;
3 . Biết rằng diện tích hình phẳng S , S , S giới 1 2 3
hạn bởi đồ thị hàm số f x và đường parabol 2 y
g x ax bx c lần lượt là , m n, p . y 5 y= g(x) S3 2 S1 -1 -5 -2 O 2 3 x S2 y= f(x) 3 Tích phân f
xdx bằng 5 208 208 208 208
A. m n p .
B. m n p
C. m n p .
D. m n p . 45 45 45 45 Trang92 Lờigiải ChọnB 2 2 2 2 2 S
f x g x dx f x dx g x dx f x dx S g x dx . 1 1 5 5 5 5 5 0 0 0 0 0 S
g x f x dx g x dx f x dx f x dx g x dx S . 2 2 2 2 2 2 2 2 3 3 3 3 S
f x g x dx f x dx g x dx f x dx S g x dx . 3 1 5 0 0 0 0 3 3 Do vậy:
f xdx S S S g x dx 1 2 3 . 5 5 3
Từ đồ thị ta thấy gxdx
là số dương. Mà 4 đáp án chỉ có B là phù hợp, nên ta chọn B. 5 3
Chúý: Có thể tính
gxdx như sau: 5
Từ đồ thị hàm số y g x ta thấy nó đi qua các điểm 5 ;2, 2
;0, 0;0 nên ta có:
25a 5b c 2 2 4 3 3 2 4 208
4a 2b c 0 a , b , c 0. Do đó: g x 2 dx x x dx . 15 15 15 15 45 c 0 5 5
Câu 46. Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng : x 2y z 1 0 ,
:2x y z 0 và điểm A1;2; 1
. Đường thẳng đi qua điểm A và song song với cả hai mặt phẳng
, có phương trình là x 1 y 2 z 1 x 1 y 2 z 1 A. . 2 4 2 . B. 1 3 5 x 1 y 2 z 1 x y 2 z 3 C. . 1 2 1 . D. 1 2 1 Lờigiải ChọnB
mp có véc tơ pháp tuyến là n 1; 2
;1 , mp có véc tơ pháp tuyến là n 2;1; 1 . 2 1
Đường thẳng có véc tơ chỉ phương là u n ;n 1;3;5 . 1 2 x 1 y 2 z 1
Phương trình của đường thẳng : . 1 3 5
Câu 47. Cho hình nón có chiều cao và bán kính đáy đều bằng 1 . Mặt phẳng P qua đỉnh của hình nón và cắt đáy
theo dây cung có độ dài bằng 1. Khoảng cách từ tâm của đáy tới mặt phẳng P bằng 7 2 3 21 A. . B. . C. . D. 7 2 3 7 Trang93 Lời giải ChọnD
Ta có l h 1
Mặt phẳng P qua đỉnh của hình nón và cắt đáy theo dây cung AB có độ dài bằng 1. I , K là hình chiếu O lên
AB ; SI . Ta có AB SIO OK SAB 2 1 3 ta có 2 2 2 IO
R OA 1 . 2 2 1 1 1 OI.SO 21 OK . 2 2 2 2 2 OK OI OS 7 OI OS
Câu 48. Có bao nhiêu cặp số nguyên dương ; x y thỏa mãn 2 x 2 cos 2.2 sin 2 y x y A. 1. B. 0 . C. 2 . D. 3 . Lời giải: Chọn B 2 2 Ta có x 2 cos y x 1 cos y 2
2.2 x sin y 2 2 x 1 2 cos y . (1)
Đặt 2t 2t f t t f t .ln 2 1 0, t 0 .
Suy ra hàm số y f t là hàm số đồng biến trên 0; .
Suy ra f x f 2 y 2 2 1 1 cos
x 1 cos y x sin y x 0 vô lí.
Vậy không tồn tại cặp số nguyên dương ;
x y nào thỏa mãn đề bài. 2 2
Câu 49. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x y 2 : 1
1 z 4 và một điểm M 2;3
;1 . Từ M kẻ được vô số các tiếp tuyến tới S , biết tập hợp các tiếp điểm là đường tròn C . Tính bán
kính r của đường tròn C . 2 3 3 2 A. r . B. r . C. r . D. 2 . 3 3 3 Hướng dẫn giải Trang94
Mặt cầu S có tâm I 1;1;0 và bán kính R 2 .
Ta có IM 1; 2; 1 và IM 6 .
Gọi H là một tiếp điểm tùy ý khi kẻ tiếp tuyến từ Oxyz đến mặt cầu, khi đó 2 2
MH IM R 2 . Gọi O là
tâm của đường tròn C khi đó IM HO và HO r . HI HM Ta có HI.HM . 2 2 2 3 H . O IM r . IM 6 3
Câu 50. Cho hàm số y = f (x) có đạo hàm 2
f x = x (x + )( 2 '( ) 1 x + 2mx + )
4 . Có bao nhiêu giá trị nguyên của
m không vượt quá 2021 để hàm số = ( 2 y
f x ) có đúng 1 điểm cực trị? A. 2021. B. 2022 . C. 5 . D. 2024 . Hướng dẫn giải Chọn D ¢ Ta có: y = ( 2 f x ) 2 4 2 4 2 5 2 4 2 ' ( ) = 2 . x f '(x ) = 2 .
x x (x + 1)(x + 2mx + 4) = 2x (x + 1)(x + 2mx + 4) ; x é = 0 Khi đó: y ' 0 ê = Û . 2 ê 4 2 t= x 2
x + 2mx + 4 = 0 ¾ ¾ ¾® t + 2mt + 4 = 0 ê ( ) 1 ë Ta thấy nghiệm của ( )
1 nếu có sẽ khác 0 . Nên x = 0 là 1 cực trị của hàm số.
Do đó để hàm số có 1 điểm cực trị thì ( )
1 hoặc vô nghiệm hoặc có nghiệm kép, hoặc có 2 nghiệm âm 2 éD ' = m - 4 £ 0 é- 2 £ m £ 2 ê ê ê 2 í ê ïê D ' = m - 4 > 0 íï m é < - 2 é- 2 £ m £ 2 ï êï Û ï Û ê ê ï Û ê Û m ³ - 2 ï êï .
ìê S = - 2m < 0 ì m ê > 2 m ê > 2 ê ë ë ï ï êï êï ïê P = 4 > 0 ïê m > 0 ïî ï ë îë íï m Î ¢ Kết hợp với ïì
Þ m Î {- 2;- 1;0;1;2;...;2018;202 } 1 ï
: có 2024 giá trị nguyên của m . m £ 2021 ïî ĐỀ 5
ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2022
BÁM SÁT ĐỀ MINH HỌA MÔN TOÁN Thời gian: 90 phút Trang95
Câu 1. Cho số phức z 3 4i . Môđun của số phức z là A. 3 . B. 5 . C. 4 . D. 9.
Câu 2. Phương trình mặt cầu có tâm I 1 ;2; 3
, bán kính R 3 là: 2 2 2 2 2 2 A. x
1 y 2 z 3 9. B. x
1 y 2 z 3 3. 2 2 2 2 2 2 C. x
1 y 2 z 3 9. D. x
1 y 2 z 3 9.
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 4 2
y x 3x 2
A. Điểm M 2; 2 .
B. Điểm N 0; 2 .
C. Điểm P 1 ;0.
D. Điểm Q 1 ; 6 .
Câu 4. Thể tích khối cầu bán kính 3 cm bằng A. 3 36 cm . B. 3 108 cm . C. 3 9 cm . D. 3 54 cm . Câu 5. Hàm số 2 x
F x e là nguyên hàm của hàm số nào trong các hàm số sau: 2 x 2 2 e A. ( ) 2 x f x xe . B. 2 ( ) x
f x x e 1. C. 2 ( ) x f x e .
D. f (x) . 2x
Câu 6. Cho hàm số f ( x) liên tục trên và có bảng xét dấu của f ( x) như sau:
Số điểm cực tiểu của hàm số đã cho là A. 2. B. 4. C. 3. D. 1.
Câu 7. Tập nghiệm của bất phương trình 2 x 13 3 27 là A. 4; . B. 4 ;4 . C. ; 4 . D. 0; 4 .
Câu 8. Công thức tính thể tích của khối chóp có diện tích đáy B và chiều cao h là 4 1 1 A. V Bh . B. V Bh .
C. V Bh . D. V Bh . 3 3 2 7 1
Câu 9. Tập xác định của hàm số y là 1 x A. . B. 1; . C. \ 1 . D. ;1 .
Câu 10. Nghiệm của phương trình log x 2 2 là 3 A. x 11. B. x 10 . C. x 7 . D. 8 . 2 2 2 Câu 11. Biết f
xdx 2 và g
xdx 6, khi đó f
x gxdx bằng 1 1 1 A. 8 . B. 4 . C. 4 . D. 8 .
Câu 12. Cho số phức z i i2 3 2 1
. Môđun của w iz z là A.2. B. 2 2 . C. 1. D. 2 . Trang96
Câu 13. Trong không gian với hê ̣ to ̣a đô ̣ Oxyz , cho mă ̣t phẳng P : 3x z 2 0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của P ? r r r r A. n 3; 0; 1 B. n 3; 1 ;2 C. n 3; 1 ;0 D. n 1 ;0; 1 4 3 1 2
Câu 14. Trong không gian với hệ tọa độ Oxyz , cho a 2; 3; 3 , b 0; 2;
1 , c 3; 1; 5 . Tìm tọa độ
của vectơ u 2a 3b 2c .
A. 10; 2;13 . B. 2 ; 2; 7 . C. 2 ; 2; 7 . D. 2 ; 2; 7 .
Câu 15. Cho số phức z 2 5i . Số phức đối của z có tọa độ điểm biểu diễn là A. 2 ; 5 . B. 2;5 . C. 5; 2 . D. 5; 2 . 2x 1
Câu 16. Tiệm cận ngang của đồ thị hàm số y x là: 1 1 A. y .
B. y 1.
C. y 1. D. y 2 . 2
Câu 17. Với a, b là các số thực dương tùy ý và a 1, log b bằng: 5 a 1 1 A. 5 log b . B. log b .
C. 5 log b . D. log b . a 5 a a 5 a
Câu 18. Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên. Số
nghiệm thực của phương trình f x 1 là A. 1 . B. 0 . C. 2 . D. 3 . x 3 y 1 z 2
Câu 19. Trong không gian Oxyz , cho đường thẳng d :
. Điểm nào dưới đây thuộc d ? 2 4 1 A. N 3; 1 ; 2 B. Q 2; 4 ;1
C. P 2; 4; 1
D. M 3;1; 2
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. A A A . D. A n k !(n . B. k)! n (k . C. n)! n k ! n (n . k)!
Câu 21. Thể tích khối lăng trụ có diện tích đáy B và có chiều cao h là 4 1 A. V . B h . B. V Bh . C. V Bh .
D. V 3Bh . 3 3
Câu 22. Tính đạo hàm của hàm số 20 x y 20x A. y . B. 1 20 x y . C. 20 x y . D. 20 . x y ln 20 . n l 20
Câu 23. Cho hàm số y f x có bảng biến thiên như sau Trang97
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? 1 ;0 ;0 1; 0; 1 A. B. C. D.
Câu 24. Cho hình trụ có diện tích xung quanh S và độ dài đường sinh 3l . Bán kính đáy r của hình trụ đã cho xq
được tính theo công thức nào sau đây? 6S S S xq xq xq 2 l A. r . B. r . C. r . D. r . l 2 l 6 l Sxq 2 3 Câu 25. Biết f
xdx 2. Giá trị của 3f xdx bằng 1 1 2 A. 5 . B. 6 . C. . D. 8 . 3
Câu 26. Cho cấp số cộng u
với u 2 và u 10
. Công sai của cấp số cộng đã cho bằng n 1 7 A. 2 . B. 3 . C. 1. D. 2 .
Câu 27. Họ nguyên hàm của hàm số f (x) x s inx là 2 x 2 x A. 2 x cos x+C B. 2 x cos x+C C. cos x+C D. cos x+C 2 2
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ. y 1 -1 1 0 x -1
Hàm số đã cho đạt cực tiểu tại A. x 0 . B. x 1 . C. x 1 . D. x 1 .
Câu 29. Tìm tập giá trị của hàm số y
x 1 9 x
A. T 1; 9 .
B. T 2 2; 4 .
C. T 1; 9 . D. T 0; 2 2 .
Câu 30. Đồ thị hàm số 3 2
y f (x) ax bx cx d . Hình nào trong 4 hình dưới đây mà hàm số luôn đồng biến trên ? Trang98 y y 3 2 x 1 O O x 1 1 A. Hình 1. B. Hình 2. y 1 y x O 1 2 1 O x 1 C. Hình 3. D. Hình 4.
Câu 31. Xét tất cả các số dương a và b thỏa mãn log a log (ab) . Mệnh đề nào dưới đây đúng? 2 8 A. 2 a b . B. 3 a b .
C. a b . D. 2 a b .
Câu 32. Cho tứ diện ABCD có AB CD 2a . Gọi M , N lần lượt là trung điểm AD và BC . Biết
MN a 3 , góc giữa hai đường thẳng AB và CD bằng. A. 0 45 . B. 0 90 . C. 0 60 . D. 0 30 . 1 1
Câu 33. Biết f
x2x dx 5
. Khi đó f xdx bằng 0 0 A. 7 . B. 3 . C. 5 . D. 4 .
Câu 34. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng đi qua điểm M 3;2; 1 và vuông x 1 2t
góc với đường thẳng d : y 2
3t (t ) . z 35t
A. 2x 3 y 5z 5 0 .
B. 2x 3y 5z 5 0 .
C. 2x 3 y 5z 5 0 . D. 2x 3y 5z 5 0 .
Câu 35. Cho số phức z 2 5i . Tìm số phức w iz z .
A. w 7 3i . B. w 3 3i .
C. w 3 3i . D. w 7 7i . Trang99
Câu 36. Cho hình hộp ABC . D A B C
D có đáy ABCD là hình vuông cạnh a , tâm O . Hình chiếu vuông góc ABCD
của A lên mặt phẳng
trùng với O . Biết tam giác A
A C vuông cân tại A . Tính khoảng cách h từ AB B A
điểm D đến mặt phẳng . 6 a 2 2 6 h a h a h a h A. 6 . B. 6 . C. 3 . D. 3 .
Câu 37. Chọn ngẫu nhiên hai số khác nhau từ 27 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng 13 14 1 365 A. . B. . C. . D. . 27 27 2 729
Câu 38. Trong không gian với hệ tọa độ Oxyz , đường thẳng đi qua điểm A 2
;4;3 và vuông góc với mặt
phẳng :2x 3y 6z 19 0 có phương trình là x 2 y 3 z 6 x 2 y 4 z 3 A. 2 . B. 4 3 2 . 3 6 x 2 y 3 z 6 x 2 y 4 z 3 C. 2 . D. 4 3 2 3 . 6 x x 1
Câu 39. Tập nghiệm của bất phương trình 2 3 9 x 1 3 3 1 0
chứa bao nhiêu số nguyên ? 27 A. 2. B. 3. C. 4. D. 5.
Câu 40. Cho hàm số y f x có đồ thị như hình vẽ:
Tìm số nghiệm của phương trình g x 0 , biết g x 3 f x 2
f x 8. A. 13 . B. 15 . C. 17 . D. 19 . 4
Câu 41. Cho hàm số f x . Biết f 0 4 và f x 2
2sin x 3, x
R , khi đó f
xdxbằng 0 2 2 2 8 8 2 8 2 2 3 2 3 A. . B. . C. . D. . 8 8 8 8 Trang100
Câu 42. Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA ABC . Mặt phẳng SBC cách A một
khoảng bằng a và hợp với mặt phẳng ABC góc 0
30 . Thể tích của khối chóp S.ABC bằng 3 8a 3 8a 3 3a 3 4a A. . B. . C. . D. . 9 3 12 9
Câu 43. Trong tập số phức, giá trị của m để phương trình bậc hai 2
z mz i 0 có tổng bình phương hai nghiệm bằng 4 i là:
A. 1 i B. 1 i
C. 1 i D. 1 i
Câu 44. Cho số phức z thoả mãn z 1 2i
5 . Giá trị lớn nhất của z 1 i bằng A. 5 . B. 5 2 . C. 20 . D. 2 5 . 1
Câu 45. Cho hai hàm số f x 3 2
ax bx cx 1 và g x 2
dx ex , a , b ,
c d, e . Biết rằng đồ thị 2
của hàm số y f (x) và y g (x) cắt nhau tại ba điểm có hoành độ lần lượt 3; 1; 2 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 253 125 253 125 A. B. C. D. 12 12 48 48
Câu 46. Trong không gian Oxyz , cho điểm A2;0; 1
và mặt phẳng P:x y 1 0 . Đường thẳng đi qua
A đồng thời song song với P và mặt phẳng Oxy có phương trình là x 3 t x 2 t x 1 2t x 3 t
A. y 2t .
B. y t . C. y 1 .
D. y 1 2t . z 1 t z 1 z t z t
Câu 47. Cho hình nón đỉnh S , đáy là đường tròn ;5 O
.Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn
đáy tại hai điểm A và B sao cho SA AB 8. Tính khoảng cách từ O đến SAB . 3 3 3 2 13 A. 2 2 . B. . C. . D. . 4 7 2 2 2 2 2
Câu 48. Số cặp nghiệm ;
x y nguyên của bất phương trình x y
5x 2 xy2 y 3 2 .2
x y 3 là A. 0 . B.1. C. 2 . D. 3 . Trang101
Câu 49. Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu S có phương trình là 2 2 2
x y z 2x 2 y 6z 7 0 . Cho ba điể
m A , M , B nằm trên mặt cầu S sao cho AMB 90 . Diện
tích tam giác AMB có giá trị lớn nhất bằng? A. 4 . B. 2 . C. 4 . D. Không tồn tại.
Câu 50. Cho hàm số f (x) có f (
¢ x)= x(x- )( 2 1 x - 2mx + )
1 . Hỏi có tất cả bao nhiêu số nguyên m không
vượt quá 2022 sao cho hàm số ( )= ( 2 g x
f x ) có 7 điểm cực trị? A. 2023. B. 2020 . C. 2021. D. 2022 .
LỜI GIẢI CHI TIẾT
Câu 1. Cho số phức z 3 4i . Môđun của số phức z là A. 3 . B. 5 . C. 4 . D. 9. Lờigiải 2 2
z 3 4i z 3 4 5
Vậy chọn đáp án B.
Câu 2. Phương trình mặt cầu có tâm I 1 ;2; 3
, bán kính R 3 là: 2 2 2 2 2 2 A. x
1 y 2 z 3 9. B. x
1 y 2 z 3 3. 2 2 2 2 2 2 C. x
1 y 2 z 3 9. D. x
1 y 2 z 3 9. Lờigiải Mặt cầu có tâm 2 2 2 I 1 ;2; 3
, bán kính R 3 có hương trình : x
1 y 2 z 3 9.
Lựa chọn đáp án A.
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 4 2
y x 3x 2
A. Điểm M 2; 2 .
B. Điểm N 0; 2 .
C. Điểm P 1 ;0.
D. Điểm Q 1 ; 6 . Lờigiải Chọn C
Câu 4. Thể tích khối cầu bán kính 3 cm bằng A. 3 36 cm . B. 3 108 cm . C. 3 9 cm . D. 3 54 cm . Lờigiải 4 4 Thể tích khối cầu là: 3 3 V . .R . .3 36 3 cm . 3 3 Câu 5. Hàm số 2 x
F x e là nguyên hàm của hàm số nào trong các hàm số sau: 2 x 2 2 e A. ( ) 2 x f x xe . B. 2 ( ) x
f x x e 1. C. 2 ( ) x f x e .
D. f (x) . 2x Lờigiải ChọnA 2 2
Ta có f x F x
x 2 x f x e xe . Trang102
Câu 6. Cho hàm số f ( x) liên tục trên và có bảng xét dấu của f ( x) như sau:
Số điểm cực tiểu của hàm số đã cho là A. 2. B. 4. C. 3. D. 1. Lời giải Chọn A
Câu 7. Tập nghiệm của bất phương trình 2 x 13 3 27 là A. 4; . B. 4 ;4 . C. ; 4 . D. 0; 4 . Lời giải Chọn B 2 2 Ta có: x 13 x 13 3 2 2 3 27 3
3 x 13 3 x 16 x 4 4 x 4 .
Vậy tập nghiệm của bất phương trình đã cho là S 4 ;4 .
Câu 8. Công thức tính thể tích của khối chóp có diện tích đáy B và chiều cao h là 4 1 1 A. V Bh . B. V Bh .
C. V Bh . D. V Bh . 3 3 2 Lời giải Chọn B 1
Công thức tính thể tích của khối chóp có diện tích đáy B và chiều cao h là V Bh . 3 7 1
Câu 9. Tập xác định của hàm số y là 1 x A. . B. 1; . C. \ 1 . D. ;1 . Lời giải Chọn D
Câu 10. Nghiệm của phương trình log x 2 2 là 3 A. x 11. B. x 10 . C. x 7 . D. 8 . Lờigiải ChọnA
Điều kiện: x 2
Phương trình tương đương với 2
x 2 3 x 11 2 2 2 Câu 11. Biết f
xdx 2 và g
xdx 6, khi đó f
x gxdx bằng 1 1 1 A. 8 . B. 4 . C. 4 . D. 8 . Lờigiải ChọnB Trang103 2 2 2 Ta có: f
x gxdx f
xdx g
xdx 26 4 . 1 1 1
Câu 12. Cho số phức z i i2 3 2 1
. Môđun của w iz z là A.2. B. 2 2 . C. 1. D. 2 . Lời giải iz
i i i z
3 2i1 i 4 6 6 4 2 3 2i
2i 4 6i z 4 6i
w iz z 6
4i 4 6i 2 2i
w 2 2 2 2 8 2 2
Vậy chọn đáp án B.
Câu 13. Trong không gian với hê ̣ to ̣a đô ̣ Oxyz , cho mă ̣t phẳng P : 3x z 2 0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của P ? r r r r A. n 3; 0; 1 B. n 3; 1 ;2 C. n 3; 1 ;0 D. n 1 ;0; 1 4 3 1 2 Lờigiải ChọnA r
Vectơ pháp tuyến của mă ̣t phẳng P : 3x z 2 0 là n 3;0; 1 . 2
Câu 14. Trong không gian với hệ tọa độ Oxyz , cho a 2; 3; 3 , b 0; 2;
1 , c 3; 1; 5 . Tìm tọa độ
của vectơ u 2a 3b 2c .
A. 10; 2;13 . B. 2 ; 2; 7 . C. 2 ; 2; 7 . D. 2 ; 2; 7 . Lờigiải Có 2a 4; 6
;6; 3b 0;6; 3
; 2c 6 ;2; 10 .
Khi đó: u 2a 3b 2c 2; 2; 7.
Câu 15. Cho số phức z 2 5i . Số phức đối của z có tọa độ điểm biểu diễn là A. 2 ; 5 . B. 2;5 . C. 5; 2 . D. 5; 2 . Lời giải
z 2 5i z 2
5i . Vậy điểm biểu diễn của z là 2 ; 5
Vậy chọn đáp án A. 2x 1
Câu 16. Tiệm cận ngang của đồ thị hàm số y x là: 1 1 A. y .
B. y 1.
C. y 1. D. y 2 . 2 Lời giải Chọn D Trang104 1 2 2x 1 Ta có lim lim
x 2 . Suy ra đồ thị hàm số có tiệmcận ngang là y 2 . x x 1 x 1 1 x
Câu 17. Với a, b là các số thực dương tùy ý và a 1, log b bằng: 5 a 1 1 A. 5 log b . B. log b .
C. 5 log b . D. log b . a 5 a a 5 a Lời giải Chọn D.
Câu 18. Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên. Số
nghiệm thực của phương trình f x 1 là A. 1 . B. 0 . C. 2 . D. 3 . Lời giải Chọn D
Từ đồ thị hàm số ta có số nghiệm thực của phương trình f x 1 là 3 . x 3 y 1 z 2
Câu 19. Trong không gian Oxyz , cho đường thẳng d :
. Điểm nào dưới đây thuộc d ? 2 4 1 A. N 3; 1 ; 2 B. Q 2; 4 ;1
C. P 2; 4; 1
D. M 3;1; 2 Lờigiải ChọnA 3 3 1 1 2 2 Ta có: 0 N 3; 1 ; 2 thuộc d . 2 4 1 . Vậy
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. A A A . D. A n k !(n . B. k)! n (k . C. n)! n k ! n (n . k)! Lời giải Chọn D n k ! A n (n k)!
Câu 21. Thể tích khối lăng trụ có diện tích đáy B và có chiều cao h là 4 1 A. V . B h . B. V Bh . C. V Bh .
D. V 3Bh . 3 3 Lời giải Chọn A
Thể tích khối lăng trụ có diện tích đáy B và có chiều cao h là: V . B h .
Câu 22. Tính đạo hàm của hàm số 20 x y Trang105 20x A. y . B. 1 20 x y . C. 20 x y . D. 20 . x y ln 20 . n l 20 Lời giải Chọn D
Áp dụng công thức: u . u a
u a ln a ta có: 20 x 2 0 .x y ln 20 .
Câu 23. Cho hàm số y f x có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? 1 ;0 ;0 1; 0; 1 A. B. C. D. Lời giải Chọn D 0; ;
Dựa vào bảng biến thiên ta có hàm số đã cho nghịch biến trên các khoảng 1 1 và .
Câu 24. Cho hình trụ có diện tích xung quanh S và độ dài đường sinh 3l . Bán kính đáy r của hình trụ đã cho xq
được tính theo công thức nào sau đây? 6S S S xq xq xq 2 l A. r . B. r . C. r . D. r . l 2 l 6 l Sxq Lờigiải Chọn C S
Bán kính đáy r của hình trụ là: xq r . 6 l 2 3 Câu 25. Biết f
xdx 2. Giá trị của 3f xdx bằng 1 1 2 A. 5 . B. 6 . C. . D. 8 . 3 Lờigiải ChọnB 2 2 Ta có : 3 f
xdx 3 f
xdx 3.2 6 . 1 1
Câu 26. Cho cấp số cộng u
với u 2 và u 10
. Công sai của cấp số cộng đã cho bằng n 1 7 A. 2 . B. 3 . C. 1. D. 2 . Lời giải Chọn D Trang106 10 2 Ta có: 7 1 6 u u u u d d hay d 2 . 7 1 6 6
Câu 27. Họ nguyên hàm của hàm số f (x) x s inx là 2 x 2 x A. 2 x cos x+C B. 2 x cos x+C C. cos x+C D. cos x+C 2 2 Lờigiải ChọnC
Theo bảng nguyên hàm cơ bản
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ. y 1 -1 1 0 x -1
Hàm số đã cho đạt cực tiểu tại A. x 0 . B. x 1 . C. x 1 . D. x 1 . Lời giải Chọn C
Câu 29. Tìm tập giá trị của hàm số y
x 1 9 x
A. T 1; 9 .
B. T 2 2; 4 .
C. T 1; 9 . D. T 0; 2 2 . Lời giải
Tập xác định: D 1; 9 1 1 x 1 y
0 9 x x 1 x 5. 2 x 1 2 9 x 9
x x 1 f
1 f 9 2 2 ; f 5 4
Vậy tập giá trị là T 2 2; 4 .
Câu 30. Đồ thị hàm số 3 2
y f (x) ax bx cx d . Hình nào trong 4 hình dưới đây mà hàm số luôn đồng biến trên ? Trang107 y y 3 2 x 1 O O x 1 1 A. Hình 1. B. Hình 2. y 1 y x O 1 2 1 O x 1 C. Hình 3. D. Hình 4.
Câu 31. Xét tất cả các số dương a và b thỏa mãn log a log (ab) . Mệnh đề nào dưới đây đúng? 2 8 A. 2 a b . B. 3 a b .
C. a b . D. 2 a b . Lời giải Chọn D Theo đề ta có: 1
log a log (ab) log a
log (ab) 3log a log (ab) 2 8 2 2 2 2 3 3 3 2
log a log (ab) a ab a b 2 2
Câu 32. Cho tứ diện ABCD có AB CD 2a . Gọi M , N lần lượt là trung điểm AD và BC . Biết
MN a 3 , góc giữa hai đường thẳng AB và CD bằng. A. 0 45 . B. 0 90 . C. 0 60 . D. 0 30 . Hướng dẫn giải Trang108
Gọi P là trung điểm AC , ta có PM //CD và PN //AB , suy ra AB,CD
PM,PN .
Dễ thấy PM PN a . 2 2 2 2 2 2
PM PN MN
a a 3a 1 Xét P
MN ta có cosMPN 2PM .PN 2. . a a 2 0 MPN AB CD 0 0 0 120 , 180 120 60 . 1 1
Câu 33. Biết f
x2x dx 5
. Khi đó f xdx bằng 0 0 A. 7 . B. 3 . C. 5 . D. 4 . Lờigiải ChọnD 1 1 1 f
x2x dx 5 f
xdx 2xdx 5 0 0 0 1 1 1 f x 1 2 dx x 5 f
xdx 15 f
xdx 4. 0 0 0 0
Câu 34. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng đi qua điểm M 3;2; 1 và vuông x 1 2t
góc với đường thẳng d : y 2
3t (t ) . z 35t
A. 2x 3 y 5z 5 0 .
B. 2x 3y 5z 5 0 .
C. 2x 3 y 5z 5 0 . D. 2x 3y 5z 5 0 .
Câu 35. Cho số phức z 2 5i . Tìm số phức w iz z .
A. w 7 3i . B. w 3 3i .
C. w 3 3i . D. w 7 7i . Hướng dẫn giải iz 5 2i
z 2 5i
w iz z 3 3i .
z 2 5i
Vậy chọn đáp án B. Trang109
Câu 36. Cho hình hộp ABC . D A B C
D có đáy ABCD là hình vuông cạnh a , tâm O . Hình chiếu vuông góc ABCD
của A lên mặt phẳng
trùng với O . Biết tam giác A
A C vuông cân tại A . Tính khoảng cách h từ AB B A
điểm D đến mặt phẳng . 6 a 2 2 6 h a h a h a h A. 6 . B. 6 . C. 3 . D. 3 . Hướng dẫn giải Chọn D 2 2 2 2 Ta có: AC
AB BC a a a 2 . AC a 2 A O Vì tam giác A
A C vuông cân tại A nên ta có: 2 2 .
Gọi M là trung điểm của AB . Suy ra OM AB . A OM Trong mặt phẳng : kẻ OH A M . AB A OM Ta có:
(vì AB OM và AB
A O ). Suy ra AB OH . OH A M
OH AB B A OH d ; O ABB A OH Vì AB . Do đó: . d ; D AB B
A 2d ; O AB B A 2OH
Do D, O, B thẳng hàng và DB 2OB nên . a 2 a . A . O OM a 6 2 2 OH 2 2 2 2 A O 6 OM
a 2 a 2 2 Ta có: . 6 ; 2 a d D ABB A h OH Vậy 3 .
Câu 37. Chọn ngẫu nhiên hai số khác nhau từ 27 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng Trang110 13 14 1 365 A. . B. . C. . D. . 27 27 2 729 Lờigiải ChọnA
Không gian mẫu có số phần tử là: 2 C 351. 27
Hai số có tổng là một số chẵn khi hai số đó là hai số chẵn hoặc hai số đó là hai số lẻ do đó ta có 2 2
C C 78 91 169 cách chọn. 13 14 169 13
Xác suất cần tính là: P . 351 27
Câu 38. Trong không gian với hệ tọa độ Oxyz , đường thẳng đi qua điểm A 2
;4;3 và vuông góc với mặt
phẳng :2x 3y 6z 19 0 có phương trình là x 2 y 3 z 6 x 2 y 4 z 3 A. 2 . B. 4 3 2 . 3 6 x 2 y 3 z 6 x 2 y 4 z 3 C. 2 . D. 4 3 2 3 . 6 Lờigiải ChọnB
Mặt phẳng :2x 3y 6z 19 0 có vectơ pháp tuyến là n 2; 3 ;6 .
Đường thẳng đi qua điểm A 2
;4;3 và vuông góc với mặt phẳng nhận n 2; 3 ;6 làm vectơ chỉ x 2 y 4 z 3
phương, khi đó phương trình đường thẳng là: . 2 3 6 x x 1
Câu 39. Tập nghiệm của bất phương trình 2 3 9 x 1 3 3 1 0
chứa bao nhiêu số nguyên ? 27 A. 2. B. 3. C. 4. D. 5. Lờigiải ChọnB Điều kiện x 1 x 1 3 1 0 3 1 x 1 . Ta có x 1
là một nghiệm của bất phương trình. x x 1 Với x 1
, bất phương trình tương đương với 2 (3 9)(3 ) 0 . 27 t 3 1 Đặt 3x t 0 2
, ta có (t 9)(t ) 1
0 (t 3)(t 3)(t ) 0 1 . Kết hợp điều kiện 27 27 t 3 27 1 3x t 0 x ta được nghiệm t 1 3 3 3 3
x 1. Kết hợp điều kiện x 1 ta được 27 27 1
x 1 suy ra trường hợp này bất phương trình có 2 nghiệm nguyên.
Vậy bất phương trình đã cho có tất cả 3 nghiệm nguyên. Trang111
Câu 40. Cho hàm số y f x có đồ thị như hình vẽ:
Tìm số nghiệm của phương trình g x 0 , biết g x 3 f x 2
f x 8. A. 13 . B. 15 . C. 17 . D. 19 . Hướng dẫn giải Chọn B
Ta có g x f x 2 3.
. f x 2. f x. f x =0
f x 0 f x 0 f x 2 3
Dựa vào đồ thị hàm số y f x ta được
+ Phương trình f x 0 có 3 nghiệm phân biệt là 1;0;1
+ Phương trình f x 0 có 4 nghiệm phân biệt
+ Phương trình f x 2
có 8 nghiệm phân biệt (để tìm nghiệm phương trình f x 2 ta kẻ đường thẳng 3 3 2 2 y
, thấy đường thẳng y
cắt đồ thị hàm số y f x tại 8 điểm phân biệt ) 3 3
Vậy phương trình có tất cả 15 nghiệm phân biệt. 4
Câu 41. Cho hàm số f x . Biết f 0 4 và f x 2
2sin x 3, x
R , khi đó f
xdxbằng 0 2 2 2 8 8 2 8 2 2 3 2 3 A. . B. . C. . D. . 8 8 8 8 Lờigiải ChọnC f
xdx 1 2
2sin x 3 dx 1 cos2x 3 dx 4 cos2x dx 4x sin 2x C . 2 Trang112 1
Ta có f 0 4 nên 4.0 sin 0 C 4 C 4 . 2 Nên f x 1
4x sin 2x 4 . 2 4 2 8 2 f x 4 1 1 2 dx
4x sin 2x 4 dx 2x cos 2x 4x 4 . 2 4 8 0 0 0
Câu 42. Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA ABC . Mặt phẳng SBC cách A một
khoảng bằng a và hợp với mặt phẳng ABC góc 0
30 . Thể tích của khối chóp S.ABC bằng 3 8a 3 8a 3 3a 3 4a A. . B. . C. . D. . 9 3 12 9 Hướng dẫn giải S H A C 300 I B Gọi I
là trung điểm sủa BC suy ra góc giữa mp SBC và mp ABC là 0 SIA 30 .
H là hình chiếu vuông góc của A trên SI suy ra d ,
A SBC AH a . AH
Xét tam giác AHI vuông tại H suy ra AI 2a . 0 sin 30 3 4a
Giả sử tam giác đều ABC có cạnh bằng x , mà AI là đường cao suy ra 2a x x . 2 3 2 2 4a 3 4a 3
Diện tích tam giác đều ABC là S . . ABC 3 4 3 2a
Xét tam giác SAI vuông tại A suy ra 0
SA AI.tan 30 . 3 2 3 1 1 4a 3 2a 8a Vậy V .S .SA . . . S.ABC 3 ABC 3 3 3 9
Câu 43. Trong tập số phức, giá trị của m để phương trình bậc hai 2
z mz i 0 có tổng bình phương hai nghiệm bằng 4 i là:
A. 1 i B. 1 i
C. 1 i D. 1 i Trang113 Lờigiải
Gọi z , z là hai nghiệm của phương trình. 1 2 b
S z z m 1 2 a Theo Viet, ta có: 2 2 2 2
z z S 2P m 2i c 1 2
P z .z i 1 2 a 2 Ta có: 2 2 2 m 2i 4
i m 2
i m 1i m 1i Ta chọn đáp án A.
Câu 44. Cho số phức z thoả mãn z 1 2i
5 . Giá trị lớn nhất của z 1 i bằng A. 5 . B. 5 2 . C. 20 . D. 2 5 . Lờigiải ChọnD Cách1.
Ta có z 1 i z 1 2i 2 i z 1 2i 2 i 2 5 .
Đẳng thức xảy ra khi z 33i .
Vậy max z 1 i 2 5 . Cách2. Đặt 2 2
z x yi, x, y thì từ điều kiện ta có: x
1 y 2 5. Gọi M ;
x y là điểm biểu diễn cho z và A 1 ;
1 là điểm biểu diễn cho số phức 1 i , khi đó
z 1 i AM với M thuộc đường tròn C tâm I 1; 2
bán kính R 5 .
Dễ thấy AC , do đó AM 2R 2 5 .
Suy ra max z 1 i 2 5 , đẳng thức xảy ra khi M K . Cách3. z 1 2i 5 *
Đặt z x yi ,
x y , khi ấy, ta có * x yi 1 2i 5 x
1 y 2i 5
x 2 y 2 1 2 5 . Trang114
x 1 5sin a Đặt 2 2
. Ta có z 1 i x 1 y
1 i x 1 y 1
y 2 5 cosa a 2 a 2 5 sin 2 5 cos 1
10 4 5 sin a 2 5 cos a 2 5 cos 2 5 5 5 10 10 sin a cos a
10 10sin a với . 5 5 5 sin 5 Vì 1
sin a 1với mọi a; 10 10 z 1 i 10 10 0 z 1 i 2 5 .
Vậy giá trị lớn nhất của z 1 i là 2 5 . Dấu " " xảy ra khi sin a 1 a k2 2 5 cos a cos
k2 sin 2 5 x x x 1 5 sin a 1 2 3 2 5
y 2 5 cosa y 2 1 y 3 sin a sin
k2 cos 2 5
z 33i . 1
Câu 45. Cho hai hàm số f x 3 2
ax bx cx 1 và g x 2
dx ex , a , b ,
c d, e . Biết rằng đồ thị 2
của hàm số y f (x) và y g (x) cắt nhau tại ba điểm có hoành độ lần lượt 3; 1; 2 (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 253 125 253 125 A. B. C. D. 12 12 48 48 Lờigiải ChọnC
Vì phương trình f (x) g(x) 0 có 3 nghiệm 3; 1; 2 nên f x g x a x 3 x 2 x 1 . 3 2 1 253
So sánh hệ số tự do ta được 6 a 1
a . Do đó S
x 3x
1 x 2 dx . 2 4 4 48 3
Câu 46. Trong không gian Oxyz , cho điểm A2;0; 1
và mặt phẳng P:x y 1 0 . Đường thẳng đi qua
A đồng thời song song với P và mặt phẳng Oxy có phương trình là Trang115 x 3 t x 2 t x 1 2t x 3 t
A. y 2t .
B. y t . C. y 1 .
D. y 1 2t . z 1 t z 1 z t z t Lờigiải ChọnB Ta có: n Oxy
1;1;0 , nOxy 0;0; 1 .
Gọi d là đường thẳng đi qua A đồng thời song song với P và mặt phẳng Oxy . Khi đó: x 2 t u d nP u d
nP, nOxy 1; 1;0 . Vậy d : y t . u d n(Oxy) z 1
Câu 47. Cho hình nón đỉnh S , đáy là đường tròn ;5
O .Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn
đáy tại hai điểm A và B sao cho SA AB 8. Tính khoảng cách từ O đến SAB . 3 3 3 2 13 A. 2 2 . B. . C. . D. . 4 7 2 Lời giải ChọnB
Gọi I là trung điểm AB . AB SO Ta có
AB SOI SAB SOI . AB OI
Trong SOI , kẻ OH SI thì OH SAB . d ;
O SAB OH . 2 8.5 Ta có: 2 2 2 SO SA OA 5 39 . 5 2 4.5 Ta có: 2 2 2
OI OA AI 5 3 . 5 Trang116 1 1 1 3 13
Tam giác vuông SOI có: OH . 2 2 2 OH OI SO 4
Vậy d O SAB 3 13 ; OH . 4 2 2 2 2
Câu 48. Số cặp nghiệm ;
x y nguyên của bất phương trình x y
5x 2 xy2 y 3 2 .2
x y 3 là A. 0 . B.1. C. 2 . D. 3 . Lờigiải Chọn D 2 2 2 2 2 2 2 2 5 x 2 xy 2 y 9 2 3
Từ 2x y .2
x y 3 2x y .2 x y x y
x y 3 0(*) a
2x y2 0 Đặ t
khi đó (*) đưa về: .2a b
0 .2a .2 b a b a b . b
x y2 3 3
Vì a 0 b 0. Xét hàm số .2t f t t
, t 0; có 2t .2t f t t .ln 2 0, t 0;.
Suy ra f a f b
a b
a b 0 . 2 2 2 2
Suy ra 2x y x y 3 0 2x y x y 3 .
Với giả thiết x, y là các số nguyên nên 2 2x y và 2 x y
chỉ có thể xẩy ra các trường hợp sau: 2x y 0 0 0 1 1 1 1 1 1 x y 0 1 1 1 1 1 1 0 0 1 1 2 2 1 1 x 0 0 0 3 3 3 3 3 3 2 2 1 1 1 1 y 0 1 1 3 3 3 3 3 3 Nhận Loại Loại Loại Nhận Nhận Loại Loại Loại
Vậy có tất cả 3 cặp nghiệm thỏa mãn.
Câu 49. Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu S có phương trình là 2 2 2
x y z 2x 2 y 6z 7 0 . Cho ba điể
m A , M , B nằm trên mặt cầu S sao cho AMB 90 . Diện
tích tam giác AMB có giá trị lớn nhất bằng? A. 4 . B. 2 . C. 4 . D. Không tồn tại. Lờigiải 2 2 2
Ta có S : x 1 y
1 z 3 4 S có tâm I 1;1;3 và bán kính R 2 .
Bài ra A , M , B nằm trên mặt cầu S và AMB 90 AB qua I AB 2R 4 . 1 2 2 MA MB 2 AB Ta có S . MA MB 4 . AMB 2 4 4 AB
Dấu " " xảy ra MA MB 2 2 và AB 4 . 2 Trang117
Do đó diện tích tam giác AMB có giá trị lớn nhất bằng 4 .
Câu 50. Cho hàm số f (x) có f (
¢ x)= x(x- )( 2 1 x - 2mx + )
1 . Hỏi có tất cả bao nhiêu số nguyên m không
vượt quá 2022 sao cho hàm số ( )= ( 2 g x
f x ) có 7 điểm cực trị? A. 2023. B. 2020 . C. 2021. D. 2022 . Lờigiải Chọn C Ta có: g ( ¢ x)= x f ( 2 ¢ x ) 2 = x x ( 2 x - )( 4 2 x - mx + ) 3 = x ( 2 x - )( 4 2 2 . 2 . 1 2 1 2 1 x - 2mx + ) 1 . x é = 0 ê ê g (
¢ x)= 0 Û x = ± 1 ê ê 4 2 x ê - 2mx + 1= 0 ( ) * ë
Do x = 0 là nghiệm bội lẻ và x = ± 1 là các nghiệm đơn nên để g (x) có 7 điểm cực trị thì phương trình (*) phải
có 4 nghiệm phân biệt khác 0 và khác ± 1 , hay phương trình 2
t - 2mt + 1 = 0 phải có 2 nghiệm dương phân biệt khác 1. íï m é > 1 2 í ï ï D ¢= m - 1> 0 ê ï ï ï ï ï m ê < - 1 ë ïï S 2m 0 ï = > ï ï Û ì Û ì m > 0 Û m > 1 ï . P = 1> 0 ï ï ï ï ï m ¹ 1 ï 2 ï ï 1 - 2 .1 m + 1 ¹ 0 ï ïî ïïïî
Kết hợp với điều kiện m nguyên, không vượt quá 2022 suy ra có 2021 giá trị của m . ĐỀ 6
ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2022
BÁM SÁT ĐỀ MINH HỌA MÔN TOÁN Thời gian: 90 phút
Câu 1. Cho số phức z 3
4i . Số phức liên hợp của z là
A. z 4 3i . B. z 3 4i .
C. z 3 4i . D. z 3 4i .
Câu 2. Mặt cầu S x y2 2 :
2xy z 1 4x có tâm là: A. I 2 ;0;0.
B. I 4;0;0. C. I 4 ;0;0.
D. I 2;0;0.
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 3 2
y x 2x 1
A. Điểm M 0 ;1 .
B. Điểm N 1; 2 .
C. Điểm P 1 ;2.
D. Điểm Q 1;0 .
Câu 4. Cho mặt cầu S có diện tích 2 2 4 a
cm . Khi đó, thể tích khối cầu S là 3 4 a 3 a 3 64 a 3 16 a A. 3 cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3 3
Câu 5. Tất cả các nguyên hàm của hàm số ( ) 3 x f x là 3x x 3 A. C
B. 3 x C
C. 3 x ln 3 C D. C ln 3 ln 3 Trang118
Câu 6. Cho hàm số f x có đạo hàm f x x x x 3 1 4 , x
. Số điểm cực đại của hàm số đã cho là A. 3 . B. 4 . C. 2 . D. 1 .
Câu 7. Tìm tập nghiệm S của bất phương trình log x 1 log 2x 1 . 1 1 2 2 1
A. S 2; . B. S 1 ;2.
C. S ; 2 . D. S ; 2 . 2
Câu 8. Khối chóp S.ABCD có A , B , C , D cố định và S chạy trên đường thẳng song song với AC . Khi đó
thể tích khối chóp S.ABCD sẽ:
A. Giảm phân nửa.. B. Tăng gấp đôi.. C. Tăng gấp bốn. D. Giữ nguyên..
Câu 9. Tập xác định của hàm số y x 3 2 1 là A. . B. ; 1 1; . C. 1 ;1 . D. \ 1 .
Câu 10. Nghiệm của phương trình log
x 9 5 là 2 A. x 41. B. x 23 . C. x 1 . D. x 16 . 1 1 1
Câu 11. Biết tích phân f
xdx 3 và gxdx 4 . Khi đó f
x gxdx bằng 0 0 0 A. 7 . B. 7 . C. 1. D. 1. 5
Câu 12. Phần thực, phần ảo của số phức z thỏa mãn z 3i 1 lần lượt là 2i A. 1;1. B.1; 2 . C. 1;2. D.1; 1 .
Câu 13. Trong không gian Oxyz , mặt phẳng P : 2x y 3z 1 0 có một vectơ pháp tuyến là:
A. n 2;1; 3
B. n 1; 3; 2
C. n 1; 3; 2 D. n 3;1; 2 1 4 2 3
Câu 14. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ x 2;1; 3 và y 1; 0; 1 . Tìm tọa độ của
vectơ a x 2y .
A. a 4;1; 1 .
B. a 3;1;4 .
C. a 0;1; 1 .
D. a 4;1; 5 .
Câu 15. Điểm M 1
;3 là điểm biểu diễn của số phức A. z 1 3i .
B. z 1 3i .
C. z 2i . D. z 2 . 3x 1
Câu 16. Tiệm cận ngang của đồ thị hàm số y x là: 1 1 A. y . B. y 3 . C. y 1. D. y 1. 3
Câu 17. Với a , b là các số thực dương tùy ý và a 1, log b bằng 2 a 1 1 A. log b . B. log b .
C. 2 log b . D. 2 log b . 2 a 2 a a a
Câu 18. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? Trang119 4 2 A. 4 2
y x 2x 1. B. 3 2
y x 3x 1. C. 3 2
y x 3x 1.
D. y x 2x 1. x 3 y 1 z 5
Câu 19. Trong không gian Oxyz , cho đường thẳng d :
. Điểm nào dưới đây thuộc d ? 2 2 1
A. M 3;1;5 .
B. N 3;1;5 .
C. P 2; 2; 1 . D. Q 2; 2 ;1 .
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n k ! n k ! k ! k ! A. C C C . D. C n k !(n . B. k)! n (n . C. k)! n k ! n k !(k . n)!
Câu 21. Chiều cao của khối lăng trụ có diện tích đáy B và thể tích V là 3V V B V A. h . B. h . C. h . D. h . B 3B V B
Câu 22. Tính đạo hàm của hàm số 1 2 2 x y . 1 2 12 x 22 x A. 2.2 x y . B. y 2 ln 2 . C. y 2 ln 2 . D. 2 1 2 .2 x y x .
Câu 23. Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây 0; 0;2 2 ;0 ; 2 A. . B. . C. . D. .
Câu 24. Cho hình trụ có bán kính đáy r và độ dài đường sinh l . Diện tích xung quanh S của hình trụ đã cho xq
được tính theo công thức nào sau đây? 1 A. S 4rl . B. S rl . C. S rl . D. S 2rl . xq xq xq 3 xq 3 3 Câu 25. Biết f
xdx 6. Giá trị của 2 f xdx bằng. 2 2 A. 36 . B. 3 . C. 12 . D. 8 .
Câu 26. Cho cấp số cộng u
với u 4 và d 8 . Số hạng u của cấp số cộng đã cho bằng n 1 20 A. 156 . B. 165 . C. 12 . D. 245 .
Câu 27. Họ nguyên hàm của hàm số x
f x e 2x là. Trang120 1 A. x 2
e x C . B. x 2
e x C . C. x 2
e x C x e C . x . D. 2 1
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ. y 2 1 -1 1 0 x -1
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 1 . C. 1. D. 0 . 2 2
Câu 29. Giá trị nhỏ nhất của hàm số y x trên đoạn 2; 3 bằng x 15 29 A. . B. 5 . C. . D. 3 . 2 3
Câu 30. Đồ thị hàm số 3 2
y f (x) ax bx cx d . Hình nào trong 4 hình dưới đây mà hàm số luôn nghịch biến trên ? A. B. C. D.
Câu 31. Xét số thực a và b thỏa mãn log 3 .
a 9b log 3. Mệnh đề nào dưới đây đúng 3 9
A. a 2b 2 .
B. 4a 2b 1.
C. 4ab 1.
D. 2a 4b 1. Trang121
Câu 32. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos AB, DM bằng 2 3 1 3 A. . B. . C. . D. . 2 6 2 2 2 2 Câu 33. Cho f
xdx 5. Tính I f
x2sin xdx 5 . 0 0
A. I 7 B. I 5
C. I 3
D. I 5 2
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua điểm M (1;1; 1) và vuông góc với đường thẳng x 1 y 2 z 1 :
có phương trình là: 2 2 1
A. 2x 2 y z 3 0
B. 2x 2 y z 3 0
C. x 2 y z 0 . D. x 2 y z 2 0
Câu 35. Cho số phức z i i2 3 2 1
. Môđun của w iz z là A.2. B. 2 2 . C. 1. D. 2 .
Câu 36. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a , o
BAD 60 , SA a và SA vuông góc với mặt
phẳng đáy. Khoảng cách tứ B đến SCD bằng? 21a 15a 21a 15a A. . B. . C. . D. . 3 3 7 7
Câu 37. Gọi S là tập các số tự nhiên có bốn chữ số khác nhau được tạo từ tập E 1; 2;3; 4; 5 . Chọn ngẫu nhiên
một số từ tập S . Tính xác suất để số được chọn là số chẵn? 3 2 3 1 A. . B. . C. . D. . 4 5 5 2
Câu 38. Trong không gian Oxyz , cho ba điểm A1;1;0, B 1;0;
1 , C 3;1;0 . Đường thẳng đi qua A và song
song với BC có phương trình là: x 1 y 1 z z 1 y 1 z A. . B. . 2 1 1 4 1 1 x 1 y 1 z x 1 y 1 z C. . 2 1 . D. 1 4 1 1
Câu 39. Tập nghiệm của bất phương trình x 2 x 2 2.7 7.2
351. 14x có dạng là đoạn S ; a b. Giá trị
b 2a thuộc khoảng nào dưới đây? 2 49
A. 3; 10 . B. 4 ;2 .
C. 7;4 10 . D. ; . 9 5 Câu 40. Cho hàm số 4 2 y
f x ax bx c có đồ thị như hình vẽ và thỏa mãn đẳng thức sau: f x
1 f x 2x 2x 1 x 1 . Cho hàm số 2
g x mx nx p và f x g 2 x 1 . Tìm nghiệm
của phương trình g x 0 . Trang122 1 1 A. . B. 2 . C. . D. 4 . 2 4 4 2
Câu 41. Cho hàm số f ( x) .Biết f (0) 4 và f (
x) 2cos x 3, x
,khi đó f (x)dx bằng? 0 2 8 8 2 8 2 2 6 8 2 2 A. . B. . C. . D. . 8 8 8 8
Câu 42. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy ABCD , góc
giữa hai mặt phẳng (SBD) và ABCD bằng 0
60 . Gọi M , N lần lượt là trung điểm của SB , SC . Tính thể tích
khối chóp S.ADNM . 3 a 6 3 a 6 3 3a 6 3 a 6 A. V = . B. V = . C. V = . D. V = . 16 24 16 8
Câu 43. Cho phương trình 2
z mz 2m 1 0 trong đó m là tham số phức. Giá trị của m để phương trình có hai
nghiệm z , z thỏa mãn 2 2 z z 10 là: 1 2 1 2
A. m 2 2 2i
B. m 2 2 2i
C. m 2 2 2i D. m 2 2 2i
Câu 44. Xét các số phức z thỏa mãn z 3 2i z 3 i 3 5 . Gọi M , m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của biểu thức P z 2 z 1 3i . Tìm M , m .
A. M 17 5 ; m 3 2 . B. M
26 2 5 ; m 2 . C. M
26 2 5 ; m 3 2 .
D. M 17 5 ; m 3 .
Câu 45. Cho hàm số y f x có đồ thị như hình vẽ và diện tích hai phần ,
A B lần lượt bằng 11 và 2. 0 Giá trị của I f 3x 1dx bằng 1 Trang123 13 A. 3. B. . C. 9. D.13. 3
Câu 46. Trong không gian Oxyz , cho điểm A3; 2 ;
4 và mặt phẳng P : 3x 2y 3z 7 0 , đường thẳng x 2 y 4 z 1 d :
. Phương trình nào sau đây là phương trình đường thẳng đi qua A , song song P và 3 2 2
cắt đường thẳng d ? x 311t
x 3 54t
x 3 47t x 311t
A. y 2 54t .
B. y 2 11t .
C. y 2 54t .
D. y 2 47t . z 4 47t z 4 47t z 4 11t z 4 54t
Câu 47. Cho hình nón có chiều cao h 20 , bán kính đáy r 25 . Một thiết diện đi qua đỉnh của hình nón có
khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 . Tính diện tích S của thiết diện đó. A. S 500 B. S 400 C. S 300 D. S 406 Câu 48. Có bao nhiêu cặp số nguyên dương
;x yvới x 2020thỏa mãn điều kiện x 2 2 2 log
x 4x 4y 8y 1 2 y . 1 A. 2020 . B. vô số. C. 1010 . D. 4040 .
Câu 49. Trong không gian với hệ tọa độ Oxyz , gọi điểm M ; a ;
b c (với a , b , c là các phân số tối giản) thuộc mặt cầu S 2 2 2
: x y z 2x 4 y 4z 7 0 sao cho biểu thức T 2a 3b 6c đạt giá trị lớn nhất. Khi đó
giá trị biểu thức P 2a b c bằng 12 51 A. . B. 8 . C. 6 . D. . 7 7
Câu 50. Cho hàm số y = f (x) có đạo hàm f (x)= ( 2 x - x)( 2 ' x - 4x + )
3 , " x Î ¡ . Tính tổng tất cả các giá trị
nguyên của tham số m để hàm số ( )= ( 2 g x f x + )
m có 3 điểm cực trị. A. 0 . B. 6 . C. 3 . D. 2 .
LỜI GIẢI CHI TIẾT
Câu 1. Cho số phức z 3
4i . Số phức liên hợp của z là
A. z 4 3i . B. z 3 4i .
C. z 3 4i . D. z 3 4i . Lờigiải z 3
4i z 3 4i
Vậy chọn đáp án D.
Câu 2. Mặt cầu S x y2 2 :
2xy z 1 4x có tâm là: A. I 2 ;0;0.
B. I 4;0;0. C. I 4 ;0;0.
D. I 2;0;0. Lờigiải
Biến đổi x y2 2 2 2 2
2xy z 1 4x x y z 4x 1 0.
Vậy mặt cầu có tâm I 2 ;0;0. Trang124
Lựa chọn đáp án A.
Câu 3. Điểm nào dưới đây thuộc đồ thị của hàm số 3 2
y x 2x 1
A. Điểm M 0 ;1 .
B. Điểm N 1; 2 .
C. Điểm P 1 ;2.
D. Điểm Q 1;0 . Lờigiải Chọn A
Câu 4. Cho mặt cầu S có diện tích 2 2 4 a
cm . Khi đó, thể tích khối cầu S là 3 4 a 3 a 3 64 a 3 16 a A. 3 cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3 3 Lờigiải
Gọi mặt cầu có bán kính R . Theo đề ta có 2 2
4 R 4 a . Vậy R a(cm) . 3 3 4 R 4 a
Khi đó, thể tích khối cầu S là: V 3 cm . 3 3
Câu 5. Tất cả các nguyên hàm của hàm số ( ) 3 x f x là 3x x 3 A. C
B. 3 x C
C. 3 x ln 3 C D. C ln 3 ln 3 Lờigiải ChọnA 3x x x Ta có
f (x)dx 3 dx 3 d(x) C . ln 3
Câu 6. Cho hàm số f x có đạo hàm f x x x x 3 1 4 , x
. Số điểm cực đại của hàm số đã cho là A. 3 . B. 4 . C. 2 . D. 1 . Lời giải Chọn D x 0
Ta có f x 0 x 1 x 4
Bảng xét dấu f x :
Từ bảng xét dấu suy ra hàm số có đúng 1 điểm cực đại.
Câu 7. Tìm tập nghiệm S của bất phương trình log x 1 log 2x 1 . 1 1 2 2 1
A. S 2; . B. S 1 ;2.
C. S ; 2 . D. S ; 2 . 2 Lờigiải Trang125
x x 1 Ta có log x 1 log 2x 1 2 1 1 x 2 . 1 1 2x10 2 2 2
Câu 8. Khối chóp S.ABCD có A , B , C , D cố định và S chạy trên đường thẳng song song với AC . Khi đó
thể tích khối chóp S.ABCD sẽ:
A. Giảm phân nửa.. B. Tăng gấp đôi.. C. Tăng gấp bốn. D. Giữ nguyên.. Lời giải. Chọn D
Gọi là đường thẳng qua S và song song AC . 1 Ta có: V . B h 3
+ song song AC nên ABCD d S, ABCD d ,
ABCD h không đổi.
+ A , B , C , D cố định nên diện tích tứ giác ABCD cũng không đổi.
Vì vậy thể tích khối chóp S.ABCD sẽ giữ nguyên.
Câu 9. Tập xác định của hàm số y x 3 2 1 là A. . B. ; 1 1; . C. 1 ;1 . D. \ 1 . Lời giải Chọn C
Câu 10. Nghiệm của phương trình log
x 9 5 là 2 A. x 41. B. x 23 . C. x 1 . D. x 16 . Lờigiải ChọnB ĐK: x 9
Ta có: log x 9 5
5 x 9 2 x 23. 2 1 1 1
Câu 11. Biết tích phân f
xdx 3 và gxdx 4 . Khi đó f
x gxdx bằng 0 0 0 A. 7 . B. 7 . C. 1. D. 1. Lờigiải ChọnC 1 1 1 Ta có f
x gxdx f
xdx g
xdx 3 4 1 . 0 0 0 5
Câu 12. Phần thực, phần ảo của số phức z thỏa mãn z 3i 1 lần lượt là 2i A. 1;1. B.1; 2 . C. 1;2. D.1; 1 . Lời giải Trang126 5 51 2i 51 2i z 3i i
i i 3i 3i 1 i 1 2 1 2 1 2 5 z 1 i
Phần thực, phần ảo của z lần lượt là 1;1.
Vậy chọn đáp án A.
Câu 13. Trong không gian Oxyz , mặt phẳng P : 2x y 3z 1 0 có một vectơ pháp tuyến là:
A. n 2;1; 3
B. n 1; 3; 2
C. n 1; 3; 2 D. n 3;1; 2 1 4 2 3 Lờigiải ChọnA
Mặt phẳng P : 2x y 3z 1 0 có một vectơ pháp tuyến là 2;1;3 .
Câu 14. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ x 2;1; 3 và y 1; 0; 1 . Tìm tọa độ của
vectơ a x 2y .
A. a 4;1; 1 .
B. a 3;1;4 .
C. a 0;1; 1 .
D. a 4;1; 5 . Lờigiải
Ta có: 2 y 2;0; 2 .
a x 2 y 2 2;1 0; 3 2 4;1; 5 .
Câu 15. Điểm M 1
;3 là điểm biểu diễn của số phức A. z 1 3i .
B. z 1 3i .
C. z 2i . D. z 2 . Lời giải
z a bi có điểm biểu diễn là M ;
a b . Ta suy ra z 1 3i
Vậy chọn đáp án A. 3x 1
Câu 16. Tiệm cận ngang của đồ thị hàm số y x là: 1 1 A. y . B. y 3 . C. y 1. D. y 1. 3 Lời giải Chọn B 3x 1 3x 1 Ta có : lim y lim 3 lim y lim 3
y là tiệm cận ngang của đồ thị hàm số. x x x và 1 x x x nên 3 1
Câu 17. Với a , b là các số thực dương tùy ý và a 1, log b bằng 2 a 1 1 A. log b . B. log b .
C. 2 log b . D. 2 log b . 2 a 2 a a a Lời giải Chọn B Trang127 1 Ta có log b log b . 2 2 a a
Câu 18. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? 4 2 A. 4 2
y x 2x 1. B. 3 2
y x 3x 1. C. 3 2
y x 3x 1.
D. y x 2x 1. Lời giải Chọn A
Dựa vào hình vẽ, ta thấy đồ thị hàm số có ba điểm cực trị nên loại các đáp án B và C. Mặt khác, ta thấy 4 2
lim x 2x
1 nên chọn đáp án A. x x 3 y 1 z 5
Câu 19. Trong không gian Oxyz , cho đường thẳng d :
. Điểm nào dưới đây thuộc d ? 2 2 1
A. M 3;1;5 .
B. N 3;1;5 .
C. P 2; 2; 1 . D. Q 2; 2 ;1 . Lờigiải ChọnB 3 3 11 5 5 Ta có 0 N 3;1; 5 d . 2 2 nên điểm 1
Câu 20. Với k và n là hai số nguyên dương k n , công thức nào sao đây đúng? n k n n k ! k ! k ! k ! A. C C C . D. C n k !(n . B. k)! n (n . C. k)! n k ! n k !(k . n)! Lời giải Chọn A n k ! C n
k !(n k)!
Câu 21. Chiều cao của khối lăng trụ có diện tích đáy B và thể tích V là 3V V B V A. h . B. h . C. h . D. h . B 3B V B Lời giải Chọn D V
Chiều cao của khối lăng trụ có diện tích đáy B và thể tích V là: h . B
Câu 22. Tính đạo hàm của hàm số 1 2 2 x y . Trang128 1 2 12 x 22 x A. 2.2 x y . B. y 2 ln 2 . C. y 2 ln 2 . D. 2 1 2 .2 x y x . Lời giải Chọn C Ta có 1 2 2.2 x y ln 2 2 2 2 x ln 2 .
Câu 23. Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây 0; 0;2 2 ;0 ; 2 A. . B. . C. . D. . Lời giải Chọn C 2 ;0
Từ bảng biến thiên, suy ra trên khoảng
hàm số đồng biến.
Câu 24. Cho hình trụ có bán kính đáy r và độ dài đường sinh l . Diện tích xung quanh S của hình trụ đã cho xq
được tính theo công thức nào sau đây? 1 A. S 4rl . B. S rl . C. S rl . D. S 2rl . xq xq xq 3 xq Lờigiải Chọn D
Diện tích xung quanh của hình trụ là: S 2rl . xq 3 3 Câu 25. Biết f
xdx 6. Giá trị của 2 f xdx bằng. 2 2 A. 36 . B. 3 . C. 12 . D. 8 . Lờigiải ChọnC 3 3 Ta có : 2 f
xdx 2 f
xdx 12.. 2 2
Câu 26. Cho cấp số cộng u
với u 4 và d 8 . Số hạng u của cấp số cộng đã cho bằng n 1 20 A. 156 . B. 165 . C. 12 . D. 245 . Lời giải Chọn A Ta có: u
u 19d 4 19.8 156 . 20 1
Câu 27. Họ nguyên hàm của hàm số x
f x e 2x là. 1 x 2 x 2 x 2 x
A. e x C .
B. e x C . C.
e x C e C . x . D. 2 1 Trang129 Lờigiải Ta có: x e x x 2 2
dx e x C
Câu 28. Cho hàm số y f x có đồ thị như hình vẽ. y 2 1 -1 1 0 x -1
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 1 . C. 1. D. 0 . Lời giải Chọn B 2 2
Câu 29. Giá trị nhỏ nhất của hàm số y x trên đoạn 2; 3 bằng x 15 29 A. . B. 5 . C. . D. 3 . 2 3 Lời giải Chọn B 2 + Ta có hàm số 2
y f (x) x
xác định và liên tục trên 2; 3 . x 2 29
+ y ' f '(x) 2x
; f '(x) 0 x 12;
3 mà f (2) 5 , f (3) . 2 x 3
+ Vậy min y 5 tại x 2 . 2; 3
Câu 30. Đồ thị hàm số 3 2
y f (x) ax bx cx d . Hình nào trong 4 hình dưới đây mà hàm số luôn nghịch biến trên ? A. B. Trang130 C. D.
Câu 31. Xét số thực a và b thỏa mãn log 3 .
a 9b log 3. Mệnh đề nào dưới đây đúng 3 9
A. a 2b 2 .
B. 4a 2b 1.
C. 4ab 1.
D. 2a 4b 1. Lời giải Chọn D Ta có:
log 3 .a9b log 3 log a 2 3 .3 b log 3 3 9 3 2 3 1 a b 1 2 2 log 3
log 3 a 2b 2a 4b 1. 3 3 2
Câu 32. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos AB, DM bằng 2 3 1 3 A. . B. . C. . D. . 2 6 2 2 Hướng dẫn giải ChọnB A N B D M C
Gọi N là trung điểm của .
AC Suy ra MN // AB Do đó: cos A ,
B DM cosMN, DM a a 3
Gọi a là độ dài cạnh của tứ diện đều ABCD , suy ra MN ; ND MD 2 2 2 2 2
MN MD ND 3
Trong tam giác MND ta có: cos NMD 2.MN.MD 6 AB DM 3 cos , cos NMD . 6 Trang131 2 2 Câu 33. Cho f
xdx 5. Tính I f
x2sin xdx 5 . 0 0
A. I 7 B. I 5
C. I 3
D. I 5 2 Lờigiải ChọnA Ta có 2 2 I f x 2
2sin x dx f x 2
dx +2 sin x dx f x 2 dx 2 cos x 5 20 1 7 . 0 0 0 0 0
Câu 34. Trong không gian Oxyz , mặt phẳng đi qua điểm M (1;1; 1) và vuông góc với đường thẳng x 1 y 2 z 1 :
có phương trình là: 2 2 1
A. 2x 2 y z 3 0
B. 2x 2 y z 3 0
C. x 2 y z 0 . D. x 2 y z 2 0
Câu 35. Cho số phức z i i2 3 2 1
. Môđun của w iz z là A.2. B. 2 2 . C. 1. D. 2 . Hướng dẫn giải iz
i 4 6i 6 4i
z 3 2i1 i2 3 2i
2i 4 6i z 4 6i
w iz z 6
4i 4 6i 2 2i
w 2 2 2 2 8 2 2
Vậy chọn đáp án B.
Câu 36. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a , o
BAD 60 , SA a và SA vuông góc với mặt
phẳng đáy. Khoảng cách tứ B đến SCD bằng? 21a 15a 21a 15a A. . B. . C. . D. . 3 3 7 7 Lờigiải Chọn C CÁCH 1: Trang132
Ta có AB / /CD d ;
B SCD d A;SCD .
Kẽ MA CD M CD ,kẻ AH SM SH SCD d ,
A SCD SH . 2S S a 3 1 1 1 21 SA a ; ACD ABCD AM SM a CD CD 2 2 2 2 SH SA AM 7 3V 3V 21a
CÁCH 2: Ta có AB / /CD d ;
B SCD d A;SCD S .BCD S .A BCD . S 2S 7 SCD SCD ( S C ;
D SD a 2; SC 2 ; a CD a )
Câu 37. Gọi S là tập các số tự nhiên có bốn chữ số khác nhau được tạo từ tập E 1; 2;3; 4; 5 . Chọn ngẫu nhiên
một số từ tập S . Tính xác suất để số được chọn là số chẵn? 3 2 3 1 A. . B. . C. . D. . 4 5 5 2 Lờigiải ChọnB
Số các số tự nhiên có bốn chữ số khác nhau được tạo từ tập E 1;2;3;4; 5 là: 5!120 .
Do đó tập S có số phần tử là: 120.
Không gian mẫu có số phần tử là: 1 C 120 . 120
Số các số chẵn có bốn chữ số khác nhau được tạo từ tập E 1;2;3;4; 5 là: 2.4! 48 . 1 C 48 2 Xác suất cần tính là: 48 P . 120 120 5
Câu 38. Trong không gian Oxyz , cho ba điểm A1;1;0, B 1;0;
1 , C 3;1;0 . Đường thẳng đi qua A và song
song với BC có phương trình là: x 1 y 1 z z 1 y 1 z A. . B. . 2 1 1 4 1 1 x 1 y 1 z x 1 y 1 z C. . 2 1 . D. 1 4 1 1 Lờigiải ChọnC
Đường thẳng đi qua A1;1;0, song song với BC nên nhận BC 2;1;
1 là véc tơ chỉ phương do đó có phương x 1 y 1 z trình là: 2 1 . 1
Câu 39. Tập nghiệm của bất phương trình x 2 x 2 2.7 7.2
351. 14x có dạng là đoạn S ; a b. Giá trị
b 2a thuộc khoảng nào dưới đây? 2 49
A. 3; 10 . B. 4 ;2 .
C. 7;4 10 . D. ; . 9 5 Lờigiải Trang133 2 x 2 7 2 x x2 x2 2.7 7.2 351. 14x 49.7x 28.2x 351. 14x 49. 28. 351 14x 14x 7x 2x x 7 28 49. 28. 351. Đặt t
, t 0 thì bpt trở thành 49t 351 2x 7x 2x t 4 7 x t 4 7 7 4
x 2 , khi đó S 4 ;2 . 49 2 49 2x 2
Giá trị b 2a 10 7;4 10 . Câu 40. Cho hàm số 4 2 y
f x ax bx c có đồ thị như hình vẽ và thỏa mãn đẳng thức sau: f x
1 f x 2x 2x 1 x 1 . Cho hàm số 2
g x mx nx p và f x g 2 x 1 . Tìm nghiệm
của phương trình g x 0 . 1 1 A. . B. 2 . C. . D. 4 . 2 4 Hướng dẫn giải Chọn C
Với x 0 thì f 1 f 0 . Vì f
1 f 0 và đồ thị hàm số 4 2 y
f x ax bx c đi qua 0; 1 , 2;1
1 nên ta có hệ phương trình: f 1 f 0
a b c c a 1 f 0 1 c 1 b 1 . f
16a 4b c 11 c 1 2 11 Vậy f x 4 2
x x 1. 2
Ta có f x g 2 x 4 2
x x m 2
x n 2 1 1 1 x 1 p 4 2 4
x x mx m n 2 1 2
x m n p m 1 m 1 2
m n 1 n 1
m n p 1 p 1
Do đó g x 2
x x 1. Trang134 g x 1
0 2x 1 0 x . 2 1 Vậy x . 2 4 2
Câu 41. Cho hàm số f ( x) .Biết f (0) 4 và f (
x) 2cos x 3, x
,khi đó f (x)dx bằng? 0 2 8 8 2 8 2 2 6 8 2 2 A. . B. . C. . D. . 8 8 8 8 Lờigiải ChọnB , x Ta có 2 f (x)
f (x)dx (2 cos x 3)dx 1 cos 2 (2. 3)dx 2 1 (cos 2x 4)dx =
sin 2x 4x C do f (0) 4 C 4 . 2 1 4 4 1
Vậy f (x) sin 2x 4x 4 nên f (x)dx ( sin 2x 4x 4)dx 2 2 0 0 2 4 1 8 2 2
( cos 2x 2x 4x) . 4 8 0
Câu 42. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy ABCD , góc
giữa hai mặt phẳng (SBD) và ABCD bằng 0
60 . Gọi M , N lần lượt là trung điểm của SB , SC . Tính thể tích
khối chóp S.ADNM . 3 a 6 3 a 6 3 3a 6 3 a 6 A. V = . B. V = . C. V = . D. V = . 16 24 16 8 Hướng dẫn giải Chọn A S M N A B O D C
Gọi O = AC Ç BD .
AO ^ BD Þ SO ^ BD . Nên góc của (SBD) 0
và ABCD là góc SOA = 60 . 1 1 1 1 1 V = .V = .V và V = . V = V . S . ADN S . ADC S . 2 4 ABCD S . AMN S . ABC S . 2 2 8 ABCD Trang135 3 Þ V = V + V = V . S . ADMN S . ADN S . AMN S . 8 ABCD 3 a 2 a 6 1 a 6 0 SA = A . O tan SOA = tan 60 = Þ V = S .SA = . 2 2 S. ABCD 3 ABCD 6 3 3 3 a 6 a 6 Þ V = . = . S. ADMN 8 6 16
Câu 43. Cho phương trình 2
z mz 2m 1 0 trong đó m là tham số phức. Giá trị của m để phương trình có hai
nghiệm z , z thỏa mãn 2 2 z z 10 là: 1 2 1 2
A. m 2 2 2i
B. m 2 2 2i
C. m 2 2 2i D. m 2 2 2i Lờigiải b
S z z m 1 2 a Theo Viet, ta có: c
P z .z 2m 1 1 2 a 2 2 2 2 z z 1
0 S 2P 1
0 m 22m 2 1 1
0 m 4m 12 0 1 2
m 22 8 0 m 2 2 2i Ta chọn đáp án A.
Câu 44. Xét các số phức z thỏa mãn z 3 2i z 3 i 3 5 . Gọi M , m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của biểu thức P z 2 z 1 3i . Tìm M , m .
A. M 17 5 ; m 3 2 . B. M
26 2 5 ; m 2 . C. M
26 2 5 ; m 3 2 .
D. M 17 5 ; m 3 . Lờigiải ChọnC
Gọi M là điểm biểu diễn số phức z , F 3 ;2 , F 3; 1 , A 2
;0 và B1;3 . 2 1
Ta có z 3 2i z 3 i 3 5 và F F 3 5 MF MF F F . 1 2 1 2 1 2
Do đó tập hợp các điểm M là đoạn thẳng F F . 1 2
Dựa vào hình vẽ, ta thấy: + M P
M A M B 26 2 5 . max 2 2 + m P
M A M B AB 3 2 . min 1 1 Trang136
Vậy M 26 2 5 ; m 3 2 .
Câu 45. Cho hàm số y f x có đồ thị như hình vẽ và diện tích hai phần ,
A B lần lượt bằng 11 và 2. 0 Giá trị của I f 3x 1dx bằng 1 13 A. 3. B. . C. 9. D.13. 3 Lờigiải ChọnA 0 dt +) Xét I f 3x
1 dx , đặt 3x
1 t dt 3dx dx 3 1 x 1 t 2 1 0 1 1 1 1 1 +) Đổi cận I f
tdt= f
tdt + f
tdt S S A B 11 2 3
x 0 t 1 3 3 3 3 2 2 0
Câu 46. Trong không gian Oxyz , cho điểm A3; 2 ;
4 và mặt phẳng P : 3x 2y 3z 7 0 , đường thẳng x 2 y 4 z 1 d :
. Phương trình nào sau đây là phương trình đường thẳng đi qua A , song song P và 3 2 2
cắt đường thẳng d ? x 311t
x 3 54t
x 3 47t x 311t
A. y 2 54t .
B. y 2 11t .
C. y 2 54t .
D. y 2 47t . z 4 47t z 4 47t z 4 11t z 4 54t Lờigiải Gọi n 3;
2; - 3 là vectơ pháp tuyến của mặt phẳng P . P
Đường thẳng d đi qua điểm M 2; 4;
1 và có vectơ chỉ phương u 3; 2; 2 . d
Giả sử d M nên M 2 3t; 4
2t;1 2t khi đó vectơ chỉ phương của đường thẳng là u AM
3t 1; 2t 6;2t 5 . Ta có AM
n AM.
n 0 nên t
t t 6 3 3 1 2 2 6 3 2 5 0 t . P P 7
11 54 47 Suy ra AM ; ; 7 7 7 Trang137
Chọn vectơ chỉ phương của đường thẳng có tọa độ là 11; 54; 4
7 do đó phương trình đường thẳng cần tìm là x 311t
y 2 54t . z 4 47t
Câu 47. Cho hình nón có chiều cao h 20 , bán kính đáy r 25 . Một thiết diện đi qua đỉnh của hình nón có
khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 . Tính diện tích S của thiết diện đó. A. S 500 B. S 400 C. S 300 D. S 406 Lời giải
Giả sử hình nón đỉnh S , tâm đáy O và có thiết diện qua đỉnh thỏa mãn yêu cầu bài toán là S AB (hình vẽ). S H B O I A
Ta có SO là đường cao của hình nón. Gọi I là trung điểm của AB OI AB .
Gọi H là hình chiếu của O lên SI OH SI .
Ta chứng minh được OH SAB OH 12. 1 1 1 1 1 1 1 1
Xét tam giác vuông SOI có 1 . 2 2 2 OH OS OI 2 2 2 OI OH OS 2 2 12 20 225 2
OI 225 OI 15 .
Xét tam giác vuông SOI có 2 2
SI OS OI 2 2 20 15 25.
Xét tam giác vuông OIA có 2 2
IA OA OI 2 2
25 15 20 AB 40 . Ta có S 1 S 1 A . B SI .40.25 500 . ABC 2 2 Câu 48. Có bao nhiêu cặp số nguyên dương
;x yvới x 2020thỏa mãn điều kiện x 2 2 2 log
x 4x 4y 8y 1 2 y . 1 A. 2020 . B. vô số. C. 1010 . D. 4040 . Lời giải Chọn C x 2 log
4y x 4x 8y 1 log x 2 log y 1 4 y 2 1 x 22 2 2 1 2 2 2 y 1 Trang138
log x 2 x 22 log 2 y 1 2 y 1 1 . 2 2 2
Xét hàm số f t 2
log t t trên 0;. 2 1
Ta có f t 2t 0 t
0; f t đồng biến trên 0; . t ln 2
1 f x 2 f 2y 2 x 2 2y 2 x 2y .
Mà 0 x 2020 0 y 1010 .
Vậy có 1010 cặp số nguyên dương ; x y .
Câu 49. Trong không gian với hệ tọa độ Oxyz , gọi điểm M ; a ;
b c (với a , b , c là các phân số tối giản) thuộc mặt cầu S 2 2 2
: x y z 2x 4 y 4z 7 0 sao cho biểu thức T 2a 3b 6c đạt giá trị lớn nhất. Khi đó
giá trị biểu thức P 2a b c bằng 12 51 A. . B. 8 . C. 6 . D. . 7 7 Hướng dẫn giải ChọnC
x y z x y z x 2 y 2 z 2 2 2 2 2 4 4 7 0 1 2 2 16 .
M a b cS a 2 b 2 c 2 ; ; 1 2 2 16 . 2 2 2 Ta có:
a b c 2 2 2 2 1 3 2 6 2
2 3 6 .a
1 b 2 c 2 .
2a 3b 6c 20 28 2a 3b 6c 20 28 2a 3b 6c 48. 15 a
2a 3b 6c 48 7
2a 3b 6c 48
a 1 b 2 26
Dấu " " xảy ra khi:
3a 2b 1 b 2 3 7 3a c 1
a 1 c 2 38 c 2 6 7 15 26 38
Vậy P 2a b c 2. 6 . 7 7 7
Câu 50. Cho hàm số y = f (x) có đạo hàm f (x)= ( 2 x - x)( 2 ' x - 4x + )
3 , " x Î ¡ . Tính tổng tất cả các giá trị
nguyên của tham số m để hàm số ( )= ( 2 g x f x + )
m có 3 điểm cực trị. A. 0 . B. 6 . C. 3 . D. 2 . Hướng dẫn giải Chọn C x é = 0 ê 2
Ta có f '(x)= x(x - ) 1 (x - )
3 ; f '(x)= 0 Û x ê = 1 ê
( x = 0, x = 3 là nghiệm đơn; x = 1 là nghiệm bội chẵn). x ê = 3 ë Trang139 x é = 0 x é = 0 ê ê 2 2 x é = 0 ê ê x + m = 0 x = - m ( ) 1 ê ê ê
Lại có g '(x)= 2 . x f '( 2
x + m); g '(x)= 0 Û Û Û ê ê ê f ' ê ( 2 x + ) 2 2 m = 0 x ê + m = 1 x ê = 1- m (2) ë ê ê 2 2 x ê + m = 3 x ê = 3- m ë ( ) 3 ë
Do (2) có nghiệm luôn là nghiệm bội chẵn; các phương trình ( ) 1 ,( )
3 có nghiệm không chung nhau và - m < 3- . m íï - m £ 0
Hàm số g (x)có 3 điểm cực trị Û g '(x)= 0 ï
có ba nghiệm bội lẻ Û ì Û 0 £ m < 3. ï 3- m > 0 ïî
Vì m Î ¢ Þ m Î {0;1; } 2 .
Vậy tổng các giá trị nguyên của tham số m bằng 3. Trang140




