Bộ đề trắc nghiệm ôn tập kiểm tra Giải tích 12 chương 3 có đáp án

Giới thiệu đến đọc giả tài liệu bộ đề trắc nghiệm ôn tập kiểm tra Giải tích 12 chương 3 có đáp án, tài liệu gồm 48 trang tuyển chọn 14 đề kiểm tra một tiết chủ đề nguyên hàm – tích phân và ứng dụng, các đề đều có cấu trúc 25 câu trắc nghiệm khách quan, tài liệu.

32 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

48 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 1
DIỄN ĐÀN GIÁO VIÊN TOÁN
OÂn taäp kieåm tra
GIAÛI TÍCH 12
NGUYEÂN HAØM - TÍCH PHAÂN
ÖÙNG DUÏNG
Naêm hoïc: 2018 - 2019
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 2
ĐỀ 1
Câu 1. Tìmnguyênhàmcủahàmsố
3
.
x
f x e
A.
3 3
1
d .
3
x x
e x e C
B.
3 3 1
1
d .
3 1
x x
e x e C
x
C.
3 3
d .
x x
e x e C
D.
3 3
d 3 .
x x
e x e C
Câu 2. Tìmnguyênhàmcủahàmsố
2 1.
f x x
A.
2
d 2 1 2 1 .
3
f x x x x C
B.
1
d 2 1 2 1 .
3
f x x x x C
C.
1
d 2 1 .
3
f x x x C
D.
1
Câu 3. Cho
( )F x
làmộtnguyênhàmcủahàmsố
( ) 2
x
f x e x
thỏamãn
3
(0)
2
F
.Tìm
( )F x
.
A.
2
3
( ) .
2
x
F x e x
B.
2
1
( ) 2 .
2
x
F x e x
C.
2
5
( ) .
2
x
F x e x
D.
2
1
( ) .
2
x
F x e x
Câu 4. Tìmnguyênhàm
( )F x
củahàmsố
( ) sin cosf x x x
thỏamãn
2.
2
F
A.
( ) cos sin 3.
F x x x
B.
( ) cos sin 3.
F x x x
C.
( ) cos sin 1.
F x x x
D.
( ) cos sin 1.
F x x x
Câu 5. Biết
( )F x
làmộtnguyênhàmcủahàmsố
1
( ) ,
1
f x
x
(2) 1
F
và
(3) ln ; , .
F a b a b
Mệnhđềnàosauđâylàđúng?
A.
1.
a b
B.
2.
a b
C.
1.
a b
D.
2.
a b
Câu 6. Chohàmsố
( )f x
thỏamãn
( ) 3 2sin ,f x x
(0) 7
f
và
; , .
3
f a b a b
Mệnhđề
nàosauđâylàđúng?
A.
2 4.
a b
B.
2 4.
a b
C.
2 2.
a b
D.
2 2.
a b
Câu 7. Chohàmsố
( )f x
cóđạohàmtrênđoạn
1;2
,
(1) 7
f
và
(2) 2
f
.Tính
2
1
( )d .I f x x
A.
5.
I
B.
5.
I
C.
9.
I
D.
7
.
2
I
Câu 8. Cho
2
1
( ) 1.
f x
Tính
2
1
2 ( ) d .I x f x x
A.
5
.
2
I
B.
7
.
2
I
C.
3
.
2
I
D.
11
.
2
I
Câu 9. Cho
6
0
( )d 12
f x x
.Tính
2
0
(3 )d .I f x x
A.
6.
I
B.
36.
I
C.
2.
I
D.
4.
I
Câu 10. Tínhtíchphân
2
2
1
2 1.d ,I x x x
bằngcáchđặt
2
1.
t x
Mệnhđềnàodướiđâyđúng?
A.
3
0
2 .d .I t t
B.
2
1
.d .I t t
C.
3
0
.d .I t t
D.
2
1
1
.d .
2
I t t
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 3
Câu 11.
Tínhtíchphân
1
ln d .
e
I x x x
A.
1
.
2
I
B.
2
2
.
2
e
I
C.
2
1
.
4
e
I
D.
2
1
.
4
e
I
Câu 12. Chotíchphân
1
0
2 3 d . ,
x
I x e x a e b
với
, a b
.Mệnhđềnàodướiđâylàđúng?
A.
2
a b
. B.
3 3
28
a b
. C.
3.
ab
D.
2 1.
a b
Câu 13. Tínhdiệntích
S
củahìnhphẳnggiớihạnbởiđồthịhàmsố
,y x
trụchoànhvàđườngthẳng
4.
x
A.
4.
S
B.
6.
S
C.
15
.
2
S
D.
8.
S
Câu 14.
Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
3
y x x
và đồ thị hàm số
2
.y x x
A.
37
.
12
S
B.
9
.
4
S
C.
81
.
12
S
D.
13.
S
Câu 15. Chohàmsố
3 2
3 2
f x x x
cóđồthị
( )C
nhưhìnhvẽ.Tínhdiệntích
S
củahìnhphẳng
(phầngạchsọc).
A.
10.
S
B.
39
.
4
S
C.
41
.
4
S
D.
13.
S
Câu 16. Cho hình phẳng D giới hạn bởi đường cong
2, 2
y y
, trục hoành vàcác đườngthẳng
0, 1.
x x
Khốitrònxoaytạo thànhkhiquayDquanhtrục hoànhcóthểtích V bằngbao
nhiêu?
A.
4
.
3
V
B.
2 .
V
C.
7
.
3
V
D.
2
.
3
V
Câu 17. ChohìnhphẳngDgiớihạnbởiđườngcong
2
y x
vàđườngthẳng
2 .y x
Khốitrònxoaytạo
thànhkhiquayDquanhtrụchoànhcóthểtíchVbằngbaonhiêu?
A.
51
.
7
V
B.
41
.
7
V
C.
64
.
15
V
D.
74
.
15
V
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 4
Câu 18. Chođồthịhàmsố
y f x
nhưhìnhvẽ.Tìmdiệntích
S
củahìnhphẳngđượcgiớihạnbởi
đồthịvàtrục
.Ox
(Phầngạchsọc).
A.
3
2
dS f x x
. B.
1 3
2 1
d d .S f x x f x x
C.
3
2
d .S f x x
D.
1 3
2 1
d dS f x x f x x
Câu 19. Chohàmsố
y f x
liêntụctrên
và
, , .
a b c
Mệnhđềnàodướiđâysai?
A.
d d d .
b c b
a a c
f x x f x x f x x
B.
d d .
b b
a a
f x x f x x
C.
d 0
a
a
f x x
D.
. d . d .
b b
a a
c f x x c f x x
Câu 20.
Tìmthểtích
V
củakhốitrònxoayđượctạorakhiquayhìnhthangcong,giớihạnbởiđồthị
hàmsố
,y f x
trục
Ox
vàhaiđườngthẳng
, ,x a x b a b
xungquanhtrục
.Ox
A.
2
d .
b
a
V f x x
B.
2
d .
b
a
V f x x
C.
d .
b
a
V f x x
D.
d .
b
a
V f x x
Câu 21. Biết
( )F x
làmộtnguyênhàmcủahàmsố
3
( ) sin cosf x x x
và
(0) .
F
Tìm
.
2
F
A.
.
2
F
B.
1
.
2 4
F
C.
1
.
2 4
F
D.
.
2
F
Câu 22. Biết
1
2
0
3 1 5
d 3ln
6 9 6
x a
x
x x b
,trongđó
a
b
làphânsốtốigiảnvới
,a b
nguyêndương.Khiđó
giátrịcủa
a b
bằngbaonhiêu?
A. 1. B.
1.
C. 37. D.
37.
Câu 23. Chobiết
1
2
0
3 2 ln 2 1 d ln ; , , .
I x x x x a b c a b c
Mệnhđềnàosauđâylàđúng?
A.
7
.
2
a b c
B.
11
.
2
a b c
C.
1
.
2
a b c
D.
1
.
2
a b c
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 5
Câu 24. Chobiết
1
2 2
0
. 4 2 d ; , .
a
I x x x a b
b
Mệnhđềnàosauđâylàđúng?
A.
log 6.
a
b
B.
log 3.
a
b
C.
log 5.
a
b
D.
log 4.
a
b
Câu 25. Tínhdiệntíchhìnhphẳnggiớihạnbởicácđường
2
2y x x
và
2.
y x
A.
9
.
2
B.
5
.
2
C.
3
.
2
D.
7
.
2
BẢNG ĐÁP ÁN
1.A
2.B
3.D
4.D
5.A
6.A
7.B
8.B
9.D
10.C
11.C
12.D
13.D
14.A
15.B
16.B
17.C
18.D
19.B
20.A
21.C 22.A 23.A 24.A 25.A
ĐỀ 2
Câu 1. Thểtíchcủavậtthểtrònxoayđượcsinhrakhiquayhìnhphẳnggiớihạnbởicácđường
2
1 ,
y x
trụchoành,trụctung,quanhtrụchoànhkhôngđượctínhbằngcôngthứcnàosau
đây?
A.
2
.
3
B.
1
3
0
.
3
x
x
C.
1
2 2
0
(1 ) d .
x x
D.
1
2
0
(1 )d .
x x
Câu 2. Nếu
( )d 5
d
a
f x x
và
( )d 2
d
b
f x x
với
a d b
thì
( )d
b
a
f x x
bằngbaonhiêu?
A. 8. B.
2.
C. 7. D. 3.
Câu 3. Diệntíchhìnhphẳnggiớihạnbởicácđường
2
1
y x
và
2
2 3 y x x
khôngđược
tínhbằngcôngthứcnàosauđây?
A.
2
2
1
( 2)d .
S x x x
B.
1
2
2
(2 2 4)d .
S x x x
C.
2
2 2
1
( 1) ( 2 3) d .
S x x x x
D.
2
2
1
2 2 4 d .
S x x x
Câu 4. Tínhdiệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố
4 2
5 4,
y x x
trụchoànhvàhai
đườngthẳng
0, 1.
x x
A.
38
.
15
B.
7
.
3
C.
8
.
5
D.
64
.
25
Câu 5. Tìmnguyênhàmcủahàmsố
3 2
2
4 5 1
.
x x
y
x
A.
2
1
2 5 . x x C
x
B.
2
1
5 . x x C
x
C.
2
1
2 5 . x x C
x
D.
2
2 5 ln . x x x C
Câu 6. Khẳngđịnhnàosauđâylàkhẳngđịnhsai?
A.
1 0
3 2 2 3
0 1
( )d ( )d .
x x x x x x
B.
1 2 1
3 2 3 2 3 2
0 0 2
( )d ( )d ( )d .
x x x x x x x x x
C.
1 1 1
3 2 3 2
0 0 0
( )d d d .
x x x x x x x
D.
1 2 1
3 2 3 2 3 2
0 0 2
( )d ( )d ( )d .
x x x x x x x x x
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 6
Câu 7. Chotíchphân
2
2
sin 3
0
sin cos d .
x
I e x x x
Nếuđổibiếnsố
2
sin
t x
thìkhẳngđịnhnàosau
đâylàkhẳngđịnhđúng?
A.
1 1
0 0
2 d d .
t t
I e t te t
B.
1
0
1
1 d .
2
t
I e t t
C.
1
0
2 1 d .
t
I e t t
D.
1
0
1
1 d .
2
t
I e t t
Câu 8. Chotíchphân
2
0
sin 8 cos d .
I x x x
Đặt
8 cos t x
thìkhẳngđịnhnàosauđâylàkhẳng
địnhđúng?
A.
8
9
1
d .
2
I t t
B.
9
8
2 d .
I t t
C.
9
8
d .
I t t
D.
8
9
d .
I t t
Câu 9. Biếttíchphân
2
2
1
1 ln d ln ; , , .
x x x a b c a b c
Khiđó
a b c
bằngbaonhiêu?
A.
26
.
9
B.
13
.
3
C. 13. D. 0.
Câu 10. Biết
2
1 sin d cos sin 2 ; , , , .
x x ax b x c x C a b c C
Khiđó,
a b c
bằngbao
nhiêu?
A.
1
.
4
B.
3
.
4
C.
29
.
12
D.
13
.
12
Câu 11. Khẳngđịnhnàosauđâylàkhẳngđịnhsai?
A.
( )d ( )d ( )d .
b c b
a a c
f x x f x x f x x
B.
( )d ( )d .
b b
a a
kf x x k f x x
C.
( )d 1.
a
a
f x x
D.
( ( ) ( ))d ( )d ( )d .
b b b
a a a
f x g x x f x x g x x
Câu 12. Tíchphân
2
0
cos 2 d
x x x
bằngbiểuthứcnàosauđây?
A.
2
2
0
1
sin 2 .
2 2
x
x
B.
2
2
0
0
1 1
sin 2 sin 2 d .
2 2
x x x x
C.
2
2
0
0
1 1
sin 2 sin 2 d .
2 2
x x x
D.
2
2
0
1
cos 2 .
2 2
x
x
Câu 13. Hàmsốnàosauđâykhônglànguyênhàmcủahàmsố
2
( 2)
( ) ?
( 1)
x x
f x
x
A.
2
1
.
1
x x
x
B.
2
.
1
x
x
C.
2
1
.
1
x x
x
D.
2
1
.
1
x x
x
Câu 14. Tínhnguyênhàm
3
4
sin
d .
cos
x
x
x
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 7
A.
3
1 1
.
3cos cos
C
x x
B.
3
1 1
.
3cos cos
C
x x
C.
3
1 1
.
cos 3cos
C
x x
D.
3
1 1
.
cos 3cos
C
x x
Câu 15. Biết
2 53 3
4
d ln ; , , .
x x a x b x C a b C
x
Khiđó,
a b
bằngbaonhiêu?
A.
23
.
5
B.
17
.
5
C.
23
.
5
D.
17
.
5
Câu 16. Thểtíchvậtthểtrònxoaysinhrakhiquayhìnhphẳngđượcgiớihạnbởicácđường
1
2 2
, 1, 2, 0,
x
y x e x x y
quanhtrụchoànhlà
2
( ).
V ae be
Khiđó,
a b
bằngbaonhiêu?
A. 1. B.
2.
C. 0. D. 2.
Câu 17. Tínhtíchphân
2
0
cos sin d .x x x

A.
3
.
2
B. 0. C.
2
.
3
D.
2
.
3
Câu 18. Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố
3 2
6 9 ,
y x x x
trụctungvàtiếptuyến
tạiđiểmcóhoànhđộthỏamãn
0
y
đượctínhbằngcôngthứcnàosauđây?
A.
3
3 2
0
( 6 10 5)d .
x x x x
B.
3
3 2
0
( 6 10 5)d .
x x x x
C.
2
3 2
0
( 6 12 8)d .
x x x x
D.
2
3 2
0
( 6 12 8)d .
x x x x
Câu 19. Tìmnguyênhàmcủahàmsố
2018
( ) 2017 .
x
f x

A.
2018
( )d 2018.2017 .ln 2017 .
x
f x x C
B.
2018
2017
( )d .
2018
x
f x x C
C.
2018
2017
( )d .
2018.ln 2017
x
f x x C
D.
2018
2017
( )d .
ln2017
x
f x x C
Câu 20. Biếtnguyênhàmcủahàmsố
2
( ) cosf x x
là
( ) sin2 ; , , .
F x ax b x C a b C
Mệnhđề
nàosauđâylàđúng?
A.
1
.
4
a b
B.
1
.
2
a b
C.
1.
a b
D.
1.
a b
Câu 21. Biết
3
0
(3 4)sin d ; , .
3
x
x x m n m n
Mệnhđềnàosauđâylàđúng?
A.
3.
m n
B.
3.
m n
C.
3
.
2
m n
D.
3
.
2
m n
Câu 22. Biết
7
2
5
ln( 4 )d ln ln ln 4; , , , , , .
x x x a b c d m n a b c d m n
Mệnhđềnàosauđâylà
đúng?
A.
27.
a b c d m n
B.
27.
a b c d m n
C.
3.
a b c d m n
D.
3.
a b c d m n
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 8
Câu 23. Biết
6
3
2
2
2
d ; , , .
2
x a b
x a b c
c
x
Mệnhđềnàosauđâylàđúng?
A.
11.
a b c
B.
27.
a b c
C.
5.
a b c
D.
3.
a b c
Câu 24. Thểtích
V
củakhốitrònxoaysinhrakhiquayhìnhphẳng(H),giớihạnbởiđồthịhàm
số
1
1
x
y
x
vàcáctrụctọađộ,quanhtrục
Ox
đượctínhbằngcôngthức
( ln ); , , .
V a b c a b c
Mệnhđềnàosauđâylàđúng?
A.
3 2 11.
a b c
B.
3 2 27.
a b c
C.
3 2 5.
a b c
D.
3 2 3.
a b c
Câu 25. TínhdiệntíchhìnhphẳnggiớihạnbởiParabol
2
2
x
y
vàđườngtròntâm
O
(gốctọa
độ),bánkính
2 2
R
đượckếtquảlà
; , .
S a b a b
Mệnhđềnàosauđâylàđúng?
A.
8
.
3
ab
B.
5.
a b
C.
7
3 .
2
a b
D.
2
1
.
2
a b
BẢNG ĐÁP ÁN
1.C
2.D
3.A
4.A
5.A
6.B
7.B
8.C
9.A
10.B
11.C 12.B 13.C 14.B 15.A 16.A 17.C 18.D 19.C 20.A
21.A 22.A 23.A 24.D 25.A
ĐỀ 3
Câu 1:TínhthểtíchVcủaphầnvậtthểgiớihạnbởihaimặtphẳng
1x
và
3
x
,biếtrằngkhi
cắtvậtthểbởimặtphẳngtùyývuônggócvớitrục
Ox
tạiđiểmcóhoànhđộ
(1 3)
x x
thìđược
mộtthiếtdiệnlàmộthìnhchữnhậtcóđộdàihaicạnhlà
3x
và
2
3 2.
x
A.
124
.
3
V
B.
32 2 15 .
V
C.
124
.
3
V
D.
32 2 15.
V
Câu 2:Tìmnguyênhàmcủahàmsố
2
2
2
( ) .
f x x
x
A.
3
1
( )d .
3
x
f x x C
x
B.
3
2
( )d .
3
x
f x x C
x
C.
3
2
( )d .
3
x
f x x C
x
D.
3
1
( )d .
3
x
f x x C
x
Câu 3:Mệnhđềnàodướiđâysai?
A.
2
íiè d .( coí ) .
2
x
x x x x C
B.
2 3
2 1
2 coí4 d íiè4 .
3 4
x x x x x C
C.
1 1
d lè 3 2 .
3 2 3
x x C
x
D.
(íiè ) d íiè .x x x C
Câu 4:Tìmnguyênhàm
( ) (1 ) cos f x x x
bằngcáchđặt
1 ,d cos d . u x v x x
Mệnhđềnàodưới
đâysai?
A.
( )d (1 )sin cos .
f x x x x x C
B.
( )d (1 )cos sin .
f x x x x x C
C.
( )d sin ( sin cos ) .
f x x x x x x C
D.
( )d (1 )sin sin d .
f x x x x x x C
Câu 5:ViếtcôngthứctínhthểtíchVcủakhốitrònxoayđượctạorakhiquayhìnhthangcong,
giớihạnbởiđồthịhàmsố
( ),y f x
trụchoànhvàhaiđườngthẳng
, ( )x a x b a b
xungquanh
trụchoành.
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 9
A.
( ) d .
b
a
V f x x
B.
2
( )d .
b
a
V f x x
C.
( )d .
b
a
V f x x
D.
2
( )d .
b
a
V f x x
Câu 6:TínhdiệntíchS củahìnhphẳngđượcgiớihạnbởiđồthịcủahàmsố
2
x
y xe
,
0
y
và
haiđườngthẳng
0; 1.
x x
A.
4 2 .S e
B.
4 .S e
C.
2 4 .S e
D.
4 2 .S e
Câu 7: Một vật đang chuyển động với vận tốc
10 /m s
thì tăng tốc với gia tốc
2 2
3 /a t t t m s
.Tínhquãngđườngs vậtđiđượctrongkhoảngthờigian10giâykểtừlúc
bắtđầutăngtốc.
A.
4300
( ).
3
s m
B.
100( ).s m
C.
400
( ).
3
s m
D.
3400
( ).
3
s m
Câu 8:Cho
4
0
( )d 16.
f x x
Tính
2
0
(2 )d .I f x x
A.
32.I
B.
8.I
C.
16.I
D.
4.I
Câu 9:Biết
d d .
( 1)(2 1) 1 2 1
x a b
x x
x x x x
.Tíchcủa
. .P a b
A.
1
.
2
P
B.
1.
P
C.
1.
P
D.
0.
P
Câu 10:Cho
2
( )
F x x
làmộtnguyênhàmcủahàmsố
2
( ) .
x
f x e
Tìmnguyênhàmcủahàmsố
2
( ) .
x
f x e
A.
2 2
( ) d 2 2 .
x
f x e x x x C
B.
2 2
( ) d 2 .
x
f x e x x x C
C.
2 2
( ) d 2 2 .
x
f x e x x x C
D.
2 2
( ) d .
x
f x e x x x C
Câu 11: Tính S diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x
và đồ thị hàm số
2
.
y x x
A.
81
.
12
S
B.
13.
S
C.
37
.
12
S
D.
4
.
9
S
Câu 12:Chohàmsố
( )f x
cóđạohàmtrênđoạn
1;2
,
(1) 1f
và
(2) 2.f
Tính
2
1
( )d .I f x x
A.
1.I
B.
3.I
C.
1.I
D.
7
.
2
I
Câu 13:Tìmhàmsố
f x( )
biết
/
( ) 2 1f x x
và
1 5.
f
A.
3
( ) 3.
3 2
x x
f x
B.
2
( ) 3.
f x x x
C.
2
( ) 3.
f x x x
D.
2
( ) 3.
2
x
f x x
Câu 14:Cho
2
0
( )d 5.
f x x
Tính
2
0
( ) 2íiè d .I f x x x
A.
5 .
2
I
B.
5 .I
C.
3.I
D.
7.I
Câu 15:Tínhtíchphân
5
2
1
4
d
x
I x
x
bằngcáchđặt
2
4.
u x
Mệnhđềnàodướiđâyđúng?
A.
3
2
5
4
1 d .
4
I u
u
B.
5
2
1
4
1 d .
4
I u
u
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 10
C.
3
2
5
4
1 d .
4
I u
u
D.
5
2
1
4
1 d .
4
I u
u
Câu 16:Tìmnguyênhàmcủahàmsố
( ) 1 cos 3 . f x x
A.
( )d 3íiè3 .f x x x x C
B.
1
( )d íiè3 .
3
f x x x x C
C.
1
( )d íiè3 .
3
f x x x x C
D.
1
( )d 1 íiè3 .
3
f x x x C
Câu 17:Chohàmsố
( )f x
thỏamãn
( ) 3 5íièf x x
và
(0) 10.f
Mệnhđềnàodướiđâyđúng?
A.
( ) 3 5coí 15.f x x x
B.
( ) 3 5coí 2.f x x x
C.
( ) 3 5coí 2.f x x x
D.
( ) 3 5coí 5.f x x x
Câu 18:Biết nguyênhàm
2 2 3 2
2
2
2
x x
c
x x e dx ax b x de C
x
x
với
, , , .
a b c d
Tính
. S a b c d
A.
1
.
6
S
B.
2.S
C.
2
.
3
S
D.
25
.
6
S
Câu 19:Cho
( )F x
làmộtnguyênhàmcủahàmsố
( ) 2
x
f x e x
thỏamãn
3
(0) .
2
F
Tìm
( ).F x
A.
2
1
( ) .
2
x
F x e x
B.
2
3
( ) .
2
x
F x e x
C.
2
5
( ) .
2
x
F x e x
D.
2
1
( ) 2 .
2
x
F x e x
Câu 20:Tìmnguyênhàmcủahàmsố
( ) 7 .
x
f x
A.
1
7
( )d .
1
x
f x x C
x
B.
( )d 7 ln 7 .
x
f x x C
C.
1
( )d 7 .
x
f x x C
D.
7
( )d .
ln 7
x
f x x C
Câu 21: Cho
1
0
3 1
d lè2 lè3
3 1 2
x a b
x x
với
,a b
là các số nguyên. Mệnh đề nào dưới đây
đúng?
A.
4.a b
B.
2 3 3.a b
C.
2 0.a b
D.
2 5 1.a b
Câu 22:Tínhtíchphân
2
1
ln dJ x x x
bằngcáchđặt
ln ,d d .u x v x x
Mệnhđềnàodướiđâysai?
A.
2
2
2
2
1
1
1
ln .
2 4
x
J x x
B.
2
2
2
1
1
ln d .
2
x
J x x x
C.
2
1
2
2
1
1
ln d .
2 2
x
J x x x
D.
3
2ln 2 .
4
J
Câu 23: Một vật chuyển động với vận tốc
1 2sin 2 ( / )v t t m s
.Tính quãng đường s vật di
chuyểntrongkhoảngthờigiantừthờiđiểm
0t
s
đếnthờiđiểm
3
4
t s
A.
1.
4
s
B.
3
1.
4
s
C.
3
1.
4
s
D.
3
.
4
s
Câu 24:Biết
4
2
3
1
d lè2 lè3 lè5,
x a b c
x x
với
, ,a b c
làcácsốnguyên.Tính
.S a b c
A.
2.S
B.
6.S
C.
0.S
D.
2.S
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 11
Câu 25:Tínhtíchphân
1
2
2
0
d
4
x
I x
x
bằngcáchđặt
2sin .x t
Mệnhđềnàodướiđâyđúng?
A.
6
0
2 1 cos 2 d .
I t t
B.
6
0
2 1 cos 2 d .
I t t
C.
6
0
1
1 cos 2 d .
2
I t t
D.
2
0
2 1 cos2 d .
I t t
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
ĐỀ 4
Câu 1: Cho
2
( )
F x x
là mộtnguyên hàm của hàm số
2
( ) .
x
f x e
Tìmnguyên hàm củahàmsố
2
( ) .
x
f x e
A.
2 2
( ) d .
x
f x e x x x C
B.
2 2
( ) d 2 2 .
x
f x e x x x C
C.
2 2
( ) d 2 .
x
f x e x x x C
D.
2 2
( ) d 2 2 .
x
f x e x x x C
Câu 2:Chohàmsố
( )f x
cóđạohàmtrênđoạn
1;4 , (1) 1
f
và
(4) 4.
f
Tính
4
1
( )d .
I f x x
A.
5.
I
B.
3.
I
C.
4.
I
D.
3.
I
Câu 3:Chohàmsố
( )f x
thỏamãn
1
0
( 1) ( )d 10
x f x x
và
2 (1) (0) 2.
f f
Tính
1
0
( )d .
I f x x
A.
8.
I
B.
8.
I
C.
12.
I
D.
12.
I
Câu 4:Tìmnguyênhàmcủahàmsố
( ) 1 sin 3 . f x x
A.
1
( )d coí3 .
3
f x x x x C
B.
1
( )d coí3 .
3
f x x x x C
C.
1
( )d 1 coí3 .
3
f x x x C
D.
( )d 3coí3 .f x x x x C
Câu 5:Tìmnguyênhàmcủahàmsố
( ) 2 1.
f x x
A.
1
( )d 2 1 .
2
f x x x C
B.
1
( )d 2 1 .
3
f x x x C
C.
1
( )d (2 1) 2 1 .
3
f x x x x C
D.
2
( )d (2 1) 2 1 .
3
f x x x x C
Câu 6:Biếtnguyênhàm
2 2
1
íiè 2 coí
x x
x e dx a x b x ce dx C
x
với
, , , .
a b c d
Tính
. S a b c d
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 12
A.
7
.
2
S
B.
11
.
2
S
C.
5.S
D.
1
.
2
S
Câu 7:Gọi
( )F x
lànguyênhàmcủahàmsố
f x x x( ) 1 coí
và
1
2
F
.Tìmhằngsố
.C
A.
.C
B.
.
2
C
C.
1 .
2
C
D.
0.C
Câu 8:Mệnhđềnàodướiđâysai?
A.
2 2
(3 ) d 3 .x x x C
B.
2
1
2 íiè4 d coí4 .
4
x x x x x C
C.
2
coí d .íiè .
2
x
x x x x C
D.
2 3
1
5(3 5 ) d (3 5 ) .
3
x x x C
Câu 9:Cho
3
1
( )
3
F x
x
làmộtnguyênhàmcủahàmsố
( )
.
f x
x
Tìmnguyênhàmcủahàmsố
( )ln .
f x x
A.
3 5
lè 1
( )lè d .
5
x
f x x x C
x x
B.
3 5
lè 1
( )lè d .
5
x
f x x x C
x x
C.
3 3
lè 1
( )lè d .
3
x
f x x x C
x x
D.
3 3
lè 1
( )lè d .
3
x
f x x x C
x x
Câu 10:Biết
2 2
1
d d .
1
( 1)
1
x a b c
x x
x x
x x
x
Tính
.S a b c
A.
2.
S
B.
3.
S
C.
4.
S
D.
1.
S
Câu 11:Tínhtíchphân
2
2
1
2 1d
I x x x
bằngcáchđặt
2
1.
u x
Mệnhđềnàodướiđâyđúng?
A.
3
0
2 d .
I u u
B.
2
1
1
d .
2
I u u
C.
3
0
d .
I u u
D.
2
1
d .
I u u
Câu 12:TínhthểtíchV củavậtthểnằmgiữahaimặtphẳng
1
x
và
1x
,biếtrằngthiếtdiện
củavậtthểbịcắtbởimặtphẳngvuônggócvớitrụcOxtạiđiểmcóhoànhđộx
( 1 1)
x
làmột
hìnhvuôngcạnhlà
2
2 1 .x
A.
16.
V
B.
25
.
3
V
C.
10
.
3
V
D.
16
.
3
V
Câu 13: Tìm nguyên hàm
( ) (1 )ln f x x x
bằng cách đặt
ln ,d (1 )d . u x v x x
Mệnh đề nào
dướiđâyđúng?
A.
2
( )d ln 1 d .
2 2
x x
f x x x x x
B.
2 2
( )d ln d .
2 2
x x
f x x x x x x
C.
2
( )d ln 1 d .
2 2
x x
f x x x x x
D.
( )d 1 ln 1 d .
2
x
f x x x x x
Câu 14:Tìmhàmsố
f x( )
biết
/
( ) 3 2
f x x
và
2 7.
f
A.
2
3
( ) 2 3.
2
f x x x
B.
2
3
( ) 2 3.
2
f x x x
C.
2
( ) 3 2 3.
f x x x
D.
2
3
( ) 2 3.
2
f x x x
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 13
Câu 15:Cho
1
0
1 1
d lè2 lè3
1 2
x a b
x x
với
,a b
làcácsốnguyên.Mệnhđềnàodướiđâyđúng
?
A.
2.a b
B.
2.a b
C.
2 0.a b
D.
2 0.a b
Câu 16:Chohàmsố
3 2
6 9 y x x x
(C).TínhdiệntíchS củahìnhphẳnggiớihạnbởiđồthị(C)
vàtrụchoành.
A.
4
.
27
S
B.
1
.
24
S
C.
27
.
4
S
D.
25
.
36
S
Câu 17:Cho
2
0
( )d 5.
f x x
Tính
2
0
( ) 2íiè d .I f x x x
A.
3.I
B.
7.I
C.
5 .I
D.
5 .
2
I
Câu 18:Biết
2 3
0
3 2 2
a
x dx a
,với
.
a
Tìm
.a
A.
1 1.
a
B.
2 5.
a
C.
3 0.
a
D.
4.
a
Câu 19:Mộtôtôđangchạyvớivậntốc
20( / )m s
thìngườingườiđạpphanh(còngọilà“thắng”).
Saukhiđạpphanh,ôtôchuyểnđộngchậmdầnđềuvớivậntốc
40 20( / )v t t m s
trong
đó
t
làkhoảngthờigiantínhbằnggiâykểtừlúcbằngđầuđạpphanh.Hỏitừlúcđạpphanhđến
khidừnghẳn,ôtôcòndichuyểnmộtquãngđườngs baonhiêumét?
A.
5 .s m
B.
10 .s m
C.
15 .s m
D.
2 .s m
Câu 20:TínhthểtíchV củavậtthểnằmgiữahaimặtphẳng
0
x
và
x
,biếtrằngthiếtdiện
củavậtthểbịcắtbởimặtphẳngvuônggócvớitrụcOxtạiđiểmcóhoànhđộx
(0 )
x
làmột
tamgiácđềucạnhlà
2 sin .x
A.
2 3.
V
B.
3.
V
C.
2 3.
V
D.
3 2.
V
Câu 21:Tínhtíchphân
0
cos d
x
F e x x
bằngcáchđặt
cos ,d d .
x
u x v e x
Mệnhđềnàodướiđây
đúng?
A.
0
0
sin cos d .
x x
F e x e x x
B.
0
0
sin cos d .
x x
F e x e x x
C.
0
0
cos sin d .
x x
F e x e x x
D.
0
0
cos sin d .
x x
F e x e x x
Câu 22: Cho hình D giới hạn bởi đường cong
2
1
y x
, trục hoành và các đường thẳng
0, 1.x x
KhốitrònxoaytạothànhkhiquayDquanhtrụchoànhcóthểtíchVbằngbaonhiêu
?
A.
4
.
3
V
B.
2 .V
C.
4
.
3
V
D.
2.V
Câu 23:Chohìnhcong(H)giớihạnbởiđường
,
x
y e
trụchoànhvàcácđườngthẳng
0x
và
lè4.x
Đườngthẳng
x k
(0 lè4)k
chia(H)thànhhaiphầncódiệntíchlà
1
S
và
2
S
nhưhình
vẽbên.Tìmkđể
1 2
2 .S S
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 14
A.
2
ln 4.
3
k
B.
ln2.k
C.
8
ln .
3
k
D.
ln3.k
Câu 24:Biết
( )F x
làmộtnguyênhàmcủahàmsố
1
( )
1
f x
x
và
(2) 1.F
Tính
(3).F
A.
7
(3) .
4
F
B.
(3) lè2 1.F
C.
1
(3) .
2
F
D.
(3) lè2 1.F
Câu 25:Cho
2
1
( )d 2f x x
và
2
1
( )d 1.g x x
Tính
2
1
2 ( ) 3 ( ) d .I x f x g x x
A.
17
.
2
I
B.
11
.
2
I
C.
7
.
2
I
D.
5
.
2
I
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
ĐỀ 5
Câu 1. Chobiết
1
2
0
3 2 ln 2 1 d ln ; , , .I x x x x a b c a b c
Mệnhđềnàosauđâylàđúng?
A.
1
.
2
a b c
B.
11
.
2
a b c
C.
7
.
2
a b c
D.
1
.
2
a b c
Câu 2. Cho
2
1
( ) 1.f x
Tính
2
1
2 ( ) d .I x f x x
A.
5
.
2
I
B.
3
.
2
I
C.
11
.
2
I
D.
7
.
2
I
Câu 3. Chohàmsố
( )f x
cóđạohàmtrênđoạn
1;2
,
(1) 7f
và
(2) 2.f
Tính
2
1
( )d .I f x x
A.
5.I
B.
5.I
C.
9.I
D.
7
.
2
I
Câu 4. Tínhtíchphân
2
2
1
2 1.d ,I x x x
bằngcáchđặt
2
1.t x
Mệnhđềnàodướiđâyđúng?
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 15
A.
3
0
.d .I t t
B.
2
1
1
.d .
2
I t t
C.
3
0
2 .d .I t t
D.
2
1
. .I t dt
Câu 5. ChohìnhphẳngDgiớihạnbởiđườngcong
2
y x
vàđườngthẳng
2 .y x
Khốitrònxoay
tạothànhkhiquayDquanhtrụchoànhcóthểtíchVbằngbaonhiêu?
A.
51
.
7
V
B.
64
.
15
V
C.
41
.
7
V
D.
74
.
15
V
Câu 6. Chohàmsố
y f x
liêntụctrên
và
, , .
a b c
Mệnhđềnàodướiđâysai?
A.
d d .
b b
a a
f x x f x x
B.
d d d .
b c b
a a c
f x x f x x f x x
C.
d 0
a
a
f x x
D.
. d . d .
b b
a a
c f x x c f x x
Câu 7. Tínhtíchphân
1
ln d .
e
I x x x
A.
2
1
.
4
e
I
B.
1
.
2
I
C.
2
2
.
2
e
I
D.
2
1
.
4
e
I
Câu 8. Tìmnguyênhàm
( )F x
củahàmsố thỏamãn
2.
2
F
A.
( ) cos sin 1.
F x x x
B.
( ) cos sin 3.
F x x x
C.
( ) cos sin 1.
F x x x
D.
( ) cos sin 3.
F x x x
Câu 9. Cho
6
0
( )d 12.
f x x
Tính
2
0
(3 )d .I f x x
A.
36.
I
B.
4.
I
C.
2.
I
D.
6.
I
Câu 10. Chotíchphân
1
0
2 3 d . ,
x
I x e x a e b
với
, .
a b
Mệnhđềnàodướiđâylàđúng?
A.
2.
a b
B.
3 3
28.
a b
C.
2 1.
a b
D.
3.
ab
Câu 11. Chobiết
1
2 2
0
. 4 2 d ; , .
a
I x x x a b
b
Mệnhđềnàosauđâylàđúng?
A.
log 5.
a
b
B.
log 3.
a
b
C.
log 4.
a
b
D.
log 6.
a
b
Câu 12. Tìmthểtích
V
củakhốitrònxoayđượctạorakhiquayhìnhthangcong,giớihạnbởiđồ
thịhàmsố
,y f x
trục
Ox
vàhaiđườngthẳng
, ,x a x b a b
xungquanhtrục
.Ox
A.
d .
b
a
V f x x
B.
2
d .
b
a
V f x x
C.
2
d .
b
a
V f x x
D.
d .
b
a
V f x x
Câu 13. Cho
( )F x
làmộtnguyênhàmcủahàmsố
( ) 2
x
f x e x
thỏamãn
3
(0)
2
F
.Tìm
( )F x
.
A.
2
5
( ) .
2
x
F x e x
B.
2
1
( ) 2 .
2
x
F x e x
C.
2
3
( ) .
2
x
F x e x
D.
2
1
( ) .
2
x
F x e x
Câu 14. Tìmnguyênhàmcủahàmsố
3
.
x
f x e
A.
3 3
d .
x x
e x e C
B.
3 3
1
d .
3
x x
e x e C
C.
3 3
d 3 .
x x
e x e C
D.
3 3 1
1
d .
3 1
x x
e x e C
x
2
1
( ) d .I f x x
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 16
Câu 15. Biết
( )F x
là một nguyên hàm của hàm số
1
( ) ,
1
f x
x
(2) 1
F
và
(3) ln ; , .
F a b a b
Mệnhđềnàosauđâylàđúng?
A.
1.
a b
B.
2.
a b
C.
1.
a b
D.
2.
a b
Câu 16. Tìmnguyênhàmcủahàmsố
2 1.
f x x
A.
1
d 2 1 2 1 .
3
f x x x x C
B.
1
d 2 1 .
3
f x x x C
C.
2
d 2 1 2 1 .
3
f x x x x C
D.
1
d 2 1 .
2
f x x x C
Câu 17. Biết
( )F x
làmộtnguyênhàmcủahàmsố
3
( ) sin cosf x x x
và
(0) .
F
Tìm
.
2
F
A.
1
.
2 4
F
B.
1
.
2 4
F
C.
.
2
F
D.
.
2
F
Câu 18. Tínhdiệntích
S
củahìnhphẳnggiớihạnbởiđồthịhàmsố
3
y x x
vàđồthịhàmsố
2
.y x x
A.
37
.
12
S
B.
9
.
4
S
C.
81
.
12
S
D.
13.
S
Câu 19. Tínhdiệntíchhìnhphẳnggiớihạnbởicácđường
2
2y x x
và
2.
y x
A.
7
.
2
B.
5
.
2
C.
3
.
2
D.
9
.
2
Câu 20. Biết
1
2
0
3 1 5
d 3ln
6 9 6
x a
x
x x b
,trongđó
a
b
làphânsốtốigiảnvới
,a b
nguyêndương.
Khiđógiátrịcủa
a b
bằngbaonhiêu?
A.
1.
B.
37.
C. 37. D. 1.
Câu 21. Cho hình phẳng D giới hạn bởi đường cong
2, 2
y y
, trục hoành và các đường
thẳng
0, 1.
x x
KhốitrònxoaytạothànhkhiquayDquanhtrụchoànhcóthểtíchV bằngbao
nhiêu?
A.
2
.
3
V
B.
4
.
3
V
C.
2 .
V
D.
7
.
3
V
Câu 22. Chođồthịhàmsố
y f x
nhưhìnhvẽ.Tìmdiệntích
S
củahìnhphẳngđượcgiớihạn
bởiđồthịvàtrục
.Ox
(Phầngạchsọc).
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 17
A.
3
2
d .S f x x
B.
3
2
dS f x x
.
C.
1 3
2 1
d dS f x x f x x
D.
1 3
2 1
d d .S f x x f x x
Câu 23. Tínhdiệntích
S
củahìnhphẳnggiớihạnbởiđồthịhàmsố
,y x
trụchoànhvàđường
thẳng
4.x
A.
8.S
B.
6.S
C.
15
.
2
S
D.
4.S
Câu 24. Chohàmsố
3 2
3 2f x x x
cóđồthị
( )C
nhưhìnhvẽ.Tínhdiệntích
S
củahình
phẳng(phầngạchsọc).
A.
39
.
4
S
B.
41
.
4
S
C.
10.S
D.
13.S
Câu 25. Chohàmsố
( )f x
thỏamãn
( ) 3 2sin ,f x x
(0) 7f
và
; , .
3
f a b a b
Mệnh
đềnàosauđâylàđúng?
A.
2 4.a b
B.
2 2.a b
C.
2 4.a b
D.
2 2.a b
Đáp án đề 001:
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 18
Câu
Chọn Câu
Chọn Câu
Chọn Câu
Chọn Câu
Chọn
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
ĐỀ 6
Câu 1. Tìmnguyênhàmcủahàmsố
3 2
2
4 5 1
.
x x
y
x
A.
2
1
5 . x x C
x
B.
2
1
2 5 . x x C
x
C.
2
2 5 ln . x x x C
D.
2
1
2 5 . x x C
x
Câu 2. Biếtnguyênhàmcủahàmsố
2
( ) cosf x x
là
( ) sin2 ; , , .F x ax b x C a b C
Mệnhđề
nàosauđâylàđúng?
A.
1
.
4
a b
B.
1
.
2
a b
C.
1.a b
D.
1.a b
Câu 3. Biếttíchphân
2
2
1
1 ln d ln ; , , .x x x a b c a b c
Khiđó
a b c
bằngbaonhiêu?
A.
13
.
3
B. 13. C.
26
.
9
D. 0.
Câu 4. Diệntíchhìnhphẳnggiớihạnbởicácđường
2
1 y x
và
2
2 3 y x x
khôngđược
tínhbằngcôngthứcnàosauđây?
A.
1
2
2
(2 2 4)d .
S x x x
B.
2
2
1
2 2 4 d .
S x x x
C.
2
2 2
1
( 1) ( 2 3) d .
S x x x x
D.
2
2
1
( 2)d .
S x x x
Câu 5. Biết
2 53 3
4
d ln ; , , .x x a x b x C a b C
x
Khiđó,
a b
bằngbaonhiêu?
A.
17
.
5
B.
23
.
5
C.
17
.
5
D.
23
.
5
Câu 6. Tínhdiệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố
4 2
5 4, y x x
trụchoànhvàhai
đườngthẳng
0, 1. x x
A.
7
.
3
B.
8
.
5
C.
64
.
25
D.
38
.
15
Câu 7. Chotíchphân
2
0
sin 8 cos d .
I x x x
Đặt
8 cos t x
thìkhẳngđịnhnàosauđâylàkhẳng
địnhđúng?
A.
8
9
d .
I t t
B.
9
8
2 d .
I t t
C.
9
8
d .
I t t
D.
8
9
1
d .
2
I t t
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 19
Câu 8. Tínhnguyênhàm
3
4
sin
d .
cos
x
x
x
A.
3
1 1
.
cos 3cos
C
x x
B.
3
1 1
.
3cos cos
C
x x
C.
3
1 1
.
3cos cos
C
x x
D.
3
1 1
.
cos 3cos
C
x x
Câu 9. Khẳngđịnhnàosauđâylàkhẳngđịnhsai?
A.
1 0
3 2 2 3
0 1
( )d ( )d .
x x x x x x
B.
1 2 1
3 2 3 2 3 2
0 0 2
( )d ( )d ( )d .
x x x x x x x x x
C.
1 1 1
3 2 3 2
0 0 0
( )d d d .
x x x x x x x
D.
1 2 1
3 2 3 2 3 2
0 0 2
( )d ( )d ( )d .
x x x x x x x x x
Câu 10. TínhdiệntíchhìnhphẳnggiớihạnbởiParabol
2
2
x
y
vàđườngtròntâm
O
(gốctọa
độ),bánkính
2 2
R
đượckếtquảlà
; , .
S a b a b
Mệnhđềnàosauđâylàđúng?
A.
5.
a b
B.
8
.
3
ab
C.
7
3 .
2
a b
D.
2
1
.
2
a b
Câu 11. Hàmsốnàosauđâykhônglànguyênhàmcủahàmsố
2
( 2)
( ) ?
( 1)
x x
f x
x
A.
2
1
.
1
x x
x
B.
2
1
.
1
x x
x
C.
2
1
.
1
x x
x
D.
2
.
1
x
x
Câu 12. Diệntíchhìnhphẳnggiớihạnbởiđồthịhàmsố
3 2
6 9 ,
y x x x
trụctungvàtiếptuyến
tạiđiểmcóhoànhđộthỏamãn
0
y
đượctínhbằngcôngthứcnàosauđây?
A.
2
3 2
0
( 6 12 8)d .
x x x x
B.
3
3 2
0
( 6 10 5)d .
x x x x
C.
2
3 2
0
( 6 12 8)d .
x x x x
D.
3
3 2
0
( 6 10 5)d .
x x x x
Câu 13. Tínhtíchphân
2
0
cos sin d .x x x

A.
2
.
3
B. 0. C.
3
.
2
D.
2
.
3
Câu 14. Khẳngđịnhnàosauđâylàkhẳngđịnhsai?
A.
( ( ) ( ))d ( )d ( )d .
b b b
a a a
f x g x x f x x g x x
B.
( )d 1.
a
a
f x x
C.
( )d ( )d .
b b
a a
kf x x k f x x
D.
( )d ( )d ( )d .
b c b
a a c
f x x f x x f x x
Câu 15. Tìmnguyênhàmcủahàmsố
2018
( ) 2017 .
x
f x

A.
2018
2017
( )d .
ln2017
x
f x x C
B.
2018
2017
( )d .
2018
x
f x x C
C.
2018
2017
( )d .
2018.ln 2017
x
f x x C
D.
2018
( )d 2018.2017 .ln 2017 .
x
f x x C
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 20
Câu 16. Chotíchphân
2
2
sin 3
0
sin cos d .
x
I e x x x
Nếuđổibiếnsố
2
sin
t x
thìkhẳngđịnhnàosau
đâylàkhẳngđịnhđúng?
A.
1
0
1
1 d .
2
t
I e t t
B.
1 1
0 0
2 d d .
t t
I e t te t
C.
1
0
2 1 d .
t
I e t t
D.
1
0
1
1 d .
2
t
I e t t
Câu 17. Thểtíchcủavậtthểtrònxoayđượcsinhrakhiquayhìnhphẳnggiớihạnbởicácđường
2
1 ,
y x
trục hoành, trụctung,quanhtrục hoànhkhôngđượctính bằngcôngthứcnàosau
đây?
A.
1
2
0
(1 )d .
x x
B.
1
3
0
.
3
x
x
C.
1
2 2
0
(1 ) d .
x x
D.
2
.
3
Câu 18. Biết
7
2
5
ln( 4 )d ln ln ln 4; , , , , , .
x x x a b c d m n a b c d m n
Mệnh đề nào sau đây là
đúng?
A.
3.
a b c d m n
B.
27.
a b c d m n
C.
3.
a b c d m n
D.
27.
a b c d m n
Câu 19. Thể tích vậtthểtrònxoaysinhrakhi quay hìnhphẳngđượcgiớihạnbởicácđường
1
2 2
, 1, 2, 0,
x
y x e x x y
quanhtrụchoànhlà
2
( ).
V ae be
Khiđó,
a b
bằngbaonhiêu?
A. 0. B. 2. C. 1. D.
2.
Câu 20. Biết
3
0
(3 4)sin d ; , .
3
x
x x m n m n
Mệnhđềnàosauđâylàđúng?
A.
3.
m n
B.
3.
m n
C.
3
.
2
m n
D.
3
.
2
m n
Câu 21. Tíchphân
2
0
cos 2 d
x x x
bằngbiểuthứcnàosauđây?
A.
2
2
0
0
1 1
sin 2 sin 2 d .
2 2
x x x x
B.
2
2
0
1
cos2 .
2 2
x
x
C.
2
2
0
0
1 1
sin 2 sin 2 d .
2 2
x x x
D.
2
2
0
1
sin 2 .
2 2
x
x
Câu 22. Nếu
( )d 5
d
a
f x x
và
( )d 2
d
b
f x x
với
a d b
thì
( )d
b
a
f x x
bằngbaonhiêu?
A.
2.
B. 8. C. 3. D. 7.
Câu 23. Biết
2
1 sin d cos sin2 ; , , , .
x x ax b x c x C a b c C
Khi đó,
a b c
bằng bao
nhiêu?
A.
13
.
12
B.
29
.
12
C.
1
.
4
D.
19
.
12
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 21
Câu 24. Thểtích
V
củakhốitrònxoaysinhrakhiquayhìnhphẳng(H),giớihạnbởiđồthịhàm
số
1
1
x
y
x
vàcáctrụctọađộ,quanhtrục
Ox
đượctínhbằngcôngthức
( ln ); , , .V a b c a b c
Mệnhđềnàosauđâylàđúng?
A.
3 2 11.a b c
B.
3 2 3.a b c
C.
3 2 5.a b c
D.
3 2 27.a b c
Câu 25. Biết
6
3
2
2
2
d ; , , .
2
x a b
x a b c
c
x
Mệnhđềnàosauđâylàđúng?
A.
11.a b c
B.
27.a b c
C.
3.a b c
D.
5.a b c
Đáp án đề 002:
Câu
Chọn Câu
Chọn Câu
Chọn Câu
Chọn Câu
Chọn
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
ĐỀ 7
Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x
và đồ thị hàm số
2
.y x x
A.
37
.
12
S
B.
81
.
12
S
C.
9
.
4
S
D.
13.S
Câu 2:Chọnkhẳngđịnhđúng.
A.
1
sin( ) cos( ) .ax b dx ax b C
a
B.
2
1
tan( ) .
cos ( )
dx
ax b C
ax b a
C.
cos sin .xdx x C
D.
2
cot .
sin
dx
x C
x
Câu 3:Cho
2 2
1
1 d 1
b
x x x x C
a
.Tính
.P a b
.
A.
6.P
B.
9.P
C.
6.P
D.
3.P
Câu 4:Tìmmộtnguyênhàm
F x
củahàmsố
3 2
4 3 4 3f x x x x
thỏa
1 10F
.
A.
4 3 2
2 3 10.
F x x x x
x
B.
4 3 2
2 3 11.
F x x x x
x
C.
2
6 4.
12
F x x
x
D.
4 3 2
2 3 .F x x x x
x
Câu 5:Mộtvậtchuyểnđộngtrong4giờvớivậntốcv(km/h)phụthuộcthời
giant (h)cóđồthịvậntốcnhưhìnhbên.Trongkhoảngthờigian3giờkểtừ
khibắtđầuchuyểnđộng,đồthịđólàmộtphầncủađườngparabolcóđỉnh
vớitrụcđốixứngsongsongvớitrụctung,khoảngthờigiancònlạiđồ
thịlàmộtđoạnthẳngsongsongvớitrụchoành.Tínhquãngđườngsmàvậtdi
chuyểnđượctrong4giờđó
A.
26,5 .km
B.
28,5 .km
C.
27 .km
D.
24 .km
(2;9)
I
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 22
Câu 6:
AnhLâmmuốnlàmcửarào
sắtcóhìnhdạngvàkíchthướcgiống
nhưhìnhvẽkếbên,biếtđườngcong
phía trên là một parabol. Giá 1 mét
vuông cửa rào sắt là 700.000 đồng.
VậyanhLâmphảitrảbaonhiêutiền
đểlàmcàicửaràosắtnhưvậy.(làm
trònđếnhàngnghìn)
A. 6.423.000. B. 6.320.000.
C.
6.523.000.
D.
6.417.000.
Câu 7:
Ngườithợgốmlàmcáichumtừmộtkhốicầucó
bánkính5dmbằngcáchcắtbỏhaichỏmcầuđốinhau.
Tínhthểtíchcủacáichum,biếtchiềucaocủanóbằng60
cm.(Quytròn2chữsốthậpphân)
A.
3
414,69 .dm
B.
3
428,74 .dm
C.
3
104,67 .dm
D.
3
135,02 .dm
Câu 8:Cho
4
0
d 10f x x
.Tính
2
0
2 df x x
.
A. 5. B.
20.
C. 10. D.
20.
Câu 9:Biết
2
4 .ln 2 .d .ln 2x x x x m x n C
.Tính
S m n
.
A.
6.S
B.
1.S
C.
3.S
D.
3.S
Câu 10:Cho2mệnhđề: P:“Nếu
f x
làhàmlẻthì
0
0
d d
a
a
f x x f x x
”.
Q:“Nếu
df x x F x C
thì
. df u x u x x F u x C
”.
Khẳngđịnhnàođúng?
A. Pđúng,Qsai. B. P, Qđềusai. C. P, Qđềuđúng. D. Psai,Qđúng.
Câu 11:Tínhdiệntíchhìnhphẳnggiớihạnbởicácđường
1
x
y e
,trụchoànhvàhaiđường
thẳng
ln 3x
,
ln 8x
.
A.
3
3 ln
2
S
. B.
3
2 ln
2
S
. C.
2
2 ln
3
S
. D.
3
2 ln
2
S
.
Câu 12:Cho
5
2
d 10f x x
.Tính
2
5
2 4 df x x
.
A. 32. B. 34. C. 36. D. 40.
Câu 13:Biết
2
( sin 3 ) cos3
x
x x dx b x C
a
.Tính
S a b
.
A.
1
.
3
S
B.
7
.
3
S
C.
5
.
3
S
D.
5.S
Câu 14:Cho
( ) 2
b
a
f x dx
và
( ) 3
b
c
f x dx
với
a b c
.Tính
( )
c
a
f x dx
.
A.
5.
B. 5. C.
1.
D. 1.
Câu 15: Cho
F x
là một nguyên hàm của
2ln , 1 2f x x F
. Tính
2
1
2 ln dK F x x x x
.
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 23
A.
1
ln 2 .
2
K
B.
1
3ln 2 .
2
K
C.
3ln 2 1.
K
D.
1
2ln 2 .
2
K
Câu 16:Tìmkhẳngđịnhsai.
A.
d .f x x f x C
B.
. d d . d .f x g x x f x x g x x
C.
. d . d .k f x x k f x x
D.
d d d .f x g x x f x x g x x
Câu 17:Tìmnguyênhàmcủahàmsố
1
5 1
f x
x
.
A.
1
ln 5 1
5
x C
B.
5ln 5 1
x C
C.
5ln(5 1)
x C
D.
1
ln 5 1
5
x C
Câu 18:Cho
2 2
cos sinf x x x
cónguyênhàm
F x
thỏa
1
4
F
.Tính
2
F
.
A.
2.
B.
5
.
2
C.
1
.
2
D.
3
.
2
Câu 19:Tìm
2016
2
x
e x dx
.
A.
2017
2
1
2 .
2017
x
e x C
B.
2017
2
1
2 .
2017
x
e x C
C.
2015
2
1 1
.
2 2015
x
e x C
D.
2017
2
1 1
.
2 2017
x
e x C
Câu 20:Biết
(1 2 ) (1 2 )
x x x
x e dx a x e be C
.Tính
S a b
.
A.
2.
S
B.
1
.
2
S
C.
1
.
3
S
D.
3.
S
Câu 21: Cho tích phân
2
2
1
2 2
d ln 2 ln 3
2
x x x
I x a b c
x
với
, ,a b c
. Chọn khẳng
địnhđúng.
A.
0
c
. B.
0
b
. C.
0
a
. D.
0
a b c
.
Câu 22:Tính
6
2
0 0
3 sin .cos .d .cos .d
x
I u u u x x
.
A.
1
.
32
B.
1
.
64
C.
1
.
16
D.
1
.
128
Câu 23:Chohình(H)giớihạnbởicácđường , vàtrụchoành.Quayhình(H)quanh
trục tađượckhốitrònxoaycóthểtíchlàbaonhiêu?
A.
.
B.
.
C.
.
D.
.
Câu 24:Cho
2
1
d
x
I x t t t
.Tínhgiátrịnhỏnhấtcủa
I x
trênđoạn
1;1
.
A.
2.
B.
5
.
6
C.
5
.
6
D.
1
.
6
y x
4
x
Ox
15
2
14
3
8
16
3
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 24
Câu 25:Kếtquảcủatíchphân
2
1
ln
d
ln 1
e
x
I x
x x
códạng
ln 2
I a b
với
,a b
.Khẳngđịnh
nàođúng?
A.
2 1.
a b
B.
2 2
4
a b
. C.
1.
a b
D.
2
ab
.
-----------HẾT----------
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
ĐỀ 8
Câu 1:Biết
1
sin 2 cos 2 sin 2
a
x xdx x x x C
b n
.Tính
2
S a b n
.
A.
4.
S
B.
2.
S
C.
10.
S
D.
6.
S
Câu 2:Cho
1 12
f
và
4
1
' d 17
f x x
.Tínhgiátrịcủa
4
f
.
A. 19. B. 29. C. 9. D. 5.
Câu 3:Cho
2
1
d 1f x x
và
4
1
d 3
f t t
.Tính
4
2
df u u
.
A.
2
. B. 4. C. 2. D.
4
.
Câu 4:Chọnkhẳngđinhsai.
A.
1
( )
( ) d .
1
ax b
ax b x C
B.
d .
x x
e x e C
C.
d .k x kx C
D.
1
d ln .x x C
x
Câu 5:Tìmkhẳngđịnhđúng.
A.
. d . d .x f x x x f x x
B.
d .f x x f x C
C.
d d d .f x g x x f x x g x x
D.
. d d . d .f x g x x f x x g x x
Câu 6:Biết
2
3 2
3 2 d
x x ax bx cx C
.Tính
S a b c
.
A.
13.
S
B.
1.
S
C.
7.
S
D.
9.
S
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 25
Câu 7:Tìmnguyênhàmcủahàmsố
2
1
3 1
f x
x
.
A.
1
.
3 1
C
x
B.
1
.
9 3
C
x
C.
1
.
9 3
C
x
D.
3
.
1 3
C
x
Câu 8:Cho
3
2 2
2
d 5 ln 5
5
x
x a x b x C
x
.Tính
P ab
.
A.
5
.
4
P
B.
5.P
C.
4
.
5
P
D.
2.P
Câu 9:Cho2mệnhđề: P:“Nếu
df x x F x C
thì
1
df ax b x F ax b C
a
”.
Q:“Nếu
f x
làhàmchẵnthì
0
0
2 2
a a
a a
f x dx f x dx f x dx
”.
Khẳngđịnhnàođúng?
A. Pđúng,Qsai. B. P, Qđềusai. C. P, Qđềuđúng. D. Psai,Qđúng.
Câu 10:Biết
2
4 .ln 2 .d .ln 2x x x x m x n C
.
.Tính
.S m n
.
A.
2.S
B.
3.S
C.
3.S
D.
6.S
Câu 11:Chobiết
3 4 4
1 1 1
d 2, d 3, d 7f x x f x x g x x
.Khẳngđịnhnàosauđâylàsai?
A.
4
1
d 10.f x g x x
B.
4
1
4 2 d 2.f x g x x
C.
3
4
d 5.f x x
D.
4
3
d 1.f x x
Câu 12:
Mộtthùngrượucóbánkínhcácđáylà30cm,thiếtdiệnvuông
gócvớitrụcvàcáchđềuhaiđáycóbánkínhlà40cm,chiềucaothùng
rượulà1m(hìnhvẽ).Biếtrằngmặtphẳngchứatrụcvàcắtmặtxung
quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu
(đơnvịlít)làbaonhiêu?
A.
lít.
B.
lít.
C.
lít.
D.
lít.
Câu 13:TìmmộtnguyênhàmF(x)củahàmsố
cosf x x x
thỏamãn
0 9F
.
A.
2
sin 9.
2
x
F x x
B.
2
sin 9.
2
x
F x x
C.
2
sin .
2
x
F x x
D.
2
sin 9.
2
x
F x x
Câu 14:Cho
2
4 5
d ln 2 ln 2 1
2 5 2
x
x a x b x C
x x
.Tính
P ab
.
A.
1.P
B.
2.P
C.
2.P
D.
1.P
Câu 15:Chotíchphân
2
2
1
2 1
d ln 2 ln3
1
x x x
I x a b c
x
với
, ,a b c
.Chọnkhẳngđịnh
sai.
A.
0a b c
. B.
0a
. C.
0b
. D.
0c
.
Câu 16:Tínhdiệntíchhìnhphẳnggiớihạnbởicácđường , và .
A.
.
B.
.
C.
.
D.
.
167,12
107,34
212,6
425,2
x
y e x
1 0
x y
ln 5
x
5 ln 4
S
4 ln 5
S
5 ln 4
S
4 ln 5
S
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 26
Câu 17:Tính
3
2
0
2
ln 2 3 3 d d
x
I u u x
.
A.
5ln 5 4ln 2 3.
B.
5ln 5 4ln 2 3.
C.
5ln 5 4ln 2 3.
D.
5ln 5 4ln 2 3.
Câu 18:Cho
2
2
3
1
1
d
x
I x b
x a
.Tính
.a b
.
A.
2.
B.
1
.
32
C.
31
.
4
D.
4.
Câu 19:
Tínhdiệntíchhìnhphẳnggiớihạnbởihaiđồthịhàmsố
2
2y x
,
2
1y x
vàtrụchoành.
A.
3 2 2 .
B.
8 2
.
3 2
C.
2 2 .
2
D.
4 2 .
Câu 20:Mộtvậtđangchuyểnđộngvớivậntốc
10 /m s
thìtăngtốcvớigiatốc
2 2
3 /a t t t m s
.
Quãngđườngvậtđiđượctrongkhoảngthời gian10giâykểtừlúcbắtđầutăngtốcbằngbao
nhiêu?
A.
4000
.
3
m
B.
4300
.
3
m
C.
1900
.
3
m
D.
2200
.
3
m
Câu 21:Cho
1
2
0
.ln 2 d ln3 ln 2I x x x a b c
với
, ,a b c
làcácsốhữutỉ.Tínhtích
. .a b c
.
A.
1.
B.
2.
C.
3
.
2
D.
3
.
4
Câu 22:
Mộtnhàhàngmuốnlàmcái
bảng hiệu là một phần của Elip có
kíchthước,hìnhdạnggiốngnhưhình
vẽvàcóchấtliệubằnggỗ.Tínhdiện
tíchbềmặtbảnghiệu.(Làmtrònđến
hàngphầntrăm,đơnvị
2
m
)
A. 2,32. B. 2,41.
C. 1,38. D. 1,61.
Câu 23: Chohình phẳng giới hạn bởiđườngcong
x
y e
, trụchoành, trục tungvà đường
thẳng
1x
. Khối tròn xoay tạo thành khi quay quanh trục hoành có thể tích bằng bao
nhiêu?
A.
2
.
2
e
V
B.
2
1
.
2
e
V
C.
2
1
.
2
e
V
D.
2
1
.
2
e
V
Câu 24:Tìm
2017
sin d
3
x
x x
.
A.
2018
1
3cos .
2018 3
x
x C
B.
2018
1 1
cos .
2018 3 3
x
x C
C.
2018
1 1
cos .
2018 3 3
x
x C
D.
2018
1
3cos .
2018 3
x
x C
Câu 25:Chobiết
2
1
3 2 d 1A f x g x x
và
2
1
2 d 3B f x g x x
.Tính
2
1
df x x
.
A. 1. B. 2. C.
5
7
. D.
1
2
.
D
D
V
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 27
-----------HẾT----------
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
ĐỀ 9
Câu 1: Công thứctính diện tích hìnhphẳnggiớihạn bởi haiđồ thị hàm số
( )y f x
,
( )y g x
liêntụctrên
[ ; ]a b
vàhaiđườngthẳng
x a
,
x b
( ).a b

A.
( ) ( ). .
b
a
S f x g x dx
B.
( ( ) ( )) .
b
a
S f x g x dx
C.
2
( ( ) ( )) . .
b
a
S f x g x dx
D.
b
a
Câu 2: ViếtcôngthứctínhthểtíchV củakhốitrònxoayđượctạorakhiquayhìnhthang
cong, giới hạn bởi đồ thị hàm số
,y f x
trục Ox và hai đường thẳng
, ,x a x b a b
xungquanhtrụcOx.
A.
2
( ) .
b
a
V f x dx
B.
2
( ) .
b
a
V f x dx
C.
( ) .
b
a
V f x dx
D.
( ) .
b
a
V f x dx
Câu 3:Hãychọnmệnhđềđúng
A.
0 1 .
ln
x
x
a
a dx C a
a
B.
1
, .
1
x
x dx C
C.
( ). ( ) ( ) . g( ) .f x g x dx f x dx x dx
D.
( )
( )
.
( )
g( )
f x dx
f x
dx
g x
x dx
Câu 4:Mệnhđềnàosauđâysai?
A.
.
x x
e dx e C
B.
1
ln , 0.
dx x C x
x
C.
,(0 1).
ln
x
x
a
a dx C a
a
D.
sin cos .xdx x C

Câu 5: Tìmnguyênhàmcủahàmsố
( ) cos3f x x
.
A.
cos3 3sin3 .x dx x C
 B.
sin3
cos3 .
3
x
x dx C

14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 28
C.
sin3
cos3 .
3
x
x dx C
D.
cos3 sin3 .xdx x C
Câu 6:Cho
2
( )
F x x
làmộtnguyênhàmcủahàmsố
2
( )
x
f x e
.Tìmnguyênhàmcủahàm
số
2
'( )
x
f x e
.
A.
2 2
'( ) 2
x
f x e dx x x C
. B.
2 2
'( )
x
f x e dx x x C
.
C.
2 2
'( ) 2 2
x
f x e dx x x C
. D.
2 2
'( ) 2 2 .
x
f x e dx x x C

Câu 7:Cho
( )F x
làmộtnguyênhàmcủahàmsố
ln
( )
x
f x
x
.Tính
( ) (1)I F e F
.
A.
I e
. B.
1
I
e
. C.
1
2
I
. D.
1I
.
Câu 8: Cho
( )F x
làmộtnguyênhàmcủahàmsố
( ) 2
x
f x e x
thỏamãn
3
(0)
2
F
.Tìm
( )F x
.
A.
2
3
( )
2
x
F x e x
. B.
2
1
( ) 2
2
x
F x e x
.
C.
2
5
( )
2
x
F x e x
. D.
2
1
( )
2
x
F x e x
.
Câu9:Cho
d
( 2) 2 ( 1) 1
2 1
x
a x x b x x C
x x
. Khiđó
3 .a b
A.
2
3
. B.
1
3
. C.
4
3
. D.
2
3
.
Câu 10:Biếtrằng
2
3
ln 1
2 1 1
x b
dx a x C
x x x
với
,a b Z
.Chọnkhẳngđịnh
đúngtrongcáckhẳngđịnhsau:
A.
1
.
2 2
a
b
B.
2.
b
a
C.
2
1.
a
b
D.
2.
b
a
Câu 11:Tìm
5a b
biết
2 3 3 5
. sin sin .sin x cos xdx a x b x C
A.
4
.
3
B.
1
.
3
C.
2
.
3
D.
2
.
3
Câu 12:Cho
0
2
1
3 5 1 2
ln
2 3
x x
I dx a b
x
.Khiđó,giátrịcủa
2 .S a b

A.
30.S
B.
40.S
C.
50.S
D.
60.S
Câu 13:Biết
4
0
2
sin3 .sin 2
2
x xdx a b
,vớia.blàcácsốnguyên.Tính
S a b
.
A.
1
.
6
 B.
3
.
10
 C.
3
.
10
D.
3
.
5

14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 29
Câu 14:Tính
2
2
1
1
ln5 ln3 ln2
4 3
x
I dx a b c
x x
với
; ;a b c
.Tínhgiátrịcủa
2 2 2
S a b c
.
A.
14.S
B.
6.S
C.
5.S
D.
9.S
Câu 15:Tìm
a
với
1a
,biết
2
2
1
6
6
a
x
dx
x
.
A.
2a
. B.
9a
. C.
4a
. D.
3a
.
Câu16:Cho
2
1
3f x dx
và
3
2
4
f x dx
.Tính
3
1
.f x dx
A.
3
1
1.
f x dx
B.
3
1
1.
f x dx
C.
3
1
7.
f x dx
D.
3
1
12.
f x dx
Câu 17:
Chohàmsố
( )f x
liêntụctrên
.Biết
2
1
( ) 3
f x dx
và
5
1
( ) 4
f x dx
.Tính
5
2
( ) 1 .f x dx
A.
5
2
( ) 1 7.
f x dx
B.
5
2
( ) 1 7.
f x dx
C.
5
2
( ) 1 1.
f x dx
D.
5
2
( ) 1 4.
f x dx
Câu 18:Gọi
F x
làmộtnguyênhàmcủa
f x
trên
2;3 ; 3 3; 2 2.
F F
Tính
3
2
( )f x dx
.
A.
1.
 B.1. C.5. D.6.
Câu 19:Cho
4
2
1.
f x dx
Tính
1
1
2
(4 ) .I f x dx
A.
1
.
2
I
 B.
1
.
4
I
 C.
1
.
4
I
 D.
1
.
2
I

Câu 20: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số
4 2
3 4
y x x
, trục
hoànhvàhaiđườngthẳng
0x
,
3.x

A.
71
5
B.
73
5
C.
72
5
D.
144
.
5
Câu 21:Diệntíchhìnhphẳngđượcgiớihạnbởiđồthịhàmsố
1
2
x
y
x
,trụchoànhvà
đườngthẳng
2.x

14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 30
A.
3 2ln2
B.
3 ln2
C.
3 2ln 2
D.
3 ln2
Câu 22:Diệntíchhìnhphẳngđượcgiớihạnbởiđồthịhàmsố
tany x
,trụchoànhvà
haiđườngthẳng
6
x
,
.
4
x

A.
3
ln
3
B.
6
ln
3
C.
3
ln
3
D.
6
ln
3

Câu 23:Gọi
1
S
làdiệntíchhìnhphẳnggiớihạnbởicác
đường
: ln ; ;C y x Ox x k
và
2
S
là diện tích hình
phẳnggiớihạnbởicácđường
1
: 1 ; ;
H y Ox x k
x
với
1k
nhưhìnhvẽbên.Biếtrằng
1 2
4S S
.Tìm
k
.
A.
2
k e
. B.
2k e
. C.
2
e
k
. D.
2k e
.
Câu 24:GọiVlàthểtíchkhốitrònxoaytạothànhkhiquayhìnhphẳnggiớihạnbởicác
đường
, 0y x y
và
4x
quanhtrục
.Ox
Đườngthẳng
x a
0 4a
cắtđồthị
hàmsố
y x
tại
M
(hìnhvẽbên).Gọi
1
V
làthểtíchkhốitrònxoaytạothànhkhiquay
tamgiác
OMH
quanhtrục
.Ox
Biếtrằng
1
2V V
.Khiđó
A.
2 2a
 B.
5
2
a
C.
2a
 D.
3a

Câu 25:ChohìnhphẳngDgiớihạnbởiđườngcong
2 sin ,y x
trụchoànhvàcác
đườngthẳng
0, .x x
KhốitrònxoaytạothànhkhiquayDquanhtrụchoànhcóthểtích
Vbằngbaonhiêu?
A.
2( 1).V
B.
2 ( 1).V
C.
2
2 .V
D.
2 .V
1
2
3
4
5
6
7
8
9
1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
2
4
2
5
D
A
A
D
B
D
C
D
C
D
A
B
D
A
D
C
D
B
B
D
C
D
A
D
B
ĐỀ 10
Câu 1:Trongcácmệnhđềsaumệnhđềnàosai?
A.
cos sin .xdx x C
B.
2
cot .
sin
dx
x C
x
C.
ln .
dx
x C
x
D.
.
ln
x
x
a
a dx C
a
Câu 2: Nguyênhàmcủahàmsố
( ) .f x x

14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 31
A.
1
.x C
B.
1
.
1
x
C
C.
1
( 1) .x C
D.
1
.
1
x
C
Câu 3:Khẳngđịnhnàosauđâylàkhẳngđịnhsai ?
A.
.f x dx F x C
 B.
.kf x dx k f x dx
C.
.kf x dx k kf x
  D.
.f x g x dx f x dx g x dx
Câu 4:Trongcácmệnhđềsauđâymệnhđềnàođúng?
(I)
2
2
1
ln( 4) .
4 2
xdx
x C
x
(II)
2
1
cot .
sin
xdx C
x
(III)
2cos 2cos
1
sin .
2
x x
e xdx e C
A. (I)và(II). B. Chỉ(III). C. (I)và(III). D. Chỉ(I).
Câu 5:Biết
( )F x
làmộtnguyênhàmcủahàmsố
2
1
x
f x
x
và
0 1.
F
Tính
(1).F

A.
1 ln 2 1.
F
 B.
1
1 ln 2 1.
2
F
 C.
1
1 ln 2 1.
2
F
 D.
1 ln 2 2.
F

Câu 6: Cho
2
2
( ) .
1
f x dx C
x
Tính
(2 ) .f x dx

A.
2
2
(2 ) .
1
f x dx C
x
B.
2
1
(2 ) .
4 1
f x dx C
x
C.
2
8
(2 ) .
4 1
f x dx C
x
D.
2
1
(2 ) .
1
f x dx C
x
Câu 7:Cho
2
1
( )
2
F x
x
làmộtnguyênhàmcủahàmsố
( )f x
x
.Tìmnguyênhàmcủa
hàmsố
( )ln .f x x
A.
2 2
ln 1
( )ln .
2
x
f x xdx C
x x
B.
2 2
ln 1
( )ln .
x
f x xdx C
x x
C.
2 2
ln 1
( )ln .
2
x
f x xdx C
x x
D.
2 2
ln 1
( )ln .
2
x
f x xdx C
x x
Câu 8:Hàmsốnàosauđâykhôngphảilànguyênhàmcủahàmsố
4
3
f x x
?
A.
5
3
5
x
F x x
. B.
5
3
5
x
F x
.
C.
5
3
2017
5
x
F x
. D.
5
3
1
5
x
F x
.
Câu 9: Giátrị
, ,a b c
để
2
( ) ( ) 2 3
g x ax bx c x
làmộtnguyênhàmcủahàmsố
2
( )
2 3
x x
f x
x
trongkhoảng
3
; .
2


A.
4, 2, 2.a b c
 B.
1, 2, 4.a b c

14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 32
 C.
2, 1, 4.a b c
D.
4, 2, 1.a b c

Câu 10:Chohàmsố
2
4
sin
m
f x x
.Tìm
m
đểnguyênhàm
F x
của
f x
thỏamãn
0 1
F
và
4 8
F
.
A.
4
3
m
. B.
3
4
m
. C.
3
4
m
. D.
4
3
m
.
Câu 11:Tìm
a b
biết
3
4
tan tan .
os
dx
a x b x C
c x
A.
3
4
B.
2
3

C.
1
3
D.
4
3
Câu 12 :Biết
2
0
1
ln
3 1
dx
b
x a
thì
2
.a b
A.2. B.14. C.10. D.12.
Câu 13: Biết
4
0
1
(1 )cos2x xdx
a b
giátrị
. .a b
A. 32. B. 2. C. 4.  D.12.
Câu 14: Biết
1
2
2
0
3
( ) ln2
x 1 2
x
e
e dx a b
,giátrị
.a b

A.
5
.
2
B.
5
.
2
C.
5
.
21
D.2.
Câu 15: Tìm
1m
saocho
1
(2 3) 2.
m
x dx

A.
17
.
9
B.
3.
  C.
18
.
9
D.4.
Câu 16: Cho
3
1
( ) 5
f x dx
.Tính
2
1
(2 1) .f x dx

A.
7
.
2
B.
5
.
2
  C.
15
.
2
 D.
17
.
9
Câu 17: Cho
2
1
( ) .f x dx a
Tính
1
2
0
. ( 1)
x f xI
dx
theo
.a
A.
.a
 B.
.
2
a
  C.
17
.
9
a
 D.
17
.
9
a
Câu 18: Cho
1
0
1
2
( )
dx
f x
.Tính
1
0
( ) 2
.
( )
f x
dx
f x
 A.
3.
B.3.  C.
12
.
9
 D.
9
.
13
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 33
Câu 19: Chohàmsố
( )f x
cónguyênhàmlà
( )F x
trênđoạn
1;2 , 2 1F
và
2
1
( ) 5F x dx
.Tính
2
1
( 1) ( ) .x f x dx

A.
4.
B.
4.
 C.
17
.
9
D.
17
.
9
Câu 20:Diệntíchhìnhphẳnggiớihạnbởiđồthịcáchàmsố
2
2y x x
,
.y x
A.
9
.
2
B.
9
.
2
C.
9
.
2
D.
81
.
10
Câu 21:Diệntíchhìnhphẳnggiớihạnbởicácđồthịhàmsố
y = ( 1)e x
và
(1 ) .
x
y e x

A. 2. B.
3
1.
e
C.
2 .
2
e
D.
1.
2
e
Câu 22:Diệntíchhìnhphẳnggiớihạnbởiđườngthẳng
4y x
vàpatabol
2
.
2
x
y

A.
28
.
3
B.
25
.
3
C.
22
.
3
D.
26
.
3
Câu 23:Tínhdiệntíchhìnhphẳngđượcđánhdấutrênhìnhbên
A.
26
.
3
S

B.
28
.
3
S
C.
2
2 3 .
3
S

D.
1
3 2 .
3
S
Câu 24:Tínhthểtíchkhốitrònxoaytạonêndoquayquanhtrục
Ox
hìnhphẳnggiớihạnbởicác
đường
2
1– ,y x 0y
,
0x
và
2.x

A.
8 2
.
3
B.
46
.
15
C.
2 .
D.
5
.
2
Câu 25:Mộtgáocóhìnhnửamặtcầubánkính
10R
cm
đựngnướccóđộcao
6h
cm
nhưhìnhvẽ.Tínhthểtíchnướctronggáo.
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 34
A.
3008
3
(đvtt)B.
3040
3
(đvtt)
C.
2048
3
(đvtt) D.
1840
3
(đvtt)
1 2 3 4 5 6 7 8 9 1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
2
4
2
5
C
B
C
C
B
B
A
A
D
C B B A B B B B A A B D A C B A
ĐỀ 11
Câu 1: Tìmnguyênhàmcủahàmsố
2
1
sin
f x
x
.
A.
d tanf x x x C
. B.
d cotf x x x C
.
C.
d cotf x x x C
. D.
d tanf x x x C
.
Câu 2: Khẳngđịnhnàosauđâylàđúng?
A.
tan .d ln cosx x x C
. B.
cot .d ln sinx x x C
.
C.
sin .d 2cos
2 2
x x
x C
. D.
cos .d 2sin
2 2
x x
x C
.
Câu 3:Cho
( )u u x
,
( )v v x
làhaihàmsốcóđạohàmliêntục,khẳngđịnhnàosauđâylà
đúng?
A.
.udv uv vdu
B.
.udv uv vdu
C.
.
u
udv vdu
v
D.
.vdu uv vdu
Câu 4: Khẳngđịnhnàosauđâylàkhẳngđịnhsai ?
A.
.f x dx F x C
B.
.kf x dx k f x dx
C.
.f x g x dx f x dx g x dx
D.
. . .f x g x dx f x dx g x dx
Câu 5:Biết
.f u du F u C
Khẳngđịnhnàođúng?
A.
3 1 3 3 1 .f x dx F x C
B.
1
3 1 .
3
f x dx F x x C
C.
3 1 3 1 .f x dx F x C
D.
1
3 1 3 1 .
3
f x dx F x C
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 35
Câu 6.Biết
( )F x
làmộtnguyênhàmcủacủahàmsố
1
( )
1
f x
x
và
(2) 1F
.Tính
(3).F
A.
(3) ln 2 1.F
B.
(3) ln2 1.F
C.
1
(3) .
2
F
D.
7
(3) .
4
F
Câu 7:Chohàmsố
F x
thỏamãn
2
' 1 .
F x x
x
Hãytính
2 1 .
F F
A.
1
2ln 2 .
2
B.
2ln 2.
C.
4ln 2 1.
D.
1
ln 4 .
2
Câu 8:Cho
2
1
( )
2
F x
x
làmộtnguyênhàmcủahàmsố
( )f x
x
.Tìmnguyênhàmcủahàm
số
( )ln .f x x
A.
2 2
ln 1
( )ln .
2
x
f x xdx C
x x

B.
2 2
ln 1
( )ln .
x
f x xdx C
x x
C.
2 2
ln 1
( )ln .
x
f x xdx C
x x
 D.
2 2
ln 1
( )ln .
2
x
f x xdx C
x x
Câu 9:Biết
.
x
F x ax b e
lànguyênhàmcủahàmsố
2 3 . .
x
y x e
Khiđó
a b
là
A.2. B.3. C.4. D.5.
Câu 10: Biết
3 2
. cos cos .
b n
sin x cos xdx a x m x C
Với
, , , , , .a b m n C b n
Tính giá
trịcủa
.T a b m n
A.
38
.
15
T
B.
32
.
3
T
C.
27
.
5
T
D.
41
.
30
T
Câu 11: Biết
sin cos sin .
3
x x x
x dx ax m C
b n
Với
, , , , .a b m n C
Tínhgiátrịcủa
.K abmn

A.
5
3 .K
 B.
4
3 .K
C.
3
3 .K
  D.
2
3 .K
Câu 12:Giảsử
2
2
1
4ln 1
ln 2 ln 2
x
dx a b
x
,với
,a b
làcácsốhữutỉ.Khiđótổng
4a b
bằng
A.3. B.5. C.7. D.9.
Câu 13: Kếtquảtíchphân
1
0
2 3
x
I x e dx
đượcviếtdướidạng
I ae b
vớia,blà
cácsốhữutỉ.Tìmkhẳngđịnhđúng.
A.
3 3
28a b
. B.
2 1a b
. C.
2a b
. D.
3ab
.
Câu 14:Giảsửrằng
0
2
1
3 5 1 2
ln
2 3
x x
I dx a b
x
.Khiđó,giátrịcủa
2 .a b

A. 30. B. 40. C. 50. D. 60.
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 36
Câu 15: Cho
4
0
( ) .f x dx a
Tính
2
4
2
0
cos ( ) 5
cos
xf x
dx
x
theo
.a
 A.
2.a
B.
5.a
  C.
.a
D.
5.a
Câu 16: Nếuđặt thì
2 2
1
dx
x x
(với
0x
)trởthành:
A.
2
1
tdt
t
. B.
2
1
tdt
t
. C.
2
1
dt
t
. D.
2
1
tdt
t
.
Câu17:Cho
5
1
( )d 5
f x x
,
5
4
( )d 2
f t t
và
4
1
1
( )d
3
g u u
.Tính
4
1
( ( ) ( ))d .f x g x x

A.
8
3
. B.
10
3
. C.
22
3
. D.
20
3
.
Câu 18:Giảsử
( )F x
làmộtnguyênhàmcủahàmsố
( )
x
e
f x
x
trênkhoảng
(0; )
và
3
3
1
x
e
I dx
x
.Khẳngđịnhnàosauđâylàkhẳngđịnhđúng?
A.
(3) (1).I F F
 B.
(6) (3).I F F

C.
(9) (3).I F F
 D.
(4) (2).I F F
Câu 19:Cho
18
0
( ) 30.
f x dx
Tính
6 9
0 0
(3 ) (2 ) .I f x dx f x dx
A.
11.I
B.
27.I
C.
25.I
D.
26.I
Câu 20:Tínhdiệntích
S
củahìnhphẳnggiớihạnbởiđườngparabol
2
3 2
y x x
và
đườngthẳng
1.y x
A.
37
.
14
S
B.
4
.
3
S
 C.
799
.
300
S
 D.
2.S
Câu 21: Diệntíchhìnhphẳnggiớihạnbởicácđường
2 , 4
y x y x
vàtrục
Ox
đượctính
bởicôngthức
A.
4 4
0 0
2 d 4 d .x x x x
B.
2 4
0 2
2 d 4 d .x x x x
C.
4
0
2 4 d .x x x
D.
2
0
4 2 d .x x x
Câu 22:Chohìnhphẳng
H
giớihạnbởicácđường
lny x
,
0y
,
x k
(
1k
).Tìm
k
đểdiệntíchhìnhphẳng
H
bằng1.
A.
2.k
B.
2
.k e
 C.
.k e
 D.
3
.k e
Câu 23:Chohìnhthangcong
( )H
giớihạn bớicácđường
, 0, 0
x
y e y x
và
ln4x
.
Đườngthẳng
(0 ln4)x k k
chia
( )H
thànhhaiphầncódiệntíchlà
1
S
2
S
vànhưhìnhvẽ
bên.Tìm
x k
để
1 2
2S S
.
1
t
x
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 37
A.
2
ln 4.
3
k
B.
ln 2.k
C.
8
ln .
3
k
D.
ln3.k
Câu 24:Gọi
H
làhìnhphẳnggiớihạnbởiđồthịhàmsố
2
4
x
y
x
,trục
Ox
vàđường
thẳng
1x
.Tínhthểtích
V
củakhốitrònxoaythuđượckhiquayhình
H
xungquanh
trục
Ox
A.
4
ln
2 3
V
. B.
1 4
ln
2 3
V
. C.
3
ln
2 4
V
. D.
4
ln
3
V
.
Câu 25:
Cho hình phẳng
H
được giới
hạn bởi các đường
2, 2, 1y x y x x
.Tínhthểtích
V
của vật thể tròn xoay khi quay hình
phẳng
H
quanhtrụchoành.
1 2 3 4 5 6 7 8 9 1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
2
4
2
5
C
A
B
D
D
B
A
A
B
A A D B B B A C C C B B C D A C
ĐỀ 12
Câu 1: KhẳngđịnhnàosauđâySai
 A.
1
( 1)
1
x
x dx C
B.
ln .
dx
x C
x
C.
sin os .xdx c x C
D.
.
x x
e dx e C
Câu 2: Khẳngđịnhnàosauđâyđúng
A.
in c s .s odx Cx x
 B.
22
.
x x
dx ee C

C.
2 2
.ln .
x x
a dx a a C
 D.
.
ln
x
x
a
a dx C
a
Câu 3: Cho
( ) ( )f u dx F u C
và
( )u u x
làhàmsốcóđạohàmliêntục,khẳngđịnh
nàosauđâylàđúng?
A.
B.
C.
D.
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 38
A.
( ( )) '( ) ( ( )) .f u x u x dx f u x C
B.
( ( )) '( ) ( ( )) .f u x u x dx F u x C

C.
'( ( )) '( ) ( ( )) .f u x u x dx f u x C
 D.
( '( )) ( ) ( ( )) .f u x u x dx F u x C
Câu 4: Khẳngđịnhnàosauđâylàkhẳngđịnhsai ?
A.
' ( ) .f x dx F x C
B.
.kf x dx k f x dx
C.
.f x g x dx f x dx g x dx
D.
.f x dx F x C
Câu 5: Tìmnguyênhàm
F x
củahàmsố
cos2f x x
,biếtrằng
2
2
F
.
A.
sin 2
F x x
. B.
3
sin 2
2
F x x x
.
C.
1
sin 2 2
2
F x x
. D.
2 2
F x x
.
Câu 6: Nguyênhàm
10
12
2
d
1
x
x
x
bằng
A.
11
1 2
11 1
x
C
x
. B.
11
1 2
3 1
x
C
x
.
C.
11
1 2
11 1
x
C
x
. D.
11
1 2
33 1
x
C
x
.
Câu 7: Tìmnguyênhàmcủahàmsố
3
.
x
f x e
A.
3 3
1
.
3
x x
e dx e C
B.
3 3 1
1
.
3 1
x x
e dx e C
x
C.
3 3
.
x x
e dx e C
D.
3 3
3 .
x x
e dx e C
Câu 8:Cho
3
1
( )
3
F x
x
làmộtnguyênhàmcủahàmsố
( )
.
f x
x
Tìmnguyênhàmcủa
hàmsố
( )lnf x x
.
A.
3 5
ln 1
( )ln .
5
x
f x xdx C
x x
B.
3 5
ln 1
( )ln .
5
x
f x xdx C
x x
C.
3 3
ln 1
( )ln .
3
x
f x xdx C
x x
D.
3 3
ln 1
( )ln .
3
x
f x xdx C
x x
Câu 9: Nếu
2
( ) ( ) 2 1F x ax bx c x
làmộtnguyênhàmcủahàmsố
2
10 7 2
( )
2 1
x x
f x
x
trênkhoảng
1
; .
2

Với
, , .a b c
Tính
2 .T a b c
A.
6.T
B.
2.T
C.
2.T
D.
6.T
Câu 10: Biết
cos3 sin cos .x xdx ax mx b nx C
Với
, , , , .a b m n C
Tính giátrị của
.K abmn
A.
1
.
3
K
 B.
2
1
.
3
K
C.
3
1
.
3
K
  D.
4
1
.
3
K
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 39
Câu 11: Biết
4
cot cot .
sin
b n
dx
a x m x C
x
Với
, , , , , .a b m n C b n
Tìm
.H a b m n
A.
3
.
4
H
B.
8
.
3
H

C.
4
.
3
H
D.
10
.
3
H
Câu 12:Biết
0
2
1
2 4
dx a
x x b
trongđóa,b, làcácsốnguyêndươngtính
.S b a
A.
15S
. B.
12S
. C.
9S
. D.
6S
.
Câu 13: Biết rằng
2
1
ln 1 d ln3 ln2
x x a b c
với
, ,a b c
là các số nguyên. Tính
.S a b c
A.
0.S
B.
1.S
C.
2.S
D.
2.S
Câu 14: Biếtrằng
1
2
2
0
2
x
x e a e
dx
b
x
với
,a b
làcácsốnguyên.Tính
2 2
.S a b
A.
0.S
B.
3.S
C.
5.S
D.
9.S
Câu 15: Biếtrằng
2
2
0
cos
với
,a b
làcácsốnguyên.Tính
2 2
.S a b
A.
0.S
B.
3.S
C.
5.S
D.
9.S
Câu 16: Chohàmsố
f x
liêntụctrên
R
vàthoảmãn
2 2cos 2 ,f x f x x
.x

Tính
3
2
3
2
d .I f x x

A.
6.I
 B.
0.I
 C.
2.I
 D.
6.I

Câu 17:Chocáctíchphân
2 4
0 2
( ) 3, ( ) 5
f x dx f x dx
.Tính
2
0
(2 ) .I f x dx
A.
2.I
B.
3.I
C.
4.I
D.
8.I

Câu 18:Cho
( )f x
liêntụctrênđoạn
0;10
thỏamãn
10 6
0 2
( )d 2017; ( )d 2016.
f x x f x x
Khiđógiátrịcủa
2 10
0 6
( )d ( )d .P f x x f x x
A.
1
B.
1
C.
0
D.
2
Câu 19:
Chohàmsố
( )f x
liêntụctrên
1;

và
8
0
( 1) 10.
f x dx
Tính
3
1
. ( ) .I x f x dx
A.
5I
.
B.
10I
.
C.
20I
.
D.
40I
.
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 40
2
y = -
1
3
x+
4
3
y =
x
2
1
4
1
y
O
x
Câu 20:Tínhdiệntíchhìnhphẳnggiớihạnbởicácđường
2
y x
,
1 4
3 3
y x
vàtrục
hoànhnhưhìnhvẽ.
A.
7
3
. B.
56
3
.
C.
39
2
. D.
11
6
.
3
y x x
Câu 21:Kíhiệu(H)làhìnhphẳnggiớihạnbởiđồthịhàmsố
vàđườngthẳng
1
2
y x
.Tínhdiệntíchhình(H).
A.
57
5
. B.
13
2
. C.
4.
D.
25
4
.
Câu 23:Tínhdiệntích
S
củahìnhphẳnggiớihạnbởiđườngparabol
2
3 2
y x x
và
đườngthẳng
1.y x
A.
37
.
14
S
B.
4
.
3
S
 C.
799
.
300
S
 D.
2.S
Câu 24:Ngườitacầntrồnghoatạiphầnđấtnằmphíangoàiđườngtròntâmgốctoạđộ,
bánkínhbằng
1
2
vàphíatrongcủaElipcóđộdàitrụclớnbằng
2 2
vàtrụcnhỏbằng
2
(nhưhìnhvẽ).Trongmỗimộtđơnvịdiệntíchcầnbón
100
2 2 1
kg
phânhữucơ.Hỏi
cầnsửdụngbaonhiêu
kg
phânhữucơđểbónchohoa?
A.
30kg
.
B.
40kg
.
C.
50kg
.
D.
45kg
.
Câu 24:Thểtíchkhốitrònxoaythuđượckhiquayhìnhphẳnggiớihạnbởicácđường
2 ,y x
, 0y x y
xungquanhtrục
Ox
đượctínhtheocôngthứcnàosauđây?
A.
1 2
2
0 1
2 d dV x x x x
. B.
2
0
2 dV x x
.
C.
1 2
0 1
d 2 dV x x x x
. D.
1 2
2
0 1
d 2 dV x x x x
.
Câu 25:Chohaiđườngtròn
1
;5
O
và
2
;3
O
cắtnhautạihaiđiểm
,A B
saocho
AB
là
mộtđườngkínhcủađườngtròn
2
.O
Gọi
D
làhìnhthẳngđượcgiớihạnbởihaiđường
tròn(ởngoàiđườngtrònlớn,phầnđượcgạchchéonhưhìnhvẽ).Quay
D
quanhtrục
1 2
O O
tađượcmộtkhốitrònxoay.Tínhthểtích
V
củakhốitrònxoayđượctạothành.
x
y
O
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 41
A.
14
.
3
V
B.
68
.
3
V
C.
40
.
3
V
D.
36 .V
1 2 3 4 5 6 7 8 9 1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
2
4
2
5
C
D
B
A
C
D
A
C
A
A D A A A B D C A A D C B C D C
ĐỀ 13
Câu 1:
Tínhdiệntíchhìnhphẳng
H
đượcgiớihạnbởicácđường
2
2 . 5, 0
y x x y
và
2.
x
A.
28.
B.
54 10 5
.
3
C.
27 5 5
.
3
D.
5273
.
500
Câu 2:
Khẳngđịnhnàosauđâylàkhẳngđịnhsai ?
A.
dx dx \ 0 .
kf x k f x k
B.
' ( ) .f x f x C
dò
C.
. dx . dx.
f x g x f x dx g x
D.
dx dx.
f x g x f x dx g x
Câu 3:
Biết
F x
làmộtnguyênhàmcủahàmsố
2 3
1
x
f x
x
và
2 2016.
F
Tính
3 .
F
A.
3 2006 5ln2.
F
B.
3 2014 5ln2.
F
C.
3 2006 5ln 2.
F
D.
3 2014 5ln2.
F
Câu 4:
Tìmnguyênhàmcủahàmsố
1 2
cos .
f x x
x
x
A.
ln sin 2 C.
f x x x x x
d
B.
2
1
d sin 4 C.
f x x x x
x
C.
2
1 1
sin C.
f x x x
x
x x
d
D.
d ln sin 4 C.
f x x x x x
Câu 5:
Dieäè tícâ ârèâ pâaúèá áiôùi âauè bôûi caùc ñö ôøèá :
4 2
3 7
y x x
vaø
2
4 5
y x
laø :
A.
608
15
B.
15
608
C.
19
4
D.
1029
15
Câu 6:
Tínhdiệntíchhìnhphẳng(S)giớihạnbởicácđường:
2
ln ; 0; 1;
y x x y x x e
khi
quayquanhOxbằng:
A.
2
1
(1 )
4
S e
B.
2
1
( 1)
4
S e
C.
2
1
S e
D.
2
1
( 1)
4
S e
1
O
2
O
B
A
D
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 42
Câu 7:
Chohìnhphẳng
H
đượcgiớihạnbởiđồthịcủahàmsố
tan ,y x
trụchoànhvà
haiđườngthẳng
0,
4
x x
. Khiquayhình
H
xungquanhtrụchoànhthì đượckhối
trònxoaycó thểtíchbằng
2
a
b
(
,a b
làcácsốnguyên).Khẳngđịnhnàosauđây là
khẳngđịnhsai?
A.
. 4.
a b
B.
2 2.a b
C.
4
1.
a
b
D.
5.
a b
Câu 8:
Cho hàm số
f x
có đạo hàm trên đoạn
1;2 , 1 2 2 1.
f và f
Tính
2
2
1
( 3 '( )) .
I x x f x
dò
A.
1.
I
B.
3.I
C.
9
.
2
I
D.
3
.
2
I
Câu 9:
Tìmthamsố
a
đểhàmsố
4 3 2
1 5 5
F x a x ax x
làmộtnguyênhàmcủa
hàmsố
3 2
4 6 10 .f x x x x
A.
4.
a
B.
4.
a
C.
2.a
D.
2.
a
Câu 10:
Bieát
( )d 10
b
a
f x x
vaø
( )d 5
b
a
g x x
. Kâi ñoù áiaù trò cuûa
3 ( ) 5 ( ) d
b
a
I f x g x x
laø :
A.
15
B.
5
C.
5
D.
10
Câu 11:
Tínhdiệntíchhìnhphẳng
H
đượcgiớihạnbởicácđồthịhàmsố
.
x
y x e
và
. .y e x
A.
9
.
25
B.
2
.
2
e
C.
7
.
20
D.
2
.
2
e
Câu 12:
Câo
3
4
2
4
1
2 d
cos
x x
I x
x
. Giaù trò
2I
baèèá :
A.
5
B.
2
C.
3
D.
4
Câu 13:
Tìmnguyênhàmcủahàmsố
2019
x
f x x x e
.
A.
2020
2
5
.
2 2020
x
e
f x x x C
dò
B.
2019
2
5
.
2 2019
x
e
f x x x C
dò
C.
2020
2
2
dx .
5 2020
x
e
f x x x C
D.
2019
2
2
.
5 2019
x
e
f x x x C
dò
Câu 14:
Chotíchphân
3
2
2
1
1 x
I dx
x
,nếuđổibiếnsố
2
1
x
t
x
thì
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 43
A.
3
2
2
1
tdt
I
t
B.
2
3
2
2
1
tdt
I
t
C.
3
2
2
2
1
t dt
I
t
D.
2
3
2
2
2
1
t dt
I
t
Câu 15:
Chotíchphân
2
1
1
(2 1)ln . ( )
e
I x x dx e b
a
trongđó
*
,a b Z
.Khiđóa+b
bằng:
A.
-1.
B.
-3.
C.
-5.
D.
5.
Câu 16:
DiệntíchScủahìnhphẳngtôđậmtronghìnhbênđượctínhtheocôngthứcnào
sauđây?

A.
2 4
0 2
( ) (x)dxS f x dx f
B.
2 4
0 2
( ) ( )S f x dx f x dx
C.
4
0
( )S f x dx
D.
2 4
0 2
( ) ( )S f x dx f x dx
Câu 17:
Cho
F x
làmộtnguyênhàmcủahàmsố
f x
liêntụctrênđoạn
; .a b
Khẳng
địnhnàosauđâysai?
A.
( )dx ( ) ( ).
b
a
f x F a F b
B.
( ) ( ) ( ).
b
a
f x F b F a
dò
C.
( ) 0.
a
a
f x
dò
D.
( )dx ( )dx.
b a
a b
f x f x
Câu 18:
Cho
( )F x
làmộtnguyênhàmcủahàmsố
ln
( )
x
f x
x
.Tính
( ) (1)I F e F
.
A.
I e
.
B.
1
2
I
.
C.
1
I
e
.
D.
1I
.
Câu 19:
Hou èáuyeâè âaøm
3
4
( ) d
1
x
F x x
x
laø :
A.
4
1
( ) lè 1
4
F x x C
B.
4
( ) ln 1F x x C
C.
4
1
( ) ln 1
3
F x x C
D.
4
1
( ) ln 1
2
F x x C
Câu 20:
Biết
2 2
1
( 3) (2 )
x x
x e dx e x n C
m
với
, m n
.khiđóTổng
2 2
S m n
bằng:
A.
41
B.
65
C.
5
D.
10
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 44
Câu 21:
Bieát tícâ pâaâè
1
0
2 1 d .
x
x e x a b e
. Tíèâ
P ab
baèèá :
A.
15.
P
B.
1.P
C.
1.P
D.
5.
P
Câu 22:
Biết
5
1
ln3 ln5.
3 1
a b
x x
dò
Tính
2 2
3 .S a ab b
A.
5.
S
B.
4.S
C.
0.
S
D.
1.S
Câu 23:
Câo ârèâ pâaúèá (S) áiôùi âauè bôûi Ox vaø
2
1
y x
. Tâek tícâ cuûa kâoái troøè òoay
kâi quay (S) quaèâ Ox laø :
A.
3
4
B.
3
2
C.
2
3
D.
4
3
Câu 24:
Cho
1
1 3ln
e
x
I dx
x
,đặt
1 3lnt x
.Khẳngđịnhnàosauđâyđúng?
A.
2
2
1
2
.
3
I t t
d
B.
2
1
2
.
3
e
I t t
d
C.
2
2
1
1
d .
3
I t t
D.
2
1
2
.
3
I t t
d
Câu 25:
Cho
1
2
0
3 2
ln3 ln6 2ln 2
x x
a b c
I dx
.Tính
S a b c
A.
17.S
B.
70.
S
C.
3.S
D.
7.
S
-----------------------------------------------
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
ĐỀ 14
Câu 1:
Tính diện tích S của hình phẳng giới hạn giới hạn bởi đồ thị hàm số
3 2
3 2
y x x
,haitrụctọađộvàđườngthẳng
2.x
A.
3
2
S
B.
4S
C.
7
2
S
D.
5
2
S
Câu 2:
Giảsửhàmsố
f x
liêntụctrênkhoảng
K
và
, , ,
a b c a b c
làbasốthựcbất
kìthuộc
.K
Khẳngđịnhnàosauđâylàsai?
A.
.
b b c
a c a
f x x f x x f x x
d d d
B.
.
b a
a b
f x x f x x
d d
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 45
C.
.
b b
a a
f x x f t t
d d
D.
0.
a
a
f x x
d
Câu 3:
Cho
( )F x
làmộtnguyênhàmcủahàmsố
( ) 2
x
f x e x
thỏamãn
3
(0)
2
F
.Tìm
( )F x
.
A.
2
3
( )
2
x
F x e x
.
B.
2
1
( ) 2
2
x
F x e x
.
C.
2
1
( )
2
x
F x e x
.
D.
2
5
( )
2
x
F x e x
.
Câu 4:
Nguyênhàmcủahàmsố
2
1
( ) 3 .
3
x
x
f x
A.
9 1
2 .
2ln
(
3 2.9
)
ln3
f x d
x
x
x
x C
B.
2
3 ln 3
.
ln3 3
( )f x d
x
x
C
x
C.
1 1
9 2 .
2l 3 9
( )
n
f x
x
Cdx x
x
D.
3
1 3 1
.
3 ln3 3 ln 3
( )
x
C
x
f x dx
Câu 5:
Diệntíchhìnhphẳnggiớihạnbởi
3
2
;
1
x
y y x
x
là:
A.
1
B.
1 – 2 lè
C.
1 2 lè
D.
2 – 2 lè
Câu 6:
GọiSlàdiệntíchcủaBanCôngcủamộtngôinhàcódạngnhưhìnhvẽ(Sđược
giớihạnbởiparabol(P)vàtrụcOx).TinhS
A.
9
2
S
B.
1S
C.
4
3
S
D.
2S
Câu 7:
Chohìnhphẳng
H
giớihạnbởiđồthịhàmsố
4 2.lny x x
,trụchoànhvà
đườngthẳng
x e
.TínhthểtíchVcủakhốitrònxoayđượctạorakhiquayhình
H
xung
quanhtrụcOx.
A.
2
2 5 .V e e
B.
2
2 5.V e e
C.
2
6 5 .V e e
D.
2
6 5.V e e
Câu 8:
Tínhtíchphân
5
2
0
3 2017
x
I x dx
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 46
A.
2017 1
15
ln2017
x
I
B.
5
125 1 2017 ln 2017
I
C.
5
15 1 2017 ln 2017
I
D.
5
2017 1
125
ln2017
I
Câu 9:
Câo âaøm íoá
( ) 2 3
x
f x x e
.Nếu
( ) ,
x
F x mx n e m n
làmộtnáuyeâè
âaøm cuûa
f x
târ hiệu
m n
bằng:
A.
6
B.
3
C.
7
D.
1
Câu 10:
TìmKhẳngđịnhsai
A.
'
b
a
f x dx f b f a
B.
b
a
f x dx F a F b
C.
0
a
a
cdx
D.
0 0
b
a
dx
Câu 11:
Diệntíchhìnhphẳngđượcgiớihạnbởihaiđường
y x
và
2
y x
là:
A.
1
5
B.
1
3
C.
1
2
D.
1
4
Câu 12:
Nếu
10
0
( ) 17
f x dx
và
8
0
( ) 12
f x dx
thì
10
8
( )f x dx
bằng:
A.
5
.
B.
29
.
C.
5
.
D.
15
.
Câu 13:
Tìmhàmsố
F x
,biếtrằng
'
2 2
2 1
2 1 1
F x
x x
A.
1 2
1 2 1
F x C
x x
B.
1 1
2 1 1
F x C
x x
C.
1 1
1 2 1
F x C
x x
D.
1
1 2 1
C
F x
x x
Câu 14:
Tínhtíchphân
4
2
1
4ln
x x
I dx
x
A.
61
100
B.
ln4 2
C.
9
ln4
2
D.
256
ln4 28
3
Câu 15:
Biết
3
1
3 1
ln
e
a
e
x xdx
b
trongđó
,a b
làcácsốnguyêndương.
Tínhgiátrịcủabiểuthức
2 2
7 1S a b a
A.
252
B.
245
C.
345
D.
315
Câu 16:
Trongcáckhẳngđịnhsau,khẳngđịnhnào sai?
A.
4ln 4 ln .x x x x
d d
B.
tan tan .x x x C
d
C.
2 1
sin 2 sin .x x x x x
x x
d d d
D.
. . .
x x
x e x x x e x
d d d
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 47
Câu 17:
Côngthứctínhdiệntíchhìnhthangconggiớihạnbởiđồthịhàmsố
y f x
,
trụchoànhvàhaiđườngthẳng
, ( )x a x b a b
là:
A.
2
b
a
S f x dx
B.
b
a
S f x dx
C.
2
b
a
S f x dx
D.
b
a
S f x dx
Câu 18:
Câo âaøm íoá
2017
( ) 2 1f x x
.Trm tất cả các hàm số
( )F x
tâỏa mãn
'
F x f x
và
1
2018
2
F
A.
2018
2 1
2018
4036
x
F x
B.
2018
2 1
2018
2018
x
F x
C.
2016
2017 2 1 2018
F x x
D.
2016
4034 2 1 2018
F x x
Câu 19:
Cho hàm số
2
( ) (6 1)
f x x
có một nguyên hàm có dạng
3 2
(x)
F ax bx cx d
thỏa điều kiện
( 1) 20F
. Giá trị của biểu thức
S a b c d
bằng
A.
21S
B.
27S
C.
46S
D.
20S
Câu 20:
Biết
2017
1 1
1
a b
x x
x x dx C
a b
với
,a b
làcácsốnguyêndương.Khi
đóTính
2P a b
bằng:
A.
2020
B.
2018
C.
2019
D.
2017
Câu 21:
Biết
1
2
0
1
ln 2 ln3.
5 6
a b
x x
dò
Tính
2 2
.M a b
A.
15.M
B.
5.M
C.
5.M
D.
3.M
Câu 22:
Biết
2
2
1
2 3 1 5
ln ,
2 1 3
x x
dx a b
x
trongđó
,a b
làcácsốhữutỉ.Tính
.S a b
A.
8.
B.
2.
C.
4
.
D.
6.
Câu 23:
Chohìnhphẳng(H)đượcgiớihạnbởiđườngcong
2 1
( ) :
1
x
C y
x
,trụcOxvà
trụcOy.Thểtíchcủakhốitrònxoaykhichohình(H)quayquanhtrụcOxlà:
A.
3
B.
4 ln2
C.
(3 4ln 2)
D.
(4 3ln2)
Câu 24:
Cho
3
1
8
f x dx
.Tínhtíchphân
4
2
0
1 2tan
cos
f x
dx
x
.
A.
4
B.
16
C.
2
D.
8
Câu 25:
Kết quả của tích phân
1
0
(2 3)
x
I x e dx
được viết dưới dạng
I ae b
với
,a b
.Khẳngđịnhnàosauđâyđúng?
A.
2a b
B.
3 3
28a b
C.
3ab
D.
2 1a b
A.
2a b
B.
3 3
28a b
C.
3ab
D.
2 1a b
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12 
Nguyễn Bảo Vươnghttps://www.facebook.com/phong.baovuong 48
-----------HẾT----------
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
21
22
23
24
25
A
B
C
D
| 1/48
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12

DIỄN ĐÀN GIÁO VIÊN TOÁN OÂn taäp kieåm tra GIAÛI TÍCH 12
NGUYEÂN HAØM - TÍCH PHAÂN ÖÙNG DUÏNG
Naêm hoïc: 2018 - 2019
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 1
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 ĐỀ 1 Câu 1.
Tìm nguyên hàm của hàm số   3x f x e . x 1 x 1 A. 3 3 d x e x eC.  B. 3 3 x 1 e dx e    C.  3 3x  1 C. 3 x 3 d x e x eC.  D. 3 x 3 d  3 x e x eC.  Câu 2.
Tìm nguyên hàm của hàm số f x  2x 1. 2 1 A.
f x dx  2x   1 2x 1  C.  B.
f x dx  2x   1 2x 1  C.  3 3 1 1 C.
f x dx   2x 1  C.  D.
f x dx  2x 1  C.  3 2 3 Câu 3.
Cho F (x) là một nguyên hàm của hàm số ( ) x
f x e  2x thỏa mãn F (0)  . Tìm F (x) . 2 x 1 x 5 x 1 x 3 A. 2
F (x)  e x  . B. 2
F (x)  2e x  . C. 2
F (x)  e x  . D. 2
F (x)  e x  . 2 2 2 2    Câu 4.
Tìm nguyên hàm F (x) của hàm số f (x)  sin x  cos x thỏa mãn F  2.    2 
A. F (x)  cos x  sin x  3.
B. F (x)   cos x  sin x  3.
C. F (x)   cos x  sin x 1.
D. F (x)   cos x  sin x 1. 1 Câu 5.
Biết F (x) là một nguyên hàm của hàm số f (x) 
, F (2)  1 và F (3)  ln a  ; b a, b  .  x  1
Mệnh đề nào sau đây là đúng?
A. a b  1.
B. a b  2. C. a b  1. D. a b  2.    Câu 6.
Cho hàm số f (x) thỏa mãn f (
x)  3  2 sin x, f (0)  7 và fa  ; b a,b  .    Mệnh đề  3  nào sau đây là đúng?
A. 2a b  4  .
B. 2a b  4. C. 2a b  2. D. 2a b  2  . 2 Câu 7.
Cho hàm số f (x) có đạo hàm trên đoạn 1; 2, f (1)  7 và f (2)  2 . Tính I f (  x)d . x  1 7 A. I  5. B. I  5. C. I  9. D. I  . 2 2 2 Câu 8. Cho f (x)  1. 
Tính I  x  2 f (x)d . x  1 1  5 7 3 11 A. I  . B. I  . C. I  . D. I  . 2 2 2 2 6 2 Câu 9. Cho
f (x)dx  12  . Tính I f (3x)d . x  0 0 A. I  6. B. I  36. C. I  2. D. I  4. 2
Câu 10. Tính tích phân 2
I  2x x 1.dx,  bằng cách đặt 2
t x 1. Mệnh đề nào dưới đây đúng? 1 3 2 3 2 1 A. I  2 t .dt.  B. I t .dt.  C. I t .dt.  D. I t .dt.  2 0 1 0 1
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 2
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 e I x ln d x . x  Tính tích phân 1 Câu 11. 1 2 e  2 2 e 1 2 e 1 A. I  . B. I  . C. I  . D. I  . 2 2 4 4 1
Câu 12. Cho tích phân  2  3 x I x e dx  . a e b, 
với a, b   . Mệnh đề nào dưới đây là đúng? 0 3 3
A. a b  2 .
B. a b  28 . C. ab  3.
D. a  2b  1.
Câu 13. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y  ,
x trục hoành và đường thẳng x  4  . 15 A. S  4. B. S  6. C. S  . D. S  8. 2
Câu 14. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x . 37 9 81 A. S  . B. S  . C. S  . D. S  13. 12 4 12
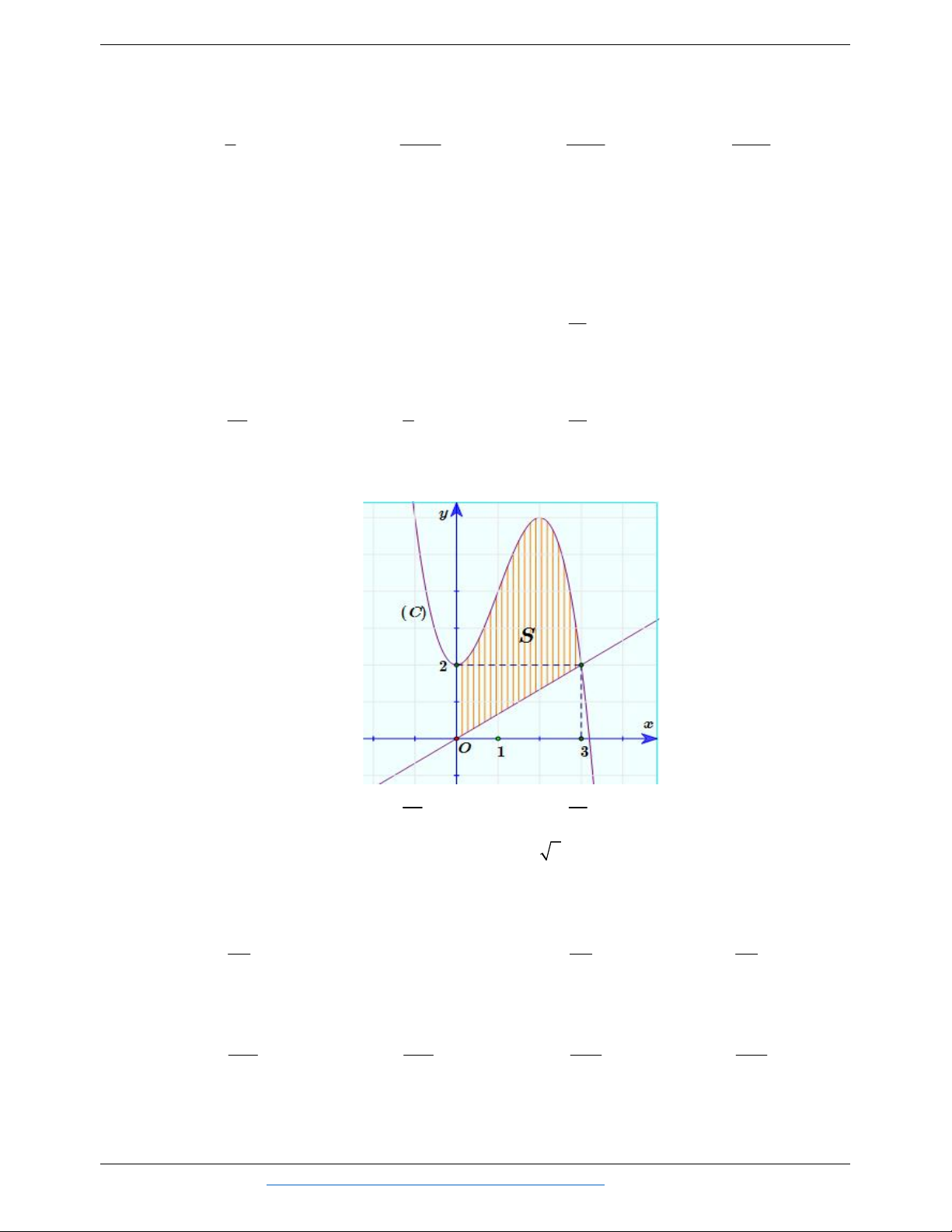
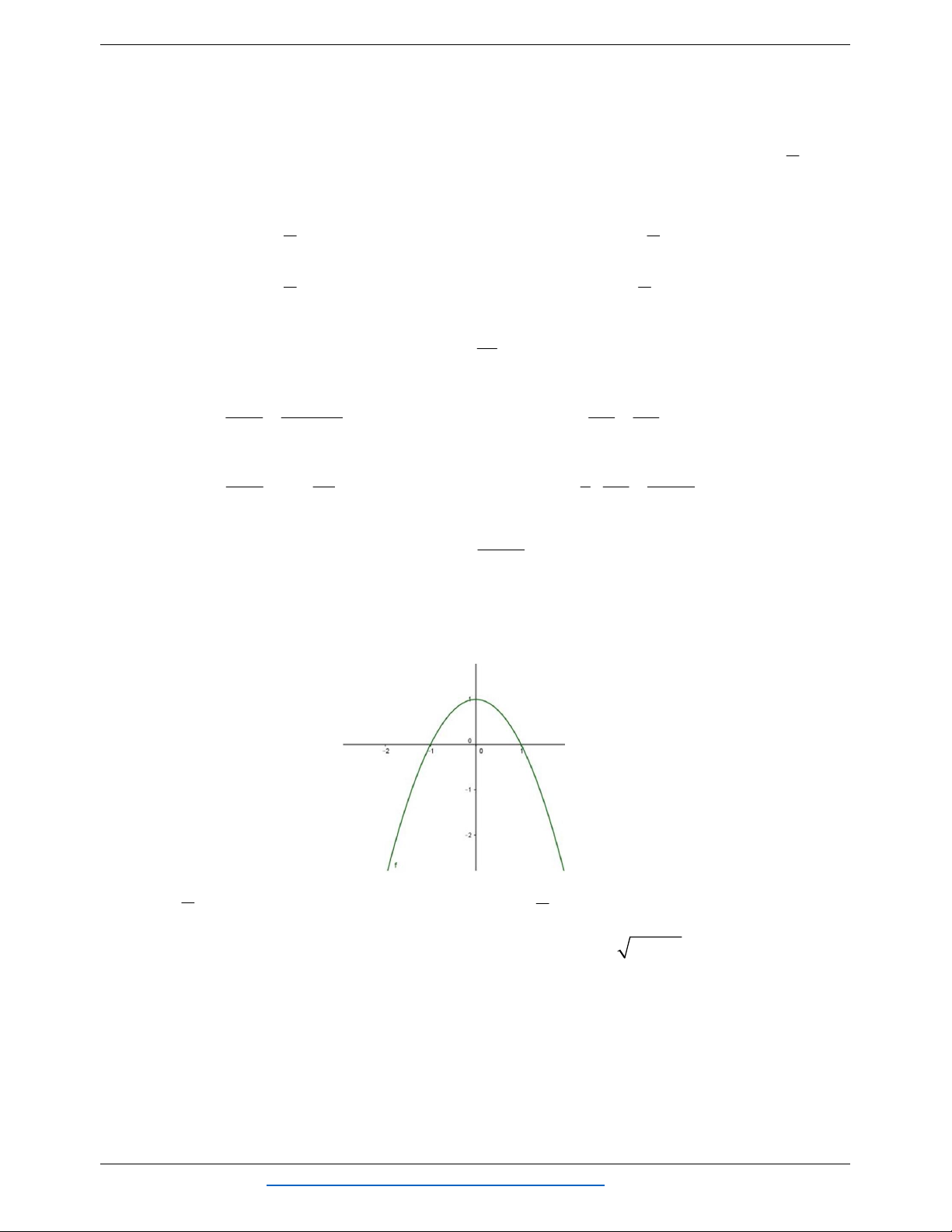
Câu 15. Cho hàm số f x 3 2
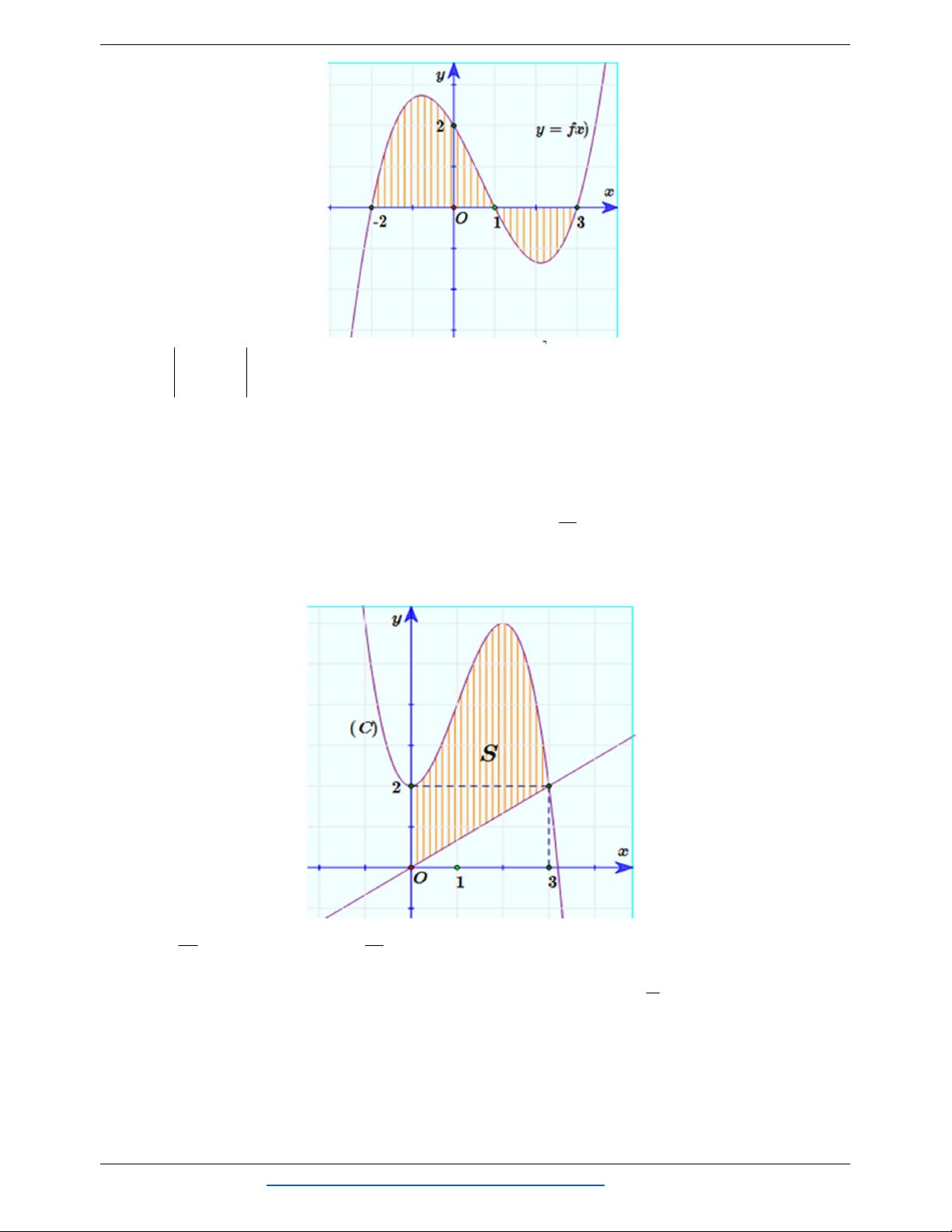
 x  3x  2 có đồ thị (C) như hình vẽ. Tính diện tích S của hình phẳng (phần gạch sọc). 39 41 A. S  10. B. S  . C. S  . D. S  13. 4 4
Câu 16. Cho hình phẳng D giới hạn bởi đường cong y
2, y  2 , trục hoành và các đường thẳng
x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 4 7 2 A. V  . B. V  2 . C. V  . D. V  . 3 3 3
Câu 17. Cho hình phẳng D giới hạn bởi đường cong 2
y x và đường thẳng y  2 .
x Khối tròn xoay tạo
thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 51 41 64 74 A. V  . B. V  . C. V  . D. V  . 7 7 15 15
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 3
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12

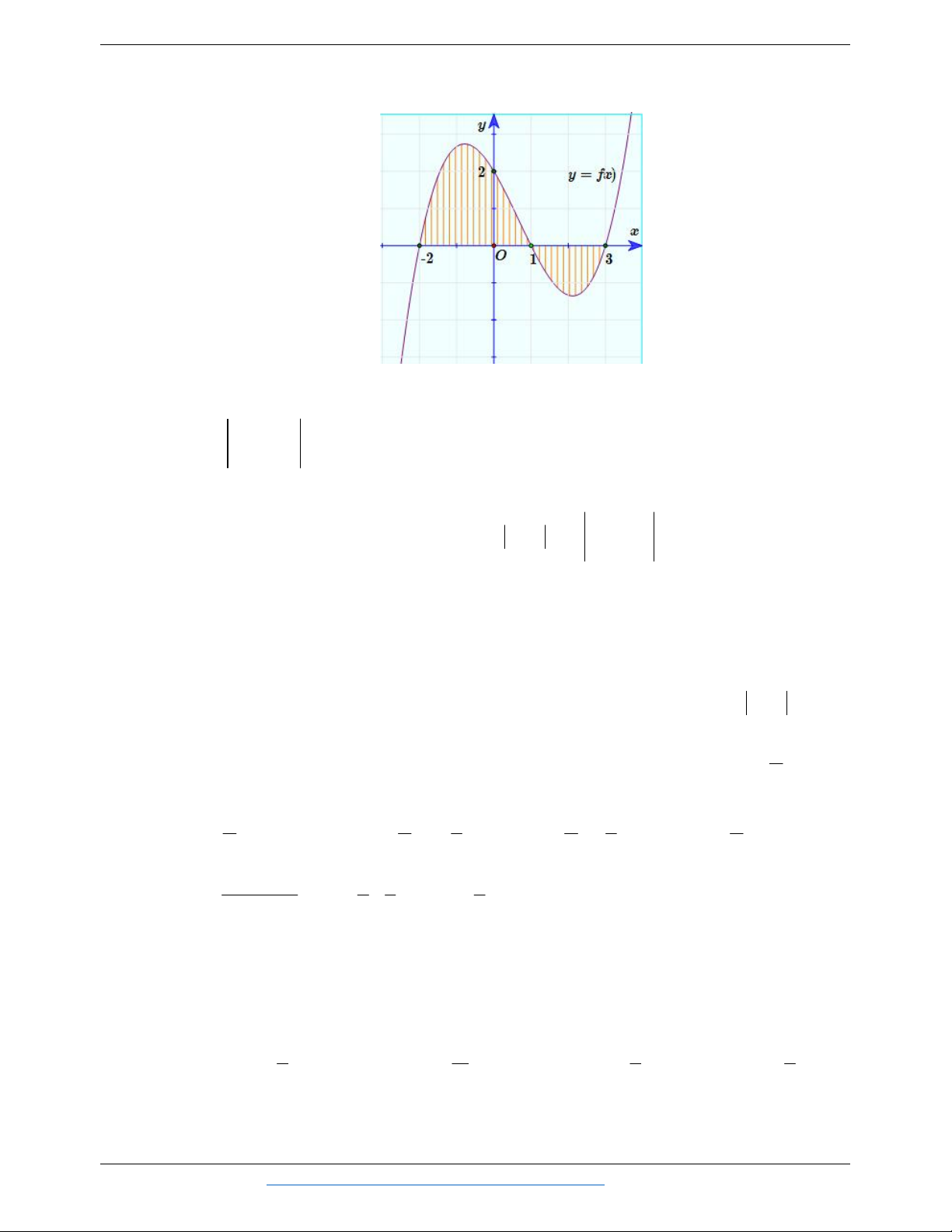
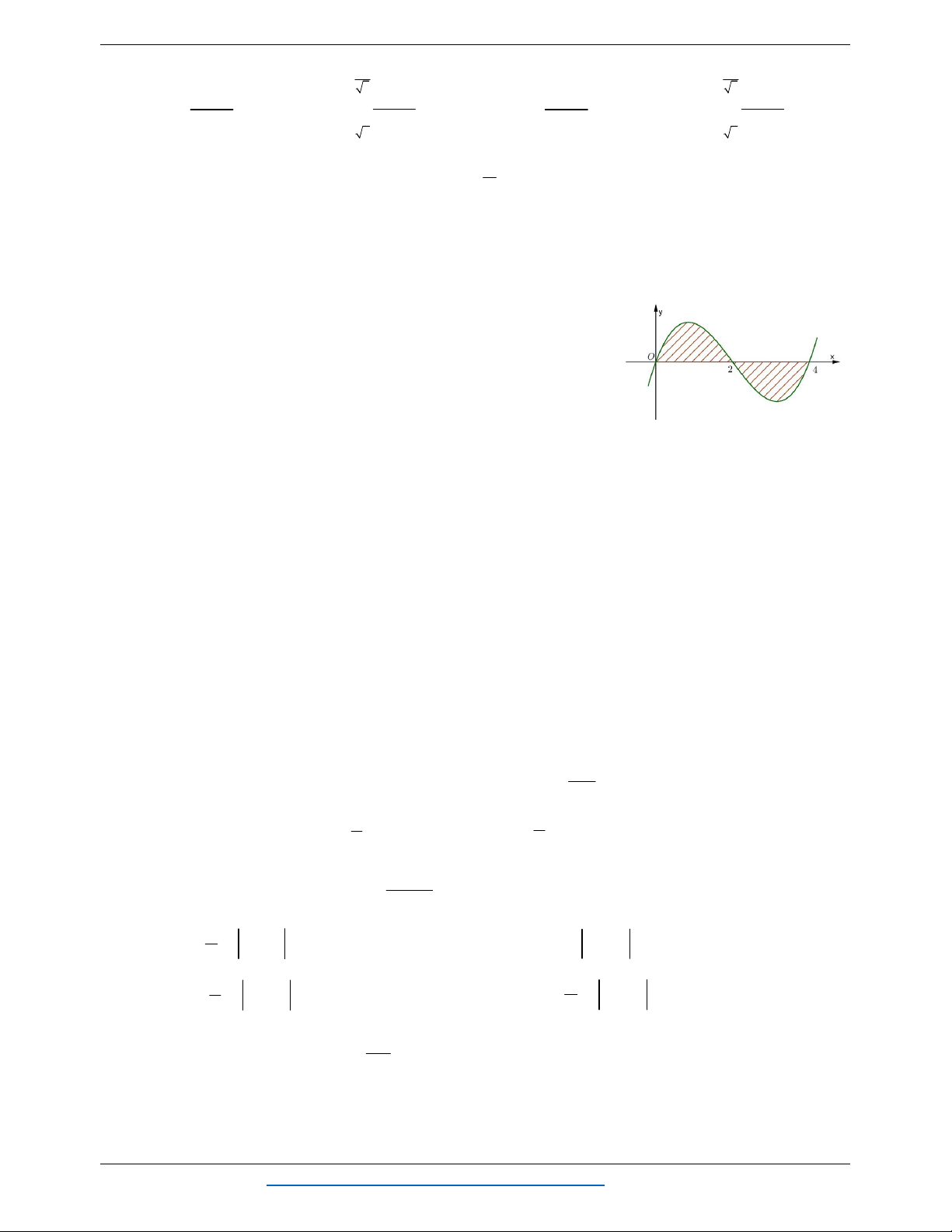
Câu 18. Cho đồ thị hàm số y f x như hình vẽ. Tìm diện tích S của hình phẳng được giới hạn bởi đồ thị và trục .
Ox (Phần gạch sọc). 3 1 3 A. S
f x dx  . B. S
f x dx f x d . x   2 2 1 3 1 3 C. S
f x dx .  D. S
f x dx f x dx   2  2 1
Câu 19. Cho hàm số y f x liên tục trên  và a,b, c  .
 Mệnh đề nào dưới đây sai? b c b b b A.
f x dx f x dx f x d . x    B.
f x dx
f x dx .   a a c a a a b b C.
f x dx  0  D. .
c f x dx  . c f x d . x   a a a
Câu 20. Tìm thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị
hàm số y f x, trục Ox và hai đường thẳng x a, x ba b, xung quanh trục . Ox b b b b A. 2 V   f x d . xB. 2 V f x d . xC. V   f x d . xD. V f x d . xa a a a   
Câu 21. Biết F (x) là một nguyên hàm của hàm số 3
f (x)  sin x cos x và F (0)   . Tìm F .    2        1    1    A. F    .   B. F     .   C. F    .   D. F   .    2   2  4  2  4  2  1 3x 1 a 5 a Câu 22. Biết dx  3ln   , trong đó
là phân số tối giản với a, b nguyên dương. Khi đó 2 x  6x  9 b 6 b 0
giá trị của a b bằng bao nhiêu? A. 1. B. 1  . C. 37. D. 3  7. 1
Câu 23. Cho biết I   2
3x  2x  ln 2x  
1 dx a ln b  ; c a, , b c  .
 Mệnh đề nào sau đây là đúng? 0 7 11 1 1
A. a b c  .
B. a b c  .
C. a b c   .
D. a b c  . 2 2 2 2
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 4
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1 a Câu 24. Cho biết 2 2
I x . 4  2x dx   ; a, b  . 
 Mệnh đề nào sau đây là đúng? b 0 log b  6. log b  3. log b  5. log b  4. A. a B. a C. a D. a
Câu 25. Tính diện tích hình phẳng giới hạn bởi các đường 2
y x  2x và y x  2. 9 5 3 7 A. . B. . C. . D. . 2 2 2 2 BẢNG ĐÁP ÁN 1.A 2.B 3.D 4.D 5.A 6.A 7.B 8.B 9.D 10.C 11.C 12.D 13.D 14.A 15.B 16.B 17.C 18.D 19.B 20.A 21.C 22.A 23.A 24.A 25.A ĐỀ 2
Câu 1. Thể tích của vật thể tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường 2
y  1 x , trục hoành, trục tung, quanh trục hoành không được tính bằng công thức nào sau đây? 1 1 1 2 3  x A. . B. x  . 2 2 2   C.  (1 ) d .  x x D.  (1 )d .  x x 3 3   0 0 0 d d b
Câu 2. Nếu f (x)dx  5 
và f (x)dx  2 
với a d b thì f (x)d  x bằng bao nhiêu? a b a A. 8. B. 2. C. 7. D. 3.
Câu 3. Diện tích hình phẳng giới hạn bởi các đường 2
y x 1 và 2
y   x  2 x  3 không được
tính bằng công thức nào sau đây? 2 1 A. 2 S
(x x  2)d .  x B. 2 S
(2x  2x  4)d .  x 1 2 2 2 C. 2 2 S
(x 1)  (x  2x  3) d .  x D. 2 S
2x  2x  4 d .  x 1 1
Câu 4. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 4 2
y x  5x  4, trục hoành và hai
đường thẳng x  0, x  1. 38 7 8 64 A. . B. . C. . D. . 15 3 5 25 3 2 4x  5x 1
Câu 5. Tìm nguyên hàm của hàm số y  . 2 x 1 1 1 A. 2 2x  5x   C. B. 2 x  5x   C. C. 2 2  x  5x   C. D. x x x 2
2 x  5x  ln x C.
Câu 6. Khẳng định nào sau đây là khẳng định sai? 1 0 1 2 1 A. 3 2 2 3
(x x )dx  (x x )d .   x B. 3 2 3 2 3 2
(x x )dx  (x x )dx  (x x )d .    x 0 1 0 0 2 1 1 1 1 2 1 C. 3 2 3 2
(x x )dx x dx x d .    x D. 3 2 3 2 3 2
(x x )dx  (x x )dx  (x x )d .    x 0 0 0 0 0 2
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 5
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
  2 2
Câu 7. Cho tích phân sin 3  sin cos d .  x I e x
x x Nếu đổi biến số 2
t  sin x thì khẳng định nào sau 0
đây là khẳng định đúng? 1 1 1 1 1 A.  2 t d  t I e t te dt.   B.  1 d .  t I e t t C.  2 1  d .  t I e t t D. 2 0 0 0 0 1 1 t I  
e 1  t  dt.  2 0  2
Câu 8. Cho tích phân I  sin x 8  cos xd . 
x Đặt t  8  cos x thì khẳng định nào sau đây là khẳng 0 định đúng? 8 1 9 9 8 A. I tdt.  B. I  2 tdt.  C. I tdt.  D. I tdt.  2 9 8 8 9 2
Câu 9. Biết tích phân  2 x   1 ln d
x x a ln b  ;
c a,b,c  .
 Khi đó a b c bằng bao nhiêu? 1 26 13 A. . B. . C. 13. D. 0. 9 3 Câu 10. Biết   x2 1 sin
dx ax b cos x csin 2x C;a, , b c,C  . 
 Khi đó, a b c bằng bao nhiêu? 1 3 29 13 A.  . B.  . C. . D.  . 4 4 12 12
Câu 11. Khẳng định nào sau đây là khẳng định sai? b c b b b
A. f (x)dx
f (x)dx f (x)d .    x
B. kf (x)dx k f (x)d .   x a a c a a a b b b
C. f (x)dx  1. 
D. ( f (x)  g(x))dx
f (x)dx g(x)d .    x a a a a  2 Câu 12. Tích phân cos 2 d  x
x x bằng biểu thức nào sau đây? 0    2 2  x 1  2 2 1 1 A.  sin 2x .   B. x sin 2x  sin 2 d x .  x 2 2   2 2 0 0 0    2 2 2 1 1 2  x 1  C. sin 2x  sin 2 d x .  x D.  cos 2x .   2 2 2 2 0 0   0 x(x  2)
Câu 13. Hàm số nào sau đây không là nguyên hàm của hàm số f (x)  ? 2 (x  1) 2 x x 1 2 x 2 x x 1 2 x x  1 A. . B. . C. . D. . x  1 x 1 x  1 x  1 3 sin x
Câu 14. Tính nguyên hàm d . x  4 cos x
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 6
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1 1 1 1 1 1 A.   C. B.   C. C.   C. D. 3 3cos x cos x 3 3cos x cos x 3 cos x 3cos x 1 1    C. 3 cos x 3cos x  4  Câu 15. Biết 3 2 3 5 x
dx a x b ln x C; a,b,C  .  
 Khi đó, a b bằng bao nhiêu?  x  23 17 23 17 A. . B. . C.  . D. . 5 5 5 5
Câu 16. Thể tích vật thể tròn xoay sinh ra khi quay hình phẳng được giới hạn bởi các đường 1 x 2 2
y x e , x  1, x  2, y  0, quanh trục hoành là 2
V   (ae be). Khi đó, a b bằng bao nhiêu? A. 1. B. 2. C. 0. D. 2. 
Câu 17. Tính tích phân 2 cos x sin xd . x  0 3 2 2 A. . B. 0. C. . D.  . 2 3 3
Câu 18. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x  6x  9x, trục tung và tiếp tuyến
tại điểm có hoành độ thỏa mãn y  0 được tính bằng công thức nào sau đây? 3 3 A. 3 2 (  6 10  5)d .  x x x x B. 3 2 (  6 10  5)d .  x x x x 0 0 2 2 C. 3 2 (  6 12  8)d .  x x x x D. 3 2 (  6 12  8)d .  x x x x 0 0
Câu 19. Tìm nguyên hàm của hàm số 2018 ( ) 2017 x f x  . 2018 2017 x A. 2018 ( )d  2018.2017 x f x x .ln 2017  C. 
B. f (x)dx   C.  2018 2018 2017 x 2018 2017 x
C. f (x)dx   C. 
D. f (x)dx   C.  2018.ln 2017 ln 2017
Câu 20. Biết nguyên hàm của hàm số 2
f (x)  cos x là F (x)  ax bsin 2x C;a, , b C  .  Mệnh đề nào sau đây là đúng? 1 1
A. a b  .
B. a b   .
C. a b  1.
D. a b  1. 4 2 3 x
Câu 21. Biết (3x  4)sin dx m  ; n m, n  . 
 Mệnh đề nào sau đây là đúng? 3 0 3 3
A. m n  3.
B. m n  3.
C. m n   .
D. m n  . 2 2 7 Câu 22. Biết 2
ln(x  4x)dx a ln b c ln d m ln n  4; a,b, c, d, , m n  . 
 Mệnh đề nào sau đây là 5 đúng?
A. a b c d m n  27.
B. a b c d m n  27.
C. a b c d m n  3.
D. a b c d m n  3.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 7
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 6 3 x a 2  b Câu 23. Biết dx  ;a, , b c  . 
 Mệnh đề nào sau đây là đúng? 2 c 2 x  2
A. a b c  11.
B. a b c  27.
C. a b c  5.
D. a b c  3.
Câu 24. Thể tích V của khối tròn xoay sinh ra khi quay hình phẳng (H), giới hạn bởi đồ thị hàm x 1 số y
và các trục tọa độ, quanh trục Ox được tính bằng công thức V   (a bln c);a, , b c  .  x 1
Mệnh đề nào sau đây là đúng?
A. 3a  2b c  11.
B. 3a  2b c  27.
C. 3a  2b c  5.
D. 3a  2b c  3. 2 x
Câu 25. Tính diện tích hình phẳng giới hạn bởi Parabol y
và đường tròn tâm O (gốc tọa 2
độ), bán kính R  2 2 được kết quả là S a  ; b a,b  .
 Mệnh đề nào sau đây là đúng? 8 7 1 A. ab  .
B. a b  5.
C. a  3b  . D. 2 a b  . 3 2 2 BẢNG ĐÁP ÁN 1.C 2.D 3.A 4.A 5.A 6.B 7.B 8.C 9.A 10.B 11.C 12.B 13.C 14.B 15.A 16.A 17.C 18.D 19.C 20.A 21.A 22.A 23.A 24.D 25.A ĐỀ 3
Câu 1: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  1 và x  3 , biết rằng khi
cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x(1  x  3) thì được
một thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 2 3x  2. 124 124 A. V  .
B. V  32  2 15. C. V  .
D. V  32  2 15. 3 3 2
Câu 2: Tìm nguyên hàm của hàm số 2
f (x)  x  . 2 x 3 x 1 3 x 2
A. f (x)dx    C. 
B. f (x)dx    C.  3 x 3 x 3 x 2 3 x 1
C. f (x)dx    C. 
D. f (x)dx    C.  3 x 3 x
Câu 3: Mệnh đề nào dưới đây sai ? 2 x 2 1 A. x íiè d x x
.( coí x)  C.  B.  2
2x  coí 4x  3 dx
x  íiè 4x C. 2 3 4 1 1 C.
dx  lè 3x  2  C.  D. (íiè x) d
x  íiè x C. 3x   2 3
Câu 4: Tìm nguyên hàm f (x)  (1 x) cos x bằng cách đặt u  1 x, dv  cos xd .
x Mệnh đề nào dưới đây sai ? A.
( )d  (1  ) sin  cos  .  f x x x x x C B.
( )d  (1  ) cos  sin  .  f x x x x x C C.
( )d  sin  ( sin  cos )  .  f x x x x x x C
D. f (x)dx  (1 x) sin x  sin d x x C.  
Câu 5: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong,
giới hạn bởi đồ thị hàm số y f (x), trục hoành và hai đường thẳng x  ,
a x b (a b) xung quanh trục hoành.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 8
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 b b b b A. V   f (x) dx.  B. 2
V f (x)dx. 
C. V   f (x)dx.  D. 2
V   f (x)dx.  a a a a x
Câu 6: Tính diện tích S của hình phẳng được giới hạn bởi đồ thị của hàm số 2
y xe , y  0 và
hai đường thẳng x  0; x  1.
A. S  4  2 e.
B. S  4  e.
C. S  2  4 e.
D. S  4  2 e.
Câu 7: Một vật đang chuyển động với vận tốc 10m / s thì tăng tốc với gia tốc a t  2  t t  2 3
m / s  . Tính quãng đường s vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc. 4300 400 3400 A. s  (m).
B. s  100(m). C. s  (m). D. s  (m). 3 3 3 4 2
Câu 8: Cho f (x)dx  16. 
Tính I f (2x)dx.  0 0 A. I  32. B. I  8. C. I  16. D. I  4. xa bCâu 9: Biết dx   dx.   . Tích của P  . a . b (x 1)(2x 1)  x 1 2x 1       1 A. P  . B. P  1. C. P  1  . D. P  0. 2 Câu 10: Cho 2
F (x)  x là một nguyên hàm của hàm số 2 ( ) x
f x e . Tìm nguyên hàm của hàm số 2 (  ) x f x e . A. x f x e
x x x   2 2 ( ) d 2 2 C. B. x f x e
x  x x   2 2 ( ) d 2 C. C. x f x e
x   x x   2 2 ( ) d 2 2 C. D. x f x e
x  x x   2 2 ( ) d C.
Câu 11: Tính S diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x . 81 37 4 A. S  . B. S  13. C. S  . D. S  . 12 12 9 2
Câu 12: Cho hàm số f (x) có đạo hàm trên đoạn 1  ;2 
 , f (1)  1 và f (2)  2. Tính I f (  x)dx.  1 7 A. I  1. B. I  3. C. I  1. D. I  . 2
Câu 13: Tìm hàm số f (x) biết /
f (x)  2x 1 và f   1  5. 3 x x 2 x
A. f (x)    3. B. 2
f (x)  x x  3. C. 2
f (x)  x x  3.
D. f (x)   x  3. 3 2 2   2 2
Câu 14: Cho f (x)dx  5. 
Tính I   f (x)  2íiè x dx.    0 0  A. I  5  .
B. I  5   . C. I  3. D. I  7. 2 5 2 x  4
Câu 15: Tính tích phân I  dx  bằng cách đặt 2 u
x  4. Mệnh đề nào dưới đây đúng ? x 1 3 5  4   4  A. I  1 d . u   B. I  1 d . u 2    2   u  4   u  4  5 1
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 9
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 3 5  4   4  C. I  1 d . u   D. I  1 d . u 2    2   u  4   u  4  5 1
Câu 16: Tìm nguyên hàm của hàm số f (x)  1 cos 3 . x 1
A. f (x)dx x  3íiè 3x C. 
B. f (x)dx x  íiè 3x C.  3 1 1
C. f (x)dx x  íiè 3x C. 
D. f (x)dx  1 íiè 3x C. 3  3
Câu 17: Cho hàm số f (x) thỏa mãn f (x)  3  5íiè x và f (0)  10. Mệnh đề nào dưới đây đúng ?
A. f (x)  3x  5 coí x  15.
B. f (x)  3x  5 coí x  2.
C. f (x)  3x  5 coí x  2.
D. f (x)  3x  5 coí x  5.  2  c
Câu 18: Biết nguyên hàm 2 2 3 2 2 x x x x   e
dx ax b x   deC 
với a,b, c, d  .  Tính 2   x x
S a b c d. 1 2 25 A. S  . B. S  2. C. S  . D. S  . 6 3 6 3
Câu 19: Cho F(x) là một nguyên hàm của hàm số ( ) x
f x e  2x thỏa mãn F(0)  . Tìm F(x). 2 x 1 x 5 x 3 x 1 A. 2
F(x)  e x  . B. 2
F(x)  e x  . C. 2
F(x)  e x  . D. 2
F(x)  2e x  . 2 2 2 2
Câu 20: Tìm nguyên hàm của hàm số ( )  7x f x . x 1 7 
A. f (x)dx   C.  B. ( )d  7 ln 7  .  x f x x C x 1 7x C. 1 ( )d 7    .  x f x x C
D. f (x)dx   C.  ln 7 1  3 1  Câu 21: Cho 
dx a lè 2    b lè3 với ,
a b là các số nguyên. Mệnh đề nào dưới đây 3x  1 x  2 0   đúng ?
A. a b  4.
B. 2a  3b  3.
C. a  2b  0.
D. 2a  5b  1. 2
Câu 22: Tính tích phân J x ln d x x
bằng cách đặt u  ln x, dv xd .
x Mệnh đề nào dưới đây sai ? 1 2 2 2 2  x  1 2 2  xA. 2 J  ln xx .   B. J  ln x  d x . x    2 4   2 1   1 1 1 2 2 1  x  1 3 C. J  ln x  d x . x   
D. J  2 ln 2  . 2 2   4 2 1
Câu 23: Một vật chuyển động với vận tốc v t   1 2sin 2t(m / s) .Tính quãng đường s vật di 3
chuyển trong khoảng thời gian từ thời điểm t  0 s đến thời điểm t  s 4  3 3 3 A. s  1. B. s  1. C. s  1. D. s  . 4 4 4 4 4 1 Câu 24: Biết
dx a lè 2  b lè3  c lè5,  với , a ,
b c là các số nguyên. Tính S a b  . c 2 x x 3 A. S  2. B. S  6. C. S  0. D. S  2.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 10
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1 2 x
Câu 25: Tính tích phân I  d 
x bằng cách đặt x  2sin t. Mệnh đề nào dưới đây đúng ? 2 0 4  x   6 6
A. I  2 1 cos 2t dt. 
B. I  2 1 cos 2t  dt.  0 0   6 1 2 C. I
1 cos 2t dt. 
D. I  2 1 cos 2t dt.  2 0 0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D ĐỀ 4 Câu 1: Cho 2
F (x)  x là một nguyên hàm của hàm số 2 ( ) x
f x e . Tìm nguyên hàm của hàm số 2 (  ) x f x e . A. x f x e
x  x x   2 2 ( ) d C. B. x f x e
x   x x   2 2 ( ) d 2 2 C. C. x f x e
x  x x   2 2 ( ) d 2 C. D. x f x e
x x x   2 2 ( ) d 2 2 C. 4
Câu 2: Cho hàm số f (x) có đạo hàm trên đoạn 1; 4, f (1)  1 và f (4)  4. Tính I f (  x)d .  x 1 A. I  5. B. I  3  . C. I  4. D. I  3. 1 1
Câu 3: Cho hàm số f (x) thỏa mãn ( 1) (  )d  10  x f x x
và 2 f (1)  f (0)  2. Tính I f (x)d .  x 0 0 A. I  8. B. I  8  . C. I  1  2. D. I  12.
Câu 4: Tìm nguyên hàm của hàm số f (x)  1 sin 3 . x 1 1
A. f (x)dx x  coí3x C. 
B. f (x)dx x  coí3x C.  3 3 1
C. f (x)dx  1 coí3x C. 
D. f (x)dx x  3 coí3x C. 3 
Câu 5: Tìm nguyên hàm của hàm số f (x)  2x 1. 1 1 A. ( )d  2 1  .  f x x x C B. ( )d   2 1  .  f x x x C 2 3 1 2 C. ( )d  (2 1) 2 1  .  f x x x x C D. ( )d  (2 1) 2 1  .  f x x x x C 3 3  1 
Câu 6: Biết nguyên hàm 2 x 2  íiè    2   coí x x e dx a
x b x ce dx C  với a, , b c, d  .  Tính  x
S a b c d.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 11
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 7 11 1 A. S  . B. S  . C. S  5. D. S  . 2 2 2   
Câu 7: Gọi F (x) là nguyên hàm của hàm số f (x)  1 xcoí x và F  1   . Tìm hằng số C.  2    A. C   . B. C  . C. C  1 . D. C  0. 2 2
Câu 8: Mệnh đề nào dưới đây sai ? 1 A. 2 2 (3x ) d
x  3x C. 
B. 2x  íiè 4x 2
dx x  coí 4x C. 4 2 x 1 C. x coí d x x  .íiè x C.  D. 2 3
5(3  5x) dx   (3  5x)  C.  2 3 1 f (x)
Câu 9: Cho F (x)  
là một nguyên hàm của hàm số
. Tìm nguyên hàm của hàm số 3 3x x f (  x) ln . x lè x 1 lè x 1 A. f (
x) lè xdx    C.  B. f (
x) lè xdx    C. 3 5  x 5x 3 5 x 5x lè x 1 lè x 1 C. f (
x) lè xdx     C.  D. f (
x) lè xdx    C. 3 3  x 3x 3 3 x 3x   x 1 a b c Câu 10: Biết dx      dx. 
S a b c 2  Tính . x(x 1)  x
x 1 x  2 1    A. S  2. B. S  3. C. S  4. D. S  1. 2
Câu 11: Tính tích phân 2 I  2x x 1d  x bằng cách đặt 2
u x 1. Mệnh đề nào dưới đây đúng ? 1 3 2 1 3 2 A. I  2 udu.  B. I udu.  C. I ud .  u D. I ud .  u 2 0 1 0 1
Câu 12: Tính thể tích V của vật thể nằm giữa hai mặt phẳng x  1
 và x  1 , biết rằng thiết diện
của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1  x  1) là một hình vuông cạnh là 2 2 1 x . 25 10 16 A. V  16. B. V  . C. V  . D. V  . 3 3 3
Câu 13: Tìm nguyên hàm f (x)  (1 x) ln x bằng cách đặt u  ln x, dv  (1 x)d . x Mệnh đề nào dưới đây đúng ? 2  x   x  2 2  x   x
A. f (x)dx x  ln x  1 d .      x
B. f (x)dx x  ln x x  d .      x 2    2  2 2     2  x   x   x
C. f (x)dx x  ln x  1 d .      x
D. f (x)dx  1 x ln x  1 d .    x 2    2   2 
Câu 14: Tìm hàm số f (x) biết /
f (x)  3x  2 và f 2  7. 3 3 A. 2 f (x)  x  2x  3. B. 2 f (x)  x  2x  3. 2 2 3 C. 2
f (x)  3x  2x  3. D. 2
f (x)  2x x  3. 2
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 12
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1  1 1  Câu 15: Cho 
dx a lè2  b lè3  với ,
a b là các số nguyên. Mệnh đề nào dưới đây đúng x 1 x 2    0   ?
A. a b  2.
B. a b  2.
C. a  2b  0.
D. a  2b  0. Câu 16: Cho hàm số 3 2
y x  6x  9x (C). Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành. 4 1 27 25 A. S  . B. S  . C. S  . D. S  . 27 24 4 36   2 2
Câu 17: Cho f (x)dx  5. 
Tính I   f (x)  2íiè x dx.    0 0  A. I  3. B. I  7.
C. I  5   . D. I  5  . 2 a
Câu 18: Biết  2 3x  2 3
dx a  2 , với a  .  Tìm . a 0 A. 1   a  1.
B. 2  a  5. C. 3   a  0. D. a  4.
Câu 19: Một ô tô đang chạy với vận tốc 20(m / s) thì người người đạp phanh (còn gọi là “thắng”).
Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc v t   40 
t  20(m / s) trong
đó t là khoảng thời gian tính bằng giây kể từ lúc bằng đầu đạp phanh. Hỏi từ lúc đạp phanh đến
khi dừng hẳn, ô tô còn di chuyển một quãng đường s bao nhiêu mét? A. s  5 . m B. s  10 . m C. s  15 . m D. s  2 . m
Câu 20: Tính thể tích V của vật thể nằm giữa hai mặt phẳng x  0 và x   , biết rằng thiết diện
của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0  x   ) là một
tam giác đều cạnh là 2 sin x. A. V  2 3. B. V  3.
C. V  2  3.
D. V  3  2. 
Câu 21: Tính tích phân x F e cos d x x  bằng cách đặt  cos , d x u x v e d .
x Mệnh đề nào dưới đây 0 đúng ?     A. x  sin x F e x e cos d x . xB. x  sin x F e x e cos d x . x  0 0 0 0     C. x  cos x F e x e sin d x . xD. x  cos x F e x e sin d x . x  0 0 0 0
Câu 22: Cho hình D giới hạn bởi đường cong 2
y x 1 , trục hoành và các đường thẳng
x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ? 4 4 A. V  . B. V  2 . C. V  . D. V  2. 3 3
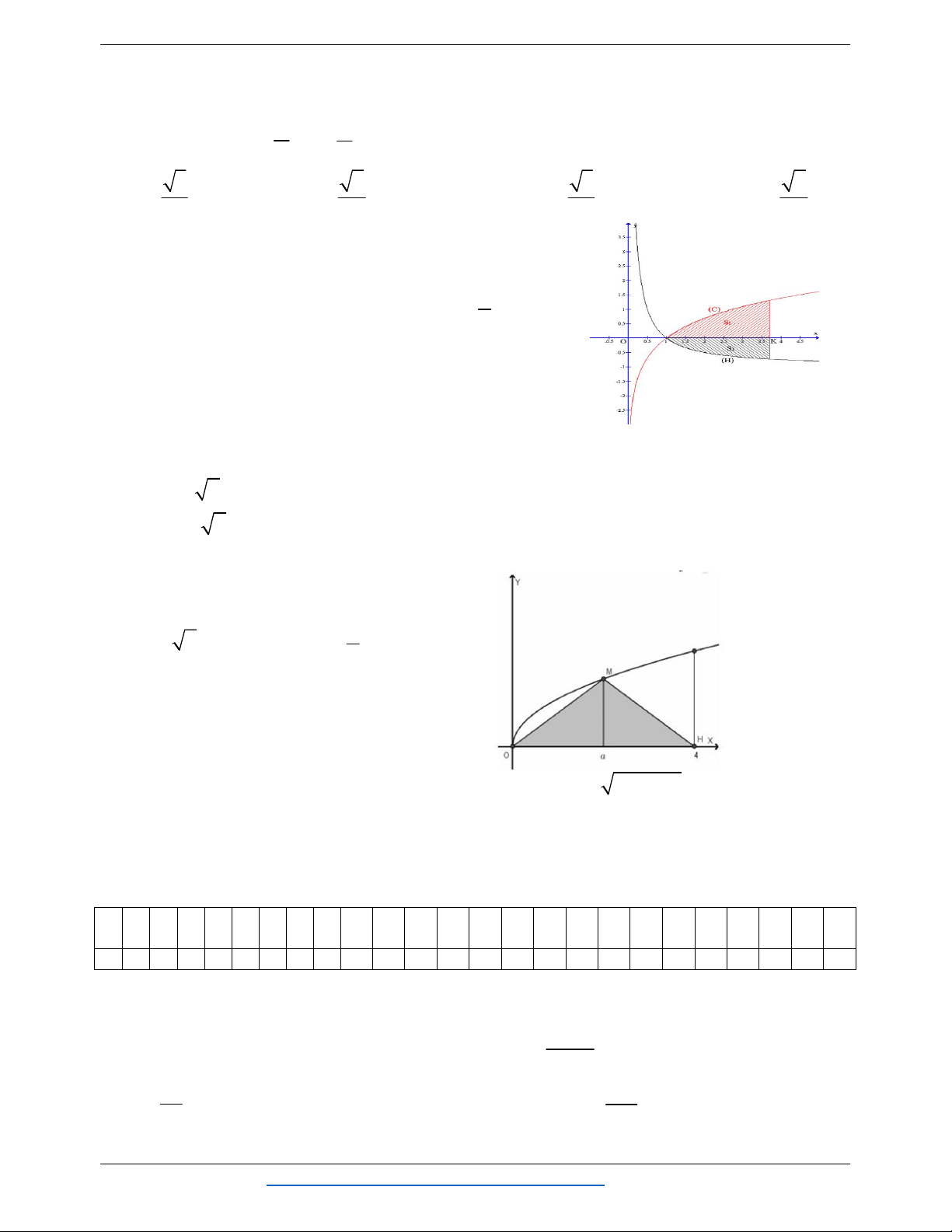
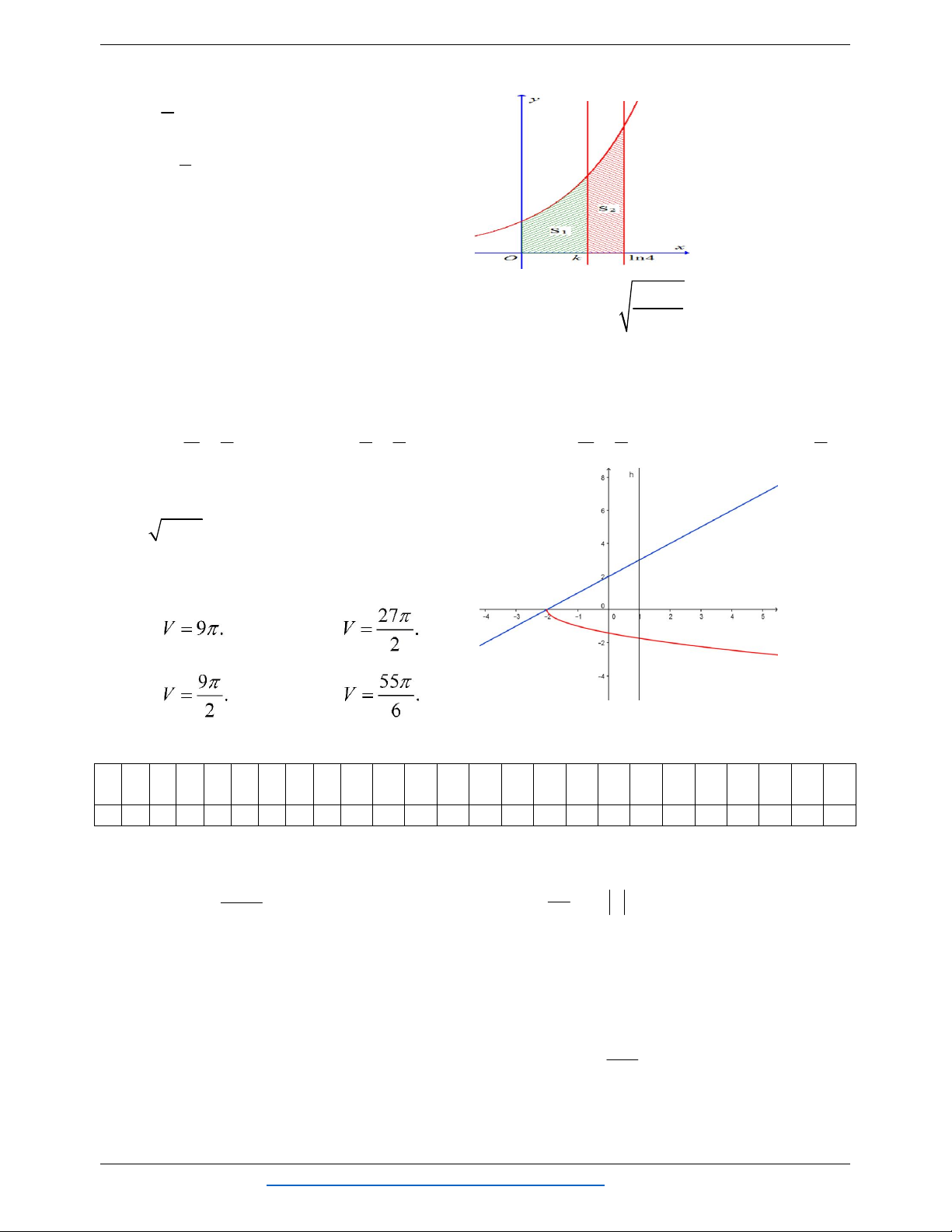
Câu 23: Cho hình cong (H) giới hạn bởi đường x
y e , trục hoành và các đường thẳng x  0 và
x  lè 4. Đường thẳng x k (0  k  lè 4) chia (H) thành hai phần có diện tích là S và S như hình 1 2
vẽ bên. Tìm k để S  2S . 1 2
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 13
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 2 A. k  ln 4. B. k  ln 2. 3 8 C. k  ln . D. k  ln 3. 3 1
Câu 24: Biết F(x) là một nguyên hàm của hàm số f (x) 
và F(2)  1. Tính F(3). x 1 7 1 A. F(3)  .
B. F(3)  lè 2 1. C. F(3)  .
D. F(3)  lè 2  1. 4 2 2 2 2
Câu 25: Cho f (x)dx  2  và ( g x)dx  1.  
Tính I  x  2 f (x)  3 ( g x) dx.    1  1  1  17 11 7 5 A. I  . B. I  . C. I  . D. I  . 2 2 2 2 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D ĐỀ 5 1
Câu 1. Cho biết I   2
3x  2x  ln 2x  
1 dx a ln b  ; c a, , b c  .
 Mệnh đề nào sau đây là đúng? 0 1 11 7 1
A. a b c   .
B. a b c  .
C. a b c  .
D. a b c  . 2 2 2 2 2 2 Câu 2. Cho f (x)  1. 
Tính I  x  2 f (x)d . x  1  1  5 3 11 7 A. I  . B. I  . C. I  . D. I  . 2 2 2 2 2
Câu 3. Cho hàm số f (x) có đạo hàm trên đoạn 1; 2, f (1)  7 và f (2)  2. Tính I f (  x)d . x  1 7 A. I  5. B. I  5. C. I  9. D. I  . 2 2
Câu 4. Tính tích phân 2
I  2x x 1.dx,  bằng cách đặt 2
t x 1. Mệnh đề nào dưới đây đúng? 1
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 14
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 3 2 1 3 2 A. I t .dt.  B. I t .dt.  C. I  2 t .dt.  D. I t .dt.  2 0 1 0 1
Câu 5. Cho hình phẳng D giới hạn bởi đường cong 2
y x và đường thẳng y  2 . x Khối tròn xoay
tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 51 64 41 74 A. V  . B. V  . C. V  . D. V  . 7 15 7 15
Câu 6. Cho hàm số y f x liên tục trên  và a,b, c  .
 Mệnh đề nào dưới đây sai? b b b c b A.
f x dx
f x dx .   B.
f xdx f xdx f xd . x    a a a a c a b b C.
f x dx  0  D. .
c f x dx  . c f x d . x   a a a e
Câu 7. Tính tích phân I x ln d x . x  1 2 e 1 1 2 e  2 2 e 1 A. I  . B. I  . C. I  . D. I  . 4 2 2 4 2   
Câu 8. Tìm nguyên hàm F ( x) của hàm số I f  ( x ) d x .  thỏa mãn F  2. 1    2 
A. F (x)   cos x  sin x 1.
B. F (x)  cos x  sin x  3.
C. F (x)   cos x  sin x 1.
D. F (x)   cos x  sin x  3. 6 2
Câu 9. Cho f (x)dx  12.  Tính I f (3x)d . x  0 0 A. I  36. B. I  4. C. I  2. D. I  6. 1
Câu 10. Cho tích phân  2  3 x I x e dx  . a e b,  với a,b  .
 Mệnh đề nào dưới đây là đúng? 0
A. a b  2. B. 3 3 a b  28.
C. a  2b  1. D. ab  3. 1 a Câu 11. Cho biết 2 2 I
x . 4  2x dx   ; a, b  . 
 Mệnh đề nào sau đây là đúng? b 0
A. log b  5.
B. log b  3.
C. log b  4. D. log b  6. a a a a
Câu 12. Tìm thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ
thị hàm số y f x, trục Ox và hai đường thẳng x a, x ba b, xung quanh trục Ox. b b b b A. V f x d . xB. 2 V   f x d . xC. 2 V
f x dx.  D. V   f xd . xa a a a 3
Câu 13. Cho F (x) là một nguyên hàm của hàm số ( ) x
f x e  2x thỏa mãn F (0)  . Tìm F (x) . 2 x 3 x 1 x 5 A. 2
F (x)  e x  . B. 2
F (x)  2e x  . C. 2
F (x)  e x  . D. 2 2 2 x 1 2
F (x)  e x  . 2
Câu 14. Tìm nguyên hàm của hàm số   3x f x e . x 1 A. 3 x 3 d x e x eC.  B. 3 3 d x e x eC.  3 x 1 C. 3 x 3 d  3 x e x eC.  D. 3 3 x 1 e dx e    C.  3x  1
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 15
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1
Câu 15. Biết F (x) là một nguyên hàm của hàm số f (x)  , F (2)  1 và x  1
F (3)  ln a  ; b a,b  .
 Mệnh đề nào sau đây là đúng?
A. a b  1.
B. a b  2.
C. a b  1.
D. a b  2.
Câu 16. Tìm nguyên hàm của hàm số f x  2x 1. 1 1 A.
f x dx  2x   1 2x 1  C.  B.
f x dx   2x 1  C.  3 3 2 1 C.
f x dx  2x   1 2x 1  C.  D.
f x dx  2x 1  C.  3 2   
Câu 17. Biết F (x) là một nguyên hàm của hàm số 3
f (x)  sin x cos x và F (0)   . Tìm F .    2     1    1       A. F     .   B. F    .   C. F   .   D. F    .    2  4  2  4  2   2 
Câu 18. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x . 37 9 81 A. S  . B. S  . C. S  . D. S  13. 12 4 12
Câu 19. Tính diện tích hình phẳng giới hạn bởi các đường 2
y x  2x và y x  2. 7 5 3 9 A. . B. . C. . D. . 2 2 2 2 1 3x 1 a 5 a Câu 20. Biết dx  3ln   , trong đó
là phân số tối giản với a,b nguyên dương. 2 x  6x  9 b 6 b 0
Khi đó giá trị của a b bằng bao nhiêu? A. 1  . B. 3  7. C. 37. D. 1.
Câu 21. Cho hình phẳng D giới hạn bởi đường cong y  2, y  2, trục hoành và các đường
thẳng x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 2 4 7 A. V  . B. V  . C. V   D. V  . 3 3 2 . 3
Câu 22. Cho đồ thị hàm số y f x như hình vẽ. Tìm diện tích S của hình phẳng được giới hạn
bởi đồ thị và trục Ox.(Phần gạch sọc).
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 16
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 3 3 A. S
f x dx .  B. S
f x dx  . 2 2 1 3 1 3 C. S
f x dx f x dx   D. S
f x dx f x d . x   2 1 2 1
Câu 23. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y x, trục hoành và đường thẳng x  4  . 15 A. S  8. B. S  6. C. S  . D. S  4. 2
Câu 24. Cho hàm số f x 3 2
 x  3x  2 có đồ thị (C) như hình vẽ. Tính diện tích S của hình
phẳng (phần gạch sọc). 39 41 A. S  . B. S  . C. S  10. D. S  13. 4 4   
Câu 25. Cho hàm số f (x) thỏa mãn f (
x)  3  2sin x, f (0)  7 và fa  ; b , a b  .    Mệnh  3 
đề nào sau đây là đúng?
A. 2a b  4.
B. 2a b  2  .
C. 2a b  4  .
D. 2a b  2. Đáp án đề 001:
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 17
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 Câu Chọn Câu Chọn Câu Chọn Câu Chọn Câu Chọn 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 ĐỀ 6 3 2 4x  5x 1
Câu 1. Tìm nguyên hàm của hàm số y  . 2 x 1 1 A. 2 x  5x   C. B. 2 2x  5x   C. C. 2
2x  5x  ln x C. D. x x 1 2 2  x  5x   C. x
Câu 2. Biết nguyên hàm của hàm số 2
f (x)  cos x là F(x)  ax bsin 2x C;a, , b C  .  Mệnh đề nào sau đây là đúng? 1 1
A. a b  .
B. a b   .
C. a b  1.
D. a b  1. 4 2 2
Câu 3. Biết tích phân  2 x   1 ln d
x x a ln b c;a, , b c  .
 Khi đó a b c bằng bao nhiêu? 1 13 26 A. . B. 13. C. . D. 0. 3 9
Câu 4. Diện tích hình phẳng giới hạn bởi các đường 2
y x 1 và 2
y   x  2x  3 không được
tính bằng công thức nào sau đây? 1 2 A. 2 S
(2x  2x  4)d .  x B. 2 S
2x  2x  4 d .  x 2 1  2 2 C. 2 2 S
(x 1)  (x  2x  3) d .  x D. 2 S
(x x  2)d .  x 1 1   4  Câu 5. Biết 3 2 3 5 x
dx a x b ln x C; a,b,C  .  
 Khi đó, a b bằng bao nhiêu?  x  17 23 17 23 A. . B. . C. . D.  . 5 5 5 5
Câu 6. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 4 2
y x  5x  4, trục hoành và hai
đường thẳng x  0, x  1. 7 8 64 38 A. . B. . C. . D. . 3 5 25 15  2
Câu 7. Cho tích phân I  sin x 8  cos xd . 
x Đặt t  8  cos x thì khẳng định nào sau đây là khẳng 0 định đúng? 8 9 9 8 1 A. I tdt.  B. I  2 tdt.  C. I tdt.  D. I tdt.  2 9 8 8 9
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 18
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 3 sin x
Câu 8. Tính nguyên hàm d . x  4 cos x 1 1 1 1 1 1 A.    C. B.   C. C.   C. D. 3 cos x 3cos x 3 3cos x cos x 3 3cos x cos x 1 1   C. 3 cos x 3 cos x
Câu 9. Khẳng định nào sau đây là khẳng định sai? 1 0 1 2 1 A. 3 2 2 3
(x x )dx  (x x )d .   x B. 3 2 3 2 3 2
(x x )dx  (x x )dx  (x x )d .    x 0 1 0 0 2 1 1 1 1 2 1 C. 3 2 3 2
(x x )dx x dx x d .    x D. 3 2 3 2 3 2
(x x )dx  (x x )dx  (x x )d .    x 0 0 0 0 0 2 2 x
Câu 10. Tính diện tích hình phẳng giới hạn bởi Parabol y
và đường tròn tâm O (gốc tọa 2
độ), bán kính R  2 2 được kết quả là S a  ; b a,b  .
 Mệnh đề nào sau đây là đúng? 8 7 1
A. a b  5. B. ab  .
C. a  3b  . D. 2 a b  . 3 2 2 x(x  2)
Câu 11. Hàm số nào sau đây không là nguyên hàm của hàm số f (x)  ? 2 (x  1) 2 x x 1 2 x x 1 2 x x  1 2 x A. . B. . C. . D. . x 1 x  1 x  1 x 1
Câu 12. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y x  6x  9x, trục tung và tiếp tuyến
tại điểm có hoành độ thỏa mãn y  0 được tính bằng công thức nào sau đây? 2 3 A. 3 2 (  6 12  8)d .  x x x x B. 3 2 (  6 10  5)d .  x x x x 0 0 2 3 C. 3 2 (  6 12  8)d .  x x x x D. 3 2 (  6 10  5)d .  x x x x 0 0 
Câu 13. Tính tích phân 2 cos x sin xd . x  0 2 3 2 A.  . B. 0. C. . D. . 3 2 3
Câu 14. Khẳng định nào sau đây là khẳng định sai? b b b a
A. ( f (x)  g(x))dx
f (x)dx g(x)d .    x
B. f (x)dx  1.  a a a a b b b c b
C. kf (x)dx k f (x)d .   x
D. f (x)dx
f (x)dx f (x)d .    x a a a a c
Câu 15. Tìm nguyên hàm của hàm số 2018 ( ) 2017 x f x  . 2018 2017 x 2018 2017 x
A. f (x)dx   C. 
B. f (x)dx   C.  ln 2017 2018 2018 2017 x
C. f (x)dx   C.  D. 2018 ( )d  2018.2017 x f x x .ln 2017  C.  2018.ln 2017
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 19
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
  2 2
Câu 16. Cho tích phân sin 3  sin cos d .  x I e x
x x Nếu đổi biến số 2
t  sin x thì khẳng định nào sau 0
đây là khẳng định đúng? 1 1 1 1 1 A.  1 d .  t I e t t B.  2 t d  t I e t te dt.   C.  2 1  d .  t I e t t D. 2 0 0 0 0 1 1 t I  
e 1  t  dt.  2 0
Câu 17. Thể tích của vật thể tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường 2
y  1 x , trục hoành, trục tung, quanh trục hoành không được tính bằng công thức nào sau đây? 1 1 3  1 x  2 A. 2  (1 )d .  x x B. x  . 2 2   C.  (1 ) d .  x x D. . 3 3 0   0 0 7 Câu 18. Biết 2
ln(x  4x)dx a ln b c ln d m ln n  4; a,b, c, d, , m n  . 
 Mệnh đề nào sau đây là 5 đúng?
A. a b c d m n  3.
B. a b c d m n  27.
C. a b c d m n  3.
D. a b c d m n  27.
Câu 19. Thể tích vật thể tròn xoay sinh ra khi quay hình phẳng được giới hạn bởi các đường 1 x 2 2
y x e , x  1, x  2, y  0, quanh trục hoành là 2
V   (ae be). Khi đó, a b bằng bao nhiêu? A. 0. B. 2. C. 1. D. 2. 3 x
Câu 20. Biết (3x  4)sin dx m  ; n m, n  . 
 Mệnh đề nào sau đây là đúng? 3 0 3 3
A. m n  3.
B. m n  3.
C. m n   .
D. m n  . 2 2  2 Câu 21. Tích phân cos 2 d  x
x x bằng biểu thức nào sau đây? 0    2 2 2 1 1 2  x 1  A. x sin 2x  sin 2 d x .  x B.  cos 2x .   2 2 2 2 0 0   0    2 2 2 1 1 2  x 1  C. sin 2x  sin 2 d x .  x D.  sin 2x .   2 2 2 2 0 0   0 d d b
Câu 22. Nếu f (x)dx  5 
và f (x)dx  2 
với a d b thì f (x)d  x bằng bao nhiêu? a b a A. 2. B. 8. C. 3. D. 7. Câu 23. Biết   x2 1 sin
dx ax bcos x c sin 2x C; a, , b c,C  . 
 Khi đó, a b c bằng bao nhiêu? 13 29 1 19 A.  . B. . C.  . D.  . 12 12 4 12
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 20
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12

Câu 24. Thể tích V của khối tròn xoay sinh ra khi quay hình phẳng (H), giới hạn bởi đồ thị hàm x 1 số y
và các trục tọa độ, quanh trục Ox được tính bằng công thức V   (a bln c); , a , b c  .  x 1
Mệnh đề nào sau đây là đúng?
A. 3a  2b c  11.
B. 3a  2b c  3.
C. 3a  2b c  5.
D. 3a  2b c  27. 6 3 x a 2  b Câu 25. Biết dx  ;a, , b c  . 
 Mệnh đề nào sau đây là đúng? 2 c 2 x  2
A. a b c  11.
B. a b c  27.
C. a b c  3.
D. a b c  5. Đáp án đề 002: Câu Chọn Câu Chọn Câu Chọn Câu Chọn Câu Chọn 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 ĐỀ 7
Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x . 37 81 9 A. S  . B. S  . C. S  . D. S  13. 12 12 4
Câu 2: Chọn khẳng định đúng. 1  dx 1
A. sin(ax b)dx
cos(ax b)  C.  B.  
tan(ax b)  C.  a 2 cos (ax b) a dx
C. cos xdx   sin x C .  D.
 cot x C .  2 sin x 1 b Câu 3: Cho 2
x 1 x d x    2
1 x   C . Tính P  . a b . a A. P  6. B. P  9. C. P  6. D. P  3.
Câu 4: Tìm một nguyên hàm F x của hàm số f x 3 2
 4x  3x  4x  3 thỏa F   1  10 .
A. F x 4 3 2
x x  2x  3x 10.
B. F x 4 3 2
x x  2x  3x 11.
C. F x 2
12x  6x  4.
D. F x 4 3 2
x x  2x  3 . x
Câu 5: Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc thời
gian t (h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ
khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh
I (2;9) với trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ
thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di
chuyển được trong 4 giờ đó
A. 26, 5km.
B. 28,5km. C. 27km. D. 24km.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 21
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12

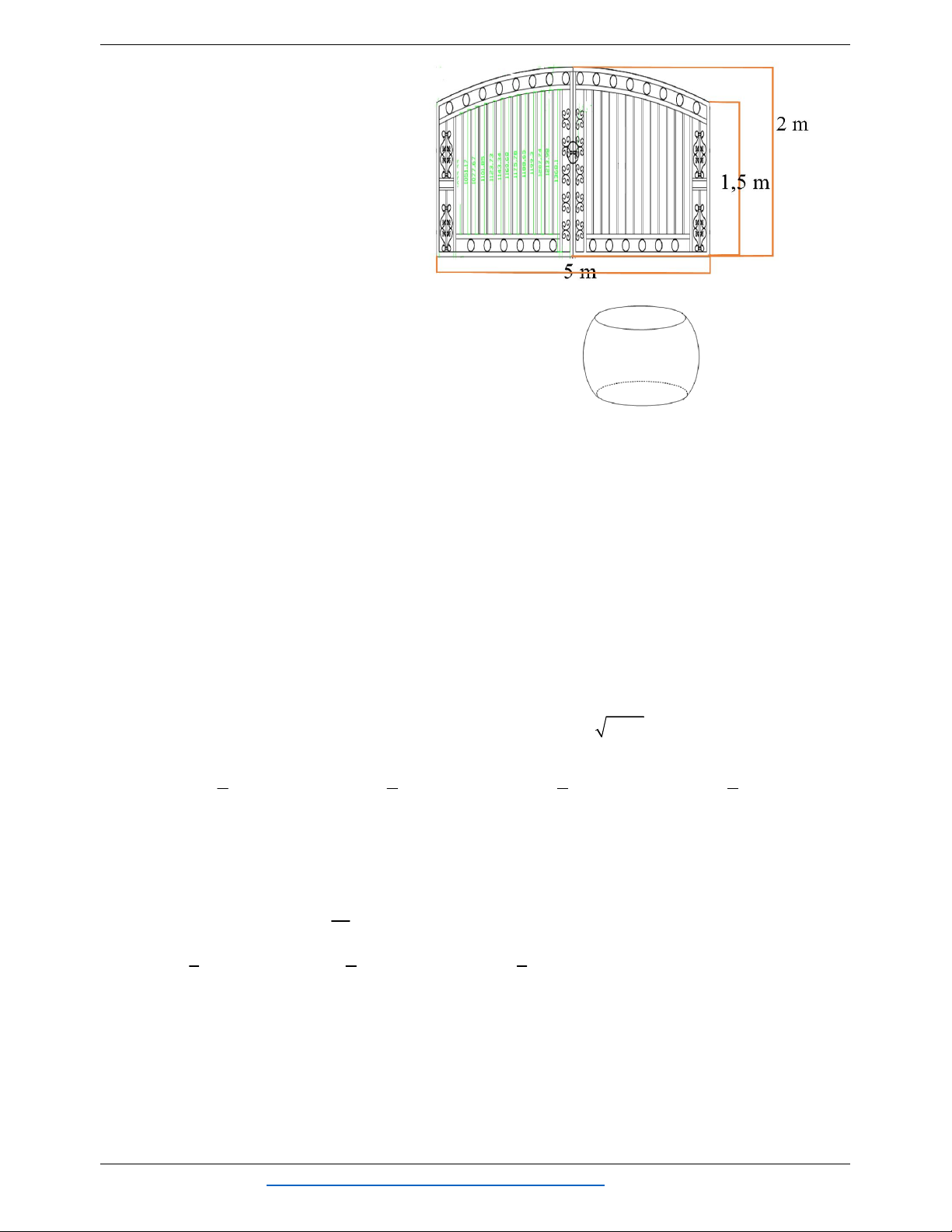
Câu 6: Anh Lâm muốn làm cửa rào
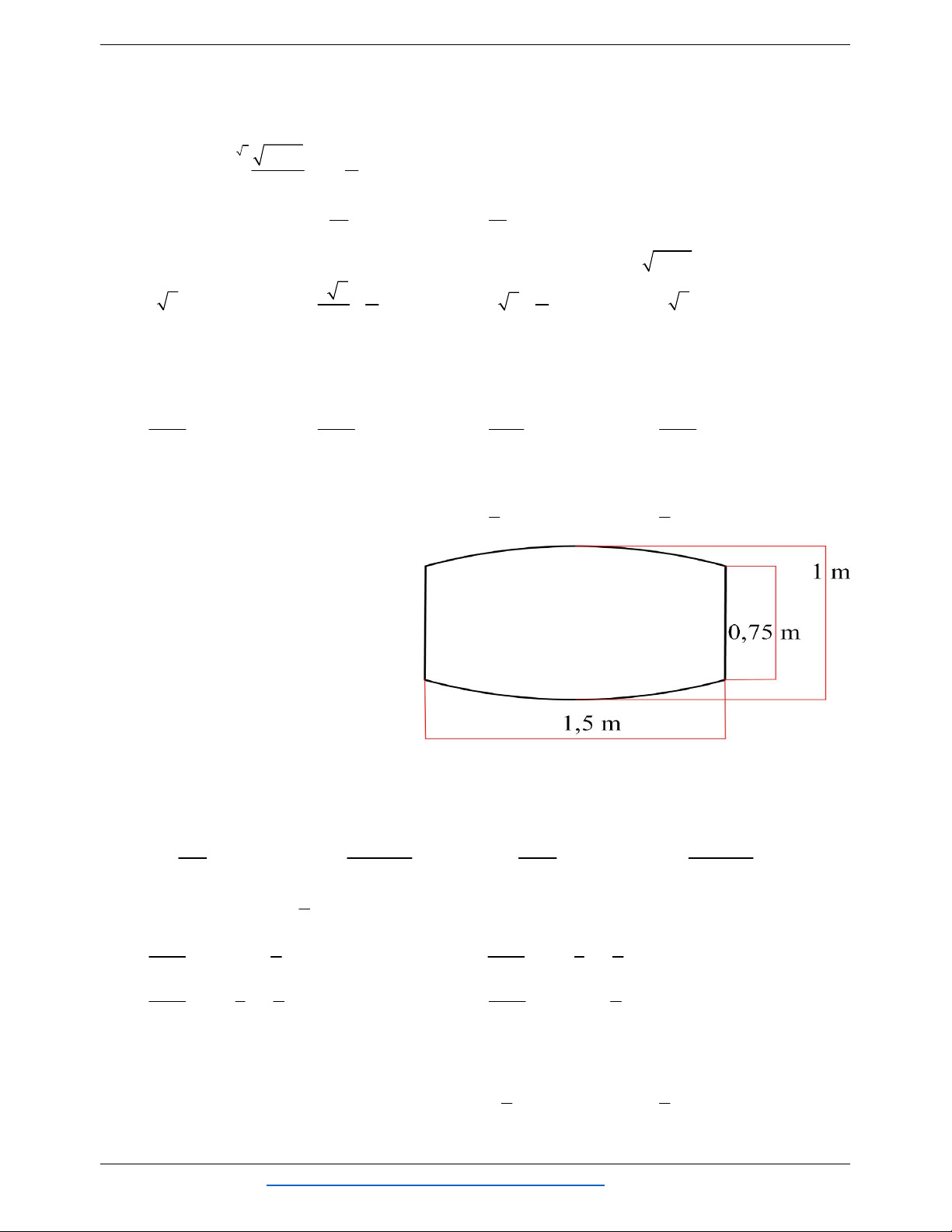
sắt có hình dạng và kích thước giống
như hình vẽ kế bên, biết đường cong
phía trên là một parabol. Giá 1 mét
vuông cửa rào sắt là 700.000 đồng.
Vậy anh Lâm phải trả bao nhiêu tiền
để làm cài cửa rào sắt như vậy. (làm tròn đến hàng nghìn) A. 6.423.000. B. 6.320.000. C. 6.523.000. D. 6.417.000.
Câu 7: Người thợ gốm làm cái chum từ một khối cầu có
bán kính 5 dm bằng cách cắt bỏ hai chỏm cầu đối nhau.
Tính thể tích của cái chum, biết chiều cao của nó bằng 60
cm.(Quy tròn 2 chữ số thập phân) A. 3 414, 69 dm . B. 3 428, 74 dm . C. 3 104, 67 dm . D. 3 135, 02 dm . 4 2
Câu 8: Cho f xdx  10 
. Tính f 2x dx  . 0 0 A. 5. B. 20. C. 10. D. 20. Câu 9: Biết 2 4 . x ln 2 .
x d x x  .
m ln 2x n  C
. Tính S m n . A. S  6. B. S  1. C. S  3. D. S  3. 0 a
Câu 10: Cho 2 mệnh đề:
P: “Nếu f x là hàm lẻ thì
f x d x   f x d x   ”. a 0
Q: “Nếu f xd x F x  C
thì f u x.u xd x F u x  C      ”. Khẳng định nào đúng?
A. P đúng, Q sai.
B. P, Q đều sai.
C. P, Q đều đúng.
D. P sai, Q đúng.
Câu 11: Tính diện tích hình phẳng giới hạn bởi các đường x
y e 1 , trục hoành và hai đường
thẳng x  ln 3 , x  ln 8 . 3 3 2 3
A. S  3  ln .
B. S  2  ln .
C. S  2  ln .
D. S  2  ln . 2 2 3 2 5 2
Câu 12: Cho f x dx  10 
. Tính 2  4 f x dx    . 2 5 A. 32. B. 34. C. 36. D. 40. 2 x
Câu 13: Biết (x  sin 3x)dx
b cos 3x C
. Tính S a b . a 1 7 5 A. S   . B. S  . C. S  . D. S  5. 3 3 3 b b c
Câu 14: Cho f (x)dx  2 
và f (x)dx  3 
với a b c . Tính f (x)dx  . a c a A. 5. B. 5. C. 1. D. 1. Câu 15: Cho F x là một nguyên hàm của
f x  2ln , x F   1  2  . Tính 2
K  F x  2x  ln x d x    . 1
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 22
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1 1 1
A. K  ln 2  .
B. K  3ln 2  .
C. K  3ln 2 1.
D. K  2 ln 2  . 2 2 2
Câu 16: Tìm khẳng định sai.
A. f  x d x f x  C. 
B. f x.g x d x f xd . x g x d . x     
C. k. f x d x k. f x d . x  
D. f x  g x d x f xd x g xd . x      1
Câu 17: Tìm nguyên hàm của hàm số f x  . 5x 1 1 1
A. ln 5x   1  C
B. 5ln 5x 1  C
C. 5ln(5x 1)  C
D. ln 5x 1  C 5 5      Câu 18: Cho  f x 2 2
 cos x  sin x có nguyên hàm F x thỏa F  1   . Tính F   .  4   2  5 1 3 A. 2. B. . C. . D.  . 2 2 2 x   Câu 19: Tìm 2016 2 e x dx   .   x 1 x 1 A. 2017 2 2e xC. B. 2017 2 2e xC. 2017 2017 1 x 1 1 x 1 C. 2015 2 e xC. D. 2017 2 e xC. 2 2015 2 2017
Câu 20: Biết (1 2 ) x  (1  2 ) x x x e dx a
x e be C
. Tính S a b . 1 1 A. S  2. B. S  . C. S  . D. S  3. 2 3  x  2 2 2 x x  2
Câu 21: Cho tích phân I
dx a b ln 2  c ln 3  với a, ,
b c   . Chọn khẳng x  2 1 định đúng. A. c  0 . B. b  0 . C. a  0 .
D. a b c  0 .  6 x   Câu 22: Tính 2
I  3 sin u.cos . u d u .cos . x d x   . 0  0  1 1 1 1 A. . B. . C. . D. . 32 64 16 128
Câu 23: Cho hình (H) giới hạn bởi các đường y
x , x  4 và trục hoành. Quay hình (H) quanh
trục Ox ta được khối tròn xoay có thể tích là bao nhiêu? 15 14 16 . . C. 8 . . A. 2 B. 3 D. 3 x
Câu 24: Cho I x   2t tdt . Tính giá trị nhỏ nhất của I x trên đoạn  1  ;  1 . 1 5 5 1 A. 2. B.  . C. . D. . 6 6 6
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 23
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 e ln x
Câu 25: Kết quả của tích phân I  dx
có dạng I a ln 2  b với ,
a b . Khẳng định x  2 ln x 1 1  nào đúng?
A. 2a b  1. B. 2 2 a b  4 .
C. a b  1. D. ab  2 . ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D ĐỀ 8 a 1
Câu 1: Biết x sin 2xdx x cos 2x  sin 2x C
. Tính S  2a b n . b n A. S  4. B. S  2. C. S  10. D. S  6. 4
Câu 2: Cho f  
1  12 và f ' x dx  17 
. Tính giá trị của f 4 . 1 A. 19. B. 29. C. 9. D. 5. 2 4 4
Câu 3: Cho f xdx  1 
và f t dt  3 
. Tính f u du  . 1 1 2 A. 2 . B. 4. C. 2. D. 4  .
Câu 4: Chọn khẳng đinh sai.  1    (ax b)
A. (ax b) d x   C.  B. x d x e
x e C.   1 1
C. k d x kx C.  D.
d x  ln x C.  x
Câu 5: Tìm khẳng định đúng. A. .
x f x d x  . x f x d . x  
B. f xd x f  x  C. 
C. f x  g x d x f xd x g xd . x     
D. f x.g x d x f xd . x g x d . x     
Câu 6: Biết  x  2 3 2 3
2 d x ax bx cx C
. Tính S a b c . A. S  13. B. S  1. C. S  7. D. S  9.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 24
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1
Câu 7: Tìm nguyên hàm của hàm số f x  . 3x  2 1 1  1 1 3 A. C. B. C. C. C. D. C. 3x 1 9x  3 9x  3 1 3x 3 x Câu 8: Cho d x a   2 x  5 2
b ln x  5  C . Tính P ab . 2 x  5 5 4 A. P   . B. P  5. C. P  . D. P  2. 4 5 1
Câu 9: Cho 2 mệnh đề: P: “Nếu
f x d x F x  C  thì
f ax b d x
F ax b  C  ”. a a 0 a
Q: “Nếu f x là hàm chẵn thì
f xdx  2 f xdx  2 f xdx    ”. aa 0 Khẳng định nào đúng?
A. P đúng, Q sai.
B. P, Q đều sai.
C. P, Q đều đúng.
D. P sai, Q đúng. Câu 10: Biết 2 4 . x ln 2 .
x d x x  .
m ln 2x n  C  . Tính S  . m n . . A. S  2. B. S  3. C. S  3. D. S  6. 3 4 4
Câu 11: Cho biết f x dx  2,
f x dx  3, g x dx  7   
. Khẳng định nào sau đây là sai? 1 1 1 4 4
A. f x  g x dx  10.   
B. 4 f x  2g x dx  2.    1 1 3 4
C. f x dx  5.  
D. f xdx  1.  4 3
Câu 12: Một thùng rượu có bán kính các đáy là 30cm, thiết diện vuông
góc với trục và cách đều hai đáy có bán kính là 40cm, chiều cao thùng
rượu là 1m (hình vẽ). Biết rằng mặt phẳng chứa trục và cắt mặt xung
quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu
(đơn vị lít) là bao nhiêu ? A. 167,12 lít. B. 107,34 lít. C. 212, 6 lít. D. 425, 2 lít.
Câu 13: Tìm một nguyên hàm F(x) của hàm số f x  x  cos x thỏa mãn F 0  9 . 2 x 2 x
A. F x  sin x   9.
B. F x  sin x   9. 2 2 2 x 2 x
C. F x   sin x  .
D. F x  sin x   9. 2 2 4x  5 Câu 14: Cho
d x a ln x  2  b ln 2x 1  C
. Tính P ab . 2 2x  5x  2 A. P  1. B. P  2. C. P  2. D. P  1.  2 2
x  2x x   1
Câu 15: Cho tích phân I
dx a b ln 2  c ln 3  với a, ,
b c  . Chọn khẳng định x 1 1 sai.
A. a b c  0 . B. a  0 . C. b  0 . D. c  0 .
Câu 16: Tính diện tích hình phẳng giới hạn bởi các đường x
y e x , x y 1  0 và x  ln 5 .
A. S  5  ln 4 .
B. S  4  ln 5 .
C. S  5  ln 4 .
D. S  4  ln 5 .
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 25
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 3 x Câu 17: Tính I ln 2    2 3u 3du    d x .  0   2
A. 5 ln 5  4 ln 2  3.
B. 5 ln 5  4 ln 2  3.
C. 5 ln 5  4 ln 2  3.
D. 5 ln 5  4 ln 2  3. 2 2 x 1 
Câu 18: Cho I  d x   b  . Tính . a b . 3 x a 1 1 31 A. 2. B.  . C. . D. 4. 32 4
Câu 19: Tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2 y  2  x , 2
y  1 x và trục hoành. 8 2   A. 3 2  2 . B.  . C. 2 2  . D. 4 2   . 3 2 2
Câu 20: Một vật đang chuyển động với vận tốc 10 m / s thì tăng tốc với gia tốc a t  2  t t  2 3 m / s  .
Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc bằng bao nhiêu? 4000 4300 1900 2200 A. . m B. . m C. . m D. . m 3 3 3 3 1
Câu 21: Cho I  . x ln   2
x  2d x a ln 3  b ln 2  c với , a ,
b c là các số hữu tỉ. Tính tích . a . b c . 0 3 3 A. 1. B. 2. C. . D. . 2 4
Câu 22: Một nhà hàng muốn làm cái
bảng hiệu là một phần của Elip có
kích thước, hình dạng giống như hình
vẽ và có chất liệu bằng gỗ. Tính diện
tích bề mặt bảng hiệu. (Làm tròn đến
hàng phần trăm, đơn vị 2 m ) A. 2,32. B. 2,41. C. 1,38. D. 1,61.
Câu 23: Cho hình phẳng D giới hạn bởi đường cong x
y e , trục hoành, trục tung và đường
thẳng x  1 . Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 2 2 2  e  e   1 2 e 1  e   1 A. V  . B. V  . C. V  . D. V  . 2 2 2 2  x Câu 24: Tìm 2017 x  sin d x   .  3  1 x 1 1 x A. 2018 x  3cos  C. B. 2018 x  cos  C. 2018 3 2018 3 3 1 1 x 1 x C. 2018 x  cos  C. D. 2018 x  3cos  C. 2018 3 3 2018 3 2 2 2
Câu 25: Cho biết A  3 f x  2g x dx  1   
và B  2 f x  g x dx  3   
. Tính f xdx  . 1 1 1 5 1 A. 1. B. 2. C.  . D. . 7 2
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 26
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D ĐỀ 9
Câu 1: Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y f (x) ,
y g(x) liên tục trên [a ; b] và hai đường thẳng x a , x b (a b). b b A. S  
f (x)  g(x) .d . x  B. S
( f (x)  g(x))d . xa a b b C. 2 S
( f (x)  g(x)) .d . x  D. S
f (x)  g (x) .d . xa a
Câu 2: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang
cong, giới hạn bởi đồ thị hàm số y f x, trục Ox và hai đường thẳng
x a, x ba b, xung quanh trục Ox. b b b A. 2
V   f (x) d . x  B. 2 V f (x) d . x
C. V   f (x) d . x  D. a a a b V   f (x) d . xa
Câu 3: Hãy chọn mệnh đề đúng x a  1   x A. x a dx
C 0  a   1 .  B. x dx   C,    .   ln a   1 f (x) ( ) dx f x
C. f (x).g(x)dx f (x)d . x g(x)d . x    D. dx  .  g(x) g(x)dx
Câu 4: Mệnh đề nào sau đây sai? 1 A. x x
e dx e C.  B.
dx  ln x C, x  0.  x x a C. x a dx
C,(0  a  1). 
D. sin xdx  cos x C.  ln a
Câu 5: Tìm nguyên hàm của hàm số f (x)  cos3x . sin 3x
A. cos3x dx  3sin 3x C.  B. cos3x dx   C.  3
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 27
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 sin 3x C. cos3x dx    C. 
D. cos3x dx sin 3x C.  3 Câu 6: Cho 2
F (x)  x là một nguyên hàm của hàm số 2 ( ) x
f x e . Tìm nguyên hàm của hàm số 2 '( ) x f x e . A. 2 x 2
f '(x)e dx  x  2x C  . B. 2 2 '( ) x
f x e dx  x x C  . C. 2 x 2
f '(x)e dx  2x  2x C  . D. 2 x 2
f '(x)e dx  2
x  2x C.  ln x
Câu 7: Cho F (x) là một nguyên hàm của hàm số f (x) 
. Tính I F (e)  F (1) . x 1 1 A. I e . B. I  . C. I  . D. I  1. e 2 3
Câu 8: Cho F (x) là một nguyên hàm của hàm số ( ) x
f x e  2x thỏa mãn F (0)  . Tìm 2 F (x) . x 1 x 3 A. 2
F (x)  e x  . B. 2
F (x)  2e x  . 2 2 x 1 x 5 C. 2
F (x)  e x  . D. 2
F (x)  e x  . 2 2 dx Câu 9: Cho
a(x  2) x  2  b(x  1) x  1  C
. Khi đó 3a  . b x  2  x  1 2  1 4 2 A. . B. . C. . D. . 3 3 3 3 x  3 b Câu 10: Biết rằng
dx a ln x  1   C
với a,b Z . Chọn khẳng định 2 x  2x  1 x  1
đúng trong các khẳng định sau: a 1 b 2a b A.   . B.  2. C.  1. D.  2.  2b 2 a b a
Câu 11: Tìm a  5b biết 2 3 3 5 sin .
x cos xdx a sin x bsin x C.  4 1 2 2 A. . B.  . C. . D.  . 3 3 3 3 0 2 3x  5x 1 2
Câu 12: Cho I dx a ln  b
. Khi đó, giá trị của S a  2 . b x  2 3 1 
A. S  30.
B. S  40.
C. S  50.
D. S  60.  4 2 Câu 13: Biết sin 3 .
x sin 2xdx a b
, với a.b là các số nguyên. Tính S a b . 2 0 1  3 3  3 A. . B. . C. . D. . 6 10 10 5
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 28
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 2 x 1
Câu 14: Tính I
dx a ln 5  b ln 3  c ln 2  với a; ;
b c   . Tính giá trị của 2 x  4x  3 1 2 2 2
S a b c . A. S  14. B. S  6. C. S  5. D. S  9. a 2 x  6
Câu 15: Tìm a với a  1, biết dx  6  . 2 x 1 A. a  2 . B. a  9 . C. a  4 . D. a  3 . 2 3 3
Câu 16: Cho f xdx  3 
và f xdx  4 
. Tính f xd . x  1 2 1 3 3 3
A. f xdx  1  . 
B. f xdx 1. 
C. f xdx  7.  D. 1 1 1 3
f xdx 12.  1 2 5
Câu 17: Cho hàm số f (x) liên tục trên  . Biết f (x)dx  3 
và f (x)dx  4   .Tính 1 1 5
f (x)   1 d . x  2 5 5
A.f (x)   1 dx  7. 
B.f (x)   1 dx  7  .  2 2 5 5
C.f (x)   1 dx  1  . 
D.f (x)   1 dx  4  .  2 2
Câu 18: Gọi F x là một nguyên hàm của f x trên 2; 
3 ; F 3  3; F 2  2. Tính 3 f (x)dx  . 2 A. 1  . B. 1. C. 5. D. 6. 1 4 Câu 19: Cho
f xdx  1.  Tính I f (4x)d . x 2 1 2 1 1 1 1 A. I   . B. I   . C. I  . D. I  . 2 4 4 2
Câu 20: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 4 2
y x  3x  4 , trục
hoành và hai đường thẳng x  0 , x  3. 71 73 72 144 A. B. C. D. . 5 5 5 5 x  1
Câu 21: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y  , trục hoành và x  2
đường thẳng x  2.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 29
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 A. 3  2ln 2 B. 3  ln 2 C. 3  2ln 2 D. 3  ln 2
Câu 22: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y  tan x , trục hoành và  
hai đường thẳng x  , x  . 6 4 3 6 3 6 A. ln B. ln C. ln D. ln 3 3 3 3
Câu 23: Gọi S là diện tích hình phẳng giới hạn bởi các 1
đường C  : y  ln ; x ;
Ox x k và S là diện tích hình 2 1
phẳng giới hạn bởi các đường  H  : y  1   ; ; Ox x k x
với k  1 như hình vẽ bên. Biết rằng S S  4 . Tìm k . 1 2 A. 2 k e . B. k  2e . C. 2e k  .
D. k e  2 .
Câu 24: Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y
x, y  0 và x  4 quanh trục O .
x Đường thẳng x a 0  a  4 cắt đồ thị hàm số y
x tại M (hình vẽ bên). Gọi V là thể tích khối tròn xoay tạo thành khi quay 1
tam giác OMH quanh trục O .
x Biết rằng V  2V . Khi đó 1 5 A. a  2 2 B. a  2 C. a  2 D. a  3
Câu 25: Cho hình phẳng D giới hạn bởi đường cong y  2  sin x, trục hoành và các
đường thẳng x  0, x   .Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
A. V  2(  1).
B. V  2 (  1). C. 2 V  2 . D. V  2 . 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 D A A D B D C D C D A B D A D C D B B D C D A D B ĐỀ 10
Câu 1: Trong các mệnh đề sau mệnh đề nào sai? dx
A. cos xdx  sin x C.  B.
 cot x C.  2 sin x dx x C.  ln x C.  D. x a a dx   C.  x ln a
Câu 2: Nguyên hàm của hàm số f (x) x  .
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 30
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
  1 x   1 x A.  1
x   C. B. C. C.  1 ( 1)x    C. D. C.   1   1
Câu 3: Khẳng định nào sau đây là khẳng định sai ? A.
f xdx F x  C. 
B. kf xdx k f xd . x  
C. kf xdx k kf x.   D.
f x  g xdx
f xdx g xd . x    
Câu 4: Trong các mệnh đề sau đây mệnh đề nào đúng ? xdx 1 1 (I) 2 
ln(x  4)  C.  (II) cot xdx    C. 2  (III) x  4 2 2 sin x x 1 2 cos 2 cos sin x e xdx   eC.  2 A. (I) và (II). B. Chỉ (III). C. (I) và (III). D. Chỉ (I). x
Câu 5: Biết F (x) là một nguyên hàm của hàm số f x 
và F 0  1. Tính F (1). 2 x  1 1 1 A. F  
1  ln 2  1. B. F   1  ln 2  1. C. F   1  ln 2 1. D. F   1  ln 2  2. 2 2 2 Câu 6: Cho
f (x)dx   C.  Tính f (2x)d . x  2 x  1 2 1 A.
f (2x)dx   C.  B.
f (2x)dx   C.  2 x  1 2 4x  1 8 1 C.
f (2x)dx   C. 
D. f (2x)dx   C.  2 4x  1 2 x  1 1 f (x)
Câu 7: Cho F (x)  
là một nguyên hàm của hàm số . Tìm nguyên hàm của 2 2x x hàm số f (  x)ln . x  ln x 1  ln x 1 A. f (
x)ln xdx     C.   B. f (  x)ln xdx    C. 2 2   2 2  x 2x x x  ln x 1   ln x 1  C. f (
x)ln xdx     C.   D. f (  x)ln xdx    C. 2 2    2 2   x 2x   x 2x
Câu 8: Hàm số nào sau đây không phải là nguyên hàm của hàm số f x   x  4 3 ?  x  5 3  x  5 3
A. F x   x .
B. F x  . 5 5  x  5 3  x  5 3
C. F x   2017 .
D. F x   1. 5 5
Câu 9: Giá trị a, b, c để 2
g(x)  (ax bx c) 2x  3 là một nguyên hàm của hàm số 2
20x  30x  7  3  f (x)  trong khoảng ; .   2x  3  2 
A. a  4, b  2, c  2.
B. a  1, b  2, c  4.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 31
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12

C. a  2, b  1, c  4.
D. a  4, b  2, c  1. 4m
Câu 10: Cho hàm số f x 2 
 sin x . Tìm m để nguyên hàm F x của f x thỏa mãn     
F 0  1 và F    .  4  8 4 3 3 4 A. m   . B. m  . C. m   . D. m  . 3 4 4 3 dx
Câu 11: Tìm a b biết 3
a tan x b tan x C.  4 o c s x 3 2 1 4 A. B. C. D. 4 3 3 3 2 dx 1
Câu 12 : Biết  ln b thì 2 a  . b 3x 1 a 0 A. 2. B. 14. C. 10. D. 12.  4 1 
Câu 13: Biết (1  x) cos 2xdx    giá trị a. . b a b 0 A. 32. B. 2. C. 4. D. 12. 1 2 e x 3 Câu 14: Biết 2 (e  )dx   a ln 2  b  , giá trị a  . b x1 2 0 5 5 5 A.  . B. . C.  . D. 2. 2 2 21 m
Câu 15: Tìm m  1 sao cho (2x  3)dx  2.  1 17 18 A. . B. 3. C. . D. 4. 9 9 3 2 Câu 16: Cho
f (x)dx  5  . Tính f (2x 1) . dx  1 1 7 5 15 17 A. . B. . C. . D. . 2 2 2 9 2 1 Câu 17: Cho
f (x)dx  . a  Tính 2 I  .
x f (x 1)dx  theo a. 1 0 a 17a 17a A. a. B. . C. . D.  . 2 9 9 1 1 1 f (x)  2 Câu 18: Cho dx  2  . Tính d . xf (x) f (x) 0 0 12 9 A. 3.  B. 3. C. . D. . 9 13
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 32
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 2
Câu 19: Cho hàm số f (x) có nguyên hàm là F (x) trên đoạn 1;2, F 2  1 và F (x)dx  5  1 2
. Tính (x 1) f (x)d . x  1 17 17 A. 4.  B. 4. C. . D.  . 9 9
Câu 20: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2
y x  2x , y  . x 9 9 9 81 A. . B. . C. . D. . 2 2 2 10
Câu 21: Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = (e  1)x và  (1 x ye ) . x 3 e e A. 2. B. 1. C. 2  . D.  1. e 2 2 2 x
Câu 22: Diện tích hình phẳng giới hạn bởi đường thẳng y  4  x và patabol y  . 2 28 25 A. . B. . 3 3 22 26 C. . D. . 3 3
Câu 23: Tính diện tích hình phẳng được đánh dấu trên hình bên 26 28 A. S  . B. S  . 3 3 2 1 C. S  2 3  .
D. S  3 2  . 3 3
Câu 24: Tính thể tích khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các đường 2
y  1 – x , y  0 , x  0 và x  2. 8 2 46 5 A. . B. . C. 2 . D. . 3 15 2
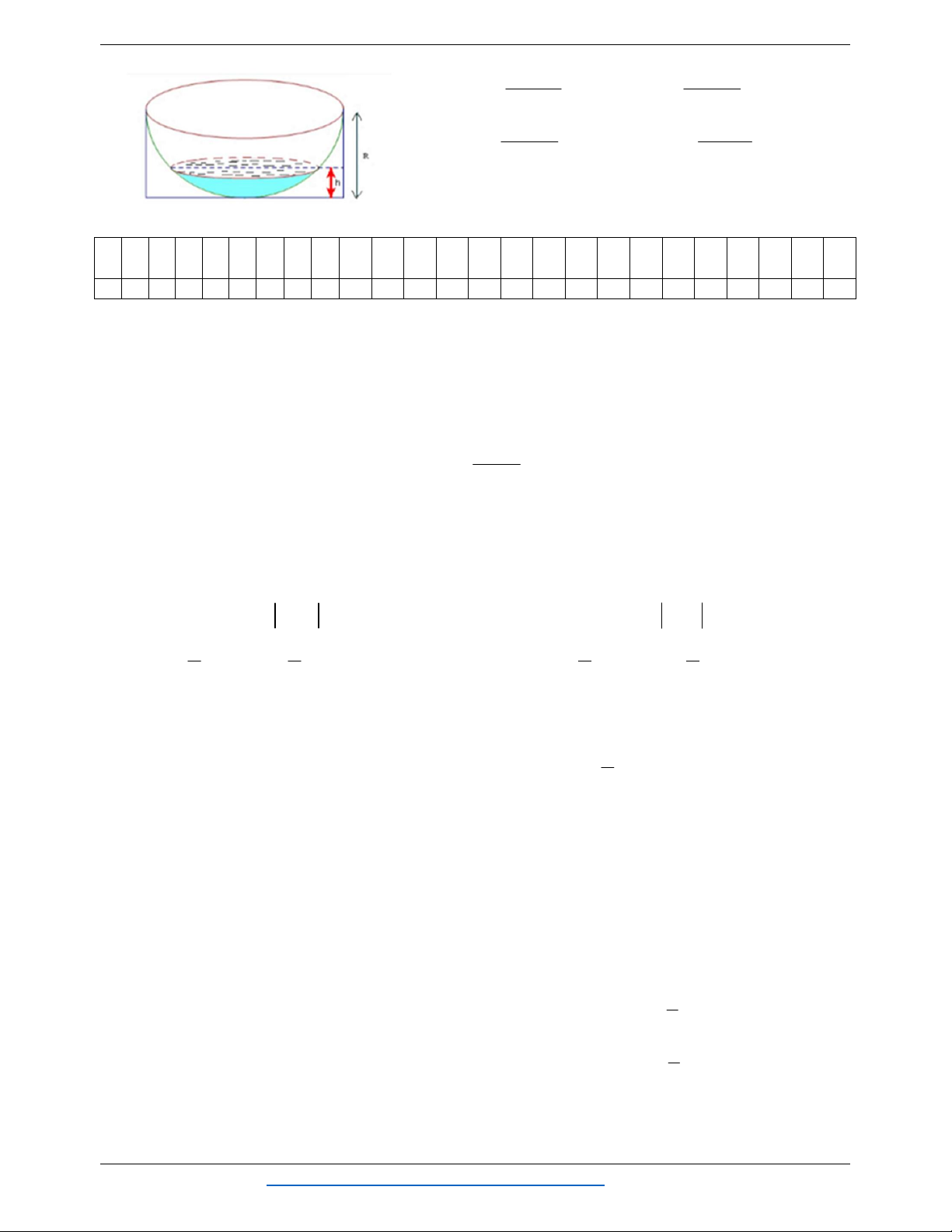
Câu 25: Một gáo có hình nửa mặt cầu bán kính R  10 cm đựng nước có độ cao h  6 cm
như hình vẽ. Tính thể tích nước trong gáo.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 33
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 3008 3040 A. (đvtt) B. (đvtt) 3 3 2048 1840 C. (đvtt) D. (đvtt) 3 3 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 C B C C B B A A D C B B A B B B B A A B D A C B A ĐỀ 11 1
Câu 1: Tìm nguyên hàm của hàm số f x  . 2 sin x
A. f xdx  tan x C
. B. f xdx  cot x C  .
C. f xdx  cot x C
. D. f xdx   tan x C  .
Câu 2: Khẳng định nào sau đây là đúng? A. tan .
x dx  ln cos x C  . B. cot .
x dx  ln sin x C  . x x x x
C. sin .dx  2cos  C  .
D. cos .dx  2sin  C  . 2 2 2 2
Câu 3: Cho u u(x) , v v(x) là hai hàm số có đạo hàm liên tục, khẳng định nào sau đây là đúng ? u
A. udv uv vd . u  
B. udv uv vd . u   C. udv   v . du   D. v
vdu uv vd . u  
Câu 4: Khẳng định nào sau đây là khẳng định sai ?
A. f xdx F x  C. 
B. kf xdx k f xd . x  
C. f x  g xdx
f xdx g xd . x    
D. f x.g xdx
f xd .
x g xd . x     
Câu 5: Biết f udu F u  C.  Khẳng định nào đúng? 1
A. f 3x  
1 dx  3F 3x   1  C. 
B. f 3x   1 dx
F x  x C.  3 1
C. f 3x  
1 dx F 3x   1  C. 
D. f 3x   1 dx F 3x   1  C.  3
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 34
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1
Câu 6. Biết F (x) là một nguyên hàm của của hàm số f (x)  và F (2) 1  . Tính x 1 F (3). 1 7
A. F(3)  ln 2 1. B. F(3)  ln 2 1. C. F (3)  . D. F (3)  . 2 4 2
Câu 7: Cho hàm số F xthỏa mãn F ' x  1 x  . Hãy tính F 2  F   1 . x 1 1 A. 2ln 2  . B. 2 ln 2. C. 4ln 2 1. D. ln 4  . 2 2 1 f (x)
Câu 8: Cho F (x) 
là một nguyên hàm của hàm số
. Tìm nguyên hàm của hàm 2 2x x số f (  x)ln . x  ln x 1  ln x 1 A. f (
x)ln xdx     C.   B. f (  x)ln xdx    C. 2 2    x 2x  2 2 x x  ln x 1  ln x 1 C. f (
x)ln xdx     C.   D. f (  x)ln xdx    C. 2 2   2 2  x x x 2x Câu 9: Biết      . x F x
ax b e là nguyên hàm của hàm số  2  3. x y x
e . Khi đó a b là A. 2. B. 3. C. 4. D. 5. Câu 10: Biết 3 2 .  cosb  cosn sin x cos xdx a x m x C.  Với a, , b , m ,
n C  ,b  . n Tính giá
trị của T a b m  . n 38 32 27 41 A. T   . B. T   . C. T   . D. T   . 15 3 5 30 x x x Câu 11: Biết x sin dx ax cos  msin  C.
a b m n C   Tính giá trị của  Với , , , , . 3 b n K abm . n A. 5 K  3 . B. 4 K  3 . C. 3 K  3 . D. 2 K  3 . 2 4 ln x  1 Câu 12: Giả sử 2
dx a ln 2  b ln 2 
, với a, b là các số hữu tỉ. Khi đó tổng 1 x
4a b bằng A. 3. B. 5. C. 7. D. 9. 1
Câu 13: Kết quả tích phân  2  3 x I x e dx
được viết dưới dạng I ae b với a,b là 0
các số hữu tỉ. Tìm khẳng định đúng. A. 3 3
a b  28 .
B. a  2b  1.
C. a b  2 . D. ab  3 . 0 2 3x  5x 1 2
Câu 14: Giả sử rằng I dx a ln  b
. Khi đó, giá trị của a  2 . b x  2 3 1  A. 30. B. 40. C. 50. D. 60.
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 35
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
   4 4 2 cos xf (x)  5
Câu 15: Cho f (x)dx  . a  Tính dx  theo a. 2 cos x 0 0 A. a  2. B. a  5. C. a. D. a  5. 1 dx
Câu 16: Nếu đặt t  thì x
(với x  0 ) trở thành: 2 2 x x 1 tdt tdt dt tdt A.  . B.  . C.  . D.  . 2 t  1 2 t  1 2 t  1 2 t  1 5 5 4 1 4 Câu 17: Cho
f (x)dx  5 
, f (t)dt  2  
và g(u)du  
. Tính ( f (x)  g(x))d . x  3 1  4 1  1  8 10 22 20  A. . B. . C. . D. . 3 3 3 3 x e
Câu 18: Giả sử F (x) là một nguyên hàm của hàm số f (x) 
trên khoảng (0; ) và x 3 3 x e I dx
. Khẳng định nào sau đây là khẳng định đúng ? x 1
A. I F (3)  F (1).
B. I F (6)  F (3).
C. I F (9)  F (3).
D. I F (4)  F (2). 18 6 9 Câu 19: Cho
f (x)dx  30.  Tính I
f (3x)dx f (2x)d . x   0 0 0 A. I 1  1. B. I  27. C. I  25. D. I  26.
Câu 20: Tính diện tích S của hình phẳng giới hạn bởi đường parabol 2
y x  3x  2 và
đường thẳng y x 1. 37 4 799 A. S  . B. S  . C. S  . D. S  2. 14 3 300
Câu 21: Diện tích hình phẳng giới hạn bởi các đường y  2x, y  4  x và trục Ox được tính bởi công thức 4 4 2 4 A.
2xdx  4  xd . x   B.
2xdx  4  xd . x   0 0 0 2 4 2
C.  2x  4  xd .x
D. 4  x  2x d .x 0 0
Câu 22: Cho hình phẳng  H  giới hạn bởi các đường y  ln x , y  0 , x k ( k  1). Tìm
k để diện tích hình phẳng  H  bằng 1. A. k  2. B. 2 k e . C. k  . e D. 3 k e .
Câu 23: Cho hình thang cong (H ) giới hạn bới các đường x
y e , y  0, x  0 và x  ln 4 .
Đường thẳng x k (0  k  ln 4) chia (H ) thành hai phần có diện tích là S S và như hình vẽ 1 2
bên. Tìm x k để S  2S . 1 2
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 36
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 2 A. k
ln 4. B. k  ln 2. 3 8
C. k  ln . D. k  ln 3. 3 x
Câu 24: Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y
, trục Ox và đường 2 4  x
thẳng x  1. Tính thể tích V của khối tròn xoay thu được khi quay hình H xung quanh trục Ox  4 1 4  3 4 A. V  ln . B. V  ln . C. V  ln . D. V   ln . 2 3 2 3 2 4 3
Câu 25: Cho hình phẳng H được giới hạn bởi các đường
y   x  2, y x  2, x 1. Tính thể tích
V của vật thể tròn xoay khi quay hình
phẳng H quanh trục hoành. A. B. C. D. 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 C A B D D B A A B A A D B B B A C C C B B C D A C ĐỀ 12
Câu 1: Khẳng định nào sau đây Sai  1  dxx A. x dx   C (  1)  B.  ln x C.    1 x
C. sin xdx  o
c sx C.  D. x x
e dx e C.
Câu 2: Khẳng định nào sau đây đúng A. in s d x x  c s o x C.  B. 2 x 2 x
e dx e C.  x a C. 2 x 2 x
a dx a .ln a C.  D. x a dx   C. ln a
Câu 3: Cho f (u)dx F (u)  C
và u u(x) là hàm số có đạo hàm liên tục, khẳng định nào sau đây là đúng ?
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 37
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12

A. f (u(x))u '(x)dx f (u(x))  C. 
B. f (u(x))u '(x)dx F (u(x))  C. 
C. f '(u(x))u '(x)dx f (u(x))  C. 
D. f (u '(x))u(x)dx F(u(x))  C. 
Câu 4: Khẳng định nào sau đây là khẳng định sai ?
A. f ' xdx F(x)  C. 
B. kf xdx k f xd . x  
C. f x  g xdx
f xdx g xd . x     
D. f xdx F x  C.    
Câu 5: Tìm nguyên hàm F x của hàm số f x  cos 2x , biết rằng F  2   .  2  3
A. F x  sin x  2 .
B. F x  x  sin 2x  . 2 1
C. F x  sin 2x  2 .
D. F x  2x  2 . 2  x  210 Câu 6: Nguyên hàm dx  bằng  x  12 1 11 11 1  x  2  1  x  2  A.     C . B.    C . 11 x  1  3  x  1  11 11 1  x  2  1  x  2  C.    C . D.    C . 11 x  1  33  x  1 
Câu 7: Tìm nguyên hàm của hàm số   3x f x e . x 1 x 1 A. 3 3x
e dx e C.  B. 3 3x 1 e dx e    C.  3 3x  1 C. 3x 3x
e dx e C.  D. 3x 3  3 x e dx e C.  1 f (x)
Câu 8: Cho F (x)  
là một nguyên hàm của hàm số . Tìm nguyên hàm của 3 3x x hàm số f (  x)ln x . ln x 1 ln x 1 A. f (  x)ln xdx    C.  B. f (  x)ln xdx    C. 3 5  x 5x 3 5 x 5x ln x 1 ln x 1 C. f (  x)ln xdx    C.  D. f (
x)ln xdx     C. 3 3  x 3x 3 3 x 3x Câu 9: Nếu 2
F (x)  (ax bx c) 2x 1 là một nguyên hàm của hàm số 2 10x  7x  2  1  f (x)  trên khoảng ; . 
 Với a,b,c  .
 Tính T  2a b  . c 2x 1  2  A. T  6.
B. T  2. C. T  2. D. T  6.
Câu 10: Biết x cos3xdx axsin mx bcos nx C.  Với a, , b , m n,C  .  Tính giá trị của K abm . n 1 1 1 1 A. K   . B. K   . C. K   . D. K   . 3 2 3 3 3 4 3
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 38
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 dx Câu 11: Biết
a cotb x m cotn x C.  Với a,b, ,
m n,C  ,b  . n Tìm 4 sin x
H a b m  . n 3 8 4 10 A. H  . B. H   . C. H   . D. H   . 4 3 3 3 0 dxa Câu 12: Biết  
trong đó a,b, là các số nguyên dương tính S b  . a 2 x  2x  4 b 1  A. S  15 . B. S  12 . C. S  9 . D. S  6 . 2
Câu 13: Biết rằng ln  x   1 dx  l a n3  l b n2  c
với a,b,c là các số nguyên. Tính 1
S a b  . c A. S  0. B. S  1. C. S  2. D. S  2. 1 2 x x e a e
Câu 14: Biết rằng dx  
với a,b là các số nguyên . Tính 2 2
S a b .  x  22 b 0 A. S  0. B. S  3. C. S  5. D. S  9. 2       2 
Câu 15: Biết rằng
cos x dx a  b
với a,b là các số nguyên . Tính 2 2
S a b . 0 A. S  0. B. S  3. C. S  5. D. S  9.
Câu 16: Cho hàm số f x liên tục trên R và thoả mãn f x  f x  2  2cos 2x, x   .  3 2 Tính I f xd . x  3  2 A. I  6.  B. I  0. C. I  2. D. I  6. 2 4 2
Câu 17: Cho các tích phân f (x)dx  3, f (x)dx  5   .Tính I f (2x)d . x  0 2 0 A. I  2. B. I  3. C. I  4. D. I  8. 10 6
Câu 18: Cho f (x) liên tục trên đoạn 0;10 thỏa mãn
f (x)dx  2017;
f (x)dx  2016.   0 2 2 10
Khi đó giá trị của P
f (x)dx f (x)d . x   0 6 A. 1 B. 1 
C. 0 D. 2 8
Câu 19: Cho hàm số f (x) liên tục trên  1
 ; và f ( x 1)dx 10.  Tính 0 3 I  .
x f (x)d . x  1 A. I  5. B. I  10. C. I  20 . D. I  40 .
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 39
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1 4
Câu 20: Tính diện tích hình phẳng giới hạn bởi các đường 2
y x , y   x  và trục 3 3 y hoành như hình vẽ. y = x2 7 56 A. . B. . 2 3 3 1 4 1 39 11 y = - x+ 3 3 C. . D. . x 2 6 O 4 1
Câu 21: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y  3 x x 1
và đường thẳng y
x . Tính diện tích hình (H). 2 57 13 25 A. . B. . C. 4. D. . 5 2 4
Câu 23: Tính diện tích S của hình phẳng giới hạn bởi đường parabol 2
y x  3x  2 và
đường thẳng y x 1. 37 4 799 A. S  . B. S  . C. S  . D. S  2. 14 3 300
Câu 24: Người ta cần trồng hoa tại phần đất nằm phía ngoài đường tròn tâm gốc toạ độ, 1 bán kính bằng
và phía trong của Elip có độ dài trục lớn bằng 2 2 và trục nhỏ bằng 2 2 100
(như hình vẽ). Trong mỗi một đơn vị diện tích cần bón
kg phân hữu cơ. Hỏi 2 2   1 
cần sử dụng bao nhiêu kg phân hữu cơ để bón cho hoa? A. 30 kg . y B. 40 kg . C. 50 kg . D. 45kg . O x
Câu 24: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường
y  2  x, y x, y  0 xung quanh trục Ox được tính theo công thức nào sau đây? 1 2 2
A. V   2  x 2
dx   x dx   .
B. V   2  xdx  . 0 1 0 1 2 1 2 C. V   d x x   2  xdx   . D. 2
V   x dx   2  xdx   . 0 1 0 1
Câu 25: Cho hai đường tròn O ;5 và O ;3 cắt nhau tại hai điểm ,
A B sao cho AB là 2  1 
một đường kính của đường tròn O . Gọi  D là hình thẳng được giới hạn bởi hai đường 2 
tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay  D quanh trục
O O ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành. 1 2
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 40
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 14 68 A. V  . B. V  . 3 3 A 40 C. V  .
D. V  36 .  D  3 O O 1 2 B 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 C D B A C D A C A A D A A A B D C A A D C B C D C ĐỀ 13
Câu 1: Tính diện tích hình phẳng  H  được giới hạn bởi các đường 2 y  2 . x
x  5, y  0 và x  2. 54 10 5 27  5 5 5273 A. 28. B. . C. . D. . 3 3 500
Câu 2: Khẳng định nào sau đây là khẳng định sai ?
A. kf xdx  k f xdx   k   \   0 . B. f ' x
f (x)  C.  dò
C. f x.g x dx   f x . dx g xdx.     
D. f x  g x dx  
f xdx g x dx.      2x  3
Câu 3: Biết F x là một nguyên hàm của hàm số f x 
và F 2  2016. Tính 1  x F 3.
A. F 3  2006  5ln 2.
B. F 3  2014  5ln 2.
C. F 3  2006  5ln 2.
D. F 3  2014  5ln 2. 1 2
Câu 4: Tìm nguyên hàm của hàm số f x   cos x  . x x 1 A.
f xx  ln x  sin x  2 x  C.  d
B. f xdx  
 sin x  4 x  C.  2 x 1 1 C.
f xx    sin x   C.  d
D. f xdx  ln x  sin x  4 x  C. 2  x x x
Câu 5: Dieäè tícâ ârèâ pâaúèá áiôùi âau è bôûi caùc ñö ôø èá : 4 2
y x  3x  7 vaø y  2 4x  5 laø : 608 15 19 1029 A. B. C. D. 15 608 4 15
Câu 6: Tính diện tích hình phẳng (S) giới hạn bởi các đường: 2 y x ln ;
x y  0; x  1; x e khi quay quanh Ox bằng: 1 1 1 A. 2 S  (1  e ) B. 2 S  (e 1) C. 2 S  1  e D. 2 S  (e 1) 4 4 4
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 41
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12

Câu 7: Cho hình phẳng  H  được giới hạn bởi đồ thị của hàm số y  tan x, trục hoành và 
hai đường thẳng x  0, x
. Khi quay hình  H  xung quanh trục hoành thì được khối 4 2 
tròn xoay có thể tích bằng a 
( a,b là các số nguyên). Khẳng định nào sau đây là b khẳng định sai ? 4a A. . a b  4  .
B. 2a b  2. C.  1  .
D. a b  5. b
Câu 8: Cho hàm số f x có đạo hàm trên đoạn  1
 ; 2, f   1  2
và f 2  1. Tính 2 2
I  (x  3x f '(x)) .  dò 1 9 3 A. I  1. B. I  3. C. I   . D. I   . 2 2
Câu 9: Tìm tham số a để hàm số F x  a   4 3 2
1 x ax  5x  5 là một nguyên hàm của
hàm số f x 3 2
 4x  6x  10 . x A. a  4. B. a  4  . C. a  2.  D. a  2. b b b Câu 10: Bieá
t f (x)d x  10  vaø
g(x)d x  5 
. Kâi ñoù áiaù trò cuûa I  3 f (x)  5g(x)d xa a a laø : A. 15 B. 5 C. 5 D. 10
Câu 11: Tính diện tích hình phẳng  H  được giới hạn bởi các đồ thị hàm số  . x y x e và y  . e . x 9 e  2 7 e  2 A. . B. . C. . D. . 25 2 20 2  4 3 x x  1
Câu 12: Câo 2I  d x
. Giaù trò I  2 baèèá : 2 cos x   4 A. 5 B. 2 C. 3 D. 4
Câu 13: Tìm nguyên hàm của hàm số     2019 x f x x x e  . 2020 5 x e 2019 5 x e A. f x 2  x x   C.  dò B. f x 2  x x   C.  dò 2 2020 2 2019 2019 x 2020 2 x e 2 e C. 2 f x 2 dx  x x   C.  D. f x  x x   C.  dò 5 2020 5 2019 3 2 1  x 2 x  1
Câu 14: Cho tích phân I dx
, nếu đổi biến số t  thì 2 x x 1
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 42
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 2 2 3 tdt 3 tdt 3 2 t dt 3 2 t dt A. I   B. I I I   2  C. D. t  1 2 t 1 2 t  1 2 t 1 2 2 2 2 e 1
Câu 15: Cho tích phân 2
I  (2x  1) ln . x dx  (e b)  trong đó *
a,b Z . Khi đó a + b a 1 bằng: A. -1. B. -3. C. -5. D. 5.
Câu 16: Diện tích S của hình phẳng tô đậm trong hình bên được tính theo công thức nào sau đây? 2 4 2 4 A. S
f (x)dx f (x) dx  
B. S   f (x)dx f (x)dx   0 2 0 2 4 2 4 C. S f (x)dx
D. S   f (x)dx f (x)dx   0 0 2
Câu 17: Cho F x là một nguyên hàm của hàm số f x liên tục trên đoạn a;b. Khẳng
định nào sau đây sai? b b
A. f (x)dx  F (a)  F(b).  B. f (x)
F (b)  F (a).  dò a a a b a C. f (x)  0.  dò
D. f (x)dx   f (x)dx.   a a b ln x
Câu 18: Cho F (x) là một nguyên hàm của hàm số f (x) 
. Tính I F (e)  F (1) . x 1 1
A. I e . B. I  . C. I  . D. I  1. 2 e 3 x Câu 19: Hou èáuyeâ è âaø m F(x)  d x  laø : 4 x 1 1 A. 4 F(x) 
lè x 1  C B. 4
F (x)  ln x 1  C 4 1 1 C. 4
F (x)  ln x 1  C D. 4 F (x) 
ln x 1  C 3 2   x 1 Câu 20: Biết 2 2 (  3)  x x e dx e
(2x n) C
với m, n   .khi đó Tổng 2 2
S m n m bằng: A. 41 B. 65 C. 5 D. 10
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 43
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 1 Câu 21: Bieá t tícâ pâaâ è 2   1 x x
e d x a  . b e
. Tíèâ P ab baèá : 0 A. P  15. B. P  1. C. P  1. D. P  5. 5 dò Câu 22: Biết
a ln 3  b ln 5.  Tính 2 2
S a ab  3b . x 3x  1 1 A. S  5. B. S  4. C. S  0. D. S  1.
Câu 23: Câo ârèâ pâaúèá (S) áiôùi âau è bôûi Ox vaø 2
y  1  x . Tâek tícâ cuûa kâoá i troø è òoay
kâi quay (S) quaèâ Ox laø : 3 3 2 4 A. B. C. D. 4 2 3 3 e 1  3ln x
Câu 24: Cho I dx
, đặt t  1  3ln x . Khẳng định nào sau đây đúng? x 1 2 2 2 e 2 2 1 2 A. 2 I t t.  d B. 2 I t t.  d C. 2 I t dt.  D. I t t.  d 3 3 3 3 1 1 1 1 1 2 a b c
Câu 25: Cho I  3x  2x dx    
. Tính S a b c ln 3 ln 6 2ln 2 0 A. S  17. B. S  70. C. S  3.  D. S  7.
----------------------------------------------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D ĐỀ 14
Câu 1: Tính diện tích S của hình phẳng giới hạn giới hạn bởi đồ thị hàm số 3 2
y  x  3x  2 , hai trục tọa độ và đường thẳng x  2. 3 7 5 A. S B. S  4 C. S D. S  2 2 2
Câu 2: Giả sử hàm số f x liên tục trên khoảng K và a, ,
b c,a b c là ba số thực bất
kì thuộc K. Khẳng định nào sau đây là sai ? b b c b a A.
f xx
d  f xx
d  f xd . x    B.
f xx
d   f xd . x   a c a a b
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 44
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 b b a C.
f xx
d  f t t d .   D.
f xx  0.  d a a a 3
Câu 3: Cho F (x) là một nguyên hàm của hàm số ( ) x
f x e  2x thỏa mãn F (0)  . Tìm 2 F (x) . x 1 x 3 A. 2
F (x)  e x  . B. 2
F (x)  2e x  . 2 2 x 5 x 1 C. 2
F (x)  e x  . D. 2
F (x)  e x  . 2 2 2  x 1 
Câu 4: Nguyên hàm của hàm số f (x)  3  .    3x x 2 x 9 1  3 ln 3 
A. f (x)dx    2x C. x
B. f (x)dx    C.  x  2 ln 3 2.9 ln 3 ln 3 3   3 x 1  1 x  1  3 1 
C. f (x)dx  9   2x C.  x
D. f (x)dx    C.  x  2 ln 3  9  3 ln 3 3 ln 3   3 x
Câu 5: Diện tích hình phẳng giới hạn bởi y  ; y x là: 2 1  x A. 1 B. 1 – lè2 C. 1  lè2 D. 2 – lè2
Câu 6: Gọi S là diện tích của Ban Công của một ngôi nhà có dạng như hình vẽ (S được
giới hạn bởi parabol (P) và trục Ox). Tinh S 9 4 A. S B. S  1 C. S D. S  2 2 3
Câu 7: Cho hình phẳng  H  giới hạn bởi đồ thị hàm số y  4x  2.ln x , trục hoành và
đường thẳng x e . Tính thể tích V của khối tròn xoay được tạo ra khi quay hình  H  xung quanh trục Ox. A. V   2
e  2e  5 .  B. 2
V e  2e  5. C. V   2
e  6e  5 .  D. 2
V e  6e  5. 5
Câu 8: Tính tích phân   2 3  2017x I xdx 0
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 45
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 2017x 1 A. I  15  B. I    5 125 1  2017 ln 2017 ln 2017 5 2017 1 C. I    5 15 1  2017 ln 2017 D. I  125  ln 2017 Câu 9: Câo âaø m íoá
( )  2  3 x f x x e .Nếu ( )     x F x mx
n e m,n    là một náuyeâè âaø
m cuûa f x târ hiệu m n bằng: A. 6 B. 3 C. 7 D. 1
Câu 10: Tìm Khẳng định sai b b A.
f ' xdx f b  f a  B.
f xdx F a  F b  a a a b C. cdx  0  D. 0dx  0  a a
Câu 11: Diện tích hình phẳng được giới hạn bởi hai đường y x và 2 y x là : 1 1 1 1 A. B. C. D. 5 3 2 4 10 8 10 Câu 12: Nếu
f (x)dx  17 
và f (x)dx  12  thì f (x)dx  bằng: 0 0 8 A. 5 . B. 29 . C. 5  . D. 15 . 2 1
Câu 13: Tìm hàm số F x , biết rằng ' F x   2x  2 1  x  2 1 1 2 1 1 F x    C
B. F x    C A. x 1 2x 1 2x 1 x 1 1 1 1 C F x    C
D. F x   C. x 1 2x 1 x 1 2x 1 4 x  4ln x
Câu 14: Tính tích phân I dx  2 x 1 61 9 256 A. B. ln 4  2 C.  ln 4 D. ln 4  28 100 2 3 e 3 a e  1 Câu 15: Biết 3 x ln xdx  
trong đó a,b là các số nguyên dương. b 1
Tính giá trị của biểu thức 2 2
S a b  7a  1 A. 252 B. 245 C. 345 D. 315
Câu 16: Trong các khẳng định sau, khẳng định nào sai ?  A. 4 ln x x d  4 ln xd . x  
B.  tan xx  tan x C.  d  2  1 C.  sin x x d  2 x d  sin xd . xx x     D. . x e x d  xd . x e d . x     xx
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 46
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12

Câu 17: Công thức tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y f x,
trục hoành và hai đường thẳng x a, x b (a b) là: b b b b A. 2 S
f xdxB. S
f xdxC. 2 S  
f xdxD. S
f xdxa a a a Câu 18: Câo âaø m íoá
f x   x  2017 ( ) 2 1
.Trm tất cả các hàm số F (x) tâỏa mãn  1 
F ' x  f x và F   2018    2   x  2018 2 1  x  2018 2 1
A. F x   2018
B. F x   2018 4036 2018
C. F x   x  2016 2017 2 1  2018
D. F x   x  2016 4034 2 1  2018 Câu 19: Cho hàm số 2
f (x)  (6x  1) có một nguyên hàm có dạng 3 2
F (x)  ax bx cx d thỏa điều kiện F ( 1
 )  20 . Giá trị của biểu thức
S a b c d bằng A. S  21 B. S  27 C. S  46 D. S  20 a b 2017 1 x 1 x
Câu 20: Biết x 1 xdx    C
với a,b là các số nguyên dương .Khi a b
đó Tính P  2a b bằng: A. 2020 B. 2018 C. 2019 D. 2017 1 1 Câu 21: Biết
a ln 2  b ln 3.  dò Tính 2 2
M a b . 2 x  5x  6 0 A. M  15. B. M  5. C. M  5. D. M  3. 2 2 2x  3x  1 5 Câu 22: Biết dx a ln  b, 
trong đó a,b là các số hữu tỉ. Tính S a  . b 2x  1 3 1 A. 8. B. 2. C. 4 . D. 6. 2x  1
Câu 23: Cho hình phẳng (H) được giới hạn bởi đường cong (C) : y  , trục Ox và x 1
trục Oy. Thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox là : A. 3 B. 4ln 2 C. (3  4 ln 2) D. (4  3ln 2)  3
4 f 1 2 tan xCâu 24: Cho
f xdx  8  . Tính tích phân dx  . 2 cos x 1 0 A. 4 B. 16 C. 2 D. 8 1
Câu 25: Kết quả của tích phân  (2  3) x I x e dx
được viết dưới dạng I ae b với 0
a,b . Khẳng định nào sau đây đúng?
A. a b  2 B. 3 3 a b  28 C. ab  3
D. a  2b  1
A. a b  2 B. 3 3 a b  28 C. ab  3
D. a  2b  1
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 47
14 ĐỀ ÔN TẬP CHƯƠNG 3 – TÍCH PHÂN 12
 ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 A B C D
Nguyễn Bảo Vương https://www.facebook.com/phong.baovuong 48