CÂU HỎI ÔN TẬP THỐNG KÊ XÃ HỘI HỌC
Câu 1. Từ 10 quả bóng đá, gồm 6 quả màu trắng và 4 quả màu da cam, người ta chọn ngẫu nhiên 1 quả
để tổ chức thi đấu. Tính xác suất để lấy được quả bóng màu trắng. A. 2/3 B. 2/5 C. 3/5 D. 1/6
Câu 2. Gieo một con xúc xắc cân đối và đồng chất 1 lần. Tính xác suất để số chấm ở mặt trên của xúc xắc lớn hơn 4. A. 1/6 B. 1/3 C. 1/2 D. 2/3
Câu 3. Một học sinh trả lời 10 câu hỏi một cách độc lập với nhau. Xác suất trả lời đúng mỗi câu bằng 0,8.
Tính xác suất để học sinh trả lời chỉ sai 2 câu trong 10 câu đó. A. C. B. D.
Câu 4. Cho Z là biến ngẫu nhiên có phân phối xác suất cho bởi bảng sau. Tính P[Z< 25]. Z 10 15 20 25 30 P 0,15 0,15 0,1 0,3 0,3 A. 0,3 B. 0,4 C. 0,7 D. 0,45
Câu 5. Cho X là biến ngẫu nhiên có phân phối xác suất cho bởi bảng sau. Tính kì vọng E[X]. X 1 3 4 6 10 P 0,1 0,3 0,1 0,3 0,2 X1.p1+X2.p2+X3.p3+… A. E[X]= 5 C. E[X]= 4,5 B. E[X]= 5,2 D. E[X]= 5,8
Câu 6. Cho Z là biến ngẫu nhiên có bảng phân phối xác suất cho bởi bảng sau. Tính phương sai Var[Z]. Z -200 -150 -100 -50 -10 P 0,1 0,05 0,15 0,5 0,2
X1bình.p1 + x2 bình.p1 + … + Xn bình.pn - (E[X]) bình C. Var[Z]=349,83. A. Var[Z]=7895. D. Var[Z]=486,89. B. Var[Z]=3064,75.
Câu 7. Chiều cao sau 1 năm tuổi của một giống cây trồng có phân phối chuẩn N(12;4). Ước lượng tỉ lệ
cây có chiều cao trên 11m.
Trang 18 – Tính gần đúng A. 40,1% C. 30,9% B. 59,9% D. 69,1%
Câu 8. Kết quả thi giữa kì môn Thống kê xã hội học của sinh viên một khoa như sau. Tính điểm trung bình. A. 4,62 C. 2,02 B. 4,086 D. 200
Câu 9. Thống kê cân nặng của 40 trẻ sơ sinh ở vùng A, ta có bảng số liệu sau. Tính trung bình mẫu (X gạch ngang). 1 Cân nặng (kg) 2,6-2,8 2,8-3,0 3,0-3,2 3,2-3,4 3,4-3,6 Số trẻ 5 10 12 4 9 A. 3,11 C. 3,45 B. 3,3 D. 3,0
Câu 10. Thống kê điểm thi của 30 bạn học sinh trong lớp, ta có bảng tần số sau. Tính phương sai mẫu (S BÌNH) A. 1,033 C. 1,895 B. 1,83 D. 1,376
Câu 11. Đo chiều cao ngẫu nhiên một số cây bạch đàn trong rừng thu được bảng sau. Tính độ lệch mẫu (S) A. 0,6427 C. 8,064 B. 0,4096 D. 35
Câu 12. Để nghiên cứu tình trạng nghỉ học của học sinh ở một trường A vào năm học trước, người ta điều
tra 40 học sinh và thu được bảng số liệu như sau: X (ngày) 0 1 2 3 4 5 Số hoc sinh 19 8 6 3 2 2
Trung vị mẫu là = MED A. 24 B. 1 C. 2 D. 0
Câu 13. Để nghiên cứu tình trạng nghỉ học của học sinh ở một trường A vào năm học trước, người ta điều
tra 40 học sinh và thu được bảng số liệu như sau: X (ngày) 0 1 2 3 4 5 Số hoc sinh 19 8 6 3 2 2
Mode của mẫu là = GTRI XUẤT HIỆN NHIỀU NHẤT A. 24 B. 3 C. 2 D. 0
Câu 14. Để nghiên cứu khối lượng một giống cam mới, người ta cân một số quả cam và thu được bảng kết quả sau.
Cam loại 2 là cam có khối lượng dưới 34g. Hãy tính tỉ lệ số cam loại 2 trong mẫu trên.
(lấy số cam của 32,33g => chia cho tổng số cam => %) A. 5% B. 20% C. 95% D. 80%
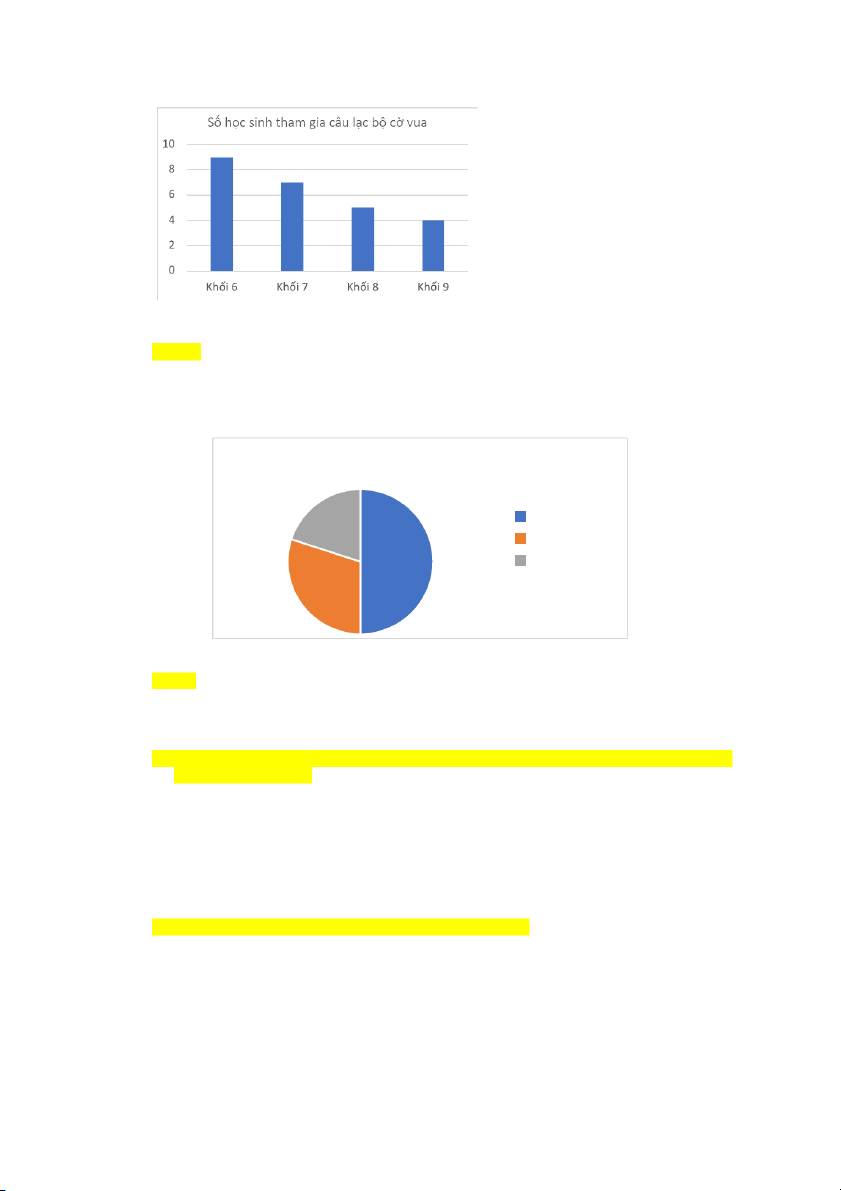
Câu 15. Biểu đồ dưới đây biểu diễn số học sinh tham gia câu lạc bộ cờ vua của một trường cấp 2 phân theo khối lớp. 2
Hãy xác định tỉ lệ học sinh khối 9 tham gia câu lạc bộ.
(số HS khối 9 chia tổng số HS 4 khối) A. 16% C. 40% B. 14% D. 4%
Câu 16. Biểu đồ dưới đây tổng kết học lực của học sinh một trường tiểu học có 500 học sinh. (20% của 500) Bi u ể đồồ h c ọ l c ự c a ủ h c ọ sinh 20.00 Gi i ỏ % Khá 50.00 Trung bình % 30.00 %
Số lượng học sinh có học lực trung bình ở trường đó là bao nhiêu? A. 1000 C. 20 B. 100 D. 200
Câu 17. Xét bài toán tìm khoảng ước lượng cho giá trị trung bình của mẫu có phân phối chuẩn với
phương sai chưa biết. Chọn khẳng định đúng => KUL trung bình = Tỉ lệ thuận
A. Nếu kích thước mẫu tăng gấp đôi thì độ dài khoảng ước lượng cũng tăng gấp đôi.
B. Với cùng một bộ số liệu thì khoảng ước lượng có độ tin cậy cao sẽ dài hơn khoảng ước lượng
có độ tin cậy thấp hơn.
C. Khi áp dụng cùng một công thức tìm khoảng ước lượng cho hai mẫu số liệu khác nhau thì sẽ
luôn được đáp số giống nhau.
D. Độ dài của khoảng ước lượng phụ thuộc vào trung bình mẫu.
Câu 18. Xét bài toán tìm khoảng ước lượng cho tỉ lệ. Chọn khẳng định đúng. => KUL tỉ lệ = tỉ lệ nghịch
A. Nếu kích thước mẫu tăng gấp đôi thì độ dài khoảng ước lượng cũng tăng gấp đôi.
B. Với cùng một bộ số liệu thì khoảng ước lượng có độ tin cậy cao sẽ ngắn hơn khoảng ước lượng
có độ tin cậy thấp hơn.
C. Nếu kích thước mẫu tăng thì độ dài khoảng ước lượng giảm.
D. Độ dài của khoảng ước lượng phụ thuộc vào kích thước của toàn bộ quẩn thể.
Câu 19. Với cùng một mẫu số liệu, tìm khoảng ước lượng cho trung bình quần thể có độ dài ngắn nhất
trong các khoảng ước lượng dưới đây. 3
A. Khoảng ước lượng với độ tin cậy 90%
B. Khoảng ước lượng với độ tin cậy 95%
C. Khoảng ước lượng với độ tin cậy 99%
D. Khoảng ước lượng với độ tin cậy 99,9%
Câu 20. Lượng nhiên liệu tiêu thụ để di chuyển quãng đường 100 km của một loại xe ô tô là một đại
lượng ngẫu nhiên có phân phối chuẩn với độ lệch chuẩn = 0,5 (lít Đo ).
25 xe ta thấy lượng nhiên liệu tiêu
thụ trung bình cho 100 km di chuyển là =8 (lít). Với độ tin cậy 95%, hãy tìm khoảng ước lượng cho
lượng nhiên liệu tiêu thụ trung bình của loại xe này. Biết =1,645; =1,96; =1,7109; 2,0639. A (7,836;8,164) C (7,829;8,171) B (7,804;8,196) D (7,794;8,206)
Câu 21. Với cùng một mẫu số liệu, tìm khoảng ước lượng cho tỉ lệ có độ dài ngắn nhất trong các khoảng
ước lượng dưới đây.
A. Khoảng ước lượng với độ tin cậy 90%
B. Khoảng ước lượng với độ tin cậy 95%
C. Khoảng ước lượng với độ tin cậy 99%
D. Khoảng ước lượng với độ tin cậy 99,9%
Câu 22. Trong các khoảng ước lượng với cùng độ tin cậy 95% cho giá trị trung bình với cỡ mẫu
n = 100, khoảng ước lượng ứng với độ lệch chuẩn nào dưới đây có độ dài lớn nhất?
=> KUL trung bình = tỉ lệ thuận A. C. B. D.
Câu 23. Sau khi khảo sát về số tiền tiêu vào các cuộc điện thoại trong một tháng của 100 sinh viên ta
được =60 (ngàn đồng), s=10 (ngàn đồng). Với độ tin cậy 95%, hãy tìm khoảng ước lượng cho lượng
tiền điện thoại trung bình trong một tháng của mỗi sinh viên. Biết =1,645; =1,96. A. (58,360;61,640) C. (58,040;61,960) B. (58,352;61,648) D. (58,030;61,970)
Câu 24. Kiểm tra ngẫu nhiên 100 sản phẩm của một lô hàng ta thấy có 10 sản phẩm không đạt tiêu
chuẩn. Với độ tin cậy 95%, hãy tìm khoảng ước lượng cho tỉ lệ s
ản phẩm không đạt tiêu chuẩn trong lô hàng. Biết =1,645; =1,96. A. (5,1%; 14,9%) C. (4,1%; 15,9%) B. (4,8%; 15,2%) D. (3,8%; 16,2%)
Câu 25. Trọng lượng của một bao gạo là đại lượng ngẫu nhiên có phân
phối chuẩn với =1 (kg). Với độ
tin cậy 95%, ta cần cân tối thiểu bao nhiêu bao gạo để xác định được khoảng ước lượng cho trọng
lượng trung bình của bao gạo có độ dài không quá 0,8 (kg)? Biết =1,645; =1,96.
XÁC ĐỊNH CỠ MẪU KUL TRUNG BÌNH A. 5 C. 7 B. 17 D. 25
Câu 26. Một công ty giới thiệu một loại hạt giống mới có tỉ lệ nảy mầm được công bố trên bao bì là
=0,9. Với độ tin cậy 95%, ta cần gieo tối thiểu bao nhiêu hạt để xác định được khoảng ước lượng cho
xác suất nảy mầm có độ dài không quá 0,2? Biết =1,645; =1,96.
XÁC ĐỊNH CỠ MẪU KUL TỈ LỆ (khi biết f) A. 7 B. 9 C. 25 D. 35 4
Câu 27. Trong bài toán kiểm định giả thuyết H với đối thuyết H 0
, ta mắc sai lầm loại 2 khi 1
A. Bác bỏ giả thuyết H trong khi H 0 đúng. 0
B. Chấp nhận giả thuyết H trong khi H 0 0 sai
C. Bác bỏ giả thuyết H trong khi H 1 sai. 1 D. Chấp nhận cả H và H 0 1.
Câu 28. Trong bài toán kiểm định giả thuyết H với đối thuyết H 0 , mức ý nghĩa là: 1
A. Xác suất bác bỏ giả thuyết H trong khi H 0 0 đúng.
B. Xác suất chấp nhận giả thuyết H trong khi H 0 sai. 0
C. Xác suất đưa ra quyết định sai.
D. Xác suất đưa ra quyết định đúng.
Câu 29. Cho là mẫu ngẫu nhiên quan sát được từ phân phối chuẩn với chưa biết, n = 10. Để kiểm định
giả thuyết thống kê ta dùng thống kê nào?
Câu 30. Giả sử tỉ lệ phần tử có tính chất A nào đó trong quần thể là
p chưa biết. Xét bài toán kiểm định
giả thuyết thống kê với đối thuyết . Với một mẫu cho trước ta có thống kê kiểm định là . Với mức ý nghĩa
, chúng ta sẽ bác bỏ giả thuyết nếu: A. C. B. D.
Câu 31. Biết rằng đại lượng ngẫu nhiên X có phân phối chuẩn với giá trị trung bình là (chưa biết) và độ
lệch chuẩn là (đã biết). Xét bài toán kiểm định giả thuyết thống kê với đối thuyết . Với một mẫu cho
trước ta có thống kê kiểm định là . Với mức ý nghĩa , chúng ta sẽ bác bỏ giả thuyết nếu: A. C. B. D.
Câu 32. Biết rằng đại lượng ngẫu nhiên X có phân phối chuẩn với giá trị trung bình là (chưa biết) và độ
lệch chuẩn là (chưa biết). Xét bài toán kiểm định giả thuyết thống kê với đối thuyết . Với một mẫu cho
trước có kích thước mẫu n = 20, ta có thống kê kiểm định là . Với mức ý nghĩa , chúng ta sẽ bác bỏ giả thuyết nếu: A. C. B. D.
Câu 33. Năm ngoái, một nhà máy sản xuất với tỉ
lệ sản phẩm loại I là 20%. Năm nay, sau khi áp dụng
phương pháp sản xuất mới, kiểm tra 500 sản phẩm thấy có 150 sản phẩm loại I. Để xác định xem phương
pháp mới có làm tăng tỉ lệ sản phẩm loại I hay không, ta xét bài toán kiểm định giả thuyết nào dưới đây?
A. Giả thuyết với đối thuyết
B. Giả thuyết với đối thuyết
C. Giả thuyết với đối thuyết
D. Giả thuyết với đối thuyết
Câu 34. Trong một nhà máy bánh kẹo, một máy tự động sản xuất ra các thanh sô cô la với trọng lượng
qui định là 250g. Biết rằng trọng lượng các thanh sô cô là được sản xuất ra có phân bố chuẩn . Trong một
ngày bộ phận kiểm tra kĩ thuật chọn một mẫu ngẫu nhiên gồm 16 thanh sô cô la và tính trọng lượng trung
bình của chúng được 244g. Hãy chọn khẳng định đúng trong các khẳng định dưới đây, cho biết và .
A. Tính được Z 0= -4,8 nên với mức ý nghĩa 5% không có đủ căn cứ để có thể kết luận rằng máy
sản xuất ra các thanh sô cô la có trọng lượng nhỏ hơn quy định.
B. Tính được Z 0= -4,8 nên với mức ý nghĩa 5% có đủ căn cứ để có thể kết luận rằng máy sản
xuất ra các thanh sô cô la có trọng lượng nhỏ hơn quy định.
C. Tính được Z = -0,96 nên 0
với mức ý nghĩa 5% không có đủ căn cứ để có thể kết luận rằng máy
sản xuất ra các thanh sô cô la có trọng lượng nhỏ hơn quy định.
D. Tính được Z 0= -0,96 nên với mức ý nghĩa 5% có đủ căn cứ để có thể kết luận rằng máy sản
xuất ra các thanh sô cô la có trọng lượng nhỏ hơn quy định. 5
Câu 35. Trong các năm trước thu nhập trung bình của công nhân là 150 (triệu/năm). Năm nay điều tra
thu nhập của 25 công nhân ta được thu nhập trung bình là 155 (triệu/năm) và độ lệch mẫu là 30
(triệu/năm). Biết rằng thu nhập của công nhân tuân theo phân phối chuẩn. Hãy chọn khẳng định đúng
trong các khẳng định dưới đây, cho biết và
A. Tính được T 0= 0,833 nên với mức ý nghĩa 5% không có đủ căn cứ để có thể kết luận rằng thu
nhập năm nay cao hơn năm ngoái. B. Tính được T0 =
0,833 nên với mức ý nghĩa 5% có đủ căn cứ để có thể kết luận rằng thu nhập năm nay cao hơn năm ngoái.
C. Tính được T0 = 4,564 nên với mức ý nghĩa 5% không có đủ căn cứ để có thể kết luận rằng thu
nhập năm nay cao hơn năm ngoái. D. Tính được T0 =
4,564 nên với mức ý nghĩa 5% có đủ căn cứ để có thể kết luận rằng thu nhập năm nay cao hơn năm ngoái.
Câu 36. Tuổi thọ sản phẩm do một doanh nghiệp sản xuất ra tuân theo phân phối chuẩn. Qua quá trình
theo dõi tuổi thọ của 100 sản phẩm thu được tuổi thọ trung bình là 378,4 giờ và độ lệch mẫu là 34,2515
giờ. Hãy chọn khẳng định đúng trong các khẳng định dưới đây, cho biết và .
A. Tính được Z 0= -6,306 nên với mức ý nghĩa 5% không có đủ căn cứ để có thể kết luận rằng
tuổi thọ trung bình nhỏ hơn 400 giờ.
B. Tính được Z 0= -6,306 nên với mức ý nghĩa 5% có đủ căn cứ để có thể kết luận rằng tuổi thọ
trung bình nhỏ hơn 400 giờ.
C. Tính được Z0 = -36,907 nên với mức ý nghĩa 5% không có đủ căn cứ để có thể kết luận rằng
tuổi thọ trung bình nhỏ hơn 400 giờ. D. Tính được Z = 0
-36,907 nên với mức ý nghĩa 5% có đủ căn cứ để có thể kết luận rằng tuổi thọ
trung bình nhỏ hơn 400 giờ.
Câu 37. Một nhà máy sản xuất sản phẩm với tỉ lệ sản phẩm loại một lúc đầu là 20%. Sau khi áp dụng
phương pháp sản xuất mới, kiểm tra 500 sản phẩm thấy có 150 sản phẩm loại một. Hãy chọn khẳng định
đúng trong các khẳng định dưới đây, cho biết
A. Tính được Z 0= 5,590 nên với mức ý nghĩa 5% không có đủ căn cứ để có thể kết luận rằng
phương pháp sản xuất mới làm thay đổi tỉ lệ sản phẩm loại một.
B. Tính được Z0 = 5,590 nên với mức ý nghĩa 5% có đủ căn cứ để có thể kết luận rằng phương
pháp sản xuất mới thay đổi tỉ lệ sản phẩm loại một.
C. Tính được Z 0= 4,480 nên với mức ý nghĩa 5% không có đủ căn cứ để có thể kết luận rằng
phương pháp sản xuất mới làm thay đổi tỉ lệ sản phẩm loại một.
D. Tính được Z 0= 4,480 nên với mức ý nghĩa 5% có đủ căn cứ để có thể kết luận rằng phương
pháp sản xuất mới làm thay đổi tỉ lệ sản phẩm loại một.
Câu 38. Những năm trước nhà máy sử dụng công nghệ A sản xuất thì có tỉ lệ phế phẩm là 6%. Năm nay
nhà máy nhập công nghệ B để sản xuất, hy vọng sẽ giảm được tỉ lệ phế phẩm. Lấy ngẫu nhiên 100 sản
phẩm để kiểm tra thì thấy có 5 phế phẩm. Hãy chọn khẳng định đúng trong các khẳng định dưới đây, cho biết
A. Tính được Z 0= -0,421 nên với mức ý nghĩa 5%, có đủ căn cứ cho rằng tỉ lệ phế phẩm của
công nghệ B nhỏ hơn công nghệ A.
B. Tính được Z 0= -0,421 nên với mức ý nghĩa 5%, không có đủ căn cứ cho rằng tỉ lệ phế phẩm
của công nghệ B nhỏ hơn công nghệ A.
C. Tính được Z 0= -0,459 nên với mức ý nghĩa 5%, có đủ căn cứ cho rằng tỉ lệ phế phẩm của
công nghệ B nhỏ hơn công nghệ A.
D. Tính được Z 0= -0,459 nên với mức ý nghĩa 5%, không có đủ căn cứ cho rằng tỉ lệ phế phẩm
của công nghệ B nhỏ hơn công nghệ A. 6
Câu 39. Chiều cao và độ rộng tán của một số cây được cho ở bảng sau: Chiều cao (mét) 14 15 17 13 15 19 21 25 Độ rộng tán (mét) 3 3,3 3,6 2,9 3,4 4,1 4,2 4,5
Gọi là hệ số tương quan giữa chiều cao và độ rộng tán của cây. Khẳng định nào dưới đây là đúng? A. B. C. D.
Câu 40. Chiều cao và độ rộng tán của một số cây được cho ở bảng sau: Chiều cao (mét) 14 15 17 13 15 19 21 25 Độ rộng tán (mét) 3 3,3 3,6 2,9 3,4 4,1 4,2 4,5
Phương trình hồi quy tuyến tính cho độ rộng tán theo chiều cao của cây là A. B. C. D. 7