BTVN1-BTVN3: Phân Tích Hàm Truyền và Phương Trình Trạng Thái Hệ Thống. Môn Lý thuyết điều khiển tự động (UET) | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội.

lOMoAR cPSD| 58833082 Bài Tập Về Nhà
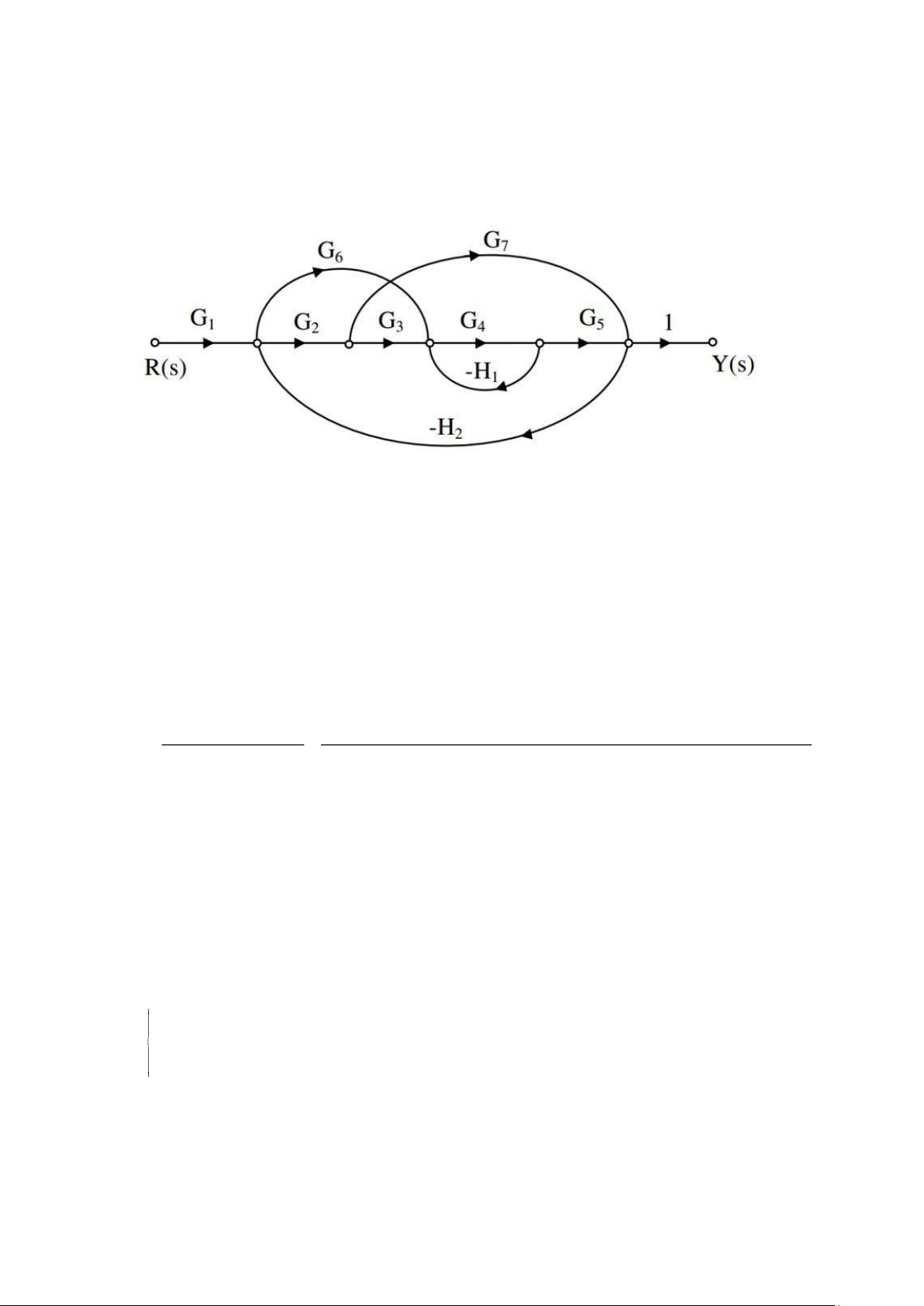
BTVN1: Tìm hàm truyền của hệ thống có sơ đồ khối như hình vẽ bằng phương pháp sơ đồ tín hiệu. Giải:
+) Đường tiến: P1=G1G2G3G4G5;P2=G1G6G4G5;P3=G1G2G7
+) Vòng kín: L1=−G4H1;L2=−G2G3G4G5H2;L3=−G6G4G5H2;L4=−G2G7 H2;
+) Chỉ có L1vàL4 không dính nhau:
→∆=1+G4 H1+G2G3G4G5 H2+G6G4G5 H2+G2G7 H2+G2G4G7 H1H2
+) ∆1=1;∆2=1;∆3=1+G4 H1 G (s)=
P1∆1+P2∆2+P3∆3=
G1G2G3G4G5+G1G6G4G5+G1G2G7(1+G4 H1) ∆
1+G4 H1+G2G3G4G5 H2+G6G4G5 H2+G2G7H2+G2G4G7H1 H2
BTVN2: Thành lập hệ phương trình trạng thái mô tả hệ thống có quan hệ giữa
tín hiệu vào và tín hiệu ra qua phương trình vi phân.
y' '' (t)+5 y' ' (t )+6 y' (t )+10 y (t )=10r' (t )+20r (t) ( ¿) Giải:
x1 (t)= y(t ) (1 )
Đặt: x2 (t)=x'1 (t )−β1r (t )(2) Đặt x'3(t )=−5 x3 (t)−6 x2 (t )−10 x1
(t )+β3r (t) x3 (t )=x'2(t )−β2r (t )(3) Từ (1) → x' ''
1 (t )=y' (t )→ y' ' (t )=x1 (t)=x'2 (t )+ β1r' (t )=x3 (t)+β2r(t )+β1r' (t)
→ y'' ' (t )=x' '' '
1 (t)=x'2 (t )+β1r' ' (t )=x'3 (t)+β2r'( t )+β1r'' (t )=−5 x3 (t )−6 x2(t )−10 x1(t )+β3r (t )+β2r' (t ) +β1r' ' (t ) lOMoAR cPSD| 58833082
Thay y' '' (t)=…, y''=…, y'=…, y=…vào (¿) ta có
−5 x3(t )−6 x2 (t )−10 x1 (t )+β3r (t )+β2r' (t ) +β1r' ' (t )+5(x3 (t)+β2r (t )+β1r' (t))+6(x2(t )+β1r (t ))+10x1 (t)=10r' (t )
Đồng nhất hệ số 2 vế của phương trình ta có:
6 β1+5 β2+β3=20 β1=0 { {
5β1+β2=10 → β32=10 β1=0 β =−30 x1' 0 1 0 x1 0 [ ] [ x23' = 0 0 ][ ] [ ] 1 x23 + 10 r (t)
x ' −10 −6 −5 x −30
→ Hệ phươngtrìnhtrạngthái: { [ ] x1 y=[1 0 0] x2 lOMoAR cPSD| 58833082 x3
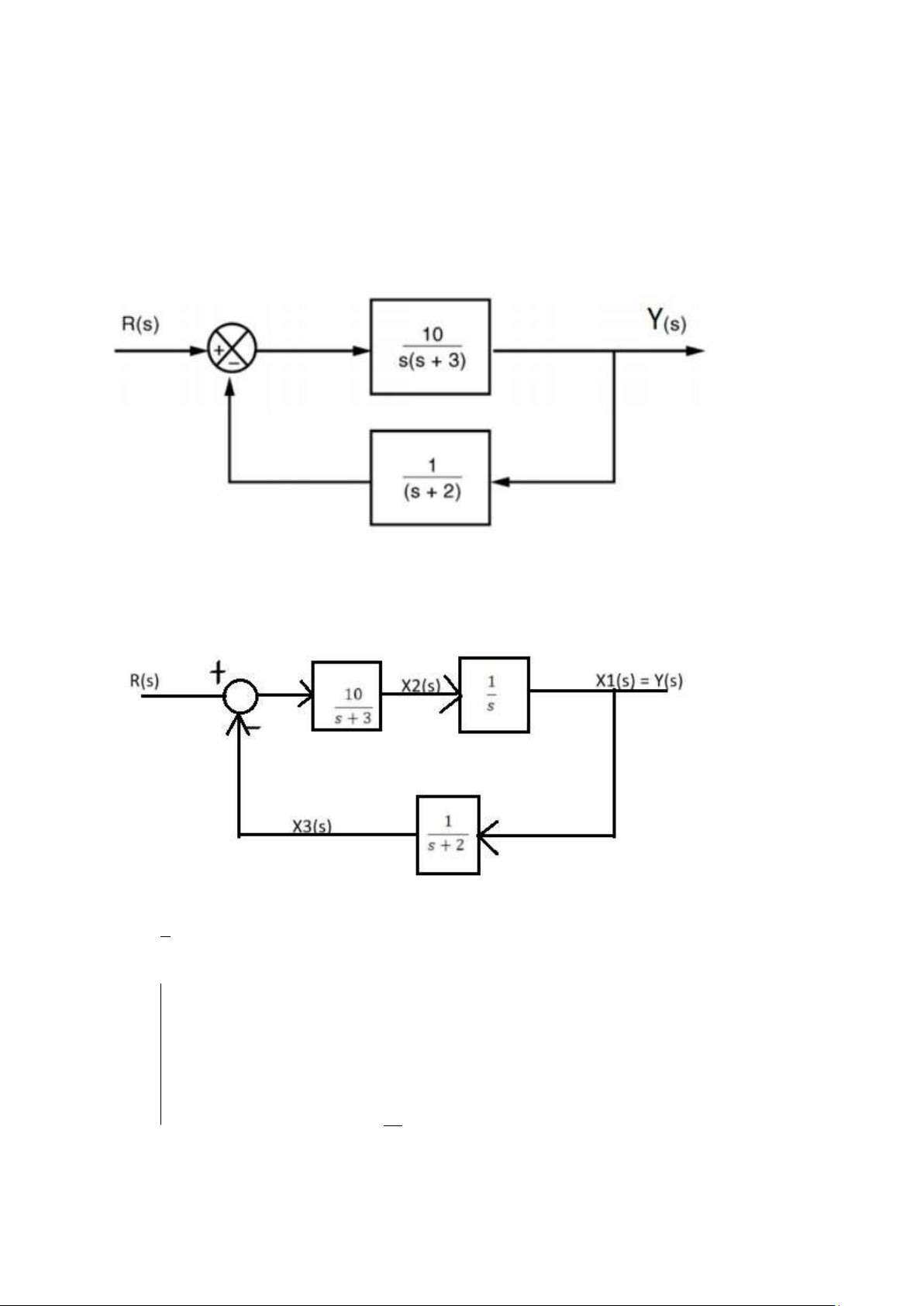
BTVN3: Hãy thành lập hệ phương trình trạng thái mô tả hệ thống có sơ đồ khối như sau: Giải:
Sơ đồ tương đương với: 1
X1( s)=X2 (s) . s
s X1 (s)= X2( s) X Ta {→
có: 2 (s)=[− X3( s)+R ( s)] . s10+3
s X2 (s)=−10 X3( s)+10 R (s)−3 X2( s) lOMoAR cPSD| 58833082
1 s X3 (s )=X1( s)−2X3(s) X3( s)=X1 (s). s+2 X1( s)=Y (s)
X1 (s)=Y (s)
Laplace ngược cả 2 vế 4 phương trình
x'1 (t)=x2 (t )
→x'2 (t )=−10x3 (t)−3x2
(t )+10r(t) x'3 (t )=x1(t )−2
x3 (t ) x1 (t )= y (t )
→Hệ phươngtrìnhtrạngthái:¿
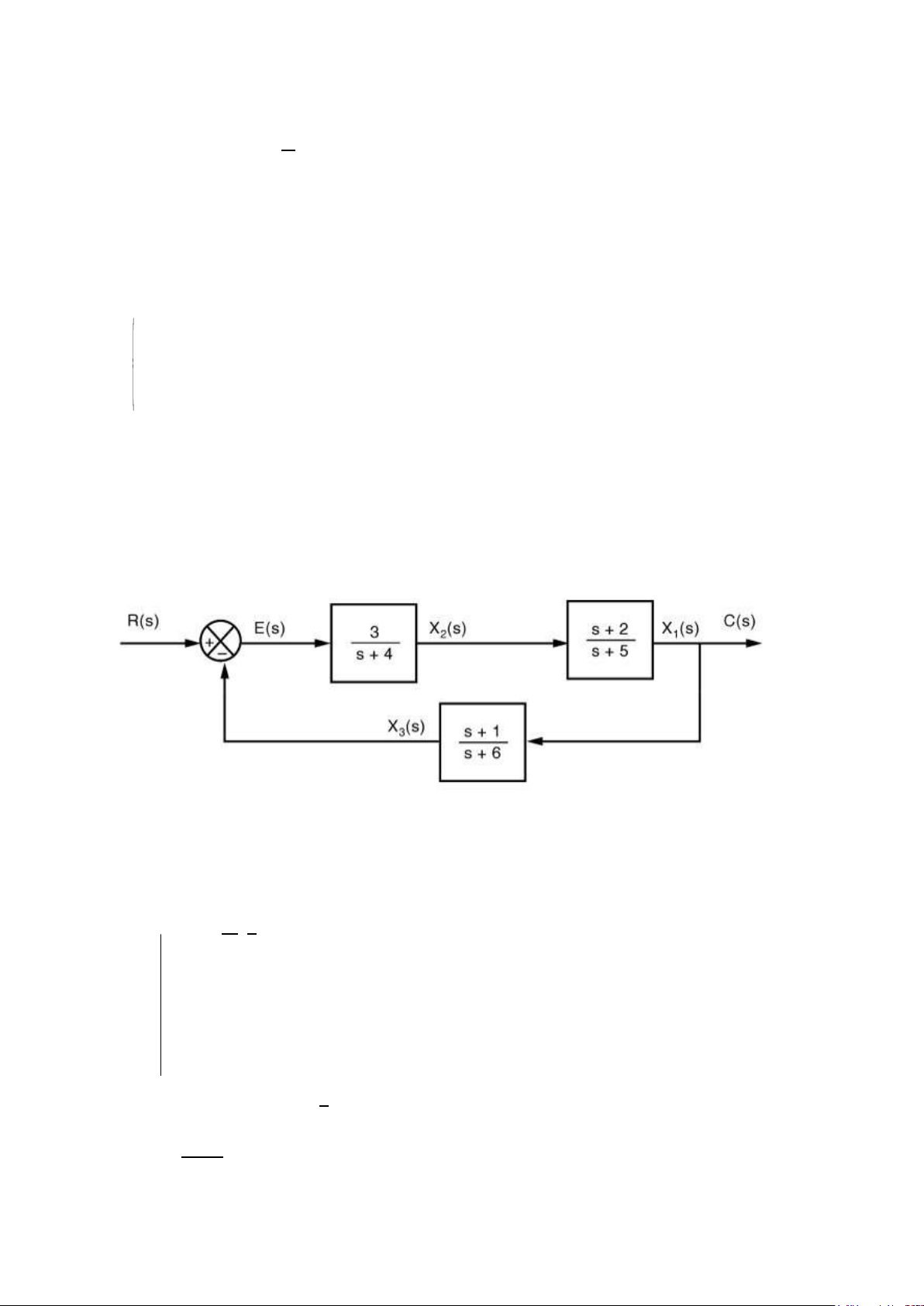
Câu 1: Hãy thành lập hệ phương trình trạng thái mô tả hệ thống với các biến
trạng thái được xác định trên sơ đồ khối sau: Giải: ( ) ) X1
s = ss++25 X2( s
s X1 (s)=s X2 (s )+2 X2 (s)−5 X1 (s) Ta {
có: 2 (s)=s+4 [ R (s)−X3( s) ] →
s X2 (s)=3 R (s)−3 X3
(s)−4 X2 (s) 3
X s+1 s X3 ( s)=s X1( s)+X1 (s )−6 X3(s) X3 (s)= s+6 X1( s) X1
(s)=Y (s) lOMoAR cPSD| 58833082
X1( s)=Y (s) Laplace ngược 2 vế
x'1 (t )=x'2 (t)+2 x2(t )−5 x1(t )(1)
→x'2 (t )=3r (t )−3 x3(t )−4 x2(t ) (2) x'3 (t)=x'1 (t )+x1 (t)−6 x3 (t )(3 ) x1(t )=y (t )
{ (1)+(2)+(3) → x'3 (t )=−4 x1 (t )−2x2 (t )−9
x3(t )+3r (t ) → x'1 (t )=−5 x1 (t )−2 x2 (t )−3 x3 (t )+3r(t ) x1' −5 −2 −3 x1 3 [ ] [ ][ ] [ ] x2' = 0−4 −3 x2 + 3 r (t ) x3' −4 −2 −9 x3 3
→ Hệ phươngtrìnhtrạng thái: ] x1 y=[1 0 0 [ ]x2 x3
Câu 2 : Cho hai hệ thống có hàm truyền, hãy thành lập phương trình trạng thái dạng chính
tắc mô tả hệ thống.
a) G1 (s)=YR (( ss))= s23+s3+s2+1 Giải :
→(s2+3s+1)Y ( s)=(3s+2) R ( s) (¿ )
ℒ ngược2vế của phươngtrình (¿ ) tacó y'
' (t )+3 y' (t )+ y(t )=3r' (t)+2r (t) ¿
x1 (t)= y (t ) (1 ) Đặt :x2
(t )=x'1 (t)−β1r (t ) (2)
x'2 (t)=−3 x2 (t )−x1(t )+ β2r (t) lOMoAR cPSD| 58833082
(1) →x'1(t )=y' (t) (2) →x' ' '
1(t )= y' (t )=x2(t )+β1r (t) →x'1 (t )=y' ' (t )=x2 (t)+β1r ' (t )=−3 x2(t )−x1(t )+β2r (t )+β1r' (t ) ¿ )
↔r (t )( β2+3 β1)=2r (t { ↔
β1=3 r' (t) β1=3r '(t ) β2=−7 →
Hệ phươngtrìnhtrạng thái:¿
b) G2 (s)=YR (( ss))= s2+3ss+2 Giải :
→(s2+3s+2)Y ( s)=sR ( s ) ℒ ngược2vế phương trìnhta có: y' '
(t )+3 y' (t )+2 y (t)=r' (t )(¿)
x1(t )= y (t )→ x'1(t )=y' (t )
Đặt x2 (t )=x'1(t )−β1r(t )→ x'1(t )=x2 (t )+β1r
(t )(2) x'2 (t)=−3x2 (t)−2x1 (t)+β2r(t ) → x' '
1 (t )= y' ' (t )=x'2 (t)+β1r ' (t )=−3 x2(t )−2 x1(t )+ β2r (t)+β1r' (t )
Thay y' '=…, y'=…, y=…vào phươngtrình (¿ ) tacó:
→−3 x2 (t )−2 x1(t )+β2r (t )+ β1r' (t )+3(x2(t )+β1r (t ))+2x1 (t)=r' (t ) ( )
→ r (tr) →{
'β(t2)+(β31β)=1)=r' (0tr) (t ββ2=1=−13
→ Hệ phươngtrìnhtrạngthái:¿
Câu 3 : Từ kết quả đã giải được từ câu 2, viết phương trình vi phân mô tả hệ thống (sử dụng PTTT).
a) G1 (s)=YR (( ss))=
s23+s3+s2+1 Hệ
phươngtrìnhtrạngthái:¿ lOMoAR cPSD| 58833082
x1(t )=y (t)
Tacó :x2 (t )=y' (t )−3r (t )
x'2 (t)=y'' (t)−3r' (t ) (¿)
Thay x'2 (t)=−3 x2 (t )−x1(t )−7r (t ) vào (¿ ) tacó:
−3( y' (t)−3r (t ))−2 y (t )−7r (t)=y'' (t)−3r' (t )
↔ y'' (t)+3 y' (t )+2 y (t )=3r' (t)+2r (t )
b) G2 (s)=YR (( ss))=
s2+3ss+2 Hệ
phươngtrìnhtrạngthái:¿
x1 (t )=y (t) Tac
ó:x2(t )=x'1(t )−r (t )=y' (t )−r(t) x' '
2(t )=x'1 (t )−r' (t)= y'' (t)−r' (t ) (¿ )
Thayx'2 (t)=−3x2 (t )−2x1 (t)−3r (t ) vào ( ¿) tacó:
−3( y' (t)−r (t ))−2 y (t )−3r (t )=y'' (t )−r' (t )
↔ y'' (t)+3 y' (t )+2 y (t )=r ' (t )