Chương II Vật dẫn môn Vật lý đại cương | Học viện Báo chí và Tuyên truyền

CHƯƠNG II: VẬT DẪN 1
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG TĨNH ĐIỆN.
ĐIỆN DUNG CỦA VẬT DẪN
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG I. Hiện tượng
II. Tụ điện và điện dung của tụ (phẳng, trụ, cầu)
§3. NĂNG LƯỢNG ĐIỆN TRƯỜNG
I. Năng lượng tương tác của một hệ điện tích điểm và của vật dẫn mang điện
II. Năng lượng tụ điện phẳng và năng lượng điện trường
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG 2
TĨNH ĐIỆN. ĐIỆN DUNG CỦA VẬT DẪN CÔ LẬP
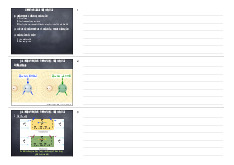
I. Điều kiện cân bằng tĩnh điện (1) Ein = 0.
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG 3
TĨNH ĐIỆN. ĐIỆN DUNG CỦA VẬT DẪN CÔ LẬP
I. Điều kiện cân bằng tĩnh điện (2)
Et = 0, En = ⃗ E .
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG 4
TĨNH ĐIỆN. ĐIỆN DUNG CỦA VẬT DẪN CÔ LẬP
II. Những tính chất của vật dẫn cân bằng tĩnh điện
(1) Vật dẫn cân bằng tĩnh điện là một vật đẳng thế. • Bên trong vật dẫn:
Et = 0, En = ⃗ E V A
M = VN N
• Trên bề mặt vật dẫn: N B
VA = VB M
• Điện thế có tính liên tục
⇒ VA = VB = VM = VN
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG 5
TĨNH ĐIỆN. ĐIỆN DUNG CỦA VẬT DẪN CÔ LẬP
II. Những tính chất của vật dẫn cân bằng tĩnh điện
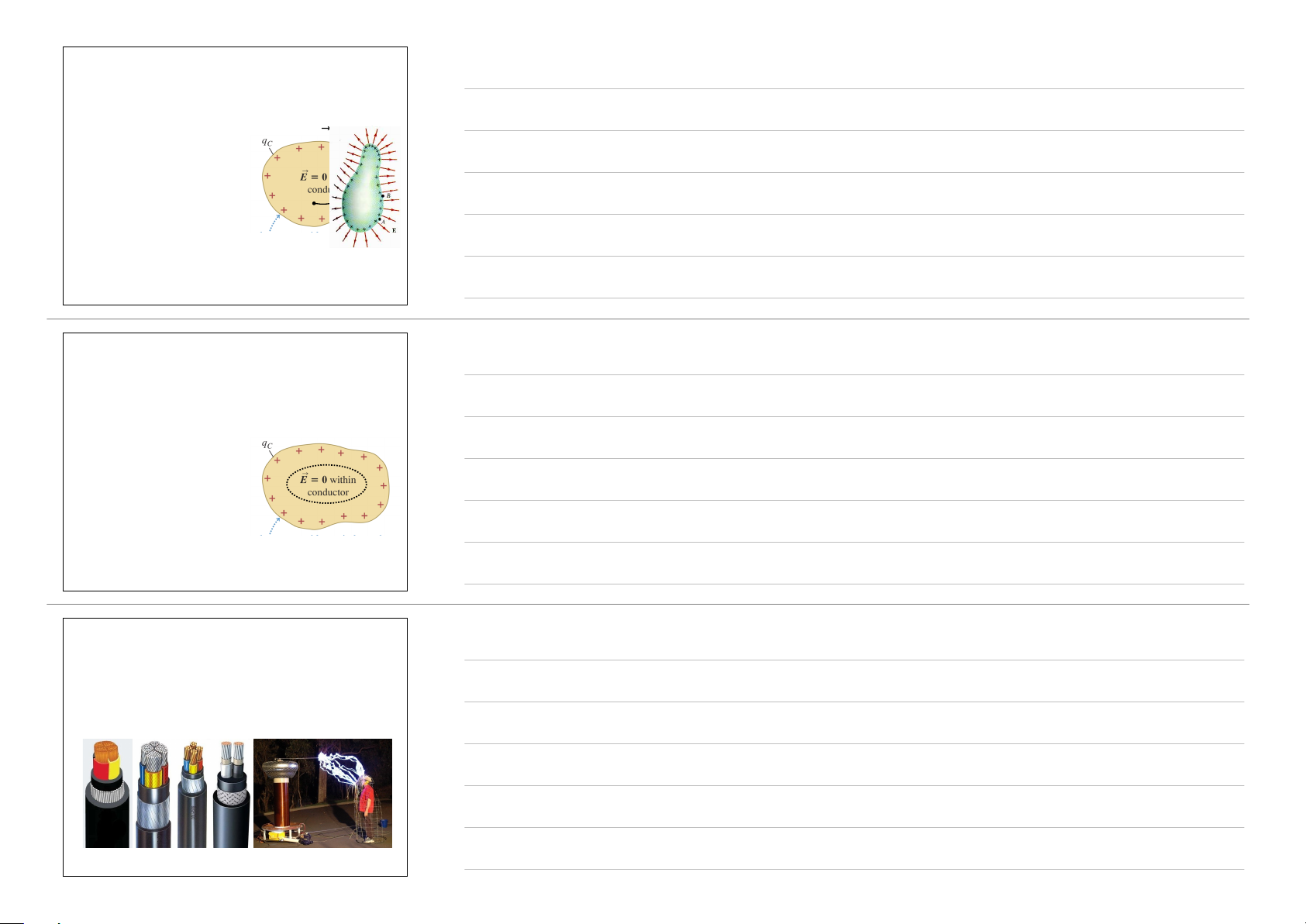
(2) Điện tích của vật dẫn cân bằng tĩnh điện chỉ phân bố trên
mặt ngoài của vật dẫn. (S) Φ ⃗
e = ∮ D . d ⃗
S = ∑qi (S) i ⇒ q ⃗ i = 0 D = ⃗ D ∑
in = ϵ0ϵ ⃗ Ein = 0 i
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG 6
TĨNH ĐIỆN. ĐIỆN DUNG CỦA VẬT DẪN CÔ LẬP
II. Những tính chất của vật dẫn cân bằng tĩnh điện
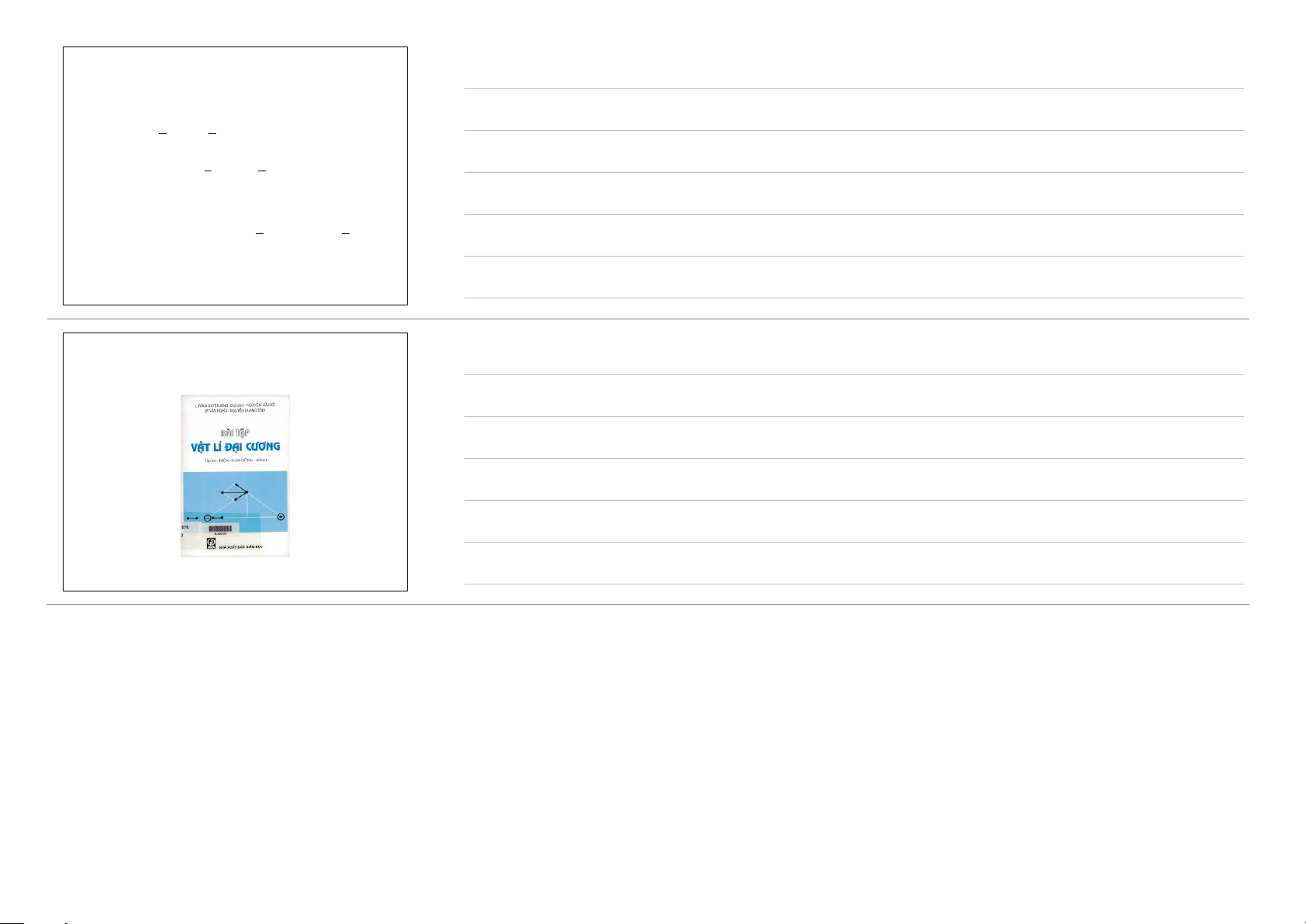
(2) Điện tích của vật dẫn cân bằng tĩnh điện chỉ phân bố trên
mặt ngoài của vật dẫn.
Dây truyền tín hiệu được bọc bởi lớp kim loại Lồng Faraday
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG 7
TĨNH ĐIỆN. ĐIỆN DUNG CỦA VẬT DẪN CÔ LẬP
II. Những tính chất của vật dẫn cân bằng tĩnh điện
(3) Sự phân bố điện tích trên bề mặt vật dẫn cân bằng tĩnh
điện phụ thuộc vào hình dạng của vật dẫn. S ( ⃗ En = ⃗ E) Φ ⃗
e = ∮ D . d ⃗
S = ∑qi (S) i (En = 0)
⇒ Dn . S = σ . S
⇒ Dn = σ ⇒ E = En = σ (1)
ϵ0ϵ S
Sears and Zeamansky’s University Physics with Modern Physics , Young, Freedman and Ford, Pearson, 2011
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG 8
TĨNH ĐIỆN. ĐIỆN DUNG CỦA VẬT DẪN CÔ LẬP
II. Những tính chất của vật dẫn cân bằng tĩnh điện
(3) Sự phân bố điện tích trên bề mặt vật dẫn cân bằng tĩnh
điện phụ thuộc vào hình dạng của vật dẫn.
E = E V
n = σ (1) 2 R2
ϵ0ϵ V R 1 1 Q1 Q2 σ1
V1 = V2 ⇒ = Q1
4πϵ0ϵR1
4πϵ0ϵR2 σ2 Q2 σ σ
⇒ 1.4πR21 = 2.4πR22
4πϵ0ϵR1
4πϵ0ϵR2 σ R E R ⇒ 1 = 2 (1) ⟹ 1 = 2 σ2 R1 E2 R1
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG 1831 9
TĨNH ĐIỆN. ĐIỆN DUNG CỦA VẬT DẪN CÔ LẬP
III. Điện dung của vật dẫn cô lập 1. Định nghĩa
“Điện dung của vật dẫn cô lập:”
C = Q (1) V
• Đơn vị điện dung: Fara (F) 1 F = 1 C 1 V
Microfara (μF),
1μF = 10−6F
Nanofara (nF),
1nF = 10−9F
Picofara (pF)
1pF = 10−12F Michael Faraday (1791-1867) (British)
§1. NHỮNG TÍNH CHẤT CỦA VẬT DẪN CÂN BẰNG 10
TĨNH ĐIỆN. ĐIỆN DUNG CỦA VẬT DẪN CÔ LẬP
III. Điện dung của vật dẫn cô lập
2. Điện dung của một quả cầu kim loại tích điện Q, bán kính R
C = 4πϵ Q 0 . R R R C 9.109m 1F
1500 x RTrái Đất 6400km
∼ 700μF RTrái Đất ∼ 0.3m
∼ 30pF Van de Graaff
V = 106 V 1cm ∼ 1pF
Q = C . V = 30.10−12.106 = 3.10−6 C
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 11 I. Hiện tượng
1. Hiện tượng điện hưởng A B C Điện tích cảm ứng
Fundamentals of Physics, D. Hal iday, Wiley, 2013
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 12 I. Hiện tượng
1. Hiện tượng điện hưởng • Định nghĩa: A B C Điện tích cảm ứng
➡ Trong trạng thái cân bằng tĩnh điện, vật dẫn là một vật đẳng thế
Fundamentals of Physics, D. Hal iday, Wiley, 2013
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 13 I. Hiện tượng
2. Định lý các phần tử tương ứng • Định nghĩa: B C A ΔS′ ΔS
✓ phần tử tương ứng.
Fundamentals of Physics, D. Hal iday, Wiley, 2013
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 14 I. Hiện tượng
2. Định lý các phần tử tương ứng
Φe = ∑qi = Δq + (− Δq′ ) (1) i (S) Φ ⃗
e = ∮ D . d ⃗ S = 0 (2) B C (S) Σ
A ΔS ΔS′
• Từ (1) & (2) ta có: Σ′ Δq Φ
−Δq′
e = Δq + (−Δq′ ) = 0
⟹ Δq = Δq′
Fundamentals of Physics, D. Hal iday, Wiley, 2013
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 15 I. Hiện tượng
3. Điện hưởng một phần và điện hưởng toàn phần
a. Điện hưởng một phần B C A −Q′ Q′
Q′ < Q
Fundamentals of Physics, D. Hal iday, Wiley, 2013
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 16 I. Hiện tượng
3. Điện hưởng một phần và điện hưởng toàn phần
a. Điện hưởng một phần
b. Điện hưởng toàn phần B C A
−Q′ Q′
Q′ = Q
Fundamentals of Physics, D. Hal iday, Wiley, 2013
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 17
II. Tụ điện và điện dung của tụ (phẳng, trụ, cầu)
Một số loại tụ điện
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 18
II. Tụ điện và điện dung của tụ (phẳng, trụ, cầu) 1. Định nghĩa
• Định nghĩa tụ điện:
• Định nghĩa điện dung của tụ điện: C = Q = Q ,
V1 − V2 U
‣ : Giá trị tuyệt đối của điện tích trên mỗi bản tụ
(điện tích trên bản dương);
‣ : Điện thế của bản tụ dương và âm;
‣ : Hiệu điện thế giữa hai bản tụ điện.
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 19
II. Tụ điện và điện dung của tụ (phẳng, trụ, cầu) 2. Cách ghép tụ điện
Cb = C1 + C2 ✦ Ghép song song
Ub = U1 = U2; Qb = Q1 + Q2 n
Cb = ∑Ci i=1 ✦ Ghép nối tiếp Cb
Ub = U1 + U2; Qb = Q1 = Q2 1 n = 1 C ∑ b C
i=1 i
Fundamentals of Physics, D. Hal iday, Wiley, 2013
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG 20
II. Tụ điện và điện dung của tụ (phẳng, trụ, cầu) 2. Cách ghép tụ điện ✦ Ghép hỗn hợp
Fundamentals of Physics, D. Hal iday, Wiley, 2013
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG C = Q = Q, 21
V1 − V2 U
II. Tụ điện và điện dung của tụ (phẳng, trụ, cầu)
3. Điện dung của tụ (phẳng, trụ, cầu) S a. Tụ phẳng (2) C = Q = Q (1) −Q V (1) 1 − V2 U • Lại có: Q (2) (2)
U = V ⃗
1 − V2 = ∫ − dV = ∫ E . dr⃗ V2 (1) (1) E d (2) r2 V = 1
∫ E . dr = E . ∫ dr = E . d (1) r1
E = σ
ϵ0ϵ
⇒ U = E . d = σ . d = Q . d (2)
ϵ0ϵ
ϵ0ϵ . S ϵ
• Từ (1) & (2) ➡ Điện dung tụ phẳng là: C = Q = 0ϵ . S U d
Fundamentals of Physics, D. Hal iday, Wiley, 2013
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG C = Q = Q, 22
V1 − V2 U
II. Tụ điện và điện dung của tụ (phẳng, trụ, cầu)
3. Điện dung của tụ (phẳng, trụ, cầu) c. Tụ cầu C = Q = Q (1) +Q
V1 − V2 U
U = Q 1 − 1
4πϵ0ϵ(R1 R2) (2)
• Từ (1) & (2), ta có: 4πϵ
C = Q =
0ϵ . R1 . R2 U
R2 − R1 4πϵ
d=R ϵ ϵ
0ϵR1R2
2−R1≪R1
0ϵ.4πR21 =
= 0ϵ . S d d d
§2. HIỆN TƯỢNG ĐIỆN HƯỞNG C = Q = Q 23
V1 − V2 U σ
E = 1R1 = Q ( * ) ϵ R 0ϵr 2πϵ 2 0ϵrl R1 b. Tụ trụ d ⃗
S M r +σ1 ⃗ D −Q M σ1
(Q = 2πR1l . σ1) Q
• Độ cao l >> d (d = R2 - R1) • Lại có: (2) (2) (2)
U = V ⃗
1 − V2 = ∫ − dV = ∫ E . dr⃗ = ∫ E . dr (1) (1) (1) R2 R2 R = Q dr 2 ∫
. dr = Q = Q ln (1)
R 2πϵ 2πϵ r 2πϵ R 1 0ϵrl
0ϵl ∫R1
0ϵ . l 1 • Theo định nghĩa: (1) 2πϵ ϵ C = Q = Q =
0ϵ . l
d=R2−R1≪R1 0ϵ . S
V1 − V2 U ln R2 d R1
§3. NĂNG LƯỢNG ĐIỆN TRƯỜNG 24
I. Năng lượng tương tác của một hệ điện tích điểm và của
vật dẫn mang điện q1 q2
1. Hệ n điện tích điểm r V1 V2
• Hệ 2 điện tích điểm q q q q W 0 . q 1 . q2 2 1 t = ⇒ W = = 1 q q 4πϵ 1( 2( 0ϵr
4πϵ0ϵr 2
4πϵ0ϵr) + 12
4πϵ0ϵr)
⇒ W = 1 q q
2 1V1 + 12 2V2 V1 V2
• Hệ n điện tích điểm
W = 1 q q q
2 1V1 + 12 2V2 + . . . + 12 nVn n hay W = 1 ∑ q 2 iVi i=1
§3. NĂNG LƯỢNG ĐIỆN TRƯỜNG 25
I. Năng lượng tương tác của một hệ điện tích điểm và của vật dẫn mang điện
1. Hệ n điện tích điểm n W = 1 ∑ q 2 iVi i=1 2. Vật dẫn mang điện
W = 1 VQ = 1 CV2 = 1 Q2 2 2 2 C
§3. NĂNG LƯỢNG ĐIỆN TRƯỜNG 26
II. Năng lượng tụ điện phẳng và năng lượng điện trường 1. Năng lượng tụ phẳng n W = 1 ∑ Q
Q . V
(−Q) . V
Q(V
2 iVi ⇒ W = 12 1 + 12 2 = 12 1 − V2) i=1
⇒ W = 1 QU = 1 CU2 = 1 Q2 2 2 2 C
§3. NĂNG LƯỢNG ĐIỆN TRƯỜNG 27
II. Năng lượng tụ điện phẳng và năng lượng điện trường 1. Năng lượng tụ phẳng
W = 1 CU2
ϵ0ϵ . S
U = E . d 2
C = d ⇒ W = 1 ( ϵ
2 0ϵ . E2)Sd = ωe . V ω ⃗
e = 1 ϵ E ⃗ D
2 0ϵ . E2 = 12
§3. NĂNG LƯỢNG ĐIỆN TRƯỜNG 28
II. Năng lượng tụ điện phẳng và năng lượng điện trường 1. Năng lượng tụ phẳng
W = 1 CU2 = 1 ϵ 2
(2 0ϵ . E2)Sd = ωe . V ω ⃗
e = 1 ϵ E ⃗ D
2 0ϵ . E2 = 12
2. Năng lượng điện trường bất kỳ W = 1 1 ⃗
∫ dW = ∫ ωe . dV = ∫
ϵ0ϵ . E2 . dV = ∫ E ⃗D.dV V V V 2 V 2
BÀI TẬP CHƯƠNG II: VẬT DẪN 29
2-1, 2-3, 2-4, 2-10, 2-12, 2-15.
Sách BT VLĐC tập II - Lương Duyên Bình