Các Dạng Toán 9 Kết Nối Tri Thức Bài 16 Vị Trí Tương Đối Của Đường Thẳng Và Đường Tròn
Nếu một đường thẳng đi qua một điểm nằm trên đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn. Cho đường thẳng a và một điểm O cách a một khoảng 8cm. Vẽ đường tròn tâm O, bán kính 10cm. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Chương 5: Đường tròn (KNTT) 5 tài liệu
Môn: Toán 9 3 K tài liệu
Sách: Kết nối tri thức
Tác giả:
Preview text:
VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN A. KIẾN THỨC
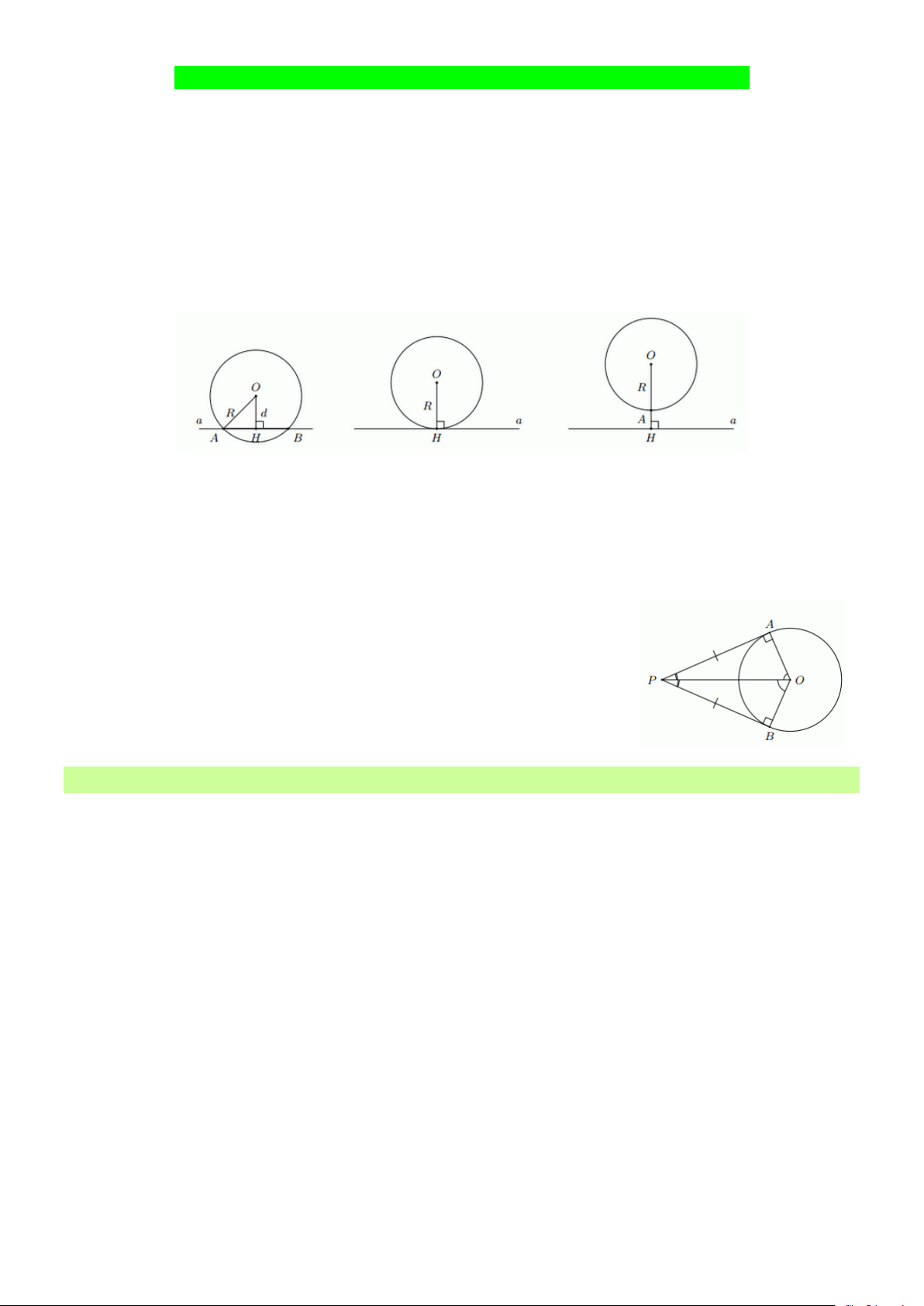
1. Vị trí tương đối của đường thẳng và đường tròn
+ Đường thẳng a và đường tròn (O) gọi là cắt nhau nếu chúng có đúng hai điểm chung
+ Đường thẳng a và đường tròn (O) gọi là tiếp xúc nhau nếu chúng có duy nhất một điểm chung
H . Điểm chung ấy gọi là tiếp điểm.
Khi đó, đường thẳng a còn gọi là tiếp tuyến của đường tròn (O) tại H .
+ Đường thẳng a và đường tròn (O) gọi là không giao nhau nếu chúng không có điểm chung,
* Nhận xét: Đường thẳng a và đường tròn (O; R) cắt nhau khi d R , tiếp xúc với nhau khi
d = R và không giao nhau khi d R
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn
* Nếu một đường thẳng đi qua một điểm nằm trên đường tròn và vuông góc với bán kính đi qua
điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
3. Hai tiếp tuyến cắt nhau của một đường tròn
* Nếu hai tiếp tuyến của đường tròn (O) cắt cắt nhau tại điểm P thì:
+ Điểm P cách đều hai tiếp điểm
+ PO là tia phân giác của góc tạo bởi hai tiếp tuyến
+ OP là tia phân giác của góc tạo bởi hai bán kính qua hai tiếp điểm. B. Các dạng toán
Dạng 1: Xác định vị trí tương đối của đường thẳng và đường tròn
Bài 1: Cho đường thẳng a và điểm O cách a một khoảng bằng 4cm . Không vẽ hình, hãy xét vị
trí tương đối của đường thẳng a và đường tròn (O) . a) (O;3cm) b) (O;5cm) c) ( ; O 4cm) Lời giải
a) Vì d R (4 3) nên đường tròn (O;3cm) không cắt đường thẳng a
b) Vì d R (4 5) nên đường tròn (O;5cm) cắt đường thẳng a
c) Vì d = R (4 = 4) nên đường tròn ( ;
O 4cm) tiếp xúc đường thẳng a
Bài 2: Cho đường thẳng b và một điểm I cách b một khoảng d = 6cm . Xác định vị trí tương
đối của b với các đường tròn sau:
a) Đường tròn (I;3cm)
b) Đường tròn (I;6cm)
c) Đường tròn (I;8cm) Lời giải Trang 1
a) Ta có d = 6cm , R = 3cm . Vì d R nên b và đường tròn (I;3cm) không giao nhau
b) Ta có d = 6cm , R = 6cm . Vì d = R nên b và đường tròn (I;6cm) tiếp xúc nhau
c) Ta có d = 6cm , R = 8cm . Vì d R nên b và đường tròn (I;8cm) cắt nhau tại hai điểm.
Bài 3: Cho đường tròn ( J;5cm) và đường thẳng c . Gọi K là chân đường vuông góc vẽ từ J
xuống c , d là độ dài của đoạn thẳng JK . Xác định vị trí tương đối của đường thẳng c và
đường tròn ( J;5cm) trong mỗi trường hợp sau: a) d = 4cm b) d = 5cm c) d = 6cm Lời giải
a) d = 4cm ; Ta có d R = 5cm , nên đoạn thẳng JK nằm trong đường tròn ( J;5cm)
Do đó, đường thẳng c cắt đường tròn tại hai điểm.
b) d = 5cm ; Ta có d = R = 5cm , nên JK tiếp xúc với đường tròn tại điểm K .
c) d = 6cm ; Ta có d R = 5cm , nên JK nằm ngoài đường tròn ( J;5cm)
Do đó, đường thẳng c cắt đường tròn không cắt nhau.
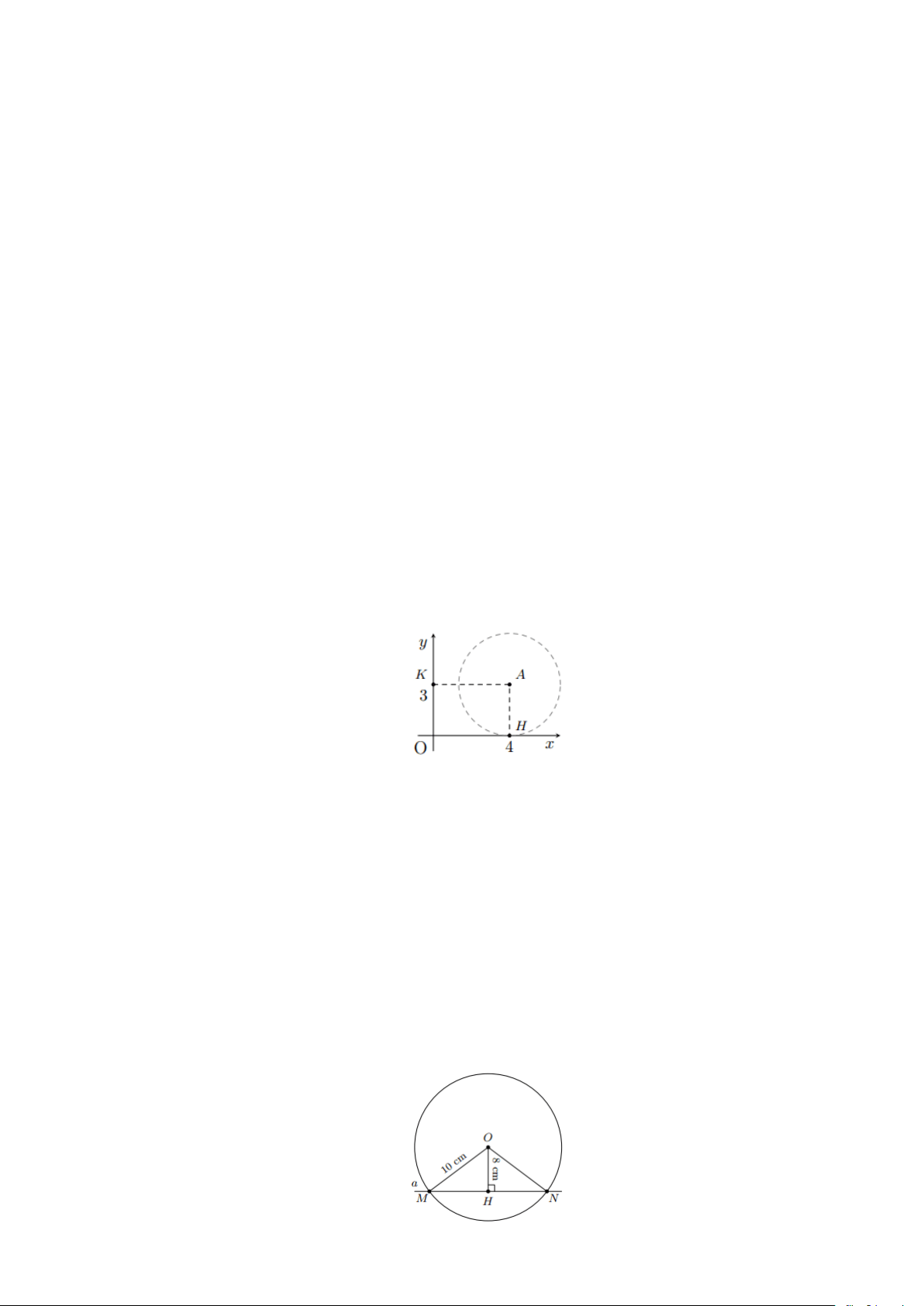
Bài 4: Trong hệ tọa độ Oxy cho điểm A(4;3) . Hãy xác định vị trí tương đối của đường tròn tâm
A , bán kính R = 3 với các hệ trục tọa độ. Lời giải
Khoảng cách từ A đến trục Ox là d = AH = OK = 3
Khoảng cách từ A đến trục Oy là d = AK = OH = 4 Do đó đường tròn ( ;3
A ) tiếp xúc với trục Ox , vì d = R = 3 Đường tròn ( ;3
A ) không cắt trục Oy vì d = 4 3 = R
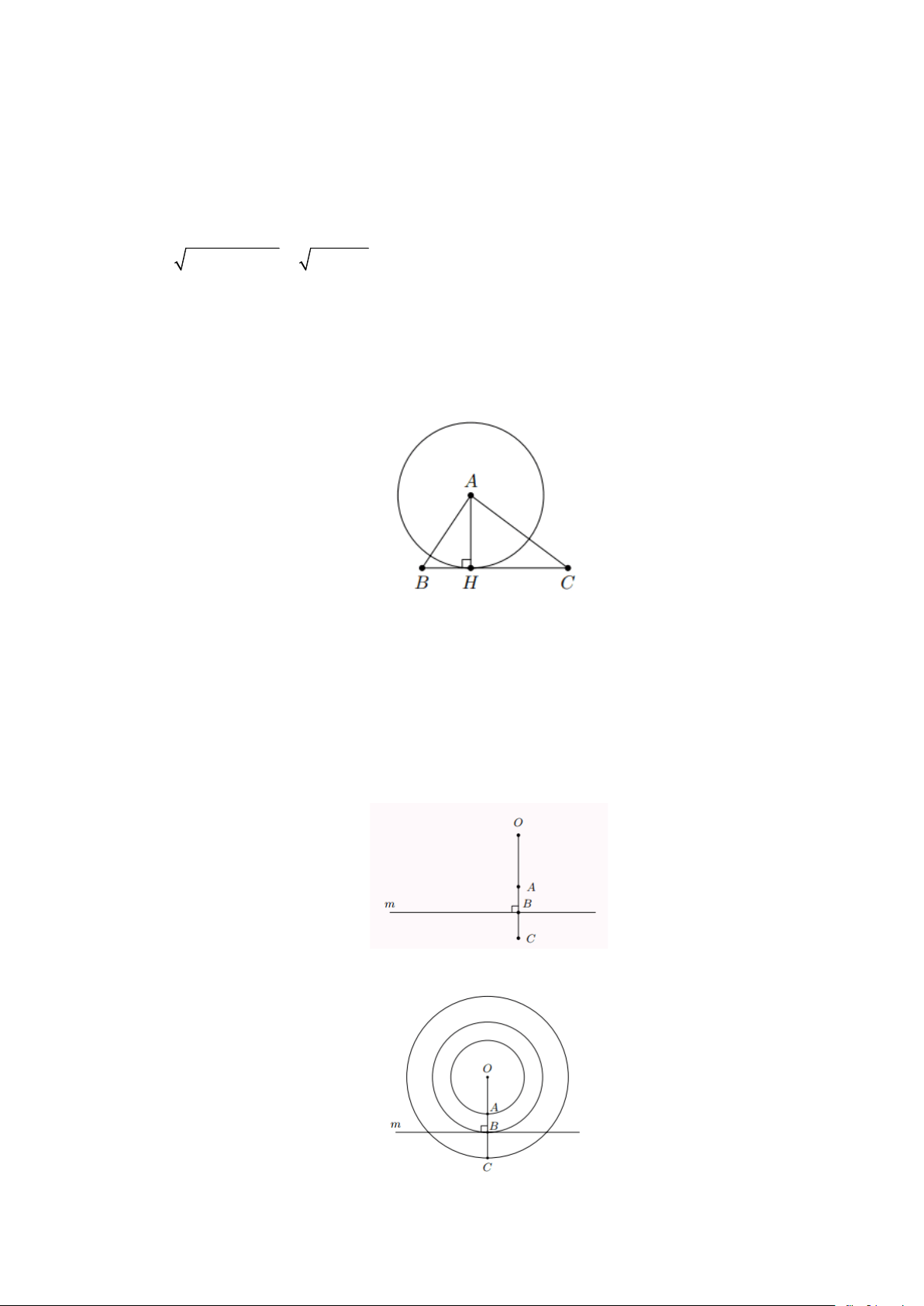
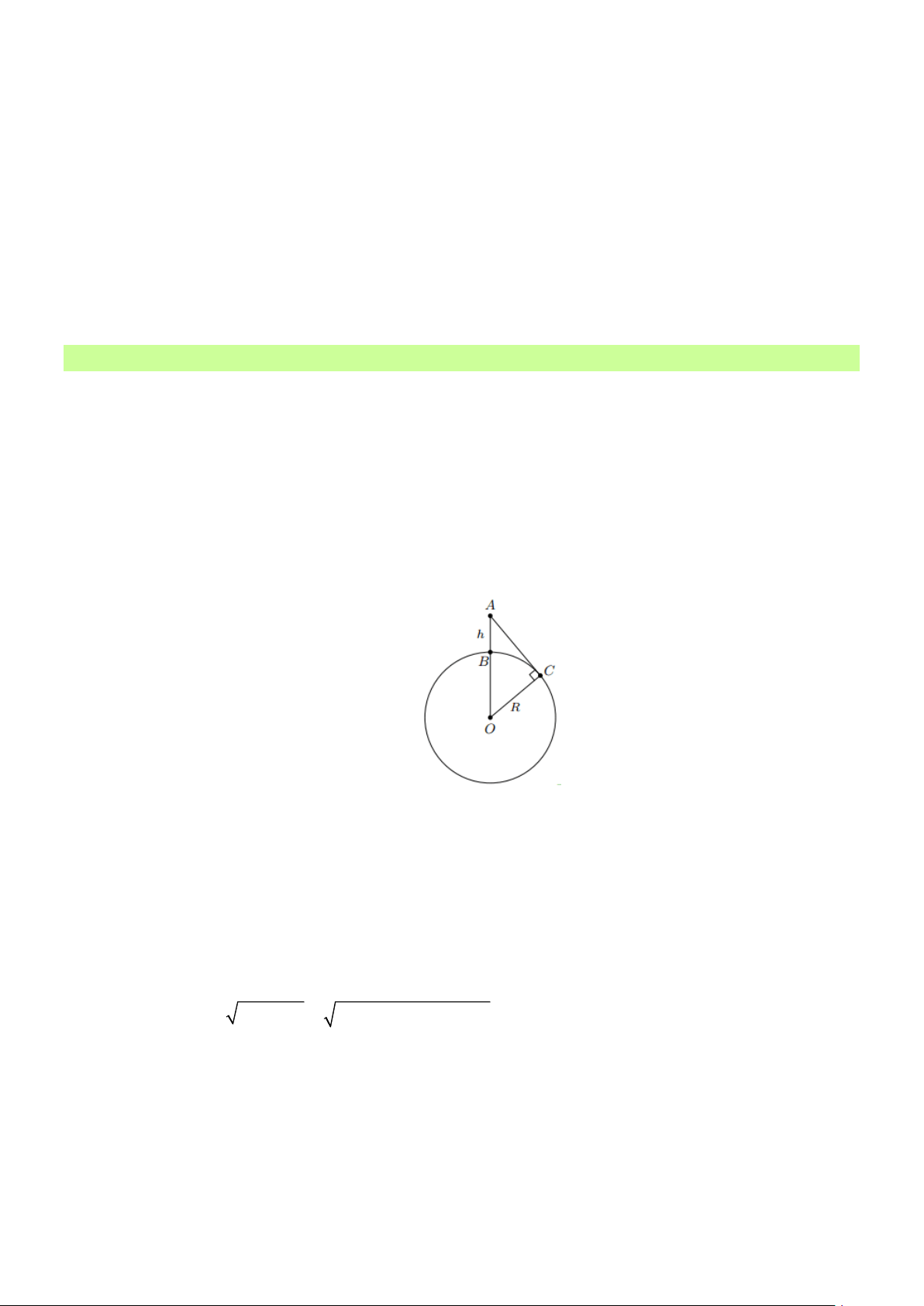
Bài 5: Cho đường thẳng a và một điểm O cách a một khoảng 8cm . Vẽ đường tròn tâm O , bán kính 10cm
a) Giải thích vì sao a và (O) cắt nhau
b) Gọi M và N là các giao điểm của đường thẳng a và đường tròn ( ;10 O cm) . Tính độ dài của dây MN . Lời giải Trang 2
a) Vẽ OH vuông góc với a tại H . Ta có OH = 8cm , R = 10cm suy ra OH R Suy ra a cắt ( ;10 O cm) tại hai điểm.
b) Do M , N thuộc (O) nên ta có OM = ON = R suy ra AMN cân tại O
Có OH là đường cao đồng thời là đường trung tuyến. Do đó, H là trung điểm của dây MN .
Trong tam giác OMH vuông tại H , ta có: 2 2 2 2
MH = OM − OH = 10 − 8 = 6(cm)
Suy ra MN = 2MH = 26 = 12(cm)
Bài 6: Cho tam giác nhọn ABC có đường cao AH . Đường thẳng BC có tiếp xúc với đường tròn ( ;
A AH ) hay không? Vì sao? Lời giải
Vì AH ⊥ BC và H thuộc đường thẳng BC nên khoảng cách từ điểm A đến đường thẳng
BC bằng AH . Do đó, khoảng cách từ tâm A của đường tròn ( ;
A AH ) đến đường thẳng
BC bằng bán kính AH của đường tròn.
Vậy đường thẳng BC tiếp xúc với đường tròn ( ; A AH ) .
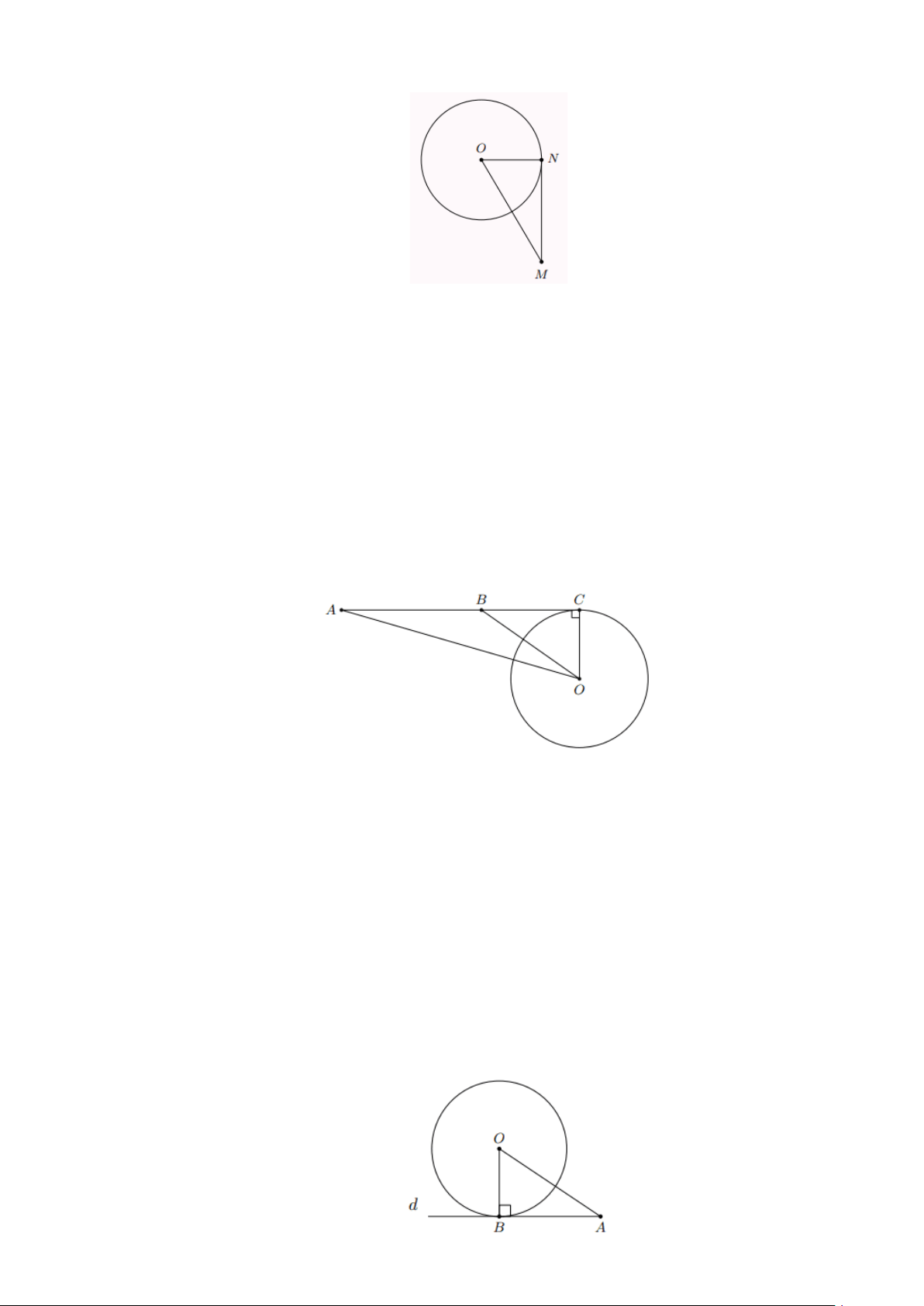
Bài 7: Cho bốn điểm O , B , C , D thẳng hàng như trong hình. Giả sử đường thẳng m đi qua B
và vuông góc với đường thẳng thẳng OC . Nêu vị trí tương đối của đường thẳng m và ba
đường tròn cùng tâm O lần lượt đi qua các điểm A , B , C . Lời giải
Đặt OB = d . Khi đó, d là khoảng cách từ điểm O đến đường thẳng m Trang 3
+ Vì OA OB và OB = d nên OA d . Vậy đường thẳng m và đường tròn (O;OA) không giao nhau
+ Vì OB = d nên đường thẳng m và đường tròn (O;OB) tiếp xúc nhau.
+ Vì OC OB và OB = d nên OC d . Vậy đường thẳng m và đường tròn (O;OC) cắt nhau
Bài 8: Cho điểm A nằm trong đường tròn (O) . Chứng minh rằng mọi đường thẳng d đi qua A
đều cắt (O) ở hai điểm phân biệt. Lời giải
Vẽ OH ⊥ d tại H OH OA (quan hệ đường xiên và đường vuông góc)
Vì A nằm trong (O) nên OA R
Suy ra OH R đường thẳng d luôn cắt (O) tại hai điểm phân biệt.
Bài 9: Chứng minh rằng một đường thẳng và một đường tròn không thể có quá hai điểm chung. Lời giải
Giả sử đường thẳng d và đường tròn (O) có ba điểm chung A , B , C theo thứ tự như hình vẽ bên.
Vì A , B , C thuộc (O) nên OA = OB = OC . Do đó tam giác OAB cân tại O
OBC = OCB 90
Suy ra OBA + OBC 90 + 90 = 180 , điều này vô lí vì A , B , C thẳng hàng theo thứ tự ấy
thì OBA + OBC = 180
Vậy điều giả sử là sai, do đó một đường thẳng và một đường tròn có không quá hai điểm chung.
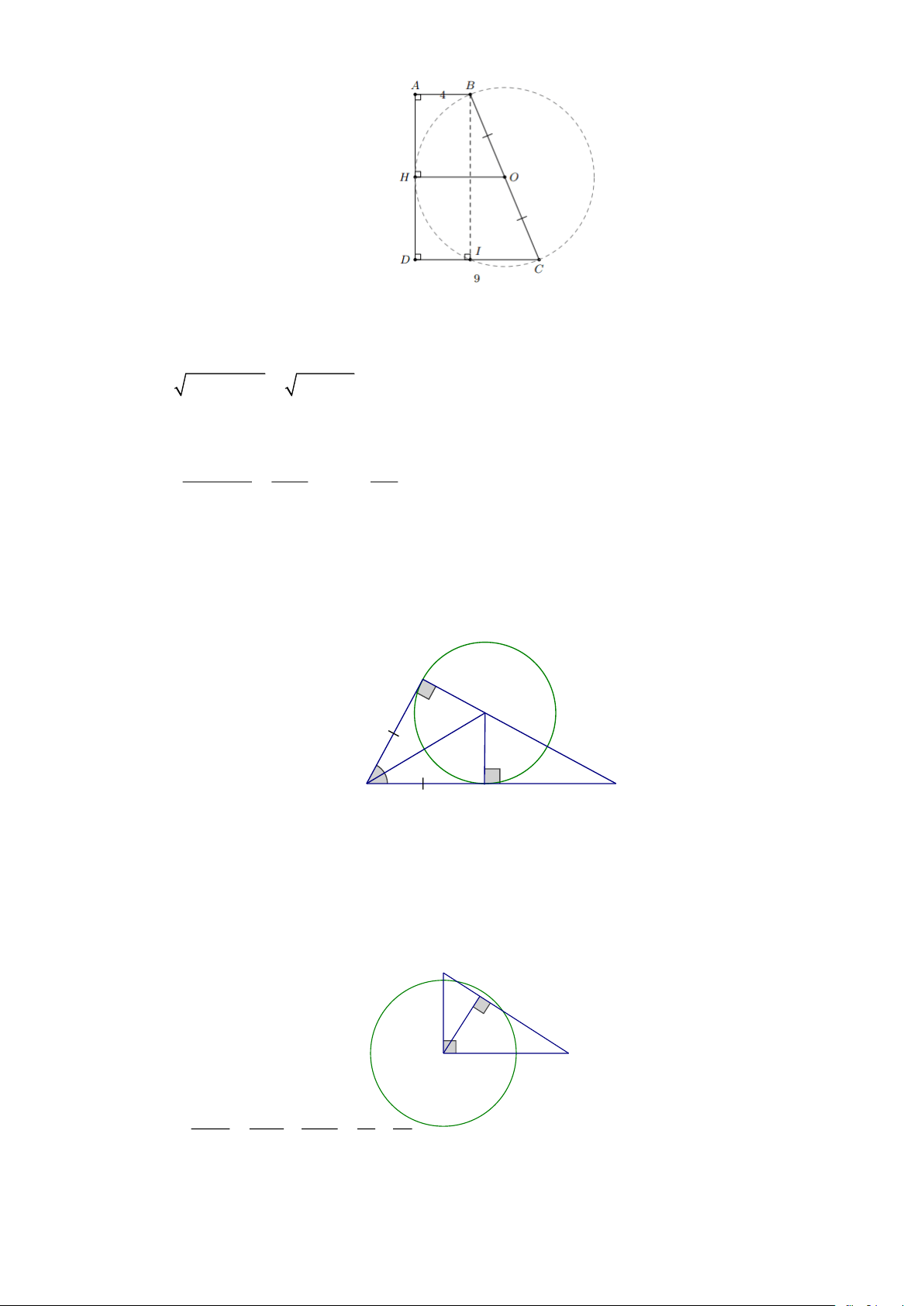
Bài 10: Cho hình thang vuông ABCD ( A = D = 90 ), AB = 4cm , BC = 13cm và CD = 9 cm. Tính
AD và chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính BC . Lời giải Trang 4
Gọi O là trung điểm của BC
Vẽ BI ⊥ CD tại I AD = BI , vẽ OH ⊥ AD tại H
Áp dụng định lí pythagore vào tam giác BIC có: 2 2 2 2
BI = BC − IC = 13 − 5 = 12 AD = 12cm
Hình thang ABCD có OH là đường trung bình nên: AB + CD 4 + 9 = = = BC OH 6,5 = = R 2 2 2
Suy ra đường tròn (O; R) tiếp xúc với AD .
Bài 11: Cho ABC vuông tại A có BD là đường phân giác. Xác định vị trí tương đối của đường
thẳng BC và đường tròn tâm D bán kính DA Lời giải A D
Vẽ DE ⊥ BC (E BC) B E C
D thuộc tia phân giác ABC; DA ⊥ AB, DE ⊥ BC DE = DA
Do đó đường thẳng BC và đường tròn tâm D bán kính DA tiếp xúc nhau.
Bài 12: Cho ABC vuông tại A có AB = 3c , m AC = 4cm
Vẽ đường tròn tâm A bán kính 2,8cm . Xác định vị trí tương đối của đường thẳng BC vầ
đường tròn tâm A bán kính 2,8cm . Lời giải B H A C
Vẽ AH là đường cao của tam giác vuông ABC Ta có: 1 1 1 1 1 = + = +
AH = 2,4cm 2,8 d r 2 2 2 2 2 ( ) AH AB AC 3 4
Do đó đường thẳng BC và đường tròn ( ;
A 2,8cm) cắt nhau Trang 5
Bài 13: Cho hình thang vuông ABCD có 0
A = B = 90 , AD = 2c , m BC = 6 ,
m CD = 8cm . Chứng minh
rằng AB tiếp xúc với đường tròn đường kính CD Lời giải A 2 D K I
Gọi I, K lần lượt là trung điểm của CD và AB B C 6 AD + Ta có: BC
IK là đường trung bình của hình thang ABCD IK = = 4(cm) 2 Lại có: CD
AD / /IK, AD ⊥ AB IK ⊥ A ; B IK =
(= 4cm),IK ⊥ AB 2
Do đó AB tiếp xúc với đường tròn tâm I đường kính CD .
Dạng 2: Nhận biết một đường thẳng là tiếp tuyến của đường tròn I. Phương pháp giải
a) Nếu một đường thẳng đi qua 1 điểm của đường tròn và vuông góc với bán kính đi qua điểm đó
thì đường thẳng ấy là một tiếp tuyến của đường tròn. Giả thiết
Đường thẳng a , điểm C thuộc (O) Trang 6
a ⊥ OC = C Kết luận
a là tiếp tuyến của đường tròn (O; R)
b) Nếu khoảng cách từ tâm đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường
thẳng đó là tiếp tuyến của đường tròn Giả thiết
Đường tròn (O; R) và đường thẳng a
d bằng khoảng cách từ O đến a và d = R Kết luận
a là tiếp tuyến của đường tròn (O; R)
c) Nếu một đường thẳng và một đường tròn chỉ có một điểm chung thì đường thẳng đó là tiếp tuyến của đường tròn II. Bài toán
Bài 1: Cho tam giác ABC có đường cao AH . Tìm tiếp tuyến của đường tròn ( ;
A AH ) tại H . Lời giải
Xét ( A) ta có AH ⊥ BC tại H ( AH là đường cao của ABC ); H ( A)
Suy ra BC là tiếp tuyến của ( A) tại H .
Bài 2: Cho hai đường tròn (O; R) và (O ; R) tiếp xúc ngoài nahu tại điểm I . Gọi d là tiếp tuyến
của (O; R) tại điểm I . Chứng minh d là tiếp tuyến của (O ; R) . Lời giải
Vì (O) và (O ') tiếp xúc ngoài tại I nên O, I,O thẳng hàng.
d là tiếp tuyến của (O; R) tại điểm I nên OI ⊥ d Hay OId = 90
Mà OId + OId = 180
Do đó OId = 180 − OId = 90
Hay d ⊥ OI . Vậy d là tiếp tuyến của (O) .
Bài 3: Cho đường tròn (O) và điểm I ở ngoài đường tròn. Gọi M là giao điểm của đường tròn
tâm K đường kính IO và đường tròn (O) . Chứng minh đường thẳng IM là tiếp tuyến của (O) tại M . Lời giải Trang 7
Vì IO, KM lần lượt là đường kính, bán kính của đường tròn (K ) nên 1 KM = IO 2
Xét IMO , ta có đường trung tuyến MK ứng với cạnh IO bằng nửa cạnh ấy.
Suy ra tam giác IMO vuông tại M
Do đó IM ⊥ MO tại M với M (O)
Vậy đường thẳng IM là một tiếp tuyến của (O) tại M .
Bài 4: Cho hai đường tròn (O) , (O) cắt nhau tại hai điểm A , B sao cho đường thẳng OA là tiếp
tuyến của đường tròn (O) . Chứng minh đường thẳng OB là tiếp tuyến của (O) . Lời giải
OA là tiếp tuyến của đường tròn (O) OA ⊥ OA Suy ra OAO = 90
Xét OAO và OBO có:
OA = OB (bán kính (O) ); OO cạnh chung; OA = OB (bán kính (O) )
Do đó OAO = OBO suy ra OAO = OBO
Mà OAO = 90 OBO = 90 hay OB ⊥ OB
Vậy OB là tiếp tuyến của đường tròn (O) .
Bài 5: Cho AB là một dây không đi qua tâm của đường tròn (O) . Đường thẳng qua O và vuông
góc với AB cắt tiếp tuyến tại A của (O) ở điểm C . Chứng minh rằng CB là một tiếp tuyến của (O) . Lời giải Trang 8
Gọi D là giao điểm của AB và OC
Trong tam giác cân AOB (OA = OB) , đường cao OD (do OC ⊥ AB ) cũng là đường phân
giác của góc O , suy ra O = O 1 2
Ta có: AOC = BOC (c-g-c), vì OC là cạnh chung, O = O và OA = OB 1 2
Từ đó OBC = OAC = 90 (do OA là tiếp tuyến)
Vậy CB vuông góc với bán kính OB tại B .
Do đó ta có CB cũng là tiếp tuyến của (O) .
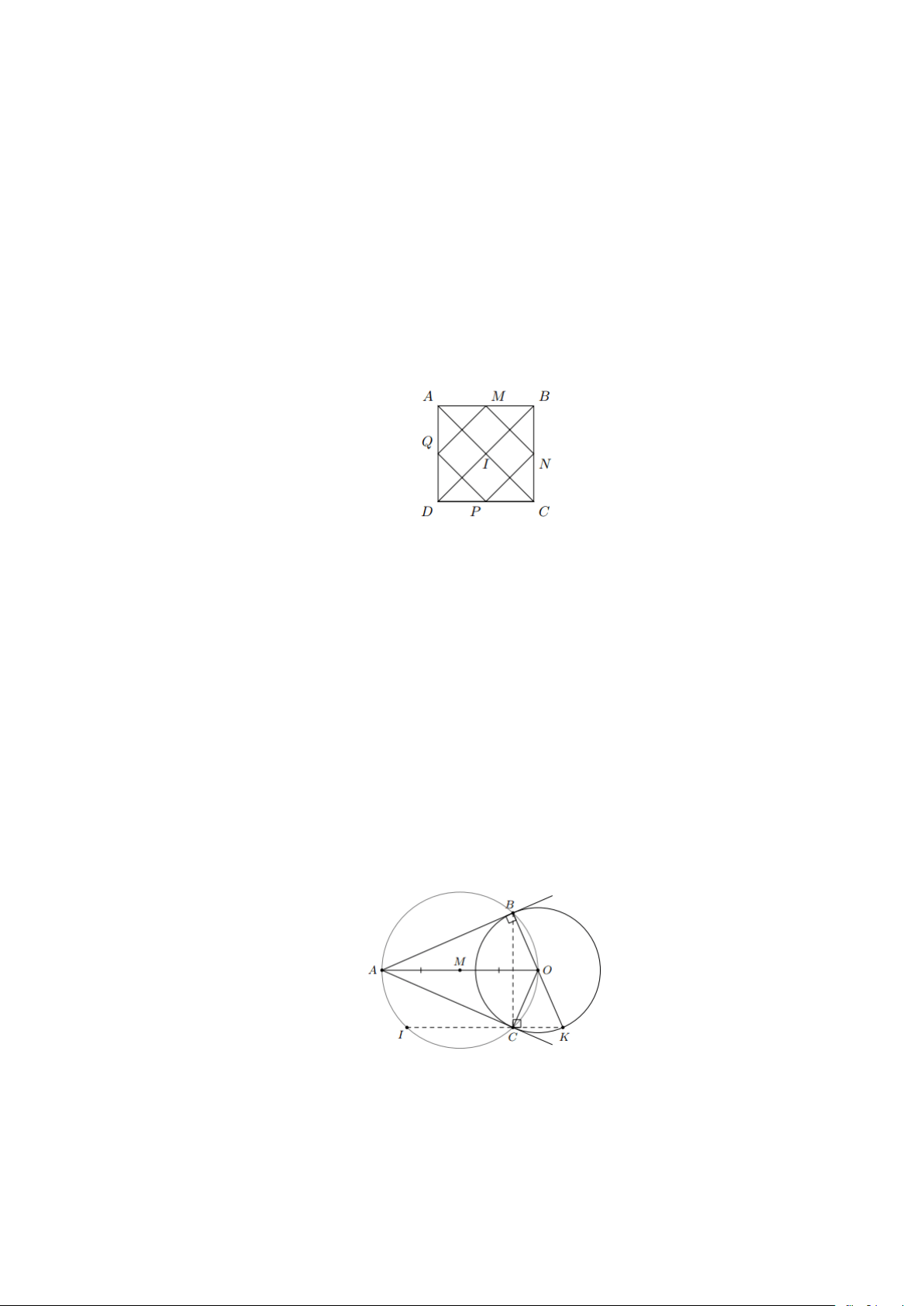
Bài 6: Cho một hình vuông có độ dài mỗi cạnh bằng 6cm và hai đường thẳng chéo cắt nhau tại I
. Chứng minh rằng đường tròn (I;3cm) tiếp xúc với cả bốn cạnh của hình vuông Lời giải
Gọi M là trung điểm của AB
Xét ABC có M là trung điểm của AB , I là trung điểm của AC
Suy ra MI là đường trung bình của ABC
Do đó MI = 3 và MI ⊥ AB tại M nên AB tiếp xúc với (I;3cm) tại M .
Chứng minh tương tự với N, P,Q lần lượt là trung điểm của BC , CD , DA .
Bài 7: Cho đường tròn (O; R) và điểm A nằm ngoài (O) . Vẽ hai đường tròn đường kính OA ,
đường tròn này cắt (O) tại hai điểm phân biệt B và C . Kẻ BI là đường kính của đường
tròn đường kính OA , kẻ BK là đường kính của đường tròn (O) . Chứng minh rằng:
a) AB , AC là hai tiếp tuyến của (O)
b) IK là tiếp tuyến của đường tròn (B; BC) Lời giải
a) B thuộc đường tròn đường kính OA nên ABO = 90
mà B thuộc (O) nên AB là tiếp tuyến của (O)
Tương tự, ta có AC là tiếp tuyến của (O)
b) C thuộc đường tròn đường kính BI nên BCI = 90 .
C thuộc đường tròn đường kính BK nên BCK = 90 Trang 9
Từ đó suy ra ba điểm I, K,C thẳng hàng và IK ⊥ BC tại C .
Mà C thuộc đường tròn (B; BC) nên IK là tiếp tuyến của (B; BC) .
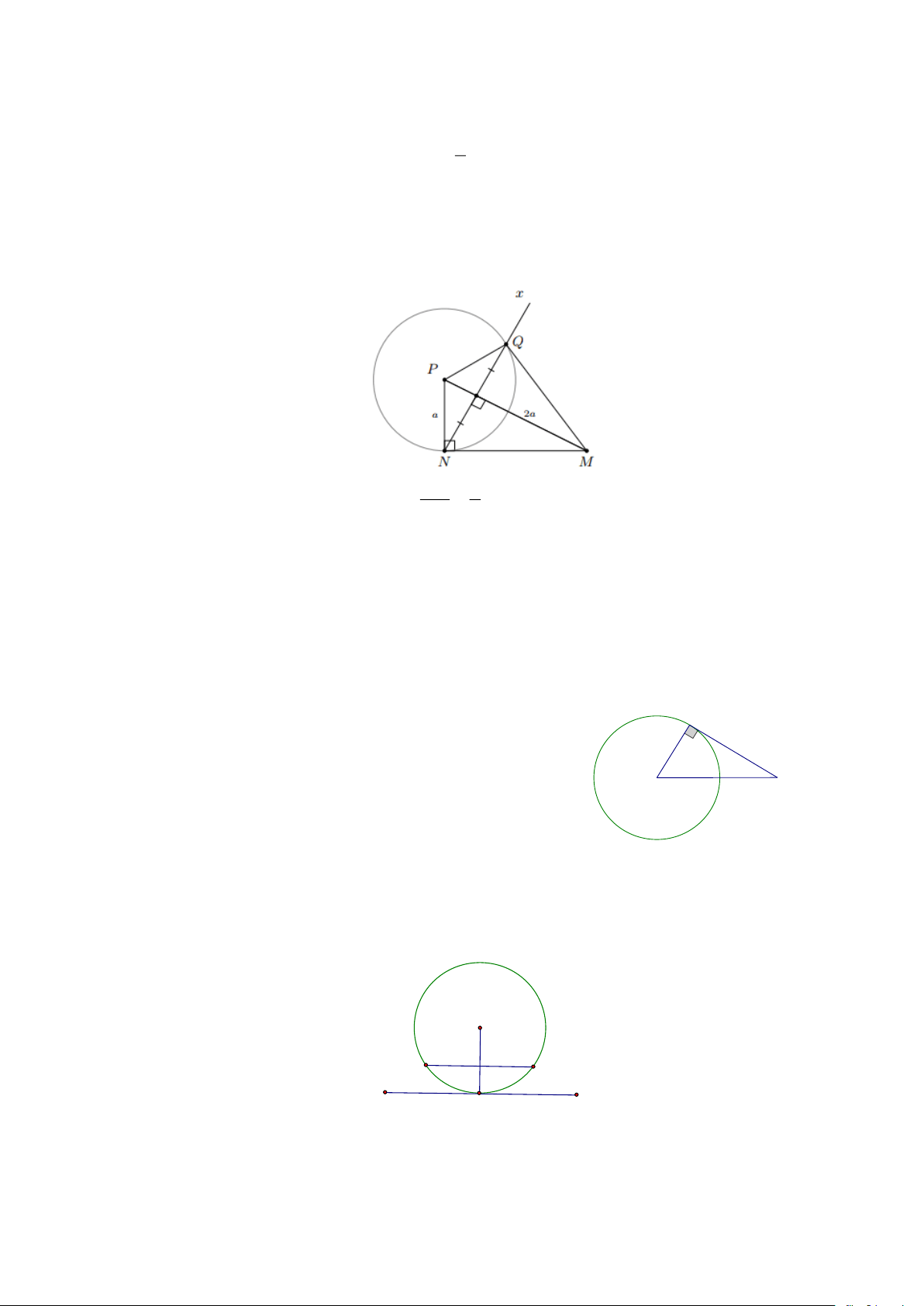
Bài 8: Cho tam giác MNP có N = 90 và 1
NP = MP = a . Vẽ đường tròn tâm P tiếp xúc với MN 2
tại N . Qua N vẽ tia Nx vuông góc với MP cắt (P) tại điểm thứ hai Q ( Q N ). Chứng
minh rằng MQ là tiếp tuyến của (P) và MNQ là tam giác đều. Lời giải Tam giác vuông NP MNP có 1 sin NMP = = MP 2
NMP = 30 NMQ = 90 − 30 = 60
Ta có hai điểm N,Q đối xứng với nhau qua MP nên MQP = MNP = 90 Và MNQ = MQN
Do đó, MQ là tiếp tuyến của (P) và MNQ là tam giác đều.
Bài 9: Cho tam giác ABC có AB = 6c , m AC = 8c , m BC = 10c .
m Vẽ đường tròn ( B; BA) . Chứng
minh AC là tiếp tuyến của đường tròn (B) A Lời giải Ta có: 2 2 2 0 0
BC = AB + AC BAC = 90 = 90 BA ⊥ AC B C
Vậy AC là tiếp tuyến của đường tròn (B) .
Bài 9: Cho đường tròn (O) và một dây AB . Gọi M là trung điểm của AB , vẽ bán kính OI đi
qua M . Từ I vẽ đường thẳng xy / / AB . Chứng minh rằng xy là tiếp tuyến của đường tròn (O) . Lời giải O
Xét đường tròn (O) , ta có OI ⊥ AB A(đường kính M đi
B qua trung điểm của dây thì vuôn góc với dây) x I y
Mà xy / / AB OI ⊥ xy xy là tiếp tuyến của đường tròn.
Bài 10: Từ điểm A ở ngoài đường tròn (O; R) vẽ tiếp tuyến AB ( B là tiếp điểm), C là điểm trên
đường tròn (O) sao cho AC = AB Trang 10
a) Chứng minh rằng AC là tiếp điểm của đường tròn (O)
b) D là điểm trên AC . Đường thẳng qua C vuông góc với OD tại M cắt đường tròn
(O) tại E ( E C ). Chứng minh rằng DE là tiếp tuyến của đường tròn (O) Lời giải
a) Xét OAC và OAB , có:
OC = OB (= R);OA: chung; AC = AB (gt)
OAC = OAB(ccc) 0
OCA = OBA = 90 AC là tiếp tuyến của đường tròn (O)
b) OD ⊥ EC (gt) M là trung điểm của EC (định lí đường kính vuông góc với dây cung)
OD là đường trung trực của đoạn thẳng 0
EC DE = DC OED = OCD = 90 (tính chất đối xứng trục)
Vậy DE là tiếp tuyến của đường tròn (O) B E A O M D
Bài 11: Cho ABC , hai đường cao BD và CE cắt nhau tại H
a) Chứng minh rằng bốn điểm ,
A D, H , E cùng n C
ằm trên một đường tròn đường kính AH
b) Gọi M là trung điểm của BC . Chứng minh rằng MD là tiếp tuyến của đường tròn đường kính AH . A Lời giải D O E H
a) Gọi O là trung điểm của AH B M C
Xét ADH và AEH vuông tại D và E ta có: 1
OD = OE = OA = OH = AH 2 Suy ra bốn điểm ,
A D, H , E cùng nằm trên một đường tròn đường kính AH
b) Tam giác DBC vuông tại D có DM là đường trung tuyến nên 1
MD = MB = BC 2
Ta có: ODA = OAD ( OAD cân)
OAD = DBC (phụ với ACB )
DBC = BDM (Vì MBD cân)
Do đó: ODA = BDM Trang 11
Ta có: ODA + ODB = 90(BD ⊥ AC)
BDM + ODB = 90(ODA = BDM )
Hay ODM = 90 MD ⊥ OD
Vậy MD là tiếp tuyến của đường tròn đường kính AH .
Tương tự ta chứng minh được ME là tiếp tuyến của đường tròn đường kính AH .
Bài 12: Cho ABC vuông tại A , đường cao AH .
Đường tròn tâm I đường kính BH cắt AB tại E , đường tròn tâm J đường kính HC cắt AC
Tại F . Chứng minh rằng:
a) AH là tiếp tuyến chung của hai đường tròn (I ) và ( J ) tại H
b) EF là tiếp tuyến của (I ) tại E , tiếp tuyến của ( J ) tại F . Lời giải A F P E B C
a) Gọi I là trung điểm của BH Ithì I là tâm c H ủa đư J
ờng tròn đường kính BH
Gọi J là trung điểm của HC thì J là tâm của đường tròn đường kính HC
Ta có: IH ⊥ AH BH là tiếp tuyến của đường tròn đường kính BH
Cũng vậy BH là tiếp tuyến của đường tròn đường kính HC
Vậy AH là tiếp tuyến chung của đường tròn (I ) và ( J ) b) Ta có: 0
A = E = F = 90 AFHE là hình chữ nhật
Gọi P là giao điểm của AH và EF
Ta có: PE = PF = PH = PA
Lại có: PEI = PHI (ccc) 0
IEP = IHP = 90 EF là tiếp tuyến của đường tròn (I )
Chứng minh được: PEJ = PHJ (ccc) 0
IFJ = PHJ = 90 EF là tiếp tuyến của đường tròn ( J )
Bài 13: Cho ABC cân tại A có các đường cao AH và BK cắt nhau tại I . Chứng minh
a) Đường tròn đường kính AI đi qua K
b) HK là tiếp tuyến của đường tròn đường kính AI Lời giải A O K I a) Chứng minh được: 0 BKA = 90 B H C Trang 12
b) Gọi O là trung điểm của AI . Ta có:
- OK = OA OKA = OAK
- OAK = HBK (cùng phụ với ACB ) 0
HB = HK HBK = HKB OKA = HBK HKO = 90
Bài 14: Cho tam giác ABC có hai đường cao BD,CE cắt nhau tại H
a. Chứng minh bốn điểm ,
A D, H , E cùng nằm trên 1 đường tròn
b. Gọi (O) là đường tròn đi qua bốn điểm ,
A D, H , E và M là trung điểm của BC .
Chứng minh ME là tiếp tuyến của (O) Lời giải A D O E H AH
a) Xét ADH (H = 90) D ; B O 2 M C AEH ( AH
E = 90) E ; O 2 Vậy 4 điểm ,
A D, H , E cùng thuộc 1 đường tròn
b) Xét BEC (E = 90) , M là trung điểm của BC EM = MC
EMC cân tại M CEM = ECM
Ta lại có AOE cân tại O AEO = EAO
Mặt khác EAO = EAM (cùng phụ với ABC ) và 0
AEO + OEC = 90 OE ⊥ ME ME là tiếp tuyến của đường tròn (O)
Bài 15: Cho (O; R) đường kính AB . Vẽ dây AC sao cho 0
CAB = 30 , trên tia đối của tia BA lấy
điểm M sao cho BM = R . Chứng minh rằng :
a. MC là tiếp tuyến của đường tròn (O) b. 2 2 MC = 3R Lời giải C A O B M a. Ta có: 0 0
ACB = 90 ABC = 60 BOC đều BC = OB = BM = R
Vậy OCM vuông tại C (đường trung tuyến ứng với cạnh huyền)
OM ⊥ OC MC là tiếp tuyến của đường tròn (O) b. BMC cân tại 0
B BCM = M = 30
BCM# CAM (g.g) Trang 13 MC MB 2 2 = MC = M . A MB = 3R MA MC
Bài 16: Cho tam giác ABC vuông tại A , có AB = 8c ,
m AC = 15cm . Vẽ đường cao AH . Gọi D là
điểm đối xứng với B qua H . Vẽ đường tròn đường kính CD cắt AC ở E
a. Chứng minh rằng HE là tiếp tuyến của đường tròn b. Tính HE A Lời giải 1 F E 1 2 B C H D O
a. Ta có E thuộc đường tròn (O) DEC = 90 DE// AB
+) Gọi F là trung điểm của AE HF là đường trung bình của hình thang
ABDE HF ⊥ AE AHE cân tại H A = E 1 1
+) Ta có EOC cân tại 0
O E = C E + E = A + C = 90 2 1 2 1 0
HEO = 90 HE ⊥ OE (đpcm)
b. Xét ABC ( A = 90) BC =17cm Ta có: 120
AH.BC = A .
B AC AH = HE = (cm) 7
Bài 17: Cho tam giác ABC cân tại A nội tiếp đường tròn tâm (O) . Vẽ hình bình hành ABCD ,
tiếp tuyến tại C của đường tròn cắt đường thẳng AD tại N . Chứng minh rằng :
a. Đường thẳng AD là tiếp tuyến của đường tròn (O) b. A D
AC, BD,ON đồng quy Lời giải N
a. Ta có ABC cân tại A OA ⊥ BC ( ) 1 I
Vì tứ giác ABCD là hình bình hành AD / //BC (2) O AD//BC (2) B Từ ( ) C
1 (2) AD ⊥ OA đpcm
b. Gọi I là giao điểm của AC và BD I là trung điểm của AC I ON ( N , A NC là tiếp tuyến)
AC, BD,ON đồng quy (đpcm)
Bài 18: Cho tam giác ABC cân tại A . Vẽ đường tròn tâm D đường kính BC cắt AC và AB lần
lượt ở E và F . Gọi H là giao điểm của BE và CF . Chứng minh rằng : a. ,
A E, H , F cùng thuộc 1 đường tròn b. A
DE là tiếp tuyến của đường tròn ở câu a Lời giải
a. Ta có D là tâm đường tròn đường kính
BC DC = DB = DE = DF BEC, BFC vuông. O F 2 E Trang 14 1 1 1 B C D
+) Gọi O là trung điểm của = = AH AH OF OE 2 Vậy 4 điểm ,
A E, H , F cùng thuộc 1 đường tròn
b. Có H là trực tâm ABC
AD là đường trung trực của BC ,
A H , D thẳng hàng
Mà B = E ; E = H = H 1 1 2 2 1 0 0
E + E = H + H = 90 OED = 90 1 2 2 1
DE là tiếp tuyến (đpcm)
Dạng 2: Bài toán liên quan đến tính độ dài I. Cách giải:
Ta nối tâm với tiếp điểm để vận dụng định lý về tính chất của tiếp điểm và sử dụng định lý pyatago. II. Bài toán
Bài 1: Cho điểm M cách đường thẳng xy 6cm, vẽ đường tròn (M;10cm) Trang 15
a. Chứng minh rằng đường tròn tâm M và đường thẳng xy cắt nhau
b. Gọi hai giao điểm là P và Q . Tính PQ M y Lời giải x P H Q
a. Kẻ MH ⊥ xy = H MH là khoảng cách từ M đến xy MH = 6cm
MH R xy cắt ( ;10 O
cm) tại P và Q R =10cm b. Ta có 1
MH ⊥ PQ HP = HQ = PQ (Quan hệ vuông góc đường kính và dây) 2 PQ = 2.HQ Xét 0
MHQ(H = 90 ) HQ = 8 c
c m (HQ 0) PQ =16(cm)
Bài 2: Cho hình vuông ABCD , trên đường chéo BD lấy điểm I sao cho BI = BA . Đường thẳng
kẻ qua I vuông góc với BD cắt AD ở E .
a. So sánh: AE, EI, ID
b. Xác định vị trí tương đối của đường thẳng BD với đường tròn (E; EA) Lời giải A B
a. Ta có : AEB = IEB (ch-cgv) AE = EI (1) E EID ( 0
I = 90 ),D = 45 vuông cân 1
IE = ID (2) I 1
Từ (1)(2) AE = EI = ID D C
b. Ta lại có EI = EA I (E; )
EA R = EI
mặt khác: EI ⊥ BD d = EI d = R đường thẳng BD tiếp xúc với (E; EA)
Bài 3: Cho nửa đường tròn tâm O , đường kính AB , M là 1 điểm thuộc nửa đường tròn, qua M
vẽ tiếp tuyến với nửa đường tròn. Gọi D và C theo thứ tự là các hình chiếu của A và B trên tiếp tuyến ấy
a. Chứng minh rằng M là trung điểm của CD
b. Chứng minh: AB = BC + AD
c. Giả sử: AOM BOM , gọi E là giao điểm của AD với nửa đường tròn. Xác định dạng của tứ giác BDCE
d. Xác định vị trí của điểm M trên nửa đường tròn sao cho tứ giác ABCD có diện tích lớn
nhất. Tính diện tích đó theo bán kính của nửa đường tròn đã cho. Lời giải D
a. Hình thang ABCD có AO = OB,OM / // AD//BC M E
là trung điểm của CD M
b. Ta có: AB = 2OM = BC + AD C
c. Tứ giác BDCE là hình chữ nhật vì có 3 góc vuông A O B Trang 16 AD + d. BC 2 S =
.BE = OM .BE OM .AB = 2R ABCD 2 2 maxS
= 2R OM ⊥ AB ABCD
Bài 4: Cho đoạn thẳng AB và trung điểm O của AB . Trên cùng một nửa mặt phẳng bờ AB vẽ
tia Ax, By vuông góc với AB . Trên các tia Ax và By lấy theo thứ tự hai điểm C và D sao
cho COD = 90 , kẻ OH ⊥ CD D
a. Chứng minh rằng H thuộc đường tròn tâm O đường kính AB
b. Xác định vị trí tương đối của CD với đường tròn (O) H C Lời giải
a. Kéo dài DO cắt AC ở E , ta có : B A
AOE = BOD (gcg) O E = ;
D OD = OE OHD = OAE(ch − gn)
OH = OA = OB H ( ; O AB)
b. Ta có H thuộc đường tròn (O) , CD ⊥ OH tại H
khoảng cách từ O đến CD bằng bán kính của (O) . Vậy CD tiếp xúc với (O) tại H .
Bài 5: Cho điểm A cách đường thẳng xy một khoảng 12 cm a. Chứng minh ( ;1
A 3cm) cắt đường thẳng xy tại hai điểm phân biệt
b. Gọi hai giao điểm của ( ;1
A 3cm) với xy là B,C . Tính độ dài đoạn thẳng BC Lời giải B H C x y A
a) Kẻ AH ⊥ xy AH = 12cm R ( )
A cắt xy tại hai điểm B và C
b) Tính được : BC = 2.HC = 10cm.
Bài 6: Cho nửa đường tròn (O) đường kính AB . Lấy điểm C là điểm thuộc (O) và gọi d là tiếp
tuyến qua C với với (O) . Kẻ AE và BF cùng vuông góc với d ; CH vuông góc với AB
a. Chứng minh: CE = CF và 2
CH = AE.BF
b. Khi C di chuyển trên một nửa đường tròn, tìm vị trí của điểm C để EF có độ dài lớn nhất. Lời giải F C E
a) Chứng minh được OC là đường trung bình của hình thang AEFB nên C là trung điểm A
của EF . Chứng minh được : O 2
AE = AH , B B
H H = BF CH = H .
A HB = AE.BF Trang 17
b) Ta có: BF (O) = H EF = AH AB EF = AB max
C là điểm chính giữa AB .
Dạng 3: Bài toán vận dụng tính chất tiếp tuyến I. Phương pháp giải
Vận dụng tính chất của tiếp tuyến. Nếu đường thẳng là tiếp tuyến của (O) tại A thì ⊥ OA tại A . II. Bài toán
Bài 1: Một thủy thủ đang ở trên cột buồm của một con tàu, cách mặt nước biển 10m . Biết bán
kính Trái Đất là khoảng 6400km . Tính tầm nhìn xa tối đa của thủy thủ đó )kết quả làm tròn đến hàng phần nghìn). Lời giải
Trên hình bên, ta có điểm B biểu diễn vị trí của con tàu, điểm A biểu diễn vị trí của thủy
thủ, điểm C biểu diễn điểm xa nhất mà thủy thủ nhìn thấy. Khi đó độ dài đoạn thẳng AC
gọi là tầm nhìn xa tối đa từ A .
Đặt h = AB, R = OB = OC . Ta tính AC theo R và h .
Do AC là tiếp tuyến với (O; R) tại C nên suy ra AC ⊥ OC
Áp dụng định lí pythagore trong tam giác ACO vuông tại C ta có:
AC = AO − OC = (R + h)2 2 2 2 2 2
− R = 2Rh + h Suy ra 2 2
AC = 2Rh + h = 264000,01+ 0,01 11,314(km)
Vậy tầm nhìn xa tối đa của thủy thủ la khoảng 11,314(km)
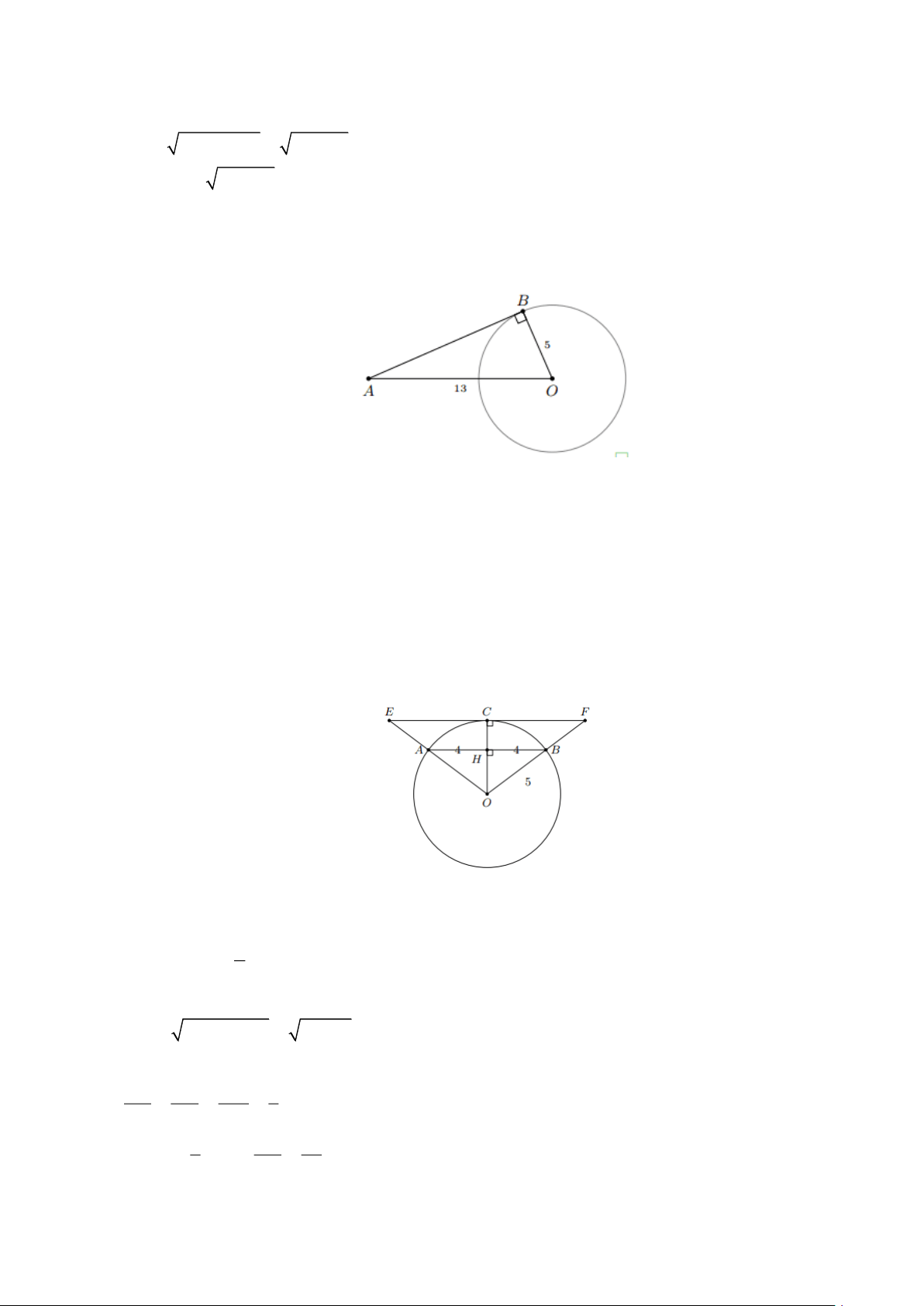
Bài 2: Cho điểm M nằm ngoài đường tròn (O;3cm) thỏa mãn OM = 5cm . Đường thẳng MN đi
qua M và tiếp xúc với đường tròn (O) tại N .
a) Tam giác OMN có phải là tam giác vuông hay không? Vì sao?
b) Tính độ dài đoạn thẳng MN . Lời giải Trang 18
a) Vì đường thẳng MN tiếp xúc với đường tròn (O) tại N nên ON ⊥ MN
Suy ra tam giác OMN vuông tại N
b) Áp dụng định lí pythagore cho tam giác OMN vuông tại N , ta có: 2 2 2
OM = ON + MN Suy ra 2 2 2 5 = 3 + MN Do đó 2 2 2
MN = 5 − 3 = 25 − 9 = 16 Vậy MN = 4(cm) .
Bài 3: Cho ba điểm A , B , C thẳng hàng, trong đó B nằm giữa A và C . Đường tròn (O) tiếp
xúc với đường thẳng AB tại điểm C . Chứng minh: 2 2 2 2
AO + BC = BO + AC Lời giải
Vì AB tiếp xúc với (O) tại C nên AC ⊥ OC
Khi đó áp dụng định lí pythagore cho AOC vuông tại C ta được: 2 2 2
AO = AC + CO Suy ra 2 2 2
CO = AO − AC (1)
Áp dụng định lí pythagore cho BOC vuông tại C ta được: 2 2 2 2 2 2
BO = BC + CO CO = BO − BC (2) Từ (1) và (2) suy ra 2 2 2 2
AO − AC = BO − BC Vậy 2 2 2 2
AO + BC = BO + AC
Bài 4: Từ điểm A cách O một khoảng d ( d R ) vẽ tiếp tuyến với đường tròn (O; R) ( B là tiếp
điểm). Tính độ dài đoạn thẳng AB theo d và R . Lời giải Trang 19
Vì AB là tiếp tuyến của (O) tại B nên AB ⊥ OB tại B
Áp dụng định lí Pythagore và AOB có: 2 2 2 2
AB = OA − OB = d − R Vậy 2 2
AB = d − R .
Bài 5: Cho đường tròn tâm O , bán kính R = 5cm và một điểm A cách O bằng 13cm . Kẻ tiếp
tuyến AB với đường tròn (O) ( B là tiếp điểm). Tính độ dài đoạn AB . Lời giải
Ta có AB là tiếp tuyến của (O) nên AB ⊥ OB
Áp dụng định lí Pythagore vào tam giác vuông ABO , ta có: 2 2 2 2 2
AB = OA − OB = 13 − 5 = 114 AB = 12 Vậy AB = 12cm
Bài 6: Cho đường tròn (O;5cm) và dây AB = 8cm . Một tiếp tuyến của (O) song song với AB cắt
tia OA tại E , cắt tia OB tại F . Tính độ dài đoạn thẳng EF . Lời giải
Gọi C là tiếp điểm của tiếp tuyến EF với (O) , H là giao điểm của OC với AB
Ta có OC ⊥ EF tại C , mà AB ⊥ EF nên OC ⊥ AB tại H 1
HA = HB = AB = 4cm 2
Áp dụng định lí Pythagore vào OHA, ta có: 2 2 2 2
OH = OA − AH = 5 − 4 = 3cm
Ta có AB//EF nên theo định lí Thales ta có: AB OB OH 3 = = = EF OF OC 5 5 58 40
EF = AB = = cm . 3 3 3 Trang 20