



Preview text:
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN A. KIẾN THỨC
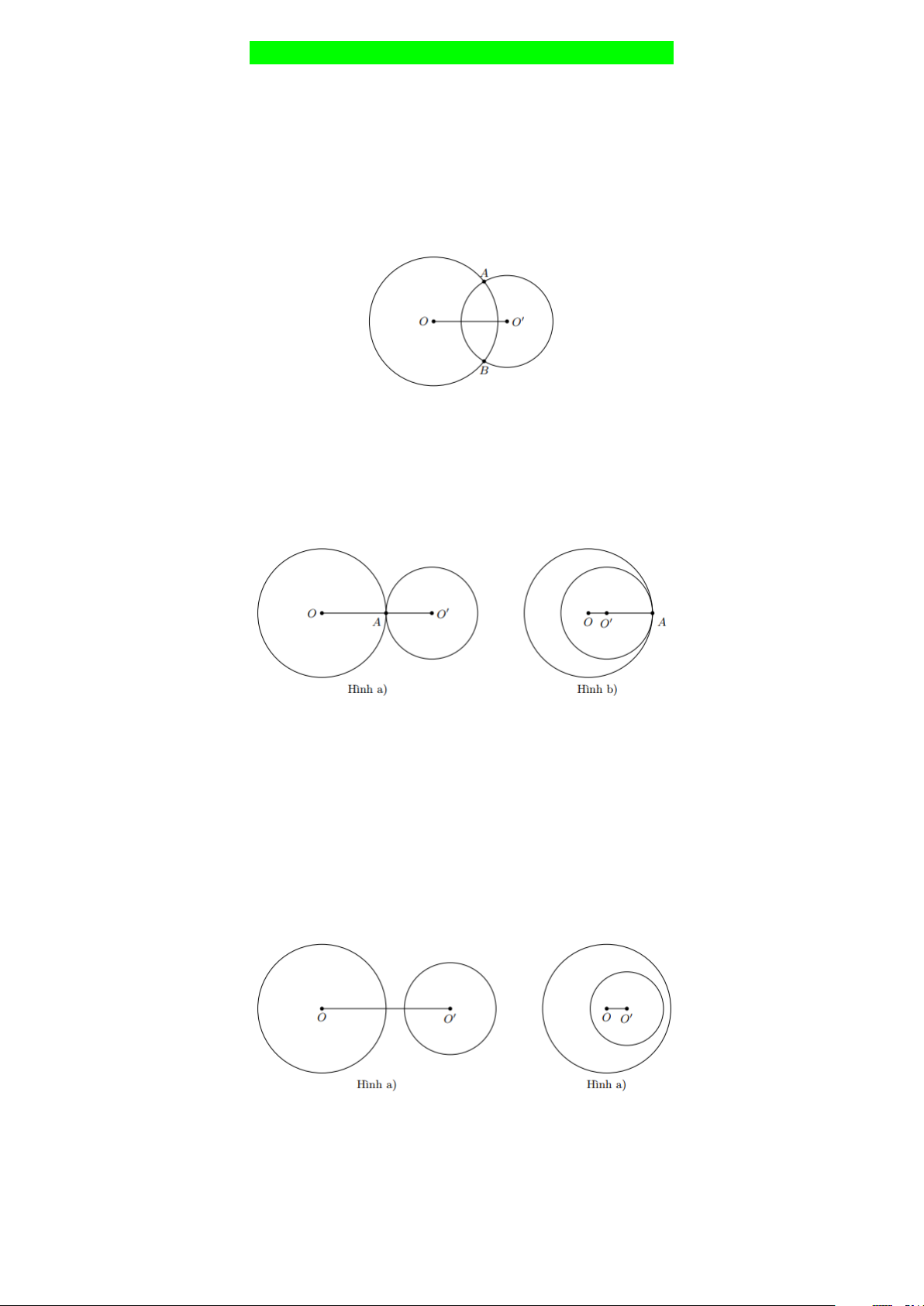
1. Hai đường tròn cắt nhau
* Nếu hai đường tròn có đúng hai điểm chung thì ta nói đó là hai đường tròn cắt nhau. Hai điểm
chung đó gọi là hai giao điểm của chúng.
* Nhận xét: Hai đường tròn (O; R) và (O ; R) cắt nhau khi:
R − R OO R + R (với R R)
2. Hai đường tròn tiếp xúc nhau
* Nếu hai đường tròn có duy nhất một điểm chung thì ta nói đó là hai đường tròn tiếp xúc nhau.
Điểm chung gọi là tiếp điểm của chúng
* Lưu ý: Người ta phân biệt hai trường hợp: Hai đường tròn tiếp xúc ngoài (hình a) và hai đường
tròn tiếp xúc trong (hình b) * Nhận xét:
+ Hai đường tròn (O; R) và (O ; R) tiếp xúc ngoài khi OO = R + R và tiếp xúc trong khi
OO = R − R (với R R)
+ Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm thẳng hàng với hai tâm.
3. Hai đường tròn không giao nhau.
* Nếu hai đường tròn không có điểm chung nào thì ta nói đó là hai đường tròn không giao nhau
* Lưu ý: Người ta phân biệt hai trường hợp: Hai đường tròn ngoài nhau (hình a) và đường tròn
này đựng đường tròn kia (hình b) * Nhận xét:
+ Hai đường tròn (O; R) và (O ; R) ngoài nhau khi OO R + R
+ Đường tròn (O; R) đựng đường tròn (O ; R) khi R R và OO R − R .
Đặc biệt khi O trùng với O và R R thì ta có hai đường tròn đồng tâm. Trang 1
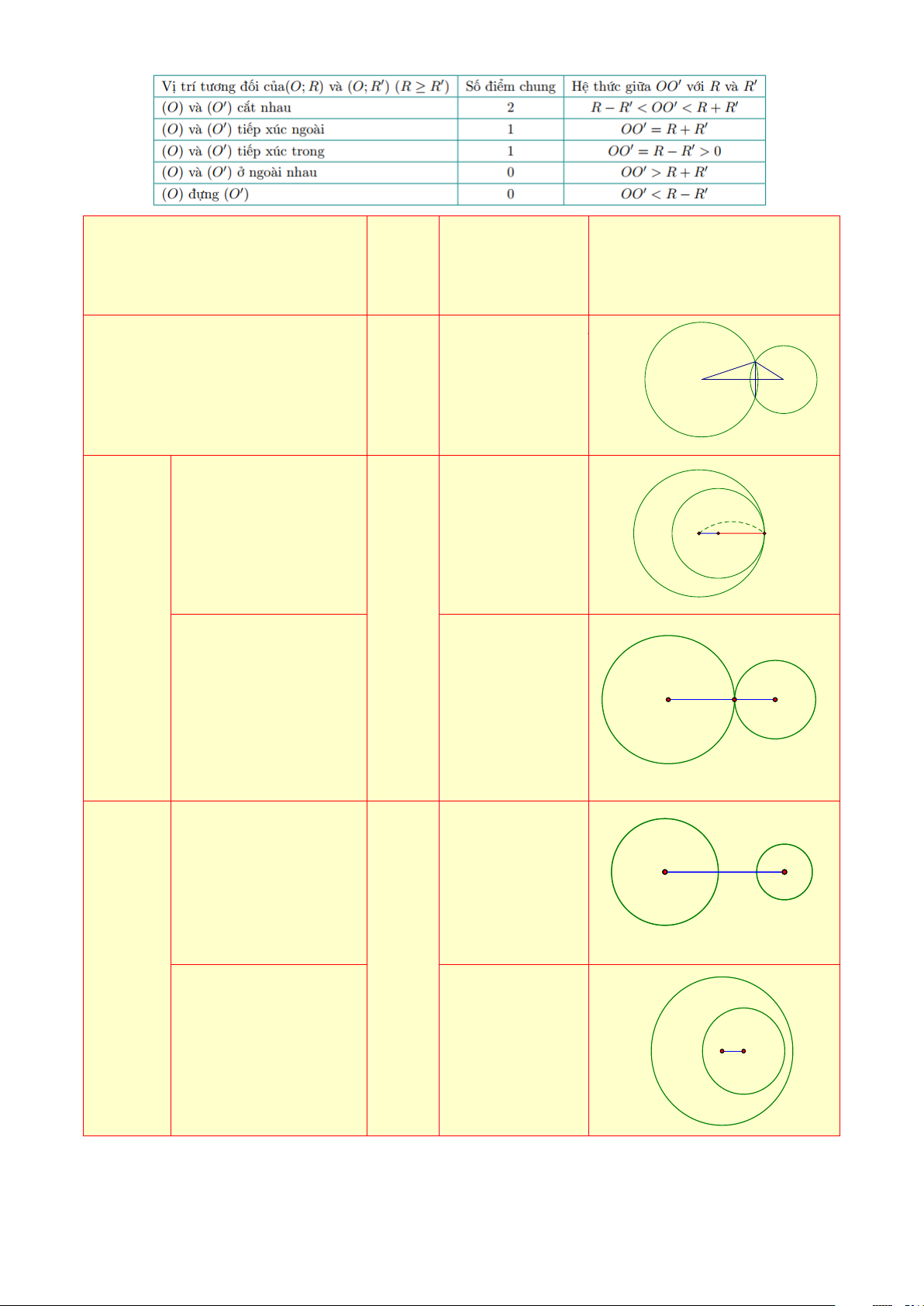
Ta có bảng tổng kết sau:
Vị trí tương đối của hai đường Số Hệ thức Hình vẽ
tròn (O; R) và (O ';r)(R r) điểm chung Cắt nhau 2
R − r OO ' R + r R r O O' Tiếp Tiếp xúc trong 1
OO ' = R − r 0 xúc R O O' r Tiếp xúc ngoài
OO ' = R + r R r O O' Không Ngoài nhau 0
OO ' R + r cắt nhau R r Đựng nhau
0 OO ' R − r O O' Trang 2 OO ' O O' O
3. Tiếp tuyến chung của hai đường tròn
Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó
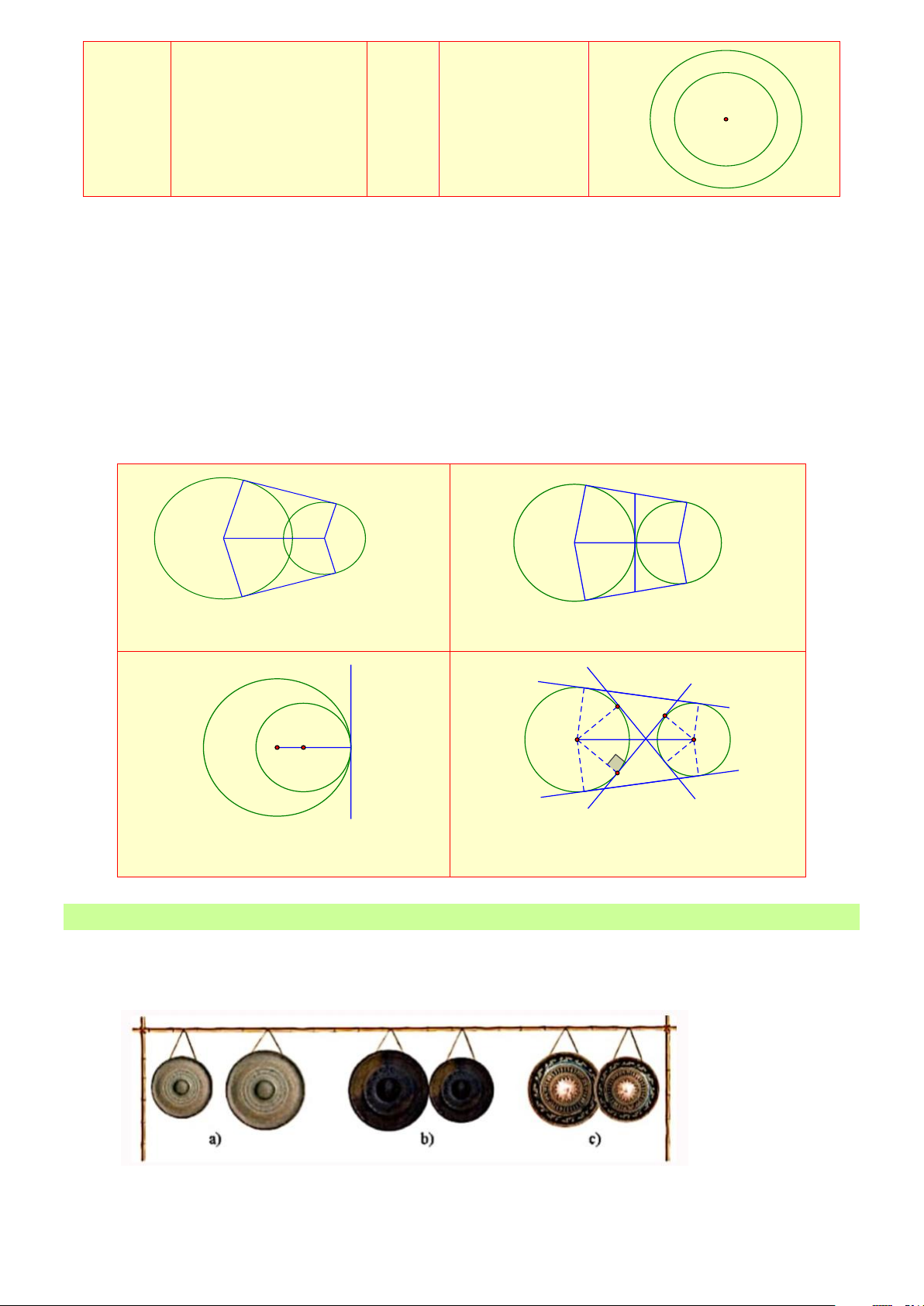
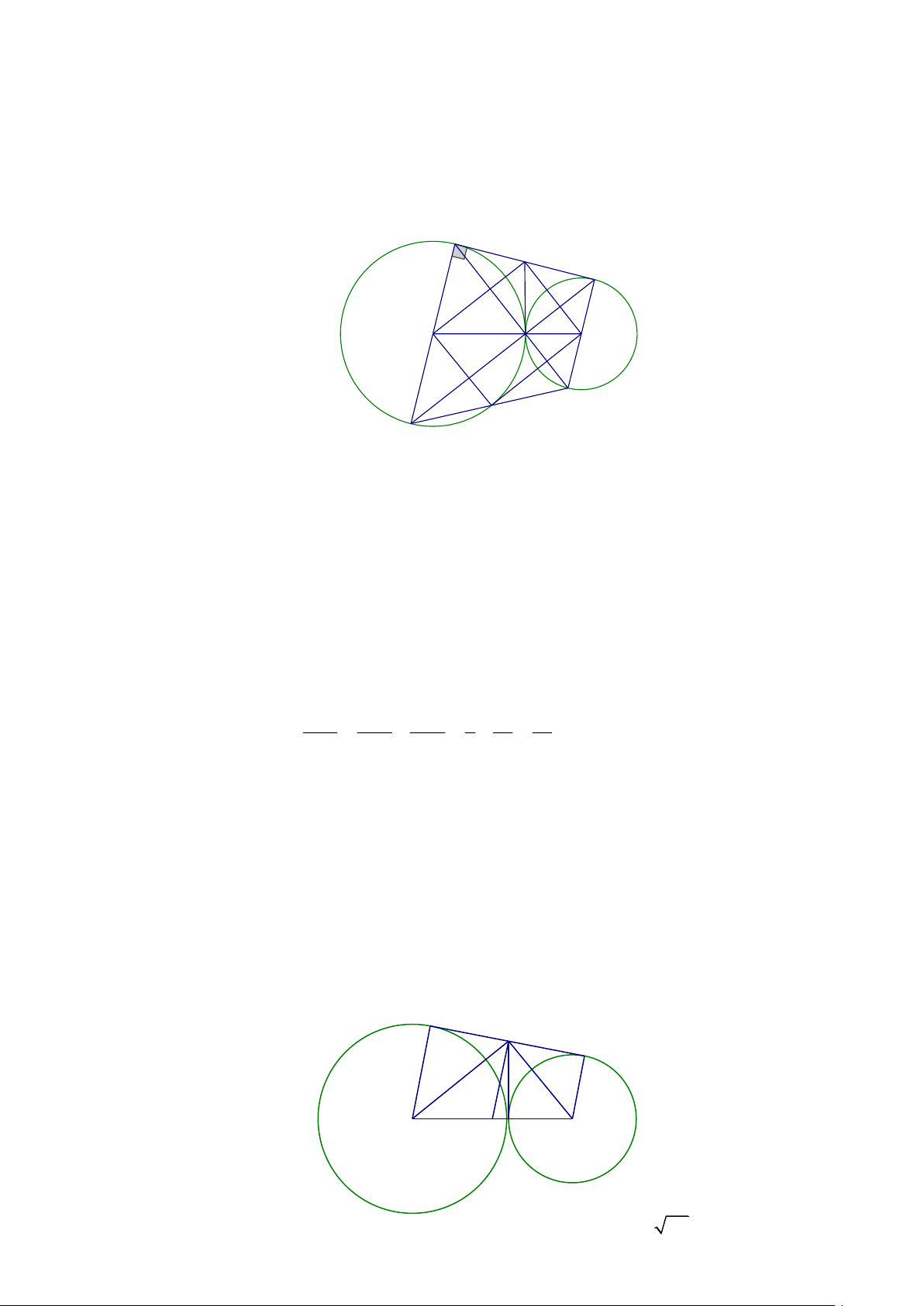
a) Hai đường tròn cắt nhau có hai tiếp tuyến chung ngoài
b) Hai đường tròn tiếp xúc ngoài có hai tiếp tuyến chung ngoài và một tiếp tuyến chung (hình vẽ b)
c) Hai đường tròn tiếp xúc trong chỉ có một tiếp tuyến chung (hình c)
d) Hai đường tròn ngoài nhau có hai tiếp tuyến chung ngoài và hai tiếp tuyến chung trong (hình vẽ d)
e) Hai đường tròn chứa nhau không có tiếp tuyến chung
f) Hai đường tròn đồng tâm không có tiếp tuyến chung O O' O O' Hình a Hình b O O' O O' Hình c Hình d B. CÁC DẠNG TOÁN
Dạng 1: Xác định vị trí tương đối của hai đường tròn
Bài 1: Mô tả vị trí tương đối giữa mỗi cặp đường tròn tròn hình chụp bộ cồng chiêng Tây Nguyên. Lời giải
Hình a) là hai đường tròn ngoài nhau
Hình b) là hai đường tròn tiếp xúc ngoài Trang 3
Hình c) là hai đường tròn ngoài nhau
Bài 2: Xác định vị trí tương đối của hai đường tròn (O; R) và (O ; R) trong mỗi trường hợp sau:
a) OO = 12 ; R = 5 ; R = 3
b) OO = 8 ; R = 5 ; R = 3
c) OO = 7 ; R = 5 ; R = 3
d) OO = 0 ; R = 5 ; R = 4 Lời giải
a) Ta có 12 5 + 3 nên OO R + R , suy ra hai đường tròn (O; R) và (O ; R) ở ngoài nhau.
b) Ta có 8 = 5 + 3 nên OO = R + R , suy ra hai đường tròn (O; R) và (O ; R) tiếp xúc ngoài.
c) Ta có 5 − 3 7 5 + 3 nên R − R OO R + R , suy ra hai đường tròn (O; R) và (O ; R) cắt nhau
d) Ta có 0 5 nên OO R − R , suy ra hai đường tròn (O; R) đựng đường tròn (O ; R) .
Bài 3: Xác định vị trí tương đối giữa hai đường tròn (I; R) và ( J; R) trong mỗi trường hợp sau:
a) IJ = 5; R = 3 ; R = 2
b) IJ = 4 ; R = 11 ; R = 7
c) IJ = 6 ; R = 9 ; R = 4
d) IJ = 10 ; R = 4 ; R = 1 Lời giải
a) Ta có 5 = 3 + 2 nên IJ = R + R , suy ra hai đường tròn (I; R) và ( J; R) tiếp xúc ngoài.
b) Ta có 4 =11− 7 nên IJ = R − R , suy ra hai đường tròn (I; R) và ( J; R) tiếp xúc trong.
c) Ta có 9 − 4 6 9 + 4 nên R − R IJ R + R , suy ra hai đường tròn (I; R) và ( J; R) cắt nhau
d) Ta có 10 4 +1 nên IJ R + R , suy ra hai đường tròn (I; R) và ( J; R) ở ngoài nhau.
Bài 4: Cho hai điểm O và O\prime sao cho OO = 5cm . Hãy giải thích tại sao hai đường tròn ( ;
O 4cm) và (O ;3cm) cắt nhau. Lời giải
Đặt R = 4cm , R = 3cm . Ta thấy 1cm 5cm<7cm , nên R − R OO R + R
Do đó, hai đường tròn đã cho cắt nhau
Bài 5: Cho đường tròn (O;5cm) và điểm I cách O một khoảng 2cm . Xác định vị trí tương đối
của đường tròn đã cho và đường tròn (I;r) trong mỗi trường hợp sau: Lời giải
a) Đặt R = 5cm , ta thấy 1cm 2cm<9cm , nên R − r OI R + r
Do đó, hai đường tròn đã cho cắt nhau
b) Đặt R = 5cm , ta thấy 1cm 2cm 11cm , nên R − r OI R + r
Do đó, hai đường tròn đã cho cắt nhau.
Bài 6: Cho hai đường tròn ( ;
O 4cm) và (O ;3cm) . Biết rằng OO = 5cm . Xét vị trí tương đối của hai đường tròn đó. Trang 4 Lời giải
Ta thấy bán kính của hai đường tròn (O) và (O) lần lượt là R = 4cm ; r = 3cm
Do R − r = 4 − 3 = 1; R + r = 4 + 3 = 7cm và 1 5 7 nên R − r OO R + r Vậy hai đường tròn ( ;
O 4cm) và (O ;3cm) cắt nhau.
Bài 7: Cho hai đường tròn ( ;14 O
cm) ; (O;5cm) với OO = 8cm . Hỏi hai đường tròn đó có cắt nhau hay không? Lời giải
Ta thấy bán kính của hai đường tròn (O) và (O) lần lượt là R =14cm ; r = 5cm
Do R − r = 14 − 5 = 9 ; R + r = 14 + 5 = 19cm và 8 9 14
Vậy hai đường tròn ( ;14 O
cm) và (O ;5cm) không cắt nhau.
Bài 8: Cho hai điểm O và O sao cho OO = 5cm . Giải thích tại sao hai đường tròn (O;3cm) và
(O ;2cm) tiếp xúc nhau. Chúng tiếp xúc trong hay tiếp xúc ngoài? Lời giải
Đặt R = 3cm , R = 2cm ta thấy 5cm = 2cm + 3cm , nghĩa là OO = R + R
Vậy hai đường tròn đã cho tiếp xúc ngoài với nhau.
Bài 9: Cho hai điểm O và O sao cho OO = 3cm . Giải thích tại sao hai đường tròn (O;8cm) và
(O ;5cm) tiếp xúc nhau. Chúng tiếp xúc trong hay tiếp xúc ngoài? Lời giải
Đặt R = 8cm , R = 5cm ta thấy 3cm = 8cm − 5cm , nghĩa là OO = R − R
Vậy hai đường tròn đã cho tiếp xúc trong với nhau.
Bài 10: Xác định vị trí tương đối của hai đường tròn (O;3cm) và (O ;5cm) biết OO 8cm Lời giải
Đặt R = 3cm , R = 5cm ta có OO = 8cm R + R
Vậy hai đường tròn đã cho là hai đường tròn ngoài nhau.
Bài 11: Cho hai điểm O và O sao cho OO = 2cm . Xác định vị trí tương đối cảu hai đường tròn
(O;5cm) và (O ;r) biết rằng r 3cm . Lời giải
Đặt R = 3cm , vì r 3 nên R − r = 5 − r 5 − 3 = 2 = OO
Vậy đường tròn (O;5cm) đừng đường tròn (O ;r) .
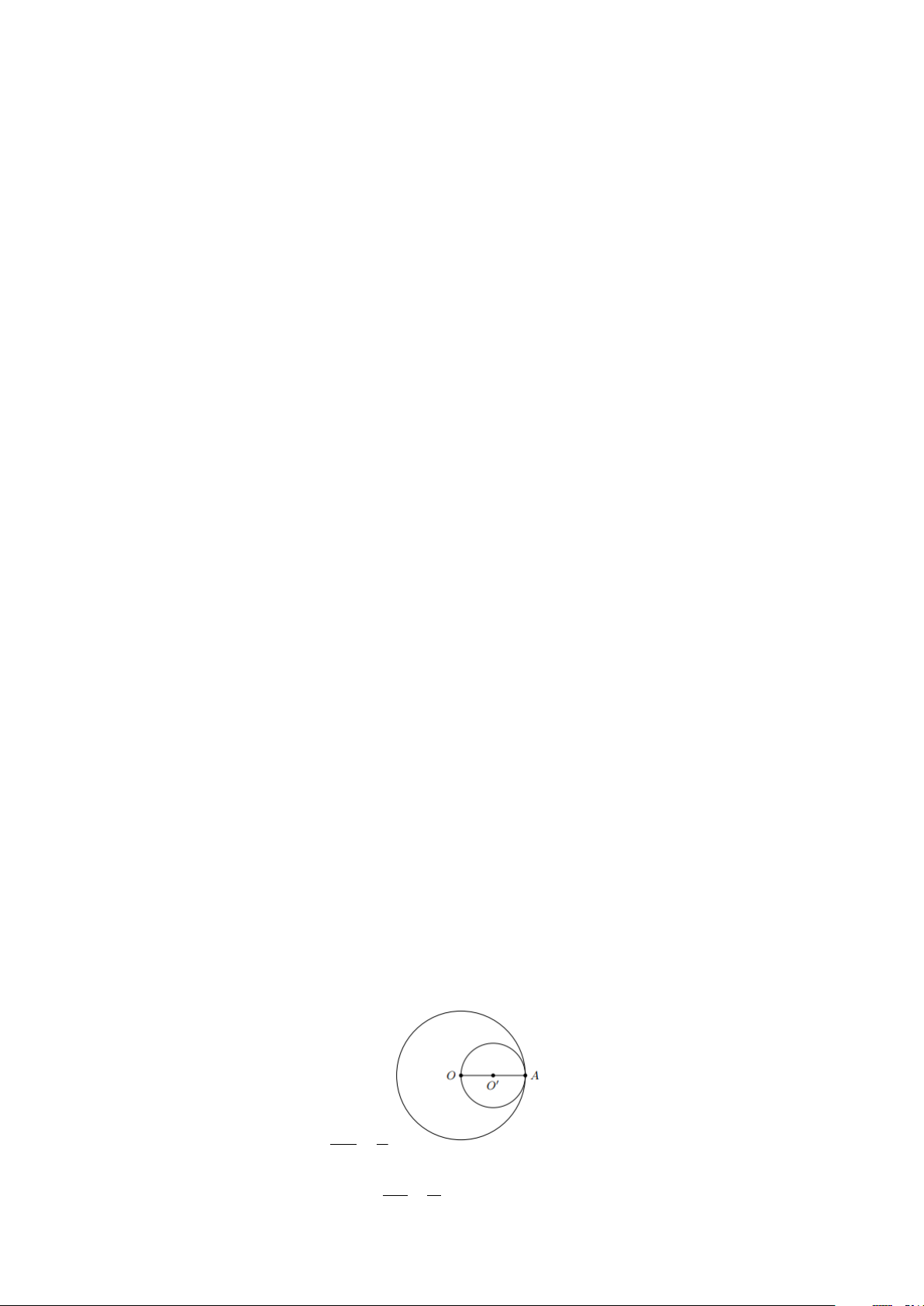
Bài 12: Cho đường tròn tâm O , bán kính R . Lấy điểm A tùy ý trên (O) . Vẽ đường tròn đường
kính OA . Xác định vị trí tương đối của hai đường tròn. Lời giải
Gọi O là tâm đường tròn đường kính OA . Ta có O là trung điểm của OA và bán kính đường tròn ( OA R O) là R = = . 2 2
Độ dài đoạn nối tâm = = OA = R d OO 2 2 Trang 5 Ta có − = R R R
= d nên (O) và (O) tiếp xúc trong tại A . 2
Bài 13: Trong mặt phẳng tọa độ Oxy cho hai điểm A(−1; )
1 và B (3;0) . Vẽ các đường tròn ( ; A r )
và (B;r). Khi r = 3 và r =1, hãy xác định vị trí tương đối của hai đường tròn. Lời giải
Độ dài đoạn nối tâm d = AB = ( + )2 2 3 1 +1 = 17 (1)
Tổng hai bán kính r + r = 3 +1 = 4 (2)
Từ (1) và (2) ta thấy 17 4 nên hai đường tròn không giao nhau
Hai đường tròn ( A) và (B) nằm ngoài nhau.
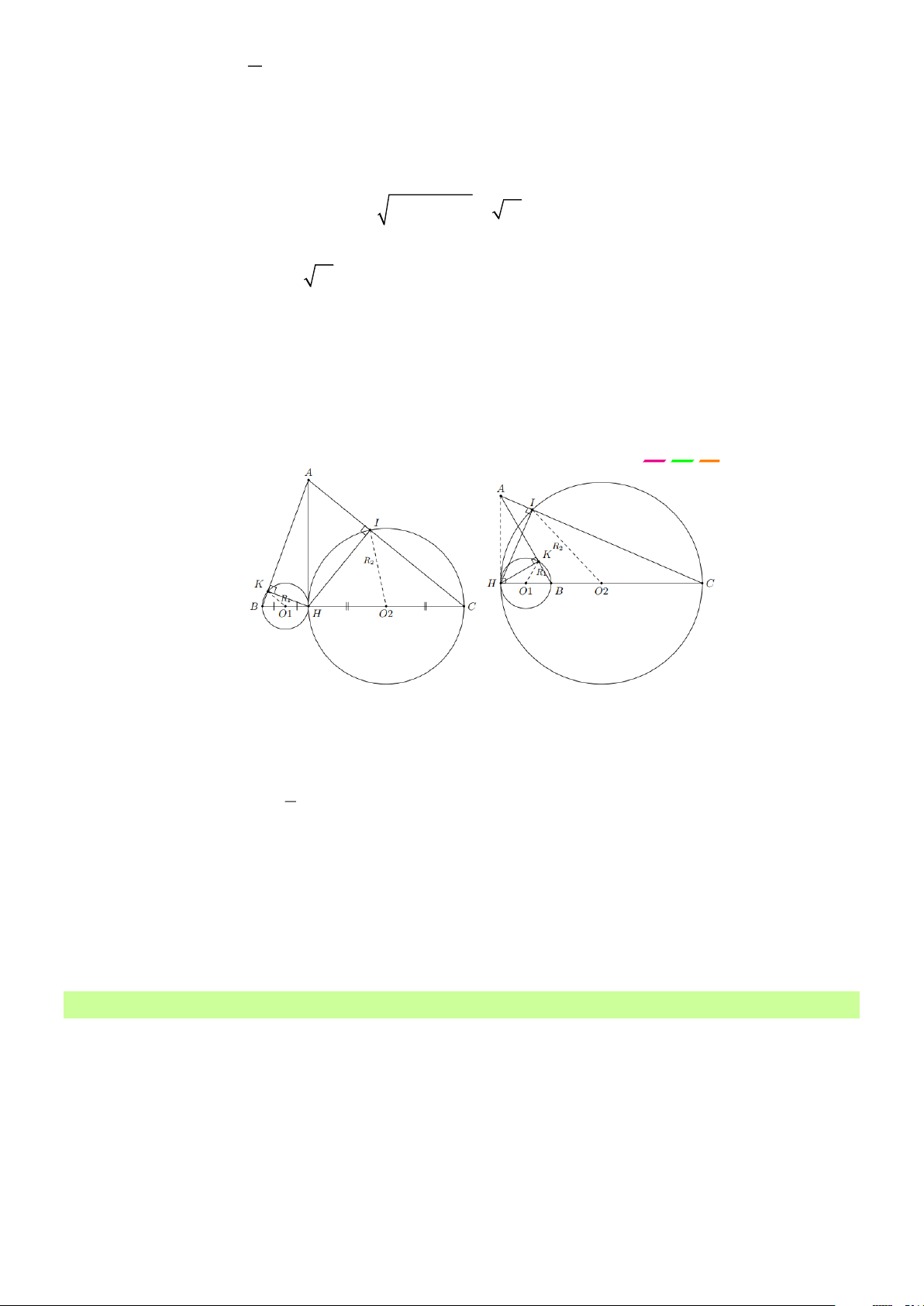
Bài 14: Cho ABC có (B ,C 90 ) , đường cao AH . Từ H kẻ HK vuông góc với AB tại K ,
HI vuông góc với AC tại I . Xác định vị trí tương đối của đường tròn ngoại tiếp tam
giác BHK và đường tròn ngoại tiếp tam giác CHI . Lời giải + Trường hợp 1:
Xét ABC có B 90 và C 90 .
Gọi O ,O lần lượt là trung điểm của BH và CH 1 2
Vì BHK vuông tại K , O là trung điểm của cạnh huyền BH nên 1 1
KO = BO = HO = BH = R 1 1 1 1 2
R + R = HO + HO = O O nên (O ; R tiếp xúc ngoài tại H với (O ;R 2 2 ) 1 1 ) 1 2 1 2 1 2 + Trường hợp 2:
Xét ABC có B = 90 (hoặc C 90 )
Tương tự trường hợp 1 ta có:
O O = R − R nên (O ; R tiếp xúc trong tại H với (O ; R . 2 2 ) 1 1 ) 1 2 1 2
Dạng 2: Các bài toán liên quan đến hai đường tròn tiếp xúc nhau
I. Cách giải: Áp dụng các kiến thức về vị trí tương đối của hai đường tròn liên quan đến trường
hợp hai đường tròn tiếp xúc nhau ABH = ANH II. Bài toán
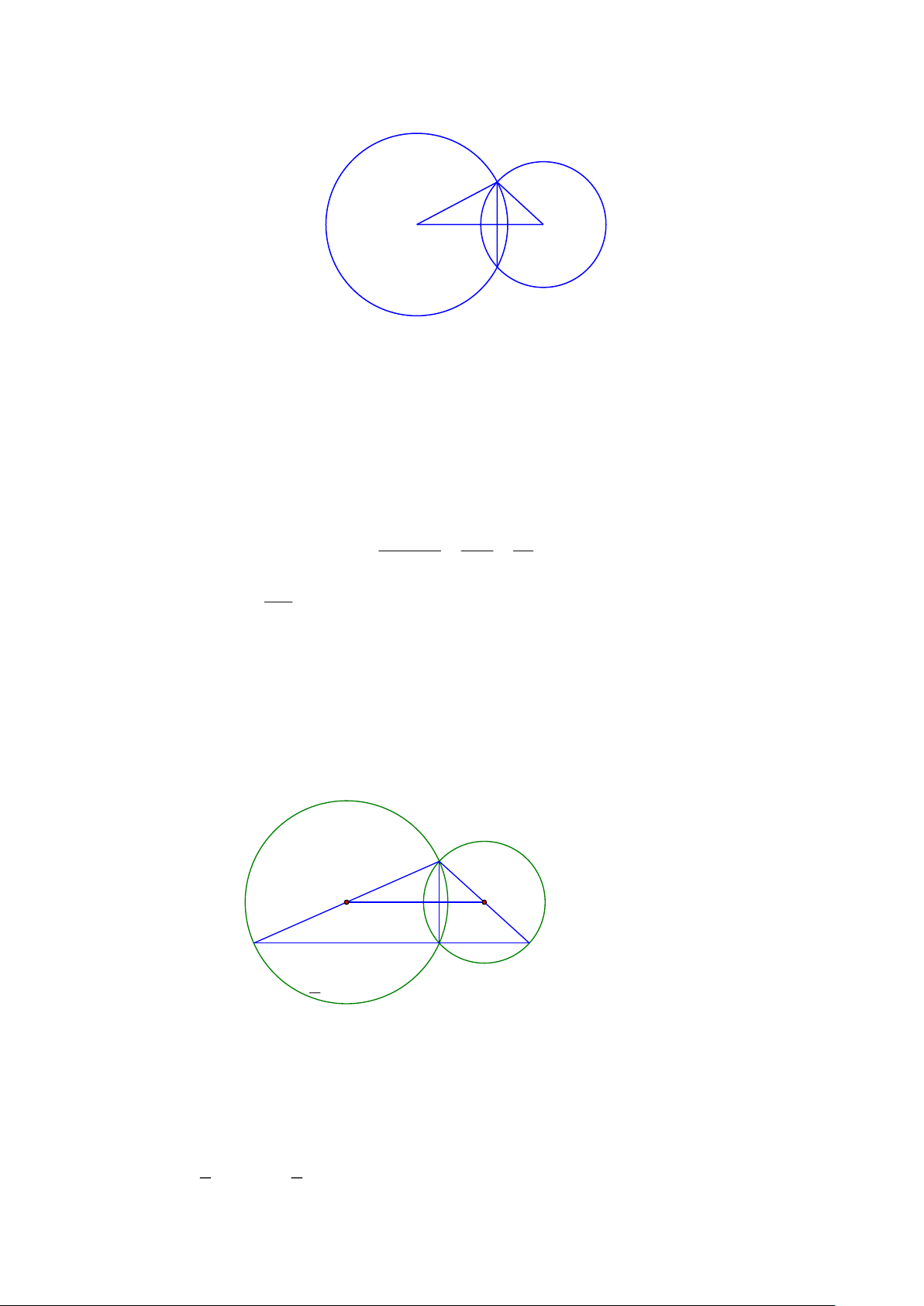
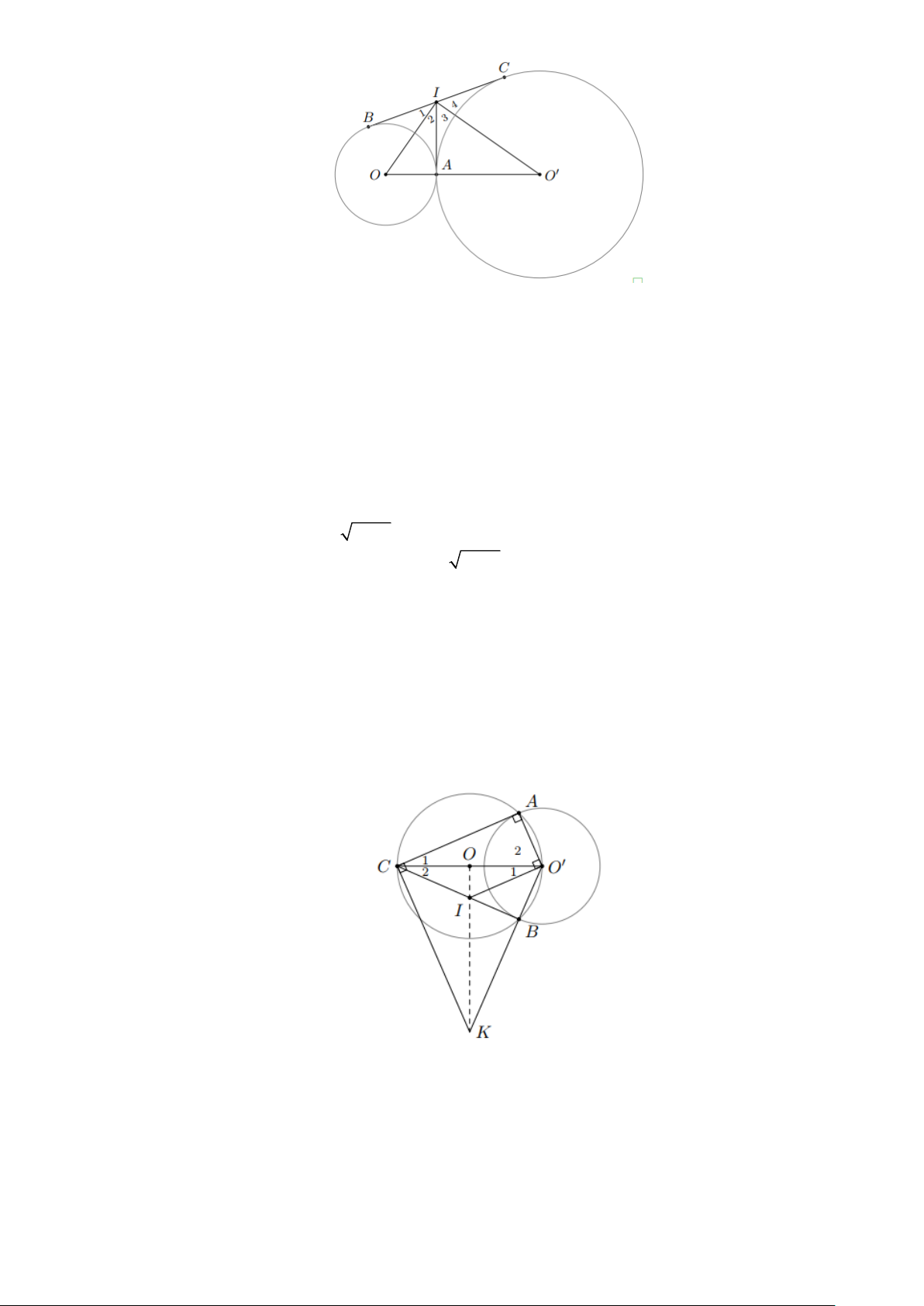
Bài 1: Cho đường tròn (O) và (O ') tiếp xúc ngoài tại A . Kẻ tiếp tuyến chung ngoài BC với B
thuộc (O) , C thuộc (O ') . Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I Trang 6
a. Vẽ đường kính BOD và CO ' E . Chứng minh các bộ ba điểm B, , A E và C, , A D thẳng hàng
b. Chứng minh BAC, DAE có diện tích bằng nhau
c. Gọi K là trung điểm của DE . Chứng minh đường tròn ngoại tiếp OKO ' tiếp xúc với BC
d. Cho OA = 4,5c ;
m O ' A = 2cm . Tính AI, BC,CA B C O O' I D K E Lời giải
a. Xét ABC , có BI = IC = AI ABC vuông tại 0 A BAC = 90 Lại có: 0
BAD = CAE = 90 đpcm
b. Ta có: BAD# EAC (gg) A . D AE = A . B AC S = S ABC DAE
c. Có OIO ' K là hình chữ nhật (hình bình hành có 1 góc vuông)
Vậy đường tròn ngoại tiếp OKO ' chính là đường tròn ngoại tiếp hình chữ nhật, có đường
kính là IK mà: IK ⊥ BC I d. Ta có: 2 AI = O .
AO ' A = 4,5.2 = 9 AI = 3cm Xét 1 1 1 1 1 5 0
BCD(B = 90 ) = + = + =
AB = 2,68cm 2 2 2 AB BC BD 9 36 36 Xét 0 2 2 2 2 2 2
ABC(A = 90 ) BC = AB + AC CA = BC − AB = 36 − 7,2 AC = 5,4cm
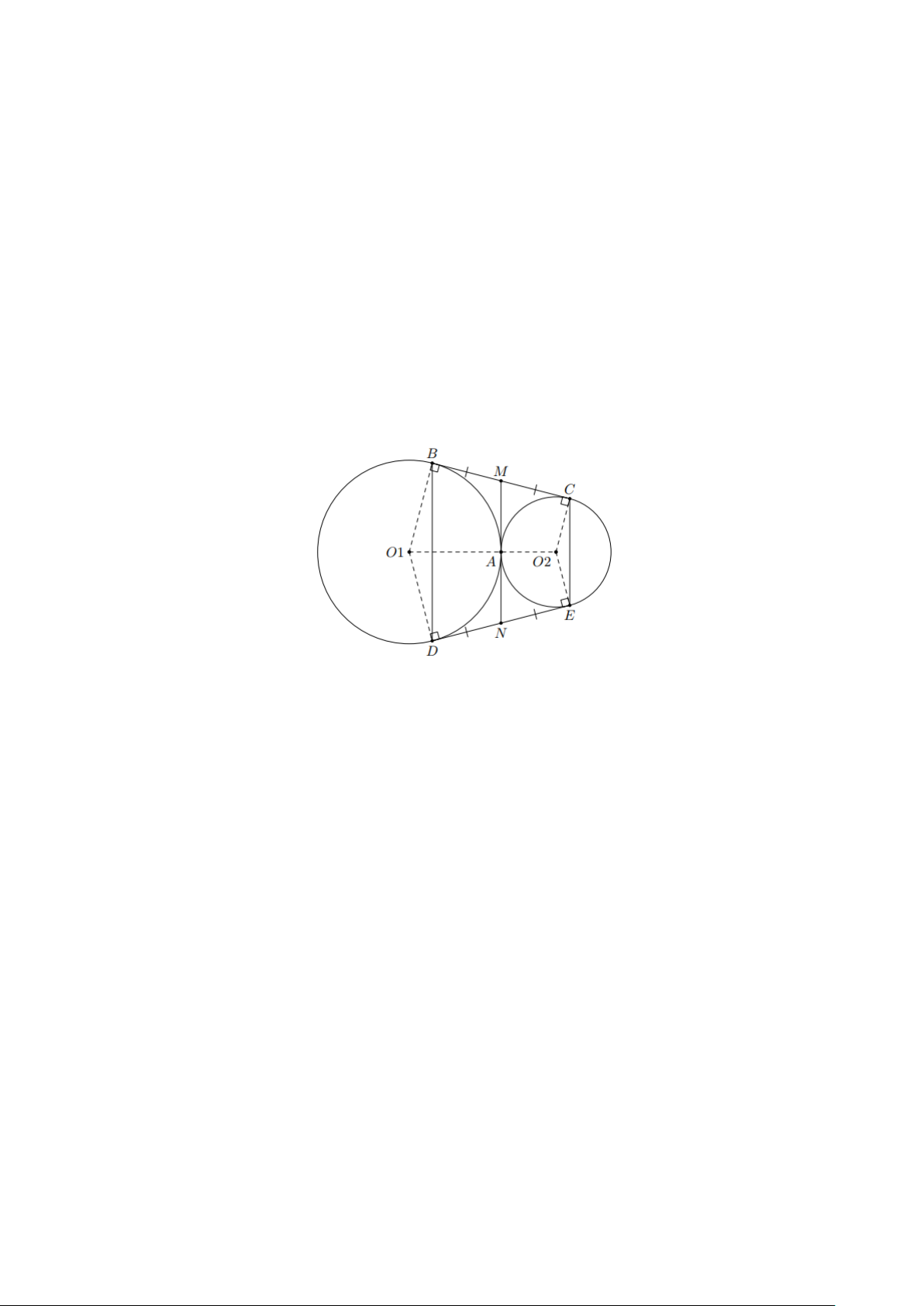
Bài 2: Cho hai đường tròn (O; R) và (O ';r) tiếp xúc ngoài với nhau tại A . Vẽ tiếp tuyến chung
ngoài BC với B (O),C (O ') . Đường thẳng vuông góc với OO ' kẻ từ A cắt BC ở M
a) Tính MA theo R và r
b) Tính diện tích tứ giác BCO 'O theo R và r
c) Tính diện tích BAC theo R và r
d) Gọi I là trung điểm của OO ' . Chứng minh rằng BC là tiếp tuyến của đường tròn (I;IM ) B Lời giải M C O I A O' a) Chứng minh được: 0 O 'MO = 90
Aps dụng hệ thức lượng trong tam giác vuông ta tính được: MA = Rr Trang 7 b) Chứng minh S = R + r Rr BCOO ' ( ) 2 2 S BC S BC Rr Rr BAC . 4 c) Chứng minh được: OMO '
BAC# OMO ' = S = = S OO ' ABC OO R r OMO ( ')2 + '
d) Tứ giác OBCO ' là hình thang vuông tại B và C có IM là đường trung bình
IM ⊥ BC = M
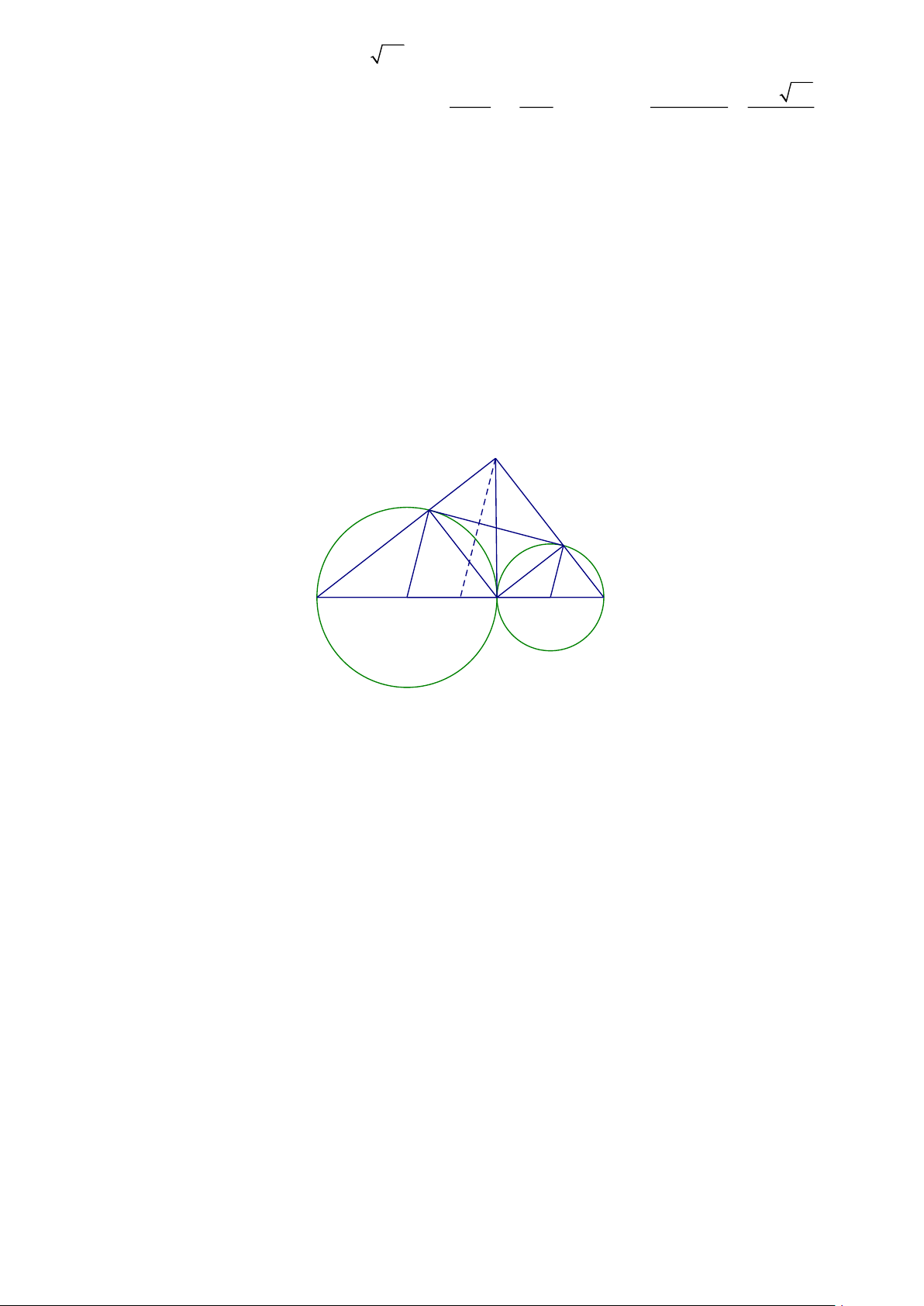
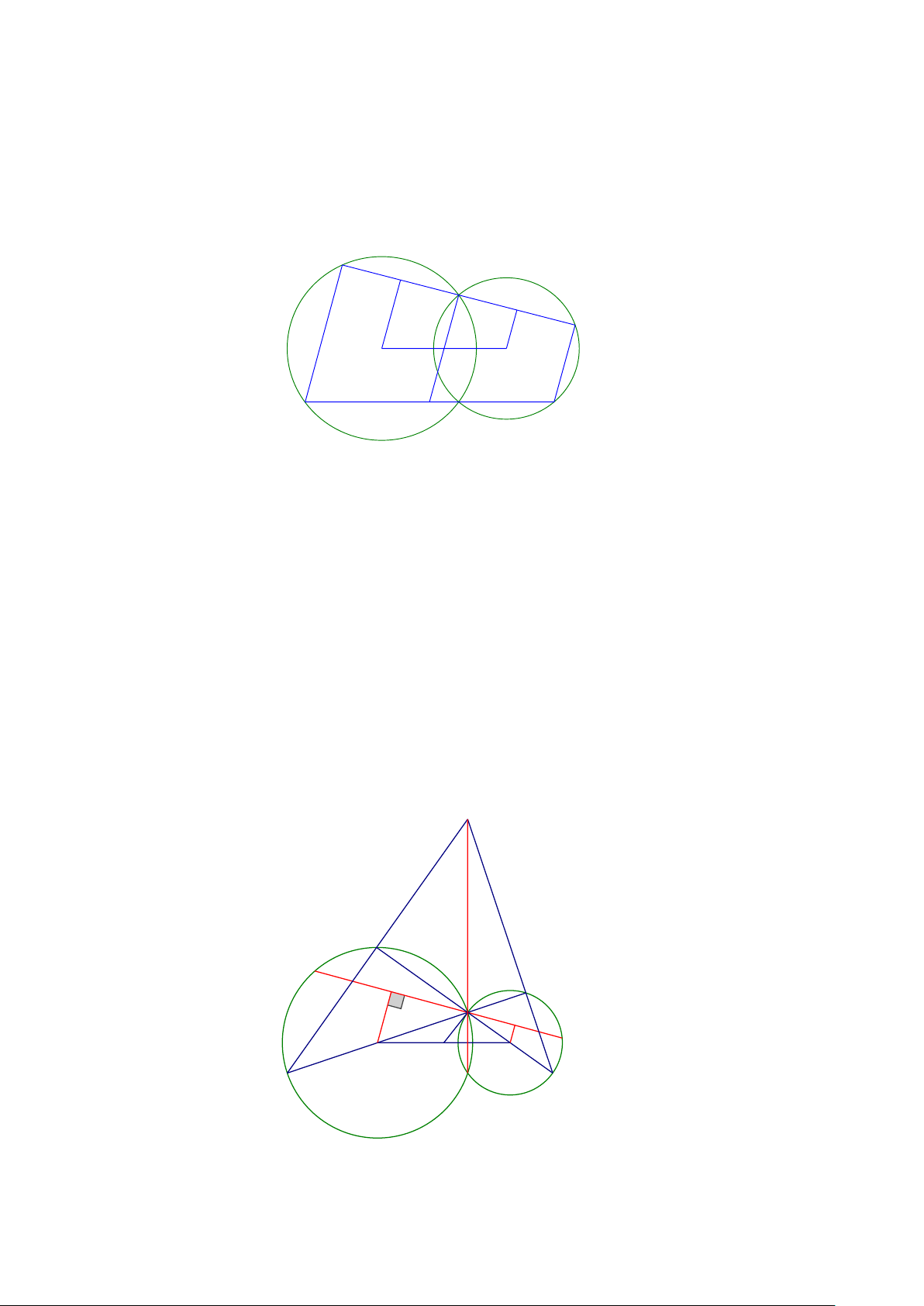
Bài 3: Cho hai đường tròn (O) và (O ') tiếp xúc ngoài tại A . Kẻ các đường kính AOB , AO 'C .
Gọi DE là tiếp tuyến chung của hai đường tròn. Gọi M là giao điểm của BD và CE a. Tính DAE
b. ADME là hình gì ? Vì sao ?
c. Chứng minh rằng MA là tiếp tuyến chung của hai đường tròn d. Chứng minh: .
MD MB = ME.MC
e. Gọi H là trung điểm của BC , chứng minh rằng MH ⊥ DE M 1 D 1 I E 1 1 2 2 B O H A C O' Lời giải A = ( 0 180 − O : 2 1 1 ) a) Ta có: 0 0 A A DAE A = ( + = = 180 − O ) 90 90 1 2 0 : 2 2 2
b) Có ADME là hình chữ nhật (tứ giác có 3 góc vuông là hình chữ nhật)
c) Gọi I là giao điểm của DE và AM ID = IA 0
IAO = IDO(ccc) IAO = IDO = 90 MA ⊥ OA A(O)
Chứng minh tương tự: MA ⊥ O ' A A(O ')
Vậy MA là tiếp tuyến chung của hai đường tròn d. Ta có: 0 2
MAB(A = 90 ), AD ⊥ MB MA = M . D MB 0 2
MAC(A = 90 ), AE ⊥ MC MA = ME.MC M .
B MD = ME.MC e) 0
M + D = B + BMA = 90 MH ⊥ DE 1 1 1
Bài 4: Cho ba điểm J , I, J ' cùng nằm trên 1 đường thẳng theo thứ tự đó. Cho biết IJ = 10cm ,
IJ ' = 4CM . Vẽ đường tròn (O) đường kính IJ và đường tròn (O ') đường kính IJ '
a. Chứng minh (O) và (O ') tiếp xúc ngoài ở I
b. Gọi A là 1 điểm trên đường tròn (O) , tia AI cắt (O ') ở A' . Chứng minh rằng
AIJ# A' IJ '
c. Qua điểm I kẻ 1 cát tuyến cắt (O) ở B ( B và A thuộc hai nửa mặt phẳng bờ IJ ), cắt
đường tròn (O ') ở B ' . Chứng minh: IAB# IA' B ' Trang 8
d. Chứng minh rằng: OAB# ; O A' B '
e. ABA' B ' là hình gì vì sao ? Lời giải B A' 2 1 J O 3 4 J' O' I B'
a) Ta có: OO ' = OI + O ' I . Vậy Hai đường tròn tiếp xúc ngoài tại I A 0
A = A' = 90
b) Xét AIJ và A' IJ ' có:
AII# A' IJ ' I = I 1 2
c) AII# A IJ (gg) IA IJ 10 5 ' ' = = = ( ) 1 IA' JI ' 4 2 # IB OB OIB
O ' IB '( gg ) 5 '
OB / /O ' B ' B = B = = 2 1 1 ( )
IB ' O ' B ' 2 Từ ( )( ) IA IB 5 1 2 =
= ; AIB = A' IB IAB# IA' B ' (cgc) IA' IB ' 2 d) AB IA 5 OA OB 5
IAB” IA' B '( cgc) = = ; = = A' B ' IA' 2 O ' A' O ' B ' 2
OA = OB = AB AOB” A'O ' B ' (ccc) O ' A' O ' B ' A' B '
e) AOB# A'O ' B ' OBA = O ' B ' A';OBI = O ' B ' I '
ABI = AB ' I ' AB// A' B '
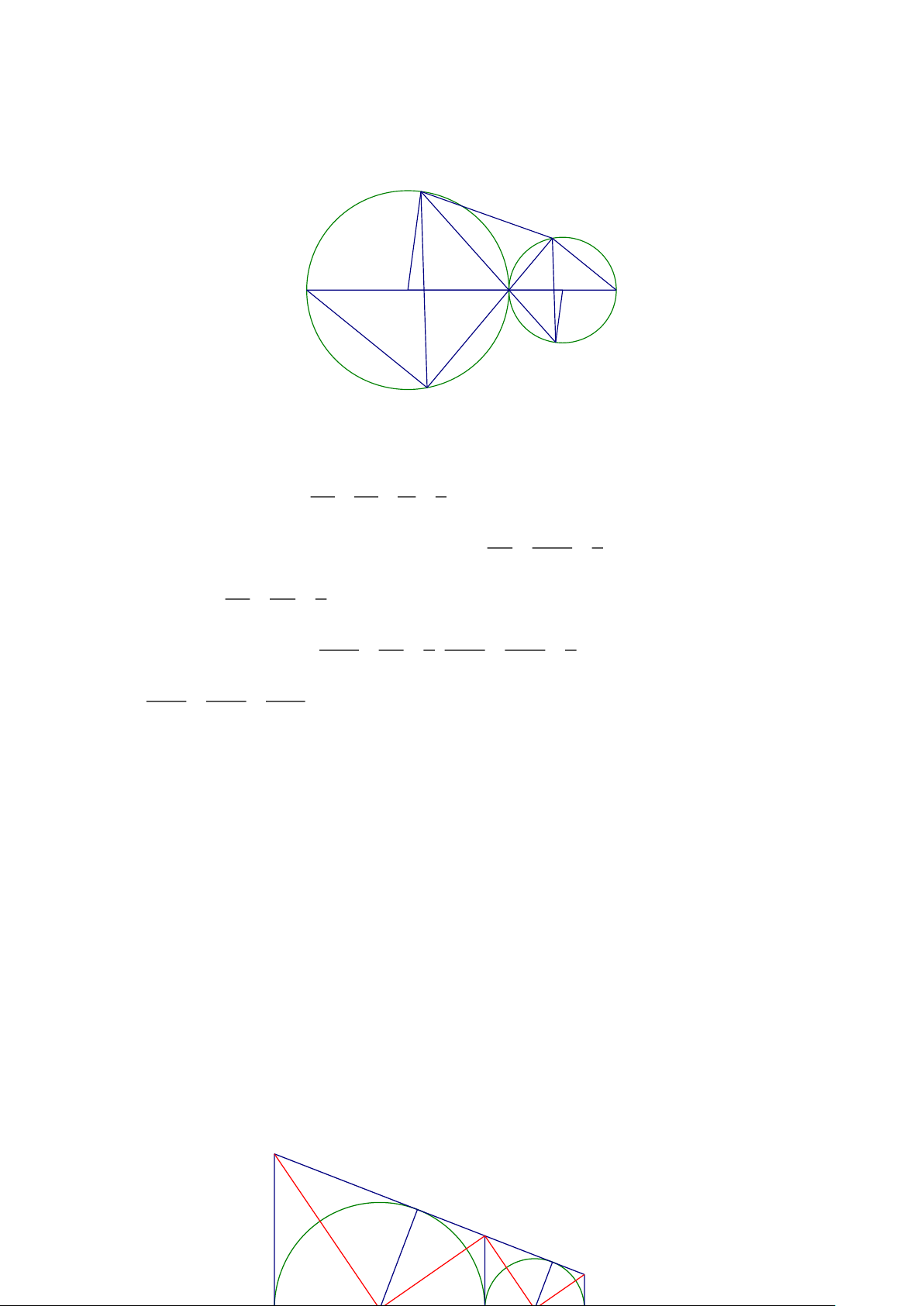
Tứ giác ABA' B ' có hai cạnh đối song song vậy là hình thang. Bài 5: Cho 3 điểm ,
A B,C theo thứ tự đó trên một đường thẳng và AB = 4BC . Trên cùng một nửa
măt phẳng bờ AC vẽ nửa đường tròn tâm O đường kính AB và nửa đường tròn tâm O ' có
đường kính BC . Tiếp tuyến chung của hai nửa đường tròn có tiếp điểm với đường tròn
(O) ở F với nửa đường tròn (O') ở G , cắt các tiếp tuyến vẽ từ A và C của hai nửa
đường tròn đó ở D và E . Tiếp tuyến chung của hai nửa đường tròn ở B cắt DE ở I
a. Chứng minh các tam giác OIO ', OID , O ' IE là các tam giác vuông
b. Đặt O 'C = a (a là độ dài cho trước). Tính BI, EG và AD theo a
c. Tính diện tích tứ giác ADEC theo a Lời giải D F I Trang 9 G E A C O B O'
a. Theo tính chất hai tia phân giác của hai góc kề bù ta có: IOO ' vuông tại I , OID
vuông tại O, IO ' E vuông tại O '
b. Ta có: OB = 2BC = 4a 0
IOO '(I = 90 ) IB ⊥ OO ' 2 2 IB = O .
B O ' B = 4a IB = 2a 2 2 O 'G a a 0 2
IO ' E(O ' = 90 ) O 'G = E . G GI GE = =
= (IG = IB = IF = 2a) AD = 8a GI 2a 2 1 1 a c) Ta có: 2 S
= (EC + AD).AC = 8a +
10a = 42,5a . ACED 2 2 2
Dạng 3: Các bài toán liên quan đến hai đường tròn cắt nhau
I. Cách giải : Áp dụng các kiến thức về vị trí tương đối của hai đường tròn liên quan đến trường
hợp hai đường tròn cắt nhau II. Bài toán
Bài 1: Cho hai đường tròn ( ;12 O
cm) và (O ';5cm) , OO ' = 13cm
a) Chứng tỏ rằng hai đưuòng tròn (O) và (O ') cắt nhua tại hai điểm phân biệt Trang 10 b) Gọi ,
A B là giao điểm của hai đường tròn (O) và (O ') . Chứng minh rằng OA là tiếp
tuyến của đường tròn (O ') , OA là tiếp tuyến của đường tròn (O) . Tính độ dài AB Lời giải A O H O'
a) Ta có: 12 − 5 13 12 + 5(R − R ' d R + R ')
B nên hai đường tròn (O) và (O ') cắt nhau
tại hai điểm phân biệt b) 2 2 2 2 2 2
OA + O ' A =12 + 5 =169;O 'O =13 =169 OAO ' có: 2 2 2
OA + O ' A = O 'O , theo định lý Pytago đảo tam giác OAO ' vuông tại A
Có OA ⊥ O ' A do đó OA là tiếp tuyến của đường tròn (O ') và O ' A là tiếp tuyến của đường tròn (O)
O 'O là đường trung trực của đoạn AB
Gọi H là giao điểm của O 'O và AB nên O . A O ' A 12.5 60
AH.O 'O = O .
A O ' A AH = = = (cm) O 'O 13 13 Vậy 120 AB = 2AH = (cm). 13
Bài 2: Cho hai đường tròn (O) và (O ') cắt nhau ở A và B (O và O ' thuộc hai nửa mặt phẳng bờ
AB ). Kẻ các đường kính BOC và BO ' D
a. Chứng minh rằng ba điểm C, , A D thẳng hàng
b. Biết OO ' = 5cm,OB = 4cm,O ' B = 3cm . Tính diện tích tam giác BCD Lời giải B O O' C D A a. Cách 1: 1
BAC(AO = BC) BAC = BAD = 90 đpcm 2
Cách 2: BCD có OO ' là đường trung bình OO '/ /CD ( ) 1
ABC có OI là đường trung bình OO'/ /CA (2) Từ ( ) 1 (2) C, , A D thẳng hàng.
b) Ta có: OBO ' vuông tại B BCD vuông tại B 1 1 2 S
= .BC.BD = .8.6 = 24(cm ) BCD 2 2 Trang 11
Bài 3: Cho hai đường tròn (O) và (O ') giao nhau tại M và N . Gọi I là trung điểm của OO ' .
Đường thẳng kẻ qua M vuông góc MI cắt đường tròn (O) và (O ') lần lượt ở A và B .
Hai đường thẳng vuông góc với AB tại A và B cắt đường tròn (O) ở P , (O ') ở Q
a. Chứng minh rằng M là trung điểm của AB
b. MI cắt PQ ở E , chứng minh: EP = EQ
c. Chứng minh: IH = IK Lời giải A H M K B O I O'
a. Kẻ: OH ⊥ AM ;O ' KP⊥ MB OH / /O E ' K Q N MI / /OH
Tứ giác HKOO ' là hình thang, MI ⊥ AB MH = MK IO / /IO'
Ta lại có: OH ⊥ AM HA = HM = MK = KB đpcm
b. Ta có ME là đường trung bình của hình thang ABQP EP = EQ
c. Xét HIK , có IM là đường trung tuyến, đường cao HIK cân tại I (đpcm).
Bài 4: Cho hai đường tròn (O) và (O ') cắt nhau tại A và B . Gọi M là trung điểm của OO ' .
Đường thẳng qua A cắt các đường tròn (O) và (O ') lần lượt ở C và D
a. Khi CD ⊥ AB . Chứng minh: AC = AD
b. Khi CD đi qua A và không vuông góc với MA
- Vẽ đường kính AE của (O) , AE cắt (O ') ở H . Vẽ đường kính AF của (O ') , AF cắt
(O) ở G . Chứng minh AB,EG,FH đồng quy
- Tìm vị trí của CD để đoạn CD có độ dài lớn nhất Lời giải G C H A D O M O'
Vẽ OP ⊥ AC;O 'Q ⊥E AD OPO 'Q là hình
B thang vuônFg tại P và Q
a. Kẻ OP,O 'Q ⊥ CD MA ⊥ CD và M là trung điểm của OO '
b. Xét EAF có AB, FG, EH là ba đường cao nên đồng quy tại 1 điểm .
+) Ta có: CD = 2PQ
Hình thang OPQO ' vuông tại P và Q nên OO ' PQ Trang 12
Vậy PQ lớn nhất khi PQ / /OO ' hay tứ giác OPQO ' là hình chữ nhật.
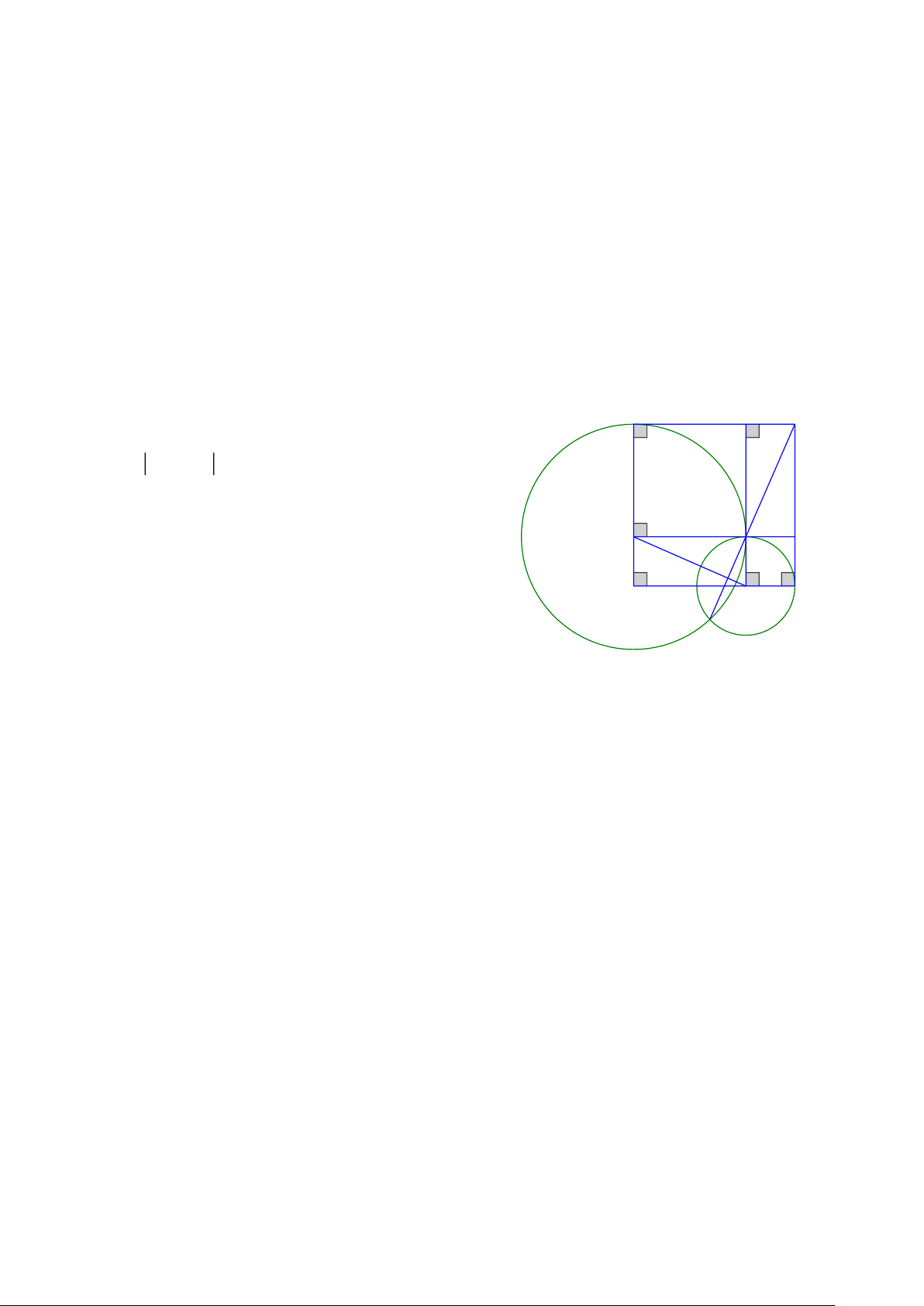
Bài 5: Cho góc vuông xOy . Lấy các điểm I và K lần lượt trên các tia Ox,Oy . Đường tròn
(I;OK ) cắt tia Ox tại M ( I nằm giữa O và M ), đường tròn (K;OI ) cắt tia Oy tại N (
K nằm giữa O và N )
a. Chứng minh (I ) và (K ) luôn cắt nhau
b. Tiếp tuyến tại M của (I ) , tiếp tuyến tại N của (K ) cắt nhau tại C . Chứng minh tứ giác OMCN là hình vuông c. Gọi ,
A B là các giao điểm của ( I ) và (K ) trong đó B ở miền trong góc xOy . Chứng minh ba điểm ,
A B,C thẳng hàng
d. Giả sử I và K theo thứ tự đi động trên các tia Ox và Oy sao cho OI + OK = a không
đổi. Chứng minh đường thẳng AB luôn đi qua một điểm cố định. N P C Lời giải
a) OI − OK IK OI + OK
Ta có ( I ) và (K ) luôn cắt nhau
b. Do OI = NK;OK = IM OM = ON B K L
Mặt khác OMCN là hình chữ nhật OMCN là hình vuông O I M
c. Gọi L là giao điểm của KB và MC ; P là A
giao điểm của IB và NC OBKI là hình chữ
nhật và BLMI là hình vuông BLC = KIO LBC = OKI = BIK Mà: 0 0
BIK + IBA = 90 LBC + IBA = 90 , có: 0
LBC + LBI + IBA =180
d) Có OMCN là hình vuông cạnh a cố định C cố định và AB luôn đi qua C . Trang 13
Dạng 3: Các bài toán về hai đường tròn không cắt nhau
I. Cách giải: Áp dụng các kiến thức về vị trí tương đối của hai đường tròn liên quan đến trường
hợp hai đường tròn không giao nhau II. Bài toán
Bài 1: Cho hai đường tròn đồng tâm O , có bán kính lần lượt là R và r . Dây MN của đường tròn
lớn cắt đường tròn nhỏ tại A và B . Gọi BC là đường
kính của đường tròn nhỏ. Tính giá trị của biểu thức ( 2 2 2
AC + AM + AN ) theo R và r C Lời giải
Kẻ OE ⊥ AB;OF ⊥ AC . Đặt AC = a, AM = b, AN = c O F R 2 2 2 2 a c − b a c + Ta có: b 2 2 r = + ; R = + 2 2 2 2 M A E N B Chứng minh được: 2 2 2
a + b + c = ( 2 2 2 r + R )
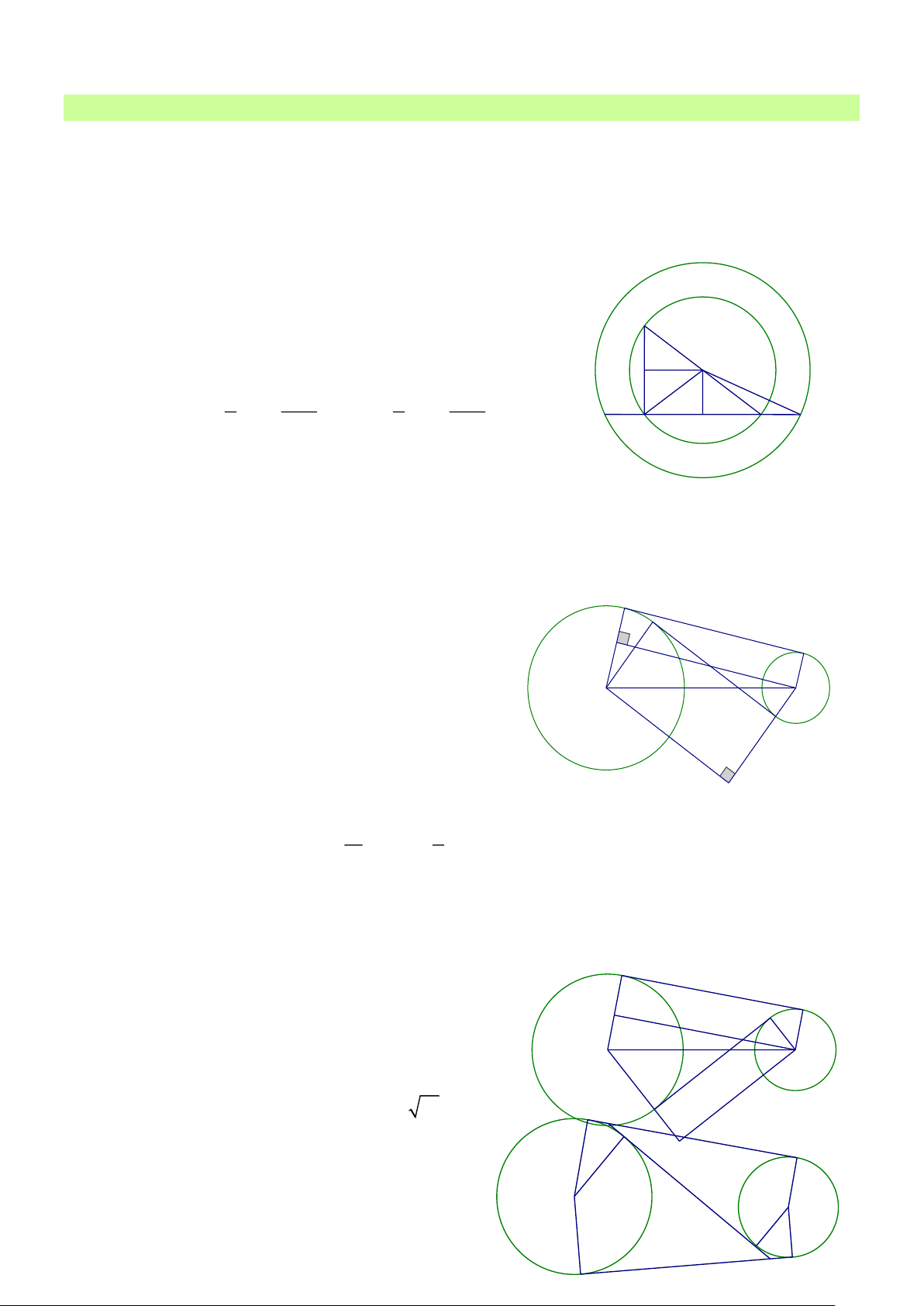
Bài 2: Cho hai đường tròn (O; R) và (O ';r) ở ngoài nhau.
Gọi MN là tiếp tuyến chung ngoài, EF
Là tiếp tuyến chung trong ( M và E thuộc (O) , N và F thuộc ( ;
O ) ). Tính bán kính của
đường tròn (O) và (O ') trong các trường hợp sau: M
a) OO ' = 10cm, MN = 8cm, EF = 6cm E H
b) OO ' = 13cm, MN = 12cm, EF = 5cm N Lời giải O O'
a) Kẻ O ' H ⊥ OM ;OK ⊥ O ' F
Ta có: OH = R − r;O ' K = R + r , mà 2 2 2 2 2 2
OH = O 'O − MN = 36;O ' K = O 'O − EF = 64 K
OH = 6;O ' K = 8 R = 7cm;r = 1cm
b) Tương tự tính được: 17 R = cm , 7 r = cm 2 2
Bài 3: Cho hai đường tròn (O;6cm) và (O ';2cm) nằm ngoài nhau. Gọi AB là tiếp tuyến chung
ngoài, CD là tiếp tuyến chung trong của hai đường tròn ( ,
A C (O); B, D (O ') ). Biết
AB = 2CD , tính độ dài đoạn nối tâm OO ' A Lời giải
a) Kẻ O ' H ⊥ O ;
A O ' K ⊥ OC B H D
Tính được: OH = 4c , m OK = 8cm , O O' Đặt 2 2
CD = x AB = 2 ;
x O 'O = 64 + x và 2 2
O 'O =16 + 4x x = 4 OO ' = 80cm . A E C
Bài 4: Cho hai đường tròn (O) và (O ') nằm K B M
ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD ( ,
A C (O); B, D (O ') ). Tiếp O O' N Trang 14 F D C
tuyến chung trong MN cắt AB,CD theo thứ tự tại E, F , (M (O), N (O ')). Chứng minh: a) AB = EF b) EM = FN Lời giải
a) Ta có: AB = AE + BE = EM + EN
và CD = FD + FC = NF + NE
AB + CD = 2EF AB = EF
b) Ta có: EM = AB − EB = EF − EN = NF .
Dạng 4: Chứng minh các tính chất về hệ thức hình học
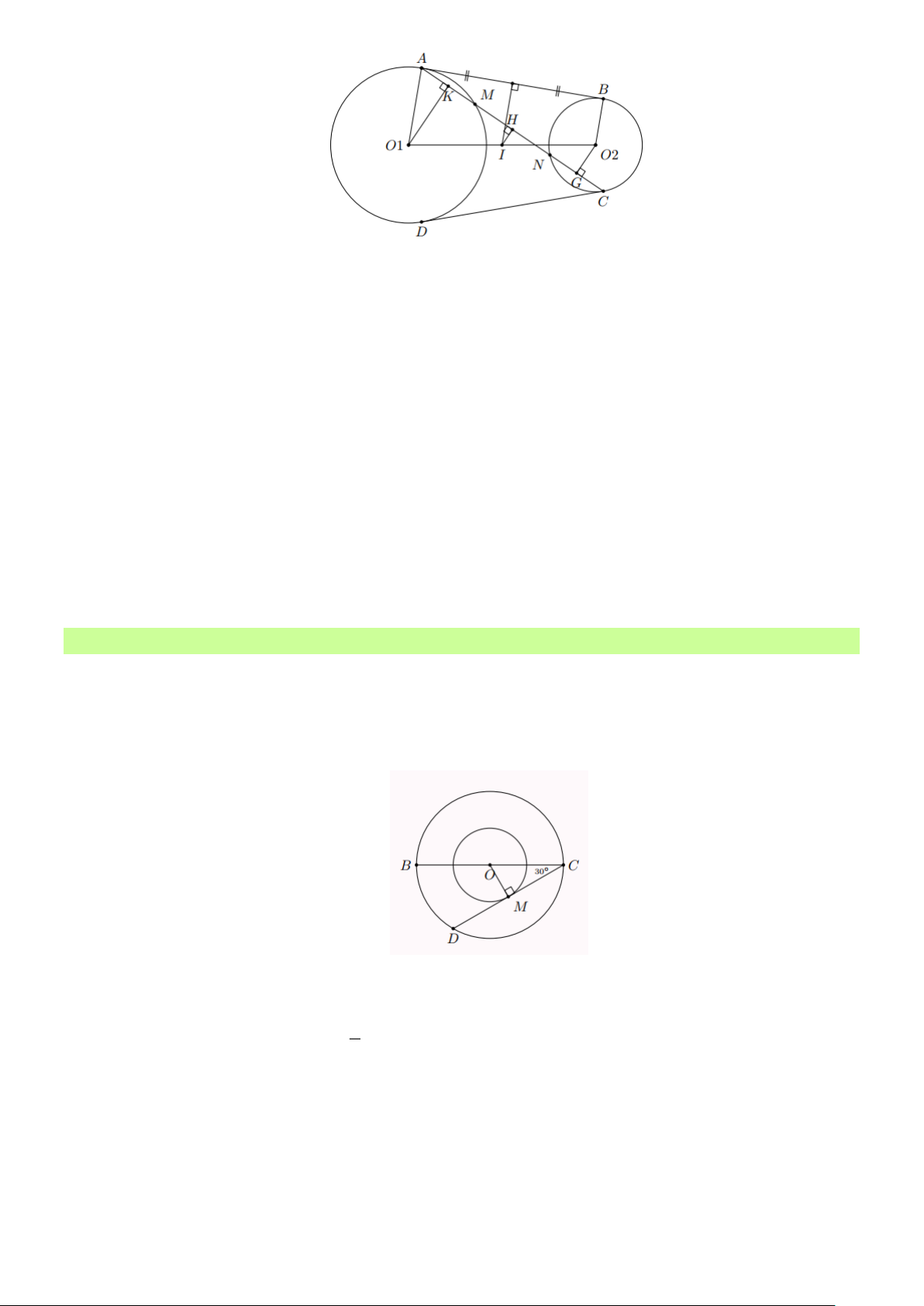
Bài 1: Cho hai đường tròn (O; R) và (O ; R) tiếp xúc ngoài tại A . Kẻ tiếp tuyến chung ngoài
BC , B (O) , C (O) . Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC tại I . Chứng minh rằng: a) OIO = 90 b) BC = 2 RR Lời giải Trang 15
a) Ta có IB , IA là hai tiếp tuyến của (O) nên I = I 1 2
IC , IA là hai tiếp tuyến của (O) nên I = I 3 4
Suy ra OIO = I + I = 180 : 2 = 90 3 4
b) Ta có IB , IA là hai tiếp tuyến của (O) nên IB = IA và IA ⊥ OA với IC , IA là hai tiếp
tuyến của (O) nên IC = IA và IA ⊥ OA. Suy ra IA = IB = IC Ba điểm O, ,
A O thẳng hàng và IA ⊥ OO . Áp dụng hệ thức 2
h = b c vào tam giác vuông OIO Ta có 2
IA = OAOA IA = R R
Mặt khác BC = IB + IC = 2IA nên BC = 2 R R
Bài 2: Cho hai đường tròn (O) và (O) cắt nhau tại A và B , trong đó O\prime nằm trên đường
tròn (O) . Kẻ đường kính OC của đường tròn (O) .
a) Chứng minh rằng CA , CB là hai tiếp tuyến của (O)
b) Đường vuông góc với AO cắt CB tại I . Đường vuông góc với AC tại C cắt đường
thẳng OB ở K . Chứng minh rằng ba điểm O , I , K thẳng hàng. Lời giải
a) Tam giác CAO có đường trung tuyến AO ứng với cạnh CO bằng nửa cạnh CO nên CAO = 90
Mà A(O) nên CA là tiếp tuyến của (O) tại A
Tương tự ta có CB là tiếp tuyến của (O) .
b) Theo tính chất hai tiếp tuyến cắt nhau thì C = C (1) 1 2 Trang 16
Ta có CA//IO (cùng vuông góc với OA ) nên C = O (2) 1 1
Từ (1) và (2) suy ra C = O . Do đó, IC = IO (3) 2 1
Theo tính chất hai tiếp tuyến cắt nhau thì COB = O 2
Mặt khác CK // AO (cùng vuông góc với AC) nên OCK = O 2
Suy ra COB = OCK . Do đó KC = KO (4)
Mà OC = OO (vì O , C cùng thuộc (O) ) (5)
Từ (3) , (4) , (5) suy ra O, I, K cùng thuộc đường trung trực của CO
Vậy ba điểm O , I , K thẳng hàng.
Bài 3: Cho hai đường tròn (O ; R và (O ; R (với R R ) tiếp xúc ngoài tại A . Kẻ các tiếp 2 2 ) 1 1 ) 1 2
tuyến chung ngoài BC và DE (với B , D thuộc (O ; C, E thuộc (O ). Chứng minh 2 ) 1 )
rằng: BC + DE = BD + CE Lời giải
Vẽ tiếp tuyến chung tại A lần lượt cắt BC , DE tại M và N . Vì MA , MB là tiếp tuyến
của (O nên MA = MB . 1 ) Vì M ,
A MC là tiếp tuyến của (O nên MA = MC MA = MB = MC 2 )
Chứng minh tương tự ta có NA = ND = NE BC + DE = 2MN ( ) 1
Gọi giao điểm của BC và DE là K , khi đó K thuộc đường thẳng O O KB = KD (tính 1 2
chất hai tiếp tuyến cắt nhau)
Mà O B = O D = R nên O K là trung trực của đoạn BC suy ra O O ⊥ BD 1 1 1 1 1 2
Chứng minh tương tự ta được O O ⊥ CE 1 2
Suy ra tứ giác BCDE là hình thang (BD//CE)
Vì M , N lần lượt là trung điểm của BC và DE nên 2MN = BD + CE (2)
Từ (1) và (2) suy ra BC + DE = BD + CE .
Bài 4: Cho hai đường tròn (O và (O ngoài nhau. Vẽ các tiếp tuyến chung ngoài AB và CD 2 ) 1 )
(với A , D thuộc (O ; B , C thuộc (O ). Nối AC với (O tại M ; cắt (O tại N với 2 ) 1 ) 2 ) 1 ) (M ,
A N C ) . Chứng minh rằng AM = NC . Lời giải Trang 17
Vẽ đường trung trực d của đoạn AB , d cắt O O tại I . Khi đó IA = IB 1 2
Ta có B và C đối xứng nhau qua O O nên IB = IC IA = IC 1 2
Kẻ IH ⊥ AC tại K , O G ⊥ AC tại G O K //IH //O G 2 1 2
Xét hình thang ABO O (vì O A//O G do cùng vuông góc với 2 1 1 2 AB)
Ta có d //O A//O B và d đi qua trung điểm của AB nên d đi qua trung điểm của O O hay 1 2 1 2
I là trung điểm của O O 1 2
Xét hình thang KGO O có IH //O K //O G và I là trung điểm của O O nên H là trung 2 1 1 2 1 2 điểm của KG
HK = HG HA − HK = HC − HG hay AG = GC 2AK = 2CG AM = AN
* Lưu ý: Trong bài toán ta đã sử dụng tính chất đường thẳng song song với hai đáy của
hình thang và đi qua trung điểm của một đường chéo thì đi qua trung điểm của đường chéo còn lại.
Dạng 5: Tính độ dài đoạn thẳng
Bài 1: Trong hình vẽ, cho hai đường tròn đồng tâm O . Cho biết BC là đường kính của đường
tròn lớn và độ dài bằng 8. Dây CD là tiếp tuyến của đường tròn nhỏ và BCD = 30 . Hãy
tính bán kính của đường tròn nhỏ. Lời giải
Ta có BC = 8 nên bán kính đường tròn lớn là OC = 4 .
Vì CD là tiếp tuyến của đường tròn nhỏ, nên CD ⊥ OM Do đó 1
OM = OC sin 30 = 4 = 2 . 2
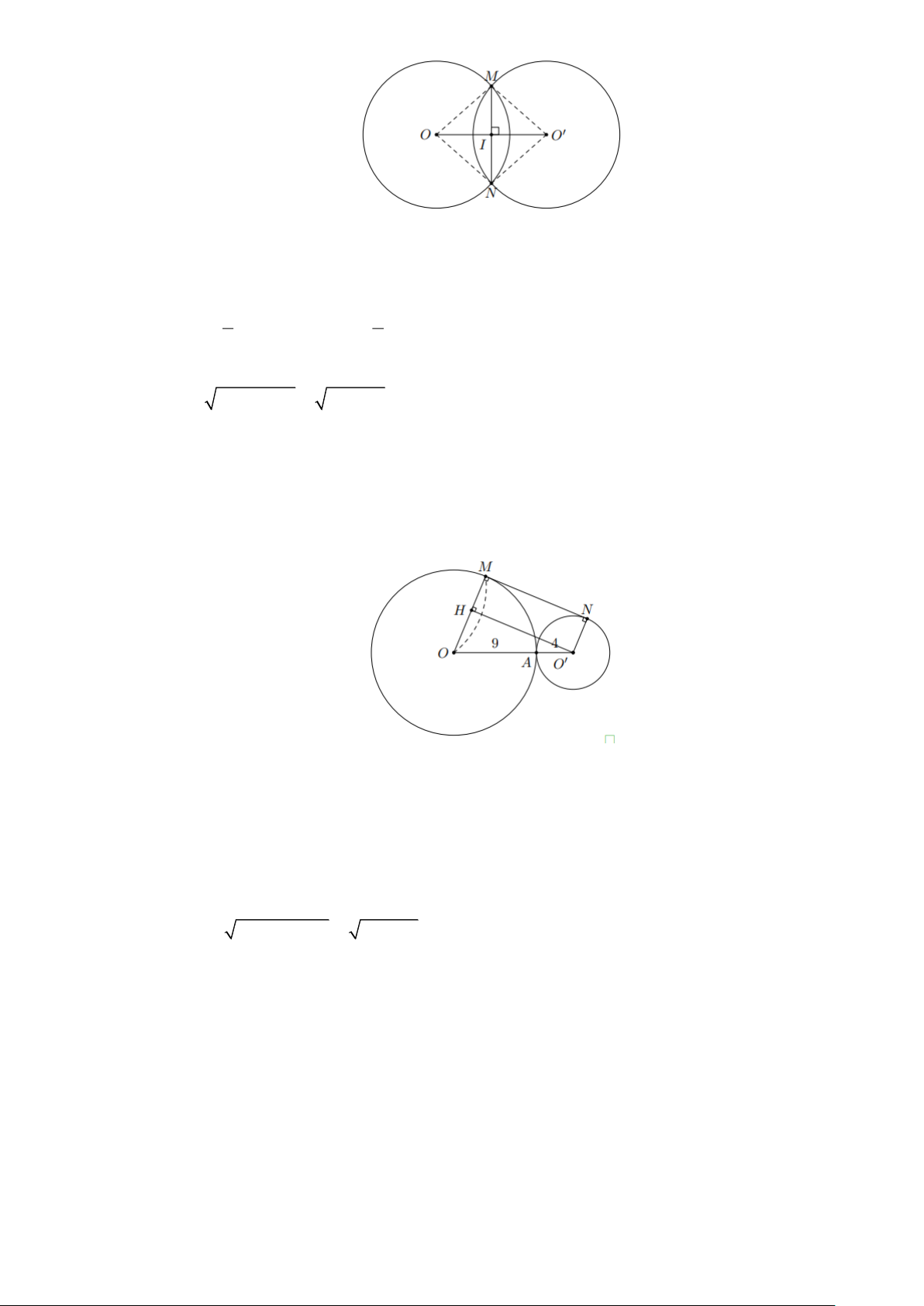
Bài 2: Cho hai đường tròn (O; R) và (O ; R) cắt nhua tại M và N . Biết OO = 24cm ,
MN = 10cm . Tính R . Lời giải Trang 18
Gọi giao điểm của OO và MN là I .
Vì OM = ON = OM = ON = R nên tứ giác OMON là hình thoi
Suy ra OO ⊥ MN tại điểm I là trung điểm của mỗi đoạn OO và MN Do đó 1 IM = MN = 5cm , 1
IO = OO = 12cm 2 2
Áp dụng định lí pythagore vào tam giác MIO , ta có: 2 2 2 2
R = OM = IM + IO = 5 +12 = 13cm Vậy R = 13cm .
Bài 3: Cho hai đường tròn (O; R) và (O ; R) tiếp xúc ngoài tại A . Kẻ tiếp tuyến chung ngoài
MN với M thuộc (O) , N thuộc (O) . Biết R = 9cm , R = 4cm . Tính độ dài đoạn MN . Lời giải
Ta có OO = OA + OA = 9 + 4 = 13cm
Kẻ OH ⊥ OM tại H
tứ giác ONMH là hình chữ nhật
MH = ON = 4cm; MN = OH
OH = OM − MH = 9 − 4 = 5cm
Áp dụng định lí pythagore vào OOH , ta có: 2 2 2 2
MN = OH = OO − OH = 13 − 5 = 12(cm) Vậy MN = 12(cm) .
Bài 4: Cho hai đường tròn (O;3cm) và (O ;4cm) cắt nhau tại A và B . Qua A kẻ một cát tuyến
cắt (O) tại M (với M A ), cắt (O) tại N ( N A ). Nếu OO = 5cm . Hãy tính giá trị lớn nhất của MN . Lời giải Trang 19
Kẻ OH ⊥ AM tại H , OK ⊥ AN tại K và OI ⊥ OK tại I
HM = HA, KA = KN và tứ giác HOIK là hình chữ nhật
MN = 2HK và KH = OI
Ta có OI OO (đường vuông góc và đường xiên)
MN = 2HK = 2OI 2OO =10cm
Dấu “=” xảy ra OI = OO I O d //OO
Vậy giá trị lớn nhất của MN bằng 10cm khi cát tuyến d song song với OO . Trang 20



