Các dạng toán trắc nghiệm góc lượng giác và công thức lượng giác

Tài liệu gồm 54 trang được biên soạn bởi thầy Nguyễn Bảo Vương, tuyển chọn các câu hỏi và bài tập trắc nghiệm chủ đề góc lượng giác và công thức lượng giác trong chương trình Đại số 10 chương 6;

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

54 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
TOÁN 10
0D6-1
Con
tents
PHẦN A
. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 1. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ ........................................................................................................ 1
DẠNG 2. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN........................................................... 2
PHẦN B. LỜI GIẢI ......................................................................................................................................................... 4
DẠNG 1. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ ........................................................................................................ 4
DẠNG 2. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN........................................................... 5
PHẦN A. CÂU HỎI
DẠNG 1. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ
Câu 1. Số đo theo đơn vị rađian của góc
31
5
là
A.
7
2
. B.
7
4
. C.
2
7
. D.
4
7
.
Câu 2. Cung tròn có số đo là
5
4
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây.
A.
5
. B.
1
5
. C.
1
72
. D.
22
5
.
Câu 3. Cung tròn có số đo là
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây.
A.
30
. B.
45
. C.
90
. D.
1
80
.
Câu 4. Góc
0
6
3 48 '
bằng (với
3
,1416
)
A.
1
,113
. B.
1
,108
. C.
1
,107
. D.
1
,114
.
Câu 5. Góc có số đo
2
5
đổi sang độ là:
A.
0
135 .
B.
0
72 .
C.
0
270 .
D.
0
240 .
Câu 6. Góc có số đo
0
108
đổi ra rađian là:
A.
3
5
. B.
10
. C.
3
2
. D.
4
.
Câu 7. Góc có số đo
9
đổi sang độ là:
A.
0
25 .
B.
0
15 .
C.
0
18 .
D.
0
20 .
Câu 8. Cho
2
2
a k
. Tìm
k
để
1
0 11
a
A.
7
k
. B.
5
k
. C.
4
k
. D.
6
k
.
Câu 9. Một bánh xe có
7
2
răng. Số đo góc mà bánh xe đã quay được khi di chuyển
1
0
răng là:
GÓC VÀ CUNG LƯỢNG GIÁC
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
A.
0
60
. B.
0
30
. C.
0
40
. D.
0
50
.
Câu 10. Đổi số đo góc
0
105
sang rađian.
A.
7
12
. B.
9
12
. C.
5
8
. D.
5
12
.
Câu 11. Số đo góc
0
22 30’
đổi sang rađian là:
A.
5
. B.
8
. C.
7
12
. D.
6
.
Câu 12. Một cung tròn có số đo là
0
45
. Hãy chọn số đo radian của cung tròn đó trong các cung tròn sau
đây.
A.
2
B.
C.
4
D.
3
Câu 13. Góc có số đo
24
đổi sang độ là:
A.
0
7 .
B.
0
7 30 .
C.
0
8 .
D.
0
8 30 .
Câu 14. Góc có số đo
0
120
đổi sang rađian là:
A.
2
3
. B.
3
2
. C.
4
. D.
10
.
DẠNG 2. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN
Câu 15. Một đồng hồ treo tường, kim giờ dài
10,57cm
và kim phút dài
13,34cm
.Trong 30 phút mũi kim
giờ vạch lên cung tròn có độ dài là
A.
2, 78cm
. B.
2, 77cm
. C.
2, 76cm
. D.
2,8cm
.
Câu 16. Cung tròn bán kính bằng
8, 43cm
có số đo
3,85
rad
có độ dài là
A.
32, 46cm
. B.
32, 47cm
. C.
32, 5cm
. D.
32, 45cm
.
Câu 17. Trên đường tròn với điểm gốc là
A
. Điểm
M
thuộc đường tròn sao cho cung lượng giác
AM
có
số đo
60
. Gọi
N
là điểm đối xứng với điểm
M
qua trục
Oy
, số đo cung
AN
là
A.
120
hoặc
240
. B.
120 360 ,k k
.
C.
120
. D.
240
.
Câu 18. Trong 20 giây bánh xe của xe gắn máy quay được 60 vòng.Tính độ dài quãng đường xe gắn máy
đã đi được trong vòng 3 phút,biết rằng bán kính bánh xe gắn máy bằng
6,5cm
(lấy
3,1416
)
A.
22043cm
. B.
. C.
. D.
.
Câu 19. Trên đường tròn bán kính
15
r
, độ dài của cung có số đo
0
50
là:
A.
180
15.l
. B.
15
.
180
l
C.
180
15. .50
l
. D.
750
l
.
Câu 20. Cho bốn cung (trên một đường tròn định hướng):
5 25 19
, , ,
6 3 3 6
, Các cung
nào có điểm cuối trùng nhau:
A.
và
;
và
. B.
, ,
. C.
, ,
.
D.
và
;
và
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
Câu 21. Cho
L
,
M
,
N
,
P
lần lượt là điểm chính giữa các cung
A
B
,
BC
,
CD
,
D
A
. Cung
có mút đầu
trùng với
A
và số đo
3
4
k
. Mút cuối của
ở đâu?
A.
L
hoặc
N
. B.
M
hoặc
P
. C.
M
hoặc
N
. D.
L
hoặc
P
.
Câu 22. Trên đường tròn bán kính
5
r
, độ dài của cung đo
8
là:
A.
8
l
. B.
8
r
l
. C.
5
8
l
. D. kết quả khác.
Câu 23. Một đường tròn có bán kính
10R
cm
. Độ dài cung
40
o
trên đường tròn gần bằng
A.
1
1cm
. B.
1
3cm
. C.
7
cm
. D.
9
cm
.
Câu 24. Biết một số đo của góc
3
, 2001
2
Ox Oy
. Giá trị tổng quát của góc
,
O
x Oy
là:
A.
3
,
2
Ox
Oy k
. B.
,
2Ox Oy k
.
C.
,
2
O
x Oy k
. D.
,
2
2
Ox Oy k
.
Câu 25. Cung nào sau đây có mút trung với B hoặc B’?
A.
0
0
90 360
a k
. B.
0
0
–90 180
a k
.
C.
2
2
k
. D.
2
2
k
.
Câu 26. Cung
có mút đầu là
A
và mút cuối là
M
thì số đo của
là:
A.
3
2
4
k
. B.
3
2
4
k
. C.
3
4
k
. D.
3
4
k
.
Câu 27. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Trên hình vẽ hai điểm
,M N
biểu diễn các cung
có số đo là:
A.
2
3
x
k
. B.
3
x
k
. C.
3
x
k
. D.
.
3
2
x k
.
Câu 28. Trên đường tròn lượng giác gốc A, cho điểm M xác định bởi sđ
3
AM
þ
. Gọi
1
M
là điểm đối
xứng của M qua trục
O
x
. Tìm số đo của cung lượng giác
1
.AM
þ
A. sđ
1
5
2 ,
3
AM k k
þ
B. sđ
1
2 ,
3
AM k k
þ
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
C. sđ
1
2 ,
3
AM k k
þ
D. sđ
1
,
3
AM k k
þ
Câu 29. Góc lượng giác nào sau đây có cùng điểm cuối với góc
7
4
?
A.
4
. B.
4
. C.
3
4
. D.
3
4
.
Câu 30. Co bao nhiêu điêm
M
trên đương tron đinh hương gôc
A
thoa man
2
6
3
k
AM
,
k
.
A.
6
. B.
4
. C.
3
. D.
8
.
PHẦN B. LỜI GIẢI
DẠNG 1. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ
Câu 1. Chọn B
Ta có
3
15 7
3
15 .
1
80 4
(rađian).
Câu 2. Chọn D
Ta có:
5
4
.1
80 .180 225
a
.
Câu 3. Chọn D
Ta có:
.180 180
a
.
Câu 4. Chọn D
Ta có
0
0
0
0
63,8 3,1416
63 48' 63,8 1,114
180
rad
Câu 5. Chọn B
Ta có:
0
0
2 2.180
72 .
5 5
Câu 6. Chọn A
Ta có:
0
0
0
108 . 3
108 .
180 5
Câu 7. Chọn D
Ta có:
0
0
180
20 .
9 9
Câu 8. Chọn B
+ Để
1
0 11
a
thì
1
9 21
2
5
2 2
k
k
Câu 9. Chọn D
+ 1 bánh răng tương ứng với
0
0
360
5
72
1
0
bánh răng là
0
50
.
Câu 10. Chọn A
0
0
0
105 . 7
105
180 12
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
Câu 11. Chọn B
0
0
0
22 30'.
22 30'
180 8
.
Câu 12. Chọn C
Ta có:
.
180 4
a
.
Câu 13. Chọn B
Ta có:
0
0
180
7 30'.
24 24
Câu 14. Chọn A
Ta có:
0
0
0
120 . 2
120
3
180
.
DẠNG 2. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN
Câu 15. Chọn B
6 giờ thì kim giờ vạch lên 1 cung có số đo nên 30 phút kim giờ vạch lên 1 cung có số đo là
1
1
2
, suy ra độ dài cung tròn mà nó vạch lên là
3
,14
10,57 2,77
12
l R
Câu 16. Chọn A
Độ dài cung tròn là
8
, 43 3,85 32, 4555l R
Câu 17. Chọn C
Ta có:
60AON ,
60MON nên
120AOM . Khi đó số đo cung
AN
bằng
120
.
Câu 18. Chọn D
3 phút xe đi được
3
60
60 540
20
vòng. Độ dài 1 vòng bằng chu vi bánh xe là
2 2 3,1416 6,5 40,8408R
. Vậy quãng đường xe đi được là
540 40,8408 22054,032cm
Câu 19. Chọn C
0
0
. .n 15.50
180 180
r
l
.
Câu 20. Chọn A
C1: Ta có:
4
2
cung
và
có điểm cuối trùng nhau.
8
hai cung
và
có điểm cuối trùng nhau.
C2: Gọi là điểm cuối của các cung
, , ,
Biểu diễn các cung trên đường tròn lượng giác ta có
,B C A D
.
Câu 21. Chọn A
Nhìn vào đường tròn lượng giác để đánh giá.
Câu 22. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
Độ dài cung AB có số đo cung AB bằng n độ:
.
5.
8
l
r n
.
Câu 23. Chọn C
Đổi đơn vị
4
0. 2
4
0
1
80 9
o
độ dài cung
2
20
.10 6,9813 7
9
9
cm cm
.
Câu 24. Chọn D
3
, 2001 2002 2
2 2 2
Ox Oy k
Câu 25. Chọn B
Nhìn vào đường tròn lượng giác để đánh giá.
Câu 26. Chọn B
Ta có
O
M
là phân giác góc
A OB
0
45
MOB
0
135
AOM
góc lượng giác
3
,
2
4
OA OM k
(theo chiều âm).
hoặc
5
, 2
4
OA OM k
(theo chiều dương).
Câu 27.
Lời giai
Chọn C
Câu 28. Chọn C
Vì
1
M
là điểm đối xứng của M qua trục
O
x
nên có 1 góc lượng giác
1
,
3
OA OM
sđ
1
2 ,
3
AM k k
þ
.
Câu 29. Chọn A
Ta có
7
2
4
4
.
Góc lượng giác có cùng điểm cuối với góc
7
4
là
4
.
Câu 30. Chọn C
Có 3 điểm
M
trên đường tròn định hướng gốc
A
thoa man
2
6
3
k
AM
,
k
, ứng với các
giá trị là số dư của phép chia
k
cho 3.
y
x
-
π
3
π
3
-K
M
1
K
H
O
A
M
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
TOÁN 10
0D6-2
Con
tents
PHẦN A
. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 1. XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC ............................................................................................ 1
DẠNG 2. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT .................................................. 2
DẠNG 3. TÍNH GIÁ TRỊ LƯỢNG GIÁC ...................................................................................................................... 3
DẠNG 4. RÚT GỌN BIỂU THỨC LƯỢNG GIÁC ....................................................................................................... 6
PHẦN B. LỜI GIẢI ......................................................................................................................................................... 9
DẠNG 1. XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC ............................................................................................ 9
DẠNG 2. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT ................................................ 10
DẠNG 3. TÍNH GIÁ TRỊ LƯỢNG GIÁC .................................................................................................................... 11
DẠNG 4. RÚT GỌN BIỂU THỨC LƯỢNG GIÁC ..................................................................................................... 15
PHẦN A. CÂU HỎI
DẠNG 1. XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC
Câu 1. Cho
2
a
. Kết quả đúng là
A.
s
in 0
a
,
c
os 0
a
. B.
s
in 0
a
,
c
os 0
a
. C.
s
in 0
a
,
c
os 0
a
. D.
s
in 0
a
,
c
os 0
a
.
Câu 2. Trong các giá trị sau,
sin
có thể nhận giá trị nào?
A.
0
,7
. B.
4
3
. C.
2
. D.
5
2
.
Câu 3. Cho
5
2 .
2
a
Chọn khẳng định đúng.
A.
tan 0, cot 0.
a a
B.
tan 0, cot 0.
a a
C.
tan 0, cot 0.
a a
D.
tan 0, cot 0
a a
.
Câu 4. Ở góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau
đây.
A.
c
ot 0
. B.
si
n 0
. C.
c
os 0
. D.
t
an 0
.
Câu 5. Ở góc phần tư thứ tư của đường tròn lượng giác. hãy chọn kết quả đúng trong các kết quả sau đây.
A.
c
ot 0
. B.
t
an 0
. C.
si
n 0
. D.
c
os 0
.
Câu 6. Cho
7
2
4
.Xét câu nào sau đây đúng?
A.
ta
n 0
. B.
c
ot 0
. C.
c
os 0
. D.
s
in 0
.
Câu 7. Xét câu nào sau đây đúng?
GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT CUNG
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
A.
2
cos 45 sin cos 60
3
.
B. Hai câu A và
C. Nếu
a
âm thì ít nhất một trong hai số
cos ,sina a
phải âm.
D. Nếu
a
dương thì
2
sin 1 cosa a
.
Câu 8. Cho . Kết quả đúng là:
A. ; . B. ; .
C. ; . D. ; .
Câu 9. Xét các mệnh đề sau:
I.
cos 0
2
. II.
sin 0
2
. III.
tan 0
2
.
Mệnh đề nào sai?
A. Chỉ I. B. Chỉ II. C. Chỉ II và III. D. Cả I, II và III.
Câu 10. Xét các mệnh đề sau đây:
I.
cos 0
2
. II.
sin 0
2
. III.
cot 0
2
.
Mệnh đề nào đúng?
A. Chỉ II và III. B. Cả I, II và III. C. Chỉ I. D. Chỉ I và II.
Câu 11. Cho góc lượng giác
2
. Xét dấu
sin
2
và
tan
. Chọn kết quả đúng.
A.
sin 0
2
tan 0
. B.
sin 0
2
tan 0
. C.
sin 0
2
tan 0
. D.
sin 0
2
tan 0
.
DẠNG 2. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT
Câu 12. Cho hai góc nhọn
và
phụ nhau. Hệ thức nào sau đây là sai?
A.
cot tan
. B.
cos sin
. C.
cos sin
. D.
sin cos
.
Câu 13. Trong các đẳng thức sau, đẳng thức nào đúng?
A.
0
sin 180 – – cosa a
. B.
0
sin 180 – sina a
.
C.
0
180 – n
si
i
n
sa a
. D.
0
180 – s
si
o
n c
a a
.
Câu 14. Chọn đẳng thức sai trong các đẳng thức sau
A.
sin cos
2
x x
. B.
sin cos
2
x x
.
C.
tan cot
2
x x
. D.
tan cot
2
x x
.
Câu 15. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
cos cosx x
. B.
sin sinx x
.
2
sin 0
cos 0
sin 0
cos 0
sin 0
cos 0
sin 0
cos 0
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
C.
cos cosx x
. D.
sin cos
2
x x
.
Câu 16. Khẳng định nào sau đây là sai?
A.
sin sin
. B.
cot cot
. C.
cos cos
. D.
tan tan
.
Câu 17. Khẳng định nào sau đây đúng?
A.
sin sin .x x
B.
cos cos .x x
C.
cot cot .x x
D.
tan tan .x x
Câu 18. Chọn hệ thức sai trong các hệ thức sau.
A.
3
tan cot
2
x x
. B.
sin 3 sin x
x
.
C.
cos 3 cos x
x
. D.
cos cosx x
.
Câu 19.
cos( 2017 )
x
bằng kết quả nào sau đây?
A.
cos x
. B.
sin x
. C.
sin x
. D.
cos x
.
DẠNG 3. TÍNH GIÁ TRỊ LƯỢNG GIÁC
Câu 20. Giá trị của
là
A.
1.
B.
1
. C.
0
. D.
5 2 5
.
Câu 21. Giá trị
cot
89
6
là
A.
3
. B.
3
. C.
3
3
. D.
–
3
3
.
Câu 22. Giá trị của
tan180
là
A.
1
. B.
0
. C.
–1
. D. Không xác định.
Câu 23. Cho biết
1
tan
2
. Tính
cot
A.
cot 2
. B.
cot
. C.
cot
. D.
cot 2
.
Câu 24. Cho
3
sin
5
và
2
. Giá trị của
cos
là:
A.
4
5
. B.
4
5
. C.
4
5
. D.
16
25
.
Câu 25. Cho
4
cos
5
với
0
2
. Tính
sin
.
A.
1
sin
5
. B.
1
sin
5
. C.
3
sin
5
. D.
3
sin
5
.
Câu 26.
Tính
biết
cos 1
A.
k k
. B.
2k k
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
C.
2
2
k k
. D.
2k k
.
Câu 27. Cho
4
tan
5
với
3
2
2
. Khi đó:
A.
4
sin
41
,
5
cos
41
. B.
4
sin
41
,
5
cos
41
.
C.
4
sin
41
5
cos
41
. D.
4
sin
41
,
5
cos
41
.
Câu 28. Cho
0
2 3
cos15
2
. Giá trị của
tan15
bằng:
A.
3 2
B.
2 3
2
C.
2 3
D.
2 3
4
Câu 29. Cho
2
cos
5
2
. Khi đó
tan
bằng
A.
21
3
. B.
21
5
. C.
21
5
. D.
21
2
.
Câu 30. Cho
tan 5
, với
3
2
. Khi đó
cos
bằng:
A.
6
6
. B.
6
. C.
6
6
. D.
1
6
.
Câu 31. Cho
3
sin 90 180
5
. Tính
cot
.
A.
cot
. B.
cot
.
C.
4
cot
3
. D.
3
cot
4
.
Câu 32. Trên nửa đường tròn đơn vị cho góc
sao cho
2
sin
3
và
cos 0
. Tính
tan
.
A.
2 5
5
. B.
2 5
5
. C.
2
5
. D.
1
.
Câu 33. Cho
1
sin
3
và
2
. Khi đó
cos
có giá trị là.
A.
2
cos
3
. B.
2 2
cos
3
. C.
8
cos
9
. D.
2 2
cos
3
.
Câu 34. Cho
cot 3 2
với
2
. Khi đó giá trị
tan cot
2 2
bằng:
A.
2 19
. B.
2 19
. C.
19
. D.
19
.
Câu 35. Nếu
3
sin cos
2
thì
sin 2
bằng
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
A.
5
4
. B.
1
2
. C.
13
4
. D.
9
4
.
Câu 36. Cho
1
sin cos
2
x x
và
0
2
x
. Tính giá trị của
sin x
.
A.
1 7
sin
6
x
. B.
1 7
sin
6
x
. C.
1 7
sin
4
x
. D.
1 7
sin
4
x
.
Câu 37. Cho sinx =
1
2
. Tính giá trị của
2
cos x
.
A.
2
3
cos
4
x
B.
2
3
cos
2
x
C.
2
1
cos
4
x
D.
2
1
cos
2
x
Câu 38. Cho
3sin cos
sin 2cos
x x
P
x x
với
tan 2
x
. Giá trị của
P
bằng
A.
8
9
. B.
2 2
3
. C.
8
9
. D.
5
4
.
Câu 39. Cho
1
sinx
2
và cosx nhận giá trị âm, giá trị của biểu thức
sin cos
sin
x x
A
x cox
bằng
A.
2 3
B.
2 3
C.
2 3
D.
2 3
Câu 40. Cho
tan 2
x
.Giá trị biểu thức
4sin 5cos
2sin 3cos
x x
P
x x
là
A.
2
. B.
13
. C.
9
. D.
2
.
Câu 41. Cho tam giác
ABC
đều. Tính giá trị của biểu thức
P cos , cos , cos ,
AB BC BC CA CA AB
.
A.
3
P
2
. B.
3
P
2
. C.
3 3
P
2
. D.
3 3
P
2
.
Câu 42. Cho
tan 2
a
. Tính giá trị biểu thức
2sin cos
sin cos
a a
P
a a
.
A.
2P
. B.
1P
. C.
5
3
P
. D.
1P
.
Câu 43. Cho cung lượng giác có số đo
x
thỏa mãn
tan 2
x
.Giá trị của biểu thức
3
3
sin 3cos
5sin 2cos
x x
M
x x
bằng
A.
7
30
. B.
7
32
. C.
7
33
. D.
7
31
.
Câu 44. Cho
1
sin
2
x
và
cos x
nhận giá trị âm, giá trị của biểu thức
sin cos
sin cos
x x
A
x x
bằng
A.
2 3
. B.
2 3
. C.
2 3
. D.
2 3
.
Câu 45. Giá trị của biểu thức
0 0
0 0
cos750 sin 420
sin 330 cos 390
A
bằng
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
A.
3 3
. B.
2 3 3
. C.
2 3
3 1
. D.
1 3
3
.
Câu 46. Cho
3
sin
5
và
0 0
90 180
. Giá trị của biểu thức
cot 2 tan
tan 3cot
E
là:
A.
2
57
. B.
2
57
. C.
4
57
. D.
4
57
.
Câu 47. Cho
tan 2
. Giá trị của
3sin cos
sin cos
A
là:
A.
5
. B.
5
3
. C.
7
. D.
7
3
.
Câu 48. Giá trị của
2 2 2 2
3 5 7
A cos cos cos cos
8 8 8 8
bằng
A.
0
. B.
1
. C.
2
. D.
1
.
Câu 49. Rút gọn biểu thức
0 0
0
0 0
sin 234 cos 216
.tan36
sin144 cos126
A
, ta có
A
bằng
A.
2
. B.
2
. C.
1
. D.
1
.
Câu 50. Biểu thức
0 0 0
0 0
0
cot 44 tan 226 .cos406
cot 72 .cot18
cos316
B
có kết quả rút gọn bằng
A.
1
. B.
1
. C.
1
2
. D.
1
2
.
Câu 51. Biết
tan 2
và
180 270
. Giá trị
cos sin
bằng
A.
3 5
5
. B. 1–
5
. C.
3 5
2
. D.
5 1
2
.
Câu 52. Cho biết
1
cot
2
x
. Giá trị biểu thức
2 2
2
sin sin .cos cos
A
x x x x
bằng
A. 6. B. 8. C. 10. D. 12.
DẠNG 4. RÚT GỌN BIỂU THỨC LƯỢNG GIÁC
Câu 53. Trong các công thức sau, công thức nào sai?
A.
2 2
sin cos 1
. B.
2
2
1
1 tan ,
cos 2
k k
.
C.
2
2
1
1 cot ,
sin
k k
. D.
tan cot 1 ,
2
k
k
.
Câu 54. Biểu thức rút gọn của A =
2 2
2 2
tan sin
cot cos
a a
a a
bằng:
A.
6
tan a
. B.
6
cos a
. C.
4
tan a
. D.
6
sin a
.
Câu 55. Biểu thức
2 2 2 2 2
cos .cot 3cos – cot 2sinD x x x x x
không phụ thuộc
x
và bằng
A. 2. B.
–2
. C. 3. D.
–3
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
Câu 56. Biểu thức
0 0 0 0
0
0
sin 328 .sin 958 cos 508 .cos 1022
cot572
tan 212
A
rút gọn bằng:
A.
1
. B.
1
. C.
0
. D.
2
.
Câu 57. Biểu thức
0 0 0 0
0 0 0 0
sin 515 .cos 475 cot 222 .cot 408
cot 415 .cot 505 tan197 .tan 73
A
có kết quả rút gọn bằng
A.
2 0
1
sin 25
2
. B.
2 0
1
cos 55
2
. C.
2 0
1
cos 25
2
. D.
2 0
1
sin 65
2
.
Câu 58. Đơn giản biểu thức
2
2cos 1
sin cos
x
x
A
x
ta có
A.
cos sinA x x
. B.
cos – sinA x x
. C.
sin – cosA x x
. D.
sin – cosA x x
.
Câu 59. Biết
sin co
2
2
s
. Trong các kết quả sau, kết quả nào sai?
A.
sin .cos –
1
4
. B.
sin co
6
2
s
.
C.
4 4
7
sin cos
8
. D.
2 2
tan cot 12
.
Câu 60. Biểu thức:
2003
cos 26 2sin 7 cos1,5 cos cos 1,5 .cot 8
2
A
có
kết quả thu gọn bằng:
A.
sin
. B.
sin
. C.
cos
. D.
cos
.
Câu 61. Đơn giản biểu thức
2 2 2
1– sin .cot 1– cot ,A x x x
ta có
A.
2
sinA x
. B.
2
cosA x
. C.
2
–sinA x
. D.
2
– cosA x
.
Câu 62. Đơn giản biểu thức
A cos sin cos sin
2 2 2 2
, ta có:
A.
2sinA a
. B.
2cosA a
. C.
sin – cosA a a
. D.
0
A
.
Câu 63. Biểu thức
3
sin cos cot 2 tan
2 2
P x x x x
có biểu thức rút gọn là
A.
2sinP x
. B.
2sinP x
. C.
0
P
. D.
2cotP x
.
Câu 64. Cho tam giác
ABC
. Đẳng thức nào sau đây sai?
A.
A B C
. B.
cos cosA B C
. C.
sin cos
2 2
A B C
. D.
sin sinA B C
.
Câu 65. Đơn giản biểu thức
A cos sin
2
, ta có
A.
s n
cos
iA a a
. B.
2sinA a
. C.
os
sin c–
A a a
. D.
0
A
.
Câu 66. Cho A, B, C là ba góc của một tam giác không vuông. Mệnh đề nào sau đây sai?
A.
tan cot
2 2
A B C
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
B.
cot tan
2 2
A B C
.
C.
cot cotA B C
.
D.
tan tanA B C
.
Câu 67. Tính giá trị của biểu thức
6 6 2 2
sin cos 3sin cosA x x x
x
.
A.
–1A
. B.
1A
. C.
4A
. D.
–4A
.
Câu 68. Biểu thức
2
2
2 2 2
1 tan
1
4 tan 4sin cos
x
x x x
A
không phụ thuộc vào
x
và bằng
A.
1
. B.
–1
. C.
1
4
. D.
1
4
.
Câu 69. Biểu thức
2 2
2 2
2 2
cos sin
cot .cot
sin .sin
x y
B x y
x y
không phụ thuộc vào
, x y
và bằng
A.
2
. B.
–2
. C.
1
. D.
–1
.
Câu 70. Biểu thức
2
4 4 2 2 8 8
2 sin cos sin cos – sin cos
C x x x x x x
có giá trị không đổi và bằng
A.
2
. B.
–2
. C.
1
. D.
–1
.
Câu 71. Hệ thức nào sai trong bốn hệ thức sau:
A.
tan tan
tan .tan
cot cot
x y
x y
x y
. B.
2
2
1 sin 1 sin
4 tan
1 sin 1 sin
a a
a
a a
.
C.
2
2
sin cos 1 cot
cos sin cos sin 1 cot
. D.
sin cos 2cos
1 cos sin cos 1
.
Câu 72. Nếu biết
4 4
98
3sin 2cos
81
x x
thì giá trị biểu thức
4 4
2sin 3cosA x x
bằng
A.
101
81
hay
601
504
. B.
103
81
hay
603
405
. C.
105
81
hay
605
504
. D.
107
81
hay
607
405
.
Câu 73. Nếu
1
sin cos
2
x x
thì
3sin 2cosx x
bằng
A.
5 7
4
hay
5 7
4
. B.
5 5
7
hay
5 5
4
.
C.
2 3
5
hay
2 3
5
. D.
3 2
5
hay
3 2
5
.
Câu 74. Biết
2
tan
b
x
a c
. Giá trị của biểu thức
2 2
cos 2 sin .cos sinA a x b x x c x
bằng
A.
–a
. B.
a
. C.
–b
. D.
b
.
Câu 75. Nếu biết
4 4
sin cos 1
a b a b
thì biểu thức
8 8
3 3
sin cos
A
a b
bằng
A.
2
1
a b
. B.
2 2
1
a b
. C.
3
1
a b
. D.
3 3
1
a b
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
Câu 76. Với mọi , biểu thức:
9
cos +cos ... cos
5 5
A
nhận giá trị bằng:
A.
–10
. B.
10
. C.
0
. D.
5
.
Câu 77. Giá trị của biểu thức
2 2 2 2
3 5 7
sin sin sin sin
8 8 8 8
A
bằng
A.
2
. B.
2
. C.
1
. D.
0
.
Câu 78. Giá trị của biểu thức A =
0 0
0 0 0
2sin 2550 .cos 188
1
tan368 2cos638 cos98
bằng:
A.
1
. B.
2
. C.
1
. D.
0
.
Câu 79. Cho tam giác ABC và các mệnh đề:
I cos sin
2 2
B C A
II tan .tan 1
2 2
A B C
III cos – – cos 2 0
A B C C
Mệnh đề đúng là:
A. Chỉ
I
. B.
II
và
III
. C.
I
và
II
. D. Chỉ
III
.
Câu 80. Rút gọn biểu thức
3
cos sin tan .sin 2
2 2
A
ta được
A.
cos
A
. B.
cos
A
. C.
A
. D.
3cos
A
.
PHẦN B. LỜI GIẢI
DẠNG 1. XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC
Câu 1. Chọn C
Vì
2
a
sin 0
a
,
cos 0
a
.
Câu 2. Chọn A.
Vì
1 sin 1
. Nên ta chọn A.
Câu 3. Chọn C
Đặt
2
a b
5
2
2
a
5
2 2
2
b
0
2
b
Có
tan tan( 2 ) tan 0
a b b
1
cot 0
tan
a
a
.
Vậy
tan 0, cot 0
a a
.
Câu 4. Chọn B
Nhìn vào đường tròn lượng giác:
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
-Ta thấy ở góc phần tư thứ nhất thì:
sin 0;cos 0;tan 0;cot 0
=> chỉ có câu A thỏa mãn.
Câu 5. Chọn D
- Ở góc phần tư thứ tư thì:
sin 0;cos 0;tan 0;cot 0
.
chỉ có C thỏa mãn.
Câu 6. Chọn C
7 3
2 2
4 2 4
nên α thuộc cung phần tư thứ IV vì vậy đáp án đúng là A
Câu 7. Chọn A
A sai vì
7
4
nhưng
2
sin cos = 0
2
.
B sai vì
5
4
nhưng
2
sin 0
2
.
C đúng vì
2
1 1
cos 45 ,sin cos60 sin
2 3 6 2
Câu 8.
Hướng dẫn giải
Chọn A
Vì nên
Câu 9. Chọn C
0
2 2
nên α thuộc cung phần tư thứ IV nên chỉ II, II sai.
Câu 10. Chọn B
3
2 2 2
nên đáp án là D
Câu 11. Chọn C
Ta có
3
cos 0
2 2
2
2
tan 0
2
.
DẠNG 2. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT
Câu 12. Chọn D
2
tan 0; cot 0
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
Thường nhớ: các góc phụ nhau có các giá trị lượng giác bằng chéo nhau
Nghĩa là
cos sin
;
cot tan
và ngược lại.
Câu 13. Chọn C.
Theo công thức.
Câu 14. Chọn D.
Câu 15. Chọn C
Ta có
cos cosx x
.
Câu 16. Chọn C
Dễ thấy C sai vì
cos cos
.
Câu 17. Chọn A
Ta có:
sin sin x x
.
Câu 18. Chọn C
cos 3 cos cosx x
x
.
Câu 19. Chọn A
Ta có
cos 2017
x
cos x
.
DẠNG 3. TÍNH GIÁ TRỊ LƯỢNG GIÁC
Câu 20. Chọn D
cot1458 cot 4.360 18 cot18 5 2 5
.
Câu 21. Chọn B
Biến đổi
89
cot 15 cot cot 3
c
6
o
6 6
t
6
.
Câu 22. Chọn B
Biến đổi
tan180 tan 0 180 tan0 0
.
Câu 23. Chọn A
Ta có:
tan .cot 1
1 1
cot 2
1
tan
2
.
Câu 24. Chọn B.
Ta có:
2 2
sin cos 1
2 2
9 16
cos =1 sin 1
25 25
4
cos
5
4
cos
5
.
Vì
2
4
cos
5
.
Câu 25. Chọn C
Ta có:
2
2 2
4 9
sin 1 cos 1
5 25
3
sin
5
.
Do
0
2
nên
sin 0
. Suy ra,
3
sin
5
.
Câu 26.
Chọn C
Ta có:
cos 1
2
2
k
k
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
Câu 27.
Chọn C
2
2
1
1 tan
cos
2
16 1
1
25 cos
2
1 41
cos 25
2
25
cos
41
5
cos
41
2 2
25 16
sin 1 cos 1
41 41
4
sin
41
3
2
2
5
cos 0 cos
41
4
sin 0 sin
41
.
Câu 28.
Chọn C
2
2 0
2 0
1 4
tan 15 1 1 2 3
cos 15
2 3
0
tan15 2 3
.
Câu 29. Chọn D
Với
2
tan 0
.
Ta có
2
2
1
1 tan
cos
2
2
1
tan 1
cos
25 21
1
4 4
21
tan
2
.
Câu 30. Chọn A
Ta có
2
2
1
1 tan
cos
2
1 5 6
.
Mặt khác
3
2
nên
6
cos
6
.
Câu 31. Chọn C
Ta có:
2
2
1
1 cot
sin
2
16
cot
9
4
cot
3
.
Vì
90 180
nên
4
cot
3
.
Câu 32. Chọn A
Có
2 2
cos 1 sin
, mà
2
sin
3
.
Suy ra
2
5
cos
9
, có
cos 0
5
cos
3
.
Có
sin 2 5
tan
cos 5
.
Câu 33. Chọn D
Vì
2
nên
0
cos
.
Ta có
2 2 2 2
8
sin 1 1 sin
9
cos co s
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
8 2 2
cos
9 3
8 2 2
cos
9 3
l
tm
Câu 34.
Chọn A
2
2
1
1 cot 1 18 19
sin
2
1
sin
19
1
sin
19
Vì
2
sin 0
1
sin
19
Suy ra
2 2
sin cos
2
2 2
tan cot 2 19
2 2 sin
sin cos
2 2
.
Câu 35. Chọn A
Ta có:
2
3 9 9 5
sin cos sin cos 1 sin 2 sin 2
2 4 4 4
.
Câu 36. Chọn C
Từ
1 1
sin cos cos sin (1)
2 2
x x x x
.
Mặt khác:
2 2
sin cos 1 (2)
x x . Thế
(1)
vào
(2)
ta được:
2
2 2
1 7
sin
1 3
4
sin sin 1 2sin sin 0
2 4
1 7
sin
4
x
x x x x
x
Vì
1 7
0 sin 0 sin
2 4
x x x
.
Câu 37. Chọn A
Ta có:
2 2
1 3
cos 1 sin 1 .
4 4
x x
Câu 38. Chọn D
Ta có
3sin cos 3tan 1 3.2 1 5
sin 2cos tan 2 2 2 4
x x x
P
x x x
.
Câu 39. Chọn A
Vì cosx nhận giá trị âm.
Ta có:
2
1 3
cos 1 sin 1
4 2
x x
Suy ra:
1 3
1 3
2 2
2 3
1 3 1 3
2 2
A
Câu 40. Chọn C
Ta có:
tan 2 cos 0
x x
.Chia tử và mẫu cho
cos x
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
Suy ra:
4sin 5cos 4 tan 5 4.2 5
13
2sin 3cos 2 tan 3 2.2 3
x x x
P
x x x
.
Câu 41. Chọn B
Ta có:
0
3
P cos , cos , cos , 3cos120
2
AB BC BC CA CA AB
Câu 42. Chọn B
Ta có:
2sin cos 2tan 1 2.2 1
1
sin cos tan 1 2 1
a a a
P
a a a
.
Câu 43. Chọn A
Do
tan 2 cos 0
x x
.
Ta có
3
2
3
3
2
1
tan . 3
sin 3cos
cos
2
5sin 2cos
5tan
cos
x
x x
x
M
x x
x
x
2
3 2
tan 1 tan 3
7
30
5tan 2 1 tan
x x
x x
.
Câu 44. Chọn A
Vì
cos x
nhận giá trị âm nên ta có
2
1 3
cos 1 sin 1
4 2
x x
Suy ra:
1 3
1 3
2 2
2 3
1 3 1 3
2 2
A
.
Câu 45. Chọn A.
0 0
0 0
cos30 sin 60 2 3
3 3
sin 30 cos30
1 3
A
.
Câu 46. Chọn B.
2 2
sin cos 1
2 2
9 16
cos =1 sin 1
25 25
4
cos
5
4
cos
5
Vì
0 0
90 180
4
cos
5
. Vậy
3
tan
4
và
4
cot
3
.
4 3
2.
cot 2 tan 2
3 4
3 4
tan 3cot 57
3.
4 3
E
.
Câu 47. Chọn C.
3sin cos 3tan 1
7
sin cos tan 1
A
.
Câu 48. Chọn C.
2 2 2 2
3 3
cos cos cos cos
8 8 8 8
A
2 2
3
2 cos cos
8 8
A
2 2
2 cos sin 2
8 8
A
.
Câu 49. Chọn C.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
0 0
0
0 0
sin 234 sin126
.tan 36
cos54 cos126
A
0 0
0
0 0
2cos180 .sin 54
.tan36
2sin 90 sin 36
A
0 0
0
0
1.sin 54 sin 36
.
cos36
1sin 36
A
1
A
.
Câu 50. Chọn B.
0 0 0
0 0
0
cot 44 tan 46 .cos 46
cot 72 .tan 72
cos44
B
0 0
0
2cot 44 .cos46
1
cos44
B
2 1 1
B
.
Câu 51. Chọn A
Do
180 270
nên
sin 0
và
cos 0
. Từ đó
Ta có
2
2
1
1 tan 5
cos
2
1
cos
5
1
cos
5
.
1 2
sin tan .cos 2.
5 5
Như vậy,
2 1 3 5
cos sin
5
5 5
.
Câu 52. Chọn C
2
2
2 2 2 2
1
2
2 1
2 1 cot
2
4
sin
10.
1 1
sin sin .cos cos 1 cot cot 1 cot cot
1
2 4
x
x
A
x x x x x x x x
DẠNG 4. RÚT GỌN BIỂU THỨC LƯỢNG GIÁC
Câu 53. Chọn D
D sai vì:
tan .cot 1 ,
2
k
k
.
Câu 54. Chọn A
2 2
2 2
tan sin
cot cos
a a
A
a a
2
2 2
2
6
2
2
2
1
sin 1
tan .tan
cos
tan
1
cot
cos 1
sin
a
a a
a
A a
a
a
.
Câu 55. Chọn A
2 2 2 2 2
cos .cot 3cos – cot 2sinD x x x x x
2 2 2
cos 2 cot cos 1
x x x
2 2 2
cos 2 cot .sinx x x
2 2
cos 2 cos 2
x x
.
Câu 56. Chọn A
0 0 0 0
0
0
sin 328 .sin 958 cos 508 .cos 1022
cot572
tan 212
A
0 0 0 0
0 0
sin 32 .sin 58 cos32 .cos58
cot32 tan32
A
0 0 0 0
2 0 2 0
0 0
sin 32 .cos32 cos32 .sin 32
sin 32 cos 32 1.
cot32 tan 32
A
Câu 57. Chọn C.
0 0 0 0
0 0 0 0
sin155 .cos115 cot 42 .cot 48
cot55 .cot 145 tan17 .cot17
A
0 0 0 0
0 0
sin 25 . sin 25 cot 42 .tan 42
cot55 .tan 55 1
A
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
2 0
sin 25 1
2
A
2 0
cos 25
2
A .
Câu 58. Chọn B
Ta có
2 2 2
2 2 2
2cos sin cos
2cos 1 cos sin
sin cos sin cos sin os
c
x x x
x x x
x x x x
A
x x
cos sin cos sin
cos sin
sin cos
x x x x
x x
x x
Như vậy,
cos – sinA x x
.
Câu 59. Chọn D
Ta có
sin co
2
2
s
2
sin co
1
2
s
1
1 2sin cos
2
1
sin cos
4
2
1 6
sin cos 1 2sin cos 1 2
4 4
6
sin cos
2
2
2
4 4 2 2 2 2
1 7
sin cos sin cos 2sin cos 1 2
4 8
4 4
2 2
2
2 2
7
sin cos
8
tan cot 14
sin cos
1
4
Như vậy,
2 2
tan cot 12
là kết quả sai.
Câu 60. Chọn B
cos 26 2sin 7 cos 1,5 cos 2003 cos 1,5 .cot 8
2
A
cos 2sin cos cos( cos .cot
2 2 2
A
cos 2sin 0 sin sin .cot cos sin cos sin .
A
Câu 61. Chọn A
2 2 2
1– sin .cot 1– cotA x x x
2 2 2
cot cos 1 cotx x x
2
sin x
.
Câu 62. Chọn A.
sin cos sin cos
A
2sin
A
.
Câu 63. Chọn B
3
sin cos cot 2 tan sin sin cot cot 2sin .
2 2
P x x x x x x x x x
Câu 64. Chọn B
Xét tam giác
ABC
ta có:
A B C A B C
.
cos cos cosA B C C
.
Câu 65. Chọn D.
cos sin
2
A
sin sin 0
A
.
Câu 66. Chọn D
Do A,B,C là ba góc của một tam giác nên
A B C A B C
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
tan tan cot
2 2 2 2
A B C C
.
cot cot tan
2 2 2 2
A B C C
.
cot cot cotA B C C
.
tan tan tan tanA B C C C
. Chọn D
Trong tam giác
ABC
ta có
A B C A B C
Do đó
tan tan tanA B C C
.
Câu 67. Chọn B
Ta có
3 3
6 6 2 2 2 2 2 2
sin cos 3sin cos sin cos 3sin cosA x x x x x x x
x
2
3
2 2 2 22 2 2
sin cos 3 3sin .cos si sin coscos
1
nx xx xx x
x x
.
Câu 68. Chọn B
Ta có
2 2
2 2
2
2 2 2 2 2 2
1 tan 1 tan
1 1 1
4 tan 4sin cos 4 tan 4 tan cos
x x
x x x x x x
A
2 2 2 2
2 2 2 2
2 2 2
1 tan 1 tan 1 tan 1 tan
4 tan 4tan 4tan
x x x x
x x x
2
2
4 tan
1
4 tan
x
x
.
Câu 69. Chọn D
Ta có
2 2 2 2 2 2
2 2
2 2 2 2 2 2
cos sin cos sin cos .cos
cot .cot
sin .sin sin sin sin .sin
x y x y x y
B x y
x y x y x y
2 2 2 2 2
2 2 2
2 2 2 2
2 2
cos 1 cos sin sin cos 1
cos sin sin
1
sin sin sin sin
1 cos sin
x y y y x
x y y
x y x y
x y
.
Câu 70. Chọn C
Ta có
2
4 4 2 2 8 8
2 sin cos sin cos – sin cos
C x x x x x x
2
2 2
42 2 42 2 4 4
2 sin cos sin cos – 2ss in cosin cosx x xx x x x
x
22
2 2
2
2 2 4 42 2
2 1 sin cos – sin co
sin cos 2sin cos
s 2x x x x xx x
x
2
2
2
2 42 42
1 sin2 1 sin
cos 2sin cos
cos – 2 x xx
x x
x
4 4 2 2 4 4 42 2 4
2 sin cos 1 sin cos 4sin cos 2sin cos
1
2 1 sin cos – 4x x xx x xx
x x x
.
Câu 71. Chọn D
A đúng vì
tan tan
tan .tan
1 1
tan tany
x y
VT x y VP
x
B đúng vì
2 2
2
2
2 2
1 sin 1 sin
1 sin 1 sin 2 2sin
2 2 2 4 tan
1 sin 1 sin 1 sin cos
a a
a a a
VT a VP
a a a a
C đúng vì
2 2 2 2 2
2 2 2 2 2
sin cos sin cos 1 cot
cos sin sin cos 1 cot
VT VP
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
Câu 72. Chọn D
Ta có
4 4
98
sin cos
81
x x A
98
cos2
81
x A
4 4
98
5 sin cos
81
x x A
2
1 1 98
1 sin 2
2 5 81
x A
2
1 1 1 98
cos 2
2 2 5 81
x A
2
98 2 98 2 98 392
81 5 81 5 81 405
A A A
Đặt
98
81
A t
2
2 13
0
5 405
t t
13
45
1
9
t
t
+)
13 607
45 405
t A
+)
1 107
.
9 81
t A
Câu 73. Chọn A
2
1 1
sin cos sin cos
2 4
x x x x
3
sin .cos
4
x x
3
sin .cos
8
x x
Khi đó
sin ,cosx x
là nghiệm của phương trình
2
1 3
0
2 8
X X
1 7
sin
4
1 7
sin
4
x
x
Ta có
1
sin cos 2 sin cos 1
2
x x x x
+) Với
1 7
sin
4
x
5 7
3sin 2cos
4
x x
+) Với
1 7 5 7
sin 3sin 2cos
4 4
x x x
.
Câu 74. Chọn B
2 2
cos 2 sin .cos sinA a x b x x c x
2
2
2 tan tan
cos
A
a b x c x
x
2 2
1 tan 2 tan tanA x a b x c x
2 2
2 2 2
1 2
b b b
A a b c
a c a c a c
2 2 2
2 2
2 2
2 4 4a c b a a c b a c c b
A
a c a c
2
2
2 2 2
2
2 2 2
. 4
2 4
a a c b
a c b a a c b a
A
a c a c a c
A a
.
Câu 75. Chọn C
Đặt
2
2
2
1
1
cos
t
t
t
a b a b
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
2
2
1
ab
b t at
a b
2 2
2
ab
at bt bt b
a b
2
2
ab
a b t bt b
a b
2
2 2
2 0
a b t b a b t b
b
t
a b
Suy ra
2 2
cos ;sin
b a
a b a b
Vậy:
8 8
4 4 3
3 3
sin cos 1
.
a b
a b
a b a b a b
Câu 76. Chọn C
9
cos +cos ... cos
5 5
A
9 4 5
cos cos ... cos cos
5 5 5
A
9 9 9 7 9
2cos cos 2cos cos ... 2cos cos
10 10 10 10 10 10
A
9 9 7 5 3
2cos cos cos cos cos cos
10 10 10 10 10 10
A
9 2
2cos 2cos cos 2cos cos cos
10 2 5 2 5 2
A
9
2cos .0 0.
10
A
Câu 77. Chọn A
3 5 7
1 cos 1 cos 1 cos 1 cos
4 4 4 4
2 2 2 2
A
1 3 5 7
2 cos cos cos cos
2 4 4 4 4
1 3 3
2 cos cos cos cos 2.
2 4 4 4 4
Câu 78. Chọn D
0 0
0 0 0
2sin 2550 .cos 188
1
tan368 2cos638 cos98
A
0 0 0 0
0 0 0 0 0 0
2sin 30 7.360 .cos 8 180
1
tan 8 360 2cos 82 2.360 cos 90 8
A
0 0
0 0 0
1 2sin 30 .cos8
tan8 2cos82 sin 8
A
0 0
0
0 0 0
1 2sin 30 .cos8
tan8
2cos 90 8 sin8
A
0 0
0 0 0
1 2sin 30 .cos8
tan8 2sin8 sin8
A
0
0 0 0
0
1.cos8
cot8 cot8 cot8 0
sin8
A
.
Câu 79. Chọn C
+) Ta có:
A B C
B C A
2 2 2
B C A
I
cos cos sin
2 2 2 2
B C A A
nên
I
đúng
+) Tương tự ta có:
2 2 2
A B C
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
tan tan cot
2 2 2 2
A B C C
tan .tan cot .tan 1
2 2 2 2
A B C C C
nên
II
đúng.
+) Ta có
2A B C C
cos cos 2 cos 2A B C C C
cos cos 2 0
A B C C
nên
III
sai.
Câu 80. Chọn B
Ta có
cos cos
sin cos
2
cot .sin cos
3
tan tan tan cot
2 2 2
sin 2 sin
A
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
TOÁN 10
0D6-3
Con
tents
PHẦN A
. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG ................................................................................................................... 1
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC ........................................................................................ 4
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH ................................. 5
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC ............................................................................................. 7
DẠNG 5. MIN-MAX ....................................................................................................................................................... 9
DẠNG 6. NHẬN DẠNG TAM GIÁC ............................................................................................................................. 9
PHẦN B. LỜI GIẢI ....................................................................................................................................................... 12
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG ................................................................................................................. 12
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC ...................................................................................... 15
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH ............................... 17
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC ........................................................................................... 18
DẠNG 5. MIN-MAX ..................................................................................................................................................... 22
DẠNG 6. NHẬN DẠNG TAM GIÁC ........................................................................................................................... 23
PHẦN A. CÂU HỎI
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG
Câu 1. Trong các công thức sau, công thức nào đúng?
A.
cos
cos .sin sin .sina b a b a b
. B.
s
in sin .cos cos .sina b a b a b
.
C.
s
in sin .cos cos .sina b a b a b
. D.
c
os cos .cos sin .sina b a b a b
.
Câu 2. Trong các công thức sau, công thức nào đúng?
A.
tan tan
tan .
1 tan tan
a b
a b
a
b
B.
ta
n – tan tan .a b a b
C.
tan tan
tan .
1 tan tan
a b
a b
a
b
D.
ta
n tan tan .a b a b
Câu 3. Biểu thức
sin cos cos sinx y x y
bằng
A.
c
os
x
y
. B.
c
os
x
y
. C.
s
in
x
y
. D.
s
in
y
x
.
Câu 4. Chọn khẳng định sai trong các khẳng định sau:
A.
cos( ) cos cos sin sina b a b a b
.
B.
si
n( ) sin cos cos sina b a b a b
.
C.
sin( ) sin cos cos sina b a b a b
.
D.
2
cos 2 1 2sina a
.
CÔNG THỨC LƯỢNG GIÁC
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
Câu 5. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Trong các khẳng định sau, khẳng định nào sai?
A.
sin sin 2cos sin
2 2
a b a b
a b
. B.
cos cos cos sin sin
a b a b a b
.
C.
sin sin cos cos sin
a b a b a b
. D.
2cos cos cos cos
a b a b a b
.
Câu 6. Biểu thức
sin
sin
a b
a b
bằng biểu thức nào sau đây? (Giả sử biểu thức có nghĩa)
A.
sin
sin sin
.
sin sin sin
a b
a b
a b a b
B.
sin
sin sin
.
sin sin sin
a b
a b
a b a b
C.
sin
tan tan
.
sin tan tan
a b
a b
a b a b
D.
sin
cot cot
.
sin cot cot
a b
a b
a b a b
Câu 7. Rút gọn biểu thức:
sin –17 .cos 13 – sin 13 .cos –17
a a a a
, ta được:
A.
sin 2 .a
B.
cos 2 .a
C.
1
.
2
D.
1
.
2
Câu 8. Giá trị của biểu thức
37
cos
12
bằng
A.
6 2
.
4
B.
6 2
.
4
C. –
6 2
.
4
D.
2 6
.
4
Câu 9. Đẳng thức nào sau đây là đúng.
A.
1
cos cos
3 2
. B.
1 3
cos sin cos
3 2 2
.
C.
3 1
cos sin cos
3 2 2
. D.
1 3
cos cos sin
3 2 2
.
Câu 10. (THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Cho
tan 2
. Tính
tan
4
.
A.
1
3
. B.
1
. C.
2
3
. D.
1
3
.
Câu 11. Kết quả nào sau đây sai?
A.
sin cos 2 sin
4
x x x
. B.
sin cos 2 cos
4
x x x
.
C.
sin2 cos2 2 sin 2
4
x x x
. D.
sin 2 cos2 2 cos 2
4
x x x
.
Câu 12. Cho
3
sin
5
x
với
2
x
khi đó
tan
4
x
bằng.
A.
2
7
. B.
1
7
.
C.
2
7
. D.
1
7
.
Câu 13. Cho sin
1
3
với
0
2
. Giá trị của
3
cos
bằng
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
A.
2 6
2 6
. B.
6 3
. C.
1 1
2
6
. D.
1
6
2
.
Câu 14. Cho hai góc
,
thỏa mãn
5
sin
13
,
2
và
3
cos
5
,
0
2
. Tính giá trị
đúng của
cos
.
A.
16
65
. B.
18
65
. C.
18
65
. D.
16
65
.
Câu 15. (THPT Cộng Hiền - Lần 1 - 2018-2019) Cho
3 3
sin , ;
5 2 2
. Tính giá trị
21
cos
4
?
A.
2
10
. B.
7 2
10
. C.
2
10
. D.
7 2
10
.
Câu 16. Biểu thức
cos –53 .sin –337 sin 307 .sin113
M
có giá trị bằng:
A.
1
.
2
B.
1
.
2
C.
3
.
2
D.
3
.
2
Câu 17. Rút gọn biểu thức:
cos54 .cos 4 – cos36 .cos86
, ta được:
A.
cos50 .
B.
cos58 .
C.
sin 50 .
D.
sin 58 .
Câu 18. Cho hai góc nhọn
a
và
b
với
tan
1
7
a
và
tan
3
4
b
. Tính
a b
.
A.
.
3
B.
.
4
C.
.
6
D.
2
.
3
Câu 19. Cho
, x y
là các góc nhọn,
cot
3
4
x
,
1
cot
7
y
. Tổng
x y
bằng:
A.
.
4
B.
3
.
4
C.
.
3
D.
.
Câu 20. Biểu thức
2 2 2
cos cos cos
3 3
x xA
x
không phụ thuộc
x
và bằng:
A.
3
.
4
B.
4
.
3
C.
3
.
2
D.
2
.
3
Câu 21. Biết
sin
,
0
2
và
k
. Giá trị của biểu thức:
4cos
3sin
3
sin
A
không phụ thuộc vào
và bằng
A.
5
.
3
B.
5
.
3
C.
3
.
5
D.
3
.
5
Câu 22. Nếu
tan 4 tan
2 2
thì
tan
2
bằng:
A.
3sin
.
5 3cos
B.
3sin
.
5 3cos
C.
3cos
.
5 3cos
D.
3cos
.
5 3cos
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
Câu 23. Cho
3
c
os
4
a
;
s
in 0
a
;
3
sin
5
b
;
c
os 0
b
. Giá trị của
c
os .a b
bằng:
A.
3
7
1 .
5 4
B.
3
7
1 .
5 4
C.
3
7
1 .
5 4
D.
3
7
1 .
5 4
Câu 24. Biết
1
c
os
2
2
b
a
và
sin
0
2
b
a
;
3
sin
2
5
a
b
và
c
os 0
2
a
b
. Giá trị
cos
a b
bằng:
A.
24
3 7
.
50
B.
7
24 3
.
50
C.
22
3 7
.
50
D.
7
22 3
.
50
Câu 25. Rút gọn biểu thức:
c
os 120 – cos 120 – cosx x x
ta được kết quả là
A.
0.
B.
– cos .x
C.
–2cos .x
D.
sin – cos .x x
Câu 26. Cho
3
sin
5
a
;
cos 0
a
;
3
c
os
4
b
;
sin 0
b
. Giá trị
si
n
a
b
bằng:
A.
1
9
7 .
5 4
B.
1
9
7 .
5 4
C.
1
9
7 .
5 4
D.
1
9
7 .
5 4
Câu 27. Biết
2
và
cot , cot , cot
theo thứ tự lập thành một cấp số cộng. Tích số
cot .cot
bằng:
A.
2
.
B.
–
2.
C.
3
.
D.
–
3.
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC
Câu 28. Đẳng thức nào không đúng với mọi
x
?
A.
2
1
cos 6
co
s 3
2
x
x
. B.
2
cos2 1 2sinx x
.
C.
s
in 2 2sin cosx x x
. D.
2
1
cos 4
sin 2
2
x
x
.
Câu 29. Trong các công thức sau, công thức nào sai?
A.
2
cot 1
cot 2
2cot
x
x
x
. B.
2
2
tan
ta
n 2
1 tan
x
x
x
.
C.
3
cos3 4cos 3cosx x x
. D.
3
sin3 3sin 4sinx x x
Câu 30. Trong các công thức sau, công thức nào sai?
A.
2
2
c
os2 cos – sin .a a a
B.
2
2
c
os2 cos sin .a a a
C.
2
cos2 2cos –1.
a a
D.
2
cos2 1– 2sin .a a
Câu 31. Mệnh đề nào sau đây đúng?
A.
2
2
cos2 cos sina a a
. B.
2
2
cos2 cos sina a a
.
C.
2
cos2 2cos 1
a a
. D.
2
cos2 2sin 1
a a
.
Câu 32. Cho góc lượng giác
.a
Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A.
2
cos 2 1 2sina a
. B.
2
2
cos 2 cos sina a a
.
C.
2
cos 2 1 2 cosa a
. D.
2
cos 2 2cos 1a a
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
Câu 33. (KSNLGV - THUẬN THÀNH 2 - BẮC NINH NĂM 2018 - 2019) Khẳng định nào dưới đây
SAI?
A.
2
2sin 1 cos 2a a
.
B.
cos2 2cos 1a a
.
C.
sin2 2sin cosa a a
.
D.
sin sin cos sin .cosa b a b b a
.
Câu 34. Chọn đáo án đúng.
A.
sin 2 2sin cosx x x
. B.
sin 2 sin cosx x x
. C.
sin 2 2cosx x
. D.
sin 2 2sinx x
.
Câu 35. Cho
4
cos , ;0
5 2
x x
. Giá trị của
sin 2x
là
A.
24
25
. B.
24
25
. C.
1
5
. D.
1
5
.
Câu 36. Nếu
1
sinx cos
2
x
thì sin2x bằng
A.
3
4
. B.
3
8
. C.
2
2
. D.
3
4
.
Câu 37. Biết rằng
6 6 2
sin cos sin 2x x a b x
, với
,a b
là các số thực. Tính
3 4T a b
.
A.
7
T
. B.
1T
. C.
0
T
. D.
7
T
.
Câu 38. Cho
3
sin 2 .
4
Tính giá trị biểu thức
tan cot
A
A.
4
3
A
. B.
2
3
A
. C.
8
3
A
. D.
16
3
A
.
Câu 39. Cho
,a b
là hai góc nhọn. Biết
1 1
cos ,cos
3 4
a b
. Giá trị của biểu thức
cos cos
a b a b
bằng
A.
119
144
. B.
115
144
. C.
113
144
. D.
117
144
.
Câu 40. (TOÁN HỌC TUỔI TRẺ SỐ 5) Cho số thực
thỏa mãn
1
sin
4
. Tính
sin 4 2sin 2 cos
A.
25
128
. B.
1
16
. C.
255
128
. D.
225
128
.
Câu 41. Cho
cot 15
a
, giá trị
sin 2a
có thể nhận giá trị nào dưới đây:
A.
11
.
113
B.
13
.
113
C.
15
.
113
D.
17
.
113
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH
Câu 42. Mệnh đề nào sau đây sai?
A.
1
cos cos cos cos
2
a b a b a b
. B.
1
sin cos sin cos
2
a b a b a b
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
C.
1
sin sin cos cos
2
a
b a b a b
. D.
1
sin cos sin sin
2
a
b a b a b
.
Câu 43. Trong các đẳng thức sau, đẳng thức nào sai?
A.
( ) cos .cos sin .sincos a b a b a b
. B.
1
cos .cos ( ) ( )
2
a b cos a b cos a b
.
C.
sin( ) sin .cos sin .cosa b a b b a
. D.
cos cos 2 ( ). ( )a b cos a b cos a b
.
Câu 44. Công thức nào sau đây là sai?
A.
co
s cos 2cos .cos
2
2
a b a b
a
b
. B.
cos
cos 2sin .sin
2
2
a b a b
a
b
.
C.
s
in sin 2sin .cos
2
2
a b a b
a
b
. D.
s
in sin 2sin .cos
2
2
a b a b
a
b
.
Câu 45. Rút gọn biểu thức
s
in3 cos 2 sin
s
in 2 0;2sin 1 0
cos sin 2 cos3
x
x x
A x x
x
x x
ta được:
A.
c
ot 6A x
. B.
c
ot 3A x
.
C.
co
t 2A x
. D.
t
an tan 2 tan 3A x x x
.
Câu 46. Rút gọn biểu thức
s
in sin
4
4
P
a a
.
A.
3
co
s 2
2
a
. B.
1
c
os 2
2
a
.
C.
2
co
s 2
3
a
. D.
1
co
s 2
2
a
.
Câu 47. Biến đổi biểu thức
s
in 1
thành tích.
A.
sin
1 2sin cos
2
2
. B.
s
in 1 2sin cos
2
4 2 4
.
C.
sin 1 2sin cos
2
2
. D.
sin 1 2sin cos
2
4 2 4
.
Câu 48. Rút gọn biểu thức
cos 2 cos 3 cos 5
sin 2 sin 3 sin 5
a a a
P
a a a
.
A.
t
anP a
. B.
c
otP a
. C.
c
ot3P a
. D.
t
an3P a
.
Câu 49. (THPT Phan Bội Châu - KTHK 1-17-18) Tính giá trị biểu thức
sin 30 .cos 60 sin 60 .cos30
o
o o o
P
.
A.
1P
. B.
0
P
. C.
3
P . D.
3
P
.
Câu 50. Giá trị đúng của
2
4 6
cos cos cos
7 7 7
bằng:
A.
1
.
2
B.
1
.
2
C.
1
.
4
D.
1
.
4
Câu 51. Giá trị đúng của
7
ta
n tan
24
24
bằng:
A.
2 6 3 .
B.
2 6 3 .
C.
2 3 2 .
D.
2 3 2 .
Câu 52. Biểu thức
0
0
1
2
sin 70
2sin10
A
có giá trị đúng bằng:
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
A.
1.
B.
–
1.
C.
2
.
D.
–
2.
Câu 53. Tích số
c
os10 .cos30 .cos50 .cos70
bằng:
A.
1
.
1
6
B.
1
.
8
C.
3
.
1
6
D.
1
.
4
Câu 54. Tích số
4
5
cos .cos .cos
7 7 7
bằng:
A.
1
.
8
B.
1
.
8
C.
1
.
4
D.
1
.
4
Câu 55. Giá trị đúng của biểu thức
t
an30 tan 40 tan50 tan 60
cos20
A
bằng:
A.
2
.
3
B.
4
.
3
C.
6
.
3
D.
8
.
3
Câu 56. Cho hai góc nhọn
a
và
b
. Biết
c
os
1
3
a
,
c
os
1
4
b
. Giá trị
c
os .cos
a
b a b
bằng:
A.
113
.
144
B.
115
.
144
C.
117
.
144
D.
119
.
144
Câu 57. Rút gọn biểu thức
sin
sin 2 sin 3
cos cos 2 cos3
x x x
A
x
x x
A.
t
an 6 .A x
B.
t
an 3 .A x
C.
tan 2 .A x
D.
tan tan 2 tan 3 .A x x x
Câu 58. Biến đổi biểu thức
sin 1a
thành tích.
A.
sin
1 2sin cos .
2 4 2 4
a
a
a
B.
sin
1 2cos sin .
2 4 2 4
a
a
a
C.
sin
1 2sin cos .
2 2
a
a a
D.
sin
1 2cos sin .
2 2
a
a a
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC
Câu 59. Cho góc
thỏa mãn
2
và
2
sin
2
5
.Tính giá trị của biểu thức
tan
2
4
A
.
A.
1
3
A
. B.
1
3
A
. C.
3
A
. D.
3
A
.
Câu 60. Cho
1
c
os 0
3 2
x x
. Giá trị của
t
an 2x
là
A.
5
2
. B.
4
2
7
. C.
5
2
. D.
4
2
7
.
Câu 61. Cho
c
os 0
x
. Tính
2
2
s
in sin
6 6
A
x x
.
A.
3
2
. B. 2. C. 1. D.
1
4
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
Câu 62. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Cho biết
2
os
3
c
. Giá trị của biểu thức
cot 3tan
2cot tan
P
bằng bao nhiêu?
A.
19
.
13
P
B.
25
.
13
P
C.
25
.
13
P
D.
19
.
13
P
Câu 63. Cho
sin .cos sin
với
2
k
,
2
l
,
,k l
. Ta có
A.
tan 2cot
. B.
tan 2cot
.
C.
tan 2 tan
. D.
tan 2 tan
.
Câu 64. Biết rằng
2 2 2
cos
1 2.tan
,
cos sin 1 tan sin
ax
x
a b
x x x b ax
. Tính giá trị của biểu thức
P a b
.
A.
4P
. B.
1P
. C.
2P
. D.
3
P
.
Câu 65. Cho
2
cos 2
3
. Tính giá trị của biểu thức
cos .cos3
P
.
A.
7
18
P
. B.
7
9
P
. C.
5
9
P
. D.
5
18
.
Câu 66. Cho
tan 2
x
3
2
x
. Giá trị của
sin
3
x
là
A.
2 3
2 5
. B.
2 3
2 5
. C.
2 3
2 5
. D.
2 3
2 5
.
Câu 67. Tổng
tan 9 cot 9 tan15 cot15 – tan 27 – cot 27
A
bằng:
A.
4.
B.
–4.
C.
8.
D.
–8.
Câu 68. Cho hai góc nhọn
a
và
b
với
sin
1
3
a
,
sin
1
2
b
. Giá trị của
sin 2
a b
là:
A.
2 2 7 3
.
18
B.
3 2 7 3
.
18
C.
4 2 7 3
.
18
D.
5 2 7 3
.
18
Câu 69. Biểu thức
2
2
2cos 2 3 sin 4 1
2sin 2 3 sin 4 1
A
có kết quả rút gọn là:
A.
cos 4 30
.
cos 4 30
B.
cos 4 30
.
cos 4 30
C.
sin 4 30
.
sin 4 30
D.
sin 4 30
.
sin 4 30
Câu 70. Kết quả nào sau đây SAI?
A.
sin 33 cos 60 co
.s3
B.
sin 9 sin12
.
sin 48 sin81
C.
2
cos 20 2sin 55 1 2 sin 65 .
D.
1 1 4
.
cos290
3 sin 250 3
Câu 71. Nếu
5sin 3sin 2
thì:
A.
tan 2 tan .
B.
tan 3tan .
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
C.
tan 4 tan .
D.
tan 5tan .
Câu 72. Cho biểu thức
2 2 2
sin – sin – si
.n
A a b a
b
Hãy chọn kết quả đúng:
A.
2cos .sin .sin .A a b a b
B.
2sin .cos .cos .A a b a b
C.
2cos .cos .cos .A a b a b
D.
2sin .sin .cos .A a b a b
Câu 73. Xác định hệ thức SAI trong các hệ thức sau:
A.
cos 40
cos40 tan .sin 40 .
cos
B.
6
sin15 tan 30 .cos15 .
3
C.
2 2 2
cos – 2cos .cos .cos cos sin .x a x a x a x a
D.
2 2 2
sin 2sin – .sin .cos sin s .
– cox a x x a a
a
x
DẠNG 5. MIN-MAX
Câu 74. Giá trị nhỏ nhất của
6 6
sin cosx x
là
A. 0. B.
1
2
. C.
1
4
. D.
1
8
.
Câu 75. Giá trị lớn nhất của
4 4
sin cosM x x
bằng:
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 76. Cho
3sin 4cosx
M x
. Chọn khẳng định đúng.
A.
5 5
M
. B.
5
M
. C.
5
M
. D.
5
M
.
Câu 77. Giá trị lớn nhất của
6 6
sin cosM x x
bằng:
A.
2
. B.
3
C.
0
. D.
1
.
Câu 78. Cho biểu thức
3
3
1 tan
1 tan
x
M
x
,
, ,
4 2
x k x k k
, mệnh đề nào trong các mệnh đề
sau đúng?
A.
1M
. B.
1
4
M
. C.
1
1
4
M
. D.
1M
.
Câu 79. Cho
2 2
6 cos 5sinM x x
. Khi đó giá trị lớn nhất của
M
là
A.
11
. B.
1
. C.
5
. D.
6
.
Câu 80. Giá trị lớn nhất của biểu thức
2 2
7 cos 2 sinM x x
là
A.
2
. B.
5
. C.
7
. D.
16
.
DẠNG 6. NHẬN DẠNG TAM GIÁC
Câu 81. Cho
, ,A B C
là các góc của tam giác
ABC
thì.
A.
sin2 sin 2 2sinA B C
. B.
sin2 sin 2 2sinA B C
.
C.
sin2 sin 2 2sinA B C
. D.
sin2 sin 2 2sinA B C
.
Câu 82. Một tam giác
ABC
có các góc
, ,A B C
thỏa mãn
3 3
sin cos sin cos 0
2 2 2 2
A B B A
thì tam giác đó có
gì đặc biệt?
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
A. Tam giác đó vuông. B. Tam giác đó đều.
C. Tam giác đó cân. D. Không có gì đặc biệt.
Câu 83. Cho
A
,
B
,
C
là các góc của tam giác
ABC
(không là tam giác vuông) thì
cot .cot cot .cot cot .cotA B B C C A
bằng :
A.
2
cot .cot .cot
A B C
. B. Một kết quả khác các kết quả đã nêu trên.
C.
1
. D.
1
.
Câu 84. Cho
A
,
B
,
C
là ba là các góc nhọn và
1
tan
2
A
;
1
tan
5
B
,
1
tan
8
C
. Tổng
A B C
bằng
A.
5
. B.
4
. C.
3
. D.
6
.
Câu 85. Biết
, ,A B C
là các góc của tam giác
,ABC
khi đó.
A.
cot cot .
2 2
A B C
B.
cos cos .
2 2
A B C
C.
cos cos .
2 2
A B C
D.
tan cot .
2 2
A B C
Câu 86.
,A
,B
,C
là ba góc của một tam giác. Hãy tìm hệ thức sai:
A.
sin sin 2
A A B C
.
B.
3
sin cos
2
A B C
A
.
C.
3
cos sin
2
A B C
C
. D.
sin sin 2C A B C
.
Câu 87. Cho
A
,
B
,
C
là các góc của tam giác
ABC
(không phải tam giác vuông) thì:
A.
tan tan tan tan .tan .tan A B C A B C
. B.
tan tan tan tan .tan .tan
2 2 2
A B C
A B C
.
C.
tan tan tan tan .tan .tan A B C A B C
. D.
tan tan tan tan .tan .tan
2 2 2
A B C
A B C
.
Câu 88. Biết
, ,A B C
là các góc của tam giác
,ABC
khi đó.
A.
sin cos .
2 2
A B C
B.
sin cos .
2 2
A B C
C.
sin sin .
2 2
A B C
D.
sin sin .
2 2
A B C
Câu 89. Nếu
2a b
và
a b c
. Hãy chọn kết quả đúng.
A.
sin sin sin sin 2b b c a
. B.
2
sin sin sin sinb b c a
.
C.
2
sin sin sin cosb b c a
. D.
sin sin sin cos2b b c a
.
Câu 90. Cho
A
,
B
,
C
là các góc của tam giác
ABC
thì:
A.
sin 2 sin2 sin 2 4sin .sin .sin A B C A B C
. B.
sin2 sin 2 sin2 4cos .cos .cos A B C A B C
.
C.
sin2 sin 2 sin 2 4cos .cos .cos A B C A B C
. D.
sin 2 sin2 sin 2 4sin .sin .sin A B C A B C
.
Câu 91.
,A
,B
,C
là ba góc của một tam giác. Hãy chỉ hệ thức sai:
A.
4 3
cot tan
2 2
A B C A
. B.
2
cos sin
2
A B C
B
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
C.
3
sin cos2
2
A
B C
C
. D.
6
5
tan cot
2 2
A B C C
.
Câu 92. Biết
, ,A B C
là các góc của tam giác
A
BC
khi đó.
A.
c
os cos
C
A B
. B.
ta
n tan
C
A B
.
C.
c
ot cot
C
A B
. D.
s
in sin
C
A B
.
Câu 93. Cho
,
,A B C
là các góc của tam giác
A
BC
(không là tam giác vuông) thì
c
ot .cot cot .cot cot .cotA B B C C A
bằng
A. Một kết quả khác các kết quả đã nêu trên. B.
1
.
C.
1
. D.
2
c
ot .cot .cot
A
B C
.
Câu 94. Cho
A
,
B
,
C
là các góc của tam giác
A
BC
(không phải tam giác vuông) thì:
A.
c
ot cot cot cot .cot .cot
2 2 2 2 2 2
A B C A B C
. B.
c
ot cot cot cot .cot .cot
2 2 2 2 2 2
A B C A B C
.
C.
c
ot cot cot cot .cot .cot
2 2 2
A B C
A
B C
. D.
c
ot cot cot cot .cot .cot
2 2 2
A B C
A
B C
.
Câu 95. Cho
A
,
B
,
C
là ba góc của một tam giác. Hãy chọn hệ thức đúng trong các hệ thức sau.
A.
2 2 2
c
os cos cos 1 cos .cos .cos .A B C A B C
B.
2
2 2
cos cos cos 1– cos .cos .cos .A B C A B C
C.
2
2 2
cos cos cos 1 2cos .cos .cos .A B C A B C
D.
2
2 2
c
os cos cos 1– 2cos .cos .cos .A B C A B C
Câu 96. Hãy chỉ ra công thức sai, nếu
,
,A B C
là ba góc của một tam giác.
A.
co
s cos sin sin sin
2 2 2 2 2
B C B C A
. B.
cos .cos sin .sin cos 0
B C B C A
.
C.
s
in cos sin cos cos
2 2 2 2 2
B C C C A
.
D.
2 2 2
c
os cos cos 2 cos cos cos 1
A
B C A B C
.
Câu 97. Cho tam giác
ABC
có
s
in sinC
s
in
c
os cos
B
A
B
C
. Khẳng định nào dưới đây đúng?
A. Tam giác
ABC
vuông tại
A
. B. Tam giác
ABC
cân tại
A
.
C. Tam giác
A
BC
đều. D. Tam giác
A
BC
là tam giác tù.
Câu 98. Cho bất đẳng thức
4
1
13
2
2cos2 4sin 0
64cos 4
c
os A B B
A
với
, ,A B C
là ba góc của tam
giác
ABC
.Khẳng định đúng là:
A.
120
o
B C
. B.
130
o
B C
. C.
120
o
A B
. D.
140
o
A C
.
Câu 99. Cho
A
,
B
,
C
là các góc nhọn và
ta
n
1
2
A
,
ta
n
B
,
ta
n
C
. Tổng
A
B C
bằng:
A.
.
6
B.
.
5
C.
.
4
D.
.
3
Câu 100. Cho
A
,
B
,
C
là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI.
A.
3
sin cos .
2
A B C
C
B.
cos – – cos 2 .A B C C
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
C.
2 3
tan cot .
2 2
A B C C
D.
2
cot tan .
2 2
A B C C
Câu 101. Cho
A
,
B
,
C
là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI.
A.
cos sin .
2 2
A B C
B.
cos 2 – cos .A B C C
C.
sin – sin .A C B
D.
cos – cos .A B C
Câu 102. Cho
A
,
B
,
C
là ba góc của một tam giác không vuông. Hệ thức nào sau đây SAI?
A.
cos cos sin sin sin .
2 2 2 2 2
B C B C A
B.
tan tan tan tan .tan .tan .A B C A B C
C.
cot cot cot cot .cot .cot .A B C A B C
D.
tan .tan tan .tan tan .tan 1.
2 2 2 2 2 2
A B B C C A
PHẦN B. LỜI GIẢI
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG
Câu 1. Chọn D
Công thức cộng:
sin sin .cos cos .sina b a b a b
Câu 2. Chọn B.
Ta có
tan tan
tan .
1 tan tan
a b
a b
a b
Câu 3. Chọn C
Áp dụng công thức cộng lượng giác ta có đáp án.
C.
Câu 4. Chon A.
Ta có công thức đúng là:
cos( ) cos cos sin sina b a b a b
.
Câu 5. Chọn B
Câu A, D là công thức biến đổi đúng
Câu C là công thức cộng đúng
Câu B sai vì
cos cos cos sin sin
a b a b a b
.
Câu 6. Chọn C.
Ta có :
sin
sin cos cos sin
sin sin cos cos sin
a b
a b a b
a b a b a b
(Chia cả tử và mẫu cho
cos cosa b
)
tan tan
tan tan
a b
a b
.
Câu 7. Chọn C.
Ta có:
sin –17 .cos 13 – sin 13 .cos –17 sin 17 13
a a a a a a
1
sin 30 .
2
Câu 8. Chọn C.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
37
c
os
12
c
os 2
12
c
os
12
c
os
12
c
os
3
4
c
os .cos sin .sin
3
4 3 4
6
2
4
.
Câu 9. Chọn D
Ta có
1 3
cos cos .cos sin .sin cos sin
3 3 3 2 2
.
Câu 10. Chọn D
Ta có
tan tan
2 1 1
4
tan
4 1 2 3
1 tan tan
4
.
Câu 11. Chọn C
Ta có
1 1
sin 2 cos2 2 sin2 cos2
2 2
x x x x
2 cos sin 2 sin cos2
4 4
x
x
2
sin 2 2 sin 2
4 4
x
x
Câu 12. Chọn D
Từ
2 2 2
9
4
s
in cos 1 cos 1 sin 1
25 5
x
x x x
.
Vì
2
x
nên
4
c
os
5
x
do đó
s
in 3
t
an
c
os 4
x
x
x
.
Ta có:
3
tan tan 1
1
4 4
tan
3
4 7
1 tan .tan 1
4 4
x
x
x
.
Câu 13. Chọn A
Ta có:
2 2 2
2
6
c
os 1 cos cos
3
3
s
in
(vì
0
nên
c
os
0
).
Ta có:
3 1 6 3 1 1 1 2 6
sin
3 2 2 3 2 2
3 6 2 6
1
cos cos
2
.
Câu 14. Chọn D
5
s
in
1
3
,
2
nên
2
5
12
c
os 1
13
13
.
3
c
os
5
,
0
2
nên
2
3
4
si
n 1
5 5
.
cos cos cos sin sin
12 3 5 4 16
.
.
1
3 5 13 5 65
.
Câu 15. Chọn A
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
Ta có:
2
2
16
4
c
os 1 sin cos
2
5 5
.Do
3
;
cos 0
2 2
nên
4
co
s
5
.
Vậy:
2
1 21 21 4 2 3 2 2
cos cos cos sin sin
4
4 4 5 2 5 2 10
.
Câu 16. Chọn A.
co
s –53 .sin –337 sin 307 .sin113
M
co
s –53 .sin 23 – 360 sin 53 360 .sin 90 23
c
os –53 .sin 23 sin 53 .cos 23
s
in 23 53
1
sin 30
2
.
Câu 17. Chọn D.
Ta có:
c
os54 .cos 4 – cos36 .cos86 cos54 .cos 4 – sin 54 .s
i
n 4 cos58 .
Câu 18. Chọn B.
t
an tan
ta
n 1
1 tan .tan
a
b
a b
a b
, suy ra
a
b
Câu 19. Chọn C.
Ta có :
4
7
tan tan
3
tan 1
4
1 tan .tan
1 .7
3
x y
x y
x y
, suy ra
3
4
x
y
.
Câu 20. Chọn C.
Ta có :
2
2
2 2
c
os cos cos
3 3
A
x
x x
2
2
3 1 3 1
cos cos sin cos sin
2 2 2 2
x x x x x
3
2
.
Câu 21. Chọn B.
Ta có
2
4
5
0
3
cos
5
sin
, thay vào biểu thức
4cos
3 sin
5
3
sin
3
A
.
Câu 22. Chọn A.
Ta có:
2
2
tan tan 3tan 3sin .cos
3sin
2 2 2 2 2
tan .
2 5 3cos
1 tan .tan 1 4 tan 1 3sin
2 2 2 2
Câu 23. Chọn A.
Ta có :
2
3
c
os
7
si
n 1 cos
4
4
sin 0
a
a a
a
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
2
3
sin
4
c
os 1 sin .
5
5
c
os 0
b
b b
b
3
4 7 3 3 7
cos cos cos sin sin . . 1 .
4 5 4 5 5 4
a b a b a b
Câu 24. Chọn A.
Ta có :
1
cos
2 2
sin 0
2
b
a
b
a
2
3
si
n 1 cos
2 2 2
b
b
a a
.
3
sin
2 5
cos
2
a
b
a
b
2
4
cos
1 sin
2 2 5
a
a
b b
.
c
os cos cos sin sin
2 2 2 2 2
a b b a b a
a
b a b
1
4 3 3 3 3 4
. . .
2 5 5 2 10
2
24
3 7
cos 2cos 1 .
2 50
a
b
a b
Câu 25. Chọn C.
cos 120 – cos 120 – cosx x x
1
3 1 3
c
os sin cos sin cos
2 2 2 2
x
x
x
x x
2cos x
Câu 26. Chọn A.
Ta có :
3
sin
5
c
os 0
a
a
2
4
cos 1 sin
5
a a
.
3
cos
4
sin 0
b
b
2
7
sin
1 cos
4
b
b
.
3 3 4 7 1 9
sin sin cos cos sin . . 7
5 4 5 4 5 4
a b a b a b
.
Câu 27. Chọn C.
Ta có :
2
, suy ra
tan tan
cot tan
1 tan tan
cot cot 2cot
cot cot 1 cot cot 1
c
ot cot 3.
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC
Câu 28. Chọn D
Ta có
2
1 cos 4
s
in 2
2
x
x
.
Câu 29. Chọn B.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
Công thức đúng là
2
2tan
tan 2
1 tan
x
x
x
.
Câu 30. Chọn B.
Ta có
2 2 2 2
cos 2 cos – sin 2cos 1 1 2sin .a a a a a
Câu 31. Chọn A
Câu 32.
Lờigiải
Chọn C
Ta có:
2 2 2 2
cos 2 cos sin 1 2sin 2cos 1a a a a a
.
Câu 33. Chọn B
Có
2
cos 2 2cos 1a a
nên đáp án B sai.
Câu 34. Chọn A
Câu 35. Chọn B
Ta có
2 2
16 9
sin 1 cos 1
25 25
x x
3
sin
5
x
vì
;0 sin 0
2
x x
.
Vậy
4 3 24
sin 2 2sin .cos 2. .
5 5 25
x x x
.
Câu 36. Chọn D
Ta có
1
sinx cos
2
x
2 2
1
sin 2sin cos cos
4
x x x x
3
sin 2
4
x
Câu 37. Chọn C
Ta có
3
6 6 2 2 2 2 2 2
sin cos sin cos 3sin .cos sin cosx x x x x x x x
2 2 2
3
1 3sin .cos 1 sin 2
4
x x x
.
Vậy
3
1,
4
a b
. Do đó
3 4 0
T a b
.
Câu 38. Chọn C
tan cot
A
2 2
sin cos sin cos
cos sin sin cos
1 1 8
1 1 3
3
sin 2 .
2 2 4
.
Câu 39. Chọn A
Từ
2
1 7
cos cos 2 2cos 1
3 9
a a a
2
1 7
cos cos 2 2cos 1
4 8
b b b
Ta có
1 1 7 7 119
cos cos cos 2 cos 2
2 2 9 8 144
a b a b a b
.
Câu 40. Ta có
sin 4 2sin 2 cos
2sin 2 cos 2 1 cos
2
4sin cos 1 2sin 1 cos
2 2
4sin 1 sin 2 2sin
2
2
8 1 sin sin
2
1 1
8 1 .
16 4
225
128
.
Câu 41. Chọn C.
cot 15
a
2
1
226
sin a
2
2
1
sin
226
225
cos
226
a
a
15
sin 2
113
a
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH
Câu 42. Chọn B
Ta có
1
s
in cos sin sin
2
a
b a b a b
.
Câu 43. Chọn D
Ta có:
co
s cos 2 . .
2 2
a b a b
a
b cos cos
Câu 44. Chọn D
Ta có
sin
sin 2cos .sin
2 2
a b a b
a
b
.
Câu 45. Chọn C
s
in 3 cos2 sin
cos sin 2 cos3
x x x
A
x
x x
2
cos 2 sin cos 2
2sin 2 sin sin 2
x x x
x x x
co
s 2 (1 2sin )
co
t 2
s
in 2 (1 2sin )
x x
x
x
x
.
Câu 46. Chọn D
Ta có:
1
1
s
in sin cos cos 2 cos 2
4
4 2 2 2
a
a a a
.
Câu 47. Chọn B
2 2
s
in 1 sin sin 2cos sin 2cos sin .
2 2 2 2 4 2 4
Câu 48. Chọn C
cos 2cos3 cos5
sin 2sin 3 sin 5
a a a
P
a
a a
2cos3 cos 2 cos3
2sin 3 cos 2sin 3
a a a
a a a
2
cos3 cos 1
2sin 3 cos 1
a
a
a a
c
os3
c
ot 3
sin 3
a
a
a
.
Câu 49. Chọn A
Ta có
sin 30 60 sin 90 1
o
o o
P
.
Câu 50. Chọn B.
Ta có
2
4 6
cos cos cos
7 7 7
2 4 6
sin cos cos cos
7 7 7 7
sin
7
3 5 3 5
sin sin sin sin sin sin
7 7 7 7 7
2sin
7
sin
1
7
2
2sin
7
.
Câu 51. Chọn A.
sin
7 3
3
tan tan 2 6 3
7
24 24
cos .cos cos cos
24 24 3 4
.
Câu 52. Chọn A.
0
0 0 0
0
0 0 0 0
1 1 4sin10 .sin 70 2sin80 2sin10
2sin 70 1
2sin10 2sin10 2sin10 2sin10
A
.
Câu 53. Chọn C.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
o
o
1
c
os10 .cos30 .cos50 .cos70 cos10 .cos30 . cos12
0
cos20
2
3 cos10 cos30 cos10
4 2 2
3
1 3
.
4
4 16
.
Câu 54. Chọn A.
4 5
cos .cos .cos
7 7 7
2 4 5
sin .cos .cos
7 7 7
2sin
7
2 2 4
sin .cos .cos
7 7 7
2sin
7
4 4
sin .cos
7 7
4sin
7
8
sin
1
7
8
8sin
7
.
Câu 55. Chọn D.
t
an30 tan 40 tan50 tan 60
cos20
A
sin 70 sin110
cos30 .cos40 cos50 .cos60
cos20
1
1
cos30 .cos40 cos50 .cos60
2 2
cos50
3 cos 40
c
os50 3 cos40
2
3 cos40 .cos50
sin 40 3 cos40
2
3
cos40 .cos50
sin100
4
3
cos10 cos90
2
8cos10 8
3 cos10 3
.
Câu 56. Chọn D.
Ta có :
2
2
2 2
1
1 1 119
cos .cos cos2 cos2 cos cos 1 1 .
2 3 4 144
a b a b a b a b
Câu 57. Chọn C.
Ta có :
sin
sin 2 sin 3
cos cos 2 cos3
x x x
A
x
x x
2
sin 2 .cos sin 2
2cos2 .cos cos2
x x x
x x x
sin
2 2cos 1
ta
n 2 .
c
os2 2cos 1
x x
x
x
x
Câu 58. Chọn D.
Ta có
s
in 1a
2
2
2sin cos sin cos
2 2 2 2
a a a a
2
sin
cos
2 2
a a
2
2
sin
2
4
a
2
sin cos
2
4 4 2
a a
2
sin cos .
2 4 2 4
a
a
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC
Câu 59. Chọn A
Vì góc
thỏa mãn
2
nên
4
2 2
suy ra
cos
0
2
.
Do
2
sin
2
5
nên
2
1
cos 1 sin
2 2
5
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
Biểu thức
tan 1
2
tan
2 4
tan 1
2
A .
Do đó
tan
2
2
.
Vậy biểu thức
2
1 1
2 1 3
A
.
Câu 60. Chọn B
2
2
1
8
s
in 1 cos 1
9
9
x
x
2 2
s
in
3
x
( vì
0
2
x
).
t
an 2 2
x
2
2
tan 4 2 4 2
tan 2 .
1 tan 7 7
x
x
x
Câu 61. Chọn A
Ta có
2
cos 2 2cos 1 1
x x
. Sử dụng công thức hạ bậc và công thức biến đổi tổng thành tích
ta được:
1 cos 2 1 cos 2
1 3
3 3
1 cos 2 cos 1
2 3 2 2
x x
A x
Câu 62.
Lời giai
Chọn A
Ta có:
2
2
2
2 1 1 5
cos tan 1 1
3 cos 4
2
3
2
2
2
2
1
1 3tan
5
3tan
1 3.
c
ot 3tan 1 3tan 19
tan tan
4
2 5
2 tan
2
cot tan 2 tan 13
ta
n 2
tan 4
tan
P
Câu 63. Chọn D
Ta có
1
s
in .cos sin sin 2 sin sin
2
sin 3sin
sin cos sin cos 3sin
s
in
3sin
cos sin
cos cos
(vì
c
os 0
)
s
in
3sin sin
*
c
os cos cos cos
(vì
cos 0
)
Mà
s
in
s
in
cos
(từ giả thiết), suy ra
3
sin sin
* tan 2tan
cos cos
Vậy
ta
n 2 tan
.
Câu 64. Chọn D
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
Ta có:
2
2
2 2
2
2
sin
1 2.tan 1
cos
s
in
cos
sin 1 tan cos 2
1
cos
x
x
x
x
x
x x x
x
2
2
1
2sin .cos
cos 2 cos sin
x x
x x x
2
1 sin 2 cos 2
1 sin 2 1 sin 2
cos2 cos 2 cos 2 cos 2
x x
x x
x x x x
2
1 sin 2 cos2
1 sin 2
x x
x
c
os2
1 sin2
x
x
. Vậy
2, 1
a b
. Suy ra
3
P a b
.
Câu 65. Chọn D
Ta có
2
2
1
1 1 2 2 5
co
s .cos3 cos 2 cos 4 2cos 2 cos 2 1 2 1
2
2 2 3 3 18
P
.
Câu 66. Chọn B
3
2
x
suy ra
sin 0, cos 0
x x
.
Ta có:
2
2
1
1
tan
c
os
x
x
2
2
1
cos
1
tan
x
x
2
1
co
s
5
x
1
cos
5
x
Do
c
os 0
x
nên nhận
1
cos
5
x .
sin 2
tan sin tan .cos
cos
5
x
x x x x
x
2
1 1 3 2 3
s
in sin .cos cos .sin . .
3 3 3 2 2
5
5 2 5
x
x x
Câu 67. Chọn C.
tan 9 cot 9 tan15 cot15 – tan 27 – cot 27
A
tan 9 cot 9 – tan 27 – cot 27 tan15 cot15
t
an 9 tan81 – tan 27 – tan 63 tan15 cot15
.
Ta có
sin18 sin18
tan9 – tan 27 tan81 – tan 63
c
os9 .cos 27 cos81 .cos63
c
os9 .cos 27 cos81 .cos63
sin
18
c
os81 .cos63 .cos9 .cos 27
sin18 cos9 .cos 27 sin 9 .sin 27
cos81 .cos63 .cos9 .cos27
4
sin18 .cos36
c
os72 cos90 cos36 cos90
4
sin18
4
c
os72
.
2
2
sin 15 cos 15 2
tan15 cot15 4
sin15 .cos15 sin 30
.
Vậy
8
A
.
Câu 68. Chọn C.
Ta có
0
2 2
2
cos
1
3
3
sin a
a
a
;
0
3
2
cos
1
s n
2
2
i b
b
b
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
si
n 2 2sin .cos
a
b a b a b
2
sin .cos sin .cos cos .cos sin .sina b b a a b a b
4
2 7 3
18
.
Câu 69. Chọn C.
Ta có :
2
2
2cos 2 3 sin 4 1
2sin 2 3 sin 4 1
A
cos4 3 sin 4
3 sin 4 cos4
sin
4 30
sin 4 30
.
Câu 70. Chọn A.
Ta có :
si
n9 sin12
sin 48 sin81
sin 9 .sin81 sin12 .sin 48 0
1
1
c
os72 cos90 cos36 cos60 0
2 2
2cos 72 2cos36 1 0
2
4cos 36 2cos36 1 0
(đúng vì
1
5
c
os36
4
). Suy ra B đúng.
Tương tự, ta cũng chứng minh được các biểu thức ở C và D đúng.
Biểu thức ở đáp án A sai.
Câu 71. Chọn C.
Ta có :
5sin 3sin 2
5sin 3sin
5
sin cos 5cos sin 3sin cos 3cos sin
2
sin cos 8cos sin
sin
sin
4
cos cos
t
an 4tan
.
Câu 72. Chọn D.
Ta có :
2 2 2
si
n – sin – sin
A
a b a
b
2
1 cos2 1 cos2
sin
2
2
a b
a b
2
1
sin 1 cos2 cos2
2
a b a b
2
cos cos cos
a b a b a b
c
os cos cos
a
b a b a b
2
sin sin cos .a b a b
Câu 73. Chọn D.
Ta có :
sin
c
os40 tan .sin 40 cos40 .sin 40
cos
cos 40
cos40 cos sin 40 sin
.
cos cos
A
đúng.
sin
15 .cos30 sin30 .cos15 sin 45 6
sin15 tan 30 .cos15 .
cos30 cos30 3
B đúng.
2 2
c
os – 2cos .cos .cos cos
x
a x a x a x
2
c
os cos 2cos cos cos
x
a x a x a x
2
cos cos cos
x a x a x
2
2 2 2 2
1
cos cos 2 cos2 cos cos cos 1 sin .
2
x a x x a x a
C đúng.
2
2
si
n 2sin – .sin .cos sin –x a x x a a x
2
si
n sin 2sin cos sin
x
a x x a a x
2
sin sin sin
x a x a x
2
1
sin
cos2 cos 2
2
x x a
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
2 2 2 2
si
n cos sin 1 sinx a x a
. D sai.
DẠNG 5. MIN-MAX
Câu 74. Chọn C
Ta có
3
6
6 2 2 2 2 2 2 2
3
3 1
sin cos sin cos 3sin cos (sin cos ) 1 sin 2 1 .
4 4 4
x
x x x x x x x x
Dấu “=” xảy ra khi và chỉ khi
2
s
in 2 1 cos2 0 2 .
2 4 2
x
x x k x k k
Câu 75.
Hương dân giai
Chọn B
Ta có
2
1
1
sin 2
2
M x
Vì
2
0
sin 1x
2
1
1
s
in 2 0
2 2
x
2
1 1
1
sin 2 1
2 2
x
.
Nên giá trị lớn nhất là
1
.
Câu 76.
Hương dân giai
Chọn A
3
4
5 sin cosx 5sin
5 5
M x x a
với
3
4
c
os ;sin
5
5
a
a
.
Ta có:
1
sin 1
x
a
5
5sin 5
x
a
.
Câu 77.
Hương dân giai
Chọn D
Ta có.
2
2 4 2 2 4
s
in cos sin sin cos cosM x x x x x x
2
2
co
s 2 1 sin cosx x x
2
1
co
s 2 1 sin 2
4
x
x
2
2
3 1 3 1 3 1
co
s 2 cos 2 cos 2 1
4
4 4 4 4 4
x x x
co
s 2 1
do
x
.
Nên giá trị lớn nhất là
1
.
Câu 78.
Hương dân giai
Chọn B
Đặt
ta
n , \ 1
t
x t
.
Ta có:
3 2
3
2
1
1
2 1
1
t
t t
M
t
t
t
2
1
2 1 1 0
M
t M t M
. (*).
Với
1M
thì (*) có nghiệm
0t
.
Với
1M
để (*) có nghiệm khác
1
thì.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
2 2
1
0 2 1 4 1 0 12 3 0
4
M M M M
.
Và
2
1 1 2 1 1 1 1 0 4
M M M
.
Câu 79.
Hương dân giai
Chọn D
2 2 2
6 1 sin 5sin 6 sinM x x x
Ta có:
2
0 sin 1x
,
x R
2
0 sin 1,
x x R
2
6 6 sin 5
x
,
x R
.
Gía trị lớn nhất là
6
.
Câu 80.
Hương dân giai
Chọn C
2 2
7 1 sin 2sinM x x
2
7 9 sin x
Ta có:
2
0 sin 1x
2
0 9sin 9,
x x R
2
7 7 2 sin 2
x
.
Gía trị lớn nhất là
7
.
DẠNG 6. NHẬN DẠNG TAM GIÁC
Câu 81. Chọn B.
Ta có:
sin 2 sin 2 2sin .cos 2sin .cos
A B A B A B C A B
2sin .cos 2sin .C A B C
Dấu đẳng thức xảy ra khi
cos 1
A B A B
.
Câu 82. Chọn C
Ta có
3 3
2 3
sin sin
2 2
sin cos sin cos 0
2 2 2 2
cos cos
2 2
A B
A B B A
A B
.
2 2
tan 1 tan tan 1 tan tan tan
2 2 2 2 2 2 2 2
A A B B A B A B
A B
.
Câu 83. Chọn C
Ta có
cot .cot cot .cot cot .cotA B B C C A
1 1 1 tan tan tan
tan .tan tan .tan tan .tan tan .tan .tan
A B C
A B B C C A A B C
.
Mặt khác
tan tan tanA B C
tan 1 tan .tan tanA B A B C
tan 1 tan .tan tanC A B C
tan 1 tan .tan tanC A B C
tan .tan .tanC A B
.
Nên
cot .cot cot .cot cot .cot 1
A B B C C A
.
Câu 84. Chọn B
Ta có
1 1
tan tan 7
2 5
tan
1 1
1 tan .tan 9
1 .
2 5
A B
A B
A B
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
Suy ra
7 1
tan tan
9 8
tan tan 1
7 1
1 tan .tan
1 .
9 8
A B C
A B C A B C
A B C
Vậy
4
A B C
.
Câu 85.
Hướng dẫn giải
Chọn D
Vì
, ,A B C
là các góc của tam giác
ABC
nên
180 180
o o
A B C C A B
.
90 .
2 2
o
C A B
Do đó
2
C
và
2
A B
là 2 góc phụ nhau.
sin cos ; cos sin ; tan cot ; cot tan .
2 2 2 2 2 2 2 2
C A B C A B C A B C A B
Câu 86. Chọn D
0 0
sin 2 sin 180 2 sin 180 sinA B C C C C C
.
Câu 87. Chọn A
Ta có:
tan tan tan A B C
tan tan tan
A B C
sin
sin
cos .cos cos
A B
C
A B C
.
cos cos .cos
sin .
cos .cos .cos
A B A B
C
A B C
sin .sin .sin
cos .cos .cos
A B C
A B C
tan .tan .tan A B C
.
Câu 88.
Hướng dẫn giải
Chọn A
Vì
, ,A B C
là các góc của tam giác
ABC
nên
180 180
o o
A B C C A B
.
90 .
2 2
o
C A B
Do đó
2
C
và
2
A B
là 2 góc phụ nhau.
sin cos ; cos sin ; tan cot ; cot tan .
2 2 2 2 2 2 2 2
C A B C A B C A B C A B
Câu 89. Chọn B
2
3
, 2 ;
2 2
1 cos2 cos(b c) cos(b c)
sin sin sin sin sin .sin =
2 2
a a
a b c a b b c
b
b b c b b c
2
1 cos cos cos 2
1 cos 2
= sin
2 2
a a a
a
a
.
Câu 90. Chọn D
Ta có:
sin2 sin 2 sin 2 A B C
sin 2 sin 2 sin 2A B C
2sin .cos 2sin .cosC
A B A B C
2sin .cos 2sin .cosC
C A B C
2sin . cos cosC
C A B
4sin .cos .cos
C A B C A B C
4sin .cos .cos
2 2
A B C A B C
C
4sin .cos .cos
2 2
C A B
4sin .sin .sin C A B
.
Câu 91. Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
0
0
2 180 2 3 3
cos cos cos 90 sin
2 2 2 2
A B C B B B B
.
Câu 92. Chọn C
Vì
, ,A B C
là các góc của tam giác
ABC
nên
180 180
A B C C A B
.
Do đó
A B
và
C
là 2 góc bù nhau.
sin sin ;cos cos
C A B C A B
.
tan tan ;cot cot
C A B C A B
Câu 93. Chọn B.
Ta có :
cot .cot cot .cot cot .cotA B B C C A
.
1 1 1
tan .tan tan .tan tan .tanA B B C C A
tan tan tan
tan .tan .tan
A B C
A B C
.
Mặt khác :
tan tan tan tan 1 tan .tan tanA B C A B A B C
.
tan 1 tan .tan tanC A B C
.
tan 1 tan .tan tanC A B C
tan tan .tanC A B
.
Nên
cot .cot cot .cot cot .cot 1
A B B C C A
.
Câu 94. Chọn A.
Ta có:
cot cot cot
2 2 2
A B C
cot cot cot
2 2 2
A B C
sin
cos
2 2
2
sin .sin sin
2 2 2
A B
C
A B C
.
sin sin .sin
2 2 2
cos .
2
sin .sin .sin
2 2 2
C A B
C
C A B
cos sin .sin
2 2 2 2
cos .
2
sin .sin .sin
2 2 2
A B A B
C
C A B
cos .cos .cos
2 2 2
sin .sin .sin
2 2 2
C B A
C A B
cot .cot .cot
2 2 2
A B C
.
Câu 95. Chọn C.
Ta có :
2 2 2
cos cos cosA B C
2
1 cos2A 1 cos2
cos
2 2
B
C
2
1 cos cos cosA B A B C
1 cos cos cos cos
C A B C A B
1 cos cos cos
C A B A B
1 2cos cos cos .A B C
Câu 96.
Hướng dẫn giải
Chọn C
2 2 2 2 2 2 2
2 2 2 2
2 2 2
cos cos cos .cos cos sin .sin
cos .cos 2cos .cos .cos cos sin .sin 1 cos 1 cos
1 cos cos cos .cos
cos cos cos 2cos .cos .cos 1
A B C A B C A B
A B A B C C A B A B
A B A B
A B C A B C
Câu 97. Chọn A
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
Ta có
2sin cos cos
sin sinC
2 2 2
sin sin sin
cos cos
2cos cos sin
2 2 2
B C B C A
B
A A A
B C B C A
B C
2
cos
2
2sin cos 2sin 1
2 2 2
sin
2
A
A A A
A
(
cos 0
2
A
vì
0 180
A
)
c
os 0 90
A
A
suy ra tam giác ABC vuông tại
A
.
Câu 98. Chọn A
Từ giả thiết suy ra:
2
2
4
1 13
2cos 2 4sin 4sin 0
64cos 4
A B B
A
2
2 2
4
1
3
c
os cos 4sin 4sin 1 *
64cos 4
A
A B B
A
AD BĐT Cauchy thì
2
2
4
1
3
cos cos (1)
64cos 4
A A
A
Mặt khác
2
2
4sin 4sin 1 2sin 1 0 2
B B B
Từ (*), (1) và (2) suy ra bđt thỏa mãn khi và chỉ khi dấu bằng ở (1) và (2) xảy ra
2
4
1
6
4
1
sin
2
cos A
c
os A
B
1
6
0
2
30 .
1
sin
9
0
2
o
o
o
A
c
osA
B
B
C
Nên
1
20
o
B
C
Chọn A.
Câu 99. Chọn C.
tan tan
tan
tan tan
1 tan .tan
tan 1
tan tan
1 tan .tan
.tan
1 tan .tan
A B
C
A B C
A B
A B C
A B
A B C
C
A B
suy ra
4
A
B C
.
Câu 100. Chọn D.
Ta có:
A
B C
3
2
2
A
B C
C
3
sin
sin cos .
2
2
A B C
C
C
A đúng.
2A
B C C
co
s – cos 2 cos 2 .A B C C C
B đúng.
2
3
2 2 2
A B C C
2
3 3
tan tan cot .
2 2 2 2
A B C C C
C đúng.
2
2
2 2
A B C C
2
c
ot cot tan .
2 2 2 2
A B C C C
D sai.
Câu 101. Chọn C.
Ta có:
2
2 2
A B C
c
os cos sin .
2 2 2 2
A B C C
A đúng.
2
A
B C C
co
s 2 cos cos .A B C C C
B đúng.
A
C B
si
n sin sin .A C B B
C sai.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng
hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
A
B C
co
s cos cos .A B C C
D đúng.
Câu 102. Chọn C.
Ta có :
+
cos cos sin sin cos cos sin .
2 2 2 2 2 2 2 2 2
B C B C B C A A
A đúng.
+
tan tan tan tan .tan .tanA B C A B C
ta
n 1 tan tan tan tanA B C B C
ta
n tan
t
an
1
tan tan
B C
A
B
C
ta
n tan
A
B C
. B đúng.
+
c
ot cot cot cot .cot .cotA B C A B C
cot cot cot 1 cot cotA B C B C
1
cot cot 1
cot cot cot
B
C
A B C
ta
n cot .A B C
C sai.
+
ta
n .tan tan .tan tan .tan 1
2 2 2 2 2 2
A
B B C C A
ta
n . tan tan 1 tan .tan
2 2 2 2 2
A B C B C
tan tan
1
2 2
tan 1 tan .tan
2 2 2
B C
A B C
c
ot tan
2
2 2
A B C
. D đúng.
| 1/54
| | Tải xuống

Có thể bạn quan tâm:

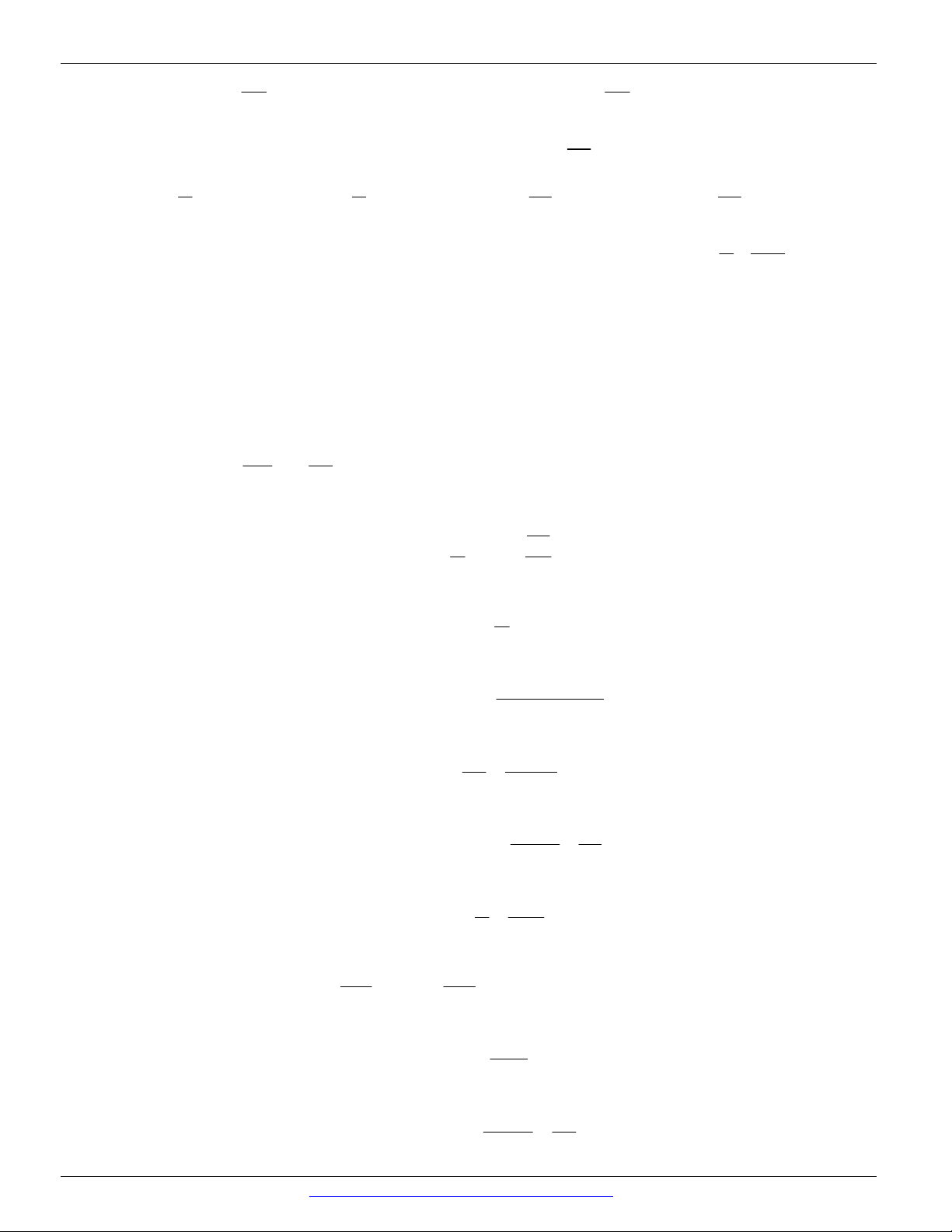
Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 10
GÓC VÀ CUNG LƯỢNG GIÁC 0D6-1 Contents
PHẦN A. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 1. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ ........................................................................................................ 1
DẠNG 2. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN........................................................... 2
PHẦN B. LỜI GIẢI ......................................................................................................................................................... 4
DẠNG 1. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ ........................................................................................................ 4
DẠNG 2. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN........................................................... 5 PHẦN A. CÂU HỎI
DẠNG 1. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ Câu 1.
Số đo theo đơn vị rađian của góc 315 là 7 7 2 4 A. . B. . C. . D. . 2 4 7 7 5 Câu 2. Cung tròn có số đo là
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây. 4 A. 5 . B. 15 . C. 172 . D. 225 . Câu 3.
Cung tròn có số đo là  . Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây. A. 30 . B. 45 . C. 90 . D. 180 . Câu 4. Góc 0
63 48 ' bằng (với   3,1416 ) A. 1,113 rad . B. 1,108 rad . C. 1,107 rad . D. 1,114 rad . 2 Câu 5. Góc có số đo đổi sang độ là: 5 A. 0 135 . B. 0 72 . C. 0 270 . D. 0 240 . Câu 6. Góc có số đo 0
108 đổi ra rađian là: 3  3  A. . B. . C. . D. . 5 10 2 4  Câu 7. Góc có số đo đổi sang độ là: 9 A. 0 25 . B. 0 15 . C. 0 18 . D. 0 20 .  Câu 8. Cho a
k 2 . Tìm k để 10  a  11 2
A. k  7 . B. k  5 .
C. k  4 .
D. k  6 . Câu 9.
Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. 0 60 . B. 0 30 . C. 0 40 . D. 0 50 .
Câu 10. Đổi số đo góc 0 105 sang rađian. 7 9 5 5 A. . B. . C. . D. . 12 12 8 12 Câu 11. Số đo góc 0
22 30’ đổi sang rađian là:   7  A. . B. . C. . D. . 5 8 12 6
Câu 12. Một cung tròn có số đo là 0
45 . Hãy chọn số đo radian của cung tròn đó trong các cung tròn sau đây.    A. B. C. D. 2 4 3 
Câu 13. Góc có số đo
đổi sang độ là: 24 A. 0 7 . B. 0 7 30 .  C. 0 8 . D. 0 8 30 . 
Câu 14. Góc có số đo 0
120 đổi sang rađian là: 2 3   A. . B. . C. . D. . 3 2 4 10
DẠNG 2. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN
Câu 15. Một đồng hồ treo tường, kim giờ dài 10, 57cm và kim phút dài 13, 34cm .Trong 30 phút mũi kim
giờ vạch lên cung tròn có độ dài là
A. 2, 78cm .
B. 2, 77cm .
C. 2, 76cm .
D. 2,8cm .
Câu 16. Cung tròn bán kính bằng 8, 43cm có số đo 3, 85 rad có độ dài là
A. 32, 46cm .
B. 32, 47cm .
C. 32, 5cm .
D. 32, 45cm .
Câu 17. Trên đường tròn với điểm gốc là A . Điểm M thuộc đường tròn sao cho cung lượng giác AM có
số đo 60 . Gọi N là điểm đối xứng với điểm M qua trục Oy , số đo cung AN là A. 1
 20 hoặc 240 .
B. 120  k360 ,  k   . C. 120 . D. 2  40 .
Câu 18. Trong 20 giây bánh xe của xe gắn máy quay được 60 vòng.Tính độ dài quãng đường xe gắn máy
đã đi được trong vòng 3 phút,biết rằng bán kính bánh xe gắn máy bằng 6, 5cm (lấy   3,1416 )
A. 22043cm .
B. 22055cm .
C. 22042cm .
D. 22054cm .
Câu 19. Trên đường tròn bán kính r  15 , độ dài của cung có số đo 0 50 là: 180 15 180 A. l  15. . B. l  . C. l  15. .50 .
D. l  750 .  180  5  25 19
Câu 20. Cho bốn cung (trên một đường tròn định hướng):   ,   ,  ,  , Các cung 6 3 3 6
nào có điểm cuối trùng nhau:
A.  và  ;  và  .
B.  ,  , .
C.  , , .
D.  và  ;  và  .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 21. Cho L , M , N , P lần lượt là điểm chính giữa các cung AB , BC , CD , DA . Cung  có mút đầu 3
trùng với A và số đo   
k . Mút cuối của  ở đâu? 4
A. L hoặc N .
B. M hoặc P .
C. M hoặc N .
D. L hoặc P . 
Câu 22. Trên đường tròn bán kính r  5 , độ dài của cung đo là: 8  r 5 A. l  . B. l  . C. l  . D. kết quả khác. 8 8 8
Câu 23. Một đường tròn có bán kính R  10cm . Độ dài cung 40o trên đường tròn gần bằng A. 11cm . B. 13cm . C. 7cm . D. 9cm . 3
Câu 24. Biết một số đo của góc  Ox,Oy 
 2001 . Giá trị tổng quát của góc  Ox,Oy là: 2 3
A.  Ox,Oy   k .
B. Ox,Oy    k 2 . 2  
C.  Ox,Oy   k .
D.  Ox,Oy   k 2 . 2 2
Câu 25. Cung nào sau đây có mút trung với B hoặc B’? A. 0 0
a  90  k360 . B. 0 0 a  –90  1 k 80 .   C.    k 2 . D.     k 2 . 2 2
Câu 26. Cung  có mút đầu là A và mút cuối là M thì số đo của  là: 3 3 3 3 A. k 2 . B.   k 2 . C.k . D.   k . 4 4 4 4
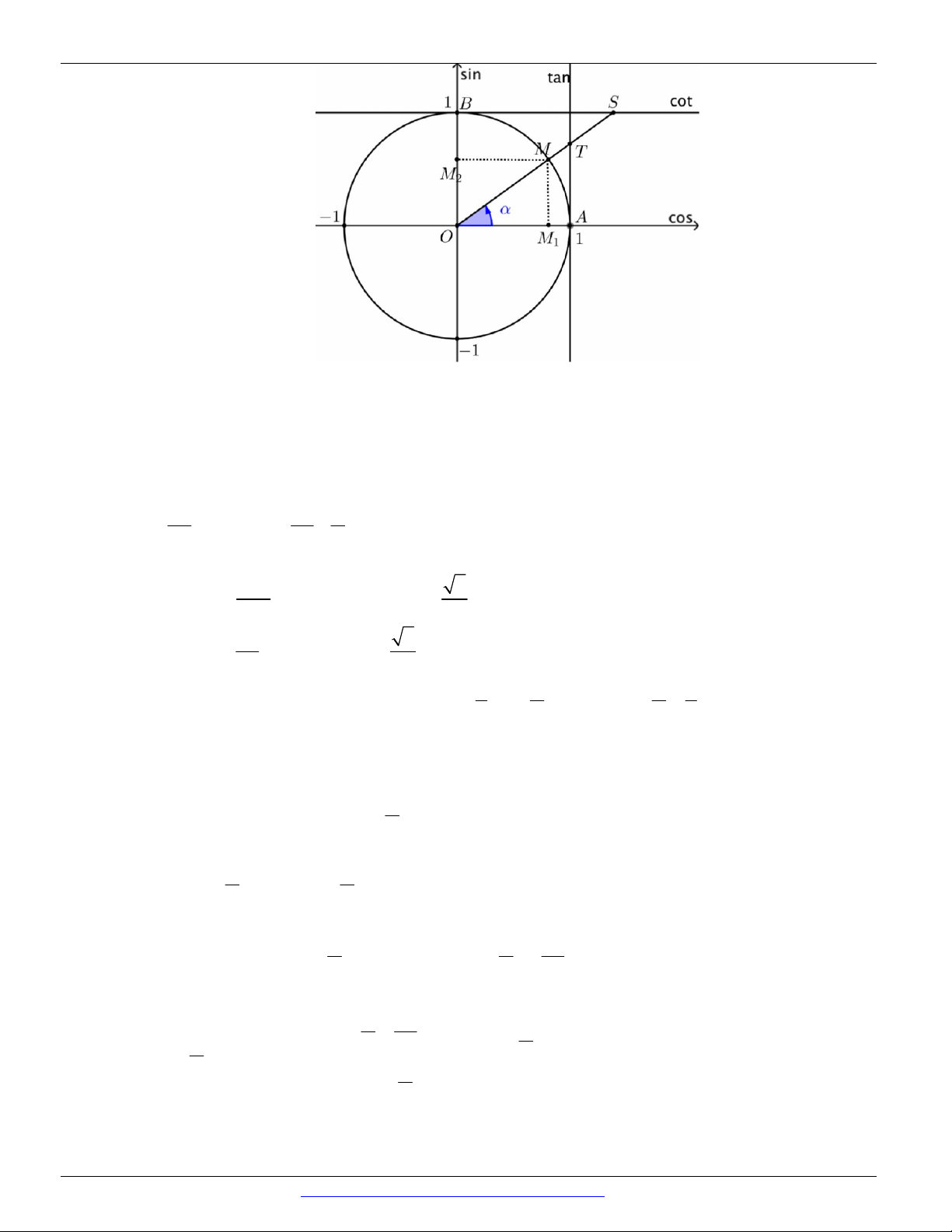
Câu 27. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Trên hình vẽ hai điểm M , N biểu diễn các cung có số đo là:      A. x   2k . B. x    k . C. x   k . D. x   k . . 3 3 3 3 2 þ 
Câu 28. Trên đường tròn lượng giác gốc A, cho điểm M xác định bởi sđ AM
. Gọi M là điểm đối 3 1 þ
xứng của M qua trục Ox . Tìm số đo của cung lượng giác AM . 1 þ 5 þ  A. sđ AM
k 2 , k   B. sđ AM
k 2 , k   1 3 1 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 þ   þ   C. sđ AM
k 2 , k   D. sđ AM
k , k   1 3 1 3 7
Câu 29. Góc lượng giác nào sau đây có cùng điểm cuối với góc ? 4   3 3 A.  . B. . C. . D.  . 4 4 4 4   k 2
Câu 30. Có bao nhiêu điểm M trên đường tròn định hướng gốc A thỏa mãn AM   , k   . 6 3 A. 6 . B. 4 . C. 3 . D. 8 . PHẦN B. LỜI GIẢI
DẠNG 1. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ Câu 1. Chọn B 315 7 Ta có 315  .  (rađian). 180 4 Câu 2. Chọn D 5  Ta có: 4 a  .180  .180  225 .   Câu 3. Chọn D  Ta có: a  .180  180 .  Câu 4. Chọn D 0 63,8  3,1416 Ta có 0 0 63 48 '  63,8   1,114rad 0 180 Câu 5. Chọn B 0 2 2.180 Ta có: 0   72 . 5 5 Câu 6. Chọn A 0 108 . 3 Ta có: 0 108   . 0 180 5 Câu 7. Chọn D 0  180 Ta có: 0   20 . 9 9 Câu 8. Chọn B 19 21
+ Để 10  a  11 thì  k 2   k  5 2 2 Câu 9. Chọn D 0 360
+ 1 bánh răng tương ứng với 0  5  10 bánh răng là 0 50 . 72 Câu 10. Chọn A 0 105 . 7 0 105   . 0 180 12
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Câu 11. Chọn B 0 22 30 '.  0 22 30 '   . 0 180 8 Câu 12. Chọn C a .    Ta có:    . 180 4 Câu 13. Chọn B 0  180 Ta có: 0   7 30 '. 24 24 Câu 14. Chọn A 0 120 . 2 Ta có: 0 120   . 0 180 3
DẠNG 2. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN Câu 15. Chọn B
6 giờ thì kim giờ vạch lên 1 cung có số đo nên 30 phút kim giờ vạch lên 1 cung có số đo là 1 3,14
 , suy ra độ dài cung tròn mà nó vạch lên là l R  10,57   2, 77 12 12 Câu 16. Chọn A
Độ dài cung tròn là l R  8, 43 3, 85  32, 4555
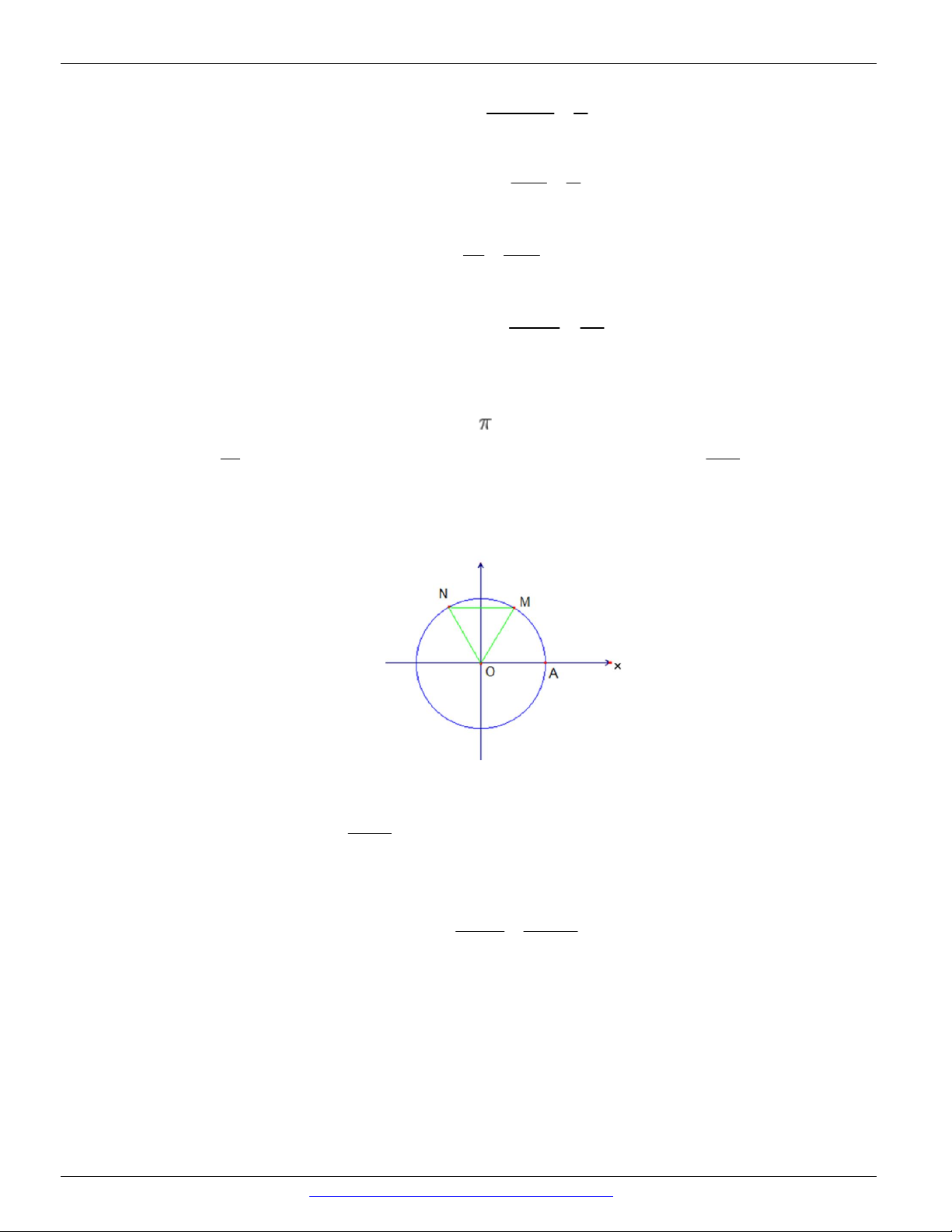
Câu 17. Chọn C Ta có:  AON  60 ,  MON  60 nên 
AOM  120 . Khi đó số đo cung AN bằng 120 . Câu 18. Chọn D 3 60 3 phút xe đi được
 60  540 vòng. Độ dài 1 vòng bằng chu vi bánh xe là 20
2 R  2  3,1416  6, 5  40,8408 . Vậy quãng đường xe đi được là 540  40, 8408  22054, 032cm Câu 19. Chọn C 0  .r.n 15.50 l   . 0 180 180 Câu 20. Chọn A
C1: Ta có:    4  2 cung  và  có điểm cuối trùng nhau.
    8  hai cung  và  có điểm cuối trùng nhau.
C2: Gọi là điểm cuối của các cung  ,  , ,
Biểu diễn các cung trên đường tròn lượng giác ta có B C, A D . Câu 21. Chọn A
Nhìn vào đường tròn lượng giác để đánh giá. Câu 22. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Độ dài cung AB có số đo cung AB bằng n độ: l r.n  5. . 8 Câu 23. Chọn C   2 20 o 40. 2 Đổi đơn vị 40    độ dài cung   .10 
 6, 9813cm  7 cm . 180 9 9 9 Câu 24. Chọn D 3  
 Ox,Oy   2001   2002   k 2 2 2 2 Câu 25. Chọn B
Nhìn vào đường tròn lượng giác để đánh giá. Câu 26. Chọn B
Ta có OM là phân giác góc  A OB     0 MOB  45   0 AOM  135 3
 góc lượng giác O , A OM   
k 2 (theo chiều âm). 4 5 hoặc O , A OM  
k 2 (theo chiều dương). 4 Câu 27. Lời giải Chọn C
Câu 28. Chọn C y M K π 3 x O π H A - 3 -K M1
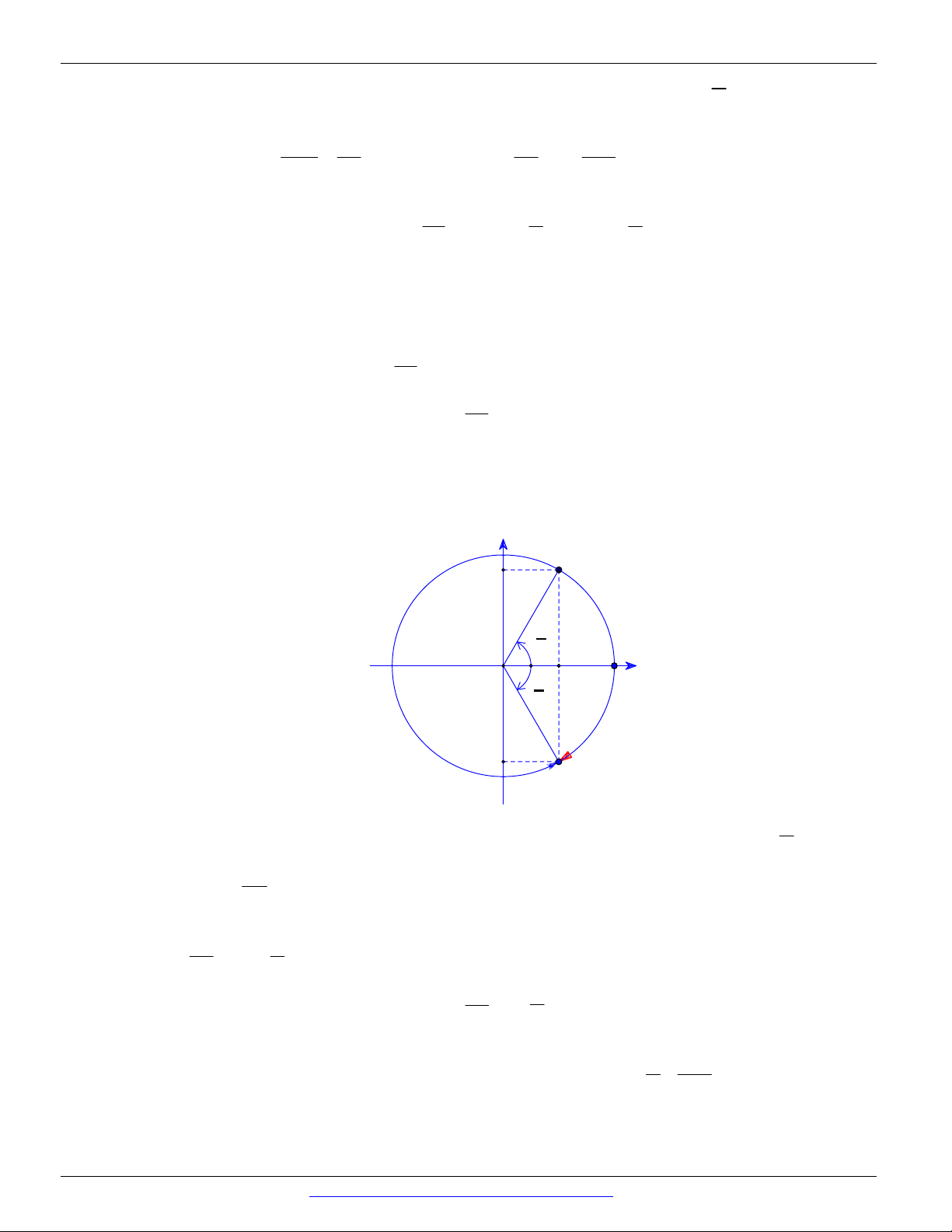
Vì M là điểm đối xứng của M qua trục Ox nên có 1 góc lượng giác O , A OM   1  1 3 þ    sđ AM
k 2 , k   . 1 3
Câu 29. Chọn A 7  Ta có  2  . 4 4 7 
Góc lượng giác có cùng điểm cuối với góc là  . 4 4
Câu 30. Chọn C   k 2
Có 3 điểm M trên đường tròn định hướng gốc A thỏa mãn AM  
, k   , ứng với các 6 3
giá trị là số dư của phép chia k cho 3.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 10
GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT CUNG 0D6-2 Contents
PHẦN A. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 1. XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC ............................................................................................ 1
DẠNG 2. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT .................................................. 2
DẠNG 3. TÍNH GIÁ TRỊ LƯỢNG GIÁC ...................................................................................................................... 3
DẠNG 4. RÚT GỌN BIỂU THỨC LƯỢNG GIÁC ....................................................................................................... 6
PHẦN B. LỜI GIẢI ......................................................................................................................................................... 9
DẠNG 1. XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC ............................................................................................ 9
DẠNG 2. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT ................................................ 10
DẠNG 3. TÍNH GIÁ TRỊ LƯỢNG GIÁC .................................................................................................................... 11
DẠNG 4. RÚT GỌN BIỂU THỨC LƯỢNG GIÁC ..................................................................................................... 15 PHẦN A. CÂU HỎI
DẠNG 1. XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC  Câu 1. Cho
a   . Kết quả đúng là 2
A. sin a  0 , cos a  0 . B. sin a  0 , cos a  0 . C. sin a  0 , cos a  0 . D. sin a  0 , cos a  0 . Câu 2.
Trong các giá trị sau, sin  có thể nhận giá trị nào? 4 5 A. 0  , 7 . B. . C.  2 . D. . 3 2 5 Câu 3. Cho 2  a
. Chọn khẳng định đúng. 2
A. tan a  0, cot a  0. B. tan a  0, cot a  0.
C. tan a  0, cot a  0. D. tan a  0, cot a  0 . Câu 4.
Ở góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây. A. cot   0 . B. sin  0 . C. cos  0 . D. tan  0 . Câu 5.
Ở góc phần tư thứ tư của đường tròn lượng giác. hãy chọn kết quả đúng trong các kết quả sau đây. A. cot   0 . B. tan  0 . C. sin  0 . D. cos  0 . 7 Câu 6. Cho
   2 .Xét câu nào sau đây đúng? 4 A. tan   0 . B. cot  0 . C. cos  0 . D. sin  0 . Câu 7.
Xét câu nào sau đây đúng?
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489    A. 2 cos 45  sin cos 60   .  3  B. Hai câu A và
C. Nếu a âm thì ít nhất một trong hai số cos ,
a sin a phải âm.
D. Nếu a dương thì 2
sin a  1 cos a . Câu 8. Cho
    . Kết quả đúng là: 2
A. sin   0 ; cos  0 . B. sin   0 ; cos  0 .
C. sin   0 ; cos  0 . D. sin   0 ; cos  0 . Câu 9. Xét các mệnh đề sau:          I. cos   0   . II. sin   0   . III. tan   0   .  2   2   2 
Mệnh đề nào sai? A. Chỉ I. B. Chỉ II.
C. Chỉ II và III.
D. Cả I, II và III.
Câu 10. Xét các mệnh đề sau đây:          I. cos    0   . II. sin    0   . III. cot    0   .  2   2   2  Mệnh đề nào đúng?
A. Chỉ II và III.
B. Cả I, II và III. C. Chỉ I.
D. Chỉ I và II.      
Câu 11. Cho góc lượng giác        . Xét dấu sin     và tan  
  . Chọn kết quả đúng.  2   2                  sin    0    sin    0    sin    0    sin    0    A.   2  . B.   2  . C.   2  . D.   2  .  tan      0     tan      0  tan      0  tan      0 
DẠNG 2. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT
Câu 12. Cho hai góc nhọn  và  phụ nhau. Hệ thức nào sau đây là sai?
A. cot  tan  .
B. cos  sin  .
C. cos   sin .
D. sin   cos  .
Câu 13. Trong các đẳng thức sau, đẳng thức nào đúng? A.  0
sin 180 – a  – cos a . B.  0
sin 180 – a  sin a . C. sin  0 180 – a  s n i a . D. sin  0 180 – a  c s o a .
Câu 14. Chọn đẳng thức sai trong các đẳng thức sau       A. sin  x  cos x   . B. sin  x  cos x   .  2   2        C. tan  x  cot x   . D. tan  x  cot x   .  2   2 
Câu 15. Trong các mệnh đề sau, mệnh đề nào đúng?
A. cos x   cos x .
B. sin  x     sin x .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489   
C. cos   x   cos x . D. sin
x   cos x   .  2 
Câu 16. Khẳng định nào sau đây là sai? A. sin  
   sin . B. cot  
    cot . C. cos 
    cos . D. tan       tan .
Câu 17. Khẳng định nào sau đây đúng?
A. sin x  s in . x
B. cos x   cos . x
C. cot x  cot . x
D. tan x  tan . x
Câu 18. Chọn hệ thức sai trong các hệ thức sau.  3  A. tan  x  cot x   .
B. sin 3  x  sin x .  2 
C. cos 3  x  cos x .
D. cos x  cos x .
Câu 19. cos(x  2017 ) bằng kết quả nào sau đây? A.  cos x . B.  sin x . C. sin x . D. cos x .
DẠNG 3. TÍNH GIÁ TRỊ LƯỢNG GIÁC
Câu 20. Giá trị của cot1458 là A. 1. B. 1  . C. 0 . D. 5  2 5 . 89 cot Câu 21. Giá trị 6 là 3 3 A. 3 . B.  3 . C. . D. – . 3 3
Câu 22. Giá trị của tan180 là A. 1. B. 0 . C. –1.
D. Không xác định. 1
Câu 23. Cho biết tan   . Tính cot  2 1 1 A. cot   2 . B. cot   . C. cot   . D. cot   2 . 4 2 3  Câu 24. Cho sin  và
    . Giá trị của cos là: 5 2 4 4 4 16 A. . B.  . C.  . D. . 5 5 5 25 4  cos  0    Câu 25. Cho 5 với 2 . Tính sin . 1 1 3 3 A. sin  . B. sin    . C. sin  . D. sin    . 5 5 5 5  
Câu 26. Tính  biết cos 1
A.   k k   .
B.   k 2 k   .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 C.  
k 2 k   . D.   
  k 2 k   . 2 4 3 tan      2 Câu 27. Cho 5 với 2 . Khi đó: 4 5 4 5 A. sin    , cos   . B. sin   , cos  . 41 41 41 41 4 5 4 5 C. sin    cos  . D. sin   , cos   . 41 41 41 41 2  3 Câu 28. Cho 0 cos15 
. Giá trị của tan15 bằng: 2 2  3 2  3 A. 3  2 B. C. 2  3 D. 2 4 2   
Câu 29. Cho cos       
 . Khi đó tan  bằng 5  2  21 21 21 21 A. . B.  . C. . D.  . 3 5 5 2 3
Câu 30. Cho tan   5 , với     . Khi đó cos bằng: 2 6 6 1 A.  . B. 6 . C. . D. . 6 6 6 3 Câu 31. Cho sin 
90    180 . Tính cot . 5 3 4 A. cot  . B. cot  . 4 3 4 3
C. cot   . D. cot   . 3 4 2
Câu 32. Trên nửa đường tròn đơn vị cho góc  sao cho sin  
và cos  0 . Tính tan  . 3 2 5 2 5 2 A. . B. . C. . D. 1. 5 5 5 1 
Câu 33. Cho sin   và
    . Khi đó cos có giá trị là. 3 2 2 2 2 8 2 2 A. cos   . B. cos  . C. cos  . D. cos   . 3 3 9 3   
Câu 34. Cho cot   3  2 với
    . Khi đó giá trị tan  cot bằng: 2 2 2 A. 2 19 . B. 2 19 . C.  19 . D. 19 . 3
Câu 35. Nếu sin  cos  thì sin  2 bằng 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 5 1 13 9 A. . B. . C. . D. . 4 2 4 4 1 
Câu 36. Cho sin x  cos x  và 0  x
. Tính giá trị của sin x . 2 2 1 7 1 7 1 7 1 7 A. sin x  . B. sin x  . C. sin x  . D. sin x  . 6 6 4 4 1 Câu 37. Cho sinx = . Tính giá trị của 2 cos x . 2 3 3 1 1 A. 2 cos x B. 2 cos x C. 2 cos x D. 2 cos x  4 2 4 2 3sin x  cos x
Câu 38. Cho P
với tan x  2 . Giá trị của P bằng
sin x  2 cos x 8 2 2 8 5 A. . B.  . C. . D. . 9 3 9 4 1 sin x  cos x Câu 39. Cho s inx 
và cosx nhận giá trị âm, giá trị của biểu thức A  bằng 2 sin x cox A. 2  3 B. 2  3 C. 2  3 D. 2  3
4 sin x  5 cos x
Câu 40. Cho tan x  2 .Giá trị biểu thức P  là
2 sin x  3cos x A. 2. B. 13 . C. 9 . D. 2  .      
Câu 41. Cho tam giác ABC đều. Tính giá trị của biểu thức P  cos  A ,
B BC   cosBC,CA  cos , CA AB . 3 3 3 3 3 3 A. P  . B. P   . C. P   . D. P  . 2 2 2 2 2sin a  cos a
Câu 42. Cho tan a  2 . Tính giá trị biểu thức P  . sin a  cos a 5 A. P  2 . B. P  1 . C. P  . D. P  1  . 3 3 sin x  3cos x
Câu 43. Cho cung lượng giác có số đo x thỏa mãn tan x  2 .Giá trị của biểu thức M  3
5sin x  2 cos x bằng 7 7 7 7 A. . B. . C. . D. . 30 32 33 31 1 sin x  cos x
Câu 44. Cho sin x
và cos x nhận giá trị âm, giá trị của biểu thức A  bằng 2 sin x  cos x A. 2   3 . B. 2  3 . C. 2   3 . D. 2  3 . 0 0 cos 750  sin 420
Câu 45. Giá trị của biểu thức A  bằng sin  0 330   cos 0 390  
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 3 1 3 A. 3   3 . B. 2  3 3 . C. . D. . 3 1 3 3 cot   2 tan Câu 46. Cho sin  và 0 0
90    180 . Giá trị của biểu thức E  là: 5 tan  3cot  2 2 4 4 A. . B.  . C. . D.  . 57 57 57 57 3sin  cos
Câu 47. Cho tan   2 . Giá trị của A  là: sin  cos 5 7 A. 5 . B. . C. 7 . D. . 3 3  3 5 7
Câu 48. Giá trị của 2 2 2 2 A  cos  cos  cos  cos bằng 8 8 8 8 A. 0 . B. 1. C. 2 . D. 1  . sin  0 234  0  cos 216
Câu 49. Rút gọn biểu thức 0 A
. tan 36 , ta có A bằng 0 0 sin144  cos126 A. 2 . B. 2 . C. 1. D. 1  .  0 0 cot 44  tan 226  0 .cos 406 Câu 50. Biểu thức 0 0 B
 cot 72 .cot18 có kết quả rút gọn bằng 0 cos 316 1  1 A. 1  . B. 1. C. . D. . 2 2  
Câu 51. Biết tan   2 và 180    270 . Giá trị cos  sin  bằng 3 5 3 5 5 1 A.  . B. 1 – 5 . C. . D. . 5 2 2 1 2
Câu 52. Cho biết cot x
. Giá trị biểu thức A  bằng 2 2 2 sin x  sin .
x cos x  cos x A. 6. B. 8. C. 10. D. 12.
DẠNG 4. RÚT GỌN BIỂU THỨC LƯỢNG GIÁC
Câu 53. Trong các công thức sau, công thức nào sai? 1    A. 2 2
sin   cos   1 . B. 2 1 tan    
k , k   . 2   cos   2  1  k  C. 2 1 cot  
  k , k   .
D. tan  cot  1   , k   . 2     sin   2  2 2 tan a  sin a
Câu 54. Biểu thức rút gọn của A = bằng: 2 2 cot a  cos a A. 6 tan a . B. 6 cos a . C. 4 tan a . D. 6 sin a . Câu 55. Biểu thức 2 2 2 2 2 D  cos .
x cot x  3cos x – cot x  2sin x không phụ thuộc x và bằng A. 2. B. –2 . C. 3. D. –3 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 sin  0 328  0 .sin 958 cos  0 508 .cos 0 1022 
Câu 56. Biểu thức A   rút gọn bằng: 0 cot 572 tan  0 212  A. 1  . B. 1. C. 0 . D. 2 . 0 sin 515 .cos  0 475   0 0  cot 222 .cot 408
Câu 57. Biểu thức A
có kết quả rút gọn bằng 0 cot 415 .cot  0 505   0 0  tan197 .tan 73 1 1 1 1 A. 2 0 sin 25 . B. 2 0 cos 55 . C. 2 0 cos 25 . D. 2 0 sin 65 . 2 2 2 2 2 2 cos x 1
Câu 58. Đơn giản biểu thức A  ta có sin x  cos x
A. A  cos x  sin x .
B. A  cos x – sin x .
C. A  sin x – cos x .
D. A   sin x – cos x . 2
Câu 59. Biết sin   cos 
. Trong các kết quả sau, kết quả nào sai? 2 1 6
A. sin .cos  – .
B. sin  cos   . 4 2 7 C. 4 4 sin   cos   . D. 2 2 tan   cot   12 . 8
Câu 60. Biểu thức:  2003 
A  cos   26   2sin   7   cos1,5  cos    cos  
 1,5 .cot  8  có  2  kết quả thu gọn bằng: A.  sin  . B. sin  . C.  cos . D. cos .
Câu 61. Đơn giản biểu thức A   2 x 2 x   2 1 – sin .cot
1 – cot x, ta có A. 2 A  sin x . B. 2 A  cos x . C. 2
A  – sin x . D. 2
A  – cos x .            
Câu 62. Đơn giản biểu thức A  cos   sin   cos    sin           , ta có:  2   2   2   2 
A. A  2 sin a .
B. A  2 cos a .
C. A  sin a – cos a .
D. A  0 .     3 
Câu 63. Biểu thức P  sin   x  cos  x  cot  
2  x  tan  x
 có biểu thức rút gọn là  2   2 
A. P  2sin x . B. P  2  sin x .
C. P  0 . D. P  2  cot x .
Câu 64. Cho tam giác ABC . Đẳng thức nào sau đây sai? A B C
A. A B C   .
B. cos  A B  cos C . C. sin  cos
. D. sin  A B  sin C . 2 2   
Câu 65. Đơn giản biểu thức A  cos    sin      , ta có  2 
A. A  cos a  sin a .
B. A  2 sin a .
C. A  sin a – cos a . D. A  0 .
Câu 66. Cho A, B, C là ba góc của một tam giác không vuông. Mệnh đề nào sau đây sai? A B C A. tan  cot   .  2  2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A B C B. cot  tan   .  2  2
C. cot  A B   cot C .
D. tan  A B  tan C .
Câu 67. Tính giá trị của biểu thức 6 6 2 2
A  sin x  cos x  3sin x cos x . A. A  –1. B. A  1 . C. A  4 . D. A  –4 . 1 tan x2 2 1
Câu 68. Biểu thức A  
không phụ thuộc vào x và bằng 2 2 2 4 tan x 4 sin x cos x 1 1 A. 1. B. –1. C. . D.  . 4 4 2 2 cos x  sin y Câu 69. Biểu thức 2 2 B   cot .
x cot y không phụ thuộc vào ,
x y và bằng 2 2 sin . x sin y A. 2 . B. –2 . C. 1. D. –1. 2
Câu 70. Biểu thức C   4 4 2 2 x x x x  8 8 2 sin cos sin cos
– sin x  cos x có giá trị không đổi và bằng A. 2 . B. –2 . C. 1. D. –1.
Câu 71. Hệ thức nào sai trong bốn hệ thức sau: 2 tan x  tan y  1 sin a 1 sin a A.  tan . x tan y . B. 2     4 tan a . cot x  cot y  1 sin a 1 sin a      2 sin  cos 1 cot  sin   cos 2 cos C.   . D.  . 2 cos  sin  cos  sin  1 cot  1 cos sin  cos 1 98 Câu 72. Nếu biết 4 4
3sin x  2 cos x
thì giá trị biểu thức 4 4
A  2sin x  3cos x bằng 81 101 601 103 603 105 605 107 607 A. hay . B. hay . C. hay . D. hay . 81 504 81 405 81 504 81 405 1
Câu 73. Nếu sin x  cos x
thì 3sin x  2 cos x bằng 2 5  7 5  7 5  5 5  5 A. hay . B. hay . 4 4 7 4 2  3 2  3 3  2 3  2 C. hay . D. hay . 5 5 5 5 2b
Câu 74. Biết tan x
. Giá trị của biểu thức 2 2
A a cos x  2b sin .
x cos x c sin x bằng a c A. –a . B. a . C. –b . D. b . 4 4 sin  cos  1 8 8 sin  cos    A   3 3 Câu 75. Nếu biết a b
a b thì biểu thức a b bằng 1 1 1 1 A. . B. . C. . D.  2 2 3 3 a b2 a ba b3 a b
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489     9 
Câu 76. Với mọi , biểu thức: A  cos + cos    ...  cos       nhận giá trị bằng:  5   5  A. –10 . B. 10 . C. 0 . D. 5 .  3 5 7
Câu 77. Giá trị của biểu thức 2 2 2 2 A  sin  sin  sin  sin bằng 8 8 8 8 A. 2 . B. 2 . C. 1. D. 0 . 0 2 sin 2550 .cos  0 188 1 
Câu 78. Giá trị của biểu thức A =  bằng: 0 0 0 tan 368 2 cos 638  cos 98 A. 1. B. 2 . C. 1  . D. 0 .
Câu 79. Cho tam giác ABC và các mệnh đề: B C A A B C I cos  sin II tan . tan
 1 III cos  A B – C  – cos 2C  0 2 2 2 2 Mệnh đề đúng là: A. Chỉ I .
B. II và III .
C. I và II . D. Chỉ III .     3 
Câu 80. Rút gọn biểu thức A  cos     sin    tan   .sin    
2   ta được  2   2 
A. A  cos .
B. A   cos .
C. A  sin .
D. A  3cos . PHẦN B. LỜI GIẢI
DẠNG 1. XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC Câu 1. Chọn C  Vì
a    sin a  0 , cos a  0 . 2 Câu 2. Chọn A.
Vì 1  sin   1 . Nên ta chọn A. Câu 3. Chọn C
Đặt a b  2 5   2  a   5 2  b  2   0  b  2 2 2
Có tan a  tan(b  2 )  tan b  0 1 cot a   0 . tan a
Vậy tan a  0, cot a  0 . Câu 4. Chọn B
Nhìn vào đường tròn lượng giác:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
-Ta thấy ở góc phần tư thứ nhất thì: sin  0;cos  0; tan  0;cot  0
=> chỉ có câu A thỏa mãn. Câu 5. Chọn D
- Ở góc phần tư thứ tư thì: sin  0;cos  0; tan  0;cot  0 .
 chỉ có C thỏa mãn. Câu 6. Chọn C 7 3     2  
   2 nên α thuộc cung phần tư thứ IV vì vậy đáp án đúng là A 4 2 4 Câu 7. Chọn A 7   2 A sai vì   nhưng sin   cos =  0 . 4 2 5 2 B sai vì   nhưng sin     0 . 4 2 1     1 C đúng vì 2 cos 45  , sin cos 60  sin    2  3  6 2 Câu 8.
Hướng dẫn giải Chọn A  Vì
    nên tan   0; cot   0 2 Câu 9. Chọn C        
   0 nên α thuộc cung phần tư thứ IV nên chỉ II, II sai. 2 2
Câu 10. Chọn B     3
            nên đáp án là D 2  2  2
Câu 11. Chọn C   3            cos    0  2 2    Ta có          2  . 2           tan      0 2   
DẠNG 2. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT
Câu 12. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Thường nhớ: các góc phụ nhau có các giá trị lượng giác bằng chéo nhau
Nghĩa là cos  sin  ; cot  tan  và ngược lại.
Câu 13. Chọn C. Theo công thức.
Câu 14. Chọn D.
Câu 15. Chọn C
Ta có cos   x   cos x .
Câu 16. Chọn C
Dễ thấy C sai vì cos      cos .
Câu 17. Chọn A
Ta có: sin x  s in x .
Câu 18. Chọn C
cos 3  x  cos  x   cos x .
Câu 19. Chọn A
Ta có cos  x  2017    cos x .
DẠNG 3. TÍNH GIÁ TRỊ LƯỢNG GIÁC
Câu 20. Chọn D
cot1458  cot 4.360 18  cot18  5  2 5 .
Câu 21. Chọn B 89        Biến đổi cot  cot  15  cot    cot   3     . 6  6   6  6
Câu 22. Chọn B
Biến đổi tan180  tan 0 180   tan 0  0.
Câu 23. Chọn A 1 1
Ta có: tan .cot   1  cot     2 . tan 1 2
Câu 24. Chọn B.  4 cos  9 16  5 Ta có: 2 2 sin   cos   1 2 2
 cos  =1 sin   1    . 25 25 4 cos    5  4 Vì
     cos   . 2 5
Câu 25. Chọn C 2  4  9 3 Ta có: 2 2
sin   1 cos   1     sin   .  5  25 5  3 Do 0   
nên sin   0 . Suy ra, sin  . 2 5
Câu 26. Chọn C
Ta có: cos  1   
k 2 k   . 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Câu 27. Chọn C 1 16 1 1 41 25 5 2 1 tan    1    2  cos    cos   2 cos  2 25 cos  2 cos  25 41 41 25 16 4 2 2
sin   1 cos   1   sin    41 41 41  5 cos  0  cos  3  41    2   2  4
sin   0  sin    .   41 Câu 28. Chọn C 1 4 tan 15  1  1  2  32 2 0 0  tan15  2  3 . 2 0 cos 15 2  3
Câu 29. Chọn D  Với
     tan  0 . 2 1 1 25 21 21 Ta có 2 1 tan   2  tan   1  1   tan    . 2 cos  2 cos  4 4 2
Câu 30. Chọn A 1 Ta có 2  1 tan     2 1 5  6 . 2 cos  3 6 Mặt khác     nên cos   . 2 6
Câu 31. Chọn C 1 16 4 Ta có: 2 1 cot   2  cot    cot   . 2 sin  9 3 4
Vì 90    180 nên cot   . 3
Câu 32. Chọn A 2 Có 2 2
cos   1  sin  , mà sin   . 3 5 5 Suy ra 2 cos  
, có cos  0  cos   . 9 3 sin  2 5 Có tan     . cos 5
Câu 33. Chọn D  Vì
    nên cos  0 . 2 8 Ta có 2 2 2 2
sin   cos   1  co s  1 sin   9
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  8 2 2 cos   l  9 3    8 2 2 cos     tm  9 3
Câu 34. Chọn A 1 1 1 2
 1 cot   118  19 2  sin    sin    2 sin  19 19 Vì  1
     sin   0  sin  2 19   2 2 sin  cos   2 Suy ra 2 2 tan  cot    2 19 . 2 2   sin sin cos 2 2
Câu 35. Chọn A 3 9 9 5 Ta có: sin  cos 
 sin  cos 2   1  sin 2   sin 2  . 2 4 4 4
Câu 36. Chọn C 1 1
Từ sin x  cos x   cos x   sin x (1) . 2 2 Mặt khác: 2 2
sin x  cos x  1 (2) . Thế (1) vào (2) ta được:  1 7 2 sin x    1  3 2 2 4 sin x   sin x
 1  2 sin x  sin x   0      2  4  1 7 sin x   4  1 7 Vì 0  x
 sin x  0  sin x  . 2 4
Câu 37. Chọn A 1 3 Ta có: 2 2
cos x  1 sin x  1  . 4 4
Câu 38. Chọn D 3sin x  cos x 3 tan x 1 3.2 1 5 Ta có P     .
sin x  2 cos x tan x  2 2  2 4
Câu 39. Chọn A
Vì cosx nhận giá trị âm. 1 3 Ta có: 2
cos x   1 sin x   1   4 2 1 3  1 3 Suy ra: 2 2 A    2  3 1 3 1 3  2 2
Câu 40. Chọn C
Ta có: tan x  2  cos x  0 .Chia tử và mẫu cho cos x
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
4 sin x  5 cos x 4 tan x  5 4.2  5 Suy ra: P     13 .
2 sin x  3cos x 2 tan x  3 2.2  3
Câu 41. Chọn B       3
Ta có: P  cos A ,
B BC cosB , C C A  cosC , A AB 0  3cos120   2
Câu 42. Chọn B 2sin a  cos a 2 tan a 1 2.2 1 Ta có: P     1. sin a  cos a tan a 1 2 1
Câu 43. Chọn A
Do tan x  2  cos x  0 . 1 3 tan . x  3 2 2 sin x  3cos x
tan x 1 tan x  3 7 Ta có cos x M     . 3
5sin x  2 cos x 2 3 2 3
5 tan x  2 1 tan x 30 5 tan x    2 cos x
Câu 44. Chọn A 1 3
Vì cos x nhận giá trị âm nên ta có 2
cos x   1 sin x   1   4 2 1 3  1 3 Suy ra: 2 2 A    2  3 . 1 3 1 3  2 2
Câu 45. Chọn A. 0 0 cos 30  sin 60 2 3 A    3   3 . 0 0 sin 30  cos 30 1 3
Câu 46. Chọn B.  4 cos  9 16  2 2 5 sin   cos   1 2 2
 cos  =1 sin   1    25 25 4 cos    5 4 3 4 Vì 0 0
90    180  cos   . Vậy tan   và cot   . 5 4 3 4  3    2.  cot  2 tan    3  4  2 E     . tan  3cot  3  4  57   3.    4  3 
Câu 47. Chọn C. 3sin  cos 3 tan 1 A    7 . sin  cos tan  1
Câu 48. Chọn C.  3 3    3 2 2 2 2  A  cos  cos  cos  cos 2 2  A  2 cos  cos   8 8 8 8  8 8     2 2   A  2 cos  sin  2   .  8 8 
Câu 49. Chọn C.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 0 0  sin 234  sin126 0 0 2 cos180 .sin 54 0 A  .tan 36 0  A  . tan 36 0 0 cos 54  cos126 0 2sin 90 sin  0 36   0 0 1.sin 54 sin 36  A  .  A  1. 1sin  0 36  0 cos 36
Câu 50. Chọn B.  0 0 cot 44  tan 46  0 .cos 46 0 0 2 cot 44 .cos 46 0 0 B
 cot 72 . tan 72  B
1  B  2 1  1. 0 cos 44 0 cos 44
Câu 51. Chọn A
Do 180    270 nên sin   0 và cos  0 . Từ đó 1 1 1 Ta có 2  1 tan   5 2  cos    cos   . 2 cos  5 5  1  2
sin   tan.cos  2.       5  5 2 1 3 5
Như vậy, cos  sin       . 5 5 5
Câu 52. Chọn C 2  1   2  2 2 1   2 1 cot 2 x sin x  4 A       10. 2 2 2 2 sin x  sin .
x cos x  cos x
1 cot x  cot x
1 cot x  cot x 1 1 1  2 4
DẠNG 4. RÚT GỌN BIỂU THỨC LƯỢNG GIÁC
Câu 53. Chọn D k 
D sai vì: tan.cot   1   , k     .  2 
Câu 54. Chọn A  1 2  sin a 1 2 2 tan a  sin a  2  2 2  cos a  tan . a tan a A  6  A    tan a . 2 2 cot a  cos a 2  1 2  cot a cos 1  2   sin a
Câu 55. Chọn A 2 2 2 2 2 D  cos .
x cot x  3cos x – cot x  2sin x 2 2  x   x  2 cos 2 cot cos x   1 2 2 2  cos x  2  cot . x sin x 2 2
 cos x  2  cos x  2 .
Câu 56. Chọn A sin  0 328  0 .sin 958 cos  0 508 .cos 0 1022  0 0 0 0 sin 32 .sin 58 cos 32 .cos 58 A    A    0 cot 572 tan  0 212  0 0 cot 32 tan 32 0 0 0 0 sin 32 .cos 32 cos 32 .sin 32 2 0 2 0 A   
  sin 32  cos 32  1.  0 0 cot 32 tan 32
Câu 57. Chọn C. 0 0 0 0 0 0 0 0
sin155 .cos115  cot 42 .cot 48
sin 25 .sin 25   cot 42 .tan 42 A   A  0 cot 55 .cot  0 145   0 0  tan17 .cot17 0 0 cot 55 .tan 55 1
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 0  sin 25 1 2 0 cos 25  A   A . 2 2
Câu 58. Chọn B 2 x    2 2 2 x x x  2 2 2 cos sin cos 2 cos 1 cos x  sin x Ta có A    sin x  cos x sin x  cos x sin x  os c x
cos x  sin xcos x  sin x 
 cos x  sin x sin x  cos x
Như vậy, A  cos x – sin x .
Câu 59. Chọn D 2 1 1 1 Ta có sin   cos      s 2 sin co   1 2 sin cos   sin  cos   2 2 2 4 6        2 1 6 sin cos
 1 2sin cos  1 2      sin   cos    4  4 2 2  
 sin   cos   sin   cos  2 1 7 4 4 2 2 2 2
 2 sin  cos   1 2      4  8 7 4 4 sin   cos  2 2 8  tan   cot     14 2 2 2 sin  cos   1      4  Như vậy, 2 2
tan   cot   12 là kết quả sai.
Câu 60. Chọn B   
A  cos   26   2sin   7   cos 1,5   cos   2003  cos  
 1,5 .cot   8   2          
A  cos  2 sin      cos  cos(    cos   .cot         2   2   2 
A  cos  2 sin   0  sin   sin .cot   cos  sin   cos  sin .
Câu 61. Chọn A A   2 x 2 x   2 1 – sin .cot 1 – cot x 2 2 2
 cot x  cos x 1 cot x 2  sin x . Câu 62. Chọn A.
A  sin   cos  sin   cos  A  2 sin  .
Câu 63. Chọn B     3 
P  sin   x  cos  x  cot  
2  x  tan
x   sin x  sin x  cot x  cot x  2 sin . x    2   2 
Câu 64. Chọn B
Xét tam giác ABC ta có:      
A B C    A B    C .
 cos  A B  cos  C    cosC .
Câu 65. Chọn D.    A  cos   sin  
   A  sin  sin  0 .  2 
Câu 66. Chọn D
Do A,B,C là ba góc của một tam giác nên A B C    A B    C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A B    C C tan  tan   cot     .  2   2 2  2  A B    C C cot  cot   tan     .  2   2 2  2
cot  A B  cot   C   cot C .
tan  A B  tan   C    tan C  tan C . Chọn D
Trong tam giác ABC ta có A B C    A B    C
Do đó tan  A B  tan   C    tan C .
Câu 67. Chọn B 3 3 Ta có 6 6 2 2 A x x x x   2 x   2 x 2 2 sin cos 3sin cos sin cos
 3sin x cos x   x x3 2 2 2 2  sin . x cos x  2 2 sin cos 3
sin x  cos x 2 2
 3sin x cos x  1.
Câu 68. Chọn B 1 tan x2 1 tan 1 x2 2 2 2 1  1  Ta có A      2 2 2 2 2  2  4 tan x 4 sin x cos x 4 tan x
4 tan x  cos x
1 tan x2 1 tan x2 1 tan x2 1 tan x2 2 2 2 2 2 4 tan x      1  . 2 2 2 4 tan x 4 tan x 4 tan x 2 4 tan x
Câu 69. Chọn D 2 2 2 2 2 2 cos x  sin y cos x  sin y cos . x cos y Ta có 2 2 B   cot . x cot y   2 2 2 2 2 2 sin . x sin y sin x sin y sin . x sin y 2 cos x  2 1 cos y  2 2  sin y sin y  2 2 2 2 cos x x y y    1 cos sin sin     1. 2 2 2 2 sin x sin y sin x sin y  2 1 cos x 2 sin y
Câu 70. Chọn C 2 Ta có C   4 4 2 2 x x x x  8 8 2 sin cos sin cos
– sin x  cos x 2  2 2 x x2 2 2  x x  4 4 2 sin cos sin cos – sin x cos x2 4 4
 2sin x cos x        2 2 2 2   x x     2 2 2 1 sin cos –
sin x  cos x2 2 2 4 4
 2sin x cos x  
 2sin x cos x   2 2 2 2 2 2 4 4  2 1
  sin x cos x – 1
  2 sin x cos x  2 sin x cos x      2  2 2 4 4
1 sin x cos x x x –  2 2 4 4  4 x x x x 4 4 2 sin cos 1 sin cos 4 sin cos
 2 sin x cos x  1 .
Câu 71. Chọn D tan x  tan y
A đúng vì VT   tan .
x tan y VP 1 1  tan x tany B đúng vì 1 sin a 1 sin a
1 sin a2  1 sin a2 2 2  2sin a 2 VT    2   2 
 2  4 tan a VP 2 2 1 sin a 1 sin a 1 sin a cos a 2 2 2 2 2  sin   cos  sin   cos  1 cot 
C đúng vì VT     VP . 2 2 2 2 2 cos   sin  sin   cos  1 cot 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 72. Chọn D 98 98 Ta có 4 4
sin x  cos x
A  cos 2x A  81 81 1 1  98  1 1 1  98  5 98 4 4
sin x  cos x   A 2  1 sin 2x   A   2   cos 2x   A   81 2 5  81  2 2 5  81  2  98  2  98  2  98  392   A   A   A          81  5  81  5  81  405  13 t  98 2 13  45 Đặt A   t 2  t t   0   81 5 405 1 t   9 13 607 +) t   A  45 405 1 107 +) t   A  . 9 81
Câu 73. Chọn A 1 1 3 3
sin x  cos x
 sin x  cos x2   sin . x cos x    sin . x cos x   2 4 4 8  1 7 sin x   1 3 4
Khi đó sin x, cos x là nghiệm của phương trình 2 X X   0   2 8  1 7 sin x   4 1
Ta có sin x  cos x
 2 sin x  cos x  1 2 1 7 5  7 +) Với sin x
 3sin x  2 cos x  4 4 1 7 5  7 +) Với sin x
 3sin x  2 cos x  . 4 4
Câu 74. Chọn B A 2 2
A a cos x  2b sin .
x cos x c sin x 2 
a  2b tan x c tan x 2 cos x 2 2  2b    2b  2b   A 2  x 2 1 tan
a  2b tan x c tan x A1 
   a  2bc     a c    a ca c   
a c2  2b2
a a c2 2
 4b a c 2  c4bA  a c2 a c2 2 2   2   2   2 2 .      4 2 4 a a c b a c b a a c b a   A    A a . a c2 a c2 a c2
Câu 75. Chọn C 1 t t 1 2  2 2
Đặt cos   t    a b a b
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 ab ab ab
b   t 2 2 1  at  2 2
at bt  2bt b
 a b 2
t  2bt b a b a b a b b
 a b2 2
t b a b 2 2
t b  0  t a b b a Suy ra 2 2 cos   ;sin   a b a b 8 8 sin  cos  a b 1 Vậy:     . 3 3 a b
a b4 a b4 a b3
Câu 76. Chọn C     9 
A  cos + cos    ...  cos        5   5    9    4   5 
A  cos  cos    ...  cos    cos           5 5 5           9  9  9  7  9   A  2 cos   cos  2 cos   cos  ...  2 cos   cos        10  10  10  10  10  10  9   9 7 5 3   A  2 cos   cos  cos  cos  cos  cos      10   10 10 10 10 10   9    2      9  A  2 cos   2 cos cos  2 cos cos  cos   
  A  2 cos   .0  0.    10   2 5 2 5 2   10 
Câu 77. Chọn A  3 5 7 1 cos 1 cos 1 cos 1 cos 4 4 4 4 1   3 5 7  A      2  cos  cos  cos  cos   2 2 2 2 2  4 4 4 4  1   3 3    2  cos  cos  cos  cos  2.   2  4 4 4 4 
Câu 78. Chọn D 0 2sin 2550 .cos  0 188 1  A   0 0 0 tan 368 2 cos 638  cos 98 2sin  0 0 30  7.360 .cos 0 0 8 180 1  0 0 1 2sin 30 .cos8  A    A   tan  0 0 8  360  2cos 0 0
82  2.360   cos 0 0 90  8  0 0 0 tan 8 2 cos 82  sin 8 0 0 1 2sin 30 .cos8 0 0 1 2sin 30 .cos 8  A    A   0 tan 8 2 cos  0 0 90  8  0  sin 8 0 0 0 tan 8 2sin 8  sin 8 0 1.cos8 0 0 0  A  cot 8   cot 8  cot 8  0 . 0 sin 8
Câu 79. Chọn C B CA
+) Ta có: A B C    B C    A    2 2 2  B C    A A I cos  cos   sin     nên I đúng  2   2 2  2 A BC
+) Tương tự ta có:   2 2 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A B   C C A B C C C tan  tan   cot    tan .tan  cot .tan  1 2  2 2  2 2 2 2 2 nên II đúng. +) Ta có
A B C    2C  cos  A B C   cos   2C    cos 2C
 cos  A B C   cos 2C   0 nên III sai.
Câu 80. Chọn B
cos      cos      sin    cos      2  Ta có 
A   cot .sin    cos  3         tan   tan     tan   cot          2    2   2  sin 
2    sin 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 10
CÔNG THỨC LƯỢNG GIÁC 0D6-3 Contents
PHẦN A. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG ................................................................................................................... 1
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC ........................................................................................ 4
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH ................................. 5
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC ............................................................................................. 7
DẠNG 5. MIN-MAX ....................................................................................................................................................... 9
DẠNG 6. NHẬN DẠNG TAM GIÁC ............................................................................................................................. 9
PHẦN B. LỜI GIẢI ....................................................................................................................................................... 12
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG ................................................................................................................. 12
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC ...................................................................................... 15
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH ............................... 17
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC ........................................................................................... 18
DẠNG 5. MIN-MAX ..................................................................................................................................................... 22
DẠNG 6. NHẬN DẠNG TAM GIÁC ........................................................................................................................... 23 PHẦN A. CÂU HỎI
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG Câu 1.
Trong các công thức sau, công thức nào đúng?
A. cos a b  cos .
a sin b  sin . a sin b .
B. sin a b  sin .
a cos b  cos . a sin b .
C. sin a b  sin .
a cos b  cos . a sin b .
D. cos a b  cos .
a cos b  sin . a sin b . Câu 2.
Trong các công thức sau, công thức nào đúng? tan a  tan b
A. tan a b  .
B. tan a – b  tan a  tan . b 1 tan a tan b tan a  tan b
C. tan a b  .
D. tan a b  tan a  tan . b 1 tan a tan b Câu 3.
Biểu thức sin x cos y  cos x sin y bằng
A. cos  x y .
B. cos  x y .
C. sin  x y .
D. sin  y x . Câu 4.
Chọn khẳng định sai trong các khẳng định sau:
A. cos(a b)  cos a cos b  sin a sin b .
B. sin(a b)  sin a cos b  cos a sin b .
C. sin(a b)  sin a cos b  cos a sin b . D. 2
cos 2a  1 2sin a .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Câu 5.
(LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Trong các khẳng định sau, khẳng định nào sai? a b a b
A. sin a  sin b  2 cos sin .
B. cos a b  cos a cos b  sin a sin b . 2 2
C. sin a b  sin a cos b  cos a sin b .
D. 2 cos a cos b  cos a b  cos a b .
sin a bCâu 6. Biểu thức
bằng biểu thức nào sau đây? (Giả sử biểu thức có nghĩa)
sin a b
sin a b sin a  sin b
sin a b sin a  sin b A.  . B.  .
sin a b sin a  sin b
sin a b sin a  sin b
sin a b tan a  tan b
sin a b cot a  cot b C.  . D.  .
sin a b tan a  tan b
sin a b cot a  cot b Câu 7.
Rút gọn biểu thức: sin a –17.cos a 13 – sin a 13.cos a –17 , ta được: 1 1 A. sin 2 . a B. cos 2 . a C.  . D. . 2 2 37 Câu 8.
Giá trị của biểu thức cos bằng 12 6  2 6  2 6  2 2  6 A. . B. . C. – . D. . 4 4 4 4 Câu 9.
Đẳng thức nào sau đây là đúng.    1    1 3 A. cos    cos    . B. cos    sin   cos   .  3  2  3  2 2    3 1    1 3 C. cos    sin   cos   . D. cos    cos  sin    .  3  2 2  3  2 2   
Câu 10. (THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Cho tan   2 . Tính tan     .  4  1 2 1 A.  . B. 1. C. . D. . 3 3 3
Câu 11. Kết quả nào sau đây sai?      
A. sin x  cosx  2 sin x    .
B. sin x  cosx   2 cos x    .  4   4       
C. sin 2x  cos2x  2 sin 2x    .
D. sin 2x  cos2x  2 cos 2x    .  4   4  3    
Câu 12. Cho sin x  với
x   khi đó tan x    bằng. 5 2  4  2 1  A. . B. . 7 7 2  1 C. . D. . 7 7 1    
Câu 13. Cho sin   với 0    . Giá trị của cos     bằng 3 2  3 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2  6 1 1 1 A. . B. 6  3 . C.  . D. 6  . 2 6 6 2 2 5    3   
Câu 14. Cho hai góc  ,  thỏa mãn sin  , 
     và cos   ,  0     . Tính giá trị 13  2  5  2 
đúng của cos     . 16 18 18 16 A. . B.  . C. . D.  . 65 65 65 65 3   3   21 
Câu 15. (THPT Cộng Hiền - Lần 1 - 2018-2019) Cho sin   ,  ; 
 . Tính giá trị cos     5  2 2   4  ? 2 7  2  2 7 2 A. . B. . C. . D. . 10 10 10 10
Câu 16. Biểu thức M  cos  –53.sin  –337  sin 307 .
 sin113 có giá trị bằng: 1 1 3 3 A.  . B. . C.  . D. . 2 2 2 2
Câu 17. Rút gọn biểu thức: cos 54 .  cos 4 – cos 36 .  cos 86 , ta được: A. cos 50 .  B. cos 58 .  C. sin 50 .  D. sin 58 .  1 3
Câu 18. Cho hai góc nhọn a và b với tan a  và tan b
. Tính a b . 7 4    2 A. . B. . C. . D. . 3 4 6 3 3 1 Câu 19. Cho ,
x y là các góc nhọn, cot x  , cot y
. Tổng x y bằng: 4 7  3  A. . B. . C. . D.  . 4 4 3       Câu 20. Biểu thức 2 2 2
A  cos x  cos  x  cos  x   
 không phụ thuộc x và bằng:  3   3  3 4 3 2 A. . B. . C. . D. . 4 3 2 3 4 cos     3 sin      4  3
Câu 21. Biết sin   , 0   
và   k . Giá trị của biểu thức: A  5 2 sin
không phụ thuộc vào  và bằng 5 5 3 3 A. . B. . C. . D. . 3 3 5 5     Câu 22. Nếu tan  4 tan thì tan bằng: 2 2 2 3sin 3sin  3cos 3cos A. . B. . C. . D. . 5  3cos 5  3cos 5  3cos 5  3cos
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3 3
Câu 23. Cho cos a
; sin a  0 ; sin b
; cos b  0 . Giá trị của cos a b. bằng: 4 5 3  7  3  7  3  7  3  7  A. 1 . B.  1 . C. 1 . D.  1 . 5  4          5 4   5 4   5 4    b  1  b   a  3  a
Câu 24. Biết cos a     và sin a   0   ; sin  b    và cos  b  0  
. Giá trị cos a b  2  2  2   2  5  2  bằng: 24 3  7 7  24 3 22 3  7 7  22 3 A. . B. . C. . D. . 50 50 50 50
Câu 25. Rút gọn biểu thức: cos 120 – x  cos 120  x – cos x ta được kết quả là A. 0. B. – cos . x C. –2 cos . x
D. sin x – cos . x 3 3
Câu 26. Cho sin a
; cos a  0 ; cos b
; sin b  0 . Giá trị sin a b bằng: 5 4 1  9  1  9  1  9  1  9  A.  7  .   B.  7  .   C. 7  .   D. 7  .   5  4  5  4  5  4  5  4  
Câu 27. Biết      
và cot  , cot  , cot  theo thứ tự lập thành một cấp số cộng. Tích số 2 cot.cot  bằng: A. 2. B. –2. C. 3. D. –3.
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC
Câu 28. Đẳng thức nào không đúng với mọi x ? x A. 2 1 cos 6 cos 3x  . B. 2
cos 2x  1 2sin x . 2  x
C. sin 2x  2sin x cos x . D. 2 1 cos 4 sin 2x  . 2
Câu 29. Trong các công thức sau, công thức nào sai? 2 cot x 1 2 tan x A. cot 2x  . B. tan 2x  . 2 cot x 2 1 tan x C. 3
cos 3x  4 cos x  3cos x . D. 3
sin 3x  3sin x  4sin x
Câu 30. Trong các công thức sau, công thức nào sai? A. 2 2
cos 2a  cos a – sin . a B. 2 2
cos 2a  cos a  sin . a C. 2
cos 2a  2 cos a –1. D. 2 cos 2a  1 – 2 sin . a
Câu 31. Mệnh đề nào sau đây đúng? A. 2 2
cos 2a  cos a  sin a . B. 2 2
cos 2a  cos a  sin a . C. 2
cos 2a  2 cos a  1 . D. 2
cos 2a  2sin a 1 .
Câu 32. Cho góc lượng giác a. Trong các khẳng định sau, khẳng định nào là khẳng định sai? A. 2
cos 2a  1  2 sin a . B. 2 2
cos 2a  cos a  sin a . C. 2
cos 2a  1  2 cos a . D. 2
cos 2a  2 cos a 1.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 33. (KSNLGV - THUẬN THÀNH 2 - BẮC NINH NĂM 2018 - 2019) Khẳng định nào dưới đây SAI? A. 2
2 sin a  1  cos 2a .
B. cos 2a  2cos a 1.
C. sin 2a  2sin a cos a .
D. sin a b  sin a cos b  sin . b cos a .
Câu 34. Chọn đáo án đúng.
A. sin 2x  2 sin x cos x . B. sin 2x  sin x cos x . C. sin 2x  2 cos x .
D. sin 2x  2 sin x . 4   
Câu 35. Cho cos x  , x   ; 0 
 . Giá trị của sin 2x là 5  2  24 24 1 1 A. . B.  . C.  . D. . 25 25 5 5 1
Câu 36. Nếu s inx  cos x  thì sin2x bằng 2 3 3 2 3  A. . B. . C. . D. . 4 8 2 4
Câu 37. Biết rằng 6 6 2
sin x  cos x a b sin 2x , với a, b là các số thực. Tính T  3a  4 b . A. T  7  . B. T 1.
C. T  0 . D. T  7 . 3
Câu 38. Cho sin 2 
. Tính giá trị biểu thức A  tan  cot 4 4 2 8 16 A. A  . B. A  . C. A  . D. A  . 3 3 3 3 1 1
Câu 39. Cho a, b là hai góc nhọn. Biết cos a  , cos b
. Giá trị của biểu thức cos a b cos a b 3 4 bằng 119 115 113 117 A.  . B.  . C.  . D.  . 144 144 144 144 1
Câu 40. (TOÁN HỌC TUỔI TRẺ SỐ 5) Cho số thực  thỏa mãn sin  . Tính 4
sin 4  2sin 2  cos 25 1 255 225 A. . B. . C. . D. . 128 16 128 128
Câu 41. Cho cot a  15 , giá trị sin 2a có thể nhận giá trị nào dưới đây: 11 13 15 17 A. . B. . C. . D. . 113 113 113 113
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH
Câu 42. Mệnh đề nào sau đây sai? 1 1
A. cos a cos b
cos a b  cosa b sin a cosb
sin a b  cos a b  2   . B.     2   .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 1
C. sin a sin b
cosa b  cosa b sin a cos b
sin a b  sin a b  2   . D.     2   .
Câu 43. Trong các đẳng thức sau, đẳng thức nào sai? 1
A. cos(a b)  cos a.cos b  sin . a sin b .
B. cos a.cos b
cos(a b)  cos(a b) . 2
C. sin(a b)  sin a.cos b  sin . b cos a .
D. cos a  cos b  2cos(a b).cos(a b) .
Câu 44. Công thức nào sau đây là sai? a b a b a b a b
A. cos a  cos b  2 cos .cos .
B. cos a  cos b  2  sin .sin . 2 2 2 2 a b a b a b a b
C. sin a  sin b  2 sin .cos .
D. sin a  sin b  2 sin .cos . 2 2 2 2
sin 3x  cos 2x  sin x
Câu 45. Rút gọn biểu thức A
sin 2x  0;2sin x  1  0 ta được:
cos x  sin 2x  cos 3x
A. A  cot 6x .
B. A  cot 3x .
C. A  cot 2x .
D. A  tan x  tan 2x  tan 3x .      
Câu 46. Rút gọn biểu thức P  sin a  sin a      .  4   4  3 1 A.  cos 2a . B. cos 2a . 2 2 2 1 C.  cos 2a . D.  cos 2a . 3 2
Câu 47. Biến đổi biểu thức sin 1 thành tích.              
A. sin  1  2 sin   cos       .
B. sin  1  2 sin  cos      .  2   2   2 4   2 4               
C. sin  1  2 sin   cos       .
D. sin  1  2 sin  cos      .  2   2   2 4   2 4 
cos a  2 cos 3a  cos 5a
Câu 48. Rút gọn biểu thức P  .
sin a  2 sin 3a  sin 5a
A. P  tan a .
B. P  cot a .
C. P  cot 3a .
D. P  tan 3a . Câu 49. (THPT Phan Bội Châu - KTHK 1-17-18) Tính giá trị biểu thức sin 30o.cos 60o sin 60o.cos 30o P   . A. P  1 . B. P  0 . C. P  3 . D. P   3 . 2 4 6
Câu 50. Giá trị đúng của cos  cos  cos bằng: 7 7 7 1 1 1 1 A. . B.  . C. . D.  . 2 2 4 4  7
Câu 51. Giá trị đúng của tan  tan bằng: 24 24 A. 2  6  3. B. 2  6  3. C. 2  3  2 . D. 2  3  2 . 1 Câu 52. Biểu thức 0 A
 2sin 70 có giá trị đúng bằng: 0 2 sin10
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. 1. B. –1. C. 2. D. –2.
Câu 53. Tích số cos10 .  cos 30 .  cos 50 .  cos 70 bằng: 1 1 3 1 A. . B. . C. . D. . 16 8 16 4  4 5 Câu 54. Tích số cos .cos .cos bằng: 7 7 7 1 1 1 1 A. . B.  . C. . D.  . 8 8 4 4
tan 30  tan 40  tan 50  tan 60
Câu 55. Giá trị đúng của biểu thức A  bằng: cos 20 2 4 6 8 A. . B. . C. . D. . 3 3 3 3 1 1
Câu 56. Cho hai góc nhọn a và b . Biết cos a  , cos b
. Giá trị cos a b.cos a b bằng: 3 4 113 115 117 119 A.  . B.  . C.  . D.  . 144 144 144 144
sin x  sin 2x  sin 3x
Câu 57. Rút gọn biểu thức A  cos x  cos2x  cos3x A. A  tan 6 . x B. A  tan 3 . x C. A  tan 2 . x
D. A  tan x  tan 2x  tan 3 . x
Câu 58. Biến đổi biểu thức sin a 1 thành tích.  a    a    a    a  
A. sin a 1  2 sin  cos  .    
B. sin a 1  2 cos  sin  .      2 4   2 4   2 4   2 4             
C. sin a 1  2sin a  cos a  .    
D. sin a 1  2 cos a  sin a  .      2   2   2   2 
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC   2    
Câu 59. Cho góc  thỏa mãn     và sin 
.Tính giá trị của biểu thức A  tan    . 2 2 5  2 4  1 1 A. A  . B. A   . C. A  3 . D. A  3  . 3 3 1   
Câu 60. Cho cos x    x  0 
 . Giá trị của tan 2x là 3  2  5 4 2 5 4 2 A. . B. . C.  . D.  . 2 7 2 7      
Câu 61. Cho cos x  0 . Tính 2 2 A  sin x   sin x      .  6   6  3 1 A. . B. 2. C. 1. D. . 2 4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2
Câu 62. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Cho biết o c s  
. Giá trị của biểu thức 3 cot   3 tan  P  bằng bao nhiêu? 2 cot   tan  19 25 25 19 A. P  . B. P  . C. P   . D. P   . 13 13 13 13  
Câu 63. Cho sin .cos      sin  với      k ,  
l , k,l   . Ta có 2 2
A. tan      2 cot  . B. tan      2 cot  .
C. tan      2 tan  . D. tan      2 tan . 1 2. tan x cos ax
Câu 64. Biết rằng  
a,b   . Tính giá trị của biểu thức 2 2 2 cos x  s in x 1 tan x
b  sin ax
P a b .
A. P  4 .
B. P  1 . C. P  2 . D. P  3 . 2
Câu 65. Cho cos 2 
. Tính giá trị của biểu thức P  cos.cos 3 . 3 7 7 5 5 A. P  . B. P  . C. P  . D. . 18 9 9 18  3    
Câu 66. Cho tan x  2   x  
 . Giá trị của sin x    là  2   3  2  3 2  3 2  3 2  3 A. . B.  . C. . D. . 2 5 2 5 2 5 2 5
Câu 67. Tổng A  tan 9  cot 9  tan15  cot15 – tan 27 – cot 27 bằng: A. 4. B. –4. C. 8. D. –8. 1 1
Câu 68. Cho hai góc nhọn a và b với sin a  , sin b
. Giá trị của sin 2 a b là: 3 2 2 2  7 3 3 2  7 3 4 2  7 3 5 2  7 3 A. . B. . C. . D. . 18 18 18 18 2 2 cos 2  3 sin 4 1
Câu 69. Biểu thức A
có kết quả rút gọn là: 2 2 sin 2  3 sin 4 1 cos 4  30 cos 4  30 sin 4  30 sin 4  30 A. . B. . C. . D. . cos 4  30 cos 4  30 sin 4  30 sin 4  30
Câu 70. Kết quả nào sau đây SAI? sin 9 sin12
A. sin 33  cos 60  cos 3 .  B.  . sin 48 sin 81 1 1 4 C. 2
cos 20  2 sin 55  1 2 sin 65 .  D.   . cos 290 3 sin 250 3
5sin   3sin   2  Câu 71. Nếu thì:
A. tan      2 tan . B. tan      3 tan .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
C. tan      4 tan . D. tan      5 tan  .
Câu 72. Cho biểu thức 2 A  a b 2 2 sin – sin a – sin .
b Hãy chọn kết quả đúng: A. A  2 cos . a sin .
b sin a b. B. A  2 sin . a cos .
b cos a b. C. A  2 cos . a cos .
b cos a b. D. A  2 sin . a sin .
b cos a b.
Câu 73. Xác định hệ thức SAI trong các hệ thức sau: cos 40  
A. cos 40  tan .sin 40  . cos 6
B. sin15  tan 30 .  cos15  . 3 C. 2 x a xa x 2  a x 2 cos – 2 cos .cos .cos cos  sin . a D. 2 x  a x 2 x a  a – x 2 sin 2 sin – .sin .cos sin  cos . a DẠNG 5. MIN-MAX
Câu 74. Giá trị nhỏ nhất của 6 6
sin x  cos x là 1 1 1 A. 0. B. . C. . D. . 2 4 8
Câu 75. Giá trị lớn nhất của 4 4
M  sin x  cos x bằng: A. 4 . B. 1. C. 2 . D. 3 .
Câu 76. Cho M  3sin x  4 cosx . Chọn khẳng định đúng. A. 5
  M  5 .
B. M  5 .
C. M  5 .
D. M  5 .
Câu 77. Giá trị lớn nhất của 6 6
M  sin x  cos x bằng: A. 2 . B. 3 C. 0 . D. 1. 3 1 tan x    
Câu 78. Cho biểu thức M  , x    k , x   k , k  
  , mệnh đề nào trong các mệnh đề 1 tan x3  4 2 
sau đúng? 1 1
A. M  1. B. M  . C. M  1.
D. M  1. 4 4 Câu 79. Cho 2 2
M  6 cos x  5 sin x . Khi đó giá trị lớn nhất của M là A. 11. B. 1. C. 5 . D. 6 .
Câu 80. Giá trị lớn nhất của biểu thức 2 2
M  7 cos x  2 sin x là A. 2  . B. 5 . C. 7 . D. 16 .
DẠNG 6. NHẬN DẠNG TAM GIÁC
Câu 81. Cho A, B, C là các góc của tam giác ABC thì.
A. sin 2A  sin 2B  2sin C .
B. sin 2A  sin 2B  2sin C .
C. sin 2A  sin 2B  2sin C .
D. sin 2A  sin 2B  2sin C . A B B A
Câu 82. Một tam giác ABC có các góc ,
A B, C thỏa mãn 3 3 sin cos  sin cos  0 thì tam giác đó có 2 2 2 2 gì đặc biệt?
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
A. Tam giác đó vuông. B. Tam giác đó đều.
C. Tam giác đó cân.
D. Không có gì đặc biệt.
Câu 83. Cho A , B , C là các góc của tam giác ABC (không là tam giác vuông) thì cot .
A cot B  cot .
B cot C  cot C.cot A bằng : A. A B C 2 cot .cot .cot
. B. Một kết quả khác các kết quả đã nêu trên. C. 1. D. 1. 1 1 1
Câu 84. Cho A , B , C là ba là các góc nhọn và tan A  ; tan B  , tan C
. Tổng A B C bằng 2 5 8     A. . B. . C. . D. . 5 4 3 6 Câu 85. Biết , A ,
B C là các góc của tam giác ABC, khi đó. A B CA B C A. cot  cot .   B. cos  cos .    2  2  2  2  A B CA B C C. cos   cos .   D. tan  cot .    2  2  2  2
Câu 86. A, B , C , là ba góc của một tam giác. Hãy tìm hệ thức sai:
3A B C
A. sin A  sin 2A B C  . sin A   cos B. 2 .
A B  3C C. cos C  sin .
D. sin C  sin  A B  2C  . 2
Câu 87. Cho A , B , C là các góc của tam giác ABC (không phải tam giác vuông) thì: A B C
A. tan A  tan B  tan C  tan . A tan .
B tan C .
B. tan A  tan B  tan C   tan . tan . tan . 2 2 2 A B C
C. tan A  tan B  tan C   tan . A tan .
B tan C .
D. tan A  tan B  tan C  tan . tan . tan . 2 2 2 Câu 88. Biết , A ,
B C là các góc của tam giác ABC, khi đó. A B CA B C A. sin  cos .   B. sin   cos .    2  2  2  2  A B CA B C C. sin  sin .   D. sin   sin .    2  2  2  2
Câu 89. Nếu a  2b và a b c   . Hãy chọn kết quả đúng.
A. sin b sin b  sin c  sin 2a . B. b b c 2 sin sin sin  sin a . C. b b c 2 sin sin sin  cos a .
D. sin b sin b  sin c  cos 2a .
Câu 90. Cho A , B , C là các góc của tam giác ABC thì:
A. sin 2A  sin 2B  sin 2C  4sin . A sin .
B sin C . B. sin 2A  sin 2B  sin 2C  4 cos . A cos . B cosC .
C. sin 2A  sin 2B  sin 2C  4  cos . A cos .
B cos C . D.
sin 2A  sin 2B  sin 2C  4sin . A sin .
B sin C .
Câu 91. A, B , C , là ba góc của một tam giác. Hãy chỉ hệ thức sai:
 4A B C  3A
A  2B C A. cot   tan   . B. cos   sin B   .  2  2  2 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
A B  3C
A B  6C  5C C. sin  cos 2C   . D. tan   cot   .  2   2  2 Câu 92. Biết ,
A B, C là các góc của tam giác ABC khi đó.
A. cos C  cos  A B . B. tan C  tan  A B .
C. cot C   cot  A B . D. sin C  sin  A B . Câu 93. Cho
A, B, C là các góc của tam giác
ABC (không là tam giác vuông) thì cot .
A cot B  cot .
B cot C  cot .
C cot A bằng
A. Một kết quả khác các kết quả đã nêu trên. B. 1. C. 1. D. A B C 2 cot .cot .cot .
Câu 94. Cho A , B , C là các góc của tam giác ABC (không phải tam giác vuông) thì: A B C A B C A B C A B C A. cot  cot  cot  cot .cot .cot . B. cot  cot  cot   cot .cot .cot . 2 2 2 2 2 2 2 2 2 2 2 2 A B C A B C C. cot  cot  cot  cot . A cot .
B cot C . D. cot  cot  cot   cot . A cot . B cot C . 2 2 2 2 2 2
Câu 95. Cho A , B , C là ba góc của một tam giác. Hãy chọn hệ thức đúng trong các hệ thức sau. A. 2 2 2
cos A  cos B  cos C  1 cos . A cos . B cos C. B. 2 2 2
cos A  cos B  cos C  1 – cos . A cos . B cos C. C. 2 2 2
cos A  cos B  cos C  1 2 cos . A cos . B cos C. D. 2 2 2
cos A  cos B  cos C  1 – 2 cos . A cos . B cos C.
Câu 96. Hãy chỉ ra công thức sai, nếu A, B, C là ba góc của một tam giác. B C B C A A. cos cos  sin sin  sin . B. cos .
B cos C  sin .
B sin C  cos A  0 . 2 2 2 2 2 B C C C A C. sin cos  sin cos  cos . 2 2 2 2 2 D. 2 2 2
cos A  cos B  cos C  2 cos A cos B cos C  1 . sin B  s inC
Câu 97. Cho tam giác ABC có sin A
. Khẳng định nào dưới đây đúng? cos B  cos C
A. Tam giác ABC vuông tại A .
B. Tam giác ABC cân tại A .
C. Tam giác ABC đều. D. Tam giác ABC là tam giác tù. 1 13
Câu 98. Cho bất đẳng thức cos2A
 2cos 2B  4sin B   0 với , A ,
B C là ba góc của tam 4   64cos A 4
giác ABC .Khẳng định đúng là: A.   120o B C . B.   130o B C . C.   120o A B . D.   140o A C . 1 1 1
Câu 99. Cho A , B , C là các góc nhọn và tan A  , tan B  , tan C
. Tổng A B C bằng: 2 5 8     A. . B. . C. . D. . 6 5 4 3
Câu 100. Cho A , B , C là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI.
A B  3C A. sin  cos C.
B. cos  A B – C   – cos 2C. 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
A B  2C 3C
A B  2C C C. tan  cot . D. cot  tan . 2 2 2 2
Câu 101. Cho A , B , C là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI. A B C A. cos  sin .
B. cos  A B  2C   – cos C. 2 2
C. sin  A C   – sin .
B D. cos  A B  – cos C.
Câu 102. Cho A , B , C là ba góc của một tam giác không vuông. Hệ thức nào sau đây SAI? B C B C A A. cos cos  sin sin  sin . 2 2 2 2 2
B. tan A  tan B  tan C  tan . A tan . B tan C.
C. cot A  cot B  cot C  cot . A cot . B cot C. A B B C C A D. tan .tan  tan .tan  tan . tan  1. 2 2 2 2 2 2 PHẦN B. LỜI GIẢI
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG Câu 1. Chọn D
Công thức cộng: sin a b  sin .
a cos b  cos . a sin b Câu 2. Chọn B. tan a  tan b
Ta có tan a b  . 1 tan a tan b Câu 3. Chọn C
Áp dụng công thức cộng lượng giác ta có đáp án. C. Câu 4. Chọn A.
Ta có công thức đúng là: cos(a b)  cos a cos b  sin a sin b . Câu 5. Chọn B
Câu A, D là công thức biến đổi đúng
Câu C là công thức cộng đúng
Câu B sai vì cos a b  cos a cos b  sin a sin b . Câu 6. Chọn C.
sin a b
sin a cos b  cos a sin b Ta có : 
(Chia cả tử và mẫu cho cos a cos b )
sin a b
sin a cos b  cos a sin b tan a  tan b  . tan a  tan b Câu 7. Chọn C.
Ta có: sin a –17.cosa 13 – sin a 13.cosa –17  sin a 17  a 13   1  sin  3  0   . 2 Câu 8. Chọn C.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 37              cos  cos 2       cos       cos     cos    12  12   12   12   3 4        6  2   cos .cos  sin .sin     .  3 4 3 4  4 Câu 9. Chọn D      1 3 Ta có cos    cos  . cos  sin . sin  cos   sin    .  3  3 3 2 2
Câu 10. Chọn D  tan  tan    2 1 1 Ta có 4 tan        .  4   1 2 3 1 tan tan 4
Câu 11. Chọn C  1 1 
Ta có sin 2x  cos2x  2 sin2x   cos2x   2 2       2 cos sin 2x   sin cos2x   4 4         2 sin 2x   2 sin 2x       4   4 
Câu 12. Chọn D 9 4 Từ 2 2 2
sin x  cos x  1 cos x   1 sin x   1   . 25 5  4 sin x 3 Vì
x   nên cos x   do đó tan x    . 2 5 cos x 4  3 tan x  tan  1    1 Ta có: 4 4 tan x       .  4  3  7 1 tan . x tan 1 4 4
Câu 13. Chọn A 2 6 1 Ta có: 2 2 2
sin   cos   1  cos    cos  (vì 0    nên cos  0 ). 3 3 2    1 3 1 6 3 1 1 1 2  6 Ta có: cos    cos  sin          .  3  2 2 2 3 2 3 6 2 2 6
Câu 14. Chọn D 2 5     5  12 sin  , 
     nên cos   1     . 13  2   13  13 2 3     3  4 cos   ,  0   
 nên sin   1    . 5  2   5  5 12 3 5 4 16
cos      cos cos   sin sin    .  .   . 13 5 13 5 65
Câu 15. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 16 4   3  4 Ta có: 2 2 cos   1 sin    cos   .Do   ;  cos  0   nên cos  . 25 5  2 2  5  21  21 21 4   2  3   2  2 Vậy: cos    cos cos  sin  sin          . 4 4 4 5  2  5  2    10    
Câu 16. Chọn A.
M  cos  –53.sin  –337  sin 307 .  sin113
 cos  –53.sin 23 – 360  sin 53  360.sin 90  23 1
 cos  –53.sin 23  sin 53.cos 23  sin 23  53   sin 30   . 2
Câu 17. Chọn D. Ta có: cos 54 .  cos 4 – cos 36 .  cos 86  cos 54 .  cos 4 – sin 54 .  sin 4  cos 58 . 
Câu 18. Chọn B. tan a  tan b
tan a b 
 1, suy ra a b  1 tan . a tan b 4
Câu 19. Chọn C. Ta có : 4  7 tan x  tan y 3  x y 3 tan  
 1 , suy ra x y  . 1 tan . x tan y 4 4 1 .7 3
Câu 20. Chọn C. Ta có : 2 2       3 1   3 1  2 2 2 
A  cos x  cos  x  cos  x 2      cos x   cos x  sin x    cos x  sin x   3   3   2 2   2 2      3  . 2
Câu 21. Chọn B.   4 cos     0     3 sin       2 3 3 5 Ta có   cos  
, thay vào biểu thức A   . 4 5 sin  3 sin      5
Câu 22. Chọn A. Ta có:      tan  tan 3 tan 3sin .cos   3sin 2 2 2 2 2  tan     . 2     2 2 5  3cos 1 tan . tan 1 4 tan 1 3sin 2 2 2 2
Câu 23. Chọn A. Ta có :  3 cos a  7 2 
4  sin a  1 cos a  . 4 si  n a  0 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  3 sin  b  4 2 
5  cos b   1 sin b   . 5 cosb  0  3 4 7 3 3  7   
cos a b  cos a cos b  sin a sin b  .   .     1 . 4 5 4 5 5  4     
Câu 24. Chọn A. Ta có :   b  1 cos a        2  2  b   b  3 2   sin a   1 cos a       .  b   2   2  2 sin  a   0      2    a  3 sin  b       2  5  a   a  4 2   cos  b  1 sin  b      .  a    2   2  5 cos  b      2  a bb   a   b   a  1 4 3 3 3 3  4 cos  cos a  cos
b  sin a  sin  b          .  .  . 2  2   2   2   2  2 5 5 2 10 a b 24 3  7
cos a b 2  2 cos 1  . 2 50
Câu 25. Chọn C. 1 3 1 3
cos 120 – x  cos 120  x – cos x   cos x  sin x  cos x
sin x  cos x  2 cos x 2 2 2 2
Câu 26. Chọn A. Ta có :  3 sin  a  4 2 
5  cos a   1 sin a   .  5 cos a  0   3 cos b  7 2 
4  sin b  1 cos b  . 4 si  n b  0  3 3  4  7 1  9 
sin a b  sin a cos b  cos a sin b  .   .  7      . 5 4  5  4 5  4 
Câu 27. Chọn C. Ta có :  tan   tan  cot   cot  2 cot       
, suy ra cot   tan        2 1 tan tan  cot  cot  1 cot  cot  1  cot  cot   3.
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC
Câu 28. Chọn D x Ta có 2 1 cos 4 sin 2x  . 2
Câu 29. Chọn B.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 tan x
Công thức đúng là tan 2x  . 2 1 tan x
Câu 30. Chọn B. Ta có 2 2 2 2
cos 2a  cos a – sin a  2 cos a 1  1 2 sin . a
Câu 31. Chọn A Câu 32. Lờigiải Chọn C Ta có: 2 2 2 2
cos 2a  cos a  sin a  1 2 sin a  2 cos a 1 .
Câu 33. Chọn B Có 2
cos 2a  2 cos a 1 nên đáp án B sai.
Câu 34. Chọn A
Câu 35. Chọn B 16 9 3    Ta có 2 2
sin x  1 cos x  1 
 sin x   vì x   ;0  sin x  0   . 25 25 5  2  4  3  24 Vậy sin 2x  2sin .
x cos x  2. .      . 5  5  25
Câu 36. Chọn D 1 1 3 
Ta có s inx  cos x  2 2
 sin x  2sin x cos x  cos x   sin 2x  2 4 4
Câu 37. Chọn C 3 Ta có 6 6 x x   2 2 x x 2 2  x x  2 2 sin cos sin cos 3sin .cos
sin x  cos x 3 2 2 2  1 3sin .
x cos x  1 sin 2x . 4 3
Vậy a  1, b  
. Do đó T  3a  4 b  0 . 4
Câu 38. Chọn C 2 2 sin  cos sin   cos  1 1 8
A  tan  cot       . cos sin sin cos 1 1 3 3 sin 2 . 2 2 4
Câu 39. Chọn A 1 7 Từ 2 cos a
 cos 2a  2 cos a 1   3 9 1 7 2 cos b
 cos 2b  2 cos b 1   4 8 1 1  7 7  119
Ta có cos a b cos a b  cos 2a  cos 2b        . 2 2  9 8  144
Câu 40. Ta có sin 4  2 sin 2  cos  2 sin 2 cos 2   1 cos     2 4 sin cos 1 2 sin    1 cos 2  1  1 225    2    2 4 sin 1 sin
2  2 sin       2 2 8 1 sin sin  8 1 .    .  16  4 128
Câu 41. Chọn C.  1 2 sin a  1   226 15 cot a  15   226   sin 2a   . 2  sin a 225 113 2 cos a    226
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH
Câu 42. Chọn B 1
Ta có sin a cos b
sin a b  sin a b 2   .
Câu 43. Chọn D a b a b
Ta có: cos a  cos b  2cos .cos . 2 2
Câu 44. Chọn D a b a b
Ta có sin a  sin b  2 cos .sin . 2 2
Câu 45. Chọn C
sin 3x  cos 2x  sin x
2 cos 2x sin x  cos 2x
cos 2x(1  2 sin x) A     cot 2x .
cos x  sin 2x  cos 3x
2 sin 2x sin x  sin 2x
sin 2x(1  2 sin x)
Câu 46. Chọn D       1    1 Ta có: sin a  sin a   cos  cos 2a   cos 2a     . 4 4 2  2        2
Câu 47. Chọn B        2 2         sin 1  sin  sin  2 cos sin  2 cos  sin  .     2 2 2  2 4   2 4 
Câu 48. Chọn C
cos a  2 cos 3a  cos 5a
2 cos 3a cos a  2 cos 3a P  
sin a  2 sin 3a  sin 5a
2 sin 3a cos a  2 sin 3a
2 cos 3a cos a   1 cos 3a    cot 3a .
2 sin 3a cos a   1 sin 3a
Câu 49. Chọn A Ta có
sin 30o 60o  sin 90o P     1.
Câu 50. Chọn B.   2 4 6  sin cos  cos  cos 2 4 6   7  7 7 7 Ta có cos  cos  cos   7 7 7  sin 7 3    5  3   5     sin  sin   sin  sin   sin   sin        sin    7  7  7  7   7   7  1     .   2 2 sin 2sin 7 7
Câu 51. Chọn A.  sin  7 3 3 tan  tan    2  6  3 . 24 24  7   cos .cos cos  cos 24 24 3 4
Câu 52. Chọn A. 0 0 0 0 1 1 4 sin10 .sin 70 2 sin 80 2 sin10 0 A   2sin 70     1. 0 0 0 0 2 sin10 2sin10 2 sin10 2 sin10
Câu 53. Chọn C.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 cos10 .  cos 30 .  cos 50 .  cos 70  cos10 .  cos 30 .   o o cos120  cos 20  2 3  cos10 cos 30  cos10  3 1 3       .  . 4  2 2  4 4 16
Câu 54. Chọn A. 2 4 5 2 2 4 4 4 sin .cos .cos sin .cos .cos sin .cos  4 5 cos .cos .cos 7 7 7  7 7 7   7 7   7 7 7    2sin 2 sin 4 sin 7 7 7 8 sin 1 7    .  8 8sin 7
Câu 55. Chọn D. sin 70 sin110 
tan 30  tan 40  tan 50  tan 60 A  cos 30 .  cos 40 cos 50 .  cos 60  cos 20 cos 20 1 1 2 2
 cos 50  3 cos 40       2   cos 30 .  cos 40 cos 50 .  cos 60 3 cos 40 cos 50  3 cos 40 .cos 50     
 sin 40  3 cos 40  sin100 8cos10 8  2    4   .  3 cos 40 .cos 50      3 3 cos10 3 cos10  cos90 2
Câu 56. Chọn D. Ta có : 2 2 1  1   1  119
cos a b.cos a b  cos 2a  cos 2b 2 2
 cos a  cos b 1   1   .     2  3   4  144
Câu 57. Chọn C. Ta có :
sin x  sin 2x  sin 3x 2 sin 2 .
x cos x  sin 2x
sin 2x 2 cos x   1 A     tan 2 . x
cos x  cos 2x  cos 3x 2 cos 2 .
x cos x  cos 2x
cos 2x 2 cos x   1
Câu 58. Chọn D. 2 a a a aa a   a   Ta có sin a 1 2 2  2 sin cos  sin  cos  sin  cos 2    2 sin    2 2 2 2  2 2   2 4   a     a   a    a    2 sin  cos       2 sin  cos  .      2 4   4 2   2 4   2 4 
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC
Câu 59. Chọn A      Vì góc  thỏa mãn     nên   suy ra cos  0 . 2 4 2 2 2  2   1 Do sin  nên 2 cos  1 sin  . 2 5 2 2 5
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  tan 1     Biểu thức 2 A  tan     .  2 4   tan 1 2  Do đó tan  2 . 2 2 1 1
Vậy biểu thức A   . 2 1 3
Câu 60. Chọn B 1 8 2 2  2 2
sin x  1 cos x  1   sin x   ( vì   x  0 ). 9 9 3 2 2 tan x 4 2 4 2
 tan x  2 2  tan 2x    . 2 1  tan x 7 7
Câu 61. Chọn A Ta có 2
cos 2x  2 cos x 1  1 . Sử dụng công thức hạ bậc và công thức biến đổi tổng thành tích ta được:       1 cos 2x  1 cos 2x       3   3   1 3 A   1 cos 2x cos  1  2 3 2 2 Câu 62.
Lời giải Chọn A 2 1 1 5 Ta có: 2 cos    tan   1  1  2 2 3 cos   2 4     3  2 1 1 3 tan  5  3 tan 2 1 3. cot   3 tan 1 3 tan  19 tan tan 4 P       2 2 2 cot   tan 2 2  tan  2  tan  5 13  tan 2  tan tan 4
Câu 63. Chọn D 1
Ta có sin.cos      sin   sin 2     sin    sin  2  
 sin         3sin   
 sin     cos  sin  cos      3sin  sin     3sin   cos  sin  
(vì cos      0 ) cos     cos     sin     3sin  sin     * (vì cos  0 ) cos     cos cos     cos sin  3sin sin Mà
 sin (từ giả thiết), suy ra  
*  tan        2 tan cos     cos cos
Vậy tan      2 tan .
Câu 64. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 sin x 1 2. tan x 1 1 2 sin . x cos x Ta có: cos x      2 2 2 2 cos x  s in x 1 tan x cos 2x s in x 2 2 cos 2x cos x  s in x 1 2 cos x 1 sin 2 x 1 sin 2 x
1 sin 2 xcos 2x
1 sin 2 xcos 2x      2 cos 2x cos 2x cos 2x cos 2x 2 1 sin 2 x cos 2x
. Vậy a  2, b  1 . Suy ra P a b  3 . 1 sin 2x
Câu 65. Chọn D 2 1 1 1  2 2    5
Ta có P  cos.cos 3 
cos 2  cos 4    2
2 cos 2  cos 2   1  2  1     2 2 2   3  3 18   .
Câu 66. Chọn B 3   x
suy ra sin x  0, cos x  0 . 2 1 1 1 1 Ta có: 2 1  tan x  2  cos x  2  cos x   cos x   2 cos x 2 1  tan x 5 5 1
Do cos x  0 nên nhận cos x   . 5 sin x 2 tan x   sin x  tan . x cos x   cos x 5       2  1  1  3 2  3 sin x   sin . x cos  cos . x sin   .   .          3  3 3  5 2   5 2  2 5
Câu 67. Chọn C.
A  tan 9  cot 9  tan15  cot15 – tan 27 – cot 27
 tan 9  cot 9 – tan 27 – cot 27  tan15  cot15
 tan 9  tan 81 – tan 27 – tan 63  tan15  cot15 . Ta có  sin18 sin18
tan 9 – tan 27  tan 81 – tan 63   cos 9 .  cos 27 cos81 .  cos 63  cos 9 .  cos 27  cos81 .  cos 63  sin18cos 9 .  cos 27  sin 9 .  sin 27  sin18    cos 81 .  cos 63 .  cos 9 .  cos 27  cos81 .  cos 63 .  cos 9 .  cos 27 4 sin18 .  cos 36 4sin18    4 .
cos 72  cos90cos36  cos90 cos 72 2 2 sin 15  cos 15 2 tan15  cot15    4 . sin15 .  cos15 sin 30 Vậy A  8 .
Câu 68. Chọn C.     0  a   0  b   2 2 2   2 3 Ta có   cos a  ;   cos b  . 1 3 1 2 sin  a  s  in b    3   2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
sin 2 a b  2sin a b.cos a b  2 sin .
a cos b  sin .
b cos acos .
a cos b  sin . a sin b 4 2  7 3  . 18
Câu 69. Chọn C. Ta có : 2 2 cos 2  3 sin 4 1 cos 4  3 sin 4 sin 4  30 A    . 2 2 sin 2  3 sin 4 1 3 sin 4  cos 4 sin 4  30
Câu 70. Chọn A. sin 9 sin12 Ta có :   sin 9 .  sin 81  sin12 .  sin 48  0 sin 48 sin 81 1 1 
cos72  cos90  cos36  cos 60  0  2cos 72  2cos36 1  0 2 2 1 5 2
 4 cos 36  2 cos 36 1  0 (đúng vì cos 36  ). Suy ra B đúng. 4
Tương tự, ta cũng chứng minh được các biểu thức ở C và D đúng.
Biểu thức ở đáp án A sai.
Câu 71. Chọn C. Ta có :
5sin   3sin   2   5sin         3sin           
 5sin     cos   5 cos    sin   3sin     cos   3cos    sin  sin     sin 
 2 sin     cos   8 cos    sin    4
 tan      4 tan  . cos     cos 
Câu 72. Chọn D. Ta có : 1 cos 2a 1 cos 2b 2 A  a b 2 2 sin
– sin a – sin b 2
 sin a b   2 2 1 2
 sin a b 1 cos 2a  cos 2b 2
  cos a b  cos a b cos a b 2
 cos a b cosa b  cosa b 
  2 sin a sin b cos a b.
Câu 73. Chọn D. Ta có : sin 
cos 40 cos  sin 40sin  cos 40  
cos 40  tan.sin 40  cos 40  .sin 40   . A cos cos cos đúng. sin15 .  cos 30  sin 30 .  cos15 sin 45 6 sin15  tan 30 .  cos15    . B đúng. cos 30 cos 30 3 2 x a xa x 2 cos – 2 cos .cos .cos
 cos a x 2
 cos x  cos a x  2
 cos a cos x  cos a x   2
 cos x  cos a x cos a x 1 2  cos x
cos 2a  cos 2x 2 2 2 2
 cos x  cos a  cos x 1  sin . a C đúng. 2 2 x  a x 2 sin 2 sin – .sin .
x cos a  sin a – x 2
 sin x  sin a x2sin x cos a  sin a x 1 2
 sin x  sin a xsin a x 2  sin x
cos 2x  cos 2a 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 2 2
 sin x  cos a  sin x 1  sin a . D sai. DẠNG 5. MIN-MAX
Câu 74. Chọn C 3 3 1
Ta có sin x  cos x  sin x  cos x3 6 6 2 2 2 2 2 2 2
 3sin x cos x(sin x  cos x)  1 sin 2x  1  . 4 4 4   
Dấu “=” xảy ra khi và chỉ khi 2
sin 2x  1  cos2x  0  2x
k  x   kk  . 2 4 2 Câu 75.
Hướng dẫn giải Chọn B 1 Ta có 2 M  1 sin 2x 2 Vì 2 0  sin x  1 1 1 2     sin 2x  0 2 2 1 1 2   1 sin 2x  1. 2 2
Nên giá trị lớn nhất là 1. Câu 76.
Hướng dẫn giải Chọn A  3 4  3 4 M  5 sin x  cosx  5sin  
x a với cos a  ;sin a  .  5 5  5 5
Ta có: 1  sin  x a  1
 5  5sin  x a  5 . Câu 77.
Hướng dẫn giải Chọn D Ta có. M   2 2 x x 4 2 2 4 sin cos
sin x  sin x cos x  cos x   x  2 2 cos 2
1 sin x cos x  1 2    cos 2x 1 sin 2x    4   3 1  3 1 3 1 2 2   cos 2x  cos 2x   cos 2x    1  
do cos 2x   1 .  4 4  4 4 4 4
Nên giá trị lớn nhất là 1. Câu 78.
Hướng dẫn giải Chọn B
Đặt t  tan x, t   \   1 . 3 2 1 t t t 1 Ta có: M    M   2
1 t  2M  
1 t M 1  0 . (*). 1 t 3 2 t  2t 1
Với M  1 thì (*) có nghiệm t  0 .
Với M  1 để (*) có nghiệm khác 1 thì.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 1
  0  2M   1  4 M   1
 0  12M  3  0  M  . 4 2 Và M   1   1  2M   1   1   
1 1  0  M  4 . Câu 79.
Hướng dẫn giải Chọn D M   2  x 2 2 6 1 sin
 5sin x  6  sin x Ta có: 2
0  sin x  1 , x   R 2
 0   sin x  1, x   R 2
 6  6  sin x  5 , x   R .
Gía trị lớn nhất là 6 . Câu 80.
Hướng dẫn giải Chọn C M   2  x 2 7 1 sin  2sin x 2  7  9 sin x Ta có: 2 0  sin x  1 2  0  9
 sin x  9, x   R 2
 7  7  2 sin x  2 .
Gía trị lớn nhất là 7 .
DẠNG 6. NHẬN DẠNG TAM GIÁC Câu 81. Chọn B.
Ta có: sin 2A  sin 2B  2sin  A B.cos A B  2sin   C .cos A B
 2sin C.cos  A B  2sin C. Dấu đẳng thức xảy ra khi cos A B  1  A B .
Câu 82. Chọn C A B sin sin A B B A Ta có 3 3 2 2 sin cos  sin cos  0   . 2 2 2 2 A B 2 3 cos cos 2 2 A A B B A B A B 2 2  tan 1 tan  tan 1 tan  tan  tan    A B     . 2  2  2  2  2 2 2 2
Câu 83. Chọn C Ta có cot .
A cot B  cot .
B cot C  cot C.cot A 1 1 1
tan A  tan B  tan C     . tan . A tan B tan . B tan C tan C. tan A tan . A tan . B tan C
Mặt khác tan A  tan B  tan C  tan  A B1 tan .
A tan B  tan C
 tan   C 1 tan .
A tan B   tan C   tan C 1 tan .
A tan B   tan C  tan C.tan . A tan B . Nên cot .
A cot B  cot .
B cot C  cot C.cot A  1.
Câu 84. Chọn B 1 1  tan A  tan B 7 Ta có  A B 2 5 tan    . 1 tan . A tan B 1 1 9 1 . 2 5
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 7 1
tan  A B tan C    Suy ra
A B C  
 A B 9 8 tan tan  C     1  
1 tan  A B.tan C 7 1 1 . 9 8 
Vậy A B C  . 4 Câu 85.
Hướng dẫn giải Chọn D Vì , A ,
B C là các góc của tam giác ABC nên    180o   180o A B C C
  A B . C A B C A B   90o  . Do đó và là 2 góc phụ nhau. 2 2 2 2 C A B C A B C A B C A B  sin  cos ; cos  sin ; tan  cot ; cot  tan . 2 2 2 2 2 2 2 2
Câu 86. Chọn D
AB C  
0  C C   0 sin 2 sin 180 2
sin 180  C   sin C .
Câu 87. Chọn A
sin  A B sin C
Ta có: tan A  tan B  tan C  tan A  tan B  tan C   . cos . A cos B cos C
  cos  A B  cos . A cos B  sin . A sin . B sin C  sin C.    tan . A tan .
B tan C . cos . A cos . B cos  C  cos . A cos . B cos C Câu 88.
Hướng dẫn giải Chọn A Vì , A ,
B C là các góc của tam giác ABC nên    180o   180o A B C C
  A B . C A B C A B   90o  . Do đó và là 2 góc phụ nhau. 2 2 2 2 C A B C A B C A B C A B  sin  cos ; cos  sin ; tan  cot ; cot  tan . 2 2 2 2 2 2 2 2
Câu 89. Chọn B a 3a
a b c   , a  2b b  ;c    2 2 1 cos 2b cos(b c)  cos(b c)
sin b sin b  sin c 2  sin b  sin . b sin c =  2 2
1 cos a  cos   a  cos 2a    1 cos 2a 2 =   sin a . 2 2
Câu 90. Chọn D
Ta có: sin 2A  sin 2B  sin 2C  sin 2A  sin 2B  sin 2C
 2sin  A B.cos A B  2sin C.cosC  2sin C.cos A B  2sin C.cosC
 2sin C.cos A B  cosC  4sin C.cos A B C.cos A B C
A B C
A B C        4 sin C.cos .cos  4 sin C.cos  A .cos    
B   4sinC.sin .
A sin B . 2 2  2   2 
Câu 91. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 0
A  2B C 180  B  2B  3B  3B 0 cos  cos  cos 90   sin   . 2 2  2  2
Câu 92. Chọn C Vì ,
A B, C là các góc của tam giác ABC nên A B C  180  C  180   A B .
Do đó  A B và C là 2 góc bù nhau.
sin C  sin  A B;cosC   cos A B .
tan C   tan  A B;cot C  cot  A B Câu 93. Chọn B. Ta có : cot .
A cot B  cot .
B cot C  cot C.cot A. 1 1 1
tan A  tan B  tan C     . tan . A tan B tan . B tan C tan C. tan A tan . A tan . B tan C
Mặt khác : tan A  tan B  tan C  tan  A B1 tan .
A tan B  tan C .
 tan   C 1 tan .
A tan B  tan C .
  tan C 1 tan .
A tan B  tan C  tan C tan . A tan B . Nên cot .
A cot B  cot .
B cot C  cot C.cot A  1. Câu 94. Chọn A. A B  sin  C   cos A B CA B C  2 2  Ta có: cot  cot  cot  cot  cot  cot 2     . 2 2 2  2 2  2 A B C sin .sin sin 2 2 2 C A BA B A B C B A sin  sin .sin cos   sin .sin cos .cos .cos C   2 2 2 C  2 2  2 2  cos .  cos . 2 2 2  2 C A B 2 C A B C A B sin .sin .sin sin .sin .sin sin .sin .sin 2 2 2 2 2 2 2 2 2 A B C  cot .cot .cot . 2 2 2
Câu 95. Chọn C. Ta có : 1 cos 2 A 1 cos 2B 2 2 2
cos A  cos B  cos C 2    cos C 2 2    A B  A B 2 1 cos cos
 cos C  1 cos C cos  A B  cos C cos  A B
 1 cos C cos  A B  cos A B 
  1 2 cos A cos B cos C. Câu 96.
Hướng dẫn giải Chọn C
cos  A B   cos C  cos .
A cos B  cos C  sin . A sin B 2 2 2 2 2  cos .
A cos B  2 cos . A cos .
B cos C  cos C  sin . A sin B   2 1 cos A 2 1 cos B 2 2 2 2
 1 cos A  cos B  cos . A cos B 2 2 2
 cos A  cos B  cos C  2 cos . A cos . B cos C  1
Câu 97. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 B C B C A 2sin cos cos sin B  s inC Ta có 2 2 2 sin A   sin A   sin A  cos B  cos C B C B C A 2 cos cos sin 2 2 2 A cos A A 2 A A 2  2 sin cos   2sin  1 ( cos
 0 vì 0  A  180 ) 2 2 A 2 2 sin 2
 cos A  0  A  90 suy ra tam giác ABC vuông tại A .
Câu 98. Chọn A 1 13 Từ giả thiết suy ra: 2 2cos A    2
2  4sin B  4sin B   0 4  64cos A 4 1 3 2 2 2
 cos A  cos A
 4sin B  4sin B 1  * 4   64cos A 4 1 3 AD BĐT Cauchy thì 2 2
cos A  cos A   (1) 4 64cos A 4 2 Mặt khác 2
4sin B  4sin B 1  2sin B   1  02
Từ (*), (1) và (2) suy ra bđt thỏa mãn khi và chỉ khi dấu bằng ở (1) và (2) xảy ra  1   o 2 1 cos A A  60  cosA  4  64cos A    2    o     B  30 . 1  1 sin B   sin B    o   2 C  90   2     Nên   120o B C Chọn A.
Câu 99. Chọn C. tan A  tan B     tan tan  tan C A B C      1 tan . A tan tan B A B C  
 1 suy ra A B C  .
1 tan  A B.tan C tan A  tan B 4 .tan C 1 tan . A tan B
Câu 100. Chọn D. Ta có:
A B  3C
A B  3C   
A B C      C  sin  sin  C  cos C.   A đúng. 2 2 2  2 
A B C    2C  cos  A B – C   cos   2C    cos 2C. B đúng.
A B  2C  3C
A B  2C   3C  3C    tan  tan   cot .   C đúng. 2 2 2 2  2 2  2
A B  2CC
A B  2C   C C    cot  cot    tan .   D sai. 2 2 2 2  2 2  2
Câu 101. Chọn C. Ta có: A BC A B   C C    cos  cos   sin .   A đúng. 2 2 2 2  2 2  2
A B  2C    C  cos  A B  2C   cos   C    cos C. B đúng.
A C    B  sin  A C   sin   B  sin . B C sai.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
A B    C  cos  A B  cos   C    cos C. D đúng.
Câu 102. Chọn C. Ta có : B C B CB C    A A + cos cos  sin sin  cos   cos   sin .     A đúng. 2 2 2 2  2 2   2 2  2
+ tan A  tan B  tan C  tan . A tan .
B tan C   tan A1 tan B tan C   tan B  tan C tan B  tan C  tan A  
 tan A   tan  B C  . B đúng. 1 tan B tan C
+ cot A  cot B  cot C  cot . A cot .
B cot C  cot Acot B cot C  
1  cot B  cot C 1 cot B cot C 1  
 tanA  cot  B C . C sai. cot A cot B  cot C A B B C C A A B C B C + tan .tan  tan .tan  tan . tan  1  tan . tan  tan  1 tan . tan   2 2 2 2 2 2 2  2 2  2 2 B C tan  tan 1 2 2 AB C     cot  tan  . D đúng. A B C   2  2 2 tan 1 tan . tan  2 2 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
Document Outline

  • 1577070199_0D6-1 GÓC VÀ CUNG LƯỢNG GIÁC
  • 1577070243_0D6-2 GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT CUNG
  • 1577070297_0D6-3 CÔNG THỨC LƯỢNG GIÁC