Preview text:
CÁC ĐỊNH LUẬT KIRCHHOFF TRONG DÒNG KHÔNG ĐỔI
I/ Các định luật Kirchhoff.
1. Định luật Kirchhoff I (Định luật bảo toàn dòng điện).
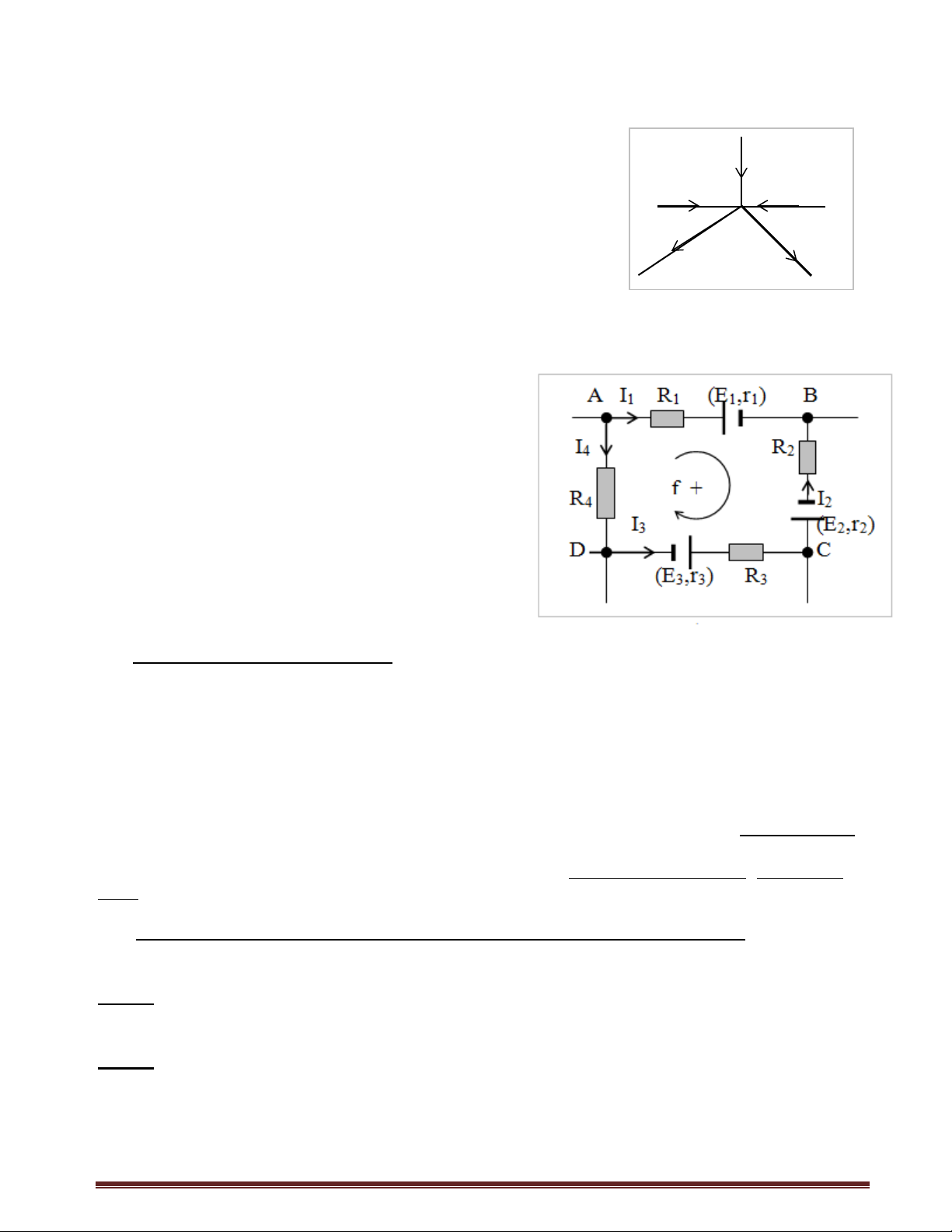
- Có nguồn gốc từ định luật bảo toàn điện tích I3
- Định luật Kirchhoff I được phát biểu như sau : I1 A I5
“Tổng số học các dòng điện đến một nút phải bằng tổng số học
các dòng điện rời khỏi nút” . I2 I4
- Trên hình vẽ bên , ta có : I1 + I3 + I5 = I2 + I4
I1 + I3 + I5 + (− I2) + (− I4) = 0
- Nếu ta quy ước dòng điện hướng tới nút là dương , dòng điện
rời nút là âm , ta có định luật Kirchhoff tổng quát như sau :
“ Tổng đại số các dòng điện đến một nút bằng không” : I = 0. (1)
2. Định luật Kirchhoff II.
- Có nguồn gốc từ định luật bảo toàn năng lượng.
- Xét một vòng kín của mạch điện , định luật Kiếchốp II được phát biểu như sau :
“ Theo một vòng kín, tổng đại số các suất điện động
bằng tổng đại số các độ giảm thế ” :
E = (I.r) (2)
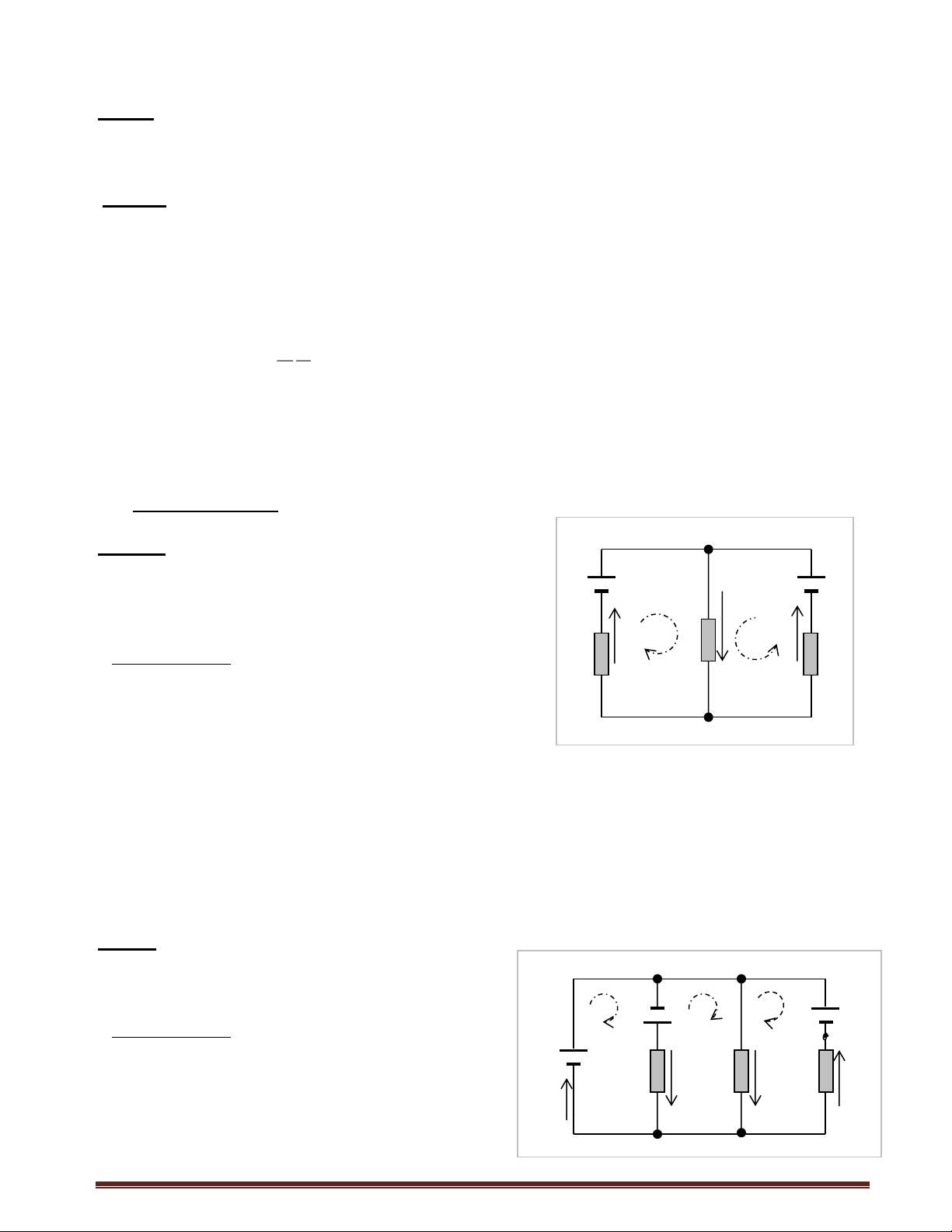
- Trên hình vẽ bên , theo định luật Kirchhoff II , ta có hệ thức : − E − −
1 + E2 − E3 = I1R1 + I1r1 − I2R2 − I2r2 − I3R3 I3r3 I4R4
II/ CÁC BÀI TOÁN VỀ MẠCH ĐIỆN.
- Mạch điện là sự chắp nối các phần tử của mạch .
- Các phần tử cấu tạo nên mạch điện là suất điện động Ei , điện trở thuần Ri (vật lí 11). Ngoài ra trong
mạch có thể có cuộn cảm, tụ điện (vật lí 12) tham gia tạo thành mạch điện.
- Nếu suất điện động của nguồn không đổi, ta có mạch điện không đổi hay mạch điện một chiều.
Ngược lại, nếu suất điện động biến đổi, ta có mạch điện với nguồn biến đổi, trong đó đáng chú yù là
mạch điện xoay chiều hình sin .
- Nếu kết cấu của mạch đã biết, tức đã biết suất điện động Ei , các thông số Ri , L, C, bài toán đặt ra là
giải tích mạch để tìm dòng I, điện áp U và công suất P... Loại toán này gọi là bài toán phân tích mạch.
- Nếu kết cấu mạch chưa biết , ta cần tìm ra kết cấu mạch để thỏa mãn yêu cầu về dòng I , về điện áp
U công suất P ở các nhánh đã định trước . Loại toán này gọi là bài toán tổng hợp mạch (hay thiết kế mạch)
III/ GỢI Ý CÁC BƯỚC TRONG VIỆC GIẢI TOÁN VỀ MẠCH ĐIỆN KHÔNG ĐỔI .
- Để vận dụng được 2 định luật Kirchhoff trong việc giải bài toán điện một chiều, ta có thể tiến hành theo các bước như sau :
Bước 1 : Vẽ một mạch điện đủ lớn để ghi được hết các kí hiệu của những đại lượng đã biết và chưa
biết của bài toán , kèm theo cả chiều giả định (tùy chọn) cho mỗi cường độ dòng và mỗi suất điện động.
Bước 2 : Thành lập hệ phương trình từ hai định luật Kirchhoff
- Nếu mạch điện có m nút thì sử dụng định luật Kirchhoff I viết (m – 1) phương trình nút .
- Nếu mạch có M mạch vòng thì sử dụng định luật Kirchhoff II viết M phương trình vòng .
Cách viết phương trình vòng như sau : Chọn một chiều dương f tùy yù cho vòng . Đi theo chiều đó , Ei
là dương khi từ cực (−) sang cực (+) và là âm khi nó qua từ cực (+) sang cực (−) . Một độ giảm thế
IiRi (kể cả điện trở nội) là âm (−) khi nó đi theo chiều dòng điện đã được chọn và là dương (+) nếu nó Các định luật Kirchhoff 1
đi theo chiều ngược lại .
Nếu mạch có n dòng điện nhánh thì số phương trình lập được từ hai định luật Kirchhoff là n
Bước 3 : Giải hệ gồm n phương trình , tìm ra đáp số là các dòng điện nhánh . Đối với đáp số âm , ta
hiểu là chiều thực tế của dòng điện ngược chiều với chiều dòng điện đã chọn ban đầu .
Đặc điểm của phương pháp này là có thể giải được mạch điện phức tạp , nhiều nguồn , nhưng nếu
số nhánh (hoặc số vòng) nhiều thì hệ phương trình nhiều ẩn, thời gian hoàn thành bài toán lâu . Ghi chú :
+ Nếu trong mạch điện có sử dụng nhiệt lượng do dòng điện tỏa ra trên điện trở để thực hiện
những quá trình nhiệt học nào đó thì có thể phải sử dụng các phương trình nhiệt để tìm các đại lượng cần thiết.
+ Hoặc mạch điện có liên quan đến việc sử dụng điện năng để thực hiện một công có ích nào đó
thì cần phải áp dụng các phương trình cơ để tính công tương ứng .
+ Hoặc mạch điện có liên quan đến hiện tượng điện phân thì cần áp dụng định luật Faraday về điện phân : 1 A m = It . F n
+ Ngoài phương pháp đã nêu trên , trong chiến lược giải toán về dòng điện không đổi người ta đã
tìm ra nhiều thủ thuật khác như : phương pháp biến đổi điện trở, phương pháp nguồn tương
đương, phương pháp điện thế nút, phương pháp xếp chồng dòng, phương pháp chuyển đổi sao tam giác,... IV/ MỘT SỐ THÍ DỤ : A
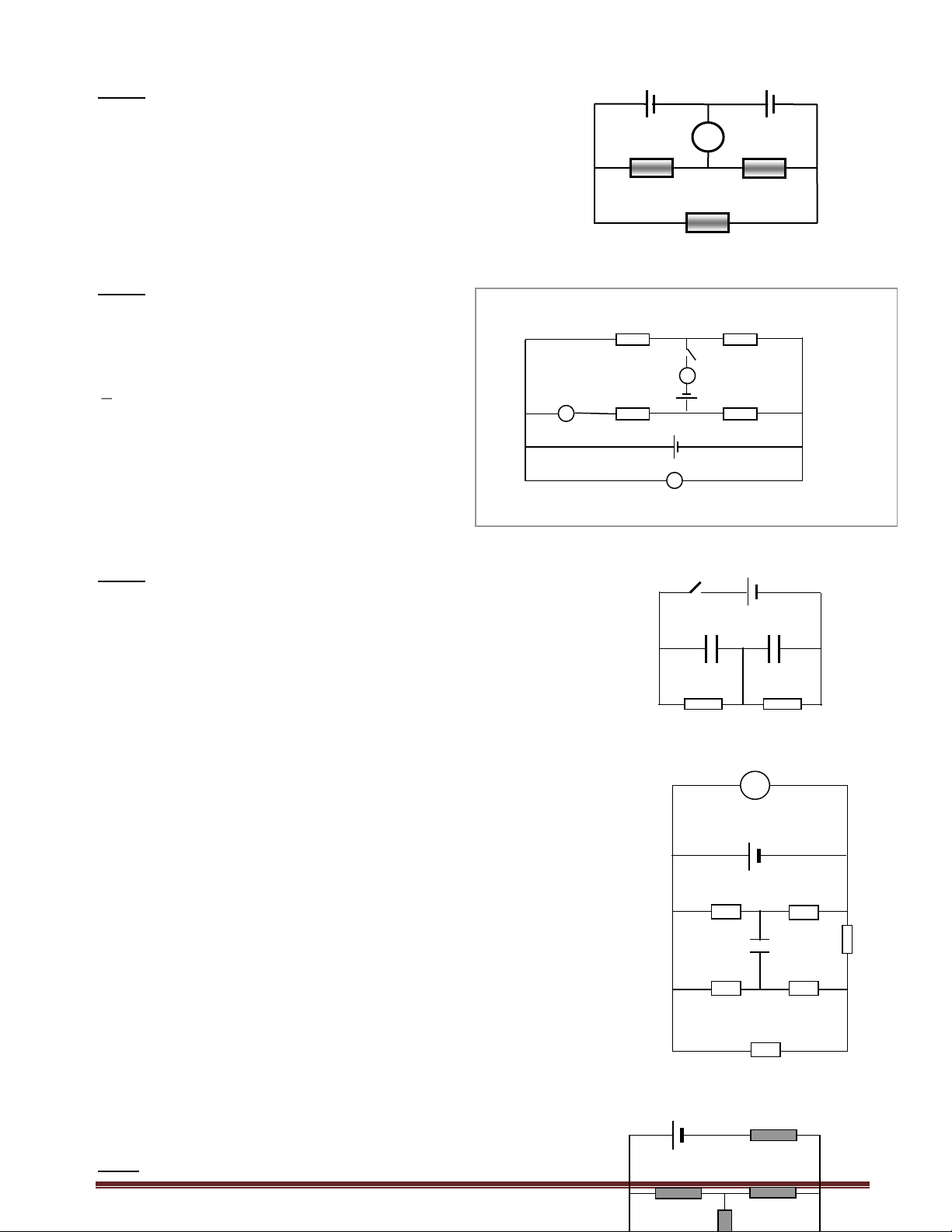
Thí dụ 1 : Cho mạch điện như hình vẽ
Cho E1 = 125V ; E2 = 90V ; r1 = r2 = 1 ; R = 4 ; E1 r1 E2 r2 R1 = 2 ; R2 = 1 ;
Tìm dòng điện trong các nhánh và hiệu điện thế đặt vào điện trở R . C • • D R1 I1 + R I + I2 R2
Hướng dẫn giải :
Chọn chiều và kí hiệu các dòng điện trên các nhánh của
mạch điện như trên hình vẽ .
- Mạch này có 2 nút nên viết được một phương trình nút : B
I = I + I (1) 1 2
- Mạch có hai mạch vòng (3 nhánh) nên viết được 2 phương trình vòng :
Chọn chiều dương của các vòng như trên hình , ta có : Trên vòng ABC : E1 = I1R1 + I1r1 + IR (2) Trên vòng ABD : E2 = I2R2 + I2r2 + IR (3)
Giải hệ 3 phương trình (1), (2), (3) ta sẽ tìm được kết quả : I1 = 15A ; I2 = 5A ; I= 20A .
Hiệu điện thế trên R là : UAB = IR = 20.4 = 80V .
(Có thể vận dụng định luật Ôm trong các loại đoạn mạch để giải quyết bài toán)
Ví dụ 2 : Cho mạch điện như hình vẽ
E1 = 35V , r1 không đáng kể ; E2 = 95V ; r2 = r4 = 2 ; B C
R2 = 48 ; R3 = R4 = 10 ; E4 = 44V ;
Tìm cường độ dòng điện qua các nhánh của mạch điện. + E2 r2 + + E4 r4
Hướng dẫn giải : D
Kí hiệu và chọn chiều dòng điện trong các nhánh như E1 r1= 0 trên hình vẽ . R2 I2 R3 I3 R4 I4
- Vì giữa B và C ; giữa M và N không có điện trở nên I1
Thực chất B và C chỉ là một nút , M và N là một nút .
Vì vậy ta viết một phương trình nút tại B (hoặc tại M): A M N I1 + I4 = I2 + I3 (1) . Các định luật Kirchhoff 2
Chọn chiều dương trong mỗi vòng theo chiều kim đồng hồ và chú rằng : điện trở trong của nguồn E1 bằng không . E + E + Xét vòng BMAB : E 1 2 I = = 1 + E2 = I2(R2 + r2) → , 2 6 (A). 2 R + r 2 2
I (R + r ) − E . 6 , 2 50 − 95 + Xét vòng BCNMB : − E 2 2 2 2 I = = = 2= I3R3 − I2(R2 + r2) → 5 , 3 (A). 3 R 10 3 E − I R 44 − 5 , 3 10 . + Xét vòng CDNC : − E 4 3 3 I = = =
4 = − I4(R4 + r4) − I3R3 → , 0 75 (A) . 4 R + r 12 4 4
+ Từ (1) suy ra : I1 = I2 + I3 – I4 = 2,6 + 3,6 – 0,75 = 5,35 (A) .
Chú yù : Có thể nhận xét điện trở trong của nguồn E1 bằng không nên UBM = UCN = E1 = 35V . Từ
đó vận dụng định luật Ôm trên các đọn mạch đề tìm các dòng điện .
Ví dụ 3 : Cho mạch điện như hình vẽ E I E
1 = 16V ; E2 = 5V ; r1 = 2 ; r2 = 1 ; 1 , r1 R
2 = 4 ; Đèn Đ có ghi : 3V – 3W ; RA = 0
Biết đèn sáng bình thường và ampe kế (A) chỉ 0 . +
Tính cường độ dòng điện qua mỗi nhánh và R R1 M R2 1 , R3 .
Hướng dẫn giải : A B
* Kí hiệu và chọn chiều các dòng điện như trên hình I1 E2 r2 I2
vẽ . Mạch điện này có 4 nút nên ta viết 3 phương + + nút độc lập . IA A - Nút A : I = I R3 IĐ 1 + I3 (1) - Nút M : I
1 + IA = I2 → I1 = I2 (2) P I3 N Đ - Nút N : I đm = 3 = IA + IĐ = IĐ = 1(A) . (3) U đm
* Chọn chiều dương trong các mắt mạng như trên hình :
+ Xét vòng BE1AMB : E1 = Ir1 + I1 (R1 + R2) → 16 = 2I + I1(R1 + 4) (4)
+ Xét vòng AMNR3A : − E2 = I1R1 – I3R3 → − 5 = I1R1 – 1.R3 (5)
+ Xét vòng MBĐNM : E2 = I2R2 – IĐRĐ → 5 = 4I
2 – 3 (6) (vì IĐRĐ = Uđm = 3V)
Từ (6) → I2 = 2A = I1. → I = 3A . Từ (4) →
R1 = ( 16 – 2.3 – 2.4 )/2 = 1 .
Từ (5) → R3 = 2.1 + 5 = 7 .
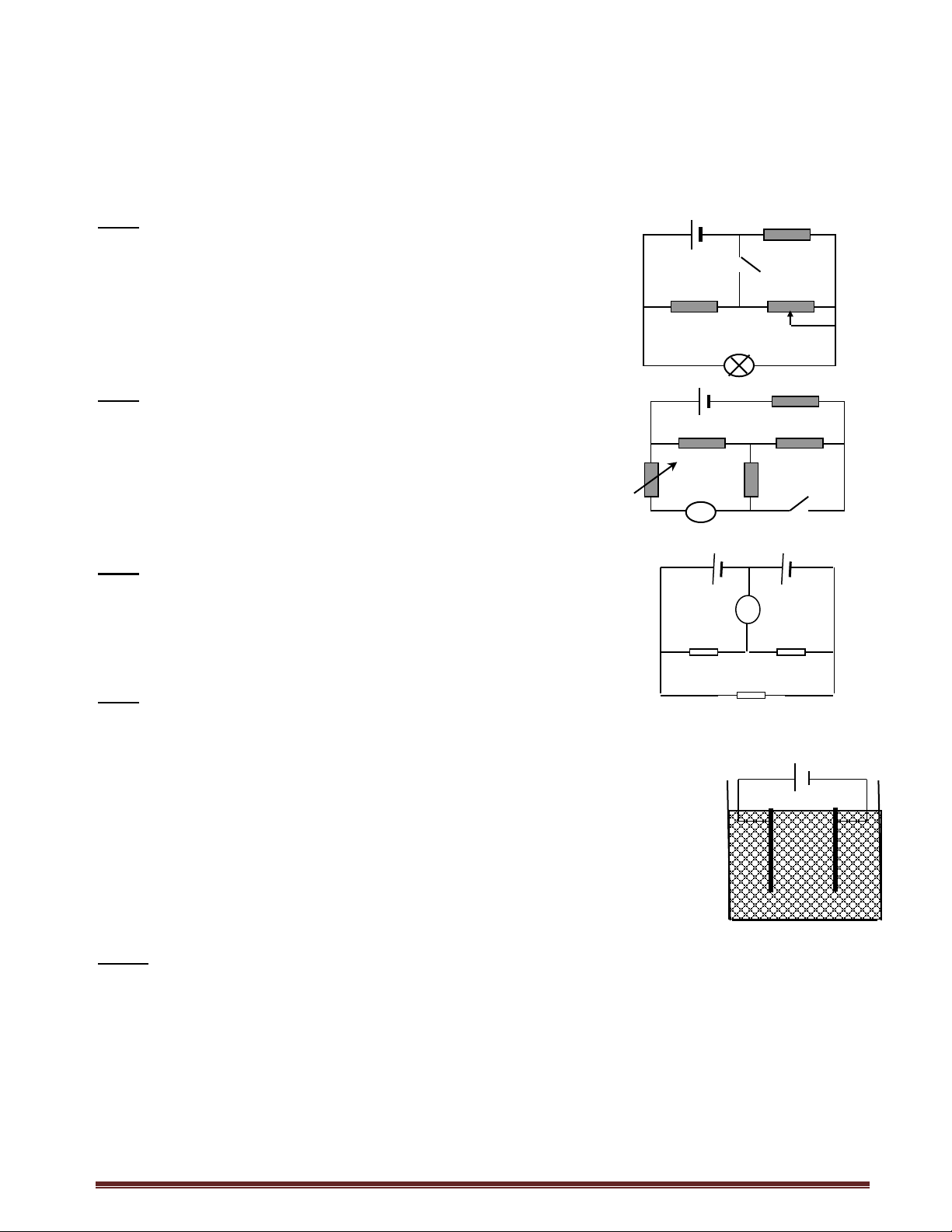
Ví dụ 4 : Cho mạch điện như hình vẽ R1 A R2 E
1 = 25V ; E2 = 16V ; r1 = r2 = 2 ; R1 = R2 = 10. I R 1 + + 3 = R4 = 5 ; R5 = 8 .
Tính cường độ dòng điện qua mỗi nhánh của mạch R 3 I3 I2 điện . (E 2,r2) R4 I4 Hướng dẫn giải B D :
* Kí hiệu và chọn chiều dòng điện như trên hình vẽ I C
Mạch điện này có 4 nút nên ta viết được 3 phương (E trình nút : 1,r1) +
- Nút B : I = I1 + I5 = I3 + I4 (1) I - Nút A : I 5 R5 1 = I2 + I3 (2) - Nút D : I4 = I2 + I5 (3)
* Chọn chiều dương trong các mắt mạng như trên hình :
- Xét vòng ACBA : E2 = I1R1 +I3R3 + Ir2 → 10I1 + 5R3 + 2I = 16 (4)
- Xét vòng ADCA : 0 = I2R2 + I4R4 – I3R3 → 10I2 + 5I4 – 5I3 = 0 (5)
- Xét vòng BR5DCB : E1 + E2 = I4R4 + I5R5 + Ir2 + I5r1 → 5I4 + 10I5 + 2I = 41 (6) Các định luật Kirchhoff 3
Giải hệ phương trình trên sẽ tìm được kết quả : I = 3A ; I3 = 1A ; I1 = 0,5 A ; I5 = 2,5 A ; I2 = - 0,5 A ; I4 = 2 A . Ví dụ 5 :
Cho một mạch điện như sơ đồ bên, trong đó : A E = V 16 , r E = 10 , r 1 1 = 1 ; V 3
3 = 2 ; R1 = 3 ; R2 = 4 ;
R3 = 6 .Mắc vào giữa hai điểm A , B nguồn 2 có điện trở + E2,r2 +
trong r2 = 2 thì thấy dòng điện qua R2 có chiều như trên E1,r1 B E3,r3
hình vẽ và có cường độ I I
2 = 1A . Tìm 2 và cách mắc ? 1 I3
Hướng dẫn giải : R1 I2 R2 R3
* Giả sử cực dương của nguồn
2 ở B , cực âm ở A . Kí hiệu
dòng điện và chọn chiều của dòng như trên hình vẽ. Mạch có 2 nút
nên viết một phương trình nút (tại A hoặc tại C): C
Tại nút C, ta có : I2 = I1 + I3 → I1 + I3 = 1 (1)
* Chọn chiều dương trong các mắt mạng như trên hình :
- Xét vòng ABCR1A : E1 + E2 = (r1 + R1) I1 + (r2 + R2)I2 → 16 + E2 = 4I1 + 6 (2)
- Xét vòng AR3CBA : − E2 – E3 = − (r2 + R2)I2 − (r3 + R3)I3 → E2 + 10 = 6 + 8I3 (3)
Giải hệ 3 phương trình trên cho kết quả của I1 , I2 và E2 .
ĐỀ BÀI DÀNH CHO BẠN (E1,r1)
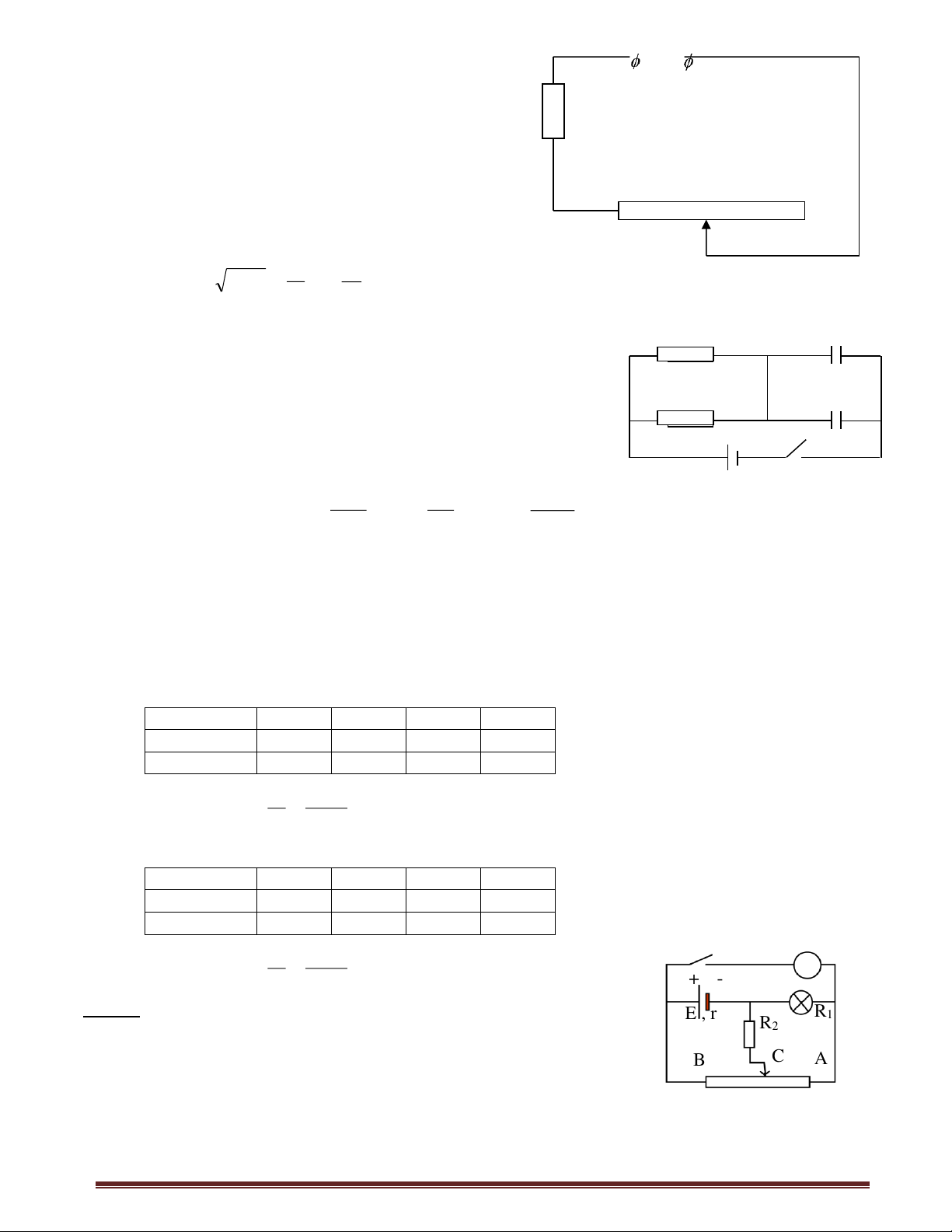
Bài 1 : Cho mạch điện như hình vẽ (H1)
E1 = 9V ; r1 = 1 ; R(A) = 0 R1 = 2 ; R2 = 6
Khi K mở ampe kế chỉ 0 ; Khi K đóng , am pe kế A M K B chỉ 8,4 A . Tìm E A 2 và r2 .
Đáp số : 6V ; 1 . R2 E2 R1 r2
Bài 2 : Cho mạch điện như hình vẽ Cho E1 = 120 V ; E2 = 110V ; N R1 = R2 = r1 = r2 = 0,5 (H1)
R3 = 2 ; R4 = 9 ; R5 = 4 . I
Xác định cường độ dòng điện trên các nhánh của 1 B I2 mạch điện . E Đáp số 1,r1 I4 I5 E2,r2
: I1 = 16,86 A ; I2 = 17,68 A ; I3 = 5,4 A ; N I4 = 11,46 A ; I5 = 23,08 A . R4 R5
Bài 3 : Cho mạch điện như hình(H3) R1 R2 C R1 = 10 . R3 R R 1 R2 2 = 20 . A C A E1 r1 B R3 = 30 . I3 R4 = 40 . (H2) R3 D R4 E2 = 105V . r1 = r2 = 0 Tìm suất điện E động 2 r2 (H3) E1 để không
có dòng điện trong đoạn mạch CD . Đáp số : 10V .
MỘT SỐ BÀI TẬP LUYỆN TẬP Các định luật Kirchhoff 4 E1,r1 E2,r2
BÀI 1 :Cho mạch điện như hình vẽ (hình 1). D
Biết E1 = 6V, r1 = 1Ω, r2 = 3 Ω, R1 = R2 = R3 = 6 Ω. Vôn kế lí tưởng. R1 R3 V
a) Vôn kế chỉ 3V. Tính suất điện động E2. A B
b) Nếu nguồn E2 có cực dương nối với B, cực âm nối C
với D thì vôn kế chỉ bao nhiêu? R2 Hình 1
BÀI 2: Cho mạch điện như hình vẽ ( H.2 ) . với R = 2 R ; R = 2 R ; E 1 2 4 3 1 = 12 v , r1 = 2 , R1 R2 R = R = o , R = ∞ a G v
a/ Khi K mở , vôn kế chỉ 10 v , Ampe kế chỉ K 1 G
A . Các điện trở đó có giá trị bằng bao nhiêu R E2,r2 3 R4 3 A A B E ? 1,r1
b/ Khi K đóng , điện kế G chỉ 0 . Tính E . 2
c/ Thay K bằng một tụ điện có điện dung C = V
3F và đổi cực của E .Tính điện tích q của tụ (H.2) 2
và xác định dấu các bản của nó ?
BÀI 3:Cho mạch điện như hình 3. Nguồn điện có suất điện động E K E r
= 12V, điện trở trong r = 5 , điện trở R1 = R = 10 , R2 = 2R,
các tụ điện có điện dung C1 = C2 = 12 F, điện trở dây nối và khoá
K không đáng kể. Ban đầu khoá K mở, các tụ điện chưa tích điện. A C1 M C2 B Sau đó đóng khoá K.
a. Tính điện lượng chuyển qua dây MN. R1 R2
b. Tính nhiệt lượng toả ra trên điện trở R1 trong thời gian 10
phút và tính hiệu suất của nguồn điện. N Hình 3
c. Tính năng lượng của mỗi tụ điện. V
BÀI 4: Cho mạch điện như hình 4. Các điện trở có giá trị
R1 = R2 = R3 = R4 = R5 = 3 ; Rx là một biến trở; nguồn điện có suất điện
động E = 5,4V; tụ điện có điện dung C = 0,01 F.
Vôn kế V có điện trở rất
lớn, các dây nối có điện trở không đáng kể. E, r 1. Ban đầu cho R R1 R3
x = 1 thì vôn kế chỉ 3,6V. M
a, Tính điện trở trong của nguồn điện.
b, Tính điện tích của bản tụ nối với M. Rx C
2. Tìm Rx để công suất tiêu thụ trên Rx cực đại. Tính công suất đó. N R2 R4 R5 Hình 4 , r R
Bài 5 : Cho mạch điện như hình 5. 1 Rx Các định luật Kirchhoff A B 5 R 2 R3 Ñ C
Cho bi ết = 18V ; r = 1Ω ; R1 = 8 Ω ; R2 = 9 Ω ; R3 = 36 Ω ; RA ≈ 0 ;
đèn Đ: 6V-6W sáng bình thường.
Tính ε , Rx và số chỉ ampe kế.GD) (H.5)
Bài 6: Cho mạch điện như hình 6 .
Cho bi ết r = 2Ω ; R1 = 18 Ω ; R2 = 2 Ω ; đèn Đ: 7V-7W R
Đóng khóa K và điều chỉnh Rbkhi đó đèn sáng bình thường. , r 1
và đạt công suất tiêu thụ cực đại. K Rb a- Tìm ε và Rb khi đó.
b- Khi K mở đèn sáng thế nào? R2 Ñ ( (H .6)
Bài 7: Cho mạch điện như hình vẽ. Biết r = 1 ; R1 = 14 ;
R2 = 4; R3 = 18; R4 = 9; RA = 1; bỏ qua điện trở dây nối và R , r 1
khóa K. Khi K đóng, điều chỉnh để R5 có công suất trÊn R5 cực đại, D A B
lúc đó ampe kế chỉ 2A. Xác định số chỉ ampe kế khi mở K. R R 2 3 R R4 5 K A (H.7) E1,r1 E2,r2
Bài 8: Cho mạch điện như hình vẽ (H8): trong đó E D 1 = 6V; r1=1Ω; r2=3Ω; R1=R2=R3=6Ω.
1.Vôn kế V (điện trở rất lớn) chỉ 3V. Tính suất điện động E2. V
2.Nếu đổi chỗ hai cực của nguồn E R
2 thì vôn kế V chỉ bao nhiêu? R1 3 A B C
Bài 9: Một tụ điện phẳng có hai bản cực hình vuông cạnh
a = 30cm, đặt cách nhau một khoảng d = 4mm nhúng chìm hoàn R2
toàn trong một thùng dầu có hằng số điện môi = , 2 4 . (H.9).Hai H.8)
bản cực được nối với hai cực của một nguồn điện có suất điện động E = 24V, điện
trở trong không đáng kể.
1. Tính điện tích của tụ.
2.Bằng một vòi ở đáy thùng dầu, người ta tháo cho dầu chảy ra ngoài và dầu
trong thùng hạ thấp dần đều với vận tốc v = 5mm/s .Tính cường độ dòng điện
chạy trong mạch trong quá trình dầu hạ thấp.
3.Nếu ta bỏ nguồn điện trước khi tháo dầu thì điện tích và hiệu điện thế của tụ thay đổi thế nào?
Bài 10: Có một số điện trở r = 5 ( ). (H.9)
a. Hỏi phải dùng tối thiểu bao nhiêu điện trở đó để mắc thành mạch có điện trở 3 ( ).
Xác định số điện trở r, lập luận vẽ sơ đồ mạch ?
b. Hỏi phải dùng tối thiểu bao nhiêu điện trở đó để mắc thành mạch có điện trở 7 ( ).
Xác định số điện trở r, lập luận vẽ sơ đồ mạch ? Bài 11: Các định luật Kirchhoff 6 + _ U
Cho mạch điện như hình 11. Biến trở AB là 1 dây
đồng chất, dài l = 1,3m, tiết diện S = 0,1mm2, điện R
trở suất = 10 - 6 m
.U là hiệu điện thế không đổi.
Nhận thấy khi con chạy ở các vị trí cách đầu A hoặc
đầu B những đoạn như nhau bằng 40cm thì công suất C
toả nhiệt trên biến trở là như nhau. Xác định R0 và A B
tỉ số công suất tỏa nhiệt trên R0 ứng với 2 vị trí của C? (H.11) ĐÁP SỐ: 6 P R = 1 = 0 = R R R ; , 2 25 1 2 13 P2 C1
Bài 12: Cho mạch điện như hình 3, nguồn điện có suất điện động E, R R M
điện trở trong r = R / 2, hai tụ điện có điện dung
C1 = C2 = C (ban đầu chưa tích điện) và hai điện trở R và 2R, lúc đầu
khóa k mở. Bỏ qua điện trở các dây nối và khoá k. Đóng k. 2R 2R C2
a.Tính điện lượng chuyển qua dây dẫn MN. N
b.Tính nhiệt lượng tỏa ra trên điện trở R. + - k E, r H×nh 12 ĐÁP SỐ: 4CE CE 8 2 CE a/ ' q = q − q = − CE = ; b/ Q . r MN 1 1 R = 3 3 21 Bài 13:
Có một số đèn (3V- 3W) và một số nguồn, mỗi nguồn có suất điện động = 4V, điện trở r = 1.
a. Cho 8 đèn. Tìm số nguồn ít nhất và cách ghép đèn, ghép nguồn để đèn sáng bình thường. Xác
định hiệu suất cách ghép.
b. Cho 15 nguồn. Tìm số đèn nhiều nhất và cách ghép đèn, ghép nguồn để đèn sáng bình
thường. Xác định hiệu suất cách ghép. ĐÁP SỐ: a/ m n P q Cách 1 2 3 4 2 Cách 2 1 6 2 4 Hiệu suất: U qUdm H = = = 50% = H 1 2 n b b/ m n P q Cách 1 5 3 10 2 Cách 2 1 15 2 10 K Hiệu suất: U qUdm H = = = 50% = H A 1 2 n + - b Bài 14: E , r R1
Cho mạch điện như hình 14. Nguồn điện R2 có E = 8V, r =2 . B C A
Điện trở của đèn là R1 = 3 ; R2 = 3 ; ampe kế có điện
trở không đáng kể. (H.14)
a, K mở, di chuyển con chạy C người ta nhận thấy khi
điện trở phần AC của biến trở AB có giá trị 1 thì đèn
tối nhất. Tính điện trở toàn phần của biến trở. Các định luật Kirchhoff 7
b, Thay biến trở trên bằng một biến trở khác và mắc
vào chỗ biến trở cũ ở mạch điện trên rồi đóng khoá K. Khi điện trở phần AC bằng 6 thì ampe kế chỉ
5 A. Tính điện trở toàn phần của biến trở mới. 3 R
BÀI 15: Cho mạch điện như hình 5 trong đó r E1,r1 1=r2=R/5 K C
RA1=RA2=R/20; E1=5E2. Bỏ qua điện trở các dây nối và khóa K. A A1 B
Khi K đóng, số chỉ Ampe kế A R
2 là 1A. Tính số chỉ các ampe kế khi R R E K mở và khi K đóng. 2,r2 A2 D R Hình 15 Các định luật Kirchhoff 8