Các phương pháp kiểm định thống kê | Đại Học Y Dược Huế

lOMoAR cPSD|59062190 LÍ THUYẾT
 CÁC ĐẶC TRƯNG MẪU – Statistics: thống kê
VỊ TRÍ TRUNG TÂM: (Central Tendency)  Mean : trung bình mẫu
 Median : trung vị - điểm nằm chính giữa
 Mode: số trội – giá trị có xác suất max-số có khả năng nhất MỨC ĐỘ PHÂN TÁN: (Dispersion)  Variance : phương sai
 Std . Devation : độ lệch chuẩn
 S.E.Mean: độ lệch chuẩn của trung bình mẫu
 Range: khoảng biến thiên
 Minimum: giá trị nhỏ nhất
 Maximum: giá trị lớn nhất
DẠNG HÌNH PHÂN PHỐI: (Distribution)
 Skewness: độ lệch, độ nghiêng
 Kurtoros: Độ nhọn-mức độ tập trung của 1 phân phối  NHẬN XÉT TÍNH CHUẨN
 FREQUENCIES: Biểu đồ với đường cong chuẩn (Histograms/Shows normal curve on histogram) :
Dạnh hình chuông đối xứng với tần số cao nhất nằm giữa và thấp dần về 2 bên. Giá trị Mean và Median gần bằng nhau và Skewness gần bằng 0.
 EXPLORE: Dùng phép kiểm định Kolmogorov-Smirnov(N>50) hoặc Shapiro-Wilk (N>50). Được coi là có phân phối chuẩn khi (p> 0.05).
Biểu đồ Normal Q-Q Plot, các trị số quan sát và trị số mong đợi đều nằm gần trên đường thẳng.
 Với N>300, giá trị tuyệt đối của Skewness < 2 và giá trị tuyệt đối của Kurtosis (proper) <7, giá trị tuyệt đối của độ nhọn dư
thừa (excess) <4 dữ liệu chắc chắn phân phối chuẩn.  CÁC TEST CẦN DÙNG:
1. One Sample T-Test: là thủ tục kiểm định 1 trung bình trong TH phương sai chưa biết. Thống kê kiểm định K= . S
n, có phân phối Student, bậc tự do df=n-1 Điều kiện: X có phân phối chuẩn.
2. Independent Samples T-Test: là thủ tục kiểm định 2 trung bình trong trường hợp phương sai chưa biết. Thống kê kiểm định K= , có phân phối Student:
 Bậc tự do df=n1+n2-2 khi σ21=σ22 S21 n1  Bậc tự do
df=(n2−1)c +(1−c) (n1−1), với c= S21 S22 , khi + n1 n2
Điều kiện: X,Y có pp chuẩn. .
3. Paired Samples T-Test: là thủ tục kiểm định trung bình mẫu ghép cặp. Thống kê kiểm định K= , có pp Student, bậc tự do df=n-1
Điều kiện: D có pp chuẩn
4. One Way ANOVA: là thủ tục kiểm định 3 trung bình trở lên
Điều kiện: 1. Các BNN độc lập với nhau
2. Các BNN có phân phối chuẩn(Explore)
3. Các phương sai bằng nhau( Test of Homogeneity of Variances)
5. Chi-Square trong Crosstabs: là thủ tục kiểm định độc lập ( mối quan hệ) giữa 2 biến định tính. Thống kê kiểm định K= Ri C j 2 r s (Oij−Eij)2 r s (n − ∑ ∑ ∑ ∑ i=1 ❑ j=1 ❑ Eij = i=1
❑ j=1 ❑, có pp Chi-Square, bậc tự do df=(r-1)(s-1) n
Điều kiện: Chi-Square đáng tin cậy nhất khi không có ô nào có tần số kì vọng <5 hoặc nếu có thì số ô có tần số kì vọng <5 phải không quá hơn 20% lOMoAR cPSD|59062190
6. Chi-Square trong Nonparametric Test: là thủ tục kiểm định sự phù hợp giữa pp lí thuyết và pp thực nghiệm. Thống kê kiểm định K= ❑(
ni−npi)2, có pp Chi-Square, bậc tự do df=k-1 i=1 Ei i=1 npi
Điều kiện: Chi-Square đáng tin cậy nhất khi không có ô nào có tần số kì vọng Ei<5 hoặc nếu có thì số ô có Ei<5 phải không quá 20% THỰC HÀNH
1) KIỂM ĐỊNH SỰ KHÁC BIỆT GIỮA GLUCOZO TRUNG BÌNH TRONG MÁU NGƯỜI VỚI 100MG%:
Gọi X là glucozo của người khỏe mạnh μ là
glucozo trung bình của người khỏe mạnh
1. Đặt giả thuyết: H0 : μ=100 (mg%) H1 : μ ≠100(mg%)
2. Lý giải việc chọn Test One Samples T-Test là phù hợp:
• One Sample T-Test là thủ tục kiểm định 1 trung bình trong TH phương sai chưa biết. Thống kê kiểm định K= S , có
phân phối Student với bậc tự do df= n-1
Điều kiện: X có pp chuẩn.
• Đối với bài toán này:
 Kiểm định tính chuẩn của X:
o Vào Analyze/ Descriptive Statistics/ Explore. o Đưa biến “Glucozo” vào
Dependent List. o Plots/ Normality Plots with test. o Nhấn Continue. Nhấn Ok.
 Đọc kết quả ở Test of Normality:
N=100(>50)  Đọc kết quả ở Kolmogorov-Smirnor: Sig. = 0,2 (>0,05)  X có pp chuẩn
 Do X có pp chuẩn nên ta chọn test One Sample T-Test để giải quyết bài toán là hoàn toàn hợp lí.
 Thao tác kiểm định trung bình trên SPSS: o Vào Analyze/ Compare Means/ One Samples
T-Test o Đưa biến”Glucozo” vào ô Test Variable o Nhập “100” vào ô Test Value o
Options/ Nhập 95% trong Confidence Interval Percentage o Nhấn Continue. Nhấn Ok.
3. Đọc kết quả bảng phân tích One Sample T-Test:
Ta có: Sig.=0.962(>0,05)  Chưa có cơ sở bác bỏ H0
 Không có sự khác biệt giữa Glucozo trung bình của người khỏe mạnh với 100 (mg%).
2) KIỂM ĐỊNH SỰ KHÁC BIỆT VỀ SỐ LƯỢNG TIỂU CẦU TRUNG BÌNH GIỮA NHÓM BỆNH NHÂN SỐT
DENGUE (SD) VÀ NHÓM BỆNH NHÂN SỐT XUẤT HUYẾT DENGUE ( SXH) : ( 2 trung bình của 2 mẫu độc lập)
Gọi X,Y là số lượng tiểu cầu của nhóm bệnh nhân SD và nhóm bệnh nhân SXH μ1, μ2 là số
lượng tiểu cầu trung bình của nhóm bệnh nhân SD và nhóm bệnh nhân SXH 1) Đặt giả thuyết: H0: μ1 = μ2 H1: μ1 ≠ μ2
2) Lý giải việc chọn Test Independent Samples T-Test là hợp lí:
 Independent Samples T-Test là thủ tục kiểm định 2 trung bình trong TH chưa biết phương sai. Thống kê kiểm định K= , có pp Student T:
 K có pp Student T có bậc tự do df = n1+n2 - 2 khi σ21=σ22 ( có pp T n1−n2−2, khi …) S21 (n1−1)(n2−1) n1
 K có pp Student T có bậc tự do df= (n ,
2−1)c2+(1−c)2(n1−1), với c= S21 S22 khi ( có pp Tm khi …) + n1 n2 lOMoAR cPSD|59062190
Điều kiện: X,Y có phân phối chuẩn  Đối với bài toán này:
 Kiểm định tính chuẩn của biến X,Y :
o Vào Analyze/ Descriptive Statistics/
Explore. o Đưa biến “tieucau” vào ô Dependent List o Đưa biến
“Nhombenhnhan” vào ô Factor List
o Plots/ Normality plots with test o Nhấn Continue. Nhấn Ok.
 Đọc kết quả ở bảng Test of Normality:
o Biến SD có: N=10(<50)  đọc kết quả ở Shapiro-Wilk: Sig.=0,238(>0,05)  Biến X có phân phối chuẩn o
Biến SXH có: N=10(<50)  đọc kết quả ở Shapiro-Wilk: Sig.=0,377(>50)  Biến Y có pp chuẩn.
 Do 2 biến X,Y đều có pp chuẩn nên việc chọn Test Independent Samples T-Test để giải quyết bài toán là hoàn toàn hợp lí.
 Thao tác kiểm định trên SPSS:
o Transform/ Record into Different Variables
o Đưa biến “ Nhom” vào ô Input VariableOutput Variable. Đổi tên thành
“nhombenhnhan” o Old and New Values/ Value(Old value): SD, Value( New
value): 1  Add, tượng tự với SXH o Nhấn Continue. Nhấn Ok.
o Vào Analyze/ Compare Means/ Independent Samples T-Test o Đưa biến
“tieucau” vào ô Test Variable(biến định lượng) o Đưa biến “nhombenhnhan” vào
ô Grouping Variable ( biến định tính) o Define Groups/ Group 1 nhập “1”,
Group 2 nhập “2”. Nhấn Continue.
o Options. Nhập 95% trong Confidence Interval Percentage o Nhấn Continue. Nhấn Ok.
3) Đọc bảng phân tích Independent Samples T-Test:
 Kiểm định Levene: Sig.=1,000(>0,05) Không có sự khác biệt giữa 2 phương sai Bài toán
so sánh 2 trung bình của tổng thể trong TH 2 phương sai bằng nhau Đọc kết quả ở Equal Variances assumed.
 Kiểm định t : Sig.=0,006(<0,05)  Bác bỏ H0, chấp nhận H1.  Có sự khác biệt giữa tiểu cầu
trung bình của 2 nhóm bệnh nhân
3) KIỂM ĐỊNH TRUNG BÌNH 2 MẪU GHÉP CẶP : GIỮA SỐ GIỜ NGỦ TRUNG BÌNH CỦA BỆNH NHÂN KHI
DÙNG THUỐC NGỦ VÀ KHI DÙNG GIẢ DƯỢC .( 2 trung bình của 2 mẫu phụ thuộc hoặc mẫu ghép cặp)
Gọi X là số giờ ngủ của bệnh nhân dùng thuốc ngủ
Y là số giờ ngủ của bệnh nhân dùng giả dược.
D=X-Y là sai biệt giữa số giờ ngủ khi dùng thuốc ngủ và khi dùng giả dược.
ED=d là sai biệt giữa số giờ ngủ trung bình khi dùng thuốc ngủ và khi dùng giả dược.
1. Đặt giả thuyết: H0: d=0 H1: d ≠ 0.
2. Lý giải việc chọn Paired Samples T-Test là hợp lí:
• Paired Samples T-Test là thủ tục kiểm định trung bình mẫu ghép cặp. Chọn thống kê kiểm định K= S(D) , có pp Student với bậc tự do df = n-1
Điều kiện: D có pp chuẩn.
• Đối với bài toán này:
 Kiểm định tính chuẩn của D (X,Y):
o Analyze/ Descriptive Statistics/ Explore o Đưa biến “sogiongucothuoc” và “
sogionguvoigiaduoc” vào ô Dependent List o Plots/ Normality plots with test o Nhấn Continue. Nhấn Ok.
 Đọc kết quả ở Test of Normality:
o Biến “sogiongucothuoc” có N=10(<50) Đọc kết quả ở Shapiro-Wilk: Sig.=0,893(>0,05)  X có pp chuẩn o
Biến “sogionguvoigiaduoc” có N=10(<50) Đọc kết quả ở Shapiro-Wilk: Sig.=0,476(>0,05) Y có pp chuẩn
 X,Y có pp chuẩn D có phân phối chuẩn
 Dùng Test Paired Samples T-Test để giải quyết bài toán là hoàn toàn hợp lí.
 Thao tác kiểm định trên SPSS:
o Analyze/ Compare Means/ Paired Sample T-Test o Đưa 2 biến
“sogiongucothuoc” và “sogionguvoigiaduoc” vào ô Paired Variable o Nhấn Ok. lOMoAR cPSD|59062190
3. Đọc kết quả bảng phân tích test Paired Samples T-Test:
Ta có: Sig.=0,011(<0,05) Bác bỏ H0, chấp nhận H1
 Có sự khác biệt giữa số giờ ngủ trung bình của bệnh nhân khi dùng thuốc ngủ và khi dùng giả dược.
4) KIỂM ĐỊNH SỰ KHÁC BIỆT BIỆT VỀ TRỊ SỐ TRUNG BÌNH TIỂU CẦU TRUNG BÌNH GIỮA 3 NHÓM BỆNH
NHÂN ( DÙNG CHO 3 NHÓM TRỞ LÊN).
Gọi X1, X2, X3 là số lượng tiểu cầu của bệnh SXH, SD và nhiễm 1 số siêu vi khác(NSV).
μ1 , μ2, μ3 là số lượng tiểu cầu trung bình của bệnh SXH, SD, NSV.
1. Đặt giả thuyết: H0: μ1 = μ2 = μ3
H1: μ1, μ2, μ3 có sự khác nhau
2. Lý giải việc chọn test One Way ANOVA là hợp lí: 
Thủ tục One Way ANOVA trong SPSS dùng để kiểm định 3 trung bình trở lên trong điều kiện:  Các BNN độc lập 
Các BNN tuân theo pp chuẩn(Explore) 
Các phương sai bằng nhau(Test of Homogeneity of variances)  Trong bài toán này: 
X1, X2, X3 độc lập với nhau. 
Kiểm định tính chuẩn của 3 biến:
o Vào Analyze/ Descriptive Statistics/ Explore o Đưa biến
“tieucau” vào ô Dependent List ( biến định lượng) o Đưa biến
“nhombenh” vào ô Factor List( biến phân loại nhóm) o Plots/
Normality plots with test o Nhấn Continue. Nhấn Ok.
 Đọc kết quả bảng Test of Normality:
Vì N=10(<50)  đọc kết quả ở Shapiro-Wilk: 
Biến ‘Nhom1’ có Sig.=0,238(>0,05)  X1 có pp chuẩn 
Biến “Nhom2” có Sig.=0,377(>0,05)  X2 có pp chuẩn 
Biến “Nhom3” có Sig.=0,7489.0,050  X3 có pp chuẩn  Kiểm định 3 phương sai trên SPSS:
o Analyze/ Compare Means/ One Way ANOVA
o Đưa biến “tieucau” vào ô Dependent List( biến định lượng) o Đưa biến “ Nhombenh” vào ô Factor List(biến
phân loại nhóm) o Options/ Homogeneity of variance test, Descriptive. o Nhấn Continue. Nhấn Ok.
Từ bảng phân tích Test of Homogeneity of Variances có: Sig.= 0,920(>0,05)  Có sự bằng nhau giữa các phương sai.
 Dùng test One Way ANOVA để giải quyết bài toán là hoàn toàn hợp lí.
3. Đọc kết quả bảng phân tích ANOVA:
Ta có: Sig.=0,001(<0,05) Bác bỏ H0, chấp nhận H1
 Có sự khác biệt giữa số lượng tiểu cầu trung bình giữa 3 nhóm bệnh nhân.
5) KIỂM ĐỊNH MỐI QUAN HỆ GIỮA 2 BIẾN ĐỊNH TÍNH: GIỮA BÚ SỮA MẸ VÀ NHIỄM HP.
Gọi X là biến bú sữa mẹ Y là biến nhiễm HP.
1. Đặt giả thuyết: H0: X,Y độc lập H1: X,Y phụ thuộc nhau.
2. Lý giải việc chọn Test Chi-Square trong Crosstabs là phù hợp:
• Test Chi-Square trong Crosstabs là thủ tục kiểm định độc lập( mối quan hệ) giữa 2 biến định tính trong trường hợp thống kê r s (Oij−Eij)2
2 kiểm định K=∑i=1 ❑∑j=1❑ Eij
, có pp Chi-Square ꭓ với df=(r-1)(s-1)
Điều kiện: Test Chi-Square đáng tin cậy nhất khi không có ô nào có tần số kì vọng Eij<5 hoặc nếu có thì số ô có tần số kì vọng < 5 không quá 20%.
• Đối với bài toán này cần kiểm định mối quan hệ giữa 2 biến định tính bằng SPSS:
 Vào Analyze/ Descriptive Statistics/ Crosstabs
 Đưa biến “NhiemHP” vào ô Row; Biến “suame” vào ô Column
Biến định lượng(hình cái thang)-ô Row; Biến định tính(3 cánh tròn)-ô Column. 
Statistics/ Chi-Square, Cells/Observed(giá trị quan sát), Cells/ Expected(giá trị kì vọng)  Nhấn Continue. Nhấn Ok.
 Đọc kết quả bảng NhiemHP*suame Crosstabution:
Ta có: N=30, không có ô nào có giá trị kì vọng Eij <5, trong đó giá trị kì vọng nhỏ nhất là 6.
 Dùng test Chi-Square trong Crosstabs để giải quyết bài toán là phù hợp, đáng tin cậy. lOMoAR cPSD|59062190
3. Đọc kết quả bảng phân tích Test Chi- Square:
Ta có: (Pearson Chi-square) Asymp. Sig.=0,03(<0,05)  Bác bỏ H0, chấp nhận H1  X, Y phụ thuộc nhau
 Việc bú sữa mẹ với nhiễm HP có liên quan đến nhau.
6) KIỂM ĐỊNH SỰ PHÙ HỢP GIỮA PHÂN PHỐI LÍ THUYẾT VÀ PHÂN PHỐI THỰC NGHIỆM: (KIỂM ĐỊNH
TỶ LỆ BỆNH NHÂN CÓ VẾT LOÉT DƯỚI DA TRONG SỐ BỆNH NHÂN NỮ BẰNG VỚI 65%)
Gọi p là tỷ lệ bệnh nhân có vết loét dưới da trong số các bệnh nhân nữ
1. Đặt giả thuyết: H0: p=0,65( tỷ lệ không có vết loét: có vết loét=0,35:0,65) H1: p≠0,65 ( tỷ lệ không
có vết loét: có vết loét ≠ 0,35:0,65)
2. Lý giải việc chọn Test Chi-Square trong Nonparametric Test là hợp lí:
 Test Chi-Square trong Nonparametric Test là thủ tục kiểm định sự phù hợp giữa pp lí thuyết và pp thực nghiệm trong TH ∑ thống kê kiểm định K= E i=k1 ❑
(Oi−Ei i)2, có pp Chi-Square ꭓ2 với bậc tự do df=k-1
Điều kiện: Test Chi-Square đáng tin cậy nhất trong TH không có ô nào có Ei<5 hoặc nếu có thì số ô có Ei<5 không quá 20%. 
Đối với bài toàn này: Bài toán kiểm định 1 tỷ lệ nhưng có thể đưa về bài toán kiểm định sự phù hợp.  Thao tác trên SPSS:
o Vào Data/ Select cases/ If condition is satisfied o If/
Đưa biến “gioi” vào ô nhập “gioi=2”.
o Vào Analyze/ Nonparametric Test/ Legacy Dialogs/ Chi-
Square o Đưa biến “covetloetda” vào ô Test Variable List
o Expected Values/ Values o Nhập 0,35Add. Nhập 0,65Add. o Nhấn Ok.
 Đọc kết quả ở Test Statistics:
Tất cả các ô có Ei>5, trong đó Ei nhỏ nhất = 19,3
 Dùng test Chi-Square trong Nonparametric Test để giải quyết bài toán này là hoàn toàn phù hợp.
3. Đọc kết quả bảng phân tích Chi-Square Test: Ta có:
Sig.=0,944(>0,05)  Chưa có cơ sở bác bỏ H0 p1:p2=0,35:0,65
 Hay tỷ lệ bệnh nhân có vết loét dưới da trong số bệnh nhân nữ là 65%.
 Kiểm định 1 tỷ lệ dùng Binomial trong Nonparametric Test, K= , có pp xấp xỉ chuẩn
Điều kiện: BNN, biến nhị phân (nếu có nhiều hơn 2 lựa chọn thì dùng lệnh Record để chuyển về 2 lựa chọn). 
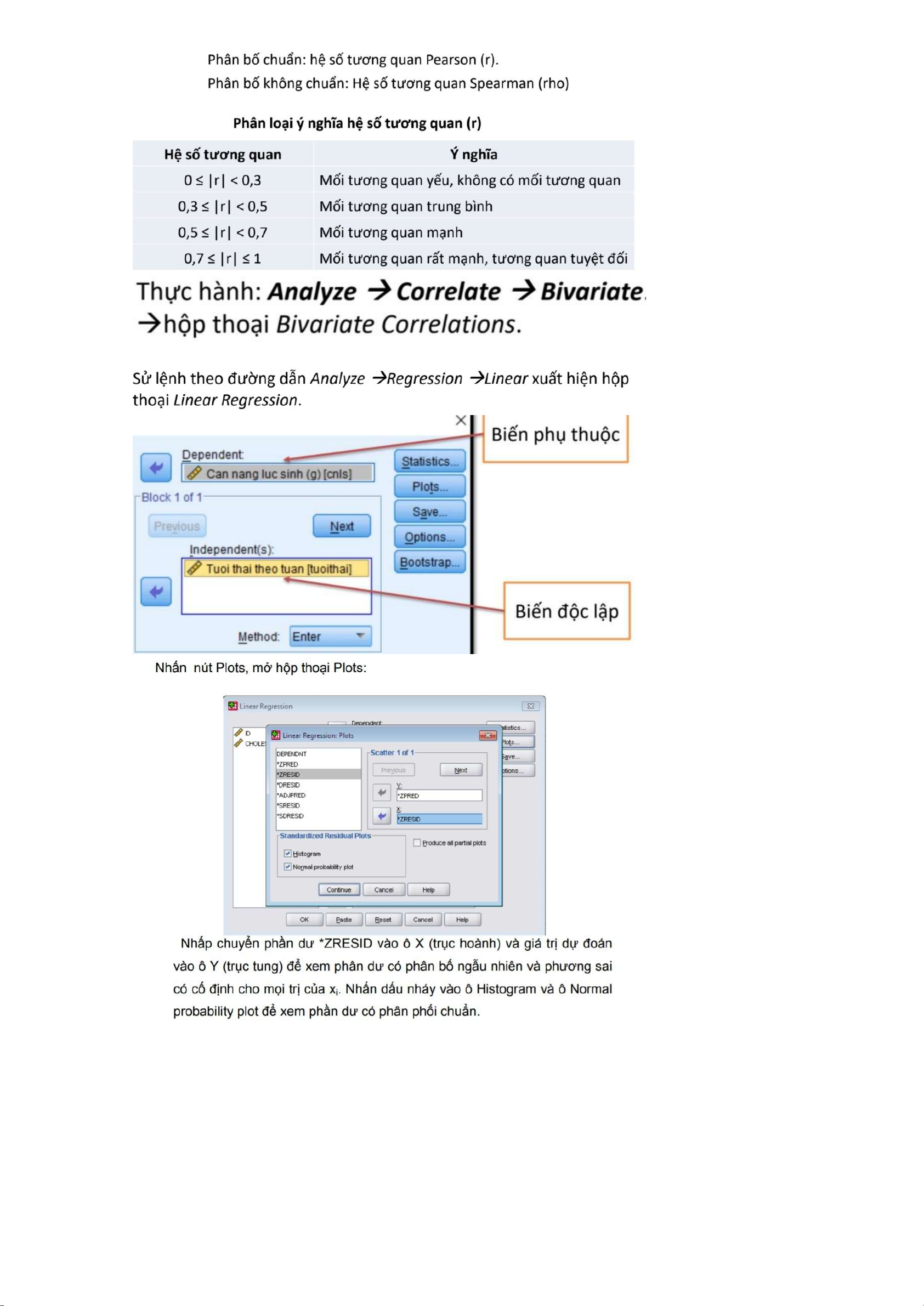
KIỂM ĐỊNH TƯƠNG QUAN HỒI QUY: lOMoAR cPSD|59062190 lOMoAR cPSD|59062190 HỒI QUY: lOMoAR cPSD|59062190