5/11/23, 3:57 PM
Cách tính và tìm ma trận nghịch đảo 2x2, 3x3, 4x4 chính xác - We Escape 5/11/23, 3:57 PM
Cách tính và tìm ma trận nghịch đảo 2x2, 3x3, 4x4 chính xác - We Escape
Ma trậ n n ghịch đả o l à gì ?
Ma tr ậ n n ghịch đả o l à gì ? : Ch o m a tr ậ n A vuôn g cấ p n . Ta nó i m a tr ậ n
A l à m a tr ậ n khả n ghịch n ế u tồn t ại m a tr ậ n B s a o ch o AB =
BA = En . Khi đ ó, B g ọ i l à m a tr ậ n n ghịch đả o c ủ a m a tr ậ n A, kí hiệ u l à A- 1.
Ma tr ậ n kh ôn g c ó dấ u p hâ n số n ê n bạ n cầ n sử d ụn g m a tr ậ n n ghịch đả o để đ ơn giả n h ó a p hé p to á n p h ức t ạ p n ày. Có hai cách
tí n h m a trậ n n ghịch đả o l à t í n h t ay và d ùn g m áy t í n h gi úp ch o kế t qu ả chí n h x ác h ơn .
M a t r ậ n n g h ị c h đ ả o l à g ì
Tí n h chấ t m a trậ n n ghịch đả o
Điề u kiệ n cầ n và đ ủ để m a tr ậ n A vuôn g cấ p n khả
n ghịch l à đị n h t h ức c ủ a A l à p hầ n tử khả n ghịch tron g và n h V.
Nế u A l à m a tr ậ n trê n một trườn g F t hì A l à khả
n ghịch khi và chỉ khi đị n h t h ức c ủ a nó khác 0.
Ma tr ậ n đ ơn v ị l à m a tr ậ n khả n ghịch .
Nế u A, B l à các m a tr ậ n khả n ghịch t hì AB khả n ghịch và ( AB) - 1 = B- 1 A- 1
Tậ p h ợp các m a tr ậ n vuôn g cấ p n trê n K khả n ghịch , đ ượ c k ý hiệ u l à GLn ( K) .
Cách t í n h m a trậ n n ghịch đả o
Dướ i đây l à h ướn g dẫ n cách t í n h ma trậ n n ghịch đả o mớ i n hấ t hãy t ha m khả o n hé
Ma trận nghịch đảo 2×2
Cách t í n h ma trậ n n ghịch đả o 2×2 t he o p h ươn g p há p sử d ụn g m a tr ậ n p h ụ h ợp ( p hé p kh ử
Ga uss -Jorda n ) t h ực hiệ n n h ư s a u : Ví d ụ :
Ma trận nghịch đảo 3×3
Ph ươn g phá p t ì m ma trậ n n ghịch đả o bằ n g cách t ạ o ma trậ n b ổ sun g :
Bước 1: Kiể m tr a đị n h t h ức c ủ a m a tr ậ n , k ý hiệ u l à de t ( A) .
Nế u de t ( A)=0 t hì A kh ôn g c ó m a tr ậ n n ghịch đả o A- 1 Nế u de t ( A)≠0 t hì
A c ó m a tr ậ n A- 1, ch uyể n s a n g b ướ c 2
Bước 2: Ch uyể n v ị m a tr ậ n g ố c tức l à đ ổ i v ị tr í c ủ a p hầ n tử t h ứ ( i , j ) và ch ỗ c ủ a p hầ n tử ( j , i ) vớ i n ha u .
Bước 3: T ì m đị n h t h ức c ủ a từ n g m a tr ậ n c on 2×2 l iê n kế t vớ i m a tr ậ n ch uyể n v ị 3×3 mớ i .
Bước 4: Tạ o m a tr ậ n các p hầ n p h ụ đại số, k ý hiệ u l à Adj ( M) .
Bước 5: Th ực hiệ n p hé p chia c ủ a to à n b ộ các p hầ n tử c ủ a m a tr ậ n b ổ sun g vớ i đị n h t h ức c ủ a m a tr ậ n l à de t ( M) .
Phương pháp tìm ma trận nghịch đảo bằng cách giảm hàng tuyến tính
Bướ c 1: Th ực hiệ n t hê m m a tr ậ n đ ơn v ị và o tron g m a tr ậ n g ố c
Bướ c 2: Tiế n hà n h p hé p giả m hà n g tuyế n t í n h và t h ực hiệ n đế n khi m a tr ậ n đ ơn v ị đ ượ c hì n h t hà n h
Bướ c 3: Viế t l ại m a tr ậ n n ghịch đả o ch o ch u ẩ n x ác
Ma trận nghịch đảo 4×4
a) Đối với ma trận 4×4 thì cách tính được áp dụng phổ biến hơn cả là phương pháp dùng các phép biến đổi sơ cấp
Cụ t hể n h ư s a u :
Nế u de t ( A)≠0 t a t í n h A- 1 bằ n g các rút g ọn m a tr ậ n - > < In : A- 1> vớ i
I l à m a tr ậ n đ ơn v ị .
b) Dùng định lý Haminton-Cayley +
Đa t h ức đặc trư n g c ủ a m a tr ậ n Anxn = l à : f ( x ) = de t ( x I – A)
Tổng qu á t : Tí n h đa t h ức đặc trư n g c ủ a m a tr ậ n A l à f ( x ) bằ n g c ôn g t h ức Bo che r n h ư s a u :
Đặ t Sp = tr ( Ap ) vớ i tr ( Ap ) = tổn g p hầ n tử trê n đ ườn g ché o chí n h c ủ a Ap
Trườn g h ợp r iê n g
c) Định lý Cayley-Hamilton
Nế u f ( x ) l à đa t h ức đặc trư n g c ủ a m a tr ậ n vuôn g A t hì f ( A)=0
Giả sử ch o A khả đả o (de t ( A)≠0) c ó đa t h ức đặc trư n g f ( x )= xn + a1 xn - 1 + a 2 xn - 2 + … + a n - 1 x + a n t hì
An + a1 An - 1 + a 2 An - 2 + … + a n - 1 A + a n =
O và a n =( - 1) n de t ( A) ≠0, t a n hâ n 2 vế ch o A- 1 đ ượ c :
Cách t ì m m a trậ n n ghịch đả o bằ n g m á y t í n h Fx 570ES Plus
Cách t ì m m a trậ n n ghịch đả o bằ n g cách d ùn g máy t í n h b ỏ tú i đ ượ c t h ực hiệ n t he o quy tr ì n h n hấ t đị n h .
Các b ướ c t h ực hiệ n ch un g c ụ t hể :
Ch ọn m áy t í n h c ó h ỗ trợ ch ức n ă n g giải m a tr ậ n
Tiế n hà n h n hậ p m a tr ậ n và o tron g m áy
Ch ọn t h ực đ ơn c on và tê n ch o m a tr ậ n
Nhậ p kích t h ướ c và từ n g p hầ n tử c ủ a m a tr ậ n
Th o á t ch ức n ă n g m a tr ậ n
T ì m m a tr ậ n n ghịch đả o bằ n g cách d ùn g p hí m n ghịch đả o c ủ a m áy
Viế t l ại m a tr ậ n n ghịch đả o ch u ẩ n x ác
Bài t ậ p m a trậ n n ghịch đả o
Bài 1: Cho ma trận A sau và tìm ma trận nghịch đảo của A Giải
de t A=(1.3.2+1.2.3+ .1.2.3) - (3.3.3+1.1.1+2.2.2)=18 - 34 = - 18 ≠0
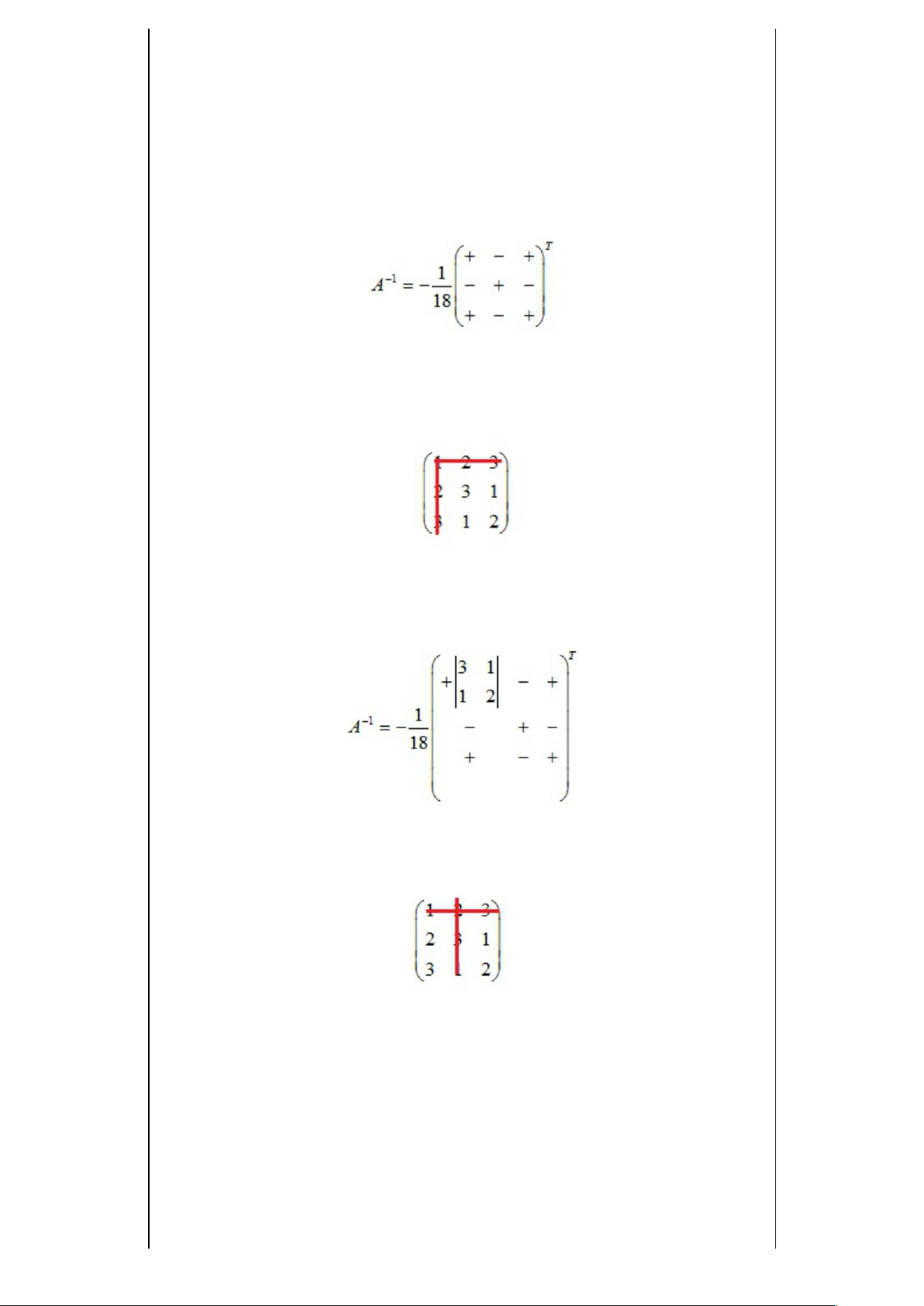
Viế t c ôn g t h ức và t h ực hiệ n đa n dấ u n h ư hì n h d ướ i :
Đố i vớ i p hầ n tử a1 1 t a lo ại b ỏ hà n g 1 và c ột 1 c ủ a m a tr ậ n A
Sa u khi lo ại b ỏ t a đ ượ c n h ư hì n h d ướ i
Đố i vớ i a 1 2 t hì lo ại b ỏ hà n g 1 c ột 2
Tươn g tự đ ố i vớ i các p hầ n tử c òn l ại t a đ ượ c :
Tí n h đị n h t h ức t a đ ượ c :
Ch uyể n v ị và t a đ ượ c kế t qu ả c uố i c ùn g : Bài 2: T ìm X Giải - 1 Ta c ó : A. X= B ⇒ X=A . B de t
A = (1. - 1.0+0.5.3+ - 2.2.1) - (2. - 1.3+1.1.5+0.0. - 2)= - 3≠0
Ch ún g tô i c ó t ha m khả o n g uồn t ại :
h ttps :// v i .w iki p edia .org / w iki / Ma _ tr %E1 %BA%ADn _ kh %E1 %B
A%A3_ n gh %E1 %BB%8 Bch
h ttps :// v i .w iki p edia .org / w iki / Ma _ tr %E1 %BA%ADn _ ( to %C3 %A 1 n _ h %E1 %BB%8 Dc )