Cách xác định tâm đường tròn ngoại tiếp tam giác đơn giản, dễ hiểu
1. Tâm đường tròn ngoại tiếp tam giác là gì?
Đường tròn ngoại tiếp tam giác là gì? a, Định nghĩa
Đường tròn ngoại tiếp tam giác được hiểu là đường tròn tiếp xúc phía ngoài của tam giác. Đường tròn
ngoại tiếp của tam giác là đường tròn đi qua 3 đỉnh của một tam giác. Tâm của đường tròn ngoại tiếp tam
giác được xác định là giao điểm của 3 đường trung trực của tam giác đó.
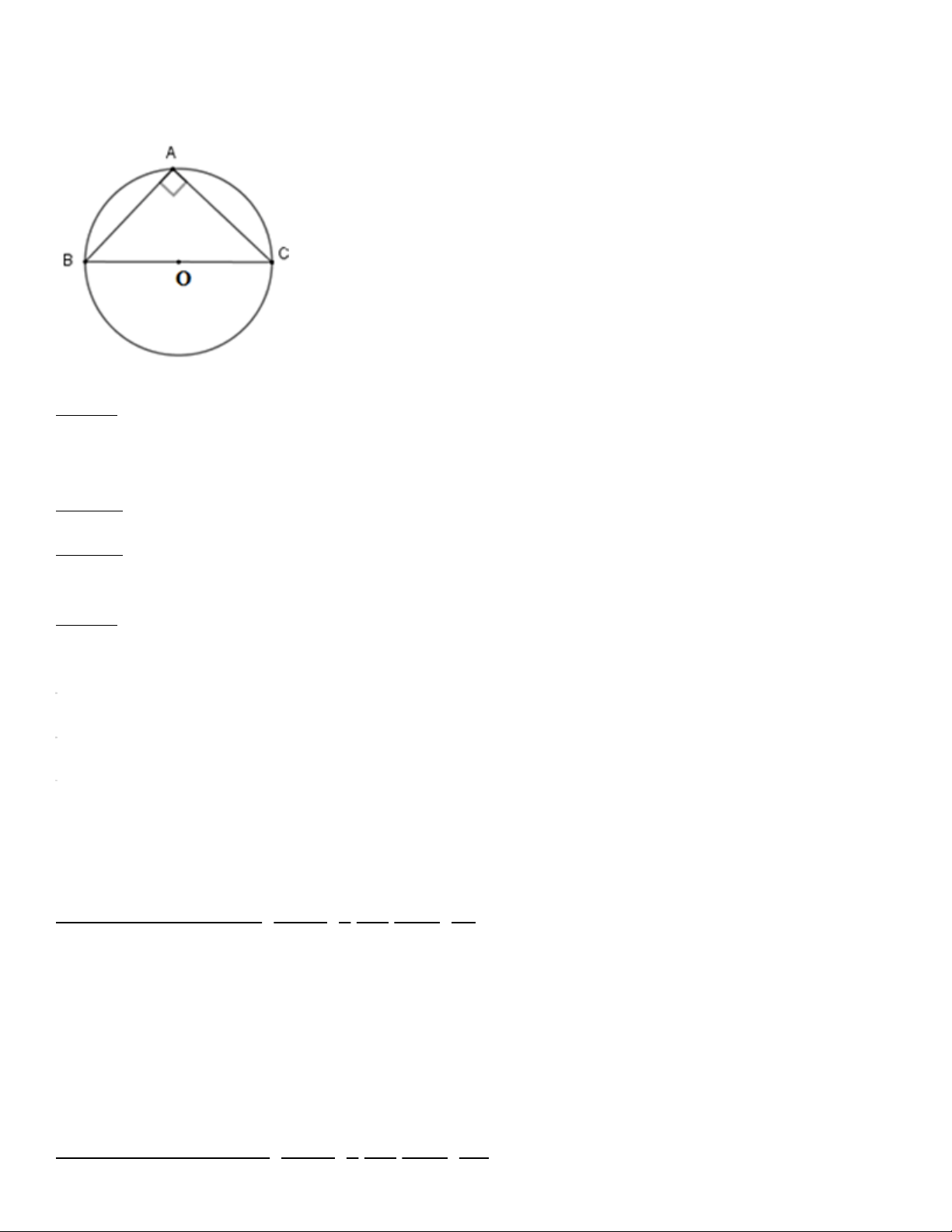
Hình ảnh minh hoạ đường tròn (O;OB) ngoài tiếp tam giác ABC
Đường tròn ngoại tiếp tam giác còn có thể được gọi với một tên khác là tam giác nội tiếp đường tròn hay
tam giác nằm trong đường tròn.
b, Tính chất của đường tròn ngoại tiếp tam giác
Thứ nhất, một tam giác chỉ có một và duy nhất một đường tròn ngoại tiếp
Hai là, giao điểm của ba đường trung trực của một tam giác bất kì chính là tâm của đường tròn ngoại tiếp tam giác đó
Ba là, đổi với tam giác vuông thì trung điểm của cạnh huyền tam giác đó chính là tâm của đường tròn ngoại tiếp của tam giác.
Bốn là, với một tam giác đều thì tâm đường tròn ngoại tiếp và nội tiếp của tam giác đó là cùng 1 điểm.
*Tâm đường tròn ngoại tiếp tam giác là gì?
Giao điểm của ba đường trung trực trong tam giác sẽ tạo thành tâm đường tròn ngoại tiếp tam giác
đó (hoặc có thể là hai đường trung trực).
2. Cách xác định tâm đường tròn ngoại tiếp tam giác.
*Cách để xác định tâm đường tròn ngoại tiếp tam giác
Để có thể xác định được tâm đường tròn ngoại tiếp tam giác, cần chú ý các vấn đề sau:
Thứ nhất, tam giác có 3 đỉnhcách đều 1 điểm thì điểm đó chính là tâm của đường tròn ngoại tiếp tam giác.
Thứ hai, quỹ tích của các điểm nhìn sang đoạn thẳng AB với một số góc vuông sẽ là đường tròn có đường kính AB.
Ta có 2 cách để có thể xác định được tâm của đường tròn ngoại tiếp tam giác là a, Cách 1:
Bước 1: Gọi K(x;y) là tâm của đường tròn ngoại tiếp tam giác EFJ. Ta có các đoạn thẳng KE = KF = KJ và bằng bán kính R.
Bước 2: Toạ độ tâm K là nghiệm của hệ phương trình KE 2 = KF2 KE2 = KJ2 b, Cách 2:
Bước 1: Tìm và viết được các phương trình đường trung trực của hai cạnh trong tam giác bất kỳ.
Bước 2: Sau đó, tìm giao điểm của hai đường trung trực đã tìm ra ở bước 1 và giao điểm của hai đường
trung trực chính là tâm đường tròn ngoại tiếp tam giác đó.
Lưu ý: Với tam giác vuông thì tâm của đường tròn ngoại tiếp tam giác này chính là trung điểm của cạnh
huyền. Cạnh huyền cũng chính là đường kính của đương tròn ngoại tiếp tam giác đó.
Để có thể xác định được tâm đường tròn ngoại tiếp tam giác theo cách 2, ta cần tìm được phương trình của
đường tròn ngoại tiếp tam giác khi biết toạ đô 3 đỉnh. Để có thể giải được bài toán về phương trình đường
tròn của ngoại tiếp tam giác ta thực hiện theo các bước như sau:
Hình ảnh minh hoạ đường tròn ngoại tiếp tam giác vuông, với OB là cạnh huyền tam giác ABC, cùng
đồng thời là tâm đường tròn O
Bước 1: Đầu tiên ta thay đổi toạ độ mỗi đỉnh của tam giác vào phương trình với ẩn a,b,c (Bởi vì các đỉnh
của tam giác thuộc đuòng tròn ngoại tiếp, vì vậy, toạ độ các đỉnh trong tam giác thoả mãn phương trình
ngoại tiếp đường tròn mà ta cần tìm
Bước 2: Giải hệ phương trình để tìm ra các hằng số a, b, c tương ứng với các đỉnh trong tam giác
Bước 3: Tiếp theo, ta thay giá trị vừa tìm được như a, b, c vào phương trình tổng quát để tìm ra phương
trình đường tròn ngoại tiếp của tam giác.
Bước 4: Do đỉnh của tam giác thuộc đường tròn ngoại tiếp nên ta có hệ phương trình sau, sau khi giải hệ
phương trình trên ta sẽ xác định được a, b, c.
Môt số dạng toán nâng cao sẽ yêu cầu các bạn học sinh phải viết được phương trình của đường tròn ngoại
tiếp tam giác. Mới nghe qua thì có thể các bạn học sinh sẽ thấy đây là dạng bài khó, tuy nhiên khi nắm vững
công thức thì việc giải bài toán này sẽ khá dễ dàng.
*Cách để có thể vẽ đường tròn ngoại tiếp tam giác
Để có thể xác định thật chính xác tâm của đường tròn ngoại tiếp tạm giác thì chúng ta cần nắm vững kiến
thức "Tâm của của đường tròn ngoại tiếp với một tam giác bất kỳ một tam giác nào luôn là giao điểm
của ba đường trung trực tam giác đó".
Vậy, khi muốn vẽ đường tròn ngoại tiếp tam giác ABC thì đầu tiên chúng ta cần vẽ tam giác. Tiếp đó kẻ các
đường trung trực xuất phát từ 3 đỉnh của tam giác đó để có thể xác định tâm I của đường tròn. Cuối cùng
chỉ cần lấy bán kính R = IA = IB = IC. Như vậy, chúng ta đã có thể vẽ được đường tròn ngoài tiếp tam giác.
*Cách tính bán kính đường tròn ngoại tiếp tam giác:
Đây là một trong những dạng bài thường gặp trong đường tròn ngoại tiếp tam giác, do đó chúng ta cần nắm
rõ và chi tiết công thức sau đây: Trong đó:
ra: Bán kính đường tròn ngoại tiếp tính theo góc A S: là diện tích p: chu vi
a, b, c: là các cạnh đối với các góc của tam giác
3. Bài tập về đường tròn ngoại tiếp tam giác
Bài tập về đường tròn ngoại tiếp tam giác có thể phân thành các dạng như sau:
Dạng 1: Xác định tâm và bán kính đường tròn ngoại tiếp
Dạng 2: Tính các đại lượng liên quan đến tam giác ngoại tiếp
Dạng 3: Chứng minh tam giác ngoại tiếp đường tròn
Một số bài tập luyện tập:
Câu 1. Cho tam giác ABC vuông tại B và AB = 6cm, BC = 8cm. Q là trung điểm cuẩC. Hãy xác định bán
kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?
Giải: Áp dụng định lý Pytago, ta có CQ = 1/2 AC
Nên AQ = QB = QC = 5cm. Gọi D là trung điểm AC
Vì tam giác ABC vuông tại B có BQ là đường trung tuyến ứng với cạnh huyền AC nên Q là tâm đường tròn ngoại tiếp tam giác ABC.
Suy ra: Đường tròn ngại tiếp tam giác ABC là trung điểm Q của cạnh huyển AC và bán kính đường tròn
ngoại tiếp ABC là R = AQ = 5cm.
Câu 2: Cho tam giác ABC với các cạnh bằng 12cm, Hãy xác định tâ và bán kính đường tròn ngoại tiếp tam giác đều ABC? MNP?
Giải :Gọi Q, I lần lượt là trung tiẻm của các cạnh BC, AB và AQ giao với CI tại O.
Vì tam giác ABC đều nên đường trung tuyến đồng thời là đường cao, đường phân giác và đường trung trực
của tam giác, theo tính chất tam giác đều.
Vậy O chính là tâm của đường tròn ngoại tiếp tam giác. Tam giác ABC có CI là đường trung tuyến nên CI
cũng là đường cao trong tam giác. Từ đó, ta áp dụng định lý Py-ta-go:
CI2=AC2 - AI2 = 122 -62 = 108 (cm) =>
Vì O là trọng tâm của tam giác ABC nên
Câu 3: Cho tam giác NMP có ba góc nhọn nội tiếp trong đường tròn (O;R). Ba đường của tam giác là NF,
ME và PD cắt nhau tại K. Chứng minh tứ giác MDEP là tức giác nội tiếp. Xác định tâm G của đường tròn ngoại tiếp đó.
Câu 4: Cho tam giác EFJ vuông tại E có EFtrung điểm của FD. Gọi A là chân đường vuông góc hạ từ J xuống đường thẳng ED. Chứng minh tứ giác
EHAJ nội tiếp và xác định vị trí tâm O của đường tròn ngoại tiếp từ tứ giác đó.
Câu 5: Cho tam giác ABC đều với cạnh bằng 10 cm, xác đinh bán kính và tâm của đường tròn ngoại tiếp tam giác ABC.
Câu 6: Cho tam giác ABC đều với cạnh bằng 10cm. Xác định bán kính và tâm của đường tròn ngoại tiếp của tam giác ABC?
Câu 7: Cho tam giác ABC vuông tại A, có AB < AC, đường cao AH (H thược BC). Lấy điểm D sao cho H là
trung điểm của BD, Gọi E là chân đường vuông góc hạ từ C xuống thẳng AD. Chứng minh tứ giác AHEC nội
tiếp và xác định vị trí tâm O của đường tròn ngoại tiếp tứ giác đó.
Cho bán kính đường tròn tâm I là 2 cm, góc BAC =50o. Tính độ dài cung EHC của đường đường tròn tâm I
và diện tích hình quạt tròn IECH.
Như vậy, trên đây là tổng hợp kiến tức về khái niệm, đặc điểm, cách xác định tâm đường tròn ngoại tiếp. Hy
vọng vọng bài viết của Luật Minh Khuê có thể giúp bạn nắm vững kiến thức và áp dụng vào bài tập.