









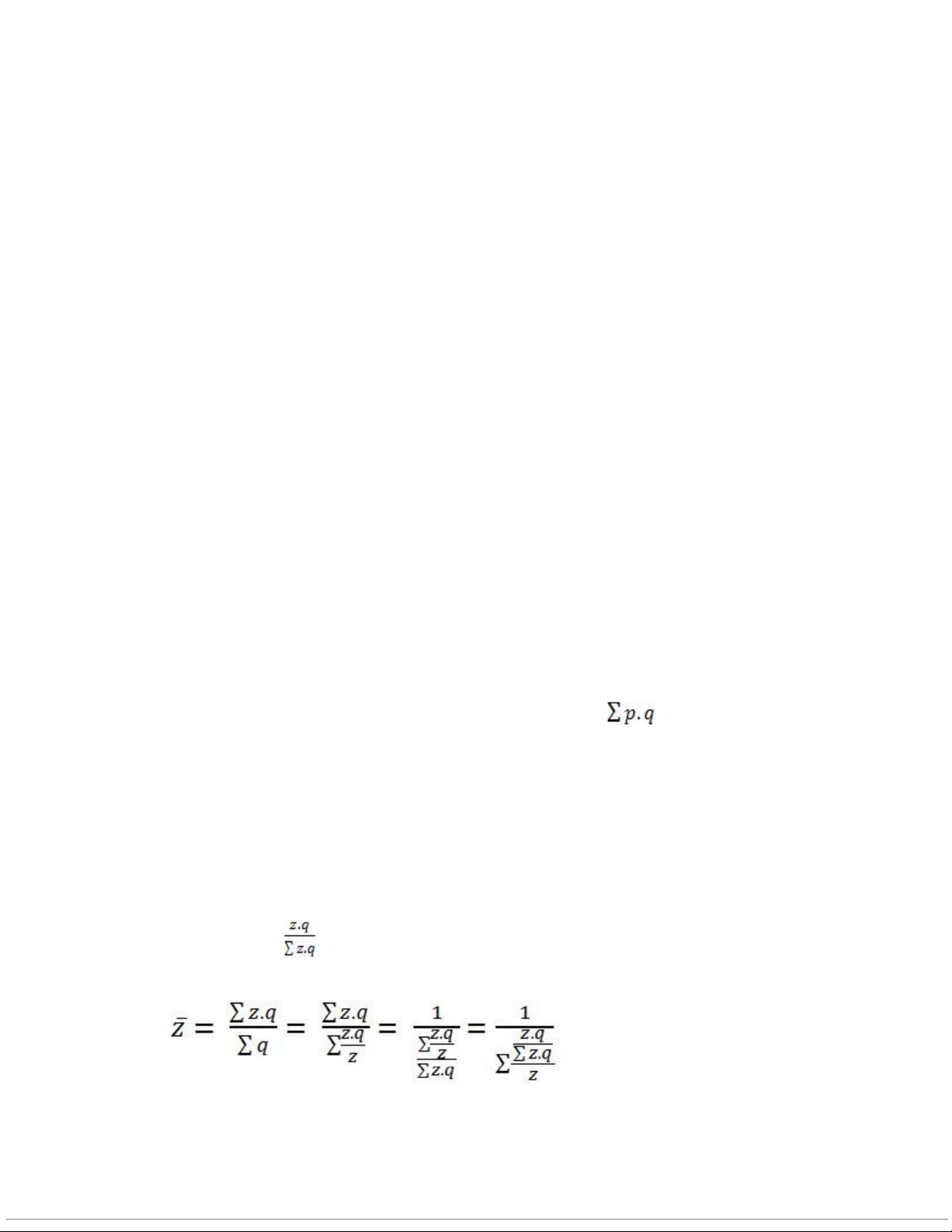







Preview text:
18. Có thể dùng số bình quân để so sánh hai cái cùng loại nhưng khác quy mô Đúng:
Số bình quân trong thống kê là mức độ biểu
hiện trị số đại biểu theo một tiêu
thức của tổng thể bao gồm nhiều đơn vị cùng loại.
Qua việc tính toán số bình quân, ta được một trị số nêu lên mức độ chung nhất,
đại biểu nhất của tiêu thức nghiên cứu nên có thể sử dụng để so sánh hai hiện tượng
cùng loại mà không cùng quy mô như so sánh năng suất lao động công nhân hai xí
nghiệp, tiền lương bình quân công nhân hai xí nghiệp, …
19. Nếu số trung bình nhỏ hơn số trung vị thì những đơn vị có lượng biến lớn hơn
số trung bình sẽ chiếm đa số.
Đúng: Số trung vị (Me) là lượng biến tiêu thức của đơn vị đứng ở chính giữa
trong dãy số lượng biến, nó phân chia
dãy số lượng biến thành hai phần, mỗi phần có số
đơn vị tổng thể bằng nhau. Khi
Me hiển nhiên những đơn vị có lượng biến lớn hơn
sẽ chiếm đa số trong tổng thể (vì những đơn vị lớn hơn Me đã chiếm một nửa tổng thể
rồi, giờ tính thêm những đơn vị nằm giữa và Me nữa thì chắc chắn phải lớn hơn một nửa tổng thể)
20. Số trung vị rất nhạy cảm với những lượng biến đột xuất trong dãy số
Sai: Số trung vị là lượng biến tiêu thức của đơn vị đứng ở chính giữa trong dãy
số lượng biến, do đó nó chỉ thay đổi khi tần số của các lượng biến thay đổi hoặc trị số
lượng biến của đơn vị đứng ở vị trí chính giữa thay đổi. Nó không phụ thuộc vào những
lượng biến đột xuất trong dãy số, vì vậy không thể nói số trung vị nhạy cảm với những lượng biến đột xuất.
21. Xác định tổ chứa mốt chỉ cần dựa vào tần số của các tổ
Sai: Trong trường hợp phân tổ có khoảng cách tổ đều nhau, thì tổ chứa Mốt được
xác định trực tiếp thông qua tần số của các tổ (tần số lớn nhất ứng với tổ chứa Mốt).
Nhưng, trong trường hợp phân tổ có khoảng cách tổ không đều nhau, tổ chứa Mốt được
xác định thông qua mật độ phân phối, tức là tổ chứa mốt là tổ có tỷ lệ tần số trên
khoảng cách tổ lớn nhất. Vì vậy, việc xác định tổ chứa Mốt phải căn cứ vào cả tần số
và khoảng cách của các tổ.
22. Hệ số biến thiên được sử dụng khi so sánh độ biến thiên giữa các chỉ tiêu khác
loại hoặc các chỉ tiêu cùng loại nhưng có số bình quân khác nhau
Đúng: Hệ số biến thiên là số tương đối rút ra từ sự so sánh giữa độ lệch tuyệt đối
bình quân (hoặc độ lệch tiêu chuẩn bình quân) với số bình quân cộng. V = x 100. Hệ
số biến thiên thể hiện bằng số tương đối nên có thể sử dụng để so sánh giữa các chỉ tiêu
khác loại như so sánh hệ số biến thiên năng suất lao động với hệ số biến thiên về tiền
lương, hoặc so sánh giữa hai chỉ tiêu cùng loại nhưng khác nhau về số bình quân.
23. Hệ số biến thiên có thể sử dụng để so sánh độ biến thiên của chỉ tiêu qua thời gian.
Đúng: Hệ số biến thiên là số tương đối rút ra từ sự so sánh giữa độ lệch tuyệt đối
bình quân (hoặc độ lệch tiêu chuẩn bình quân) với số bình quân cộng. V = x 100, nên
nó được coi như chỉ tiêu tốt nhất đo độ biến thiên của tiêu thức để so sánh. Vì vậy, có
thể sử dụng hệ số biến thiên để so sánh độ biến thiên của chỉ tiêu qua thời gian.
24. Trong công thức số bình quân cộng X (trung bình) = tổng xi/n thì tổng xi luôn
là tổng lượng biến thiêu thức
Sai: Trong công thức số bình quân cộng giản đơn, tổng xi là tổng của lượng biến tiêu thức.
Nhưng trong công thức số bình quân cộng gia quyền, do có quyền số của mỗi xi
nên tổng xi không còn chỉ đơn thuần là tổng lượng biến tiêu thức, nó là tổng lượng biến
tiêu thức có tính đến quyền số của mỗi lượng biến.
25. Việc xác định tổ chứa Mốt luôn căn cứ vào mật độ tổ chứa mốt.
Sai: Đối với dãy số phân phối có khoảng cách tổ đều nhau, việc xác định
tổ chứa Mốt chỉ cần
xác định thông qua tần số mỗi tổ, tổ chứa Mốt là tổ có tần số
lớn nhất. Còn trong dãy số phân phối có khoảng cách tổ không đều nhau thì việc
xác định tổ chứa Mốt mới cần xác định thông qua mật độ tần số các tổ, tổ nào có
mật độ tần số lớn nhất là tổ chứa Mốt.
26. Phương sai có thể được dùng để đánh giá độ biến thiên giữa Năng suất lao
động và Tiền lương một công nhân
Sai: Phương sai là số bình quân cộng của bình phương các độ lệch giữa các lượng biến với
với số bình quân cộng của các lượng biến đó. Phương sai chỉ được
sử dụng để đánh giá sự biến thiên của bản thân từng tiêu thức, xem xét mức độ
phân tán so với giá trị trung tâm. Vì phương sai sẽ có đơn vị là bình phương đơn vị
của lượng biến, nên nhìn chung không dùng để so sánh giữa các chỉ tiêu khác loại.
Vì vậy, không thể dùng phương sai để đánh giá độ biến thiên giữa Năng suất lao
động và Tiền lương một công nhân.
27. Phương sai là chênh lệch giữa bình quân của bình phương các lượng biến
và bình phương của số trung bình
Đúng: Phương sai là số bình quân cộng của bình phương các độ lệch giữa các lượng
biến với số bình quân cộng của các lượng biến đó:
Khai triển công thức trên tương đương với:
Vậy phương sai là chênh lệch giữa bình quân của bình phương các lượng
biến và bình phương của số trung bình.
28. Phương sai của lượng biến lớn thì lượng biến thay đổi nhiều
Đúng: Phương sai của lượng biến đại diện cho mức độ phân tán của lượng biến xung quanh
giá trị trung bình. Phương sai càng lớn chứng tỏ các lượng biến
thay đổi càng nhiều xung quanh giá trị trung bình, hay nói cách khác phương sai
càng lớn thì lượng biến thay đổi càng nhiều.
29. Số trung vị phụ thuộc vào tất cả các lượng biến
Sai: Số trung vị là lượng biến tiêu thức của đơn vị đứng ở vị trí chính giữa trong dãy số lượng
biến, tức là nó chỉ phụ thuộc vào các tần số trong dãy số phân
phối và lượng biến của đơn vị đứng ở vị trí chính giữa dãy số, mà không phụ thuộc
vào các lượng biến khác. Vì thể không thể cho rằng số trung vị phụ thuộc vào tất cả các lượng biến.
30. Mốt chỉ được xác định từ dãy số phân phối theo tiêu thức số lượng
Sai: Mốt là biểu hiện của tiêu thức được gặp lại nhiều lần nhất trong một tổng thể hay trong
một dãy số phân phối. Như vậy, khái niệm Mốt chỉ nhắc đến số
lần lặp lại của tiêu thức mà không hề có sự phân biệt giữa tiêu thức số lượng hay
tiêu thức thuộc tính. Trên thực tế, với dãy số phân phối theo tiêu thức thuộc tính, ta
vẫn có thể tìm được Mốt theo đúng định nghĩa, dựa vào tần số lớn nhất trong phân phối đó.
31. Số trung bình nên kết hợp với dãy số phân phối
Đúng: Số trung bình đặc trưng cho mức độ đại diện, phổ biến nhất của tiêu thức nghiên cứu,
nhưng nó không phải là một chỉ tiêu hoàn hảo. Do nó đã loại trừ
đi ảnh hưởng của các phần tử cá biệt. Trong phân tích, đánh giá, vẫn nên kết hợp
với dãy số phân phối để có những kết luận chính xác nhất. Ví dụ như việc xem xét
doanh thu không chỉ xem doanh thu bình quân mà nên kết hợp với dãy số phân
phối để xem liệu doanh thu có đều theo thời gian hay không, những thời kì nào có biến động lớn
43. Điều kiện của phương pháp xu hướng phát triển cơ bản là loại bỏ sự
tác động của các yếu tổ ngẫu nhiên
Sai: Xu hướng phát triển cơ bản được hiểu là chiều hướng tiến triển chung kéo dài theo thời
gian, phản ánh tính quy luật của sự phát triển, vì vậy phương
pháp xu hướng phát triển được áp dụng nhằm mục đích loại bỏ tác động của các
yếu tố ngẫu nhiên, tìm ra quy luật chung. Vì vậy “loại bỏ tác động của các yếu tố
ngẫu nhiên” là mục đích chứ không phải điều kiện của phương pháp xu hướng phát triển
44. Lượng tăng (giảm) tuyệt đối trung bình chỉ nên tính khi dãy số thời gian
có các lượng tăng (giảm) tuyệt đối liên hoàn xấp xỉ nhau
Đúng: Lượng tăng (giảm) tuyệt đối trung bình được tính bằng công thức:
(Ghi công thức tính ra nhá)
Do lượng tăng giảm tuyệt đối trung bình san bằng các chênh lệch giữa các
lượng tăng giảm tuyệt đối liên hoàn nên nó sẽ mang tính chất đại diện cao khi
các lượng tăng giảm tuyệt đối liên hoàn xấp xỉ nhau, và kết quả có thể được sử dụng để dự đoán.
45. Lượng tăng (giảm) bình quân chính là bình quân của các tốc độ tăng (giảm) liên hoàn
Sai: Lượng tăng (giảm) tuyệt đối bình quân chính là bình quân của các
lượng tăng (giảm) tuyệt đối liên hoàn: (Ghi công thức ra nhá)
Chứ không phải là bình quân của các tốc độ tăng (giảm) liên hoàn.
46. Khi tính mức độ bình quân từ một dãy số thời điểm có khoảng cách không
bằng nhau thì quyền số được xác định bằng mức độ của dãy số.
Sai: Khi tính mức độ bình quân từ dãy số thời điểm có khoảng cách thời gian không bằng
nhau thì phải sử dụng quyền số là khoảng thời gian có mức độ
chứ không phải mức độ của dãy số: Công thức: trong đó:
yi: mức độ của dãy số
hi: khoảng thời gian có mức độ yi
47. Có thể tính tốc độ tăng giảm bình quân theo công thức tính bình quân
cộng hoặc bình quân nhân.
Sai: Tốc độ tăng giảm bình quân được tính thông qua tốc độ phát triển bình quân:
– 1. Trong đó tốc độ phát triển bình quân được tính bằng bình quân nhân của
các tốc độ phát triển liên hoàn.
Không thể tính tốc độ tăng giảm bình quân trực tiếp bằng công thức bình
quân cộng hay bình quân nhân được.
48. Giá trị tuyệt đối của 1% tốc độ tăng giảm liên hoàn là một số không đổi
Sai: Giá trị tuyệt đối của 1% tốc độ tăng giảm liên hoàn được tính bằng cách
chia lượng tăng giảm tuyệt đối liên hoàn cho tốc độ tăng giảm liên hoàn: gi =
gi phụ thuộc vào giá trị của yi-1, do đó không thể nói giá trị tuyệt đối của
1% tốc độ tăng giảm liên hoàn là một số không đổi.
49. Giá trị tuyệt đối của 1% tăng giảm định gốc bằng tổng các giá trị tuyệt đối
của 1% tăng giảm liên hoàn
Sai: Giá trị tuyệt đối của 1% tốc độ tăng giảm liên hoàn được tính bằng công thức: gi =
Giá trị tuyệt đối của 1% tốc độ tăng giảm định gốc luôn luôn bằng
Vì vậy không thể nói giá trị tuyệt đối của 1% tốc độ tăng giảm định gốc
bằng tổng các giá trị tuyệt đối của 1% tốc độ tăng giảm liên hoàn
50. Tốc độ tăng (giảm) bình quân được tính khi dãy số có các lượng tăng
(giảm) tuyệt đối liên hoàn xấp xỉ nhau
Sai: Tốc độ tăng (giảm) bình quân được tính bằng công thức: – 1. Tức
là nó được tính thông qua tốc độ phát triển bình quân. Tốc độ phát triển bình quân
chính là bình quân nhân của các tốc độ phát triển liên hoàn, nó đại diện cho các tốc
độ phát triển liên hoàn. Để đảm bảo cho khả năng đại diện cao và có thể sử dụng
để dự báo thì các tốc độ phát triển liên hoàn nên xấp xỉ nhau. Vậy tốc độ tăng
(giảm) bình quân được tính khi dãy số có tốc độ phát triển liên hoàn xấp xỉ nhau
chứ không phải lượng tăng (giảm) tuyệt đối liên hoàn xấp xỉ nhau.
51. Tốc độ phát triển bình quân là trung bình cộng của các tốc độ phát triển liên hoàn
Sai: Tốc độ phát triển liên hoàn là số tương đối so sánh sự biến động của hiện
tượng ở thời gian sau so với thời gian liền trước đó: ti =
. Do đó khi tính tốc độ
phát triển bình quân phải sử dụng bình quân nhân của các tốc độ phát triển liên
hoàn thì mới đảm bảo tính đại diện cho các tốc độ phát triển liên hoàn. Vậy, tốc độ
phát triển bình quân là trung bình nhân của các tốc độ phát triển liên hoàn chứ
không phải là trung bình cộng.
52. Đơn vị của 1% tăng giảm tuyệt đối là %
Sai: Giá trị tuyệt đối của 1% tốc độ tăng giảm liên hoàn được tính bằng công thức: gi =
Từ công thức ta thấy đơn vị của gi sẽ giống với đơn vị của yi-1. Nên
không thể nói đơn vị của 1% tăng giảm tuyệt đối là % được. Chương 7: Chỉ số
53. Chỉ số tổng hợp về giá của một nhóm các mặt hàng vừa có tính tổng hợp,
vừa có tính phân tích.
Đúng: Chỉ số tổng hợp về giá của một nhóm các mặt hàng biểu hiện quan hệ so sánh giữa
giá bán của một nhóm các mặt hàng ở kỳ nghiên cứu so với kỳ gốc
qua đó phản ánh biến động chung về giá bán của các mặt hàng. Vì vậy nó vừa
mang tính tổng hợp: nói lên biến động chung về giá bán các mặt hàng, vừa mang
tính chất phân tích: phân tích biến động riêng của các
54. Chỉ số tổng hợp về lượng qua thời gian thực chất là trung bình cộng giản
đơn của các chỉ số đơn về lượng.
Sai: Chỉ số tổng hợp về lượng qua thời gian được tính bằng công thức:
+ Chỉ số tổng hợp về lượng theo Las:
: Chỉ số tổng hợp về lượng theo Las là
trung bình cộng gia quyền của các chỉ số đơn về lượng.
+ Chỉ số tổng hợp về lượng theo Pass:
: Chỉ số tổng hợp về lượng theo Pass là trung bình
điều hòa của các chỉ số đơn về lượng.
Vậy chỉ số tổng hợp về lượng qua thời gian không phải là trung bình cộng
giản đơn của các chỉ số đơn về lượng.
55. Chỉ số tổng hợp về giá của Fisher qua thời gian là trung bình cộng của chỉ
số tổng hợp về giá của Las và Pass
Sai: Chỉ số tổng hợp giá của Fisher qua thời gian phản ánh biến động chung giá bán của các
mặt hàng dựa trên cơ sở san bằng chênh lệch giữa các chỉ số Las
và Pass, được tính theo công thức bình quân nhân của các chỉ số tổng hợp về giá của Las và Pass:
(Ghi công thức của chỉ số Fisher ra)
57. Việc tính chỉ số tổng hợp về giá theo công thức của Las và Pass sẽ không
chênh lệch nhiều khi kết cấu lượng hàng hóa tiêu thụ giữa hai kỳ thay đổi lớn.
Sai: Chỉ số tổng hợp về giá theo công thức của Las được tính với quyền số
là lượng hàng hóa kỳ gốc (ghi công thức ra)
Chỉ số tổng hợp về giá theo công thức của Pass được tính với quyền số là
lượng hàng hóa tiêu thụ kỳ nghiên cứu (ghi công thức ra)
Vì vậy, khi kết cấu lượng hàng hóa tiêu thụ giữa hai kỳ thay đổi lớn, hai chỉ
số giá theo Las và Pass sẽ cho ra kết quả chênh lệch nhau nhiều.
58. Phương pháp chỉ số là phương pháp phân tích mối liên hệ, cho phép
nghiên cứu cái chung và các bộ phận một cách kết hợp.
Đúng: Chỉ số là số tương đối biểu hiện quan hệ so sánh giữa hai mức độ của một hiện tượng
nghiên cứu. Phương pháp chỉ số cho phép nghiên cứu cái chung:
nghiên cứu tổng thể khi so sánh giữa tử số và mẫu số và nghiên cứu bộ phận: khi
phân tích ảnh hưởng của đối tượng nghiên cứu bởi các bộ phận cấu thành. Ví dụ
phương pháp chỉ số dùng để nghiên cứu doanh thu: M = . (Viết công thức của IM = Ip. Iq)
54. Chỉ số tổng hợp về giá của một nhóm các mặt hàng vừa có tính tổng hợp,
vừa có tính phân tích.
Đúng: Chỉ số tổng hợp về giá của một nhóm các mặt hàng biểu hiện quan hệ so sánh giữa
giá bán của một nhóm các mặt hàng ở kỳ nghiên cứu so với kỳ gốc
qua đó phản ánh biến động chung về giá bán của các mặt hàng. Vì vậy nó vừa
mang tính tổng hợp: nói lên biến động chung về giá bán các mặt hàng, vừa mang
tính chất phân tích: phân tích biến động riêng của các
55. Chỉ số tổng hợp về lượng qua thời gian thực chất là trung bình cộng giản
đơn của các chỉ số đơn về lượng.
Sai: Chỉ số tổng hợp về lượng qua thời gian được tính bằng công thức:
+ Chỉ số tổng hợp về lượng theo Las:
: Chỉ số tổng hợp về lượng theo Las là
trung bình cộng gia quyền của các chỉ số đơn về lượng.
+ Chỉ số tổng hợp về lượng theo Pass:
: Chỉ số tổng hợp về lượng theo Pass là trung bình.
điều hòa của các chỉ số đơn về lượng.
Vậy chỉ số tổng hợp về lượng qua thời gian không phải là trung bình cộng
giản đơn của các chỉ số đơn về lượng.
56. Chỉ số tổng hợp về giá của Fisher qua thời gian là trung bình cộng của chỉ
số tổng hợp về giá của Las và Pass
Sai: Chỉ số tổng hợp giá của Fisher qua thời gian phản ánh biến động chung giá bán của các
mặt hàng dựa trên cơ sở san bằng chênh lệch giữa các chỉ số Las
và Pass, được tính theo công thức bình quân nhân của các chỉ số tổng hợp về giá
của Las và Pass: (Ghi công thức của chỉ số Fisher ra)
58. Việc tính chỉ số tổng hợp về giá theo công thức của Las và Pass sẽ không
chênh lệch nhiều khi kết cấu lượng hàng hóa tiêu thụ giữa hai kỳ thay đổi lớn.
Sai: Chỉ số tổng hợp về giá theo công thức của Las được tính với quyền số
là lượng hàng hóa kỳ gốc (ghi công thức ra)
Chỉ số tổng hợp về giá theo công thức của Pass được tính với quyền số là
lượng hàng hóa tiêu thụ kỳ nghiên cứu (ghi công thức ra)
Vì vậy, khi kết cấu lượng hàng hóa tiêu thụ giữa hai kỳ thay đổi lớn, hai chỉ
số giá theo Las và Pass sẽ cho ra kết quả chênh lệch nhau nhiều.
58. Phương pháp chỉ số là phương pháp phân tích mối liên hệ, cho phép
nghiên cứu cái chung và các bộ phận một cách kết hợp.
Đúng: Chỉ số là số tương đối biểu hiện quan hệ so sánh giữa hai mức độ của một hiện tượng
nghiên cứu. Phương pháp chỉ số cho phép nghiên cứu cái chung:
nghiên cứu tổng thể khi so sánh giữa tử số và mẫu số và nghiên cứu bộ phận: khi
phân tích ảnh hưởng của đối tượng nghiên cứu bởi các bộ phận cấu thành. Ví dụ
phương pháp chỉ số dùng để nghiên cứu doanh thu: M = . (Viết công thức của IM = Ip. Iq)
59. Khi có số liệu về giá thành đơn vị sản phẩm và tỷ trọng chi phí sản xuất
của từng phân xưởng có thể tính giá thành bình quân chung của các phân xưởng
Đúng: Khi có số liệu về giá thành đơn vị sản phẩm: z và tỷ trọng chi phí sản xuất từng phân xưởng:
. Ta có thể tính giá thành bình quân chung của các phân xưởng theo công thức:
60. Chỉ số tổng hợp về giá của Fisher được sử dụng khi có sự khác biệt lớn về
cơ cấu tiêu thụ các mặt hàng giữa 2 kỳ nghiên cứu
Đúng: Chỉ số tổng hợp về giá của Fisher phản ánh biến động chung giá bán của các mặt hàng
dựa trên cơ sở san bằng chênh lệch giữa các chỉ số Las và Pass (ghi công thức ra)
Chỉ số tổng hợp giá của Las tính với quyền số là lượng hàng hóa tiêu thụ kỳ
gốc, và chỉ số tổng hợp giá của Pass tính với quyền số là lượng hàng hóa tiêu thụ
kỳ nghiên cứu. Nên khi cơ cấu tiêu thụ các mặt hàng giữa hai kỳ thay đổi thì chỉ số
giá của Las và Pass sẽ có sự khác biệt lớn nên cần sử dụng chỉ số tổng hợp về giá
của Fisher để có một chỉ số mang tính chất đại diện chung.
61. Phương pháp chỉ số là phương pháp mang tính tổng hợp, không mang tính chất phân tích
Sai: Chỉ số là số tương đối biểu hiện quan hệ so sánh giữa hai mức độ của một hiện tượng
nghiên cứu. Phương pháp chỉ số cho phép nghiên cứu cái chung:
nghiên cứu tổng thể khi so sánh giữa tử số và mẫu số và nghiên cứu bộ phận: khi
phân tích ảnh hưởng của đối tượng nghiên cứu bởi các bộ phận cấu thành. Ví dụ
phương pháp chỉ số dùng để nghiên cứu doanh thu: M = . (Viết công thức của IM = Ip. Iq)
62. Chỉ số cấu thành cố định nghiên cứu đồng thời biến động của bản thân
tiêu thức và kết cấu tổng thể nghiên cứu.
Sai: Chỉ số cấu thành cố định chỉ phản ánh biến động của chỉ tiêu bình quân do ảnh
hưởng của tiêu thức nghiên cứu, trong điều kiện kết cấu tổng thể cố định. Công thức: I = Ix. . Trong đó: Ix =
. Kết cấu tổng thể được cố định ở kỳ nghiên cứu trong phân tích ảnh
hưởng của bản thân tiêu thức nghiên cứu đến chỉ tiêu bình quân.
63. Theo chỉ số tổng hợp giá của Las, quyền số có thể là lượng hàng hóa tiêu
thụ ở kỳ gốc hoặc doanh thu kỳ gốc
Đúng: Công thức chỉ số tổng hợp giá của Las:
(Sửa lại chỗ kia là Ip nhá, anh đánh máy nhầm thành Iq)
Theo công thức thứ nhất, quyền số của chỉ số tổng hợp giá của Las là lượng
hàng tiêu thụ kỳ gốc. Hoặc theo công thức thức 3, quyền số là doanh thu tiêu thụ kỳ gốc.
64. Chỉ số tổng hợp về giá của Fisher là chỉ số dựa trên chênh lệch của chỉ số Las và Pass
Đúng: Chỉ số tổng hợp về giá của Fisher phản ánh biến động chung giá bán của các mặt hàng
dựa trên cơ sở san bằng chênh lệch giữa các chỉ số Las và Pass
(ghi công thức ra). Khi chỉ số giá của Las và Pass có sự khác biệt lớn cần sử dụng
chỉ số tổng hợp về giá của Fisher để có một chỉ số mang tính chất đại diện chung.
65. Chỉ số tổng hợp lượng hàng tiêu thụ của mặt hàng A và B, quyền số chỉ có
thể là giá cố định được nhà nước đặt ra.
Sai: Trong công thức chỉ số tổng hợp lượng hàng tiêu thụ của hai mặt hàng A và B, quyền
số là giá cố định, giá này có thể là giá cố định do nhà nước đặt ra
hoặc là giá trung bình của hai mặt hàng A và B. Trong trường hợp sử dụng quyền
số là giá trung bình. Công thức xác định chỉ số như sau: . Trong đó p = CÓ THỂ KO THI
Chương 1: Điều tra chọn mẫu – Ước lượng
32. Điều tra chọn mẫu là 1 trường hợp vận dụng quy luật số lớn
Đúng: Điều tra chọn mẫu là một loại điều tra thống kê không toàn bộ mà trong đó một số đơn
vị được chọn tra đủ lớn để điều tra thực tế và dựa vào kết quả điều
ra được có thể tính toán suy rộng cho toàn bộ hiện tượng. (Đây là khái niệm gt).
Vậy muốn số liệu có thể dùng đế suy rộng cho tổng thể, thì kết quả rút ra từ
mẫu phải có tính đại diện, tức là hạn chế ảnh hưởng của yếu tổ ngẫu nhiên, nên nó
là sự áp dụng quy luật số lớn.
33. Khi xác định số đơn vị mẫu điều tra để ước lượng tỷ lệ, người ta chọn tỷ lệ
lớn nhất trong các lần điều tra trước.
Sai: Khi xác định số đơn vị mẫu điều tra để ước lượng tỷ lệ mà chưa biết tỷ lệ tổng thể, có
thể dựa vào số liệu từ các cuộc điều tra trước và chọn tỷ lệ gần 0.5
nhất trong các lần điều tra để làm tỷ lệ tổng thể. Với cách chọn như vậy sẽ làm
tăng tính đại diện của tổng thể mẫu.
34. Trong điều tra chọn mẫu, sai số theo phương án chọn 1 lần nhỏ hơn sai số
theo phương pháp chọn nhiều lần. Đúng:
Sai số chọn mẫu trung bình về trung bình:
- Theo cách chọn 1 lần (chọn không lặp): (Chép công thức ra)
- Theo cách chọn nhiều lần (chọn lặp): (Chép công thức ra)
Sai số chọn mẫu theo cách chọn 1 lần nhỏ hơn sai số chọn mẫu theo cách
chọn nhiều lần do 0 < 1 -
Sai số chọn mẫu trung bình về tỷ lệ: (Viết công thức và làm tương tự)
35. Điều tra trọng điểm có thể được dùng để suy rộng thành đặc điểm chung
của toàn bộ tổng thể.
Sai: Trong điều tra trọng điểm, người ta chỉ tiến hành điều tra ở bộ phận chủ yếu nhất của
tổng thể chung, vì vậy các đơn vị được lựa chọn để điều tra không
mang tính chất đại diện cho toàn bộ tổng thể chung được, do đó kết quả trong điều
tra trọng điểm không được dùng để suy rộng cho các đặc điểm chung của tổng thể.
Trong các phương pháp điều tra không toàn bộ, chỉ có điều tra chọn mẫu kết quả
mới được sử dụng để suy rộng thành đặc điểm chung của tổng thể.
Chương 5: Phân tích hồi quy tương quan
36. Hệ số tương quan và hệ số hồi quy cho phép xây dựng cượng độ và chiều
hướng của mối liên hệ tương quan tuyến tính.
Sai: Cả hai hệ số điều được sử dụng để xác định chiều hướng của mối liên hệ
tương quan tuyến tính: khi r, b1 > 0: quan hệ tương quan tuyến tính là quan hệ
thuận, khi r. b1 < 0: quan hệ tương quan tuyến tính là quan hệ nghịch; nhưng chỉ có hệ số
tương quan mới được sử dụng để xác định cường độ của mối liên hệ này thôi
37. Khi mối liên hệ tương quan tuyến tính giữa hai tiêu thức số lượng là
nghịch thì không thể sử dụng tỷ số tương quan để đánh giá trình độ chặt chẽ
của mối liên hệ này.
Sai: Tỷ số tương quan ( : đọc là êta) được sử dụng để đánh giá mức độ chặt
chẽ của mối liên hệ tương quan phi tuyến tính và tuyến tính giữa hai tiêu thức số
lượng. nhận các giá trị trong khoảng [0;1], và càng gần 1 thì quan hệ giữa hai
tiêu thức là càng chặt chẽ. Vì vậy, ngay cả khi quan hệ tuyến tính giữa hai tiêu thức
số lượng là nghịch thì vẫn có thể sử dụng tỷ số tương quan để đánh giá trình độ
chặt chẽ của mối liên hệ này.
38. Khi mối liên hệ tương quan tuyến tính giữa hai tiêu thức số lượng là thuận
thì có thể thay thế hệ số tương quan bằng tỷ số tương quan để đánh giá mức
độ chặt chẽ giữa x và y.
Đúng: Hệ số tương quan (r) và tỷ số tương quan ( cùng được sử dụng để
đánh giá mức độ chặt chẽ của mối quan hệ tương quan, nhưng r có thể nhận giá trị
âm hoặc dương (tùy thuộc vào quan hệ giữa hai tiêu thức là thuận hay nghịch),
nhưng luôn nhận giá trị dương. Vì vậy, khi mối liên hệ giữa hai tiêu thức số
lượng là thuận thì r > 0, khi đó có thể thay hệ số tương quan bằng tỷ số tương quan
để đánh giá mức độ chắt chẽ giữa x và y.
39. Khi xem xét các nhân tố ảnh hưởng tới một hiện tượng cần phân tích chỉ
có thể sử dụng phương pháp hồi quy tương quan
Sai: Hồi quy tương quan chỉ là một trong những phương pháp có thể sử
dụng để xem xét ảnh hưởng của các nhân tố tới hiện tượng cần phân tích, thường là
quan hệ dưới dạng tiêu thức nguyên nhân – tiêu thức kết quả. Ngoài ra, còn có các
phương pháp khác để xác định ảnh hưởng của các nhân tố tới hiện tượng cần phân
tích ví dụ như phương pháp chỉ số. Ví dụ: Phân tích ảnh hưởng của giá bán và sản
lượng hàng hóa tới doanh thu của doanh nghiệp, ta có thể sử dụng hệ thống chỉ số để phân tích.
40. Phương pháp bình phương nhỏ nhất chính là sự tối thiểu hóa trong
các bình phương các chênh lệch giữa các giá trị thực tế và giá trị trung bình
của tiêu thức kết quả.
Sai: Phương pháp bình phương nhỏ nhất được áp dụng khi xác định các yếu tố của một mô
hình hồi quy dựa trên cơ sở tìm giá trị nhỏ nhất của tổng bình
phương các chênh lệch giữa các giá trị thực tế và các giá trị tương ứng được tính
ra theo mô hình hồi quy chứ không phải giá trị trung bình của tiêu thức kết quả.
41. Tỷ số tương quan và hệ số hồi quy dùng để đánh giá chiều hướng của mối liên hệ
Sai: Chỉ có hệ số hồi quy (b1) mới được sử dụng để đánh giá chiều hướng của mối liên hệ.
b1 > 0: mối liên hệ thuận, b1 < 0: mối liên hệ nghịch. Còn tỷ số
tương quan (ƞ) chỉ được sử dụng để đánh giá mức độ chặt chẽ của mối liên hệ mà
không được sử dụng để đánh giá chiều hướng của mối liên hệ vì luôn nhận giá tr ƞ ị dương.
42. Mối liên hệ tương quan là mối liên hệ không hoàn toàn chặt chẽ
Đúng: Mối liên hệ tương quan không hoàn toàn chặt chẽ, tức là mỗi giá trị của tiêu thức
nguyên nhân sẽ có nhiều giá trị tương ứng của tiêu thức kết quả, các
mối quan hệ này không biểu hiện rõ ràng trên từng đơn vị cá thể, do đó để phản
ánh mối liên hệ tương quan thì phải nghiên cứu trên hiện tượng số lớn. Dự đoán
66. Dự đoán dựa vào lượng tăng (giảm) tuyệt đối thực hiện đối với dãy số có
tốc độ tăng (giảm) liên hoàn xấp xỉ nhau
Sai: Dự đoán dựa vào lượng tăng (giảm) tuyệt đối được xây dựng trên giả thuyết lượng
tăng (giảm) của các năm sẽ tương tự nhau, do đó người ta có thể lấy
năm cuối cùng theo số liệu đã có để tính trị số của năm tiếp theo bằng công thức: yn+1 = yn +
Dự đoán sẽ cho kết quả có độ tin cậy cao khi lượng tăng (giảm) liên hoàn
xấp xỉ nhau chứ không phải tốc độ tăng (giảm) liên hoàn xấp xỉ nhau.




