Câu hỏi trắc nghiệm môn thống kê ứng dụng

lOMoARcPSD| 36207943
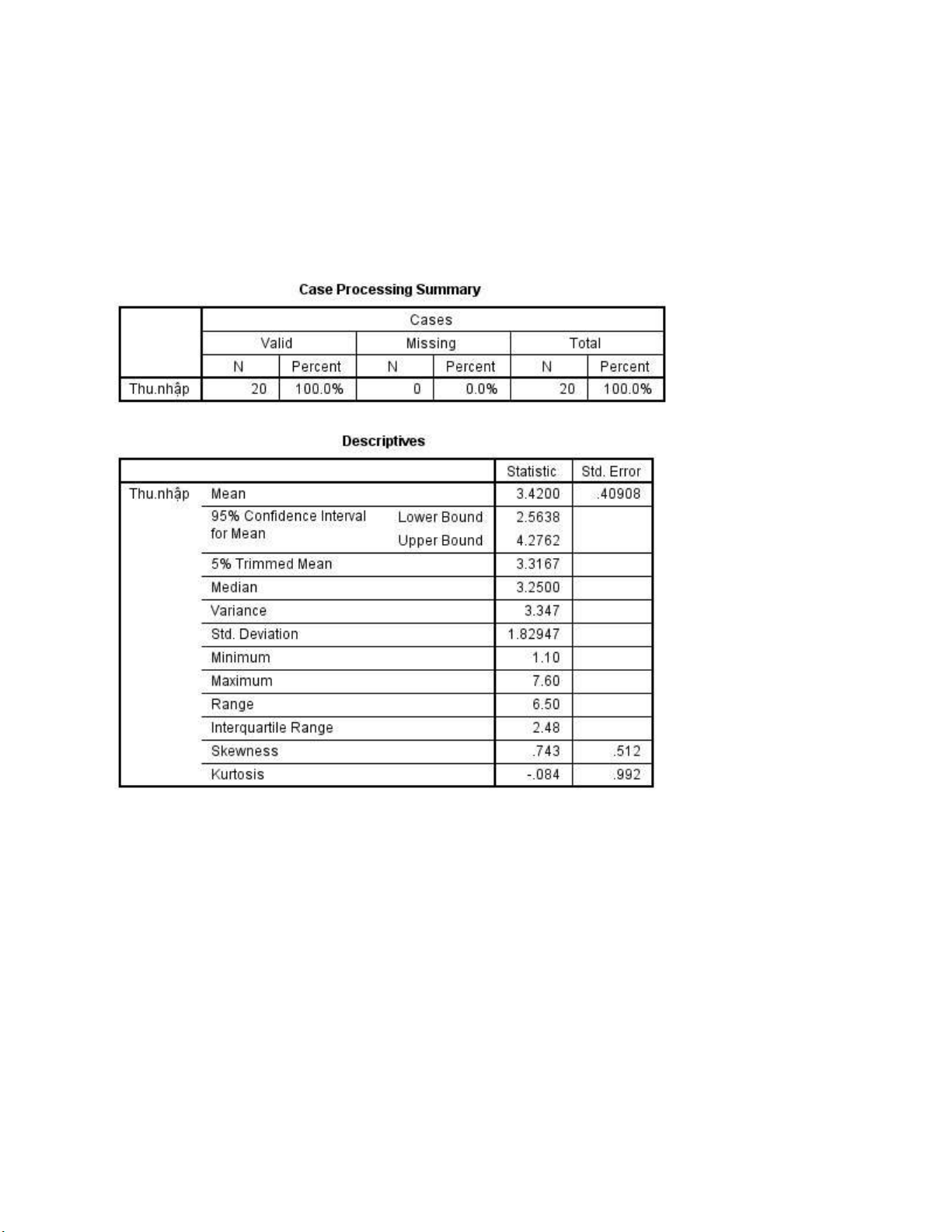
Câu 1. Một cuộc khảo sát về thu nhập (triệu ồng/tháng) của một nhóm sinh viên với kết quả như sau
Dựa vào bảng phân tích kết quả SPSS ở trên, thì trung bình mẫu, ộ lệch chuẩn, ộ xiên Skewnees
và ộ nhọn Kurtosis của bộ dữ liệu lần lượt là bao nhiêu? a. 3.42, 3.347, 0.743, -0.084
b. 3.42, 1.82947, 0.743, -0.084 c. 3.25, 3.347, -0.084, 0.743
d. 3.25, 1.82947, -0.084, 0.743 Câu 2.
Đối với bộ dữ liệu thu nhập này, dữ liệu có hình dạng như thế nào? a. Phân phối cân ối lOMoARcPSD| 36207943
b. Phân phối lệch trái, do trung bình nhỏ hơn trung vị
c. Phân phối lệch phải, do trung bình lớn hơn trung vị
d. Không ủ thông tin ể ưa ra kết luận
Câu 3. Để kiểm tra bộ dữ liệu thu nhập có phân phối chuẩn hay không, người ta dùng kiểm ịnh
phi tham số Jarque Bera. Khi ó, giá trị kiểm ịnh JB nhận giá trị là a. 0.5201 b. 10.4025 c. 0.1983 d. 3.9650 Câu 4.
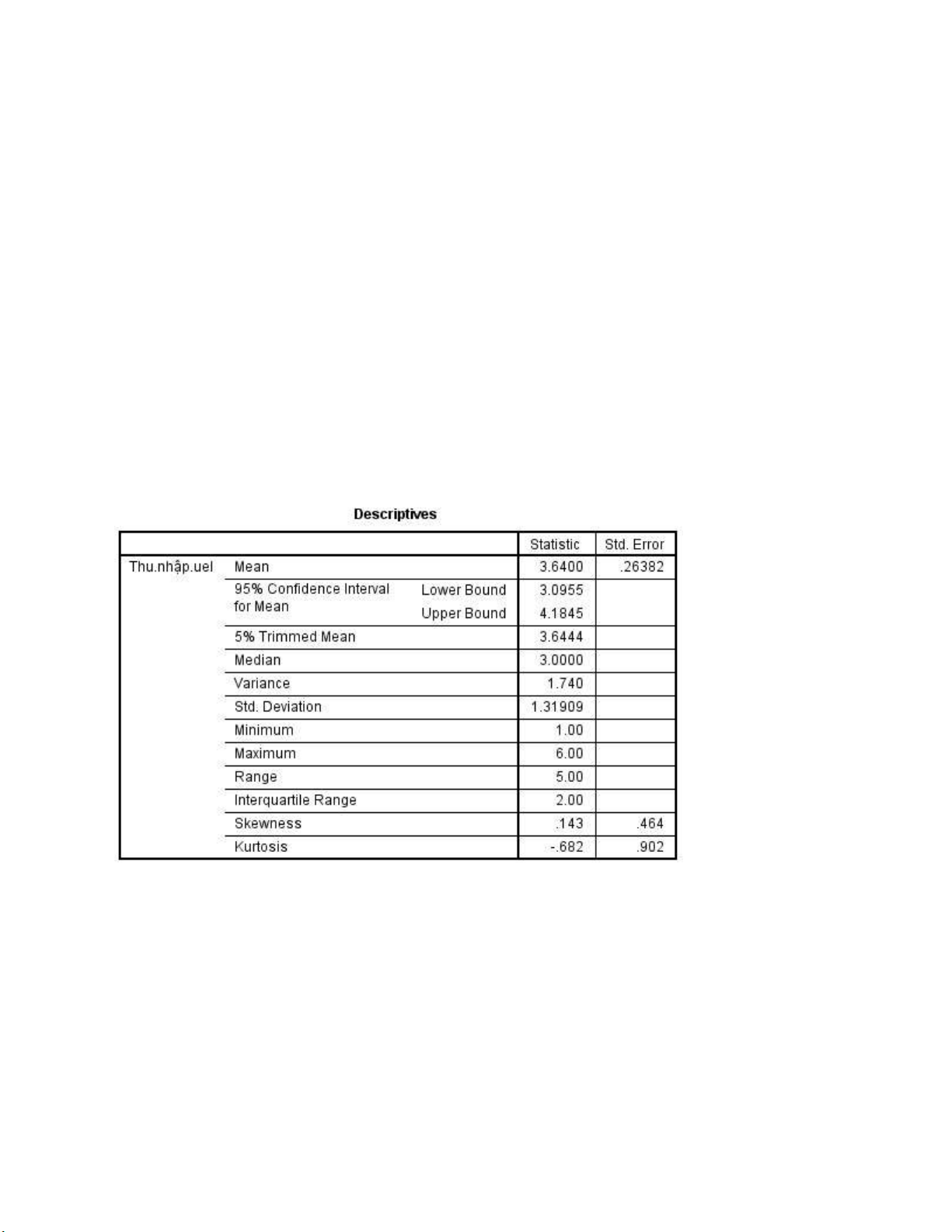
Và một mẫu thứ hai khảo sát về thu nhập của sinh viên Trường Đại học Kinh tế -
Luật, có kết quả như sau
Để so sánh sự biến thiên của thu nhập hai nhóm sinh viên: một nhóm sinh viên nói chung và một
nhóm sinh viên UEL thì cần sử dụng:
a. Hệ số biến thiên 𝐶𝑉, thì thấy nhóm sinh viên nói chung có ộ biến ộng lớn hơn.
b. Độ lệch chuẩn 𝑆, thì thấy nhóm sinh viên nói chung có ộ biến ộng lớn hơn.
c. Vì trung bình khác nhau, nên chỉ có thể dùng hệ số biến thiên 𝐶𝑉. lOMoARcPSD| 36207943
d. Sử dụng ộ lệch chuẩn hay hệ số biến thiên ều ược khi so sánh về ộ biến thiên của hai bộ dữ liệu.
Câu 5. Nếu khi hỏi về con số thu nhập cụ thể, người ược phỏng vấn không sẵn lòng trả lời cho
câu hỏi. Vậy chúng ta nên chuyển câu hỏi về dưới dạng mức thu nhập nằm trong
các khoảng (dưới 3 triệu ồng/tháng, từ 3 ến 10 triệu ồng/tháng, trên 10 triệu ồng/tháng).
Đối với câu hỏi như vậy, người phỏng vấn ang sử dụng thang o gì? a. Thang o ịnh danh b. Thang o tỷ lệ c. Thang o khoảng d. Thang o thứ bậc
Câu 6. Một mẫu ngẫu nhiên thu ược từ cuộc iều tra về thời gian sử dụng Internet trong ngày như sau Thời gian Ít hơn 2 Từ 2 ến 4 Từ 4 ến 8 Trên 8 (giờ/ngày) Số người 25 40 50 35
Giả sử thời gian sử dụng Internet có phân phối chuẩn. Tìm khoảng ước lượng ối xứng trung
bình thời gian sử dụng với mức ý nghĩa 5%. Biết 𝑧0.025 = 1.96, 𝑧0.05 = 1.645 a. (4.7971, 5.8029) b. (4.8779, 5.7221) c. (3.9735, 6.6265) d. (3.7195, 6.8805)
Câu 7. Thời gian sử dụng Internet trong ngày ược coi là bình thường nếu thời gian sử dụng từ
4 ến 8 giờ/ngày. Hãy tìm khoảng tin cậy ối xứng nhằm ước lượng tỷ lê những người có thời
gian sử dụng là bình thường, với ộ tin cậy 99%. Biết 𝑧0.01 = 2.33, 𝑧0.005 = 2.575 a. (0.497, 0.703) b. (0.297, 0.503) c. (0.3068, 0.4932) d. (0.5068, 0.6932) lOMoARcPSD| 36207943
Câu 8. Có hai mẫu khảo sát về số liệu của các sản phẩm X bán ược trong khoảng thời gian bốn
tháng ở hai cửa hàng Co.op food và Vin mart như sau Cửa hàng Co.op food Số lượng 12 14 15 17 22 24 26 29 (gói) Số ngày 10 15 15 20 30 20 5 5 Cửa hàng Vin mart Số lượng (gói) 11 13 16 20 28 Số ngày 15 20 40 30 15
Có thông tin cho rằng, ộ phân tán số lượng hàng hóa bán ược của hai cửa hàng trên là bằng
nhau. Hãy kiểm ịnh lại thông tin trên với mức ý nghĩa 0.05, biết
𝐹119,119,0.025 = 1.4349 và 𝐹119,119,0.975 = 0.6969.
a. Giá trị kiểm ịnh là 1.1024, chứng tỏ ộ phân tán của hai cửa hàng bằng nhau
b. Giá trị kiểm ịnh là 1.0499, chứng tỏ ộ phân tán của hai cửa hàng bằng nhau
c. Độ phân tán của hai cửa hàng khác nhau với mức ý nghĩa 0.05
d. Chưa ủ cơ sở ể kết luận.
Câu 9. Đối với mẫu khảo sát ở trên, giả sử hai mẫu khảo sát về số liệu của các sản phẩm X
bán ược trong khoảng thời gian bốn tháng ở hai cửa hàng Co.op food và Vin mart ở trên
có phương sai bằng nhau. Giá trị phương sai chung cho hai mẫu trên là a. 4.8769 b. 23.7841 c. 11.313 d. 12.4711
Câu 10. Ở mức ý nghĩa 95%, nếu muốn ước lượng tỷ lệ cá nhiễm nấm trong một hồ nuôi, cần
kiểm tra tổi thiểu bao nhiêu con cá ể ảm bảo ộ sai lệch của tỷ lệ không quá 0.01, biết 𝑧0.025 = 1.96 a. 9640
b. Không ủ thông tin về tỷ lệ mẫu ể tính toán lOMoARcPSD| 36207943
c. Cần sử dụng công thức 𝑓+(1−𝑓) 2 d. 964000
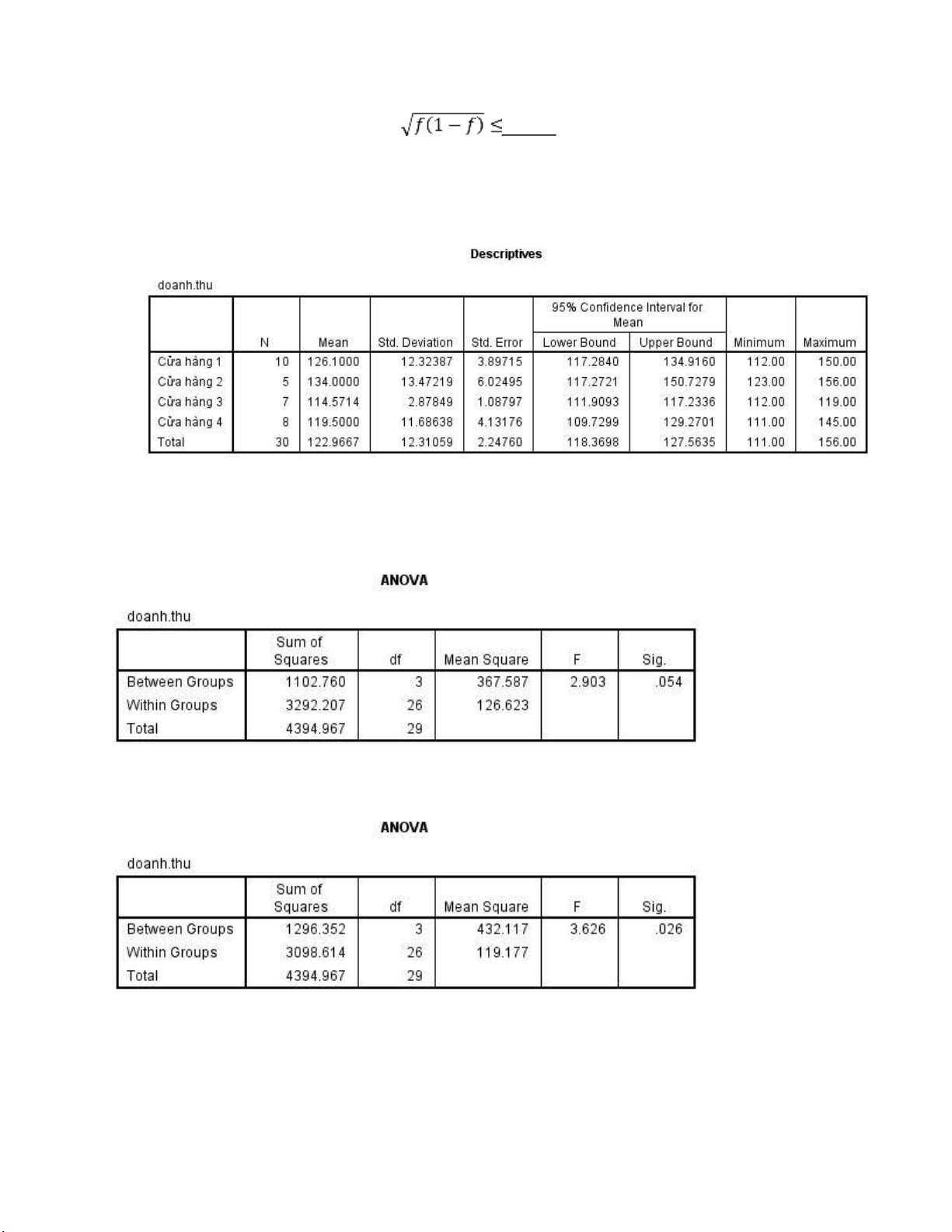
Câu 11. Bảng khảo sát doanh thu của bốn cửa hàng tóm tắt qua bảng dữ liệu sau.
Giả sử doanh thu ảm bảo các iều kiện của phương pháp phân tích phương sai ANOVA. Bảng phân
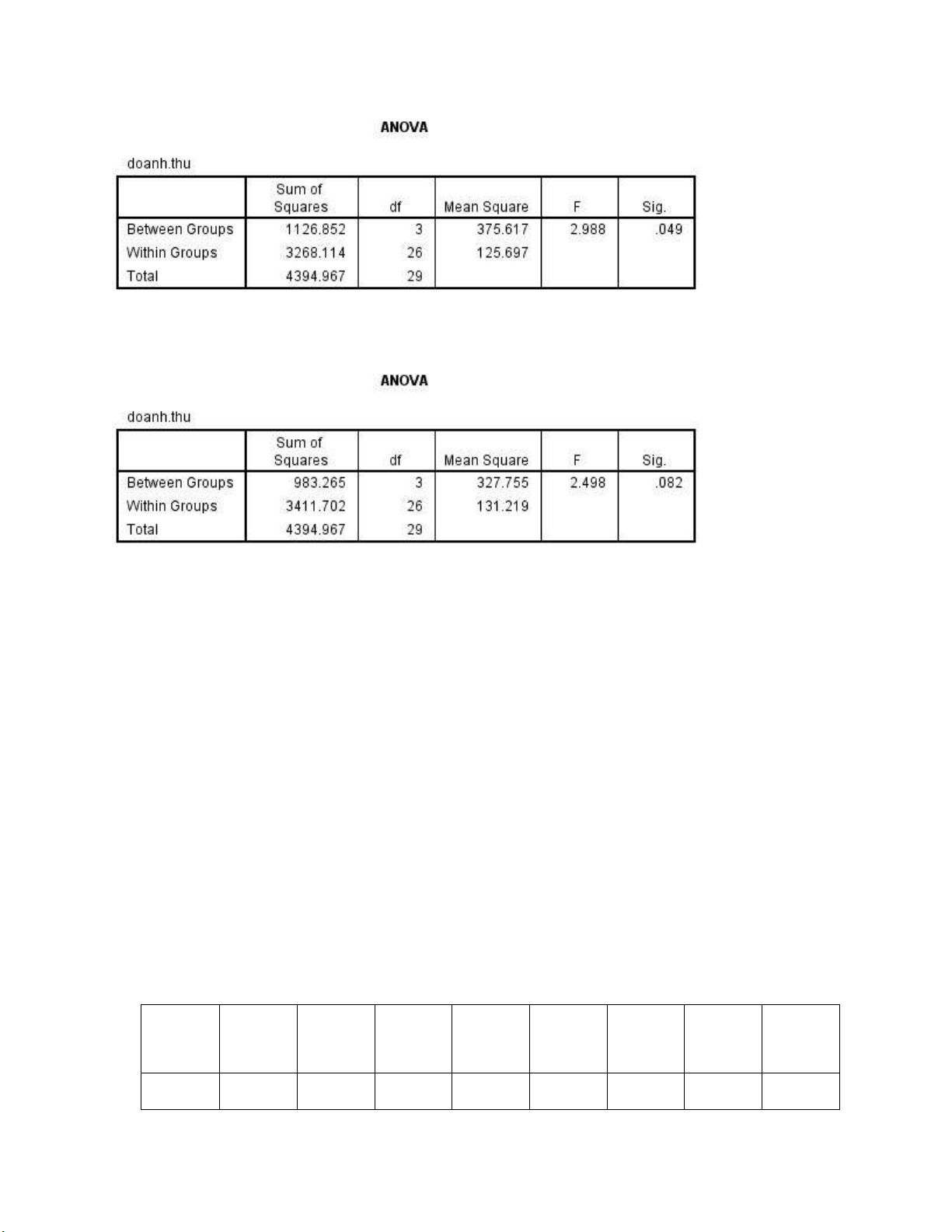
tích phương sai ANOVA cho kết quả ở trên tương ương với bảng nào sau ây: a. b. c. lOMoARcPSD| 36207943 d.
Câu 12. Biết giá trị tra bảng Fisher như sau 𝐹3,26,0.01 = 4.6366, 𝐹3,26,0.025 = 3.6697, 𝐹3,26,0.05 = 2.9752, 𝐹3,26,0.1 = 2.3075
a. Ở mức ý nghĩa 1% và 2.5%, chứng tỏ doanh thu trung bình của bốn cửa hàng là bằng nhau
b. Ở mức ý nghĩa 1% và 5%, chứng tỏ doanh thu trung bình của bốn cửa hàng là bằng nhau
c. Ở mức ý nghĩa 1% và 10%, chứng tỏ doanh thu trung bình của bốn cửa hàng là bằng nhau
d. Ở mức ý nghĩa 5% và 10%, chứng tỏ doanh thu trung bình của bốn cửa hàng là bằng nhau
Câu 13. Sử dụng kiểm ịnh dấu hạng Wilconxon cho bảng kết quả khảo sát về số lượng hồ sơ
(hồ sơ) sang tên ổi chủ của xe gắn máy sau khi có thông tin phạt xe không chính chủ, tại 8
quận huyện trong khoảng thời gian hai tháng kề nhau trước và sau thông tin trên Trước 100 120 130 120 102 100 104 126 𝑥𝑖 Sau 𝑦𝑖 120 200 160 105 92 110 130 107 lOMoARcPSD| 36207943
Bảng xếp hạng tính giá trị sai lệch 𝑑𝑖 = 𝑥𝑖 − 𝑦𝑖. Tổng các hạng của 𝑅− là a. 8.5 b. 36 c. 8 d. 27.5 Câu 14.
Trong bài toán kiểm ịnh Chi bình phương về sự phụ thuộc giữa hai biến ịnh tính,
tần số lý thuyết 𝐸11, 𝐸12, 𝐸21, 𝐸22 (𝐸𝑖𝑗 là ở vị trí hàng thứ 𝑖 và cột thứ 𝑗) lần lượt là
Th ờ i gian h ọ c Dướ i 8 (gi ờ/ngày) Trên 8 (gi ờ/ngày) X ế p lo ạ i Dưới Khá 100 50 T ừ khá trở lên 200 250 a. 150, 150, 150, 150 b. 75, 75, 225, 225 c. 75, 225, 75, 225 d. 225, 225, 75, 75
Câu 15. Với số lượng 560 sản phẩm có trọng lượng trung bình là 140 gam và mức ộ dao ộng
là 40 gam. Hỏi có bao nhiêu sản phẩm thuộc khoảng (100, 180) gam? a. 95% b. 90% c. 532 sản phẩm d. 504 sản phẩm
Câu 16. Phỏng vấn ngẫu nhiên 1000 người thấy có 43% cho rằng an toàn vệ sinh thực phẩm là
không áng quan tâm. Sau một thời gian vận ộng về tuyên truyền các vấn ề liên quan ến sức
khỏe thấy rằng tỷ lệ người quan tâm ến vệ sinh an toàn thực phẩm là 67% trong tổng số
2000 người ược phỏng vấn. Trong bài toán ước lượng về sự sai khác giữa hai tỷ
lệ tổng thể thì tỷ lệ chung về quan tâm ến vệ sinh an toàn thực phẩm nhận giá trị là a. 55.53% b. 59.06% lOMoARcPSD| 36207943 c. 63.67% d. 62.33% Câu 17.
Trong bài toán ước lượng phương sai của tổng thể có mẫu iều tra như sau 20 21 23 24 25 26 21 21 23 24 25 26 23 24 22 21 21 24 25 23
Biết trung bình của tổng thể là 22. Khi ó giá trị phương sai ược sử dụng trong bài toán này nhận giá trị bằng bao nhiêu a. 3.3578 b. 3.19 c. 4.4 d. 4.6316 Câu 18.
Trong các phát biểu sau, phát biểu nào úng
a. Kiểm ịnh dấu hạng Wilconxon là áp dụng cho bài toán kiểm ịnh trung bình trên một
tổng thể, kiểm ịnh sự sai khác trung bình trên tổng thể với iều kiện hai mẫu phụ thuộc
với nhau, nhưng vi phạm iều kiện tổng thể có phân phối chuẩn
b. Kiểm ịnh tổng hạng Wilconxon và kiểm ịnh dấu hạng Wilconxon ều giống nhau
c. Kiểm ịnh Kruskal – Wallis áp dụng so sánh trung bình của nhiều tổng thể cần phải thỏa
mãn iều kiện là các tổng thể này có phân phối chuẩn.
d. Kiểm ịnh Chi bình phương cho phép kiểm ịnh về giá trị trung bình tổng thể Câu 19.
Biểu ồ nhánh lá nào phù hợp với bảng giá trị sau 12 13 14 24 12 25 36 27 38 27 13 12 25 12 24 36 36 28 29 21 lOMoARcPSD| 36207943 VAR00001 Stem-and-Leaf Plot VAR00001 Stem-and-Leaf Plot Frequency Stem & Leaf Frequency Stem & Leaf 7.00 1 . 2222334 7.00 1 . 2222334 .00 1 . .00 1 . 3.00 2 . 144 3.00 2 . 144 6.00 2 . 557789 6.00 2 . 557789 .00 3 . .00 3 . 4.00 3 . 6668 4.00 3 . 6668 Stem width: 10.00 Stem width: 100.00 Each leaf: 1 case(s) Each leaf: 1 case(s) b. a. VAR00001 Stem-and-Leaf Plot VAR00001 Stem-and-Leaf Plot Frequency Stem & Leaf Frequency Stem & Leaf 7.00 1 . 2222334 7.00 1 . 2222334 .00 1 . .00 1 . 3.00 2 . 144 3.00 2 . 144 6.00 2 . 557789 6.00 2 . 557789 .00 3 . .00 3 . 4.00 3 . 6668 4.00 3 . 6668 Stem width: 0.10 Stem width: 10.00 Each leaf: 1 case(s) Each leaf: 2 case(s) c. d.
Câu 20. Đại lượng thống kê mô tả nào là phù hợp nhất trong câu hỏi
Đánh giá chất lượng của căn tin trường với (1: rất không hài lòng, 2: ít hài lòng, 3: bình
thường, 4: hài lòng, 5: rất hài lòng)
a. Trung bình và sử dụng trong các bài toán ước lượng và kiểm ịnh tham số
b. Trung bình, trung vị và sử dụng trong các bài toán ước lượng và kiểm ịnh tham số
c. Trung bình, mode và sử dụng trong các bài toán ước lượng và kiểm ịnh tham số
d. Trung vị, tứ phân vị và sử dụng trong các bài toán phi tham số. lOMoARcPSD| 36207943