Câu hỏi trắc nghiệm ôn tập - Cơ sở Vật lí | Đại học Sư Phạm Hà Nội

Untitled Translated by Meng Ngày 2 tháng 8 năm 2023 Bài 1: Mission to Mars
1. Trong một nhiệm vụ phóng phi thuyền từ Trái Đất tới Hoả tinh, cách hiệu quả nhất để thực hiện nhiệm
vụ là sử dụng chuyển quỹ đạo Hohmann. Giả sử rằng quỹ đạo của Hoả tinh và Trái Đất là hai đường
tròn đồng tâm là Mặt trời, quỹ đạo chuyển tiếp sẽ có dạng nửa ellipse với cận điểm là điểm phóng và
viễn điểm là điểm đến. Cho bán kính quỹ đạo của Trái Đất và Hoả tinh quanh Mặt Trời lần lượt là RE
và R , và khối lượng mặt trời là MS. M
(a) Tìm vận tốc tối thiểu của phi thuyền tại vị trí phóng trên Trái Đất để có thể chuyển quỹ đạo.
(b) Tìm thời gian chuyển quỹ đạo TH.
(c) Thời gian ngắn nhất của nhiệm vụ (tới Hoả tinh và quay lại) bằng bao nhiêu ? Bài 2: Sao chổi
1. Một quỹ đạo sao chổi cắt quỹ đạo Trái Đất (coi là đường tròn bán kính R0 = 1.5 · 108km) dưới góc
θ = 45o. Quỹ đạo sao chổi và Trái Đất nằm cùng 1 mặt phẳng.
(a) Tìm khoảng cách cận điểm R
của quỹ đạo sao chổi quanh Mặt Trời. Giả thiết viễn điểm của quỹ min đạo Rmax >> R0.
(b) Trong bao ngày thì khoảng cách từ sao chổi tới Mặt Trời sẽ nhỏ hơn R0? Bài 3: Lost in space
1. Giả thiết coi Trái Đất là một quả cầu đồng chất có khối lượng phân bố đều, bỏ qua mọi tác động của
việc Trái Đất tự quay quanh mình và ảnh hưởng của các yếu tố thời tiết. Từ trạm không gian cách mặt
đất một độ cao h người ta bắn ra vật thể nhỏ. Vật nhỏ chuyển động so với Trái Đất với vận tốc ban đầu
có phương vuông góc với đường thẳng nối vật và tâm Trái Đất. Biết bán kính Trái Đất là R, khối lượng
Trái Đất là M, hằng số G.
(a) Để vật nhỏ chuyển động tuần hoàn quanh Trái Đất thì vận tốc ban đầu của nó phải thoả mãn điều kiện gì?
(b) Giả sử vận tốc ban đầu của vật là v , vật có khả năng rơi xuống đất. Tìm độ lớn và hướng của vận 0
tốc lúc vật chạm đất(tức góc hợp bởi vector vận tốc của vật và phương ngang) và thời gian kể từ
khi vật bắn ra cho đến khi rơi xuống đất.
Cho tích phân sau (Điều kiện: c<0, ∆ = b2 − 4ac > 0): √ Z x a + bx + cx2 b 2cx + b √ dx = − arcsin( √ ) + C 3 a + bx + cx2 c 2(−c)2 ∆ Bài 4: To infinity and beyond
1. Một tàu vũ trụ chuyển động theo quỹ đạo ellipse với Mặt Trời là tiêu điểm, V và C lần lượt là viễn
điểm và cận điểm của quỹ đạo. Khi tàu đến C, người ta thay đổi tức thời vận tốc của nó, tàu chuyển
động theo quỹ đạo tròn với tâm là Mặt Trời. Gọi θ là góc hợp giữa đường thẳng nối điểm V với tàu và
đường thẳng nối điểm V với Mặt Trời. Khi tàu chuyển động tròn quanh Mặt Trời, góc θ có giá trị lớn
nhất là θ0 = 35o. Cho khoảng cách từ Mặt Trời đến viễn điểm là R = 149.6 · 109 m, hằng số hấp dẫn
G = 6.67 · 10( − 11) N · m2/kg2, khối lượng Mặt Trời MS = 1.99 · 1030kg
(a) Tìm thời gian ngắn nhất tàu đi từ V đến C
(b) Tính độ biến thiên vận tốc tàu khi nó thay đổi quỹ đạo chuyển động
(c) Để thoát khỏi Mặt Trời, khi tàu chuyển động tròn đến vị trí M có θ = θ , người ta thay đổi tức thời 0
vận tốc của nó sao cho tàu chuyển động theo quỹ đạo parabol với Mặt Trời là tiêu điểm. Gọi N là
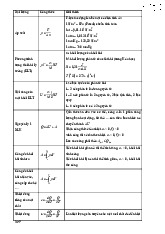
vị trí tiếp theo của tàu có θ = θ . Cho phương trình đường parabol trong hệ toạ độ Oxy có dạng 0
y2 = 2ax, với A là tiêu điểm, a=2OA là tham số tiêu (Hình 1). Hãy tính:
i. Thời gian tàu đi từ M đến N ii. Vận tốc tàu tại N Bài 5: Voyage of discovery
1. Trong một tương lai xa, công nghệ du hành vũ trụ đã phát triển lên tầm cao mới và đã đưa con người
vượt hàng vạn năm ánh sáng để khám phá ra rất nhiều hành tinh khác nhau. Trong bài tập này, chúng
ta sẽ xem xét một vài hành tinh kì lạ mà một phi hành đoàn đã khám phá ra được.
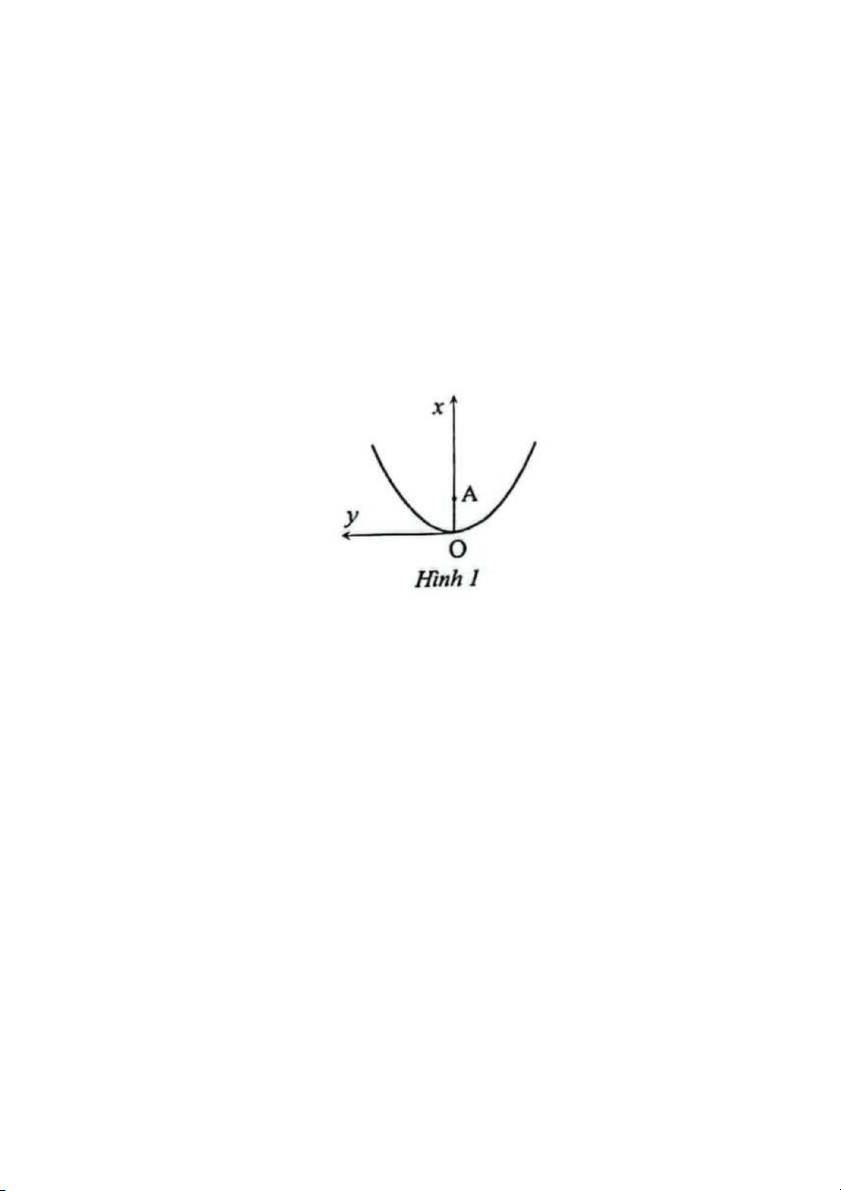
(a) Ở đằng xa, đội trưởng của phi hành đoàn phát hiện ra một hành tinh kì lạ có dạng hình hộp với
đáy hình vuông cạnh a và bề dày h << a. Ông ta liền ra lệnh đi tới tâm của hành tinh theo hướng như hình vẽ.
Phi hành đoàn phát hiện ra rằng, khi tắt động cơ của tàu vũ trụ đi thì gia tốc rơi tự do của tàu do
hành tinh gây ra ở khoảng cách H >> h, tỉ lệ với góc khối Ω (nhìn từ tàu), cho bởi công thức: g = αΩ
Sau khi đáp xuống bề mặt hành tinh và phân tích các mẫu đất, các nhà khoa học phát hiện ra rằng
hành tinh là đồng chất và có khối lượng riêng là ρ1 = 3000kg/m3 và gia tốc rơi tự do tại bề mặt mà
đoàn thám hiểm đáp xuống gần như là đều và có giá trị bằng g1 = 9.81 · 10−2m/s2 i. Tính bề dày hành tinh ii. Tính α
(b) Sau khi rời khỏi hành tinh thứ nhất, phi hành đoàn lại gặp 1 hành tinh độc lạ khác có hình dạng
kim tự tháp với đáy hình vuông cạnh a=10000 km và chiều cao a. 2
i. Tính gia tốc trọng trường của hành tinh tại đỉnh chóp của nó, biết rằng hành tinh là đồng chất
và có khối lượng riêng ρ2 = 4500kg/m3
ii. Sau khi đi khỏi hành tinh kim tự tháp, các nhà thám hiểm phát hiện ra thêm 1 hành tinh là 1
khối lập phương cạnh a. Sau khi thực hiện các đo đạc, họ tìm được khối lượng riêng của hành
tinh này là ρ3 = 5000kg/m3. Biết rằng vận tốc thoát của hành tinh kim tự tháp tại chóp là
v1 = 3.45km/s, tìm vận tốc thoát của hành tinh lập phương tại các đỉnh của nó.
(c) Rất lâu sau đó, phi hành đoàn đáp xuống một hành tinh có các đặc điểm tương đồng với Trái Đất
như bán kính R, chu kì tự quay, khối lượng riêng trung bình. Tuy nhiên, hình dạng hành tinh lại
là 1 hình trụ. Tính gia tốc trọng trường của hành tinh tại bề mặt. Biện luận tính khả thi để thoát khỏi hành tinh này? Bài 6: Wonderland
1. Trong một giấc mơ kì lạ, bạn vô tình lạc vào một xứ sở tên "Wonderland", nơi mà định luật vạn vật hấp
dẫn hơi khác đi so với ở thế giới thực. Khi được một cư dân ở Wonderland dẫn đi thăm quan vũ trụ của
họ, bạn nhận ra rằng chuyển động của các hành tinh của vũ trụ Wonderland cũng tuân theo ’Các định luật Kepler’:
(a) Các hành tinh di chuyển theo quỹ đạo ellipse với ’Mặt Trời’ ở tâm.
(b) Trong cùng một khoảng thời gian, diện tích quét của 1 hành tinh là
(c) Chu kì của các hành tinh là như nhau, không phụ thuộc vào kích thước bán trục lớn và bán trục nhỏ.
Biện luận về định luật vạn vật hấp dẫn ở Wonderland và chuyển động của các hành tinh ở Wonderland.
Từ đó rút ra phát biểu cho định luật II ’Kepler’ ở Wonderland. Bài 7: Bài toán ba vật
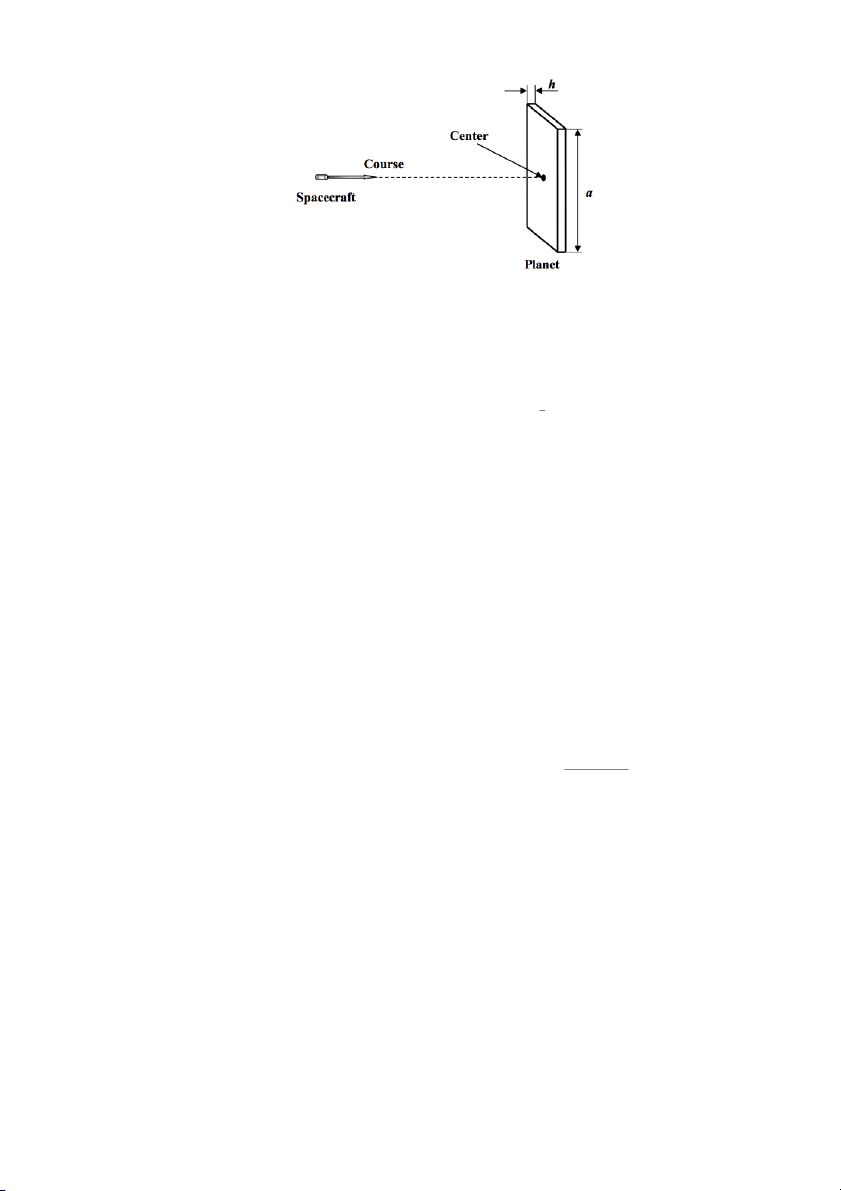
1. Hai thiên thể khối lượng M và m chuyển động tròn quanh khối tam của chúng với bán kính tương ứng R
và r. Một thiên thể thứ ba có khối lượmg µ sao cho µ « m, M được đặt vào quỹ đạo tròn có tâm là khối
tâm hệ, sao cho không có lực tác động vào µ theo phương tiếp tuyến quỹ đạo. Tìm khoảng cách giữa µ đến m, M và khối tâm O.
2. Tìm chu kỳ dao động của µ khi m=M
Bài 8: Vệ tinh địa tĩnh trong bầu khí quyển
1. Vệ tinh địa tĩnh là các vệ tinh quay trên một quỹ đạo trong trong mặt phẳng xích đạo của Trái Đất, và
có cùng vận tốc góc tự quay của Trái Đất quanh trục. Ở bài tập này, ta coi Trái Đất là vật hình cầu,
khối lượng M, bán kính R) trong đó z là độ cao của vệ tinh. Gọi g là gia tốc trọng trường tại mặt đất.
(a) Tìm độ cao quỹ đạo địa tĩnh.
(b) Khi chuyển động, vệ tinh chịu tác dụng của lực ma sát tỉ lệ với bình phương vận tốc của nó:
F = km v2 . Tính biến thiên độ cao theo thời gian dz và giải thích nghịch lý dù có ma sát nhưng tốc z dt độ vẫn tăng?
(c) Thực tế, biểu thức lực có dạng f = f
và n là những hằng số dương), lực ma sát này kéo theo 0vn (f0
một sự biến thiên nhỏ của độ cao vệ tinh trong khoảng thời gian dt: dz=-Cdt(C là hằng số dương nhỏ).
Tìm n và tìm biểu thức f theo m, C, g, và R 0
Bài 9: Trọng trường nhân tạo
1. Để có thể tạo ra một môi trường trọng lực ở trong không gian, các nhà khoa học trong tương lai đã nghĩ
ra một cách là quay một tàu vũ trụ hình trụ rất dài và to, nặng quanh trục đối xứng của nó. Chu kì
quay của nó được điều chỉnh sao cho các phi hành gia trong tàu cảm nhận được một ’trọng lực’ như ở
Trái Đất (g = 10m/s−2) ở phần rìa tàu.
Trong một nhiệm vụ dài, các phi hành gia tập thể dục ở một phòng gym cao 5m, với sàn là phần rìa tàu.
(a) Tính công thực hiện bởi 1 phi hành gia (coi là chất điểm) khối lượng 80 kg, khi anh ta trèo đến trần
của phòng gym bằng 1 cái cột. Tính biến thiên động năng của phi hành gia trong hệ quy chiếu quán
tính gắn với khối tâm của tàu vũ trụ. Kết quả có tuân theo định luật bảo toàn năng lượng không?
Nếu không, thì phần năng lượng kia đã biến đi đâu?
(b) Nếu phi hành gia ngã từ đỉnh của cột thì anh ta sẽ rơi trong bao lâu? Vị trí anh ta ngã xuống cách
chân cột bao xa (đo dọc theo sàn)?
Bài 10: Thiên thực của vệ tinh sao Mộc
1. Trong quá khứ, khi chưa có các công cụ hiện đại để đo được chính xác vận tốc ánh sáng, O Romer-một
nhà thiên văn học người Đan Mạch đã quan sát và ghi chép về thiên thực của một vệ tinh sao Mộc và
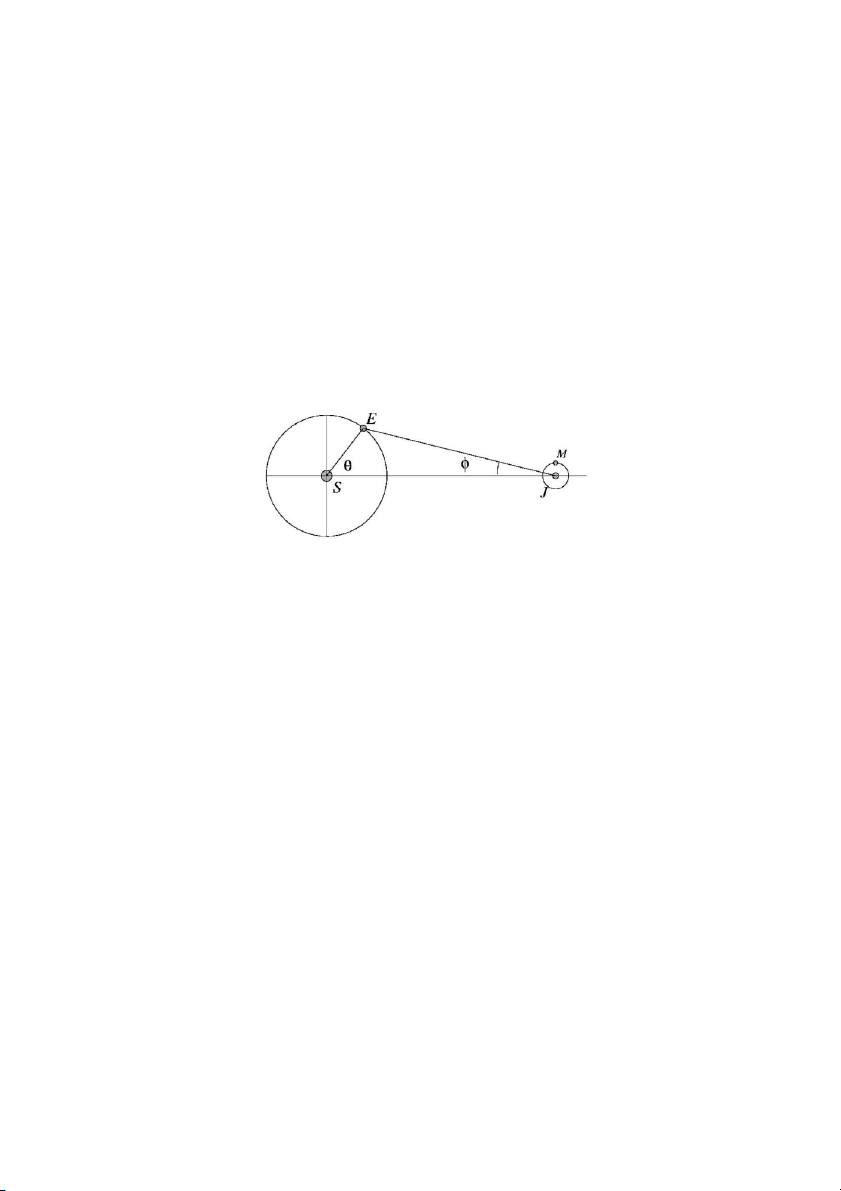
đã có thể xác định được vận tốc ánh sáng. Ông ấy đã quan sát thời điểm giữa hai lần ló của vệ tinh M
từ Mộc tinh(xem hình vẽ). Bằng cách thực hiện rất nhiều lần quan sát, ta có thể thu được một giá trị
gần đúng cho chu kì của M. Chu kì quan sát được sẽ phụ thuộc vào vị trí tương đối của Trái Đất trong
hệ quy chiếu SJ. Thời gian trung bình của 1 chu kì là T0 = 42h28m16s và chu kì dài nhất quan sát được là T0 + 15s Các thông số đã biết:
Khoảng cách từ Trái Đất->Mặt Trời:RE = 149.6 · 106
Khoảng cách tối đa: RE,max = 1.015RE
Chu kì Trái Đất quanh Mặt Trời: 365 ngày
Chu kì Mộc tinh quanh Mặt Trời: 11.9 năm
Khoảng cách từ vệ tinh M đến Mộc tinh: RM = 422 · 103km
(a) Tính khoảng cách từ Mộc tinh tới Trái Đất. Tính vận tốc góc tương đối ω của Trái Đất trong HQC Mặt Trời-Mộc tinh.
(b) Giả sử rằng một nhà thiên văn học thấy M ló dạng từ từ khỏi Mộc tinh khi vị trí ông ấy đang là Θk
và các lần ló dạng khác khi ông ấy đang ở vị trí Θ
, k=1, 2, 3,...Từ các quan sát này ông ấy thu k+1
được chu kì tức thời T (t
, sau đó sử dụng các phép xấp xỉ để chỉ ra
k) là một hàm của thời gian tk
cách khoảng cách ảnh hưởng tới chu kì quỹ đạo của M. Tính lỗi xấp xỉ khi sử dụng phép xấp xỉ đó.
(c) Tìm liên hệ hàm khoảng cách giữa Trái Đất và Mộc tinh(d(t ). Vẽ đồ thị hàm k)) và hàm chu kì T(tk
T(t ) theo thời gian quan sát . Tìm vị trí quan sát mà ở đó có thể quan sát được chu kì dài nhất, k tk
ngắn nhất, và chu kì chính xác của vệ tinh M.
(d) Tính vận tốc ánh sáng từ kết quả thu được ở các câu trên Bài 11: Wobble
1. Ở bài tập này, chúng ta sẽ tìm hiểu một phương pháp để khám phá các ngoại hành tinh có tên "Astro-
metric Wobble". Phương pháp này dựa vào việc đo đạc sự thay đổi vị trí của một ngôi sao trên bầu trời
do trường hấp dẫn của các hành tinh xung quanh nó. Phương pháp này đã trở nên dễ dàng hơn với sự
xuất hiện của các thiết bị đo hiện đại, chính xác.
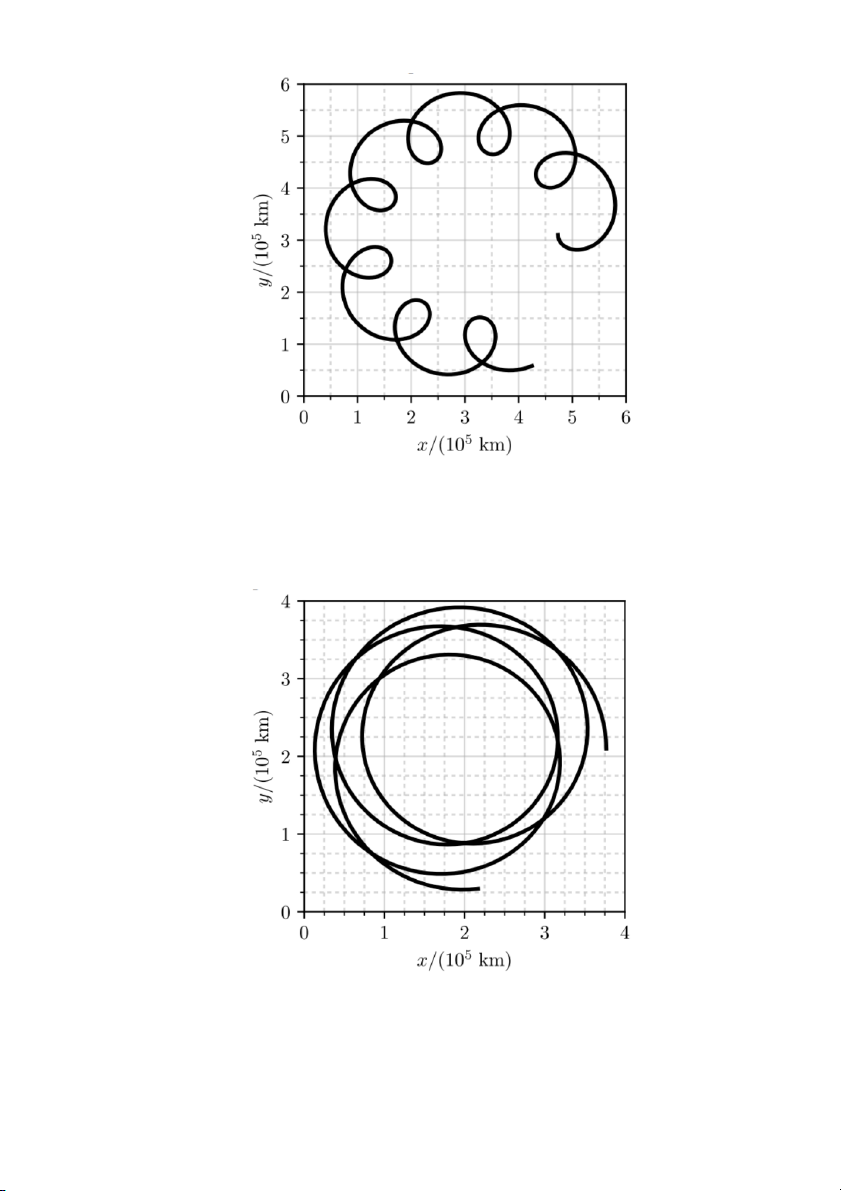
(a) Xét một hệ bao gồm 1 ngôi sao trung tâm, một hành tinh A, và 1 hành tinh B (bán kính quỹ đạo A
nhỏ hơn bán kính quỹ đạo B). Hình vẽ bên dưới là quỹ đạo của khối tâm ngôi sao trong mặt phẳng
vuông góc với tia ngắm, được đo trong khoảng thời gian 10 năm. Giả sử rằng quỹ đạo của cả hai
hành tinh đều là tròn. Tìm chu kì T và của các hành tinh. A TB
(b) Dựa vào các hình ảnh của hành tinh A, người ta đo được bán kĩnh quỹ đạo của nó là aA = 1.5AU =
2.2 · 108km. Tìm khối lượng M của sao trung tâm, và tìm khối lượng m của hành tinh A. A
(c) Tìm khối lượng hành tinh B.
(d) Xem xét 1 hệ sao và 2 hành tinh khác, cũng được quan sát và đo đạc trong thời gian 10 năm. Quỹ đạo
của khối tâm ngôi sao đó được cho ở hình dưới. Tìm khối lượng M của ngôi sao này, và khối lượng mA,
m của hai hành tinh. Cho bán kính quỹ đạo của hành tinh nằm trong là B aA = 1.3AU = 2.0 · 108km
Bài 12: Quỹ đạo đồng bộ
1. Chu kỳ quanh của Mặt trăng quanh trục của nó hiện tại bằng chu kỳ quay của nó quanh Trái Đất sao
cho cùng một phía của Mặt trăng luôn hướng về Trái Đất. Sự bằng nhau của hai chu kỳ này có lẽ đã
xảy ra do tác động của các lực thuỷ triều trong lịch sử lâu dài của hệ Trái Đất-Mặt Trăng.
Tuy nhiên, chu kỳ quay của Trái Đất quanh trục nó hiện tại ngắn hơn chu kỳ quay của Mặt trăng. Do
đó, các lực thuỷ triều của Mặt trăng tiếp tục hoạt động theo cách có xu hướng làm chậm tốc độ quay
của Trái Đất và đẩy Mặt trăng ra xa hơn.
Trong câu hỏi này, chúng ta quan tâm đến việc ước tính xem sẽ mất thêm bao nhiêu thời gian nữa để
chu kỳ quay của Trái Đất bằng với chu kỳ quay của Mặt trăng. Lúc đó, Mặt trăng đã trở thành vệ tinh
đồng bộ. Chúng ta sẽ tìm hiểu xem Trái Đất sẽ mất bao lâu để hoàn thành một vòng quay khi hai chu kỳ nói trên bằng nhau.
Hai hệ toạ độ sẽ được sử dụng làm HQC. Trục toạ độ thứ của hai hệ thống này song song với nhau và
vuông góc với mặt phẳng quỹ đạo của Mặt trăng.
(II) HQC thứ nhất, gọi là HQC khối tâm, là HQC quán tính có gốc toạ độ tại khối tâm C của hệ Trái Đất-Mặt trăng.
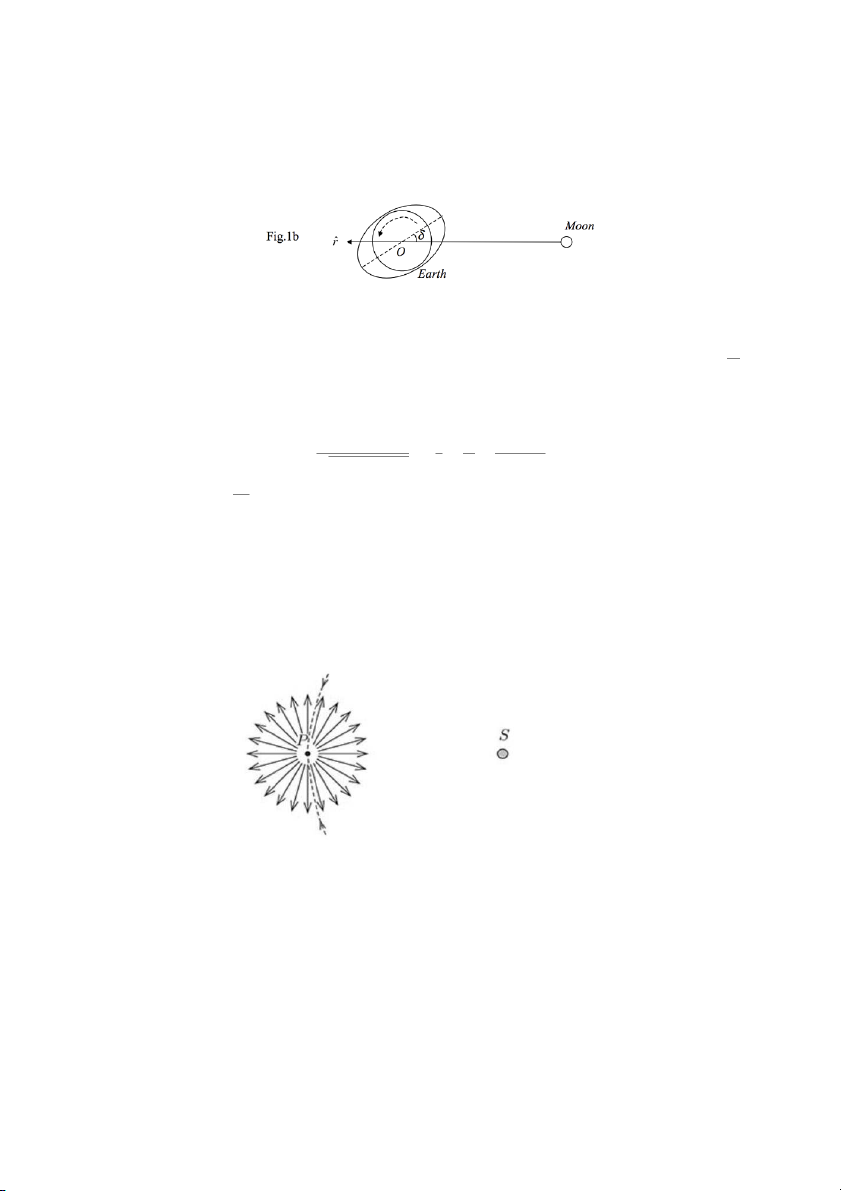
(II) HQC thứ hai, gọi là HQC xyz, có gốc toạ độ cố định tại tâm O của Trái Đất. Trục z của nó trùng
với trục quay của Trái Đất. Trục x của nó nằm dọc theo đường nối tâm của Mặt trăng và Trái Đất, và
chỉ theo hướng của vector đơn vị ˆr như hình vẽ. Mặt trăng luôn nằm trên trục x âm trong HQC này.
Lưu ý rằng khoảng cách trong hình không được vẽ theo tỉ lệ. Các mũi tên cong cho thấy hướng quay
của Trái Đất và vòng quay của Mặt trăng. Khoảng cách Trái Đất-Mặt trăng được ký hiệu là r.
Các dữ liệu sau đây được cho:
(a) Hiện tại, khoảng cách giữa Mặt trăng và Trái Đất là r0 = 3.85 · 108 và tăng với tốc độ 0.038 m mỗi năm.
(b)Chu kỳ quay của Mặt trăng hiện nay là =27.322 ngày
(c)Khối lượng Mặt trăng là M = 7.35 · 1022kg
(d)Bán kính Mặt trăng RM = 1.74 · 106m
(e)Chu kỳ tự quay của Trái Đất hiện tại TE = 23.933 giờ
(f)Khối lượng Trái Đất ME = 5.97 · 1024
(g)Bán kính Trái Đất RE = 6.37 · 106m
Các giả định sau đây có thể được thực hiện khi trả lời câu hỏi:
(i)Hệ thống Trái Đất-Mặt trăng là hệ cô lập.
(ii)Quỹ đạo của Mặt trăng quanh Trái Đất là tròn.
(iii)Trục quay của Trái Đất vuông góc với mặt phẳng quỹ đạo của Mặt trăng.
(iv)Phân bố khối lượng Trái Đất là đều. Trái Đất là hình cầu bán kính RE
(v)Đối với Trái Đất hoặc Mặt trăng, momen quán tính I đối với bất kỳ trục nào đi qua tâm của nó là
của một quả cầu đồng chất khối lượng M và bán kính R.
(vi)Nước quanh Trái Đất đứng yên trong hệ quy chiếu xyz.
Trả lời các câu hỏi sau:
(a) Đối với khối tâm C, giá trị hiện tại của tổng momen động lượng L của hệ Trái Đất-Mặt Trăng là bao nhiêu?
(b) Khi chu kỳ quay của Trái Đất và chu kỳ quay của Mặt Trăng bằng nhau thì một vòng quay của
Trái Đất là bao lâu? Biểu thị câu trả lời là T và diễn đạt theo đơn vị ngày hiện tại. Chỉ cần phương
pháp gần đúng để sử dụng phương pháp lặp.
(c) Coi Trái Đất là một quả cầu rắn quay được bao phủ một lớp nước trên bề mặt và giả sử rằng khi
Mặt trăng chuyển động quanh Trái đất, lớp nước đứng yên trong HQC xyz. Trong một mô hình,
lực ma sát giữa quả cầu rắn quay và lớp nước được tính đến. Trái đất rắn quay nhanh hơn được
cho là sẽ kéo theo thuỷ triều của Mặt trăng sao cho đường nối các chỗ phình ra của thuỷ triều tạo
một góc δ với trục x, như thể hiện trong hình bên. Do đó, các lực thuỷ triều của Mặt Trăng tác
dụng lên Trái Đất sẽ tạo ra một momen xoắn Γ quanh O để làm chậm chuyển động quay của Trái Đất.
Góc δ được coi là không đổi và không phụ thuộc vào khoảng cách Trái Đất-Mặt trăng r cho đến khi
nó biến mất khi vòng quay của Mặt trăng đồng bộ với vòng quay của Trái Đất để lực ma sát không
còn tồn tại. Momen xoắn Γ do đó tỷ lệ với khoảng cách Trái Đất-Mặt trăng và tỷ lệ thuận với 1 . r6
Theo mô hình này, khi nào chu kỳ quay của Trái Đất và chu kỳ quay của Mặt Trăng sẽ bằng nhau?
Biểu thị câu trả lời là t và thể hiện kết qủa theo đơn vị năm hiện tại. f
Cho: Với 0 ≤ s < r và x=scos(θ): 1 1 x 3x2 − s2 √ ≈ ( − + + ...) r2 + s2 + 2rx r r2 2r3
Nếu a = 0 và dω = bω1−a thì ωa(t′) − ωa(t) = (t′ − t)ab dt Bài 13: Bantumlum
1. Hai sao chổi có khối lượng và vận tốc bằng nhau được phát hiện bởi các nhà thiên văn học. Trong lúc
quan sát, họ nhận ra rằng hai thiên thạch đang bay qua mặt trời theo hai quỹ đạo parabol giống nhau
nằm trong cùng một mặt phẳng. Hai thiên thạch sau đó đã va chạm với nhau tại cận điểm của quỹ đạo
và nổ tung thành từng mảnh vụn. Những mảnh vụn này bắn đi khắp mọi hướng và cùng một vận tốc đầu (Xem hình vẽ).
(a) Hình bao quanh Mặt trời tạo bởi tập hợp quỹ đạo của các mảnh vụn sau vụ nổ là hình gì? Bài 14: Gravitational Lensing
1. Gravitational Lensing là hiện tượng khi mà ánh sáng từ một nguồn sáng rất xa bị ảnh hưởng bởi trường
hấp dẫn rất lớn của một thiên thể nằm giữa hoặc nằm gần tia ngắm giữa người quan sát và nguồn sáng.
Hiện tượng này lần đầu được phát hiện ra vào sự kiện Nhật thực năm 1919, khi vị trí của các ngôi sao ở
sau Mặt Trời khác với vị trí đo được của chúng trong vũ trụ, sự kiện này đã chứng minh thuyết tương
đối của Einstein là chính xác.
Khi ánh sáng đi qua một thiên thể có khối lượng lớn M, hướng đi của nó sẽ bị chệch đi một góc: 4GM α = rc2
Hiện tượng này đã giúp nhân loại trong việc tìm ra các ngoại hành tinh. Phương pháp này có tên "Exoplanet Microlensing".
(a) Xét một ngôi sao S ở vị trí D tính từ Trái Đất là nguồn sáng. Một ngôi sao L khác có khối lượng s
M và ở vị trí D < ( ) từ Trái Đất làm "thấu kính". Đường nối EL và ES tạo một góc nhỏ l Ds β giữa
chúng. Kẻ một đường vuông góc với EL qua L(coi đó là "thấu kính"), gọi góc nhìn của ngôi sao S
quan sát từ Trái Đất là Θ. Vẽ hình và tính góc Θ theo các thông số đã cho(D ), coi s, Dl, G, M , c, β
rằng đường truyền ánh sáng từ S đến thấu kính và từ thấu kính đến E là thẳng.
(b) Khi ba vật trên thẳng hàng nhau(Trái Đất, S, và L), thì ảnh quan sát được của S sẽ là một cái
vòng. Người ta gọi đấy là "nhẫn Einstein". Tìm bán kính góc Θ của nhẫn Einstein. Vẽ ảnh quan E
sát được của S khi ba vật nằm thẳng hàng nhau.
(c) Khi ba vật không thẳng hàng, ảnh quan sát được của S sẽ trông như thế nào?
2. Xét một trường hợp mà Mặt trời của ta là một "thấu kính". Tính khoảng cách nhỏ nhất, f (đơn vị min
A.U), tính từ tâm Mặt trời, mà các tia sáng từ xa vô cùng hội tụ.
Cho bán kính Mặt Trời là 1 RS = AU . 125
3. Trong vũ trụ, có rất nhiều vật thể có khối lượng phân bố không đồng đều mà ánh sáng có thể đi qua
và bị bẻ cong, , ví dụ như vật chất tối ở các cụm thiên hà. Để đơn giản hoá tính toán, giả sử rằng với
khoảng cách r(tính từ đường truyền ánh sáng ban đầu tới tâm vật thể), thì chỉ khối lượng bên trong bán
kính r đó mới ảnh hưởng tới đường truyền ánh sáng.
Tìm phân bố khối lượng M(r), sao cho các vật thể này có tính chất giống với thấu kính quang học lý tưởng.
Bài 15: Newton-Laplace Cosmology
1. Sau khi Isaac Newton phát hiện ra định luật vạn vật hấp dẫn, Pierre-Simón Laplace đã thử mô hình hoá
vũ trụ là một đám mây chứa vật chất chuyển động. Laplace giả thiết rằng: ở khoảng cách rất xa giữa
các vật chất, chỉ có tương tác hấp dẫn là đáng kể. Tuy nhiên, Laplace thiếu các thông số thực tế để có
thể hoàn thiện mô hình vũ trụ này.
Vào thế kỉ 10, các quan sát thiên văn học cho ta biết rằng ở các vị trí quan sát được của vũ trụ, vật
chất được phân bố đồng đều và đẳng hướng(ví dụ: ở những nơi có nhiều thiên hà thì khối lượng riêng
trung bình ở đó là gần như bằng nhau). Ngoài ra, Edwin Hubble đã phát hiện ra một định luật: vận tốc
xuyên tâm V (vận tốc của các thiên thể theo phương ngắm), tỉ lệ với khoảng cách r: r Vr = H · r, với H
là hằng số Hubble (hằng số này không phụ thuộc vào khoảng cách và xấp xỉ bằng H −1 t ≈ 7 · 10−11năm .
George Gamow cho rằng lí do phân bố vận tốc có giá trị như vậy vì Big Bang(vụ nổ khai sinh vũ trụ)
đã xảy ra ở một không gian nhỏ, và sau đó vật chất đã bay đi theo các mọi hướng với các vận tốc khác
nhau. Do đó, các hạt vật chất có vận tốc lớn hơn, thì giờ đã ở rất xa khỏi vị trí ban đầu.
(a) Dựa vào phát biểu của định luật Hubble, liệu có thể khẳng định rằng thái dương hệ là nơi mà vụ
nổ Big Bang đã xảy ra (vì Hubble đã quan sát từ Trái Đất)? Giải thích?
Trong vật lí lý thuyết, thuyết tương đối rộng của Einstein đã được dùng để mô tả sự giãn nở của vũ trụ
sau Big Bang. Tuy nhiên, trong bài tập này, ta sẽ thử tìm một số kết luận mà Laplace đã có thể rút ra
nếu ông sử dụng mô hình vũ trụ của mình kết hợp định luật Hubble, các định luật của Newton, và các
dữ kiện về sự đồng nhất của vũ trụ.
Xét sự giãn nở của mô hình vũ trụ cổ điển (Newtonian Universe-NU). NU là một khối cầu đồng chất có
khối lượng M = 1055kg, trong đó, tương tác giữa các hạt vật chất chỉ có tương tác hấp dẫn, và vận tốc
của vật chất tuân thủ định luật Hubble. Tuy nhiên, hằng số H lại là một hàm phụ thuộc vào thời gian H(t).
(a) Tính thế năng hấp dẫn E của NU ở thời điểm t theo M và R, với R là bán kính tại thời điểm T G của NU.
(b) Tính động năng E của NU ở cùng thời điểm theo M, H, và R. K
Ta có thể thấy rằng, quá trình giãn nở của NU sẽ dần chậm lại bởi trọng lực. Giả sử rằng, vào thời điểm
t nào đó (tính từ Big Bang), "cư dân"của NU đã đo được khối lượng riêng trung bình ρ(t)của vật chất
trong NU và hằng số Hubble H(t).
(a) Tìm liên hệ giữa ρ(t) và H(t) để sự giãn nở của NU có thể dừng lại và thay bằng sự co lại (trong
một khoảng thời gian hữu hạn). Viết câu trả lời dưới dạng bất đẳng thức.
(b) Giả sử rằng tổng năng lượng của NU(bao gồm động năng và thế năng hấp dẫn) là −2 E = M c2, với 15
c là tốc độ ánh sáng trong chân không. Tìm bán kính tối đa của NU trong quá trình giãn nở. Viết
kết quả trong đơn vị parsecs(1 parsec bằng 3.2 năm ánh sáng, hoặc 3 · 106m)
(c) Dựa vào điều kiện câu trên, tìm tuổi thọ của NU từ Big Bang tới Big Implosion. Viết câu trả lời trong đơn vị năm. Cho biết: √ Z 1 x Z 1 √ dx = 2 p1 − y2 dy 0 1 − x 0
(d) Tìm các trường hợp khả dĩ khác cho chuyển động vật chất trong NU với các mức năng lượng E khác
nhau. Mô tả định tính sự thay đổi của bán kính NU cho từng trường hợp. Để làm được điều này,
hãy vẽ phác đồ thị của hàm R(t) và hàm dR V
cho từng trường hợp(cho biết rằng vào thời R(t) = dt
điểm vụ nổ Big Bang t=0 thì bán kính của NU có thể coi là bằng 0). Bài 16: Thần Châu 12
1. Việc ghép thành công tên lửa có người lái Thần Châu 12 với trạm vũ trụ Thiên Cung vào tháng 6 năm
2021 liên quan đến bài toán đuổi bắt giữa tên lửa đuổi (mô-đun Thần Châu 12) và mục tiêu (trạm vũ
trụ) trên quỹ đạo quanh Trái đất. Bài toán này sử dụng sơ đồ thay đổi quỹ đạo đuổi bắt để nghiên cứu
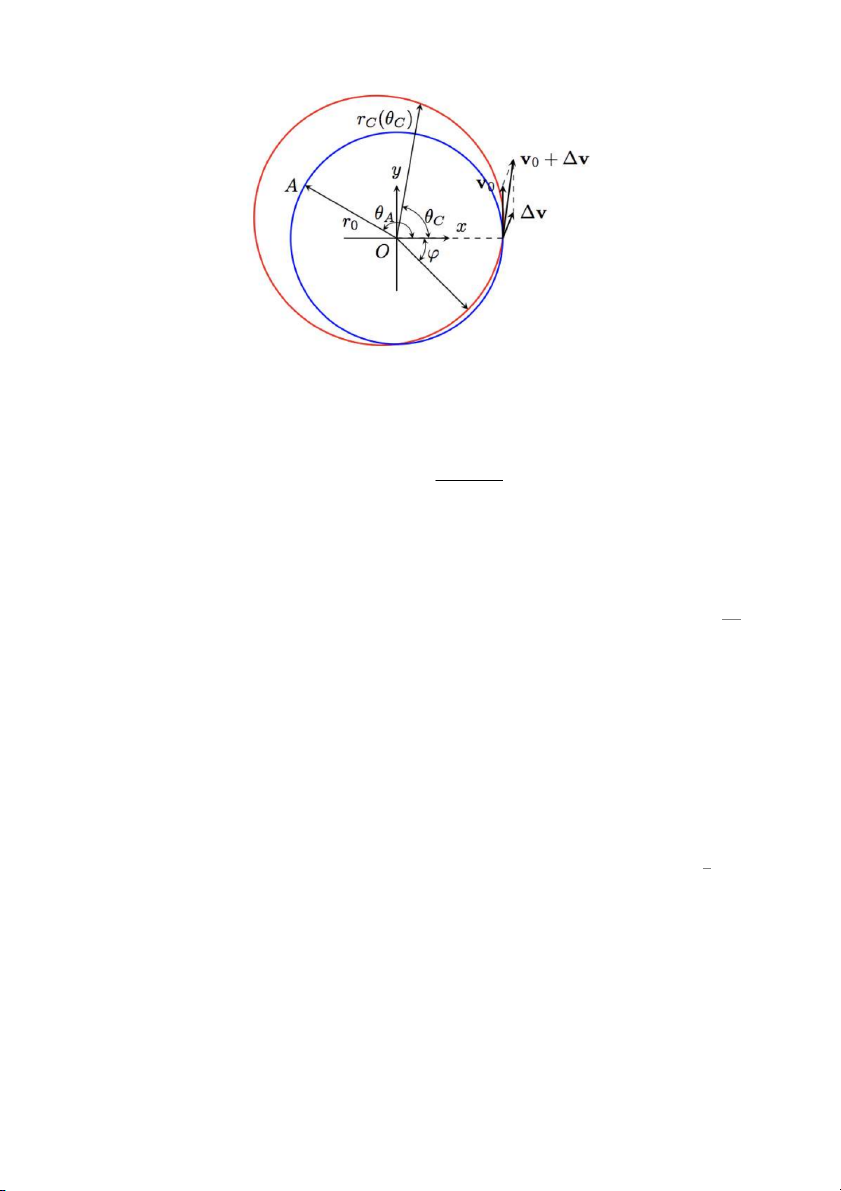
cách tên lửa thay đổi vận tốc để cập bến với mục tiêu theo quỹ đạo cố định. Như được minh hoạ trong
hình vẽ, mục tiêu A và tên lửa đuổi C đều đang chuyển động ngược chiều kim đồng hồ với tốc độ v0
theo quỹ đạo tròn bán kính r . Vị trí của hai vật thể tại thời điểm 0 là 0
θA,i = θ0, θc,i = 0, rA,i = rc, i = r0
Tại thời điểm này, tên lửa C phụt nhiên liệu ngay lập tức và vận tốc thay đổi ngay lập tức một lượng
∆v (xem hình vẽ); quỹ đạo C cũng thay đổi tức thì từ quỹ đạo tròn bán kính r sang quỹ đạo elip như 0
trong hình. Góc giữa trục chính của quỹ đạo hình elip và hướng của trục cực(đường từ tâm đến vị trí
C tại thời điểm phụt) là ϕ (ϕ được đo theo chiều kim đồng hồ). Góc giữa hướng chuyển động của C và
hướng của trục cực là θ (
theo chiều dương ngược chiều kim đồng hồ), khoảng cách giữa tâm O và C C θC là rC(θC).
(a) Nếu biết khối lượng m, năng lượng E (thực chất là tổng cơ năng của hệ vật và Trái đất) và momen
động lượng L của vật, hãy biểu diễn các thông số quỹ đạo p, ε theo E, L, m và các tham số đã biết r ,
, v.v. được đưa ra trong câu hỏi. Biết rằng hình dạng của một quỹ đạo elip dương(có trục dài 0 v0
dọc theo trục cực) trong hệ toạ độ cựuc(lấy gốc toạ độ làm trọng tâm) tuân theo định luật I Kepler là p r(θ) = 1 + εcos(θ)
trong đó p là bán trục vuông và ε là tâm sai, được gọi chung là tham số quỹ đạo.
(b) Viết biểu thức cho quỹ đạo r , tâm sai
c(θC ) của tên lửa đuổi C sau khi phụt khí (xem hình) theo r0 ε và ϕ. (c) Viết tỷ số T của chu kỳ quỹ đạo
của tên lửa sau khi phụt khí với chu kỳ của mục tiêu C /TA TC TA A theo ε và ϕ
(d) Xác định hai tham số phụt khí (xem Hình): Tốc độ thay đổi không thứ nguyên của vận tốc ∆v δ = | |, v0 góc α giữa ∆v và v ( 0
α = 0 khi trùng hợp, lấy theo chiều kim đồng hồ làm chiều dương). Cố gắng
sử dụng các thông số δ và α để biểu thị tâm sai ε và εcosϕ của quỹ đạo của kẻ săn đuổi C.
(e) Hãy xem xét trường hợp mà tên lửa đuổi C và mục tiêu A gặp nhau tại điểm giao quỹ đạo của lớp
quỹ đạo đầu tiên. Giả sử số lần mục tiêu A vượt qua điểm giao quỹ đạo đầu tiên kể từ thời điểm
0 là n và số lần tên lửa C vượt qua điểm giao quỹ đạo đầu tiên (không tính điểm bắt đầu) là nC. A Tại thời điểm 0, θ theo A,i = θ0, θc,i = 0. Tìm nA nC, θ0, ε, và ϕ. (f) Biểu diễn n theo cho A
δ và α, giữ nguyên δ và cố gắng tìm hai điểm cực trị đơn giản, khác biệt α0
sự thay đổi của hàm nA(α) (do đó, mặc dù góc α tại thời điểm tia lửa phun có một số độ lệch so
với α , giải pháp vẫn giữ ở mức xấp xỉ, tạo điều kiện cho việc ghép thành công). 0
(g) Nếu một trong hai giá trị α trên được sử dụng: 0
i. Giá trị của δ có giới trên δ (tức là nếu
, việc ghép sẽ thất bại), tìm max δ > δmax δmax
ii. Đặt giá trị ban đầu của π θ là , tìm liên hệ giữa , , ; tìm giá trị A θ0 δ và θ0 nA nC δ khi θ0 = , n 2 A = 2, nC = 1.
Bản dịch của bài tập này được tham khảo từ anh Kiên T. Phạm.