
Preview text:
lOMoARcPSD| 36207943
CÂU HỎI PHẦN TỰ LUẬN của ĐỀ THI GIỮA KỲ
1. Trưởng phòng nhân sự của một công ty tuyên bố rằng tiền lương của tấtcả
nhân viên làm việc ở công ty này sau 3 năm sẽ tăng gấp đôi so với khi họ vừa
được tuyển dụng vào công ty? Dựa vào kiến thức đã học của môn
Thống kê Ứng dụng, làm thế nào để kiểm tra xem tuyên bố trên có đáng tin cậy không?
2. Quan sát số hoa hồng bán ra trong một ngày của một cửa hàng bán hoasau
một thời gian, người ta ghi được số liệu sau: Số hoa hồng ( đoá ) 12 13 15 16 17 18 19 Số ngày 3 2 7 7 3 2 1
(a) Tìm ước lượng điểm của số hoa hồng trung bình bán được trong mộtngày.
(b) Sau khi tính toán, ông chủ cửa hàng nói rằng nếu trung bình mộtngày
không bán được 15 đoá hoa thì chẳng thà đóng cửa còn hơn. Dựa vào số
liệu trên, hãy kết luận giúp ông chủ cửa hàng xem có nên tiếp tục bán hay
không với mức ý nghĩa 5%.
(c) Giả sử những ngày bán được từ 13 đến 17 đoá hồng là những ngày“bình
thường”. Hãy ước lượng tỉ lệ của những ngày bình thường của cửa hàng
với độ tin cậy 90%. (Giả thiết rằng số hoa bán ra trong ngày có phân phối chuẩn).
3. (THÊM ) Một giảng viên nhận xét rằng kết quả học môn Thống kê có phụ thuộc
vào giới tính của sinh viên. Dựa vào kiến thức đã học của môn Thống kê Ứng
dụng, làm thế nào để kiểm tra xem nhận xét của giảng viên này có đúng hay không?
GỢI Ý CHO ĐÁP ÁN PHẦN TỰ LUẬN
1. Câu 1 cần trả lời xoay quanh các ý chính sau:
- Xác định dữ liệu: lương của các nhân viên trong công ty, lúc vừa được tuyển
dụng và lương sau 3 năm.
- Thống kê mô tả dữ liệu: như trung bình, phương sai (độ lệch chuẩn), các bảng biểu đồ thị.
- Dạng bài toán khác biệt hai trung bình, mẫu cặp.
- Thiết kế bài toán kiểm định 1
2. Đây là gợi ý giải bài toán 2
Gọi X số đoá hoa hồng được bán ra trong một ngày.
Khi đó, X ∼N(µ,σ2). a. x¯ = 15,4
Downloaded by nn nmr (janccokoorc@hotmail.com) lOMoARcPSD| 36207943 b. •
(H01 : µ = 15 H : µ < 15
• Thống kê kiểm định: Khi H0 đúng
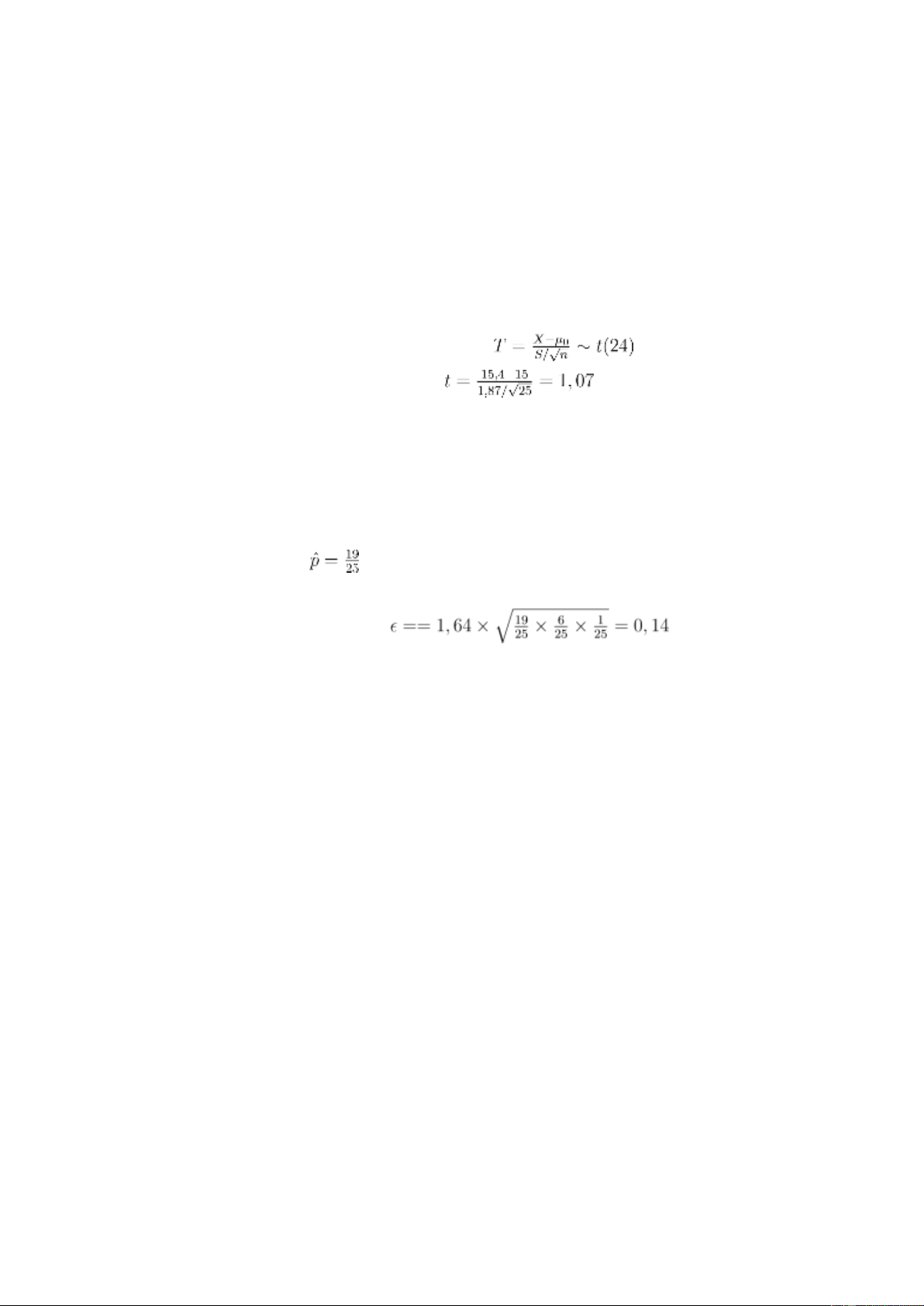
• Giá trị thống kê kiểm định:
• Với mức ý nghĩa 5%, ta thấy t = 1,07 > −1,7109 = −t0,95;24 nên chưa
đủ cơ sở bác bỏ H0. Vậy với mức ý nghĩa 5%, ông chủ cửa hàng nên tiếp tục bán.
c. Gọi p là tỷ lệ những ngày cửa hàng bán bình thường. • Tỉ lệ mẫu
• Kiểm tra điều kiện: np >ˆ 5 và n(1 − pˆ) > 5 • Dung sai ước lượng
• Kết luận: Vậy khoảng tin cậy 90% cho tỷ lệ những ngày bán bình
thường là p ∈ (0,62;0,9).
3. Câu 3 cần trả lời xoay quanh các ý chính sau:
- Xác định dữ liệu: kết quả học tập của sinh viên nam và nữ. - Thống kê mô tả
dữ liệu: như trung bình, phương sai (độ lệch chuẩn), các bảng biểu đồ thị.
- Dạng bài toán khác biệt hai trung bình, mẫu độc lập. - Thiết kế bài toán kiểm định. 2
Downloaded by nn nmr (janccokoorc@hotmail.com)




