










































































Preview text:
lOMoARcPSD| 36207943
Câu 1: Cho A là ma trận vuông cấp n thỏa điều kiện 𝟐𝐀𝟐 − 𝐀 = 𝐈𝐧. Phát biểu nào sau đây là sai? A. 𝐀 khả đảo
B. 𝐈𝐧 − 𝟐𝐀 khả đảo
2A2 − A = In ⇒ A. 2A − A = In ⇒ A(2A − I) = I ⇒ A và 2A-I đều khả đảo
C. 𝐈𝐧 + 𝐀 khả đảo
2A2 − A = In ⇒ In + A = 2A2 ⇒ |In + A| = |2A2| = 2n. |A|2 ≠ 0 ⇒ In + A khả đảo. D. 𝐈𝐧 = 𝐀
2A2 − A = In ⇒ 2A2 − A − In = θ ⇒ 2A2 − 2A + A − In = θ ⇒ 2A(A − In) + (A − In) = θ
⇒ (2A + I)(A − I) = θ ⇒ [2A + I = 0 ⇒ [A = −I A − I = 0 A = I
Kết luận In = A là chưa chính xác, vì cũng có thể A = − I.
Câu 2: Tìm m để hàm số 𝐟(𝐱) = 𝟏
𝐦𝐱 − 𝟏 có giới hạn hữu hạn khi x tiến đến vô cùng. 𝐞 −𝟏 𝐱
-Điều kiện xác định của hàm số emx − 1 ≠ 0 ⇒ m ≠ 0
-Xét trường hợp mx → −∞, tức khi { m > 0 và , ta có: x → −∞
lim emx = 0 ⇒ lim f(x) = −1 x→∞ x→∞
-Xét trường hợp mx → +∞, tức khi , ta có: x − emx + 1 −memx −m2emx −m lim f(x) = lim
mx − x = x→∞lim emx + mxemx − 1 = x→∞lim memx + memx + m2xemx = x→∞lim 2 + mx x→∞ x→∞ xe = 0
-Vậy ∀m ≠ 0 thì lim f(x) là hữu hạn. x→∞
Phần 1: ĐẠI SỐ TUYẾN TÍNH K41 – MÃ ĐỀ 209 lOMoARcPSD| 36207943 Câu 1: Cho 𝐀 = (𝟏
𝟐) và 𝐁 = 𝐀𝟓 + 𝐦𝐀𝟔. Tìm điều kiện của m để B không khả đảo. 𝟐 𝟏
B không khả đảo ⇔ |B| = 0 ⇔ |A
= 0 ⇔ |A (I + mA) = 0 ⇔ |A| .|I + mA|
|A| = 0 (không thỏa)m1 + m ⇔ [ ⇔ |I + mA| |I + mA| = 0 2m m2m 1 + m
⇔ (1 + m)2 − 4m2 = 0 ⇔ −3m
Câu 2: Cho A, B, C là các ma trận vuông cấp 3 có 𝐝𝐞𝐭𝐀 = 𝟓, 𝐝𝐞𝐭𝐁 = 𝟏𝟎, 𝐝𝐞𝐭𝐂 = 𝟓𝟎 và 𝐌 = 𝟓𝐀𝐁𝟐𝐂−𝟏. Tính định thức của ma trận M?
|M3x3| = |5AB2C−1| = 53.|A|. |B2|.|C−1| = 53.|A|. |B|2. |C|−1 = 53. 5.102.50−1 = 1250
Câu 3: Tìm m để không gian nghiệm của hệ phương trình sau có số chiều lớn nhất:
𝐱𝟏 + 𝐱𝟐 + 𝐱𝟑 + 𝐱𝟒 + 𝐱𝟓 = 𝟎 {
𝟐𝐱𝟏 + 𝟑𝐱𝟐 + 𝟒𝐱𝟑 + 𝟓𝐱𝟒 + 𝟔𝐱𝟓 = 𝟎
(𝐦 − 𝟏)𝐱𝟏 + 𝟓𝐱𝟐 + 𝟔𝐱𝟑 + 𝟕𝐱𝟒 + 𝟐(𝐦 − 𝟏)𝐱𝟒 = 𝟎 1 1 1 1 1
-Ta có: 𝐝𝐢𝐦𝐕 = 𝐧 − 𝐫𝐚𝐧𝐤(𝐀) với n = 5 là số ẩn của hệ phương trình và A = ( 2 3 4 5 6 ) m − 1 5 6 7 2(m − 1)
Như vậy: dimV → max ⇔ rank(A) → min.
-Rõ ràng hai dòng đầu của A đã độc lập với nhau. Muốn rank(A) nhỏ nhất thì ta phải tìm m sao cho dòng 3 được
tạo ra bởi hai dòng đầu. Nhìn các hệ số của các ẩn x2,x3, x4, ta dễ dàng nhận thấy: d3 = 2d1 + d2, suy ra: 1.2 + 2 = m − 1 ⇒ m = 5
Thật vậy, khi m = 5 thì d3 = 2d1 + d2, tức dòng 3 phụ thuộc tuyến tính vào 2 dòng trên, làm cho hạng của ma trận
A bằng 2, đạt cực tiểu.
-Vậy dimV → max ⇔ m = 5.
Công thức 𝒅𝒊𝒎𝑾 = 𝒏 − 𝒓𝒂𝒏𝒌(𝑨) có vẻ lạ đối với nhiều bạn, vì ta thường học 𝒅𝒊𝒎𝑾 = 𝒓𝒂𝒏𝒌(𝑨) và 𝒅𝒊𝒎𝑾 =
𝒏. Thật ra, điều lạ đó xảy ra do ta viết công thức mà không hiểu A và n ở đây là gì.
Mình có 3 bài toán như sau:
Bài toán 1: Cho không gian con W = . Tìm số chiều của W?
𝐝𝐢𝐦𝐕 = 𝐧 = 𝟐, 𝐯ớ𝐢 𝐧 𝐥à 𝐬ố 𝐛𝐢ế𝐧 𝐭𝐫𝐨𝐧𝐠 𝐯é𝐜𝐭ơ 𝐧𝐠𝐡𝐢ệ𝐦
Bài toán 2: Cho W là không gian sinh bởi hệ {(1,0,0),(0,1,0),(1,1,0),(1,1,1)}. Tìm số chiều của W?
𝐝𝐢𝐦𝐖 = 𝐫𝐚𝐧𝐤(𝐀) = 𝟑, 𝐯ớ𝐢 𝐀 𝐥à 𝐦𝐚 𝐭𝐫ậ𝐧 𝐠ồ𝐦 𝐜á𝐜 𝐯é𝐜𝐭ơ 𝐬𝐢𝐧𝐡 x + y + z = 0
Bài toán 3: W là không gian nghiệm của hệ phương trình {x + 2y + 4z = 0 . Tìm số chiều của W?
Muốn tìm số chiều của W, ta phải tìm nghiệm của hệ phương trình đã cho. Đó là: lOMoARcPSD| 36207943 3x x (x, − , ) 2 2 Khi đó, ta viết: W = Kết luận: dimW = 1 Dễ dàng nhận thấy:
(với n là số ẩn của hệ phương trình)
(với A là ma trận đặc trưng cho hệ phương trình) Vậy thật sự thì:
𝐝𝐢𝐦𝐖 = 𝐧 − 𝐫𝐚𝐧𝐤(𝐀)
Với n là số ẩn trong hệ phương trình và A là ma trận đặc trưng cho hệ phương trình.
Khi dùng công thức, hãy chú ý đề bài và hiểu rõ ý nghĩa của n và rank(A) nhé, để tránh bị nhầm lẫn.
Câu 4: Cho A và B là các ma trận vuông cấp n thỏa 𝐀 = 𝐏𝐁𝐏−𝟏, với P là ma trận vuông cấp n khả nghịch. Phát biểu nào sau đây là sai?
A. A khả nghịch khi và chỉ khi B khả nghịch
B. 𝐁𝟓 = (𝐏−𝟏)𝟓𝐀𝟓𝐏𝟓
C. 𝐝𝐞𝐭(𝐀−𝟏) = 𝐝𝐞𝐭(𝐁−𝟏)
D. 𝐁𝟓 = 𝐏−𝟏𝐁𝟓𝐏𝟓
-Trước tiên, ta tìm B theo A:
A = PBP−1 ⇒ P−1.(A). P = P−1.(PBP−1).P ⇔ P−1AP = B hay 𝐁 = 𝐏−𝟏𝐀𝐏
-Xét câu A, ta lập luận: A khả nghịch ⇔ |A| |PBP
-Xét câu C, ta lập luận:
det(A−1) = |A|−1 = |PBP−1|−1 = (|P|. |B|. |P|−1)−1 = |B|−1 = det(B−1) -Chú ý câu B va D:
B5 = (P−1AP).(P−1AP).(P−1AP). (P−1AP). (P−1AP) = P−1APP−1APP−1APP−1APP−1AP
= P−1A(PP−1)A(PP−1)A(PP−1)A(PP−1)AP = P−1A5P
Tóm lại: 𝑩 = 𝑷−𝟏𝑨𝑷 ⇒ 𝑩𝒏 = 𝑷−𝟏𝑨𝒏𝑷
Câu 5: Cho hệ phương trình tuyến tính 𝐀𝐗 = 𝐁 (𝟏) với 𝐀𝐦×𝐧 (𝐦 > 𝐧) . Ta có: lOMoARcPSD| 36207943 A. Các câu kia đều sai.
B. Tập nghiệm của (1) là không gian con của ℝ𝐧. C. Hệ vô nghiệm. D. 𝐑
Xét câu B: (1) có thể vô nghiệm
Xét câu C: (1) cũng có thể có vô số nghiệm, khả năng này cao khi số phương trình > số ẩn.
Xét câu D: Điều này là không thể, vì khi thêm 1 cột vào thì hạng của ma trận không thể giảm được, tức R R(A). Câ 6 u : C h o A
, B là 2 không gian con của ℝ𝐧. Tìm trong những tập hợp sau, tất cả những tập hợp không là không gian con c ủ a ℝ . 𝐧
-Chúng ta cứ hiểu đơn giản rằng không gian n chính là không gian n chiều, có tính đối xứng và phải chứa vector
không (gốc tọa độ). Quen thuộc nhất chính là:
-Không gian 1 chiều ℝ1: đường thẳng đi qua gốc tọa độ.
-Không gian 2 chiều ℝ2: mặt phẳng đi qua gốc tọa độ.
-Không gian 3 chiều ℝ3: hình khối, không gian chúng ta đang tồn tại, không kể thời gian. - :
+Theo tính chất đã thừa nhận thì giao của hai không gian con của ℝ𝑛 cũng là một không gian con của ℝ𝑛. Mình xin
giải thích dài dòng thêm một chút ở dưới.
+Nếu A và B là hai không gian con có cùng số chiều thì giao của chúng sẽ là không gian con bằng chính chúng hoặc
không gian con có số chiều thấp hơn 1 chiều. Ví dụ: 2 mặt phẳng trùng nhau thì giao nhau ra chính chúng. 2 mặt
phẳng cắt nhau cho ra một đường thẳng đi qua gốc tọa độ (vì mặt phẳng phải đi qua gốc tọa độ). Chú ý rằng không
có trường hợp song song vì 2 mặt phẳng đều phải đi qua gốc tọa độ (chứa vector không).
+Nếu số chiều của A lớn hơn B (hoặc ngược lại) thì giao của chúng sẽ cho ra chính A hoặc không gian con với số
chiều bằng hiệu số chiều. Ví dụ: 1 mặt phẳng chứa 1 đường thẳng thì giao cho ra chính đường thẳng. Còn nếu mặt
phẳng bị đường thẳng cắt thì chắc chắn phải cắt tại gốc tọa độ, tức không gian cho ra cuối cùng chỉ còn vector
không, cũng là một không gian con của ℝ𝑛.
+Tóm lại, C chính là không gian con cũa ℝ𝑛. -Xét 𝐃 = 𝐀\𝐁.
Vì A, B là 2 không gian con của Rn nên chắc chắc chúng chứa vector không. Loại B ra khỏi A cũng chính là
loại vector không ra khỏi A, nên kết quả cho ra không phải không gian con của ℝn nữa. - .
ại đi x mà không loại đi -x thì -x sẽ không còn ai để bắt cặp nữa. Vậy nên E không phải là không gian con của n. -
A đã có vector không rồi, gộp thêm vector không vào nữa cũng ra chính nó thôi. Hay F = A. -Xét 𝐇 = 𝐁\𝐀.
Tương tự như A\B, trong H không có vector không nên H không phải không gian con của ℝn. lOMoARcPSD| 36207943
Câu 7: Giả sử hệ phương trình tuyến tính 𝐀𝐗 = 𝐁 (có n phương trình và n ẩn số) là hệ vô nghiệm. Phát biểu nào sau đây là sai?
A) Hệ vector cột của ma trận A là hệ phụ thuộc tuyến tính
B) Ma trận A là ma trận suy biến
C) Vector cột B nằm trong không gian con sinh bởi hệ vector cột của A.
D) Hệ vector dòng của ma trận A không phải cơ sở của ℝ𝒏.
-Hệ phương trình có n phương trình n ẩn vô nghiệm (Hệ Cramer) ⇔ |A| = 0
⇔ Hệ vector cột và hệ vector dòng của A là hệ phụ thuộc tuyến tính, hay ma trận A suy biến.
⇒ Hệ vector dòng của A không phải cơ sở của n (vì cơ sở là hệ những vector độc lập tuyến tính) -Mặt khác, ta có: r
(Chú ý rằng A̅T có n+1 dòng và dòng của A̅T là cột của A̅)
Vậy nên hệ vector dòng của A̅T là hệ phụ thuộc tuyến tính, suy ra hệ vector cột của A là hệ phụ thuộc tuyến tính,
hay có thể nói rằng vector cột B được sinh ra bởi hệ vector cột của A.
Câu 8: Cho A, B là 2 ma trận vuông cấp 2 thỏa 𝐀𝐁 . Phát biểu nào sai? A) 𝐀𝟑𝐁𝟑 = 𝛉
A3B3 = AAABBB = AA(AB)BB = AA. θ. BB = θ B) 𝐁𝐀 = 𝛉
Phép nhân ma trận không có tính giao hoán và điều kiện đề bài cũng không đủ để kết luận BA = θ. C) A và B là hai ma trận suy biến.
Giả sử A không suy biến thì A−1 tồn tại. Nhân vào hai vế của gia thiết, ta có:
AB = θ ⇒ A−1.AB = A−1.θ ⇒ B = 0 (vô lý)
Vậy A phải suy biến, chứng minh tương tự được B suy biến. D. (𝐁𝐀)𝟐 = 𝛉
(BA)2 = BA. BA = B. (AB). A = B. θ. A = θ
Câu 9: Cho ma trận 𝐀 = (𝐚𝐢𝐣)𝟒𝐱𝟒 và ma trận 𝐁 = (𝐛𝐢𝐣)𝟒𝐱𝟒 với 𝐛𝐢𝐣
. Ký hiệu 𝐀𝐓 là ma trận chuyển vị của
ma trận A. Phát biểu nào sau đây là sai? C) 𝐀𝐓 = 𝐁
Chính đề bài đã nói lên điều này, theo đúng định nghĩa của ma trận chuyển vị. B) Nếu B suy biến thì A suy biến.
B suy biến ⇒ |B| = 0 ⇒ |AT| = 0 ⇒ |A| = 0 ⇒ A suy biến lOMoARcPSD| 36207943
A) Nếu A có 3 dòng bằng 0 thì 𝐀𝐁 = 𝛉
D. Nếu 𝐀. 𝐁 = 𝛉 thì 𝐀 = 𝐁 = 𝛉
-Xét phần tử (AB)ij của ma trận tích AB, ta có:
(AB)ij = Dòng i của A . Cột j của B = ai1b1i + ai2b2i + ai3b3i + ai4b4i
Mà B = AT nên ai1 = b1i,ai2 = b2i, ai3 4i, suy ra:
Điều này chứng tỏ trong ma trận tích của một ma trận và ma trận chuyển vị của chính nó, các phần tử luôn không âm.
-Xét câu A, chỉ cần có một phần tử khác 0 ở hàng còn lại thì sẽ có một phần tử trong ma trận tích khác 0.
-Xét câu D, muốn ma trận tích bằng 0 thì buộc toàn bộ các phần từ của ma trận A phải bằng 0. Câu 10: Cho 𝐀 = (𝟐
𝟑) , 𝐁 = (𝟏 −𝟑) , 𝐂 = (𝟐𝟎 −𝟏𝟓). 𝟓 𝟒 𝟐 −𝟏 𝟒𝟓 𝟏𝟎
Giả sử M là ma trận vuông cấp 2 thỏa 𝐌𝐀 = (−𝟑 −𝟏). Tìm ma trận MB, MC? 𝟖 𝟓
Ta sẽ đi tìm ma trận M bằng cách nhân cả hai vế của giả thiết cho A : M = MA. A ⇒ MB Chú ý rằng:
, vì hai ma trận này hoàn toàn khác nhau.
“Hai ma trận gọi là bằng nhau khi chúng có cùng kích cỡ và các phần tử tương ứng bằng nhau”
Câu 11: Cho A, B là các ma trận vuông cùng cấp khả nghịch. Đặt 𝐂 = (𝟓 𝐀𝐓)(𝟕 𝐁). Tìm 𝐂−𝟏? 𝟐 𝟑 −1 C−1 = (ATB) =B−1(AT)−1 =B−1(A−1)T
Câu 12: Hệ vector nào sau đây không là hệ nghiệm cơ bản của hệ {𝐱𝐱𝟏 + + + − 𝟏
+ 𝐱𝐱𝟐𝟐 + 𝟐𝐱𝟑𝐱𝟑𝟑 + 𝟑𝐱𝟓𝐱𝟒𝟒 − 𝟒𝐱𝟓𝐱𝟓𝟓 == 𝟎𝟎
A. 𝐕𝟏 = (𝟏, 𝟎, −𝟐,𝟏, 𝟎), 𝐕𝟐 = (−𝟐,𝟓, −𝟔, 𝟑, 𝟎), 𝐕𝟑 = (𝟑, 𝟐, 𝟎, 𝟏, 𝟐)
B. 𝐕𝟏 = (𝟏, 𝟎,−𝟐, 𝟏, 𝟎), 𝐕𝟐 = (𝟏, 𝟏, 𝟏, 𝟎, 𝟏), 𝐕𝟑 = (𝟑, 𝟐, 𝟎, 𝟏, 𝟐)
C. 𝐕𝟏 = (𝟏, 𝟎, −𝟐,𝟏, 𝟎), 𝐕𝟐 = (−𝟐,𝟓, −𝟏,𝟏, 𝟏), 𝐕𝟑 = (𝟑,𝟐, 𝟎, 𝟏, 𝟐)
D. 𝐕𝟏 = (𝟏, 𝟎, −𝟐,𝟏, 𝟎), 𝐕𝟐 = (𝟎 − 𝟏, 𝟐,−𝟏, 𝟎), 𝐕𝟑 = (𝟑, 𝟐, 𝟎, 𝟏, 𝟐) lOMoARcPSD| 36207943
-Chắc chắn là thay vector nào vô hệ cũng đúng hết, chú ý đến vector V2 và nhớ rằng: “Hệ nghiệm cơ bản chỉ gồm
những vector độc lập tuyến tính”, tức không có vector nào được tạo ra từ các vector khác.
-Nhẩm là thấy ngay vector V2 ở câu B được tạo ra hai vector V1 và V3.
-Vậy hệ vector ở câu B không phải là hệ nghiệm cơ bản. 𝐱 + 𝐲 − 𝐳 = 𝟏
Câu 13: Cho hệ phương trình tuyến tính { 𝟐𝐱 + 𝟑𝐲 + 𝐳 = 𝟐. Phát biểu nào sau đây sai?
𝟐𝐱 + 𝐲 + 𝐦𝐳 = 𝟐 A. Tồn tại m để hệ số vô số nghiệm.
B. Tồn tại m để hệ có nghiệm duy nhất.
C. Tồn tại m để hệ vô nghiệm.
D. Tồn tại m để hệ có nghiệm.
-Trước tiên, ta kiểm tra xem điều kiện để r(A) < 3 có tồn tại không, tức kiểm tra có tồn tại giá trị nào của m để |A| = 0. |12 13 −11 | = 0 ⇔ |12 01
03 | = |−11 m + 23| = m + 2 + 3 = 0 ⇔ m = −5 2 1 m 2 −1 m + 2
-Thay m = −5 vào ma trận vuông cấp 3 còn lại và kiểm tra xem r có xảy ra hay không? | -Như vậy, r
< 3. Đồng thời thấy rằng hai dòng đầu của hệ độc lập tuyến tính nên ta kết luận: r
= 2 < 3 ⇔ m = −5, tức tồn tại m để hệ có vô số nghiệm. -Với các trường hợp thì |A|
, chứng tỏ chỉ có thể là r(A) = r(A̅) = 3, tức hệ có nghiệm duy nhất.
-Tóm lại, hệ này không thể vô nghiệm được.
Câu 14: Cho A là ma trận vuông các n với . A. |𝟔𝐀| = 𝟔|𝐀|
Sai tính chất. |6A| = 6n|A|
B. Nếu |𝐀| = 𝟎 thì có 1 vector dòng của A là tổ hợp tuyến tính của các vector còn lại.
Điều này đúng với tính chất. D. |−𝐀| = |𝐀|
|−A| = |(−1).A| = (−1)n|A| = [|A| ⇔ n chẵn −|A| ⇔ n lẻ
Câu 15: Trong mô hình Input – Output mở, cho ma trận hệ số đầu vào là:
𝟎, 𝟏 𝟎, 𝟐 𝟎, 𝟑
𝐀 = (𝟎, 𝟐 𝟎, 𝟑 𝟎, 𝟐)
𝟎, 𝟑 𝟎, 𝟏 𝟎, 𝟐
Đặt 𝐁 = 𝟏𝟎(𝐈𝟑 − 𝐀) = [𝐛𝐢𝐣]𝟑×𝟑. Gọi 𝐌𝐢𝐣 là định thức con bù của 𝐛𝐢𝐣. lOMoARcPSD| 36207943
a) Tính tất cả các 𝐁𝐢𝐣 = (−𝟏)𝐢+𝐣𝐌𝐢𝐣 và tính 𝐁−𝟏. -Tìm B. 1 0 0 0,1 0,2 0,3 0,9 −0,2 −0,3 9 −2 −3 B = 10(I3 − A) = 10[(0 1 0) − (0,2 0,3 0,2)] = 10.(−0,2 0,7 −0,2) = (−2 7 −2) 0 0 1 0,3 0,1 0,2 −0,3 −0,1 0,8 −3 −1 8 Tính tất cả các Bij: 7 | = 23 B11 = (−1)1+1.|−17
−28 | = 54 B12 = (−1)1+2.|−2−3 −28 | = 22
B13 = (−1)1+3.|−2−3 −1 −2 B | = 15
21 = (−1)2+1.|−2−1 −38 | = 19
B22 = (−1)2+2.|−39 −38 | = 63 B23 = (−1)2+3.|−39 −1
B31 = (−1)3+1.|−27 −3−2| = 25 B B 33 = (−1)3+3.|−9−2 −2
32 = (−1)3+2.|−29 −2−3| = 24 | = 59 7 -Tính B−1. 9 −2 −3 15 −2 −19 |B| = |−2 7 −2| = |−23 7 54 | = (−1).(−1)3+2 | 15 −19| = 373 −3 −1 −23 54 8 0 −1 0 1 54 19 25 B−1 = |B| . PB = 373(2223 63152459)
b) Tìm giá trị sản lượng của ba ngành biết yêu cầu của ngành mở đối với ba ngành là 𝐃 = (𝟐𝟏𝟎, 𝟐𝟒𝟎,𝟏𝟏𝟎).
Ta có công thức tính sản lượng của ba ngành: X = (I − A)−1.D
Trong đó, (I − A)−1 được tính như sau: I − A = B ⇒ (I − A)−1 = 10 373 23 15 59 10.B−1 = (5422 Từ đó tính được: 1963 2524) 54 19 25 210 500 X =(22 63 24). (240) = (600) 373 23 15 59 110 400
Vậy sản lượng của 3 ngành lần lượt là: 500,600,400.
Câu 16: Cho hệ phương trình tuyến tính 𝐀𝐗 = 𝐁 (𝟏) và hệ thuần nhất tương ứng 𝐀𝐗 = 𝛉 có dạng:
𝐱𝟏 + 𝐱𝟐 + 𝟐𝐱𝟑 + 𝟑𝐱𝟒 + 𝟒𝐱𝟓 = 𝟎
{𝟑𝐱𝟏 + 𝟒𝐱𝟐 + 𝟒𝐱𝟑 + 𝟓𝐱𝟒 + 𝟐𝐱𝟓 = 𝟎 𝟓𝐱𝟏 +
𝟕𝐱𝟐 + 𝟔𝐱𝟑 + 𝟕𝐱𝟒 + 𝟔𝐱𝟓 = 𝟎
a) Tìm nghiệm tổng quát và tìm 1 nghiệm cơ bản của hệ thuần nhất trên. lOMoARcPSD| 36207943
Đưa hệ phương trình đã cho vào ma trận, ta có: d −5d 𝑑 𝑑 → Đặt x3 = a, x4 = b, với
, ta có nghiệm tổng quát của hệ (1):
−4a − 7b, 2a + 4b, a, b, 0)
Cho a = b = 1, ta được 1 nghiệm cơ bản của hệ trên:
(x1, x2,x3, x4,x5) = (−11; 6; 1; 1; 0) 𝟓
b) Giả sử 𝐗 = 𝟒𝟑 là 1 nghiệm riêng của hệ phương trình tuyến tính 𝐀𝐗 = 𝐁 (𝟏). 𝟐 [𝟏]
Tìm B và tìm nghiệm tổng quát của hệ (1). Tìm ma trận B: 1 1 1 2 3 4 2 41 B = AX = (3 4 4 5 2 ) 3 = (53) 5 7 6 7 6 4 95 (5)
Thay B ngược vào phương trình AX = B, ta đưa hệ vào ma trận: −5d 𝑑 → Đặt x = b, với
, ta có nghiệm tổng quát của hệ phương trình đã cho:
41 − 4a − 7b, −20 + 2a + 4b, a,b, 5) K41 CLC – MÃ ĐỀ 209 𝐦 − 𝟓 𝟏 𝟏 Câu 1: Cho 𝐀 = ( 𝟏 𝟏
𝐦 − 𝟓). Tìm điều kiện của m để A không khả đảo. lOMoARcPSD| 36207943 𝟏 𝐦 − 𝟓 𝟏 m − 5 1 1 m − 5 1 1 m − 5 1 1 −|A| = | 1 m − 5 1 | = | 1 m − 5 1 | = (m − 3). | 1 m − 5 1| 1 1 m − 5 m − 3 m − 3 m − 3 1 1 1 m − 6 0 0 = (m − 3) 0 m − 6 0 (m − 3)(m − 6)2 1 1 1
Vậy nên: A không khả đảo ⇔ |A|
Câu 2: Cho A, B là các ma trận vuông cùng cấp khả nghịch. Đặt 𝐂 = (𝟐 𝐀𝐓) (𝟕 𝐁). Tìm 𝐂−𝟏? 𝟓 𝟑 −1 C−1 = (ATB) =B−1(AT)−1 =B−1(A−1)T
Câu 3: Giả sử hệ phương trình tuyến tính 𝐀𝐗 = 𝐁 (có n phương trình và n ẩn số) là hệ vô nghiệm. Phát biểu nào sau đây là sai?
A) Ma trận A là ma trận suy biến.
B) Hệ vector cột B nằm trong không gian con sinh bởi hệ vector cột của A.
C) Hệ vector cột của ma trận A là hệ phụ thuộc tuyến tính.
D. Hệ vertor dòng của ma trận A không phải là cơ sở của ℝ𝐧.
-Hệ phương trình có n phương trình n ẩn vô nghiệm (Hệ Cramer) ⇔ |A| = 0
⇔ Hệ vector cột và hệ vector dòng của A là hệ phụ thuộc tuyến tính, hay ma trận A suy biến.
⇒ Hệ vector dòng của A không phải cơ sở của n (vì cơ sở là hệ những vector độc lập tuyến tính) -Mặt khác, ta có: r
(Chú ý rằng A̅T có n+1 dòng và dòng của A̅T là cột của A̅)
Vậy nên hệ vector dòng của A̅T là hệ phụ thuộc tuyến tính, suy ra hệ vector cột của A là hệ phụ thuộc tuyến tính,
hay có thể nói rằng vector cột B được sinh ra bởi hệ vector cột của A. 𝐱 + 𝐲 − 𝐳 = 𝟏
Câu 4: Cho hệ phương trình tuyến tính {𝟐𝐱 + 𝟑𝐲 + 𝐳 = 𝟐. Phát biểu nào sau đây sai?
𝟐𝐱 + 𝐲 + 𝐦𝐳 = 𝟐
A) Tồn tại m để hệ số vô số nghiệm.
B) Tồn tại m để hệ có nghiệm duy nhất.
C) Tồn tại m để hệ vô nghiệm.
D) Tồn tại m để hệ có nghiệm.
-Trước tiên, ta kiểm tra xem điều kiện để r(A) < 3 có tồn tại không, tức kiểm tra có tồn tại giá trị nào của m để |A| = 0. |12 13 −11 | = 0 ⇔ |12 01
03 | = |−11 m + 23| = m + 2 + 3 = 0 ⇔ m = −5 2 1 m 2 −1 m + 2 lOMoARcPSD| 36207943
-Thay m = −5 vào ma trận vuông cấp 3 còn lại và kiểm tra xem r có xảy ra hay không? | -Như vậy, r
< 3. Đồng thời thấy rằng hai dòng đầu của hệ độc lập tuyến tính nên ta kết luận: r
= 2 < 3 ⇔ m = −5, tức tồn tại m để hệ có vô số nghiệm. -Với các trường hợp thì |A|
, chứng tỏ chỉ có thể là r(A) = r(A̅) = 3, tức hệ có nghiệm duy nhất.
-Tóm lại, hệ này không thể vô nghiệm được.
Câu 5: Tìm m để không gian nghiệm của hệ phương trình sau có số chiều lớn nhất:
𝐱𝟏 + 𝐱𝟐 + 𝐱𝟑 + 𝐱𝟒 + 𝐱𝟓 = 𝟎 {
𝟐𝐱𝟏 + 𝟑𝐱𝟐 + 𝟒𝐱𝟑 + 𝟓𝐱𝟒 + 𝟔𝐱𝟓 = 𝟎
(𝐦 − 𝟏)𝐱𝟏 + 𝟓𝐱𝟐 + 𝟔𝐱𝟑 + 𝟕𝐱𝟒 + 𝟐(𝐦 − 𝟏)𝐱𝟒 = 𝟎 1 1 1 1 1
-Ta có: 𝐝𝐢𝐦𝐕 = 𝐧 − 𝐫𝐚𝐧𝐤(𝐀) với n = 5 là số ẩn của hệ phương trình và A = ( 2 3 4 5 6 ) m − 1 5 6 7 2(m − 1)
Như vậy: dimV → max ⇔ rank(A) → min.
-Rõ ràng hai dòng đầu của A đã độc lập với nhau. Muốn rank(A) nhỏ nhất thì ta phải tìm m sao cho dòng 3 được
tạo ra bởi hai dòng đầu. Nhìn các hệ số của các ẩn x2,x3, x4, ta dễ dàng nhận thấy: d3 = 2d1 + d2, suy ra: 1.2 + 2 = m − 1 ⇒ m = 5
Thật vậy, khi m = 5 thì d3 = 2d1 + d2, tức dòng 3 phụ thuộc tuyến tính vào 2 dòng trên, làm cho hạng của ma trận
A bằng 2, đạt cực tiểu.
-Vậy dimV → max ⇔ m = 5.
Câu 6: Cho A, B, C là các ma trận vuông cấp 3 có 𝐝𝐞𝐭𝐀 = 𝟓, 𝐝𝐞𝐭𝐁 = 𝟏𝟎, 𝐝𝐞𝐭𝐂 = 𝟓𝟎 và 𝐌 = 𝟓𝐀𝐁𝟐𝐂−𝟏. Tính định thức của ma trận M.
|M3x3| = |5AB2C−1| = 53.|A|. |B2|.|C−1| = 53.|A|. |B|2. |C|−1 = 53. 5.102.50−1 = 1250
Câu 7: Cho hệ phương trình tuyến tính 𝐀𝐗 = 𝐁 (𝟏) với 𝐀𝐦×𝐧 (𝐦 > 𝐧),𝐀 = (𝐀|𝐁). Ta có: A) 𝐑 B) Hệ vô nghiệm.
C) Tập nghiệm của (1) là không gian con của ℝ𝐧. D) Các câu kia đều sai.
Xét câu A: Điều này là không thể, vì khi thêm 1 cột vào thì hạng của ma trận không thể giảm được, tức R R(A).
Xét câu B: (1) có thể vô nghiệm
Xét câu C: (1) cũng có thể có vô số nghiệm, khả năng này cao khi số phương trình > số ẩn, khi đó tập nghiệm của
(1) hiển nhiên là không gian con của ℝ𝑛.
Câu 8: Cho hệ phương trình tuyến tính {𝐱𝐱 𝟏 𝟐 𝟑 𝟒
𝟏 ++ 𝐱𝐱𝟐 ++ 𝟑𝐱𝟐𝐱𝟑 ++ 𝟓𝐱𝟑𝐱𝟒 == 𝟎𝟎 lOMoARcPSD| 36207943
Hệ vector nào sau đây không là hệ nghiệm cơ bản của hệ.
𝐀. 𝐕𝟏 = (𝟏, 𝟎,−𝟐, 𝟏), 𝐕𝟐 = (−𝟑, 𝟎,𝟔, −𝟑)
𝐁) 𝐕𝟏 = (𝟏, 𝟎,−𝟐, 𝟏), 𝐕𝟐 = (−𝟐,𝟓, −𝟔, 𝟑)
𝐂) 𝐕𝟏 = (𝟏, 𝟎, −𝟐, 𝟏), 𝐕𝟐 = (𝟏, 𝟏, −𝟒,𝟐)
𝐃) 𝐕𝟏 = (𝟏, 𝟎, −𝟐, 𝟏), 𝐕𝟐 = (𝟎, −𝟏,𝟐, −𝟏)
-2 phương trình 4 ẩn độc lập tuyến tính, ta hoàn toàn có thể viết 2 ẩn này theo 2 ẩn còn lại.
Đặt k = −x1 − x2, ta có giải hệ 2 phương trình 2 ẩn theo k:
{23xx33 + 3+ 5xx44 == kk ⇒ {2xx33+ 2+ 3xx44= 0= k ⇒ {xx34= −2= −kx4 ⇒ {xx43 = −= 2kk
-Vậy nghiệm tổng quát của hệ này là:
(x1, x2,−2x1 − 2x2,x1 + x2) Và cả
4 đáp án đều đúng (thay vào cũng thấy điều đó).
Câu 9: Cho A là ma trận vuông các n với . A) |𝟔𝐀| = 𝟔|𝐀|
Sai tính chất. |6A| = 6n|A|
B) Nếu |𝐀| = 𝟎 thì có 1 vector cột của A là tổ hợp tuyến tính của các vector cột còn lại.
Điều này đúng với tính chất. D) |−𝐀| = |𝐀|
|−A| = |(−1).A| = (−1)n|A| = [|A| ⇔ n chẵn −|A| ⇔ n lẻ Câu 1 0 : C h o A , không B gi là 2 an
con của ℝ𝐧. Tìm trong những tập hợp sau, tất cả những tập hợp không là không gian n của . ℝ 𝐧
-Chúng ta cứ hiểu đơn giản rằng không gian n chính là không gian n chiều, có tính đối xứng và phải chứa vector
không (gốc tọa độ). Quen thuộc nhất chính là:
-Không gian 1 chiều ℝ1: đường thẳng đi qua gốc tọa độ.
-Không gian 2 chiều ℝ2: mặt phẳng đi qua gốc tọa độ.
-Không gian 3 chiều ℝ3: hình khối, không gian chúng ta đang tồn tại, không kể thời gian. - :
+Theo tính chất đã thừa nhận thì giao của hai không gian con của ℝ𝑛 cũng là một không gian con của ℝ𝑛. Mình xin
giải thích dài dòng thêm một chút ở dưới. lOMoARcPSD| 36207943
+Nếu A và B là hai không gian con có cùng số chiều thì giao của chúng sẽ là không gian con bằng chính
chúng hoặc không gian con có số chiều thấp hơn 1 chiều. Ví dụ: 2 mặt phẳng trùng nhau thì giao nhau ra chính
chúng. 2 mặt phẳng cắt nhau cho ra một đường thẳng đi qua gốc tọa độ (vì mặt phẳng phải đi qua gốc tọa độ).
Chú ý rằng không có trường hợp song song vì 2 mặt phẳng đều phải đi qua gốc tọa độ (chứa vector không).
+Nếu số chiều của A lớn hơn B (hoặc ngược lại) thì giao của chúng sẽ cho ra chính A hoặc không gian con với số
chiều bằng hiệu số chiều. Ví dụ: 1 mặt phẳng chứa 1 đường thẳng thì giao cho ra chính đường thẳng. Còn nếu
mặt phẳng bị đường thẳng cắt thì chắc chắn phải cắt tại gốc tọa độ, tức không gian cho ra cuối cùng chỉ còn
vector không, cũng là một không gian con của ℝ𝑛.
+Tóm lại, C chính là không gian con cũa ℝ𝑛. -Xét 𝐃 = 𝐀\𝐁.
Vì A, B là 2 không gian con của Rn nên chắc chắc chúng chứa vector không. Loại B ra khỏi A cũng chính là
loại vector không ra khỏi A, nên kết quả cho ra không phải không gian con của ℝn nữa. - .
ại đi x mà không loại đi -x thì -x sẽ không còn ai để bắt cặp nữa. Vậy nên E không phải là không gian con của n. -
A đã có vector không rồi, gộp thêm vector không vào nữa cũng ra chính nó thôi. Hay F = A. -Xét 𝐇 = 𝐁\𝐀.
Tương tự như A\B, trong H không có vector không nên H không phải không gian con của ℝn.
Câu 11: Cho A, B là 2 ma trận vuông cấp 2 thỏa 𝐀𝐁 . Phát biểu nào sai? A) 𝐀𝟑𝐁𝟑 = 𝛉
A3B3 = AAABBB = AA(AB)BB = AA. θ. BB = θ B) (𝐁𝐀)𝟐 = 𝛉
(BA)2 = BA. BA = B. (AB). A = B. θ. A = θ
C) A và B là hai ma trận suy biến.
Giả sử A không suy biến thì A−1 tồn tại. Nhân vào hai vế của gia thiết, ta có:
AB = θ ⇒ A−1.AB = A−1.θ ⇒ B = 0 (vô lý)
Vậy A phải suy biến, chứng minh tương tự được B suy biến. D) 𝐁𝐀 = 𝛉
Phép nhân ma trận không có tính giao hoán và điều kiện đề bài cũng không đủ để kết luận BA = θ.
Câu 12: Cho A và B là các ma trận vuông cấp n thỏa 𝐀 = 𝐏𝐁𝐏−𝟏, với P là ma trận vuông cấp n khả nghịch. Phát biểu nào sau đây là sai?
A) A khả nghịch khi và chỉ khi B khả nghịch
B) 𝐁𝟑 = (𝐏−𝟏)𝟑𝐀𝟑𝐏𝟑
C) 𝐝𝐞𝐭(𝐀−𝟏) = 𝐝𝐞𝐭(𝐁−𝟏) lOMoARcPSD| 36207943
D) 𝐁𝟑 = 𝐏−𝟏𝐁𝟑𝐏𝟑
-Trước tiên, ta tìm B theo A:
A = PBP−1 ⇒ P−1.(A). P = P−1.(PBP−1).P ⇔ P−1AP = B hay B = P−1AP
-Xét câu A, ta lập luận: A khả nghịch ⇔ |A| |PBP
-Xét câu C, ta lập luận:
det(A−1) = |A|−1 = |PBP−1|−1 = (|P|. |B|. |P|−1)−1 = |B|−1 = det(B−1) -Xét câu B và D, ta tìm:
B3 = (P−1AP).(P−1AP). (P−1AP) = P−1APP−1APP−1AP
= P−1A(PP−1)A(PP−1)AP = P−1A3P
Tóm lại: B = P−1AP ⇒ Bn = P−1AnP
Câu 13: Cho ma trận 𝐀 = (𝐚𝐢𝐣)𝟒𝐱𝟒 và ma trận 𝐁 = (𝐛𝐢𝐣)𝟒𝐱𝟒 với 𝐛𝐢𝐣
. Ký hiệu 𝐀𝐓 là ma trận chuyển vị
của ma trận A. Phát biểu nào sau đây là sai? C) 𝐀𝐓 = 𝐁
Chính đề bài đã nói lên điều này, theo đúng định nghĩa của ma trận chuyển vị. B) Nếu B suy biến thì A suy biến.
B suy biến ⇒ |B| = 0 ⇒ |AT| = 0 ⇒ |A| = 0 ⇒ A suy biến
A) Nếu A có 3 dòng bằng 0 thì 𝐀𝐁 = 𝛉
D. Nếu 𝐀. 𝐁 = 𝛉 thì 𝐀 = 𝐁 = 𝛉
-Xét phần tử (AB)ij của ma trận tích AB, ta có:
(AB)ij = Dòng i của A . Cột j của B = ai1b1i + ai2b2i + ai3b3i + ai4b4i
Mà B = AT nên ai1 = b1i,ai2 = b2i, ai3 4i, suy ra:
Điều này chứng tỏ trong ma trận tích của một ma trận và ma trận chuyển vị của chính nó, các phần tử luôn không âm.
-Xét câu A, chỉ cần có một phần tử khác 0 ở hàng còn lại thì sẽ có một phần tử trong ma trận tích khác 0.
-Xét câu D, muốn ma trận tích bằng 0 thì buộc toàn bộ các phần từ của ma trận A phải bằng 0. 𝟎, 𝟐 𝟎, 𝟑
Câu 14: Trong mô hình Input-Output mở cho ma trận hệ số đầu vào 𝐀 = (𝟎, 𝟓 𝟎, 𝟒). Gọi 𝐱𝟏, 𝐱𝟐 lần lượt là giá trị sản
lượng đầu ra của ngành 1 và 2, 𝐝𝟏, 𝐝𝟐 lần lượt là yêu cầu của ngành mở đối với ngành 1, 2. Cho (𝐱𝟏, 𝐱𝟐) = (𝟐𝟎𝟎;
𝟑𝟎𝟎). Hãy tìm (𝐝𝟏, 𝐝𝟐)?
d1) = D = (I − A)X = [(1 0) − (00,,5200,,43)] (300200) = (−00,8,5−00,6,3)(300200) = (7080) (d2 0 1 lOMoARcPSD| 36207943
Câu 15: Trong mô hình Input – Output mở, cho ma trận hệ số đầu vào là:
𝟎, 𝟑 𝟎, 𝟐 𝟎, 𝟏
𝐀 = (𝟎, 𝟏 𝟎, 𝟑 𝟎, 𝟐)
𝟎, 𝟏 𝟎, 𝟐 𝟎, 𝟑 Đặt 𝐁
= 𝟏𝟎(𝐈𝟑 − 𝐀) = [𝐛𝐢𝐣] . Gọi 𝐌𝐢𝐣 là định thức con bù của 𝐛𝐢𝐣. 𝟑×𝟑
a) Tính tất cả các 𝐁𝐢𝐣 = (−𝟏)𝐢+𝐣𝐌𝐢𝐣 và tính 𝐁−𝟏. -Tìm B. 1 0 0
𝟎, 𝟑 𝟎, 𝟐 𝟎, 𝟏 0,7 −0,2 −0,1 7 −2 −1 B = 10(I3 − A) = 10[(0
1 0) − (𝟎, 𝟏 𝟎, 𝟑 𝟎, 𝟐)] = 10.(−0,1 0,7 −0,2) = (−1 7 −2) 0 0 1
𝟎, 𝟏 𝟎, 𝟐 𝟎, 𝟑 −0,1 −0,2 0,7 −1 −2 7 Tính tất cả các Bij:
B11 = (−1)1+1.|−27 −27 | = 45
B12 = (−1)1+2.|−1−1 −27 | = 9
B13 = (−1)1+3.|−1−1 −27 | = 9
B21 = (−1)2+1.|−2−2−17 | = 16
B22 = (−1)2+2.|−17 −17 | = 48
B23 = (−1)2+3.|−17 −2−2| = 16
B31 = (−1)3+1.|−27 −1−2| = 11
B32 = (−1)3+2.|−17 −2−1| = 15
B33 = (−1)3+3.|−17 −27 | = 47 -Tính B−1. 7 −2 −1 0 0 −1 −15 11 | = 288 |B| = |−1 7 −2| = |−15 11 −2| = (−1).(−1)1+3 | 48 −16 −1 −2 7 48 −16 7 1 45 16 11
B−1 = |B| . PB = 288 ( 99 116481547)
b) Tìm giá trị sản lượng của ba ngành biết yêu cầu của ngành mở đối với ba ngành là 𝐃 = (𝟏𝟕𝟎, 𝟕𝟎, 𝟐𝟓𝟎).
Ta có công thức tính sản lượng của ba ngành: X = (I − A)−1.D
Trong đó, (I − A)−1 được tính như sau: I − A =⇒ (I − A) = 10. B =( 9 48 15) B −1 −1 10 288 9 116 47 45 16 11 Từ đó tính được: 45 16 11 170 400 X =( 9 48 15) . ( 70 ) = (300) 288 9 116 47 250 500
Vậy sản lượng của 3 ngành lần lượt là: 400,300,500. lOMoARcPSD| 36207943
Câu 16: Biện luận theo m hạng của ma trận sau: 𝒎 𝟑 𝟑 𝟑 𝟑 𝟑 𝒎 𝟑 𝟑 𝟑 𝑨 = 𝟑 𝟑 𝒎 𝟑 𝟑 𝟑 𝟑 𝟑 𝒎 𝟑 ( 𝟑 𝟑 𝟑 𝟑 𝒎) Ta có: m 3 3 3 3 m 3 3 3 3 m 3 3 3 3
3 m 3 3 3 3 m 3 3 3 3 m 3 3 3 |A| = |3 3 m 3 3| = | 3 3 m 3 3 | = (m + 3). |3 3 m 3 3| 3 3 3 m 3 3 3 3 m 3 3 3 3 m 3 3 3 3 3 m
m + 3 m + 3 m + 3 m + 3 m + 3 1 1 1 1 1 m − 3 0 0 0 m − 3 0 0 0 = (m + 3) m − 3 0 0| = (m + 3)(m − 3)4 0 m − 3 0 1 1 1 Xét khi , ta có: |A|
Xét khi m = 3, dễ dàng thấy r
Xét khi m = −3, ta tìm được r . Vậy Khi . Khi . Khi m = 3 thì r . K40 – MÃ ĐỀ 624
Câu 1: Giả sử hệ phương trình tuyến tính AX=B có nghiệm duy nhất. Chọn phát biểu đúng?
A) Hệ véctơ dòng của A độc lập tuyến tính
B) Hệ véctơ cột của A phụ thuộc tuyến tính
C) Hệ véctơ dòng của A phụ thuộc tuyến tính
D) Hệ véctơ cột của A độc lập tuyến tính
Phương trình tuyến tính AX=B có nghiệm duy nhất ⇔ r(A) = n ⇔ r(AT) = n lOMoARcPSD| 36207943
⇔ Hệ véctơ dòng của AT độc lập tuyến tính
⇔ Hệ véctơ cột của A độc lập tuyến tính
(Vì dòng của A là cột của AT và ngược lại. Nếu Am×n thì ATn×m)
Có ý kiến: Tại sao từ "𝑟(𝐴) = 𝑛" ta không suy thẳng ra “hệ véctơ dòng của A độc lập tuyến tính”? Mình xin
giải thích ngắn gọn thế này:
Trong tính chất “Nếu 𝑟(𝐴) = 𝑛 thì hệ véctơ dòng của A độc lập tuyến tính” thì ý nghĩa của n chính là số dòng
của A. Còn trong bài toán trên, n là số ẩn (tức số cột), còn m mới là số phương trình (tức số dòng). Vì vậy
mình buộc phải dùng đến ma trận chuyển vị để n biến thành số phương trình của ma trận chuyển vị.
Vì vậy, khi sử dụng các tính chất, chún ta cần chú ý đến ý nghĩa của các chữ cái đại diện!
Câu 2: Cho u, v, w là các véctơ khác 0 trong ℝ𝟑. Tập hợp nào sau đây là không gian con của ℝ𝟑. A)
Nếu u và v không cùng phương thì không thể tồn tại số thực x để 𝑢 + 𝑥𝑣 = 𝜃, tức có thể trong không gian W1 không có vector không.
Vì vậy, không thể khẳng định W1 là không gian con của ℝ3. B)
Điều kiện 1 hiển nhiên thỏa mãn, vì luôn tìm được 2 số thực x, y để w + xu + yv = θ.
Điều kiện 2: Giả sử A = w + xu
. Ta cần kiểm tra xem αA có thuộc W2 hay không?
Ta có: αA = αw + αxu + αyv Đặt thì αA = αw + Xu + Yv
Điều kiện 2 không thỏa mãn nên W2 không phải không gian con của
C) 𝐖𝟑 = {𝐱𝐮 + 𝐲(𝐯 + 𝐰)
Điều kiện 1 hiển nhiên thỏa mãn
Điều kiện 2: Giả sử A = xu + y(v + w)
. Ta cần kiểm tra xem αA có thuộc W3 hay không?
Ta có: αA = αxu + αy(v + w) Đặt thì αA = Xu + Y(v + w)
Vậy W là không gian con của D)
Điều kiện 1 hiển nhiên thỏa mãn khi n=0.
Điều kiện 2: Giả sử A = nu
. Ta cần kiểm tra xem αA có thuộc W3 hay không? Ta có: αA = αnu Đặt thì αA = Nu (chứ không phải như điều kiện)
Vậy W3 là không phải là không gian con của
Có thể nói rằng, 2 điều kiện tối thiểu cần phải xét đến đối với không gian con, đó là: -Tồn tại vector không -N . lOMoARcPSD| 36207943 −𝟐 𝟏 𝟑
Câu 3: Cho ma trận 𝐀 = ( 𝟐
𝐦 𝟒). Với giá trị nào của m thì ma trận 𝐀𝟑𝐀𝐓 có hạng bé hơn 3? −𝟏 −𝟑 𝟏
Thấy A3AT chắc chắn là ma trận vuông cấp 3. Ta có:
r(A3AT) < 3 ⇔ |A3AT| = 0 ⇔ |A3||AT| = 0 ⇔ |A|3.|A| = 0 ⇔ |A|4 = 0 ⇔ |A| = 0 −2 1 3 0 7 1
⇔ | 2 m 4| = 0 ⇔ | 0 m − 6 6| = 0 ⇔ | 7 1| = 0 ⇔ m − 6 = 42 ⇔ m = 48 m − 6 6 −1 −3 1 −1 −3 1 Câu 4: Cho 𝐀 = (𝟐
𝟒). Tìm m để 𝐀𝟓 + 𝐦𝐀𝟒 khả đảo. 𝟑 𝟑
Chắc rằng A5 + mA4 là ma trận vuông cấp 2. A5 + mA4 khả đảo ⇔ |A (A + mI)| .|A + mI| |A + mI| ⇔ | 2 + m 4
−𝟐𝐱 + 𝟑𝐲 + 𝐳 = 𝟏
Câu 5: Cho hệ phương trình {
𝐱 + 𝟐𝐲 − 𝟑𝐳 = 𝟐
. Phát biểu nào sau đây là đúng?
−𝟑𝐱 + 𝟖𝐲 + 𝐦𝐳 = 𝐦 + 𝟓
A) Với mọi m, hệ luôn có nghiệm.
B) Với mọi m, hệ có nghiệm duy nhất.
C) Với mọi m, hệ có vô số nghiệm.
D) Tồn tại m để hệ có đúng hai nghiệm.
-Trước tiên, ta kiểm tra xem điều kiện để r(A) < 3 có tồn tại không, tức kiểm tra có tồn tại giá trị nào của m để |A| = 0 không. −2 3 1 0 7 −5 | 1 2 −3| = 0 ⇔ |1 2 −3 | = − | 7
−5 | = 7(m − 9) + 70 = 0 ⇔ m = −1 −3 8 m 0 14 𝑚 − 9 14 m − 9
-Thay m = −1 vào ma trận vuông cấp 3 còn lại và kiểm tra xem r(A̅) < 3 có xảy ra hay không? 3 1 1 0 0 1
|2 −3 2| = |−4 −5 2| = |−4 −5| = 0 8 −1 4 −4 −5 4 −4 −5
-Như vậy, r(A) < 3 và r(A̅) < 3.
Đồng thời thấy rằng hai dòng đầu của hệ độc lập tuyến tính nên ta kết luận: r
= 2 < 3 ⇔ m = −1, tức tồn tại m để hệ có vô số nghiệm. -Với các trường hợp thì |A|
, chứng tỏ chỉ có thể là r(A) = r(A̅) = 3, tức hệ có nghiệm duy nhất. lOMoARcPSD| 36207943
-Tóm lại, hệ này luôn có nghiệm.
𝐱 + 𝐲 + 𝟐𝐳 + 𝟑𝐭 = 𝟒
Câu 7: Cho hệ phương trình { 𝟐𝐱 + 𝟑𝐲 + 𝟑𝐳 = 𝟔 . Tìm z?
𝐱 + 𝟒𝐲 − 𝐳 + 𝐭 = −𝟐
−𝟑𝐱 + 𝟒𝐳 − 𝟐𝐭 = 𝟖 Dùng
công thức đối với hệ Cramer: 1 1 4 3 1 1 4 3 2 3 6 0 0 1 1 −2 −6 1 −6 1 −6 16| | | 1 4 −2 | |0 3 −6 |3 −2 −2| |0 −2 −2| −6 0 0 16| −3 0 8 −2 z = 1 1 2 3 = = = = || = 2
| 21 34 −13 01 | |00 13 −1 −6| |3 −3 −2| |0 0 16| 13 25 −3 −2 3 10 7 0 13 25 −3 0 4 −2 0 3 10 7 Câu 8: Cho các ma trận: 𝐀 = (𝟏
𝟐) ; 𝐁𝟏 = (𝟒𝟓) ; 𝐁𝟐 = (𝟔𝟑) 𝟒 𝟗
Gọi 𝐗𝟏,𝐗𝟐 lần lượt là nghiệm của hệ A𝐗 = 𝐁𝟏 và A𝐗 = 𝐁𝟐. Khi đó 𝟐𝐗𝟏 + 𝟑𝐗𝟐 là: X1 = A−1B1 ; X2 = A−1B2
⇒ 2X1 + 3X2 = A−1(2B1 + 3B2) = (−49−21 ) (2619) = (−85196)
Câu 9: Cho A, B là hai ma trận vuông cấp n thỏa mãn điều kiện 𝐀𝟐𝐁 = 𝐀𝐁𝟐 = 𝐈. Khẳng định nào sau đây sai? A) (𝐀𝐁)−𝟏 = 𝐁
Ta có: AB2 = I ⇔ (AB). B = I ⇔ AB và B là ma trận nghịch đảo của nhau B) 𝐀 = 𝐁
Ta có: A2B = AB2 ⇔ AAB = ABB ⇔ A−1.AAB. B−1 = A−1.ABB. B−1 ⇔ A = B C) A, B không suy biến
Như câu A, ta đã biết B khả đảo, chứng tỏ B không suy biến
Chứng minh tương tự, ta được A cũng không suy biến.
D) 𝐝𝐞𝐭𝐀 + 𝐝𝐞𝐭𝐁 = 𝟎
Dùng kết quả từ câu B) và C), chứng minh được |𝐴|
Thật ra ngay từ đầu, ta đã nhận ra tính đối xứng trong đề bài và dễ dàng chứng minh được: 𝐴 = 𝐵
Khi đó, thay vào đề bài thì: 𝐴3 = 𝐵3 = 𝐼 ⇒ 𝐴 = 𝐵 = 𝐼
Từ đó thay vào các câu A, B, C, D ta dễ dàng thấy D là phát biểu sai.
Câu 10: Cho ma trận 𝐀 = (
. Biết 𝐀𝐀𝐓 khả đảo. Hãy tìm hạng của 𝐀𝐓. lOMoARcPSD| 36207943 𝟐 𝐦 −𝟒 AAT khả đảo ⇔ |AAT| | ) | ⇔ 6 (m + 8)
Khi đó, ta biến đổi: AT Vì
nên d1 và d2 độc lập tuyến tính, suy ra r
Câu 11: Trong ℝ𝟑 cho hệ véctơ 𝐁 = {𝐮𝟏 = (−𝟏, 𝟐,𝟑), 𝐮𝟐 = (𝟐, 𝟓,𝟏), 𝐮𝟑 = (𝟏,𝟗, 𝟕), 𝐮𝟒 = (𝟓,𝟖, −𝟏)}. Phát biểu nào sau đây là sai?
A) Hệ {𝐮𝟏,𝐮𝟐, 𝐮𝟑} độc lập tuyến tính. u Xét |u | | Hệ độc lập tuyến tính. u
B) Hệ {𝐮𝟏,𝐮𝟐, 𝐮𝟒} phụ thuộc tuyến tính. u Xét |u |
| = 0 ⇒ Hệ {u1,u2,u4} phụ thuộc tuyến tính. u
C) Số chiều của không gian con sinh bởi hệ {𝐮𝟏, 𝐮𝟐, 𝐮𝟑,𝐮𝟒} có số chiều là 2. Theo câu A, trong hệ
có ít nhất 3 véctơ độc lập tuyến tính, nên số chiều tối thiểu của không gian con sinh bởi hệ trên là 3.
D) {𝐮𝟏,𝐮𝟐, 𝐮𝟑} là hệ véctơ độc lập tuyến tính cực đại của B.
Theo câu B, u4 có được từ u1,u2 nên u4 xem như bị loại. Hệ B còn lại ba véctơ độc lập tuyến tính.
Vậy {u1,u2,u3} là hệ véctơ độc lập tuyến tính cực đại của B.
Câu 12: Cho A, B là hai ma trận vuông cùng cấp và khả nghịch. Đặt 𝐂 = (𝟐 𝐀𝐓) (𝟒 𝐁−𝟏). Khi đó 𝐂−𝟏 =? 𝟑 𝟓 C = ATB−1 ⇒ C−1 = (ATB−1)−1 = (B−1)−1.(AT)−1 = B. (A−1)T 𝟏 𝐱𝟐 𝐱𝟑 𝐱
Câu 13: Đặt 𝐏(𝐱) = |−𝟏 𝟑 𝟐
𝟓 |. Tìm bậc của đa thức 𝐏(𝐱)? 𝟐 𝟏 −𝟐 𝟏 𝟑 𝟒 −𝟏 𝟑 Khai triển đa thức P theo dòng 1, ta có: lOMoARcPSD| 36207943 P | x + | Xét hệ số của x có bậc bé hơn 3. Xét hệ số của x là đa thức bậc 2.
𝟐𝐱𝟏 − 𝐱𝟐 + 𝐱𝟑 − 𝐱𝟒 = 𝟎
Câu 14: Gọi W là không gian nghiệm của hệ phương trình tuyến tính thuần nhất { 𝐱𝟏−+𝐱 𝟐𝐱 𝐱 𝟏
+𝟐𝟑𝐱+𝟐 +𝟑 +𝟒𝐱𝟑𝐱𝟒 𝟒==𝟎𝟎 . Phát
𝟑𝐱𝟏 − 𝟒𝐱𝟐 + 𝐱𝟑 + 𝐦𝐱𝟒 = 𝟎 biểu nào sau đây là sai? A) 𝐝𝐢𝐦𝐖 với mọi m.
Rõ ràng d3 = d2 − d1 nên phương trình thứ 3 bị loại. Hệ phương trình trên thực sự chỉ còn: 2x1 − x2 + x3 − x4 = 0 { x1 + 2x2 + x3 + 3x4 = 0 3x1 − 4x2 + x3 + mx4 = 0
Nhận thấy hai phương trình đầu của hệ này độc lập tuyến tính nên: rank Ta lại có: dimW = n − rank Vậy với mọi m.
B) Với mọi m thì W luôn có cơ sở
Hệ phương trình trên luôn tồn tại nghiệm nên không gian W luôn tồn tại. Vậy nên W luôn có cơ sở. C) Tồn tại m sao cho 𝟒
Rõ ràng ở câu A ta đã chứng minh được
với mọi m. Nên không thể xảy ra .
D) Mọi hệ gồm 3 phần tử của W đều phụ thuộc tuyến tính.
Số chiều của W tối đa bằng 2 nên W được xây dựng chỉ từ tối đa 2 véctơ độc lập tuyến tính.
Vậy nên mọi hệ gồm 3 phần tử của W đều phụ thuộc tuyến tính.
Câu 15: Trong mô hình Input-output mở, cho ma trận hệ số đầu vào:
𝟎,𝟏 𝟎, 𝟐 𝟎, 𝟏 lOMoARcPSD| 36207943
𝑨 = (𝟎,𝟐 𝟎, 𝟐 𝟎, 𝟏) 𝟎,𝟑 𝟎, 𝟏 𝟎, 𝟐 a)
Tìm tổng giá trị lượng nguyên liệu mà ba ngành cung cấp cho ngành 1 để ngành 1 làm ra lượng sản phẩm trị giá 100 (đvt).
Tổng giá trị lượng nguyên liệu cung cấp cho ngành 1:
𝑦1 = (𝑎11 + 𝑎21 + 𝑎31).𝑥1 = (0,1 + 0,2 + 0,3).100 = 60 b)
Tìm giá trị sản lượng 3 ngành, biết yêu cầu của ngành mở đối với 3 ngành là 𝑫 = (𝟏𝟏, 𝟑𝟖,𝟏𝟕).
Ta có công thức tính sản lượng: 𝑋 = (𝐼 − 𝐴)−1𝐷. 0,9 𝐼 − 𝐴 = (−0,2 0,8 69 11)
−0,1) ⇒ (𝐼 − 𝐴) = = (19 −0,2 0,8 |𝐼 − 𝐴| 503 26
−0,3 Từ đó tính được: −0,1 15 68 −0,1 −1 𝑃𝐼−𝐴 63 17 10 63 17 10 11 30 𝑋 =(19 69 11). (38) = (60) 503 26 15 68 17 40
Câu 16: Trong không gian ℝ𝟒, gọi W là không gian sinh bởi các véctơ:
𝐮𝟏 = (𝟏, 𝟐, −𝟏,𝟏) ; 𝐮𝟐 = (𝟐, 𝟑, 𝟏, 𝟑) ; 𝐮𝟑 = (𝟑, 𝟕,−𝟔, 𝟐) ; 𝐮𝟒 = (𝟒, 𝟕, −𝟏, 𝟓)
a) Tìm số chiều và một cơ sở của W. 1 2 −1 1 2 −1 1 1 −1 −1 1 ) Ta có: dimW = rank 1 −3 −1 (23 4 3 1 3) = rank (00 −1 3 1 7 −6 2 7 −1 5 0 1 2 −1 1 1 2 −1 1 −1 1 1
= rank (00 −10 −1−4 ) = rank (00 −10 −4 ) = 3 0 0 0 4 0 0 0 0 0 Vậy W có 3 chiều. 0 Xét: u1 1 2 −1 1 1 1 3) = 2 −1 1 rank (u2) = rank (2 3 rank (0 −1 −1 1) = 3 u3 3 7 −6 2 0 0 −4 0
⇒ u1, u2,u3 độc lập tuyến tính ⇒ {u1,u2,u3} là một cơ sở của W
b) Véctơ 𝐯 = (𝟏, 𝟏, 𝟐, 𝟐) có thuộc W hay không? Tại sao? Giả sử: v = α ⇔ 1,2,−1,1) 3,7,−6,2) lOMoARcPSD| 36207943 ⇔
Vậy v = (1,1,2,2) có thuộc W. K39 – MÃ ĐỀ 12
Câu 1: Cho A, B là hai ma trận vuông cấp 5. Giả sử dòng 2 của A bằng 0 và cột 3 của B bằng 0. Đặt C=AB, khi đó:
A) Dòng 2 và cột 2 của C bằng 0
B) Dòng 3 và cột 3 của C bằng 0
C) Dòng 2 và cột 3 của C bằng 0
D) Dòng 3 và cột 2 của C bằng 0
Dòng 2 của A làm cho toàn bộ dòng 2 của C bằng 0. Cột 3 của B làm cho toàn bộ cột 3 của C bằng 0.
Câu 2: Gọi V là không gian nghiệm của hệ
𝐱𝟏 + 𝐱𝟐 + 𝐱𝟑 + 𝐱𝟒 + 𝐱𝟓 = 𝟎 {
𝟐𝐱𝟏 + 𝟑𝐱𝟐 + 𝟒𝐱𝟑 + 𝟓𝐱𝟒 + 𝟔𝐱𝟓 = 𝟎
(𝐦 + 𝟏)𝐱𝟏 + 𝟓𝐱𝟐 + 𝟔𝐱𝟑 + 𝟕𝐱𝟒 + 𝟐(𝐦 + 𝟏)𝐱𝟓 = 𝟎 Tìm m để dimV lớn nhất? dimV = n − rank(A)
⇒ dimV → max ⇔ rank(A) → min
Rõ ràng hai phương trình đầu đã độc lập tuyến tính nên để hạng của A nhỏ nhất thì phương trình thứ 3 phải là tổ
hợp từ hai phương trình trên.
Dễ dàng nhận ra, 2d1 + d2 = 4x1 + 5x2 + 6x3 + 7x4 + 8x5 = 0 là một phương trình tương tự d3.
Đồng nhất nó với d3, ta được m=3. Vậy dimV → max ⇔ m = 3
Câu 3: Cho 2 hệ phương trình AX=0 (1) và AX=B (2) với 𝐀𝐦×𝐧. Phát biểu nào sai? A)
Nếu m=n và (1) có nghiệm duy nhất thì (2) có nghiệm duy nhất Khi m = n và (1) có
nghiệm duy nhất thì r(A) = n Mà r = n. Vậy r
= n, tức (2) có nghiệm duy nhất. B)
) có duy nhất nghiệm thì (2) có nghiệm.
Xét vế trái: (1) có nghiệm duy nhất ⇔ r(A) = n Xét
vế phải: (2) có nghiệm ⇔ r(A) = r(A̅)
Vì r(A̅) = n; m nên ta không có đủ cơ sở để từ vế trái suy ra vế phải, tức (1) có nghiệm thì chưa chắc (2) có nghiệm.
C) Nếu (1) có vô số nghiệm thì chưa chắc (2) có nghiệm.
Xét vế trái: (1) có vô số nghiệm ⇒ r(A) < n
Xét vế phải: (2) có nghiệm ⇔ r(A) = r(A̅) lOMoARcPSD| 36207943
Ta chưa chắc được (2) có nghiệm hay không vì không biết chắc hạng của A̅. D)
Nếu (2) có vô số nghiệm thì ) có vô số nghiệm. (2) có vô số nghiệm⇔ r
< n ⇒ (1) có vô số nghiệm.
Câu 4: Hệ véctơ nào sau đây không phải là không gian con của ℝ𝟑? A)
𝐕 = {(𝐱 − 𝐲,𝐲, 𝟎)
Trong V có véctơ không, khi x=y=z=0 Xét A = (x − y, y, 0)
(αx − αy, αy, 0) = (X − Y, Y, 0)
Vậy V là không gian con của . B)
𝐕 = {(𝐱 − 𝐲 + 𝐳, 𝐳 − 𝐲, 𝐱)
Trong V có véctơ không, khi x=y=0
Xét A = (x − y + z, z − y, x)
(αx − αy + αz, αz − αy, αx) = (X − Y + Z, Z − Y, X)
Vậy V là không gian con của . C)
V gồm tất cả các véctơ được sinh ra bởi hệ {(𝟏,𝟐, 𝟏), (−𝟐, 𝟎,𝟏), (𝟏, 𝟐, −𝟑), (𝟑, −𝟐,𝟏)} Hệ véctơ thuộc
bất kỳ đều có thể sinh ra không gian con của ℝ3. D) 𝐕 = {(𝐱, 𝐲, 𝐱𝐲)
Trong V có véctơ không, khi x=y=0 Xét A = (x, y, xy) (αx, αy, αxy)
Vậy V không là không gian con của ℝ3.
Câu 5: Cho A, B là hai ma trận vuông cùng cấp và khả nghịch. Đặt
𝐂 = (𝟑 𝐀𝐓) (𝟕 𝐁). Khi đó 𝐂−𝟏 =? 𝟓 𝟒 C = ATB ⇒ C−1 = (ATB)−1 = B−1.(AT)−1 = B−1.(A−1)T
Câu 7: Hệ vector nào sau đây là hệ nghiệm cơ bản của hệ phương trình tuyến tính {𝐱𝐱𝟏 + + + 𝟏
+ 𝐱𝐱𝟐𝟐 + 𝟐𝐱𝟑𝐱𝟑𝟑 + 𝟑𝐱𝟓𝐱𝟒 = 𝟒 = 𝟎𝟎.
A) 𝐕𝟏 = (𝟏, 𝟎, −𝟐, 𝟏)
B) 𝐕𝟏 = (𝟏, 𝟎, −𝟐, 𝟏), 𝐕𝟐 = (−𝟐,−𝟐, 𝟎, 𝟎), 𝐕𝟑 = (𝟎, 𝟏, −𝟐,𝟏)
C) 𝐕𝟏 = (𝟏, 𝟎, −𝟐,𝟏), 𝐕𝟐 = (𝟏, 𝟏,𝟏, 𝟎)
D) 𝐕𝟏 = (𝟏, 𝟎, −𝟐,𝟏), 𝐕𝟐 = (𝟎, 𝟏, −𝟐, 𝟏)
Hệ trên gồm 2 phương trình độc lập tuyến tính 4 ẩn. Như vậy số véctơ trong hệ nghiệm cơ bản sẽ là 4-2=2 (véctơ)
thỏa mãn hệ phương trình. Chỉ có đáp án D là phụ hợp điều kiện. lOMoARcPSD| 36207943 𝟒𝐱 + 𝟑𝐲 = −𝟔
Câu 8: Hệ { 𝟓𝐱 + 𝟖𝐲 = 𝟏 có đúng 1 nghiệm khi và chỉ khi a=? 𝐚𝟐𝐱 + 𝟑𝐚𝐲 = −𝟗
Giải hai phương trình đầu ta được nghiệm: (x, y) = (−3,2)
Để hệ phương trình đã cho có đúng 1 nghiệm thì phương trình cuối phải thỏa (x, y) = (−3,2).
Thay (x, y) = (−3,2) vào, ta tìm được điều kiện của a:
Câu 9: Cho các ma trận: 𝐀 = (𝟏𝟑 𝟐𝟗) ; 𝐃𝟏 = (𝟓𝟔) ; 𝐃𝟐 = (𝟓𝟗)
Gọi 𝐗𝟏,𝐗𝟐 lần lượt là nghiệm của hệ A𝐗 = 𝐁𝟏 và A𝐗 = 𝐁𝟐. Khi đó 𝐗𝟐 − 𝐗𝟏 là: X1 = A−1D1 ; X2 = A−1D2
⇒ X2 − X1 = A−1(D2 − D1) = (−39 −21 )(30) = (−63 ) → (−21 ) 𝟎, 𝟐 𝟎, 𝟏
Câu 10: Trong mô hình Input-Output mở, cho ma trận hệ số đầu vào 𝐀 = [𝟎, 𝟑 𝟎, 𝟒]. Gọi 𝐱𝟏,𝐱𝟐 lần lượt là giá trị sản
lượng đầu ra của ngành 1 và 2, 𝐝𝟏, 𝐝𝟐 lần lượt là yêu cầu của ngành mở đối với ngành 1, 2. Khi đó, nếu (𝐱𝟏, 𝐱𝟐) =
(𝟐𝟎𝟎, 𝟑𝟎𝟎) thì (𝐝𝟏, 𝐝𝟐) sẽ là:
D = (I − A). X = [(10 01) − (00,,2300,,14)] . (300200) = (−00,8,3−00,6,1)(200300) = (130; 120)
Câu 11: Cho A là ma trận vuông cấp n với . A) |𝟑𝐀| = 𝟑|𝐀|
Theo công thức: |3A| = 3n|A| B) |−𝐀| = −|𝐀|
Cũng công thức trên: |−A| = |(−1)A| = (−1)n|A| = [−|A|A| khi n =| khi n =
C) Nếu |𝐀| = 𝟎 thì có 1 véctơ cột của A là tổ hợp tuyến tính của các véctơ cột còn lại.
Điều này đúng, rút ra từ điều vi. Trong sách giáo trình, trang 41.
Nếu có 1 véctơ cột là tổ hợp tuyến tính của các véctơ khác thì ta hoàn toàn có thể biến nó thành véctơ y hệt như
các véctơ tạo ra nó. Khi đó, định thức có hai cột giống nhau nên có giá trị bằng 0. D) Các câu kia đều sai. Câu C đúng cơ mà =]]
Câu 12: Cho hệ phương trình tuyến tính AX=B (1) với 𝐀𝐦×𝐧 (𝐦 > 𝐧), 𝐀 = (𝐀|𝐁). Ta có: A)
Tập nghiệm của (1) là không gian con của ℝ𝐧. lOMoARcPSD| 36207943
Khi số phương trình > số ẩn, hệ phương trình có thể vô nghiệm.
Khi đó, tập nghiệm của (1) là tập rỗng, không phải không gian con của ℝn.
B) 𝐫(𝐀) > 𝐫(𝐀 )
Hệ phương trình tuyến tính AX=B chỉ xảy ra trường hợp r C) Hệ vô nghiệm
Hệ vẫn có thể có nghiệm nếu r(A) = n 𝐦 − 𝟏 𝟏 𝟏 Câu 13: Cho 𝐀 = ( 𝟏 𝟏
𝐦 − 𝟏). A không khả đảo khi và chỉ khi: 𝟏 𝐦 − 𝟏 𝟏 m − 1 1 1 m − 1 1 1
|A| không khả đảo ⇔ |𝐴| = 0 ⇔ | 1 1 m − 1| = − | 1 m − 1 1 | = 0 1 m − 1 1 1 1 m − 1 m + 1 m + 1 m + 1 1 1 1 | 1 m − 1
1 | = 0 ⇔ (m + 1) |1 m − 1 1 | = 0 1 1 m − 1 1 1 m − 1 1 1 1 ⇔ (m + 1) |0 m − 2 0
| = 0 ⇔ (m + 1)(m − 2)2 = 0 ⇔ [m = −1 m = 2 0 0 m − 2 𝑚 − 1 1 1 𝑚 − 1 1 1
Chú ý dấu từ ở biểu thức: | 1 1 𝑚 − 1| = − | 1 𝑚 − 1
1 | vì ta đã đổi chỗ hai hàng. 1 𝑚 − 1 1 1 1 𝑚 − 1
Dù có hay không có dấu trừ thì kết quả vẫn vậy, như sẽ dẫn đến việc ta quên mất quy tắc: “Khi đổi chỗ hai
hàng hoặc hai cột của định thức thì định thức đổi dấu” – có thể sẽ gây nên nhiều sai lẫm trong các bài toán.
Câu 14: Trong không gian ℝ𝟑, xét các tập hợp:
𝐖𝟏 = {(𝐱, 𝐲, 𝟏) | 𝐱 = 𝟐𝐲} ; 𝐖𝟐 = {(𝐱,𝐲, 𝐳) | 𝐳 = 𝟐𝐱 − 𝐲} ; 𝐖𝟑 = {(𝐱, 𝐲,𝐳) | 𝐱 + 𝐲 + 𝐳 = 𝟎} Chọn mệnh đề đúng:
A) 𝐖𝟏 và 𝐖𝟐 là không gian con của ℝ𝟑
B) 𝐖𝟏 và 𝐖𝟑 là không gian con của ℝ𝟑
C) 𝐖𝟐 và 𝐖𝟑 là không gian con của ℝ𝟑
D) Cả ba mệnh đề trên đều sai.
W1 không chứa véctơ không nên W1 không phải không gian con của ℝ3. Còn lại W2 và W3 đều là không gian con của ℝ3.
Câu 15: Trong mô hình Input – Output mở, cho ma trận hệ số đầu vào là:
𝟎, 𝟒 𝟎, 𝟐 𝟎, 𝟏
𝐀 = (𝟎, 𝟏 𝟎, 𝟑 𝟎, 𝟐)
𝟎, 𝟐 𝟎, 𝟐 𝟎, 𝟑 a) Đặt 𝐁 = 𝟏𝟎(𝐈𝟑 − 𝐀). Tính 𝐁−𝟏. -Tìm B. lOMoARcPSD| 36207943 1 0 0
𝟎, 𝟒 𝟎, 𝟐 𝟎, 𝟏 0,6 −0,2 −0,1 6 −2 −1 B = 10(I3 − A) = 10[(0
1 0) − (𝟎, 𝟏 𝟎, 𝟑 𝟎, 𝟐)] = 10.(−0,1 0,7 −0,2) = (−1 7 −2) 0 0 1
𝟎, 𝟐 𝟎, 𝟐 𝟎, 𝟑 −0,2 −0,2 0,7 −2 −2 7 Tính tất cả các Bij:
B11 = (−1)1+1.|−27 −27 | = 45
B12 = (−1)1+2.|−2−1 −27 | = 11
B13 = (−1)1+3.|−1−2 −27 | = 16
B21 = (−1)2+1.|−2−2−17 | = 16
B22 = (−1)2+2.|−26 −17 | = 40
B23 = (−1)2+3.|−26 −2−2| = 16
B31 = (−1)3+1.|−27 −1−2| = 11
B32 = (−1)3+2.|−16 −2−1| = 13
B33 = (−1)3+3.|−16 −27 | = 40 -Tính B−1. 6 −2 −1 0 0 −1 −13 11 | = 232 |B| = |−1 7 −27| = |−1340 −1611
−27 | = (−1).(−1)1+3 | 40 −16 −2 −2 1 45 16 11 B−1 = |B| . PB = 232(1116 40161340)
b) Tìm giá trị sản lượng của ba ngành biết yêu cầu của ngành mở đối với ba ngành là 𝐃 = (𝟖𝟓, 𝟐𝟎, 𝟒𝟓).
Ta có công thức tính sản lượng của ba ngành: X = (I − A)−1.D
Trong đó, (I − A)−1 được tính như sau: I − A = B −1 = 10 232 16 16 40 10.B−1 = (4511 1640 1113) Từ đó tính được: ⇒ (I − A) 45 16 11 85 200 X =(11 40 13) . (20) = (100) 232 16 16 40 45 150
Vậy sản lượng của 3 ngành lần lượt là: 200,100,150.
Câu 16: Biện luận hạng của ma trận sau theo tham số m. 𝐦 − 𝟏 𝟑 𝟑 𝟑
𝐀 = [ 𝟑𝟑 𝐦 − 𝟏𝟑 𝐦 − 𝟏𝟑 𝟑𝟑 ] 𝟑 𝟑 𝟑 𝐦 − 𝟏
Ta tính định thức cấp 4 của A theo m: lOMoARcPSD| 36207943 m − 1 3 3 3 | 33 m − 13 m − 13 33 | 3 3 3 m − 1 m + 8 m + 8 m + 8 m + 8 | m − 1m − 1 33 | m − 1 1 m − 1 = (m + 8) | m − 1 33 | m − 1 1 = (m + 8) | m − 4m − 4 00 | m − 4 (m + 8)(m − 4) Xét . Ta có |A|
Xét m = 4. Dễ dàng thấy rank Xét m
= −8. Ta có |A| = 0 ⇒ rank Ta tính: |A Vậy khi và thì rank khi m = 4 thì rank khi m = −8 thì rank K38 – MÃ ĐỀ 357 𝟏 (𝐢 < 𝐣)
Câu 1: Cho ma trận 𝐀 = (𝐚𝐢𝐣)𝟒×𝟒 với 𝐚𝐢𝐣 = [ 𝟎 (𝐢 = 𝐣) và ma trận 𝐁 = (𝐛𝐢𝐣)𝟑×𝟑 với 𝐛𝐢𝐣 = 𝐚𝐢𝐣. −𝟏 (𝐢 > 𝐣)
Ký hiệu 𝐀𝐓 là ma trận chuyển vị của A. Phát biểu nào sau đây đúng? A) Ma trận A suy biến. B) 𝐀𝐓 = 𝐀. C) Ma trận B suy biến.
D) Các câu trên đều sai.
Ta dễ dàng viết ra được: 0 1 1 lOMoARcPSD| 36207943 A = ; AT ; B = [−1 0 1] −1 −1 0 Dễ dàng tính được: |A|
và |B| = 0 ⇒ B suy biến.
Câu 2: Với giá trị nào của m thì véctơ x là tổ hợp tuyến tính của các véctơ u, v, w.
Biết rằng 𝐱 = (𝟕, −𝟐, 𝐦); 𝐮 = (𝟐, 𝟑,𝟓); 𝐯 = (𝟑, 𝟕, 𝟖); 𝐰 = (𝟏, −𝟔,𝟏).
x là tổ hợp tuyến tính của các véctơ u, v, w
⇔ (7, −2, m) = α(2,3,5) + β(3,7,8) + γ(1,−6,1) có nghiệm (α, β, γ)
Giải phương trình, hoặc tinh ý nhận ra x = u + v + 2w, ta dễ dàng tìm được m=15.
Câu 3: Cho hệ phương trình tuyến tính AX=B (I) gồm 4 phương trình và 3 ẩn số. Biết rằng hệ (I) có nghiệm duy
nhất. Ký hiệu r(A) là hạng của ma trận A và ký hiệu 𝐀 là ma trận hệ số mở rộng của hệ (I). Khi đó: A) 𝐀 không suy biến.
A̅ là ma trận cấp 4x4 nên max[r(A̅ )] = 4.
Nhưng vì (I) có nghiệm duy nhất nên r(A) = r(A̅ ) = 3 < 4.
Điều đó chứng tỏ A̅ suy biến. B) 𝐫(𝐀) = 𝟒
Theo cách giải thích ở câu A thì r(A) = 3.
Thật vậy, hệ phương trình có 4 phương trình 3 ẩn, tức ma trận A là ma trận cấp 4x3 nên max[r(A)] = 3. C) Hệ
véctơ cột của ma trận A là hệ độc lập tuyến tính.
Hệ véctơ cột không có ý nghĩa đối với ma trận.
D) Hệ véctơ dòng của ma trận A là hệ độc lập tuyến tính. r(A) = 3
Ta có: {max[r(A)] = 3 ⇒ A là hệ độc lập tuyến tính
Câu 4: Tập hợp nào sau đây là không gian con của ℝ𝟑? A) Xét A = B) Xét A = −x, −y3) C) Xét A = −x, −y2) D) 𝐕 = Xét A = lOMoARcPSD| 36207943
𝐱 + 𝟐𝐲 − 𝟑𝐳 = 𝐚
Câu 5: Cho hệ phương trình tuyến tính {𝟐𝐱 + 𝟔𝐲 − 𝟏𝟏𝐳 = 𝐛 với
. Điều kiện của a, b, c để hệ phương trình
𝐱 − 𝟐𝐲 + 𝟕𝐳 = 𝐜 đã cho có nghiệm là: -Ta tính được: 1 2 −3 |A| = |2 6
−11| = 0 ⇒ r(A) < 3 ⇒ Hệ không thể có duy nhất nghiệm 1 −2 7
-Mà theo đề bài, hệ có nghiệm. Vậy bắt buộc, hệ phải có vô số nghiệm, tức: r(A̅) = r(A) = 2 -Ta có: 1 2 −3 a 1 2 −3 a A̅ = (2 6 −11|b) → (0 2 −5|b − 2a) 1 −2 7 c 0 −4 10 c − a
-Nhận thấy, để r(A̅) = 2 thì ta cần d3 = −2d2. Từ đó, ta có liên hệ:
b − 2a = −2(c − a) ⇔ 5a = 2b + c
𝟐𝐱 + 𝟑𝐲 + 𝟓𝐳 = 𝟎
Câu 6: Cho hệ phương trình tuyến tính thuần nhất { 𝐱 + 𝐲 + 𝟐𝐳
. Với giá trị nào của m thì
𝟑𝐱 + 𝟐𝐲 + 𝐦𝐳 = 𝟎
không gian nghiệm của hệ (I) có cơ sở khác rỗng?
Không gian nghiệm của hệ (I) có cơ sở khác rỗng
⇔ Không gian nghiệm của hệ (I) khác rỗng ⇔ (I) có vô số nghiệm 2 3 5 ⇔ |1 1
2 | = 0 ⇔ (𝑚 − 5) = 0 ⇔ 𝑚 = 5 3 2 𝑚
Câu 7: Cho A và B là các ma trận vuông cấp n không suy biến. Ký hiệu 𝐫(𝐀𝐁), (𝐁𝐀), 𝐫(𝐀−𝟏𝐁),𝐫(𝐁−𝟏𝐀) lần lượt là
hạng của ma trận 𝐀𝐁, 𝐁𝐀, 𝐀−𝟏𝐁,𝐁−𝟏𝐀. Phát biểu nào sau đây là sai?
A) 𝐝𝐞𝐭𝐀𝐁 = 𝐝𝐞𝐭𝐁𝐀
Ta có: |AB| = |A|. |B| = |B|. |A| = |BA| ⇒ detAB = detBA
B) 𝐫(𝐀𝐁) = 𝐫(𝐁𝐀)
A, B không suy biến ⇒ |A| = n
C) 𝐫(𝐀−𝟏𝐁) = 𝐫(𝐁−𝟏𝐀) |A ||AB|| A, B không suy biến ⇒ |A| {|A|⇒ r = n |B A| |B|
D) 𝐝𝐞𝐭(𝐀−𝟏𝐁) = 𝐝𝐞𝐭(𝐁−𝟏𝐀) lOMoARcPSD| 36207943 |A B| ||AB|| Ta có: {|A| . |B A| |B|
Câu 8: Với giá trị nào của a, b, c thì hệ véctơ 𝐔 = {𝐮𝟏 = (𝟐, 𝐚 + 𝐛, 𝐜); 𝐮𝟐 = (𝟐, 𝐛 + 𝐜, 𝐚); 𝐮𝟑 = (𝟐, 𝐜 + 𝐚,𝐛)} là cơ sở của không gian ℝ𝟑. u
U là cơ sở của ℝ3 ⇔ u1,u2,u3 độc lập tuyến tính ⇔ |u u 2 a + b c1 a + b c ⇔ |2 b + c a| 1 b + c a| 2 c + a b 1 c + a b 1 a + b a + b + c + 1 1 a + b 1 ⇔ 2.|1 b + c a + b + c + 1| (a + b + c + 1) |1 b + c 1 1 c + a a + b + c + 1 1 c + a 1 1 a + b 1 1 a + b 1
Vì |1 b + c 1| = 0 do có hai cột giống nhau nên ta luôn có (a + b + c + 1) |1 b + c 1 . 1 c + a 1 1 c + a 1
Vậy không tồn tại a, b, c thỏa mãn yêu cầu đề bài.
Câu 9: Gọi V là một khôn
on của không gian ℝ𝟑. Giả sử V có một cơ sở là 𝐌 = {𝐮𝟏 = (𝟏, 𝟎, −𝟐), 𝐮𝟐 = (𝟐, 𝟏,
𝟎)}. Điều kiện để véctơ 𝐮 = (𝐱, 𝐲,𝐳) : u = có nghiệm ⇒ ⇒ x − 2y + z = 0 ⇒ 2x − 4y + z = 0
Câu 10: Cho A và B là các ma trận vuông cấp n thỏa 𝐀 = 𝐏𝐁𝐏−𝟏 với P là ma trận vuông cấp n khả nghịch. Phát biểu nào sau đây là sai?
A) 𝐝𝐞𝐭𝐀 = 𝐝𝐞𝐭𝐁
Ta có: |A| = |PBP−1 | = |P|. |B|. |P−1| = |P|. |B|. | P1| = |B| ⇒ detA = detB
B) 𝐀𝟐 = 𝐏𝟐𝐁𝟐(𝐏−𝟏)𝟐
Không có không thức (XYZ)2 = X2Y2Z2 đâu nhé!
C) 𝐀𝟐 = 𝐏𝐁𝟐𝐏−𝟏 lOMoARcPSD| 36207943
Ta có: A2 = (PBP−1)2 = (PBP−1)(PBP−1) = PB(P−1P)BP−1 = PB2P−1
D) Nếu A khả nghịch thì B khả nghịch
Theo phân tích ở câu câu A thì |A| |B| A khả nghịch ⇒ |A| B khả nghịch.
Câu : Biết rằng hệ véctơ 𝐌 = {𝐮𝟏 = (𝟏, 𝟐, −𝟏), 𝐮𝟐 = (𝟎, −𝟏,𝟑), 𝐮𝟑 = (𝟏, 𝟏, 𝟎)} là một cơ sở cả không gian ℝ𝟑 và véct
𝟑 có tọa độ theo cơ sở M là [𝐮]𝐌 = (𝟏, 𝟐, −𝟏). Khi đó u=?
Chú ý rằng các véctơ u1,u2,u3 chưa được giao rõ nhiệm vụ trong ℝ3 (là trục nào trong ℝ3).
Nên hai khả năng sau đều có thể xảy ra:
u = 1u1 + 2u2 + (−1)u3 hoặc u = 1u2 + 2u3 + (−1)u1
Vậy, ta không xác định được u.
Tuy nhiên, nếu mặc định rằng 𝑢1,𝑢2,𝑢3 là các vector đơn vị của các trục tương ứng thì: 𝑢 =
1𝑢1 + 2𝑢2 − 1𝑢3 = (0,−1,5) 𝟏 𝟐 𝟑 𝟏 𝟏 𝟑
Câu 12: Cho các ma trận 𝐀 = (−𝟏) , 𝐁 = (𝟏) , 𝐂 = (𝟎
𝟐) và M là một ma trận sao cho 𝐌𝐀 = (𝟏) , 𝐌𝐁 = (𝟒). 𝟎 𝟏 𝟏 𝟏 𝟏 𝟔 Hãy tìm ma trận MC?
Nếu tinh ý, ta sẽ nhận ra: 3 1 C = (0 2) = (A + B|B − A) 1 1 Vậy nên: 4 2
MC = M(A + B|B − A) = (M(A + B)|(B − A)) = (MA + MB|MB − MA) = (5 3) 7 5
Câu 13: Cho S là hệ véctơ trong không gian ℝ𝐧 thỏa S phụ thuộc tuyến tính và S chứa một hệ véctơ con độc lập
tuyến tính gồm đúng n véctơ. Ký hiệu r(S) là hạng của hệ véctơ S. Khi đó:
A) Mọi hệ véctơ con độc lập tuyến tính cực đại của S chứa nhiều hơn n véctơ.
Theo đề bài, S chứa một hệ gồm n véctơ độc lập tuyến tính, nên rõ ràng S là không gian n chiều hay n. Như
vậy hệ véctơ con độc lập tuyến tính cực đại của S chỉ có thể chứa tối đa n véctơ. B) Mọi hệ véctơ con độc lập tuyến
tính của S gồm đúng n véctơ.
Tùy theo cách chọn véctơ, nếu chỉ chọn n-1 véctơ độc lập tuyến tính trong n véctơ độc lập tuyến tính thì hệ vừa
chọn cũng chỉ có n-1 véctơ. C) r(S)>n. r(S) = dimS = n
D) Mọi hệ véctơ con độc lập tuyến tính cực đại của S gồm đúng n véctơ.
Phần phân tích ở câu A đã khẳng định câu D là đúng. lOMoARcPSD| 36207943
Câu 14: Giả sử hệ phương trình tuyến tính AX=B (có n phương trình và n ẩn số) là hệ vô nghiệm. Phát biểu nào sau đây là sai?
A) Hệ véctơ dòng của ma trận A không phải cơ sở của ℝ𝐧.
B) Hệ véctơ cột của ma trận A là hệ phụ thuộc tuyến tính
C) Ma trận A là ma trận suy biến
D) Véctơ cột B nằm trong không gian con sinh bởi véctơ cột của A. -AX=B là hệ vô nghiệm ⇒ r(A) < n ⇒ |A| = 0
⇒ Hệ vector dòng và hệ vector cột của ma trận A phụ thuộc tuyến tính.
⇒ Hệ vector dòng của A không phải cơ sở của ℝ𝑛. -Mặt khác, ta có: r
(Chú ý rằng A̅T có n+1 dòng và dòng của A̅T là cột của A̅)
Vậy nên hệ vector dòng của A̅T là hệ phụ thuộc tuyến tính, suy ra hệ vector cột của A là hệ phụ thuộc tuyến tính,
hay có thể nói rằng vector cột B được sinh ra bởi hệ vector cột của A. K37 – MÃ ĐỀ 483
Câu 1: Giả sử A và B là các ma trận vuông cấp n thỏa mãn
là ma trận không). Khi đó: A) 𝐁𝟐𝐀𝟐 = 𝟎 B2A2 = BB. AA = B. 0. A = 0 B) (𝐀𝐁)𝟐 = 𝟎 (AB)2 = AB. AB = A. 0. B = 0 C) A và B đều suy biến
Giả sử A không suy biến thì |A| , suy ra tồn tại A−1.
Nhân cả hai vế của B. A = 0 cho A , ta được:
B. A. A−1 = 0. A−1 ⇒ B = 0 (trái giả thiết) Và
chứng minh tương tự, cuối cùng suy ra A, B đều suy biến. D) Tất cả đều đúng
Câu 2: Cho hệ phương trình tuyến tính AX=B với 𝐀𝐦×𝐧. Nếu hệ phương trình có nghiệm duy nhất thì: A) 𝐦 = 𝐧 lOMoARcPSD| 36207943 B)
C) Hệ véctơ cột của A độc lập tuyến tính
D) Hệ véctơ dòng của A độc lập tuyến tính.
Phương trình tuyến tính AX=B có nghiệm duy nhất ⇔ r(A) = n ⇔ r(AT) = n
⇔ Hệ véctơ dòng của AT độc lập tuyến tính
⇔ Hệ véctơ cột của A độc lập tuyến tính
Câu 3: Cho không gian véctơ V có chiều bằng
độc lập tuyến tính. Khẳng định nào sau đây luôn đúng?
A) Tập {𝐱, 𝐲, 𝐳, 𝐭} phụ thuộc tuyến tính.
dimV = 3 < số véctơ = 4 ⇒ Tập {x,y, z, t} phụ thuộc tuyến tính.
B) Hệ {𝐱,𝐲, 𝐳} độc lập tuyến tính.
Ta chỉ biết trong V có hệ 3 véctơ độc lập tuyến tính, 2 trong 3 véctơ đó là x và y. Nhưng véctơ còn lại thì chưa biết chắc là z hay t.
C) 𝐕 = {𝐱, 𝐲, 𝐱 + 𝟐𝐲}
Nếu vậy thì dimV = 2 (trái với đề bài).
D) {𝐱, 𝐲, 𝐱 − 𝟐𝐲} sinh ra không gian ba chiều.
Chỉ có hai ẩn x và y nên hệ này chỉ sinh được không gian hai chiều. Phần hai: GIẢI TÍCH K41 – MÃ ĐỀ 213
Câu 1: Tìm cực trị của hàm hai biến 𝐟(𝐱, 𝐲) = 𝐱 + 𝐲 + 𝟐𝟕 . 𝐱𝐲 Dùng định lý Cauchy: f(x, y) = x + y +
Dấu “=” xảy ra khi x = y = 27 ⇒ x = y = 3. xy
Vậy min f = 9 khi x = y = 3.
Không khuyến khích dùng phương pháp Lagrange cho bài toán này.
Câu 2: Cho hàm số 𝐟(𝐱) = 𝟐|𝐱 − 𝟑| + (𝐱 − 𝟑)𝟐. Tính 𝐟′(𝟐). lOMoARcPSD| 36207943
Khi x → 2 thì x − 3 < 0 nên ta bỏ trị tuyệt đối của hàm số:
f(x) = 2(3 − x) + (x − 3)2 ⇒ f ′(x) = −2 + 2(x − 3) ⇒ f ′(2) = −4
Câu 3: Cho 𝐟(𝐱) = 𝐱𝟗𝐬𝐢𝐧𝐱. Tính 𝐟 . f i=0 Câu 4: Tính
𝐬𝐢𝐧𝟐 𝐱 − 𝟓𝐱𝟑 𝐋 = 𝐥𝐢𝐦
𝐱→𝟎 𝟕𝐱𝟑 + 𝟐 𝐭𝐚𝐧𝟐 𝐱 − 𝟑 √
𝟑 𝐱 . 𝐭𝐚𝐧𝟒𝐱
Sử dụng tính xấp xỉ của các đại lượng vô cùng bé, ta viết lại: x2 + 24x4/3 x2/3
L = lim= lim= − 2 x→0 7 x 3 +2 x 2 −12 x 4 / 3 x→0 7 x 5 / 3 +2 x 2 / 3 −12
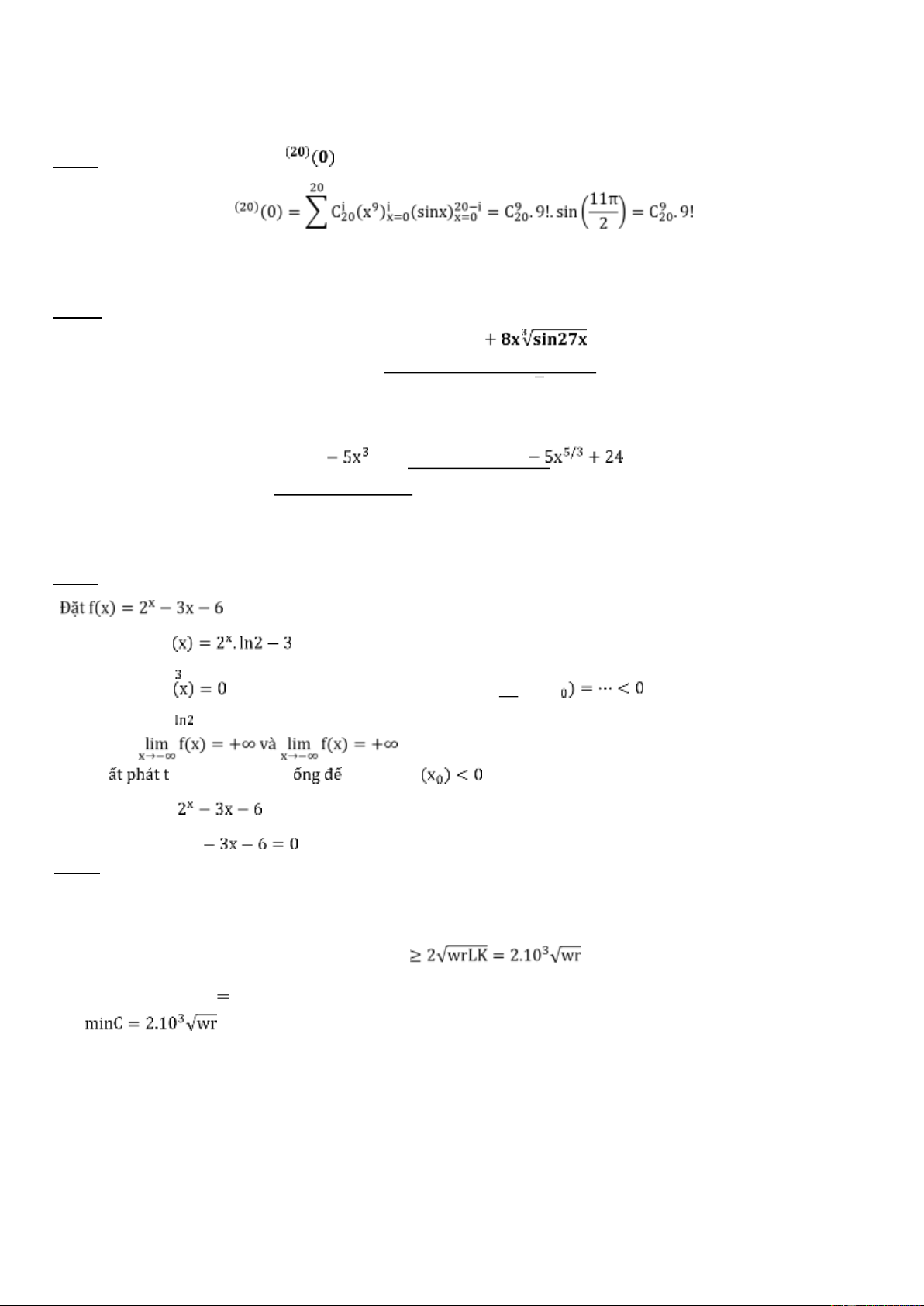
Câu 5: Phương trình 𝟐𝐱 − 𝟑𝐱 − 𝟔 = 𝟎 có bao nhiêu nghiệm trên ℝ? - -Lấy đạo hàm: f ′ -Phương trình f ′
cho ta duy nhất một nghiệm x0 = log2 ⇒ f(x -Nhận thấy
nên ta có thể dùng bảng biến thiên để mô tả hình dạng đồ thị của f(x): Xu ừ trên cao, lao xu n cực tiểu f
rồi lại quay ngược trở lên cao, giống như parabol. Như vậy, hàm số
cắt trục hoành tại 2 điểm. Vậy phương trình 2x
có đúng 2 nghiệm trên ℝ.
Câu 6: Chi phí của một công ty là 𝐂(𝐋, 𝐊) = 𝐰𝐋 + 𝐫𝐊 trong đó là L là lượng lao động, K là tiền vốn, w và r là các
hằng số thực dương. Điều kiện cần để C nhỏ nhất thỏa điều kiện 𝐋𝐊 = 𝟏𝟎𝟔 là: Theo định lý Cauchy: C(L, K) = wL + rK = const
Dấu “=” xảy ra khi wL rK Vậy khi wL = rK Câu 7: Tính giới hạn 𝟏 𝐥𝐢𝐦 (𝟏 + 𝐱→𝟎 lOMoARcPSD| 36207943 1 8 sin 2 lim (1 + tan 8x − sin8x)
x = lim 𝐭𝐚𝐧𝟖𝐱−𝐬𝐢𝐧𝟖𝐱
𝟖𝐬𝐢𝐧 𝟐 𝐱 eln(1+tan 8x−sin 8xx ) x = ) 1 𝐱
lim e8 sin 2 xln(1+tan 8x−sin 8xx ) x→0 x x→0 x→0 1
Xét phần mũ, sử dụng tính chất lượng vô cùng 8 sin 2 bé tương đương: tan 8x − sin 8x limx ) = lim= lim 8 sin 2 8 xsin 2 8 xsin 2 x→0 x x→0 x x→0 x . cos 8x 4x 2 8.2.16 = lim 8 x.x 2 .cos8x 8 = x lsiin m 2 = lim= 32 x→0 x . cos 8x x→0 x→0 8 .cos8x Vậy lim (1 + tan 8x−sin 8x ) x = e32 x→0 x
Đây là cách làm mình trích từ cách làm của cô Bùi Thị Lệ Thủy – Khoa Toán - Thống Kế UEH.
Bài giải của cô hơi khác mình một tí, mình chỉ mượn bước sụ dụng công thức lượng giác 1 − 𝑐𝑜𝑠 8𝑥 = 2 𝑠𝑖𝑛2
4𝑥 của cô trong phần tính số mũ thôi. Nếu mình có vô tình giải sai thì không có nghĩa là cô giải sai nhé!
Câu 8: Giả sử 𝐲 = 𝐟(𝐱) là nghiệm của phương trình vi phân 𝐲′ −
𝟏+𝐱𝐱𝐲 𝟐 = 𝟎 thỏa điều kiện 𝐟(𝟎) = 𝟏. Tính 𝐟(𝟏)?
-Nghiệm của phương trình vi phân thuần nhất trên: y = e -Theo đề bài: f = 1 ⇒ C = 1 -Từ đó tính được: f
Câu 9: Trong khai triển Mac-Laurin đến cấp 5 của hàm số 𝐟
= 𝐱. 𝐥𝐧 (𝟏 + 𝟐𝐱), hệ số của 𝐱𝟓 là: K 5.16.6 f 5! = −5.16.6 ⇒ K5 = −= −4 i=0 𝐞𝟐𝐱 Câu 10: Cho 𝐟 . Tính 𝐟′(𝟎). 𝟒 𝐤𝐡𝐢 𝐱 = 𝟎 2 − 4 e lOMoARcPSD| 36207943
f ′(0) = x→0lim f(xx − 0) − f(0) = x→0lim e2x − 1 −xlnx(1 + 2x) = x→0lim
2x − 1 − ln(x1 + 23x) − 4x2 = 2 2 e 2 x − 1+2 x − 8x 4e2x + − 8 8e2x − 3 x 2 = lim = lim = lim = − x→0 x→0 6x x→0 6
Câu 11: Dùng khai triển Mac-Laurin đến cấp 2 của hàm số 𝐟 để tính . f(x + Δx) = f Δ𝑥 ⇒. 2! Thay x = , ta có: ⇒
Câu 12: Cho hàm lợi ích 𝐔(𝐱, 𝐲) có các đạo hàm riêng cấp hai liên tục trên ℝ𝟐. Giả sử ta có điều kiện 𝐱𝟐 + 𝟐𝐲𝟐 = 𝐓
(𝟏) với T là hằng số dương cho trước. Điều kiện cần để U đạt cực đại tại (𝐱, 𝐲) thỏa điều kiện (1) là:
L(x, y, λ) = U(x, y) + λ(T − x2 − 2y2)
Điều kiện cần để hàm số đạt cực đại là: ⇒ {UUyx′′⇒ λ =
U2xx′ = Uyy′ ⇒ 2yUx′ = xUy′ 4
Câu 13: Xét phương trình vi phân 𝐲′′ − 𝟒𝐲′ + 𝟓𝐲 = 𝐞𝟐𝐱(𝐱𝐜𝐨𝐬𝐱 + 𝟑𝐬𝐢𝐧𝐱). Phương trình này có một nghiệm riêng với dạng là:
Phương trình đặc trưng k2 − 4k + 5 = 0 ⇒ k = 2 ± i
Xét vế trái của phương trình, nhận thấy 2 + i là nghiệm của phương trình đặc trưng nên nghiệm riêng của phương trình đã cho có dạng:
y1 = x. e2x[(ax + b)cosx + (cx + d)sinx]
Câu 14: Xét phương trình vi phân 𝒚′′ − 𝟒𝒚′ + 𝟒𝒚 = 𝒆𝟐𝒙(𝟑𝒙 + 𝟏). Phương trình này có một nghiệm riêng với dạng là:
Phương trình đặc trưng: 𝑘2 − 4𝑘 + 4 = 0 ⇒ 𝑘 = 2 lOMoARcPSD| 36207943
Xét vế trái của phương trình, nhận thấy 2 là nghiệm kép của phương trình đặc trưng nên nghiệm riêng của phương
trình vi phân đã cho có dạng:
𝑦1 = 𝑒2𝑥𝑥2(𝑎𝑥 + 𝑏) ℎ𝑎𝑦 𝑦1 = 𝑒2𝑥(𝑎𝑥3 + 𝑏𝑥2) 𝟏 𝟏
Câu 15: w, r là các hằn số dương cho trước. Tìm (𝐋; 𝐊) theo w và r để hàm 𝐅(𝐋, 𝐊) = 𝟔𝐋𝟑𝐊𝟑 − 𝐰𝐋 − 𝐫𝐊 đạt cực
đại toàn cục trên 𝐃 =
𝐧|𝐋 > 𝟎, 𝐊 > 𝟎} Xét hàm F(L, K) = 6L − wL − rK, ta có: − w ; − r ∂ 2 F 4 1 F L − 5 3 K 3 ∂L 2 =− 3 ; ; Tìm điểm dừng, ta có: w6r3 −33 3 2 L = ( ) = 2 2 2 2 ⇒ = w ⇒ = r LK = r ⇒ 29 r3 − w r ⇒ { K =L = wr 3wr = r { K = (23L) Mặt khác, ta có: a |H̅| | F F Suy ra hàm số
đã cho đạt cực đại toàn cục trên D khi: 3 3 (L, K) = (;) w r r w 2 2 Giá trị cực đạt: 24 8w 8r 8 2 − r2)
maxF(L, K) = − − = (3 − w wr r w wr lOMoARcPSD| 36207943 lOMoARcPSD| 36207943
16: Cho phương trình vi phân 𝐲′′ − 𝟔𝐲′ + 𝟖𝐲 = 𝟖𝐱𝐞𝟐𝐱 (𝟏).
a) Giải phương trình (1).
-Nghiệm của phương trình đặc trưng:
k2 − 6k + 8 = 0 ⇒ [k = 2 k = 4
-Ta có nghiệm của phương trình thuần nhất liên kết y′′ là: y = c 4x với c
-Xét vế phải của (1), thấy α = 2 là 1 nghiệm đơn của phương trình đặc trưng nên (1) có một nghiệm riêng:
y1 = e2x.x. (ax + b) = e2x(ax2 + bx) ⇒ y ′
1 = 2e2x(ax2 + bx) + e2x(2ax + b) = e2x[2ax2 + (2a + 2b)x + b]
⇒ y1′′ = 2e2x[2ax2 + (2a + 2b)x + b] + e2x(4ax + 2a + 2b) = e2x[4ax2 + (8a + 4b)x + 2a + 4b]
-Thay vào phương trình (1), ta có:
e2x[4ax2 + (8a + 4b)x + 2a + 4b] − 6e2x[2ax2 + (2a + 2b)x + b] + 8e2x(ax2 + bx) = 8xe2x
⇒ (−4a − 8) + 2a − 2b = 0 ⇒ {−4a − 8 = 0 ⇒ {a = −2 2a − 2b = 0 b = −2 ⇒ y1′ = −2xe2x(x + 1)
-Vậy nghiệm tổng quát của phương trình đã cho là:
y = y + y1 = c1e2x + c2e4x − 2xe2x(x + 1) với c
b) Tìm nghiệm riêng của (1) thỏa điều kiện 𝐲(𝟎) = 𝟏 và 𝐲′(𝟎) = 𝟏. Ta có:
y = c1e2x + c2e4x − e2x(2x2 + 2x) ⇒ y′ = 2c1e2x
+ 4c2e4x − 2e2x(2x2 + 2x) − e2x(4x + 2) Theo đề bài: yy(0) = 1 c1 + c2 = 1
⇒ {2cc11 ++ 4c2c2= 1= 3 ⇒ c1 = c2
= { ′(0) = 1 ⇒ {2c1 + 4c2 − 2 = 1
Vậy nghiệm riêng cần tìm là:
y = e2x + e4x − e2x(2x2 + 2x) K40 – MÃ ĐỀ 460
Câu 1: Giả sử 𝐏(𝐱) là hàm số liên tục trên
là một nguyên hàm của 𝐏 và lOMoARcPSD| 36207943 Câu 𝐥𝐢𝐦 𝐏
Gọi 𝛗(𝐱) là một nghiệm của phương trình vi phân 𝐲′
. 𝐲 = 𝟎. Khi đó 𝐥𝐢𝐦 𝐱. 𝛗(𝐱) có giá trị:
Vì φ(x) là nghiệm của phương trình y′ nên: C C x. Ce 0.∞ e e.F′ Vì nên = 0 (dạng C )
Câu 2: Cho hàm sản lượng =(𝐊,𝐋) = 𝟑𝐊𝟏/𝟑𝐋𝟐/𝟑, trong đó K là lượng vốn và L là lượng lao động. Tính sản lượng biên
theo lao động khi 𝐊 = 𝟏𝟐𝟓,𝐋 = 𝟐𝟕 biết lúc đó hệ số co giãn của Q theo L là 3/20. dQ
Sản lượng biên theo lao động: MQ(L) = dQ LdL
{ Hệ số co giãn của Q theo L: εQL = dL . Q Q 3.
⇒ MQ(L) = εQL. L =.⇒ MQ(L) = 0,75 20 27
Có một bạn đề nghị mình giải tuần tự ra hết để so sánh với bài làm của thầy bạn ấy. Vì thầy bạn ấy làm tuần
tự ra thì kết quả lại là 3/10. Sau đây mình xin trả lời yêu cầu của bạn: Theo định nghĩa: 𝑑𝑄 𝐿 𝑑(𝐾1/3) 𝑑(𝐿2/3) 𝐿𝐾−2/3.𝑑𝐾 2 3 3
𝜀𝑄𝐿 = 𝑑𝐿 . 𝑄 = 3 [ 𝑑𝐿 . 𝐿2/3 + 𝐾1/3.
𝑑𝐿 ] . 3𝐾1/3𝐿2/3 =
𝑑𝐿𝐾. 𝐿1/23/𝐿3−1+/𝐾3 1/3.𝐿−1/3
−1.𝐿. 𝑑𝐾 + = 𝐿 . 𝑑𝐾 + ⇒ 𝜀 3 𝑄𝐿 = 𝐾 𝑑𝐿 3 3𝐾 𝑑𝐿 𝑑𝐾 𝑑𝐾 ⇒=. +⇒ = − 20 375 3 108 𝑑𝐿 𝑑𝐿 Theo định nghĩa: 𝑀𝑄(𝐿) = 𝑑𝑄 𝑑(𝐾1/3)
2/3 + 𝐾1/3.𝑑(𝐿2/3)] = 3 [ 𝐾−2/3.𝑑𝐾 . 𝐿2/3 + 𝐾1/3. 𝐿−1/3] = 3 [ . 𝐿 𝑑𝐿 𝑑𝐿 𝑑𝐿 3 𝑑𝐿 3 lOMoARcPSD| 36207943
−2/3.𝐿2/3.𝑑𝐾 + 2. 𝐾1/3.𝐿−1/3 ⇒ 𝑀𝑄(𝐿) = 𝐾 𝑑𝐿
⇒ 𝑀𝑄(𝐿) = 125−2/3.272/3.(− ) + 2. 1251/3.27−1/3 = 0,75
3: Giả sử 𝐲 = 𝐲(𝐱) là nghiệm của phương trình vi phân 𝐲′ − 𝐲 = 𝐞𝐱 + 𝟏, thỏa điều kiện 𝐲(𝟎) = −𝟏. Phát biểu nào sau đây là sai?
-Trước tiên, ta cần tìm nghiệm tổng quát của phương trình y′ − y = ex + 1.
-Nghiệm của phương trình thuần nhất tương ứng y′ là: y = C. e = C. ex
-Xem C = C(x) ⇒ y = C(x). ex. Thay vào phương trình đã cho và rút gọn ta được: C′ + 1 ⇒ dC .dx ⇒ C = x − e
-Vậy nghiệm tổng quát của phương trình y′ − y = ex là: y = -Theo đề bài:
y(0) = −1 ⇒ K − 1 = −1 ⇒ K = 0 -Vậy cuối cùng thì: y(x) = x. ex − 1 A) 𝐲(𝟏) > 𝟎
y(1) = 1. e − 1 = e − 1 > 0 B) 𝐲′(𝟎) = 𝟏
y′(x) = (x + 1)ex ⇒ y′(0) = 1 C) 𝐲 = 𝟎 D) 𝐲
Câu 4: Một xí nghiệp sản xuất một loại sản phẩm. Hàm sản lượng được cho bởi =(𝐱) = 𝟒,𝟎𝟐𝐱𝟏/𝟐, trong đó x là
lượng nguyên liệu chính tạo ra sản phẩm. Tỉ lệ hao hụt nguyên liệu khi sản xuất là 5%. Giả sử đơn giá bán sản
phẩm là 100 và đơn giá mua nguyên liệu là 20. Để xí nghiệp thu được lợi nhuận lớn nhất thì lượng nguyên liệu
cần sử dụng là bao nhiêu?
-Gọi N là lượng nguyên liệu cần sử dụng.
-Để mua lượng nguyên liệu này, xí nghiệp tốn chi phí: C = 20N
-Do hao hụt nguyên liệu khi sản xuất nên lượng nguyên liệu chính tạo ra sản phẩm chỉ còn lại lOMoARcPSD| 36207943 Câu N′ = 95%.N = 0,95N
-Lượng sản phẩm này cho ra sản lượng: Q
= 4,02.N′ = 4,02.(0,95N)1/2 -Sản
lượng này đem bán sẽ mang về doanh thu: R = 100Q = 402.(0,95N)1/2
-Lợi nhuận của xí nghiệp được tính:
π = doanh thu − chi phí = R − C = 402. (0,95N) − 20N
-Ta cần tìm lượng nguyên liệu N để lợi nhuận π đạt cực đại.
-Sử dụng phương pháp tìm cực trị như hồi Trung học: 1
π′(N) = 0 ⇔ 201(0,95N)−2 − 20 = 0 ⇔ N = (
Câu 5: Bằng cách sử dụng vi phân toàn phần, ta có thể xấp xỉ hàm số 𝐟 nằm trong lân
cận của (𝟒, 𝟐) bởi đa thức:
Với (x, y) nằm trong lân cận của (4,2), ta có thể biểu diễn:
x = x0 + Δx ; y = y0 + Δy với (x0,y0) = (4,2) và (Δx, Δy) → (0,0) Áp
dụng công thức Taylor cho hàm nhiều biến đến đạo hàm cấp 1, ta có: f(x, y) = f(x0 + Δx, y
⇒ f(x, y) = f(x0,y0) + (x − x0) ⇒ f ⇒ f ⇒ f y
Nhìn quá trời vậy thôi chứ thật ra dễ hiểu lắm! Đừng vội nản nhé!
Cảm ơn bạn Nguyễn Văn Quang Phú đã giúp đỡ mình bài toán này (nhờ dịp này mới gặp được người quen,
hê hê). Bạn ấy không nói công thức làm bài này nằm ở trang 187 sách giáo trình chắc tới hết đời mình cũng
không thèm tách hai trang sách 188 và 189 đang bị dính của mình. Cảm ơn bạn rất nhiều!
Cách làm trên là mình lấy từ ý tưởng của bạn Phú, nhưng đã sắp xếp lại cho chặt chẽ hơn.
Câu 6: Trong khai triển Maclaurin của hàm số 𝐟
thì hệ số của 𝐱𝟑 là: Theo công thức Maclaurin: ( 0 ) (2) ( 0 ) f (3) ( 0 ) f ( n ( 0 ) f(x) = f(0) + f (1) .x 2 + .x 3 + ⋯ + .x n + . x + f f. x 2! 3! n! n+1 lOMoARcPSD| 36207943 1! (n + 1)!
Hệ số của x3 chính là: f (3) − K3 = 3! = = −32
7: Phương trình vi phân 𝐲′′ − 𝟐𝐲′ + 𝐲 = 𝐱. (𝐞𝐱 − 𝟏) có một nghiệm riêng dạng:
-Ta viết lại phương trình đã cho thành: y′′ + y = xex − x
-Gọi y1 là nghiệm riêng của phương trình y′′ + y = xex.
-Phương trình đặc trưng k
có nghiệm kép k = 1 nên y1 có dạng: y hay y1 = ex(a1x3 + b1x2)
-Gọi y2 là nghiệm riêng của phương trình y′′ + y = −x.
-Phương trình đặc trưng k có nghiệm kép nên y2 có dạng: y2 = a2x + b2
-Theo nguyên lý chồng chất nghiệm, nghiệm riêng của phương trình đã cho có dạng:
y = y1 + y2 = ex(a1x3 + b1x2) + a2x + b2
-Có thể đặt lại: a1 = a, b1 = b, a2 = c và a2 = d cho giống đáp án: y = ex(ax3 + bx2) + cx + d
Câu 8: Cho hàm số 𝐟(𝐱) khả vi trong một lân cận của 0, 𝐟(𝟎) = 𝟎 và 𝐟′(𝐱) là một vô cùng bé bậc cao hơn x khi 𝐱 → 𝟎. Hãy tính: − 𝐜𝐨𝐬𝐱 𝐋 = 𝐥𝐢𝐦𝐱→𝟎 𝐱𝟐
f ′(x) là một vô cùng bé bậc cao hơn x khi x → 0, tức là f ′ khi x → 0, hay ta viết: f ′
Ta sẽ dùng quy tắc L’hospital cho bài toán này: f ′ √ 1+ f ( x ) − cosx 2 √ 1+ f ( x ) L=lim x→0 x 2 = lim x→0 f ′ lOMoARcPSD| 36207943 Câu 2x Vì f(0) = 0, lim f ′(x) = 0 và lim nên: x→0 x x→0 x f ′ = 0 và lim=⇒ L = 2 x→0 2x 2
Câu 9: Cho hàm số 𝐟(𝐱) =
𝟏+𝐬𝐢𝐧𝐱|𝐱|. Phát biểu nào sau đây là
sai? A) f không có đạo hàm tại 0.
′(0) = lim f(x) − f(0) = lim = lim sinx .
= 1 ⇒ f ′(0) = 1 ⇒ f có đạo hàm tại 0 f x→0 x − 0 x→0 x x→0 1+ | x x | B) f liên tục tại 0
lim+ 1+ |x| = lim− |x| = f(0) = 0 ⇒) f liên tục tại 0 x→0 1+ x→0 C) f bị chặn trên Ta có: .
D) f có giới hạn hữu hạn khi Vì nên
Vậy f có giới hạn hữu hạn khi . Câu 10: Cho hàm số 𝐚 𝐟(𝐱) = {𝟑𝐱. 𝐱 𝐛 (𝐱 = 𝟎)
Trong đó a, b là các hằng số. Tìm điều kiện của a và b để f liên tục tại 0.
f liên tục tại 0 ⇔ limx→0+ f(x) = x→0lim− f(x) = f(0) = b Ta xét: a lOMoARcPSD| 36207943 lim+ f(x) = x→0lim+ 3x. x x→0
Nhận thấy, với mỗi trường hợp hằng số a dương, âm, hoặc bằng không đều ảnh hưởng đến kết quả.
Ta chia thành 3 trường hợp:
-Trường hợp 1: a>0. Khi đó:
Bài toán rơi vào dạng vô định 0. ∞ nên ta cần khử dạng vô định bằng quy tắc L’hospital: a1 a x x lim 3x.x = lim= lim= 1 1 x→0+ x→0+x→0+ x x 1
Để tính đạo hàm của (3a)x, ta phải dùng phương pháp ln hóa hai vế như sau. 1 y = (3a)x a)1x] = 1 ln3a ⇒ lny = ln [(3 x ⇒ 1 ′ = − a 2 . y y x a ⇒ y′ = −. y 2 x a 1 ⇒ y′ = −. (3a)x 2 x lOMoARcPSD| 36207943 Khi đó: 1 ln3 a 1 ( 3 a ) x − x 1 lim = lim x 2 . ( 3 a ) = lim x =+ ∞ x→0 + 1 x→0 + 1 x→0 + ln3 a . ( 3 a ) x − x 2
Như vậy, với trường hợp a>0 thì không tồn tại b.
Trường hợp 2: a=0. Khi đó:
lim+ f(x) = x→0lim− f(x) = 0 ⇒ b =
0 x→0 Vậy a=0, b=0 là một trường hợp thỏa mãn.
Trường hợp 3: a<0. Khi đó: = 0 ; lim x→0 x→0 x→0
Vậy khi a<0 thì hàm số không liên tục tại x=0.
Câu 11: Với ràng buộc 𝐱𝟐 + 𝐲 = 𝟑 thì hàm số 𝐟(𝐱, 𝐲) = 𝐱𝐲 sẽ:
A) Đạt cực đại tại (-1,2)
B) Đạt cực đại tại (1,2)
C) Đạt cực tiểu tại (1,-2)
D) Đạt cực tiểu tại (1,-2)
Cách 1: Kiến thức Trung học phổ thông f 3x − x3 f ′(x) = 0 ⇔ [ x = 1 x = −1
f ′′(1) = −6 < 0 ⇒ f(x) đạt cực đại tại x = 1 f
′′(−1) = 6 > 0 ⇒ f(x) đạt cực tiểu tại x = −1
Hay f(x, y) đạt cực đại tại (x, y) = (1,2) và đạt cực tiểu tại (x, y) = (−1,2) Cách
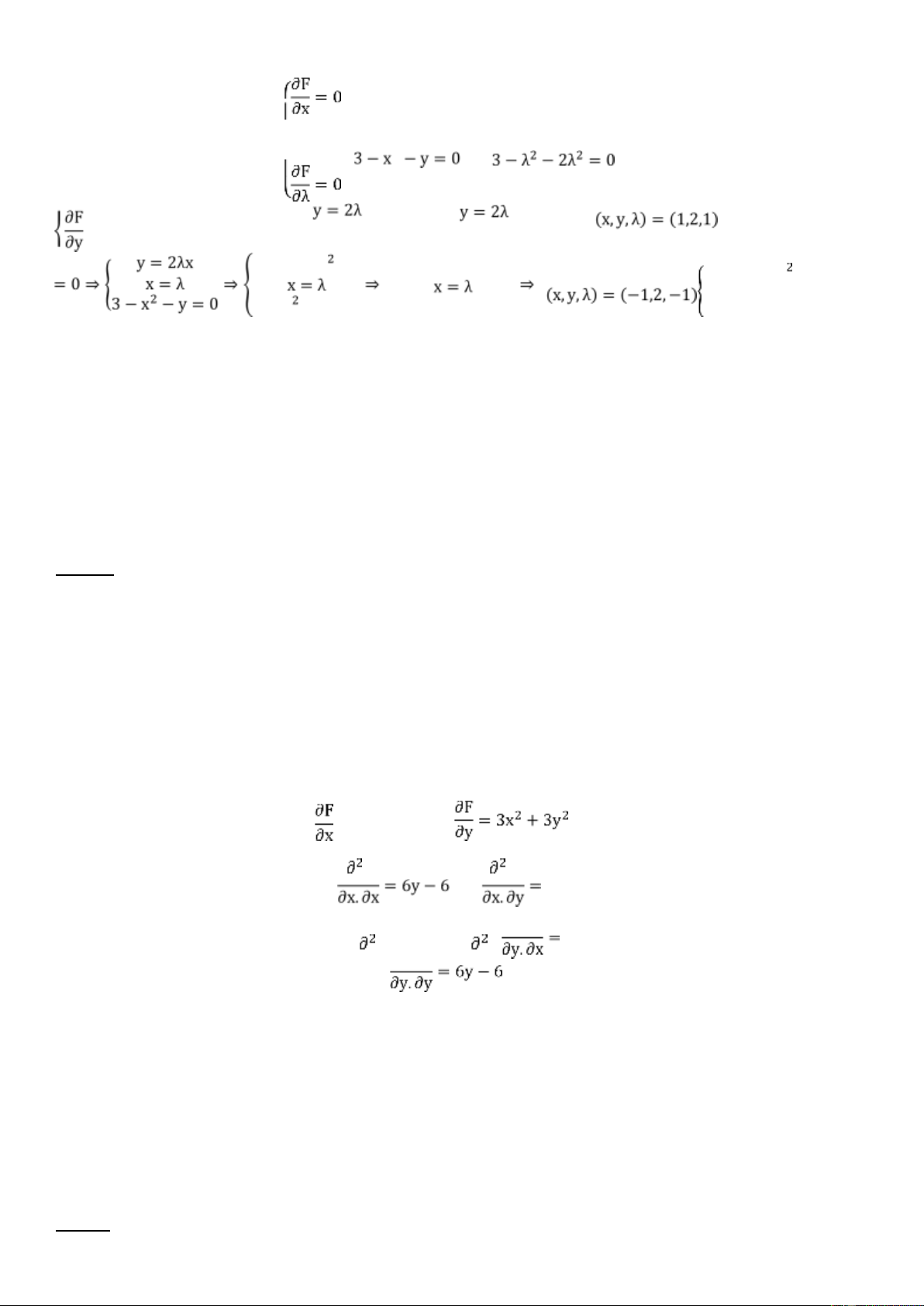
2: Sử dụng phương pháp nhân tử Lagrange. g(x, y) = 3 − x2 − y
F(x, y, λ) = f(x, y) + λ. g(x, y) = xy + λ(3 − x2 − y) Ta tìm các đạo hàm: = y − 2λx − y F lOMoARcPSD| 36207943 Tìm các điểm dừng: [
Điều kiện đủ để các điểm dừng là cực trị: −2 1 0 H2(1,2,1) = | 1 0
−1| = 4 > 0 ⇒ (−1)2.H2(1,2,1) > 0 ⇒ f(x, y) đạt cực đại tại (x, y) = (1,2) −2 −1 0 2 1 0 H2(−1,2,−1) = |1 0
−1| = −4 < 0 ⇒ (−1)1.H2(−1,2,−1) > 0 ⇒ f(x, y) đạt cực tiểu tại (x,y) = (−1,2) 2 −1 0
Câu 12: Cho biết 𝐌(𝟏, 𝟏) 𝐯à 𝐍(𝟎,𝟐) là hai trong số các điểm dừng của hàm số:
𝐟(𝐱, 𝐲) = 𝟑𝐱𝟐𝐲 + 𝐲𝟑 − 𝟑𝐱𝟐 − 𝟑𝐲𝟐 + 𝟐 Phát biểu nao sau đây là sai? A)
f đạt cực đại tại M, đạt cực tiểu tại N B)
f đạt cực tiểu tại M, đạt cực đại tại N C)
f không đạt cực trị tại M, đạt cực đại tại N D) f không đạt cực trị tại M, đạt cực tiểu tại N Ta tìm các đạo hàm:. = 6xy − 6x ; − 6y F F 6x FF 6x Ta xét:
HM(1,1) = |06 60| = −36 < 0 ⇒ f không đạt cực trị tại M
HN(0,2) = |60 06| = 36 > 0 và a11(0,2) = 6 > 0 ⇒ f đạt cực tiểu tại N
Câu 13: Giả sử hàm số 𝐟(𝐱) có đạo hàm cấp hai trong một lân cận của 0 và: lOMoARcPSD| 36207943 𝐟(𝟎) = 𝟎, 𝐟′(𝟎) = 𝟎, 𝐟′′(𝟎) = −𝟐
Giới hạn 𝐥𝐢𝐦𝐱→𝟎
𝐟(𝐱𝟐𝐱)−𝟐 𝐟(𝐱) có giá trị là:
Chú ý đạo hàm của hàm hợp: df(x2) = df . d(x2) ′(x2).2x = f dx d ( x 2 ) dx
Như vậy, ta sẽ sử dụng liên tục quy tắc L’hospital để giải quyết bài toán này: f f ′ .2x − f ′ f ′′ lim= lim = lim x→0 2 x x→0 2x x→0 2 f f ′′ ⇒ lim= = = 1 x→0 2 2 2 x Vậy lim f= 2 1 x→0 x
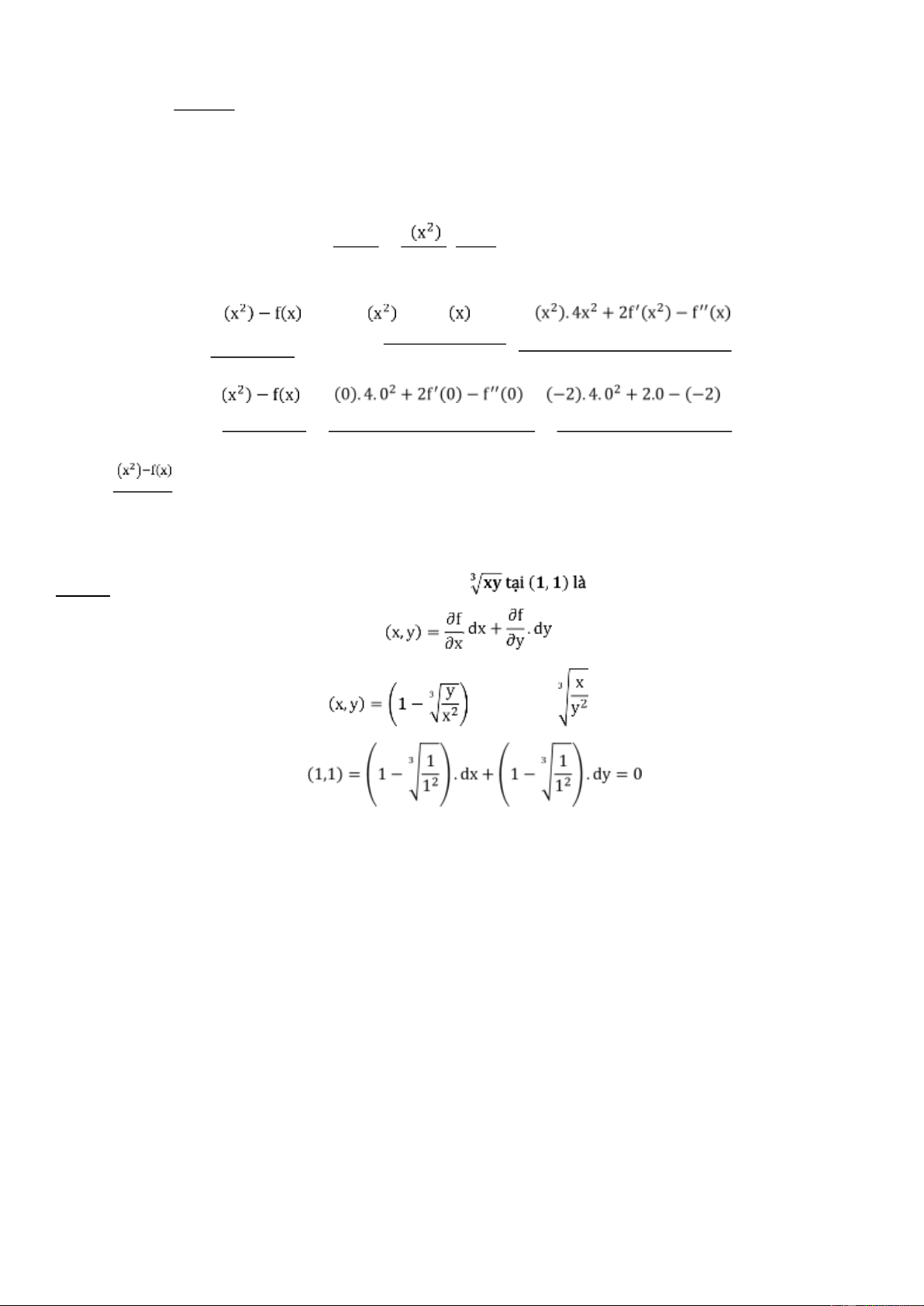
Câu 14: Vi phân toàn phần của hàm số 𝐟(𝐱, 𝐲) = 𝐱 + 𝐲 − 𝟑 : df ⇒ df . dx + (1 − ) . dy ⇒ df lOMoARcPSD| 36207943
Câu 15: Sử dụng phương pháp nhân tử Lagrange tìm cực trị địa phương của hàm số:
𝐳 = 𝐟(𝐱, 𝐲) = 𝐞𝐱𝐲 Với
điều kiện 𝐱𝟐 + 𝐲𝟐 = 𝟖 𝐯à 𝐱, 𝐲 > 𝟎. Bước 1: Đặt: g(x, y) = x2 + y2 − 8
F(x, y, λ) = f(x, y) + λ. g(x, y) = exy + λ. (x2 + y2 − 8)
Bước 2: Tìm các đạo hàm: = yexy = xexy F F exy F 2x F exy F F 2y F F 2x 2y
Bước 3: Giải hệ phương trình: ∂F =0 ⇒ { xe xy ∂y x 2 + y 2 =8 xe ∂F { x 2 + y 2 =8 = −2= −2λyλx ⇒ xy = −2y
λyx ⇒ { xλ = −2x+2 =y2xey2= 82yxy ⇒ {λ = −y = 2x = 2e24 (chú ý: x, y > 0)
B ư ớ c 4 : Xét định thức:
H2 (2,2, − e24) = |35ee4453ee44 44| = 32.5e4 − 32.3e4 = 32.2e4 > 0 ⇒ (−1)2.H2 > 0 4 4 0
⇒ Hàm số đã cho đạt cực đại tại (x,y) = (2,2) Bước 5: Kết luận
Vậy hàm số f(x, y) = exy với điều kiện x2 + y2 = 8; x, y > 0 đạt cực trị địa phương tại (x, y) = (2,2). Chú ý:
𝐇𝐧 𝐥à đị𝐧𝐡 𝐭𝐡ứ𝐜 𝐜ủ𝐚 𝐦𝐚 𝐭𝐫ậ𝐧 𝐜ấ𝐩 (𝐧 + 𝟏)×(𝐧 + 𝟏) 𝐧ằ𝐦 ở 𝐠ó𝐜 𝐭𝐫ê𝐧 𝐛ê𝐧 𝐭𝐫á𝐢 𝐜ủ𝐚 𝐦𝐚 𝐭𝐫ậ𝐧 đạ𝐨 𝐡à𝐦 𝐜ấ𝐩 𝟐 lOMoARcPSD| 36207943 - 𝐦.𝐇𝐤 thì f đạt cực tiểu - thì f đạt cực đại
Với n số ẩn của hàm số cần tìm cực trị và m là số điều kiện.
Câu 16: Tìm nghiệm tổng quát của phương trình vi phân: 𝐲′′ + 𝟒𝐲 = 𝐱𝐞𝟐𝐱 (𝟏𝟔)
Bước 1: Tìm nghiệm của phương trình đặc trưng k2 + 4 = 0 ⇔ [ k = 2i k = −2i
Bước 2: Tìm nghiệm tổng quát của phương trình vi phân thuần nhất tương ứng Vậy
nghiệm tổng quát của phương trình thuần nhất tương ứng y′′ là:
y = c1.cos2x + c2.sin2x với c
Bước 3: Tìm nghiệm riêng của phương trình vi phân đã cho
Vì α = 2 không là nghiệm của phương trình đặc trưng nên nghiệm riêng của (16) có dạng: y1 = e2x.(ax + b)
⇒ y1′ = 2e2x.(ax + b) + ae2x = e2x.(2ax + a + 2b) y1′′ =
2e2x.(2ax + a + 2b) + e2x.2a = e2x.(4ax + 4a + 4b)
Thay vào phương trình (16), rồi rút gọn:
e2x.(4ax + 4a + 4b) + e2x.(4ax + 4b) = xe2x
⇔ (8a − 1)x + (4a + 8b) = 0 ⇔ { 8a − 1 = 0 ⇔ { a = 4a + 8b = 0 b = − 16
Ta được một nghiệm riêng của (16) là: y1 =e2x.(2x − 1) 16
Bước 4: Kết luận nghiệm tổng quát Vậy
nghiệm tổng quát của (16) là: y = y1 + y =
e2x. (2x − 1) + c1.cos2x + c2.sìn2x K39 – MÃ ĐỀ 17
Câu 1: Cho 𝐟(𝐱) = 𝐱𝟒𝐬𝐢𝐧𝐱. Tính 𝐟(𝟏𝟗)(𝟎). Áp dụng công thức: 𝐤 lOMoARcPSD| 36207943 𝐢=𝟎 Ta có: f i=0
Nhận thấy với i < 4 thì số hạng trong biểu thức khai triển sẽ chứa x và khi thay x=0 vào thì giá trị sẽ bằng 0. Với
i>4 thì đạo hàm của x4 bằng 0, kéo theo giá trị của số hạng chứa nó cũng bằng 0.
Như vậy, trong khai triển thành tổng trên, chỉ có i=4 thì số hạng mới có nghĩa. Tức”
f (19)(0) = C194 .(x4)(x=04) .[sinx](x=015) = C194 .(4.3.2.1)x=0.[sin(x + 15)] = −24.C194
x=0 Ta có thể làm tổng quát: k (xn.sinax) (x = 0) i=0
= Ckn. (n!)x=0.an.[sin (ax + (k − n))] = Ckn. n! an. sin[(k − n)] x=0
𝐧. 𝐬𝐢𝐧𝐚𝐱)(𝐤)(𝐱 = 𝟎) = 𝐂𝐤𝐧. 𝐧! 𝐚𝐧. 𝐬𝐢𝐧[(𝐤 − 𝐧) 𝛑𝟐] ⇒ (𝐱
Áp dụng vào bài toán trên, thay n=4, k=19 và a=1, ta được:
f (19)(0) = C194 .4! 1n. sin(15 ) = −24.C194
Câu 2: Chi phí của một công ty là 𝐂(𝐋, 𝐊) = 𝐰𝐋 + 𝐫𝐊 trong đó L là lượng lao động, K là tiền vốn, w và r là các số
thực dương. Điều kiện cần để C nhỏ nhất thỏa điều kiện 𝐋𝐊 = 𝟏𝟎𝟔 là:
Cách 1: Sử dụng định lý Cauchy: C(L, K) = wL + rK
Dấu “=” xảy ra ⇔ wL = rK ⇔ w = K r L
Cách 2: Sử dụng phương pháp nhân tử Lagrange: g(L, K) = 106 − LK
F(L, K, λ) = C(L, K) + λ. g(L, K) = wL + rK + λ. (106 − LK)
Điều kiện cần để C nhỏ nhất là: w − λK = 0 w = λK w K ⇒ { r − λL = 0 ⇒ { r = λL ⇒ lOMoARcPSD| 36207943 LK
Câu 3: Tính giá trị của:
𝐬𝐢𝐧𝟐𝐱 − 𝟓𝐱𝟑 + 𝟐𝐬𝐢𝐧𝟑𝐱 𝐋
= 𝐥𝐢𝐦𝐱→𝟎 𝟕𝐱𝟑 + 𝟐𝐭𝐚𝐧𝟐𝐱 − 𝟑𝐭𝐚𝐧𝟒𝐱 Cách 1: Khi x → 0 thì nên ta có thể viết: x 2 −5 x 3 x−5x 2 +6 6 1 + 6x L=lim = lim = =− 7 x 3 +2 x 2 −12 x x→0 7 x 2 +2x−12 −12 2 x→0
Cách này cho ta đáp án đúng và nhanh nhưng lại vi phạm trầm trọng quy tắc sử dụng các đại lượng vô cùng bé
tương đương: “Không áp dụng thay thế các đại lượng cho một tổng ở mẫu hoặc các đại lượng đang nằm trong
một hàm khác”. Không khuyến khích dùng cách này khi thi. Khi nào bí quá thì đành vi phạm thôi, nhưng không
chắc kết quả sẽ đúng.
Cách 2: Dùng quy tắc L’hospital: 2x − 5x3 L = lim= lim== − x→0 −12 2 7 x 3 +2 tan 2 x−3tan4x x→0
Cách 3: Sử dụng máy tính: Nhập vào màn hình: 2x − 5x3 7 x 3 +2 tan 2 x−3tan4x
Nhấn CALC, nhập X=0,0001. Nhấn “=”, ta được kết quả xấp xỉ -0,5.
Câu 4: Cho hàm số 𝐟(𝐱) = 𝟐|𝐱𝟐 − 𝟒| + (𝐱 − 𝟐)𝟐. Tính 𝐟′(𝟏)?
′(1) = lim f(x) − f(1) = lim 2(4 −
x2) + (x − 2)2 − 7 = lim −x2 − 4x + 5 = lim(−x − 5) = −6 f x→1 x − 1 x→1 x − 1 x→1 x − 1 x→1
Câu 5: Tính giá trị của:
𝐋 = 𝐥𝐢𝐦𝐱→𝟎 𝟐𝐱𝐭𝐚𝐧𝟑𝐜𝐨𝐬𝟐𝟐𝐱𝟑𝐱
Ta tách thành tích của hai giới hạn: x→0 Ta có thể sử d : lOMoARcPSD| 36207943 x→0x→0 Vì lim x = 0 và nên: x→0 3 L = limx tan = 2 0 x→0 2x lOMoARcPSD| 36207943 Câu 6: Cho hàm số 𝐟
= 𝐞𝟓𝐱−𝟐𝐲. Tìm 𝐝𝟐𝐟 ? df . dx +
5x−2y.dx − 2e5x−2y.dy = e5x−2y(5dx − 2dy) ⇒ d . dx +
5dx − 2dy). dx − 2e5x−2y(5dx − 2dy). dy ⇒ d − 20. dx. dy + 4dy2)
𝐞𝟑𝐱−𝐜𝐨𝐬𝐱 Câu 7: Cho 𝐟 { 𝐱 . Tính 𝐟′(𝟎). 𝟑 𝐤𝐡𝐢 𝐱 = 𝟎 e3x − cosx
f ′(0) = x→0lim f(xx − 0) − f(0 = x→0lim x x − 3 = x→0lim e 3x − cosx − 3xx2 ) = lim = lim = = 5 x→0 2x x→0
Câu 8: Giả sử 𝐲 = 𝐟(𝐱) là nghiệm của phương trình vi phân 𝐲′ −
𝟑+𝐱𝐱𝐲 𝟐 = 𝟎 thỏa điều kiện 𝐟(𝟏) = 𝟐. Khi đó 𝐟(𝟐)
có giá trị bằng bao nhiêu?
Nghiệm tổng quát của phương trình vi phân đã cho là: y = C. e Theo đề bài: f ⇒ y = f
Câu 9: Xét phương trình vi phân 𝐲′′ − 𝟓𝐲′ + 𝟔𝐲 = 𝐞𝟐𝐱(𝟑𝐱 + 𝟏). Phương trình này có một nghiệm riêng với dạng:
Nghiệm của phương trình đặc trưng:
k2 − 5k + 6 = 0 ⇔ [x = 2 x = 3
Nhận thấy α = 2 là nghiệm đơn của phương trình đặc trưng nên nghiệm riêng của phương trình đã cho có dạng:
y = x. e2x(Ax + B) hay y = e2x(Ax2 + Bx)
Đáp án câu này lừa tình ghê thật!
u(x) = e2x+1(ax2 + bx) = e2x.e(ax2 + bx) = e2x.(eax2 + ebx)
So sánh với đáp án ta vừa giải được thì: ea Vậy hóa ra: lOMoARcPSD| 36207943 Câu e
Hãy nhớ rằng: Số mũ của hàm e trong các bài toán không bao giờ chứa hệ số tự do. Nếu có thì hãy tách nó ra thành hằng số như trên.
10: Trong khai triển Maclaurin đến cấp 4 của hàm số 𝐟(𝐱) = 𝐱. 𝐬𝐢𝐧𝟐𝐱, hệ số của 𝐱𝟒 là: Theo công thức Maclaurin: f(x) = f(0) + f (1) ( 0 ) (2) ( 0 ) f (3) ( 0 ) f ( n ( 0 ) . x + f f . .x 2 + .x 3 + ⋯ + .x n + xn+1 2! 3! n! 1! (n + 1)!
Thì hệ số của x4 chính là: f (4) (−32cos2x + 16x. sinx)x=0 K == == − 24 4! 3 4!
Câu 11: Giới hạn 𝐋 = 𝐥𝐢𝐦
𝐭𝐚𝐧𝟐𝐱𝟏/𝐬𝐢𝐧𝟐𝐱 có giá trị: 𝐱→𝟎 𝐱 x→0 x = +∞ x
Cảm ơn bạn Vu Thi Ngoc Anh đã tìm ra lỗi sai trong cách giải tưởng chừng như hoàn hảo dưới đây:
Sử dụng phương pháp ln hóa:
𝐿 = 𝑙𝑖𝑚 (𝑡𝑎𝑛2𝑥)1/𝑠𝑖𝑛2𝑥 = 𝑙𝑖𝑚 𝑒𝑙𝑛[(𝑡𝑎𝑛2𝑥𝑥 )1/𝑠𝑖𝑛2𝑥] 𝑠𝑖𝑛
2 𝑥𝑙𝑛(𝑡𝑎𝑛2𝑥𝑥 ) = 𝑙𝑖𝑚 𝑒 𝑥→0 𝑥 𝑥→0 𝑥→0
Ta cần tìm số mũ (áp dụng quy tắc L’hospital): 2𝑥 𝑡𝑎𝑛2𝑥 𝑙𝑛 (
𝑙𝑖𝑚𝑥→0 𝑠𝑖𝑛 𝑥 𝑙𝑛 ( 𝑥 ) = 𝑙𝑖𝑚𝑥→0𝑠𝑖𝑛𝑡𝑎𝑛2𝑥2𝑥𝑥) = 𝑙𝑖𝑚𝑥→0 𝑡𝑎𝑛2𝑥𝑥2.𝑠𝑖𝑛𝑥. 𝑐𝑜𝑠𝑥𝑐𝑜𝑠22𝑥𝑥−2 𝑡𝑎𝑛2𝑥 = 𝑥→0𝑙𝑖𝑚 2𝑥 2
(𝑥2𝑐𝑜𝑠.𝑡𝑎𝑛2𝑥. 𝑠𝑖𝑛𝑥. 𝑐𝑜𝑠𝑥22𝑥2𝑥 − 𝑡𝑎𝑛2𝑥) lOMoARcPSD| 36207943 Câu Mẫu gồ
ể sử dụng phương pháp lượng vô cùng bé tương đương cho cả tử và mẫu với
𝑥→0𝑙𝑖𝑚𝑠𝑖𝑛𝑡𝑎𝑛2𝑥2𝑥𝑥→0 𝑥 (𝑐𝑜𝑠4𝑥22𝑥2𝑥 − 2𝑥) = 𝑙𝑖𝑚 𝑐𝑜𝑠1222.𝑐𝑜𝑠𝑥𝑥 − 1 = 𝑙𝑖𝑚𝑥→0 2𝑡𝑎𝑛𝑥2.𝑐𝑜𝑠𝑥22𝑥= 𝑙𝑖𝑚𝑥→0
2𝑥24.𝑐𝑜𝑠𝑥𝑥2= 𝑥→0𝑙𝑖𝑚 𝑐𝑜𝑠𝑥2
𝑙𝑛 ( 𝑥 ) = 𝑙𝑖𝑚 4.𝑐𝑜𝑠𝑥 𝑥→0 2𝑥 Vì số mũ 𝑙𝑖𝑚
𝑙𝑛 (𝑡𝑎𝑛2𝑥) = 2 nên: 2 𝑥→0 𝑠𝑖𝑛 𝑥 𝑥
𝐿 = 𝑙𝑖𝑚 (𝑡𝑎𝑛2𝑥)1/𝑠𝑖𝑛2𝑥 = 𝑒2 𝑥→0 𝑥 𝒕𝒂𝒏𝟐𝒙
𝒍𝒏( 𝒙 ) không phải dạng
𝟎 ha nên không thể áp dụng quy tắc L’hospital. Các này sai bởi vì 𝒍𝒊𝒎𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟎
Trong đề 16 của K39 cũng có một câu tương tự, nhưng kết quả hoàn toàn khác. Đây mới thực sự là một bài
tính giới hạn từ dạng vô định
7 (K49 – Mã đề 16): Tính giới hạn: 𝟏
𝐭𝐚𝐧𝐱 𝐬𝐢𝐧𝟐𝐱 𝐥𝐢𝐦 ( ) 𝐱→𝟎 𝐱 lim (tanx ln(tanxx 1 ) )= lim e sin 2 x x→0 x x→0 Xét riêng phần mũ: tanx tanx tanx x→0lim sin 2 xx= x→0lim sin 2 xx= x→0lim xsin2− 1x = x→0lim tanx − xx. sin2x 1 cos 2 x − 1 2x 2x
= x→0lim sin2x + sin2x.x = x→0 ( li sin m 2 x + sin2x.x).c os 2x = x→0li ( sin m 2 x + sin2x.x).c os 2 x = x2 = x→0lim (x ( 1+2 ) .cos 2 3 2 + 2x2).cos2x = x→0lim x = lOMoARcPSD| 36207943 Câu tanx 1/3 ⇒ lim ( )= e x→0 x
Câu 12: Cho 𝐟(𝐱, 𝐲) = 𝐱 + 𝐲 − 𝟐𝟕. 𝐱𝐲
A) Hàm f đạt cực đại tại 𝐌(𝟑; 𝟑)
B) Hàm f đạt cực đại tại 𝐌(−𝟑;−𝟑)
C) Hàm f đạt cực tiểu tại 𝐌(𝟑; 𝟑)
D) Hàm f đạt cực tiểu tại 𝐌(−𝟑; −𝟑)
Nói chung, ta không thể dùng định lý Cauchy cho bài toán này được! Đành dùng phương pháp Lagrange.
Ta tiến hành tìm các đạo hàm: ; y F x y F Tìm các điểm dừng” x ⇒ { xy Ta xét: 54 27 − − 2 81 81 54 2 −27 H(−3, −3) = | | =
> 0 và a11(−3,−3) < 0 ⇒ f 27 54 81 2
đạt cực đại tại (−3;−3) 81 81 − −
Câu 13: Cho hàm lợi ích 𝐔′(𝐱,𝐲) có các đạo hàm riêng cấp hai liên tục trên ℝ𝟐. Giả sử ta có điều kiện
𝟑𝐱 + 𝟔𝐲 = 𝐓 (𝟏)
với T là hằng số dương cho trước. Điều kiện cần để U đạt cực trị tại (𝐱, 𝐲) thỏa điều kiện (1) là: lOMoARcPSD| 36207943 Đặt các hàm: g(x, y) = T − 3x − 6y
F(x, y, λ) = U(x,y) + λ. g(x, y) = U(x, y) + λ. (T − 3x − 6y) Tìm các đạo hàm: = T − 3x − 6y
Điều kiện cần để U đạt cực trị tại
thỏa điều kiện (1) là: ∂x = 3λ ∂F =0 ⇒ { U ′ ′ ′ y = 6λ ⇒U y =2 U x ∂y 3 x+6y = T ∂F =0 { ∂λ A) 𝐱 = 𝐓 , 𝐲 = 𝐓 𝟔 𝟏𝟐
Chưa đủ cơ sở để kết luận.
B) 𝐔𝐱′ = 𝟐𝐔𝐲′
C) 𝟐𝐔𝐱′ = 𝐔𝐲′
Cách làm trên đã cho ta đáp án
D) Các câu kia đều sai Câu C đúng mà!
Câu 14: Cho hàm số 𝐟(𝐱) có 𝐟(𝟖) = 𝟐 𝐯à 𝐟′(𝟖) = −𝟏 và 𝐠(𝐱) = 𝐝 [𝐱𝟑𝐟(𝟒𝐱)]. Tính 𝐠(𝟐)? 𝐝𝐱
g(x) = d [x3f(4x)] = d(x3). f(4x) + x3. df(4x) = 3x2.f(4x) + x3. f ′(4x). 4 dx dx dx
⇒ g(2) = 3. 22.f(8) + 23.f ′(8).4 = 12.2 + 8.(−1).4 = −8
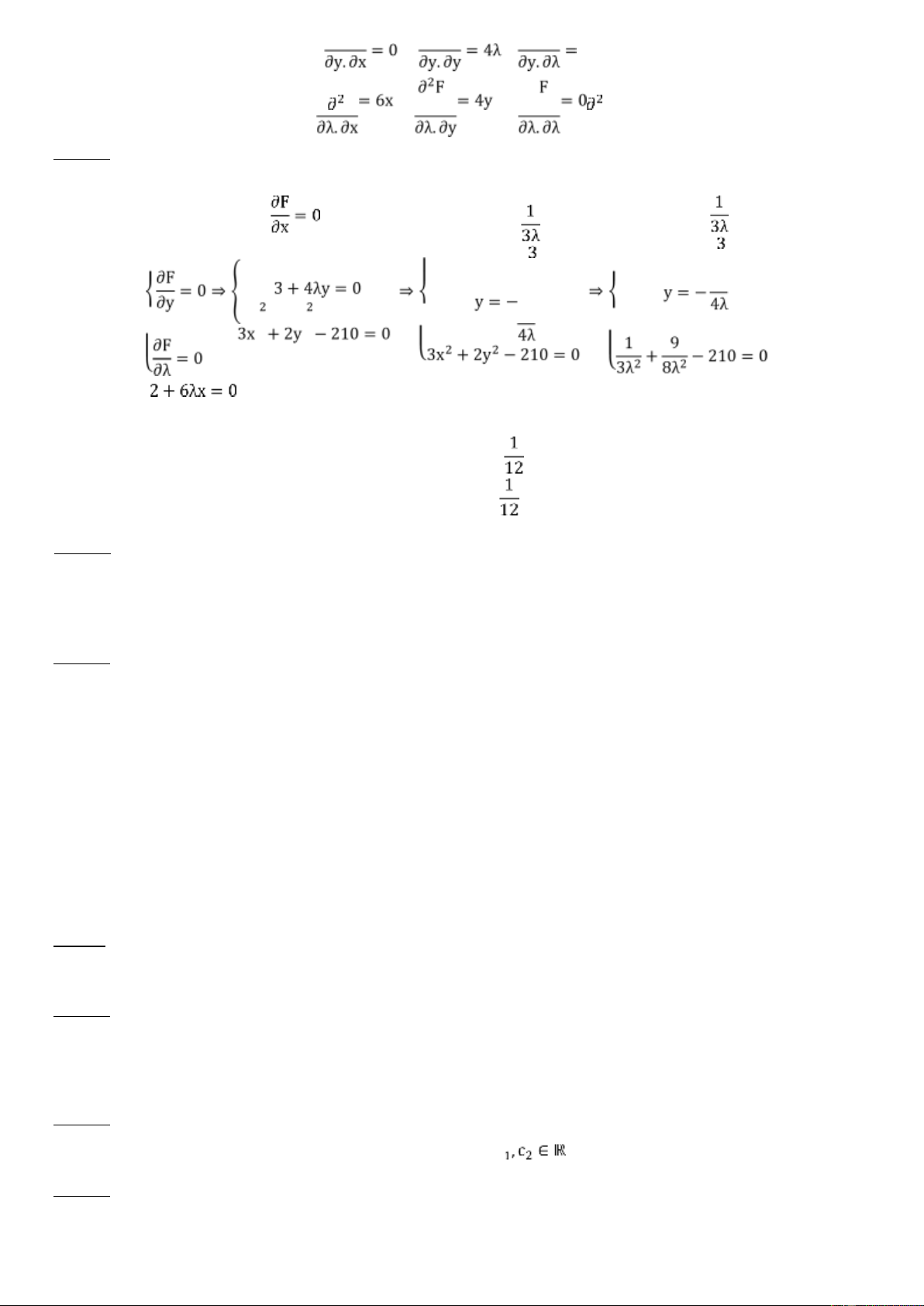
Câu 15: Dùng phương pháp nhân tử Lagrange để tìm cực trị hàm 𝐟(𝐱, 𝐲) = 𝟐𝐱 + 𝟑𝐲 thỏa điều kiện
𝟑𝐱𝟐 + 𝟐𝐲𝟐 = 𝟐𝟏𝟎 Bước 1: Đặt các hàm: g(x, y) = 3x2 + 2y2 − 210
F(x, y, λ) = f(x, y) + λ.g(x, y) = 2x + 3y + λ. (3x2 + 2y2 − 210)
Bước 2: Tìm các đạo hàm: F F F 6x F F F lOMoARcPSD| 36207943 4y F
Bước 3: Giải hệ phương trình: x = − x = −
(x1, y1,λ1) = (−4; −9;) (λ1 > 0) ⇒ [
(x2,y2, λ2) = (4; 9; −) (λ2 < 0) Bước 4: Ta xét: 6λ 0 6x H2 = | 0 4λ
4y| = −36.4x2λ − 24.4y2λ = −4(36x2 + 24y2).λ 6x 4y 0 Bước 5: Như vậy:
(−1)1.H2(x1,y1,λ1) > 0 nên f(x, y) đạt cực tiểu tại (x1,y1) = (−4; −9)
(−1)2.H2(x2,y2,λ2) > 0 nên f(x, y) đạt cực đại tại (x2,y2) = (4; 9)
Vậy hàm số đã cho đạt cực tiểu tại (x, y) = (−4;−9) và đạt cực đại tại (x, y) = (4; 9)
Cảm ơn Tee Nguyễn và Lê Quỳnh Duyên đã đóng góp đáp án giúp mình nhận ra một sai lầm khủng khiếp!
Bài 16: Cho phương trình vi phân 𝐲′′ − 𝟓𝐲′ + 𝟒𝐲 = (𝟔𝐱 − 𝟓).𝐞𝐱 (𝟏𝟔) a) Giải phương trình (16)
Bước 1: Nghiệm của phương trình đặc trưng:
k2 − 5k + 4 = 0 ⇔ [k = 1 k = 4
Bước 2: Vậy nghiệm tổng quát của phương trình tuyến tính tương ứng là: y = c1ex + c2e4x với c
Bước 3: Vì α = 1 là nghiệm đơn của phương trình đặc trưng nên nghiệm riêng của (16) có dạng:
y1 = x. ex. (ax + b) = ex. (ax2 + bx) lOMoARcPSD| 36207943
⇒ y1′ = ex.(ax2 + bx) + ex.(2ax + b) = ex. [ax2 + (2a + b). x + b]
⇒ y1′′ = ex. [ax2 + (2a + b). x + b] + ex.[2ax + (2a + b)] = ex.[ax2 + (4a + b). x + 2a + 2b]
Thay hết vào phương trình (16), ta được:
ex.[ax2 + (4a + b). x + 2a + 2b] − 5ex.[ax2 + (2a + b). x + b] + 4ex.(ax2 + bx) = (6x − 5). ex
⇒ x. (−6a − 6) + 2a − 3b + 5 = 0 ⇒ { −6a − 6 = 0 ⇒ {a = −1 2a − 3b + 5 = 0 b = 1
Ta được nghiệm riêng của (16) là: y1 = ex.(−x2 + x)
Bước 5: Vậy nghiệm tổng quát của (16) là:
y = y1 + y = (−x2 + x + c1). ex + c2.e4x với c
b) Tìm nghiệm riêng của (1) thỏa điều kiện 𝐲(𝟎) = 𝟏 và 𝐲′(𝟎) = −𝟐.
y = (−x2 + x + c1).ex + c2.e4x ; y′ = (−x2 − x + c1 + 1). ex + 4c2.e4x
{y′y((00))= −2= 1⇒ {c1 + 1 + 4c1 + c2c= 12 = −2 ⇒ {c1c1+ 4+cc22 = −3= 1 ⇒ { c1 = c2 = −
Vậy nghiệm riêng cần tìm là:
y = (−x2 − x + ) . ex − . e4x
Cảm ơn bạn Cuxi Libra đã giúp mình tìm ra lỗi sai! K38 – MÃ ĐỀ 110
Câu 1: Cho g là một hàm khả vi thỏa điều kiện 𝐠
. Phát biểu nào sau đây là đúng? A)
f đạt cực tiểu địa phương tại -2, đạt cực đại địa phương tại 2 B)
f đạt cực đại địa phương tại -2, đạt cực tiểu địa phương tại 2 C)
f đạt cực đại và cực tiểu địa phương tại -2 D)
f đạt cực đại và cực tiểu địa phương tại 2 -Tương tự như hồi Trung học:
f đạt cực trị ⇔ f ′(x) = 0 ⇔ x2 − 4 = 0 ⇔ [ x = 2 x = −2
-Ta tìm đạo hàm cấp hai của f(x):
f ′′(x) = 2x. g(x) + (x2 − 4). g(x) lOMoARcPSD| 36207943 -Ta có:
f ′′(2) = 4. g(x) < 0 ⇒ f đạt cực đại địa phương tại x = 2 f
′′(−2) = −4.g(x) > 0 ⇒ f đạt cực tiểu địa phương tại x = −2
Câu 2: Xét phương trình 𝐲′′ + 𝟒𝐲 = 𝟎. Phát biểu nào sau đây là sai?
Xét phương trình y′′ + 4y = 0.
Nghiệm của phương trình đặc trưng: k2 + 4k = 0 ⇔ [ k = 2i k = −2i Suy ra nghiệm tổng quát: y = c cos2x + c sin2x với c Nếu đặt C a = Asinφ và C b thì: y = Asin
Thật ra, nếu chú ý, ta sẽ nhận ra 𝑦′′
chính là phương trình vi phân của dao động điều hòa như khi
học Dao động điều hòa ở lớp 12:
Phương trình 𝑥′′ + 𝜔2𝑥 = 0 có nghiệm tổng quát:
𝑥 = 𝐴𝑐𝑜𝑠(𝜔𝑡 + 𝜑) ℎ𝑜ặ𝑐 𝑥 = 𝐴𝑠𝑖𝑛(𝜔𝑡 + 𝜑′) Tóm lại,
giải phương trình 𝑦′′ + 4𝑦 = 0, ta được nghiệm tổng quát:
𝑦 = 𝐴𝑠𝑖𝑛(2𝑥 + 𝜑) A)
Mọi nghiệm đều là hàm bị chặn trên B)
Có một nghiệm riêng là hàm hằng Cho A=0 thì y=0 là hàm hằng. C)
Có một nghiệm riêng là 3sin2x. Đương nhiên! Khi A=3 và φ = 0. D)
Mọi nghiệm đều có giới hạn khi
Hàm sinx và cosx không có giới hạn khi . Tức không xác định.
Câu 3: Cho f là một hàm số liên tục và 𝐅′ . Giả sử 𝐥𝐢𝐦 𝐅 = 𝟎. Hãy tính:
(𝐱/𝟐𝟎𝟏𝟑).𝐝𝐱 𝟎
Áp dụng những nguyên tắc tính tích phân đơn giản hồi Trung học phổ thông: (x/2013) lOMoARcPSD| 36207943 (Chú ý
rằng: (ax + b). dx = 1 F(ax + b)) a
Câu 4: Trong khai triển Maclaurin cho hàm số 𝐟(𝐱) = 𝐱. 𝐬𝐢𝐧𝟐𝐱, hệ số của số hạng chứa 𝐱𝟑 là: f (3)
(−8sin2x − 4sin2x − 8x. cos2x)x=0 K3 = 3! = 3! = 0 Câu 5: Cho hàm số: 𝟏
𝐟(𝐱, 𝐲) = 𝐱 + 𝐲 + 𝐱𝐲
Khẳng định nào sau đây đúng? A) Có hai điểm dừng
B) Đạt cực tiểu địa phương
C) Đạt cực đại địa phương D) Không đạt cực trị Tìm điểm dừng: x y x y = 1 x = 1
⇒ ⇒ {y x = 1 ⇒ {y = 1 ⇒ f chỉ có một điểm dừng Xét: f H = | f | |
> 0 ⇒ f đạt cực tiểu tại (1; 1)
Câu 6: Tìm tất cả các giá trị của m để hàm số 𝐟 f liên
tục tại 0 ⇔ lim f(x) = f(0) = m2. x→0 Ta có: 𝐞𝐦𝐱−𝟏 { 𝐱 liên tục tại 0.
𝐦𝟐 𝐤𝐡𝐢 𝐱 = 𝟎 emx − 1 memx lim f(x) = lim = lim = m x→0 x→0 x x→0 1 lOMoARcPSD| 36207943 Từ đó suy ra: m = m2 ⇔ [m = 0 m = 1 C â u 7 : C
h o f, g là các hàm số khả vi trên ℝ thỏa 𝐟(𝟎) = 𝟏 và 𝐠
. Nếu 𝐡(𝐱) = 𝐟(𝐱). 𝐠(𝐱) và 𝐡′(𝐱) = 𝐟 : A) B) C) D)
Theo đúng công thức đạo hàm:
h(x) = f(x). g(x) ⇒ h′(x) = f′(x). g(x) + f(x). g′(x) Nhưng theo đề bài:
h′(x) = f(x). g′(x) Chứng tỏ rằng: f ′ Vì f nên f Câu 8: Đặt ( 𝐱 𝛂 𝐱 ) = ∫ √ 𝟎
𝐭 𝟑 + 𝟏. 𝐝𝐭. Tính giá trị của:
𝛂(𝐱) − 𝐬𝐢𝐧𝐱 𝐥𝐢𝐦𝐱→𝟎 𝐱𝟑 Gọi F . dt là nguyên hàm của . Khi đó (lưu ý F là hằng số thực): ⇒ α′
Như vậy, áp dụng quy tắc L’hospital, ta có: 3x 6x 6x 6
Câu 9: Xét phương trình vi phân 𝒚′ + 𝟐𝒙𝒚 = 𝒆−𝒙𝟐. Phát biểu nào sau đây là đúng?
Trước hết, ta tìm nghiệm tổng quát của phương trình trên.
Nghiệm tổng quát của phương trình liên kết có dạng: y = Ce lOMoARcPSD| 36207943
Xem C = C(x) rồi thay vào phương trình đã cho, ta giải được: C(x) = x + K
Vậy nghiệm tổng quát của phương trình y′ + 2xy = e−x2 là: y = (x + K). e−x2
Sau đó, theo ý chung của các phát biểu, ta tìm thêm giới hạn: (x + K) e
A) Tồn tại một nghiệm riêng không có giới hạn khi
B) Mọi nghiệm đều có giới hạn khác
D) Mọi nghiệm có giới hạn hữu hạn khi Rõ ràng y = 0 (hữu hạn)
(tức với mọi nghiệm riêng)
C) Nghiệm tổng quát là 𝐲 = 𝐱𝐞−𝐱𝟐 + 𝐂
Thay vào thấy đúng nhưng nó chưa chắc đã là nghiệm tổng quát nhé!
Câu 1 : Với giá trị nào của 𝛂, tích phân suy rộng 𝐞
𝛂𝐱𝐞𝛂𝐱+𝟏 . 𝐝𝐱 sẽ hội tụ?
Để tích phân trên hội tụ thì
. dx phải có giá trị là một hằng số. Điều đó xảy ra khi: eαK = const ⇔ lim eαK = const ⇔ lim eαK Tuy nhiên, chú ý, với
thì quay lại biểu thức tính giới hạn, ta lại phải dạng vô định và giới hạn tính được không phải hằng số.
Vậy chỉ α < 0 là thỏa mãn yêu cầu đề bài.
Câu 12: Một sản phẩm được tạo ra từ hai loại nguyên liệu A, B. Sản lượng Q của loại sản phẩm này được cho bởi
hàm =(𝐱, 𝐲), với x, y là lượng nguyên liệu A, B, một cách tương ứng. Giá bán của sản phẩm này là P. Hàm chi phí
là 𝐂(𝐱, 𝐲) = 𝐚𝐱 + 𝐛𝐲 + 𝐝, 𝐯ớ𝐢 𝐝 > 𝟎. Để lợi nhuận lớn nhất thì:
Lợi nhuận = Doanh thu – Chi phí = Sản lượng × đơn giá – Chi phí
π = Q. P − C = Q(x, y). P − (ax + by + d)
Điều kiện cần để hàm đạt cực trị: P. P. a Q′x a lOMoARcPSD| 36207943 ⇒⇒ ⇒ hay Q′y = b lOMoARcPSD| 36207943 Câu 1 3: Cho hàm số
𝐟(𝐱) = {𝛂 + 𝐞𝟐𝐱
𝟒 + 𝛃𝐱, 𝐱 < 𝟎
Giả sử 𝐟(𝐱) khả vi tại 0. Khi đó giá trị của 𝐟(𝛂 − 𝛃) là: f(x) khả vi tại 0 ⇔ limx→0
f(xx−0)−f(0) tồn tại ⇔ limx→0+ f (x)−xf(0) = x→0lim− f (x)−xf(0) Ta có: lim+ f (x) −x f(0) = x→0lim+ α +
e2x −x (α + 1) = x→0lim+
e2xx− 1 () = x→0lim+ 2e2x = 2 x→0 f(x) − f(0) 4 + βx − (α + 1) 3 − α x→0lim− x= x→0lim− x= x→0lim− (β + x ) Nhận thấy: f(x) − f(0) f(x) − f(0) x→0lim+ x= x→0lim− x⇔ α = 3 và β = 2
và hàm đã cho sẽ không khả vi) Ta có thể viết lại: f 4 + 2x, x < 0 ⇒ f
Câu 14: Phương trình 𝐲′′ − 𝟔𝐲′ + 𝟗𝐲 = 𝐱. 𝐞𝟑𝐱 có một nghiệm riêng dạng:
Phương trình đặc trưng:
k2 − 6k + 9 = 0 ⇔ k = 3 (nghiệm kép)
Vì α = 3 là nghiệm kép của phương trình đặc trưng nên phương trình đã cho có nghiệm riêng dạng:
y = x2. (ax + b). e3x hay y = (ax3 + bx2).e3x
5: Giải phương trình vi phân
𝐲′′ − 𝟑𝐲′ + 𝟐𝐲 = 𝐱. 𝐞𝐱 lOMoARcPSD| 36207943 Câu 1
Bước 1: Nghiệm của phương trình đặc trưng:
k2 − 3k + 2 = 0 ⇔ {k = 1 k = 2
Bước 2: Nghiệm tổng quát của phương trình tuyến tính liên kết y′′ là: y = c1ex + c2e2x với c
Bước 3: Tìm nghiệm riêng của phương trình đã cho.
Vì α = 1 là nghiệm đơn của phương trình đặc trưng nên nghiệm riêng của phương trình đã cho có dạng:
y1 = x. ex.(ax + b) hay y1 = ex.(ax2 + bx)
⇒ y1′ = ex(ax2 + 2ax + bx + b) ⇒ y1′′ = ex(ax2 + 4ax + bx + 2a + 2b)
Thay vào phương trình đã cho:
ex(ax2 + 4ax + bx + 2a + 2b) − 3ex(ax2 + 2ax + bx + b) + 2ex. (ax2 + bx) = x. ex
⇒ (−2a − 1). x + (2a − b) = 0 ⇒ {−2a − 1 = 0 ⇒ {a = − 2a − b = 0 b = −1
Nghiệm riêng của phương trình đã cho là: y1 = ex.(− x2 − x)
Vậy nghiệm tổng quát của phương trình đã cho là:
y = y1 + y = ex.(− x2 − x + c1) + c2e2x với c
6: Tìm cực trị của hàm số 𝐳 = 𝐟(𝐱, 𝐲) = 𝟐𝐱𝐲 với điều kiện 𝐱𝟐 + 𝐲𝟐 = 𝟗 bàng phương pháp nhân tử Lagrange. Bước 1: Đặt: g(x, y) = x2 + y2 − 9
F(x, y, λ) = f(x, y) + λ. g(x, y) = 2xy + λ. (x2 + y2 − 9)
Bước 2: Tìm các đạo hàm: 2y + 2λx 2x + 2λy F F F 2x F F F lOMoARcPSD| 36207943 Câu 1 2y F
Bước 3: Giải hệ phương trình: 3 3 ( x,y,λ ) =( ; ;−1) √ 2 √ 2 3 3 ( x,y,λ ) =(− ; √ 2 √ 2 3 3 ( x,y,λ ) =( ;− √ 2 √ 2 3 3 y x = y ; 1) ( x,y,λ ) =(− ;− ;−1) [ √ 2 √ 2 ⇒x x ⇒ x ; 1)
Bước 4: Xét định thức: 2x H Với hai điểm dừng ; −1) và thì H2 > 0 ⇒
> 0 ⇒ f đạt cực đại tại cả 2 điểm dừng trên. Với hai điểm dừng ; 1) và ; 1) thì H2 < 0 ⇒
> 0 ⇒ f đạt cực tiểu tại cả 2 điểm dừng trên. Bước 5: Kết luận Vậy hàm số f = 2xy với điều kiện x đạt: -Cực đại tại -Cực tiểu tại lOMoARcPSD| 36207943
PHÂN BIỆT ĐẠO HÀM THƯỜNG VÀ ĐẠO HÀM RIÊNG
Xét hàm 𝐟(𝐱, 𝐲) = 𝐱𝐲. Khi đó:
-Đạo hàm thường, ta vẫn xem y là biến: df d(xy) dx dy dy = = . y + x.= y + x. dx dx dx dx dx
-Đối với đạo hàm riêng, y trở thành hằng: . y + x. = 1.y + x. 0 = y
Cái ta sai chính là không phân biệt rõ ký hiệu đạo hàm thường hay riêng trong công thức nên khi đạo hàm thường bị nhầm. lOMoARcPSD| 36207943 )
GIẢI BÀI TẬP THEO YÊU CẦU 1)
(K37 – 485): Xét phương trình vi phân 𝐲′′ − 𝟒𝐲′ + 𝟒𝐲 = 𝟐𝐱. (𝟑𝐱 − 𝟏). Nghiệm riêng của phương trình này có dạng:
Trước tiên, ta cần biến đổi một chút: 2x = eln2x = ex.ln2 Khi
đó, phương trình đã cho trở thành:
y′′ − 4y′ + 4y = ex.ln2. (3x − 1) Vậy ở đây, hệ số α = ln2.
Dễ dàng tìm được nghiệm riêng của phương trình đã cho là: y1 = eln2.x.(ax + b) 2)
Câu 3 (K37 – 485): Giả sử 𝐲 = 𝐟(𝐱) là nghiệm của phương trình vi phân 𝐲′ + 𝐲 = 𝐬𝐢𝐧𝐱 thỏa điều kiện 𝐟(𝛑) = 𝟏. 𝐱
Khi đó 𝐟 (𝛑) có giá trị? 𝟐
Nghiệm của phương trình thuần nhất y′ + y = 0 là: x dx −lnx C C y = C. e e x Xem C = C(x) thì y = C
(x). Thay vào phương trình đã cho: x C′ . x − C 2 x x dC(x) = sinx.x. dx ⇒ C = −x. cosx + sinx + K Vậy nên: K + sinx y = −cosx + x Theo đề bài: y(π) = 1 ⇒ −cosπ + = 1 ⇒ K = 0 π sin π 2 2 ⇒ y () = −cos + = 2 π π 2 lOMoARcPSD| 36207943
3) Câu 5 (K37 – 485): Hàm 𝐟(𝐱, 𝐲) nào sau đây thỏa phương trình 𝐱. 𝛛𝐟 + 𝐲. 𝛛𝐟 = 𝟎? 𝛛𝐱 𝛛𝐲
Câu này mình chỉ có thể thay đáp án vào thôi! Chứ còn giải phương trình chứa đạo hàm riêng thì mình chưa thể. A) . y = ⇒ x. (không thỏa)
B 𝐟 ( 𝐱,𝐲 ) = √𝐱 𝟐 + 𝐲𝟐 y ⇒ x. (không thỏa) 𝐟 𝐱 𝐲 ( 𝐱,𝐲 ) = √ + √ C) 𝐲 𝐱 ⇒ x. (không thỏa)
Ở đây, nếu x, y > 0 thì điều đã cho đúng. Nhưng khi x, y < 0 thì: x |x|
4) Câu 11: Cho các hàm số 𝐟 𝟏𝐱+𝟏
𝐭𝟐−𝐭.𝐝𝐭𝟐𝐭+𝟐 và 𝐠(𝐱) = 𝐥𝐧(𝐱 + 𝟏). Hãy tính giá trị của: ∫ 𝐱+𝟏 𝐭. 𝐝𝐭 𝟏 𝐭 𝟐 − 𝟐𝐭+𝟐 𝐟 𝐥𝐧(𝐱 + 𝟏)
Nếu gọi F(x) là nguyên hàm của t 2−2tt+2, tức viết: t. dt F t 2 −2 t +2
Thì rõ ràng, ta có thể viết:
f(x) = F(t)|1x+1 = F(x + 1) − F(1) lOMoARcPSD| 36207943 ) ⇒ f ′(x) = F′(x + 1) =
(Chú ý F(1) là một hằng số)
Đến đây, ta hoàn toàn có thể áp dụng quy tác L’hospital cho giới hạn cần tính:
Có thể tham khảo thêm bài 8 – K38. lOMoARcPSD| 36207943 )
5 Câu 16 (K37 – 485): Cho phương trình vi phân sau: 𝐲′ + 𝟐𝐱𝐲 = 𝐞−𝐱𝟐 (𝟏)
a) Tìm nghiệm tổng quát 𝐲 = 𝐲
Nghiệm của phương trình thần nhất liên kết y′ là: y = C. e
Coi C là hàm, tức C = C(x) thì nghiệm tổng quát của (1) có dạng: y = C(x). e−x2 Thay
vào (1) và rút gọn, ta được: C′
Vậy nghiệm tổng quát của (1) là: y = (x + K ). e−x2 b) Tìm .
Ta sử dụng quy tắc L’hospital: (x + K ) ex
6) Câu 1 (K36 – 134): Cho hàm chi phí 𝐂 = 𝟏𝟎 𝟐 + 𝟐𝟎 + 𝟓𝟎. Tính chi phí biên tế và độ co dãn tại Q=10. dC
MC(Q) == 20Q + 20 ⇒ MC(10) = 220 dQ dC Q dC Q ε 1000+200+50
CL = dQ . C = dQ . 10Q2 + 20Q + 50 ⇒ εCL(10) = 220. = 1,76 7) Câu 1
: Viết khai triển Maclaurin của hàm 𝐲 = 𝐬𝐢𝐧𝐱 đến cấp 5. Áp dụng tính gần đúng 𝐬𝐢𝐧𝟏°.
Nếu thích, các bạn có thể tìm hiểu định nghĩa của hàm sinx, dựa theo khai triển Maclaurin: x x x 3 x 5 x 7 sinx= − + + + ⋯ =∑ 1! 3! 5! 7! 2i + 1 ! i=0 Như vậy: ( ) lOMoARcPSD| 36207943 )
7 Tìm nghiệm riêng của phương trình:
𝐲′′ + 𝐲 = 𝟒𝐱. 𝐬𝐢𝐧𝐱
Biết 𝐲(𝟎) = 𝟎, 𝐲′ (𝛑) = 𝟎. 𝟔
Phương trình đặc trưng có nghiệm: k2 + 1 = 0 ⇔ k = ±i
Nghiệm tổng quát của phương trình thuần nhất: y = c1cosx + c2sinx
Vì α = i (lấy được từ vế phải của phương trình đã cho) là nghiệm đơn của phương trình đặc trưng nên nghiệm
riêng của phương trình đã cho là:
y1 = x. [(ax + b). cosx + (cx + d). sinx] = (ax2 + bx). cosx + (cx2 + dx). sinx
⇒ y1′ = (2ax + b + cx2 + dx). cosx + (−ax2 − bx + 2cx + d). sinx
⇒ y1′′ = (−ax2 − bx + 4cx + 2a + 2d).cosx + (−cx2 − dx − 4ax − 2b + 2c). sinx
Thay vào phương trình đã cho:
(4cx + 2a + 2d).cosx + (−4ax − 2b + 2c).sinx = 4x. sinx
⇔ (4cx + 2a + 2d). cosx + (−4ax − 4x − 2b + 2c).sinx = 0 4c = 0 a = −1 ⇔ { 4cx + 2a + 2d = 0 ⇔ { 2a + 2d = 0 ⇔ { b = 0 −4ax − 4x − 2b + 2c = 0 −4a − 4 = 0 c = 0 −2b + 2c = 0 d = 1 ⇒ y1 = −x2.cosx + x. sinx
Nghiệm tổng quát của phương trình đã cho:
y = y1 + y = (c1 − x2).cosx + (c2 + x). sinx
⇒ y′ = (−c1 + x2 + 1). sinx + (c2 − x). cosx Theo đề bài: y c c ⇒ { c
Vậy nghiệm riêng theo yêu cầu đề bài là: lOMoARcPSD| 36207943 y = y1 + y = −x
8) Cho A là ma trận vuông cấp n thỏa điều kiện 𝟐𝐀𝟐 − 𝐀 = 𝐈𝐧. Phát biểu nào sau đây là sai? A. 𝐀 khả đảo
B. 𝐈𝐧 − 𝟐𝐀 khả đảo
2A2 − A = In ⇒ A. 2A − A = In ⇒ A(2A − I) = I ⇒ A và 2A-I đều khả đảo
C. 𝐈𝐧 + 𝐀 khả đảo
2A2 − A = In ⇒ In + A = 2A2 ⇒ |In + A| = |2A2| = 2n. |A|2 ≠ 0 ⇒ In + A khả đảo. D. 𝐈𝐧 = 𝐀
2A2 − A = In ⇒ 2A2 − A − In = θ ⇒ 2A2 − 2A + A − In = θ ⇒ 2A(A − In) + (A − In) = θ
⇒ (2A + I)(A − I) = θ ⇒ [2A + I = 0 ⇒ [A = −I A − I = 0 A = I
Kết luận In = A là chưa chính xác, vì cũng có thể A = − I.
9) Tìm m để hàm số 𝐟(𝐱) = 𝐞 𝟏
𝐦𝐱 −𝟏 − 𝟏𝐱 có giới hạn hữu hạn khi x tiến đến vô cùng.
-Điều kiện xác định của hàm số emx − 1 ≠ 0 ⇒ m ≠ 0
-Xét trường hợp mx → −∞, tức khi { m > 0 và , ta có: x → −∞ f(x) = −1
-Xét trường hợp mx → +∞, tức khi { m > 0 và { m < 0 , ta có: x → +∞ x → −∞ x − emx + 1 −memx −m2emx −m lim f(x) = lim
mx − x = x→∞lim emx + mxemx − 1 = x→∞lim memx + memx + m2xemx = x→∞lim 2 + mx x→∞ x→∞ xe = 0
-Vậy ∀m ≠ 0 thì lim f(x) là hữu hạn. x→∞ lOMoARcPSD| 36207943
MỘT SỐ MẸO DÙNG MÁY TÍNH
Mẹo 1: Tìm số nghiệm của phương trình.
Ví dụ: Phương trình 𝟐𝐱 + 𝟑𝐱 + 𝟔 = 𝟎 có bao nhiêu nghiệm?
Hàm số này liên tục trên ℝ
Sử dụng máy tính, ở Mode TABLE.
Nhập biểu thức y(x) = 2x + 3x + 6
Cho x chạy từ -7 đến 8. Ta được bảng kết quả: X -7 -6 -5 -4 -3 -2 -1 0 Y -15.0 -12.0 -8.9 -5.9 -2.8 0.25 3.5 7 X 1 2 3 4 5 6 7 8 Y 11 16 23 34 53 88 155 286
Như vậy, ta dễ dàng hình dung giá trị hàm số tăng từ âm vô cùng đến dương vô cùng. Từ x=-3 sang x=-2, hàm
số đổi dấu. Chứng tỏ nó vừa cắt trục hoành. Sau đó nó đi đến tận dương vô cùng. Vậy có thể kết luận hàm số này
chỉ có tối đa 1 nghiệm.
Tuy nhiên cách này chỉ là dự phòng và thiếu cơ sở (nhưng nói chung xài thì rất ổn).
Nếu muốn làm một cách tường minh, bạn hãy chứng minh rằng hàm số liên tục và đạo hàm của nó không đổi dấu,
tức luôn âm hoạc luôn dương. Sau đó chỉ ra hai giá trị a, b sao cho: f(a). f(b) < 0 Tương
tự, với hàm số: y(x) = 2x + 3x − 6. X -7 -6 -5 -4 -3 -2 -1 0 Y -27 -24 -21 -17 -14 -11 -8.5 -5 X 1 2 3 4 5 6 7 8 Y -1 4 11 22 41 76 143 274
Hàm số đổi dấu khi đi từ x=1 đến x=2. Vậy phương trình có 1 nghiệm.
Tương tự, với hàm số: y(x) = 2x − 3x − 6. X -7 -6 -5 -4 -3 -2 -1 0 Y + + + + + + - - X 1 2 3 4 5 6 7 8 Y - - - - + + + +
Hàm số đổi dấu khi đi từ x=-2 đến x=-1 và x=4 đến x=5. Vậy phương trình có 2 nghiệm. Mẹo 2: Tính giới hạn
Mẹo này có lẽ nhiều bạn cũng biết, nhưng đọc tiếp chút nữa xem có cần thiết không đã nhé :D Ví dụ 1: Tính giới hạn lOMoARcPSD| 36207943
𝐬𝐢𝐧𝟐𝐱 − 𝟓𝐱𝟑 + 𝟐𝐬𝐢𝐧𝟑𝐱
𝐥𝐢𝐦𝐱→𝟎 𝟕𝐱𝟑 + 𝟐𝐭𝐚𝐧𝟐𝐱 − 𝟑𝐭𝐚𝐧𝟒𝐱 Nhập vào máy tính: x − 5x 7 x 3 +2 tan 2 x−3tan4x
Nhấn CALC, nhập 𝑋 = 0,0101, nhấn =, ta nhận được kết quả:
Ví dụ 2: Tính giới hạn e3x − cosx lim x − 3 x→0 x
Đừng vội nhập vào, hãy biến đổi tí đã. x→0 e3x −xcosxx
− 3 = x→0lim e3x − cosx − 3xx2 lim Bây giờ mới nhập vào
e3x−cosx−3xx2 và cho 𝑥 = 0,0001. Ta thu được kết quả
Nếu quên đổi đơn vị sang radian, ta sẽ ra kết quả bằng 4,5. Cẩn thận đấy! Ví dụ 3: Tính giới hạn 𝟏
𝐭𝐚𝐧 𝟖𝐱 − 𝐬𝐢𝐧𝟖𝐱 𝟖 𝐬𝐢𝐧𝟐 𝐱 𝐥𝐢𝐦 (𝟏 + ) 𝐱→𝟎 𝐱
Đừng dại dột nhập y chang vào, bấm ra số tùm lum luôn cho xem.
Chịu khó biến đổi cái đã, để lát chỉ cần tìm mũ thôi. 1 8 sin 2 1
lim (1 + tan 8x − sin8x) x = lim e8 sin 2 xln(1+tan 8x−sin 8xx ) x→0 x x→0
Lúc này, ta chỉ cần tính giới hạn của mẫu: tan8x−sin8x 1 tan8x−sin8x tan8x−sin8x lim ln(1+ )= lim x = lim x→0 8 sin 2 x x x→0 8 sin 2 x x→0 8 xsin 2 x Nhập vào và cho
(chú ý đơn vị radian). Ta thu được kết quả . x 1 8 tan 8x − sin 8x sin 2 x 32 lOMoARcPSD| 36207943 lim (1 + ) = e x→0 x
Cho máy tính thở một chút thì nó sẽ giúp ta làm việc hiệu quả hơn, đúng không?




