Câu hỏi tự luận Vector cường độ điện trường và Định lí Gauss môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
Câu hỏi tự lu¿n V¾T LÍ ĐẠI CƯƠNG II Câu 1:
1. Nêu dịnh nghĩa và ý nghĩa cÿa vector cường độ điện trường
Giả sử ta đặt một điện tích ÿą tại một điểm M nào đó trong điện trường. ⇨
ÿą sẽ bị điện trường tác dụng một lực Ă
Tỉ sá Ă không phụ thuộc vào qo mà phụ thuộc vào vị trí điểm M, nghĩa là ÿą
tại mỗi điểm M thì tỉ sá ā = Ă = const ÿą
ā : vector cường độ điện trường
E: cường độ điện trường Nếu chọn ÿ0= +1 thì ā Ă = nghĩa là :
Vector cường độ điện trường tai một điểm là một đại lượng vector bằng lực
tác dụng cÿa điện trường lên một đơn vị điện tích dương tại điểm đó
ā đặc trưng cho điện trường về phương diện tác dụng lực tại điểm đang xét.
●Công thāc xác định vector cường độ điện trường gây ra bởi điện tích điểm ¸Ā2.Ā
Ta có : lực tác dụng lên điện tích ÿ0 lên bằng: .ÿ.ÿ0 Ă = 1 4¸Ā2.Ā 4ø0 Ā
( Ā : bán kính vector hướng từ điện tích q tới điểm M ) ā = Ă = 1 .ÿ ( 1) ÿ0 4ø0 Ā
Từ (1) nhận thấy rằng :
q > 0 => ā cùng hướng với Ā => hướng ā ra xa điện tích q
q < 0 => ā ngược hướng với Ā => hướng vào ā điện tích q
⇨Cường độ điện trường tại điểm M tỉ lệ thuận với độ lớn cÿa q và tỉ lệ nghịch
với bình phương khoảng cách từ điểm đang xét đến q E = | ÿ| 4ø¸ Ā 0 2
●Công thāc xác định vector cường độ điện trường gây ra bởi hệ điện tích điểm:
Xét một hệ điện tích điểm ÿ1 ,ÿ2ÿ ,3ÿĄ , … ,
được phân bá liên tục trong không gian.
Đặt tại M một điện tích thử ÿ0 1
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/ Ą Ă
= ∑ Ăÿ (Ăÿ là lực tác dụng cÿa ÿÿÿ0 lên ) ÿ=1 Ą ā = Ă ∑ = Ăÿ ÿ0 ÿ0 ÿ=1 Nhưng āÿ
= Ăÿ chính là vector cường độ điện
trường gây ra bởi tại M nên ÿÿ
⇨Vector cường độ điện trường gây ra bởi một hệ điện tích điểm bằng tổng các
vector cường độ điện trường gây ra bởi từng điện tích điểm cÿa hệ.
( Nguyên lí chồng chất điện trường )
●Công thāc xác định vector cường độ điện trường gây ra bởi một vật mang điện.
Chia vật mang điện thành nhiều phần nhß sao cho điện tích dq mang trên mỗi phần đó
có thể coi là điện tích điểm.
Gọi dā là vector cường độ điện trường gây ra bởi điện tích dq tại một điểm M cách
dq một khoảng r, Ā là bán kính vector hướng từ dq tới M.
⇨Vector cường độ điện trường do vật mang điện gây ra tại điểm M ā = ∫ Ăā = ∫1 .Ăÿ ĂĀ 4ø0 ¸Ā2 Ā ĂąàĄ Āộ �㕣ậĂ ĂąàĄ Āộ �㕣ậĂ
2. ā1 là vector cường độ điện trường gây ra tại ÿ1 A do
ā2 là vector cường độ điện trường gây ra tại ÿ2 A do
⇨Vector cường độ điện trường gây ra tại A là ā = ā1 + ā2 2 2 . => E = ā ÿ1 ýþ4+ÿ2 1 2+ ā2 21 = 4ø0 þÿ4
Thay sá => E = 2,5 . 104 V/m 1 .ÿ2 Cos θā= 2 4ø0 ¸.þÿ2 = 0,8 ā= ā ⇨θ = 36, 87° ā hợp với ā2 một góc θ = 36, 87° Câu 2:
1. Lưỡng cực điện là một hệ 2 điện tích điểm có độ lớn bằng nhau nhưng trái dấu +q và
–q (q > 0) cách nhau một đoạn l rất nhß so với khoảng cách từ lưỡng cực điện tới
những điểm đang xét cÿa trường. Để đặc trưng cho tính chất điện ca lưỡng cực điện, 2
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
người ta dùng đại lượng vector momen lưỡng cực điện hay momen điện cÿa lưỡng cực, kí hiệu là Āă . Āă = ÿĂ
Ă : là vector hướng từ -q đến +q
Ă : có độ lớn bằng khoảng cách từ -q đến +q.
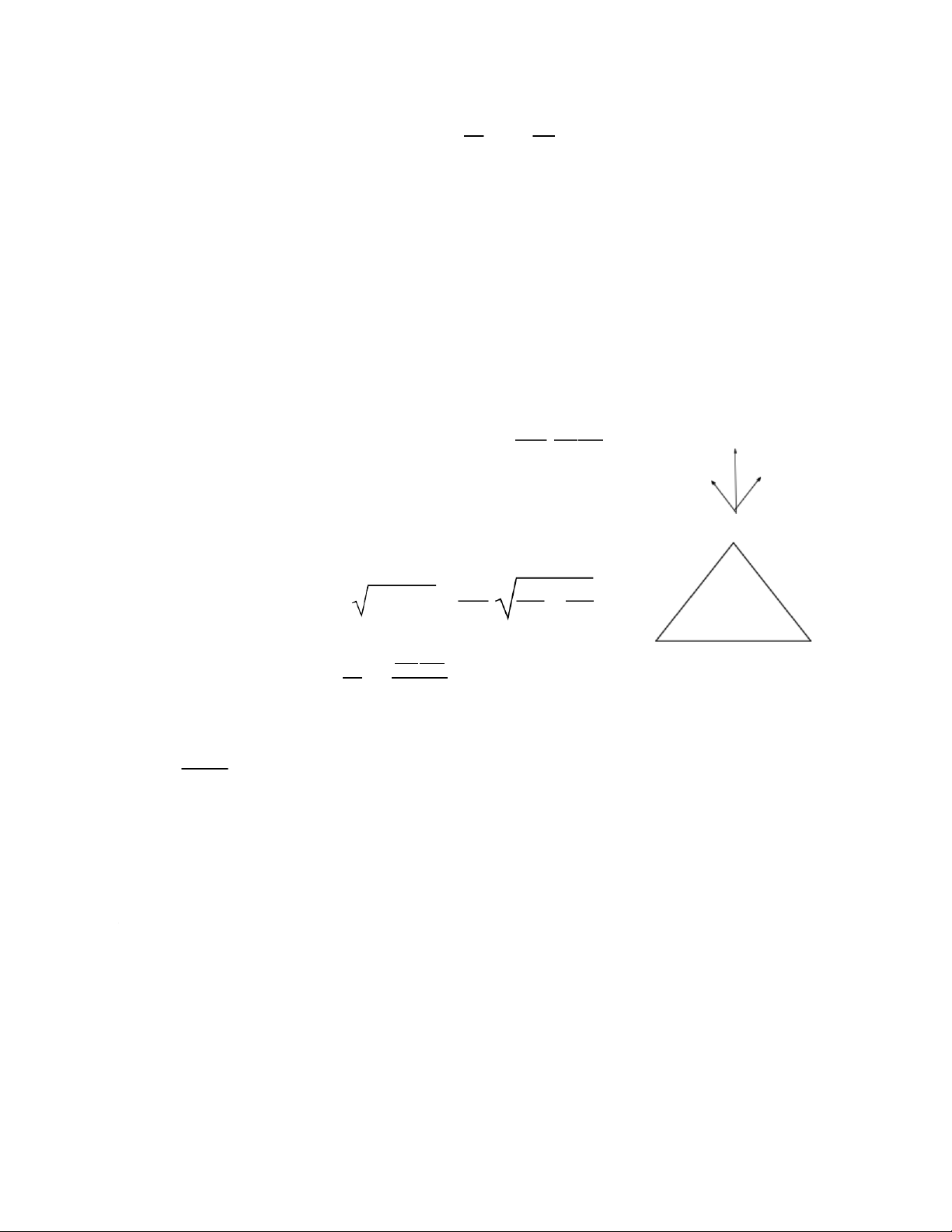
●Xác định ā tại M thuộc đường trung trực cách O một khoảng h khá lớn.
Theo nguyên lí chồng chất điện trường, vector cường độ điện trường ā gây ra bởi
lưỡng cực tại M bằng tổng vector cường độ điện trường gây ra bởi –q và +q cÿa lưỡng cực. ā = ā1 + ā2 ā1 ,ā2 hướng như hình vẽ, Ā1= Ā2 ā1= ā2= 1 .ÿ 4ø0 2 ¸Ā1
Theo quy tắc tổng hợp vector => ā song song, ngược chiều với Ă E = 2.ā1 .cos α Cos α = Ă => E = 1 .ÿĂ 2Ā1 4ø0 3 ¸Ā1 Vì h ≫ l nên Ā1~ ℎ . Mà ql = Ā 1 Āă ă => E = 4ø 3 0 ¸Ā1
Do ā song song, ngược chiều với nên Ă ā = 1.Āă 4ø0 ¸Ā 31
●Ý nghĩa cÿa Āă : Biết vector momen điện Āă
ta có thể xác định được vector cường độ
điện trường do lưỡng cực gây ra. Do đó, ta nói vector momen điện đặc trưng cho tính
chất điện cÿa lưỡng cực điện.
2. –Tại tâm O: chia dây thành những phần tử mang điện tích dq, tại phần tử điện tích A
gây ra tại O một điện trườngāý, ta có thể cho một phần tử điện tích B đái xāng với A
qua O, gây ra tại O một điện trường, vector cường độ điện trường do phần tử B gây ra tại O là āþ 3
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/ āý, ā ⇨
þ cùng độ lớn nhưng ngược chiều. āý ā ⇨ þ +0=
Tương tự cho các phần tử điện khác
Áp dụng nguyên lí chồng chất điện trường Ą āÿ = ∑ āÿ = 0 => āÿ= 0 ÿ=1 - Tại M
Chia dây thành những phần tử mang điện dq nhß.
Āng với mỗi phần tử điện tích A, ta có thể chọn được một phần tử điện tích B đái
xāng với A qua O. Phần tử điện tích B sẽ có điện tích dq cách M mội khoảng r’ = AM. Do đái xāng nên dā1 , d ā2 āđái xāng qua 1= Ăā2 OM => d
Cường độ điện trường tổng hợp tại M: Dā = d ā1 + d ā2 => dE = 2 d ā1α cos cos α = ℎĀ= ℎ ℎ2+ Ā2 ⇨dE = ℎ ℎ ℎ.Ăÿ 2+ Ā2.Ăÿ = 4ø0. ℎ + 2 Ā2 ( ) 4ø ( 0 ℎ2+ Ā ) 2 3/2
Áp dụng nguyên lí chồng chất điện trường: ā āý= ∫ Ăā = ∫ℎ.Ăÿ 4ø ( 0 ℎ2+ Ā ) 2 3/2 = ℎā 4ø . 0 (ℎ2+ Ā ) 2 3/2 0
Thay sá, ta tính được āý= 0,, 4. 105 þ/ă
Câu 3: 1. Công cÿa lực tĩnh điện trong chuyển dời vô cùng nhß ds bằng: dA = Ă . Ăā = ÿ0. ā . hay dA Ăā = ÿ40. ø ¸0Ā3 ÿ Ā . Ăā = ÿ0.ÿ ( 4ø¸ Ā 0 2Ăā. āąāα α = ( Ā ; Ăā)
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
Từ hình vẽ ta thấy ds.cosα = dr, do đó: dA = ÿ . 0 ÿ 4ø¸ Ā 0 2ĂĀ
⇨Công cÿa lực tĩnh điện trong sự dịch chuyển điện tích ÿ0 từ M tới N là: þ ∫ ý ÿ 4 0 Ã.ÿ ¸¸ Ā 0 2ĂĀ ÿ0.ÿ ÿ . 0 ÿ ýþ = = - 4ø¸ Ā 0 ý 4ø¸ Ā 0 þ ý
⇨Công cÿa lực tĩnh điện trong sự dịch chuyển điện tích q0 trong điện trường
tĩnh cÿa một điện tích điểm không phụ thuộc vào dạng đường cong dịch
chuyển mà phụ thuộc vào vị trí điểm đầu và điểm cuái cÿa chuyển dời. A = ∮. ā = 0 (1) ĂĂ
Lưu sá cÿa vector cường độ điện trường dọc theo đường cong kín bằng 0.
⇨Ý nghĩa biểu thāc (1) và phát biểu trên đặc trưng cho tính chất thế cÿa điện trường tĩnh.
2.Chia MN thành các phần tử vô cùng nhß Ăā
Công cÿa lực tĩnh điện trong chuyển dời vô cùng nhß ds bằng: dA = Ă . Ăā = ÿ0. ā . = Ăā ds.cos 2ÿ0.āƛ , mà ds.cos ¸ý α α = Ăý Āþ ∫2ÿ ⇨A = 0.āƛ
¸ý Ăý = 2ÿ0.āƛ¸ý . ln ĂĄ Āþ Āý Āý
Thay sá => A = 5. 10−6 ( J ) Câu 4:
1. - Định lí Ostrogradski Gauss:
Điện thông qua 1 mặt kín bằng tổng đại sá các điện tích chāa trong mặt kín ấy. Ą θă= ∫ Ā . Ăă = ∑ ÿÿ ă ÿ=1
∑ ÿÿLà phép lấy tổng đại sá các điện tích chāa trong mặt kín S
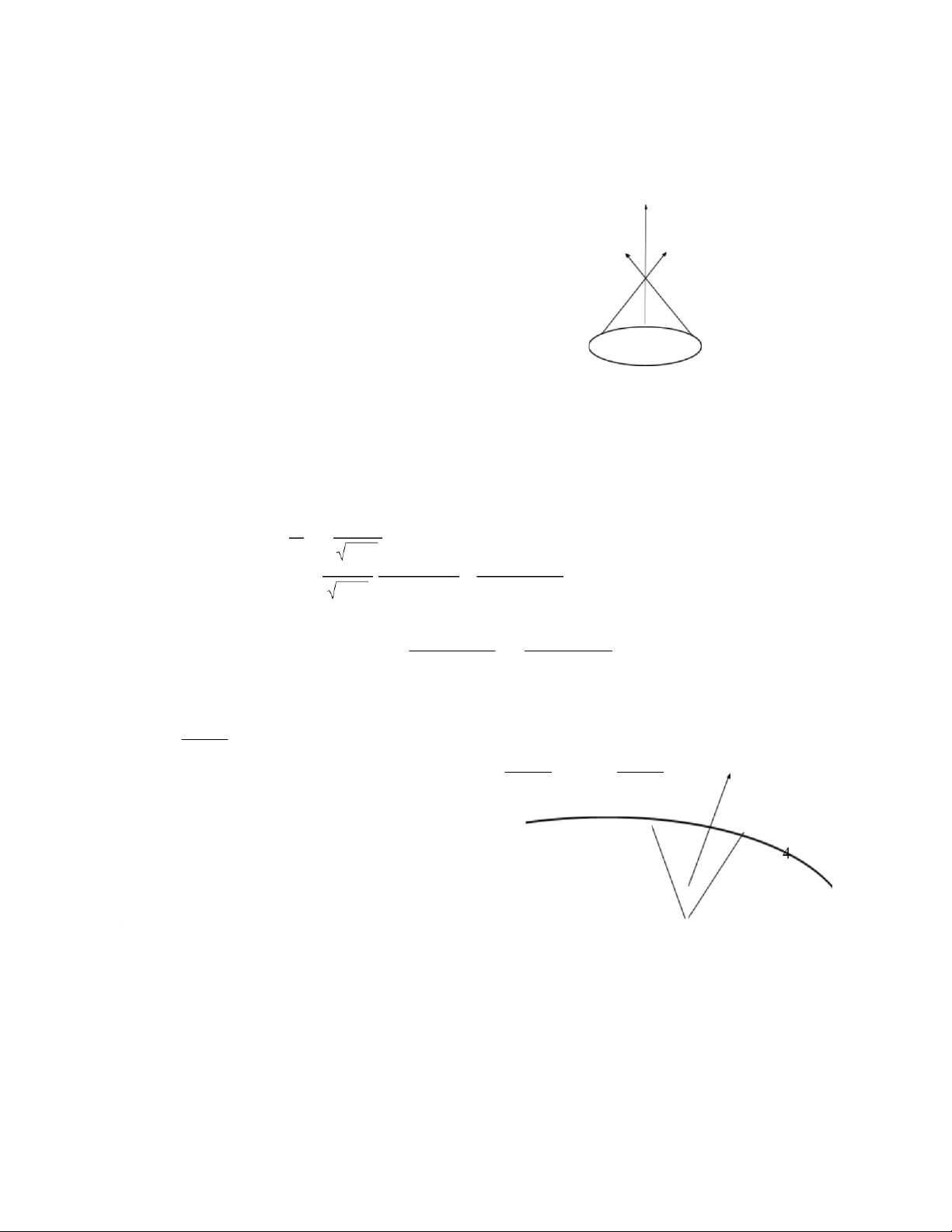
- Dựng mặt trụ ( S ) cùng trục với mặt trụ đã cho, ∆ 5
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
đường sinh song song với và ∆
∆ vuông góc với 2 đáy , M ϵ ( S )
Thông lượng cảm āng điện gửi qua mặt trụ kín ( S ) bằng : Tại 2 mặt đáy
Áp dụng định lí Ostragradski Gauss:
●Dựng mặt trụ ( S ) ( hình vẽ )
Thông lượng cảm āng điện từ qua ( S ) Mặt đáy:
Áp dụng định lí Ostragradski gauss: ∅ă= ∫ Ā ĄĂā = ∫ Ā ĄĂā + ∫ Ā ĄĂā ăặĂ ĂĀụ ăặĂ 2 ăặĂ đáþ Tại 2 mặt đáy ( ĀĄ ; ) = Ăā => à ∫ Ā 22 ăặĂ đáþ ĄĂā = 0 ∅ă= ⇨= ∫ Ā =ĄĂā ∫ = D ĀĄĂā = D.2π.rl ∫ ĀĂā ∫ Ăā ăặĂ ĀêĄ ăặĂ ĀêĄ ăặĂ ĀêĄ ăặĂ ĀêĄ = D.2πr. ā 2ÃσĂ = ĀāĀ (l: độ dài mặt trụ ). σĂ
Áp dụng định lí Ostragradski Gauss: ∅ă= ĀāĀ σĂ = ā σĂ σĂ ⇨D =
=> E = ¸¸0Āσ2ÃĂĂ ) ( Q = λl = Ã
2. Dựng mặt trụ (S) (hình vẽ )
Thông lượng cảm āng điện từ qua (S) ∅ă= ∫ Ā ĄĂā = ∫ Ā ĄĂā + ∫ Ā ĄĂā ăặĂ ĂĀụ ăặĂ ĀêĄ 2 ăặĂ đáþ mặt đáy ( ĀĄ ; ) = Ăā => à 2 ∫ Ā ĄĂā = 0 2 ăặĂ đáþ ∅ă= ⇨= ∫ Ā =ĄĂā ∫ = D ĀĄĂā = D.2π.rl ∫ ĀĂā ∫ Ăā ăặĂ ĀêĄ ăặĂ ĀêĄ ăặĂ ĀêĄ ăặĂ ĀêĄ = D.2πr. 2 āÃσĂ = ĀāĀ σĂ
Áp dụng định lí Ostragradski Gauss: 6
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/ σĂ ∅ 1 ă= ĀāĀ = ā => D =σĂ1 => E = => E = σĂ1 à ¸¸ Ā 0 ý = 200 ĀĂĄ 3.10−2ĂĄ2 = 9618 þ/ă Ă2 Ă1 Câu 5:
1. – Định lí Ostragradski Gauss trong điện trường:
Điện thông qua 1 mặt kín bằng tổng đại sá các điện tích chāa trong mặt kín ấy. Ą θă= ∫ Ā . Ăă = ∑ ÿÿ ă ÿ=1
∑ ÿÿLà phép lấy tổng đại sá các điện tích chāa trong mặt kín S
- Vẽ qua M một mặt trụ kín ( hình vẽ ), mặt trụ có đường sinh vuông góc mặt phẳng, 2
đáy song song, bằng nhau và cách đều mặt phẳng.
Thông lượng cảm āng điện qua mặt trụ kín bằng: ∅ă= ∫ Ā 1Ą1 Ăā + ∫ Ā 2Ą2 Ăā + ∫ Ā 3Ą3 Ăā ăặĂ ĀêĄ ăặĂ đáþ ăặĂ đáþ = ∫ Ā2Ăā + ∫ Ā3Ăā ăặĂ ĀêĄ ăặĂ đáþ
Do D2, D3không đổi trên 2 đáy
∅ă= Ā1∆ă1+ Ā2∆ă2 ⇨= 2 Ā∆ă σ = Q => D = E = σ 2 ¸¸0
- Ā1 , Ā2 lần lượt là vector cảm āng điện do từng mặt gây ra
Vector cảm āng điện do 2 mặt phẳng mang điện gây ra Ā =Ā1 + Ā2
( Theo nguyên lí chồng chất điện trường )
Ā1 , Ā2 có phương vuông góc với mặt phẳng Ā1= Ā2= · mang điện, có độ lớn 2 Ā1 , Ā2 cùng chiều => Ā
có phương vuông góc với 2 mặt phẳng. ⇨Và D =D Ā σ 1+ D2= => E = σ = ¸¸0 ¸¸0
2. Cường độ điện trường gây ra bởi tụ điện: 7
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/ E = σ => U = Ed = σ.Ă ¸¸0 ¸¸0
Công cÿa e khi bay từ bản âm sang bản dương. A = eU = e. σĂ = …. ¸¸0 Câu 6:
1. Tỉ sá W/qokhông phụ thuộc vào độ lớn cÿa điện tích q0 mà chỉ phụ thuộc vào độ lớn
cÿa các điện tích gây ra điện trường và vào vị trí điểm đang xét trong điện trường. Vì
vậy, có thể dùng tỉ sá đó để đặc trưng cho điện trường tại điểm đang xét. V = W/q0
Được gọi là điện thế cÿa điện trường tại điểm đang xét.
●Điện thế gây ra bởi một vật tích điện có điện tích phân bá liên tục. V = ∫ Ăþ = ∫ 1
r: khoảng cách từ vật đến điểm đang xét 4ø¸0ĀĂÿ ●Ý nghĩa: ∞
VM= ∫ ā Ăā : Điện thế tại một điểm M bất kì trong điện trường. ý ýýþ = (þý− þþ) q0 ýýþ ⇨=þý− þþ ÿ0
Nếu ÿ0 = +1 => þý− þþýýþ =
Hiệu điện thế giữa hai điểm M và N trong điện trường là một đại lượng về trị sá =
công cÿa lực tĩnh điện trong sự dịch chuyển 1 đơn vị diện tích + từ M đến N. þýþ-∞ =ýý∞
Nếu lấy q0 = +1 đơn vị điện tích và chọn N ở xa vô cùng thì
Điện thế tại 1 điêm trong điện trường là một đại lượng về trị sá bằng công cÿa lực tĩnh
điện trong dịch chuyển 1 đơn vị điện tích dương từ M đến vô cùng.
2. a, Chia đĩa thành những vành khăn tâm O, bán kính x và x + dx, dS = 2 x à mang điện tích dq = σds
Điện thế do dq gây ra tại M, dV = Ăÿ = σĂā = σ2ÃĂý = σýĂý 4ø¸ Ā 0 4ø¸ ý 0 + 2 ℎ2 4ø¸ ý 0 + 2 ℎ2 2¸¸0ý + 2 ℎ2 8
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/ Ă Ă ⇨V= ∫ Ăþ = ∫ σýĂ 2¸ ý ¸ ý . ý 0 + 2 ℎ2= σ 2+ ℎ2 ( ) 2¸¸0 0 0 = ( σ Ă2+ ℎ2− = ℎ) ā 2¸(¸ à 0 Ă2Ă2+ ℎ2− ℎ) 2¸¸0 = 2ā¸āĂ2 ( Ă2+ ℎ2− ℎ) = ….
b. Công cÿa lực điện khi cho qora xa vô cực: VM-þ∞= ýý∞ ÿą
do þ∞= 0 => ý. ý∞ = ÿąþý= … Câu 7:
1. Xét 2 điểm M, N rất gần nhau trong điện trường ā . Giả sử điện thế tại M,N lân lượt là V, V+ dV (dV> 0) dA = qo ā Ăā = Ăā ýþ Mặt khác: dA = qo[V – (V +dV)] = -qodV ⇨ā Ăā = − Ăþ => ā = −Ăþ Ăā Vì dV > 0 nên ā Ăā
= ā. Ăāāąāα < 0 ℎÿþ āąāα < 0 ; α = (ā, Ăā )
Do đó α là góc tù véc tơ cường độ điện trường luôn luôn hướng theo chiều giảm cÿa điện thế.
⇨Hình chiếu cÿa véc tơ cường độ điện trường trên 1 phương nào đó về trị sá
bằng độ giảm điện thế trên 1 đơn vị dài cÿa phương đó.
Ex, Ey, Ezlà hình chiếu cÿa ā lên Ox, Oy, Oz.
āý= −∂þ∂ý ; āþ= −∂þ ∂þ ; āÿ= −∂þ ∂ÿ ā = āýÿ + āþĀ + āÿā =− ÿ .∂ ý ∂ +þ Ā . ∂ ∂ þ þ + ā . ∂þ ( ) = −∂þ ∂ÿ ∂ý = − �㕔ĀÿĂ þ
⇨Công thāc hiệu điện thế giữa 22 bản cực cÿa tụ điện phẳng : U = σĂ ¸¸0 9
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
2. Xét mặt Gauss đòng tâm với khái cầu bán kính r (r trường trên mặt này như nhau và vuông góc với mặt cầu.
Theo định lý Ostrograd ski – Gauss: ∅
∫ Ăā = ¸¸ąā4ÃĀ2 = ∑ ÿ = Ä ă=
∫ Ā Ăā = ∫ ¸¸ąā Ăā = ¸¸ąā 4 3ÃĀ3 āả �㕣ậĂ āả �㕣ậĂ āả �㕣ậĂ ⇨ā = Ä3¸¸ą
Hiệu điện thế giữa 2 điểm cách tâm lần lượt những khoảng R/2 và R là: Ă Ă Ăā þĂ2 34ÃĂ3 U= V ∫ ĂĀ = Ā2 a/2 – Va= =∫ āĂĀ = ÄĀ Ä = 3¸¸ą 6¸¸ą 8¸¸ą 8¸¸ą Ă Ă 2 2 Ă 2 =3ā34¸¸ąĂ Câu 8:
1. * Điều kiện cân bằng tĩnh điện:
-Vector cường độ điện trường bên trong vật bằng 0. : āĂĀąĄ�㕔 = 0
-Thành phần tiếp tuyến Et cÿa vector cường độ điện trường tại mọi điểm trên vật dẫn bằng 0 . āĂ = 0; ā = āĄ
●Tính chất cÿa vật dẫn cân bằng tĩnh điện:
-Vật dẫn cân bằng tĩnh điện là một khái đẳng thế. Mặt vât dẫn là một mặt đẳng thế.
-Giả sử truyền cho vật một điện tích q nào đó. Khi vật dẫn đã ở trạng thái cân bằng
tĩnh điện, ta có thể coi rằng điện tích q chỉ được phân bá trên bề mặt vật dẫn, bên
trong vật dẫn điện tích bằng 0.
-Đái với vật dẫn rỗng đã ở trạng thái cân bằng tĩnh điện, điện trường cÿa vật rỗng
và trong thành cÿa vật rỗng bằng không. ÿ Ă.4ø¸ąĂ2 ą.ā = 2. a) F = => Q = øĂ2 =… 4ø¸ąĂ2 ÿą āÿą
b.) Công A = q o( VR- VM) ( VR= kQ/R ; VM= kQ/r )
=> VR= A/qo+ VM=> kQ/R = A/qo+ VM => R =… 10
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/ Câu 9:
1. – Hiện tượng các điện tích cảm āng xuất hiện trên vật dẫn ( lúc đầu không mang
điện ) khi đặt trong điện trường ngoài gọi là hiện tượng điện hưởng.
-Định lí các phần tử tương āng :
Điện tích cảm āng trên các phần tử tương āng có độ lớn bằng nhau và trái dấu.
-Tụ điện là một hệ 2 vật dẫn A, B sao cho vật dẫn B được bao bọc hoàn toàn bên
trong vật dẫn A. ( A, B thường được gọi là 2 cát hoặc 2 bản tụ điện ). A, B ở trạng
thái điện hưởng toàn phần.
-Tụ điện phẳng có hai bản cùng diện tích S, cách nhau 1 khoảng d.
Nếu d rất nhß so với kích thước mỗi bản, ta có thể coi điện trường giữa hai bản tụ
là điện trường gây bởi 2 mặt phẳng song song vô hạn tích điện đều. þ1− þ2= Ăσ = Ăā ¸¸0 ¸¸ ă 0 ⇨ÿ = ā = ¸¸0ă þ1− þ2 Ă
Xét mặt cầu ( S ) đồng tâm với 2 mặt cầu cÿa tụ bán kính Ă1< Ā < Ă2
Áp dụng định lí O – G : Ą θ ∫ Ā . Ăă = Ā. 4ÃĀ ă= 2= ∑ ÿÿ= ā ÿả �㕣ậĂ ÿ=1 ā ā ⇨D = => E = 4ÃĀ2 4ø¸ Ā 0 2
Q: trị sá điện tích trên bản cực cÿa tụ cầu. 4ø¸0Ă1Ă2 4ø¸0Ă1Ă2ý C = āý= => Q = Ă − 1 Ă2 Ă − 1 Ă2 Ă Ă 1 ý 2 ⇨E = = 32k V/m (Ă − 1 Ă ) 2 Ā2 Câu 10:
1. – Hiện tượng trên thanh điện môi đặt trong điện trường có xuất hiện điện tích gọi là
hiện tượng phân cực điện môi.
-Giả sử trong thể tích cÿa khổi điện môi đồng chất có n phân tử điện môi. Gọi Pe là
vector momen điện cÿa phần tử thā i. 11
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
Vector phân cực điện môi là một đại lượng đo bằng tổng momen điện cÿa các phần tử
có trong 1 đơn vị V cÿa khái điện môi. Ą ∑ Āăÿ Āă = ÿ=1 ∆þ
-Mái liên hệ giữa vector phân cực điện môi và mật độ điện tích liên kết trên bề mặt điện môi: σ = Āă. Ą
Mật độ điện tích liên kết xuất hiện trên mặt giới hạn cÿa khổi điện môi có giá trị
bằng hình chiếu cÿa vector phân cực điện môi trên pháp tuyến cÿa mặt giới hạn đó. 2. Bài toán:
F = qE = q.U/d => d = ÿý = ..= 1 cm Ă ¸¸ ă 0 C = Ă => ¸ = Ăÿ =…=2 ¸ ă 0 Q = CU = …= 3,84.10−9 C Câu 11:
1. - Giả sử ta có một điện trường đều Eo giữa 2 mặt phẳng song song vô hạn, mang điện
đều nhưng trái dấu, chất điện môi được lấp đầy khoảng không gian giữa hai mặt phẳng.
Trên các mặt giới hạn xuất hiện điện tích liên kết. Điện tích liên kết gây ra điện trường phụ E’
Theo nguyên lí chồng chất điện trường, vector cường độ điện trường E tại một điểm bất kì bằng: ā = ā0 +ā'
Chiếu lên phương ā0ā: E = 0− ā' ā'= σ ¸0
Mặt khác: σ'= Āă. Ą =¸0 ℵăā ⇨E’ = ℵăā ⇨E = ā0 1+ℵăā
-Hiệu āng áp điện thuận: 12
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
Khi nén hoặc kéo dãn mẫu tinh thể điện môi theo những phương đặc biệt trong tinh
thể thì trên các mặt giới hạn cÿa tinh thể có xuất hiện những điện tích trái dấu,
tương tự như những điện tích trong hiện tượng phân cực điện.
-Hiệu āng áp điện nghịch:
Nếu ta đặt lên hai mặt cÿa một tinh thể một hiệu điện thế thì nó sẽ bị dãn hoặc nén.
Nếu hiệu điện thế này là một hiệu điện thế xoay chiều thì bản tinh thể sẽ bị dãn,
nén liên tiếp và dao động theo tần sá cÿa hiệu điện thế xoay chiều. 2. Bài toán: ā = ā0 +ā' E = ā0− ā' ā0 = σ , ā'= σ' ¸0 ¸0 ⇨ā = σ− σ' ¸0 Mặt khác: E = ý = σ Ă ¸¸0 σ = σ− σ'
=> σ'= ¸0(¸ − 1) ý Ă = 8,86. 10−6 ă2 C/ ¸¸0 ¸0 Câu 12: 1.
●Thế năng tương tác giữa 2 điện tích điểm:
2 điện tích điểm q1, q2 đặt cách nhau một khoảng r thì thế năng tương tác cÿa q1
trong điện trường q2 bằng thế năng tương tác cÿa q2 trong điện trường q1. ÿ . Ă= 1 ÿ1.ÿ2 = 12. (ÿ1þ1+ ÿ2þ2) 4ø0 ¸Ā
●Năng lượng cÿa hệ điện tích điểm: Ą W = 1 ∑ ÿÿþÿ 2ÿ=1
●Năng lượng cÿa vật dẫn cô lập:
Chia vật dẫn thành những điện tích điểm dq
⇨Năng lượng cÿa vật dẫn đó là: W = 12∫ þĂÿ 13
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
Đái với vật cân bằng điện tích, V = const: ÿ2
W = 12þ∫ Ăÿ =1 2ÿþ = 1 2 ÿ
( q = CV , C: điện dung vật dẫn) 2. Bài toán:
a, Xét mặt cầu ( S ) bán kính r:
Áp dụng định lí O – G : θ ∫ Ā . Ăă = Ā. 4ÃĀ ă= 2= Äþ ÿả �㕣ậĂ ā 3ÃĂ3.4 3ÃĀ3 4 E = Äþ 4ø ¸ 4ø ¸ 0 Ā2= āĀ4ø ¸ 0 Ă3105 þ/ă 0 Ā2= = 9. Ă Ă b. W = 12∫ Ăÿ
= ∫1 2¸0¸ā2Ăþ = ∫1 2¸0¸ā24ÃĀ2ĂĀ (�㕣ớÿ Ăþ = 4ÃĀ2ĂĀ) 0 0 Ă Ă
= ∫1 2¸0¸( āĀ4ø ¸0Ă3) 24ÃĀ2ĂĀ = ∫ā2Ā84ø ¸0Ă6ĂĀ = ā2 40¸0¸ÃĂ = 1 10− 12,5. 3 J 0 0 Câu 13:
1. Năng lượng điện trường cÿa tụ điện phẳng: W = 12ÿý2
Xét 1 tụ điện phắngdxdxdxđ Câu 14:
1. – Xét 2 điện tích nhß dSn nằm vuông góc với các đường dòng và cách nhau một khoảng nhß dl.
Gọi V, V + dV là điện thế tại hai điện tích ấy.
dI là cường độ dòng điện chạy qua chúng.
Theo định luật Ohm ta có:
-Nguồn điện là một cơ chế tạo ra điện thế nhằm duy trì dòng điện lâu dài trong mạch
-Gọi E là vector cường độ điện trường tĩnh, E* là vector cường độ điện trường lạ tại
cùng một điểm bất kì trong mạch. 14
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
⇨Công cÿa lực điện trường tổng hợp trong sự dịch chuyển cÿa điện tích q 1 vòng mạch kín: Câu 15:
1. Định luật Bio – Xava – Laplace
Vector cảm āng điện từ B do một phần tử dòng điện Idl gây ra tại điểm M, cách phần
tử một khoảng r là một vector có: + Gác tại M
+ Phương vuông góc với mặt phẳng chāa phần tử dòng điện Idl và điểm M.
+ Chiều sao cho vector dl, r, dB theo thā tự hợp thành một tam diện thuận
-Độ lớn dB xác định bởi:
Vector cảm āng từ B do AB gây ra
Vì các vector dB do các phần tử dòng điện cÿa AB sinh ra có cùng phương chiều
nên B có cùng phương chiều như dB. Câu 16:
1. Toàn bộ dòng điện tròn có thể phân thành từng cặp phân tử dl1, dl2, có chiều dài bằng
nhau và nằm đái xāng nhau qua tâm 0 cÿa vòng tròn.
⇨Các vector dB1, dB2 do chúng gây ra tại một điểm M trên trục dòng điện
cũng nằm đái xāng nhau với trục đó.
Vector cảm āng từ tổng hợp db1 + dB2 nằm trên trục cÿa dòng điện, B do cả
dòng điện tròn gây ra cùng nằm trên trục ấy.
Gọi dBn hình chiếu cÿa dB lên trục dòng điện.
Cảm āng từ B do dòng điện tròn gây ra tại M là
Gọi S là một vector nằm trên trục cÿa dòng điện tròn, chiều là chiều tiến cÿa cái
vặn nút chai khi ta quay nó theo chiều cÿa dòng điện. Câu 17:
1. – Lưu sá cÿa vector cường độ từ trường dọc theo một đường cong kín ( C ) bất kì ( 1
vòng ) bằng tổng đại sá cường độ cÿa các dòng điện xuyên qua điện tích giới hạn bởi đường cong đó:
Trong đó Ii mang dấu dương nếu dòng thā I nhận chiều dịch chuyển trên đường cong
làm chiều quay thuận xung quanh nó, Ii mang dấu âm nếu dòng điện thā I nhận chiều
dịch chuyển trên đường cong làm chiều quay nghịch xung quanh nó. 15
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
-Công thāc tính cảm āng từ trong lòng dây điện hình xuyến cho cuộn dây điện hình xuyến gồm n vòng R1: bán kính trong R2: bán kính ngoài
-Công thāc cảm āng từ trong lòng áng dây điện thẳng dài vô tận:
àng dây thẳng dài vô tận có thể xem như một cuộn dây điện hình xuyến có bán kính vô cùng lớn: R1 = R2 =
Do đó, cường độ từ trường tại mọi điểm bên trong áng dây đều bằng nhau và bằng : Câu 18: Câu 19:
1. Xét thanh kim loại AB dài l, có thể trượt trên 2 dây kim loại song song cÿa một mạch
điện. Giả sử mạch điện này nằm trong một từ trường đều và vuông góc vector cảm
āng từ B cÿa từ trường
Lực Ampe tác dụng lên thanh có độ lớn:
Khi thanh dịch chuyển một đoạn nhß ds, công cÿa lực Ampe là:
dS = l.ds : diện tích quét bởi đoạn dòng điện AB
Nếu thanh AB dịch chuyển một đoạn hữu hạn từ (1) => (2), cường độ dòng điện qua
thanh coi như không thay đổi
-Áp dụng định luật Ohm cho mạch điện trong quá trình dòng điện đang được thành lập, ta có: R : điện trở toàn mạch
Nhân cả 2 vế với idt, ta có:
…. Là năng lương do nguồn điện sinh ra trong khoảng thời gian dt, năng lương này
một phần tßa thành nhiệt trong mạch, một phần tiềm tang dưới dạng năng lượng từ trường
- Chia không gian cÿa từ trường thành các phần thể tích vô cùng nhß dV
Năng lượng từ trường trong mỗi thể tích dV là :
⇨Năng lượng từ trường bất kì là Câu 20:
1. – Khi từ thông gửi qua một mạch kín thay đổi thì trong mạch điện xuất hiện một dòng
điện ( dòng điện cảm āng) => hiện tượng cảm āng điện từ. 16
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/ - Định luật Len xơ:
Dòng điện cảm āng phải có chiều sao cho từ trường do nó sinh ra có tác dụng
cháng lại nguyên nhân sinh ra nó.
- Thiết lập công thāc tính suất điện động cảm āng: Giả sử trong dt:
+ từ thông gửi qua vòng dây biến thiên
+ dòng điện cảm āng xuất hiện trong vòng dây có cường độ Ic
⇨Công cÿa từ lực tác dụng lên dòng điện cảm āng là:
Áp dụng định luật Len xơ :
Áp dụng định luật bảo toàn năng lượng:
Công dA’ được chuyển thành năng lượng cÿa dòng điện cảm āng. Câu 21:
1. –Hiện tượng tự cảm: Khi làm thay đổi cường độ dòng điện trong một mạch điện để từ
thông do chính dòng điện đó gửi qua diện tích cÿa mạch thay đổi thì trong mạch cũng
xuất hiện dòng điện cảm āng. Dòng điện này do sự cảm āng cÿa dòng trong mạch sinh
ra nên được gọi là dòng điện tự cảm và hiện tượng này gọi là hiện tượng tự cảm.
- Thiết lập biểu thāc tính suất điện động tự cảm:
VD: Āng dụng cÿa hiện tượng tự cảm trong tôi kim loại ở lớp bề mặt.
Nhiều chi tiết máy như biên, trục máy, bánh răng khía.. cần đạt yêu cầu kĩ thuật là :
bề mặt phải thật cāng bên trong vẫn còn độ dẻo thích hợp, do đó, cho dòng điện
cao tần chạy qua một cuộn dây điện bên trong có đặt chi tiết máy cần tôi. Dòng
điện cao tần sinh ra trong chi tiết máy, những dòng điện cảm āng biến đổi với tần
sá cao tần. Do hiện tượng tự cảm, những dòng điện này chỉ chạy ở lớp bề mặt cÿa
chi tiết máy. Khi lớp bề mặt này đã được nung đß đến māc cần thiết, ta nhúng chi
tiết máy vào nước tôi và như vậy, ta được một lớp mặt ngoài cāng còn bên trong chi tiết máy vẫn dẻo. Câu 22:
Dòng điện xoay chiều sinh ra từ trường biến thiên cũng xoay chiều qua mặt khung, dẫn tới
trong khung có suất điện động cảm āng xoay chiều và có dòng điện cảm āng xoay chiều qua được tụ.
Chia khung dây thành các dải nhß song song với dòng điện thẳng. Xét dải cách dòng điện
một đoạn x có diện tích dS = adx
⇨Từ thông do dòng điện gửi qua khung dây: Câu 23:
1. –Luận điểm 1 cÿa Maxwell 17
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
Bất kì một từ trường nào biến đổi theo thời gian cũng sinh ra một điện trường xoáy.
- Phân biệt điện trường tĩnh và điện trường xoáy:
+ Điện trường tĩnh: có đường sāc là các đường cong hở, công cÿa điện trường tĩnh
trong sự dịch chuyển hạt điện theo đường cong kín bằng 0.
+ Điện trường xoáy: có đường sāc là các đường cong kín, công cÿa điện trường
trong sự dịch chuyển hạt điện theo đường cong kín khác 0.
- Thiết lập phương trình Maxwell – Pharaday
Xét 1 vòng dây kín nằm trong từ trường þ đang biến đổi.
Suất điện động cảm āng xuất hiện trong vòng dây đó là:
Là từ thông diện tích S giới hạn bởi vòng dây dẫn mà ta xét. Câu 24:
1. –Luận điểm 2 cÿa Maxwell :
Bất kì 1 điện trường nào biến đổi theo thời gian cũng sinh ra một từ trường.
- Dòng điện dịch: là dòng điện tương đương với điện trường biến đổi theo thời gian
về phương diện sinh ra từ trường.
- Dòng điện dẫn: là dòng chuyển dời có hường cÿa các hạt mang điện. Dòng điện dịch - Dòng điện dẫn -
Tương đương với điện trường -
Là dòng chuyển dời có hường
biến đổi theo thời gian về phương diện cÿa các hạt mang điện
sinh ra từ trường tồn tại trong chân không - Không gây tßa nhiệt - Gây tßa nhiệt Jun Len-xơ -
Không chịu tác dụng cÿa từ -
Chịu tác dụng cÿa từ trường bên trường bên ngoài ngoài -
Sinh ra từ trường, điện trường - Sinh ra từ trường
thay đổi, sinh ra từ trường thay đổi theo thời gian
- Thiết lập công thāc Maxwell – Ampere dạng tích phân
J là vector mật độ dòng điện dẫn.
Jd là vector mật độ dòng điện dịch.
⇨Mật độ dòng điện toàn phần tại một điểm:
Xét đường cong kín bất kì ( C ) nằm trong miền không gian có cả dòng điện
dịch và dòng điện dẫn chạy qua. 18
BK- Đại Cương Môn Phái - https://www.facebook.com/groups/249046605455122/
Itp là cường độ dòng điện toàn phần chạy qua diện tích ( S ) giới hạn bởi đường cong ( C ). 19