Câu hỏi và đáp án tự luận vật lý đại cương III môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
Bán kính mặt cầu của thấu kính phẳng-lồi trong hệ vân tròn Newton là R. Chiếu một chùm tia sáng đơn sắc, song song đơn sắc bước sóng λ. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Môn: Vật lý đại cương 2 298 tài liệu
Trường: Học viện Công Nghệ Bưu Chính Viễn Thông 1.7 K tài liệu
Tác giả:
Preview text:
VŨ TIẾN LÂM
CÂU HỎI VÀ ĐÁP ÁN TỰ LUẬN
VẬT LÝ ĐẠI CƯƠNG III – PH1130 Câu 1: 1. n 1T,rnìn
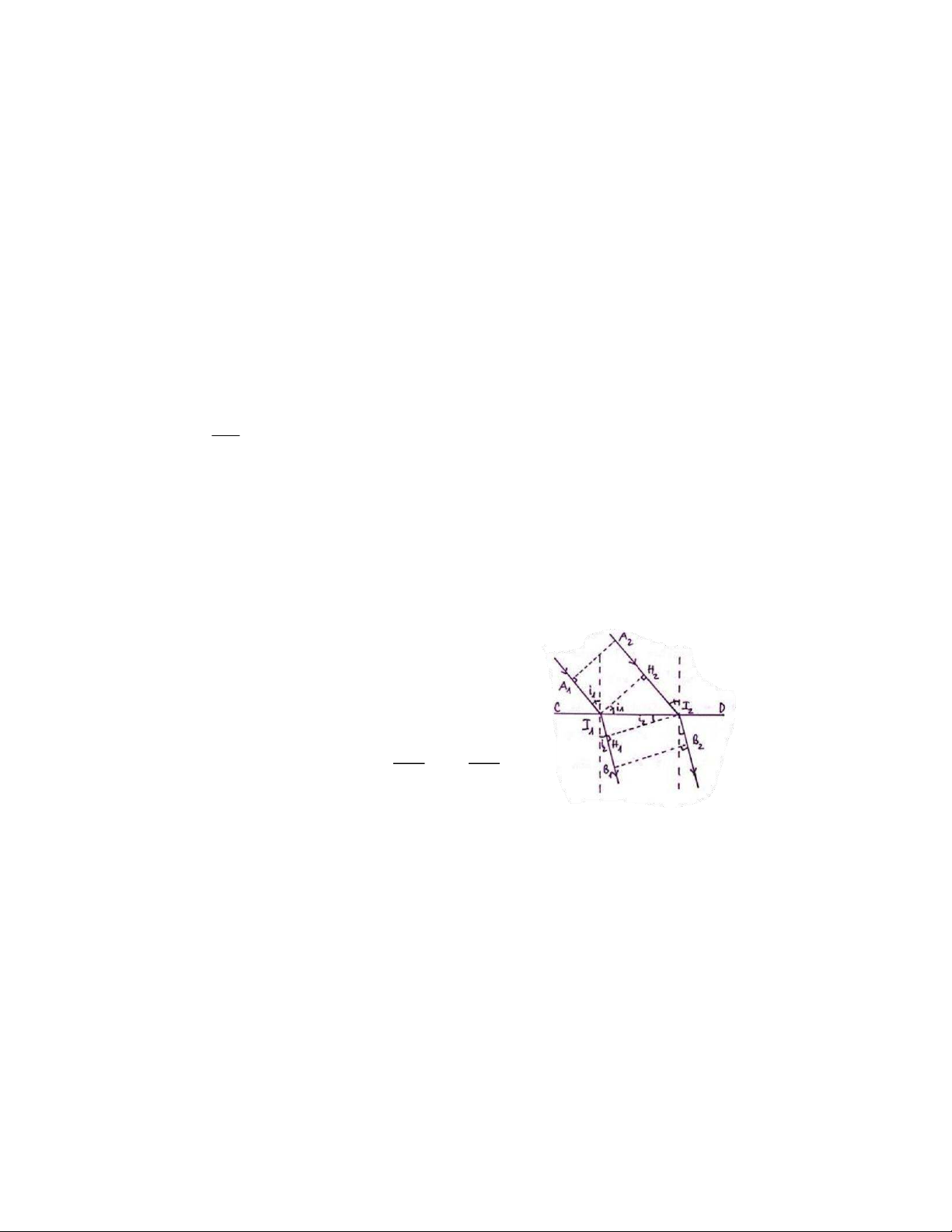
2. h bày khái niệm quang lộ và mặt trực giao của một chùm sáng. Phát biểu đị 2.n h M lu ột ậ tc M hù al m ussá, ncgh ứ c n ó gb m ướin c hs óđịnng hλ lu=ật 0M ,5 a5l uμs mc hđoư tợrcư ờ c n hi gế h u ợvpu tôrnùgm g sóác nvg ớsi on m gặt so n n ê g m kth h ú ủ c y txiạn q h ucaó m chặitế tp hsâunất cá n ch = c1,ủa 5. ha N ig m ườ ôi ir tar ưqờ
u nagn tsráot nhgệ stuhốốtn cgó vcâhni ếgti sau o ấtth oa i = 0,21 mm.
gây bởi chùm tia phản chiếu và thấy rằng khoảng cách giữa hai vân tối liên tiếp
a/ Xác định góc nghiêng của nêm.
b/ Xác định vị trí của ba vân tối đầu tiên. Biết rằng vân tối số 1 là cạnh của nêm. Giải
1. – Quang lộ giữa hai điểm A,B (trong môi trường đồng tính, có chiết suất n,
cách nhau một đoạn bằng d) là đoạn đường ánh sáng truyền được trong chân
không trong khoảng thời gian bằng khoảng thời gian mà ánh sáng đi hết đoạn
đường AB trong môi trường chiết suất n.
- Mặt trực giao: là mặt vuông góc với các tia sáng của một chùm sáng . Nếu
chùm sáng là chùm đồng quy thì những mặt trực giao là những mặt cầu đồng tâ {m L 1m = à ntâ 1 m A1 Il1à đ + iể ( m n2 Iđ1ồ Hn1g + qu n2y H đ1ó B .1 N ) ếu ( c1hù
) m sáng là chùm song song thì mặt
trực giao là những đường mặt phẳng song song.
- Định luật Malus: Quang lộ củ I1I a2 c = ác n 2t.iIa1 s
Há1ng giữa hai mặt trực giao của một chLù2m = s(án n1g At2hìH 2bằ + ng n1 nHh2aIu2. ) C+hứ n2nIg2 m B2 i n h : +n T Q a1 . ucsiaón: n gAi1 l1ộI1 = h= n a2.i Astii2an His2á;nH →g1 Bn11.=H I22IB 2 2 I1I2 M H ặat yk h
n1á.c:H 2I2= n2.H1I1 thay vào (1)→ L1= L2 VŨ TIẾN LÂM 2. Tóm tắt Giải
λ = 0,55 μm a/ + Vị trí vân tối thứ k: n = 1,5 dt= k. λ i = 0,21 mm 2n (k ∈ Z) a/ α =? b/ xt(1→3) =? Ta có: sin α = dk
xt với xt là vị trí vân xét (1)
Mà xt=ki (k ∈ Z); sin α ≈ α (với α nhỏ) (2) Từ (1) và (2) =>
α = λ2ni hay khoảng vân: i = λ 2na
+ Thay vào công thức => góc nghiêng của màn là:, α = λ2ni =0,55.10−6
2.1,5.0,21.10−3 = 8,73.10−4 rad
b/ Vị trí vân tối: Ta có xt=ki = k.λ2nα (với k=0,1,2,…)
→ Vị trí của ba vân tối đầu tiên là: x1= 0 mm; x2= 0,21 mm; x3= 0,42 mm. Câu 2:
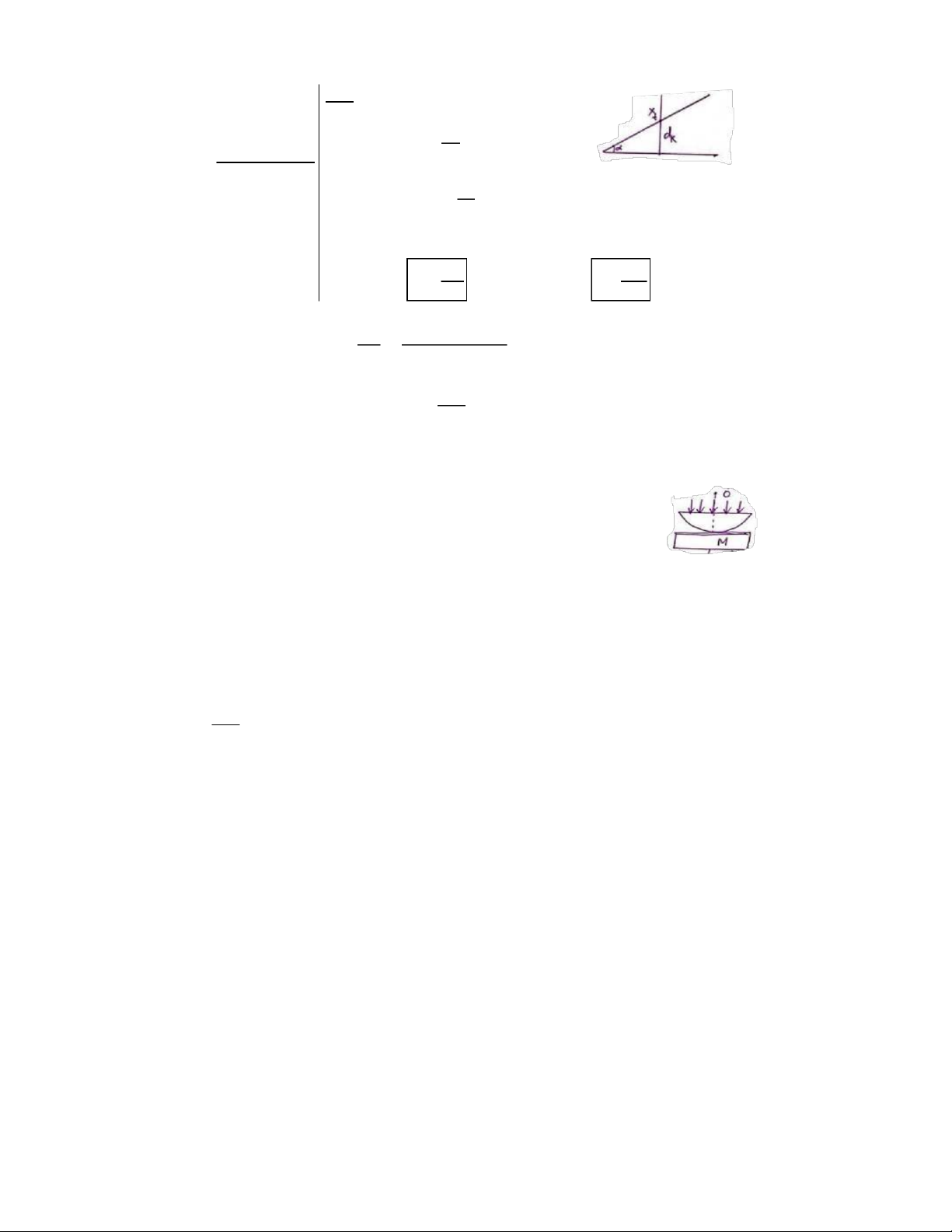
1. Bán kính mặt cầu của thấu kính phẳng-lồi trong hệ vân tròn
Newton là R. Chiếu một chùm tia sáng đơn sắc, song song đơn sắc
bước sóng λ theo phương vuông góc với bản thủy tinh (hình vẽ).
Giải thích sự tạo thành vân giao thoa và tìm biểu thức xác định bán kính của vân tối thứ k.
2. Cho R=100cm, chiết suất của thấu kính và bản thủy tinh lần lượt là n1= 1,5
và n2= 1,7; vùng không gian giữa mặt cong của thấu kính và bản thủy tinh
chứa đầy một chất có chiết suất n = 1,63. Xác định bán kính vân tối thứ 5 nếu
quan sát vân giao thoa bằng ánh sáng phản xạ, cho biết bước sóng của ánh sáng λ = 0,55 μm. Giải
1. – Hệ mặt cầu và bản thủy tinh tạo thành một lớp không khí ở giữa là một bản
mỏng có bề dày không đổi. Rọi lên thấu kính một chùm sáng đơn sáng song
song vuông góc với bản thủy tinh. Tương tự như nêm không khí, tại mặt cong
của thấu kính sẽ có sự gặp nhau của các tia phản xạ và quan sát được các vân
giao thoa, ở đây là các vòng tròn đồng tâm. VŨ TIẾN LÂM
+ Hiệu quang lộ hai tia sáng giao thoa với nhau tại
bề mặt cầu lồi ΔL =L2−L1=2d+λ2
Tại I điều kiện là vân tối:
→ ΔL = (2k + 1).λ2→2d +λ2=(2k + 1).λ2
→ Bề dày của bản nêm không khí ứng với các vân tối:
dt= k. λ2 (k = 0,1,2,3, … ) + Theo hình vẽ ta có:
rk2= R2−(R − dk)2= R2− R2+2Rdk− dk 2=2Rdk− dk 2=(2R − dk). dk
Vì bán kính mặt cầu khá lớn (R ≫ dk)→ rk2≈2Rdk hay rk=√2Rdk (∗)
Ta có {rk=√2Rdk2→ rk=√Rλ.√k (với k = 0,1,2,3,…) dk= k. λ
Tiếp điểm M là điểm tối, các vân tối càng xa M càng sít nhau 2. Tóm tắt Giải
R = 100 cm + n > n1→ Quang lộ của tia phản n1= 1,5
xạ tại mặt phân cách n1− n sẽ kéo n2= 1,7 dài thêm λ2; n2> n1→ Quang lộ n = 1,63
λ = 0,55 μm của tia phản xạ tại mặt phân cách
___________ n2− n sẽ kéo dài thêm λ2. Khi đó hiệu quang lộ của hai tia r5=?
phản xạ: ΔL = L2− L1=2n. d (1)
+ Vân xác định là vân tối → ΔL = (2k + 1).2λ (2) Từ (1) và (2) suy ra
2ndk=(2k + 1).λ2→ dk=(2k + 1).λ4n (3) Thay (3) vào (*) ta được rk=√2Rdk
Vậy ta có bán kính của vân tối thứ k: rk=√(2k + 1). λ. R
2n . Thay số ta được r5= 1,36mm VŨ TIẾN LÂM Câu 3:
1. Định nghĩa hiện tượng nhiễu xạ ánh sáng. Phát biểu nguyên lý Huygens-
Fersnel. Trình bày phương pháp đới cầu Fresnel, nêu các tính chất của đới cầu.
Tính biên độ dao động sáng tại một điểm do nguồn sáng điểm gây ra theo các đới cầu Fresnel.
2. Chiếu một chùm tia sáng song song, bước sóng λ = 0,45 μm thẳng góc với
một lỗ tròn bán kính r = 0,9 mm, sau lỗ tròn đặt một màn quan sát. Xác định
khoảng cách lớn nhất từ lỗ tròn tới màn quan sát để tâm nhiễu xạ trên màn là một vệt tối. Giải
1. – Hiện tượng nhiễu xạ ánh sáng là hiện tượng ánh sáng lệch khỏi phương
truyền thẳng khi đi gần các chướng ngại vật.
- Nguyên lý Huygens-Frosnel:
+ Phát biểu của Huygens: Bất kỳ một điểm nào mà ánh sáng truyền đến đều trở
thành nguồn sáng thứ cấp phát ra ánh sáng về phía trước.
+ Phát biểu của Frosnel: Biên độ và pha của nguồn thứ cấp là biên độ và pha do
nguồn thực gây ra tại vị trí của nguồn thứ cấp.
- Phương pháp đới cầu Frosnel và tính chất
+ Xét một nguồn điểm O phát ra ánh sáng có bước sóng λ
+ Điểm được chiếu sáng M
+ Dựng mặt cầu ∑ có tâm là O, bán kính
R+ Dựng các mặt cầu ∑,0∑, 1∑, … 2 , ∑ ncó bán
kính tương ứng là b; b + λ2; b + 2λ2; … ; b + nλ2 . Cắt mặt cầu ∑ → tạo ra các đới
cầu gọi là các đới cầu Fresnel:
+ Diện tích mỗi đới cầu đều bằng nhau: ΔΣ =(πR. b) R + b . λ
+ Bán kính của đới cầu thứ k: rk=√k.√Rbλ R + b (với k = 1,2,3, … )
+ Ta coi mỗi đới cầu là một nguồn thứ cấp phát sáng đến M
+ Theo nguyên lý Huygens, mỗi đới cầu có thể coi là một nguồn thứ cấp gửi
ánh sáng đến M. Các đới cầu càng xa M thì biên độ sáng giảm dần. Biên độ
sáng do đới thứ k gây ra tại M bằng trung bình cộng của biên độ dao động sáng
do hai đới bên cạnh gây ra VŨ TIẾN LÂM ak=12(ak−1 + ak+1)
+ Khoảng cách từ hai đới cầu liên tiếp tới điểm M khác nhau λ 2; có hiệu pha dao động
Δφ =2πλ(L2− L1)=2πλ.λ2= π (ngược pha)
Như vậy hai đới cầu liên tiếp ngược pha nhau nên chúng sẽ khử lẫn nhau
- Biên độ sáng tại Mi. Gọi a là biên độ sáng tại M (tổng hợp do các đới cầu gây
ra), ta có M ở khá xa mặt ∑, do đó dao động sáng do các đới cầu gây ra tại M có
thể coi là cùng phương → a = a1− a2+ a3− a4+ a5− a6+ ⋯
→ an=a12+(a12− a2+a3 2)+(a32− a4+a5 2)+ ⋯ + an2
Do a thay đổi khá nhỏ nên có thể coi:
ak=ak−12+ak+1 2 nên an=a1 2±an2
Khi n → ∞ thì an→ 0 nên ta có: a∞=a1 2 2. Tóm tắt Giải
λ = 0,45 μm + Để tâm của hình nhiễu xạ là tối nhất thì bán kính lỗ tròn
r = 0,9 mm phải có giá trị sao cho chỉ có 2 đới cầu đi qua bmax =? rlỗ = r2=√2. √Rbλ R + b (1)
+ Vì R → ∞ nên ta có r2=√2. √bλ
+ Khoảng cách lớn nhất từ lỗ tròn tới màn quan sát để tâm của hình nhiễu xạ là vệt tối là: bmax =r22λ =(0,9.10−3)2 2.0,45.10−6 = 0,9 (m)
Câu 4: Trình bày hiện tượng nhiễu xạ của sóng phẳng ánh sáng đơn sắc qua
một khe hẹp. Tìm công thức xác định cực tiểu và cực đại nhiễu xạ. Vẽ đồ thị
biểu diễn cường độ sáng của các cực đại nhiễu xạ và nêu các nhận xét. Giải - Hiện tượng:
+ Rọi một chùm sáng song song vuông góc với
một khe hẹp bề rộng b. Sau khe, các tia nhiễu xạ theo nhiều phương.
+ φ = 0: Các tia đều cùng pha và hội tụ tại F. Khi
đó điểm F rất sáng, gọi là cực đại giữa. VŨ TIẾN LÂM
+ φ ≠ 0: Các tia nhiễu xạ hội tụ tại M.
+ Chia mặt phẳng khe thành các dải sáng Fresnel bởi các mặt Σ0; Σ1; Σ2; …
vuông góc với chùm nhiễu xạ, cách nhau từng λ2.
• Mỗi dải được coi là một nguồn thứ cấp gửi ánh sáng đến M.
• Hiệu quang lộ của hai dải kế tiếp bằng λ 2→ dao động của hai dải kế tiếp khử nhau. + Bề rộng mỗi dải: Δb = λ/ si 2
n φ → số dải trên khe: n = b Δb =2b.sin φ λ
- Cực tiểu và cực đại nhiễu xạ
+ Nếu khe chứa số chẵn dải => M tối (Do các dải sáng triệt tiêu nhau) n = 2b. siλn=φ
2k → sin φ = kλ b (với k = ±1;±2;±3;…)
Đặc biệt: Khi k = 0 → sin φ = 0; M ≡ F: là vị trí cực đại giữa → loại
+ Nếu khe chứa số lẽ dải => M sáng n = 2b. siλn=φ
2k + 1 → sin φ = (2k + 1).λ 2b (với k = 1;±2;±3;…)
Đặc biệt: Khi k = 0 và k = −1 → sin φ = ± λ2b :vì giữa sin φ = 0 và sin φ =
±λ2b không thể có cực tiểu nhiễu xạ → loại
- Đồ thị phân bố cường độ sáng * Nhận xét:
+ Cường độ sáng tập trung chủ yếu ở cực đại giữa: I0I1=1 0,045
+ Bề rộng cực đại giữa rộng gấp 2 lần các cực đại khác.
+ Vị trí cực đại, cực tiểu không thay đổi khi di chuyển khi đi song song với
chính nó (L và E cố định). VŨ TIẾN LÂM Câu 5:
1. Khảo sát hiện tượng nhiễu xạ của sóng ánh sáng đơn sắc qua cách tử truyền
qua. Tìm công thức xác định cực đại, cực tiểu nhiễu xạ qua cách tử.
2. Vẽ và giải thích đồ thị biểu diễn cường độ sáng của các cực đại nhiễu xạ của
sóng ánh sáng phẳng đơn sắc qua năm khe hẹp giống nhau trên màn chắn P, biết
khoảng cách giữa hai khe kế tiếp nhau là d, bề rộng một khe là b và d/b=3. Giải
1.- Thí nghiệm khảo sát hiện tượng nhiễu xạ
+ Cách tử là một tập hợp các khe hẹp giống
nhau, song song, cách đều nhau và cùng nằm
trong một mặt phẳng. Khoảng cách giữa hai khe
kế tiếp nhau được gọi là chu kỳ của cách tử.
+ Rọi một chùm sáng song song, vuông góc với
mặt phẳng cách tử có chu kỳ d, bề rộng giữa hai khe là b.
Khi đó sẽ xảy ra các hiện tượng:
• Nhiễu xạ qua từng khe hẹp.
• Giao thoa giữa các khe hẹp.
• Ảnh nhiễu xạ là sự chồng chất ảnh nhiễu xạ qua từng khe.
+ Tại những điểm trên màn quan sát: góc φ phải thỏa mãn điều kiện sin φ = kλ
b (với k = ±1; ±2; ±3; … )
Khi đó, các khe đều cho cực tiểu nhiễu xạ gọi là các cực tiểu chính.
+ Xét 2 tia sáng từ 2 khe kế tiếp tới M. Hiệu quang lộ là: ΔL = L2− L1= d. sin φ
+ Nếu ΔL = d. sin φ = k. λ thì dao động do hai tia đố gây ra tại điểm M đồng
pha nhau, kết quả là điểm M sẽ sáng. Các điểm sáng đó được gọi là các cực đại
chính. Vị trí của các cực đại chính được xác định bởi công thức: sin φ = kλ
d (với k = 0; ±1; ±2; ±3; … )
+ Tại F (k = 0; sin φ = 0) khi đó F là cực đại chính giữa. Do d>b nên giữa hai
cực tiểu chính có thể có nhiều cực đại chính.
- Xác định vị trí các cực đại chính, cực tiểu chính và số cực đại phụ, cực tiểu phụ
+ Tại điểm chính giữa hai cực đại chính kế tiếp, góc nhiễu xạ φ thoả mãn điều kiện: sin φ = (2k + 1).λ
2d (với k = 0; ±1; ±2; ±3; … ) VŨ TIẾN LÂM
Tại các điểm đó, hiệu quang lộ của hai tia gửi tới từ hai khe kế tiếp có giá trị là
ΔL = L2− L1= d. sin φ = (2k + 1).λ2, dao động do hai tia đó khử lẫn nhau
nhưng điểm này có thể là điểm tối, gọi là cực tiểu phụ hoặc sáng gọi là cực đại
phụ tùy vào số lượng khe chẵn hay lẻ.
+ Nếu có N khe, giữa hai khe cực đại chính kế tiếp có (N-1) cực tiểu phụ và (N-2) cực đại phụ. 2. Tóm tắt Giải d
- Khi N=5, ta có: giữa hai cực đại chính liên tiếp có 4 cực tiểu b= 3
phụ và 3 cực đại phụ N = 5 - Hình vẽ: Vẽ đồ thị ? Câu 6:
1. Phân biệt ánh sáng tự nhiên, ánh sáng phân cực một phần và toàn phần. Trình
bày sự quay của mặt phẳng phân cực khi cho ánh sáng phân cực toàn phần đi
qua tinh thể đơn trục và qua dung dịch hoạt quang. Viết công thức xác định góc
quay trong các trường hợp trên.
2. Chiếu một chùm sáng song song đơn sắc có bước sóng λ vuông góc vào mặt
phẳng một cách tử truyền qua, cho biết trên 1cm chiều dài của cách tử có n=500
vạch. Phía sau cách tử đặt một thấu kính hội tụ có tiêu cự f=0,5m và màn ảnh có
đặt ở tiêu diện của thấu kính.
a/ Biết khoảng cách giữa hai cực đại chính bậc 1 trên màn ảnh là Δx = 3,4 cm. Tính bước sóng λ?
b/ Nếu thay chùm sáng đơn sắc trên bằng chùm sáng trắng có bước sóng từ
0,40 μm đến 0,76 μm thì bề rộng của quang phổ bậc một trên màn là bao nhiêu? Giải
1. – Các loại ánh sáng:
+ Ánh sáng tự nhiên: Là ánh sáng có phương dao động của vector cường độ
điện trường dao động đều đặn theo mọi phương vuông góc với tia sáng. VŨ TIẾN LÂM
+ Ánh sáng phân cực toàn phần: Là ánh sáng có vector cường độ điện trường
chỉ dao động theo một phương xác định (còn gọi là ánh sáng phân cực thẳng).
+ Ánh sáng phân cực một phần: Là ánh sáng có vector cường độ điện trường
dao động theo mọi phương vuông góc với tia sáng, nhưng có phương dao động
mạnh, có phương dao động yếu.
- Sự quay của mặt phẳng phân cực
* Trường hợp các tinh thể đơn trục
+ Khi rọi ánh sáng phân cực toàn phần theo quang trục của tinh thể thì vector
dao động sáng không bị tách đôi nhưng bị quay đi một góc α xung quanh tia
sáng, do đó mặt phẳng phân cực cũng bị quay đi một góc α.
+ Thực nghiệm chứng tỏ rằng đối với một ánh sáng đơn sắc nhất định thì góc α
tỷ lệ với bề dày d của bản tinh thể mà ánh sáng truyền qua với khối lượng riêng của bản. α = [α]. p. d
Trong đó [α] là hệ số tỷ lệ
* Trường hợp các chất vô định hình (quang hoạt)
+ Thực nghiệm chứng tỏ rằng đối với một ánh sáng đơn sắc nhất định, góc quay
α của mặt phẳng phân cực tỷ lệ với bề dày l của lớp dung dịch mà ánh sáng
truyền qua và tỷ lệ với nồng độ C của chất quang hoạt trong dung dịch. α = [α]. l. C
Trong đó [α] là hệ số tỷ lệ 2. Tóm tắt Giải l = 1 cm → n = 500
a/ - Ta có: Chu kỳ của cách tử là: f = 0,5 m d = ln=10−2 Δx = 3,4 cm 500 = 2.10 −5 (m)
____________________ - Vị trí cực đại chính bậc 1 là: a/ λ =? sin φ1=λd b/ λ = (0,4 → 0,76)μm ΔDbậc 1 =?
- Mà khoảng cách giữa hai cực đại chính bậc 1 trên màn là:
Δx = 2. f. tan φ1≈ 2. f. sin φ1= 2. f. λd
→Bước sóng ánh sáng: λ = Δx.2df=3,4.10−2. 2.10−5 2.0,5 = 6,8.10−7 (m)
b/ Thay bằng ánh sáng trắng, bề rộng của quang phổ bậc một là: ΔD - Ta có:
+ Vị trí quang phổ bậc 1 (cực đại chính) ứng với λ1= 0,4 μm là:
D1= f. tan φ1≈ f. sin φ1=fd. λ1 (1)
+ Vị trí quang phổ bậc 1 (cực đại chính) ứng với λ2= 0,76 μm là: VŨ TIẾN LÂM
D2= f. tan φ2≈ f. sin φ2=fd. λ2 (2)
Từ (1) và (2) suy ra bề rộng của quang phổ bậc 1 là:
ΔD = D2− D1=fd(λ2− λ1)=0,52.10−5(0,76−0,4).10−6 = 9.10−3 (m) Câu 7:
1. Định nghĩa năng suất phát xạ đơn sắc và hệ số hấp thụ đơn sắc. Phát biểu và
viết biểu thức định luật Kirchhoff.
2. Định nghĩa vật đen tuyệt đối. Phát biểu các định luật thực nghiệm về sự phát
xạ của vật đen tuyệt đối và ứng dụng của chúng. Giải
1. – Năng suất phát xạ đơn sắc và hệ số hấp thụ đơn sắc
+ Giả sử trong một đơn vị thời gian, một bức xạ đơn sắc có bước sóng trong
khoảng (λ; λ + dλ) do một đơn vị diện tích của vật ở nhiệt độ T không đổi,
mang năng lượng dRT. Khi đó năng suất phát xạ đơn sắc của vật là: rλ;T =dRdTλ (W m2)
rλ;T phụ thuộc vào bản chất, nhiệt độ của vật, bước sóng bức xạ phát ra
→ Năng suất phát xạ đơn sắc đặc trưng cho mức độ mang năng lượng của bức xạ đơn sắc.
+ Giả sử trong một đơn vị thời gian, một bức xạ đơn sắc có bước sóng trong
khoảng (λ; λ + dλ) gửi tới một đơn vị diện tích của vật một năng lương dϕλ;T
nhưng vật chỉ hấp thụ một phần là dϕ ố ấ ụ đơn sắ ở nhiệt λ′. Khi đó hệ s h p th c ;T
độ T ứng với bước sóng λ là: aλ;T =dϕλ;T′ dϕλ;T
aλ;T < 1: phụ thuộc vào bản chất, nhiệt độ của vật và bước sóng bức xạ gửi tới
vật. Hệ số hấp thụ đơn sắc đặc trưng cho mức độ hấp thụ năng lượng của bức xạ đơn sắc. - Định luật Kirchhoff
+ Nội dung định luật: Tỷ số giữa năng suất phát xạ
đơn sắc và hệ số hấp thụ đơn sắc của một vật ở
một nhiệt độ nhất định là một hàm chỉ phụ thuộc
vào bước sóng của bức xạ và nhiệt độ mà không
phụ thuộc vào bản chất của vật. + Biểu thức: VŨ TIẾN LÂM ε(λ; T)=r(λ; T)
a(λ; T)→ ε(λ; T) là hàm phổ biến + Đồ thị:
Ta có: Vật đen tuyệt đối: a(λ; T)= 1 → r(λ; T)= ε(λ; T)
→ Hàm phổ biến là năng suất phát xạ đơn sắc của vật đen tuyệt đối ứng với bức
xạ bước sóng λ và nhiệt độ T.
2. – Vật đen tuyệt đối: là vật hấp thụ toàn bộ năng lượng của mọi chùm tia bức
xạ chiếu tới (a(λ; T)= 1). Hệ số hấp thụ đơn sắc a(λ; T) của vật đen tuyệt đối
không phụ thuộc vào bước sóng của chùm bức xạ và nhiệt độ của vật (vì nó luôn xấp xỉ bằng 1).
- Định luật Steffan-Boltzmann
+ Nội dung định luật: Năng suất phát xạ toàn phần của vật đen tuyệt đối tỷ lệ
thuận với lũy thừa bậc bốn của nhiệt độ tuyệt đối của vật đó. + Biểu thức: RT= σ. T4 với σ = 5,67.10−8 (W
m2.K4) là hằng số Steffan-Boltzmann - Định luật Wien
+ Nội dung định luật: Đối với vật đen tuyệt đối bước sóng của chùm bức xạ đơn
sắc mang nhiều năng lượng nhất tỷ lệ nghịch với nhiệt độ tuyệt đối của vật. + Biểu thức: λmax =bT
với b = 2,8978.10−3 (m. K) là hằng số Wien
- Ứng dụng của định luật Stefan-Boltzmann và định luật Wien: Đo nhiệt độ. Câu 8:
1. Trình bày thuyết lượng tự năng lượng của Plauck và thuyết photon của
Einstein. Nêu các đặc trưng động lực học của photon.
2. Nhiệt độ của một vật đen tuyệt đối tăng từ 227oC đến 727oC
a/ Năng suất phát xạ toàn phần của nó tăng lên bao nhiêu lần?
b/ Bước sóng ứng với năng suất phát xạ đơn sắc cực đại của nó tăng hay giảm?
Tính độ tăng hay giảm đó. Biết rằng hằng số Wien b = 2,896.10−3 mK. Giải
1. – Thuyết lượng tử năng lượng của Plauck
+ Nội dung: Các nguyên tử và phân tử của vật chất phát xạ và hấp thụ năng
lượng một cách gians đoạn. Nghĩa là năng lượng do chúng phát xạ hay hấp thụ
chỉ có thể bằng một số nguyên lần của một lượng nhỏ năng lượng xác định, gọi là lượng tử (quantum). VŨ TIẾN LÂM + Biểu thức: ε = hf =hcλ
với h = 6,625.10−34 J. s là hằng số Plauck.
- Thuyết photon của Einstein
+ Nội dung: Ánh sáng gồm những hạt rất nhỏ gọi là photon (hay lượng tử ánh
sáng), mang một năng lượng xác định
ε = hf =hcλ (h = 6,625.10−34 J.s)
Trong chân không cũng như trong mọi môi trường khác, photon chuyển động
với cùng một vận tốc xác định c = 3.108 m/s.
Cường độ của chùm sáng tỷ lệ với số photon phát ra từ nguồn sáng trong một đơn vị thời gian.
- Các đặc trưng động lực học của photon
+ Theo thuyết tương đối Einstein, photon có khối lượng cho bởi
ε = mc2→ m = εc2=hfc2=hc. λ với m = m0 √1 − v2 c2
m0 là khối lượng nghỉ: m0= m√1 − v2c2
+ Đối với photon: v = c → m0= 0
+ Photon luôn chuyển động với vận tốc c, do đó nó có động lượng bằng p = mc =hλ 2. Tóm tắt Giải
227oC < T < 727oC a/ Áp dụng định luật Stefan-Boltzmann cho vật đen
_________________ tuyệt đối: a/ RT2 RT1 =? {RTT12 = σ. T1244→RT2
RT1 =(T2T1)4=(10500)4=16 lần b/Δλmax =?
b/ Áp dụng định luật Wien ta có λ1=bT1=2,896.10−3 500 = 5,792.10−6 (m)
1000 = 2,896.10−6 (m)→Δλ = λ1− λ2= 2,896 μm λ 2=bT2=2,896.10−3 {
Vậy bước sóng ứng với năng suất phức xạ cực đại của vật giảm một lượng Δλ = 2,896 μm VŨ TIẾN LÂM Câu 9:
1. Chiếu một chùm tia X qua một khối parafin, coupton nhận thấy khi đi qua
khối chất, chùm tia X bị tán xạ. Hãy nêu đặc điểm của chùm tia X bị tán xạ.
Giải thích hiệu ứng coupton.
2. Dựa vào định luật bảo toàn động lượng, hãy chứng minh công thức liên hệ
giữa góc tán xạ θ của photon và góc bay ra φ của electron trong sự tán xạ.
Coupton của photon lên electron đúng yên là tan φ = cot θ2
1 + λλ với λc là bước sóng coupton c Giải
1. – Đặc điểm của chùm tia X tán xạ
+ Chiếu một chùm tia X, bước sóng λ vào khối parafin. Trong phổ tia X bị tán
xạ, ngoài vạch có bước sóng λ của chùm tia tới còn có vạch ứng với bước sóng
λ′> λ không phụ thuộc vào cấu tạo của khối chất mà chỉ phụ thuốc với góc tán
xạ θ gây ra hiệu ứng coupton. - Giải thích
+ Bước sóng λ′ phụ thuộc vào góc tán xạ θ đàn hội của tia X với các e− trong nguyên tử
+ Tia X có năng lượng lớn, mà e− có khối lượng rất nhỏ → động lượng của e−
phụ thuộc vào vận tốc
→ Hiệu ứng coupton là kết quả của sự va chạm đàn hồi giữa photon và electron - Biểu thức
+ Vách có bước sóng λ là do sự tán xạ của photon lên electron liên kết mạnh với
hạt nhân. Vạch có bước sóng λ′> λ là do sự tán xạ của photon của tia X có
năng lượng lớn với electron liên kết yếu với hạt nhân (xem như tự do, đứng yên).
+ Áp dụng định luật bảo toàn động lượng và bảo toàn năng lượng ta có: λ′= λ + 2. λc. sin2(θ2)
với λc=hm0.c = 2,426.10−12 m là bước sóng coupton VŨ TIẾN LÂM
2. – Gọi Pγ ; Pγ′ là động lượng của photon trước và sau khi
tán xạ, Pe′ là động lượng của electron bay ra. Áp dụng
định luật bảo toàn động lượng của electron và photon ta có:
Pγ = Pγ′ + Pe (có P
e= 0:động lượng e ban đầu)
+ Từ giản đồ vector bên ta có: tan φ = Pγ′. sin θ Pγ− Pγ′. cos θ (1)
+ Lại có: Pγ=h λ; Pγ′=h λ′. Thay vào (1) ta có: tan φ = sin θ λλ− cos θ (2) ′
+ Theo định luật Coupton có: λ′= λ + 2. λc. sin2(θ2) (3) {sin θ = sin (2. θ 2)= 2. sin (θ 2). cos (θ 2) cos θ = cos (2. θ 2)= 1 − 2. sin2(θ2) (4)
Thay (3) và (4) vào (2) ta được: tan φ = 2. sin (θ 2). cos (θ 2) λ + 2. λc. sin2(θ2) λ− 1 + 2 sin2(θ 2)
Rút gọn ta được: tan φ = cot θ2 1 + λλ (đpcm) c Câu 10:
1. Phát biểu những kết luận về lưỡng tính sóng hạt của ánh sáng, trình bày nội
dung giả thuyết De Broglie về lưỡng tính sóng hạt của vi hạt.
2. Một chùm electron được gia tốc bởi một hiệu điện thế 104 V. Xác định bước
sóng De Broglie của electron sau khi được gia tốc. Nếu hạt được gia tốc bởi
hiệu điện thế 510 kV thì bước sóng De Broglie bằng bao nhiêu? Cho h = 6,625.10−34 J. s Giải
1. – Lưỡng tính sóng hạt của ánh sáng
+ Ánh sáng vừa có tính chất sóng, vừa có tính chất hạt. Tính chất sóng được thể
hiện rõ trong các hiện tượng như giao thoa, nhiễu xạ,… Còn tính chất hạt được
thể hiện rõ trong các hiện tượng quang điện, Coupton,… Lưỡng tính sóng hạt VŨ TIẾN LÂM
của ánh sáng đã được Einstein nêu lên trong thuyết lượng tử ánh sáng. - Giả thuyết De Broglie
+ Một vi hạt tự do có năng lượng xác định, động lượng xác định tương ứng với
một sóng phẳng đơn sắc xác định:
• Năng lượng của vi hạt liên hệ với tần số dao động của sóng theo hệ thức:
E = h. f hay E = ℏ. ω với ℏ = h 2π = 1,055.10−34 J. s
• Động lượng của vi hạt liên hệ với bước sóng tương ứng theo hệ thức:
P = hλ hay P = ℏ.k 2. Tóm tắt Giải U = 104 V → λ =? - Với: U = 104 V
U = 510 kV → λ =? →eU =104 eV < 0,51 MeV = mc2
Áp dụng công thức trong cơ học phi tương đối tính. Ta có P = √2meU
→ λ = hP=h√2meU =6,625.10−34
√2.9,1.10−31. 1,6.10−19.104= 1,23.10−11 m
- Với U = 510 kV →eU =510 keV = 0,51 MeV
Áp dụng công thức trong cơ học phi tương đối tính. Ta có λ = hP=hc√eU(eU +2mc2)=hc
√mc2(mc2+2mc2)=h√3mc2=1√3.hmc =1√3.λc
→ λ = 1√3.2,4.10−12 = 1,40.10−12 (m)= 0,014 Aom Câu 11:
1. Trình bày hệ thức bất định Heisenberg và ý nghĩa của nó.
2. Một hạt vi mô có m = 10−16 kg chuyển động trong phạm vi 10−8 m, tìm độ
bất định về tốc độ. Nếu hạt là electron có me= 9,1.10−31 kg chuyển động trong
phạm vi 10−10 m thì độ bất định về tốc độ là bao nhiêu? Từ hai ví dụ trên rút ra
kết luận gì? (sử dụng hệ thức Δx. ΔPx= h). Giải
1. – Xét sự nhiễu xạ của chùm vi hạt qua một khe hẹp. Sau khi qua khe, vị trí và
động lượng P của hạt thay đổi. Sau khi qua khe, hạt
sẽ bị nhiễu xạ theo những phương khác nhau. Tùy
theo giá trị của góc nhiễu xạ φ, mật độ chùm hạt
nhiễu xạ trên màn sẽ cực đại hoặc cực tiểu (bằng không). VŨ TIẾN LÂM
+ Xét tọa độ của hạt theo phương x nằm trên mặt phẳng của khe, song song với
chiều rộng của khe. Vị trí tọa độ của hạt trong khe sẽ có giá trị trong khoảng từ 0
đến b: 0 ≤ x ≤ b hay Δx ≈ b. Nói cách khác thì vị trí của hạt trong khe được
xác định với độ bất định Δx = b.
+ Sau khi qua khe, phương động lượng P của hạt thay đổi. Hình chiếu của P
theo phương x sẽ có giá trị trong khoảng: 0 ≤ Px≤ p. sin φ1. Nghĩa là sau khi
qua khe, hạt có thể rơi vào cực đại giữa hoặc phụ.
+ Hình chiếu Px được xác định với độ bất định nhỏ nhất (ΔPx nhỏ nhất) ứng với
trường hợp hạt rơi vào cực đại giữa, nghĩa là ΔPx= p. sin φ1
với φ1 là góc ứng với cực tiểu thứ nhất: sin φ1=λ b
+ Như vậy: Δx. ΔPx≈ p. λ
Theo giả thuyết De Broglie có p = hλ, do đó ta có: Δx. ΔPx≈ h
+ Tương tự có: Δy. ΔPy≈ h và Δz. ΔPz≈ h
Tóm lại: Hệ thức bất định giữa tọa độ và động lượng là: {Δxz. ΔPx
Pz≈ h hoặc {Δz. ΔPz≈ ℏ Δy. ΔPy≈ h Δz. ΔPz≈ ℏ Δz. ΔPz≈ ℏ
- Ý nghĩa của hệ thức bất định Heisenberg
+ Vị trí và động lượng không được xác định chính xác đồng thời, vị trí xác định
càng chính xác thì động lượng càng bất định và ngược lại.
+ Không có khái niệm quỹ đạo trong thế giới vi mô. 2. Tóm tắt Giải m1=10−16 kg
− Ta có: Δx. ΔPx= h → Δx. m. Δvx= h Δx1=10−8 m → Δvx=h m2= 9,1.10−31 kg m. Δx Δx2=10−10 m
- Với hạt có khối lượng m1=10−16 kg; Δx1=10−8 m _____________ ta có: Δv1; Δv2=? Δvx=hm. Δx =6,625.10−34
10−16.10−8 = 6,625.10−10 (m/s)
- Với hạt có khối lượng m2= 9,1.10−31 kg; Δx2= 10−10 m ta có: Δvx=hm. Δx =6,625.10−34
9,1. 10−31.10−10 = 7.106 (m/s) - Kết luận:
+ Với hạt vĩ mô thì vị trí và động lượng có thể xác định chính xác đồng thời.
+ Với hạt vi mô thì vị trí và động lượng không thể xác định chính xác đồng thời. VŨ TIẾN LÂM Câu 12:
1. Phát biểu giả thuyết De Broglie; viết biểu thức hàm sóng của một vi hạt chuyển động tự do.
2. Một vi hạt chuyển động tự do trong giếng thế năng một chiều U(x) có dạng U(x)= { 0 khi 0 < x < a
∞ khi x ≤ 0 và a < x. Tìm năng lượng và hàm sóng của hạt? Giải
1. – Giả thuyết De Broglie:
+ Một vi hạt tự do có năng lượng xác định, động lượng xác định tương ứng với
một sóng phẳng đơn sắc xác định.
• Năng lượng của vi hạt liên hệ với tần số dao động của sóng tương ứng theo hệ thức: E = hf hay E = ℏω
• Động lượng của vi hạt liên hệ với bước sóng của sóng tương ứng theo hệ thức: P = hλ hay P = ℏ.k
- Hàm sóng trong cơ học lượng tử
+ Chuyển động của vi hạt tự do được mô tả bởi hàm sóng tương tụ như sóng phẳng đơn sắc:
ψ = ψ0. e−i(ωt−2πλ.r .n ) {f = Eh
λ = hP→ ψ = ψ0. e−iℏ(E.t−P .r )
với ψ02=|ψ|2= ψ. ψ∗ là biên độ của hàm sóng
ψ∗ là liên hợp phức của ψ 2. U(x)= { 0 khi 0 < x < a ∞ khi x ≤ 0 và a < x
- Phương trình Schrodinger của hạt trong giếng thế năng có dạng
Δψ(r )+2mℏEψ(r )= 0 → d2ψ dx2+2mℏ2Eψ = 0 (1) Đặt 2mE ℏ2= k2 thay vào (1) →d2ψ dx2+ k2ψ = 0 (2)
Nghiệm của PT vi phân (2) có dạng: VŨ TIẾN LÂM
ψ(x)= A sin(kx) + B cos(kx) (3)
Vì hàm sóng phải liên tục và giới nội, ta có: {ψ(0)= B = 0 ψ(a)= A sin ka = 0
Nếu A=0, phương trình có nghiệm tầm thường nên A ≠ 0; B = 0 → sin(ka) = 0 → k = n a π
(n = 1,2,3, … )→ ψn(x)= A. sin (nπ ax)
- Hệ số A được xác định từ điều kiện chuẩn hóa: a a ∫|0ψ = 1 → ∫ A2. sin2(nπ ax)dx = 1 → A = √2a n(x)|2dx 0
→ Hàm sóng ψn(x)=√2a. sin (nπ ax) Câu 13:
1. Nêu các kết luận về năng lượng và hàm sóng của electron trong nguyên tử Hydro?
2. Hàm sóng của electron trong nguyên tử Hydro ở trạng thái cơ bản 1s có dạng:
ψ1s = A. e−ra0 với A là hằng số;a0= 0,53 Ao. Tìm khoảng cách r ứng với xác
suất tìm hạt lớn nhất? Giải
1. – Hàm sóng ψ và năng lượng của electron trong nguyên tử Hydro là nghiệm
của phương trình Schrodinger. + Hàm sóng:
ψ = ψn,l,m(r; θ; φ)= Rnl(r). Ylm(θ; φ)
+ Ý nghĩa các số lượng tử l,n,m
• l = 0,1,2,3, … n − 1: số lượng tử quỹ đạo (orbital)
• n = 1,2,3,4, … : số lượng tử chính
• m = 0, ±1, ±2, … ± l: số lượng tử từ
- Năng lượng của electron trong nguyên tử Hydro + Năng lượng:
En= − 1n2.mee4 2)2ℏ2 hay En= − Rh n2= − 13,6 2(4πε n2 eV (n = 1,2,3, … ) 0
Với R là hằng số Rydberg: R = mee4
(4πε2)4πℏ3= 3,27.1015 (s−1) 0
+ Năng lượng bị lượng tử hóa có giá trị âm chứng tỏ electron liên kết với hạt nhân trong nguyên tử. VŨ TIẾN LÂM 2. Tóm tắt Giải ψ1s = A. e−ra
- Xác suất tìm thấy hạt trong khoảng r → r + dr là: 0 A = const
dW =|ψ1s|2dV = A2. e−2ra0.4π.r2.dr
a0= 0,53 Ao → Xác suất cực đại ứng với cực trị của hàm P(r)= e−2r a0. r2 (1) Đạo hàm (1) ta được: dP( dr r) = − 2a ( 1 a 0. e−2ra 0);dP(r)
0. r2+ 2. e−2ra0. r2= 2. e−2ra0. r 1 − dr = 0 → r = a0
Câu 14: Trình bày về momen động lượng orbital và momen từ orbital của
electron trong nguyên tử. Hiệu ứng Zeeman và giải thích. Giải
- Momen động lượng quỹ đạo (orbital)
+ Vector momen động lượng không có hướng xác định.
+ Giá trị của momen động lượng của electron lại là một đại lượng xác định và
nó nhận các giá trị gián đoạn.
+ Độ lớn: L = ℏ. √l(l + 1)
+ Hình chiếu lên phương z của momen động lượng Lz bị lượng tử hóa Lz= ±m. ℏ
- Momen từ quỹ đạo (orbital) trong nguyên tử
+ Momen từ orbital dạng vector: μ = − e L 2meL
+ Độ lớn momen từ orbital:
|μL |=eℏ2me√l(l + 1)=μB√l(l + 1)
Với μB=eℏ2me=10−23 A. m2 là hằng số Magneton Bohr. - Hiệu ứng Zeeman
+ Hiệu ứng Zeeman là hiện tượng tách vạch quang phổ nguyên tử thành nhiều
vạch sít nhau khi nguyên tử phát sáng đặt trong từ trường. Để quan sát hiện
tượng đó, ta hãy đặt một nguồn khí Hydro phát sáng vào giữa hai cực một nam
châm điện. Nam châm điện tạo nên từ trường mạnh. Khi quan sát các bức xạ
phát ra theo phương vuông góc với các vector từ trường thì thấy mỗi vạch quang
phổ của nguyên tử Hydro bị tách thành ba vạch sít nhau.
- Giải thích hiện tượng Zeeman
+ Vì e− có momen từ μ nên có thêm năng lượng phụ khi đặt trong từ trường B : VŨ TIẾN LÂM ΔW = −(μ . B )
+ Giả sử phương z là phương của từ trường H nên ta có: ΔW = −μz. B = m. μB. B
+ Như vật khi nguyên tử Hydro đặt trong từ trường, năng lượng W’ còn phụ
thuộc vào số lượng tử từ m: W′= W + mμB. B
với W là năng lượng của e− khi không có từ trường
+ Khi chuyển từ trạng thái có năng lượng cao W2′ sang trạng thái có năng lượng
thấp W1′. e− phát ra bức xạ có tần số f′: f′=(W2′− W h 1′ =) W2− W1 h+(m2− m1)μB h . B = f + Δm hμB. B
Với f: tần số của vạch quang phổ khi không có từ trường
+ Vì năng lượng còn phụ thuộc vào số lượng tử từ cho nên khi e− chuyển từ
trạng thái cao xuống thấp nó còn phải tuân theo quy tắc lựa chọn đối với m đã
được xác định trong cơ học lượng tử. Δm = 0; ±1
Vậy tần số f’ xác định ba giá trị f−μBhB (Δm=−1) f′= f (Δm = 0) f + μBhB (Δm = 1) { + Như vậy
• Một vạch quang phổ (khi không có từ trường) bị tách thành ba vạch (khi
có từ trường). Trong dó vạch giữa (Δm = 0) trùng với vạch cũ.
• Độ rộng giữa hai mức năng lượng kế tiếp ở mọi trạng thái tương ứng giá trị của μB. Câu 15:
1. Trình bày về năng lượng của electron hóa trị và quang phổ trong nguyên tử kim loại kiềm.
2. Xét nguyên tử Liti năng lượng liên kết ở trạng thái 2s là 5,59 eV; ở trạng thái
2p là 3,54 eV. Tính các số bổ chính Rydberg đối với các số hạng s và p của Li. Cho biết Rh=13,6 eV. Giải
1. – Năng lượng của electron hóa trị
+ Trong kim loại kiềm, vòng ngoài cùng có một electron hóa trị, e− hóa trị này
liên kết yếu với phần còn lại của nguyên tử (hạt nhân và các e− khác). Do đó
Tài liệu liên quan:
-
Bài tập Vật lý nguyên tử môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
11 6 -
Bài tập Vật lý nguyên tử môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
12 6 -
Tán xạ ánh sáng và Hiệu ứng Tyndall - Lý thuyết và Ứng dụng môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
20 10 -
Chương 23: Quang học lượng tử môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
18 9 -
Chương 24: Cơ Học Lượng Tử - Tính Sóng-Hạt và Phương Trình Schrödinger môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông
19 10