Chapter 19 The first law of thermodynamics môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Chapter 19 The first law of thermodynamics HUST – CTTT PH 1026 Thermal Contact Thermal Equilibrium Two cups of water are in
Two systems have the same temperature if they are in contact. thermal equilibrium. •Heat one cup •Equilibrium between systems heater •Compare macroscopic properties
•Measure of macroscopic properties If they are the same they are
If two systems are not in thermodynamic equilibrium, in thermal contact.
they are not in thermal contact. heater •eg. metal cups
If different they are insulated. HUST – CTTT PH 1026 HUST – CTTT PH 1026
If two systems are each in thermodynamic equilibrium
with a third system, then they are in thermodynamic equilibrium with each other.
This is the Zeroth Law of Thermodynamics.
A is in thermal equilibrium with B. ABC
C is in thermal equilibrium with B. Therefore, A is in thermal equilibrium with C. HUST – CTTT PH 1026 HUST – CTTT PH 1026
Internal Energy of an Ideal Gas with fdegrees of freedom: Nk T f =
The internal energy of an ideal gas UB 2
f ⇒3 (monatomic), 5 (diatomic), 6 (polyatomic)
(here we consider only trans.+rotat. degrees of freedom, and neglect
the vibrational ones that can be excited at very high temperatures)
How does the internal energy of air in this (not-air-tight) room change
with Tif the external P = const? = = ⎡= ⎤ f2 in room B in room ⎢ PV = ⎥ f2 U N k T N PV ⎣ k T ⎦ B
- does not change at all, an increase of the kinetic energy of individual
molecules with Tis compensated by a decrease of their number. HUST – CTTT PH 1026 HUST – CTTT PH 1026 Mechanical work involves a force acting through a distance. Work is an energy transfer Work can involve a change in that is not due to a internal energy. temperature difference. •Temperature may change Heat is an energy transfer that is due to a •Temperature did not cause temperature difference. the work HUST – CTTT PH 1026 HUST – CTTT PH 1026 PV Diagram Slow Motion The ideal gas law links During rapid change the pressure, volume, and macroscopic state temperature. variables are not well defined. •PV = nRT For fixed quantity of gas, P any two of the three On a PV diagram it is determine the third. 2 P , 2 V , 2 T assumed that the system changes slowly. 1 P, 1 V, 1 T Graph of pressure vs volume describes the V This is a quasi-static system. change. HUST – CTTT PH 1026 HUST – CTTT PH 1026 Measuring Work The mechanical work can be measured on the PV diagram. W = ∑ Δ F x P W = ∑ P Δ A x P V, 2 T , 2 2 P , V 1T, 1 1 W = ∑ Δ P V The work done is the area V under the PV curve describing the system. work done HUST – CTTT PH 1026 HUST – CTTT PH 1026 HUST – CTTT PH 1026 HUST – CTTT PH 1026
W and Q are not State Functions Comment on State Functions
U, P, T, and Vare the state functions, Qand Ware not. Specifying an initial and final V W - we can P br = 2 T ing t V Vhd e V system from state 1 to
states of a system does not fix the values of Qand W, we need to know the whole − 1 2 ∫ − ( , )
process (the intermediate states). Analogy: in classical mechanics, if a force is not 1
state 2 along infinite # of paths, and for
conservative (e.g., friction), the initial and final positions do not determine the work, the
each path P(T,V)will be different. P entire path must be specified. 2
Since the work done on a system depends not
In math terms, Qand Ware not exact differentials of some
only on the initial and final states, but also on the U
functions of macroparameters. To emphasize that Wand Qare V T1
intermediate states, it is not a state function.
NOT the state functions, we will use sometimes the curled symbols
δ(instead of d)for their increments (δQand δW). V
U is a state function, W -is not ⇒ ΔU = Q + W = d U − T d S P dV S - an exact differential
thus, Qis not a state function either P . = - it y i z s ( x an , ex+
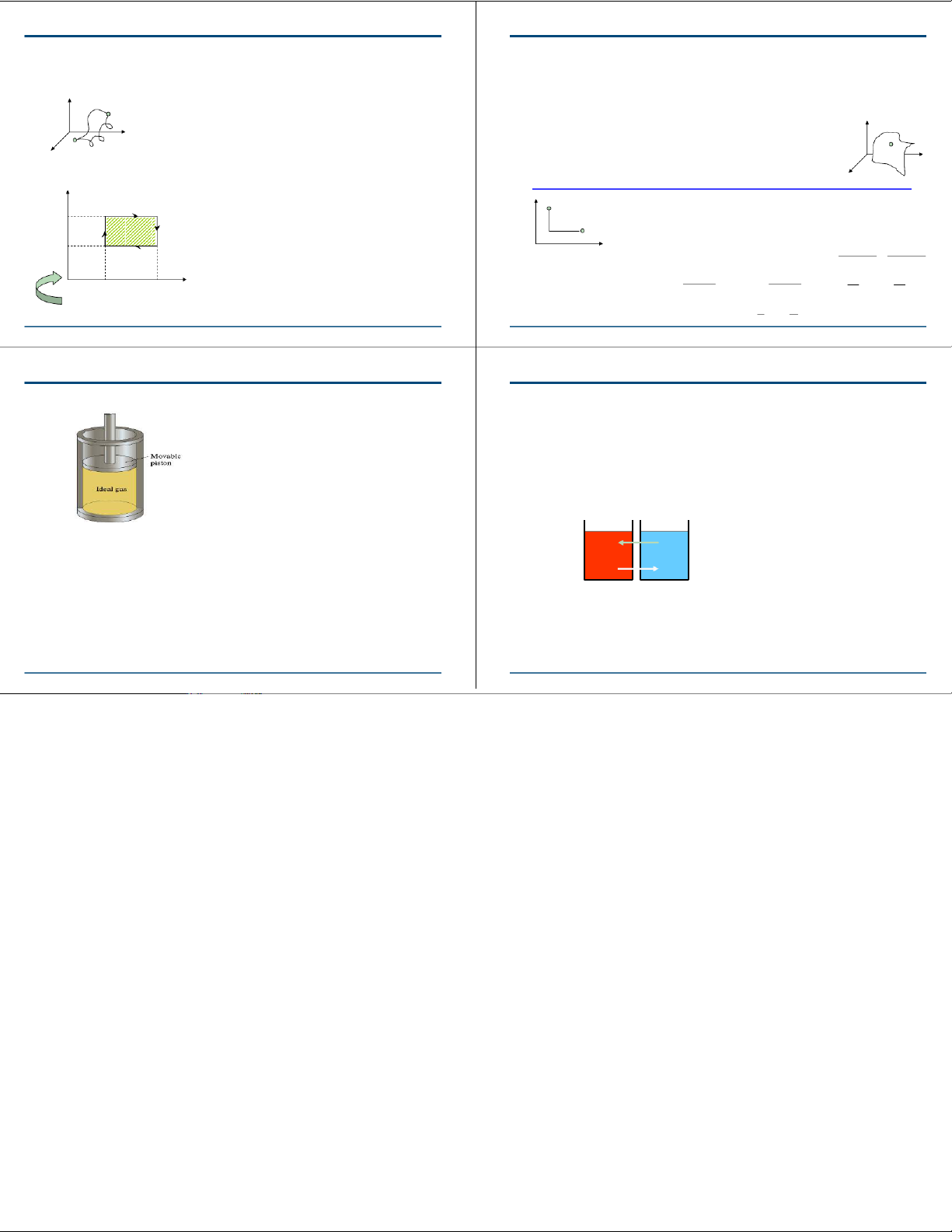
act differe xn ,tial if it is d ay ( A ) ( x ) AB 1,y1) y dx A x y dy net AB W = CD W + W = − P V V P V V 2 ( ( ) ) − − − P2 2 1 1 1 2
the difference between the values of some (state) function () = ( − )P − P V −V < 0 z(x2,y2) = + )+ , − ( d a, (z)x dx y dy z x y 2 1 2 1 z(x,y) at these points: P1 ∂ A , ()x y , () y ∂A x y D C x x
A necessary and sufficient condition for this: =
- the work is negative for the “clockwise” y ∂ x ∂
cycle; if the cyclic process were carried out If this condition () () (=), ( ∂ ) z x, y ∂z x y ⎛ z ∂ ⎞ ⎛ z ∂ ⎞ , , = V x ∂ A x y y A x y d z = ⎜ ⎟ dx + ⎜ ⎜ ⎟ ⎟ dy 1V2 V
in the reverse order (counterclockwise), the holds: x ∂ y ⎝ x ∂ ⎠ ⎝ y ∂ y ⎠x PV diagram
net work done on the gas would be positive. i ⎛ T ⎞ e.g., for an ideal gas: δQ = d + U = PdV N + k 2 dT ⎜⎟ dV - cross derivatives B ⎝⎠ V are not equal HUST – CTTT PH 1026 HUST – CTTT PH 1026 Constant Temperature Internal Energy Conserved An ideal gas only changes Changes often involve internal energy with holding one variable temperature change. constant. •ΔU= 0 Moving a piston slowly changes pressure and Work done volume. by gas Base is kept at a constant Temperature remains the temperature same. From the first law, work done equals heat flow. Heat flow into gas •ΔU= Q–W •Q= W HUST – CTTT PH 1026 HUST – CTTT PH 1026
Isothermal Process in an Ideal Gas Constant Volume Fixing the piston keeps the volume constant. P isothermal ( T= const ) : PV= NkBT dU = 0 hold fixed If heat flows in then W V V 2 2 dV V temperature remains the 2 ( , ) V2 ∫ 1 l W 2n →B V1 = −∫ P V T dV = −Nk T B = −Nk T V same. 1 V V V V 1 1 heat flows at base to change V Q = W i = W l → − 1 2 → 1 2 temperature − n Nk T i f V B f
Wi-f > 0 if Vi>Vf(compression)
Wi-f < 0 if ViHUST – CTTT PH 1026 HUST – CTTT PH 1026 Isochoric Process
Specific Heat at Constant Volume For a constant volume process At constant volume the heat there is no work. equals the change in internal energy. •ΔV= 0 •W = 0 P A molar specific heat at Q = nC Δ V T
constant volume relates to the P , V 1 , T 1 The internal energy change is change in temperature. nC T Δ = ΔU only due to heat. V P , V 2 , T 2 •ΔU = Q–W= Q C 1 U Δ V Vcan be defined from the C = internal energy. V n T Δ isotherms HUST – CTTT PH 1026 HUST – CTTT PH 1026 Constant Pressure Isobaric Process Allow the piston to move to For a constant pressure keep the pressure constant. process the work is a simple product. •Same on both sides •W= P(V2–V1) move to P maintain pressure Heat flows in and the piston can do work.
The heat can be related to the heat flows at base to change internal energy change and P V, 2 T P, 2 , V 1 T, 1 temperature volume change. •Q = ΔU + W V •Q = ΔU + PΔV isotherms HUST – CTTT PH 1026 HUST – CTTT PH 1026
Specific Heat at Constant Pressure
Quasistatic Processes in an Ideal Gas The internal energy was related to the temperature isochoric ( V= const ) P change. 2 1 2 = → W 0 3 PV= Nk Q = U Δ + P V Δ = − > = B ΔBT2 Q V →0 Nk 1 2 ()(T2 )T C T 1 PV= NkBT1 2 1 Q = nC T Δ + P V Δ (see the last slide) V V1,2 V dU =Q A molar specific heat at 1 2 → Q = nC Δ + Δ V T nR T constant pressure relates to isobaric ( P= const ) the change in temperature. Q = nC Δ P 2 P T W P V T dV PV →V 2 = −∫ =− − 1 2 < ( 1, ) () 0 2 1 C = C + R 1 PV= NkBT2 5 P V = − > = B Δ Q P →0 PV= NkBT1 1 2 Nk()( T2 )T1 C T For and ideal gas, CPcan be 2 defined from C V1 V2 V V. dU W = Q → + 1 2 → 1 2 HUST – CTTT PH 1026 HUST – CTTT PH 1026 No Heat
Quasistatic Processes in an Ideal Gas Completely insulate the
adiabatic (thermally isolated system) 1 1 Q2 → 2 = → 0 dU =W system.
The amount of work needed to change the state of a thermally isolated system
depends only on the initial and final states and not on the intermediate states. 2 V Allow the piston to move. W P V T dV 1→ = 2 ∫ − ( , ) P V1 2
to calculate W1-2 , we need to know P(V,T) for an adiabatic process Heat can’t flow, but work PV= NkBT2 1 PV= NkBT1 f f completely 2 =2 ⇒ = B = − UB Nk T dU Nk dT PdV insulate to can be done. V2 V1 V block heat flow
( f– the # of “unfrozen” degrees of freedom ) + 2 = − PdV ÷VdP PdV =PV ⇒ + B = PV B Nk T PdV VdP Nk dT f Equivalent process occurs dV 2 V +∫2 ⎞ dP + = = 1 ∫ dV dP ⎜ ⎜ ⎛ + ⎟ ⎟ 0 , γ 1 P + ∫ = γ 0 when change is quick so V ⎝ f ⎠ P f VPV P ⎛ ⎞γ 1 1 ⎛ ⎞ little heat flows. ⇒ = V= P1 γ γ ln⎜ ⎜ ⎟ ⎟ = ln⎜ ⎟ PV V P1 1 const V ⎝ 1 ⎠ P ⎝ ⎠ HUST – CTTT PH 1026 HUST – CTTT PH 1026
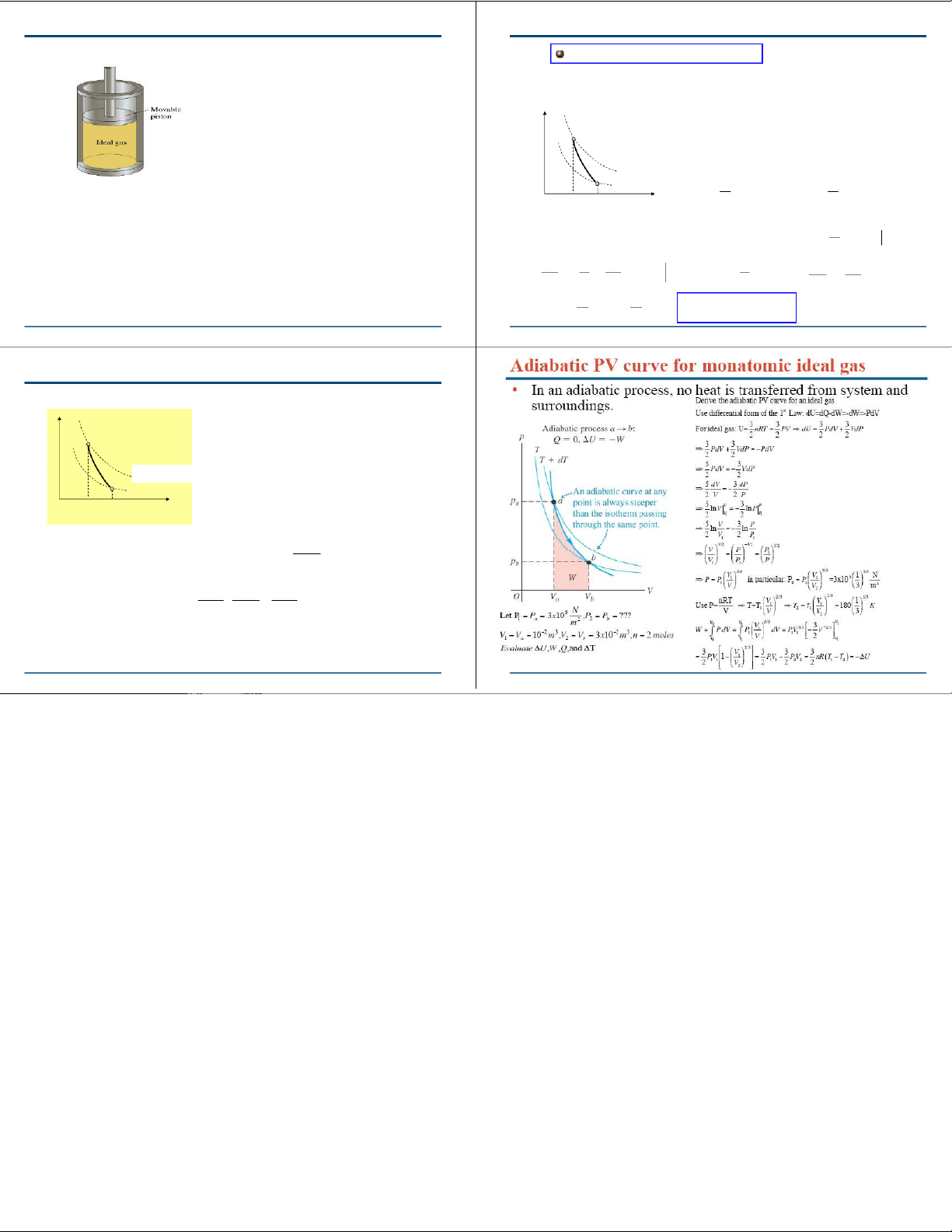
Quasistatic Processes in an Ideal Gas γ γ P = PV = V P const 1 1 2
An adiabata is “steeper” than an isotherma: PV= NkBT2
in an adiabatic process, the work flowing 1 PV= Nk
out of the gas comes at the expense of its BT1
thermal energy ⇒its temperature will V2 V1 V decrease. 2 V 2 V γ V P W = − ( P , V ) T dV = − ∫ 1 1 dV → 1 ∫2 γ V 1 V 1 V ⎛− ⎞ γ 1 ⎜ 1 1 ⎟ = V P1 1 ⎜ γ −1 γ −1 ⎟ γ −1 ⎝V V 2 1 ⎠
⇒1+2/3≈1.67 (monatomic), 1+2/5 =1.4 (diatomic), 1+2/6 ≈1.33 (polyatomic) γ
(again, neglecting the vibrational degrees of freedom) HUST – CTTT PH 1026 HUST – CTTT PH 1026 HUST – CTTT PH 1026 HUST – CTTT PH 1026 HUST – CTTT PH 1026 HUST – CTTT PH 1026 Heat Capacity CV and CP for an Ideal Gas ⎛∂U ⎞
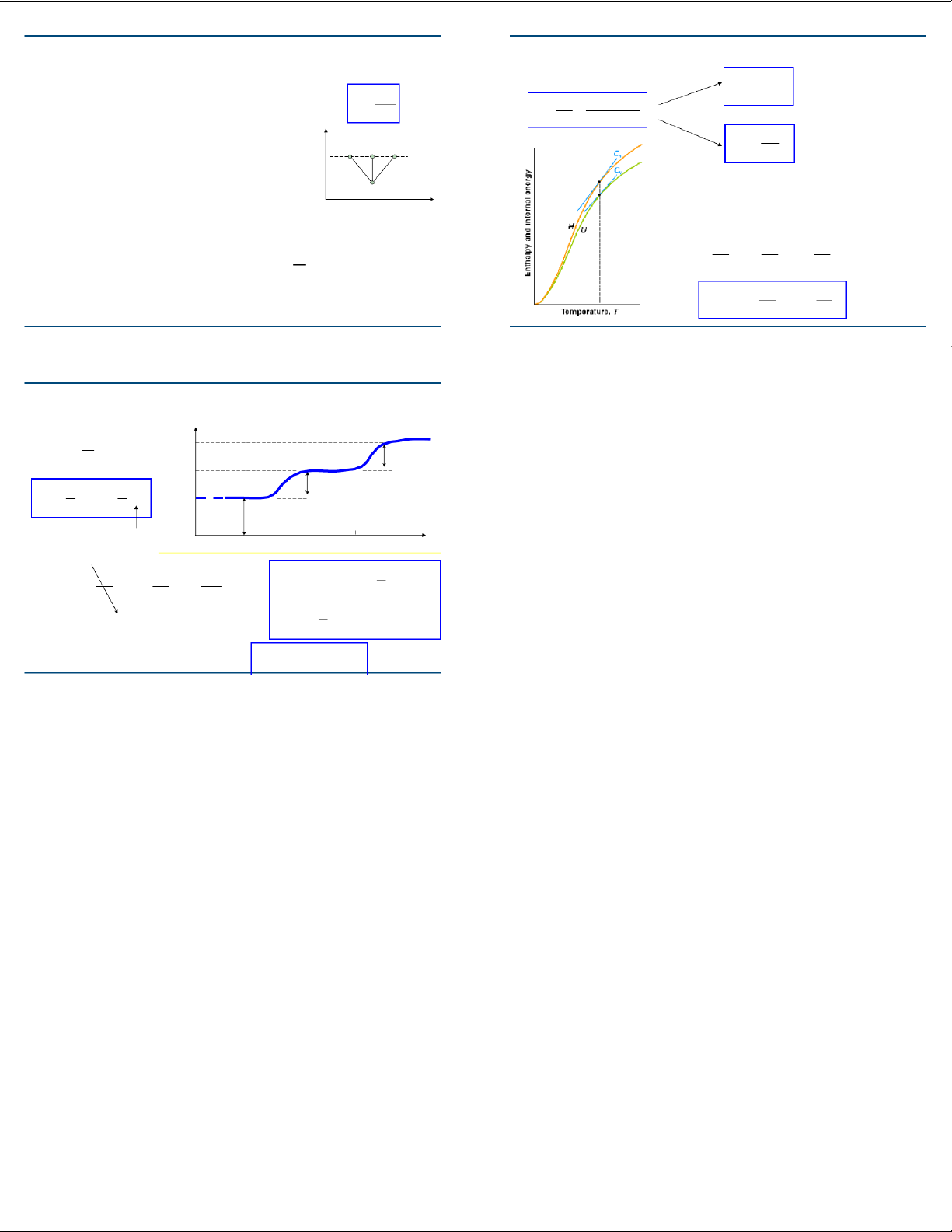
The heat capacity of a system - the amount of energy C⎟=⎜ the heat capacity at Q δ V = const VT ⎝∂ ⎠
transfer due to heating required to produce a unit CΔ≡ C+ δQ dU PdV V constant volume = =
temperature rise in that system T dT dT P = const T
⎛∂H ⎞ the heat capacity at f C⎟= ⎜ 1f2f3 PT ⎝∂ ⎠ constant pressure
Cis NOT a state function (since Qis not a T1+dT P
state function) – it depends on the path
between two states of a system ⇒ T1 To find C = (V,T) i
Pand CV, we need f (P,V,T) = 0 and U U V dU + PdV ⎡⎟ ⎛∂U ⎞ ⎛∂ U ⎤ ⎞
( isothermic – C = ∞, adiabatic – C = 0 ) C = = dU = ⎜ ⎟ dT + ⎜ dV dT ⎢ ⎣ ⎝∂T ⎥ ⎠ ∂ V ⎝ V T ⎠ ⎦ ⎛∂U ⎞ ⎡+⎛ U ∂ ⎞ ⎤ dV C = ⎜ ⎟ + ⎢ ⎜ ⎟ P⎥ The specific heat capacity m c≡ ⎝ T ∂ ⎠ ∂ V ⎣ ⎝ V T ⎠ ⎦ dT ⎡+ ⎛∂U ⎞ ⎤ d ⎛ V C ⎞ ⎟− C = ⎢⎜ ⎟ P ⎜ ⎥ P dT V ⎝ V ∂ ⎠ ⎝ ⎠ ⎣ T ⎦ P HUST – CTTT PH 1026 HUST – CTTT PH 1026 CV and CP for an Ideal Gas For an ideal gas CV = dU/dT CVof one mole of H2 f 7/2NkB UB= Nk T Vibration 2 5/2NkB ii Rotation R k C n N VB 22 3/2NkB Translation # of moles 10 100 1000 T, K ⎡+ i ⎛⎞ ⎛∂U ⎤ ⎞ d ⎛ V ⎞ Nk C C C =+ N = k + ⎜⎟ 1 Nk B −C = ⎜ ⎟ P ⎜ ⎟ ⎢ ⎥ = P B = Nk PV B B P V 2 ⎝⎠ ⎣⎝∂V T ⎠ ⎦ d ⎝ T P ⎠ P i ⎛ nR ⎞ 0 =+⎜⎟ 1 = R ( for one mole ) 2 ⎝⎠ = 3= 5
For one mole of a monatomic ideal Vga 2 s: C P R C R 2