














Preview text:
lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Chương 2. THỦY TĨNH
Dạng 1: Phương trình thủy tĩnh phương pháp áp suất tại điểm
Kiến thức nhắc lại p = p + h : khi B thấp hơn A. B A p = p − h : khi B cao hơn A. B A Lưu ý:
Áp suất dư của mặt phân cách tiếp xúc khi hở trời p = 0 . du
Áp suất tại các điểm trong cùng một khối khí sẽ bằng nhau.
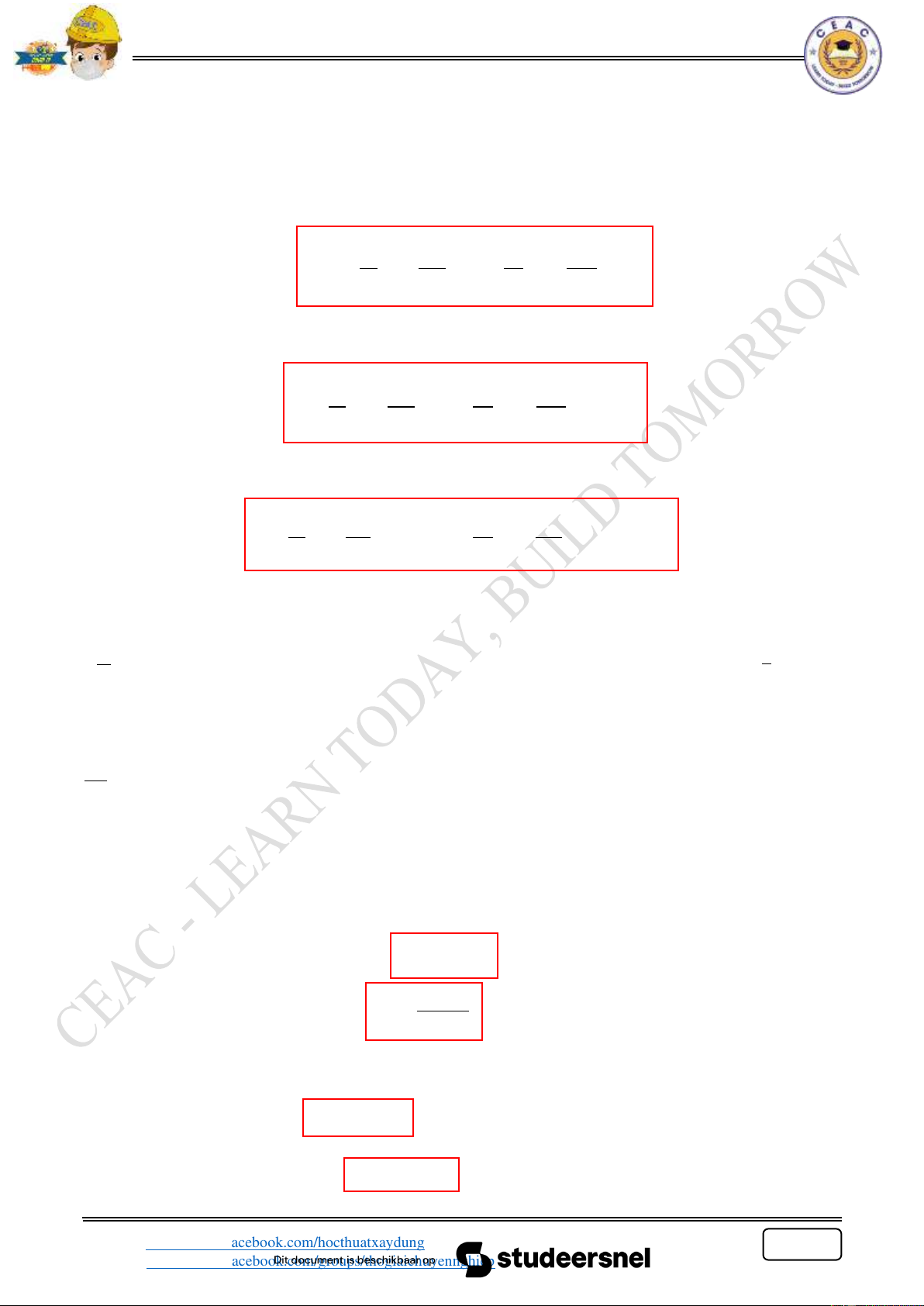
Ví dụ 1: Bình kín chưa dầu (0.8) và khí ốn đo áp như Hình 1.
Cho l = 40cm , l = 100cm và l = 60cm , tỷ khối của thủy 1 2 3
ngân bằng 13.6, áp suất khí trong bình bằng bao nhiêu? Lưu ý:
Áp suất tại điểm trong của cùng một khối khí sẽ bằng nhau: = = 9810 N/m3 H2O H2O Giải: p = 0 Pa 1 ( ) p = p + l + l 2 1 1 dau 3 Hg
= 0 +13.698100.6 + 0.898100.4 = 83.19(KPa)
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 1
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Ví dụ 2: Xác định chênh áp suất p − p trong 2 bình kín như hình dưới, biết A B 3
= 9000N / m , = 10000 N/m3, = 10500 N/m3, = 9750 N/m3, h = 28cm , h = 32cm , 1 2 3 4 1 2 h = 7cm và h = 21cm. 3 4 Lưu ý:
Áp suất tại các điểm trong
cùng một khối khí sẽ bằng nhau 4
1at = 10mH O = 9.8110 Pa = 735mmHg 2 Gi ải: Cách gi
ải dạng bài này chúng ta nên đi liên tục từ đầu đến cuối bình. p + h − h + h − h − h = p A 2 1 ( 1 2 ) 2 3 3 4 4 B
p − p = h + h + h + h + h A B 2 1 ( 1 2 ) 2 3 3 4 4 = 0.3 −
2 9000 + (0.28 + 0.32) 10000 + 0.07 10500 + 0.21 9700 = 5892 Pa 5892 0.6mH O 2 9810
Ví dụ 3: Piston có đường kính 8cm đẩy dầu (0.827) dâng lên trong mốt ống đo áp nghiêng, như
hình bên. Khi vậy nặng W được thêm vào trên Piston, đầu trong ống đo áp dân lên thêm một đoạn
10cm. Hãy tính trọng lượng của vật W. Lưu ý:
“Trong lưu chất không nén được, liên tục, ở trạng thái cân
bằng trong trường trọng lực áp suất tại mọi điểm sẽ được
truyền đi nguyên vẹn đến mọi điểm trong lưu chất đó.” Gi ải: Khoảng cách: = ( o) = ( o h H s in 15 0.1 sin 15 ) 2 2 D 0.08 Diện tích Piston: A = = 4 4
Trọng lượng của vật W: W = A 0.08
= 0.827 + 9810 0.1Sin (15 ) 2 o 4 =1.055N
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 2
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Dạng 2: Tính áp lực thủy tĩnh
2.1. Đối với diện tích phẳng
Độ lớn: P = p A = h A c c
Trong đó: p là áp suất tại trọng tâm C của diện tích A (*) c
A là diện tích mặt chịu lực Điểm đặ I t: x'x' y = y + D C y A C Trong đó I
là momen quán tính của diện tích A đối với trục đi qua trọng tâm song song x ' x '
với mặt tọa độ Ox (thường đề cho) (*) Lưu ý:
Gốc tọa độ O phải là giao điểm của mặt phẳng chứ diện tích A với mặt thoáng có pdư = 0
( p = 0 , có thể là mặt tự do tiếp xúc khí trời hở) 0 p
p 0 đổi sang bài toán tương đương: 0 h = 0 0
Phần diện tích nằm dưới mặt thoáng p = 0 thì p 0
dư > 0 (hướng vào trong mặt phẳng chịu lực)
Phần diện tích nằm trên mặt thoáng p = 0 thì p 0
dư < 0 (hướng ngược lại)
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 3
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
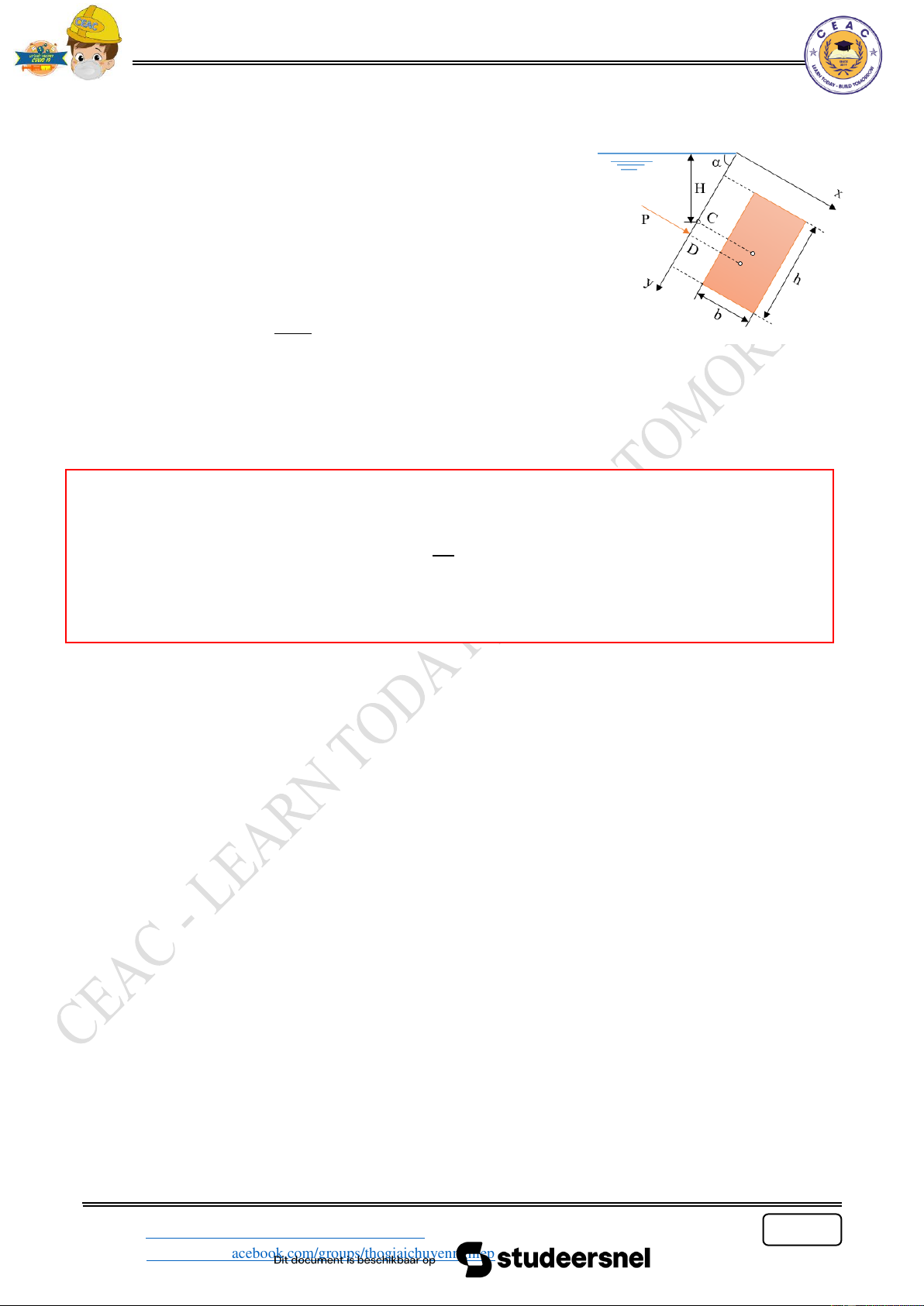
Ví dụ 4: Diện tích phẳng hình thang như hình 4, H là khoảng cách thẳng đứng từ mặt thoáng
đến tâm C của diện tích. Biết các số liệu: H = 1.3m , p = 0.6at , h = 1.8m , B = 2.2m , b = 1.8m và tỷ 0
trọng chất lỏng = 0.8.Áp lực thủy tĩnh trên diện tích là: Lưu ý:
p 0 đổi sang bài toán tương đương. (Đối với một số bài 0
nếu chỉ cần tính áp lực thì có thể không cần dời) B + b
Diện tích hình thang: S = h 2 Giải:
Cách 1: chuyển thành bài toán tương đương p 0.06 98100 0 h = = = 0.75m 0 0.8 9810 dau P = p A = h A c c ( + ) 1.8+ 2.2 = 0.8 9810 0.75 1.3 1.8 2 = 57.9kN
Cách 2: không cần chuyển bài toán thành bài toán tương đương P = p A = h A c c ( + ) 1.8+ 2.2 = 0.06 98100 0.8 9810 1.3 1.8 2 = 57.9kN
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 4
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
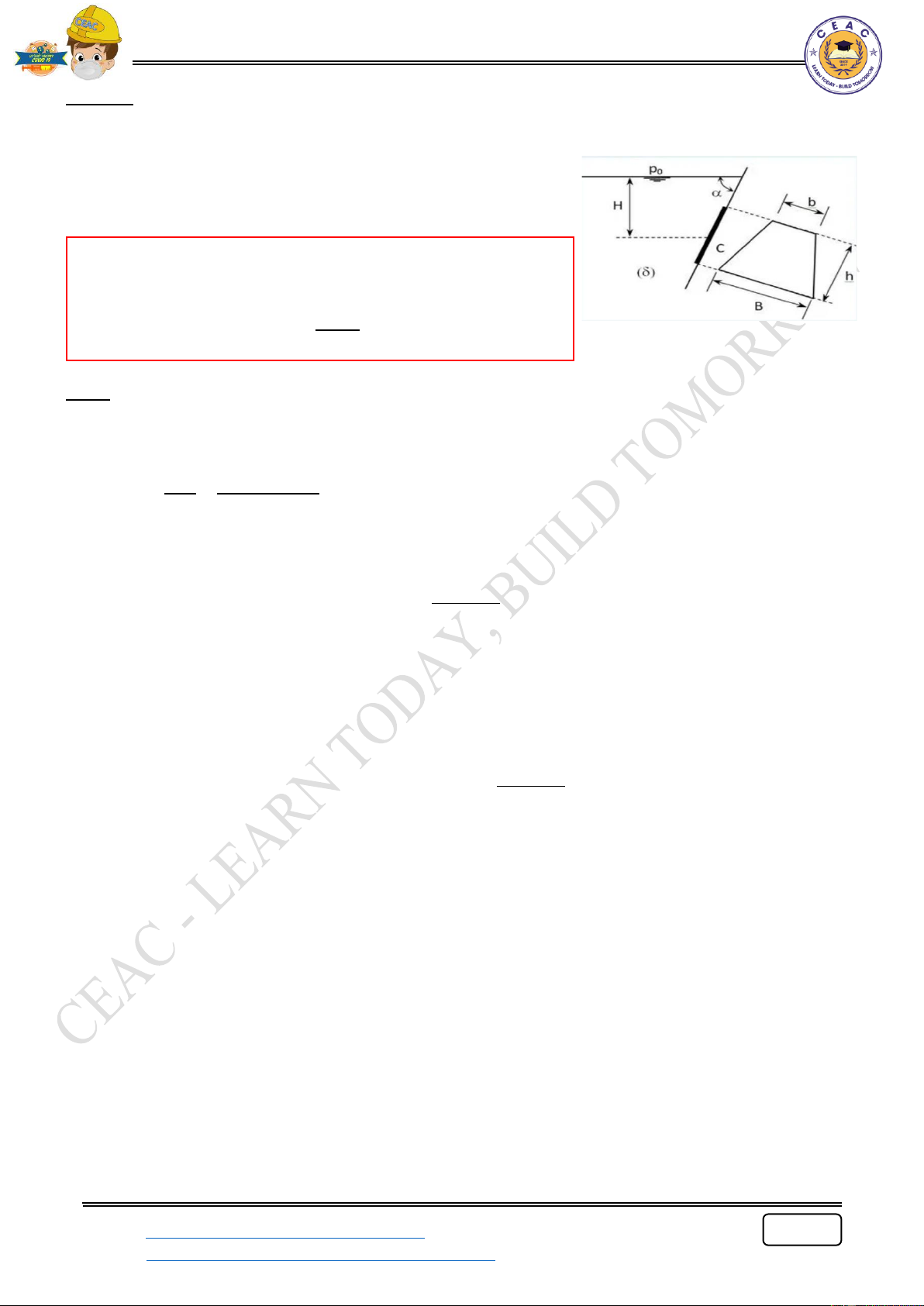
Ví dụ 5: Van AB hình chữ nhật có chiều dài 10m, chiều rộng
4m (chiều vuông góc với mặt giấy), nặng 300kg được giữ cố
định bằng một dây cáp căng ngang như hình dưới. Van AB
có bản lề tại điểm A. Ma sát trong dây cáp không đáng kể.
Lực căng dây cáp có giá trị bằng bao nhiêu? Lưu ý:
Công thức tính momen M= F × d
Trong đó: F - lực tác dụng (N),
d - cánh tay đòn = khoảng cách từ trục quay đến giá của lực (m) Giải: Tóm tắt l = 10 m b = 4 m m = 300kg T = ?
Để van AB giữ cố định thì moment làm van quay theo chiều kim đồng hồ bằng moment quay ngược chiều kim đồng hồ: M = M + M T F P
T d = F AD + P OA (1) T + d = 10sin 60 = 5 3m T 3 + Điểm đặ J 4 8 16 t tại F: c y = y + = 4 + = m D C y s 12 4 8 4 3 D 16 8 AD = 8 − = m 3 3 + OA = 5cos 60 = 2.5m 2 3 + F = Pc A = 9810 8 4 =1087450.8N mc 2
+ P = mg = 300 9.81 = 2943N
Thế vào (1) ta có: T = 335.7 (kN)
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 5
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
2.2. Đối với mặt cong
Tính toán áp lực thủy tĩnh trên diện tích cong là xác định 3 thành phần Px, Py, Pz
+ Lực theo phương x (phương ngang): P = p A x cx x
Trong đó: p là áp suất tại trọng tâm C của diện tích A cx x
A là diện tích hình chiếu của mặt cong lên mặt x = 0 cx
+ Lực theo phương y: P = p A (thường bằng 0) x cx x
+ Lực theo phương z (phương đứng): P = W z
Trong đó: W là thể tích biểu đồ áp lực khi chiếu lên mặt z = 0 (Oxy) Tổng lực 2 2 2 P = P + P + P x y z
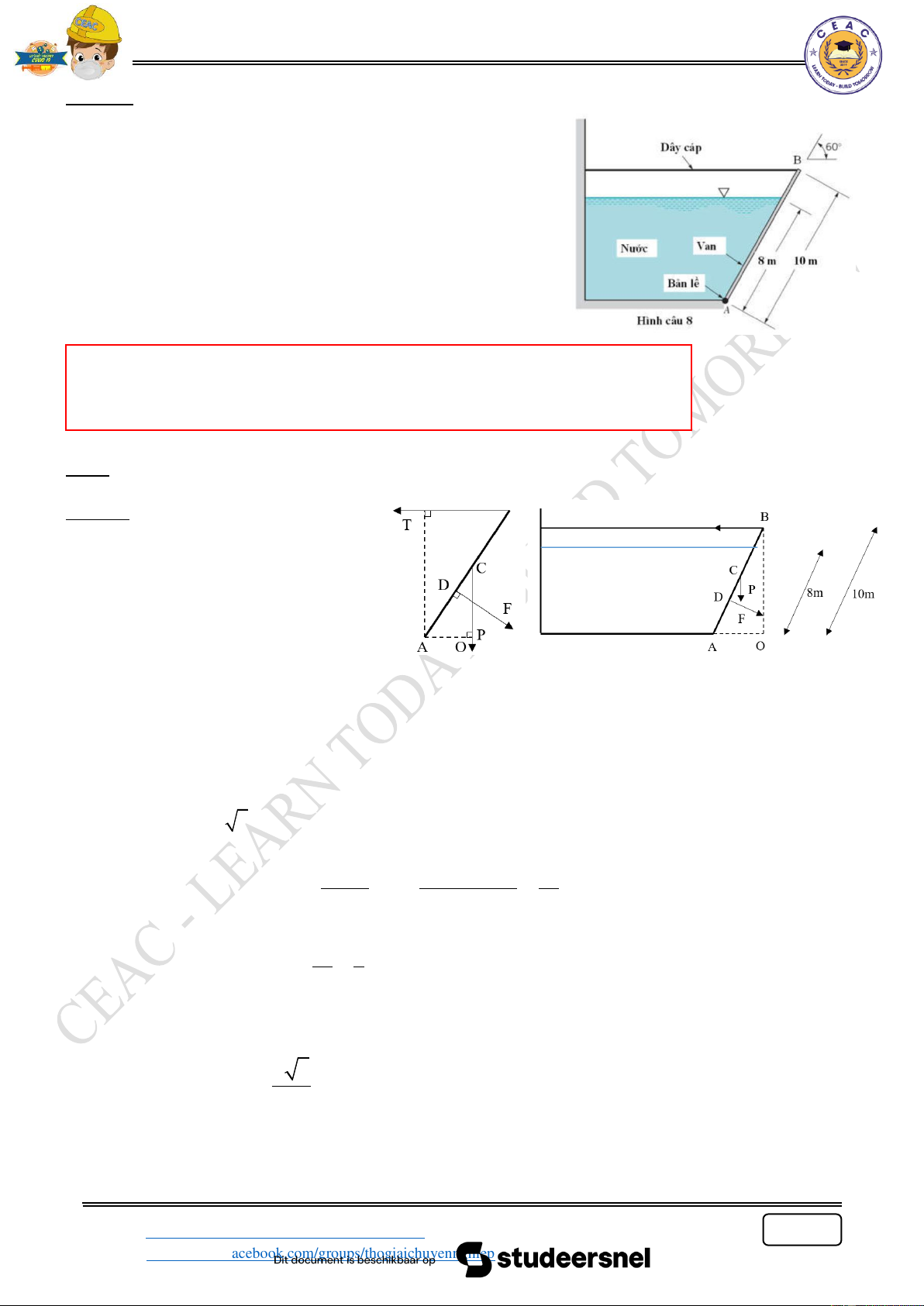
Ví dụ 6: Tính thành phần thẳng đứng của áp lực thủy tĩnh của nước, tác dụng trên ¼ mặt trụ, biết
các kích thước R = 1.2m, H = 1.5m và bề rộng b = 2m Lưu ý:
W là thể tích tích biểu đồ áp lực khi chiếu lên mắt z = 0 (Oxy) 1 W = V − V hinhhop tru 4 Giải: Tóm tắt: R = 1.2m 1 Pz = W = V − V hinhhop tru H = 1.5m 4 b = 2m = 9810 (1.2 +1.5) 1 2 1.2 − 1.2 4 = 41.4(kN)
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 6
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Dạng 3: Lực đẩy Acsimet
Kiến thức nhắc lại: Công thức: Pz = V = gV
Trong đó: V là thể tích vật chiếm chỗ
Ví dụ 7: Một khối trụ đồng chất tỷ trọng 0.8 thả cân bằng trong nước. Đường kính đáy của khối
trụ bằng 0.2m, chiều cao khối trụ bằng 0.8m. Gọi V là thể tích khối trụ, Vn là thể tích phần nước bị
khối trụ chiếm chỗ. Tỷ số Vn/V bằng bao nhiêu? Giải:
Fz = P nước × g × Vchìm = m × g nướ c
g Vchìm = dầu Vvật g V 0.81000 chim dau = = = 0.8 V 1000 nuoc Chúc bạn qua môn nè
----------------- From CEAC with love -----------------
Tài liệu có sử dụng các bài tập trên BkeL, tham khảo tài liệu của CLB Chúng ta cùng tiến,
giáo trình và bài giảng của quý Giảng viên ĐH Bách Khoa – ĐHQG TP.HCM.
Fan page: https://www.facebook.com/hocthuatxaydung Trang 7
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Chương 3. ĐỘNG HỌC
Dạng 1: TÍNH CHẤT DÒNG CHẢY TRONG LƯU CHẤT
1.1. Xác định loại chuyển động
Loại 1: Chuyển động ổn định hay không ổn định
Kiến thức nhắc lại:
Chuyển động ổn định là chuyển động không phụ thuộc vào thời gian nhưng có thể thay đổi theo
không gian. (cụ thể là phương trình vận tốc không có biến t nhưng có thể có các biến không gian như (x, y, z)
Cách phân biệt chuyển động được miêu tả theo phương pháp Lagrange hay phương pháp Euler:
+ Trong phương pháp Lagrange các yếu tố chuyển động chỉ phụ thuộc vào thời gian.
Có thể có biến t mà không có các biến không gian là x, y, z.
+ Trong phương pháp Euler các yếu tố dòng chảy được mô tả tại từng điểm trong không gian,
do đó các thông số phụ thuộc cả không gian và thời gian. Có thể có cả biến thời gian t và
các biến không gian là x, y, z.
Ví dụ 1: Xác định loại chuyển động trong thông qua phương trình mô tả vận tốc sau: 2 2
U = 6xt + yz ; U = 3t + xy ; U = xy − 2xyz − 6z X y z
Tính ổn định: ta thấy rằng có xuất hiện biến thời gian (t) → Chuyển động không ổn định
Phương pháp mô tả: P/trình trên có cả biến số thời gian (t) và không gian (x, y, z) → PP Euler
Loại 2: Chuyển động tầng hay chuyển động rối
Kiến thức nhắc lại:
Dựa vào số Reynolds (Re) ta phân loại như sau:
+ Chuyển động tầng: R R e e,toi han
+ Chuyển động rối: R R e e,toi han l V Vl Công thức tính R = = e
Re toi han là giá trị tới hạn.
Trong đó: ta tính toán số Re thông qua khối lượng riêng của lưu chất (kg/m3),
chiều dài đặc trưng của dòng chảy l (m), vận tốc dòng chảy V (m/s),
hệ số nhớt động lực học (Pa.s), hệ số nhớt động học (m2/s). VD Lưu ý:
Dòng chảy trong ống tròn có đường kính D là R = ; R = 2300 e etoihan
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 1
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Loại 3: Chuyển động quay hay không quay 1 u u y z = − x 2 y z 1 u u
Công thức xác định vận tốc quay của của 1 điểm: x z = − (1) y 2 z x 1 u y ux = − z 2 x y Lưu ý:
Xét chuyển động có x = y = z = 0 → chuyển động không quay.
Ngược lại là chuyển động quay (tồn tại 1 thành phần vận tốc quay khác 0) y x
Ví dụ 2: Lưu chất chuyển động với vận tốc: U = − ; U = X 2 y 2 b a
Tìm các thành phần vận tốc quay.
Giải: Áp dụng công thức (1) ta có: x 1 (0) 2 a = − = 0 x 2 y z −y 2 1 b (0) = − = 0 y 2 z x x −y 2 2 1 a b 1 1 1 = − = + z 2 2 2 x y 2 a b
1.2. Tìm phương trình đường dòng
Kiến thức nhắc lại: dx dy dz
Phương trình vi phân đường dòng có dạng = = (2) U U U x y z
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 2
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Ví dụ 3: Cho phương trình vận tốc của một lưu chất chuyển động phẳng ổn định không nén u = −y / 4
được với vận tốc u = (u ; u như sau: x
. Tìm pt đường dòng đi qua điểm (1, -2) x y ) u = x / 9 y
Giải: Áp dụng công thức (2) ta có: 2 2 dx dy −y x y x = u dy = u dx dy = dx − = + C x y u u 4 9 8 18 x y (− )2 ( )2 2 1 5
Do đường dòng đi qua điểm (1, -2) nên ta có − = + C C = − 8 18 9 2 2 y x 5
Vậy phương trình đường dòng cần tìm có dạng 2 2 − = − hay 4x + 9y = 40 8 18 9 1.3. Tìm gia tốc
Kiến thức nhắc lại: du u u u u x x x x x a = = u + u + u + x x y z dt x y z t du u u u + y y y y u Phương pháp Euler: x a = = u + u + u + y x y z dt x y z t du u u u u z z z z x a = = u + u + u + z x y z dt x y z t u u u u Trong đó thành phần i i i u + u + u x y z x y z
là gia tốc đối lưu và i t là gia tốc cục bộ 2 2 2 a = a + a + a x y z + du u Phương pháp Lagrange: a = = dt t u = 2.5x + y (cm / s) x
Ví dụ 4: Một lưu chất chuyển động phương trình vận tốc: u = 3x − 2.5y (cm / s) y
Tìm gia tốc tại điểm M(2cm, 3cm). du u u u x x x x a = = u + u + x x y dt x y t
Giải: Áp dụng công thức Euler ta có: du u u y y y u x a = = u + u + y x y dt x y t
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 3
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC (2.5x + y) 2.5x + y 2.5x + y a = 2.5x + y + 3x − 2.5y + x ( ) ( ) ( ) ( ) x y t (3x − 2.5y) 3x − 2.5y 3x − 2.5y a = 2.5x + y + 3x − 2.5y + y ( ) ( ) ( ) ( ) x y t
a = 2.5 2.5x + y +1 3x − 2.5y + 0 = 9.25x x ( ) ( )
a =3 2.5x + y −2.5 3x −2.5y +0 =9.25y y ( ) ( ) 2 a = 9.25 2 = 18.5 cm / s x
Thay tọa độ (2, 3) và ta được: 2 2 a = a + a = 33.35cm/s2 2 x y a = 9.25 3 = 27 7 . 5 cm / s y
Dạng 2: TÌM LƯU LƯỢNG VẬN TỐC TRUNG BÌNH
Kiến thức nhắc lại:
Công thức tính lưu lượng qua mặt cắt ướt:
Đối với dòng lưu chất ổn định không nén được ( = const) Q = V A; Q = u dA n Q = Q V A = V A 1 2 1 1 2 2
Phương trình liên tục lưu chất không nén được, chuyển động ổn định tại nút: Q = Q vao ra
Ví dụ 5: Nước chảy từ một ống tròn vào giữa khe của 2 mặt tròn như hình vẽ. Ống tròn có đường
kính d = 4 cm và mặt tròn có đường kính D = 20 cm.
Cho vận tốc đi trong ống v = o
3 m/s, khoảng cách giữa 2 mặt tròn
a = 1cm.Vận tốc v đi ra khỏi mặt tròn là: A. 0.8 m/s B. 0.4 m/s C. 1.0 m/s D. 0.6 m/s E. 1.2 m/s
Giải: Bảo toàn lưu lượng ta có: Q = Q 0 A
V A = V A(löu yù maët caét A vuoâng goùc vôùi V) 0 0 2 d V = V D a → Chọn đáp án D. 0 4 2 2 d 1 0.04 1 V = V = 3 = 0.6(m / s) 0 4 D a 4 0.2 0.01
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 4
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Ví dụ 6: Phân bố vận tốc dòng khí từ bình vào ống tròn tại hai
mặt cắt được mô tả như trên hình. Ở mặt cắt số 1 ngay lối vào
vận tốc U xem như phân bố 0
đều. Ở mặt cắt số 2, phân bố vận 2 r
tốc có dạng parabol: u = u 1− max 2 R
Với umax là vận tốc ở tâm ống, r tính từ tâm ống, R là bán kính ống. Biết U = u 0
15 cm/s, max bằng bao nhiêu? Chọn đáp án đúng A. 0.1 m/s B. 0.4 m/s C. 0.05 m/s D. 0.2 m/s E. 0.3 m/s Giải: Ta có: Q = Q A Z U dA = udA 0 R 2 r U A = u
2 1− rdr 0 max 2 R 0 2 4 → Chọn đáp án E R R 2 U R = u 2 − 0 max 2 2 4R 2 R 2 U R = u 2 0 max 4 u = 2U = 2 0.15 = 0.3m / s max 0 Nhận xét:
Lưu lượng chính là thể tích của biểu đồ phân bố vận tốc
Giải lại ví dụ 6 theo nhận xét trên:
Thể tích phân bố vận tốc tại 1 bằng với thể tích phân bố vận tốc tại 2.
Thể tích hình trụ 1 bằng thể tích parabolic 2. 1 2 2
R U = R U 0 max 2 2U = U = 0.15 2 = 0.3(m / s) 0 max
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 5
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Ví dụ 7: Chất lỏng chuyển động trong khe hẹp có vận tốc phân bố tuyến tính từ thành khe
hẹp tới tâm khe hẹp. Chiều cao của khe hẹp là h = 0.6 m. Tại tâm khe hẹp vận tốc đạt giá trị u
=1.4 m/s. Vận tốc trung bình của chất lỏng là: max A. 0.5 m/s B. 0.9 m/s C. 0.7m/s D. 0.6 m/s E. 0.8 m/s Giải: Ta có: Q = udA = V A tb 1 u h b = V h b → Chọn đáp án C max tb 2 u 1.4 max V = = = 0.7(m / s) tb 2 2
Ví dụ 8: Dòng nước chảy trong hệ thống đường ống tròn, đi vào và ra tại nút I, có lắp một máy
bơm ở nhánh 1 như hình. Cho lưu lượng qua bơm Q = Q b
60l/s và lưu lượng ở các nhánh = 2 15l/s Q = D = 10cm. 3
25l/s với quy ước chiều dương như hình. Cho đường kính ở ống 4 là 4
Vận tốc ở mặt cắt 4 là: A. 4.046 m/s B. 3.046 m/s C. 2.546 m/s D. 2.046 m/s E. 3.546 m/s
Giải: Tại nút I ta có: Q = Q + Q + Q 1 2 3 4 Q = Q − Q − Q 4 1 2 3 A V = Q − Q − Q 4 4 1 2 3 2 (D ) 4 V = Q − Q − Q → Chọn đáp án C 4 1 2 3 4 4 V = (Q − Q − Q ) 4 1 2 3 2 (D ) 4 4 = (60 −15 − 25) 2 1 = 25.46dm / s = 2.546m / s Chúc bạn qua môn nè
----------------- From CEAC with love -----------------
Tài liệu có sử dụng các bài tập trên BkeL, tham khảo tài liệu của CLB Chúng ta cùng tiến,
giáo trình và bài giảng của quý Giảng viên ĐH Bách Khoa – ĐHQG TP.HCM.
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 6
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
TÀI LIỆU ÔN TẬP CƠ LƯU CHẤT
Tài liệu được tổng hợp bởi CEAC – CLB Học thuật Xây dựng Bách Khoa
có sử dụng các bài tập trên BKel, giáo trình và bài giảng
của quý Giảng viên trường ĐH Bách Khoa – ĐHQG TP.HCM
Tài liệu còn nhiều thiếu sót mong được sự góp ý tích cực của mọi người để hoàn thiện
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 1
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Chương 4: ĐỘNG LỰC HỌC LƯU CHẤT 4.1 Lý thuyết
• Cho lưu chất lý tưởng ( = 0): 2 2 P V P V 1 1 2 2 z + + = z + + 1 1 2 2 2g 2g
• Cho lưu chất thực ( 0) : 2 2 P V P V 1 1 2 2 z + + = z + + + h 1 1 2 2 f (1−2) 2g 2g
• Cho lưu chất thực có thiết bị thủy lực: 2 2 P V P V 1 1 2 2 z + + + H = z + + + H + h 1 1 B 2 2 T f (1 2) 2g − 2g Với: P z +
: là thế năng đơn vị trọng lượng lưu chất (m). Bao gồm z là vị năng đơn vị (m) và 𝑝 là áp năng 𝛾 đơn vị (m) 2 v
: là động năng đơn vị trong lượng lưu chất (m) 2g
hf(1− : là tổn thất năng lượng của dòng chảy khi đi từ mặt cắt 1 đến mặt cắt 2 2)
H : là năng lượng của máy bơm cung cấp cho đơn vị trọng lượng lưu chất (m) B
• Công suất hữu ích của máy bơm: N = QH (W) B B • QH
Công suất trên trục máy bơm: B N =
với η là hiệu suất máy bơm (≤ 1) B
H : là năng lượng tuabin lấy đi từ đơn vị trọng lượng lưu chất (m) T
• Công suất của tuabin: N = QH (W) T T
• Công suất trên trục tua bin: N = QH
với η là hiệu suất tua bin (≤ 1) T T
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 2
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Điều kiện áp dụng phương trình năng lượng:
• Lưu chất chuyển động ổn định
• Lưu chất chỉ bị ảnh hưởng bởi trường trọng lực
• Dòng chảy không trao đổi nhiệt
• Tại mặt cắt 1-1 và 2-2, đường dòng thẳng song song và biến đổi chậm
• Lưu chất không nén được
• Lưu lượng qua mặt cắt 1-1 và 2-2 bằng nhau
• Đoạn dòng chảy giữa 2 mặt cắt 1-1 và 2-2 không có nhập lưu và tách lưu
4.1.2 Phương trình biến thiên động lượng
• Xét lưu chất chuyển động ổn định, không nén được, đi vào mặt cắt 1-1 và ra mặt cắt 2-2: F = − ngoailuc Q( V
V = Động năng ra – Động năng vào 2 2 1 1 )
• Đối với dòng chảy có nhiều mặt cắt vào và nhiều mặt cắt ra: F = ngoailuc
Động năng ra – Động năng vào
Phân tích ngoại lực thường bao gồm: + Trọng lực G
+ Lực ma sát Fms giữa chất lỏng và thành rắn
+ Phản lực vuông góc của thành rắn tác dụng lên dòng chảy
+ Áp lực Pi tác dụng vào mặt cắt mà dòng chảy ra vào (tính như áp lực thủy tĩnh)
** Lưu ý: thông thường lực ma sát Fms và phản lực vuông góc được gom chung thành lực R thành
rắn tác dụng lên dòng chảy
Còn trọng lượng G có giá trị nhỏ nên thường bỏ qua, hoặc bị triệt tiêu với phản lực của đáy kênh
(dành cho bài toán dòng chảy qua cửa kênh, cống) ** Bài tập áp dụng:
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 3
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
+ Bài toán xác định lực tác dụng lên vòi, ống nước: bao gồm ống thẳng, ống cong
(α =90° hoặc α khác 90°)
+ Bài toán xác định lực tác dụng lên đập tràn, cửa cống, cửa kênh
+ Chuyển động của tia nước chạm thành phẳng: chuyển động tuyệt đối và tương đối 4.2 Bài tập
CÁC BÀI TOÁN LIÊN QUAN ĐẾN PHƯƠNG TRÌNH NĂNG LƯỢNG
DẠNG 1: DÒNG CHẢY ỔN ĐỊNH QUA LỖ THÀNH MỎNG
Dòng chảy từ bể chảy qua lỗ tháo có diện tích A. Chiều cao cột chất lỏng là H tính từ tâm lỗ là
không đổi. Xác định vận tốc và lưu lượng chất lỏng chảy qua lỗ tháo. 0 0 H c A c Giải:
Chọn mặt cắt 0-0 và c-c như trong hình vẽ
Ta có phương trình năng lượng cho đoạn dòng giữa hai mặt cắt 0-0 và c-c, mặt chuẩn qua tâm A của lỗ: 2 2 p V p V 1 1 c c z + + = z + +
+ h (Xem = = 1) 1 1 c 2 c g 2 f g
Và V 0 , p = p = 0 , Suy ra vận tốc chảy ra khỏi lỗ tháo: 1 1 c V = 2g(z − z − h ) = 2g(H − h ) = C 2gH c 1 c f f V
C <1 do mất năng sinh ra khi đi qua lỗ hẹp, gọi là hệ số lưu tốc V
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 4
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC
Lưu lượng: Q = V A = C C A 2gH = C A 2gH c c v c d
Với C <1 do dòng chảy bị co hẹp khi ra khỏi lỗ tháo, gọi là hệ số co hẹp c
C = C C : hệ số lưu lượng d v c
Ví dụ 1: Một lỗ thành mỏng được lắp vào bên trong của một bể chứa nước kín khí ở trên, đựng
nước đến cao trình H so với trục lỗ. Mực nước trong ống đo áp lên đến cao độ là H1 so với mặt
nước trong bể. Đường kính lỗ thành mỏng là d. Hệ số co hẹp là Cc; hệ số lưu tốc là Cv. H 1 Po 1 1 H c A c
Cho H=4m; H1=4m; d=6 cm; Cc=0,64; Cv=0,97. Lưu lượng chảy ra khỏi lỗ là?
( Lưu ý: Lưu lượng của lỗ Q=CcCvQLT trong đó QLT là lưu lượng tính với giả thiết bỏ qua tổn thất
năng lượng và không có co hẹp dòng chảy) Giải:
Áp dụng phương trình năng lượng Bernoulli cho thể tích ướt giữa mặt cắt 1-1 và c-c ta có: 2 2 P V P V 1 1 c c Z + + = Z + + 1 c 2g 2g 2 Vc H + H + 0 = 0 + 0 + 1 2g V = 2g(H + H ) c 1
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 5
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC 2 d 3 Q = V A = 2g(H + H ). . 0,0354(m / s) LT c c 1 4 Q = C .C .Q = 22(l / s) c v LT
DẠNG 2: DÒNG CHẢY QUA VÒI LẮP NGOÀI
Dòng chảy từ bể qua một đoạn ống ngắn chảy ra ngoài không khí. Tìm công thức tính lưu lượng
qua vòi. Tính lưu lượng dòng chảy qua vòi và vận tốc tại mặt cắt c-c 0 0 pck H c 1 A c 1 Giải:
Tính lưu lượng Q
Viết phương trình năng lượng cho đoạn dòng giới hạn bởi hai mặt cắt 0-0 và 1-1, mặt chuẩn qua trục vòi: 2 2 p V p V 0 0 1 1 z + + = z + + + h 0 1 0 1 2g − 2 f g
Có z = H ; z = 0 ; p = p = p = 0 ; V 0 0 1 0 1 a 0
Do đó V = 2g(H − h ) = C 2gH 1 f 0 1 − v
Lưu lượng Q = V A = C A 2gH = C A 2gH 1 1 v 1 d 1 Với C = C v d
Tính vận tốc tại mặt cắt c-c
Viết phương trình năng lượng cho đoạn dòng giới hạn bởi hai mặt cắt 0-0 và c-c, mặt chuẩn qua trục vòi:
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 6
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com) lOMoARcPSD|54133207
CƠ LƯU CHẤT ÔN TẬP KIẾN THỨC CÙNG CEAC 2 2 p V p V 0 0 c c z + + = z + + + h (xem = = 1) 0 c f 0 0 c 2g − 2 c g
Với z = H ; z = 0 ; V 0 ; p = 0 ta được: 0 c c 0 p p V = 2 c g H − h − = C 2 c g H − c f 0−c v
Với C <1 do mất năng sinh ra khi đi qua lỗ hẹp, gọi là hệ số lưu tốc V NOTE:
+ Đề bỏ qua mất năng thì C = C = 1 v c
+ Áp suất tại mặt cắt C-C là áp suất chân không
DẠNG 3: ỐNG PITÔ ĐO LƯU TỐC ĐIỂM
Ống Pito gồm 2 đoạn ống như hình vẽ. Xác định lưu tốc tại điểm A theo độ chênh cột áp thẳng
đứng h, bỏ qua mất năng. Giải:
Áp dụng phương trình năng lượng cho đường dòng qua 2 điểm A, B 2 2 p u p u A A B B z + + = z + + A 2 B g 2g
(trong đó uB=0 do điểm B nằm trong ống)
Lưu chất trong 2 ống đo áp ở trạng thái tĩnh, ta áp dụng phương trình thủy tĩnh: p p A M z + = z + ( p = p = 0 ) A M M a
Fanpage: https://www.facebook.com/hocthuatxaydung Trang 7
Diễn đàn: https://www.facebook.com/groups/thogiaichuyennghiep
Downloaded by Tài Li?u Thanh Hi?n By PDF (kaidz9987@gmail.com)




