Chủ đề 1: Điện trường trong điện môi - Lưỡng cực điện và ứng dụng môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Chủ đề 1: Điện trường trong điện môi
I. Lý thuyết:
1. Lưỡng cực điện: a. Định nghĩa:
- Lưỡng cực điện là một hệ hai điện tích có độ lớn bằng nhau nhưng trái dấu q và
– q, cách nhau một đoạn rất nhỏ so với khoảng cách từ lưỡng cực tới các điểm đang xét trong điện trường.
- Vector momen lưỡng cực điện, gọi tắt là momen điện của lưỡng cực:
hướng từ - q đến + q và có độ dài bằng khoảng cách giữa hai điện tích, e Trong đó l
đường thẳng nối hai điện tích gọi là trục của lưỡng cực.
- Đơn vị của pe trong hệ SI là C.m (Coulomb nhân mét).
- Lưỡng cực điện thường gặp trong các vật thể, do bản thân các nguyên tử khi chịu
tác dụng của điện trường ngoài thì thường bị biến dạng, khiến cho về mặt phân bố điện
tích có thể coi chúng như lưỡng cực điện. Ngoài ra, một số phân tử có cấu tạo mà cả
phân tử trung hòa điện, trong đó phân tử có thể được coi như một lưỡng cực do tính
không đối xứng của phân tử.
b. Cường độ điện trường và điện thế gây ra
bởi lưỡng cực điện:
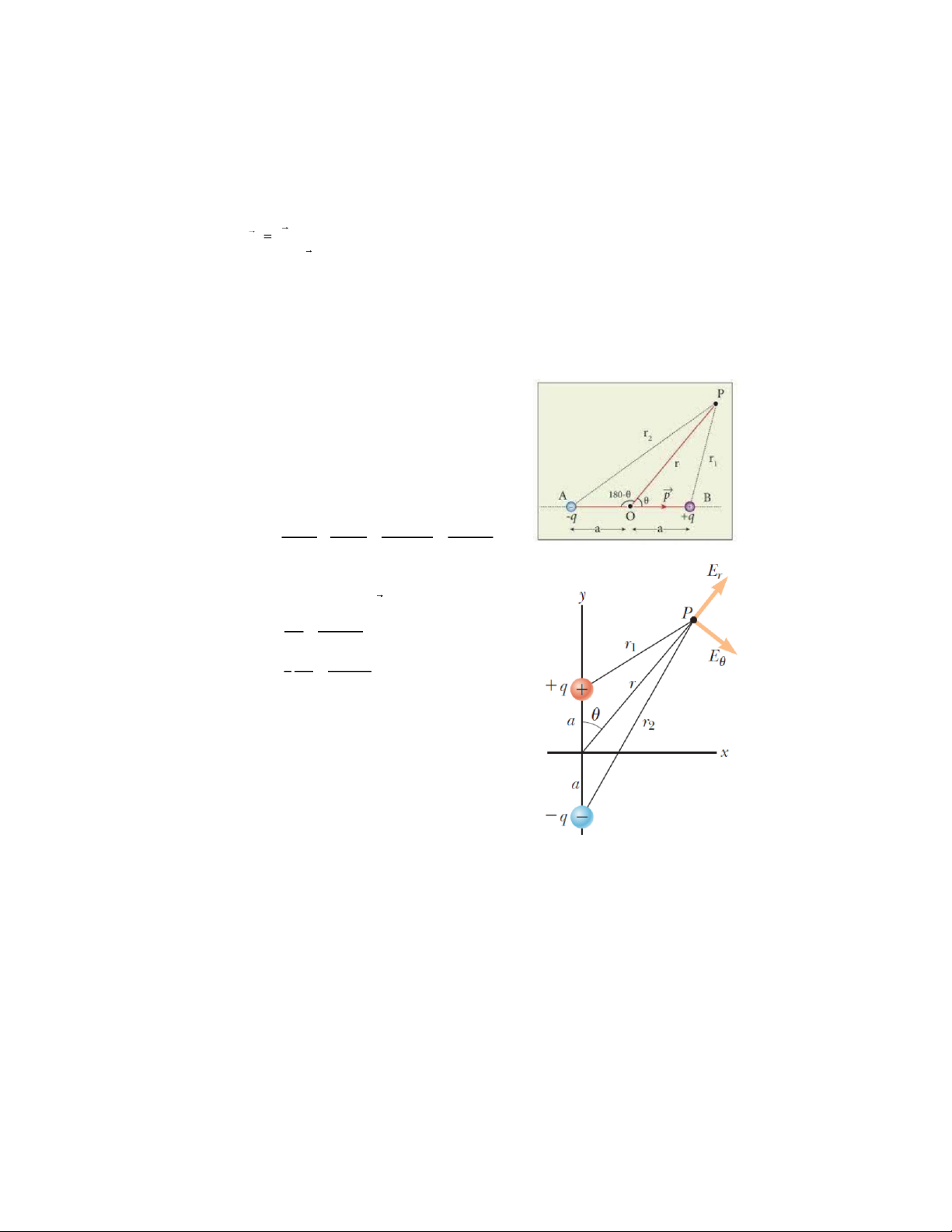
- Coi điện tích tại A âm, tại B dương.
- Ta xét vector cường độ điện trường gây bởi
lưỡng cực điện tại điểm P cách trung điểm O của
đoạn thẳng AB đoạn r và góc POB  .
Điện thế tại điểm P: 4 4 4  4e q q q r r p cos Vr .  r  rr r    2  1  M 2 0 1 0 2 0 1 2 0
Các thành phần tiếp tuyến En và pháp tuyến Et
của cường độ điện trườ 2e
ng E có biểu thức: V  p cos ; Er   r   4e r 3 1 V  p 0sin  Er   r    t 3 0
c. Lực tác dụng lên lưỡng cực điện đặt
trong điện trường:
- Xét trường hợp điện trường đều, khi đó
điện trường tác dụng lên lưỡng cực một ngẫu lực
có momen M  qEl sin si  n p E với α là góc e
tạo bởi vector l và vector E . Vector momen
ngẫu lực có phương trùng trục quay lưỡng cực
điện, có tác dụng làm cho lưỡng cực quay trong trong điện trường.
- Khi đặt lưỡng cực trong điện trường không đều, giả sử lưỡng
cực nằm dọc theo một đường sức điện, khi đó cường độ điện trường
tại nơi đặt điện tích – q là E, còn tại nơi đặt điện tích + q là 'E  E E l
, khi đó tổng hợp lực tác dụng lên lưỡng cực là: x  E  E  E  F          1
F 2 F 1 2F F q E l qE ql p e  x  x  x
lực này hướng về phía điện trường mạnh.
Như vậy tổng quát, khi đặt lưỡng cực điện vào trong điện
trường không đều, thì nó chịu tác dụng của lực và ngẫu lực. Ngẫu
lực có xu hướng làm lưỡng cực quay cho đến khi có phương trùng
với E , còn lực có tác dụng kéo lưỡng cực về phía điện trường mạnh.
=> Đũa thủy tinh hoặc ebonide nhiễm điện có thể hút các vật nhẹ.
d. Thế năng của lưỡng cực điện trong điện trường:
- Quy ước thế năng của lưỡng cực điện bằng 0 khi nó vuông góc với các đường
sức điện. Như vật, thế năng W của lưỡng cực bằng công mà điện trường cần thực hiện
để làm lưỡng cực quay từ 
  đến α. Phép tính chi tiết cho ta: 02 W  p  E  e e cos   . II. Bài tập:
Bài 1 (1): Một lưỡng cực điện có momen p , có tâm O, được đặt dọc theo trục
x’Ox. Lưỡng cực nằm trong một điện trường đều E0 hướng theo trục x’Ox.
a. Tìm biểu thức cho điện thế V của hệ gồm lưỡng cực và điện trường, tại một
điểm M có tọa độ cực r và , ở đủ xa lưỡng cực. Người ta giả thiết điện thế của điện  trường đều E b
0 ằng không tại điểm O.
b. Xác định mặt đẳng thế V = 0.
c. Chứng minh rằng cường độ điện trường trên mặt đẳng thế V=0 có giá trị 3E0cos.
Bài 2 (2): Một lưỡng cực điện điểm, với mô men điện p định hướng theo chiều
dương trục z, được đặt tại gốc tọa độ O. Hãy tìm hình chiếu của vec tơ cường độ điện trường E E z và
 lên một mặt phẳng vuông góc với trục z tại điểm S.
Bài 3 (3): Hai đầu một đòn cân nhẹ chiều dài 2L có gắn điện tích +Q và – Q với
cùng khối lượng M. Đòn cân có thể quay không ma sát quanh trục thẳng đứng.  dưới
đòn cân, trên đường thẳng nối +Q và – Q có một lưỡng cực điện nhỏ gồm hai điện tích
+q và – q cách nhau 2a (với a << L) cố định.  thời điểm ban đầu đòn cân nằm ở vị trí
cân bằng. Tính tần số dao động nhỏ của đòn cân trong mặt phẳng thẳng đứng.
Bài 4 (9): Lưỡng cực điện có mô men p hướng theo trục Ox, được đặt cố định ở 1
điểm O. Lưỡng cực điện có mô men p t
2 đặ ở điểm M có tọa độ M(r, 1) chỉ có thể quay quanh M. 1)  vị trí cân bằng,    2
p lập với OM một góc 2. Tìm mối liên hệ giữa 1 và 2. ππ
Tính toán cho trường hợp 1 = 0, ; 4 2
2) a) Biểu diễn năng lượng W = - p21.E của lưỡng cực p nằm cân b 2 ằng trong điện trường E của p . 1 1
b) Tìm giá trị của 1 sao cho năng lượng đó là cực tiểu. Xác định lực hút giữa hai
lưỡng cực ứng với giá trị 1 này.
3) Tính năng lượng cực tiểu và lực hút nếu các lưỡng cực là hai phân tử nước đặt
cách nhau 3 oA . Cho biết mối liên kết OH trong phân tử nước có mômen p = 4.10-30C.m
và hai liên kết OH lập với nhau góc  = 150o.
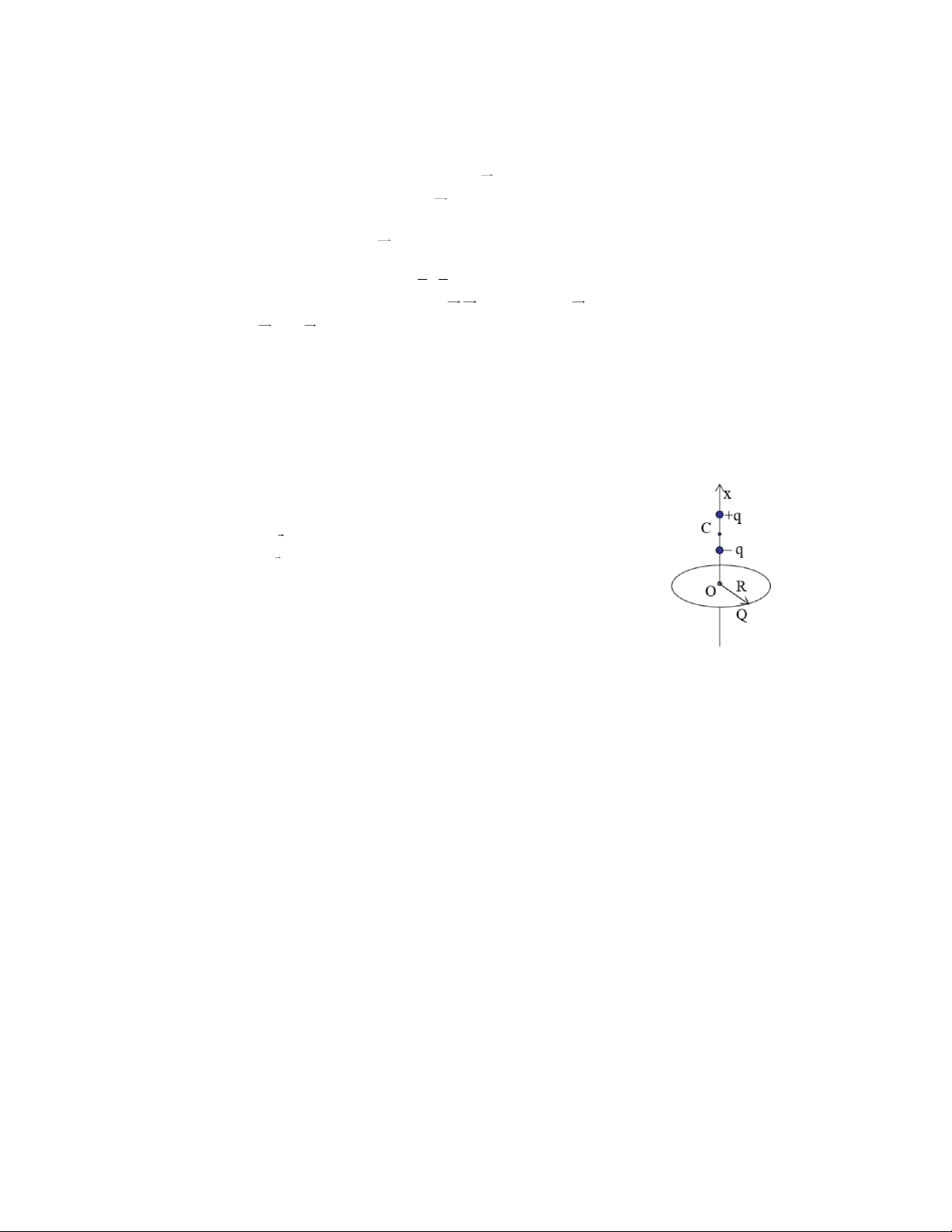
Bài 5 (10): Đặt trong chân không một vòng dây mảnh, tròn, bán kính
R, tâm O, mang điện tích dương Q phân bố đều. Dựng trục Oz vuông góc
với mặt phẳng của vòng dây và hướng theo chiều vec tơ cường độ điện
trường của vòng dây tại O (hình vẽ). Một lưỡng cực điện có vec tơ mô men
lưỡng cực p , tâm C và có khối lượng m chuyển động dọc theo trục Oz mà
chiều của p luôn trùng với chiều dương của trục Oz. Bỏ qua tác dụng của trọng lực.
a) Xác định tọa độ z0 của C khi lưỡng cực ở vị trí cân bằng bền và
khi lưỡng cực ở vị trí cân bằng không bền. Tính chu kì T của dao động nhỏ
của lưỡng cực quanh vị trí cân bằng bền.
b) Giả sử ban đầu điểm C nằm ở điểm O và vận tốc của lưỡng cực bằng không.
Tính vận tốc cực đại của lưỡng cực khi nó chuyển động trên trục Oz.