Chủ đề 2: Tụ Điện - Lý Thuyết và Ứng Dụng Cơ Bản môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Chủ đề 2: Tụ điện A. Lý thuyết
I. Tụ điện: 1. Ứng dụng tụ điện:
- Tụ điện được dùng để lọc các
dòng một chiều đi qua một mạch xoay chiều nào đó.
- Tụ điện có thể được dùng để
tích và phóng điện trong mạch điện.
- Tụ điện được dùng để lưu trữ
điện tích một cách ổn định và ít khi
mất mát, có thể được dùng để sạc các thiết bị điện. 2. Khái niệm tụ điện:
- Tụ điện là một hệ hai vật dẫn đặt gần nhau và ngăn cách nhau bằng môt lớp cách
điện sao cho giữa chúng xảy ra hiện tượng hưởng ứng toàn phần.
- Hai vật dẫn tạo nên tụ điện gọi là các bản của tụ điện.
- Có nhiều cách phân chia tụ điện: theo hình dáng, theo bản chất lớp điện môi của tụ điện.
3. Cách tích điện cho tụ điện:
- Nối các cực của tụ điện vào nguồn điện.
- Điện tích của bản dương được gọi là điện tích của tụ điện.
- Do hiện tượng hưởng ứng toàn phần, các đường sức xuất phát từ một bản và kết
thúc ở bản kia, nên điện tích trên hai bản bằng nhau nhưng khác dấu.
II. Điện dung của tụ điện: 1. Định nghĩa:
- Là đại lượng đặc trưng cho khả năng tích điện của tụ điện ở một hiệu điện thế
nhất định. Nó được xác định bằng thương số của điện tích của tụ điện và hiệu điện thế giữa hai bản của nó. Q CU 2. Đơn vị: F (Fara)
3. Năng lượng điện trường trong tụ điện
- Khi tụ điện tích điện thì điện trường trong tụ điện sẽ dự trữ một năng lượng. Đó
là năng lượng điện trường. CU W 2 2
III. Công thức tính điện dung của một số tụ điện:
Điện dung của tụ phụ thuộc vào hình dạng, kích thước, vị trí tương đối của các
bản và môi trường giữa hai bản. 1. Tụ điện phẳng:
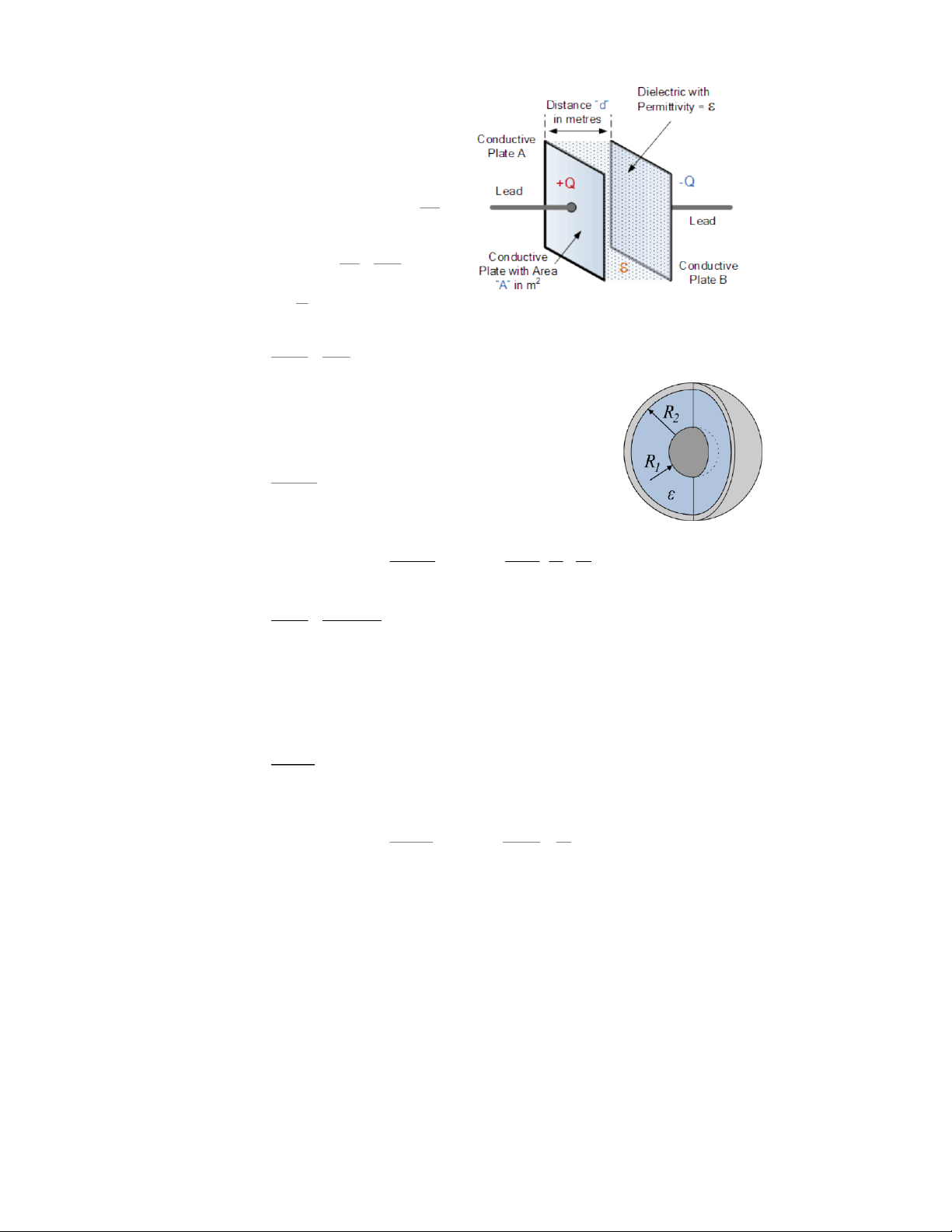
- Xét một tụ điện phẳng có hai bản là
hai tấm kim loại mỏng có cùng diện tích S
đặt song song và cách nhau đoạn d. Nếu d
nhỏ có thể xem điện trường giữa hai bản là đều:  Khi đó  với  (áp 1 V 2V Ed E 0 dụng định lý O-G) Suy ra d d Q    1 V 2V S   0 0 với Q  
là mật độ điện tích trên S
mỗi bản, ε là hằng số điện môi của môi trường lấp đầy giữa hai bản. Từ đó suy ra: Q 0S CVV  d  1 2 2. Tụ điện cầu:
- Hai bản tụ điện là hai mặt kim loại đồng tâm bán kính R1 và
R2. Áp dụng định lý O-G ta tính được cường độ điện trường giữa hai bản tụ điện: q Er 2 40
(q là điện tích của tụ điện). Ta tính được điện thế giữa hai bản tụ: 2 V 2R q q 1 1
dV  Edr   dV  V  V    2 1 2  r R   R V R 4 4 0 0 1 2 1 1
Do đó điện dung của tụ cầu bằng: Q 4R  R 0 1 2 CV V  R R  1 2 2 1 3. Tụ điện trụ:
- Hai bản của tụ điện trụ là hai mặt trụ kim loại đồng trục bán kính lần lượt là R1
và R2 và có chiều cao bằng l. Nếu chiều cao l rất lớn so với các bán kính R1 và R2 ta có
thể coi điện trường giữa hai bản như điện trường gây ra bởi hai mặt trụ mang điện dài vô hạn.
Áp dụng định lý O – G ta tính được cường độ điện trường giữa hai bản tụ điện: q Elr 20
(q là điện tích của tụ điện, r là khoảng cách từ điểm tính cường độ điện trường đến
trục khối trụ). Ta tính được điện thế giữa hai bản tụ: 2 V 2R q q 2 R
dV  Edr   dV  V     1 2 V ln  lr l R V R 2 2 0 0 1 1 1
Do đó điện dung của tụ trụ bằng: q 20l CR V V 2 1 2 ln 1 R 4. Chú ý:
- Các tụ có thể bị đánh thủng nếu điện trường giữa hai bản rất lớn.
- Hiệu điện thế lớn nhất mà một tụ điện có thể chịu được để không bị đánh thủng
được gọi là hiệu điện thế đánh thủng. B. Bài tập:
Bài 0: Tính và so sánh điện dung các tụ sau trong trường hợp chúng có cùng diện
tích các bản tụ và cùng độ dày.
Bài 1: Khoảng không gian giữa hai bản tụ điện phẳng được đổ đầy chất điện môi
với hằng số điện môi biến đổi theo hàm bậc nhất từ ε1 ở gần bản tụ thứ nhất đến ε2 ở
gần bản tụ thứ hai. Cho khoảng cách giữa hai bản tụ là d, diện tích mỗi bản là S. Tìm điện dung C của tụ.
Bài 2: Trong một tụ phẳng, mỗi bản tụ có mật độ điện mặt σ, mỗi bản tụ có mật
độ điện mặt σ, đặt một điện môi tích điện dương sao cho mật độ điện tích khối thay đổi t  x
ừ 0 ở gần bản tụ đến ρ0 ở gần bản tụ âm theo quy luật  x  d  , trong đó d là khoảng 2
cách giữa hai bản tụ. Tìm sự phân bố của điện trường E trong không gian, biết hằng số điện môi là ε.
Bài 3: Trong không gian giữa hai bản
của một tụ điện trụ được lấp đầy bởi hai điện
môi đồng chất có hằng số điện môi lần lượt
là ε0 và ε1. Tụ có bán kính trong là a, bán kính
ngoài là b, chiều cao của tụ là L, mỗi điện
môi lấp đầy một nửa không gian giữa các bản tụ như hình vẽ.
a. Tính điện dung của tụ.
b. Mở rộng bài toán trong trường hợp
các mặt phân cách đều đi qua trục đối xứng
của trụ, nhưng góc hợp bởi hai mặt phân cách của hai loại điện môi là α. Tính điện dung của tụ khi đó. Bài 4:
a. Khoảng không gian giữa hai bản tụ điện trụ
được lấp đầy bởi hai chất điện môi, trong đó điện môi
có hằng số ε1 lấp đầy khoảng không gian từ bán kính R1
đến R2, điện môi có hằng số ε2 lấp đầy khoảng không
gian từ bán kính R2 đến R3. Mặt cắt vuông góc với trục
khối trụ được cho trên hình vẽ. Cho chiều dài trụ là L.
Tính điện dung của tụ điện.
b. Khoảng không gian giữa hai bản tụ điện trụ được đổ đầy chất điện môi với hằng
số điện môi biến đổi theo hàm bậc nhất của khoảng cách đến trục từ ε1 ở gần bản tụ
trong bán kính a đến ε2 ở gần bản tụ ngoài bán kính b. Cho chiều dài trụ là L. Tìm điện dung C của tụ.
Bài 5: Một tụ hình trụ dài được đổ đầy điện môi có hằng số điện môi phụ thuộc vào kho R
ảng cách đến trục r theo hàm 1  , trong đó R 1 r
1 là bán kính của trụ bên
trong. Bỏ qua các hiệu ứng bờ.
a. Tính điện dung của tụ điện biết bán kính ngoài R2 = 1,25R1.
b. Đặt vào giữa hai bản tụ hiệu điện thế U0. Tìm hàm mật độ phân bố điện tích khối bên trong tụ.
Bài 6: Một tụ cầu được đổ đầy chất điện môi có hằng số điện môi phụ thuộc vào 2 R
bán kính r được cho bởi hàm số 1  , trong đó R ủ ụ ỏ 12
1 là bán kính trong c a t . B qua r các hiệu ứng bờ.
a. Tính điện dung của tụ điện biết bán kính ngoài R2 = 1,25R1.
b. Đặt vào giữa hai bản tụ hiệu điện thế U0. Tìm hàm mật độ phân bố điện tích khối bên trong tụ.
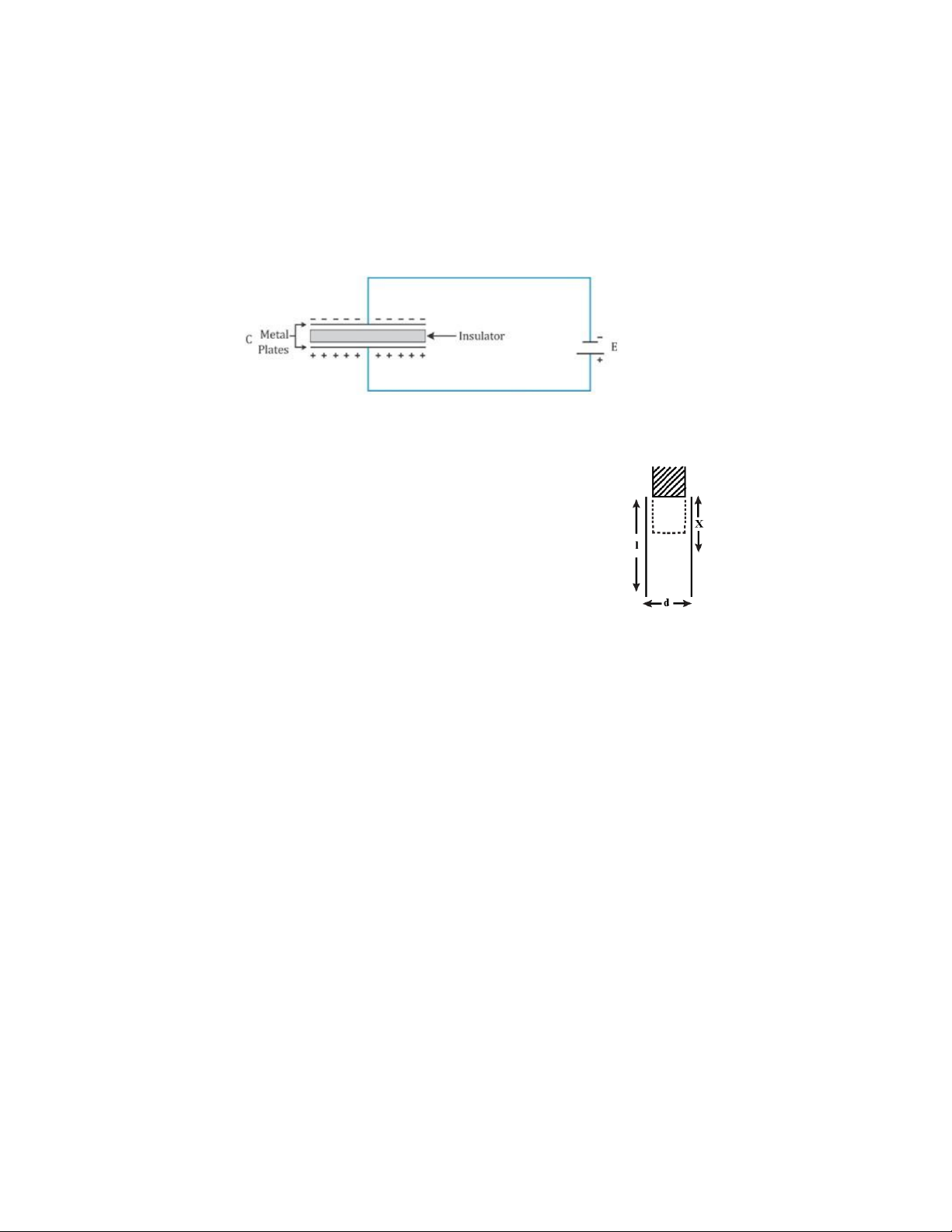
Bài 7: Người ta tích điện cho một tụ phẳng không khí đến hiệu điện thế U0. Bên
trong tụ đó người ta đưa vào một tấm kính hình hộp đứng có hằng số điện môi ε (tấm
kính có độ dày d và có hình dạng giống với các bản tụ) sao cho các mặt đáy của nó song
song với các bản tụ. Cho biết khoảng cách giữa hai bản tụ là D.
a. Nối tụ với nguồn. Xác định điện tích của tụ sau khi đưa tấm thủy tinh vào và
năng lượng cần thiết để làm việc đó.
b. Ngắt tụ khỏi nguồn. Xác định hiệu điện thế của tụ sau khi đưa tấm thủy tinh vào
và năng lượng cần thiết để làm việc đó.
Bài 8: Giải lại bài 7 trong trường hợp ta thay tấm thủy tinh bằng 1 tấm kim loại có cùng kích thước.
Bài 9: Giải lại bài toán số 7 trong trường hợp tấm thủy
tinh có độ dày bằng khoảng cách giữa hai bản, và được đưa
một phần có độ dài x vào trong bản hình vuông cạnh a.