Chữa bài tập thực hành - Môn hệ thống thông tin quản lý | Đại học Kinh Tế Quốc Dân
Đại học Kinh tế Quốc dân với những kiến thức và thông tin bổ ích giúp các bạn định hướng và học tập dễ dàng hơn. Mời bạn đọc đón xem. Chúc bạn ôn luyện thật tốt và đạt điểm cao trong kì thi sắp tới.
Môn: Hệ thống thông tin quản lý (HTTTQL(120)_01) 80 tài liệu
Trường: Đại học Kinh Tế Quốc Dân 3 K tài liệu
Tác giả:
Preview text:
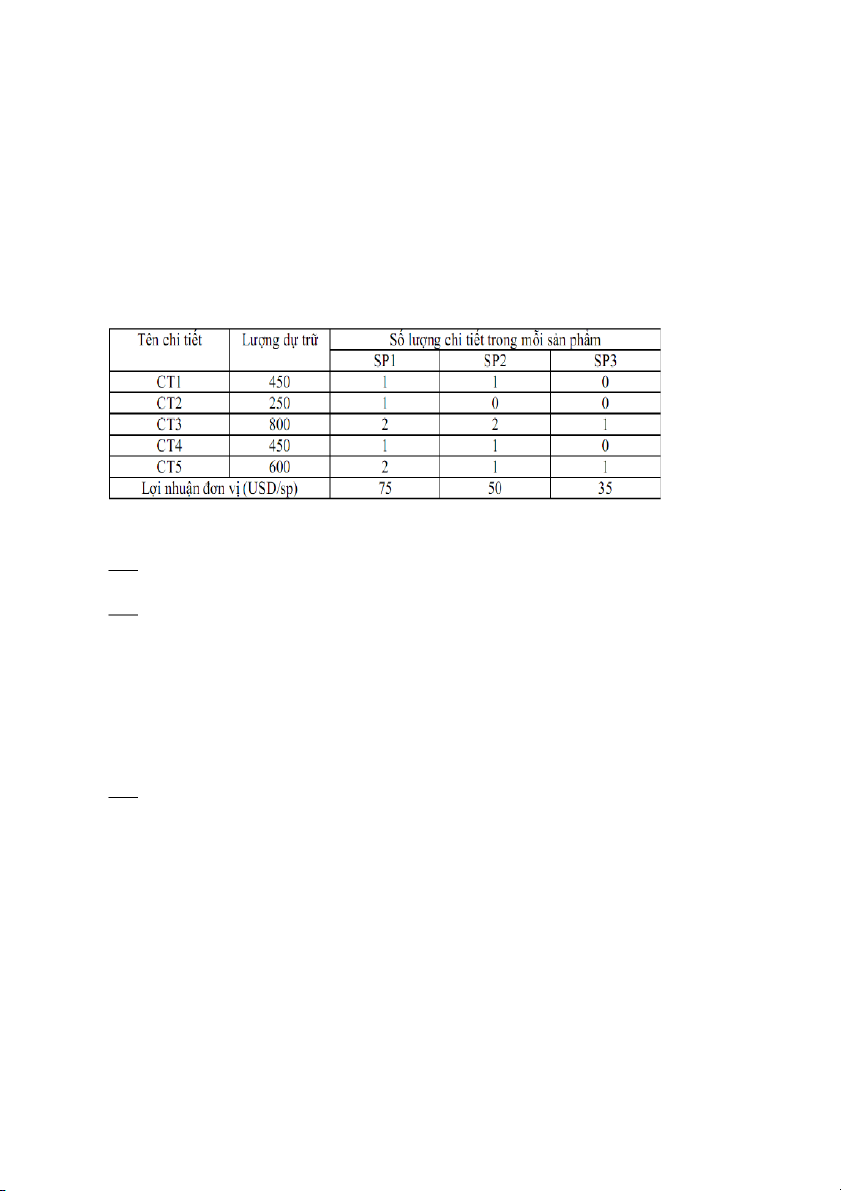
Một công ty sản xuất 3 loại sản phẩm ký hiệu lần lượt là SP1, SP2, SP3 bằng
cách lắp ráp từ các chi tiết tiêu chuẩn hóa ký hiệu CT1, CT2, CT3, CT4, CT5.
Số lượng mỗi chi tiết trong từng sản phẩm, số lượng dự trữ của từng loại chi
tiết và lợi nhuận đơn vị của từng loại sản phẩm cho trong bảng sau. Giả sử thị
trường có khả năng tiêu thụ hết số sản phẩm được sản xuất. Hãy tìm phương án
sản xuất để tối đa hóa lợi nhuận. Lợi nhuận ứng với phương án đó bằng bao nhiêu? F(min)= -10 khi X1=2, X2
B1: Hàm mục tiêu: F(x) = 75X1 + 50X2 + 35X3 ---> F(max) = ?
B2: Các điều kiện ràng buộc
X1, X2, X3 là số nguyên >=0 X1+X2 <= 450 X1 <= 250 2X1 +2X2+X3 <= 800 X1+X2 <= 450 2X1 + X2+X3 <= 600 B3
: F(max)= 25000 khi X1= 200, X2= 200, X3=0