Chương 1, Bài 3: Hàm Số Liên Tục - Tài Liệu Giải Tích 1. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.

lOMoAR cPSD| 58833082
TRƯỜNG ĐẠI HỌC GIAO THÔNG VẬN TẢI THÀNH PHỐ HỒ CHÍ MINH
KHOA CƠ BẢN – BỘ MÔN TOÁN
BÀI GIẢNG GIẢI TÍCH 1
CHƯƠNG I. GIỚI HẠN VÀ SỰ LIÊN
TỤC CỦA HÀM MỘT BIẾN
§ 3 . H m số liŒn t ục
GV: Đinh Tiến Dũng lOMoAR cPSD| 58833082 NỘI DUNG CHÍNH
 CÆc định nghĩa về h m số liŒn tục tại một điểm,
trŒn một khoảng, đoạn, nửa đoạn.  CÆc t nh
chất của h m số liŒn tục.
 Ph n loại điểm giÆn đoạn. lOMoAR cPSD| 58833082
§ 4 . Hm số liŒn t ục
1 . CÆc địnhnghĩa
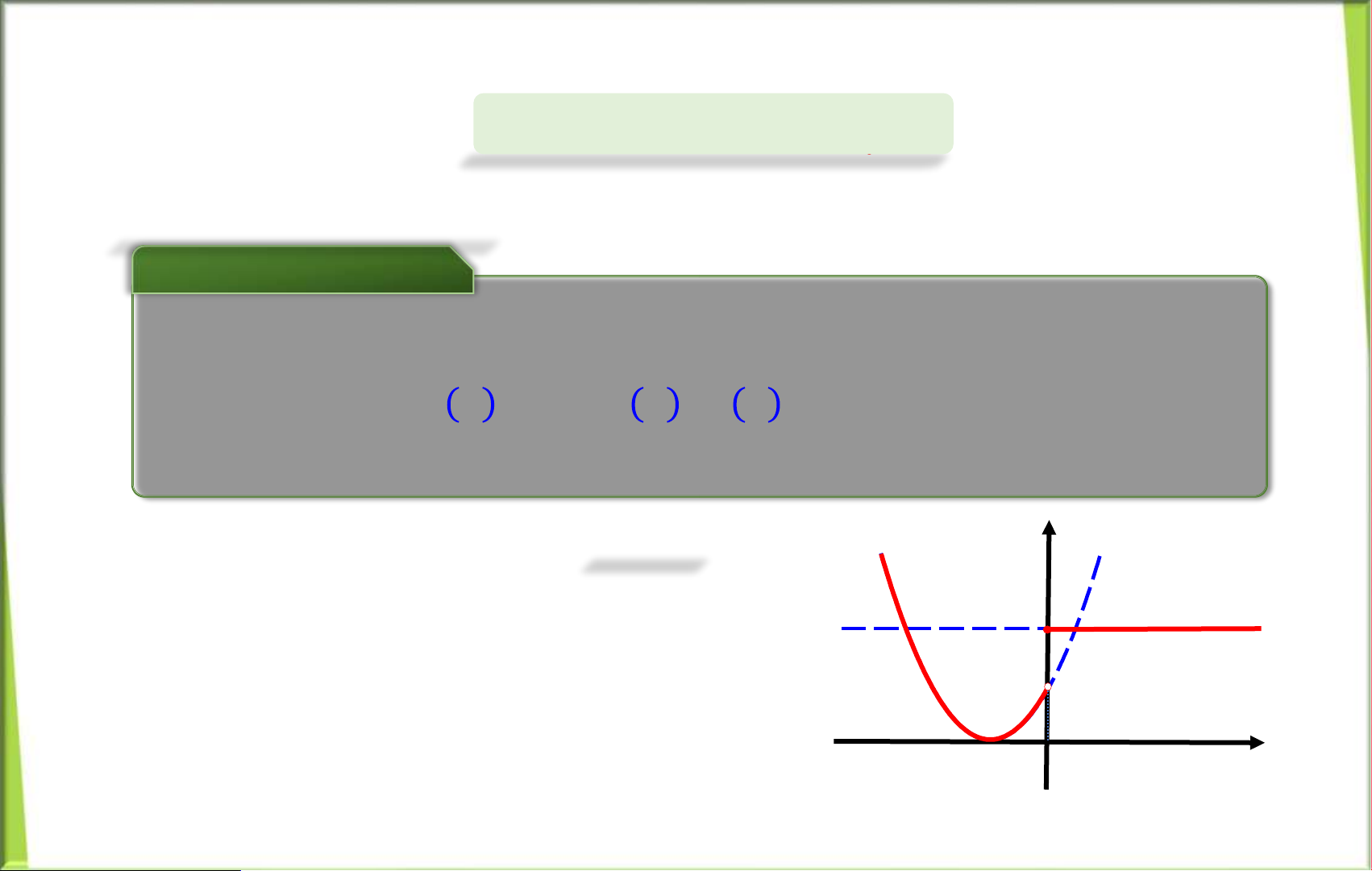
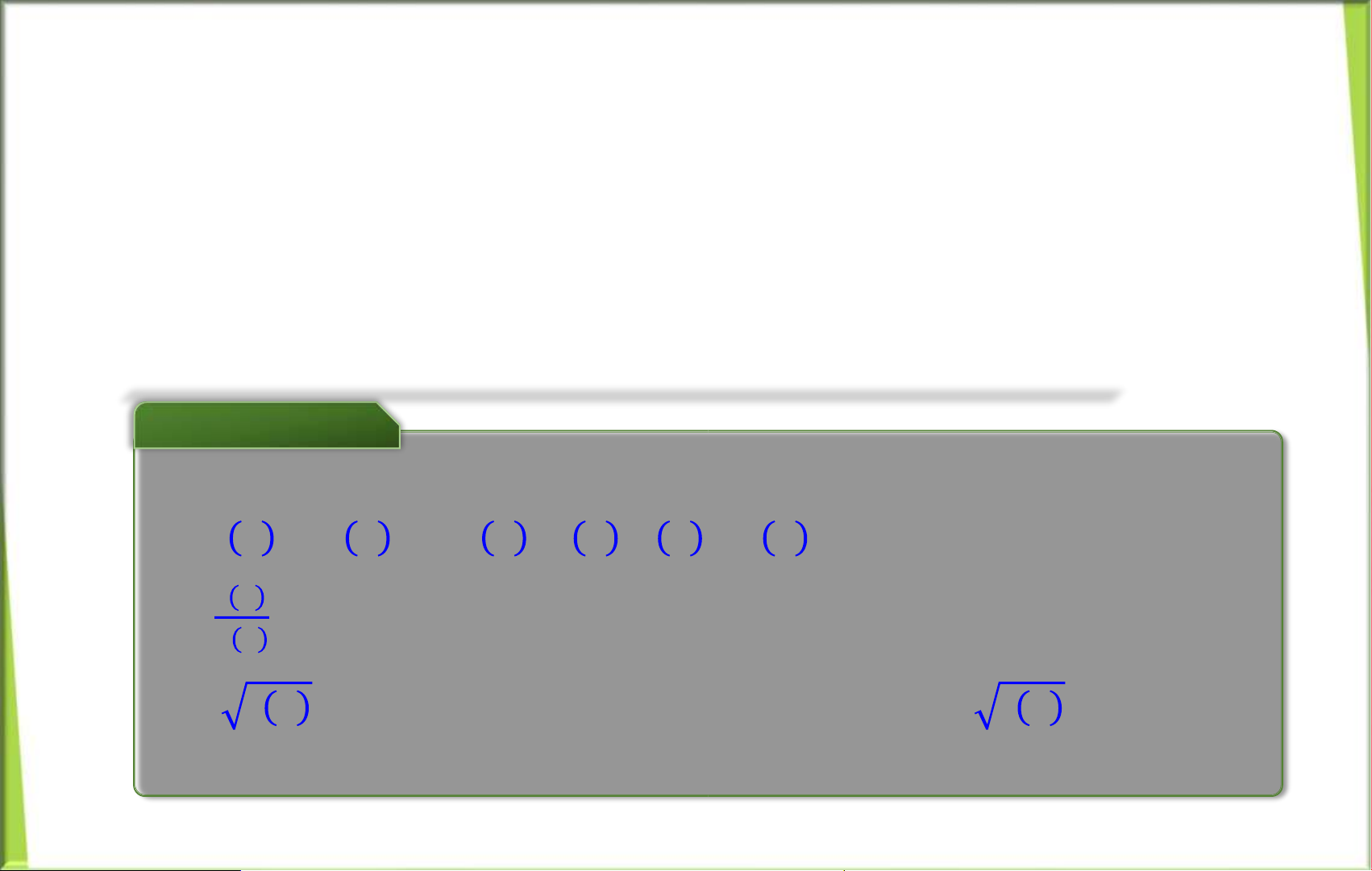
 V dụ mở đầu (𝑥+1) 2 ,𝑛ế𝑢𝑥<0 Cho hàm số: 𝑓(𝑥)=ቊ . Hãy 2 vẽ đồ thịhàm , 𝑛ế𝑢𝑥≥0 số. Tính lim 𝑓 lim 𝑓 𝑥 ; 𝑥;𝑓 0 . So sánhcác 𝑥→0 − + giá trịtrên để 𝑥→0 lý 𝑥 =0
giảinguyên nhân đồ thịhàm số bị giánđoạntại 0 . Giải 𝑦
Đồ thị hm số l hợpcủa hai đồ thị : 𝟐 𝑦= 2 𝑥 + 2 𝑥 +1 ,𝑥<0 𝟏 𝑦=2,𝑥≥0 𝟎 − 𝟏 𝑥 lOMoAR cPSD| 58833082
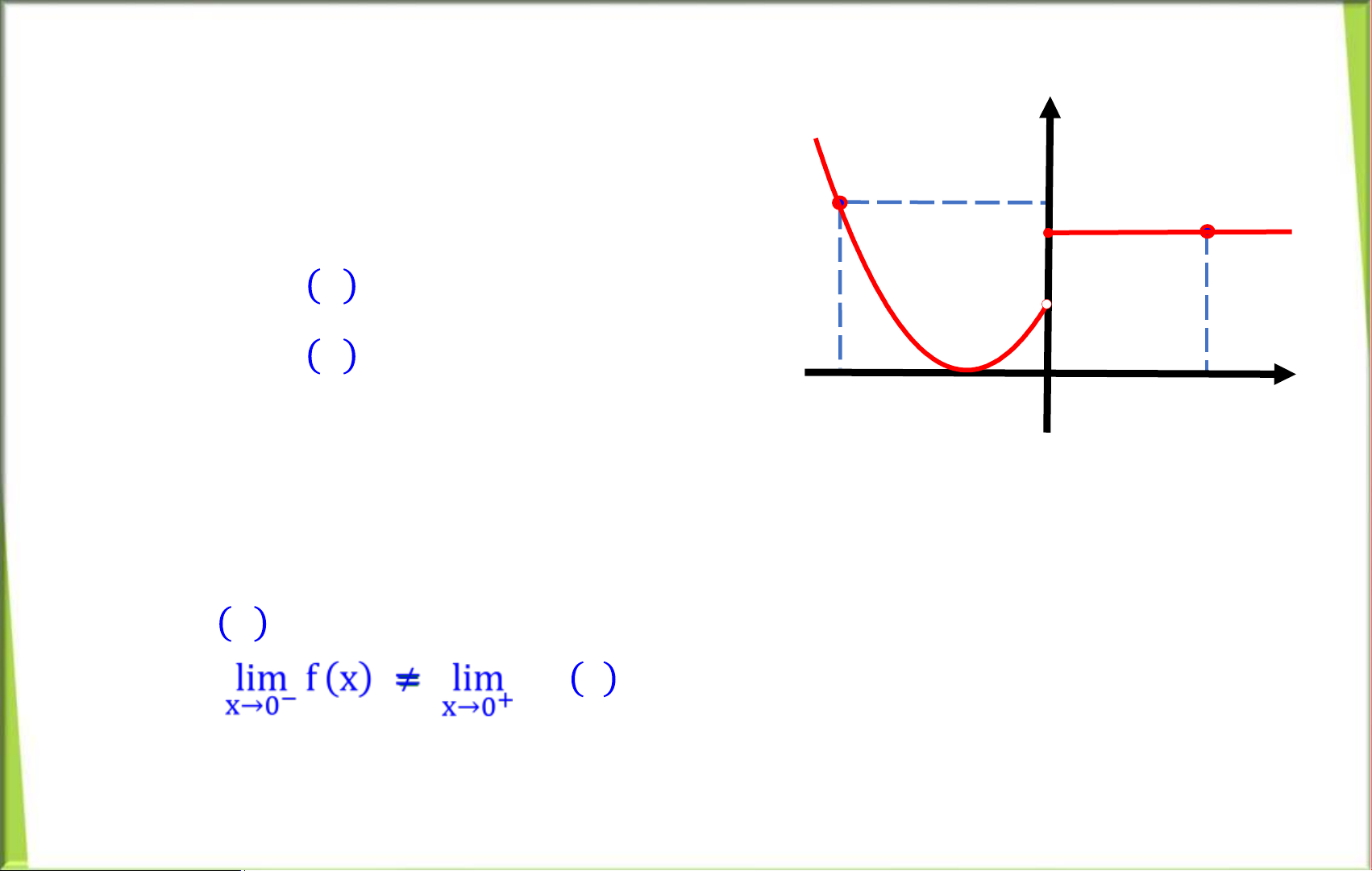
(𝑥 + 1)2, 𝑛ế𝑢 𝑥 < 0 𝑦 𝑓(𝑥) = ቊ 𝒇(𝒙)
12𝟐 , 𝑛ế𝑢 𝑥 ≥ 0 Ta c : 𝟐 ▪ 𝑥→0lim− 𝑓 𝑥 𝟏
==?𝑥→0lim−(𝑥 + 1)2 = 𝟏 𝒙 − 𝒙 𝟏 𝟎 𝑥
▪ lim+ 𝑓 𝑥 ==?𝑥→0lim+ 2 =12 = 122 𝑥→0
▪ 𝑓 0 ==?212 Suy ra f x = f(0)
Sự khÆc nhau của giới hạn trÆi v giới hạn phải tại 𝑥0=0 l nguyŒn nh
n dẫn đến sự đứt (giÆn đoạn) của h m số tại 𝑥0=0. lOMoAR cPSD| 58833082
 Hỏi: Cần điều chỉnh c ng thức h m số như thế n o để h m số liŒn tục tại
𝑥𝟎 = 𝟎?
NX: f(𝑥) liên tục tại 𝑥 = 𝑥0 ⇔ lim𝑥→𝑥0− 𝑓 𝑥 = lim+ 𝑓 𝑥 = 𝑓 𝑥0 . 𝑥→𝑥0 hay lim 𝑓 𝑥 = 𝑓 𝑥0 . 𝑥→𝑥0
Định nghĩa 1 điểm giÆn đoạn
▪ H m số f(𝑥) gọi l liŒn tục tại điểm 𝒙 của h m số f. 𝟎 
nếu f 𝑥Æc định trong một l n cận Tóm tắt: đ
(𝒙𝟎−𝛿; 𝒙𝟎 + 𝛿) v
lim 𝑓(𝑥) = 𝑓 𝒙𝟎 . n 𝑥→𝒙𝟎 𝐟(𝐱) 𝐟(𝒙𝟎)
▪ H m số f(𝑥) gọi l giÆn đoạn tại 𝒙𝟎 nếu
n kh ng liŒn tục tại 𝒙𝟎. Khi đó 𝒙𝟎 gọi l lOMoAR cPSD| 58833082
𝒙 → 𝒙𝟎 thì 𝐟(𝒙) → 𝒇(𝒙𝟎) ( 𝒙𝟎 𝒙 𝑥)0+ 𝛿 𝟎 𝑥0- 𝛿
f(𝑥) liên tục tại 𝒙𝟎 ⇔ lim 𝑓 𝑥 = 𝑓 𝑥0 𝑥→𝑥0 đn
Hay: f(𝑥) liên tục tại 𝒙𝟎 ⇔ 𝑥→𝑥lim0− 𝑓 (𝑥) = lim+ 𝑓 (𝑥) = 𝑓(𝑥0) 𝑥→𝑥0  Lưu :
• Nếu f liŒn tục tại 𝑥0 th đồ thị h m y=f(𝑥) liền nØt tại 𝑥0.
• f giÆn đoạn tại 𝑥0 nếu 𝑥→lim𝒙𝟎 𝑓(𝑥) kh ng tồn tại hữu hạn hoặc 𝑓 𝒙𝟎 kh ng
tồn tại ( f kh ng𝑥Æc định tại 𝑥0) hoặc hai giÆ trị ấy khÆc nhau. lOMoAR cPSD| 58833082 
Địnhnghĩa 2 đn f(𝑥 𝒙 ⇔ lim f 𝑥 𝒙 .
) liêntục phải tại 𝟎 = f 𝟎 𝑥→ + 𝒙 𝟎 đn f(𝑥 𝒙 ⇔ lim f .
) liêntụctráitại 𝟎 𝑥 = f 𝒙 𝟎 𝑥→ − 𝒙 𝟎
 Nhận xØt: f liŒn tục tại 𝒙𝟎 ⇔ f liŒn tục trÆi v liŒn tục phải tại 𝒙𝟎.
 Định nghĩa 3 đn
▪ f(𝑥) liŒn tục trŒn (𝒂; 𝒃) ⇔ f(𝑥) liŒn tục tại mọi điểm 𝒙𝟎 ∈ (𝑎; 𝑏). đn
▪ f(𝑥) liŒn tục trŒn (𝒂; 𝒃] ⇔ f(𝑥) liŒn tục trŒn (𝑎; 𝑏) đồng thời
liŒn tục trÆi tại 𝑏. đn lOMoAR cPSD| 58833082
▪ f(𝑥) liŒn tục trŒn [𝒂; 𝒃) ⇔ f(𝑥) liŒn tục trŒn (𝑎; 𝑏) đồng thời
liŒn tục phải tại a. đn
▪ f(𝑥) liŒn tục trŒn [𝒂; 𝒃] ⇔ f(𝑥) liŒn tục trŒn (𝑎; 𝑏) đồng thời
liŒn tục phải tại 𝑎 v liŒn tục trÆi tại b.  Ví dụ: 𝒚
Hàm 𝑓(𝑥) = arcsin𝑥 liên tục trên [−1; 1] vì: 𝝅 𝟐
• f liên tục tại mọi điểm thuộc (−1; 1);
• f không liên tục tại -1 mà chỉ liên tục phải -1 − 𝟏 𝟎 𝟏 𝒙 𝝅 − 𝟐 lOMoAR cPSD| 58833082
• f không liên tục tại 1 mà chỉ liên tục trái tại 1; Ngoài ra 𝑓(𝑥)
không 𝑥ác định ngoài [−1; 1] nên nó gián đoạn tại mọi 𝑥 không
thuộc [−1; 1]. 𝒚 = 𝒂𝒓𝒄𝒔𝒊𝒏𝒙
2. Tính chất của hàm số liên tục tại một điểm  Định l 1
Giả sử cÆc h m f(𝑥) v g(𝑥) cøng liŒn tục tại điểm 𝐱𝟎, khi đó:
a) f x ± g x , C. f x , f x . g x , [f x ]n liŒn tục tại điểm 𝐱𝟎; f x
b) g x liŒn tục tại điểm 𝐱𝟎 nếu 𝐠(𝐱𝟎) ≠ 0; lOMoAR cPSD| 58833082
c) n f x cũng liŒn tục tại 𝐱𝟎 nếu biểu thức n f x 𝑥Æc định trong một l
n cận n o đó của điểm 𝐱𝟎.
3. Tính liên tục của các hm số sơ cấp
 Định nghĩa 1 (Hàm sơ cấp cơ bản)
CÆc h m số đơn giản nhất khi kết hợp với cÆc phØp toÆn giải t ch ta
c thể x y dựng nŒn mọi h m sơ cấp, ta gọi chœng l cÆc h m sơ cấp
cơ bản. Hiện nay cÆc h m sơ cấp cơ bản đã được tạo lập trŒn hầu hết
cÆc thế hệ mÆy t nh bỏ tœi, phần mềm t nh toÆn v được giảng dạy
kỹ trong chương tr nh phổ th ng. Đó l :
1) Hàm số hằng f 𝑥 = 𝐶
𝑣ớ𝑖 𝑚ọ𝑖 𝑥 ∈ 𝑅 .
2) Hàm số luỹ thừa f 𝑥 = 𝑥𝛼 𝛼 ∈ 𝑅 .
3) Hàm số mũ 𝑦 = 𝑎𝑥; 0 < 𝑎 ≠ 1 . lOMoAR cPSD| 58833082
4) Hàm số logarit y = log𝑎𝑥, 0 < 𝑎 ≠ 1 .
5)Hàm lượng giác cơ bản: 𝑓(𝑥)=sinx, f(𝑥)=cosx, f(𝑥)=tanx,f(𝑥)=cotx.
6) Các hàm lượng giác ngược: 𝑓(𝑥)=arcsinx, f(𝑥)=arccosx,
f(𝑥)=arctanx, f(𝑥)=arccotx.
7) H m hyperbolic, h m hyperbolic ngược (Xem GT)
 Định nghĩa 2 (Hàm sơ cấp)
H m số sơ cấp l m số số được cho bằng một biểu thức giải t ch v
được x y dựng từ cÆc h m số sơ cấp cơ bản bằng một số phØp
toÆn số học cộng, trừ, nh n, chia, phØp lấy h m hợp.  V dụ 2 𝑥− 3 +2 x.tan (2 𝑥 ) lOMoAR cPSD| 58833082
▪ Hàm đa thức 𝑦 = 𝑥3 + 𝑥 − 3 l tổng-hiệu cÆc h m lũy thừa v h
m hằng nŒn n một h m số sơ cấp.
▪ H m số 𝑦 = sin( ⅇ𝑥) l hợp của h m y= sinx với h m 𝑦 = ⅇ𝑥 nŒn n cũng l h m sơ cấp.
▪ H m số 𝑦 = l h m sơ cấp. 𝑥−1
▪ Hàm số 𝑓 𝑥 = 𝑥 = ቊ 𝑥 , 𝑛ế𝑢 𝑥 ≥ 0 nhiều hơn một c ng
−𝑥 , 𝑛ế𝑢 𝑥 < 0
thức nŒn kh ng phải l h m số sơ cấp. lOMoAR cPSD| 58833082
 Định l 2 Cáchàm 𝑥
sốsơ cấpliêntụctrêntừngkhoảng ácđịnhcủa chúng. V 𝒚
dụ 1: XØt t nh liŒn t
ục cÆc h m số : 𝑥+1 a) (𝑥 4 2 ) 𝑥 𝑥 ( f
= −2 +1
b) g 𝑥 ) = 𝑥−1 𝟏 Giải a) 𝑥 𝑥 - 𝟏 𝟎 𝟏 𝒙
f( ) là hàm sơ cấp ác địnhtrên 𝒚 R= − ∞;∞ .Suy 𝑥 𝑅 ra f( ) liên tục trên . b) g(𝑥 𝑥 (−
) là hàm sơ cấp ác định trên ∞,1), (1 𝟏 ,+∞ ) . Vậy g(𝑥 ) liŒn t ục trŒn t ừngkhoảng (−∞,1),(1,+∞ 𝟏 𝟏 ) vgiÆn 𝑥=1 𝒙 đoạntại . - 𝟏 lOMoAR cPSD| 58833082 V 𝑥
dụ 2. XØt tnh liŒn
t ục của hm số sau tại điểm =0: 2 𝑒 𝑥
− 𝑐𝑜𝑠(2𝑥 ) ,𝑥≠0 𝑓(𝑥)=ቐ 𝑙𝑛(1+𝑥 2 ) . 3 𝑥 −1 ,𝑥 =0 Giải Đ𝑛
AD Định nghĩa: f(𝑥) liên tục tại 𝒙𝟎 ⇔ lim 𝑓 𝑥 = 𝑓 𝑥0 . 𝑥→𝑥0
▪ T𝑥đ: D = R. Ta có :f 0 = −1; ⅇx2 − cos(2x) ex2−1+1−cos2x x→0lim f (x)= x→0lim ln(1 + x2)= x→0lim x2 ex2−1 1−cos2x lOMoAR cPSD| 58833082 = lim + lim . x→0 x x→0 x VCB x2 2x2 = lim + lim = lim1 + lim2 = 3. x→0 x→0
▪ Ta thấy: lim f(x) ≠ f(0) ⇒ f giÆn đoạn tại điểm 𝑥=0. x→0
2 𝑠𝑖𝑛(1−𝑥 ) ,𝑥<1 1−𝑥 2 3 V 𝑓 3𝑥−2−1 .
dụ 3. Tm
m đê hm số 𝑥 = ,𝑥>1
liŒn t ục trŒn R 𝑥−1 2 𝑚, 𝑥=1 lOMoAR cPSD| 58833082 Giải ▪ T𝑥đ: D = R.
▪ TrŒn −∞; 1 và 1;+∞ thì 𝑓 𝑥 l h m sơ cấp nŒn f liŒn tục trŒn
từng khoảng ấy. Để f liŒn tục trŒn R th chỉ cần n liŒn tục tại x=1. ▪ Tại 𝑥 = 1: f(1) = 2m; 2sin(1−x) 2(1−x) 2 lim f x = lim = lim = lim = 1; x→1−x→1− 1−x2 x→1− 1−x2 x→1− 1+x
lim+f x =x→1lim+3 1+(3𝑥−𝟑)−1𝑥−1 VCB= x→1lim+13(3x−3)x−1 = x→1lim+ 11 = 1. x→1 lOMoAR cPSD| 58833082
▪ YCBT ⇔ limx→1− f(x) = limx→1+ f(x) = f(1) ⇔ 2m = 1 ⇔ m = 1/2. lOMoAR cPSD| 58833082
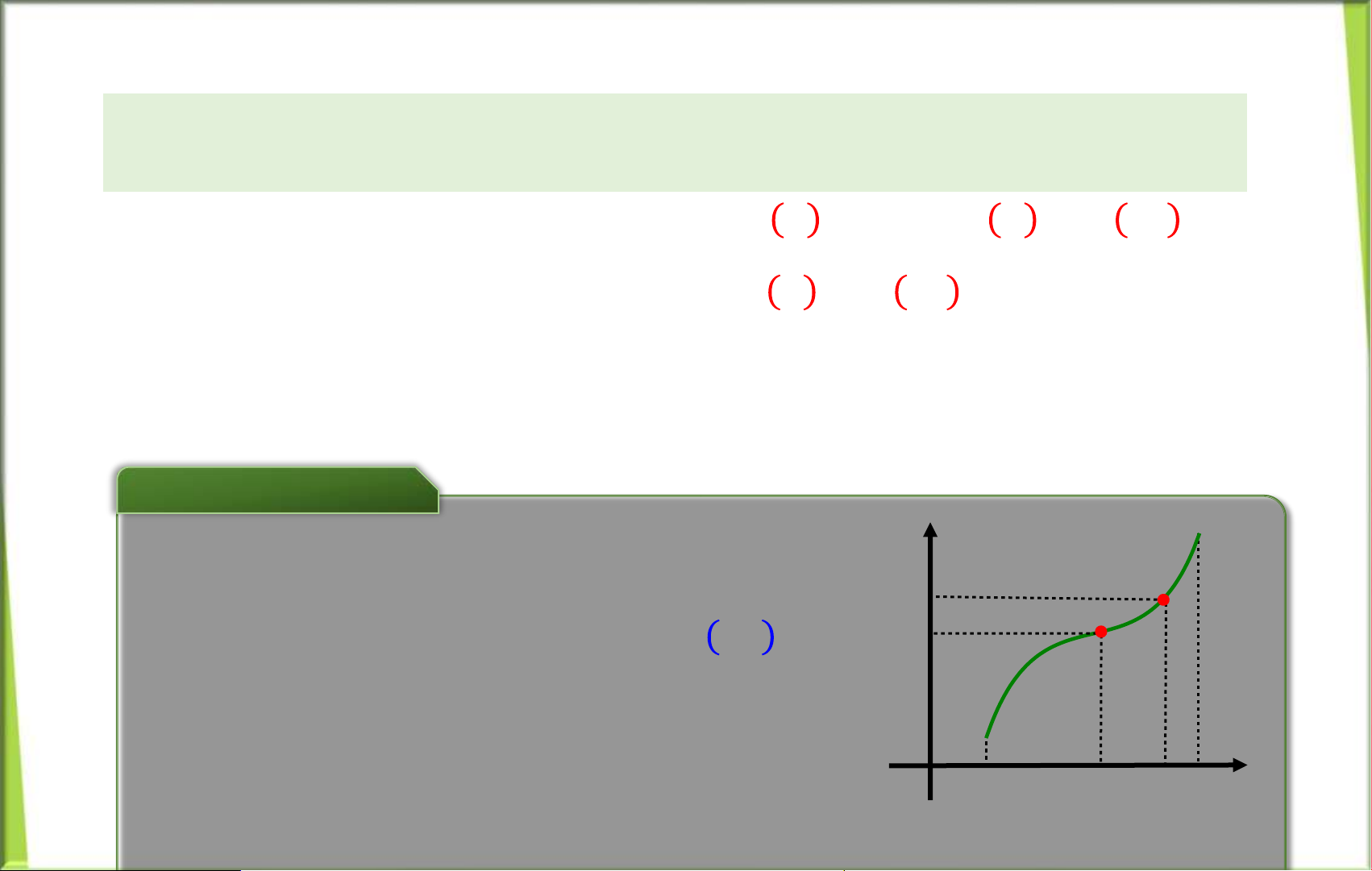
 Hệ quả 1: (Qui tắc tnh giới hạn hm sơ cấp ) Chof(x)l
hm sốsơ cấp .Khi đó : Nếu 𝑥 ( − + f(x)
Æ định trong một ln cậnbất kỳ 𝒙 𝟎 𝛿; 𝒙 𝟎 𝛿 ) củađiểm 𝐱 c 𝟎 th: 𝒙 𝟎 lim 𝑓(𝑥)=𝑓 𝒙 𝟎
//////////////// ( 𝑥→ .
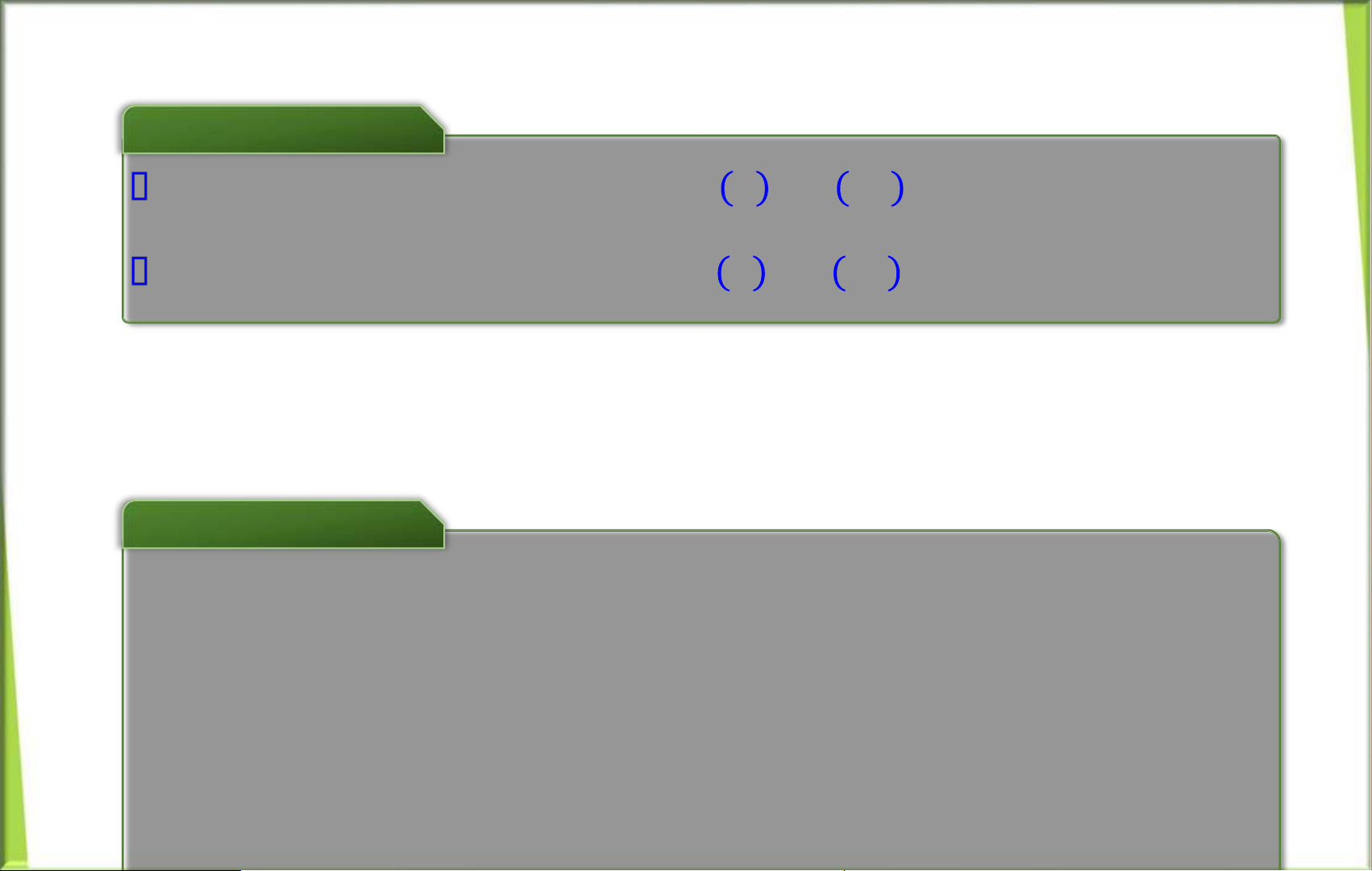
) ////////////// 𝒙 𝟎 𝒙 𝒙 + 𝛿 𝟎 − 𝛿 𝟎 Nếu [ ; + 𝛿 f(x)xÆc định trŒn
nửa ln cậnphải 𝒙 𝟎 𝒙 𝟎 ) th:
lim 𝑓(𝑥)=𝑓 𝒙 𝟎 .
/////////////////////////////////// [ 𝑥→ +
) ////////////// 𝒙 𝟎 𝒙 𝟎 𝒙 𝟎 + 𝛿 Nếu ( − ] f(x)xÆc định trŒn
nửa ln cận trÆi 𝒙 𝟎 𝛿; 𝒙 𝟎 th: lim 𝑓(𝑥)=𝑓 𝒙 𝟎 𝑥→ − . //////////////// 𝒙 ( 𝟎 ] 𝒙
////////////////////////////////// 𝟎 − 𝒙 𝛿 𝟎 lOMoAR cPSD| 58833082 VD. Cho h m f 𝑥 =
9 − 𝑥2. T nh lim𝒇(𝒙); lim𝒇(𝒙); nếu c . 𝑥→𝟏 𝑥→𝟑 Giải .𝟏 ]
Tập 𝑥Æc định D = [−3; 3]. /////////////////////[ ///////////////////// -3 3
lim𝑓 𝑥 = lim 9 − 𝒙2 = 9 − 𝟏 = 𝟖. 𝑥→1𝑥→1 lOMoAR cPSD| 58833082
𝑥→3lim−𝑓 𝑥 = 𝑥→3lim− 9 − 𝑥2 = 9 − 𝟑2 = 𝟎. Hàm số không xác định
khi 𝑥 > 3 nên không tồn tại lim+𝑓(𝑥) vậy 𝑥→3
lim𝒇(𝒙) cũng không tồn tại. 𝑥→𝟑
 Hệ quả 2. (Quy tắc tính giới hạn hàm số hợp liŒn tục)
Giả sử lim 𝑔 𝒙 = 𝒂 v h m 𝑓(𝑥) liŒn tục tại x = 𝒂. Khi đó: 𝑥→𝒙𝟎
lim 𝑓[𝑔 𝑥 ] = 𝑓( lim g(x)) = 𝑓 𝒂 . 𝑥→𝒙𝟎 𝑥→𝒙𝟎