




























































Preview text:
lOMoAR cPSD| 40425501
TRƯỜNG ĐẠI HỌC GIAO THÔNG VẬN TẢI THÀNH PHỐ HỒ CHÍ MINH
KHOA CƠ BẢN – BỘ MÔN TOÁN
Năm học 2023 -2024 BÀI GIẢNG
XÁC SUẤT THỐNG KÊ
VÀ XỬ LÝ SỐ LIỆU THỰC NGHIỆM
ThS. Đinh Tiến Dũng lOMoAR cPSD| 40425501
Giới thiệu học phần
Học phần n y cung cấp cÆc kiến thức về l thuyết xÆc suất, biến ngẫu nhiŒn v
luật ph n phối xÆc suất, l thuyết mẫu, cÆc b i toÆn ước lượng tham số, cÆc b i
toÆn kiểm định giả thuyết thống kŒ; b i toÆn ph n t ch tương quan v ph n t ch
hồi quy. Qua đó rŁn luyện cho sinh viŒn cÆc kỹ năng về tư duy, đánh giÆ được
khả năng xảy ra của một số cÆc biến cố ngẫu nhiŒn c thể xảy ra trong cÆc b i
toÆn thực tế; ứng dụng kiến thức về biến ngẫu nhiŒn v thống kŒ toÆn học cũng
như nghiŒn cứu được sự phụ thuộc của cÆc biến số để giải quyết một số vấn đề c
liŒn quan đến số liệu thống kŒ, l thuyết dự bÆo trong cÆc lĩnh vực giÆo dục,
sản xuất, dinh dưỡng, kinh tế, kỹ thuật… lOMoAR cPSD| 40425501
TÀI LIỆU THAM KHẢO
• [1] Bộ m n ToÆn, B i giảng XÆc suất thống kŒ v
ứng dụng, Trường đại
Học GTVT TP.HCM, 2021
• [2] LŒ Sĩ Đồng, XÆc suất thống kŒ v
ứng dụng, NXB Khoa học Kỹ thuật, 2011.
• [3] Nguyễn Cao Văn, Trần ThÆi Ninh, NXB Khoa học Kỹ thuật, 1996.
• [4] Đặng Høng Thắng, Thống kŒ v ứng dụng, NXB GiÆo dục, 1999.
• [5] Đào Hữu Hồ, XÆc suất thống kŒ, NXB Đại học Quốc gia H Nội, 2006.
• [6] Aczel, Amir D, and Jayavel Sounderpandian, Complete Business
Statistics, McGraw-Hill/Irwin Boston, 1999.
Giới thiệu giảng viŒn lOMoAR cPSD| 40425501
• ThS: Đinh Tiến Dũng
• SĐT: 0793112122 (Zalo)
• Mail: dung.dinh@ut.edu.vn CHƯƠNG I
BIẾN CỐ VÀ XÁC SUẤT CỦA BIẾN CỐ NỘI DUNG CHÍNH
§ 1. Bổ túc về giải tích tổ hợp.
§ 2. Phép thử ngẫu nhiên và biến cố.
§ 3. Xác suất của biến cố.
§ 4. Một số công thức xác suất quan trọng. lOMoAR cPSD| 40425501
CHƯƠNG I. BIẾN CỐ VÀ XÁC SUẤT CỦA BIẾN CỐ
§1. Bổ túc về giải tích tổ hợp
1.1. Các quy tắc đếm
• Quy tắc cộng: Nếu c m cÆch chọn đối tượng x,n cÆch chọn đối
tượng y v nếu mỗi cÆch chọn đối tượng x kh ng trøng với bất kỳ
cÆch chọn đối tượng y n o th c m+n cÆch chọn đối tượng “ x hoặc y ".
• Tổng quÆt: Nếu c 𝑛𝑖 cÆch chọn đối tượng 𝑥𝑖(𝑖 = 1, … , 𝑘), v nếu
cÆch chọn đối tượng 𝑥𝑖 kh ng trøng với bất kỳ cÆch chọn đối tượng
𝑥𝑗 n o th c 𝑁 = 𝑛1 + ⋯ + 𝑛𝑘 cÆch chọn đối tượng “ 𝑥1 hoặc 𝑥2 … hoặc 𝑥𝑘 ". lOMoAR cPSD| 40425501
• Quy tắc nh n: Nếu một c ng việc được chia l m 𝑘 giai đoạn, giai
đoạn thứ 𝑖(𝑖 = 1, … , 𝑘) c 𝑛𝑖 cÆch thực hiện, th sẽ c 𝑁 = 𝑛1 … 𝑛𝑘
cÆch thực hiện xong to n bộ c ng việc.
• Tổ hợp: Tổ hợp chập 𝑘 của 𝑛 phần tử l một nh m gồm 𝑘 phần tử kh
ng c thứ tự, đôi một khÆc nhau được lấy từ 𝑛 phần tử đã cho. Số
cÆc tổ hợp 𝑛 chọn 𝑘 l :
𝐶𝑛𝑘 = 𝑘!(𝑛−𝑘)!𝑛! .
• Chỉnh hợp: Chỉnh hợp chập 𝑘 của n phần tử l một nh m gồm 𝑘 phần
tử c thứ tự, đôi một khÆc nhau được lấy từ 𝑛 phần tử đã cho. Số
cÆc tổ hợp 𝑛 chọn 𝑘 l : lOMoAR cPSD| 40425501
𝐴𝑘𝑛 = (𝑛−𝑘𝑛! )!. 1.2. Ví dụ
Một lớp c 10 nam v 20 nữ. Hỏi c bao nhiŒu cÆch a)
Chọn một người (nam hoặc nữ)?
b) Chọn một ban cÆn sự gồm 3 nam v 2 nữ? Giải
a) Đối tượng 𝑥 là “nam”: có 10 cách chọn, đối tượng 𝑦 là “nữ”: có
20 cách chọn, và chọn nam thì không chọn nữ và ngược lại. Do
đó theo quy tắc cộng sẽ có:
N = 10 + 20 = 30 (cách chọn một người − nam hoặc nữ).
b) Số cách chọn 3 nam từ 10 nam là: C .
Số cách chọn 2 nữ từ 15 nữ là: C . lOMoAR cPSD| 40425501
Theo quy tắc nhân sẽ có: N = C 3 2 10 ⋅ C15 = 12600 cách chọn một
ban cán sự lớp gồm 3 nam và 2 nữ.
§2. Phép thử ngẫu nhiên và biến cố
2.1. Khái niệm về phép thử ngẫu nhiên
PhØp thử ngẫu nhiŒn (gọi tắt l phØp thử) l một khÆi niệm cơ bản
của bộ m n xÆc suất. Kh ng thể định nghĩa, ta m tả bởi cÆc v dụ sau: V dụ 1:
• Gieo 1 đồng tiền c n đối v đồng chất để xem kết quả mặt
ph a trŒn xuất hiện sấp hay mặt ngửa.
• Gieo 1 con xœc xắc c n đối v đồng chất để xem kết quả mặt
ph a trŒn xuất hiện số chấm n o. lOMoAR cPSD| 40425501
• Rœt ngẫu nhiŒn lần lượt 3 lÆ b i trong một bộ b i để xem
kết quả được lÆ b i n o.
Mỗi h nh động trŒn đều c nhiều kết quả ngẫu nhiŒn đồng khả năng
xảy ra. Ta gọi đó l phØp thử ngẫu nhiŒn (gọi tắt l phØp thử). V dụ 2:
• Thả một vật từ trŒn cao để xem kết quả vật rơi theo hướng n o.
• Quan sÆt xem mặt trời mọc ở hướng đông hay t y.
• Đun nước đến nhiệt độ 1000𝐶 để xem kết quả xảy ra.
Mỗi h nh động hoặc th nghiệm ở trŒn lu n biết trước c đúng 1 kết quả
nŒn n kh ng phải l phØp thử ngẫu nhiŒn. lOMoAR cPSD| 40425501
Khi thực hiện một phØp thử ngẫu nhiŒn, ta kh ng thể biết trước được
kết quả tuy vậy ta c thể liệt kê được cụ thể hoặc biểu diễn tất cả cÆc kết
quả c thể xảy ra của phØp thử.
2.2. Khái niệm không gian mẫu
Định nghĩa: Tập hợp cÆc kết quả c thể xảy ra của một phØp thử được
gọi l kh ng gian mẫu của phØp thử. K hiệu: .
Ph n loại: C 2 loại kh ng gian mẫu
- Kh ng gian mẫu rời rạc: l tập hợp hữu hạn hay v hạn đếm được cÆc phần tử.
- Kh ng gian mẫu liŒn tục: l tập hợp v hạn kh ng đếm được. Ví dụ 1
T m kh ng gian mẫu của phØp thử gieo 1 đồng tiền c n đối v đồng chất. lOMoAR cPSD| 40425501 Giải:
K hiệu 𝑆 l mặt sấp, 𝑁 l mặt ngửa của
đồng tiền. Kh ng gian mẫu của phØp
thử sẽ l : = 𝑆, 𝑁 . lOMoAR cPSD| 40425501 Ví dụ 2
M tả khnggian mẫucủa phØp thử gieo một conxœc xắc cn đối v đồngchất . Giải:
Với số chấmđượcbiểudiễnbằng cÆ số tự
nhiŒn,khnggian mẫucủa phØp c
thử l một
tậprời rạc : ={1;2 ;3;4;5; 6} . Ví dụ 3
M tả khnggian
mẫucủa phØp thửđothời gian sốngcủamột con
chip điện tử . Giải:
Thời gian được t nh bằng số thực kh ng m nŒn kh ng gian mẫu của phØp
thử l : = 0; ∞ . Đây l kh ng gian mẫu liŒn tục. lOMoAR cPSD| 40425501 Ví dụ 4
Viết khnggian mẫucủa phØp thử gieo đồngthời haiconxœc xắc cn
đối v đồngchất . Giải: = {(𝑖; 𝑗)|𝑖 = 1; 6 và 𝑗 = 1; 6}.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 1 2 3 4 5 6 1
(1; 1) (1; 2) (1; 3) (1; 4) (1; 5) (1; 6) 2 (2; 1) (2; 4) (2; 2) (2; 3) (2; 5) (2; 6) 3 (3; 3) (3; 1) (3; 4) (3; 2) (3; 5) (3; 6) 4 (4; 1) (4; 4) (4; 2) (4; 3) (4; 5) (4; 6) 5
(5; 1) (5; 2) (5; 3) (5; 4) (5; 5) (5; 6) 6 (6; 1)
(6; 2) (6; 3) (6; 4) (6; 5) (6; 6)
2.3. Các khái niệm về biến cố:
Trong một phép thử với không gian mẫu :
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
▪ Biến cố ngẫu nhiên là một tập con của không gian mẫu . Biến cố
ngẫu nhiên gọi tắt là biến cố. Ký hiệu biến cố: A,B,C,D,…
▪ Mỗi phần tử của biến cố gọi là một kết quả thuận lợi của biến cố.
Trái lại, ta gọi là các kết quả không thuận lợi.
▪ Nếu biến cố chỉ chứa không quá một phần tử thì ta gọi đó là biến cố sơ cấp.
▪ Hai biến cố bằng nhau về tập hợp gọi là hai biến cố tương đương.
▪ Hai biến cố có khả năng xuất hiện như nhau gọi là hai biến cố đồng khả năng.
▪ Tập ∅ đgl biến cố không thể.
▪ Tập đgl biến cố chắc chắn.
Chœ : Với mọi biến cố 𝐴, ta lu n c 𝐴 ⊂ Ω, ∅ ⊂ 𝐴, 𝐴 ⊂ 𝐴.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 V dụ
XØt phØp thử gieo một con xœc xắc
c n đối v đồng chất lŒn mặt b n. Biến cố
Biểu diễn tập hợp
𝐴𝑖(𝑖 = 1,6) là biến cố được mặt 𝑖 chấm
𝐿 là biến cố được mặt có số
chấm lẻ; 𝑃 là biến cố được
𝐴 là biến cố được mặt có số chấm ≤ 6
mặt có số chấm nguyên tố. 𝐴1 = 1 ; 𝐴2 = 2 ; 𝐴3 = 3 ;
𝐵 là biến cố được mặt có số chấm ≥ 7 𝐴 4 = 4 ; 𝐴5 = 5 ; 𝐴6 = 6
Các biến cố sơ cấp đồng khả 𝐶 năng
là biến cố được mặt có số chấm chẵn
𝐴 = 1; 2; 3; 4; 5; 6 = 𝛺
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Biến cố chắc chắn. 𝑃 = 2; 3; 5 𝐵 = ∅
Các biến cố ngẫu nhiên
đồng khả năng.
Biến cố không thể 𝐶 = 2; 4; 6 𝐿 = 1; 3; 5
2.4. Các phép toán trên biến cố
Cho 𝐴,𝐵, 𝐴1, … , 𝐴𝑛 l cÆc biến cố trong một phØp thử. Khi đó:
Tập 𝑨 𝑩 đgl hợp hay tổng của cÆc biến cố A v B. C n k hiệu l
A+B, n xảy ra khi v chỉ khi c t nhất một biến cố A hoặc B xảy ra.
Tổng quÆt: Tổng 𝐴 = 𝐴1 + ⋯ + 𝐴𝑛 (hay 𝐴 = 𝐴1 ∪ 𝐴2 ∪ ⋯ ∪ 𝐴𝑛 )
xảy ra khi v chỉ khi c t nhất một trong 𝑛 biến cố 𝐴1, … , 𝐴𝑛 xảy ra.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Tập 𝑨 𝑩 đgl giao hay t ch của cÆc biến cố A v B. C n k hiệu l
𝐴𝐵, n xảy ra khi v chỉ khi cả 𝐴 v 𝐵 đồng thời xảy ra.
Tổng quÆt: T ch 𝐴 = 𝐴1𝐴2 … 𝐴𝑛 (hay 𝐴 = 𝐴1 ∩ 𝐴2 ∩ ⋯ ∩ 𝐴𝑛 ) xảy
ra khi v chỉ khi cả 𝑛 biến cố đó cøng xảy ra.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 V dụ
PhØp thử gieo một con xœc xắc c n đối v đồng chất lŒn mặt b n. K hiệu:
• 𝐴𝑖(𝑖 = 1, … , 6) l biến cố được mặt 𝑖 chấm;
• 𝐴 l biến cố được mặt c số chấm ≤ 6;
• 𝐵 l biến cố được mặt c số chấm ≥ 7;
• 𝐶 l biến cố được mặt c số chấm chẵn;
• 𝐿 l biến cố được mặt c số chấm lẻ;
• 𝑃 l biến cố được mặt c số chấm l số nguyŒn tố.
𝐶 = 𝐴2 + 𝐴4 + 𝐴6 Khi đó: 𝑃 = 𝐴 2 + 𝐴3 + 𝐴5 𝐿 = 𝐴1 + 𝐴3 + 𝐴5 𝑃𝐶 = 𝐴2
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 𝑃𝐿 = 𝐴3 + 𝐴5 𝐿𝐶 = ∅ v 𝐿 + 𝐶 = Ω
𝐴𝑖𝐴𝑗 = ∅, 𝑖 ≠ 𝑗
𝐴1 + 𝐴2 + 𝐴3 + 𝐴4 + 𝐴5 + 𝐴6 = Ω
2.5. Quan hệ giữa các biến cố
Hai biến cố 𝑨 v 𝑩 được gọi l xung khắc nếu chœng kh ng đồng thời
xảy ra khi thực hiện phØp thử, nghĩa l 𝐴𝐵 = ∅. Tổng quÆt:
▪ Nh m 𝒏 biến cố 𝑨𝟏, … , 𝑨𝒏 được gọi l xung khắc từng đôi (hay
đôi một xung khắc) nếu hai biến cố khÆc nhau bất kỳ trong 𝑛 biến
cố l xung khắc với nhau, nghĩa l 𝐴𝑖𝐴𝑗 = ∅, ∀𝑖 ≠ 𝑗.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
▪ Nh m 𝒏 biến cố 𝑨𝟏, … , 𝑨𝒏 được gọi l nh m biến cố đầy đủ v xung
khắc từng đôi nếu trong phØp thử bắt buộc c đúng một biến cố
xảy ra, nghĩa l 𝐴1 + ⋯ + 𝐴𝑛 = 𝛺 v 𝐴𝑖𝐴𝑗 = ∅, ∀𝑖 ≠ 𝑗.
Hai biến cố 𝑨 v 𝑩 được gọi l đối lập nhau nếu trong phØp thử c
đúng một biến cố xảy ra, nghĩa l : 𝐴 + 𝐵 = 𝛺; 𝐴𝐵 = ∅. Biến cố đối lập
của biến cố 𝐴 k hiệu l 𝐴᪄. Ví dụ
PhØp thử gieo một con xœc xắc c n đối v đồng chất lŒn mặt b n. K hiệu:
• 𝐴𝑖(𝑖 = 1, … , 6) l biến cố được mặt 𝑖 chấm;
• 𝐴 l biến cố được mặt c số chấm ≤ 6;
• 𝐵 l biến cố được mặt c số chấm ≥ 7;
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• 𝐶 l biến cố được mặt c số chấm chẵn;
• 𝐿 l biến cố được mặt c số chấm lẻ;
• 𝑃 l biến cố được mặt c số chấm l số nguyŒn tố. Ta c :
• 𝐴1, 𝐴2, 𝐴3, 𝐴4, 𝐴5, 𝐴6 là nhóm đầy đủ và xung khắc từng đôi;
• 𝐶 = 𝐿,᪄ 𝐿 = 𝐶᪄ ;
• 𝑃 v 𝐿 là hai biến cố không xung khắc nhau.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 2.6. Các tí
nh chất của biến cố 1) ഥ ᪄ 𝐀=𝐀; 9) 𝐀⋅∅=∅; 2) 𝑨.𝑨=𝑨;
10) 𝐀+𝐁=𝐁+𝐀; 3) 𝑨+𝑨=𝑨; 11) 𝐀+ 𝐁+𝐂 = 𝐀+𝐂 + 𝐁; 4) 𝑨.𝜴=𝑨;
1 2 ) 𝐀⊂𝐁⇒𝐀+𝐁=𝐁,𝐀𝐁 = 𝐀; 5) 𝑨+∅=𝑨; 1 3 ) 𝐀 𝐁+𝐂 = 𝐀𝐁 + 𝐀𝐂 6) 𝑨.𝑩=𝑩.𝑨;
1 4 ) 𝐀+ 𝐁.𝐂 = 𝐀+𝐁. 𝐀+𝐂; ᪄ ᪄ 7) 𝑨+ ᪄ 𝑨=𝜴;
15) 𝐀 𝟏 …𝐀 𝐧 = 𝐀 𝟏 + ⋯ + 𝐀 𝐧; ᪄ ᪄ 8) 𝑨+𝜴=𝜴;
16) 𝐀 𝟏 + ⋯+𝐀 𝐧 = 𝐀 𝟏 … 𝐀 𝐧;
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
§3. Xác suất của biến cố
3.1. Khái niệm chung về xác suất
▪ Để so sÆnh hay đánh giÆ một hay nhiều biến cố về khả năng xuất
hiện trong một phØp thử tương ứng, người ta gÆn cho mỗi biến cố
một con số thuộc đoạn [0; 1] sao cho với hai biến cố bất kỳ, biến cố n o
c khả năng xuất hiện nhiều hơn th gÆn số lớn hơn, cÆc biến cố đồng
khả năng xuất hiện th gÆn cøng một số.
▪ Số gÆn cho biến cố A, k hiệu l P(A), được gọi l xÆc suất
(Probability) của biến cố A. Ví dụ 1 Xét phép thử 2
gieo đồng xu. Gọi A là biến cố được mặt sấp thì
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 𝑃(𝐴) = 50% = .
3.2. Định nghĩa cổ điển về xác suất
XÆc suất của biến cố 𝐴 trong một phØp thử với kh ng gian mẫu 𝜴, k
hiệu 𝑷(𝑨) v được t nh theo c ng thức sau: 𝒏𝑨
Số phần tử của biến cố 𝑨 𝑷(𝑨)= = .
𝒏𝜴 Số phần tử của không gian mẫu 𝜴
Hạn chế của định nghĩa cổ điển:
Chỉ t nh được xÆc suất của biến cố trong phØp thử c kh ng gian mẫu
rời rạc v hữu hạn. 25×105 525
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) 9880 1976 lOMoAR cPSD| 40425501 Ví dụ
Chọn ngẫu nhiên 3 sinh viên từ một lớp học có 25 nam và 15 sinh viên
nữ. Gọi A là biến cố chọn được một nam và hai nữ. Tính 𝑃(𝐴)=? 𝐶151 ×𝐶152 𝑃(𝐴) = 3 = = . 𝐶40
3.3. Định nghĩa hình học về xác suất
XÆc suất của biến cố A trong một phØp thử m cÆc phần tử của kh
ng gian mẫu 𝛺 c thể biểu diễn bởi cÆc điểm trong kh ng gian, được định nghĩa bởi c ng thức: 𝝁 𝑨
Độ đo của tập hợp 𝑨 𝑷(𝑨) = = . 𝝁 𝜴
Độ đo của tập hợp 𝜴
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chœ : Theo lý thuyết cơ bản về Độ đo
Độ đo trên đường thẳng thực R:
▪ Chiều dài đoạn thẳng gọi là độ đo của đoạn thẳng đó.
▪ Tập hợp các điểm rời rạc có độ đo bằng 0.
Độ đo trong mặt phẳng 𝑹𝟐:
▪ Diện tích hình phẳng gọi là độ đo của hình phẳng đó.
▪ Các đường (cong hoặc thẳng) diện tích bằng 0 nên độ đo bằng 0.
Độ đo trong không gian 𝑹𝟑
▪ Thể tích của một hình khối gọi là độ đo của hình khối đó. ▪ Các đường,
các mặt có thể tích bằng 0 nên độ đo bằng 0. Ví dụ 1
Hai người hẹn nhau tại một địa điểm xÆc định v o khoảng 19 đến
20 giờ. Người đến trước sẽ đợi người kia 15 phœt, sau đó nếu kh
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
ng gặp th sẽ đi khỏi điểm hẹn. Hªy t m xÆc suất để hai người gặp
nhau, nếu biết rằng mỗi người c thể đến chỗ hẹn trong khoảng thời
gian quy định một cÆch ngẫu nhiŒn v kh ng tøy thuộc v o người kia đến v o lœc n o.
Giải: Gọi 𝐴 l biến cố: “Hai người gặp nhau” v
𝑥, 𝑦 tương ứng l thời gian người thứ nhất,
người thứ hai đến điểm hẹn. Ta c : • 𝛺 = 𝑥, 𝑦
∈ 𝑅2: 19 ≤ 𝑥, 𝑦 ≤ 20 ⇒ 𝜇 𝛺 = 1. • A = 𝑥, 𝑦 ∈ 𝛺: 𝑥 − 𝑦 ≤ 1 1 1 = 𝑥,𝑦 ∈𝛺:− ≤𝑥−𝑦≤ 4 4 4
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ⇒ 𝜇 𝐴. Vậy 𝑃 𝐴 = 𝜇 𝐴 =. 𝜇 𝛺 Ví dụ 2
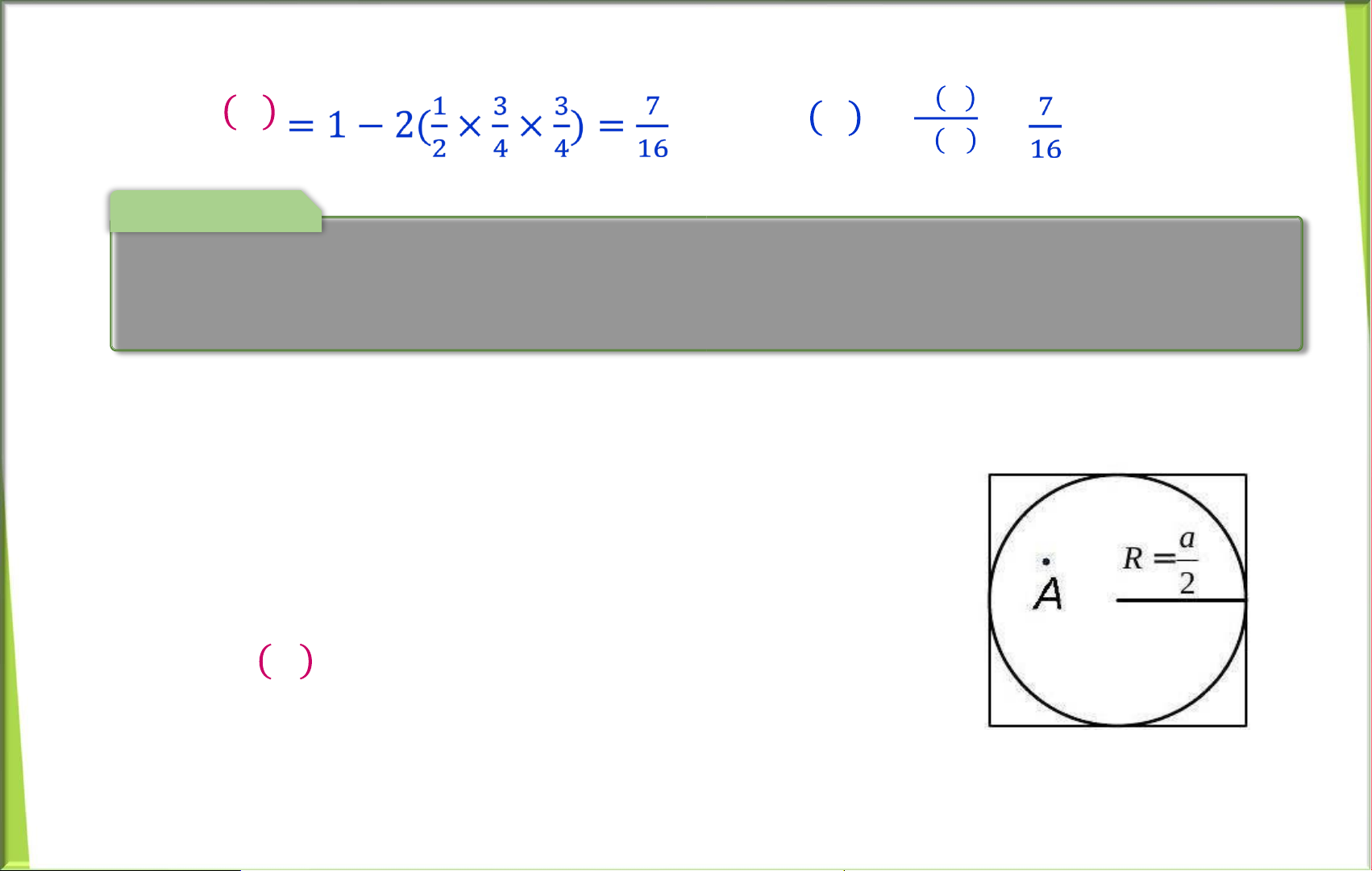
Chọn ngẫu nhiŒn một điểm A trong h nh vu ng cạnh a. T nh xÆc
suất để A thuộc h nh tr n nội tiếp h nh vu ng trŒn. Giải:
Gọi B l biến cố: “Điểm A thuộc h nh tr n nội tiếp h nh vuông”. Ta c :
• 𝛺 l hình vuông cạnh bằng a
⇒ 𝜇 𝛺 = 𝑎2 (diện tích hình vuông).
• B l hình tròn nội tiếp hình vuông
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
⇒ 𝜇 𝐵 = 𝜋(𝑎/2)2 (diện tích hình tròn bán kính 𝑎/2). 𝜇 𝐵 𝜋(𝑎/2)2 𝜋
• Vậy 𝑃 B = 𝜇 𝛺 = 𝑎2 = 4.
3.4. Định nghĩa xác suất theo thống kê Giả sử trong 𝑛 phØp thử
với điều kiện giống nhau, biến cố 𝐴 xuất
𝑚 hiện 𝑚 lần. Khi đó tỷ số 𝑓𝑛(𝐴)
= 𝑛 được gọi l tần suất xuất hiện biến cố 𝐴 trong 𝑛 lần thử. XÆc
suất của biến cố 𝐴 l :
𝑷(𝑨) = lim 𝑓𝑛(𝐴). 𝑛→∞
Trong thực tế, ta thường chọn 𝑃(𝐴) ≈ 𝑓𝑛(𝐴) khi 𝑛 đủ lớn.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ
a) Khi kiểm tra ngẫu nhiŒn 100 sản phẩm ở một l h ng, người ta
phÆt hiện ra 7 phế phẩm.
Gọi 𝐴 l biến cố sản phẩm được kiểm tra l phế phẩm th xÆc suất 𝑃(𝐴) = = 7%.
Ví dụ (tt)
b) Để nghiŒn cứu khả năng xuất hiện mặt sấp (S) khi tung một đồng
xu, người ta tiến h nh tung đồng xu nhiều lần v thu được kết quả cho ở bảng sau:
Người tung Số lần xuất Tần suất Số lần tung 𝑺 𝒇(𝑺)
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Đồng xu hiện mặt
Buyffon 4040 2048 0.5069 Pearson 12000 6019 0.5016 Pearson 24000 12012 0.5005
Khi số lần tung đồng xu tăng lên thì tần suất 𝑓(𝑆) cũng dần dần hội tụ về con số 0,5.
Vậy xác xuất để 1 lần tung được mặt sấp là 0,5.
Bá tước Buffon (1707-1788)
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
BÆ tước Buffon hay đúng hơn l BÆ tước của xứ
Buffon l một nh BÆc học người PhÆp, tŒn thật của ng l
Georges Louis Leclerc. ng sinh ng y 07 thÆng 09 năm 1707
tại Monbard, C te d’Or, PhÆp v mất v o ng y 16 thÆng 04 năm 1788 tại Paris.
Buffon nổi tiếng với vai tr l một nh tự nhiŒn học nhưng
thời trẻ ng c niềm đam mŒ với toÆn học mặc dø khi đó ng
đang theo đuổi tham vọng của cha m nh l trở th nh một luật sư.
Từ năm 1739, Buffon trở th nh người quản l của Vườn Thực Vật Ho ng Gia
(Jardin du Roi) v ng l m việc ở đây cho đến cuối đời. TÆc phẩm nổi tiếng nhất của
Buffon l Histoire Naturelle (Lịch Sử Tự NhiŒn, 1749 – 1785) tr nh b y mọi vấn đề
về thiŒn nhiŒn từ con người, động vật, thực vật tới khoÆng vật. }
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Karl Pearson (1857 – 1936)
Karl Pearson l một nh toÆn học v thống kŒ sinh học
người Anh. ng đã được ghi nhận với việc thiết lập kỷ lục thống kŒ toÆn học.
ng th nh lập khoa thống kŒ đại học đầu tiŒn trŒn
thế giới tại Đại học College London v o năm 1911, v đóng
g p đáng kể cho lĩnh vực sinh trắc học v kh tượng học.
Pearson cũng l người ủng hộ chủ nghĩa xª hội Darwin v
thuyết ưu sinh, v suy nghĩ của ng l một v dụ về những g ng y nay được m tả l
chủ nghĩa ph n biệt chủng tộc trong khoa học. Pearson l người bảo hộ v l người
viết tiểu sử của Ng i Francis Galton. ng đã biŒn tập v ho n thiện cả Common
Sense of the Exact Sciences (1885) của William Kingdon Clifford v History of the
Theory of Elasticity của Isaac Todhunter, Tập. 1 (1886–1893) v Tập. 2 (1893),
sau cÆi chết của họ.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
3.5 . Các tính chất cơ bản của xác suất
1) 0 ≤𝑃(𝐴)≤ 1 với mọi biến cố 𝐴 . 2) 𝑃 Ω =1 , 3) 𝑃(∅)=0 . 4) 𝐴⊂𝐵 𝑃(𝐴)≤𝑃(𝐵) Nếu th . 5) 𝐴 𝑃(𝐴)+𝑃( Với mọi biến cố , ta lun c: 𝐴)=1 ҧ
§4. Công thức xác suất
4.1. Công thức cộng xác suất
Công thức cộng cho 2 biến cố: 𝑃(𝐴 + 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴𝐵) Đặc
biệt: Nếu 𝐴, 𝐵 là hai biến cố xung khắc thì: 𝐴𝐵 = 𝜙 nŒn:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 𝑃 𝐴 + 𝐵 = 𝑃 𝐴 + 𝑃 𝐵
Công thức cộng cho 3 biến cố: 𝑃 𝐴 + 𝐵 + 𝐶 = 𝑃 𝐴 + 𝑃 𝐵
+ 𝑃 𝐶 − 𝑃 𝐴𝐵 − 𝑃 𝐴𝐶 − 𝑃 𝐵𝐶 + 𝑃 𝐴𝐵𝐶 .
Đặc biệt: Nếu 𝐴, 𝐵, 𝐶 là ba biến cố xung khắc từng đôi một thì: 𝑃 𝐴 + 𝐵 + 𝐶 = 𝑃 𝐴 + 𝑃 𝐵 + 𝑃 𝐶
Tổng quát: Công thức cộng cho n biến cố:
𝑃 ∑𝑛𝑖=1𝐴𝑖 = ∑𝑛𝑖=1𝑃 𝐴𝑖 − ∑𝑖<𝑗 𝑃 𝐴𝑖𝐴𝑗 + ∑𝑖<𝑗<𝑘 𝑃 𝐴𝑖𝐴𝑗𝐴𝑘 + ⋯ +
(−1)𝑛−1𝑃 𝐴1 … 𝐴𝑛 .
Đặc biệt: Nếu 𝐴𝑖 𝑖 = 1, … . , 𝑛 xung khắc từng đôi thì:
𝑃 𝐴1 + ⋯ + 𝐴𝑛 = 𝑃 𝐴1 + ⋯ + 𝑃 𝐴𝑛
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ
Từ một hộp có 6 viên bi màu đỏ và 8 viên bi màu xanh cùng hình
dáng bên ngoài, lấy ngẫu nhiên ra 4 viên bi. Tính xác suất để:
a) C đúng 3 viŒn bi cøng m u trong 4 viŒn bi lấy ra.
b) C kh ng quÆ 3 bi đỏ trong 4 viŒn bi lấy ra. Giải:
Gọi 𝐷𝑖 là biến cố có 𝑖 bi đỏ và (4 − 𝑖) bi xanh.
𝑋𝑖 là biến cố có 𝑖 bi xanh v 4 − 𝑖 bi đỏ, với 𝑖 = 0,1,2,3,4.
a) Gọi 𝐴 là biến cố lấy được 3 viên bi cùng màu thì 𝐴 = 𝐷3 + 𝑋3. 𝑥𝑘 𝐶63 × 8 6 × 𝐶83
𝑃(𝐴) = 𝑃 𝐷3 + 𝑋3 = 𝑃 𝐷3 + 𝑃 𝑋3 = 𝐶4 + 𝐶144 = 1001
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 14
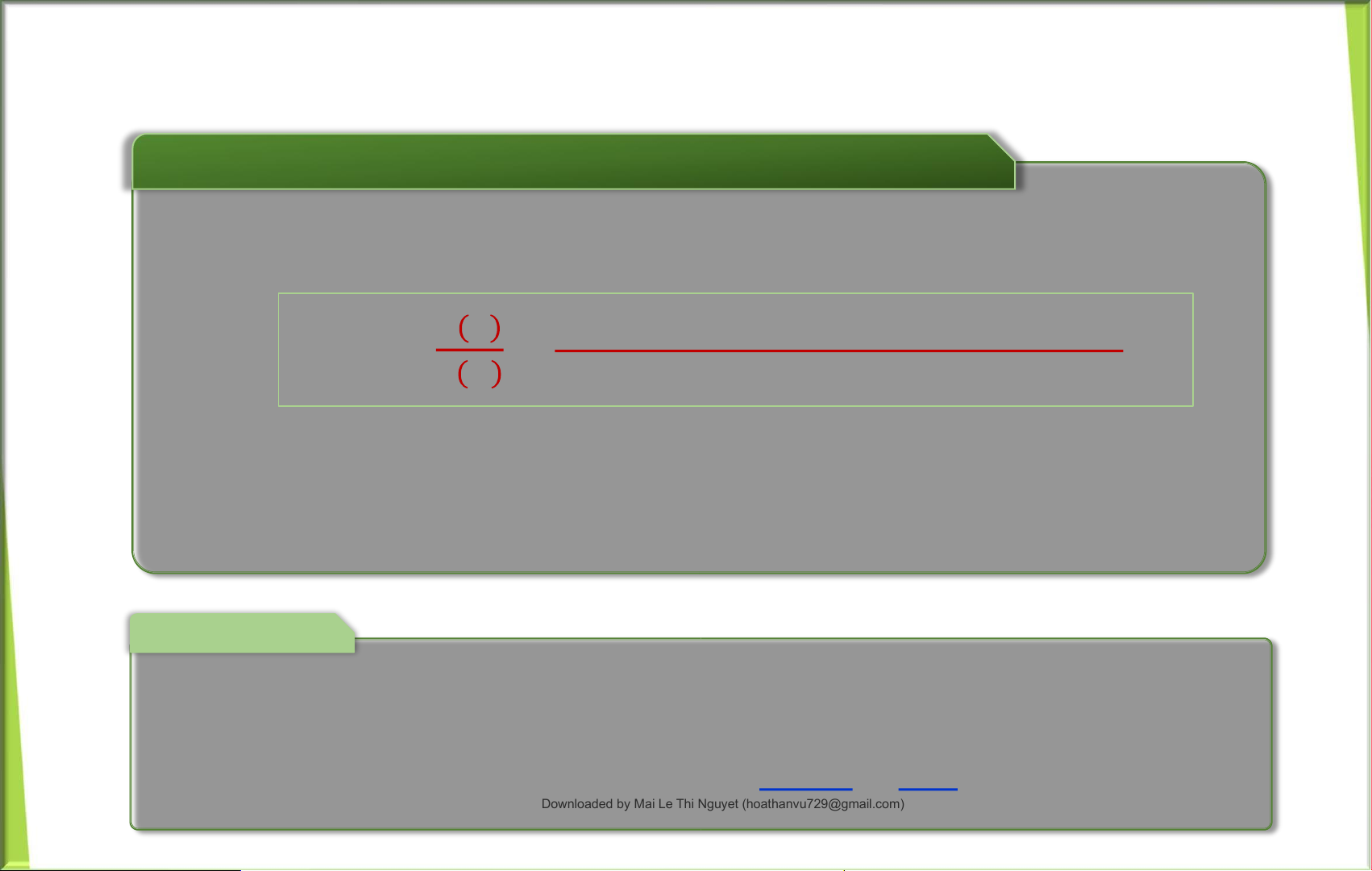
b) Gọi 𝐵 là biến cố có không quá 3 bi đỏ th 𝐵᪄ là biến cố có hơn 3 bi
đỏ, tức là 𝐵 = 𝐷᪄ 4
𝑃(𝐵) = 𝑃᪄ 𝐷4 = 𝐶𝐶14464 =
⇒ 𝑃(𝐵) = 1 − 𝑃(𝐵) =᪄ .
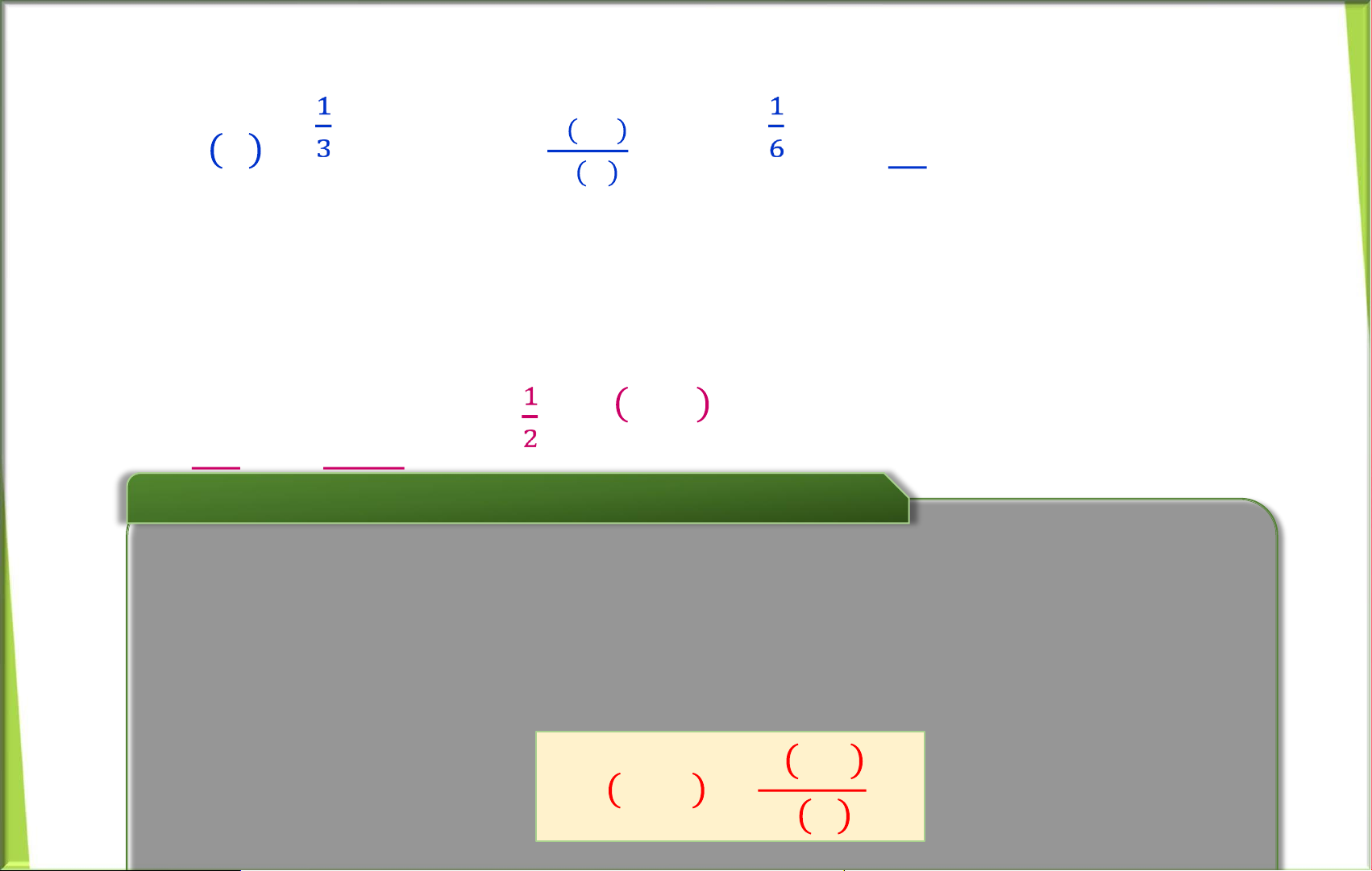
Giới thiệu về Xác suất có điều kiện B i toÆn:
Một chiếc tœi đựng 3 viŒn bi gồm 1 bi đỏ, 1 bi xanh v 1 bi v ng. Cậu bØ
lần lượt lấy mỗi lần một viŒn bi kh ng ho n lại. Hỏi xÆc suất lấy được
viŒn bi xanh sau khi lấy được viŒn bi đỏ l bao nhiŒu? Gọi A l biến cố:
”lần đầu lấy được viŒn bi đỏ”; B l biến cố: “lần sau lấy được bi xanh”.
Khi đó A.B l biến cố: “Lần đầu lấy được bi đỏ v lần sau lấy được bi xanh”. Ta thấy:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 𝑛 𝐴𝐵 1.1 𝑃 𝐴 = ; 𝑃(𝐴𝐵) = = = . 𝑛 𝛺 3.2
P(B) kh ng thể t nh v kh ng biết trong tœi c n 2 bi m u g !
Giả sử cố A đã xảy ra tức l cậu bØ đã lấy ra 1 viŒn bi đỏ, trong tœi chỉ
c n hai viŒn bi m u xanh v v ng. Khi đó xÆc xuất của B với điều kiện A
1 6Τ 𝑃(𝐴𝐵) đã xảy ra l : 𝑃 𝐵/𝐴 = = 1Τ3 = 𝑃(𝐴) .
4.1. Công thức xác suất có điều kiện
Giả sử c hai biến cố A, B v biến cố A xảy ra sẽ ảnh hưởng đến khả
năng xảy ra biến cố B sau đó. XÆc suất xảy ra biến cố B với điều
kiện l biến cố A đã xảy ra tức l 𝑃(𝐴) > 0 được gọi l xÆc xuất của B
với điều kiện A. Được k hiệu l 𝑃(𝐵/𝐴) được định nghĩa l :
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
𝑃 𝐴𝐵 𝑃 𝐴 𝑃 𝐵/𝐴 = .
Tương tự nếu 𝑃(𝐵) > 0, ta c xÆc suất của 𝐴 với điều kiện 𝐵: 𝑃 𝐴𝐵 𝑃 𝐴/𝐵 = . 𝑃 𝐵 *
Nhận xØt: 𝑃 𝐴 /𝐵ഥ = 1 − 𝑃(A/B). Ví dụ 1
Một lớp học c 96 sinh viŒn, gồm 46 nam v 50 nữ. Trong đó c 23
sinh viŒn giỏi gồm c 13 nam v 10 nữ. Chọn ngẫu nhiŒn một sinh viŒn trong lớp.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
a) T nh xÆc suất để chọn được sinh viŒn giỏi.
b) Biết rằng sinh viŒn chọn được l sinh viŒn giỏi. T nh xÆc suất để sinh viŒn đó l nữ. Giải:
a) Gọi A l biến cố “chọn được sinh viŒn giỏi”. Ta c : 𝑃 𝐴 = .
b) Gọi B l biến cố “chọn được sinh viŒn nữ”. Khi đó:
AB là biến cố “Chọn được SV vừa giỏi vừa là nữ” nên ta có: 𝑃 𝐴𝐵 = . 10 P(𝐴𝐵)
Ta cần tính: 𝑃 𝐵/𝐴 = = = . 𝑃 𝐴 96
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ 2
Một l h ng c 100 sản phẩm, trong đó c 5 phế phẩm. Lấy ngẫu nhiŒn kh
ng ho n lại lần lượt ra 2 sản phẩm. T m xÆc suất để: a) Lần đầu lấy được ch nh phẩm.
b) Lần đầu lấy được ch nh phẩm v lần sau lấy được phế phẩm.
c) Lần thứ hai lấy được phế phẩm, biết rằng lần thứ nhất đã lấy được ch nh phẩm. Giải:
Gọi 𝐴𝑖 là biến cố lần thứ 𝑖 lấy được chính phẩm,
𝐵𝑖 là biến cố lần thứ 𝑖 lấy được phế phẩm với 𝑖 = 1,2.
a) Xác suất để lần đầu lấy được chính phẩm: 𝑃 𝐴1 = .
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
b) Xác suất để lần đầu lấy được chính phẩm và lần sau lấy được phế phẩm: P(𝐴1. 𝐵2) = .
c) Xác suất để lần thứ hai lấy được phế phẩm, biết rằng lần thứ nhất lấy
được chính phẩm: 𝑃 𝐵2/𝐴1 = P(𝐴1. 𝐵2) = 5/99. 𝑃 𝐴 1
4.3. Công thức nhân xác suất, biến cố độc lập
a) Khái niệm biến cố độc lập:
• Hai biến cố 𝐴 v 𝐵 được gọi l độc lập nhau nếu sự xuất hiện hay kh
ng xuất hiện của biến cố n y kh ng phụ thuộc v o sự xuất hiện hay
kh ng xuất hiện của biến cố kia, nghĩa l :
𝑃(𝐴/𝐵) = 𝑃(𝐴) và 𝑃(𝐵/𝐴) = 𝑃(𝐵)
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Hệ 3 biến cố 𝐴, 𝐵, 𝐶 gọi l độc lập từng đôi nếu 𝐴 độc lập với 𝐵, B
độc lập với C v C độc lập với A.
• Hệ 𝑛 biến cố 𝐴1, … , 𝐴𝑛 gọi l độc lập to n phần nếu mỗi biến cố độc
lập với cÆc biến cố c n lại v độc lập với t ch bất kỳ của hai hay
nhiều biến cố c n lại.
• Từ định nghĩa trŒn ta thấy hệ độc lập to n phần th độc lập từng
đôi nhưng điều ngược lại n i chung l kh ng đúng. Khi n i họ 𝐴1,
𝐴2, … , 𝐴𝑛 độc lập m kh ng n i g thŒm th ta hiểu đó l độc lập to n phần. Ví dụ
a) XØt phØp thử: Bạn An gieo một đồng xu v đồng thời bạn B nh gieo một con xœc xắc.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Gọi A l biến cố: “An gieo được mặt sấp” th 𝑃(𝐴) = 1/2. • Gọi B l
biến cố: “Bình gieo được mặt 6 chấm” th 𝑃(𝐵) = 1/6.
Rı r ng xÆc suất của biến cố B kh ng thay đổi khi biến cố A xảy ra hay kh
ng xảy ra v ngược lại. Vậy hai biến cố A v B độc lập nhau. b) Trong b nh
c 4 quả cầu trắng v 5 quả cầu xanh.
• Lấy ngẫu nhiŒn từ trong b nh ra 1 quả cầu. Gọi A l biến cố “lấy
được quả cầu xanh”. Hiển nhiŒn P(A) = 5/9.
• Quả cầu lấy ra được bỏ lại v o b nh v tiếp tục lấy 1 quả cầu. Gọi B l
biến cố “lần thứ 2 lấy được quả cầu xanh”, khi đó P(B) = 5/9.
Rı r ng xÆc suất của biến cố B kh ng thay đổi khi biến cố A xảy ra hay kh
ng xảy ra v ngược lại. Vậy hai biến cố A v B độc lập nhau.
b) Công thức nhân xác xuất:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Từ công thức xác suất có điều kiện, ta có các công thức nhân sau:
Công thức nhân cho 2 biến cố bất kỳ:
𝑃 𝐴𝐵 = 𝑃 𝐵 . 𝑃 𝐴/𝐵
Đặc biệt: Nếu A,B là các biến cố độc lập thì: 𝑃 𝐴𝐵 = 𝑃 𝐴 . 𝑃(𝐵)
Công thức nhân cho 3 biến cố bất kỳ: 𝑃 𝐴𝐵𝐶
= 𝑃 𝐴 . 𝑃 𝐵/𝐴 . 𝑃(𝐶/𝐴𝐵)
Đặc biệt: Nếu A,B,C là các biến cố độc lập toàn phần thì:
𝑃 𝐴𝐵𝐶 = 𝑃 𝐴 . 𝑃 𝐵 . 𝑃(𝐶) Tổng
quát: Công thức nhân cho n biến cố bất kỳ: 𝑃 𝐴1 … 𝐴𝑛
= 𝑃 𝐴1 . 𝑃 𝐴2/𝐴1 . 𝑃 𝐴3/𝐴1𝐴2 … 𝑃 𝐴𝑛/𝐴1 … 𝐴𝑛−1
Đặc biệt: Nếu hệ các biến cố 𝐴1, … , 𝐴𝑛 độc lập toàn phần thì
𝑃 𝐴1𝐴2 … 𝐴𝑛 = 𝑃 𝐴1
⋅ 𝑃 𝐴2 … 𝑃 𝐴𝑛
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ 1
Một doanh nghiệp c 3 t hoạt động độc lập. Từ tần suất xe hỏng
người ta c được xÆc suất để trong một ng y cÆc t bị hỏng lần lượt
l 0,1; 0,15 v 0,2. T m xÆc suất để trong một ng y: a) Cả 3 t bị hỏng;
b) C t nhất một t bị hỏng.
Giải: Gọi A,B,C lần lượt l cÆc biến cố trong một ng y t thứ nhất, thứ hai v thứ ba bị hỏng.
𝑃(𝐴) = 0,1; 𝑃(𝐵) = 0,15; 𝑃(𝐶) = 0,2
a) Gọi D l biến cố: “Cả 3 t bị đều bị hỏng trong một ngày” th
𝐷 = 𝐴 ∩ 𝐵 ∩ 𝐶 = 𝐴. 𝐵. 𝐶
V A,B,C độc lập: 𝑷 𝑫
= 𝑷 𝑨 . 𝑷 𝑩 . 𝑷 𝑪
= 𝟎, 𝟏 × 𝟎, 𝟏𝟓 × 𝟎, 𝟐 = 𝟎, 𝟎𝟎𝟑.
b) Gọi E l biến cố: “C t nhất một t bị hỏng trong ng y” th
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
𝐸 = 𝐴 ∪ 𝐵 ∪ 𝐶 = 𝐴 + 𝐵 + 𝐶 𝑃 𝐸 = 𝑃 𝐴 + 𝑃 𝐵
+ 𝑃 𝐶 − 𝑃 𝐴𝐵 − 𝑃 𝐴𝐶 − 𝑃 𝐵𝐶
+ 𝑃 𝐴𝐵𝐶 = 0,388.
CÆch giải khÆc:
Gọi E l biến cố: “C t nhất một t bị hỏng trong ng y” th
Eഥ l biến cố: “Không c t n o bị hỏng trong ng y” nŒn:
E =ഥA ∩ഥB ∩ഥ C =ഥ A .ഥ B .ഥ Cഥ. Ta c :
𝑃 𝐸 = 1 − 𝑃 𝐸ഥ= 1 − 𝑃 𝐴 .ഥ 𝐵 .ഥ 𝐶ഥ
= 1 − 𝑃 𝐴ഥ . 𝑃 𝐵 . 𝑃ഥ𝐶ഥ
= 1 − 0,9 × 0,85 × 0,8 = 0,388.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ 2
C hai l h ng, mỗi l chứa 10 sản phẩm. L I c 3 sản phẩm lỗi. L II c 4
sản phẩm lỗi. Chọn ngẫu nhiŒn từ mỗi l ra 2 sản phẩm.
a) T nh xÆc suất để trong 4 sản phẩm chọn ra c 2 sản phẩm đạt
chuẩn v 2 sản phẩm lỗi.
b) Giả sử đã chọn được 2 sản phẩm đạt chuẩn v 2 sản phẩm lỗi.
T nh xÆc suất chọn được 1 sản phẩm đạt chuẩn v 1 sản phẩm lỗi từ l II. Giải:
• Gọi 𝐴𝑖(𝑖 = 0,1,2) là biến cố có 𝑖 sản phẩm đạt chuẩn và (2 − 𝑖) sản
phẩm lỗi có trong 2 sản phẩm được chọn ra từ lô I.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Gọi 𝐵𝑖(𝑖 = 0,1,2) là biến cố có 𝑖 sản phẩm đạt chuẩn và 2 − 𝑖 sản phẩm
lỗi có trong 2 sản phẩm được chọn ra từ lô II.
• Ta c : 𝐴0, 𝐴1, 𝐴2 xung khắc từng đôi.
• 𝐵0, 𝐵1, 𝐵2 xung khắc từng đôi.
• 𝐴𝑖 v 𝐵𝑗 độc lập nhau. 𝐶2
Ta c : 𝑃 𝐴0 = 𝐶1023 ==; 𝐶
7 chính phẩm 1 3 phế phẩm 𝑃 𝐴1 = 7𝐶× 𝐶2 31 = 2145 = 157 ;
Lô sản phẩm I 10
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 𝐶2 𝑃 𝐴2= 𝐶1027 = 2145 = 157 ; 𝐶2 𝑃 𝐵0= 𝐶24 = 456 = 152 ; 10
6 chính phẩm 𝐶1 4 phế phẩm 𝑃 𝐵1 = 6𝐶× 𝐶2 41 = 2445 = 158 ;
Lô sản phẩm II 10
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 𝐶2 𝑃 𝐵 6 15 1 2 = 𝐶102 ==. 45 3 a) Gọi 𝐴 l
biến cố được 2 sản phẩm đạt chuẩn v 2 sản phẩm lỗi.
Ta c : 𝐴 = 𝐴0𝐵2 + 𝐴1𝐵1 + 𝐴2𝐵0;
𝑃 𝐴 = 𝑃 𝐴0𝐵2 + 𝐴1𝐵1 + 𝐴2𝐵0 𝑥𝑘= 𝑃 𝐴0𝐵2
+ 𝑃 𝐴1𝐵1 + 𝑃 𝐴2𝐵0 đ𝒍 = 𝑃 𝐴0 𝑃 𝐵2 + 𝑃 𝐴1 𝑃 𝐵1 + 𝑃 𝐴2 𝑃 𝐵0 = 1/3.
b) Giả sử đã chọn được 2 sản phẩm đạt chuẩn v 2 sản phẩm lỗi. T nh
xÆc suất chọn được 1 sản phẩm đạt chuẩn v 1 sản phẩm lỗi từ l II.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
`p dụng c ng thức xÆc suất c điều kiện, ta c : 𝑃 𝐴𝐵1 𝑃
(𝐴0𝐵2 + 𝐴1𝐵1 + 𝐴2𝐵0)𝐵1 𝑃 𝐵1/𝐴 = = 𝑃(𝐴) 𝑃(𝐴) (7/15)(8/15) 56 𝑃 𝐴1 𝑃 𝐵1 = = = . 1/3 𝑃(𝐴) 75
4.4. Công thức xác suất đầy đủ và công thức Bayes
▪ Cho 𝐴1, 𝐴2, … , 𝐴𝑛, 𝐴 l cÆc biến cố v 𝛺 l kh ng gian mẫu. Nếu dªy
biến cố 𝐴1, 𝐴2, … , 𝐴𝑛 đầy đủ v xung khắc từng đôi, tức l :
𝐴1 ∪ 𝐴2 ∪ ⋯ ∪ 𝐴𝑛 = 𝛺 v 𝐴𝑖 ∩ 𝐴𝑗 = 𝜙, ∀𝑖 ≠ 𝑗 th 𝑃(𝐴) = 𝑃 𝐴1
𝑃 𝐴/𝐴1 + 𝑃 𝐴2 𝑃 𝐴/𝐴2 … + 𝑃 𝐴𝑛 𝑃 𝐴/𝐴𝑛 . Viết thu gọn l : 𝑃 𝐴
= ∑𝑛𝑖=1 𝑃 𝐴𝑖 𝑃 𝐴/𝐴𝑖 .
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
C ng thức trŒn gọi l c ng thức xÆc suất đầy đủ. CÆc xÆc suất
𝑃 𝐴1 , 𝑃 𝐴2 , … 𝑃 𝐴𝑛 thường gọi l cÆc “xác suất của giả thiết” hay
“xác xuất tiŒn nghiệm”.
▪ Sau khi biết biến cố A đã xảy ra, cÆc xÆc suất 𝑃 𝐴𝑘/𝐴 gọi l cÆc
“xác suất hậu nghiệm” được t nh bởi c ng thức sau đây v gọi l c ng thức Bays:
𝑃 𝐴𝑘/𝐴 = 𝑃 𝐴/𝐴𝑃𝑘𝐴.𝑃 𝐴𝑘 =
𝑃𝑛 𝐴/𝐴𝑘 .𝑃 𝐴𝑘 .
᪄𝑖=1 𝑃 𝐴𝑖 𝑃 𝐴/𝐴𝑖
Chứng minh
Từ giả thiết 𝐴1 ∪ 𝐴2 ∪ ⋯ ∪ 𝐴𝑛 = 𝛺 tức l
𝐴1 + 𝐴2 + ⋯ + 𝐴𝑛 = 𝛺
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
⇒ 𝐴 = 𝐴. 𝛺 = 𝐴 𝐴1 + 𝐴2 + ⋯ + 𝐴𝑛
= A𝐴1 + 𝐴𝐴2 + ⋯ + 𝐴𝐴𝑛
Do nh m 𝐴1, 𝐴2, … , 𝐴𝑛 xung khắc từng đôi nên A𝐴1; 𝐴𝐴2; … ; 𝐴𝐴𝑛 cũng
xung khắc từng đôi. Vậy nên:
𝑃 𝐴 = P A𝐵1 + 𝐴𝐵2 + ⋯ + 𝐴𝐵𝑛 = P A𝐵1 + 𝑃 𝐴𝐵2 + ⋯ + 𝑃 𝐴𝐵𝑛 = 𝑃 𝐴1 𝑃 𝐴/𝐴1
+ 𝑃 𝐴2 𝑃 𝐴/𝐴2 … + 𝑃 𝐴𝑛 𝑃 𝐴/𝐴𝑛
= ∑𝑛𝑖=1 𝑃 𝐴𝑖 𝑃 𝐴/𝐴𝑖 (1)
Tiếp tục Æp dụng c ng thức xác xuất có điều kiện và công thức nh n xÆc suất ta c : 𝑃 𝐴. 𝐴𝑘
𝑃 𝐴/𝐴𝑘 𝑃 𝐴𝑘
𝑃 𝐴𝑘/𝐴 = 𝑃(𝐴) = 𝑃(𝐴) (2)
Thế P(A) từ (1) v o (2): 𝑃 𝐴𝑘/𝐴 =
𝑃𝑛 𝐴/𝐴𝑘 .𝑃 𝐴𝑘 .
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
᪄𝑖=1 𝑃 𝐴𝑖 𝑃 𝐴/𝐴𝑖
Thomas Bayes, 1702 - 1761 Ví dụ 1
C 3 l h ng cøng h nh dÆng bŒn ngo i, tỉ lệ phế phẩm của từng l
tương ứng l 6%, 2%, 1%. Chọn ngẫu nhiŒn một l rồi từ l đã chọn
lấy ngẫu nhiŒn ra một sản phẩm.
a) T nh xÆc suất để lấy được một phế phẩm.
b) Giả sử lấy được phế phẩm. T nh x.suất để phế phẩm đó của l thứ ba.
Giải: Gọi 𝐴𝑖(𝑖 = 1,2,3) là biến cố: “Chọn được lô hàng thứ 𝑖” thì họ
𝐴1, 𝐴2, 𝐴3 đầy đủ, xung khắc từng đôi và: 𝑃 𝐴1 =𝑃 𝐴2 =𝑃 𝐴3 = .
a) Gọi 𝐴 là biến cố: “Lấy được phế phẩm”, ta có:
𝑃 𝐴/𝐴1 = 0,06; 𝑃 𝐴/𝐴2 = 0,02; 𝑃 𝐴/𝐴3 = 0,01.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Áp dụng công thức xác suất đầy đủ, ta có:
𝑃 𝐴 =𝑃 𝐴1 𝑃𝐴 𝐴Τ 1 +𝑃 𝐴2 𝑃 𝐴 𝐴Τ 2 + 𝑃 𝐴3 𝑃 𝐴 𝐴Τ 3 = 0,06 + 0,02 + 0,01 = 0,03. Τ 13 ×0,01 b) ADCT Bayes: 𝑃 𝐴 𝑃 𝐴 𝐴Τ 3Τ𝐴 = 𝑃 𝐴3𝑃 𝐴 3 = 0 ,03 = .
Ví dụ 2*
Một hộp c 3 sản phẩm kh ng rı chất lượng. Lấy ngẫu nhiŒn kh
ng ho n lại một sản phẩm từ hộp th được sản phẩm tốt. Sau đó
chọn ngẫu nhiŒn từ hộp một sản phẩm nữa. T m xÆc suất để
sản phẩm lấy ra từ hộp lần thứ hai l sản phẩm tốt? Giải:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
▪ Gọi 𝐴𝑖 l biến cố trong hộp c 𝑖 sản phẩm tốt 𝑖 = 0,1,2,3 th 𝐴𝑖
𝑖=0,3 l hệ biến cố đầy đủ v xung khắc từng đôi.
▪ V kh ng biết rı chất lượng sản phẩm trong hộp nŒn ta c thể coi
cÆc biến cố 𝐴0, 𝐴1, 𝐴2, 𝐴3 c khả năng xảy ra như nhau. Tức l :
𝑃 𝐴0 = 𝑃 𝐴1 = 𝑃 𝐴2 = 𝑃 𝐴3 = .
▪ Gọi 𝐵 l biến cố sản phẩm lấy ra từ hộp lần đầu l sản phẩm tốt. ta c
: 𝑃 𝐵/𝐴0 = 0; 𝑃 𝐵/𝐴1 = ; 𝑃 𝐵/𝐴2 = ; 𝑃 𝐵/𝐴3 = .
▪ ADCT xÆc suất đầy đủ: 1 3 4 3
𝑃(𝐵) = ∑3𝑖=0 𝑃 𝐴𝑖 𝑃 𝐵/𝐴𝑖 = 0 + + + = 0,5.
▪ Theo giả thiết th 𝐵 đã xảy ra nŒn theo c ng thức Bayes:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 1 1 𝑃 ⋅ 𝐴 1 𝑃 𝐵/𝐴 1 1 = 4 3 =
𝑃 𝐴0/𝐵 = 𝑃 𝐴0𝑃(𝐵)𝑃 𝐵/𝐴0 = 0; 𝑃 𝐴1/𝐵 = 0 ,5 6𝑃 (𝐵) 1 2 1 3 𝑃 ⋅ ⋅ 𝐴 2 𝑃 𝐵/𝐴 2 2 𝑃 3 = 4 3 𝐴 3 𝑃 𝐵/𝐴 3 4 3 = = = 𝑃 𝐴2/𝐵 = 0 ,5 6𝑃 (𝐵); 𝑃 𝐴3/𝐵 = 0 ,5 6 𝑃(𝐵)
▪ Gọi 𝐶 l biến cố lấy được sản phẩm tốt ở lần sau. `p dụng c ng thức
xÆc suất đầy đủ ta c : 3 𝑃 𝐶
= ∑3𝑖=0 𝑃 𝐴𝑖/𝐵 𝑃 C/(𝐴𝑖/𝐵) = ∑𝑖=0
𝑃 𝐴𝑖/𝐵 𝑃 𝐶/𝐴𝑖𝐵) Lưu : .
CÆc xÆc suất tiŒn nghiệm l 𝑃 𝐴0 = 𝑃 𝐴1 = 𝑃 𝐴2 = 𝑃 𝐴 , sau khi
lấy một sản phẩm từ hộp v biết được đó l sản phẩm tốt đã l m cho cÆc xÆc
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
suất tiŒn nghiệm n y thay đổi th nh 𝑃 𝐴0/𝐵 , 𝑃 𝐴1/𝐵 , 𝑃 𝐴2/𝐵 , 𝑃 𝐴3/𝐵
ch nh l cÆc xÆc suất hậu nghiệm.
4.5. Công thức Bernoulli
a) PhØp thử Bernoulli:
Tiến h nh 𝑛 phØp thử độc lập trong những điều kiện như nhau. Nếu
trong mỗi phØp thử, biến cố 𝐴 xuất hiện với xÆc suất kh ng đổi 𝑝 ∈
(0; 1) th phØp thử n y gọi l phØp thử Bernoulli v dªy gồm 𝑛 phØp thử
như trŒn được gọi l dªy phØp thử Bernoulli. XÆc suất 𝑝 được gọi l
xÆc suất th nh c ng của biến cố 𝐴. b) C ng thức Bernoulli:
XÆc suất để biến cố 𝐴 xuất hiện 𝑘 lần trong 𝑛 phØp thử của dªy
phØp thử Bernoulli, k hiệu l 𝑃𝑛(𝑘, 𝑝) hoặc 𝑃𝑛(𝑘) được t nh theo c ng
thức sau v gọi l c ng thức Bernoulli:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 𝑃 𝑘
𝑛(𝑘, 𝑝) = 𝐶𝑛 𝑝𝑘. (1 − 𝑝)𝑛−𝑘
Chứng minh
Gọi Ai l biến cố “Ở phØp thử thứ i biến cố A xảy ra" (i = 1,2, … , n).
𝐴𝑖 sẽ l biến cố “Ở phØp thử thứ i biến cố A kh ng xảy ra”.
Gọi 𝐵 l biến cố "trong n phØp thử, 𝐴 xảy ra đúng 𝑘 lần".
Khi đó B c thể xảy ra theo nhiều cÆch khÆc nhau. Chẳng hạn, 𝑘 phØp
thử đầu, 𝐴 xảy ra, c n n-k phØp thử sau 𝐴 kh ng xảy ra. Do đó cÆc biến
cố thuận lợi cho B c dạng:
𝐴1. 𝐴2 … 𝐴𝑘. 𝐴 𝑘+1. 𝐴 𝑘+2 … 𝐴𝑛
Hoặc 𝑛 − 𝑘 phØp thử đầu 𝐴 kh ng xảy ra, c n 𝑛 − 𝑘 phØp thử cuối 𝐴 xảy
ra: 𝐴1. 𝐴2 … 𝐴 𝑛−𝑘. 𝐴 𝑛−𝑘+1. 𝐴𝑛−𝑘 … 𝐴𝑛
Do đó, biến cố B l tổng gồm 𝐶𝑛𝑘 số hạng m mỗi số hạng l một t ch c dạng như trŒn.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Đối với mỗi t ch, ta thấy biến cố A xảy ra đúng k lần, c n 𝐴 xảy ra đúng
(n-k) lần. Do đó xÆc suất của mỗi t ch đều bằng 𝑝𝑘(1 − 𝑝)𝑛−𝑘.
V cÆc biến cố t ch l cÆc biến cố xung khắc từng đôi, nŒn ta c :
𝑃𝑛(𝑘, 𝑝) = 𝑃(𝐵) = 𝐶𝑛𝑘𝑝𝑘(1 − 𝑝)𝑛−𝑘.
c) Số c khả năng nhất:
XØt c ng thức xÆc suất Bernoulli: 𝑘
𝑃𝑛(𝑘, 𝑝) = 𝐶𝑛 𝑝𝑘. (1 − 𝑝)𝑛−𝑘 với 𝑘 ∈ 0,1,2, … , 𝑛 . 𝑚 0 𝑚 0 Số 𝑚 −𝑚
0 ∈ {0,1,2, … , 𝑛} m 𝑃𝑛 𝑚 (1 0,𝑝 − 𝑝)𝑛= 𝐶 0 đạ 𝑝 𝑛
t giÆ trị lớn nhất được gọi
l số c khả năng nhất của dªy n phØp thử. Số c khả năng nhất được t nh bởi c ng thức:
ቊ𝑚0 = 𝑛𝑝 − 𝑞 hay 𝑚0 = 𝑛𝑝 − 𝑞 + 1, khi 𝑛𝑝 − 𝑞 ∈ N
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
𝑚0 = 𝑛𝑝 − 𝑞 + 1, khi 𝑛𝑝 − 𝑞 ∉ N
Trong đó 𝑞 = 1 − 𝑝 v k hiệu [𝑥] để chỉ phần nguyŒn của 𝑥.
Lưu : 𝑃𝑛 𝑚0, 𝑝 l số hạng trung t m của ph n bố nhị thức m ta sẽ học ở chương sau.
Chứng minh 𝑃𝑛(𝑚,𝑝)
𝐶𝑛𝑚𝑝𝑚.𝑞𝑛−𝑚 𝑚+1 𝑞
XØt tỷ số: 𝑃 (𝑚+1,𝑝) 𝐶 𝑝𝑚+1.𝑞 𝑛−𝑚 𝑝 suy ra: 𝑛 𝑛
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• 𝑃𝑛 𝑚, 𝑝 = 𝑃𝑛(𝑚 + 1, 𝑝) ⇔ 𝑃𝑛𝑃(𝑛𝑚+1,𝑝(𝑚,𝑝) ) = 1 ⇔ 𝑚 = 𝑛𝑝 − 𝑞;
• 𝑃𝑛(𝑚, 𝑝) ≤ 𝑃𝑛(𝑚 + 1, 𝑝) ⇔ 𝑃𝑛𝑃(𝑛𝑚+1,𝑝(𝑚,𝑝) ) ≤ 1 ⇔ 𝑚 ≤ 𝑛𝑝 − 𝑞;
• 𝑃𝑛(𝑚, 𝑝) ≥ 𝑃𝑛(𝑚 + 1, 𝑝) ⇔ 𝑃𝑛𝑃(𝑛𝑚+1,𝑝(𝑚,𝑝) ) ≥ 1 ⇔ 𝑚 ≥ 𝑛𝑝 − 𝑞.
Ta thấy 𝑃𝑛(𝑚, 𝑝) biến thiŒn như l h m đồng biến khi 𝑚 ≤ 𝑛𝑝 − 𝑞 v
nghịch biến khi 𝑚 ≥ 𝑛𝑝 − 𝑞.
Do đó xÆc suất 𝑃𝑛(𝑚, 𝑝) đạt giÆ trị lớn nhất tại 𝑚 = 𝑛𝑝 − 𝑞 v
𝑃𝑛(𝑚, 𝑝) = 𝑃𝑛(𝑚 + 1, 𝑝).
Mặt khác do 𝑚 là số tự nhiên nên ta có các trường hợp sau:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Nếu 𝑛𝑝 − 𝑞 ∈ N th 𝑚0 = 𝑛𝑝 − 𝑞 hay 𝑚0 = 𝑛𝑝 − 𝑞 + 1 • Nếu 𝑛𝑝
− 𝑞 ∉ N, ta c : [𝑛𝑝 − 𝑞] < 𝑛𝑝 − 𝑞 < [𝑛𝑝 − 𝑞] + 1 nŒn 𝑚0 = [𝑛𝑝 − 𝑞] + 1. Ví dụ 1
Đề thi THPTQG m n ToÆn c 50 c u hỏi trắc nghiệm khÆch quan,
mỗi c u c 4 phương Æn, trong đó chỉ c một phương Æn đúng.
Giả sử mỗi c u trả lời đúng được 0,2 điểm c n mỗi c u trả lời sai
được 0 điểm. Một học sinh l m b i bằng cÆch chọn ngẫu nhiŒn.
a) T nh xÆc suất để học sinh đó được 5 điểm.
b) T nh xÆc suất sinh viŒn đó đạt điểm lớn hơn hoặc bằng 5.
c) T m số c u đúng c xÆc xuất lớn nh t. Giải:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
a) SV cần trả lời đúng 25 c u v 25 c u sai. Xác suất cần tìm là: 𝑃 .
b) Xác suất để SV đó đạt điểm lớn hơn hoặc bằng 5 là: 50k50−𝑘 1 3 𝑝 = ᪄ 𝑝(𝑘,) = ᪄ 𝐶50 4 4 50𝑘=25 k ⋅⋅. 𝑘=25
c) Áp dụng công thức tìm số có khả năng nhất:
ቊ𝑚0 = 𝑛𝑝 − 𝑞 hay 𝑚0 = 𝑛𝑝 − 𝑞 + 1, khi 𝑛𝑝 − 𝑞 ∈ N
𝑚0 = 𝑛𝑝 − 𝑞 + 1, khi 𝑛𝑝 − 𝑞 ∉ N Ta thấy: 𝑛𝑝
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
⇒ 𝑚0 = 𝑛𝑝 − 𝑞 + 1 = [11,75] + 1 = 12.
Vậy số câu đúng có xác xuất lớn nh t là 12 câu. Tức là học sinh l
m b i theo cÆch đánh hœ họa th có khả năng cao nhất sẽ đạt
2,4 điểm. Tuy vậy xác xuất đạt điểm 2,4 cũng sẽ rất rất nhỏ.
Mở rộng b i toÆn: T nh xác suất để biến cố 𝐴 trong 𝑛 phép thử của
dãy phép thử Bernoulli
1) Biến cố 𝐴 xảy ra từ 𝑘1 đến 𝑘2 lần.
2)𝐴 xảy ra t nhất một lần.
3) T m số lần thực hiện phØp thử tối thiểu để thỏa mªn điều kiện n o đó. Cách giải:
1) XÆc suất để biến cố 𝐴 xảy ra từ 𝑘1 đến 𝑘2 lần l :
𝑃𝑛 𝑘1 ≤ 𝑘 ≤ 𝑘2 = 𝑃𝑛 𝑘1
+ 𝑃𝑛 𝑘1 + 1 + ⋯ . +𝑃𝑛 𝑘2
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
2) XÆc suất để biến cố 𝐴 xảy ra t nhất một lần l :
𝑃𝑛(1 ≤ 𝑘 ≤ 𝑛) = 1 − 𝑃𝑛(0) = 1 − (1 − 𝑝)𝑛.
3) Phương pháp giải sẽ được xét trong từng bài toán cụ thể. Ví dụ 2
Một xạ thủ bắn lần lượt 6 viŒn đạn v o một mục tiŒu với xÆc
suất trœng trong mỗi lần bắn l 0,8. T m xÆc suất sao cho: a) C
kh ng quÆ 2 viŒn trœng mục tiŒu.
b) C t nhất 1 viŒn trœng mục tiŒu.
c) Phải bắn bao nhiŒu lần để xÆc suất c t nhất 1 viŒn trœng mục tiŒu l 99,968%? Giải:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Dãy phép thử ở đây là dãy phép thử Bernoulli với n = 6 và p = 0,8. a)
Xác suất có không quá 2 viên trúng mục tiêu là: 𝑘
𝑃6 0 ≤ 𝑘 ≤ 2 = ∑𝑘=02 𝑃6 𝑘 = ᪄𝑘=02 𝐶6k 0,8 0,2 6−𝑘 ≈ 0,01696.
a) Xác suất có ít nhất 1 viên trúng mục tiêu:
𝑃6 1 ≤ 𝑘 ≤ 6 = 1 − 𝑃6 0 = 1 − 0,2 6 ≈ 0,999936.
c) YCBT ⇔ 𝑃𝑛 1 ≤ 𝑘 ≤ 𝑛 = 0,99968 ⇔ 1 − 0,2 𝑛 = 0,99968
⇔ 0,2 𝑛 = 0,00032 ⇔ n = log0,2(0,00032) = 5. Vậy cần bắn 5 lần. Ví dụ 3
Đề thi trắc nghiệm m n XÆc suất c 50 c u hỏi, mỗi c u c 4 phương
Æn, trong đó chỉ c một phương Æn đúng. Giả sử mỗi c u trả lời
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
đúng được 0,2 điểm c n mỗi c u trả lời kh ng đúng bị trừ 0,05
điểm. Một SV l m b i bằng cÆch chọn ngẫu nhiŒn.
a) T nh xÆc suất sinh viŒn đó được 5 điểm.
b) T nh xÆc suất sinh viŒn đó đạt điểm lớn hơn hoặc bằng 5. Giải:
a) Gọi 𝑘 là số câu đúng thì 50 − 𝑘 là số câu sai:
Để được 5 điểm th 0,2𝑘 − 0,05 50 − 𝑘 = 5 ⇔ k = 30. Tức là
SV cần trả lời đúng 30 c u v 20 c u sai. Xác suất cần tìm là: 𝑃 .
b) Xác suất để SV đó đạt điểm lớn hơn hoặc bằng 5 là: 50k50−𝑘
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 50𝑘=30 k ⋅⋅≈ 1 3 0,000000164. 4 4 𝑝 = ᪄ 𝑝(𝑘,) = ᪄ 𝐶50 𝑘=30
BÀI KHẢO SÁT MỨC ĐỘ TIẾP THU BÀI TẠI LỚP
1) Một máy sản xuất với tỉ lệ sản phẩm đạt tiêu chuẩn là 60%.
a)Cho mÆy sản xuất ra 10 sản phẩm. T nh xÆc suất được t nhất 4
sản phẩm đạt tiŒu chuẩn.
b)Nếu mÆy sản xuất ra 210 sản phẩm th số sản phẩm đạt tiŒu
chuẩn c khả năng nhất l bao nhiŒu?
2) C ng ty chuyển phÆt nhanh Xpress hoạt động trŒn ba khu vực I,
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
II, III với tỉ lệ bưu phẩm của ba khu vực n y lần lượt l 35%, 45%, 20%.
Biết rằng tỉ lệ chuyển phÆt th nh c ng ở khu vực I l 95%, khu vực II l 93%, v khu vực III l 97%;
a)T nh tỉ lệ bưu phẩm được chuyển phÆt th nh c ng bởi c ng ty.
b)Giả sử c ng ty cần chuyển phÆt 20 bưu phẩm. T nh xÆc suất để
số bưu phẩm bị thất lạc kh ng quÆ 2 bưu phẩm.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)




