Chương 1: Các nguyên lý thuyết cổ điển về cấu trúc nguyên tử - Cơ sở vật lí | Đại học Sư Phạm Hà Nội

CHƯƠNG 1.
CÁC LÝ THUYẾT CỔ ĐIỂN VỀ CẤU TRÚC NGUYÊN TỬ
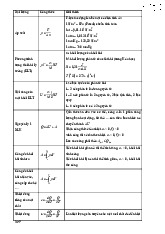
1.1. Mẫu Thomson về cấu trúc nguyên tử
- Nguyên tử có dạng hình cầu với kích thước cỡ amstrong (Å)
- Hình cầu này tích điện dương dạng môi trường đồng nhất
- Các electron mang điện tích âm phân bố rải rác và đối xứng trong hình cầu
- Tổng điện tích âm bằng tổng điện tích dương nên nguyên tử trung hoà về điện.
 Mẫu này (Hình 1.1) chỉ tồn tại trong một thời gian ngắn vì có
những mâu thuẫn với thực nghiệm. Hình 1.1
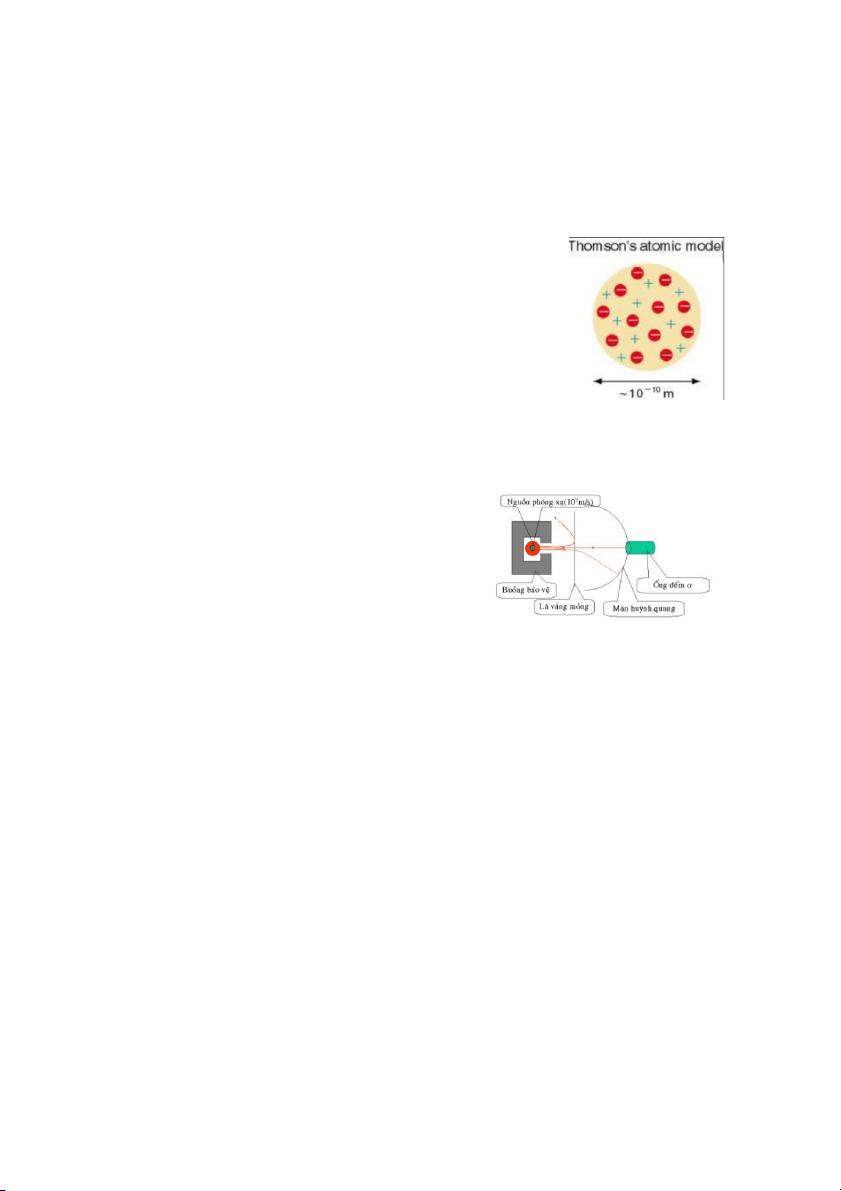
1.2. Thí nghiệm tán xạ hạt α của Rutherford
- Sơ đồ thí nghiệm (Hình 1.2):
+ Nguồn phóng xạ chứa các hạt α.
- Tiến hành thí nghiệm: Bắn các hạt α vào lá vàng
mỏng và quan sát, thí nghiệm cho thấy:
+ Đa số hạt α xuyên thẳng qua lá vàng,
+ Một số hạt α bị lệch hướng (tán xạ) khi xuyên qua lá vàng, Hình 1.2
+ Một số rất ít hạt α bị bật trở lại. - Lập luận:
+ Đa số hạt α xuyên qua lá vàng, chứng tỏ nguyên tử rất nhỏ bé (khoảng cách giữa các
nguyên tử lớn hơn nhiều so với kích thước nguyên tử).
+ Một số hạt α bị lệch hướng khi xuyên qua lá vàng chứng tỏ nó đã bị va chạm trước khi ra khỏi lá vàng.
+ Một số rất ít hạt α bị bật trở lại chứng tỏ nó đã va chạm trực diện với một hạt có khối lượng lớn so với nó. - Giải thích:
+ Thực tế cấu tạo nguyên tử không giống như mẫu Thomson vì nếu nguyên tử phân bố
đồng nhất như mẫu Thomson thì không thể có một số hạt nhân giật lùi như trong thí nghiệm.
+ Như vậy, nguyên tử phải có phần lõi ở giữa có kích thước nhỏ nhưng khối lượng lớn và
mang điện tích dương. Chính điện tích dương này đẩy hạt α giật lùi khi gặp nó. Phần lõi
này được gọi là hạt nhân nguyên tử.
+ Hạt nhân có kích thước bé nên chỉ một số ít hạt α bị lệch hướng truyền; đặc biệt chỉ có
rất ít hạt va chạm đối diện với hạt nhân và bị bật trở lại.
1.3. Công thức tán xạ Rutherford 1.3.1. Các giả thiết
- Lá vàng rất mỏng → coi như 1 lớp nguyên tử → mỗi hạt α chỉ tán xạ 1 lần.
- Hạt α bị tán xạ là do tương tác điện (bỏ qua tương tác hấp dẫn) vì Fđ >> Fhd.
- Bỏ qua tương tác giữa ê và hạt nhân vì mê << mhn.
- Hạt α được coi như đạn, lá vàng mỏng đứng yên coi như bia vì Au m > hơn nhiều  m . hn hn
1.3.2. Quỹ đạo chuyển động của hạt α
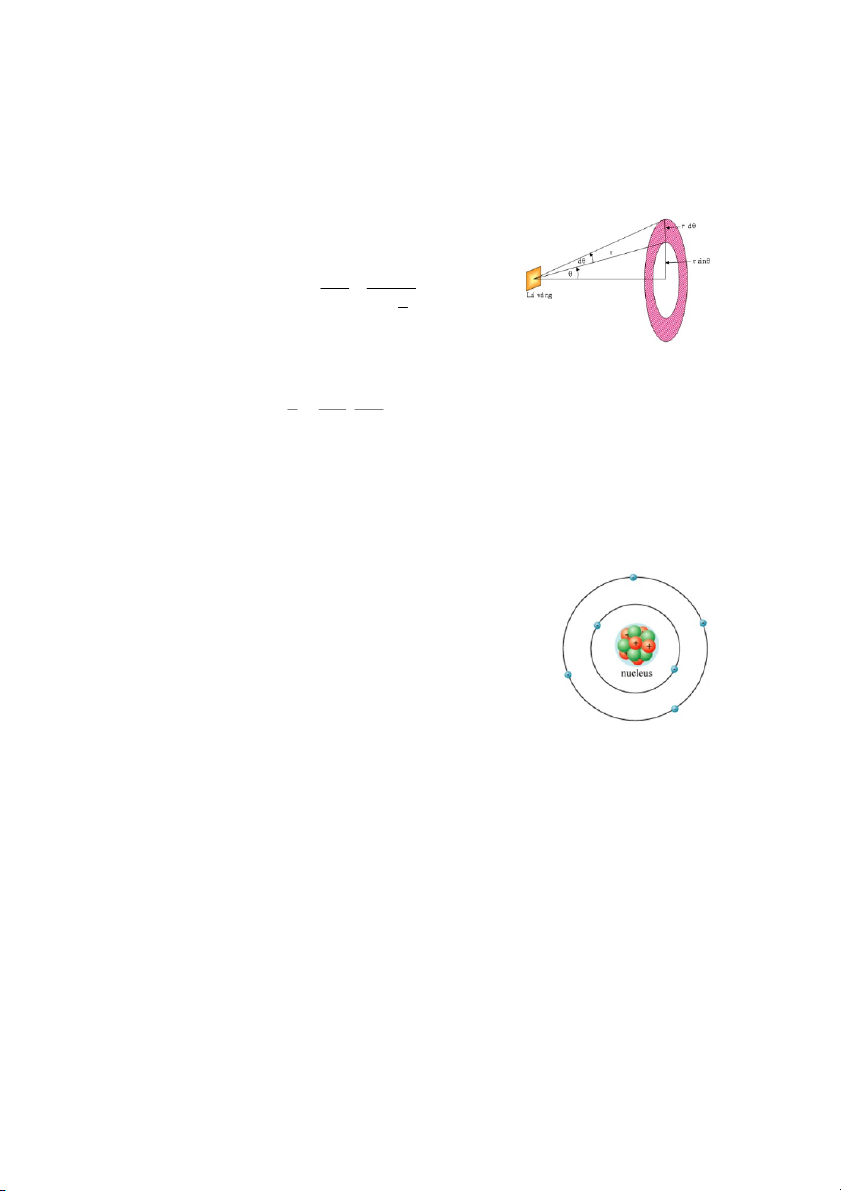
- Giả sử hạt α có động năng T chuyển động đến gần 1 hạt nhân của lá vàng (đặt tại O) theo
phương AB cách hạt nhân 1 khoảng b – gọi là khoảng nhằm (Hình 1.3)
- Kết quả chứng minh cho thấy, quỹ
đạo của hạt α là đường hyperbol có 2 I D α θ
đường tiệm cận AB và CD và hạt A C B b
nhân Au nằm ở 1 trong 2 tiêu điểm. φ
- Góc θ hợp bởi 2 đường tiệm cận của O r
hyperbol gọi là góc tán xạ, được xác
Hình 1.3. Quỹ đạo của hạt α
định theo biểu thức sau:   cot Tb    (1.1) 2  2  kZe
- Theo (1.1), b càng nhỏ thì θ càng lớn và đến 1 giá trị nào đó của b thì θ > π/2 → hạt α sẽ bị bật trở lại.
1.3.3. Công thức tán xạ Rutherford
- Gọi n là số hạt α đến lá vàng trong một đơn vị thời gian; N là mật độ nguyên tử thể tích
của vàng; d là độ dày lá vàng.
- Hạt α bị tán xạ trên lá vàng theo nhiều hướng khác nhau và nó phụ thuộc vào góc tán xạ θ:
+ Số hạt α bị tán xạ trong một đơn vị thời gian: 2  kZe2  sin dN   2 n . N . d . . d .    (1.2)  T 2     sin4    2 
+ Số hạt α bị tán xạ trên một đơn vị diện tích (N(θ))
thỏa mãn hệ thức: Hình 1.4 2 2     4 N  .sin    nNd kZe , (1.3) ( ) 2  2   r  2  T 
với, r là khoảng cách từ hạt nhân vàng đến vị trí quan sát trên màn (Hình 1.4);
(1.3) là công thức Rutherford, công thức này cho phép xác định số hạt α có động năng T
bị tán xạ theo góc θ trên một đơn vị diện tích nghiên cứu.
1.4. Mẫu nguyên tử hành tinh
1.4.1. Mẫu nguyên tử của Rutherford
- Nguyên tử gồm có hạt nhân mang điện tích dương (Ze) có kích
thước rất nhỏ ở chính giữa và chiếm hầu hết khối lượng nguyên tử.
- Xung quanh hạt nhân là các electron chuyển động theo quỹ đạo tròn.
- Số electron quay xung quanh hạt nhân đúng bằng nguyên tử số
Z của nguyên tử nên nguyên tử trung hoà về điện (Hình 1.5) Hình 1.5
→ Mẫu nguyên tử của Rutherford có cấu trúc giống như cấu trúc của hệ Mặt Trời nên
còn được gọi là mẫu hành tinh nguyên tử.
1.4.2. Đánh giá mẫu nguyên tử Rutherford
- So với mẫu Thomson, mẫu Rutherford đã có những phát triển vượt bậc (sự tập trung điện
tích dương ở hạt nhân, sự chuyển động của ê xung quanh hạt nhân,…). Tuy nhiên, nó vẫn
còn một số hạn chế sau:
1. Theo mẫu nguyên tử Rutherford thì các ê quay tròn xung quanh hạt nhân nên có gia tốc
hướng tâm → nó sẽ bức xạ sóng điện từ → năng lượng của ê giảm liên tục → ê chuyển
động theo đường trôn ốc và sau 10-8s nó sẽ rơi vào hạt nhân và nguyên tử bị phá hủy → trái với thực nghiệm
→ Không giải thích được sự tồn tại bền vững của nguyên tử trong tự nhiên.
2. Theo mẫu nguyên tử Rutherford thì do ê trong nguyên tử luôn bức xạ sóng điện từ → ta
chỉ có thể thu được quang phổ liên tục → trái với thực nghiệm
→ Không giải thích được sự tạo thành quang phổ vạch của nguyên tử.
1.5. Quy luật quang phổ của nguyên tử Hyđrô. Công thức Balmer
1.5.1. Các dãy quang phổ của nguyên tử Hyđrô
Bằng thực nghiệm các nhà khoa học đã xác định được quang phổ của nguyên tử Hyđrô là
quang phổ vạch và sắp xếp thành các dãy riêng biệt. Gồm có 5 dãy sau:
- Dãy Lyman: Các vạch phổ thuộc vùng tử ngoại, có số sóng S (hay bước sóng λ) được xác định theo công thức: 1  1 1  S   R  
; với n là số nguyên và n > 1   2 2 1 n 
Trong đó, R là hằng số Ridberg (R = 1,096776.107 m-1).
- Dãy Balmer: Các vạch phổ thuộc vùng ánh sáng nhìn thấy và vùng tử ngoại, có số sóng S
(hay bước sóng λ) được xác định theo công thức: 1  1 1  S   R   ; với n > 2   2 2 2 n 
- Dãy Paschen: Các vạch phổ thuộc vùng hồng ngoại gần, có số sóng S (hay bước sóng λ)
được xác định theo công thức: 1  1 1  S   R   ; với n > 3   2 2 3 n 
- Dãy Brackett: Các vạch phổ thuộc vùng hồng ngoại xa, có số sóng S (hay bước sóng λ)
được xác định theo công thức: 1  1 1  S   R   ; với n > 4   2 2 4 n 
- Dãy Pfund: Các vạch phổ thuộc vùnghồng ngoại rất xa, có số sóng S (hay bước sóng λ)
được xác định theo công thức: 1  1 1  S    R   ; với n > 5   2 2 5 n 
1.5.2. Công thức Balmer tổng quát
- Từ các công thức thức nghiệm ở trên, Balmer đã xây dựng một công thức tổng quát gọi là công thức Balmer: 1  1 1  S   R  (1.4) 2 2     n n  i k
trong đó: ni là số nguyên nhận các giá trị 1, 2, 3, 4, 5 ứng với các dãy quang phổ Lyman,
Balmer, Paschen, Brackett và Pfum; nk là số nguyên (nk > ni).
- Trong 1 dãy phổ (ni = const): + λmax khi nk = ni + 1 (liền kề) 1 + λ R min khi nk = ∞ →  2  min ni
1.6. Thuyết Bohr về cấu trúc nguyên tử
1.6.1. Các tiên đề của Bohr
- Tiên đề về trạng thái dừng: Nguyên tử chỉ tồn tại trong những trạng thái có năng lượng
xác định và gián đoạn (E1, E2, ..., En) gọi là trạng thái dừng. Trong trạng thái dừng
nguyên tử không bức xạ mà các ê chỉ chuyển động trên quỹ đạo tròn có bán kính xác định
gọi là quỹ đạo lượng tử (quỹ đạo dừng). Các quỹ đạo này thỏa mãn điều kiện lượng tử hóa của Bohr:  L  n , (1.5)
trong đó: L là mô men xung lượng; n là số nguyên dương (n = 1, 2, 3,..) gọi là số lượng tử chính; h 34    0 , 1 54.10
Js gọi là hằng số Plank rút gọn. 2
- Tiên đề về tần số bức xạ: Nguyên tử chỉ phát xạ hay hấp thụ năng lượng dưới dạng bức
xạ điện từ khi nó chuyển từ trạng thái dừng này sang trạng thái dừng khác. Tần số của
bức xạ điện từ mà nguyên tử phát xạ hay hấp thụ được tính theo biểu thức: E  E i k   , (1.6) h
Ei và Ek là năng lượng của trạng thái đầu và trạng thái cuối của quá trình chuyển trạng thái.
1.6.2. Cấu trúc nguyên tử hidro và các ion tương tự theo lý thuyết Bohr
- Nguyên tử hidro và các ion tương tự là những hệ bao gồm 1 hạt nhân mang điện tích +Ze
đứng yên tại tâm và 1 ê chuyển động tròn xung quanh hạt nhân.
- Bán kính quỹ đạo dừng n: 2. n r r 0  , (1.7) n Z 2  với r 10   5 , 0 3 1
. 0 m là bán kính Bohr thứ nhất. 0 kme2
- Vận tốc của ê trên quỹ đạo dừng n: 2 ke v  Z . , (1.8) n n
- Năng lượng của các trạng thái dừng: E0 2 E   .Z , (1.9) n 2 n 2 4 với k me E   13 6 , eV . 0 2 2 
 Từ (1.7), (1.8) và (1.9) ta thấy bán kính quỹ đạo, vận tốc và năng lượng của các trạng thái
dừng bị lượng tử hóa, tức là chúng chỉ có thể nhận các giá trị gián đoạn.
- Với nguyên tử hidro, Z = 1 nên từ (1.7), (1.8) và (1.9) ta có: 2 2 ke E r  n , v  và 0 E   (1.10) n 0 r n n  n 2 n
+ Một số trạng thái dừng của nguyên tử hidro: n 1 2 3 4 5 6 Tên quỹ đạo K L M N O P rn (Å) r0 4 r0 9 r0 16 r0 25 r0 36 r0 En (eV) - E0 - E0/4 - E0/9 - E0/16 - E0/25 - E0/36
+ Thay En từ (1.9) vào công thức Balmer (1.4), ta tìm được hằng số Ridberg: 2 4 k me R  4   c 3 , (1.11)
thay số vào (1.11) ta tìm được hằng số Ridberg trùng khớp với giá trị thực nghiệm.
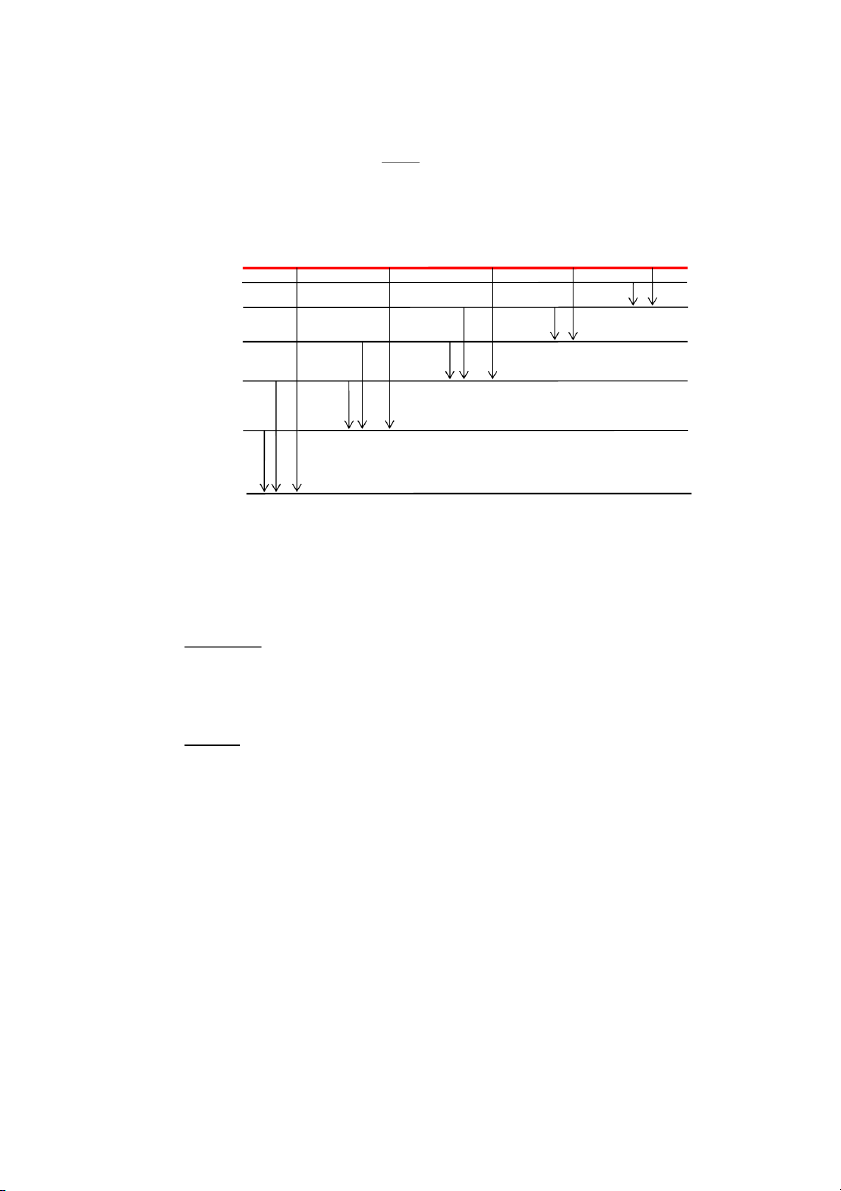
+ Các dãy quang phổ của nguyên tử hidro: n = ∞ P n = 6 O n = 5 Pfund Hβ n = 4 N Brackett H M α n = 3 Paschen L n = 2 Balmer K n = 1 Lyman
Hình 1.6. Các dãy quang phổ của nguyên tử hiđrô
1.6.3. Thí nghiệm Franck-Hertz
- Nhằm kiểm tra bằng thực nghiệm sự tồn tại của các trạng thái dừng trong nguyên tử. 1.6.4. Đánh giá mẫu Bohr - Thành công:
+ Giải thích được tính bền vững của nguyên tử
+ Giải thích thành công sự tạo thành quang phổ vạch của các nguyên tử
+ Tính chính xác tần số của các vạch quang phổ theo công thức (1.6) - Hạn chế:
+ Không giải thích được sự phân bố cường độ sáng của các vạch phổ
+ Không giải thích được sự phân cực của các vạch phổ
+ Với các nguyên tử không phải hydro thì kết quả sai lệch nhiều so với thực nghiệm
 Mẫu Bohr có mâu thuẫn nội tại: thừa nhận một số vấn đề của lí thuyết hiện đại (sự lượng
tử hóa) nhưng vẫn vận dụng những quy luật của cơ học cổ điển:    L mvr n (1.12) BÀI TẬP CHƯƠNG I
1.1. Tìm khoảng cách ngắn nhất r0 mà một hạt α có năng lượng K = 5 MeV có thể đến gần hạt
nhân nguyên tử bạc (Ag) có Z = 47 trong va chạm trực diện giữa chúng.
1.2. Hiệu các số sóng của hai vạch đầu tiên thuộc dãy Balmer trong quang phổ của hydro là
5,326.105 m-1. Hãy tính giá trị của hằng số Ridberg.
1.3. Tìm khoảng cách ngắn nhất mà một hạt α có động năng 0,8 MeV có thể đến gần:
1. Hạt nhân nguyên tử chì (Pb) có Z = 82
2. Hạt nhân nguyên tử liti (Li) có Z = 3
trong va chạm trực diện giữa chúng.
1.4. Bước sóng lớn nhất của vạch quang phổ hidro trong dãy Balmer bằng 656,3 nm. Dựa vào
bước sóng đó, hãy tìm bước sóng lớn nhất của dãy Lyman.
1.5. Trong thí nghiệm Rutherford, người ta cho chùm hạt α với cường độ 104 hạt/s và động năng
ban đầu 6 MeV tới đập vào lá vàng mỏng (Z = 79, A = 197) có bề dày 0,5μm và khối lượng
riêng ρ = 19,4.103 kg/m3. Hãy tính số hạt α bị tán xạ trong khoảng góc từ 590 đến 610 trong thời gian 30 phút.
1.6. Người ta quan sát số hạt α tán xạ theo một góc cố định θ; lúc đầu dùng một lá kim loại mỏng
có nguyên tử số Z1, nguyên tử lượng A1, khối lượng riêng ρ1; sau đó dùng một lá kim loại
mỏng khác có nguyên tử số Z2, nguyên tử lượng A2, khối lượng riêng ρ2. Biết hai lá kim loại
có cùng diện tích và cùng khối lượng. Hãy tìm tỉ số của số hạt α quan sát được trong hai trường hợp đó.
1.7. Sau khi xuyên qua lá vàng (Z = 79), một hạt α có động năng ban đầu 4 MeV bị tán xạ dưới
góc tán xạ θ = 600. Hãy tính khoảng nhằm của hạt α.
1.8. Chứng minh rằng, tần số bức xạ phát ra khi nguyên tử hydro chuyển dời từ quỹ đạo thứ (n +
1) về quỹ đạo thứ n với n → ∞ sẽ tiến tới tần số quay của electron trên quỹ đạo thứ n.
1.9. Một hạt meson π- có điện tích –e và khối lượng mπ = 273me, có thể kết hợp với một proton
để tạo thành một nguyên tử (meson nguyên tử), giống như một electron kết hợp với một
proton để tạo thành nguyên tử hydro. Hãy xác định mức năng lượng cơ bản ứng với quỹ đạo
dừng gần hạt nhân nhất.
1.10. Tìm tỉ số giữa các hằng số Ridberg đối với hydro và heli, biết rằng khối lượng hạt nhân hydro là m -27 -27 H = 1,672.10
kg, khối lượng hạt nhân liti là mHe = 6,644.10 kg, khối lượng electron là m -31 e = 9,1.10 kg.
1.11. Cho biết hằng số Ridberg của hydro và heli tương ứng là R 7 -1 H = 1,096776.10 m và RHe = m m
1,077223.107 m-1. Hãy tìm tỉ số H và He . m m He H
1.12. Những vạch quang phổ nào có thể xuất hiện khi dùng chùm electron có năng lượng 12,5
eV bắn phá các nguyên tử hydro ở trạng thái cơ bản?
1.13. Cho một chùm electron bắn phá các nguyên tử hydro ở trạng thái cơ bản để kích thích chúng:
1. Tìm vận tốc cực tiểu của electron sao cho có thể làm xuất hiện tất cả các vạch phổ bức xạ của nguyên tử hydro.
2. Muốn cho quang phổ của hydro chỉ có duy nhất một vạch thì năng lượng của electron kích
thích phải nằm trong khoảng nào?
1.14. Một photon có năng lượng 20 eV đã làm bứt một electron ra khỏi nguyên tử hydro từ
trạng thái cơ bản. Hãy tìm vận tốc của electron đó sau khi rời nguyên tử.
1.15. Trong thí nghiệm kiểm nghiệm định đề của Bohr, khi dùng electron bắn vào nguyên tử
hydro ở trạng thái cơ bản để kích thích nó, người ta đo được giá trị của các hiệu điện thế kích
thích là 10,2eV và 12,1eV và có 3 vạch quang phổ phát xạ. Tính bước sóng của 3 vạch quang
phổ đó và cho biết các vạch này thuộc dãy quang phổ nào?
1.16. Động năng của electron trong nguyên tử hydro thay đổi bao nhiêu khi nguyên tử đó bức
xạ ra một photon có bước sóng λ = 4,86.10-7m?
1.17. Vẫn với giả thuyết như bài 1.16 nhưng hãy xác định xem thế năng của electron tăng hay giảm bao nhiêu?
1.18. Mô men xung lượng quỹ đạo của electron trong nguyên tử hydro thay đổi bao nhiêu lần
khi electron chuyển từ trạng thái kích thích về trạng thái cơ bản để phát ra lượng tử có bước sóng λ = 9,725.10-8 m?
1.19. Tính năng lượng tối thiểu cần truyền cho nguyên tử hydro để dãy Balmer trong quang
phổ của nó chỉ có duy nhất một vạch.
1.20. Hằng số Ridberg của hydro R=109677,58 cm-1. Hãy xác định bước sóng của vạch Hα
trong quang phổ của hydro.