Chương 1: Đại cương hóa vô cơ | Tài Liệu Học Tập Hóa Học 1

lOMoAR cPSD| 45315597 CHƢƠNG 1 ĐẠI CƢƠNG HÓA VÔ CƠ
1.1. Các khái niệm mở đầu và định luật hóa học cơ bản
1.1.1. Các khái niệm cơ bản
❖ Chất là dạng tồn tại của vật chất dưới dạng các hạt có khối lượng như electron, nguyên tử…
Ví dụ 1: Khí nitơ, khí oxi, muối ăn, đá vôi, đường saccarozơ
Chất có hai đặc tính quan trọng là đồng nhất và có thành phần xác định.
Ví dụ 2: Xi măng, gỗ và thép không được gọi là chất mà được gọi là vật liệu vì
chúng không đồng nhất. Dầu hoả đồng nhất nhưng cũng không phải là một chất vì nó không
có thành phần xác định, dầu hoả là hỗn hợp của nhiều chất có tính chất khác nhau, người
ta có thể tách riêng ra từng chất khi chưng cất.
❖ Nguyên tử là hạt nhỏ nhất của nguyên tố hoá học không thể chia nhỏ hơn
được nữa về mặt hoá học.
Trong các phản ứng hoá học, nguyên tử của các nguyên tố vẫn được bảo toàn về khối lượng.
Tuy nhiên, xét về mặt vật lý, nguyên tử cấu tạo rất phức tạp. Trong nguyên tử có
các electron mang điện tích âm và hạt nhân mang điện tích dương. Có các hạt nơtron không
mang điện. Nguyên tử trung hoà về điện.
Electron (e) có khối lượng vô cùng nhỏ bé so với khối lượng của nguyên tử và
bằng 9,11. 10 – 31 Kg, nghĩa là bằng
khối lượng của nguyên tử hyđro và có điện tích bằng - 1,6. 10 – 19 C.
Hạt nhân nguyên tử gồm các hạt proton (p) và nơtron (n). Proton có khối lượng
là 1,671. 10 – 24 gam. Nơtron có khối lượng là 1,675. 10 – 24 gam và không mang điện. A = P + N
❖ Nguyên tố hoá học: Gồm tất cả các nguyên tử có cùng điện tích hạt nhân.
Nhiều nguyên tố là hỗn hợp của các đồng vị. Những nguyên tử của các đồng vị của một
nguyên tố có cùng số proton nên có cùng một điện tích hạt nhân và có cùng số electron
nhưng có số nơtron khác nhau nên khác nhau về số khối và khối lượng nguyên tử.
❖ Phân tử: Là hạt nhỏ nhất của một chất có tất cả tính chất hoá học của chất
đó. Phân tử có thể có từ hai đến hàng ngàn nguyên tử liên kết với nhau (trừ các khí hiếm
tồn tại dưới dạng nguyên tử tự do).
Những nguyên tử của cùng một nguyên tố liên kết với nhau tạo nên phân tử của
đơn chất. Các nguyên tử của các nguyên tố khác nhau liên kết với nhau tạo nên phân tử của hợp chất. 1 lOMoAR cPSD| 45315597
❖ Khối lƣợng nguyên tử, khối lƣợng phân tử và mol.
Đơn vị khối lượng nguyên tử bằng khối lượng nguyên tử đồng vị 12C của cac bon là 1,6603. 10 –24 gam.
Khối lượng nguyên tử của một nguyên tố là khối lượng trung bình của các đồng vị của nguyên tố đó.
Ví dụ 3: Khối lượng nguyên tử của H là 1,0079; khối lượng nguyên tử của N là
14,0067; khối lượng nguyên tử của O là 15,9994; khối lượng nguyên tử của Fe là 55,847;
khối lượng nguyên tử của Cu là 63,546.
Khối lượng phân tử của một chất là khối lượng của một phân tử chất và bằng tổng
khối lượng nguyên tử của các nguyên tố trong phân tử.
Ví dụ 4: Khối lượng phân tử của H2O là 18,0152; khối lượng phân tử của NH3 là 17,0304.
Mol nguyên tử : Là lượng của một nguyên tố được tính bằng gam có giá trị về số
bằng khối lượng nguyên tử của nguyên tố đó.
Ví dụ 5: Mol nguyên tử của H là 1,0079 gam; mol nguyên tử của O là 15,994 gam.
Mol phân tử: Là lượng chất được tính bằng gam và có giá trị về số bằng khối
lượng phân tử của chất đó.
Ví dụ 6: Mol phân tử của H2O là 18,0152 gam; mol phân tử của NH3 là 17,0304 gam.
❖ Nguyên chất và hỗn hợp.
Nguyên chất chỉ có một chất. Hỗn hợp gồm hai chất trở lên ❖
Đƣơng lƣợng lƣợng và đƣơng lƣợng gam.
Các chất luôn luôn tác dụng với nhau theo những tỷ lệ nhất định về khối lượng. Ví dụ 7: Xét phản ứng H2 + Cl2 as 2HCl 1 35,5 *
Đƣơng lƣợng của một nguyên tố là số phần khối lượng của nguyên tố đó
kết hợp (hay thay thế) vừa đủ với một phần khối lượng của hiđro hoặc 8 phần khối lượng của oxy. *
Đƣơng lƣợng của một hợp chất là số phần khối lượng của hợp chất đó tác
dụng vừa đủ với một đương lượng hiđro hoặc với một đương lượng oxy hoặc với một
đương lượng của một hợp chất bất kỳ nào khác đã biết đương lượng. *
Đƣơng lƣợng gam của một chất chính là khối lượng tính ra gam của một
đương lượng chất đó. 2 lOMoAR cPSD| 45315597 *
Công thức tính đƣơng lƣợng gam của một nguyên tố Đ = A , n
trong đó: Đ là đương lượng gam của nguyên tố,
A là khối lượng mol nguyên tử của nguyên tố đó,
n là hóa trị nguyên tố.
Ví dụ 8: Fe có mol nguyên tử bằng 55,84, ứng với 2 hóa trị 2, 3 ĐFe = = 27,92g, ĐFe = = 18,61g. *
Công thức tính đƣợng lƣợng gam của một hợp chất: Đ = M , trong
đó: M là khối lượng mol phân tử, n
n: Có ý nghĩa khác nhau tùy loại phản ứng.
+ Trong phản ứng trao đổi: n là tổng số đơn vị điện tích trao đổi.
Ví dụ 9: Tính đương lượng của H3PO4 trong các phản ứng sau :
H3PO4 + 3 NaOH → Na3PO4 + 3 H2O (1)
H3PO4 + 2 NaOH → Na2HPO4 + 2 H2O (2)
H3PO4 + NaOH → NaH2PO4 + H2O (3)
Đương lượng của H3PO4 lần lượt là : M 98 Đ(1) = = , 3 3 M 98 Đ(2) = = , 2 2 M 98 Đ(3 ) = = . 1 1 Tổng quát ta có : 3 lOMoAR cPSD| 45315597
Ví dụ 10: Xét phản ứng: KOH + HCl → KCl + H 2O Đ KOH = MKOH = 56 g, 1
Ba(OH)2 + 2HCl → BaCl 2 + 2H 2O ĐBa(OH)2 = M 85,5g. 2
Ví dụ 11 : Xét phản ứng : 2AgNO3 + MgCl2 → 2AgCl + Mg(NO3) 2 MAgNO 3 ĐAgNO3 = 170 g, 1 MAgCl Đ AgCl = 143,5 g, 1
ĐMg(NO3)2 = MMg(NO3)2 148 74g , 2 2 M MgCl2 95 ĐMgCl = 47,5g . 2 2 2
Trong những phản ứng khác nhau, đương lượng gam của cùng một chất có thể
khác nhau. Cho nên không thể áp dụng máy móc các quy tắc trên.
+ Trong phản ứng oxy hóa khử: n là số e mà một phân tử chất đó trao đổi với chất khác , .
Ví dụ 12: Tính đương lượng gam của chất oxi hóa và chất khử trong phản ứng SO2 + 2H2S → 3S + 2H2O
Chất oxi hóa: SO2, chất khử H2S
Ta có: S+4 + 4e → S0 do đó ĐSO 16(g). 2
Ta có: S-2 → S0 + 2e do đó ĐH2S 17(g) . 4 lOMoAR cPSD| 45315597
* Định luật đƣơng lƣợng: Các chất tương tác với nhau hay thay thế nhau theo
những lượng tỷ lệ với đương lượng của chúng hay khi hai chất tác dụng với nhau, số đương
lượng của chúng phải bằng nhau.
Xét phản ứng tổng quát: A + B → C + D mA §A mB §B
1.1.2. Các định luật hóa học cơ bản
❖ Định luật bảo toàn khối lƣợng
―Khối lượng của các chất trong mọi quá trình hoá học là luôn luôn không đổi‖.
Đó là nội dung của định luật bảo toàn khối lượng do nhà hoá học người Pháp là A.
L. Lavoisier; (1743 – 1794) đề ra năm 1785.
Tổng khối lượng của các chất tham gia bằng tổng khối lượng của các chất thu được sau phản ứng .
m chất phản ứng = m chất sản phẩm.
❖ Định luật thành phần không đổi.
Một chất dù điều chế bằng cách nào cũng có thành phần không đổi.
❖ Định luật Avôgdrô.
Ở cùng điều kiện về nhiệt độ, áp suất, những thể tích bằng nhau của các chất khí
đều chứa cùng một số phân tử.
1.2. Cấu tạo nguyên tử - Định luật tuần hoàn và hệ thống tuần hoàn các nguyên tố
1.2.1. Cấu tạo nguyên tử theo các thuyết cổ điển và theo quan điểm hiện đại.
1.2.1.1. Mẫu hành tinh nguyên tử của Rơzefor.
Mỗi nguyên tử có một hạt nhân mang điện dương và các electron quay xung quanh.
Hạt nhân được cấu tạo từ các hạt p,n. Các hạt p; n liên kết với nhau bằng một loại lực đặc
biệt gọi là lực hạt nhân. Khối lượng nguyên tử hầu như tập trung ở hạt nhân. 5 lOMoAR cPSD| 45315597
Hình 1.1. Mô hình mẫu hành tinh nguyên tử của Rơzefor
Theo thuyết của Rơzefor thì khi nguyên tử hấp thụ năng lượng thì electron chuyển
động từ quỹ đạo gần nhân hơn ra quỹ đạo xa nhân hơn như vậy nguyên tử sẽ phát c
ra sóng điện từ có năng lượng = h . . Do đó nguyên tử sẽ phát ra sóng điện từ có tần
số tăng dần và quang phổ của chúng phát ra sẽ là quang phổ liên tục nhưng thực tế quang
phổ của các chất là quang phổ vạch.
Kết quả và hạn chế của thuyết Rơzefor: Mẫu của Rơzefor giải thích được sự cấu
tạo tuần hoàn của các nguyên tố hoá học song không giải thích được sự tạo thành quang
phổ vạch của các nguyên tố.
1.2.1.2. Thuyết Bo (Borh)
❖ Trong nguyên tử, electron chỉ có thể chuyển động trên quỹ đạo xác định; có
bán kính xác định. Khi quay trên các quỹ đạo đó năng lượng của electron được bảo toàn.
❖ Mỗi quỹ đạo ứng với một mức năng lượng của electron. Quỹ đạo gần hạt
nhân nhất ứng với năng lượng thấp nhất. Quỹ đạo càng xa nhân, mức năng lượng càng cao.
❖ Khi electron chuyển từ quỹ đạo này sang quỹ đạo khác thì xảy ra sự hấp thụ
hoặc giải phóng năng lượng. Electron hấp thụ năng lượng khi chuyển từ quỹ đạo gần nhân
ra quỹ đạo xa nhân hơn và giải phóng năng lượng khi chuyển theo chiều ngược lại. c = h . = E 1 - E 2
trong đó: E1; E2 là những mức năng lượng khác nhau.
Kết quả và hạn chế của thuyết Bohr.
Kết quả: Thuyết Bohr đã giải thích được cấu tạo quang phổ vạch của nguyên tử
hiđro. Nó cũng cho phép tính được bán kính nguyên tử hiđro ở trạng thái cơ bản: r
= 0,529. 10—10 m = 0,529. 10—8 cm = 0,529 A0.
Hạn chế: Không giải thích được cấu tạo của quang phổ của các nguyên tử phức
tạp. Không giải thích được sự tách các vạch quang phổ dưới tác dụng của điện trường và từ trường.
1.2.1.3. Lƣợng tử năng lƣợng (Do M.Plank tìm ra).
Năng lượng bức xạ được giải phóng hoặc hấp thụ dưới dạng những lượng gián
đoạn gọi là các lượng tử năng lượng.
Với các tia đơn sắc có tần số : = h.
trong đó: là tần số; h là hằng số Plank = 6,6256 10—34 J.s 6 lOMoAR cPSD| 45315597
Lượng tử năng lượng của bức xạ được giải phóng hoặc hấp thụ bằng hiệu giữa hai
mức năng lượng có tần số và bước sóng được xác định khi electron chuyển từ mức E1 đến mức E2: = h. = h. C = E1- E2
trong đó: C là vận tốc ánh sáng, λ là bước sóng ánh sáng.
1.2.1.4. Bản chất sóng hạt của hạt vi mô ❖ Các hạt cơ bản.
Electron (e): Do Thompson tìm ra năm 1897 có khối lượng là 9,1095.10—31 kg,
điện tích: 1,602. 10—19 C. Electron quay xung quanh hạt nhân nguyên tử.
Hạt nhân nguyên tử gồm 2 loại hạt:
Proton ( p) mang điện dương.
Nơtron ( n) không mang điện.
❖ Các hạt cơ bản có lƣỡng tính sóng – hạt
* Tính chất hạt: Hiệu ứng quang điện. Hiệu ứng Compton.
Trong các hiệu ứng này, ánh sáng thể hiện tính chất như các dòng hạt có khối l-
ượng và dung lượng xác định, với động năng được tính bằng công thức: = mC2
trong đó: m là khối lượng hạt ánh sáng, C là vận tốc ánh sáng *
Tính chất sóng: Thể hiện ở tính nhiễu xạ và giao thoa. Đối với ánh sáng: = h. = hC/λ = mC2 = hC/ λ h = mC
Đối với các hạt vi mô: = h/mv.
1.2.1.5. Nguyên lý bất định Heisenberg.
Về nguyên tắc không thể xác định đồng thời chính xác cả toạ độ và vận tốc hạt.
Do đó không thể vẽ hoàn toàn chính xác quỹ đạo chuyển động của hạt. h x . vx m
trong đó: x là sai số của phép đo toạ độ theo phương x 7 lOMoAR cPSD| 45315597
vx là sai số của phép đo thành phần vận tốc hạt theo phương x
m là khối lượng hạt h là hằng số Planck.
1.2.1.6. Cơ học lƣợng tử - Phƣơng trình sóng Schrodinger.
Electron có thể chuyển động trong cả thể tích nguyên tử và có mặt ở bất kỳ vị trí
nào xung quanh nhân. Khả năng tìm thấy electron ở một khu vực nào đó có thể nhiều hay
ít. (Xác suất tìm thấy electron ở một khu vực nào đó lớn hay nhỏ).
Electron chuyển động rất nhanh nên điện tích của nó được dãn ra thành những
đám mây mang điện âm ở xung quanh hạt nhân. Ở nơi nào đó, xác suất tìm thấy electron
lớn thì mật độ đám mây electron sẽ lớn.
Ngoài việc chuyển động xung quanh hạt nhân, có thể coi electron còn tham gia
chuyển động nội tại. Các đại lượng vật lý đặc trưng cho trạng thái của electron trong nguyên tử gồm: + Năng lượng.
+ Véc tơ mômen động lượng quỹ đạo
+ Véc tơ mômen động lượng riêng ứng với chuyển động nội tại.
Các đại lượng trên được biểu diễn bằng các thông số xác định. Trong hoá học gọi là số lượng tử.
Đối với các hạt vi mô, cơ học lượng tử sử dụng phương pháp khảo sát dựa vào những khái niệm sau: ❖ Hàm sóng.
Trạng thái chuyển động của hạt vi mô (ví dụ: electron trong nguyên tử), nằm tại
điểm M(x,y,z,) ở thời điểm được mô tả bởi hàm: │ (x,y,z, )│
Hàm có thể âm, dương hoặc hàm phức.
2 = . * có ý nghĩa vật lý.
Hàm │ (x,y,z, )│2 dx dy dz cho biết xác suất tìm thấy hạt tại thời điểm trong
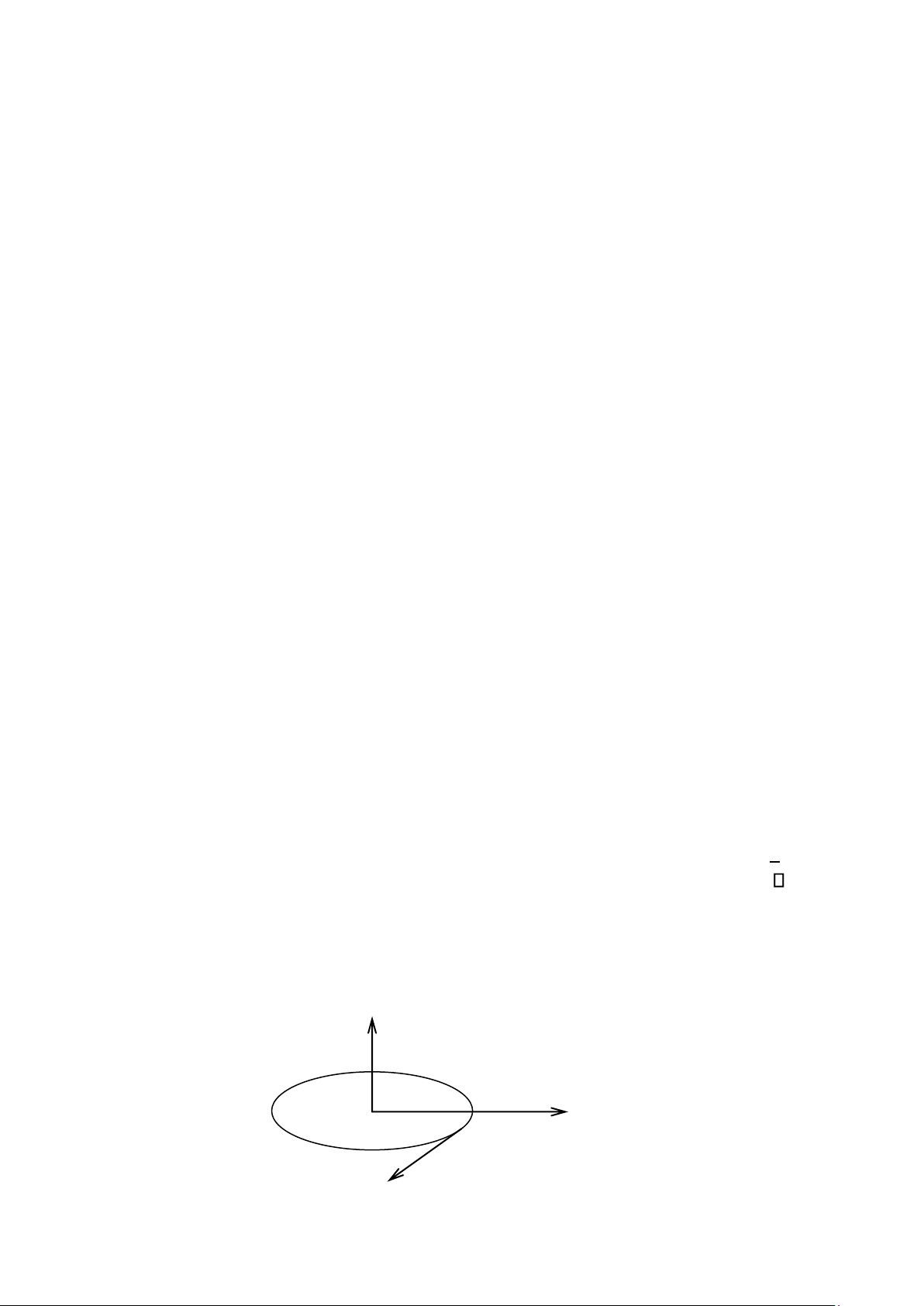
nguyên tử có thể tích d = dx dy dz; có tâm M(x,y,z) Z M ө r r x 8 lOMoAR cPSD| 45315597 y O φ x
Hình 1.2. Mô phỏng tọa độ hạt trong thể tích nguyên tử
Trong cơ học lượng tử không còn khái niệm quỹ đạo nên người ta tìm cách xác
định xác suất tìm thấy hạt ở các thời điểm khác nhau trong không gian. Nếu trạng thái của
hạt không phụ thuộc vào thời gian (được gọi trạng thái dừng) thì hàm sóng không phụ thuộc thời gian .
Khi đó biểu thức│ (x,y,z, )│2 biểu thị mật độ, xác suất tìm thấy hạt tại một điểm
có toạ độ │ (x,y,z, )│2 hay (q) 2 chỉ phụ thuộc toạ độ.
Vì xác suất tìm thấy hạt trong toàn bộ không gian bằng 1 nên: 2d =1
Đây là điều kiện của hàm sóng.
❖ Phƣơng trình Schrodinger. h2 8 2m V . = E. 2 2 2
trong đó: Toán tử Laplace: = x + y2 + z2
V : Thế năng của hạt E : Năng lượng toàn phần của hạt
❖ Orbitan nguyên tử và ý nghĩa các số lƣợng tử
* Số lượng tử chính n, n : 1, 2, 3, 4…
Xác định năng lượng của electron trong nguyên tử. 1 mZ2 . e4
En = - n2 8 2o . h2 trong đó: M là
khối lượng electron e là điện tích
electron Z là điện tích hạt nhân
H là hằng số Planck n là các số nguyên dương 1,2,3,4.. .
Năng lượng được đặc trưng bởi số lượng tử n gọi là số lượng tử chính.
Ứng với mỗi giá trị n có một mức năng lượng. Các e có giá trị như nhau coi như
cùng một lớp electron. n : 1 2 3 4 5 6 7 Mức En : K L M N O P Q 9 lOMoAR cPSD| 45315597
Vì n là các số nguyên dương nên năng lượng electron trong nguyên tử chỉ có thể
nhận các giá trị gián đoạn.
* Số lƣợng tử phụ l.
Đối với hệ có nhiều electron thì mỗi mức năng lượng lại được chia thành n phân mức.
Ví dụ 1: Mức thứ nhất n = 1 sẽ có 1 phân mức.
Mức thứ hai n =2 sẽ có 2 phân mức.
Mỗi phân mức được đặc trưng bằng số lượng tử phụ, ký hiệu: l
nhận các giá trị 0 , 1 , 2 , 3 …. n - 1
ứng với các ký hiệu s p d f
Mức thứ nhất n = 1 sẽ có 1 phân mức. Ký hiệu 1s Mức
thứ hai n = 2 sẽ có 2 phân mức. Ký hiệu 2s 2p
Mức thứ ba n = 3 sẽ có 3 phân mức. Ký hiệu 3s 3p 3d
Mức thứ tư n = 4 sẽ có 4 phân mức. Ký hiệu 4s 4p 4d 4f
Trong cùng một mức năng lượng, các phân mức có năng lượng hơi khác nhau.
Phân mức nào có trị số l càng lớn sẽ có năng lượng càng lớn.
Trong cùng một mức năng lượng : s < p < d < f
* Số lượng tử từ m
Các electron trong cùng một phân mức năng lượng (cùng trị số l), vectơ mômen
động lượng quỹ đạo có độ lớn như nhau nhưng có thể có chiều ngược nhau. Vì electron
chuyển động trong trường hạt nhân là một trường đối xứng tâm, mọi phương đều có ý
nghĩa như nhau. Khi có từ trường hay điện trường ngoài, người ta phân biệt các phương
bằng cách chiếu các vectơ momen động lượng lên phương từ trường. h
Bằng tính toán người ta tìm được độ lớn của hình chiếu đó: M z = m 2
trong đó: Mz là hình chiếu của vectơ M lên trục Z P = m.v (Động lượng) 10 lOMoAR cPSD| 45315597
Hình 1.3. Mô phỏng vectơ momen động lượng của electron trong nguyên tử.
Số lượng tử từ m phải là số nguyên có (2l +1) giá trị từ - l qua 0 đến + l Ví
dụ 2: Khi l = 2 thì m có 2. 2 + 1 = 5 giá trị đó là: -2, -1 , 0 , +1 , +2.
Mỗi giá trị của m được gọi là một trạng thái. Ví dụ 3:
- Phân mức s (l = 0) có 2 . 0 +1 = 1 trạng thái ứng với m = 0
- Phân mức p (l =1) có 2 . 1 +1 = 3 trạng thái ứng với m = -1, 0, + 1
Như vậy: Mỗi phân mức (phân lớp) gồm những vùng được định hướng trong
không gian, ở đó xác suất có mặt electron cao nhất gọi là Orbitan nguyên tử (AO) và
Số lượng AO trong mỗi phân mức bằng trị số m. Ví dụ 4: n l m Lớp Phân lớp Số AO Ký hiệu 1 1(K) 0 S 0 1s 2 2(L) 1 s 0 - 2s p 1, 0, +1 2p
* Số lƣợng tử spin ms.
Các electron ngoài chuyển động quanh hạt nhân còn có sự chuyển động nội tại 1 h
ứng với một mômen động lượng riêng có độ lớn là
. Những hình chiếu của véc tơ 2 2
này lên trục z xác định các giá trị + , - . Và được gọi là số lượng tử spin (số lượng tử quay).
Chiều quay thuận ứng với s = + , Chiều quay ngược ứng với s = -
Số lượng tử quay hình dung gần đúng chiều tự quay của electron.
❖ Hình dạng các đám mây electron .
Phụ thuộc vào số lượng tử n, l, m.
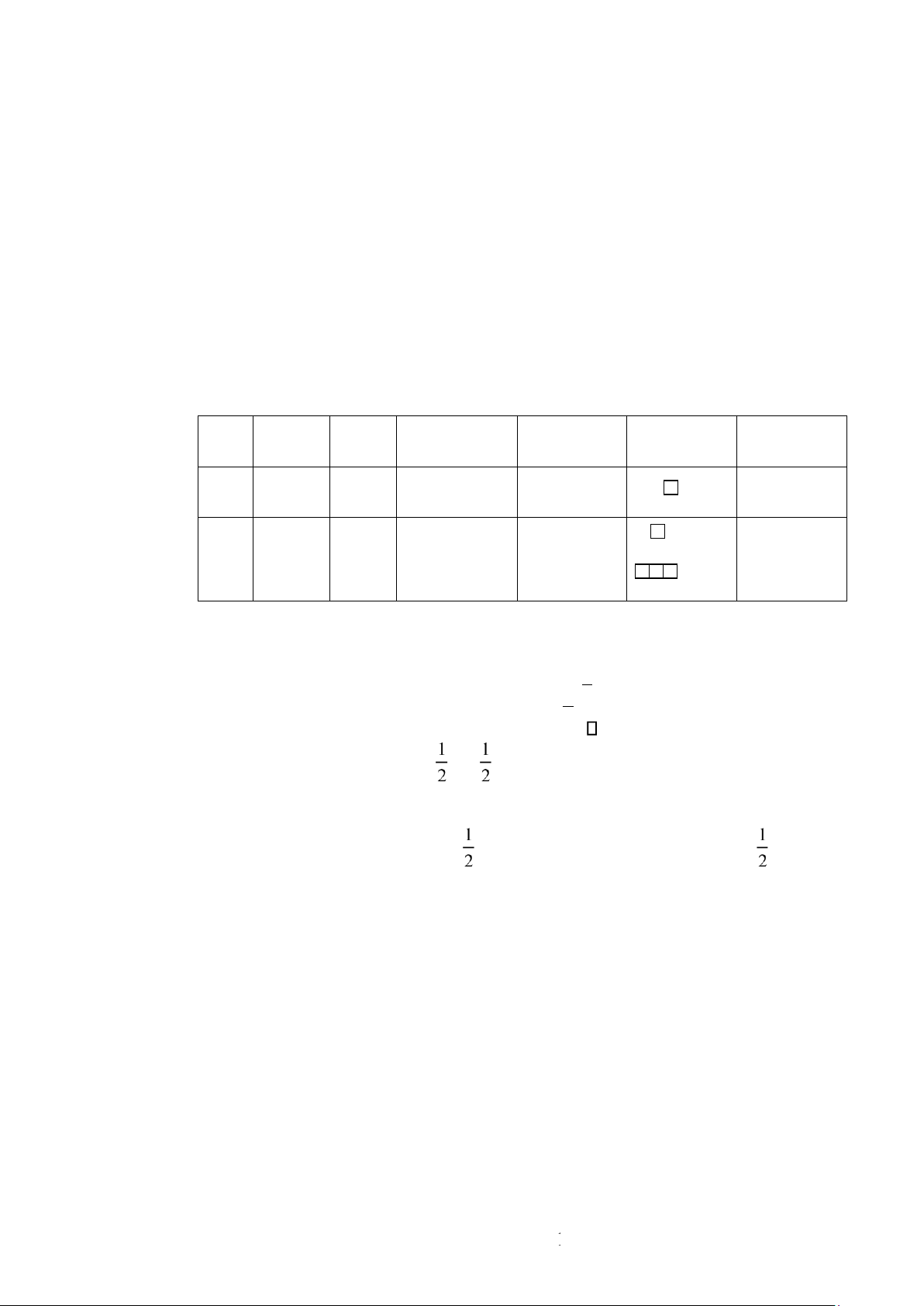
Đám mây electron s có dạng đối xứng cầu. Mật độ đám mây chỉ phụ thuộc vào
khoảng cách tới nhân ( không phụ thuộc vào phương). Xác suất tìm electron trên mặt cầu là lớn nhất. 11 lOMoAR cPSD| 45315597
Hình 1.4. Mô hình đám mây electron s
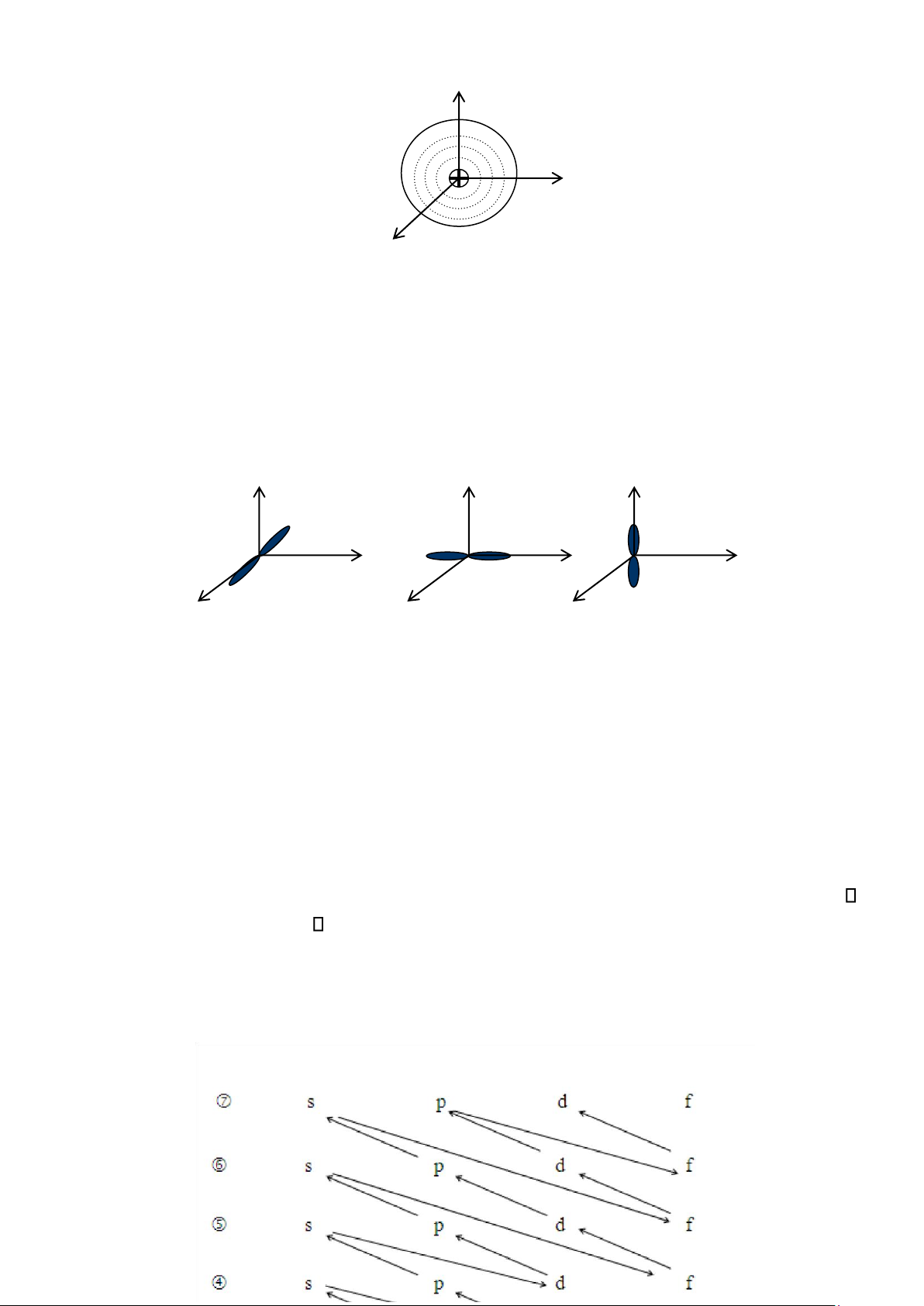
Đám mây electron p có dạng quả tạ đôi có 3 trạng thái px, py, pz (3 trị số của m).
3 đám mây p phân bố theo 3 trục toạ độ.
Đám mây p có trục đối xứng. Mật độ đám mây không phụ thuộc khoảng cách tới nhân.
Hình 1.5. Mô hình đám mây electron p ❖
Sự phân bố các electron trong nguyên tử có nhiều electron.
Electron có trong nguyên tử không những bị hạt nhân hút mà còn chịu lực đẩy từ
phía các electron. Các lớp electron bên trong thành màng đặc biệt làm giảm lực hút của
electron đối với hạt nhân.
Trong nguyên tử nhiều electron, năng lượng phụ thuộc số lượng tử chính n và số
lượng tử phụ l. Sự tăng năng lượng theo các phân mức như sau:
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f
5d < 6p < 7s < 5f 5d < 7p. 12 lOMoAR cPSD| 45315597
Hình 1.6. Sơ đồ quy tắc Klechcopxki ❖
Sự phân bố các e trong nguyên tử ở trạng thái cơ bản tuân theo các
nguyên lý và các qui tắc sau: * Nguyên lý Pauli.
Trong cùng nguyên tử không thể có hai electron hoàn toàn giống nhau. Tức là các
electron trong cùng nguyên tử phải khác nhau ít nhất một số lượng tử.
+ Số electron tối đa ứng với một trạng thái có nhiều nhất là 2e.
Các electron có 3 số lượng tử n, l, m giống nhau được gọi là có cùng trạng thái.
Chúng phải khác nhau ở số lượng tử ms (một electron nhận + , một electron nhận – )
+ Số electron tối đa trong một phân mức có 2l + 1 trạng thái.
Mỗi trạng thái tối đa chỉ có 2 electron . Cụ thể như sau:
- Phân mức s ( l = 0) có 2. 0 + 1 = 1 trạng thái nên chỉ có 2e.
- Phân mức p ( l = 1) có 2 . 1 +1 = 3 trạng thái nên chỉ có tối đa 6e.
- Phân mức d ( l = 2) có 2 . 2 +1 = 5 trạng thái nên chỉ có tối đa 10e.
- Phân mức f ( l = 3) có 2 . 3 +1 = 7 trạng thái nên chỉ có tối đa 14e.
+ Số electron tối đa trong một mức năng lƣợng.
Một mức có n phân mức. Số electron tối đa trong một mức bằng tổng số các
electron tối đa trong các phân mức. n - 1
2 (2l + 1) = 2n2 (Viết gọn N = 2n2 ) l = 0
Ví dụ 5: Mức 2 (n = 2 ) tối đa có N = 2n2 = 2 .22 = 8e.
Mức 3 (n = 3 ) tối đa có N = 2n2 = 2 .32 = 18e.
Mức 4 (n = 4 ) tối đa có N = 2n2 = 2 .42 = 32e.
Lớp thứ nhất: ( n = 1 ) Lớp K tối đa 2e.
Lớp thứ hai: ( n = 2 ) Lớp L tối đa 8e.
Lớp thứ ba: ( n = 3 ) Lớp M tối đa 18e. 13 lOMoAR cPSD| 45315597
Lớp thứ tư: ( n = 4 ) Lớp N tối đa 32e.
* Nguyên lý vững bền.
Electron sẽ vững bền nhất nếu có năng lượng dự trữ thấp nhất.
Năng lượng phụ thuộc số lượng tử n, l. Phân mức ứng vào số (n + l) lớn hơn có năng lượng lớn hơn.
Nếu hai phân mức có (n + l) bằng nhau. Phân mức nào có n lớn hơn, có mức năng
lượng cao hơn sẽ xếp sau.
Ví dụ 6: 3p có n + l = 3 + 1 = 4 4s có n + l = 4 + 0 = 4
4s phải xếp sau 3p vì 4s > 3p
Ví dụ 7: 4s có n + l = 4 + 0 = 4 3d có n + l = 3 + 2 = 5
3d phải xếp sau 4s vì 3d > 4s * Quy tắc Hund.
Trong một phân lớp, các electron có khuynh hướng chiếm các orbitan sao cho tổng
số spin của chúng là cực đại ( tổng số electron độc thân là cực đại ).
❖ Công thức electron và cấu trúc vỏ electron .
Dựa vào nguyên lý Pau li, nguyên lý vững bền và quy tắc Hund, biểu diễn cấu trúc
vỏ electron của nguyên tử bằng công thức electron theo hai cách.
Cách 1. Dùng ký hiệu để chỉ phân lớp có ghi số electron trên mỗi phân lớp dưới dạng số mũ:
Ví dụ 8: Biểu diễn cấu trúc electron của oxy.
Cấu hình electron : 1s2 2s2 2p4 O6 2
Lớp 1 : (Lớp K) n = 1 có 2e.
Lớp 2 : (Lớp L) n = 2 có 6e ( lớp ngoài cùng).
2e đầu tiên điền vào phân mức 1s
2e tiếp theo điền vào phân mức 2s
4e sau cùng điền vào phân mức 2p. Ví dụ 9:
Biểu diễn cấu trúc electron của Titan. 2 14 lOMoAR cPSD| 45315597 10
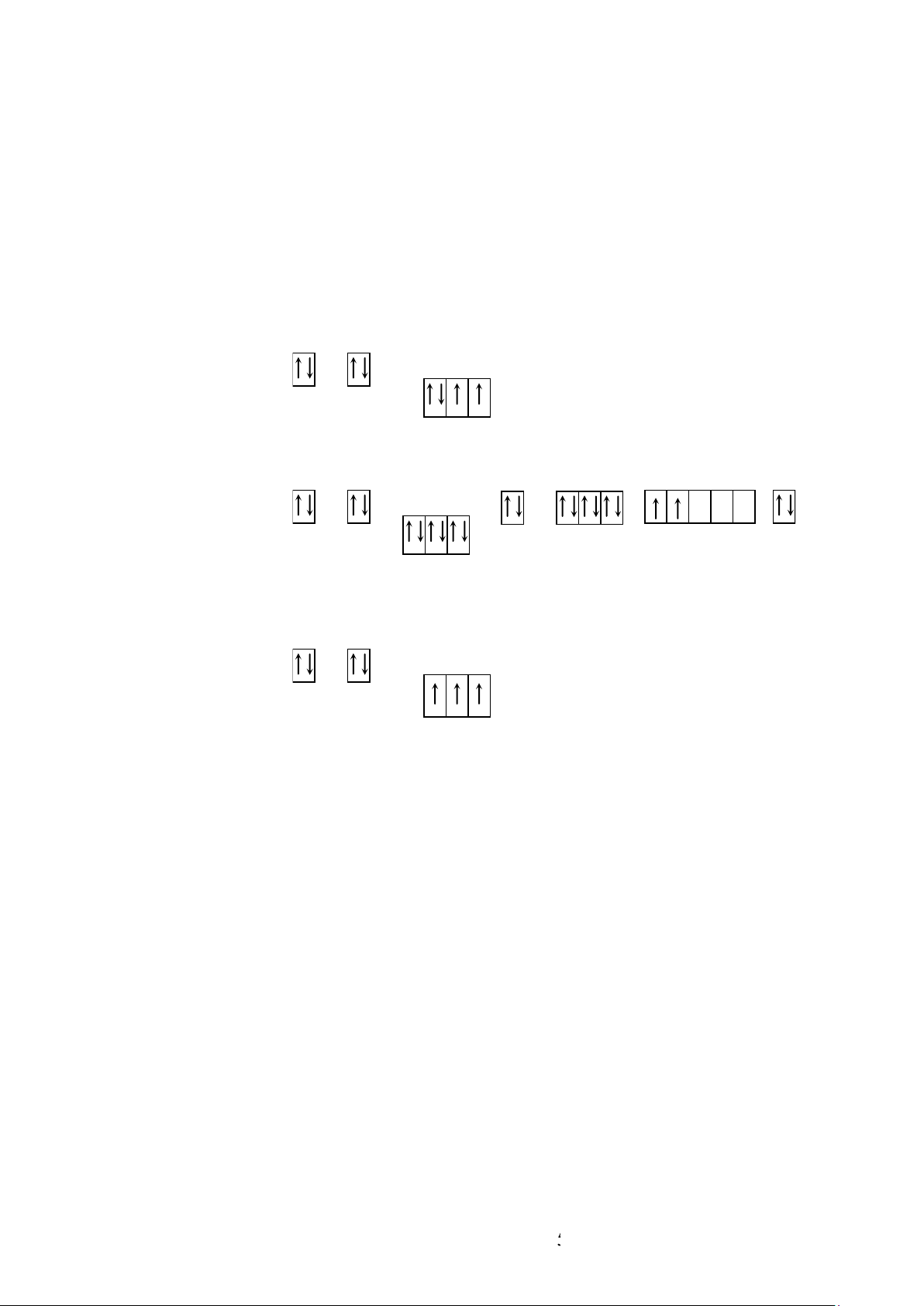
Cấu hình electron : 1s2 2s2 2p6 3s2 3p6 3d2 4s2 Ti 8 2 Cách 2.
Mỗi orbitan được biểu diễn bằng một ô vuông (ô lượng tử ).
Mỗi electron được ký hiệu bằng một mũi tên.
Hai electron trong một orbitan có spin ngược chiều nhau được biểu diễn bằng hai mũi tên ngược chiều. 6 O 2 1s2 2s2 2p4 2 10 Ti 8 2 1s2 2s2 2p6 3s2 3p6 3d2 4s2 5 N 2 1s2 2s2 2p3 15