

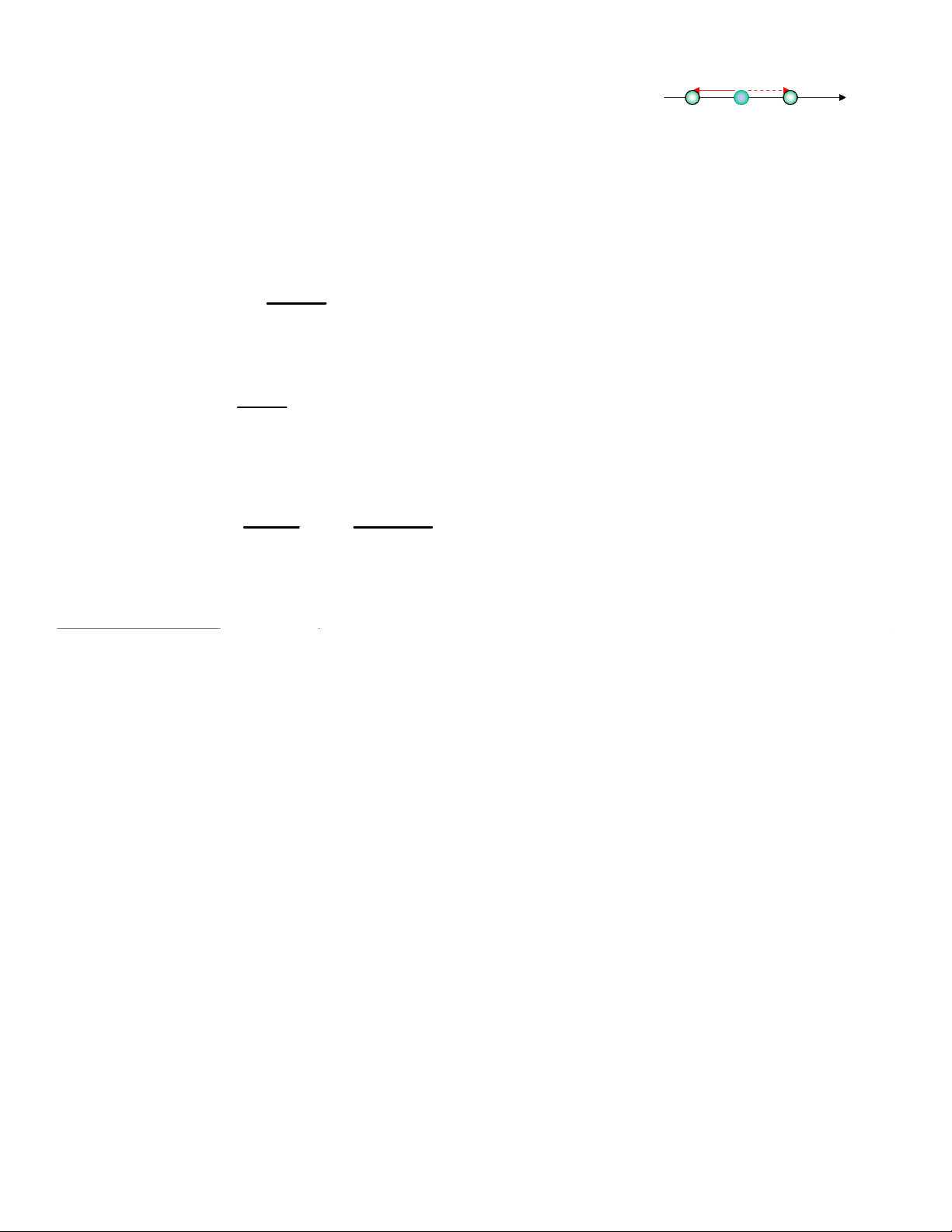

Preview text:
§éng häc: N/C c¸c ®Æc tr−ng cña chuyÓn
®éng vμnh÷ng chuyÓn ®éng kh¸c nhau
(kh«ng tÝnh ®Õn lùc t¸c dông)
§éng lùc häc: N/C mèi quan hÖ gi÷a
chuyÓn ®éng víi t−¬ng t¸c gi÷a c¸c vËt (
cã tÝnh ®Õn lùc t¸c dông)
TÜnh häc lμmét phÇn cña §éng lùc häc
N/C tr¹ng th¸i c©n b»ng cña c¸c vËt
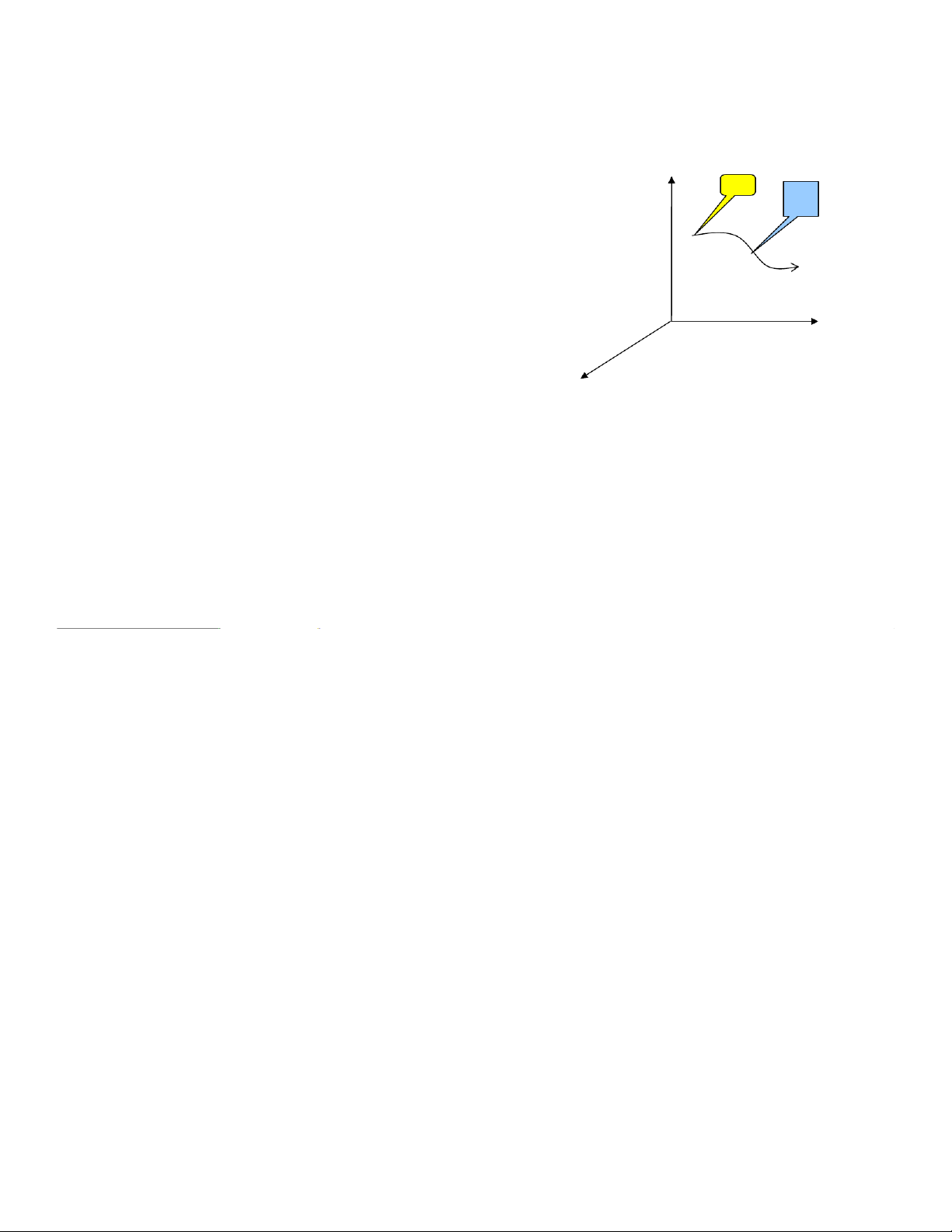
1.4. QuÜ ®¹o: §−êng t¹o bëi tËp hîp c¸c vÞ
trÝ cña chÊt ®iÓm trong kh«ng gian
F/t quÜ ®¹o:Khö tham sè t trong f/t c®: z A M VÝ dô: F/t chuyÓn ®éng: x=a.cos(ωt+ϕ) y=a.sin(ωt+ϕ) y x F/t quÜ ®¹o: x2+y = 2 a21.5. Hoμnh ®é cong:
VÞ trÝ chÊt ®iÓm x¸c ®Þnh bëi cung AM=s
Qu·ng ®−êng s lμhμm cña thêi gian s=s(t)
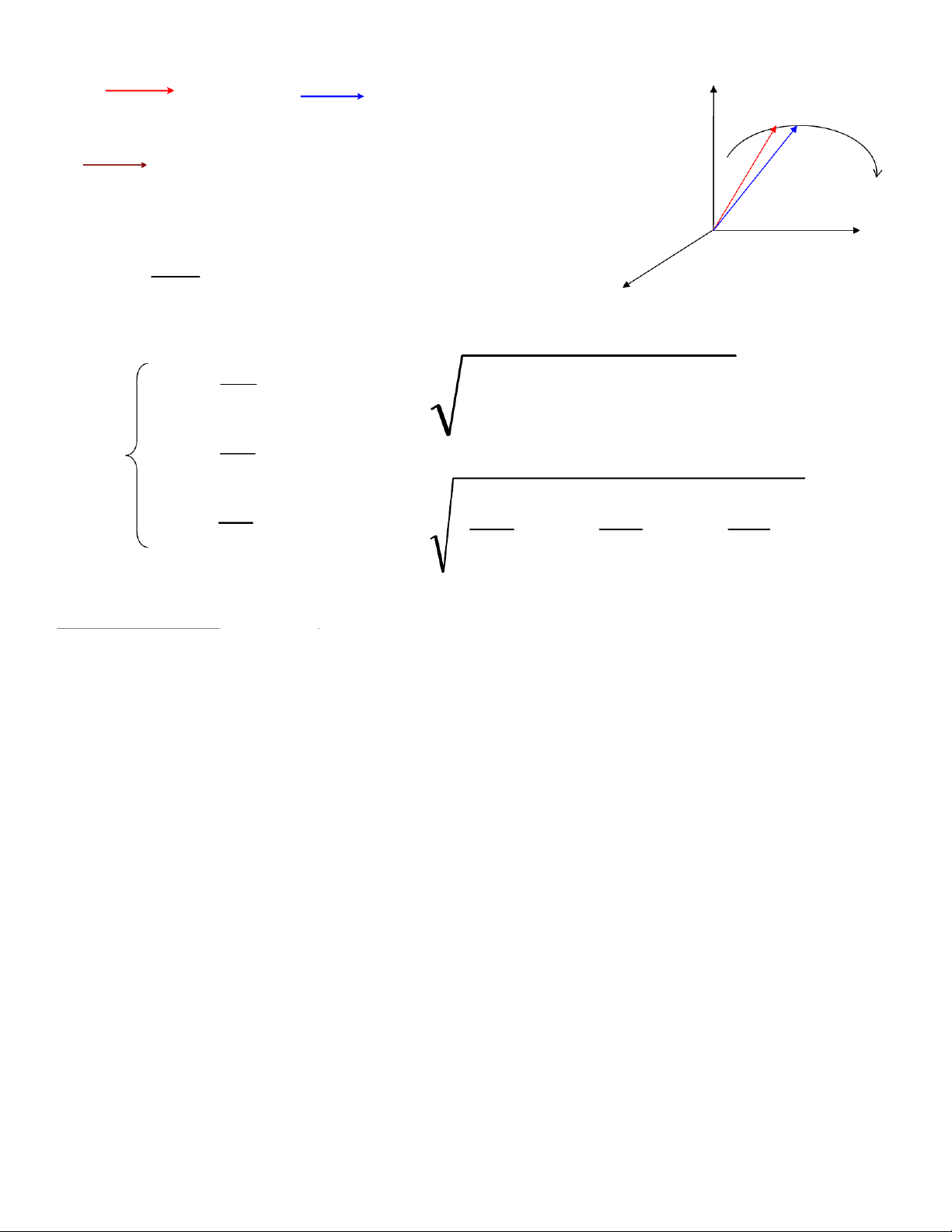
2.2. VÐc t¬ vËn tèc trong hÖ to¹ ®é ®Ò c¸c: r' OM r d rr =r r r = = + z MM’ r r M ds M'd drr rr =r = rr' = drr r §¹o hμm vect¬ to¹ v O y x dt ®é theo thêi gian dx v =2 2 2 x + v dt + v v xv dy y z vr = v = y dt dz v = dx dy dz z= dt + (+ )2 ) ( )2 ( 2 dt dt dt
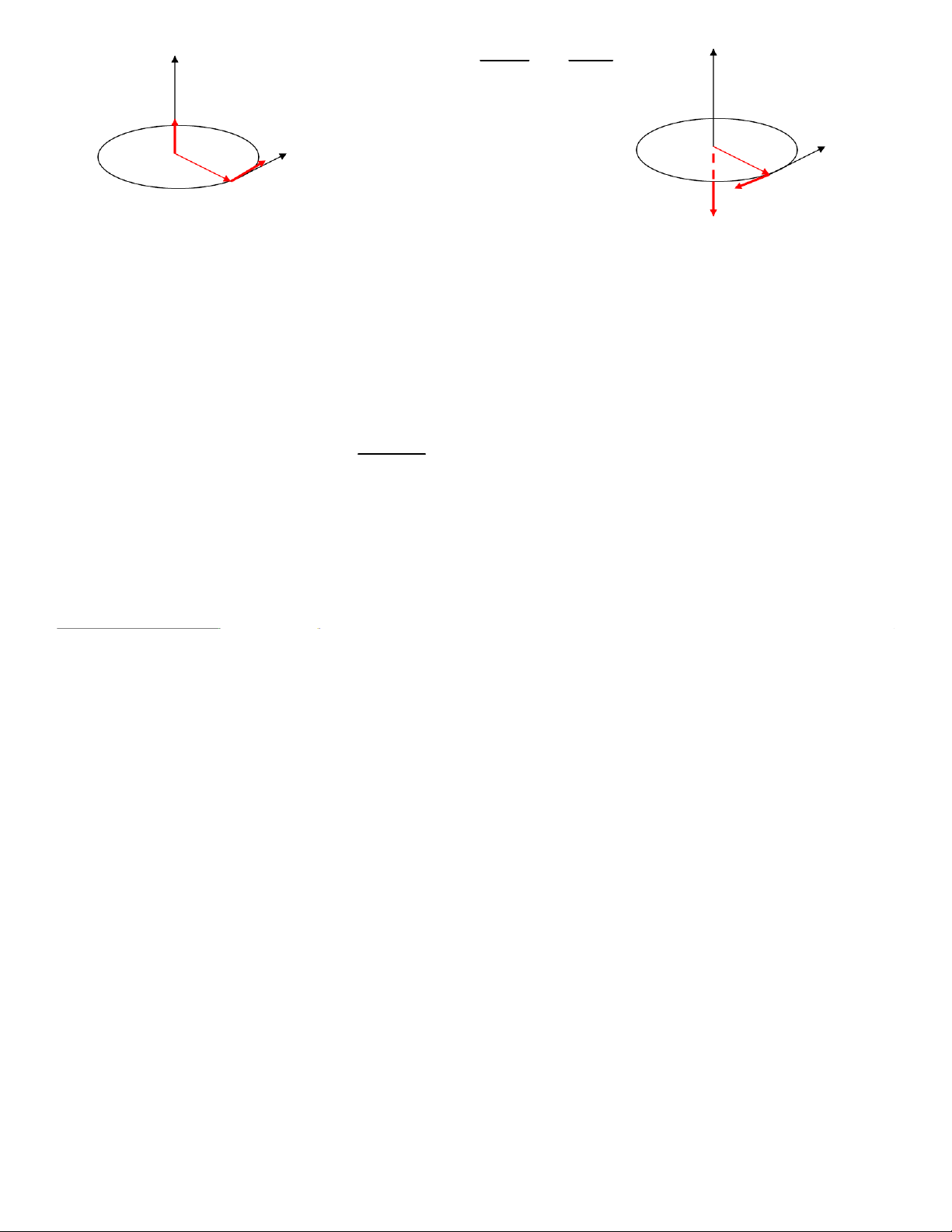
3.2 Gia tèc tiÕp tuyÕn vμgia tèc ph¸p tuyÕn t n art arn ar
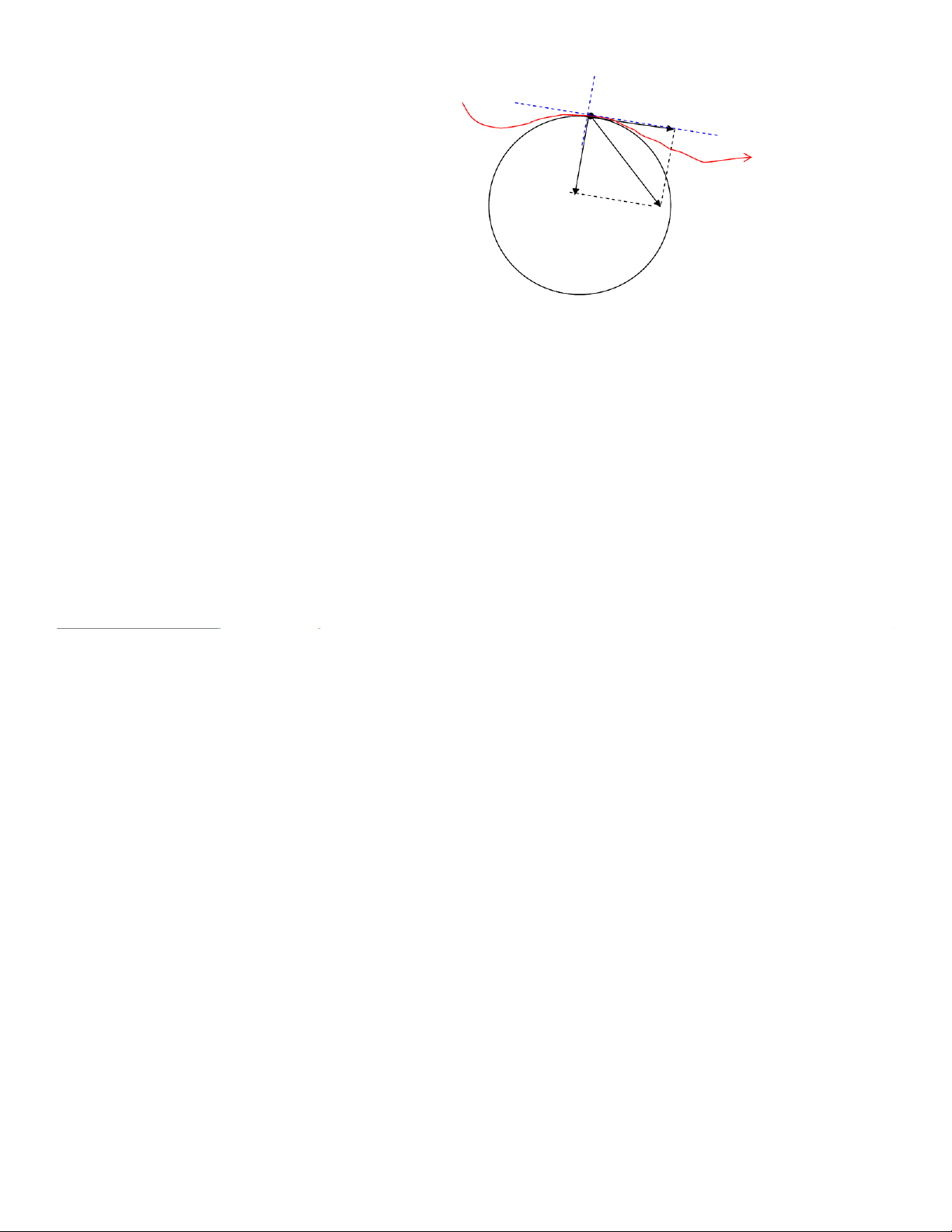
ChiÕu vÐc t¬ gia tèc lªn tiÕp tuyÕn vμph¸p tuyÕn cña quü ®¹o a ra r r = t a+ n ar Gia tèc tiÕp tuyÕn t ar gia tèc ph¸p tuyÕn n ¾Gia tèc ph¸p tuyÕn
- Møc ®é thay ®æi ph−¬ng cña vËn tèc
- Cã ph−¬ng trïng ph¸p tuyÕn cña quü ®¹o
- H−íng vÒ phÝa lâm cña quü ®¹o - Cã gi¸ trÞa2 v n= R M
4. Mét sè d¹ng chuyÓn ®éng c¬ ®Æc biÖt
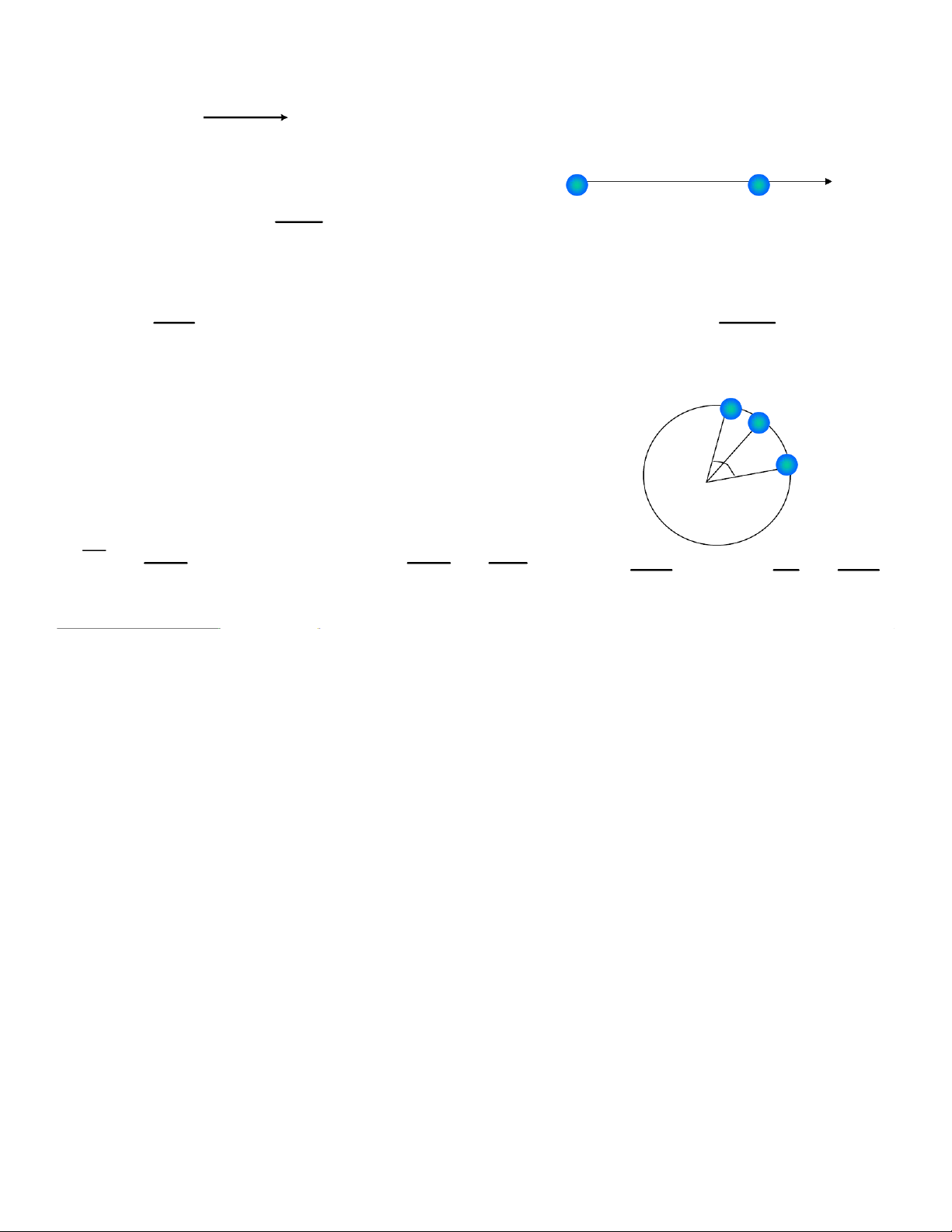
4.1. ChuyÓn ®éng th¼ng biÕn ®æi ®Òu: ar v -v = const 2 20=2as a 0 OM dv const = + a t=a dt v adt at v ds at2 ⇒v0 = a+t v0 =s ∫+(at v0)dt dt 2 4.2. ChuyÓn ®éng trßn M’ T¹i M: t Δθ M
T¹i M’: t’=t+Δt=> OM quÐt Δθ O Δθ θ Δ dθ 2 1 ω =dt ω = π ω Δ l → πim t 0 = TT ;= 2 ν = = Δt t Δ ω r r r r ω Δ ω r d ω β = Δ l → im t 0 = ω r t Δ dt r β r r r a = β × t R r O a r r O r t R v R r v r M M at Qui t¾c tam diÖn thuËn β
T−¬ng tù nh−trong chuyÓn ®éng th¼ng: ω = βt + ω 20 βt θ = + ω0t 2 ω2 − ω2 = β 0 2 θ
4.4. Dao ®éng th¼ng ®iÒu hoμ ph−¬ng tr×nh dao ®éng 0 x x = . A cos( t ω + ϕ)
TuÇn hoμn theo thêi gian: x(t)=x(t+nT) =2 π T ω dx = dt = − v ω ω . A+ si ϕ n( t ) 2 = = − d ω v d x ω 2 + ϕ a . A cos( t ) dt dt d a v' r + r r r d A vr' dV ⇒ = + dt dt dt a Vt¬ gia tèc M trong hqc O
a’ Vt¬ gia tèc M trong hqc O’
A Vt¬ gia tèc O’ ®èi víi hqc O
VÐc t¬ gia tèc cña chÊt ®iÓm ®èi víi mét hÖ
qchiÕu O b»ng tæng hîp vÐc t¬ gia tèc cña chÊt
®iÓm ®ã ®èi víi hÖ qc O’chuyÓn ®éng tÞnh tiÕn
®èi víi hÖ qc O vμvt¬ gia tèc tÞnh tiÕn cña hÖ qc O’ ®èi víi hÖ qc O




