Chương 1: Vi phân toàn phần | Tài liệu nội dung môn Toán Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh
Trong kinh tế học, ta hầu như làm việc với các mô hình toán học. Theo bản chất của chúng thì các mô hình này chứa các biến được chia thành hai loại: biến nội sinh (endogenous variables) và biến ngoại sinh (exogenous variables). Biến nội sinh (endogenous variables) (theo tiếng Hy Lạp “endo” có nghĩa là bên trong, “genous” có nghĩa là được sinh ra): là biến mà mô hình cố gắng giải thích. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: Toán 1
Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm
Mục lục . . .. .. .. .. .. . . . .. .. . . . .. . . . .. .. . . . .. . . . .. .. . .. .. .. .. .. .. .. .. . . . .. .. . . . .. . . . .. .. . . . .. 1
1.1. Biến nội sinh và biến ngoại sinh .............................................................................. 2
1.2. Dạng cấu trúc và dạng thu gọn của mô hình ........................................................... 3
1.2.1. Dạng cấu trúc ........................................................................................... 3
1.2.2. Dạng thu gọn ............................................................................................. 3
1.2.3. Hàm ẩn và hàm hiện ................................................................................. 4
1.2.4. Tính đạo hàm ............................................................................................ 6
1.3. Vi phân toàn phần cho người mới bắt đầu .............................................................. 7 dy 1.3.1. Phương pháp tính
................................................................................ 8 dx
1.4. Vi phân toàn phần cho người trung bình ............................................................... 11
1.4.1. Phương pháp tính ................................................................................... 12
1.5. Vi phân toàn phần cho người thông thạo ............................................................. 15
1.5.1. Hệ các hàm ẩn ......................................................................................... 15 y
1.5.2. Cách tính i ......................................................................................... 18 x j
1.6. Vi phân toàn phần và tối ưu hóa ........................................................................... 23
1.6.1. Một hệ quả từ ngyên lý chính ................................................................ 23
1.6.2. Cực đại hóa lợi nhuận ............................................................................ 24
1.6.3. Tối ưu hóa có ràng buộc ........................................................................ 27
1.6.4. Cực đại hóa hàm tiện ích ....................................................................... 28
1.6.5. Cực tiểu hóa chi phí ............................................................................... 30
Bài tập chương 1 .......................................................................................................... 33 Trang 1
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm Chương 1 VI PHÂN TOÀN PHẦN
1.1 Biến nội sinh và biến ngoại sinh
Trong kinh tế học, ta hầu như làm việc với các mô hình toán học. Theo bản chất
của chúng thì các mô hình này chứa các biến được chia thành hai loại: biến nội sinh
(endogenous variables) và biến ngoại sinh (exogenous variables).
Biến nội sinh (endogenous variables) (theo tiếng Hy Lạp “endo” có nghĩa là bên
trong, “genous” có nghĩa là được sinh ra): là biến mà mô hình cố gắng giải thích. Ví dụ
Trong mô hình cung và cầu, cả hai giá cân bằng P và đại lượng Q được xác định
bởi mô hình, nghĩa là tại giao điểm của các đường cong cung và cầu. Chúng là các biến nội sinh.
Biến ngoại sinh (exogenous variables) (theo tiếng Hy Lạp “exo” có nghĩa là bên
ngoài, “genous” có nghĩa là được sinh ra): là biến mà mô hình không nói gì về việc xác
định nó cả. Tuy nhiên, các biến này có ảnh hưởng đến các biến nội sinh. Ví dụ
Trong mô hình cung và cầu, thời tiết là biến ngoại sinh. Thời tiết xấu làm thay đổi
đường cong cung các quả cam về bên trái và làm cho P đi lên và Q đi xuống. Do đó, thời tiết
ảnh hưởng đến P và Q nhưng P và Q không ảnh hưởng đến thời tiết. Mô hình cung và
cầu thì không nói gì về việc thời tiết được xác định như thế nào.
Thường các biến về chính sách như thuế, việc chi tiêu chính phủ hay việc cung
cấp tiền là các biến ngoại sinh.
Về mặt toán học, bạn có thể nghĩ các biến ngoại sinh như “ x ” hay biến độc lập,
trong khi các biến nội sinh là các biến phụ thuộc hay “y ”.
Điển hình trong kinh tế ta không sử dụng các biến x và y trong ký hiệu của
chúng ta, vì thế thường bạn sẽ cần suy nghĩ một cách cẩn thận về những gì là các biến Trang 2
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm
ngoại sinh và những gì là các biến nội sinh trong bất kỳ mô hình riêng biệt nào.
1.2 Các dạng cấu trúc và các dạng thu gọn của mô hình
1.2.1 Dạng cấu trúc của mô hình
Đầu tiên khi ta viết một mô hình kinh tế, đó là trước khi thực hiện bất kỳ việc rút
ra một điều phức tạp nào, ta thường gặp trường hợp là các biến nội sinh y [y ] ( n1 i
vector) và các biến ngoại sinh x [x ( m1 vector) đều lẫn lộn nhau và xuất hiện ở cả i ] hai vế của dấu =:
M ( y, x) N (y, x)
Dạng này của mô hình thường được xem như dạng cấu trúc của mô hình vì trong
dạng này các điều giả sử (hay cấu trúc) của mô hình thường là dễ thấy.
1.2.2 Dạng thu gọn của mô hình
Trong kinh tế học ta thường quan tâm đến các thay đổi của biến x , là các biến
ngoại sinh có ảnh hưởng như thế nào đối với biến y , là các biến nội sinh.
Ví dụ ta có thể xem sự gia tăng tốc độ thuế t (một biến ngoại sinh) có ảnh hưởng
như thế nào đến giá P và sản lượng Q (các biến nội sinh).
Thường thì khó đối với dạng cấu trúc của mô hình để thực hiện những thử nghiệm
như thế. Bài toán đó là các biến y và x đều lẫn lộn với nhau. Điều đó sẽ là có ích hơn
nếu có dạng rút gọn của mô hình:
y h(x )
sao cho y nằm ở vế bên trái và một hàm số nào đó theo biến x nằm ở vế bên phải.
Nếu biết trước dạng của (
h x) , ta có thể xét bất kỳ số thay đổi nào theo x và khi đó
thấy biến y thay đổi như thế nào. Ví dụ
Giả sử y là số công nhân mà công ty sử dụng, x là giá hàng hoá mà công ty bán 1
ra và x là lương danh nghĩa. Từ mô hình ta thấy biên tế thu nhập của việc sử dụng thêm 2 một công nhân là: Trang 3
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm 1 2
M ( y, x , x ) x y 1 2 1
trong khi biên tế chi phí là: 1 2
N( y, x , x ) x y 1 2 2
Đồng nhất biên tế thu nhập M và biên tế chi phí N ta đi đến mô hình cấu trúc:
M (y, x , x ) N(y, x , x ) 1 2 1 2 hay 1 1 2 2 x y x y 1 2
Để nhận dạng rút gọn ta cần để y một mình bên vế trái. Trong trường hợp này,
điều này không khó thực hiện. Khi đó, ta thấy: x 1
y h(x , x ) 1 2 x 2
Giả sử x x 1. Khi đó, ta có y . Xét ba thử nghiệm sau: 1 2 1
1) Nhân đôi x trong khi giữ x cố định. 1 2
2) Nhân đôi x trong khi giữ x cố định. 2 1
3) Nhân đôi cả hai x và x . 1 2
Ta thấy từ dạng rút gọn là thử nghiệm đầu tiên đưa đến việc nhân đôi y cho 2, thử 1
nghiệm thứ hai đưa đến việc giảm phân nửa y cho , trong khi trong thử nghiệm thứ ba 2
không có gì xảy ra đối với y .
1.2.3 Hàm ẩn và hàm hiện
Liên quan một cách mật thiết đến khái niệm của các dạng rút gọn và dạng cấu trúc
là các hàm hiện và các hàm ẩn.
Định nghĩa 1: Hàm ẩn là hàm được viết như sau:
g( y, x) 0
trong đó các biến y và x xuất hiện lẫn lộn với nhau ở vế trái và 0 ở bên vế phải.
Cho trước dạng cấu trúc của mô hình. Điều đó là dễ dàng để viết lại nó dưới dạng Trang 4
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm
một hàm ẩn. Do đó từ dạng cấu trúc M (y,x) N (y,x) ta có thể tìm hàm ẩn g (y ,x ) như sau: ( g , y ) x M( , y ) x N( , y ) x 0 Dùng ví dụ: 1 1 2
M (y ,x ,x ) x y và 2
N (y ,x ,x ) x y 1 2 1 1 2 2 Ta có: 1 1 2 2 g( ,
y x , x ) x y x y 0 1 2 1 2
Định nghĩa 2: Một hàm ẩn phục hồi trật tự các biến y và x sao cho y nằm một mình ở
vế trái như sau:
y h(x )
Cho trước hàm hiện hay dạng rút gọn, ta luôn luôn có thể viết nó dưới dạng một hàm ẩn như sau:
g( y, x) y h(x) 0
Tuy nhiên, thường ta không thể tìm một hàm hiện hay dạng rút gọn từ một hàm ẩn hay mô hình cấu trúc. Ví dụ Cho trước hàm ẩn:
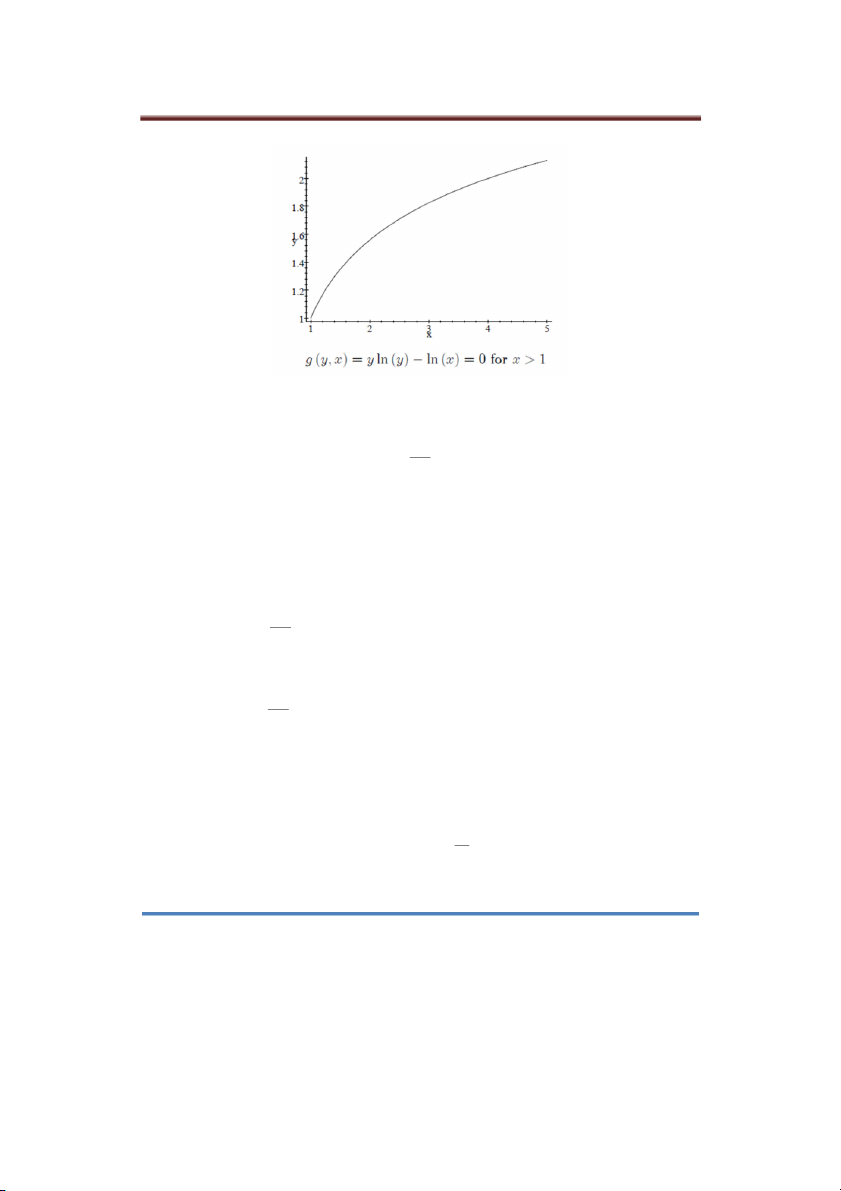
g( y, x) y ln(y) ln(x) 0, x 1
Không có cách nào để làm cho y nằm một mình bên vế trái. Cách tốt nhất ta có thể làm là:
y ln(y) ln(x) hay y y x
Tuy nhiên, g(y, x) y ln(y) ln(x) 0 là một hàm số hoàn hảo. Chẳng hạn ta có thể chứng
tỏ rằng nó là tăng và lõm. Ta có thể vẽ nó như sau: Trang 5
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm
1.2.4 Tính đạo hàm
Trong kinh tế học, ta thường chú ý đến việc tính đạo hàm riêng: y i x j
Đạo hàm riêng này nói cho chúng ta mối quan hệ giữa biến ngoại sinh thứ j và
biến nội sinh thứ i khi tất cả các biến ngoại sinh khác giữ không đổi. Điều này tương ứng
với việc thử nghiệm giữ tất cả các biến ngoại sinh khác, ngoại trừ biến x , không đổi, j
thay đổi nhỏ biến x và ta sẽ thấy biến y thay đổi như thế nào. j i y
Định nghĩa 3: Nếu i 0 thì mối liên hệ dương tồn tại giữa x và y ; nghĩa là một sự x j i j
tăng (giảm) theo x dẫn đến sự tăng (giảm) theo y . j i y
Định nghĩa 4: Nếu i 0 thì mối liên hệ âm tồn tại giữa x và y ; nghĩa là một sự tăng x j i j
(giảm) theo x dẫn đến sự giảm (tăng) theo y . j i Ví dụ
Trong ví dụ trên ta thấy x1
y h(x , x ) 1 2 x2 Ta có: Trang 6
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm y 1 y x1 0, 0 2 x x x ( x ) 1 2 2 2
Do đó, có mối liên hệ dương giữa x và y và mối liên hệ âm giữa x và y . 1 2
Bởi vì thường ta không thể tìm được dạng rút gọn của mô hình, nghĩa là thường ta
không thể phục hồi mô hình đủ để nhận nó mà trong đó y xuất hiện một mình ở vế trái y và ( h )
x xuất hiện ở vế phải và ta luôn không thể tính được
i theo cách thông thường. xj
Một cách may mắn, dù dạng cấu trúc của mô hình hay hàm ẩn có lộn xộn ta vẫn có y
thể tính được i một cách gián tiếp bằng cách dùng vi phân toàn phần. Trong phần dưới x j
đây ta sẽ học kỹ thuật này bắt đầu với những trường hợp đơn giản nhất và xây dựng đến
trường hợp tổng quát hơn.
1.3 Vi phân toàn phần cho người bắt đầu
Giả sử cho trước hàm ẩn:
g(y, x) 0
trong đó cả hai y và x là các số vô hướng sao cho có một biến nội sinh y và một biến
ngoại sinh x . Dưới điều kiện này, điều này xác định một hàm hiện:
y h(x )
Lý do mà chúng ta biết điều này chính là Định Lý Hàm Ẩn (Implicit Function Theorem):
Định Lý 5: (Định Lý Hàm Ẩn I) g y x Hàm hiện (
h x) là tồn tại nếu
( , ) 0. Khi đó, ta có: y
dy h '(x) dx
Ta thực hiện được điều này bằng cách lấy vi phân toàn phần của g (y ,x) .
Định nghĩa 6: Vi phân toàn phần được xác định như sau:
g(y, x)
g(y, x) dy dx 0 y x Trang 7
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm dy
Vi phân toàn phần có thể được sử dụng để tính
bằng cách sử dụng phương pháp sau: dx dy
1.3.1 Phương pháp tính dx
Bước 1: Hãy xác định biến nội sinh y và biến ngoại sinh x trong mô hình của bạn.
Bước 2: Nếu mô hình cấu trúc không được viết như một hàm ẩn dưới dạng
g(y, x) 0 thì viết lại nó sao cho nó ở dưới dạng này. g (y ,x )
Bước 3: Lấy đạo hàm riêng g(y, x) theo y và gọi là a . Do đó, a . Hãy y
kiểm tra a 0 mà bảo đảm rằng hàm hiện tồn tại theo Định Lý Hàm Ẩn. Nhân a cho dy để nhận được: a dy g (y ,x)
Bước 4: Lấy đạo hàm riêng g (y ,x) theo x và gọi là b . Do đó, b . Hãy x
kiểm tra a 0 mà bảo đảm rằng hàm hiện tồn tại theo Định Lý Hàm Ẩn. Nhân b cho dx để nhận được: b dx
Bước 5: Cộng các kết quả ở bước 3 và 4 và cho chúng bằng 0 để nhận được vi phân toàn phần:
a dy b dx 0
Bước 6: Giải tỉ số dy để nhận được: dx dy b dx a
hay bằng cách sử dụng định nghĩa của a và b :
g(y, x) dy x dx
g(y, x) y Trang 8
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm
Chú ý nếu a 0 thì tỉ số này sẽ không được xác định.
Ví dụ 1: (Hàm tuyến tính). Cho mô hình cấu trúc: 3Q 4R 9
trong đó Q là sản lượng của táo được trồng trong một vườn cây và R là lượng mưa rơi. Giải
Áp dụng bước 1 trong phương pháp, Q là biến nội sinh và R là biến ngoại sinh.
Điều này suy ra từ nghĩa thông thường là lượng mưa có thể ảnh hưởng đến sản lượng của
táo nhưng sản lượng của táo thì không ảnh hưởng đến lượng mưa.
Áp dụng bước 2 ta có thể viết điều này như một hàm ẩn bằng cách đặt số 9 vào vế
khác của dấu bằng để nhận được: ( g , Q )
R 3Q 4 R 9 0
Từ các bước 3,4, và 5, vi phân toàn phần của g (Q,R) là: 3dQ 4dR 0 vì g( , Q ) R g( , Q ) R a 3,b 4 Q R
Chú ý a 3 0 và do đó hàm hiện tồn tại theo Định Lý Hàm Ẩn. Q Giải đối với
từ vi phân toàn phần khi đó suy ra được: R Q 4 R 3
Đây là câu trả lời giống nhau mà ta sẽ nhận được khi làm việc với dạng hiện của
hàm số hay dạng rút gọn. Ta thu được điều này bằng cách giải g(Q, R) 3Q 4R 9 0
đối với Q để nhận được: 4 Q R 3 3 Từ đó dễ dàng suy ra: Q 4 R 3 Trang 9
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm
Ví dụ 2: Cho phương trình cấu trúc dưới dạng: y y x
ở đây y là biến nội sinh và x là biến ngoại sinh.
Từ bước 2 bằng cách lấy ln( ) cả hai vế, ta có thể viết phương trình này như một hàm ẩn:
g(y, x) y ln(y) ln(x) 0
mà không thể được viết như một hàm hiện y h(x).
Từ các bước 3,4 và 5 vi phân toàn phần của ( g , y ) x là: 1
(1 ln(y))dy dx 0 x vì g ( , y ) x g ( , y ) x 1 a 1 ln( ) y , b y x x
Giải đối với dy : dx dy 1 dx x(1 ln(y))
Ta có thể dùng kết quả này để chứng tỏ rằng dy 0 1
với x 1 và do đó mối liên hệ dx
dương tồn tại giữa x và y . Điều này được suy ra vì:
x 1 ln( y) y ln(x) 0
kéo theo y 1 vì nếu y 1 thì ln( y) 0 . Do đó, từ x 1 và (1 ln( ) y ) 1 ta có: dy 1 x 1 0 1 dx x(1 ln(y))
Như một bài tập, lấy đạo hàm một lần nữa theo x và chứng tỏ rằng: 2 d y 1 1 1 dy 0 2 dx
x (1 ln(y )) x
y (1 ln(y )) dx sao cho hàm số là lõm.
Ví dụ 3: (Nhu cầu Lao Động Ngắn Hạn)
Giả sử một công ty có hàm sản xuất ngắn hạn Q f( )
L trong đó f '( ) L 0 và Trang 10
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm W
f "(L) 0 và trong đó Q là sản lượng và L là số lao động. Nếu w là lương thực sự P
thì công ty sẽ chọn L thoả mãn:
f '( L) w
Ở đây w là biến ngoại sinh và L là biến nội sinh. Ta có thể viết dạng cấu trúc
này của mô hình như một hàm ẩn sau:
g (L,w ) f '(L ) w 0
Điều này xác định hàm nhu cầu lao động hay là hàm hiện hay dạng rút gọn sau: L L (w) Vi phân toàn phần là:
f "(L )dL dw 0 vì g ( L, ) w g ( L , ) w a f "(L ),b 1 L w
Chú ý a 0 và vì thế hàm hiện tồn tại.
Chú ý hệ số của dL là âm vì biên tế sản phẩm lao động giảm kéo theo f "(L) 0 .
Giải đối với dL ta thấy: dw dL 1 0 dw f "(L )
và do đó đường cong cầu lao động có độ dốc hướng xuống.
1.4 Vi Phân Toàn Phần cho Người Trung Bình
Bây giờ xét một hàm ẩn có m biến ngoại sinh x ,x ,...,x (mà ta có thể viết như 1 2 m
m 1 vector x ) và biến nội sinh y . Hàm ẩn bây giờ được viết như sau:
g(y, x , x ,..., x m ) 0 1 2 và xác định hàm hiện: y (
h x , x ,..., x ) 1 2 m Trang 11
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm
vì Định Lý Hàm Ẩn được thoả.
Định Lý 7: (Định Lý Hàm Ẩn II) g
(y ,x ,x ,...,x )
Hàm hiện y h(x ,x ,...,x ) tồn tại nếu 1 2 m 0 . 1 2 m y
Định nghĩa 8: Vi phân toàn phần của ( g , y )
x 0 được cho bởi:
a dy b dx b dx ... b dx 0 1 1 2 2 m m trong đó ,
a b , b ,..., b được định nghĩa như dưới đây: 1 2 m
1.4.1 Phương pháp tính
Ta tiến hành như sau:
Bước 1: Nếu không rõ ràng, bạn hãy xác định biến nội sinh y và các biến ngoại
sinh x , x ,..., x trong mô hình của bạn. 1 2 m
Bước 2: Hãy viết dạng cấu trúc của mô hình như một hàm ẩn dưới dạng:
g(y, x , x ,..., x ) 0 1 2 m
Một cách tổng quát, điều này có nghĩa là chuyển tất cả các số hạng về bên vế trái
của mô hình cấu trúc và cho bằng 0.
Bước 3: Lấy đạo hàm riêng g (y ,x) theo y và gọi đạo hàm riêng này là a . Hãy
chắc chắn là a 0 sao cho hàm hiện tồn tại theo Định Lý Hàm Ẩn. Nhân a cho dy để nhận được: a dy
Bước 4: Lấy đạo hàm riêng g(y, x) theo x và gọi đạo hàm riêng này là b . Nhân 1 1
b cho dx để nhận được b dx . Lặp lại điều này với x ,x ,...,x và cộng chúng lại với 1 1 1 1 2 3 m nhau để nhận được:
b dx b dx ...b dx 1 1 2 2 m m
Bước 5: Cộng các kết quả của các bước 3 và 4 với nhau và cho chúng bằng zero
để nhận được vi phân toàn phần:
a dy b dx b dx ... b dx m m 0 1 1 2 2 Trang 12
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm y
Bước 6: Để nhận được đạo hàm riêng
, cho tất cả các dx bằng zero ngoại trừ x j
dx và sau đó thay các d còn lại trong vi phân toàn phần bằng các . j
Do đó, ta đặt dy y ,dx x
và dx với i j trong vi phân toàn phần để nhận được: i 0 j j
ay b x 0 j j y Bây giờ giải với : x j
g(y, x) y b x j j x a g (y, x) j y
Ví dụ 1: (Hàm Tuyến Tính Đơn Giản). Xét mô hình cấu trúc:
3Q 4R 7S 9
trong đó Q là sản lượng của táo, R là lượng mưa rơi và S là lượng ánh sang mặt trời
chiếu xuống. Theo bước 1, Q là biến nội sinh và R và S là hai biến ngoại sinh.
Mô hình cấu trúc có thể được viết lại như một hàm ẩn như sau:
g (Q,R,S ) 3Q 4R 7S 9 0
Theo các bước 3,4 và 5 vi phân toàn phần là:
3dQ 4dR 7dS 0 vì
g(Q, R, S)
g(Q, R, S)
g(Q, R, S) a 3,b 4 ,b 7 1 2 Q R S
Giả sử ta muốn tính Q. Theo bước 6, trước tiên đặt dR 0 và sau đó thay các d S
còn lại bằng sao cho dQ Q và dS S
. Khi đó, ta thu được: 3 Q 7 S 0 Do đó, Trang 13
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm Q 7 . S 3
Trong ví dụ này ta cũng có thể tính Q từ dạng rút gọn. Từ 3Q 4R 7S 9 0 ta S
có thể đi đến dạng rút gọn (hay hàm hiện) như sau: 4 7
Q h(R, S) R S 3 3 3
Từ đó hiển nhiên tính được: Q 7 S 3
Ví dụ 2: Xét hàm ẩn: 1 1 2 2
g(y, x , x ) x y x y 1 2 1 2
Ta thấy hàm này có dạng rút gọn: x1
y h(x , x ) 1 2 x2
Từ đó dễ dàng tính y và y . x x 1 2
Ta hãy tìm các đạo hàm riêng này từ hàm ẩn. Vi phân toàn phần là: 3 1 1 1 1 2 2 2 2
(x y x y )dy y dx y dx 0 1 2 1 2 2 vì: 3 1
g(y, x , x ) 1 1 1 2 2 2 a
x y x y 1 2 y 2 2 1 g
(y, x , x ) 1 2 2 b y 1 x1 1
g(y, x , x ) 1 2 2 b y 2 x2
Để tính y ta đặt dx 0 và thay các d còn lại bằng sao cho dy y và dx x . Khi x 2 1 1 1 đó, ta thu được: Trang 14
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm 3 1 1 1 2 2 2
(x y x y ) y y x 0 1 2 1 2 y Giải đối với ta thu được: x 1 1 2 y 2 y 3 1 x 1 2 2 x y x y 1 2
Như một bài tập hãy dùng dạng rút gọn x1 y
để chứng minh rằng biểu thức ở trên đối x2 y với bằng 1 . x x 1 2
Để tính y hãy đặt dx 0 và thay các d còn lại bằng để thu được: x 1 2 3 1 1 1 2 2 2
(x y x y )y y x 0 1 2 2 2 y Giải đối với ta thu được: x 2 1 2 y 2 y 0 3 1 x 2 2 2 x y x y 1 2
Như một bài tập hãy dùng dạng rút gọn x1 y
để chứng minh rằng biểu thức ở trên đối x2 y x với bằng 1 . x 2 (x ) 2 2
1.5 Vi Phân Toàn Phần cho Người Thông Thạo
1.5.1 Hệ các hàm ẩn
Giả sử ta có một mô hình trong đó có n biến nội sinh y , y ,..., y và m biến ngoại 1 2 n
sinh x , x ,..., x . Ta có thể viết điều này một cách ngắn gọn hơn bằng cách đặt y [y ] là 1 2 m i
n 1 vector của các biến nội sinh và x [x ] là m 1 vector của các biến ngoại sinh. i Trang 15
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm
Giả sử cho trước n hàm ẩn:
g (y ,x) 0,i 1, 2,...,n i
Điều này xác định n dạng rút gọn hay các hàm hiện được cho bởi: y h x i n i i ( ), 1, 2,...,
nếu Định Lý Hàm Ẩn được thỏa.
Định Lý 9 (Định Lý Hàm Ẩn III)
Các hàm hiện y h (x ,x ,...,x ),i 1, 2,...,n tồn tại nếu det[ ]
A 0 trong đó i i 1 2 m
g (y.x) g (y.x) g (y.x) 1 1 1 ... y y y 1 2 n g (y.x) g (y.x) g (y.x) 2 2 2 ... A y y y 1 2 n g (y.x) g (y.x) g (y.x) n n ... n y y y 1 2 n
Ví dụ: Giả sử ta có mô hình cấu trúc trong đó sản lượng táo Q và sản lượng mật ong Q 1 2
có liên quan với lượng mưa rơi R , lượng ánh sáng mặt trời chiếu xuống S và nhiệt độ T như sau:
3Q 2Q 3S 5T 2R 7 1 2
Q 2Q 6 R 3T 2 S 4 1 2
ở đây Q và Q là các biến nội sinh và R ,S và T là các biến ngoại sinh. Chú ý ta có hai 1 2
phương trình và hai biến nội sinh.
Khi đó, điều này có thể được viết như hai hàm ẩn như sau:
g (Q ,Q R, S,T) 3Q 2Q 2R 3S 5T 7 0 1 1 2 1 2
g (Q , Q , R ,
S T) Q 2Q 6 R 2 S 3T 4 0 2 1 2 1 2 ở đây:
g ( y, x)
g (y, x) 1 1 Q Q 3 2 1 2 A g ( , y ) x g ( , y ) x 1 2 2 2 Q Q 1 2 Trang 16
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm và 3 2 det 8 0 1 2 và do đó các hàm hiện: Q h ( , R S, T) 1 1 Q h ( , R S,T) 2 2
tồn tại theo Định Lý Hàm Ẩn. Q h
(R,S,T )
Do đó, ta có lẻ muốn tính 2 2
, nghĩa là lượng ánh sáng mặt trời S S
chiếu xuống có ảnh hưởng như thế nào đến sản lượng mật ong. y
Tổng quát, ta có lẻ muốn tính
i để xác định bản chất của mối quan hệ giữa biến x j
ngoại sinh thứ j là x và biến nội sinh thứ i là y . Ta thực hiện điều này bằng cách tính j i
vi phân toàn phần được định nghĩa như sau:
Định nghĩa 10: Vi phân toàn phần của g (y, x) 0,i 1, 2,..., n được định nghĩa như sau: i
Ady Bdx 0 trong đó dy dx 1 1 dy dx 2 2 dy , dx dy dx n m
và A là n n ma trận được định nghĩa ở trên và B là n m ma trận được cho bởi: g ( . y x) g ( . y x) g ( . y x) 1 1 1 ... x x x 1 2 m g ( . y ) x g ( . y ) x g ( .y ) x 2 2 2 ... B x x x 1 2 m g y x g y x g y x n( . ) n( . ) n( . ) ... x x x 1 2 m Trang 17
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm y
Phương pháp để tính vi phân toàn phần và từ đạo hàm riêng i này là như sau: x j y 1.5.2
Cách tính i xj
Bước 1: Nhận biết n biến nội sinh y ,y ,...,y và m biến ngoại sinh x ,x ,...,x 1 2 n 1 2 m trong mô hình của bạn.
Bước 2: Nếu mô hình cấu trúc không được viết như một hệ các hàm ẩn, hãy viết chúng dưới dạng:
g ( y , y ,..., y x x x n , , ,..., m) 0 1 1 2 1 2
g (y , y ,..., y x x x n , , ,..., m) 0 2 1 2 1 2
g (y , y ,..., y , x , x ,..., x ) 0 n 1 2 n 1 2 m
Chú ý bạn sẽ có số hàm ẩn bằng với số biến nội sinh.
Bước 3: Lấy đạo hàm riêng của hàm ẩn đầu tiên g (y,x) 0 theo y . Gọi đạo hàm 1 1 g y x riêng này là ( , ) a sao cho 1 a
. Nhân a với dy để nhận a dy . Tiếp tục điều 11 11 y 11 1 11 1 1
này với các biến nội sinh còn lại y , y ,..., y và cộng các kết quả với nhau để thu được: 2 3 n
a dy a dy ... a dy 11 1 12 2 1n n g y x Chú ý ( , ) 1 a
của hệ số dy theo hàm ẩn thứ nhất. 1 j y j j
Bước 4: Lấy đạo hàm riêng của g (y, x) theo x và gọi đạo hàm riêng này là b . 1 1 11
Nhân b với dx để nhận b dx . Lặp lại với x ,x ,...,x để nhận được: 11 1 11 1 2 3 m
b dx b dx ... b dx 11 1 12 2 1m m
Bước 5: Cộng các kết quả của các bước 3 và 4 với nhau và cho chúng bằng zero.
Điều này cho bạn vi phân toàn phần đối với hàm ẩn thứ nhất:
a dy a dy ... a dy b dx b dx ... b dx 0 11 1 12 2 1 n n 11 1 12 2 1 m m
Bây giờ lặp lại điều này với hàm ẩn thứ hai để nhận được:
a dy a dy ... a dy b dx b dx ... b dx 0 21 1 22 2 2 n n 21 1 22 2 2 m m Trang 18
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm g y x g y x sao cho ( , ) ( , ) 2 a và 2 b . 2 j y 2 j x j j
Thực hiện điều này với n phương trình ẩn để nhận được n vi phân toàn phần:
a dy a dy ... a dy b dx b dx b dx n n ... m m 0 11 1 12 2 1 11 1 12 2 1
a dy a dy ... a dy b dx b dx ... b dx 0 21 1 22 2 2 n n 21 1 22 2 2 m m
a dy a dy a dy b dx b dx b dx n n ... nn n n n ... nm m 0 1 1 2 2 1 1 2 2 g y x g y x sao cho i ( , ) a và i ( , ) b
là các hệ số của dy và dx theo vi phân toàn phần ij y ij x j j j j thứ i .
Do đó, có n vi phân toàn phần, mỗi vi phân toàn phần cho một phương trình ẩn. y
Bước 6: Để nhận đạo hàm riêng
i từ vi phân toàn phần ta cho tất cả các dx xj
bằng zero ngoại trừ dx và sau đó thay các d còn lại bằng các để thu được: j a y a y ... a y b x n n j j 0 11 1 12 2 1 1
a y a y ... a y b x n n j j 0 21 1 22 2 2 2
a y a y a y b x n n ... nn n nj j 0 1 2 2
Bây giờ chuyển các số hạng chứa x
về vế bên phải để nhận được: j a y a y ...a y b x 11 1 12 2 1n n 1 j j a y a y ... a y b x 21 1 22 2 2n n 2j j a y a y a y b x n n ... 1 2 2 nn n nj j hay: a a
... a y b 11 12 1n 1 1j a a ... a y b 21 22 2 n 2 2 j A x j a a ... a y b 1 n n2 nn n nj Trang 19
Chương 1: Vi phân toàn phần GV: Huỳnh Tấn Liêm
Chia hai vế cho vô hướng x và viết lại hệ thức này theo ký hiệu ma trận: j y A b j x j y trong đó
và b là các n 1
các vector cột lần lượt cho bởi: x j j y 1 x j b 1 j y 2 y b 2 x , j b j j x j b nj y n x j
Chú ý b là cột thứ j của ma trận B . j y
Để giải i ta dùng công thức Cramer để thu được: x j y det[A b i ( j )] i x det[A] j trong đó A ( b
) là ma trận mà bạn thu được bằng cách thay cột thứ i của ma trận A với i j vector b . j
Ví dụ 1: Lấy ví dụ hàm sản xuất táo/mật ong ở trên, ta có hai phương trình ẩn tuyến tính:
g (Q , Q , , R ,
S T) 3Q 2Q 2 R 3S 5T 7 0 1 1 2 1 2
g (Q , Q , , R ,
S T) Q 2Q 3 R 2 S 3T 4 0 2 1 2 1 2
Giả sử ta muốn tính Q2 . S
Dùng Vi Phân Toàn Phần
Theo các bước 3,4 và 5 ta có: g g 1 1 a 3,a 2 11 12 Q Q 1 2 g g g 1 1 1 b 2,b 3,b 5 11 12 13 R S T Trang 20