Chương 1: Xác suất ngẫu nhiên, phép tính xác suất - Xác suất thống kê (MI2020) | Trường Đại học Bách khoa Hà Nội
Xây dựng mô hình v, n sao cho x gần với đáp án nhất -> Ước lượng tham số
Preview text:
lOMoAR cPSD| 45254322
Chap1_SKNgauNhien_PhepTinhXS BT: x = f(t,u) x = v ∗ t + n ∗ u
Xây dựng mô hình v, n sao cho x gần với đáp án nhất
-> Ước lượng tham số
Để tìm được tuyến tính của pt x = f(t) -> cực tiểu hoá n ∑(xi − v ∗ t)2 → min i=1
<=> ∑2(xi − v ∗ t) = 0
<=> ∑xi − (∑ti) ∗ v = 0
Trong trường hợp không tuyến tính Kiểm định: Mô hình Tham số
-> Kết quả đầu ra phụ thuộc rất nhiều vào dữ liệu đầu vào.
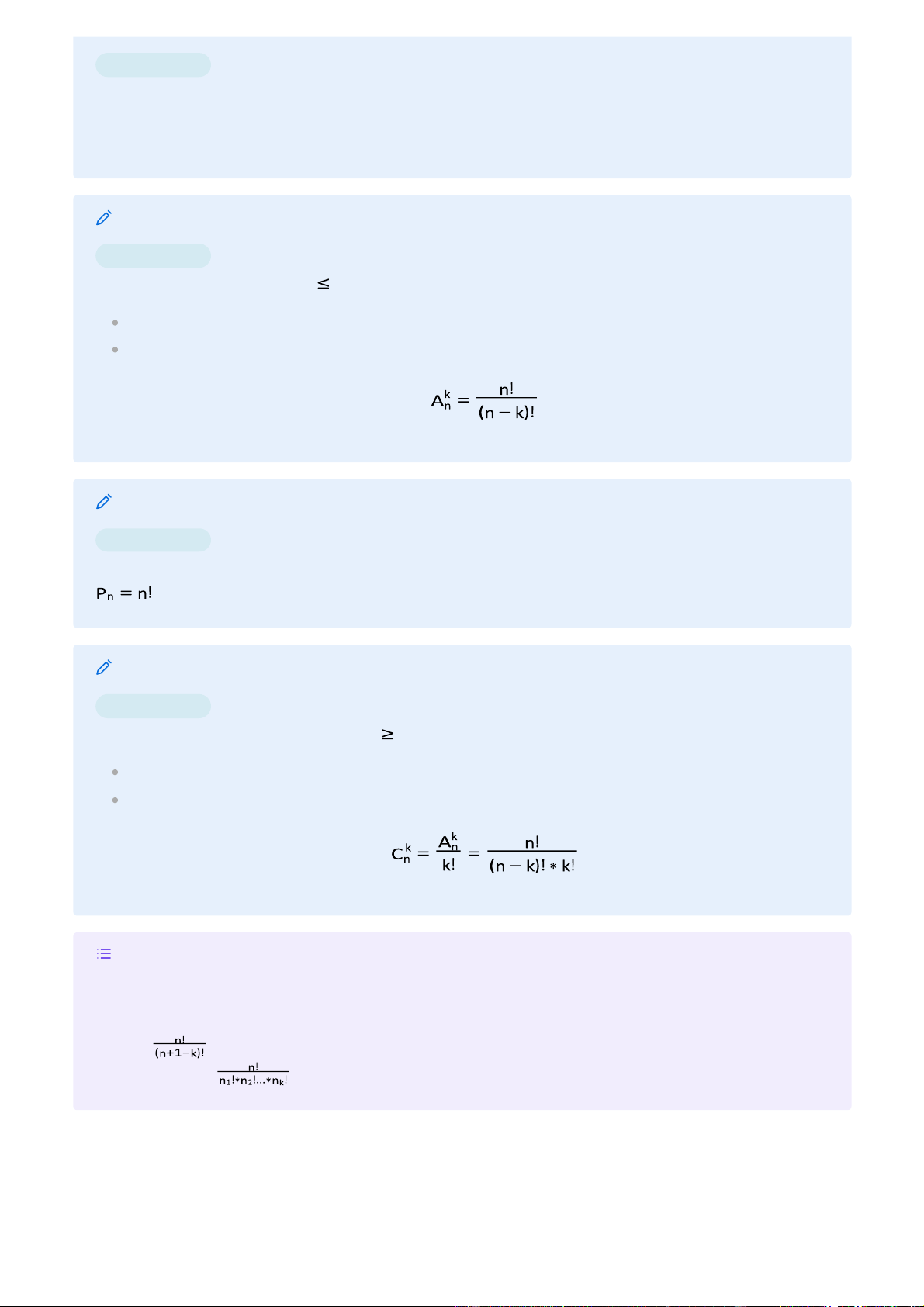
I. Giải tích kết hợp Quy tắc cộng #xstk_fomula
Một cv có thể chia là k TH : có cách giải quyết, - , ... -> Có
cách giải quyết công việc trên Quy tắc nhân #xstk_fomula
Một cv có thể chia là k giai đoạn : có cách giải quyết, - ... - > Có cách giải quyết cv
BT: cần lấy ra k phần tử từ n phần tử Có thứ tự:
Có lặp -> Chỉnh hợp lặp
Không lặp: -> chỉnh hợp ( ) || Hoán vị ( ) Không có thứ tự: Không lặp -> tổ hợp Chỉnh hợp lặp lOMoAR cPSD| 45254322 #xstk_fomula
Một tập hợp có n phần tử, có bao nhiêu cách chọn để có được dãy k phần tử (có
thứ tự, có thể lặp lại) = A~k_n = n^k Chỉnh hợp #xstk_fomula
Chập k của n phần tử (k n) là số cách chọn k phần tử: Có thứ tự Không lặp lại Hoán vị #xstk_fomula
Số cách sắp xếp n phần tử đã cho theo một thứ tự nhất định Tổ hợp #xstk_fomula
Tổ hợp chập k của n phần tử (n k) Không có thứ tự Không lặp lại Example
Có một tập hợp có n phần tử, có bao nhiêu cách để chia thành k nhóm với n1, n2, ... nk phần tử -> có (Sai) Đáp án thầy: (Đúng)
Ex: Sắp xếp 5 quyển sách khác nhau vào 3 ngăn sao cho mỗi ngăn có ít nhất 1
quyển sách B1. Đếm số cách đưa 5 quyển sách vào 3 ngăn B2. Đếm số cách đưa 5
quyển sách sao cho có đúng 1 ngăn trống b2.1 chọn 1 ngăn trống lOMoAR cPSD| 45254322
b2.2 xếp 5 quyển sách vào 2 ngăn sao cho mỗi ngăn có ít nhất 1
quyển b2.2.a Đếm số cách xếp 5 q vào 2 ngăn b2.2.b Trừ số cách xếp
5 q sách vào 1 ngăn B3. Đếm số cách đưa 5 quyển sách sao cho có đúng 2 ngăn trống -> Quá dài dòng
II. Sự kiện và các phép toán Định nghĩa
Phép thử - Việc thực hiện một nhóm các điều kiện cơ bản để quan sát một hiện tượng nào đó.
Kết cục - Kết quả của phép thử mà không thể chia nhỏ hơn
Không gian mẫu (Ω)- tập gồm tất cả các kết cục
Sự kiện (A,B,C ...) - tập con của không gian mẫu
Sự kiện sơ cấp - sự kiện không thể phân tích được nữa
Sự kiện chắc chắn - sự kiện luôn xảy ra trong phép thử (Ω)
Sự kiện không thể - sự kiện không bh xảy ra khi thực hiện phép thử (∅) Sự
kiện ngẫu nhiên - Sự kiện có thể xảyg ra hoặc không khi thực hiện phép thử
Phép thử ngẫu nhiên - phép thử mà các kết quả là các sự kiện ngẫu nhiên.
Quan hệ của các SK Quan hệ kéo theo #xstk_fomula
Nếu A xảy ra thì B xảy ra: hoặc
Quan hệ tương đương #xstk_fomula Nếu && : hoặc Sự kiện TỔNG #xstk_fomula
C là tổng A và B khi C xảy ra, khi và chỉ khi, ít nhất 1 trong 2 sự kiện A,B xảy lOMoAR cPSD| 45254322 – – lOMoAR cPSD| 45254322
Các phép toán sự kiện #xstk_fomula Note Giao hoán : Kết hợp : Phân phối Đặc biệt
III. Các định nghĩa xác suất –
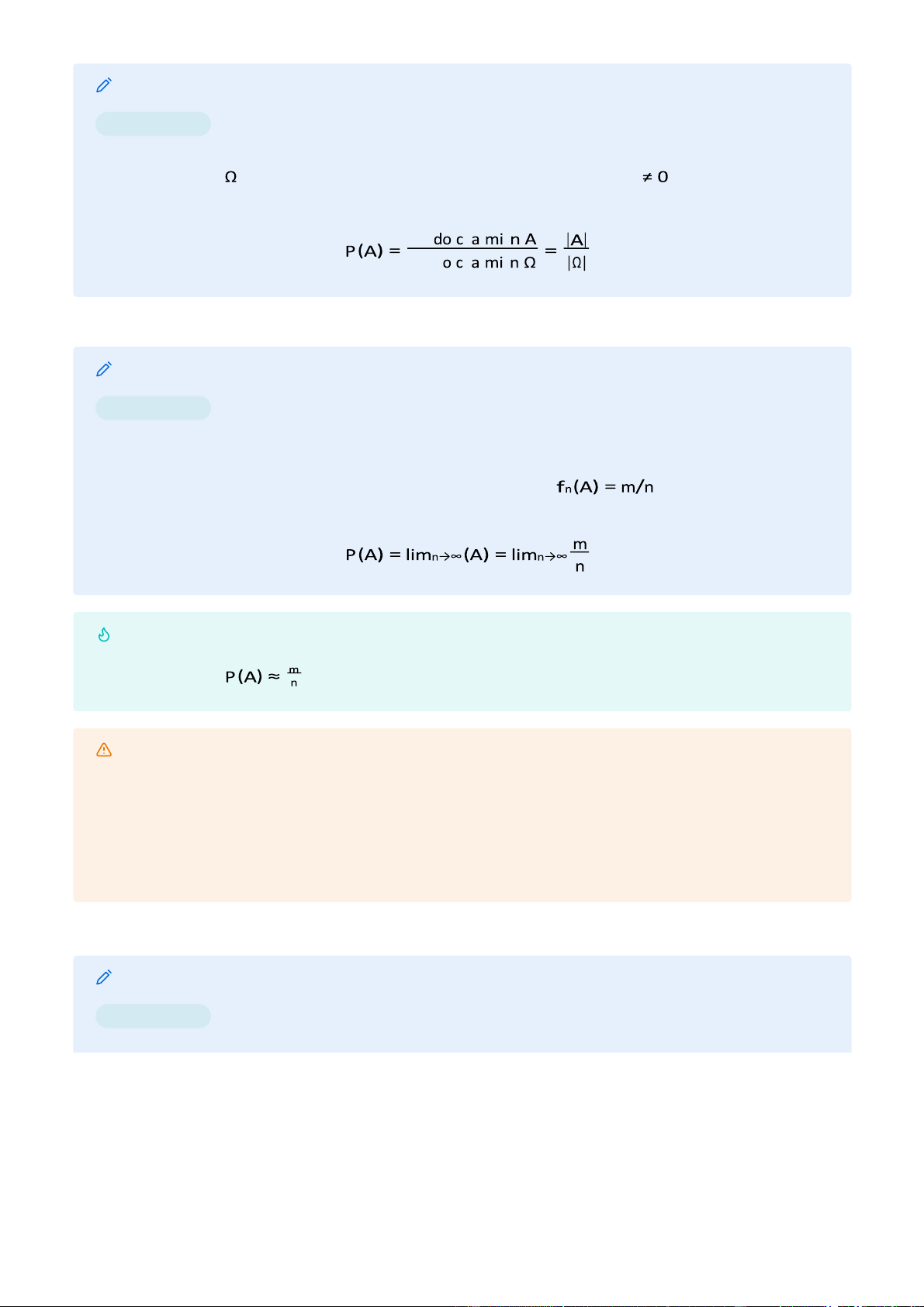
Định nghĩa xác suất cổ điển
Định nghĩa x ác suất cổ điể n #xstk_fomula
Một phép thử có hữu hạn kết cục, các kết cục có đồng khả năng xuất hiện. ố ế ụ ậ ợ ố ế ụ ó ể ả lOMoAR cPSD| 45254322
Định nghĩa xác suất theo quan điểm hình học
Định nghĩa xác suất theo quan điểm hình học #xstk_fomula
G\s tập hợp các kết cục đồng khả năng của một phép thử có thể biểu thị bởi một
miền hình học có độ đo (độ dài, diện tích, thể tích .. ) , còn tập các kết
cục thuận lợi cho sự kiện A là một miền A. Độ ủ ề Độ ủ ề
Định nghĩa xác suất theo tần suất (thống kê)
Định nghĩa xác suất theo tần suất #xstk_fomula
G\s một phép thử có thể thực hiện lặp lại nhiều lần trong những điều kiện giống
nhau. Nếu trong n lần thực hiện, phép thử có m lần xuất hiện sự kiện A. Khi đó
tần suất xuất hiện của sự kiện A trong n phép thử .
Cho số phép thử tăng lên vô hạn: Thực tế Với n đủ lớn, Warning
Xs theo freq chỉ được dùng cho các phép thử ngẫu nhiên, lặp lại nhiều lần một
cách độc lập trong các điều kiện giống nhau.
Việc thực hiện xác định tương đối chính xác giá trị của sx cần số lượng phép thử
đủ lớn -> thời gian và chi phí
IV. Một số công thức tính sx Công thức cộng XS #xstk_fomula lOMoAR cPSD| 45254322 –
Từ công thức xs có điều kiện, ta có được công thức nhân xs – lOMoAR cPSD| 45254322
TH đặc biệt: với các sự kiện n độc lập tổng thể (sự xảy ra hay không xảy ra của
một nhóm sự kiện bất kì không làm ảnh hưởng tới việc xảy ra hay không xảy ra của các sự kiện còn lại.)
P(A1A2...An) = P(A1).P(A2).P(A3)...P(An) Công thức Bernoulli
Dãy phép thử Bernoulli
Là việc tiến hành n phép thử độc lập, với mỗi phép thử chỉ xảy ra 1 trong 2 trường hợp: Sự kiện A xảy ra
hoặc sự kiện A không xảy ra
Xác suất xảy ra sự kiện A trong mỗi phép thử luôn bằng p . Công thức Bernoulli #xstk_fomula
Xác suất để sự kiện A xuất hiện đúng k lần trong n phép thử của dãy phép thử Bernoulli – với
Ví dụ về ct Bernoulli
Xác suất thành công của một thí nghiệm sinh hóa là 40%. Một nhóm gồm 9 sinh viên
tiến hành cùng thí nghiệm trên độc lập với nhau. Tìm xác suất để:
Có đúng 6 thí nghiệm thành công
Có ít nhất 1 thí nghiệm thành công -- Giải --
A: thí nghiệm sinh hóa thành công ->
a. Có 6 thí nghiệm thành công:
b. B: có ít nhất 1 thí nghiệm thành công – - >
: không có thí nghiệm nào thành công – lOMoAR cPSD| 45254322
V. Công thức xác suất đầy đủ và công thức Bayes Nhóm đầy đủ Nhóm các sự kiện
của một phép thử được gọi là
Nhóm đầy đủ nếu thỏa mãn 2 điều kiện: (không gian mẫu) Tính chất:
Ví dụ: với 2 sự kiện A, B thì nhóm đầy đủ: {AB,AB,AB,AB}.
Công thức xác suất đầy đủ #xstk_fomula Giả sử
là một nhóm đầy đủ các sự kiện. Xét sự kiện H sao cho H chỉ
xảy ra khi một trong các sự kiện
xảy ra. Nói cách khác, H xảy ra thì
một sự kiện nào đó xảy ra. Khi đó, có công thức xác suất đầy đủ: –
Trong công thức xác suất đầy đủ, H là sự kiện kết quả, còn các sự kiện i
là các sự kiện nguyên nhân.
Khi biết nguyên nhân nào xảy ra -> xác định đuợc xác suất xảy ra H.
Giờ biết đuợc kết quả xảy ra H, muốn tính xác suất để nguyên nhân thứ i xảy ra (ngược lại) lOMoAR cPSD| 45254322
- xác suất tiên nghiệm
- xác suất hậu nghiệm Công thức Bayes #xstk_fomula ớ