

















Preview text:
lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
CHƯƠNG 2 PHÉP TÍNH VI PHÂN HÀM MỘT BIẾN
2.1. Đạo hàm và vi phân (derivative and differentiation) 2.1.1.
Hai bài toán thực tế dẫn đến bài toán đạo hàm
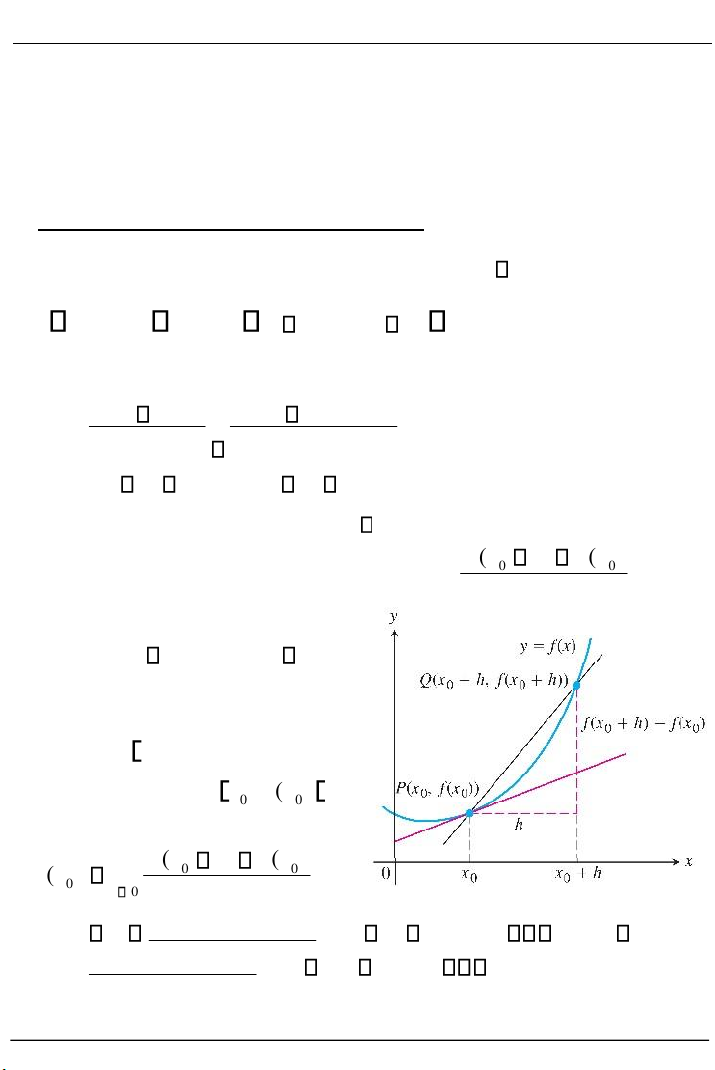
a) Bài toán tiếp tuyến (tangent problem):
Cho đường cong C có phương trình y f x( ) . Lấy hai điểm P x 0; f x( 0) và Q x 0 h f x; ( 0
h) nằm trên C . Cát tuyến PQ có phương trình là: x x0 y f x( 0 ) (x 0 h) x0 f x( 0 h) f x( 0 ) h
Hệ số góc (slope) của cát tuyến ( fx h ) ( fx PQ là: 0 0 ) h
Khi Q P hay h 0
thì cát tuyến PQ tiến về vị trí tiếp tuyến của C tại điểm . Khi đó hệ số góc 0 )
của tiếp tuyến tại Px ; ( fx 0 ) 0 ( fx h ) ( fx ) 0 0 ( mx ) lim 0 h 0 h Hình 2.1 y f x( 0
h) f x( 0 ) x f x( 0 ) x0 f x( 0 hh) f x( 0 ) Trang 63 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM P x 0; f x( là:
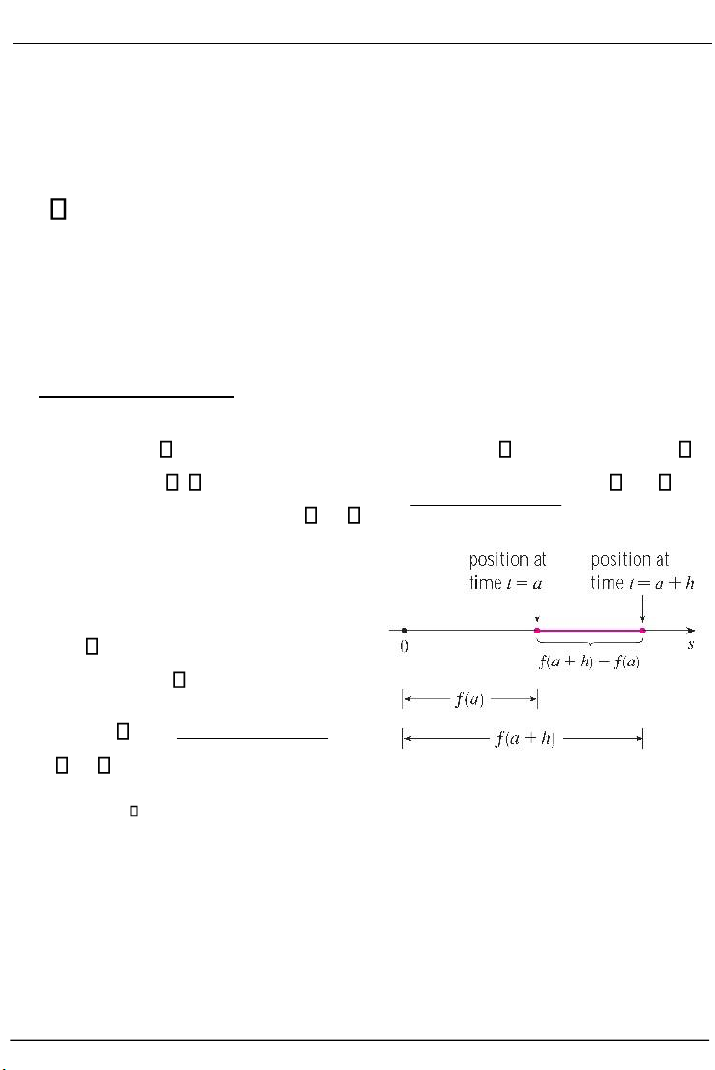
b) Vận tốc (velocities):
Giả sử một vật di chuyển trên một đường thẳng có phương trình
chuyển động s f t( ) . Trong khoảng thời gian h 0 từ thời điểm t a
đến thời điểm t a h vật đi được một quãng đường là : f a( h) f a(
) với vận tốc trung bình: f a( h) h f a( ) .
Vận tốc tức thời v a( ) tại thời
điểm t a là giới hạn của vận tốc
trung bình khi h 0 , nghĩa là: v a( ) lim f a( h) f a( ) h h 0 Hình 2.2
Từ hai bài toán thực tế trên ta có định nghĩa về đạo hàm như sau.
2.1.2. Đạo hàm tại một điểm (derivative at a point)
Cho hàm số f x( ) xác định trong lân cận của điểm x . Đạo hàm 0 Trang 64 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
(derivative) của f tại x , ký hiệu là 0
f / (x0) , và được tính theo công thức sau: f / (x )
lim f x( 0 h) f x( 0 ) 0 0 h h
Nếu đặt x x . Kh đó đạo hàm 0
h h x x h0; 0 x x0
của hàm f tại x0 còn được tính theo công thức sau:
f / (x0 ) xlim x0 f x( )x xf x0( 0 )
Định lý: Nếu hàm f có đạo hàm tại x x0 thì f liên tục tại x x0 .
Chứng minh: Giả sử rằng f / (x0 ) tồn tại, chúng ta cần chỉ ra rằng lim f x( ) f x( ). x x 0 0 Ta có: f / (x0 ) limh 0 f x( 0 hh) f x( 0 ) f x( ) f x( 0 ) f x( )
f x( 0 ) (x x0 ) x x0 Suy ra: f x( ) f
xlim x0 f x( )
xlim x0 f x( 0 ) xlim x0 x x x ( ) 0 0
.lim(x x0 x x0 )
f x( 0 ) f / (x0 ) 0 f x( 0 ) Vậy
hàm f liên tục tại x x0 . Một số lưu ý: Trang 65 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
1) Theo các định nghĩa đạo hàm, ta suy ra hệ số góc tiếp tuyến tại điểm P x ) 0 , f x( 0
của đường cong f x( ) là: m f / (x0 ) .
Khi đó phương trình tiếp tuyến tại P x 0 , f x( 0 ) là: y
f x( 0 ) f / (x0 ).(x x0 )
2) Vận tốc tức thời của vật chuyển động thẳng với phương trình
chuyển động s f t( ) tại thời điểm t a là: v a( ) f / ( )a .
3) Tốc độ biến thiên (rates of change)
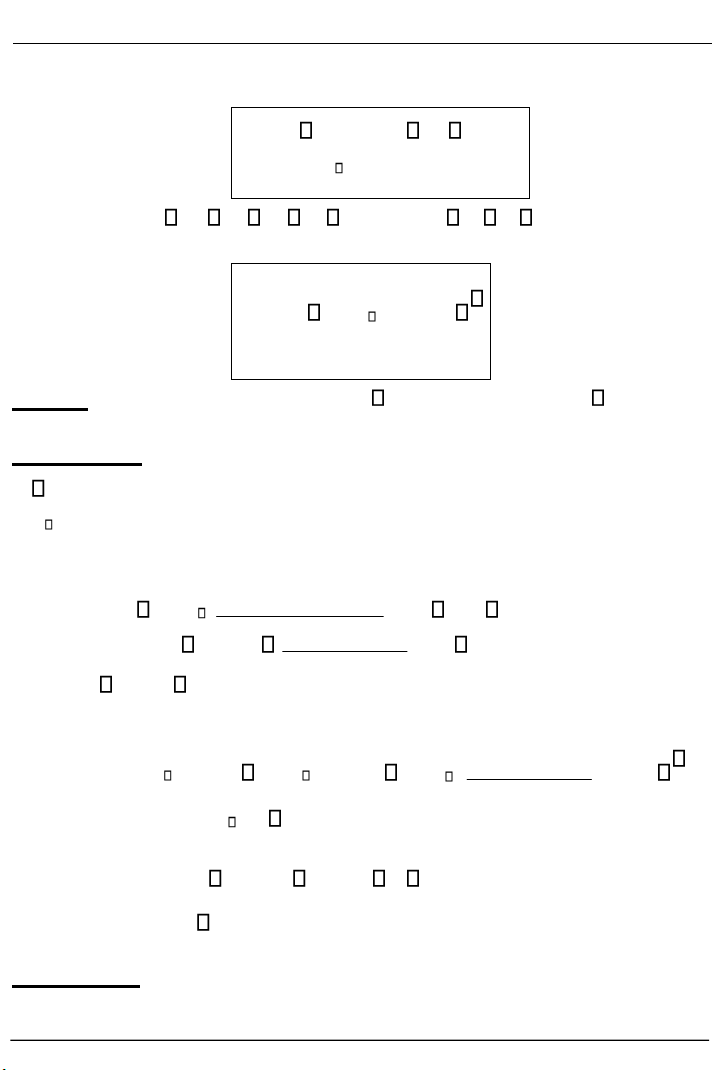
Gọi P x f x 1, ( 1) , Q x 2, f x( 2)
là hai điểm trên đường cong y f x( ) . Hệ số
góc tiếp tuyến tại P Q, lần lượt là f / (x1) và f /
(x2 ) . Do đó, khi f / (x1) lớn (đường cong dốc,
như tại điểm P ) thì giá trị của y thay đổi
nhanh; khi f / (x2 ) nhỏ (đường
cong phẳng, như tại điểm Q) thì giá trị của y thay đổi chậm. Hình 2.3
Vì vậy, đạo hàm f / (x0 ) được gọi là tốc độ biến thiên của hàm số theo biến
x tại điểm x x0 . Trang 66 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
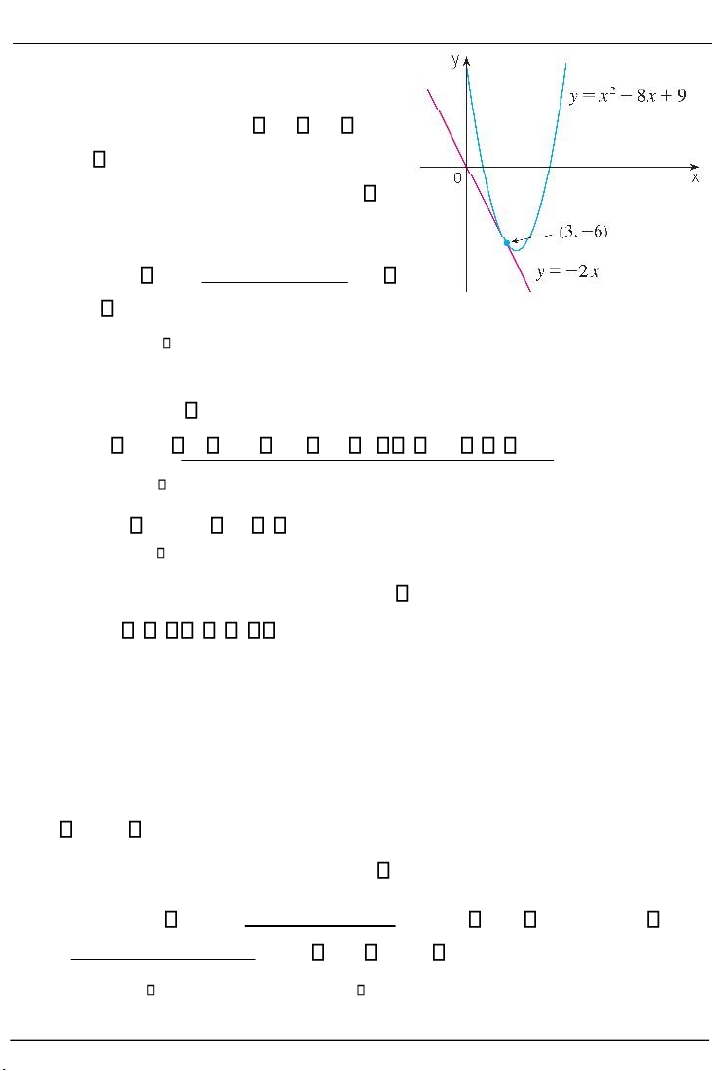
Trường ĐH GTVT TP.HCM Ví dụ 2.1
Viết phương trình đường tiếp
tuyến với parabola f x( ) x2 8x 9 tại điểm (3, 6).
Giải. Hệ số góc của tiếp tuyến tại (3, 6) là: f / (3) lim f (3 h) f (3) h 0 h Hình 2.4
f / (3) lim (3 h)2 8(3 h) 9 (32 8 3 9) h 0 h lim(h 2) 2 h 0
Phương trình của tiếp tuyến tại điểm (3, 6) là: y ( 6) 2(x 3) y 2x
Ví dụ 2.2. Giả sử một quả bóng rơi từ đài quan sát phía trên của tháp CN, cách mặt đất 450m.
a) Tính vận tốc của bóng sau 5 giây.
b) Tốc độ của bóng như thế nào khi nó chạm đất?
Giải. Theo định luật Galileo, phương trình chuyển động của quả bóng sẽ
là: s f t( ) 4,9t 2 (m/s).
Vận tốc tức thời tại thời điểm t a là: v a( ) lim f a( h) f a( ) lim
4,9(a h)2 4,9a2 9,8a h 0 h h 0 h Trang 67 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
4,9lim(2a h) 9,8a h 0
a) Vận tốc tức thời sau 5s: v(5) 49(m s/ ) .
b) Vì tầng quan sát cách mặt đất 450m nên quả bóng chạm mặt đất tại
thời điểm t1 thỏa mãn phương trình: s t( ) 2 1 450 4,9t1 450 t1 9,58s
Vậy vận tốc tức thời của quả bóng lúc chạm đất là: v t( ) 1 9,8t1 93,884(m s/ ).
2.1.3. Đạo hàm là một hàm số (the derivative as a function)
Trong mục 2.1.2, chúng ta đã biết đạo hàm của hàm f tại x0 là
f / (x0 ) limh 0
f x( 0 hh) f x( 0)
Trong công thức trên, thay x0 bởi x , ta có:
f / ( )x lim f x( h) f x( ) h 0 h
Cứ mỗi x , nếu giới hạn trên tồn tại, ta có f / ( )x . Ta có thể xem f /
như là một hàm mới và gọi là đạo hàm (derivative) của hàm f .
Lưu ý: Cho hàm số y f x( ) trong đó x là biến độc lập, y là biến phụ
thuộc, thì đạo hàm của y theo x còn có thể được ký hiệu bằng nhiều cách khác như sau:
f / ( )x y/ dy df d f x( ) Df x( ) D f xx ( ) dx dx dx Trang 68 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Để chỉ giá trị cụ thể của đạo hàm tại một giá trị x a, chúng ta sử
dụng kí hiệu: f / ( )a dy df d f x dx x a dx x a dx x a d 3 ) 3x2 12 Chẳng hạn: (x dx x 2 x 2
Ví dụ 2.3. Tính đạo hàm mỗi hàm số sau bằng định nghĩa:
a) f x( ) x3
b) f x( ) x c) f x( ) ex 2 2 x h x ( x h ) ( x ) / b) ( x ) lim lim h 0 h 0 h h( x h x ) d) f x( ) ln x 1 1 lim h 0 x h x 2 x
Giải. Ta có : f / ( xh x h e e e h x 1 x x x )x lim c) / ( e ) lim e lim e lim e h 0 h 0 h 0 h h h f x( h) f x( ) h 0 h a) (x 3 )/ lim (x h)3 x3
lim(3x2 3hx h2 ) 3x2 h 0 h h 0
(vì eh 1h h, 0) d) (ln x) /
lim ln(x h) ln x lim ln 1 hx lim h x/ 1 Trang 69 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM h 0 h h 0 h h 0 h x (vì ln 1 hx
hx , h 0 với một x 0 cố định)
2.1.4. Đạo hàm vô cùng; Tiếp tuyến thẳng đứng
f x( 0 h) f x( 0 ) thì
Xét tại x0 mà hàm f liên tục, nếu limh 0 h ta nói f có đạo hàm vô cùng
(infinite derivative) tại x . Khi đó ta nói rằng đường cong liên tục 0 y f x(
) có tiếp tuyến thẳng đứng (vertical tangent) tại x x0 .
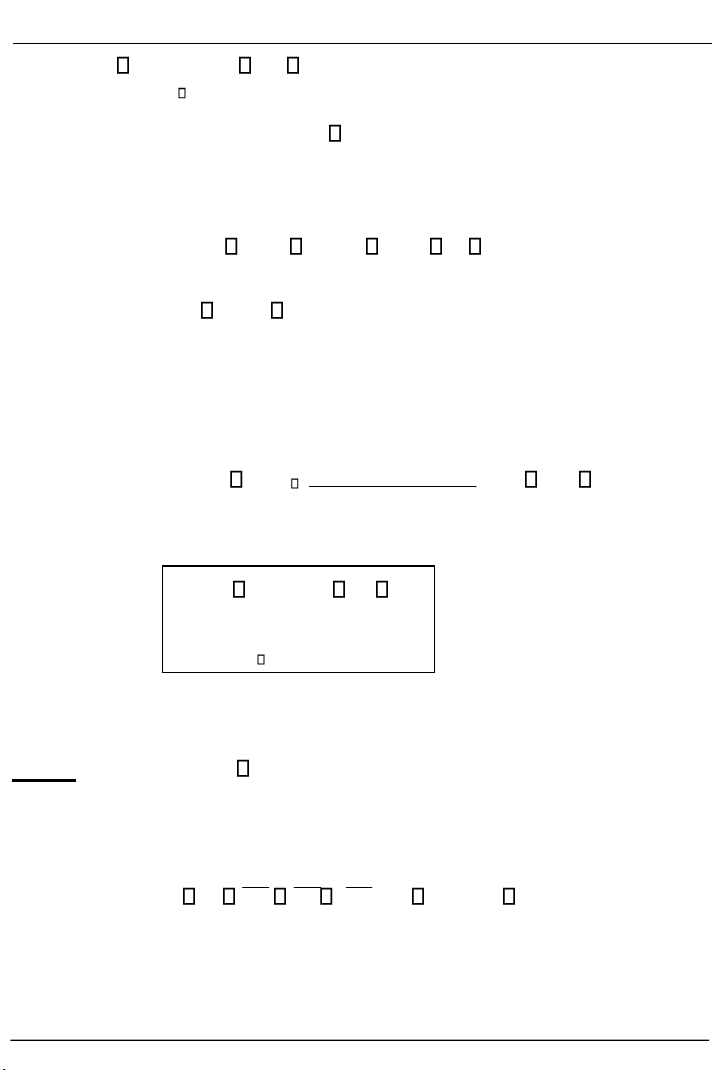
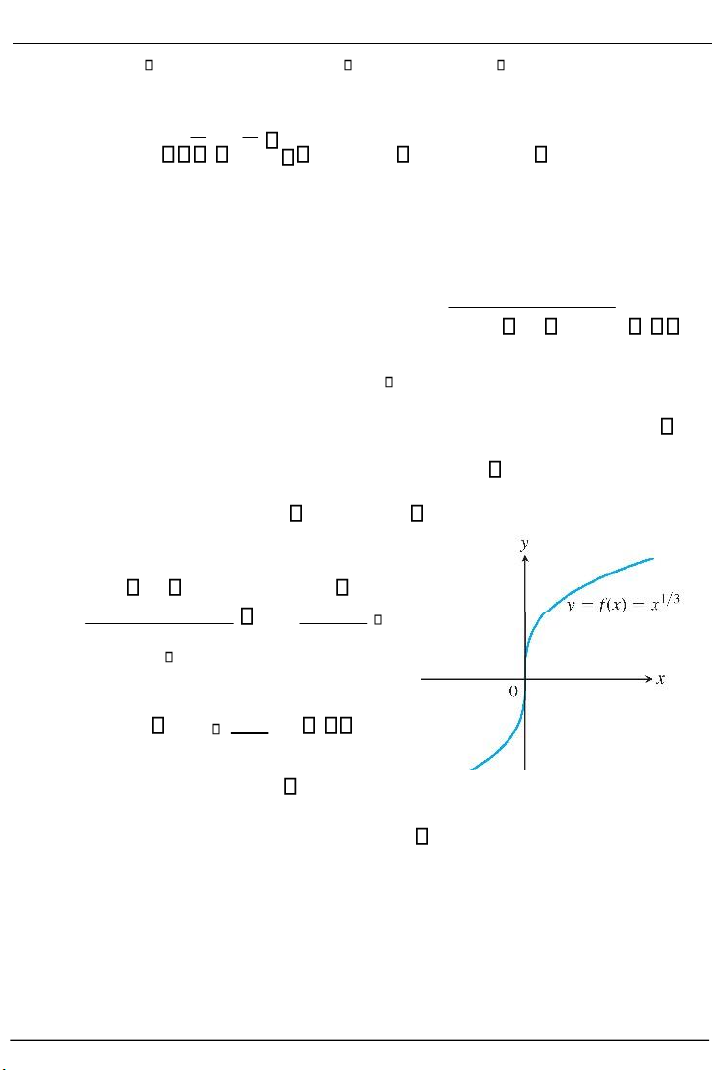
Ví dụ 2.4. Cho hàm số f x( ) x1/3 . Tại x 0 , hàm f liên tục. Ta có:
f (0 h) f (0) h1/3 0 lim lim h 0 h h h 0 1 lim h 0 h2/3
Vậy đồ thị hàm số f x( ) x1/3 có
tiếp tuyến thẳng đứng tại điểm ứng với (hình 2.5). x 0 Hình 2.5 Trang 70 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
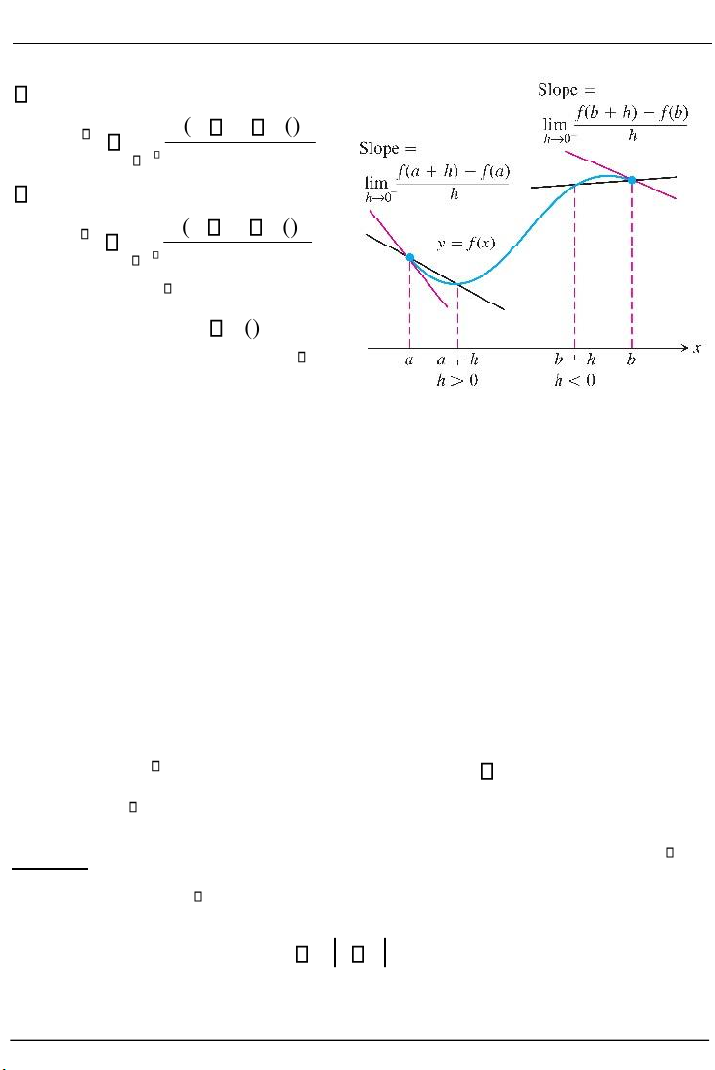
2.1.5. Đạo hàm một phía; Tiếp tuyến một phía là hệ số góc của
Đạo hàm bên phải tại a : ( fa h ) () fa / f ( a ) lim h 0 h
Đạo hàm bên trái tại b : ( fb h ) () fb / f ( b ) lim h 0 h Nếu /
f ( a ) tồn tại thì ta
nói đồ thị hàm số y () fx có
tiếp tuyến phải tại a và / f ( a ) tiếp tuyến phải.
Hình 2.6. Tiếp tuyến trái, phải
Nếu f / (b ) tồn tại thì ta nói đồ thị hàm số y f x( ) có tiếp tuyến trái
tại b và f / (b ) là hệ số góc của tiếp tuyến trái.
Định lý : Hàm f có đạo hàm tại x0 khi và chỉ khi đạo hàm trái f / (x0 ) và
đạo hàm phải f / (x0 ) cùng tồn tại hữu hạn và chúng bằng nhau.
Ví dụ 2.5. Cho hàm số f x( ) x x 2 . Trang 71 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
a) Tính đạo hàm bên trái, đạo hàm bên phải tại x 2. Kết luận gì về đạo
hàm của f tại x 2?
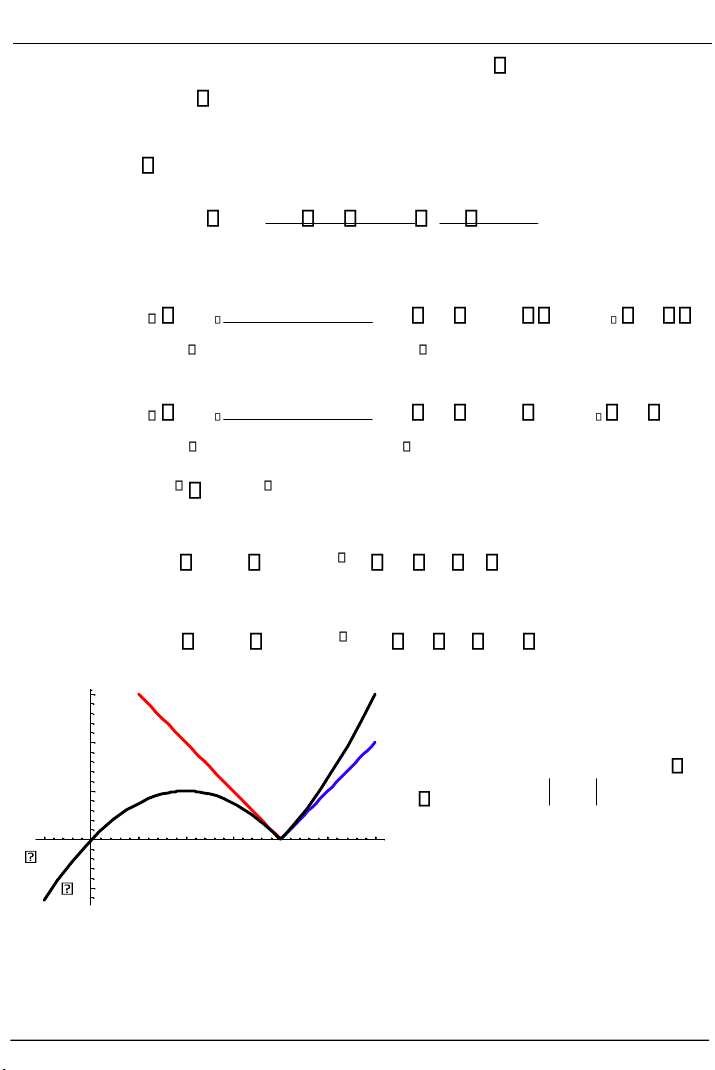
b) Viết phương trình tiếp tuyến trái, tiếp tuyến phải tại P(2,0). Vẽ đồ thị
hàm số y f x( ) và các tiếp tuyến trên cùng một hệ trục tọa độ.
Giải. a) Ta có f (2) 0; f (2 h) f (2) (2 h) | h | h h f / (2 ) lim
f (2 h) f (2) lim(2 h) 2 h 0 h h 0 f / (2 ) lim
f (2 h) f (2) lim(2 h) 2 h 0 h h 0
Do f / (2 ) f / (2 ) nên không tồn tại f / (2) .
b) Tiếp tuyến trái tại P(2,0) có phương trình:
y f (2) f / (2 ).( x 2) y 4 2x
Tiếp tuyến phải tại P(2,0) có phương trình:
y f (2) f / (2 ).(
x 2) y 2x 4 y 3 2
Hình 2.7. Đồ thị hàm số f x( ) x 1
x 2 và các tiếp tuyến tại điểm P(2,0) . 0.5 0.5 1 1.5 2 2.5 3 x 1
Đoạn code bằng Mathematica để vẽ hình 2.7
In[45]:= p1 Plot xAbs x 2 , x, 0.5,3 ,PlotStyle Thickness 0.01 Trang 72 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM p2 Plot 4 2 x, x,0.5,2 ,PlotStyle 2 /3 Thickness 0.01 ,Hue 0
p3 Plot 2x 4, x,2,3 ,PlotStyle Thickness 0.01 ,Hue 0.7 Show
p2,p3,p1 ,PlotRange All,AxesLabel x,y , TextStyle
FontFamily "Times",FontSize 14
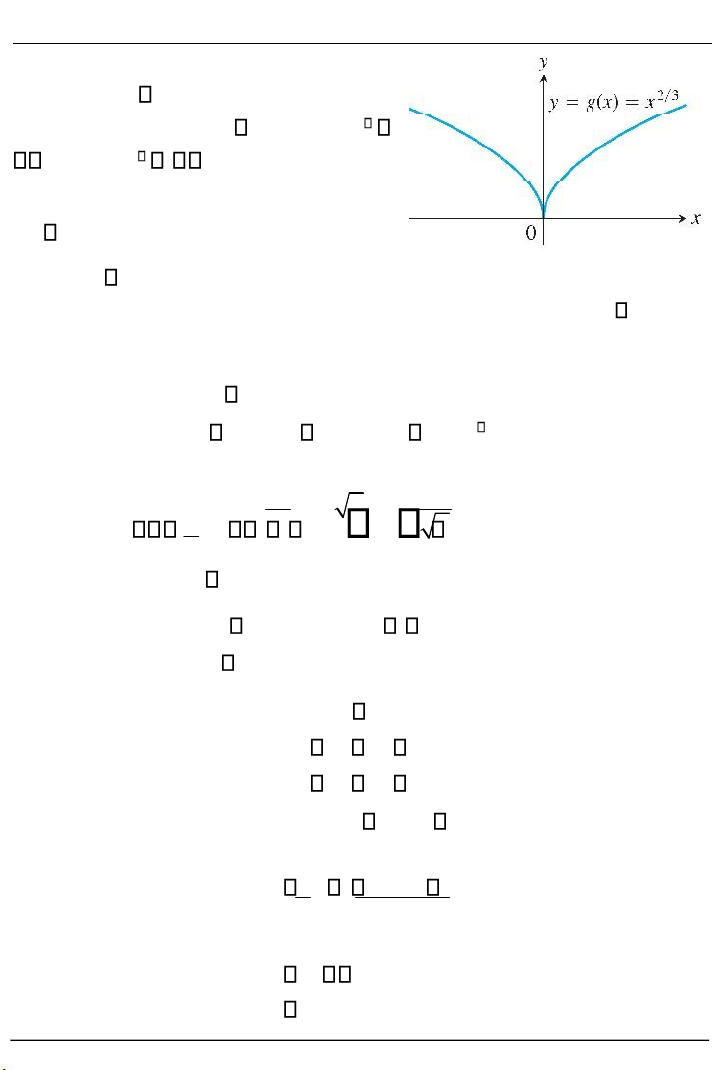
Ví dụ 2.6. Cho hàm số y g x( ) x .
a) Tính đạo hàm bên trái, đạo hàm bên phải tại x 0 . Kết luận gì về đạo
hàm của g tại x 0 ?
b) Viết phương trình tiếp tuyến trái, tiếp tuyến phải tại (0,0) . Vẽ đồ thị
hàm số y g x( ) và các tiếp tuyến trên cùng một hệ trục tọa độ.
Giải. a) Ta có g(0) 0; g(0 h) g(0) h 2/3 11/3 h h h g / (0 ) hlim 0
g(0 h) g(0) hlim 0 11/3 h h g / (0 ) hlim 0
g(0 h) g(0) hlim 0 11/3 h h Trang 73 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Vậy hàm g không tồn tại đạo hàm
vô cùng tại x 0 , nhưng nó có đạo hàm
vô cùng một phía tại x 0 là: g / (0 ) và g / (0 ) .
b) Tiếp tuyến đứng bên trái và bên phải
tại (0,0) cùng có phương
trình là x 0 , hình 2.8. 2/3
Hình 2.8. Hàm g x( ) x
2.1.6. Một số công thức và quy tắc lấy đạo hàm Hàm hằng: ( )C / 0
Hàm lũy thừa: ( )x / 1 ; (x2 )/ 2x ; (xn )/ n x. n 1 1x / 1 2 ; x / 1 x 2 x Hàm số mũ:
(ax )/ ax lna , với 0 a 1
(ex )/ ex
Quy tắc nhân với hằng số: ( . )C u / C u. / , C là hằng số Quy tắc tổng:
(u v)/ u/ v/ Quy tắc hiệu:
(u v)/ u/ v/ Quy tắc tích:
( . )u v / u v/ . u v. / u / u v/ . 2u v. / Quy tắc thương: v v Trang 74 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Quy tắc hàm nghịch đảo: 1v / v12 v/
Ví dụ 2.7. Cho đường cong C có phương trình y x4 2x2 2 . Tìm tất
cả các điểm trên C mà tại đó có tiếp tuyến nằm ngang.
Giải. Phương trình tiếp tuyến tại điểm (x0 , y0 ) C là : y
f x( 0 ) f / (x0 ).(x x0 )
Do đó, khi f / (x0 ) 0 thì đồ thị có tiếp tuyến nằm ngang y y0 . y/
(x4 2x2 2)/ 4x3 4x
y/ 0 4x3 4x 0 4 (x x2 1) 0 x 0;1; 1
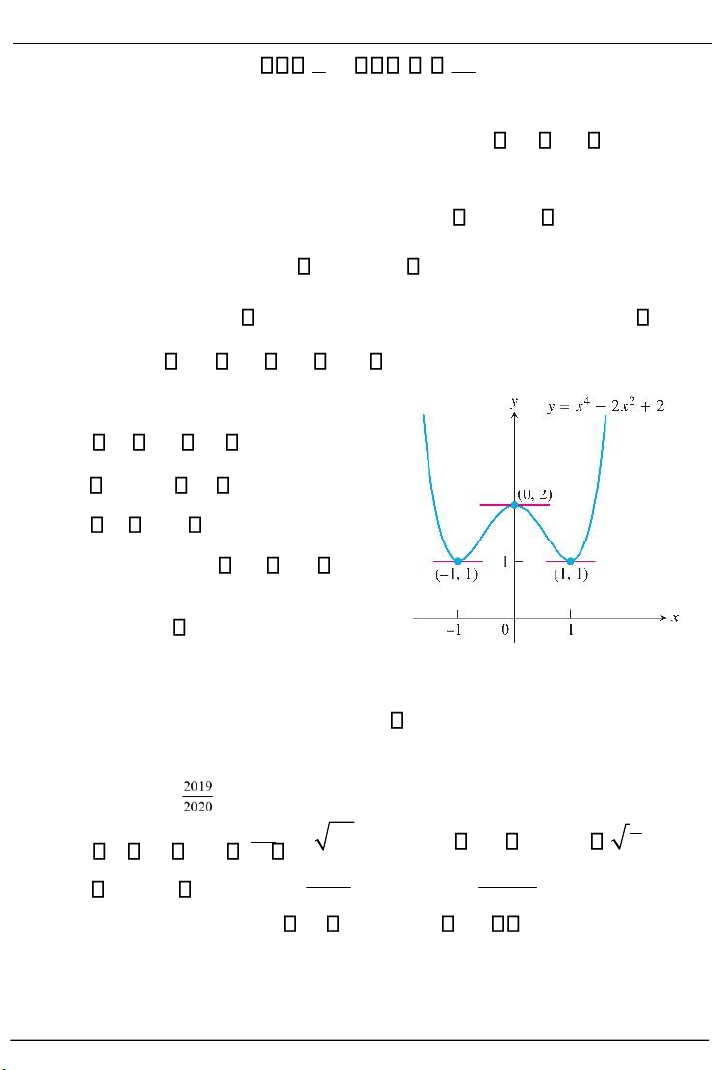
Đường cong y x4 2x2 2 có
tiếp tuyến nằm ngang tại các điểm
(0;2),(1;1) và ( 1 ;1) , hình 2.9.
Hình 2.9. Các tiếp tuyến ngang Ví
dụ 2.8. Tìm đạo hàm của các hàm số y f x( ) sau:
a) y 2 3x 2x4 15 6.3 x2 x
b) y (x3 3 )(4xx x)
c) y 2020.x x
2.2x xx 1 d) y xx3 exx Giải Trang 75 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
a) Ta có: y 2 3x 2x4 x 5 6.x2/3 y/ (2)/ 3( )x / 2(x4 )/ (x 5
)/ 6(x2/3 )/ y /
3 8x3 5x 6 4x 1/3
b) y/ (x3 3 ) (4x / x x) / x ) (x3 3 )(4x x 1 ) 2 x
(3x2 3x ln3)(4x x) (x3 3 )(4x / / ()( x x 1) .( xx 1)
c) y/ 2020(x
)/ (x2 ) .2/ x x2.(2 )x / (x 1)2 2019.x 20201
2 .2x x x2.2x.ln2 d) y / (x ex ) (/ x3 (xx3)
(xx)2 ex )(x3 x)/
(1 ex )(x3 (xx)3
(xx) 2 ex )(3x2 1) ex (x3 3(xx 2 3
xx) 2 1) 2x3
2.1.7. Quy tắc xích (the chain rule)
Đây là quy tắc tìm đạo hàm của hàm hợp
Định lý: Nếu u là hàm khả vi tại x và f là hàm khả vi tại u x( ) thì hàm
hợp F x( ) f u x( ) khả vi tại x và ta có:
F / ( )x f u / ( )x f / u x( ) . u/ ( )x Trang 76 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM d Viết ngắn gọn là: ( )
f / u x( ) . u x/ ( ) f u x dx
Ví dụ 2.9. Áp dụng quy tắc xích, tính đạo
hàm mỗi hàm số sau:
a) f x( )
b) f x( ) (5x3 x4 )2019 9 2 x 1
c) f x( ) d) f x( ) 2xx 21 1 3 2 x x 1 1
Giải. a) f / ( )x 2 .(x2 1)/ x 2 x 1 x2 1
b) f / ( )x 2019(5x3 x4 2018) .(5x3 x4 )/
2019(5x3 x4 )2018.(15x2 4x3 )
c) Ta có: f x( ) (x2 x 1) 1/3 f / ( )x
1(x2 x 1) 4/3.(x2 x 1)/
1(x2 x 1) 4/3 (2x 1) 3 3 d) f / ( )x 9 2xx 21 8 2xx 21 / 9 2xx 21 8 (2x5 1)2 45((2xx 1)2)108
2.1.8. Đạo hàm của hàm lượng giác – lượng giác ngược
a) Đạo hàm của hàm lượng giác: Trang 77 lOMoARcPSD| 36006477 Giải Nhắ tcích 1 lại: t–a C n hươn x sin x g 2 cos x cot x cos
Trường ĐH GTVT TP.HCM x sin x sin x 1 sec x csc x 1 cos x sin x
Ta có các công thức đạo hàm sau: (sin x)/ cos x (cos x)/ sin x (tan x)/ 1 2 x
sec2 x (sec x)/ sec xtan x cos (cot x)/
csc2 x (csc x)/ csc xcot x
b) Đạo hàm hàm lượng giác ngược:
Xét hàm số y arcsin x sin y x, y . Lấy đạo hàm 2 2
hai vế của phương trình sin y x theo biến x, ta được: d dy dy 1 1
(sin y) 1 cos .y
1 dx dx dx cos y 1 x2
Tương tự ta có công thức đạo hàm các hàm lượng giác ngược sau: 1 1 2 2 arcsin x / 1 x arccos x / 1 x arctan x / arccot /
Ví dụ 2.10. Tính đạo hàm mỗi hàm số sau: cos x
a) y sin xcos x b) y 1 sin x c) y tan x2 sin2 x
d) y sin cos(tan ) x
Giải. a) y/ (sin ) cosx / x sin .(cos )xx / cos2 x sin2 x Trang 78 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM b) y / (cos x) .(1/
sin )x cos .(12 x sin )x / (1 sin )x
( sin x)(1 sin )x cos ( cos ) 2 x x 1 sin x 2 1 (1 sin )x (1 sin )x 1 sin x c) y/ sec2 x2 sin2 x
. x2 sin2 x /
sec2 x2 sin2 x . 2 x 2sin xcos x
d) y/ cos cos(tan ) . cos(tan ) x x / cos cos(tan ) x sin(tan ) .(tan )x x / cos cos tan x sin tan x sec2 x
Ví dụ 2.11. Tìm đạo hàm của mỗi hàm số sau: 1 a) f x( )
b) f x( ) xarcsin( x) arctan x Giải. a) f / ( )x (arctan x)2/
2 1 2 (arctan x) (1 x ).(arctan x) ( x)
b) f / ( )x arcsin( x) x.[arcsin( x)]/ arcsin( x) x / . 1 x 1 1 arcsin( x) x arcsin( x) x Trang 79 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM 2 x 1 x 2 1 x
2.1.9. Đạo hàm hàm logarit
Xét hàm số y loga x, (0 a 1). Khi đó ay x
Lấy đạo hàm hai vế đối với biến x : y dy dy 1 1 a .ln .a 1 y dx dx a lna xlna Vậy ta có loga x / 1 công thức (ln x)/ 1 xlna : x Đặc biệt:
Lưu ý: Ta có: u v eln(uv ) ev.lnu
d (uv ) d (ev.lnu ) ev.lnu.
d (v.lnu) dx dx dx
Vậy ta có công thức đạo hàm: d d ) v x() v x( u x( ) [ ( )]u x [ ( )]u x . dx dx v x( ).ln
Ví dụ 2.12. Tính đạo hàm mỗi hàm số sau:
a) f x( ) ln sin x b) f x( ) log (1 3 x10 ) 1
c) f x( ) ln x d) f x( ) ln xx 2 Trang 80 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
e) f x( ) (x 1)x2
f) f x( ) (3x2 1)sin(2x) Giải. a) 1 1 f / ( )x sin x /
cos x cot x sin x sin x b) f / ( )x
(1 x101).ln3(1 x10 )/ (1 10x10x)9.ln3 1
c) f / ( )x 1 d ln x 1 .
1 2 ln x dx 2 ln x x 2x ln x d 1
d) f / ( )x dx ln x 1 12 ln x 2 x 1 1 1 2 x 2
/ ( )x (x 1) .x 2 x2 ln(x 1) / (x 1) . 2x2
x.ln(x 1) xx 21 e) f
f) f / ( )x (3x2 1)sin(2x). sin(2 ).ln(3 x x2 1) / 6 x
(3x2 1)sin(2 )x . 2
cos(2 ).lnx(3x2 1) 3x 2 1.sin(2 )x 2.1.10. Hàm khả vi
Định nghĩa 1: Cho hàm số f : (a b, ) . Hàm f được gọi là khả vi
(differentiable) tại x (a b, ) nếu:
f f x( x) f x( ) A. xo( x) (*)
trong đó, A là chỉ phụ thuộc vào x và hàm f ; o( x) là vô cùng Trang 81 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
bé cấp cao hơn x khi x 0.
Hàm f khả vi trên (a b, ) nếu f khả vi tại mọi x (a b, ) .
Định nghĩa 2: Cho y f x( ) là hàm khả vi trên (a b, ). Vi phân
(diferential) df (hay dy ) được định nghĩa: df f / ( )x dx trong đó, dx là
vi phân của biến x , nó là một biến độc lập. Định lý: Hàm f khả vi tại điểm
x (a b, ) khi và chỉ khi f có đạo hàm tại x và A f / ( )x . Chứng minh:
- Giả sử hàm f khả vi tại x . Từ (1), ta suy ra: f / ( )x limx0 fx limx0 A o( xx) A
- Giả sử f có đạo hàm tại x . Ta có: f f /
/ lim f ( )x f ( )x
( x) , với lim ( x) 0. x 0 x x x 0 Suy ra:
f f / ( )x xx ( x) A. xo( x)
Ví dụ 2.13. Xét sự khả vi của hàm số f x( ) | x | trên .
Giải. Hàm f xác định trên .
Với x 0 , f x( ) x f / ( )x 1
Với x 0 , f x( ) x f / ( )x 1 Tại x 0 , f (0) 0. f / (0 ) lim
f (0 h) f (0) lim | h| 1 h h 0 h h 0 f / (0 ) lim
f (0 h) f (0) lim | h| 1 Trang 82 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM h 0 h h 0 h
f / (0 ) f / (0 ) , suy ra hàm f không có đạo hàm tại x 0 .
Kết luận: Hàm f khả vi trên các khoảng ( ,0) và (0, ), không khả vi tại x 0 .
2.1.11. Đạo hàm cấp cao (higher derivatives) a)
Định nghĩa đạo hàm cấp cao:
Cho f là hàm khả vi. Đạo hàm của số f / (nếu có) được gọi là đạo
hàm cấp 2 (the second derivative) của hàm f , các ký hiệu: f // d ydx2 2 ( f / )/ dx dxd dy
Đạo hàm cấp n là đạo hàm của đạo hàm cấp n 1: f (n) d ydxn n f (n 1) / dxd ddxn n1 y1
Ví dụ 2.14. Cho f x( ) 2x4 3x2 2x 1. Tìm f (n) ( )x , n 1,2,... Giải. Ta có:
f / ( )x 8x3 6x 2
f // ( )x 24x2 6
f /// ( )x 48x f (n) ( f (4) ( )x 48 )x 0, n 5 b)
Gia tốc (acceleration): Nếu s s t( ) là phương
trình chuyển động của một vật trên đường thẳng thì v t( ) s t/ ( )
ds là vận tốc tức thời dt
của vật tại thời điểm t . Tốc độ biến thiên tức thời của vận tốc theo thời
gian được gọi là gia tốc (acceleration), nghĩa là: Trang 83 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
a t( ) v t/ ( ) s// ( )t hay viết a dvdt d sdt22 c)
Tính chất của đạo hàm cấp cao: 1) . ( )f x . ( )g x (n)
.f (n) ( )x
.g (n) ( )x Trong đó
, là các hằng số, n 2,3,... 2) ( f g. ) (n)
Cn0. f (n).g Cn1. f (n 1).g / Cn2. f (n 2).g // ... Cnn. f g. (n)
(Tính chất 2 còn được gọi là quy tắc Leibnitz)
d) Đạo hàm cấp n của một số hàm số cơ bản:
Chứng minh bằng phương pháp quy nạp toán học, ta có các công
thức đạo hàm cấp n sau: 1) (e ax b )(n) a en ax b n 2)
sin(ax b) ( )n an sin ax b 2 n 3)
cos(ax b) ( )n an cos ax b 2 4) (ax b) (n) an
( 1)...( n 1)(ax b) n 5) ax1 b (n)
( 1) .( ax n ba n)nn. ! 1 6) ln(ax b) (n)
( 1) (nax 1.a n.(b)nn 1)!
Đạo hàm cấp cao trong Mathematica: Trang 84 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Khai báo hàm f : f[x_ ] = biểu thức
Đạo hàm cấp 1, 2, 3: f [ ]x , f [ ]x , f [
]x Đạo hàm cấp n : D f x [ ],{ ,x n}
Ví dụ 2.15. Tính đạo hàm cấp n của các hàm số sau: 1 x a) f x( )
b) f x( ) (2x2 x 1)e2x (x 1)(x 2)
c) f x( ) ln(x2 5x 6), x 2 d) f x( ) 2x 1
Giải. a) Phân tích hàm f thành tổng các phân thức cơ bản f x( ) 1 x A B (1)
(x 1)(x 2) x 1 x 2
Cách tìm các hằng số A B, đơn giản như sau: B
Nhân hai vế của (1) cho x 1, ta được: 1 x A (x 1) x 2 x 2 Cho x 1, thu được: A 2
Người ta thường viết gọn là: A 1 x 2 x 2x 1
Tương tự: B 1 x 3 x 1 x 2 Trang 85 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM Vậy f x( ) 2 3 x 1 x 2 f (n) ( )x 2 x1 1 (n) 3 x 1 2 (n) (2( 1)x 1)nnn 1! (3( 1)x 2)nnn !1
Sử dụng Mathematica các phân thức cơ bản 1 x 2 x Phân tích thành tổng Apart 1 x
b) Với n 1, f / ( )x (4x 1)e2x 2(2x2 x 1)e2x (4x2 2x 1)e2x
Với n 2 , áp dụng quy tắc Leibnitz, ta có : f ( )n ( )x
Cn0.(e2x n)( ).(2x2 x 1) Cn1.(e2x n)( 1).(2x2 x 1)/ 2).(2x2 x 1)//
Cn2.(e2x n)( 2 ne2x(2x2
x 1) n.2n 1e2x(4x 1) n n( 1)
.2n 2.e2x.4 2
2ne2x(2x2 x 1) n.2n 1e2x(4x 1) n n( 1).2n 1.e2x 2n 1e2x
2(2x2 x 1) n(4x 1) n n( 1) 2n 1e2x
4x2 2(2n 1)x n2 2n 2
Kết hợp hai trường hợp trên, ta có:
f (n) ( )x 2n 1e2x
4x2 2(2n 1)x n2 2n 2 , n 1 Trang 86 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
c) f x( ) ln(x2 5x 6) ln[(x 2)(x 3)] 2 x 0
Với x 2 3 x 0 .
Do đó: f x( ) ln(2 x) ln(3 x) f (n) ( )x ln(2 x) (n) ln(3 x) (n)
( 1) n 1.( 1) .( n n 1)!( 1) n 1.( 1) .( n n 1)! (2 x) n (3 x)n 1 1 (n 1)! (2 x) n (3 x)n d) f x( ) 2x 1 (2x 1)1/ 2
f (n) ( )x 2n 12 12 1 ... 12 n 1 (2 x 1) 12 n 1 ( 1)( 3)...( 2
n 3)(2x 1)2 n 1 2
( 1)n 11.3.5....(2n 3).(2x 1) n Ví
dụ 2.16. Tính f (100) 2
biết f x( ) x2 sin x .
Giải. Áp dụng quy tắc Leibnitz (với n 2 ), ta có :
f ( )n ( )x C xn0. 2.(sin x)( )n Cn1.(x2 ) .(/ sin x)(n 1) Cn2.(x2 ) .(// sin x)(n 2) Trang 87 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM x2 sin x n2 2nxsin x (n 21) n n( 1)sin x (n 22)
Thay n 100 và x , ta được: 2 f (100) 2 42 .sin 2 50 100 .sin 50 100.99.sin 2 49 2 9900 4
Ví dụ 2.17. Chứng tỏ rằng hàm số x f x( ) cos(2 ) 2 thỏa phương trình : x 1
(x2 1) f (3) ( )x 6 .x f // ( )x 6 f / ( )x 8sin(2 )x Giải. x f x( ) cos(2 ) 2
(x2 1) ( )f x cos(2 )x (1) x 1
Lấy đạo hàm cấp 3 hai vế của (1) và áp dụng quy tắc Leinitz, ta được : C f 0 (3) 1 // 2 / 3
( ).(x x2 1) C f3
( ).(x x2 1)/ C f3 ( ).(x x2 1)// [cos(2 )]x
(3) (x2 1) f (3) ( )x 6 .x f // ( )x 6 f / ( )x 8sin(2 )x
Chú ý rằng: có thể tính đạo hàm trực tiếp từ hàm f rồi thế vào biểu thức
và rút gọn. Cách này sẽ rất phức tạp, Sinh viên làm theo cách này hầu hết
không đến kết quả cuối cùng. Trang 88 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Sử dụng Mathematica Cos2 x fx_ 2 2 ; x 1
Together x 1 f'''x 6 xf''x 6 f'x
2.2. Ứng dụng của đạo hàm (applications of differentiation)
2.2.1. Định lý giá trị trung bình
Định lý 1: (Định lý Rolle – Rolle’s theorem)
Giả sử hàm f liên tục trên đoạn [a b, ] và khả vi trên (a b, ). Nếu f a(
) f b( ) , thì có ít nhất một điểm c (a b, ) sao cho f / ( )c 0 .
Ý nghĩa hình học: Trong khoảng (a b, ), nếu hàm f thỏa định lý Rolle thì
tồn tại ít nhất một điểm c mà tại đó tiếp tuyến nằm ngang. Đồ thị của các
kiểu hàm dưới đây thỏa mãn các điều kiện của định lý Rolle.
Ví dụ 2.18. Ứng dụng định lý Rolle cho hàm vị trí s f t( ) của một vật
chuyển động. Nếu vật có cùng một vị trí tại hai thời điểm khác nhau t
a , t b, tức là: f a( ) f b( ) thì sẽ có ít nhất một thời điểm c (a b, ) mà
vận tốc của vật bằng không: f / ( )c 0, chẳng hạn khi
ném thẳng một quả bóng lên trên.
Định lý 2: (Định lý giá trị trung bình – the mean value theorem)
Giả sử hàm f liên tục trên đoạn [a b, ] và khả vi trên (a b, ). Khi đó
tồn tại ít nhất một điểm c thuộc khoảng (a b, ) sao cho: f / ( )c
f b( ) f a( ) hay f b( ) f a( ) f / ( )(c b a) b a Trang 89 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
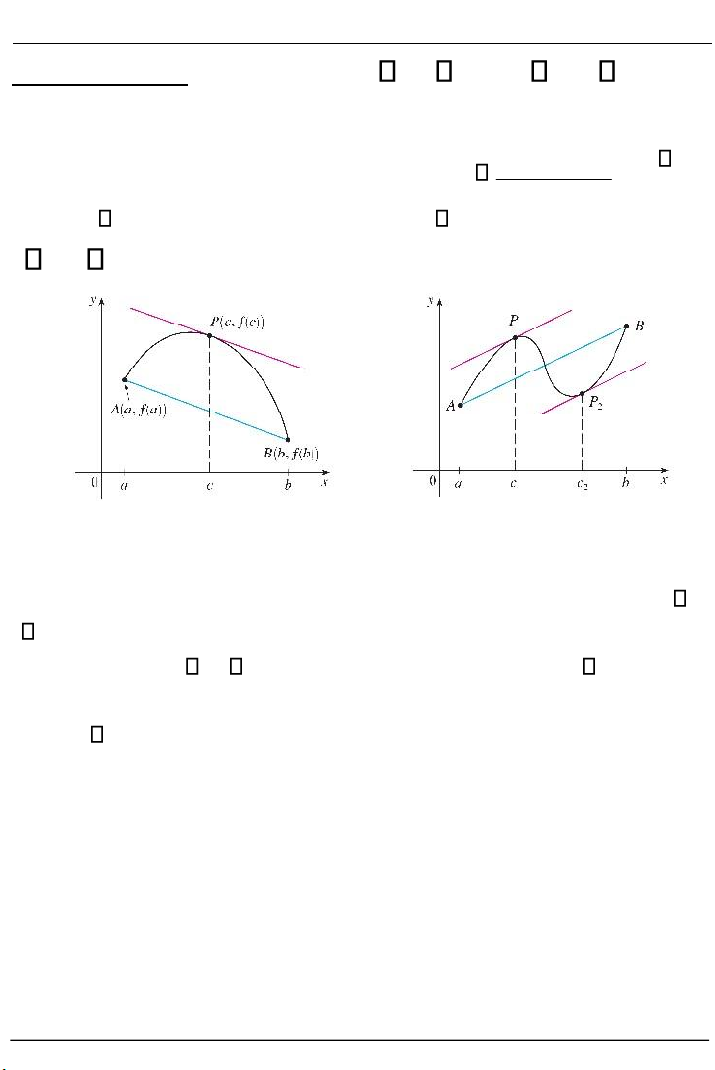
Ý nghĩa hình học: Xét 2 điểm A a f a ,( ) , B b f b , ( ) là 2 điểm thuộc
đồ thị hàm f . Hệ số góc của cát tuyến AB là m f b( ) f a( AB
) . Vậy b a định lý khẳng định là có điểm c (a,b) mà tiếp tuyến tại P c f
c , ( ) song song với cát tuyến AB , hình 2.10a. (a) (b)
Hình 2.10. Định lý giá trị trung bình
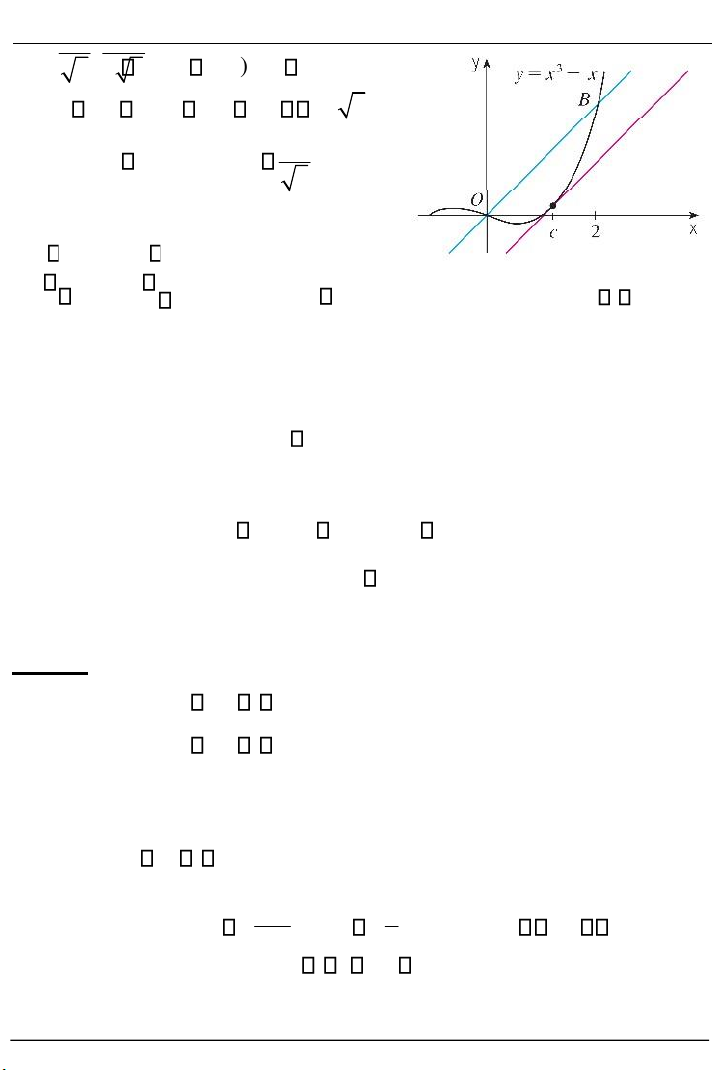
Ví dụ 2.19. Minh họa định lý giá trị trung bình đối với hàm số f x( ) x3
x trên đoạn [0;2] .
Giải. Hàm f x( ) x3 x liên tục và có đạo hàm với mọi x . Do đó f
liên tục trên [0,2], khả vi trong (0,2). Theo định lý giá trị trung bình,
tồn tại c (0;2) thỏa: Trang 90 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM / f (2) f (0) f ()(2 c 0) 2 6 (3 c 1)2 c 2 / 3 2 Vì c (0 ; 2) nên c . 3
Tiếp tuyến với đường cong f 2 2 tại 3 3 3, song song với B .
Hình 2.11. Hàm y x3 x
2.2.2. Hàm đơn điệu (monotonic functions)
Giả sử hàm f liên tục trên đoạn [a b, ] và khả vi trên (a b, ). Lấy bất kỳ x
. Áp dụng định lý giá trị trung bình cho
1 và x2 thuộc [a,b] với x1 x2
hàm f trên [x x1, 2 ], ta có: f x( 2 )
f x( 1) f / ( )(cx2 x1) (1)
Từ (1), ta thấy rằng hiệu f x(
) cùng dấu với đạo hàm 2 ) f x( 1 f / ( )c
. Do đó, ta có định lý sau về tính đơn điệu của hàm số: Định lý:
1) Nếu f / ( )x 0, x (a b, ), thì f là hàm tăng trên [a b, ] .
2) Nếu f / ( )x 0, x (a b, ) , thì f là hàm giảm trên [a b, ].
Ví dụ 2.20. Áp dụng tính đơn điệu của hàm số, hãy chứng minh các bất đẳng thức sau:
a) sin x x, x 0. b) arcsin(3 )x 3x 92x3 0;1 . , x 3 Trang 91 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Giải. a) Đặt f x( ) sin x x
Với x 1 thì sin x 1 x. Suy ra: sin x x, x 1
Với 0 x 1, f / ( )x cos x 1 0
f x( ) f (0) 0 sin x x
b) Đặt g x( ) arcsin(3 )x 3x 9x3 2 Ta cần chứng minh rằng: 1 g x( ) 0, x 0; 3 , ta có: g / ( )x 3 3 27x2 2 2 1 9 x 27 x g // ( )x 2 3/ 2 27x 27x 1 1 (1 9 x2 )3/ 2 1 0, x 0; 3 (1 9x ) 1
g / ( )x g / (0) 0, x 0; 3
g x( ) g(0) 0, x 0;1/3
2.2.3. Giá trị cực trị của hàm số (Extreme Values of Functions)
a) Số tới hạn: Số thực c thuộc miền xác định của hàm f được gọi
là số tới hạn (critical number) của f nếu thỏa f / ( )c 0 hoặc f /
( )c không tồn tại. Trang 92 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Ví dụ 2.21. Tìm các số tới hạn của hàm số f x( ) x3/5 (4 x) . Giải.
Hàm f xác định trên . Ta có: f / ( )x
3 x 2/5 (4 x) x3/5 12 8x 5 5
f / ( )x 0 12 8x 0 x
f / (0) không tồn tại.
Vậy hàm f có 2 số tới hạn là 0 và 3/ 2.
b) Cực trị địa phương: Định nghĩa:
Hàm f đạt cực đại địa phương (local maximum) tại điểm c nếu: f c( )
f x( ) với mọi x trong một lân cận của điểm c.
Hàm f đạt cực tiểu địa phương (local minimum) tại điểm c nếu: f c(
) f x( ) với mọi x trong một lân cận của điểm c.
Quy ước: Khi nói đến cực trị của hàm số mà không đề cập gì thêm thì ta
hiểu là cực trị địa phương.
Định lý 1: (Định lý Fermat – Fermat’s theorem)
Nếu hàm f đạt cực đại hay cực tiểu địa phương tại c và nếu f / ( )c
tồn tại thì f / ( )c 0.
Lưu ý: Chiều ngược lại của định lý Fermat là không đúng, chẳng hạn:
hàm y x3 , ta có y/ 3x2 , y/ 0 3x2 0 x 0, nhưng hàm y không
đạt cực đại hay cực tiểu tại x 0 .
Định lý 2: (Tiêu chuẩn đạo hàm cấp 1 - The first derivative test)
Giả sử c là một số tới hạn của hàm liên tục f .
1) Nếu f / đổi dấu từ âm sang dương khi qua c, thì f đạt cực tiểu địa phương tại c.
2) Nếu f / đổi dấu từ dương sang âm khi qua c, thì f đạt cực đại địa phương tại c; Trang 93 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
3) Nếu f / không đổi dấu khi qua c (nghĩa là, f / dương cả hai phía
hoặc âm cả hai phía của c), thì f không đạt cực trị tại c.
c) Cực trị tuyệt đối (giá trị lớn nhất, giá trị nhỏ nhất):
Cho hàm y f x( ) có miền xác định D . Định nghĩa:
Hàm f đạt cực đại tuyệt đối (absolute maximum) trên D tại điểm c
nếu: f c( ) f x( ), x D . Khi đó ta nói f c( ) là giá trị lớn nhất
(maximum value) của f trên D .
Hàm f đạt cực tiểu tuyệt đối (absolute minimum) trên D tại điểm c
nếu: f c( ) f x( ), x D . Khi đó ta nói f c( ) là giá trị nhỏ nhất
(minimum value) của f trên D .
Định lý: (sự tồn tại giá trị lớn nhất, giá trị nhỏ nhất)
Nếu hàm f liên tục trên khoảng đóng [a b, ] thì f đạt được đồng thời
giá trị lớn nhất M và giá trị nhỏ nhất m trên [a b, ]. Nghĩa là, tồn tại các
số x1 và x2 thuộc [a b, ] sao cho:
f x( 1) m f x,( 2 ) M, và m f x( ) M , x[a,b]
Các bước tìm giá trị lớn nhất, giá trị nhỏ nhất:
Cho hàm f liên tục trên khoảng đóng [a b, ].
Bước 1: Tìm giá trị của f tại các số tới hạn của f trong (a b, ).
Bước 2: Tính các giá trị tại hai điểm biên: f a( ), f b( ) .
Bước 3: Giá trị lớn nhất (nhỏ nhất) của f tìm được trong 2 bước trên là
giá trị lớn nhất (nhỏ nhất) của f trên [a b, ]. Ví dụ 2.22
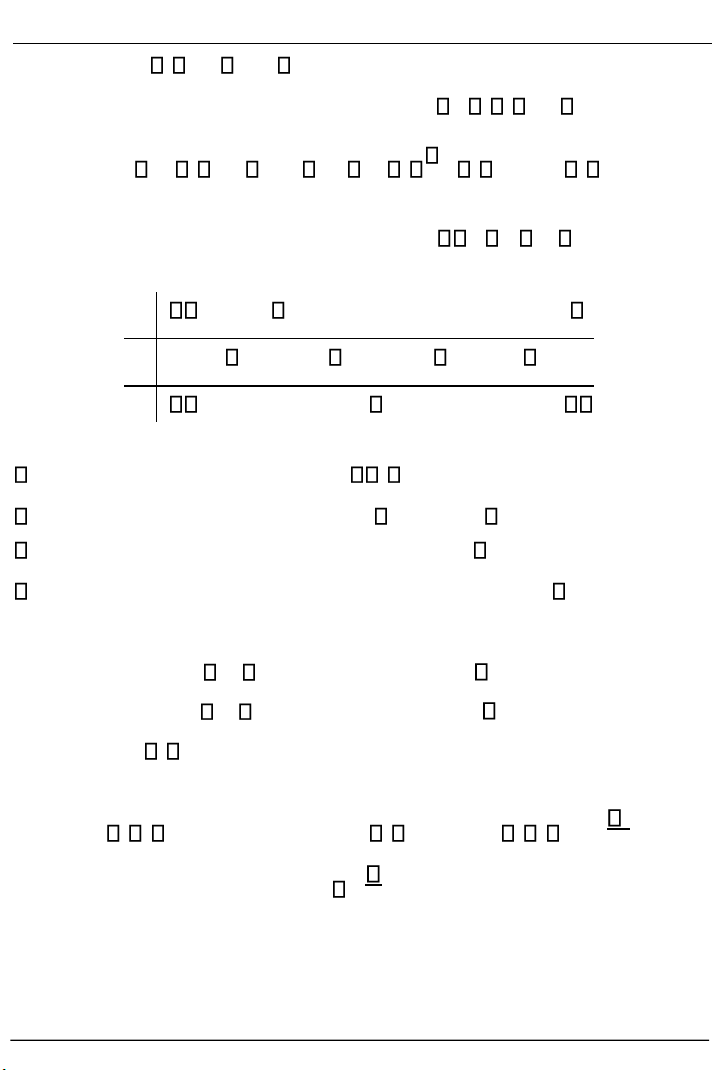
1) (Hình 2.12) Hàm số y x2 có tập xác định D , tập giá trị R [0; )
. Hàm đạt cực tiểu tại x 0 với f (0) 0, đây cũng giá trị nhỏ nhất
của hàm số trên D . Hàm không có điểm cực đại, và cũng không có giá trị lớn nhất. Trang 94 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
2) (Hình 2.13) Hàm số y x3 có tập xác định D , tập giá trị R .
Hàm số không có điểm cực trị, và cũng không có giá trị lớn nhất,
không có giá trị nhỏ nhất.
Hình 2.12. Hàm y x2
Hình 2.13. Hàm y x3
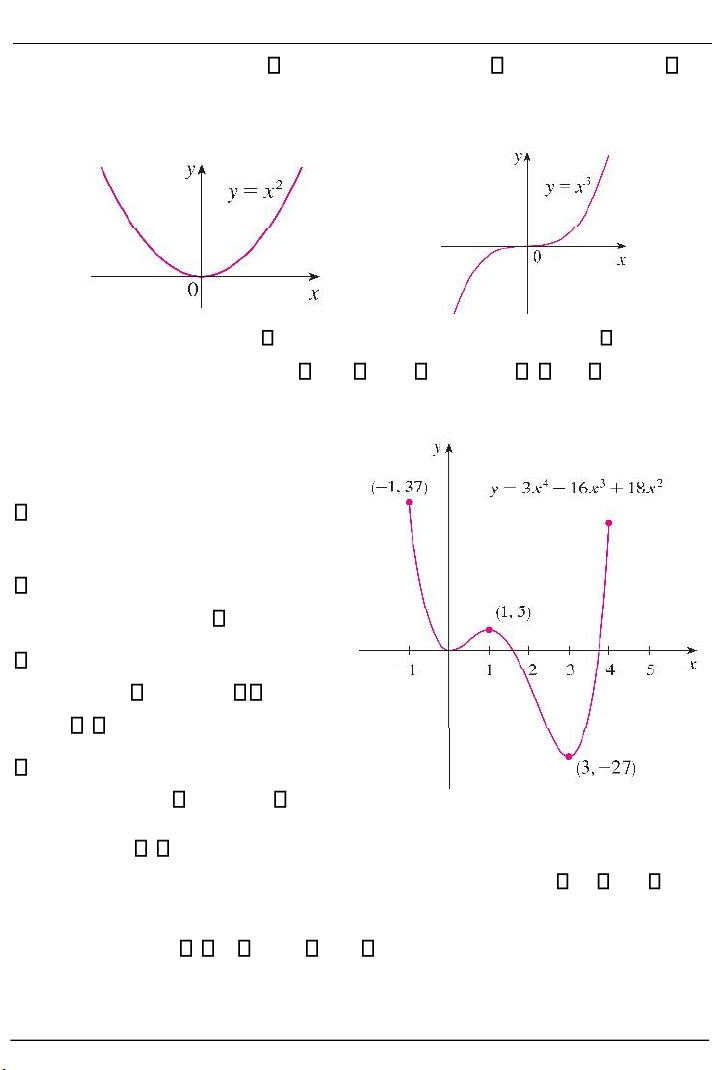
Ví dụ 2.23. Xét hàm số f x( ) 3x4 16x3 18x2 với 1 x 4 có đồ thị hình 2.14.
Dựa vào đồ thị, ta có các kết luận sau:
Hàm số đạt cực đại tại điểm (1;5).
Hàm số đạt cực tiểu tại các điểm (0;0) và (3; 27) .
Hàm số đạt giá trị lớn nhất trên
đoạn [ 1 ;4] tại x 1 với f ( 1) 37 .
Hàm số đạt giá trị nhỏ nhất
trên đoạn [ 1 ;4] tại x 3 với f (3) 27 . 4 3 2
Hình 2.14. Hàm y 3x 16x 18x
Ví dụ 2.24. Tìm các khoảng tăng, giảm và các điểm cực trị địa phương
của hàm số f x( ) x4 26x2 48x 1.
Giải. Hàm f xác định trên . Trang 95 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Ta có: f / ( )x 4x3 52x 48 x 4 y 353
f / ( )x 0 4x3 52x 48 0 x 1 y 22 x 3 y 10 Lập bảng biến thiên: x 4 1 3 y/ 0 0 0 y 353 22 10
Dựa vào bảng biến thiên, ta có kết luận:
Hàm số tăng trên các khoảng: ( ; 4) và (1;3) .
Hàm số giảm trên các khoảng: ( 4 ;1) và (3; ).
Hàm số đạt cực tiểu địa phương tại điểm (1; 22) .
Hàm số đạt cực đại địa phương tại hai điểm ( 4;353) và (3,10)
Ví dụ 2.25. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f
x( ) x 2sin x trên đoạn [0;2 ]
Giải. Hàm số f x( ) x 2sin x liên tục trên [0,2 ] .
Ta có: f / ( )x 1 2cos x f / ( )x 0 1 2cos x 0 cos x 1 x , x 5 2 3 3 Trang 96 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM f 3 3 2sin 3 3 3 0,684853 f 53 53 2sin 53 53 3 6,968039
Giá trị của hàm f tại các điểm biên: f (0) 0, f (2 ) 2 6,28
Vậy, giá trị nhỏ nhất f 3 3 3 và lớn nhất f 53 53 3 .
Ví dụ 2.26. Kính viễn vọng không gian Hubble được đưa vào sử dụng
ngày 24 tháng 8 năm 1990, bởi tàu con thoi Discovery. Mô hình toán cho
vận tốc (tính bằng ft/s) của tàu trong thời gian thực thi nhiệm vụ, từ lúc
phóng ở thời điểm t 0 cho đến lúc các tên lửa đẩy nhiên liệu rắn được
vứt bỏ ở thời điểm t 126 s , cho bởi
v t( ) 0,001302t3 0,09029t 2 23,61t 3,083
Sử dụng mô hình này, xấp xỉ các giá trị lớn nhất và nhỏ nhất của gia
tốc tàu trong thời gian làm nhiệm vụ. Giải. Gia tốc của tàu con thoi:
a t( ) v t/ ( ) 0,003906t 2 0,18058t 23,61; 0 t
126 a t/ ( ) 0,007812t 0,18058 a t/ ( ) 0 t 23,12
Tính giá trị a t( ) tại các điểm biên và điểm tới hạn: a(0) 23,61 Trang 97 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM a(23,12) 21,52 a(126) 62,87
Vậy gia tốc cực đại khoảng 62,87 ( ft s/ 2 ) và gia tốc cực tiểu khoảng 21,52 ( ft s/ 2 ).
2.2.4. Quy tắc L’Hospital (L’Hospital’s rule) 0
(Quy tắc L’Hospital dùng để khử các dạng vô định và trong 0 việc tính giới hạn hàm số)
a) Định lý (Quy tắc L’Hospital):
Cho f g, là hai vô cùng bé khi x x0 (nghĩa là : xlim x0 f x( ) 0 và
lim 0 g x( ) 0) hoặc hai vô cùng lớn x x0 ( lim | 0 f x( )| và x x x x lim | g x( )| ). Giả sử f g,
khả vi và g x( ) 0 trên khoảng mở x x 0 chứa x ). Khi đó :
0 (có thể trừ tại x0
f x( ) f / ( )x lim0 lim0 / ( )x x x g x( ) x x g Chú ý :
1) Trước khi áp dụng quy tắc L’Hospital, chúng ta nên áp dụng quy
tắc thay thế vô cùng bé tương đương hoặc vô cùng lớn tương
đương (nếu có) để làm giảm độ phức tạp của biểu thức khi tính giới hạn. Trang 98 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
2) Có thể áp dụng quy tắc L’Hospital nhiều lần, liên tục trong một bài toán giới hạn.
b) Khử dạng vô định 0.∞
Xét lim f x g x( ) ( ) , trong đó lim f x( ) 0, lim | g x( )| . x x 0 x x0 x x0
Để áp dụng được quy tắc L’Hospital, ta biến đổi giới hạn về một
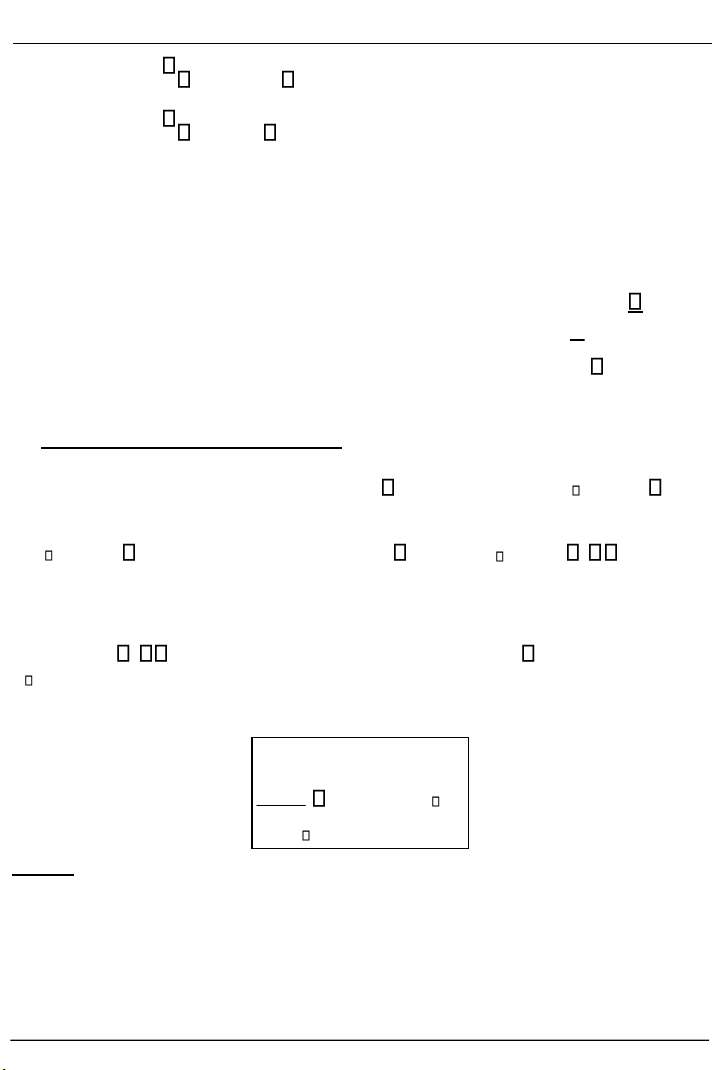
trong hai dạng sau : có dạng Hoặc có dạng
c) Khử dạng vô định ∞ - ∞ : Cố gắng biến đổi hiệu thành dạng thương 0 hoặc để sử dụng quy tắc L’Hospital. 0
d) Khử các dạng vô định 00 , 0 ,1 : ( )
Xét giới hạn A lim f x g x( ) x x0
Áp dụng tính liên tục của hàm số y ln x , nên ta có: ln(A)
lim 0 g x( ).ln f x( ) x x 0 Trang 99 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Ví dụ 2.27 (dạng và ). Áp dụng quy tắc L’Hospital, tính các giới 0 hạn sau : ln x ex a) limx 1 x 1 b) xlim x2 ln x tan x x c) xlim 3 x d) limx 0 x3
Giải. a) Vì limln x 0, lim(x 1) 0, Áp dụng quy tắc L’Hospital, ta x 1 x 1 có: lim x 1
xln x1 limx 1 ((xln x1))// limx 1 1 1/ x limx 1 1x 1
b) Vì lim ex , lim x2 , Áp dụng quy tắc L’Hospital liên tiếp 2 x x lần, ta có: ex ex ex xlim
x2 xlim 2x xlim 2 c) Vì ln x và 3 x khi x .
Áp dụng quy tắc L’Hospital, ta có: 1/ x 3 lim ln x lim lim 0 x 3 x x x 2/3 x 3 x Trang 100 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM d) Vì lim tan x
x x 0 và lim 0 x3 0, Áp dụng quy tắc L’Hospital, ta 0 x có: lim tanxx 3
x limx 0 (1 tan3x22 x) 1 limx 0 tan3x 22 x
limx 0 3xx22 13 x 0
(vì tan x x x, 0)
Ví dụ 2.28. (dạng ) Áp dụng quy tắc L’Hospital, hãy chứng minh một
số vô cùng bé tương đương thường dùng (chương 1)
(1) sin x x , x 0
(6) ex 1x, x 0
(2) 1 cos x
x2 , x 0 (7) (1 x)
1 x, x 0 2
(3) tan x x , x 0
(8) ax 1x.lna, x 0
(4) arcsin x x , x 0
(9) ln(1 x) x, x 0
(5) arctan x x , x 0
Giải. Để chứng minh hai vô cùng bé f x( ) và g x( ) là tương đương khi x
0 , ta chứng minh giới hạn lim
f x( ) 1 bằng cách áp dụng quy tắc
x 0 g x( ) L’Hospital. cos x (1) lim sin x lim 1 x 0 x x 0 1 1 cos x sin x Trang 101 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM (2) limx 0 x2 /2 limx 0 x 1 tan x 1 (3) limx 0 x limx 0 cos2 x 1 1 (4) lim arcsin x lim 1 x 0 x x 0 1 x2 arctan x 1 (5) lim x lim 1 x2 1 x 0 x 0 ex 1 ex (6) lim lim
1 x 0 x x 0 1 (1 x) 1 (1 x) 1 (7) lim lim 1 x 0 x x 0 ax 1 ax lna (8) lim lim 1 x 0 x.lna x 0 lna ln(1 x) 1 (9) lim lim 1 x 0 x x 0 1 x
Ví dụ 2.29. (dạng 0. ) Tính các giới hạn sau: lim | a) x 0 xln | x b) xlim 2arctanx x Giải. |
a) A lim xln | x (dạng 0. ) x 0 Trang 102 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM 1 / x A lim ln | x | (dạng ) lim x 0 1 / x2
limx 0 x 0 x 0 1/ x b) B lim 2arctan x x (dạng 0. ) x 2arctan x B xlim x 1/ 2 (dạng ) 2 1 1 x lim 1 x 1 2 x 2 lim 2 x x 3/ 2 x 1 x 2 Ví dụ 2.30. (dạng
) Tính các giới hạn sau: a) lim x 0 x12 tan12 x b) xlim x ln(x 1) Giải. a) 1 1 A lim x 0 x 2 tan 2 x (dạng ) tan2 x x2 tan2 x x2 0 lim
x2.tan2 x limx 0 x4 (dạng 0 ) x 0
(vì tan x x x, 0) Trang 103 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM lim lim A lim 2 3 x 0 2tan .x (1
4xtan3 x) 2x 12
x 0 tanx3 x 12 x 0 tanxx 3 x tan3 x x3 tan x x 1 lim lim x 0 x3 limx 0 x3 1 ; x 0 x3 3 (ví dụ 2.27) Vậy A 1 1 2 2 6 3
b) B lim x ln(x 1) (dạng ) x B 1 xlim ln(xx 1) xlim x ln(x 1) 1 lim lim
0 (quy tắc L’Hospital) x x x x 1 B (1 0) ( )
Ví dụ 2.31. (00 , 0 ,1 ) Tính các giới hạn sau: 1
b) lim xx a) lim cot x lnx x 0 x 0 1 x cos x x2 d) lim 1 sin x
c) lim arcsin x tanx x 0 x 0 Trang 104 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
esin x 1 ln| |x f*) lim x e) lim 1
sin 4x cotx x 0 x 0 1
Giải. a) A lim cot (dạng 0 ) x ln x x 0 ln A lim ln(cot )x x 0 (dạng ) ln x 1
ln A lim sin2 x.cot x x 0 1/ x (quy tắc L’Hospital) x x 2 lim 2 lim
1 (vì sin(2 )x 2x x,
0 ) x 0 sin(2 )x x 0 2x Vậy A e 1 .
b) A lim xx (dạng 00 ) x 0
ln A lim xln x 0 (ví dụ 2.29a) x 0 Vậy A 1.
c) A lim arcsin x tanx (dạng 00 ) x 0
ln A lim tan x ln(arcsin )x lim xln(arcsin )x x 0 x 0
(vì tan x x x, 0 ) Trang 105 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM 1 xlim 0
ln(arcsin )1/ x x limx 0 arcsin . 1 1x/ x2 x2 (quy tắc L’Hospital) x2 x2
lim lim (vìarcsin x x x, 0) x 0 arcsin . 1x x2 x 0 x. 1 x2 x lim 0 x 0 1 x2 Vậy A 1. 1 d) A lim x 0 x1 sincosxx x2 (dạng 1 ) ln A lim
ln(x cos )x x 2 ln(1 sin )x (dạng 00 ) x 0 1 sin x cos x x cos x 1 sin x lim (quy tắc
L’Hospital) x 0 2x 1
(1 sin2 x) cos (x x cos )x lim 2 x 0
x x( cos )(1x sin )x 1 lim xcos x
2 x 0 x x( cos )(1x sin )x cos x 1 lim 1 Trang 106 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
2 x 0 (x cos )(1x sin )x 2
Vậy A e 1/ 2 . e) A lim 1
sin 4x cotx (dạng 1 ) x 0 ln A lim cot .ln(1 x sin4 )x (dạng 0. ) x 0 ln A lim ln(1 sin4 )x lim 4x 4 x 0 tan x x 0 x
(Vì tan x x x, 0 ; ln(1 sin 4 )x sin 4x 4x x, 0 ) Vậy A e4 . f*) A lim esinxx 1
ln| |x (dạng 1 ) x 0 Ta có : lim
esin x 1 lim x 1 (vì esin x 1sin x x x, 0) x 0 x x 0 x e sin x 1 esin x 1 x Đặt ( )x
1 thì lim ( )x 0 . x x x 0 Mặt khác ta có: e sin x 1 x cos .x esin x 1 lim x lim 2 x 0 2x x 0 lim sin .x e sin x cos2 x e. sin x 1 (quy tắc L’Hospital) Trang 107 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM x 0 2 2 esin x 1 x x Suy ra ( )x , x 0 x 2 A limx 0 1 ( )x (1x)
(x)ln| |x 1 lim 1 0 ( )x (x) e x lim
( )x ln | x | 1 lim 0 x.ln | x | 0 (ví dụ 2.29a) x 0 2 x
Vậy A e0 1.
2.2.5. Công thức Taylor (Taylor's Formula)
a) Định lý Taylor: Nếu hàm f liên tục trên [a b, ], khả vi đến cấp n 1
trong trong (a b, ) thì với mọi x0 ,x (a b, ) , ta có công thức sau và gọi là
công thức Taylor của hàm f tại điểm x0 đến cấp n :
f / (x0 ) (x x0 ) f // (x0 ) (x x0 )2 f x( ) f x( 0 ) 1! 2!
f (n) (x0 ) (x x 0 )n
Rn ( )x ... n! Trong đó: Trang 108 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM ( )c R xn ( ) f (n 1)
n 1 với c nằm giữa x0 và x , được gọi
là (x x0 ) (n 1)! phần dư Lagrange.
Hoặc Rn ( )x o ( x x0 )n , là vô cùng bé cấp cao hơn (x x0
)n khi x x , được gọi là phần dư Peano 0
. b) Công thức Maclaurin:
Công thức Taylor tại x 0 được gọi là công thức Maclaurin 0 : f / (0)
f // (0)2 . f (n) (0) xn R xn ( ) f x( ) f (0) x x 1! 2! n!
c) Ý nghĩa hình học của công thức Taylor :
Đặt Tn ( )x f x( 0 )
f / (x0 ) (x x0 ) ...
f (n) (x0 ) (x x0 )n 1! n!
Thì f x( ) Tn ( )x Rn ( )x
Trong lân cận của điểm x , phần dư 0
Rn ( )x là “rất nhỏ” nên ta có xấp
xỉ f x( ) Tn ( )x . Do đó, đồ thị của hai hàm số y f x( ) và y Tn ( )x rất
“gần nhau” trong lân cận của điểm x0 .
d) Công thức Maclaurin của một số hàm số: x 1 x x x k 2
x3 ... xn o(xn) n o(xn) 1) e 2! 3! n! k 0 k!
2) sin x x ... ( 1)n 1 x2n 1
o(x2n 1),n 1,2,... x3 x5 3! 5! (2n 1)! Trang 109 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM x2 x4 x2n 3) cos x 1 ... ( 1) n
o(x2n ),n 0,1,...
2! 4! (2 )!n x2 x3
4) ln(1 x) x ... ( 1)n 1
xn o(xn ),n 1,2,... 2 3 n n ( 1)...( k 1) 5) (1 x) 1
xk o(xn ) k 1 k! 1 n 6) 1
x x2 ... xn o(xn ) xk o(xn ) 1 x k 0 1 n 7) 1
x x2 ... ( 1)n xn o(xn ) ( 1) k xk o(xn ) 1 x k 0
Ví dụ 2.32. Tìm công thức Taylor của hàm số f x( ) x2 e2(x 1) tại điểm
x 1 đến cấp 4 với phần dư Peano. Giải. Ta có : (1) f x( ) f (1) f / (1) (x 1) f // (x 1)2 1! 2! f /// (1) (x 1)3
f (4) (1) (x 1)4 o ( x 1)4 3! 4! Trang 110 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
f / ( )x 2x 2e2(x 1) f // ( )x 2 4e2(x 1) f /// ( )x 8e2(x 1)
f (4) ( )x 16e2(x 1) f (1) 2; f / (1)
4; f // (1) 6 ; f /// (1) 8 ; f (4) (1) 16
Vậy f x( ) 2 4(x 1) 3(x 1)2 4 (x 1)3 2 (x 1)4 o ( x 1)4 3 3
Có thể sử dụng Mathematica theo cấu trúc sau : In[1]:= Seriesxx 2 x 1 , x,1,4 3 3 4 2 Out[1]= 2 4 x 1 3 x 1 2 x 1 3 x 1 4 O x 1 5
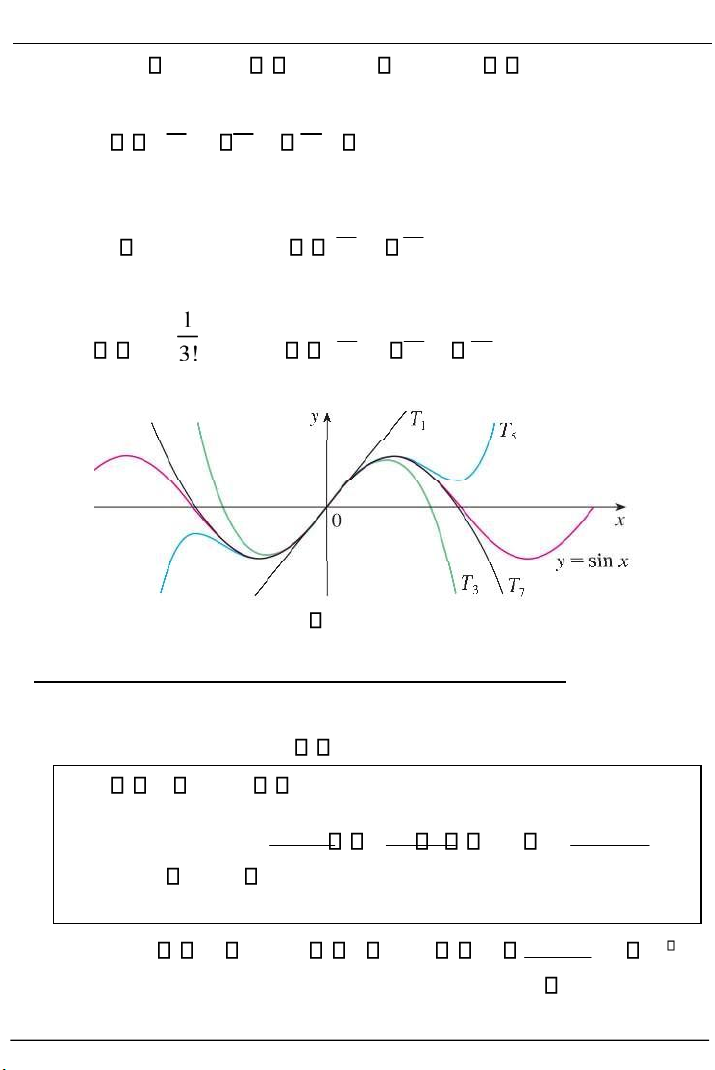
Ví dụ 2.33. Tìm công thức Maclaurin của hàm số f x( ) sin x đến cấp n 7 với phần dư Peano. Giải. f (0) Ta có : f x( ) 7 (k k 0 k)! xk o(x7 )
f (k ) ( )x (sin x)(k ) sin x k 2 , k 1,2,...
f // (0) f (4) (0) f (6) (0) 0 Trang 111 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
f / (0) 1, f /// (0) 1, f (5) (0) 1, f (7) (0) 1 Vậy 1 f x( ) x
x3 1 x5 1 x7 o(x7 ) 3! 5! 7! Đặt 1 T x1( ) x
T x5( ) x x3 1 x5 3! 5! 1 T x3( ) xx3 T x7 ( ) x
x3 1 x5 1 x7 3! 5! 7!
Hình 2.15. Hàm f x( ) sin x và các hàm T T T T1, 3, 5, 7
f) Áp dụng công thức Taylor tính xấp xỉ giá trị hàm số:
Một trong những ứng dụng của công thức Taylor là tính gần đúng
giá trị của hàm số tại điểm x 0
x . Công thức xấp xỉ bậc n là: f x( 0 x) T xn ( 0 x)
f / (x0 ) xf / (x0 ) ( x)2 .. f (n) (x0 ) ( x)n f x( 0 ) 1! 2! n! Sai số: | R n (x0 x)| | f x( 0
x) Tn (x0 x)|
M ( x)n 1 (n 1)! Trang 112 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
Trong đó | f (n 1) ( )x | M với mọi x nằm giữa x 0 và x0 x
Ví dụ 2.34. Tìm công thức Maclaurin của hàm số f x( ) sin x đến cấp
9. Áp dụng tính gần đúng giá trị sin(1) và đánh giá sai số. x3 x5 x7 x9
Giải. Ta có: sin x x R9 ( )x 3! 5! 7! 9! 1 Suy ra : sin(1) 1 1 1 1 0,8414710097 3! 5! 7! 9!
Giá trị đúng: sin(1) 0,8414709848078965... Sai số: x 0
0, x1, sin(10) ( )x sin x 10 2 sin(x 5 ) sin x
| sin(10) ( )x | | sin x | 1 | R9(1) | 2,75.10 7 Trang 113 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
g) Áp dụng công thức Taylor để tính giới hạn: Ví dụ 2.35
1) Tìm công thức Maclaurin các hàm sau đến cấp 3 với phần dư Peano
a) f x( ) e2x
b) f x( ) ln(1 x) c) f x( ) ex sin x
ex sinx e2x
2) Áp dụng câu 1, hãy tính : A limx 0 2ln(1 x) 2x x2
Giải. 1a) Áp dụng công thức: t et 1 t 2 t3 o( )t3 2! 3! Suy ra: e 2x 1(2 )x (2 )x 2
(2 )x 3 o (1 x3 ) 2! 3!
1b) ln(1 x) x x 2 x3 o (2 3 ) x 2 3
1c) f x( ) ex sin x f (0) 1 f / ( )x (1 cos ).x ex sin x (1 cos ). ( )x
f x f / (0) 2 f // ( )x sin . ( )x f x (1 cos ).x
f / ( )x f // (0) 4
f /// ( )x cos . ( )x f x sin .x f / ( )x sin .x f / ( )x (1 cos ).x f // ( )x f /// (0) 1 8 7
f x( ) f (0) f / (0).x f // (0) x2
f /// (0) x3 o (3 x3 ) 2! 3!
12x 2x2 x3 o (3 x3 ) Trang 114 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM 7
2) A limx 0 1 2x 2x2 2
6xx 3 2o ( 3 xx33) o 4 x ( 1x 3 3)2 x 22x xx 2 2 3 o (1 x3) x 2 3 2 A lim 16 1 2
x3 o (x3 ) o (x3 ) 16 o (3xx3 3 ) o 3 (1xx3 3 ) 2 x 3 2 o ( x ) 2 x x 0 limx 0 o (2 3 ) 3 3 3 2 x3
16 limx2 0 o (3xx3 3 ) limx 30)o (1xx3 3 ) 21//36 14
3 2limx 0 o (2xx3
Ví dụ 2.36. Tìm công thức Maclaurin của hàm số f x( ) sin x đến
1 x cấp 7 với phần dư Peano. Từ đó suy ra các đạo hàm f (k ) (0),k 1,...,7 . Giải. Ta có:
f x( ) f (0) f / (0) x f // (0) x2 ...
f (7) (0) x7 o(x7 ) (1) 1! 2! 7!
Mặt khác, áp dụng các công thức ) Trang 115 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
1 x 2 x3 x4 x5 x6 x7 o (1 x7 ) 1 x 1 x
sin x x x 3 x5 x7 o (2 x7 ) 3! 5! 7! Ta thu được: 1 f x( ) 1 x sin x
1 x x2 x3 x4 x5 x6 x7 o (1 x7 ) x x 3! 3 x5!5 x7!7 o (x7 ) 2 f x( ) x x3! 3 x5!5 x7!7 x x x3!3 x5!5 x2 x x3! 3 x5!5 x3 x x3
x4 x x3
x x5. x x6. o(x7 ) 3! 3!
f x( ) x x 2 5 x3 5 x4 101 x5 101 x6
4241 x7 o(x7 ) (2) 6 6 120 120 5040
So sánh hệ số của xk ở (1) và (2), ta suy ra: Trang 116 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
f / (0) 1 ; f // (0) 2 ; f (3) (0) 5 ; f (4) (0) 20 f (5)
(0) 101 ; f (6) (0) 606 ; f (7) (0) 4241 BÀI TẬP CHƯƠNG 2
2.1. Tính đạo hàm f / ( )x bằng định nghĩa, biết:
a) f x( ) cos 2x
b) f x( ) 1 3x
c) f x( ) 2e3x 1
d) f x( ) ln(x 2)
2.2. Cho hàm số y f x( ) x 2(x 1)2/3
a) Tính đạo hàm của hàm f / ( )x ,x 1. Viết phương trình tiếp tuyến
nằm ngang của đồ thị hàm số f .
b) Tính đạo hàm vô cùng tại x 1.
c) Vẽ đồ thị hàm f và tiếp tuyến đứng x 1 trên cùng đồ thị (bằng Mathematica).
2.3. (Kinh tế) Giả sử c x( ) biểu diễn chi phí để sản xuất x đơn vị sản
phẩm. Chi phí trung bình để sản xuất thêm 1 đơn vị sản phẩm khi c
x( h) c x( )
đã sản xuất x đơn vị sản phẩm là . Giới hạn của h
phân thức này khi h 0 được gọi là chi phí sản xuất cận biên của x
đơn vị sản phẩm. Vậy chi phí sản xuất cận biên sẽ là c/ ( )x . Áp dụng:
Giả sử rằng chi phí sản xuất (USD) x chiếc máy giặt là c x( ) 2000 100x 0,1x2
Doanh thu khi bán x chiếc máy giặt là: r x( ) 20,000 1 1x ) Trang 117 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
a) Tìm chi phí sản xuất trung bình trên mỗi máy giặt của 100 chiếc đầu tiên.
b) Tìm chi phí sản xuất cận biên khi 100 chiếc máy giặt được sản xuất.
c) Hãy chỉ ra rằng, chi phí sản xuất cận biên khi 100 chiếc máy giặt
được sản xuất xấp xỉ chi phí sản xuất thêm một chiếc máy giặt
sau khi đã sản xuất được 100 chiếc, bằng cách tính toán trực tiếp chi phí sản xuất sau.
d) Tìm thu nhập cận biên khi 100 chiếc máy giặt được bán ra.
e) Sử dụng hàm r x ( ) để ước lượng doanh thu tăng thêm khi tăng
lượng sản phẩm bán ra từ 100 chiếc mỗi tuần lên 101 chiếc mỗi tuần.
f) Tìm giới hạn của r x ( ) khi x . Giải thích gì về giá trị số vừa tìm được?
2.4. (Sự rơi tự do trên sao Hỏa và sao Mộc) Phương trình rơi
tự do trên bề mặt của sao Hỏa và sao Mộc (s có đơn vị đo là
mét, t có đơn vị giây) là s 1,86t 2 trên sao Hỏa và s 11,44t
2 trên sao Mộc. Hỏi mất thời gian bao lâu thì một viên đá rơi
từ trạng thái nghỉ đạt đến vận tốc 27,8 m/giây (tương đương
100km/giờ) trên mỗi hành tinh trên?
2.5. (Chuyển động phóng trên mặt trăng) Một viên đá được
ném lên theo phương thẳng đứng từ bề mặt của mặt trăng với
vận tốc ban đầu 24m/giây (khoảng 86km/giờ) và đạt tới độ
cao s 24t 0,8t 2 (m) sau t giây.
a) Hãy tìm vận tốc và gia tốc của viên đá tại thời điểm t . (Gia tốc
trong trường hợp này chính là gia tốc trọng trường trên mặt trăng).
b) Mất thời gian bao lâu thì viên đá đạt độ cao lớn nhất? và tính độ
cao mà viên đá bay được?
c) Mất thời gian bao lâu thì viên đá đạt một nữa độ cao tối đa?
d) Viên đá ở trên cao bao lâu? Trang 118 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
2.6. (Áp suất mặt trụ) Nếu gas được chứa trong một
chiếc bình dạng khối trụ (hình 2.16) ở một mức
nhiệt độ cố định là T , thì áp suất P phụ thuộc vào
thể tích V theo công thức dạng: nRT an2 P 2 V nb V
trong đó, a b n, , và R đều là các hằng số. Tìm dP dV/ . Hình 2.16
2.7. (Bài toán chuyển động) Cho hàm vị trí s f t( ) của một vật thể
chuyển động thẳng theo một trục tọa độ, với s (mét) và t (giây).
a) Tìm quãng đường đi được của vật và vận tốc trung bình trong các
khoảng thời gian được chỉ ra.
b) Tìm tốc độ (giá trị tuyệt đối của vận tốc) chuyển động của vật và
gia tốc tại điểm cuối của khoảng.
c) Tìm gia tốc của vật tại thời điểm mà vận tốc bằng không.
d) Tìm tốc độ của vật tại thời điểm mà gia tốc bằng không.
e) Thời điểm nào trong suốt khoảng thời gian chuyển động vật đổi chiều?
1) s t3 3t 2 3t, 0 t 3
2) s 1 t 4 t3 t 2 , 0 t 3 3) s 25 5 2 , 1 t 5 4) s , 4 t 0 t t t 5
2.8. (Rơi tự do từ đỉnh tháp Pisa) Nhà thiên văn học Galileo đã thả một
viên đạn súng thần công từ trên đỉnh tháp Pisa, ở độ cao 179 feet so
với mặt đất, độ cao của viên đạn so với mặt đất sau t giây rơi xuống
là s 179 16t 2 feet.
a) Xác định vận tốc, tốc độ, gia tốc của viên đạn tại thời điểm t .
b) Mất khoảng bao lâu thì viên đạn chạm mặt đất?
c) Tính gia tốc của viên đạn đạt được tại thời điểm chạm mặt đất? ) Trang 119 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
2.9. (Quần thể vi khuẩn) Khi thuốc diệt khuẩn được cho thêm vào canh
dinh dưỡng đó là môi trường mà vi khuẩn có thể sinh sôi, quần thể
vi khuẩn tiếp tục nảy nở và phát triển được một khoảng thời gian,
nhưng sau đó ngừng nảy nở và bắt đầu suy giảm. Kích thước tổng
thể tại thời điểm t (giờ) là b t( ) 106 104 t 103t 2 .
a) Tìm tốc độ phát triển của vi khuẩn tại mỗi thời điểm: 0;4;9 giờ.
b) Tại thời điểm nào thì vi khuẩn bắt đầu ngừng phát triển?
2.10. (Tháo nước bồn) Lượng nước trong bồn sau thời gian tháo t phút
là Q t( ) 200(30 t)2 (đơn vị: gallon).
a) Tính tốc độ chảy ra của nước tại thời điểm 10 phút sau khi tháo.
b) Tính tốc độ nước chảy trung bình trong 10 phút tháo đầu tiên.
2.11. (Máy bay cất cánh) Giả sử khoảng cách máy bay chuyển
động dọc theo đường băng trước khi cất cánh là D (10/9)t
2 , ở đây D là số đo quãng đường (met) từ điểm bắt đầu và t
là thời gian (giây) tính từ thời điểm nhả phanh. Máy bay sẽ
cất cánh khi tốc độ đạt đến 200 km/h. Phải mất thời gian
bao lâu để máy nay cất cánh được, và quãng đường mà máy
bay chuyển động trong khoảng thời gian này?
2.12. Tính đạo hàm các hàm số sau:
a) y 5x 2x b) y x12 2 x (4 1)(x x 1)
c) y x3 sin xcos x
d) y (2 x)tan2 x e) y cot x
f) y log2 x sin x 1 sin x x cos x
2.13. Áp dụng quy tắc xích (quy tắc đạo hàm hàm hợp), hãy tính đạo hàm các hàm số sau:
a) y 4 3x 2x x3
b) y 1 cos(x2 )
c) y (x2 x) 2019 e2020x
d) y x2 sin4 x xcos 2 x Trang 120 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
e) y x tan(2 x)
f) y tan (sin2 3 x)
g) y sin sin(sin ) x
h) y 4sin( 1 x )
i) y 3x 2 1 x
j) y sin(e2x x2) k) y x x sin2 x 3 4 l) y sin xx 1 m) y x 3 x 24x 3 sin x 2 n) y 1 cos x
2.14. Tính đạo hàm các hàm số sau:
a) y (x 1)x x 2
b) y (x sin )x cos2x
c) y arcsin( x)
d) y arctan( sin x) 1
e) y arccos( 1 x2 )
f) y arccot x arccot x
g) y log (2 e x cos x) h) y ln arctanx 2x
i) y ln(sin2 x) f) y ln(1 ex ) 8
2.15. Tìm giá trị của tham số a để hàm số sau khả vi trên : ax, x 0 f x( ) 2 x 3x x, 0 ) Trang 121 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
2.16. Tìm các giá trị của các tham số a và b làm cho hàm số sau khả ax b, x 1
vi trên, biết : f x( ) 2 bx 3, x 1 1 x2 1
2.17. Cho hàm số f x( ) 2 , x 0 x a , x 0
a) Tìm giá trị của tham số a để hàm f x( ) liên tục .
b) Với a tìm được, tính f / ( )x và xét tính liên tục của hàm f / ( )x .
c) Tính f // (0) (nếu có). 3 x2 , x 1
2.18. Cho hàm số f x( ) a x/ , x 1
a) Tìm giá trị của tham số a để f x( ) liên tục tại x 1.
b) Với a tìm được, hãy tính f / (1) (nếu có) .
2.19. Xét sự khả vi của mỗi hàm số sau trên tập xác định của nó: x
a) f x( ) sin 3 b) f x( ) e 1x (x 2) 23 x 1
c) f x( ) x2 5x x x| 3|
d) f x( ) | x 2 | sin( x)
2.20. Tính đạo hàm cấp 2 của mỗi hàm số sau:
a) y x2 (x3 1)5
b) y tan 3x
c) y ln(1 1 x2 )
d) y ln(2x x2 ) 1 e) y 1 1x 3 f) y 1 x Trang 122 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
g) y e x sin x
h) y ecos2x
2.21. Tính đạo hàm tất cả các bậc của các hàm số sau: x4 x5 b) y a) y 3 x2 x 120 2 2
(x2 x)(x2 d) y
c) y (4x3 3 )(2x x) 4 x 1) x x 3 x x2
e) y 122 x 4x3 f) y 3 1 (3x 1)3 (x 1)
2.22. Tính đạo hàm cấp n của các hàm số sau
a) y x2 ln(x 1)
b) y (x2 x)cos3x d) y c) y 23x 5 23x 1 x x 5x 6 4x
e) y x2 x.sin2x
f) y (xcos x)2 e 1 x2 x3 sin x
g) y xln(x2 6x 5),x 1 h) y 2x 2.23. Cho hàm số y x2 1
. Chứng minh rằng hàm y thỏa
phương trình: (x2 1).y(4) 8 .x y(3) 12y// sin x
2.24. Cho hàm số y
cos2x . Chứng minh rằng hàm y thỏa phương x 2 ) Trang 123 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
trình: (x 2).y(4) 4.y(3) 16cos2x
2.25. Chứng tỏ các hàm sau thỏa mãn ba giả thuyết của định lí Rolle trên
khoảng chỉ ra. Sau đó tìm tất cả các số c thỏa mãn kết luận của định lý.
a) f x( ) x x, [0;9]
b) f x( ) x3 x2 6x 2, [0;3]
2.26. Chứng tỏ các hàm sau thỏa các giả thuyết của định lý giá trị trung
bình trên khoảng chỉ ra. Sau đó tìm tất cả các số c thỏa mãn kết luận của định lý.
a) f x( ) 3x2 2x 5, [ 1; 1] b) f x( ) e 2x, [0;3]
c) f x( ) x3 x2 , [ 1,2]
d) f x( ) x2/3, [0,1] 1
e) f x( ) x 1 , [ ,2] f) f x( ) x 1, [1,3] x 2
2.27. Áp dụng định lý giá trị trung bình chứng minh bất đẳng thức sau: a)
sina sinb a b , a b, b)
| cos x 1| | x |, x c)
arctan x arctan y x y , x y, d)
x y 1 x y , x y, [1, ) 2 a e) a b ln
a b (a b 0) a b b
2.28. Áp dụng tính đơn điệu của hàm số, chứng minh các bất đẳng thức:
a) tan x x với 0 x / 2
b) cos2x 1 2x2 , x 0 x sin x x2 c)
ln(1 x) x, x 0 d) e 1 x , x 0 x 1 2
e) (1 x)ln(1 x) arctan x, x 0 Trang 124 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
2.29. Tìm các khoảng tăng hoặc giảm và cực trị địa phương của mỗi hàm
số sau trên tập xác định của nó:
a) f x( ) x(4 x)3
b) f x( ) (x 1) (2 x 3)2
c) f x( ) x2 32 x
d) f x( ) x2 5 x
e) f x( ) x 1 x
f) f x( ) x x 3
g) f x( ) x2 2 h) f x( ) x 1 x x2 2x 2
i) f x( ) | x3 9x |
j) f x( ) x1/3 (x2 4)
k) f x( ) x e2 3x
l) f x( ) e2x e x
2.30. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x( ) sau:
a) f x( ) ln(x2 x 1) trên [ 1 ;1]
b) f x( ) 3 x(8 x) trên [0;8]
c) f x( ) 2tan x tan2 x trên [0, / 2)
d) f x( ) 3ln(x 2) ln(1 x2 ) trên [ 1 ;4]
e) f x( ) x ln(x2 1) 4arctan x trên [ 4 ;3] 15 f) f x( ) x 1 2 x 2 arctan( x 1) trên [0;5]
g) f x( ) (x 20) x 1 45arctan( x 1) trên [ 1 ;4]
2.31. (Sự kháng thuốc ở người) Trong một số trường hợp sự kháng
thuốc xảy ra ở cơ thể người được biểu diễn bởi một phương trình có dạng R M 2 C2 M3
. Trong đó, C là một hằng số dương và ) Trang 125 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM
M là lượng thuốc hấp thụ trong máu. dR a)
Tìm mức độ mẫn cảm của cơ thể với thuốc, nghĩa là tính . dM b)
Tìm lượng thuốc cho cơ thể nhạy cảm nhất bằng cách giải
tìm dR giá trị của M để cực đại . dM
2.32. Một thùng đựng hàng hình hộp chữ nhật không nắp có thể
tích 10m3. Chiều dài đáy gấp đôi chiều rộng. Chi phí cho
vật liệu làm mặt đáy là $10 /m2; mặt bên là $6 /m2 vuông.
Tìm chi phí rẻ nhất có thể để sản xuất thùng đựng hàng đó.
2.33. Một dây kim loại dài 10 m được cắt làm hai. Một miếng
được bẻ cong thành một hình vuông và miếng còn lại được
bẻ cong thành một tam giác đều. Ta nên cắt dây kim loại
này như thế nào để tổng diện tích bị chắn là (a) lớn nhất? (b) nhỏ nhất?
2.34. Áp dụng quy tắc L’Hospital, hãy tính các giới hạn có dạng vô 0 định hoặc sau: 0 e sin x 1 x sin3 x a) lim
b) lim x 0 ln(1 sin )x x x 0 x tan x 1 2x1 15 1 16 x9 1 c) limx 0 ln(cos )x
d) limx 0 sin(x3 ) x3
1 .36. Tìm công thức Maclaurin đến số hạng chứa xn với phần dư Peano của các hàm số sau: Trang 126 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM e 1/x2 lim 0 e) xlim 0 f) x x6 x3 ln(1 x5 ) ln(ln )x h) lim g) lim 2 e2x x x x x
2.35. Áp dụng quy tắc L’Hospital, hãy tính các giới hạn có dạng vô định ,0. ,1 ,0 , 0 0 sau:
b) lim sin xln x a) lim x x2 x 0 x 0 2 x 1 lim c) arctan x x d) lim x ex x x 0 ln(1 x) 1/ x
(1 x)1/ x 1/ x e) lim x x 0 f) lim e x 0 x ln 2 tan g) lim(2 x) 2
h) lim x1 ln x x x 1 x 1/x 1 tanx i) lim tan j) lim ) Trang 127 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM cot x 1 x 2x 1 x 0 x 1 1
k) lim (1 x2 )ln| |x x
l) lim x x x 1 1
n) lim(1 x3 ) ln m) lim x e. x x x ln 1 x x
p) lim(tan2 )x x
o) lim sin x x x 0 x 0 Trang 128 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM a) f x( ) 1 b) f x( ) 5 3 x 2x 2 (x 1)(x 9) (x 1)(x 2)
f x( ) (2x 1)e2x
f x( ) (x 1)ln(x 2) 2.37.
Tìm công thức Taylor đến số hạng chứa (x x0 )n với phần dư Peano của các hàm số sau:
a) y ln(x2 3x 2), x 0 3
b) y xln(3 x),x0 2 x 1 c) y ,x0 1
d) y (x 4)ex 2 , x 0 2 (x 2)(x 3)
2.38. Tìm công thức Maclaurin đến số hạng chứa x2 với phần dư Peano của mỗi hàm số sau: 1 x a) f x( ) 1 e2x
b) f x( ) (x 2)sin x 2 x 1 c) f x( ) 1 x 1
d) f x( ) (x 1)ln 1 x x 1
2.39. Tìm công thức Taylor đến số hạmg chứa (x x0 )2 với phần dư
Peano của mỗi hàm số sau: ) Trang 129 lOMoARcPSD| 36006477
Giải tích 1 – Chương 2
Trường ĐH GTVT TP.HCM a) f x( ) cos 3x2
, x0 1 b) f x( ) 3 x2 , x0 1 e x2 3x c) f x( ) , x 0
3 d) f x( ) ln( x 1), x0 4 x 2
2.40. Tìm công thức Maclaurin đến số hạng chứa x10 với phần dư Peano
của mỗi hàm số sau. Áp dụng kết quả tìm được, hãy tính các
đạo hàm f (k ) (0), k 1,10
a) f x( ) (2 x e) 2x2
b) f x( ) sin(x2 )ln(x2 1) 3x2 5x 2 cos(2 )x c) f x( )
(x 1)(x2 1) d) f x( ) x3 1
2.41. Áp dụng khai triển Maclaurin để tính các giới hạn sau ln(1 x3 ) x3 x6 a) limx 0
sin(x2 ) x2 b) limx 0 x e 2 x2
x4 sin(x2 ) Trang 130


![[TCC] - Tóm tắt lý thuyết chương 1 dãy số - Giải tích 1. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.](https://docx.com.vn/storage/uploads/images/documents/banner/ed538236c0435a2addd79b216bf0ad19.jpg)

