Chương 2 Tích phân bội - Công nghệ thông tin | Đại học Mở Hà Nội
Bài toán. Giả sử hàm số 𝑧 = 𝑓(𝑥, 𝑦) là hàm số xác định, liên tục và không âm trong miền D đóng, bị chặn, có biên là đường kín L trong mặt phẳng Oxy. Hãy tính thể tích vật thể giới hạn dưới bởi mp (Oxy) (miền D), giới hạn trên bởi mặt cong có phương trình 𝑧 = 𝑓(𝑥, 𝑦), xung quanh là mặt trụ có đường sinh song song với Oz tựa trên biên L của D. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Môn: Công nghệ thông tin (Mở HN)
Trường: Đại học Mở Hà Nội
Thông tin:
Tác giả:
Preview text:
Chương 2. TÍCH PHÂN BỘI
2.1 TÍCH PHÂN HAI LỚP
2.1.1 Khái niệm tích phân hai lớp (tích phân kép)
a. Bài toán thể tích vật thể hình trụ.
Bài toán. Giả sử hàm số 𝑧 = 𝑓(𝑥, 𝑦) là hàm số xác định, liên tục và không âm trong miền D đóng,
bị chặn, có biên là đường kín L trong mặt phẳng Oxy. Hãy tính thể tích vật thể giới hạn dưới bởi mp
(Oxy) (miền D), giới hạn trên bởi mặt cong có phương trình 𝑧 = 𝑓(𝑥, 𝑦), xung quanh là mặt trụ có đường
sinh song song với Oz tựa trên biên L của D.
Chia D một cách tùy ý thành n mảnh nhỏ không giao nhau 𝑆1, 𝑆2, … , 𝑆𝑛 có diện tích tương ứng là
∆𝑆1, ∆𝑆2, … , ∆𝑆𝑛. Lấy mỗi mảnh đó làm đáy, dựng các vật thể hình trụ mà mặt xung quanh là hình trụ có
đường sinh song song với Oz , phía trên giới hạn bởi một phần mặt cong 𝑧 = 𝑓(𝑥, 𝑦). Hình trụ ban đầu
được chia thành n thể trụ nhỏ.
Lấy một điểm 𝑀𝑖 ∈ 𝑆𝑖, 𝑖 = 1, 𝑛 tùy ý. Tích 𝑓(𝑥𝑖, 𝑦𝑖)∆𝑆𝑖 là thể tích hình trụ thẳng thứ i có đáy 𝑆𝑖 và
chiều cao 𝑓(𝑥𝑖, 𝑦𝑖). Gọi 𝑑𝑖 là đường kính của mảnh 𝑆𝑖. Khi 𝑑𝑖 khá nhỏ, có thể xấp xỉ thể tích thể trụ thứ
i là ∆𝑉𝑖 bởi thể trụ thẳng thứ i nói trên, nghĩa là: ∆𝑉𝑖 ≈ 𝑓(𝑥𝑖, 𝑦𝑖)∆𝑆𝑖. Khi đó thể tích vật thể hình trụ ban đầu là: n
V f (x , y )S i i i i=1
Phép xấp xỉ này càng chính xác khi n càng lớn và các 𝑑𝑖 càng nhỏ.
Do đó thể tích V của vật thể ban đầu được định nghĩa bằng giới hạn nếu có của tổng trên khi 𝑛 →
∞ sao cho đường kính lớn nhất trong các đường kính 𝑑𝑖 của các mảnh 𝑆𝑖 dần tới 0, giới hạn ấy không
phụ thuộc cách chia miền D và cách chọn các điểm 𝑀𝑖.
b. Định nghĩa tích phân hai lớp
Cho hàm số 𝑧 = 𝑓(𝑥, 𝑦) là hàm số xác định, bị chặn trong miền compact 𝐷 ⊂ ℝ2.
Chia D một cách tùy ý thành n mảnh nhỏ không giao nhau 𝐷1, 𝐷2, … , 𝐷𝑛 có diện tích tương ứng là
∆𝑆1, ∆𝑆2, … , ∆𝑆𝑛. Lấy điểm
𝑀𝑖 ∈ 𝐷𝑖, 𝑖 = 1, 𝑛 tùy ý. Lập tổng: 𝐼𝑛 = ∑𝑛
𝑓(𝑥𝑖, 𝑦𝑖)∆𝑆𝑖 𝑖=1
𝐼𝑛 được gọi là tổng tích phân của hàm số 𝑧 = 𝑓(𝑥, 𝑦) tương ứng với cách chia miền D và cách chọn các điểm 𝑀𝑖.
Gọi 𝑑𝑖 là đường kính của các mảnh 𝐷𝑖 (đường kính của một miền là khoảng cách lớn nhất giữa hai
điểm bất kỳ của miền đó), và 𝑑 = 𝑚𝑎𝑥𝑑𝑖. Cho 𝑛 → ∞ sao cho 𝑑 → 0, nếu tồn tại lim 𝐼𝑛 = 𝐼 (hữu hạn, xác định) 𝑑→0
không phụ thuộc cách chia D và cách chọn các điểm 𝑀𝑖, thì ta nói giới hạn đó được gọi là tích phân hai
lớp (tích phân kép) của hàm số 𝑓(𝑥, 𝑦) trong miền D và ký hiệu:
I = f (x, y)dS (2.1) D
trong đó D là miền lấy tích phân, f(x,y) là hàm số dưới dấu tích phân, dS là yếu tố diện tích. Trong trường
hợp này ta nói hàm sô f(x,y) khả tích trong miền D.
Chú ý. Vì tích phân hai lớp tồn tại không phụ thuộc cách chia miền D, nên ta có thể chia D bởi hai
họ đường thẳng song song với các trục tọa độ. Do đó ∆𝑆𝑖 = ∆𝑥𝑖∆𝑦𝑖 𝑛ê𝑛 𝑑𝑆 = 𝑑𝑥. 𝑑𝑦, và ta có thể viết:
I = f (x, y)dS = f (x, y)dxdy = f (x, y)dydx (2.2) D D D
c. Ý nghĩa hình học 1
Giả sử hàm số 𝑓(𝑥, 𝑦) xác định trên miền đóng, bị chặn 𝐷 ⊂ ℝ2, nghĩa là cho mặt S có phương
trình 𝑧 = 𝑓(𝑥, 𝑦), mặt này có hình chiếu trên mặt phẳng (Oxy) là miền D. Người ta gọi hình giới hạn bởi
mặt S, mặt xung quanh tạo bởi đường sinh song song với trục Oz tựa trên biên L của D và mặt phẳng
Oxy là một hình trụ cong. Giả sử 𝑓(𝑥, 𝑦 ≥ 0, ∀(𝑥, 𝑦) ∈ 𝐷, từ bài toán thể tích vât thể hình trụ và định
nghĩa tich phân hai lớp. thì tích phân ∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 chính là thể tích hình trụ cong đó, tức là: 𝐷
V = f (x, y)dxdy D
d. Điều kiện khả tích
Đặt 𝑚𝑖 = 𝑖𝑛𝑓(𝑥,𝑦)∈𝑆 𝑓(𝑥, 𝑦),
𝑀𝑖 = 𝑠𝑢𝑝(𝑥,𝑦)∈𝑆 𝑓(𝑥, 𝑦) 𝑖 𝑖
Các tổng 𝑠 = ∑𝑛 𝑖=1 𝑚𝑖∆𝑆𝑖 và 𝑆 = ∑𝑛 𝑀 𝑖=1
𝑖∆𝑆𝑖 lần lượt được gọi là tổng Darboux dưới và trên của
hàm f(x,y) ứng với cách chia miền D.
Đặt 𝐼∗ = 𝑠𝑢𝑝{𝑠} và 𝐼∗ = 𝑖𝑛𝑓{𝑆} thì ta luôn có 𝑠 ≤ 𝐼∗ ≤ 𝐼∗ ≤ 𝑆.
Định lý 2.1 (Điều kiện khả tích). Điều kiện cần và đủ để hàm số f(x,y) khả tích trong miền D là: lim (𝑆 − 𝑠) = 0 𝑚𝑎𝑥𝑑𝑖→0
Hệ quả. Nếu hàm số f(x,y) liên tục trong miền đóng, bị chặn D thì khả tích trong miền đó. 2.1.2 Tính chất
1. f (x, y) + g(x, y)dxdy = f (x, y)dxdy + g(x, y)dxdy D D D
2. k. f (x, y)dxdy = k. f (x, y)dxdy D D
3. Nếu chia D thành hai miền rời nhau 𝐷 = 𝐷1 ∪ 𝐷2 thì:
f (x, y)dxdy = f (x, y)dxdy + f (x, y)dxdy D D1 D2
4. Nếu f (x, y) g(x, y) (x, y) D thì f (x, y)dxdy g(x, y)dxdy D D
5. Nếu m f (x, y) M , (x, y) D thì mS f (x, y)dxdy MS , S là diện tích miền D. D
(m, M là các hằng số).
6. (Định lý về giá trị trung bình) Nếu 𝑓(𝑥, 𝑦) là hàm số liên tục trong miền đóng và bị chặn D thì
tồn tại điểm (𝑥0, 𝑦0) ∈ 𝐷 sao cho:
f (x, y)dxdy = f (x , y ).S , S là diện tích miền D. 0 0 D
2.1.3 Cách tính tích phân kép
a) Miền lấy tích phân D là hình chữ nhật 𝐷 = [𝑎, 𝑏] × [𝑐, 𝑑]
Định lý 2.2 Nếu f(x,y) liên tục trên 𝐷 = [𝑎, 𝑏] × [𝑐, 𝑑] thì: b d d b
f (x, y)dxdy = f (x, y)dy dx = f (x, y)dxdy D a c c a
Công thức trên được gọi là công thức đổi thứ tự lấy tích phân. • Chú ý.
Nếu 𝑓(𝑥, 𝑦) = ℎ(𝑥). 𝑔(𝑦) thì luôn luôn có: 2 b d
f (x, y)dxdy = h(x)dx. g( y)dy D a c Ví dụ 2.1 𝑑𝑥𝑑𝑦 1. Tính 𝐼 = ∬ , 𝐷 = [1,2] × [1,2] 𝐷 (𝑥+𝑦)2 𝑑𝑥𝑑𝑦 2 2 2 1 1 1 𝐼 = ∬ − (𝑥 + 𝑦)2 = ∫ [∫ ] 𝑑𝑥
(𝑥 + 𝑦)2 𝑑𝑦] 𝑑𝑥 = ∫ [𝑥 + 1 𝐷 1 1 1 𝑥 + 2 𝑥 + 1 2 9 = 𝑙𝑛 | || = 𝑙𝑛 𝑥 + 2 8 1 𝜋 2. Tính
𝐼 = ∬ 2𝑦. 𝑠𝑖𝑛2𝑥𝑑𝑥𝑑𝑦, 𝐷 = [0, ] × [ 1,2 ] 𝐷 𝜋 2 𝑦 2 𝑦 Ta có:
𝐼 = ∬ 2 . 𝑠𝑖𝑛2𝑥𝑑𝑥𝑑𝑦 = ∫2 𝑠𝑖𝑛2𝑥𝑑𝑥 ∫ 2 𝑑𝑦 𝐷 0 1 𝜋 𝑦 2
= −𝑐𝑜𝑠2𝑥|2 . 2 | = 3 2 0 𝑙𝑛2 1 𝑙𝑛2
b) Miền lấy tích phân D là miền bị chặn bất kỳ
Định lý 2.2 Giả sử miền lấy tích phân là hình thang cong:
D =(x, y) | a x b, y1(x) y(x) y2(x),
trong đó các hàm số 𝑦1(𝑥), 𝑦2(𝑥) là các hàm số liên tục trên [a,b], 𝑓(𝑥, 𝑦) khả tích trên D và tồn 𝑦
tại tích phân 𝐼(𝑥) = ∫ 2(𝑥) 𝑓(𝑥, 𝑦)𝑑𝑦, ∀𝑥 ∈ [𝑎, 𝑏], thì tồn tại tích phân lặp: 𝑦1(𝑥) 𝑏 𝑦2(𝑥)
∫ [ ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 ] 𝑑𝑥 𝑎 và ta có: 𝑦1(𝑥 ) 𝑦2(𝑥) 𝑏
∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫ [ ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 ] 𝑑𝑥 (2.3) 𝐷 𝑎 𝑦1(𝑥)
Tương tự, khi thay đổi vai trò của x và y trong định lý 2.2, ta có kết quả tương tự.
Định lý 2.3 Giả sử miền lấy tích phân là hình thang cong
D =(x, y) | c y d, x1( y) x x2(y) ,
trong đó các hàm số 𝑥1(𝑦), 𝑥(𝑦) là các hàm số liên tục trên [c,d]. Giả sử 𝑓(𝑥, 𝑦) khả tích trên D
và tồn tại tích phân 𝐼(𝑦) = 𝑥(𝑦) ∫
𝑓(𝑥, 𝑦)𝑑𝑥, ∀𝑦 ∈ [𝑐, 𝑑], thì tồn tại tích phân lặp: 𝑥1(𝑦) 𝑑 𝑥2(𝑦)
∫ [ ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 ] 𝑑𝑦 𝑐 𝑥1(𝑦) và ta có: 𝑑 𝑥2(𝑦)
∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫ [ ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 ] 𝑑𝑦 (2.4) 𝐷 𝑐 𝑥1(𝑦) 3
Nếu D là miền phẳng giới hạn bởi đường cong kín L, sao cho mỗi đường thẳng song song với một
trong hai trục tọa độ cắt L ở nhiều nhất hai điểm. Dựng hình chữ nhật: a x b, c y d , mà các
cạnh của nó tiếp xúc với biên L tại các điểm M, N, P, Q. Các điểm M, P chia biên L của D thành hai cung 𝑀
̂𝑁𝑃, 𝑀̂𝑄𝑃 có phương trình theo thứ tự là 𝑦 = 𝑦1(𝑥), 𝑦 = 𝑦2(𝑥), các điểm N, Q chia L thành hai cung 𝑄̂𝑀𝑁, 𝑄
̂𝑃𝑁 có phương trình theo thứ tự là 𝑥 = 𝑥1(𝑦), 𝑥 = 𝑥2(𝑦) , trong trường hợp này ta có thể tính ∬ 𝑓(𝑥, theo cả hai công thức: 𝐷 𝑦)𝑑𝑥𝑑𝑦
∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫𝑏 𝑑𝑥 ∫𝑦2(𝑥) 𝑓(𝑥, 𝑦)𝑑𝑦 = ∫𝑑 𝑑𝑦 ∫𝑥2(𝑦) 𝑓(𝑥, 𝑦)𝑑𝑥 , nghĩa là ta có thể thay đổi 𝐷 𝑎 𝑦1(𝑥) 𝑐 𝑥1(𝑦) thứ tự lấy tích phân.
Chú ý. Miền D trong các trường hợp trên được gọi là miền đơn giản. Nếu D không phải là miền
đơn giản, để tính ∬𝐷 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦, ta phải chia D thành các miền đơn giản đã xét, tích phân trên miền D
sẽ bằng tổng các tích phân trên các miền đơn giản. Ví dụ 2.2
1. Xác định các cận của tích phân ∬𝐷 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦, trong đó D là miền giới hạn bởi các đường 1
𝑥 = 2, 𝑦 = , 𝑦 = 𝑥. 𝑥
Giải. Từ hình vẽ ta thấy, D được xác định như sau: 1 ≤ 𝑥 ≤ 2 {1 ≤ 𝑦 ≤ 𝑥 𝑥 Vậy: 2 𝑥
∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 𝐷 1 1 𝑥
Nếu đổi thứ tự lấy tích pân ta có: 1 2 2 2
∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 + ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 𝐷 1/2 1 1 𝑦 𝑦
2. Tính 𝐼 = ∬ (𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦, trong đó D giới hạn bởi các đường: 𝐷
𝑦 = 𝑥, 𝑦 = 𝑥 + 1, 𝑦 = 1, 𝑦 = 3. 1 ≤ 𝑦 ≤ 3 Giải. 𝐷 = { 𝑦 − 1 ≤ 𝑥 ≤ 𝑦 3 y
I = (x2 + y2 )dxdy ==
(x2 + y2 )dx dy = ... = 14 D 1 y−1
3. Tính I = x2 ( y − x)dxdy , D là miền giới hạn bởi các đường 𝑦 = 𝑥2 𝑣à 𝑥 = 𝑦2. D Giải.
I = x2 ( y − x)dxdy D 1 1 x4 x = x2 dx =
( y − x)dy
x2 − + x3 + − x x dx = ... 0 2 2 x2 0 4
4. Tính I = xydxdy , D là miền tam giác OAB, với O(0,0), A(1,1), B(2,0). D 0 x 1 1 x 2
Giải. Cách 1. D = D1 D2 , với D1 : và D2 :
0 y x
0 y 2 − x 1 x 2 2−x Khi đó:
I = xydxdy + xydxdy == xdx ydy + xdx ydy D1 D2 0 0 1 0 1 = x3 2 x(2 − x)2 1 dx + dx = ... = 2 2 3 0 1
Cách 2. Nếu nhìn miền D theo phương của trục Ox thì ta được tích phân thuận lợi hơn. Vì: 0 y 1 1 1 2− y
x2 y 2 − y D : I =
ydy xdx = dy 2 y
y x 2 − y 0 y 0
1 (2 − y)2 y y3 1 2 1 1 =
− dy = (2 y − 2 y2 )dy = y2 − y3 = 0 2 2 0 3 3 0
5. Đổi thứ tự lấy tích phân các tích phân sau: 2 4 4 √ 𝑦
a. ∫ 𝑑𝑥 ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 ⟺ ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 −2 𝑥2 0 −√𝑦
b. ∫3 𝑑𝑦 ∫2𝑦 𝑓(𝑥, 𝑦)𝑑𝑥 ⟺ ∫2 𝑑𝑥 ∫3 𝑓(𝑥, 𝑦)𝑑𝑦 + ∫6 𝑑𝑥 ∫3 𝑓(𝑥, 𝑦)𝑑𝑦 1 0 0 1 2 𝑥/2
c. ∫1 𝑑𝑦 ∫1+√1−𝑦2 𝑓(𝑥, 𝑦)𝑑𝑥 ⟺ ∫2 𝑑𝑥 ∫1+√2𝑥−𝑥2 𝑓(𝑥, 𝑦)𝑑𝑦 1 2−𝑦 1 2−𝑥
2.1.4 Đổi biến số trong tích phân hai lớp
a. Công thức đổi biến tổng quát Xét tích phân:
f (x, y)dxdy D
trong đó 𝑓(𝑥, 𝑦) là hàm số liên tục trên miền đóng và bị chặn 𝐷 ⊂ ℝ2.
Đặt: {𝑥 = 𝑥(𝑢, 𝑣) . Giả sử: 𝑦 = 𝑦(𝑢, 𝑣)
- 𝑥(𝑢, 𝑣), 𝑦(𝑢, 𝑣) là các hàm số liên tục và có đạo hàm riêng liên tục trên miền đóng và bị chặn
trong 𝐷′ ⊂ (𝑂𝑢𝑣)
- Các hàm số 𝑥(𝑢, 𝑣), 𝑦(𝑢, 𝑣) xác định một song ánh từ 𝐷′ 𝑙ê𝑛 𝐷. 𝐷(𝑥,𝑦) 𝑥′ 𝑥′ - Định thức Jacobi: 𝐽 = = | 𝑢 𝑣| ≠ 0 trong 𝐷′. 𝐷(𝑢,𝑣) 𝑦′ 𝑦′ 𝑢 𝑣
Khi đó, ta có công thức đổi biến số tổng quát trong tích phân hai lớp:
f (x, y)dxdy = f x(u,v), y(u,v). | J | dxdy (2.5) D D ' Ví dụ 2.3
1. Tính ∬ (𝑥 + 𝑦)𝑑𝑥𝑑𝑦, trong đó D giới hạn bởi các đường: 𝐷
𝑦 = −𝑥, 𝑦 = −𝑥 + 3, 𝑦 = 2𝑥 − 1, 𝑦 = 2𝑥 + 1 5 Giải.
Đổi biến { 𝑢 = 𝑥 + 𝑦 𝑥 = 𝑢−𝑣 - { 3 𝑣 = −2𝑥 + 𝑦 𝑦 = 2𝑢+𝑣 3
Phép đổi biến trên là một song ánh từ
𝐷 → 𝐷′ xác định bởi { 0 ≤ 𝑢 ≤ 3 −1 ≤ 𝑣 ≤ 1
Định thức Jacobi của phép đổi biến là:
J = ... = 1 ≠ 0 3 Suy ra 3 1 1
𝐼 = ∬(𝑥 + 𝑦)𝑑𝑥𝑑𝑦 = ∫ ∫ 𝑢𝑑𝑢 𝑑𝑣 = 3 3 𝐷 0 −1
2. Tương tự ví dụ trên nhưng với D giới hạn bởi các đường
𝑦 = 𝑥 + 2, 𝑦 = −2𝑥 + 1, 𝑦 = 𝑥 − 1, 𝑦 = −2𝑥 + 4
b. Đổi biến trong hệ tọa độ cực
𝑥 = 𝑟𝑐𝑜𝑠𝜑
Công thức liên hệ giữa tọa độ Dercaster (x,y) và tọa độ cực (𝑟, 𝜑) của cùng một điểm là: { 𝑦 = 𝑟𝑠𝑖𝑛𝜑
Nếu 𝑟 > 0, 0 ≤ 𝜑 < 2𝜋 thì các công thức ấy xác định một song ánh giữa các tọa độ Dercaster và
tọa độ cực. riêng gốc O có 𝑟 = 0, 𝜑 tùy ý.
Xem các công thức trên như là một phép đổi biến số, ta có:
Định thức Jacobi của phép đổi biến là: 𝐷(𝑥,𝑦) 𝑥′ 𝑥′
𝑐𝑜𝑠𝜑 −𝑟𝑠𝑖𝑛𝜑 𝐽 = = | 𝑟 𝜑| = |
| = 𝑟 ≠ 0 (trừ ra tại O(0,0) 𝐷(𝑟,𝜑) 𝑦′ 𝑦′ 𝑠𝑖𝑛𝜑 𝑟𝑐𝑜𝑠𝜑 𝑟 𝜑
Do đó, từ công thức đổi biến tổng quát, ta có công thức đổi biến trong tọa độ cực:
𝐼 = ∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∬ 𝑓(𝑟𝑐𝑜𝑠𝜑, 𝑟𝑠𝑖𝑛𝜑). 𝑟𝑑𝑟𝑑𝜑 (2.6) 𝐷 𝐷′ Chú ý.
- Theo công thức (5), dù miền D có chứa gốc O hay không, ta luôn có công thức (6). Nếu miền D
có dạng hình quạt ta nhận được 𝐷′ = {𝛼 ≤ 𝜑 ≤ 𝛽, 𝑟1(𝜑) ≤ 𝑟 ≤ 𝑟2(𝜑)} và 𝛽 𝑟2(𝜑)
∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫
∫ 𝑓(𝑟𝑐𝑜𝑠𝜑, 𝑟𝑠𝑖𝑛𝜑)𝑑𝜑 𝑑𝜑 𝐷 𝛼 𝑟1(𝜑)
Nếu O nằm trong miền D và mọi tia xuất phát từ O đều cắt biên của D tại một điểm có bán kính vecto là 𝑟(𝜑) thì: 2𝜋 𝑟(𝜑)
∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫ 𝑓(𝑟𝑐𝑜𝑠𝜑, 𝑟𝑠𝑖𝑛𝜑)𝑑𝜑 𝐷 0 0
- Thường dùng tọa độ cực khi phương trình biên miền D có chứa biểu thức 𝑥2 + 𝑦2. Khi đó thay
𝑥2 + 𝑦2 = 𝑟2 sẽ được phương trình đơn giản hơn theo 𝑟, 𝜑.
- Trong một số trường hợp ta đổi biến theo công thức:
{𝑥 = 𝑥0 + 𝑟𝑐𝑜𝑠𝜑
𝑦 = 𝑦0 + 𝑟𝑠𝑖𝑛𝜑
(tọa độ cực tịnh tiến) 6
Sẽ có |𝐽| = 𝑟, (𝑥 − 𝑥0)2 + (𝑦 − 𝑦0)2 = 𝑟2, nên thường dùng khi gặp biểu thức
(𝑥 − 𝑥0)2 + (𝑦 − 𝑦0)2
trong phương trình biên miền D. Cận của 𝑟, 𝜑 xác định theo gốc cực mới là điểm 𝐼0(𝑥0, 𝑦0).
𝑥 = 𝑎𝑟𝑐𝑜𝑠𝜑 𝑥2 𝑦2 2 - Cũng có thể đặt { + =
𝑦 = 𝑏𝑟𝑠𝑖𝑛𝜑
(tọa độ cực co giãn), sẽ có 𝐽 = 𝑎𝑏𝑟 và 𝑟 , nên thường 𝑎2 𝑏2
dùng tọa độ cực co giãn khi D là miền elip. Ví dụ 2.4 𝑑𝑥𝑑𝑦 1. Tính 𝐼 = ∬
trong đó D là miền 𝑥2 + 𝑦2 ≤ 1, 𝑥 ≥ 0, 𝑦 ≥ 0. 𝐷 1+𝑥2+𝑦2 𝑥 = 𝑟𝑐𝑜𝑠𝜑 Giải.
Đổi biến tọa độ cực: { 𝑦 = 𝑟𝑠𝑖𝑛𝜑 0 ≤ 𝑟 ≤ 1
Ta có: 𝐷 → 𝐷′ = {0 ≤ 𝜑 ≤ 𝜋 , 𝐽 = 𝑟 2 dxdy π /2 1 rdr π = Do đó: = ln 2
1 + x2 + y2 dφ 1 + r2 4 D 0 0 2. Tính ∬ √ 𝐷
𝑥2 + 𝑦2𝑑𝑥𝑑𝑦, D là miền 𝑥2 + 𝑦2 ≤ 𝑎2 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đổi biến tọa độ cực: { 𝑦 = 𝑟𝑠𝑖𝑛𝜑 0 ≤ 𝑟 ≤ 𝑎 Ta có: 𝐷 → 𝐷′ = { 0 ≤ , 𝐽 = 𝑟 𝜑 ≤ 2𝜋 2𝜋 𝑎 2𝜋𝑎3
∬ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫ 𝑟. 𝑟𝑑𝑟 = ⋯ = 3 𝐷 0 0
3. 𝐼 = ∬ (𝑥 + 𝑦)𝑑𝑥𝑑𝑦, trong đó D là miền 𝑥2 + 𝑦2 ≤ 𝑥 + 𝑦. 𝐷 1 1 2 2
Miền lấy tích phân là miền tròn 1 + y − x − 2 2 2 1
𝑥 − = 𝑟𝑐𝑜𝑠𝜑
Chuyển sang tọa độ cực suy rộng ta có: { 2 , 𝐽 = 𝑟
𝑦 − 1 = 𝑟𝑠𝑖𝑛𝜑 2 1 Khi đó 0 r D ' = ; J = r 0 2 1 2𝜋 √2 𝜋
𝐼 = ∬(𝑥 + 𝑦)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫[1 + 𝑟(𝑐𝑜𝑠𝜑 + 𝑠𝑖𝑛𝜑)]𝑟𝑑𝑟 = ⋯ = 2 𝐷 0 0
4. Tính 𝐼 = ∬ √1 − 𝑥2 − 𝑦2 𝑑𝑥𝑑𝑦, trong đó D là miền elip 𝐷 𝑎2
𝑏2 𝑥 = 𝑎𝑟𝑐𝑜𝑠𝜑 ′ 0 ≤ 𝜑 ≤ 2𝜋
Chuyển sang tọa độ cực { = {
𝑦 = 𝑏𝑟𝑠𝑖𝑛𝜑 ; 𝐽 = 𝑎𝑏𝑟 𝐷 0 ≤ 𝑟 ≤ 1 Do đó: 2𝜋 1 𝑥2 𝑦2 2𝜋𝑎𝑏 𝐼 = ∬ √1 − −
𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫ √1 − 𝑟2𝑎𝑏𝑟𝑑𝑟 = ⋯ = 𝑎2 𝑏 2 3 𝐷 0 0 7
2.2 TÍCH PHÂN BA LỚP
2.2.1. Định nghĩa tích phân ba lớp. Điều kiện tồn tại. a. Bài toán
Cho vật thể V trong không gian, biết khối lượng riêng tại mỗi điểm của nó là 𝜌(𝑥, 𝑦, 𝑧). Tính khối lượng của vật thể.
Chia miền V một cách tùy ý thành n miền nhỏ 𝑉1, 𝑉2, … , 𝑉𝑛 có thể tích tương ứng là
∆𝑉1, ∆𝑉2, … , ∆𝑉𝑛. Lấy các điểm 𝑀𝑖(𝑥𝑖, 𝑦𝑖, 𝑧𝑖) ∈ 𝑉𝑖, khối lượng riêng của miền đó tại 𝑀𝑖 là 𝜌(𝑀𝑖) =
𝜌(𝑥𝑖, 𝑦𝑖, 𝑧𝑖). Nếu 𝑉𝑖 khá nhỏ, khối lượng phần vật thể thứ i là 𝑚𝑖 ≈ 𝜌(𝑥𝑖, 𝑦𝑖, 𝑧𝑖). ∆𝑉𝑖, và khối lượng gần
đúng của toàn bộ vật thể là n n
m = m i
(xi , yi , zi )Vi i=1 i=1
Cho 𝑛 → ∞ sao cho 𝑚𝑎𝑥𝑑𝑖 → 0 (𝑑𝑖- đường kính của 𝑉𝑖), thì : n
m = lim (xi , yi , zi )Vi max di→0 i=1
Để tính được giới hạn của tổng đặc biệt này, ta đi đến định nghĩa sau:
b. Định nghĩa tích phân ba lớp
Cho hàm số 𝑓(𝑥, 𝑦, 𝑧) xác định trong miền V đóng và giới nội của không gian Oxyz. Chia miền V
thành n miền nhỏ 𝑉1, 𝑉2, … , 𝑉𝑛 có thể tích tương ứng là ∆𝑉1, ∆𝑉2, … , ∆𝑉𝑛. Lấy 𝑀𝑖(𝑥𝑖, 𝑦𝑖, 𝑧𝑖) ∈ 𝑉𝑖, 𝑖 = 1, 𝑛. Lập tổng:
𝐼𝑛 = ∑𝑛 𝑖=1 𝑓(𝑥𝑖, 𝑦𝑖, 𝑧𝑖). ∆𝑉𝑖 gọi là tổng tích phân của hàm số 𝑓(𝑥, 𝑦, 𝑧) trong miền V.
Gọi 𝑑𝑖 là đường kính của 𝑉𝑖. Cho 𝑛 → ∞ sao cho 𝑚𝑎𝑥𝑑𝑖 → 0, nếu
lim 𝐼𝑛 = 𝐼 (hữu hạn) không 𝑚𝑎𝑥𝑑𝑖→0
phụ thuộc vào cách chia miền V và cách chọn các điểm 𝑀𝑖(𝑥𝑖, 𝑦𝑖, 𝑧𝑖) ∈ 𝑉𝑖, thì giới hạn đó được gọi là tích
phân ba lớp của hàm số 𝑓(𝑥, 𝑦, 𝑧) trong miền V, ký hiệu là:
𝐼 = ∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑉, dV là yếu tố vi phân thể tích. 𝑉
Trong trường hợp tích phân này tồn tại, ta nói hàm só 𝑓(𝑥, 𝑦, 𝑧) khả tích trong miền V. • Ý nghĩa.
- Ý nghĩa hình học: Nếu 𝑓(𝑥, 𝑦, 𝑧) = 1, thì: 𝐼 = ∭ 𝑑𝑉 =
lim ∑𝑛 ∆𝑉𝑖 = 𝑉 là thể tích miền V. 𝑉
𝑚𝑎𝑥𝑑𝑖→0 𝑖=1
- Ý nghĩa cơ học: Giả sử 𝑓(𝑥, 𝑦, 𝑧) > 0 được coi là khối lượng riêng của miền V, khi ∆𝑉𝑖 đủ nhỏ có
thể coi khối lượng gần đúng của nó là 𝑓(𝑥𝑖, 𝑦𝑖, 𝑧𝑖). ∆𝑉𝑖 với 𝑀𝑖(𝑥𝑖, 𝑦𝑖, 𝑧𝑖) ∈ 𝑉𝑖. Theo định nghĩa tích
phân ba lớp, khối lượng gần đúng của V là:
𝐼 = ∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑉 = 𝑚 là khối lượng miền V. 𝑉
Chú ý. Vì giá trị tích phân ba lớp tồn tại không phụ thuộc cách chia miền V, nên ta có thể chia V
bởi họ các mặt phẳng song song với các mặt phẳng tọa độ, mỗi ∆𝑉𝑖 nói chung là một hình hộp chữ nhật.
Do đó: 𝑑𝑉 = 𝑑𝑥𝑑𝑦𝑑𝑧, vì vậy:
𝐼 = ∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑉 = ∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧. 𝑉 𝑉
• Điều kiện tồn tại tích phân ba lớp
Đặt 𝑚𝑖 = 𝑖𝑛𝑓(𝑥,𝑦,𝑧)∈𝑉 𝑓(𝑥, 𝑦, 𝑧),
𝑀𝑖 = 𝑠𝑢𝑝(𝑥,𝑦,𝑧)∈𝑉 𝑓(𝑥, 𝑦, 𝑧) 𝑖 𝑖
Các tổng 𝑠 = ∑𝑛 𝑖=1 𝑚𝑖∆𝑉𝑖 và 𝑆 = ∑𝑛 𝑀 𝑖=1
𝑖∆𝑉𝑖 lần lượt được gọi là tổng Darboux dưới và trên của
hàm f(x,y,z) ứng với cách chia miền V.
Đặt 𝐼∗ = 𝑠𝑢𝑝{𝑠} và 𝐼∗ = 𝑖𝑛𝑓{𝑆} thì ta luôn có 𝑠 ≤ 𝐼∗ ≤ 𝐼∗ ≤ 𝑆. 8
Định lý 2.4 (Điều kiện khả tích). Điều kiện cần và đủ để hàm số f(x,y,z) khả tích trong miền D là: lim (𝑆 − 𝑠) = 0 𝑚𝑎𝑥𝑑𝑖→0
Hệ quả. Nếu hàm số f(x,y,z) liên tục trong miền đóng, bị chặn V thì khả tích trong miền đó. 2.2.2. Tính chất
Tích phân ba lớp có các tính chất tương tự như tích phân hai lớp đã được phát biểu.
2.2.3. Cách tính tích phân ba lớp 𝐼 = ∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
a. Miền lấy tích phân là hình hộp chữ nhật
Giả sử V là hình hộp chữ nhật 𝑉 = [𝑎, 𝑏] × [𝑐, 𝑑] × [𝑒, 𝑓], 𝑓(𝑥, 𝑦, 𝑧) là hàm số liên tục trên V. Khi đó: 𝑏 𝑑 𝑓
𝐼 = ∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝑥 ∫ 𝑑𝑦 ∫ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑧 (2.7) 𝑉 𝑎 𝑐 𝑒
Trong trường hợp V là hình hộp chữ nhật, ta có thể đổi sang một thứ tự lấy tích phân khác một cách tùy ý.
b. Miền lấy tích phân là hình trụ cong
Giả sử V được giới hạn bởi các mặt 𝑧1(𝑥, 𝑦), 𝑧2(𝑥, 𝑦), với 𝑧1(𝑥, 𝑦), 𝑧2(𝑥, 𝑦) liên tục trên miền
phẳng D, 𝑧1(𝑥, 𝑦) ≤ 𝑧2(𝑥, 𝑦) ∀(𝑥, 𝑦) ∈ 𝐷, D là hình chiếu của V lên mặt phẳng (Oxy). Khi đó:
z2 ( x, y)
I = f (x, y, z)dxdydz = dxdy f (x, y, z)dz V D
z1( x, y)
Nếu 𝐷 = {𝑎 ≤ 𝑥 ≤ 𝑏, 𝑦1(𝑥) ≤ 𝑦 ≤ 𝑦2(𝑥)}, trong đó 𝑦1(𝑥), 𝑦2(𝑥) là các hàm liên tục trên [a,b], thì: b y 2 ( x)
z2 ( x, y)
I = dx dy f (x, y, z)dz (2.8) a y z 1( x) 1( x, y) Ví dụ 2.5 dV
1. Tính, I =
(1+ x + y + z)3 V
trong đó V được giới hạn bởi các mặt phẳng tọa độ và mặt phẳng 𝑥 + 𝑦 + 𝑧 = 1. 0 ≤ 𝑥 ≤ 1
Giải. Miền V xác định như sau: { 0 ≤ 𝑦 ≤ 1
0 ≤ 𝑧 ≤ 1 − 𝑥 − 𝑦 1 1− x 1− x− y 1 1 5
I = dx dy dz = ... = ln 2 −
(1 + x + y + z)3 2 16 0 0 0 2. Tính 𝐼 = ∭
𝑥𝑑𝑥𝑑𝑦𝑑𝑧, trong đó V giới hạn bởi các mặt 𝑉
𝑥 = 0, 𝑦 = 0, 𝑧 = 𝑥2 + 𝑦2, 𝑧 = 4 (trong góc 1/8 thứ nhất). 0 ≤ 𝑥 ≤ 2
Giải. Miền V xác định như sau: {0 ≤ 𝑦 ≤ √4 − 𝑥2 𝑥2 + 𝑦2 ≤ 𝑧 ≤ 4 9 2 √4−𝑥2 4 2 √4−𝑥2
𝐼 = ∭ 𝑥𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝑥 ∫ 𝑑𝑦
∫ 𝑥𝑑𝑧 = ∫ 𝑑𝑥
∫ 𝑥(4 − 𝑥2 − 𝑦2)𝑑𝑦 𝑉 0 0 𝑥2+𝑦2 0 0 2 1 64
= − ∫(4 − 𝑥2)3/2𝑑(4 − 𝑥2) = ⋯ = 3 15 0
2.2.4 Đổi biến số trong tích phân ba lớp
1. Đổi biến tổng quát
Cho hàm số 𝑓(𝑥, 𝑦, 𝑧) liên tục trong miền đóng, bị chặn V trong không gian Oxyz. Để tính tích phân
I = f (x, y, z)dxdydz V 𝑥 = 𝑥(𝑢, 𝑣, 𝑤) Đặt:
{𝑦 = 𝑦(𝑢, 𝑣, 𝑤)
(𝑢, 𝑣, 𝑤) ∈ 𝑉′ 𝑧 = 𝑧(𝑢, 𝑣, 𝑤) Giả sử:
- Các hàm 𝑥 = 𝑥(𝑢, 𝑣, 𝑤), 𝑦 = 𝑦(𝑢, 𝑣, 𝑤), 𝑧 = 𝑧(𝑢, 𝑣, 𝑤) liên tục, có đạo hàm riêng liên tục trong 𝑉′.
- Các hàm 𝑥 = 𝑥(𝑢, 𝑣, 𝑤), 𝑦 = 𝑦(𝑢, 𝑣, 𝑤), 𝑧 = 𝑧(𝑢, 𝑣, 𝑤) xác định song ánh từ 𝑉 → 𝑉′. - Định thức Jacobi: 𝑥′ 𝑥′ 𝑥′ 𝑢 𝑣 𝑤
𝐽 = 𝐷(𝑥,𝑦,𝑧) = |𝑦′
𝑦′ 𝑦′ | ≠ 0 trong 𝑉′ (trừ ra một số điểm) 𝐷(𝑢,𝑣,𝑤) 𝑢 𝑣 𝑤 𝑧′ 𝑧′ 𝑧′ 𝑢 𝑣 𝑤 Khi đó ta có:
I = f (x, y, z)dxdydz = f [x(u,v, w), y(u,v, w), z(u,v, w)] J dudvdw (2.9) V V '
2. Đổi biến tọa độ trụ
a) Hệ tọa độ trụ
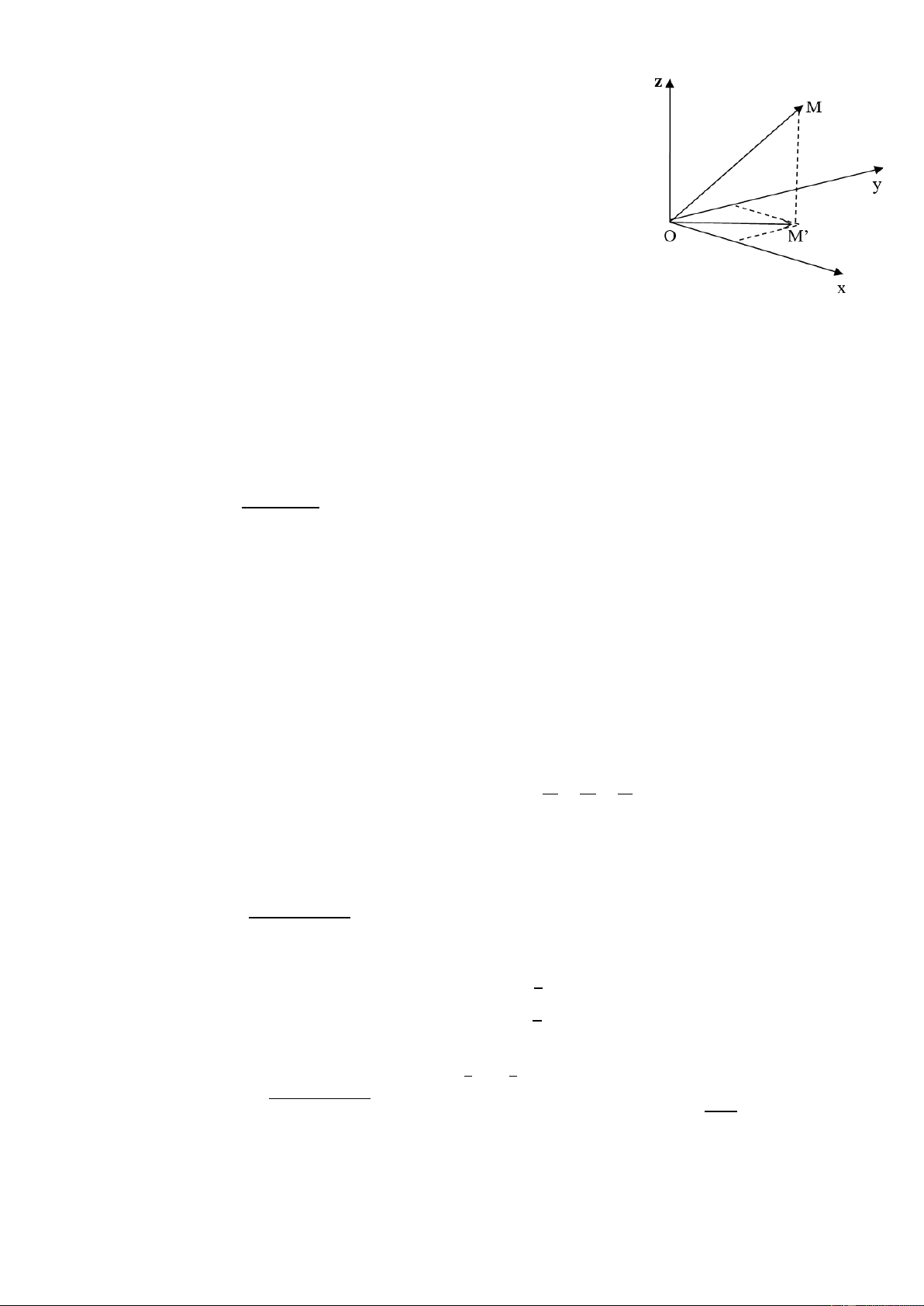
Cho điểm 𝑀(𝑥, 𝑦, 𝑧) ∈ ℝ3, gọi 𝑀′(𝑥, 𝑦, 0) là hình chiếu của M lên (Oxy). Đặt
𝜑 = (𝑂𝑥, ⃗𝑂⃗⃗⃗𝑀
⃗⃗⃗⃗→′ ) , 0 ≤ 𝜑 ≤ 2𝜋 𝑟 = | ⃗𝑂⃗⃗⃗𝑀
⃗⃗⃗⃗→′| , 0 ≤ 𝑟 < +∞
𝑧 = 𝑂𝑀, −∞ ≤ 𝑧 ≤ +∞
Bộ (𝑟, 𝜑, 𝑧) được gọi là tọa độ trụ của điểm M, ký hiệu là 𝑀(𝑟, 𝜑, 𝑧). Ta có công thức liên hệ
giữa tọa độ Đecac (𝑥, 𝑦, 𝑧) và tọa độ trụ (𝑟, 𝜑, 𝑧) của M là: 𝑥 = 𝑟𝑐𝑜𝑠𝜑
{𝑦 = 𝑟𝑠𝑖𝑛𝜑 (0 ≤ 𝑟, 0 ≤ 𝜑 ≤ 2𝜋, 𝑧 ∈ ℝ) 𝑧 = 𝑧
b) Đổi biến trong tọa độ trụ
Từ công thức đổi biến tổng quát, với 𝑢 = 𝑟, 𝑣 = 𝜑, 𝑤 = 𝑧.
𝑐𝑜𝑠𝜑 −𝑟𝑠𝑖𝑛𝜑 0
Ta có định thức Jacobi của phép đổi biến là:
𝐽 = 𝐷(𝑥,𝑦,𝑧) = |𝑠𝑖𝑛𝜑 𝑟𝑐𝑜𝑠𝜑 0| = 𝑟 𝐷(𝑟,𝜑,𝑧) 0 0 1
Vậy công thức chuyển tích phân ba lớp từ tọa độ đề các sang tọa độ trụ là: 10
I = f (x, y, z)dxdydz = f [r cos(φ), r sin(φ), (2.10) Ví dụ z)].rdrdφvdz 2.6 V V '
1. Tính 𝐼 = ∭ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧, V là miền hình trụ 𝑥2 + 𝑦2 = 2𝑦, giới hạn bởi các mặt phẳng 𝑉
𝑧 = 0, 𝑧 = 𝑎 (𝑎 > 0). 𝑥 = 𝑟𝑐𝑜𝑠𝜑 0 ≤ 𝜑 ≤ 𝜋
Giải. Đổi biến tọa độ trụ: {𝑦 = 𝑟𝑠𝑖𝑛𝜑
. Khi đó: 𝑉′ = {0 ≤ 𝑟 ≤ 2𝑠𝑖𝑛𝜑 𝑧 = 𝑧 0 ≤ 𝑧 ≤ 𝑎 𝜋 2𝑠𝑖𝑛𝜑 𝑎
𝐼 = ∭ √𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑟2𝑑𝑧 𝑉 0 0 0 𝜋 2𝑠𝑖𝑛𝜑 𝜋 3 2𝑠𝑖𝑛𝜑 𝜋 3 𝑟 8𝑠𝑖𝑛 𝜑
= ∫ 𝑑𝜑 ∫ 𝑎𝑟2𝑑𝑟 = 𝑎 ∫ 3 | 𝑑𝜑 = 𝑎 ∫ 3 𝑑𝜑 0 0 0 0 0 𝜋 8𝑎 32 = −
∫(1 − 𝑐𝑜𝑠2𝜑)𝑑(𝑐𝑜𝑠𝜑) = 𝑎 3 9 0 2. Tính 𝐼 = ∭
√𝑥2 + 𝑦2. 𝑧𝑑𝑥𝑑𝑦𝑑𝑧, V là miền giới hạn bởi các mặt 𝑉
𝑧 = √𝑥2 + 𝑦2, 𝑧 = 1.
Giải. Đổi biến tọa độ trụ: 𝑥 = 𝑟𝑐𝑜𝑠𝜑 0 ≤ 𝜑 ≤ 2𝜋
V= {𝑦 = 𝑟𝑠𝑖𝑛𝜑
Khi đó: 𝑉′ = { 0 ≤ 𝑟 ≤ 1 𝑧 = 𝑧 𝑟 ≤ 𝑧 ≤ 1 Khi đó: 2𝜋 1 1
𝐼 = ∭ √𝑥2 + 𝑦2. 𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝑟 ∫ 𝑧. 𝑟. 𝑟𝑑𝑧 𝑉 0 0 𝑟
= 2𝜋. 1 ∫1 𝑟2(1 − 𝑟2)𝑑𝑟 = 2𝜋 2 0 15
3. Tính 𝐼 = ∭ (𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦𝑑𝑧, V là miền giới hạn bởi các mặt 𝑉
2𝑧 = 𝑥2 + 𝑦2, 𝑧 = 2 .
Giải. Hinh chiếu của V xuống mặt phẳng (Oxy) là miền 𝐷: 𝑥2 + 𝑦2 ≤ 𝒙 = 𝒓𝒄𝒐𝒔𝝋 𝟎 ≤ 𝝋 ≤ 𝟐𝝅
Đổi biến: {𝒚 = 𝒓𝒔𝒊𝒏𝝋 ⟹ 𝑽′ { 𝟎 ≤ 𝒓 ≤ 𝟐 𝒓𝟐 𝒛 = 𝒛 ≤ 𝒛 ≤ 𝟐 𝟐 𝟐𝝅 𝟐 𝟐
𝑰 = ∭(𝒙𝟐 + 𝒚𝟐)𝒅𝒙𝒅𝒚𝒅𝒛 = ∫ 𝒅𝝋 ∫ 𝒓𝟑𝒅𝒓 ∫ 𝒅𝒛 𝑽 𝟎 𝟎 𝒓𝟐 𝟐 𝟐 𝒓 𝟏𝟔
= 𝟐𝝅 ∫ 𝒓𝟑 (𝟐 − 𝟐 ) 𝒅𝒓 = 𝝅 𝟎 𝟐 𝟑 11
3. Đổi biến tọa độ cầu
a) Hệ tọa độ cầu
Cho điểm 𝑀(𝑥, 𝑦, 𝑧) ∈ ℝ3, gọi 𝑀′(𝑥, 𝑦, 0) là hình chiếu của M lên (Oxy).
Đặt 𝜑 = (𝑂𝑥, ⃗𝑂⃗⃗⃗𝑀
⃗⃗⃗⃗→′) , 0 ≤ 𝜑 ≤ 2𝜋
𝜃 = (𝑂𝑧, ⃗𝑂⃗⃗⃗𝑀
⃗⃗→ ), 0 ≤ 𝜃 ≤ 𝜋 𝜌 = | ⃗𝑂⃗⃗⃗𝑀
⃗⃗⃗⃗→′| , 0 ≤ 𝜌 < +∞
Bộ (𝜌, 𝜃, 𝜑) được gọi là tọa độ cầu của điểm M, ký hiệu
𝑀(𝜌, 𝜑, 𝜃). Ta có công thức liên hệ giữa tọa độ Decac (x,y,z) và tọa
độ cầu (𝜌, 𝜑, 𝜃) của M là:
𝑥 = 𝜌𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃
{𝑦 = 𝜌𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃 (0 ≤ 𝑟,
0 ≤ 𝜑 ≤ 2𝜋, 0 ≤ 𝜃 ≤ 𝜋) 𝑧 = 𝜌𝑐𝑜𝑠𝜃
b) Đổi biến tọa độ cầu
Từ công thức đổi biến tổng quát, với 𝑢 = 𝜌, 𝑣 = 𝜃, 𝑤 = 𝜑.
Ta có định thức Jacobi của phép đổi biến là: 𝐷(𝑥, 𝑦, 𝑧)
𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃 −𝜌𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃 𝜌𝑐𝑜𝑠𝜑𝑐𝑜𝑠𝜃 𝐽 =
= |𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃
𝜌𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃
𝜌𝑠𝑖𝑛𝜑𝑐𝑜𝑠𝜃| = −𝜌2𝑠𝑖𝑛𝜃 𝐷(𝜌, 𝜃, 𝜑) 𝑐𝑜𝑠𝜃 0 −𝜌𝑠𝑖𝑛𝜃
𝐽 ≠ 0 khi 𝜌 ≠ 0 và 𝑠𝑖𝑛𝜃 ≠ 0.
Vậy ta có công thức đổi biến từ hệ tọa độ đề các sang hệ tọa độ cầu:
𝐼 = ∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 = ∭ 𝑓(𝜌𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜑, 𝜌𝑠𝑖𝑛𝜃𝑠𝑖𝑛𝜑, 𝜌𝑐𝑜𝑠𝜃). 𝜌2𝑠𝑖𝑛𝜃𝑑𝜌𝑑𝜃𝑑𝜑 𝑉 𝑉
Công thức vẫn đúng khi miền V chứa những điểm trên trục Oz. Chú ý.
-Từ công thức đổi biến tọa độ cầu ta có: 𝑥2 + 𝑦2 + 𝑧2 = 𝜌, nên thường dùng đổi biến tọa độ cầu
khi phương trình giới hạn miền V có chứa biểu thức 𝑥2 + 𝑦2 + 𝑧2. 𝑥2 𝑦2 𝑧2
- Trường hợp mặt giới hạn miền V có chứa biểu thức + + 𝑎2 𝑏2
𝑐2 thì có thể sử dụng đổi biến:
𝑥 = 𝑎𝜌𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜑
{𝑦 = 𝑏𝜌𝑠𝑖𝑛𝜃𝑠𝑖𝑛𝜑 ⟹ |𝐽| = 𝑎𝑏𝑐𝜌2𝑠𝑖𝑛𝜃
𝑧 = 𝑐𝜌𝑐𝑜𝑠𝜃 Ví dụ 2.7
1. Tính ∭ √𝑥2 + 𝑦2 + 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧, trong đó 𝑉
a. V là góc phần tám thứ nhất của hình cầu 𝑥2 + 𝑦2 + 𝑧2 = 𝑅2
𝑥 = 𝜌𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜑 0 ≤ 𝜑 ≤ 𝜋 2
Đổi biến tọa độ cầu: {𝑦 = 𝜌𝑠𝑖𝑛𝜃𝑠𝑖𝑛𝜑 ⟹ {0 ≤ 𝜃 ≤ 𝜋
|𝐽| = 𝜌2𝑠𝑖𝑛𝜃 𝑧 = 𝜌𝑐𝑜𝑠𝜃 2 0 ≤ 𝜌 ≤ 𝑅 𝜋 𝜋 2 2 𝑅 𝜋𝑅4
∭ √𝑥2 + 𝑦2 + 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑠𝑖𝑛𝜃𝑑𝜃 ∫ 𝜌3𝑑𝜃 = ⋯ = 8 𝑉 0 0 0 12
b. V là hình cầu 𝑥2 + 𝑦2 + 𝑧2 = 𝑧
𝑥 = 𝜌𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜑
Đổi biến tọa độ cầu: {𝑦 = 𝜌𝑠𝑖𝑛𝜃𝑠𝑖𝑛𝜑 𝑧 = 𝜌𝑐𝑜𝑠𝜃 0 ≤ 𝜑 ≤ 2𝜋 𝜋
⟹ { 0 ≤ 𝜃 ≤ |𝐽| = 𝜌2𝑠𝑖𝑛𝜃 2
0 ≤ 𝜌 ≤ 𝑐𝑜𝑠𝜃 𝜋 2𝜋 2 𝑐𝑜𝑠𝛩 2𝜋
∭ √𝑥2 + 𝑦2 + 𝑧2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑠𝑖𝑛𝜃𝑑𝜃 ∫ 𝜌3𝑑𝜃 = ⋯ = 5 𝑉 0 0 0 𝑥2+𝑦2
2. ∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧, V là miền giới hạn bởi nửa trên của elipxoit + 𝑧2 = 1 và mặt 𝑉 𝑎2 𝑐2 phẳng 𝑧 = 0.
Cách 1. Dùng tọa độ trụ 2
Từ x +y2 + z2 = 1 ⟹ z = c √a2 − (x2 + y2) (z ≥ 0) a2 c2 a 𝑥 = 𝑟𝑐𝑜𝑠𝜑 0 ≤ 𝜑 ≤ 2𝜋
Đổi biến tọa độ trụ: {𝑦 = 𝑟𝑠𝑖𝑛𝜑 ⟹ 𝑉′ = { 0 ≤ 𝑟 ≤ 𝑎 𝑧 = 𝑧 0 ≤ 𝑧 ≤ c √a2 − r2 a c 2 √a2−r2 𝜋 𝑎 a 2𝜋𝑎3𝑐2
∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑟2𝑑𝑟 ∫ 𝑧𝑑𝑧 = ⋯ = 15 𝑉 0 0 0
Cách 2. Đổi biến tọa độ cầu mở rộng
𝑥 = 𝑎𝜌𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜑 0 ≤ 𝜑 ≤ 2𝜋 𝜋
{𝑦 = 𝑎𝜌𝑠𝑖𝑛𝜃𝑠𝑖𝑛𝜑 ⟹ |𝐽| = 𝑎2𝑐𝜌2𝑠𝑖𝑛𝜃 ⟹ { 0 ≤ 𝜃 ≤ 2
𝑧 = 𝑐𝜌𝑐𝑜𝑠𝜃 0 ≤ 𝜌 ≤ 1 𝜋 2𝜋 ⁄2 1 2𝜋𝑎3𝑐2
∭ 𝑧√𝑥2 + 𝑦2𝑑𝑥𝑑𝑦𝑑𝑧 = ∫ 𝑑𝜑 ∫ 𝑑𝜃 ∫ 𝑐𝜌𝑐𝑜𝑠𝜃. 𝑎𝜌𝑠𝑖𝑛𝜃. 𝑎2𝑐𝜌2𝑠𝑖𝑛𝜃𝑑𝜌 = 15 𝑉 0 0 0
Chú ý. Để xác định các cận tích phân thuận lợi, ta xác định theo thứ tự 𝜑 → 𝜃 → 𝑟. Ta cho nửa
mặt phẳng (P) tựa trên trục Oz quay xung quanh trục này sao cho góc 𝜑 tăng dần, lần đầu tiên (P) tiếp
xúc với vật thể V cho ta cận dưới của 𝜑 là 𝜑1, lần cuối cùng rời khỏi V cho cận trên là 𝜑2. Tại vị trí ứng
với góc 𝜑 giữa 𝜑1và 𝜑2, (P) cắt V theo một thiết diện L. Cho tia Ot trên (P) quay từ trên xuống dưới (góc
𝜃 tăng dần), lần đầu tiên tia Ot chạm vào thiết diện (L) ta nhận được góc 𝜃(𝜑1), lần cuối cùng tia Ot ra
khỏi thiết diện cho cận trên 𝜃(𝜑2). Khi tia ứng với 𝜑 nằm giữa 𝜃(𝜑1), 𝜃(𝜑2) thì biến 𝜌 sẽ chạy từ
𝜌1(𝜑, 𝜃) đế𝑛 𝜌1(𝜑 𝜃).
Trong trường hợp miền lấy tích phân khó vẽ, ta có thể tìm các cận tích phân từ các bất đẳng thức
xác định miền, hay những điều kiện để biểu thức có nghĩa.
2.3 ỨNG DỤNG CỦA TÍCH PHÂN BỘI
2.3.1 Tính diện tích hình phẳng
Từ ý nghĩa hình học của tích phân hai lớp, miền phẳng D giới hạn bởi đường cong kín, thì có diện
tích được xác định bởi công thức: 13
𝑆(𝐷) = ∬ 𝑑𝑥𝑑𝑦 (2.11) 𝐷
Nếu đường cong giới hạn miền D có phương trình trong tọa độ cực thì:
𝑆(𝐷) = ∬ 𝑟𝑑𝑟𝑑𝜑 (2.12) 𝐷′ Ví dụ 2.8
1. Tính diện tích miền phẳng giới hạn bởi các đường 1 1 𝑦2 = 𝑥, 𝑦 = , 𝑦 = 𝑥 2 Giải. 1 1/𝑦 7
𝑆 = ∫ 𝑑𝑦 ∫ 𝑑𝑥 = 𝑙𝑛2 − 24 1/2 𝑦2
2. Tính diện tích hình phẳng giới hạn bởi đường:
(𝑥2 + 𝑦2)2 = 2𝑎𝑥3 (𝑎 > 0)
Ta thấy đường cong giới hạn miền nằm bên phải Oy, đối xứng qua Ox.
Vì vậy: 𝑆 = 2𝑆(𝐷′), 𝐷′ là phần hình phẳng nằm bên phải Oy.
Đổi biến tọa độ cực, ta có: 𝜋 𝑥 = 𝑟𝑐𝑜𝑠𝜑 { 0 ≤ 𝜑 ≤
𝑦 = 𝑟𝑠𝑖𝑛𝜑 ⟹ 𝐷′ = { 2
0 ≤ 𝑟 ≤ 2𝑎𝑐𝑜𝑠3𝜑
Vậy 𝑆 = 2𝑆(𝐷′) = 2 2𝜋 𝑑 𝜑
2𝑎𝑐𝑜𝑠3𝜑 𝑟𝑑𝑟 = 5𝜋𝑎2 ∫ ∫ 0 0 8
3. Tính diện tích hình phẳng giới hạn bởi các đường sau: 𝑦2 = 𝑝𝑥,
𝑦2 = 𝑞𝑥, 𝑥2 = 𝑎𝑦, 𝑥2 = 𝑏𝑦,
0 < 𝑝 < 𝑞; 0 < 𝑎 < 𝑏 𝑢 = 𝑦2 𝑥 𝑝 ≤ 𝑢 ≤ 𝑞 Giải.
Đổi biến: { 𝑣 = 𝑥2 ⟹ {𝑎 ≤ 𝑣 ≤ 𝑏 𝑦 𝑥 = 3√𝑢𝑣2 1 Ta có: { ⟹ |𝐽| = 𝑦 = 3√𝑢2𝑣 3 Do đó: 𝑞 𝑏 1 1 𝑆 = ∫ 𝑑𝑢 ∫ 𝑑𝑣 = 3
(𝑞 − 𝑝)(𝑏 − 𝑎) 3 𝑝 𝑎
2.3.2 Tính thể tích vật thể
- Nếu hình trụ cong V giới hạn trên bởi mặt cong có phương trình 𝑧 = 𝑓(𝑥, 𝑦), giới hạn dưới bởi
miền phẳng D (D là hình chiếu của V xuống mặt phẳng (Oxy)), xung quanh là mặt trụ có đường sinh song
song với Oz tựa trên biên của D, có thể tích là:
𝑉 = ∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 (2.13) 𝐷 14
Trong trường hợp miền V giới hạn bởi các mặt cong 𝑧1(𝑥, 𝑦), 𝑧2(𝑥, 𝑦), trong đó D là hình chiếu của
V xuống mặt phẳng (Oxy), 𝑧1 ≤ 𝑧2 ∀(𝑥, 𝑦) ∈ 𝐷 thì thể tích vật thể là:
𝑉 = ∬[𝑧2(𝑥, 𝑦) − 𝑧1(𝑥, 𝑦)]𝑑𝑥𝑑𝑦 (2.14) 𝐷
Chú ý. Có trường hợp miền V phải chia thành nhiều miền nhỏ rồi cộng lại.
Ngoài ra, từ ý nghĩa hình học của tích phân ba lớp, ta có công thức tính thể tích của vật thể Ω đóng
và bị chặn trong không gian là:
𝑉 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 (2.15) Ω
Ví dụ 2.9 Tính thể tích vật thể giới hạn bởi các mặt sau:
1. 𝑧 = √1 − 𝑥2 − 𝑦2, 𝑦 = 𝑥, 𝑦 = √3𝑥, 𝑧 = 0.
2. {𝑥2 + 𝑦2 + 𝑧2 = 2𝑧, 𝑧 = √𝑥2 + 𝑦2} Giải.
1. Chiếu miền V xuống mp(Oxy) ta được miền D xác định bởi
𝐷 = {𝑥2 + 𝑦2 ≤ 1, 𝑥 ≤ 𝑦 ≤ √3𝑥}
Đổi biến tọa độ cực ta có: 𝑥 = 𝑟𝑐𝑜𝑠𝜑 𝜋 𝜋 ≤ 𝜑 ≤
{𝑦 = 𝑟𝑠𝑖𝑛𝜑 ⟹ |𝐽| = 𝑟; 𝐷′ = {4 3 0 ≤ 𝑟 ≤ 1 𝜋 3 1 𝜋
𝑉 = ∬ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫(1 − 𝑟2)𝑟𝑑𝑟 = ⋯ = (đ𝑣𝑡𝑡) 48 𝐷 𝜋 0 4
2. Mặt cầu 𝑥2 + 𝑦2 + 𝑧2 = 2𝑧 và mặt nón 𝑧 = √𝑥2 + 𝑦2 cắt nhau theo đường tròn {𝑥2 + 𝑦2 = 1 𝑧 = 1
Miền V giới hạn dưới bởi mặt 𝑧 = √𝑥2 + 𝑦2, giới hạn trên bởi mặt 𝑧 = 1 + √1 − 𝑥2 − 𝑦2. Khi
đó thể tích miền V là:
𝑉 = ∭ 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
Đổi biến tọa độ cầu, ta có:
𝑥 = 𝜌𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜑 0 ≤ 𝜑 ≤ 2𝜋 𝜋
{𝑦 = 𝜌𝑠𝑖𝑛𝜃𝑠𝑖𝑛𝜑 ⟹ 𝑽′ = { 0 ≤ 𝜃 ≤
|𝐽| = 𝜌2𝑠𝑖𝑛𝜃 𝑧 = 𝜌𝑐𝑜𝑠𝜃 4
0 ≤ 𝜌 ≤ 2𝑐𝑜𝑠𝜃 Khi đó: 𝜋 𝜋 2 𝜋 4 2𝑐𝑜𝑠𝛩 4 2𝜋
𝑉 = ∫ 𝑑𝜑 ∫ 𝑑𝜃
∫ 𝜌2𝑠𝑖𝑛𝜃𝑑𝜌 =
∫ 8𝑐𝑜𝑠3𝜃. 𝑠𝑖𝑛𝜃𝑑𝜃 = 𝜋 (đ𝑣𝑡𝑡) 3 0 0 0 0
2.3.3. Diện tích mặt cong
Mặt cong đơn trị S có phương trình 𝑧 = 𝑓(𝑥, 𝑦), trong đó 𝑓(𝑥, 𝑦) là hàm số liên tục, có các đạo hàm
riêng liên tục trên D, D là hình chiếu của S xuống mặt phẳng (Oxy), có diện tích xác định bởi công thức: 15
𝑆 = ∬ √1 + 𝑧′2 + 𝑧′2𝑑𝑥𝑑𝑦 (2.16) 𝑥 𝑦 𝐷 Ví dụ 2.10
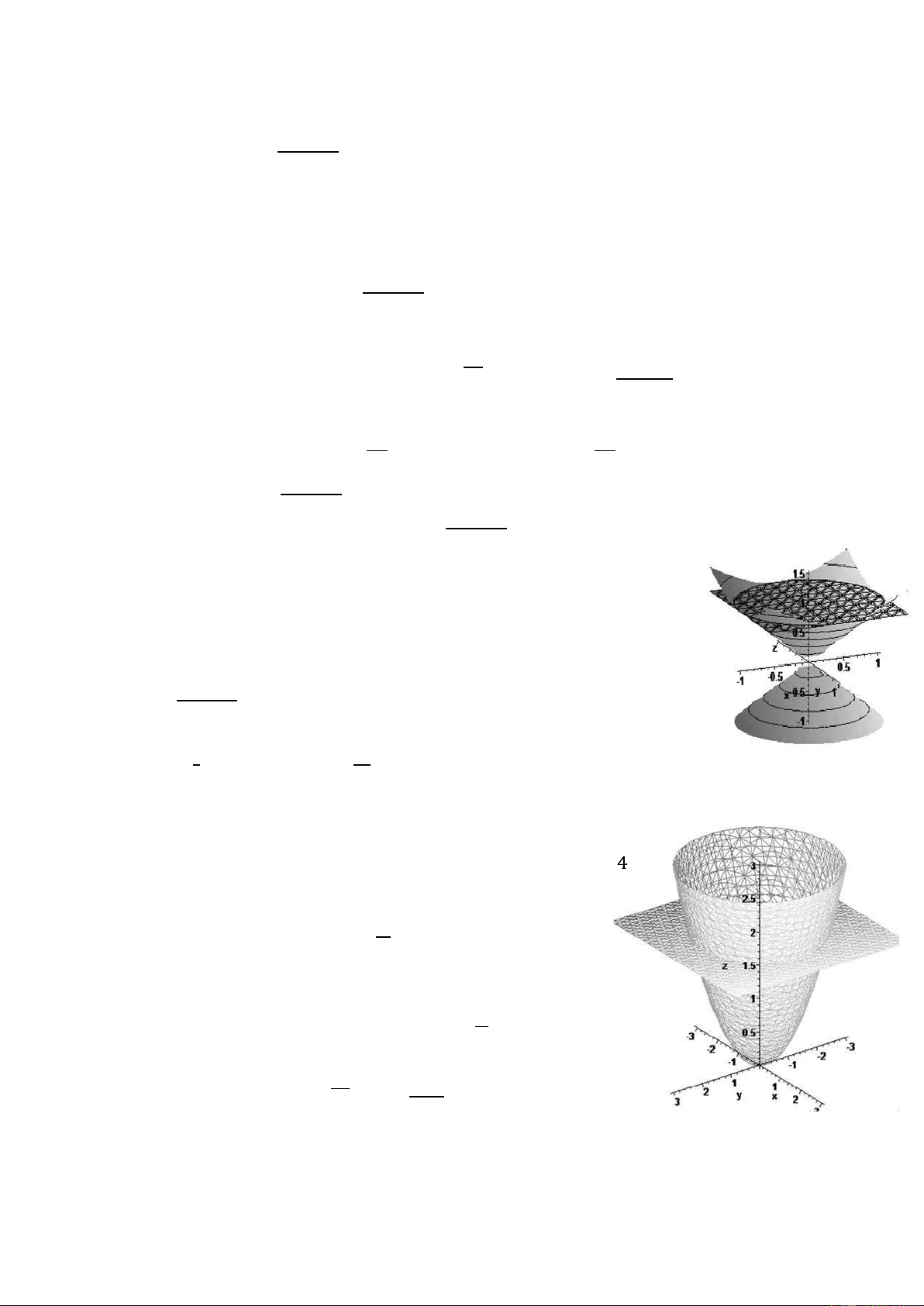
1. Tính diện tích của phần mặt paraboloit tròn xoay 2𝑧 = 𝑥2 + 𝑦2 nằm giữa các mặt 𝑧 = 0; 𝑧 = 2
Giải. Hình chiếu của phần mặt paraboloit bị chắn giữa hai
mặt phẳng xuông (Oxy) là hình tròn : 𝐷 = {𝑥2 + 𝑦2 ≤ 4}
Diện tích phần mặt cần tìm là:
𝑆 = ∬ √1 + 𝑧′2 + 𝑧′2𝑑𝑥𝑑𝑦 𝑥 𝑦 𝐷
=∬ √1 + 𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 𝐷 𝑥 = 𝑟𝑐𝑜𝑠𝜑
Đổi biến tọa độ cực {
|𝐽 = 𝑟; 𝐷′ = {0 ≤ 𝜑 ≤ 2𝜋 0 ≤
𝑦 = 𝑟𝑠𝑖𝑛𝜑 ⟹ | 𝑟 ≤ 2 2𝜋 2 2𝜋
𝑆 = ∬ √1 + 𝑥2 + 𝑦2𝑑𝑥𝑑𝑦 = ∫ 𝑑𝜑 ∫ √1 + 𝑟2. 𝑟𝑑𝑟 = ⋯ = (5√5 − 1) 3 𝐷 0 0
2. Tính diện tích phần mặt cầu 𝑥2 + 𝑦2 + 𝑧2 = 4 bị chắn bởi mặt trụ : 𝑥2 + 𝑦2 = 2𝑥 Giải.
Do tính đối xứng của phần mặt cầu bị chắn bởi mặt trụ qua các mặt phẳng (Oxy), (Oxz), ta chỉ cần 1
xét phần mặt cầu bị chắn trong góc ⁄8 thứ nhất. Khi đó phương trình của mặt là 𝑧 = √4 − 𝑥2 − 𝑦2. Suy ra:
𝑆 = 4 ∬ √1 + 𝑧′2 + 𝑧′2𝑑𝑥𝑑𝑦 𝑥 𝑦 𝐷
Trong đó 𝐷 = {𝑥2 + 𝑦2 ≤ 2𝑥; 𝑦 ≥ 0} 𝑥 = 𝑟𝑐𝑜𝑠𝜑 0 ≤ 𝜑 ≤ 𝜋
Đổi biến tọa độ cực ta có: { 2
𝑦 = 𝑟𝑠𝑖𝑛𝜑 ⟹ |𝐽| = 𝑟; 𝐷′ = {
0 ≤ 𝑟 ≤ 2𝑐𝑜𝑠𝜑 𝜋 2 2𝑐𝑜𝑠𝜑 2 𝑟𝑑𝑟 𝜋 𝑆 = 4 ∬
𝑑𝑥𝑑𝑦 = 8 ∫ 𝑑𝜑 ∫ = ⋯ = 16 ( √4 − 𝑥2 − 𝑦2 √4 − 𝑟2 2 − 1) 𝐷 0 0
2.4 TÍCH PHÂN PHỤ THUỘC THAM SỐ (Tham khảo)
2.4.1 Tích phân phụ thuộc tham số với cận là hằng số
Định nghĩa. Giả sử hàm số f(x,y) xác định trên hình chữ nhật [𝑎, 𝑏] × [𝑐, 𝑑], sao cho 𝑓(𝑥, 𝑦) khả
tích theo x trên [a,b] ∀𝑦 ∈ [𝑐, 𝑑]. Khi đó:
𝐼(𝑦) = ∫𝑏 𝑓(𝑥,
tồn tại phụ thuộc tham số y, được gọi là tích phân phụ thuộc tham số với cận 𝑎 𝑦)𝑑𝑥 là hằng số.
Định lý 2.4 Nếu hàm số 𝑓(𝑥, 𝑦) xác định, liên tục trên hình chữ nhật [𝑎, 𝑏] × [𝑐, 𝑑] thì 𝐼(𝑦) là hàm số liên tục trên [c,d]. 16
Định lý 2.5 Nếu hàm số 𝑓(𝑥, 𝑦) xác định trên hình chữ nhật [𝑎, 𝑏] × [𝑐, 𝑑], liên tục theo 𝑥 ∈ [𝑎, 𝑏] ∀𝑦 ∈
[𝑐, 𝑑], và tồn tại đạo hàm riêng 𝑓′(𝑥, 𝑦) 𝑦
liên tục trên hình chữ nhật [𝑎, 𝑏] × [𝑐, 𝑑], thì: 𝑏 𝐼′(𝑦) = ∫ ( 𝑦 𝑓′ 𝑥, 𝑦)𝑑𝑥 𝑎
Định lý 2.6 Nếu hàm số 𝑓(𝑥, 𝑦) xác định, liên tục trên hình chữ nhật [𝑎, 𝑏] × [𝑐, 𝑑] thì: 𝑑 𝑑 𝑏
∫ 𝐼(𝑦)𝑑𝑦 = ∫ (∫ 𝑓(𝑥, 𝑦)𝑑𝑥) 𝑑𝑦 𝑐 𝑐 𝑎
Hay ∫𝑏 (∫𝑑 𝑓(𝑥, 𝑦)𝑑𝑦) 𝑑𝑥 = ∫𝑑 (∫𝑏 𝑓(𝑥, 𝑦)𝑑𝑥) 𝑑𝑦 𝑎 𝑐 𝑐 𝑎
Đây là công thức đổi thứ tự lấy tích phân (Tham khảo GT [1]). Ví dụ 2.11 Tính 1 𝑥𝑏−𝑥𝑏 1. 𝐼 = ∫ 𝑑𝑥 0 𝑙𝑛𝑥 Giải.
Vì 𝐽 = ∫𝑏 𝑥𝑦𝑑𝑦 = 𝑥𝑏−𝑥𝑏 ⟹ 𝐼 = ∫1 (∫𝑏 𝑥𝑦𝑑𝑦) 𝑑𝑥 = ∫𝑏 (∫1 𝑥𝑦𝑑𝑥) 𝑑𝑦 = 𝑙𝑛 𝑏+1 𝑎 𝑙𝑛𝑥 0 𝑎 𝑎 0 𝑎+1
2. Cho biết 𝐼(𝑦) = ∫1 1 1 1 1 1
𝑑𝑥 = 𝑎𝑟𝑐𝑡𝑎𝑛 . Tính ∫ 𝑑𝑥 0 𝑥2+𝑦2 𝑦 𝑦 0 (𝑥2+𝑦2)2
Lấy đạo hàm hai vế của 𝐽(𝑦) theo y ta được: 1 1 1 1 1 𝐽′(𝑦) = −2𝑦 ∫ 𝑑𝑥 = − − (𝑥2 + 𝑦2)2
𝑦2 𝑎𝑟𝑐𝑡𝑎𝑛 𝑦 𝑦(1 + 𝑦2) 0 1 1 1 1 1 ⟹ ∫ ( +
𝑥2 + 𝑦2)2 𝑑𝑥 = 2𝑦3 𝑎𝑟𝑐𝑡𝑎𝑛 𝑦 2𝑦3(1 + 𝑦2) (𝑦 ≠ 0) 0
2.4.2 Tích phân phụ thuộc tham số với cận hàm số
Xét tích phân xác định phụ thuộc tham số 𝐼(𝑦) = ∫𝑏(𝑦) 𝑓(𝑥, 𝑦)𝑑𝑥, y là tham số trong đó 𝑓(𝑥, 𝑦) 𝑎(𝑦 )
xác định trên [𝑎, 𝑏] × [𝑐, 𝑑], các hàm số 𝑎(𝑦), 𝑏(𝑦) xác định trên [𝑐, 𝑑] và thỏa mãn:
𝑎 ≤ 𝑎(𝑦) ≤ 𝑏; 𝑎 ≤ 𝑏(𝑦) ≤ 𝑏; ∀𝑦 ∈ [𝑐, 𝑑] (*)
Tương tự như tích phân phụ thuộc tham số với cận hằng số, ta có:
Định lý 2.7 Nếu hàm số 𝑓(𝑥, 𝑦) xác định, liên tục trên [𝑎, 𝑏] × [𝑐, 𝑑], các hàm số 𝑎(𝑦), 𝑏(𝑦) liên tục
trên [𝑐, 𝑑] và thỏa mãn điều kiện (*) thì 𝐼(𝑦) là một hàm số liên tục đối với y trên [𝑐, 𝑑].
Định lý 2.8 Nếu hàm số 𝑓(𝑥, 𝑦) liên tục trên [𝑎, 𝑏] × [𝑐, 𝑑], các hàm số 𝑎(𝑦), 𝑏(𝑦) liên tục trên [𝑐, 𝑑],
nhận giá trị trên [𝑎, 𝑏], và nếu đạo hàm riêng 𝑓′(𝑥, 𝑦) 𝑦
liên tục trên [𝑐, 𝑑] thì hàm số 𝐼(𝑦) khả vi
theo y trên [𝑐, 𝑑] và ta có: 𝑏(𝑦)
𝐼′(𝑦) = ∫ 𝑓′(𝑦 𝑥, 𝑦) 𝑑𝑥 + 𝑓(𝑏(𝑦), 𝑦). 𝑏′(𝑦) − 𝑓(𝑎(𝑦), 𝑦). 𝑎′(𝑦) 𝑎(𝑦)
2.4.3 Tích phân suy rộng phụ thuộc tham số
Xét tích phân suy rông phụ thuộc tham số: 𝐼(𝑦) = ∫+∞ 𝑓(𝑥, 𝑦)𝑑𝑥 (1) 𝑎
với y là tham số, hàm số 𝑓(𝑥, 𝑦) xác định trên [𝑎, +∞) × [𝑐, 𝑑].
Định nghĩa. Giả sử tồn tại tích phân 17 𝑏
𝐼𝑏(𝑦) = ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 ∀𝑦 ∈ [𝑐, 𝑑], 𝑎
- Tích phân suy rộng (1) gọi là hội tụ tại 𝑦 ∈ [𝑐, 𝑑] nếu tồn tại giới hạn hữu hạn 𝑏
lim 𝐼𝑏(𝑦) = lim ∫ 𝑓(𝑥, 𝑦)𝑑𝑥 = 𝐼(𝑦) 𝑏→+∞ 𝑏→+∞ 𝑎
Nghĩa là ∀𝜀 > 0, ∃𝐵 > 0 ∶ ∀𝑏 > 𝐵 ⟹ |𝐼𝑏(𝑦) − 𝐼(𝑦)| < 𝜀 (B phụ thuộc 𝜀, 𝑦) hay
|∫+∞ 𝑓(𝑥, 𝑦)𝑑𝑥| < 𝜀. 𝑏
- Tích phân suy rộng (1) gọi là hội tụ đều trên [𝑐, 𝑑] nếu ∀𝜀 > 0, ∃𝐵(𝜀) > 0 (Số B chỉ phụ thuộc
𝜀) sao cho ∀𝑏 > 𝐵(𝜀) thì |∫+∞ 𝑓(𝑥, 𝑦)𝑑𝑥| < 𝜀. 𝑏 Định lý 2.9
Nếu tồn tại hàm số 𝑔(𝑥) sao cho:
- |𝑓(𝑥, 𝑦)| ≤ 𝑔(𝑥)
∀(𝑥, 𝑦) ∈ [𝑎, +∞) × [𝑐, 𝑑]
- ∫+∞ 𝑔(𝑥)𝑑𝑥 hội tụ 𝑎
thì tích phân suy rộng (1) hội tụ đều trên [c,d]
Ví dụ 2.12 Xét tích phân ∫+∞ cos (𝑥𝑦) 𝑑𝑥 0 1+𝑥2+𝑦2 cos (𝑥𝑦) 1 +∞ 1 Do | | ≤ 2 2
2 ∀𝑦 và tích phân ∫0
2 𝑑𝑥 hội tụ. Vậy, tích phân đã cho hội tụ đều trên ℝ. 1+𝑥 +𝑦 1+𝑥 1+𝑥
Định lý 2.10 Giả sử 𝑓(𝑥, 𝑦) xác định và liên tục trên [𝑎, +∞) × [𝑐, 𝑑] và nếu tích phân 𝐼(𝑦) =
∫+∞ 𝑓(𝑥, 𝑦)𝑑𝑥 hội tụ đều trên [c,d] thì 𝐼(𝑦) là hàm liên tục trên [c,d]. 𝑎
Định lý 2.11 Giả sử 𝑓(𝑥, 𝑦) xác định và liên tục trên [𝑎, +∞) × [𝑐, 𝑑] và nếu tích phân 𝐼(𝑦) hội tụ đều
trên [c,d] thì 𝐼(𝑦) khả tích trên [c,d] và ta có công thức: 𝑑 𝑑 +∞ +∞ 𝑑
∫ 𝐼(𝑦)𝑑𝑦 = ∫ (∫ 𝑓(𝑥, 𝑦)𝑑𝑥) 𝑑𝑦 = ∫ (∫ 𝑓(𝑥, 𝑦)𝑑𝑦) 𝑑𝑥 𝑐 𝑐 𝑎 𝑎 𝑐
(Công thức đổi thứ tự lấy tích phân)
Định lý 2.12 Giả sử
- Hàm số 𝑓(𝑥, 𝑦) liên tục trên [𝑎, +∞) × [𝑐, 𝑑] - ( 𝑦
𝑓′ 𝑥, 𝑦) liên tục trên [𝑎, +∞) × [𝑐, 𝑑]
- ∫+∞ 𝑓(𝑥, 𝑦)𝑑𝑥 hội tụ với mọi 𝑦 ∈ [𝑐, 𝑑] 𝑎
- ∫+∞ 𝑓′(𝑥, 𝑦)𝑑𝑥
hội tụ đều trên [𝑐, 𝑑] 𝑎 𝑦
Khi đó 𝐼(𝑦) khả vi trên [c,d] và 𝐼′(𝑦) = ∫+∞ 𝑓′(𝑥, 𝑦)𝑑𝑥 ∀𝑦 ∈ [𝑐, 𝑑] 𝑎 𝑦
(Công thức đạo hàm dưới dấu tích phân) Ví dụ 2.12 1. Tính tích phân:
𝐽 = ∫𝑏 𝑒−𝑡𝑥𝑑𝑥 từ đó tính tích phân 𝐼(𝑎, 𝑏) = ∫+∞ 𝑒−𝑎𝑥−𝑒−𝑏𝑥 𝑑𝑥 (𝑎 < 𝑏) 𝑎 0 𝑥 Ta có: 𝑏 +∞ 𝑏
𝑒−𝑎𝑥 − 𝑒−𝑏𝑥
𝐽 = ∫ 𝑒−𝑡𝑥𝑑𝑡 =
→ 𝐼(𝑎, 𝑏) = ∫ (∫ 𝑒−𝑡𝑥𝑑𝑡) 𝑑𝑥 𝑥 𝑎 0 𝑎 18
Xét tích phân phụ thuộc tham số ∫+∞ 𝑒−𝑡𝑥𝑑𝑥, 𝑡 ∈ [𝑎, 𝑏] 0
. Vì 𝑒−𝑡𝑥 < 𝑒−𝑎𝑥 và ∫+∞ 𝑒−𝑎𝑥𝑑𝑥, (𝑎 > 0) 0
hội tụ nên suy ra ∫+∞ 0 𝑒−𝑡𝑥𝑑𝑥
hội tụ đều với ∈ [𝑎, 𝑏] .
Mặt khác hàm 𝑓(𝑥, 𝑡) = 𝑒−𝑡𝑥 liên tục trên miền [0, +∞) × [𝑎, 𝑏]. Do đó ta có thể lấy tích phân
dưới dấu tích phân như sau: +∞ 𝑏 𝑏 +∞ 𝑏
𝐼(𝑎, 𝑏) = ∫ (∫ 𝑒−𝑡𝑥𝑑𝑡) 𝑑𝑥 = ∫ (∫ 𝑒−𝑡𝑥 𝑑𝑥) 𝑑𝑡 = 𝑙𝑛 𝑎 0 𝑎 𝑎 0
+∞ 𝑒−𝑎𝑥2−𝑒−𝑏𝑥2 2. Tính 𝐼(𝑎) = ∫ ( 0 𝑑𝑥 𝑎, 𝑏 > 0) (*) 𝑥 2
Ta có: 𝑓(𝑎, 𝑥) = 𝑒−𝑎𝑥2−𝑒−𝑏𝑥2 𝑎
liên tục trong miền 𝐷: 𝑥 ≥ 𝑥0 > 0, 𝑎 ≥ 𝑎0 > 0. 𝑥
và 𝐾′ (𝑎, 𝑥) = −𝑥𝑒−𝑎𝑥 2 2
𝐼(𝑎) hội tụ và ∫+∞ 𝑥𝑒−𝑎𝑥 𝑑𝑥 ≤ 𝑥𝑒−𝑎0𝑥2 0
hội tụ đều ∀𝑎 ≥ 𝑎0 > 0 do 𝑥𝑒−𝑎𝑥 Vậy: +∞ +∞ 1 2 1 2
𝐼′(𝑎) = − ∫ 𝑥𝑒−𝑎𝑥 𝑑𝑥 =
∫ 𝑒−𝑎𝑥 𝑑(−𝑎𝑥2) = − 2 2𝑎 0 𝑎 0 ( = − 1 Và 𝐼 𝑎 𝑙𝑛𝑎 + 𝐶 ) 2
Theo (*): 𝐼(𝑏) = 0, do đó: 0 = − 1 𝑙𝑛𝑏 + 𝐶 hay 𝐶 = 1 𝑙𝑛𝑏 . Suy ra: 𝐼 = 𝐼(𝑎) = 𝑙𝑛√𝑏. 2 2 𝑎 19 BÀI TẬP CHƯƠNG 2
1. Tính các tích phân kép:
a. I = (6x2y3 − 5y4)dxdy trong đó D =(x, y): 0 x 3,0 y 1 D b. I = xy2 2 dxdy
trong đó D =(x, y): 0 x 1, −3 y 3 x + 1 D
c. I = e x−y dxdy trong đó D =(x, y): 0 x 1,0 y 1 D
d. I = (x2 + 3xy − y x)dxdy trong đó D = 0,2−2,2 D
2. Tính tích phân kép
a. I = x3y2dxdy trong đó D =(x, y): 0 x 2, −x y x D y b. I = dxdy
trong đó D = (x, y) : 0 x 1,0 y x x2 + 1 D
c. I = xsin(x + y) dxdy trong đó D =(x, y): 0 x / 2,0 y x D d. I = (x2 + y2 )3/ 2 dxdy x2 + y2 4
3. Đổi thứ tự lấy tích phân rồi tính các tích phân sau: 1 3 3 9 2 a. I = dy ex dx b. I = dy ycosx2dx 0 3y 0 y2 1 1 1 1 c. I = dxcos y2dy d. I = dxxydy 0 x 0 x
4. Dùng các phép đổi biến thích hợp tính các tích phân:
a. I = (x2 − y2)dxdy trong đó D là hình vuông với các đỉnh (0,2),(1,1),(2,2),(1,3) ; D
b. I = xydxdy , trong đó D là miền trong góc phần tư thứ nhất của mặt phẳng xOy giới D
hạn bởi các đường thẳng y = x, y = 3xvà các hypebol xy =1, xy = 3. x − 2y c. I =
dxdy trong đó D giới hạn bởi các đường 3x − y D
x − 2y = 0, x − 2y = 4, 3x − y =1, 3x − y = 8. 20