Chương 2 - Trình Bày Dữ Liệu Bằng Bảng Và Đồ Thị môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Bài 2 TRÌNH BÀY DỮ LIỆU BẰNG BẢNG VÀ ĐỒ THỊ 1 Nội dung chính I II III TRÌNH BÀY TRÌNH BÀY ỨNG DỤNG DỮ LIỆU DỮ LIỆU SPSS TRONG ĐƠN BIẾN ĐA BIẾN TRÌNH BÀY DỮ LIỆU 2 1 2/27/2025
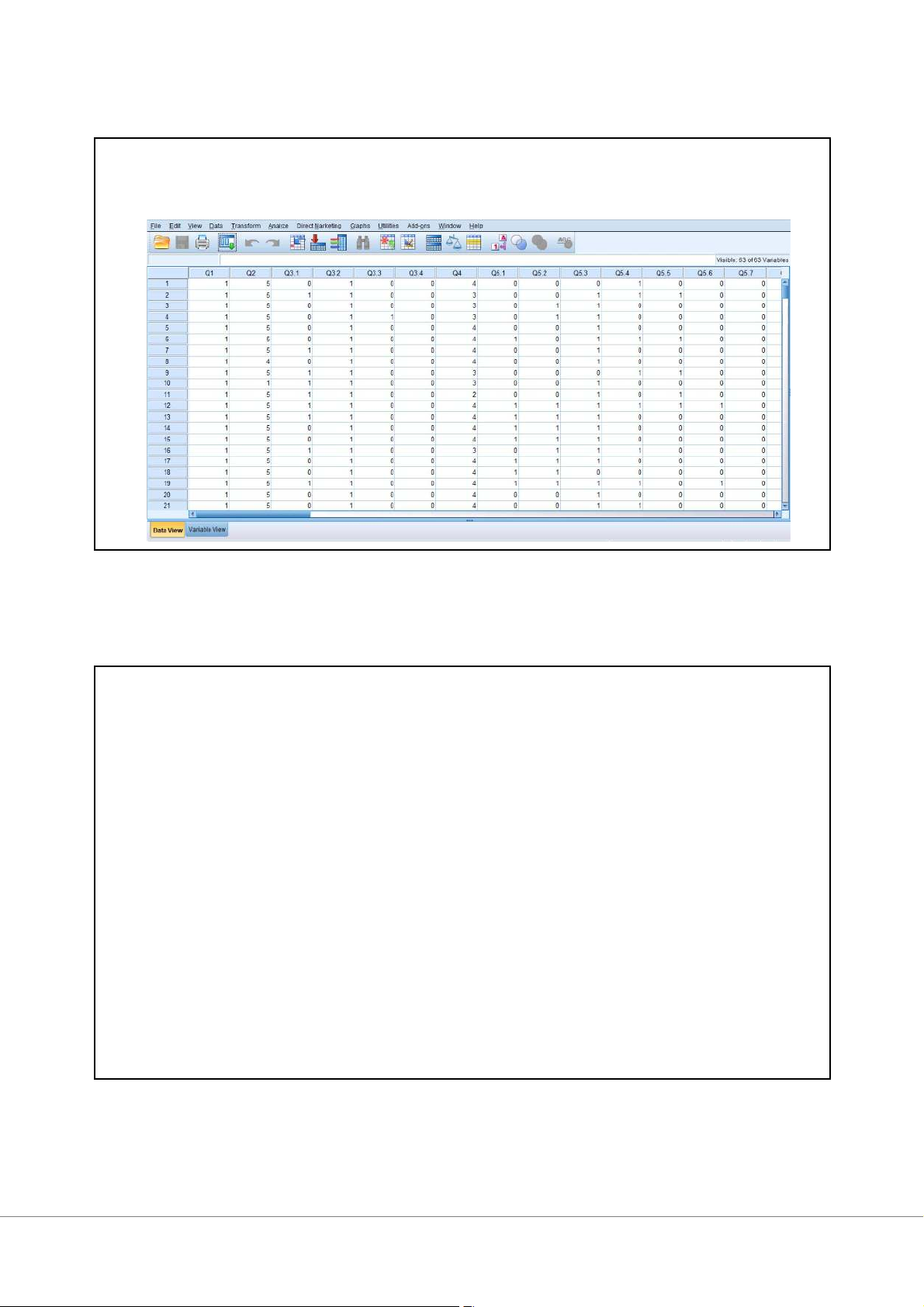
Dữ liệu thu được qua điều tra 3
Tóm tắt và trình bày dữ liệu
Tại sao cần phải tóm tắt và trình bày dữ liệu?
Dữ liệu thu được qua điều tra được gọi là dữ liệu 'thô’.
Dữ liệu thô có thể bao gồm hàng nghìn, hàng triệu quan sát và thường cung cấp rất nhiều thông tin
không dễ sử dụng để ra các quyết định.
Cần phải tóm tắt và trình bày dữ liệu. 4 2 2/27/2025
Tóm tắt và trình bày dữ liệu Mục đích
Cho biết đặc điểm chung của một tổng thể hoặc một mẫu nghiên cứu. Yêu cầu
Tóm tắt dữ liệu loại bỏ các chi tiết nhưng phải cung cấp đặc điểm chung của
tổng thể hoặc mẫu nghiên cứu.
Thông tin được tóm tắt cần ngắn gọn nhưng phải phản ánh chính xác bản chất của dữ liệu gốc 5
Tóm tắt và trình bày dữ liệu Nhiệm vụ
Tổ chức, sắp xếp dữ liệu theo một trật tự nhất định
Tính toán một số giá trị Phương pháp Bảng Đồ thị
Các mức độ thống kê mô tả (bài 3)
Loại bảng hoặc đồ thị được sử dụng phụ thuộc vào biến được tóm tắt 6 3 2/27/2025
Trình bày dữ liệu đơn biến
Một số khái niệm cơ bản
Trình bày dữ liệu định tính
Trình bày dữ liệu định lượng 7
Một số khái niệm cơ bản
Bảng tần số phân phối, còn gọi là Dãy số phân phối (Frequency table)
ghi lại số lần xuất hiện của mỗi giá trị và được trình bày dưới dạng bảng.
Tần số (Frequency) là số lần xuất hiện của mỗi giá trị nhất định hay là số
quan sát được sắp xếp vào mỗi tổ tương ứng với một giá trị.
Khi lấy tần số của mỗi tổ chia cho tổng số quan sát, ta được tần suất của
tổ đó tính theo đơn vị lần (Relative frequency).
• Khi lấy tần suất tính theo đơn vị lần của mỗi tổ nhân với 100, ta được tần
suất tính theo đơn vị % hay còn gọi là tỷ trọng của mỗi tổ trong tổng thể
hoặc mẫu nghiên cứu (Percent frequency). 8 4 2/27/2025
Trình bày dữ liệu định tính
Ví dụ: Phỏng vấn 50 sinh viên về loại đồ uống ưa thích nhất. Coca Coca Coca Coca Fanta Coca ăn kiêng Fanta Coca ăn kiêng Sprite Coca Pepsi Sprite Coca Fanta Coca ăn kiêng Coca ăn kiêng Coca Sprite Pepsi Pepsi Coca Coca ăn kiêng Sprite Coca ăn kiêng Pepsi Coca Coca Pepsi Pepsi Pepsi Fanta Coca Coca Coca Pepsi Coca ăn kiêng Sprite Coca Coca Coca Pepsi Coca Coca Coca Fanta Pepsi Coca ăn kiêng Pepsi Pepsi Pepsi 9
Trình bày dữ liệu định tính
Bảng tần số phân phối với dữ liệu định tính, còn gọi là dãy số thuộc tính Loại đồ uống Tần số Tần suất (lần) Tần suất (%) Coca 19 0,38 38 Coca ăn kiêng 8 0,16 16 Fanta 5 0,10 10 Pepsi 13 0,26 26 Sprite 5 0,10 10 Tổng số 50 1 100 10 5 2/27/2025 Lưu ý
Khi mỗi biểu hiện (thuộc tính) của biến định tính hình thành một tổ: bảng
tần số phân phối giản đơn
Trong một số trường hợp, có thể ghép một số biểu hiện có đặc điểm
tương tự nhau vào trong cùng một tổ. 11
Trình bày dữ liệu định tính
Đồ thị hình cột (Bar chart)
Một trục dùng để biểu diễn các thuộc tính cho từng tổ. Trục còn lại biểu diễn
tần số hoặc tần suất.
Mỗi thuộc tính được biểu diễn bằng một cột có chiều rộng cố định, chiều cao
tương ứng với tần số hoặc tần suất của thuộc tính đó.
Các cột thường được tách ra để nhấn mạnh: mỗi tổ là một nhóm riêng biệt.
Đồ thị hình tròn (Pie chart)
Vẽ một vòng tròn và thường sử dụng tần suất (%) của các thuộc tính để chia
vòng tròn thành các phần tương ứng. 12 6 2/27/2025
Trình bày dữ liệu định tính Đồ thị phân phối 40 38 35 30 26 25 10% Coca 20 16 38% Coca ăn kiêng T1 ầ 5 n suất (%) 26% 10 10 Fanta 10 Pepsi 5 Sprite 10% 16% 0 Coca Coca ăn Fanta Pepsi Sprite kiêng Loại đồ uống Đồ thị hình cột Đồ thị hình tròn 13
Trình bày dữ liệu định tính
Nên sử dụng đồ thị hình cột hay đồ thị hình tròn?
Chọn đồ thị trình bày thông tin hiệu quả nhất (‘Learning by doing’) 14 7 2/27/2025
Trình bày dữ liệu định lượng
Bảng tần số phân phối với dữ liệu định lượng, còn gọi là dãy số
lượng biến: được sắp xếp theo trình tự biến động của lượng biến
Khi mỗi lượng biến hình thành 1 tổ: bảng tần số phân phối giản đơn.
Khi nhiều lượng biến cùng nằm trong 1 tổ: bảng tần số phân phối có khoảng cách tổ
• Khoảng cách tổ bằng nhau
• Khoảng cách tổ không bằng nhau 15
Bảng tần số phân phối giản đơn
Áp dụng với dữ liệu định lượng có ít các lượng biến rời rạc.
Ví dụ: Có số lượng đơn hàng đã thực hiện của 20 nhân viên giao hàng
Tiki trong 1 giờ đồng hồ như sau
7, 7, 10, 8, 5, 4, 5, 6, 4, 9, 8, 7, 6, 4, 8, 5, 7, 10, 10, 9
• Xây dựng bảng tần số phân phối. 16 8 2/27/2025
Bảng tần số phân phối giản đơn
Sắp xếp dữ liệu theo thứ tự từ thấp đến cao
Xác định các tổ và đếm số lượng nhân viên trong từng tổ đó. Số lượng đơn hàng Số nhân viên 4 3 Tần số 5 3 6 2 7 4 8 3 9 2 10 3 Tổng số 20 17
Bảng tần số phân phối có khoảng cách tổ
Áp dụng với dữ liệu định lượng có nhiều lượng biến rời rạc hoặc lượng biến liên tục. Kỹ thuật
• Ghép một phạm vi lượng biến vào một tổ
Tại sao phải phân tổ có khoảng cách tổ? 18 9 2/27/2025
Bảng tần số phân phối có khoảng cách tổ Các thuật ngữ:
• Giới hạn dưới (lower class limit): giá trị thấp nhất trong một tổ
• Giới hạn trên (upper class limit): giá trị cao nhất trong một tổ
→ Giới hạn dưới và giới hạn trên của một tổ thường được làm tròn
• Khoảng cách tổ (class width): phạm vi lượng biến của một tổ từ giới hạn
dưới đến giới hạn trên 19
Bảng tần số phân phối có khoảng cách tổ Các bước xây dựng
• Sắp xếp dữ liệu theo thứ tự từ thấp đến cao
• Xác định lượng biến lớn nhất, lượng biến nhỏ nhất và khoảng biến thiên của lượng biến (R)
R = Lượng biến lớn nhất – lượng biến nhỏ nhất • Xác định số tổ
• Xác định khoảng cách tổ
• Xác định giới hạn dưới của tổ đầu tiên
• Xây dựng bảng tần số phân phối 20 10 2/27/2025
Bảng tần số phân phối có khoảng cách tổ bằng nhau
Xác định khoảng cách tổ bằng nhau
𝐡 ≈ 𝐱𝐦𝐚𝐱 − 𝐱𝐦𝐢𝐧 𝐤 Trong đó: h: khoảng cách tổ
x: giá trị của lượng biến lớn nhất
x: giá trị của lượng biến nhỏ nhất k: số tổ định chia 21
Bảng tần số phân phối có khoảng cách tổ bằng nhau
Ví dụ: Có số liệu về doanh số bình quân một tháng (triệu đồng) trong năm
2024 của 50 nhân viên trong một doanh nghiệp 91 78 93 57 75 52 99 80 97 62 71 69 72 89 66 75 79 75 72 76 104 74 62 68 97 105 77 65 80 109 85 97 88 68 83 68 71 69 67 74 62 82 98 101 79 105 79 69 62 73 22 11 2/27/2025
Bảng tần số phân phối có khoảng cách tổ bằng nhau
Giả sử, chia thành 6 tổ
Khoảng cách tổ: h = (109 - 52)/6 = 9,5 ≈ 10 Doanh sốbq (Trđ) Sốnhân viên Khoảng cách tổ 50-<60 2 =60-50=10 60-<70 13 Giới hạn 70-<80 16 trên 80-<90 7 90-<100 7 Giới hạn 100-110 5 dưới Tổng số 50 23
Bảng tần số phân phối có khoảng cách tổ không bằng nhau
Ví dụ: Lương bình quân tháng (triệu đồng) năm 2024 của 25 nhân viên có
độ tuổi từ 25-30 trong một doanh nghiệp Lương bq tháng (trđ) Số nhân viên 5 - < 6 4 6 - < 8 6 8 - < 9 6 9 - < 12 6 12 - 15 3 Tổng số 25
Mỗi tổ phản ánh sự khác biệt trong bản chất của dữ liệu 24 12 2/27/2025
Bảng tần số phân phối có khoảng cách tổ mở
Tổ mở (open-ended class): tổ đầu tiên không có giới hạn dưới và/hoặc tổ
cuối cùng không có giới hạn trên
Thường sử dụng khi có các dữ liệu đột xuất (outlier) (giá trị quá thấp hoặc
quá cao) hoặc trong một số trường hợp không quá quan tâm đến các giá
trị nhỏ nhất hoặc lớn nhất của biến nghiên cứu. 25
Bảng tần số phân phối có khoảng cách tổ mở
Ví dụ: Có số liệu về mức thu nhập bình quân năm (triệu đồng) của 30
nhân viên trong một chi nhánh ngân hàng A năm 2024 202 277 654 145 361 457 77 64 240 144 310 391 362 437 429 176 325 221 374 216 480 120 274 398 282 153 470 303 338 209 26 13 2/27/2025
Bảng tần số phân phối có khoảng cách tổ mở Thu nhập (trđ) Số nhân viên <100 2 100 - <200 5 Tổmở, không ạ 200 - <300 có giới h n 8 dưới 300 - <400 9 400 - <500 5 ≥500 1 Tổng số 30 Tổmở, không có giới hạn trên 27 Câu hỏi
Tại sao giới hạn trên của tổ đứng trước thường trùng với giới hạn dưới của tổ đứng sau?
Tính khoảng cách tổ của những tổ mở như thế nào? 28 14 2/27/2025
Dãy số lượng biến tổng quát 𝒙𝒊 𝒇𝒊 𝒅𝒊=𝒇𝒊 𝑺𝒊 𝒎𝒊=𝒇𝒊 ∑𝒇𝒊 (𝟏𝟎𝟎) 𝒉𝒊 Lượng biến Tần số Tần suất Tần số tích lũy Mật độ phân phối Là biểu hiện bằng Là số lần xuất hiện
Là tần số được biểu Là tần số cộng dồn Dùng để so sánh số của biến định của lượng biến hoặc hiện bằng số tương các tần số khi lượng dùng để số quan sát phân đối (lần, %) khoảng cách tổ phân tổ phối vào mỗi tổ không bằng nhau x1 f1 d1 S1= f1 m1 … … … … … xn fn dn Sn = f1+ f2+ … + fn mn Tổng 𝒅𝒊  𝒇𝒊 29
Trị số giữa = (Giới hạn trên + Giới hạn dưới) / 2
Dãy số lượng biến tổng quát: các tính toán khác
Trị số giữa (Class midpoint) của một tổ: là trung bình của giới hạn trên và
giới hạn dưới của tổ đó.
Tần số tích lũy (Cummulative frequency) của một tổ: là tổng tần số của tổ
đó và các tổ trước đó, cho biết số lượng quan sát có giá trị nhỏ hơn hoặc
bằng giới hạn trên của một tổ.
Tần suất tích lũy (Cummulative percent frequency) của một tổ (%): là tổng
tần suất của tổ đó và các tổ trước đó, cho biết phần trăm số quan sát có
giá trị nhỏ hơn hoặc bằng giới hạn trên của một tổ. 30 15 2/27/2025 Ví dụ Doanh số bq Trị số giữa Tần số Tần suất (%) Tần số tích Tần suất tích (Tr.đ) lũy lũy (%) 50-<60 55 2 4 2 4 60-<70 65 13 26 15 30 70-<80 75 16 32 31 62 80-<90 85 7 14 38 76 90-<100 95 7 14 45 90 100-110 100 5 10 50 100 Tổng 50 100 (90+100)/2 7/50x100 38+7 76+14 31
Trình bày dữ liệu định lượng
Đồ thị phân phối với dữ liệu định lượng
• Đồ thị điểm (Dot plot)
• Biểu đồ tần số phân phối (Histogram)
• Đa giác tần số (Polygon)
• Đa giác tần số/tần suất tích lũy (Ogive)
• Biểu đồ hộp (Box-plot) (Bài 3) 32 16 2/27/2025 Đồ thị điểm
• Trục hoành biểu diễn biến động của các lượng biến.
• Mỗi giá trị được thể hiện bằng một điểm trên trục. Doanh sốbình quân . . .. . . . . .. .. .. .. . .
. . . ..... .......... .. . .. . . ... . .. . 50 60 70 80 90 50 100 60 70 8 1 0 1 9 0 0 100 110 Doanh Doanh s s ố ố (Tr.đ) (Tr.đ) 33
Biểu đồ tần số phân phối Doanh sốbình quân 18 1
• Mô tả thông tin trong các bảng tần
số phân phối có khoảng cách tổ 16 1 dưới dạng đồ thị 14 1
• Chiều cao của cột biểu thị tần số 12 1 của mỗi tổ 10 1 Tần số Tần s
• Độ rộng của cột là khoảng cách tổ 8 6
• Các cột không tách rời mà dính liền nhau. 4 2 Do D a o n a h n số s bq b (t ( r t đ r ) đ 505 0    6  0  6 0    7  0  7 0    8  0  8 0    9  0  9 0    1  0  0- 1 1 0 1 0 0 -110 34 17 2/27/2025
Biểu đồ tần số phân phối
Tầm quan trọng của Histogram
• Cho biết hình dáng phân phối của dữ liệu
• Cho biết vị trí trung tâm của dữ liệu
• Cho biết sự biến thiên của dữ liệu
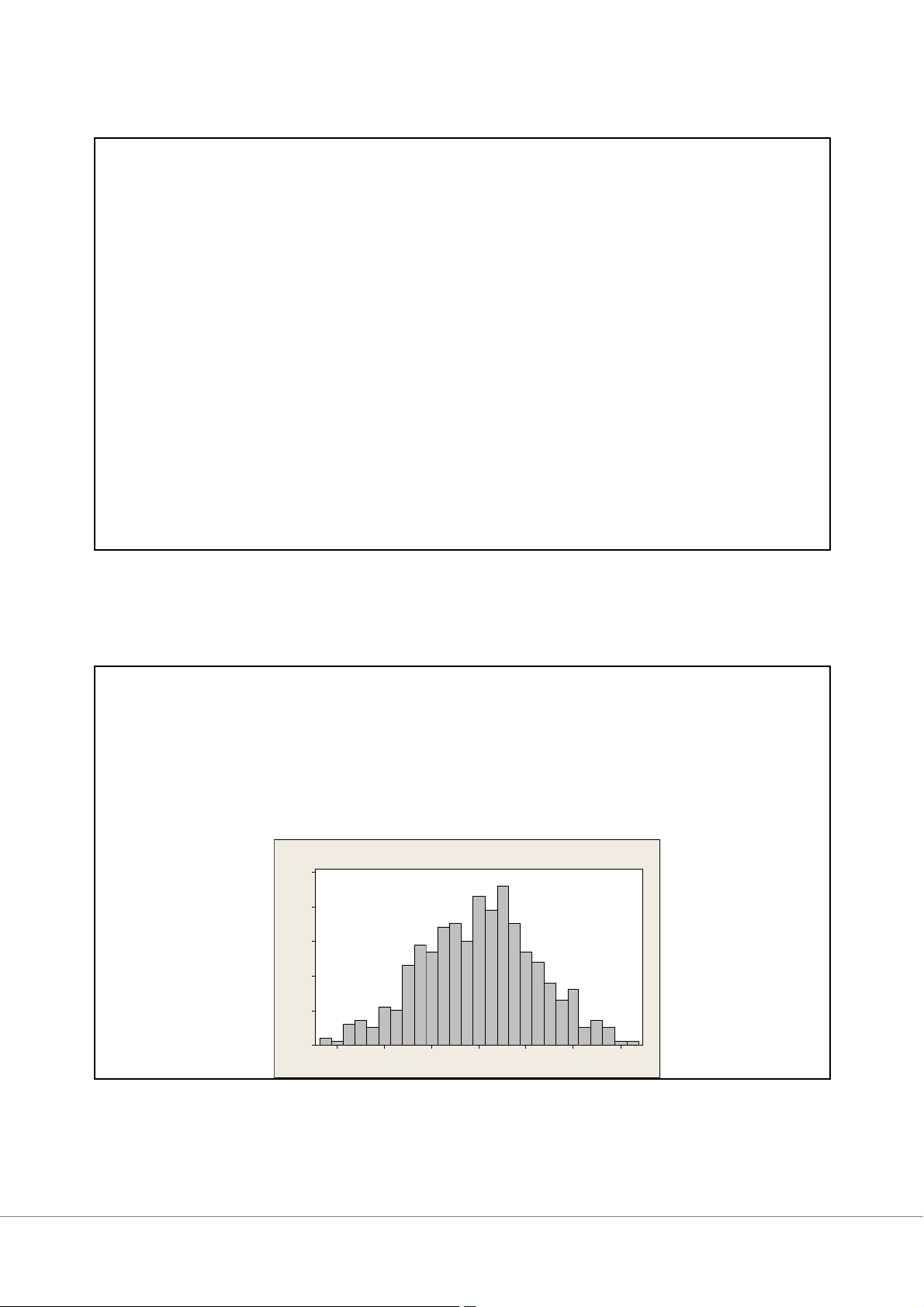
• Dùng để xác định dữ liệu đột xuất (outliers) 35 Hình dáng của Histogram Đối xứng
Ví dụ: chiều cao và cân nặng Histogr am of Symmetr ic 50 40 30 Freq 20 uency 10 0 -2.4 -1.6 -0.8 0.0 0.8 1.6 2.4 Sy mme t ric 36 18 2/27/2025 Hình dáng của Histogram Lệch trái Ví dụ: điểm thi Histogram of Negative skew 35 30 25 20 15 Frequency 10 5 0 3.0 4.5 6.0 7.5 9.0 Negat ive skew 37 Hình dáng của Histogram Lệch phải
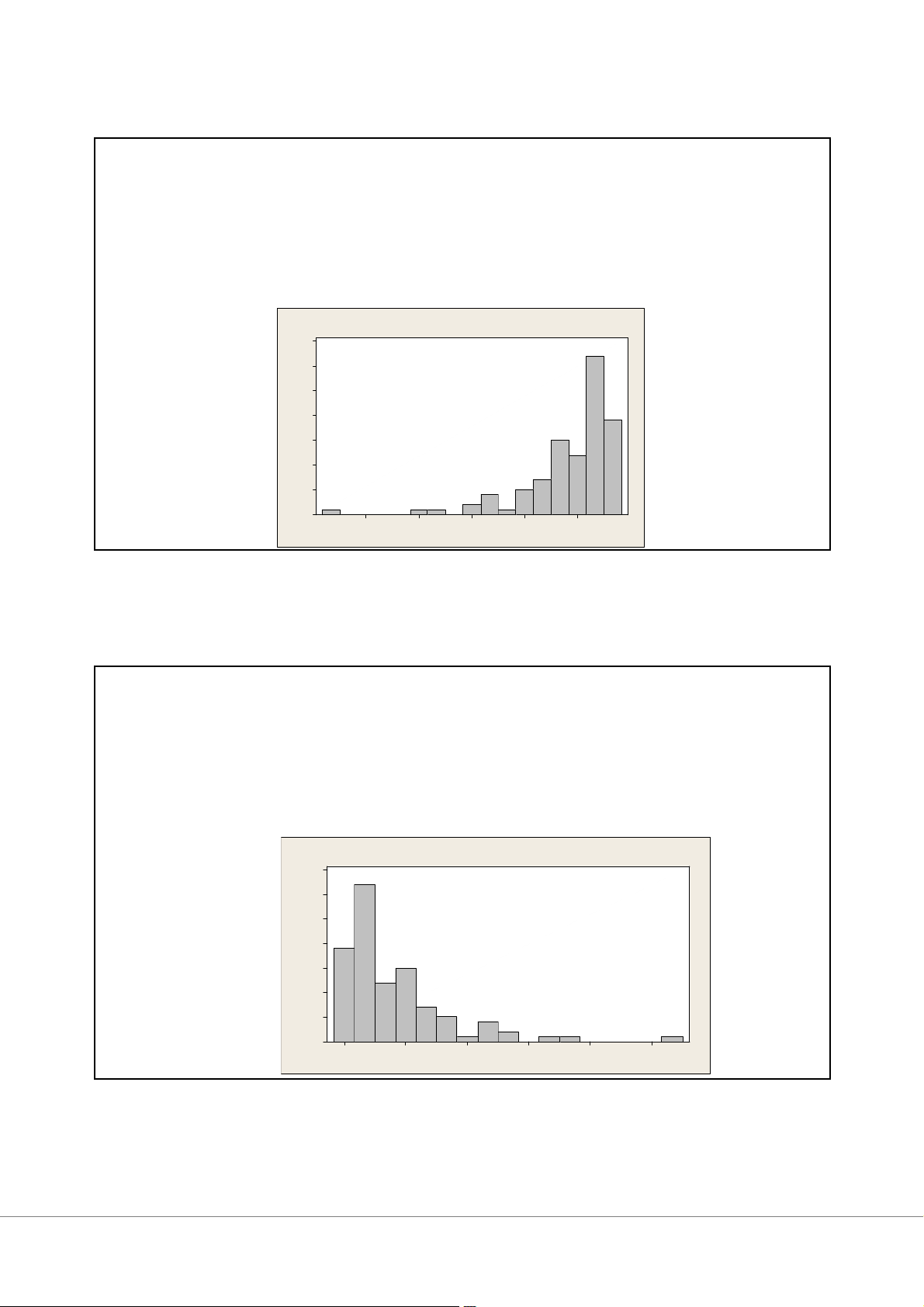
Ví dụ: giá nhà, thu nhập
Hi s to gr a m o f P o s iti v e s ke w 35 30 25 20 15 Frequency 10 5 0 0 .0 1 .5 3 .0 4 .5 6 .0 7 .5 P o s it iv e s ke w 38 19 2/27/2025 Hình dáng của Histogram Hai mốt
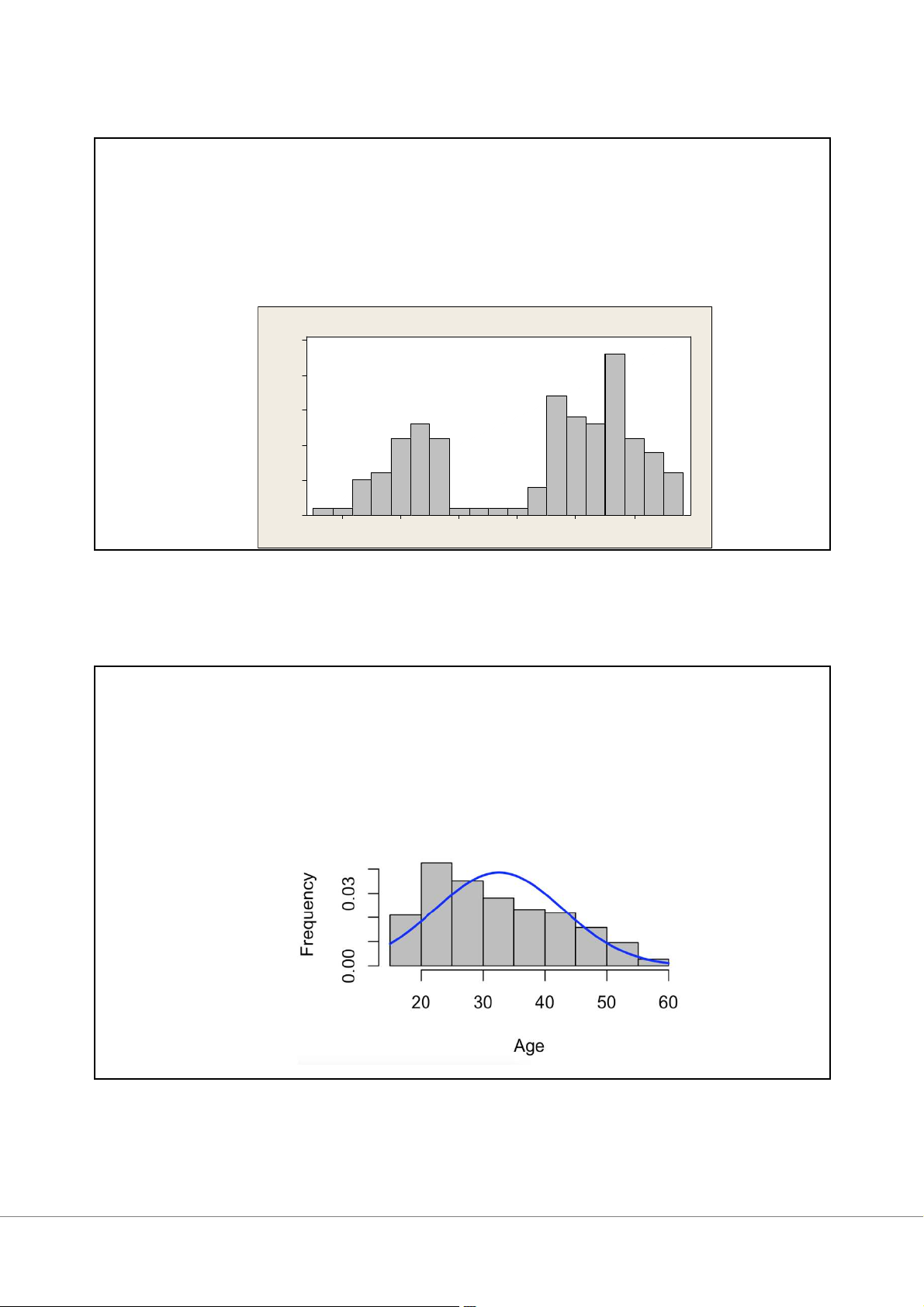
Ví dụ: điểm thi tiếng Anh H is to gr a m o f B im oda l 2 5 2 0 1 5 Freq 1 u 0ency 5 0 - 1 .5 0 .0 1 .5 3 .0 4 .5 6 .0 B im o d a l 39 Hình dáng của Histogram
Histogram với đường cong phân phối chuẩn 40 20