Chương 2: Ứng Lực Trong Bài Toán Thanh | Môn Sức bền vật liệu - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58970315 09-Aug-22
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI
KHOA XÂY DỰNG DÂN DỤNG VÀ CÔNG NGHIỆP
www : xaydung.huce.edu.vn
Sức bền Vật liệu
Bộ môn Sức bền Vật liệu – Khoa Xây dựng Dân dụng và Công nghiệp
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI 1
CHƯƠNG 2: ỨNG LỰC TRONG BÀI TOÁN THANH
2.1 . Bài toán phẳng, các thành phần ứng lực trong bài toán phẳng
2.2 . Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
2.3 . Quan hệ vi phân giữa lực cắt, mô men uốn và tải trọng
phân bố, các ứng dụng
2.4 . Phương pháp vẽ biểu đồ ứng lực theo điểm đặc biệt 2 lOMoAR cPSD| 58970315 09-Aug-22
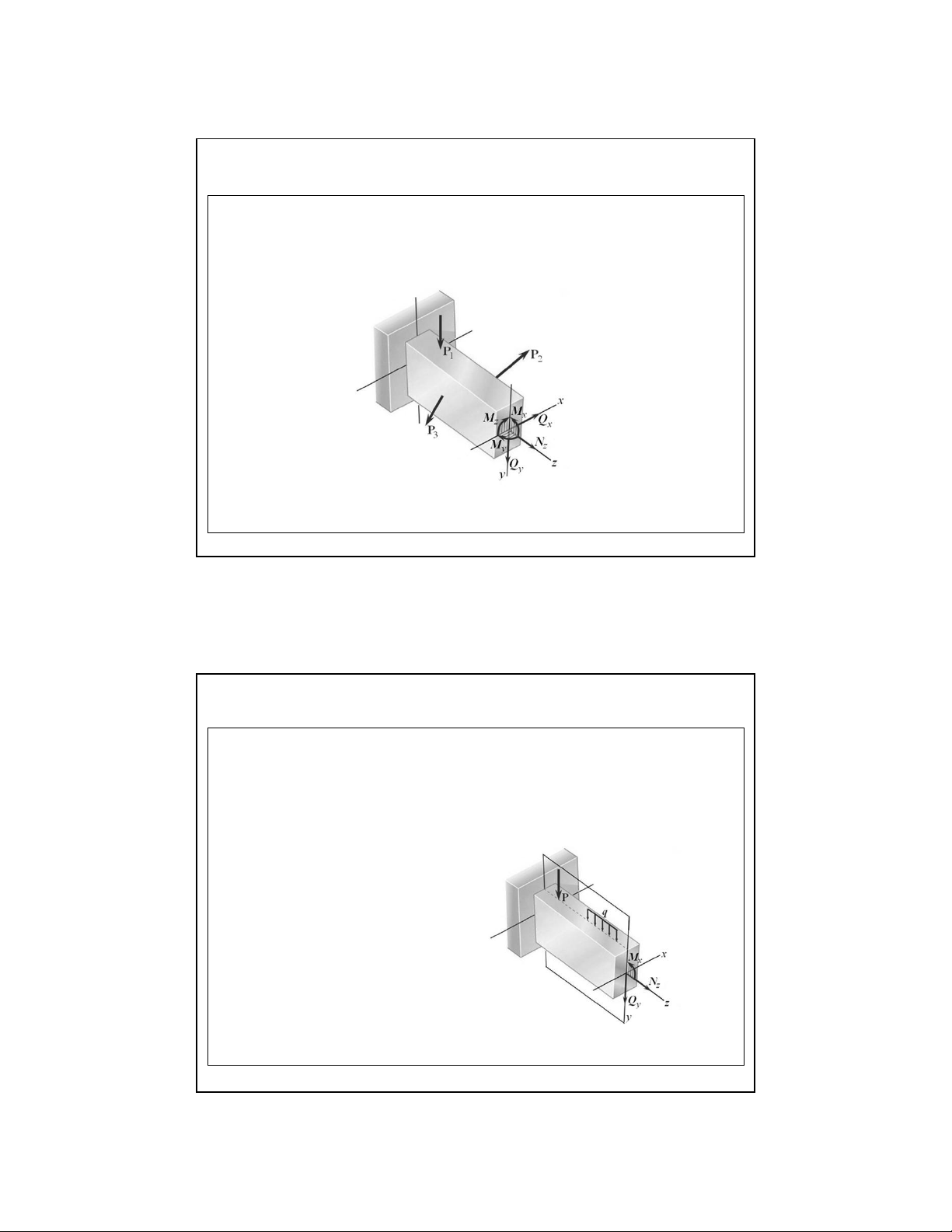
2.1. Bài toán phẳng, các thành phần ứng lực trong bài toán phẳng
Trong trường hợp tổng quát, dưới tác dụng của ngoại lực,
trên mặt cắt ngang của thanh có 6 thành phần ứng lực . 3
2.1. Bài toán phẳng, các thành phần ứng lực trong bài toán phẳng
2 . 1 . 1 Bài toán phẳng :
Bài toán phẳng : Tất cả các ngoại lực cùng nằm trong mặt phẳng
đối xứng của thanh ( z O y ) → Khi đó trên mặt cắt ngang chỉ tồn
tại các thành phần ứng lực nằm trong vào mặt phẳng này , gồm :
N z ; Q y ; M x
N – lực dọc ; Q – lực cắt ; M – mô men uốn z y x lOMoAR cPSD| 58970315 09-Aug-22
2.1. Bài toán phẳng, các thành phần ứng lực trong bài toán phẳng 4 5 lOMoAR cPSD| 58970315 09-Aug-22
2.1. Bài toán phẳng, các thành phần ứng lực trong bài toán phẳng
2.1. Bài toán phẳng, các thành phần ứng lực trong bài toán phẳng
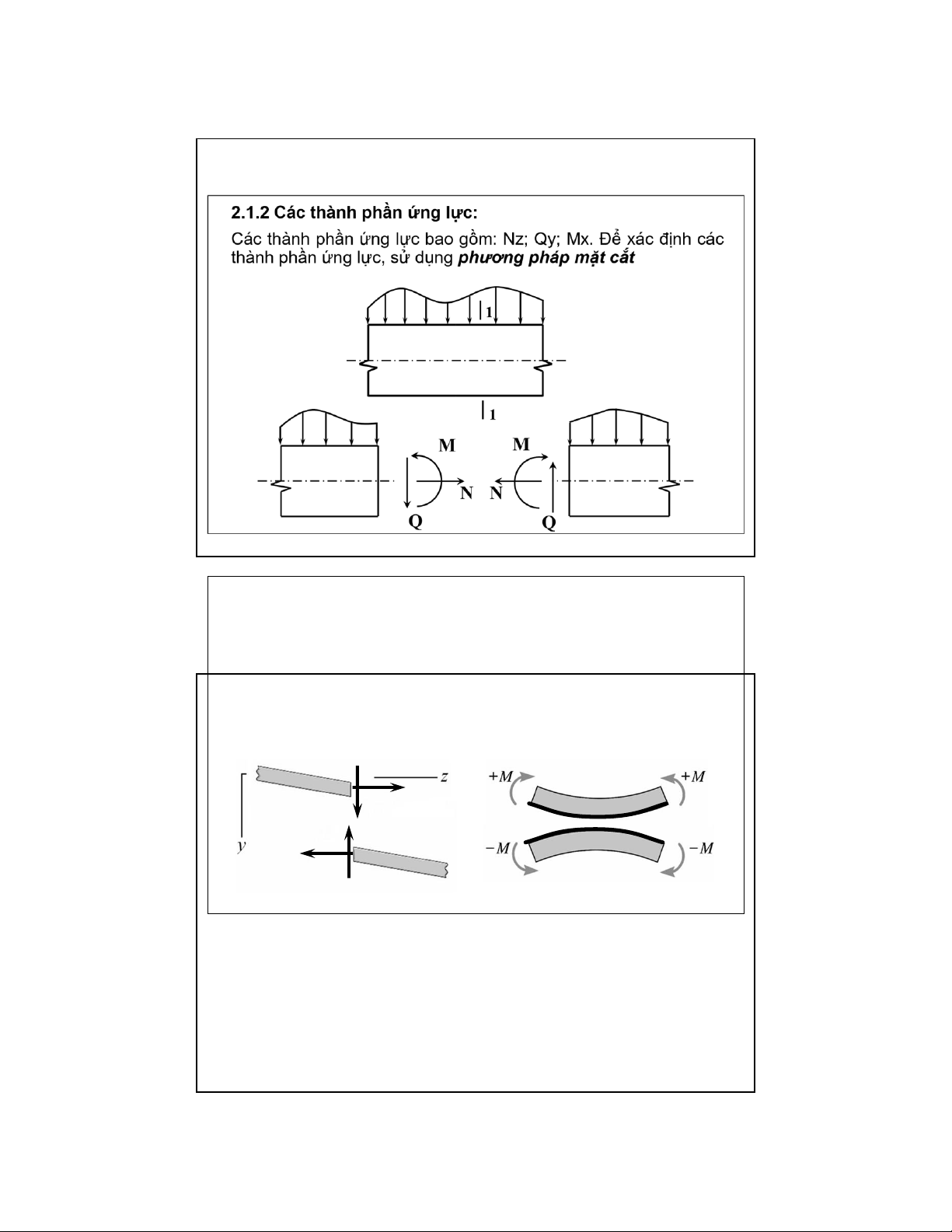
2 . 1 . 3 Quy ước dấu cho các thành phần ứng lực :
• Lực dọc : N > 0 hướng ra khỏi mặt cắt ( gây kéo)
• Lực cắt : Q > 0 quay quanh phần đang xét thuận chiều kim đồng hồ • Mô men uốn :
M > 0 làm căng thớ dưới
M < 0 làm căng thớ trên + N + Q + Q + N 6 7 lOMoAR cPSD| 58970315 09-Aug-22
2.1. Bài toán phẳng, các thành phần ứng lực trong bài toán phẳng
2 . 1 . 4 Cách xác định các thành phần ứng lực :
• Giả thiết chiều của các thành phần ứng lực N , Q , M là dương như quy ước
• Viết phương trình cân bằng hình chiều lên phương trục z, y và
phương trình mô - men đối với trọng tâm O của mặt cắt ngang
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
• Khi tính toán kết cấu thanh , người thiết kế cần tìm vị trí mặt
cắt ngang có trị số ứng lực cực trị → cần biết sự phân bố của
nội lực dọc theo chiều dài thanh
• Biểu đồ nội lực là đồ thị biểu diễn sự biến thiên của các thành
phần ứng lực theo toạ độ mặt cắt ngang
✓ Biểu đồ lực dọc và lực cắt vẽ theo quy tắc toán học thông thường,
dương trên, âm dưới. Biểu đồ phải ghi dấu
N , Q z
✓ Biểu đồ mô men vẽ về phía thớ căng, không ghi dấu z M 8 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
Các bước vẽ biểu đồ - Phương pháp mặt cắt biến thiên
• Xác định phản lực tại các liên kết
• Phân đoạn thanh sao cho biểu thức của các thành phần
ứng lực trên từng đoạn là liên tục
• Viết biểu thức xác định các thành phần ứng lực N, Q, M
theo toạ độ mặt cắt ngang bằng phương pháp mặt cắt
• Vẽ biểu đồ cho từng đoạn căn cứ vào biểu thức đã được
xác định ở bước trên
• Kiểm tra biểu đồ nhờ vào các nhận xét mang tính trực quan, kinh nghiệm 9 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
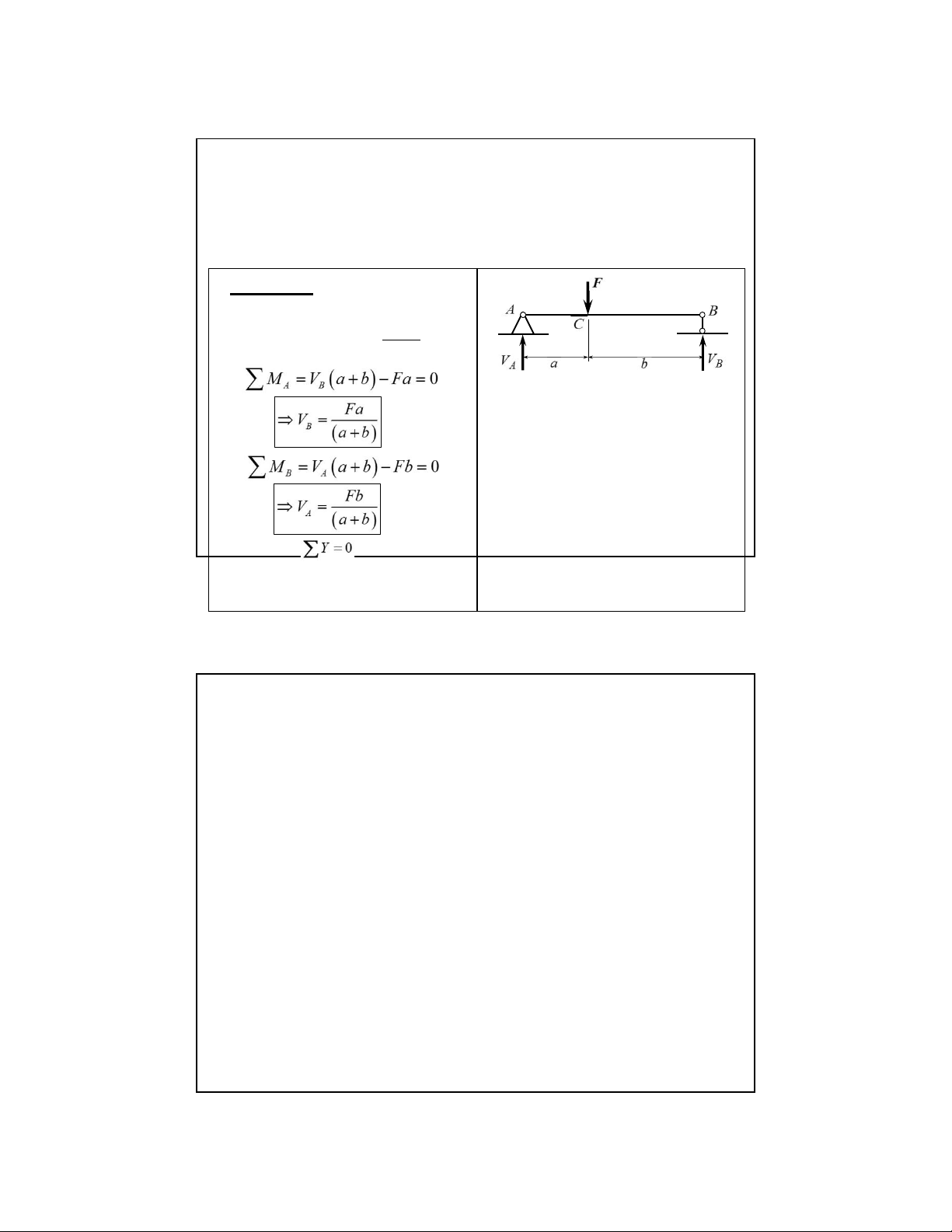
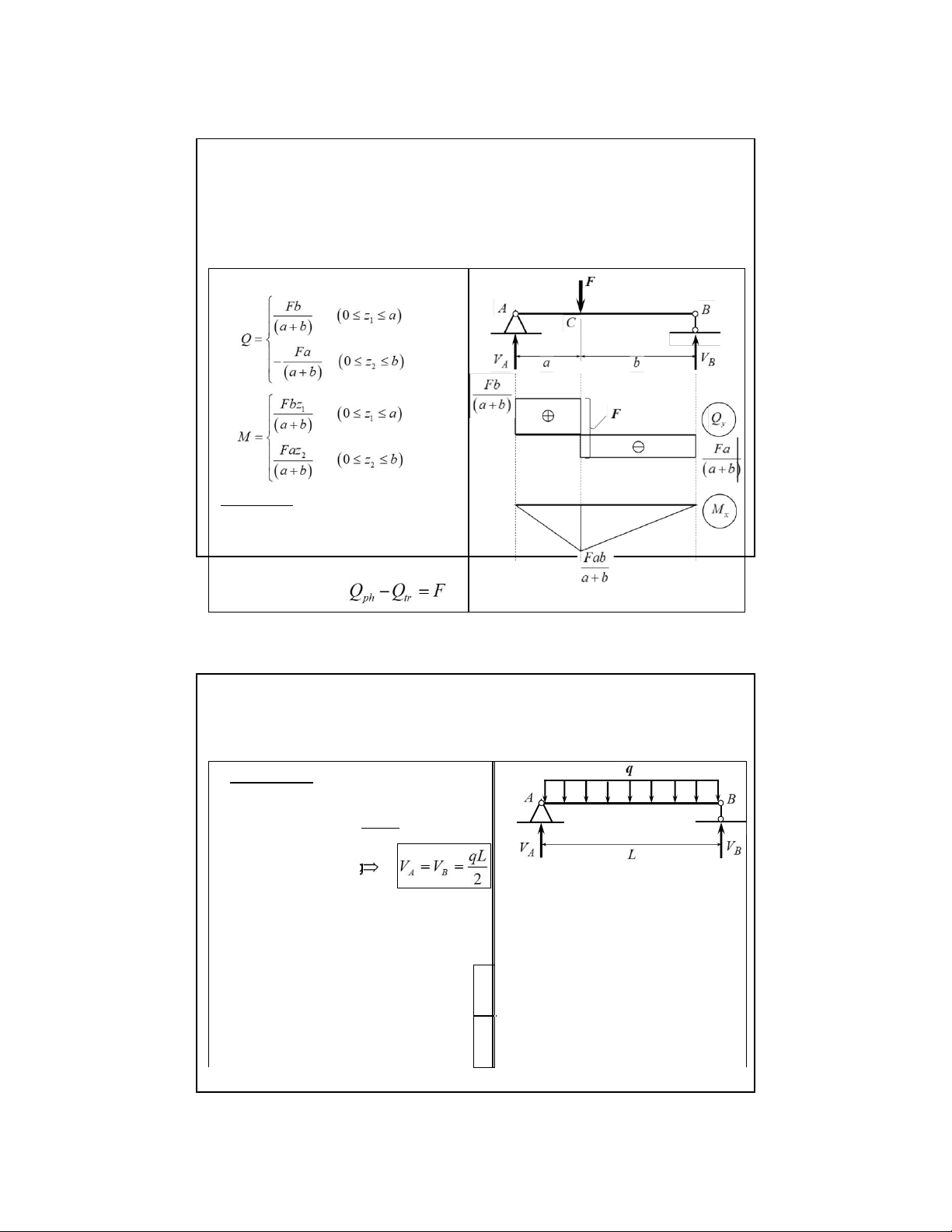
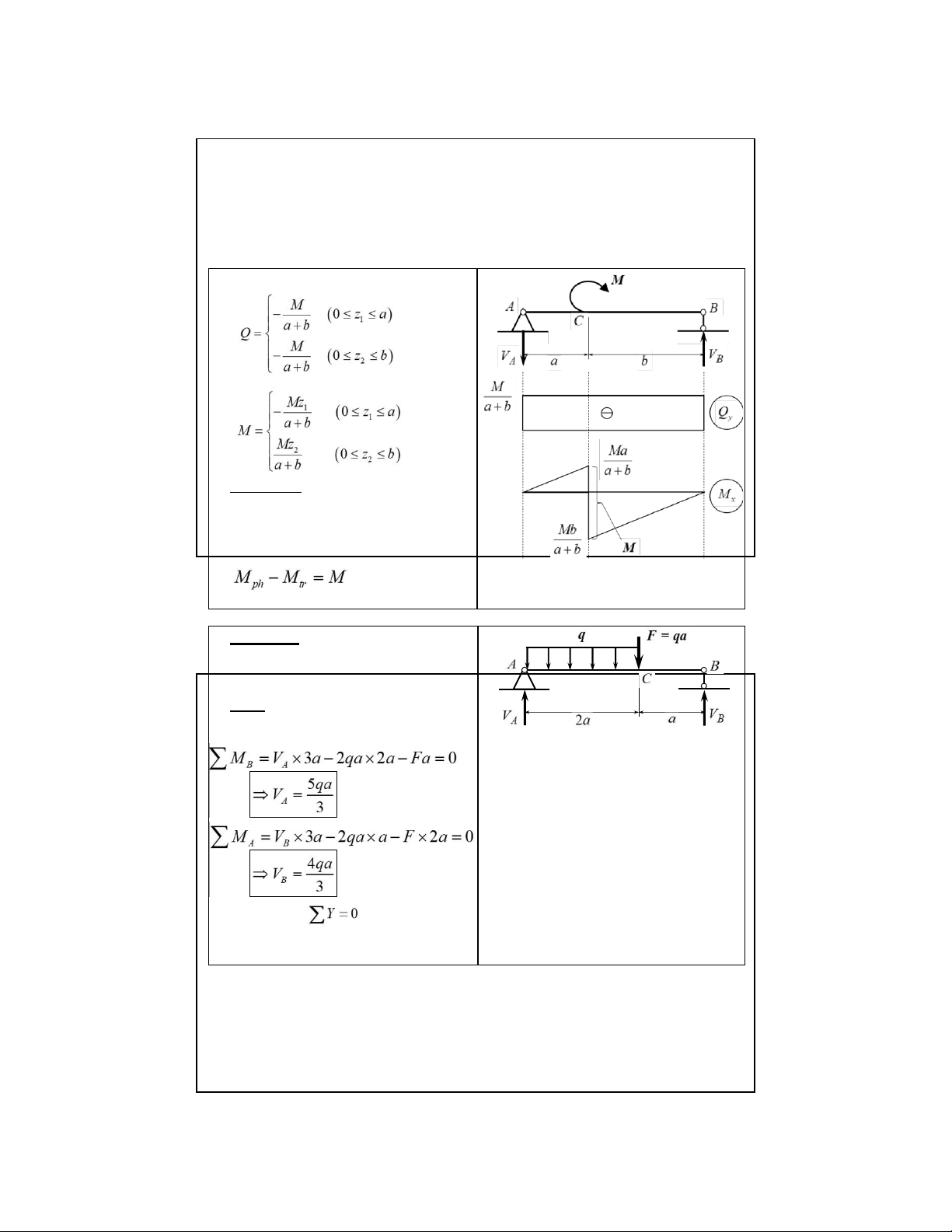
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên Ví dụ 2.1:
Vẽ biểu đồ ứng lực cho dầm chịu
tải trọng như hình vẽ. Giải: 1. Xác định phản lực Kiểm tra: 10 lOMoAR cPSD| 58970315 09-Aug-22
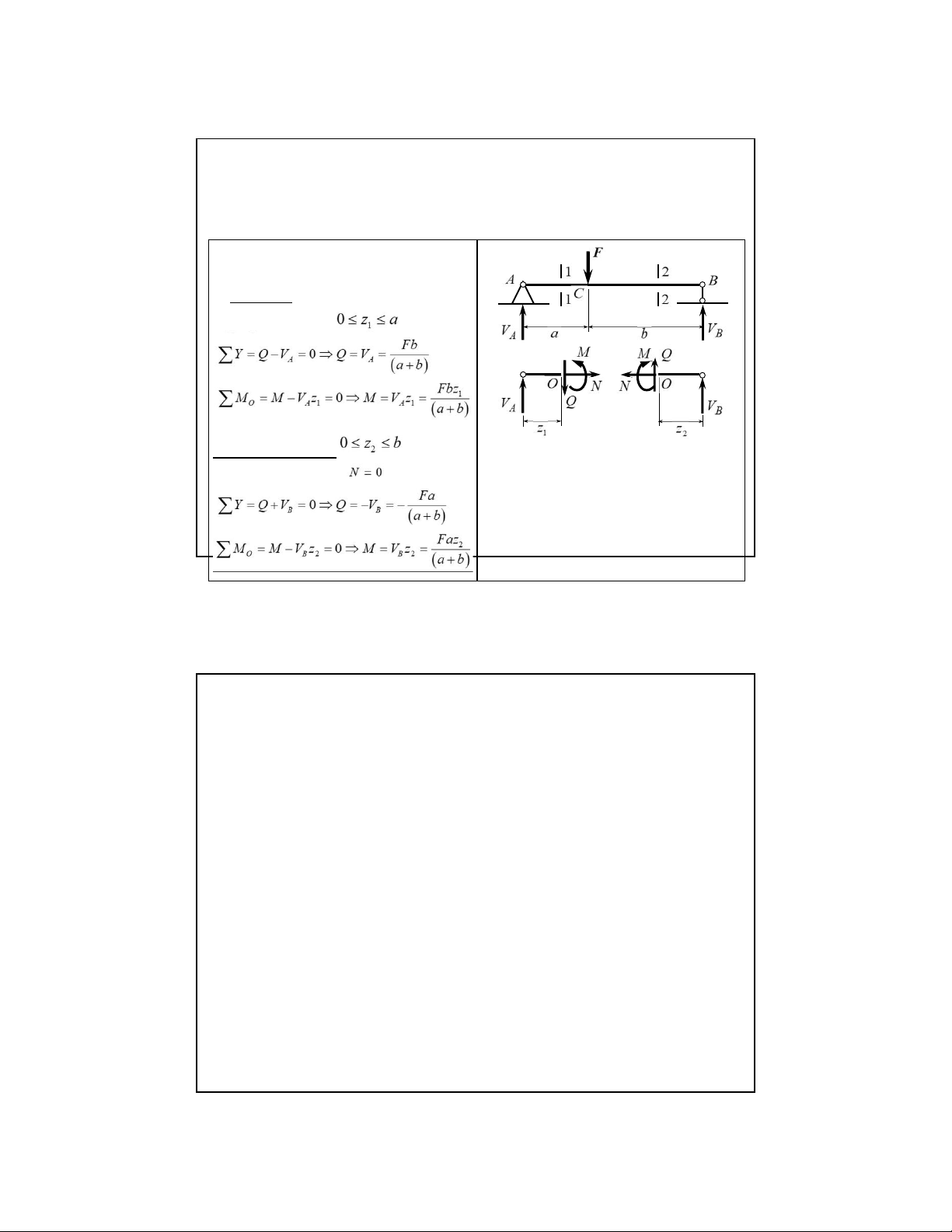
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
2. Phân đoạn và lập biểu thức cho mỗi đoạn như hình vẽ Đoạn AC Mặt cắt 1-1: Đoạn BC Mặt cắt 2-2: 11 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên 3. Vẽ biểu đồ Nhận xét 1:
Tại mặt cắt ngang có lực tập trung,
biểu đồ lực cắt có bước nhảy, giá trị
bằng giá trị của lực tập trung, chiều
hướng theo chiều của lực tập trung
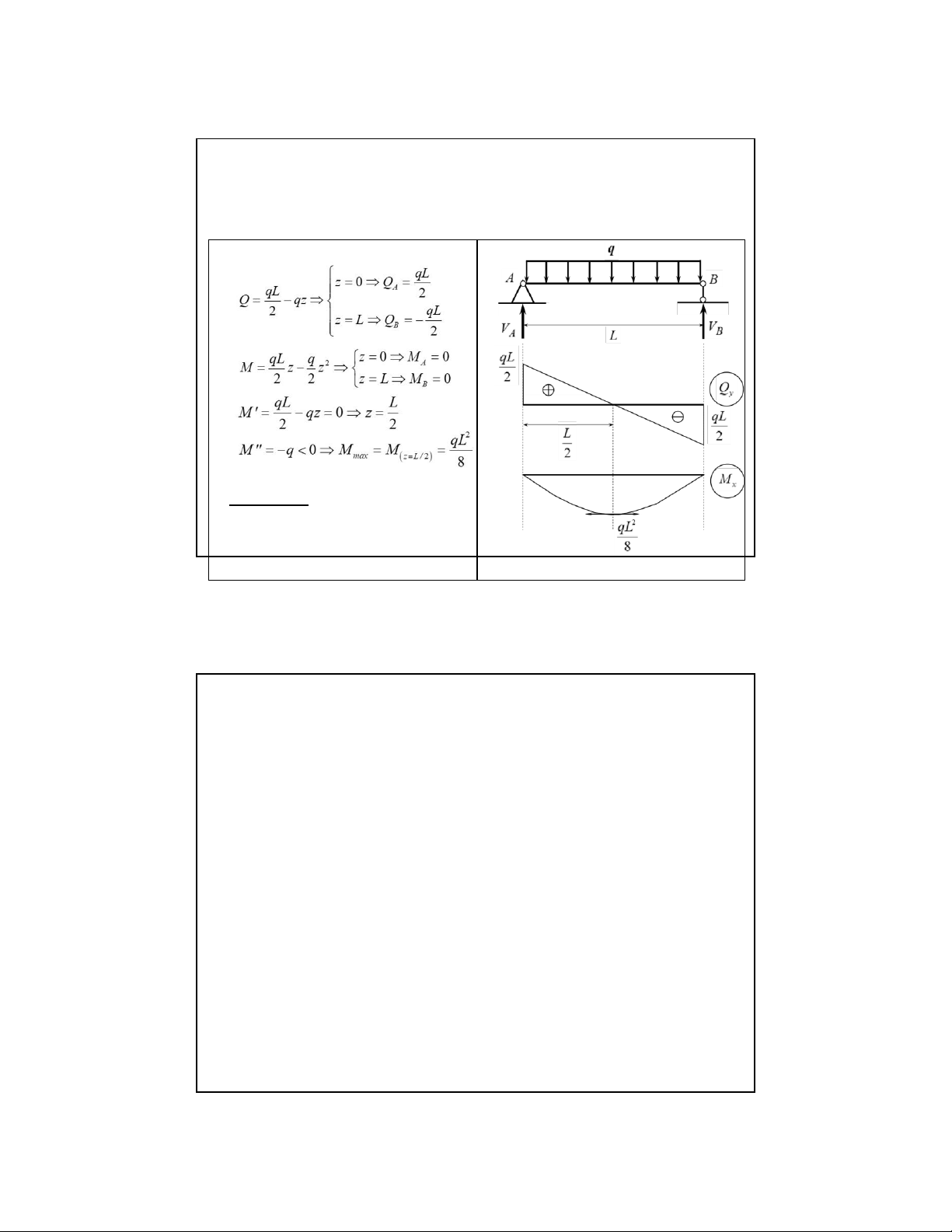
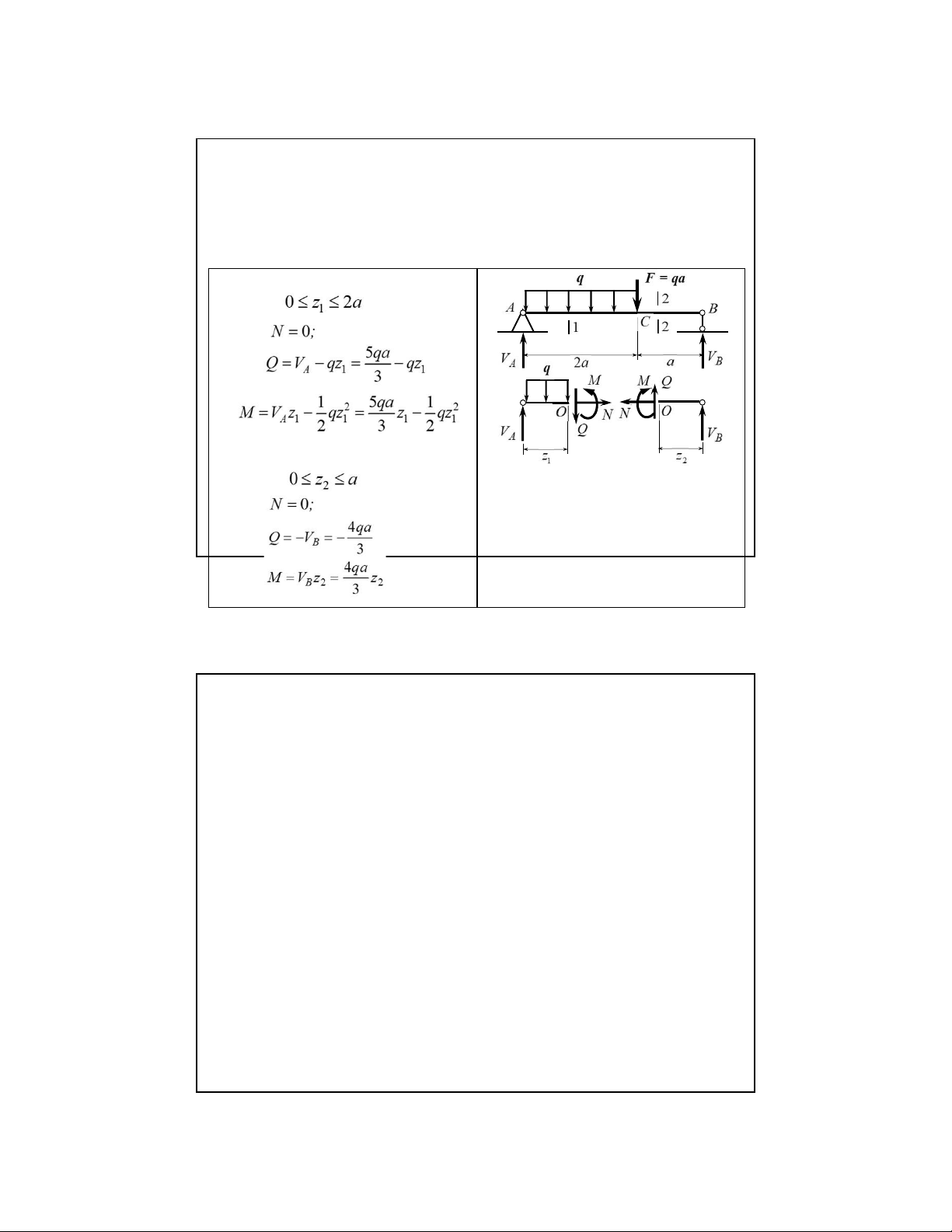
tính từ trái qua phải 12 Ví dụ 2.2:
Vẽ biểu đồ ứng lực cho dầm chịu tải
trọng như hình vẽ. Giải: 1. Phản lực Do tính đối xứng Hoặc: lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên Kiểm tra: 13
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
2. Phân đoạn và lập biểu thức cho mỗi đoạn như hình vẽ Đoạn 1-1: 14 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên 3. Vẽ biểu đồ Nhận xét 2:
Tại mặt cắt có lực cắt bằng 0, biểu
đồ mô men đạt cực trị 15 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
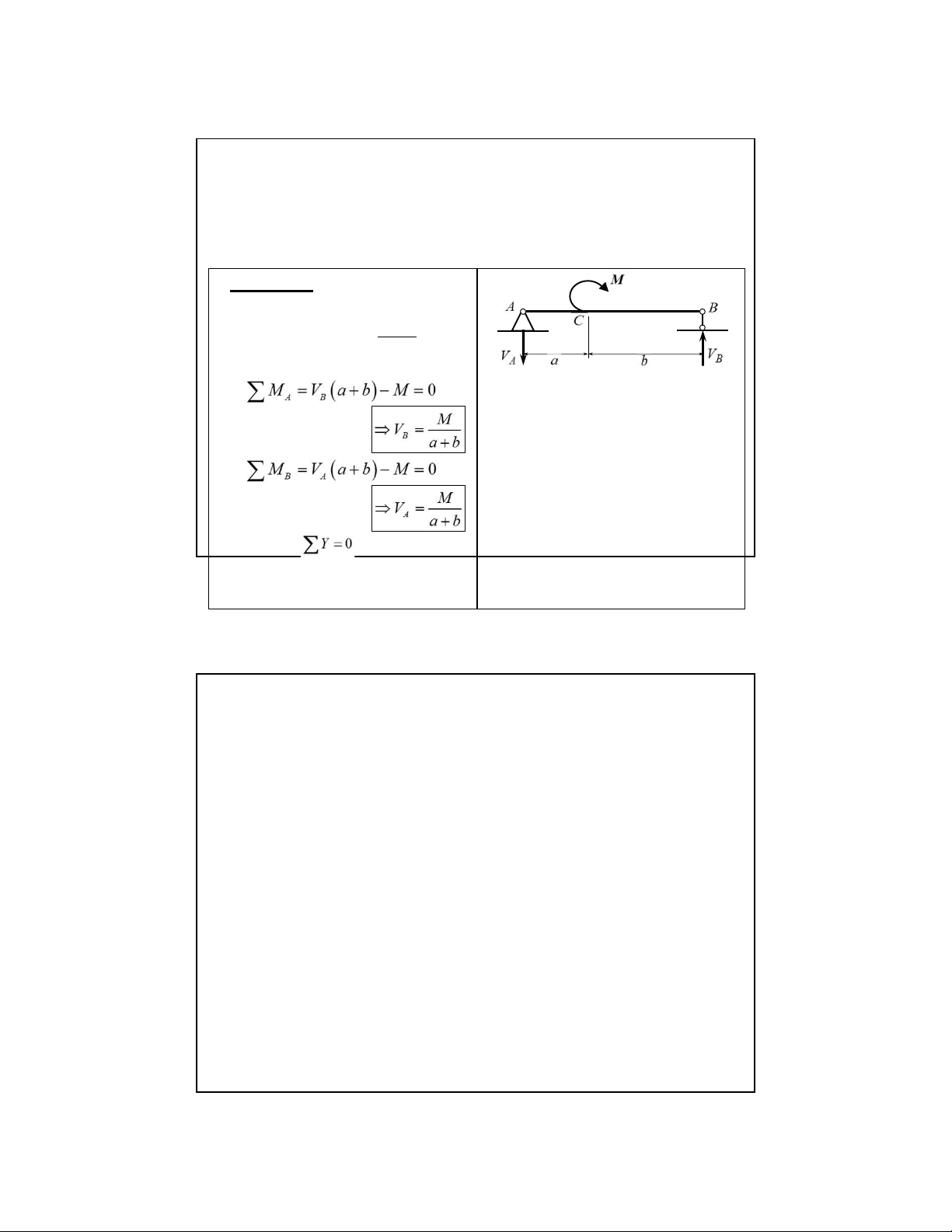
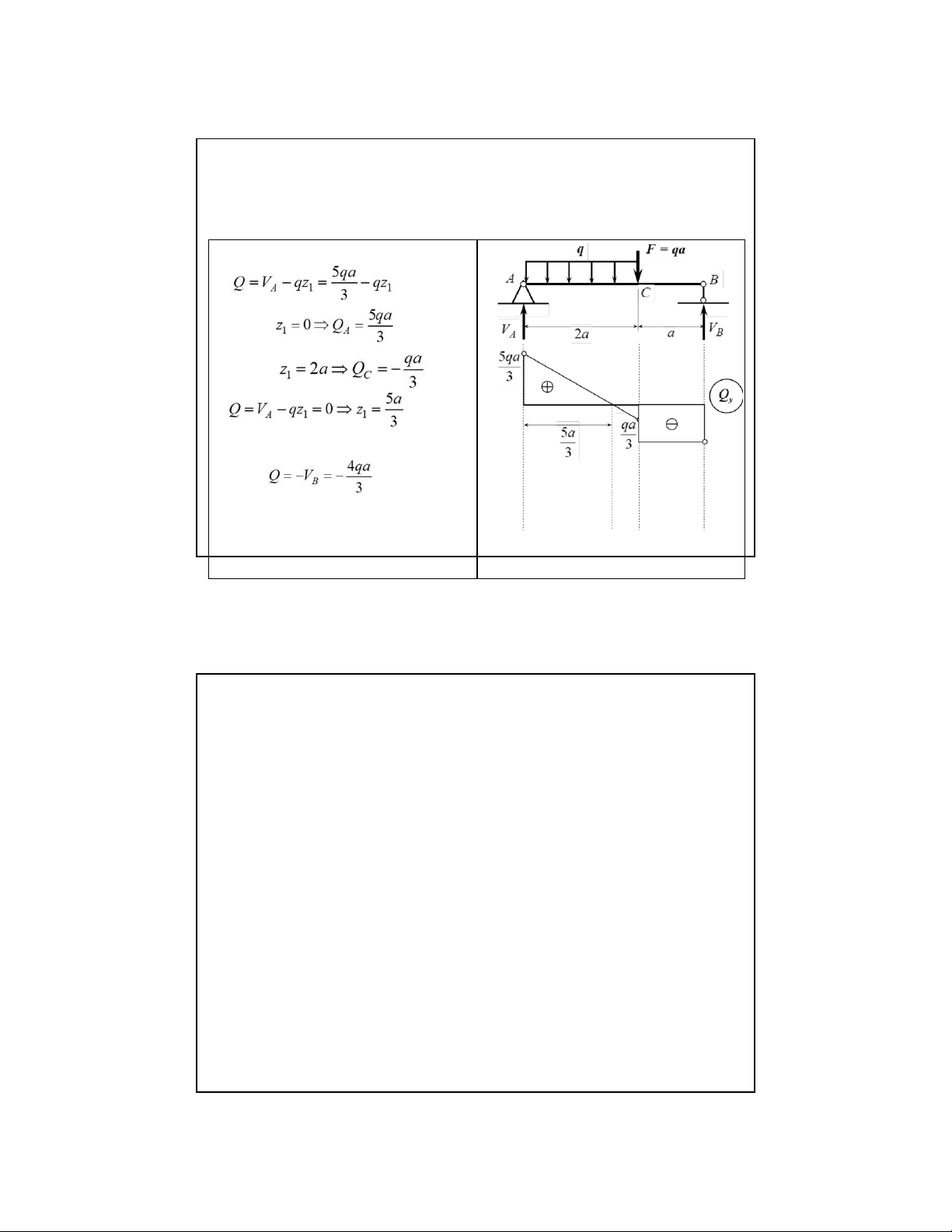
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên Ví dụ 2.3:
Vẽ biểu đồ ứng lực cho dầm chịu
tải trọng như hình vẽ Giải: 1 . Phản lực Kiểm tra: 16 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
2. Phân đoạn và lập biểu thức cho mỗi đoạn như hình vẽ Đoạn AC Mặt cắt 1 - 1 : Đoạn CB Mặt cắt 2-2: 17 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên 3. Vẽ biểu đồ Nhận xét 3:
Tại mặt cắt có mô men tập trung, biểu
đồ moomen có bước nhảy, giá trị bằng
giá trị của mô men tập trung, theo chiều
mô-men tập trung tính từ trái qua phải
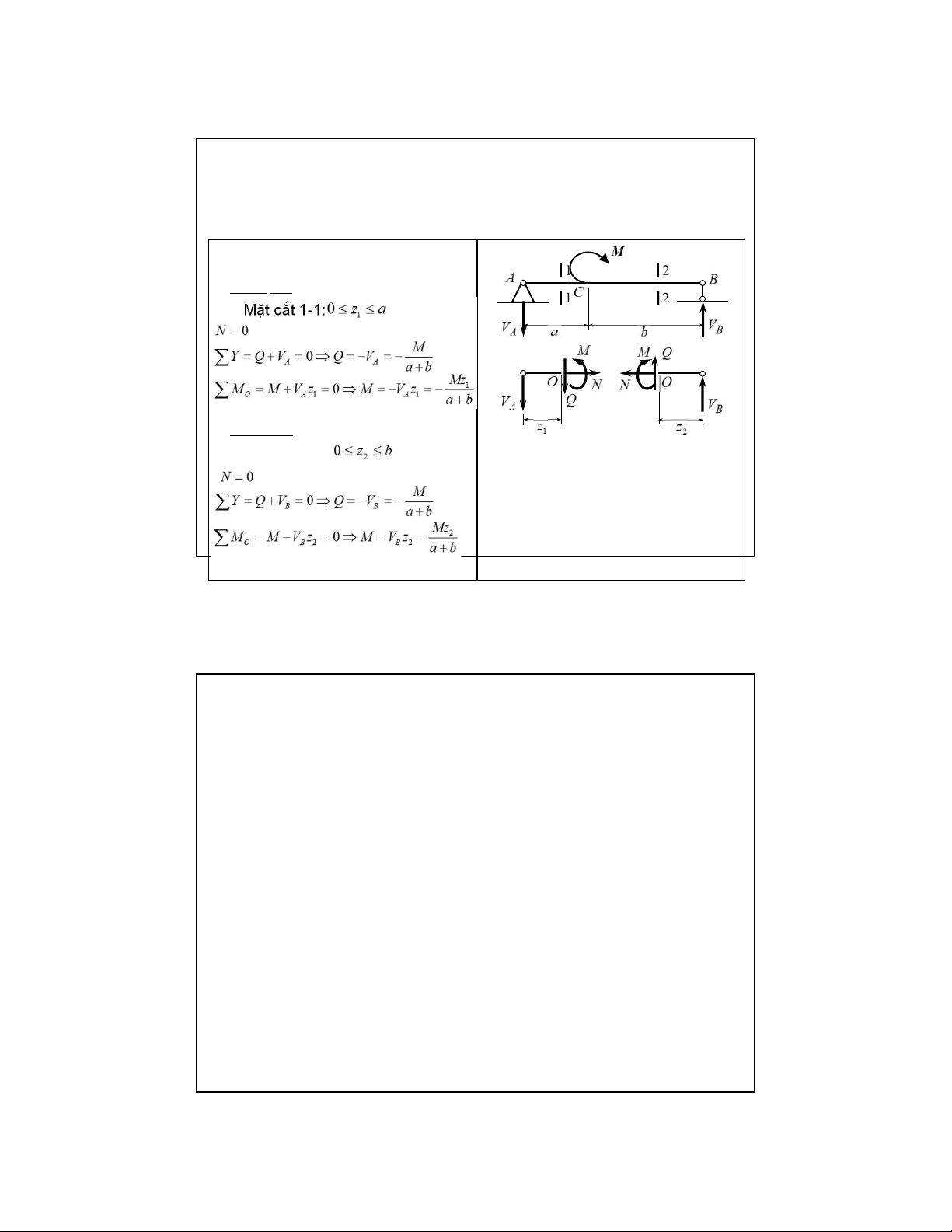
T.M Tu; N.H Tan; H.T Phuong - NUCE 18 Ví dụ 2.4:
Vẽ biểu đồ ứng lực cho dầm chịu tải trọng như hình vẽ. Giải: 1. Phản lực liên kết: Check: 19 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
2. Xét đoạn AC: mặt cắt 1-1 Ta có:
3. Xét đoạn BC: mặt cắt 2-2 Ta có: 20 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên 4. Vẽ biểu đồ Đoạn BC 21 lOMoAR cPSD| 58970315 09-Aug-22
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên
2.2. Biểu đồ ứng lực, phương pháp mặt cắt biến thiên Đoạn BC 22 lOMoAR cPSD| 58970315 09-Aug-22
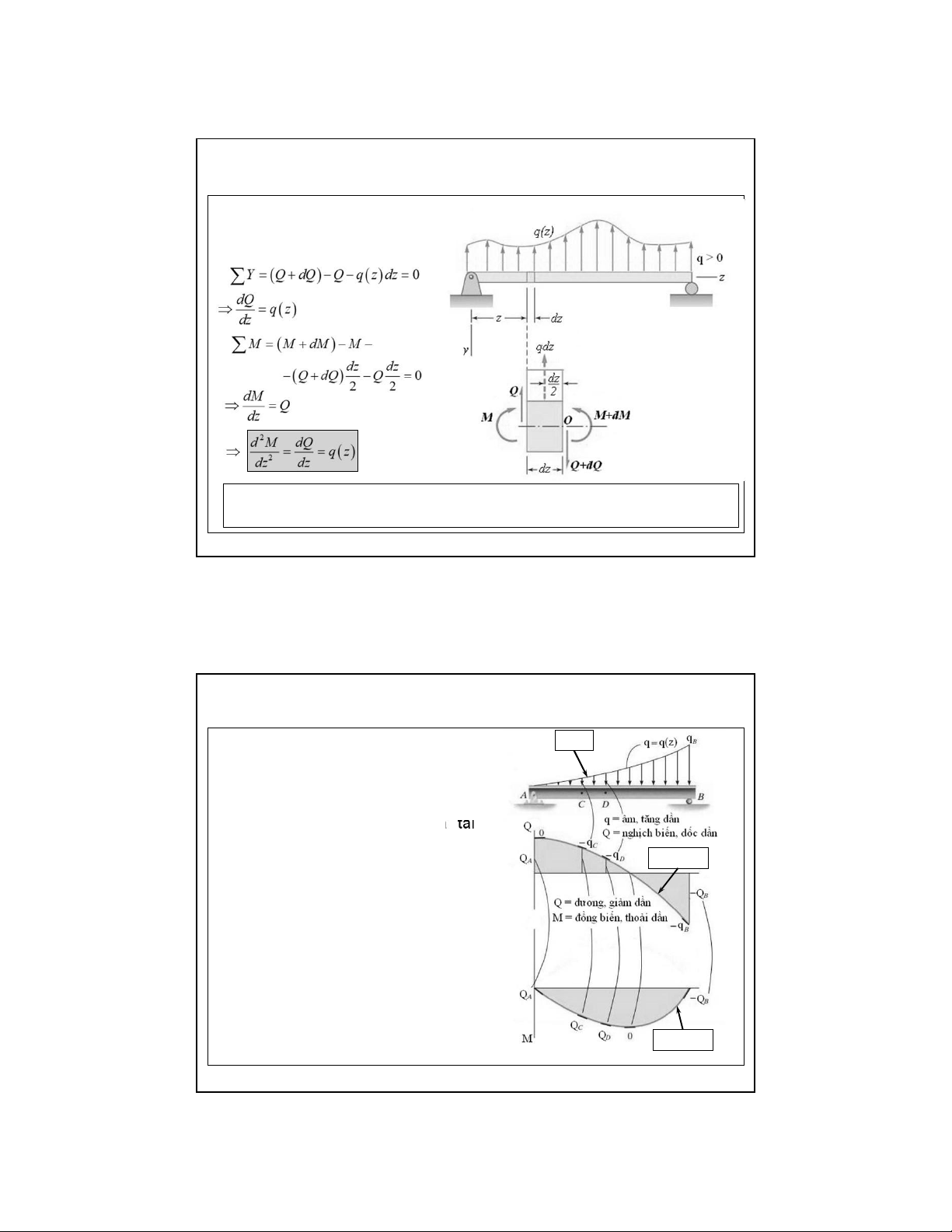
2.3. Quan hệ vi phân giữa lực cắt, mô men uốn và tải trọng phân bố, các ứng dụng
Xét dầm chịu tải trọng q ( z ) > 0 ( hướng lên) :
Xét cân bằng của đoạn thanh dz như hình vẽ :
Đạo hàm bậc hai của mô men bằng đạo hàm bậc nhất của lực cắt và
bằng cường độ của tải trọng phân bố 23
2.3. Quan hệ vi phân giữa lực cắt, mô men uốn và tải trọng phân bố, các ứng dụng Ứng dụng : bậc n
• Nhận dạng các biểu đồ Q, M khi
biết quy luật phân bố của tải
trọng phân bố q(z) : Nếu trên một
đoạn thanh , biểu thức của tải
trọng q(z) có bậc n thì biểu thức của Q có bậc ( + n 1 ) và biểu thức bậc (n+1) của M có bậc ( n + 2 )
• Tính nghịch biến / đồng biến và độ
dốc của các biểu đồ Q, M cũng
phụ thuộc vào quy luật phân bố của q(z)
• Tại mặt cắt có q= 0 → Q đạt cực
trị ; Tại mặt cắt có Q= 0 → M đạt cực trị bậc (n+2) lOMoAR cPSD| 58970315 09-Aug-22
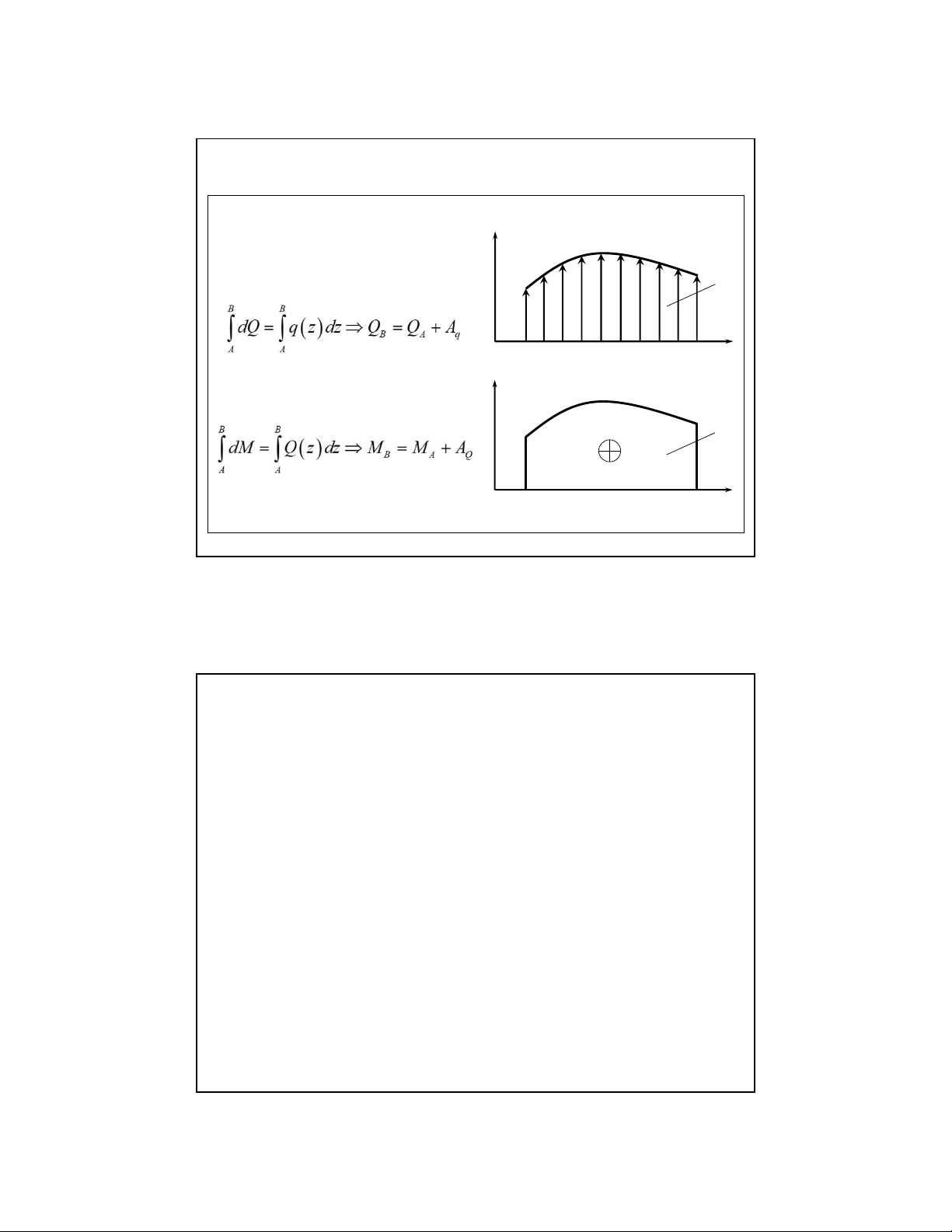
2.3. Quan hệ vi phân giữa lực cắt, mô men uốn và tải trọng phân bố, các ứng dụng Nhận xét :
❖ Có thể tính giá trị ứng lực tại q 1 q
tiết diện khi biết giá trị ứng ( z )
lực tại tiết diện khác A q z A B Q Q ( z ) A Q z A B 24 25
2.3. Quan hệ vi phân giữa lực cắt, mô men uốn và tải trọng phân bố, các ứng dụng lOMoAR cPSD| 58970315 09-Aug-22
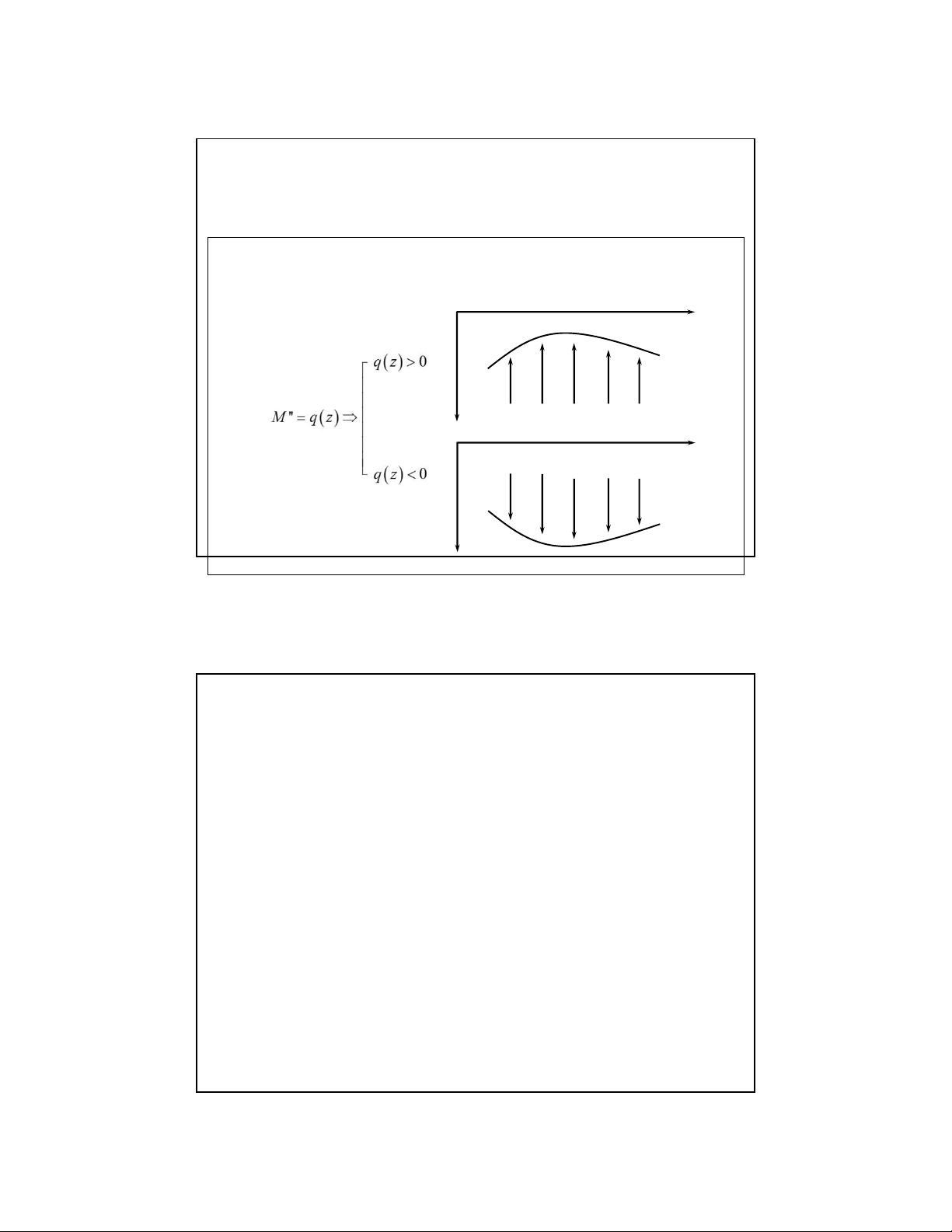
2.3. Quan hệ vi phân giữa lực cắt, mô men uốn và tải trọng phân bố, các ứng dụng Ứng dụng :
• Tính lồi / lõm của biểu đồ mômen uốn : biểu đồ mômen luôn có xu
hướng hứng tải trọng phân bố z → M lõm M z → M lồi M 26 27